Plate Theories for Classical and Laminated plates Weak Formulation and Element Calculations
|
|
|
- Corey Griffin
- 5 years ago
- Views:
Transcription
1 Plate heores for Classcal and Lamnated plates Weak Formulaton and Element Calculatons PM Mohte Department of Aerospace Engneerng Indan Insttute of echnolog Kanpur EQIP School on Computatonal Methods n Engneerng Applcaton Knowledge Incubaton for EQIP
2 Plate lke Elements n Structural Applcatons
3 Classcal Plate heor
4 Classcal Plate heor: Plate Geometr and notatons, n-plane coordnates coordnate plane md-plane or md-surface h q(,) z coordnate n thckness drecton h thckness of the plate u, v and w deformatons/dsplacements along, and z aes, respectvel z - doman of the plate, - boundng surface
5 Classcal Plate heor: Basc Features: Deformaton feld s based on the of Krchhoff-Love assumptons Applcable to thn plates Plane stress condton 1. Normal to the md-plane (.e., transverse normals) before deformaton reman straght and normal after deformaton. ransverse normals to the md-plane are netensble 3. Materal s homogeneous and sotropc
6 Classcal Plate heor: Knematcs of Deformaton Geometr of Deformaton Approach Undeformed Geometr: a b Or z Deformaton Stretchng acton due to load the edges of plate and parallel to the md-surface Bendng acton due to loads the top and bottom surface
7 Classcal Plate heor: Knematcs of Deformaton Deformaton due to Stretchng: An normal to the mdplane s translated horzontall as a rgd lne n the plane Undeformed Geometr a X Deformed Geometr z b u (,) a X z Vew n drecton b
8 Classcal Plate heor: Knematcs of Deformaton Deformaton due to Bendng: An normal to the mdplane s translated vertcall as rgd lne mantanng, coordnates then rotates as a rgd element Undeformed Geometr a b Deformed Geometr z a w (,) z Vew n drecton b
9 Classcal Plate heor: Knematcs of Deformaton Deformaton due to Stretchng and Bendng: Undeformed Geometr a z b u (,) w (,) Deformed Geometr a z Vew n drecton b
10 Classcal Plate heor: Knematcs of Deformaton Deformaton of a Generc Pont on the Normal: z α w tan For small deformatons, w tan w z a a p p In-plane deformaton due to rgd rotaton of the normal z b α w b z w Vew n drecton
11 Classcal Plate heor: Knematcs of Deformaton Deformaton of a Generc Pont on the Normal due to both Stretchng and Bendng:,,, u z u z w Smlarl, the deformaton vewed n drecton can be gven as,,, v z v z w Stretchng part Bendng part And the deformaton n the transverse drecton,,, w z w Bendng part
12 Classcal Plate heor: Knematcs of Deformaton Alternate Approach: Small deformatons, Strans are nfntesmal he frst assumpton leads to the condton that transverse shear strans are zero. z and z Inetensblt of a transverse normal mples the transverse normal stran s zero. hat s, zz Integratng ths wth respect to z, w z, z w w,, - functon of and onl
13 Classcal Plate heor: Knematcs of Deformaton Deformaton feld: From the frst assumpton z u w z u z w Integratng wth respect to z w,,z z u, u Smlarl, z v w z v z w
14 Classcal Plate heor: Deformaton feld: Integratng wth respect to z w,,z z v, v Snce,, v, and w, are ndependent of z, u, ther varaton along thckness s zero or these are constants along z. herefore, u,, v, and w, are taken as md-plane or md-surface dsplacements.
15 Classcal Plate heor: Stran Feld All other stran components are zero. hs also mples that the transverse shear stresses are zero w z v u v u w z v v w z u u 1 1 z z
16 Classcal Plate heor: Consttutve Relatons Stran Feld: where, z u v u v Md-plane strans w w w Md-plane Curvatures
17 Classcal Plate heor: Consttutve Relatons Isotropc Materals: Strans n terms of stresses ν Posson s rato, E- Young s Modulus Stresses n terms of strans E 1 1 E 1 1 1
18 Classcal Plate heor: Stress Resultants z Defne shear force resultants as z z z Q h h z dz
19 Classcal Plate heor: Stress Resultants z z z Q h h z dz
20 Classcal Plate heor: Stress Resultants Resultant Forces: h h h N dz, N dz, N dz h h h Resultant Moments: h h h M z dz, M z dz, M z dz h h h
21 Classcal Plate heor: Stress Resultants Resultant Forces: N 1 N A 1 N 1 where, A Eh 1 Resultant Moments: M 1 M D 1 M 1 where, D Eh Bendng Rgdt 3 1 1
22 Classcal Plate heor: Equlbrum Equatons Equaton n -drecton wthout an bod force: z z Multpl wth z and ntegrate over plate thckness h h h z dz z dz z dz z z h h h M M z z dz z h h
23 Classcal Plate heor: Equlbrum Equatons Smplfng, h h h z z dz z z h z z dz Q z h h No shear stress on the top and bottom of the plate. M M Q a Smlarl, equlbrum equaton n drecton s M M Q b
24 Classcal Plate heor: Equlbrum Equatons Integratng the equlbrum equaton n z drecton over the plate thckness In terms of resultants h h h z z h h h ransverse load s appled on top face onl. zz dz dz dz z Q Q zz z z h h z zz z zz z h and z h q, z zz z
25 Classcal Plate heor: Equlbrum Equatons hs gves Q Q q, c Combnng Eqs. (a), (b) and (c) nto a sngle equaton and elmnatng Q and Q M M M q, Fnall, epressng the resultant moments n terms of dsplacement w 4 q w Nonhomogeneous Bharmonc Equaton frst developed b Sophe German n D
26 Fnte Element Formulaton of Classcal Plate heor
27 Classcal Plate heor: Fnte Element Formulaton Let the doman be dvded nto (3 noded) trangular or (4 noded) quadrlateral elements e k e l j j k Each node has three nodal dsplacements or 3 degrees of freedom (DOF) or prmar varables w w θ w θ e w a w z
28 Classcal Plate heor: Fnte Element Formulaton Each node has three nodal forces (secondar varables) q z (q θ ) (q θ ) z e q q q q z
29 Classcal Plate heor: Fnte Element Formulaton otal Potental Energ of an element π: D w w w w 1 d d a q he frst varaton of π w w w 1 D w w w w d d a q 1 w w
30 Classcal Plate heor: Fnte Element Formulaton he frst varaton of otal Potental Energ of an element usng resultant moments and curvatures w w w M M M d d a q Moments and Curvatures n matr forms usng assumed dsplacement over an element M d d a q
31 Classcal Plate heor: Fnte Element Formulaton Re-arrangement of Stran Feld: s a lnear operator For eample, for the element shown the DOFS are a L w L w w w L j k e w , c c c c c c c c c w
32 Classcal Plate heor: Fnte Element Formulaton Nodal dsplacement for th node: Or can be found as ([A] s nvertble) c w e e c A a e e a A c 1 e c
33 Classcal Plate heor: Fnte Element Formulaton Md-plane curvatures for e th element: Or where, c c c c c c c c c w w w e e e c H H
34 Classcal Plate heor: Fnte Element Formulaton Md-plane curvatures for e th element n terms of nodal varables: e 1 H A a e Let B H A 1 Now the resultant moments are epressed as M 1 M D 1 M 1 or where, M D* D* 1 D 1 1
35 Classcal Plate heor: Fnte Element Formulaton he frst varaton of otal Potental Energ of an element usng resultant moments and curvatures a B D Ba d d a q Usng the relatons developed for resultant moments and md-plane curvatures a B D* B a dd a q or a B D * Bdd a q
36 Classcal Plate heor: Fnte Element Formulaton hs can be further wrtten as where, e a K a q e k B D* Bdd as a s arbtrar. Fnall, for an element e we wrte K e a e q e
37 Classcal Plate heor: Fnte Element Formulaton Element load vector calculaton: From Prncpal of vrtual work Now, re-wrte the dsplacement over the element,,,,, a q p w dd P w r w ds M w ds n , c c c c c c c c c w j k P P 1 M r(,) p(,)
38 Classcal Plate heor: Fnte Element Formulaton Dsplacement n an element or 3 3, 1,,,,,,,, w c e, 1,,,,,,,, * 1 w A a C A a e e Let herefore, and N C * A 1 e w N a a N e w a N
39 Classcal Plate heor: Fnte Element Formulaton Puttng these n vrtual work of eternal forces a q a p, N dd a P N, N, a r, N, ds a M ds n Snce a s arbtrar e q p, N dd P N, N, r, N, ds M ds n
40 Classcal Lamnated Plate heor
41 Classcal Lamnated Plate heor: Nomenclature H otal lamnate thckness 13 Prncpal materal drectons z Global materal drectons θ k Pl orentaton of k th pl z k bottom z-coordnate of k th pl Abbrevated as CL or Classcal Lamnated Plate heor - CLP
42 Classcal Lamnated Plate heor: Assumptons hs s a drect etenson of classcal plate theor to lamnates Same assumptons as n classcal plate theor wth Laers are perfectl bonded. here s no slp between adjacent laers. he dsplacements are contnuous through the thckness. Each laer s consdered to be homogeneous and can be sotropc, orthotropc or transversel sotropc wth known propertes.
43 Classcal Lamnated Plate heor: Lamna Consttutve Relatons Orthotropc Materals, Prncpal Materal Drectons Strans n k th lamna n terms of stress Stresses n k th lamna n terms of strans Q G E E E E E E and G E E E E
44 Classcal Lamnated Plate heor: Lamna Consttutve Relatons Global Drectons ransformaton of stresses ransformaton of strans n m mn mn mn m n mn n m 1 11 and cos m where, sn n n m mn mn mn m n mn n m 1 11
45 Classcal Lamnated Plate heor: Lamna Consttutve Relatons Stresses n Global Drectons Q Q 1 1 Q Reduced transformed stffness matr: 1 Q Q Q Q Q Q Q Q 1 6 Q Q Q Q
46 Classcal Lamnated Plate heor: Lamna Consttutve Relatons Strans n Global Drectons S Reduced transformed stffness matr: S Q Q S S S S S S 1 6 S S S Q, Q, S are smmetrc matrces
47 Classcal Lamnated Plate heor: Lamna Consttutve Relatons Stresses n k th lamna k Q k k Usng defnton of strans k k k k Q Q z
48 Classcal Lamnated Plate heor: Lamnate Consttutve Relatons Resultant Forces: H H H N dz, N dz, N dz Usng defnton of stresses H H H where N N N N H k k k k N Q dz Q Q z dz H H H Stresses var pecewse lnearl n each laer.
49 Classcal Lamnated Plate heor: Lamnate Consttutve Relatons k are constant n each laer Q, and Integraton over lamnate thckness s evaluated as sum of ntegratons over laer thcknesses Nla k k k k N Q dz Q Q z dz z k Nla k1 z k1 k1 k1 z z k where, Nla N A B k 1 A Q z k zk1, B Q zk zk1 k1 k1 Nla k
50 Classcal Lamnated Plate heor: Lamnate Consttutve Relatons Resultant Moments: H H H M zdz, M zdz, M zdz H H H where M M M M Usng defnton of stresses H H k k k k M Q zdz Q Q z zdz H H Stresses var pecewse lnearl n each laer.
51 Classcal Lamnated Plate heor: Lamnate Consttutve Relatons Integraton over lamnate thckness s evaluated as sum of ntegratons over laer thcknesses Nla k k k k M Q zdz Q Q z zdz z k Nla k1 z k1 k1 k1 M B D z z k where, Nla Nla 1 k B Q z k zk1, D Q zk zk1 k1 k1 k A, B and D are smmetrc.
52 Classcal Lamnated Plate heor: Lamnate Consttutve Relatons Stress Resultants Moment Resultants
53 Classcal Lamnated Plate heor: Lamnate Consttutve Relatons Lamnate Consttutve Relatons: B D N A B M Equatons of moton: N N M N N M M q,
54 Classcal Lamnated Plate heor: Weak Formulaton From the frst equaton of moton: e u u v u v w w w A11 A1 A16 B11 B 1 B 16 dd u u v u v w w w A16 A6 A66 B16 B 6 B 66 e N u ds n n
55 Classcal Lamnated Plate heor: Weak Formulaton From the second equaton of moton: e e v u v u v w w w A1 A A6 B1 B B 6 v u v u v w w w N A16 A6 A66 B16 B 6 B 66 s u ds s dd
56 Classcal Lamnated Plate heor: Weak Formulaton From the thrd equaton of moton: e w u v u v w w w A11 A1 A16 B11 B 1 B 16 w w u v u v w w w A16 A6 A66 B16 B 6 B 66 dd w u v u v w w w A1 A A6 B1 B B 6 w w u v u v w w w A16 A6 A66 B16 B 6 B 66
57 Classcal Lamnated Plate heor: Weak Formulaton From the thrd equaton of moton: w u v u v w w w B11 B1 B16 D11 D 1 D 16 w u v u v w w w B1 B B6 D1 D D 6 dd e w u v u v w w w B B B D D D 66 wq w Vn w M n ds n e
58 Classcal Lamnated Plate heor: Weak Formulaton where, N N n N n, N N n N n n s M ns Vn Qn P s M M n M n, M M n M n n s w w w w P N N n N N n (n, n ) denote the drecton cosnes of the unt normal on the element boundar Γ e
59 Classcal Plate heor: Fnte Element Formulaton Let the doman be dvded nto (3 noded) trangular or (4 noded) quadrlateral elements e k e l j j k Each node has fve nodal dsplacements or 5 degrees of freedom (DOF) or prmar varables v u θ w z θ a e u v w w w
60 Classcal Plate heor: Fnte Element Formulaton Each node has fve nodal forces (secondar varables) q q q z (q θ ) (q θ ) z Nodal force vector: e q q q q q q z
61 Classcal Lamnated Plate heor: Fnte Element Formulaton Appromaton of soluton n an element: u Node, 1, u N Smlarl, for the other varables v, w, w and w hat s, appromaton of soluton vector: Node Number of nodes n an element e N (,) Interpolaton functon assocated wth node a a value of correspondng to node Node a N, a 1
62 Classcal Lamnated Plate heor: Weak Formulaton otal Potental Energ Nelem Number of elements Nelem e1 d e e e d U W e U e - Stran energ of an element W e - work done b eternal forces n an element
63 Classcal Lamnated Plate heor: Fnte Element Formulaton Md-plane strans: or where, E stands for etenson. E L a w v u
64 Classcal Lamnated Plate heor: Fnte Element Formulaton Md-plane curvatures: or where, B stands for bendng. w v u a L B
65 Classcal Lamnated Plate heor: Fnte Element Formulaton Generalzed Md-plane strans: where, and BE LE N Node B E B E 1 L a L N a Node 1 B E E E Node 1 B E d a and d a a a a 1 3 Node
66 Classcal Lamnated Plate heor: Fnte Element Formulaton Generalzed Md-plane curvatures: where, and BB LB N Node B B B B 1 L a L N a Node B 1 B B B Node 1 B B d a and d a a a a 1 3 Node
67 Classcal Lamnated Plate heor: Fnte Element Formulaton Stran Energ of an element: Stran energ due to etenson Stran energ due to bendng Usng the notatons, B E e U U U e A e da M N U 1 e A B B B E E B E E e da d B D B d d B B B d d B B B d d B A B d U 1
68 Classcal Lamnated Plate heor: Fnte Element Formulaton Stran Energ of an element n a concse form e 1 e U d K d where, K e s the element stffness matr 1 K B A B B B B B B B B D B da e E E B E E B B B e A
69 Classcal Lamnated Plate heor: Fnte Element Formulaton Eternal work done: e N W d N q, da d N r, ds d M ds n A e e e Also can be wrtten concsel as e W d q e where, q e s the element load vector N q N q da N r ds M ds n e,, A e e e
70 Classcal Lamnated Plate heor: Fnte Element Formulaton Numercal Integraton of Stffness Matr (for quadrlateral element): 11 e * j j K B D B J dd 11 NIN NIN e * j J j l m l1 m1 K B D B W W NIN - s the number of Gauss quadrature ponts nξ and η drectons W weght ponts n drecton J - Determnant of the Jacoban matr
71 Classcal Lamnated Plate heor: Fnte Element Formulaton where, B BE B B and D * A B B D
72 Classcal Lamnated Plate heor: Fnte Element Formulaton Numercal ntegraton of Load vector: wo parts: Area ntegral and lne ntegral N q N q da N r ds M ds n e,, where, area ntegral part of the load vector: And lne ntegral part of the load vector: A e e e e q e q e q 1 e q N q, 1 e A e q N r, e ds e da N n M ds
73 Classcal Lamnated Plate heor: Fnte Element Formulaton Numercal ntegraton of Load vector: 11 e q N, q J d d 1, 1 1 NIN NIN e q N q,,, J l m l m l, 1 l1 m1 m W l W m All other terms have same meanng as n stffness matr numercal ntegraton
74 Classcal Lamnated Plate heor: Fnte Element Formulaton Numercal ntegraton of Load vector: Lne ntegral 1D Numercal ntegraton q 1 e N 1D N r M J d n 1 NIN1D N l l l M l l J l1 n e q N r NIN1D - s the number of Gauss quadrature ponts nξ drecton 1D 1D W D W 1 l 1D J weght ponts n drecton - Jacoban for one dmensonal ntegratons (=length/)
75 Hgher Order Shear Deformable Plate heores
76 Hgher Order Plate heor: Dsplacement feld: u,,z u, zu, z u, z u, v,,z v, zv, z v, z v, w,,z w, zw, z w, z w, Hgher order representaton of strans n the thckness drecton ransverse strans are non-zero. Stran components: zz z z
77 Frst Order Shear Deformaton heor: Dsplacement feld: 1 1 u,,z u, zu, v,,z v, zv, w,,z w, 1 Hgher order representaton of strans n the thckness drecton ransverse shear strans are non-zero but transverse normal stran s zero. Stran components: z z
78 hrd Order Plate heor: Dsplacement feld: u,,z u, zu, z u, z u, v,,z v, zv, z v, z v, w,,z w, 1 No transverse stresses on top and bottom face of plate. z z v w w v zv z v z u w w u zu z u z
79 hrd Order Plate heor: Dsplacement feld: u v : s used smplf the feld w1 3 w1 v4 4 : also used to smplf the feld v, u u 4 h 4h For the (earler) dsplacement feld the resultant moments and shear force H H H * 3 * 3 * 3,, M z dz M z dz M z dz H H H H H H H * * z, z, z, z Q dz Q dz Q z dz Q z dz H H H H
80 hrd Order Plate heor: Fnte Element Formulaton In the FE formulaton the defntons of are changed: Now there are seven varables per node! Dsplacement vector changed. L E, L B d s also L S s defned for shear part. Stran energ s d B AB d d B BB d E E B E e 1 U d BE BBB d d BB DBB d da A e d BS DS BS d
81 hrd Order Plate heor: Fnte Element Formulaton Stran Energ of an element n a concse form e 1 e U d K d where, K e s the element stffness matr K e 1 B E A BE BB B BE BE B BB BB D B B da A e BS DS BS
82 Hgher Order Plate heor: Most popular hgher order theores have constant or lnear varaton of transverse dsplacement. hat s, the transverse normal stran s zero or constant! he development of these theores was domnated b bendng loadng. he stretchng of aal part s not gven mportance. In case of unsmmetrc lamnates there s stretchng bendng couplng. hese theores ma not be sutable.
83 Hgher Order Plate heor: Dsplacement feld: u v w p, p, p p u z 1, u z 1 u,,z v pz 1 v,,z v, z w,,z 1 w pz 1 w, z 1 z z z - order of polnomal drector functons n z-drecton for u, v and w hese orders can be dfferent.
84 Hgher Order Plate heor: In general, p u z For bendng domnated problems p v z, v,,z u,,z w,,z - antsmmetrc wth respect to z (odd powers) - smmetrc wth respect to z (even powers) For frst order shear deformable theor hs s Denoted as: 1,1, u v w z z z p p 1, p For thrd order shear deformable theor hs s Denoted as: 3,3,
85 Hgher Order Plate heor: Natural Herarch of models for bendng domnated problems: 1,1,, 1,1,, 3,3,, 3,3,4, For membrane domnated problems: u,,z, v,,z - smmetrc wth respect to z (even powers) w,,z - antsmmetrc wth respect to z (odd powers) Natural Herarch of models for membrane domnated problems:,,1,,,1,,,3, 4,4,3,
86 Hgher Order Plate heor: For both bendng and membrane domnated problems: 1,1,1,,,, 3,3,3, 4,4,4, he sequences of the models were based on the convergence of ther solutons to the three dmensonal soluton n a sutable norm.
87 hank ou
One Dimensional Axial Deformations
 One Dmensonal al Deformatons In ths secton, a specfc smple geometr s consdered, that of a long and thn straght component loaded n such a wa that t deforms n the aal drecton onl. The -as s taken as the
One Dmensonal al Deformatons In ths secton, a specfc smple geometr s consdered, that of a long and thn straght component loaded n such a wa that t deforms n the aal drecton onl. The -as s taken as the
C PLANE ELASTICITY PROBLEM FORMULATIONS
 C M.. Tamn, CSMLab, UTM Corse Content: A ITRODUCTIO AD OVERVIEW mercal method and Compter-Aded Engneerng; Phscal problems; Mathematcal models; Fnte element method. B REVIEW OF -D FORMULATIOS Elements and
C M.. Tamn, CSMLab, UTM Corse Content: A ITRODUCTIO AD OVERVIEW mercal method and Compter-Aded Engneerng; Phscal problems; Mathematcal models; Fnte element method. B REVIEW OF -D FORMULATIOS Elements and
Instituto Tecnológico de Aeronáutica FINITE ELEMENTS I. Class notes AE-245
 Insttuto Tecnológco de Aeronáutca FIITE ELEMETS I Class notes AE-5 Insttuto Tecnológco de Aeronáutca 5. Isoparametrc Elements AE-5 Insttuto Tecnológco de Aeronáutca ISOPARAMETRIC ELEMETS Introducton What
Insttuto Tecnológco de Aeronáutca FIITE ELEMETS I Class notes AE-5 Insttuto Tecnológco de Aeronáutca 5. Isoparametrc Elements AE-5 Insttuto Tecnológco de Aeronáutca ISOPARAMETRIC ELEMETS Introducton What
PLATE BENDING ELEMENTS
 8. PLATE BENING ELEMENTS Plate Bendng s a Smple Etenson of Beam Theor 8. INTROUCTION { XE "Plate Bendng Elements" }Before 960, plates and slabs were modeled usng a grd of beam elements for man cvl engneerng
8. PLATE BENING ELEMENTS Plate Bendng s a Smple Etenson of Beam Theor 8. INTROUCTION { XE "Plate Bendng Elements" }Before 960, plates and slabs were modeled usng a grd of beam elements for man cvl engneerng
Chapter Eight. Review and Summary. Two methods in solid mechanics ---- vectorial methods and energy methods or variational methods
 Chapter Eght Energy Method 8. Introducton 8. Stran energy expressons 8.3 Prncpal of statonary potental energy; several degrees of freedom ------ Castglano s frst theorem ---- Examples 8.4 Prncpal of statonary
Chapter Eght Energy Method 8. Introducton 8. Stran energy expressons 8.3 Prncpal of statonary potental energy; several degrees of freedom ------ Castglano s frst theorem ---- Examples 8.4 Prncpal of statonary
Finite Element Modelling of truss/cable structures
 Pet Schreurs Endhoven Unversty of echnology Department of Mechancal Engneerng Materals echnology November 3, 214 Fnte Element Modellng of truss/cable structures 1 Fnte Element Analyss of prestressed structures
Pet Schreurs Endhoven Unversty of echnology Department of Mechancal Engneerng Materals echnology November 3, 214 Fnte Element Modellng of truss/cable structures 1 Fnte Element Analyss of prestressed structures
Application to Plane (rigid) frame structure
 Advanced Computatonal echancs 18 Chapter 4 Applcaton to Plane rgd frame structure 1. Dscusson on degrees of freedom In case of truss structures, t was enough that the element force equaton provdes onl
Advanced Computatonal echancs 18 Chapter 4 Applcaton to Plane rgd frame structure 1. Dscusson on degrees of freedom In case of truss structures, t was enough that the element force equaton provdes onl
APPENDIX F A DISPLACEMENT-BASED BEAM ELEMENT WITH SHEAR DEFORMATIONS. Never use a Cubic Function Approximation for a Non-Prismatic Beam
 APPENDIX F A DISPACEMENT-BASED BEAM EEMENT WITH SHEAR DEFORMATIONS Never use a Cubc Functon Approxmaton for a Non-Prsmatc Beam F. INTRODUCTION { XE "Shearng Deformatons" }In ths appendx a unque development
APPENDIX F A DISPACEMENT-BASED BEAM EEMENT WITH SHEAR DEFORMATIONS Never use a Cubc Functon Approxmaton for a Non-Prsmatc Beam F. INTRODUCTION { XE "Shearng Deformatons" }In ths appendx a unque development
Professor Terje Haukaas University of British Columbia, Vancouver The Q4 Element
 Professor Terje Haukaas Unversty of Brtsh Columba, ancouver www.nrsk.ubc.ca The Q Element Ths document consders fnte elements that carry load only n ther plane. These elements are sometmes referred to
Professor Terje Haukaas Unversty of Brtsh Columba, ancouver www.nrsk.ubc.ca The Q Element Ths document consders fnte elements that carry load only n ther plane. These elements are sometmes referred to
Elshaboury SM et al.; Sch. J. Phys. Math. Stat., 2015; Vol-2; Issue-2B (Mar-May); pp
 Elshabour SM et al.; Sch. J. Phs. Math. Stat. 5; Vol-; Issue-B (Mar-Ma); pp-69-75 Scholars Journal of Phscs Mathematcs Statstcs Sch. J. Phs. Math. Stat. 5; (B):69-75 Scholars Academc Scentfc Publshers
Elshabour SM et al.; Sch. J. Phs. Math. Stat. 5; Vol-; Issue-B (Mar-Ma); pp-69-75 Scholars Journal of Phscs Mathematcs Statstcs Sch. J. Phs. Math. Stat. 5; (B):69-75 Scholars Academc Scentfc Publshers
In this section is given an overview of the common elasticity models.
 Secton 4.1 4.1 Elastc Solds In ths secton s gven an overvew of the common elastcty models. 4.1.1 The Lnear Elastc Sold The classcal Lnear Elastc model, or Hooean model, has the followng lnear relatonshp
Secton 4.1 4.1 Elastc Solds In ths secton s gven an overvew of the common elastcty models. 4.1.1 The Lnear Elastc Sold The classcal Lnear Elastc model, or Hooean model, has the followng lnear relatonshp
COMPOSITE BEAM WITH WEAK SHEAR CONNECTION SUBJECTED TO THERMAL LOAD
 COMPOSITE BEAM WITH WEAK SHEAR CONNECTION SUBJECTED TO THERMAL LOAD Ákos Jósef Lengyel, István Ecsed Assstant Lecturer, Professor of Mechancs, Insttute of Appled Mechancs, Unversty of Mskolc, Mskolc-Egyetemváros,
COMPOSITE BEAM WITH WEAK SHEAR CONNECTION SUBJECTED TO THERMAL LOAD Ákos Jósef Lengyel, István Ecsed Assstant Lecturer, Professor of Mechancs, Insttute of Appled Mechancs, Unversty of Mskolc, Mskolc-Egyetemváros,
CIVL 8/7117 Chapter 10 - Isoparametric Formulation 42/56
 CIVL 8/77 Chapter 0 - Isoparametrc Formulaton 4/56 Newton-Cotes Example Usng the Newton-Cotes method wth = ntervals (n = 3 samplng ponts), evaluate the ntegrals: x x cos dx 3 x x dx 3 x x dx 4.3333333
CIVL 8/77 Chapter 0 - Isoparametrc Formulaton 4/56 Newton-Cotes Example Usng the Newton-Cotes method wth = ntervals (n = 3 samplng ponts), evaluate the ntegrals: x x cos dx 3 x x dx 3 x x dx 4.3333333
STATIC ANALYSIS OF TWO-LAYERED PIEZOELECTRIC BEAMS WITH IMPERFECT SHEAR CONNECTION
 STATIC ANALYSIS OF TWO-LERED PIEZOELECTRIC BEAMS WITH IMPERFECT SHEAR CONNECTION Ákos József Lengyel István Ecsed Assstant Lecturer Emertus Professor Insttute of Appled Mechancs Unversty of Mskolc Mskolc-Egyetemváros
STATIC ANALYSIS OF TWO-LERED PIEZOELECTRIC BEAMS WITH IMPERFECT SHEAR CONNECTION Ákos József Lengyel István Ecsed Assstant Lecturer Emertus Professor Insttute of Appled Mechancs Unversty of Mskolc Mskolc-Egyetemváros
Module 3: Element Properties Lecture 1: Natural Coordinates
 Module 3: Element Propertes Lecture : Natural Coordnates Natural coordnate system s bascally a local coordnate system whch allows the specfcaton of a pont wthn the element by a set of dmensonless numbers
Module 3: Element Propertes Lecture : Natural Coordnates Natural coordnate system s bascally a local coordnate system whch allows the specfcaton of a pont wthn the element by a set of dmensonless numbers
C PLANE ELASTICITY PROBLEM FORMULATIONS
 C M.. Tamn, CSMLab, UTM Corse Content: A ITRODUCTIO AD OVERVIEW mercal method and Compter-Aded Engneerng; Phscal problems; Mathematcal models; Fnte element method. B REVIEW OF -D FORMULATIOS Elements and
C M.. Tamn, CSMLab, UTM Corse Content: A ITRODUCTIO AD OVERVIEW mercal method and Compter-Aded Engneerng; Phscal problems; Mathematcal models; Fnte element method. B REVIEW OF -D FORMULATIOS Elements and
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM
 ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
MEMBRANE ELEMENT WITH NORMAL ROTATIONS
 9. MEMBRANE ELEMENT WITH NORMAL ROTATIONS Rotatons Mst Be Compatble Between Beam, Membrane and Shell Elements 9. INTRODUCTION { XE "Membrane Element" }The comple natre of most bldngs and other cvl engneerng
9. MEMBRANE ELEMENT WITH NORMAL ROTATIONS Rotatons Mst Be Compatble Between Beam, Membrane and Shell Elements 9. INTRODUCTION { XE "Membrane Element" }The comple natre of most bldngs and other cvl engneerng
Frame element resists external loads or disturbances by developing internal axial forces, shear forces, and bending moments.
 CE7 Structural Analyss II PAAR FRAE EEET y 5 x E, A, I, Each node can translate and rotate n plane. The fnal dsplaced shape has ndependent generalzed dsplacements (.e. translatons and rotatons) noled.
CE7 Structural Analyss II PAAR FRAE EEET y 5 x E, A, I, Each node can translate and rotate n plane. The fnal dsplaced shape has ndependent generalzed dsplacements (.e. translatons and rotatons) noled.
(5.1.1) v Here, u and v are the displacements parallel to x and y directions respectively.
 Lecture : Constant Stran rangle he trangular elements wth dfferent numbers of nodes are used for solvng two dmensonal sold members. he lnear trangular element was the frst tpe of element developed for
Lecture : Constant Stran rangle he trangular elements wth dfferent numbers of nodes are used for solvng two dmensonal sold members. he lnear trangular element was the frst tpe of element developed for
EVALUATION OF THE VISCO-ELASTIC PROPERTIES IN ASPHALT RUBBER AND CONVENTIONAL MIXES
 EVALUATION OF THE VISCO-ELASTIC PROPERTIES IN ASPHALT RUBBER AND CONVENTIONAL MIXES Manuel J. C. Mnhoto Polytechnc Insttute of Bragança, Bragança, Portugal E-mal: mnhoto@pb.pt Paulo A. A. Perera and Jorge
EVALUATION OF THE VISCO-ELASTIC PROPERTIES IN ASPHALT RUBBER AND CONVENTIONAL MIXES Manuel J. C. Mnhoto Polytechnc Insttute of Bragança, Bragança, Portugal E-mal: mnhoto@pb.pt Paulo A. A. Perera and Jorge
Physics 5153 Classical Mechanics. D Alembert s Principle and The Lagrangian-1
 P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
Section 8.3 Polar Form of Complex Numbers
 80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
Indeterminate pin-jointed frames (trusses)
 Indetermnate pn-jonted frames (trusses) Calculaton of member forces usng force method I. Statcal determnacy. The degree of freedom of any truss can be derved as: w= k d a =, where k s the number of all
Indetermnate pn-jonted frames (trusses) Calculaton of member forces usng force method I. Statcal determnacy. The degree of freedom of any truss can be derved as: w= k d a =, where k s the number of all
THE SMOOTH INDENTATION OF A CYLINDRICAL INDENTOR AND ANGLE-PLY LAMINATES
 THE SMOOTH INDENTATION OF A CYLINDRICAL INDENTOR AND ANGLE-PLY LAMINATES W. C. Lao Department of Cvl Engneerng, Feng Cha Unverst 00 Wen Hwa Rd, Tachung, Tawan SUMMARY: The ndentaton etween clndrcal ndentor
THE SMOOTH INDENTATION OF A CYLINDRICAL INDENTOR AND ANGLE-PLY LAMINATES W. C. Lao Department of Cvl Engneerng, Feng Cha Unverst 00 Wen Hwa Rd, Tachung, Tawan SUMMARY: The ndentaton etween clndrcal ndentor
Week 9 Chapter 10 Section 1-5
 Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Grid Generation around a Cylinder by Complex Potential Functions
 Research Journal of Appled Scences, Engneerng and Technolog 4(): 53-535, 0 ISSN: 040-7467 Mawell Scentfc Organzaton, 0 Submtted: December 0, 0 Accepted: Januar, 0 Publshed: June 0, 0 Grd Generaton around
Research Journal of Appled Scences, Engneerng and Technolog 4(): 53-535, 0 ISSN: 040-7467 Mawell Scentfc Organzaton, 0 Submtted: December 0, 0 Accepted: Januar, 0 Publshed: June 0, 0 Grd Generaton around
coordinates. Then, the position vectors are described by
 Revewng, what we have dscussed so far: Generalzed coordnates Any number of varables (say, n) suffcent to specfy the confguraton of the system at each nstant to tme (need not be the mnmum number). In general,
Revewng, what we have dscussed so far: Generalzed coordnates Any number of varables (say, n) suffcent to specfy the confguraton of the system at each nstant to tme (need not be the mnmum number). In general,
So far: simple (planar) geometries
 Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Physics 5153 Classical Mechanics. Principle of Virtual Work-1
 P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
Fastener Modeling for Joining Composite Parts
 AM-VPD09-006 Fastener Modelng for Jonng Composte Parts Alexander Rutman, Assocate Techncal Fellow, Sprt AeroSystems Chrs Boshers, Stress ngneer, Sprt AeroSystems John Parady, Prncpal Applcaton ngneer,
AM-VPD09-006 Fastener Modelng for Jonng Composte Parts Alexander Rutman, Assocate Techncal Fellow, Sprt AeroSystems Chrs Boshers, Stress ngneer, Sprt AeroSystems John Parady, Prncpal Applcaton ngneer,
PHYS 705: Classical Mechanics. Calculus of Variations II
 1 PHYS 705: Classcal Mechancs Calculus of Varatons II 2 Calculus of Varatons: Generalzaton (no constrant yet) Suppose now that F depends on several dependent varables : We need to fnd such that has a statonary
1 PHYS 705: Classcal Mechancs Calculus of Varatons II 2 Calculus of Varatons: Generalzaton (no constrant yet) Suppose now that F depends on several dependent varables : We need to fnd such that has a statonary
OFF-AXIS MECHANICAL PROPERTIES OF FRP COMPOSITES
 ICAMS 204 5 th Internatonal Conference on Advanced Materals and Systems OFF-AXIS MECHANICAL PROPERTIES OF FRP COMPOSITES VLAD LUPĂŞTEANU, NICOLAE ŢĂRANU, RALUCA HOHAN, PAUL CIOBANU Gh. Asach Techncal Unversty
ICAMS 204 5 th Internatonal Conference on Advanced Materals and Systems OFF-AXIS MECHANICAL PROPERTIES OF FRP COMPOSITES VLAD LUPĂŞTEANU, NICOLAE ŢĂRANU, RALUCA HOHAN, PAUL CIOBANU Gh. Asach Techncal Unversty
CHAPTER 6. LAGRANGE S EQUATIONS (Analytical Mechanics)
 CHAPTER 6 LAGRANGE S EQUATIONS (Analytcal Mechancs) 1 Ex. 1: Consder a partcle movng on a fxed horzontal surface. r P Let, be the poston and F be the total force on the partcle. The FBD s: -mgk F 1 x O
CHAPTER 6 LAGRANGE S EQUATIONS (Analytcal Mechancs) 1 Ex. 1: Consder a partcle movng on a fxed horzontal surface. r P Let, be the poston and F be the total force on the partcle. The FBD s: -mgk F 1 x O
Rigid body simulation
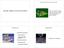 Rgd bod smulaton Rgd bod smulaton Once we consder an object wth spacal etent, partcle sstem smulaton s no longer suffcent Problems Problems Unconstraned sstem rotatonal moton torques and angular momentum
Rgd bod smulaton Rgd bod smulaton Once we consder an object wth spacal etent, partcle sstem smulaton s no longer suffcent Problems Problems Unconstraned sstem rotatonal moton torques and angular momentum
Lecture 13 APPROXIMATION OF SECOMD ORDER DERIVATIVES
 COMPUTATIONAL FLUID DYNAMICS: FDM: Appromaton of Second Order Dervatves Lecture APPROXIMATION OF SECOMD ORDER DERIVATIVES. APPROXIMATION OF SECOND ORDER DERIVATIVES Second order dervatves appear n dffusve
COMPUTATIONAL FLUID DYNAMICS: FDM: Appromaton of Second Order Dervatves Lecture APPROXIMATION OF SECOMD ORDER DERIVATIVES. APPROXIMATION OF SECOND ORDER DERIVATIVES Second order dervatves appear n dffusve
SCALARS AND VECTORS All physical quantities in engineering mechanics are measured using either scalars or vectors.
 SCALARS AND ECTORS All phscal uanttes n engneerng mechancs are measured usng ether scalars or vectors. Scalar. A scalar s an postve or negatve phscal uantt that can be completel specfed b ts magntude.
SCALARS AND ECTORS All phscal uanttes n engneerng mechancs are measured usng ether scalars or vectors. Scalar. A scalar s an postve or negatve phscal uantt that can be completel specfed b ts magntude.
Inductance Calculation for Conductors of Arbitrary Shape
 CRYO/02/028 Aprl 5, 2002 Inductance Calculaton for Conductors of Arbtrary Shape L. Bottura Dstrbuton: Internal Summary In ths note we descrbe a method for the numercal calculaton of nductances among conductors
CRYO/02/028 Aprl 5, 2002 Inductance Calculaton for Conductors of Arbtrary Shape L. Bottura Dstrbuton: Internal Summary In ths note we descrbe a method for the numercal calculaton of nductances among conductors
Chapter 6 Elastic -Plastic Fracture Mechanics
 Chapter 6 Elastc -Plastc Fracture Mechancs The hgh stresses at the crack tp cannot be sustaned b, practcall, an materal. Thus, f the materal does not fracture, a plastc zone (or damage zone or process
Chapter 6 Elastc -Plastc Fracture Mechancs The hgh stresses at the crack tp cannot be sustaned b, practcall, an materal. Thus, f the materal does not fracture, a plastc zone (or damage zone or process
CHAPTER 4. Vector Spaces
 man 2007/2/16 page 234 CHAPTER 4 Vector Spaces To crtcze mathematcs for ts abstracton s to mss the pont entrel. Abstracton s what makes mathematcs work. Ian Stewart The man am of ths tet s to stud lnear
man 2007/2/16 page 234 CHAPTER 4 Vector Spaces To crtcze mathematcs for ts abstracton s to mss the pont entrel. Abstracton s what makes mathematcs work. Ian Stewart The man am of ths tet s to stud lnear
Lecture 12: Discrete Laplacian
 Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Interconnect Modeling
 Interconnect Modelng Modelng of Interconnects Interconnect R, C and computaton Interconnect models umped RC model Dstrbuted crcut models Hgher-order waveform n dstrbuted RC trees Accuracy and fdelty Prepared
Interconnect Modelng Modelng of Interconnects Interconnect R, C and computaton Interconnect models umped RC model Dstrbuted crcut models Hgher-order waveform n dstrbuted RC trees Accuracy and fdelty Prepared
General displacement arch-cantilever element method for stress analysis of arch dam
 Water Scence and Engneerng, 009, (): 3-4 do:0.388/j.ssn.674-370.009.0.004 http://kkb.hhu.edu.cn e-mal: wse@hhu.edu.cn General dsplacement arch-cantlever element method for stress analyss of arch dam Hao
Water Scence and Engneerng, 009, (): 3-4 do:0.388/j.ssn.674-370.009.0.004 http://kkb.hhu.edu.cn e-mal: wse@hhu.edu.cn General dsplacement arch-cantlever element method for stress analyss of arch dam Hao
PART 8. Partial Differential Equations PDEs
 he Islamc Unverst of Gaza Facult of Engneerng Cvl Engneerng Department Numercal Analss ECIV 3306 PAR 8 Partal Dfferental Equatons PDEs Chapter 9; Fnte Dfference: Ellptc Equatons Assocate Prof. Mazen Abualtaef
he Islamc Unverst of Gaza Facult of Engneerng Cvl Engneerng Department Numercal Analss ECIV 3306 PAR 8 Partal Dfferental Equatons PDEs Chapter 9; Fnte Dfference: Ellptc Equatons Assocate Prof. Mazen Abualtaef
DUE: WEDS FEB 21ST 2018
 HOMEWORK # 1: FINITE DIFFERENCES IN ONE DIMENSION DUE: WEDS FEB 21ST 2018 1. Theory Beam bendng s a classcal engneerng analyss. The tradtonal soluton technque makes smplfyng assumptons such as a constant
HOMEWORK # 1: FINITE DIFFERENCES IN ONE DIMENSION DUE: WEDS FEB 21ST 2018 1. Theory Beam bendng s a classcal engneerng analyss. The tradtonal soluton technque makes smplfyng assumptons such as a constant
χ x B E (c) Figure 2.1.1: (a) a material particle in a body, (b) a place in space, (c) a configuration of the body
 Secton.. Moton.. The Materal Body and Moton hyscal materals n the real world are modeled usng an abstract mathematcal entty called a body. Ths body conssts of an nfnte number of materal partcles. Shown
Secton.. Moton.. The Materal Body and Moton hyscal materals n the real world are modeled usng an abstract mathematcal entty called a body. Ths body conssts of an nfnte number of materal partcles. Shown
Bezier curves. Michael S. Floater. August 25, These notes provide an introduction to Bezier curves. i=0
 Bezer curves Mchael S. Floater August 25, 211 These notes provde an ntroducton to Bezer curves. 1 Bernsten polynomals Recall that a real polynomal of a real varable x R, wth degree n, s a functon of the
Bezer curves Mchael S. Floater August 25, 211 These notes provde an ntroducton to Bezer curves. 1 Bernsten polynomals Recall that a real polynomal of a real varable x R, wth degree n, s a functon of the
Buckling analysis of single-layered FG nanoplates on elastic substrate with uneven porosities and various boundary conditions
 IOSR Journal of Mechancal and Cvl Engneerng (IOSR-JMCE) e-issn: 78-1684,p-ISSN: 30-334X, Volume 15, Issue 5 Ver. IV (Sep. - Oct. 018), PP 41-46 www.osrjournals.org Bucklng analyss of sngle-layered FG nanoplates
IOSR Journal of Mechancal and Cvl Engneerng (IOSR-JMCE) e-issn: 78-1684,p-ISSN: 30-334X, Volume 15, Issue 5 Ver. IV (Sep. - Oct. 018), PP 41-46 www.osrjournals.org Bucklng analyss of sngle-layered FG nanoplates
Modal Identification of the Elastic Properties in Composite Sandwich Structures
 Modal Identfcaton of the Elastc Propertes n Composte Sandwch Structures M. Matter Th. Gmür J. Cugnon and A. Schorderet School of Engneerng (STI) Ecole poltechnque fédérale f de Lausanne (EPFL) Swterland
Modal Identfcaton of the Elastc Propertes n Composte Sandwch Structures M. Matter Th. Gmür J. Cugnon and A. Schorderet School of Engneerng (STI) Ecole poltechnque fédérale f de Lausanne (EPFL) Swterland
CinChE Problem-Solving Strategy Chapter 4 Development of a Mathematical Model. formulation. procedure
 nhe roblem-solvng Strategy hapter 4 Transformaton rocess onceptual Model formulaton procedure Mathematcal Model The mathematcal model s an abstracton that represents the engneerng phenomena occurrng n
nhe roblem-solvng Strategy hapter 4 Transformaton rocess onceptual Model formulaton procedure Mathematcal Model The mathematcal model s an abstracton that represents the engneerng phenomena occurrng n
MODELLING OF ELASTO-STATICS OF POWER LINES BY NEW COMPOSITE BEAM FINITE ELEMENT Bratislava
 ODING OF ASTO-STATICS OF POW INS BY NW COPOSIT BA FINIT NT urín Justín 1 rabovský Jura 1 Gogola oman 1 utš Vladmír 1 Paulech Jura 1 1 Insttute of Automotve echatroncs FI STU n Bratslava Ilkovčova 3 812
ODING OF ASTO-STATICS OF POW INS BY NW COPOSIT BA FINIT NT urín Justín 1 rabovský Jura 1 Gogola oman 1 utš Vladmír 1 Paulech Jura 1 1 Insttute of Automotve echatroncs FI STU n Bratslava Ilkovčova 3 812
A Quantum Gauss-Bonnet Theorem
 A Quantum Gauss-Bonnet Theorem Tyler Fresen November 13, 2014 Curvature n the plane Let Γ be a smooth curve wth orentaton n R 2, parametrzed by arc length. The curvature k of Γ s ± Γ, where the sgn s postve
A Quantum Gauss-Bonnet Theorem Tyler Fresen November 13, 2014 Curvature n the plane Let Γ be a smooth curve wth orentaton n R 2, parametrzed by arc length. The curvature k of Γ s ± Γ, where the sgn s postve
Moments of Inertia. and reminds us of the analogous equation for linear momentum p= mv, which is of the form. The kinetic energy of the body is.
 Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Physics 181. Particle Systems
 Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Tensor Analysis. For orthogonal curvilinear coordinates, ˆ ˆ (98) Expanding the derivative, we have, ˆ. h q. . h q h q
 For orthogonal curvlnear coordnates, eˆ grad a a= ( aˆ ˆ e). h q (98) Expandng the dervatve, we have, eˆ aˆ ˆ e a= ˆ ˆ a h e + q q 1 aˆ ˆ ˆ a e = ee ˆˆ ˆ + e. h q h q Now expandng eˆ / q (some of the detals
For orthogonal curvlnear coordnates, eˆ grad a a= ( aˆ ˆ e). h q (98) Expandng the dervatve, we have, eˆ aˆ ˆ e a= ˆ ˆ a h e + q q 1 aˆ ˆ ˆ a e = ee ˆˆ ˆ + e. h q h q Now expandng eˆ / q (some of the detals
12. The Hamilton-Jacobi Equation Michael Fowler
 1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
ORIGIN 1. PTC_CE_BSD_3.2_us_mp.mcdx. Mathcad Enabled Content 2011 Knovel Corp.
 Clck to Vew Mathcad Document 2011 Knovel Corp. Buldng Structural Desgn. homas P. Magner, P.E. 2011 Parametrc echnology Corp. Chapter 3: Renforced Concrete Slabs and Beams 3.2 Renforced Concrete Beams -
Clck to Vew Mathcad Document 2011 Knovel Corp. Buldng Structural Desgn. homas P. Magner, P.E. 2011 Parametrc echnology Corp. Chapter 3: Renforced Concrete Slabs and Beams 3.2 Renforced Concrete Beams -
Effects of Boundary Conditions on Cross-Ply Laminated Composite Beams
 Internatonal Journal of Engneerng Research And Advanced Technology (IJERAT) DOI: http://dx.do.org/0.734/ijerat.344 E-ISSN : 454-635 Vol.3 (0) Oct -07 Effects of Boundary Condtons on Cross-Ply Lamnated
Internatonal Journal of Engneerng Research And Advanced Technology (IJERAT) DOI: http://dx.do.org/0.734/ijerat.344 E-ISSN : 454-635 Vol.3 (0) Oct -07 Effects of Boundary Condtons on Cross-Ply Lamnated
5.76 Lecture #21 2/28/94 Page 1. Lecture #21: Rotation of Polyatomic Molecules I
 5.76 Lecture # /8/94 Page Lecture #: Rotaton of Polatomc Molecules I A datomc molecule s ver lmted n how t can rotate and vbrate. * R s to nternuclear as * onl one knd of vbraton A polatomc molecule can
5.76 Lecture # /8/94 Page Lecture #: Rotaton of Polatomc Molecules I A datomc molecule s ver lmted n how t can rotate and vbrate. * R s to nternuclear as * onl one knd of vbraton A polatomc molecule can
( ) [ ( k) ( k) ( x) ( ) ( ) ( ) [ ] ξ [ ] [ ] [ ] ( )( ) i ( ) ( )( ) 2! ( ) = ( ) 3 Interpolation. Polynomial Approximation.
![( ) [ ( k) ( k) ( x) ( ) ( ) ( ) [ ] ξ [ ] [ ] [ ] ( )( ) i ( ) ( )( ) 2! ( ) = ( ) 3 Interpolation. Polynomial Approximation. ( ) [ ( k) ( k) ( x) ( ) ( ) ( ) [ ] ξ [ ] [ ] [ ] ( )( ) i ( ) ( )( ) 2! ( ) = ( ) 3 Interpolation. Polynomial Approximation.](/thumbs/84/90601477.jpg) 3 Interpolaton {( y } Gven:,,,,,, [ ] Fnd: y for some Mn, Ma Polynomal Appromaton Theorem (Weerstrass Appromaton Theorem --- estence ε [ ab] f( P( , then there ests a polynomal
3 Interpolaton {( y } Gven:,,,,,, [ ] Fnd: y for some Mn, Ma Polynomal Appromaton Theorem (Weerstrass Appromaton Theorem --- estence ε [ ab] f( P( , then there ests a polynomal
PHYS 705: Classical Mechanics. Canonical Transformation II
 1 PHYS 705: Classcal Mechancs Canoncal Transformaton II Example: Harmonc Oscllator f ( x) x m 0 x U( x) x mx x LT U m Defne or L p p mx x x m mx x H px L px p m p x m m H p 1 x m p m 1 m H x p m x m m
1 PHYS 705: Classcal Mechancs Canoncal Transformaton II Example: Harmonc Oscllator f ( x) x m 0 x U( x) x mx x LT U m Defne or L p p mx x x m mx x H px L px p m p x m m H p 1 x m p m 1 m H x p m x m m
NUMERICAL RESULTS QUALITY IN DEPENDENCE ON ABAQUS PLANE STRESS ELEMENTS TYPE IN BIG DISPLACEMENTS COMPRESSION TEST
 Appled Computer Scence, vol. 13, no. 4, pp. 56 64 do: 10.23743/acs-2017-29 Submtted: 2017-10-30 Revsed: 2017-11-15 Accepted: 2017-12-06 Abaqus Fnte Elements, Plane Stress, Orthotropc Materal Bartosz KAWECKI
Appled Computer Scence, vol. 13, no. 4, pp. 56 64 do: 10.23743/acs-2017-29 Submtted: 2017-10-30 Revsed: 2017-11-15 Accepted: 2017-12-06 Abaqus Fnte Elements, Plane Stress, Orthotropc Materal Bartosz KAWECKI
Inner Product. Euclidean Space. Orthonormal Basis. Orthogonal
 Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
Solution of Linear System of Equations and Matrix Inversion Gauss Seidel Iteration Method
 Soluton of Lnear System of Equatons and Matr Inverson Gauss Sedel Iteraton Method It s another well-known teratve method for solvng a system of lnear equatons of the form a + a22 + + ann = b a2 + a222
Soluton of Lnear System of Equatons and Matr Inverson Gauss Sedel Iteraton Method It s another well-known teratve method for solvng a system of lnear equatons of the form a + a22 + + ann = b a2 + a222
BAR & TRUSS FINITE ELEMENT. Direct Stiffness Method
 BAR & TRUSS FINITE ELEMENT Drect Stness Method FINITE ELEMENT ANALYSIS AND APPLICATIONS INTRODUCTION TO FINITE ELEMENT METHOD What s the nte element method (FEM)? A technqe or obtanng approxmate soltons
BAR & TRUSS FINITE ELEMENT Drect Stness Method FINITE ELEMENT ANALYSIS AND APPLICATIONS INTRODUCTION TO FINITE ELEMENT METHOD What s the nte element method (FEM)? A technqe or obtanng approxmate soltons
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Lectures - Week 4 Matrix norms, Conditioning, Vector Spaces, Linear Independence, Spanning sets and Basis, Null space and Range of a Matrix
 Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
The Feynman path integral
 The Feynman path ntegral Aprl 3, 205 Hesenberg and Schrödnger pctures The Schrödnger wave functon places the tme dependence of a physcal system n the state, ψ, t, where the state s a vector n Hlbert space
The Feynman path ntegral Aprl 3, 205 Hesenberg and Schrödnger pctures The Schrödnger wave functon places the tme dependence of a physcal system n the state, ψ, t, where the state s a vector n Hlbert space
Finite Element Solution Algorithm for Nonlinear Elasticity Problems by Domain Decomposition Method
 Fnte Element Soluton Algorthm for Nonlnear Elastcty Problems by Doman Decomposton Method Bedřch Sousedík Department of Mathematcs, Faculty of Cvl Engneerng, Czech Techncal Unversty n Prague, Thákurova
Fnte Element Soluton Algorthm for Nonlnear Elastcty Problems by Doman Decomposton Method Bedřch Sousedík Department of Mathematcs, Faculty of Cvl Engneerng, Czech Techncal Unversty n Prague, Thákurova
APPENDIX A Some Linear Algebra
 APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
Finite Difference Method
 7/0/07 Instructor r. Ramond Rump (9) 747 698 rcrump@utep.edu EE 337 Computatonal Electromagnetcs (CEM) Lecture #0 Fnte erence Method Lecture 0 These notes ma contan coprghted materal obtaned under ar use
7/0/07 Instructor r. Ramond Rump (9) 747 698 rcrump@utep.edu EE 337 Computatonal Electromagnetcs (CEM) Lecture #0 Fnte erence Method Lecture 0 These notes ma contan coprghted materal obtaned under ar use
Bézier curves. Michael S. Floater. September 10, These notes provide an introduction to Bézier curves. i=0
 Bézer curves Mchael S. Floater September 1, 215 These notes provde an ntroducton to Bézer curves. 1 Bernsten polynomals Recall that a real polynomal of a real varable x R, wth degree n, s a functon of
Bézer curves Mchael S. Floater September 1, 215 These notes provde an ntroducton to Bézer curves. 1 Bernsten polynomals Recall that a real polynomal of a real varable x R, wth degree n, s a functon of
Lecture Notes Introduction to Cluster Algebra
 Lecture Notes Introducton to Cluster Algebra Ivan C.H. Ip Updated: Ma 7, 2017 3 Defnton and Examples of Cluster algebra 3.1 Quvers We frst revst the noton of a quver. Defnton 3.1. A quver s a fnte orented
Lecture Notes Introducton to Cluster Algebra Ivan C.H. Ip Updated: Ma 7, 2017 3 Defnton and Examples of Cluster algebra 3.1 Quvers We frst revst the noton of a quver. Defnton 3.1. A quver s a fnte orented
Army Ants Tunneling for Classical Simulations
 Electronc Supplementary Materal (ESI) for Chemcal Scence. Ths journal s The Royal Socety of Chemstry 2014 electronc supplementary nformaton (ESI) for Chemcal Scence Army Ants Tunnelng for Classcal Smulatons
Electronc Supplementary Materal (ESI) for Chemcal Scence. Ths journal s The Royal Socety of Chemstry 2014 electronc supplementary nformaton (ESI) for Chemcal Scence Army Ants Tunnelng for Classcal Smulatons
9. Complex Numbers. 1. Numbers revisited. 2. Imaginary number i: General form of complex numbers. 3. Manipulation of complex numbers
 9. Comple Numbers. Numbers revsted. Imagnar number : General form of comple numbers 3. Manpulaton of comple numbers 4. The Argand dagram 5. The polar form for comple numbers 9.. Numbers revsted We saw
9. Comple Numbers. Numbers revsted. Imagnar number : General form of comple numbers 3. Manpulaton of comple numbers 4. The Argand dagram 5. The polar form for comple numbers 9.. Numbers revsted We saw
Geometrically exact multi-layer beams with a rigid interconnection
 Geometrcally exact mult-layer beams wth a rgd nterconnecton Leo Škec, Gordan Jelenć To cte ths verson: Leo Škec, Gordan Jelenć. Geometrcally exact mult-layer beams wth a rgd nterconnecton. 2nd ECCOMAS
Geometrcally exact mult-layer beams wth a rgd nterconnecton Leo Škec, Gordan Jelenć To cte ths verson: Leo Škec, Gordan Jelenć. Geometrcally exact mult-layer beams wth a rgd nterconnecton. 2nd ECCOMAS
Increase Decrease Remain the Same (Circle one) (2 pts)
 ME 270 Sample Fnal Eam PROBLEM 1 (25 ponts) Prob. 1 questons are all or nothng. PROBLEM 1A. (5 ponts) FIND: A 2000 N crate (D) s suspended usng ropes AB and AC and s n statc equlbrum. If θ = 53.13, determne
ME 270 Sample Fnal Eam PROBLEM 1 (25 ponts) Prob. 1 questons are all or nothng. PROBLEM 1A. (5 ponts) FIND: A 2000 N crate (D) s suspended usng ropes AB and AC and s n statc equlbrum. If θ = 53.13, determne
Module 2. Random Processes. Version 2 ECE IIT, Kharagpur
 Module Random Processes Lesson 6 Functons of Random Varables After readng ths lesson, ou wll learn about cdf of functon of a random varable. Formula for determnng the pdf of a random varable. Let, X be
Module Random Processes Lesson 6 Functons of Random Varables After readng ths lesson, ou wll learn about cdf of functon of a random varable. Formula for determnng the pdf of a random varable. Let, X be
Introduction to Density Functional Theory. Jeremie Zaffran 2 nd year-msc. (Nanochemistry)
 Introducton to Densty Functonal Theory Jereme Zaffran nd year-msc. (anochemstry) A- Hartree appromatons Born- Oppenhemer appromaton H H H e The goal of computatonal chemstry H e??? Let s remnd H e T e
Introducton to Densty Functonal Theory Jereme Zaffran nd year-msc. (anochemstry) A- Hartree appromatons Born- Oppenhemer appromaton H H H e The goal of computatonal chemstry H e??? Let s remnd H e T e
Calculus of Variations Basics
 Chapter 1 Calculus of Varatons Bascs 1.1 Varaton of a General Functonal In ths chapter, we derve the general formula for the varaton of a functonal of the form J [y 1,y 2,,y n ] F x,y 1,y 2,,y n,y 1,y
Chapter 1 Calculus of Varatons Bascs 1.1 Varaton of a General Functonal In ths chapter, we derve the general formula for the varaton of a functonal of the form J [y 1,y 2,,y n ] F x,y 1,y 2,,y n,y 1,y
Poisson brackets and canonical transformations
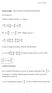 rof O B Wrght Mechancs Notes osson brackets and canoncal transformatons osson Brackets Consder an arbtrary functon f f ( qp t) df f f f q p q p t But q p p where ( qp ) pq q df f f f p q q p t In order
rof O B Wrght Mechancs Notes osson brackets and canoncal transformatons osson Brackets Consder an arbtrary functon f f ( qp t) df f f f q p q p t But q p p where ( qp ) pq q df f f f p q q p t In order
Estimation of the composition of the liquid and vapor streams exiting a flash unit with a supercritical component
 Department of Energ oltecnco d Mlano Va Lambruschn - 05 MILANO Eercses of Fundamentals of Chemcal rocesses rof. Ganpero Gropp Eercse 8 Estmaton of the composton of the lqud and vapor streams etng a unt
Department of Energ oltecnco d Mlano Va Lambruschn - 05 MILANO Eercses of Fundamentals of Chemcal rocesses rof. Ganpero Gropp Eercse 8 Estmaton of the composton of the lqud and vapor streams etng a unt
THEOREMS OF QUANTUM MECHANICS
 THEOREMS OF QUANTUM MECHANICS In order to develop methods to treat many-electron systems (atoms & molecules), many of the theorems of quantum mechancs are useful. Useful Notaton The matrx element A mn
THEOREMS OF QUANTUM MECHANICS In order to develop methods to treat many-electron systems (atoms & molecules), many of the theorems of quantum mechancs are useful. Useful Notaton The matrx element A mn
1 Matrix representations of canonical matrices
 1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
One-sided finite-difference approximations suitable for use with Richardson extrapolation
 Journal of Computatonal Physcs 219 (2006) 13 20 Short note One-sded fnte-dfference approxmatons sutable for use wth Rchardson extrapolaton Kumar Rahul, S.N. Bhattacharyya * Department of Mechancal Engneerng,
Journal of Computatonal Physcs 219 (2006) 13 20 Short note One-sded fnte-dfference approxmatons sutable for use wth Rchardson extrapolaton Kumar Rahul, S.N. Bhattacharyya * Department of Mechancal Engneerng,
Linear Regression Analysis: Terminology and Notation
 ECON 35* -- Secton : Basc Concepts of Regresson Analyss (Page ) Lnear Regresson Analyss: Termnology and Notaton Consder the generc verson of the smple (two-varable) lnear regresson model. It s represented
ECON 35* -- Secton : Basc Concepts of Regresson Analyss (Page ) Lnear Regresson Analyss: Termnology and Notaton Consder the generc verson of the smple (two-varable) lnear regresson model. It s represented
PHYS 705: Classical Mechanics. Newtonian Mechanics
 1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
1 PHYS 705: Classcal Mechancs Newtonan Mechancs Quck Revew of Newtonan Mechancs Basc Descrpton: -An dealzed pont partcle or a system of pont partcles n an nertal reference frame [Rgd bodes (ch. 5 later)]
VEKTORANALYS. GAUSS s THEOREM and STOKES s THEOREM. Kursvecka 3. Kapitel 6-7 Sidor 51-82
 VEKTORANAY Kursvecka 3 GAU s THEOREM and TOKE s THEOREM Kaptel 6-7 dor 51-82 TARGET PROBEM EECTRIC FIED MAGNETIC FIED N + Magnetc monopoles do not est n nature. How can we epress ths nformaton for E and
VEKTORANAY Kursvecka 3 GAU s THEOREM and TOKE s THEOREM Kaptel 6-7 dor 51-82 TARGET PROBEM EECTRIC FIED MAGNETIC FIED N + Magnetc monopoles do not est n nature. How can we epress ths nformaton for E and
Lecture 5.8 Flux Vector Splitting
 Lecture 5.8 Flux Vector Splttng 1 Flux Vector Splttng The vector E n (5.7.) can be rewrtten as E = AU (5.8.1) (wth A as gven n (5.7.4) or (5.7.6) ) whenever, the equaton of state s of the separable form
Lecture 5.8 Flux Vector Splttng 1 Flux Vector Splttng The vector E n (5.7.) can be rewrtten as E = AU (5.8.1) (wth A as gven n (5.7.4) or (5.7.6) ) whenever, the equaton of state s of the separable form
Lecture Note 3. Eshelby s Inclusion II
 ME340B Elastcty of Mcroscopc Structures Stanford Unversty Wnter 004 Lecture Note 3. Eshelby s Incluson II Chrs Wenberger and We Ca c All rghts reserved January 6, 004 Contents 1 Incluson energy n an nfnte
ME340B Elastcty of Mcroscopc Structures Stanford Unversty Wnter 004 Lecture Note 3. Eshelby s Incluson II Chrs Wenberger and We Ca c All rghts reserved January 6, 004 Contents 1 Incluson energy n an nfnte
UNIVERSITY OF BOLTON RAK ACADEMIC CENTRE BENG(HONS) MECHANICAL ENGINEERING SEMESTER TWO EXAMINATION 2017/2018 FINITE ELEMENT AND DIFFERENCE SOLUTIONS
 OCD0 UNIVERSITY OF BOLTON RAK ACADEMIC CENTRE BENG(HONS) MECHANICAL ENGINEERING SEMESTER TWO EXAMINATION 07/08 FINITE ELEMENT AND DIFFERENCE SOLUTIONS MODULE NO. AME6006 Date: Wednesda 0 Ma 08 Tme: 0:00
OCD0 UNIVERSITY OF BOLTON RAK ACADEMIC CENTRE BENG(HONS) MECHANICAL ENGINEERING SEMESTER TWO EXAMINATION 07/08 FINITE ELEMENT AND DIFFERENCE SOLUTIONS MODULE NO. AME6006 Date: Wednesda 0 Ma 08 Tme: 0:00
MEEM 3700 Mechanical Vibrations
 MEEM 700 Mechancal Vbratons Mohan D. Rao Chuck Van Karsen Mechancal Engneerng-Engneerng Mechancs Mchgan echnologcal Unversty Copyrght 00 Lecture & MEEM 700 Multple Degree of Freedom Systems (ext: S.S.
MEEM 700 Mechancal Vbratons Mohan D. Rao Chuck Van Karsen Mechancal Engneerng-Engneerng Mechancs Mchgan echnologcal Unversty Copyrght 00 Lecture & MEEM 700 Multple Degree of Freedom Systems (ext: S.S.
ASME2015 IDETC/CIE, 11th International Conference on Multibody Systems, Nonlinear Dynamics, and Control (MSNDC) MSNDC-10 Vehicle Dynamics
 UNCLASSIFIED: Dstrbuton Statement A. Approved for publc release. #26261 ASME215 IDETC/CIE, 11th Internatonal Conference on Multbody Systems, Nonlnear Dynamcs, and Control (MSNDC) MSNDC-1 Vehcle Dynamcs
UNCLASSIFIED: Dstrbuton Statement A. Approved for publc release. #26261 ASME215 IDETC/CIE, 11th Internatonal Conference on Multbody Systems, Nonlnear Dynamcs, and Control (MSNDC) MSNDC-1 Vehcle Dynamcs
PHYS 705: Classical Mechanics. Hamilton-Jacobi Equation
 1 PHYS 705: Classcal Mechancs Hamlton-Jacob Equaton Hamlton-Jacob Equaton There s also a very elegant relaton between the Hamltonan Formulaton of Mechancs and Quantum Mechancs. To do that, we need to derve
1 PHYS 705: Classcal Mechancs Hamlton-Jacob Equaton Hamlton-Jacob Equaton There s also a very elegant relaton between the Hamltonan Formulaton of Mechancs and Quantum Mechancs. To do that, we need to derve
Optimum design of laminated composite under axial compressive load
 Sādhanā Vol. 36, Part 1, February 2011, pp. 73 85. Indan Academy of Scences Optmum desgn of lamnated composte under axal compressve load NGRIYENGAR 1, and NILESH VYAS 2 1 Department of Aerospace Engneerng,
Sādhanā Vol. 36, Part 1, February 2011, pp. 73 85. Indan Academy of Scences Optmum desgn of lamnated composte under axal compressve load NGRIYENGAR 1, and NILESH VYAS 2 1 Department of Aerospace Engneerng,
Relaxation Methods for Iterative Solution to Linear Systems of Equations
 Relaxaton Methods for Iteratve Soluton to Lnear Systems of Equatons Gerald Recktenwald Portland State Unversty Mechancal Engneerng Department gerry@pdx.edu Overvew Techncal topcs Basc Concepts Statonary
Relaxaton Methods for Iteratve Soluton to Lnear Systems of Equatons Gerald Recktenwald Portland State Unversty Mechancal Engneerng Department gerry@pdx.edu Overvew Techncal topcs Basc Concepts Statonary
Pre-Calculus Summer Assignment
 Pre-Calculus Summer Assgnment Dear Future Pre-Calculus Student, Congratulatons on our successful completon of Algebra! Below ou wll fnd the summer assgnment questons. It s assumed that these concepts,
Pre-Calculus Summer Assgnment Dear Future Pre-Calculus Student, Congratulatons on our successful completon of Algebra! Below ou wll fnd the summer assgnment questons. It s assumed that these concepts,
GEO-SLOPE International Ltd, Calgary, Alberta, Canada Vibrating Beam
 GEO-SLOPE Internatonal Ltd, Calgary, Alberta, Canada www.geo-slope.com Introducton Vbratng Beam Ths example looks at the dynamc response of a cantlever beam n response to a cyclc force at the free end.
GEO-SLOPE Internatonal Ltd, Calgary, Alberta, Canada www.geo-slope.com Introducton Vbratng Beam Ths example looks at the dynamc response of a cantlever beam n response to a cyclc force at the free end.
Numerical analysis of buried pipes subjected to lateral soil movements
 Numercal analss of bured ppes subjected to lateral sol movements P. Casamchele, M. Mauger & E. Motta Department of Cvl and Envronmental Engneerng, Catana Unverst, Ital Abstract he response of bured ppes
Numercal analss of bured ppes subjected to lateral sol movements P. Casamchele, M. Mauger & E. Motta Department of Cvl and Envronmental Engneerng, Catana Unverst, Ital Abstract he response of bured ppes
CHAPTER-5 INFORMATION MEASURE OF FUZZY MATRIX AND FUZZY BINARY RELATION
 CAPTER- INFORMATION MEASURE OF FUZZY MATRI AN FUZZY BINARY RELATION Introducton The basc concept of the fuzz matr theor s ver smple and can be appled to socal and natural stuatons A branch of fuzz matr
CAPTER- INFORMATION MEASURE OF FUZZY MATRI AN FUZZY BINARY RELATION Introducton The basc concept of the fuzz matr theor s ver smple and can be appled to socal and natural stuatons A branch of fuzz matr
