arxiv: v1 [math.gt] 13 Mar 2008
|
|
|
- Sylvia Clark
- 5 years ago
- Views:
Transcription
1 arxiv: v1 [math.gt] 13 Mar 2008 Conformal invariance of the writhe of a knot R. Langevin Institut de Mathématiques de Bourgogne, Université de Bourgogne J. O Hara Department of Mathematics, Tokyo Metropolitan University June 8, 2018 Abstract We give a new proof of the conformal invariance of the writhe of a knot from a conformal geometric vewpoint. Key words and phrases. writhe, conformal invariant Mathematics Subject Classification. Primary 57M25, Secondary 53A30. 1 Introduction Suppose K is a framed knot, i.e. there is a unit normal vector field e 2 along K. A 2-component link K K +εe 2 ( ε 1) can be considered a closed ribbon. Let Lk and Tw be the linking number and the total twist of K K +εe 2, and Wr the writhe of K. Then we have Lk = Wr+Tw. (1) When the knot K has nowhere vanishing curvature and e 2 is the principal normal vector, Lk is called the self-linking number of the knot and denoted by Sl. The equation (1) was proved in this case in [Cǎ1, Cǎ2, Cǎ3, Po], and in [Wh] in general. It plays an important role in the application of the knot theory to molecular biology ([Ful1, Ful2, Wh-Ba]). When the knot K is given by K = f(s 1 ) the writhe is given by the Gauss integral: Wr(f) = 1 det(f (s),f (t),f(s) f(t)) 4π S 1 S f(s) f(t) 3 dsdt (2) 1 This joint work was done during the second author s stay in Dijon which was supported by JSPS. 1
2 (the reader is referred to [AKT] for the details concerning writhe). Banchoff and White showed that the absolute value of the writhe is conformally invariant ([BW]). To be precise, they showed Theorem 1.1 ([BW]) Suppose I is an inversion in a sphere. Then we have It is a corollary of Wr(I(K)) = Wr(K). (3) Theorem 1.2 ([BW]) Suppose I is an inversion in a sphere. Then we have Tw(I(K)) Tw(K) (mod Z). (4) In this paper, using techniques in conformal geometry, we give new proofs of Theorem 1.1 and a special case of Theorem 1.2 when K has nowhere vanishing curvature and e 2 is the unit principal normal vector field. 2 Notations Throughout the paper we use the following notations. We assume that a knot K = f(s 1 ) is oriented. We denote the positive tangent vector f by v = v(x). We denote the circle through x,y, and z by Γ(x,y,z). When one of x,y, and z, say z is, Γ(x,y, ) means the line through x and y. When x is a point on a knot K, Γ(x,x,y) denotes the circle (or line) which is tangent to K at x that passes through y. We assume that it is oriented by v at x. Especially, when y = x Γ(x,x,x) denotes the oriented osculating circle. (We consider lines as circles through.) The union of osculating circles Γ(x,x,x) is called the curvature tube x K ([BW]). Suppose x is a point on a knot K. We denote a sphere through the osculating circle Γ(x,x,x) and y (y x) by Σ(x,x,x,y). It is uniquely determined generically, i.e. unless y Γ(x,x,x). When y = Σ(x,x,x, ) means the plane through Γ(x,x,x). 3 Proof of Theorem 1.2 in special case In this section we assume that a knot K = f(s 1 ) has nowhere vanishing curvature and the unit normal vector field e 2 along K is given by the principal normal vectors. In this case the total twist is equal to 1 2π times the total torsion which we denote by Tω: Tω = 1 τ dx, 2π K where τ denotes the torsion of the knot. We will show in this section 2
3 Proposition 3.1 If both K and I(K) have nowhere vanishing curvatures then where I is an inversion in a sphere. Tω(I(K)) Tω(K) (mod Z), (5) We remark that the above proposition can be proved by Theorem 6.3 of [CSW] which gives Tω(K) = 1 τdx 1 Tdρ (mod Z), 2π K 2π K where T is the conformal torsion and ρ is the conformal arc-length. Lemma 3.2 Suppose a point P does not belong to the osculating circle Γ(x 0,x 0,x 0 ) of a knot K at x 0. (We allow P =.) Then, infinitesimally speaking, the sphere Σ(x,x,x,P) rotates aroundthe circle Γ(x 0,x 0,P) at x = x 0 as x travels in K. In other words, lim (Σ(x 0,x 0,x 0,P) Σ(x 1,x 1,x 1,P)) Γ(x 0,x 0,P). (6) x 1 x 0 Proof: Let Σ(x,y,z,w) denote a sphere through x,y,z, and w. Then lim (Σ(x 0,x 0,x 0,P) Σ(x 1,x 1,x 1,P)) x 1 x 0 ( ( lim Σ(y0,x 0,x 1,P) Σ(x 0,x 1,y 1,P) ) y 0 x 0,y 1 x 1 = lim x 1 x 0 lim Γ(x 0,x 1,P) = Γ(x 0,x 0,P). x 1 x 0 There is an alternative computational proof using the Lorentzian exterior product introduced in [LO]. We show that the total torsion of the image of K by an inversion in a sphere with center P is equal to the total angle variation of the rotation of the sphere Σ(x,x,x,P) as x goes around in K. In order to take into accound the sign of the torsion, we have to consider the orientations. Fix P Γ(x,x,x), where we allow P =. The osculating circle Γ(x,x,x) divide the sphere Σ(x,x,x,P) into two domains. Let D 1 be one of the two that does not contain P (gray disc of Figure 1 left). Assume Σ(x,x,x,P) is given the orientation such that the restriction to D 1 induces the same orientation to the boundary D 1 as that of Γ(x,x,x) which is fixed in the previous section. Let n(x) and n P (x) be the positive unit normal vectors to Σ(x,x,x,P) at x and P respectively (Figure 1 left). Let Π(x) and Π P (x) be the normal planes to Γ(x,x,P) at x and P respectively. We assume that Π(x) (or Π P (x)) is oriented so that the algebraic intersection number of Γ(x,x,P) and Π(x) (or Π P (x)) at x (or respectively, at P) is equal to +1. Since Π(x) Γ(x,x,P), Lemma 3.2 implies ) 3
4 Corollary 3.3 Infinitesimally, the normal vector n(x) to the sphere Σ(x, x, x, P) rotates in the plane Π(x) to K: d n(x) Π(x). (7) dx Let I be an inversion in a sphere with center P. We denote I(x) and I(K) by x and K. Then I maps the osculating circle Γ(x,x,x) to the osculating circle Γ( x, x, x) of K at x, and the sphere Σ(x,x,x,P) to the plane Σ( x, x, x, ). Let ñ( x) be the positive unit normal vector to Σ( x, x, x, ). Then (Figure 1). ñ( x) = n P (x) (8) Figure 1: The above convention of orientation implies that ñ( x) is equal to the unit binormal vector of K. Lemma 3.2 implies that ñ( x) rotates in Π( x) at x. Our convention of the orientation of Π( x) implies Lemma 3.4 The torsion of K is equal to the angle velocity of ñ with respect to the arc-length s: τ( K)( x) = ε( x) dñ d s ( x) (ε( x) {+1, 1}), (9) where ε( x) is the signature of the rotation of ñ at x with respect to the orientation of Π( x). In other words, we have ( τ( K)( x) = ṽ ñ dñ ), d s 4
5 where ṽ denotes the positive unit tangent vector to K. Figure 2: Since the positive unit tangent vector to Γ(x,x,P) at P is equal to ṽ( x), theorientationsofπ P (x) isoppositetothatofπ( x). Therefore,(8) andlemma 3.4 imply τ( K)( x) = ε P ds d s dn P ds (ε P {+1, 1}), where ε P is the signature of the rotation of n P with respect to the orientation of Π P (x). Then Lemma 3.2 implies dn P ds = dn ds (Figure 3), therefore we have Lemma 3.5 The torsion of K at x is equal to the negative of the angle velocity of n in Π(x) with respect to the arc-length s of K up to the multiplication by the Jacobian: τ( K)( x) = ε(x) ds d s dn ds (x) (ε(x) {+1, 1}), (10) where ε(x) is the signature of the rotation of n at x with respect to the orientation of Π(x). In other words, we have τ( K)( x) = ds ( d s v n dn ). ds Thus we are led to 5
6 Figure 3: n(x) n(x 1 ) = n P (x) n P (x 1 ) = Σ(x,x,x,P) Σ(x 1,x 1,x 1,P) Proposition 3.6 Let K be a knot with nowhere vanishing curvature, I an inversion in a sphere with center P, and K = I(K). Assume that K has nowhere vanishing curvature, which happens if and only if P is not contained in the curvature tube of K. Then the total torsion of K is the negative of the total angle variation of the positive unit normal vector n(x) to the sphere Σ(x,x,x,P) as x goes around in K: τ( K)( x)d x = ε dn = v (n dn). (11) K ek K Corollary 3.7 Let K be a knot with nowhere vanishing curvature, and I j (j = 1,2) an inversion in a sphere with center P j which is not contained in the curvature tube of K. Then the total torsion of I 1 (K) and I 2 (K) coincide modulo 2πZ: τd x 1 τd x 2 (mod 2πZ). In other words, I 1(K) I 2(K) Tω(I 1 (K)) Tω(I 2 (K)) Z. Proof: Let n j (j = 1,2) be the positive unit normal vector to Σ(x,x,x,P j ) at x, and θ 21 the angle from n 1 to n 2 in the oriented plane Π(x). Then Corollary 3.3 and the above Proposition imply τd x 1 τd x 2 = dθ 21, I 1(K) I 2(K) K which is equal to 2πk (k Z) since K is closed. Proof of Proposition 3.1: Put P 2 = in the above Corollary. 6
7 4 Proof of Theorem 1.1 We first prove the following fact in our context, which implies Theorem 3.1 in the case when the knot has nowhere vanishing curvature. Proposition 4.1 ([Cǎ1], [Po]) Suppose K has nowhere vanishing curvature. Then 4πWr(K) = 2 τ +4πk for some k Z. In other words, Wr+Tω is an integer. K Proof: Assume K = f(s 1 ) is parametrized by the arc-length. Suppose S 1 = [0,L]/, where L is the length of K. Let ϕ be a map from S 1 S 1 \ to S 2 given by ϕ(s,t) = f(s) f(t) (s t). f(s) f(t) Then the integrand of the writhe is equal to the pull-back of the standard area element of S 2 by ϕ: det(f (s),f (t),f(s) f(t)) f(s) f(t) 3 = ϕ (ϕ s ϕ t ), where ϕ s = ϕ and ϕ t = ϕ. Therefore, 4π times the writhe is equal to the s t signed area of the image of D = {(s,t) 0 s L,s < t < s+l} by ϕ. Let S be the closure of ϕ(d). Then S is an oriented surface (a continuous image of S 1 [0,L]) possibly with self-overlaps in S 2 whose boundary (the image of S 1 {0,L}) is given by S = C + ( C ), where C + and C denote the positive and negative tangential indicatrices: C + =ϕ( + ) = {v(s) = f(s) 0 s L}, C =ϕ( ) = { v(s) = f(s) 0 s L}. We assume that the indicatirices are oriented so that s increases in the positive direction. Let Γ(s) denote a great circle in S 2 which is tangent to C + at v(s) (and to C at v(s)). We remark that C + has nowhere vanishing tangent vector since the knot has nowhere vanishing curvature. Note that C + C is the envelope of the family {Γ(s)} 0 s L. We assume that Γ(s) has an orientation compatible with that of C + at v(s). Let Γ + (s) be a semi-circle of Γ(s) from v(s) C + to 7
8 v(s) C in the positive direction of Γ(s), and S a region in S 2 swept by Γ + (s) as s varies in [0,L]. Then S is given by S = {w(s,t) = (cost)v(s)+(sint) v (s) 0 s L, 0 t π}. v It is an oriented surface (a continuous image of S 1 [0,π]) possibly with selfoverlaps in S 2 whose boundary (the image of S 1 {0,π}) is C + ( C ). The signed area of S is given by Area(S ) = L π 0 0 w (w s w t )dsdt. Since v/ v is equal to the principal normal vector e 2 of the knot K, we have w (w s w t )=det((cost)e 1 +(sint)e 2,(cost)κe 2 +(sint) e 2, (sint)e 1 +(cost)e 2 ) which implies = τ sint, Area(S ) = 2 L 0 τ ds = 4πTω(K). Since both S and S have the boundary C + ( C ), S ( S ) is a cycle of S 2, i.e. an oriented surface (a continuous image of a torus) possibly with self-overlaps without a boundary. Therefore, the signed area of S ( S ) is equal to 4πk for some integer k. It follows that Area(S ( S )) = Area(S) Area(S ) = 4πWr+4πTω = 4πk (k Z), which completes the proof. Corollary 4.2 If both K and I(K) have nowhere vanishing curvatures then Wr(I(K)) = Wr(K). Proof: Let I j (j = 0,1) be an inversion in a sphere with center P j which is not contained in the curvature tube of K. Then Proposition 4.1 implies that Then Corollary 3.7 implies Wr(I 0 (K))+Tω(I 0 (K)) Z, Wr(I 1 (K))+Tω(I 1 (K)) Z. Wr(I 0 (K)) Wr(I 1 (K)) Z. Join P 0 and P 1 by a smooth path P t. Let I t be an inversion in a sphere with center P t. Then Wr(I t (K)) is a continuous function of t ([Po]), and hence Wr(I 0 (K)) = Wr(I 1 (K)). 8
9 When P 1 goes to and the radius of the sphere of the inversion also goes to +, I 1 (K) approachesthe mirrorimageof K and hence Wr(I 1 (K)) approaches Wr(K), which completes the proof. Proof of Theorem 1.1: Suppose the curvature of K vanishes somewhere. We have only to show that K can be approximated, with respect to the C 2 - topology, by a knot with non-vanishing curvature. This can be done as follows. The curvature tube of K is non-compact as it contains a line. But we can still find a point P with a very big distance from K which is not contained in the cuvature tube. Let I be an inversion in a sphere with center P and radius approximately equal to the distance between P and K. We can get a desired knot by taking the mirror image of I(K) thus constructed. References [AKT] J. Aldinger, I. Klapper, and M. Tabor, Formulae for the calculation and estimation of writhe, J. Knot Theory Ramifications. 4(1995), [BW] [Cǎ1] [Cǎ2] [Cǎ3] T. Banchoff and J. H. White, The behavior of the total twist and selflinking number of a closed space curve under inversions, Math. Scand. 36 (1975), G. Cǎlugǎreanu, L intégrale de Gauss et l analyse des nœuds tridimensionnels, Rev. Math. Pures Appl. 4 (1959), G. Cǎlugǎreanu, Sur les classes d isotopie des noeuds tridimensionnels et leur invariants, Czechoslovak Math. J. 11 (1961), G. Cǎlugǎreanu, O teoremǎ asupra înlǎnţuirilor tridimensionale de curbe închise, Comm. Acad. R. P. Romîne (1961), [CSW] G. Cairns, R. W. Sharpe and L. Webb, Conformal invariants for curves and surfaces in three dimensional space forms, Rocky Mountain Journal of Math. 24 (1994), [Ful1] F. B. Fuller, The writhing number of a space curve, Proc. Natl. Acad. Sci. USA 68 (1971), [Ful2] F. B. Fuller, Decomposition of the linking of a closed ribbon: a problem from molecular biology, Proc. Natl. Acad. Sci. USA 75 (1978), [LO] [Po] [Wh] R. Langevin and J. O Hara, Conformally invariant energies of knots, J. Inst. Math. Jussieu 4 (2005), W. F. Pohl, The self-linking number of a closed space curves, J. of Math. Mech. 17 (1968), J. H. White, Self-linking and the Gauss integral in higher dimensions, Amer. J. Math. 91 (1969),
10 [Wh-Ba] J. H. White and W. R. Bauer, Calculation of the twist and the writhe for representative models of DNA, J. Mol. Biol. 189 (1989),
arxiv:math/ v1 [math.gt] 8 Jun 2004
![arxiv:math/ v1 [math.gt] 8 Jun 2004 arxiv:math/ v1 [math.gt] 8 Jun 2004](/thumbs/89/98823437.jpg) Journal of Knot Theory and Its Ramifications c World Scientific Publishing Company COMPUTING THE WRITHE OF A KNOT arxiv:math/46148v1 [math.gt] 8 Jun 24 DAVID CIMASONI Section de mathématiques Université
Journal of Knot Theory and Its Ramifications c World Scientific Publishing Company COMPUTING THE WRITHE OF A KNOT arxiv:math/46148v1 [math.gt] 8 Jun 24 DAVID CIMASONI Section de mathématiques Université
Geometry of Călugăreanu s theorem
 461, 3245 3254 doi:10.1098/rspa.2005.1527 Published online 26 August 2005 Geometry of Călugăreanu s theorem BY M. R. DENNIS 1 AND J. H. HANNAY 2 1 School of Mathematics, University of Southampton, Highfield,
461, 3245 3254 doi:10.1098/rspa.2005.1527 Published online 26 August 2005 Geometry of Călugăreanu s theorem BY M. R. DENNIS 1 AND J. H. HANNAY 2 1 School of Mathematics, University of Southampton, Highfield,
arxiv:math-ph/ v1 7 Mar 2005
 Geometry of Călugăreanu s theorem By M. R. Dennis 1 and J. H. Hannay 2 arxiv:math-ph/0503012v1 7 Mar 2005 1 School of Mathematics, University of Southampton, Highfield, Southampton SO17 1BJ, UK 2 H.H.
Geometry of Călugăreanu s theorem By M. R. Dennis 1 and J. H. Hannay 2 arxiv:math-ph/0503012v1 7 Mar 2005 1 School of Mathematics, University of Southampton, Highfield, Southampton SO17 1BJ, UK 2 H.H.
AN ESTIMATE OF THE TRIPLE POINT NUMBERS OF SURFACE-KNOTS BY QUANDLE COCYCLE INVARIANTS
 AN ESTIMATE OF THE TRIPLE POINT NUMBERS OF SURFACE-KNOTS BY QUANDLE COCYCLE INVARIANTS ERI HATAKENAKA Abstract. The triple point number of a surface-knot is defined to be the minimal number of triple points
AN ESTIMATE OF THE TRIPLE POINT NUMBERS OF SURFACE-KNOTS BY QUANDLE COCYCLE INVARIANTS ERI HATAKENAKA Abstract. The triple point number of a surface-knot is defined to be the minimal number of triple points
QUALIFYING EXAMINATION Harvard University Department of Mathematics Tuesday, February 25, 1997 (Day 1)
 QUALIFYING EXAMINATION Harvard University Department of Mathematics Tuesday, February 25, 1997 (Day 1) 1. Factor the polynomial x 3 x + 1 and find the Galois group of its splitting field if the ground
QUALIFYING EXAMINATION Harvard University Department of Mathematics Tuesday, February 25, 1997 (Day 1) 1. Factor the polynomial x 3 x + 1 and find the Galois group of its splitting field if the ground
arxiv: v1 [math.gt] 17 Aug 2010
![arxiv: v1 [math.gt] 17 Aug 2010 arxiv: v1 [math.gt] 17 Aug 2010](/thumbs/89/97921390.jpg) A SYMMETRIC MOTION PICTURE OF THE TWIST-SPUN TREFOIL arxiv:1008.2819v1 [math.gt] 17 Aug 2010 AYUMU INOUE Abstract. With the aid of a computer, we provide a motion picture of the twist-spun trefoil which
A SYMMETRIC MOTION PICTURE OF THE TWIST-SPUN TREFOIL arxiv:1008.2819v1 [math.gt] 17 Aug 2010 AYUMU INOUE Abstract. With the aid of a computer, we provide a motion picture of the twist-spun trefoil which
On end rotation for open rods undergoing. large deformations. G.H.M. van der Heijden, M.A. Peletier and. R. Planqué
 ARMA manuscript No. (will be inserted by the editor) On end rotation for open rods undergoing large deformations G.H.M. van der Heijden, M.A. Peletier and R. Planqué Abstract We give a careful discussion
ARMA manuscript No. (will be inserted by the editor) On end rotation for open rods undergoing large deformations G.H.M. van der Heijden, M.A. Peletier and R. Planqué Abstract We give a careful discussion
8. THE FARY-MILNOR THEOREM
 Math 501 - Differential Geometry Herman Gluck Tuesday April 17, 2012 8. THE FARY-MILNOR THEOREM The curvature of a smooth curve in 3-space is 0 by definition, and its integral w.r.t. arc length, (s) ds,
Math 501 - Differential Geometry Herman Gluck Tuesday April 17, 2012 8. THE FARY-MILNOR THEOREM The curvature of a smooth curve in 3-space is 0 by definition, and its integral w.r.t. arc length, (s) ds,
arxiv: v3 [math.dg] 19 Jun 2017
![arxiv: v3 [math.dg] 19 Jun 2017 arxiv: v3 [math.dg] 19 Jun 2017](/thumbs/78/78609060.jpg) THE GEOMETRY OF THE WIGNER CAUSTIC AND AFFINE EQUIDISTANTS OF PLANAR CURVES arxiv:160505361v3 [mathdg] 19 Jun 017 WOJCIECH DOMITRZ, MICHA L ZWIERZYŃSKI Abstract In this paper we study global properties
THE GEOMETRY OF THE WIGNER CAUSTIC AND AFFINE EQUIDISTANTS OF PLANAR CURVES arxiv:160505361v3 [mathdg] 19 Jun 017 WOJCIECH DOMITRZ, MICHA L ZWIERZYŃSKI Abstract In this paper we study global properties
Section Arclength and Curvature. (1) Arclength, (2) Parameterizing Curves by Arclength, (3) Curvature, (4) Osculating and Normal Planes.
 Section 10.3 Arclength and Curvature (1) Arclength, (2) Parameterizing Curves by Arclength, (3) Curvature, (4) Osculating and Normal Planes. MATH 127 (Section 10.3) Arclength and Curvature The University
Section 10.3 Arclength and Curvature (1) Arclength, (2) Parameterizing Curves by Arclength, (3) Curvature, (4) Osculating and Normal Planes. MATH 127 (Section 10.3) Arclength and Curvature The University
ON OSCULATING, NORMAL AND RECTIFYING BI-NULL CURVES IN R 5 2
 Novi Sad J. Math. Vol. 48, No. 1, 2018, 9-20 https://doi.org/10.30755/nsjom.05268 ON OSCULATING, NORMAL AND RECTIFYING BI-NULL CURVES IN R 5 2 Kazım İlarslan 1, Makoto Sakaki 2 and Ali Uçum 34 Abstract.
Novi Sad J. Math. Vol. 48, No. 1, 2018, 9-20 https://doi.org/10.30755/nsjom.05268 ON OSCULATING, NORMAL AND RECTIFYING BI-NULL CURVES IN R 5 2 Kazım İlarslan 1, Makoto Sakaki 2 and Ali Uçum 34 Abstract.
RE-NORMALIZED LINK INVARIANTS FROM THE UNROLLED QUANTUM GROUP. 1. Introduction
 RE-NORMALIZED LINK INARIANS FROM HE UNROLLED QUANUM GROUP NAHAN GEER 1 Introduction In the last several years, C Blanchet, F Costantino, B Patureau, N Reshetikhin, uraev and myself (in various collaborations)
RE-NORMALIZED LINK INARIANS FROM HE UNROLLED QUANUM GROUP NAHAN GEER 1 Introduction In the last several years, C Blanchet, F Costantino, B Patureau, N Reshetikhin, uraev and myself (in various collaborations)
On surface-knots with triple point number at most three
 On surface-knots with triple point number at most three A. Al Kharusi and T. Yashiro Abstract arxiv:1711.04838v1 [math.at] 13 Nov 2017 In this paper, we show that if a diagram of a surface-knot F has at
On surface-knots with triple point number at most three A. Al Kharusi and T. Yashiro Abstract arxiv:1711.04838v1 [math.at] 13 Nov 2017 In this paper, we show that if a diagram of a surface-knot F has at
arxiv: v1 [math.gt] 5 Aug 2015
![arxiv: v1 [math.gt] 5 Aug 2015 arxiv: v1 [math.gt] 5 Aug 2015](/thumbs/93/112116148.jpg) HEEGAARD FLOER CORRECTION TERMS OF (+1)-SURGERIES ALONG (2, q)-cablings arxiv:1508.01138v1 [math.gt] 5 Aug 2015 KOUKI SATO Abstract. The Heegaard Floer correction term (d-invariant) is an invariant of
HEEGAARD FLOER CORRECTION TERMS OF (+1)-SURGERIES ALONG (2, q)-cablings arxiv:1508.01138v1 [math.gt] 5 Aug 2015 KOUKI SATO Abstract. The Heegaard Floer correction term (d-invariant) is an invariant of
AN INTEGRAL FORMULA FOR TRIPLE LINKING IN HYPERBOLIC SPACE
 AN INTEGRAL FORMULA FOR TRIPLE LINKING IN HYPERBOLIC SPACE PAUL GALLAGHER AND TIANYOU ZHOU Abstract. We provide a geometrically natural formula for the triple linking number of 3 pairwise unlinked curves
AN INTEGRAL FORMULA FOR TRIPLE LINKING IN HYPERBOLIC SPACE PAUL GALLAGHER AND TIANYOU ZHOU Abstract. We provide a geometrically natural formula for the triple linking number of 3 pairwise unlinked curves
arxiv: v2 [math.gt] 25 Jan 2018
![arxiv: v2 [math.gt] 25 Jan 2018 arxiv: v2 [math.gt] 25 Jan 2018](/thumbs/78/77343233.jpg) arxiv:1603.03728v2 [math.gt] 25 Jan 2018 SOME NUMERICAL COMPUTATIONS ON REIDEMEISTER TORSION FOR HOMOLOGY 3-SPHERES OBTAINED BY DEHN SURGERIES ALONG THE FIGURE-EIGHT KNOT TERUAKI KITANO Abstract. This
arxiv:1603.03728v2 [math.gt] 25 Jan 2018 SOME NUMERICAL COMPUTATIONS ON REIDEMEISTER TORSION FOR HOMOLOGY 3-SPHERES OBTAINED BY DEHN SURGERIES ALONG THE FIGURE-EIGHT KNOT TERUAKI KITANO Abstract. This
KNOTS, LINKS and GEOMETRY
 KNOTS, LINKS and GEOMETRY Herman Gluck Knots in Washington, May 2013 My mathematical life began with knots and low-dim'l topology, then moved into differential geometry, and later came back to knots and
KNOTS, LINKS and GEOMETRY Herman Gluck Knots in Washington, May 2013 My mathematical life began with knots and low-dim'l topology, then moved into differential geometry, and later came back to knots and
Solutions for Math 348 Assignment #4 1
 Solutions for Math 348 Assignment #4 1 (1) Do the following: (a) Show that the intersection of two spheres S 1 = {(x, y, z) : (x x 1 ) 2 + (y y 1 ) 2 + (z z 1 ) 2 = r 2 1} S 2 = {(x, y, z) : (x x 2 ) 2
Solutions for Math 348 Assignment #4 1 (1) Do the following: (a) Show that the intersection of two spheres S 1 = {(x, y, z) : (x x 1 ) 2 + (y y 1 ) 2 + (z z 1 ) 2 = r 2 1} S 2 = {(x, y, z) : (x x 2 ) 2
ON END ROTATION FOR OPEN RODS UNDERGOING LARGE DEFORMATIONS
 QUARTERLY OF APPLIED MATHEMATICS VOLUME LXV, NUMBER 2 JUNE 27, PAGES 385 42 S 33-569X(7)149-X Article electronically published on April 1, 27 ON END ROTATION FOR OPEN RODS UNDERGOING LARGE DEFORMATIONS
QUARTERLY OF APPLIED MATHEMATICS VOLUME LXV, NUMBER 2 JUNE 27, PAGES 385 42 S 33-569X(7)149-X Article electronically published on April 1, 27 ON END ROTATION FOR OPEN RODS UNDERGOING LARGE DEFORMATIONS
ANALYTIC DEFINITIONS FOR HYPERBOLIC OBJECTS. 0. Introduction
 Trends in Mathematics Information Center for Mathematical Sciences Volume 5, Number 1,June 00, Pages 11 15 ANALYTIC DEFINITIONS FOR HYPERBOLIC OBJECTS YUNHI CHO AND HYUK KIM Abstract We can extend the
Trends in Mathematics Information Center for Mathematical Sciences Volume 5, Number 1,June 00, Pages 11 15 ANALYTIC DEFINITIONS FOR HYPERBOLIC OBJECTS YUNHI CHO AND HYUK KIM Abstract We can extend the
arxiv: v1 [math.gt] 2 Jun 2015
![arxiv: v1 [math.gt] 2 Jun 2015 arxiv: v1 [math.gt] 2 Jun 2015](/thumbs/78/77343186.jpg) arxiv:1506.00712v1 [math.gt] 2 Jun 2015 REIDEMEISTER TORSION OF A 3-MANIFOLD OBTAINED BY A DEHN-SURGERY ALONG THE FIGURE-EIGHT KNOT TERUAKI KITANO Abstract. Let M be a 3-manifold obtained by a Dehn-surgery
arxiv:1506.00712v1 [math.gt] 2 Jun 2015 REIDEMEISTER TORSION OF A 3-MANIFOLD OBTAINED BY A DEHN-SURGERY ALONG THE FIGURE-EIGHT KNOT TERUAKI KITANO Abstract. Let M be a 3-manifold obtained by a Dehn-surgery
How circular are generalized circles
 How circular are generalized circles Mario Ponce A plane circle is defined as the locus of points that have constant distance (radius) from a distinguished point (center). In this short note we treat with
How circular are generalized circles Mario Ponce A plane circle is defined as the locus of points that have constant distance (radius) from a distinguished point (center). In this short note we treat with
arxiv: v1 [math.gt] 2 Jun 2016
![arxiv: v1 [math.gt] 2 Jun 2016 arxiv: v1 [math.gt] 2 Jun 2016](/thumbs/96/126774048.jpg) CONVERTING VIRTUAL LINK DIAGRAMS TO NORMAL ONES NAOKO KAMADA arxiv:1606.00667v1 [math.gt] 2 Jun 2016 Abstract. A virtual link diagram is called normal if the associated abstract link diagram is checkerboard
CONVERTING VIRTUAL LINK DIAGRAMS TO NORMAL ONES NAOKO KAMADA arxiv:1606.00667v1 [math.gt] 2 Jun 2016 Abstract. A virtual link diagram is called normal if the associated abstract link diagram is checkerboard
Stable tangential families and singularities of their envelopes
 Stable tangential families and singularities of their envelopes arxiv:math/0406584v1 [math.dg] 28 Jun 2004 Gianmarco Capitanio Abstract We study tangential families, i.e. systems of rays emanating tangentially
Stable tangential families and singularities of their envelopes arxiv:math/0406584v1 [math.dg] 28 Jun 2004 Gianmarco Capitanio Abstract We study tangential families, i.e. systems of rays emanating tangentially
Ravello GNFM Summer School September 11-16, Renzo L. Ricca. Department of Mathematics & Applications, U. Milano-Bicocca
 Ravello GNFM Summer School September 11-16, 2017 Renzo L. Ricca Department of Mathematics & Applications, U. Milano-Bicocca renzo.ricca@unimib.it Course contents 1. Topological interpretation of helicity
Ravello GNFM Summer School September 11-16, 2017 Renzo L. Ricca Department of Mathematics & Applications, U. Milano-Bicocca renzo.ricca@unimib.it Course contents 1. Topological interpretation of helicity
ON THE RULED SURFACES WHOSE FRAME IS THE BISHOP FRAME IN THE EUCLIDEAN 3 SPACE. 1. Introduction
 International Electronic Journal of Geometry Volume 6 No.2 pp. 110 117 (2013) c IEJG ON THE RULED SURFACES WHOSE FRAME IS THE BISHOP FRAME IN THE EUCLIDEAN 3 SPACE ŞEYDA KILIÇOĞLU, H. HILMI HACISALIHOĞLU
International Electronic Journal of Geometry Volume 6 No.2 pp. 110 117 (2013) c IEJG ON THE RULED SURFACES WHOSE FRAME IS THE BISHOP FRAME IN THE EUCLIDEAN 3 SPACE ŞEYDA KILIÇOĞLU, H. HILMI HACISALIHOĞLU
GLOBAL PROPERTIES OF PLANE AND SPACE CURVES
 GLOBAL PROPERTIES OF PLANE AND SPACE CURVES KEVIN YAN Abstract. The purpose of this paper is purely expository. Its goal is to explain basic differential geometry to a general audience without assuming
GLOBAL PROPERTIES OF PLANE AND SPACE CURVES KEVIN YAN Abstract. The purpose of this paper is purely expository. Its goal is to explain basic differential geometry to a general audience without assuming
(1) * "?; y«= hfï? ~ A'í>v + r^>>
 proceedings of the american mathematical society Volume 33, Number 2, June 1972 CONVEX FUNCTIONS AND HARMONIC MAPS WILLIAM B. GORDON Abstract. A subset D of a riemannian manifold Y is said to be convex
proceedings of the american mathematical society Volume 33, Number 2, June 1972 CONVEX FUNCTIONS AND HARMONIC MAPS WILLIAM B. GORDON Abstract. A subset D of a riemannian manifold Y is said to be convex
Index. Bertrand mate, 89 bijection, 48 bitangent, 69 Bolyai, 339 Bonnet s Formula, 283 bounded, 48
 Index acceleration, 14, 76, 355 centripetal, 27 tangential, 27 algebraic geometry, vii analytic, 44 angle at a corner, 21 on a regular surface, 170 angle excess, 337 angle of parallelism, 344 angular velocity,
Index acceleration, 14, 76, 355 centripetal, 27 tangential, 27 algebraic geometry, vii analytic, 44 angle at a corner, 21 on a regular surface, 170 angle excess, 337 angle of parallelism, 344 angular velocity,
Topological properties
 CHAPTER 4 Topological properties 1. Connectedness Definitions and examples Basic properties Connected components Connected versus path connected, again 2. Compactness Definition and first examples Topological
CHAPTER 4 Topological properties 1. Connectedness Definitions and examples Basic properties Connected components Connected versus path connected, again 2. Compactness Definition and first examples Topological
MA304 Differential Geometry
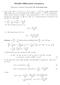 MA34 Differential Geometr Homework solutions, Spring 8, 3% of the final mark Let I R, where I = (a, b) or I = [a, b] Let α : I R 3 be a regular parameterised differentiable curve (not necessaril b arc
MA34 Differential Geometr Homework solutions, Spring 8, 3% of the final mark Let I R, where I = (a, b) or I = [a, b] Let α : I R 3 be a regular parameterised differentiable curve (not necessaril b arc
arxiv: v1 [math.gt] 23 Apr 2014
![arxiv: v1 [math.gt] 23 Apr 2014 arxiv: v1 [math.gt] 23 Apr 2014](/thumbs/75/72058242.jpg) THE NUMBER OF FRAMINGS OF A KNOT IN A 3-MANIFOLD PATRICIA CAHN, VLADIMIR CHERNOV, AND RUSTAM SADYKOV arxiv:1404.5851v1 [math.gt] 23 Apr 2014 Abstract. In view of the self-linking invariant, the number
THE NUMBER OF FRAMINGS OF A KNOT IN A 3-MANIFOLD PATRICIA CAHN, VLADIMIR CHERNOV, AND RUSTAM SADYKOV arxiv:1404.5851v1 [math.gt] 23 Apr 2014 Abstract. In view of the self-linking invariant, the number
GEOMETRY HW 7 CLAY SHONKWILER
 GEOMETRY HW 7 CLAY SHONKWILER 4.5.1 Let S R 3 be a regular, compact, orientable surface which is not homeomorphic to a sphere. Prove that there are points on S where the Gaussian curvature is positive,
GEOMETRY HW 7 CLAY SHONKWILER 4.5.1 Let S R 3 be a regular, compact, orientable surface which is not homeomorphic to a sphere. Prove that there are points on S where the Gaussian curvature is positive,
Space curves, vector fields and strange surfaces. Simon Salamon
 Space curves, vector fields and strange surfaces Simon Salamon Lezione Lagrangiana, 26 May 2016 Curves in space 1 A curve is the path of a particle moving continuously in space. Its position at time t
Space curves, vector fields and strange surfaces Simon Salamon Lezione Lagrangiana, 26 May 2016 Curves in space 1 A curve is the path of a particle moving continuously in space. Its position at time t
MATH 332: Vector Analysis Summer 2005 Homework
 MATH 332, (Vector Analysis), Summer 2005: Homework 1 Instructor: Ivan Avramidi MATH 332: Vector Analysis Summer 2005 Homework Set 1. (Scalar Product, Equation of a Plane, Vector Product) Sections: 1.9,
MATH 332, (Vector Analysis), Summer 2005: Homework 1 Instructor: Ivan Avramidi MATH 332: Vector Analysis Summer 2005 Homework Set 1. (Scalar Product, Equation of a Plane, Vector Product) Sections: 1.9,
Classical differential geometry of two-dimensional surfaces
 Classical differential geometry of two-dimensional surfaces 1 Basic definitions This section gives an overview of the basic notions of differential geometry for twodimensional surfaces. It follows mainly
Classical differential geometry of two-dimensional surfaces 1 Basic definitions This section gives an overview of the basic notions of differential geometry for twodimensional surfaces. It follows mainly
CURVATURE VIA THE DE SITTER S SPACE-TIME
 SARAJEVO JOURNAL OF MATHEMATICS Vol.7 (9 (20, 9 0 CURVATURE VIA THE DE SITTER S SPACE-TIME GRACIELA MARÍA DESIDERI Abstract. We define the central curvature and the total central curvature of a closed
SARAJEVO JOURNAL OF MATHEMATICS Vol.7 (9 (20, 9 0 CURVATURE VIA THE DE SITTER S SPACE-TIME GRACIELA MARÍA DESIDERI Abstract. We define the central curvature and the total central curvature of a closed
REGULAR TRIPLETS IN COMPACT SYMMETRIC SPACES
 REGULAR TRIPLETS IN COMPACT SYMMETRIC SPACES MAKIKO SUMI TANAKA 1. Introduction This article is based on the collaboration with Tadashi Nagano. In the first part of this article we briefly review basic
REGULAR TRIPLETS IN COMPACT SYMMETRIC SPACES MAKIKO SUMI TANAKA 1. Introduction This article is based on the collaboration with Tadashi Nagano. In the first part of this article we briefly review basic
arxiv:math/ v3 [math.dg] 1 Jul 2007
![arxiv:math/ v3 [math.dg] 1 Jul 2007 arxiv:math/ v3 [math.dg] 1 Jul 2007](/thumbs/92/108985523.jpg) . SKEW LOOPS IN FLAT TORI. BRUCE SOLOMON arxiv:math/0701913v3 [math.dg] 1 Jul 2007 Abstract. We produce skew loops loops having no pair of parallel tangent lines homotopic to any loop in a flat torus or
. SKEW LOOPS IN FLAT TORI. BRUCE SOLOMON arxiv:math/0701913v3 [math.dg] 1 Jul 2007 Abstract. We produce skew loops loops having no pair of parallel tangent lines homotopic to any loop in a flat torus or
MATH 423/ Note that the algebraic operations on the right hand side are vector subtraction and scalar multiplication.
 MATH 423/673 1 Curves Definition: The velocity vector of a curve α : I R 3 at time t is the tangent vector to R 3 at α(t), defined by α (t) T α(t) R 3 α α(t + h) α(t) (t) := lim h 0 h Note that the algebraic
MATH 423/673 1 Curves Definition: The velocity vector of a curve α : I R 3 at time t is the tangent vector to R 3 at α(t), defined by α (t) T α(t) R 3 α α(t + h) α(t) (t) := lim h 0 h Note that the algebraic
Tangent and Normal Vectors
 Tangent and Normal Vectors MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Navigation When an observer is traveling along with a moving point, for example the passengers in
Tangent and Normal Vectors MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Navigation When an observer is traveling along with a moving point, for example the passengers in
µ INVARIANT OF NANOPHRASES YUKA KOTORII TOKYO INSTITUTE OF TECHNOLOGY GRADUATE SCHOOL OF SCIENCE AND ENGINEERING 1. Introduction A word will be a sequ
 µ INVARIANT OF NANOPHRASES YUKA KOTORII TOKYO INSTITUTE OF TECHNOLOGY GRADUATE SCHOOL OF SCIENCE AND ENGINEERING 1. Introduction A word will be a sequence of symbols, called letters, belonging to a given
µ INVARIANT OF NANOPHRASES YUKA KOTORII TOKYO INSTITUTE OF TECHNOLOGY GRADUATE SCHOOL OF SCIENCE AND ENGINEERING 1. Introduction A word will be a sequence of symbols, called letters, belonging to a given
EACAT7 at IISER, Mohali Homology of 4D universe for every 3-manifold
 EACAT7 at IISER, Mohali Homology of 4D universe for every 3-manifold Akio Kawauchi Osaka City University Advanced Mathematical Institute December 2, 2017 1. Types I, II, full and punctured 4D universes
EACAT7 at IISER, Mohali Homology of 4D universe for every 3-manifold Akio Kawauchi Osaka City University Advanced Mathematical Institute December 2, 2017 1. Types I, II, full and punctured 4D universes
Tangent and Normal Vector - (11.5)
 Tangent and Normal Vector - (.5). Principal Unit Normal Vector Let C be the curve traced out bythe vector-valued function r!!t # f!t, g!t, h!t $. The vector T!!t r! % r! %!t!t is the unit tangent vector
Tangent and Normal Vector - (.5). Principal Unit Normal Vector Let C be the curve traced out bythe vector-valued function r!!t # f!t, g!t, h!t $. The vector T!!t r! % r! %!t!t is the unit tangent vector
ON POSITIVITY OF KAUFFMAN BRACKET SKEIN ALGEBRAS OF SURFACES
 ON POSITIVITY OF KAUFFMAN BRACKET SKEIN ALGEBRAS OF SURFACES THANG T. Q. LÊ Abstract. We show that the Chebyshev polynomials form a basic block of any positive basis of the Kauffman bracket skein algebras
ON POSITIVITY OF KAUFFMAN BRACKET SKEIN ALGEBRAS OF SURFACES THANG T. Q. LÊ Abstract. We show that the Chebyshev polynomials form a basic block of any positive basis of the Kauffman bracket skein algebras
arxiv: v2 [math.gt] 17 May 2018
![arxiv: v2 [math.gt] 17 May 2018 arxiv: v2 [math.gt] 17 May 2018](/thumbs/94/121838866.jpg) FAMILIES OF NOT PERFECTLY STRAIGHT KNOTS arxiv:1804.04799v2 [math.gt] 17 May 2018 NICHOLAS OWAD Abstract. We present two families of knots which have straight number higher than crossing number. In the
FAMILIES OF NOT PERFECTLY STRAIGHT KNOTS arxiv:1804.04799v2 [math.gt] 17 May 2018 NICHOLAS OWAD Abstract. We present two families of knots which have straight number higher than crossing number. In the
Mathematics for Economists
 Mathematics for Economists Victor Filipe Sao Paulo School of Economics FGV Metric Spaces: Basic Definitions Victor Filipe (EESP/FGV) Mathematics for Economists Jan.-Feb. 2017 1 / 34 Definitions and Examples
Mathematics for Economists Victor Filipe Sao Paulo School of Economics FGV Metric Spaces: Basic Definitions Victor Filipe (EESP/FGV) Mathematics for Economists Jan.-Feb. 2017 1 / 34 Definitions and Examples
13.3 Arc Length and Curvature
 13 Vector Functions 13.3 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. We have defined the length of a plane curve with parametric equations x = f(t),
13 Vector Functions 13.3 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. We have defined the length of a plane curve with parametric equations x = f(t),
PSEUDO DIAGRAMS OF KNOTS, LINKS AND SPATIAL GRAPHS
 PSEUDO DIAGRAMS OF KNOTS, LINKS AND SPATIAL GRAPHS RYO HANAKI Abstract. A pseudo diagram of a spatial graph is a spatial graph projection on the 2-sphere with over/under information at some of the double
PSEUDO DIAGRAMS OF KNOTS, LINKS AND SPATIAL GRAPHS RYO HANAKI Abstract. A pseudo diagram of a spatial graph is a spatial graph projection on the 2-sphere with over/under information at some of the double
Polynomial mappings into a Stiefel manifold and immersions
 Polynomial mappings into a Stiefel manifold and immersions Iwona Krzyżanowska Zbigniew Szafraniec November 2011 Abstract For a polynomial mapping from S n k to the Stiefel manifold Ṽk(R n ), where n k
Polynomial mappings into a Stiefel manifold and immersions Iwona Krzyżanowska Zbigniew Szafraniec November 2011 Abstract For a polynomial mapping from S n k to the Stiefel manifold Ṽk(R n ), where n k
arxiv:math/ v1 [math.gt] 14 Dec 2004
![arxiv:math/ v1 [math.gt] 14 Dec 2004 arxiv:math/ v1 [math.gt] 14 Dec 2004](/thumbs/86/93466553.jpg) arxiv:math/0412275v1 [math.gt] 14 Dec 2004 AN OPEN BOOK DECOMPOSITION COMPATIBLE WITH RATIONAL CONTACT SURGERY BURAK OZBAGCI Abstract. We construct an open book decomposition compatible with a contact
arxiv:math/0412275v1 [math.gt] 14 Dec 2004 AN OPEN BOOK DECOMPOSITION COMPATIBLE WITH RATIONAL CONTACT SURGERY BURAK OZBAGCI Abstract. We construct an open book decomposition compatible with a contact
arxiv: v3 [math.gt] 23 Dec 2014
![arxiv: v3 [math.gt] 23 Dec 2014 arxiv: v3 [math.gt] 23 Dec 2014](/thumbs/88/115838398.jpg) THE RASMUSSEN INVARIANT, FOUR-GENUS AND THREE-GENUS OF AN ALMOST POSITIVE KNOT ARE EQUAL arxiv:1411.2209v3 [math.gt] 23 Dec 2014 KEIJI TAGAMI Abstract. An oriented link is positive if it has a link diagram
THE RASMUSSEN INVARIANT, FOUR-GENUS AND THREE-GENUS OF AN ALMOST POSITIVE KNOT ARE EQUAL arxiv:1411.2209v3 [math.gt] 23 Dec 2014 KEIJI TAGAMI Abstract. An oriented link is positive if it has a link diagram
arxiv:math/ v1 [math.gt] 14 Nov 2003
![arxiv:math/ v1 [math.gt] 14 Nov 2003 arxiv:math/ v1 [math.gt] 14 Nov 2003](/thumbs/93/111283059.jpg) AUTOMORPHISMS OF TORELLI GROUPS arxiv:math/0311250v1 [math.gt] 14 Nov 2003 JOHN D. MCCARTHY AND WILLIAM R. VAUTAW Abstract. In this paper, we prove that each automorphism of the Torelli group of a surface
AUTOMORPHISMS OF TORELLI GROUPS arxiv:math/0311250v1 [math.gt] 14 Nov 2003 JOHN D. MCCARTHY AND WILLIAM R. VAUTAW Abstract. In this paper, we prove that each automorphism of the Torelli group of a surface
Exercise 1 (Formula for connection 1-forms) Using the first structure equation, show that
 1 Stokes s Theorem Let D R 2 be a connected compact smooth domain, so that D is a smooth embedded circle. Given a smooth function f : D R, define fdx dy fdxdy, D where the left-hand side is the integral
1 Stokes s Theorem Let D R 2 be a connected compact smooth domain, so that D is a smooth embedded circle. Given a smooth function f : D R, define fdx dy fdxdy, D where the left-hand side is the integral
Geometry of Skeletal Structures and Symmetry Sets
 Geometry of Skeletal Structures and Symmetry Sets Azeb Zain Jafar Alghanemi Submitted in accordance with the requirements for the degree of Doctor of Philosophy The University of Leeds Department of Pure
Geometry of Skeletal Structures and Symmetry Sets Azeb Zain Jafar Alghanemi Submitted in accordance with the requirements for the degree of Doctor of Philosophy The University of Leeds Department of Pure
MEAN CURVATURE FLOW OF ENTIRE GRAPHS EVOLVING AWAY FROM THE HEAT FLOW
 MEAN CURVATURE FLOW OF ENTIRE GRAPHS EVOLVING AWAY FROM THE HEAT FLOW GREGORY DRUGAN AND XUAN HIEN NGUYEN Abstract. We present two initial graphs over the entire R n, n 2 for which the mean curvature flow
MEAN CURVATURE FLOW OF ENTIRE GRAPHS EVOLVING AWAY FROM THE HEAT FLOW GREGORY DRUGAN AND XUAN HIEN NGUYEN Abstract. We present two initial graphs over the entire R n, n 2 for which the mean curvature flow
Polynomials in knot theory. Rama Mishra. January 10, 2012
 January 10, 2012 Knots in the real world The fact that you can tie your shoelaces in several ways has inspired mathematicians to develop a deep subject known as knot theory. mathematicians treat knots
January 10, 2012 Knots in the real world The fact that you can tie your shoelaces in several ways has inspired mathematicians to develop a deep subject known as knot theory. mathematicians treat knots
Tangent and Normal Vector - (11.5)
 Tangent and Normal Vector - (.5). Principal Unit Normal Vector Let C be the curve traced out by the vector-valued function rt vector T t r r t t is the unit tangent vector to the curve C. Now define N
Tangent and Normal Vector - (.5). Principal Unit Normal Vector Let C be the curve traced out by the vector-valued function rt vector T t r r t t is the unit tangent vector to the curve C. Now define N
Defining the Energy of a Knot
 Defining the Energy of a Knot The University of Iowa August 4, 2016 Overview Möbius energy Definition: A knot is a closed curve in R 3. Although knots are often defined diagrammatically, they can be given
Defining the Energy of a Knot The University of Iowa August 4, 2016 Overview Möbius energy Definition: A knot is a closed curve in R 3. Although knots are often defined diagrammatically, they can be given
Minimizing properties of geodesics and convex neighborhoods
 Minimizing properties of geodesics and convex neighorhoods Seminar Riemannian Geometry Summer Semester 2015 Prof. Dr. Anna Wienhard, Dr. Gye-Seon Lee Hyukjin Bang July 10, 2015 1. Normal spheres In the
Minimizing properties of geodesics and convex neighorhoods Seminar Riemannian Geometry Summer Semester 2015 Prof. Dr. Anna Wienhard, Dr. Gye-Seon Lee Hyukjin Bang July 10, 2015 1. Normal spheres In the
Final Exam Topic Outline
 Math 442 - Differential Geometry of Curves and Surfaces Final Exam Topic Outline 30th November 2010 David Dumas Note: There is no guarantee that this outline is exhaustive, though I have tried to include
Math 442 - Differential Geometry of Curves and Surfaces Final Exam Topic Outline 30th November 2010 David Dumas Note: There is no guarantee that this outline is exhaustive, though I have tried to include
LECTURE 15: COMPLETENESS AND CONVEXITY
 LECTURE 15: COMPLETENESS AND CONVEXITY 1. The Hopf-Rinow Theorem Recall that a Riemannian manifold (M, g) is called geodesically complete if the maximal defining interval of any geodesic is R. On the other
LECTURE 15: COMPLETENESS AND CONVEXITY 1. The Hopf-Rinow Theorem Recall that a Riemannian manifold (M, g) is called geodesically complete if the maximal defining interval of any geodesic is R. On the other
MATH DIFFERENTIAL GEOMETRY. Contents
 MATH 3968 - DIFFERENTIAL GEOMETRY ANDREW TULLOCH Contents 1. Curves in R N 2 2. General Analysis 2 3. Surfaces in R 3 3 3.1. The Gauss Bonnet Theorem 8 4. Abstract Manifolds 9 1 MATH 3968 - DIFFERENTIAL
MATH 3968 - DIFFERENTIAL GEOMETRY ANDREW TULLOCH Contents 1. Curves in R N 2 2. General Analysis 2 3. Surfaces in R 3 3 3.1. The Gauss Bonnet Theorem 8 4. Abstract Manifolds 9 1 MATH 3968 - DIFFERENTIAL
Metrics on the space of shapes
 Metrics on the space of shapes IPAM, July 4 David Mumford Division of Applied Math Brown University Collaborators Peter Michor Eitan Sharon What is the space of shapes? S = set of all smooth connected
Metrics on the space of shapes IPAM, July 4 David Mumford Division of Applied Math Brown University Collaborators Peter Michor Eitan Sharon What is the space of shapes? S = set of all smooth connected
Variations of the Nonuniform Möbius Energy
 Variations of the Nonuniform The University of Iowa March 26, 2016 Overview Möbius energy Nonuniform Möbius energy Variations Definition: A knot is a closed curve in R 3. Although knots are often defined
Variations of the Nonuniform The University of Iowa March 26, 2016 Overview Möbius energy Nonuniform Möbius energy Variations Definition: A knot is a closed curve in R 3. Although knots are often defined
THEp 1 -CENTRALEXTENSIONOF THE MAPPING CLASS GROUP OF ORIENTABLE SURFACES
 KNOT THEORY BANACH CENTER PUBLICATIONS, VOLUME 42 INSTITUTE OF MATHEMATICS POLISH ACADEMY OF SCIENCES WARSZAWA 1998 THEp 1 -CENTRALEXTENSIONOF THE MAPPING CLASS GROUP OF ORIENTABLE SURFACES SYLVAIN GERVAIS
KNOT THEORY BANACH CENTER PUBLICATIONS, VOLUME 42 INSTITUTE OF MATHEMATICS POLISH ACADEMY OF SCIENCES WARSZAWA 1998 THEp 1 -CENTRALEXTENSIONOF THE MAPPING CLASS GROUP OF ORIENTABLE SURFACES SYLVAIN GERVAIS
j=1 ωj k E j. (3.1) j=1 θj E j, (3.2)
 3. Cartan s Structural Equations and the Curvature Form Let E,..., E n be a moving (orthonormal) frame in R n and let ωj k its associated connection forms so that: de k = n ωj k E j. (3.) Recall that ωj
3. Cartan s Structural Equations and the Curvature Form Let E,..., E n be a moving (orthonormal) frame in R n and let ωj k its associated connection forms so that: de k = n ωj k E j. (3.) Recall that ωj
Linear Ordinary Differential Equations
 MTH.B402; Sect. 1 20180703) 2 Linear Ordinary Differential Equations Preliminaries: Matrix Norms. Denote by M n R) the set of n n matrix with real components, which can be identified the vector space R
MTH.B402; Sect. 1 20180703) 2 Linear Ordinary Differential Equations Preliminaries: Matrix Norms. Denote by M n R) the set of n n matrix with real components, which can be identified the vector space R
Cross-index of a graph
 Cross-index of a graph Akio Kawauchi, Ayaka Shimizu, and Yoshiro Yaguchi Abstract. A family of topological invariants of a connected graph associated to every tree is introduced and called the cross-index.
Cross-index of a graph Akio Kawauchi, Ayaka Shimizu, and Yoshiro Yaguchi Abstract. A family of topological invariants of a connected graph associated to every tree is introduced and called the cross-index.
e 2 = e 1 = e 3 = v 1 (v 2 v 3 ) = det(v 1, v 2, v 3 ).
 3. Frames In 3D space, a sequence of 3 linearly independent vectors v 1, v 2, v 3 is called a frame, since it gives a coordinate system (a frame of reference). Any vector v can be written as a linear combination
3. Frames In 3D space, a sequence of 3 linearly independent vectors v 1, v 2, v 3 is called a frame, since it gives a coordinate system (a frame of reference). Any vector v can be written as a linear combination
Chapter 31. The Laplace Transform The Laplace Transform. The Laplace transform of the function f(t) is defined. e st f(t) dt, L[f(t)] =
![Chapter 31. The Laplace Transform The Laplace Transform. The Laplace transform of the function f(t) is defined. e st f(t) dt, L[f(t)] = Chapter 31. The Laplace Transform The Laplace Transform. The Laplace transform of the function f(t) is defined. e st f(t) dt, L[f(t)] =](/thumbs/82/86733502.jpg) Chapter 3 The Laplace Transform 3. The Laplace Transform The Laplace transform of the function f(t) is defined L[f(t)] = e st f(t) dt, for all values of s for which the integral exists. The Laplace transform
Chapter 3 The Laplace Transform 3. The Laplace Transform The Laplace transform of the function f(t) is defined L[f(t)] = e st f(t) dt, for all values of s for which the integral exists. The Laplace transform
A METHOD OF THE DETERMINATION OF A GEODESIC CURVE ON RULED SURFACE WITH TIME-LIKE RULINGS
 Novi Sad J. Math. Vol., No. 2, 200, 10-110 A METHOD OF THE DETERMINATION OF A GEODESIC CURVE ON RULED SURFACE WITH TIME-LIKE RULINGS Emin Kasap 1 Abstract. A non-linear differential equation is analyzed
Novi Sad J. Math. Vol., No. 2, 200, 10-110 A METHOD OF THE DETERMINATION OF A GEODESIC CURVE ON RULED SURFACE WITH TIME-LIKE RULINGS Emin Kasap 1 Abstract. A non-linear differential equation is analyzed
Gauss Theorem Egregium, Gauss-Bonnet etc. We know that for a simple closed curve in the plane. kds = 2π.
 Gauss Theorem Egregium, Gauss-Bonnet etc. We know that for a simple closed curve in the plane kds = 2π. Now we want to consider a simple closed curve C in a surface S R 3. We suppose C is the boundary
Gauss Theorem Egregium, Gauss-Bonnet etc. We know that for a simple closed curve in the plane kds = 2π. Now we want to consider a simple closed curve C in a surface S R 3. We suppose C is the boundary
SPLIT QUATERNIONS and CANAL SURFACES. in MINKOWSKI 3-SPACE
 INTERNATIONAL JOURNAL OF GEOMETRY Vol. 5 (016, No., 51-61 SPLIT QUATERNIONS and CANAL SURFACES in MINKOWSKI 3-SPACE SELAHATTIN ASLAN and YUSUF YAYLI Abstract. A canal surface is the envelope of a one-parameter
INTERNATIONAL JOURNAL OF GEOMETRY Vol. 5 (016, No., 51-61 SPLIT QUATERNIONS and CANAL SURFACES in MINKOWSKI 3-SPACE SELAHATTIN ASLAN and YUSUF YAYLI Abstract. A canal surface is the envelope of a one-parameter
Contents. 1. Introduction
 FUNDAMENTAL THEOREM OF THE LOCAL THEORY OF CURVES KAIXIN WANG Abstract. In this expository paper, we present the fundamental theorem of the local theory of curves along with a detailed proof. We first
FUNDAMENTAL THEOREM OF THE LOCAL THEORY OF CURVES KAIXIN WANG Abstract. In this expository paper, we present the fundamental theorem of the local theory of curves along with a detailed proof. We first
The Frenet Serret formulas
 The Frenet Serret formulas Attila Máté Brooklyn College of the City University of New York January 19, 2017 Contents Contents 1 1 The Frenet Serret frame of a space curve 1 2 The Frenet Serret formulas
The Frenet Serret formulas Attila Máté Brooklyn College of the City University of New York January 19, 2017 Contents Contents 1 1 The Frenet Serret frame of a space curve 1 2 The Frenet Serret formulas
A Note on Dormant Opers of Rank p 1 in Characteristic p
 A Note on Dormant Opers of Rank p 1 in Characteristic p Yuichiro Hoshi May 2017 Abstract. In the present paper, we prove that the set of equivalence classes of dormant opers of rank p 1 over a projective
A Note on Dormant Opers of Rank p 1 in Characteristic p Yuichiro Hoshi May 2017 Abstract. In the present paper, we prove that the set of equivalence classes of dormant opers of rank p 1 over a projective
Engineering Mechanics Prof. U. S. Dixit Department of Mechanical Engineering Indian Institute of Technology, Guwahati Kinematics
 Engineering Mechanics Prof. U. S. Dixit Department of Mechanical Engineering Indian Institute of Technology, Guwahati Kinematics Module 10 - Lecture 24 Kinematics of a particle moving on a curve Today,
Engineering Mechanics Prof. U. S. Dixit Department of Mechanical Engineering Indian Institute of Technology, Guwahati Kinematics Module 10 - Lecture 24 Kinematics of a particle moving on a curve Today,
27. Folds (I) I Main Topics A What is a fold? B Curvature of a plane curve C Curvature of a surface 10/10/18 GG303 1
 I Main Topics A What is a fold? B Curvature of a plane curve C Curvature of a surface 10/10/18 GG303 1 http://upload.wikimedia.org/wikipedia/commons/a/ae/caledonian_orogeny_fold_in_king_oscar_fjord.jpg
I Main Topics A What is a fold? B Curvature of a plane curve C Curvature of a surface 10/10/18 GG303 1 http://upload.wikimedia.org/wikipedia/commons/a/ae/caledonian_orogeny_fold_in_king_oscar_fjord.jpg
NON-TRIVIALITY OF GENERALIZED ALTERNATING KNOTS
 Journal of Knot Theory and Its Ramifications c World Scientific Publishing Company NON-TRIVIALITY OF GENERALIZED ALTERNATING KNOTS MAKOTO OZAWA Natural Science Faculty, Faculty of Letters, Komazawa University,
Journal of Knot Theory and Its Ramifications c World Scientific Publishing Company NON-TRIVIALITY OF GENERALIZED ALTERNATING KNOTS MAKOTO OZAWA Natural Science Faculty, Faculty of Letters, Komazawa University,
MÖBIUS INVARIANT ENERGIES AND AVERAGE LINKING WITH CIRCLES
 MÖBIUS INVARIANT ENERGIES AND AVERAGE LINKING WITH CIRCLES Jun O Hara and Gil Solanes Abstract We introduce a Möbius invariant energy associated to planar domains, as well as a generalization to space
MÖBIUS INVARIANT ENERGIES AND AVERAGE LINKING WITH CIRCLES Jun O Hara and Gil Solanes Abstract We introduce a Möbius invariant energy associated to planar domains, as well as a generalization to space
Math 32A Discussion Session Week 5 Notes November 7 and 9, 2017
 Math 32A Discussion Session Week 5 Notes November 7 and 9, 2017 This week we want to talk about curvature and osculating circles. You might notice that these notes contain a lot of the same theory or proofs
Math 32A Discussion Session Week 5 Notes November 7 and 9, 2017 This week we want to talk about curvature and osculating circles. You might notice that these notes contain a lot of the same theory or proofs
LECTURE 16: CONJUGATE AND CUT POINTS
 LECTURE 16: CONJUGATE AND CUT POINTS 1. Conjugate Points Let (M, g) be Riemannian and γ : [a, b] M a geodesic. Then by definition, exp p ((t a) γ(a)) = γ(t). We know that exp p is a diffeomorphism near
LECTURE 16: CONJUGATE AND CUT POINTS 1. Conjugate Points Let (M, g) be Riemannian and γ : [a, b] M a geodesic. Then by definition, exp p ((t a) γ(a)) = γ(t). We know that exp p is a diffeomorphism near
ABSOLUTE CONTINUITY OF FOLIATIONS
 ABSOLUTE CONTINUITY OF FOLIATIONS C. PUGH, M. VIANA, A. WILKINSON 1. Introduction In what follows, U is an open neighborhood in a compact Riemannian manifold M, and F is a local foliation of U. By this
ABSOLUTE CONTINUITY OF FOLIATIONS C. PUGH, M. VIANA, A. WILKINSON 1. Introduction In what follows, U is an open neighborhood in a compact Riemannian manifold M, and F is a local foliation of U. By this
1 First and second variational formulas for area
 1 First and second variational formulas for area In this chapter, we will derive the first and second variational formulas for the area of a submanifold. This will be useful in our later discussion on
1 First and second variational formulas for area In this chapter, we will derive the first and second variational formulas for the area of a submanifold. This will be useful in our later discussion on
QUALIFYING EXAMINATION Harvard University Department of Mathematics Tuesday August 31, 2010 (Day 1)
 QUALIFYING EXAMINATION Harvard University Department of Mathematics Tuesday August 31, 21 (Day 1) 1. (CA) Evaluate sin 2 x x 2 dx Solution. Let C be the curve on the complex plane from to +, which is along
QUALIFYING EXAMINATION Harvard University Department of Mathematics Tuesday August 31, 21 (Day 1) 1. (CA) Evaluate sin 2 x x 2 dx Solution. Let C be the curve on the complex plane from to +, which is along
HOMEWORK 2 SOLUTIONS
 HOMEWORK SOLUTIONS MA11: ADVANCED CALCULUS, HILARY 17 (1) Find parametric equations for the tangent line of the graph of r(t) = (t, t + 1, /t) when t = 1. Solution: A point on this line is r(1) = (1,,
HOMEWORK SOLUTIONS MA11: ADVANCED CALCULUS, HILARY 17 (1) Find parametric equations for the tangent line of the graph of r(t) = (t, t + 1, /t) when t = 1. Solution: A point on this line is r(1) = (1,,
PRACTICE PROBLEMS. Please let me know if you find any mistakes in the text so that i can fix them. 1. Mixed partial derivatives.
 PRACTICE PROBLEMS Please let me know if you find any mistakes in the text so that i can fix them. 1.1. Let Show that f is C 1 and yet How is that possible? 1. Mixed partial derivatives f(x, y) = {xy x
PRACTICE PROBLEMS Please let me know if you find any mistakes in the text so that i can fix them. 1.1. Let Show that f is C 1 and yet How is that possible? 1. Mixed partial derivatives f(x, y) = {xy x
Exotic spheres. Overview and lecture-by-lecture summary. Martin Palmer / 22 July 2017
 Exotic spheres Overview and lecture-by-lecture summary Martin Palmer / 22 July 2017 Abstract This is a brief overview and a slightly less brief lecture-by-lecture summary of the topics covered in the course
Exotic spheres Overview and lecture-by-lecture summary Martin Palmer / 22 July 2017 Abstract This is a brief overview and a slightly less brief lecture-by-lecture summary of the topics covered in the course
On constant isotropic submanifold by generalized null cubic
 On constant isotropic submanifold by generalized null cubic Leyla Onat Abstract. In this paper we shall be concerned with curves in an Lorentzian submanifold M 1, and give a characterization of each constant
On constant isotropic submanifold by generalized null cubic Leyla Onat Abstract. In this paper we shall be concerned with curves in an Lorentzian submanifold M 1, and give a characterization of each constant
arxiv: v6 [math.gt] 8 May 2017
![arxiv: v6 [math.gt] 8 May 2017 arxiv: v6 [math.gt] 8 May 2017](/thumbs/87/96683054.jpg) RECTANGLE CONDITION AND ITS APPLICATIONS BO-HYUN KWON arxiv:404.765v6 [math.gt] 8 May 07 Abstract. In this paper, we define the rectangle condition on the bridge sphere for a n-bridge decomposition of
RECTANGLE CONDITION AND ITS APPLICATIONS BO-HYUN KWON arxiv:404.765v6 [math.gt] 8 May 07 Abstract. In this paper, we define the rectangle condition on the bridge sphere for a n-bridge decomposition of
HARMONIC CLOSE-TO-CONVEX MAPPINGS
 Applied Mathematics Stochastic Analysis, 15:1 (2002, 23-28. HARMONIC CLOSE-TO-CONVEX MAPPINGS JAY M. JAHANGIRI 1 Kent State University Department of Mathematics Burton, OH 44021-9500 USA E-mail: jay@geauga.kent.edu
Applied Mathematics Stochastic Analysis, 15:1 (2002, 23-28. HARMONIC CLOSE-TO-CONVEX MAPPINGS JAY M. JAHANGIRI 1 Kent State University Department of Mathematics Burton, OH 44021-9500 USA E-mail: jay@geauga.kent.edu
CHAPTER 3. Gauss map. In this chapter we will study the Gauss map of surfaces in R 3.
 CHAPTER 3 Gauss map In this chapter we will study the Gauss map of surfaces in R 3. 3.1. Surfaces in R 3 Let S R 3 be a submanifold of dimension 2. Let {U i, ϕ i } be a DS on S. For any p U i we have a
CHAPTER 3 Gauss map In this chapter we will study the Gauss map of surfaces in R 3. 3.1. Surfaces in R 3 Let S R 3 be a submanifold of dimension 2. Let {U i, ϕ i } be a DS on S. For any p U i we have a
SELECTED SAMPLE FINAL EXAM SOLUTIONS - MATH 5378, SPRING 2013
 SELECTED SAMPLE FINAL EXAM SOLUTIONS - MATH 5378, SPRING 03 Problem (). This problem is perhaps too hard for an actual exam, but very instructional, and simpler problems using these ideas will be on the
SELECTED SAMPLE FINAL EXAM SOLUTIONS - MATH 5378, SPRING 03 Problem (). This problem is perhaps too hard for an actual exam, but very instructional, and simpler problems using these ideas will be on the
Practice Final Solutions
 Practice Final Solutions Math 1, Fall 17 Problem 1. Find a parameterization for the given curve, including bounds on the parameter t. Part a) The ellipse in R whose major axis has endpoints, ) and 6, )
Practice Final Solutions Math 1, Fall 17 Problem 1. Find a parameterization for the given curve, including bounds on the parameter t. Part a) The ellipse in R whose major axis has endpoints, ) and 6, )
THEODORE VORONOV DIFFERENTIAL GEOMETRY. Spring 2009
 [under construction] 8 Parallel transport 8.1 Equation of parallel transport Consider a vector bundle E B. We would like to compare vectors belonging to fibers over different points. Recall that this was
[under construction] 8 Parallel transport 8.1 Equation of parallel transport Consider a vector bundle E B. We would like to compare vectors belonging to fibers over different points. Recall that this was
Lectures in Discrete Differential Geometry 2 Surfaces
 Lectures in Discrete Differential Geometry 2 Surfaces Etienne Vouga February 4, 24 Smooth Surfaces in R 3 In this section we will review some properties of smooth surfaces R 3. We will assume that is parameterized
Lectures in Discrete Differential Geometry 2 Surfaces Etienne Vouga February 4, 24 Smooth Surfaces in R 3 In this section we will review some properties of smooth surfaces R 3. We will assume that is parameterized
Boundedness and Regularizing Effects of O Hara s Knot Energies
 March, 2 2:24 WSPC/INSTRUCTION FILE OHarasEnergies Boundedness and Regularizing Effects of O Hara s Knot Energies Simon Blatt Departement Mathematik ETH Zürich Rämistrasse CH-84 Zürich Switzerland simon.blatt@math.ethz.ch
March, 2 2:24 WSPC/INSTRUCTION FILE OHarasEnergies Boundedness and Regularizing Effects of O Hara s Knot Energies Simon Blatt Departement Mathematik ETH Zürich Rämistrasse CH-84 Zürich Switzerland simon.blatt@math.ethz.ch
UNIVERSITY OF DUBLIN
 UNIVERSITY OF DUBLIN TRINITY COLLEGE JS & SS Mathematics SS Theoretical Physics SS TSM Mathematics Faculty of Engineering, Mathematics and Science school of mathematics Trinity Term 2015 Module MA3429
UNIVERSITY OF DUBLIN TRINITY COLLEGE JS & SS Mathematics SS Theoretical Physics SS TSM Mathematics Faculty of Engineering, Mathematics and Science school of mathematics Trinity Term 2015 Module MA3429
Dynamical Systems Analysis Using Differential Geometry
 Dynamical Systems Analysis Using Differential Geometry Jean-Marc GINOUX and Bruno ROSSETTO Laboratoire P.R.O.T.E.E., équipe EBMA / ISO Université du Sud Toulon-Var, B.P. 3, 83957, La Garde, ginoux@univ-tln.fr,
Dynamical Systems Analysis Using Differential Geometry Jean-Marc GINOUX and Bruno ROSSETTO Laboratoire P.R.O.T.E.E., équipe EBMA / ISO Université du Sud Toulon-Var, B.P. 3, 83957, La Garde, ginoux@univ-tln.fr,
