MA304 Differential Geometry
|
|
|
- Katherine Adela McDaniel
- 5 years ago
- Views:
Transcription
1 MA34 Differential Geometr Homework solutions, Spring 8, 3% of the final mark Let I R, where I = (a, b) or I = [a, b] Let α : I R 3 be a regular parameterised differentiable curve (not necessaril b arc length), and let β : J R 3 be a reparameterisation of α(i) b the arc length s = s(t), measured from a Let t = t(s) be the inverse function of s and set dα = dt α, d α = α, d3 α = α Assume that α (t) and α (t) dt dt 3 for all t I Prove that (a) dt ds = α and d t ds = α α α 4 (b) The curvature of α at t I is (c) The torsion of α at t I is k(t) = α α α 3 τ(t) = (α α ) α α α Solution (a) dt ds = ds follows from the definition that α dt = α We have d t ds = d ds α = dt d ds dt (α α ) / = ( ) α (α α ) 3/ (α α α α ) = ) ( α α = α α α α 3 α 4 (b) Note that for an two vectors a, b R 3, we have a b = (a b) (a b) = a (b (a b)) = a ((b b)a (b a)b) = (a a)(b b) (a b) = a b (a b), () b the scalar and vector triple products (see homework, question ) Since β(s) = (α t)(s), β (s) = α (t(s))t (s) = α α, () β (s) = α (t(s))t (s) α (t(s))t (s) = α α (α α )α, (3) α 4 β (s) β (s) = α α (α α ) (α α ) (α α ) α 4 α 6 α 8 = α 6 ( α α (α α ) ) = α α α 6,
2 where we have applied () for the last equalit Therefore, the curvature of α is (c) Note that the torsion of α is k(t) = β (s) = α α α 3 (4) τ(t) = τ β (s) = (β (s) β (s)) β (s) k β (s), b homework, question 4, where k β (s) and τ β (s) are the curvature and torsion of β(s) We compute the expression on the right B () and (3), we have ( ) β (s) β (s) = α α α α (α α )α = α α, α 4 α 3 β (s) = d [ α (t(s))t (s) α (t(s))t (s) ] ds dt = α ds t (s) α t (s)t dt (s) α ds t (s) α t (s), (β (s) β (s)) β (s) = α α α 3 α Together with (4), we have dt ds t (s) = (α α ) α α 6 τ(t) = (β (s) β (s)) β (s) k β (s) = (α α ) α α α Find the curvature and torsion of the following curves For parts (b) and (c), find also all of the vertices (a) α : (, ) R 3, where α(t) = (cos t, sin t, log(t )) (b) α : [, π] R, where α(t) = (a cos t, b sin t) and < b < a (c) α : [, π] R, where α(t) = (( cos t) cos t, ( cos t) sin t) Solution We use the expressions for curvature and torsion from question (a) We have α (t) = ( ) sin t, cos t, t e e e 3 α α = sin t cos t t cos t sin t (t) ( cos t = (t ) sin t ) e t ( cos t α α = (t ) sin t ) t = (t ) 4 (t ), and α (t) = ( cos t, sin t, ) (t ) ( sin t (t ) cos t t ( sin t (t ) cos t ) t ) e (sin t cos t)e 3
3 and Therefore, the curvature of α is Also, (α α ) α = Therefore, the torsion of α is α = sin t cos t (t ) = (t ) k(t) = α α α 3 = ((t ) 4 (t ) ) / ((t ) ) 3/ α (t) = ( ) sin t, cos t,, (t ) 3 ( cos t (t ) sin t ) ( sin t sin t t (t ) cos t ) cos t t (t ) 3 = (t ) (t ) 3 τ(t) = (α α ) α α α = (t ) (t ) 3 (t ) 4 (t ) For parts (b) and (c), we note that the torsion of α should be, since a plane curve cannot have an twisting Indeed, α α is in the direction of e 3, and α has zero e 3 component, so (α α ) α =, which implies τ(t) = It remains to find the curvature and the vertices in parts (b) and (c) (b) We have and α (t) = ( a sin t, b cos t) and α (t) = ( a cos t, b sin t) Therefore, the curvature of α is We have e e e 3 α α = a sin t b cos t = abe 3, a cos t b sin t α = a sin t b cos t k(t) = α α α 3 = ab (a sin t b cos t) 3/ k (t) = 3 ab(a sin t b cos t) / (a sin t cos t b cos t sin t) = 3 ab(a sin t b cos t) / (a b ) sin t, 3
4 so k (t) = when sin t =, t =, π, π, 3π It follows that the vertices of α are (a, ), (, b), ( a, ) and (, b) (c) We have α(t) = ( cos t cos t, sin t cos t sin t) = ( cos t cos t, sin t sin t ), α (t) = ( sin t cos t sin t, cos t cos t) = ( sin t sin t, cos t cos t), α (t) = ( cos t cos t, sin t sin t), e e e 3 α α = sin t sin t cos t cos t cos t cos t sin t sin t and = [( sin t sin t)( sin t sin t) ( cos t cos t)( cos t cos t)]e 3 = (4 sin t sin t 6 sin t sin t 4 cos t cos t 6 cos t cos t)e 3 = (6 6 cos t)e 3 α = ( sin t sin t) ( cos t cos t) = 4 sin t sin t 4 sin t sin t 4 cos t cos t 4 cos t cos t = 4 cos t Therefore, the curvature of α is We have k(t) = α α α 3 = 6 6 cos t ( 4 cos t) 3/ k (t) = 6 sin t( 4 cos t)3/ (6 6 cos t) 3 ( 4 cos t)/ ( 4 sin t) ( 4 cos t) 3 Since 4 cos t >, we have k (t) = when the numerator is equal to The numerator simplifies to 6( 4 cos t) / sin t( cos t), which is when sin t = or cos t =, giving t =, π, π, 4π It follows that the vertices of α are (3, ), ( 3, 3 3), (, ) and 3 3 ( 3, 3 3 ) 3 Determine if the following surfaces in xz-space are regular, and explain our reasoning carefull For those surfaces that are regular, give a local parameterisation and show how to cover the surface with several such parameterisations You ma use an of the propositions that were proved in class (a) The surface T, obtained b rotating the circle (x a) z = b in the xz-plane about the z-axis b π, where < b < a 4
5 (b) The surface C given b z = x, where x > and < x (c) The surface S given b { x z = for z, x = for < z Solution (a) The surface T is a torus, and is given b the equation ( x a) z = b B letting f(x,, z) = ( x a) z, we see that T is the set f (b ) (x, ) (, ), we have For f x = x( x a), x f = ( x a), x f z = z, so the three partial derivatives vanish simultaneousl at (x,, ) such that x = a These points do not belong to f (b ), b is a regular value of f B Proposition 3, T is a regular surface Finall, T can be covered b three parameterisations For example, x (u, v) = ((a b cos u) cos v, (a b cos u) sin v, b sin u), < u, v < π, x (ũ, ṽ) = ( (a b cos ũ) cos ṽ, (a b cos ũ) sin ṽ, b sin ũ), < ũ, ṽ < π, x 3 (û, ˆv) = ((a b sin û) sin ˆv, (a b sin û) cos ˆv, b cos û), < û, ˆv < π The parameters u, v, ũ, etc can be chosen, x (u, v) covers T except for the circles C = {(x,, z) : x = (ab), z = } and C = {(x,, z) : (x a) z = b, = }; x (ũ, ṽ) covers T except for the circles C = {(x,, z) : x = (a b), z = } and C = {(x,, z) : (x a) z = b, = }; and x 3 (û, ˆv) covers T except for the circles C 3 = {(x,, z) : x = a, z = b} and C 3 = {(x,, z) : ( a) z = b, x = } It is eas to see that ever point of T is covered b at least one of the three parameterisations (b) Since C is the graph of f(x, ) = x on the open set U = {(x, ) R : x >, < x}, C is regular b Proposition Clearl, the single parameterisation x(x, ) = (x,, x ), for (x, ) U covers the whole of C (c) We show that S is not a regular surface Otherwise if S is regular, then b Proposition, there is a neighbourhood V S of (,, ) which is the graph of a differentiable function in one of the forms z = f(x, ), = g(x, z) or x = h(, z) The first two cases are not possible since the projections of V onto the x-plane and the xz-plane are not one-to-one Indeed, for the first case we would have both (,, ), (,, ε) V being projected to (, ), for some small ε > For the second case we would have both ( ε, ( ε), ), ( ε, ( ε), ) V being projected to ( ε, ), for some small ε > In the final case, we have { z x = h(, z) = for z, for < z
6 We have { x ( z = z ) 3/ z ( z ) / for z, for < z, x z = (,z)=(,) { for z, for < z We see that x = h(, z) is not differentiable at (, z) = (, ), which is a contradiction 4 Verif the Cauch-Crofton formula for the following curves (a) x = where x (b) (Optional, for bonus) = x where x Solution In both parts, let f(p, ) denote the multiplicit of the line with parameters (p, ), with respect to the curve in consideration Let R = {(p, ) R : p and < π, or p > and π < π} (a) The curve is a semi-circle with radius, so its arc length is π We must show that f(p, ) dp d = π We note that, since the curve is smmetric about the x- R axis, we have f(p, ) = f(p, π ) for π < < π Thus, it suffices to show that π f(p, ) dp d = π (a) (b) d x x d Figure For < π, we have d = sin in Figure (a), f(p, ) = { for p < sin or p =, for sin p < For π < π, we have d = cos( π ) = sin in Figure (b), f(p, ) = for p sin Therefore, f(p, ) dp d = / (sin ( sin )) d = [ cos ] π/ [ cos ] π π/ = π π/ sin d 6
7 (b) We first find the arc length of the curve We can parameterise the curve b α(t) = (t, t ) for t, the arc length is α (t) dt = (t) ( ) / dt = ( u ) / du [ = 4 u( u ) / 4 log u ( u ) / ] = 4 log( ) 4 log( ) = ( ) 4 log = 4 log [ ( ) ] = log( ) We now simplif the task slightl We ma instead consider the curve x = for, which has the same arc length and is smmetric about the x-axis, so that f(p, ) = f(p, π ) for π < < π Similar to part (a), it suffices to show that f(p, ) dp d = log( ) Furthermore, it suffices to determine f(p, ) for < < π For the lines corresponding to, let m denote their common gradient, so that m = cot (a) (b) d 3 (c) L 4 d x x d 4 x L d L (d) d L 6 d 6 x (e) d 7 x Figure Let < π In Figure (a), the equation of the line L 4 is = cot (x ), the x-intercept is tan, and d = ( tan ) cos = cos sin The equation of the line L is = cot (x ), the x-intercept is tan, and d = ( tan ) cos = cos sin Therefore, { for cos sin < p cos sin, f(p, ) = for p cos sin 7
8 Let π < α < 3π be the angle such that tan α = For π < π, we have d 3 = cos sin in Figure (b), as before For π < α, in Figure (c), the x-intercept of the line L 4 is again tan <, d 4 = (tan ) cos(π ) = cos sin Since the tangent line to the curve at (, ) has gradient, we conclude that for π < α, 4 f(p, ) = for p cos sin Let α < 3π In Figure (d), we have d 4 = cos sin as before We compute the value of d 6 The line L 6 has gradient m and is tangent to the curve At the point of contact, we have x / = m, which gives x = and = x / = 4m m The equation of L 6 is therefore m = m (x be 4m < Therefore, d 6 = 4m f(p, ) = ) Setting =, we obtain the x-intercept of L 4m 6 to cos(π ) = 4 tan cos = cos sec, and { for p < cos sin or p = cos sec, for cos sin p < cos sec Let 3π 4 < < π We have d 7 = cos sec in Figure (e), as before Therefore, { for p = 4 f(p, ) = cos sec, 4 for p < cos sec Note that tan α = implies sin α =, cos α =, and sec α = We have as required f(p, ) dp d = = /4 /4 ( sin (cos sin )) d 3π/4 α α π/4 (cos sin ) d ( cos sin ( 34 cos 4 )) sec sin d ( 3π/ cos ) 4 sec d 3π/4 cos d (cos sin ) d ( ) sec d 3π/4 α π/4 ( 3 cos sin ) d 3π/4 α cos d [ = [ sin ] π/4 [sin cos ] 3π/4 π/4 ] π log sec tan α [ 3 ] 3π/4 sin cos α [ ] π sin 3π/4 = log log 3 3 = log( ), 8
Find the indicated derivative. 1) Find y(4) if y = 3 sin x. A) y(4) = 3 cos x B) y(4) = 3 sin x C) y(4) = - 3 cos x D) y(4) = - 3 sin x
 Assignment 5 Name Find the indicated derivative. ) Find y(4) if y = sin x. ) A) y(4) = cos x B) y(4) = sin x y(4) = - cos x y(4) = - sin x ) y = (csc x + cot x)(csc x - cot x) ) A) y = 0 B) y = y = - csc
Assignment 5 Name Find the indicated derivative. ) Find y(4) if y = sin x. ) A) y(4) = cos x B) y(4) = sin x y(4) = - cos x y(4) = - sin x ) y = (csc x + cot x)(csc x - cot x) ) A) y = 0 B) y = y = - csc
Solutionbank Edexcel AS and A Level Modular Mathematics
 Page of Exercise A, Question The curve C, with equation y = x ln x, x > 0, has a stationary point P. Find, in terms of e, the coordinates of P. (7) y = x ln x, x > 0 Differentiate as a product: = x + x
Page of Exercise A, Question The curve C, with equation y = x ln x, x > 0, has a stationary point P. Find, in terms of e, the coordinates of P. (7) y = x ln x, x > 0 Differentiate as a product: = x + x
Find the slope of the curve at the given point P and an equation of the tangent line at P. 1) y = x2 + 11x - 15, P(1, -3)
 Final Exam Review AP Calculus AB Find the slope of the curve at the given point P and an equation of the tangent line at P. 1) y = x2 + 11x - 15, P(1, -3) Use the graph to evaluate the limit. 2) lim x
Final Exam Review AP Calculus AB Find the slope of the curve at the given point P and an equation of the tangent line at P. 1) y = x2 + 11x - 15, P(1, -3) Use the graph to evaluate the limit. 2) lim x
MATH 332: Vector Analysis Summer 2005 Homework
 MATH 332, (Vector Analysis), Summer 2005: Homework 1 Instructor: Ivan Avramidi MATH 332: Vector Analysis Summer 2005 Homework Set 1. (Scalar Product, Equation of a Plane, Vector Product) Sections: 1.9,
MATH 332, (Vector Analysis), Summer 2005: Homework 1 Instructor: Ivan Avramidi MATH 332: Vector Analysis Summer 2005 Homework Set 1. (Scalar Product, Equation of a Plane, Vector Product) Sections: 1.9,
MTH 122: Section 204. Plane Trigonometry. Test 1
 MTH 122: Section 204. Plane Trigonometry. Test 1 Section A: No use of calculator is allowed. Show your work and clearly identify your answer. 1. a). Complete the following table. α 0 π/6 π/4 π/3 π/2 π
MTH 122: Section 204. Plane Trigonometry. Test 1 Section A: No use of calculator is allowed. Show your work and clearly identify your answer. 1. a). Complete the following table. α 0 π/6 π/4 π/3 π/2 π
Multiple Choice. 1.(6 pts) Find symmetric equations of the line L passing through the point (2, 5, 1) and perpendicular to the plane x + 3y z = 9.
 Multiple Choice.(6 pts) Find smmetric equations of the line L passing through the point (, 5, ) and perpendicular to the plane x + 3 z = 9. (a) x = + 5 3 = z (c) (x ) + 3( 3) (z ) = 9 (d) (e) x = 3 5 =
Multiple Choice.(6 pts) Find smmetric equations of the line L passing through the point (, 5, ) and perpendicular to the plane x + 3 z = 9. (a) x = + 5 3 = z (c) (x ) + 3( 3) (z ) = 9 (d) (e) x = 3 5 =
HOMEWORK 2 SOLUTIONS
 HOMEWORK SOLUTIONS MA11: ADVANCED CALCULUS, HILARY 17 (1) Find parametric equations for the tangent line of the graph of r(t) = (t, t + 1, /t) when t = 1. Solution: A point on this line is r(1) = (1,,
HOMEWORK SOLUTIONS MA11: ADVANCED CALCULUS, HILARY 17 (1) Find parametric equations for the tangent line of the graph of r(t) = (t, t + 1, /t) when t = 1. Solution: A point on this line is r(1) = (1,,
This exam will be over material covered in class from Monday 14 February through Tuesday 8 March, corresponding to sections in the text.
 Math 275, section 002 (Ultman) Spring 2011 MIDTERM 2 REVIEW The second midterm will be held in class (1:40 2:30pm) on Friday 11 March. You will be allowed one half of one side of an 8.5 11 sheet of paper
Math 275, section 002 (Ultman) Spring 2011 MIDTERM 2 REVIEW The second midterm will be held in class (1:40 2:30pm) on Friday 11 March. You will be allowed one half of one side of an 8.5 11 sheet of paper
Mth Review Problems for Test 2 Stewart 8e Chapter 3. For Test #2 study these problems, the examples in your notes, and the homework.
 For Test # study these problems, the examples in your notes, and the homework. Derivative Rules D [u n ] = nu n 1 du D [ln u] = du u D [log b u] = du u ln b D [e u ] = e u du D [a u ] = a u ln a du D [sin
For Test # study these problems, the examples in your notes, and the homework. Derivative Rules D [u n ] = nu n 1 du D [ln u] = du u D [log b u] = du u ln b D [e u ] = e u du D [a u ] = a u ln a du D [sin
3.4 Conic sections. Such type of curves are called conics, because they arise from different slices through a cone
 3.4 Conic sections Next we consider the objects resulting from ax 2 + bxy + cy 2 + + ey + f = 0. Such type of curves are called conics, because they arise from different slices through a cone Circles belong
3.4 Conic sections Next we consider the objects resulting from ax 2 + bxy + cy 2 + + ey + f = 0. Such type of curves are called conics, because they arise from different slices through a cone Circles belong
Math 20C Homework 2 Partial Solutions
 Math 2C Homework 2 Partial Solutions Problem 1 (12.4.14). Calculate (j k) (j + k). Solution. The basic properties of the cross product are found in Theorem 2 of Section 12.4. From these properties, we
Math 2C Homework 2 Partial Solutions Problem 1 (12.4.14). Calculate (j k) (j + k). Solution. The basic properties of the cross product are found in Theorem 2 of Section 12.4. From these properties, we
Coordinate goemetry in the (x, y) plane
 Coordinate goemetr in the (x, ) plane In this chapter ou will learn how to solve problems involving parametric equations.. You can define the coordinates of a point on a curve using parametric equations.
Coordinate goemetr in the (x, ) plane In this chapter ou will learn how to solve problems involving parametric equations.. You can define the coordinates of a point on a curve using parametric equations.
" $ CALCULUS 2 WORKSHEET #21. t, y = t + 1. are A) x = 0, y = 0 B) x = 0 only C) x = 1, y = 0 D) x = 1 only E) x= 0, y = 1
 CALCULUS 2 WORKSHEET #2. The asymptotes of the graph of the parametric equations x = t t, y = t + are A) x = 0, y = 0 B) x = 0 only C) x =, y = 0 D) x = only E) x= 0, y = 2. What are the coordinates of
CALCULUS 2 WORKSHEET #2. The asymptotes of the graph of the parametric equations x = t t, y = t + are A) x = 0, y = 0 B) x = 0 only C) x =, y = 0 D) x = only E) x= 0, y = 2. What are the coordinates of
Examiner: D. Burbulla. Aids permitted: Formula Sheet, and Casio FX-991 or Sharp EL-520 calculator.
 University of Toronto Faculty of Applied Science and Engineering Solutions to Final Examination, June 017 Duration: and 1/ hrs First Year - CHE, CIV, CPE, ELE, ENG, IND, LME, MEC, MMS MAT187H1F - Calculus
University of Toronto Faculty of Applied Science and Engineering Solutions to Final Examination, June 017 Duration: and 1/ hrs First Year - CHE, CIV, CPE, ELE, ENG, IND, LME, MEC, MMS MAT187H1F - Calculus
MAC2313 Final A. (5 pts) 1. How many of the following are necessarily true? i. The vector field F = 2x + 3y, 3x 5y is conservative.
 MAC2313 Final A (5 pts) 1. How many of the following are necessarily true? i. The vector field F = 2x + 3y, 3x 5y is conservative. ii. The vector field F = 5(x 2 + y 2 ) 3/2 x, y is radial. iii. All constant
MAC2313 Final A (5 pts) 1. How many of the following are necessarily true? i. The vector field F = 2x + 3y, 3x 5y is conservative. ii. The vector field F = 5(x 2 + y 2 ) 3/2 x, y is radial. iii. All constant
Examiner: D. Burbulla. Aids permitted: Formula Sheet, and Casio FX-991 or Sharp EL-520 calculator.
 University of Toronto Faculty of Applied Science and Engineering Solutions to Final Examination, June 216 Duration: 2 and 1/2 hrs First Year - CHE, CIV, CPE, ELE, ENG, IND, LME, MEC, MMS MAT187H1F - Calculus
University of Toronto Faculty of Applied Science and Engineering Solutions to Final Examination, June 216 Duration: 2 and 1/2 hrs First Year - CHE, CIV, CPE, ELE, ENG, IND, LME, MEC, MMS MAT187H1F - Calculus
Name Class. (a) (b) (c) 4 t4 3 C
 Chapter 4 Test Bank 77 Test Form A Chapter 4 Name Class Date Section. Evaluate the integral: t dt. t C (a) (b) 4 t4 C t C C t. Evaluate the integral: 5 sec x tan x dx. (a) 5 sec x tan x C (b) 5 sec x C
Chapter 4 Test Bank 77 Test Form A Chapter 4 Name Class Date Section. Evaluate the integral: t dt. t C (a) (b) 4 t4 C t C C t. Evaluate the integral: 5 sec x tan x dx. (a) 5 sec x tan x C (b) 5 sec x C
Calculus I Sample Exam #01
 Calculus I Sample Exam #01 1. Sketch the graph of the function and define the domain and range. 1 a) f( x) 3 b) g( x) x 1 x c) hx ( ) x x 1 5x6 d) jx ( ) x x x 3 6 . Evaluate the following. a) 5 sin 6
Calculus I Sample Exam #01 1. Sketch the graph of the function and define the domain and range. 1 a) f( x) 3 b) g( x) x 1 x c) hx ( ) x x 1 5x6 d) jx ( ) x x x 3 6 . Evaluate the following. a) 5 sin 6
Homework 6. (x 3) 2 + (y 1) 2 = 25. (x 5) 2 + (y + 2) 2 = 49
 245 245 Name: Solutions Due Date: Monday May 16th. Homework 6 Directions: Show all work to receive full credit. Solutions always include the work and problems with no work and only answers will receive
245 245 Name: Solutions Due Date: Monday May 16th. Homework 6 Directions: Show all work to receive full credit. Solutions always include the work and problems with no work and only answers will receive
Math 3c Solutions: Exam 2 Fall 2017
 Math 3c Solutions: Exam Fall 07. 0 points) The graph of a smooth vector-valued function is shown below except that your irresponsible teacher forgot to include the orientation!) Several points are indicated
Math 3c Solutions: Exam Fall 07. 0 points) The graph of a smooth vector-valued function is shown below except that your irresponsible teacher forgot to include the orientation!) Several points are indicated
2.2 The derivative as a Function
 2.2 The derivative as a Function Recall: The derivative of a function f at a fixed number a: f a f a+h f(a) = lim h 0 h Definition (Derivative of f) For any number x, the derivative of f is f x f x+h f(x)
2.2 The derivative as a Function Recall: The derivative of a function f at a fixed number a: f a f a+h f(a) = lim h 0 h Definition (Derivative of f) For any number x, the derivative of f is f x f x+h f(x)
a k 0, then k + 1 = 2 lim 1 + 1
 Math 7 - Midterm - Form A - Page From the desk of C. Davis Buenger. https://people.math.osu.edu/buenger.8/ Problem a) [3 pts] If lim a k = then a k converges. False: The divergence test states that if
Math 7 - Midterm - Form A - Page From the desk of C. Davis Buenger. https://people.math.osu.edu/buenger.8/ Problem a) [3 pts] If lim a k = then a k converges. False: The divergence test states that if
IMPLICIT DIFFERENTIATION
 IMPLICIT DIFFERENTIATION Section.5 Calculus AP/Dual, Revised 017 viet.dang@humbleisd.net 7/30/018 1:47 AM.5: Implicit Differentiation 1 REVIEW Solve or d of 4 + 3 = 6 4 3 6 4 3 6 4 3 4 ' 3 3 7/30/018 1:47
IMPLICIT DIFFERENTIATION Section.5 Calculus AP/Dual, Revised 017 viet.dang@humbleisd.net 7/30/018 1:47 AM.5: Implicit Differentiation 1 REVIEW Solve or d of 4 + 3 = 6 4 3 6 4 3 6 4 3 4 ' 3 3 7/30/018 1:47
MTH 277 Test 4 review sheet Chapter , 14.7, 14.8 Chalmeta
 MTH 77 Test 4 review sheet Chapter 13.1-13.4, 14.7, 14.8 Chalmeta Multiple Choice 1. Let r(t) = 3 sin t i + 3 cos t j + αt k. What value of α gives an arc length of 5 from t = 0 to t = 1? (a) 6 (b) 5 (c)
MTH 77 Test 4 review sheet Chapter 13.1-13.4, 14.7, 14.8 Chalmeta Multiple Choice 1. Let r(t) = 3 sin t i + 3 cos t j + αt k. What value of α gives an arc length of 5 from t = 0 to t = 1? (a) 6 (b) 5 (c)
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES Before starting this section, you might need to review the trigonometric functions. DIFFERENTIATION RULES In particular, it is important to remember that,
3 DIFFERENTIATION RULES DIFFERENTIATION RULES Before starting this section, you might need to review the trigonometric functions. DIFFERENTIATION RULES In particular, it is important to remember that,
Solutions Of Homework 4
 Solutions Of Homework 1. Two parallel sides of a rectangle are being lengthened at the rate of 3 in/sec, while the other two sides are shortened in such a way that the figure remains a rectangle with constant
Solutions Of Homework 1. Two parallel sides of a rectangle are being lengthened at the rate of 3 in/sec, while the other two sides are shortened in such a way that the figure remains a rectangle with constant
Section Arclength and Curvature. (1) Arclength, (2) Parameterizing Curves by Arclength, (3) Curvature, (4) Osculating and Normal Planes.
 Section 10.3 Arclength and Curvature (1) Arclength, (2) Parameterizing Curves by Arclength, (3) Curvature, (4) Osculating and Normal Planes. MATH 127 (Section 10.3) Arclength and Curvature The University
Section 10.3 Arclength and Curvature (1) Arclength, (2) Parameterizing Curves by Arclength, (3) Curvature, (4) Osculating and Normal Planes. MATH 127 (Section 10.3) Arclength and Curvature The University
Solutions for Math 348 Assignment #4 1
 Solutions for Math 348 Assignment #4 1 (1) Do the following: (a) Show that the intersection of two spheres S 1 = {(x, y, z) : (x x 1 ) 2 + (y y 1 ) 2 + (z z 1 ) 2 = r 2 1} S 2 = {(x, y, z) : (x x 2 ) 2
Solutions for Math 348 Assignment #4 1 (1) Do the following: (a) Show that the intersection of two spheres S 1 = {(x, y, z) : (x x 1 ) 2 + (y y 1 ) 2 + (z z 1 ) 2 = r 2 1} S 2 = {(x, y, z) : (x x 2 ) 2
M273Q Multivariable Calculus Spring 2017 Review Problems for Exam 3
 M7Q Multivariable alculus Spring 7 Review Problems for Exam Exam covers material from Sections 5.-5.4 and 6.-6. and 7.. As you prepare, note well that the Fall 6 Exam posted online did not cover exactly
M7Q Multivariable alculus Spring 7 Review Problems for Exam Exam covers material from Sections 5.-5.4 and 6.-6. and 7.. As you prepare, note well that the Fall 6 Exam posted online did not cover exactly
Math 152 Take Home Test 1
 Math 5 Take Home Test Due Monday 5 th October (5 points) The following test will be done at home in order to ensure that it is a fair and representative reflection of your own ability in mathematics I
Math 5 Take Home Test Due Monday 5 th October (5 points) The following test will be done at home in order to ensure that it is a fair and representative reflection of your own ability in mathematics I
Things you should have learned in Calculus II
 Things you should have learned in Calculus II 1 Vectors Given vectors v = v 1, v 2, v 3, u = u 1, u 2, u 3 1.1 Common Operations Operations Notation How is it calculated Other Notation Dot Product v u
Things you should have learned in Calculus II 1 Vectors Given vectors v = v 1, v 2, v 3, u = u 1, u 2, u 3 1.1 Common Operations Operations Notation How is it calculated Other Notation Dot Product v u
Thursday 14 June 2012 Morning
 Thursday 14 June 01 Morning A GCE MATHEMATICS (MEI) 4757 Further Applications of Advanced Mathematics (FP3) QUESTION PAPER *471575061* Candidates answer on the Printed Answer Book. OCR supplied materials:
Thursday 14 June 01 Morning A GCE MATHEMATICS (MEI) 4757 Further Applications of Advanced Mathematics (FP3) QUESTION PAPER *471575061* Candidates answer on the Printed Answer Book. OCR supplied materials:
Vectors, dot product, and cross product
 MTH 201 Multivariable calculus and differential equations Practice problems Vectors, dot product, and cross product 1. Find the component form and length of vector P Q with the following initial point
MTH 201 Multivariable calculus and differential equations Practice problems Vectors, dot product, and cross product 1. Find the component form and length of vector P Q with the following initial point
Contents. MATH 32B-2 (18W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables. 1 Multiple Integrals 3. 2 Vector Fields 9
 MATH 32B-2 (8W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Multiple Integrals 3 2 Vector Fields 9 3 Line and Surface Integrals 5 4 The Classical Integral Theorems 9 MATH 32B-2 (8W)
MATH 32B-2 (8W) (L) G. Liu / (TA) A. Zhou Calculus of Several Variables Contents Multiple Integrals 3 2 Vector Fields 9 3 Line and Surface Integrals 5 4 The Classical Integral Theorems 9 MATH 32B-2 (8W)
Linearization and Extreme Values of Functions
 Linearization and Extreme Values of Functions 3.10 Linearization and Differentials Linear or Tangent Line Approximations of function values Equation of tangent to y = f(x) at (a, f(a)): Tangent line approximation
Linearization and Extreme Values of Functions 3.10 Linearization and Differentials Linear or Tangent Line Approximations of function values Equation of tangent to y = f(x) at (a, f(a)): Tangent line approximation
Faculty of Engineering, Mathematics and Science School of Mathematics
 Faculty of Engineering, Mathematics and Science School of Mathematics GROUPS Trinity Term 06 MA3: Advanced Calculus SAMPLE EXAM, Solutions DAY PLACE TIME Prof. Larry Rolen Instructions to Candidates: Attempt
Faculty of Engineering, Mathematics and Science School of Mathematics GROUPS Trinity Term 06 MA3: Advanced Calculus SAMPLE EXAM, Solutions DAY PLACE TIME Prof. Larry Rolen Instructions to Candidates: Attempt
MATH 2433 Homework 1
 MATH 433 Homework 1 1. The sequence (a i ) is defined recursively by a 1 = 4 a i+1 = 3a i find a closed formula for a i in terms of i.. In class we showed that the Fibonacci sequence (a i ) defined by
MATH 433 Homework 1 1. The sequence (a i ) is defined recursively by a 1 = 4 a i+1 = 3a i find a closed formula for a i in terms of i.. In class we showed that the Fibonacci sequence (a i ) defined by
1 are perpendicular to each other then, find. Q06. If the lines x 1 z 3 and x 2 y 5 z
 Useful for CBSE Board Examination of Math (XII) for 6 For more stuffs on Maths, please visit : www.theopgupta.com Time Allowed : 8 Minutes Max. Marks : SECTION A 3 Q. Evaluate : sin cos 5. Q. State the
Useful for CBSE Board Examination of Math (XII) for 6 For more stuffs on Maths, please visit : www.theopgupta.com Time Allowed : 8 Minutes Max. Marks : SECTION A 3 Q. Evaluate : sin cos 5. Q. State the
Jim Lambers MAT 169 Fall Semester Practice Final Exam
 Jim Lambers MAT 169 Fall Semester 2010-11 Practice Final Exam 1. A ship is moving northwest at a speed of 50 mi/h. A passenger is walking due southeast on the deck at 4 mi/h. Find the speed of the passenger
Jim Lambers MAT 169 Fall Semester 2010-11 Practice Final Exam 1. A ship is moving northwest at a speed of 50 mi/h. A passenger is walking due southeast on the deck at 4 mi/h. Find the speed of the passenger
Solutions of homework 1. 2 a) Using the stereographic projection from the north pole N = (0, 0, 1) introduce stereographic coordinates
 Solutions of homework 1 1 a) Using the stereographic projection from the north pole N (0, 1) introduce stereographic coordinate for the part of the circle S 1 ( + 1) without the north pole. b) Do the same
Solutions of homework 1 1 a) Using the stereographic projection from the north pole N (0, 1) introduce stereographic coordinate for the part of the circle S 1 ( + 1) without the north pole. b) Do the same
Math Vector Calculus II
 Math 255 - Vector Calculus II Review Notes Vectors We assume the reader is familiar with all the basic concepts regarding vectors and vector arithmetic, such as addition/subtraction of vectors in R n,
Math 255 - Vector Calculus II Review Notes Vectors We assume the reader is familiar with all the basic concepts regarding vectors and vector arithmetic, such as addition/subtraction of vectors in R n,
Objective Mathematics
 Chapter No - ( Area Bounded by Curves ). Normal at (, ) is given by : y y. f ( ) or f ( ). Area d ()() 7 Square units. Area (8)() 6 dy. ( ) d y c or f ( ) c f () c f ( ) As shown in figure, point P is
Chapter No - ( Area Bounded by Curves ). Normal at (, ) is given by : y y. f ( ) or f ( ). Area d ()() 7 Square units. Area (8)() 6 dy. ( ) d y c or f ( ) c f () c f ( ) As shown in figure, point P is
Multivariable Calculus Notes. Faraad Armwood. Fall: Chapter 1: Vectors, Dot Product, Cross Product, Planes, Cylindrical & Spherical Coordinates
 Multivariable Calculus Notes Faraad Armwood Fall: 2017 Chapter 1: Vectors, Dot Product, Cross Product, Planes, Cylindrical & Spherical Coordinates Chapter 2: Vector-Valued Functions, Tangent Vectors, Arc
Multivariable Calculus Notes Faraad Armwood Fall: 2017 Chapter 1: Vectors, Dot Product, Cross Product, Planes, Cylindrical & Spherical Coordinates Chapter 2: Vector-Valued Functions, Tangent Vectors, Arc
DIFFERENTIATION RULES
 3 DIFFERENTIATION RULES DIFFERENTIATION RULES Before starting this section, you might need to review the trigonometric functions. DIFFERENTIATION RULES In particular, it is important to remember that,
3 DIFFERENTIATION RULES DIFFERENTIATION RULES Before starting this section, you might need to review the trigonometric functions. DIFFERENTIATION RULES In particular, it is important to remember that,
MAY THE FORCE BE WITH YOU, YOUNG JEDIS!!!
 Final Exam Math 222 Spring 2011 May 11, 2011 Name: Recitation Instructor s Initials: You may not use any type of calculator whatsoever. (Cell phones off and away!) You are not allowed to have any other
Final Exam Math 222 Spring 2011 May 11, 2011 Name: Recitation Instructor s Initials: You may not use any type of calculator whatsoever. (Cell phones off and away!) You are not allowed to have any other
Mathematical Techniques: Revision Notes
 Differentiation Dr A. J. Bevan October 20, 200 Mathematical Techniques: Revision Notes Dr A. J. Bevan, These notes contain the core of the information conveed in the lectures. The are not a substitute
Differentiation Dr A. J. Bevan October 20, 200 Mathematical Techniques: Revision Notes Dr A. J. Bevan, These notes contain the core of the information conveed in the lectures. The are not a substitute
4. We accept without proofs that the following functions are differentiable: (e x ) = e x, sin x = cos x, cos x = sin x, log (x) = 1 sin x
 4 We accept without proofs that the following functions are differentiable: (e x ) = e x, sin x = cos x, cos x = sin x, log (x) = 1 sin x x, x > 0 Since tan x = cos x, from the quotient rule, tan x = sin
4 We accept without proofs that the following functions are differentiable: (e x ) = e x, sin x = cos x, cos x = sin x, log (x) = 1 sin x x, x > 0 Since tan x = cos x, from the quotient rule, tan x = sin
Answer Key 1973 BC 1969 BC 24. A 14. A 24. C 25. A 26. C 27. C 28. D 29. C 30. D 31. C 13. C 12. D 12. E 3. A 32. B 27. E 34. C 14. D 25. B 26.
 Answer Key 969 BC 97 BC. C. E. B. D 5. E 6. B 7. D 8. C 9. D. A. B. E. C. D 5. B 6. B 7. B 8. E 9. C. A. B. E. D. C 5. A 6. C 7. C 8. D 9. C. D. C. B. A. D 5. A 6. B 7. D 8. A 9. D. E. D. B. E. E 5. E.
Answer Key 969 BC 97 BC. C. E. B. D 5. E 6. B 7. D 8. C 9. D. A. B. E. C. D 5. B 6. B 7. B 8. E 9. C. A. B. E. D. C 5. A 6. C 7. C 8. D 9. C. D. C. B. A. D 5. A 6. B 7. D 8. A 9. D. E. D. B. E. E 5. E.
MA304 Differential Geometry
 MA304 Differential Geoetry Hoework 4 solutions Spring 018 6% of the final ark 1. The paraeterised curve αt = t cosh t for t R is called the catenary. Find the curvature of αt. Solution. Fro hoework question
MA304 Differential Geoetry Hoework 4 solutions Spring 018 6% of the final ark 1. The paraeterised curve αt = t cosh t for t R is called the catenary. Find the curvature of αt. Solution. Fro hoework question
SELECTED SAMPLE FINAL EXAM SOLUTIONS - MATH 5378, SPRING 2013
 SELECTED SAMPLE FINAL EXAM SOLUTIONS - MATH 5378, SPRING 03 Problem (). This problem is perhaps too hard for an actual exam, but very instructional, and simpler problems using these ideas will be on the
SELECTED SAMPLE FINAL EXAM SOLUTIONS - MATH 5378, SPRING 03 Problem (). This problem is perhaps too hard for an actual exam, but very instructional, and simpler problems using these ideas will be on the
16.2 Line Integrals. Lukas Geyer. M273, Fall Montana State University. Lukas Geyer (MSU) 16.2 Line Integrals M273, Fall / 21
 16.2 Line Integrals Lukas Geyer Montana State University M273, Fall 211 Lukas Geyer (MSU) 16.2 Line Integrals M273, Fall 211 1 / 21 Scalar Line Integrals Definition f (x) ds = lim { s i } N f (P i ) s
16.2 Line Integrals Lukas Geyer Montana State University M273, Fall 211 Lukas Geyer (MSU) 16.2 Line Integrals M273, Fall 211 1 / 21 Scalar Line Integrals Definition f (x) ds = lim { s i } N f (P i ) s
ANSWERS, Homework Problems, Fall 2014: Lectures Now You Try It, Supplemental problems in written homework, Even Answers. 24x + 72 (x 2 6x + 4) 4
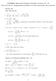 ANSWERS, Homework Problems, Fall 014: Lectures 19 35 Now You Try It, Supplemental problems in written homework, Even Answers Lecture 19 1. d [ 4 ] dx x 6x + 4) 3 = 4x + 7 x 6x + 4) 4. a) P 0) = 800 b)
ANSWERS, Homework Problems, Fall 014: Lectures 19 35 Now You Try It, Supplemental problems in written homework, Even Answers Lecture 19 1. d [ 4 ] dx x 6x + 4) 3 = 4x + 7 x 6x + 4) 4. a) P 0) = 800 b)
MATH 2053 Calculus I Review for the Final Exam
 MATH 05 Calculus I Review for the Final Exam (x+ x) 9 x 9 1. Find the limit: lim x 0. x. Find the limit: lim x + x x (x ).. Find lim x (x 5) = L, find such that f(x) L < 0.01 whenever 0 < x
MATH 05 Calculus I Review for the Final Exam (x+ x) 9 x 9 1. Find the limit: lim x 0. x. Find the limit: lim x + x x (x ).. Find lim x (x 5) = L, find such that f(x) L < 0.01 whenever 0 < x
12.4. Curvature. Introduction. Prerequisites. Learning Outcomes
 Curvature 12.4 Introduction Curvature is a measure of how sharpl a curve is turning. At a particular point along the curve a tangent line can be drawn; this tangent line making an angle ψ with the positive
Curvature 12.4 Introduction Curvature is a measure of how sharpl a curve is turning. At a particular point along the curve a tangent line can be drawn; this tangent line making an angle ψ with the positive
MATH DIFFERENTIAL GEOMETRY. Contents
 MATH 3968 - DIFFERENTIAL GEOMETRY ANDREW TULLOCH Contents 1. Curves in R N 2 2. General Analysis 2 3. Surfaces in R 3 3 3.1. The Gauss Bonnet Theorem 8 4. Abstract Manifolds 9 1 MATH 3968 - DIFFERENTIAL
MATH 3968 - DIFFERENTIAL GEOMETRY ANDREW TULLOCH Contents 1. Curves in R N 2 2. General Analysis 2 3. Surfaces in R 3 3 3.1. The Gauss Bonnet Theorem 8 4. Abstract Manifolds 9 1 MATH 3968 - DIFFERENTIAL
 4 TANGENTS AND NORMALS OBJECTIVE PROBLEMS. For a curve = f(x) if = x then the angle made b the tangent at (,) with OX is ) π / 4 ) π / tan tan / ) 4). The angle made b the tangent line at (,) on the curve
4 TANGENTS AND NORMALS OBJECTIVE PROBLEMS. For a curve = f(x) if = x then the angle made b the tangent at (,) with OX is ) π / 4 ) π / tan tan / ) 4). The angle made b the tangent line at (,) on the curve
f(x)
 Calculus m y_0e1^y jkdudtdaw ZS[oifntCwxaCrJej ilhl[cq.k i qatlplm mrpiyg^hztbsz YrmePsqeWrNvxeEdG. Calculus Ch. 3 Review Given the graph of f '(x), sketch a possible graph of f (x). 1) f '(x) f(x) 8 8
Calculus m y_0e1^y jkdudtdaw ZS[oifntCwxaCrJej ilhl[cq.k i qatlplm mrpiyg^hztbsz YrmePsqeWrNvxeEdG. Calculus Ch. 3 Review Given the graph of f '(x), sketch a possible graph of f (x). 1) f '(x) f(x) 8 8
DO NOT BEGIN THIS TEST UNTIL INSTRUCTED TO START
 Math 265 Student name: KEY Final Exam Fall 23 Instructor & Section: This test is closed book and closed notes. A (graphing) calculator is allowed for this test but cannot also be a communication device
Math 265 Student name: KEY Final Exam Fall 23 Instructor & Section: This test is closed book and closed notes. A (graphing) calculator is allowed for this test but cannot also be a communication device
Calculus III. Math 233 Spring Final exam May 3rd. Suggested solutions
 alculus III Math 33 pring 7 Final exam May 3rd. uggested solutions This exam contains twenty problems numbered 1 through. All problems are multiple choice problems, and each counts 5% of your total score.
alculus III Math 33 pring 7 Final exam May 3rd. uggested solutions This exam contains twenty problems numbered 1 through. All problems are multiple choice problems, and each counts 5% of your total score.
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. D) D: (-, 0) (0, )
 Midterm Practice Test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the domain and graph the function. ) G(t) = t - 3 ) 3 - -3 - - 3 - - -3
Midterm Practice Test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the domain and graph the function. ) G(t) = t - 3 ) 3 - -3 - - 3 - - -3
True or False. Circle T if the statement is always true; otherwise circle F. for all angles θ. T F. 1 sin θ
 Math 90 Practice Midterm III Solutions Ch. 8-0 (Ebersole), 3.3-3.8 (Stewart) DISCLAIMER. This collection of practice problems is not guaranteed to be identical, in length or content, to the actual exam.
Math 90 Practice Midterm III Solutions Ch. 8-0 (Ebersole), 3.3-3.8 (Stewart) DISCLAIMER. This collection of practice problems is not guaranteed to be identical, in length or content, to the actual exam.
1 + f 2 x + f 2 y dy dx, where f(x, y) = 2 + 3x + 4y, is
 1. The value of the double integral (a) 15 26 (b) 15 8 (c) 75 (d) 105 26 5 4 0 1 1 + f 2 x + f 2 y dy dx, where f(x, y) = 2 + 3x + 4y, is 2. What is the value of the double integral interchange the order
1. The value of the double integral (a) 15 26 (b) 15 8 (c) 75 (d) 105 26 5 4 0 1 1 + f 2 x + f 2 y dy dx, where f(x, y) = 2 + 3x + 4y, is 2. What is the value of the double integral interchange the order
Chapter 2 Section 3. Partial Derivatives
 Chapter Section 3 Partial Derivatives Deinition. Let be a unction o two variables and. The partial derivative o with respect to is the unction, denoted b D1 1 such that its value at an point (,) in the
Chapter Section 3 Partial Derivatives Deinition. Let be a unction o two variables and. The partial derivative o with respect to is the unction, denoted b D1 1 such that its value at an point (,) in the
Math 5378, Differential Geometry Solutions to practice questions for Test 2
 Math 5378, Differential Geometry Solutions to practice questions for Test 2. Find all possible trajectories of the vector field w(x, y) = ( y, x) on 2. Solution: A trajectory would be a curve (x(t), y(t))
Math 5378, Differential Geometry Solutions to practice questions for Test 2. Find all possible trajectories of the vector field w(x, y) = ( y, x) on 2. Solution: A trajectory would be a curve (x(t), y(t))
Find the domain and range of each function. Use interval notation (parenthesis or square brackets).
 Page of 10 I. Functions & Composition of Functions A function is a set of points (x, y) such that for every x, there is one and only one y. In short, in a function, the x-values cannot repeat while the
Page of 10 I. Functions & Composition of Functions A function is a set of points (x, y) such that for every x, there is one and only one y. In short, in a function, the x-values cannot repeat while the
GEOMETRY HW (t, 0, e 1/t2 ), t > 0 1/t2, 0), t < 0. (0, 0, 0), t = 0
 GEOMETRY HW CLAY SHONKWILER Consider the map.5.0 t, 0, e /t ), t > 0 αt) = t, e /t, 0), t < 0 0, 0, 0), t = 0 a) Prove that α is a differentiable curve. Proof. If we denote αt) = xt), yt), zt0), then it
GEOMETRY HW CLAY SHONKWILER Consider the map.5.0 t, 0, e /t ), t > 0 αt) = t, e /t, 0), t < 0 0, 0, 0), t = 0 a) Prove that α is a differentiable curve. Proof. If we denote αt) = xt), yt), zt0), then it
g(t) = f(x 1 (t),..., x n (t)).
 Reading: [Simon] p. 313-333, 833-836. 0.1 The Chain Rule Partial derivatives describe how a function changes in directions parallel to the coordinate axes. Now we shall demonstrate how the partial derivatives
Reading: [Simon] p. 313-333, 833-836. 0.1 The Chain Rule Partial derivatives describe how a function changes in directions parallel to the coordinate axes. Now we shall demonstrate how the partial derivatives
MATH Final Review
 MATH 1592 - Final Review 1 Chapter 7 1.1 Main Topics 1. Integration techniques: Fitting integrands to basic rules on page 485. Integration by parts, Theorem 7.1 on page 488. Guidelines for trigonometric
MATH 1592 - Final Review 1 Chapter 7 1.1 Main Topics 1. Integration techniques: Fitting integrands to basic rules on page 485. Integration by parts, Theorem 7.1 on page 488. Guidelines for trigonometric
Here is a link to the formula booklet:
 IB MATH SL2 SUMMER ASSIGNMENT review of topics from year 1. We will be quizzing on this when you return to school. This review is optional but you will earn bonus points if you complete it. Questions?
IB MATH SL2 SUMMER ASSIGNMENT review of topics from year 1. We will be quizzing on this when you return to school. This review is optional but you will earn bonus points if you complete it. Questions?
Practice Exam 1 Solutions
 Practice Exam 1 Solutions 1a. Let S be the region bounded by y = x 3, y = 1, and x. Find the area of S. What is the volume of the solid obtained by rotating S about the line y = 1? Area A = Volume 1 1
Practice Exam 1 Solutions 1a. Let S be the region bounded by y = x 3, y = 1, and x. Find the area of S. What is the volume of the solid obtained by rotating S about the line y = 1? Area A = Volume 1 1
Summary for Vector Calculus and Complex Calculus (Math 321) By Lei Li
 Summary for Vector alculus and omplex alculus (Math 321) By Lei Li 1 Vector alculus 1.1 Parametrization urves, surfaces, or volumes can be parametrized. Below, I ll talk about 3D case. Suppose we use e
Summary for Vector alculus and omplex alculus (Math 321) By Lei Li 1 Vector alculus 1.1 Parametrization urves, surfaces, or volumes can be parametrized. Below, I ll talk about 3D case. Suppose we use e
Directional derivatives and gradient vectors (Sect. 14.5) Directional derivative of functions of two variables.
 Directional derivatives and gradient vectors (Sect. 14.5) Directional derivative of functions of two variables. Partial derivatives and directional derivatives. Directional derivative of functions of three
Directional derivatives and gradient vectors (Sect. 14.5) Directional derivative of functions of two variables. Partial derivatives and directional derivatives. Directional derivative of functions of three
Math 180 Written Homework Solutions Assignment #4 Due Tuesday, September 23rd at the beginning of your discussion class.
 Math 180 Written Homework Solutions Assignment #4 Due Tuesday, September 23rd at the beginning of your discussion class. Directions. You are welcome to work on the following problems with other MATH 180
Math 180 Written Homework Solutions Assignment #4 Due Tuesday, September 23rd at the beginning of your discussion class. Directions. You are welcome to work on the following problems with other MATH 180
Technical Calculus I Homework. Instructions
 Technical Calculus I Homework Instructions 1. Each assignment is to be done on one or more pieces of regular-sized notebook paper. 2. Your name and the assignment number should appear at the top of the
Technical Calculus I Homework Instructions 1. Each assignment is to be done on one or more pieces of regular-sized notebook paper. 2. Your name and the assignment number should appear at the top of the
(a) The points (3, 1, 2) and ( 1, 3, 4) are the endpoints of a diameter of a sphere.
 MATH 4 FINAL EXAM REVIEW QUESTIONS Problem. a) The points,, ) and,, 4) are the endpoints of a diameter of a sphere. i) Determine the center and radius of the sphere. ii) Find an equation for the sphere.
MATH 4 FINAL EXAM REVIEW QUESTIONS Problem. a) The points,, ) and,, 4) are the endpoints of a diameter of a sphere. i) Determine the center and radius of the sphere. ii) Find an equation for the sphere.
Homework 3. (33-40) The graph of an exponential function is given. Match each graph to one of the following functions.
 Homework Section 4. (-40) The graph of an exponential function is given. Match each graph to one of the following functions. (a)y = x (b)y = x (c)y = x (d)y = x (e)y = x (f)y = x (g)y = x (h)y = x (46,
Homework Section 4. (-40) The graph of an exponential function is given. Match each graph to one of the following functions. (a)y = x (b)y = x (c)y = x (d)y = x (e)y = x (f)y = x (g)y = x (h)y = x (46,
An Introduction to Gaussian Geometry
 Lecture Notes in Mathematics An Introduction to Gaussian Geometry Sigmundur Gudmundsson (Lund University) (version 2.068-16th of November 2017) The latest version of this document can be found at http://www.matematik.lu.se/matematiklu/personal/sigma/
Lecture Notes in Mathematics An Introduction to Gaussian Geometry Sigmundur Gudmundsson (Lund University) (version 2.068-16th of November 2017) The latest version of this document can be found at http://www.matematik.lu.se/matematiklu/personal/sigma/
Math 221 Examination 2 Several Variable Calculus
 Math Examination Spring Instructions These problems should be viewed as essa questions. Before making a calculation, ou should explain in words what our strateg is. Please write our solutions on our own
Math Examination Spring Instructions These problems should be viewed as essa questions. Before making a calculation, ou should explain in words what our strateg is. Please write our solutions on our own
TABLE OF CONTENTS 2 CHAPTER 1
 TABLE OF CONTENTS CHAPTER 1 Quadratics CHAPTER Functions 3 CHAPTER 3 Coordinate Geometry 3 CHAPTER 4 Circular Measure 4 CHAPTER 5 Trigonometry 4 CHAPTER 6 Vectors 5 CHAPTER 7 Series 6 CHAPTER 8 Differentiation
TABLE OF CONTENTS CHAPTER 1 Quadratics CHAPTER Functions 3 CHAPTER 3 Coordinate Geometry 3 CHAPTER 4 Circular Measure 4 CHAPTER 5 Trigonometry 4 CHAPTER 6 Vectors 5 CHAPTER 7 Series 6 CHAPTER 8 Differentiation
Exercise: concepts from chapter 3
 Reading:, Ch 3 1) The natural representation of a curve, c = c(s), satisfies the condition dc/ds = 1, where s is the natural parameter for the curve. a) Describe in words and a sketch what this condition
Reading:, Ch 3 1) The natural representation of a curve, c = c(s), satisfies the condition dc/ds = 1, where s is the natural parameter for the curve. a) Describe in words and a sketch what this condition
Calculus First Semester Review Name: Section: Evaluate the function: (g o f )( 2) f (x + h) f (x) h. m(x + h) m(x)
 Evaluate the function: c. (g o f )(x + 2) d. ( f ( f (x)) 1. f x = 4x! 2 a. f( 2) b. f(x 1) c. f (x + h) f (x) h 4. g x = 3x! + 1 Find g!! (x) 5. p x = 4x! + 2 Find p!! (x) 2. m x = 3x! + 2x 1 m(x + h)
Evaluate the function: c. (g o f )(x + 2) d. ( f ( f (x)) 1. f x = 4x! 2 a. f( 2) b. f(x 1) c. f (x + h) f (x) h 4. g x = 3x! + 1 Find g!! (x) 5. p x = 4x! + 2 Find p!! (x) 2. m x = 3x! + 2x 1 m(x + h)
APPLICATIONS OF DIFFERENTIABILITY IN R n.
 APPLICATIONS OF DIFFERENTIABILITY IN R n. MATANIA BEN-ARTZI April 2015 Functions here are defined on a subset T R n and take values in R m, where m can be smaller, equal or greater than n. The (open) ball
APPLICATIONS OF DIFFERENTIABILITY IN R n. MATANIA BEN-ARTZI April 2015 Functions here are defined on a subset T R n and take values in R m, where m can be smaller, equal or greater than n. The (open) ball
d (5 cos 2 x) = 10 cos x sin x x x d y = (cos x)(e d (x 2 + 1) 2 d (ln(3x 1)) = (3) (M1)(M1) (C2) Differentiation Practice Answers 1.
 . (a) y x ( x) Differentiation Practice Answers dy ( x) ( ) (A)(A) (C) Note: Award (A) for each element, to a maximum of [ marks]. y e sin x d y (cos x)(e sin x ) (A)(A) (C) Note: Award (A) for each element.
. (a) y x ( x) Differentiation Practice Answers dy ( x) ( ) (A)(A) (C) Note: Award (A) for each element, to a maximum of [ marks]. y e sin x d y (cos x)(e sin x ) (A)(A) (C) Note: Award (A) for each element.
Lecture Wise Questions from 23 to 45 By Virtualians.pk. Q105. What is the impact of double integration in finding out the area and volume of Regions?
 Lecture Wise Questions from 23 to 45 By Virtualians.pk Q105. What is the impact of double integration in finding out the area and volume of Regions? Ans: It has very important contribution in finding the
Lecture Wise Questions from 23 to 45 By Virtualians.pk Q105. What is the impact of double integration in finding out the area and volume of Regions? Ans: It has very important contribution in finding the
Geometry of Cylindrical Curves over Plane Curves
 Applied Mathematical Sciences, Vol 9, 015, no 113, 5637-5649 HIKARI Ltd, wwwm-hikaricom http://dxdoiorg/101988/ams01556456 Geometry of Cylindrical Curves over Plane Curves Georgi Hristov Georgiev, Radostina
Applied Mathematical Sciences, Vol 9, 015, no 113, 5637-5649 HIKARI Ltd, wwwm-hikaricom http://dxdoiorg/101988/ams01556456 Geometry of Cylindrical Curves over Plane Curves Georgi Hristov Georgiev, Radostina
Solve the problem. 2) If tan = 3.7, find the value of tan + tan ( + ) + tan ( + 2 ). A) 11.1 B) 13.1 C) D) undefined
 Assignment Bonus Chs 6,,8 Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. In the problem, t is a real number and P = (x, y) is the point on the
Assignment Bonus Chs 6,,8 Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. In the problem, t is a real number and P = (x, y) is the point on the
Math 180, Final Exam, Fall 2012 Problem 1 Solution
 Math 80, Final Exam, Fall 0 Problem Solution. Find the derivatives of the following functions: (a) ln(ln(x)) (b) x 6 + sin(x) e x (c) tan(x ) + cot(x ) (a) We evaluate the derivative using the Chain Rule.
Math 80, Final Exam, Fall 0 Problem Solution. Find the derivatives of the following functions: (a) ln(ln(x)) (b) x 6 + sin(x) e x (c) tan(x ) + cot(x ) (a) We evaluate the derivative using the Chain Rule.
Preview from Notesale.co.uk Page 2 of 42
 . CONCEPTS & FORMULAS. INTRODUCTION Radian The angle subtended at centre of a circle by an arc of length equal to the radius of the circle is radian r o = o radian r r o radian = o = 6 Positive & Negative
. CONCEPTS & FORMULAS. INTRODUCTION Radian The angle subtended at centre of a circle by an arc of length equal to the radius of the circle is radian r o = o radian r r o radian = o = 6 Positive & Negative
Arc Length and Surface Area in Parametric Equations
 Arc Length and Surface Area in Parametric Equations MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2011 Background We have developed definite integral formulas for arc length
Arc Length and Surface Area in Parametric Equations MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2011 Background We have developed definite integral formulas for arc length
SOLVING TRIGONOMETRIC INEQUALITIES (CONCEPT, METHODS, AND STEPS )
 SOLVING TRIGONOMETRIC INEQUALITIES (CONCEPT, METHODS, AND STEPS ) Definition. A trig inequality is an inequality in standard form: R(x) > 0 (or < 0) that contains one or a few trig functions of the variable
SOLVING TRIGONOMETRIC INEQUALITIES (CONCEPT, METHODS, AND STEPS ) Definition. A trig inequality is an inequality in standard form: R(x) > 0 (or < 0) that contains one or a few trig functions of the variable
Curves I: Curvature and Torsion. Table of contents
 Math 48 Fall 07 Curves I: Curvature and Torsion Disclaimer. As we have a textbook, this lecture note is for guidance and sulement only. It should not be relied on when rearing for exams. In this lecture
Math 48 Fall 07 Curves I: Curvature and Torsion Disclaimer. As we have a textbook, this lecture note is for guidance and sulement only. It should not be relied on when rearing for exams. In this lecture
Final Exam Review Problems
 Final Exam Review Problems Name: Date: June 23, 2013 P 1.4. 33. Determine whether the line x = 4 represens y as a function of x. P 1.5. 37. Graph f(x) = 3x 1 x 6. Find the x and y-intercepts and asymptotes
Final Exam Review Problems Name: Date: June 23, 2013 P 1.4. 33. Determine whether the line x = 4 represens y as a function of x. P 1.5. 37. Graph f(x) = 3x 1 x 6. Find the x and y-intercepts and asymptotes
Disclaimer: This Final Exam Study Guide is meant to help you start studying. It is not necessarily a complete list of everything you need to know.
 Disclaimer: This is meant to help you start studying. It is not necessarily a complete list of everything you need to know. The MTH 234 final exam mainly consists of standard response questions where students
Disclaimer: This is meant to help you start studying. It is not necessarily a complete list of everything you need to know. The MTH 234 final exam mainly consists of standard response questions where students
APPM 1360 Final Exam Spring 2016
 APPM 36 Final Eam Spring 6. 8 points) State whether each of the following quantities converge or diverge. Eplain your reasoning. a) The sequence a, a, a 3,... where a n ln8n) lnn + ) n!) b) ln d c) arctan
APPM 36 Final Eam Spring 6. 8 points) State whether each of the following quantities converge or diverge. Eplain your reasoning. a) The sequence a, a, a 3,... where a n ln8n) lnn + ) n!) b) ln d c) arctan
0, otherwise. Find each of the following limits, or explain that the limit does not exist.
 Midterm Solutions 1, y x 4 1. Let f(x, y) = 1, y 0 0, otherwise. Find each of the following limits, or explain that the limit does not exist. (a) (b) (c) lim f(x, y) (x,y) (0,1) lim f(x, y) (x,y) (2,3)
Midterm Solutions 1, y x 4 1. Let f(x, y) = 1, y 0 0, otherwise. Find each of the following limits, or explain that the limit does not exist. (a) (b) (c) lim f(x, y) (x,y) (0,1) lim f(x, y) (x,y) (2,3)
arxiv:math/ v1 [math.dg] 6 Mar 1998
![arxiv:math/ v1 [math.dg] 6 Mar 1998 arxiv:math/ v1 [math.dg] 6 Mar 1998](/thumbs/85/93034393.jpg) TORUS CURVES WITH VANISHING CURVATURE arxiv:math/9803021v1 [math.dg] 6 Mar 1998 EDGAR J. FULLER, JR. Abstract. Let T be the standard torus of revolution in R 3 with radii b and 1. Let α be a (p,q) torus
TORUS CURVES WITH VANISHING CURVATURE arxiv:math/9803021v1 [math.dg] 6 Mar 1998 EDGAR J. FULLER, JR. Abstract. Let T be the standard torus of revolution in R 3 with radii b and 1. Let α be a (p,q) torus
MAT137 Calculus! Lecture 6
 MAT137 Calculus! Lecture 6 Today: 3.2 Differentiation Rules; 3.3 Derivatives of higher order. 3.4 Related rates 3.5 Chain Rule 3.6 Derivative of Trig. Functions Next: 3.7 Implicit Differentiation 4.10
MAT137 Calculus! Lecture 6 Today: 3.2 Differentiation Rules; 3.3 Derivatives of higher order. 3.4 Related rates 3.5 Chain Rule 3.6 Derivative of Trig. Functions Next: 3.7 Implicit Differentiation 4.10
TRIGONOMETRIC FUNCTIONS. Copyright Cengage Learning. All rights reserved.
 12 TRIGONOMETRIC FUNCTIONS Copyright Cengage Learning. All rights reserved. 12.2 The Trigonometric Functions Copyright Cengage Learning. All rights reserved. The Trigonometric Functions and Their Graphs
12 TRIGONOMETRIC FUNCTIONS Copyright Cengage Learning. All rights reserved. 12.2 The Trigonometric Functions Copyright Cengage Learning. All rights reserved. The Trigonometric Functions and Their Graphs
Review Exercises for Chapter 3. Review Exercises for Chapter r v 0 2. v ft sec. x 1 2 x dx f x x 99.4.
 Review Eercises for Chapter 6. r v 0 sin. Let f, 00, d 0.6. v 0 00 ftsec changes from 0 to dr 00 cos d 6 0 d 0 r dr 80 00 6 96 feet 80 cos 0 96 feet 8080 f f fd d f 99. 00 0.6 9.97 00 Using a calculator:
Review Eercises for Chapter 6. r v 0 sin. Let f, 00, d 0.6. v 0 00 ftsec changes from 0 to dr 00 cos d 6 0 d 0 r dr 80 00 6 96 feet 80 cos 0 96 feet 8080 f f fd d f 99. 00 0.6 9.97 00 Using a calculator:
4.3 TRIGONOMETRY EXTENDED: THE CIRCULAR FUNCTIONS
 4.3 TRIGONOMETRY EXTENDED: THE CIRCULAR FUNCTIONS MR. FORTIER 1. Trig Functions of Any Angle We now extend the definitions of the six basic trig functions beyond triangles so that we do not have to restrict
4.3 TRIGONOMETRY EXTENDED: THE CIRCULAR FUNCTIONS MR. FORTIER 1. Trig Functions of Any Angle We now extend the definitions of the six basic trig functions beyond triangles so that we do not have to restrict
