(8) 1f = f. can be viewed as a real vector space where addition is defined by ( a1+ bi
|
|
|
- Laura Daniel
- 5 years ago
- Views:
Transcription
1 Geeral Liear Spaes (Vetor Spaes) ad Solutios o ODEs Deiitio: A vetor spae V is a set, with additio ad salig o elemet deied or all elemets o the set, that is losed uder additio ad salig, otais a zero elemet (), ad satisies the ollowig axioms: For all, gh, Vad salars,, () ( + g) + h= + ( g+ h) (5) ( + g) = + g () + g = g+ (6) ( + ) = + (3) + = (7) ( ) = ( ) (4) + ( ) = (8) = We ll deal iitially with the ase where the salars are real umbers. Suh a vetor spae is alled a real vetor spae. We will also use omplex salars i whih ase we ll all this a omplex vetor spae. Though we a give deiitios ad prove theorems about vetor spaes i geeral, it s helpul to develop a library o examples to whih we a reer.. R is a vetor spae. Ideed, the motivatio or our deiitio ad axioms is to deie vetor spaes to be spaes whih a udametally lie R. All o the required axioms are amiliar ats about vetors i R.. Ay subspae o R is a vetor spae. All o the axioms are iherited ad every subspae otais the zero vetor, ad the deiitio o subspae esures that a subspae is losed uder additio ad salig. 3. The omplex umbers = { a + bi : a, b are real umbers, i =} a be viewed as a real vetor spae where additio is deied by ( a+ bi ) + ( a + bi ) = ( a+ a) + ( b+ b) i ad salig by a real umber is deied by ( a + bi) = a + bi. Note that we do ot deie multipliatio o omplex umbers i this otext. The omplex umbers otai the zero elemet = + i ad all o the axioms ollow rom orrespodig ats about real umbers. m 4. = M( m, ) = { m matries with real etries} R is a real vetor spae with additio ad salig o matries deied ompoet-wise. The m zero matrix is the zero elemet ad the axioms are all ow properties o matrix algebra. Note that i this otext we do ot deie the produt o matries. 5. F(, ) = F( ) = { utios : with domai } RR R R R R is a real vetor spae where additio o utios ad salig o utios are deied by poitwise by ( + g)( x) = ( x) + gx ( ) ad ( )( x) = ( x). The zero elemet i this ase is the utio that is idetially zero or all x. (This is quite dieret tha just the real umber.) Oe agai, the axioms all ollow rom amiliar ats about real umbers. 6. P = { real polyomials o degree } = { a + ax + + ax : a, a,, a R} is a real vetor spae. Note that we must allow all polyomials less tha or equal to beause we might add two polyomials (or sale by ) ad get a polyomial o lesser degree. 7. C (, ) = C ( ) = { otiuous utios : } RR R R R is a real vetor spae. Closure ollows rom theorems o Calulus that the sum o otiuous utios is otiuous ad a salar multiple o a otiuous utio is also otiuous. The zero utio is learly otiuous, ad the axioms are all easily veriied. Deiitio: A subspae W o a vetor spae V is a subset that is losed uder additio ad salig o elemets. That is, or ay vetors v, v W ad salars,, it must be the ase that v+ v W. We write W V. 8. C (, ) = C ( ) = { dieretiable utios : } RR R R R is a real vetor spae. Closure ollows rom the theorems o Calulus that ( + g) = + g ad ( ) =. The zero utio is learly dieretiable.
2 Note: All polyomials are dieretiable, ad a (hopeully) amiliar theorem o Calulus tells us that dieretiable utios must be otiuous, so or ay, P C ( R) C ( R) F( R ). 9. C (, ) = C ( ) = { utios : that are at least times dieretiable} RR R R R is a real vetor spae. This ollows similarly rom Calulus theorems. The zero utio is dieretiable to all orders.. C (, ) = C ( ) = { utios : that are dieretiable to all orders} RR R R R is a real vetor spae. This also ollows rom the Calulus theorems above. The zero utio is dieretiable to all orders. Note: For ay, P P P P P C ( R) C ( R) C ( R) C ( R) F( R). It s also importat to ote that whe dealig with spaes o utios, these spaes are muh larger that R. To better uderstad this, we ll eed some more deiitios, but some o the importat details will have to wait util you tae ourse i aalysis ad topology. May o the deiitios whe worig with vetors spaes are essetially the same as those i R. Deiitio: Give a olletio o elemets {,,, } V spa {,, } = { + + where, are salars} Deiitio: A set o elemets { }, we deie the spa o these elemets as:.,,, V is alled liearly idepedet i give ay liear ombiatio o the orm + + =, this implies that = = =. That is, there is o otrivial way to ombie these vetors to yield the zero elemet. Deiitio: Give a subspae W V, a olletio o elemets {,,, } W is alled a basis o W i Spa {,,, } = W ad {,,, } are liearly idepedet. A basis is a miimal spaig set ad, as was the ase i R, i a basis or W osists o iitely may elemets the ay other basis will have the same umber o elemets, the dimesio o W. It is importat to ote, however, that it will ote be the ase, espeially i the ase o utio spaes, that a subspae might ot be spaed by iitely may elemets. Coordiates relative to a basis Deiitio: I B = {,, } is a basis or a iite dimesioal vetor spae V (or a subspae o V), ad i V, the a be expressed uiquely as = + + or salars {,, }. These uiquely determied salars are alled the oordiates o relative to this basis. I we express these oordiates as a olum vetor (eetively a vetor i. B R ), we deote this oordiate vetor by [ ] Deiitio: Give two vetors spaes V ad W, a utio T : V W is alled a liear trasormatio i or all elemets, V ad or all salars,, T satisies T( + ) = T ( ) + T( ). This a also be expressed by sayig that T preserves additio ad salar multipliatio. We all the iput spae V the domai o T ad we all the output spae W the odomai. Deiitio: Suppose T : V W is a liear trasormatio. We deie: image( T ) im( T ) T ( ): V W erel( T) = er( T) = V : T( ) = V = = { } ad { } These are both subspaes. The argumet is the same as we ve see beore.
3 Deiitio: Give a liear trasormatio T : V W, we deie: ra( T) = dim(im T) ad ullity( T) = dim(er T) whe these subspaes have iite dimesio. We a also state (without proo) the orrespodig at regardig the relatioship betwee ra ad ullity. Ra-Nullity Theorem: I T : V ra( T) + ullity( T) = dim( V). W is a liear trasormatio ad V has iite dimesio, the Deiitio: A liear trasormatio T : V W is alled a isomorphism i it is oe-to-oe ad oto its odomai. That is, or every g W there is a uique V suh that T( ) = g. Appliatio to Liear Ordiary Dieretial Equatios I ay spae osistig o dieretiable utios, the dieretiatio operator D( ) = is a liear trasormatio. This ollows rom the Calulus ats that D( + g) = ( + g) = + g = D( ) + D( g) ad D( ) = ( ) = = D( ). The erel o this liear trasormatio osists o the ostat utios. This liear trasormatio is thereore NOT a isomorphism. I ay spae o utios, aother importat liear trasormatio is multipliatio by a ixed utio g. That is, i we deie Mg ( ) = g, the or ay salars, ad ay utios, we have: M ( + ) = g( + ) = g + g = M ( ) + M ( ) g g g I we ombie the dieretiatio operator ad various multipliatio operators via additio ad ompositio, we a build more ompliated liear dieretial operators. For example, D = D D is a liear operator orrespodig to taig the d derivative. Similarly, D = D D D orrespods with taig the th derivative. I pt () is a utio, the T = D + pi is a irst order liear dieretial operator alulated by: T( xt ()) = ( D+ pi)( xt ()) = + ptxt () () More geerally, give utios p (), t, p(), t p() t, we a orm the liear dieretial operator T= D + p D + + pd+ pi. Whe applied to a suiietly dieretial utio xt (), this gives: d x d = + x = T ( xt ()) ( D p D pd pi )( xt ()) p () t p () t p () txt () Solvig a th order liear ODE o the orm + () () () () () p t p t p txt qt = a thus be see as solvig T( xt ()) = qt (). I the ase o a homogeeous liear ODE, the beomes simply T( xt ( )) =, i.e. we are tryig to id the erel o the liear dieretial operator. 3 d x d x Perhaps the greatest beeit o this ormulatio is that i we a id several (liearly idepedet) homogeeous solutios x (), t x () t [that is, T( x( t)) = T( x( t)) = = T( x ( t)) = ], the or ay salars,, we have (by liearity) T( x() t + + x()) t = T ( x()) t + + T( x()) t =. That is, ay liear ombiatio o solutios will also be a solutio [Priiple o Superpositio]. Liear ODEs with ostat oeiiets A importat (ad easily solvable) ase is where all o the oeiiet utios are ostat, i.e. a operator o the orm T= D + a D + + ad + ai where a,, a, a are ostats. We ll irst osider the homogeeous ase, i.e. solvig a homogeeous liear ODE with ostat oeiiets o the orm d x a d + x + + a + ax =. We a geerate solutios to suh a ODE by (iitially) osiderig rt expoetial utios o the orm xt () = e where r is ostat. Substitutig this ito the ODE gives:
4 d x d x rt rt rt rt rt + a + + a + a x = r e + a r e + + are + ae = ( r + a r + + ar + a ) e = The polyomial P() r = r + a r + + ar + a is alled the harateristi polyomial o this ODE. Ay root o this polyomial will yield a expoetial solutio to the ODE, ad the Fudametal Theorem o Algebra guaratees roots, though some may be omplex ad some may be repeated. The roots o the harateristi polyomial are alled the harateristi roots or harateristi values o the ODE. Our strategy will be to try to reate a basis out o suh expoetial solutios rom whih ALL homogeeous solutios a be ostruted. First Order Example: I we solve x =, we have the harateristi polyomial Pr () = r = ad t t harateristi value r =. This yields the expoetial solutio e. By liearity, x() t = e will also be a t solutio ad, i at, this yields ALL homogeeous solutios. That is { e } is a basis or all suh solutios. Seod Order Example: Suppose we wat to solve the ODE x =. The orrespodig liear dieretial operator is T = D + 3D+ I ad the harateristi polyomial is Pr ( ) = r + 3r+ = ( r+ )( r+ ). t This yields the harateristi values r = ad r = ad expoetial solutios e t ad e. By liearity, ay t t utio o the orm x() t = e + e will also be a homogeeous solutio or ay salars,. Does this t t give ALL solutios? That is, does { e, e } ostitute a basis or all solutios? We a show that this is atually the ase by thiig o T = D + 3D+ I = ( D+ ) I ( D+ I), i.e. as a ompositio o irst-order liear operators. We are seeig a solutio xt () suh that ( D+ I)[( D+ I)( xt ( ))] =. I we let yt ( ) = ( D+ I)( xt ( )), the we a irst solve ( D+ I)[ yt ( ))] = y + y = to get all solutios o the orm t y() t e t =. Next, or ay suh solutio we ll have ( D+ I)( x( t)) = x + x= e. This is a ihomogeeous t irst-order ODE. The homogeeous solutios are all o the orm xh () t = e ad we a use the Method o t Udetermied Coeiiets to produe a partiular solutio to the ihomogeeous equatio, i.e. xp () t = Ae t t t or some salar A. Substitutio gives x + x = ( A + A) e = Ae = e, so A=. We the add the t t homogeeous ad partiular solutios to get that all solutios must be o the orm x() t = e e. I we t t t t ow simply reame the oeiiets we see that all solutios are o the orm x() t = e + e, i.e. { e, e } does ostitute a basis or all solutios. (It s straightorward to show that these utios are liearly idepedet.) The above argumet wors the same i the ase o a th order liear homogeeous ODE with ostat oeiiets as alog as all the roots o the harateristi polyomial are distit. It s eve valid i the ase o omplex roots (though it s geerally preerable to use Euler s Formula to re-express the expoetial solutios i terms o sie ad osie utios). Repeated roots have to be hadled dieretly. A example will illustrate what should be doe i that ase. Repeated root example: Suppose we wat to solve the ODE dieretial operator is T = D + 4D+ 4I ad the harateristi polyomial is yields oly the harateristi value r = with orrespodig expoetial solutios x =. The orrespodig liear Pr ( ) r 4r 4 ( r ) = + + = +. This t e t. Does x() t = e yield ALL homogeeous solutios, i.e. does { e t } ostitute a basis or all solutios? The aswer is NO. I we proeed i the same maer as the previous example, we write ( D+ I)[( D+ I)( x( t))] = ad let t yt ( ) = ( D+ I)( xt ( )). We solve ( D+ I)[ yt ( ))] = y + y = to get y() t = e ad the see solutios o t ( D+ I)( x( t)) = x + x= e. I this ase, it may ot be so lear how to use Udetermied Coeiiets to
5 guess a partiular solutio to this ihomogeeous equatio. We a use Variatio o Parameters to id t t e solutios. I we see a solutio o the orm xp () t = vte (), the method gives that v () t = = t, so e v() t = t + (we atually do t eed to ilude the + i we re just seeig a partiular solutio). So we a t hoose xp () t = te t. The homogeeous solutios are all o the orm xh () t = e. Thereore, ALL solutios t t t t are o the orm x() t = te + e. That is, { e, te } orms a basis or ALL solutios. This a be geeralized or ay repeated root o ay multipliity. For example, a similar alulatio shows that 3 3t 3t 3t or the homogeeous liear ODE ( D+ 3 I) ( xt ( )) =, { e, te, t e } gives a basis or all solutios. That is, 3t 3t 3t all solutios are expressible (uiquely) i the orm x() t = e + te + t e } 3 As log as we a easily ator the harateristi polyomial, the above example illustrate how we a simply geerate a basis or all homogeeous solutios or i the ase o ostat oeiiets. Example: Fid all solutios to the ODE: d4x d3x x =. 4 3 Solutio: The harateristi polyomial i the ase is Pr ( ) = r + r + 5r + 8r+ 4 = ( r+ ) ( r + 4) =. The harateristi values are r = (with multipliity ), r = i, ad r = i. From these we get a basis or all t t it it t t it it solutios { e, te, e, e }. We ould express all solutios i the orm x() t = e + te + 3e + 4e where we eessarily have to allow or omplex oeiiets. However, i we ote (usig Euler s Formula) that it it e = os( t) + isi( t) ad e = os( t) isi( t) we a easily see that we ould also (perhaps more simply) use { t t e, te,os t,si t} as a basis or all solutios, i.e. all solutios may be expressed i the orm ( ) t t x t = e + te + os t+ si t where all the oeiiets are real salars. 3 4 Our ext several tass will be to osider ihomogeeous equatios ad iitial value problems. This will eessitate a slightly more uaed view o what we mea by liearly idepedet utios or the purpose o idig uique solutios to well-posed iitial value problems. This will ivolve what is ow as the Wrosia assoiated with a give basis o homogeeous solutios. Notes by Robert Witers 5
Sx [ ] = x must yield a
![Sx [ ] = x must yield a Sx [ ] = x must yield a](/thumbs/96/128993958.jpg) Math -b Leture #5 Notes This wee we start with a remider about oordiates of a vetor relative to a basis for a subspae ad the importat speial ase where the subspae is all of R. This freedom to desribe vetors
Math -b Leture #5 Notes This wee we start with a remider about oordiates of a vetor relative to a basis for a subspae ad the importat speial ase where the subspae is all of R. This freedom to desribe vetors
Class #25 Wednesday, April 19, 2018
 Cla # Wedesday, April 9, 8 PDE: More Heat Equatio with Derivative Boudary Coditios Let s do aother heat equatio problem similar to the previous oe. For this oe, I ll use a square plate (N = ), but I m
Cla # Wedesday, April 9, 8 PDE: More Heat Equatio with Derivative Boudary Coditios Let s do aother heat equatio problem similar to the previous oe. For this oe, I ll use a square plate (N = ), but I m
After the completion of this section the student. V.4.2. Power Series Solution. V.4.3. The Method of Frobenius. V.4.4. Taylor Series Solution
 Chapter V ODE V.4 Power Series Solutio Otober, 8 385 V.4 Power Series Solutio Objetives: After the ompletio of this setio the studet - should reall the power series solutio of a liear ODE with variable
Chapter V ODE V.4 Power Series Solutio Otober, 8 385 V.4 Power Series Solutio Objetives: After the ompletio of this setio the studet - should reall the power series solutio of a liear ODE with variable
, then cv V. Differential Equations Elements of Lineaer Algebra Name: Consider the differential equation. and y2 cos( kx)
 Cosider the differetial equatio y '' k y 0 has particular solutios y1 si( kx) ad y cos( kx) I geeral, ay liear combiatio of y1 ad y, cy 1 1 cy where c1, c is also a solutio to the equatio above The reaso
Cosider the differetial equatio y '' k y 0 has particular solutios y1 si( kx) ad y cos( kx) I geeral, ay liear combiatio of y1 ad y, cy 1 1 cy where c1, c is also a solutio to the equatio above The reaso
Where do eigenvalues/eigenvectors/eigenfunctions come from, and why are they important anyway?
 Where do eigevalues/eigevectors/eigeuctios come rom, ad why are they importat ayway? I. Bacgroud (rom Ordiary Dieretial Equatios} Cosider the simplest example o a harmoic oscillator (thi o a vibratig strig)
Where do eigevalues/eigevectors/eigeuctios come rom, ad why are they importat ayway? I. Bacgroud (rom Ordiary Dieretial Equatios} Cosider the simplest example o a harmoic oscillator (thi o a vibratig strig)
McGill University Math 354: Honors Analysis 3 Fall 2012 Solutions to selected problems. x y
 McGill Uiversity Math 354: Hoors Aalysis 3 Fall 212 Assigmet 3 Solutios to selected problems Problem 1. Lipschitz uctios. Let M K be the set o all uctios cotiuous uctios o [, 1] satisyig a Lipschitz coditio
McGill Uiversity Math 354: Hoors Aalysis 3 Fall 212 Assigmet 3 Solutios to selected problems Problem 1. Lipschitz uctios. Let M K be the set o all uctios cotiuous uctios o [, 1] satisyig a Lipschitz coditio
CHAPTER 5. Theory and Solution Using Matrix Techniques
 A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
ANOTHER PROOF FOR FERMAT S LAST THEOREM 1. INTRODUCTION
 ANOTHER PROOF FOR FERMAT S LAST THEOREM Mugur B. RĂUŢ Correspodig author: Mugur B. RĂUŢ, E-mail: m_b_raut@yahoo.om Abstrat I this paper we propose aother proof for Fermat s Last Theorem (FLT). We foud
ANOTHER PROOF FOR FERMAT S LAST THEOREM Mugur B. RĂUŢ Correspodig author: Mugur B. RĂUŢ, E-mail: m_b_raut@yahoo.om Abstrat I this paper we propose aother proof for Fermat s Last Theorem (FLT). We foud
Bernoulli Numbers. n(n+1) = n(n+1)(2n+1) = n(n 1) 2
 Beroulli Numbers Beroulli umbers are amed after the great Swiss mathematiia Jaob Beroulli5-705 who used these umbers i the power-sum problem. The power-sum problem is to fid a formula for the sum of the
Beroulli Numbers Beroulli umbers are amed after the great Swiss mathematiia Jaob Beroulli5-705 who used these umbers i the power-sum problem. The power-sum problem is to fid a formula for the sum of the
Explicit and closed formed solution of a differential equation. Closed form: since finite algebraic combination of. converges for x x0
 Chapter 4 Series Solutios Epliit ad losed formed solutio of a differetial equatio y' y ; y() 3 ( ) ( 5 e ) y Closed form: sie fiite algebrai ombiatio of elemetary futios Series solutio: givig y ( ) as
Chapter 4 Series Solutios Epliit ad losed formed solutio of a differetial equatio y' y ; y() 3 ( ) ( 5 e ) y Closed form: sie fiite algebrai ombiatio of elemetary futios Series solutio: givig y ( ) as
Observer Design with Reduced Measurement Information
 Observer Desig with Redued Measuremet Iformatio I pratie all the states aot be measured so that SVF aot be used Istead oly a redued set of measuremets give by y = x + Du p is available where y( R We assume
Observer Desig with Redued Measuremet Iformatio I pratie all the states aot be measured so that SVF aot be used Istead oly a redued set of measuremets give by y = x + Du p is available where y( R We assume
Computational Methods CMSC/AMSC/MAPL 460. Quadrature: Integration
 Computatioal Metods CMSC/AMSC/MAPL 6 Quadrature: Itegratio Ramai Duraiswami, Dept. o Computer Siee Some material adapted rom te olie slides o Eri Sadt ad Diae O Leary Numerial Itegratio Idea is to do itegral
Computatioal Metods CMSC/AMSC/MAPL 6 Quadrature: Itegratio Ramai Duraiswami, Dept. o Computer Siee Some material adapted rom te olie slides o Eri Sadt ad Diae O Leary Numerial Itegratio Idea is to do itegral
ε > 0 N N n N a n < ε. Now notice that a n = a n.
 4 Sequees.5. Null sequees..5.. Defiitio. A ull sequee is a sequee (a ) N that overges to 0. Hee, by defiitio of (a ) N overges to 0, a sequee (a ) N is a ull sequee if ad oly if ( ) ε > 0 N N N a < ε..5..
4 Sequees.5. Null sequees..5.. Defiitio. A ull sequee is a sequee (a ) N that overges to 0. Hee, by defiitio of (a ) N overges to 0, a sequee (a ) N is a ull sequee if ad oly if ( ) ε > 0 N N N a < ε..5..
Taylor Polynomials and Approximations - Classwork
 Taylor Polyomials ad Approimatios - Classwork Suppose you were asked to id si 37 o. You have o calculator other tha oe that ca do simple additio, subtractio, multiplicatio, or divisio. Fareched\ Not really.
Taylor Polyomials ad Approimatios - Classwork Suppose you were asked to id si 37 o. You have o calculator other tha oe that ca do simple additio, subtractio, multiplicatio, or divisio. Fareched\ Not really.
CHAPTER I: Vector Spaces
 CHAPTER I: Vector Spaces Sectio 1: Itroductio ad Examples This first chapter is largely a review of topics you probably saw i your liear algebra course. So why cover it? (1) Not everyoe remembers everythig
CHAPTER I: Vector Spaces Sectio 1: Itroductio ad Examples This first chapter is largely a review of topics you probably saw i your liear algebra course. So why cover it? (1) Not everyoe remembers everythig
Topic 9 - Taylor and MacLaurin Series
 Topic 9 - Taylor ad MacLauri Series A. Taylors Theorem. The use o power series is very commo i uctioal aalysis i act may useul ad commoly used uctios ca be writte as a power series ad this remarkable result
Topic 9 - Taylor ad MacLauri Series A. Taylors Theorem. The use o power series is very commo i uctioal aalysis i act may useul ad commoly used uctios ca be writte as a power series ad this remarkable result
CS537. Numerical Analysis and Computing
 CS57 Numerical Aalysis ad Computig Lecture Locatig Roots o Equatios Proessor Ju Zhag Departmet o Computer Sciece Uiversity o Ketucky Leigto KY 456-6 Jauary 9 9 What is the Root May physical system ca be
CS57 Numerical Aalysis ad Computig Lecture Locatig Roots o Equatios Proessor Ju Zhag Departmet o Computer Sciece Uiversity o Ketucky Leigto KY 456-6 Jauary 9 9 What is the Root May physical system ca be
CS321. Numerical Analysis and Computing
 CS Numerical Aalysis ad Computig Lecture Locatig Roots o Equatios Proessor Ju Zhag Departmet o Computer Sciece Uiversity o Ketucky Leigto KY 456-6 September 8 5 What is the Root May physical system ca
CS Numerical Aalysis ad Computig Lecture Locatig Roots o Equatios Proessor Ju Zhag Departmet o Computer Sciece Uiversity o Ketucky Leigto KY 456-6 September 8 5 What is the Root May physical system ca
Zeros of Polynomials
 Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
Math 160 www.timetodare.com 4.5 4.6 Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered with fidig the solutios of polyomial equatios of ay degree
M A T H F A L L CORRECTION. Algebra I 1 4 / 1 0 / U N I V E R S I T Y O F T O R O N T O
 M A T H 2 4 0 F A L L 2 0 1 4 HOMEWORK ASSIGNMENT #4 CORRECTION Algebra I 1 4 / 1 0 / 2 0 1 4 U N I V E R S I T Y O F T O R O N T O P r o f e s s o r : D r o r B a r - N a t a Correctio Homework Assigmet
M A T H 2 4 0 F A L L 2 0 1 4 HOMEWORK ASSIGNMENT #4 CORRECTION Algebra I 1 4 / 1 0 / 2 0 1 4 U N I V E R S I T Y O F T O R O N T O P r o f e s s o r : D r o r B a r - N a t a Correctio Homework Assigmet
Chapter Vectors
 Chapter 4. Vectors fter readig this chapter you should be able to:. defie a vector. add ad subtract vectors. fid liear combiatios of vectors ad their relatioship to a set of equatios 4. explai what it
Chapter 4. Vectors fter readig this chapter you should be able to:. defie a vector. add ad subtract vectors. fid liear combiatios of vectors ad their relatioship to a set of equatios 4. explai what it
Properties and Tests of Zeros of Polynomial Functions
 Properties ad Tests of Zeros of Polyomial Fuctios The Remaider ad Factor Theorems: Sythetic divisio ca be used to fid the values of polyomials i a sometimes easier way tha substitutio. This is show by
Properties ad Tests of Zeros of Polyomial Fuctios The Remaider ad Factor Theorems: Sythetic divisio ca be used to fid the values of polyomials i a sometimes easier way tha substitutio. This is show by
SOME NOTES ON INEQUALITIES
 SOME NOTES ON INEQUALITIES Rihard Hoshio Here are four theorems that might really be useful whe you re workig o a Olympiad problem that ivolves iequalities There are a buh of obsure oes Chebyheff, Holder,
SOME NOTES ON INEQUALITIES Rihard Hoshio Here are four theorems that might really be useful whe you re workig o a Olympiad problem that ivolves iequalities There are a buh of obsure oes Chebyheff, Holder,
N A N A ( ) We re-arrange and collapse the random variables into a set corresponding to the weighted
 7- trodutio Note that rom 08bx0v3.do (p6) while rom page 7, ad Title Bo Xu Y = μ T B E N N ( Y ) = ( ) UV N μ Commet: Bo, Write a brie itrodutio explaiig what this doumet will do. You a opy parts rom the
7- trodutio Note that rom 08bx0v3.do (p6) while rom page 7, ad Title Bo Xu Y = μ T B E N N ( Y ) = ( ) UV N μ Commet: Bo, Write a brie itrodutio explaiig what this doumet will do. You a opy parts rom the
Basic Probability/Statistical Theory I
 Basi Probability/Statistial Theory I Epetatio The epetatio or epeted values of a disrete radom variable X is the arithmeti mea of the radom variable s distributio. E[ X ] p( X ) all Epetatio by oditioig
Basi Probability/Statistial Theory I Epetatio The epetatio or epeted values of a disrete radom variable X is the arithmeti mea of the radom variable s distributio. E[ X ] p( X ) all Epetatio by oditioig
ALGEBRAIC GEOMETRY COURSE NOTES, LECTURE 5: SINGULARITIES.
 ALGEBRAIC GEOMETRY COURSE NOTES, LECTURE 5: SINGULARITIES. ANDREW SALCH 1. The Jacobia criterio for osigularity. You have probably oticed by ow that some poits o varieties are smooth i a sese somethig
ALGEBRAIC GEOMETRY COURSE NOTES, LECTURE 5: SINGULARITIES. ANDREW SALCH 1. The Jacobia criterio for osigularity. You have probably oticed by ow that some poits o varieties are smooth i a sese somethig
Fluids Lecture 2 Notes
 Fluids Leture Notes. Airfoil orte Sheet Models. Thi-Airfoil Aalysis Problem Readig: Aderso.,.7 Airfoil orte Sheet Models Surfae orte Sheet Model A aurate meas of represetig the flow about a airfoil i a
Fluids Leture Notes. Airfoil orte Sheet Models. Thi-Airfoil Aalysis Problem Readig: Aderso.,.7 Airfoil orte Sheet Models Surfae orte Sheet Model A aurate meas of represetig the flow about a airfoil i a
A brief introduction to linear algebra
 CHAPTER 6 A brief itroductio to liear algebra 1. Vector spaces ad liear maps I what follows, fix K 2{Q, R, C}. More geerally, K ca be ay field. 1.1. Vector spaces. Motivated by our ituitio of addig ad
CHAPTER 6 A brief itroductio to liear algebra 1. Vector spaces ad liear maps I what follows, fix K 2{Q, R, C}. More geerally, K ca be ay field. 1.1. Vector spaces. Motivated by our ituitio of addig ad
Recursive Algorithms. Recurrences. Recursive Algorithms Analysis
 Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
Recursive Algorithms Recurreces Computer Sciece & Egieerig 35: Discrete Mathematics Christopher M Bourke cbourke@cseuledu A recursive algorithm is oe i which objects are defied i terms of other objects
POWER SERIES METHODS CHAPTER 8 SECTION 8.1 INTRODUCTION AND REVIEW OF POWER SERIES
 CHAPTER 8 POWER SERIES METHODS SECTION 8. INTRODUCTION AND REVIEW OF POWER SERIES The power series method osists of substitutig a series y = ito a give differetial equatio i order to determie what the
CHAPTER 8 POWER SERIES METHODS SECTION 8. INTRODUCTION AND REVIEW OF POWER SERIES The power series method osists of substitutig a series y = ito a give differetial equatio i order to determie what the
Lecture 8. Dirac and Weierstrass
 Leture 8. Dira ad Weierstrass Audrey Terras May 5, 9 A New Kid of Produt of Futios You are familiar with the poitwise produt of futios de ed by f g(x) f(x) g(x): You just tae the produt of the real umbers
Leture 8. Dira ad Weierstrass Audrey Terras May 5, 9 A New Kid of Produt of Futios You are familiar with the poitwise produt of futios de ed by f g(x) f(x) g(x): You just tae the produt of the real umbers
ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 4 Solutions [Numerical Methods]
![ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 4 Solutions [Numerical Methods] ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 4 Solutions [Numerical Methods]](/thumbs/89/97848596.jpg) ENGI 3 Advaced Calculus or Egieerig Facult o Egieerig ad Applied Sciece Problem Set Solutios [Numerical Methods]. Use Simpso s rule with our itervals to estimate I si d a, b, h a si si.889 si 3 si.889
ENGI 3 Advaced Calculus or Egieerig Facult o Egieerig ad Applied Sciece Problem Set Solutios [Numerical Methods]. Use Simpso s rule with our itervals to estimate I si d a, b, h a si si.889 si 3 si.889
Maclaurin and Taylor series
 At the ed o the previous chapter we looed at power series ad oted that these were dieret rom other iiite series as they were actually uctios o a variable R: a a + + a + a a Maclauri ad Taylor series +
At the ed o the previous chapter we looed at power series ad oted that these were dieret rom other iiite series as they were actually uctios o a variable R: a a + + a + a a Maclauri ad Taylor series +
Recurrence Relations
 Recurrece Relatios Aalysis of recursive algorithms, such as: it factorial (it ) { if (==0) retur ; else retur ( * factorial(-)); } Let t be the umber of multiplicatios eeded to calculate factorial(). The
Recurrece Relatios Aalysis of recursive algorithms, such as: it factorial (it ) { if (==0) retur ; else retur ( * factorial(-)); } Let t be the umber of multiplicatios eeded to calculate factorial(). The
9.3 Taylor s Theorem: Error Analysis for Series. Tacoma Narrows Bridge: November 7, 1940
 9. Taylor s Theorem: Error Aalysis or Series Tacoma Narrows Bridge: November 7, 940 Last time i BC So the Taylor Series or l x cetered at x is give by ) l x ( ) ) + ) ) + ) ) 4 Use the irst two terms o
9. Taylor s Theorem: Error Aalysis or Series Tacoma Narrows Bridge: November 7, 940 Last time i BC So the Taylor Series or l x cetered at x is give by ) l x ( ) ) + ) ) + ) ) 4 Use the irst two terms o
Inverse Matrix. A meaning that matrix B is an inverse of matrix A.
 Iverse Matrix Two square matrices A ad B of dimesios are called iverses to oe aother if the followig holds, AB BA I (11) The otio is dual but we ofte write 1 B A meaig that matrix B is a iverse of matrix
Iverse Matrix Two square matrices A ad B of dimesios are called iverses to oe aother if the followig holds, AB BA I (11) The otio is dual but we ofte write 1 B A meaig that matrix B is a iverse of matrix
Digital Signal Processing. Homework 2 Solution. Due Monday 4 October Following the method on page 38, the difference equation
 Digital Sigal Proessig Homework Solutio Due Moda 4 Otober 00. Problem.4 Followig the method o page, the differee equatio [] (/4[-] + (/[-] x[-] has oeffiiets a0, a -/4, a /, ad b. For these oeffiiets A(z
Digital Sigal Proessig Homework Solutio Due Moda 4 Otober 00. Problem.4 Followig the method o page, the differee equatio [] (/4[-] + (/[-] x[-] has oeffiiets a0, a -/4, a /, ad b. For these oeffiiets A(z
8. Applications To Linear Differential Equations
 8. Applicatios To Liear Differetial Equatios 8.. Itroductio 8.. Review Of Results Cocerig Liear Differetial Equatios Of First Ad Secod Orders 8.3. Eercises 8.4. Liear Differetial Equatios Of Order N 8.5.
8. Applicatios To Liear Differetial Equatios 8.. Itroductio 8.. Review Of Results Cocerig Liear Differetial Equatios Of First Ad Secod Orders 8.3. Eercises 8.4. Liear Differetial Equatios Of Order N 8.5.
Series: Infinite Sums
 Series: Ifiite Sums Series are a way to mae sese of certai types of ifiitely log sums. We will eed to be able to do this if we are to attai our goal of approximatig trascedetal fuctios by usig ifiite degree
Series: Ifiite Sums Series are a way to mae sese of certai types of ifiitely log sums. We will eed to be able to do this if we are to attai our goal of approximatig trascedetal fuctios by usig ifiite degree
Lecture 11. Solution of Nonlinear Equations - III
 Eiciecy o a ethod Lecture Solutio o Noliear Equatios - III The eiciecy ide o a iterative ethod is deied by / E r r: rate o covergece o the ethod : total uber o uctios ad derivative evaluatios at each step
Eiciecy o a ethod Lecture Solutio o Noliear Equatios - III The eiciecy ide o a iterative ethod is deied by / E r r: rate o covergece o the ethod : total uber o uctios ad derivative evaluatios at each step
If we want to add up the area of four rectangles, we could find the area of each rectangle and then write this sum symbolically as:
 Sigma Notatio: If we wat to add up the area of four rectagles, we could fid the area of each rectagle ad the write this sum symbolically as: Sum A A A A Liewise, the sum of the areas of te triagles could
Sigma Notatio: If we wat to add up the area of four rectagles, we could fid the area of each rectagle ad the write this sum symbolically as: Sum A A A A Liewise, the sum of the areas of te triagles could
Linear Differential Equations of Higher Order Basic Theory: Initial-Value Problems d y d y dy
 Liear Differetial Equatios of Higher Order Basic Theory: Iitial-Value Problems d y d y dy Solve: a( ) + a ( )... a ( ) a0( ) y g( ) + + + = d d d ( ) Subject to: y( 0) = y0, y ( 0) = y,..., y ( 0) = y
Liear Differetial Equatios of Higher Order Basic Theory: Iitial-Value Problems d y d y dy Solve: a( ) + a ( )... a ( ) a0( ) y g( ) + + + = d d d ( ) Subject to: y( 0) = y0, y ( 0) = y,..., y ( 0) = y
The Phi Power Series
 The Phi Power Series I did this work i about 0 years while poderig the relatioship betwee the golde mea ad the Madelbrot set. I have fially decided to make it available from my blog at http://semresearch.wordpress.com/.
The Phi Power Series I did this work i about 0 years while poderig the relatioship betwee the golde mea ad the Madelbrot set. I have fially decided to make it available from my blog at http://semresearch.wordpress.com/.
MATH 205 HOMEWORK #2 OFFICIAL SOLUTION. (f + g)(x) = f(x) + g(x) = f( x) g( x) = (f + g)( x)
 MATH 205 HOMEWORK #2 OFFICIAL SOLUTION Problem 2: Do problems 7-9 o page 40 of Hoffma & Kuze. (7) We will prove this by cotradictio. Suppose that W 1 is ot cotaied i W 2 ad W 2 is ot cotaied i W 1. The
MATH 205 HOMEWORK #2 OFFICIAL SOLUTION Problem 2: Do problems 7-9 o page 40 of Hoffma & Kuze. (7) We will prove this by cotradictio. Suppose that W 1 is ot cotaied i W 2 ad W 2 is ot cotaied i W 1. The
Organic Electronic Devices
 Orgai letroi Devies Week 3: Charge rasport Leture 3.3: Multiple rap ad Release MR Model Brya W. Boudouris Chemial gieerig Purdue Uiversity Leture Overview ad Learig Objetives Coepts to be Covered i this
Orgai letroi Devies Week 3: Charge rasport Leture 3.3: Multiple rap ad Release MR Model Brya W. Boudouris Chemial gieerig Purdue Uiversity Leture Overview ad Learig Objetives Coepts to be Covered i this
Introduction to Algorithms
 Itroductio to Algorithms 6.046J/8.40J/SMA5503 Lecture 9 Pro. Charles E. Leiserso Biary-search-tree sort T Create a empty BST or i to do TREE-INSERT(T, A[i]) Perorm a iorder tree wal o T. Eample: A [3 8
Itroductio to Algorithms 6.046J/8.40J/SMA5503 Lecture 9 Pro. Charles E. Leiserso Biary-search-tree sort T Create a empty BST or i to do TREE-INSERT(T, A[i]) Perorm a iorder tree wal o T. Eample: A [3 8
PRELIMINARY MATHEMATICS LECTURE 5
 SCHOOL OF ORIENTAL AND AFRICAN STUDIES UNIVERSITY OF LONDON DEPARTMENT OF ECONOMICS 5 / - 6 5 MSc Ecoomics PRELIMINARY MATHEMATICS LECTURE 5 Course website: http://mercur.soas.ac.uk/users/sm97/teachig_msc_premath.htm
SCHOOL OF ORIENTAL AND AFRICAN STUDIES UNIVERSITY OF LONDON DEPARTMENT OF ECONOMICS 5 / - 6 5 MSc Ecoomics PRELIMINARY MATHEMATICS LECTURE 5 Course website: http://mercur.soas.ac.uk/users/sm97/teachig_msc_premath.htm
The Method of Least Squares. To understand least squares fitting of data.
 The Method of Least Squares KEY WORDS Curve fittig, least square GOAL To uderstad least squares fittig of data To uderstad the least squares solutio of icosistet systems of liear equatios 1 Motivatio Curve
The Method of Least Squares KEY WORDS Curve fittig, least square GOAL To uderstad least squares fittig of data To uderstad the least squares solutio of icosistet systems of liear equatios 1 Motivatio Curve
11. FINITE FIELDS. Example 1: The following tables define addition and multiplication for a field of order 4.
 11. FINITE FIELDS 11.1. A Field With 4 Elemets Probably the oly fiite fields which you ll kow about at this stage are the fields of itegers modulo a prime p, deoted by Z p. But there are others. Now although
11. FINITE FIELDS 11.1. A Field With 4 Elemets Probably the oly fiite fields which you ll kow about at this stage are the fields of itegers modulo a prime p, deoted by Z p. But there are others. Now although
g () n = g () n () f, f n = f () n () x ( n =1,2,3, ) j 1 + j 2 + +nj n = n +2j j n = r & j 1 j 1, j 2, j 3, j 4 = ( 4, 0, 0, 0) f 4 f 3 3!
 Higher Derivative o Compositio. Formulas o Higher Derivative o Compositio.. Faà di Bruo's Formula About the ormula o the higher derivative o compositio, the oe by a mathematicia Faà di Bruo i Italy o about
Higher Derivative o Compositio. Formulas o Higher Derivative o Compositio.. Faà di Bruo's Formula About the ormula o the higher derivative o compositio, the oe by a mathematicia Faà di Bruo i Italy o about
Abstract Vector Spaces. Abstract Vector Spaces
 Astract Vector Spaces The process of astractio is critical i egieerig! Physical Device Data Storage Vector Space MRI machie Optical receiver 0 0 1 0 1 0 0 1 Icreasig astractio 6.1 Astract Vector Spaces
Astract Vector Spaces The process of astractio is critical i egieerig! Physical Device Data Storage Vector Space MRI machie Optical receiver 0 0 1 0 1 0 0 1 Icreasig astractio 6.1 Astract Vector Spaces
PAPER : IIT-JAM 2010
 MATHEMATICS-MA (CODE A) Q.-Q.5: Oly oe optio is correct for each questio. Each questio carries (+6) marks for correct aswer ad ( ) marks for icorrect aswer.. Which of the followig coditios does NOT esure
MATHEMATICS-MA (CODE A) Q.-Q.5: Oly oe optio is correct for each questio. Each questio carries (+6) marks for correct aswer ad ( ) marks for icorrect aswer.. Which of the followig coditios does NOT esure
3.2 Properties of Division 3.3 Zeros of Polynomials 3.4 Complex and Rational Zeros of Polynomials
 Math 60 www.timetodare.com 3. Properties of Divisio 3.3 Zeros of Polyomials 3.4 Complex ad Ratioal Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered
Math 60 www.timetodare.com 3. Properties of Divisio 3.3 Zeros of Polyomials 3.4 Complex ad Ratioal Zeros of Polyomials I these sectios we will study polyomials algebraically. Most of our work will be cocered
Eigenvalues and Eigenvectors
 5 Eigevalues ad Eigevectors 5.3 DIAGONALIZATION DIAGONALIZATION Example 1: Let. Fid a formula for A k, give that P 1 1 = 1 2 ad, where Solutio: The stadard formula for the iverse of a 2 2 matrix yields
5 Eigevalues ad Eigevectors 5.3 DIAGONALIZATION DIAGONALIZATION Example 1: Let. Fid a formula for A k, give that P 1 1 = 1 2 ad, where Solutio: The stadard formula for the iverse of a 2 2 matrix yields
Computational Methods in the Theory of Synthesis of Radio and Acoustic Radiating Systems
 Applied Mathematis 3 4 53-549 http://dxdoiorg/436/am34378 Published Olie Marh 3 (http://wwwsirporg/joural/am) omputatioal Methods i the Theory o Sythesis o Radio ad Aousti Radiatig Systems Petro Sаveko
Applied Mathematis 3 4 53-549 http://dxdoiorg/436/am34378 Published Olie Marh 3 (http://wwwsirporg/joural/am) omputatioal Methods i the Theory o Sythesis o Radio ad Aousti Radiatig Systems Petro Sаveko
Study on Solution of Non-homogeneous Linear Equation based on Ordinary Differential Equation Driving Jing Zhang
 Iteratioal Coeree o Automatio Meaial Cotrol ad Computatioal Egieerig AMCCE 05 Stud o Solutio o No-omogeeous Liear Equatio based o Ordiar Dieretial Equatio Drivig Jig Zag Meaial ad Eletrial Egieerig College
Iteratioal Coeree o Automatio Meaial Cotrol ad Computatioal Egieerig AMCCE 05 Stud o Solutio o No-omogeeous Liear Equatio based o Ordiar Dieretial Equatio Drivig Jig Zag Meaial ad Eletrial Egieerig College
EEO 401 Digital Signal Processing Prof. Mark Fowler
 EEO 40 Digital Sigal Processig Prof. Mark Fowler Note Set #3 Covolutio & Impulse Respose Review Readig Assigmet: Sect. 2.3 of Proakis & Maolakis / Covolutio for LTI D-T systems We are tryig to fid y(t)
EEO 40 Digital Sigal Processig Prof. Mark Fowler Note Set #3 Covolutio & Impulse Respose Review Readig Assigmet: Sect. 2.3 of Proakis & Maolakis / Covolutio for LTI D-T systems We are tryig to fid y(t)
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
TEACHER CERTIFICATION STUDY GUIDE
 COMPETENCY 1. ALGEBRA SKILL 1.1 1.1a. ALGEBRAIC STRUCTURES Kow why the real ad complex umbers are each a field, ad that particular rigs are ot fields (e.g., itegers, polyomial rigs, matrix rigs) Algebra
COMPETENCY 1. ALGEBRA SKILL 1.1 1.1a. ALGEBRAIC STRUCTURES Kow why the real ad complex umbers are each a field, ad that particular rigs are ot fields (e.g., itegers, polyomial rigs, matrix rigs) Algebra
LECTURE 8: ORTHOGONALITY (CHAPTER 5 IN THE BOOK)
 LECTURE 8: ORTHOGONALITY (CHAPTER 5 IN THE BOOK) Everythig marked by is ot required by the course syllabus I this lecture, all vector spaces is over the real umber R. All vectors i R is viewed as a colum
LECTURE 8: ORTHOGONALITY (CHAPTER 5 IN THE BOOK) Everythig marked by is ot required by the course syllabus I this lecture, all vector spaces is over the real umber R. All vectors i R is viewed as a colum
Last time, we talked about how Equation (1) can simulate Equation (2). We asserted that Equation (2) can also simulate Equation (1).
 6896 Quatum Complexity Theory Sept 23, 2008 Lecturer: Scott Aaroso Lecture 6 Last Time: Quatum Error-Correctio Quatum Query Model Deutsch-Jozsa Algorithm (Computes x y i oe query) Today: Berstei-Vazirii
6896 Quatum Complexity Theory Sept 23, 2008 Lecturer: Scott Aaroso Lecture 6 Last Time: Quatum Error-Correctio Quatum Query Model Deutsch-Jozsa Algorithm (Computes x y i oe query) Today: Berstei-Vazirii
Math 155 (Lecture 3)
 Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
ECE-S352 Introduction to Digital Signal Processing Lecture 3A Direct Solution of Difference Equations
 ECE-S352 Itroductio to Digital Sigal Processig Lecture 3A Direct Solutio of Differece Equatios Discrete Time Systems Described by Differece Equatios Uit impulse (sample) respose h() of a DT system allows
ECE-S352 Itroductio to Digital Sigal Processig Lecture 3A Direct Solutio of Differece Equatios Discrete Time Systems Described by Differece Equatios Uit impulse (sample) respose h() of a DT system allows
Math 61CM - Solutions to homework 3
 Math 6CM - Solutios to homework 3 Cédric De Groote October 2 th, 208 Problem : Let F be a field, m 0 a fixed oegative iteger ad let V = {a 0 + a x + + a m x m a 0,, a m F} be the vector space cosistig
Math 6CM - Solutios to homework 3 Cédric De Groote October 2 th, 208 Problem : Let F be a field, m 0 a fixed oegative iteger ad let V = {a 0 + a x + + a m x m a 0,, a m F} be the vector space cosistig
CHAPTER 6c. NUMERICAL INTERPOLATION
 CHAPTER 6c. NUMERICAL INTERPOLATION A. J. Clark School o Egieerig Departmet o Civil ad Evirometal Egieerig y Dr. Irahim A. Assakka Sprig ENCE - Computatio Methods i Civil Egieerig II Departmet o Civil
CHAPTER 6c. NUMERICAL INTERPOLATION A. J. Clark School o Egieerig Departmet o Civil ad Evirometal Egieerig y Dr. Irahim A. Assakka Sprig ENCE - Computatio Methods i Civil Egieerig II Departmet o Civil
Fourier Series and the Wave Equation
 Fourier Series ad the Wave Equatio We start with the oe-dimesioal wave equatio u u =, x u(, t) = u(, t) =, ux (,) = f( x), u ( x,) = This represets a vibratig strig, where u is the displacemet of the strig
Fourier Series ad the Wave Equatio We start with the oe-dimesioal wave equatio u u =, x u(, t) = u(, t) =, ux (,) = f( x), u ( x,) = This represets a vibratig strig, where u is the displacemet of the strig
A widely used display of protein shapes is based on the coordinates of the alpha carbons - - C α
 Nice plottig of proteis: I A widely used display of protei shapes is based o the coordiates of the alpha carbos - - C α -s. The coordiates of the C α -s are coected by a cotiuous curve that roughly follows
Nice plottig of proteis: I A widely used display of protei shapes is based o the coordiates of the alpha carbos - - C α -s. The coordiates of the C α -s are coected by a cotiuous curve that roughly follows
Fall 2013 MTH431/531 Real analysis Section Notes
 Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
M 340L CS Homew ork Set 6 Solutions
 1. Suppose P is ivertible ad M 34L CS Homew ork Set 6 Solutios A PBP 1. Solve for B i terms of P ad A. Sice A PBP 1, w e have 1 1 1 B P PBP P P AP ( ).. Suppose ( B C) D, w here B ad C are m matrices ad
1. Suppose P is ivertible ad M 34L CS Homew ork Set 6 Solutios A PBP 1. Solve for B i terms of P ad A. Sice A PBP 1, w e have 1 1 1 B P PBP P P AP ( ).. Suppose ( B C) D, w here B ad C are m matrices ad
M 340L CS Homew ork Set 6 Solutions
 . Suppose P is ivertible ad M 4L CS Homew ork Set 6 Solutios A PBP. Solve for B i terms of P ad A. Sice A PBP, w e have B P PBP P P AP ( ).. Suppose ( B C) D, w here B ad C are m matrices ad D is ivertible.
. Suppose P is ivertible ad M 4L CS Homew ork Set 6 Solutios A PBP. Solve for B i terms of P ad A. Sice A PBP, w e have B P PBP P P AP ( ).. Suppose ( B C) D, w here B ad C are m matrices ad D is ivertible.
EECS 455 Solutions to Problem Set 8
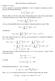 . Problem 7.55 o text EECS 455 Solutios to Problem Set 8 a) For repeaters i asade, the probability o i out o repeaters to produe a error is give by the biomial distributio P i p i p i However, there is
. Problem 7.55 o text EECS 455 Solutios to Problem Set 8 a) For repeaters i asade, the probability o i out o repeaters to produe a error is give by the biomial distributio P i p i p i However, there is
Chapter 4. Fourier Series
 Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Introduction to Algorithms
 Itroductio to Algorithms 6.046J/8.40J LECTURE 9 Radomly built biary search trees Epected ode depth Aalyzig height Coveity lemma Jese s iequality Epoetial height Post mortem Pro. Eri Demaie October 7, 2005
Itroductio to Algorithms 6.046J/8.40J LECTURE 9 Radomly built biary search trees Epected ode depth Aalyzig height Coveity lemma Jese s iequality Epoetial height Post mortem Pro. Eri Demaie October 7, 2005
On The Stability and Accuracy of Some Runge-Kutta Methods of Solving Second Order Ordinary Differential Equations
 Iteratioal Joural o Computatioal Egieerig Resear Vol Issue 7 O Te Stabilit ad Aura o Some Ruge-Kutta Metods o Solvig Seod Order Ordiar Dieretial Euatios S.O. Salawu R.A. Kareem ad O.T. Arowolo Departmet
Iteratioal Joural o Computatioal Egieerig Resear Vol Issue 7 O Te Stabilit ad Aura o Some Ruge-Kutta Metods o Solvig Seod Order Ordiar Dieretial Euatios S.O. Salawu R.A. Kareem ad O.T. Arowolo Departmet
Linearly Independent Sets, Bases. Review. Remarks. A set of vectors,,, in a vector space is said to be linearly independent if the vector equation
 Liearly Idepedet Sets Bases p p c c p Review { v v vp} A set of vectors i a vector space is said to be liearly idepedet if the vector equatio cv + c v + + c has oly the trivial solutio = = { v v vp} The
Liearly Idepedet Sets Bases p p c c p Review { v v vp} A set of vectors i a vector space is said to be liearly idepedet if the vector equatio cv + c v + + c has oly the trivial solutio = = { v v vp} The
Summation Method for Some Special Series Exactly
 The Iteratioal Joural of Mathematis, Siee, Tehology ad Maagemet (ISSN : 39-85) Vol. Issue Summatio Method for Some Speial Series Eatly D.A.Gismalla Deptt. Of Mathematis & omputer Studies Faulty of Siee
The Iteratioal Joural of Mathematis, Siee, Tehology ad Maagemet (ISSN : 39-85) Vol. Issue Summatio Method for Some Speial Series Eatly D.A.Gismalla Deptt. Of Mathematis & omputer Studies Faulty of Siee
APPENDIX F Complex Numbers
 APPENDIX F Complex Numbers Operatios with Complex Numbers Complex Solutios of Quadratic Equatios Polar Form of a Complex Number Powers ad Roots of Complex Numbers Operatios with Complex Numbers Some equatios
APPENDIX F Complex Numbers Operatios with Complex Numbers Complex Solutios of Quadratic Equatios Polar Form of a Complex Number Powers ad Roots of Complex Numbers Operatios with Complex Numbers Some equatios
Chapter 2. Periodic points of toral. automorphisms. 2.1 General introduction
 Chapter 2 Periodic poits of toral automorphisms 2.1 Geeral itroductio The automorphisms of the two-dimesioal torus are rich mathematical objects possessig iterestig geometric, algebraic, topological ad
Chapter 2 Periodic poits of toral automorphisms 2.1 Geeral itroductio The automorphisms of the two-dimesioal torus are rich mathematical objects possessig iterestig geometric, algebraic, topological ad
4 The Sperner property.
 4 The Sperer property. I this sectio we cosider a surprisig applicatio of certai adjacecy matrices to some problems i extremal set theory. A importat role will also be played by fiite groups. I geeral,
4 The Sperer property. I this sectio we cosider a surprisig applicatio of certai adjacecy matrices to some problems i extremal set theory. A importat role will also be played by fiite groups. I geeral,
In algebra one spends much time finding common denominators and thus simplifying rational expressions. For example:
 74 The Method of Partial Fractios I algebra oe speds much time fidig commo deomiators ad thus simplifyig ratioal epressios For eample: + + + 6 5 + = + = = + + + + + ( )( ) 5 It may the seem odd to be watig
74 The Method of Partial Fractios I algebra oe speds much time fidig commo deomiators ad thus simplifyig ratioal epressios For eample: + + + 6 5 + = + = = + + + + + ( )( ) 5 It may the seem odd to be watig
Principal Component Analysis. Nuno Vasconcelos ECE Department, UCSD
 Priipal Compoet Aalysis Nuo Vasoelos ECE Departmet, UCSD Curse of dimesioality typial observatio i Bayes deisio theory: error ireases whe umber of features is large problem: eve for simple models (e.g.
Priipal Compoet Aalysis Nuo Vasoelos ECE Departmet, UCSD Curse of dimesioality typial observatio i Bayes deisio theory: error ireases whe umber of features is large problem: eve for simple models (e.g.
Appendix: The Laplace Transform
 Appedix: The Laplace Trasform The Laplace trasform is a powerful method that ca be used to solve differetial equatio, ad other mathematical problems. Its stregth lies i the fact that it allows the trasformatio
Appedix: The Laplace Trasform The Laplace trasform is a powerful method that ca be used to solve differetial equatio, ad other mathematical problems. Its stregth lies i the fact that it allows the trasformatio
In number theory we will generally be working with integers, though occasionally fractions and irrationals will come into play.
 Number Theory Math 5840 otes. Sectio 1: Axioms. I umber theory we will geerally be workig with itegers, though occasioally fractios ad irratioals will come ito play. Notatio: Z deotes the set of all itegers
Number Theory Math 5840 otes. Sectio 1: Axioms. I umber theory we will geerally be workig with itegers, though occasioally fractios ad irratioals will come ito play. Notatio: Z deotes the set of all itegers
Principle Of Superposition
 ecture 5: PREIMINRY CONCEP O RUCUR NYI Priciple Of uperpositio Mathematically, the priciple of superpositio is stated as ( a ) G( a ) G( ) G a a or for a liear structural system, the respose at a give
ecture 5: PREIMINRY CONCEP O RUCUR NYI Priciple Of uperpositio Mathematically, the priciple of superpositio is stated as ( a ) G( a ) G( ) G a a or for a liear structural system, the respose at a give
6 Integers Modulo n. integer k can be written as k = qn + r, with q,r, 0 r b. So any integer.
 6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
6 Itegers Modulo I Example 2.3(e), we have defied the cogruece of two itegers a,b with respect to a modulus. Let us recall that a b (mod ) meas a b. We have proved that cogruece is a equivalece relatio
Notes on iteration and Newton s method. Iteration
 Notes o iteratio ad Newto s method Iteratio Iteratio meas doig somethig over ad over. I our cotet, a iteratio is a sequece of umbers, vectors, fuctios, etc. geerated by a iteratio rule of the type 1 f
Notes o iteratio ad Newto s method Iteratio Iteratio meas doig somethig over ad over. I our cotet, a iteratio is a sequece of umbers, vectors, fuctios, etc. geerated by a iteratio rule of the type 1 f
FIR Filter Design: Part I
 EEL3: Discrete-Time Sigals ad Systems FIR Filter Desig: Part I. Itroductio FIR Filter Desig: Part I I this set o otes, we cotiue our exploratio o the requecy respose o FIR ilters. First, we cosider some
EEL3: Discrete-Time Sigals ad Systems FIR Filter Desig: Part I. Itroductio FIR Filter Desig: Part I I this set o otes, we cotiue our exploratio o the requecy respose o FIR ilters. First, we cosider some
NUMERICAL METHODS FOR SOLVING EQUATIONS
 Mathematics Revisio Guides Numerical Methods for Solvig Equatios Page 1 of 11 M.K. HOME TUITION Mathematics Revisio Guides Level: GCSE Higher Tier NUMERICAL METHODS FOR SOLVING EQUATIONS Versio:. Date:
Mathematics Revisio Guides Numerical Methods for Solvig Equatios Page 1 of 11 M.K. HOME TUITION Mathematics Revisio Guides Level: GCSE Higher Tier NUMERICAL METHODS FOR SOLVING EQUATIONS Versio:. Date:
Recurrences: Methods and Examples
 Reurrees: Methods ad Examples CSE 30 Algorithms ad Data Strutures Alexadra Stefa Uiversity of exas at Arligto Updated: 308 Summatios Review Review slides o Summatios Reurrees Reursive algorithms It may
Reurrees: Methods ad Examples CSE 30 Algorithms ad Data Strutures Alexadra Stefa Uiversity of exas at Arligto Updated: 308 Summatios Review Review slides o Summatios Reurrees Reursive algorithms It may
Solutions 3.2-Page 215
 Solutios.-Page Problem Fid the geeral solutios i powers of of the differetial equatios. State the reurree relatios ad the guarateed radius of overgee i eah ase. ) Substitutig,, ad ito the differetial equatio
Solutios.-Page Problem Fid the geeral solutios i powers of of the differetial equatios. State the reurree relatios ad the guarateed radius of overgee i eah ase. ) Substitutig,, ad ito the differetial equatio
Definition 4.2. (a) A sequence {x n } in a Banach space X is a basis for X if. unique scalars a n (x) such that x = n. a n (x) x n. (4.
 4. BASES I BAACH SPACES 39 4. BASES I BAACH SPACES Sice a Baach space X is a vector space, it must possess a Hamel, or vector space, basis, i.e., a subset {x γ } γ Γ whose fiite liear spa is all of X ad
4. BASES I BAACH SPACES 39 4. BASES I BAACH SPACES Sice a Baach space X is a vector space, it must possess a Hamel, or vector space, basis, i.e., a subset {x γ } γ Γ whose fiite liear spa is all of X ad
ON THE SM -OPERATORS
 Soepara d O The SM-operators ON THE SM -OPERTORS Soepara Darawijaya Musli sori da Supaa 3 3 Matheatis Departeet FMIP UGM Yogyaarta eail: aspoo@yahoo.o Matheatis Departeet FMIP Uiversitas Lapug Jl. Soeatri
Soepara d O The SM-operators ON THE SM -OPERTORS Soepara Darawijaya Musli sori da Supaa 3 3 Matheatis Departeet FMIP UGM Yogyaarta eail: aspoo@yahoo.o Matheatis Departeet FMIP Uiversitas Lapug Jl. Soeatri
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
 Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Principal Component Analysis
 Priipal Compoet Aalysis Nuo Vasoelos (Ke Kreutz-Delgado) UCSD Curse of dimesioality Typial observatio i Bayes deisio theory: Error ireases whe umber of features is large Eve for simple models (e.g. Gaussia)
Priipal Compoet Aalysis Nuo Vasoelos (Ke Kreutz-Delgado) UCSD Curse of dimesioality Typial observatio i Bayes deisio theory: Error ireases whe umber of features is large Eve for simple models (e.g. Gaussia)
Complex Numbers Solutions
 Complex Numbers Solutios Joseph Zoller February 7, 06 Solutios. (009 AIME I Problem ) There is a complex umber with imagiary part 64 ad a positive iteger such that Fid. [Solutio: 697] 4i + + 4i. 4i 4i
Complex Numbers Solutios Joseph Zoller February 7, 06 Solutios. (009 AIME I Problem ) There is a complex umber with imagiary part 64 ad a positive iteger such that Fid. [Solutio: 697] 4i + + 4i. 4i 4i
CS 270 Algorithms. Oliver Kullmann. Growth of Functions. Divide-and- Conquer Min-Max- Problem. Tutorial. Reading from CLRS for week 2
 Geeral remarks Week 2 1 Divide ad First we cosider a importat tool for the aalysis of algorithms: Big-Oh. The we itroduce a importat algorithmic paradigm:. We coclude by presetig ad aalysig two examples.
Geeral remarks Week 2 1 Divide ad First we cosider a importat tool for the aalysis of algorithms: Big-Oh. The we itroduce a importat algorithmic paradigm:. We coclude by presetig ad aalysig two examples.
1 Approximating Integrals using Taylor Polynomials
 Seughee Ye Ma 8: Week 7 Nov Week 7 Summary This week, we will lear how we ca approximate itegrals usig Taylor series ad umerical methods. Topics Page Approximatig Itegrals usig Taylor Polyomials. Defiitios................................................
Seughee Ye Ma 8: Week 7 Nov Week 7 Summary This week, we will lear how we ca approximate itegrals usig Taylor series ad umerical methods. Topics Page Approximatig Itegrals usig Taylor Polyomials. Defiitios................................................
A Probabilistic Analysis of Quicksort
 A Probabilistic Aalysis of Quicsort You are assumed to be familiar with Quicsort. I each iteratio this sortig algorithm chooses a pivot ad the, by performig comparisios with the pivot, splits the remaider
A Probabilistic Aalysis of Quicsort You are assumed to be familiar with Quicsort. I each iteratio this sortig algorithm chooses a pivot ad the, by performig comparisios with the pivot, splits the remaider
Enumerative & Asymptotic Combinatorics
 C50 Eumerative & Asymptotic Combiatorics Notes 4 Sprig 2003 Much of the eumerative combiatorics of sets ad fuctios ca be geeralised i a maer which, at first sight, seems a bit umotivated I this chapter,
C50 Eumerative & Asymptotic Combiatorics Notes 4 Sprig 2003 Much of the eumerative combiatorics of sets ad fuctios ca be geeralised i a maer which, at first sight, seems a bit umotivated I this chapter,
Solutions to Final Exam Review Problems
 . Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
. Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
