Lecture 2: Recurrence relations and population dynamics
|
|
|
- Corey Jack McGee
- 5 years ago
- Views:
Transcription
1 Lecture 2: Recurrence relations and population dynamics Daniel Chan UNSW Semester Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
2 Sample real-world problem In this lecture, we study the important Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
3 Sample real-world problem In this lecture, we study the important Problem How is the population of hobbits in the Shire changing? Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
4 Sample real-world problem In this lecture, we study the important Problem How is the population of hobbits in the Shire changing? We will approach this down-to-middle-earth question using a type of mathematical model called a recurrence relation. Those of you studying MATH1081 will see more of the mathematical aspects of this. Our goal is not so much to deal with the mathematics, but to see where the concept can be useful. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
5 Our basic assumption and ensuing recurrence relation Recurrence relations can be used when you know how a variable changes say from day to day, or year to year. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
6 Our basic assumption and ensuing recurrence relation Recurrence relations can be used when you know how a variable changes say from day to day, or year to year. Basic assumption The yearly increase in the hobbit population is proportional to the population. DISCUSS Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
7 Our basic assumption and ensuing recurrence relation Recurrence relations can be used when you know how a variable changes say from day to day, or year to year. Basic assumption The yearly increase in the hobbit population is proportional to the population. DISCUSS The recurrence relation Let P n be the hobbit population in year n. Then for some constant of proportionality α we have P n+1 P n = αp n or equivalently, where a = α + 1. P n+1 = ap n Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
8 Our basic assumption and ensuing recurrence relation Recurrence relations can be used when you know how a variable changes say from day to day, or year to year. Basic assumption The yearly increase in the hobbit population is proportional to the population. DISCUSS The recurrence relation Let P n be the hobbit population in year n. Then for some constant of proportionality α we have P n+1 P n = αp n or equivalently, where a = α + 1. P n+1 = ap n This is a recurrence relation for the variable/sequence P n which expresses P n+1 in terms of earlier values of the variable, namely P n. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
9 The abstract solution Note that if you know the initial population P 0, you can use the recurrence relation to determine P 1 and then P 2, P 3,.... Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
10 The abstract solution Note that if you know the initial population P 0, you can use the recurrence relation to determine P 1 and then P 2, P 3,.... In this case however, it is also easy to determine the formula for P n as an explicit function of n. Formula P n = a n P 0. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
11 The abstract solution Note that if you know the initial population P 0, you can use the recurrence relation to determine P 1 and then P 2, P 3,.... In this case however, it is also easy to determine the formula for P n as an explicit function of n. Formula P n = a n P 0. There is a natural Question What is the value of a? Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
12 Using data The other natural question is, how accurate is our model? In other words, is our basic assumption a decent approximation of the real world? Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
13 Using data The other natural question is, how accurate is our model? In other words, is our basic assumption a decent approximation of the real world? For this, we need access to some hobbit population data. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
14 Using data The other natural question is, how accurate is our model? In other words, is our basic assumption a decent approximation of the real world? For this, we need access to some hobbit population data. Year, n Population, P n Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
15 Determining a. Validating the model We may re-write the recurrence relation as P n+1 P n = a. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
16 Determining a. Validating the model We may re-write the recurrence relation as P n+1 P n = a. Test for model Our mathematical model will be a good approximation to real life if the ratio P n+1 /P n is approximately constant. Picking an appropriate value for this constant will give our parameter a. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
17 Determining a. Validating the model We may re-write the recurrence relation as P n+1 P n = a. Test for model Our mathematical model will be a good approximation to real life if the ratio P n+1 /P n is approximately constant. Picking an appropriate value for this constant will give our parameter a. n P n+1 /P n Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
18 Determining a. Validating the model We may re-write the recurrence relation as P n+1 P n = a. Test for model Our mathematical model will be a good approximation to real life if the ratio P n+1 /P n is approximately constant. Picking an appropriate value for this constant will give our parameter a. n P n+1 /P n Conclusion: The model seems reasonably accurate as the ratio hovers around the constant 1.06 which we can take for a. (Alternatively, we can average the ratios above in some way). In other words, the population increases by about 6% a year. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
19 Comparing the mathematical model with reality Once we fix a value for a, say 1.06, we can also test the model by comparing the actual population P n to the model s predicted value P n = P n 1. Year Actual population Predicted population Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
20 Comparing the mathematical model with reality Once we fix a value for a, say 1.06, we can also test the model by comparing the actual population P n to the model s predicted value P n = P n 1. Year Actual population Predicted population actual population = +, predicted population = Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
21 Enter the orcs The hobbits have new neighbours, the orcs! Q Do you think the hobbit population will be affected? If so, how? Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
22 Enter the orcs The hobbits have new neighbours, the orcs! Q Do you think the hobbit population will be affected? If so, how? New model Let P n = hobbit population in year n, O n = orc population in year n. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
23 Enter the orcs The hobbits have new neighbours, the orcs! Q Do you think the hobbit population will be affected? If so, how? New model Let P n = hobbit population in year n, O n = orc population in year n. New recurrence relation P n+1 = ap n bp n O n O n+1 = co n dp n O n for some real positive constants a, b, c, d. This is a coupled system of recurrence relations in two variables. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
24 Enter the orcs The hobbits have new neighbours, the orcs! Q Do you think the hobbit population will be affected? If so, how? New model Let P n = hobbit population in year n, O n = orc population in year n. New recurrence relation P n+1 = ap n bp n O n O n+1 = co n dp n O n for some real positive constants a, b, c, d. This is a coupled system of recurrence relations in two variables. Warning Don t try to solve this explicitly! However, remember that given parameter and initial values, we can get the computer to work out as many values as we like. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
25 Understanding the parameters To make the model work we will need to fix values of the parameters. To do this well, it is best to understand their physical significance. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
26 Understanding the parameters To make the model work we will need to fix values of the parameters. To do this well, it is best to understand their physical significance. Before the orcs moved in, there was no interaction between the hobbits and orcs, so we may assume that b = d = 0 and a, c represent the growth rates of the two populations when left to themselves. If you have data on this before the arrival of the orcs, we can determine a, c as before. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
27 Understanding the parameters To make the model work we will need to fix values of the parameters. To do this well, it is best to understand their physical significance. Before the orcs moved in, there was no interaction between the hobbits and orcs, so we may assume that b = d = 0 and a, c represent the growth rates of the two populations when left to themselves. If you have data on this before the arrival of the orcs, we can determine a, c as before. The parameters b, d measure the extent of hostile interaction and should be determined from data after the orcs move in. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
28 Understanding the parameters To make the model work we will need to fix values of the parameters. To do this well, it is best to understand their physical significance. Before the orcs moved in, there was no interaction between the hobbits and orcs, so we may assume that b = d = 0 and a, c represent the growth rates of the two populations when left to themselves. If you have data on this before the arrival of the orcs, we can determine a, c as before. The parameters b, d measure the extent of hostile interaction and should be determined from data after the orcs move in. Q What is the physical significance of b > d or b < d? Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
29 Understanding the parameters To make the model work we will need to fix values of the parameters. To do this well, it is best to understand their physical significance. Before the orcs moved in, there was no interaction between the hobbits and orcs, so we may assume that b = d = 0 and a, c represent the growth rates of the two populations when left to themselves. If you have data on this before the arrival of the orcs, we can determine a, c as before. The parameters b, d measure the extent of hostile interaction and should be determined from data after the orcs move in. Q What is the physical significance of b > d or b < d? Hypothesis Let s suppose we have prior data which give the growth rates of hobbit and orc populations at 6% and 4% respectively. Then a = 1.06, c = Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
30 Equilibrium analysis Alhough we cannot compute explicit solutions, we can determine some information when the situation is in equilibrium, that is, there is no change in population. In formulas Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
31 Equilibrium analysis Alhough we cannot compute explicit solutions, we can determine some information when the situation is in equilibrium, that is, there is no change in population. In formulas P n def = P n+1 P n = 0, O n def = O n+1 O n = 0 Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
32 Equilibrium analysis Alhough we cannot compute explicit solutions, we can determine some information when the situation is in equilibrium, that is, there is no change in population. In formulas P n def = P n+1 P n = 0, O n def = O n+1 O n = 0 Equilibrium population Suppose that several years after the orcs arrive, the hobbit and orc populations are holding steady at P e = 2322 and O e = Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
33 Equilibrium analysis Alhough we cannot compute explicit solutions, we can determine some information when the situation is in equilibrium, that is, there is no change in population. In formulas P n def = P n+1 P n = 0, O n def = O n+1 O n = 0 Equilibrium population Suppose that several years after the orcs arrive, the hobbit and orc populations are holding steady at P e = 2322 and O e = = P e+1 P e = (a 1)P e bp e O e = P e ((a 1) bo e ) = P e (.06 bo e ) so solving.06 = 1596b gives b =.06/ Also Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
34 Equilibrium analysis Alhough we cannot compute explicit solutions, we can determine some information when the situation is in equilibrium, that is, there is no change in population. In formulas P n def = P n+1 P n = 0, O n def = O n+1 O n = 0 Equilibrium population Suppose that several years after the orcs arrive, the hobbit and orc populations are holding steady at P e = 2322 and O e = = P e+1 P e = (a 1)P e bp e O e = P e ((a 1) bo e ) = P e (.06 bo e ) so solving.06 = 1596b gives b =.06/ Also so d =.04/ = O e = O e (.04 dp e ) Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
35 Perturbation from equilibrium Oh no! A large crop of pipeweed was diseased and led to the sudden deaths of 225 hobbits. Q What will happen to the hobbit and orc populations now? Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
36 Perturbation from equilibrium Oh no! A large crop of pipeweed was diseased and led to the sudden deaths of 225 hobbits. Q What will happen to the hobbit and orc populations now? We have now determined values of the parameter a, b, c, d. We also have new initial values, P 0 = P e 225 = = 2097, O 0 = O e = Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
37 Perturbation from equilibrium Oh no! A large crop of pipeweed was diseased and led to the sudden deaths of 225 hobbits. Q What will happen to the hobbit and orc populations now? We have now determined values of the parameter a, b, c, d. We also have new initial values, P 0 = P e 225 = = 2097, O 0 = O e = We can use the new recurrence relations with the aid of an appropriate computer package. It s easiest to plot the result over the next 100 years. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
38 Conclusion hobbits = blue, orcs = green. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
39 Conclusion hobbits = blue, orcs = green. It seems that the hobbit population will be killed off and the orc population will grow exponentially. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
40 Some basic principles of mathematical modelling When making a mathematical model, you may wish to consider the following guidelines. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
41 Some basic principles of mathematical modelling When making a mathematical model, you may wish to consider the following guidelines. Identify some variables that you wish to analyse quantitatively or qualitatively. In our example, P n and O n. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
42 Some basic principles of mathematical modelling When making a mathematical model, you may wish to consider the following guidelines. Identify some variables that you wish to analyse quantitatively or qualitatively. In our example, P n and O n. Use your understanding of the physical situation to introduce relations between the variables. There may be parameters involved at this stage. In our example, we have recurrence relations, and a, b, c, d were parameters which depended on the precise situation. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
43 Some basic principles of mathematical modelling When making a mathematical model, you may wish to consider the following guidelines. Identify some variables that you wish to analyse quantitatively or qualitatively. In our example, P n and O n. Use your understanding of the physical situation to introduce relations between the variables. There may be parameters involved at this stage. In our example, we have recurrence relations, and a, b, c, d were parameters which depended on the precise situation. Identify parameters using data if need be. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
44 Some basic principles of mathematical modelling When making a mathematical model, you may wish to consider the following guidelines. Identify some variables that you wish to analyse quantitatively or qualitatively. In our example, P n and O n. Use your understanding of the physical situation to introduce relations between the variables. There may be parameters involved at this stage. In our example, we have recurrence relations, and a, b, c, d were parameters which depended on the precise situation. Identify parameters using data if need be. Use your relations to study the variables. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
45 Some basic principles of mathematical modelling When making a mathematical model, you may wish to consider the following guidelines. Identify some variables that you wish to analyse quantitatively or qualitatively. In our example, P n and O n. Use your understanding of the physical situation to introduce relations between the variables. There may be parameters involved at this stage. In our example, we have recurrence relations, and a, b, c, d were parameters which depended on the precise situation. Identify parameters using data if need be. Use your relations to study the variables. Verify your predictions with given data to see if your model is reliable or not. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
46 Some basic principles of mathematical modelling When making a mathematical model, you may wish to consider the following guidelines. Identify some variables that you wish to analyse quantitatively or qualitatively. In our example, P n and O n. Use your understanding of the physical situation to introduce relations between the variables. There may be parameters involved at this stage. In our example, we have recurrence relations, and a, b, c, d were parameters which depended on the precise situation. Identify parameters using data if need be. Use your relations to study the variables. Verify your predictions with given data to see if your model is reliable or not. Comment on theoretical limitations of your model which may come from inaccuracies in your assumptions or elsewhere. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
47 Some basic principles of mathematical modelling When making a mathematical model, you may wish to consider the following guidelines. Identify some variables that you wish to analyse quantitatively or qualitatively. In our example, P n and O n. Use your understanding of the physical situation to introduce relations between the variables. There may be parameters involved at this stage. In our example, we have recurrence relations, and a, b, c, d were parameters which depended on the precise situation. Identify parameters using data if need be. Use your relations to study the variables. Verify your predictions with given data to see if your model is reliable or not. Comment on theoretical limitations of your model which may come from inaccuracies in your assumptions or elsewhere. In our example, we posit exponential population growth if the hobbits are left to themselves. GROUP WORK: Is this reasonable? Discuss. Daniel Chan (UNSW) Lecture 2: Recurrence relations Semester / 13
Lecture 3: Graphical analysis- Arms race
 Lecture 3: Graphical analysis- Arms race Daniel Chan UNSW Semester 1 2014 Daniel Chan (UNSW) Lecture 3: Graphical analysis Semester 1 2014 1 / 12 Scenario Event 1 Saruman has taught the orcs the secrets
Lecture 3: Graphical analysis- Arms race Daniel Chan UNSW Semester 1 2014 Daniel Chan (UNSW) Lecture 3: Graphical analysis Semester 1 2014 1 / 12 Scenario Event 1 Saruman has taught the orcs the secrets
Introduction to Population Dynamics
 MATH235: Differential Equations with Honors Introduction to Population Dynamics Quote of Population Dynamics Homework Wish I knew what you were looking for. Might have known what you would find. Under
MATH235: Differential Equations with Honors Introduction to Population Dynamics Quote of Population Dynamics Homework Wish I knew what you were looking for. Might have known what you would find. Under
reversed chain is ergodic and has the same equilibrium probabilities (check that π j =
 Lecture 10 Networks of queues In this lecture we shall finally get around to consider what happens when queues are part of networks (which, after all, is the topic of the course). Firstly we shall need
Lecture 10 Networks of queues In this lecture we shall finally get around to consider what happens when queues are part of networks (which, after all, is the topic of the course). Firstly we shall need
Math 122 Fall Handout 11: Summary of Euler s Method, Slope Fields and Symbolic Solutions of Differential Equations
 1 Math 122 Fall 2008 Handout 11: Summary of Euler s Method, Slope Fields and Symbolic Solutions of Differential Equations The purpose of this handout is to review the techniques that you will learn for
1 Math 122 Fall 2008 Handout 11: Summary of Euler s Method, Slope Fields and Symbolic Solutions of Differential Equations The purpose of this handout is to review the techniques that you will learn for
Old & new co-ordinates
 Old & new co-ordinates Aim lecture: A wise choice of co-ordinates can make life much easier. We give some examples showing how to make a linear change of co-ords to facilitate calculations. Suppose we
Old & new co-ordinates Aim lecture: A wise choice of co-ordinates can make life much easier. We give some examples showing how to make a linear change of co-ords to facilitate calculations. Suppose we
Math 111, Introduction to the Calculus, Fall 2011 Midterm I Practice Exam 1 Solutions
 Math 111, Introduction to the Calculus, Fall 2011 Midterm I Practice Exam 1 Solutions For each question, there is a model solution (showing you the level of detail I expect on the exam) and then below
Math 111, Introduction to the Calculus, Fall 2011 Midterm I Practice Exam 1 Solutions For each question, there is a model solution (showing you the level of detail I expect on the exam) and then below
Calculus II. Calculus II tends to be a very difficult course for many students. There are many reasons for this.
 Preface Here are my online notes for my Calculus II course that I teach here at Lamar University. Despite the fact that these are my class notes they should be accessible to anyone wanting to learn Calculus
Preface Here are my online notes for my Calculus II course that I teach here at Lamar University. Despite the fact that these are my class notes they should be accessible to anyone wanting to learn Calculus
Orthogonal complement
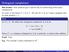 Orthogonal complement Aim lecture: Inner products give a special way of constructing vector space complements. As usual, in this lecture F = R or C. We also let V be an F-space equipped with an inner product
Orthogonal complement Aim lecture: Inner products give a special way of constructing vector space complements. As usual, in this lecture F = R or C. We also let V be an F-space equipped with an inner product
Examples of Countable State Markov Chains Thursday, October 16, :12 PM
 stochnotes101608 Page 1 Examples of Countable State Markov Chains Thursday, October 16, 2008 12:12 PM Homework 2 solutions will be posted later today. A couple of quick examples. Queueing model (without
stochnotes101608 Page 1 Examples of Countable State Markov Chains Thursday, October 16, 2008 12:12 PM Homework 2 solutions will be posted later today. A couple of quick examples. Queueing model (without
1 (t + 4)(t 1) dt. Solution: The denominator of the integrand is already factored with the factors being distinct, so 1 (t + 4)(t 1) = A
 Calculus Topic: Integration of Rational Functions Section 8. # 0: Evaluate the integral (t + )(t ) Solution: The denominator of the integrand is already factored with the factors being distinct, so (t
Calculus Topic: Integration of Rational Functions Section 8. # 0: Evaluate the integral (t + )(t ) Solution: The denominator of the integrand is already factored with the factors being distinct, so (t
Math 216 First Midterm 19 October, 2017
 Math 6 First Midterm 9 October, 7 This sample exam is provided to serve as one component of your studying for this exam in this course. Please note that it is not guaranteed to cover the material that
Math 6 First Midterm 9 October, 7 This sample exam is provided to serve as one component of your studying for this exam in this course. Please note that it is not guaranteed to cover the material that
Dynamical Systems: Lecture 1 Naima Hammoud
 Dynamical Systems: Lecture 1 Naima Hammoud Feb 21, 2017 What is dynamics? Dynamics is the study of systems that evolve in time What is dynamics? Dynamics is the study of systems that evolve in time a system
Dynamical Systems: Lecture 1 Naima Hammoud Feb 21, 2017 What is dynamics? Dynamics is the study of systems that evolve in time What is dynamics? Dynamics is the study of systems that evolve in time a system
Algorithms CMSC The Method of Reverse Inequalities: Evaluation of Recurrent Inequalities
 Algorithms CMSC 37000 The Method of Reverse Inequalities: Evaluation of Recurrent Inequalities László Babai Updated 1-19-2014 In this handout, we discuss a typical situation in the analysis of algorithms:
Algorithms CMSC 37000 The Method of Reverse Inequalities: Evaluation of Recurrent Inequalities László Babai Updated 1-19-2014 In this handout, we discuss a typical situation in the analysis of algorithms:
Exact Inference by Complete Enumeration
 21 Exact Inference by Complete Enumeration We open our toolbox of methods for handling probabilities by discussing a brute-force inference method: complete enumeration of all hypotheses, and evaluation
21 Exact Inference by Complete Enumeration We open our toolbox of methods for handling probabilities by discussing a brute-force inference method: complete enumeration of all hypotheses, and evaluation
Rings, Paths, and Cayley Graphs
 Spectral Graph Theory Lecture 5 Rings, Paths, and Cayley Graphs Daniel A. Spielman September 16, 2014 Disclaimer These notes are not necessarily an accurate representation of what happened in class. The
Spectral Graph Theory Lecture 5 Rings, Paths, and Cayley Graphs Daniel A. Spielman September 16, 2014 Disclaimer These notes are not necessarily an accurate representation of what happened in class. The
Infinity Unit 2: Chaos! Dynamical Systems
 Infinity Unit 2: Chaos! Dynamical Systems Iterating Linear Functions These questions are about iterating f(x) = mx + b. Seed: x 1. Orbit: x 1, x 2, x 3, For each question, give examples and a symbolic
Infinity Unit 2: Chaos! Dynamical Systems Iterating Linear Functions These questions are about iterating f(x) = mx + b. Seed: x 1. Orbit: x 1, x 2, x 3, For each question, give examples and a symbolic
INTERPRETING POPULATION DYNAMICS GRAPH
 INTERPRETING POPULATION DYNAMIS GRAPH OJETIVES TASKS Name: To learn about three types of population dynamics graphs To determine which type of graph you constructed from the Pike and Perch Game To interpret
INTERPRETING POPULATION DYNAMIS GRAPH OJETIVES TASKS Name: To learn about three types of population dynamics graphs To determine which type of graph you constructed from the Pike and Perch Game To interpret
Data fitting. Ideal equation for linear relation
 Problem Most likely, there will be experimental error so you should take more than 2 data points, & they will not lie on a line so the ideal eqn above has no solution. The question is what is the best
Problem Most likely, there will be experimental error so you should take more than 2 data points, & they will not lie on a line so the ideal eqn above has no solution. The question is what is the best
Math 90 Lecture Notes Chapter 1
 Math 90 Lecture Notes Chapter 1 Section 1.1: Introduction to Algebra This textbook stresses Problem Solving! Solving problems is one of the main goals of mathematics. Think of mathematics as a language,
Math 90 Lecture Notes Chapter 1 Section 1.1: Introduction to Algebra This textbook stresses Problem Solving! Solving problems is one of the main goals of mathematics. Think of mathematics as a language,
Math 112 Section 10 Lecture notes, 1/7/04
 Math 11 Section 10 Lecture notes, 1/7/04 Section 7. Integration by parts To integrate the product of two functions, integration by parts is used when simpler methods such as substitution or simplifying
Math 11 Section 10 Lecture notes, 1/7/04 Section 7. Integration by parts To integrate the product of two functions, integration by parts is used when simpler methods such as substitution or simplifying
AUTOMATIC CONTROL. Andrea M. Zanchettin, PhD Spring Semester, Introduction to Automatic Control & Linear systems (time domain)
 1 AUTOMATIC CONTROL Andrea M. Zanchettin, PhD Spring Semester, 2018 Introduction to Automatic Control & Linear systems (time domain) 2 What is automatic control? From Wikipedia Control theory is an interdisciplinary
1 AUTOMATIC CONTROL Andrea M. Zanchettin, PhD Spring Semester, 2018 Introduction to Automatic Control & Linear systems (time domain) 2 What is automatic control? From Wikipedia Control theory is an interdisciplinary
CPSC 490 Problem Solving in Computer Science
 CPSC 490 Problem Solving in Computer Science Lecture 6: Recovering Solutions from DP, Bitmask DP, Matrix Exponentiation David Zheng and Daniel Du Based on CPSC490 slides from 2014-2017 2018/01/23 Announcements
CPSC 490 Problem Solving in Computer Science Lecture 6: Recovering Solutions from DP, Bitmask DP, Matrix Exponentiation David Zheng and Daniel Du Based on CPSC490 slides from 2014-2017 2018/01/23 Announcements
Non-square diagonal matrices
 Non-square diagonal matrices Aim lecture: We apply the spectral theory of hermitian operators to look at linear maps T : V W which are not necessarily endomorphisms. This gives useful factorisations of
Non-square diagonal matrices Aim lecture: We apply the spectral theory of hermitian operators to look at linear maps T : V W which are not necessarily endomorphisms. This gives useful factorisations of
Math Spring 2011 Final Exam
 Math 471 - Spring 211 Final Exam Instructions The following exam consists of three problems, each with multiple parts. There are 15 points available on the exam. The highest possible score is 125. Your
Math 471 - Spring 211 Final Exam Instructions The following exam consists of three problems, each with multiple parts. There are 15 points available on the exam. The highest possible score is 125. Your
Jordan blocks. Defn. Let λ F, n Z +. The size n Jordan block with e-value λ is the n n upper triangular matrix. J n (λ) =
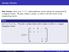 Jordan blocks Aim lecture: Even over F = C, endomorphisms cannot always be represented by a diagonal matrix. We give Jordan s answer, to what is the best form of the representing matrix. Defn Let λ F,
Jordan blocks Aim lecture: Even over F = C, endomorphisms cannot always be represented by a diagonal matrix. We give Jordan s answer, to what is the best form of the representing matrix. Defn Let λ F,
Math Precalculus I University of Hawai i at Mānoa Spring
 Math 135 - Precalculus I University of Hawai i at Mānoa Spring - 2013 Created for Math 135, Spring 2008 by Lukasz Grabarek and Michael Joyce Send comments and corrections to lukasz@math.hawaii.edu Contents
Math 135 - Precalculus I University of Hawai i at Mānoa Spring - 2013 Created for Math 135, Spring 2008 by Lukasz Grabarek and Michael Joyce Send comments and corrections to lukasz@math.hawaii.edu Contents
3.3 Accumulation Sequences
 3.3. ACCUMULATION SEQUENCES 25 3.3 Accumulation Sequences Overview. One of the most important mathematical ideas in calculus is that of an accumulation of change for physical quantities. As we have been
3.3. ACCUMULATION SEQUENCES 25 3.3 Accumulation Sequences Overview. One of the most important mathematical ideas in calculus is that of an accumulation of change for physical quantities. As we have been
Ordinary Di erential Equations Lecture notes for Math 133A. Slobodan N. Simić
 Ordinary Di erential Equations Lecture notes for Math 133A Slobodan N. Simić c Slobodan N. Simić 2016 Contents Chapter 1. First order di erential equations 1 1.1. What is a di erential equation? 1 1.2.
Ordinary Di erential Equations Lecture notes for Math 133A Slobodan N. Simić c Slobodan N. Simić 2016 Contents Chapter 1. First order di erential equations 1 1.1. What is a di erential equation? 1 1.2.
Lecture 8: Conditional probability I: definition, independence, the tree method, sampling, chain rule for independent events
 Lecture 8: Conditional probability I: definition, independence, the tree method, sampling, chain rule for independent events Discrete Structures II (Summer 2018) Rutgers University Instructor: Abhishek
Lecture 8: Conditional probability I: definition, independence, the tree method, sampling, chain rule for independent events Discrete Structures II (Summer 2018) Rutgers University Instructor: Abhishek
Hypothesis testing I. - In particular, we are talking about statistical hypotheses. [get everyone s finger length!] n =
![Hypothesis testing I. - In particular, we are talking about statistical hypotheses. [get everyone s finger length!] n = Hypothesis testing I. - In particular, we are talking about statistical hypotheses. [get everyone s finger length!] n =](/thumbs/86/94764601.jpg) Hypothesis testing I I. What is hypothesis testing? [Note we re temporarily bouncing around in the book a lot! Things will settle down again in a week or so] - Exactly what it says. We develop a hypothesis,
Hypothesis testing I I. What is hypothesis testing? [Note we re temporarily bouncing around in the book a lot! Things will settle down again in a week or so] - Exactly what it says. We develop a hypothesis,
MAT1302F Mathematical Methods II Lecture 19
 MAT302F Mathematical Methods II Lecture 9 Aaron Christie 2 April 205 Eigenvectors, Eigenvalues, and Diagonalization Now that the basic theory of eigenvalues and eigenvectors is in place most importantly
MAT302F Mathematical Methods II Lecture 9 Aaron Christie 2 April 205 Eigenvectors, Eigenvalues, and Diagonalization Now that the basic theory of eigenvalues and eigenvectors is in place most importantly
MA 1128: Lecture 08 03/02/2018. Linear Equations from Graphs And Linear Inequalities
 MA 1128: Lecture 08 03/02/2018 Linear Equations from Graphs And Linear Inequalities Linear Equations from Graphs Given a line, we would like to be able to come up with an equation for it. I ll go over
MA 1128: Lecture 08 03/02/2018 Linear Equations from Graphs And Linear Inequalities Linear Equations from Graphs Given a line, we would like to be able to come up with an equation for it. I ll go over
MAT 1302B Mathematical Methods II
 MAT 1302B Mathematical Methods II Alistair Savage Mathematics and Statistics University of Ottawa Winter 2015 Lecture 19 Alistair Savage (uottawa) MAT 1302B Mathematical Methods II Winter 2015 Lecture
MAT 1302B Mathematical Methods II Alistair Savage Mathematics and Statistics University of Ottawa Winter 2015 Lecture 19 Alistair Savage (uottawa) MAT 1302B Mathematical Methods II Winter 2015 Lecture
STUDENT VERSION DISEASE SPREAD
 STUDENT VERSION DISEASE SPREAD STATEMENT We offer a modeling opportunity in which the phenomenon of the spread of disease can be described by one differential equation. First, let us consider growth in
STUDENT VERSION DISEASE SPREAD STATEMENT We offer a modeling opportunity in which the phenomenon of the spread of disease can be described by one differential equation. First, let us consider growth in
Student Exploration: Food Chain
 Name: Date: Student Exploration: Food Chain Vocabulary: consumer, ecosystem, equilibrium, food chain,, predator, prey, producer Prior Knowledge Questions (Do these BEFORE using the Gizmo.) The Food Chain
Name: Date: Student Exploration: Food Chain Vocabulary: consumer, ecosystem, equilibrium, food chain,, predator, prey, producer Prior Knowledge Questions (Do these BEFORE using the Gizmo.) The Food Chain
A. Incorrect! Check your algebra when you solved for volume. B. Incorrect! Check your algebra when you solved for volume.
 AP Chemistry - Problem Drill 03: Basic Math for Chemistry No. 1 of 10 1. Unlike math problems, chemistry calculations have two key elements to consider in any number units and significant figures. Solve
AP Chemistry - Problem Drill 03: Basic Math for Chemistry No. 1 of 10 1. Unlike math problems, chemistry calculations have two key elements to consider in any number units and significant figures. Solve
P (E) = P (A 1 )P (A 2 )... P (A n ).
 Lecture 9: Conditional probability II: breaking complex events into smaller events, methods to solve probability problems, Bayes rule, law of total probability, Bayes theorem Discrete Structures II (Summer
Lecture 9: Conditional probability II: breaking complex events into smaller events, methods to solve probability problems, Bayes rule, law of total probability, Bayes theorem Discrete Structures II (Summer
Lecture 1. Scott Pauls 1 3/28/07. Dartmouth College. Math 23, Spring Scott Pauls. Administrivia. Today s material.
 Lecture 1 1 1 Department of Mathematics Dartmouth College 3/28/07 Outline Course Overview http://www.math.dartmouth.edu/~m23s07 Matlab Ordinary differential equations Definition An ordinary differential
Lecture 1 1 1 Department of Mathematics Dartmouth College 3/28/07 Outline Course Overview http://www.math.dartmouth.edu/~m23s07 Matlab Ordinary differential equations Definition An ordinary differential
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER / Lines and Their Equations
 ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER 1 017/018 DR. ANTHONY BROWN. Lines and Their Equations.1. Slope of a Line and its y-intercept. In Euclidean geometry (where
ACCESS TO SCIENCE, ENGINEERING AND AGRICULTURE: MATHEMATICS 1 MATH00030 SEMESTER 1 017/018 DR. ANTHONY BROWN. Lines and Their Equations.1. Slope of a Line and its y-intercept. In Euclidean geometry (where
Math 231E, Lecture 25. Integral Test and Estimating Sums
 Math 23E, Lecture 25. Integral Test and Estimating Sums Integral Test The definition of determining whether the sum n= a n converges is:. Compute the partial sums s n = a k, k= 2. Check that s n is a convergent
Math 23E, Lecture 25. Integral Test and Estimating Sums Integral Test The definition of determining whether the sum n= a n converges is:. Compute the partial sums s n = a k, k= 2. Check that s n is a convergent
First-Order Differential Equations
 CHAPTER 1 First-Order Differential Equations 1. Diff Eqns and Math Models Know what it means for a function to be a solution to a differential equation. In order to figure out if y = y(x) is a solution
CHAPTER 1 First-Order Differential Equations 1. Diff Eqns and Math Models Know what it means for a function to be a solution to a differential equation. In order to figure out if y = y(x) is a solution
Markov Chain Monte Carlo
 Department of Statistics The University of Auckland https://www.stat.auckland.ac.nz/~brewer/ Emphasis I will try to emphasise the underlying ideas of the methods. I will not be teaching specific software
Department of Statistics The University of Auckland https://www.stat.auckland.ac.nz/~brewer/ Emphasis I will try to emphasise the underlying ideas of the methods. I will not be teaching specific software
Basic Thermodynamics Prof. S. K. Som Department of Mechanical Engineering Indian Institute of Technology, Kharagpur. Lecture No 16
 Basic Thermodynamics Prof. S. K. Som Department of Mechanical Engineering Indian Institute of Technology, Kharagpur Lecture No 16 Properties of Pure Substances-I Good afternoon. In the last class, we were
Basic Thermodynamics Prof. S. K. Som Department of Mechanical Engineering Indian Institute of Technology, Kharagpur Lecture No 16 Properties of Pure Substances-I Good afternoon. In the last class, we were
CS 237: Probability in Computing
 CS 237: Probability in Computing Wayne Snyder Computer Science Department Boston University Lecture 13: Normal Distribution Exponential Distribution Recall that the Normal Distribution is given by an explicit
CS 237: Probability in Computing Wayne Snyder Computer Science Department Boston University Lecture 13: Normal Distribution Exponential Distribution Recall that the Normal Distribution is given by an explicit
Math 138: Introduction to solving systems of equations with matrices. The Concept of Balance for Systems of Equations
 Math 138: Introduction to solving systems of equations with matrices. Pedagogy focus: Concept of equation balance, integer arithmetic, quadratic equations. The Concept of Balance for Systems of Equations
Math 138: Introduction to solving systems of equations with matrices. Pedagogy focus: Concept of equation balance, integer arithmetic, quadratic equations. The Concept of Balance for Systems of Equations
Joint, Conditional, & Marginal Probabilities
 Joint, Conditional, & Marginal Probabilities The three axioms for probability don t discuss how to create probabilities for combined events such as P [A B] or for the likelihood of an event A given that
Joint, Conditional, & Marginal Probabilities The three axioms for probability don t discuss how to create probabilities for combined events such as P [A B] or for the likelihood of an event A given that
A population is modeled by the differential equation
 Math 2, Winter 2016 Weekly Homework #8 Solutions 9.1.9. A population is modeled by the differential equation dt = 1.2 P 1 P ). 4200 a) For what values of P is the population increasing? P is increasing
Math 2, Winter 2016 Weekly Homework #8 Solutions 9.1.9. A population is modeled by the differential equation dt = 1.2 P 1 P ). 4200 a) For what values of P is the population increasing? P is increasing
Chapter 2: Vector Geometry
 Chapter 2: Vector Geometry Daniel Chan UNSW Semester 1 2018 Daniel Chan (UNSW) Chapter 2: Vector Geometry Semester 1 2018 1 / 32 Goals of this chapter In this chapter, we will answer the following geometric
Chapter 2: Vector Geometry Daniel Chan UNSW Semester 1 2018 Daniel Chan (UNSW) Chapter 2: Vector Geometry Semester 1 2018 1 / 32 Goals of this chapter In this chapter, we will answer the following geometric
UCI MATH CIRCLE: POPULATION DYNAMICS
 UCI MATH CIRCLE: POPULATION DYNAMICS ADAPTED FROM A SESSION OF THE UNIVERSITY OF UTAH MATH CIRCLE When Europeans first arrived in the Americas, Passenger Pigeons were perhaps the most populous bird in
UCI MATH CIRCLE: POPULATION DYNAMICS ADAPTED FROM A SESSION OF THE UNIVERSITY OF UTAH MATH CIRCLE When Europeans first arrived in the Americas, Passenger Pigeons were perhaps the most populous bird in
Matrices related to linear transformations
 Math 4326 Fall 207 Matrices related to linear transformations We have encountered several ways in which matrices relate to linear transformations. In this note, I summarize the important facts and formulas
Math 4326 Fall 207 Matrices related to linear transformations We have encountered several ways in which matrices relate to linear transformations. In this note, I summarize the important facts and formulas
CS1800: Strong Induction. Professor Kevin Gold
 CS1800: Strong Induction Professor Kevin Gold Mini-Primer/Refresher on Unrelated Topic: Limits This is meant to be a problem about reasoning about quantifiers, with a little practice of other skills, too
CS1800: Strong Induction Professor Kevin Gold Mini-Primer/Refresher on Unrelated Topic: Limits This is meant to be a problem about reasoning about quantifiers, with a little practice of other skills, too
Pumps, Maps and Pea Soup: Spatio-temporal methods in environmental epidemiology
 Pumps, Maps and Pea Soup: Spatio-temporal methods in environmental epidemiology Gavin Shaddick Department of Mathematical Sciences University of Bath 2012-13 van Eeden lecture Thanks Constance van Eeden
Pumps, Maps and Pea Soup: Spatio-temporal methods in environmental epidemiology Gavin Shaddick Department of Mathematical Sciences University of Bath 2012-13 van Eeden lecture Thanks Constance van Eeden
Here are some additional properties of the determinant function.
 List of properties Here are some additional properties of the determinant function. Prop Throughout let A, B M nn. 1 If A = (a ij ) is upper triangular then det(a) = a 11 a 22... a nn. 2 If a row or column
List of properties Here are some additional properties of the determinant function. Prop Throughout let A, B M nn. 1 If A = (a ij ) is upper triangular then det(a) = a 11 a 22... a nn. 2 If a row or column
Math 2930 Worksheet Introduction to Differential Equations
 Math 2930 Worksheet Introduction to Differential Equations Week 1 August 24, 2017 Question 1. Is the function y = 1 + t a solution to the differential equation How about the function y = 1 + 2t? How about
Math 2930 Worksheet Introduction to Differential Equations Week 1 August 24, 2017 Question 1. Is the function y = 1 + t a solution to the differential equation How about the function y = 1 + 2t? How about
Assignment 2.1. Exponent Properties: The Product Rule
 Assignment.1 NAME: Exponent Properties: The Product Rule What is the difference between x and x? Explain in complete sentences and with examples. Product Repeated Multiplication Power of the form a b 5
Assignment.1 NAME: Exponent Properties: The Product Rule What is the difference between x and x? Explain in complete sentences and with examples. Product Repeated Multiplication Power of the form a b 5
Nonlinear System Analysis
 Nonlinear System Analysis Lyapunov Based Approach Lecture 4 Module 1 Dr. Laxmidhar Behera Department of Electrical Engineering, Indian Institute of Technology, Kanpur. January 4, 2003 Intelligent Control
Nonlinear System Analysis Lyapunov Based Approach Lecture 4 Module 1 Dr. Laxmidhar Behera Department of Electrical Engineering, Indian Institute of Technology, Kanpur. January 4, 2003 Intelligent Control
Chapter 4: Linear Equations
 Chapter 4: Linear Equations Daniel Chan UNSW Semester 1 2018 Daniel Chan (UNSW) Chapter 4: Linear Equations Semester 1 2018 1 / 42 An Ancient Chinese Problem The following maths problem was taken from
Chapter 4: Linear Equations Daniel Chan UNSW Semester 1 2018 Daniel Chan (UNSW) Chapter 4: Linear Equations Semester 1 2018 1 / 42 An Ancient Chinese Problem The following maths problem was taken from
One sided tests. An example of a two sided alternative is what we ve been using for our two sample tests:
 One sided tests So far all of our tests have been two sided. While this may be a bit easier to understand, this is often not the best way to do a hypothesis test. One simple thing that we can do to get
One sided tests So far all of our tests have been two sided. While this may be a bit easier to understand, this is often not the best way to do a hypothesis test. One simple thing that we can do to get
8. Statistical Equilibrium and Classification of States: Discrete Time Markov Chains
 8. Statistical Equilibrium and Classification of States: Discrete Time Markov Chains 8.1 Review 8.2 Statistical Equilibrium 8.3 Two-State Markov Chain 8.4 Existence of P ( ) 8.5 Classification of States
8. Statistical Equilibrium and Classification of States: Discrete Time Markov Chains 8.1 Review 8.2 Statistical Equilibrium 8.3 Two-State Markov Chain 8.4 Existence of P ( ) 8.5 Classification of States
CSE332: Data Structures & Parallelism Lecture 2: Algorithm Analysis. Ruth Anderson Winter 2018
 CSE332: Data Structures & Parallelism Lecture 2: Algorithm Analysis Ruth Anderson Winter 2018 Today Algorithm Analysis What do we care about? How to compare two algorithms Analyzing Code Asymptotic Analysis
CSE332: Data Structures & Parallelism Lecture 2: Algorithm Analysis Ruth Anderson Winter 2018 Today Algorithm Analysis What do we care about? How to compare two algorithms Analyzing Code Asymptotic Analysis
Lecture 6: Recurrent Algorithms:
 Lecture 6: Recurrent Algorithms: Divide-and-Conquer Principle Georgy Gimel farb COMPSCI 220 Algorithms and Data Structures 1 / 20 1 Divide-and-conquer 2 Math induction 3 Telescoping 4 Examples 5 Pros and
Lecture 6: Recurrent Algorithms: Divide-and-Conquer Principle Georgy Gimel farb COMPSCI 220 Algorithms and Data Structures 1 / 20 1 Divide-and-conquer 2 Math induction 3 Telescoping 4 Examples 5 Pros and
Sections 6.1 and 6.2: Systems of Linear Equations
 What is a linear equation? Sections 6.1 and 6.2: Systems of Linear Equations We are now going to discuss solving systems of two or more linear equations with two variables. Recall that solving an equation
What is a linear equation? Sections 6.1 and 6.2: Systems of Linear Equations We are now going to discuss solving systems of two or more linear equations with two variables. Recall that solving an equation
Matrix-valued functions
 Matrix-valued functions Aim lecture: We solve some first order linear homogeneous differential equations using exponentials of matrices. Recall as in MATH2, the any function R M mn (C) : t A(t) can be
Matrix-valued functions Aim lecture: We solve some first order linear homogeneous differential equations using exponentials of matrices. Recall as in MATH2, the any function R M mn (C) : t A(t) can be
Math 016 Lessons Wimayra LUY
 Math 016 Lessons Wimayra LUY wluy@ccp.edu MATH 016 Lessons LESSON 1 Natural Numbers The set of natural numbers is given by N = {0, 1, 2, 3, 4...}. Natural numbers are used for two main reasons: 1. counting,
Math 016 Lessons Wimayra LUY wluy@ccp.edu MATH 016 Lessons LESSON 1 Natural Numbers The set of natural numbers is given by N = {0, 1, 2, 3, 4...}. Natural numbers are used for two main reasons: 1. counting,
Markov Chains. X(t) is a Markov Process if, for arbitrary times t 1 < t 2 <... < t k < t k+1. If X(t) is discrete-valued. If X(t) is continuous-valued
 Markov Chains X(t) is a Markov Process if, for arbitrary times t 1 < t 2
Markov Chains X(t) is a Markov Process if, for arbitrary times t 1 < t 2
CSE332: Data Structures & Parallelism Lecture 2: Algorithm Analysis. Ruth Anderson Winter 2018
 CSE332: Data Structures & Parallelism Lecture 2: Algorithm Analysis Ruth Anderson Winter 2018 Today Algorithm Analysis What do we care about? How to compare two algorithms Analyzing Code Asymptotic Analysis
CSE332: Data Structures & Parallelism Lecture 2: Algorithm Analysis Ruth Anderson Winter 2018 Today Algorithm Analysis What do we care about? How to compare two algorithms Analyzing Code Asymptotic Analysis
t. y = x x R² =
 A4-11 Model Functions finding model functions for data using technology Pre-requisites: A4-8 (polynomial functions), A4-10 (power and exponential functions) Estimated Time: 2 hours Summary Learn Solve
A4-11 Model Functions finding model functions for data using technology Pre-requisites: A4-8 (polynomial functions), A4-10 (power and exponential functions) Estimated Time: 2 hours Summary Learn Solve
CSE332: Data Structures & Parallelism Lecture 2: Algorithm Analysis. Ruth Anderson Winter 2019
 CSE332: Data Structures & Parallelism Lecture 2: Algorithm Analysis Ruth Anderson Winter 2019 Today Algorithm Analysis What do we care about? How to compare two algorithms Analyzing Code Asymptotic Analysis
CSE332: Data Structures & Parallelism Lecture 2: Algorithm Analysis Ruth Anderson Winter 2019 Today Algorithm Analysis What do we care about? How to compare two algorithms Analyzing Code Asymptotic Analysis
Handout 1 Systems of linear equations Gaussian elimination
 06-21254 Mathematical Techniques for Computer Science The University of Birmingham Autumn Semester 2017 School of Computer Science c Achim Jung September 27, 2017 Handout 1 Systems of linear equations
06-21254 Mathematical Techniques for Computer Science The University of Birmingham Autumn Semester 2017 School of Computer Science c Achim Jung September 27, 2017 Handout 1 Systems of linear equations
Math 123, Week 2: Matrix Operations, Inverses
 Math 23, Week 2: Matrix Operations, Inverses Section : Matrices We have introduced ourselves to the grid-like coefficient matrix when performing Gaussian elimination We now formally define general matrices
Math 23, Week 2: Matrix Operations, Inverses Section : Matrices We have introduced ourselves to the grid-like coefficient matrix when performing Gaussian elimination We now formally define general matrices
Definition of a Logarithm
 Chapter 17 Logarithms Sec. 1 Definition of a Logarithm In the last chapter we solved and graphed exponential equations. The strategy we used to solve those was to make the bases the same, set the exponents
Chapter 17 Logarithms Sec. 1 Definition of a Logarithm In the last chapter we solved and graphed exponential equations. The strategy we used to solve those was to make the bases the same, set the exponents
Elements of Vector Calculus : Scalar Field & its Gradient
 Elements of Vector Calculus : Scalar Field & its Gradient Lecture 1 : Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Introduction : In this set of approximately 40 lectures
Elements of Vector Calculus : Scalar Field & its Gradient Lecture 1 : Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Introduction : In this set of approximately 40 lectures
MAT01B1: Separable Differential Equations
 MAT01B1: Separable Differential Equations Dr Craig 3 October 2018 My details: acraig@uj.ac.za Consulting hours: Tomorrow 14h40 15h25 Friday 11h20 12h55 Office C-Ring 508 https://andrewcraigmaths.wordpress.com/
MAT01B1: Separable Differential Equations Dr Craig 3 October 2018 My details: acraig@uj.ac.za Consulting hours: Tomorrow 14h40 15h25 Friday 11h20 12h55 Office C-Ring 508 https://andrewcraigmaths.wordpress.com/
PRACTICE PROBLEMS FOR EXAM 2
 PRACTICE PROBLEMS FOR EXAM 2 Math 3160Q Fall 2015 Professor Hohn Below is a list of practice questions for Exam 2. Any quiz, homework, or example problem has a chance of being on the exam. For more practice,
PRACTICE PROBLEMS FOR EXAM 2 Math 3160Q Fall 2015 Professor Hohn Below is a list of practice questions for Exam 2. Any quiz, homework, or example problem has a chance of being on the exam. For more practice,
Matrix-valued functions
 Matrix-valued functions Aim lecture: We solve some first order linear homogeneous differential equations using exponentials of matrices. Recall as in MATH2, the any function R M mn (C) : t A(t) can be
Matrix-valued functions Aim lecture: We solve some first order linear homogeneous differential equations using exponentials of matrices. Recall as in MATH2, the any function R M mn (C) : t A(t) can be
Modeling with differential equations
 Mathematical Modeling Lia Vas Modeling with differential equations When trying to predict the future value, one follows the following basic idea. Future value = present value + change. From this idea,
Mathematical Modeling Lia Vas Modeling with differential equations When trying to predict the future value, one follows the following basic idea. Future value = present value + change. From this idea,
ECE 440 Lecture 28 : P-N Junction II Class Outline:
 ECE 440 Lecture 28 : P-N Junction II Class Outline: Contact Potential Equilibrium Fermi Levels Things you should know when you leave Key Questions What is the contact potential? Where does the transition
ECE 440 Lecture 28 : P-N Junction II Class Outline: Contact Potential Equilibrium Fermi Levels Things you should know when you leave Key Questions What is the contact potential? Where does the transition
Bayesian Updating with Discrete Priors Class 11, Jeremy Orloff and Jonathan Bloom
 1 Learning Goals ian Updating with Discrete Priors Class 11, 18.05 Jeremy Orloff and Jonathan Bloom 1. Be able to apply theorem to compute probabilities. 2. Be able to define the and to identify the roles
1 Learning Goals ian Updating with Discrete Priors Class 11, 18.05 Jeremy Orloff and Jonathan Bloom 1. Be able to apply theorem to compute probabilities. 2. Be able to define the and to identify the roles
Definition of a Logarithm
 Chapter 17 Logarithms Sec. 1 Definition of a Logarithm In the last chapter we solved and graphed exponential equations. The strategy we used to solve those was to make the bases the same, set the exponents
Chapter 17 Logarithms Sec. 1 Definition of a Logarithm In the last chapter we solved and graphed exponential equations. The strategy we used to solve those was to make the bases the same, set the exponents
Math 353, Fall 2017 Study guide for the final
 Math 353, Fall 2017 Study guide for the final December 12, 2017 Last updated 12/4/17. If something is unclear or incorrect, please let me know so I can update the documents. Updates 12/4: De-emphasized
Math 353, Fall 2017 Study guide for the final December 12, 2017 Last updated 12/4/17. If something is unclear or incorrect, please let me know so I can update the documents. Updates 12/4: De-emphasized
Math Assignment 2
 Math 2280 - Assignment 2 Dylan Zwick Spring 2014 Section 1.5-1, 15, 21, 29, 38, 42 Section 1.6-1, 3, 13, 16, 22, 26, 31, 36, 56 Section 2.1-1, 8, 11, 16, 29 Section 2.2-1, 10, 21, 23, 24 1 Section 1.5
Math 2280 - Assignment 2 Dylan Zwick Spring 2014 Section 1.5-1, 15, 21, 29, 38, 42 Section 1.6-1, 3, 13, 16, 22, 26, 31, 36, 56 Section 2.1-1, 8, 11, 16, 29 Section 2.2-1, 10, 21, 23, 24 1 Section 1.5
MATH3203 Lecture 1 Mathematical Modelling and ODEs
 MATH3203 Lecture 1 Mathematical Modelling and ODEs Dion Weatherley Earth Systems Science Computational Centre, University of Queensland February 27, 2006 Abstract Contents 1 Mathematical Modelling 2 1.1
MATH3203 Lecture 1 Mathematical Modelling and ODEs Dion Weatherley Earth Systems Science Computational Centre, University of Queensland February 27, 2006 Abstract Contents 1 Mathematical Modelling 2 1.1
Math Bootcamp 2012 Miscellaneous
 Math Bootcamp 202 Miscellaneous Factorial, combination and permutation The factorial of a positive integer n denoted by n!, is the product of all positive integers less than or equal to n. Define 0! =.
Math Bootcamp 202 Miscellaneous Factorial, combination and permutation The factorial of a positive integer n denoted by n!, is the product of all positive integers less than or equal to n. Define 0! =.
Computational Fluid Dynamics Prof. Dr. SumanChakraborty Department of Mechanical Engineering Indian Institute of Technology, Kharagpur
 Computational Fluid Dynamics Prof. Dr. SumanChakraborty Department of Mechanical Engineering Indian Institute of Technology, Kharagpur Lecture No. #11 Fundamentals of Discretization: Finite Difference
Computational Fluid Dynamics Prof. Dr. SumanChakraborty Department of Mechanical Engineering Indian Institute of Technology, Kharagpur Lecture No. #11 Fundamentals of Discretization: Finite Difference
6.867 Machine Learning
 6.867 Machine Learning Problem set 1 Solutions Thursday, September 19 What and how to turn in? Turn in short written answers to the questions explicitly stated, and when requested to explain or prove.
6.867 Machine Learning Problem set 1 Solutions Thursday, September 19 What and how to turn in? Turn in short written answers to the questions explicitly stated, and when requested to explain or prove.
1 Glaciers and climate
 1 Glaciers and climate 1.1 Equilibrium length For a glacier to be in equilibrium with climate the (integrated) mass balance must be equal to zero. For a glacier of a uniform width and length l this implies
1 Glaciers and climate 1.1 Equilibrium length For a glacier to be in equilibrium with climate the (integrated) mass balance must be equal to zero. For a glacier of a uniform width and length l this implies
Lecture 16 : Fully Developed Pipe flow with Constant Wall temperature and Heat Flux
 Module 2 : Convection Lecture 16 : Fully Developed Pipe flow with Constant Wall temperature and Heat Flux Objectives In this class: The fully developed temperature profile for uniform circumferential heating
Module 2 : Convection Lecture 16 : Fully Developed Pipe flow with Constant Wall temperature and Heat Flux Objectives In this class: The fully developed temperature profile for uniform circumferential heating
Recitation 9: Probability Matrices and Real Symmetric Matrices. 3 Probability Matrices: Definitions and Examples
 Math b TA: Padraic Bartlett Recitation 9: Probability Matrices and Real Symmetric Matrices Week 9 Caltech 20 Random Question Show that + + + + +... = ϕ, the golden ratio, which is = + 5. 2 2 Homework comments
Math b TA: Padraic Bartlett Recitation 9: Probability Matrices and Real Symmetric Matrices Week 9 Caltech 20 Random Question Show that + + + + +... = ϕ, the golden ratio, which is = + 5. 2 2 Homework comments
Data for a vector space
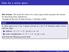 Data for a vector space Aim lecture: We recall the notion of a vector space which provides the context for describing linear phenomena. Throughout the rest of these lectures, F denotes a field. Defn A
Data for a vector space Aim lecture: We recall the notion of a vector space which provides the context for describing linear phenomena. Throughout the rest of these lectures, F denotes a field. Defn A
Jordan chain. Defn. E.g. T = J 3 (λ) Daniel Chan (UNSW) Lecture 29: Jordan chains & tableaux Semester / 10
 Jordan chain Aim lecture: We introduce the notions of Jordan chains & Jordan form tableaux which are the key notions to proving the Jordan canonical form theorem. Throughout this lecture we fix the following
Jordan chain Aim lecture: We introduce the notions of Jordan chains & Jordan form tableaux which are the key notions to proving the Jordan canonical form theorem. Throughout this lecture we fix the following
MATH 10 INTRODUCTORY STATISTICS
 MATH 10 INTRODUCTORY STATISTICS Ramesh Yapalparvi It is Time for Homework! ( ω `) First homework + data will be posted on the website, under the homework tab. And also sent out via email. 30% weekly homework.
MATH 10 INTRODUCTORY STATISTICS Ramesh Yapalparvi It is Time for Homework! ( ω `) First homework + data will be posted on the website, under the homework tab. And also sent out via email. 30% weekly homework.
MATH 104, HOMEWORK #3 SOLUTIONS Due Thursday, February 4
 MATH 104, HOMEWORK #3 SOLUTIONS Due Thursday, February 4 Remember, consult the Homework Guidelines for general instructions. GRADED HOMEWORK: 1. Give direct proofs for the two following its. Do not use
MATH 104, HOMEWORK #3 SOLUTIONS Due Thursday, February 4 Remember, consult the Homework Guidelines for general instructions. GRADED HOMEWORK: 1. Give direct proofs for the two following its. Do not use
Math Precalculus I University of Hawai i at Mānoa Spring
 Math 135 - Precalculus I University of Hawai i at Mānoa Spring - 2014 Created for Math 135, Spring 2008 by Lukasz Grabarek and Michael Joyce Send comments and corrections to lukasz@math.hawaii.edu Contents
Math 135 - Precalculus I University of Hawai i at Mānoa Spring - 2014 Created for Math 135, Spring 2008 by Lukasz Grabarek and Michael Joyce Send comments and corrections to lukasz@math.hawaii.edu Contents
Markov chains. Randomness and Computation. Markov chains. Markov processes
 Markov chains Randomness and Computation or, Randomized Algorithms Mary Cryan School of Informatics University of Edinburgh Definition (Definition 7) A discrete-time stochastic process on the state space
Markov chains Randomness and Computation or, Randomized Algorithms Mary Cryan School of Informatics University of Edinburgh Definition (Definition 7) A discrete-time stochastic process on the state space
Chapter Usual types of questions Tips What can go ugly. and, common denominator will be
 C3 Cheat Sheet Chapter Usual types of questions Tips What can go ugly 1 Algebraic Almost always adding or subtracting Factorise everything in each fraction first. e.g. If denominators Blindly multiplying
C3 Cheat Sheet Chapter Usual types of questions Tips What can go ugly 1 Algebraic Almost always adding or subtracting Factorise everything in each fraction first. e.g. If denominators Blindly multiplying
A Simple Model of Evolution with Variable System Size
 A Simple Model of Evolution with Variable System Size Claus Wilke and Thomas Martinetz Institut für Neuroinformatik Ruhr-Universität Bochum (Submitted: ; Printed: September 28, 2001) A simple model of
A Simple Model of Evolution with Variable System Size Claus Wilke and Thomas Martinetz Institut für Neuroinformatik Ruhr-Universität Bochum (Submitted: ; Printed: September 28, 2001) A simple model of
MATHEMATICS ENRICHMENT CLUB. Solution Sheet 6, June 10, Let x be a natural number, then we wish to know whether
 MATHEMATICS ENRICHMENT CLUB. Solution Sheet 6, June 10, 2014 1 1. Let x be a natural number, then we wish to know whether x 3 + (x + 1) 3 + (x + 2) 3 is divisible by 18. Letting the above sum be n x 3
MATHEMATICS ENRICHMENT CLUB. Solution Sheet 6, June 10, 2014 1 1. Let x be a natural number, then we wish to know whether x 3 + (x + 1) 3 + (x + 2) 3 is divisible by 18. Letting the above sum be n x 3
Maximum and Minimum Values
 Maimum and Minimum Values y Maimum Minimum MATH 80 Lecture 4 of 6 Definitions: A function f has an absolute maimum at c if f ( c) f ( ) for all in D, where D is the domain of f. The number f (c) is called
Maimum and Minimum Values y Maimum Minimum MATH 80 Lecture 4 of 6 Definitions: A function f has an absolute maimum at c if f ( c) f ( ) for all in D, where D is the domain of f. The number f (c) is called
2: SIMPLE HARMONIC MOTION
 2: SIMPLE HARMONIC MOTION Motion of a Mass Hanging from a Spring If you hang a mass from a spring, stretch it slightly, and let go, the mass will go up and down over and over again. That is, you will get
2: SIMPLE HARMONIC MOTION Motion of a Mass Hanging from a Spring If you hang a mass from a spring, stretch it slightly, and let go, the mass will go up and down over and over again. That is, you will get
Physics 20 Homework 3 SIMS 2016
 Physics 20 Homework 3 SIMS 2016 Due: Thursday, August 25 th Special thanks to Sebastian Fischetti for problems 1, 5, and 6. Edits in red made by Keith Fratus. 1. The ballistic pendulum is a device used
Physics 20 Homework 3 SIMS 2016 Due: Thursday, August 25 th Special thanks to Sebastian Fischetti for problems 1, 5, and 6. Edits in red made by Keith Fratus. 1. The ballistic pendulum is a device used
