Section 1.2: A Single Server Queue
|
|
|
- Aron Jordan
- 5 years ago
- Views:
Transcription
1 Section 12: A Single Server Queue Discrete-Event Simulation: A First Course c 2006 Pearson Ed, Inc Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 1/ 30
2 Section 12: A Single-Server Queue arrivals queue server departures service node A single-server service node consists of a server plus its queue If there is only one service technician, the machine shop model from section 11 is a single-server queue Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 2/ 30
3 Queue Discipline Queue discipline: the algorithm used when a job is selected from the queue to enter service FIFO first in, first out LIFO last in, first out SIRO serve in random order Priority typically shortest job first (SJF) Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 3/ 30
4 Assumptions FIFO is also known as first come, first serve (FCFS) The order of arrival and departure are the same This observation can be used to simplify the simulation Unless otherwise specified, assume FIFO with infinite queue capacity Service is non-preemptive Once initiated, service of a job will continue until completion Service is conservative Server will never remain idle if there is one or more jobs in the service node Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 4/ 30
5 Specification Model For a job i: The arrival time is a i The delay in the queue is d i The time that service begins is b i = a i + d i The service time is s i The wait in the node is w i = d i + s i The departure time is c i = a i + w i w i d i s i time a i b i c i Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 5/ 30
6 Arrivals The interarrival time between jobs i 1 and i is where, by definition, a 0 = 0 r i = a i a i 1 r i a i 2 a i 1 a i a i+1 Note that a i = a i 1 + r i and so (by induction) time a i = r 1 + r r i i = 1,2,3, Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 6/ 30
7 Algorithmic Question Given the arrival times and service times, can the delay times be computed? For some queue disciplines, this question is difficult to answer If the queue discipline is FIFO, d i is determined by when a i occurs relative to c i 1 There are two cases to consider: Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 7/ 30
8 Cases If a i < c i 1, job i arrives before job i 1 completes: d i 1 s i 1 a i 1 b i 1 c i 1 a i b i c i r i d i s i If a i c i 1, job i arrives after job i 1 completes: d i 1 s i 1 a i 1 b i 1 c i 1 r i s i a i c i t t Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 8/ 30
9 Calculating Delay for Each Job Algorithm 121 c 0 = 00; /* assumes that a 0 = 00 */ i = 0; while ( more jobs to process ) { i++; a i = GetArrival(); if (a i < c i 1 ) d i = c i 1 a i ; else d i = 00; s i = GetService(); c i = a i + d i + s i ; } n = i; return d 1, d 2,, d n ; Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 9/ 30
10 Example 122 Algorithm 121 used to process n = 10 jobs i read from file a i from algorithm d i read from file s i For future reference, note that for the last job a n = 320 c n = a n + d n + s n = = 376 Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 10/ 30
11 Output Statistics The purpose of simulation is insight gained by looking at statistics The importance of various statistics varies on perspective: Job perspective: wait time is most important Manager perspective: utilization is critical Statistics are broken down into two categories Job-averaged statistics Time-averaged statistics Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 11/ 30
12 Job-Averaged Statistics Job-averaged statistics: computed via typical arithmetic mean Average interarrival time: r = 1 n n i=1 r i = a n n 1/r is the arrival rate Average service time: s = 1 n n i=1 s i 1/s is the service rate Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 12/ 30
13 Example 123 For the 10 jobs in Example 122 average interarrival time is r = a n /n = 320/10 = 320 seconds per job average service is s = 347 seconds per job arrival rate is 1/r 0031 jobs per second service rate is 1/s 0029 jobs per second The server is not quite able to process jobs at the rate they arrive on average Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 13/ 30
14 Job-Averaged Statistics The average delay and average wait are defined as d = 1 n n i=1 d i Recall w i = d i + s i for all i w = 1 n n i=1 w i w = 1 n n w i = 1 n i=1 n (d i + s i ) = 1 n i=1 n d i + 1 n i=1 n s i = d + s i=1 Sufficient to compute any two of w, d, s Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 14/ 30
15 Example 124 From the data in Example 122, d = 267 From Example 123, s = 347 Therefore w = = 614 Recall verification is one (difficult) step of model development Consistency check: used to verify that a simulation satisfies known equations Compute w, d, and s independently Then verify that w = d + s Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 15/ 30
16 Time-Averaged Statistics Time-averaged statistics: defined by area under a curve (integration) For SSQ, need three additional functions l(t): number of jobs in the service node at time t q(t): number of jobs in the queue at time t x(t): number of jobs in service at time t By definition, l(t) = q(t) + x(t) l(t) = 0,1,2, q(t) = 0,1,2, x(t) = 0,1 Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 16/ 30
17 Time-Averaged Statistics All three functions are piece-wise constant 4 3 l(t) t Figures for q( ) and x( ) can be deduced q(t) = 0 and x(t) = 0 if and only if l(t) = 0 Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 17/ 30
18 Time-Averaged Statistics Over the time interval (0,τ): time-averaged number in the node: l = 1 τ time-averaged number in the queue: q = 1 τ time-averaged number in service: x = 1 τ Since l(t) = q(t) + x(t) for all t > 0 l = q + x τ 0 τ 0 τ 0 l(t)dt q(t)dt x(t)dt Sufficient to calculate any two of l, q, x Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 18/ 30
19 Example 125 From Example 122 (with τ = c 10 = 376), l = 1633 q = 0710 x = 0923 The average of numerous random observations (samples) of the number in the service node should be close to l Same holds for q and x Server utilization: time-averaged number in service (x) x also represents the probability the server is busy Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 19/ 30
20 Little s Theorem How are job-averaged and time-average statistics related? Theorem (Little, 1961) If (a) queue discipline is FIFO, (b) service node capacity is infinite, and (c) server is idle both at t = 0 and t = c n then cn 0 l(t)dt = n i=1 w i and cn 0 q(t)dt = n i=1 d i and cn 0 x(t)dt = n i=1 s i Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 20/ 30
21 Little s Theorem Proof Proof For each job i = 1, 2,, define an indicator function { 1 ai < t < c ψ i (t) = i 0 otherwise Then and so l(t) = n ψ i (t) i=1 0 < t < c n cn 0 l(t)dt = cn 0 n ψ i (t)dt = i=1 n cn i=1 0 ψ i (t)dt = n (c i a i ) = n i=1 i=1 w i The other two equations can be derived similarly Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 21/ 30
22 Example w 1 cumulative number w 2 of arrivals w 3 w 4 w 5 w w 7 w 8 cumulative number of departures w 9 w 10 t l(t)dt = 10 i=1 w i = 614 Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 22/ 30
23 Little s Equations Using τ = c n in the definition of the time-averaged statistics, along with Little s Theorem, we have c n l = cn 0 l(t)dt = n w i = nw i=1 We can perform similar operations and ultimately have ( n l = c n ) ( ) ( ) n n w and q = d and x = s c n c n Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 23/ 30
24 Computational Model The ANSI C program ssq1 implements Algorithm 121 Data is read from the file ssq1dat consisting of arrival times and service times in the format a1 s 1 a 2 s 2 a n s n Since queue discipline is FIFO, no need for a queue data structure Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 24/ 30
25 Example 128 Running program ssq1 with ssq1dat 1/r 010 and 1/s 014 If you modify program ssq1 to compute l,q, and x x 028 Despite the significant idle time, q is nearly 2 Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 25/ 30
26 Traffic Intensity Traffic intensity: ratio of arrival rate to service rate 1/r 1/s = s r = s ( ) a n /n = cn x a n Assuming c n /a n is close to 10, the traffic intensity and utilization will be nearly equal Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 26/ 30
27 Case Study Sven and Larry s Ice Cream Shoppe owners considering adding new flavors and cone options concerned about resulting service times and queue length Can be modeled as a single-server queue ssq1dat represents 1000 customer interactions Multiply each service time by a constant In the following graph, the circled point uses unmodified data Moving right, constants are 105, 110, 115, Moving left, constants are 095, 090, 085, Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 27/ 30
28 Sven and Larry q x Modest increase in service time produces significant increase in queue length Non-linear relationship between q and x Sven and Larry will have to assess the impact of the increased service times Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 28/ 30
29 Graphical Considerations q x Since both x and q are continuous, we could calculate an infinite number of points Few would question the validity of connecting the dots Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 29/ 30
30 Guidelines If there is essentially no uncertainty and the resulting interpolating curve is smooth, connecting the dots is OK Leave the dots as a reminder of the data points If there is essentially no uncertainty but the curve is not smooth, more dots should be generated If the dots correspond to uncertain (noisy) data, then interpolation is not justified Use approximation of a curve or do not superimpose at all Discrete data should never have a solid curve Discrete-Event Simulation: A First Course Section 12: A Single Server Queue 30/ 30
Section 3.3: Discrete-Event Simulation Examples
 Section 33: Discrete-Event Simulation Examples Discrete-Event Simulation: A First Course c 2006 Pearson Ed, Inc 0-13-142917-5 Discrete-Event Simulation: A First Course Section 33: Discrete-Event Simulation
Section 33: Discrete-Event Simulation Examples Discrete-Event Simulation: A First Course c 2006 Pearson Ed, Inc 0-13-142917-5 Discrete-Event Simulation: A First Course Section 33: Discrete-Event Simulation
CPSC 531: System Modeling and Simulation. Carey Williamson Department of Computer Science University of Calgary Fall 2017
 CPSC 531: System Modeling and Simulation Carey Williamson Department of Computer Science University of Calgary Fall 2017 Motivating Quote for Queueing Models Good things come to those who wait - poet/writer
CPSC 531: System Modeling and Simulation Carey Williamson Department of Computer Science University of Calgary Fall 2017 Motivating Quote for Queueing Models Good things come to those who wait - poet/writer
NATCOR: Stochastic Modelling
 NATCOR: Stochastic Modelling Queueing Theory II Chris Kirkbride Management Science 2017 Overview of Today s Sessions I Introduction to Queueing Modelling II Multiclass Queueing Models III Queueing Control
NATCOR: Stochastic Modelling Queueing Theory II Chris Kirkbride Management Science 2017 Overview of Today s Sessions I Introduction to Queueing Modelling II Multiclass Queueing Models III Queueing Control
Queueing Theory I Summary! Little s Law! Queueing System Notation! Stationary Analysis of Elementary Queueing Systems " M/M/1 " M/M/m " M/M/1/K "
 Queueing Theory I Summary Little s Law Queueing System Notation Stationary Analysis of Elementary Queueing Systems " M/M/1 " M/M/m " M/M/1/K " Little s Law a(t): the process that counts the number of arrivals
Queueing Theory I Summary Little s Law Queueing System Notation Stationary Analysis of Elementary Queueing Systems " M/M/1 " M/M/m " M/M/1/K " Little s Law a(t): the process that counts the number of arrivals
Queueing Review. Christos Alexopoulos and Dave Goldsman 10/6/16. (mostly from BCNN) Georgia Institute of Technology, Atlanta, GA, USA
 1 / 24 Queueing Review (mostly from BCNN) Christos Alexopoulos and Dave Goldsman Georgia Institute of Technology, Atlanta, GA, USA 10/6/16 2 / 24 Outline 1 Introduction 2 Queueing Notation 3 Transient
1 / 24 Queueing Review (mostly from BCNN) Christos Alexopoulos and Dave Goldsman Georgia Institute of Technology, Atlanta, GA, USA 10/6/16 2 / 24 Outline 1 Introduction 2 Queueing Notation 3 Transient
Slides 9: Queuing Models
 Slides 9: Queuing Models Purpose Simulation is often used in the analysis of queuing models. A simple but typical queuing model is: Queuing models provide the analyst with a powerful tool for designing
Slides 9: Queuing Models Purpose Simulation is often used in the analysis of queuing models. A simple but typical queuing model is: Queuing models provide the analyst with a powerful tool for designing
Queueing Theory. VK Room: M Last updated: October 17, 2013.
 Queueing Theory VK Room: M1.30 knightva@cf.ac.uk www.vincent-knight.com Last updated: October 17, 2013. 1 / 63 Overview Description of Queueing Processes The Single Server Markovian Queue Multi Server
Queueing Theory VK Room: M1.30 knightva@cf.ac.uk www.vincent-knight.com Last updated: October 17, 2013. 1 / 63 Overview Description of Queueing Processes The Single Server Markovian Queue Multi Server
Queueing Systems: Lecture 3. Amedeo R. Odoni October 18, Announcements
 Queueing Systems: Lecture 3 Amedeo R. Odoni October 18, 006 Announcements PS #3 due tomorrow by 3 PM Office hours Odoni: Wed, 10/18, :30-4:30; next week: Tue, 10/4 Quiz #1: October 5, open book, in class;
Queueing Systems: Lecture 3 Amedeo R. Odoni October 18, 006 Announcements PS #3 due tomorrow by 3 PM Office hours Odoni: Wed, 10/18, :30-4:30; next week: Tue, 10/4 Quiz #1: October 5, open book, in class;
Networking = Plumbing. Queueing Analysis: I. Last Lecture. Lecture Outline. Jeremiah Deng. 29 July 2013
 Networking = Plumbing TELE302 Lecture 7 Queueing Analysis: I Jeremiah Deng University of Otago 29 July 2013 Jeremiah Deng (University of Otago) TELE302 Lecture 7 29 July 2013 1 / 33 Lecture Outline Jeremiah
Networking = Plumbing TELE302 Lecture 7 Queueing Analysis: I Jeremiah Deng University of Otago 29 July 2013 Jeremiah Deng (University of Otago) TELE302 Lecture 7 29 July 2013 1 / 33 Lecture Outline Jeremiah
Richard C. Larson. March 5, Photo courtesy of Johnathan Boeke.
 ESD.86 Markov Processes and their Application to Queueing Richard C. Larson March 5, 2007 Photo courtesy of Johnathan Boeke. http://www.flickr.com/photos/boeke/134030512/ Outline Spatial Poisson Processes,
ESD.86 Markov Processes and their Application to Queueing Richard C. Larson March 5, 2007 Photo courtesy of Johnathan Boeke. http://www.flickr.com/photos/boeke/134030512/ Outline Spatial Poisson Processes,
Queueing Review. Christos Alexopoulos and Dave Goldsman 10/25/17. (mostly from BCNN) Georgia Institute of Technology, Atlanta, GA, USA
 1 / 26 Queueing Review (mostly from BCNN) Christos Alexopoulos and Dave Goldsman Georgia Institute of Technology, Atlanta, GA, USA 10/25/17 2 / 26 Outline 1 Introduction 2 Queueing Notation 3 Transient
1 / 26 Queueing Review (mostly from BCNN) Christos Alexopoulos and Dave Goldsman Georgia Institute of Technology, Atlanta, GA, USA 10/25/17 2 / 26 Outline 1 Introduction 2 Queueing Notation 3 Transient
11 The M/G/1 system with priorities
 11 The M/G/1 system with priorities In this chapter we analyse queueing models with different types of customers, where one or more types of customers have priority over other types. More precisely we
11 The M/G/1 system with priorities In this chapter we analyse queueing models with different types of customers, where one or more types of customers have priority over other types. More precisely we
Massachusetts Institute of Technology
 .203J/6.28J/3.665J/5.073J/6.76J/ESD.26J Quiz Solutions (a)(i) Without loss of generality we can pin down X at any fixed point. X 2 is still uniformly distributed over the square. Assuming that the police
.203J/6.28J/3.665J/5.073J/6.76J/ESD.26J Quiz Solutions (a)(i) Without loss of generality we can pin down X at any fixed point. X 2 is still uniformly distributed over the square. Assuming that the police
PBW 654 Applied Statistics - I Urban Operations Research
 PBW 654 Applied Statistics - I Urban Operations Research Lecture 2.I Queuing Systems An Introduction Operations Research Models Deterministic Models Linear Programming Integer Programming Network Optimization
PBW 654 Applied Statistics - I Urban Operations Research Lecture 2.I Queuing Systems An Introduction Operations Research Models Deterministic Models Linear Programming Integer Programming Network Optimization
Queues and Queueing Networks
 Queues and Queueing Networks Sanjay K. Bose Dept. of EEE, IITG Copyright 2015, Sanjay K. Bose 1 Introduction to Queueing Models and Queueing Analysis Copyright 2015, Sanjay K. Bose 2 Model of a Queue Arrivals
Queues and Queueing Networks Sanjay K. Bose Dept. of EEE, IITG Copyright 2015, Sanjay K. Bose 1 Introduction to Queueing Models and Queueing Analysis Copyright 2015, Sanjay K. Bose 2 Model of a Queue Arrivals
Chapter 6 Queueing Models. Banks, Carson, Nelson & Nicol Discrete-Event System Simulation
 Chapter 6 Queueing Models Banks, Carson, Nelson & Nicol Discrete-Event System Simulation Purpose Simulation is often used in the analysis of queueing models. A simple but typical queueing model: Queueing
Chapter 6 Queueing Models Banks, Carson, Nelson & Nicol Discrete-Event System Simulation Purpose Simulation is often used in the analysis of queueing models. A simple but typical queueing model: Queueing
5/15/18. Operations Research: An Introduction Hamdy A. Taha. Copyright 2011, 2007 by Pearson Education, Inc. All rights reserved.
 The objective of queuing analysis is to offer a reasonably satisfactory service to waiting customers. Unlike the other tools of OR, queuing theory is not an optimization technique. Rather, it determines
The objective of queuing analysis is to offer a reasonably satisfactory service to waiting customers. Unlike the other tools of OR, queuing theory is not an optimization technique. Rather, it determines
IEOR 6711, HMWK 5, Professor Sigman
 IEOR 6711, HMWK 5, Professor Sigman 1. Semi-Markov processes: Consider an irreducible positive recurrent discrete-time Markov chain {X n } with transition matrix P (P i,j ), i, j S, and finite state space.
IEOR 6711, HMWK 5, Professor Sigman 1. Semi-Markov processes: Consider an irreducible positive recurrent discrete-time Markov chain {X n } with transition matrix P (P i,j ), i, j S, and finite state space.
ISyE 2030 Practice Test 1
 1 NAME ISyE 2030 Practice Test 1 Summer 2005 This test is open notes, open books. You have exactly 90 minutes. 1. Some Short-Answer Flow Questions (a) TRUE or FALSE? One of the primary reasons why theoretical
1 NAME ISyE 2030 Practice Test 1 Summer 2005 This test is open notes, open books. You have exactly 90 minutes. 1. Some Short-Answer Flow Questions (a) TRUE or FALSE? One of the primary reasons why theoretical
Queueing Theory and Simulation. Introduction
 Queueing Theory and Simulation Based on the slides of Dr. Dharma P. Agrawal, University of Cincinnati and Dr. Hiroyuki Ohsaki Graduate School of Information Science & Technology, Osaka University, Japan
Queueing Theory and Simulation Based on the slides of Dr. Dharma P. Agrawal, University of Cincinnati and Dr. Hiroyuki Ohsaki Graduate School of Information Science & Technology, Osaka University, Japan
Class 11 Non-Parametric Models of a Service System; GI/GI/1, GI/GI/n: Exact & Approximate Analysis.
 Service Engineering Class 11 Non-Parametric Models of a Service System; GI/GI/1, GI/GI/n: Exact & Approximate Analysis. G/G/1 Queue: Virtual Waiting Time (Unfinished Work). GI/GI/1: Lindley s Equations
Service Engineering Class 11 Non-Parametric Models of a Service System; GI/GI/1, GI/GI/n: Exact & Approximate Analysis. G/G/1 Queue: Virtual Waiting Time (Unfinished Work). GI/GI/1: Lindley s Equations
Computer Networks More general queuing systems
 Computer Networks More general queuing systems Saad Mneimneh Computer Science Hunter College of CUNY New York M/G/ Introduction We now consider a queuing system where the customer service times have a
Computer Networks More general queuing systems Saad Mneimneh Computer Science Hunter College of CUNY New York M/G/ Introduction We now consider a queuing system where the customer service times have a
Computer Science, Informatik 4 Communication and Distributed Systems. Simulation. Discrete-Event System Simulation. Dr.
 Simulation Discrete-Event System Simulation Chapter 9 Verification and Validation of Simulation Models Purpose & Overview The goal of the validation process is: To produce a model that represents true
Simulation Discrete-Event System Simulation Chapter 9 Verification and Validation of Simulation Models Purpose & Overview The goal of the validation process is: To produce a model that represents true
Photo: US National Archives
 ESD.86. Markov Processes and their Application to Queueing II Richard C. Larson March 7, 2007 Photo: US National Archives Outline Little s Law, one more time PASTA treat Markov Birth and Death Queueing
ESD.86. Markov Processes and their Application to Queueing II Richard C. Larson March 7, 2007 Photo: US National Archives Outline Little s Law, one more time PASTA treat Markov Birth and Death Queueing
Introduction to Queueing Theory with Applications to Air Transportation Systems
 Introduction to Queueing Theory with Applications to Air Transportation Systems John Shortle George Mason University February 28, 2018 Outline Why stochastic models matter M/M/1 queue Little s law Priority
Introduction to Queueing Theory with Applications to Air Transportation Systems John Shortle George Mason University February 28, 2018 Outline Why stochastic models matter M/M/1 queue Little s law Priority
Performance Evaluation of Queuing Systems
 Performance Evaluation of Queuing Systems Introduction to Queuing Systems System Performance Measures & Little s Law Equilibrium Solution of Birth-Death Processes Analysis of Single-Station Queuing Systems
Performance Evaluation of Queuing Systems Introduction to Queuing Systems System Performance Measures & Little s Law Equilibrium Solution of Birth-Death Processes Analysis of Single-Station Queuing Systems
CPU scheduling. CPU Scheduling
 EECS 3221 Operating System Fundamentals No.4 CPU scheduling Prof. Hui Jiang Dept of Electrical Engineering and Computer Science, York University CPU Scheduling CPU scheduling is the basis of multiprogramming
EECS 3221 Operating System Fundamentals No.4 CPU scheduling Prof. Hui Jiang Dept of Electrical Engineering and Computer Science, York University CPU Scheduling CPU scheduling is the basis of multiprogramming
Advanced Computer Networks Lecture 3. Models of Queuing
 Advanced Computer Networks Lecture 3. Models of Queuing Husheng Li Min Kao Department of Electrical Engineering and Computer Science University of Tennessee, Knoxville Spring, 2016 1/13 Terminology of
Advanced Computer Networks Lecture 3. Models of Queuing Husheng Li Min Kao Department of Electrical Engineering and Computer Science University of Tennessee, Knoxville Spring, 2016 1/13 Terminology of
Chapter 2 Queueing Theory and Simulation
 Chapter 2 Queueing Theory and Simulation Based on the slides of Dr. Dharma P. Agrawal, University of Cincinnati and Dr. Hiroyuki Ohsaki Graduate School of Information Science & Technology, Osaka University,
Chapter 2 Queueing Theory and Simulation Based on the slides of Dr. Dharma P. Agrawal, University of Cincinnati and Dr. Hiroyuki Ohsaki Graduate School of Information Science & Technology, Osaka University,
M/G/1 and Priority Queueing
 M/G/1 and Priority Queueing Richard T. B. Ma School of Computing National University of Singapore CS 5229: Advanced Compute Networks Outline PASTA M/G/1 Workload and FIFO Delay Pollaczek Khinchine Formula
M/G/1 and Priority Queueing Richard T. B. Ma School of Computing National University of Singapore CS 5229: Advanced Compute Networks Outline PASTA M/G/1 Workload and FIFO Delay Pollaczek Khinchine Formula
EE 368. Weeks 3 (Notes)
 EE 368 Weeks 3 (Notes) 1 State of a Queuing System State: Set of parameters that describe the condition of the system at a point in time. Why do we need it? Average size of Queue Average waiting time How
EE 368 Weeks 3 (Notes) 1 State of a Queuing System State: Set of parameters that describe the condition of the system at a point in time. Why do we need it? Average size of Queue Average waiting time How
BIRTH DEATH PROCESSES AND QUEUEING SYSTEMS
 BIRTH DEATH PROCESSES AND QUEUEING SYSTEMS Andrea Bobbio Anno Accademico 999-2000 Queueing Systems 2 Notation for Queueing Systems /λ mean time between arrivals S = /µ ρ = λ/µ N mean service time traffic
BIRTH DEATH PROCESSES AND QUEUEING SYSTEMS Andrea Bobbio Anno Accademico 999-2000 Queueing Systems 2 Notation for Queueing Systems /λ mean time between arrivals S = /µ ρ = λ/µ N mean service time traffic
Queuing Theory. Using the Math. Management Science
 Queuing Theory Using the Math 1 Markov Processes (Chains) A process consisting of a countable sequence of stages, that can be judged at each stage to fall into future states independent of how the process
Queuing Theory Using the Math 1 Markov Processes (Chains) A process consisting of a countable sequence of stages, that can be judged at each stage to fall into future states independent of how the process
Queueing systems. Renato Lo Cigno. Simulation and Performance Evaluation Queueing systems - Renato Lo Cigno 1
 Queueing systems Renato Lo Cigno Simulation and Performance Evaluation 2014-15 Queueing systems - Renato Lo Cigno 1 Queues A Birth-Death process is well modeled by a queue Indeed queues can be used to
Queueing systems Renato Lo Cigno Simulation and Performance Evaluation 2014-15 Queueing systems - Renato Lo Cigno 1 Queues A Birth-Death process is well modeled by a queue Indeed queues can be used to
1.225 Transportation Flow Systems Quiz (December 17, 2001; Duration: 3 hours)
 1.225 Transportation Flow Systems Quiz (December 17, 2001; Duration: 3 hours) Student Name: Alias: Instructions: 1. This exam is open-book 2. No cooperation is permitted 3. Please write down your name
1.225 Transportation Flow Systems Quiz (December 17, 2001; Duration: 3 hours) Student Name: Alias: Instructions: 1. This exam is open-book 2. No cooperation is permitted 3. Please write down your name
Exact Simulation of the Stationary Distribution of M/G/c Queues
 1/36 Exact Simulation of the Stationary Distribution of M/G/c Queues Professor Karl Sigman Columbia University New York City USA Conference in Honor of Søren Asmussen Monday, August 1, 2011 Sandbjerg Estate
1/36 Exact Simulation of the Stationary Distribution of M/G/c Queues Professor Karl Sigman Columbia University New York City USA Conference in Honor of Søren Asmussen Monday, August 1, 2011 Sandbjerg Estate
Queuing Theory. The present section focuses on the standard vocabulary of Waiting Line Models.
 Queuing Theory Introduction Waiting lines are the most frequently encountered problems in everyday life. For example, queue at a cafeteria, library, bank, etc. Common to all of these cases are the arrivals
Queuing Theory Introduction Waiting lines are the most frequently encountered problems in everyday life. For example, queue at a cafeteria, library, bank, etc. Common to all of these cases are the arrivals
Fluid Models of Parallel Service Systems under FCFS
 Fluid Models of Parallel Service Systems under FCFS Hanqin Zhang Business School, National University of Singapore Joint work with Yuval Nov and Gideon Weiss from The University of Haifa, Israel Queueing
Fluid Models of Parallel Service Systems under FCFS Hanqin Zhang Business School, National University of Singapore Joint work with Yuval Nov and Gideon Weiss from The University of Haifa, Israel Queueing
Systems Simulation Chapter 6: Queuing Models
 Systems Simulation Chapter 6: Queuing Models Fatih Cavdur fatihcavdur@uludag.edu.tr April 2, 2014 Introduction Introduction Simulation is often used in the analysis of queuing models. A simple but typical
Systems Simulation Chapter 6: Queuing Models Fatih Cavdur fatihcavdur@uludag.edu.tr April 2, 2014 Introduction Introduction Simulation is often used in the analysis of queuing models. A simple but typical
Continuous Time Processes
 page 102 Chapter 7 Continuous Time Processes 7.1 Introduction In a continuous time stochastic process (with discrete state space), a change of state can occur at any time instant. The associated point
page 102 Chapter 7 Continuous Time Processes 7.1 Introduction In a continuous time stochastic process (with discrete state space), a change of state can occur at any time instant. The associated point
Queuing Theory. Queuing Theory. Fatih Cavdur April 27, 2015
 Queuing Theory Fatih Cavdur fatihcavdur@uludag.edu.tr April 27, 2015 Introduction Introduction Simulation is often used in the analysis of queuing models. A simple but typical model is the single-server
Queuing Theory Fatih Cavdur fatihcavdur@uludag.edu.tr April 27, 2015 Introduction Introduction Simulation is often used in the analysis of queuing models. A simple but typical model is the single-server
Single-Server Service-Station (G/G/1)
 Service Engineering July 997 Last Revised January, 006 Single-Server Service-Station (G/G/) arrivals queue 000000000000 000000000000 departures Arrivals A = {A(t), t 0}, counting process, e.g., completely
Service Engineering July 997 Last Revised January, 006 Single-Server Service-Station (G/G/) arrivals queue 000000000000 000000000000 departures Arrivals A = {A(t), t 0}, counting process, e.g., completely
Queuing Analysis. Chapter Copyright 2010 Pearson Education, Inc. Publishing as Prentice Hall
 Queuing Analysis Chapter 13 13-1 Chapter Topics Elements of Waiting Line Analysis The Single-Server Waiting Line System Undefined and Constant Service Times Finite Queue Length Finite Calling Problem The
Queuing Analysis Chapter 13 13-1 Chapter Topics Elements of Waiting Line Analysis The Single-Server Waiting Line System Undefined and Constant Service Times Finite Queue Length Finite Calling Problem The
QUEUING SYSTEM. Yetunde Folajimi, PhD
 QUEUING SYSTEM Yetunde Folajimi, PhD Part 2 Queuing Models Queueing models are constructed so that queue lengths and waiting times can be predicted They help us to understand and quantify the effect of
QUEUING SYSTEM Yetunde Folajimi, PhD Part 2 Queuing Models Queueing models are constructed so that queue lengths and waiting times can be predicted They help us to understand and quantify the effect of
Module 5: CPU Scheduling
 Module 5: CPU Scheduling Basic Concepts Scheduling Criteria Scheduling Algorithms Multiple-Processor Scheduling Real-Time Scheduling Algorithm Evaluation 5.1 Basic Concepts Maximum CPU utilization obtained
Module 5: CPU Scheduling Basic Concepts Scheduling Criteria Scheduling Algorithms Multiple-Processor Scheduling Real-Time Scheduling Algorithm Evaluation 5.1 Basic Concepts Maximum CPU utilization obtained
Lecture 7: Simulation of Markov Processes. Pasi Lassila Department of Communications and Networking
 Lecture 7: Simulation of Markov Processes Pasi Lassila Department of Communications and Networking Contents Markov processes theory recap Elementary queuing models for data networks Simulation of Markov
Lecture 7: Simulation of Markov Processes Pasi Lassila Department of Communications and Networking Contents Markov processes theory recap Elementary queuing models for data networks Simulation of Markov
Chapter 6: CPU Scheduling
 Chapter 6: CPU Scheduling Basic Concepts Scheduling Criteria Scheduling Algorithms Multiple-Processor Scheduling Real-Time Scheduling Algorithm Evaluation 6.1 Basic Concepts Maximum CPU utilization obtained
Chapter 6: CPU Scheduling Basic Concepts Scheduling Criteria Scheduling Algorithms Multiple-Processor Scheduling Real-Time Scheduling Algorithm Evaluation 6.1 Basic Concepts Maximum CPU utilization obtained
Analysis of Software Artifacts
 Analysis of Software Artifacts System Performance I Shu-Ngai Yeung (with edits by Jeannette Wing) Department of Statistics Carnegie Mellon University Pittsburgh, PA 15213 2001 by Carnegie Mellon University
Analysis of Software Artifacts System Performance I Shu-Ngai Yeung (with edits by Jeannette Wing) Department of Statistics Carnegie Mellon University Pittsburgh, PA 15213 2001 by Carnegie Mellon University
CPU Scheduling. CPU Scheduler
 CPU Scheduling These slides are created by Dr. Huang of George Mason University. Students registered in Dr. Huang s courses at GMU can make a single machine readable copy and print a single copy of each
CPU Scheduling These slides are created by Dr. Huang of George Mason University. Students registered in Dr. Huang s courses at GMU can make a single machine readable copy and print a single copy of each
Classification of Queuing Models
 Classification of Queuing Models Generally Queuing models may be completely specified in the following symbol form:(a/b/c):(d/e)where a = Probability law for the arrival(or inter arrival)time, b = Probability
Classification of Queuing Models Generally Queuing models may be completely specified in the following symbol form:(a/b/c):(d/e)where a = Probability law for the arrival(or inter arrival)time, b = Probability
Contents Preface The Exponential Distribution and the Poisson Process Introduction to Renewal Theory
 Contents Preface... v 1 The Exponential Distribution and the Poisson Process... 1 1.1 Introduction... 1 1.2 The Density, the Distribution, the Tail, and the Hazard Functions... 2 1.2.1 The Hazard Function
Contents Preface... v 1 The Exponential Distribution and the Poisson Process... 1 1.1 Introduction... 1 1.2 The Density, the Distribution, the Tail, and the Hazard Functions... 2 1.2.1 The Hazard Function
Fuzzy Queues with Priority Discipline
 Applied Mathematical Sciences, Vol. 4,, no., 575-58 Fuzzy Queues with Priority Discipline W. Ritha* and Lilly Robert Department of Mathematics Holy Cross College (Autonomous) Trichirapalli, Tamilnadu,
Applied Mathematical Sciences, Vol. 4,, no., 575-58 Fuzzy Queues with Priority Discipline W. Ritha* and Lilly Robert Department of Mathematics Holy Cross College (Autonomous) Trichirapalli, Tamilnadu,
IOE 202: lectures 11 and 12 outline
 IOE 202: lectures 11 and 12 outline Announcements Last time... Queueing models intro Performance characteristics of a queueing system Steady state analysis of an M/M/1 queueing system Other queueing systems,
IOE 202: lectures 11 and 12 outline Announcements Last time... Queueing models intro Performance characteristics of a queueing system Steady state analysis of an M/M/1 queueing system Other queueing systems,
Section 7.3: Continuous RV Applications
 Section 7.3: Continuous RV Applications Discrete-Event Simulation: A First Course c 2006 Pearson Ed., Inc. 0-13-142917-5 Discrete-Event Simulation: A First Course Section 7.3: Continuous RV Applications
Section 7.3: Continuous RV Applications Discrete-Event Simulation: A First Course c 2006 Pearson Ed., Inc. 0-13-142917-5 Discrete-Event Simulation: A First Course Section 7.3: Continuous RV Applications
GI/M/1 and GI/M/m queuing systems
 GI/M/1 and GI/M/m queuing systems Dmitri A. Moltchanov moltchan@cs.tut.fi http://www.cs.tut.fi/kurssit/tlt-2716/ OUTLINE: GI/M/1 queuing system; Methods of analysis; Imbedded Markov chain approach; Waiting
GI/M/1 and GI/M/m queuing systems Dmitri A. Moltchanov moltchan@cs.tut.fi http://www.cs.tut.fi/kurssit/tlt-2716/ OUTLINE: GI/M/1 queuing system; Methods of analysis; Imbedded Markov chain approach; Waiting
4.7 Finite Population Source Model
 Characteristics 1. Arrival Process R independent Source All sources are identical Interarrival time is exponential with rate for each source No arrivals if all sources are in the system. OR372-Dr.Khalid
Characteristics 1. Arrival Process R independent Source All sources are identical Interarrival time is exponential with rate for each source No arrivals if all sources are in the system. OR372-Dr.Khalid
Elementary queueing system
 Elementary queueing system Kendall notation Little s Law PASTA theorem Basics of M/M/1 queue M/M/1 with preemptive-resume priority M/M/1 with non-preemptive priority 1 History of queueing theory An old
Elementary queueing system Kendall notation Little s Law PASTA theorem Basics of M/M/1 queue M/M/1 with preemptive-resume priority M/M/1 with non-preemptive priority 1 History of queueing theory An old
Non Markovian Queues (contd.)
 MODULE 7: RENEWAL PROCESSES 29 Lecture 5 Non Markovian Queues (contd) For the case where the service time is constant, V ar(b) = 0, then the P-K formula for M/D/ queue reduces to L s = ρ + ρ 2 2( ρ) where
MODULE 7: RENEWAL PROCESSES 29 Lecture 5 Non Markovian Queues (contd) For the case where the service time is constant, V ar(b) = 0, then the P-K formula for M/D/ queue reduces to L s = ρ + ρ 2 2( ρ) where
57:022 Principles of Design II Final Exam Solutions - Spring 1997
 57:022 Principles of Design II Final Exam Solutions - Spring 1997 Part: I II III IV V VI Total Possible Pts: 52 10 12 16 13 12 115 PART ONE Indicate "+" if True and "o" if False: + a. If a component's
57:022 Principles of Design II Final Exam Solutions - Spring 1997 Part: I II III IV V VI Total Possible Pts: 52 10 12 16 13 12 115 PART ONE Indicate "+" if True and "o" if False: + a. If a component's
Scheduling I. Today Introduction to scheduling Classical algorithms. Next Time Advanced topics on scheduling
 Scheduling I Today Introduction to scheduling Classical algorithms Next Time Advanced topics on scheduling Scheduling out there You are the manager of a supermarket (ok, things don t always turn out the
Scheduling I Today Introduction to scheduling Classical algorithms Next Time Advanced topics on scheduling Scheduling out there You are the manager of a supermarket (ok, things don t always turn out the
Kendall notation. PASTA theorem Basics of M/M/1 queue
 Elementary queueing system Kendall notation Little s Law PASTA theorem Basics of M/M/1 queue 1 History of queueing theory An old research area Started in 1909, by Agner Erlang (to model the Copenhagen
Elementary queueing system Kendall notation Little s Law PASTA theorem Basics of M/M/1 queue 1 History of queueing theory An old research area Started in 1909, by Agner Erlang (to model the Copenhagen
Introduction to Queueing Theory
 Introduction to Queueing Theory Raj Jain Washington University in Saint Louis Jain@eecs.berkeley.edu or Jain@wustl.edu A Mini-Course offered at UC Berkeley, Sept-Oct 2012 These slides and audio/video recordings
Introduction to Queueing Theory Raj Jain Washington University in Saint Louis Jain@eecs.berkeley.edu or Jain@wustl.edu A Mini-Course offered at UC Berkeley, Sept-Oct 2012 These slides and audio/video recordings
Queueing. Chapter Continuous Time Markov Chains 2 CHAPTER 5. QUEUEING
 2 CHAPTER 5. QUEUEING Chapter 5 Queueing Systems are often modeled by automata, and discrete events are transitions from one state to another. In this chapter we want to analyze such discrete events systems.
2 CHAPTER 5. QUEUEING Chapter 5 Queueing Systems are often modeled by automata, and discrete events are transitions from one state to another. In this chapter we want to analyze such discrete events systems.
Generation of Discrete Random variables
 Simulation Simulation is the imitation of the operation of a realworld process or system over time. The act of simulating something first requires that a model be developed; this model represents the key
Simulation Simulation is the imitation of the operation of a realworld process or system over time. The act of simulating something first requires that a model be developed; this model represents the key
Control of Fork-Join Networks in Heavy-Traffic
 in Heavy-Traffic Asaf Zviran Based on MSc work under the guidance of Rami Atar (Technion) and Avishai Mandelbaum (Technion) Industrial Engineering and Management Technion June 2010 Introduction Network
in Heavy-Traffic Asaf Zviran Based on MSc work under the guidance of Rami Atar (Technion) and Avishai Mandelbaum (Technion) Industrial Engineering and Management Technion June 2010 Introduction Network
UNIVERSITY OF YORK. MSc Examinations 2004 MATHEMATICS Networks. Time Allowed: 3 hours.
 UNIVERSITY OF YORK MSc Examinations 2004 MATHEMATICS Networks Time Allowed: 3 hours. Answer 4 questions. Standard calculators will be provided but should be unnecessary. 1 Turn over 2 continued on next
UNIVERSITY OF YORK MSc Examinations 2004 MATHEMATICS Networks Time Allowed: 3 hours. Answer 4 questions. Standard calculators will be provided but should be unnecessary. 1 Turn over 2 continued on next
Verification and Validation. CS1538: Introduction to Simulations
 Verification and Validation CS1538: Introduction to Simulations Steps in a Simulation Study Problem & Objective Formulation Model Conceptualization Data Collection Model translation, Verification, Validation
Verification and Validation CS1538: Introduction to Simulations Steps in a Simulation Study Problem & Objective Formulation Model Conceptualization Data Collection Model translation, Verification, Validation
Waiting Line Models: Queuing Theory Basics. Metodos Cuantitativos M. En C. Eduardo Bustos Farias 1
 Waiting Line Models: Queuing Theory Basics Cuantitativos M. En C. Eduardo Bustos Farias 1 Agenda Queuing system structure Performance measures Components of queuing systems Arrival process Service process
Waiting Line Models: Queuing Theory Basics Cuantitativos M. En C. Eduardo Bustos Farias 1 Agenda Queuing system structure Performance measures Components of queuing systems Arrival process Service process
The Transition Probability Function P ij (t)
 The Transition Probability Function P ij (t) Consider a continuous time Markov chain {X(t), t 0}. We are interested in the probability that in t time units the process will be in state j, given that it
The Transition Probability Function P ij (t) Consider a continuous time Markov chain {X(t), t 0}. We are interested in the probability that in t time units the process will be in state j, given that it
Figure 10.1: Recording when the event E occurs
 10 Poisson Processes Let T R be an interval. A family of random variables {X(t) ; t T} is called a continuous time stochastic process. We often consider T = [0, 1] and T = [0, ). As X(t) is a random variable
10 Poisson Processes Let T R be an interval. A family of random variables {X(t) ; t T} is called a continuous time stochastic process. We often consider T = [0, 1] and T = [0, ). As X(t) is a random variable
Stationary remaining service time conditional on queue length
 Stationary remaining service time conditional on queue length Karl Sigman Uri Yechiali October 7, 2006 Abstract In Mandelbaum and Yechiali (1979) a simple formula is derived for the expected stationary
Stationary remaining service time conditional on queue length Karl Sigman Uri Yechiali October 7, 2006 Abstract In Mandelbaum and Yechiali (1979) a simple formula is derived for the expected stationary
6 Solving Queueing Models
 6 Solving Queueing Models 6.1 Introduction In this note we look at the solution of systems of queues, starting with simple isolated queues. The benefits of using predefined, easily classified queues will
6 Solving Queueing Models 6.1 Introduction In this note we look at the solution of systems of queues, starting with simple isolated queues. The benefits of using predefined, easily classified queues will
2/5/07 CSE 30341: Operating Systems Principles
 page 1 Shortest-Job-First (SJR) Scheduling Associate with each process the length of its next CPU burst. Use these lengths to schedule the process with the shortest time Two schemes: nonpreemptive once
page 1 Shortest-Job-First (SJR) Scheduling Associate with each process the length of its next CPU burst. Use these lengths to schedule the process with the shortest time Two schemes: nonpreemptive once
THE STRUCTURE AND PERFORMANCE OF OPTIMAL ROUTING SEQUENCES. Proefschrift
 THE STRUCTURE AND PERFORMANCE OF OPTIMAL ROUTING SEQUENCES Proefschrift ter verkrijging van de graad van Doctor aan de Universiteit Leiden, op gezag van de Rector Magnificus Dr. D. D. Breimer, hoogleraar
THE STRUCTURE AND PERFORMANCE OF OPTIMAL ROUTING SEQUENCES Proefschrift ter verkrijging van de graad van Doctor aan de Universiteit Leiden, op gezag van de Rector Magnificus Dr. D. D. Breimer, hoogleraar
Sandwich shop : a queuing net work with finite disposable resources queue and infinite resources queue
 Sandwich shop : a queuing net work with finite disposable resources queue and infinite resources queue Final project for ISYE 680: Queuing systems and Applications Hongtan Sun May 5, 05 Introduction As
Sandwich shop : a queuing net work with finite disposable resources queue and infinite resources queue Final project for ISYE 680: Queuing systems and Applications Hongtan Sun May 5, 05 Introduction As
Solutions to COMP9334 Week 8 Sample Problems
 Solutions to COMP9334 Week 8 Sample Problems Problem 1: Customers arrive at a grocery store s checkout counter according to a Poisson process with rate 1 per minute. Each customer carries a number of items
Solutions to COMP9334 Week 8 Sample Problems Problem 1: Customers arrive at a grocery store s checkout counter according to a Poisson process with rate 1 per minute. Each customer carries a number of items
Data analysis and stochastic modeling
 Data analysis and stochastic modeling Lecture 7 An introduction to queueing theory Guillaume Gravier guillaume.gravier@irisa.fr with a lot of help from Paul Jensen s course http://www.me.utexas.edu/ jensen/ormm/instruction/powerpoint/or_models_09/14_queuing.ppt
Data analysis and stochastic modeling Lecture 7 An introduction to queueing theory Guillaume Gravier guillaume.gravier@irisa.fr with a lot of help from Paul Jensen s course http://www.me.utexas.edu/ jensen/ormm/instruction/powerpoint/or_models_09/14_queuing.ppt
Intro to Queueing Theory
 1 Intro to Queueing Theory Little s Law M/G/1 queue Conservation Law 1/31/017 M/G/1 queue (Simon S. Lam) 1 Little s Law No assumptions applicable to any system whose arrivals and departures are observable
1 Intro to Queueing Theory Little s Law M/G/1 queue Conservation Law 1/31/017 M/G/1 queue (Simon S. Lam) 1 Little s Law No assumptions applicable to any system whose arrivals and departures are observable
Scheduling I. Today. Next Time. ! Introduction to scheduling! Classical algorithms. ! Advanced topics on scheduling
 Scheduling I Today! Introduction to scheduling! Classical algorithms Next Time! Advanced topics on scheduling Scheduling out there! You are the manager of a supermarket (ok, things don t always turn out
Scheduling I Today! Introduction to scheduling! Classical algorithms Next Time! Advanced topics on scheduling Scheduling out there! You are the manager of a supermarket (ok, things don t always turn out
Lecture 20: Reversible Processes and Queues
 Lecture 20: Reversible Processes and Queues 1 Examples of reversible processes 11 Birth-death processes We define two non-negative sequences birth and death rates denoted by {λ n : n N 0 } and {µ n : n
Lecture 20: Reversible Processes and Queues 1 Examples of reversible processes 11 Birth-death processes We define two non-negative sequences birth and death rates denoted by {λ n : n N 0 } and {µ n : n
A Fuzzy Approach to Priority Queues
 International Journal of Fuzzy Mathematics and Systems. ISSN 2248-9940 Volume 2, Number 4 (2012), pp. 479-488 Research India Publications http://www.ripublication.com A Fuzzy Approach to Priority Queues
International Journal of Fuzzy Mathematics and Systems. ISSN 2248-9940 Volume 2, Number 4 (2012), pp. 479-488 Research India Publications http://www.ripublication.com A Fuzzy Approach to Priority Queues
Introduction to queuing theory
 Introduction to queuing theory Claude Rigault ENST claude.rigault@enst.fr Introduction to Queuing theory 1 Outline The problem The number of clients in a system The client process Delay processes Loss
Introduction to queuing theory Claude Rigault ENST claude.rigault@enst.fr Introduction to Queuing theory 1 Outline The problem The number of clients in a system The client process Delay processes Loss
Simulation of Process Scheduling Algorithms
 Simulation of Process Scheduling Algorithms Project Report Instructor: Dr. Raimund Ege Submitted by: Sonal Sood Pramod Barthwal Index 1. Introduction 2. Proposal 3. Background 3.1 What is a Process 4.
Simulation of Process Scheduling Algorithms Project Report Instructor: Dr. Raimund Ege Submitted by: Sonal Sood Pramod Barthwal Index 1. Introduction 2. Proposal 3. Background 3.1 What is a Process 4.
Queuing Theory. 3. Birth-Death Process. Law of Motion Flow balance equations Steady-state probabilities: , if
 1 Queuing Theory 3. Birth-Death Process Law of Motion Flow balance equations Steady-state probabilities: c j = λ 0λ 1...λ j 1 µ 1 µ 2...µ j π 0 = 1 1+ j=1 c j, if j=1 c j is finite. π j = c j π 0 Example
1 Queuing Theory 3. Birth-Death Process Law of Motion Flow balance equations Steady-state probabilities: c j = λ 0λ 1...λ j 1 µ 1 µ 2...µ j π 0 = 1 1+ j=1 c j, if j=1 c j is finite. π j = c j π 0 Example
CSCE 313 Introduction to Computer Systems. Instructor: Dezhen Song
 CSCE 313 Introduction to Computer Systems Instructor: Dezhen Song Schedulers in the OS CPU Scheduling Structure of a CPU Scheduler Scheduling = Selection + Dispatching Criteria for scheduling Scheduling
CSCE 313 Introduction to Computer Systems Instructor: Dezhen Song Schedulers in the OS CPU Scheduling Structure of a CPU Scheduler Scheduling = Selection + Dispatching Criteria for scheduling Scheduling
Homework 1 - SOLUTION
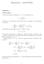 Homework - SOLUTION Problem M/M/ Queue ) Use the fact above to express π k, k > 0, as a function of π 0. π k = ( ) k λ π 0 µ 2) Using λ < µ and the fact that all π k s sum to, compute π 0 (as a function
Homework - SOLUTION Problem M/M/ Queue ) Use the fact above to express π k, k > 0, as a function of π 0. π k = ( ) k λ π 0 µ 2) Using λ < µ and the fact that all π k s sum to, compute π 0 (as a function
Chapter 1. Introduction. 1.1 Stochastic process
 Chapter 1 Introduction Process is a phenomenon that takes place in time. In many practical situations, the result of a process at any time may not be certain. Such a process is called a stochastic process.
Chapter 1 Introduction Process is a phenomenon that takes place in time. In many practical situations, the result of a process at any time may not be certain. Such a process is called a stochastic process.
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.265/15.070J Fall 2013 Lecture 22 12/09/2013. Skorokhod Mapping Theorem. Reflected Brownian Motion
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.265/15.7J Fall 213 Lecture 22 12/9/213 Skorokhod Mapping Theorem. Reflected Brownian Motion Content. 1. G/G/1 queueing system 2. One dimensional reflection mapping
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.265/15.7J Fall 213 Lecture 22 12/9/213 Skorokhod Mapping Theorem. Reflected Brownian Motion Content. 1. G/G/1 queueing system 2. One dimensional reflection mapping
The Queue Inference Engine and the Psychology of Queueing. ESD.86 Spring 2007 Richard C. Larson
 The Queue Inference Engine and the Psychology of Queueing ESD.86 Spring 2007 Richard C. Larson Part 1 The Queue Inference Engine QIE Queue Inference Engine (QIE) Boston area ATMs: reams of data Standard
The Queue Inference Engine and the Psychology of Queueing ESD.86 Spring 2007 Richard C. Larson Part 1 The Queue Inference Engine QIE Queue Inference Engine (QIE) Boston area ATMs: reams of data Standard
Introduction to Markov Chains, Queuing Theory, and Network Performance
 Introduction to Markov Chains, Queuing Theory, and Network Performance Marceau Coupechoux Telecom ParisTech, departement Informatique et Réseaux marceau.coupechoux@telecom-paristech.fr IT.2403 Modélisation
Introduction to Markov Chains, Queuing Theory, and Network Performance Marceau Coupechoux Telecom ParisTech, departement Informatique et Réseaux marceau.coupechoux@telecom-paristech.fr IT.2403 Modélisation
I, A BRIEF REVIEW ON INFINITE QUEUE MODEL M.
 A BRIEF REVIEW ON INFINITE QUEUE MODEL M. Vasuki*, A. Dinesh Kumar** & G. Vijayaprabha** * Assistant Professor, Department of Mathematics, Srinivasan College of Arts and Science, Perambalur, Tamilnadu
A BRIEF REVIEW ON INFINITE QUEUE MODEL M. Vasuki*, A. Dinesh Kumar** & G. Vijayaprabha** * Assistant Professor, Department of Mathematics, Srinivasan College of Arts and Science, Perambalur, Tamilnadu
Chapter 10. Queuing Systems. D (Queuing Theory) Queuing theory is the branch of operations research concerned with waiting lines.
 Chapter 10 Queuing Systems D. 10. 1. (Queuing Theory) Queuing theory is the branch of operations research concerned with waiting lines. D. 10.. (Queuing System) A ueuing system consists of 1. a user source.
Chapter 10 Queuing Systems D. 10. 1. (Queuing Theory) Queuing theory is the branch of operations research concerned with waiting lines. D. 10.. (Queuing System) A ueuing system consists of 1. a user source.
Routing and Staffing in Large-Scale Service Systems: The Case of Homogeneous Impatient Customers and Heterogeneous Servers 1
 Routing and Staffing in Large-Scale Service Systems: The Case of Homogeneous Impatient Customers and Heterogeneous Servers 1 Mor Armony 2 Avishai Mandelbaum 3 June 25, 2008 Abstract Motivated by call centers,
Routing and Staffing in Large-Scale Service Systems: The Case of Homogeneous Impatient Customers and Heterogeneous Servers 1 Mor Armony 2 Avishai Mandelbaum 3 June 25, 2008 Abstract Motivated by call centers,
NEW FRONTIERS IN APPLIED PROBABILITY
 J. Appl. Prob. Spec. Vol. 48A, 209 213 (2011) Applied Probability Trust 2011 NEW FRONTIERS IN APPLIED PROBABILITY A Festschrift for SØREN ASMUSSEN Edited by P. GLYNN, T. MIKOSCH and T. ROLSKI Part 4. Simulation
J. Appl. Prob. Spec. Vol. 48A, 209 213 (2011) Applied Probability Trust 2011 NEW FRONTIERS IN APPLIED PROBABILITY A Festschrift for SØREN ASMUSSEN Edited by P. GLYNN, T. MIKOSCH and T. ROLSKI Part 4. Simulation
Che-Wei Chang Department of Computer Science and Information Engineering, Chang Gung University
 Che-Wei Chang chewei@mail.cgu.edu.tw Department of Computer Science and Information Engineering, Chang Gung University } 2017/11/15 Midterm } 2017/11/22 Final Project Announcement 2 1. Introduction 2.
Che-Wei Chang chewei@mail.cgu.edu.tw Department of Computer Science and Information Engineering, Chang Gung University } 2017/11/15 Midterm } 2017/11/22 Final Project Announcement 2 1. Introduction 2.
λ, µ, ρ, A n, W n, L(t), L, L Q, w, w Q etc. These
 Queuing theory models systems with servers and clients (presumably waiting in queues). Notation: there are many standard symbols like λ, µ, ρ, A n, W n, L(t), L, L Q, w, w Q etc. These represent the actual
Queuing theory models systems with servers and clients (presumably waiting in queues). Notation: there are many standard symbols like λ, µ, ρ, A n, W n, L(t), L, L Q, w, w Q etc. These represent the actual
Solutions to Homework Discrete Stochastic Processes MIT, Spring 2011
 Exercise 6.5: Solutions to Homework 0 6.262 Discrete Stochastic Processes MIT, Spring 20 Consider the Markov process illustrated below. The transitions are labelled by the rate q ij at which those transitions
Exercise 6.5: Solutions to Homework 0 6.262 Discrete Stochastic Processes MIT, Spring 20 Consider the Markov process illustrated below. The transitions are labelled by the rate q ij at which those transitions
THE HEAVY-TRAFFIC BOTTLENECK PHENOMENON IN OPEN QUEUEING NETWORKS. S. Suresh and W. Whitt AT&T Bell Laboratories Murray Hill, New Jersey 07974
 THE HEAVY-TRAFFIC BOTTLENECK PHENOMENON IN OPEN QUEUEING NETWORKS by S. Suresh and W. Whitt AT&T Bell Laboratories Murray Hill, New Jersey 07974 ABSTRACT This note describes a simulation experiment involving
THE HEAVY-TRAFFIC BOTTLENECK PHENOMENON IN OPEN QUEUEING NETWORKS by S. Suresh and W. Whitt AT&T Bell Laboratories Murray Hill, New Jersey 07974 ABSTRACT This note describes a simulation experiment involving
10.2 For the system in 10.1, find the following statistics for population 1 and 2. For populations 2, find: Lq, Ls, L, Wq, Ws, W, Wq 0 and SL.
 Bibliography Asmussen, S. (2003). Applied probability and queues (2nd ed). New York: Springer. Baccelli, F., & Bremaud, P. (2003). Elements of queueing theory: Palm martingale calculus and stochastic recurrences
Bibliography Asmussen, S. (2003). Applied probability and queues (2nd ed). New York: Springer. Baccelli, F., & Bremaud, P. (2003). Elements of queueing theory: Palm martingale calculus and stochastic recurrences
7. Queueing Systems. 8. Petri nets vs. State Automata
 Petri Nets 1. Finite State Automata 2. Petri net notation and definition (no dynamics) 3. Introducing State: Petri net marking 4. Petri net dynamics 5. Capacity Constrained Petri nets 6. Petri net models
Petri Nets 1. Finite State Automata 2. Petri net notation and definition (no dynamics) 3. Introducing State: Petri net marking 4. Petri net dynamics 5. Capacity Constrained Petri nets 6. Petri net models
