On a Grouping Method for Constructing Mixed Orthogonal Arrays
|
|
|
- Annabel Sherman
- 6 years ago
- Views:
Transcription
1 Ope Joural of Saiic hp://dxdoiorg/1046/oj010 Publihed Olie April 01 (hp://wwwscirporg/joural/oj) O a Groupig Mehod for Corucig Mixed Orhogoal Array Chug-Yi Sue Depare of Maheaic Clevelad Sae Uiveriy Clevelad USA Eail: cue@cuohioedu Received Jauary 0 01; revied February 19 01; acceped March 8 01 ABSTRACT Mixed orhogoal array of regh wo ad ize are coruced by groupig poi i he fiie projecive geoery PG 1 PG 1 ca be pariioed io fla i aociaed wih a poi i PG 1 -fla uch ha each A orhogoal array 1 1 uig 1 1 poi i PG 1 fla over GF() if i i ioorphic o PG 1 If here exi a A e of 1 1 poi i ca be coruced by PG i called a 1 - -fla over GF() i PG 1 he we ca replace he correpodig by 1 1 -level colu ad obai a ixed orhogoal array May ew ixed orhogoal array ca be obaied by hi procedure I hi paper we udy ehod for fidig dijoi 1 -fla over GF() i PG 1 i order o co- ruc ore ixed orhogoal array of regh wo I paricular if ad are relaively prie he we ca co- 1 ruc a i 1 i for ay 0 i New orhogoal array of ize ad 104 are obaied by uig PG(7 ) PG(8 ) ad PG(9 ) repecively -level colu i 1 1 Keyword: Fiie Field; Fiie Projecive Geoery; 1 -Fla over GF() i PG 1 ; Geoeric Orhogoal Array; Marix Repreeaio; Miial Polyoial; Orhogoal Mai-Effec Pla; Priiive Elee; Tigh 1 Iroducio Orhogoal array of regh wo are ued a orhogoal ai-effec pla i fracioal facorial experie I a orhogoal ai-effec pla he ai effec of each facor ca be opially eiaed auig he ieracio of all facor are egligible e N 1 k deoe a orhogoal array of regh wo wih N row k colu ad i level i he ih colu for i 1 k I every N ubarray of N 1 k all poible cobiaio of level occur equally ofe a row I i kow ha N 1 i 1 i a N 1k ad he orhogoal array i called igh if he equaliy hold Orhogoal array N 1 k i called yeric if 1 oherwie i i called k ayeric or ixed Syeric orhogoal array have bee coruced i [1-] Mixed orhogoal array were iroduced i [4] ad hey have draw he aeio of ay reearcher i rece year Mehod for corucig ixed orhogoal array of regh wo have bee developed i [5-9] ad ay oher auhor Thee ehod ue Hadaard arice differece chee geeralized Kroecker u fiie projecive geoerie ad orhogoal projecio arice We refer o [10] for ore corucio ad applicaio of orhogoal array The ehod of groupig wa ued i [11] o replace hree wo-level colu i yeric orhogoal array by oe four-level colu for corucig ixed orhogoal array havig wo-level ad four-level colu A yeaic ehod [1] wa developed for ideifyig Copyrigh 01 SciRe
2 C-Y SUEN 189 dijoi e of hree wo-level colu for corucig N ( 4 ) The ehod wa geeralized i [6] for co- rucig 1 k r1 r where i a prie power Mixed orhogoal array of regh were coruced by uig ixed pread of regh i fiie geoerie i [1] Thi ehod wa alo idepedely dicovered i [14] for corucig ixed orhogoal array of regh hree ad four Orhogoal array coruced by hi ehod are called geoeric Geoeric orhogoal array 64 ( ) 64 ( ) 64 ( ) ad 64 ( ) were coruced i [1] However he ehod i rericed o corucig ixed orhogoal array wih he uber of level i each colu a power of I hi paper we hall ue fiie projecive geoerie o develop a geeral procedure for corucig ore ixed orhogoal array Moreover he procedure allow u o coruc ixed orhogoal array wih he uber of level i each colu a power of ay give prie uber We ar wih a yeric orhogoal array 1 1 ad he coruc ixed orhogoal array by replacig a group of colu wih aoher group of colu Our groupig ehod ue properie of fiie projecive geoerie which i differe fro he groupig ehod i [6] Hece we are able o obai oe ew erie of ixed orhogoal array Geoeric Orhogoal Array For r 1 ad a prie power le PG r 1 deoe he r 1-dieioal fiie projecive geoery over he Galoi field GF() A poi i PG r 1 i deoed by a r-uple x 1 xr where x i are elee of GF() ad a lea oe x i i o 0 Two r-uple repree he ae poi i PG r 1 if oe i a uliple r of he oher Hece here are 1 1 poi i PG r 1 A 1 -fla i PG r 1 i a e of 1 1 poi which are liear cobiaio of idepede poi A pread F of 1-fla of PG r 1 i a e of 1-fla which pariio PG r 1 I i kow [15] ha here exi a pread F of 1-fla of PG r 1 if ad oly if divide r We call a e of fla F1 Fk a ixed pread of PG r 1 if i pariio PG r 1 ad a lea wo fla i F have differe dieio Mixed pread are ueful for corucig ixed orhogoal array of regh wo Specifically we give he followig heore for corucig a orhogoal array fro a (ixed) pread The heore i he pecial cae of regh wo of Theore 1 [14] i fiie projecive geoery laguage Theore 1 e F 1 Fk of PG r 1 be a (ixed) pread where F i i a i 1-fla for i 1 k The we ca coruc a orhogoal array 1 k r We ow decribe he procedure o coruc he orhogoal array i Theore 1 For i 1 k le G i be a r i arix uch ha he i colu are ay choice of i idepede poi of he i 1-fla F i e G be he r i arix k G1 Gk The r 1 coi of r row which are he elee of he row pace of G where he i -level colu of G i i replaced by a i -level colu for each i 1 k We call orhogoal array geoeric if hey ca be obaied by Theore 1 Geoeric orhogoal array have bee coruced i [1 9116] Exaple of geoeric orhogoal array are: r 1 1 1) r ; ) r 1 1 r if divide r; r 1 r ) r if r ; ad k l 4) r where 1 1 j l 1 1 k j i j 1 r i j 0 j Mai Reul I i proved i ea 1 [1] ha if V 1 V V are hree dijoi 1 -fla of PG 1 he heir uio ca be regrouped io 1 dijoi 1-fla Hece hree 1 -level colu i a ca be replaced by 1 4-level colu By applyig hi reul o a pread of -fla of PG(5 ) 64 ( ) ad 64 ( ) were coruced Geeralizig he idea we would like o fid a ufficie codiio ha a e of fla i PG 1 ca be regrouped io a e of fla Sice here exi a pread of 1-fla of PG 1 we ca by Theore 1 coruc a If here exi 1 -fla i he pread uch ha heir uio ca be 1 1 -fla he we 1 regrouped io ca replace he correpodig 1 1 -level Copyrigh 01 SciRe
3 190 C-Y SUEN colu i he by -level colu ad obai a By repeaig hi proce ay orhogoal array ca be obaied Fir we would like o eablih a oe-o-oe corre podece bewee he 1 1 dijoi 1 - fla i PG 1 ad he 1 1 poi i PG 1 e ω be a priiive elee of GF( ) ad le he iiu polyoial of GF be where 0 1 are elee of GF() The copaio arix of he iiu polyoial i a arix W If ω i a priiive elee of GF he 01 are he elee of GF The elee of GF ca be repreeed by arice wih erie fro GF() The elee ω i i repreeed by W i ad he elee 0 ad 1 are repreeed by he zero arix ad he ideiy arix repecively Deoe he arix repreeaio of a elee x i GF by W(x) e each poi x 1 x PG 1 correpod o he 1 PG 1 -fla i which coi of poi ha are liear cobiaio of row vecor of he arix W x1 W x over GF() I ca be how ha he fla correpodig o he 1 1 poi of PG 1 pariio PG 1 Thi eablihe a oe-o-oe corre podece bewee he 1 1 dijoi 1-fla i PG 1 ad he 1 1 poi i PG 1 Defiiio 1 A e of 1 1 poi i PG 1 i aid o be a 1 -fla over GF() if i i poible o fid coordiae for hi e of 1 1 poi uch ha i i ioorphic o PG 1 over GF() i Noe ha wheher a e of 1 1 poi i PG 1 i ioorphic o PG 1 over GF() deped o oly o he choice of he poi bu alo o he choice of he coordiae for hee poi For exa- ple he e S1 1 1 i Exaple 1 (give afer Theore ) i a 1-fla over GF() i PG 1 8 ice i i ioorphic o PG 1 over GF() Bu if we chooe differe coordiae for 4 S he i i o ioorphic o PG 1 over GF() Hece i i ipora o pecify he correc coordiae whe a 1 -fla over GF() i PG 1 i eioed Alo we oe ha i i poible o have > for a 1 -fla over GF() i PG 1 For exaple S 1 ad S i Exaple (give afer Theore ) are -fla over GF() i PG 1 16 We ow give a ufficie codiio ha a e of 1 1 dijoi 1 -fla i PG 1 ca be regrouped io a e of 1 1 dijoi 1 -fla Theore A e of 1 1 dijoi 1 - fla i PG 1 ca be regrouped io a e of fla if he e of dijoi 1 1 correpodig poi i PG 1 i a 1 -fla over GF() Proof e he coordiae of he 1 1 correpodig poi of he 1 -fla over GF() i PG 1 x x for be 1j j j 1 Alo le be a arix uch ha he row are he poi of PG 1 The he 1 -fla i PG 1 correpodig o he poi x 1 j xj coi of poi which are he row of he 1 1 arix M j W x1 j W x j where W(x) i he arix repreeaio of x We ca verify ha for each i poi he e of which coi of he ih row of M M 1 i a fla i PG(-1 ) Noe ha i geeral here are ore way of regroupig 1 1 dijoi 1-fla i a e of Copyrigh 01 SciRe
4 C-Y SUEN 191 PG 1 io dijoi fla if he 1 1 i a 1-fla over GF() e P ij be he poi i PG 1 wih he ih row of M j a i coordiae The array of poi P P ij ha he followig properie: 1) Each row (colu) of P i a 1-fla ( 1 - fla) u 1 1 poi i a give row (colu) correpodig poi i PG 1 ) If for a 1 u u -fla he he 1 1 poi a he ae poiio i ay oher row (colu) alo for a u 1-fla For exaple if here exi a -fla over GF() i PG(1 16) he each of he 7 poi i he -fla over GF() correpod o 15 poi i PG(7 ) The 105 poi i PG(7 ) correpodig o he -fla over GF() i PG(1 16) ca be arraged io a 15 7 array uch ha each row i a -fla ad each colu i a -fla Sice a -fla ca be pariioed io five 1-fla he 15 7 array of poi ca be pariioed io five 7 ubarray uch ha each colu i a 1-fla ad each row i a -fla Alo coider a 15 ubarray of he 15 7 array uch ha each row i a 1-fla We ca elec a 7 ubarray uch ha each colu i a -fla Each of he reaiig eigh row i a 1-fla Hece he 15 ubarray ca be pariioed io hree -fla ad eigh 1-fla Therefore hee 105 poi ca be grouped io: 1) 7 i -fla ad 5i 1-fla for i 0 7 ; ) 15 i -fla ad 7i 1-fla for i 0 5 ; or ) four -fla hree -fla ad eigh 1-fla 6 Exaple 1 e 01 be he 8 elee of GF(8) wih 1 Coider PG(1 8) wih ie poi (0 1) (1 0) (1 1) (1 ω) (1 ω ) (1 ω ) (1 ω 4 ) (1 ω 5 ) ad (1 ω 6 ) Each poi of PG(1 8) correpod o a -fla i PG(5 ) ad he ie -fla pariio PG(5 ) We ca coruc a 64 (8 9 ) by Theore 1 e S1 1 1 S 1 1 S ad We ca verify ha S 1 S ad S are dijoi 1-fla over GF() i PG(1 8) The arix repreeaio W of ω ad he 7 arix give i he proof of Theore are W ; The hree poi of S 1 correpod o he hree -fla i PG(5 ) which are row of he followig hree arice M 1 M ad M repecively M1 W 1 W M W W M W W We oberve ha for each i 1 7 he ih row of M 1 M ad M are hree poi of a 1-fla i PG(5 ) Hece we ca replace he hree 8-level colu correpodig o S 1 i 64 (8 9 ) by eve 4-level colu o obai a ( ) Coiuig hi procedure we ca replace he hree 8-level colu correpodig o S i 64 ( ) by eve 4-level colu o obai a 64 ( ) Noe ha 64 ( ) ad 64 ( ) were alo coruc i [1] uig a differe ehod However Theore i ore veraile a how i followig exaple 14 Exaple e 01 be he 16 elee of GF(16) wih 4 1 Coider PG(1 16) wih 17 poi (0 1) (1 0) (1 1) (1 ω) (1 ω 14 ) Each poi of PG(1 16) correpod o a -fla i PG(7 ) ad he eveee -fla pariio PG(7 ) We ca coruc a 56 (16 17 ) by Theore 1 e S1 1 1 S 1 T Copyrigh 01 SciRe
5 19 C-Y SUEN ad T 1 1 xw i xw j xw i W j xw l T T 1 1 T 1 1 T We ca verify ha S 1 ad S are dijoi -fla ad T1 T5 are dijoi 1-fla over GF() i PG(1 16) Moreover S 1 S ad T 1 pariio PG(1 16) By he difollowig Theore we ca replace he ubar- cuio ray 56 (16 7 ) correpodig o S 1 or S i 56 (16 17 ) by 56 ( ) or 56 (8 15-i 4 7i ) 0 i 5 Siilarly we ca replace he ubarray 56 (16 ) correpodig o T1 T5 i 56 (16 17 ) by 56 (8 4 8 ) May ixed orhogoal array uch a 56 ( ) 56 ( ) 56 ( ) 56 ( ) 56 ( ) 56 ( ) 56 ( ) ca be obaied by hi procedure 4 Corucio of More Orhogoal Array I hi ecio ehod for fidig dijoi fla over GF() i PG 1 are developed o coruc ore orhogoa l array e α be a priiive elee of GF( ) ad le he arix repreeaio of α i GF() be W Sice ad i a elee of GF() W i he arix repreeaio of we have W I where I i he ideiy arix The for ay fixed poi x x 1 x i PG 1 he e i S xw : i 0 co i a o 1 1 poi x a 1 1 i PG 1 ice ( x I x) ad x repree he ae poi Moreover if β ad γ are ay elee of GF() ad xw i ad xw j are elee of S x he xw for oe l ice i j i βw + γw i he arix repreeaio of he elee βα + γα j of GF S x ha he rucure of a fla over GF() i 1 PG ice liear cobiaio of poi i S x are alo poi i S x I fac S x i a 1-fla over GF PG 1 if ad oly if he uber of () i poi i S x i 1 1 x ad y are wo poi i PG 1 for oe ieger Now if ad Sx Sy he here exi i ad j uch ha xw i = yw j i j We have y xw S x hece S x = Sy PG 1 ad le Theore e x be a poi i i x xw : i 0 1 i PG 1 uber of S x i 1 1 ay wo poi x ad y i PG 1 or Sx Sy Hece PG 1 S The S x i a -fla over GF() if ad oly if he poi i for oe ieger Moreover for eiher S x = S y ca be pariioed io dijoi e of S x Exaple We illurae how we obai he hree di- joi 1-fla over GF() i PG(1 8) i Exaple 1 e ω be a priiive elee of GF(8) wih ω = ω + 1 ad le α be a priiive elee of GF(4) wih α = α + 1 ad arix repreeaio The 0 1 W 1 1 S W 01W S 1 1 W 1 1 W 1 1 ad S 1 1 W 1 W S GF(4) 8 8 S S ad S ve dijoi 1-fla over GF() are T Exaple Theore 4 If i a prie power a 8 8 relaively prie he we ca coruc ixe 1 1 are hree dijoi 1-fla over GF() i PG(1 8) Exaple 4 e ω be a priiive elee of GF(16) wih ω 4 = ω + 1 ad le α be a priiive elee of wih α = α + 1 ad arix repreeaio W give i Exaple The 17 poi of PG(1 16) ca be pariioed io he followig fla over GF(): S S S 1 1 The fi T i array 1 5 d ad are d orhogoal Copyrigh 01 SciRe
6 C-Y SUEN 19 1 i 1 1 i for i Proof We ca coruc a 1 1 fro PG 1 Fro he proof of Theore 46 [15] if ad are relaively prie he S x i a 1 -fla over GF() i PG 1 for PG 1 PG 1 riioed io poi x i every Hece ca be pa 1-fla over GF() Each S x repree 1 1 -level colu i 1 1 ad by Theore i ca be re- placed by 1 1 -level colu The followig reul which follow fro Theore 4 i a geeralizaio of Theore 4 Corollary 1 If i a prie power ad d i he greae coo divior of ieger ad he we ca coruc ixed orhogoal array d d 1 1 d i 1 1 i 1 1 for 0 d d i Proof If d i he greae coo divior of ad he d ad d are relaively prie By ubiud d ad d repecively i ig ad wih Theore 4 we obai he ixed orhogoal array By uig Theore 4 ad Corollary 1 we obai he followig ew erie of igh orhogoal array for ay prie power 1) 6 ) 10 1 i 1 0 i + 1; 10 1 i ) i i i 1 ; 1 i i i 1 ; 4) i i 4 + 1; 14 1 i ) 6) i i i 1 i i 1 1 ; ad i 1 1 The followig heore give a e of 1 dijoi 1 -fla over GF() i PG(1 ) Theore 5 For i 0 le Ti i : GF \ 0 ive elee of GF The T T 0 are 1 di- joi 1 -fla over GF() i PG (1 ) Proof Ti i a e of 1 1 poi i PG(1 i i ( ) ice where ω i a prii- ) repree he ae poi for each ozero elee α of GF() To how ha T i i a 1 -fla over GF( ) we prove ha ay liear cobiaio of elee i Ti i agai i T i If i i GF he 1 1 T i ad 1 i i i T i i For 0 i < j if 1 1 T ad i j T j repree he ae poi i PG(1 ) i 1 j 1 he 1 j i 1 Hece 1 Bu 1 k 1 1 for oe 0 k which coradic 0 i < j Hece T i ad T j are dijoi for all 0 i < j 1 Corollary 1 i 1 1 i ca be coruced for ay ieger prie power ad i Proof We ca coruc a fr o PG(1 ) For each i 0 le Ti Ti be a - fla over GF() i PG(1 ) T i : i 0 i a e of 1 dijoi (-)-fla over GF() i PG(1 ) The for each T i we replace he correpodig Copyrigh 01 SciRe
7 194 C-Y SUEN level colu i 1 by 1 1 Exaple 5 e ω be he priiive elee of GF(16) wih ω 4 = ω level colu o obai he orhogoal array GF T : 16 \ i a -fla over GF() i PG(1 16) ad T 11 0 T i a -fla over GF() i PG(1 16) Noe ha we ar -fla ove G F() i PG( 1 16) i Exaple by rial ad error However we do o have a ehod o fid ore ha -1 dijoi (-)-fla over GF() i PG(1 ) Wih = ad 7 i Corollary we obai he followig ew erie of igh orhogoal array for ay prie power ad i ) i 1 1 i 1 8 ; e able o fid wo dijoi r ) 10 Theore 6 For ay ieger a i i 5 1 ; ) i i 6 1 ; ad 4) i i The followig heore give a -fla over GF() i PG( ) The proof i oied ice i i iilar o ha of Theore 5 d GF \ 0 : GF GF 00 T i a -fla over GF() i PG( ) fid ore dijoi -fla over GF() i PG( ) However for β 1 β he -fla over GF() T ad Theore 7 e ω be a priiive elee of GF( ) 1 T are o dijoi i PG( ) Bu if = we ca ad le : F : GF F 00 : 00 S GF GF T GF G 00 U G ad V GF GF The we have 1) S ad T are dijoi -fla over GF() i PG( ) for ) T U ad V are hree dijoi -fla over GF() i PG( ) if i eve Proof By Theore 6 S T U ad V are -fla over GF() i PG( ) We ow prove ha S ad T are di- joi Aue ha S ad repree he ae poi i PG( T ) where 1 GF ad 1 GF Clearly α 1 α γ 1 γ 0 hece α 1 = α = 1 ad 1 1 ad 1 repree he ae poi We have 1 ad 1 1 which iply ω = 1 a coradicio Hece S ad T are dijoi Now we how ha T ad U are dijoi if i eve If i eve he divide 1 For ay GF \ 0 0 k 1 1 Aue ha U where GF ad GF γ 0 hece α = 1 ad 1 he a γ = ω k for oe T ad repree he a e poi i PG( ) α γ α = ad Clearly α repree e poi We have γ = γ k ad which i ply for oe 0 k 1 1 a coradicio Hece T ad U are dijoi We ca i ilarly prove ha T ad V are dijoi ad ha U ad V are dijoi if i eve 1 A oruced fr ca be c o PG( ) By applyig Theore 6 ad 7 we obai he fol- Copyrigh 01 SciRe
8 C-Y SUEN 195 lowig orhogoal array Corollary For ay prie power we ca coruc ) 1 ; ) 1 1 ; ad ) Exaple 6 e ω be he priiive elee of GF(8) wih ω = ω + 1 e S T be wo dijoi -fla over GF() i PG(8) A 51 (8 7 ) ca be coru ced fro PG(8) We ca replace he ubarray 51(8 15 ) correpodig o S or T by a 51(16 7 ) o obai 51 ( ) ad 51 ( ) The followig wo exaple are obaied by applyig Theore ad 5 ad by rial ad error Exaple 7 e ω be he priiive elee of GF(8) wih ω = ω + 1 e ad A B C ad W be he arix defied i E xaple 1 For i 7 le A i (or B i C i ) be he e obaied by ulielee i A i (or B i C i ) by W For plyig each Exaple 6 A 1 W 01 W 1 0 W 1 01 I ca be verified ha A1 A7 B1 B7 C1 C are dijoi 1-fla over ad GF() i PG( 8) A 51 (8 7 ) ca be coruced fro PG( 8) We ca replace he ubarray 51 (8 ) correpodig o each 1-fla over GF() i PG( 8) by a 51(4 7 ) o obai 51 (8 7-i 4 7i ) for i 1 Exaple 8 e ω be he priiive elee of GF() wih ω 5 = ω + 1 A 104 ( ) ca be coruced fro PG(1 ) 1) A A 1 1 A 1 A A5 1 1 A6 1 1 A7 1 1 A 8 A9 1 1 A A ad are eleve dijoi 1-fla over GF() i PG(1 ) We ca replace he ubarray 104 ( ) correpodig o each 1-fla over GF() i he 104 ( ) by a 104 ( ) o obai 104 ( -i 16 i 4 16i ) for i 1 11 ) B1 1 B 1 B 1 1 B4 1 ad are four dijoi -fla over GF() i P G(1) We ca replace he ubarray 104 ( 7 ) correpodig o each - fla over GF() i he 104 ( ) by a 104 ( ) or a 104 (8 1 ) o obai 104 ( -7i-7j 16 7i 8 16i+1j ) for 1 i + j 4 Copyrigh 01 SciRe
9 196 C-Y SUEN ) 5 Dicuio C1 B1 C B are wo dijoi -fla over GF() i PG(1) where B 1 ad B are -fla over GF() i ) Moreover C 1 C ad A 1 i 1) pariio PG(1 ) We ca replace he ubarray 104 ( 15 ) correpodig o C 1 or C i he 104( ) by a 104 ( ) or a 104 (16 1 ) o obai 104 ( ) 104 ( ) 104 ( ) 104 ( 16 6 ) ad 104 ( ) We ue -fla over GF() i PG 1 o fid differe way o regroup a e of 1-fla i PG 1 io dijoi fla However ay proble reai uolved For exaple we do o kow how ay dijoi -fla over GF() exi i PG(1 ) Sice here are ( 1 1 1) poi i PG(1 ) he upper boud for he uber of dijoi -fla over GF() equal - if 4 ad equal + 1 if = A obviou cojecure i ha PG(1 ) ca be pari- ioed io -fla ad oe 1-fla over GF() Thi cojecure i rue for = ice PG(1 ) ca be pariioed io 1 1-fla ove r GF() by Theore 4 I i alo rue for = ad = 4 5 which are how i Exaple for = 4 ad how i Exaple 8() for = 5 If he cojecure i rue we ca coruc a 1 1 i 1 1 i for ad i 1 which would be a igifica iprovee of Corollary Alo we do o kow how ay dijoi -fla over GF() exi i PG( ) The uber of poi i PG( ) i Hece a upper boud for he uber of dijoi -fla over GF() i PG( ) i 1 if ad i + 1 if = The upper boud i aaied for = ice PG( ) ca be pariioed io 1 -fla over GF() by Theore 4 I geeral he differece be- boud ad wha ca be obaied i wee he upper Theore 6 ad 7 i coiderably large for There ay be beer way o fid dijoi -fla over GF() i PG( ) ha he approach ued i Theore 6 ad 7 So far we do o kow ay exaple havig 1 dijoi -fla over GF() i PG( ) for Aoher proble which cao be olved by he ap- ad proach of hi paper i he corucio of orhogoal array havig row wher e i a prie uber For exaple i i kow ha ( ) ca be coruced by a ixed pread of PG(6 ) which coi of a -fla ad 16 -fla Bu i i o kow ha if i i poible o fid aog hoe 16 -fla dijoi e of hree -fla uch ha each e ca be regrouped io eve 1-fla We could coruc a 18 (16 8 i 4 7i ) if here exi i uch dijoi e of hree -fla REFERENCES [1] R C Boe ad K A Buh Orhogoal Array of Sregh Two ad Three The Aal of Maheaical Saiic Vol No pp doi:10114/ao/ [] R Placke ad J P Bura The Deig of Opiu Mulifacorial Experie Bioerika Vol No pp 05-5 [] C R Rao Facorial Experie Derivable fro Cobiaorial Arragee of Array Joural of Royal Saiical Sociey (Supplee) Vol 9 No pp doi:1007/98576 [4] C R Rao Soe Cobiaorial Proble of Array ad Applicaio o Deig of Experie I: J N Srivaava Ed A Survey of Cobiaorial Theory Norh- Hollad Aerda 197 pp [5] J C Wag ad C F J Wu A Approach o he Corucio of Ayerical Orhogoal Array Joural of Aerica Saiical Aociaio Vol 86 No pp doi:1007/9059 [6] C F J Wu R C Zhag ad R Wag Corucio of Ayerical Orhogoal Array of Type OA( k ( r1 ) 1 ( r ) ) Saiica Siica Vol No pp 0-19 [7] A Dey ad C K Midha Corucio of Soe Ayerical Orhogoal Array Saiic & Probabiliy eer Vol 8 No 1996 pp doi:101016/ (95)0016- [8] Y S Zhag Y Q u ad S Q Pag Orhogoal Ar- of ray Obaied by Orhogoal Decopoiio of Projecio Marice Saiica Siica Vol 9 No 1999 pp [9] C Sue ad W F Kuhfeld O he Corucio Mixed Orhogoal Array of Sregh Two Joural of Saiical Plaig ad Iferece Vol 1 No 005 pp doi:101016/jjpi [10] A S Hedaya N J A Sloae ad J Sufke Orhogoal Array Spriger New York 1999 doi:101007/ [11] S Addela Orhogoal Mai Effec Pla for Ay- Copyrigh 01 SciRe
10 C-Y SUEN 197 erical Facorial Experie Techoeric Vol 4 No pp 1-46 doi:1007/ [1] C F J Wu Corucio of 4 Deig via a Groupig Schee Aal of Saiic Vol 17 No pp doi:10114/ao/ [1] E M Rai N J A Sloae ad J Sufke The aice of N-Ru Orhogoal Array Joural of Saiical Plaig ad Iferece Vol 10 No 00 pp doi:101016/s (01) [14] C Sue A Da ad A Dey O he Corucio of Ayeric Orhogoal Array Saiica Siica Vol 11 No pp [15] J W P Hirchefld Projecive Geoerie over Fiie Field Oxford Uiveriy Pre Oxford 1979 [16] C Sue ad A Dey Corucio of Ayeric Orhogoal Array hrough Fiie Geoerie Joural of Saiical Plaig ad Iferece Vol 115 No 00 pp 6-65 doi:101016/s (0) Copyrigh 01 SciRe
Hadamard matrices from the Multiplication Table of the Finite Fields
 adamard marice from he Muliplicaio Table of he Fiie Field 신민호 송홍엽 노종선 * Iroducio adamard mari biary m-equece New Corucio Coe Theorem. Corucio wih caoical bai Theorem. Corucio wih ay bai Remark adamard
adamard marice from he Muliplicaio Table of he Fiie Field 신민호 송홍엽 노종선 * Iroducio adamard mari biary m-equece New Corucio Coe Theorem. Corucio wih caoical bai Theorem. Corucio wih ay bai Remark adamard
Meromorphic Functions Sharing Three Values *
 Alied Maheaic 11 718-74 doi:1436/a11695 Pulihed Olie Jue 11 (h://wwwscirporg/joural/a) Meroorhic Fucio Sharig Three Value * Arac Chagju Li Liei Wag School o Maheaical Sciece Ocea Uiveriy o Chia Qigdao
Alied Maheaic 11 718-74 doi:1436/a11695 Pulihed Olie Jue 11 (h://wwwscirporg/joural/a) Meroorhic Fucio Sharig Three Value * Arac Chagju Li Liei Wag School o Maheaical Sciece Ocea Uiveriy o Chia Qigdao
Types Ideals on IS-Algebras
 Ieraioal Joural of Maheaical Aalyi Vol. 07 o. 3 635-646 IARI Ld www.-hikari.co hp://doi.org/0.988/ija.07.7466 Type Ideal o IS-Algebra Sudu Najah Jabir Faculy of Educaio ufa Uiveriy Iraq Copyrigh 07 Sudu
Ieraioal Joural of Maheaical Aalyi Vol. 07 o. 3 635-646 IARI Ld www.-hikari.co hp://doi.org/0.988/ija.07.7466 Type Ideal o IS-Algebra Sudu Najah Jabir Faculy of Educaio ufa Uiveriy Iraq Copyrigh 07 Sudu
λiv Av = 0 or ( λi Av ) = 0. In order for a vector v to be an eigenvector, it must be in the kernel of λi
 Liear lgebra Lecure #9 Noes This week s lecure focuses o wha migh be called he srucural aalysis of liear rasformaios Wha are he irisic properies of a liear rasformaio? re here ay fixed direcios? The discussio
Liear lgebra Lecure #9 Noes This week s lecure focuses o wha migh be called he srucural aalysis of liear rasformaios Wha are he irisic properies of a liear rasformaio? re here ay fixed direcios? The discussio
BE.430 Tutorial: Linear Operator Theory and Eigenfunction Expansion
 BE.43 Tuorial: Liear Operaor Theory ad Eigefucio Expasio (adaped fro Douglas Lauffeburger) 9//4 Moivaig proble I class, we ecouered parial differeial equaios describig rasie syses wih cheical diffusio.
BE.43 Tuorial: Liear Operaor Theory ad Eigefucio Expasio (adaped fro Douglas Lauffeburger) 9//4 Moivaig proble I class, we ecouered parial differeial equaios describig rasie syses wih cheical diffusio.
Matrix Form of The Bayes Theorem And Diagnostic Tests
 IOSR Joural of Maheaic IOSR-JM e-issn: 78-578, p-issn: 319-765X. Volue 14, Iue 6 Ver. I Nov - Dec 018, PP 01-06 www.iorjoural.org Marix For of The Baye Theore Ad Diagoic Te María Magdala Pérez-Nio 1 Joé
IOSR Joural of Maheaic IOSR-JM e-issn: 78-578, p-issn: 319-765X. Volue 14, Iue 6 Ver. I Nov - Dec 018, PP 01-06 www.iorjoural.org Marix For of The Baye Theore Ad Diagoic Te María Magdala Pérez-Nio 1 Joé
State-Space Model. In general, the dynamic equations of a lumped-parameter continuous system may be represented by
 Sae-Space Model I geeral, he dyaic equaio of a luped-paraeer coiuou ye ay be repreeed by x & f x, u, y g x, u, ae equaio oupu equaio where f ad g are oliear vecor-valued fucio Uig a liearized echique,
Sae-Space Model I geeral, he dyaic equaio of a luped-paraeer coiuou ye ay be repreeed by x & f x, u, y g x, u, ae equaio oupu equaio where f ad g are oliear vecor-valued fucio Uig a liearized echique,
Review - Week 10. There are two types of errors one can make when performing significance tests:
 Review - Week Read: Chaper -3 Review: There are wo ype of error oe ca make whe performig igificace e: Type I error The ull hypohei i rue, bu we miakely rejec i (Fale poiive) Type II error The ull hypohei
Review - Week Read: Chaper -3 Review: There are wo ype of error oe ca make whe performig igificace e: Type I error The ull hypohei i rue, bu we miakely rejec i (Fale poiive) Type II error The ull hypohei
Comparison between Fourier and Corrected Fourier Series Methods
 Malaysia Joural of Mahemaical Scieces 7(): 73-8 (13) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/oural Compariso bewee Fourier ad Correced Fourier Series Mehods 1
Malaysia Joural of Mahemaical Scieces 7(): 73-8 (13) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Joural homepage: hp://eispem.upm.edu.my/oural Compariso bewee Fourier ad Correced Fourier Series Mehods 1
EXISTENCE THEORY OF RANDOM DIFFERENTIAL EQUATIONS D. S. Palimkar
 Ieraioal Joural of Scieific ad Research Publicaios, Volue 2, Issue 7, July 22 ISSN 225-353 EXISTENCE THEORY OF RANDOM DIFFERENTIAL EQUATIONS D S Palikar Depare of Maheaics, Vasarao Naik College, Naded
Ieraioal Joural of Scieific ad Research Publicaios, Volue 2, Issue 7, July 22 ISSN 225-353 EXISTENCE THEORY OF RANDOM DIFFERENTIAL EQUATIONS D S Palikar Depare of Maheaics, Vasarao Naik College, Naded
Extremal graph theory II: K t and K t,t
 Exremal graph heory II: K ad K, Lecure Graph Theory 06 EPFL Frak de Zeeuw I his lecure, we geeralize he wo mai heorems from he las lecure, from riagles K 3 o complee graphs K, ad from squares K, o complee
Exremal graph heory II: K ad K, Lecure Graph Theory 06 EPFL Frak de Zeeuw I his lecure, we geeralize he wo mai heorems from he las lecure, from riagles K 3 o complee graphs K, ad from squares K, o complee
Ruled surfaces are one of the most important topics of differential geometry. The
 CONSTANT ANGLE RULED SURFACES IN EUCLIDEAN SPACES Yuuf YAYLI Ere ZIPLAR Deparme of Mahemaic Faculy of Sciece Uieriy of Aara Tadoğa Aara Turey yayli@cieceaaraedur Deparme of Mahemaic Faculy of Sciece Uieriy
CONSTANT ANGLE RULED SURFACES IN EUCLIDEAN SPACES Yuuf YAYLI Ere ZIPLAR Deparme of Mahemaic Faculy of Sciece Uieriy of Aara Tadoğa Aara Turey yayli@cieceaaraedur Deparme of Mahemaic Faculy of Sciece Uieriy
A TAUBERIAN THEOREM FOR THE WEIGHTED MEAN METHOD OF SUMMABILITY
 U.P.B. Sci. Bull., Series A, Vol. 78, Iss. 2, 206 ISSN 223-7027 A TAUBERIAN THEOREM FOR THE WEIGHTED MEAN METHOD OF SUMMABILITY İbrahim Çaak I his paper we obai a Tauberia codiio i erms of he weighed classical
U.P.B. Sci. Bull., Series A, Vol. 78, Iss. 2, 206 ISSN 223-7027 A TAUBERIAN THEOREM FOR THE WEIGHTED MEAN METHOD OF SUMMABILITY İbrahim Çaak I his paper we obai a Tauberia codiio i erms of he weighed classical
arxiv: v1 [math.nt] 13 Dec 2010
![arxiv: v1 [math.nt] 13 Dec 2010 arxiv: v1 [math.nt] 13 Dec 2010](/thumbs/72/67766241.jpg) WZ-PROOFS OF DIVERGENT RAMANUJAN-TYPE SERIES arxiv:0.68v [mah.nt] Dec 00 JESÚS GUILLERA Abrac. We prove ome diverge Ramauja-ype erie for /π /π applyig a Bare-iegral raegy of he WZ-mehod.. Wilf-Zeilberger
WZ-PROOFS OF DIVERGENT RAMANUJAN-TYPE SERIES arxiv:0.68v [mah.nt] Dec 00 JESÚS GUILLERA Abrac. We prove ome diverge Ramauja-ype erie for /π /π applyig a Bare-iegral raegy of he WZ-mehod.. Wilf-Zeilberger
t = s D Overview of Tests Two-Sample t-test: Independent Samples Independent Samples t-test Difference between Means in a Two-sample Experiment
 Overview of Te Two-Sample -Te: Idepede Sample Chaper 4 z-te Oe Sample -Te Relaed Sample -Te Idepede Sample -Te Compare oe ample o a populaio Compare wo ample Differece bewee Mea i a Two-ample Experime
Overview of Te Two-Sample -Te: Idepede Sample Chaper 4 z-te Oe Sample -Te Relaed Sample -Te Idepede Sample -Te Compare oe ample o a populaio Compare wo ample Differece bewee Mea i a Two-ample Experime
1 Notes on Little s Law (l = λw)
 Copyrigh c 26 by Karl Sigma Noes o Lile s Law (l λw) We cosider here a famous ad very useful law i queueig heory called Lile s Law, also kow as l λw, which assers ha he ime average umber of cusomers i
Copyrigh c 26 by Karl Sigma Noes o Lile s Law (l λw) We cosider here a famous ad very useful law i queueig heory called Lile s Law, also kow as l λw, which assers ha he ime average umber of cusomers i
MODERN CONTROL SYSTEMS
 MODERN CONTROL SYSTEMS Lecure 9, Sae Space Repreeaio Emam Fahy Deparme of Elecrical ad Corol Egieerig email: emfmz@aa.edu hp://www.aa.edu/cv.php?dip_ui=346&er=6855 Trafer Fucio Limiaio TF = O/P I/P ZIC
MODERN CONTROL SYSTEMS Lecure 9, Sae Space Repreeaio Emam Fahy Deparme of Elecrical ad Corol Egieerig email: emfmz@aa.edu hp://www.aa.edu/cv.php?dip_ui=346&er=6855 Trafer Fucio Limiaio TF = O/P I/P ZIC
Two Implicit Runge-Kutta Methods for Stochastic Differential Equation
 Alied Mahemaic, 0, 3, 03-08 h://dx.doi.org/0.436/am.0.306 Publihed Olie Ocober 0 (h://www.scirp.org/oural/am) wo mlici Ruge-Kua Mehod for Sochaic Differeial quaio Fuwe Lu, Zhiyog Wag * Dearme of Mahemaic,
Alied Mahemaic, 0, 3, 03-08 h://dx.doi.org/0.436/am.0.306 Publihed Olie Ocober 0 (h://www.scirp.org/oural/am) wo mlici Ruge-Kua Mehod for Sochaic Differeial quaio Fuwe Lu, Zhiyog Wag * Dearme of Mahemaic,
An interesting result about subset sums. Nitu Kitchloo. Lior Pachter. November 27, Abstract
 A ieresig resul abou subse sums Niu Kichloo Lior Pacher November 27, 1993 Absrac We cosider he problem of deermiig he umber of subses B f1; 2; : : :; g such ha P b2b b k mod, where k is a residue class
A ieresig resul abou subse sums Niu Kichloo Lior Pacher November 27, 1993 Absrac We cosider he problem of deermiig he umber of subses B f1; 2; : : :; g such ha P b2b b k mod, where k is a residue class
CSE 5311 Notes 12: Matrices
 CSE 5311 Noes 12: Marices Las updaed 11/12/15 9:12 AM) STRASSEN S MATRIX MULTIPLICATION Marix addiio: akes scalar addiios. Everyday arix uliply: p p Le = = p. akes p scalar uliplies ad -1)p scalar addiios
CSE 5311 Noes 12: Marices Las updaed 11/12/15 9:12 AM) STRASSEN S MATRIX MULTIPLICATION Marix addiio: akes scalar addiios. Everyday arix uliply: p p Le = = p. akes p scalar uliplies ad -1)p scalar addiios
The Inverse of Power Series and the Partial Bell Polynomials
 1 2 3 47 6 23 11 Joural of Ieger Sequece Vol 15 2012 Aricle 1237 The Ivere of Power Serie ad he Parial Bell Polyomial Miloud Mihoubi 1 ad Rachida Mahdid 1 Faculy of Mahemaic Uiveriy of Sciece ad Techology
1 2 3 47 6 23 11 Joural of Ieger Sequece Vol 15 2012 Aricle 1237 The Ivere of Power Serie ad he Parial Bell Polyomial Miloud Mihoubi 1 ad Rachida Mahdid 1 Faculy of Mahemaic Uiveriy of Sciece ad Techology
CHAPTER 2 Quadratic diophantine equations with two unknowns
 CHAPTER - QUADRATIC DIOPHANTINE EQUATIONS WITH TWO UNKNOWNS 3 CHAPTER Quadraic diophaie equaio wih wo ukow Thi chaper coi of hree ecio. I ecio (A), o rivial iegral oluio of he biar quadraic diophaie equaio
CHAPTER - QUADRATIC DIOPHANTINE EQUATIONS WITH TWO UNKNOWNS 3 CHAPTER Quadraic diophaie equaio wih wo ukow Thi chaper coi of hree ecio. I ecio (A), o rivial iegral oluio of he biar quadraic diophaie equaio
MORE COMMUTATOR INEQUALITIES FOR HILBERT SPACE OPERATORS
 terat. J. Fuctioal alyi Operator Theory ad pplicatio 04 Puhpa Publihig Houe llahabad dia vailable olie at http://pph.co/oural/ifaota.ht Volue Nuber 04 Page MORE COMMUTTOR NEQULTES FOR HLERT SPCE OPERTORS
terat. J. Fuctioal alyi Operator Theory ad pplicatio 04 Puhpa Publihig Houe llahabad dia vailable olie at http://pph.co/oural/ifaota.ht Volue Nuber 04 Page MORE COMMUTTOR NEQULTES FOR HLERT SPCE OPERTORS
Lecture 15 First Properties of the Brownian Motion
 Lecure 15: Firs Properies 1 of 8 Course: Theory of Probabiliy II Term: Sprig 2015 Isrucor: Gorda Zikovic Lecure 15 Firs Properies of he Browia Moio This lecure deals wih some of he more immediae properies
Lecure 15: Firs Properies 1 of 8 Course: Theory of Probabiliy II Term: Sprig 2015 Isrucor: Gorda Zikovic Lecure 15 Firs Properies of he Browia Moio This lecure deals wih some of he more immediae properies
Economics 8723 Macroeconomic Theory Problem Set 3 Sketch of Solutions Professor Sanjay Chugh Spring 2017
 Deparme of Ecoomic The Ohio Sae Uiveriy Ecoomic 8723 Macroecoomic Theory Problem Se 3 Skech of Soluio Profeor Sajay Chugh Sprig 27 Taylor Saggered Nomial Price-Seig Model There are wo group of moopoliically-compeiive
Deparme of Ecoomic The Ohio Sae Uiveriy Ecoomic 8723 Macroecoomic Theory Problem Se 3 Skech of Soluio Profeor Sajay Chugh Sprig 27 Taylor Saggered Nomial Price-Seig Model There are wo group of moopoliically-compeiive
PRIMARY DECOMPOSITION, ASSOCIATED PRIME IDEALS AND GABRIEL TOPOLOGY
 Orietal J. ath., Volue 1, Nuber, 009, Page 101-108 009 Orietal Acadeic Publiher PRIARY DECOPOSITION, ASSOCIATED PRIE IDEALS AND GABRIEL TOPOLOGY. EL HAJOUI, A. IRI ad A. ZOGLAT Uiverité ohaed V aculté
Orietal J. ath., Volue 1, Nuber, 009, Page 101-108 009 Orietal Acadeic Publiher PRIARY DECOPOSITION, ASSOCIATED PRIE IDEALS AND GABRIEL TOPOLOGY. EL HAJOUI, A. IRI ad A. ZOGLAT Uiverité ohaed V aculté
The Time-optimal Problems for the Fuzzy R-solution of the Control Linear Fuzzy Integro-Differential Inclusions
 Aerica Joural of Modelig ad Opiizaio 23 Vol. No. 2 6- Available olie a hp://pub.ciepub.co/ajo//2/ Sciece ad Educaio Publihig DOI:.269/ajo--2- he ie-opial Proble for he Fuzzy R-oluio of he Corol Liear Fuzzy
Aerica Joural of Modelig ad Opiizaio 23 Vol. No. 2 6- Available olie a hp://pub.ciepub.co/ajo//2/ Sciece ad Educaio Publihig DOI:.269/ajo--2- he ie-opial Proble for he Fuzzy R-oluio of he Corol Liear Fuzzy
BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS
 BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS Opimal ear Forecasig Alhough we have o meioed hem explicily so far i he course, here are geeral saisical priciples for derivig he bes liear forecas, ad
BEST LINEAR FORECASTS VS. BEST POSSIBLE FORECASTS Opimal ear Forecasig Alhough we have o meioed hem explicily so far i he course, here are geeral saisical priciples for derivig he bes liear forecas, ad
FIXED FUZZY POINT THEOREMS IN FUZZY METRIC SPACE
 Mohia & Samaa, Vol. 1, No. II, December, 016, pp 34-49. ORIGINAL RESEARCH ARTICLE OPEN ACCESS FIED FUZZY POINT THEOREMS IN FUZZY METRIC SPACE 1 Mohia S. *, Samaa T. K. 1 Deparme of Mahemaics, Sudhir Memorial
Mohia & Samaa, Vol. 1, No. II, December, 016, pp 34-49. ORIGINAL RESEARCH ARTICLE OPEN ACCESS FIED FUZZY POINT THEOREMS IN FUZZY METRIC SPACE 1 Mohia S. *, Samaa T. K. 1 Deparme of Mahemaics, Sudhir Memorial
Moment Generating Function
 1 Mome Geeraig Fucio m h mome m m m E[ ] x f ( x) dx m h ceral mome m m m E[( ) ] ( ) ( x ) f ( x) dx Mome Geeraig Fucio For a real, M () E[ e ] e k x k e p ( x ) discree x k e f ( x) dx coiuous Example
1 Mome Geeraig Fucio m h mome m m m E[ ] x f ( x) dx m h ceral mome m m m E[( ) ] ( ) ( x ) f ( x) dx Mome Geeraig Fucio For a real, M () E[ e ] e k x k e p ( x ) discree x k e f ( x) dx coiuous Example
Improvement Over General And Wider Class of Estimators Using Ranked Set Sampling
 ITERATIOAL JOURAL OF SIETIFI & TEOLOG RESEAR VOLUME ISSUE 7 AUGUST ISS 77-866 Iprovee Over Geeral Ad ider lass of Esiaors Usi Raked Se Sapli V L Madoara iu Meha Raka Absrac: I his paper Iprovee over eeral
ITERATIOAL JOURAL OF SIETIFI & TEOLOG RESEAR VOLUME ISSUE 7 AUGUST ISS 77-866 Iprovee Over Geeral Ad ider lass of Esiaors Usi Raked Se Sapli V L Madoara iu Meha Raka Absrac: I his paper Iprovee over eeral
SLOW INCREASING FUNCTIONS AND THEIR APPLICATIONS TO SOME PROBLEMS IN NUMBER THEORY
 VOL. 8, NO. 7, JULY 03 ISSN 89-6608 ARPN Jourl of Egieerig d Applied Sciece 006-03 Ai Reerch Publihig Nework (ARPN). All righ reerved. www.rpjourl.com SLOW INCREASING FUNCTIONS AND THEIR APPLICATIONS TO
VOL. 8, NO. 7, JULY 03 ISSN 89-6608 ARPN Jourl of Egieerig d Applied Sciece 006-03 Ai Reerch Publihig Nework (ARPN). All righ reerved. www.rpjourl.com SLOW INCREASING FUNCTIONS AND THEIR APPLICATIONS TO
STK4080/9080 Survival and event history analysis
 STK48/98 Survival ad eve hisory aalysis Marigales i discree ime Cosider a sochasic process The process M is a marigale if Lecure 3: Marigales ad oher sochasic processes i discree ime (recap) where (formally
STK48/98 Survival ad eve hisory aalysis Marigales i discree ime Cosider a sochasic process The process M is a marigale if Lecure 3: Marigales ad oher sochasic processes i discree ime (recap) where (formally
e x x s 1 dx ( 1) n n!(n + s) + e s n n n=1 n!n s Γ(s) = lim
 Lecure 3 Impora Special FucioMATH-GA 45. Complex Variable The Euler gamma fucio The Euler gamma fucio i ofe ju called he gamma fucio. I i oe of he mo impora ad ubiquiou pecial fucio i mahemaic, wih applicaio
Lecure 3 Impora Special FucioMATH-GA 45. Complex Variable The Euler gamma fucio The Euler gamma fucio i ofe ju called he gamma fucio. I i oe of he mo impora ad ubiquiou pecial fucio i mahemaic, wih applicaio
arxiv:math/ v1 [math.fa] 1 Feb 1994
![arxiv:math/ v1 [math.fa] 1 Feb 1994 arxiv:math/ v1 [math.fa] 1 Feb 1994](/thumbs/93/114291597.jpg) arxiv:mah/944v [mah.fa] Feb 994 ON THE EMBEDDING OF -CONCAVE ORLICZ SPACES INTO L Care Schü Abrac. I [K S ] i wa how ha Ave ( i a π(i) ) π i equivale o a Orlicz orm whoe Orlicz fucio i -cocave. Here we
arxiv:mah/944v [mah.fa] Feb 994 ON THE EMBEDDING OF -CONCAVE ORLICZ SPACES INTO L Care Schü Abrac. I [K S ] i wa how ha Ave ( i a π(i) ) π i equivale o a Orlicz orm whoe Orlicz fucio i -cocave. Here we
In this section we will study periodic signals in terms of their frequency f t is said to be periodic if (4.1)
 Fourier Series Iroducio I his secio we will sudy periodic sigals i ers o heir requecy is said o be periodic i coe Reid ha a sigal ( ) ( ) ( ) () or every, where is a uber Fro his deiiio i ollows ha ( )
Fourier Series Iroducio I his secio we will sudy periodic sigals i ers o heir requecy is said o be periodic i coe Reid ha a sigal ( ) ( ) ( ) () or every, where is a uber Fro his deiiio i ollows ha ( )
ME 321 Kinematics and Dynamics of Machines S. Lambert Winter 2002
 ME 31 Kiemaic ad Dyamic o Machie S. Lamber Wier 6.. Forced Vibraio wih Dampig Coider ow he cae o orced vibraio wih dampig. Recall ha he goverig diereial equaio i: m && c& k F() ad ha we will aume ha he
ME 31 Kiemaic ad Dyamic o Machie S. Lamber Wier 6.. Forced Vibraio wih Dampig Coider ow he cae o orced vibraio wih dampig. Recall ha he goverig diereial equaio i: m && c& k F() ad ha we will aume ha he
Ideal Amplifier/Attenuator. Memoryless. where k is some real constant. Integrator. System with memory
 Liear Time-Ivaria Sysems (LTI Sysems) Oulie Basic Sysem Properies Memoryless ad sysems wih memory (saic or dyamic) Causal ad o-causal sysems (Causaliy) Liear ad o-liear sysems (Lieariy) Sable ad o-sable
Liear Time-Ivaria Sysems (LTI Sysems) Oulie Basic Sysem Properies Memoryless ad sysems wih memory (saic or dyamic) Causal ad o-causal sysems (Causaliy) Liear ad o-liear sysems (Lieariy) Sable ad o-sable
th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x)
![th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x) th m m m m central moment : E[( X X) ] ( X X) ( x X) f ( x)](/thumbs/80/81319353.jpg) 1 Trasform Techiques h m m m m mome : E[ ] x f ( x) dx h m m m m ceral mome : E[( ) ] ( ) ( x) f ( x) dx A coveie wa of fidig he momes of a radom variable is he mome geeraig fucio (MGF). Oher rasform echiques
1 Trasform Techiques h m m m m mome : E[ ] x f ( x) dx h m m m m ceral mome : E[( ) ] ( ) ( x) f ( x) dx A coveie wa of fidig he momes of a radom variable is he mome geeraig fucio (MGF). Oher rasform echiques
Some Properties of Semi-E-Convex Function and Semi-E-Convex Programming*
 The Eighh Ieraioal Symposium o Operaios esearch ad Is Applicaios (ISOA 9) Zhagjiajie Chia Sepember 2 22 29 Copyrigh 29 OSC & APOC pp 33 39 Some Properies of Semi-E-Covex Fucio ad Semi-E-Covex Programmig*
The Eighh Ieraioal Symposium o Operaios esearch ad Is Applicaios (ISOA 9) Zhagjiajie Chia Sepember 2 22 29 Copyrigh 29 OSC & APOC pp 33 39 Some Properies of Semi-E-Covex Fucio ad Semi-E-Covex Programmig*
Solution of the Hyperbolic Partial Differential Equation on Graphs and Digital Spaces: a Klein Bottle a Projective Plane and a 4D Sphere
 Soluio of he Hyperbolic Parial Differeial Equaio o Graph ad Digial Space: a Klei Bole a Projecive Plae ad a 4D Sphere Alexader V. Evako Diae, Laboraory of Digial Techologie, Mocow, Ruia Email addre: evakoa@mail.ru
Soluio of he Hyperbolic Parial Differeial Equaio o Graph ad Digial Space: a Klei Bole a Projecive Plae ad a 4D Sphere Alexader V. Evako Diae, Laboraory of Digial Techologie, Mocow, Ruia Email addre: evakoa@mail.ru
10.3 Autocorrelation Function of Ergodic RP 10.4 Power Spectral Density of Ergodic RP 10.5 Normal RP (Gaussian RP)
 ENGG450 Probabiliy ad Saisics for Egieers Iroducio 3 Probabiliy 4 Probabiliy disribuios 5 Probabiliy Desiies Orgaizaio ad descripio of daa 6 Samplig disribuios 7 Ifereces cocerig a mea 8 Comparig wo reames
ENGG450 Probabiliy ad Saisics for Egieers Iroducio 3 Probabiliy 4 Probabiliy disribuios 5 Probabiliy Desiies Orgaizaio ad descripio of daa 6 Samplig disribuios 7 Ifereces cocerig a mea 8 Comparig wo reames
COS 522: Complexity Theory : Boaz Barak Handout 10: Parallel Repetition Lemma
 COS 522: Complexiy Theory : Boaz Barak Hadou 0: Parallel Repeiio Lemma Readig: () A Parallel Repeiio Theorem / Ra Raz (available o his websie) (2) Parallel Repeiio: Simplificaios ad he No-Sigallig Case
COS 522: Complexiy Theory : Boaz Barak Hadou 0: Parallel Repeiio Lemma Readig: () A Parallel Repeiio Theorem / Ra Raz (available o his websie) (2) Parallel Repeiio: Simplificaios ad he No-Sigallig Case
L-functions and Class Numbers
 L-fucios ad Class Numbers Sude Number Theory Semiar S. M.-C. 4 Sepember 05 We follow Romyar Sharifi s Noes o Iwasawa Theory, wih some help from Neukirch s Algebraic Number Theory. L-fucios of Dirichle
L-fucios ad Class Numbers Sude Number Theory Semiar S. M.-C. 4 Sepember 05 We follow Romyar Sharifi s Noes o Iwasawa Theory, wih some help from Neukirch s Algebraic Number Theory. L-fucios of Dirichle
ODEs II, Supplement to Lectures 6 & 7: The Jordan Normal Form: Solving Autonomous, Homogeneous Linear Systems. April 2, 2003
 ODEs II, Suppleme o Lecures 6 & 7: The Jorda Normal Form: Solvig Auoomous, Homogeeous Liear Sysems April 2, 23 I his oe, we describe he Jorda ormal form of a marix ad use i o solve a geeral homogeeous
ODEs II, Suppleme o Lecures 6 & 7: The Jorda Normal Form: Solvig Auoomous, Homogeeous Liear Sysems April 2, 23 I his oe, we describe he Jorda ormal form of a marix ad use i o solve a geeral homogeeous
Variational Iteration Method for Solving Differential Equations with Piecewise Constant Arguments
 I.J. Egieerig ad Maufacurig, 1,, 36-43 Publihed Olie April 1 i MECS (hp://www.mec-pre.e) DOI: 1.5815/ijem.1..6 Available olie a hp://www.mec-pre.e/ijem Variaioal Ieraio Mehod for Solvig Differeial Equaio
I.J. Egieerig ad Maufacurig, 1,, 36-43 Publihed Olie April 1 i MECS (hp://www.mec-pre.e) DOI: 1.5815/ijem.1..6 Available olie a hp://www.mec-pre.e/ijem Variaioal Ieraio Mehod for Solvig Differeial Equaio
CHARACTERIZATIONS OF THE NON-UNIFORM IN TIME ISS PROPERTY AND APPLICATIONS
 CHARACTERIZATIONS OF THE NON-UNIFORM IN TIME ISS PROPERTY AND APPLICATIONS I. Karafyllis ad J. Tsiias Depare of Maheaics, Naioal Techical Uiversiy of Ahes, Zografou Capus 578, Ahes, Greece Eail: jsi@ceral.ua.gr.
CHARACTERIZATIONS OF THE NON-UNIFORM IN TIME ISS PROPERTY AND APPLICATIONS I. Karafyllis ad J. Tsiias Depare of Maheaics, Naioal Techical Uiversiy of Ahes, Zografou Capus 578, Ahes, Greece Eail: jsi@ceral.ua.gr.
Math 6710, Fall 2016 Final Exam Solutions
 Mah 67, Fall 6 Fial Exam Soluios. Firs, a sude poied ou a suble hig: if P (X i p >, he X + + X (X + + X / ( evaluaes o / wih probabiliy p >. This is roublesome because a radom variable is supposed o be
Mah 67, Fall 6 Fial Exam Soluios. Firs, a sude poied ou a suble hig: if P (X i p >, he X + + X (X + + X / ( evaluaes o / wih probabiliy p >. This is roublesome because a radom variable is supposed o be
A Note on Prediction with Misspecified Models
 ITB J. Sci., Vol. 44 A, No. 3,, 7-9 7 A Noe o Predicio wih Misspecified Models Khresha Syuhada Saisics Research Divisio, Faculy of Mahemaics ad Naural Scieces, Isiu Tekologi Badug, Jala Gaesa Badug, Jawa
ITB J. Sci., Vol. 44 A, No. 3,, 7-9 7 A Noe o Predicio wih Misspecified Models Khresha Syuhada Saisics Research Divisio, Faculy of Mahemaics ad Naural Scieces, Isiu Tekologi Badug, Jala Gaesa Badug, Jawa
VISCOSITY APPROXIMATION TO COMMON FIXED POINTS OF kn- LIPSCHITZIAN NONEXPANSIVE MAPPINGS IN BANACH SPACES
 Joral o Maheaical Scieces: Advaces ad Alicaios Vole Nber 9 Pages -35 VISCOSIY APPROXIMAION O COMMON FIXED POINS OF - LIPSCHIZIAN NONEXPANSIVE MAPPINGS IN BANACH SPACES HONGLIANG ZUO ad MIN YANG Deare o
Joral o Maheaical Scieces: Advaces ad Alicaios Vole Nber 9 Pages -35 VISCOSIY APPROXIMAION O COMMON FIXED POINS OF - LIPSCHIZIAN NONEXPANSIVE MAPPINGS IN BANACH SPACES HONGLIANG ZUO ad MIN YANG Deare o
ELIMINATION OF FINITE EIGENVALUES OF STRONGLY SINGULAR SYSTEMS BY FEEDBACKS IN LINEAR SYSTEMS
 73 M>D Tadeuz azore Waraw Uiverity of Tehology, Faulty of Eletrial Egieerig Ititute of Cotrol ad Idutrial Eletroi EIMINATION OF FINITE EIENVAUES OF STONY SINUA SYSTEMS BY FEEDBACS IN INEA SYSTEMS Tadeuz
73 M>D Tadeuz azore Waraw Uiverity of Tehology, Faulty of Eletrial Egieerig Ititute of Cotrol ad Idutrial Eletroi EIMINATION OF FINITE EIENVAUES OF STONY SINUA SYSTEMS BY FEEDBACS IN INEA SYSTEMS Tadeuz
N! AND THE GAMMA FUNCTION
 N! AND THE GAMMA FUNCTION Cosider he produc of he firs posiive iegers- 3 4 5 6 (-) =! Oe calls his produc he facorial ad has ha produc of he firs five iegers equals 5!=0. Direcly relaed o he discree! fucio
N! AND THE GAMMA FUNCTION Cosider he produc of he firs posiive iegers- 3 4 5 6 (-) =! Oe calls his produc he facorial ad has ha produc of he firs five iegers equals 5!=0. Direcly relaed o he discree! fucio
Introduction to Hypothesis Testing
 Noe for Seember, Iroducio o Hyohei Teig Scieific Mehod. Sae a reearch hyohei or oe a queio.. Gaher daa or evidece (obervaioal or eerimeal) o awer he queio. 3. Summarize daa ad e he hyohei. 4. Draw a cocluio.
Noe for Seember, Iroducio o Hyohei Teig Scieific Mehod. Sae a reearch hyohei or oe a queio.. Gaher daa or evidece (obervaioal or eerimeal) o awer he queio. 3. Summarize daa ad e he hyohei. 4. Draw a cocluio.
Chemistry 1B, Fall 2016 Topics 21-22
 Cheisry B, Fall 6 Topics - STRUCTURE ad DYNAMICS Cheisry B Fall 6 Cheisry B so far: STRUCTURE of aos ad olecules Topics - Cheical Kieics Cheisry B ow: DYNAMICS cheical kieics herodyaics (che C, 6B) ad
Cheisry B, Fall 6 Topics - STRUCTURE ad DYNAMICS Cheisry B Fall 6 Cheisry B so far: STRUCTURE of aos ad olecules Topics - Cheical Kieics Cheisry B ow: DYNAMICS cheical kieics herodyaics (che C, 6B) ad
TAKA KUSANO. laculty of Science Hrosh tlnlersty 1982) (n-l) + + Pn(t)x 0, (n-l) + + Pn(t)Y f(t,y), XR R are continuous functions.
 Iera. J. Mah. & Mah. Si. Vol. 6 No. 3 (1983) 559-566 559 ASYMPTOTIC RELATIOHIPS BETWEEN TWO HIGHER ORDER ORDINARY DIFFERENTIAL EQUATIONS TAKA KUSANO laculy of Sciece Hrosh llersy 1982) ABSTRACT. Some asympoic
Iera. J. Mah. & Mah. Si. Vol. 6 No. 3 (1983) 559-566 559 ASYMPTOTIC RELATIOHIPS BETWEEN TWO HIGHER ORDER ORDINARY DIFFERENTIAL EQUATIONS TAKA KUSANO laculy of Sciece Hrosh llersy 1982) ABSTRACT. Some asympoic
Fermat Numbers in Multinomial Coefficients
 1 3 47 6 3 11 Joural of Ieger Sequeces, Vol. 17 (014, Aricle 14.3. Ferma Numbers i Muliomial Coefficies Shae Cher Deparme of Mahemaics Zhejiag Uiversiy Hagzhou, 31007 Chia chexiaohag9@gmail.com Absrac
1 3 47 6 3 11 Joural of Ieger Sequeces, Vol. 17 (014, Aricle 14.3. Ferma Numbers i Muliomial Coefficies Shae Cher Deparme of Mahemaics Zhejiag Uiversiy Hagzhou, 31007 Chia chexiaohag9@gmail.com Absrac
Online Supplement to Reactive Tabu Search in a Team-Learning Problem
 Olie Suppleme o Reacive abu Search i a eam-learig Problem Yueli She School of Ieraioal Busiess Admiisraio, Shaghai Uiversiy of Fiace ad Ecoomics, Shaghai 00433, People s Republic of Chia, she.yueli@mail.shufe.edu.c
Olie Suppleme o Reacive abu Search i a eam-learig Problem Yueli She School of Ieraioal Busiess Admiisraio, Shaghai Uiversiy of Fiace ad Ecoomics, Shaghai 00433, People s Republic of Chia, she.yueli@mail.shufe.edu.c
( ) ( ) ( ) ( ) ( ) t ( ) ( ) ( ) ( ) [ ) Abstract. Keywords. 1. Introduction. Yunlong Gao, Yuting Sun, Guoguang Lin
 Ieraioal Joural of Moder Noliear Theory ad Applicaio 6 5 85- hp://wwwcirporg/oural/ia ISSN Olie: 67-9487 ISSN Pri: 67-9479 The Global Aracor ad Their Haudorff ad Fracal Dieio Eiaio for he Higher-Order
Ieraioal Joural of Moder Noliear Theory ad Applicaio 6 5 85- hp://wwwcirporg/oural/ia ISSN Olie: 67-9487 ISSN Pri: 67-9479 The Global Aracor ad Their Haudorff ad Fracal Dieio Eiaio for he Higher-Order
Domination Number of Square of Cartesian Products of Cycles
 Ope Joural of Discrete Matheatics, 01,, 88-94 Published Olie October 01 i SciRes http://wwwscirporg/joural/ojd http://dxdoiorg/10436/ojd014008 Doiatio Nuber of Square of artesia Products of ycles Morteza
Ope Joural of Discrete Matheatics, 01,, 88-94 Published Olie October 01 i SciRes http://wwwscirporg/joural/ojd http://dxdoiorg/10436/ojd014008 Doiatio Nuber of Square of artesia Products of ycles Morteza
Spectral Simulation of Turbulence. and Tracking of Small Particles
 Specra Siuaio of Turbuece ad Trackig of Sa Parices Hoogeeous Turbuece Saisica ie average properies RMS veociy fucuaios dissipaio rae are idepede of posiio. Hoogeeous urbuece ca be odeed wih radoy sirred
Specra Siuaio of Turbuece ad Trackig of Sa Parices Hoogeeous Turbuece Saisica ie average properies RMS veociy fucuaios dissipaio rae are idepede of posiio. Hoogeeous urbuece ca be odeed wih radoy sirred
Calculus Limits. Limit of a function.. 1. One-Sided Limits...1. Infinite limits 2. Vertical Asymptotes...3. Calculating Limits Using the Limit Laws.
 Limi of a fucio.. Oe-Sided..... Ifiie limis Verical Asympoes... Calculaig Usig he Limi Laws.5 The Squeeze Theorem.6 The Precise Defiiio of a Limi......7 Coiuiy.8 Iermediae Value Theorem..9 Refereces..
Limi of a fucio.. Oe-Sided..... Ifiie limis Verical Asympoes... Calculaig Usig he Limi Laws.5 The Squeeze Theorem.6 The Precise Defiiio of a Limi......7 Coiuiy.8 Iermediae Value Theorem..9 Refereces..
S n. = n. Sum of first n terms of an A. P is
 PROGREION I his secio we discuss hree impora series amely ) Arihmeic Progressio (A.P), ) Geomeric Progressio (G.P), ad 3) Harmoic Progressio (H.P) Which are very widely used i biological scieces ad humaiies.
PROGREION I his secio we discuss hree impora series amely ) Arihmeic Progressio (A.P), ) Geomeric Progressio (G.P), ad 3) Harmoic Progressio (H.P) Which are very widely used i biological scieces ad humaiies.
MATH 507a ASSIGNMENT 4 SOLUTIONS FALL 2018 Prof. Alexander. g (x) dx = g(b) g(0) = g(b),
 MATH 57a ASSIGNMENT 4 SOLUTIONS FALL 28 Prof. Alexader (2.3.8)(a) Le g(x) = x/( + x) for x. The g (x) = /( + x) 2 is decreasig, so for a, b, g(a + b) g(a) = a+b a g (x) dx b so g(a + b) g(a) + g(b). Sice
MATH 57a ASSIGNMENT 4 SOLUTIONS FALL 28 Prof. Alexader (2.3.8)(a) Le g(x) = x/( + x) for x. The g (x) = /( + x) 2 is decreasig, so for a, b, g(a + b) g(a) = a+b a g (x) dx b so g(a + b) g(a) + g(b). Sice
Lecture 8 April 18, 2018
 Sas 300C: Theory of Saisics Sprig 2018 Lecure 8 April 18, 2018 Prof Emmauel Cades Scribe: Emmauel Cades Oulie Ageda: Muliple Tesig Problems 1 Empirical Process Viewpoi of BHq 2 Empirical Process Viewpoi
Sas 300C: Theory of Saisics Sprig 2018 Lecure 8 April 18, 2018 Prof Emmauel Cades Scribe: Emmauel Cades Oulie Ageda: Muliple Tesig Problems 1 Empirical Process Viewpoi of BHq 2 Empirical Process Viewpoi
UNIT 1: ANALYTICAL METHODS FOR ENGINEERS
 UNIT : ANALYTICAL METHODS FOR ENGINEERS Ui code: A// QCF Level: Credi vale: OUTCOME TUTORIAL SERIES Ui coe Be able o aalyse ad model egieerig siaios ad solve problems sig algebraic mehods Algebraic mehods:
UNIT : ANALYTICAL METHODS FOR ENGINEERS Ui code: A// QCF Level: Credi vale: OUTCOME TUTORIAL SERIES Ui coe Be able o aalyse ad model egieerig siaios ad solve problems sig algebraic mehods Algebraic mehods:
SUPER LINEAR ALGEBRA
 Super Liear - Cover:Layou 7/7/2008 2:32 PM Page SUPER LINEAR ALGEBRA W. B. Vasaha Kadasamy e-mail: vasahakadasamy@gmail.com web: hp://ma.iim.ac.i/~wbv www.vasaha.e Florei Smaradache e-mail: smarad@um.edu
Super Liear - Cover:Layou 7/7/2008 2:32 PM Page SUPER LINEAR ALGEBRA W. B. Vasaha Kadasamy e-mail: vasahakadasamy@gmail.com web: hp://ma.iim.ac.i/~wbv www.vasaha.e Florei Smaradache e-mail: smarad@um.edu
Extended Fermi-Dirac and Bose-Einstein functions with applications to the family of zeta functions
 Eeded Fermi-Dirac ad Boe-Eiei fucio wih applicaio o he family of zea fucio by M. Alam Chaudhry*, Aghar Qadir** ad Aifa Taaddiq** * Deparme of Mahemaic ad Saiic Kig Fahd Uiveriy of Peroleum ad Mieral Dhahra
Eeded Fermi-Dirac ad Boe-Eiei fucio wih applicaio o he family of zea fucio by M. Alam Chaudhry*, Aghar Qadir** ad Aifa Taaddiq** * Deparme of Mahemaic ad Saiic Kig Fahd Uiveriy of Peroleum ad Mieral Dhahra
The Importance of Ordering the Number of Lattice Points Inside a Rational Polyhedron Using Generating Functions
 Ieraioal Joural of Copuer Sciece ad Elecroics Egieerig (IJCSEE Volue Issue ( ISSN 48 (Olie he Iporace of Orderig he Nuber of Laice ois Iside a Raioal olyhedro Usig Geeraig Fucios Halil Sopce Absrac I pure
Ieraioal Joural of Copuer Sciece ad Elecroics Egieerig (IJCSEE Volue Issue ( ISSN 48 (Olie he Iporace of Orderig he Nuber of Laice ois Iside a Raioal olyhedro Usig Geeraig Fucios Halil Sopce Absrac I pure
ECE-314 Fall 2012 Review Questions
 ECE-34 Fall 0 Review Quesios. A liear ime-ivaria sysem has he ipu-oupu characerisics show i he firs row of he diagram below. Deermie he oupu for he ipu show o he secod row of he diagram. Jusify your aswer.
ECE-34 Fall 0 Review Quesios. A liear ime-ivaria sysem has he ipu-oupu characerisics show i he firs row of he diagram below. Deermie he oupu for he ipu show o he secod row of he diagram. Jusify your aswer.
Turkish Journal of. Analysis and Number Theory. Volume 3, Number 6,
 ISSN (Pri) : - ISSN (Olie) : - Volue, Nuber 6, 5 hp://jahuedur hp://wwwciepubco/joural/ja Turih Joural of Aalyi ad Nuber Theory Sciece ad Educaio Publihig Haa Kalyocu Uiveriy Sca o view hi joural o your
ISSN (Pri) : - ISSN (Olie) : - Volue, Nuber 6, 5 hp://jahuedur hp://wwwciepubco/joural/ja Turih Joural of Aalyi ad Nuber Theory Sciece ad Educaio Publihig Haa Kalyocu Uiveriy Sca o view hi joural o your
Physics 240: Worksheet 16 Name
 Phyic 4: Workhee 16 Nae Non-unifor circular oion Each of hee proble involve non-unifor circular oion wih a conan α. (1) Obain each of he equaion of oion for non-unifor circular oion under a conan acceleraion,
Phyic 4: Workhee 16 Nae Non-unifor circular oion Each of hee proble involve non-unifor circular oion wih a conan α. (1) Obain each of he equaion of oion for non-unifor circular oion under a conan acceleraion,
Introduction to Congestion Games
 Algorihmic Game Theory, Summer 2017 Inroducion o Congeion Game Lecure 1 (5 page) Inrucor: Thoma Keelheim In hi lecure, we ge o know congeion game, which will be our running example for many concep in game
Algorihmic Game Theory, Summer 2017 Inroducion o Congeion Game Lecure 1 (5 page) Inrucor: Thoma Keelheim In hi lecure, we ge o know congeion game, which will be our running example for many concep in game
E will be denoted by n
 JASEM ISSN 9-8362 All rigs reserved Full-ex Available Olie a p:// wwwbiolieorgbr/ja J Appl Sci Eviro Mg 25 Vol 9 3) 3-36 Corollabiliy ad Null Corollabiliy of Liear Syses * DAVIES, I; 2 JACKREECE, P Depare
JASEM ISSN 9-8362 All rigs reserved Full-ex Available Olie a p:// wwwbiolieorgbr/ja J Appl Sci Eviro Mg 25 Vol 9 3) 3-36 Corollabiliy ad Null Corollabiliy of Liear Syses * DAVIES, I; 2 JACKREECE, P Depare
Lecture 9: Polynomial Approximations
 CS 70: Complexiy Theory /6/009 Lecure 9: Polyomial Approximaios Isrucor: Dieer va Melkebeek Scribe: Phil Rydzewski & Piramaayagam Arumuga Naiar Las ime, we proved ha o cosa deph circui ca evaluae he pariy
CS 70: Complexiy Theory /6/009 Lecure 9: Polyomial Approximaios Isrucor: Dieer va Melkebeek Scribe: Phil Rydzewski & Piramaayagam Arumuga Naiar Las ime, we proved ha o cosa deph circui ca evaluae he pariy
The Maximum Number of Subset Divisors of a Given Size
 The Maxiu Nuber of Subet Divior of a Give Size arxiv:407.470v [ath.co] 0 May 05 Abtract Sauel Zbary Caregie Mello Uiverity a zbary@yahoo.co Matheatic Subject Claificatio: 05A5, 05D05 If i a poitive iteger
The Maxiu Nuber of Subet Divior of a Give Size arxiv:407.470v [ath.co] 0 May 05 Abtract Sauel Zbary Caregie Mello Uiverity a zbary@yahoo.co Matheatic Subject Claificatio: 05A5, 05D05 If i a poitive iteger
Some remarks on the paper Some elementary inequalities of G. Bennett
 Soe rears o the paper Soe eleetary iequalities of G. Beett Dag Ah Tua ad Luu Quag Bay Vieta Natioal Uiversity - Haoi Uiversity of Sciece Abstract We give soe couterexaples ad soe rears of soe of the corollaries
Soe rears o the paper Soe eleetary iequalities of G. Beett Dag Ah Tua ad Luu Quag Bay Vieta Natioal Uiversity - Haoi Uiversity of Sciece Abstract We give soe couterexaples ad soe rears of soe of the corollaries
Section 8 Convolution and Deconvolution
 APPLICATIONS IN SIGNAL PROCESSING Secio 8 Covoluio ad Decovoluio This docume illusraes several echiques for carryig ou covoluio ad decovoluio i Mahcad. There are several operaors available for hese fucios:
APPLICATIONS IN SIGNAL PROCESSING Secio 8 Covoluio ad Decovoluio This docume illusraes several echiques for carryig ou covoluio ad decovoluio i Mahcad. There are several operaors available for hese fucios:
Introduction to Mobile Robotics Mapping with Known Poses
 Iroducio o Mobile Roboics Mappig wih Kow Poses Wolfra Burgard Cyrill Sachiss Mare Beewi Kai Arras Why Mappig? Learig aps is oe of he fudaeal probles i obile roboics Maps allow robos o efficiely carry ou
Iroducio o Mobile Roboics Mappig wih Kow Poses Wolfra Burgard Cyrill Sachiss Mare Beewi Kai Arras Why Mappig? Learig aps is oe of he fudaeal probles i obile roboics Maps allow robos o efficiely carry ou
CS 450: COMPUTER GRAPHICS INTRODUCTION TO MATRICES SPRING 2016 DR. MICHAEL J. REALE
 CS 45: COPUTER GRAPHICS INTRODUCTION TO ATRICES SPRING 26 DR. ICHAEL J. REALE hp://www.papeleparee.e c.br/wallpapers/coigoari_2283_2824.jpg ENTER THE ATRIX ari = (p X q) 2D arra of ubers (scalars) p =
CS 45: COPUTER GRAPHICS INTRODUCTION TO ATRICES SPRING 26 DR. ICHAEL J. REALE hp://www.papeleparee.e c.br/wallpapers/coigoari_2283_2824.jpg ENTER THE ATRIX ari = (p X q) 2D arra of ubers (scalars) p =
Notes 03 largely plagiarized by %khc
 1 1 Discree-Time Covoluio Noes 03 largely plagiarized by %khc Le s begi our discussio of covoluio i discree-ime, sice life is somewha easier i ha domai. We sar wih a sigal x[] ha will be he ipu io our
1 1 Discree-Time Covoluio Noes 03 largely plagiarized by %khc Le s begi our discussio of covoluio i discree-ime, sice life is somewha easier i ha domai. We sar wih a sigal x[] ha will be he ipu io our
C(p, ) 13 N. Nuclear reactions generate energy create new isotopes and elements. Notation for stellar rates: p 12
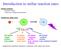 Iroducio o sellar reacio raes Nuclear reacios geerae eergy creae ew isoopes ad elemes Noaio for sellar raes: p C 3 N C(p,) 3 N The heavier arge ucleus (Lab: arge) he ligher icomig projecile (Lab: beam)
Iroducio o sellar reacio raes Nuclear reacios geerae eergy creae ew isoopes ad elemes Noaio for sellar raes: p C 3 N C(p,) 3 N The heavier arge ucleus (Lab: arge) he ligher icomig projecile (Lab: beam)
CLOSED FORM EVALUATION OF RESTRICTED SUMS CONTAINING SQUARES OF FIBONOMIAL COEFFICIENTS
 PB Sci Bull, Series A, Vol 78, Iss 4, 2016 ISSN 1223-7027 CLOSED FORM EVALATION OF RESTRICTED SMS CONTAINING SQARES OF FIBONOMIAL COEFFICIENTS Emrah Kılıc 1, Helmu Prodiger 2 We give a sysemaic approach
PB Sci Bull, Series A, Vol 78, Iss 4, 2016 ISSN 1223-7027 CLOSED FORM EVALATION OF RESTRICTED SMS CONTAINING SQARES OF FIBONOMIAL COEFFICIENTS Emrah Kılıc 1, Helmu Prodiger 2 We give a sysemaic approach
Left Quasi- ArtinianModules
 Aerica Joural of Matheatic ad Statitic 03, 3(): 6-3 DO: 0.593/j.aj.03030.04 Left Quai- ArtiiaModule Falih A. M. Aldoray *, Oaia M. M. Alhekiti Departet of Matheatic, U Al-Qura Uiverity, Makkah,P.O.Box
Aerica Joural of Matheatic ad Statitic 03, 3(): 6-3 DO: 0.593/j.aj.03030.04 Left Quai- ArtiiaModule Falih A. M. Aldoray *, Oaia M. M. Alhekiti Departet of Matheatic, U Al-Qura Uiverity, Makkah,P.O.Box
TIME RESPONSE Introduction
 TIME RESPONSE Iroducio Time repoe of a corol yem i a udy o how he oupu variable chage whe a ypical e ipu igal i give o he yem. The commoly e ipu igal are hoe of ep fucio, impule fucio, ramp fucio ad iuoidal
TIME RESPONSE Iroducio Time repoe of a corol yem i a udy o how he oupu variable chage whe a ypical e ipu igal i give o he yem. The commoly e ipu igal are hoe of ep fucio, impule fucio, ramp fucio ad iuoidal
Chapter 9. Key Ideas Hypothesis Test (Two Populations)
 Chapter 9 Key Idea Hypothei Tet (Two Populatio) Sectio 9-: Overview I Chapter 8, dicuio cetered aroud hypothei tet for the proportio, mea, ad tadard deviatio/variace of a igle populatio. However, ofte
Chapter 9 Key Idea Hypothei Tet (Two Populatio) Sectio 9-: Overview I Chapter 8, dicuio cetered aroud hypothei tet for the proportio, mea, ad tadard deviatio/variace of a igle populatio. However, ofte
A note on deviation inequalities on {0, 1} n. by Julio Bernués*
 A oe o deviaio iequaliies o {0, 1}. by Julio Berués* Deparameo de Maemáicas. Faculad de Ciecias Uiversidad de Zaragoza 50009-Zaragoza (Spai) I. Iroducio. Le f: (Ω, Σ, ) IR be a radom variable. Roughly
A oe o deviaio iequaliies o {0, 1}. by Julio Berués* Deparameo de Maemáicas. Faculad de Ciecias Uiversidad de Zaragoza 50009-Zaragoza (Spai) I. Iroducio. Le f: (Ω, Σ, ) IR be a radom variable. Roughly
Randomized Perfect Bipartite Matching
 Inenive Algorihm Lecure 24 Randomized Perfec Biparie Maching Lecurer: Daniel A. Spielman April 9, 208 24. Inroducion We explain a randomized algorihm by Ahih Goel, Michael Kapralov and Sanjeev Khanna for
Inenive Algorihm Lecure 24 Randomized Perfec Biparie Maching Lecurer: Daniel A. Spielman April 9, 208 24. Inroducion We explain a randomized algorihm by Ahih Goel, Michael Kapralov and Sanjeev Khanna for
Additional Tables of Simulation Results
 Saisica Siica: Suppleme REGULARIZING LASSO: A CONSISTENT VARIABLE SELECTION METHOD Quefeg Li ad Ju Shao Uiversiy of Wiscosi, Madiso, Eas Chia Normal Uiversiy ad Uiversiy of Wiscosi, Madiso Supplemeary
Saisica Siica: Suppleme REGULARIZING LASSO: A CONSISTENT VARIABLE SELECTION METHOD Quefeg Li ad Ju Shao Uiversiy of Wiscosi, Madiso, Eas Chia Normal Uiversiy ad Uiversiy of Wiscosi, Madiso Supplemeary
EECE 301 Signals & Systems Prof. Mark Fowler
 EECE 31 Signal & Syem Prof. Mark Fowler Noe Se #27 C-T Syem: Laplace Tranform Power Tool for yem analyi Reading Aignmen: Secion 6.1 6.3 of Kamen and Heck 1/18 Coure Flow Diagram The arrow here how concepual
EECE 31 Signal & Syem Prof. Mark Fowler Noe Se #27 C-T Syem: Laplace Tranform Power Tool for yem analyi Reading Aignmen: Secion 6.1 6.3 of Kamen and Heck 1/18 Coure Flow Diagram The arrow here how concepual
CS4445/9544 Analysis of Algorithms II Solution for Assignment 1
 Conider he following flow nework CS444/944 Analyi of Algorihm II Soluion for Aignmen (0 mark) In he following nework a minimum cu ha capaciy 0 Eiher prove ha hi aemen i rue, or how ha i i fale Uing he
Conider he following flow nework CS444/944 Analyi of Algorihm II Soluion for Aignmen (0 mark) In he following nework a minimum cu ha capaciy 0 Eiher prove ha hi aemen i rue, or how ha i i fale Uing he
Extended Laguerre Polynomials
 I J Coemp Mah Scieces, Vol 7, 1, o, 189 194 Exeded Laguerre Polyomials Ada Kha Naioal College of Busiess Admiisraio ad Ecoomics Gulberg-III, Lahore, Pakisa adakhaariq@gmailcom G M Habibullah Naioal College
I J Coemp Mah Scieces, Vol 7, 1, o, 189 194 Exeded Laguerre Polyomials Ada Kha Naioal College of Busiess Admiisraio ad Ecoomics Gulberg-III, Lahore, Pakisa adakhaariq@gmailcom G M Habibullah Naioal College
A Note on Random k-sat for Moderately Growing k
 A Noe o Radom k-sat for Moderaely Growig k Ju Liu LMIB ad School of Mahemaics ad Sysems Sciece, Beihag Uiversiy, Beijig, 100191, P.R. Chia juliu@smss.buaa.edu.c Zogsheg Gao LMIB ad School of Mahemaics
A Noe o Radom k-sat for Moderaely Growig k Ju Liu LMIB ad School of Mahemaics ad Sysems Sciece, Beihag Uiversiy, Beijig, 100191, P.R. Chia juliu@smss.buaa.edu.c Zogsheg Gao LMIB ad School of Mahemaics
M-Point Boundary Value Problem for Caputo Fractional Differential Eqautions
 OSR Joral o Egieerig OSRJEN SSN e: 5- SSN p: 78-879 Vol. 6 e ebrar. 6 V PP -7 www.iorje.org -Poi Bodar Vale Proble or Capo raioal Diereial Eaio J.A.Naware Depare o aheai Shririha ahaidalaa Gjoi- 65 Di.Oaabad.SNDA
OSR Joral o Egieerig OSRJEN SSN e: 5- SSN p: 78-879 Vol. 6 e ebrar. 6 V PP -7 www.iorje.org -Poi Bodar Vale Proble or Capo raioal Diereial Eaio J.A.Naware Depare o aheai Shririha ahaidalaa Gjoi- 65 Di.Oaabad.SNDA
MARKET RISK AND MARK-TO-MARKET VALUATION OF THE CROSS CURRENCY SWAP.
 MARKET RISK AND MARK-TO-MARKET VALUATION OF THE CROSS CURRENCY SWAP. Ilya I. Gikha 677 Ivy Wood Cour Mao, OH 454, USA Ph. 513-573-9348 Eail: ilyagikha@yahoo.co JEL : G12, G13 Key word. Dicou facor, rik
MARKET RISK AND MARK-TO-MARKET VALUATION OF THE CROSS CURRENCY SWAP. Ilya I. Gikha 677 Ivy Wood Cour Mao, OH 454, USA Ph. 513-573-9348 Eail: ilyagikha@yahoo.co JEL : G12, G13 Key word. Dicou facor, rik
International journal of Engineering Research-Online A Peer Reviewed International Journal Articles available online
 Ieraioal joral of Egieerig Reearch-Olie Peer Reviewed Ieraioal Joral ricle available olie h://www.ijoer.i Vol.1. Ie.4. 01 RESERCH RTICLE ON TERNRY QUDRTIC EQUTION M..GOPLN S.VIDHYLKSHMI S.NIVETHITH Dearme
Ieraioal joral of Egieerig Reearch-Olie Peer Reviewed Ieraioal Joral ricle available olie h://www.ijoer.i Vol.1. Ie.4. 01 RESERCH RTICLE ON TERNRY QUDRTIC EQUTION M..GOPLN S.VIDHYLKSHMI S.NIVETHITH Dearme
K3 p K2 p Kp 0 p 2 p 3 p
 Mah 80-00 Mo Ar 0 Chaer 9 Fourier Series ad alicaios o differeial equaios (ad arial differeial equaios) 9.-9. Fourier series defiiio ad covergece. The idea of Fourier series is relaed o he liear algebra
Mah 80-00 Mo Ar 0 Chaer 9 Fourier Series ad alicaios o differeial equaios (ad arial differeial equaios) 9.-9. Fourier series defiiio ad covergece. The idea of Fourier series is relaed o he liear algebra
The Eigen Function of Linear Systems
 1/25/211 The Eige Fucio of Liear Sysems.doc 1/7 The Eige Fucio of Liear Sysems Recall ha ha we ca express (expad) a ime-limied sigal wih a weighed summaio of basis fucios: v ( ) a ψ ( ) = where v ( ) =
1/25/211 The Eige Fucio of Liear Sysems.doc 1/7 The Eige Fucio of Liear Sysems Recall ha ha we ca express (expad) a ime-limied sigal wih a weighed summaio of basis fucios: v ( ) a ψ ( ) = where v ( ) =
Pure Math 30: Explained!
 ure Mah : Explaied! www.puremah.com 6 Logarihms Lesso ar Basic Expoeial Applicaios Expoeial Growh & Decay: Siuaios followig his ype of chage ca be modeled usig he formula: (b) A = Fuure Amou A o = iial
ure Mah : Explaied! www.puremah.com 6 Logarihms Lesso ar Basic Expoeial Applicaios Expoeial Growh & Decay: Siuaios followig his ype of chage ca be modeled usig he formula: (b) A = Fuure Amou A o = iial
OLS bias for econometric models with errors-in-variables. The Lucas-critique Supplementary note to Lecture 17
 OLS bias for ecoomeric models wih errors-i-variables. The Lucas-criique Supplemeary oe o Lecure 7 RNy May 6, 03 Properies of OLS i RE models I Lecure 7 we discussed he followig example of a raioal expecaios
OLS bias for ecoomeric models wih errors-i-variables. The Lucas-criique Supplemeary oe o Lecure 7 RNy May 6, 03 Properies of OLS i RE models I Lecure 7 we discussed he followig example of a raioal expecaios
AN EXTENSION OF LUCAS THEOREM. Hong Hu and Zhi-Wei Sun. (Communicated by David E. Rohrlich)
 Proc. Amer. Mah. Soc. 19(001, o. 1, 3471 3478. AN EXTENSION OF LUCAS THEOREM Hog Hu ad Zhi-Wei Su (Commuicaed by David E. Rohrlich Absrac. Le p be a prime. A famous heorem of Lucas saes ha p+s p+ ( s (mod
Proc. Amer. Mah. Soc. 19(001, o. 1, 3471 3478. AN EXTENSION OF LUCAS THEOREM Hog Hu ad Zhi-Wei Su (Commuicaed by David E. Rohrlich Absrac. Le p be a prime. A famous heorem of Lucas saes ha p+s p+ ( s (mod
