Series of functions. Chapter The Dirichlet kernel
|
|
|
- Mavis McCarthy
- 6 years ago
- Views:
Transcription
1 Chapter 3 Series of fuctios 3.9 The Dirichlet kerel Our argumets so far have bee etirely abstract we have ot really used ay properties of the fuctios e (x) = e ix except that they are orthoormal. To get better results, we eed to take a closer look at these fuctios. I some of our argumets, we shall eed to chage variables i itegrals, ad such chages may take us outside our basic iterval [, π], ad hece outside the regio where our fuctios are defied. To avoid these problems, we exted our fuctios periodically outside the basic iterval such that f(x + 2π) = f(x) for all x R. The figure shows the extesio graphically; i part a) we have the origial fuctio, ad i part b) (a part of ) the periodic extesio. As there is o dager of cofusio, we shall deote the origial fuctio ad the extesio by the same symbol f. a) b) π 3π π 3π Figure Let us begi by lookig at the partial sums N s N (x) = f, e e (x) = N
2 2 CHAPTER 3. SERIES OF FUNCTIONS of the Fourier series. Sice we have s N (x) = 2π N = N α = f, e = 2π ( f(t)e it dt ) f(t)e it dt e ix = 2π = 2π f(x u) N = N e iu du f(t) N = N e i(x t) dt = where we i the last step has substituted u = x t ad used the periodicity of the fuctios to remai i the iterval [, π]. If we itroduce the Dirichlet kerel N D N (u) = e iu we may write this as s N (x) = 2π = N f(x u)d N (u) du Note that the sum N = N eiu = N = N (eiu ) is a geomtric series. For u = 0, all the terms are ad the sum is 2N +. For u 0, we use the sum formula for a fiite geometric series to get: D (u) = e inu e i(n+)u e iu = e i(n+ 2 )u e i(n+ 2 )u e i u 2 e i u 2 = si((n + 2 )u) si u 2 where we have used the formula si x = eix e ix 2i twice i the last step. This formula gives us a ice, compact expressio for D N (u). If we substitute it ito the formula above, we get s N (x) = f(x u) si((n + 2 )u) 2π si u du 2 If we wat to prove that partial sums s N (x) coverge to f(x) (i.e. that the Fourier series coverges poitwise to f), the obvious strategy is to prove that itegral above coverges to f. I 829, Dirichlet used this approach to prove: Theorem 3.9. (Dirichlet s Theorem) If f D has oly a fiite umber of local miima ad maxima, the the Fourier series of f coverges poitwise to f.
3 3.9. THE DIRICHLET KERNEL 3 Dirichlet s result must have come as somethig of a surprise; it probably seemed ulikely that a theorem should hold for fuctios with jumps, but ot for cotiuous fuctios with a ifiite umber of extreme poits. Through the years that followed, a umber of mathematicias tried ad failed to prove that the Fourier series of a periodic, cotiuous fuctio always coverges to the fuctio. I 873, the Germa mathematicia Paul Du Bois-Reymod explaied why they failed by costructig a periodic, cotiuous fuctio whose Fourier series diverges at a dese set of poits. It turs out that the theory for poitwise covergece of Fourier series is quite complicated, ad we shall ot prove Dirichlet s theorem here. Istead we shall prove a result kow as Dii s test which allows us to prove covergece for may of the fuctios that appear i practice. But before we do that, we shall take a look at a differet otio of covergece which is easier to hadle, ad which will also give us some tools that are useful i the proof of Dii s test. This alterative otio of covergece is called Cesaro covergece or covergece i Cesaro mea. But first of all we shall collect some properties of the Dirichlet kerels that will be useful later. Let us first see what they look like. The figure below shows Dirichlet s kerel D for = 5, 0, 5, 20. Note the chagig scale o the y-axis; as we have alresdy observed, the maximum value of D is 2 +. As grows, the graph becomes more ad more domiated by a sharp peak at the origi. The smaller peaks ad valleys shrik i size relative to the big peak, but the problem with the Dirichlet kerel is that they do ot shrik i absolute terms as goes to ifiity, the area betwee the curve ad the x-axis (measured i absolute value) goes to ifiity. This makes the Dirichlet kerel very difficult to work with. Whe we tur to Cesaro covergece i the ext sectio, we get aother set of kerels the Fejér kerels ad they tur out ot to have this problem. This is the mai reaso why Cesaro covergece works much better tha ordiary covergece for Fourier series.
4 4 CHAPTER 3. SERIES OF FUNCTIONS Let us ow prove some of the crucial properties of the Dirichlet kerel. Recall that a fuctio g is eve if g(t) = g( t) for all t i the domai: Lemma The Dirichlet kerel D (t) is a eve, realvalued fuctio such that D (t) D (0) = 2 + for all t. For all, π D (t) dt = 2π but lim D (t) dt Proof: That D N is realvalued ad eve, follows immediately from the formula D (t) = si((+ 2 )t) To prove that D si t (t) D (0) = 2 +, we just 2 observe that D (t) = k= Similarly for the itegral e ikt π D (t) dt = 2π k= k= e ikt = 2 + = D (0) π e ikt dt = 2π
5 3.0. THE FEJÉR KERNEL 5 as all itegrals except the oe for k = 0 is zero. To prove the last part, we observe that sice si u u for all u, we have D (t) = si(( + 2 )t) si t 2 2 si(( + 2 )t) t Usig the symmetry ad the substitutio z = ( + 2 )t, we see that D (t) dt = 0 2 D (t) dt 0 4 si(( + 2 )t) t dt = = (+ 2 )π 0 4 si z z dz k= kπ (k )π 4 si z kπ dz = 8 π The expressio o the right goes to ifiity sice the series diverges. k= k The last part of the lemma is bad ews. It tells us that whe we are doig calculatios with the Dirichlet kerel, we have to be very careful i puttig i absolute values as the itegrals are likely to diverge. For this reaso we shall ow itroduce aother kerel the Fejér kerel where this problem does ot occur. Exercises for Sectio 3.9. Let f : [, π] C be the fuctio f(x) = x. Draw the periodic extesio of f. Do the same with the fuctio g(x) = x 2. si((+ 2. Check that D (0) = 2 + by computig lim 2 )t) t 0. si t 2 3. Work out the details of the substitutio u = x t i the derivatio of the formula D N = si((n+ 2 )t). si t 2 4. Explai the details i the last part of the proof of Lemma (the part that proves that lim D (t) dt ). 3.0 The Fejér kerel Before studyig the Fejér kerel, we shall take a look at a geeralized otio of covergece for sequeces. Certai sequeces such at 0,, 0,, 0,, 0,,... do ot coverge i the ordiary sese, but they do coverge i average i the sese that the average of the first elemets approaches a limit as goes to ifiity. I this sese, the sequece above obviously coverges to 2. Let us make this otio precise:
6 6 CHAPTER 3. SERIES OF FUNCTIONS Defiitio 3.0. Let {a k } be a sequece of complex umbers, ad let S = a k. We say that the sequece coverges to a C i Cesaro mea if a = lim S a 0 + a + + a = lim We shall write a = C- lim a. The sequece at the begiig of the sectio coverges to 2 i Cesaro mea, but diverges i the ordiary sese. Let us prove that the opposite ca ot happe: Lemma If lim a = a, the C-lim a = a. Proof: Give a ɛ > 0, we must fid a N such that S a < ɛ whe N. Sice {a } coverges to a, there is a K N such that a a < ɛ 2 whe K. If we let M = max{ a k a : k = 0,, 2,...}, we have for ay K: S a = (a 0 a) + (a a) + + (a K a) + (a K a) + (a a) (a 0 a) + (a a) + + (a K a) + (a K a) + (a a) MK + ɛ 2 Choosig large eough, we get MK < ɛ 2, ad the lemma follows, The idea behid the Fejér kerel is to show that the partial sums s (x) coverge to f(x) i Cesaro middel; i.e. that the sums coverge to f(x). Sice S (x) = s 0(x) + s (x) + + s (x) s k (x) = 2π where D k is the Dirichlet kerel, we get S (x) = ( ) π f(x u) D k (u) 2π f(x u)d k (u) du du = f(x u)f (u) du 2π where F (u) = D k(u) is the Fejér kerel. We ca fid a closed expressio for the Fejér kerel as we could for the Dirichlet kerel, but the argumets are a little loger:
7 3.0. THE FEJÉR KERNEL 7 Lemma The Fejér kerel is give by for u 0 ad F (0) =. Proof: Sice F (u) = si2 ( u 2 ) si 2 ( u 2 ) F (u) = D k (u) = si( u 2 ) si((k + 2 )u) we have to fid si((k + 2 )u) = 2i ( ) e i(k+ 2 )u e i(k+ 2 )u The series are geometric ad ca easily be summed: ad e i(k+ 2 )u = e i u 2 e iku = e i u 2 e i(k+ 2 )u = e i u 2 e iku = e i u 2 Hece e iu e iu = e iu e iu = e iu e i u 2 e i u 2 e iu e i u 2 e i u 2 si((k + 2 )u) = ( e iu + e iu ) 2i e i u 2 e i = ( e iu 2 + e iu ) u 2 2i e i u 2 e i = u 2 ad thus = 2i (ei u 2 e u 2 ) 2 e i u 2 e i u 2 = ( ) e i u 2 e u 2 2 ) 2i e i u 2 e i u 2 2i = si2 ( u 2 ) si u 2 F (u) = si( u 2 ) si((k + 2 )u) = si2 ( u 2 ) si 2 u 2 To prove that F (0) =, we just have to sum a arithmetic series F (0) = D k (0) = (2k + ) =
8 8 CHAPTER 3. SERIES OF FUNCTIONS The figure below shows the Fejer kerels F for = 5, 0, 5, 20. At first glace they look very much like the Dirichlet kerels i the previous sectio. The peak i the middle is growig slower tha before i absolute terms (the maximum value is compared to 2+ for the Dirichlet kerel), but relative to the smaller peaks ad values, it is much more domiat. The fuctios are ow positive, ad the areas betwee their graphs ad the x-axis is always equal to oe. As gets big, almost all this area belogs to the domiat peak i the middle. The positivity ad the cocetratio of all the area i the ceter peak make the Fejér kerels much easier to hadle tha their Dirichlet couterparts. Let us ow prove some of the properties of the Fejér kerels. Propositio For all, the Fejér kerel F fuctio such that π F (x) dx = 2π is a eve, positive For all ozero x [, π] 0 F (x) π2 x 2
9 3.0. THE FEJÉR KERNEL 9 Proof: That F is eve ad positive follows directly from the formula i the lemma. By Propositio 3.9.2, we have π F (x) dx = 2π 2π D k dx = π D k dx = 2π = For the last formula, observe that for u [ π 2, π 2 ], we have 2 π u si u (make a drawig). Thus F (x) = si2 ( x 2 ) si 2 x 2 ( 2 π π2 x 2 )2 x 2 We shall ow show that S (x) coverges to f(x), i.e. that the Fourier series coverges to f i Cesaro mea. We have already observed that S (x) = 2π f(x u)f (u) du If we itroduce a ew variable t = u ad use that F is eve, we get S (x) = f(x + t)f ( t) ( dt) = 2π π = f(x + t)f (t) dt = f(x + u)f (u) du 2π 2π If we combie the two expressios we ow have for S (x), we get S (x) = (f(x + u) + f(x u)) F (u) du Sice 2π F (u) du =, we also have f(x) = f(x)f (u) du 2π Hece S (x) f(x) = (f(x + u) + f(x u) 2f(x)) F (u) du To prove that S (x) coverges to f(x), we oly eed to prove that the itegral goes to 0 as goes to ifiity. The ituitive reaso for this is that for large, the kerel F (u) is extremely small except whe u is close to 0, but whe u is close to 0, the other factor i the itegral, f(x+u)+f(x u) 2f(x), is very small. Here are the techical details.
10 0 CHAPTER 3. SERIES OF FUNCTIONS Theorem If f D, the S coverges to f o [, π], i.e. the Fourier series coverges i Cesaro mea. The covergece is uiform o each subiterval [a, b] [, π] where f is cotiuous. Proof: Give ɛ > 0, we must fid a N N such that S (x) f(x) < ɛ whe N. Sice f is i D, there is a δ > 0 such that f(x + u) f(x u) 2f(x) < ɛ whe u < δ (keep i mid that sice f D, f(x) = 2 lim u 0(f(x + u) f(x u))). We have S (x) f(x) = = + + δ δ δ δ For the first itegral we have δ δ f(x + u) + f(x u) 2f(x) F (u) du = f(x + u) + f(x u) 2f(x) F (u) du+ f(x + u) + f(x u) 2f(x) F (u) du+ f(x + u) + f(x u) 2f(x) F (u) du f(x + u) + f(x u) 2f(x) F (u) du δ ɛf (u) du δ For the secod itegral we get δ ɛf (u) du = ɛ 2 f(x + u) + f(x u) 2f(x) F (u) du δ π 2 4 f δ 2 du = π2 f δ 2 Exactly the same estimate holds for the third itegral, ad by choosig N > 2 f, we get the sum of the last two itegrals less tha ɛ ɛδ 2 2. But the S (x) f(x) < ɛ, ad the covergece is proved. So what about the uiform covergece? We eed to check that we ca choose the same N for all x [a, b]. Note that N oly depeds o x through the choice of δ, ad hece it suffices to show that we ca use the same δ for all x [a, b]. Oe might thik that this follows immediately from the fact that a cotiuous fuctio o a compact iterval [a, b] is uiformly cotiuous, but we eed to be a little careful as x + u or x u may be outside the
11 3.. THE RIEMANN-LEBESGUE LEMMA iterval [a, b] eve if x is iside. The quickest way to fix this, is to observe that sice f is i D, it must be cotiuous ad hece uiformly cotiuous o a slightly larger iterval [a η, b + η]. This meas that we ca use the same δ < η for all x ad x ± u i [a η, d + η], ad this cliches the argumet. We have ow fially proved Theorem which we restate here: Corollary The trigoometric polyomials are dese i C p i - orm, i.e. for ay f C P there is a sequece of trigoometric polyomials covergig uiformly to f. Proof: Accordig to the theorem, the sums S N (x) = N N =0 s (x) coverge uiformly to f. Sice each s is a trigoometric polyomial, so are the S N s. Exercises to Sectio 3.0. Let {a } be the sequece, 0,, 0,, 0,, 0,.... Prove that C-lim a = Show that C-lim (a + b ) = C lim a + C lim b 3. Check that F (0) = by computig lim u 0 si 2 ( u 2 ) si 2 u 2 4. Show that S N (x) = N = (N ) α ( N )e (x), where α = f, e is the Fourier coefficiet. 5. Assume that f C P. Work through the details of the proof of Theorem ad check that S coverges uiformly to f.. 3. The Riema-Lebesgue lemma The Riema-Lebesgue lemma is a seemigly simple observatio about the size of the Fourier coefficiets, but it turs out to be a very efficiet tool i the study of poitwise covergece. Theorem 3.. (Riema-Lebesgue Lemma) If f D ad α = 2π f(x)e ix dx, Z, are the Fourier coefficiets of f, the lim α 0. Proof: Accordig to Bessel s iequality 3.6.9, = α 2 f 2 2 <, ad hece α 0 as. Remark: We are cheatig a little here as we oly prove the Riema- Lebesgue lemma for fuctio which are i D ad hece square itegrable.
12 2 CHAPTER 3. SERIES OF FUNCTIONS The lemma holds for itegrable fuctios i geeral, but eve i that case the proof is quite easy. The Riema-Lebesgue lemma is quite deceptive. It seems to be a result about the coefficiets of certai series, ad it is proved by very geeral ad abstract methods, but it is really a theorem about oscillatig itegrals as the followig corollary makes clear. Corollary 3..2 If f D ad [a, b] [, π], the Also b lim a b lim a f(x) cos(x) dx = f(x)e ix dx = 0 b lim a f(x) si(x) dx = 0 Proof: Let g be the fuctio (this looks more horrible tha it is!) 0 if x / [a, b] the g is i D, ad b a f(x) if x (a, b) g(x) = 2 lim x a f(x) if x = a 2 lim x b f(x) if x = b f(x)e ix dx = g(x)e ix dx = 2πα where α is the Fourier coefficiet of g. By the Riema-Lebesgue lemma, α 0. The last two parts follows from what we have just proved ad the idetities si(x) = eix e ix 2i ad cos(x) = eix +e ix 2 Let us pause for a momet to discuss why these results hold. The reaso is simply that for large values of, the fuctios si x, cos x, ad e ix (if we cosider the real ad imagiary parts separately) oscillate betwee positive ad egative values. If the fuctio f is relatively smooth, the positive ad egative cotributios cacel more ad more as icreases, ad i the limit there is othig left. This argumet also idicates why rapidly oscillatig, cotiuous fuctios are a bigger challege for Fourier aalysis tha jump discotiuities fuctios with jumps average out o each side of the jump, while for wildly oscillatig fuctios the averagig procedure may ot work. Sice the Dirichlet kerel cotais the factor si(( + 2 )x), the followig result will be useful i the ext sectio:
13 3.2. DINI S TEST 3 Corollary 3..3 If f D ad [a, b] [, π], the b lim a f(x) si ( ( + 2 )x) dx = 0 Proof: Follows from the corollary above ad the idetity si ( ( + 2 )x) = si(x) cos x 2 + cos(x) si x 2 Exercises to Sectio 3.. Work out the details of the si(x)- ad cos(x)-part of Corollary Work out the details of the proof of Corollary a) Show that if p is a trigoometric polyomial, the the Fourier coefficiets β = p, e are zero whe is sufficietly large. b) Let f be a itegrable fuctio, ad assume that for each ɛ > 0 there is a trigoometric polyomial such that π 2π f(t) p(t) dt < ɛ. Show that if α = π 2π f(t)e it dt are the Fourier coefficiets of f, the lim α = Dii s test We shall fially take a serious look at poitwise covergece of Fourier series. As aready idicated, this is a rather tricky busiess, ad there is o ultimate theorem, just a collectio of scattered results useful i differet settigs. We shall cocetrate o a criterio called Dii s test which is relatively easy to prove ad sufficietly geeral to cover a lot of differet situatios. Recall from Sectio 3.9 that if s N (x) = N = N is the partial sum of a Fourier series, the s N (x) = 2π f, e e (x) f(x u)d N (u) du If we chage variable i the itergral ad use the symmetry of D N, we see that we also get s N (x) = f(x + u)d N (u) du 2π
14 4 CHAPTER 3. SERIES OF FUNCTIONS Combiig these two expressios, we get s N (x) = ( f(x + u) + f(x u) ) DN (u) du Sice 2π D N(u) du, we also have f(x) = f(x)d N (u) du 2π ad hece s N (x) f(x) = (f(x + u) + f(x u) 2f(x)) D N (u) du (ote that the we are ow doig exactly the same to the Dirichlet kerel as we did to the Fejér kerel i Sectio 3.0). To prove that the Fourier series coverges poitwise to f, we just have to prove that the itegral coverges to 0. The ext lemma simplifies the problem by tellig us that we ca cocetrate o what happes close to the origi: Lemma 3.2. Let f D ad assume that there is a η > 0 such that lim N η η (f(x + u) + f(x u) 2f(x)) D N (u) du = 0 The the Fourier series {s N (x)} coverges to f(x). Proof: Note that sice si x 2 tells us that lim N is a bouded fuctio o [η, π], Corollary 3..3 π (f(x + u) + f(x u) 2f(x)) D N (u) du = η π [ = lim (f(x + u) + f(x u) 2f(x)) N η si u 2 ] si ( (N + 2 )u) du = 0 The same obviously holds for the itegral from to η, ad hece s N (x) f(x) = = + η η η (f(x + u) + f(x u) 2f(x)) D N (u) du = (f(x + u) + f(x u) 2f(x)) D N (u) du+ (f(x + u) + f(x u) 2f(x)) D N (u) du+
15 3.2. DINI S TEST 5 + (f(x + u) + f(x u) 2f(x)) D N (u) du η = 0 Theorem (Dii s test) Let x [, π], ad assume that there is a δ > 0 such that δ f(x + u) + f(x u) 2f(x) u du < δ The the Fourier series coverges to the fuctio f at the poit x, i.e. s N (x) f(x). Proof: Accordig to the lemma, it suffices to prove that lim N δ δ (f(x + u) + f(x u) 2f(x)) D N (u) du = 0 Give a ɛ > 0, we have to show that if N N is large eough, the δ δ (f(x + u) + f(x u) 2f(x)) D N (u) du < ɛ Sice the itegral i the theorem coverges, there is a η > 0 such that η f(x + u) + f(x u) 2f(x) u du < ɛ η Sice si v 2 v π for v [ π 2, π 2 ] (make a drawig), we have D N(u) = si((n+ 2 )u) si u π 2 u for u [, π]. Hece η (f(x + u) + f(x u) 2f(x)) D N (u) du η η η By Corollary 3..3 we ca get δ η f(x + u) + f(x u) 2f(x) π u du < ɛ 2 (f(x + u) + f(x u) 2f(x)) D N (u) du as small as we wat by choosig N large eough ad similarly for the itegral from δ to η. I particular, we ca get δ δ (f(x + u) + f(x u) 2f(x)) D N (u) du =
16 6 CHAPTER 3. SERIES OF FUNCTIONS = η + + δ η η δ η (f(x + u) + f(x u) 2f(x)) D N (u) du+ (f(x + u) + f(x u) 2f(x)) D N (u) du+ (f(x + u) + f(x u) 2f(x)) D N (u) du less tha ɛ, ad hece the theorem is proved. Dii s test have some immediate cosequeces that we leave to the reader to prove. Corollary If f D is differetiable at a poit x, the the Fourier series coverges to f(x) at this poit. We may eve exted this result to oe-sided derivatives: Corollary Assume f D ad that the limits ad f(x + u) f(x + ) lim u 0 u f(x + u) f(x ) lim u 0 u exist at a poit x. The the Fourier series s N (x) coverges to f(x) at this poit. Exercises to Sectio 3.2 2( ) +. Show that the Fourier series = si(x) i Example 3.7. coverges to f(x) = x for x (, π). What happes i the edpoits? 2. Prove Corollary Prove Corollary Termwise operatios I Sectio 3.3 we saw that power series ca be itegrated ad differetiated term by term, ad we ow wat to take a quick look at the correspodig questios for Fourier series. Let us begi by itegratio which is by far the easiest operatio to deal with. The first thig we should observe, is that whe we itegrate a Fourier series α e ix term by term, we do ot get a ew Fourier series sice the costat term α 0 itegrates to α 0 x, which is ot a term i a Fourier
17 3.3. TERMWISE OPERATIONS 7 series whe α 0 0. However, we may, of course, still itegrate term by term to get the series α 0 x + ( iα ) e ix Z, 0 The questio is if this series coverges to the itegral of f. Propositio 3.3. Let f D, ad defie g(x) = x 0 f(t) dt. If s is the partial sums of the Fourier series of f, the the fuctios t (x) = x 0 s (t) dt coverge uiformly to g o [, π]. Hece x g(x) = f(t) dt = α 0 x + ( iα ) e ix 0 Z, 0 where the covergece of the series is uiform. Proof: By Cauchy-Schwarz s iequality we have g(x) t (x) = 0 (f(t) s (t)) dt f(t) s (t) dt ( π ) 2π f(s) s (s) ds = 2π f s, 2π 2π f s 2 2 = 2π f s 2 By Theorem 3.8.6, we see that f s 2 0, ad hece t coverges uiformly to g(x). If we move the term α 0 x to the other side i the formula above, we get g(x) α 0 x = ( iα ) e ix Z, 0 where the series o the right is the Fourier series of g(x) α 0 x. As always, termwise differetiatio is a must trickier subject. I Example of Sectio 3.7, we showed that the Fourier series of x is 2( ) + si(x), = ad by what we ow kow, it is clear that the series coverges poitwise to x o (, π). However, if we differetiate term by term, we get the hopelessly diverget series 2( ) + cos(x) = Fortuately, there is more hope whe f C p, i.e. whe f is cotiuous ad f() = f(π):
18 8 CHAPTER 3. SERIES OF FUNCTIONS Propositio Assume that f C P ad that f is cotiuous o [, π]. If =0 α e ix is the Fourier series of f, the the differetiated series =0 iα e ix is the Fourier series of f, ad it coverges poitwise to f at ay poit x where f (x) exists. Proof: Let β be the Fourier coefficiet of f. By itegratio by parts β = 2π f (t)e it dt = [ f(t)e it ] π 2π f(t)( ie it ) dt = 2π = 0 + i f(t)e it dt = iα 2π which shows that =0 iα e ix is the Fourier series of f. The covergece follows from Corollary Fial remark: I this chapter we have developed Fourier aalysis over the iterval [, π]. If we wat to study Fourier series over aother iterval [a r, a + r], all we have to do is to move ad rescale the fuctios: The basis ow cosists of the fuctios the ier product is defied by f, g = 2r ad the Fourier series becomes e (x) = e iπ r (x a), = a+r a r f(x)g(x) dx α e iπ r (x a) Note that whe the legth r of the iterval icreases, the frequecies iπ r of the basis fuctios e iπ r (x a) get closer ad closer. I the limit, oe might imagie that the sum = α e iπ r (x a) turs ito a itegral (thik of the case a = 0): α(t)e ixt dt This leads to the theory of Fourier itegrals ad Fourier trasforms, but we shall ot look ito these topics here. Exercises for Sectio 3.3. Use itegratio by parts to check that Z, 0 ( iα ) e ix is the Fourier series of g(x) α 0 x (see the passage after the proof of Propositio 3.3.).
19 3.3. TERMWISE OPERATIONS 9 2. Show that si 2x k= cos((2k )x) = 2 si x. 3. I this problem we shall study a feature of Fourier series kow as Gibbs pheomeo. Let f : [, π] R be give by for x < 0 f(x) = 0 for x = 0 for x > The figure shows the partial sums s (x) of order = 5,, 7, 23. We see that although the approximatio i geeral seems to get better ad better, the maximal distace betwee f ad s remais more or less costat it seems that the partial sums have bumps of more or less costat height ear the jump i fuctio values. We shall take a closer look at this pheomeo. Alog the way you will eed the solutio of problem 2. a) Show that the partial sums ca be expressed as s 2 (x) = 4 si((2k )x) π 2k k= b) Use problem 2 to fid a short expressio for s 2 (x). c) Show that the local miimum ad maxima of s 2 closest to 0 are x = π 2 ad x + = π 2. d) Show that s 2 (± π 2 ) = ± 4 si (2k )π 2 π 2k k=
20 20 CHAPTER 3. SERIES OF FUNCTIONS e) Show that s 2 (± π 2 ) ± 2 π as a Riema sum. 0 si x x dx by recogizig the sum above f) Use a calculator or a computer or whatever you wat to show that dx.8 2 π 0 si x x These calculatios show that the size of the bumps is 9% of the size of the jump i the fuctio value. Gibbs showed that this umber holds i geeral for fuctios i D.
Sequences and Series of Functions
 Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges
Chapter 6 Sequeces ad Series of Fuctios 6.1. Covergece of a Sequece of Fuctios Poitwise Covergece. Defiitio 6.1. Let, for each N, fuctio f : A R be defied. If, for each x A, the sequece (f (x)) coverges
6.3 Testing Series With Positive Terms
 6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
6.3. TESTING SERIES WITH POSITIVE TERMS 307 6.3 Testig Series With Positive Terms 6.3. Review of what is kow up to ow I theory, testig a series a i for covergece amouts to fidig the i= sequece of partial
Ma 4121: Introduction to Lebesgue Integration Solutions to Homework Assignment 5
 Ma 42: Itroductio to Lebesgue Itegratio Solutios to Homework Assigmet 5 Prof. Wickerhauser Due Thursday, April th, 23 Please retur your solutios to the istructor by the ed of class o the due date. You
Ma 42: Itroductio to Lebesgue Itegratio Solutios to Homework Assigmet 5 Prof. Wickerhauser Due Thursday, April th, 23 Please retur your solutios to the istructor by the ed of class o the due date. You
Chapter 6 Infinite Series
 Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
f(x)g(x) dx is an inner product on D.
 Ark9: Exercises for MAT2400 Fourier series The exercises o this sheet cover the sectios 4.9 to 4.13. They are iteded for the groups o Thursday, April 12 ad Friday, March 30 ad April 13. NB: No group o
Ark9: Exercises for MAT2400 Fourier series The exercises o this sheet cover the sectios 4.9 to 4.13. They are iteded for the groups o Thursday, April 12 ad Friday, March 30 ad April 13. NB: No group o
MATH4822E FOURIER ANALYSIS AND ITS APPLICATIONS
 MATH48E FOURIER ANALYSIS AND ITS APPLICATIONS 7.. Cesàro summability. 7. Summability methods Arithmetic meas. The followig idea is due to the Italia geometer Eresto Cesàro (859-96). He shows that eve if
MATH48E FOURIER ANALYSIS AND ITS APPLICATIONS 7.. Cesàro summability. 7. Summability methods Arithmetic meas. The followig idea is due to the Italia geometer Eresto Cesàro (859-96). He shows that eve if
Infinite Sequences and Series
 Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Chapter 6 Ifiite Sequeces ad Series 6.1 Ifiite Sequeces 6.1.1 Elemetary Cocepts Simply speakig, a sequece is a ordered list of umbers writte: {a 1, a 2, a 3,...a, a +1,...} where the elemets a i represet
Fall 2013 MTH431/531 Real analysis Section Notes
 Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
Math 113, Calculus II Winter 2007 Final Exam Solutions
 Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
(A sequence also can be thought of as the list of function values attained for a function f :ℵ X, where f (n) = x n for n 1.) x 1 x N +k x N +4 x 3
 MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
Ma 530 Introduction to Power Series
 Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Ma 530 Itroductio to Power Series Please ote that there is material o power series at Visual Calculus. Some of this material was used as part of the presetatio of the topics that follow. What is a Power
Math 341 Lecture #31 6.5: Power Series
 Math 341 Lecture #31 6.5: Power Series We ow tur our attetio to a particular kid of series of fuctios, amely, power series, f(x = a x = a 0 + a 1 x + a 2 x 2 + where a R for all N. I terms of a series
Math 341 Lecture #31 6.5: Power Series We ow tur our attetio to a particular kid of series of fuctios, amely, power series, f(x = a x = a 0 + a 1 x + a 2 x 2 + where a R for all N. I terms of a series
Additional Notes on Power Series
 Additioal Notes o Power Series Mauela Girotti MATH 37-0 Advaced Calculus of oe variable Cotets Quick recall 2 Abel s Theorem 2 3 Differetiatio ad Itegratio of Power series 4 Quick recall We recall here
Additioal Notes o Power Series Mauela Girotti MATH 37-0 Advaced Calculus of oe variable Cotets Quick recall 2 Abel s Theorem 2 3 Differetiatio ad Itegratio of Power series 4 Quick recall We recall here
Fourier Series and their Applications
 Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Sequences A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece 1, 1, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet
A sequence of numbers is a function whose domain is the positive integers. We can see that the sequence
 Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
Sequeces A sequece of umbers is a fuctio whose domai is the positive itegers. We ca see that the sequece,, 2, 2, 3, 3,... is a fuctio from the positive itegers whe we write the first sequece elemet as
1.3 Convergence Theorems of Fourier Series. k k k k. N N k 1. With this in mind, we state (without proof) the convergence of Fourier series.
 .3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
.3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
Mathematical Methods for Physics and Engineering
 Mathematical Methods for Physics ad Egieerig Lecture otes Sergei V. Shabaov Departmet of Mathematics, Uiversity of Florida, Gaiesville, FL 326 USA CHAPTER The theory of covergece. Numerical sequeces..
Mathematical Methods for Physics ad Egieerig Lecture otes Sergei V. Shabaov Departmet of Mathematics, Uiversity of Florida, Gaiesville, FL 326 USA CHAPTER The theory of covergece. Numerical sequeces..
Math 113 Exam 3 Practice
 Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
Solutions to Final Exam Review Problems
 . Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
. Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
Ma 530 Infinite Series I
 Ma 50 Ifiite Series I Please ote that i additio to the material below this lecture icorporated material from the Visual Calculus web site. The material o sequeces is at Visual Sequeces. (To use this li
Ma 50 Ifiite Series I Please ote that i additio to the material below this lecture icorporated material from the Visual Calculus web site. The material o sequeces is at Visual Sequeces. (To use this li
Lesson 10: Limits and Continuity
 www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
www.scimsacademy.com Lesso 10: Limits ad Cotiuity SCIMS Academy 1 Limit of a fuctio The cocept of limit of a fuctio is cetral to all other cocepts i calculus (like cotiuity, derivative, defiite itegrals
Integrable Functions. { f n } is called a determining sequence for f. If f is integrable with respect to, then f d does exist as a finite real number
 MATH 532 Itegrable Fuctios Dr. Neal, WKU We ow shall defie what it meas for a measurable fuctio to be itegrable, show that all itegral properties of simple fuctios still hold, ad the give some coditios
MATH 532 Itegrable Fuctios Dr. Neal, WKU We ow shall defie what it meas for a measurable fuctio to be itegrable, show that all itegral properties of simple fuctios still hold, ad the give some coditios
MATH301 Real Analysis (2008 Fall) Tutorial Note #7. k=1 f k (x) converges pointwise to S(x) on E if and
 MATH01 Real Aalysis (2008 Fall) Tutorial Note #7 Sequece ad Series of fuctio 1: Poitwise Covergece ad Uiform Covergece Part I: Poitwise Covergece Defiitio of poitwise covergece: A sequece of fuctios f
MATH01 Real Aalysis (2008 Fall) Tutorial Note #7 Sequece ad Series of fuctio 1: Poitwise Covergece ad Uiform Covergece Part I: Poitwise Covergece Defiitio of poitwise covergece: A sequece of fuctios f
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
Advanced Analysis. Min Yan Department of Mathematics Hong Kong University of Science and Technology
 Advaced Aalysis Mi Ya Departmet of Mathematics Hog Kog Uiversity of Sciece ad Techology September 3, 009 Cotets Limit ad Cotiuity 7 Limit of Sequece 8 Defiitio 8 Property 3 3 Ifiity ad Ifiitesimal 8 4
Advaced Aalysis Mi Ya Departmet of Mathematics Hog Kog Uiversity of Sciece ad Techology September 3, 009 Cotets Limit ad Cotiuity 7 Limit of Sequece 8 Defiitio 8 Property 3 3 Ifiity ad Ifiitesimal 8 4
1 Approximating Integrals using Taylor Polynomials
 Seughee Ye Ma 8: Week 7 Nov Week 7 Summary This week, we will lear how we ca approximate itegrals usig Taylor series ad umerical methods. Topics Page Approximatig Itegrals usig Taylor Polyomials. Defiitios................................................
Seughee Ye Ma 8: Week 7 Nov Week 7 Summary This week, we will lear how we ca approximate itegrals usig Taylor series ad umerical methods. Topics Page Approximatig Itegrals usig Taylor Polyomials. Defiitios................................................
4x 2. (n+1) x 3 n+1. = lim. 4x 2 n+1 n3 n. n 4x 2 = lim = 3
 Exam Problems (x. Give the series (, fid the values of x for which this power series coverges. Also =0 state clearly what the radius of covergece is. We start by settig up the Ratio Test: x ( x x ( x x
Exam Problems (x. Give the series (, fid the values of x for which this power series coverges. Also =0 state clearly what the radius of covergece is. We start by settig up the Ratio Test: x ( x x ( x x
Chapter 10: Power Series
 Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Convergence of random variables. (telegram style notes) P.J.C. Spreij
 Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Sequences, Series, and All That
 Chapter Te Sequeces, Series, ad All That. Itroductio Suppose we wat to compute a approximatio of the umber e by usig the Taylor polyomial p for f ( x) = e x at a =. This polyomial is easily see to be 3
Chapter Te Sequeces, Series, ad All That. Itroductio Suppose we wat to compute a approximatio of the umber e by usig the Taylor polyomial p for f ( x) = e x at a =. This polyomial is easily see to be 3
Seunghee Ye Ma 8: Week 5 Oct 28
 Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
University of Colorado Denver Dept. Math. & Stat. Sciences Applied Analysis Preliminary Exam 13 January 2012, 10:00 am 2:00 pm. Good luck!
 Uiversity of Colorado Dever Dept. Math. & Stat. Scieces Applied Aalysis Prelimiary Exam 13 Jauary 01, 10:00 am :00 pm Name: The proctor will let you read the followig coditios before the exam begis, ad
Uiversity of Colorado Dever Dept. Math. & Stat. Scieces Applied Aalysis Prelimiary Exam 13 Jauary 01, 10:00 am :00 pm Name: The proctor will let you read the followig coditios before the exam begis, ad
CHAPTER 10 INFINITE SEQUENCES AND SERIES
 CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
lim za n n = z lim a n n.
 Lecture 6 Sequeces ad Series Defiitio 1 By a sequece i a set A, we mea a mappig f : N A. It is customary to deote a sequece f by {s } where, s := f(). A sequece {z } of (complex) umbers is said to be coverget
Lecture 6 Sequeces ad Series Defiitio 1 By a sequece i a set A, we mea a mappig f : N A. It is customary to deote a sequece f by {s } where, s := f(). A sequece {z } of (complex) umbers is said to be coverget
Section 11.8: Power Series
 Sectio 11.8: Power Series 1. Power Series I this sectio, we cosider geeralizig the cocept of a series. Recall that a series is a ifiite sum of umbers a. We ca talk about whether or ot it coverges ad i
Sectio 11.8: Power Series 1. Power Series I this sectio, we cosider geeralizig the cocept of a series. Recall that a series is a ifiite sum of umbers a. We ca talk about whether or ot it coverges ad i
Chapter 6 Overview: Sequences and Numerical Series. For the purposes of AP, this topic is broken into four basic subtopics:
 Chapter 6 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals (which is what most studets
Chapter 6 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals (which is what most studets
HOMEWORK #10 SOLUTIONS
 Math 33 - Aalysis I Sprig 29 HOMEWORK # SOLUTIONS () Prove that the fuctio f(x) = x 3 is (Riema) itegrable o [, ] ad show that x 3 dx = 4. (Without usig formulae for itegratio that you leart i previous
Math 33 - Aalysis I Sprig 29 HOMEWORK # SOLUTIONS () Prove that the fuctio f(x) = x 3 is (Riema) itegrable o [, ] ad show that x 3 dx = 4. (Without usig formulae for itegratio that you leart i previous
Carleton College, Winter 2017 Math 121, Practice Final Prof. Jones. Note: the exam will have a section of true-false questions, like the one below.
 Carleto College, Witer 207 Math 2, Practice Fial Prof. Joes Note: the exam will have a sectio of true-false questios, like the oe below.. True or False. Briefly explai your aswer. A icorrectly justified
Carleto College, Witer 207 Math 2, Practice Fial Prof. Joes Note: the exam will have a sectio of true-false questios, like the oe below.. True or False. Briefly explai your aswer. A icorrectly justified
Math 113 Exam 3 Practice
 Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
2 Banach spaces and Hilbert spaces
 2 Baach spaces ad Hilbert spaces Tryig to do aalysis i the ratioal umbers is difficult for example cosider the set {x Q : x 2 2}. This set is o-empty ad bouded above but does ot have a least upper boud
2 Baach spaces ad Hilbert spaces Tryig to do aalysis i the ratioal umbers is difficult for example cosider the set {x Q : x 2 2}. This set is o-empty ad bouded above but does ot have a least upper boud
Chapter 6: Numerical Series
 Chapter 6: Numerical Series 327 Chapter 6 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals
Chapter 6: Numerical Series 327 Chapter 6 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals
The minimum value and the L 1 norm of the Dirichlet kernel
 The miimum value ad the L orm of the Dirichlet kerel For each positive iteger, defie the fuctio D (θ + ( cos θ + cos θ + + cos θ e iθ + + e iθ + e iθ + e + e iθ + e iθ + + e iθ which we call the (th Dirichlet
The miimum value ad the L orm of the Dirichlet kerel For each positive iteger, defie the fuctio D (θ + ( cos θ + cos θ + + cos θ e iθ + + e iθ + e iθ + e + e iθ + e iθ + + e iθ which we call the (th Dirichlet
x x x Using a second Taylor polynomial with remainder, find the best constant C so that for x 0,
 Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
A Proof of Birkhoff s Ergodic Theorem
 A Proof of Birkhoff s Ergodic Theorem Joseph Hora September 2, 205 Itroductio I Fall 203, I was learig the basics of ergodic theory, ad I came across this theorem. Oe of my supervisors, Athoy Quas, showed
A Proof of Birkhoff s Ergodic Theorem Joseph Hora September 2, 205 Itroductio I Fall 203, I was learig the basics of ergodic theory, ad I came across this theorem. Oe of my supervisors, Athoy Quas, showed
Roberto s Notes on Series Chapter 2: Convergence tests Section 7. Alternating series
 Roberto s Notes o Series Chapter 2: Covergece tests Sectio 7 Alteratig series What you eed to kow already: All basic covergece tests for evetually positive series. What you ca lear here: A test for series
Roberto s Notes o Series Chapter 2: Covergece tests Sectio 7 Alteratig series What you eed to kow already: All basic covergece tests for evetually positive series. What you ca lear here: A test for series
Lecture 3 The Lebesgue Integral
 Lecture 3: The Lebesgue Itegral 1 of 14 Course: Theory of Probability I Term: Fall 2013 Istructor: Gorda Zitkovic Lecture 3 The Lebesgue Itegral The costructio of the itegral Uless expressly specified
Lecture 3: The Lebesgue Itegral 1 of 14 Course: Theory of Probability I Term: Fall 2013 Istructor: Gorda Zitkovic Lecture 3 The Lebesgue Itegral The costructio of the itegral Uless expressly specified
MATH 10550, EXAM 3 SOLUTIONS
 MATH 155, EXAM 3 SOLUTIONS 1. I fidig a approximate solutio to the equatio x 3 +x 4 = usig Newto s method with iitial approximatio x 1 = 1, what is x? Solutio. Recall that x +1 = x f(x ) f (x ). Hece,
MATH 155, EXAM 3 SOLUTIONS 1. I fidig a approximate solutio to the equatio x 3 +x 4 = usig Newto s method with iitial approximatio x 1 = 1, what is x? Solutio. Recall that x +1 = x f(x ) f (x ). Hece,
Math 2784 (or 2794W) University of Connecticut
 ORDERS OF GROWTH PAT SMITH Math 2784 (or 2794W) Uiversity of Coecticut Date: Mar. 2, 22. ORDERS OF GROWTH. Itroductio Gaiig a ituitive feel for the relative growth of fuctios is importat if you really
ORDERS OF GROWTH PAT SMITH Math 2784 (or 2794W) Uiversity of Coecticut Date: Mar. 2, 22. ORDERS OF GROWTH. Itroductio Gaiig a ituitive feel for the relative growth of fuctios is importat if you really
The Growth of Functions. Theoretical Supplement
 The Growth of Fuctios Theoretical Supplemet The Triagle Iequality The triagle iequality is a algebraic tool that is ofte useful i maipulatig absolute values of fuctios. The triagle iequality says that
The Growth of Fuctios Theoretical Supplemet The Triagle Iequality The triagle iequality is a algebraic tool that is ofte useful i maipulatig absolute values of fuctios. The triagle iequality says that
( 1) n (4x + 1) n. n=0
 Problem 1 (10.6, #). Fid the radius of covergece for the series: ( 1) (4x + 1). For what values of x does the series coverge absolutely, ad for what values of x does the series coverge coditioally? Solutio.
Problem 1 (10.6, #). Fid the radius of covergece for the series: ( 1) (4x + 1). For what values of x does the series coverge absolutely, ad for what values of x does the series coverge coditioally? Solutio.
Math 21B-B - Homework Set 2
 Math B-B - Homework Set Sectio 5.:. a) lim P k= c k c k ) x k, where P is a partitio of [, 5. x x ) dx b) lim P k= 4 ck x k, where P is a partitio of [,. 4 x dx c) lim P k= ta c k ) x k, where P is a partitio
Math B-B - Homework Set Sectio 5.:. a) lim P k= c k c k ) x k, where P is a partitio of [, 5. x x ) dx b) lim P k= 4 ck x k, where P is a partitio of [,. 4 x dx c) lim P k= ta c k ) x k, where P is a partitio
MAT1026 Calculus II Basic Convergence Tests for Series
 MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
Product measures, Tonelli s and Fubini s theorems For use in MAT3400/4400, autumn 2014 Nadia S. Larsen. Version of 13 October 2014.
 Product measures, Toelli s ad Fubii s theorems For use i MAT3400/4400, autum 2014 Nadia S. Larse Versio of 13 October 2014. 1. Costructio of the product measure The purpose of these otes is to preset the
Product measures, Toelli s ad Fubii s theorems For use i MAT3400/4400, autum 2014 Nadia S. Larse Versio of 13 October 2014. 1. Costructio of the product measure The purpose of these otes is to preset the
Z ß cos x + si x R du We start with the substitutio u = si(x), so du = cos(x). The itegral becomes but +u we should chage the limits to go with the ew
 Problem ( poits) Evaluate the itegrals Z p x 9 x We ca draw a right triagle labeled this way x p x 9 From this we ca read off x = sec, so = sec ta, ad p x 9 = R ta. Puttig those pieces ito the itegralrwe
Problem ( poits) Evaluate the itegrals Z p x 9 x We ca draw a right triagle labeled this way x p x 9 From this we ca read off x = sec, so = sec ta, ad p x 9 = R ta. Puttig those pieces ito the itegralrwe
Definition 4.2. (a) A sequence {x n } in a Banach space X is a basis for X if. unique scalars a n (x) such that x = n. a n (x) x n. (4.
 4. BASES I BAACH SPACES 39 4. BASES I BAACH SPACES Sice a Baach space X is a vector space, it must possess a Hamel, or vector space, basis, i.e., a subset {x γ } γ Γ whose fiite liear spa is all of X ad
4. BASES I BAACH SPACES 39 4. BASES I BAACH SPACES Sice a Baach space X is a vector space, it must possess a Hamel, or vector space, basis, i.e., a subset {x γ } γ Γ whose fiite liear spa is all of X ad
Part I: Covers Sequence through Series Comparison Tests
 Part I: Covers Sequece through Series Compariso Tests. Give a example of each of the followig: (a) A geometric sequece: (b) A alteratig sequece: (c) A sequece that is bouded, but ot coverget: (d) A sequece
Part I: Covers Sequece through Series Compariso Tests. Give a example of each of the followig: (a) A geometric sequece: (b) A alteratig sequece: (c) A sequece that is bouded, but ot coverget: (d) A sequece
Analytic Continuation
 Aalytic Cotiuatio The stadard example of this is give by Example Let h (z) = 1 + z + z 2 + z 3 +... kow to coverge oly for z < 1. I fact h (z) = 1/ (1 z) for such z. Yet H (z) = 1/ (1 z) is defied for
Aalytic Cotiuatio The stadard example of this is give by Example Let h (z) = 1 + z + z 2 + z 3 +... kow to coverge oly for z < 1. I fact h (z) = 1/ (1 z) for such z. Yet H (z) = 1/ (1 z) is defied for
MA131 - Analysis 1. Workbook 3 Sequences II
 MA3 - Aalysis Workbook 3 Sequeces II Autum 2004 Cotets 2.8 Coverget Sequeces........................ 2.9 Algebra of Limits......................... 2 2.0 Further Useful Results........................
MA3 - Aalysis Workbook 3 Sequeces II Autum 2004 Cotets 2.8 Coverget Sequeces........................ 2.9 Algebra of Limits......................... 2 2.0 Further Useful Results........................
Math 120 Answers for Homework 23
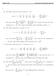 Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
Math 0 Aswers for Homewor. (a) The Taylor series for cos(x) aroud a 0 is cos(x) x! + x4 4! x6 6! + x8 8! x0 0! + ( ) ()! x ( ) π ( ) ad so the series ()! ()! (π) is just the series for cos(x) evaluated
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
 Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Introductory Analysis I Fall 2014 Homework #7 Solutions
 Itroductory Aalysis I Fall 214 Homework #7 Solutios Note: There were a couple of typos/omissios i the formulatio of this homework. Some of them were, I believe, quite obvious. The fact that the statemet
Itroductory Aalysis I Fall 214 Homework #7 Solutios Note: There were a couple of typos/omissios i the formulatio of this homework. Some of them were, I believe, quite obvious. The fact that the statemet
The picture in figure 1.1 helps us to see that the area represents the distance traveled. Figure 1: Area represents distance travelled
 1 Lecture : Area Area ad distace traveled Approximatig area by rectagles Summatio The area uder a parabola 1.1 Area ad distace Suppose we have the followig iformatio about the velocity of a particle, how
1 Lecture : Area Area ad distace traveled Approximatig area by rectagles Summatio The area uder a parabola 1.1 Area ad distace Suppose we have the followig iformatio about the velocity of a particle, how
Chapter 7: Numerical Series
 Chapter 7: Numerical Series Chapter 7 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals
Chapter 7: Numerical Series Chapter 7 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals
Series III. Chapter Alternating Series
 Chapter 9 Series III With the exceptio of the Null Sequece Test, all the tests for series covergece ad divergece that we have cosidered so far have dealt oly with series of oegative terms. Series with
Chapter 9 Series III With the exceptio of the Null Sequece Test, all the tests for series covergece ad divergece that we have cosidered so far have dealt oly with series of oegative terms. Series with
It is often useful to approximate complicated functions using simpler ones. We consider the task of approximating a function by a polynomial.
 Taylor Polyomials ad Taylor Series It is ofte useful to approximate complicated fuctios usig simpler oes We cosider the task of approximatig a fuctio by a polyomial If f is at least -times differetiable
Taylor Polyomials ad Taylor Series It is ofte useful to approximate complicated fuctios usig simpler oes We cosider the task of approximatig a fuctio by a polyomial If f is at least -times differetiable
TR/46 OCTOBER THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION A. TALBOT
 TR/46 OCTOBER 974 THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION by A. TALBOT .. Itroductio. A problem i approximatio theory o which I have recetly worked [] required for its solutio a proof that the
TR/46 OCTOBER 974 THE ZEROS OF PARTIAL SUMS OF A MACLAURIN EXPANSION by A. TALBOT .. Itroductio. A problem i approximatio theory o which I have recetly worked [] required for its solutio a proof that the
MIDTERM 3 CALCULUS 2. Monday, December 3, :15 PM to 6:45 PM. Name PRACTICE EXAM SOLUTIONS
 MIDTERM 3 CALCULUS MATH 300 FALL 08 Moday, December 3, 08 5:5 PM to 6:45 PM Name PRACTICE EXAM S Please aswer all of the questios, ad show your work. You must explai your aswers to get credit. You will
MIDTERM 3 CALCULUS MATH 300 FALL 08 Moday, December 3, 08 5:5 PM to 6:45 PM Name PRACTICE EXAM S Please aswer all of the questios, ad show your work. You must explai your aswers to get credit. You will
1 Lecture 2: Sequence, Series and power series (8/14/2012)
 Summer Jump-Start Program for Aalysis, 202 Sog-Yig Li Lecture 2: Sequece, Series ad power series (8/4/202). More o sequeces Example.. Let {x } ad {y } be two bouded sequeces. Show lim sup (x + y ) lim
Summer Jump-Start Program for Aalysis, 202 Sog-Yig Li Lecture 2: Sequece, Series ad power series (8/4/202). More o sequeces Example.. Let {x } ad {y } be two bouded sequeces. Show lim sup (x + y ) lim
Chapter 3. Strong convergence. 3.1 Definition of almost sure convergence
 Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
SUMMARY OF SEQUENCES AND SERIES
 SUMMARY OF SEQUENCES AND SERIES Importat Defiitios, Results ad Theorems for Sequeces ad Series Defiitio. A sequece {a } has a limit L ad we write lim a = L if for every ɛ > 0, there is a correspodig iteger
SUMMARY OF SEQUENCES AND SERIES Importat Defiitios, Results ad Theorems for Sequeces ad Series Defiitio. A sequece {a } has a limit L ad we write lim a = L if for every ɛ > 0, there is a correspodig iteger
Convergence: nth-term Test, Comparing Non-negative Series, Ratio Test
 Covergece: th-term Test, Comparig No-egative Series, Ratio Test Power Series ad Covergece We have writte statemets like: l + x = x x2 + x3 2 3 + x + But we have ot talked i depth about what values of x
Covergece: th-term Test, Comparig No-egative Series, Ratio Test Power Series ad Covergece We have writte statemets like: l + x = x x2 + x3 2 3 + x + But we have ot talked i depth about what values of x
Lecture Chapter 6: Convergence of Random Sequences
 ECE5: Aalysis of Radom Sigals Fall 6 Lecture Chapter 6: Covergece of Radom Sequeces Dr Salim El Rouayheb Scribe: Abhay Ashutosh Doel, Qibo Zhag, Peiwe Tia, Pegzhe Wag, Lu Liu Radom sequece Defiitio A ifiite
ECE5: Aalysis of Radom Sigals Fall 6 Lecture Chapter 6: Covergece of Radom Sequeces Dr Salim El Rouayheb Scribe: Abhay Ashutosh Doel, Qibo Zhag, Peiwe Tia, Pegzhe Wag, Lu Liu Radom sequece Defiitio A ifiite
(a) (b) All real numbers. (c) All real numbers. (d) None. to show the. (a) 3. (b) [ 7, 1) (c) ( 7, 1) (d) At x = 7. (a) (b)
 Chapter 0 Review 597. E; a ( + )( + ) + + S S + S + + + + + + S lim + l. D; a diverges by the Itegral l k Test sice d lim [(l ) ], so k l ( ) does ot coverge absolutely. But it coverges by the Alteratig
Chapter 0 Review 597. E; a ( + )( + ) + + S S + S + + + + + + S lim + l. D; a diverges by the Itegral l k Test sice d lim [(l ) ], so k l ( ) does ot coverge absolutely. But it coverges by the Alteratig
Archimedes - numbers for counting, otherwise lengths, areas, etc. Kepler - geometry for planetary motion
 Topics i Aalysis 3460:589 Summer 007 Itroductio Ree descartes - aalysis (breaig dow) ad sythesis Sciece as models of ature : explaatory, parsimoious, predictive Most predictios require umerical values,
Topics i Aalysis 3460:589 Summer 007 Itroductio Ree descartes - aalysis (breaig dow) ad sythesis Sciece as models of ature : explaatory, parsimoious, predictive Most predictios require umerical values,
Power Series: A power series about the center, x = 0, is a function of x of the form
 You are familiar with polyomial fuctios, polyomial that has ifiitely may terms. 2 p ( ) a0 a a 2 a. A power series is just a Power Series: A power series about the ceter, = 0, is a fuctio of of the form
You are familiar with polyomial fuctios, polyomial that has ifiitely may terms. 2 p ( ) a0 a a 2 a. A power series is just a Power Series: A power series about the ceter, = 0, is a fuctio of of the form
AP Calculus Chapter 9: Infinite Series
 AP Calculus Chapter 9: Ifiite Series 9. Sequeces a, a 2, a 3, a 4, a 5,... Sequece: A fuctio whose domai is the set of positive itegers = 2 3 4 a = a a 2 a 3 a 4 terms of the sequece Begi with the patter
AP Calculus Chapter 9: Ifiite Series 9. Sequeces a, a 2, a 3, a 4, a 5,... Sequece: A fuctio whose domai is the set of positive itegers = 2 3 4 a = a a 2 a 3 a 4 terms of the sequece Begi with the patter
1. (25 points) Use the limit definition of the definite integral and the sum formulas 1 to compute
 Math, Calculus II Fial Eam Solutios. 5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute 4 d. The check your aswer usig the Evaluatio Theorem. ) ) Solutio: I this itegral,
Math, Calculus II Fial Eam Solutios. 5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute 4 d. The check your aswer usig the Evaluatio Theorem. ) ) Solutio: I this itegral,
FINAL EXAMINATION IN FOUNDATION OF ANALYSIS (TMA4225)
 Norwegia Uiversity of Sciece ad Techology Departmet of Mathematical Scieces Page of 7 Cotact durig exam: Eugeia Maliikova (735) 52 57 FINAL EXAMINATION IN FOUNDATION OF ANALYSIS (TMA4225) Moday, December
Norwegia Uiversity of Sciece ad Techology Departmet of Mathematical Scieces Page of 7 Cotact durig exam: Eugeia Maliikova (735) 52 57 FINAL EXAMINATION IN FOUNDATION OF ANALYSIS (TMA4225) Moday, December
f(x) dx as we do. 2x dx x also diverges. Solution: We compute 2x dx lim
 Math 3, Sectio 2. (25 poits) Why we defie f(x) dx as we do. (a) Show that the improper itegral diverges. Hece the improper itegral x 2 + x 2 + b also diverges. Solutio: We compute x 2 + = lim b x 2 + =
Math 3, Sectio 2. (25 poits) Why we defie f(x) dx as we do. (a) Show that the improper itegral diverges. Hece the improper itegral x 2 + x 2 + b also diverges. Solutio: We compute x 2 + = lim b x 2 + =
FUNDAMENTALS OF REAL ANALYSIS by
 FUNDAMENTALS OF REAL ANALYSIS by Doğa Çömez Backgroud: All of Math 450/1 material. Namely: basic set theory, relatios ad PMI, structure of N, Z, Q ad R, basic properties of (cotiuous ad differetiable)
FUNDAMENTALS OF REAL ANALYSIS by Doğa Çömez Backgroud: All of Math 450/1 material. Namely: basic set theory, relatios ad PMI, structure of N, Z, Q ad R, basic properties of (cotiuous ad differetiable)
Problem Cosider the curve give parametrically as x = si t ad y = + cos t for» t» ß: (a) Describe the path this traverses: Where does it start (whe t =
 Mathematics Summer Wilso Fial Exam August 8, ANSWERS Problem 1 (a) Fid the solutio to y +x y = e x x that satisfies y() = 5 : This is already i the form we used for a first order liear differetial equatio,
Mathematics Summer Wilso Fial Exam August 8, ANSWERS Problem 1 (a) Fid the solutio to y +x y = e x x that satisfies y() = 5 : This is already i the form we used for a first order liear differetial equatio,
Math 113 Exam 4 Practice
 Math Exam 4 Practice Exam 4 will cover.-.. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for
Math Exam 4 Practice Exam 4 will cover.-.. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for
MA131 - Analysis 1. Workbook 2 Sequences I
 MA3 - Aalysis Workbook 2 Sequeces I Autum 203 Cotets 2 Sequeces I 2. Itroductio.............................. 2.2 Icreasig ad Decreasig Sequeces................ 2 2.3 Bouded Sequeces..........................
MA3 - Aalysis Workbook 2 Sequeces I Autum 203 Cotets 2 Sequeces I 2. Itroductio.............................. 2.2 Icreasig ad Decreasig Sequeces................ 2 2.3 Bouded Sequeces..........................
Fourier Series and the Wave Equation
 Fourier Series ad the Wave Equatio We start with the oe-dimesioal wave equatio u u =, x u(, t) = u(, t) =, ux (,) = f( x), u ( x,) = This represets a vibratig strig, where u is the displacemet of the strig
Fourier Series ad the Wave Equatio We start with the oe-dimesioal wave equatio u u =, x u(, t) = u(, t) =, ux (,) = f( x), u ( x,) = This represets a vibratig strig, where u is the displacemet of the strig
Math Solutions to homework 6
 Math 175 - Solutios to homework 6 Cédric De Groote November 16, 2017 Problem 1 (8.11 i the book): Let K be a compact Hermitia operator o a Hilbert space H ad let the kerel of K be {0}. Show that there
Math 175 - Solutios to homework 6 Cédric De Groote November 16, 2017 Problem 1 (8.11 i the book): Let K be a compact Hermitia operator o a Hilbert space H ad let the kerel of K be {0}. Show that there
Math 10A final exam, December 16, 2016
 Please put away all books, calculators, cell phoes ad other devices. You may cosult a sigle two-sided sheet of otes. Please write carefully ad clearly, USING WORDS (ot just symbols). Remember that the
Please put away all books, calculators, cell phoes ad other devices. You may cosult a sigle two-sided sheet of otes. Please write carefully ad clearly, USING WORDS (ot just symbols). Remember that the
Indian Statistical Institute, Bangalore Centre Solution set of M.Math II Year, End-Sem Examination 2015 Fourier Analysis
 Idia Statistical Istitute, Bagalore Cetre Solutio set of M.Math II Year, Ed-Sem Examiatio 05 Fourier Aalysis Note: We use the followig otatios L () L ad L () L.. Prove that f, ˆf L the f L. Proof. Sice
Idia Statistical Istitute, Bagalore Cetre Solutio set of M.Math II Year, Ed-Sem Examiatio 05 Fourier Aalysis Note: We use the followig otatios L () L ad L () L.. Prove that f, ˆf L the f L. Proof. Sice
REAL ANALYSIS II: PROBLEM SET 1 - SOLUTIONS
 REAL ANALYSIS II: PROBLEM SET 1 - SOLUTIONS 18th Feb, 016 Defiitio (Lipschitz fuctio). A fuctio f : R R is said to be Lipschitz if there exists a positive real umber c such that for ay x, y i the domai
REAL ANALYSIS II: PROBLEM SET 1 - SOLUTIONS 18th Feb, 016 Defiitio (Lipschitz fuctio). A fuctio f : R R is said to be Lipschitz if there exists a positive real umber c such that for ay x, y i the domai
MTH 122 Calculus II Essex County College Division of Mathematics and Physics 1 Lecture Notes #20 Sakai Web Project Material
 MTH 1 Calculus II Essex Couty College Divisio of Mathematics ad Physics 1 Lecture Notes #0 Sakai Web Project Material 1 Power Series 1 A power series is a series of the form a x = a 0 + a 1 x + a x + a
MTH 1 Calculus II Essex Couty College Divisio of Mathematics ad Physics 1 Lecture Notes #0 Sakai Web Project Material 1 Power Series 1 A power series is a series of the form a x = a 0 + a 1 x + a x + a
INFINITE SEQUENCES AND SERIES
 INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES I geeral, it is difficult to fid the exact sum of a series. We were able to accomplish this for geometric series ad the series /[(+)]. This is
INFINITE SEQUENCES AND SERIES INFINITE SEQUENCES AND SERIES I geeral, it is difficult to fid the exact sum of a series. We were able to accomplish this for geometric series ad the series /[(+)]. This is
Math 19B Final. Study Aid. June 6, 2011
 Math 9B Fial Study Aid Jue 6, 20 Geeral advise. Get plety of practice. There s a lot of material i this sectio - try to do as may examples ad as much of the homework as possible to get some practice. Just
Math 9B Fial Study Aid Jue 6, 20 Geeral advise. Get plety of practice. There s a lot of material i this sectio - try to do as may examples ad as much of the homework as possible to get some practice. Just
Lecture 3: Convergence of Fourier Series
 Lecture 3: Covergece of Fourier Series Himashu Tyagi Let f be a absolutely itegrable fuctio o T : [ π,π], i.e., f L (T). For,,... defie ˆf() f(θ)e i θ dθ. π T The series ˆf()e i θ is called the Fourier
Lecture 3: Covergece of Fourier Series Himashu Tyagi Let f be a absolutely itegrable fuctio o T : [ π,π], i.e., f L (T). For,,... defie ˆf() f(θ)e i θ dθ. π T The series ˆf()e i θ is called the Fourier
Sequences I. Chapter Introduction
 Chapter 2 Sequeces I 2. Itroductio A sequece is a list of umbers i a defiite order so that we kow which umber is i the first place, which umber is i the secod place ad, for ay atural umber, we kow which
Chapter 2 Sequeces I 2. Itroductio A sequece is a list of umbers i a defiite order so that we kow which umber is i the first place, which umber is i the secod place ad, for ay atural umber, we kow which
The second is the wish that if f is a reasonably nice function in E and φ n
 8 Sectio : Approximatios i Reproducig Kerel Hilbert Spaces I this sectio, we address two cocepts. Oe is the wish that if {E, } is a ierproduct space of real valued fuctios o the iterval [,], the there
8 Sectio : Approximatios i Reproducig Kerel Hilbert Spaces I this sectio, we address two cocepts. Oe is the wish that if {E, } is a ierproduct space of real valued fuctios o the iterval [,], the there
4.1 Sigma Notation and Riemann Sums
 0 the itegral. Sigma Notatio ad Riema Sums Oe strategy for calculatig the area of a regio is to cut the regio ito simple shapes, calculate the area of each simple shape, ad the add these smaller areas
0 the itegral. Sigma Notatio ad Riema Sums Oe strategy for calculatig the area of a regio is to cut the regio ito simple shapes, calculate the area of each simple shape, ad the add these smaller areas
11.6 Absolute Convergence and the Ratio and Root Tests
 .6 Absolute Covergece ad the Ratio ad Root Tests The most commo way to test for covergece is to igore ay positive or egative sigs i a series, ad simply test the correspodig series of positive terms. Does
.6 Absolute Covergece ad the Ratio ad Root Tests The most commo way to test for covergece is to igore ay positive or egative sigs i a series, ad simply test the correspodig series of positive terms. Does
Chapter 4. Fourier Series
 Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Riemann Sums y = f (x)
 Riema Sums Recall that we have previously discussed the area problem I its simplest form we ca state it this way: The Area Problem Let f be a cotiuous, o-egative fuctio o the closed iterval [a, b] Fid
Riema Sums Recall that we have previously discussed the area problem I its simplest form we ca state it this way: The Area Problem Let f be a cotiuous, o-egative fuctio o the closed iterval [a, b] Fid
Chapter 7 Isoperimetric problem
 Chapter 7 Isoperimetric problem Recall that the isoperimetric problem (see the itroductio its coectio with ido s proble) is oe of the most classical problem of a shape optimizatio. It ca be formulated
Chapter 7 Isoperimetric problem Recall that the isoperimetric problem (see the itroductio its coectio with ido s proble) is oe of the most classical problem of a shape optimizatio. It ca be formulated
