The Effect of a Basal-friction Parameterization on. Grounding-line Dynamics in Ice-sheet Models.
|
|
|
- Melvyn Watts
- 6 years ago
- Views:
Transcription
1 The Effect of a Basal-friction Parameterization on Grounding-line Dynamics in Ice-sheet Models. by Gunter Leguy Submitted in Partial Fulfillment of the Requirements for the Degree of Ph.D of Applied & Industrial Mathematics New Mexico Institute of Mining and Technology Socorro, New Mexico August, 5
2 ABSTRACT Keywords: KEYWORD; KEYWORD; KEY PHRASE 3;...
3 CONTENTS LIST OF TABLES LIST OF FIGURES v vi. INTRODUCTION. The Antarctic ice sheet Modeling ice sheets Thesis goals LITERATURE REVIEW 9 3. MODEL DERIVATION 4 3. Stokes flow model The Blatter-Pattyn model One-dimensional shallow-shelf flow line model The continuity equation The conservation of momentum The boundary conditions Effective pressure parameterization and friction law Chapter summary STEADY STATE PROPERTIES In the ice sheet Asymptotic Method and series formula At the ice divide and its vicinity At the grounding line In the bulk of the ice sheet in the ice Shelf Chapter summary ii
4 5. NUMERICS The fixed grid models Fixed-grid model without a GLP Addition of the GLP A pseudo-spectral Benchmark model Motivation The numerics Chapter Summary STABILITY ANALYSIS 8 6. Linearization around steady state Normal mode analysis The momentum equation The continuity equation A method for finding the fastest growing or slowest decaying eigenmode Chapter summary PARAMETER SENSITIVITY Steady-state experiments over a linear bed rock topography Varying the ice softness A Varying the shear stress factor C Varying the bed slope b x Varying the wavelength of bedrock bumps λ max Varying the Channel width W Steady-state experiments over a polynomial bed rock topography Transient Experiment over a linear bed rock topography Varying the shear stress factor C Melting ice shelves Chapter summary THREE-DIMENSIONAL MODEL EXPERIMENT The Community Ice Sheet Model CISM) The MISMIP3D experiment Chapter summary iii
5 9. CONCLUSION 57 REFERENCES 6 iv
6 LIST OF TABLES 3. Parameter values Ice softness values for the MISMIP experiments and Shear stress factor sample Bedrock slope sample Wavelength of bedrock bumps sample Channel width sample Values of the shear stress factor C used in the transient experiments Parameter values for MISMIP3d v
7 LIST OF FIGURES. Antarctic geography and characteristics Dependence of ice geometry and effective pressure on the parameter p over a linear bed Dependence of ice geometry and effective pressure on the parameter p over a polynomial bed Basal stress representation and its asymptotic limits Asymptotic results for bed rock topography at ice divide Asymptotic results for ice thickness at ice divide Asymptotic results for bed rock topography at grounding line Asymptotic results for ice thickness at grounding line Difference between shallow ice and shallow shelf models Staggered grid illustration Eigenvalue problem results Numerical eigenvalue results Benchmark grounding-line positions differences, varying ice softness Grounding-line position analytical comparison for p= over a linear bed, varying ice softness Grounding-line position signed difference over a linear bed, varying Ice softness Grounding-line maximum error as a function of resolution over a linear bed, varying ice softness Shear stress factor distribution Grounding-line position analytical comparison over a linear bed, varying C vi
8 7.7 Grounding-line position signed difference over a linear bed, varying C Grounding-line maximum error as a function of resolution over a linear bed, varying C Grounding-line position analytical comparison over a linear bed, varying b x Grounding-line maximum error as a function of resolution over a linear bed, varying b x Grounding-line position at 5m resolution over a linear bed, varying b x Grounding-line positions over a linear bed, varying the wavelength of bedrock bumps Transition zone length using a linear bed and varying the wavelength of bedrock bumps Grounding-line maximum error as a function of resolution over a linear bed, varying the wavelength of bedrock bumps Grounding-line maximum error as a function of resolution over a linear bed, varying the wavelength of bedrock bumps second experiment) Channel width distribution over the Antarctic ice sheet Grounding-line position at 5m resolution over a linear bed, varying W Grounding-line maximum error as a function of resolution over a linear bed, varying W Polynomial bed Grounding-line position comparison over a polynomial bed, varying ice softness Grounding-line root-mean-square error as a function of resolution over a polynomial bed, varying ice softness Grounding-line position signed difference over a polynomial bed, varying Ice softness Grounding-line position benchmark evolution over 5 years and varying C Grounding-line position signed difference over 5 years and varying C Grounding-line maximum error as a function of resolution over 5 years, for experiments a and a, and when varying C Grounding-line maximum error as a function of resolution over 5 years, for experiments b and b, and when varying C vii
9 7.7 Grounding-line position evolution of the benchmark for the iceshelf melt experiment Grounding-line position signed difference for the ice shelf-melt experiment Grounding-line maximum error as a function of resolution over 5 years for the ice-shelf melt experiment Basal shear stress factor spatial perturbation for the MISMIP3d experiments MISMIP3d results for SSA, at km resolution MISMIP3d results for DIVA and BP, for p = and at km resolution MISMIP3d results comparison between SSA and DIVA, for all p and at km resolution viii
10 This thesis is accepted on behalf of the faculty of the Institute by the following committee: Whilliam D. Stone, Advisor I release this document to the New Mexico Institute of Mining and Technology. Gunter Leguy Date
11 CHAPTER INTRODUCTION The purpose of this work is to propose a new basal-stress parameterization and analyze its effect on ice sheet models with the ultimate goal to better forecast sea-level rise. In this introduction we give a general background and the necessary terminology to understand the physical framework and the motivation of this dissertation. An ice sheet is a mass of ice resting on solid ground with a surface area greater than 5. km. There are two of them on Earth: Antarctica and Greenland. If the ice of each ice sheet was to be dropped in the ocean, either in the form of melted ice or a block of ice, sea level would rise by 58 m Fretwell et al., 3) and 7 m Letrégully et al., 99a) respectively in comparison, all glaciers on Earth combined represent a sea-level rise increase of.6 m), impacting coastal areas around the globe. This fact drives the motivation of understanding the conditions under which sea level would rise significantly in the future and the timescale over which it would happen. In order to provide such information, it is crucial to accurately model ice-sheet dynamics. Although Greenland has a strong sea-level rise potential, our work focuses on Antarctica.. The Antarctic ice sheet Antarctica is a continent with a surface area of 6 km and can be divided in two regions, as shown in figure., that each have their own characteristics: The East Antarctic Ice Sheet EAIS) and the West Antarctic Ice Sheet WAIS). The EAIS is a desert and contains most of the Antarctic Ice. The ice thickness averages 3 km and its sea level rise equivalent is about fifty meters. The WAIS reaches an elevation of about.5 km in average figure.). It is often referred to as a marine ice sheet as its bedrock topography lies below sea level figure.) and its ice flows into ice shelves which are floating ice surfaces attached to the ice sheet. WAIS is surrounded by the two biggest in the continent: the Rohne-Filchner and the Ross ice shelves. WAIS also includes the Antarctic
12 Peninsula AP) which is surrounded by ocean water. In contrast with the EAIS, and because of its immersed bed topography, the WAIS is very vulnerable to ocean warming and climate change. Figure. shows the ice velocity in Antarctica. The ice in the anterior of the ice sheet moves slowly and is even quasi static at some location. However, some ice flows faster because they sit on more lubricated bed that has less resistance than the surrounding ice. This ice then forms rivers of ice that are called ice streams. Even though ice streams represent % of Antarctica, they drive more than 9% of the inland ice to the ocean. The state of an ice sheet highly depends on ice stream flows. Once the ice sheet reaches the ocean, the ice eventually loses contact with the bed to become an ice shelf. The location where it happens is called the grounding line GL). This boundary plays an important role in understanding sea level rise as it is the area that controls the flow from grounded to floating ice and therefore the contribution to sea level rise. The outer boundary of an ice shelf is called the calving front. When a part of the ice shelf calves, it becomes an iceberg. Calving accounts for 9% of the ablation process in Antarctica. It results from initiation of fractures and their propagation through the ice thickness. Another source of ice loss is via basal melting. Basal melting is due to warm water interaction with the ice and occurs below an ice shelf. Deep water has a higher pressure and therefore a lower freezing point. For example, the freezing point under the Rohne-Filshner ice shelf is about.4 C. However, the temperature of upwelling water is about -3 C. This difference leads to basal melting. This melted ice could eventually refreeze while coming up closer to the water surface. Antarctica s contribution to sea level rise has increased in the past decade. While the contribution of the East Antarctic Ice Sheet EAIS) remains steady, mass loss from the West Antarctic Ice Sheet WAIS) has more than doubled Velicogna, 9; Rignot et al., ). Theoretical models suggest that marine ice sheets like WAIS are susceptible to instabilities when they lie on bedrock that slopes upward in the direction of ice flow Weertman, 974; Schoof, 7a). At the grounding line, the net upstream accumulation needs to equal the outflow. Schoof 7b) showed that the ice flux at the grounding line is proportional to the depth of the ice-sheet bed below sea level to the power 5. An inland perturbation of the grounding line increases the depth of the ice sheet which leads to an increase in ice flux. Such a perturbation creates an instability that cannot be stopped. If these instabilities are triggered, mass loss will accelerate, exacerbating future sea-level rise and potentially leading to WAIS collapse Vaughan and Spouge, ; Joughin and Alley, ). Once WAIS collapses nothing would prevent grounded ice with bedrock above sea level to flow rapidly into the ocean and further contribute to sea-level rise. For this reason it is important to understand the dynamic processes that drive ice sheets in the region.
13 . Modeling ice sheets The glaciology community has developed many ice-sheet models of varying complexity. Ice is considered to be a very viscous fluid which deforms in two ways, by stretching and shearing. The deformation of ice is typically represented by a stress tensor which defines the state of stress of a point in the ice. Stokes models Durand et al., 9; Favier et al., ), which include all components of the stress tensor, are the most accurate of the widely used ice-flow models. However, they can be impractical at continental scales because of their large computational cost, especially in three dimensions. By neglecting terms in the stress tensor, modelers have derived and applied several simpler, computationally cheaper approximations to the Stokes equations, including the first-order model Pattyn, 3; Perego et al., ), the so-called LL model Hindmarsh, 4; Schoof and Hindmarsh, ; Cornford et al., 3), the shallow-ice approximation Rutt et al., 9), the shallow-shelf approximation MacAyeal, 989; Schoof, 7a); and hybrid models that combine the shallow-ice and shallow-shelf approximations Bueler and Brown, 9; Pollard and DeConto, ). Shallow-ice models do not include extensional stresses and therefore cannot accurately represent shelf flow. Even the more accurate flow approximations require very fine resolution < km) in the transition zone the region where ice-sheet flow dominated by vertical shear stress transitions to ice-shelf flow dominated by extensional stress) in order to obtain numerically accurate ice sheet ice shelf simulations Durand et al., 9; Cornford et al., 3). Several studies have investigated the effects of different friction laws on ice dynamics using one-dimensional, depth-integrated models Muszynski and Birchfield, 987; MacAyeal, 989; Schoof, 7a). Vieli and Payne 5) and Schoof 7a) prescribed a discontinuous friction law across the grounding line where the ice loses contact with the bed. In these models the friction is nonzero in the ice sheet, but abruptly falls to zero at the grounding line. These models have the drawback that very high grid resolution near the grounding line is required for convergence. In models with fixed grids, a tolerance of a few kilometers in the grounding-line location requires a resolution on the order of tens to hundreds of meters Durand et al., 9; Gladstone et al., a,b; Cornford et al., 3), which is computationally prohibitive for large-scale simulations. This requirement was confirmed by the Marine Ice Sheet Model Intercomparison Project MISMIP, Pattyn et al., ) which used the same basal friction law as in Schoof 7a). In this project, participants using a variety of fixed-grid models found that the errors in grounding-line position were unacceptably high km or more) at resolutions that were computationally feasible in three-dimensional models km). One way to reduce the computational cost is to use adaptive mesh refinement Goldberg et al., 9; Gladstone et al., b; Cornford et al., 3), i.e., to subdivide the horizontal mesh near features where high resolution is needed. Durand et al. 9) investigated this approach in a Stokes model with the basal friction law of Schoof 7a). They performed a set of experiments based on the MISMIP experiments with the goal of reaching steady state when using very high resolution near the grounding line. Even with grid resolution of 3 m in 3
14 the transition zone, they found differences in the grounding-line position over an advance-and-retreat cycle of km, whereas theoretical arguments predict that there should be no difference. In order to reduce the need for high resolution near the grounding line, Pattyn et al. 6) proposed a smooth basal-friction parameter that decays exponentially to zero as the ice flows across the grounding line into the ice shelf. This approach gave promising results, as the transition zone could be partially resolved even at.5 km grid resolution. However, the model introduced an arbitrary length scale of exponential decay, and the basal friction remained nonzero though small) in the ice shelf. Gladstone et al. ) showed that the need for high resolution could also be relaxed by decreasing the value of the basal drag coefficient, the ice softness, or channel width when buttressing is included in the model), or by steepening the slope of the bedrock topography. Pattyn et al. 6) and Gladstone et al. a) also showed that higher-order interpolation at the grounding line, where the grounded ice sheet meets the floating ice shelf, could greatly reduce the error in the grounding-line position, implying convergence at coarser resolution. In the case of rapidly sliding ice streams, basal resistance is controlled by the underlying water-laden plastic till Tulaczyk et al., a,b; van der Wel et al., 3). The presence of liquid water lowers the effective pressure at the ice base, leading to reduced basal friction Tulaczyk et al., b; Carter and Fricker, ; van der Wel et al., 3), an effect not accounted for in many ice sheet models. Recent observations confirm the existence of basal drainage channels that connect subglacial lake systems Wingham et al., 6; Fricker et al., 9). Some of these drainage systems are found near grounding lines Fricker and Scambos, 9; Carter and Fricker, ), meaning that they are likely to connect to the ocean Le Brocq et al., 3). In a detailed hydrology/till model, van der Wel et al. 3) found that subglacial conduits can extend to the grounding line if sufficient water is available from local melting and upstream transport. They concluded that the Kamb Ice Stream currently does not have conduit systems but that the Rutford Ice Stream is connected to the ocean via a permanent conduit system. Cuffey and Paterson, p. 83) suggested that a free connection between subglacial water and the ocean is likely near the grounding line, though not plausible at 5 or km upstream. Several previous models have included the effect of basal water pressure or meltwater depth in their friction laws. Bueler and Brown 9) assumed plastic flow with a yield stress proportional to the effective pressure N the difference between the ice overburden pressure and the basal water pressure). They parameterized basal water pressure as a linear function of water depth, with a maximum value equal to 95 % of overburden pressure. Pimentel et al. ) used the friction law of Schoof 5), which predicts a basal shear stress proportional to N in the limit of fast flow and small N. They treated basal water pressure as a nonlinear function of water depth, capped at the overburden pressure. Martin et al. ) assumed plastic flow with a yield stress proportional to N, with basal water pressure prescribed to be 96 % of overburden pressure under the marine 4
15 portion of the Antarctic Ice Sheet including close to grounding lines). This parameterization reduced but did not eliminate the discontinuity in basal friction at the grounding line. The earlier models of Budd et al. 979) and Budd and Jenssen 989) included the effect of hydrological connectivity between basal channels and the ocean. These models assumed that the basal water pressure is equal to the ocean pressure at the same depth, or equivalently, that the effective pressure is proportional to the thickness above flotation. This implies N = at the grounding line, where the ice begins to float. Although Schoof 5) later showed that the friction law in Budd et al. 979) and Budd and Jenssen 989) was unphysical, the parameterization of N as a function of thickness above flotation inspired our own study..3 Thesis goals The main goal of this thesis is to propose and investigate a new treatment of effective pressure near the grounding line, combined with an established friction law Schoof, 5) linking basal stress and sliding to the effective pressure. We begin our work in In chapter with a literature review and summarize the key points of publications relevant to the development of this research. We only present the works that was essential to the full understanding of our work. Some other important publications are cited throughout the work and given in the bibliography. Chapter 3 presents the one-dimensional vertically-integrated model we use in this study. In a first part we show how we derive our model from the Stokes flow model, which most accurately represent ice-sheet dynamic, along with the assumptions required for our model to be valid. Our model solves for two unknowns: the ice sheet thickness and velocity. In a second part we describe the physical motivation and derivation of the basal-friction law which includes our new parameterization. We discuss mathematical limits of the basal-friction law which is proportional to the sliding velocity in the vicinity of the ice sheet and asymptotes to a Coulomb friction law close to the grounding line. In chapter 4 we investigate the steady-state properties of our one-dimensional model. Our model lacks an analytical solution. Thus, in the first section, we use an asymptotic analysis method to determines qualitative behavior of our model at the ice divide and at the grounding line; we show that only using 4 terms in our expansion is enough to approximate the steady-state model. We then use the Shallow Ice approximation SIA) - a further approximation of our model that only requires to solve an ODE system - to approximate our solution in the bulk of the ice sheet. We finally derive a close form solution of our equation in the ice shelf. With the qualitative and quantitative results from chapter 4 we can derive and test our numerical model presented in chapter 5. We use finite difference 5
16 and a staggered grid to discretize two fixed-grid models. The models differ in the treatment of the equations in the cell containing the grounding line: the first model treats that cell as fully grounded and the grounding line is located using linear interpolation between the first grounded and the first floating point. The second model uses a grounding-line parameterization GLP) Gladstone et al., a) which partitioned that cell into a grounded and a floating portion. Finally, we present a stretched-grid, pseudo-spectral model using Chebyshev polynomials. This model is used as a benchmark solution to compare with the fixed-grid results. Chapter 6 presents the numerical stability properties of our fixed-grid models. To this end we suppose the existence of a steady-state solution and linearize our system of equation around them. Using this linearized model, we perform a normal-mode analysis and attest on the stability of our numerical model. In chapter 7 we simulate ice streams using the numerical models described in chapter 5. We begin with a study of their steady-state behavior while varying different model parameters presented in chapter 3. We then perform a set of transient simulations over time frame similar used to simulate sea level rise. We perform these simulations at numerical resolutions varying between 3. km and.5 km. To this end we observe how model resolution impacts model convergence. We want to show that very high resolution at the grounding line is not necessary in order to perform reliable ice-sheet simulations. We discuss the role played by our new basal parameterization in these conclusions. Using a one-dimensional ice-sheet model is only practical in determining general properties of ice-sheet dynamics. To this end we investigate whether some results from chapter 7 remains valid in three-dimensional models which is the purpose of chapter??. Using the Community Ice Sheet Model CISM) Rutt et al., 9; Perego et al., ; Lipscomb et al., 3) and the MISMIP3D experiments Pattyn et al., 3) we perform experiments varying the basal stress specially and including our new parameterization. We perform these experiments using the extension of our model in two dimensions and compare the results with two other three-dimensional models. In chapter 9 we finally summarize our main results, discuss the limitations of our parameterization and the implications for future development of threedimensional ice-sheet models. Background: The big picture: climate change and sea-level rise. The ice sheets in the Earth s system The Antarctic Ice sheet: bed topography, climate,... The dynamic of the West Antarctic Ice Sheet WAIS): definition of the main component of an ice stream. the marine ice sheet instability. numerical models and challenges. 6
17 The role of the grounding-line: Why we care about parameterizing the effective pressure: mention the origin of including effective pressure in basal shear stress expression Bud). I can include some part of paper introduction here. Introduce the layout of my dissertation. 7
18 Figure.: The geography and characteristics of Antarctica. 8
19 CHAPTER LITERATURE REVIEW Adhikari, S. and Marshall S. J.: Parameterization of lateral drag in flowline models of glaciers dynamics, J. Glaciol., 58, doi:.389/jogj8,. Flowline model are often used as an approximation to Stokes-flow model as they are computationally inexpensive and provide good approximation in specific flow regimes. The drawback of these models is heir lack of lateral drag representation. This work shows how a correction factor can be applied, given some knowledge of the bed geometry, to account for most of the lateral drag effect in a flow line model. It confirmed that for any type of bed geometry, the ice velocity is maximum at the centerline of the glacier. Budd, W. F., Keage, P. L., and Blundy, N. A.: Empirical studies of ice sliding, J. Glaciol., 3, 57 7, 979. The basal sliding relations presented in this paper are derived empirically. The tests showed that, using different physical constraint, the basal sliding velocity can be derived as a power law involving basal stress and effective pressure. These power laws assume that the basal water pressure is equal to the ocean pressure at the same depth, in other words that the effective pressure is proportional to the thickness above flotation. Later on, Schoof 5) will show that such a power law is not physical everywhere in the ice-sheet domain but remains a good approximation close to the grounding line. Cornford, S. L., Martin, D. F., Graves, D. T., Ranken, D. F., Brocq, A. M. L., Gladstone, R. M., Payne, A. J., Ng, E. G., and Lipscomb, W. H.: Adaptive mesh, finite volume modeling of marine ice sheets, J. Comput. Phys., 3, , 3. This paper presents the capability of a 3-dimensional adaptive mesh refinement model using the shallow-shelf approximation. Using adaptive mesh refinement, the mesh spacing can be kept small at the grounding line, where high resolution is needed, while it can be incrementally increased away from the grounding line. Compared to a fixed-grid model, this techniques avoid unnecessary computational cost while it accurately model grounding-line motion. The 9
20 authors showed that the computational cost can be reduced by factors 7 to 4 depending on the grid and the problem that was solved. Dukowicz, John K. and Price, Stephen F. and Lipscomb, William H.: Consistent approximations and boundary conditions for ice-sheet dynamics from a principle of least action, J. Glaciol., 56, ,. Many model are used to simulate ice-sheet flow. The Stoke model is considered to be the most accurate model as it accounts for all shear and strain forces. Dukowicz et al. ) uses a variational principle of least action approach to show under which condition the different approximations are valid. This work completes the work from Schoof and Hindmarsh ) and provides a mathematical proof on assumptions that modeler had taken for granted for many years. This paper provides with a very nice figure summarizing the validity of different models. Durand, G., Gagliardini, O., de Fleurian, B., Zwinger, T., and Le Meur, E.: Marine ice sheet dynamics: hysteresis and neutral equilibrium, J. Geophys. Res.- Earth, 4, F39, doi:.9/8jf7, 9. In this paper the authors investigate grounding line dynamics using a Stokes flow model and the the basal sliding law of Schoof 7a). Their model is discretized using a fixed-grid model with adaptive mesh refinement near the grounding line. They performed a set of experiments based on the MISMIP experiments with the goal of reaching steady state when using very high resolution near the grounding line. Even with grid resolution of 3 m in the transition zone, they found differences in the grounding-line position over an advance-andretreat cycle of km whereas theoretical arguments predict that there should be no difference. Their numerical results shed light on discrepancies due to model formulation. They found poor agreement between their model and the boundary-layer Model B from Schoof 7b) which might reflect the differences between a Stokes-flow model and a depth integrated model. Gagliardini, O., Cohen, D., Raaback, P., and Zwinger, T.: Finite-element modeling of subglacial cavities and re- lated friction law, J. Geophys. Res.-Earth,, F7, doi:.9/6jf576, 7. The authors propose a general formulation of a basal friction law that captures the main features of sliding with cavitation. To this end, they numerically validate the ad-hoc formulation of Schoof 5) as a limiting case of their own and show that it is appropriate for sawtooth terrain confirming the appropriateness for rough terrain stated in Schoof 5). This limitation may lead to better behavior in numerical model because the relation between basal stress and sliding velocity is monotonic. Gladstone, R. M., Payne, A. J., and Cornford, S. L.: Parameterising the grounding line in flow-line ice sheet models, The Cryosphere, 4, 65 69, doi:.594/tc , a.
21 This paper introduces the use of grounding-line parameterization in a onedimensional ice sheet model using both linear and nonlinear sliding laws. It investigates the use of interpolation techniques on accurately locating the groundingline position and their effect on model resolutions. Regardless of the order of accuracy of a technique, the convergence with respect to model resolution is linear. However, the use of any of the grounding-line parameterization decreases the need of resolution in the vicinity of the grounding line. Gladstone, R. M., Payne, A. J., and Cornford, S. L.: Resolution requirements for grounding-line modelling: sensitivity to basal drag and ice-shelf buttressing, Ann. Glaciol., 53, 97 5, doi:.389/aog6a48,. In this paper, Gladstone et al. ) investigates the impact of different parameters rate factor, basal drag coefficient, bed gradient, accumulation and channel width) on grounding-line position and model resolution using a linear sliding law in a one-dimensional ice-sheet model. The result show that the grounding-line position is sensitive to all parameters but accumulation considering the range of accumulation investigated in this paper). They also show that the required resolution of a fixed-grid model near the grounding line can be relaxed with a smaller rate factor, a smaller basal drag coefficient, a steeper bed gradient and a narrower channel width. Pattyn, F., Huyghe, A., De Brabander, S., and De Smedt, B.: Role of transition zones in marine ice sheet dynamics, J. Geophys. Res.- Earth,, F4, doi:.9/jb39, 6. Pattyn et al. 6) propose a smooth basal friction parameter that decays exponentially to zero as the ice flows across the grounding line into the ice shelf. This approach give promising results as it decreases the need of very high resolution near the grounding line in fixed-grid model as the transition zone could be resolved at.5 km grid resolution. However, the model introduces an arbitrary length scale of exponential decay, and the basal friction remains nonzero though small) in the ice shelf. Pattyn, F., Schoof, C., Perichon, L., Hindmarsh, R. C. A., Bueler, E., de Fleurian, B., Durand, G., Gagliardini, O., Gladstone, R., Goldberg, D., Gudmundsson, G. H., Huybrechts, P., Lee, V., Nick, F. M., Payne, A. J., Pollard, D., Rybak, O., Saito, F., and Vieli, A.: Results of the Marine Ice Sheet Model Intercomparison Project, MISMIP, The Cryosphere, 6, , doi:.594/tc ,. This paper gathers the numerical capabilities of one-dimensional models to accurately capture grounding-line migration using a basal sliding law as in? during a set of advance and retreat experiment. An advance of the ice is triggered by reducing the flow rate factor while a retreat is triggered by increasing that same factor. Experiments are done using two different bed topographies: a linear downward sloping bed and a polynomial bed that includes an overdeepening. The results -compared to a semi-analytic boundary-layer solution- show that the numerical method used to discretize a vertically integrated marine ice-sheet model strongly affect the model accuracy; numerical models using a moving grid
22 approach always returned more accurate grounding-line position compared to fixed-grid models at a given resolution. Also, the results of this experiment suggest that very high resolution is needed in the transition zone in order to accurately model grounding-line dynamic. Pattyn, F., Perichon, L., Durand, G., Favier, L., Gagliardini, O, Hindmarsh, R. C. A., Zwinger, T., Albrecht, T., Cornford, S., Docquier, D., and others.: Groundingline migration in plan-view marine ice-sheet models: results of the icesea MISMIP3d intercomparison, J. Glaciol., 59, doi:.389/3jogj9, 3. This paper follows up on Pattyn et al. ) which proposed numerical results from one-dimensional flow line model. This paper shows results on the MISMIP 3D inter comparison project for three-dimensional ice sheet models. The experiments starts from a steady state based on the flow line model with no variation in the y velocity. The ice is then subject to a change in basal sliding law: A spatial Gaussian-type perturbation is applied with the goal of making the grounding at the center line very slippery compared to the rest of the ice. This perturbation induces a variation in y-velocity and results in a grounding line advance at the center line and a grounding line retreat at the boundary of the domain. This project further test the robustness and numerical capabilities of numerical models under strong constraints. Schoof, C.: The effect of cavitation on glacier sliding, Proc. R. Soc. A, 46, 69 67, doi:.98/rspa.4.35, 5. Schoof 5) shows that the basal friction law of the form τ b = Cu m b Nn, as the one used in Budd et.al 979, is unphysical. This relation allows arbitrary high shear stress at the bed while in nature it has to satisfy an upper bound Iken 98)) proportional to the geometry of the bed. He investigates the influence of bed bumps using a sinusoidal-bed form with different wavelength and observes that obstacles with the steepest slopes control the dependency of the bed on the basal sliding law. However he underlines that Iken s bound prevents obstacle of the shape of a staircase. He concludes by suggesting an ad-hoc nonlinear friction law which links basal stress and sliding to the effective pressure. The friction law has the correct limits for large values of the effective pressure and slow flow, and reduces to Coulomb friction law in the limit of small effective pressure and fast flow; it is also an appropriate simplification for rough terrains. Schoof, C.: Ice sheet grounding line dynamics: steady states, stability, and hysteresis, J. Geophys. Res,, F3S8, doi:.9/6jf664, 7a. Schoof 7a) studies the effect of a one-dimensional vertically integrated marine ice-sheet model that prescribes a discontinuous friction law across the grounding line. He shows that the steady-state grounding-line position on a bed sloping monotonically downward in the direction of the ice flow is unique for a given ice softness. Further, a stable grounding-line location does not exist on an upward sloping bed in absence of buttressing. This missing stress can provide the necessary stress to stabilize the grounding line on an upward sloping bed.
23 Last, the author shows that marine ice sheets can undergo hysteresis under the perturbation of material parameters or external forcing. Schoof, C.: Marine ice-sheet dynamics Part : The case of rapid sliding, J. Fluid Mech., 573, 7 55, 7b. This paper follows up the work done in Schoof 7a); it provides the derivation of the semi-analytic solutions to the non-linear system of equation of the marine ice-sheet using a boundary layer method. A dimensional analysis shows that the longitudinal stress is small compared to the driving and the basal shear stresses. Close to the grounding line, a boundary layer exists over which the longitudinal stress has to compensate for the loss of basal shear stress. The size of the boundary layer determines where high resolution is needed to accurately solve the nonlinear system of equation numerically. Further analysis is provided to show that the ice thickness at the grounding line has to be small compared to the mean thickness of the interior ice. van der Wel, N., Christoffersen, P., and Bougamont, M.: The influence of subglacial hydrology on the flow of Kamb Ice Stream, West Antarctica, J. Geophys. Res.-Earth, 8, 97, doi:.9/jf57, 3. In this paper the authors developed a -dimensional flow line model that couples hydrology, ice thermodynamics and till rheology. At the ice-till interface they allowed the presence of a subglacial conduit. Using observation and their model, they found that subglacial conduits can extend to the grounding line if enough water is available from local melting and upstream transport. They draw the conclusion that the Ruttford Ice Stream is connected to the ocean via permanent conduit system. Vieli, A. and Payne, A. J.: Assessing the ability of numerical ice sheet models to simulate grounding line migration, J. Geophys. Res.-Earth,, F3, doi:.9/4jf, 5. Vieli and Payne 5) use a vertically integrated one-dimensional icesheet model to investigate the capabilities of numerical models to accurately model grounding-line dynamic prescribing a discontinuous friction law across the grounding line. They compare fixed-grid to moving-grid models. The experiments performed suggest that for both type of model numerics, the groundingline position converges with increasing resolution. At a given resolution movinggrid models are more accurate compared to fixed-grid model. The fixed-grid model shows to be more sensitive to grid size and bed topography compared to moving-grid models. 3
24 CHAPTER 3 MODEL DERIVATION In this chapter we briefly derive the field equations that will be used to investigate the effect of ocean-water connectivity on ice sheet flow. It is intended to give a better understanding of the origin of the problem and of the validity of the approach of the work. The goal is not to rewrite the entire ice-sheet dynamic theory but to give an overview of the origin of the equation that are used for modeling ice-sheet flow. In depth details of ice sheet dynamic theory, can be found in Greve and Blatter 9) and Cuffey and Paterson ). While deriving the ice-flow equations, our ultimate goal is to obtain a system of equations that solves for ice velocity and ice thickness which are best to describe ice motion. 3. Stokes flow model In glaciology, an ice-sheet is considered to be a very viscous fluid which motion is described by two modes of stress deformation: shearing and stretching. To this extend we can use the Navier-Stokes equations to model its motion. The latter are derived considering the conservation of mass, the conservation of linear momentum and the conservation of angular momentum which leads to: ρ i t + ρ iv =, 3.) ρ i V t + ρ iv )V T F =, 3.) T ij = T ji, 3.3) where ρ i is the ice density, V the ice velocity, T the stress tensor and F the body force acting on the ice. 4
25 A complete model includes the conservation of energy equation which is used to calculate the temperature of the ice in the system. However, for the purpose of our work, we will assume the ice to be isothermal with the possibility to adjust the ice temperature at the bed as we will discuss in section 3.3.) and averaged over the full ice-sheet depth. We will account for the ice temperature with the ice softness coefficient also called the flow law coefficient) that will be introduced in section 3.. In the case of fast-flowing ice such as an ice stream, this assumption remains valid over more than the first half of the top layer of the ice and sometimes more). At the bed, the ice is at or close to) melting temperature. The ice temperature evolves from cold ice at the top of the ice to warm temperature at its base, creating steep temperature gradients at the bottom layer of the ice. Such a profile can be observed for the Bindschadler ice stream in Antarctica Engelhardt, 4a). This observation shows some limitation of our model in this respect. The system of equations 3.) 3.3) can be simplified when accounting for physical ice properties and making reasonable assumptions. First, we will assume that the ice of an ice sheet has a constant density. An ice layer is composed of two principal layers: an ice layer with constant density, and a firn layer, a layer of ice being in an intermediate stage between snow and ice through which ice undergoes a strong density change from approximately 4 to 9 kg.m 3 Maeno et al., 983)). In the interior of the ice sheet, as at the Sipple station located at Pine Island Glacier in West Antarctica), the thickness of the full ice layer is about 3 km Fretwell et al., 3) while the one of the firn layer is about 7 m Schwander et al., 984), representing about % of the total thickness. In the ice shelf, where the ice is floating, the ice could be as thin as 3 m Fretwell et al., 3) as at Little America which where a series of exploration at the edge of the Ross Ice Shelf) with a firn thickness of about 5 m Gow, 968), representing about 6 % of the total thickness layer. We acknowledge this assumption to be strong in the ice shelf. In most of our case study, the ice shelf dynamics will not impact the dynamic in the ice sheet, the main focus of our study. Under the assumption of the density to be constant, equation 3.) reduces to the incompressible condition by neglecting its first term. Further, since ice is a very viscous fluid and its Froude number, the ratio of ice acceleration and pressure gradient, is very small 5 ), the term accounting for inertia can be neglected in equation 3.). Last, if we consider the flow to be steady, equations 3.)-3.3) reduce to: V =, 3.4) T + F = 3.5) T ij = T ji, 3.6) where equation 3.5) is the Stokes equation. A model which solve this system of equation is referred to as Stokes-flow model. This model is accepted to be very 5
26 accurate for representing ice-sheet flows but is usually computationally expensive to run at resolution high enough to observe grounding-line migration. In order to reduce this cost further assumptions can be made to simplify the system given by equations 3.4)-3.6). One cheaper model is the so-called Blatter-Pattyn model which is the subject of the next section. 3. The Blatter-Pattyn model Here we present the Blatter-Pattyn model Pattyn, 3), which is a simplified version of the Stokes-flow model, which is obtained by making further assumptions on the conservation of momentum given by equation 3.5). If we rewrite equation 3.5) in cartesian coordinates, and set F = ρ i g = ρ i g z, where g is the gravitational acceleration, we obtain: x : T xx x y : T yy y + T xy y + T xy x + T xz z = 3.7) + T yz z = 3.8) z : T zz z + T zy y + T zx x = ρ ig. 3.9) The stress tensor T is related to the deviatoric stress τ by: τ ij = T ij + P δ ij, 3.) where P is the pressure and δ the Kroenecker delta symbol. Substituting equation 3.) into equations 3.7)-3.9) leads to: x : τ xx x P x + τ xy y + τ xz z = 3.) y : τ yy y P y + τ yx x + τ yz z = 3.) z : τ zz z P z + τ zy y + τ zx x = ρ ig. 3.3) 6
27 Dukowicz et al. ) and Schoof and Hindmarsh ) showed that when the ratio between the vertical and the horizontal length scale is small equation 3.3) can be simplified as: z : τ zz z P z = ρ ig. 3.4) If this assumption fails to be valid, we would need to use the Stokes model to provide a good representation of ice flow dynamics. Equation 3.4) only involve partial derivative with respect to the z-coordinate such that we can derive an expression for the pressure P by integrating through the depth of the ice sheet. Assuming a stress free boundary condition at the ice surface and that the atmospheric surface pressure is negligeable, Equation 3.4) becomes: P = ρ i g sx, y) z) + τ zz, 3.5) where s represents the surface of the ice sheet. Equation 3.5) represents the hydrostatic approximation, where the vertical normal stress is balanced by the hydrostatic pressure. We can now substitute equation 3.5) into equations 3.)-3.). For the x component we have: x : τ xx x + τ xy y + τ xz z x : τ xx x + τ xy y + τ xz z = P x x : τ xx x τ zz x + τ xy y + τ xz z 3.6) = x [ρ igs z) + τ zz z)] 3.7) = ρ ig s x. 3.8) For an incompressible material, the sum of the normal components of the deviatoric stresses is zero, i.e, τ xx + τ yy + τ zz =. Thus, substituting τ zz in equation 3.8) leads to: x : τ xx x + τ yy x + τ xy y + τ xz z = ρ ig s x. 3.9) The y component can be obtained analogously. Since we used the vertical component to derive the hydrostatic approximation, we are now left with horizontal 7
28 components only: x : τ xx x + τ yy x + τ xy y + τ xz z y : τ yy y + τ xx y + τ yx x + τ yz z = ρ ig s x 3.) = ρ ig s y. 3.) Ultimately we would like to solve a system of equations in terms of ice velocities. In the case of a Newtonian fluid, the strain rate tensor ɛ ij is proportional to the stress tensor τ ij as τ ij =η ɛ ij, 3.) where η is the effective viscosity or ice viscosity in our case). Ice does not behave as a Newtonian fluid but becomes more fluid the more it deforms. This physical behavior can be expressed using the constitutive law for ice, which was empirically derived assuming a power law by Glen 955), and links strain rates to stresses as τ ij = A n n ɛ n e ɛ ij, 3.3) where ɛ ij is the strain rate tensor, n Glen s exponent, A the ice softness or flow law) coefficient which accounts for ice temperature) and ɛ e the effective strain rate defined as: ɛ e [ ] ɛ xx + ɛ yy + ɛ zz + ɛ xz + ɛ xy + ɛ yz, ɛ xx + ɛ yy + ɛ xx ɛ yy + ɛ xz + ɛ xy + ɛ yz, 3.4) where we used the incompressibility property to substitute ɛ zz = ɛ xx ɛ yy. A definition of the effective ice viscosity is then given by η = A n n ɛ n e, 3.5) 8
29 such that, combined with the definition that relates the strain rate tensor in terms of velocity gradients ɛ ij = u i + u ) j, 3.6) x j x i we obtain: τ ij = η u i + u ) j. 3.7) x j x i Before continuing further, we will assume that w x u z and w y v z Pattyn, 3), i.e that horizontal gradients of the vertical velocity are small compared to the vertical gradient of the horizontal velocity. These assumptions are valid over most of the ice sheet domain, besides at the ice divide. With these assumptions we now substitute equation 3.7) into equations 3.)-3.) and obtain our new system of equations in terms of velocities: x :4 η u ) + η v ) + [ u η x x x y y y + v )] + η u ) = ρ x z z i g s x 3.8) y :4 η v ) + η u ) + [ v η y y y x x x + u )] + η v ) = ρ y z z i g s y 3.9) 3.3 One-dimensional shallow-shelf flow line model In this section we derive the one-dimensional vertically integrated icesheet model that will be used in this study. There is very little variation in acrossflow direction in ice which is the reason why we will consider an ice flow that takes into account one horizontal component along the x-axis. We want to derive an equation of motion that models an ice streams fast flowing ice) flowing to the right of a symmetric ice divide, the origin of the domain, connected at a grounding line one point in one dimension) with a single ice shelf. 9
30 3.3. The continuity equation The goal here is to derive an equation for the conservation of mass, also known as the continuity equation, that links the ice sheet thickness to the vertically averaged ice-sheet velocity. To achieve this goal we start from the incompressibility condition given in equation 3.4) and rewrite it in cartesian coordinates: u x + w z =, 3.3) where u, w) represent the velocity components in the x, z) directions. Equation 3.3) is now vertically integrated between the bed or ice sheet base) z = b) and the surface z = s) of the ice sheet: s w s) w b) = b = x u dz 3.3) x s ) udz + u s) s b u b) x x, 3.3) b where we used Leibnitz s rule to switch the order of integration and differentiation in equation 3.3). By definition, the vertical velocity at the surface is the sum of the rate of change of ice surface elevation and the ice accumulation rate. A positive accumulation rate corresponds to a negative downward) velocity negative advection) at the surface in situations where the surface elevation is steady and the ice geometry is not altered. Thus w s) ds dt ṁ a 3.33) = s s + u s) t x ṁ a, 3.34) where ṁ a represents ice accumulation or ice ablation if the accumulation is negative) and where we used the definition of the material derivative from equation 3.33) to equation 3.34). Similarly, at the bed of the ice sheet the vertical velocity is w b) db dt ṁ b 3.35) = b t + u b) b x ṁ b, 3.36)
31 where ṁ b represents the basal ablation rate positive for melting, negative for freezing). Substituting equations 3.34) and 3.36) into equation 3.3) leads, after simplification, to s t b t = s ) udz + ṁ a ṁ x b. 3.37) b Using the relation for the ice thickness H = s b, and the definition of the depthaveraged velocity ū = H udz, equation 3.37) is rewritten as s b H t + x Hū) = ṁ a ṁ b. 3.38) The right hand side terms of equation 3.38) are usually combined into a single term called surface mass balance; it accounts for all physical effect besides of ice motion that induce a change of ice thickness at a given time and space. Equation 3.38) is the conservation of mass for an ice geometry throughout the entire ice thickness. Due to its dependency of time derivative, this equation is prognostic: we can predict the ice geometry in the future by considering the present ice geometry, velocity and surface mass balance. This equation apply to both the ice sheet and the ice shelf. In the absence of ocean interaction on ice shelves and when considering constant accumulation, we will simply right the continuity equation as: H t + x Hū) = ṁ a. 3.39) 3.3. The conservation of momentum Using the results from section 3. we can now derive the one-dimensional momentum equation used in this study. To begin we will ignore the shear stresses due to friction between the ice and side walls similar to river banks) or adjacent slower flowing ice; these frictions are usually referred to as lateral drags. From these two assumptions, it follows that the deviatoric stresses equal zero, i.e, τ xy =. Furthermore, if we restrain our model to not vary in the y-direction we can then write τ yy = τ yx =. Before we continue the derivation of our model, let us express the effective strain rate, which we will need later. Under these assumptions and the one we made in the previous sections, it can be rewritten in
32 terms of velocities as: ɛ e ɛ xx + ɛ xz, u x ) + 4 ) u. 3.4) z We could further simplify equation 3.4) under the assumption that u z u x. Consequently, this assumption neglects vertical shear and the new system is then design to model fast sliding ice sheet with no slip condition at the bed, which is appropriate for modeling ice streams. A model that includes vertical shear would be more accurate anywhere else in the ice sheet where the ice is subject to high basal friction and slow velocities. Adding this new assumption, the model is referred to as the Shallow-Shelf Approximation model SSA). We now have made all the necessary assumptions to derive our one-dimensional model. We can now rewrite equation 3.) as: τ xx x + τ xz z = ρ ig s x. 3.4) We can now integrate equation 3.4) from the bed b of the ice to its surface s: s b τ xx x dz + s b τ xz z dz = s b ρ i g s dz. 3.4) x Using Leibniz rule for integral on the first left hand side term, and that both s and b are only functions of x, equation 7.) can be rewritten as: s τ xx dz τ xx s) s x b x + τ xx b) b x + τ xz s) τ xz b) = ρ i g s s b). x 3.43) There is no deviatoric stress at the surface s such that τ xx s) = τ xz s) =. The integral term in equation 7.3) can be rewritten as a product of ice thickness and depth-averaged value of the deviatoric stress τ xx which we will denote τ xx. Thus, equation 7.3) becomes: x Hτ l) τ b + τ d =, 3.44)
33 where we used the relation for the ice thickness H = s b and where τ l = τ xx, 3.45) τ b = τ xx b) b x + τ xz b), 3.46) τ d = ρ i gh s x. 3.47) In equations 3.45)-3.47), τ l is the vertically averaged longitudinal stress which represents the horizontal ice stretching effects, τ b is the basal stress and τ d is the driving stress. This model of the momentum equation neglects lateral drags, and thus is best used to simulate fast-flowing ice streams. While additional physics would be required to model realistic ice sheets, this model is a simple, computationally efficient tool for idealized studies of grounding-line dynamics. To make use of equation 3.45) we rewrite in terms of the vertically averaged velocity ū, which from now on we will simply denote u, τ l = Ā n u n u x x. 3.48) In equation 3.48), the stress τ l includes the nonlinear viscosity given by Glen s flow law, where Ā is the depth-averaged ice softness and n is the Glen s flow law exponent. In equation 3.47), τ d is the gravitational stress that drives ice flow in the direction of decreasing surface elevation. Equations 3.44)-3.48) apply to both the ice sheet and the ice shelf. The surface elevation s is computed differently in the two regions from the bedrock elevation and ice thickness in the ice sheet, and from exact flotation in the ice shelf: s = H + b x < x g ), 3.49) ρ i ρ w H x x g where x g denotes the grounding-line position. We define b to be negative below sea level. In reality, ice is at exact flotation in the ice shelf but not at the grounding line but we will assume it is as another approximation. In fact, ice is elastic but our model assumptions do not allow to account for the stresses that represent this physical property and Stokes model should be used for this purpose Nowicki and Wingham, 8). Equation 3.47) accounts for physical representation that occur at length 3
34 scales that cannot be resolved numerically such as local bedrock obstacles, debris, undulation in the ice at the bed, which all contribute to basal drag. Instead they are parameterized in the form of a friction law which expresses the averaged drag τ b at the bed to in our case) the vertically averaged velocity u as τ b = f u), where f is an increasing function of u. Schoof 5) showed that at low velocity, and when the ice is frozen at the bed, τ b u n, where n is Glen s exponent. At faster velocity the basal stress has to satisfy Iken s bound Iken, 98), τ b N, where N is the effective pressure. Beneath ice shelves the basal stress is zero everywhere. Thus, under the ice sheet, the basal-friction law takes the form given in Schoof 5): τ b =C u n u N n m max λ max A b u + N n ) n, 3.5) where C is the constant shear stress factor defined in Schoof 7a), the effective pressure N p i p w is the difference between the overburden pressure p i ρ i gh and the basal water pressure p w, A b is the ice softness at the bed chosen based on an ice temperature of - C, and λ max and m max are the wavelength of bedrock bumps and the maximum bed obstacle slope, respectively. These last two parameters represent bedrock roughness at scales too small to be resolved in the model. The model parameter values used in this model are given in Table. 3.. As we will discuss further in section 3.3.4, equation 3.5) was proposed in Schoof 5) as an ad hoc non-linear extension of the linear friction law n = ) with the appropriate behavior in the limits of both slower-flowing, thicker ice in the ice-sheet interior and more rapidly sliding, thinner ice near grounding lines. Gagliardini et al. 7) numerically validated this ad hoc formulation as a limiting case of their own friction law. We have modified the notation from Schoof 5) to match that of Schoof 7a) in the limit of slow flow and large effective pressure The boundary conditions From now on the subscripts x and t denote partial derivatives e.g.,h x H x ). We assume the ice sheet to be symmetric at the ice divide, the origin of the domain, leading to the following boundary conditions: u = at x =, 3.5) H + b) x = at x =, 3.5) 4
35 Table 3.: Parameter values used for all experiments. Parameters Value Units Definition ρ i 9 kg m 3 Ice density ρ w kg m 3 Water density A see tables Pa 3 s Ice softness A b Pa 3 s Ice softness at the bed C Pam s) /3 Shear stress factor ṁ a.3 m a Ice accumulation rate g 9.8 m s Gravitational acceleration n 3 Glen s flaw low exponent m max.5 Maximum bed obstacle slope λ max m Wavelength of bedrock bumps At the grounding line, the requirement of exact flotation leads to the boundary condition H = ρ w ρ i b at x = x g. 3.53) Combining equations 3.47) 3.49), the stress balance in the ice shelf is given by [Ā n H ux n u x ] x ρ i ρ ) i ghh x =. 3.54) ρ w At the calving front, the ice shelf is subject to the ocean backpressure, p w = ρ w gz, between the ice shelf base, z = ρ i /ρ w )H, and sea level, z =. The ocean pressure partially but not completely) balances the hydrostatic pressure of the ice, p i = ρ i gz s). The force on the ice shelf due to the difference in hydrostatic pressure between the ice shelf and the ocean is: s f p x c ) = = ρ i ρ i /ρ w )H ρ i ρ w ρ i gz s)dz ρ w gzdz ρ i /ρ w )H ) gh. 3.55) The force on the calving face due to longitudinal viscous) stress must compen- 5
36 sate for this imbalance in hydrostatic pressure: Ā n H ux n u x = ρ i ρ ) i gh at x = x c. 3.56) ρ w Following Schoof 7a), we integrate equation 3.54) from the calving front x = x c ) to the grounding line x = x g ), and use equation 3.56) to show that the same condition holds at the grounding line as at the calving front: Ā n H ux n u x = ρ i ρ ) i gh at x = x g. 3.57) ρ w In order for the stresses to remain finite, H, u and u x must be continuous across the grounding line. These are additional constraints that must be satisfied in order for the longitudinal stress to be continuous across the grounding line and the continuity equation to remain valid Effective pressure parameterization and friction law Most models of marine ice sheets assume that the basal friction jumps discontinuously to zero across the grounding line. We propose a simple parameterization that removes the discontinuity, yielding a smooth transition between grounded and floating ice. We adopt the friction law from Schoof 5), validated and extended in Gagliardini et al. 7). This formulation, given by equation 3.5), has the correct limits for large values of the effective basal pressure N and slow flow, and reduces to Coulomb friction in the limit of small N and fast flow. Schoof 5) suggested that this friction law is an appropriate simplification for rough terrain; Gagliardini et al. 7) showed that this limiting case of their more general friction law corresponding to their decay parameter q = ) was appropriate for sawtooth terrain. They also argued that this limit of their friction law may lead to better behavior in numerical models than more realistic q values because the relation between basal stress and sliding velocity is monotonic. This is a desirable feature that enforces τ b to have a unique solution in u and vice versa. If the effective pressure is continuous across the grounding line, the basal shear stress smoothly approaches zero at the grounding line. Assuming that the subglacial drainage system is connected to the ocean, the water pressure at the ice-sheet base will be close to the ocean pressure at that depth, reaching the ocean pressure at the grounding line with pressure differences driving flow through the drainage system). A simple function for the effective pressure that accounts 6
37 for connectivity between the subglacial drainage system and the ocean is Np) = ρ i gh H ) p f, 3.58) H in which we introduce a parameter p that varies between zero no basal water pressure) and one the subglacial drainage system is hydrologically well connected ) to the ocean). The flotation thickness is defined by H f max, ρ w ρi b. The effective basal pressure Np) has the following desired limits: When p =, Np) = ρ i gh no water-pressure support). When p =, Np) = ρ i g H H f ) full water-pressure support from the ocean wherever the ice-sheet base is below sea level). At the grounding line when p >, Np) = τ b is continuous across the grounding line). Far from the grounding line where the bed is above sea level and H f = ), Np) = ρ i gh. When H f /H and the bedrock is below sea level b < ), the basal water pressure is attenuated to a fraction p of the full ocean pressure at the depth of the bed inland of the grounding line. We can combine the definition of the effective pressure, N p i p w, and the overburden pressure, p i ρ i gh, with equation 3.58) to solve for the basal water pressure p w : p w = ρ i gh [ H ) p ] f. 3.59) H In the limit H f H, this expression can be approximated by the first term in the Taylor series p w ρ i gh p H ) f, H pρ i gh f, 3.6) which is p times the ocean water pressure at the depth of the bed, p ocean = ρ w gb = ρ i gh f. These conditions will typically hold on the inland side of the transition zone, since a rapid increase in H is usually needed to produce the driving stress that balances the relatively large basal friction in this region. One way 7
38 such attenuation might occur is by a gradual loss of connectivity between the basal hydrological system and the ocean. Equation 3.58) can be regarded as a mathematical regularization, ensuring that the basal friction transitions smoothly from a finite value in the ice sheet interior to zero in the ice shelf. It can also be viewed as a simple parameterization of basal hydrology, motivated by the hydrological connectivity that may exist between the ice bed and the ocean near the grounding line. By parameterization we mean the replacement of small-scale or complex physical processes with a simplified process.) The functional form of equation 3.58) is ad hoc, since there are no detailed observations to show how N varies near grounding lines, but the limits are physically based. We emphasize that equation 3.58) does not represent all the processes that might be included in a complex hydrology or till model. It represents only the portion of water-pressure support related to the ocean; basal water pressure in the model falls to zero when the bedrock reaches sea level b = ). More sophisticated models of basal till find that the basal water pressure remains a significant fraction of the overburden pressure in much of the ice-sheet interior Tulaczyk et al., b; van der Wel et al., 3). A more complex model might include a network of channels as well as water-laden till at the base of ice streams. This hydrological network would influence the basal friction through water-pressure support outside the transition zone. Thus, our parameterization predicts a larger N away from the grounding line than would likely be observed in much of the interior of ice sheets. We do not think this is a critical model weakness, however, because we are mainly interested in ice dynamics near the grounding line. In the interior, where N is larger, the basal shear stress is described by a power law see equation 3.6) below) and is relatively insensitive to N. Figures 3. and 3. show typical ice-sheet geometry, thickness, H f /H and N for five values of p over linear and polynomial bedrock topography, respectively. In both cases, the smaller the p value the greater the effective pressure, which tends to move the grounding line seaward. The jump in effective pressure is to be expected for p = because of the limit defined above. For small values of p >, the transition in basal stress occurs over a narrow region of order km or less, and is thus resolved only at high model resolution. The figures show that N drops to zero more smoothly as p increases, meaning that the basal stress will also be increasingly smooth. Parameterized in terms of p, equation 3.5) becomes τ b = C u n Np) n ) n u, 3.6) κ u + Np) n where κ m max λ max A. This formulation does not require the introduction of an arbitrary length scale of basal transition, as in the parameterization proposed by b Pattyn et al. 6). Equation 3.6) has two asymptotic behaviors. In the ice 8
39 N kpa) H f /H H km) -b, s, zb km) 4 a b c d Ice sheet domain 3 km) b Hf p= p=.5 p=.5 p=.75 p= Figure 3.: Dependence of ice geometry and effective pressure on the parameter p over a linear bed as in Schoof 7b). All panels show the fixed-grid solution at.8 km resolution without a grounding-line parameterization see section??) and with ice softness A = 5 Pa 3 s. a) Ice surface and bedrock colors), and basal elevation black) over the full ice-sheet domain. b) Ice sheet thickness colors) and flotation thickness black) over the marine portion of the ice sheet. c) The ratio between the flotation thickness and the ice-sheet thickness. d) The effective pressure N, which approaches zero more smoothly with increasing p. Plots in panels c) and d) include only grounded cells, as the ice is exactly at flotation and effective pressure is zero elsewhere. The plotted effective pressure does not go to zero for all p > because the grounding line lies between the last grounded cell and the first floating cell. sheet interior, the ice is thick and slow-moving, so that κu Np) n and τ b C u n u. 3.6) 9
40 N kpa) H f /H H km) -b, s, zb km) 4 Region Region Region a b c p= p=.5 p=.5.8 p=.75 p= d Ice sheet domain 3 km) Figure 3.: Dependence of ice geometry and effective pressure on p, as in figure 3. but with the polynomial bed as in Schoof 7b), containing two stable regions and 3) and an unstable region ). b Hf In this limit, τ b is independent of p. Many models define the basal-friction law throughout the ice sheet to have the form of equation 3.6), as in Schoof 7a) and the MISMIP experiments. This simplified friction law leads to a set of equations with an accurate semi-analytic approximation Schoof, 7a,b), whereas the more complex friction law in equation 3.6) does not lend itself to a similar semi-analytic solution. A boundary-layer solution could be computed numerically, but we have instead opted to compute a high-accuracy benchmark solution over the full domain, as described in the next section. The semi-analytic solution of Schoof 7a) closely approximates our model as p approaches zero. Figure 3.3a shows that the basal-stress term blue) closely matches the limit of high overburden pressure red) given by equation 3.6) when p =. In this limit, the boundary-layer solution and our high-resolution benchmark solution differ by a few kilometers or less. 3
41 5 5 Basal stress term kpa) Distance to grounding line km) 4 a) p = b) p=.5 c) p= Figure 3.3: Basal stress given by equation 3.6) blue) and its asymptotic limits, equation 3.6) red) and equation 3.63) green) for ice softness A = 5 Pa 3 s and using the Chebyshev benchmark solution. a) When p =, the second green) asymptote is never reached, the red and blue curves overlap almost exactly, and there is no friction transition zone basal stress falls abruptly to zero at the grounding line). b) and c) When p =.5 and p =, the length of the friction transition zone, defined as the region where Np) n κu roughly speaking, the region where the blue curve differs from the red curve), ranges from several hundred meters to km depending on A, p and bedrock topography. The second asymptote, the Coulomb-friction limit, occurs near the grounding line where the ice is thin and fast-flowing, so that κu Np) n and τ b C κ n Np) u u. 3.63) By construction, when p = the effective pressure is equal to the full overburden pressure, p i, and the basal stress discontinuously drops to zero across the grounding line. When p >, the effective pressure N smoothly approaches zero at the grounding line over a distance that increases as p increases. Just inland of the grounding line, the basal stress is proportional to the effective pressure. We define the friction transition zone as the part of the ice sheet where Np) n < κu, where Coulomb friction is dominant. The friction transition zone is closely related to the transition zone defined in section, since the transition 3
42 from flow dominated by vertical shear to flow dominated by extensional stress must occur in the region where the basal shear stress drops from a large value high N) to a small value low N). For the range of parameters we studied, the size of the friction transition zone varies between and km, depending on p, the bedrock topography, and the ice softness. Importantly, the size of the friction transition zone is an increasing function of p, meaning that, at a given resolution, this zone is better resolved when p is larger. Figure 3.3b and 3.3c show the basal-stress terms and their two asymptotic limits for p =.5 and p =, respectively. Equation 3.6), the red curve, dominates in the bulk of the ice sheet, while equation 3.63), shown in green, dominates in the friction transition zone. Figures show that although the friction transition zone is small compared to the whole ice sheet, its effects are far-reaching. As p increases from to other things being equal), the grounding line retreats by more than km, and the steady-state surface elevation is reduced hundreds of km upstream. 3.4 Chapter summary Stokes flow model are computationally expensive to run and be used as numerical models. With reasonable assumptions, we can derive ice sheet models that are good approximations to the Stokes model and cheaper to run. The goal of this work is to study grounding line migration for fast flowing ice such as ice streams since they are driving most of the ice from the interior of the ice sheet to the ocean. A model that represents ice streams reasonably well, and is cheap to run, is the so-called Shallow-Ice Approximation model. It can be derived from the conservation of linear and angular momentum by assuming: the ice is in hydrostatic equilibrium, the horizontal length scales dominate compared to vertical length scales and the vertical shear stresses are negligible. We then obtain a model in one dimension by neglecting the effect of the y-coordinate and by vertically integrating the model from the base of the ice sheet to its surface. It results in the momentum equation which is the balance of three stresses: the longitudinal stress, the basal stress and the driving stress. The basal stress has to be parameterize as its effect occurs at sub-grid scale precision. To do so we use the formulation of Schoof 5) to which we add a parameterization of the effective pressure depending on ocean-water penetration at the bed across the grounding line. This parameterization has the property to lubricate the bed inland of the grounding line allowing for a smooth transition in the basal stress between grounded and floating ice. The momentum equation, together with the continuity equation that is derived from the conservation of mass, leads to a system of equations and two unknowns that are the vertically average velocity and the ice thickness. In this work we will study how the effective pressure parameterization affect these two variables and impacts grounding line migration. 3
43 CHAPTER 4 STEADY STATE PROPERTIES To the best of our knowledge, our system of equations does not lead to an analytical solution. However, physical arguments and mathematical analysis can provide some clues on the qualitative and quantitative properties of H and u at steady state when the grounding-line position is known. This chapter describes how to obtain these properties which in turn can be used as a comparison for the steady-state profile simulations. To begin this analysis we first non-dimensionalize our system of equations. We rewrite equations 3.39), 3.44), 3.5)-3.53) and 3.57) by substituting X = X [X] where X represents a model variable, X its nondimentionalization and [X] its characteristic value. For a typical ice sheet [H] m and [x] 6 m. With a characteristic accumulation rate [ṁ a ] =.3 ma we deduce from equation 3.39) that [u] 3 ma and the typical time response of an ice sheet is [T] 3 a. Defining b = b [H] we obtain [τ l ] = Ā n [H][u] n, [τ b ] = C[u] n [x] n + and [τ d ] = ρ ig[h]. Thus, by dropping the asterisks, our problem can be written as [x] H t + uh) x = ṁ a, 4.) ] 4ε [H u x n u x n N n ) n u x κ u + N n u u Hs x =, 4.) u = at x =, 4.3) H + b) x = at x =, 4.4) H = ρ w ρ i b at x = x g, 4.5) 4ε u x n u x = δ H at x x g. 4.6) 33
44 where γ = [τ b] [τ d ], ε = [τ l] [τ d ] and δ = ρ i ρ w ). Physically, ε represents the ratio of the deviatoric stress and the hydrostatic pressure. The faster the ice slides, the larger ε. With an ice softness value Ā = Pa 3 s, we find γ 8 and ε 3. At steady state equation 4.) becomes uh) x =ṁ a, 4.7) or, in its integrated form uh =ṁ a x, 4.8) where we have, from the boundary condition, uh = at the ice divide. For obvious reason the ice thickness H has to be positive everywhere in the ice sheet domain in order for an ice sheet to exist. If we suppose ice accumulation to be strictly positive which we will assume in most of our case studies) it results from equation 4.8) that u has to be positive as well throughout the whole domain with the exception of the boundary condition at the ice divide. If u was equal to zero somewhere else in the domain, the ice thickness would be unbounded in steady state at that location. The signs of H x and u x require a more careful analysis. Throughout the entire domain, the surface slope of the ice sheet, H + b) x, has to be negative at steady state in the direction of the ice flow, with the exception of the boundary condition at the ice divide. Otherwise there would be a dip in the ice at the surface which in time would be filled up by ice accumulation and convergence of ice flow. This means that H x is locally bounded from above by b x. At the ice divide, the boundary condition equations 4.3)-4.4) apply. Expanding equation 4.) and making use of equation 4.3), we obtain, u x =ṁa H >, at x = 4.9) Furthermore, from the boundedness of H x we can deduce that u x is bounded from below by ṁa b x u in the entire domain. H 4. In the ice sheet We can gain further insights of the solution s behavior by expanding the system locally and by simplifying the momentum equation in the bulk of the ice 34
45 sheet. In this section we will perform asymptotic analyses at the ice divide and the grounding line, making use of the boundary conditions at these locations. 4.. Asymptotic Method and series formula The asymptotic expansion method consists in expanding a variable as a power series, which power and coefficient have to be determined. In our case we want to expend u and H. We begin the expansion using integer powers. However we find in some cases that some terms cannot be balanced. Thus, in order to find the right expansion, we expand our variable, say H, with an unknown rational power, say α, as H = H + H α x α. 4.) The power α is found by substituting the relations 4.) in the system of equation to be solved. There exists an m N that satisfies the relation m < α < m +. Since α is rational, we can then rewrite α = m + q r, where q, r) N. Using a change of variable y x r, the expansion carries on by considering the power series of general form H = H + H i y i, 4.) i= where H,..., H mr+q =. This method remains valid even if more than one power are integers but the others are not. If α was irrational, this method could not be used. Before we begin the analysis we recall some results involving power series. 35
46 The multiplication and division of power series are: hx) = f x)gx) = = c n = n= n i= c n x n, ) ) a n x n b n x n, 4.) n= n= a i b n i, 4.3) gx) = hx) f x), 4.4) b = c a, and b n = c n n i= a ib n i a. 4.5) We will also use the recurrence relationship for a series raised to a power also called the JCP Miller s algorithm Knuth, 98)): n n r i = f x) = + ng f x = f g x, [ m=m + )a m+ x m ] i r + )a i +b r i = r i= i= a m x m, and gx) = [ f x)] n = + b m x m, m= m= + ) b m x m = + m= a i r i)b r i, r nia i b r i =a rb r + a r r r)b + r nia i b r i =a rb r + i= Equation 4.6) leads to the recurrence relation: a = b = i= [ ] a m x m) m + )b m+ x m, m= m= a i r i)b r i, r a i r i)b r i. 4.6) i= b r = ra r i= ni r + i)a ib r i. 4.7) 36
47 In this and the following sections, we will illustrate results using a linear bedrock topography as in Schoof 7a): b x) = 7.38x) m, 4.8) and a steady state ice thickness profile obtained using an ice softness Ā = Pa 3 s. For numerical stability we need the bed slope topography to be zero at the divide which property will be discussed in the next section). Therefore we regularize the bedrock by replacing x by x + ɛ, where ɛ is a small regularizing term. 4.. At the ice divide and its vicinity In the vicinity of the ice divide we can perform an asymptotic analysis described in section 4.. to learn more about the qualitative behavior of the solution. We will focus on obtaining the first four terms of the power series and identify the trend of the remaining powers. Obtaining the generalized expression of the coefficients is a rather tedious algebraic exercise which does not add any comprehensive results to the qualitative description of our solution. Using the method described in section 4.., we find the first nonzero dominant power to be α = + n. Thus we will expand H x) in powers of y x n as: Hy) = H + H q y q, 4.9) q= where H q are to be found. Instead of immediately setting H q =, q =,.., n, we will keep the general form of equation 4.9) and derive the origin of these constraints. In our study we are assuming n = 3. The boundary condition at the ice divide involving H is given by equa- 37
48 tion 4.4). We need to examine the lim x H x : H x =H y dy dx, = ny n = n qh q y q, q= qh q y q n. 4.) q= The limit of H x as x goes to zero will only remain finite if H q =, q =,.., n. Therefore, the next dominant term in H must be H n y n = H n x. If we assume the bed to be purely linear even at the divide), we obtain a contradiction in our problem setup: at the ice divide we τ d = because of the boundary condition 4.4). Thus, if b x x = ) = then H x x = ) =. When we perform the asymptotic analysis with these requirements, a term in the longitudinal stress term expansion is unbalanced leading to Hτ l )x = ) = which is contrary to equation 4.). Therefore we need to enforce H x x = ) = b x x = ) =. Consequently we cannot use an exact linear bed for this problem and we need to enforce a regularization as mentioned in section 4... Finally, these assumptions lead to H n =. We can rewrite H as: or as Hy) = H + Hy) = H + H n+ y n+ + H n+ y n+ + H n+3 y n+3 + O H q y q, 4.) q=n+ y n+4), 4.) if we only want to keep four terms in the expansion. Since we have a Neumann boundary condition in H, the first term H cannot be directly determined. Instead, for a given set of parameters, we choose H to match the ice thickness at the ice divide from our numerical simulation. We assume the bedrock elevation is a known function of x. Its properties at the ice divide are similar to those of H, meaning it can be evaluated as an analogous series: by) = b + b n+ y n+ + b n+ y n+ + b n+3 y n+3 + O y n+4) 4.3) 38
49 We can rewrite u x) from equation 4.8) in terms of y using equation 4.4): u x) = ṁax H x), = ṁay n H y), u y) = ṁa H y n H n+ H y n+ H n+ H y n+ H n+3 H y n+3 ) + O y n+4). 4.4) The expression of u in equation 4.4) shows that the boundary condition in equation 4.3) will always be satisfied. Furthermore, if we rewrite u as a similar series to H we deduce that u q =, q =,.., n, n +,.., n and or u y) =u n y n + u q y q, 4.5) q=n+ uy) = u n y n + u n+ y n+ + u n+ y n+ + u n+3 y n+3 + O y n+4), 4.6) if we only want to keep four terms in the expansion. By identification, we deduce from equation 4.4) that, u n = ṁa H, 4.7) u n+ = ṁah n+ H, 4.8) u n+ = ṁah n+ H, 4.9) u n+3 = ṁah n+3 H. 4.3) 39
50 We can easily obtain the expression for u x : u x = dy dx u y, = ny n u n + O ny n + n + ) u n+ y n + n + ) u n+ y n+ + n + 3) u ) n+3 y n+ u n u n u n y n+3), n + ) u =u n + n+ y n+ n + ) u + n+ y n+ n + 3) u + n+3 y n+3 n u n n u n n u n ) + O 4.3) y n+4). The first term to expand in equation 4.) is the vertically integrated longitudinal stress term: [ Hτ l ) x 4ɛ H u x ) /n]. 4.3) x Using the relation given by equation 4.7), we have u x ) n = u n ) n + O n + ) + ) n + ) u n+ n y n+ n + 3) u + n+3 u n n y n+3 u n u n+ n y n+ + u n y n+4). 4.33) Using the recurrence relation equation 4.3) we find H u x ) n =H u n ) n + [ n + ) + n + 3) n u n+3 u n + H n+3 H u n+ n + H n+ u n H ) ] y n+3 + O ) n + ) y n+ + n u n+ u n + H n+ H y n+4). 4.34) ) y n+ 4
51 Thus we have Hτ l ) x = t l y + t l y + t l3 y 3 + O y 4), 4.35) t l 4εH u n ) n n + n + ) u n+ n n + H ) n+, u n H t l 4εH u n ) n n + n + ) u n+ n n + H ) n+, u n H t l3 4εH u n ) n n + 3 n + 3) u n+3 n n + H ) n+3. u n H The second term to expand in equation 4.) is the basal stress term: We start with expanding: τ b = γu n N n ) n, κu + N n = γu n n + κu. 4.36) N n u n =u nn y + n u n+ y n+ + u n n u n+ y n+ + ) u n+3 y n+3 + O y n+5). 4.37) u n n u n The effective pressure is defined by equation 3.58), where H f = anywhere that b <. We will assume that the bedrock is above sea level at and in the vicinity of) the ice divide, so that N = H in this region. Under this assumption, the parameter p does not affect this asymptotic analysis. In view of equation 4.37) we only need to keep terms up to order O y n+5) or O y n+) since we ve considered n = 3) while expanding the second factor in τ b : κu N n =κu n H n y n + u n+ y n+ + O y n+)) u n n H n+ y n+ n H n+ y n+ n H n+3 y n+3 n H n+4 y n+4 + O H H H H = κu [ n H n y n un+ + n H ] ) n+ y n+ + O y n+). u n H y n+5)), 4
52 In the vicinity of the ice divide u, H and κ 3 so that N κu n which allows us write: + κu N n n = n ) [ κu n H n y n n κun H n y n un+ + n H ] ) n+ y n+ + O y n+). u n H Keeping the first four non-zero terms in τ b, we have: τ b =t b y + t bn+ y n+ + t bn+ y n+ + t bn+3 y n+3 + O t b γu n n, t bn+ γ κ n u + n H n, t bn+ γ n u n n u n+, t bn+3 γ n u n n u n+. y n+4), 4.38) The last term to expand in equation 4.) is the driving stress: τ d = H H + b) x. 4.39) We have n + H + b) x = n s n+y + n + n s n+y + n + 3 n s n+3y 3 + n + 4 ) n s n+4y 4 + O y 5), where s q = H q + b q, q. The first four nonzero terms of the driving-stress 4
53 expansion are then: τ d =t d y + t d y + t d3 y 3 + t d4 y 4 + O t d n + n H s n+, t d n + n H s n+, t d3 n + 3 n H s n+3, t d4 n + 4 n H s n+4. y 5), 4.4) We now require that equation 4.) holds at each order of y. In view of equations 4.35), 4.38) and 4.4), the longitudinal stress term and the driving stress are represented by two expansions of the same order with terms that are nonzero at each order of y. The basal stress would also have a same order order expansion as the two other stresses only if we consider a linear problem and n =. Equating the terms of order y leads to: t l + t b + t d =. 4.4) We can solve for H n+ by substituting equation 4.7) and equation 4.8) into equation 4.4): H n+ = n n+ γ ṁa H ) n + H b n+ 4ε ṁa H ) n n n n H. 4.4) We can solve for H n+ and H n+3 by equating the terms of order y and y 3, which results in: H H n+ = b n+ ), 4.43) 4ε ṁa n n n H H n 43
54 and H H n+3 = b n+3 ). 4.44) 4ε ṁa n n n 3 H H n These results are not linked to a particular case. Thus, given H, we can determine the shape of the ice thickness and ice velocity) at the ice divide. b km) Comparison between asymptotic and numerical bed rock topography 35 asymptotic terms asymptotic terms asymptotic 3 terms asymptotic 3 terms asymptotic 4 terms 3 asymptotic 4 terms analytic 5 Difference m) Ice sheet domain km) Ice sheet domain km) Figure 4.: left) Comparison between the analytic, equation 4.8), and the asymptotic bed rock topography in the vicinity of the ice divide when including terms cyan), 3 terms yellow) and 4 terms brown) in the expansion given by equation 4.3). At the ice divide the bed is not exactly linear due to symmetry at the ice divide. The coefficients b i were obtained using a least square fit to equation 4.8). right) The difference between the asymptotic and the analytical bed when including terms cyan), 3 terms yellow) and 4 terms brown) in the expansion given by equation 4.3). Using two terms in the expansion introduces an error of 35 m at the ice divide. Using 4 terms in the expansion shows a maximum of about 3 m over a range of 4 km, dividing by the difference when only including terms. Figure 4. compares the analytic bedrock topography to its asymptotic solution. Using 4 terms in the expansion proves to be accurate within 5 m to the bedrock profile in equation 4.8). Our results showed that the value of p has no impact on the asymptotic expansion at the ice divide. We will illustrate our results for one value of p only; the results are similar for other values of p. Figure 4. 44
55 Ice thickness km) Comparison between asymptotic and numerical steady-state ice thickness for p= asymptotic terms asymptotic 3 terms asymptotic 4 terms steady state Ice sheet domain km) Difference m) asymptotic terms asymptotic 3 terms asymptotic 4 terms 3 4 Ice sheet domain km) Figure 4.: left) Comparison between the asymptotic ice thickness when including terms cyan), 3 terms yellow) and 4 terms brown) in the expansion given by equation 4.) and a steady-state ice-thickness profile in the vicinity of the ice divide for ice softness Ā = Pa 3 s and p= and.4 km resolution. The asymptotic coefficient H = 4.47 km at the ice divide was chosen to be the same as of the one of the steady state solution. The asymptotic expression evolves towards the steady state solution as more terms are added. right) The difference between the asymptotic ice thickness and the steady state solution. Using only 4 terms in the asymptotic expression generates a difference of about -5 m compared to -5 m with only terms. Using 4 terms deems to be relatively accurate within the range of 4 km but not beyond. compares the ice thickness steady-state solution for p = at.4 km resolution. The asymptotic expansion becomes more accurate while adding more terms, as predicted. Using only four terms in the expansion, the error the absolute difference) between the steady-state solution and the expansion is less than 5 m. The coefficient H is chosen to be the same as the ice thickness steady-state value at the ice divide. Typically, an asymptotic results is highly accurate locally. The fact that our four-term results is accurate within 4 km of the ice divide may be a coincidence. The non-dimensional ratio ε 3 while H at the ice divide. Thus, the denominators in equations 4.4) 4.44) are proportional to H. In view of equation 4.4) both basal and driving stresses play an important role in the solution at the ice divide. Furthermore, equations 4.4) 4.44) show that the shape of the series of H will largely be determined by the bed topography. This 45
56 is further emphasized when neglecting the terms factors of ε as equations 4.43) 4.44) become: H n+ b n+, 4.45) H n+3 b n ) Using the same numerical configuration as the one used to generate figures 4. and 4. we find the numerical values: b =.7 H = 4.5 b n+ = 4.8 H n+ =.8 b n+ = 7.59 H n+ = ) b n+3 = 4.3 H n+3 = 4.3 The numerical values in 4.47) shows that the series of H and b are alternating series. However, we will need more terms to have a sense of their possible convergence. However, the numerics confirm the approximations 4.45) and 4.46). According to the expression of the power of y, this analysis shows that the shape of the ice thickness strongly depends on n at the ice divide. In our case we have set n = 3 but the expressions we have derived would remain valid for any integers n. If n 3, the balance between each term would happen very close to the ice divide and we would most likely need to obtain the derivation of many terms for this analysis to be meaningful away from the ice divide At the grounding line At the grounding line we can perform a similar analysis as in section 4... However this technique does not work when p =. A remedy to this problem is to use a boundary-layer method to capture the behavior of the solution Zauderer, 989). This work has been done and we will refer to Schoof 7a) for further details. Asymptotic analysis provides information on the solution when p >. Here again, we will focus on obtaining the first four coefficients of the power series solution and discuss its general form. We first need to define a local hori- 46
57 zontal coordinate relative to the grounding-line position. This is done by defining ˆx x g x. 4.48) This coordinate has been chosen to be positive toward the ice sheet. We can then expand the power series solution around ˆx =. The cases < p < and p = have to be treated separately. We will use a similar process as in section 4.. to perform the analysis. The case p = Using the method described in section 4.. we found that the series expand with positive integer powers of ˆx. Thus we expand H ˆx) and u ˆx) as: H ˆx) = u ˆx) = i= i= H i ˆx i, 4.49) u i ˆx i. 4.5) The boundary condition given by equation 4.6) requires u x to remain finite. It follows by expanding the continuity equation 4.7) that H x has to remain finite as well. These two conditions imply that the basal and driving stress are also finite. Therefore the vertically integrated longitudinal stress term has to remain finite as well in order for equation 4.) to be valid. Expanding this term, assuming u x >, leads to: [ [ ] ] [Hτ l ] x =4ε H x u x ) n + H u x ) n, x =4ε [H x u x ) n + n ] H u x) n u xx. 4.5) Equation 4.5) also implies that u xx must remain finite. Since in this case the powers are integers, these requirements do not restricts the series of u ˆx) and H ˆx) in any ways. Considering only four terms in the expansion, we can rewrite: H ˆx) =H + H ˆx + H ˆx + H 3 ˆx 3 + O ˆx 4), 4.5) u ˆx) =u + u ˆx + u ˆx + u 3 ˆx 3 + O ˆx 4). 4.53) 47
58 For the same reason as in section 4.. we rewrite the expression of the bed topography following the same power series as H: b ˆx) =b + b ˆx + b ˆx + b 3 ˆx 3 + O ˆx 4). 4.54) From equations 4.5) 4.53) we can derive H x, u x and u xx : i= H x = d ˆx dx H ˆx = ih i ˆx i, = H H ˆx 3H 3 ˆx + O ˆx 3), = H + H ˆx + 3 H 3 ˆx + O H H i= u x = d ˆx dx u ˆx = iu i ˆx i, = u u ˆx 3u 3 ˆx + O ˆx 3), = u + u ˆx + 3 u 3 ˆx + O u u u xx = d ˆx dx [u x] ˆx = =u + 6u 3 ˆx + O i i ) u i ˆx i, i= ˆx 3)), 4.55) ˆx 3)), 4.56) ˆx ). 4.57) 48
59 Using the continuity equation we can expand u in terms of H: xg ˆx ) u ˆx) =ṁa, H ˆx) ṁ a xg ˆx ) = ), H + H H ˆx + H H ˆx + H 3 H ˆx 3 + O ˆx 4 ) ) =ṁax g ṁa H + x g ˆx + ṁa H H H H H H ṁa H + O H 3 [ + x g H H ] + [ + x g H H H ) [ + x g H H ] ) H x g ˆx H ] ) ˆx 3 x g H H H H ˆx 4), 4.58) such that, using identification, u = ṁax g, 4.59) H ) u = ṁa H + x g, 4.6) H H [ ] ) u = ṁa H H + x H g x g, 4.6) H H H H u 3 = ṁa H H 3 H x g H H [ + x g H H ] + H H ) [ ] ) H + x g. 4.6) H From the boundary conditions equations 4.5)-4.6) we have: H ) = H = H f ) = b δ, 4.63) ) n δh u x x = ) = u =. 4.64) 8ɛ Using equation 4.6) we deduce the expression for H : H = H x g [ H ṁ a ) n δh ], 4.65) 8ɛ 49
60 where H is known from equation 4.63). The vertically integrated longitudinal stress term is [ ] Hτ l ) x = 4ɛ H u x ) n. 4.66) x We need to expand u x ) n in order to express Hτ l ) x. The negative sign in equation 4.56) could pose algebraic problems. However, as we discussed at the beginning of this chapter, u is a monotonically increasing function in the direction of the ice flow at steady state. The change of coordinate in this section implies that u is monotonically decreasing as a function of ˆx. Thus the first coefficient, u, in equation 4.56) has to be negative, meaning that u is positive. We then have: u x ) n = u ) n + u ˆx + 3 u 3 ˆx + O u u [ = u ) n + u 3 u ˆx n u n u n [ =H u ) n u + + H ] ˆx n u H [ 3 u H + u n u H n u n H u x ) n [ ] H u x ) n = H u ) n x ˆx ), n u u + H H + ˆx 3)) n, n ) u [ 3 n ) ) ] ) u ˆx + O u + H )] ) ˆx + O ˆx 3), u H u 3 + H + u u H n u n ˆx 3), ) u u + H H + O Hτ l ) x =t l + t l ˆx + O ˆx ), 4.67) [ t l = 4ɛH u ) n u + H ], n u H [ t l = 8ɛH u ) n 3 u 3 + H + ) u n u H n u n u + H )]. u H )] ) ˆx The second derivative in the vertically integrated longitudinal stress restricts the order to which we need to expand the two remaining stresses. The 5
61 driving stress expands as τ d = H H b) x, H b) x = H b ) H b ) ˆx + O ˆx ), τ d =t d + t d ˆx + O ˆx ), 4.68) t d =H H b ), t d =H H b ) + H H b ). The last term to expand is the basal stress. Again, in view of equation 4.67) we expand the term up to O ˆx ). When p =, N = H H f. Since H f = b δ, we expand H f using equation 4.54): H f y) = b δ + b δ ˆx + O ˆx ), H f y) = H f + H f ˆx + O ˆx ), 4.69) where H f = H f ). Using equation 4.63) we expand N as N = H H f ) ˆx + O ˆx ). 4.7) Close to the grounding line, the basal stress asymptotes to equation 3.63). Thus the basal stress expands as τ b =t b ˆx + O t b = γ κ n ˆx ), 4.7) H H f ). Equations 4.67), 4.68) and 4.7) show that the dominant balance is between the vertically integrated longitudinal stress and the driving stress terms, both O ), 5
62 from which we can solve for u and obtain: [ n H u =u b ) 4ɛ u ) n H H ]. 4.7) We solve for H in equation 4.6): H = H x g ) H + x g H u. 4.73) H ax g The next dominant balance is O ˆx) and appears in all three terms from which we can solve for u 3 : u 3 = n td + t b u ) n + H u + [ ) 3 8ɛH H n u n u + H ]). 4.74) u H We solve for H 3 in equation 4.6) H 3 = H u 3 + H + ) H ax g H x g H H ) [ ] H + H. 4.75) x g Other than for H the expressions that determine the coefficients H i, i =,.., 3 do not show a strong dependence on the bedrock topography. The dependence is stronger with p at the grounding line. This will be easier to see when we treat the case < p < next. Also, the powers of ˆx are independent of n and the derivation of u i and H i do not strongly depend on n as well. These two observations are opposite to what we observed at the ice divide. b =.39 H =.434 b =.38 H = 3.8 b =.6 8 H = ) b 3 = H 3 = The coefficients b i and H i are shown in 4.76). The power series for H is clearly diverging. 5
63 The case < p < The asymptotic analysis becomes more complicated to obtain when < p <. Let us assume that p is a rational number that can be written as p = q r, q, r) N. For this derivation, we exclude the possibility of p = meaning that r and q < r. Using the method described in section 4.. we expand H and u in powers of y = ˆx r : H = u = i= H i y i, u i y i. i= For the same reasons as in the case p =, u x and u xx have to remain finite across the grounding line. These requirements restricts the coefficients of u as: u x = dy d ˆx u y = r y r = r requiring that u i = for i =,.., r. Similarly, iu i y i, i= iu i y i r, 4.77) i= u xx = dy d ˆx [u x] y = r i i r) u i y i r, 4.78) i= requiring that u i = for i = r +,.., r. The goal remains to derive the expression of the first four terms in the expansions of u and H. However it isn t clear right now which power of y dominates after r as it will depends on the values of q and r. To ensure we will keep four terms, we write the expansion up to i = 3r, and for readability we will keep the summation notation and write u y) = u + u r y r + u r y r + 3r u i y i + O y 3r+). 4.79) i=r+ 53
64 From the continuity equation H can be expressed in terms of u: x y r ) H y) =ṁa, u y) ṁ a x y = r ) u + u r u y r + i=r =ṁax g yr u x g =ṁax g + u [ ur ), u i u y i ) u r u y r u r u + x g [ u 3r u + u ru r u ] y r + x g [ ur u u y r [ ur ur 3r i=r+ ) + u r u u x g u ) ]] u r y 3r + O u u i u y i u 3r y 3r + O u ] y r 3r u i y i u i=r+ y 3r+)), y 3r+)), 4.8) such that, using identification, H =ṁax g, 4.8) u H r = ṁax [ g ur + ], 4.8) u u x g [ H r =ṁax g ur ur + ) u ] r, 4.83) u u u x g u u i H i = ṁax g, i = r +,.., 3r 4.84) u u [ [ H 3r =ṁax g u 3r + u ru r u u u ) ]] ur u r. 4.85) x g u u By identification, equation 4.8) shows that the same restrictions on u applies to H, namely H i = for i =,.., r, r +,.., r and H can be expressed as: H y) = H + H r y r + H r y r + 3r H i y i + O y 3r+). 4.86) i=r+ 54
65 Once again, the bed is expressed similarly as H: b y) = b + b r y r + b r y r + 3r b i y i + O y 3r+). 4.87) i=r+ The expressions for u and H remain unchanged. The expressions for u r and H r are similar to equations 4.6) and 4.65) by replacing u and H by u r and H r respectively. For clarity we rewrite here the expression for u x, u xx and H x using equations 4.77) 4.78): [ u x = ru r + ru r y r + r [ = u r + u r y r + u r u xx =u r [ u r u r + =u r [ + H x = H r [ 3r iu i y i r + O y r+)], i=r+ 3r i u i y i r + O r u i=r+ r 3r i i r) u i r i=r+ y i r + O u r 3r i i r) r i=r+ + H r H r y r + y r+)], 4.88) y r+)], u i y i r + O y r+)], 4.89) u r 3r i H i y i r + O y r+)]. 4.9) r H i=r+ r For the same reasons as in the case p =, u r > and there will be no confusion later on when considering nonlinear terms in u x. In this section, it is clearer to expand the longitudinal stress terms last and begin with expanding the driving 55
66 stress terms: H b) x = H r b r ) H r b r ) y r τ d =t d + t dr y r + t d =H H r b r ), 3r t di y i r + t dr y r + O i=r+ t dr =H H r b r ) + H r H r b r ), t di = i r H H i b i ), i = r +,.., 3r 3r i r H i b i ) y i r + O y r+), i=r+ t dr =3H H 3r b 3r ) + H r H r b r ) + H r H r b r ). y r+), 4.9) In the vicinity of the grounding line it is useful to rewrite the basal stress term as The effective pressure is where H f = τ b = γ κ n N =H N ) κu n. 4.9) κu + N n [ H ] p f, 4.93) H b δ. Using equation 4.87), H f can be expressed as a power series: H f y) = H f + H fr y r + H fr y r + 3r H fi y i + O y 3r+). 4.94) i=r+ In view of equation 4.9) we only need to keep terms up to order O y r+) when expanding the basal stress terms. The derivation that follows will show that keeping terms up to order O y r+) in u and H despite the nonlinearities 56
67 will suffice to rich our goal. Using the results H = H f we have H f H = + H f r y r + H f r y r + O H H +O y r+)), ) H fr H r = + y r + H y r+)) H r H y r + [ ) ] Hr H r H H H fr r H ) ) r H fr H r y r + O H H H y r y r+), H ) p ) ) f Hr H p fr Hr = y q H fr + p H r y r + O y r+)), H H H r H fr H ) [ Hr H p fr N =H y q + p) H r + p H ] r H fr y r + O y r+)), H H H r H fr ) [ Hr N n =H n H np fr y nq + n p) H r + p H ] r H fr y r + O y r+)), H H H r H fr N n ) [ κu = Hn Hr H np fr y nq + n p) H r + p H ] r H fr y r + O y r+)) κu H H H r H fr = Hn κu u r +O y r + O y r+)), u ) [ Hr H np fr y nq + H n p) H r H + np H r H fr H r H fr u r u y r+)). 4.95) ] y r The left hand side of equation 4.95) is O y qn ). This term is negligibly small compared with terms that are O y r ) when p > n but remains important as p 57
68 . Finally we have ) + Nn n H = n κu n κu +O ) [ Hr H np fr y nq + H n p) H r H + np H r H fr H r H fr y r+)), 4.96) τ b = γ ) [ Hr H p fr H κ n y q + p) H r + p H ] r H fr y r + O H H H r H fr H n ) [ Hr H np fr y nq + n p) H r + np H r H fr n κu H H H r H fr +O y r+))). 4.97) u r u ] y r y r+)) u r u ] y r Before expanding equation 4.97) we need to determine which terms dominate. Since n, q) N, r + nq > r + and y r+nq = O y r+). We further need to compare nq to r +. Equating these two values after substituting pr for q leads to p = r+ nr. Therefore ynq = O y r+) whenever p r+ nr, which would never happen when n =. In our case study n = 3 and r and y nq = O y r+) whenever p. Therefore we need to keep this term in our expansion. The basal stress expands as: τ b = γ ) [ Hr H p fr H κ n y q + p) H r + p H ] r H fr y r H H H r H fr H n ) Hr H np fr y nq + O y r+)), n κu H =t bq y q + t bq+r y q+r + t bq+nq y q+nq + O y r+), 4.98) t bq = γ ) Hr H p fr H κ n, H t bq+r = γ ) [ Hr H p fr H κ n p) H r + p H ] r H fr, H H H r H fr t bq+nq = n+ ) γ H Hr H p+np fr. n κ n + u H 58
69 The expansion of the vertically integrated longitudinal stress terms are: u x ) n = u r ) n + u r y r + u r H u x ) n = u r ) n + n [ + n n =H u r ) n + u r u r y r + n ) ur + u r [ Hr [ H r + H r u r H n [ ] H u x ) n = H u r ) n x + 3r i u i y i r + O y r+)) n, r u i=r+ r ) + 3 n H + n + H u r n [ Hr + H n [ H r + H r u r + H n H u r n 3r i=r+ u r u r u 3r u r n u r ũ r i r ] u i u r y i r y r + O ] y r + n ) ur u r ] + 3r n ) ur n i=r+ 3r i=r+ u r y r+)), i u i r ) + 3 n u r y i r u 3r u r ] y r + O ii r) u i r y i r u r ) ] + 3 u 3r n u r y r + O y r+)), y r+)). We finally obtain 3r Hτ l ) x =t l + t li y i r + t lr y r + O y r+), 4.99) i=r+ t l = 4ɛH u r ) n Hr + ) u r, H n u r t li = 4ɛH u r ) n i i r) u i nr, i = r +,.., 3r u r t lr = 8ɛH u r ) n H r + H r u r + ) ) ) H n H u r n n ur + 3 u 3r. u r n u r Equations 4.9), 4.98) and 4.99) show that the dominant balance is between the vertically integrated longitudinal stress and the driving stress terms, 59
70 both O ), leading to u r = nu r [ ] H r H r b r ). 4.) H 4ɛ u r ) n We obtain the value of H r using equation 4.83). The next dominant balance term in driving stress is in terms of y r. Since q < r, the term of power y q in the expansion of τ b equation 4.98)) has to be balanced with a term from the vertically integrated longitudinal stress term in equation 4.99), namely t lr+q y q. Consequently, some terms in equation 4.99) cannot be balanced, meaning u i =, i = r +,.., r + q. Therefore we obtain u r+q = γ κ n Hr H ) p f r nr u r ) n H H 4ɛ r + q) r + q). 4.) The expression of H r+q is then given using equation 4.84). Thus, in terms of x, the power series of u and H rewrites as: H x) = H + H r xg x ) + H r xg x ) + Hr+p xg x ) +p + O x 3), 4.) u x) = u + u r xg x ) + u r xg x ) + ur+p xg x ) +p + O x 3). 4.3) It is difficult to generalize the power series expressions as they strongly depend on p. In fact, in equation 4.98) the two following powers of y after q) are q + r and q + nq. However, q + r > q + nq whenever p < n. Also, the next dominant balance in driving stress is O y r ). If p < n+, q + nq < r and the next dominant balance in the power series expansion remains between the basal and the longitudinal stress terms. Otherwise, the next dominant balance is O y r ) and is between the longitudinal and the driving stress terms again. Thus, in order to obtain an accuracy of say O x g x) 3) or smaller, the power series expansions require more terms for very small values of p than for larger values of p. Figure 4.3 compares the analytic bedrock topography to its asymptotic solution. The power series solution approximate the analytic solution equation 4.8) within m while using four terms or less in the expansion. Figure 4.4 compares the ice thickness steady-state solution for p =.5 top), p =.5 middle) 6
71 Comparison between asymptotic and numerical bed rock topography asymptotic terms asymptotic 3 terms asymptotic 4 terms analytic b km) Difference - m) asymptotic terms asymptotic 3 terms asymptotic 4 terms Distance to grounding line km) Distance to grounding line km) Figure 4.3: left) Comparison between the analytic, equation 4.8), and the asymptotic bed rock topography in the vicinity of the grounding line when including terms cyan), 3 terms yellow) and 4 terms brown) in the expansion given by equation 4.54). The coefficients b q were obtained using a least square fit to equation 4.8). right) The difference between the asymptotic and the analytical bed when including terms cyan), 3 terms yellow) and 4 terms brown) in the expansion given by equation 4.3). Regardless of the number of terms, the power series expansion remains very accurate, within m of the analytic expression. and p = bottom) at.5 km resolution. The expansion is more accurate while adding more terms to it with increasing p. Using only four terms in the expansion, the error the absolute difference) between the steady-state solution and the expansion is less than 3 m within 3 km of the grounding line when p = while the solution diverges away from the grounding line when p =.5. We would need many more terms in order to match the solution further inland of the grounding line assuming the power series do not diverge. In the case when p =.5 the expansion with only terms is overall more accurate than with more terms. This is just a coincidence of the numerics. 6
72 p = Comparison between asymptotic and numerical ice thickness Ice thickness km) 3 Difference m) p = p = Distance to grounding line km) Distance to grounding line km) Figure 4.4: left) Comparison between the asymptotic ice thickness when including terms cyan), 3 terms yellow) and 4 terms brown) in the expansion given by equation 4.) and a steady state ice thickness profile for ice softness Ā = Pa 3 s for p =.5 top), p =.5 middle), p = bottom) at.5 km resolution. right) The difference between the asymptotic ice thickness and the steady state solution. In this particular case, using terms only is more accurate within 3 km from the grounding line. However this might just be a coincidence based on the numerics. Adding more terms is beneficial only locally. 6
73 4..4 In the bulk of the ice sheet The asymptotic analysis method typically applies locally usually at the boundaries of the problem) and does not provide any insights of the solution over the entire domain. However, we can make further assumptions to remedy this problem. In the bulk of the ice sheet the nonlinearity of the problem in the stress balance equation prevents us from finding an analytical solution to the ice flow problem. However, the dimensional analysis of equation 3.44) at the beginning of this chapter shows that the vertically integrated longitudinal stress is negligible and the stress equilibrium is between the basal stress and the driving stress. The stress balance equation then simplifies to the shallow ice approximation γ u n u N n κ u + N n ) n u u H H b) x =. 4.4) The shallow-ice approximation simplifies the momentum equation to a lower order ordinary differential equation ODE) in u. Solving for u in equation 4.8) and substitute the result into equation 4.4), results in solving a nonlinear ODE in H: H x =b x γṁax H ṁ a x H n κ ṁ a x H N n n + Nn. 4.5) Since we assume the grounding-lie position known, we use the flotation condition, equation 4.5) as a boundary condition. Equation 4.5) is then integrated from the grounding line to the ice divide. Figure 4.5 shows the difference in ice sheet thickness between the shallowice approximation and the full model for p = upper panel) and p = lower panel) between the ice divide and the grounding line, assuming the latter known. The shallow-ice approximation captures the solution of the full model within m when p = over the given domain meaning the shallow ice is a good approximation of the full model. In this particular situation, the basal stress remains in the asymptotic state of equation 3.6). The boundary layer, where the basal stress goes to zero and where the new equilibrium between the longitudinal and driving stress occurs, is not resolved when p = and the largest error would be seen there. Instead the stress balance transitions as a step function at the grounding line and the numerics do not capture the phenomena. When p =, the shallow ice model approximates the full model within a m over the full domain outside of the friction transition zone. The difference becomes noticeable in the friction transition zone upstream of the grounding line. The basal stress evolves 63
74 5 Difference in ice thickness between shallow ice and full model p = p = Difference m) Difference m) Ice sheet domain 3 km) Figure 4.5: Difference m) in ice sheet thickness at steady state between the solution of the shallow ice model given by equation 4.4) and the full model given by equation 4.) for p = upper panel) and p = lower panel) at 5 m resolution over a domain between the ice divide and the grounding line. The shallow-ice solution was generated using the steady state grounding line position of the full model and an ice softness Ā = When p = the shallow ice model remains a good approximation throughout the entire domain. When p = the shallow ice model remains a good approximation in the bulk of the ice sheet x < ) but not inland of the grounding line < x <.7). The difference is due to the change in asymptotic behavior of the basal friction law in the friction transition zone. smoothly from one asymptotic behavior to the other and during this transition the longitudinal stress becomes no longer negligible. The shallow-ice approximation is in agreement with the results obtained using the asymptotic analysis at the ice divide. In fact, in the vicinity of the ice divide where κu N n and x is small, equation 4.5) simplifies to H x b x, 4.6) 64
75 confirming the strong dependency of the ice thickness with respect to the bed topography there. 4. in the ice Shelf The asymptotic analysis and the shallow-ice approximation were useful results in the ice-sheet domain because of the lack of analytical solution there. However this is no longer true in the ice shelf where an analytical solution can be derived. In the ice shelf the stress balance equation reduces to equation 3.57) such that, at steady state, the problem reduces to uh) x =ṁ a, 4.7) Ā n H ux n u x = ρ i ρ ) i gh. 4.8) ρ w As the ice thickness always remains a positive quantity, the term u x in equation 4.8) is positive as well and we can omit the absolute value notation. At steady state we can use the integrated form of equation 4.7) given by equation 4.8). Substituting the latter into equation 4.8) leads to u x u n =K n xn. 4.9) ) where K = 4 ρ i ρ i ρ w gṁ a Ā n. We can now integrate equation 4.9) over the entire shelf and obtain u n+ =K n xn+ + C, 4.) where C is a constant of integration that can be evaluated at the grounding line as C = u n+ x g K nxn+ g. Equation 4.) then becomes ) ) u shelf = K n x n+ x n+ g + u n+ n+ x g. 4.) 65
76 Using equation 4.7) the ice thickness in the ice shelf at steady steady reads ) ) H shelf =ṁ a x K n x n+ x n+ g + u n+ n+ x g. 4.) Equations 4.) and 4.) show that u and H respectively grow and decay linearly away from the grounding line. The expressions of u shelf and H shelf require to know the ice velocity or the ice thickness) at the grounding line. If the grounding-line location is known, the ice thickness at the grounding line is known using the flotation condition, equation 4.5). The ice velocity can then be found using the continuity equation. In the absence of buttressing, this analysis shows that the solution can be solved in the ice shelf without knowing anything from the ice sheet. 4.3 Chapter summary In this chapter we discussed the steady-state properties of our ice-flow problem. In the ice-sheet domain, where the ice is grounded, the steady-state solution does not lend itself to an analytical solution. At the boundaries of the ice-sheet domain, the ice divide and the grounding line, where the solution of our system is known due to boundary conditions, we used an asymptotic analysis to characterize the nature of the solution. At the ice divide, the solution expands as a polynomial of non-integer powers, describing the nonlinear behavior of the solution. The nonlinear powers are strong functions of Glen s exponent n but are independent of p as the bed lies above sea level. At the grounding line, the solution behaves linearly when p =. When < p <, the solution is nonlinear and the polynomial powers are functions of p and n. When p = the asymptotic method fails and a boundary layer analysis should be used instead. In the bulk of the ice sheet, the asymptotic method does not work in general. Instead, we can neglect the vertically integrated longitudinal stress and solve the shallow-ice approximation model. This model returns a good approximation the full model solution. When < p the difference becomes large upstream of the grounding line, in the friction transition zone. In the ice sheet, for both the asymptotic analysis and the shallow-ice model, the solution is a strong function of the bedrock topography. In the ice shelf, the steady state solution can be solved analytically independently of the ice sheet solution providing the most accurate comparison possible to our numerical solution. 66
77 CHAPTER 5 NUMERICS In the absence of analytic solutions we need to numerically solve the system of equations 4.) 4.6). In chapter 4 we have shown: how the solution behaves near the boundaries of the domain; that neglecting the longitudinal stress in the ice sheet, the solution to the system returns a good approximation to the full ice flow model; and, the system can be solved analytically in the ice shelf. However, the goal is not to describe our solution as a piecewise valid solution but rather as a continuous function throughout the entire domain. Nonetheless, these information can prove to be useful when validating our numerical solution. Vieli and Payne 5) and Pattyn et al. ) showed that the numerical method used to discretize equations 4.) 4.) with a friction law given by equation 3.6) affects model accuracy. They noted that moving-grid models are significantly more accurate at reproducing grounding-line dynamics than fixedgrid models. Although a one-dimensional moving-grid model is easy to implement, moving grids are hard to incorporate in three-dimensional ice-sheet models, whereas fixed grids are well suited for this purpose. To mimic the constraints on realistic 3-D models, we aim to produce a solution of acceptable accuracy using a fixed-grid model with the lowest possible computational cost. As we will show in chapter 7, depending on the values of the parameter p, our parameterization of effective pressure can considerably reduce the computational cost of an accurate fixed-grid simulation. Pattyn et al. 6) and Gladstone et al. a) showed that numerical errors or alternatively, the computational cost of a simulation with a given numerical error) could be reduced through the use of numerical grounding line parameterizations GLPs). GLPs involve sub-grid-scale interpolation of the groundingline position, which is used in the grid cell containing the grounding line to compute a stress that varies continuously as the grounding line moves. In the following section, we present results both with and without a GLP in order to compare our findings with those of Gladstone et al. a) and to investigate the possible benefit of combining the GLP with our effective-pressure parameterization. We implemented a GLP similar to the PA GB GLP in Gladstone et al. a). 67
78 5. The fixed grid models 5.. Fixed-grid model without a GLP Δx H H u 3/ H N u N+/ H N+M un+m+/ x= x=x c Ice Sheet Ice shelf Figure 5.: Illustration of the staggered grid used in the model. The H-grid points are represented by solid circles and the u-grid points by empty circles. x is the grid spacing on both H- and u-grids). H N is the ice thickness in the last grounded point. The ice divide is at x = and the calving front at x = x c. We use centered differences to discretize equations 4.) 4.6) on a uniform grid. To insure numerical stability, we use a first-order upwinding scheme and a semi-implicit time stepping scheme to discretize equation 4.) when computing steady state results. We use the partially implicit, second-order accurate in time, Crank-Nicholson scheme for transient simulations as in section 7.3. We compute u and H on staggered grids separated by half a grid cell, as shown on figure 5.. The ice-sheet-ice-shelf domain contains N + M points, where N is the number of points in the ice sheet changing in time as the grounding line migrates) and M the number of points in the ice shelf both on the H-grid. Since the boundary conditions in equation 4.3) and 4.4) are most easily satisfied at a u-grid point, we place the ice divide, x = x d =, at the first point on the u-grid. In general, the grounding-line position, x = x g, lies between two grid points and is diagnosed from H using equation 4.5), the flotation condition. We found that it simplified computations near the ice divide to place a ghost H-grid point to the left of the divide; we enforce symmetry by requiring that the ice thickness is symmetric across the ice divide, that is H = H, satisfying equation 4.4). Similarly, we find that a ghost point beyond the calving-front, this time on the u-grid, makes it easier to simultaneously solve equation 4.) at the last real u-grid point and equation 4.6) at the calving front. This ghost point is also needed to solve equation 4.) at the calving front. 68
79 Excluding the two half-cells associated with these ghost points, there are N + M) 3 half-cells between the ice divide and the calving front on the staggered grid. Thus, the spacing between points on both the H- and u-grids is given by x = L N + M 3, 5.) where L = x c x d denotes the length of the domain and x c the calving front location. For an integer index i [, N + M], we define the location of H-grid points by x i i 3/) x and those of u-grid points by x i+/ i ) x. Similarly, we introduce a time index j [, T], where T is the number of time steps in a given simulation, so that t j = j t for a constant time step t. Discrete values of thickness and velocity, are H j i Hx i, t j ) and u j i+/ ux i+/, t j ), respectively. The grounding line position is defined as xg j = x g j t). The depth of the ice-sheet bed is defined as b i bx i ) at H-points and by b g = bx g ) at the grounding line. The effective pressure, Nx, t; p), is located on an H-grid point and is defined by N j i Nx i, t j ; p) not to be confused with the number of ice-sheet grid points N): N j i = H j i H f i H j i The flotation thickness, H f, is defined at H-grid points as ) p. 5.) H fi H f x i ) = max, b i ρ w /ρ i ). 5.3) For numerical stability purposes we regularize the absolute value and maximum operators for any real number as: ) x s = x + ɛs, 5.4) max x, ) max s x) = x s + x), 5.5) where ɛ s is a very small number of order 8 or smaller). Equation 4.) is 69
80 discretized at H-grid points throughout the domain both ice sheet and ice shelf): H j+ i H j i t + θf j+ i + θ) F j i = ṁ a, 5.6) where F j i ) H j u j H j u j up,i+ i+ up,i i, 5.7) x and where we have used first-order upwinding, with the upwind thickness defined by H j H j i if u j, i+ = up,i+ 5.8) H j i+ if u j. i+ The time centering is determined by θ : If θ =, the time stepping is fully implicit; if θ =, we are using a fully explicit scheme; and if θ = /, the method is the partially implicit, second-order accurate in time Crank Nicholson scheme. Equation 4.) is most naturally discretized at u-grid points, requiring that the thickness, H, in the driving stress and the effective pressure, N, in the friction law be averaged to the u-grid, e.g. H j = H j i+ i + Hj i+ )/. In the grounded ice sheet, equation 4.) in discrete form is 4ε x + n γ [ uj i+ H j i+ uj i+ 3 n u j i+ ) H j i+ + Hj i u j i+ n u j i+ 3 u j i+ j N i+ +N j i κ u j + i+ N j ) n ) i+ +N j n i ) H j i+ + b i+ H j i b i x ) H j i n uj i+ u j n ) ] i u j u j i+ i =. 5.9) 7
81 In the ice shelf, equation 4.) is discretized as 4ε x + n [ H j i+ uj i+ 3 H j i+ + Hj i ) u j i+ H j i+ Hj i x n ) u j i+ 3 ) u j H j i+ i uj i+ u j i n u j i+ u j i =. 5.) The boundary conditions, equations 4.3), 4.4) and 4.6), are expressed as ) ] 4ε x n uj N+M+ u j N+M n u j N+M+ u j 3 =, 5.) ) H j + b H j b =, 5.) x ) u j δ N+M Hj N+M =, 5.3) We solve the stress balance equation for u j+ i+/ and the continuity equation for H j+ i using Picard fixed-point iteration. We use the thickness and velocity from the previous time step as the initial guesses: H j, i H j i, 5.4) u j, i+/ uj i+/, 5.5) At each iteration, we first solve for the new velocity u j,k+ i+/ from the stress-balance equation using the iterate on viscosity method which can be found in Goldberg et al. 9). The longitudinal stress at iteration k + is defined as τ j,k+ l,i+ [ x H j,k i+ νj,k i+ u j,k+ i+ 3 ν j,k i 4ε x n uj,k i+ u j,k i ) u j,k+ i+ H j,k i ν j,k i u j,k+ i+ )] u j,k+, 5.6) i n. 5.7) 7
82 The basal-friction law at iteration k + in the ice sheet is given by τ j,k+ b,i+ γ uj,k i+ n N j,k κ u j,k + i+ i+ +N j,k i N j,k ) n ) i+ +N j,k n i n u j,k+, 5.8) i+ Basal stress in the ice shelf is zero for all iterations. Driving stress does not depend explicitly on u; it is computed entirely from time-independent quantities and thicknesses at iteration k. Boundary conditions are x νj,k N+M u j,k+ u j,k+ N+M+ u j,k+ 3 N+M =, 5.9) ) = δ Hj,k N+M. 5.) The result is a linear system involving a tridiagonal matrix M k u u k+ = r k u. 5.) We use a sparse matrix solver to compute the new velocities. Next, we solve the continuity equation for the new thicknesses H j,k+ i : H j,k+ i H j i t + θf j,k+ i + θ) F j i = a, 5.) where F j,k+ i ) H j,k+ u j,k+ H j,k+ u j,k+ up,i+ i+ up,i i, 5.3) x 7
83 and where H j,k+ up,i+ H j,k+ i if u j,k+, i+ H j,k+ i+ if uj,k+. i+ 5.4) The remaining boundary condition, given by equation 4.4), here is H j,k+ H j,k+ = b + b. 5.5) The tridiagonal linear system actually u is typically strictly positive so the system is bidiagonal since negative velocity typically occur when the advection is negative as well) is solved for the new thickness. Iteration continues until the the residual M k+ H H k+ = r H. 5.6) R k M k u u k r u k < max τ j,k d,i+ ). 5.7) Note that all terms are evaluated at iteration k. 5.. Addition of the GLP A few simple modifications to the numerical method from the previous section are required to add a GLP. The basal and driving stresses in the grid cell containing the grounding line are modified so that the stresses transition smoothly between their grounded and floating values as the grounding line passes through the cell. Following Pattyn et al. 6), we define the grounding-line position to be the location where the function f Pattyn x) = H f x)/hx) is equal to one. Values of f Pattyn at arbitrary x values are computed by linear interpolation between values at H-grid points: f Pattyn x) = x x ) i f x i + ) x xi f x i+ x i x < x i+, 5.8) f i H f x i )/H i. 5.9) 73
84 With this definition, the grounding-line position x g is given by f Pattyn x g ), 5.3) x g = x i + f i f i+ f i x. 5.3) In the cell containing the grounding line, we compute the basal and driving stresses once each assuming the cell is entirely grounded and then entirely floating. Then, the stresses are linearly interpolated between their grounded and floating values, based on the fraction of the cell that is grounded vs. floating. Following Gladstone et al. a), we define the fraction of the u-grid cell that is grounded as: λ g f i f i+ f i. 5.3) Assuming the u-grid cell at N + / contains the grounding line, the three stresses at the center of this cell are τ l,n+ = 4ε x + n [ H j N uj N+ τ b,n+ = λ g γ τ d,n+ = H j N+ uj N+ 3 uj N+ u j N ) H j N+ + Hj N + λ g ) δ n u j N+ u j N+ n u j N+ 3 n u j u j N+ N κ u j + N+ j N N+ +N j N u j N+ ) ) ], 5.33) ) n N j N+ +N N j ) n ) H j N+ λ + b N+ H j N b N g x H j N+ Hj N x ) n, 5.34), 5.35) 74
85 where, as usual, the stresses must balance: τ l,n+ + τ b,n+ + τ d,n+ =. 5.36) In simulations without a GLP, the model computes basal and driving stresses as if the cell containing the grounding line were entirely grounded. Note that τ l has not been modified as part of the GLP because longitudinal stress takes the same form in the ice sheet and the ice shelf. The other equations of the system are unchanged from the previous section. We chose not to use the quadrature methods employed in Gladstone et al. a) because they would likely be too cumbersome and costly in 3-D ice-sheet model. 5. A pseudo-spectral Benchmark model 5.. Motivation To evaluate the performance of the fixed-grid model, we need a benchmark solution to compare with our fixed-grid results. To this end we implemented a stretched-grid, pseudo-spectral method using Chebyshev polynomials Boyd, ) to produce spectrally accurate steady-state benchmark results. The Chebyshev collocation points are non-uniformly distributed over the ice-sheet domain, with the highest resolution at the grounding line and ice divide. Using 5 Chebyshev modes, the grid spacing continuously decreases from 8 m at a distance of km from the grounding line to.5 m at the grounding line. We verified the numerical convergence of the Chebyshev benchmark by comparing grounding-line positions with those computed using 49 modes at various values of p and A. We found that results changed by at most 5 cm when doubling the resolution, suggesting that numerical errors in the Chebyshev grounding-line position are negligible compared to those from the fixed-grid model. We compute errors in our fixed-grid results by comparing them to Chebyshev benchmark solutions. In order to give us further confidence that the benchmark solutions are accurate, we compared the Chebyshev results with the semianalytic boundary-layer model from Schoof 7a) known as Model A. We can reproduce the grounding-line position in Model A to within fractions of a millimeter if we neglect longitudinal stresses, use the friction law from equation 3.6), and apply boundary conditions given by equations 4.5) and 4.6). This approach can be used to reproduce the grounding-line position from Model A but not the velocity and thickness solutions.) When we included the full longitudinal stress in the Chebyshev model, the differences with the Model A grounding-line position increased to km. 75
86 Switching to the more complex basal friction law, equations 3.58) and 3.6), introduced further differences of km or less. We attribute the differences between Model A and the Chebyshev solution with full longitudinal stress and our friction law to the simplifying assumptions of Model A, rather than to errors in the Chebyshev model. These results give us confidence that the Chebyshev model is producing solutions with errors that should be negligible of order meters or less) compared to those from the fixed-grid model order kilometers or more). This close agreement between the boundary-layer model and our benchmark sheds some light on possible sources of discrepancies between numerical solutions in Pattyn et al. ). While some discrepancies are due to numerical error, others are due to different model formulations. The latter is evident in Durand et al. 9). Whereas they found poor agreement between their Stokes-flow model and the boundary-layer Model B from Schoof 7a) which might reflect the differences between a Stokes model and a depth-integrated model we find excellent agreement between our benchmark with p = ) and the boundarylayer model, both of which aim to solve the same equations. The boundary-layer solution from Schoof 7a) is only valid for an unbuttressed ice stream when p = and the basal shear stress never asymptotes to a Coulomb friction regime. Tsai et al. 5) showed that a boundary-layer results can be derived for an un-buttressed ice stream when the basal shear stress asymptotes to a Coulomb friction law equivalent to ours when p = ). They obtained their results considering a different friction law: τ b = min Cu n, C This expression satisfies the same asymptotic limits 3.6) and 3.63) from the basal-friction law used in this study, and our formulation can be interpreted as a regularization of theirs. However, the distance over which the transition from one limit to another occurs is key in order for the boundary layer to be used with our parameterization: the shorter the friction transition zone, the better the agreement between Tsai et al. 5) boundary layer results and our model results when p =. For some parameter values that we will experiment with in chapter 7, we found differences by more than 3 km between the boundary-layer and the Chebyshev results. While this difference is too large to consider this boundary layer as a benchmark, it can be used qualitatively. More works needs to be addressed to fully understand how we could adapt Tsai et al. 5) results to our formulation but this will be the focus of future research. κ n N ). 5.. The numerics The Chebyshev model is a Python code that finds steady-state solutions to the equations of motion. The code is pseudo-spectral Boyd, ): integrals and derivatives are computed in spectral space i.e., using Chebyshev modes), whereas products and quotients are computed in physical space on a collocation grid. The 76
87 collocation points are the Chebyshev Gauss Lobatto nodes, defined as: x k = x g cos ) πk N k =,,..., N, 5.37) where N = 4 is the order of the Chebyshev polynomials that form the set of basis functions. This choice of collocation grids means that there are collocation points on the domain boundaries the ice divide x = ) and the grounding line x N = x g ) which makes applying boundary conditions at these locations relatively straightforward. We used open-source code from PyBlog von Winckel, 3) for transformations between physical and spectral space and for recurrence relations for integrals and derivatives. The code uses the derivative of thickness, H x, as its primary computational variable. This choice reduces numerical noise because we never need to compute the second derivative of the primary variable. Higher-order derivatives introduce increasing amounts of numerical noise, whereas integrals tend to remove noise. The thickness H is derived from H x by integration H = Hx g ) + x x g H x dx, 5.38) where Hx g ) is known from the flotation boundary condition, equation 4.5). The velocity u is determined from H using the integral of the steady-state continuity equation, uh = ṁ a x, and the velocity derivative u x is computed from the continuity equation, equation 4.), with H t : u = ṁa x H, 5.39) u x = ṁa uh x. 5.4) H Given u, H and their derivatives, we use Picard iteration to solve stress-balance, equation 4.). Each Picard iteration involves solving the following linear system for H x,k+, based on the results computed at the previous iteration k: M khx,k+ = c k, 5.4) ) D ν x, k u k + ν k u x, k + Hk D ν k u k ) D x, 5.4) M k c k ν x, k a τ b, k Hk bx, k, 5.43) 77
88 ν 4ε u x n, 5.44) where quantities with arrows over them are vectors of N + values from each collocation point, quantities that are bold and in capital letters are N + ) N + ) matrices, D is an operator that puts the vector elements along the diagonal of a matrix, D x is the Chebyshev derivative operator expressed as a matrix, and τ b, k is given by equation 3.5) with all quantities evaluated at iteration k. Products of vectors are defined element-wise in these equations, rather than as dot products. Picard iteration requires an initial guess at H x, which we define as H x, [ ] x Hx g ) H xg, 5.45) H 3 m. 5.46) An outer iterative loop uses Brent s root-finding method Brent, 973) to find the grounding-line position x g where the final boundary condition, equation 4.5), is satisfied. Brent s method requires bounds on x g : we break the domain into segments of downward-sloping bedrock topography and search for steady states independently on each segment. The method is also capable of finding unstable steady states on upward-sloping bedrock. The method is considered to have converged when both the residual r = max M k Hx, k c k ) and the residual in equation 4.5) are less than. All computational variables are non-dimensionalized to be of order unity. 5.3 Chapter Summary This chapter describes the numerical schemes used to discretize the iceflow problem. We use a fixed-grid model approach for this purpose. The ice velocity and ice thickness are computed on a staggered grid separated by half a grid cell. The first velocity point is most naturally placed at the ice divide. The continuity equation is discretized using a first-order upwind scheme and a fullyimplicit time stepping scheme when running simulations to steady state. The time stepping scheme is switched to the partially implicit, second order accurate in time Crank-Nicholson scheme when running transient simulations. The momentum equation and the boundary conditions are discretized using a centered difference scheme. A grounding-line parameterization GLP) has proved to be beneficial in reducing numerical error when using a friction law as in equation 3.6). It smoothes the transition of the basal and driving stresses between their last grounded and first floating cell. We implement a simple GLP which uses a linear reconstruction of the stresses from the last fully grounded cell to 78
89 the grounding line, which is located using an interpolation based on Pattyn function. We will test whether the GLP is complementary to our hydrology parameterization p. Due to the lack of analytical solution, we use a spectrally accurate Chebyshev method as a benchmark solution. This solution was compared, under matching assumptions, to a semi-analytical boundary-layer solution and proved to be accurate to within fractions of millimeter. 79
90 CHAPTER 6 STABILITY ANALYSIS Before exploring the model s behavior properties and sensitivities with respect to different physical parameters, we investigate the numerical stability of the fixed-grid model developed in sections 5.. and 5... We will show that adding a small perturbation to a steady-state solution does not cause a large deviation of that solution. To achieve this, two steps are necessary: first, we need to linearize our problem around steady state. Second, we compute a semi-discrete normal mode perturbations to the steady-state solution and show that the eigenvalue with the largest magnitude has a negative real part, meaning the steadystate solution is stable. In this chapter we will only show results for the model without the GLP. The addition of the GLP does not alter the conclusion of this analysis. 6. Linearization around steady state Let us assume the existence of the steady-state solutions of the ice thickness H and the ice velocity ū. We denote their perturbation respectively by ɛĥ and ɛû, where Ĥ and û are of order unity. We can now linearize our problem by rewriting Hx, t) = Hx) + ɛ Ĥx, t), 6.) ux, t) = ūx) + ɛ ûx, t), 6.) where ɛ denotes a small perturbation term. In general we denote by X = X + ɛ ˆX the decomposition of a given quantity X in its steady-state and perturbed components. Expanding the different expressions in the ice-flow problem and only keeping terms of order ɛ, we obtain a new linear system of equations. 8
91 We first linearize the numerical smoothing operators given by equation 5.4): x + ɛ ˆx s = x + ɛ ˆx) + ɛs, = x + ɛs ) + ɛ = x s + ɛ x x s ˆx + O ) x ˆx x + ɛs + O ɛ ), ɛ ). 6.3) The linearization of the continuity equation is: H + ɛĥ ) t + [ ū + ɛû) H + ɛĥ )] x =ṁ a, Ĥ t + [û H + ūĥ] x = + O ɛ ). 6.4) H t = and ū H) x = ṁ a. The lin- where we used the relations at steady state: earization of the longitudinal stress term is n τ l =4ε ū x + ɛû x s ū x + ɛû x ), ) ) ] n =4ε ū x s ū x [ + ɛ + ū x n ūx ū x û x + O ɛ ) s = τ l + ɛ ˆτ l + O ɛ ), 6.5) where n τ l =4ε ū x s ū x 6.6) ) ) n ˆτ l =4ε ū x 3 s ū x s n + ū x û x. 6.7) We can now derive the expression for the vertically integrated longitudinal stress: [Hτ l ] x = [ H + ɛĥ) τ l + ɛ ˆτ l ) ] ɛ x + O ), = [ H τ l ] x + ɛ [ ] Ĥ τ l + H ˆτ l ɛ x + O ). 6.8) 8
92 Before linearizing the basal stress it is useful to linearize its main components: N = H + ɛĥ) H ) p f, H + ɛĥ = H + ɛĥ) H f H f Ĥ H )p + pɛ H H H f ) ) + Oɛ ), = H [ )] f H f Ĥ H )p H + ɛ Ĥ + p + Oɛ H ), H f ) κ u N n = N + ɛ ˆN + Oɛ ), 6.9) N = H H f H )p, 6.) ˆN = N ) H f + p Ĥ, 6.) H H H f = κ ū + ɛû s N + ɛ ˆN ) n + O ɛ ), = κ ū s ū N n + ɛ ū s + κ u N n = + κ ū ) s N n + κ u N n [ ) n = + κ ū ) n s N n = + κ ū ) n s N n = ḡ + ɛĝ + O û n ˆN ]) + O ɛ N ), [ κ ū s ū + ɛ κ ū s + N n ū u n ˆN ]) + O ɛ N ), s [ ɛ κ ū s ū n κ ū s + N n ū û n ˆN ]) + O N s [ ]) κ ū + ɛ s ˆN κ ū s + N n N ū n ū û + O s ɛ ), ɛ ), ɛ ), 6.) ḡ = + κ ū ) n s, 6.3) N n [ ]) κ ū ĝ = g s ˆN s κ ū s + N n N ū n ū u. 6.4) s 8
93 The linearization of the basal stress is then: n τ b =γ ū + ɛû s ū + ɛû) ḡ + ɛĝ) + O ɛ ), ) ) n =γ ū ū s ūḡ + ɛ n ū û + ɛ s n =γ ū n s ūḡ + ɛγ ū s ūḡ ū ū + κ ū s H κ ū s + N n ) = τ b + ɛ ˆτ b + O û n ū + ĝ )) ḡ ɛ ), + O ) ū + ū N n n s ū κ ū s s + N n û ) ) H f + p Ĥ + O ɛ H ) H f ɛ ), 6.5) where n τ b =γ ū s ūḡ, 6.6) ) ) ) ˆτ b = τ b ū ū ū + ū N n κ ū n s ū κ ū s s + N n û + s H f H κ ū s + N n + p Ĥ. ) H H f 6.7) The driving stress linearization is: τ d = H + ɛĥ ) s + ɛŝ) x = H s x ɛ ) Ĥ s x + Hŝ x + Oɛ ) = τ d + ɛ ˆτ d + O ɛ ), 6.8) where τ d = H s x, 6.9) ˆτ d = Ĥ s x Hŝ x, 6.) H + b x < x g s = δ H x x g, 6.) 83
94 ŝ = Ĥ x < x g. 6.) δĥ x x g The linearization of the boundary conditions at the ice divide leads to: u = ū + ɛû =, û =, 6.3) H + b) x = H + ɛĥ + b) x =, Ĥ x =, 6.4) Equations 6.3)-6.4) show that the linearization process did not alter the ice dynamic at the ice divide: the perturbed velocity is zero and the perturbation ice thickness is symmetric just as for the steady-state solution. At the calving front and more generally in the ice shelf, the balance between the vertically integrated longitudinal stress and the driving stress becomes: 8ε δ ū n x + ɛû x s ū x + ɛû x ) = H + ɛĥ ) ) ] 8ε δ ū n x s ū x [ + ɛ + ū x n ūx ū x û x = H + ɛĥ + O s At steady state we have 8ε δ ū n x s ū x = H, which allows us to rewrite equation 6.5) as ɛ ). 6.5) û x = ū x ū x s ) H ū x s + n ū x ) Ĥ + O ɛ). 6.6) We do not need to know the grounding-line position in order to solve the system of equations 4.)-4.) unless we include the GLP in our numerics. Rather, the grounding-line is found using equation 4.5). However, if we want to determine the perturbed grounding-line position once the perturbed ice thickness is 84
95 known, we need to introduce a grounding-line perturbation term in the form x g = x g + ɛx g. Introducing this perturbation in equation 4.5) leads to: H x g + ɛ ˆx g ) + ɛĥ x g + ɛ ˆx g ) = H f x g + ɛ ˆx g ), H x g ) + ɛ ˆx g H x x g ) + ɛĥ x g ) = H f x g ) + ɛ ˆx g H fx x g ) + Oɛ ), ˆx g H x x g ) + Ĥ x g ) = ˆx g H fx x g ) + Oɛ), ˆx g = Ĥ x g ) + Oɛ). 6.7) H fx x g ) H x x g ) where we used the relation H x g ) = H f x g ) at steady state and a Taylor expansion in order to obtain the final expression of ˆx g. With the formulation given by equation 6.7) the perturbed grounding line position can be determined explicitly rather than implicitly once Ĥ is known. 6. Normal mode analysis as: Using the results from section 6. the linearized system can be rewritten Ĥ t + [û H + ūĥ] x =, 6.8) [ ] H ˆτ l + Ĥ τ l x ˆτ b + ˆτ d =, 6.9) û = at x =, 6.3) Ĥ x = at x =, 6.3) û x ū x ū x s ) H ū x s + n ū x ) Ĥ = at x =x c. 6.3) Normal mode analysis is commonly used to perform a stability analysis on differential equations. Typically, this consists in expressing the system in terms of Fourier modes and determining the sign of the real part of the eigenvalues. If any real parts is positive, the system s solution grows without bound in time once perturbed; if all real parts are negative, the perturbed system evolves to 85
96 it s unperturbed solution. However, this method is usually used when dealing with constant coefficients which is not the case in our problem. With nonconstant coefficients, the stability analysis requires solving a more general eigenvalue/eigenmode problem which connote typically be solved analytically. Following Petersson ) we will consider our perturbed problem being discrete in space but continuous in time. We will then obtain an eigenvalue problem which can be solved numerically. In what follows, we introduce the position vector X = x,..., x N+M ) T, where the exponent T denotes the transpose of a vector, and x i = x hi or x i = x ui, corresponds to the location of an H- or u- grid point as illustrated in figure 5.. We will denote X h = x h,..., x hn+m ) T and X u = x u,..., x un+m ) T. We now express our perturbed parameters as: Ĥ X) He λ Ht, 6.33) û X) ũe λ ut, 6.34) where H and ũ are eigenvectors of the spatially discretized problem and λ H and λ u are the eigenmode also called mode number) relative to û and Ĥ respectively. Equations 6.33) 6.34) are then substituted in equations 6.8) 6.3). The momentum equation will become a linear system of equation relating ũ to H. This relation will be substituted in the linearized continuity equation which will result in an eigenvalue problem for H. The stability results we seek will be the solution of this problem. For clarity and to derive the eigenvalue problem, It is practical to define the following R N+M) N+M) matrices: D + i, j) = D i, j) = x when j = i, i =,.., N + M, x when j = i +, i =,.., N + M, elsewhere, x when j = i, i =,.., N + M, x when j = i, i =,.., N + M, elsewhere, 6.35) 6.36) 86
97 D + D i, j) = i, j) = when j = i, i =,.., N + M, when j = i +, i =,.., N + M, elsewhere, when j = i, i =,.., N + M, when j = i, i =,.., N + M, elsewhere, 6.37) 6.38) where D + and D respectively are the discrete forward and backward firstderivative operators in space; D + and D are two operators that average vectors expressed on the H-grid onto the u-grid and vectors expressed on the u-grid onto the H-grid respectively. From now on a vector quantity is denoted in bold as V = V X), where V represents a given function in our equation. For any given vectors V = v,.., v N+M ) T and W = w,.., w N+M ) T, we will assume that exponentiation, multiplication, division, etc. apply element-wise as follows: V m = v m,.., vm N+M) T, m R, 6.39) V = v,.., v N+M ) T, 6.4) V W = v,.., v ) T N+M, w w N+M 6.4) VW = v w,.., v N+M w N+M ) T. 6.4) We further denote the unit vector R N+M and the identity matrix I R N+M) N+M). We recall that the operator D is an operator that puts a vector element along the diagonal of a matrix. In the sections that follow, we recall, unless stated otherwise, that only the subscripts x and t refer to derivatives. Other subscript notations are arbitrary. 6.. The momentum equation We now vectorize the linear system 6.8) 6.3) and substitute equations 6.33)- 6.34) in it. We will use the same discretization in space as in section 5... The 87
98 matrices presented in this section and the next one simply represents the vectorization of the numerical finite difference scheme introduced in chapter 5. We begin with the linear momentum equation 6.9): If we denote ) ) n t lu =4ε H ū x 3 s ū x s n + ū x, t lh =4ε ū x n s ū x, T lu =D + D t lu ) D, 6.43) T lh =D + D t lh ), 6.44) the linearized vertically integrated longitudinal stress becomes [ Hτ l + H τ l ] We can write the basal-friction law in a similar fashion: n t b =γ ū s ū + κ ū s D N n t bu = t b ū ū ū + ū n s ū s κ ū t bh = t b s H κ ū s + D N ) n x T l u ũe λ ut + T lh He λ Ht. 6.45) ), D N n κ ū s + D N n + p ), ) H f, H H f T bu =D t bu ), 6.46) T bh =D t bh ) D, 6.47) and the linearized basal-friction law is: τ b T bu ũe λ ut + T bh He λ Ht. 6.48) 88
99 Similarly, if we denote: ŝ x = x < x g, δ x x g T dh = D H ŝ x ) D + D s x ) D, 6.49) the linearized driving stress becomes: τ d T dh He λ Ht. 6.5) The substitution of equations 6.45), 6.48) and 6.5) into equation 6.9) returns a linear system linking ũ and H as: M u ũe λ ut + M H He λ Ht =, 6.5) where M u = T lu T bu and M H = T lh T bh + T dh are two real square matrices of sizes N + M) N + M). The boundary conditions given by equations 6.3) and 6.3) are enforced by replacing the first and last row of M u and M H with: M u, ) =, M u, j) =, M H, j) =, j [, N + M], j [, N + M], M u N + M, j) =, j [, N + M ], M u N + M, N + M ) = dx, M u N + M, N + M) = dx, M H N + M, j) =, j [, N + M ], M H N + M, N + M) = ū x ū x s ) H ū x s + n ū x ). 89
100 Equation 6.5) remains valid t R. Thus we have M u ũ + M H H = at t =, 6.5) M u ũe λ u + M H He λ H = at t =. 6.53) Combining equation 6.5) into equation 6.53) leads to the relation λ u = λ H. 6.54) From now on, we will simply write λ instead of λ u and λ H. The matrix M u is a derivative operator including boundary conditions for the momentum equation. By construction it is then invertible. From these results we deduce that ũ = M u M H H. 6.55) 6.. The continuity equation Substituting equations 6.33)-6.34) in equation 6.8) leads to λi + T ch ) H + T cu ũ =, 6.56) where T ch =D ū) D + D + D ū x), T cu =D H) D + + D H x ) D +. Before continuing further we need to enforce the boundary condition 6.3) which is done by setting: T ch, ) = dx, T ch, ) = dx, 9
101 T ch, j) =, T cu, j) =, j [3, N + M], j [, N + M]. Substituting equation 6.55) into equation 6.56) returns: λi + T ch ) H + T cu M u M H H =, 6.57) which is equivalent, after simplification, in solving the eigenvalue problem λ H =C H H, 6.58) where C H = T ch + T cu M u M H ). 6.59) By definition, the steady-state solution of the system 4.)-4.6) is strictly stable if the real part of all eigenvalues in equation 6.58) are negative. It would be tedious to show the stability results for all the experiments done in this work Therefore we will only show the result for 3 values of p p =, p =.5, p = ) using the set of parameter given in table 3. for an ice softness A = Pa 3 s and a resolution of 4 m; the stability results remain valid for all resolutions not shown). Figure 6. shows the 7 largest eigenvalues left panel) with their corresponding eigenvectors right panel), of the eigenvalue problem 6.58), in decreasing order, for p = top), p =.5 middle), and p = bottom). In all cases the 7 eigenvalues are real and the eigenvectors resemble a Fourier series-type set of solution: we observe one additional zero for each subsequent eigenvector. The eigenvalues, in all three cases, are negative, meaning the steady-state solution is strictly stable when subject to a small perturbation. In all three cases, the first eigenvector has a shape that is similar to an ice-thickness profile we obtained at steady state. All the eigenvectors, starting from the fourth eigenvector and thereafter, show a growing solution in the ice shelf. However, these growing solutions are associated to shorter decaying time compared to the slowest decaying mode meaning their effect rapidly becomes negligible. The characteristic decaying time scale of our perturbation is proportional to [λ] = [T] 3 a. If we consider, for example, the fourth larger eigenvalue when p =, λ 4 35, the decaying timescale is approximately years which is small compared to the characteristic decaying time scale of the slowest-decaying mode. 9
102 Real part of the 7 eigenvalues of largest magnitude and their corresponding eigenvectors, Res =.4 km Eigenvalues Eigenvectors p= Reλ) Reλ) p = λ λ λ3 λ4 λ5 λ6 λ p= Reλ) Number of eigenvalues Ice sheet domain 3 km) Figure 6.: The 7 smallest eigenvalues left) and their corresponding eigenvectors right) for p = top), p =.5 middle), and p = bottom), for an ice softness A = Pa 3 s and 4 m resolution. The eigenvalue with largest magnitude is λ =.558 when p =, λ =.696 when p =.5, λ =.783 when p =. In this section we showed that numerical steady-state modes obtained with a fixed-grid model are stable. The asymptotic analysis performed in sections showed that the steady-state solutions are highly nonlinear at 9
103 the ice divide and at the grounding line. We have not shown that the transient solution of our problem asymptotically behaves similarly to the steady-state solutions. If we assume that a similar expansion extends to the transient solution, sections show that the next coefficient in the linearization is of order ɛ + n or ɛ + p, not ɛ. Thus nonlinear perturbation residual could remain after a linear perturbation that are big enough to cross contaminate the linearization. A numerical method exists for finding the eigenvalue of a problem with the largest magnitude and its corresponding eigenvector. Such a results can be used as a confirmation of the stability of the system and help determine the contribution of nonlinear terms in the stability analysis. This method is the purpose of the next section A method for finding the fastest growing or slowest decaying eigenmode In this section we discuss a numerical method that can find the slowest decaying eigenmode which we will call the finite amplitude numerical method. The method consists in adding a small constant perturbation to the steady-state solution and letting the new solution evolve for a fixed time T long enough for the perturbations corresponding to smaller eigenmodes to have decayed significantly with respect to the slowest decaying mode. Once this first step is done, we continue the perturbation process by adding to the steady-state solution a scaled difference between the steady state and the solution we have obtained after the first perturbation. The new perturbed term should have a maximum amplitude corresponding to the same order of the initial perturbation. We re-iterate this latter step J times to obtain the largest eigenvalue and its corresponding eigenvector; it is typically enough to choose J =3 or 4. Let us denote H j) t) the perturbed ice thickness and H j) t) the ice perturbation of the process at time t and at the j-th iteration of the method. An algorithm that describes this process is 93
104 Algorithm 6.6) Step :choose a small ɛ and set H ) ) = ɛ, Step :For j = to J : end H j) ) = H + H j) ), run to time T, H j) T) = H j) T) H, compute γ j+) a = H j+) ) = γ j+) a ɛ max H j) T)), H j) T), step 3 : compute λ using least squares fit. This numerical approach has the benefit of confirming the numerical stability without requiring linearization of the system. If the steady state were unstable, the perturbation would exponentially grow rather than decay but the process would be the same. At step 3 of this algorithm, the largest eigenvalue λ is obtained by computing the slope of the maximum difference between the perturbed ice thickness and the steady-state solution over a time iteration using a least square fit. Then, we can compare this value with the one found semianalytically in section 6.. We perform tests using the finite amplitude numerical method for p =, p =.5 and p =. In view of the largest eigenvalues found in section 6. we choose T = a. We performed a set of simulation using ɛ = and found that this amplitude was too large in order to observe exponential decay. We then experimented using a smaller constant amplitude perturbation term ɛ = 3. Figure 6. shows the results of the numerical experiments for p = top), p =.5 middle), p = bottom). The comparison between the semi-analytical value obtained in section 6. and the one obtained using the least square fit of the maximum residual of the ice thickness over time show that the best agreement is when p = by approximately % with a difference of.3. For the two other values of p, the method differs by approximately 4% and the decay is, in both cases, faster when using the finite amplitude numerical method. There are several possible reasons to explain the discrepancies between 94
105 the two methods. Let us first mention that it is very unlikely that some residual of the second largest eigenvalue of the system is causing this discrepancy, since its value is λ 7 in all three cases which is approximately 4 times smaller than the largest eigenmode. Consequently, and considering λ T, at time T the mode associated with λ would be e 3 times smaller than the one associated to the largest eigenmode. After 4T, this ratio becomes e 3) 4 times smaller. It is possible that a constant perturbation of ɛ = 3 remains too large in some cases as when p =. In order to verify this assumption we perturbed the system by adding the eigenvector corresponding to the largest eigenvalue such that the biggest magnitude corresponded to 3. We applied the algorithm 6.6) with J = 4 and found similar numerical eigenvalue as when simply applying a constant perturbation when p =.5 and p =. However we found a better match when p = with the numerical eigenvalue matching the semi-analytical eigenvalue by approximately 4%. This means that the constant perturbation method could work when p = if we choose a smaller perturbation term. However with such a small perturbation the method becomes numerically restricted. Another plausible explanation of the discrepancies lies, once again, within the nonlinearity of the steady-state solutions as shown in sections 4.. and The next order of the linearization in section 6. should be of order ɛ. If we assume the asymptotic expansion is valid for transient solution, then at the ice divide, and for all p, we showed that the next coefficient is in fact of order ɛ n +. This nonlinearity and the one at the grounding line when p =.5 can diffuse over time and cross contaminate the results at high mode number. The finite amplitude numerical method shows to be difficult to apply to our problem. However it has clearly shown that adding small constant to our steady-state solution lead to a non-divergent solution over time, confirming the stability of the steady-state solution. So far we have only mentioned adding a negative perturbation to our system. We could have done the same analysis by adding a positive perturbation instead. However, the constant amplitude numerical method shows its limit in this situation due to numerical artifact. The numerical grid shows to be sticky and allows new solution to be numerically acceptable to be considered as steady state solution. This numerical feature has been observed in Pattyn et al. ) and will be observed and further explained in chapter Chapter summary In this chapter we discussed the stability of the steady-state solution of our ice-flow problem. To achieve this goal we first linearized the analytical steadystate solution by adding a small perturbation to the ice thickness and ice velocity. This resulted in a coupled system in perturbed ice thickness and ice velocity. The stability result was achieved by writing the perturbed ice thickness and velocity 95
106 as a product of a discrete function in space and a continuous exponential function in time. We could not find the eigenvalues of the system analytically and had to solve an eigenvalue problem numerically using numerical steady-state solution. We found that the largest eigenvalue for all values of p were negative meaning that the steady-state solutions were stable. Due to the lack of analytical solution, we tried to verify these results using a numerical method that did not involve calculus derivation, a method we called the finite amplitude numerical method. This method consists in adding a small constant perturbation to a steady-state solution and let it evolve over time. In theory, the perturbed solution should either grow expoentially or relax back to the steady-state solution. For long enough time, the decay should be exponential with a coefficient being close to the largest eigenvalue of the system. We found this method to be useful when applying a negative perturbation; all the experiments we performed relaxed back to the steady-state solution. However it was of limited use in our case as the nonlinearity of the system is most likely cross-contaminating the results at high mode number. Consequently, we did not obtain good agreement between the largest eigenvalues obtained semi-analytically and numerically. The differences were largest for p = and p =.5. When we applied a positive perturbation to the system, the solution did not relax back to the steady-state solution due to the numerical grid being sticky. This phenomenon will be observed in chapter 7. 96
107 p = p =.5 p = Comparison between semi-analytical and numerical fit to ice thickness perturbation, for ε = λannal = λnum = -.69 maxlogh-hs)) λannal = -.69 λnum = maxlogh-hs)) λannal = -.78 λnum = maxlogh-hs)) Time 3 a) Thickness residual comparison, ε = H Hs at time = ) H Hs at time = ) Ice sheet domain 3 km) Figure 6.: Both panels show numerical results for p = top), p =.5 middle), and p = bottom), an ice softness A = Pa 3 s and 4 m resolution. left) Comparison between the largest eigenvalue obtained semi-analytically in section 6. red) and the numerical eigenvalue obtained numerically green). The maximum residuals blue) were obtained after 4 iterations J=4) of the algorithm 6.6). The numerical eigenvalue is the least square fit of the maximum residual. The numerical eigenvalue corresponds to an approximately 4% steeper slope compared to the semi-analytical results. right) The Ice thickness residual at the fourth iteration at initial time blue) and final time red). The shape of the residual is conserved throughout the experiment. However, the shape differs from the eigenvector corresponding to λ in figure?? in the grounding line region. 97
108 CHAPTER 7 PARAMETER SENSITIVITY Using the numerical setup from section 5 we can now test our model and the impact of the basal stress parameterization on both ice-sheet behavior and model resolution. In this chapter we will perform three sets of experiments. The first set will consist in integrating the transient model until it reaches a steady state over a linear bedrock topography while varying 5 different parameters, one at a time: the ice softness A, the basal constant C, the bed slope b x, the wavelength of bedrock bumps λ max and the channel width W. The second set will be similar to the first set but varying only the ice softness and using a polynomial bedrock topography. The third set of experiments will consist in observing the transient model behavior over a linear bedrock topography forced by change in basal friction or ice shelf melting over human timescales 5 to years. These forcing mechanisms are more relevant to shorter-term changes in ice sheets such as those caused by anthropogenic climate change. The results described in this chapter are based on the MISMIP Marine Ice Sheet Model Intercomparison Project) experiments Pattyn et al., ), which are designed to study the transient behavior of marine ice-sheet models. Although the MISMIP experiments specifically vary the ice softness A, we will use the same setup while varying each of our parameters. Each set of experiments consist in a set of advance and retreat steps as in the MISMIP experiments. For a given parameter we obtain a steady ice-sheet profile. This profile is then used as the initial condition for the next experiment, which evolves to a new steady state with a new value of the parameter. For each parameter, the list of values is given such that the grounding-line position advances from one value to another. The retreat experiment is obtained by doing the advance experiment in reverse back to the original value, resulting in grounding-line retreat. Results have shown Pattyn et al., ) that fixed-grid models are more accurate during advance experiments compared to retreat experiments. A full description of the MISMIP experiments can be found at Models participating in the MISMIP intercomparison used the friction law of Schoof 7a), which is equivalent to equation 3.6). For our experiments we test two model configurations, non-glp and GLP, both of which include the fric- 98
109 GL difference km) without GLP with GLP p= p=.5 p=.5 p=.75 p= ^4 ^5 ^6 /A ^5 ^4 ^4 ^5 ^6 /A ^5 ^4 Figure 7.: The difference in grounding-line position between the Chebyshev and fixedgrid model at 5 m resolution during advance and retreat experiments over a linear bed for five values of p. We show here the example of varying the ice softness as a typical example of the differences. With the GLP, the error is always within 5 km and the error is a decreasing function of increasing p. Without the GLP the maximum error occurs during the retreat experiment for low values of p and can be of up to 3 km as shown here). Typically, this maximum occurs either at the beginning or the end of the experiments, when simulating for an extreme parameter value. Otherwise a typical range of error is about 5 km. The larger the value of p the smaller the error. tion law from equation 3.6), with effective pressure defined by equation 3.58). The GLP configuration includes the grounding-line parameterization discussed in section 5, while the non-glp configuration does not. We tested five values of the parameter p, equally spaced between zero and one, at seven resolutions between 3. and.5 km, each a factor of two smaller than the previous. Only the results with p = can be directly compared with the results of Pattyn et al. ). By changing p we are changing the physics, not just the numerics, of the problem. Aside from the modified friction law and associated parameterization of effective pressure, we used the standard MISMIP protocols except as specifically stated below. In these experiments, unless stated otherwise, the parameter values of our model are shown in table 3.. Typically, differences in grounding-line positions are used to compare the accuracy of ice-sheet model results Pattyn et al., ). This error metric is practical for us as well, since the grounding-line position is easily diagnosed from both our Chebyshev benchmark and fixed-grid codes. In realistic simulations, errors in grounding-line position are not as important as those in volume above flotation, which is directly related to the ice sheet s contribution to sea-level change. However, we found not shown) that the behavior of both metrics is qualitatively similar: larger errors in grounding-line position correspond to larger errors in volume above flotation. Gladstone et al. ) performed a similar sensitivity analysis using a similar flow line model as ours. The main difference lies in the choice of the basal friction law which they chose to be a linear function of ice velocity. Nevertheless, we will show that for varying a given parameter we obtain similar conclusions. Unless stated otherwise, we use the Chebyshev solution as the benchmark 99
110 in our experiment. If the Chebyshev solution has not converged for a given parameter, we use the fixed-grid solution at a resolution of 5 m as a benchmark solution. Figure 7. shows the difference in grounding-line position between both benchmark solutions during and advance and retreat experiment while varying the ice softness parameter; this figure is a typical representation of the difference between both benchmarks, which is used as an estimate of the error in the benchmarks. The difference is typically larger during a retreat experiment, at the beginning or the end of the experiment, without the GLP and for low values of p. With the GLP, the error is always within 5 km and the error decreases with increasing p. Without the GLP the maximum error occurs during the retreat experiment for low values of p and can be of up to 3 km. Typically, this maximum occurs either at the beginning or the end of the experiments, when simulating for an extreme parameter value. Otherwise a typical range of error is about 5 km. The larger the value of p the smaller the error. 7. Steady-state experiments over a linear bed rock topography The first bedrock topography we consider slopes linearly downward toward the ocean. Unless otherwise specified, we define the bedrock as in equation 4.8): b x) = 7.38x) m, 7.. Varying the ice softness A The experiments varying the ice softness are based on the MISMIP experiment Pattyn et al., ). We forced the ice sheet first to advance and then to retreat by varying the ice softness A, in analogy to MISMIP experiments and. To force ice-sheet advance, we incrementally decreased A through the values listed in table 7., allowing the ice sheet to evolve to steady state each time A was changed. Then, to force retreat, we increased A through the same values in reverse order, again evolving to steady state at each step. Schoof 7a,b) showed that the steady-state grounding-line position on a bed sloping monotonically downward in the direction of the ice flow is unique for a given ice softness. Figure 7. shows the grounding-line positions derived from the boundary-layer solution of Schoof 7a) and those from advanceand-retreat cycles using our Chebyshev and fixed-grid models with p = at.5 km resolution. The grounding-line position in our Chebyshev simulation differs from that of the boundary-layer solution by less than. km. As mentioned in section 5.., this difference appears to be mostly due to the fact that the boundary-layer model neglects longitudinal stresses in the bulk of the ice sheet.
111 Step no. A 6 s Pa 3 ) Table 7.: Values of the ice softness A used in the MISMIP experiment linear bed). These are the same values prescribed in Pattyn et al. ). The grounding-line position in the fixed-grid model advances relatively accurately, whether or not the GLP is applied, with errors of no more than. km. During the retreat experiment, the grounding-line position is overestimated as much as 6 km when the GLP is not used, but by no more than 5 km with the GLP included, showing its potential benefit. Figure 7.3 shows the differences between the grounding-line position from the fixed-grid and benchmark models in several configurations: both without left) and with right) the GLP, and at three different resolutions,.6 km top),.4 km middle) and. km bottom). We show differences rather than estimated errors the absolute value of the differences), because the sign of the difference is important in telling whether the grounding line is too far advanced or too far retreated. During the retreat phase of each experiment the right-hand side of each plot), the fixed-grid grounding line is always too advanced, whereas during the advance phase the left-hand side of each plot), the grounding line may be too advanced or too retreated depending on the values of p and A. For simulations with p <.5 with and without the GLP, the grounding-line position is not sufficiently advanced during the advance phase. For simulations with p >.5, the grounding-line position is always too advanced during the full experiment. The differences between experiments are most apparent during the retreat phase of each experiment right-hand side of each panel in figure 7.3). The experiments most similar to typical MISMIP fixed-grid results experiments without GLP and with p = show huge estimated errors during retreat on the order of hundreds of kilometers. The maximum error is approximately a factor of ten smaller in both the experiments with a GLP at p = red dots in the right-hand column) and the experiments without a GLP but with p =. Surprisingly, the combination of the GLP and effective-pressure parameterization with p = does not seem to produce smaller errors than p = without the GLP, showing diminished performance particularly during retreat. The GLP has essentially no impact on the advance phase left-hand side of each panel in figure 7.3), whereas
112 Grounding-line position for p = and Res =.5 km.8.7 analytic numeric without GLP numeric with GLP numeric Cheb analytic numeric without GLP numeric with GLP numeric Cheb.6 Position 3 km) /A 5 4 Figure 7.: The grounding-line position during advance and retreat experiments over a linear bed at 5 m resolution with p = from the boundary-layer solution by Schoof 7a) solid black), the Chebyshev benchmark model pluses), the fixed-grid model without the GLP dots) and the fixed-grid model with the GLP stars). The boundarylayer solution is in close agreement with the Chebyshev benchmark maximum difference of. km), as are the fixed-grid results with or without the GLP. Both fixed-grid models closely agree with the Chebyshev benchmark during advance maximum difference of. km). During retreat, the model with the GLP matches the benchmark maximum difference of 5 km) better than the model without the GLP maximum error of 6 km). the error during advance does tend to decrease as p increases. Figure 7.4 shows the maximum error over an advance-and-retreat cycle at a given value of p and resolution without the GLP left) and with the GLP right). The error map was obtained by bilinear interpolation from our 35 experiments. The figure shows that the maximum errors decrease approximately linearly with the grid-cell size for each value of p, either with or without the GLP. Linear convergence of grounding-line errors with resolution has been seen in other fixedgrid models Gladstone et al., a; Cornford et al., 3). Compared with resolution, the application of the GLP and larger values of the parameter p produce a much more dramatic reduction in maximum error. The black line in figure 7.4 shows a maximum error in grounding-line position of 3 km 5 % of the difference between the most advanced and most
113 Difference km) Res =. km Res =.4 km Res =.6 km Difference in grounding line position Without GLP p= p=.5 p=.5 p=.75 p= With GLP /A /A 5 4 Figure 7.3: The signed difference between the fixed-grid and benchmark grounding-line positions over a linear bed at.6 km top row),.4 km middle row) and. km bottom row) resolution for simulations without GLP left column) and with GLP right column). Each column contains both advance sub left column) and retreat sub right column) experiments. The dashed line at 5 km) in each panel shows the location of a transition in scale of the y-axis, which allows the same figure to present both very large and relatively small errors. Errors the magnitude of the differences) are approximately inversely proportional to the resolution and decrease with increasing p, strongly so without the GLP. The GLP reduces the most egregious errors during retreat occurring when p is small). retreated grounding-line positions of the benchmark). We chose this as a somewhat arbitrary) threshold below which we deem the error to be acceptable. In experiments without the GLP, smoother basal friction larger values of p) means that this error threshold is reached at a coarser resolution. This is not the case when the GLP is included. Instead we reach our threshold error at roughly the same resolution for all values of p. As it turns out, using the GLP is always beneficial when p.5 but becomes disadvantageous when p >.5. 3
114 3. Maximum Error in grounding line position Without GLP With GLP Resolution km) p p Figure 7.4: The maximum error over the advance and retreat experiments between the fixed-grid and benchmark grounding-line position over a linear bed for simulation without the GLP left column) and with the GLP right column). The errors are bilinear interpolations of our 35 experiments 5 values of p and 7 resolutions). The black line shows a contour of 3 km error 5 % of the difference between the most advanced and the most retreated positions of the benchmark), below which we deem the error to be sufficiently small. Note that each panel uses a different nonlinear color bar. Without the GLP, the maximum error decreases approximately linearly with resolution and superlinearly with p. With the GLP the maximum error decreases weakly with respect to p but approximately linearly with resolution. 6 5 C value sampling Schoof 7 C value C-value distribution Number of elements C value log) Figure 7.5: Distribution of the shear stress factor obtained by inversion using BISICLES on a log scale in Pam s) /3. The value used in Schoof 7a) is plotted in dashed red lines as a reference. 4
115 Step no. C 5 Pa m /3 s /3 ) Table 7.: Values of the shear stress factor C used in experiment linear bed). 7.. Varying the shear stress factor C In order to vary C in a meaningful way, we computed its likely range using a basal friction map Martin, 4) which was derived using BISICLES Cornford et al., 3). The basal friction map was obtained by using the ice thickness data from Fretwell et al. 3), the surface ice velocity from Rignot et al. ) and considering a linear basal friction law in the form τ b = βu. We then used equation 3.6), wrote it as linear function of velocity, and solved for the basal stress factor C using the β-value map. The value of p barely influenced the distribution of C. This does not come as a surprise since p only plays a role very near grounding lines and the basal friction zone is somewhat small compared to the length of the ice stream. The distribution of C is given in figure 7.5. Based on the histogram we perform a similar set of experiments as in section 7.. which includes advance and retreat experiments. The values of the shear stress factor for these experiments are given in table 7.. To force the ice sheet advance, we incrementally increase the value of C. The ice sheet retreats while decreasing the value of C. It is worth mentioning that the sample of C-values was chosen to be representative of the distribution shown in figure 7.5, spanning a range varying by orders of magnitude between the lowest and the highest values of C. However, the largest value of C in table 7. produces an ice sheet profile with an ice thickness of 8 km or higher which is not realistic considering Antarctica as of today. This thick ice occurs because C is not a constant in reality but depends on space as well. Figures 7.6, 7.7 and 7.8 are the same as figures 7., 7.3 and 7.4 respectively but for varying C. The inferences we established when varying the ice softness parameter A are similar to when varying C. Figure 7.6 shows that the groundingline position in our Chebyshev simulation differs from that of the boundary-layer 5
116 Grounding line position for p= and Res =.5 km.5 analytic analytic numeric without GLP) numeric without GLP) numeric with GLP) numeric with GLP) numeric Cheb) numeric Cheb).4 GL position 3 km) C Pams - ) /3 ) Figure 7.6: The same as figure 7., but varying the shear stress factor C. The boundarylayer solution is in close agreement with the Chebyshev benchmark maximum difference of.8 km), as are the fixed-grid results with or without the GLP. Both fixed-grid models closely agree with the Chebyshev benchmark during advance maximum difference of.5 km). During retreat, the model with the GLP matches the benchmark maximum difference of 6 km) better than the model without the GLP maximum error of 3 km). solution by less than.7 km. The grounding-line position in the fixed-grid model advances relatively accurately, whether or not the GLP is applied, with errors of no more than.5 km. During the retreat experiment, the grounding-line position is overestimated as much as 3 km when the GLP is not used, but by no more than 6 km with the GLP included, showing, again, its potential benefit. Figure 7.7 shows increasing errors with increasing C for all p-values. During advance simulation, the grounding line is always too advanced when p >.5 and too retreated otherwise. During the retreat simulation, the grounding line is always too advanced. Without the GLP the maximum error always occurs for p = during the retreat experiment for large value of C. With the GLP, the largest error occurs during the retreat experiment as well but mainly when p =.5 at coarse resolution and p = at high resolution. We observed a peculiarity during the retreat experiments: by decreasing C the grounding line advance first before retreating. This phenomenon possibly increases the hysteretic behavior of the solution. We will explain this further in the transient simulation section. 6
117 Difference km) Res =.4 km Res =.6 km Res =. km p= p=.5 p=.5 p=.75 p= Without GLP Difference in grounding lnie position C C 3-3 With GLP 7 6 Figure 7.7: As in figure 7.3 but varying the basal constant C. Errors the magnitude of the differences) are approximately inversely proportional to the resolution and decrease with increasing p, strongly so without the GLP. The GLP reduces the most egregious errors during retreat occurring when p is small). We observe a peculiarity during the retreat experiment though. The first retreating step, when p <, with or without the GLP, shows a grounding line position difference always larger compared to the difference of the last advanced step. This feature has a physical explanation that will be observed and explained in section 7.3. Figure 7.8 shows that the maximum errors decrease approximately linearly with the grid-cell size for each value of p, either with or without the GLP. This result was also observed in Gladstone et al. ) for the specific case p =. The variation in shear stress factor shows the benefit of the parameterization. The maximum error is a strong function of p without the GLP, meaning that the 3 km 7
118 3. Maximum Error in grounding line position Without GLP 3. With GLP Resolution km) p p Figure 7.8: As in figure 7.4, but varying the shear stress factor. Note that each panel uses the same nonlinear color bar. Without the GLP, the maximum error decreases approximately linearly with resolution and superlinearly with p. With the GLP the maximum error decreases weakly with respect to p but approximately linearly with resolution. threshold is reached at coarser resolution for larger values of p, and a weak function of p with the GLP. Compared with resolution, the application of the GLP and/or larger values of the parameter p produce a much more dramatic reduction in maximum errors. The maximum error in these experiments are larger than when varying A. These large errors are mainly associated with the large values of C. In a more realistic scenario, high values of C only occur in part of the ice sheet with very slow moving ice and bed topography above sea level. If we only consider constant values of C that results in a physically valid ice sheet, an ice sheet with a maximum ice thickness of 5 km, we obtain similar results as in section 7.. both qualitatively and quantitatively: without the GLP the error is a strong function of resolution and p; the coarsest resolution that results in a 3 km error is m when p = and. km when p =. With the GLP, the error is a weak function of p but a stronger function of resolution; a 3 km error is reached at a resolution of 8 m when p = and. km when p =. In these experiments we have not allowed C to vary with space. We have chosen not to do this as it would complicate our analysis substantially since basal stress already varies spatially with u and H. We would also have to consider different functions for C with different limits at the grounding line depending on its smoothness) which effect could compete with the ocean pressure parameterization and complicate the analysis of the impact of C or p on the system. However, functions for C could potentially be obtained by inversion given a specific form of the basal sliding law. Such an analysis is beyond the scope of this work and is left for future research. 8
119 7..3 Varying the bed slope b x Step no. b x m/km) Table 7.3: Values of the bedrock slope used in experiment linear bed). In these experiments we are varying the bed slope b x by keeping the location where b x) = constant and we rewrite equation 4.8) as: b x) =b x.9 x) m, 7.) where b x is the slope of the bedrock. The bed slope values for this experiment are given in table 7.3. The range of slopes in our sample varies by a factor of 3 between the shallowest and the steepest slope. The steepest slope we consider here is times steeper than in equation 4.8). Adding steeper values to the sample does not yield any extra information as the grounding-line position with the current steepest bed slope is very close to sea level where bx) = ). Shallower slopes will advance the grounding-line location seaward. Figure 7.9 is the same as figure 7. but for varying the bed slope topography b x. It shows that the grounding-line position in our Chebyshev simulation differs from that of the boundary-layer solution by less than. km. The grounding-line position in the fixed-grid model advances relatively accurately compared to the Chebyshev solution with an error of about. km during advance and retreats with a maximum error of about 4 km, without the GLP. When the GLP is applied the maximum error during advance and retreat is the same, about 6.3 km. Figure 7. is the same as figure 7.4 but for varying b x and the observations are similar: without the GLP, the resolution needed to accurately model grounding-line migration is a strong function of p. The smoother the basal friction law, the coarser the resolution needed. In order to obtain an error of less than 3 km, a resolution of m is needed when p = and.4 km when p =. Without the GLP, the error is a weak function of p: in order to obtain an error within 3 km, a resolution of 8 m is needed when p = and. km when 9
120 Grounding line position for p = and Res =.5 km.5.4 analytic numeric without GLP numeric with GLP numeric Cheb analytic numeric without GLP numeric with GLP numeric cheb.3 Position 3 km) b x m/km) Figure 7.9: The same as figure 7., but varying the bed slope b x. The boundary-layer solution is in close agreement with the Chebyshev benchmark maximum difference of. km), as are the fixed-grid results with or without the GLP. During advance, the model without the GLP matches the benchmark maximum difference of. km) better than the model with the GLP maximum error of 6.3 km). During retreat, the model with the GLP matches the benchmark maximum difference of 6.3 km) better than the model without the GLP maximum error of 4 km). p =. In both panels, at p =.5 and at high resolution, one value of the maximum error breaks the monotonicity with respect to resolution that we should theoretically observe. This is an artifact of using the maximum error which created a noisier set of values compared to the L-norm for example). We could have chosen a sample with twice as many values to create a better error sampling and gotten rid of this plotting artifact. This would not change the conclusion we can infer from these results. With or without the GLP, the maximum error decreases somewhat linearly with resolution. Without the GLP and for a given resolution, the maximum error always occurs during the first retreat experiment, for a bed slope value b x =.38 m/km and for p =. The same observations holds true with the GLP but for p =.5 and at resolution coarser than m. At higher resolution, the
121 3. Maximum Error in grounding line position Without GLP 3. With GLP Resolution km) p p Figure 7.: The same as figure 7.4, but varying the bed slope topography. Note that each panel uses the same nonlinear color bar. Without the GLP, the maximum error decreases approximately linearly with resolution and superlinearly with p. With the GLP the maximum error decreases weakly with respect to p but approximately linearly with resolution. maximum error occurs during the advance experiment at the same bed slope but for p =.5 but the error is no greater than km. We did not explicitly display these results. Figure 7. shows the grounding line position for all value of p without the GLP and at 5 m resolution. The grounding line position is a strong function of decreasing bed slope. At very steep bed slope topography, the value of p has a weak impact on the grounding line location. These observations are similar when the GLP is applied and therefore are not shown. We observe that the steeper the gradient, the closer the grounding line location to sea level. In fact, when we chose a steeper bed gradient, our model could not find a solution with any floating ice. These results suggest that basal physics have little influence on the model on steep bedrock. These observations are in agreement with what we found in section 4..: our basal parameterization does not impact the ice flow solution when the ice is grounded above sea level and the basal stress τ b asymptotes to equation 3.6). Further, this result suggests that the knowledge of bed gradient at the grounding line could act as a constraint on model resolution requirement, allowing the use of a coarse resolution over steeper topography. Over a constant, steep bedrock topography, the contribution to sea level change of an ice sheet is small. In fact, compared to a shallower bed slope, over a steep bedrock the driving stress is larger and therefore leads to faster flow. This will results in thinner ice which in turns creates a grounding line retreat. Therefore, a small variation in grounding-line position implies a large variation in ice thickness but a small variation of ice flux because of the continuity equation, thus a small change in sea level rise.
122 Position 3 km) Grounding line position for all p at Res =.5 km p= p=.5 p=.5 p=.75 p= b x m/km) Figure 7.: The grounding line position for all values of p without the GLP and at 5 m resolution. The grounding line position is a strong function of p for decreasing bed slopes. The value of p matters less as the bed steepens Varying the wavelength of bedrock bumps λ max In this section we will show how bedrock properties at sub-grid scale, which are represented by κ in equation 3.6), impact grounding-line motion. We choose to vary λ max to perform this analysis keeping in mind that it would be equivalent to vary m max, A b or κ: an increase/decrease in λ max is equivalent to an increase/decrease in A b and a decrease/increase in m max or κ. To the best of our knowledge, there exist no data to constrain κ and therefore λ max. Thus we choose to vary λ max by more than three orders of magnitude and follow the experimental setup as in section 7... The values for this experiment are given in table 7.4. The results are not qualitatively different when using other value of ice softness A and. In this set of experiments we will simply use one specific ice softness A = Pa 3 s. The grounding line position advances when λ max increases. Away from the grounding line the basal stress takes the form of equation 3.6) and is independent of λ max. Near the grounding line the basal stress is expressed as the
123 Step no. λ max m) Table 7.4: Values of the wavelength of bedrock bumps used in section Coulomb friction limit, equation 3.63). An increase in λ max there is equivalent to an increase of the basal shear stress factor C which in turn induces a groundingline position advance as we experienced in section 7... Unlike the other parameters we have investigated in the previous sections, we cannot derive a semi-analytic solution for λ max as a function of the groundingline position. When p = the basal stress remains in the asymptotic limit given by equation 3.6) and the momentum equation remains independent of λ max. Instead, we use our Chebyshev solution as a benchmark in this experiment. Figure 7. shows the grounding line position from the fixed-grid models in several configuration: both without left column) and with right column) GLP, and at three different resolutions,.6 km top),.4 km middle) and. km bottom). The grounding line position is a strong function of the wavelength of bedrock bumps for large p-values but not for low p-values regardless of resolution, with or without the GLP. The results also show that the grounding line position advances as λ max increases for all values of p > and converges to the grounding-line position with p =. When p =, the grounding line advances by km over the full experiment meaning that varying λ max by three orders of magnitude has a negligible impact on the asymptotic state of the basal shear stress. Figure 7.3 shows the length of the friction transition zone using the Chebyshev solution. Its size decreases with increasing values of λ max and asymptotes to zero. When p = the friction transition zone length remains invariant over the range of λ max chosen in this study. For large values of λ max and for large values of p, the friction transition zone shrinks and eventually reaches zero. Consequently the lubrication in basal sliding will not impact the basal sliding anymore and the 3
124 .4 Difference in grounding line transition Without GLP With GLP.4 Res =.6 km p= p=.5 p=.5 p=.75 p= Difference km) Res =.4 km Res =. km λ log) λ log) Figure 7.: The fixed-grid grounding line positions over a linear bed at.6 km top row),.4 km middle row) and. km bottom row) resolution for simulations without GLP left column) and with GLP right column). Each column contains both advance sub left column) and retreat sub right column) experiments. The grounding line position is a stronger function of the wavelength of bedrock bumps for large p-values but not for low p-values regardless of resolution, with or without the GLP. transition between grounded and floating ice will have a discontinuity just as for the case when p =. This is why the grounding-line position when p = asymptotes to the one when p = in figure 7.. Figure 7.4 is the same as figure 7.4 but for varying λ max. We are still observing linear convergence with resolution in both cases, with and without the GLP. However, we do not observe a decreasing error as a function of p and the smallest errors are in both cases when p =. This results contradicts our assumption that a smooth transition in basal stress is a desirable feature in an 4
125 4 3 Friction transition zone length km) p= p=.5 p=.5 p=.75 p= λ log) Figure 7.3: The friction transition zone length using a linear bed, the Chebyshev solution, and an ice softness A = The Chebyshev solution resolves the friction transition zone when p = and low values of λ max. The friction transition zone is a decreasing function of increasing λ max for all values of p. Resolution km) Maximum Error in grounding line position Without GLP 3. With GLP p p Figure 7.4: The same as figure 7.4, but varying the wavelength of bedrock bumps. Note that each panel uses the same nonlinear color bar. Without the GLP, the maximum error decreases approximately linearly with resolution and superlinearly with p > ; the error is the smallest when p =. With the GLP the maximum error decreases approximately linearly with resolution but increases as a function of p. 5
126 ice sheet model. However, figure 7. shows little grounding line motion when p =. The benchmark of 3 km chosen at the beginning of this chapter represents an error of 5% of grounding-line motion while the grounding line moved over 6 km within a set of experiments. We claim that the small error we observe in this case is due to a lack of grounding-line dynamic which has not been observed with any parameters so far. In order to validate the assumption about the grounding line dynamic importance in the error analysis, we perform another set of experiments that will induce grounding line motion for all values of p. For the advance experiment, we chose an ice-sheet profile with a grounding-line position located at 9 km. We use this profile as an initial state and run the experiment for all the different values of λ max separately. The retreat experiment is performed in a similar fashion but choosing an initial ice sheet profile with a grounding-line location at 4 km. We only ran this experiment for p = and p = since this was sufficient to validate our hypothesis. 3. MaximumError in grounding line position Without GLP 3. With GLP 5 Resolution km) p p Figure 7.5: The same as figure 7.4, but for the second experiment. We only present results for the values of p = and p =. Note that each panel uses the same nonlinear color bar. With this new experiment, the grounding line has the possibility to move over a distance of 5 km from its initial position to its steady state. With such a range of motion, the error plot resemble the one of figure 7.4. On the left panel the contour line looks linear by part, but this is a plotting artifact from the bilinear interpolation. Figure 7.5 is the same as figure 7.4 but for the second experiment of varying λ max and showing results only for p = and p =. With a grounding-line motion of 5 km the maximum error results are similar to those when varying A and the results shown in figure 7.5 resemble the one shown in Figure 7.4. In this second set of experiments, the maximum error always occurs during the retreat experiment with or without the GLP and for p =. Also, the grounding-line location remains constant as a function of λ max when p = confirming the lack of change in the friction transition zone in this case. Again, these results are stated but not displayed. 6
127 This experiments points out the importance of grounding-line dynamics when testing an ice sheet model. If the error in grounding-line position is used as a validation metric, a threshold has to be a function of the total grounding-line migration Varying the Channel width W So far we have only considered an ice stream flowing within a very wide channel which allowed us to neglect lateral drag. Realistic ice streams are more constrained and the effect of lateral drag, the friction of the ice against the side wall of the bed, is often non-negligible. In this set of experiments we suppose our ice stream to be embedded within a channel of half width W. For simplicity in section 3.3 we omitted ice motion in the y-direction. In this section, we will derive and apply a parameterization of lateral drag in our model. Let us first state that we still assume no velocity in the y-direction, meaning v =. If v was part of our unknowns it would be more natural to solve the two-dimensional problem. We also continue to assume that vertical shear is negligible. We will further assume the following: the ice thickness and ice velocity are symmetric with respect to the axis y = ; zero velocity at the side wall, u x, ±W) = ; W is constant in x; the ice thickness does not vary significantly in the y direction such that H = Hx); bedrock topography is independent of y within the channel meaning b = bx) thus, the surface s = H b is also a function of x only). In order to include lateral drag in our model we need to go back to the Blatter-Pattyn equations 3.8) and 3.9). The next step is to integrate both equations vertically as it was done in section 3.3.)) and then average them with respect to y over the width of the channel. Applying these two steps along with our assumptions to equation 3.9) leads to each terms being equal to zero due to symmetry. We are now left with applying both steps to equation 3.8). We begin by integrating vertically from the bed b of the ice to its surface s as in section 3.3.) it is understood that the velocities and stresses are vertically integrated and we will not use the overbar notation at this stage of the derivation which leads to s b τ xx x dz + s b τ xy y dz + s b τ xz z dz = s b ρ i g s dz. 7.) x Using Leibnitz rule for integrals on the first two left hand side terms, and that both s and b are only functions of x and y, equation 7.) can be rewritten as: s τ xx dz + s τ xy dz τ x b y b = ρ i g s s b), 7.3) b x 7
128 where τ b = τ xx b) b x + τ xz b), 7.4) and τ xx s) = τ xy s) = τ xz s) =. 7.5) Since there is no variation along the y-direction in the bed slope topography, the expression of the basal sliding law remains unchanged compared to the one we obtained in section 3.3.). The integral terms in equation 7.3) can be rewritten as a product of ice thickness and depth-averaged value as x Hτ l) + y Hτ k) τ b + τ d =, 7.6) where we used the relation for the ice thickness H = s b and where τ l = τ xx, 7.7) τ k = τ xy, 7.8) τ d = ρ i gh s x. 7.9) In order to express the integrals of stresses in terms of the integrals of u and H in y we suppose a general separation of variables for the ice velocity ux, y) = Ux)Yy). Without this assumption we found it not possible to show, in general, how the two-dimensional model asymptotes to our one-dimensional model for very wide channels. This choice further satisfies the property that ice velocity at the center line of the channel is independent of the channel width as it is the case in our one-dimensional model. We define Y such that Y W) = Y W) = and W Yy)dy =. 7.) W W The boundary conditions satisfied by Y enforce no ice velocity at the side wall of the channel. Equation 7.) ensures that U x) is the channel-averaged value of u x, y). In what follows we will use the standard derivative notation of 8
129 a function of one variable: U du dx and Y dy dy. Under these assumptions, the y-averaged continuity equation 3.39) remains unchanged and we only need to derive the momentum equation. We will y-average each terms of equation 7.6) separately. The effective strain rate is then: ɛ e ɛ xx + ɛ yx. 7.) The effective viscosity is now: η = A n = A n = A n ) ɛ xx + ɛ yx n n, Y U + U n Y ) n, YU ) n n + U U ) Y Y ) ) n n. 7.) The y-averaged first term in equation 3.39) is then: W I W = [ H x W = [ 4H x W = x x Hτ l) dy, η u ] W x dy, ηy du ] x dy, W W W W H W A n U ) n W Y n W + U U ) Y Y ) ) n n dy. 7.3) Our goal is to show that the one-dimensional model we derived in section 3.3. is a limiting case of this model for infinitely wide channel. To simplify the analysis we make the change of variable y = y W in equation 7.3) and it becomes: I = H x A n U ) n Y n + ) U Y ) ) n n W U Y dy. 7.4) 9
130 If we now define the functional G β) as G β) Y n Y + β x) Y ) ) n n dy, 7.5) equation 7.4) becomes: I = [ HA n U ) )] n U G x W U. 7.6) We can easily rewrite the y-averaged expression of the second term in equation 7.6): I W W W Given equation 7.8), τ k x, ±W) = y Hτ k) dy, = H W [τ k x, W) τ k x, W)]. 7.7) [ η u y ] ±W and we need to express η ±W). We assumed u x, y) to be symmetric about y = and that u x, ±W) =. This means that the longitudinal strain rate at the walls ɛ xx ±W = u/ x ±W =, so that only the lateral strain rate contributes to η at the walls: η ±W) = A n = A n ɛ xy ±W) n n, [ ] u y ±W n n. 7.8) By symmetry of u and the assumption that u has a maximum at the center of the channel, [ u/ y] W = [ u/ y] W = u/ y W, and therefore η W) = η W). Equation 7.7) becomes I = H [[ η u ] [ η u ] W y W y = H ) W A n u n y, W W ],
131 = H W τ s, 7.9) where we denoted τ k x, W) = τ s x), and τ s = A n ) u n y. 7.) W The basal stress expression in equation 7.6) is similar to the one we derived in section 3.3.4, but the velocity now has a y-dependance. We will assume that the basal stress takes the same form as in section since, as we will show, it satisfies the one-dimensional limit of our model. We will denote τ b W W W τ bdy. If we define the functional F β) as F β) the width averaged basal stress can be written as β x) ) n dy, 7.) Y + β x) τ b = C N n ) NF. 7.) κ n κu The functional F is independent of W. When p =, we have shown that the basal stress expression yields to equation 3.6): τ b C u n u. In this case the basal stress leads to τ b = W CU n Y n dy, W W = CU n W Y n dy, W W = CU n G ). 7.3) ) When p > we need to consider equation 3.6): τ b = C u n Np) n n u. κ u +Np) n Since we assumed H and b to be functions of x only, N = N x). When κu N, equation 3.6) asymptotes to equation 3.6) and therefore equation 7.) asymptotes to equation 7.3). When κu N, equation 3.6) asymptotes to
132 equation 3.63): τ b C Np) u. Its width average expression becomes: κ n u τ b = W W W C Ndy, κ n = C κ n N. 7.4) In the same asymptotic limit, equation 7.) asymptotes to τ b = C F ) =, equation 7.) then asymptotes to equation 7.4). κ n NF ). Since In both asymptotic limits the basal stress remains independent of the channel width. Further, we have shown that the asymptotic limit in two dimensions satisfy our asymptotic limits in one dimension apart from a constant. If W, G ) is a constant and it can be incorporated in the value of C. In between the two asymptotic limit the value of τ b remains somewhat ad-hoc. This is not of great concern as our one-dimensional expression of τ b was built based on asymptotic limit as well. Finally, the last term to average in equation 7.6) is driving stress. However, with our assumption, this term in independent of y and remains unchanged from its non-integrated form. After averaging over the channel width, equation 7.6) becomes: [ HA n U ) )] n U G x W U H W τ s x) C N n ) NF + τ κ n κu d =. 7.5) For very wide channels, the lateral stress term goes to zero and equation 7.5) becomes similar to equation 3.44) apart from constants of integration which depend on the value of G ). Equation 7.5) represents the most general form of the vertically integrated and y-averaged one-dimensional equation. At this point we still cannot express equation 7.) or evaluate both functionals G or F without further assumptions. We could go further by assuming a specific expression for u x, y). From here on, let us assume that u x, y) has the functional form: [ u x, y) = u x) y W q ], 7.6) where q is a parameter and u x) is a function that satisfies the requirement,
133 using equation 7.), U x) = W u x, y) dy. W W Note that expression 7.6) is somewhat arbitrary but we will show it satisfies the assumption that the lateral strain rate varies linearly as a function of y across the channel width Van der Veen 3), ch.4). Also, this form of velocity satisfies the requirement of u being maximal at the centerline Adhikari and Marshall, ). Further, it is worth mentioning that our choice of u satisfies the boundary conditions u x, ±W) = u/ x ±W = under the condition that q is even. Given equation 7.6), the width average velocity is then U x) = W W = u x) = u x) = u x) W [ u x) y W y q dy, q ] dy, y q dy + ] [ [y y q+ + q + y ) ) q dy y + y ) q+ q + = q q + u x). 7.7) Using equations 7.6) and 7.7) we can derive an expression for Y: Y y) = q + q [ y W ],, q ]. 7.8) The expression of Y in equation 7.8) satisfies relation 7.). The derivative of u x, y) with respect to y is then u y = q u x) y W W q sgn y), 3
134 where sgn x) is the sign function. Thus u y = q u x) W W. It follows from equations 7.) and 7.7) that ) qu x) n τ s =, AW ) q + )U x) n =. 7.9) AW If we choose q = n + where n = 3 in our case), we obtain a similar expression than Van der Veen 3). With this value of q the lateral drag in equation 7.5) is then: τ W = H W τ s x), ) n + )U x) n. 7.3) = H W AW Step no. W 4 m) Table 7.5: Values of the channel widths used in experiment linear bed). We have derived a model which includes lateral drag over the whole icesheet domain and can now determine the effect of the channel width on groundingline migration. The values of the channel widths for this experiments are given in table 7.5. The experiment using the widest channel should result in grounding- 4
135 line positions that are similar to those from the flowline model that does not include any lateral drag. 8 Width sampling km) 7 6 Number of elements Channel width km) Figure 7.6: Distribution of channel width for Antarctic ice streams in km. This sampled was done given a map of Antarctica where ice streams could be identified. The channel-width values were chosen by sampling ice stream width in Antarctica, figure 7.6). For this purpose we used a velocity map of 8 km resolution on which ice streams could be identified courtesy of Dan Martin). The boundaries of a channel can be identified by shear margins with strong velocity gradients, resulting from a sudden drop from large velocities in the stream to nearly zero velocity on either side. Using Matlab, we selected two points representing the extremities of a perpendicular cross section to the ice flow; using the coordinate of these two points we then obtained the width of the channel at that location. We sampled values at several locations along a given ice stream: at the grounding line, the ice stream margin, upstream and downstream of tributary inflows into bigger ice river bed. Our Chebyshev benchmark code did not converge for these simulations. Instead we are using our fixed-grid model with a 5 m resolution as benchmark for these experiments. Figure 7.7 shows the grounding line position for all values of p without the GLP and at 5 m resolution. The grounding line position appears to be a strong function of decreasing channel width. This figure also shows that the grounding line position converges to a value independent of p for narrow chan- 5
136 ..9 Grounding line position for all p at Res =.5 km p= p=.5 p=.5 p=.75 p=.8 Position 3 km) W 4 km) Figure 7.7: The grounding line position for all values of p without the GLP and at 5 m resolution when varying W. The grounding line position is a stronger function of p as the channel widens. For small width, the grounding-line position becomes independent of p. nels. These observations are similar with the GLP and therefore not shown. In the ice sheet, the lateral stress is a resistive force, along with the basal stress, and balances the driving stress while the longitudinal stress remains negligible. In the ice shelf, the resistive stress remains via lateral drag as the basal stress no longer resists the ice flow. The lateral drag remains more dominant than the longitudinal stress and the force balance happens mostly between the lateral drag and the driving stress. The lateral drag becomes stronger for a narrower channel. Consequently, ice has time to accumulate, leading to thickening and grounding line advance. The lubrication at the bed is not strong enough to induce a grounding line signal for narrow channels. This result suggests that the knowledge of channel width at the grounding line could act as a constraint on model resolution requirement, allowing the use of coarse resolution for narrower channels. Figure 7.8 is the same as figure 7.4 but varying W, and shows similar observations: without the GLP, the resolution needed to accurately model groundingline migration is a strong function of p. The required resolution is coarser as the basal friction law is smoother. The 3 km error threshold is obtained at a reso- 6
137 3. Maximum Error in grounding line position Without GLP With GLP Resolution km) p p Figure 7.8: The same as figure 7.4, but varying the channel width. Note that each panel uses the same nonlinear color bar. Without the GLP, the maximum error decreases approximately linearly with resolution and superlinearly with p. With the GLP the maximum error decreases weakly with respect to p but approximately linearly with resolution. lution of 5 m resolution when p = and.8 km when p =. Without the GLP, the error is a weaker function of p and a resolution of about 8 m is needed when p = as opposed to.6 km when p =. Typically the maximum error happens for wide channels. In our experiments the widest channel is large enough to reproduce results close to our model without lateral drag. Thus figure 7.8 really reflects the errors for wide channels and does not add any comprehensiveness on results for narrower channels. 7. Steady-state experiments over a polynomial bed rock topography In this section we performed a series of grounding-line advance-and-retreat cycles using our lateral drag stress-free model and with bedrock topography shown in figure 7.9 and given by the following polynomial function Schoof, 7a): bx) = [ x x x 6] m. 7.3) These experiments are analogous to MISMIP experiment 3 Pattyn et al., ), but with our modified friction law and effective-pressure parameterization and with more values of the ice softness A. The bed topography has three distinct 7
138 Polynomial bed rock topography Elevation km).5.5 Region Region Region Horizontal position 3 km) Figure 7.9: The polynomial bed used in the second set of MISMIP experiments. The bed consists in three distinct regions: regions and slope downward toward the ocean and, in absence of lateral drag, a stable grounding-line position is possible. Region slope upward toward the ocean and is unstable and the theory predicts that no grounding-line position can be found there. regions. Region slopes downward from the ice divide toward a local minimum, region slopes upward, and region 3 slopes downward again, forming a steep continental-shelf break. In this experimental setup we only varied the ice softness A as varying other parameters does not lead to new results or comprehension of the model. Theoretical arguments Weertman, 974; Schoof, 7a) suggest that, in the absence of buttressing, stable steady-state grounding-line positions can be found in regions and 3 with downward-sloping beds) but not in region with an upward-sloping bed). Our numerical results are consistent with theory. We found that steady-state grounding-line positions do not exist on upward-sloping beds in region but that new steady state solutions are found in region 3 when the grounding line has been forced to advance through region. Starting with a grounding line in region, we varied the ice softness A to induce grounding-line motion. In his boundary layer model, Schoof 7a) showed that the grounding-line position exhibits hysteresis: The grounding line jumps across the unstable region at significantly smaller values of A during the advance phase than during the retreat phase. When p.5 we varied A between 3 5 and.5 6 s Pa 3, the bounds of MISMIP experiment 3, over nineteen values approximately equally spaced in log space. For values of p >.5, our experiment did not show the full hysteresis behavior within this range of A. In fact, for a given ice softness, lower basal friction i.e., larger p) tends to move the grounding line inland, as shown in Fig, 3., so that the grounding line never reaches the unstable region for larger values of p. In order to obtain hysteresis we extended the range of A to.5 7 s Pa 3 and varied A over 34 values approximately equally spaced in log space. For all experiments, we used more values of A than MISMIP in order to obtain a better statistical sampling of the 8
139 error within each experiment and to reduce the influence of particularly large errors that occur as the grounding line approaches the unstable region. The largest errors occur when the fixed-grid solution is in region while the benchmark is in region 3 or vice versa. Grounding-line position for p = and Res =.5 km.4.3. analytic numeric without GLP numeric with GLP numeric Cheb analytic numeric without GLP numeric with GLP numeric Cheb Position 3 km) /A 5 Figure 7.: The same as figure 7. but with the polynomial bed shown in figure 3.a. The boundary-layer solution closely agrees with Chebyshev results maximum difference of.4 km). Fixed-grid results both with and without the GLP closely agree with the Chebyshev benchmark during advance maximum difference of km without the GLP and.6 km with the GLP). During retreat, the model with GLP is the better match to the benchmark maximum difference of 4 km). Without the GLP, the fixed-grid grounding-line position matches the benchmark reasonably well when both solutions are on the same side of the unstable region maximum difference of 38 km) but not in the vicinity of the local maximum where the solutions are on different side of the unstable region, maximum difference of 57 km). When p =, the boundary-layer solution, model A of Schoof 7a), again 9
140 provides a good approximation of our equations of motion. Figure 7. shows the grounding-line positions derived from the boundary-layer solution together with the positions from experiments using our Chebyshev and fixed-grid models with p =. The grounding line of the boundary-layer solution differs from that in our Chebyshev benchmark simulations by less than.4 km, similar to the linear bed experiments. The fixed-grid model at.5 km resolution performs well during the advance phase both with and without the GLP; the grounding line is always in the same region either or 3) as the benchmark solution. The maximum error is about.9 km without the GLP and about.6 km with the GLP. However, without the GLP, the model does not perform as well during the retreat phase. The error in the fixed-grid solution is as large as 38 km when the fixed-grid and benchmark grounding lines are in the same region. The fixed-grid model with the GLP follows the Chebyshev solution more accurately, with a maximum error of 4 km and grounding-line positions that always lie in the same region as the benchmark. During the retreat experiment, the model configuration without GLP shows a grounding-line position located in the wrong region for two values of A, leading to an error of about 57 km. Although this behavior is not seen when the GLP is included, we would likely see similar discrepancies between this configuration and the benchmark if we had sampled an even larger number of A values. In other words, the GLP would appear to reduce the likelihood of these large errors but it is unlikely that they have been eliminated entirely. The polynomial bed in these experiments represents a more realistic topography than the linear bed. Local maxima and minima, absent in the linear topography, have a significant impact on both model dynamics and numerical errors. Figure 7. shows the root-mean-square RMS) error between the fixedgrid and benchmark grounding-line position for simulation without the GLP left plot) and with the GLP right plot). The error map was obtained by bilinear interpolation from our 35 experiments. Here, we used the RMS error instead of the maximum error because the latter is typically dominated by cases in which the benchmark and fixed-grid grounding lines lie in different regions and is highly sensitive to the particular choice of A values. The gray area in each panel indicates experiments which are not reversible the fixed-grid grounding line position fails to retreat back to region at the end of the retreat experiment). The figure shows that, without the GLP, the RMS error decreases linearly with resolution and rapidly with increasing p. When the GLP is included, the RMS error decreases linearly with resolution, while increasing p has a less dramatic impact. As was the case for the linear bed experiments, including the GLP improves the error for small values but not necessarily for large values of p. For small p, including the GLP improves the ability of the model to retreat past the unstable region, as shown by the reduced grey area on the right-hand side of figure 7.. All experiments with the GLP and a resolution of km or higher show reversibility, whereas a resolution of between and m is required without GLP when p =. Similarly to the previous sections, we use a threshold of 3 km as the maximum allowable RMS error, indicated by the black contour line in figure 7.. Our 3
141 3. RMS Error in grounding line position Without GLP With GLP Resolution km) p p Figure 7.: The root-mean-square RMS) error between the fixed-grid and benchmark grounding-line position over a polynomial bed for simulation without the GLP left column) and with the GLP right column). The errors are bilinear interpolations of our 35 experiments. The gray area shows experiments that were not reversible i.e. for which the fixed-grid grounding line position did not retreat from region 3 to region during the retreat experiment). The black line shows a contour of 3 km error, below which the error is deemed acceptable, as in figure 7.4. The RMS error without the GLP is approximately inversely proportional to the resolution and decreases strongly with increasing p. With the GLP, the RMS error is inversely proportional to the resolution and decreases, though less steeply, with increasing p results show that even with the GLP, resolution as high as m is required in locations with large effective pressure near the grounding line p ). On the other hand, a resolution of km is sufficient where the effective pressure is low p ). In general, the results from the linear section remain valid when using a polynomial bed: When p.5, using the GLP leads to smaller RMS errors and better reversibility. However, when p >.5, using a GLP is disadvantageous. Figure 7. shows the error in grounding-line position as a function of the benchmark grounding-line position during the retreat phase. The figure makes clear that the error increases as the grounding line approaches the unstable region. These results suggest that the fixed-grid model can capture hysteresis with increasing fidelity as p increases and to a lesser extent) as resolution increases, and that errors nearly always decrease at a given value of x g as p increases. Figure 7. also suggests that errors may be a strong function of bedrock slope. The largest errors occur near the local maximum in bed elevation at around x =.5 3 km, and decrease sharply as the bedrock steepens further into region 3. This behavior is to be expected as the grounding line approaches a bifur- 3
142 Error estimate km) Res =. km Res =.4 km Res =.6 km Error estimate in grounding line position Without GLP p= p=.5 p=.5 p=.75 p= With GLP GL position 3 km) GL position 3 km) Figure 7.: The same as figure 7.3, but showing only the retreat experiment over the polynomial bed and with benchmark grounding-line position instead of A along the x- axis. The dashed line at 4 km) in each panel shows the location of a transition in scale of the y-axis used to show large errors without losing the differences between smaller errors. The error in grounding-line position is consistently lower at a given groundingline position when p = than for smaller values of p. The figure shows that errors tend to increase as the grounding line approaches the unstable region empty gap in each figure). cation point. No stable steady-state solution will exist near that maximum if A is decreased further; small changes in A will lead to large changes in groundingline position. Similar inverse correlation between bed slope and error can be seen 3
143 in region, though the bedrock steepens more gradually in this region. These observations are in agreement with the results we observed in section 7..3: the largest error occurred where the bedrock is flatter while the smallest error occurred where the bedrock is the steepest. 7.3 Transient Experiment over a linear bed rock topography So far we have investigated the model sensitivity by running our model to steady state at each step in an experiment. Typically steady-state runs require thousands to tens of thousands of years to come to steady state for each step. On the other hand, typical timescales for climate projections are on the order of a century or two. The transient experiments are meant to investigate whether the dependence of errors on model parameters is both qualitatively and quantitatively similar over century timescales as it is for steady-state simulations. For this set of experiments, we will evaluate the impact of two parameters, the basal friction constant C and the melt rate underneath an ice shelf. For each of these experiments we start from a steady state ice sheet. At time we change a parameter and advance the model forward in time over 5 years Varying the shear stress factor C In section 7.. we studied the effect of increasing and decreasing the shear stress factor on steady-state solutions. These experiments did not look at glacier behavior such as the monotonicity of the grounding line response to the perturbation, the time the system needs to react to the perturbation, etc. In these experiments, we will give more insights into these behaviors. Step no. C 6 Pa m /3 s /3 ) a b Table 7.6: Values of the shear stress factor C used in the transient experiments. We consider two sets of two experiments with values of C given in table 7.6. The first set begins with a steady-state profile of an ice sheet with a shear stress factor given in a. At time, the shear stress factor is then switched to the value of C in b and the model is ran forward in time. The second experiment is similar but begins with the C-value in b which is switched to the C-value in a. We denotes these two experiments Experiment a and Experiment b 33
144 respectively. The second set of experiments is similar but using the values of C in row and called Experiment a and Experiment b. These experiments are performed without lateral drag and we use the Chebyshev solution as the benchmark. The values of C used in these experiments are somewhat arbitrary. The high C-value is unlikely to represent a C-value in Antarctica figure 7.5). This high value created enough grounding-line motion for us to analyze error estimation. Position 3 km) Position 3 km) Grounding line position of the Chebyshev Benchark for all p Experiment a p= p=.5 p=.5 p=.75 p=.6 Experiment a Time a).6 Experiment b Experiment b Time a) Figure 7.3: The grounding line position of the benchmark for all values of p while varying C over 5 years for experiments a left column) and b right column), and experiments top) and bottom). The horizontal lines are the steady-state grounding-line positions for the end of each experiment and for each p each color correspond to the value of p given in the legend). During experiments a and a, and for all p-values, the grounding line retreats by km. During experiments b and b, and for all p- values, the grounding line advances by km before retreating top left panel). After 5 years, the grounding line positions remains hundreds of kilometers away from their steady-state location. Figure 7.3 shows the grounding-line position over 5 years from the benchmark model over a linear bed for experiments a left column) and b right column), and experiments top) and bottom). During experiments a and a, the grounding line retreats by tens of kilometer and never re-advances over the 5 years time period. During experiments b and b, the grounding line moves 34
145 in the opposite direction, advancing by hundreds of kilometers before retreating. At the end of the experiments, the grounding lines remain hundreds of kilometers away from their steady-state location horizontal lines in figure 7.3). As we showed in section 7.. with the steady-state simulation, an increase in shear stress factor should result in a grounding-line advance while a decrease should result in a grounding-line retreat. These observations are the opposite of the initial grounding-line behavior shown in figure 7.3. By increasing the shear stress constant a experiments) we increase the friction of the ice at the bed. This lead to a reduced flow of the ice sheet because thickness and therefore driven stress) can t change instantly. Consequently, the flux at the grounding line is weaker and leads to a grounding line retreat. In time, the lower fluxes will lead to a gradual thickening of the ice via accumulation over 3 years) and the grounding line will advance as seen in section 7... Similarly, decreasing the shear stress constant increases the ice velocity in the ice sheet region and at the grounding line. The flux increases at the grounding line which thins the ice more quickly than it can thickness due to decreased flux. consequently the grounding line advances. In time, the ice will thin by advection and the grounding line will retreat as seen in section 7... Neither in experiment a nor a do we observe any grounding line advance. This does not come as too much of a surprise since ice needs thousands of years to accumulate significantly given our accumulation rate. The small accumulation rate which are typical for Antarctica) compared to other mass fluxes explains why an advance process is typically slower compared to a retreat process. Similarly, experiment b is not long enough to observe any retreat because of the relatively small fluxes due to high value of C. However, the experiments was long enough to observe a small retreat in experiment b. Figure 7.4 shows the signed difference between the fixed-grid and the benchmark grounding line position over a linear bed for 5 years at.6 km top row),.4 km middle row) and. km bottom row) resolution. We show results for experiments a and b without GLP left columns respectively) and experiments a and b with GLP right columns respectively). During experiment a, with and without the GLP, the grounding line of the lower-resolution solution is always too advanced and grow approximately linearly with time; the differences are most apparent for small p-values without the GLP. During experiment b, with and without the GLP, the differences are always positive the grounding line is too advanced relative to the benchmark) and saturate rather quickly for large values of p. For small values of p the differences are non monotonic in time. The grounding-line differences for experiments a and b are qualitatively similar and therefore not shown. Figure 7.3 showed, for experiment b and all p-values, an advance of the grounding line prior to a retreat. For low p-values the grounding line advances more quickly, reaches its maximum sooner and retreats more slowly than the benchmark, leading to the s-shaped curves in figure 7.4. In other words, the non-monotonicity in grounding line differences for low p-values is inherent to the stickiness of the fixed-grid creating a time delay in grounding line response. The local minimum in the s-shaped curves suggests an underestimation 35
146 3 Difference in grounding line position Without GLP With GLP Exp a Exp b Exp a Exp b 3 Difference km) Res =. km Res =.4 km Res =.6 km p= p=.5 p=.5 p=.75 p= Time a) Time a) 5 5 Figure 7.4: The signed difference between the fixed-grid and the benchmark grounding line position over a linear bed and for 5 a at.6 km top row),.4 km middle row) and. km bottom row) resolution for experiments a and b without GLP left columns respectively) and experiments a and b with GLP right columns respectively). During experiment a, with and without the GLP, the differences are one sided and grow approximately linearly with time; the differences are most apparent for small p-values without the GLP. During experiment b, with and without the GLP, the differences saturate rather quickly for large values of p. For small values of p the differences are non monotonic in time. of the error in time due to error cancelation, meaning we do not have a good error estimate for low p-values. In contrast such non-monotonic behaviors are not seen for simulations with high values of p meaning they better capture transient grounding line behavior. Figure 7.5 is the same as figure 7.4 but for the transient simulation while varying C, and for experiment a top row), a bottom row), without the GLP left column), and with the GLP right column). The plots are qualitatively similar between experiment a and a with and without the GLP: the maximum error decreases as a strong function of p without the GLP and is a week function of 36
147 Resolution km) Without GLP Exp a Maximum Error in grounding line position With GLP Exp a Resolution km) p Exp a Exp a p Figure 7.5: The same as figure 7.4 but for the transient simulation while varying C, and for experiment a top row), a bottom row), without the GLP left column), and with the GLP right column). Note that each panel uses the same color bar. The black contour lines distinguish errors at,, 3, 4, and 5 km. The plots are qualitatively similar between experiment a and a with and without the GLP: the maximum error decreases as a strong function of p without the GLP and is a week function of p with the GLP, while it decreases somewhat linearly with resolution. p with the GLP, while it decreases somewhat linearly with resolution. Experiments a and a would have grounding-line advance over thousands of years but show a grounding line retreat over the 5 years of the experiments. Thus it does not come as a surprise the errors to resemble those of a retreat experiment in section 7.. Figure 7.6 is the same as figure 7.5 but for experiments b and b. The maximum grounding-line position plots are qualitatively similar between experiment and with and without the GLP: the largest error occurs for large values of p at coarse resolution. At higher resolution, the error decreases as a function of p without the GLP; with the GLP the error increases as a function with increasing p during experiment b while it is a weak function of p for experiment b. These error plots are consistent with the results in figure 7.7 where we observed larger errors for high p-values during the advance experiments. The error plot of 37
148 Resolution km) Resolution km) Without GLP Exp b Exp b p Maximum Error in grounding line position With GLP Exp b Exp b p Figure 7.6: The same as figure 7.5 but for experiments b and b. Note that each panel uses the same color bar. The black contour lines distinguish errors at,, 3, 4, and 5 km. The maximum grounding line position plots are qualitatively similar between experiment and with and without the GLP: the largest error occurs for large values of p at coarse resolution. At higher resolution, the error decreases as a strong function of p without the GLP. With the GLP the error increases as a strong function with increasing p during experiment b while it is a weak function of p for experiment b. experiment b comes somewhat as a surprise to us as it is the first time we observe results to be more accurate for low p-values at higher resolution. However, it does not alter the general observation we have seen so far. For high p-values, adding the GLP had little effect on the maximum error compared to the results without the GLP. This is no longer valid for low p-values for which the effect of the GLP relaxes the need of resolution by a factor of 4 or more. The local maximum we observe in experiment b at p =.5 might be the result of a relatively small grounding-line motion in this experiment. Figures 7.5 and 7.6 show contour lines of the maximum error at,, 3, 4, and 5 km. In section 7. we used an error threshold of 3 km which we deemed to be acceptable for determining resolution requirement; it represented about 5% of grounding line motion. In these experiments we cannot use the same requirement. Although figure 7.3 shows a grounding line motion of km or more for experiments b and b, it only shows one of km for experiments a and 38
149 a. Using a 5% error in grounding line motion implies a km error threshold which is not realistic to expect at coarse resolution. With this threshold, the linear interpolation used to locate the grounding line i.e equation 5.3) contributes to a grounding-line error of order unity at coarse resolution. Therefore, instead of fixing an error threshold in these experiments the contour lines are plotted with the only goal to provide more information on resolution requirement. We let modelers decide which resolution will satisfy their needs e.g. for sea-level prediction or for comparison with observed grounding line behavior, based on the model they are using Melting ice shelves Ocean warming impacts ice-sheet dynamic by melting the base of ice shelf Rignot et al., 4). Unless the calving front coincides with the grounding line, direct melting at the grounding line is almost non-existent as warm water moves up to a given water column. The warm water underneath an ice shelf melts the ice vertically and its horizontal impact is negligible. In the absence of buttressing, basal melting applied to a free floating ice shelf does not affect the grounded ice sheet as it does not impact the ice flux at the grounding line or stresses in the grounded ice Gudmundsson, 3). To allow melting to drive grounding-line motion, for this experiment, we use a flowline model that includes lateral drag as in section We choose to experiment with a channel width W = 5 km. The melt rate is added to the continuity equation as H t + uh) x =ṁ a ṁ b, 7.3) where ṁ b represents the melt rate. We choose to experiment with a single melt rate value of m a. The values of channel width and melt rate are typical in the Amundsen Sea sector in West Antarctica Rignot et al., 3). We now need to determine how to discretize the continuity equation 7.3) with melting. Clearly, no melt occurs at fully grounded cells, while melt does occur at fully floating cells. The cell containing the grounding line is grounded upstream, and floating downstream of it; the portion representing the grounded part is determined by λ equation 5.3)). This suggests scaling the melt rate by λ for that cell. This is not always a good idea in practice. Allowing melting in a cell containing the grounding line will likely lead to thinning in that cell and thus grounding line retreat. This thinning modifies the driving stress upstream of the grounding line. In other words, scaling the melt rate differs from scaling the stresses in the momentum equation as it thins the ice shelf and affects the driving stress significantly as a result, while this is not the case for the basal shear stress. This numerical artifact could trigger Marine Ice Sheet Instability MISI) for unphysical reasons and is therefore not desirable. 39
150 The fixed-grid model without the GLP considers the ice-thickness point in the cell containing the grounding line to be fully grounded. Thus it is also natural to consider that cell to be fully grounded in the continuity equation in part due to the numerical reasons argued previously. In contrast, the fixed-grid model with the GLP rescales the stresses accounting for the floating fraction of the cell containing the grounding line. It is then consistent to believe that the melt rate should also be rescaled in the continuity equation. To shed light on the numerical effect of scaling the melt rate, we performed a series of experiments on an un-buttressed ice sheet, for a melt rate of ma at.6 km resolution over years. We considered four different scenarios: ) without GLP and without melt scaling; ) without GLP and with melt scaling; 3) with GLP and without melt scaling; 4) with GLP and with melt scaling. As mentioned above, we should not observe any grounding line motion in any of the 4 scenarios. We found not shown) that the grounding line retreated several hundred of meters within the first decade but stabilized afterwords for scenarios, 3 and 4 for all values of p. However the grounding line retreated by several kilometers for high values of p without settling at the end of the experiment for scenario. For low p-values we showed in the previous section that it takes a strong forcing at coarse resolution for the grounding line to move. The lack of motion here might be the result of error cancelation). This retreat effect is less significant with higher resolution. Because of these larges differences for high values of p and at coarse resolution, we chose not to apply any scaling factor to the melt rate in the continuity equation. Thus the melt rate is given as a step function and is defined as: ṁ b = x < x i, 7.33) x x i where x i is the first floating point. The experiments we consider in the rest of this section start with a buttressed ice-sheet steady-state profile that does not include any melt rate. We chose to experiment with only one melt rate value on the assumption that other values would not change the results qualitatively. Since these experiments involve lateral drag parameterization, we use the 5 m resolution fixed-grid as a benchmark. In these experiments we expect the grounding line position to retreat over time as melting occurs downstream of its location. Figure 7.7 shows the benchmark grounding-line position for all values of p without the GLP the result with the GLP are similar therefore not shown). The figure shows two behaviors in grounding line motion for all values of p: first, the grounding line retreats somewhat linearly with time over the 5 year simulation. Second, we observe a lag in grounding-line response of about years at the beginning of each simulation. Such a behavior has been observed by more sophisticated models that account for full land-ice-ocean coupling Goldberg et al., 4
151 .93 Grounding line position for all p at Res =.5 km.9 Position 3 km) Time a) Figure 7.7: The grounding line position for all values of p without the GLP and at 5 m resolution the results with the GLP are very similar therefore not shown) over 5 years while melting the ice shelf at a rate of m a. The grounding line position decreases somewhat linearly over time. At the beginning of the experiment we observe a time lag in grounding-line response of years. ). This time lag is likely a physical property of the system that we have not investigated and is left for future work. Figure 7.8 is the same as figure 7.3 but for our transient simulation when thinning the ice shelf with a melt rate of ma. Each experiment shows a grounding line that is too advanced compared to the benchmark and a difference that is monotonic with p. Without the GLP, and at coarse resolutions, the difference grows linearly with time for small values of p while it saturates at higher resolutions. With the GLP and for all p, as for high p without the GLP, the difference saturates very fast. At coarse resolution, with and without the GLP, and for p =, the difference oscillates like a wave that stretches over time without growing in magnitude. In the fixed-grid model in the cell containing the grounding line, only the thickness grid-point downstream of the grounding line is subject to melting when no GLP is applied to the melt rate. As the ice thins there, the grounding line retreats within that cell and the linear interpolation that determines the grounding line location equation 5.3)) drives the differences in figure 7.8. As the grounding line retreats it eventually moves to another grid cell and that previ- 4
152 Difference km) Res =. km Res =.4 km Res =.6 km Difference in grounding line position Without GLP 5 p= With GLP p=.5 p=.5 p=.75 5 p= Time a) Time a) 5 Figure 7.8: The same as figure 7.3 but for our transient ice shelf melting experiment and a melt rate of ma. The differences are non-monotonic with p. Without the GLP, and at coarse resolutions, the difference accumulates somewhat linearly over time for small values of p while it saturates slowly at higher resolutions. With the GLP and for all p, as for high p without the GLP, the difference saturates very fast. At coarse resolution, with and without the GLP, and for high values of p we notice a wavy behavior of the difference that stretches but not grow over time. ously grounded thickness point becomes afloat. The linear interpolation is most accurate close to this new floating point. The jump from one cell to another coincide with the jump we observe in the difference. The fact that the difference always returns to a similar value shows that the grounding line retreats at a similar rate for both the fixed grid and the benchmark. This wavy behavior decreases in amplitude with higher resolution and the stretch of the difference over time coincide with the grounding-line motion slowing down. Figure 7.7 shows a grounding line retreat of about 5 to km over 5 years depending on the value of p. This signifies, based on figure 7.8, that the grounding-line difference at coarse resolution, without the GLP and at low p- values, represents % of the grounding-line motion. This type of error is similar to those observed in section 7.. However, steady-state is achieved over tens of thousands of years. These results insinuate that large errors accumulates early on in the simulation and continue to accumulate all the way on to steady state. 4
153 These large error can be reduced using the GLP and for high values of p with and without the GLP. 3. Maximum Error in grounding line position Without GLP With GLP Resolution km) p p Figure 7.9: The same as figure 7.4 but for the transient simulation and the ice shelf melt experiment. Note that each panel uses the same nonlinear color bar. Without the GLP, the maximum error decreases approximately linearly with resolution and superlinearly with p. With the GLP the maximum error decreases weakly with respect to p but approximately linearly with resolution. The black contour lines distinguish errors at,, 3, 4, and 5 km Figure 7.9 is the same as figure 7.4 but for the transient ice shelf melt simulation. The results are similar to those observed in section 7.: the maximum error decreases somewhat linearly with grid-cell size for each value of p, with or without the GLP. The error decreases more dramatically as a function of p at coarse resolution without the GLP and approximately linearly otherwise. Similarly to the previous section, we do not give a suggested acceptable resolution as it will vary depending on the modeler s need. However, we should point out that even with a threshold of km error, a resolution of km or coarser remains acceptable to reproduce grounding line migration for high values of p, with and without the GLP. In general, the lack of grounding line motion indicates that this experiment is not well designed to test grounding line motion in our code. Instead it provides qualitative information and warnings in view of sea level rise forecast simulations. We could have chosen a threshold based on grounding line retreat observed in Rignot et al. 4) but some extreme grounding line retreat events took place which were most likely caused by complex physical systems with twodimensional topography and three-dimensional stresses that are phenomenon that cannot be reproduced using our model. Instead we leave it to the reader to choose a threshold that would be adequate for specific simulation setup involving ice shelf melting based on the properties shown in figure
Ocean Ice Interactions: A
 Ocean Ice Interactions: A Cryospheric Perspective Tony Payne a.j.payne@bristol.ac.uk Steph Cornford, Rupert Gladstone and Dan Martin (LLNL) KISS short course Sept. 2013 Slide number 1/37 Outline Evidence
Ocean Ice Interactions: A Cryospheric Perspective Tony Payne a.j.payne@bristol.ac.uk Steph Cornford, Rupert Gladstone and Dan Martin (LLNL) KISS short course Sept. 2013 Slide number 1/37 Outline Evidence
Modeled and observed fast flow in the Greenland ice sheet
 Modeled and observed fast flow in the Greenland ice sheet Ed Bueler 1 Constantine Khroulev 1 Andy Aschwanden 2 Ian Joughin 3 1 Dept of Mathematics and Statistics, University of Alaska Fairbanks 2 Arctic
Modeled and observed fast flow in the Greenland ice sheet Ed Bueler 1 Constantine Khroulev 1 Andy Aschwanden 2 Ian Joughin 3 1 Dept of Mathematics and Statistics, University of Alaska Fairbanks 2 Arctic
Summary for the Greenland ice sheet
 Contribution of Greenland and Antarctica to future sea level change Catherine Ritz, Gaël Durand, Fabien Gillet-Chaulet, Olivier Gagliardini, Vincent Peyaud EDGe team, LGGE, CNRS/UJF Grenoble, France Ice
Contribution of Greenland and Antarctica to future sea level change Catherine Ritz, Gaël Durand, Fabien Gillet-Chaulet, Olivier Gagliardini, Vincent Peyaud EDGe team, LGGE, CNRS/UJF Grenoble, France Ice
Assessing the ability of numerical ice sheet models to simulate grounding line migration
 JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 110,, doi:10.1029/2004jf000202, 2005 Assessing the ability of numerical ice sheet models to simulate grounding line migration A. Vieli and A. J. Payne Centre for Polar
JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 110,, doi:10.1029/2004jf000202, 2005 Assessing the ability of numerical ice sheet models to simulate grounding line migration A. Vieli and A. J. Payne Centre for Polar
Decay of the Greenland Ice Sheet due to surface-meltwater-induced acceleration of basal sliding
 Decay of the Greenland Ice Sheet due to surface-meltwater-induced acceleration of basal sliding arxiv:0905.07v [physics.geo-ph] May 009 Ralf Greve Shin Sugiyama Institute of Low Temperature Science, Hokkaido
Decay of the Greenland Ice Sheet due to surface-meltwater-induced acceleration of basal sliding arxiv:0905.07v [physics.geo-ph] May 009 Ralf Greve Shin Sugiyama Institute of Low Temperature Science, Hokkaido
Glacier Hydrology II: Theory and Modeling
 Glacier Hydrology II: Theory and Modeling McCarthy Summer School 2018 Matt Hoffman Gwenn Flowers, Simon Fraser Operated by Los Alamos National Security, LLC for the U.S. Department of Energy's NNSA Observations
Glacier Hydrology II: Theory and Modeling McCarthy Summer School 2018 Matt Hoffman Gwenn Flowers, Simon Fraser Operated by Los Alamos National Security, LLC for the U.S. Department of Energy's NNSA Observations
Frank PATTYN Laboratoire de Glaciologie Université Libre de Bruxelles Belgium
 Frank PATTYN Laboratoire de Glaciologie Université Libre de Bruxelles Belgium 200 x 10 6 people living in coastal floodplains IPCC, 2007 2 x 10 6 km 2 and 10 12 US$ worth of assets lying
Frank PATTYN Laboratoire de Glaciologie Université Libre de Bruxelles Belgium 200 x 10 6 people living in coastal floodplains IPCC, 2007 2 x 10 6 km 2 and 10 12 US$ worth of assets lying
Ice in the climate system. Summary so far. Today. The Cryosphere. 1. Climate history of the Earth. 2. Paleo observations (1)
 Ice in the climate system 1. Climate history of the Earth 2. Paleo observations (1) 3. Paleo observations (2) 4. Ice ages 5. Climate sensitivity 6. Ice in the climate system Summary so far Radiation (Milankovitch
Ice in the climate system 1. Climate history of the Earth 2. Paleo observations (1) 3. Paleo observations (2) 4. Ice ages 5. Climate sensitivity 6. Ice in the climate system Summary so far Radiation (Milankovitch
Elmer/Ice Chinese-Finnish seminar, October 30 th 2012
 Elmer/Ice Chinese-Finnish seminar, October 30 th 2012 NEW GENERATION ICE SHEET MODELS Shallow ice approximation is so 80 s! Thomas Zwinger 1) and... 1) CSC IT Center for Science Ltd. Espoo, Finland ...
Elmer/Ice Chinese-Finnish seminar, October 30 th 2012 NEW GENERATION ICE SHEET MODELS Shallow ice approximation is so 80 s! Thomas Zwinger 1) and... 1) CSC IT Center for Science Ltd. Espoo, Finland ...
PISM, a Parallel Ice Sheet Model: Current status of our Antarctic ice sheet simulation
 PISM, a Parallel Ice Sheet Model: Current status of our Antarctic ice sheet simulation Craig Lingle, 1 Ed Bueler, 2 Jed Brown, 1 and David Covey, 1 1 Geophysical Institute, Univ. of Alaska, Fairbanks 2
PISM, a Parallel Ice Sheet Model: Current status of our Antarctic ice sheet simulation Craig Lingle, 1 Ed Bueler, 2 Jed Brown, 1 and David Covey, 1 1 Geophysical Institute, Univ. of Alaska, Fairbanks 2
Effect of Ocean Warming on West Antarctic Ice Streams and Ice Shelves. Bryan Riel December 4, 2008
 Effect of Ocean Warming on West Antarctic Ice Streams and Ice Shelves Bryan Riel December 4, 2008 Ice Sheet Mass Balance/WAIS Dynamics -Mass Balance = (Ice/Snow Accumulation) (Surface melting, ice outflux,
Effect of Ocean Warming on West Antarctic Ice Streams and Ice Shelves Bryan Riel December 4, 2008 Ice Sheet Mass Balance/WAIS Dynamics -Mass Balance = (Ice/Snow Accumulation) (Surface melting, ice outflux,
Modelling of surface to basal hydrology across the Russell Glacier Catchment
 Modelling of surface to basal hydrology across the Russell Glacier Catchment Sam GAP Modelling Workshop, Toronto November 2010 Collaborators Alun Hubbard Centre for Glaciology Institute of Geography and
Modelling of surface to basal hydrology across the Russell Glacier Catchment Sam GAP Modelling Workshop, Toronto November 2010 Collaborators Alun Hubbard Centre for Glaciology Institute of Geography and
Title. Author(s)Greve, Ralf. Issue Date Doc URL. Type. Note. File Information.
 Title Increased future sea level rise due to rapid decay o Author(s)Greve, Ralf CitationProceedings of the First International Symposium on Issue Date 008--04 Doc URL http://hdl.handle.net/5/4868 Type
Title Increased future sea level rise due to rapid decay o Author(s)Greve, Ralf CitationProceedings of the First International Symposium on Issue Date 008--04 Doc URL http://hdl.handle.net/5/4868 Type
Ice Sheet Modeling and Sea Level Rise. William Lipscomb, NCAR CESM Sea Level Session 10 January 2018
 Ice Sheet Modeling and Sea Level Rise William Lipscomb, NCAR CESM Sea Level Session 10 January 2018 Ice sheets in IPCC AR4 The IPCC Fourth Assessment Report (AR4) projected 0.18 to 0.59 m of sea level
Ice Sheet Modeling and Sea Level Rise William Lipscomb, NCAR CESM Sea Level Session 10 January 2018 Ice sheets in IPCC AR4 The IPCC Fourth Assessment Report (AR4) projected 0.18 to 0.59 m of sea level
Multi-Modal Flow in a Thermocoupled Model of the Antarctic Ice Sheet, with Verification
 Multi-Modal Flow in a Thermocoupled Model of the Antarctic Ice Sheet, with Verification Craig Lingle 1 Jed Brown 2 Ed Bueler 2 1 Geophysical Institute University of Alaska Fairbanks, USA 2 Department of
Multi-Modal Flow in a Thermocoupled Model of the Antarctic Ice Sheet, with Verification Craig Lingle 1 Jed Brown 2 Ed Bueler 2 1 Geophysical Institute University of Alaska Fairbanks, USA 2 Department of
Modelling ice shelf basal melt with Glimmer-CISM coupled to a meltwater plume model
 Modelling ice shelf basal melt with Glimmer-CISM coupled to a meltwater plume model Carl Gladish NYU CIMS February 17, 2010 Carl Gladish (NYU CIMS) Glimmer-CISM + Plume February 17, 2010 1 / 24 Acknowledgements
Modelling ice shelf basal melt with Glimmer-CISM coupled to a meltwater plume model Carl Gladish NYU CIMS February 17, 2010 Carl Gladish (NYU CIMS) Glimmer-CISM + Plume February 17, 2010 1 / 24 Acknowledgements
The effect of bottom boundary conditions in the ice-sheet to ice-shelf transition zone problem
 Journal of Glaciology, Vol. 53, No. 182, 2007 363 The effect of bottom boundary conditions in the ice-sheet to ice-shelf transition zone problem Alexander V. WILCHINSKY Centre for Polar Observation and
Journal of Glaciology, Vol. 53, No. 182, 2007 363 The effect of bottom boundary conditions in the ice-sheet to ice-shelf transition zone problem Alexander V. WILCHINSKY Centre for Polar Observation and
Ice on Earth: An overview and examples on physical properties
 Ice on Earth: An overview and examples on physical properties - Ice on Earth during the Pleistocene - Present-day polar and temperate ice masses - Transformation of snow to ice - Mass balance, ice deformation,
Ice on Earth: An overview and examples on physical properties - Ice on Earth during the Pleistocene - Present-day polar and temperate ice masses - Transformation of snow to ice - Mass balance, ice deformation,
A finite element solver for ice sheet dynamics to be integrated with MPAS
 A finite element solver for ice sheet dynamics to be integrated with MPAS Mauro Perego in collaboration with FSU, ORNL, LANL, Sandia February 6, CESM LIWG Meeting, Boulder (CO), 202 Outline Introduction
A finite element solver for ice sheet dynamics to be integrated with MPAS Mauro Perego in collaboration with FSU, ORNL, LANL, Sandia February 6, CESM LIWG Meeting, Boulder (CO), 202 Outline Introduction
Dynamics of Glaciers
 Dynamics of Glaciers McCarthy Summer School 01 Andy Aschwanden Arctic Region Supercomputing Center University of Alaska Fairbanks, USA June 01 Note: This script is largely based on the Physics of Glaciers
Dynamics of Glaciers McCarthy Summer School 01 Andy Aschwanden Arctic Region Supercomputing Center University of Alaska Fairbanks, USA June 01 Note: This script is largely based on the Physics of Glaciers
SUPPLEMENTARY INFORMATION
 SUPPLEMENTARY INFORMATION DOI: 1.138/NGEO1218 Supplementary information Ice speed of a calving glacier modulated by small fluctuations in basal water pressure Shin Sugiyama 1, Pedro Skvarca 2, Nozomu Naito
SUPPLEMENTARY INFORMATION DOI: 1.138/NGEO1218 Supplementary information Ice speed of a calving glacier modulated by small fluctuations in basal water pressure Shin Sugiyama 1, Pedro Skvarca 2, Nozomu Naito
Greenland subglacial drainage evolution regulated by weakly-connected regions of the bed
 Greenland subglacial drainage evolution regulated by weakly-connected regions of the bed Matthew Hoffman Stephen Price Lauren Andrews Ginny Catania Weakly-connected Drainage Distributed Drainage Channelized
Greenland subglacial drainage evolution regulated by weakly-connected regions of the bed Matthew Hoffman Stephen Price Lauren Andrews Ginny Catania Weakly-connected Drainage Distributed Drainage Channelized
ANTARCTIC SUBGLACIAL PROCESSES AND INTERACTIONS: ASPI F. PATTYN, J.-L. TISON, P. HUYBRECHTS ROLE OF TRANSITION ZONES IN ICE SHEET STABILITY
 ANTARCTIC SUBGLACIAL PROCESSES AND INTERACTIONS: ROLE OF TRANSITION ZONES IN ICE SHEET STABILITY ASPI F. PATTYN, J.-L. TISON, P. HUYBRECHTS SCIENCE FOR A SUSTAINABLE DEVELOPMENT (SSD) Antarctica - Climate
ANTARCTIC SUBGLACIAL PROCESSES AND INTERACTIONS: ROLE OF TRANSITION ZONES IN ICE SHEET STABILITY ASPI F. PATTYN, J.-L. TISON, P. HUYBRECHTS SCIENCE FOR A SUSTAINABLE DEVELOPMENT (SSD) Antarctica - Climate
Parameterization of lateral drag in flowline models of glacier dynamics
 Journal of Glaciology, Vol. 58, No. 212, 2012 doi: 10.3189/2012JoG12J018 1119 Parameterization of lateral drag in flowline models of glacier dynamics Surendra ADHIKARI, Shawn J. MARSHALL Department of
Journal of Glaciology, Vol. 58, No. 212, 2012 doi: 10.3189/2012JoG12J018 1119 Parameterization of lateral drag in flowline models of glacier dynamics Surendra ADHIKARI, Shawn J. MARSHALL Department of
The State of the cryosphere
 The State of the cryosphere Course outline Introduction The cryosphere; what is it? The Earth; a unique planet Cryospheric components Classifications Lecture outlines The State of the cryosphere The State
The State of the cryosphere Course outline Introduction The cryosphere; what is it? The Earth; a unique planet Cryospheric components Classifications Lecture outlines The State of the cryosphere The State
OCN/ATM/ESS 587. The wind-driven ocean circulation. Friction and stress. The Ekman layer, top and bottom. Ekman pumping, Ekman suction
 OCN/ATM/ESS 587 The wind-driven ocean circulation. Friction and stress The Ekman layer, top and bottom Ekman pumping, Ekman suction Westward intensification The wind-driven ocean. The major ocean gyres
OCN/ATM/ESS 587 The wind-driven ocean circulation. Friction and stress The Ekman layer, top and bottom Ekman pumping, Ekman suction Westward intensification The wind-driven ocean. The major ocean gyres
Large-scale changes in Greenland outlet glacier dynamics triggered at the terminus
 PUBLISHED ONLINE: JANUARY 2 DOI:./NGEO Large-scale changes in Greenland outlet glacier dynamics triggered at the terminus Faezeh M. Nick 1 *, Andreas Vieli 1, Ian M. Howat 2 and Ian Joughin The recent
PUBLISHED ONLINE: JANUARY 2 DOI:./NGEO Large-scale changes in Greenland outlet glacier dynamics triggered at the terminus Faezeh M. Nick 1 *, Andreas Vieli 1, Ian M. Howat 2 and Ian Joughin The recent
Chapter 9: Differential Analysis of Fluid Flow
 of Fluid Flow Objectives 1. Understand how the differential equations of mass and momentum conservation are derived. 2. Calculate the stream function and pressure field, and plot streamlines for a known
of Fluid Flow Objectives 1. Understand how the differential equations of mass and momentum conservation are derived. 2. Calculate the stream function and pressure field, and plot streamlines for a known
Subglacial topography inferred from ice surface terrain analysis reveals a large un-surveyed basin below sea level in East Antarctica
 GEOPHYSICAL RESEARCH LETTERS, VOL. 35, L16503, doi:10.1029/2008gl034728, 2008 Subglacial topography inferred from ice surface terrain analysis reveals a large un-surveyed basin below sea level in East
GEOPHYSICAL RESEARCH LETTERS, VOL. 35, L16503, doi:10.1029/2008gl034728, 2008 Subglacial topography inferred from ice surface terrain analysis reveals a large un-surveyed basin below sea level in East
Chapter 9: Differential Analysis
 9-1 Introduction 9-2 Conservation of Mass 9-3 The Stream Function 9-4 Conservation of Linear Momentum 9-5 Navier Stokes Equation 9-6 Differential Analysis Problems Recall 9-1 Introduction (1) Chap 5: Control
9-1 Introduction 9-2 Conservation of Mass 9-3 The Stream Function 9-4 Conservation of Linear Momentum 9-5 Navier Stokes Equation 9-6 Differential Analysis Problems Recall 9-1 Introduction (1) Chap 5: Control
Marine ice sheet dynamics: Hysteresis and neutral equilibrium
 JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 114,, doi:10.1029/2008jf001170, 2009 Marine ice sheet dynamics: Hysteresis and neutral equilibrium G. Durand, 1 O. Gagliardini, 1 B. de Fleurian, 1 T. Zwinger, 2 and
JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 114,, doi:10.1029/2008jf001170, 2009 Marine ice sheet dynamics: Hysteresis and neutral equilibrium G. Durand, 1 O. Gagliardini, 1 B. de Fleurian, 1 T. Zwinger, 2 and
Effect of Ocean Warming on West Antarctic Ice Streams and Ice Shelves
 Effect of Ocean Warming on West Antarctic Ice Streams and Ice Shelves By Bryan Riel GEO 387H Physical Climatology Dr. Zong-Liang Yang November 18, 2008 Abstract The Intergovernmental Panel on Climate Change
Effect of Ocean Warming on West Antarctic Ice Streams and Ice Shelves By Bryan Riel GEO 387H Physical Climatology Dr. Zong-Liang Yang November 18, 2008 Abstract The Intergovernmental Panel on Climate Change
Ice Sheets and Climate Change. William H. Lipscomb Los Alamos National Laboratory
 Ice Sheets and Climate Change William H. Lipscomb Los Alamos National Laboratory What is an expert? An expert is somebody who is more than 50 miles from home, has no responsibility for implementing the
Ice Sheets and Climate Change William H. Lipscomb Los Alamos National Laboratory What is an expert? An expert is somebody who is more than 50 miles from home, has no responsibility for implementing the
Numerical simulations of glacier evolution performed using flow-line models of varying complexity
 Numerical simulations of glacier evolution performed using flow-line models of varying complexity Antonija Rimac 1, 2, Sharon van Geffen 1, 2, and Johannes Oerlemans 1 1 Institute for Marine and Atmospheric
Numerical simulations of glacier evolution performed using flow-line models of varying complexity Antonija Rimac 1, 2, Sharon van Geffen 1, 2, and Johannes Oerlemans 1 1 Institute for Marine and Atmospheric
Glacier Thermodynamics: Ice Temperature and Heat Transfer Processes
 Glacier Thermodynamics: Ice Temperature and Heat Transfer Processes ESS431: Principles of Glaciology ESS505: The Cryosphere Wednesday, 10/24 Ben Hills Today s Objectives: Why do we care about ice temperature?
Glacier Thermodynamics: Ice Temperature and Heat Transfer Processes ESS431: Principles of Glaciology ESS505: The Cryosphere Wednesday, 10/24 Ben Hills Today s Objectives: Why do we care about ice temperature?
Marine ice sheet profiles and stability under Coulomb basal conditions
 Journal of Glaciology, Vol., No., 1 Marine ice sheet profiles and stability under Coulomb basal conditions Victor C. TSAI, 1 Andrew L. STEWART, 2 Andrew F. THOMPSON, 3 1 Seismological Laboratory, California
Journal of Glaciology, Vol., No., 1 Marine ice sheet profiles and stability under Coulomb basal conditions Victor C. TSAI, 1 Andrew L. STEWART, 2 Andrew F. THOMPSON, 3 1 Seismological Laboratory, California
THE SCIENCE OF ICE SHEETS: THE MATHEMATICAL MODELING AND COMPUTATIONAL SIMULATION OF ICE FLOWS
 THE SCIENCE OF ICE SHEETS: THE MATHEMATICAL MODELING AND COMPUTATIONAL SIMULATION OF ICE FLOWS Max Gunzburger Department of Scientific Computing, Florida State University Collaborators: Mauro Perego (Florida
THE SCIENCE OF ICE SHEETS: THE MATHEMATICAL MODELING AND COMPUTATIONAL SIMULATION OF ICE FLOWS Max Gunzburger Department of Scientific Computing, Florida State University Collaborators: Mauro Perego (Florida
Understanding and Modelling Rapid Dynamic Changes of Tidewater Outlet Glaciers: Issues and Implications
 Surv Geophys (211) 32:437 458 DOI 1.17/s1712-11-9132-4 Understanding and Modelling Rapid Dynamic Changes of Tidewater Outlet Glaciers: Issues and Implications Andreas Vieli Faezeh M. Nick Received: 5 November
Surv Geophys (211) 32:437 458 DOI 1.17/s1712-11-9132-4 Understanding and Modelling Rapid Dynamic Changes of Tidewater Outlet Glaciers: Issues and Implications Andreas Vieli Faezeh M. Nick Received: 5 November
Evolution of a coupled marine ice sheet sea level model
 JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 117,, doi:10.1029/2011jf002128, 2012 Evolution of a coupled marine ice sheet sea level model Natalya Gomez, 1 David Pollard, 2 Jerry X. Mitrovica, 1 Peter Huybers,
JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 117,, doi:10.1029/2011jf002128, 2012 Evolution of a coupled marine ice sheet sea level model Natalya Gomez, 1 David Pollard, 2 Jerry X. Mitrovica, 1 Peter Huybers,
Manuscript prepared for The Cryosphere with version 2014/09/ Copernicus papers of the L A TEX class copernicus.cls. Date: 5 August 2016
 Manuscript prepared for The Cryosphere with version 14/9/16 7.15 Copernicus papers of the L A TEX class copernicus.cls. Date: 5 August 16 Balance between driving stress and basal drag results in linearity
Manuscript prepared for The Cryosphere with version 14/9/16 7.15 Copernicus papers of the L A TEX class copernicus.cls. Date: 5 August 16 Balance between driving stress and basal drag results in linearity
Röthlisberger channel model accounting for antiplane shear loading and undeforming bed
 öthlisberger channel model accounting for antiplane shear loading and undeforming bed Matheus C. Fernandes Colin. Meyer Thibaut Perol James. ice,2 John A. Paulson School of Engineering and Applied Sciences
öthlisberger channel model accounting for antiplane shear loading and undeforming bed Matheus C. Fernandes Colin. Meyer Thibaut Perol James. ice,2 John A. Paulson School of Engineering and Applied Sciences
A posteriori estimator for the accuracy of the shallow shelf approximation
 Math Geosci manuscript No. will be inserted by the editor A posteriori estimator for the accuracy of the shallow shelf approximation Guillaume Jouvet Marco Picasso Received: date / Accepted: date Abstract
Math Geosci manuscript No. will be inserted by the editor A posteriori estimator for the accuracy of the shallow shelf approximation Guillaume Jouvet Marco Picasso Received: date / Accepted: date Abstract
ESS 431 Principles of Glaciology ESS 505 The Cryosphere
 MID-TERM November 9, 2015 ESS 431 Principles of Glaciology ESS 505 The Cryosphere Instructions: Please answer the following 5 questions. [The actual 5 questions will be selected from these 12 questions
MID-TERM November 9, 2015 ESS 431 Principles of Glaciology ESS 505 The Cryosphere Instructions: Please answer the following 5 questions. [The actual 5 questions will be selected from these 12 questions
Ice-stream stability on a reverse bed slope
 SUPPLEMENTARY INFORMATION DOI: 10.1038/NGEO1600 Supplementary Information: Ice stream stability on a reverse bed Ice-stream stability on a reverse bed slope slope Stewart S.R. Jamieson 1, Andreas Vieli
SUPPLEMENTARY INFORMATION DOI: 10.1038/NGEO1600 Supplementary Information: Ice stream stability on a reverse bed Ice-stream stability on a reverse bed slope slope Stewart S.R. Jamieson 1, Andreas Vieli
SUPPLEMENTARY INFORMATION
 SUPPLEMENTARY INFORMATION DOI: 10.1038/NGEO1887 Diverse calving patterns linked to glacier geometry J. N. Bassis and S. Jacobs 1. Supplementary Figures (a) (b) (c) Supplementary Figure S1 Schematic of
SUPPLEMENTARY INFORMATION DOI: 10.1038/NGEO1887 Diverse calving patterns linked to glacier geometry J. N. Bassis and S. Jacobs 1. Supplementary Figures (a) (b) (c) Supplementary Figure S1 Schematic of
Antarctic ice-rise formation, evolution and stability
 GEOPHYSICAL RESEARCH LETTERS, VOL.???, XXXX, DOI:10.1002/, 1 Antarctic ice-rise formation, evolution and stability Lionel Favier, 1 Frank Pattyn, 1 Corresponding author: L. Favier, Laboratoire de Glaciologie,
GEOPHYSICAL RESEARCH LETTERS, VOL.???, XXXX, DOI:10.1002/, 1 Antarctic ice-rise formation, evolution and stability Lionel Favier, 1 Frank Pattyn, 1 Corresponding author: L. Favier, Laboratoire de Glaciologie,
Modeling Antarctic subglacial lake filling and drainage cycles
 The Cryosphere,, 38 393, 6 www.the-cryosphere.net//38/6/ doi:.594/tc--38-6 Author(s) 6. CC Attribution 3. License. Modeling Antarctic subglacial lake filling and drainage cycles Christine F. Dow,a, Mauro
The Cryosphere,, 38 393, 6 www.the-cryosphere.net//38/6/ doi:.594/tc--38-6 Author(s) 6. CC Attribution 3. License. Modeling Antarctic subglacial lake filling and drainage cycles Christine F. Dow,a, Mauro
This is an author produced version of Actively evolving subglacial conduits and eskers initiate ice shelf channels at an Antarctic grounding line.
 This is an author produced version of Actively evolving subglacial conduits and eskers initiate ice shelf channels at an Antarctic grounding line. White Rose Research Online URL for this paper: http://eprints.whiterose.ac.uk/113417/
This is an author produced version of Actively evolving subglacial conduits and eskers initiate ice shelf channels at an Antarctic grounding line. White Rose Research Online URL for this paper: http://eprints.whiterose.ac.uk/113417/
UNSTOPPABLE COLLAPSE OF THE WEST ANTARCTIC ICE SHEET IS NOT HAPPENING
 UNSTOPPABLE COLLAPSE OF THE WEST ANTARCTIC ICE SHEET IS NOT HAPPENING Dr. Don J. Easterbrook, Western Washington University, Bellingham, WA May 19, 2014 A New York Times headline reads Scientists Warn
UNSTOPPABLE COLLAPSE OF THE WEST ANTARCTIC ICE SHEET IS NOT HAPPENING Dr. Don J. Easterbrook, Western Washington University, Bellingham, WA May 19, 2014 A New York Times headline reads Scientists Warn
Numerical simulations of cyclic behaviour in the Parallel Ice Sheet Model (PISM)
 Journal of Glaciology, Vol. 58, No. 208, 2012 doi: 10.3189/2012JoG11J217 347 Numerical simulations of cyclic behaviour in the Parallel Ice Sheet Model (PISM) Ward J.J. VAN PELT, Johannes OERLEMANS Institute
Journal of Glaciology, Vol. 58, No. 208, 2012 doi: 10.3189/2012JoG11J217 347 Numerical simulations of cyclic behaviour in the Parallel Ice Sheet Model (PISM) Ward J.J. VAN PELT, Johannes OERLEMANS Institute
UQ Benchmark Problems for Multiphysics Modeling
 SIAMUQ UQ Challenge Benchmarks UQ Benchmark Problems for Multiphysics Modeling Maarten Arnst March 31, 2014 SIAMUQ UQ Challenge Benchmarks 1 / 25 Motivation Previous presentation at USNCCM2013 UQ Challenge
SIAMUQ UQ Challenge Benchmarks UQ Benchmark Problems for Multiphysics Modeling Maarten Arnst March 31, 2014 SIAMUQ UQ Challenge Benchmarks 1 / 25 Motivation Previous presentation at USNCCM2013 UQ Challenge
Ice-flow characteristics over a rough bedrock: implications for ice-core interpretation
 Ice-flow characteristics over a rough bedrock: implications for ice-core interpretation Frank PATTYN Department of Geography Vrije Universiteit Brussel Pleinlaan 2, B-5 Brussel, Belgium POLAR METEOROLOGY
Ice-flow characteristics over a rough bedrock: implications for ice-core interpretation Frank PATTYN Department of Geography Vrije Universiteit Brussel Pleinlaan 2, B-5 Brussel, Belgium POLAR METEOROLOGY
Sea level projections with semiempirical and earth system models
 Sea level projections with semiempirical and earth system models John C. Moore College of Global Change and Earth System Science, Beijing Normal University, Beijing, China and Arctic Centre, University
Sea level projections with semiempirical and earth system models John C. Moore College of Global Change and Earth System Science, Beijing Normal University, Beijing, China and Arctic Centre, University
The Shallow Water Equations
 The Shallow Water Equations Clint Dawson and Christopher M. Mirabito Institute for Computational Engineering and Sciences University of Texas at Austin clint@ices.utexas.edu September 29, 2008 The Shallow
The Shallow Water Equations Clint Dawson and Christopher M. Mirabito Institute for Computational Engineering and Sciences University of Texas at Austin clint@ices.utexas.edu September 29, 2008 The Shallow
Basal topography and thinning rates of Petermann Gletscher, northern Greenland, measured by ground-based phase-sensitive radar
 Basal topography and thinning rates of Petermann Gletscher, northern Greenland, measured by ground-based phase-sensitive radar Craig Stewart British Antarctic Survey, Natural Environment Research Council,
Basal topography and thinning rates of Petermann Gletscher, northern Greenland, measured by ground-based phase-sensitive radar Craig Stewart British Antarctic Survey, Natural Environment Research Council,
Dropping Ice Shelves onto an Ocean Model and Moving Grounding Lines. Robert Hallberg NOAA / GFDL
 Dropping Ice Shelves onto an Ocean Model and Moving Grounding Lines Robert Hallberg NOAA / GFDL Projected Global Mean Sea Level Rise Sources of uncertainty in 2100 global mean sea level projections: Forcing
Dropping Ice Shelves onto an Ocean Model and Moving Grounding Lines Robert Hallberg NOAA / GFDL Projected Global Mean Sea Level Rise Sources of uncertainty in 2100 global mean sea level projections: Forcing
ANTARCTIC SUBGLACIAL PROCESSES AND INTERACTIONS: ROLE OF TRANSITION ZONES IN ICE SHEET STABILITY ASPI
 ANTARCTIC SUBGLACIAL PROCESSES AND INTERACTIONS: ROLE OF TRANSITION ZONES IN ICE SHEET STABILITY ASPI T. BOEREBOOM, B. DE SMEDT, PH. HUYBRECHTS, A. HUYGHE, F. PATTYN, L. PERICHON, J.-PH. REMY, D. SAMYN,
ANTARCTIC SUBGLACIAL PROCESSES AND INTERACTIONS: ROLE OF TRANSITION ZONES IN ICE SHEET STABILITY ASPI T. BOEREBOOM, B. DE SMEDT, PH. HUYBRECHTS, A. HUYGHE, F. PATTYN, L. PERICHON, J.-PH. REMY, D. SAMYN,
Ice Sheets and Glaciers
 Ice Sheets and Glaciers Technical University of Denmark Kees van der Veen Department of Geography University of Kansas Why are glaciers and ice sheets important? Large volume of fresh water stored in ice
Ice Sheets and Glaciers Technical University of Denmark Kees van der Veen Department of Geography University of Kansas Why are glaciers and ice sheets important? Large volume of fresh water stored in ice
ORE Open Research Exeter
 ORE Open Research Exeter TITLE Retreat of Pine Island Glacier controlled by marine ice-sheet instability AUTHORS Favier, L; Durand, G; Cornford, Stephen; et al. JOURNAL Nature Climate Change DEPOSITED
ORE Open Research Exeter TITLE Retreat of Pine Island Glacier controlled by marine ice-sheet instability AUTHORS Favier, L; Durand, G; Cornford, Stephen; et al. JOURNAL Nature Climate Change DEPOSITED
Understanding Glacier-Climate Interaction with Simple Models
 Understanding Glacier-Climate Interaction with Simple Models 65-4802-00L / FS 203 Rhonegletscher, Switzerland, 2007-202 (VAW/ETHZ) A proglacial lake is forming in the terminus area of Rhonegletscher (Furkapass,
Understanding Glacier-Climate Interaction with Simple Models 65-4802-00L / FS 203 Rhonegletscher, Switzerland, 2007-202 (VAW/ETHZ) A proglacial lake is forming in the terminus area of Rhonegletscher (Furkapass,
Greenland and Antarctic ice sheets under 1.5 C global warming
 Greenland and Antarctic ice sheets under 1.5 C global warming Frank Pattyn, Catherine Ritz, Edward Hanna, Xylar Asay-Davis, Rob DeConto, Gaël Durand, Lionel Favier, Xavier Fettweis, Heiko Goelzer, Nicholas
Greenland and Antarctic ice sheets under 1.5 C global warming Frank Pattyn, Catherine Ritz, Edward Hanna, Xylar Asay-Davis, Rob DeConto, Gaël Durand, Lionel Favier, Xavier Fettweis, Heiko Goelzer, Nicholas
NASA Images of Antarctica and the Arctic covered in both land and sea ice
 ICE SHELVES ACTIVITY 1: DECODING THE ROLE OF ANTARCTIC ICE IN GLOBAL CLIMATE Ice Shelves play a critical role in Antarctica, serving as a buffer between the ocean and the continental ice sheet covering
ICE SHELVES ACTIVITY 1: DECODING THE ROLE OF ANTARCTIC ICE IN GLOBAL CLIMATE Ice Shelves play a critical role in Antarctica, serving as a buffer between the ocean and the continental ice sheet covering
University of Bristol - Explore Bristol Research
 Cornford, S., Martin, D., Lee, V., Payne, T., & Ng, E. (2016). Adaptive mesh refinement versus subgrid friction interpolation in simulations of Antarctic ice dynamics. Annals of Glaciology, 57(73), 1-9.
Cornford, S., Martin, D., Lee, V., Payne, T., & Ng, E. (2016). Adaptive mesh refinement versus subgrid friction interpolation in simulations of Antarctic ice dynamics. Annals of Glaciology, 57(73), 1-9.
ATOC OUR CHANGING ENVIRONMENT Class 19 (Chp 6) Objectives of Today s Class: The Cryosphere [1] Components, time scales; [2] Seasonal snow
![ATOC OUR CHANGING ENVIRONMENT Class 19 (Chp 6) Objectives of Today s Class: The Cryosphere [1] Components, time scales; [2] Seasonal snow ATOC OUR CHANGING ENVIRONMENT Class 19 (Chp 6) Objectives of Today s Class: The Cryosphere [1] Components, time scales; [2] Seasonal snow](/thumbs/95/126309683.jpg) ATOC 1060-002 OUR CHANGING ENVIRONMENT Class 19 (Chp 6) Objectives of Today s Class: The Cryosphere [1] Components, time scales; [2] Seasonal snow cover, permafrost, river and lake ice, ; [3]Glaciers and
ATOC 1060-002 OUR CHANGING ENVIRONMENT Class 19 (Chp 6) Objectives of Today s Class: The Cryosphere [1] Components, time scales; [2] Seasonal snow cover, permafrost, river and lake ice, ; [3]Glaciers and
Modelling historical and recent mass loss of McCall Glacier, Alaska, USA
 The Cryosphere, 2, 23 31, 2008 Author(s) 2008. This work is distributed under the Creative Commons Attribution 3.0 License. The Cryosphere Modelling historical and recent mass loss of McCall Glacier, Alaska,
The Cryosphere, 2, 23 31, 2008 Author(s) 2008. This work is distributed under the Creative Commons Attribution 3.0 License. The Cryosphere Modelling historical and recent mass loss of McCall Glacier, Alaska,
Glacier (and ice sheet) Mass Balance
 Glacier (and ice sheet) Mass Balance The long-term average position of the highest (late summer) firn line is termed the Equilibrium Line Altitude (ELA) Firn is old snow How an ice sheet works (roughly):
Glacier (and ice sheet) Mass Balance The long-term average position of the highest (late summer) firn line is termed the Equilibrium Line Altitude (ELA) Firn is old snow How an ice sheet works (roughly):
Changing Landscapes: Glaciated Landscapes. How do glaciers move?
 Changing Landscapes: Glaciated Landscapes How do glaciers move? What you need to know Differences between cold-and warm-based glaciers, their locations and rates of movement Glacier ice movement including
Changing Landscapes: Glaciated Landscapes How do glaciers move? What you need to know Differences between cold-and warm-based glaciers, their locations and rates of movement Glacier ice movement including
Dynamical processes involved in the retreat of marine ice sheets
 Journal ofglaciology, Vol. 47, No. 157, 2001 Dynamical processes involved in the retreat of marine ice sheets Richard C.A. Hindmarsh, E. Le Meur British Antarctic Survey, Natural Environment Research Council,
Journal ofglaciology, Vol. 47, No. 157, 2001 Dynamical processes involved in the retreat of marine ice sheets Richard C.A. Hindmarsh, E. Le Meur British Antarctic Survey, Natural Environment Research Council,
PEAT SEISMOLOGY Lecture 2: Continuum mechanics
 PEAT8002 - SEISMOLOGY Lecture 2: Continuum mechanics Nick Rawlinson Research School of Earth Sciences Australian National University Strain Strain is the formal description of the change in shape of a
PEAT8002 - SEISMOLOGY Lecture 2: Continuum mechanics Nick Rawlinson Research School of Earth Sciences Australian National University Strain Strain is the formal description of the change in shape of a
Glacial Geomorphology Lecture 1: Glaciers & Glacial Environments. GGY 166: Geomorphology of Southern Africa
 Glacial Geomorphology Lecture 1: Glaciers & Glacial Environments GGY 166: Geomorphology of Southern Africa Relevance in Southern African Context South African landscape has been influenced by glacial action
Glacial Geomorphology Lecture 1: Glaciers & Glacial Environments GGY 166: Geomorphology of Southern Africa Relevance in Southern African Context South African landscape has been influenced by glacial action
Basal Processes (i.e. boundary conditions)
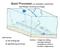 Basal Processes (i.e. boundary conditions) Alan Rempel, University of Oregon Motivation: a) the sliding law b) weathering & erosion Outline: - temperate sliding - drainage elements - intemperate effects
Basal Processes (i.e. boundary conditions) Alan Rempel, University of Oregon Motivation: a) the sliding law b) weathering & erosion Outline: - temperate sliding - drainage elements - intemperate effects
Ice stream stabilization through a meltwater channel in the shear margin
 JOURNAL OF GEOPHYSICAL RESEARCH, VOL.???, XXXX, DOI:10.1029/, Ice stream stabilization through a meltwater channel in the shear margin John D. Platt 1,2, Thibaut Perol, 1, Jenny Suckale 3, and James R.
JOURNAL OF GEOPHYSICAL RESEARCH, VOL.???, XXXX, DOI:10.1029/, Ice stream stabilization through a meltwater channel in the shear margin John D. Platt 1,2, Thibaut Perol, 1, Jenny Suckale 3, and James R.
Glaciers form wherever snow and ice can accumulate High latitudes High mountains at low latitudes Ice temperatures vary among glaciers Warm
 The Cryosphere Glaciers form wherever snow and ice can accumulate High latitudes High mountains at low latitudes Ice temperatures vary among glaciers Warm (temperate) glaciers: at pressure melting point,
The Cryosphere Glaciers form wherever snow and ice can accumulate High latitudes High mountains at low latitudes Ice temperatures vary among glaciers Warm (temperate) glaciers: at pressure melting point,
How do glaciers form?
 Glaciers What is a Glacier? A large mass of moving ice that exists year round is called a glacier. Glaciers are formed when snowfall exceeds snow melt year after year Snow and ice remain on the ground
Glaciers What is a Glacier? A large mass of moving ice that exists year round is called a glacier. Glaciers are formed when snowfall exceeds snow melt year after year Snow and ice remain on the ground
Determining conditions that allow a shear margin to coincide with a Röthlisberger channel
 JOURNAL OF GEOPHYSICAL RESEARCH, VOL.???, XXXX, DOI:10.1029/, Determining conditions that allow a shear margin to coincide with a Röthlisberger channel John D. Platt 1,2, Thibaut Perol, 1, Jenny Suckale
JOURNAL OF GEOPHYSICAL RESEARCH, VOL.???, XXXX, DOI:10.1029/, Determining conditions that allow a shear margin to coincide with a Röthlisberger channel John D. Platt 1,2, Thibaut Perol, 1, Jenny Suckale
BELISSIMA: BELgian Ice Sheet- Shelf Ice Measurements in Antarctica
 BELISSIMA: BELgian Ice Sheet- Shelf Ice Measurements in Antarctica Frank PATTYN 1, Jean-Louis TISON 1, Denis SAMYN 1, Kenichi MATSUOKA², Howard CONWAY², Bryn HUBBARD³ (1)Laboratoire de Glaciologie, DSTE,
BELISSIMA: BELgian Ice Sheet- Shelf Ice Measurements in Antarctica Frank PATTYN 1, Jean-Louis TISON 1, Denis SAMYN 1, Kenichi MATSUOKA², Howard CONWAY², Bryn HUBBARD³ (1)Laboratoire de Glaciologie, DSTE,
Chapter 5. The Differential Forms of the Fundamental Laws
 Chapter 5 The Differential Forms of the Fundamental Laws 1 5.1 Introduction Two primary methods in deriving the differential forms of fundamental laws: Gauss s Theorem: Allows area integrals of the equations
Chapter 5 The Differential Forms of the Fundamental Laws 1 5.1 Introduction Two primary methods in deriving the differential forms of fundamental laws: Gauss s Theorem: Allows area integrals of the equations
Continuum mechanism: Stress and strain
 Continuum mechanics deals with the relation between forces (stress, σ) and deformation (strain, ε), or deformation rate (strain rate, ε). Solid materials, rigid, usually deform elastically, that is the
Continuum mechanics deals with the relation between forces (stress, σ) and deformation (strain, ε), or deformation rate (strain rate, ε). Solid materials, rigid, usually deform elastically, that is the
ACTIVITY II: THE FATE OF THE LARSEN S, A FAMILY OF ANTARCTIC ICE SHELVES
 ACTIVITY II: THE FATE OF THE LARSEN S, A FAMILY OF ANTARCTIC ICE SHELVES Ice Shelves play a critical role in Antarctica, serving as a buffer between the ocean and the continental ice sheet covering the
ACTIVITY II: THE FATE OF THE LARSEN S, A FAMILY OF ANTARCTIC ICE SHELVES Ice Shelves play a critical role in Antarctica, serving as a buffer between the ocean and the continental ice sheet covering the
Rock Rheology GEOL 5700 Physics and Chemistry of the Solid Earth
 Rock Rheology GEOL 5700 Physics and Chemistry of the Solid Earth References: Turcotte and Schubert, Geodynamics, Sections 2.1,-2.4, 2.7, 3.1-3.8, 6.1, 6.2, 6.8, 7.1-7.4. Jaeger and Cook, Fundamentals of
Rock Rheology GEOL 5700 Physics and Chemistry of the Solid Earth References: Turcotte and Schubert, Geodynamics, Sections 2.1,-2.4, 2.7, 3.1-3.8, 6.1, 6.2, 6.8, 7.1-7.4. Jaeger and Cook, Fundamentals of
Simulating a glacier: application to Engabreen
 Utrecht University Institute for Marine and Atmospheric Research Utrecht Bachelor thesis Simulating a glacier: application to Engabreen Supervisors: Carleen Tijm-Reijmer Hans Oerlemans Author: Jesse Reusen
Utrecht University Institute for Marine and Atmospheric Research Utrecht Bachelor thesis Simulating a glacier: application to Engabreen Supervisors: Carleen Tijm-Reijmer Hans Oerlemans Author: Jesse Reusen
( ) = 1005 J kg 1 K 1 ;
 Problem Set 3 1. A parcel of water is added to the ocean surface that is denser (heavier) than any of the waters in the ocean. Suppose the parcel sinks to the ocean bottom; estimate the change in temperature
Problem Set 3 1. A parcel of water is added to the ocean surface that is denser (heavier) than any of the waters in the ocean. Suppose the parcel sinks to the ocean bottom; estimate the change in temperature
Name. 4. The diagram below shows a soil profile formed in an area of granite bedrock. Four different soil horizons, A, B, C, and D, are shown.
 Name 1. In the cross section of the hill shown below, which rock units are probably most resistant to weathering? 4. The diagram below shows a soil profile formed in an area of granite bedrock. Four different
Name 1. In the cross section of the hill shown below, which rock units are probably most resistant to weathering? 4. The diagram below shows a soil profile formed in an area of granite bedrock. Four different
ENIGMA: something that is mysterious, puzzling, or difficult to understand.
 Lecture 12. Attempts to solve the Eccentricity Enigma ENIGMA: something that is mysterious, puzzling, or difficult to understand. Milankovitch forcing glacier responses pre-900,000 yr BP glacier responses
Lecture 12. Attempts to solve the Eccentricity Enigma ENIGMA: something that is mysterious, puzzling, or difficult to understand. Milankovitch forcing glacier responses pre-900,000 yr BP glacier responses
V (r,t) = i ˆ u( x, y,z,t) + ˆ j v( x, y,z,t) + k ˆ w( x, y, z,t)
 IV. DIFFERENTIAL RELATIONS FOR A FLUID PARTICLE This chapter presents the development and application of the basic differential equations of fluid motion. Simplifications in the general equations and common
IV. DIFFERENTIAL RELATIONS FOR A FLUID PARTICLE This chapter presents the development and application of the basic differential equations of fluid motion. Simplifications in the general equations and common
Glaciers Earth 9th Edition Chapter 18 Glaciers: summary in haiku form Key Concepts Glaciers Glaciers Glaciers Glaciers
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Earth 9 th Edition Chapter 18 : summary in haiku form Ten thousand years thence big glaciers began to melt - called "global warming." Key Concepts and types of glaciers.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 Earth 9 th Edition Chapter 18 : summary in haiku form Ten thousand years thence big glaciers began to melt - called "global warming." Key Concepts and types of glaciers.
Glaciers. (Shaping Earth s Surface, Part 6) Science 330 Summer 2005
 Glaciers (Shaping Earth s Surface, Part 6) Science 330 Summer 2005 1 Glaciers Glaciers are parts of two basic cycles Hydrologic cycle Rock cycle Glacier a thick mass of ice that originates on land from
Glaciers (Shaping Earth s Surface, Part 6) Science 330 Summer 2005 1 Glaciers Glaciers are parts of two basic cycles Hydrologic cycle Rock cycle Glacier a thick mass of ice that originates on land from
ESS314. Basics of Geophysical Fluid Dynamics by John Booker and Gerard Roe. Conservation Laws
 ESS314 Basics of Geophysical Fluid Dynamics by John Booker and Gerard Roe Conservation Laws The big differences between fluids and other forms of matter are that they are continuous and they deform internally
ESS314 Basics of Geophysical Fluid Dynamics by John Booker and Gerard Roe Conservation Laws The big differences between fluids and other forms of matter are that they are continuous and they deform internally
A Numerical Model Investigation of the Role of the Glacier Bed in Regulating Grounding Line Retreat of Thwaites Glacier, West Antarctica
 Portland State University PDXScholar Dissertations and Theses Dissertations and Theses Winter 3-20-2017 A Numerical Model Investigation of the Role of the Glacier Bed in Regulating Grounding Line Retreat
Portland State University PDXScholar Dissertations and Theses Dissertations and Theses Winter 3-20-2017 A Numerical Model Investigation of the Role of the Glacier Bed in Regulating Grounding Line Retreat
A Study on Numerical Solution to the Incompressible Navier-Stokes Equation
 A Study on Numerical Solution to the Incompressible Navier-Stokes Equation Zipeng Zhao May 2014 1 Introduction 1.1 Motivation One of the most important applications of finite differences lies in the field
A Study on Numerical Solution to the Incompressible Navier-Stokes Equation Zipeng Zhao May 2014 1 Introduction 1.1 Motivation One of the most important applications of finite differences lies in the field
Dynamic controls on glacier basal motion inferred from surface ice motion
 JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 113,, doi:10.1029/2007jf000925, 2008 Dynamic controls on glacier basal motion inferred from surface ice motion Ian M. Howat, 1 Slawek Tulaczyk, 2 Edwin Waddington,
JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 113,, doi:10.1029/2007jf000925, 2008 Dynamic controls on glacier basal motion inferred from surface ice motion Ian M. Howat, 1 Slawek Tulaczyk, 2 Edwin Waddington,
Chapter 1. Governing Equations of GFD. 1.1 Mass continuity
 Chapter 1 Governing Equations of GFD The fluid dynamical governing equations consist of an equation for mass continuity, one for the momentum budget, and one or more additional equations to account for
Chapter 1 Governing Equations of GFD The fluid dynamical governing equations consist of an equation for mass continuity, one for the momentum budget, and one or more additional equations to account for
2/23/2009. Visualizing Earth Science. Chapter Overview. Deserts and Drylands. Glaciers and Ice Sheets
 Visualizing Earth Science By Z. Merali and B. F. Skinner Chapter 6 Deserts, Glaciers and Ice Sheets Chapter Overview Deserts and Drylands Glaciers and Ice Sheets Deserts Geography Categorization of deserts
Visualizing Earth Science By Z. Merali and B. F. Skinner Chapter 6 Deserts, Glaciers and Ice Sheets Chapter Overview Deserts and Drylands Glaciers and Ice Sheets Deserts Geography Categorization of deserts
Comparison of hybrid schemes for the combination of shallow approximations in numerical simulations of the Antarctic Ice Sheet
 doi:10.5194/tc-11-247-2017 Author(s) 2017. CC Attribution 3.0 License. Comparison of hybrid schemes for the combination of shallow approximations in numerical simulations of the Antarctic Ice Sheet Jorge
doi:10.5194/tc-11-247-2017 Author(s) 2017. CC Attribution 3.0 License. Comparison of hybrid schemes for the combination of shallow approximations in numerical simulations of the Antarctic Ice Sheet Jorge
1 Glaciers and climate
 1 Glaciers and climate 1.1 Equilibrium length For a glacier to be in equilibrium with climate the (integrated) mass balance must be equal to zero. For a glacier of a uniform width and length l this implies
1 Glaciers and climate 1.1 Equilibrium length For a glacier to be in equilibrium with climate the (integrated) mass balance must be equal to zero. For a glacier of a uniform width and length l this implies
Sand Ripple Dynamics on the Inner Shelf
 Sand Ripple Dynamics on the Inner Shelf Donald N. Slinn Department of Civil and Coastal Engineering, University of Florida Gainesville, FL 32611-6590, Phone: (352) 392-9537 x 1431 Fax: (352) 392-3466 E-mail:
Sand Ripple Dynamics on the Inner Shelf Donald N. Slinn Department of Civil and Coastal Engineering, University of Florida Gainesville, FL 32611-6590, Phone: (352) 392-9537 x 1431 Fax: (352) 392-3466 E-mail:
verification, validation, and basal strength in models for the present state of ice sheets
 verification, validation, and basal strength in models for the present state of ice sheets Ed Bueler 1 Constantine Khroulev 2 Andy Aschwanden 3 1 Dept of Mathematics and Statistics, University of Alaska
verification, validation, and basal strength in models for the present state of ice sheets Ed Bueler 1 Constantine Khroulev 2 Andy Aschwanden 3 1 Dept of Mathematics and Statistics, University of Alaska
Insights into ice stream dynamics through modelling their response to tidal forcing
 The Cryosphere, 8, 1763 1775, 214 www.the-cryosphere.net/8/1763/214/ doi:1.5194/tc-8-1763-214 Author(s) 214. CC Attribution 3. License. Insights into ice stream dynamics through modelling their response
The Cryosphere, 8, 1763 1775, 214 www.the-cryosphere.net/8/1763/214/ doi:1.5194/tc-8-1763-214 Author(s) 214. CC Attribution 3. License. Insights into ice stream dynamics through modelling their response
SUPPLEMENTARY INFORMATION
 This section includes additional information for the model parameters as well as the results of a set of sensitivity experiments to illustrate the dependence of the model behavior on different parameter
This section includes additional information for the model parameters as well as the results of a set of sensitivity experiments to illustrate the dependence of the model behavior on different parameter
Cronfa - Swansea University Open Access Repository
 Cronfa - Swansea University Open Access Repository This is an author produced version of a paper published in : Geoscientific Model Development Cronfa URL for this paper: http://cronfa.swan.ac.uk/record/cronfa32207
Cronfa - Swansea University Open Access Repository This is an author produced version of a paper published in : Geoscientific Model Development Cronfa URL for this paper: http://cronfa.swan.ac.uk/record/cronfa32207
