MAXIMA, MINIMA AND POINTS OF INFLEXION
|
|
|
- Magnus Lee
- 6 years ago
- Views:
Transcription
1 Page of 8 MAXIMA, MINIMA AND POINTS OF INFLEXION Introduction 0 M Q S f( x) P I I R I I T 5 7 a 0 b x The diagram shows the graph of y domain a x b. The points Q and S are called local maxima. The points P, R and T are called local minima. x = f ( x) where f ( x) is a continuous function defined on the The points are designated local maxima or local minima to distinguish from the gobal maximum and global minimum. The latter refer to the greatest and least values attained by f ( x) over the domain. Thus in the diagram M is the global maximum and R, in addition to being a local minimum is also the global minimum. At P, Q, R, S and T the tangent to the curve is horizontal, i.e. the gradient of the curve is zero, so that at any local maxima or local minima the following condition holds : dy dx ( x) = f All points at which f ( x) are called stationary points but as shown in the sketch below there are stationary points which are neither local maxima nor local minima.. P dy At P 0 dx = P is in fact an example of a type of point known as a point of inflexion.
2 Page of 8 Other examples of points of inflexion are the points I, I, I and I in the diagram at the top of page. These are the points at which the curve crosses the tangent to the curve as can be seen in the blown up sketch of the curve in the region of I shown below. I To the left of increasing x so that I the gradient, f ( x), decreases with increasing x and to the right increases with I is a local minimum of f ( x). Similarly and so on for I and I. Hence finding the points of inflexion of f( x) local maxima and minima of f ( x) I is a local maximum of f( x) is equivalent to finding the. For this reason we do not consider points of inflexion further in these notes and concentrate solely on the max/min problem. Local Maxima and L P R At P, f ( x) y = f ( x) At L, f ( x) > 0 At R, f ( x) < 0 As x increases from L to R the gradient of the curve decreases or in other words the rate of change of the gradient with respect to x is non-positive. We cannot say that the rate of change of the gradient is strictly negative since, as we shall see, in some cases it is zero at P. But the rate of change of the gradient with respect to x is d f ( x ) = f ( x ) dx From this we can deduce the following:- At a local maximum f( x) and f( x) 0 y = f ( x) At P, f ( x) At L, f ( x) < 0 L P R At R, f ( x) > 0 In this case the gradient is increasing as x increases from L to R from which we can deduce the following:- At a local minimum
3 Page of 8 f( x) and f( x) 0 Thus to identify the local maxima and minima of a given function we proceed as follows:- Find all the stationary points i.e. solve f ( x). At each stationary point evaluate f x ( ), then (i) if f ( x) < 0; Local Maximum (ii) if f ( x) > 0; Local Minimum (iii) if f ( x) ; examine the behaviour of f ( x) in the neighbourhood of the point as Examples shown in the examples below.. Find and classify the stationary points of the following functions and give also the global maximum and global minimum. (i) f ( x) = x x x+ 5, x The stationary points are given by f ( x) = 6x 6x i.e. 6( x )( x + ) i.e. x = and x = f ( ) = 5 and f ( ) = To classify:- f ( x) = x 6 f ( ) = 8> 0 and f ( ) = 8< 0 On the graph of y = f ( x) the point (,-5) is a local minimum the point (-,) is a local maximum To help sketch the graph we note that at x, y = f(0) = 5 x=, y = f( ) = x=, y = f() = 7 Using all the above information we obtain the graph below.
4 Page of 8 0 ( 7, ) (, ) 0 (, ) 0 0 (, 5) The global minimum is at (,-5) and the global maximum at (,7) (ii) f( x) = ( x ) (x+ ), x To find the stationary points f ( x) = ( x ) ( x+ ) + ( x ) ( x ) ( x+ + x ) 0xx ( ) i.e. x and x = f ( 0) = and f () To classify, f ( x) ( x ) + 60x( x ) f ( 0) < 0 f () Thus (0,) is a local maximum To classify the point (,0) we need to examine the behaviour of f ( x) near x =. = so that if x is slightly less than, f ( x) < 0 We have f ( x) 0 x( x ) and if x is slightly greater than, f ( x) > 0. (,0) is a local minimum In addition we have that f and f() = 9 Hence we obtain the sketch of y f( x) = shown below..
5 Page 5 of 8 ( 9, ) y = (x-) (x+) 5 ( 0, ) ( 0.5, 0) Global maximum at (, 9) Global minimum at, 0 and (, 0 ). (iii) f x x x x x x ( ) = 8 6 +, f x = x x x+ = x x x+ ( ) ( ) We can cancel the so that the stationary points are given by x x x+ = 0 To find the roots notice that putting x = satisfies the equation so that x is a factor of the left hand side. This leads to ( x )( x x ) = ( x )( x+ )( x ) The stationary points are x=, x=, x= f () =, f ( ) = 9, f () = 8 To classify them we need the second derivative f x = x x ( ) ( ) From which we find that (,) is a local maximum, (-,-9) is a local minimum, (,8) is a local minimum. To help sketch the curve y = f( x) notice that f(0), f( ), f() = 5 5
6 Page 6 of 8 (, 0) 0 y = x - 8x -6x + x ( 5, ) 0 (, ) ( 8, ) 0 (, 9) 0 Global maximum at (,5) Global minimum at (-,-9) (iv) f ( x) ( x ) ( x ) 5, x = + + < < ( ) f x = x + x x+ = x x + x+ ( ) ( ) ( ) ( ) ( ) ( ) ( ) = + = + The stationary points are x=, x= f () = 5, f ( ) = ( x ) (x 8) ( x ) ( x ) To classify : f ( x) = {( x ) + ( x )( x+ ) } f () and f (-)=6>0 Hence (-,-) is a local minimum. To classify the point (,5) we need to examine the behaviour of f( x) f ( x) = ( x ) ( x+ ) so in the neighbourhood of x =. We have that f ( x) > 0 whether x is slightly bigger than or slightly less than from which we deduce that (,5) is a point of inflexion. To help sketch the curve y = f( x) notice that f (0) = and also As x ±, f( x) +. Hence we obtain the sketch below : 6
7 Page 7 of 8 y = (x - ) (x + ) (, ) 0 (, ) 0 Global maximum is at ( ±, ) Global minimum is at (-,-). A company is producing closed cylindrical containers of volume of m. In order to minimise costs they need the surface area of a container to be as small as possible. Find the required dimemions (radius and height) correct to four decimal places. If we neglect the thickness of the material from which the containers are constructed we may proceed as follows: Let the radius be r m., the height h m., the surface area A m. and the volume V m. A r rh = + and V = r h= r A= r + = r + r r r da = r for stationary points. dr r This gives r = 0.59 = m. d A = + which is positive for the above value of r dr r Hence h = so that Therefore this value of r gives a local minimum of A.In this type of problem we need to ask is it also the global minimum. In this case we can argue as follows. If a function has only one stationary point and that point is a local minimum it is clearly also the global minimum. r.59m. and h= =.080m. r Therefore the required dimensions are Tutorial ( Solutions on page 9.). Find and classify the stationary points of the following functions and sketch their graphs. Give the global maximum and global minimum. (i) f( x) = x x+, x (ii) f( x) = ( x ) ( x+ ) 0, x (iii) f ( x) x x x 60, x = + + < < (iv) f x x x x ( ) = ( ) +, 7
8 Page 8 of 8. A piece of flexible wire of length 0cm is bent into the shape of an isoscelese triangle.what is the maximum area of the triangle. (Hint: Let the two equal sides be x cm long and the third side y cm so that y+ x. Express the area of the triangle in terms of x and y and substitute for y.). A company produces closed rectangular boxes of height h m with a square base and top of side length x m. (a) If each box is to contain a volume of m find the minimum surface area of material used in its construction. (b) If each box is to be constructed from 0m of material find the dimensions which will maximise the volume contained. (Neglect the thickness of the material.) To go to the tutorial solutions directly click here. (To return to this spot after viewing the solutions just use the Back Button). To return to the main list click here. 8
2015 Math Camp Calculus Exam Solution
 015 Math Camp Calculus Exam Solution Problem 1: x = x x +5 4+5 = 9 = 3 1. lim We also accepted ±3, even though it is not according to the prevailing convention 1. x x 4 x+4 =. lim 4 4+4 = 4 0 = 4 0 = We
015 Math Camp Calculus Exam Solution Problem 1: x = x x +5 4+5 = 9 = 3 1. lim We also accepted ±3, even though it is not according to the prevailing convention 1. x x 4 x+4 =. lim 4 4+4 = 4 0 = 4 0 = We
Math 180, Final Exam, Fall 2007 Problem 1 Solution
 Problem Solution. Differentiate with respect to x. Write your answers showing the use of the appropriate techniques. Do not simplify. (a) x 27 x 2/3 (b) (x 2 2x + 2)e x (c) ln(x 2 + 4) (a) Use the Power
Problem Solution. Differentiate with respect to x. Write your answers showing the use of the appropriate techniques. Do not simplify. (a) x 27 x 2/3 (b) (x 2 2x + 2)e x (c) ln(x 2 + 4) (a) Use the Power
One variable optimization
 Università Ca Foscari di Venezia - Dipartimento di Economia - A.A.06-07 Mathematics (Curriculum Economics, Markets and Finance) Luciano Battaia October 9, 06 These notes are a summary of chapter 8 of the
Università Ca Foscari di Venezia - Dipartimento di Economia - A.A.06-07 Mathematics (Curriculum Economics, Markets and Finance) Luciano Battaia October 9, 06 These notes are a summary of chapter 8 of the
EDEXCEL ANALYTICAL METHODS FOR ENGINEERS H1 UNIT 2 - NQF LEVEL 4 OUTCOME 3 - CALCULUS TUTORIAL 2 MAXIMA AND MINIMA
 EDEXCEL ANALYTICAL METHODS FOR ENGINEERS H1 UNIT - NQF LEVEL 4 OUTCOME 3 - CALCULUS TUTORIAL MAXIMA AND MINIMA The calculus: the concept of the limit and continuity; definition of the derivative; derivatives
EDEXCEL ANALYTICAL METHODS FOR ENGINEERS H1 UNIT - NQF LEVEL 4 OUTCOME 3 - CALCULUS TUTORIAL MAXIMA AND MINIMA The calculus: the concept of the limit and continuity; definition of the derivative; derivatives
Solutionbank C1 Edexcel Modular Mathematics for AS and A-Level
 Heinemann Solutionbank: Core Maths C Page of Solutionbank C Exercise A, Question Find the values of x for which f ( x ) = x x is a decreasing function. f ( x ) = x x f ( x ) = x x Find f ( x ) and put
Heinemann Solutionbank: Core Maths C Page of Solutionbank C Exercise A, Question Find the values of x for which f ( x ) = x x is a decreasing function. f ( x ) = x x f ( x ) = x x Find f ( x ) and put
MAT 122 Homework 7 Solutions
 MAT 1 Homework 7 Solutions Section 3.3, Problem 4 For the function w = (t + 1) 100, we take the inside function to be z = t + 1 and the outside function to be z 100. The derivative of the inside function
MAT 1 Homework 7 Solutions Section 3.3, Problem 4 For the function w = (t + 1) 100, we take the inside function to be z = t + 1 and the outside function to be z 100. The derivative of the inside function
MATHEMATICS FOR ENGINEERING TUTORIAL 4 MAX AND MIN THEORY
 MATHEMATICS FOR ENGINEERING TUTORIAL 4 MAX AND MIN THEORY This tutorial is essential pre-requisite material for anyone studying mechanical engineering. This tutorial uses the principle of learning by example.
MATHEMATICS FOR ENGINEERING TUTORIAL 4 MAX AND MIN THEORY This tutorial is essential pre-requisite material for anyone studying mechanical engineering. This tutorial uses the principle of learning by example.
AP Calculus BC Chapter 4 AP Exam Problems A) 4 B) 2 C) 1 D) 0 E) 2 A) 9 B) 12 C) 14 D) 21 E) 40
 Extreme Values in an Interval AP Calculus BC 1. The absolute maximum value of x = f ( x) x x 1 on the closed interval, 4 occurs at A) 4 B) C) 1 D) 0 E). The maximum acceleration attained on the interval
Extreme Values in an Interval AP Calculus BC 1. The absolute maximum value of x = f ( x) x x 1 on the closed interval, 4 occurs at A) 4 B) C) 1 D) 0 E). The maximum acceleration attained on the interval
Exam A. Exam 3. (e) Two critical points; one is a local maximum, the other a local minimum.
 1.(6 pts) The function f(x) = x 3 2x 2 has: Exam A Exam 3 (a) Two critical points; one is a local minimum, the other is neither a local maximum nor a local minimum. (b) Two critical points; one is a local
1.(6 pts) The function f(x) = x 3 2x 2 has: Exam A Exam 3 (a) Two critical points; one is a local minimum, the other is neither a local maximum nor a local minimum. (b) Two critical points; one is a local
Learning Target: I can sketch the graphs of rational functions without a calculator. a. Determine the equation(s) of the asymptotes.
 Learning Target: I can sketch the graphs of rational functions without a calculator Consider the graph of y= f(x), where f(x) = 3x 3 (x+2) 2 a. Determine the equation(s) of the asymptotes. b. Find the
Learning Target: I can sketch the graphs of rational functions without a calculator Consider the graph of y= f(x), where f(x) = 3x 3 (x+2) 2 a. Determine the equation(s) of the asymptotes. b. Find the
Applications of Differentiation
 MathsTrack (NOTE Feb 2013: This is the old version of MathsTrack. New books will be created during 2013 and 2014) Module9 7 Introduction Applications of to Matrices Differentiation y = x(x 1)(x 2) d 2
MathsTrack (NOTE Feb 2013: This is the old version of MathsTrack. New books will be created during 2013 and 2014) Module9 7 Introduction Applications of to Matrices Differentiation y = x(x 1)(x 2) d 2
Differentiation Practice Questions
 A. Chain, product and quotient rule 1. Differentiate with respect to x Differentiation Practice Questions 3 4x e sin x Answers:...... (Total 4 marks). Differentiate with respect to x: (x + l). 1n(3x 1).
A. Chain, product and quotient rule 1. Differentiate with respect to x Differentiation Practice Questions 3 4x e sin x Answers:...... (Total 4 marks). Differentiate with respect to x: (x + l). 1n(3x 1).
2009 A-level Maths Tutor All Rights Reserved
 2 This book is under copyright to A-level Maths Tutor. However, it may be distributed freely provided it is not sold for profit. Contents the derivative formula 3 tangents & normals 7 maxima & minima 10
2 This book is under copyright to A-level Maths Tutor. However, it may be distributed freely provided it is not sold for profit. Contents the derivative formula 3 tangents & normals 7 maxima & minima 10
Taylor Series and stationary points
 Chapter 5 Taylor Series and stationary points 5.1 Taylor Series The surface z = f(x, y) and its derivatives can give a series approximation for f(x, y) about some point (x 0, y 0 ) as illustrated in Figure
Chapter 5 Taylor Series and stationary points 5.1 Taylor Series The surface z = f(x, y) and its derivatives can give a series approximation for f(x, y) about some point (x 0, y 0 ) as illustrated in Figure
Sections 4.1 & 4.2: Using the Derivative to Analyze Functions
 Sections 4.1 & 4.2: Using the Derivative to Analyze Functions f (x) indicates if the function is: Increasing or Decreasing on certain intervals. Critical Point c is where f (c) = 0 (tangent line is horizontal),
Sections 4.1 & 4.2: Using the Derivative to Analyze Functions f (x) indicates if the function is: Increasing or Decreasing on certain intervals. Critical Point c is where f (c) = 0 (tangent line is horizontal),
Applications of Derivatives
 Applications of Derivatives Extrema on an Interval Objective: Understand the definition of extrema of a function on an interval. Understand the definition of relative extrema of a function on an open interval.
Applications of Derivatives Extrema on an Interval Objective: Understand the definition of extrema of a function on an interval. Understand the definition of relative extrema of a function on an open interval.
x x implies that f x f x.
 Section 3.3 Intervals of Increase and Decrease and Extreme Values Let f be a function whose domain includes an interval I. We say that f is increasing on I if for every two numbers x 1, x 2 in I, x x implies
Section 3.3 Intervals of Increase and Decrease and Extreme Values Let f be a function whose domain includes an interval I. We say that f is increasing on I if for every two numbers x 1, x 2 in I, x x implies
Math 241 Final Exam, Spring 2013
 Math 241 Final Exam, Spring 2013 Name: Section number: Instructor: Read all of the following information before starting the exam. Question Points Score 1 5 2 5 3 12 4 10 5 17 6 15 7 6 8 12 9 12 10 14
Math 241 Final Exam, Spring 2013 Name: Section number: Instructor: Read all of the following information before starting the exam. Question Points Score 1 5 2 5 3 12 4 10 5 17 6 15 7 6 8 12 9 12 10 14
Integration - Past Edexcel Exam Questions
 Integration - Past Edexcel Exam Questions 1. (a) Given that y = 5x 2 + 7x + 3, find i. - ii. - (b) ( 1 + 3 ) x 1 x dx. [4] 2. Question 2b - January 2005 2. The gradient of the curve C is given by The point
Integration - Past Edexcel Exam Questions 1. (a) Given that y = 5x 2 + 7x + 3, find i. - ii. - (b) ( 1 + 3 ) x 1 x dx. [4] 2. Question 2b - January 2005 2. The gradient of the curve C is given by The point
In order to master the techniques explained here it is vital that you undertake plenty of practice exercises so that they become second nature.
 Maima and minima In this unit we show how differentiation can be used to find the maimum and minimum values of a function. Because the derivative provides information about the gradient or slope of the
Maima and minima In this unit we show how differentiation can be used to find the maimum and minimum values of a function. Because the derivative provides information about the gradient or slope of the
APPLICATIONS OF DERIVATIVES
 9 APPLICATIONS OF DERIVATIVES In the previous lesson, we have learnt that the slope of a line is the tangent of the angle which the line makes with the positive direction of x-axis. It is denoted by the
9 APPLICATIONS OF DERIVATIVES In the previous lesson, we have learnt that the slope of a line is the tangent of the angle which the line makes with the positive direction of x-axis. It is denoted by the
We saw in the previous lectures that continuity and differentiability help to understand some aspects of a
 Module 3 : Differentiation and Mean Value Theorems Lecture 9 : Roll's theorem and Mean Value Theorem Objectives In this section you will learn the following : Roll's theorem Mean Value Theorem Applications
Module 3 : Differentiation and Mean Value Theorems Lecture 9 : Roll's theorem and Mean Value Theorem Objectives In this section you will learn the following : Roll's theorem Mean Value Theorem Applications
WJEC LEVEL 2 CERTIFICATE 9550/01 ADDITIONAL MATHEMATICS
 Surname Centre Number Candidate Number Other Names 0 WJEC LEVEL 2 CERTIFICATE 9550/01 ADDITIONAL MATHEMATICS A.M. MONDAY, 22 June 2015 2 hours 30 minutes S15-9550-01 For s use ADDITIONAL MATERIALS A calculator
Surname Centre Number Candidate Number Other Names 0 WJEC LEVEL 2 CERTIFICATE 9550/01 ADDITIONAL MATHEMATICS A.M. MONDAY, 22 June 2015 2 hours 30 minutes S15-9550-01 For s use ADDITIONAL MATERIALS A calculator
5.3. Exercises on the curve analysis of polynomial functions
 .. Exercises on the curve analysis of polynomial functions Exercise : Curve analysis Examine the following functions on symmetry, x- and y-intercepts, extrema and inflexion points. Draw their graphs including
.. Exercises on the curve analysis of polynomial functions Exercise : Curve analysis Examine the following functions on symmetry, x- and y-intercepts, extrema and inflexion points. Draw their graphs including
Suppose that f is continuous on [a, b] and differentiable on (a, b). Then
![Suppose that f is continuous on [a, b] and differentiable on (a, b). Then Suppose that f is continuous on [a, b] and differentiable on (a, b). Then](/thumbs/74/71325034.jpg) Lectures 1/18 Derivatives and Graphs When we have a picture of the graph of a function f(x), we can make a picture of the derivative f (x) using the slopes of the tangents to the graph of f. In this section
Lectures 1/18 Derivatives and Graphs When we have a picture of the graph of a function f(x), we can make a picture of the derivative f (x) using the slopes of the tangents to the graph of f. In this section
SUMMER KNOWHOW STUDY AND LEARNING CENTRE
 SUMMER KNOWHOW STUDY AND LEARNING CENTRE Differential Calculus 2 Contents Limits..5 Gradients, Tangents and Derivatives.6 Differentiation from First Principles.8 Rules for Differentiation..10 Chain Rule.12
SUMMER KNOWHOW STUDY AND LEARNING CENTRE Differential Calculus 2 Contents Limits..5 Gradients, Tangents and Derivatives.6 Differentiation from First Principles.8 Rules for Differentiation..10 Chain Rule.12
MA202 Calculus III Fall, 2009 Laboratory Exploration 2: Gradients, Directional Derivatives, Stationary Points
 MA0 Calculus III Fall, 009 Laboratory Exploration : Gradients, Directional Derivatives, Stationary Points Introduction: This lab deals with several topics from Chapter. Some of the problems should be done
MA0 Calculus III Fall, 009 Laboratory Exploration : Gradients, Directional Derivatives, Stationary Points Introduction: This lab deals with several topics from Chapter. Some of the problems should be done
Math 1314 Lesson 24 Maxima and Minima of Functions of Several Variables
 Math 1314 Lesson 24 Maxima and Minima of Functions of Several Variables We learned to find the maxima and minima of a function of a single variable earlier in the course We had a second derivative test
Math 1314 Lesson 24 Maxima and Minima of Functions of Several Variables We learned to find the maxima and minima of a function of a single variable earlier in the course We had a second derivative test
APPLICATION OF DERIVATIVES
 94 APPLICATION OF DERIVATIVES Chapter 6 With the Calculus as a key, Mathematics can be successfully applied to the explanation of the course of Nature. WHITEHEAD 6. Introduction In Chapter 5, we have learnt
94 APPLICATION OF DERIVATIVES Chapter 6 With the Calculus as a key, Mathematics can be successfully applied to the explanation of the course of Nature. WHITEHEAD 6. Introduction In Chapter 5, we have learnt
Calculus Example Exam Solutions
 Calculus Example Exam Solutions. Limits (8 points, 6 each) Evaluate the following limits: p x 2 (a) lim x 4 We compute as follows: lim p x 2 x 4 p p x 2 x +2 x 4 p x +2 x 4 (x 4)( p x + 2) p x +2 = p 4+2
Calculus Example Exam Solutions. Limits (8 points, 6 each) Evaluate the following limits: p x 2 (a) lim x 4 We compute as follows: lim p x 2 x 4 p p x 2 x +2 x 4 p x +2 x 4 (x 4)( p x + 2) p x +2 = p 4+2
cos t 2 sin 2t (vi) y = cosh t sinh t (vii) y sin x 2 = x sin y 2 (viii) xy = cot(xy) (ix) 1 + x = sin(xy 2 ) (v) g(t) =
 MATH1003 REVISION 1. Differentiate the following functions, simplifying your answers when appropriate: (i) f(x) = (x 3 2) tan x (ii) y = (3x 5 1) 6 (iii) y 2 = x 2 3 (iv) y = ln(ln(7 + x)) e 5x3 (v) g(t)
MATH1003 REVISION 1. Differentiate the following functions, simplifying your answers when appropriate: (i) f(x) = (x 3 2) tan x (ii) y = (3x 5 1) 6 (iii) y 2 = x 2 3 (iv) y = ln(ln(7 + x)) e 5x3 (v) g(t)
MAXIMA AND MINIMA CHAPTER 7.1 INTRODUCTION 7.2 CONCEPT OF LOCAL MAXIMA AND LOCAL MINIMA
 CHAPTER 7 MAXIMA AND MINIMA 7.1 INTRODUCTION The notion of optimizing functions is one of the most important application of calculus used in almost every sphere of life including geometry, business, trade,
CHAPTER 7 MAXIMA AND MINIMA 7.1 INTRODUCTION The notion of optimizing functions is one of the most important application of calculus used in almost every sphere of life including geometry, business, trade,
Math 180, Final Exam, Fall 2012 Problem 1 Solution
 Math 80, Final Exam, Fall 0 Problem Solution. Find the derivatives of the following functions: (a) ln(ln(x)) (b) x 6 + sin(x) e x (c) tan(x ) + cot(x ) (a) We evaluate the derivative using the Chain Rule.
Math 80, Final Exam, Fall 0 Problem Solution. Find the derivatives of the following functions: (a) ln(ln(x)) (b) x 6 + sin(x) e x (c) tan(x ) + cot(x ) (a) We evaluate the derivative using the Chain Rule.
Workbook for Calculus I
 Workbook for Calculus I By Hüseyin Yüce New York 2007 1 Functions 1.1 Four Ways to Represent a Function 1. Find the domain and range of the function f(x) = 1 + x + 1 and sketch its graph. y 3 2 1-3 -2-1
Workbook for Calculus I By Hüseyin Yüce New York 2007 1 Functions 1.1 Four Ways to Represent a Function 1. Find the domain and range of the function f(x) = 1 + x + 1 and sketch its graph. y 3 2 1-3 -2-1
d (5 cos 2 x) = 10 cos x sin x x x d y = (cos x)(e d (x 2 + 1) 2 d (ln(3x 1)) = (3) (M1)(M1) (C2) Differentiation Practice Answers 1.
 . (a) y x ( x) Differentiation Practice Answers dy ( x) ( ) (A)(A) (C) Note: Award (A) for each element, to a maximum of [ marks]. y e sin x d y (cos x)(e sin x ) (A)(A) (C) Note: Award (A) for each element.
. (a) y x ( x) Differentiation Practice Answers dy ( x) ( ) (A)(A) (C) Note: Award (A) for each element, to a maximum of [ marks]. y e sin x d y (cos x)(e sin x ) (A)(A) (C) Note: Award (A) for each element.
MATH 135 Calculus 1 Solutions/Answers for Exam 3 Practice Problems November 18, 2016
 MATH 35 Calculus Solutions/Answers for Exam 3 Practice Problems November 8, 206 I. Find the indicated derivative(s) and simplify. (A) ( y = ln(x) x 7 4 ) x Solution: By the product rule and the derivative
MATH 35 Calculus Solutions/Answers for Exam 3 Practice Problems November 8, 206 I. Find the indicated derivative(s) and simplify. (A) ( y = ln(x) x 7 4 ) x Solution: By the product rule and the derivative
11.1 Absolute Maximum/Minimum: Definition:
 Module 4 : Local / Global Maximum / Minimum and Curve Sketching Lecture 11 : Absolute Maximum / Minimum [Section 111] Objectives In this section you will learn the following : How to find points of absolute
Module 4 : Local / Global Maximum / Minimum and Curve Sketching Lecture 11 : Absolute Maximum / Minimum [Section 111] Objectives In this section you will learn the following : How to find points of absolute
Candidates are expected to have available a calculator. Only division by (x + a) or (x a) will be required.
 Revision Checklist Unit C2: Core Mathematics 2 Unit description Algebra and functions; coordinate geometry in the (x, y) plane; sequences and series; trigonometry; exponentials and logarithms; differentiation;
Revision Checklist Unit C2: Core Mathematics 2 Unit description Algebra and functions; coordinate geometry in the (x, y) plane; sequences and series; trigonometry; exponentials and logarithms; differentiation;
Calculus 221 worksheet
 Calculus 221 worksheet Graphing A function has a global maximum at some a in its domain if f(x) f(a) for all other x in the domain of f. Global maxima are sometimes also called absolute maxima. A function
Calculus 221 worksheet Graphing A function has a global maximum at some a in its domain if f(x) f(a) for all other x in the domain of f. Global maxima are sometimes also called absolute maxima. A function
Differentiation 2. The METRIC Project, Imperial College. Imperial College of Science Technology and Medicine, 1996.
 Differentiation 2 The METRIC Project, Imperial College. Imperial College of Science Technology and Medicine, 1996. 1 Launch Mathematica. Type
Differentiation 2 The METRIC Project, Imperial College. Imperial College of Science Technology and Medicine, 1996. 1 Launch Mathematica. Type
14 Increasing and decreasing functions
 14 Increasing and decreasing functions 14.1 Sketching derivatives READING Read Section 3.2 of Rogawski Reading Recall, f (a) is the gradient of the tangent line of f(x) at x = a. We can use this fact to
14 Increasing and decreasing functions 14.1 Sketching derivatives READING Read Section 3.2 of Rogawski Reading Recall, f (a) is the gradient of the tangent line of f(x) at x = a. We can use this fact to
4.1 Analysis of functions I: Increase, decrease and concavity
 4.1 Analysis of functions I: Increase, decrease and concavity Definition Let f be defined on an interval and let x 1 and x 2 denote points in that interval. a) f is said to be increasing on the interval
4.1 Analysis of functions I: Increase, decrease and concavity Definition Let f be defined on an interval and let x 1 and x 2 denote points in that interval. a) f is said to be increasing on the interval
Math 140 Final Sample A Solutions. Tyrone Crisp
 Math 4 Final Sample A Solutions Tyrone Crisp (B) Direct substitution gives, so the limit is infinite. When is close to, but greater than,, the numerator is negative while the denominator is positive. So
Math 4 Final Sample A Solutions Tyrone Crisp (B) Direct substitution gives, so the limit is infinite. When is close to, but greater than,, the numerator is negative while the denominator is positive. So
Solving related rates problems
 Solving related rates problems 1 Draw a diagram 2 Assign symbols to all quantities that are functions of time 3 Express given information and the required rate in terms of derivatives 4 Write down a relation
Solving related rates problems 1 Draw a diagram 2 Assign symbols to all quantities that are functions of time 3 Express given information and the required rate in terms of derivatives 4 Write down a relation
Section 2.1 : Solution Curves without a Solution. - allow us to sketch solution curves to first-order ODEs. dy dx. = f (x, y) (1)
 Section 2.1 : Solution Curves without a Solution Direction Fields (Slope Fields) - allow us to sketch solution curves to first-order ODEs. General first-order ODE: dy dx = f (x, y) (1) Let y = y(x) be
Section 2.1 : Solution Curves without a Solution Direction Fields (Slope Fields) - allow us to sketch solution curves to first-order ODEs. General first-order ODE: dy dx = f (x, y) (1) Let y = y(x) be
MAXIMA AND MINIMA - 2
 MAXIMA AND MINIMA - GREATEST AND LEAST VALUES Definition: Let f be a function defined on a set A and l f( A ). Then l is said to be (i) the maimum value or the greatest value of f in A if f( ) l A. (ii)
MAXIMA AND MINIMA - GREATEST AND LEAST VALUES Definition: Let f be a function defined on a set A and l f( A ). Then l is said to be (i) the maimum value or the greatest value of f in A if f( ) l A. (ii)
Please do not start working until instructed to do so. You have 50 minutes. You must show your work to receive full credit. Calculators are OK.
 Loyola University Chicago Math 131, Section 009, Fall 2008 Midterm 2 Name (print): Signature: Please do not start working until instructed to do so. You have 50 minutes. You must show your work to receive
Loyola University Chicago Math 131, Section 009, Fall 2008 Midterm 2 Name (print): Signature: Please do not start working until instructed to do so. You have 50 minutes. You must show your work to receive
Department of Mathematics
 Department of Mathematics TIME: Hours Setter: JH/CF DATE: 4 July 017 GRADE 1 PRELIM EXAMINATION MATHEMATICS: PAPER I Total marks: 150 Moderator: DAS Name of student: PLEASE READ THE FOLLOWING INSTRUCTIONS
Department of Mathematics TIME: Hours Setter: JH/CF DATE: 4 July 017 GRADE 1 PRELIM EXAMINATION MATHEMATICS: PAPER I Total marks: 150 Moderator: DAS Name of student: PLEASE READ THE FOLLOWING INSTRUCTIONS
CURVE SKETCHING M.K. HOME TUITION. Mathematics Revision Guides Level: AS / A Level. AQA : C1 Edexcel: C1 OCR: C1 OCR MEI: C1
 Mathematics Revision Guides Curve Sketching Page 1 of 11 M.K. HOME TUITION Mathematics Revision Guides Level: AS / A Level AQA : C1 Edexcel: C1 OCR: C1 OCR MEI: C1 CURVE SKETCHING Version :.1 Date: 03-08-007
Mathematics Revision Guides Curve Sketching Page 1 of 11 M.K. HOME TUITION Mathematics Revision Guides Level: AS / A Level AQA : C1 Edexcel: C1 OCR: C1 OCR MEI: C1 CURVE SKETCHING Version :.1 Date: 03-08-007
(c) Find the gradient of the graph of f(x) at the point where x = 1. (2) The graph of f(x) has a local maximum point, M, and a local minimum point, N.
 Calculus Review Packet 1. Consider the function f() = 3 3 2 24 + 30. Write down f(0). Find f (). Find the gradient of the graph of f() at the point where = 1. The graph of f() has a local maimum point,
Calculus Review Packet 1. Consider the function f() = 3 3 2 24 + 30. Write down f(0). Find f (). Find the gradient of the graph of f() at the point where = 1. The graph of f() has a local maimum point,
8/6/2010 Assignment Previewer
 Week 9 Friday Homework (32849) Question 23456789234567892. Question DetailsSCalcET6 4.2.AE.3. [29377] EXAMPLE 3 To illustrate the Mean Value Theorem with a specific function, let's consider f(x) = 5x 3
Week 9 Friday Homework (32849) Question 23456789234567892. Question DetailsSCalcET6 4.2.AE.3. [29377] EXAMPLE 3 To illustrate the Mean Value Theorem with a specific function, let's consider f(x) = 5x 3
Applied Calculus I Practice Final Exam
 AMS 151 (Fall, 2009) Applied Calculus I Practice Final Exam Joe Mitchell IN ORDER TO RECEIVE FULL CREDIT, YOU MUST SHOW YOUR WORK AND GIVE YOUR REASONING. NO CREDIT WILL BE GIVEN FOR A NUMERICAL ANSWER
AMS 151 (Fall, 2009) Applied Calculus I Practice Final Exam Joe Mitchell IN ORDER TO RECEIVE FULL CREDIT, YOU MUST SHOW YOUR WORK AND GIVE YOUR REASONING. NO CREDIT WILL BE GIVEN FOR A NUMERICAL ANSWER
1,3. f x x f x x. Lim. Lim. Lim. Lim Lim. y 13x b b 10 b So the equation of the tangent line is y 13x
 1.5 Topics: The Derivative lutions 1. Use the limit definition of derivative (the one with x in it) to find f x given f x 4x 5x 6 4 x x 5 x x 6 4x 5x 6 f x x f x f x x0 x x0 x xx x x x x x 4 5 6 4 5 6
1.5 Topics: The Derivative lutions 1. Use the limit definition of derivative (the one with x in it) to find f x given f x 4x 5x 6 4 x x 5 x x 6 4x 5x 6 f x x f x f x x0 x x0 x xx x x x x x 4 5 6 4 5 6
Higher Mathematics Course Notes
 Higher Mathematics Course Notes Equation of a Line (i) Collinearity: (ii) Gradient: If points are collinear then they lie on the same straight line. i.e. to show that A, B and C are collinear, show that
Higher Mathematics Course Notes Equation of a Line (i) Collinearity: (ii) Gradient: If points are collinear then they lie on the same straight line. i.e. to show that A, B and C are collinear, show that
Universidad Carlos III de Madrid
 Universidad Carlos III de Madrid Question 1 3 4 5 6 Total Grade Economics Department Final Exam, Mathematics I January 14, 011 Total length: hours. SURNAME: NAME: DNI: Degree: Group: { 4(x 4) if 3 x 4
Universidad Carlos III de Madrid Question 1 3 4 5 6 Total Grade Economics Department Final Exam, Mathematics I January 14, 011 Total length: hours. SURNAME: NAME: DNI: Degree: Group: { 4(x 4) if 3 x 4
Math 180, Exam 2, Spring 2013 Problem 1 Solution
 Math 80, Eam, Spring 0 Problem Solution. Find the derivative of each function below. You do not need to simplify your answers. (a) tan ( + cos ) (b) / (logarithmic differentiation may be useful) (c) +
Math 80, Eam, Spring 0 Problem Solution. Find the derivative of each function below. You do not need to simplify your answers. (a) tan ( + cos ) (b) / (logarithmic differentiation may be useful) (c) +
MATH 115 SECOND MIDTERM
 MATH 115 SECOND MIDTERM March 31, 2009 NAME: SOLUTIONS INSTRUCTOR: SECTION NUMBER: 1. Do not open this exam until you are told to begin. 2. This exam has 9 pages including this cover. There are 9 questions.
MATH 115 SECOND MIDTERM March 31, 2009 NAME: SOLUTIONS INSTRUCTOR: SECTION NUMBER: 1. Do not open this exam until you are told to begin. 2. This exam has 9 pages including this cover. There are 9 questions.
y2 + 4y - 5 c a + b 27 i C) ) (16, ) B) (16 3 3, )
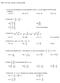 MAT 107 Final, Version A, Spring 2008 1) If (4, 4) is the endpoint of a line segment, and (2, 1) is its midpoint, find the other endpoint. A) (0, 7) B) (-2, 0) C) (8, 10) D) (0, -2) 2) Solve for x: A)
MAT 107 Final, Version A, Spring 2008 1) If (4, 4) is the endpoint of a line segment, and (2, 1) is its midpoint, find the other endpoint. A) (0, 7) B) (-2, 0) C) (8, 10) D) (0, -2) 2) Solve for x: A)
MATH 18.01, FALL PROBLEM SET # 6 SOLUTIONS
 MATH 181, FALL 17 - PROBLEM SET # 6 SOLUTIONS Part II (5 points) 1 (Thurs, Oct 6; Second Fundamental Theorem; + + + + + = 16 points) Let sinc(x) denote the sinc function { 1 if x =, sinc(x) = sin x if
MATH 181, FALL 17 - PROBLEM SET # 6 SOLUTIONS Part II (5 points) 1 (Thurs, Oct 6; Second Fundamental Theorem; + + + + + = 16 points) Let sinc(x) denote the sinc function { 1 if x =, sinc(x) = sin x if
DEPARTMENT OF MATHEMATICS
 DEPARTMENT OF MATHEMATICS AS level Mathematics Core mathematics 2 - C2 2015-2016 Name: Page C2 workbook contents Algebra Differentiation Integration Coordinate Geometry Logarithms Geometric series Series
DEPARTMENT OF MATHEMATICS AS level Mathematics Core mathematics 2 - C2 2015-2016 Name: Page C2 workbook contents Algebra Differentiation Integration Coordinate Geometry Logarithms Geometric series Series
Chapter 3: Inequalities, Lines and Circles, Introduction to Functions
 QUIZ AND TEST INFORMATION: The material in this chapter is on Quiz 3 and Exam 2. You should complete at least one attempt of Quiz 3 before taking Exam 2. This material is also on the final exam and used
QUIZ AND TEST INFORMATION: The material in this chapter is on Quiz 3 and Exam 2. You should complete at least one attempt of Quiz 3 before taking Exam 2. This material is also on the final exam and used
Calculus I: Practice Midterm II
 Calculus I: Practice Mierm II April 3, 2015 Name: Write your solutions in the space provided. Continue on the back for more space. Show your work unless asked otherwise. Partial credit will be given for
Calculus I: Practice Mierm II April 3, 2015 Name: Write your solutions in the space provided. Continue on the back for more space. Show your work unless asked otherwise. Partial credit will be given for
Multiple Choice. at the point where x = 0 and y = 1 on the curve
 Multiple Choice 1.(6 pts.) A particle is moving in a straight line along a horizontal axis with a position function given by s(t) = t 3 12t, where distance is measured in feet and time is measured in seconds.
Multiple Choice 1.(6 pts.) A particle is moving in a straight line along a horizontal axis with a position function given by s(t) = t 3 12t, where distance is measured in feet and time is measured in seconds.
DEPARTMENT OF MATHEMATICS
 DEPARTMENT OF MATHEMATICS AS level Mathematics Core mathematics 1 C1 2015-2016 Name: Page C1 workbook contents Indices and Surds Simultaneous equations Quadratics Inequalities Graphs Arithmetic series
DEPARTMENT OF MATHEMATICS AS level Mathematics Core mathematics 1 C1 2015-2016 Name: Page C1 workbook contents Indices and Surds Simultaneous equations Quadratics Inequalities Graphs Arithmetic series
Chapter 6 Overview: Applications of Derivatives
 Chapter 6 Overview: Applications of Derivatives There are two main contets for derivatives: graphing and motion. In this chapter, we will consider the graphical applications of the derivative. Much of
Chapter 6 Overview: Applications of Derivatives There are two main contets for derivatives: graphing and motion. In this chapter, we will consider the graphical applications of the derivative. Much of
Solutionbank Edexcel AS and A Level Modular Mathematics
 Page of Exercise A, Question The curve C, with equation y = x ln x, x > 0, has a stationary point P. Find, in terms of e, the coordinates of P. (7) y = x ln x, x > 0 Differentiate as a product: = x + x
Page of Exercise A, Question The curve C, with equation y = x ln x, x > 0, has a stationary point P. Find, in terms of e, the coordinates of P. (7) y = x ln x, x > 0 Differentiate as a product: = x + x
( ) 9 b) y = x x c) y = (sin x) 7 x d) y = ( x ) cos x
 NYC College of Technology, CUNY Mathematics Department Spring 05 MAT 75 Final Eam Review Problems Revised by Professor Africk Spring 05, Prof. Kostadinov, Fall 0, Fall 0, Fall 0, Fall 0, Fall 00 # Evaluate
NYC College of Technology, CUNY Mathematics Department Spring 05 MAT 75 Final Eam Review Problems Revised by Professor Africk Spring 05, Prof. Kostadinov, Fall 0, Fall 0, Fall 0, Fall 0, Fall 00 # Evaluate
JUST THE MATHS UNIT NUMBER DIFFERENTIATION APPLICATIONS 2 (Local maxima and local minima) & (Points of inflexion) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 11.2 DIFFERENTIATIN APPLICATINS 2 (Local maxima and local minima) & (Points of inflexion) b A.J.Hobson 11.2.1 Introduction 11.2.2 Local maxima 11.2.3 Local minima 11.2.4 Points
JUST THE MATHS UNIT NUMBER 11.2 DIFFERENTIATIN APPLICATINS 2 (Local maxima and local minima) & (Points of inflexion) b A.J.Hobson 11.2.1 Introduction 11.2.2 Local maxima 11.2.3 Local minima 11.2.4 Points
3.1 ANALYSIS OF FUNCTIONS I INCREASE, DECREASE, AND CONCAVITY
 MATH00 (Calculus).1 ANALYSIS OF FUNCTIONS I INCREASE, DECREASE, AND CONCAVITY Name Group No. KEYWORD: increasing, decreasing, constant, concave up, concave down, and inflection point Eample 1. Match the
MATH00 (Calculus).1 ANALYSIS OF FUNCTIONS I INCREASE, DECREASE, AND CONCAVITY Name Group No. KEYWORD: increasing, decreasing, constant, concave up, concave down, and inflection point Eample 1. Match the
7a3 2. (c) πa 3 (d) πa 3 (e) πa3
 1.(6pts) Find the integral x, y, z d S where H is the part of the upper hemisphere of H x 2 + y 2 + z 2 = a 2 above the plane z = a and the normal points up. ( 2 π ) Useful Facts: cos = 1 and ds = ±a sin
1.(6pts) Find the integral x, y, z d S where H is the part of the upper hemisphere of H x 2 + y 2 + z 2 = a 2 above the plane z = a and the normal points up. ( 2 π ) Useful Facts: cos = 1 and ds = ±a sin
Math Exam 03 Review
 Math 10350 Exam 03 Review 1. The statement: f(x) is increasing on a < x < b. is the same as: 1a. f (x) is on a < x < b. 2. The statement: f (x) is negative on a < x < b. is the same as: 2a. f(x) is on
Math 10350 Exam 03 Review 1. The statement: f(x) is increasing on a < x < b. is the same as: 1a. f (x) is on a < x < b. 2. The statement: f (x) is negative on a < x < b. is the same as: 2a. f(x) is on
c) xy 3 = cos(7x +5y), y 0 = y3 + 7 sin(7x +5y) 3xy sin(7x +5y) d) xe y = sin(xy), y 0 = ey + y cos(xy) x(e y cos(xy)) e) y = x ln(3x + 5), y 0
 Some Math 35 review problems With answers 2/6/2005 The following problems are based heavily on problems written by Professor Stephen Greenfield for his Math 35 class in spring 2005. His willingness to
Some Math 35 review problems With answers 2/6/2005 The following problems are based heavily on problems written by Professor Stephen Greenfield for his Math 35 class in spring 2005. His willingness to
Partial Derivatives. w = f(x, y, z).
 Partial Derivatives 1 Functions of Several Variables So far we have focused our attention of functions of one variable. These functions model situations in which a variable depends on another independent
Partial Derivatives 1 Functions of Several Variables So far we have focused our attention of functions of one variable. These functions model situations in which a variable depends on another independent
x n+1 = ( x n + ) converges, then it converges to α. [2]
![x n+1 = ( x n + ) converges, then it converges to α. [2] x n+1 = ( x n + ) converges, then it converges to α. [2]](/thumbs/92/110299841.jpg) 1 A Level - Mathematics P 3 ITERATION ( With references and answers) [ Numerical Solution of Equation] Q1. The equation x 3 - x 2 6 = 0 has one real root, denoted by α. i) Find by calculation the pair
1 A Level - Mathematics P 3 ITERATION ( With references and answers) [ Numerical Solution of Equation] Q1. The equation x 3 - x 2 6 = 0 has one real root, denoted by α. i) Find by calculation the pair
MATH Midterm 1 Sample 4
 1. (15 marks) (a) (4 marks) Given the function: f(x, y) = arcsin x 2 + y, find its first order partial derivatives at the point (0, 3). Simplify your answers. Solution: Compute the first order partial
1. (15 marks) (a) (4 marks) Given the function: f(x, y) = arcsin x 2 + y, find its first order partial derivatives at the point (0, 3). Simplify your answers. Solution: Compute the first order partial
The region enclosed by the curve of f and the x-axis is rotated 360 about the x-axis. Find the volume of the solid formed.
 Section A ln. Let g() =, for > 0. ln Use the quotient rule to show that g ( ). 3 (b) The graph of g has a maimum point at A. Find the -coordinate of A. (Total 7 marks) 6. Let h() =. Find h (0). cos 3.
Section A ln. Let g() =, for > 0. ln Use the quotient rule to show that g ( ). 3 (b) The graph of g has a maimum point at A. Find the -coordinate of A. (Total 7 marks) 6. Let h() =. Find h (0). cos 3.
AP Calculus. Analyzing a Function Based on its Derivatives
 AP Calculus Analyzing a Function Based on its Derivatives Student Handout 016 017 EDITION Click on the following link or scan the QR code to complete the evaluation for the Study Session https://www.surveymonkey.com/r/s_sss
AP Calculus Analyzing a Function Based on its Derivatives Student Handout 016 017 EDITION Click on the following link or scan the QR code to complete the evaluation for the Study Session https://www.surveymonkey.com/r/s_sss
SOLUTIONS FOR PRACTICE FINAL EXAM
 SOLUTIONS FOR PRACTICE FINAL EXAM ANDREW J. BLUMBERG. Solutions () Short answer questions: (a) State the mean value theorem. Proof. The mean value theorem says that if f is continuous on (a, b) and differentiable
SOLUTIONS FOR PRACTICE FINAL EXAM ANDREW J. BLUMBERG. Solutions () Short answer questions: (a) State the mean value theorem. Proof. The mean value theorem says that if f is continuous on (a, b) and differentiable
APPLICATIONS OF DIFFERENTIATION
 4 APPLICATIONS OF DIFFERENTIATION APPLICATIONS OF DIFFERENTIATION Many applications of calculus depend on our ability to deduce facts about a function f from information concerning its derivatives. APPLICATIONS
4 APPLICATIONS OF DIFFERENTIATION APPLICATIONS OF DIFFERENTIATION Many applications of calculus depend on our ability to deduce facts about a function f from information concerning its derivatives. APPLICATIONS
TIME TRIAL 4 H2 MATHEMATICS 9758 PAPER 1
 TIME TRIAL H MATHEMATICS 9758 PAPER Additional Materials: Writing papers Duration: 3 Hours MF6 DO NOT OPEN THIS BOOKLET UNTIL YOU ARE TOLD TO DO SO READ THESE INSTRUCTIONS FIRST Write in dark blue or black
TIME TRIAL H MATHEMATICS 9758 PAPER Additional Materials: Writing papers Duration: 3 Hours MF6 DO NOT OPEN THIS BOOKLET UNTIL YOU ARE TOLD TO DO SO READ THESE INSTRUCTIONS FIRST Write in dark blue or black
Math 16A Second Midterm 6 Nov NAME (1 pt): Name of Neighbor to your left (1 pt): Name of Neighbor to your right (1 pt):
 Math 16A Second Mierm 6 Nov 2008 NAME (1 pt): TA (1 pt): Name of Neighbor to your left (1 pt): Name of Neighbor to your right (1 pt): Instructions: This is a closed book, closed notes, closed calculator,
Math 16A Second Mierm 6 Nov 2008 NAME (1 pt): TA (1 pt): Name of Neighbor to your left (1 pt): Name of Neighbor to your right (1 pt): Instructions: This is a closed book, closed notes, closed calculator,
MATH 151, Fall 2015, Week 12, Section
 MATH 151, Fall 2015, Week 12, Section 5.1-5.3 Chapter 5 Application of Differentiation We develop applications of differentiation to study behaviors of functions and graphs Part I of Section 5.1-5.3, Qualitative/intuitive
MATH 151, Fall 2015, Week 12, Section 5.1-5.3 Chapter 5 Application of Differentiation We develop applications of differentiation to study behaviors of functions and graphs Part I of Section 5.1-5.3, Qualitative/intuitive
AB CALCULUS SEMESTER A REVIEW Show all work on separate paper. (b) lim. lim. (f) x a. for each of the following functions: (b) y = 3x 4 x + 2
 AB CALCULUS Page 1 of 6 NAME DATE 1. Evaluate each it: AB CALCULUS Show all work on separate paper. x 3 x 9 x 5x + 6 x 0 5x 3sin x x 7 x 3 x 3 5x (d) 5x 3 x +1 x x 4 (e) x x 9 3x 4 6x (f) h 0 sin( π 6
AB CALCULUS Page 1 of 6 NAME DATE 1. Evaluate each it: AB CALCULUS Show all work on separate paper. x 3 x 9 x 5x + 6 x 0 5x 3sin x x 7 x 3 x 3 5x (d) 5x 3 x +1 x x 4 (e) x x 9 3x 4 6x (f) h 0 sin( π 6
Spring 2015 Sample Final Exam
 Math 1151 Spring 2015 Sample Final Exam Final Exam on 4/30/14 Name (Print): Time Limit on Final: 105 Minutes Go on carmen.osu.edu to see where your final exam will be. NOTE: This exam is much longer than
Math 1151 Spring 2015 Sample Final Exam Final Exam on 4/30/14 Name (Print): Time Limit on Final: 105 Minutes Go on carmen.osu.edu to see where your final exam will be. NOTE: This exam is much longer than
Unit V Applications of Derivatives
 Unit V Applications of Derivatives Curve Sketching Inequalities (Not covered in 3205) Polynomial Rational Functions Related Rate Problems Optimization (Max/Min) Problems 1 Inequalities Linear Polynomial
Unit V Applications of Derivatives Curve Sketching Inequalities (Not covered in 3205) Polynomial Rational Functions Related Rate Problems Optimization (Max/Min) Problems 1 Inequalities Linear Polynomial
Unit V Applications of Derivatives
 Unit V Applications of Derivatives Curve Sketching Inequalities (Covered in 2200) Polynomial Rational Functions Related Rate Problems Optimization (Max/Min) Problems 1 Inequalities Linear Polynomial Rational
Unit V Applications of Derivatives Curve Sketching Inequalities (Covered in 2200) Polynomial Rational Functions Related Rate Problems Optimization (Max/Min) Problems 1 Inequalities Linear Polynomial Rational
Question. [The volume of a cone of radius r and height h is 1 3 πr2 h and the curved surface area is πrl where l is the slant height of the cone.
 Q1 An experiment is conducted using the conical filter which is held with its axis vertical as shown. The filter has a radius of 10cm and semi-vertical angle 30. Chemical solution flows from the filter
Q1 An experiment is conducted using the conical filter which is held with its axis vertical as shown. The filter has a radius of 10cm and semi-vertical angle 30. Chemical solution flows from the filter
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY 31 OCTOBER 2018
 SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY OCTOBER 8 Mark Scheme: Each part of Question is worth marks which are awarded solely for the correct answer. Each
SOLUTIONS FOR ADMISSIONS TEST IN MATHEMATICS, COMPUTER SCIENCE AND JOINT SCHOOLS WEDNESDAY OCTOBER 8 Mark Scheme: Each part of Question is worth marks which are awarded solely for the correct answer. Each
MIDTERM 2 REVIEW: ADDITIONAL PROBLEMS. 1 2 x + 1. y = + 1 = x 1/ = 1. y = 1 2 x 3/2 = 1. into this equation would have then given. y 1.
 MIDTERM 2 REVIEW: ADDITIONAL PROBLEMS ) If x + y =, find y. IMPLICIT DIFFERENTIATION Solution. Taking the derivative (with respect to x) of both sides of the given equation, we find that 2 x + 2 y y =
MIDTERM 2 REVIEW: ADDITIONAL PROBLEMS ) If x + y =, find y. IMPLICIT DIFFERENTIATION Solution. Taking the derivative (with respect to x) of both sides of the given equation, we find that 2 x + 2 y y =
Final Exam Study Guide
 Final Exam Study Guide Final Exam Coverage: Sections 10.1-10.2, 10.4-10.5, 10.7, 11.2-11.4, 12.1-12.6, 13.1-13.2, 13.4-13.5, and 14.1 Sections/topics NOT on the exam: Sections 10.3 (Continuity, it definition
Final Exam Study Guide Final Exam Coverage: Sections 10.1-10.2, 10.4-10.5, 10.7, 11.2-11.4, 12.1-12.6, 13.1-13.2, 13.4-13.5, and 14.1 Sections/topics NOT on the exam: Sections 10.3 (Continuity, it definition
Lecture 9 - Increasing and Decreasing Functions, Extrema, and the First Derivative Test
 Lecture 9 - Increasing and Decreasing Functions, Extrema, and the First Derivative Test 9.1 Increasing and Decreasing Functions One of our goals is to be able to solve max/min problems, especially economics
Lecture 9 - Increasing and Decreasing Functions, Extrema, and the First Derivative Test 9.1 Increasing and Decreasing Functions One of our goals is to be able to solve max/min problems, especially economics
CHAPTER 3 APPLICATIONS OF THE DERIVATIVE
 CHAPTER 3 APPLICATIONS OF THE DERIVATIVE 3.1 Maxima and Minima Extreme Values 1. Does f(x) have a maximum or minimum value on S? 2. If it does have a maximum or a minimum, where are they attained? 3. If
CHAPTER 3 APPLICATIONS OF THE DERIVATIVE 3.1 Maxima and Minima Extreme Values 1. Does f(x) have a maximum or minimum value on S? 2. If it does have a maximum or a minimum, where are they attained? 3. If
Differential Calculus Average Rate of Change (AROC) The average rate of change of y over an interval is equal to
 Differential Calculus Average Rate of Change (AROC) The average rate of change of y over an interval is equal to change in y y y1 f ( x) f ( x1 ) f ( b) f ( a). changein x x x x x b a 1 Example: Find the
Differential Calculus Average Rate of Change (AROC) The average rate of change of y over an interval is equal to change in y y y1 f ( x) f ( x1 ) f ( b) f ( a). changein x x x x x b a 1 Example: Find the
3.3 Increasing & Decreasing Functions and The First Derivative Test
 3.3 Increasing & Decreasing Functions and The First Derivative Test Definitions of Increasing and Decreasing Functions: A funcon f is increasing on an interval if for any two numbers x 1 and x 2 in the
3.3 Increasing & Decreasing Functions and The First Derivative Test Definitions of Increasing and Decreasing Functions: A funcon f is increasing on an interval if for any two numbers x 1 and x 2 in the
Review Guideline for Final
 Review Guideline for Final Here is the outline of the required skills for the final exam. Please read it carefully and find some corresponding homework problems in the corresponding sections to practice.
Review Guideline for Final Here is the outline of the required skills for the final exam. Please read it carefully and find some corresponding homework problems in the corresponding sections to practice.
IMP 13 First Hour Exam Solutions
 IMP 13 First Hour Exam Solutions 1. Two charges are arranged along the x-axis as shown, with q 1 = 4 µc at x = -4 m and q 2 = -9 µc at x = +2 m. (Remember 1 µc = 10-6 C). y * q 1 * q 2 x a. What is the
IMP 13 First Hour Exam Solutions 1. Two charges are arranged along the x-axis as shown, with q 1 = 4 µc at x = -4 m and q 2 = -9 µc at x = +2 m. (Remember 1 µc = 10-6 C). y * q 1 * q 2 x a. What is the
AP Calculus AB Worksheet - Differentiability
 Name AP Calculus AB Worksheet - Differentiability MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. The figure shows the graph of a function. At the
Name AP Calculus AB Worksheet - Differentiability MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. The figure shows the graph of a function. At the
Math Essentials of Calculus by James Stewart Prepared by Jason Gaddis
 Math 231 - Essentials of Calculus by James Stewart Prepared by Jason Gaddis Chapter 3 - Applications of Differentiation 3.1 - Maximum and Minimum Values Note We continue our study of functions using derivatives.
Math 231 - Essentials of Calculus by James Stewart Prepared by Jason Gaddis Chapter 3 - Applications of Differentiation 3.1 - Maximum and Minimum Values Note We continue our study of functions using derivatives.
Math 75B Practice Problems for Midterm II Solutions Ch. 16, 17, 12 (E), , 2.8 (S)
 Math 75B Practice Problems for Midterm II Solutions Ch. 6, 7, 2 (E),.-.5, 2.8 (S) DISCLAIMER. This collection of practice problems is not guaranteed to be identical, in length or content, to the actual
Math 75B Practice Problems for Midterm II Solutions Ch. 6, 7, 2 (E),.-.5, 2.8 (S) DISCLAIMER. This collection of practice problems is not guaranteed to be identical, in length or content, to the actual
AP Calculus BC Fall Final Part IIa
 AP Calculus BC 18-19 Fall Final Part IIa Calculator Required Name: 1. At time t = 0, there are 120 gallons of oil in a tank. During the time interval 0 t 10 hours, oil flows into the tank at a rate of
AP Calculus BC 18-19 Fall Final Part IIa Calculator Required Name: 1. At time t = 0, there are 120 gallons of oil in a tank. During the time interval 0 t 10 hours, oil flows into the tank at a rate of
