Gauss-Bonnet Theorem on Moduli Spaces. 陆志勤 Zhiqin Lu, UC Irvine
|
|
|
- Benedict Mathews
- 6 years ago
- Views:
Transcription
1 Gauss-Bonnet Theorem on Moduli Spaces 陆志勤 Zhiqin Lu, UC Irvine 台大数学科学中心 July 28, 2009 Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 1/57
2 Background Calabi-Yau 3-folds are one of the most important objects in mathematics and string theory They are defined as the Kähler manifolds with zero first Chern class Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 2/57
3 Background Calabi-Yau 3-folds are one of the most important objects in mathematics and string theory They are defined as the Kähler manifolds with zero first Chern class By the work of Yau, we know that within any fixed Kähler class, there is a unique Ricci flat metric Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 2/57
4 Background Calabi-Yau 3-folds are one of the most important objects in mathematics and string theory They are defined as the Kähler manifolds with zero first Chern class By the work of Yau, we know that within any fixed Kähler class, there is a unique Ricci flat metric The fundamental question is that, Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 2/57
5 Background Calabi-Yau 3-folds are one of the most important objects in mathematics and string theory They are defined as the Kähler manifolds with zero first Chern class By the work of Yau, we know that within any fixed Kähler class, there is a unique Ricci flat metric The fundamental question is that, how to write out the Ricci-flat metric explicitly? Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 2/57
6 A K3 surface is a Calabi-Yau 2-fold Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 3/57
7 A K3 surface is a Calabi-Yau 2-fold Currently it is not possible to write down the Ricci flat metric explicitly even for K3 surfaces Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 3/57
8 A K3 surface is a Calabi-Yau 2-fold Currently it is not possible to write down the Ricci flat metric explicitly even for K3 surfaces Indirect way (or the standard way): Linerization moduli space of Calabi-Yau manifold, Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 3/57
9 A K3 surface is a Calabi-Yau 2-fold Currently it is not possible to write down the Ricci flat metric explicitly even for K3 surfaces Indirect way (or the standard way): Linerization moduli space of Calabi-Yau manifold, Calabi-Yau moduli 模空间的理论之所以会成功是因为它是某些东西的线性化! Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 3/57
10 A K3 surface is a Calabi-Yau 2-fold Currently it is not possible to write down the Ricci flat metric explicitly even for K3 surfaces Indirect way (or the standard way): Linerization moduli space of Calabi-Yau manifold, Calabi-Yau moduli 模空间的理论之所以会成功是因为它是某些东西的线性化! It is well motivated in mathematics as well as in string theory! Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 3/57
11 Why moduli space (CY moduli)? Moduli space gives a way to compare CY manifolds that are close to each other So it gives a platform of linearization Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 4/57
12 有两类模空间是适合微分几何的研究的 Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 5/57
13 有两类模空间是适合微分几何的研究的 1 一类是黎曼面的模空间 ( 它的万有覆盖就是 Teichmüller 空间 ) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 5/57
14 有两类模空间是适合微分几何的研究的 1 一类是黎曼面的模空间 ( 它的万有覆盖就是 Teichmüller 空间 ) 2 另一类就是卡拉比 - 丘成桐空间的模空间 Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 5/57
15 有两类模空间是适合微分几何的研究的 1 一类是黎曼面的模空间 ( 它的万有覆盖就是 Teichmüller 空间 ) 2 另一类就是卡拉比 - 丘成桐空间的模空间 因为这两类空间都是光滑的 Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 5/57
16 By a theorem of Tian-Todorov, the Calabi-Yau moduli is smooth Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 6/57
17 By a theorem of Tian-Todorov, the Calabi-Yau moduli is smooth We shall study the Differential Geometry of CY moduli Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 6/57
18 By a theorem of Tian-Todorov, the Calabi-Yau moduli is smooth We shall study the Differential Geometry of CY moduli with respect to the so-called Weil-Petersson metric Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 6/57
19 Weil-Petersson metric The metric is an L 2 metric, defined by the following Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 7/57
20 Weil-Petersson metric The metric is an L 2 metric, defined by the following Definition Let Z be a polarized Calabi-Yau manifold with the Ricci flat Kähler metric µ whose Kähler form defines the polarization Let X, Y H 1 (Z, T (1,0) Z) Define the L 2 inner product by (X, Y) = 1 X, Y µ n n! For a Calabi-Yau manifold, via the Kodaira-Spencer map: T Z M H 1 (Z, T (1,0) Z), which is an isomorphism, the above inner product defines a metric on the smooth part of M The metric happens to be Kählerian, and is called the Weil-Petersson metric of M Z Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 7/57
21 A very quick review of Kodaira-Spencer theory A complex structure J is a real operator such that J 2 = I J : T C Z T C Z Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 8/57
22 A very quick review of Kodaira-Spencer theory A complex structure J is a real operator J : T C Z T C Z such that J 2 = I For fixed frames, we have ( 1I J = 1I ) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 8/57
23 A very quick review of Kodaira-Spencer theory A complex structure J is a real operator J : T C Z T C Z such that J 2 = I For fixed frames, we have ( 1I J = 1I ) A variation of the complex structure is a real matrix A such that (J + εa) 2 = I Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 8/57
24 A very quick review of Kodaira-Spencer theory-2 Or we have Thus we have AJ + JA = 0 ( A = Ā1 A 1 ) for some A 1 : T 1,0 Z T 0,1 Z, or equivalently A 1 can be represented by φ Λ 0,1 (T 1,0 Z) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 9/57
25 A very quick review of Kodaira-Spencer theory-2 Or we have Thus we have AJ + JA = 0 ( A = Ā1 A 1 ) for some A 1 : T 1,0 Z T 0,1 Z, or equivalently A 1 can be represented by φ Λ 0,1 (T 1,0 Z) Roughly speaking, the Kodaira-Spencer map is defined as ε φ Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 9/57
26 The differential geometry of the Weil-Petersson metric on Calabi-Yau moduli is called the Weil-Petersson geometry Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 10/57
27 The differential geometry of the Weil-Petersson metric on Calabi-Yau moduli is called the Weil-Petersson geometry The Aim: We want to be able to tell the properties of the moduli space through geometric analysis Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 10/57
28 Local Weil-Petersson geometry Good properties Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 11/57
29 Local Weil-Petersson geometry Good properties Kählerian Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 11/57
30 Local Weil-Petersson geometry Good properties Kählerian Formula of Strominger and 王金龙 Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 11/57
31 Local Weil-Petersson geometry Good properties Kählerian Formula of Strominger and 王金龙 很多其他的性质 Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 11/57
32 Local Weil-Petersson geometry Good properties Kählerian Formula of Strominger and 王金龙 很多其他的性质 Bad property Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 11/57
33 Local Weil-Petersson geometry Good properties Kählerian Formula of Strominger and 王金龙 很多其他的性质 Bad property The curvature is neither positive nor negative Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 11/57
34 Rebuilding the local geometry The following result was proved in my thesis (1997) Theorem Let M be the moduli space of a CY 3-fold with dimension m Then We define the the following metric ω H = (m + 3)ω WP + Ric(ω WP ) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 12/57
35 Rebuilding the local geometry The following result was proved in my thesis (1997) Theorem Let M be the moduli space of a CY 3-fold with dimension m Then We define the the following metric which I called it Hodge metric ω H = (m + 3)ω WP + Ric(ω WP ) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 12/57
36 Rebuilding the local geometry The following result was proved in my thesis (1997) Theorem Let M be the moduli space of a CY 3-fold with dimension m Then We define the the following metric ω H = (m + 3)ω WP + Ric(ω WP ) which I called it Hodge metric The curvature has good properties (non-positive bisectional curvature, negative Ricci and holomorphic sectional curvature, etc) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 12/57
37 Rebuilding the local geometry The following result was proved in my thesis (1997) Theorem Let M be the moduli space of a CY 3-fold with dimension m Then We define the the following metric ω H = (m + 3)ω WP + Ric(ω WP ) which I called it Hodge metric The curvature has good properties (non-positive bisectional curvature, negative Ricci and holomorphic sectional curvature, etc) 对于高维的 CY 流形, 霍奇度量也可以定义, 只是没有一个简洁的公式了 Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 12/57
38 We are not able to prove that the sectional curvature is non-positive However, we don t expect that, otherwise the CY moduli may be too restrictive Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 13/57
39 Hodge theory helps us! Recall that for any compact complex manifold, we can define the cohomology groups H p,q By Hodge theorem, they are made from harmonic forms Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 14/57
40 If we deform the CY manifolds, we deform the Hodge flags This is called the variation of Hodge structure Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 15/57
41 We want to study the differential geometric properties of the moduli space with respect to the Weil-Petersson metric Local theory Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 16/57
42 We want to study the differential geometric properties of the moduli space with respect to the Weil-Petersson metric Local theory Semi-global theory Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 16/57
43 We want to study the differential geometric properties of the moduli space with respect to the Weil-Petersson metric Local theory Semi-global theory The BCOV conjecture (settled by Zinger-07 方浩 - 陆 -Yoshikawa-06) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 16/57
44 We want to study the differential geometric properties of the moduli space with respect to the Weil-Petersson metric Local theory Semi-global theory The BCOV conjecture (settled by Zinger-07 方浩 - 陆 -Yoshikawa-06) Incompleteness of the Weil-Petersson metric ( 王 -96 for 1d, L-Wang-09 in preparation) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 16/57
45 We want to study the differential geometric properties of the moduli space with respect to the Weil-Petersson metric Local theory Semi-global theory The BCOV conjecture (settled by Zinger-07 方浩 - 陆 -Yoshikawa-06) Incompleteness of the Weil-Petersson metric ( 王 -96 for 1d, L-Wang-09 in preparation) A lot of others Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 16/57
46 We want to study the differential geometric properties of the moduli space with respect to the Weil-Petersson metric Local theory Semi-global theory The BCOV conjecture (settled by Zinger-07 方浩 - 陆 -Yoshikawa-06) Incompleteness of the Weil-Petersson metric ( 王 -96 for 1d, L-Wang-09 in preparation) A lot of others Global theory Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 16/57
47 We want to study the differential geometric properties of the moduli space with respect to the Weil-Petersson metric Local theory Semi-global theory The BCOV conjecture (settled by Zinger-07 方浩 - 陆 -Yoshikawa-06) Incompleteness of the Weil-Petersson metric ( 王 -96 for 1d, L-Wang-09 in preparation) A lot of others Global theory Freed Conjecture (L-99) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 16/57
48 We want to study the differential geometric properties of the moduli space with respect to the Weil-Petersson metric Local theory Semi-global theory The BCOV conjecture (settled by Zinger-07 方浩 - 陆 -Yoshikawa-06) Incompleteness of the Weil-Petersson metric ( 王 -96 for 1d, L-Wang-09 in preparation) A lot of others Global theory Freed Conjecture (L-99) Gauss-Bonnet Theorem (Joint/w M R Douglas) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 16/57
49 We want to study the differential geometric properties of the moduli space with respect to the Weil-Petersson metric Local theory Semi-global theory The BCOV conjecture (settled by Zinger-07 方浩 - 陆 -Yoshikawa-06) Incompleteness of the Weil-Petersson metric ( 王 -96 for 1d, L-Wang-09 in preparation) A lot of others Global theory Freed Conjecture (L-99) Gauss-Bonnet Theorem (Joint/w M R Douglas) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 16/57
50 The BCOV Conjecture BCOV=Bershadsky-Cecotti-Ooguri-Vafa Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 17/57
51 The BCOV Conjecture BCOV=Bershadsky-Cecotti-Ooguri-Vafa Definition The mirror map is the holomorphic map from a neighborhood of P 1 to a neighborhood of 0 defined by the following formula q := (5ψ) 5 exp 5 y 0 (ψ) n=1 (5n)! (n!) 5 5n j=n j (5ψ) 5n, where ψ 1, and y 0 (ψ) := n=0 (5n)! (n!) 5, ψ > 1 (5ψ) 5n The inverse of the mirror map is denoted by ψ(q) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 17/57
52 Define the multi-valued function F top 1,B (ψ) as ( ) 62 ψ F top 1,B (ψ) := 3 (ψ 5 1) 1 dψ 6 q y 0 (ψ) dq, and F top 1,A (q) := Ftop 1,B (ψ(q)) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 18/57
53 Conjecture (A) Conjecture (A) Let n g (d) be the genus-g degree-d instanton number of a quintic in CP 4 for g = 0, 1 Then the following identity holds: q d log Ftop 1,A dq (q) = nd qnd n 1 (d) 1 q nd n,d=1 d=1 n 0 (d) 2d q d 12(1 q d ) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 19/57
54 Conjecture (A) was proved by Aleksey Zinger Aleksey Zinger The Reduced Genus-One Gromov-Witten Invariants of Calabi-Yau Hypersurfaces ArXiv: v2, 2007 Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 20/57
55 Setup of Conjecture (B) Let X be a compact Kähler manifold Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 21/57
56 Setup of Conjecture (B) Let X be a compact Kähler manifold Let = p,q be the Laplacian on (p, q) forms; Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 21/57
57 Setup of Conjecture (B) Let X be a compact Kähler manifold Let = p,q be the Laplacian on (p, q) forms; By compactness, the spectrum of are eigenvalues: 0 λ 0 λ 1 λ n + Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 21/57
58 Setup of Conjecture (B) Let X be a compact Kähler manifold Let = p,q be the Laplacian on (p, q) forms; By compactness, the spectrum of are eigenvalues: 0 λ 0 λ 1 λ n + Define det = λ i 0 λ i Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 21/57
59 Setup of Conjecture (B) Let X be a compact Kähler manifold Let = p,q be the Laplacian on (p, q) forms; By compactness, the spectrum of are eigenvalues: 0 λ 0 λ 1 λ n + Define det = λ i 0 λ i Not well-defined? Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 21/57
60 Setup of Conjecture (B) Let X be a compact Kähler manifold Let = p,q be the Laplacian on (p, q) forms; By compactness, the spectrum of are eigenvalues: 0 λ 0 λ 1 λ n + Define det = λ i 0 λ i Not well-defined? ζ function regularization (for example: Riemann ζ-function) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 21/57
61 Setup of Conjecture B Bershadsky-Ceccotti-Ooguri-Vafa defined T def = p,q (det p,q ) ( 1)p+q pq Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 22/57
62 Setup of Conjecture B Bershadsky-Ceccotti-Ooguri-Vafa defined T def = p,q (det p,q ) ( 1)p+q pq Why define such a strange quantity? Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 22/57
63 Setup of Conjecture B Bershadsky-Ceccotti-Ooguri-Vafa defined T def = p,q (det p,q ) ( 1)p+q pq Why define such a strange quantity? Answer: Riemann-Roch-Grothendieck theorem Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 22/57
64 Conjecture (B) Let be the Hermitian metric on the line bundle (π K W/CP 1) 62 (T(CP 1 )) 3 CP 1 \D induced from the L 2 -metric on π K W/CP 1 and from the Weil-Petersson metric on T(CP 1 ) Then the following identity holds: 1 τ BCOV (W ψ ) = Const F top 1,B (ψ)3 ( ) 62 ( Ωψ q d y 0 (ψ) dq where Ω is the local holomorphic section of the (3, 0) forms ) 3 2 3, Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 23/57
65 Conjecture B was proved by Fang-L-Yoshikawa 方浩 -L-Yoshikawa( 吉川谦一 ) Asymptotic behavior of the BCOV torsion of Calabi-Yau moduli ArXiv: JDG (80), 2008, , Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 24/57
66 In fact, there is only one conjecture: By counting the instanton numbers we get the function F top 1,A, and by computing the BCOV torsion we get the function F top 1,B These two functions are the same Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 25/57
67 In fact, there is only one conjecture: By counting the instanton numbers we get the function F top 1,A, and by computing the BCOV torsion we get the function F top 1,B These two functions are the same Combining Conjecture A and B, we verified the Mirror Symmetry prediction of the case g = 1 For higher genus, the B-side of the conjectures have not been set up (Yau-Yamagochi, Huang-Klemn-Quakenbush, and many others) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 25/57
68 Chern classes A quick review We assume that E M is a holomorphic vector bundle over a compact complex manifold M Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 26/57
69 Chern classes A quick review We assume that E M is a holomorphic vector bundle over a compact complex manifold M Let h be a Hermitian metric on E Let be the matrix of the connection Γ = h h 1 Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 26/57
70 Chern classes A quick review We assume that E M is a holomorphic vector bundle over a compact complex manifold M Let h be a Hermitian metric on E Let Γ = h h 1 be the matrix of the connection Let R = Γ be the curvature matrix Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 26/57
71 Let f be an invariant polynomial That is, f is a polynomial on C r2 that f(a) = f(t 1 AT) such Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 27/57
72 Let f be an invariant polynomial That is, f is a polynomial on C r2 that f(a) = f(t 1 AT) such The Chern-Weil form with respect to the polynomial f is defined by f(r) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 27/57
73 If in addition, we assume that f has integer coefficients, then we have the following results: 1 f(r) is closed This is the Chern-Weil form; Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 28/57
74 If in addition, we assume that f has integer coefficients, then we have the following results: 1 f(r) is closed This is the Chern-Weil form; 2 [f(r)] H (M, Z), and is independent of the choice of the connection Gauss-Bonnet-Chern Theorem Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 28/57
75 This is joint with Michael R Douglas Zhiqin Lu and Michael R Douglas Gauss-Bonnet-Chern theorem on moduli spaces preprint, 2008, arxiv: Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 29/57
76 This is joint with Michael R Douglas Zhiqin Lu and Michael R Douglas Gauss-Bonnet-Chern theorem on moduli spaces preprint, 2008, arxiv: Theorem Let f be an invariant polynomial with rational coefficients Let R be the curvature tensor with respect the Weil-Petersson metric Then f(r) is a rational number M Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 29/57
77 Some remarks The moduli space is often non-compact Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 30/57
78 Some remarks The moduli space is often non-compact If the moduli space were compact, then the Chern-Weil forms define Chern classes, and the theorem follows Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 30/57
79 Some remarks The moduli space is often non-compact If the moduli space were compact, then the Chern-Weil forms define Chern classes, and the theorem follows If the growth of the Chern-Weil forms and the connection were mild at infinity, the theorem follows from a theorem of Mumford Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 30/57
80 Important! We realized that Theorem Let E M be a Hodge bundle over the moduli space of a polarized Kähler manifold Let R be the curvature tensor with respect to the Hodge bundle Then f(r) is a rational number M Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 31/57
81 Previous results For the first Chern class of the Weil-Petersson metric, the result is by Sun-L (CMP, 06); Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 32/57
82 Previous results For the first Chern class of the Weil-Petersson metric, the result is by Sun-L (CMP, 06); For general moduli space, if the dimension is 1, the result is by Peters, Zucker, Mumford (independently) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 32/57
83 Previous results For the first Chern class of the Weil-Petersson metric, the result is by Sun-L (CMP, 06); For general moduli space, if the dimension is 1, the result is by Peters, Zucker, Mumford (independently) For general moduli space, in the case of first Chern class, the result is by J Kollár Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 32/57
84 Our result is true for the Weil-Petersson metric on Calabi-Yau moduli and the Chern-Weil forms on general moduli spaces We proved the theorems of this kind to the full generality, with the introduction of new techniques Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 33/57
85 The idea of Mumford Let M be the compactification of M We suppose E can be extended to M Let Γ 0 be a smooth connection of the extended bundle Let ρ be a cut-off function We can compare the two integrals: ρf(r) and ρf(r 0 ) M M where R 0 = Γ 0 is the curvature of Γ 0 Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 34/57
86 The idea of Mumford Let M be the compactification of M We suppose E can be extended to M Let Γ 0 be a smooth connection of the extended bundle Let ρ be a cut-off function We can compare the two integrals: ρf(r) and ρf(r 0 ) M M where R 0 = Γ 0 is the curvature of Γ 0 When ρ 1, M ρf(r) goes to M f(r), and M ρf(r 0 ) goes to M f(r 0), which is an integer by the fact that the Chern-Weil form defines a rational class Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 34/57
87 Let f be the polarization of f That is, f(a,, A) = f(a) and Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 35/57
88 Let f be the polarization of f That is, f(a,, A) = f(a) and f(, Ai,, A j, ) = f(, A j,, A i, ) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 35/57
89 Let f be the polarization of f That is, f(a,, A) = f(a) and f(, Ai,, A j, ) = f(, A j,, A i, ) and f(ta1 T 1,, TA j T 1, ) = f(a 1,, A j, ) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 35/57
90 Let f be the polarization of f That is, f(a,, A) = f(a) and f(, Ai,, A j, ) = f(, A j,, A i, ) and f(ta1 T 1,, TA j T 1, ) = f(a 1,, A j, ) f is linear with respect to all the components Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 35/57
91 Let f be the polarization of f That is, f(a,, A) = f(a) and f(, Ai,, A j, ) = f(, A j,, A i, ) and f(ta1 T 1,, TA j T 1, ) = f(a 1,, A j, ) f is linear with respect to all the components For example, if f = tr(a 2 ), then f = 1 2tr(AB + BA) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 35/57
92 Let f be the polarization of f That is, f(a,, A) = f(a) and f(, Ai,, A j, ) = f(, A j,, A i, ) and f(ta1 T 1,, TA j T 1, ) = f(a 1,, A j, ) f is linear with respect to all the components For example, if f = tr(a 2 ), then f = 1 2tr(AB + BA)In general, all invariant polynomials have a unique polarization Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 35/57
93 Then we have the following identity: ρ(f(r) f(r 0 )) M = ρf(r,, R, R R 0, R 0,, R 0 ) i M = ρ f(r,, R, Γ Γ 0, R 0,, R 0 ) i M Apparently, if the growth of R, R 0, Γ, Γ 0 are mild, then the right hand side will go to zero Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 36/57
94 Then we have the following identity: ρ(f(r) f(r 0 )) M = ρf(r,, R, R R 0, R 0,, R 0 ) i M = ρ f(r,, R, Γ Γ 0, R 0,, R 0 ) i M Apparently, if the growth of R, R 0, Γ, Γ 0 are mild, then the right hand side will go to zero If a connection whose growth is mild, Mumford called it good Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 36/57
95 Unfortunately, the Hodge metrics are not good in the sense of Mumford Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 37/57
96 Unfortunately, the Hodge metrics are not good in the sense of Mumford What do we need to do? Control ρ; Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 37/57
97 Unfortunately, the Hodge metrics are not good in the sense of Mumford What do we need to do? Control ρ; Control Γ, R; Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 37/57
98 Unfortunately, the Hodge metrics are not good in the sense of Mumford What do we need to do? Control ρ; Control Γ, R; Control Γ 0, R 0 Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 37/57
99 Unfortunately, the Hodge metrics are not good in the sense of Mumford What do we need to do? Control ρ; Control Γ, R; Control Γ 0, R 0 Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 37/57
100 The P-boundedness Definition Let U be a neighborhood and let z 1,, z n be the holomorphic coordinate system The divisor D = {z 1 = 0} A smooth form on U\D is called P bounded (refer to Poincaré Bounded), if it is bounded under the frame d log z 1 / log 1 z 1, d log z 1/ log 1 z 1, dz j, d z j for j > 1 Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 38/57
101 The P-boundedness Definition Let U be a neighborhood and let z 1,, z n be the holomorphic coordinate system The divisor D = {z 1 = 0} A smooth form on U\D is called P bounded (refer to Poincaré Bounded), if it is bounded under the frame d log z 1 / log 1 z 1, d log z 1/ log 1 z 1, dz j, d z j for j > 1 For example, a one form η = a i dz i is P bounded iff a 1 C r 1 log 1/r 1, a k C, for k > 1 Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 38/57
102 If η 1, η 2 are P bounded, then so is η 1 η 2 Furthermore, if η is an (n, n) form which is P-bounded, then η C n i=1 1 z 2 i (log 1 z i )2 Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 39/57
103 If η 1, η 2 are P bounded, then so is η 1 η 2 Furthermore, if η is an (n, n) form which is P-bounded, then In particular, η is finite U η C n i=1 1 z 2 i (log 1 z i )2 Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 39/57
104 If η 1, η 2 are P bounded, then so is η 1 η 2 Furthermore, if η is an (n, n) form which is P-bounded, then In particular, η is finite U η C n i=1 1 z 2 i (log 1 z i )2 It is standard to prove that one can choose a cut-off function ρ so that ρ is P-bounded with the Lebesgue of supp ( ρ) going to zero For example, we can pick ρ = g(log 1/r) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 39/57
105 If η 1, η 2 are P bounded, then so is η 1 η 2 Furthermore, if η is an (n, n) form which is P-bounded, then In particular, η is finite U η C n i=1 1 z 2 i (log 1 z i )2 It is standard to prove that one can choose a cut-off function ρ so that ρ is P-bounded with the Lebesgue of supp ( ρ) going to zero For example, we can pick ρ = g(log 1/r) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 39/57
106 We consider a neighborhood U at the infinity of the moduli space, where the divisor D can be written as {z 1 = 0} By the nilpotent orbit theorem of Schmid, we have the expansion of the Hodge metric ( ) log 1 α1 r 1 h = + lower order terms ) αr (log 1r1 Without loss of generality, we assume that α 1 α 2 α r Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 40/57
107 We let ) α1 /2 (log 1r1 Λ = ( ) log 1 αr /2 r 1 Then we have h = Λh Λ Then we have h = I + lower order terms, and the connection is hh 1 = ΛΛ 1 + Λ h (h ) 1 Λ 1 + Λh ΛΛ 1 (h ) 1 Λ 1 Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 41/57
108 Go back to the previous expression ρ f(r,, R, Γ Γ 0, R 0,, R 0 ) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 42/57
109 Since Γ 0, R 0 are smooth, they are bounded Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 43/57
110 Since Γ 0, R 0 are smooth, they are bounded However, even in the above simplest case, the connection and hence the curvature are not P bounded: hh 1 = ΛΛ 1 + Λ h (h ) 1 Λ 1 + Λh ΛΛ 1 (h ) 1 Λ 1 Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 43/57
111 Since Γ 0, R 0 are smooth, they are bounded However, even in the above simplest case, the connection and hence the curvature are not P bounded: hh 1 = ΛΛ 1 + Λ h (h ) 1 Λ 1 + Λh ΛΛ 1 (h ) 1 Λ 1 But is P bounded Ad(Λ 1 )( hh 1 ) = Λ 1 Λ + h (h ) 1 + h ΛΛ 1 (h ) 1 Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 43/57
112 Since Γ 0, R 0 are smooth, they are bounded However, even in the above simplest case, the connection and hence the curvature are not P bounded: hh 1 = ΛΛ 1 + Λ h (h ) 1 Λ 1 + Λh ΛΛ 1 (h ) 1 Λ 1 But Ad(Λ 1 )( hh 1 ) = Λ 1 Λ + h (h ) 1 + h ΛΛ 1 (h ) 1 is P bounded In fact, this is a special case of the Cattani-Kaplan-Schmid theorem Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 43/57
113 The problem is that, when Ad(Λ 1 )( hh 1 ) is P bounded, then in general 0 Λ = log 1 r 1 «α1 /2 1 «C α log r 1 r/2a 1 Ad(Λ 1 )(Γ 0 ) and Ad(Λ 1 )(R 0 ) are not bounded Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 44/57
114 Let Γ 0 = (a ij ) Then Ad(Λ 1 )(Γ 0 ) = (a ij (log 1/r 1 ) αi αj ), and they are bounded if and only if Γ 0 is of lower triangular Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 45/57
115 Let Then Γ 0 = (a ij ) Ad(Λ 1 )(Γ 0 ) = (a ij (log 1/r 1 ) αi αj ), and they are bounded if and only if Γ 0 is of lower triangular The technical heart of the proof is that We are able to find such a connection Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 45/57
116 Let Ω α be the frame defined by the nilpotent theorem and let A αβ be the transition functions We proved that the connection Γ α = ψ γ A αγ A 1 αγ is the Correct connection! Or roughly speaking, they are all of lower triangular! Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 46/57
117 The proof is very technical and uses the full power of the SL 2 -orbit theorem of several variables Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 47/57
118 The proof is very technical and uses the full power of the SL 2 -orbit theorem of several variables Continue Ṣkip Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 47/57
119 The key technical lemma of this section is the following: Lemma Let U = U γ be an open set such that U C Let A = A αγ Then on U C, Ad((e 1 ) t )Ad(A 1 C )( AA 1 ) is Poincaré bounded Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 48/57
120 Sketch of the Proof Let Ω = Ω γ be the local frame of U defined by the nilpotent orbit theorem Let C be a fixed cone of U and let Ω C be the frame of the cone We assume that C C We just need to prove the assertion of the lemma on C C because as C is running over all the cones, the whole U C will be covered Let e be the matrix under the frame Ω C Let A C be the constant matrix defined as Ω = Ω C At C Then we have Ω C = Ω C At C At (A 1 C )t Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 49/57
121 We let B = A 1 C AA C and let h be the metric matrix of Ω C Then Ω C = Ω C Bt Thus h = Ω t CΩ C = Bh Bt (1) It follows that hh 1 = BB 1 + Ad(B)( h (h ) 1 ) (2) Since A C, A C are constant matrices, we have BB 1 = Ad(A 1 C )( AA 1 ) Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 50/57
122 In order to prove the lemma, we only need to prove that Ad((e 1 ) t )Ad(B) h (h ) 1 = D(Ad(((e ) 1 ) t ))( h (h ) 1 )D 1 is Poincaré bounded, where D = (e 1 ) t B(e ) t Thus we only need to prove that D and D 1 are bounded Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 51/57
123 To prove the claim in the last slide, we observe that if and if then by (1) h = e t kē, h = (e ) t k ē, k = Dk Dt As a consequence of the SL 2 orbit theorem of Cattani-Kaplan-Schmid, Since both k and k are positive definite, D and D 1 must be bounded Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 52/57
124 Physics Background In the paper of Ashok-Douglas the index of all supersymmetric vacua was given The index is given by I vac (L L max ) = const det( R WP ω WP ), M H where M is the Calabi-Yau moduli and H is the moduli space of elliptic curves Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 53/57
125 In the paper of Douglas-Shiffman-Zelditch, the following strengthened result of the above was given Theorem Let K be a compact subset of M with piecewise smooth boundary Then [ ] Ind χk (L) = const(l 2m ) c m (T (M) F 3 ) + O(L 1/2 ) K Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 54/57
126 By our results, we have Theorem The indices I vac and Ind χk are all finite Moreover, Ind χk is bounded from above uniformly with respect to K They are all bounded, up to an absolute constant, by the Hodge volume of the Calabi-Yau moduli Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 55/57
127 In Layman words, if string theory is true, the the number of feasible Universes is finite Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 56/57
128 Thank you! Zhiqin Lu, UC Irvine Gauss-Bonnet Theorem 57/57
Geometry of the Calabi-Yau Moduli
 Geometry of the Calabi-Yau Moduli Zhiqin Lu 2012 AMS Hawaii Meeting Department of Mathematics, UC Irvine, Irvine CA 92697 March 4, 2012 Zhiqin Lu, Dept. Math, UCI Geometry of the Calabi-Yau Moduli 1/51
Geometry of the Calabi-Yau Moduli Zhiqin Lu 2012 AMS Hawaii Meeting Department of Mathematics, UC Irvine, Irvine CA 92697 March 4, 2012 Zhiqin Lu, Dept. Math, UCI Geometry of the Calabi-Yau Moduli 1/51
On the BCOV Conjecture
 Department of Mathematics University of California, Irvine December 14, 2007 Mirror Symmetry The objects to study By Mirror Symmetry, for any CY threefold, there should be another CY threefold X, called
Department of Mathematics University of California, Irvine December 14, 2007 Mirror Symmetry The objects to study By Mirror Symmetry, for any CY threefold, there should be another CY threefold X, called
Geometry of the Moduli Space of Curves and Algebraic Manifolds
 Geometry of the Moduli Space of Curves and Algebraic Manifolds Shing-Tung Yau Harvard University 60th Anniversary of the Institute of Mathematics Polish Academy of Sciences April 4, 2009 The first part
Geometry of the Moduli Space of Curves and Algebraic Manifolds Shing-Tung Yau Harvard University 60th Anniversary of the Institute of Mathematics Polish Academy of Sciences April 4, 2009 The first part
K-stability and Kähler metrics, I
 K-stability and Kähler metrics, I Gang Tian Beijing University and Princeton University Let M be a Kähler manifold. This means that M be a complex manifold together with a Kähler metric ω. In local coordinates
K-stability and Kähler metrics, I Gang Tian Beijing University and Princeton University Let M be a Kähler manifold. This means that M be a complex manifold together with a Kähler metric ω. In local coordinates
Elements of Topological M-Theory
 Elements of Topological M-Theory (with R. Dijkgraaf, S. Gukov, C. Vafa) Andrew Neitzke March 2005 Preface The topological string on a Calabi-Yau threefold X is (loosely speaking) an integrable spine of
Elements of Topological M-Theory (with R. Dijkgraaf, S. Gukov, C. Vafa) Andrew Neitzke March 2005 Preface The topological string on a Calabi-Yau threefold X is (loosely speaking) an integrable spine of
The structure of algebraic varieties
 The structure of algebraic varieties János Kollár Princeton University ICM, August, 2014, Seoul with the assistance of Jennifer M. Johnson and Sándor J. Kovács (Written comments added for clarity that
The structure of algebraic varieties János Kollár Princeton University ICM, August, 2014, Seoul with the assistance of Jennifer M. Johnson and Sándor J. Kovács (Written comments added for clarity that
A complex geometric proof of Tian-Yau-Zelditch expansion
 A complex geometric proof of Tian-Yau-Zelditch expansion Zhiqin Lu Department of Mathematics, UC Irvine, Irvine CA 92697 October 21, 2010 Zhiqin Lu, Dept. Math, UCI A complex geometric proof of TYZ expansion
A complex geometric proof of Tian-Yau-Zelditch expansion Zhiqin Lu Department of Mathematics, UC Irvine, Irvine CA 92697 October 21, 2010 Zhiqin Lu, Dept. Math, UCI A complex geometric proof of TYZ expansion
Remarks on hypersurface K-stability. Complex Geometry: A Conference Honoring Simon Donaldson
 Remarks on hypersurface K-stability Zhiqin Lu, UC Irvine Complex Geometry: A Conference Honoring Simon Donaldson October 26, 2009 Zhiqin Lu, UC. Irvine Hypersurface K-stability 1/42 The Result Theorem
Remarks on hypersurface K-stability Zhiqin Lu, UC Irvine Complex Geometry: A Conference Honoring Simon Donaldson October 26, 2009 Zhiqin Lu, UC. Irvine Hypersurface K-stability 1/42 The Result Theorem
Enumerative Geometry: from Classical to Modern
 : from Classical to Modern February 28, 2008 Summary Classical enumerative geometry: examples Modern tools: Gromov-Witten invariants counts of holomorphic maps Insights from string theory: quantum cohomology:
: from Classical to Modern February 28, 2008 Summary Classical enumerative geometry: examples Modern tools: Gromov-Witten invariants counts of holomorphic maps Insights from string theory: quantum cohomology:
Mirror Symmetry: Introduction to the B Model
 Mirror Symmetry: Introduction to the B Model Kyler Siegel February 23, 2014 1 Introduction Recall that mirror symmetry predicts the existence of pairs X, ˇX of Calabi-Yau manifolds whose Hodge diamonds
Mirror Symmetry: Introduction to the B Model Kyler Siegel February 23, 2014 1 Introduction Recall that mirror symmetry predicts the existence of pairs X, ˇX of Calabi-Yau manifolds whose Hodge diamonds
Topics in Geometry: Mirror Symmetry
 MIT OpenCourseWare http://ocw.mit.edu 8.969 Topics in Geometry: Mirror Symmetry Spring 2009 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MIRROR SYMMETRY:
MIT OpenCourseWare http://ocw.mit.edu 8.969 Topics in Geometry: Mirror Symmetry Spring 2009 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MIRROR SYMMETRY:
Geometry of the Moduli Space of Curves
 Harvard University January, 2007 Moduli spaces and Teichmüller spaces of Riemann surfaces have been studied for many years, since Riemann. They have appeared in many subjects of mathematics, from geometry,
Harvard University January, 2007 Moduli spaces and Teichmüller spaces of Riemann surfaces have been studied for many years, since Riemann. They have appeared in many subjects of mathematics, from geometry,
SUMMARY OF THE KÄHLER MASS PAPER
 SUMMARY OF THE KÄHLER MASS PAPER HANS-OACHIM HEIN AND CLAUDE LEBRUN Let (M, g) be a complete n-dimensional Riemannian manifold. Roughly speaking, such a space is said to be ALE with l ends (l N) if there
SUMMARY OF THE KÄHLER MASS PAPER HANS-OACHIM HEIN AND CLAUDE LEBRUN Let (M, g) be a complete n-dimensional Riemannian manifold. Roughly speaking, such a space is said to be ALE with l ends (l N) if there
How to count universes in string theory.
 Random Complex Geometry, or How to count universes in string theory. Steve Zelditch Department of Mathematics Johns Hopkins University AMS meeting Atlanta Friday, January 7, 2005: 10: 05-10: 55 Joint work
Random Complex Geometry, or How to count universes in string theory. Steve Zelditch Department of Mathematics Johns Hopkins University AMS meeting Atlanta Friday, January 7, 2005: 10: 05-10: 55 Joint work
Some new torsional local models for heterotic strings
 Some new torsional local models for heterotic strings Teng Fei Columbia University VT Workshop October 8, 2016 Teng Fei (Columbia University) Strominger system 10/08/2016 1 / 30 Overview 1 Background and
Some new torsional local models for heterotic strings Teng Fei Columbia University VT Workshop October 8, 2016 Teng Fei (Columbia University) Strominger system 10/08/2016 1 / 30 Overview 1 Background and
Two simple ideas from calculus applied to Riemannian geometry
 Calibrated Geometries and Special Holonomy p. 1/29 Two simple ideas from calculus applied to Riemannian geometry Spiro Karigiannis karigiannis@math.uwaterloo.ca Department of Pure Mathematics, University
Calibrated Geometries and Special Holonomy p. 1/29 Two simple ideas from calculus applied to Riemannian geometry Spiro Karigiannis karigiannis@math.uwaterloo.ca Department of Pure Mathematics, University
Rational Curves On K3 Surfaces
 Rational Curves On K3 Surfaces Jun Li Department of Mathematics Stanford University Conference in honor of Peter Li Overview of the talk The problem: existence of rational curves on a K3 surface The conjecture:
Rational Curves On K3 Surfaces Jun Li Department of Mathematics Stanford University Conference in honor of Peter Li Overview of the talk The problem: existence of rational curves on a K3 surface The conjecture:
This theorem gives us a corollary about the geometric height inequality which is originally due to Vojta [V].
![This theorem gives us a corollary about the geometric height inequality which is originally due to Vojta [V]. This theorem gives us a corollary about the geometric height inequality which is originally due to Vojta [V].](/thumbs/83/87985628.jpg) 694 KEFENG LIU This theorem gives us a corollary about the geometric height inequality which is originally due to Vojta [V]. Corollary 0.3. Given any ε>0, there exists a constant O ε (1) depending on ε,
694 KEFENG LIU This theorem gives us a corollary about the geometric height inequality which is originally due to Vojta [V]. Corollary 0.3. Given any ε>0, there exists a constant O ε (1) depending on ε,
From Random Polynomials to String Theory
 From Random Polynomials to String Theory Steve Zelditch Department of Mathematics Johns Hopkins University Madison, Wisconsin Friday, October 7, 4PM B239 Joint work with M. R. Douglas and B. Shiffman 1
From Random Polynomials to String Theory Steve Zelditch Department of Mathematics Johns Hopkins University Madison, Wisconsin Friday, October 7, 4PM B239 Joint work with M. R. Douglas and B. Shiffman 1
Topics in Geometry: Mirror Symmetry
 MIT OpenCourseWare http://ocw.mit.edu 18.969 Topics in Geometry: Mirror Symmetry Spring 2009 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MIRROR SYMMETRY:
MIT OpenCourseWare http://ocw.mit.edu 18.969 Topics in Geometry: Mirror Symmetry Spring 2009 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. MIRROR SYMMETRY:
Non-Kähler Calabi-Yau Manifolds
 Non-Kähler Calabi-Yau Manifolds Shing-Tung Yau Harvard University String-Math 2011 University of Pennsylvania June 6, 2011 String and math have had a very close interaction over the past thirty years.
Non-Kähler Calabi-Yau Manifolds Shing-Tung Yau Harvard University String-Math 2011 University of Pennsylvania June 6, 2011 String and math have had a very close interaction over the past thirty years.
Generalized Tian-Todorov theorems
 Generalized Tian-Todorov theorems M.Kontsevich 1 The classical Tian-Todorov theorem Recall the classical Tian-Todorov theorem (see [4],[5]) about the smoothness of the moduli spaces of Calabi-Yau manifolds:
Generalized Tian-Todorov theorems M.Kontsevich 1 The classical Tian-Todorov theorem Recall the classical Tian-Todorov theorem (see [4],[5]) about the smoothness of the moduli spaces of Calabi-Yau manifolds:
The Strominger Yau Zaslow conjecture
 The Strominger Yau Zaslow conjecture Paul Hacking 10/16/09 1 Background 1.1 Kähler metrics Let X be a complex manifold of dimension n, and M the underlying smooth manifold with (integrable) almost complex
The Strominger Yau Zaslow conjecture Paul Hacking 10/16/09 1 Background 1.1 Kähler metrics Let X be a complex manifold of dimension n, and M the underlying smooth manifold with (integrable) almost complex
A Bird Eye s view: recent update to Extremal metrics
 A Bird Eye s view: recent update to Extremal metrics Xiuxiong Chen Department of Mathematics University of Wisconsin at Madison January 21, 2009 A Bird Eye s view: recent update to Extremal metrics Xiuxiong
A Bird Eye s view: recent update to Extremal metrics Xiuxiong Chen Department of Mathematics University of Wisconsin at Madison January 21, 2009 A Bird Eye s view: recent update to Extremal metrics Xiuxiong
The geometry of Landau-Ginzburg models
 Motivation Toric degeneration Hodge theory CY3s The Geometry of Landau-Ginzburg Models January 19, 2016 Motivation Toric degeneration Hodge theory CY3s Plan of talk 1. Landau-Ginzburg models and mirror
Motivation Toric degeneration Hodge theory CY3s The Geometry of Landau-Ginzburg Models January 19, 2016 Motivation Toric degeneration Hodge theory CY3s Plan of talk 1. Landau-Ginzburg models and mirror
Recent Results on the Moduli Spaces of Riemann Surfaces
 Recent Results on the Moduli Spaces of Riemann Surfaces Kefeng Liu JDG Conference May 14, 2005 Harvard Twenty years ago, at his Nankai Institute of Mathematics, a lecture of Prof. S.-S. Chern on the Atiyah-Singer
Recent Results on the Moduli Spaces of Riemann Surfaces Kefeng Liu JDG Conference May 14, 2005 Harvard Twenty years ago, at his Nankai Institute of Mathematics, a lecture of Prof. S.-S. Chern on the Atiyah-Singer
Statistics of supersymmetric vacua in string/m theory
 Statistics of supersymmetric vacua in string/m theory Steve Zelditch Department of Mathematics Johns Hopkins University Joint Work with Bernard Shiffman Mike Douglas 1 Supergravity theory An effective
Statistics of supersymmetric vacua in string/m theory Steve Zelditch Department of Mathematics Johns Hopkins University Joint Work with Bernard Shiffman Mike Douglas 1 Supergravity theory An effective
Kähler Potential of Moduli Space. of Calabi-Yau d-fold embedded in CP d+1
 March 2000 hep-th/000364 Kähler Potential of Moduli Space arxiv:hep-th/000364v 20 Mar 2000 of Calabi-Yau d-fold embedded in CP d+ Katsuyuki Sugiyama Department of Fundamental Sciences Faculty of Integrated
March 2000 hep-th/000364 Kähler Potential of Moduli Space arxiv:hep-th/000364v 20 Mar 2000 of Calabi-Yau d-fold embedded in CP d+ Katsuyuki Sugiyama Department of Fundamental Sciences Faculty of Integrated
Overview of classical mirror symmetry
 Overview of classical mirror symmetry David Cox (notes by Paul Hacking) 9/8/09 () Physics (2) Quintic 3-fold (3) Math String theory is a N = 2 superconformal field theory (SCFT) which models elementary
Overview of classical mirror symmetry David Cox (notes by Paul Hacking) 9/8/09 () Physics (2) Quintic 3-fold (3) Math String theory is a N = 2 superconformal field theory (SCFT) which models elementary
Hyperkähler geometry lecture 3
 Hyperkähler geometry lecture 3 Misha Verbitsky Cohomology in Mathematics and Physics Euler Institute, September 25, 2013, St. Petersburg 1 Broom Bridge Here as he walked by on the 16th of October 1843
Hyperkähler geometry lecture 3 Misha Verbitsky Cohomology in Mathematics and Physics Euler Institute, September 25, 2013, St. Petersburg 1 Broom Bridge Here as he walked by on the 16th of October 1843
THE QUANTUM CONNECTION
 THE QUANTUM CONNECTION MICHAEL VISCARDI Review of quantum cohomology Genus 0 Gromov-Witten invariants Let X be a smooth projective variety over C, and H 2 (X, Z) an effective curve class Let M 0,n (X,
THE QUANTUM CONNECTION MICHAEL VISCARDI Review of quantum cohomology Genus 0 Gromov-Witten invariants Let X be a smooth projective variety over C, and H 2 (X, Z) an effective curve class Let M 0,n (X,
d) There is a Web page that includes links to both Web page A and Web page B.
 P403-406 5. Determine whether the relation R on the set of all eb pages is reflexive( 自反 ), symmetric( 对 称 ), antisymmetric( 反对称 ), and/or transitive( 传递 ), where (a, b) R if and only if a) Everyone who
P403-406 5. Determine whether the relation R on the set of all eb pages is reflexive( 自反 ), symmetric( 对 称 ), antisymmetric( 反对称 ), and/or transitive( 传递 ), where (a, b) R if and only if a) Everyone who
Galileo Galilei ( ) Title page of Galileo's Dialogue concerning the two chief world systems, published in Florence in February 1632.
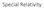 Special Relativity Galileo Galilei (1564-1642) Title page of Galileo's Dialogue concerning the two chief world systems, published in Florence in February 1632. 2 Galilean Transformation z z!!! r ' = r
Special Relativity Galileo Galilei (1564-1642) Title page of Galileo's Dialogue concerning the two chief world systems, published in Florence in February 1632. 2 Galilean Transformation z z!!! r ' = r
Counting black hole microstates as open string flux vacua
 Counting black hole microstates as open string flux vacua Frederik Denef KITP, November 23, 2005 F. Denef and G. Moore, to appear Outline Setting and formulation of the problem Black hole microstates and
Counting black hole microstates as open string flux vacua Frederik Denef KITP, November 23, 2005 F. Denef and G. Moore, to appear Outline Setting and formulation of the problem Black hole microstates and
The Calabi Conjecture
 The Calabi Conjecture notes by Aleksander Doan These are notes to the talk given on 9th March 2012 at the Graduate Topology and Geometry Seminar at the University of Warsaw. They are based almost entirely
The Calabi Conjecture notes by Aleksander Doan These are notes to the talk given on 9th March 2012 at the Graduate Topology and Geometry Seminar at the University of Warsaw. They are based almost entirely
On the Quark model based on virtual spacetime and the origin of fractional charge
 On the Quark model based on virtual spacetime and the origin of fractional charge Zhi Cheng No. 9 Bairong st. Baiyun District, Guangzhou, China. 510400. gzchengzhi@hotmail.com Abstract: The quark model
On the Quark model based on virtual spacetime and the origin of fractional charge Zhi Cheng No. 9 Bairong st. Baiyun District, Guangzhou, China. 510400. gzchengzhi@hotmail.com Abstract: The quark model
BERGMAN KERNEL ON COMPACT KÄHLER MANIFOLDS
 BERGMAN KERNEL ON COMPACT KÄHLER MANIFOLDS SHOO SETO Abstract. These are the notes to an expository talk I plan to give at MGSC on Kähler Geometry aimed for beginning graduate students in hopes to motivate
BERGMAN KERNEL ON COMPACT KÄHLER MANIFOLDS SHOO SETO Abstract. These are the notes to an expository talk I plan to give at MGSC on Kähler Geometry aimed for beginning graduate students in hopes to motivate
Riemannian Curvature Functionals: Lecture III
 Riemannian Curvature Functionals: Lecture III Jeff Viaclovsky Park City Mathematics Institute July 18, 2013 Lecture Outline Today we will discuss the following: Complete the local description of the moduli
Riemannian Curvature Functionals: Lecture III Jeff Viaclovsky Park City Mathematics Institute July 18, 2013 Lecture Outline Today we will discuss the following: Complete the local description of the moduli
Constructing compact 8-manifolds with holonomy Spin(7)
 Constructing compact 8-manifolds with holonomy Spin(7) Dominic Joyce, Oxford University Simons Collaboration meeting, Imperial College, June 2017. Based on Invent. math. 123 (1996), 507 552; J. Diff. Geom.
Constructing compact 8-manifolds with holonomy Spin(7) Dominic Joyce, Oxford University Simons Collaboration meeting, Imperial College, June 2017. Based on Invent. math. 123 (1996), 507 552; J. Diff. Geom.
Knots and Mirror Symmetry. Mina Aganagic UC Berkeley
 Knots and Mirror Symmetry Mina Aganagic UC Berkeley 1 Quantum physics has played a central role in answering the basic question in knot theory: When are two knots distinct? 2 Witten explained in 88, that
Knots and Mirror Symmetry Mina Aganagic UC Berkeley 1 Quantum physics has played a central role in answering the basic question in knot theory: When are two knots distinct? 2 Witten explained in 88, that
Knot Homology from Refined Chern-Simons Theory
 Knot Homology from Refined Chern-Simons Theory Mina Aganagic UC Berkeley Based on work with Shamil Shakirov arxiv: 1105.5117 1 the knot invariant Witten explained in 88 that J(K, q) constructed by Jones
Knot Homology from Refined Chern-Simons Theory Mina Aganagic UC Berkeley Based on work with Shamil Shakirov arxiv: 1105.5117 1 the knot invariant Witten explained in 88 that J(K, q) constructed by Jones
Takao Akahori. z i In this paper, if f is a homogeneous polynomial, the correspondence between the Kodaira-Spencer class and C[z 1,...
 J. Korean Math. Soc. 40 (2003), No. 4, pp. 667 680 HOMOGENEOUS POLYNOMIAL HYPERSURFACE ISOLATED SINGULARITIES Takao Akahori Abstract. The mirror conjecture means originally the deep relation between complex
J. Korean Math. Soc. 40 (2003), No. 4, pp. 667 680 HOMOGENEOUS POLYNOMIAL HYPERSURFACE ISOLATED SINGULARITIES Takao Akahori Abstract. The mirror conjecture means originally the deep relation between complex
Complex manifolds, Kahler metrics, differential and harmonic forms
 Complex manifolds, Kahler metrics, differential and harmonic forms Cattani June 16, 2010 1 Lecture 1 Definition 1.1 (Complex Manifold). A complex manifold is a manifold with coordinates holomorphic on
Complex manifolds, Kahler metrics, differential and harmonic forms Cattani June 16, 2010 1 Lecture 1 Definition 1.1 (Complex Manifold). A complex manifold is a manifold with coordinates holomorphic on
Topic: First Chern classes of Kähler manifolds Mitchell Faulk Last updated: April 23, 2016
 Topic: First Chern classes of Kähler manifolds itchell Faulk Last updated: April 23, 2016 We study the first Chern class of various Kähler manifolds. We only consider two sources of examples: Riemann surfaces
Topic: First Chern classes of Kähler manifolds itchell Faulk Last updated: April 23, 2016 We study the first Chern class of various Kähler manifolds. We only consider two sources of examples: Riemann surfaces
On Flux Quantization in F-Theory
 On Flux Quantization in F-Theory Raffaele Savelli MPI - Munich Bad Honnef, March 2011 Based on work with A. Collinucci, arxiv: 1011.6388 Motivations Motivations The recent attempts to find UV-completions
On Flux Quantization in F-Theory Raffaele Savelli MPI - Munich Bad Honnef, March 2011 Based on work with A. Collinucci, arxiv: 1011.6388 Motivations Motivations The recent attempts to find UV-completions
Contributors. Preface
 Contents Contributors Preface v xv 1 Kähler Manifolds by E. Cattani 1 1.1 Complex Manifolds........................... 2 1.1.1 Definition and Examples.................... 2 1.1.2 Holomorphic Vector Bundles..................
Contents Contributors Preface v xv 1 Kähler Manifolds by E. Cattani 1 1.1 Complex Manifolds........................... 2 1.1.1 Definition and Examples.................... 2 1.1.2 Holomorphic Vector Bundles..................
Cohomology jump loci of quasi-projective varieties
 Cohomology jump loci of quasi-projective varieties Botong Wang joint work with Nero Budur University of Notre Dame June 27 2013 Motivation What topological spaces are homeomorphic (or homotopy equivalent)
Cohomology jump loci of quasi-projective varieties Botong Wang joint work with Nero Budur University of Notre Dame June 27 2013 Motivation What topological spaces are homeomorphic (or homotopy equivalent)
Calabi-Yau Fourfolds with non-trivial Three-Form Cohomology
 Calabi-Yau Fourfolds with non-trivial Three-Form Cohomology Sebastian Greiner arxiv: 1512.04859, 1702.03217 (T. Grimm, SG) Max-Planck-Institut für Physik and ITP Utrecht String Pheno 2017 Sebastian Greiner
Calabi-Yau Fourfolds with non-trivial Three-Form Cohomology Sebastian Greiner arxiv: 1512.04859, 1702.03217 (T. Grimm, SG) Max-Planck-Institut für Physik and ITP Utrecht String Pheno 2017 Sebastian Greiner
Moduli space of smoothable Kähler-Einstein Q-Fano varieties
 Moduli space of smoothable Kähler-Einstein Q-Fano varieties Chi Li joint work with Xiaowei Wang and Chenyang Xu Mathematics Department, Stony Brook University University of Tokyo, July 27, 2015 Table of
Moduli space of smoothable Kähler-Einstein Q-Fano varieties Chi Li joint work with Xiaowei Wang and Chenyang Xu Mathematics Department, Stony Brook University University of Tokyo, July 27, 2015 Table of
VARIATION OF HODGE STRUCTURES, FROBENIUS MANIFOLDS AND GAUGE THEORY
 VARIATION OF HODGE STRUCTURES, FROBENIUS MANIFOLDS AND GAUGE THEORY SI LI ABSTRACT. We explain the homological relation between the Frobenius structure on the deformation space of Calabi-Yau manifold and
VARIATION OF HODGE STRUCTURES, FROBENIUS MANIFOLDS AND GAUGE THEORY SI LI ABSTRACT. We explain the homological relation between the Frobenius structure on the deformation space of Calabi-Yau manifold and
Shafarevich s Conjecture for CY Manifolds I
 Pure and Applied Mathematics Quarterly Volume 1, Number 1, 28 67, 2005 Shafarevich s Conjecture for CY Manifolds I Kefeng Liu, Andrey Todorov Shing-Tung Yau and Kang Zuo Abstract Let C be a Riemann surface
Pure and Applied Mathematics Quarterly Volume 1, Number 1, 28 67, 2005 Shafarevich s Conjecture for CY Manifolds I Kefeng Liu, Andrey Todorov Shing-Tung Yau and Kang Zuo Abstract Let C be a Riemann surface
String-Theory: Open-closed String Moduli Spaces
 String-Theory: Open-closed String Moduli Spaces Heidelberg, 13.10.2014 History of the Universe particular: Epoch of cosmic inflation in the early Universe Inflation and Inflaton φ, potential V (φ) Possible
String-Theory: Open-closed String Moduli Spaces Heidelberg, 13.10.2014 History of the Universe particular: Epoch of cosmic inflation in the early Universe Inflation and Inflaton φ, potential V (φ) Possible
Uniform K-stability of pairs
 Uniform K-stability of pairs Gang Tian Peking University Let G = SL(N + 1, C) with two representations V, W over Q. For any v V\{0} and any one-parameter subgroup λ of G, we can associate a weight w λ
Uniform K-stability of pairs Gang Tian Peking University Let G = SL(N + 1, C) with two representations V, W over Q. For any v V\{0} and any one-parameter subgroup λ of G, we can associate a weight w λ
Donaldson Invariants and Moduli of Yang-Mills Instantons
 Donaldson Invariants and Moduli of Yang-Mills Instantons Lincoln College Oxford University (slides posted at users.ox.ac.uk/ linc4221) The ASD Equation in Low Dimensions, 17 November 2017 Moduli and Invariants
Donaldson Invariants and Moduli of Yang-Mills Instantons Lincoln College Oxford University (slides posted at users.ox.ac.uk/ linc4221) The ASD Equation in Low Dimensions, 17 November 2017 Moduli and Invariants
A TRANSCENDENTAL METHOD IN ALGEBRAIC GEOMETRY
 Actes, Congrès intern, math., 1970. Tome 1, p. 113 à 119. A TRANSCENDENTAL METHOD IN ALGEBRAIC GEOMETRY by PHILLIP A. GRIFFITHS 1. Introduction and an example from curves. It is well known that the basic
Actes, Congrès intern, math., 1970. Tome 1, p. 113 à 119. A TRANSCENDENTAL METHOD IN ALGEBRAIC GEOMETRY by PHILLIP A. GRIFFITHS 1. Introduction and an example from curves. It is well known that the basic
Deligne s functorial Riemann-Roch theorem
 Deligne s functorial Riemann-Roch theorem PIMS, Sept. 13th 2007 D. Rössler (joint with V. Maillot) () Deligne s functorial Riemann-Roch theorem PIMS, Sept. 13th 2007 1 / 14 The Adams-Riemann-Roch theorem
Deligne s functorial Riemann-Roch theorem PIMS, Sept. 13th 2007 D. Rössler (joint with V. Maillot) () Deligne s functorial Riemann-Roch theorem PIMS, Sept. 13th 2007 1 / 14 The Adams-Riemann-Roch theorem
INSTANTON MODULI AND COMPACTIFICATION MATTHEW MAHOWALD
 INSTANTON MODULI AND COMPACTIFICATION MATTHEW MAHOWALD () Instanton (definition) (2) ADHM construction (3) Compactification. Instantons.. Notation. Throughout this talk, we will use the following notation:
INSTANTON MODULI AND COMPACTIFICATION MATTHEW MAHOWALD () Instanton (definition) (2) ADHM construction (3) Compactification. Instantons.. Notation. Throughout this talk, we will use the following notation:
As always, the story begins with Riemann surfaces or just (real) surfaces. (As we have already noted, these are nearly the same thing).
 An Interlude on Curvature and Hermitian Yang Mills As always, the story begins with Riemann surfaces or just (real) surfaces. (As we have already noted, these are nearly the same thing). Suppose we wanted
An Interlude on Curvature and Hermitian Yang Mills As always, the story begins with Riemann surfaces or just (real) surfaces. (As we have already noted, these are nearly the same thing). Suppose we wanted
Pietro Fre' SISSA-Trieste. Paolo Soriani University degli Studi di Milano. From Calabi-Yau manifolds to topological field theories
 From Calabi-Yau manifolds to topological field theories Pietro Fre' SISSA-Trieste Paolo Soriani University degli Studi di Milano World Scientific Singapore New Jersey London Hong Kong CONTENTS 1 AN INTRODUCTION
From Calabi-Yau manifolds to topological field theories Pietro Fre' SISSA-Trieste Paolo Soriani University degli Studi di Milano World Scientific Singapore New Jersey London Hong Kong CONTENTS 1 AN INTRODUCTION
Lecture Note on Linear Algebra 14. Linear Independence, Bases and Coordinates
 Lecture Note on Linear Algebra 14 Linear Independence, Bases and Coordinates Wei-Shi Zheng, wszheng@ieeeorg, 211 November 3, 211 1 What Do You Learn from This Note Do you still remember the unit vectors
Lecture Note on Linear Algebra 14 Linear Independence, Bases and Coordinates Wei-Shi Zheng, wszheng@ieeeorg, 211 November 3, 211 1 What Do You Learn from This Note Do you still remember the unit vectors
Vanishing theorems and holomorphic forms
 Vanishing theorems and holomorphic forms Mihnea Popa Northwestern AMS Meeting, Lansing March 14, 2015 Holomorphic one-forms and geometry X compact complex manifold, dim C X = n. Holomorphic one-forms and
Vanishing theorems and holomorphic forms Mihnea Popa Northwestern AMS Meeting, Lansing March 14, 2015 Holomorphic one-forms and geometry X compact complex manifold, dim C X = n. Holomorphic one-forms and
Algebraic geometry over quaternions
 Algebraic geometry over quaternions Misha Verbitsky November 26, 2007 Durham University 1 History of algebraic geometry. 1. XIX centrury: Riemann, Klein, Poincaré. Study of elliptic integrals and elliptic
Algebraic geometry over quaternions Misha Verbitsky November 26, 2007 Durham University 1 History of algebraic geometry. 1. XIX centrury: Riemann, Klein, Poincaré. Study of elliptic integrals and elliptic
ERRATUM TO AFFINE MANIFOLDS, SYZ GEOMETRY AND THE Y VERTEX
 ERRATUM TO AFFINE MANIFOLDS, SYZ GEOMETRY AND THE Y VERTEX JOHN LOFTIN, SHING-TUNG YAU, AND ERIC ZASLOW 1. Main result The purpose of this erratum is to correct an error in the proof of the main result
ERRATUM TO AFFINE MANIFOLDS, SYZ GEOMETRY AND THE Y VERTEX JOHN LOFTIN, SHING-TUNG YAU, AND ERIC ZASLOW 1. Main result The purpose of this erratum is to correct an error in the proof of the main result
CHARACTERISTIC CLASSES
 1 CHARACTERISTIC CLASSES Andrew Ranicki Index theory seminar 14th February, 2011 2 The Index Theorem identifies Introduction analytic index = topological index for a differential operator on a compact
1 CHARACTERISTIC CLASSES Andrew Ranicki Index theory seminar 14th February, 2011 2 The Index Theorem identifies Introduction analytic index = topological index for a differential operator on a compact
HYPERKÄHLER MANIFOLDS
 HYPERKÄHLER MANIFOLDS PAVEL SAFRONOV, TALK AT 2011 TALBOT WORKSHOP 1.1. Basic definitions. 1. Hyperkähler manifolds Definition. A hyperkähler manifold is a C Riemannian manifold together with three covariantly
HYPERKÄHLER MANIFOLDS PAVEL SAFRONOV, TALK AT 2011 TALBOT WORKSHOP 1.1. Basic definitions. 1. Hyperkähler manifolds Definition. A hyperkähler manifold is a C Riemannian manifold together with three covariantly
Gromov-Witten invariants and Algebraic Geometry (II) Jun Li
 Gromov-Witten invariants and Algebraic Geometry (II) Shanghai Center for Mathematical Sciences and Stanford University GW invariants of quintic Calabi-Yau threefolds Quintic Calabi-Yau threefolds: X =
Gromov-Witten invariants and Algebraic Geometry (II) Shanghai Center for Mathematical Sciences and Stanford University GW invariants of quintic Calabi-Yau threefolds Quintic Calabi-Yau threefolds: X =
Dualities and Topological Strings
 Dualities and Topological Strings Strings 2006, Beijing - RD, C. Vafa, E.Verlinde, hep-th/0602087 - work in progress w/ C. Vafa & C. Beasley, L. Hollands Robbert Dijkgraaf University of Amsterdam Topological
Dualities and Topological Strings Strings 2006, Beijing - RD, C. Vafa, E.Verlinde, hep-th/0602087 - work in progress w/ C. Vafa & C. Beasley, L. Hollands Robbert Dijkgraaf University of Amsterdam Topological
Source mechanism solution
 Source mechanism solution Contents Source mechanism solution 1 1. A general introduction 1 2. A step-by-step guide 1 Step-1: Prepare data files 1 Step-2: Start GeoTaos or GeoTaos_Map 2 Step-3: Convert
Source mechanism solution Contents Source mechanism solution 1 1. A general introduction 1 2. A step-by-step guide 1 Step-1: Prepare data files 1 Step-2: Start GeoTaos or GeoTaos_Map 2 Step-3: Convert
Eigenvalues of Collapsing Domains and Drift Laplacian
 Eigenvalues of Collapsing Domains and Drift Laplacian Zhiqin Lu Dedicate to Professor Peter Li on his 60th Birthday Department of Mathematics, UC Irvine, Irvine CA 92697 January 17, 2012 Zhiqin Lu, Dept.
Eigenvalues of Collapsing Domains and Drift Laplacian Zhiqin Lu Dedicate to Professor Peter Li on his 60th Birthday Department of Mathematics, UC Irvine, Irvine CA 92697 January 17, 2012 Zhiqin Lu, Dept.
Stable bundles on CP 3 and special holonomies
 Stable bundles on CP 3 and special holonomies Misha Verbitsky Géométrie des variétés complexes IV CIRM, Luminy, Oct 26, 2010 1 Hyperkähler manifolds DEFINITION: A hyperkähler structure on a manifold M
Stable bundles on CP 3 and special holonomies Misha Verbitsky Géométrie des variétés complexes IV CIRM, Luminy, Oct 26, 2010 1 Hyperkähler manifolds DEFINITION: A hyperkähler structure on a manifold M
David R. Morrison. String Phenomenology 2008 University of Pennsylvania 31 May 2008
 : : University of California, Santa Barbara String Phenomenology 2008 University of Pennsylvania 31 May 2008 engineering has been a very successful approach to studying string vacua, and has been essential
: : University of California, Santa Barbara String Phenomenology 2008 University of Pennsylvania 31 May 2008 engineering has been a very successful approach to studying string vacua, and has been essential
Conjectures in Kahler geometry
 Conjectures in Kahler geometry S.K. Donaldson Abstract. We state a general conjecture about the existence of Kahler metrics of constant scalar curvature, and discuss the background to the conjecture 1.
Conjectures in Kahler geometry S.K. Donaldson Abstract. We state a general conjecture about the existence of Kahler metrics of constant scalar curvature, and discuss the background to the conjecture 1.
Generalized Hitchin-Kobayashi correspondence and Weil-Petersson current
 Author, F., and S. Author. (2015) Generalized Hitchin-Kobayashi correspondence and Weil-Petersson current, International Mathematics Research Notices, Vol. 2015, Article ID rnn999, 7 pages. doi:10.1093/imrn/rnn999
Author, F., and S. Author. (2015) Generalized Hitchin-Kobayashi correspondence and Weil-Petersson current, International Mathematics Research Notices, Vol. 2015, Article ID rnn999, 7 pages. doi:10.1093/imrn/rnn999
Refined Donaldson-Thomas theory and Nekrasov s formula
 Refined Donaldson-Thomas theory and Nekrasov s formula Balázs Szendrői, University of Oxford Maths of String and Gauge Theory, City University and King s College London 3-5 May 2012 Geometric engineering
Refined Donaldson-Thomas theory and Nekrasov s formula Balázs Szendrői, University of Oxford Maths of String and Gauge Theory, City University and King s College London 3-5 May 2012 Geometric engineering
Conjectures on counting associative 3-folds in G 2 -manifolds
 in G 2 -manifolds Dominic Joyce, Oxford University Simons Collaboration on Special Holonomy in Geometry, Analysis and Physics, First Annual Meeting, New York City, September 2017. Based on arxiv:1610.09836.
in G 2 -manifolds Dominic Joyce, Oxford University Simons Collaboration on Special Holonomy in Geometry, Analysis and Physics, First Annual Meeting, New York City, September 2017. Based on arxiv:1610.09836.
Recent results on the moduli space of Riemann surfaces
 Surveys in Differential Geometry X Recent results on the moduli space of Riemann surfaces Kefeng Liu Abstract. In this paper we briefly discuss some of our recent results in the study of moduli space of
Surveys in Differential Geometry X Recent results on the moduli space of Riemann surfaces Kefeng Liu Abstract. In this paper we briefly discuss some of our recent results in the study of moduli space of
Recall for an n n matrix A = (a ij ), its trace is defined by. a jj. It has properties: In particular, if B is non-singular n n matrix,
 Chern characters Recall for an n n matrix A = (a ij ), its trace is defined by tr(a) = n a jj. j=1 It has properties: tr(a + B) = tr(a) + tr(b), tr(ab) = tr(ba). In particular, if B is non-singular n n
Chern characters Recall for an n n matrix A = (a ij ), its trace is defined by tr(a) = n a jj. j=1 It has properties: tr(a + B) = tr(a) + tr(b), tr(ab) = tr(ba). In particular, if B is non-singular n n
Heterotic Flux Compactifications
 Heterotic Flux Compactifications Mario Garcia-Fernandez Instituto de Ciencias Matemáticas, Madrid String Pheno 2017 Virginia Tech, 7 July 2017 Based on arxiv:1611.08926, and joint work with Rubio, Tipler,
Heterotic Flux Compactifications Mario Garcia-Fernandez Instituto de Ciencias Matemáticas, Madrid String Pheno 2017 Virginia Tech, 7 July 2017 Based on arxiv:1611.08926, and joint work with Rubio, Tipler,
Invariance Theory, the Heat Equation, and the Atiyah-Singer Index Theorem
 PETER B. GILKEY Department of Mathematics, University of Oregon Invariance Theory, the Heat Equation, and the Atiyah-Singer Index Theorem Second Edition CRC PRESS Boca Raton Ann Arbor London Tokyo Contents
PETER B. GILKEY Department of Mathematics, University of Oregon Invariance Theory, the Heat Equation, and the Atiyah-Singer Index Theorem Second Edition CRC PRESS Boca Raton Ann Arbor London Tokyo Contents
Cohomology of the Mumford Quotient
 Cohomology of the Mumford Quotient Maxim Braverman Abstract. Let X be a smooth projective variety acted on by a reductive group G. Let L be a positive G-equivariant line bundle over X. We use a Witten
Cohomology of the Mumford Quotient Maxim Braverman Abstract. Let X be a smooth projective variety acted on by a reductive group G. Let L be a positive G-equivariant line bundle over X. We use a Witten
arxiv: v1 [math.dg] 11 Jan 2009
![arxiv: v1 [math.dg] 11 Jan 2009 arxiv: v1 [math.dg] 11 Jan 2009](/thumbs/92/107852357.jpg) arxiv:0901.1474v1 [math.dg] 11 Jan 2009 Scalar Curvature Behavior for Finite Time Singularity of Kähler-Ricci Flow Zhou Zhang November 6, 2018 Abstract In this short paper, we show that Kähler-Ricci flows
arxiv:0901.1474v1 [math.dg] 11 Jan 2009 Scalar Curvature Behavior for Finite Time Singularity of Kähler-Ricci Flow Zhou Zhang November 6, 2018 Abstract In this short paper, we show that Kähler-Ricci flows
2012 AP Calculus BC 模拟试卷
 0 AP Calculus BC 模拟试卷 北京新东方罗勇 luoyong@df.cn 0-3- 说明 : 请严格按照实际考试时间进行模拟, 考试时间共 95 分钟 Multiple-Choice section A 部分 : 无计算器 B 部分 : 有计算器 Free-response section A 部分 : 有计算器 B 部分 : 无计算器 总计 45 题 /05 分钟 8 题,55 分钟
0 AP Calculus BC 模拟试卷 北京新东方罗勇 luoyong@df.cn 0-3- 说明 : 请严格按照实际考试时间进行模拟, 考试时间共 95 分钟 Multiple-Choice section A 部分 : 无计算器 B 部分 : 有计算器 Free-response section A 部分 : 有计算器 B 部分 : 无计算器 总计 45 题 /05 分钟 8 题,55 分钟
Finite-Difference Methods (FDM)
 Finite-Diffeence Methods (FDM) Finite-diffeence Appoimations Assuming a 1D f() as in Fig.4.14 witing f 1 and f as Talo seies epansions aound = 0 Appoimating deivatives at f f (1) () ( 0) = f h f + h 1
Finite-Diffeence Methods (FDM) Finite-diffeence Appoimations Assuming a 1D f() as in Fig.4.14 witing f 1 and f as Talo seies epansions aound = 0 Appoimating deivatives at f f (1) () ( 0) = f h f + h 1
arxiv:alg-geom/ v1 29 Jul 1993
 Hyperkähler embeddings and holomorphic symplectic geometry. Mikhail Verbitsky, verbit@math.harvard.edu arxiv:alg-geom/9307009v1 29 Jul 1993 0. ntroduction. n this paper we are studying complex analytic
Hyperkähler embeddings and holomorphic symplectic geometry. Mikhail Verbitsky, verbit@math.harvard.edu arxiv:alg-geom/9307009v1 29 Jul 1993 0. ntroduction. n this paper we are studying complex analytic
BPS states, Wall-crossing and Quivers
 Iberian Strings 2012 Bilbao BPS states, Wall-crossing and Quivers IST, Lisboa Michele Cirafici M.C.& A.Sincovics & R.J. Szabo: 0803.4188, 1012.2725, 1108.3922 and M.C. to appear BPS States in String theory
Iberian Strings 2012 Bilbao BPS states, Wall-crossing and Quivers IST, Lisboa Michele Cirafici M.C.& A.Sincovics & R.J. Szabo: 0803.4188, 1012.2725, 1108.3922 and M.C. to appear BPS States in String theory
FAKE PROJECTIVE SPACES AND FAKE TORI
 FAKE PROJECTIVE SPACES AND FAKE TORI OLIVIER DEBARRE Abstract. Hirzebruch and Kodaira proved in 1957 that when n is odd, any compact Kähler manifold X which is homeomorphic to P n is isomorphic to P n.
FAKE PROJECTIVE SPACES AND FAKE TORI OLIVIER DEBARRE Abstract. Hirzebruch and Kodaira proved in 1957 that when n is odd, any compact Kähler manifold X which is homeomorphic to P n is isomorphic to P n.
AFFINE SPHERES AND KÄHLER-EINSTEIN METRICS. metric makes sense under projective coordinate changes. See e.g. [10]. Form a cone (1) C = s>0
![AFFINE SPHERES AND KÄHLER-EINSTEIN METRICS. metric makes sense under projective coordinate changes. See e.g. [10]. Form a cone (1) C = s>0 AFFINE SPHERES AND KÄHLER-EINSTEIN METRICS. metric makes sense under projective coordinate changes. See e.g. [10]. Form a cone (1) C = s>0](/thumbs/88/115605861.jpg) AFFINE SPHERES AND KÄHLER-EINSTEIN METRICS JOHN C. LOFTIN 1. Introduction In this note, we introduce a straightforward correspondence between some natural affine Kähler metrics on convex cones and natural
AFFINE SPHERES AND KÄHLER-EINSTEIN METRICS JOHN C. LOFTIN 1. Introduction In this note, we introduce a straightforward correspondence between some natural affine Kähler metrics on convex cones and natural
FROM HOLOMORPHIC FUNCTIONS TO HOLOMORPHIC SECTIONS
 FROM HOLOMORPHIC FUNCTIONS TO HOLOMORPHIC SECTIONS ZHIQIN LU. Introduction It is a pleasure to have the opportunity in the graduate colloquium to introduce my research field. I am a differential geometer.
FROM HOLOMORPHIC FUNCTIONS TO HOLOMORPHIC SECTIONS ZHIQIN LU. Introduction It is a pleasure to have the opportunity in the graduate colloquium to introduce my research field. I am a differential geometer.
MIFPA PiTP Lectures. Katrin Becker 1. Department of Physics, Texas A&M University, College Station, TX 77843, USA. 1
 MIFPA-10-34 PiTP Lectures Katrin Becker 1 Department of Physics, Texas A&M University, College Station, TX 77843, USA 1 kbecker@physics.tamu.edu Contents 1 Introduction 2 2 String duality 3 2.1 T-duality
MIFPA-10-34 PiTP Lectures Katrin Becker 1 Department of Physics, Texas A&M University, College Station, TX 77843, USA 1 kbecker@physics.tamu.edu Contents 1 Introduction 2 2 String duality 3 2.1 T-duality
Perspective on Geometric Analysis: Geometric Structures III
 Perspective on Geometric Analysis: Geometric Structures III Shing-Tung Yau Harvard University Talk in UCLA 1 When the topological method of surgery and gluing fails, we have to find a method that does
Perspective on Geometric Analysis: Geometric Structures III Shing-Tung Yau Harvard University Talk in UCLA 1 When the topological method of surgery and gluing fails, we have to find a method that does
Gradient Estimates and Sobolev Inequality
 Gradient Estimates and Sobolev Inequality Jiaping Wang University of Minnesota ( Joint work with Linfeng Zhou) Conference on Geometric Analysis in honor of Peter Li University of California, Irvine January
Gradient Estimates and Sobolev Inequality Jiaping Wang University of Minnesota ( Joint work with Linfeng Zhou) Conference on Geometric Analysis in honor of Peter Li University of California, Irvine January
Heterotic Torsional Backgrounds, from Supergravity to CFT
 Heterotic Torsional Backgrounds, from Supergravity to CFT IAP, Université Pierre et Marie Curie Eurostrings@Madrid, June 2010 L.Carlevaro, D.I. and M. Petropoulos, arxiv:0812.3391 L.Carlevaro and D.I.,
Heterotic Torsional Backgrounds, from Supergravity to CFT IAP, Université Pierre et Marie Curie Eurostrings@Madrid, June 2010 L.Carlevaro, D.I. and M. Petropoulos, arxiv:0812.3391 L.Carlevaro and D.I.,
On the Convergence of a Modified Kähler-Ricci Flow. 1 Introduction. Yuan Yuan
 On the Convergence of a Modified Kähler-Ricci Flow Yuan Yuan Abstract We study the convergence of a modified Kähler-Ricci flow defined by Zhou Zhang. We show that the modified Kähler-Ricci flow converges
On the Convergence of a Modified Kähler-Ricci Flow Yuan Yuan Abstract We study the convergence of a modified Kähler-Ricci flow defined by Zhou Zhang. We show that the modified Kähler-Ricci flow converges
Ω Ω /ω. To these, one wants to add a fourth condition that arises from physics, what is known as the anomaly cancellation, namely that
 String theory and balanced metrics One of the main motivations for considering balanced metrics, in addition to the considerations already mentioned, has to do with the theory of what are known as heterotic
String theory and balanced metrics One of the main motivations for considering balanced metrics, in addition to the considerations already mentioned, has to do with the theory of what are known as heterotic
0.1 Complex Analogues 1
 0.1 Complex Analogues 1 Abstract In complex geometry Kodaira s theorem tells us that on a Kähler manifold sufficiently high powers of positive line bundles admit global holomorphic sections. Donaldson
0.1 Complex Analogues 1 Abstract In complex geometry Kodaira s theorem tells us that on a Kähler manifold sufficiently high powers of positive line bundles admit global holomorphic sections. Donaldson
Aspects on Calabi Yau moduli
 Aspects on Calabi Yau moduli Chin-Lung Wang National Taiwan University The 90th Anniversary of Tsinghua Math. April 23, 2017 1 / 24 Contents Distance Curvature Singularities Transitions Invariance 2 /
Aspects on Calabi Yau moduli Chin-Lung Wang National Taiwan University The 90th Anniversary of Tsinghua Math. April 23, 2017 1 / 24 Contents Distance Curvature Singularities Transitions Invariance 2 /
Generalized N = 1 orientifold compactifications
 Generalized N = 1 orientifold compactifications Thomas W. Grimm University of Wisconsin, Madison based on: [hep-th/0602241] Iman Benmachiche, TWG [hep-th/0507153] TWG Madison, Wisconsin, November 2006
Generalized N = 1 orientifold compactifications Thomas W. Grimm University of Wisconsin, Madison based on: [hep-th/0602241] Iman Benmachiche, TWG [hep-th/0507153] TWG Madison, Wisconsin, November 2006
Moduli spaces of log del Pezzo pairs and K-stability
 Report on Research in Groups Moduli spaces of log del Pezzo pairs and K-stability June 20 - July 20, 2016 Organizers: Patricio Gallardo, Jesus Martinez-Garcia, Cristiano Spotti. In this report we start
Report on Research in Groups Moduli spaces of log del Pezzo pairs and K-stability June 20 - July 20, 2016 Organizers: Patricio Gallardo, Jesus Martinez-Garcia, Cristiano Spotti. In this report we start
Perspectives and Advances in Kähler Geometry
 Perspectives and Advances in Kähler Geometry Shing-Tung Yau Harvard University 30th Shanks Lecture, Vanderbilt University May 19, 2015 1. Introduction of the concept of Kähler manifolds The foundation
Perspectives and Advances in Kähler Geometry Shing-Tung Yau Harvard University 30th Shanks Lecture, Vanderbilt University May 19, 2015 1. Introduction of the concept of Kähler manifolds The foundation
Chern numbers and Hilbert Modular Varieties
 Chern numbers and Hilbert Modular Varieties Dylan Attwell-Duval Department of Mathematics and Statistics McGill University Montreal, Quebec attwellduval@math.mcgill.ca April 9, 2011 A Topological Point
Chern numbers and Hilbert Modular Varieties Dylan Attwell-Duval Department of Mathematics and Statistics McGill University Montreal, Quebec attwellduval@math.mcgill.ca April 9, 2011 A Topological Point
