ADDITIVELY SEPARABLE FUNCTIONS
|
|
|
- Monica Thompson
- 6 years ago
- Views:
Transcription
1 ADDITIVELY SEPARABLE FUNCTIONS FUNCTIONS OF THE FORM F (, ) =f()+g() STEVEN F. BELLENOT Abstract. A sample project similar to the project for Spring 25. The picture below has a hortizontal space coordinate s and vertical time coordinate t. We see two waves, a raised hump moving to the left and a depression moving to the right. At t =,the middle hortizontal bold black line, the two waves cancel each other briefl. From another viewpoint, the red line is the -aes and the red curve above it is f() =ep( 2 ), the blue line is the -aes and the blue curve below it is g() = ep( 2 ). The surface is the graph of F (, ) =f()+g(), a additivel separable function; but also a solution to awaveequation.
2 2 Additivel Separable Functions Introduction We consider a simple special class of functions of two variables, those that can be written in the form F (, ) =f()+g(). (Your project will be about functions that can be written in the form F (, ) =f()g().) This is perhaps the simplest collection of functions of two variables that depends on both variables. Our first step is to give a name to the collection, since this collection is not usuall studied, we get to make up a name. Definition. A function of two variables F (, ) will be called additivel separable if it can written as f()+g() for some single-variable functions f() and g(). After a definition one usuall adds some simple observations to aid the reader to get a feel for the topic. Note that constant functions like F (, ) =5orfunctionsofonevariable F(, ) =h() are additivel separable. Indeed, let f() =andg()=5org()=h()in the definition. But not all functions are additivel separable, later we will see F (, ) = is not additivel separable. Finall, the functions f() andg() in the definition are never unique, since if F (, ) =f()+g(), then also F (, ) =(f()+c)+(g() C) for an constant C. This collection is surprisingl rich. We start with a few eamples, Figure shows that such functions can look full three dimensional. This is surprising, since for fied = a, each cross section F (a, ) isg()+c a translate of the function g() withc=f(a). That is the sections = a for different parameters a all wave to the same time steps. The tangent plane to z = h(, ) atanpoint(a, b, h(a, b)) is additivel separable since is alwas of the form z = h (a, b)( a) +h (a, b)( b) +h(a, b). (So we could take f() =h (a, b)( a) andg()=h (a, b)( b)+h(a, b). Remember a, b, h(a, b), h (a, b) and h (a, b) are all constants and not variables.) The three basic etrema, local minimums, local maimums and saddle points, are often drawn like in Figure 2. These are graphs of the functions F (, ) = 2 2, showing a local maimum at (, ), F (, ) = 2 2, showing a saddle point at (, ), and F (, ) = 2 + 2, showing a local minimum (, ). All three functions are additivel separable. The last function in polar coordinates is just r 2 which is curious. A function of one variable in one coordinate sstem which is a nice additivel separable in a radicall different coordinate sstem. Neither r = 2 + 2, r 3, nor even r = is additivel separable. Rectangle Conditions When is a function F (, ) additivel separable? A simple necessar condition is obtained b assuming F (, ) =f()+g() and then plaing with its values at the four corners of Figure. The graph of sin + sin (left) and selected cross sections (right)
3 Additivel Separable Functions Figure 2. Local Ma, Saddle and Local Min a rectangle {(a, b), (c, b), (c, d), (a, d)} (see Figure 3). We have F (c, b)+f(a, d) F (a, b) =(f(c)+g(b))+(f(a)+g(d)) (f(a)+g(b)) = f(c)+g(d) =F(c, d) which we can write as a theorem. Theorem 2. If F (, ) is additivel separable, then for all a, b, c, d, F (c, b) +F(a, d) F (a, b) =F(c, d). Using a = b =andc=d=weseef(, ) = is not additivel separable. as the left hand side is zero, while the right hand side is one. Theorem 2 has a converse which is also true. Let f() =F(, ) and g() =F(,) F(, ) and use the theorem with = c, = d and a = b =. Wehave F(, ) =F(, ) + F (,) F(, ) = f()+g() which we can write as another theorem. Theorem 3. If for all a, b, c, d, F (c, b)+f (a, d) F (a, b) =F(c, d), thenf(, ) is additivel separable. Derivative conditions Obviousl if F (, ) =f()+g() then the partial derivatives of F are eas to compute. F = f () sinceg() is constant as a function of. Similarl F = g (), F = f (), F = g () and more importantl F = F =. Again lets make this a theorem. Theorem. If F (, ) is additivel separable, then = Again we see F (, ) = is not additivel separable since F =. Theorem sas all additivel separable functions satisf a simple PDE (Partial Differential Equation). The converse is also true. First remember from one variable that f () = (a, d) (c, d) (a, b) (c, b) Figure 3. The sum of the values at the diagonall opposite corners are equal
4 Additivel Separable Functions means that f() is a constant. For a function of two variables G (, ) = means that G(, ) is a constant function of but can be an arbitrar function of. SoF =(F ) = means F = h() some arbitrar function of and hence F (, ) =f()+g()whereg() is some arbitrar function of and f () =h()(sof()= a h(t)dt). Lets state this as another theorem Theorem 5. If F (, ) satisfs the PDE then F (, ) is additivel separable, = The Wave Equation It turns out this PDE is reall a famous PDE in disguise. With a a change of coordinates, this PDE becomes the one dimensional wave equation. The solutions to the one dimension wave equation can have two components, a wave function moving to the right (the g()) and another wave function moving to the left (the f()). Figure shows the function f() =ep( 2 ),g()= ep( 2 ),F(, ) =f()+g() along with the curve at several times. The t = graph is the bold straight line in the middle. Times before zero are below andinfrontoft= and times after zero are above and behind. So time increase as we go up Figure The space dimension shows the leftward motion of the wave. This is too important a fact to not show the connection, and it is a good application of the chain rule for several variables, but this section is not used in the sequel. The graph in Figure (also on the cover) page shows raised wave moving to the left and depression moving to the right. The -aisisred,the-ais is blue and the function is F (, ) =ep( 2 ) ep( 2 ). Time increases as one goes up the page and the one space dimension is hortizontal. The change of coordinates is given b t = + (time) and s = is the one space dimension. Inverting this transformation gives =(s+ t)/2and=(t s)/2. Using the chain rule F s = F s + F ( F s = F t = F t + F t = F ) 2 ( F + F ) 2 To take second partials F ss, the equation becomes mess since we have to appl the chain rule to F and F since the are functions of both and as well as appling the product rule. s 2 = ( 2 s + 2 F Since F = ss = ss = This simplifs to ) s s + F 2 ( 2 ) s 2 + F s + 2 F 2 s s + F 2 s 2 Similarl s 2 = 2 F 2 ( ) F s 2 t 2 == ( F 2 ) ( ) 2 =( 2 F s F 2 )
5 Additivel Separable Functions 5 Figure. The space dimension is hortizontal, the time vertical, the red line is the -aes and the blue line is the -aes and we have the one dimensional wave equation s 2 = 2 F t 2 The two forms of the wave equation are equivalent, although we have shown onl one direction. Usuall the wave equation has a constant c which represents the speed of the waves, in our case this c =. It is more common to see the wave equation written as s 2 = c 2 t 2 Critical Points and local etrema Here is one of sections that ou will need to do for our project on functions of the form f()g(). We want to characterize the local etrema of additivel separable functions F (, ) =f()+g() in terms of the critical points of f() andg(). From the derivatives section we have Theorem 6. The point (a, b) is a critical point of F (, ), ifandonlifboth=ais a critical point of f() and = b is a critical point of g(). To use the several variables classification function, big D = F F F 2, weusef = and the other second partials from the derivatives section to compute big D = f ()g (). As long as big D is not zero, namel when both f (a) g (b). We cover all cases in the table below which is onl for critical points (a, b).
6 6 Additivel Separable Functions Figure 5. The four basic cases: when big D f (a) g (b) big D Classification Local Min + Saddle + Saddle + Local Ma Clearl these crition are nicel illustrated b sin + sin in Figure at the points (π/2,π/2), (π/2, 3π/2), (3π/2,π/2) and (3π/2, 3π/2). The additivel separable functions are simple enough we can handle the general case with Talor series. If a is a critical point for f() thenf (a)=,letf (n) (a)=a n bethefirst non-zero higher derivative of f at a. (Similarl let m be the first non-zero higher derivative of g at b and let g (m) (b) =b m.) Talor sas f() f(a)+a n ( a) n. So if n is odd this is like 3 at, the critical point = a is neither a local min nor a a local ma. This is because a n ( a) n will be positive on one side of a and negative on the other side of a. If nis even, the point is a local min if a n > andalocalmaifa n <. Our more complete collection is summarized in Table below. n a n m b m Classification even + even + Local Min even + even Saddle even + odd ± Saddle even even + Saddle even even Local Ma even odd ± Saddle odd ± even + Saddle odd ± even Saddle odd ± odd ± Saddle But a better statement is the following theorem Theorem 7. The critical point (a, b) of the additive separable function F (, ) =f()+g() is a local ma [respectivel local min], if and onl if, both a is a local ma [respectivel local min] for f() and b is a local ma[respectivel local min] for g(). Otherwise the point (a, b) is a saddle point for F (, ). Basicall this sas if F (, ) F (a, b) for(, ) nearb(a, b) thenf()+g(b)=f(, b) F (a, b) =f(a)+g(b)sof() f(a) and similarl g() g(b). Conversel if f() f(a) and g() g(b) thenf()+g() f(a)+g(b)orf(, ) F (a, b). Theorem 7 is false for functions in general. The function F (, ) = has both F (, ) = andf(,)=sothat= is both a local min and local ma for F (, ) = and =
7 Additivel Separable Functions 7 Figure 6. Some of the odd power cases: note big D = is both a local min and local ma for F (,)=andet(,) is clearl a saddle point for F. Closure and Uniqueness Properties This is a bonus section and is off the topic. Closure properties sa what can ou do a class or collection and still remain in the collection. For eample, if F (, ) andg(, ) are both additivel separable then so is F (, )+G(, ), but not ever product F (, )G(, ) is additivel separate. Multiplication b a constant C is ok, since CF(, ) is additivel separable whenever F is additivel separable. Also partial derivatives and integrals of additivel separable functions are additivel separable. We summarize in the net theorem. Theorem 8. The collection of additivel separable functions is closed under the following operations. (The first two make the collection a Linear space.) () addition (2) multiplication b constants (3) partial derivatives with respect to or () integrals with respect to d or d Here is a uniqueness question, let L be an line in the -plane which is not parallel to the or ais. If the additivel separable function F (, ) is zero on all points on L and the directional derivative of F in the direction normal to L is also zero on L, then must F (, ) be identicall zero everwhere? The picture on the cover page, shows it is not enough for F to be zero on one line.
8 8 Additivel Separable Functions Your optional group assignment This is a group project. Groups are 3- people ecept in unusual cases. Individual projects are not accepted. The work on the project must be a true collaboration in which each member of the team will carr their own weight. It is NOT acceptable for the team members to split the project between them and work on them independentl. Instead all members must activel work together on all parts of the assignment. The fact that group members have to work together means that ou need to carefull consider a potential group member s schedule before forming the group. You cannot be a group if ou cannot find large chunks of time to spend together. Your assignment is to write in prose, in understandable English, a tped report about separation of variables, that is functions of the form F (, ) = f()g(). There are three parts to the assignment. First ou must do the local etrema for functions of the form f()g(), note that this is harder than the case for functions of the form f() +g() done above. Second, ou must find something interesting about about such functions, unfortunatel one cannot just take logs and translate a additivel separable result via ln(f()g()) = ln f() +lng() since logs are onl defined for positive values. This fact must be strong enough to show that + cannot be written in the form f()g(). Third, ou must research and find a place where separation of variables is used outside the ordinar differential equation case ou might have learned in Calculus 2. The project has two due dates: A hardcop outline which lists who is in our group and what our project is going to contain is due on Frida 25 March at 3pm and the completed hardcop project itself is due on Frida 8 April also at 3pm. (The project must be bound or stapled and not loose, nor dog-eared. Part of the grade will be based on presentation and clarit. There are a few bonus points available for wow value.) In addition to the project, EACH team member will write a separate evaluation of the relative contributions of all the team members.
MAT 127: Calculus C, Fall 2010 Solutions to Midterm I
 MAT 7: Calculus C, Fall 00 Solutions to Midterm I Problem (0pts) Consider the four differential equations for = (): (a) = ( + ) (b) = ( + ) (c) = e + (d) = e. Each of the four diagrams below shows a solution
MAT 7: Calculus C, Fall 00 Solutions to Midterm I Problem (0pts) Consider the four differential equations for = (): (a) = ( + ) (b) = ( + ) (c) = e + (d) = e. Each of the four diagrams below shows a solution
Section 4.1 Increasing and Decreasing Functions
 Section.1 Increasing and Decreasing Functions The graph of the quadratic function f 1 is a parabola. If we imagine a particle moving along this parabola from left to right, we can see that, while the -coordinates
Section.1 Increasing and Decreasing Functions The graph of the quadratic function f 1 is a parabola. If we imagine a particle moving along this parabola from left to right, we can see that, while the -coordinates
Systems of Linear Equations: Solving by Graphing
 8.1 Sstems of Linear Equations: Solving b Graphing 8.1 OBJECTIVE 1. Find the solution(s) for a set of linear equations b graphing NOTE There is no other ordered pair that satisfies both equations. From
8.1 Sstems of Linear Equations: Solving b Graphing 8.1 OBJECTIVE 1. Find the solution(s) for a set of linear equations b graphing NOTE There is no other ordered pair that satisfies both equations. From
INTRODUCTION TO DIFFERENTIAL EQUATIONS
 INTRODUCTION TO DIFFERENTIAL EQUATIONS. Definitions and Terminolog. Initial-Value Problems.3 Differential Equations as Mathematical Models CHAPTER IN REVIEW The words differential and equations certainl
INTRODUCTION TO DIFFERENTIAL EQUATIONS. Definitions and Terminolog. Initial-Value Problems.3 Differential Equations as Mathematical Models CHAPTER IN REVIEW The words differential and equations certainl
Section 3.1. ; X = (0, 1]. (i) f : R R R, f (x, y) = x y
![Section 3.1. ; X = (0, 1]. (i) f : R R R, f (x, y) = x y Section 3.1. ; X = (0, 1]. (i) f : R R R, f (x, y) = x y](/thumbs/83/88503328.jpg) Paul J. Bruillard MATH 0.970 Problem Set 6 An Introduction to Abstract Mathematics R. Bond and W. Keane Section 3.1: 3b,c,e,i, 4bd, 6, 9, 15, 16, 18c,e, 19a, 0, 1b Section 3.: 1f,i, e, 6, 1e,f,h, 13e,
Paul J. Bruillard MATH 0.970 Problem Set 6 An Introduction to Abstract Mathematics R. Bond and W. Keane Section 3.1: 3b,c,e,i, 4bd, 6, 9, 15, 16, 18c,e, 19a, 0, 1b Section 3.: 1f,i, e, 6, 1e,f,h, 13e,
Math 180, Exam 2, Spring 2013 Problem 1 Solution
 Math 80, Eam, Spring 0 Problem Solution. Find the derivative of each function below. You do not need to simplify your answers. (a) tan ( + cos ) (b) / (logarithmic differentiation may be useful) (c) +
Math 80, Eam, Spring 0 Problem Solution. Find the derivative of each function below. You do not need to simplify your answers. (a) tan ( + cos ) (b) / (logarithmic differentiation may be useful) (c) +
We have examined power functions like f (x) = x 2. Interchanging x
 CHAPTER 5 Eponential and Logarithmic Functions We have eamined power functions like f =. Interchanging and ields a different function f =. This new function is radicall different from a power function
CHAPTER 5 Eponential and Logarithmic Functions We have eamined power functions like f =. Interchanging and ields a different function f =. This new function is radicall different from a power function
Engineering Mathematics I
 Engineering Mathematics I_ 017 Engineering Mathematics I 1. Introduction to Differential Equations Dr. Rami Zakaria Terminolog Differential Equation Ordinar Differential Equations Partial Differential
Engineering Mathematics I_ 017 Engineering Mathematics I 1. Introduction to Differential Equations Dr. Rami Zakaria Terminolog Differential Equation Ordinar Differential Equations Partial Differential
11.4 Polar Coordinates
 11. Polar Coordinates 917 11. Polar Coordinates In Section 1.1, we introduced the Cartesian coordinates of a point in the plane as a means of assigning ordered pairs of numbers to points in the plane.
11. Polar Coordinates 917 11. Polar Coordinates In Section 1.1, we introduced the Cartesian coordinates of a point in the plane as a means of assigning ordered pairs of numbers to points in the plane.
Limits and Continuous Functions. 2.2 Introduction to Limits. We first interpret limits loosely. We write. lim f(x) = L
 2 Limits and Continuous Functions 2.2 Introduction to Limits We first interpret limits loosel. We write lim f() = L and sa the limit of f() as approaches c, equals L if we can make the values of f() arbitraril
2 Limits and Continuous Functions 2.2 Introduction to Limits We first interpret limits loosel. We write lim f() = L and sa the limit of f() as approaches c, equals L if we can make the values of f() arbitraril
CHAPTER 2: Partial Derivatives. 2.2 Increments and Differential
 CHAPTER : Partial Derivatives.1 Definition of a Partial Derivative. Increments and Differential.3 Chain Rules.4 Local Etrema.5 Absolute Etrema 1 Chapter : Partial Derivatives.1 Definition of a Partial
CHAPTER : Partial Derivatives.1 Definition of a Partial Derivative. Increments and Differential.3 Chain Rules.4 Local Etrema.5 Absolute Etrema 1 Chapter : Partial Derivatives.1 Definition of a Partial
Vectors and the Geometry of Space
 Chapter 12 Vectors and the Geometr of Space Comments. What does multivariable mean in the name Multivariable Calculus? It means we stud functions that involve more than one variable in either the input
Chapter 12 Vectors and the Geometr of Space Comments. What does multivariable mean in the name Multivariable Calculus? It means we stud functions that involve more than one variable in either the input
1.2 Functions and Their Properties PreCalculus
 1. Functions and Their Properties PreCalculus 1. FUNCTIONS AND THEIR PROPERTIES Learning Targets for 1. 1. Determine whether a set of numbers or a graph is a function. Find the domain of a function given
1. Functions and Their Properties PreCalculus 1. FUNCTIONS AND THEIR PROPERTIES Learning Targets for 1. 1. Determine whether a set of numbers or a graph is a function. Find the domain of a function given
Ch 3 Alg 2 Note Sheet.doc 3.1 Graphing Systems of Equations
 Ch 3 Alg Note Sheet.doc 3.1 Graphing Sstems of Equations Sstems of Linear Equations A sstem of equations is a set of two or more equations that use the same variables. If the graph of each equation =.4
Ch 3 Alg Note Sheet.doc 3.1 Graphing Sstems of Equations Sstems of Linear Equations A sstem of equations is a set of two or more equations that use the same variables. If the graph of each equation =.4
Week #6 - Taylor Series, Derivatives and Graphs Section 4.1
 Week #6 - Talor Series, Derivatives and Graphs Section 4.1 From Calculus, Single Variable b Hughes-Hallett, Gleason, McCallum et. al. Copright 2005 b John Wile & Sons, Inc. This material is used b permission
Week #6 - Talor Series, Derivatives and Graphs Section 4.1 From Calculus, Single Variable b Hughes-Hallett, Gleason, McCallum et. al. Copright 2005 b John Wile & Sons, Inc. This material is used b permission
y = ± x 2 + c. ln y = 2 ln x + 2C sin(x) dx
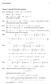 Worked Solutions Chapter 4: Separable First-Order Equations 43 a Factoring out 2, we get 3 sinx)) 2, which is f x)g), ds with f x) 3 sinx) and g) 2 So the equation is separable 43 c x x )2 x )2 f x)g)
Worked Solutions Chapter 4: Separable First-Order Equations 43 a Factoring out 2, we get 3 sinx)) 2, which is f x)g), ds with f x) 3 sinx) and g) 2 So the equation is separable 43 c x x )2 x )2 f x)g)
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION INTEGRATED ALGEBRA. Student Name: School Name:
 INTEGRATED ALGEBRA The Universit of the State of New York REGENTS HIGH SCHOOL EXAMINATION INTEGRATED ALGEBRA Wednesda, August 18, 2010 8:30 to 11:30 a.m., onl Student Name: School Name: Print our name
INTEGRATED ALGEBRA The Universit of the State of New York REGENTS HIGH SCHOOL EXAMINATION INTEGRATED ALGEBRA Wednesda, August 18, 2010 8:30 to 11:30 a.m., onl Student Name: School Name: Print our name
1.2 Functions and Their Properties PreCalculus
 1. Functions and Their Properties PreCalculus 1. FUNCTIONS AND THEIR PROPERTIES Learning Targets for 1. 1. Determine whether a set of numbers or a graph is a function. Find the domain of a function given
1. Functions and Their Properties PreCalculus 1. FUNCTIONS AND THEIR PROPERTIES Learning Targets for 1. 1. Determine whether a set of numbers or a graph is a function. Find the domain of a function given
Intermediate Math Circles Wednesday November Inequalities and Linear Optimization
 WWW.CEMC.UWATERLOO.CA The CENTRE for EDUCATION in MATHEMATICS and COMPUTING Intermediate Math Circles Wednesda November 21 2012 Inequalities and Linear Optimization Review: Our goal is to solve sstems
WWW.CEMC.UWATERLOO.CA The CENTRE for EDUCATION in MATHEMATICS and COMPUTING Intermediate Math Circles Wednesda November 21 2012 Inequalities and Linear Optimization Review: Our goal is to solve sstems
MEP Pupil Text 16. The following statements illustrate the meaning of each of them.
 MEP Pupil Tet Inequalities. Inequalities on a Number Line An inequalit involves one of the four smbols >,, < or. The following statements illustrate the meaning of each of them. > : is greater than. :
MEP Pupil Tet Inequalities. Inequalities on a Number Line An inequalit involves one of the four smbols >,, < or. The following statements illustrate the meaning of each of them. > : is greater than. :
Green s Theorem Jeremy Orloff
 Green s Theorem Jerem Orloff Line integrals and Green s theorem. Vector Fields Vector notation. In 8.4 we will mostl use the notation (v) = (a, b) for vectors. The other common notation (v) = ai + bj runs
Green s Theorem Jerem Orloff Line integrals and Green s theorem. Vector Fields Vector notation. In 8.4 we will mostl use the notation (v) = (a, b) for vectors. The other common notation (v) = ai + bj runs
MATH Line integrals III Fall The fundamental theorem of line integrals. In general C
 MATH 255 Line integrals III Fall 216 In general 1. The fundamental theorem of line integrals v T ds depends on the curve between the starting point and the ending point. onsider two was to get from (1,
MATH 255 Line integrals III Fall 216 In general 1. The fundamental theorem of line integrals v T ds depends on the curve between the starting point and the ending point. onsider two was to get from (1,
Math 123 Summary of Important Algebra & Trigonometry Concepts Chapter 1 & Appendix D, Stewart, Calculus Early Transcendentals
 Math Summar of Important Algebra & Trigonometr Concepts Chapter & Appendi D, Stewart, Calculus Earl Transcendentals Function a rule that assigns to each element in a set D eactl one element, called f (
Math Summar of Important Algebra & Trigonometr Concepts Chapter & Appendi D, Stewart, Calculus Earl Transcendentals Function a rule that assigns to each element in a set D eactl one element, called f (
8. BOOLEAN ALGEBRAS x x
 8. BOOLEAN ALGEBRAS 8.1. Definition of a Boolean Algebra There are man sstems of interest to computing scientists that have a common underling structure. It makes sense to describe such a mathematical
8. BOOLEAN ALGEBRAS 8.1. Definition of a Boolean Algebra There are man sstems of interest to computing scientists that have a common underling structure. It makes sense to describe such a mathematical
8.1 Exponents and Roots
 Section 8. Eponents and Roots 75 8. Eponents and Roots Before defining the net famil of functions, the eponential functions, we will need to discuss eponent notation in detail. As we shall see, eponents
Section 8. Eponents and Roots 75 8. Eponents and Roots Before defining the net famil of functions, the eponential functions, we will need to discuss eponent notation in detail. As we shall see, eponents
Quick Review 4.1 (For help, go to Sections 1.2, 2.1, 3.5, and 3.6.)
 Section 4. Etreme Values of Functions 93 EXPLORATION Finding Etreme Values Let f,.. Determine graphicall the etreme values of f and where the occur. Find f at these values of.. Graph f and f or NDER f,,
Section 4. Etreme Values of Functions 93 EXPLORATION Finding Etreme Values Let f,.. Determine graphicall the etreme values of f and where the occur. Find f at these values of.. Graph f and f or NDER f,,
Maximum and Minimum Values - 3.3
 Maimum and Minimum Values - 3.3. Critical Numbers Definition A point c in the domain of f is called a critical number offiff c or f c is not defined. Eample a. The graph of f is given below. Find all possible
Maimum and Minimum Values - 3.3. Critical Numbers Definition A point c in the domain of f is called a critical number offiff c or f c is not defined. Eample a. The graph of f is given below. Find all possible
Unit 26 Solving Inequalities Inequalities on a Number Line Solution of Linear Inequalities (Inequations)
 UNIT Solving Inequalities: Student Tet Contents STRAND G: Algebra Unit Solving Inequalities Student Tet Contents Section. Inequalities on a Number Line. of Linear Inequalities (Inequations). Inequalities
UNIT Solving Inequalities: Student Tet Contents STRAND G: Algebra Unit Solving Inequalities Student Tet Contents Section. Inequalities on a Number Line. of Linear Inequalities (Inequations). Inequalities
on Œ0; 1, p p p q q p C q.p C q/ pcq :
 388 C HAPTER 4 APPLICATIONS OF THE DERIVATIVE 0 0 30 4 4 4 0 (A) (B) FIGURE Cubic polnomials Let f./ D 3 3 C a C b C c. UsingEercise9,wehaveg./ D f 0./ D C a C b>0for all provided b> 4 a, in which case
388 C HAPTER 4 APPLICATIONS OF THE DERIVATIVE 0 0 30 4 4 4 0 (A) (B) FIGURE Cubic polnomials Let f./ D 3 3 C a C b C c. UsingEercise9,wehaveg./ D f 0./ D C a C b>0for all provided b> 4 a, in which case
9.2. Cartesian Components of Vectors. Introduction. Prerequisites. Learning Outcomes
 Cartesian Components of Vectors 9.2 Introduction It is useful to be able to describe vectors with reference to specific coordinate sstems, such as the Cartesian coordinate sstem. So, in this Section, we
Cartesian Components of Vectors 9.2 Introduction It is useful to be able to describe vectors with reference to specific coordinate sstems, such as the Cartesian coordinate sstem. So, in this Section, we
Exact Differential Equations. The general solution of the equation is f x, y C. If f has continuous second partials, then M y 2 f
 APPENDIX C Additional Topics in Differential Equations APPENDIX C. Eact First-Order Equations Eact Differential Equations Integrating Factors Eact Differential Equations In Chapter 6, ou studied applications
APPENDIX C Additional Topics in Differential Equations APPENDIX C. Eact First-Order Equations Eact Differential Equations Integrating Factors Eact Differential Equations In Chapter 6, ou studied applications
8 Differential Calculus 1 Introduction
 8 Differential Calculus Introduction The ideas that are the basis for calculus have been with us for a ver long time. Between 5 BC and 5 BC, Greek mathematicians were working on problems that would find
8 Differential Calculus Introduction The ideas that are the basis for calculus have been with us for a ver long time. Between 5 BC and 5 BC, Greek mathematicians were working on problems that would find
Section 1.2: A Catalog of Functions
 Section 1.: A Catalog of Functions As we discussed in the last section, in the sciences, we often tr to find an equation which models some given phenomenon in the real world - for eample, temperature as
Section 1.: A Catalog of Functions As we discussed in the last section, in the sciences, we often tr to find an equation which models some given phenomenon in the real world - for eample, temperature as
f x, y x 2 y 2 2x 6y 14. Then
 SECTION 11.7 MAXIMUM AND MINIMUM VALUES 645 absolute minimum FIGURE 1 local maimum local minimum absolute maimum Look at the hills and valles in the graph of f shown in Figure 1. There are two points a,
SECTION 11.7 MAXIMUM AND MINIMUM VALUES 645 absolute minimum FIGURE 1 local maimum local minimum absolute maimum Look at the hills and valles in the graph of f shown in Figure 1. There are two points a,
12.2. Maxima and Minima. Introduction. Prerequisites. Learning Outcomes
 Maima and Minima 1. Introduction In this section we analse curves in the local neighbourhood of a stationar point and, from this analsis, deduce necessar conditions satisfied b local maima and local minima.
Maima and Minima 1. Introduction In this section we analse curves in the local neighbourhood of a stationar point and, from this analsis, deduce necessar conditions satisfied b local maima and local minima.
Table of Contents. Module 1
 Table of Contents Module 1 11 Order of Operations 16 Signed Numbers 1 Factorization of Integers 17 Further Signed Numbers 13 Fractions 18 Power Laws 14 Fractions and Decimals 19 Introduction to Algebra
Table of Contents Module 1 11 Order of Operations 16 Signed Numbers 1 Factorization of Integers 17 Further Signed Numbers 13 Fractions 18 Power Laws 14 Fractions and Decimals 19 Introduction to Algebra
Math 214 Spring problem set (a) Consider these two first order equations. (I) dy dx = x + 1 dy
 Math 4 Spring 08 problem set. (a) Consider these two first order equations. (I) d d = + d (II) d = Below are four direction fields. Match the differential equations above to their direction fields. Provide
Math 4 Spring 08 problem set. (a) Consider these two first order equations. (I) d d = + d (II) d = Below are four direction fields. Match the differential equations above to their direction fields. Provide
Introduction to Differential Equations
 Introduction to Differential Equations. Definitions and Terminolog.2 Initial-Value Problems.3 Differential Equations as Mathematical Models Chapter in Review The words differential and equations certainl
Introduction to Differential Equations. Definitions and Terminolog.2 Initial-Value Problems.3 Differential Equations as Mathematical Models Chapter in Review The words differential and equations certainl
Coordinate geometry. + bx + c. Vertical asymptote. Sketch graphs of hyperbolas (including asymptotic behaviour) from the general
 A Sketch graphs of = a m b n c where m = or and n = or B Reciprocal graphs C Graphs of circles and ellipses D Graphs of hperbolas E Partial fractions F Sketch graphs using partial fractions Coordinate
A Sketch graphs of = a m b n c where m = or and n = or B Reciprocal graphs C Graphs of circles and ellipses D Graphs of hperbolas E Partial fractions F Sketch graphs using partial fractions Coordinate
Vector Fields. Field (II) Field (V)
 Math 1a Vector Fields 1. Match the following vector fields to the pictures, below. Eplain our reasoning. (Notice that in some of the pictures all of the vectors have been uniforml scaled so that the picture
Math 1a Vector Fields 1. Match the following vector fields to the pictures, below. Eplain our reasoning. (Notice that in some of the pictures all of the vectors have been uniforml scaled so that the picture
Algebra II Notes Unit Six: Polynomials Syllabus Objectives: 6.2 The student will simplify polynomial expressions.
 Algebra II Notes Unit Si: Polnomials Sllabus Objectives: 6. The student will simplif polnomial epressions. Review: Properties of Eponents (Allow students to come up with these on their own.) Let a and
Algebra II Notes Unit Si: Polnomials Sllabus Objectives: 6. The student will simplif polnomial epressions. Review: Properties of Eponents (Allow students to come up with these on their own.) Let a and
Pure Core 1. Revision Notes
 Pure Core Revision Notes Ma 06 Pure Core Algebra... Indices... Rules of indices... Surds... 4 Simplifing surds... 4 Rationalising the denominator... 4 Quadratic functions... 5 Completing the square....
Pure Core Revision Notes Ma 06 Pure Core Algebra... Indices... Rules of indices... Surds... 4 Simplifing surds... 4 Rationalising the denominator... 4 Quadratic functions... 5 Completing the square....
FIRST- AND SECOND-ORDER IVPS The problem given in (1) is also called an nth-order initial-value problem. For example, Solve: Solve:
 .2 INITIAL-VALUE PROBLEMS 3.2 INITIAL-VALUE PROBLEMS REVIEW MATERIAL Normal form of a DE Solution of a DE Famil of solutions INTRODUCTION We are often interested in problems in which we seek a solution
.2 INITIAL-VALUE PROBLEMS 3.2 INITIAL-VALUE PROBLEMS REVIEW MATERIAL Normal form of a DE Solution of a DE Famil of solutions INTRODUCTION We are often interested in problems in which we seek a solution
Introduction to Differential Equations. National Chiao Tung University Chun-Jen Tsai 9/14/2011
 Introduction to Differential Equations National Chiao Tung Universit Chun-Jen Tsai 9/14/011 Differential Equations Definition: An equation containing the derivatives of one or more dependent variables,
Introduction to Differential Equations National Chiao Tung Universit Chun-Jen Tsai 9/14/011 Differential Equations Definition: An equation containing the derivatives of one or more dependent variables,
LESSON #42 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART 2 COMMON CORE ALGEBRA II
 LESSON #4 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART COMMON CORE ALGEBRA II You will recall from unit 1 that in order to find the inverse of a function, ou must switch and and solve for. Also,
LESSON #4 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART COMMON CORE ALGEBRA II You will recall from unit 1 that in order to find the inverse of a function, ou must switch and and solve for. Also,
1 x
 Unit 1. Calculus Topic 4: Increasing and decreasing functions: turning points In topic 4 we continue with straightforward derivatives and integrals: Locate turning points where f () = 0. Determine the
Unit 1. Calculus Topic 4: Increasing and decreasing functions: turning points In topic 4 we continue with straightforward derivatives and integrals: Locate turning points where f () = 0. Determine the
MATRIX TRANSFORMATIONS
 CHAPTER 5. MATRIX TRANSFORMATIONS INSTITIÚID TEICNEOLAÍOCHTA CHEATHARLACH INSTITUTE OF TECHNOLOGY CARLOW MATRIX TRANSFORMATIONS Matri Transformations Definition Let A and B be sets. A function f : A B
CHAPTER 5. MATRIX TRANSFORMATIONS INSTITIÚID TEICNEOLAÍOCHTA CHEATHARLACH INSTITUTE OF TECHNOLOGY CARLOW MATRIX TRANSFORMATIONS Matri Transformations Definition Let A and B be sets. A function f : A B
CCSSM Algebra: Equations
 CCSSM Algebra: Equations. Reasoning with Equations and Inequalities (A-REI) Eplain each step in solving a simple equation as following from the equalit of numbers asserted at the previous step, starting
CCSSM Algebra: Equations. Reasoning with Equations and Inequalities (A-REI) Eplain each step in solving a simple equation as following from the equalit of numbers asserted at the previous step, starting
6 = 1 2. The right endpoints of the subintervals are then 2 5, 3, 7 2, 4, 2 9, 5, while the left endpoints are 2, 5 2, 3, 7 2, 4, 9 2.
 5 THE ITEGRAL 5. Approimating and Computing Area Preliminar Questions. What are the right and left endpoints if [, 5] is divided into si subintervals? If the interval [, 5] is divided into si subintervals,
5 THE ITEGRAL 5. Approimating and Computing Area Preliminar Questions. What are the right and left endpoints if [, 5] is divided into si subintervals? If the interval [, 5] is divided into si subintervals,
Chapter Nine Chapter Nine
 Chapter Nine Chapter Nine 6 CHAPTER NINE ConcepTests for Section 9.. Table 9. shows values of f(, ). Does f appear to be an increasing or decreasing function of? Of? Table 9. 0 0 0 7 7 68 60 0 80 77 73
Chapter Nine Chapter Nine 6 CHAPTER NINE ConcepTests for Section 9.. Table 9. shows values of f(, ). Does f appear to be an increasing or decreasing function of? Of? Table 9. 0 0 0 7 7 68 60 0 80 77 73
DIFFERENTIATION. 3.1 Approximate Value and Error (page 151)
 CHAPTER APPLICATIONS OF DIFFERENTIATION.1 Approimate Value and Error (page 151) f '( lim 0 f ( f ( f ( f ( f '( or f ( f ( f '( f ( f ( f '( (.) f ( f '( (.) where f ( f ( f ( Eample.1 (page 15): Find
CHAPTER APPLICATIONS OF DIFFERENTIATION.1 Approimate Value and Error (page 151) f '( lim 0 f ( f ( f ( f ( f '( or f ( f ( f '( f ( f ( f '( (.) f ( f '( (.) where f ( f ( f ( Eample.1 (page 15): Find
Symmetry Arguments and the Role They Play in Using Gauss Law
 Smmetr Arguments and the Role The la in Using Gauss Law K. M. Westerberg (9/2005) Smmetr plas a ver important role in science in general, and phsics in particular. Arguments based on smmetr can often simplif
Smmetr Arguments and the Role The la in Using Gauss Law K. M. Westerberg (9/2005) Smmetr plas a ver important role in science in general, and phsics in particular. Arguments based on smmetr can often simplif
Review: critical point or equivalently f a,
 Review: a b f f a b f a b critical point or equivalentl f a, b A point, is called a of if,, 0 A local ma or local min must be a critical point (but not conversel) 0 D iscriminant (or Hessian) f f D f f
Review: a b f f a b f a b critical point or equivalentl f a, b A point, is called a of if,, 0 A local ma or local min must be a critical point (but not conversel) 0 D iscriminant (or Hessian) f f D f f
Lab 5 Forces Part 1. Physics 211 Lab. You will be using Newton s 2 nd Law to help you examine the nature of these forces.
 b Lab 5 Forces Part 1 Phsics 211 Lab Introduction This is the first week of a two part lab that deals with forces and related concepts. A force is a push or a pull on an object that can be caused b a variet
b Lab 5 Forces Part 1 Phsics 211 Lab Introduction This is the first week of a two part lab that deals with forces and related concepts. A force is a push or a pull on an object that can be caused b a variet
Additional Material On Recursive Sequences
 Penn State Altoona MATH 141 Additional Material On Recursive Sequences 1. Graphical Analsis Cobweb Diagrams Consider a generic recursive sequence { an+1 = f(a n ), n = 1,, 3,..., = Given initial value.
Penn State Altoona MATH 141 Additional Material On Recursive Sequences 1. Graphical Analsis Cobweb Diagrams Consider a generic recursive sequence { an+1 = f(a n ), n = 1,, 3,..., = Given initial value.
Ordinary Differential Equations
 58229_CH0_00_03.indd Page 6/6/6 2:48 PM F-007 /202/JB0027/work/indd & Bartlett Learning LLC, an Ascend Learning Compan.. PART Ordinar Differential Equations. Introduction to Differential Equations 2. First-Order
58229_CH0_00_03.indd Page 6/6/6 2:48 PM F-007 /202/JB0027/work/indd & Bartlett Learning LLC, an Ascend Learning Compan.. PART Ordinar Differential Equations. Introduction to Differential Equations 2. First-Order
2.2 Equations of Lines
 660_ch0pp07668.qd 10/16/08 4:1 PM Page 96 96 CHAPTER Linear Functions and Equations. Equations of Lines Write the point-slope and slope-intercept forms Find the intercepts of a line Write equations for
660_ch0pp07668.qd 10/16/08 4:1 PM Page 96 96 CHAPTER Linear Functions and Equations. Equations of Lines Write the point-slope and slope-intercept forms Find the intercepts of a line Write equations for
Introduction to Vector Spaces Linear Algebra, Spring 2011
 Introduction to Vector Spaces Linear Algebra, Spring 2011 You probabl have heard the word vector before, perhaps in the contet of Calculus III or phsics. You probabl think of a vector like this: 5 3 or
Introduction to Vector Spaces Linear Algebra, Spring 2011 You probabl have heard the word vector before, perhaps in the contet of Calculus III or phsics. You probabl think of a vector like this: 5 3 or
Lab 5 Forces Part 1. Physics 225 Lab. You will be using Newton s 2 nd Law to help you examine the nature of these forces.
 b Lab 5 orces Part 1 Introduction his is the first week of a two part lab that deals with forces and related concepts. A force is a push or a pull on an object that can be caused b a variet of reasons.
b Lab 5 orces Part 1 Introduction his is the first week of a two part lab that deals with forces and related concepts. A force is a push or a pull on an object that can be caused b a variet of reasons.
v t t t t a t v t d dt t t t t t 23.61
 SECTION 4. MAXIMUM AND MINIMUM VALUES 285 The values of f at the endpoints are f 0 0 and f 2 2 6.28 Comparing these four numbers and using the Closed Interval Method, we see that the absolute minimum value
SECTION 4. MAXIMUM AND MINIMUM VALUES 285 The values of f at the endpoints are f 0 0 and f 2 2 6.28 Comparing these four numbers and using the Closed Interval Method, we see that the absolute minimum value
Chapter 8 Notes SN AA U2C8
 Chapter 8 Notes SN AA U2C8 Name Period Section 8-: Eploring Eponential Models Section 8-2: Properties of Eponential Functions In Chapter 7, we used properties of eponents to determine roots and some of
Chapter 8 Notes SN AA U2C8 Name Period Section 8-: Eploring Eponential Models Section 8-2: Properties of Eponential Functions In Chapter 7, we used properties of eponents to determine roots and some of
Directional derivatives and gradient vectors (Sect. 14.5). Directional derivative of functions of two variables.
 Directional derivatives and gradient vectors (Sect. 14.5). Directional derivative of functions of two variables. Partial derivatives and directional derivatives. Directional derivative of functions of
Directional derivatives and gradient vectors (Sect. 14.5). Directional derivative of functions of two variables. Partial derivatives and directional derivatives. Directional derivative of functions of
2.1 The Rectangular Coordinate System
 . The Rectangular Coordinate Sstem In this section ou will learn to: plot points in a rectangular coordinate sstem understand basic functions of the graphing calculator graph equations b generating a table
. The Rectangular Coordinate Sstem In this section ou will learn to: plot points in a rectangular coordinate sstem understand basic functions of the graphing calculator graph equations b generating a table
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. Section. Rolle s Theorem and the Mean Value Theorem. 7 Section. Increasing and Decreasing Functions and the First Derivative
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. Section. Rolle s Theorem and the Mean Value Theorem. 7 Section. Increasing and Decreasing Functions and the First Derivative
Practice Questions for Midterm 2 - Math 1060Q - Fall 2013
 Eam Review Practice Questions for Midterm - Math 060Q - Fall 0 The following is a selection of problems to help prepare ou for the second midterm eam. Please note the following: anthing from Module/Chapter
Eam Review Practice Questions for Midterm - Math 060Q - Fall 0 The following is a selection of problems to help prepare ou for the second midterm eam. Please note the following: anthing from Module/Chapter
4.3 Mean-Value Theorem and Monotonicity
 .3 Mean-Value Theorem and Monotonicit 1. Mean Value Theorem Theorem: Suppose that f is continuous on the interval a, b and differentiable on the interval a, b. Then there eists a number c in a, b such
.3 Mean-Value Theorem and Monotonicit 1. Mean Value Theorem Theorem: Suppose that f is continuous on the interval a, b and differentiable on the interval a, b. Then there eists a number c in a, b such
2.5 CONTINUITY. a x. Notice that Definition l implicitly requires three things if f is continuous at a:
 SECTION.5 CONTINUITY 9.5 CONTINUITY We noticed in Section.3 that the it of a function as approaches a can often be found simpl b calculating the value of the function at a. Functions with this propert
SECTION.5 CONTINUITY 9.5 CONTINUITY We noticed in Section.3 that the it of a function as approaches a can often be found simpl b calculating the value of the function at a. Functions with this propert
AP Calculus AB Summer Assignment
 AP Calculus AB Summer Assignment Name: When you come back to school, you will be epected to have attempted every problem. These skills are all different tools that you will pull out of your toolbo this
AP Calculus AB Summer Assignment Name: When you come back to school, you will be epected to have attempted every problem. These skills are all different tools that you will pull out of your toolbo this
Autonomous Equations / Stability of Equilibrium Solutions. y = f (y).
 Autonomous Equations / Stabilit of Equilibrium Solutions First order autonomous equations, Equilibrium solutions, Stabilit, Longterm behavior of solutions, direction fields, Population dnamics and logistic
Autonomous Equations / Stabilit of Equilibrium Solutions First order autonomous equations, Equilibrium solutions, Stabilit, Longterm behavior of solutions, direction fields, Population dnamics and logistic
1.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS
 .6 Continuit of Trigonometric, Eponential, and Inverse Functions.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS In this section we will discuss the continuit properties of trigonometric
.6 Continuit of Trigonometric, Eponential, and Inverse Functions.6 CONTINUITY OF TRIGONOMETRIC, EXPONENTIAL, AND INVERSE FUNCTIONS In this section we will discuss the continuit properties of trigonometric
x y plane is the plane in which the stresses act, yy xy xy Figure 3.5.1: non-zero stress components acting in the x y plane
 3.5 Plane Stress This section is concerned with a special two-dimensional state of stress called plane stress. It is important for two reasons: () it arises in real components (particularl in thin components
3.5 Plane Stress This section is concerned with a special two-dimensional state of stress called plane stress. It is important for two reasons: () it arises in real components (particularl in thin components
Chapter Eleven. Chapter Eleven
 Chapter Eleven Chapter Eleven CHAPTER ELEVEN Hughes Hallett et al c 005, John Wile & Sons ConcepTests and Answers and Comments for Section. For Problems, which of the following functions satisf the given
Chapter Eleven Chapter Eleven CHAPTER ELEVEN Hughes Hallett et al c 005, John Wile & Sons ConcepTests and Answers and Comments for Section. For Problems, which of the following functions satisf the given
9-1. The Function with Equation y = ax 2. Vocabulary. Graphing y = x 2. Lesson
 Chapter 9 Lesson 9-1 The Function with Equation = a BIG IDEA The graph of an quadratic function with equation = a, with a 0, is a parabola with verte at the origin. Vocabular parabola refl ection-smmetric
Chapter 9 Lesson 9-1 The Function with Equation = a BIG IDEA The graph of an quadratic function with equation = a, with a 0, is a parabola with verte at the origin. Vocabular parabola refl ection-smmetric
8.7 Systems of Non-Linear Equations and Inequalities
 8.7 Sstems of Non-Linear Equations and Inequalities 67 8.7 Sstems of Non-Linear Equations and Inequalities In this section, we stud sstems of non-linear equations and inequalities. Unlike the sstems of
8.7 Sstems of Non-Linear Equations and Inequalities 67 8.7 Sstems of Non-Linear Equations and Inequalities In this section, we stud sstems of non-linear equations and inequalities. Unlike the sstems of
University of Toronto Mississauga
 Surname: First Name: Student Number: Tutorial: Universit of Toronto Mississauga Mathematical and Computational Sciences MATY5Y Term Test Duration - 0 minutes No Aids Permitted This eam contains pages (including
Surname: First Name: Student Number: Tutorial: Universit of Toronto Mississauga Mathematical and Computational Sciences MATY5Y Term Test Duration - 0 minutes No Aids Permitted This eam contains pages (including
November 13, 2018 MAT186 Week 8 Justin Ko
 1 Mean Value Theorem Theorem 1 (Mean Value Theorem). Let f be a continuous on [a, b] and differentiable on (a, b). There eists a c (a, b) such that f f(b) f(a) (c) =. b a Eample 1: The Mean Value Theorem
1 Mean Value Theorem Theorem 1 (Mean Value Theorem). Let f be a continuous on [a, b] and differentiable on (a, b). There eists a c (a, b) such that f f(b) f(a) (c) =. b a Eample 1: The Mean Value Theorem
LESSON #28 - POWER FUNCTIONS COMMON CORE ALGEBRA II
 1 LESSON #8 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
1 LESSON #8 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
y = f(x + 4) a) Example: A repeating X by using two linear equations y = ±x. b) Example: y = f(x - 3). The translation is
 Answers Chapter Function Transformations. Horizontal and Vertical Translations, pages to. a h, k h, k - c h -, k d h 7, k - e h -, k. a A (-,, B (-,, C (-,, D (,, E (, A (-, -, B (-,, C (,, D (, -, E (,
Answers Chapter Function Transformations. Horizontal and Vertical Translations, pages to. a h, k h, k - c h -, k d h 7, k - e h -, k. a A (-,, B (-,, C (-,, D (,, E (, A (-, -, B (-,, C (,, D (, -, E (,
Rolle s Theorem. THEOREM 3 Rolle s Theorem. x x. then there is at least one number c in (a, b) at which ƒ scd = 0.
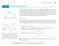 4.2 The Mean Value Theorem 255 4.2 The Mean Value Theorem f '(c) 0 f() We know that constant functions have zero derivatives, ut could there e a complicated function, with man terms, the derivatives of
4.2 The Mean Value Theorem 255 4.2 The Mean Value Theorem f '(c) 0 f() We know that constant functions have zero derivatives, ut could there e a complicated function, with man terms, the derivatives of
f x,y da ln 1 y ln 1 x dx. To evaluate this integral, we use integration by parts with dv dx
 MATH (Calculus III) - Quiz 4 Solutions March, 5 S. F. Ellermeer Name Instructions. This is a take home quiz. It is due to be handed in to me on Frida, March at class time. You ma work on this quiz alone
MATH (Calculus III) - Quiz 4 Solutions March, 5 S. F. Ellermeer Name Instructions. This is a take home quiz. It is due to be handed in to me on Frida, March at class time. You ma work on this quiz alone
Trigonometric Functions
 TrigonometricReview.nb Trigonometric Functions The trigonometric (or trig) functions are ver important in our stud of calculus because the are periodic (meaning these functions repeat their values in a
TrigonometricReview.nb Trigonometric Functions The trigonometric (or trig) functions are ver important in our stud of calculus because the are periodic (meaning these functions repeat their values in a
Unit 9: Symmetric Functions
 Haberman MTH 111 Section I: Functions and Their Graphs Unit 9: Symmetric Functions Some functions have graphs with special types of symmetries, and we can use the reflections we just studied to analyze
Haberman MTH 111 Section I: Functions and Their Graphs Unit 9: Symmetric Functions Some functions have graphs with special types of symmetries, and we can use the reflections we just studied to analyze
MAT 1275: Introduction to Mathematical Analysis. Graphs and Simplest Equations for Basic Trigonometric Functions. y=sin( x) Function
 MAT 275: Introduction to Mathematical Analsis Dr. A. Rozenblum Graphs and Simplest Equations for Basic Trigonometric Functions We consider here three basic functions: sine, cosine and tangent. For them,
MAT 275: Introduction to Mathematical Analsis Dr. A. Rozenblum Graphs and Simplest Equations for Basic Trigonometric Functions We consider here three basic functions: sine, cosine and tangent. For them,
Vertex. March 23, Ch 9 Guided Notes.notebook
 March, 07 9 Quadratic Graphs and Their Properties A quadratic function is a function that can be written in the form: Verte Its graph looks like... which we call a parabola. The simplest quadratic function
March, 07 9 Quadratic Graphs and Their Properties A quadratic function is a function that can be written in the form: Verte Its graph looks like... which we call a parabola. The simplest quadratic function
UNIVERSIDAD CARLOS III DE MADRID MATHEMATICS II EXERCISES (SOLUTIONS )
 UNIVERSIDAD CARLOS III DE MADRID MATHEMATICS II EXERCISES (SOLUTIONS ) CHAPTER : Limits and continuit of functions in R n. -. Sketch the following subsets of R. Sketch their boundar and the interior. Stud
UNIVERSIDAD CARLOS III DE MADRID MATHEMATICS II EXERCISES (SOLUTIONS ) CHAPTER : Limits and continuit of functions in R n. -. Sketch the following subsets of R. Sketch their boundar and the interior. Stud
Functions of Several Variables
 Chapter 1 Functions of Several Variables 1.1 Introduction A real valued function of n variables is a function f : R, where the domain is a subset of R n. So: for each ( 1,,..., n ) in, the value of f is
Chapter 1 Functions of Several Variables 1.1 Introduction A real valued function of n variables is a function f : R, where the domain is a subset of R n. So: for each ( 1,,..., n ) in, the value of f is
2.1 Rates of Change and Limits AP Calculus
 . Rates of Change and Limits AP Calculus. RATES OF CHANGE AND LIMITS Limits Limits are what separate Calculus from pre calculus. Using a it is also the foundational principle behind the two most important
. Rates of Change and Limits AP Calculus. RATES OF CHANGE AND LIMITS Limits Limits are what separate Calculus from pre calculus. Using a it is also the foundational principle behind the two most important
14.5 The Chain Rule. dx dt
 SECTION 14.5 THE CHAIN RULE 931 27. w lns 2 2 z 2 28. w e z 37. If R is the total resistance of three resistors, connected in parallel, with resistances,,, then R 1 R 2 R 3 29. If z 5 2 2 and, changes
SECTION 14.5 THE CHAIN RULE 931 27. w lns 2 2 z 2 28. w e z 37. If R is the total resistance of three resistors, connected in parallel, with resistances,,, then R 1 R 2 R 3 29. If z 5 2 2 and, changes
Trigonometry Outline
 Trigonometr Outline Introduction Knowledge of the content of this outline is essential to perform well in calculus. The reader is urged to stud each of the three parts of the outline. Part I contains the
Trigonometr Outline Introduction Knowledge of the content of this outline is essential to perform well in calculus. The reader is urged to stud each of the three parts of the outline. Part I contains the
AP Calculus AB Summer Assignment
 AP Calculus AB Summer Assignment Name: When you come back to school, it is my epectation that you will have this packet completed. You will be way behind at the beginning of the year if you haven t attempted
AP Calculus AB Summer Assignment Name: When you come back to school, it is my epectation that you will have this packet completed. You will be way behind at the beginning of the year if you haven t attempted
Unit 3 NOTES Honors Common Core Math 2 1. Day 1: Properties of Exponents
 Unit NOTES Honors Common Core Math Da : Properties of Eponents Warm-Up: Before we begin toda s lesson, how much do ou remember about eponents? Use epanded form to write the rules for the eponents. OBJECTIVE
Unit NOTES Honors Common Core Math Da : Properties of Eponents Warm-Up: Before we begin toda s lesson, how much do ou remember about eponents? Use epanded form to write the rules for the eponents. OBJECTIVE
Constant no variables, just a number. Linear Note: Same form as f () x mx b. Quadratic Note: Same form as. Cubic x to the third power
 Precalculus Notes: Section. Modeling High Degree Polnomial Functions Graphs of Polnomials Polnomial Notation f ( ) a a a... a a a is a polnomial function of degree n. n n 1 n n n1 n 1 0 n is the degree
Precalculus Notes: Section. Modeling High Degree Polnomial Functions Graphs of Polnomials Polnomial Notation f ( ) a a a... a a a is a polnomial function of degree n. n n 1 n n n1 n 1 0 n is the degree
3.7 InveRSe FUnCTIOnS
 CHAPTER functions learning ObjeCTIveS In this section, ou will: Verif inverse functions. Determine the domain and range of an inverse function, and restrict the domain of a function to make it one-to-one.
CHAPTER functions learning ObjeCTIveS In this section, ou will: Verif inverse functions. Determine the domain and range of an inverse function, and restrict the domain of a function to make it one-to-one.
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 0 Section. Rolle s Theorem and the Mean Value Theorem. 07 Section. Increasing and Decreasing Functions and the First
CHAPTER Applications of Differentiation Section. Etrema on an Interval.............. 0 Section. Rolle s Theorem and the Mean Value Theorem. 07 Section. Increasing and Decreasing Functions and the First
2.2 SEPARABLE VARIABLES
 44 CHAPTER FIRST-ORDER DIFFERENTIAL EQUATIONS 6 Consider the autonomous DE 6 Use our ideas from Problem 5 to find intervals on the -ais for which solution curves are concave up and intervals for which
44 CHAPTER FIRST-ORDER DIFFERENTIAL EQUATIONS 6 Consider the autonomous DE 6 Use our ideas from Problem 5 to find intervals on the -ais for which solution curves are concave up and intervals for which
NST1A: Mathematics II (Course A) End of Course Summary, Lent 2011
 General notes Proofs NT1A: Mathematics II (Course A) End of Course ummar, Lent 011 tuart Dalziel (011) s.dalziel@damtp.cam.ac.uk This course is not about proofs, but rather about using different techniques.
General notes Proofs NT1A: Mathematics II (Course A) End of Course ummar, Lent 011 tuart Dalziel (011) s.dalziel@damtp.cam.ac.uk This course is not about proofs, but rather about using different techniques.
CHAPTER 3 Applications of Differentiation
 CHAPTER Applications of Differentiation Section. Etrema on an Interval................... 0 Section. Rolle s Theorem and the Mean Value Theorem...... 0 Section. Increasing and Decreasing Functions and
CHAPTER Applications of Differentiation Section. Etrema on an Interval................... 0 Section. Rolle s Theorem and the Mean Value Theorem...... 0 Section. Increasing and Decreasing Functions and
A function from a set D to a set R is a rule that assigns a unique element in R to each element in D.
 1.2 Functions and Their Properties PreCalculus 1.2 FUNCTIONS AND THEIR PROPERTIES Learning Targets for 1.2 1. Determine whether a set of numbers or a graph is a function 2. Find the domain of a function
1.2 Functions and Their Properties PreCalculus 1.2 FUNCTIONS AND THEIR PROPERTIES Learning Targets for 1.2 1. Determine whether a set of numbers or a graph is a function 2. Find the domain of a function
Finding Limits Graphically and Numerically. An Introduction to Limits
 60_00.qd //0 :05 PM Page 8 8 CHAPTER Limits and Their Properties Section. Finding Limits Graphicall and Numericall Estimate a it using a numerical or graphical approach. Learn different was that a it can
60_00.qd //0 :05 PM Page 8 8 CHAPTER Limits and Their Properties Section. Finding Limits Graphicall and Numericall Estimate a it using a numerical or graphical approach. Learn different was that a it can
Math Notes on sections 7.8,9.1, and 9.3. Derivation of a solution in the repeated roots case: 3 4 A = 1 1. x =e t : + e t w 2.
 Math 7 Notes on sections 7.8,9., and 9.3. Derivation of a solution in the repeated roots case We consider the eample = A where 3 4 A = The onl eigenvalue is = ; and there is onl one linearl independent
Math 7 Notes on sections 7.8,9., and 9.3. Derivation of a solution in the repeated roots case We consider the eample = A where 3 4 A = The onl eigenvalue is = ; and there is onl one linearl independent
