Systems of Linear Equations: Solving by Graphing
|
|
|
- Tyrone Gibbs
- 6 years ago
- Views:
Transcription
1 8.1 Sstems of Linear Equations: Solving b Graphing 8.1 OBJECTIVE 1. Find the solution(s) for a set of linear equations b graphing NOTE There is no other ordered pair that satisfies both equations. From our work in Section 6.1, we know that an equation of the form 3 is a linear equation. Remember that its graph is a straight line. Often we will want to consider two equations together. The then form a sstem of linear equations. An eample of such a sstem is A solution for a linear equation in two variables is an ordered pair that satisfies the equation. Often there is just one ordered pair that satisfies both equations of a sstem. It is called the solution for the sstem. For instance, there is one solution for the sstem above, and it is (2, 1) because, replacing with 2 and with 1, we have Because both statements are true, the ordered pair (2, 1) satisfies both equations. One approach to finding the solution for a sstem of linear equations is the graphical method. To use this, we graph the two lines on the same coordinate sstem. The coordinates of the point where the lines intersect is the solution for the sstem. Eample 1 Solving b Graphing NOTE Use the intercept method to graph each equation. Solve the sstem b graphing. 6 4 First, we determine solutions for the equations of our sstem. For 6, two solutions are (6, 0) and (0, 6). For 4, two solutions are (4, 0) and (0, 4). Using these intercepts, we graph the two equations. The lines intersect at the point (5, 1). NOTE B substituting 5 for and 1 for into the two original equations, we can check that (5, 1) is indeed the solution for our sstem Both statements must be true for (5, 1) to be a solution for the sstem. 4 (5, 1) 6 (5, 1) is the solution of the sstem. It is the onl point that lies on both lines. 621
2 622 CHAPTER 8 SYSTEMS OF LINEAR EQUATIONS CHECK YOURSELF 1 Solve the sstem b graphing Eample 2 shows how to graph a sstem when one of the equations represents a horizontal line. Eample 2 Solving b Graphing Solve the sstem b graphing For 3 2 6, two solutions are (2, 0) and (0, 3). These represent the and intercepts of the graph of the equation. The equation 6 represents a horizontal line that crosses the ais at the point (0, 6). Using these intercepts, we graph the two equations. The lines will intersect at the point ( 2, 6). So this is the solution to our sstem
3 SYSTEMS OF LINEAR EQUATIONS: SOLVING BY GRAPHING SECTION CHECK YOURSELF 2 Solve the sstem b graphing The sstems in Eamples 1 and 2 both had eactl one solution. A sstem with one solution is called a consistent sstem. It is possible that a sstem of equations will have no solution. Such a sstem is called an inconsistent sstem. We present such a sstem here. Eample 3 Solving an Inconsistent Sstem Solve b graphing We can graph the two lines as before. For 2 2, two solutions are (0, 2) and (1, 0). For 2 4, two solutions are (0, 4) and (2, 0). Using these intercepts, we graph the two equations. NOTE In slope-intercept form, our equations are 2 2 and 2 4 Both lines have slope Notice that the slope for each of these lines is 2, but the have different intercepts. This means that the lines are parallel (the will never intersect). Because the lines have no points in common, there is no ordered pair that will satisf both equations. The sstem has no solution. It is inconsistent.
4 624 CHAPTER 8 SYSTEMS OF LINEAR EQUATIONS CHECK YOURSELF 3 Solve b graphing There is one more possibilit for linear sstems, as Eample 4 illustrates. Eample 4 Solving a Dependent Sstem NOTE Notice that multipling the first equation b 2 results in the second equation. Solve b graphing Graphing as before and using the intercept method, we find The two equations have the same graph! Because the graphs coincide, there are infinitel man solutions for this sstem. Ever point on the graph of 2 4 is also on the graph of 2 4 8, so an ordered pair satisfing 2 4 also satisfies This is called a dependent sstem, and an point on the line is a solution.
5 SYSTEMS OF LINEAR EQUATIONS: SOLVING BY GRAPHING SECTION CHECK YOURSELF 4 Solve b graphing The following summarizes our work in this section. Step b Step: To Solve a Sstem of Equations b Graphing Step 1 Step 2 Graph both equations on the same coordinate sstem. Determine the solution to the sstem as follows. a. If the lines intersect at one point, the solution is the ordered pair corresponding to that point. This is called a consistent sstem. A consistent sstem NOTE There is no ordered pair that lies on both lines. b. If the lines are parallel, there are no solutions. This is called an inconsistent sstem. An inconsistent sstem
6 626 CHAPTER 8 SYSTEMS OF LINEAR EQUATIONS NOTE An ordered pair that corresponds to a point on the line is a solution. c. If the two equations have the same graph, then the sstem has infinitel man solutions. This is called a dependent sstem. A dependent sstem Step 3 Check the solution in both equations, if necessar. CHECK YOURSELF ANSWERS ( 5, 8) 8 (3, 2) There is no solution. The lines are parallel, so the sstem is inconsistent A dependent sstem
7 Name 8.1 Eercises Section Date Solve each of the following sstems b graphing ANSWERS
8 ANSWERS
9 ANSWERS
10 ANSWERS
11 ANSWERS 25. Find values for m and b in the following sstem so that the solution to the sstem is (1, 2) m b Find values for m and b in the following sstem so that the solution to the sstem is ( 3, 4). 5 7 b m Complete the following statements in our own words: To solve an equation means to.... To solve a sstem of equations means to A sstem of equations such as the one below is sometimes called a 2-b-2 sstem of linear equations Eplain this term. 29. Complete this statement in our own words: All the points on the graph of the equation Echange statements with other students. Do ou agree with other students statements? 30. Does a sstem of linear equations alwas have a solution? How can ou tell without graphing that a sstem of two equations graphs into two parallel lines? Give some eamples to eplain our reasoning. 631
12 ANSWERS a. b. c. d. e. f. Getting Read for Section 8.2 [Section 1.6] Simplif each of the following epressions. (a) (2 ) ( ) (b) ( ) ( ) (c) (3 2) ( 3 3) (d) ( 5) (2 5) (e) 2( ) (3 2) (f ) 2(2 ) ( 4 3) (g) 3(2 ) 2( 3 ) (h) 3(2 4) 4( 3) g. h. Answers (5, 1) (1, 4) (2, 1) (2, 4) 632
13 (6, 2) (2, 3) Dependent (4, 2) (4, 3) Inconsistent 633
14 , (4, 6) 25. m 2, b a. 3 b. 2 c. d. 3 e. 5 f. 5 g. 5 h
Unit 12 Study Notes 1 Systems of Equations
 You should learn to: Unit Stud Notes Sstems of Equations. Solve sstems of equations b substitution.. Solve sstems of equations b graphing (calculator). 3. Solve sstems of equations b elimination. 4. Solve
You should learn to: Unit Stud Notes Sstems of Equations. Solve sstems of equations b substitution.. Solve sstems of equations b graphing (calculator). 3. Solve sstems of equations b elimination. 4. Solve
14.1 Systems of Linear Equations in Two Variables
 86 Chapter 1 Sstems of Equations and Matrices 1.1 Sstems of Linear Equations in Two Variables Use the method of substitution to solve sstems of equations in two variables. Use the method of elimination
86 Chapter 1 Sstems of Equations and Matrices 1.1 Sstems of Linear Equations in Two Variables Use the method of substitution to solve sstems of equations in two variables. Use the method of elimination
12.1 Systems of Linear equations: Substitution and Elimination
 . Sstems of Linear equations: Substitution and Elimination Sstems of two linear equations in two variables A sstem of equations is a collection of two or more equations. A solution of a sstem in two variables
. Sstems of Linear equations: Substitution and Elimination Sstems of two linear equations in two variables A sstem of equations is a collection of two or more equations. A solution of a sstem in two variables
7.5 Solve Special Types of
 75 Solve Special Tpes of Linear Sstems Goal p Identif the number of of a linear sstem Your Notes VOCABULARY Inconsistent sstem Consistent dependent sstem Eample A linear sstem with no Show that the linear
75 Solve Special Tpes of Linear Sstems Goal p Identif the number of of a linear sstem Your Notes VOCABULARY Inconsistent sstem Consistent dependent sstem Eample A linear sstem with no Show that the linear
The slope, m, compares the change in y-values to the change in x-values. Use the points (2, 4) and (6, 6) to determine the slope.
 LESSON Relating Slope and -intercept to Linear Equations UNDERSTAND The slope of a line is the ratio of the line s vertical change, called the rise, to its horizontal change, called the run. You can find
LESSON Relating Slope and -intercept to Linear Equations UNDERSTAND The slope of a line is the ratio of the line s vertical change, called the rise, to its horizontal change, called the run. You can find
( 7, 3) means x = 7 and y = 3. ( 7, 3) works in both equations so. Section 5 1: Solving a System of Linear Equations by Graphing
 Section 5 : Solving a Sstem of Linear Equations b Graphing What is a sstem of Linear Equations? A sstem of linear equations is a list of two or more linear equations that each represents the graph of a
Section 5 : Solving a Sstem of Linear Equations b Graphing What is a sstem of Linear Equations? A sstem of linear equations is a list of two or more linear equations that each represents the graph of a
1. Solutions to Systems of Linear Equations. Determine whether the ordered pairs are solutions to the system. x y 6. 3x y 2
 78 Chapter Sstems of Linear Equations Section. Concepts. Solutions to Sstems of Linear Equations. Dependent and Inconsistent Sstems of Linear Equations. Solving Sstems of Linear Equations b Graphing Solving
78 Chapter Sstems of Linear Equations Section. Concepts. Solutions to Sstems of Linear Equations. Dependent and Inconsistent Sstems of Linear Equations. Solving Sstems of Linear Equations b Graphing Solving
Chapter 6: Systems of Equations and Inequalities
 Chapter 6: Sstems of Equations and Inequalities 6-1: Solving Sstems b Graphing Objectives: Identif solutions of sstems of linear equation in two variables. Solve sstems of linear equation in two variables
Chapter 6: Sstems of Equations and Inequalities 6-1: Solving Sstems b Graphing Objectives: Identif solutions of sstems of linear equation in two variables. Solve sstems of linear equation in two variables
For questions 5-8, solve each inequality and graph the solution set. You must show work for full credit. (2 pts each)
 Alg Midterm Review Practice Level 1 C 1. Find the opposite and the reciprocal of 0. a. 0, 1 b. 0, 1 0 0 c. 0, 1 0 d. 0, 1 0 For questions -, insert , or = to make the sentence true. (1pt each) A. 5
Alg Midterm Review Practice Level 1 C 1. Find the opposite and the reciprocal of 0. a. 0, 1 b. 0, 1 0 0 c. 0, 1 0 d. 0, 1 0 For questions -, insert , or = to make the sentence true. (1pt each) A. 5
Chapter 11. Systems of Equations Solving Systems of Linear Equations by Graphing
 Chapter 11 Sstems of Equations 11.1 Solving Sstems of Linear Equations b Graphing Learning Objectives: A. Decide whether an ordered pair is a solution of a sstem of linear equations. B. Solve a sstem of
Chapter 11 Sstems of Equations 11.1 Solving Sstems of Linear Equations b Graphing Learning Objectives: A. Decide whether an ordered pair is a solution of a sstem of linear equations. B. Solve a sstem of
11.1 Solving Linear Systems by Graphing
 Name Class Date 11.1 Solving Linear Sstems b Graphing Essential Question: How can ou find the solution of a sstem of linear equations b graphing? Resource Locker Eplore Tpes of Sstems of Linear Equations
Name Class Date 11.1 Solving Linear Sstems b Graphing Essential Question: How can ou find the solution of a sstem of linear equations b graphing? Resource Locker Eplore Tpes of Sstems of Linear Equations
Section 3.1 Solving Linear Systems by Graphing
 Section 3.1 Solving Linear Sstems b Graphing Name: Period: Objective(s): Solve a sstem of linear equations in two variables using graphing. Essential Question: Eplain how to tell from a graph of a sstem
Section 3.1 Solving Linear Sstems b Graphing Name: Period: Objective(s): Solve a sstem of linear equations in two variables using graphing. Essential Question: Eplain how to tell from a graph of a sstem
RELATIONS AND FUNCTIONS through
 RELATIONS AND FUNCTIONS 11.1.2 through 11.1. Relations and Functions establish a correspondence between the input values (usuall ) and the output values (usuall ) according to the particular relation or
RELATIONS AND FUNCTIONS 11.1.2 through 11.1. Relations and Functions establish a correspondence between the input values (usuall ) and the output values (usuall ) according to the particular relation or
Engineering Mathematics I
 Engineering Mathematics I_ 017 Engineering Mathematics I 1. Introduction to Differential Equations Dr. Rami Zakaria Terminolog Differential Equation Ordinar Differential Equations Partial Differential
Engineering Mathematics I_ 017 Engineering Mathematics I 1. Introduction to Differential Equations Dr. Rami Zakaria Terminolog Differential Equation Ordinar Differential Equations Partial Differential
Name Class Date. Solving Special Systems by Graphing. Does this linear system have a solution? Use the graph to explain.
 Name Class Date 5 Solving Special Sstems Going Deeper Essential question: How do ou solve sstems with no or infinitel man solutions? 1 A-REI.3.6 EXAMPLE Solving Special Sstems b Graphing Use the graph
Name Class Date 5 Solving Special Sstems Going Deeper Essential question: How do ou solve sstems with no or infinitel man solutions? 1 A-REI.3.6 EXAMPLE Solving Special Sstems b Graphing Use the graph
10.4 Nonlinear Inequalities and Systems of Inequalities. OBJECTIVES 1 Graph a Nonlinear Inequality. 2 Graph a System of Nonlinear Inequalities.
 Section 0. Nonlinear Inequalities and Sstems of Inequalities 6 CONCEPT EXTENSIONS For the eercises below, see the Concept Check in this section.. Without graphing, how can ou tell that the graph of + =
Section 0. Nonlinear Inequalities and Sstems of Inequalities 6 CONCEPT EXTENSIONS For the eercises below, see the Concept Check in this section.. Without graphing, how can ou tell that the graph of + =
Lecture 5. Equations of Lines and Planes. Dan Nichols MATH 233, Spring 2018 University of Massachusetts.
 Lecture 5 Equations of Lines and Planes Dan Nichols nichols@math.umass.edu MATH 233, Spring 2018 Universit of Massachusetts Februar 6, 2018 (2) Upcoming midterm eam First midterm: Wednesda Feb. 21, 7:00-9:00
Lecture 5 Equations of Lines and Planes Dan Nichols nichols@math.umass.edu MATH 233, Spring 2018 Universit of Massachusetts Februar 6, 2018 (2) Upcoming midterm eam First midterm: Wednesda Feb. 21, 7:00-9:00
Can a system of linear equations have no solution? Can a system of linear equations have many solutions?
 5. Solving Special Sstems of Linear Equations Can a sstem of linear equations have no solution? Can a sstem of linear equations have man solutions? ACTIVITY: Writing a Sstem of Linear Equations Work with
5. Solving Special Sstems of Linear Equations Can a sstem of linear equations have no solution? Can a sstem of linear equations have man solutions? ACTIVITY: Writing a Sstem of Linear Equations Work with
EOC Review. Algebra I
 EOC Review Algebra I Order of Operations PEMDAS Parentheses, Eponents, Multiplication/Division, Add/Subtract from left to right. A. Simplif each epression using appropriate Order of Operations.. 5 6 +.
EOC Review Algebra I Order of Operations PEMDAS Parentheses, Eponents, Multiplication/Division, Add/Subtract from left to right. A. Simplif each epression using appropriate Order of Operations.. 5 6 +.
8.4. If we let x denote the number of gallons pumped, then the price y in dollars can $ $1.70 $ $1.70 $ $1.70 $ $1.
 8.4 An Introduction to Functions: Linear Functions, Applications, and Models We often describe one quantit in terms of another; for eample, the growth of a plant is related to the amount of light it receives,
8.4 An Introduction to Functions: Linear Functions, Applications, and Models We often describe one quantit in terms of another; for eample, the growth of a plant is related to the amount of light it receives,
Section 4.1 Increasing and Decreasing Functions
 Section.1 Increasing and Decreasing Functions The graph of the quadratic function f 1 is a parabola. If we imagine a particle moving along this parabola from left to right, we can see that, while the -coordinates
Section.1 Increasing and Decreasing Functions The graph of the quadratic function f 1 is a parabola. If we imagine a particle moving along this parabola from left to right, we can see that, while the -coordinates
UNIT 5. SIMULTANEOUS EQUATIONS
 3º ESO. Definitions UNIT 5. SIMULTANEOUS EQUATIONS A linear equation with two unknowns is an equation with two unknowns having both of them degree one. Eamples. 3 + 5 and + 6 9. The standard form for these
3º ESO. Definitions UNIT 5. SIMULTANEOUS EQUATIONS A linear equation with two unknowns is an equation with two unknowns having both of them degree one. Eamples. 3 + 5 and + 6 9. The standard form for these
Math 084 Spring 2014 Exam 3 (Final) Preperation Ch 4 et al v01 Dressler. Name
 Math 0 Spring 01 Eam 3 (Final) Preperation Ch et al v01 Dressler Name Determine whether the ordered pair is a solution of the sstem. 1) (-3, ) + = 3 - = -9 Solve the sstem b graphing. If there is no solution
Math 0 Spring 01 Eam 3 (Final) Preperation Ch et al v01 Dressler Name Determine whether the ordered pair is a solution of the sstem. 1) (-3, ) + = 3 - = -9 Solve the sstem b graphing. If there is no solution
Mth Quadratic functions and quadratic equations
 Mth 0 - Quadratic functions and quadratic equations Name Find the product. 1) 8a3(2a3 + 2 + 12a) 2) ( + 4)( + 6) 3) (3p - 1)(9p2 + 3p + 1) 4) (32 + 4-4)(2-3 + 3) ) (4a - 7)2 Factor completel. 6) 92-4 7)
Mth 0 - Quadratic functions and quadratic equations Name Find the product. 1) 8a3(2a3 + 2 + 12a) 2) ( + 4)( + 6) 3) (3p - 1)(9p2 + 3p + 1) 4) (32 + 4-4)(2-3 + 3) ) (4a - 7)2 Factor completel. 6) 92-4 7)
MA 15800, Summer 2016 Lesson 25 Notes Solving a System of Equations by substitution (or elimination) Matrices. 2 A System of Equations
 MA 800, Summer 06 Lesson Notes Solving a Sstem of Equations b substitution (or elimination) Matrices Consider the graphs of the two equations below. A Sstem of Equations From our mathematics eperience,
MA 800, Summer 06 Lesson Notes Solving a Sstem of Equations b substitution (or elimination) Matrices Consider the graphs of the two equations below. A Sstem of Equations From our mathematics eperience,
Chapter 13. Overview. The Quadratic Formula. Overview. The Quadratic Formula. The Quadratic Formula. Lewinter & Widulski 1. The Quadratic Formula
 Chapter 13 Overview Some More Math Before You Go The Quadratic Formula The iscriminant Multiplication of Binomials F.O.I.L. Factoring Zero factor propert Graphing Parabolas The Ais of Smmetr, Verte and
Chapter 13 Overview Some More Math Before You Go The Quadratic Formula The iscriminant Multiplication of Binomials F.O.I.L. Factoring Zero factor propert Graphing Parabolas The Ais of Smmetr, Verte and
Section 5.1: Functions
 Objective: Identif functions and use correct notation to evaluate functions at numerical and variable values. A relationship is a matching of elements between two sets with the first set called the domain
Objective: Identif functions and use correct notation to evaluate functions at numerical and variable values. A relationship is a matching of elements between two sets with the first set called the domain
Math 3201 UNIT 5: Polynomial Functions NOTES. Characteristics of Graphs and Equations of Polynomials Functions
 1 Math 301 UNIT 5: Polnomial Functions NOTES Section 5.1 and 5.: Characteristics of Graphs and Equations of Polnomials Functions What is a polnomial function? Polnomial Function: - A function that contains
1 Math 301 UNIT 5: Polnomial Functions NOTES Section 5.1 and 5.: Characteristics of Graphs and Equations of Polnomials Functions What is a polnomial function? Polnomial Function: - A function that contains
4 The Cartesian Coordinate System- Pictures of Equations
 The Cartesian Coordinate Sstem- Pictures of Equations Concepts: The Cartesian Coordinate Sstem Graphs of Equations in Two Variables -intercepts and -intercepts Distance in Two Dimensions and the Pthagorean
The Cartesian Coordinate Sstem- Pictures of Equations Concepts: The Cartesian Coordinate Sstem Graphs of Equations in Two Variables -intercepts and -intercepts Distance in Two Dimensions and the Pthagorean
STUDY KNOWHOW PROGRAM STUDY AND LEARNING CENTRE. Functions & Graphs
 STUDY KNOWHOW PROGRAM STUDY AND LEARNING CENTRE Functions & Graphs Contents Functions and Relations... 1 Interval Notation... 3 Graphs: Linear Functions... 5 Lines and Gradients... 7 Graphs: Quadratic
STUDY KNOWHOW PROGRAM STUDY AND LEARNING CENTRE Functions & Graphs Contents Functions and Relations... 1 Interval Notation... 3 Graphs: Linear Functions... 5 Lines and Gradients... 7 Graphs: Quadratic
Systems of Linear Inequalities
 . Sstems of Linear Inequalities sstem of linear inequalities? How can ou sketch the graph of a ACTIVITY: Graphing Linear Inequalities Work with a partner. Match the linear inequalit with its graph. + Inequalit
. Sstems of Linear Inequalities sstem of linear inequalities? How can ou sketch the graph of a ACTIVITY: Graphing Linear Inequalities Work with a partner. Match the linear inequalit with its graph. + Inequalit
Chapter 1 Graph of Functions
 Graph of Functions Chapter Graph of Functions. Rectangular Coordinate Sstem and Plotting points The Coordinate Plane Quadrant II Quadrant I (0,0) Quadrant III Quadrant IV Figure. The aes divide the plane
Graph of Functions Chapter Graph of Functions. Rectangular Coordinate Sstem and Plotting points The Coordinate Plane Quadrant II Quadrant I (0,0) Quadrant III Quadrant IV Figure. The aes divide the plane
Chapter 18 Quadratic Function 2
 Chapter 18 Quadratic Function Completed Square Form 1 Consider this special set of numbers - the square numbers or the set of perfect squares. 4 = = 9 = 3 = 16 = 4 = 5 = 5 = Numbers like 5, 11, 15 are
Chapter 18 Quadratic Function Completed Square Form 1 Consider this special set of numbers - the square numbers or the set of perfect squares. 4 = = 9 = 3 = 16 = 4 = 5 = 5 = Numbers like 5, 11, 15 are
Summer Math Packet (revised 2017)
 Summer Math Packet (revised 07) In preparation for Honors Math III, we have prepared a packet of concepts that students should know how to do as these concepts have been taught in previous math classes.
Summer Math Packet (revised 07) In preparation for Honors Math III, we have prepared a packet of concepts that students should know how to do as these concepts have been taught in previous math classes.
5 Systems of Equations
 Systems of Equations Concepts: Solutions to Systems of Equations-Graphically and Algebraically Solving Systems - Substitution Method Solving Systems - Elimination Method Using -Dimensional Graphs to Approximate
Systems of Equations Concepts: Solutions to Systems of Equations-Graphically and Algebraically Solving Systems - Substitution Method Solving Systems - Elimination Method Using -Dimensional Graphs to Approximate
APPENDIX D Rotation and the General Second-Degree Equation
 APPENDIX D Rotation and the General Second-Degree Equation Rotation of Aes Invariants Under Rotation After rotation of the - and -aes counterclockwise through an angle, the rotated aes are denoted as the
APPENDIX D Rotation and the General Second-Degree Equation Rotation of Aes Invariants Under Rotation After rotation of the - and -aes counterclockwise through an angle, the rotated aes are denoted as the
Maintaining Mathematical Proficiency
 Name Date Chapter 5 Maintaining Mathematical Proficienc Graph the equation. 1. + =. = 3 3. 5 + = 10. 3 = 5. 3 = 6. 3 + = 1 Solve the inequalit. Graph the solution. 7. a 3 > 8. c 9. d 5 < 3 10. 8 3r 5 r
Name Date Chapter 5 Maintaining Mathematical Proficienc Graph the equation. 1. + =. = 3 3. 5 + = 10. 3 = 5. 3 = 6. 3 + = 1 Solve the inequalit. Graph the solution. 7. a 3 > 8. c 9. d 5 < 3 10. 8 3r 5 r
x. 4. 2x 10 4x. 10 x
 CCGPS UNIT Semester 1 COORDINATE ALGEBRA Page 1 of Reasoning with Equations and Quantities Name: Date: Understand solving equations as a process of reasoning and eplain the reasoning MCC9-1.A.REI.1 Eplain
CCGPS UNIT Semester 1 COORDINATE ALGEBRA Page 1 of Reasoning with Equations and Quantities Name: Date: Understand solving equations as a process of reasoning and eplain the reasoning MCC9-1.A.REI.1 Eplain
3.2 Understanding Relations and Functions-NOTES
 Name Class Date. Understanding Relations and Functions-NOTES Essential Question: How do ou represent relations and functions? Eplore A1.1.A decide whether relations represented verball, tabularl, graphicall,
Name Class Date. Understanding Relations and Functions-NOTES Essential Question: How do ou represent relations and functions? Eplore A1.1.A decide whether relations represented verball, tabularl, graphicall,
Chapter 5: Systems of Equations
 Chapter : Sstems of Equations Section.: Sstems in Two Variables... 0 Section. Eercises... 9 Section.: Sstems in Three Variables... Section. Eercises... Section.: Linear Inequalities... Section.: Eercises.
Chapter : Sstems of Equations Section.: Sstems in Two Variables... 0 Section. Eercises... 9 Section.: Sstems in Three Variables... Section. Eercises... Section.: Linear Inequalities... Section.: Eercises.
2 variables. is the same value as the solution of. 1 variable. You can use similar reasoning to solve quadratic equations. Work with a partner.
 9. b Graphing Essential Question How can ou use a graph to solve a quadratic equation in one variable? Based on what ou learned about the -intercepts of a graph in Section., it follows that the -intercept
9. b Graphing Essential Question How can ou use a graph to solve a quadratic equation in one variable? Based on what ou learned about the -intercepts of a graph in Section., it follows that the -intercept
Algebra 1 Skills Needed for Success in Math
 Algebra 1 Skills Needed for Success in Math A. Simplifing Polnomial Epressions Objectives: The student will be able to: Appl the appropriate arithmetic operations and algebraic properties needed to simplif
Algebra 1 Skills Needed for Success in Math A. Simplifing Polnomial Epressions Objectives: The student will be able to: Appl the appropriate arithmetic operations and algebraic properties needed to simplif
Systems of Linear and Quadratic Equations. Check Skills You ll Need. y x. Solve by Graphing. Solve the following system by graphing.
 NY- Learning Standards for Mathematics A.A. Solve a sstem of one linear and one quadratic equation in two variables, where onl factoring is required. A.G.9 Solve sstems of linear and quadratic equations
NY- Learning Standards for Mathematics A.A. Solve a sstem of one linear and one quadratic equation in two variables, where onl factoring is required. A.G.9 Solve sstems of linear and quadratic equations
Using Intercept Form
 8.5 Using Intercept Form Essential Question What are some of the characteristics of the graph of f () = a( p)( q)? Using Zeros to Write Functions Work with a partner. Each graph represents a function of
8.5 Using Intercept Form Essential Question What are some of the characteristics of the graph of f () = a( p)( q)? Using Zeros to Write Functions Work with a partner. Each graph represents a function of
MATH SPEAK - TO BE UNDERSTOOD AND MEMORIZED
 FOM 11 T GRAPHING LINEAR INEQUALITIES & SET NOTATION - 1 1 MATH SPEAK - TO BE UNDERSTOOD AND MEMORIZED 1) INEQUALITY = a mathematical statement that contains one of these four inequalit signs: ,.
FOM 11 T GRAPHING LINEAR INEQUALITIES & SET NOTATION - 1 1 MATH SPEAK - TO BE UNDERSTOOD AND MEMORIZED 1) INEQUALITY = a mathematical statement that contains one of these four inequalit signs: ,.
Objectives To solve quadratic equations using the quadratic formula To find the number of solutions of a quadratic equation
 9-6 The Quadratic Formula and the Discriminant Content Standards A.REI..a Use the method of completing the square to transform an quadratic equation in into an equation of the form ( p) 5 q... Derive the
9-6 The Quadratic Formula and the Discriminant Content Standards A.REI..a Use the method of completing the square to transform an quadratic equation in into an equation of the form ( p) 5 q... Derive the
11.4 Polar Coordinates
 11. Polar Coordinates 917 11. Polar Coordinates In Section 1.1, we introduced the Cartesian coordinates of a point in the plane as a means of assigning ordered pairs of numbers to points in the plane.
11. Polar Coordinates 917 11. Polar Coordinates In Section 1.1, we introduced the Cartesian coordinates of a point in the plane as a means of assigning ordered pairs of numbers to points in the plane.
ACCUPLACER MATH 0311 OR MATH 0120
 The University of Teas at El Paso Tutoring and Learning Center ACCUPLACER MATH 0 OR MATH 00 http://www.academics.utep.edu/tlc MATH 0 OR MATH 00 Page Factoring Factoring Eercises 8 Factoring Answer to Eercises
The University of Teas at El Paso Tutoring and Learning Center ACCUPLACER MATH 0 OR MATH 00 http://www.academics.utep.edu/tlc MATH 0 OR MATH 00 Page Factoring Factoring Eercises 8 Factoring Answer to Eercises
Derivatives 2: The Derivative at a Point
 Derivatives 2: The Derivative at a Point 69 Derivatives 2: The Derivative at a Point Model 1: Review of Velocit In the previous activit we eplored position functions (distance versus time) and learned
Derivatives 2: The Derivative at a Point 69 Derivatives 2: The Derivative at a Point Model 1: Review of Velocit In the previous activit we eplored position functions (distance versus time) and learned
3.2 LOGARITHMIC FUNCTIONS AND THEIR GRAPHS
 Section. Logarithmic Functions and Their Graphs 7. LOGARITHMIC FUNCTIONS AND THEIR GRAPHS Ariel Skelle/Corbis What ou should learn Recognize and evaluate logarithmic functions with base a. Graph logarithmic
Section. Logarithmic Functions and Their Graphs 7. LOGARITHMIC FUNCTIONS AND THEIR GRAPHS Ariel Skelle/Corbis What ou should learn Recognize and evaluate logarithmic functions with base a. Graph logarithmic
Absolute Value Equations(One Absolute Value) Objectives. Absolute Value Inequalities (> or ) Absolute Value Inequalities (< or )
 Section 5 Absolute Value Equations and Inequalities Solve Absolute Value Equations Solve Absolute Value Inequalities Involving < or Solve Absolute Value Inequalities Involving > or Absolute Value Equations(One
Section 5 Absolute Value Equations and Inequalities Solve Absolute Value Equations Solve Absolute Value Inequalities Involving < or Solve Absolute Value Inequalities Involving > or Absolute Value Equations(One
3 Polynomial and Rational Functions
 3 Polnomial and Rational Functions 3.1 Quadratic Functions and Models 3.2 Polnomial Functions and Their Graphs 3.3 Dividing Polnomials 3.4 Real Zeros of Polnomials 3.5 Comple Zeros and the Fundamental
3 Polnomial and Rational Functions 3.1 Quadratic Functions and Models 3.2 Polnomial Functions and Their Graphs 3.3 Dividing Polnomials 3.4 Real Zeros of Polnomials 3.5 Comple Zeros and the Fundamental
Chapter 1: Linear Equations and Functions
 Chapter : Answers to Eercises Chapter : Linear Equations and Functions Eercise.. 7= 8+ 7+ 7 8 = 8+ + 7 8 = 9. + 8= 8( + ). + 8= 8+ 8 8 = 8 8 7 = 0 = 0 9 = = = () = 96 = 7. ( 7) = ( + ) 9.. = + + = + =
Chapter : Answers to Eercises Chapter : Linear Equations and Functions Eercise.. 7= 8+ 7+ 7 8 = 8+ + 7 8 = 9. + 8= 8( + ). + 8= 8+ 8 8 = 8 8 7 = 0 = 0 9 = = = () = 96 = 7. ( 7) = ( + ) 9.. = + + = + =
Essential Question How can you solve a nonlinear system of equations?
 .5 Solving Nonlinear Sstems Essential Question Essential Question How can ou solve a nonlinear sstem of equations? Solving Nonlinear Sstems of Equations Work with a partner. Match each sstem with its graph.
.5 Solving Nonlinear Sstems Essential Question Essential Question How can ou solve a nonlinear sstem of equations? Solving Nonlinear Sstems of Equations Work with a partner. Match each sstem with its graph.
Exact Differential Equations. The general solution of the equation is f x, y C. If f has continuous second partials, then M y 2 f
 APPENDIX C Additional Topics in Differential Equations APPENDIX C. Eact First-Order Equations Eact Differential Equations Integrating Factors Eact Differential Equations In Chapter 6, ou studied applications
APPENDIX C Additional Topics in Differential Equations APPENDIX C. Eact First-Order Equations Eact Differential Equations Integrating Factors Eact Differential Equations In Chapter 6, ou studied applications
8.1 Exponents and Roots
 Section 8. Eponents and Roots 75 8. Eponents and Roots Before defining the net famil of functions, the eponential functions, we will need to discuss eponent notation in detail. As we shall see, eponents
Section 8. Eponents and Roots 75 8. Eponents and Roots Before defining the net famil of functions, the eponential functions, we will need to discuss eponent notation in detail. As we shall see, eponents
Math098 Practice Final Test
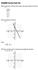 Math098 Practice Final Test Find an equation of the line that contains the points listed in the table. 1) 0-6 1-2 -4 3-3 4-2 Find an equation of the line. 2) 10-10 - 10 - -10 Solve. 3) 2 = 3 + 4 Find the
Math098 Practice Final Test Find an equation of the line that contains the points listed in the table. 1) 0-6 1-2 -4 3-3 4-2 Find an equation of the line. 2) 10-10 - 10 - -10 Solve. 3) 2 = 3 + 4 Find the
( 3x. Chapter Review. Review Key Vocabulary. Review Examples and Exercises 6.1 Properties of Square Roots (pp )
 6 Chapter Review Review Ke Vocabular closed, p. 266 nth root, p. 278 eponential function, p. 286 eponential growth, p. 296 eponential growth function, p. 296 compound interest, p. 297 Vocabular Help eponential
6 Chapter Review Review Ke Vocabular closed, p. 266 nth root, p. 278 eponential function, p. 286 eponential growth, p. 296 eponential growth function, p. 296 compound interest, p. 297 Vocabular Help eponential
Solving Systems Using Tables and Graphs
 3-1 Solving Sstems Using Tables and Graphs Vocabular Review 1. Cross out the equation that is NOT in slope-intercept form. 1 5 7 r 5 s a 5!3b 1 5 3 1 7 5 13 Vocabular Builder linear sstem (noun) LIN ee
3-1 Solving Sstems Using Tables and Graphs Vocabular Review 1. Cross out the equation that is NOT in slope-intercept form. 1 5 7 r 5 s a 5!3b 1 5 3 1 7 5 13 Vocabular Builder linear sstem (noun) LIN ee
Vertex. March 23, Ch 9 Guided Notes.notebook
 March, 07 9 Quadratic Graphs and Their Properties A quadratic function is a function that can be written in the form: Verte Its graph looks like... which we call a parabola. The simplest quadratic function
March, 07 9 Quadratic Graphs and Their Properties A quadratic function is a function that can be written in the form: Verte Its graph looks like... which we call a parabola. The simplest quadratic function
Basic Pr actice Final Exam #3 Page 1 / 20
 Basic Practice Final Eam #3 Class Name : M Test Retake Instructor Name : Mr. Becke Student Name : Instructor Note : 1. Graph the inequalit. < 3 + 1 - - - - - - - -. Graph the sstem below and write its
Basic Practice Final Eam #3 Class Name : M Test Retake Instructor Name : Mr. Becke Student Name : Instructor Note : 1. Graph the inequalit. < 3 + 1 - - - - - - - -. Graph the sstem below and write its
Solving Quadratic Equations by Graphing 9.1. ACTIVITY: Solving a Quadratic Equation by Graphing. How can you use a graph to solve a quadratic
 9. Solving Quadratic Equations b Graphing equation in one variable? How can ou use a graph to solve a quadratic Earlier in the book, ou learned that the -intercept of the graph of = a + b variables is
9. Solving Quadratic Equations b Graphing equation in one variable? How can ou use a graph to solve a quadratic Earlier in the book, ou learned that the -intercept of the graph of = a + b variables is
Ch 3 Alg 2 Note Sheet.doc 3.1 Graphing Systems of Equations
 Ch 3 Alg Note Sheet.doc 3.1 Graphing Sstems of Equations Sstems of Linear Equations A sstem of equations is a set of two or more equations that use the same variables. If the graph of each equation =.4
Ch 3 Alg Note Sheet.doc 3.1 Graphing Sstems of Equations Sstems of Linear Equations A sstem of equations is a set of two or more equations that use the same variables. If the graph of each equation =.4
Are You Ready? Find Area in the Coordinate Plane
 SKILL 38 Are You Read? Find Area in the Coordinate Plane Teaching Skill 38 Objective Find the areas of figures in the coordinate plane. Review with students the definition of area. Ask: Is the definition
SKILL 38 Are You Read? Find Area in the Coordinate Plane Teaching Skill 38 Objective Find the areas of figures in the coordinate plane. Review with students the definition of area. Ask: Is the definition
A. Simplifying Polynomial Expressions
 A. Simplifing Polnomial Epressions I. Combining Like Terms - You can add or subtract terms that are considered "like", or terms that have the same variable(s) with the same eponent(s). E. 1: 5-7 + 10 +
A. Simplifing Polnomial Epressions I. Combining Like Terms - You can add or subtract terms that are considered "like", or terms that have the same variable(s) with the same eponent(s). E. 1: 5-7 + 10 +
MATH GRADE 8 UNIT 4 LINEAR RELATIONSHIPS EXERCISES
 MATH GRADE 8 UNIT LINEAR RELATIONSHIPS Copright 01 Pearson Education, Inc., or its affiliate(s). All Rights Reserved. Printed in the United States of America. This publication is protected b copright,
MATH GRADE 8 UNIT LINEAR RELATIONSHIPS Copright 01 Pearson Education, Inc., or its affiliate(s). All Rights Reserved. Printed in the United States of America. This publication is protected b copright,
Linear Equation Theory - 2
 Algebra Module A46 Linear Equation Theor - Copright This publication The Northern Alberta Institute of Technolog 00. All Rights Reserved. LAST REVISED June., 009 Linear Equation Theor - Statement of Prerequisite
Algebra Module A46 Linear Equation Theor - Copright This publication The Northern Alberta Institute of Technolog 00. All Rights Reserved. LAST REVISED June., 009 Linear Equation Theor - Statement of Prerequisite
SOLVING SYSTEMS OF EQUATIONS
 SOLVING SYSTEMS OF EQUATIONS 4.. 4..4 Students have been solving equations even before Algebra. Now the focus on what a solution means, both algebraicall and graphicall. B understanding the nature of solutions,
SOLVING SYSTEMS OF EQUATIONS 4.. 4..4 Students have been solving equations even before Algebra. Now the focus on what a solution means, both algebraicall and graphicall. B understanding the nature of solutions,
The Coordinate Plane and Linear Equations Algebra 1
 Name: The Coordinate Plane and Linear Equations Algebra Date: We use the Cartesian Coordinate plane to locate points in two-dimensional space. We can do this b measuring the directed distances the point
Name: The Coordinate Plane and Linear Equations Algebra Date: We use the Cartesian Coordinate plane to locate points in two-dimensional space. We can do this b measuring the directed distances the point
10.3 Solving Nonlinear Systems of Equations
 60 CHAPTER 0 Conic Sections Identif whether each equation, when graphed, will be a parabola, circle, ellipse, or hperbola. Then graph each equation.. - 7 + - =. = +. = + + 6. + 9 =. 9-9 = 6. 6 - = 7. 6
60 CHAPTER 0 Conic Sections Identif whether each equation, when graphed, will be a parabola, circle, ellipse, or hperbola. Then graph each equation.. - 7 + - =. = +. = + + 6. + 9 =. 9-9 = 6. 6 - = 7. 6
Northwest High School s Algebra 2/Honors Algebra 2
 Northwest High School s Algebra /Honors Algebra Summer Review Packet 0 DUE Frida, September, 0 Student Name This packet has been designed to help ou review various mathematical topics that will be necessar
Northwest High School s Algebra /Honors Algebra Summer Review Packet 0 DUE Frida, September, 0 Student Name This packet has been designed to help ou review various mathematical topics that will be necessar
12x y (4) 2x y (4) 5x y is the same as
 Name: Unit #6 Review Quadratic Algebra Date: 1. When 6 is multiplied b the result is 0 1 () 9 1 () 9 1 () 1 0. When is multiplied b the result is 10 6 1 () 7 1 () 7 () 10 6. Written without negative eponents
Name: Unit #6 Review Quadratic Algebra Date: 1. When 6 is multiplied b the result is 0 1 () 9 1 () 9 1 () 1 0. When is multiplied b the result is 10 6 1 () 7 1 () 7 () 10 6. Written without negative eponents
PACKET Unit 4 Honors ICM Functions and Limits 1
 PACKET Unit 4 Honors ICM Functions and Limits 1 Day 1 Homework For each of the rational functions find: a. domain b. -intercept(s) c. y-intercept Graph #8 and #10 with at least 5 EXACT points. 1. f 6.
PACKET Unit 4 Honors ICM Functions and Limits 1 Day 1 Homework For each of the rational functions find: a. domain b. -intercept(s) c. y-intercept Graph #8 and #10 with at least 5 EXACT points. 1. f 6.
Review of Elementary Algebra Content
 Review of Elementar Algebra Content 0 1 Table of Contents Fractions...1 Integers...5 Order of Operations...9 Eponents...11 Polnomials...18 Factoring... Solving Linear Equations...1 Solving Linear Inequalities...
Review of Elementar Algebra Content 0 1 Table of Contents Fractions...1 Integers...5 Order of Operations...9 Eponents...11 Polnomials...18 Factoring... Solving Linear Equations...1 Solving Linear Inequalities...
SOLVING SYSTEMS OF EQUATIONS
 SOLVING SYSTEMS OF EQUATIONS 3.. 3..4 In this course, one focus is on what a solution means, both algebraicall and graphicall. B understanding the nature of solutions, students are able to solve equations
SOLVING SYSTEMS OF EQUATIONS 3.. 3..4 In this course, one focus is on what a solution means, both algebraicall and graphicall. B understanding the nature of solutions, students are able to solve equations
(2.5) 1. Solve the following compound inequality and graph the solution set.
 Intermediate Algebra Practice Final Math 0 (7 th ed.) (Ch. -) (.5). Solve the following compound inequalit and graph the solution set. 0 and and > or or (.7). Solve the following absolute value inequalities.
Intermediate Algebra Practice Final Math 0 (7 th ed.) (Ch. -) (.5). Solve the following compound inequalit and graph the solution set. 0 and and > or or (.7). Solve the following absolute value inequalities.
Math Intermediate Algebra
 Math 095 - Intermediate Algebra Final Eam Review Objective 1: Determine whether a relation is a function. Given a graphical, tabular, or algebraic representation for a function, evaluate the function and
Math 095 - Intermediate Algebra Final Eam Review Objective 1: Determine whether a relation is a function. Given a graphical, tabular, or algebraic representation for a function, evaluate the function and
The letter m is used to denote the slope and we say that m = rise run = change in y change in x = 5 7. change in y change in x = 4 6 =
 Section 4 3: Slope Introduction We use the term Slope to describe how steep a line is as ou move between an two points on the line. The slope or steepness is a ratio of the vertical change in (rise) compared
Section 4 3: Slope Introduction We use the term Slope to describe how steep a line is as ou move between an two points on the line. The slope or steepness is a ratio of the vertical change in (rise) compared
9.2. Cartesian Components of Vectors. Introduction. Prerequisites. Learning Outcomes
 Cartesian Components of Vectors 9.2 Introduction It is useful to be able to describe vectors with reference to specific coordinate sstems, such as the Cartesian coordinate sstem. So, in this Section, we
Cartesian Components of Vectors 9.2 Introduction It is useful to be able to describe vectors with reference to specific coordinate sstems, such as the Cartesian coordinate sstem. So, in this Section, we
UNCORRECTED SAMPLE PAGES. 3Quadratics. Chapter 3. Objectives
 Chapter 3 3Quadratics Objectives To recognise and sketch the graphs of quadratic polnomials. To find the ke features of the graph of a quadratic polnomial: ais intercepts, turning point and ais of smmetr.
Chapter 3 3Quadratics Objectives To recognise and sketch the graphs of quadratic polnomials. To find the ke features of the graph of a quadratic polnomial: ais intercepts, turning point and ais of smmetr.
Graphing Linear Functions The collection of all input values is called the of a function.
 Math /7 NTES (9.3) Name Graphing Linear Functions The collection of all input values is called the of a function. The collection of all output values is called the of a function. Make a table for the function.
Math /7 NTES (9.3) Name Graphing Linear Functions The collection of all input values is called the of a function. The collection of all output values is called the of a function. Make a table for the function.
4.3 Exercises. local maximum or minimum. The second derivative is. e 1 x 2x 1. f x x 2 e 1 x 1 x 2 e 1 x 2x x 4
 SECTION 4.3 HOW DERIVATIVES AFFECT THE SHAPE OF A GRAPH 297 local maimum or minimum. The second derivative is f 2 e 2 e 2 4 e 2 4 Since e and 4, we have f when and when 2 f. So the curve is concave downward
SECTION 4.3 HOW DERIVATIVES AFFECT THE SHAPE OF A GRAPH 297 local maimum or minimum. The second derivative is f 2 e 2 e 2 4 e 2 4 Since e and 4, we have f when and when 2 f. So the curve is concave downward
Solving Systems of Linear Equations by Graphing. ESSENTIAL QUESTION How can you solve a system of equations by graphing? 8.9 Slope-intercept form
 ? LESSN. Solving Sstems of Linear Equations b Graphing ESSENTIAL QUESTIN How can ou solve a sstem of equations b graphing? Epressions, equations, and relationships.9 Identif and verif the values of and
? LESSN. Solving Sstems of Linear Equations b Graphing ESSENTIAL QUESTIN How can ou solve a sstem of equations b graphing? Epressions, equations, and relationships.9 Identif and verif the values of and
2 x = You try: 1a) Simplify: 6x 5+ 8x 5. 1 a) Simplify: 5x 4+ 3x+ You try: 2a) Solve: x 6= 2 a) Solve: 4+ x = 10. b) Solve: 3 12.
 1 a) Simplif: 5 + + 7 1 1a) Simplif: 6 5+ 5. b) Simplif: 6 ( + 5) ( 6+ 5) 1b) Simplif: 5 ( ) 65 ( ) A.SSE. a) Solve: + 10 a) Solve: 6 10 b) Solve: 1 b) Solve: 5 A.REI. Page 1 of 19 MCC@WCCUSD (AUSD) 10/1/1
1 a) Simplif: 5 + + 7 1 1a) Simplif: 6 5+ 5. b) Simplif: 6 ( + 5) ( 6+ 5) 1b) Simplif: 5 ( ) 65 ( ) A.SSE. a) Solve: + 10 a) Solve: 6 10 b) Solve: 1 b) Solve: 5 A.REI. Page 1 of 19 MCC@WCCUSD (AUSD) 10/1/1
Math RE - Calculus I Functions Page 1 of 10. Topics of Functions used in Calculus
 Math 0-03-RE - Calculus I Functions Page of 0 Definition of a function f() : Topics of Functions used in Calculus A function = f() is a relation between variables and such that for ever value onl one value.
Math 0-03-RE - Calculus I Functions Page of 0 Definition of a function f() : Topics of Functions used in Calculus A function = f() is a relation between variables and such that for ever value onl one value.
FACULTY OF MATHEMATICAL STUDIES MATHEMATICS FOR PART I ENGINEERING. Lectures AB = BA = I,
 FACULTY OF MATHEMATICAL STUDIES MATHEMATICS FOR PART I ENGINEERING Lectures MODULE 7 MATRICES II Inverse of a matri Sstems of linear equations Solution of sets of linear equations elimination methods 4
FACULTY OF MATHEMATICAL STUDIES MATHEMATICS FOR PART I ENGINEERING Lectures MODULE 7 MATRICES II Inverse of a matri Sstems of linear equations Solution of sets of linear equations elimination methods 4
Glossary. Also available at BigIdeasMath.com: multi-language glossary vocabulary flash cards. An equation that contains an absolute value expression
 Glossar This student friendl glossar is designed to be a reference for ke vocabular, properties, and mathematical terms. Several of the entries include a short eample to aid our understanding of important
Glossar This student friendl glossar is designed to be a reference for ke vocabular, properties, and mathematical terms. Several of the entries include a short eample to aid our understanding of important
Linear algebra in turn is built on two basic elements, MATRICES and VECTORS.
 M-Lecture():.-. Linear algebra provides concepts that are crucial to man areas of information technolog and computing, including: Graphics Image processing Crptograph Machine learning Computer vision Optimiation
M-Lecture():.-. Linear algebra provides concepts that are crucial to man areas of information technolog and computing, including: Graphics Image processing Crptograph Machine learning Computer vision Optimiation
Eigenvectors and Eigenvalues 1
 Ma 2015 page 1 Eigenvectors and Eigenvalues 1 In this handout, we will eplore eigenvectors and eigenvalues. We will begin with an eploration, then provide some direct eplanation and worked eamples, and
Ma 2015 page 1 Eigenvectors and Eigenvalues 1 In this handout, we will eplore eigenvectors and eigenvalues. We will begin with an eploration, then provide some direct eplanation and worked eamples, and
Summer Review For Students Entering Algebra 2
 Summer Review For Students Entering Algebra Teachers and administrators at Tuscarora High School activel encourage parents and communit members to engage in children s learning. This Summer Review For
Summer Review For Students Entering Algebra Teachers and administrators at Tuscarora High School activel encourage parents and communit members to engage in children s learning. This Summer Review For
74 Maths Quest 10 for Victoria
 Linear graphs Maria is working in the kitchen making some high energ biscuits using peanuts and chocolate chips. She wants to make less than g of biscuits but wants the biscuits to contain at least 8 g
Linear graphs Maria is working in the kitchen making some high energ biscuits using peanuts and chocolate chips. She wants to make less than g of biscuits but wants the biscuits to contain at least 8 g
Solving Linear Systems
 1.4 Solving Linear Sstems Essential Question How can ou determine the number of solutions of a linear sstem? A linear sstem is consistent when it has at least one solution. A linear sstem is inconsistent
1.4 Solving Linear Sstems Essential Question How can ou determine the number of solutions of a linear sstem? A linear sstem is consistent when it has at least one solution. A linear sstem is inconsistent
Solve each system by graphing. Check your solution. y =-3x x + y = 5 y =-7
 Practice Solving Sstems b Graphing Solve each sstem b graphing. Check our solution. 1. =- + 3 = - (1, ). = 1 - (, 1) =-3 + 5 3. = 3 + + = 1 (, 3). =-5 = - 7. = 3-5 3 - = 0 (1, 5) 5. -3 + = 5 =-7 (, 7).
Practice Solving Sstems b Graphing Solve each sstem b graphing. Check our solution. 1. =- + 3 = - (1, ). = 1 - (, 1) =-3 + 5 3. = 3 + + = 1 (, 3). =-5 = - 7. = 3-5 3 - = 0 (1, 5) 5. -3 + = 5 =-7 (, 7).
Course 15 Numbers and Their Properties
 Course Numbers and Their Properties KEY Module: Objective: Rules for Eponents and Radicals To practice appling rules for eponents when the eponents are rational numbers Name: Date: Fill in the blanks.
Course Numbers and Their Properties KEY Module: Objective: Rules for Eponents and Radicals To practice appling rules for eponents when the eponents are rational numbers Name: Date: Fill in the blanks.
R = { } Fill-in-the-Table with the missing vocabulary terms: 1) 2) Fill-in-the-blanks: Function
 Name: Date: / / QUIZ DAY! Fill-in-the-Table with the missing vocabular terms: ) ) Input Fill-in-the-blanks: 3) Output Function A special tpe of where there is one and onl one range () value for ever domain
Name: Date: / / QUIZ DAY! Fill-in-the-Table with the missing vocabular terms: ) ) Input Fill-in-the-blanks: 3) Output Function A special tpe of where there is one and onl one range () value for ever domain
LESSON #42 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART 2 COMMON CORE ALGEBRA II
 LESSON #4 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART COMMON CORE ALGEBRA II You will recall from unit 1 that in order to find the inverse of a function, ou must switch and and solve for. Also,
LESSON #4 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART COMMON CORE ALGEBRA II You will recall from unit 1 that in order to find the inverse of a function, ou must switch and and solve for. Also,
Lesson 8.2 Exercises, pages
 Lesson 8. Eercises, pages 38 A Students should verif the solutions to all equations.. Which values of are not roots of each equation? a) ƒ - 3 ƒ = 7 = 5 or =- Use mental math. 5: L.S. 7 R.S. 7 : L.S. 7
Lesson 8. Eercises, pages 38 A Students should verif the solutions to all equations.. Which values of are not roots of each equation? a) ƒ - 3 ƒ = 7 = 5 or =- Use mental math. 5: L.S. 7 R.S. 7 : L.S. 7
Essential Question How can you solve a system of linear equations? $15 per night. Cost, C (in dollars) $75 per Number of. Revenue, R (in dollars)
 5.1 Solving Sstems of Linear Equations b Graphing Essential Question How can ou solve a sstem of linear equations? Writing a Sstem of Linear Equations Work with a partner. Your famil opens a bed-and-breakfast.
5.1 Solving Sstems of Linear Equations b Graphing Essential Question How can ou solve a sstem of linear equations? Writing a Sstem of Linear Equations Work with a partner. Your famil opens a bed-and-breakfast.
1.3. Absolute Value and Piecewise-Defined Functions Absolutely Piece-ful. My Notes ACTIVITY
 Absolute Value and Piecewise-Defined Functions Absolutel Piece-ful SUGGESTED LEARNING STRATEGIES: Activating Prior Knowledge, Create Representations, Quickwrite. Graph both = - for < 3 and = - + 7 for
Absolute Value and Piecewise-Defined Functions Absolutel Piece-ful SUGGESTED LEARNING STRATEGIES: Activating Prior Knowledge, Create Representations, Quickwrite. Graph both = - for < 3 and = - + 7 for
3.7 InveRSe FUnCTIOnS
 CHAPTER functions learning ObjeCTIveS In this section, ou will: Verif inverse functions. Determine the domain and range of an inverse function, and restrict the domain of a function to make it one-to-one.
CHAPTER functions learning ObjeCTIveS In this section, ou will: Verif inverse functions. Determine the domain and range of an inverse function, and restrict the domain of a function to make it one-to-one.
