Linear Differential Equations. Driven by Delta Functions
|
|
|
- Maude Cole
- 6 years ago
- Views:
Transcription
1 Gauge Istitute Joural H. Vic Dao Liear Differetial Equatios Drive by Delta Fuctios H. Vic Dao May, 4 Abstract We solve the liear differetial equatio LG ( ) (, ) = d( -), for the Hyper-real Gree fuctio G (, ), where L ( ) is a liear differetial operator, ad d( - ) is the hyper-real Delta fuctio. Keywords: Sturm-Liouville Epasios, Ifiitesimal, Ifiite- Hyper-Real, Hyper-Real, ifiite Hyper-real, Ifiitesimal Calculus, Delta Fuctio, Fourier Series, Laguerre Polyomials, Legedre Fuctios, Bessel Fuctios, Delta Fuctio, Mathematics Subject Classificatio 6E35; 6E3; 6E5; 6E; 6A6; 6A; 3E; 3E55; 3E7; 3H5; 46S; 97I4; 97I3.
2 Gauge Istitute Joural H. Vic Dao Cotets. Liear differetial Equatio Drive by Delta Fuctios. Hyper-real lie.. Hyper-real Fuctio 3. Itegral of a Hyper-real Fuctio 4. Delta Fuctio 5. Coverget Series 6. Gree s Fuctio for y'( ) + P( ) y( ) = f( ), with y () = 7. Gree s Fuctio for y"( ) + P( ) y'( ) + Q( ) y( ) = f( ), with y () =, & y '() = 8. Gree s Fuctio for y"( ) + P( ) y'( ) + Q( ) y( ) = f( ), with ya () =, & yb () = 9. Hyper-real Sturm-Liouville Problem. Delta Epasio i No-Normalized Eige-Fuctios. Gree s Fuctio Epasio i No-Normalized Eige- Fuctios. Gree Fuctio for Sie Sturm-Liouville y"( ) + ly( ) = & a = b = 3. Gree Fuctio for Cosie Sturm-Liouville y"( ) + ly( ) = & a = b = p 4. Gree s Fuctio for Bessel Sturm-Liuoville
3 Gauge Istitute Joural H. Vic Dao y"( ) + ly( ) = & a = 5. Gree s Fuctio for Bessel Sturm-Liuoville - 4 u"( ) + ( l - ) u( ) = & a = b = 6. Delta Epasio i Orthoormal Eige-fuctios 7. Gree s Fuctio Epasio i Orthoormal Eige-fuctios 8. Gl (,, ) Aalytic Cotiuatio i l ito the Comple Plae 9. Gree Fuctio for Hermit Sturm-Liuoville u u "( ) + ( l - ) ( ) = for ay real. Gree Fuctio for Legedre Sturm-Liuoville u"( q) + [ l + ] u( q) =, - p < q < p 4 cos q. Gree Fuctio for Legedre Sturm-Liuoville y"( q) + [ l + ( - m ) ] y( q) =, - p < q < p 4 cos q. Gree Fuctio for Bessel Sturm-Liuoville - 4 u"( ) + ( l - ) u( ) = & < < b 3. Gree Fuctio for Bessel Sturm-Liuoville y"( ) + ( l - ) y( ) =, < < & a = 4. Gree Fuctio for Bessel Sturm-Liuoville y"( ) + ( m - ) y( ) =, < < & a = p 5. Gree s Fuctio Itegral Epasio i Eige-fuctios 6. Gree s Fuctio Itegral Epasio i Cosie Fuctios of y"( ) + ly( ) =, < < 3
4 Gauge Istitute Joural H. Vic Dao 7. Gree s Fuctio Itegral Epasio for Weber Equatio - 4 y"( ) + ( l - ) y( ) =, a < <, a > 8. Gree s Fuctio for Hakel s - 4 y"( ) + ( l - ) y( ) =, < < 9. Gree s Fuctio for Bessel s y"( ) + ( l + ) y( ) =, - < < 3. Gree s Fuctio for Bessel s y"( ) + ( l + e ) y( ) =, - < < 3. Gree s Fuctio for Bessel s y"( ) + ( l - e ) y( ) =, - < < Refereces 4
5 Gauge Istitute Joural H. Vic Dao. Liear Differetial Equatio drive by Delta Fuctio A liear Differetial Equatio for the Hyper-real fuctio y ( ), forced by the Hyper-real fuctio f ( ) is LDy (, )() = f(), where the Differetial Operator LD (, ) is liear. If there is a Hyper-real Gree fuctio, that satisfies the equatio G (, ) LDG (, ) (, ) = d(, ), with the same Boudary coditio that y ( ) satisfies the, G (, ) is the Kerel of a Itegral Operator that trasforms a fuctio f ( ) ito the solutio y ( ) of the liear differetial equatio L (,Dy )() = f(). Ideed, if the = b y ( ) = ò G (, ) f( ) d, = a 5
6 Gauge Istitute Joural H. Vic Dao = b LDy (, )() = LD (, ) ò G (, )() f d, = a = b = LD (, ) åg (, )() f d, = b = a = å LDG (, ) (, )() f d = a = f ( ). d( -) We shall see that the epasio of d( - ) i series, or itegrals guaratees the eistece of a Gree Fuctio that ca be epaded similarly. The Delta Fuctio ca be defied oly as a hyper-real fuctio i ifiitesimal Calculus. We proceed with the defiitio of the Hyper-real lie. 6
7 Gauge Istitute Joural H. Vic Dao. Hyper-real Lie Each real umber a ca be represeted by a Cauchy sequece of ratioal umbers, ( r, r, r3,...) so that r a. The costat sequece ( aaa,,,...) is a costat hyper-real. I [Da] we established that,. Ay totally ordered set of positive, mootoically decreasig to zero sequeces ifiitesimal hyper-reals. ( i, i, i3,...) costitutes a family of. The ifiitesimals are smaller tha ay real umber, yet strictly greater tha zero. 3. Their reciprocals (,,,...) i i i 3 are the ifiite hyper-reals. 4. The ifiite hyper-reals are greater tha ay real umber, yet strictly smaller tha ifiity. 5. The ifiite hyper-reals with egative sigs are smaller tha ay real umber, yet strictly greater tha The sum of a real umber with a ifiitesimal is a o-costat hyper-real. 7. The Hyper-reals are the totality of costat hyper-reals, a family of ifiitesimals, a family of ifiitesimals with 7
8 Gauge Istitute Joural H. Vic Dao egative sig, a family of ifiite hyper-reals, a family of ifiite hyper-reals with egative sig, ad o-costat hyper-reals. 8. The hyper-reals are totally ordered, ad aliged alog a lie: the Hyper-real Lie. 9. That lie icludes the real umbers separated by the ocostat hyper-reals. Each real umber is the ceter of a iterval of hyper-reals, that icludes o other real umber.. I particular, zero is separated from ay positive real by the ifiitesimals, ad from ay egative real by the ifiitesimals with egative sigs, - d.. Zero is ot a ifiitesimal, because zero is ot strictly greater tha zero.. We do ot add ifiity to the hyper-real lie. 3. The ifiitesimals, the ifiitesimals with egative sigs, the ifiite hyper-reals, ad the ifiite hyper-reals with egative sigs are semi-groups with respect to additio. Neither set icludes zero. 4. The hyper-real lie is embedded i, ad is ot homeomorphic to the real lie. There is o bi-cotiuous oe-oe mappig from the hyper-real oto the real lie. 8
9 Gauge Istitute Joural H. Vic Dao 5. I particular, there are o poits o the real lie that ca be assiged uiquely to the ifiitesimal hyper-reals, or to the ifiite hyper-reals, or to the o-costat hyperreals. 6. No eighbourhood of a hyper-real is homeomorphic to a ball. Therefore, the hyper-real lie is ot a maifold. 7. The hyper-real lie is totally ordered like a lie, but it is ot spaed by oe elemet, ad it is ot oe-dimesioal. 9
10 Gauge Istitute Joural H. Vic Dao. Hyper-real Fuctio. Defiitio of a hyper-real fuctio f () is a hyper-real fuctio, iff it is from the hyper-reals ito the hyper-reals. This meas that ay umber i the domai, or i the rage of a hyper-real f ( ) is either oe of the followig real real + ifiitesimal real ifiitesimal ifiitesimal ifiitesimal with egative sig ifiite hyper-real ifiite hyper-real with egative sig Clearly,. Every fuctio from the reals ito the reals is a hyper-real fuctio.
11 Gauge Istitute Joural H. Vic Dao 3. Itegral of a Hyper-real Fuctio I [Da3], we defied the itegral of a Hyper-real Fuctio. Let f () be a hyper-real fuctio o the iterval [ ab],. The iterval may ot be bouded. f ( ) may take ifiite hyper-real values, ad eed ot be bouded. At each a b, there is a rectagle with base [ -, + d ], height f ( ), ad area d f ( d. ) We form the Itegratio Sum of all the areas for the s that start at = a, ad ed at = b, å f ( d ). Î[ a, b] If for ay ifiitesimal d, the Itegratio Sum has the same hyper-real value, the f ( ) is itegrable over the iterval [ ab],. The, we call the Itegratio Sum the itegral of f () from = a, to = b, ad deote it by
12 Gauge Istitute Joural H. Vic Dao = b ò f ( d ). = a If the hyper-real is ifiite, the it is the itegral over [, ab], If the hyper-real is fiite, = b ò fd ( ) = real part of the hyper-real. = a 3. The coutability of the Itegratio Sum I [Da], we established the equality of all positive ifiities: We proved that the umber of the Natural Numbers, Card, equals the umber of Real Numbers, Card = Card, ad we have Card Card Card = ( Card ) =... = = =... º. I particular, we demostrated that the real umbers may be well-ordered. Cosequetly, there are coutably may real umbers i the iterval [ ab],, ad the Itegratio Sum has coutably may terms. While we do ot sequece the real umbers i the iterval, the summatio takes place over coutably may f ( d. ) The Lower Itegral is the Itegratio Sum where f ( ) is replaced
13 Gauge Istitute Joural H. Vic Dao by its lowest value o each iterval [ -, + ] d d 3. å Î[ a, b] æ ö if f ( t) d ç çè- t + ø d d The Upper Itegral is the Itegratio Sum where f ( ) is replaced by its largest value o each iterval [ -, + ] d d 3.3 å Î[ a, b] æ ö sup f ( t) d ç è- t + ø d d If the itegral is a fiite hyper-real, we have 3.4 A hyper-real fuctio has a fiite itegral if ad oly if its upper itegral ad its lower itegral are fiite, ad differ by a ifiitesimal. 3
14 Gauge Istitute Joural H. Vic Dao 4. Delta Fuctio I [Da5], we have defied the Delta Fuctio, ad established its properties. The Delta Fuctio is a hyper-real fuctio defied from the hyper-real lie ito the set of two hyper-reals ì ï ü í, ï ý. The ïî d ïþ hyper-real is the sequece,,,.... The ifiite hyperreal d depeds o our choice of d.. We will usually choose the family of ifiitesimals that is spaed by the sequeces,, 3, It is a semigroup with respect to vector additio, ad icludes all the scalar multiples of the geeratig sequeces that are o-zero. That is, the family icludes ifiitesimals with egative sig. Therefore, d will mea the sequece. Alteratively, we may choose the family spaed by the sequeces, 3,, The, 4 d will mea the 4
15 Gauge Istitute Joural H. Vic Dao sequece. Oce we determied the basic ifiitesimal d, we will use it i the Ifiite Riema Sum that defies a Itegral i Ifiitesimal Calculus. 3. The Delta Fuctio is strictly smaller tha 4. We defie, c d ( ) º d ( ), d d é ù, ê- ë úû where c é ê- ë d, d ì, Î é-d, d ù ( ) = ï ê ú í ë û. ïï, otherwise î ù úû 5. Hece, for <, d ( ) = at for d =-, d ( ) jumps from to d, d, d ê ë ú û, ( ) Î é- ù d =. d at =, d () = d at d =, d ( ) drops from d for >, d ( ) =. to. d ( ) = 6. If d =, ( ) = ( ), ( ),3 ( )... [-, ] [-, ] [-, ] d c c c If d =, 3 d ( ) =,,,... cosh cosh cosh 3 5
16 Gauge Istitute Joural H. Vic Dao 8. If d =, d( ) = e c [, ), e c[, ), 3 e c[, ),... = ò 9. d( d ) =. =- k = -ik( - ). d ( - ) = e dk p ò k =- 6
17 Gauge Istitute Joural H. Vic Dao 5. Coverget Series I [Da8], we defied covergece of ifiite series i Ifiitesimal Calculus 5. Sequece Covergece to a fiite hyper-real a a a iff a - a = ifiitesimal. 5. Sequece Covergece to a ifiite hyper-real A a A iff a represets the ifiite hyper-real A. 5.3 Series Covergece to a fiite hyper-real s a + a +... s iff a a - s = ifiitesimal. 5.4 Series Covergece to a Ifiite Hyper-real S a + a +... S iff a a represets the ifiite hyper-real S. 7
18 Gauge Istitute Joural H. Vic Dao 6. Gree s Fuctio for y'( ) + P( ) y( ) = f( ), with y () = q= q= q= ò - ò ò q= q= q= 6. G (, ) = e e = e Proof: We solve the equatio P( q) dq P( q) dq P( q) dq G (, ) + PG () (, ) = d ( - ), with G(, ) = Multiplyig both sides by the itegratig factor q= ò e q= P( q) dq q= q= q= ò P( q) dq ò P( q) dq ò P( q) dq q= q= q= e G(, ) + e P() G(, ) = e d( - ) q= q= ò = P( q) dq P( q) dq { e q= G (, )} e q= d( ò -) Itegratig with respect to, q= q= P( q) dq = ò ò P( q) dq q= q= e G(, ) = e d( -) d ò =- 8
19 Gauge Istitute Joural H. Vic Dao q= = P( q) dq å ( ) d q= = d - =- ò e Therefore, q= ò = e q= P( q) dq q= q= ò G (, ) = e e ò P( q) dq - P( q) dq q= q= q= ò P( q) dq q= = e. 6. = ò P( q) dq q= y ( ) = ò e f( d ) = q= 9
20 Gauge Istitute Joural H. Vic Dao 7. Gree s Fuctio for y"( ) + P( ) y'( ) + Q( ) y( ) = f( ) ad y '() = y () =, with, 7. y"( ) + P( ) y'( ) + Q( ) y( ) = f( ), with y () =, y '() = u ( )solves u"( ) + P( ) u'( ) + Q( ) u( ) =, with u () = v ( )solves v"( ) + P( ) v'( ) + Q( ) v( ) =, with v () = The, G (, ) = u() v() u ( ) v ( ) u() v() u'( ) v'( ) Proof: We solve the equatio G (, ) + P () G (, ) + QG () (, ) = d( - ), with G(, ) =, ad G (, ) = = Let u ( ) solve the equatio The, u"( ) + P( ) u'( ) + Q( ) u( ) = ug " + PuG ' + QuG = ud( - ),, with u () =
21 Gauge Istitute Joural H. Vic Dao Subtractig, Gu " + PGu ' + QGu =, ug "- Gu " + P( ug '- Gu ') = ud( -) ( ug '-Gu ')' ò P( q) dq q= Multiplyig by the itegratig factor e, P( ) d P( ) d { e ò q q [ u ( ) G '(, ) G (, ) u '( )]} e ò q q q= q= - = u ( ) d( -). Itegratig, P( q) dq t= ò ò P( q) dq q= q= e [ u( ) G'(, ) - G(, ) u'( )] = ò e u( t) d( t -) dt. (I) q= q= q= q= q= t t = Similarly, for v ( ) that solves the equatio v"( ) + P( ) v'( ) + Q( ) v( ) =, with v () = q= q= t P( q) dq t = ò ò P( q) dq q= q= e [() v G'(, ) - G(, )'()] v = ò e v()( t d t -) dt. (II) t = To elimiate G ', subtract (I) v ( )-(II) u( ), q= q= t P( q) dq t = ò P( ) d u ( ) v ( ) ò q q [ u( t) v( t) q= q= e G(, ) = e d( ) u'( ) v'( ) ò t -dt u ( ) v ( ) Substitutig, by Abel equality, t= q= ò e q= P( q) dq u ( ) v ( ) u() v() =, u'( ) v'( ) u'() v'() ad
22 Gauge Istitute Joural H. Vic Dao q= t ò e q= P( q) dq = u() v() u'() v'() u( t) v( t) u'( t) v'( t) t = u() v() t= u() v() u'() v'() [ u( t) v( t) G (, ) = ( ) d u'() v'() ò d t - t u( t) v( t) u( ) v( ) u'( t) v'( t) t= [ u( t) v( t) G (, ) = ò d( t -) dt u( t) v( t) u ( ) v ( ) t = u'( t) v'( t) [ u( ) v( ) u ( ) v ( ) =. u() v() u'( ) v'( )
23 Gauge Istitute Joural H. Vic Dao 8. Gree s Fuctio for y"( ) + P( ) y'( ) + Q( ) y( ) = f( ) ad yb () = ya () =, with, 8. y"( ) + P( ) y'( ) + Q( ) y( ) = f( ), with ya () =, yb () =, u"( ) + P( ) u'( ) + Q( ) u( ) =, with ua () =, ub () ¹, v"( ) + P( ) v'( ) + Q( ) v( ) =, with va () ¹, vb () = Proof: The, G (, ) ìï ()(), u v a = ï í u() v() ïï ïuu ( ) ( ), b³ ³ u'( ) v'( ) ïî We solve the equatio Let u ( ) solve the equatio y"( ) + P( ) y'( ) + Q( ) y( ) = f( ), with ya () =, ad yb () =. u"( ) + P( ) u'( ) + Q( ) u( ) = ad let v ( ) solve the equatio, with ua () =, ad ub () ¹, v"( ) + P( ) v'( ) + Q( ) v( ) =, with va () ¹, ad vb () =. 3
24 Gauge Istitute Joural H. Vic Dao By 7 a particular solutio to the equatio for y ( ) is = [ u( ) v( ) y ( ) = ( ) p ò f d, u() v() u ( ) v ( ) = a ad the geeral solutio is u'( ) v'( ) y ( ) = cu ( ) + cv ( ) + y( ). = ya ( ) = c ua ( ) + c va ( ) + y( p a) c = ¹ p = yb ( ) = c ub ( ) + c vb ( ) + y( p b) ¹ c =- y ub () p() b = b =- ub () ò u() v() = a u'( ) v'( ) [ u( ) v( ) f () d ub () vb () u( ) v( b) -u( b) v( ) = b = ò = a v() u() v() u'( ) v'( ) f () d = b = v() u()() v - u()() v y( ) = u( ) ò f( ) d + f( ) d u() v() ò u() v() = a = a u'( ) v'( ) u'( ) v'( ) 4
25 Gauge Istitute Joural H. Vic Dao Therefore, = b = uv ( ) ( ) u( ) v ( ) = ò f () d + f() u() v() ò d u() v() = = a u'( ) v'( ) u'( ) v'( ) G (, ) ìï u()(), v a = ï í u() v() ïï ïuu ( ) ( ), b³ ³ u'( ) v'( ) ïî. 5
26 Gauge Istitute Joural H. Vic Dao 9. Hyper-real Sturm-Liouville Problem The Hyper-real Sturm-Liouville equatio is the secod order Hyper-real liear differetial equatio for the Hyper-real fuctio y ( ), - y"( ) + q( ) = ly( ), o a iterval that may be bouded, or may be the whole Hyper-real lie. The hyper-real fuctio q ( ) is (assumed i the literature to be) cotiuous o the iterval, ad bouded at its edpoits. The choice of the umber l (which may be real or comple), allows the equatio with boudary coditios, at the iterval edpoits to become a eige-value problem: l is a eige-value, ad y ( ) is the correspodig Hyper-real eige-fuctio iff - y "( )( ) + q( ) y ( ) = l ( ) y. The eige-fuctios are orthogoal, over the iterval. = b ò y ( ) y ( ) d =, for ¹ m. m = a 6
27 Gauge Istitute Joural H. Vic Dao. Delta Epasio i No-Normalized Eige-fuctios As described i [Titchmarsh, Chapter I], give umbers a, ad b, the Sturm-Liouville Problem o the iterval with edpoits a, ad b has solutios f (, l ), with f (, a l ) = sia, ad f '( a, l ) =-cosa, a a c (, l ), with c (, b l ) = sib, ad c '( b, l ) =-cosb,, b which are etire fuctios of l. The, b a b d d f (, l) c (, l) f '(, l) c '(, l) f (, l) c (, l) a b a b a b = + f '(, l) c '(, l) f '(, l) c '(, l) f "(, l) c "(, l) a b a b a b W [ f, c ] a b = fc "-cf " a b b a = f ( q -l) c -c ( q -l) f a b b a =. Hece, the Wroskia W[ f a, c b ] is a fuctio of l aloe: [ f, c ] = w( l). W a b 7
28 Gauge Istitute Joural H. Vic Dao Now, if the oly zeros of wl ( ) are the simple zeros The, for each =,,, 3,... l,,, l,, l l 3 f (, l ) c (, l ) a b = wl ( ) =. f '(, l ) c '(, l ) That is, for each =,,, 3,... there is a umber k so that a c (, l ) = k f (, l ). b Titchmarsh applied the Residue Theorem to obtai the coefficiets i the Sturm-Liouville epasio of f ( ). Followig Titchmarsh, we coclude that the Hyper-real Sturm- a b Liouville epasio of a Hyper-real fuctio f ( ) i the Hyperreal eige-fuctios fa (, l ) is = æ = b k ö f ( ) = å f( f ) ( l, ) d f(, l) a a = ç w'( l ) ò çè = a ø = æ = b k ö = å f() f(, l) d f(, l) ç å a a w'( l ) çè ø = = a Echagig summatio order = b= k = åå f (, l ) f (, l )() f d a a w'( l ) = a = = b = k ò a a w'( l ) = a = d( -) = å f (, l ) f (, l )() f d 8
29 Gauge Istitute Joural H. Vic Dao Therefore,. The Hyper-real Delta Fuctio Epasio i o-ormalized eige-fuctios is = k d( - ) = å f (, l ) f (, l ) a a w'( l ) = That is,. The Hyper-real Delta Fuctio is the ifiite sequece k a a a a '( ) w'( l ) w l k f (, l ) f (, l ) f (, l ) f (, l ). 9
30 Gauge Istitute Joural H. Vic Dao. Gree s Fuctio Epasio i No-Normalized Eige-fuctios Gree s Fuctio is defied by DG(,, l) + [ l- q ()] G(,, l) = d( - ) with the Boudary coditios at the itervals edpoits. Substitutig Delta from., k DG(,, ) [ q ()] G(,, ) (, ) (, ) = l + l- l = å f l f l a a = w'( l ) Thus, Gree s Fuctio must have a epasio i f (, l ) f (, l ), = G (,, l) = å a() lf(, l) f(, l). = a a a a To determie the a ( l ), we substitute the epasio ito the Sturm-Liouville equatio for Gl (,, ), k (){ l f "(, l ) [ l ()] f (, l )} f (, l ) f (, l ) f (, l ) = = åa + - q = a a a å a = = w'( l ) -[ l-q ( )] f (, ) a l [ l-l] fa (, l) k ()[ l l l ] f (, l ) f (, l ) f (, l ) f (, l ) = = a - = a a a a = = w'( l ) å å, Equatig the coefficiets, for each =,,, 3,... a 3
31 Gauge Istitute Joural H. Vic Dao k a ( l)[ l - l ] =, w'( l ) a ( l) = k l - l w'( l ).. The Hyper-real Gree Fuctio is = k G (,, l) = å f(, l) f(, l). a a l - l w'( l ) = That is,. The Hyper-real Gree Fuctio is the ifiite sequece k k f (, l ) f (, l ) f (, l ) f (, l ) l -l w l l -l w l = a a a a '( ) '( ) =..3 The Hyper-real yl (, ) for No-Normalized Eige-fuctios = b y (, l) = ò G (,, l)() f d = a Proof: We substitute it ito the Sturm-Liouville equatio = b "(, l) (,, l) ( ) = a y = ò D G f d, = b y"(, l) + [ l - q()](, y l) = ò { D G(,, l) + [ l -q()] G(,, l)}() f d = a d( -) = f ( ). 3
32 Gauge Istitute Joural H. Vic Dao. Gree Fuctio for Sie Sturm- Liuoville y"( ) + ly( ) = & a = b = Two idepedet solutios are cos l, ad si l. For a =, f l l (, ) =- si ( -a) l satisfies the Boudary coditios ad f (, a l ) = si =, f '( a, l ) =- cos =-. For b =, c l l satisfies the Boudary coditios (, ) = si ( b -) l ad c (, b l ) = si =, c '( b, l ) =- cos =-, Therefore, 3
33 Gauge Istitute Joural H. Vic Dao si l( -a) si l( b -) - wl ( ) = l l -cos l( -a) -cos l( b -) = si l( b - a). l Hece, the zeros of wl ( ) are l æ p ö = çèb - a ø, =,,3,... d w'( l) = si ( - ) l dl { l b a } { écos ( ) b a l b a ù - l si l( b a) } = l ê ë úû l l w'( l ) = ( b -a)cos l ( b -a) l = - - ). ( b a)( l p. k = c (, l ) f (, l ) si l ( b - ) =- si l ( - a) si =- si b- b-a -a b-a p p -a si[ p - p] b-a =- -a si p b-a 33
34 Gauge Istitute Joural H. Vic Dao -a -a = {- si( p)cos p + cos( p)si p } -a b-a b-a si p b-a = (-). (-) Therefore,. The Hyper-real Gree Fuctio i [ ab], = æ -a a G (,, l) sip ö æ - sip ö = å b -a ç = l è b -a ø èç b a - - ø p ( ) b-a = k Proof: G (,, l) = å f(, l) f(, l) a a l - l w'( l ) = = = å (-) (-) p ( ) b-a = l - b-a l si l ( -a) si l ( -a) l l Namely, = æ -aö æ -a = å si p si p ö = l b -a çè b -a ø èç b a - - ø. p ( ) b-a. The Hyper-real Gree Fuctio i [ ab], is the ifiite sequece æ aö æ aö si - p - si p +... b -a çè b -a ø çè b a - - ø p ( ) l b-a æ -aö æ -aö + si p si p ç ç l - = p ( ) è b -a ø è b -a ø b- a = 34
35 Gauge Istitute Joural H. Vic Dao 3. Gree Fuctio for Cosie Sturm- Liuoville y"( ) + ly( ) = & a = b = p Similarly to the former sectio, for a = b = p, we obtai 3. The Hyper-real Gree Fuctio i [ ab], ì = ü a a G (,, l) ï æ - cosp ö æ - cosp ö = í + ý ï b a å - l = p l ( ) ç b a ç b a - è - ø è - ø ïî b-a ïþ Namely, 3. The Hyper-real Gree Fuctio i [ ab], is the ifiite sequece æ -aö æ -aö cos p cos p b -a l ç l b -a ç b a - - = p ( ) è ø è ø b- a = 35
36 Gauge Istitute Joural H. Vic Dao 4. Gree s Fuctio for Bessel Sturm-Liuoville y"( ) ly( ) & + = a = For a =, si f (, l) =- satisfies the Boudary coditios l l ad f (, a l ) = si =, f '( a, l ) =- cos =-. The solutio c l = l - b + l - b (, ) si ( b )cos cos[ ( b )]si b l satisfies the Boudary coditios ad c (, b l ) = sib, b c '( b, l ) =- cos b, b Therefore, at = b, wl ( ) - si lb si b l = - cos lb - cos b 36
37 Gauge Istitute Joural H. Vic Dao Hece, the zeros of wl ( ) are the roots of That is, si lbcos b =-cos lbsi b. l ta l b =- l ta b. [Titchmarsh, p. 7] obtais Therefore, w'( l ) = bcos bcos( b l ){ + l ta b + ta b} k l b = cos bcos( b l ){ + l ta b } 4. The Gree Fuctio epasio i [ ab], is + l ta b G (,, l) = si( l)si( l) b l l l b b = å = - + ta + ta b Proof: = k G (,, l) = å f(, l) f(, l). a a l - l w'( l ) = Namely, 4. The Hyper-real Gree Fuctio i [ ab], is the ifiite sequece = j= + l ta b j å si( l )si( l ) j j j = l - l + l ta b + tab j b = b 37
38 Gauge Istitute Joural H. Vic Dao 5. Gree s Fuctio for Bessel Sturm Liuoville - 4 u"( ) + ( l - ) u( ) = & a = b = Put u ( ) = y ( ), to obtai Bessel s y"( ) + y'( ) + ( l - ) y( ) =. Two idepedet solutios to Bessel s equatio are J ( l), ad Y ( l ). Two idepedet solutios to - 4 u"( ) + ( l - ) u( ) = are For a =, J ( l), ad Y ( l ). f (, l) = p a{ J ( l) Y ( a l) - Y ( l) J ( a l) } satisfies the Boudary coditios ad For b =, f (, a l ) = si =, f '( a, l ) =- cos =-. c (, l) = p b{ J ( l) Y ( b l) - Y ( l) J ( b l) } satisfies the Boudary coditios 38
39 Gauge Istitute Joural H. Vic Dao ad c (, b l ) = si =, c '( b, l ) =- cos =-, [Titchmarsh, p.8] obtais wl ( ) f (, l) c (, l) = f (, l) c (, l) = p ab J a ly b l -Y a l J b l. { ( ) ( ) ( ) ( )} ì a J '( a l) b J '( b l) ü ab ìj ( b l) J ( a ) w'( l) ï ï w( l) ï l = ü ï í ý í ïýïï ï l J ( b l) l J ( b l) l î J ( a l) J ( b l) ïþ ïî þ ab ì J ( b l ) J ( a l ü w'( l ) ï - ) =- í ï ý l ï J ( a l ) J ( b l ) î ïþ k b J ( b l ) =, a J ( a l ) l are the zeros of wl ( ). 5. The Hyper-real Gree Fuctio i [ ab], is G (,, l) p l J ( b l ) = = å = l - l J ( a l )- J ( b l ) { J ( l ) Y ( a l ) Y ( l ) J ( a l ) } - { J ( l ) Y ( a l ) Y ( l ) J ( a l ) } - 39
40 Gauge Istitute Joural H. Vic Dao Proof: = k G (,, l) = å f(, l) f(, l). a a l - l w'( l ) = Namely, 5. The Hyper-real Gree Fuctio i [ ab], is the ifiite sequece p lj ( b l ) ( ) ( ) j= j j å j = l - l J a l - J b l j j { J ( l ) Y ( a l ) Y ( l ) J ( a l ) j j j j } - { J ( l ) Y ( a l ) Y ( l ) J ( a l ) j j j j } = - = 4
41 Gauge Istitute Joural H. Vic Dao 6. Delta Epasio i Orthoormal Eige-fuctios The Hyper-real eige-fuctios of a Hyper-real Sturm-Liouville problem over the iterval with edpoits a, ad b, ca be ormalized so that y ( ), y ( ), y ( ), = b ò y ( ) y ( ) d = d. m m = a The, a hyper-real fuctio f ( ) may be epaded i them by = æ = b ö f () = f() y() d y() = ç çè = a ø å ò. = = b = åå = = a Echagig summatio order, f y() dy() = b ì= ü = ï y () y () ï åí f() ý = a å d ïî = ïþ = b = = ò å y () y ()() f d. = a = d( -) 4
42 Gauge Istitute Joural H. Vic Dao Therefore, 6. The Hyper-real Delta Fuctio epasio i orthoormal Sturm-Liuoville eige-fuctios is = d( - ) = å y ( ) y ( ). = That is, 6. The Hyper-real Delta Fuctio is the ifiite sequece y ( ) y ( ) + y( ) y( ) y ( ) y ( ). 4
43 Gauge Istitute Joural H. Vic Dao 7. Gree s Fuctio Epasio i Orthoormal Eige-fuctios Gree s Fuctio is defied as the solutio to Sturm-Liuoville problem. Namely, the Sturm-Liouville equatio DG(,, l) + [ l- q ()] G(,, l) = d( - ) with the Boudary coditios at the itervals edpoits. That is, = DG(,, l) + [ l- q ()] G (,, l) = y() y() å = Hece, Gree s Fuctio must have a epasio i y ( ) y ( ), = G (,, l) = å a() ly() y(). = To determie the a ( l ), we substitute ito the Sturm-Liouville equatio for G(,, l), = = å a ( l){ y "( ) + [ l - q( )] y ( )} y ( ) = y ( ) y ( ) = = -[ l -q ( )] y ( ) [ l-l ] y ( ) å = = åa ()[ l l - l ] y () y () = () () å y y, = = 43
44 Gauge Istitute Joural H. Vic Dao Equatig the coefficiets, for each =,,, 3,... a ( l)[ l - l ] =, a ( l ) = l - l. 7. The Hyper-real Gree Fuctio is = G (,, l) = å y() y(). l - l = That is, 7. The Hyper-real Gree Fuctio is the ifiite sequece y ( ) y ( ) + y( ) y( ) y ( ) y ( ). l l l l l l = = 7.3 The Hyper-real yl (, ) for Orthoormal Eige-fuctios Proof:.3. = b y (, l) = ò G (,, l)() f d = a 44
45 Gauge Istitute Joural H. Vic Dao 8. Gl (,, ) Aalytic Cotiuatio i l ito the Comple Plae 8. Fi, ad, cosider l i the comple plae, ad let = G (,, z) = å y() y() z - l = be the Hyper-Comple Aalytic Cotiuatio of Gl (,, ) ito the z Hyper-comple plae. Let g be a cotour that ecloses all the l s. ò The G (,, z) dz= pd i( -) g First Proof: (that uses the Residue Theorem) By Sturm-Liuoville Oscillatio Theorem [Ic..6], l are the simple poles of Gz (,, ) o the positive real lie. Applyig the Residue Theorem = ò G (,, z) dz= piå Res { G (,, z) }. z= l g = Sice the Residue of Gz (,, ) at each l is y ( ) y ( ), = = piå y ( ) y ( ) = 45
46 Gauge Istitute Joural H. Vic Dao = pd i ( - ). Sice we do ot supply here a proof of the Residue Theorem, we shall give a direct proof: Secod Proof (that uses the Circular Comple Delta) g = G (,, z) dz= ò å y() y() dz z - l ò g = = = å y ( ) y ( ) d ò z. z - l = g Now, by [Da], pi z - l is the Hyper-comple Circular Delta Fuctio, ad Therefore, ò dz =, for each pi z - l g =,, 3,... g = G (,, z) dz= å y() y() d ò z = z - l g ò = = piå y ( ) y ( ) = = pd i ( - ). pi 46
47 Gauge Istitute Joural H. Vic Dao 9. Gree Fuctio for Hermit Sturm- Liouville Put u"( ) + ( l - ) u( ) =, real - u ( ) = e y ( ), ad obtai Hermit s equatio y"( ) + y'( ) + ( l - ) y( ) =, The, the eige values are l = +, =,,, 3,.. ad the correspodig eige fuctios are Hermit Polyomials of degree, H ( ). Therefore, - e H ( ) solve u"( ) + ( l - ) u( ) =. [Titchmarsh, p. 75] shows that 9. The Normalized eige fuctios are Therefore, - y ( ) = e H ( ).! p 47
48 Gauge Istitute Joural H. Vic Dao 9. = - - G (,, l) = e e å H() H() p = ( l - -)! = Proof: G (,, l) = å y() y(). l - l = Namely, 9.3 The Hyper-real Gree Fuctio i real, ad is the ifiite sequece - - e e H ( ) H ( ) H ( ) H ( ) p ( l - ) ( l - -)! = = 48
49 Gauge Istitute Joural H. Vic Dao. Gree Fuctio for Legedre Sturm-Liouville u "( q) + [ l + ] u( q) =, 4 cos q - p < q < p Legedre s equatio with m = is The eige values are (- ) y"( ) + y'( ) + ( l - ) y( ) =. 4 l = ( + ), =,,, 3,... ad the correspodig eige fuctios are Legedre Polyomials of degree, Put to obtai Put to obtai P ( ). = si q, y"( q) - y'( q)ta q + ( l - ) y( q) =. u 4 y() q = u() q, cos q "( q) [ l ( ta q)] u( q) =. Substitutig cos q = + ta q, 49
50 Gauge Istitute Joural H. Vic Dao Therefore, u"( q) + [ l + ] u( q) =. 4 cos q cos qp (si q ) solve u"( q) + ( l + ) u( q) =. [Titchmarsh, p. 79] shows that. The Normalized eige fuctios are 4cos y () q = + cos qp (si q). q Therefore,. for - p < q ad j < p G(, qjl, ) = cosq cos j ( + ) (si q) (si j) = å P P = l -( + ) Namely,.3 The Hyper-real Gree Fuctio i - p < q, j < p is the ifiite sequece cos q cos j P(si q) P(si j) ( + ) P (si q) P (si j) l = l ( ) 4 = 5
51 Gauge Istitute Joural H. Vic Dao. Gree Fuctio for Legedre Sturm-Liouville u "( q ) + [ l + ( - m ) ] u ( q ) =, - p < q < p 4 cos q Legedre s equatio with for m =,,, 3..., is (- ) y "( ) + y '( ) + [ l - - m ] y ( ) =. The eige values are 4 - m l = ( - m + ), = m,m +,... ad the correspodig eige fuctios are Legedre Fuctios Put to obtai Put to obtai P ( ). m = si q, y"( q) - y'( q)ta q + [ l - - m ] y( q) =. 4 cos q y() q = u() q, cos q u"( q) + [ l + ( + ta q) - m ] u ( q) =. 4 4 cos q Substitutig cos q = + ta q, 5
52 Gauge Istitute Joural H. Vic Dao Therefore, u"( q) + [ l + ( - m ) ] u( q) =. 4 cos q m cos q (si q ) solve u"( q) + [ l + ( - m ) ] u( q) =. P [Titchmarsh, p. 8] shows that. The Normalized eige fuctios are 4 cos q Therefore, ( - m)! m y () q = cos (si ) - m + q P q.!. For - p < q j <, = m p, ad for m =,,, 3..., G(, qjl, ) = cosq cosj = ( - m)! ( m ) P m (si ) m å - + q P (si j ) l -( - m + )! Namely,.3 The Hyper-real Gree Fuctio i - p < q, j < p is the ifiite sequece cos q cosj k= ( k - m)! ( ) m (si ) m å k - m + P q k P k (si j ) l -( - m + ) k! k= m = = m 5
53 Gauge Istitute Joural H. Vic Dao. Gree Fuctio for Bessel Sturm- Liouville y"( ) + [ l - ( - )] y( ) =, 4 < < b Two idepedet solutios are J ( l), ad Y ( l ) By [Titchmarsh, p. 85], J ( b l) J ( l) y (, l) = p J( )() f d ò l J ( b l) Y ( b l) Y ( l) = = Therefore,. + = b J ( b l) J ( l) p J ( l) f ( ) d ò J ( b l) Y ( b l) Y ( l) = G (,, l) p = í J ( b l) ïïïï ìï J ( b l) J ( l) J ( l), ï Y ( b l) Y ( l) ï J ( b l) J ( l) J ( l), ³ ï Y ( b l) Y ( l) ïî 53
54 Gauge Istitute Joural H. Vic Dao Alteratively, we may epad Gl (,, ) i eige fuctios: For ³ By [Titchmarsh, p. 8],. The eige-values l are the zeros of J ( b l ), =,, 3,... ad the ormalized eige-fuctios are Therefore, bj.3 For ³, i < < b b = - J b J ( l ). '( b l ) = G (,, l) = å J( l) J( l), ³ ( l l ) '( l ) Namely,.4 For ³ the Hyper-real Gree Fuctio i <, < b is the ifiite sequece k= å J ( l ) J ( l ) = k k b k = ( l - l ) J '( b l ) k = For < <, ¹ 54
55 Gauge Istitute Joural H. Vic Dao By [Titchmarsh, p. 83],.5 The eige-values l are the zeros of cj ( b l) - l J ( b l), where c = c ost. - r ì - c l J '( b l) - l J '( b l) ü - =- Re sï í l + ï ý - ï c l J ( b l) - l J ( b l) b î ïþ - l= l ad the ormalized eige-fuctios are Therefore, p b - r J ( b l ){ cl J ( l )- J ( l ) }. - sip < < ¹, the i < < b.6 If, p b G = r J b = (,, l) ( ) å l 4si p = l - l Namely,.7 If - - { cl J ( l ) J ( l )}{ cl J ( l ) J ( l ) - - } - - < <, ¹, the the Hyper-real Gree Fuctio i <, <b is the ifiite sequece p b 4si p k= - å r J ( b l ){ cl J ( l )- J ( l ) k k k k - k } l - l k = 55
56 Gauge Istitute Joural H. Vic Dao - { cl J ( l ) J ( l ) k k - k } - = =.8 If < <, ¹, the For c = ifiite hyper-real, the epasio is i J : p b G c r J b J J = - (,, l) = ( ) ( ) ( ) å l l l l 4si p = l - l For c = ifiitesimal, the epasio is i J : - p b G r J b J J = (,, l) = ( ) ( ) ( ) å l l l - - 4si p = l - l 56
57 Gauge Istitute Joural H. Vic Dao 3. Gree Fuctio for Bessel Sturm Liouville y"( ) + [ l - ] y( ) =, < <, with a = By [Titchmarsh, p. 9], 3. The eige-values l are the zeros of l J 3 l - 3 J ( ) + ( ), =,, 3,... ad the ormalized eige-fuctios are - l é J ( l ) J 3 ( l ) ù ê ë ú û Therefore, { ( [ ]) ( [ ]) 3-3 } l - J l - + J l - 3. The Hyper-real Gree Fuctio i < < is G (,, l) = l - l = å l l - = - l é J ( l ) ( l ) ù êë - J 3-3 { J ( [ l ] ) J 3 ( [ l ] ) - 3 } { J ( [ l ] ) J 3 ( [ l ] ) - 3 } úû 57
58 Gauge Istitute Joural H. Vic Dao Namely, 3.3 The Hyper-real Gree Fuctio i <, < is the ifiite sequece k= å l - l - k k k = l - l l é J ( ) ( ) l k l ù k êë - J 3-3 úû { J ( [ l ]) J 3 ( [ l ]) k - 3 k } { J ([ l ]) J 3 ([ l ]) k - 3 k } = = 58
59 Gauge Istitute Joural H. Vic Dao 4. Gree Fuctio for Bessel Sturm- Liouville y"( ) [ m ] y( ), + - = < < with a = p By [Titchmarsh, p. 9], 4. The eige-values m are the zeros of J ( )- ( ), =,, 3,... m J 3 m - 3 ad the ormalized eige-fuctios are - m é J ( m ) J 3 ( m ) ù ê ë ú û Therefore, { ([ ]) 3 ([ ]) - 3 } m - J m - + J m - 4. the Hyper-real Gree Fuctio i < < is G (,, m) = m - m = å - = m - m m é J ( ) ( ) m m ù êë + J 3-3 { J ( [ m ] ) J 3 ( [ m ] ) - 3 } { J ( [ m ] ) J 3 ( [ m ] ) - 3 } úû 59
60 Gauge Istitute Joural H. Vic Dao Namely, 4.3 the Hyper-real Gree Fuctio i <, < is the ifiite sequece k= å m - m - k k k = m - m m é J ( ) ( ) m k m ù k êë + J 3-3 úû { J ([ m ]) J 3 ([ m ]) k - 3 k } { J ( [ m ]) J ( [ m ]) 3 k - 3 k } = = 6
61 Gauge Istitute Joural H. Vic Dao 5. Gree s Fuctio Itegral Epasio i Eige-fuctios If the eige-values are oly ifiitesimally separated from each other, the series summatio of eige-fuctios over discrete eige values is replaced by Hyper-real itegratio over the cotiuum of eige-values. The, the epasio is represeted by a itegral. Titchmarsh applied the Residue Theorem to obtai the projectios of a fuctio f ( ) o the eige-fuctios of Sturm-Liouville problems, with cotiuous spectrum of eige-values. This yields the Itegral epasio of the Delta Fuctio i Sturm- Liuoville eige-fuctios. The Delta Fuctio Epasio determies the Gree s Fuctio itegral epasio i Sturm-Liuoville eige-fuctios. 6
62 Gauge Istitute Joural H. Vic Dao 6. Gree s Fuctio Itegral Epasio i Cosie Fuctios of y"( ) + ly( ) =, < < We may solve Gree s Equatio by Fourier Trasformig it DG(,, l) + lg(,, l) = d( -) DG(,, l) + lg (,, l) = d( -) = ( w) ˆ( w,, l) ˆ( w,, l) d( ) i G G - e d = e ò =- -iw -iw ( ) ˆ(,, ) ˆ -i iw G wl + lg( wl,, ) = e w, ˆ(,, ) -i G wl = e w, l - w The, Iverse Trasformig it, w= ì ü -iw iw G (,, l) = ï e ïe dw p ò í ý ïîl - w ïþ w=- 6
63 Gauge Istitute Joural H. Vic Dao = w= iw( -) ò e dw. - w=- p l w That is, 6. The Hyper-real Gree Fuctio is w= iw( -) G (,, l) = e d p ò l - w w=- w Sice Fourier Trasformig applies oly to Liear Differetial Equatios with costat coefficiets, we demostrate a method that applies to equatios with variable coefficiets: The eige-values l º w, are the iterval of hyper-real positive umbers (, ). By [Titchmarsh, p. 7], the Hyper-real fuctio f ( ) is give for ay hyper-real by = l= f ( ) = cos( l)cos( l) dlf( ) d + l p ò ò =- l= ì ï = + p ïî = l= + si( l)si( l) dl ( ) l p ò ò f d =- l= = l= ï {cos( l)cos( l) si( l)si( l)} dlï ò í ý ( ) ò f d l =- ï l= cos[( -) l] ï üï ïþ 63
64 Gauge Istitute Joural H. Vic Dao = w= = ò cos w( ) dwf( ) d p ò - =- w= d( -) Hece, the Hyper-real Delta i - <, < is w= d( - ) = ò cos w( -) dw p w= ( iw( -) -iw( -) e + e ) w= = p ò p Sice Gree s Fuctio satisfies w=- e iw( -) dw w= iw( -) = å e dw. w=- DG(,, l) + lg (,, l) = d( - ), i ( ) the Hyper-real Gree Fuctio must have a epasio i - : l = å w w. p w= iw( -) G (,, ) a( ) e d w=- Substitutig i the Gree s Fuctio Differetial Equatio å a( w){ - w + l} e dw = å e p p w= w= iw( -) iw( - w=- w=- ) dw. e w Equatig each term, a( w){ - w + l} =, a( w) = l - w 64
65 Gauge Istitute Joural H. Vic Dao å w, w= iw( -) G (,, l) = e d p w=- l - w = w= iw( -) ò e dw. - w=- p l w 65
66 Gauge Istitute Joural H. Vic Dao 7. Gree s Fuctio Itegral Epasio for Weber Equatio y"( ) + [ l - ( - )] y( ) =, a < < a > 4 The eige-values - l º s, are the iterval of hyper-real egative umbers (-,). By [Titchmarsh, p. 87], the Hyper-real fuctio f ( ) is give for hyper-real a < < by = s = f ( ) = J( sy ) ( as) -J( asy ) ( s) ( ) ( ) J as + Y as = a s= { } ò ò { } J ( sy ) ( as) -J ( asy ) ( s) sds f( ) d Therefore, the Hyper-real Delta i a <, < is s= J ( sy ) ( as) - J ( asy ) ( s) d( - ) = J ( sy ) ( as) -J ( asy ) ( s) sds ò s= J ( as) + Y ( as) Sice Gree s Fuctio satisfies { } 66
67 Gauge Istitute Joural H. Vic Dao - 4 G (,, l) + [ l- ] G (,, l) = d( - ), the Hyper-real Gree Fuctio must have a epasio i J ( sy ) ( as) - J ( as) Y ( s) y (,, s) = J ( s) Y ( as) -J ( as) Y ( s) { } J ( as) + Y ( as). Substitutig s = G (,, l) = å as (){ y(,,)} s sds s = i the Gree s Fuctio Differetial Equatio, - as (){ y [ l ] y } sds y (,, ssds ) s= s= = s= s= å å. Now, s is the eige-value associated with J ( s), with Y ( s) with J ( s) Y ( as) - J ( as) Y ( s), ad thus with y (,,) s. Hece, - 4 y = -[ s - ] y. Substitutig i the Gree s Fuctio differetial Equatio s= s= å å as (){ l - s} y sds= y (,, ssds ) s= s=, Equatig each term, as (){ l - s} =, as () = l - s 67
68 Gauge Istitute Joural H. Vic Dao s = G (,, l) = å y(,,) ssds. l - s s = 7. s = J ( sy ) ( as) - J ( asy ) ( s) G(, l, ) = ò { J ( s) Y ( as) -J ( as) Y ( s) } sds l - + s = s J ( as) Y ( as) 68
69 Gauge Istitute Joural H. Vic Dao 8. Gree s Fuctio for Hakel s y"( ) + [ l - ( - )] y( ) =, 4 < < By [Titchmarsh, p. 88], = () ( ) =- p ( l) ( ) ( ) ò l = y i H J f d Therefore, - = () ip J ( l) H ( ) f( ) d ò l = 8. G (,, l) ìï () H ( l) J ( l), ip =- ï í ïïï () H ( l) J ( l), ³ ïî 69
70 Gauge Istitute Joural H. Vic Dao 9. Gree s Fuctio for Bessel s y"( ) + [ l + )] y( ) =, - < < By [Titchmarsh, p. 93], () () y (, l) =- ip + lh ([ + l]) + lh ([ + l])() f d = 6 =- ò Therefore, 9. = () () - ip + lh ( [ + l] ) + lh ( [ + l] ) f( ) d 6 = ò ìï () () H ([ + l]) H ([ + l]), ip G (,, l) =- + l + lï í 6 ïïï () () ïh ( [ + l]) H 3 ( [ + l]), 3 ïî ³ 7
71 Gauge Istitute Joural H. Vic Dao 3. Gree s Fuctio for Bessel s y"( ) + [ l + e )] y( ) =, - < < By [Titchmarsh, p. 95], ip y (, l) =- { J ( e) + J ( e)} J ( e) f( ) d i l -i l ò -i l sih( p l) = =- Therefore, = ip - J ( e ) { J ( e ) J ( e )} f( ) d -i l ò + i l -i l sih( p l) =- 3. G (,, l) ìï { J ( e ) + J ( e )} J ( e ), i l -i l -i l ip =- ï í sih( p l) ïï { ( ) ( )} ( ï J e + J e J e i i i ), ³ ïî l - l - l 7
72 Gauge Istitute Joural H. Vic Dao 3. Gree s Fuctio for Bessel s y"( ) + [ l - e )] y( ) =, - < < By [Titchmarsh, p. 96], = = ò ò y(, l) =-K ( e ) I ( e )() f d -I ( e ) K ( e )() f d Therefore, i l -i l -i l i l =- =- 3. G (,, l) ìï K ( e ) I ( e ), i l -i l =-í ï ïï ïk ( e ) I ( e ), ³ ïî i l -i l 7
73 Gauge Istitute Joural H. Vic Dao Refereces [Abramowitz] Abramowitz, M., ad Stegu, I., Hadbook of Mathematical Fuctios with Formulas Graphs ad Mathematical Tables, U.S. Departmet of Commerce, Natioal Bureau of Stadards, 964. [Da] Dao, H. Vic, Well-Orderig of the Reals, Equality of all Ifiities, ad the Cotiuum Hypothesis i Gauge Istitute Joural Vol. 6 No., May ; Well-Orderig of the Reals, Equality of all Ifiities, ad the Cotiuum Hypothesis [Da] Dao, H. Vic, Ifiitesimals i Gauge Istitute Joural Vol.6 No. 4, November ; Ifiitesimals [Da3] Dao, H. Vic, Ifiitesimal Calculus i Gauge Istitute Joural Vol. 7 No. 4, November ; Ifiitesimal Calculus [Da4] Dao, H. Vic, Riema s Zeta Fuctio: the Riema Hypothesis Origi, the Factorizatio Error, ad the Cout of the Primes, i Gauge Istitute Joural of Math ad Physics, Vol. 5, No. 4, November 9. Riema Zeta Fuctio: the Riema Hypothesis Origi, the Factorizatio Error, ad the Cout of the Primes [Da5] Dao, H. Vic, The Delta Fuctio i Gauge Istitute Joural Vol. 8, No., February, ; The Delta Fuctio [Da6] Dao, H. Vic, Riemaia Trigoometric Series, Gauge Istitute Joural, Volume 7, No. 3, August. Riemaia Trigoometric Series 73
74 Gauge Istitute Joural H. Vic Dao [Da7] Dao, H. Vic, Delta Fuctio the Fourier Trasform, ad the Fourier Itegral Theorem i Gauge Istitute Joural Vol. 8, No., May, ; Delta Fuctio, the Fourier Trasform, ad Fourier Itegral Theorem [Da8] Dao, H. Vic, Ifiite Series with Ifiite Hyper-real Sum i Gauge Istitute Joural Vol. 8, No. 3, August, ; Ifiite Series with Ifiite Hyper-real Sum [Da9] Dao, H. Vic, Sturm-Liuoville Epasios of the Delta Fuctio Sturm-Liouville Epasios of the Delta Fuctio [Da] H. Vic Dao, Comple Delta Fuctio, Comple Fourier Trasform, ad Fourier Itegral Theorem. Comple Delta Fuctio, Comple Fourier Trasform, ad Fourier Itegral Theorem [Ferrers] Ferrers, N., M., A Elemetary treatmet o Spherical Harmoics, Macmilla, 877. [Gradshtey] Gradshtey, I., S., ad Ryzhik, I., M., Tables of Itegrals Series ad Products, 7 th Editio, edited by Alla Jeffery, ad Daiel Zwilliger, Academic Press, 7 [Hardy] Hardy, G. H., Diverget Series, Chelsea 99. [Jackso] Jackso, Duham, Fourier Series ad Orthogoal Polyomials, Mathematical associatio of America, 94. [Magus] Magus, W., Oberhettiger, F., Soy, R., P., Formulas ad Theorems for the Special Fuctios of Mathematical Physics Third Editio, Spriger-Verlag, 966. [Sasoe] Sasoe, Giovai, Orthogoal Fuctios, Revised Editio, Krieger,
75 Gauge Istitute Joural H. Vic Dao [Spiegel] Spiegel, Murray, Mathematical Hadbook of formulas ad tables Schaum s Outlie Series, McGraw Hill, 968. [Spaier] Spaier, Jerome, ad Oldham, Keith, A Atlas of Fuctios, Hemisphere, 987. [Szego] Szego, Gabor, Orthogoal Polyomials Revised Editio, America Mathematical Society,959. [Szego4] Szego, Gabor, Orthogoal Polyomials Fourth Editio, America Mathematical Society,975. [Titchmarsh], E. C. Titchmarsh, Eigefuctio Epasios Associated with Secod-order Differetial Equatios, Part I, Secod Editio, Oford, 96. [Weisstei], Weisstei, Eric, W., CRC Ecyclopedia of Mathematics, Third Editio, CRC Press, 9. 75
Sturm-Liouville Expansions. of the Delta Function
 Gauge Istitute Joural H. Vic Dao Sturm-Liouville Expasios of the Delta Fuctio H. Vic Dao vic0@comcast.et May, 04 Abstract We expad the Delta Fuctio i Series, ad Itegrals of Sturm-Liouville Eige-fuctios.
Gauge Istitute Joural H. Vic Dao Sturm-Liouville Expasios of the Delta Fuctio H. Vic Dao vic0@comcast.et May, 04 Abstract We expad the Delta Fuctio i Series, ad Itegrals of Sturm-Liouville Eige-fuctios.
Periodic Delta Function. in Bessel Functions
 Gauge Istitute Joural H. Vic Dao Periodic Delta Fuctio ad Fourier Epasio i Bessel Fuctios H. Vic Dao vic@comcast.et Jue, Abstract Let f ( be itegrable o [,]. The zeros of the Bessel Fuctio J (. < l < l
Gauge Istitute Joural H. Vic Dao Periodic Delta Fuctio ad Fourier Epasio i Bessel Fuctios H. Vic Dao vic@comcast.et Jue, Abstract Let f ( be itegrable o [,]. The zeros of the Bessel Fuctio J (. < l < l
Gauge Institute Journal, Volume 8, No. 1, February The Delta Function. H. Vic Dannon. September, 2010
 Gauge Istitute Joural, Volume 8, No., February 0 H. Vic Dao The Delta Fuctio H. Vic Dao vic0@comcast.et September, 00 Abstract The Dirac Delta Fuctio, the idealizatio of a impulse i Radar circuits, is
Gauge Istitute Joural, Volume 8, No., February 0 H. Vic Dao The Delta Fuctio H. Vic Dao vic0@comcast.et September, 00 Abstract The Dirac Delta Fuctio, the idealizatio of a impulse i Radar circuits, is
Notes 19 Bessel Functions
 ECE 638 Fall 17 David R. Jackso Notes 19 Bessel Fuctios Notes are from D. R. Wilto, Dept. of ECE 1 Cylidrical Wave Fuctios Helmholtz equatio: ψ + k ψ = I cylidrical coordiates: ψ 1 ψ 1 ψ ψ ρ ρ ρ ρ φ z
ECE 638 Fall 17 David R. Jackso Notes 19 Bessel Fuctios Notes are from D. R. Wilto, Dept. of ECE 1 Cylidrical Wave Fuctios Helmholtz equatio: ψ + k ψ = I cylidrical coordiates: ψ 1 ψ 1 ψ ψ ρ ρ ρ ρ φ z
MAT1026 Calculus II Basic Convergence Tests for Series
 MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
MAT026 Calculus II Basic Covergece Tests for Series Egi MERMUT 202.03.08 Dokuz Eylül Uiversity Faculty of Sciece Departmet of Mathematics İzmir/TURKEY Cotets Mootoe Covergece Theorem 2 2 Series of Real
PAPER : IIT-JAM 2010
 MATHEMATICS-MA (CODE A) Q.-Q.5: Oly oe optio is correct for each questio. Each questio carries (+6) marks for correct aswer ad ( ) marks for icorrect aswer.. Which of the followig coditios does NOT esure
MATHEMATICS-MA (CODE A) Q.-Q.5: Oly oe optio is correct for each questio. Each questio carries (+6) marks for correct aswer ad ( ) marks for icorrect aswer.. Which of the followig coditios does NOT esure
Quiz. Use either the RATIO or ROOT TEST to determine whether the series is convergent or not.
 Quiz. Use either the RATIO or ROOT TEST to determie whether the series is coverget or ot. e .6 POWER SERIES Defiitio. A power series i about is a series of the form c 0 c a c a... c a... a 0 c a where
Quiz. Use either the RATIO or ROOT TEST to determie whether the series is coverget or ot. e .6 POWER SERIES Defiitio. A power series i about is a series of the form c 0 c a c a... c a... a 0 c a where
Calculus 2 - D. Yuen Final Exam Review (Version 11/22/2017. Please report any possible typos.)
 Calculus - D Yue Fial Eam Review (Versio //7 Please report ay possible typos) NOTE: The review otes are oly o topics ot covered o previous eams See previous review sheets for summary of previous topics
Calculus - D Yue Fial Eam Review (Versio //7 Please report ay possible typos) NOTE: The review otes are oly o topics ot covered o previous eams See previous review sheets for summary of previous topics
x x x Using a second Taylor polynomial with remainder, find the best constant C so that for x 0,
 Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
We are mainly going to be concerned with power series in x, such as. (x)} converges - that is, lims N n
 Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
Review of Power Series, Power Series Solutios A power series i x - a is a ifiite series of the form c (x a) =c +c (x a)+(x a) +... We also call this a power series cetered at a. Ex. (x+) is cetered at
CHAPTER 5. Theory and Solution Using Matrix Techniques
 A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
A SERIES OF CLASS NOTES FOR 2005-2006 TO INTRODUCE LINEAR AND NONLINEAR PROBLEMS TO ENGINEERS, SCIENTISTS, AND APPLIED MATHEMATICIANS DE CLASS NOTES 3 A COLLECTION OF HANDOUTS ON SYSTEMS OF ORDINARY DIFFERENTIAL
A) is empty. B) is a finite set. C) can be a countably infinite set. D) can be an uncountable set.
 M.A./M.Sc. (Mathematics) Etrace Examiatio 016-17 Max Time: hours Max Marks: 150 Istructios: There are 50 questios. Every questio has four choices of which exactly oe is correct. For correct aswer, 3 marks
M.A./M.Sc. (Mathematics) Etrace Examiatio 016-17 Max Time: hours Max Marks: 150 Istructios: There are 50 questios. Every questio has four choices of which exactly oe is correct. For correct aswer, 3 marks
PRELIM PROBLEM SOLUTIONS
 PRELIM PROBLEM SOLUTIONS THE GRAD STUDENTS + KEN Cotets. Complex Aalysis Practice Problems 2. 2. Real Aalysis Practice Problems 2. 4 3. Algebra Practice Problems 2. 8. Complex Aalysis Practice Problems
PRELIM PROBLEM SOLUTIONS THE GRAD STUDENTS + KEN Cotets. Complex Aalysis Practice Problems 2. 2. Real Aalysis Practice Problems 2. 4 3. Algebra Practice Problems 2. 8. Complex Aalysis Practice Problems
Comparison Study of Series Approximation. and Convergence between Chebyshev. and Legendre Series
 Applied Mathematical Scieces, Vol. 7, 03, o. 6, 3-337 HIKARI Ltd, www.m-hikari.com http://d.doi.org/0.988/ams.03.3430 Compariso Study of Series Approimatio ad Covergece betwee Chebyshev ad Legedre Series
Applied Mathematical Scieces, Vol. 7, 03, o. 6, 3-337 HIKARI Ltd, www.m-hikari.com http://d.doi.org/0.988/ams.03.3430 Compariso Study of Series Approimatio ad Covergece betwee Chebyshev ad Legedre Series
62. Power series Definition 16. (Power series) Given a sequence {c n }, the series. c n x n = c 0 + c 1 x + c 2 x 2 + c 3 x 3 +
 62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
62. Power series Defiitio 16. (Power series) Give a sequece {c }, the series c x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + is called a power series i the variable x. The umbers c are called the coefficiets of
MIDTERM 3 CALCULUS 2. Monday, December 3, :15 PM to 6:45 PM. Name PRACTICE EXAM SOLUTIONS
 MIDTERM 3 CALCULUS MATH 300 FALL 08 Moday, December 3, 08 5:5 PM to 6:45 PM Name PRACTICE EXAM S Please aswer all of the questios, ad show your work. You must explai your aswers to get credit. You will
MIDTERM 3 CALCULUS MATH 300 FALL 08 Moday, December 3, 08 5:5 PM to 6:45 PM Name PRACTICE EXAM S Please aswer all of the questios, ad show your work. You must explai your aswers to get credit. You will
Chapter 10: Power Series
 Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Chapter : Power Series 57 Chapter Overview: Power Series The reaso series are part of a Calculus course is that there are fuctios which caot be itegrated. All power series, though, ca be itegrated because
Chapter 4. Fourier Series
 Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
MTH Assignment 1 : Real Numbers, Sequences
 MTH -26 Assigmet : Real Numbers, Sequeces. Fid the supremum of the set { m m+ : N, m Z}. 2. Let A be a o-empty subset of R ad α R. Show that α = supa if ad oly if α is ot a upper boud of A but α + is a
MTH -26 Assigmet : Real Numbers, Sequeces. Fid the supremum of the set { m m+ : N, m Z}. 2. Let A be a o-empty subset of R ad α R. Show that α = supa if ad oly if α is ot a upper boud of A but α + is a
1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y
![1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y 1 1 2 = show that: over variables x and y. [2 marks] Write down necessary conditions involving first and second-order partial derivatives for ( x0, y](/thumbs/95/125864248.jpg) Questio (a) A square matrix A= A is called positive defiite if the quadratic form waw > 0 for every o-zero vector w [Note: Here (.) deotes the traspose of a matrix or a vector]. Let 0 A = 0 = show that:
Questio (a) A square matrix A= A is called positive defiite if the quadratic form waw > 0 for every o-zero vector w [Note: Here (.) deotes the traspose of a matrix or a vector]. Let 0 A = 0 = show that:
Math Solutions to homework 6
 Math 175 - Solutios to homework 6 Cédric De Groote November 16, 2017 Problem 1 (8.11 i the book): Let K be a compact Hermitia operator o a Hilbert space H ad let the kerel of K be {0}. Show that there
Math 175 - Solutios to homework 6 Cédric De Groote November 16, 2017 Problem 1 (8.11 i the book): Let K be a compact Hermitia operator o a Hilbert space H ad let the kerel of K be {0}. Show that there
1 lim. f(x) sin(nx)dx = 0. n sin(nx)dx
 Problem A. Calculate ta(.) to 4 decimal places. Solutio: The power series for si(x)/ cos(x) is x + x 3 /3 + (2/5)x 5 +. Puttig x =. gives ta(.) =.3. Problem 2A. Let f : R R be a cotiuous fuctio. Show that
Problem A. Calculate ta(.) to 4 decimal places. Solutio: The power series for si(x)/ cos(x) is x + x 3 /3 + (2/5)x 5 +. Puttig x =. gives ta(.) =.3. Problem 2A. Let f : R R be a cotiuous fuctio. Show that
ENGI Series Page 6-01
 ENGI 3425 6 Series Page 6-01 6. Series Cotets: 6.01 Sequeces; geeral term, limits, covergece 6.02 Series; summatio otatio, covergece, divergece test 6.03 Stadard Series; telescopig series, geometric series,
ENGI 3425 6 Series Page 6-01 6. Series Cotets: 6.01 Sequeces; geeral term, limits, covergece 6.02 Series; summatio otatio, covergece, divergece test 6.03 Stadard Series; telescopig series, geometric series,
Math 113 Exam 3 Practice
 Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
Math Exam Practice Exam 4 will cover.-., 0. ad 0.. Note that eve though. was tested i exam, questios from that sectios may also be o this exam. For practice problems o., refer to the last review. This
CHAPTER 10 INFINITE SEQUENCES AND SERIES
 CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
CHAPTER 10 INFINITE SEQUENCES AND SERIES 10.1 Sequeces 10.2 Ifiite Series 10.3 The Itegral Tests 10.4 Compariso Tests 10.5 The Ratio ad Root Tests 10.6 Alteratig Series: Absolute ad Coditioal Covergece
(a) (b) All real numbers. (c) All real numbers. (d) None. to show the. (a) 3. (b) [ 7, 1) (c) ( 7, 1) (d) At x = 7. (a) (b)
 Chapter 0 Review 597. E; a ( + )( + ) + + S S + S + + + + + + S lim + l. D; a diverges by the Itegral l k Test sice d lim [(l ) ], so k l ( ) does ot coverge absolutely. But it coverges by the Alteratig
Chapter 0 Review 597. E; a ( + )( + ) + + S S + S + + + + + + S lim + l. D; a diverges by the Itegral l k Test sice d lim [(l ) ], so k l ( ) does ot coverge absolutely. But it coverges by the Alteratig
f(w) w z =R z a 0 a n a nz n Liouville s theorem, we see that Q is constant, which implies that P is constant, which is a contradiction.
 Theorem 3.6.4. [Liouville s Theorem] Every bouded etire fuctio is costat. Proof. Let f be a etire fuctio. Suppose that there is M R such that M for ay z C. The for ay z C ad R > 0 f (z) f(w) 2πi (w z)
Theorem 3.6.4. [Liouville s Theorem] Every bouded etire fuctio is costat. Proof. Let f be a etire fuctio. Suppose that there is M R such that M for ay z C. The for ay z C ad R > 0 f (z) f(w) 2πi (w z)
Fourier Series and their Applications
 Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Fourier Series ad their Applicatios The fuctios, cos x, si x, cos x, si x, are orthogoal over (, ). m cos mx cos xdx = m = m = = cos mx si xdx = for all m, { m si mx si xdx = m = I fact the fuctios satisfy
Most text will write ordinary derivatives using either Leibniz notation 2 3. y + 5y= e and y y. xx tt t
 Itroductio to Differetial Equatios Defiitios ad Termiolog Differetial Equatio: A equatio cotaiig the derivatives of oe or more depedet variables, with respect to oe or more idepedet variables, is said
Itroductio to Differetial Equatios Defiitios ad Termiolog Differetial Equatio: A equatio cotaiig the derivatives of oe or more depedet variables, with respect to oe or more idepedet variables, is said
Inverse Nodal Problems for Differential Equation on the Half-line
 Australia Joural of Basic ad Applied Scieces, 3(4): 4498-4502, 2009 ISSN 1991-8178 Iverse Nodal Problems for Differetial Equatio o the Half-lie 1 2 3 A. Dabbaghia, A. Nematy ad Sh. Akbarpoor 1 Islamic
Australia Joural of Basic ad Applied Scieces, 3(4): 4498-4502, 2009 ISSN 1991-8178 Iverse Nodal Problems for Differetial Equatio o the Half-lie 1 2 3 A. Dabbaghia, A. Nematy ad Sh. Akbarpoor 1 Islamic
Mathematical Methods for Physics and Engineering
 Mathematical Methods for Physics ad Egieerig Lecture otes Sergei V. Shabaov Departmet of Mathematics, Uiversity of Florida, Gaiesville, FL 326 USA CHAPTER The theory of covergece. Numerical sequeces..
Mathematical Methods for Physics ad Egieerig Lecture otes Sergei V. Shabaov Departmet of Mathematics, Uiversity of Florida, Gaiesville, FL 326 USA CHAPTER The theory of covergece. Numerical sequeces..
Ma 4121: Introduction to Lebesgue Integration Solutions to Homework Assignment 5
 Ma 42: Itroductio to Lebesgue Itegratio Solutios to Homework Assigmet 5 Prof. Wickerhauser Due Thursday, April th, 23 Please retur your solutios to the istructor by the ed of class o the due date. You
Ma 42: Itroductio to Lebesgue Itegratio Solutios to Homework Assigmet 5 Prof. Wickerhauser Due Thursday, April th, 23 Please retur your solutios to the istructor by the ed of class o the due date. You
Apply change-of-basis formula to rewrite x as a linear combination of eigenvectors v j.
 Eigevalue-Eigevector Istructor: Nam Su Wag eigemcd Ay vector i real Euclidea space of dimesio ca be uiquely epressed as a liear combiatio of liearly idepedet vectors (ie, basis) g j, j,,, α g α g α g α
Eigevalue-Eigevector Istructor: Nam Su Wag eigemcd Ay vector i real Euclidea space of dimesio ca be uiquely epressed as a liear combiatio of liearly idepedet vectors (ie, basis) g j, j,,, α g α g α g α
lim za n n = z lim a n n.
 Lecture 6 Sequeces ad Series Defiitio 1 By a sequece i a set A, we mea a mappig f : N A. It is customary to deote a sequece f by {s } where, s := f(). A sequece {z } of (complex) umbers is said to be coverget
Lecture 6 Sequeces ad Series Defiitio 1 By a sequece i a set A, we mea a mappig f : N A. It is customary to deote a sequece f by {s } where, s := f(). A sequece {z } of (complex) umbers is said to be coverget
Section 11.8: Power Series
 Sectio 11.8: Power Series 1. Power Series I this sectio, we cosider geeralizig the cocept of a series. Recall that a series is a ifiite sum of umbers a. We ca talk about whether or ot it coverges ad i
Sectio 11.8: Power Series 1. Power Series I this sectio, we cosider geeralizig the cocept of a series. Recall that a series is a ifiite sum of umbers a. We ca talk about whether or ot it coverges ad i
Subject: Differential Equations & Mathematical Modeling-III
 Power Series Solutios of Differetial Equatios about Sigular poits Subject: Differetial Equatios & Mathematical Modelig-III Lesso: Power series solutios of differetial equatios about Sigular poits Lesso
Power Series Solutios of Differetial Equatios about Sigular poits Subject: Differetial Equatios & Mathematical Modelig-III Lesso: Power series solutios of differetial equatios about Sigular poits Lesso
Ma 530 Infinite Series I
 Ma 50 Ifiite Series I Please ote that i additio to the material below this lecture icorporated material from the Visual Calculus web site. The material o sequeces is at Visual Sequeces. (To use this li
Ma 50 Ifiite Series I Please ote that i additio to the material below this lecture icorporated material from the Visual Calculus web site. The material o sequeces is at Visual Sequeces. (To use this li
Chapter 10 Partial Differential Equations and Fourier Series
 Math-33 Chapter Partial Differetial Equatios November 6, 7 Chapter Partial Differetial Equatios ad Fourier Series Math-33 Chapter Partial Differetial Equatios November 6, 7. Boudary Value Problems for
Math-33 Chapter Partial Differetial Equatios November 6, 7 Chapter Partial Differetial Equatios ad Fourier Series Math-33 Chapter Partial Differetial Equatios November 6, 7. Boudary Value Problems for
Chapter 6 Infinite Series
 Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Chapter 6 Ifiite Series I the previous chapter we cosidered itegrals which were improper i the sese that the iterval of itegratio was ubouded. I this chapter we are goig to discuss a topic which is somewhat
Abstract Vector Spaces. Abstract Vector Spaces
 Astract Vector Spaces The process of astractio is critical i egieerig! Physical Device Data Storage Vector Space MRI machie Optical receiver 0 0 1 0 1 0 0 1 Icreasig astractio 6.1 Astract Vector Spaces
Astract Vector Spaces The process of astractio is critical i egieerig! Physical Device Data Storage Vector Space MRI machie Optical receiver 0 0 1 0 1 0 0 1 Icreasig astractio 6.1 Astract Vector Spaces
8. Applications To Linear Differential Equations
 8. Applicatios To Liear Differetial Equatios 8.. Itroductio 8.. Review Of Results Cocerig Liear Differetial Equatios Of First Ad Secod Orders 8.3. Eercises 8.4. Liear Differetial Equatios Of Order N 8.5.
8. Applicatios To Liear Differetial Equatios 8.. Itroductio 8.. Review Of Results Cocerig Liear Differetial Equatios Of First Ad Secod Orders 8.3. Eercises 8.4. Liear Differetial Equatios Of Order N 8.5.
Generating Functions for Laguerre Type Polynomials. Group Theoretic method
 It. Joural of Math. Aalysis, Vol. 4, 2010, o. 48, 257-266 Geeratig Fuctios for Laguerre Type Polyomials α of Two Variables L ( xy, ) by Usig Group Theoretic method Ajay K. Shula* ad Sriata K. Meher** *Departmet
It. Joural of Math. Aalysis, Vol. 4, 2010, o. 48, 257-266 Geeratig Fuctios for Laguerre Type Polyomials α of Two Variables L ( xy, ) by Usig Group Theoretic method Ajay K. Shula* ad Sriata K. Meher** *Departmet
AP Calculus Chapter 9: Infinite Series
 AP Calculus Chapter 9: Ifiite Series 9. Sequeces a, a 2, a 3, a 4, a 5,... Sequece: A fuctio whose domai is the set of positive itegers = 2 3 4 a = a a 2 a 3 a 4 terms of the sequece Begi with the patter
AP Calculus Chapter 9: Ifiite Series 9. Sequeces a, a 2, a 3, a 4, a 5,... Sequece: A fuctio whose domai is the set of positive itegers = 2 3 4 a = a a 2 a 3 a 4 terms of the sequece Begi with the patter
Definition 4.2. (a) A sequence {x n } in a Banach space X is a basis for X if. unique scalars a n (x) such that x = n. a n (x) x n. (4.
 4. BASES I BAACH SPACES 39 4. BASES I BAACH SPACES Sice a Baach space X is a vector space, it must possess a Hamel, or vector space, basis, i.e., a subset {x γ } γ Γ whose fiite liear spa is all of X ad
4. BASES I BAACH SPACES 39 4. BASES I BAACH SPACES Sice a Baach space X is a vector space, it must possess a Hamel, or vector space, basis, i.e., a subset {x γ } γ Γ whose fiite liear spa is all of X ad
2. Fourier Series, Fourier Integrals and Fourier Transforms
 Mathematics IV -. Fourier Series, Fourier Itegrals ad Fourier Trasforms The Fourier series are used for the aalysis of the periodic pheomea, which ofte appear i physics ad egieerig. The Fourier itegrals
Mathematics IV -. Fourier Series, Fourier Itegrals ad Fourier Trasforms The Fourier series are used for the aalysis of the periodic pheomea, which ofte appear i physics ad egieerig. The Fourier itegrals
Math 113 Exam 3 Practice
 Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
Math Exam Practice Exam will cover.-.9. This sheet has three sectios. The first sectio will remid you about techiques ad formulas that you should kow. The secod gives a umber of practice questios for you
NBHM QUESTION 2007 Section 1 : Algebra Q1. Let G be a group of order n. Which of the following conditions imply that G is abelian?
 NBHM QUESTION 7 NBHM QUESTION 7 NBHM QUESTION 7 Sectio : Algebra Q Let G be a group of order Which of the followig coditios imply that G is abelia? 5 36 Q Which of the followig subgroups are ecesarily
NBHM QUESTION 7 NBHM QUESTION 7 NBHM QUESTION 7 Sectio : Algebra Q Let G be a group of order Which of the followig coditios imply that G is abelia? 5 36 Q Which of the followig subgroups are ecesarily
Power Series: A power series about the center, x = 0, is a function of x of the form
 You are familiar with polyomial fuctios, polyomial that has ifiitely may terms. 2 p ( ) a0 a a 2 a. A power series is just a Power Series: A power series about the ceter, = 0, is a fuctio of of the form
You are familiar with polyomial fuctios, polyomial that has ifiitely may terms. 2 p ( ) a0 a a 2 a. A power series is just a Power Series: A power series about the ceter, = 0, is a fuctio of of the form
Additional Notes on Power Series
 Additioal Notes o Power Series Mauela Girotti MATH 37-0 Advaced Calculus of oe variable Cotets Quick recall 2 Abel s Theorem 2 3 Differetiatio ad Itegratio of Power series 4 Quick recall We recall here
Additioal Notes o Power Series Mauela Girotti MATH 37-0 Advaced Calculus of oe variable Cotets Quick recall 2 Abel s Theorem 2 3 Differetiatio ad Itegratio of Power series 4 Quick recall We recall here
Complex Analysis Spring 2001 Homework I Solution
 Complex Aalysis Sprig 2001 Homework I Solutio 1. Coway, Chapter 1, sectio 3, problem 3. Describe the set of poits satisfyig the equatio z a z + a = 2c, where c > 0 ad a R. To begi, we see from the triagle
Complex Aalysis Sprig 2001 Homework I Solutio 1. Coway, Chapter 1, sectio 3, problem 3. Describe the set of poits satisfyig the equatio z a z + a = 2c, where c > 0 ad a R. To begi, we see from the triagle
3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,
![3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense, 3. Z Transform. Recall that the Fourier transform (FT) of a DT signal xn [ ] is ( ) [ ] = In order for the FT to exist in the finite magnitude sense,](/thumbs/82/85448051.jpg) 3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
3. Z Trasform Referece: Etire Chapter 3 of text. Recall that the Fourier trasform (FT) of a DT sigal x [ ] is ω ( ) [ ] X e = j jω k = xe I order for the FT to exist i the fiite magitude sese, S = x [
Subject: Differential Equations & Mathematical Modeling -III. Lesson: Power series solutions of Differential Equations. about ordinary points
 Power series solutio of Differetial equatios about ordiary poits Subject: Differetial Equatios & Mathematical Modelig -III Lesso: Power series solutios of Differetial Equatios about ordiary poits Lesso
Power series solutio of Differetial equatios about ordiary poits Subject: Differetial Equatios & Mathematical Modelig -III Lesso: Power series solutios of Differetial Equatios about ordiary poits Lesso
Archimedes - numbers for counting, otherwise lengths, areas, etc. Kepler - geometry for planetary motion
 Topics i Aalysis 3460:589 Summer 007 Itroductio Ree descartes - aalysis (breaig dow) ad sythesis Sciece as models of ature : explaatory, parsimoious, predictive Most predictios require umerical values,
Topics i Aalysis 3460:589 Summer 007 Itroductio Ree descartes - aalysis (breaig dow) ad sythesis Sciece as models of ature : explaatory, parsimoious, predictive Most predictios require umerical values,
THE SOLUTION OF NONLINEAR EQUATIONS f( x ) = 0.
 THE SOLUTION OF NONLINEAR EQUATIONS f( ) = 0. Noliear Equatio Solvers Bracketig. Graphical. Aalytical Ope Methods Bisectio False Positio (Regula-Falsi) Fied poit iteratio Newto Raphso Secat The root of
THE SOLUTION OF NONLINEAR EQUATIONS f( ) = 0. Noliear Equatio Solvers Bracketig. Graphical. Aalytical Ope Methods Bisectio False Positio (Regula-Falsi) Fied poit iteratio Newto Raphso Secat The root of
Seunghee Ye Ma 8: Week 5 Oct 28
 Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
Week 5 Summary I Sectio, we go over the Mea Value Theorem ad its applicatios. I Sectio 2, we will recap what we have covered so far this term. Topics Page Mea Value Theorem. Applicatios of the Mea Value
(A sequence also can be thought of as the list of function values attained for a function f :ℵ X, where f (n) = x n for n 1.) x 1 x N +k x N +4 x 3
 MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
MATH 337 Sequeces Dr. Neal, WKU Let X be a metric space with distace fuctio d. We shall defie the geeral cocept of sequece ad limit i a metric space, the apply the results i particular to some special
f t dt. Write the third-degree Taylor polynomial for G
 AP Calculus BC Homework - Chapter 8B Taylor, Maclauri, ad Power Series # Taylor & Maclauri Polyomials Critical Thikig Joural: (CTJ: 5 pts.) Discuss the followig questios i a paragraph: What does it mea
AP Calculus BC Homework - Chapter 8B Taylor, Maclauri, ad Power Series # Taylor & Maclauri Polyomials Critical Thikig Joural: (CTJ: 5 pts.) Discuss the followig questios i a paragraph: What does it mea
Chapter 6 Overview: Sequences and Numerical Series. For the purposes of AP, this topic is broken into four basic subtopics:
 Chapter 6 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals (which is what most studets
Chapter 6 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals (which is what most studets
The Bilateral Laplace Transform of the Positive Even Functions and a Proof of Riemann Hypothesis
 The Bilateral Laplace Trasform of the Positive Eve Fuctios ad a Proof of Riema Hypothesis Seog Wo Cha Ph.D. swcha@dgu.edu Abstract We show that some iterestig properties of the bilateral Laplace trasform
The Bilateral Laplace Trasform of the Positive Eve Fuctios ad a Proof of Riema Hypothesis Seog Wo Cha Ph.D. swcha@dgu.edu Abstract We show that some iterestig properties of the bilateral Laplace trasform
Chapter 7: Numerical Series
 Chapter 7: Numerical Series Chapter 7 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals
Chapter 7: Numerical Series Chapter 7 Overview: Sequeces ad Numerical Series I most texts, the topic of sequeces ad series appears, at first, to be a side topic. There are almost o derivatives or itegrals
1.3 Convergence Theorems of Fourier Series. k k k k. N N k 1. With this in mind, we state (without proof) the convergence of Fourier series.
 .3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
.3 Covergece Theorems of Fourier Series I this sectio, we preset the covergece of Fourier series. A ifiite sum is, by defiitio, a limit of partial sums, that is, a cos( kx) b si( kx) lim a cos( kx) b si(
Solutions to Tutorial 5 (Week 6)
 The Uiversity of Sydey School of Mathematics ad Statistics Solutios to Tutorial 5 (Wee 6 MATH2962: Real ad Complex Aalysis (Advaced Semester, 207 Web Page: http://www.maths.usyd.edu.au/u/ug/im/math2962/
The Uiversity of Sydey School of Mathematics ad Statistics Solutios to Tutorial 5 (Wee 6 MATH2962: Real ad Complex Aalysis (Advaced Semester, 207 Web Page: http://www.maths.usyd.edu.au/u/ug/im/math2962/
Assignment 1 : Real Numbers, Sequences. for n 1. Show that (x n ) converges. Further, by observing that x n+2 + x n+1
 Assigmet : Real Numbers, Sequeces. Let A be a o-empty subset of R ad α R. Show that α = supa if ad oly if α is ot a upper boud of A but α + is a upper boud of A for every N. 2. Let y (, ) ad x (, ). Evaluate
Assigmet : Real Numbers, Sequeces. Let A be a o-empty subset of R ad α R. Show that α = supa if ad oly if α is ot a upper boud of A but α + is a upper boud of A for every N. 2. Let y (, ) ad x (, ). Evaluate
MATHEMATICS Code No. 13 INSTRUCTIONS
 DO NOT OPEN THIS TEST BOOKLET UNTIL YOU ARE ASKED TO DO SO COMBINED COMPETITIVE (PRELIMINARY) EXAMINATION, 0 Serial No. MATHEMATICS Code No. A Time Allowed : Two Hours Maimum Marks : 00 INSTRUCTIONS. IMMEDIATELY
DO NOT OPEN THIS TEST BOOKLET UNTIL YOU ARE ASKED TO DO SO COMBINED COMPETITIVE (PRELIMINARY) EXAMINATION, 0 Serial No. MATHEMATICS Code No. A Time Allowed : Two Hours Maimum Marks : 00 INSTRUCTIONS. IMMEDIATELY
1. (25 points) Use the limit definition of the definite integral and the sum formulas 1 to compute
 Math, Calculus II Fial Eam Solutios. 5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute 4 d. The check your aswer usig the Evaluatio Theorem. ) ) Solutio: I this itegral,
Math, Calculus II Fial Eam Solutios. 5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute 4 d. The check your aswer usig the Evaluatio Theorem. ) ) Solutio: I this itegral,
Prof. Dr. I. Nasser Phys 571, T131 5-Nov-13 Green function.doc. 2 ρ(r)
 Gree fuctio.doc Solutio of ihomogeeous ordiary differetial equatios usig Gree's fuctios G(, ') (9.7, 10.5) Historical Itroductio: Gree's fuctios are auiliary fuctios i the solutio of liear partial differetial
Gree fuctio.doc Solutio of ihomogeeous ordiary differetial equatios usig Gree's fuctios G(, ') (9.7, 10.5) Historical Itroductio: Gree's fuctios are auiliary fuctios i the solutio of liear partial differetial
j=1 dz Res(f, z j ) = 1 d k 1 dz k 1 (z c)k f(z) Res(f, c) = lim z c (k 1)! Res g, c = f(c) g (c)
 Problem. Compute the itegrals C r d for Z, where C r = ad r >. Recall that C r has the couter-clockwise orietatio. Solutio: We will use the idue Theorem to solve this oe. We could istead use other (perhaps
Problem. Compute the itegrals C r d for Z, where C r = ad r >. Recall that C r has the couter-clockwise orietatio. Solutio: We will use the idue Theorem to solve this oe. We could istead use other (perhaps
Lecture Notes for Analysis Class
 Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
THE ZETA FUNCTION AND THE RIEMANN HYPOTHESIS. Contents 1. History 1
 THE ZETA FUNCTION AND THE RIEMANN HYPOTHESIS VIKTOR MOROS Abstract. The zeta fuctio has bee studied for ceturies but mathematicias are still learig about it. I this paper, I will discuss some of the zeta
THE ZETA FUNCTION AND THE RIEMANN HYPOTHESIS VIKTOR MOROS Abstract. The zeta fuctio has bee studied for ceturies but mathematicias are still learig about it. I this paper, I will discuss some of the zeta
Math 61CM - Solutions to homework 3
 Math 6CM - Solutios to homework 3 Cédric De Groote October 2 th, 208 Problem : Let F be a field, m 0 a fixed oegative iteger ad let V = {a 0 + a x + + a m x m a 0,, a m F} be the vector space cosistig
Math 6CM - Solutios to homework 3 Cédric De Groote October 2 th, 208 Problem : Let F be a field, m 0 a fixed oegative iteger ad let V = {a 0 + a x + + a m x m a 0,, a m F} be the vector space cosistig
CHAPTER 1 SEQUENCES AND INFINITE SERIES
 CHAPTER SEQUENCES AND INFINITE SERIES SEQUENCES AND INFINITE SERIES (0 meetigs) Sequeces ad limit of a sequece Mootoic ad bouded sequece Ifiite series of costat terms Ifiite series of positive terms Alteratig
CHAPTER SEQUENCES AND INFINITE SERIES SEQUENCES AND INFINITE SERIES (0 meetigs) Sequeces ad limit of a sequece Mootoic ad bouded sequece Ifiite series of costat terms Ifiite series of positive terms Alteratig
Løsningsførslag i 4M
 Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side 1 av 6 Løsigsførslag i 4M Oppgave 1 a) A sketch of the graph of the give f o the iterval [ 3, 3) is as follows: The Fourier
Norges tekisk aturviteskapelige uiversitet Istitutt for matematiske fag Side 1 av 6 Løsigsførslag i 4M Oppgave 1 a) A sketch of the graph of the give f o the iterval [ 3, 3) is as follows: The Fourier
MATHEMATICAL SCIENCES PAPER-II
 MATHEMATICAL SCIENCES PAPER-II. Let {x } ad {y } be two sequeces of real umbers. Prove or disprove each of the statemets :. If {x y } coverges, ad if {y } is coverget, the {x } is coverget.. {x + y } coverges
MATHEMATICAL SCIENCES PAPER-II. Let {x } ad {y } be two sequeces of real umbers. Prove or disprove each of the statemets :. If {x y } coverges, ad if {y } is coverget, the {x } is coverget.. {x + y } coverges
MATH 6101 Fall 2008 Series and a Famous Unsolved Problem
 MATH 60 Fall 2008 Series ad a Famous Usolved Problem Problems = + + + + = (2- )(2+ ) 3 3 5 5 7 7 9 2-Nov-2008 MATH 60 2 Problems ( 4) = + 25 48 2-Nov-2008 MATH 60 3 Problems ( )! = + 2-Nov-2008 MATH 60
MATH 60 Fall 2008 Series ad a Famous Usolved Problem Problems = + + + + = (2- )(2+ ) 3 3 5 5 7 7 9 2-Nov-2008 MATH 60 2 Problems ( 4) = + 25 48 2-Nov-2008 MATH 60 3 Problems ( )! = + 2-Nov-2008 MATH 60
SOLUTIONS TO EXAM 3. Solution: Note that this defines two convergent geometric series with respective radii r 1 = 2/5 < 1 and r 2 = 1/5 < 1.
 SOLUTIONS TO EXAM 3 Problem Fid the sum of the followig series 2 + ( ) 5 5 2 5 3 25 2 2 This series diverges Solutio: Note that this defies two coverget geometric series with respective radii r 2/5 < ad
SOLUTIONS TO EXAM 3 Problem Fid the sum of the followig series 2 + ( ) 5 5 2 5 3 25 2 2 This series diverges Solutio: Note that this defies two coverget geometric series with respective radii r 2/5 < ad
Riemann Hypothesis Proof
 Riea Hypothesis Proof H. Vic Dao 43 rd West Coast Nuber Theory Coferece, Dec 6-0, 009, Asiloar, CA. Revised 0/8/00. Riea Hypothesis Proof H. Vic Dao vic0@cocast.et March, 009 Revised Deceber, 009 Abstract
Riea Hypothesis Proof H. Vic Dao 43 rd West Coast Nuber Theory Coferece, Dec 6-0, 009, Asiloar, CA. Revised 0/8/00. Riea Hypothesis Proof H. Vic Dao vic0@cocast.et March, 009 Revised Deceber, 009 Abstract
n 3 ln n n ln n is convergent by p-series for p = 2 > 1. n2 Therefore we can apply Limit Comparison Test to determine lutely convergent.
 06 微甲 0-04 06-0 班期中考解答和評分標準. ( poits) Determie whether the series is absolutely coverget, coditioally coverget, or diverget. Please state the tests which you use. (a) ( poits) (b) ( poits) (c) ( poits)
06 微甲 0-04 06-0 班期中考解答和評分標準. ( poits) Determie whether the series is absolutely coverget, coditioally coverget, or diverget. Please state the tests which you use. (a) ( poits) (b) ( poits) (c) ( poits)
In this section, we show how to use the integral test to decide whether a series
 Itegral Test Itegral Test Example Itegral Test Example p-series Compariso Test Example Example 2 Example 3 Example 4 Example 5 Exa Itegral Test I this sectio, we show how to use the itegral test to decide
Itegral Test Itegral Test Example Itegral Test Example p-series Compariso Test Example Example 2 Example 3 Example 4 Example 5 Exa Itegral Test I this sectio, we show how to use the itegral test to decide
Introduction to Optimization Techniques
 Itroductio to Optimizatio Techiques Basic Cocepts of Aalysis - Real Aalysis, Fuctioal Aalysis 1 Basic Cocepts of Aalysis Liear Vector Spaces Defiitio: A vector space X is a set of elemets called vectors
Itroductio to Optimizatio Techiques Basic Cocepts of Aalysis - Real Aalysis, Fuctioal Aalysis 1 Basic Cocepts of Aalysis Liear Vector Spaces Defiitio: A vector space X is a set of elemets called vectors
2.4.2 A Theorem About Absolutely Convergent Series
 0 Versio of August 27, 200 CHAPTER 2. INFINITE SERIES Add these two series: + 3 2 + 5 + 7 4 + 9 + 6 +... = 3 l 2. (2.20) 2 Sice the reciprocal of each iteger occurs exactly oce i the last series, we would
0 Versio of August 27, 200 CHAPTER 2. INFINITE SERIES Add these two series: + 3 2 + 5 + 7 4 + 9 + 6 +... = 3 l 2. (2.20) 2 Sice the reciprocal of each iteger occurs exactly oce i the last series, we would
Chapter 8. Euler s Gamma function
 Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
LATEST TRENDS on APPLIED MATHEMATICS, SIMULATION, MODELLING. P. Sawangtong and W. Jumpen. where Ω R is a bounded domain with a smooth boundary
 Eistece of a blow-up solutio for a degeerate parabolic iitial-boudary value problem P Sawagtog ad W Jumpe Abstra Here before blow-up occurs we establish the eistece ad uiueess of a blow-up solutio of a
Eistece of a blow-up solutio for a degeerate parabolic iitial-boudary value problem P Sawagtog ad W Jumpe Abstra Here before blow-up occurs we establish the eistece ad uiueess of a blow-up solutio of a
Regn. No. North Delhi : 33-35, Mall Road, G.T.B. Nagar (Opp. Metro Gate No. 3), Delhi-09, Ph: ,
 . Sectio-A cotais 30 Multiple Choice Questios (MCQ). Each questio has 4 choices (a), (b), (c) ad (d), for its aswer, out of which ONLY ONE is correct. From Q. to Q.0 carries Marks ad Q. to Q.30 carries
. Sectio-A cotais 30 Multiple Choice Questios (MCQ). Each questio has 4 choices (a), (b), (c) ad (d), for its aswer, out of which ONLY ONE is correct. From Q. to Q.0 carries Marks ad Q. to Q.30 carries
Real Numbers R ) - LUB(B) may or may not belong to B. (Ex; B= { y: y = 1 x, - Note that A B LUB( A) LUB( B)
 Real Numbers The least upper boud - Let B be ay subset of R B is bouded above if there is a k R such that x k for all x B - A real umber, k R is a uique least upper boud of B, ie k = LUB(B), if () k is
Real Numbers The least upper boud - Let B be ay subset of R B is bouded above if there is a k R such that x k for all x B - A real umber, k R is a uique least upper boud of B, ie k = LUB(B), if () k is
Sequences, Mathematical Induction, and Recursion. CSE 2353 Discrete Computational Structures Spring 2018
 CSE 353 Discrete Computatioal Structures Sprig 08 Sequeces, Mathematical Iductio, ad Recursio (Chapter 5, Epp) Note: some course slides adopted from publisher-provided material Overview May mathematical
CSE 353 Discrete Computatioal Structures Sprig 08 Sequeces, Mathematical Iductio, ad Recursio (Chapter 5, Epp) Note: some course slides adopted from publisher-provided material Overview May mathematical
Math 113, Calculus II Winter 2007 Final Exam Solutions
 Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
Math, Calculus II Witer 7 Fial Exam Solutios (5 poits) Use the limit defiitio of the defiite itegral ad the sum formulas to compute x x + dx The check your aswer usig the Evaluatio Theorem Solutio: I this
Dupuy Complex Analysis Spring 2016 Homework 02
 Dupuy Complex Aalysis Sprig 206 Homework 02. (CUNY, Fall 2005) Let D be the closed uit disc. Let g be a sequece of aalytic fuctios covergig uiformly to f o D. (a) Show that g coverges. Solutio We have
Dupuy Complex Aalysis Sprig 206 Homework 02. (CUNY, Fall 2005) Let D be the closed uit disc. Let g be a sequece of aalytic fuctios covergig uiformly to f o D. (a) Show that g coverges. Solutio We have
Numerical Conformal Mapping via a Fredholm Integral Equation using Fourier Method ABSTRACT INTRODUCTION
 alaysia Joural of athematical Scieces 3(1): 83-93 (9) umerical Coformal appig via a Fredholm Itegral Equatio usig Fourier ethod 1 Ali Hassa ohamed urid ad Teh Yua Yig 1, Departmet of athematics, Faculty
alaysia Joural of athematical Scieces 3(1): 83-93 (9) umerical Coformal appig via a Fredholm Itegral Equatio usig Fourier ethod 1 Ali Hassa ohamed urid ad Teh Yua Yig 1, Departmet of athematics, Faculty
Chapter 8. Euler s Gamma function
 Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s) that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Chapter 8 Euler s Gamma fuctio The Gamma fuctio plays a importat role i the fuctioal equatio for ζ(s) that we will derive i the ext chapter. I the preset chapter we have collected some properties of the
Fourier Series and the Wave Equation
 Fourier Series ad the Wave Equatio We start with the oe-dimesioal wave equatio u u =, x u(, t) = u(, t) =, ux (,) = f( x), u ( x,) = This represets a vibratig strig, where u is the displacemet of the strig
Fourier Series ad the Wave Equatio We start with the oe-dimesioal wave equatio u u =, x u(, t) = u(, t) =, ux (,) = f( x), u ( x,) = This represets a vibratig strig, where u is the displacemet of the strig
A 2nTH ORDER LINEAR DIFFERENCE EQUATION
 A 2TH ORDER LINEAR DIFFERENCE EQUATION Doug Aderso Departmet of Mathematics ad Computer Sciece, Cocordia College Moorhead, MN 56562, USA ABSTRACT: We give a formulatio of geeralized zeros ad (, )-discojugacy
A 2TH ORDER LINEAR DIFFERENCE EQUATION Doug Aderso Departmet of Mathematics ad Computer Sciece, Cocordia College Moorhead, MN 56562, USA ABSTRACT: We give a formulatio of geeralized zeros ad (, )-discojugacy
Math 341 Lecture #31 6.5: Power Series
 Math 341 Lecture #31 6.5: Power Series We ow tur our attetio to a particular kid of series of fuctios, amely, power series, f(x = a x = a 0 + a 1 x + a 2 x 2 + where a R for all N. I terms of a series
Math 341 Lecture #31 6.5: Power Series We ow tur our attetio to a particular kid of series of fuctios, amely, power series, f(x = a x = a 0 + a 1 x + a 2 x 2 + where a R for all N. I terms of a series
where c is a scaling constant, 0, 0,. r c sinh cos csinh cos cos, csinh cos sin, ccosh sin U csinh sin sin, csinh sin cos,0
 MATH 38:Partial Differetial Equatios Solutios to The Secod Midterm DEGENERATE ELLIPSOID COORDINATES. Problem PROOF: Give csih si cos, y csihsi si, z ccoshcos, where c is a scalig costat,,,. r We compute
MATH 38:Partial Differetial Equatios Solutios to The Secod Midterm DEGENERATE ELLIPSOID COORDINATES. Problem PROOF: Give csih si cos, y csihsi si, z ccoshcos, where c is a scalig costat,,,. r We compute
f(x) dx as we do. 2x dx x also diverges. Solution: We compute 2x dx lim
 Math 3, Sectio 2. (25 poits) Why we defie f(x) dx as we do. (a) Show that the improper itegral diverges. Hece the improper itegral x 2 + x 2 + b also diverges. Solutio: We compute x 2 + = lim b x 2 + =
Math 3, Sectio 2. (25 poits) Why we defie f(x) dx as we do. (a) Show that the improper itegral diverges. Hece the improper itegral x 2 + x 2 + b also diverges. Solutio: We compute x 2 + = lim b x 2 + =
A collocation method for singular integral equations with cosecant kernel via Semi-trigonometric interpolation
 Iteratioal Joural of Mathematics Research. ISSN 0976-5840 Volume 9 Number 1 (017) pp. 45-51 Iteratioal Research Publicatio House http://www.irphouse.com A collocatio method for sigular itegral equatios
Iteratioal Joural of Mathematics Research. ISSN 0976-5840 Volume 9 Number 1 (017) pp. 45-51 Iteratioal Research Publicatio House http://www.irphouse.com A collocatio method for sigular itegral equatios
ECE-S352 Introduction to Digital Signal Processing Lecture 3A Direct Solution of Difference Equations
 ECE-S352 Itroductio to Digital Sigal Processig Lecture 3A Direct Solutio of Differece Equatios Discrete Time Systems Described by Differece Equatios Uit impulse (sample) respose h() of a DT system allows
ECE-S352 Itroductio to Digital Sigal Processig Lecture 3A Direct Solutio of Differece Equatios Discrete Time Systems Described by Differece Equatios Uit impulse (sample) respose h() of a DT system allows
An application of a subset S of C onto another S' defines a function [f(z)] of the complex variable z.
![An application of a subset S of C onto another S' defines a function [f(z)] of the complex variable z. An application of a subset S of C onto another S' defines a function [f(z)] of the complex variable z.](/thumbs/82/84763354.jpg) Diola Bagaoko (1 ELEMENTARY FNCTIONS OFA COMPLEX VARIABLES I Basic Defiitio of a Fuctio of a Comple Variable A applicatio of a subset S of C oto aother S' defies a fuctio [f(] of the comple variable z
Diola Bagaoko (1 ELEMENTARY FNCTIONS OFA COMPLEX VARIABLES I Basic Defiitio of a Fuctio of a Comple Variable A applicatio of a subset S of C oto aother S' defies a fuctio [f(] of the comple variable z
Sequences and Limits
 Chapter Sequeces ad Limits Let { a } be a sequece of real or complex umbers A ecessary ad sufficiet coditio for the sequece to coverge is that for ay ɛ > 0 there exists a iteger N > 0 such that a p a q
Chapter Sequeces ad Limits Let { a } be a sequece of real or complex umbers A ecessary ad sufficiet coditio for the sequece to coverge is that for ay ɛ > 0 there exists a iteger N > 0 such that a p a q
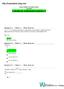 FINALTERM EXAMINATION Fall 9 Calculus & Aalytical Geometry-I Questio No: ( Mars: ) - Please choose oe Let f ( x) is a fuctio such that as x approaches a real umber a, either from left or right-had-side,
FINALTERM EXAMINATION Fall 9 Calculus & Aalytical Geometry-I Questio No: ( Mars: ) - Please choose oe Let f ( x) is a fuctio such that as x approaches a real umber a, either from left or right-had-side,
