Professor Terje Haukaas University of British Columbia, Vancouver System Reliability
|
|
|
- Moses Parker
- 6 years ago
- Views:
Transcription
1 System Reliability This material was first described to me in a course taught by Professor Armen Der iureghian at the University of California at Berkeley. In 2005 he made an excellent description available in Chapter 14 First- and second-order reliability methods of the CRC Engineering Design Reliability Handbook edited by Nikolaidis, Ghiocel and Singhal, published by the CRC Press in Boca Raton, Florida. System reliability analysis deals with problems where failure is defined in terms of more than one limit-state function. One example is a structural element with two failure modes, say, shear and bending. Suppose one limit-state function is defined for shear failure and another for bending failure. The failure event is if any of the two limit-state functions are negative. Thus, this is an example of a system reliability problem. Conversely, reliability problems with only one limit-state function are called component reliability problems. Formulation of System Reliability Problems For reference, the component reliability problem, i.e., the problem when only one limitstate function is involved, reads = P( g(x 0 (1 In contrast, a series system reliability problem is characterized by failure occurring if any of several limit-state functions are negative: = P ( g k (x 0 (2 where is the number of limit-state functions. Another special case of system reliability problems is the parallel system, in which failure occurs only when all the limit-state functions are negative: = P ( g k (x 0 (3 However, neither the series system nor the parallel system describes the general system reliability problem. Rather the general system reliability problem is formulated as a series system of parallel systems: = P ( g j (x 0 (4 j c m where is the number of parallel systems and c m is the number of so-called cut sets. The terminology is further developed in the field of operations research. In the context of reliability analysis, cut set is another name for a sub parallel system. The logical operator in Eq. (4 j c m means that only limit-state functions within cut set number m is included. The cut set formulation in Eq. (4 can be replaced by the equally general link System Reliability Updated February 22, 2014 Page 1
2 set formulation, in which the problem is defined as a parallel system of sub series systems. However, this is uncommon and less efficient in structural reliability analysis. To this end, unless the problem at hand is a pure series or parallel system, it is an important task to identify the cut sets of the problem. Three types exist: general cut sets, minimum cut sets, and disjoint cut sets. The following step-wise procedure is suggested: 1. Identify all cut sets: Identify all failure scenarios, i.e., all combinations of component failure that would cause system failure. A general cut set is any set of components whose joint failure constitutes failure of the system. 2. Identify the minimum cut sets: A minimum cut set contains the minimum number of components; if any component is removed from the set then it ceases to be a cut set. Usually, when care is exercised in Ste then the minimum cut sets are already specified in that step. 3. If possible, identify the disjoint cut sets: By definition, two cut sets are disjoint when their intersection is the null event. In other words, if two cut sets are disjoint then they cannot occur simultaneously. An important consequence of this is that the failure probability for a general system with disjoint cut sets is that the system failure probability is simply the sum of the cut set failure probabilities. However, it is rarely efficient to pursue disjoint cut sets for efficiency reasons. The reason is that to establish disjoint cut sets it is necessary to include the complement of component failure events in the cut sets. This increases the number of components in the cut sets, which increases the cost of computing their failure probability. Reliability Block Diagrams Reliability block diagrams (RBDs are sometimes helpful to visualize system reliability problems and identify cut sets. An RBD is a sketch that connects the components in the same way as a road map. Figure 1 shows an example of a simple RBD. The top of the figure shows the physical problem, namely the road network between two cities. The RBD is shown at the bottom. For road network problems the sketch of the physical problem is particularly close to the RBD. However, the direct mapping of the physical problem into an RBD is not generally possible. The road network problem is utilized here for pedagogical reasons because any RBD is best interpreted as a road network between two cities. This interpretation helps when identifying cut sets; the failure of any set of components that would close the connection between the two cities is a cut set. The road network analogy is why it is more straightforward to identify cut sets after the RBD has been sketched. For the example in Figure 1 it is relatively easy to see that failure of Tunnel 2 is one cut set, and the simultaneous failure of the bridge and Tunnel 1 is another cut set. The failure of any of these two cut sets will sever the connection between the two cities. Hence, the system failure event is written BT 1 T 2. System Reliability Updated February 22, 2014 Page 2
3 Tunnel 1 City A Tunnel 2 City B Bridge T 1 T 2 B Figure 1: Reliability block diagram. FOR Solution for Series and Parallel Problems The series system reliability problem is written in Eq. (2. It is equivalently written in the standard normal space: = P ( G k (y 0 (5 where y is the vector of standard normal random variables. Linearizing each limit-state function according to FOR component reliability analysis yields: = P α T k y 0 (6 where β k and α k are, respectively, the reliability index and alpha-vector for each limitstate function. For each limit-state function, the random variable z k = α k T y (7 is now defined. According to the joint uncorrelated standard normal distribution for y the z k variables have zero mean. Also, because the alpha-vectors are normalized the z k variables have unit variances. The covariance between z i and z j is Cov α T i y,α T j y = α T i Σ yy α j = α T i α j (8 i.e., the dot product of the two alpha-vectors. This covariance is equal to the correlation because the z k variables have unit standard deviation. Substitution of Eq. (7 into Eq. (6 yields the following expression for the system failure probability: = P z k (9 System Reliability Updated February 22, 2014 Page 3
4 To arrive at an expression involving the intersection operator rather than the union operator, the complementary probability rule is first invoked: = 1 P z k followed by the application of one of de organ s rules: = 1 P z k = 1 P (10 ( z < β k k (11 Because z k are correlated standard normal random variables the k-dimensional joint standard normal CDF is identified: = 1 Φ ( β,r (12 where β is the vector of reliability indices for all the limit-state functions and R is the correlation matrix for the random variables z k. The correlation matrix contains the covariances in Eq. (8 because the standard deviations are equal to one. Unfortunately, it is difficult to evaluate the joint CDF in Eq. (12. The development of accurate approximations remains an open research area. For k=2 the following analytical solution is available: Φ 2 ( β,r = Φ( β 1 Φ( β 2 + ρ π 1 ρ exp β β ρ β 1 β (1 ρ 2 dρ (13 0 where the last term is the integral of the bivariate standard normal PDF with correlation, and the correlation between the two limit-states according to Eq. (8 is ρ 12 = α 1 T α 2 (14 It is noted that the correlation coefficient must exceed, say, 0.5 before the intersection probability becomes significant. In Eq. (13 it is also observed that the joint CDF is equal to the product of the two component failure probabilities when the two failure modes are uncorrelated. Otherwise an integral must be evaluated to obtain the joint failure probability. Carrying out the derivations above for parallel systems yields: = Φ ( β,r (15 Sampling Analysis Although sampling analysis is usually computationally expensive it is appealingly straightforward to implement for system reliability problems. For each sample is it checked whether the any of the limit-states are violated and if this caused system failure. Depending on the result the indicator variable is set to zero or one and another sample is generated. Hence, for limit-state functions that are computationally inexpensive to evaluate, mean-centred sampling is a straightforward alternative to obtain an estimate of the failure probability. System Reliability Updated February 22, 2014 Page 4
5 System Reliability Bounds The difficulties associated with evaluating the system failure probability even for series and parallel systems have led to the exploration of probability bounds. For series systems there are uni-modal, bi-modal, and tri-modal bounds. These three options are understood by considering the inclusion-exclusion rule of probability for the series system problem: = P C m = P(C m P(C m C i + P(C m C i (16 i<m j <i<m where C m denote the event that limit-state number m is violated, or more generally the event that cut set number m is in the failure state. Uni-modal bounds are formulated by retaining only the first term in Eq. (16: max(p m min 1, p m (17 where the shorthand notation p m = P(C m is introduced. Bi-modal bounds is an extension where also the two-component joint probabilities are included: m 1 + max 0, p m p mj + p m max j <m (p mj (18 m=2 j =1 m=2( where the shorthand notation p ij = P(C i is introduced and evaluated according to Eq. (13. To make the bi-modal bounds more accessible they are here illustrated for up to four components: ( ( ( + max 0, p 2 p 21 + max 0, p 3 (p 31 + p 32 + max 0, p 4 (p 41 + p 42 + p 43 + p 2 p 21 + p 3 max(p 31, p 32 + p 4 max(p 41, p 42, p 43 In theory the bounds will vary somewhat depending on the ordering of the limit-state functions. Hence, all combinations should be checked to ensure that the bounds are not falsely narrow. Beyond uni-modal and bi-modal bounds, tri-modal bounds are also formulated in the literature in terms of p ijk = P(C i C k but not covered here because of the additional complexity in evaluating p ijk. (19 System Reliability Updated February 22, 2014 Page 5
Professor Terje Haukaas University of British Columbia, Vancouver Sampling ( ) = f (x)dx
 Sampling There exist several sampling schemes to address the reliability problem. In fact, sampling is equally applicable to component and system reliability problems. For this reason, the failure region
Sampling There exist several sampling schemes to address the reliability problem. In fact, sampling is equally applicable to component and system reliability problems. For this reason, the failure region
component risk analysis
 273: Urban Systems Modeling Lec. 3 component risk analysis instructor: Matteo Pozzi 273: Urban Systems Modeling Lec. 3 component reliability outline risk analysis for components uncertain demand and uncertain
273: Urban Systems Modeling Lec. 3 component risk analysis instructor: Matteo Pozzi 273: Urban Systems Modeling Lec. 3 component reliability outline risk analysis for components uncertain demand and uncertain
Multivariate Distribution Models
 Multivariate Distribution Models Model Description While the probability distribution for an individual random variable is called marginal, the probability distribution for multiple random variables is
Multivariate Distribution Models Model Description While the probability distribution for an individual random variable is called marginal, the probability distribution for multiple random variables is
DETERMINATION OF RELIABILITY BOUNDS FOR STRUCTURAL SYSTEMS USING LINEAR PROGRAMMING
 An. Şt. Univ. Ovidius Constanţa Vol. 11(2), 2003, 171 182 DETERMINATION OF REIABIITY BOUNDS FOR STRUCTURA SYSTEMS USING INEAR PROGRAMMING Romică Trandafir, Sorin Demetriu and Ion Mierlus-Mazilu Abstract
An. Şt. Univ. Ovidius Constanţa Vol. 11(2), 2003, 171 182 DETERMINATION OF REIABIITY BOUNDS FOR STRUCTURA SYSTEMS USING INEAR PROGRAMMING Romică Trandafir, Sorin Demetriu and Ion Mierlus-Mazilu Abstract
Basics of Uncertainty Analysis
 Basics of Uncertainty Analysis Chapter Six Basics of Uncertainty Analysis 6.1 Introduction As shown in Fig. 6.1, analysis models are used to predict the performances or behaviors of a product under design.
Basics of Uncertainty Analysis Chapter Six Basics of Uncertainty Analysis 6.1 Introduction As shown in Fig. 6.1, analysis models are used to predict the performances or behaviors of a product under design.
The main results about probability measures are the following two facts:
 Chapter 2 Probability measures The main results about probability measures are the following two facts: Theorem 2.1 (extension). If P is a (continuous) probability measure on a field F 0 then it has a
Chapter 2 Probability measures The main results about probability measures are the following two facts: Theorem 2.1 (extension). If P is a (continuous) probability measure on a field F 0 then it has a
Multiple Random Variables
 Multiple Random Variables This Version: July 30, 2015 Multiple Random Variables 2 Now we consider models with more than one r.v. These are called multivariate models For instance: height and weight An
Multiple Random Variables This Version: July 30, 2015 Multiple Random Variables 2 Now we consider models with more than one r.v. These are called multivariate models For instance: height and weight An
Theorem 2.1 (Caratheodory). A (countably additive) probability measure on a field has an extension. n=1
 Chapter 2 Probability measures 1. Existence Theorem 2.1 (Caratheodory). A (countably additive) probability measure on a field has an extension to the generated σ-field Proof of Theorem 2.1. Let F 0 be
Chapter 2 Probability measures 1. Existence Theorem 2.1 (Caratheodory). A (countably additive) probability measure on a field has an extension to the generated σ-field Proof of Theorem 2.1. Let F 0 be
Chapter 5 continued. Chapter 5 sections
 Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
Summary of basic probability theory Math 218, Mathematical Statistics D Joyce, Spring 2016
 8. For any two events E and F, P (E) = P (E F ) + P (E F c ). Summary of basic probability theory Math 218, Mathematical Statistics D Joyce, Spring 2016 Sample space. A sample space consists of a underlying
8. For any two events E and F, P (E) = P (E F ) + P (E F c ). Summary of basic probability theory Math 218, Mathematical Statistics D Joyce, Spring 2016 Sample space. A sample space consists of a underlying
IEOR 4701: Stochastic Models in Financial Engineering. Summer 2007, Professor Whitt. SOLUTIONS to Homework Assignment 9: Brownian motion
 IEOR 471: Stochastic Models in Financial Engineering Summer 27, Professor Whitt SOLUTIONS to Homework Assignment 9: Brownian motion In Ross, read Sections 1.1-1.3 and 1.6. (The total required reading there
IEOR 471: Stochastic Models in Financial Engineering Summer 27, Professor Whitt SOLUTIONS to Homework Assignment 9: Brownian motion In Ross, read Sections 1.1-1.3 and 1.6. (The total required reading there
Preliminary statistics
 1 Preliminary statistics The solution of a geophysical inverse problem can be obtained by a combination of information from observed data, the theoretical relation between data and earth parameters (models),
1 Preliminary statistics The solution of a geophysical inverse problem can be obtained by a combination of information from observed data, the theoretical relation between data and earth parameters (models),
Multivariate Random Variable
 Multivariate Random Variable Author: Author: Andrés Hincapié and Linyi Cao This Version: August 7, 2016 Multivariate Random Variable 3 Now we consider models with more than one r.v. These are called multivariate
Multivariate Random Variable Author: Author: Andrés Hincapié and Linyi Cao This Version: August 7, 2016 Multivariate Random Variable 3 Now we consider models with more than one r.v. These are called multivariate
Topic 2: Probability & Distributions. Road Map Probability & Distributions. ECO220Y5Y: Quantitative Methods in Economics. Dr.
 Topic 2: Probability & Distributions ECO220Y5Y: Quantitative Methods in Economics Dr. Nick Zammit University of Toronto Department of Economics Room KN3272 n.zammit utoronto.ca November 21, 2017 Dr. Nick
Topic 2: Probability & Distributions ECO220Y5Y: Quantitative Methods in Economics Dr. Nick Zammit University of Toronto Department of Economics Room KN3272 n.zammit utoronto.ca November 21, 2017 Dr. Nick
Single Sample Means. SOCY601 Alan Neustadtl
 Single Sample Means SOCY601 Alan Neustadtl The Central Limit Theorem If we have a population measured by a variable with a mean µ and a standard deviation σ, and if all possible random samples of size
Single Sample Means SOCY601 Alan Neustadtl The Central Limit Theorem If we have a population measured by a variable with a mean µ and a standard deviation σ, and if all possible random samples of size
Chapter 5. Chapter 5 sections
 1 / 43 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
1 / 43 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions
STAT 302 Introduction to Probability Learning Outcomes. Textbook: A First Course in Probability by Sheldon Ross, 8 th ed.
 STAT 302 Introduction to Probability Learning Outcomes Textbook: A First Course in Probability by Sheldon Ross, 8 th ed. Chapter 1: Combinatorial Analysis Demonstrate the ability to solve combinatorial
STAT 302 Introduction to Probability Learning Outcomes Textbook: A First Course in Probability by Sheldon Ross, 8 th ed. Chapter 1: Combinatorial Analysis Demonstrate the ability to solve combinatorial
Chapter 3 Discrete Random Variables
 MICHIGAN STATE UNIVERSITY STT 351 SECTION 2 FALL 2008 LECTURE NOTES Chapter 3 Discrete Random Variables Nao Mimoto Contents 1 Random Variables 2 2 Probability Distributions for Discrete Variables 3 3 Expected
MICHIGAN STATE UNIVERSITY STT 351 SECTION 2 FALL 2008 LECTURE NOTES Chapter 3 Discrete Random Variables Nao Mimoto Contents 1 Random Variables 2 2 Probability Distributions for Discrete Variables 3 3 Expected
Table of Contents. Multivariate methods. Introduction II. Introduction I
 Table of Contents Introduction Antti Penttilä Department of Physics University of Helsinki Exactum summer school, 04 Construction of multinormal distribution Test of multinormality with 3 Interpretation
Table of Contents Introduction Antti Penttilä Department of Physics University of Helsinki Exactum summer school, 04 Construction of multinormal distribution Test of multinormality with 3 Interpretation
ENGI 3423 Introduction to Probability; Sets & Venn Diagrams Page 3-01
 ENGI 3423 Introduction to Probability; Sets & Venn Diagrams Page 3-01 Probability Decision trees θ 1 u 1 α 1 θ 2 u 2 Decision α 2 θ 1 u 3 Actions Chance nodes States of nature θ 2 u 4 Consequences; utility
ENGI 3423 Introduction to Probability; Sets & Venn Diagrams Page 3-01 Probability Decision trees θ 1 u 1 α 1 θ 2 u 2 Decision α 2 θ 1 u 3 Actions Chance nodes States of nature θ 2 u 4 Consequences; utility
Dependence. Practitioner Course: Portfolio Optimization. John Dodson. September 10, Dependence. John Dodson. Outline.
 Practitioner Course: Portfolio Optimization September 10, 2008 Before we define dependence, it is useful to define Random variables X and Y are independent iff For all x, y. In particular, F (X,Y ) (x,
Practitioner Course: Portfolio Optimization September 10, 2008 Before we define dependence, it is useful to define Random variables X and Y are independent iff For all x, y. In particular, F (X,Y ) (x,
Chapter 1 Statistical Reasoning Why statistics? Section 1.1 Basics of Probability Theory
 Chapter 1 Statistical Reasoning Why statistics? Uncertainty of nature (weather, earth movement, etc. ) Uncertainty in observation/sampling/measurement Variability of human operation/error imperfection
Chapter 1 Statistical Reasoning Why statistics? Uncertainty of nature (weather, earth movement, etc. ) Uncertainty in observation/sampling/measurement Variability of human operation/error imperfection
A Probability Review
 A Probability Review Outline: A probability review Shorthand notation: RV stands for random variable EE 527, Detection and Estimation Theory, # 0b 1 A Probability Review Reading: Go over handouts 2 5 in
A Probability Review Outline: A probability review Shorthand notation: RV stands for random variable EE 527, Detection and Estimation Theory, # 0b 1 A Probability Review Reading: Go over handouts 2 5 in
Dynamic System Identification using HDMR-Bayesian Technique
 Dynamic System Identification using HDMR-Bayesian Technique *Shereena O A 1) and Dr. B N Rao 2) 1), 2) Department of Civil Engineering, IIT Madras, Chennai 600036, Tamil Nadu, India 1) ce14d020@smail.iitm.ac.in
Dynamic System Identification using HDMR-Bayesian Technique *Shereena O A 1) and Dr. B N Rao 2) 1), 2) Department of Civil Engineering, IIT Madras, Chennai 600036, Tamil Nadu, India 1) ce14d020@smail.iitm.ac.in
Professor Terje Haukaas University of British Columbia, Vancouver Notation
 Notation This document establishes the notation that is employed throughout these notes. It is intended as a look-up source during the study of other documents and software on this website. As a general
Notation This document establishes the notation that is employed throughout these notes. It is intended as a look-up source during the study of other documents and software on this website. As a general
Set Operations. Combining sets into new sets
 Set Operations Combining sets into new sets Union of Sets The union of two sets is the set of all elements that are in one or the other set: A B = {x x A x B} The union is the set theoretic equivalent
Set Operations Combining sets into new sets Union of Sets The union of two sets is the set of all elements that are in one or the other set: A B = {x x A x B} The union is the set theoretic equivalent
Network Simulation Chapter 6: Output Data Analysis
 Network Simulation Chapter 6: Output Data Analysis Prof. Dr. Jürgen Jasperneite 1 Contents Introduction Types of simulation output Transient detection When to terminate a simulation 2 Prof. Dr. J ürgen
Network Simulation Chapter 6: Output Data Analysis Prof. Dr. Jürgen Jasperneite 1 Contents Introduction Types of simulation output Transient detection When to terminate a simulation 2 Prof. Dr. J ürgen
Semiparametric Regression
 Semiparametric Regression Patrick Breheny October 22 Patrick Breheny Survival Data Analysis (BIOS 7210) 1/23 Introduction Over the past few weeks, we ve introduced a variety of regression models under
Semiparametric Regression Patrick Breheny October 22 Patrick Breheny Survival Data Analysis (BIOS 7210) 1/23 Introduction Over the past few weeks, we ve introduced a variety of regression models under
Background on Coherent Systems
 2 Background on Coherent Systems 2.1 Basic Ideas We will use the term system quite freely and regularly, even though it will remain an undefined term throughout this monograph. As we all have some experience
2 Background on Coherent Systems 2.1 Basic Ideas We will use the term system quite freely and regularly, even though it will remain an undefined term throughout this monograph. As we all have some experience
Stress, Strain, Mohr s Circle
 Stress, Strain, Mohr s Circle The fundamental quantities in solid mechanics are stresses and strains. In accordance with the continuum mechanics assumption, the molecular structure of materials is neglected
Stress, Strain, Mohr s Circle The fundamental quantities in solid mechanics are stresses and strains. In accordance with the continuum mechanics assumption, the molecular structure of materials is neglected
Probability theory. References:
 Reasoning Under Uncertainty References: Probability theory Mathematical methods in artificial intelligence, Bender, Chapter 7. Expert systems: Principles and programming, g, Giarratano and Riley, pag.
Reasoning Under Uncertainty References: Probability theory Mathematical methods in artificial intelligence, Bender, Chapter 7. Expert systems: Principles and programming, g, Giarratano and Riley, pag.
First Year Examination Department of Statistics, University of Florida
 First Year Examination Department of Statistics, University of Florida August 19, 010, 8:00 am - 1:00 noon Instructions: 1. You have four hours to answer questions in this examination.. You must show your
First Year Examination Department of Statistics, University of Florida August 19, 010, 8:00 am - 1:00 noon Instructions: 1. You have four hours to answer questions in this examination.. You must show your
Introduction to Computational Finance and Financial Econometrics Probability Theory Review: Part 2
 Introduction to Computational Finance and Financial Econometrics Probability Theory Review: Part 2 Eric Zivot July 7, 2014 Bivariate Probability Distribution Example - Two discrete rv s and Bivariate pdf
Introduction to Computational Finance and Financial Econometrics Probability Theory Review: Part 2 Eric Zivot July 7, 2014 Bivariate Probability Distribution Example - Two discrete rv s and Bivariate pdf
MULTINOMIAL PROBABILITY DISTRIBUTION
 MTH/STA 56 MULTINOMIAL PROBABILITY DISTRIBUTION The multinomial probability distribution is an extension of the binomial probability distribution when the identical trial in the experiment has more than
MTH/STA 56 MULTINOMIAL PROBABILITY DISTRIBUTION The multinomial probability distribution is an extension of the binomial probability distribution when the identical trial in the experiment has more than
PROBABILITY AND RANDOM VARIABLES
 CHAPTER PROBABILIT AND RANDOM VARIABLES. Introduction.. Basics of Probability.3.. Terminology.3.. Probability of an event.5.3 Random Variables.3.3. Distribution function.3.3. Probability density function.7.3.3
CHAPTER PROBABILIT AND RANDOM VARIABLES. Introduction.. Basics of Probability.3.. Terminology.3.. Probability of an event.5.3 Random Variables.3.3. Distribution function.3.3. Probability density function.7.3.3
ASM Study Manual for Exam P, First Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA Errata
 ASM Study Manual for Exam P, First Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA (krzysio@krzysio.net) Errata Effective July 5, 3, only the latest edition of this manual will have its errata
ASM Study Manual for Exam P, First Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA (krzysio@krzysio.net) Errata Effective July 5, 3, only the latest edition of this manual will have its errata
Continuous Random Variables
 1 / 24 Continuous Random Variables Saravanan Vijayakumaran sarva@ee.iitb.ac.in Department of Electrical Engineering Indian Institute of Technology Bombay February 27, 2013 2 / 24 Continuous Random Variables
1 / 24 Continuous Random Variables Saravanan Vijayakumaran sarva@ee.iitb.ac.in Department of Electrical Engineering Indian Institute of Technology Bombay February 27, 2013 2 / 24 Continuous Random Variables
EE4601 Communication Systems
 EE4601 Communication Systems Week 2 Review of Probability, Important Distributions 0 c 2011, Georgia Institute of Technology (lect2 1) Conditional Probability Consider a sample space that consists of two
EE4601 Communication Systems Week 2 Review of Probability, Important Distributions 0 c 2011, Georgia Institute of Technology (lect2 1) Conditional Probability Consider a sample space that consists of two
Safety Envelope for Load Tolerance and Its Application to Fatigue Reliability Design
 Safety Envelope for Load Tolerance and Its Application to Fatigue Reliability Design Haoyu Wang * and Nam H. Kim University of Florida, Gainesville, FL 32611 Yoon-Jun Kim Caterpillar Inc., Peoria, IL 61656
Safety Envelope for Load Tolerance and Its Application to Fatigue Reliability Design Haoyu Wang * and Nam H. Kim University of Florida, Gainesville, FL 32611 Yoon-Jun Kim Caterpillar Inc., Peoria, IL 61656
Counting principles, including permutations and combinations.
 1 Counting principles, including permutations and combinations. The binomial theorem: expansion of a + b n, n ε N. THE PRODUCT RULE If there are m different ways of performing an operation and for each
1 Counting principles, including permutations and combinations. The binomial theorem: expansion of a + b n, n ε N. THE PRODUCT RULE If there are m different ways of performing an operation and for each
Introduction to Normal Distribution
 Introduction to Normal Distribution Nathaniel E. Helwig Assistant Professor of Psychology and Statistics University of Minnesota (Twin Cities) Updated 17-Jan-2017 Nathaniel E. Helwig (U of Minnesota) Introduction
Introduction to Normal Distribution Nathaniel E. Helwig Assistant Professor of Psychology and Statistics University of Minnesota (Twin Cities) Updated 17-Jan-2017 Nathaniel E. Helwig (U of Minnesota) Introduction
Turbulent Flows. U (n) (m s 1 ) on the nth repetition of a turbulent flow experiment. CHAPTER 3: THE RANDOM NATURE OF TURBULENCE
 U (n) (m s ) 5 5 2 4 n Figure 3.: Sketch of the value U (n) of the random velocity variable U on the nth repetition of a turbulent flow experiment. (a) x (t) 2-2 (b) (c) x (t) 2-2 4 2 x (t) x (t) -2-4
U (n) (m s ) 5 5 2 4 n Figure 3.: Sketch of the value U (n) of the random velocity variable U on the nth repetition of a turbulent flow experiment. (a) x (t) 2-2 (b) (c) x (t) 2-2 4 2 x (t) x (t) -2-4
ASM Study Manual for Exam P, Second Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA Errata
 ASM Study Manual for Exam P, Second Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA (krzysio@krzysio.net) Errata Effective July 5, 3, only the latest edition of this manual will have its errata
ASM Study Manual for Exam P, Second Edition By Dr. Krzysztof M. Ostaszewski, FSA, CFA, MAAA (krzysio@krzysio.net) Errata Effective July 5, 3, only the latest edition of this manual will have its errata
a. See the textbook for examples of proving logical equivalence using truth tables. b. There is a real number x for which f (x) < 0. (x 1) 2 > 0.
 For some problems, several sample proofs are given here. Problem 1. a. See the textbook for examples of proving logical equivalence using truth tables. b. There is a real number x for which f (x) < 0.
For some problems, several sample proofs are given here. Problem 1. a. See the textbook for examples of proving logical equivalence using truth tables. b. There is a real number x for which f (x) < 0.
Structural Reliability
 Structural Reliability Thuong Van DANG May 28, 2018 1 / 41 2 / 41 Introduction to Structural Reliability Concept of Limit State and Reliability Review of Probability Theory First Order Second Moment Method
Structural Reliability Thuong Van DANG May 28, 2018 1 / 41 2 / 41 Introduction to Structural Reliability Concept of Limit State and Reliability Review of Probability Theory First Order Second Moment Method
Stochastic optimization - how to improve computational efficiency?
 Stochastic optimization - how to improve computational efficiency? Christian Bucher Center of Mechanics and Structural Dynamics Vienna University of Technology & DYNARDO GmbH, Vienna Presentation at Czech
Stochastic optimization - how to improve computational efficiency? Christian Bucher Center of Mechanics and Structural Dynamics Vienna University of Technology & DYNARDO GmbH, Vienna Presentation at Czech
A Study of System Reliability Analysis Using Linear Programming
 A Study of System Reliability Analysis Using Linear Programming Yi Chang* 1 and Yasuhiro Mori 2 1 Graduate Student, Department of Environmental Engineering and Architecture, Nagoya University, Japan 2
A Study of System Reliability Analysis Using Linear Programming Yi Chang* 1 and Yasuhiro Mori 2 1 Graduate Student, Department of Environmental Engineering and Architecture, Nagoya University, Japan 2
Learning Objectives for Stat 225
 Learning Objectives for Stat 225 08/20/12 Introduction to Probability: Get some general ideas about probability, and learn how to use sample space to compute the probability of a specific event. Set Theory:
Learning Objectives for Stat 225 08/20/12 Introduction to Probability: Get some general ideas about probability, and learn how to use sample space to compute the probability of a specific event. Set Theory:
Example: An experiment can either result in success or failure with probability θ and (1 θ) respectively. The experiment is performed independently
 Chapter 3 Sufficient statistics and variance reduction Let X 1,X 2,...,X n be a random sample from a certain distribution with p.m/d.f fx θ. A function T X 1,X 2,...,X n = T X of these observations is
Chapter 3 Sufficient statistics and variance reduction Let X 1,X 2,...,X n be a random sample from a certain distribution with p.m/d.f fx θ. A function T X 1,X 2,...,X n = T X of these observations is
1 Presessional Probability
 1 Presessional Probability Probability theory is essential for the development of mathematical models in finance, because of the randomness nature of price fluctuations in the markets. This presessional
1 Presessional Probability Probability theory is essential for the development of mathematical models in finance, because of the randomness nature of price fluctuations in the markets. This presessional
EECS 126 Probability and Random Processes University of California, Berkeley: Spring 2015 Abhay Parekh February 17, 2015.
 EECS 126 Probability and Random Processes University of California, Berkeley: Spring 2015 Abhay Parekh February 17, 2015 Midterm Exam Last name First name SID Rules. You have 80 mins (5:10pm - 6:30pm)
EECS 126 Probability and Random Processes University of California, Berkeley: Spring 2015 Abhay Parekh February 17, 2015 Midterm Exam Last name First name SID Rules. You have 80 mins (5:10pm - 6:30pm)
BOOLEAN ALGEBRA INTRODUCTION SUBSETS
 BOOLEAN ALGEBRA M. Ragheb 1/294/2018 INTRODUCTION Modern algebra is centered around the concept of an algebraic system: A, consisting of a set of elements: ai, i=1, 2,, which are combined by a set of operations
BOOLEAN ALGEBRA M. Ragheb 1/294/2018 INTRODUCTION Modern algebra is centered around the concept of an algebraic system: A, consisting of a set of elements: ai, i=1, 2,, which are combined by a set of operations
Why study probability? Set theory. ECE 6010 Lecture 1 Introduction; Review of Random Variables
 ECE 6010 Lecture 1 Introduction; Review of Random Variables Readings from G&S: Chapter 1. Section 2.1, Section 2.3, Section 2.4, Section 3.1, Section 3.2, Section 3.5, Section 4.1, Section 4.2, Section
ECE 6010 Lecture 1 Introduction; Review of Random Variables Readings from G&S: Chapter 1. Section 2.1, Section 2.3, Section 2.4, Section 3.1, Section 3.2, Section 3.5, Section 4.1, Section 4.2, Section
Local and Global Sensitivity Analysis
 Omar 1,2 1 Duke University Department of Mechanical Engineering & Materials Science omar.knio@duke.edu 2 KAUST Division of Computer, Electrical, Mathematical Science & Engineering omar.knio@kaust.edu.sa
Omar 1,2 1 Duke University Department of Mechanical Engineering & Materials Science omar.knio@duke.edu 2 KAUST Division of Computer, Electrical, Mathematical Science & Engineering omar.knio@kaust.edu.sa
Statistical Inference
 Statistical Inference Lecture 1: Probability Theory MING GAO DASE @ ECNU (for course related communications) mgao@dase.ecnu.edu.cn Sep. 11, 2018 Outline Introduction Set Theory Basics of Probability Theory
Statistical Inference Lecture 1: Probability Theory MING GAO DASE @ ECNU (for course related communications) mgao@dase.ecnu.edu.cn Sep. 11, 2018 Outline Introduction Set Theory Basics of Probability Theory
G12MAN Mathematical Analysis Fully-justified answers to Revision Quiz questions
 G12MAN Mathematical Analysis Fully-justified answers to Revision Quiz questions Remember that, unless otherwise specified or not applicable for some reason), you MUST justify your answers to questions
G12MAN Mathematical Analysis Fully-justified answers to Revision Quiz questions Remember that, unless otherwise specified or not applicable for some reason), you MUST justify your answers to questions
Similarity Beyond Correlation: Symmetry-Based Approach
 University of Texas at El Paso DigitalCommons@UTEP Departmental Technical Reports (CS) Department of Computer Science 6-2016 Similarity Beyond Correlation: Symmetry-Based Approach Ildar Batyrshin Instituto
University of Texas at El Paso DigitalCommons@UTEP Departmental Technical Reports (CS) Department of Computer Science 6-2016 Similarity Beyond Correlation: Symmetry-Based Approach Ildar Batyrshin Instituto
Making Hard Decision. Probability Basics. ENCE 627 Decision Analysis for Engineering
 CHAPTER Duxbury Thomson Learning Making Hard Decision Probability asics Third Edition A. J. Clark School of Engineering Department of Civil and Environmental Engineering 7b FALL 003 y Dr. Ibrahim. Assakkaf
CHAPTER Duxbury Thomson Learning Making Hard Decision Probability asics Third Edition A. J. Clark School of Engineering Department of Civil and Environmental Engineering 7b FALL 003 y Dr. Ibrahim. Assakkaf
STT 843 Key to Homework 1 Spring 2018
 STT 843 Key to Homework Spring 208 Due date: Feb 4, 208 42 (a Because σ = 2, σ 22 = and ρ 2 = 05, we have σ 2 = ρ 2 σ σ22 = 2/2 Then, the mean and covariance of the bivariate normal is µ = ( 0 2 and Σ
STT 843 Key to Homework Spring 208 Due date: Feb 4, 208 42 (a Because σ = 2, σ 22 = and ρ 2 = 05, we have σ 2 = ρ 2 σ σ22 = 2/2 Then, the mean and covariance of the bivariate normal is µ = ( 0 2 and Σ
Probability Theory and Statistics. Peter Jochumzen
 Probability Theory and Statistics Peter Jochumzen April 18, 2016 Contents 1 Probability Theory And Statistics 3 1.1 Experiment, Outcome and Event................................ 3 1.2 Probability............................................
Probability Theory and Statistics Peter Jochumzen April 18, 2016 Contents 1 Probability Theory And Statistics 3 1.1 Experiment, Outcome and Event................................ 3 1.2 Probability............................................
Estimating Risk of Failure of Engineering Structures using Predictive Likelihood
 Dublin Institute of Technology ARROW@DIT Conference papers School of Civil and Structural Engineering 2006-1 Estimating Risk of Failure of Engineering Structures using Predictive Likelihood Colin C. Caprani
Dublin Institute of Technology ARROW@DIT Conference papers School of Civil and Structural Engineering 2006-1 Estimating Risk of Failure of Engineering Structures using Predictive Likelihood Colin C. Caprani
Chapter 2. Vectors and Vector Spaces
 2.1. Operations on Vectors 1 Chapter 2. Vectors and Vector Spaces Section 2.1. Operations on Vectors Note. In this section, we define several arithmetic operations on vectors (especially, vector addition
2.1. Operations on Vectors 1 Chapter 2. Vectors and Vector Spaces Section 2.1. Operations on Vectors Note. In this section, we define several arithmetic operations on vectors (especially, vector addition
Midterm #1 - Solutions
 Midterm # - olutions Math/tat 94 Quizzes. Let A be the event Andrea and Bill are both in class. The complementary event is (choose one): A c = Neither Andrea nor Bill are in class A c = Bill is not in
Midterm # - olutions Math/tat 94 Quizzes. Let A be the event Andrea and Bill are both in class. The complementary event is (choose one): A c = Neither Andrea nor Bill are in class A c = Bill is not in
EE/CpE 345. Modeling and Simulation. Fall Class 9
 EE/CpE 345 Modeling and Simulation Class 9 208 Input Modeling Inputs(t) Actual System Outputs(t) Parameters? Simulated System Outputs(t) The input data is the driving force for the simulation - the behavior
EE/CpE 345 Modeling and Simulation Class 9 208 Input Modeling Inputs(t) Actual System Outputs(t) Parameters? Simulated System Outputs(t) The input data is the driving force for the simulation - the behavior
CME 106: Review Probability theory
 : Probability theory Sven Schmit April 3, 2015 1 Overview In the first half of the course, we covered topics from probability theory. The difference between statistics and probability theory is the following:
: Probability theory Sven Schmit April 3, 2015 1 Overview In the first half of the course, we covered topics from probability theory. The difference between statistics and probability theory is the following:
Ph/CS 219b. Exercises Due: Thursday 22 February 2018
 Ph/CS 219b 3.1 Bound on D-dimensional codes Exercises Due: Thursday 22 February 2018 In class we proved a bound on [[n, k, d]] for local stabilizer codes in 2 dimensions: kd 2 = O(n), where k is the number
Ph/CS 219b 3.1 Bound on D-dimensional codes Exercises Due: Thursday 22 February 2018 In class we proved a bound on [[n, k, d]] for local stabilizer codes in 2 dimensions: kd 2 = O(n), where k is the number
4 CONNECTED PROJECTIVE-PLANAR GRAPHS ARE HAMILTONIAN. Robin Thomas* Xingxing Yu**
 4 CONNECTED PROJECTIVE-PLANAR GRAPHS ARE HAMILTONIAN Robin Thomas* Xingxing Yu** School of Mathematics Georgia Institute of Technology Atlanta, Georgia 30332, USA May 1991, revised 23 October 1993. Published
4 CONNECTED PROJECTIVE-PLANAR GRAPHS ARE HAMILTONIAN Robin Thomas* Xingxing Yu** School of Mathematics Georgia Institute of Technology Atlanta, Georgia 30332, USA May 1991, revised 23 October 1993. Published
Probability: Sets, Sample Spaces, Events
 Probability: Sets, Sample Spaces, Events Engineering Statistics Section 2.1 Josh Engwer TTU 01 February 2016 Josh Engwer (TTU) Probability: Sets, Sample Spaces, Events 01 February 2016 1 / 29 The Need
Probability: Sets, Sample Spaces, Events Engineering Statistics Section 2.1 Josh Engwer TTU 01 February 2016 Josh Engwer (TTU) Probability: Sets, Sample Spaces, Events 01 February 2016 1 / 29 The Need
3 PROBABILITY TOPICS
 Chapter 3 Probability Topics 135 3 PROBABILITY TOPICS Figure 3.1 Meteor showers are rare, but the probability of them occurring can be calculated. (credit: Navicore/flickr) Introduction It is often necessary
Chapter 3 Probability Topics 135 3 PROBABILITY TOPICS Figure 3.1 Meteor showers are rare, but the probability of them occurring can be calculated. (credit: Navicore/flickr) Introduction It is often necessary
MAS3301 Bayesian Statistics
 MAS3301 Bayesian Statistics M. Farrow School of Mathematics and Statistics Newcastle University Semester, 008-9 1 13 Sequential updating 13.1 Theory We have seen how we can change our beliefs about an
MAS3301 Bayesian Statistics M. Farrow School of Mathematics and Statistics Newcastle University Semester, 008-9 1 13 Sequential updating 13.1 Theory We have seen how we can change our beliefs about an
BACKGROUND NOTES FYS 4550/FYS EXPERIMENTAL HIGH ENERGY PHYSICS AUTUMN 2016 PROBABILITY A. STRANDLIE NTNU AT GJØVIK AND UNIVERSITY OF OSLO
 ACKGROUND NOTES FYS 4550/FYS9550 - EXERIMENTAL HIGH ENERGY HYSICS AUTUMN 2016 ROAILITY A. STRANDLIE NTNU AT GJØVIK AND UNIVERSITY OF OSLO efore embarking on the concept of probability, we will first define
ACKGROUND NOTES FYS 4550/FYS9550 - EXERIMENTAL HIGH ENERGY HYSICS AUTUMN 2016 ROAILITY A. STRANDLIE NTNU AT GJØVIK AND UNIVERSITY OF OSLO efore embarking on the concept of probability, we will first define
College Algebra Through Problem Solving (2018 Edition)
 City University of New York (CUNY) CUNY Academic Works Open Educational Resources Queensborough Community College Winter 1-25-2018 College Algebra Through Problem Solving (2018 Edition) Danielle Cifone
City University of New York (CUNY) CUNY Academic Works Open Educational Resources Queensborough Community College Winter 1-25-2018 College Algebra Through Problem Solving (2018 Edition) Danielle Cifone
MA/ST 810 Mathematical-Statistical Modeling and Analysis of Complex Systems
 MA/ST 810 Mathematical-Statistical Modeling and Analysis of Complex Systems Review of Basic Probability The fundamentals, random variables, probability distributions Probability mass/density functions
MA/ST 810 Mathematical-Statistical Modeling and Analysis of Complex Systems Review of Basic Probability The fundamentals, random variables, probability distributions Probability mass/density functions
COMPOSITE RELIABILITY MODELS FOR SYSTEMS WITH TWO DISTINCT KINDS OF STOCHASTIC DEPENDENCES BETWEEN THEIR COMPONENTS LIFE TIMES
 COMPOSITE RELIABILITY MODELS FOR SYSTEMS WITH TWO DISTINCT KINDS OF STOCHASTIC DEPENDENCES BETWEEN THEIR COMPONENTS LIFE TIMES Jerzy Filus Department of Mathematics and Computer Science, Oakton Community
COMPOSITE RELIABILITY MODELS FOR SYSTEMS WITH TWO DISTINCT KINDS OF STOCHASTIC DEPENDENCES BETWEEN THEIR COMPONENTS LIFE TIMES Jerzy Filus Department of Mathematics and Computer Science, Oakton Community
Review of probability
 Review of probability Computer Sciences 760 Spring 2014 http://pages.cs.wisc.edu/~dpage/cs760/ Goals for the lecture you should understand the following concepts definition of probability random variables
Review of probability Computer Sciences 760 Spring 2014 http://pages.cs.wisc.edu/~dpage/cs760/ Goals for the lecture you should understand the following concepts definition of probability random variables
Math 180B Problem Set 3
 Math 180B Problem Set 3 Problem 1. (Exercise 3.1.2) Solution. By the definition of conditional probabilities we have Pr{X 2 = 1, X 3 = 1 X 1 = 0} = Pr{X 3 = 1 X 2 = 1, X 1 = 0} Pr{X 2 = 1 X 1 = 0} = P
Math 180B Problem Set 3 Problem 1. (Exercise 3.1.2) Solution. By the definition of conditional probabilities we have Pr{X 2 = 1, X 3 = 1 X 1 = 0} = Pr{X 3 = 1 X 2 = 1, X 1 = 0} Pr{X 2 = 1 X 1 = 0} = P
Problem 1. Problem 2. Problem 3. Problem 4
 Problem Let A be the event that the fungus is present, and B the event that the staph-bacteria is present. We have P A = 4, P B = 9, P B A =. We wish to find P AB, to do this we use the multiplication
Problem Let A be the event that the fungus is present, and B the event that the staph-bacteria is present. We have P A = 4, P B = 9, P B A =. We wish to find P AB, to do this we use the multiplication
1 Basic Combinatorics
 1 Basic Combinatorics 1.1 Sets and sequences Sets. A set is an unordered collection of distinct objects. The objects are called elements of the set. We use braces to denote a set, for example, the set
1 Basic Combinatorics 1.1 Sets and sequences Sets. A set is an unordered collection of distinct objects. The objects are called elements of the set. We use braces to denote a set, for example, the set
Math 180B, Winter Notes on covariance and the bivariate normal distribution
 Math 180B Winter 015 Notes on covariance and the bivariate normal distribution 1 Covariance If and are random variables with finite variances then their covariance is the quantity 11 Cov := E[ µ ] where
Math 180B Winter 015 Notes on covariance and the bivariate normal distribution 1 Covariance If and are random variables with finite variances then their covariance is the quantity 11 Cov := E[ µ ] where
Value of Information Analysis with Structural Reliability Methods
 Accepted for publication in Structural Safety, special issue in the honor of Prof. Wilson Tang August 2013 Value of Information Analysis with Structural Reliability Methods Daniel Straub Engineering Risk
Accepted for publication in Structural Safety, special issue in the honor of Prof. Wilson Tang August 2013 Value of Information Analysis with Structural Reliability Methods Daniel Straub Engineering Risk
ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page α 2 θ 1 u 3. wear coat. θ 2 = warm u 2 = sweaty! θ 1 = cold u 3 = brrr!
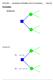 ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page 2-01 Probability Decision trees u 1 u 2 α 2 θ 1 u 3 θ 2 u 4 Example 2.01 θ 1 = cold u 1 = snug! α 1 wear coat θ 2 = warm u 2 = sweaty! θ
ENGI 4421 Introduction to Probability; Sets & Venn Diagrams Page 2-01 Probability Decision trees u 1 u 2 α 2 θ 1 u 3 θ 2 u 4 Example 2.01 θ 1 = cold u 1 = snug! α 1 wear coat θ 2 = warm u 2 = sweaty! θ
Name of the Student: Problems on Discrete & Continuous R.Vs
 Engineering Mathematics 08 SUBJECT NAME : Probability & Random Processes SUBJECT CODE : MA645 MATERIAL NAME : University Questions REGULATION : R03 UPDATED ON : November 07 (Upto N/D 07 Q.P) (Scan the
Engineering Mathematics 08 SUBJECT NAME : Probability & Random Processes SUBJECT CODE : MA645 MATERIAL NAME : University Questions REGULATION : R03 UPDATED ON : November 07 (Upto N/D 07 Q.P) (Scan the
STAT T&E COE-Report Reliability Test Planning for Mean Time Between Failures. Best Practice. Authored by: Jennifer Kensler, PhD STAT T&E COE
 Reliability est Planning for Mean ime Between Failures Best Practice Authored by: Jennifer Kensler, PhD SA &E COE March 21, 2014 he goal of the SA &E COE is to assist in developing rigorous, defensible
Reliability est Planning for Mean ime Between Failures Best Practice Authored by: Jennifer Kensler, PhD SA &E COE March 21, 2014 he goal of the SA &E COE is to assist in developing rigorous, defensible
Section 8.1. Vector Notation
 Section 8.1 Vector Notation Definition 8.1 Random Vector A random vector is a column vector X = [ X 1 ]. X n Each Xi is a random variable. Definition 8.2 Vector Sample Value A sample value of a random
Section 8.1 Vector Notation Definition 8.1 Random Vector A random vector is a column vector X = [ X 1 ]. X n Each Xi is a random variable. Definition 8.2 Vector Sample Value A sample value of a random
Linear Regression Models
 Linear Regression Models Model Description and Model Parameters Modelling is a central theme in these notes. The idea is to develop and continuously improve a library of predictive models for hazards,
Linear Regression Models Model Description and Model Parameters Modelling is a central theme in these notes. The idea is to develop and continuously improve a library of predictive models for hazards,
WISE Power Tutorial Answer Sheet
 ame Date Class WISE Power Tutorial Answer Sheet Power: The B.E.A.. Mnemonic Select true or false for each scenario: (Assuming no other changes) True False 1. As effect size increases, power decreases.
ame Date Class WISE Power Tutorial Answer Sheet Power: The B.E.A.. Mnemonic Select true or false for each scenario: (Assuming no other changes) True False 1. As effect size increases, power decreases.
Probability and Stochastic Processes
 Probability and Stochastic Processes A Friendly Introduction Electrical and Computer Engineers Third Edition Roy D. Yates Rutgers, The State University of New Jersey David J. Goodman New York University
Probability and Stochastic Processes A Friendly Introduction Electrical and Computer Engineers Third Edition Roy D. Yates Rutgers, The State University of New Jersey David J. Goodman New York University
L2: Review of probability and statistics
 Probability L2: Review of probability and statistics Definition of probability Axioms and properties Conditional probability Bayes theorem Random variables Definition of a random variable Cumulative distribution
Probability L2: Review of probability and statistics Definition of probability Axioms and properties Conditional probability Bayes theorem Random variables Definition of a random variable Cumulative distribution
CHAPTER 1. Preliminaries. 1 Set Theory
 CHAPTER 1 Preliminaries 1 et Theory We assume that the reader is familiar with basic set theory. In this paragraph, we want to recall the relevant definitions and fix the notation. Our approach to set
CHAPTER 1 Preliminaries 1 et Theory We assume that the reader is familiar with basic set theory. In this paragraph, we want to recall the relevant definitions and fix the notation. Our approach to set
2012 Assessment Report. Mathematics with Calculus Level 3 Statistics and Modelling Level 3
 National Certificate of Educational Achievement 2012 Assessment Report Mathematics with Calculus Level 3 Statistics and Modelling Level 3 90635 Differentiate functions and use derivatives to solve problems
National Certificate of Educational Achievement 2012 Assessment Report Mathematics with Calculus Level 3 Statistics and Modelling Level 3 90635 Differentiate functions and use derivatives to solve problems
Venn Diagrams; Probability Laws. Notes. Set Operations and Relations. Venn Diagram 2.1. Venn Diagrams; Probability Laws. Notes
 Lecture 2 s; Text: A Course in Probability by Weiss 2.4 STAT 225 Introduction to Probability Models January 8, 2014 s; Whitney Huang Purdue University 2.1 Agenda s; 1 2 2.2 Intersection: the intersection
Lecture 2 s; Text: A Course in Probability by Weiss 2.4 STAT 225 Introduction to Probability Models January 8, 2014 s; Whitney Huang Purdue University 2.1 Agenda s; 1 2 2.2 Intersection: the intersection
EE/CpE 345. Modeling and Simulation. Fall Class 10 November 18, 2002
 EE/CpE 345 Modeling and Simulation Class 0 November 8, 2002 Input Modeling Inputs(t) Actual System Outputs(t) Parameters? Simulated System Outputs(t) The input data is the driving force for the simulation
EE/CpE 345 Modeling and Simulation Class 0 November 8, 2002 Input Modeling Inputs(t) Actual System Outputs(t) Parameters? Simulated System Outputs(t) The input data is the driving force for the simulation
Introductory Analysis I Fall 2014 Homework #5 Solutions
 Introductory Analysis I Fall 2014 Homework #5 Solutions 6. Let M be a metric space, let C D M. Now we can think of C as a subset of the metric space M or as a subspace of the metric space D (D being a
Introductory Analysis I Fall 2014 Homework #5 Solutions 6. Let M be a metric space, let C D M. Now we can think of C as a subset of the metric space M or as a subspace of the metric space D (D being a
RESPONSE SPECTRUM METHOD FOR ESTIMATION OF PEAK FLOOR ACCELERATION DEMAND
 RESPONSE SPECTRUM METHOD FOR ESTIMATION OF PEAK FLOOR ACCELERATION DEMAND Shahram Taghavi 1 and Eduardo Miranda 2 1 Senior catastrophe risk modeler, Risk Management Solutions, CA, USA 2 Associate Professor,
RESPONSE SPECTRUM METHOD FOR ESTIMATION OF PEAK FLOOR ACCELERATION DEMAND Shahram Taghavi 1 and Eduardo Miranda 2 1 Senior catastrophe risk modeler, Risk Management Solutions, CA, USA 2 Associate Professor,
Mathematics Review for Business PhD Students
 Mathematics Review for Business PhD Students Anthony M. Marino Department of Finance and Business Economics Marshall School of Business Lecture 1: Introductory Material Sets The Real Number System Functions,
Mathematics Review for Business PhD Students Anthony M. Marino Department of Finance and Business Economics Marshall School of Business Lecture 1: Introductory Material Sets The Real Number System Functions,
In this initial chapter, you will be introduced to, or more than likely be reminded of, a
 1 Sets In this initial chapter, you will be introduced to, or more than likely be reminded of, a fundamental idea that occurs throughout mathematics: sets. Indeed, a set is an object from which every mathematical
1 Sets In this initial chapter, you will be introduced to, or more than likely be reminded of, a fundamental idea that occurs throughout mathematics: sets. Indeed, a set is an object from which every mathematical
E X A M. Probability Theory and Stochastic Processes Date: December 13, 2016 Duration: 4 hours. Number of pages incl.
 E X A M Course code: Course name: Number of pages incl. front page: 6 MA430-G Probability Theory and Stochastic Processes Date: December 13, 2016 Duration: 4 hours Resources allowed: Notes: Pocket calculator,
E X A M Course code: Course name: Number of pages incl. front page: 6 MA430-G Probability Theory and Stochastic Processes Date: December 13, 2016 Duration: 4 hours Resources allowed: Notes: Pocket calculator,
Product measure and Fubini s theorem
 Chapter 7 Product measure and Fubini s theorem This is based on [Billingsley, Section 18]. 1. Product spaces Suppose (Ω 1, F 1 ) and (Ω 2, F 2 ) are two probability spaces. In a product space Ω = Ω 1 Ω
Chapter 7 Product measure and Fubini s theorem This is based on [Billingsley, Section 18]. 1. Product spaces Suppose (Ω 1, F 1 ) and (Ω 2, F 2 ) are two probability spaces. In a product space Ω = Ω 1 Ω
Econometrics of financial markets, -solutions to seminar 1. Problem 1
 Econometrics of financial markets, -solutions to seminar 1. Problem 1 a) Estimate with OLS. For any regression y i α + βx i + u i for OLS to be unbiased we need cov (u i,x j )0 i, j. For the autoregressive
Econometrics of financial markets, -solutions to seminar 1. Problem 1 a) Estimate with OLS. For any regression y i α + βx i + u i for OLS to be unbiased we need cov (u i,x j )0 i, j. For the autoregressive
Two hours. To be supplied by the Examinations Office: Mathematical Formula Tables and Statistical Tables THE UNIVERSITY OF MANCHESTER.
 Two hours MATH38181 To be supplied by the Examinations Office: Mathematical Formula Tables and Statistical Tables THE UNIVERSITY OF MANCHESTER EXTREME VALUES AND FINANCIAL RISK Examiner: Answer any FOUR
Two hours MATH38181 To be supplied by the Examinations Office: Mathematical Formula Tables and Statistical Tables THE UNIVERSITY OF MANCHESTER EXTREME VALUES AND FINANCIAL RISK Examiner: Answer any FOUR
