Lovász Local Lemma a new tool to asymptotic enumeration?
|
|
|
- Dylan Ray
- 6 years ago
- Views:
Transcription
1 Lovász Local Lemma a ew tool to asymptotic eumeratio? Liyua Licol Lu László Székely Uiversity of South Carolia Supported by NSF DMS
2 Overview LLL ad its geeralizatios LLL a istace of the Poisso paradigm New egative depedecy graphs Applicatios: Permutatio eumeratio Lati rectagle eumeratio Regular graph eumeratio A joke
3 Whe oe of the evets happe Assume that A 1,A 2,,A are evets i a probability space Ω. How ca we ifer A i? i=1 If A i s are mutually idepedet, P(A i )<1, the P A i i=1 = P ( A ) i = ( 1 P( A i )) > 0 i=1 i=1 If ( ), the P A i < 1 i=1 P i=1 A i = P i=1 A i = 1 P i=1 A i 1 ( ) P A i > 0 i=1
4 A way to combie argumets: Assume that A 1,A 2,,A are evets i a probability space Ω. Graph G is a depedecy graph of the evets A 1,A 2,,A, if V(G)={1,2,,} ad each A i is idepedet of the elemets of the evet algebra geerated by { A j :ij E( G) }
5 Lovász Local Lemma (Erdős-Lovász 1975) Assume G is a depedecy graph for A 1,A 2,,A, ad d=max degree i G If for i=1,2,,, P(A i )<p, ad e(d+1)p<1, the P i=1 A i > 0
6 Lovász Local Lemma (Specer) Assume G is a depedecy graph for A 1,A 2,,A If there exist x 1,x 2,,x i [0,1) such that the P ( ) x i 1 x j P A i i=1 A i ( ) ij E G ( ) ( ) 1 x i > 0 i=1
7 Negative depedecy graphs Assume that A 1,A 2,,A are evets i a probability space Ω. Graph G with V(G)={1,2,,} is a egative depedecy graph for evets A 1,A 2,,A, if i S { j :ij E( G) } P j S A j implies > 0 P A i A j j S P A i ( )
8 LLL: Erdős-Specer 1991, Albert-Freeze-Reed 1995, Ku Assume G is a egative depedecy graph for A 1,A 2,,A, exist x 1,x 2,,x i [0,1) such that, P( A i ) x ( i 1 x ) j, the P i=1 A i ( ) ( ) ij E G 1 x i > 0 i=1 Settig x i =1/(d+1) implies the uiform versio both for depedecy ad egative depedecy
9 Needle i the haystack LLL has bee i use for existece proofs to exhibit the existece of evets of tiy probability. Is it good for other purposes? Where to fid egative depedecy graphs that are ot depedecy graphs?
10 Poisso paradigm Assume that A 1,A 2,,A are evets i a probability space Ω, p(a i )=p i. Let X deote the sum of idicator variables of the evets. If depedecies are rare, X ca be approximated with Poisso distributio of mea Σ p i. X~Poisso meas usig k=0, P i=1 A i ( ) = e µ µ k / k! P X = k e µ = e i=1 p i
11 Models for the Poisso paradigm Che-Stei method Jaso iequality 1990 Bru s sieve Now: LLL. Assume G is egative depedecy graph, 0<ε<0.14. i : P A i ( ) < ε; P A j 1+ 3ε ( ) < ε imply P A j e j=1 ( ) ij E G j =1 ( ) ( ) P A j
12 Two egative depedecy graphs H is a complete graph K N or a complete bipartite graph K N,L ; Ω is the uiform probability space of maximal matchigs i H. For a partial matchig M, the caoical evet A M = F Ω M F { } Caoical evets A M ad A M* are i coflict: M ad M* have o commo extesio ito maximal matchig, i.e. A M A M * =
13 Mai theorem For a graph H=K N or K N,L, ad a family of caoical evets, if the edges of the graph G are defied by coflicts, the G is a egative depedecy graph. This theorem fails to exted for the hexago H=C 6
14 Hexago example Two perfect matchigs e p( A ) e = p( A ) f = 1 2 f ( ) = p A e A f p A e A f ( ) p( A ) f = 1 2 = 1 p( A ) 1 e 2
15 Relevace for permutatio eumeratio problems Deragemets avoid: 2-cycle free avoids: 3-cycle free avoids: i i i j i j i j k i j k
16 ε-ear-positive depedecy graphs Assume that A 1,A 2,,A are evets i a probability space Ω. Graph G with V(G)={1,2,,} is a ε ear-positive depedecy graph of the evets A 1,A 2,,A, ( ) = 0 ij E(G) implies P A i A j i S { j :ij E( G) } P A j j S > 0 implies P A i j S A j ( 1 ε)p A i ( )
17 Quotiet graphs Assume G is a egative depedecy graph for A 1,A 2,,A. Assume further that V(G) is partitioed ito classes such that evets i the same class are disjoit. For every partitio class J, let B J = A j. The quotiet graph of G is a j J egative depedecy graph for the evets B J
18 Quotiet graphs of ε-ear-positive depedecy graphs If the oly edges of the quotiet graph of a ε ear-positive depedecy graph are loops, the the quotiet graph is also a ε-ear-positive depedecy graph.
19 Asymptotic results A collectio of matchigs M is regular, if for every i, every vertex is covered d i times by i-elemet matchigs from M A collectio of matchigs M is δ-sparse (details avoided!) Negative depedecy graphs of δ- sparse collectios of matchigs are also ε-ear-positive depedecy graphs
20 Asymptotic results a theorem A collectio of matchigs M i K N or K N,N is regular, r is the largest matchig size, M is δ-sparse. Set µ = P( A ) M over M. Suppose δ=o(µ -1 ), µ is separated from 0, ad r = o( N ) The P M A M ( ) µ = o Nr 3/2 = ( 1 + o(1) )e µ
21 Cosequeces for permutatio eumeratio For k fixed, the proportio of k-cycle free permutatios is ( 1 o( 1) )e 1 k (Beder 70 s) If max K grows slowly with, the proportio of permutatios free of cycles of legth from set K is ( 1 o( 1) )e k K 1 k
22 Lati rectagles Lati rectagle: k times array filled with etries 1,2,,; puttig a permutatio ito every row ad ot repeatig a etry i ay colum (k ) L(k,)= umber of k times Lati rectagles
23 Eumeratio of Lati rectagles L(2,)=! (# of deragemets) (!) 2 e -1 Riorda 1944 L(3,) (!) 3 e -3 Erdős-Kaplasky 1946 L( k,) (! ) k e k 2 for k = o (( log) 3 ) 2 Yamamoto 1951 exteded to ( ) k = o 1 3 ε
24 Eumeratio of Lati rectagles Stei 1978 (usig Che-Stei method) L( k,) (! ) k e k 2 k3 6 ( ) for k = o 1 2 Godsil ad McKay 1990 refied the asymptotics to make it work for ( ) k = o 6 7
25 Eumeratio of Lati rectagles Skau 1990 (usig va der Waerde s iequality for the permaet) (! ) k k 1 1 r r =1 ad with this matched Stei s lower boud o a slightly smaller rage: L( k,) ( 1 o(1) )(! ) k e L( k,) k 2 k3 6 ( for k = o 1 2 ) log
26 Eumeratio of Lati rectagles Quotiet graph versio of the egative depedecy graph LLL yields Skau s lower boud: matches the rage of Stei s lower boud: L k, (! ) k k 1 1 r r =1 ( ) ( 1 o(1) )(! ) k e L( k,) k 2 k3 6 ( for k = o 1 2 ) log
27 Eumeratio of Lati rectagles Quotiet graph versio of the ear ε- positive depedecy graph argumet yields tight asymptotic upper boud i Yamamoto s rage: L( k,) ( 1 o(1) )(! ) k e k 2 for k = o( 1 3 ε )
28 Relevace for Lati rectagle eumeratio Try to fill i the fourth row with a permutatio of [5]. Complete bipartite graph: 1st class colums, 2d class etries Caoical evets defied by the edges 11, 13, 14; 23, 22, 25; 34, 35, 31; 42, 44, 43; 55, 51, 52
29 Eumeratio of labeled regular graphs Beder-Cafield, idepedetly Wormald 1978: d fix, d eve ( 2e 1 d2 )/4 d d d e d ( d! ) 2 2
30 Cofiguratio model (Bollobás 1980) Put d (d eve) vertices ito equal clusters Pick a radom matchig of K d Cotract every cluster ito a sigle vertex gettig a multigraph or a simple graph Observe that all simple graphs are equiprobable
31 Eumeratio of labeled regular graphs Bollobás 1980: d eve, d < 2log ( 1+ o( 1) )e 1 d2 ( ( )/4 d 1)!! ( d! ) McKay 1985: for ( d = o 1 ) 3
32 Eumeratio of labeled regular graphs McKay ad Wormald: d eve, ( ( 1 + o( 1) )e 1 d2 )/4 d 3 /( 12)+O d 2 / ( ) d 1 Wormald 1981: fix d 3, g 3 girth ( 1+ o( 1) )e g 1 ( d 1) i ( 2i d 1)!! i=1 ( d! ) d = o 1 2 ( )!! ( d! ) ( )
33 Theorem I the cofiguratio model, if d 3 ad g 3 d 2g-3 =o(), the the probability that the resultig radom d-regular multigraph after the cotractio has girth at least g, is ( 1 + o( 1) )e hece the umber of d-regular graphs with girth at least g is ( 1+ o( 1) )e g 1 i=1 g 1 i=1 ( d 1) i ( d 1) i 2i ( 2i d 1)!! ( d! )
34 Specer s joke Specer s joke i Te Lectures o the Probabilistic Method : uiformly selected radom fuctio from [a] to [b] is ijectio whp, if b>>a 2, but: LLL ca show the existece of a ijectio whe 2ea < b.
35 Our joke Our joke: usig egative depedecy graph LLL, a uiformly selected radom fuctio [a] to [a] is ijectio with probability at least a! a a > 1 e o(1) Combiatorial proof to the slightly weakeed Stirlig formula a
36 Symmetric evets Evets A 1,A 2,,A are symmetric, if the probability of their Boolea expressios do ot chage, whe A π(i) is substituted for A i simultaeously for ay permutatio π.
37 A Lemma for symmetric evets If evets A 1,A 2,,A are symmetric p i = P i j =1 A j ad p = 1, 0 i = 1,2,..., 1 p i 2 p i 1 p i+1 the LLL applies with empty egative depedecy graph, x i =p 1
38 Proof to our joke Cosider a uiform radom fuctio f from [a] to [b] with a b. Let A u deote the evet that f(u) occurs with multiplicity 2 or higher. P( A ) u = 1 b ( ) 1 P A 1 P ij (b 1)a 1 ad p b a i = i! ( ( ) ) a = 1 1 a a(a 1) b i (b i) a i b a = 1 e o(1) a
39
Connected Balanced Subgraphs in Random Regular Multigraphs Under the Configuration Model
 Coected Balaced Subgraphs i Radom Regular Multigraphs Uder the Cofiguratio Model Liyua Lu Austi Mohr László Székely Departmet of Mathematics Uiversity of South Carolia 1523 Greee Street, Columbia, SC 29208
Coected Balaced Subgraphs i Radom Regular Multigraphs Uder the Cofiguratio Model Liyua Lu Austi Mohr László Székely Departmet of Mathematics Uiversity of South Carolia 1523 Greee Street, Columbia, SC 29208
Randomized Algorithms I, Spring 2018, Department of Computer Science, University of Helsinki Homework 1: Solutions (Discussed January 25, 2018)
 Radomized Algorithms I, Sprig 08, Departmet of Computer Sciece, Uiversity of Helsiki Homework : Solutios Discussed Jauary 5, 08). Exercise.: Cosider the followig balls-ad-bi game. We start with oe black
Radomized Algorithms I, Sprig 08, Departmet of Computer Sciece, Uiversity of Helsiki Homework : Solutios Discussed Jauary 5, 08). Exercise.: Cosider the followig balls-ad-bi game. We start with oe black
On Random Line Segments in the Unit Square
 O Radom Lie Segmets i the Uit Square Thomas A. Courtade Departmet of Electrical Egieerig Uiversity of Califoria Los Ageles, Califoria 90095 Email: tacourta@ee.ucla.edu I. INTRODUCTION Let Q = [0, 1] [0,
O Radom Lie Segmets i the Uit Square Thomas A. Courtade Departmet of Electrical Egieerig Uiversity of Califoria Los Ageles, Califoria 90095 Email: tacourta@ee.ucla.edu I. INTRODUCTION Let Q = [0, 1] [0,
Math778P Homework 2 Solution
 Math778P Homework Solutio Choose ay 5 problems to solve. 1. Let S = X i where X 1,..., X are idepedet uiform { 1, 1} radom variables. Prove that E( S = 1 ( 1 1 Proof by Day Rorabaugh: Let S = X i where
Math778P Homework Solutio Choose ay 5 problems to solve. 1. Let S = X i where X 1,..., X are idepedet uiform { 1, 1} radom variables. Prove that E( S = 1 ( 1 1 Proof by Day Rorabaugh: Let S = X i where
Lecture 2. The Lovász Local Lemma
 Staford Uiversity Sprig 208 Math 233A: No-costructive methods i combiatorics Istructor: Ja Vodrák Lecture date: Jauary 0, 208 Origial scribe: Apoorva Khare Lecture 2. The Lovász Local Lemma 2. Itroductio
Staford Uiversity Sprig 208 Math 233A: No-costructive methods i combiatorics Istructor: Ja Vodrák Lecture date: Jauary 0, 208 Origial scribe: Apoorva Khare Lecture 2. The Lovász Local Lemma 2. Itroductio
Problem Set 2 Solutions
 CS271 Radomess & Computatio, Sprig 2018 Problem Set 2 Solutios Poit totals are i the margi; the maximum total umber of poits was 52. 1. Probabilistic method for domiatig sets 6pts Pick a radom subset S
CS271 Radomess & Computatio, Sprig 2018 Problem Set 2 Solutios Poit totals are i the margi; the maximum total umber of poits was 52. 1. Probabilistic method for domiatig sets 6pts Pick a radom subset S
ACO Comprehensive Exam 9 October 2007 Student code A. 1. Graph Theory
 1. Graph Theory Prove that there exist o simple plaar triagulatio T ad two distict adjacet vertices x, y V (T ) such that x ad y are the oly vertices of T of odd degree. Do ot use the Four-Color Theorem.
1. Graph Theory Prove that there exist o simple plaar triagulatio T ad two distict adjacet vertices x, y V (T ) such that x ad y are the oly vertices of T of odd degree. Do ot use the Four-Color Theorem.
Lecture 12: November 13, 2018
 Mathematical Toolkit Autum 2018 Lecturer: Madhur Tulsiai Lecture 12: November 13, 2018 1 Radomized polyomial idetity testig We will use our kowledge of coditioal probability to prove the followig lemma,
Mathematical Toolkit Autum 2018 Lecturer: Madhur Tulsiai Lecture 12: November 13, 2018 1 Radomized polyomial idetity testig We will use our kowledge of coditioal probability to prove the followig lemma,
Disjoint Systems. Abstract
 Disjoit Systems Noga Alo ad Bey Sudaov Departmet of Mathematics Raymod ad Beverly Sacler Faculty of Exact Scieces Tel Aviv Uiversity, Tel Aviv, Israel Abstract A disjoit system of type (,,, ) is a collectio
Disjoit Systems Noga Alo ad Bey Sudaov Departmet of Mathematics Raymod ad Beverly Sacler Faculty of Exact Scieces Tel Aviv Uiversity, Tel Aviv, Israel Abstract A disjoit system of type (,,, ) is a collectio
Polynomial identity testing and global minimum cut
 CHAPTER 6 Polyomial idetity testig ad global miimum cut I this lecture we will cosider two further problems that ca be solved usig probabilistic algorithms. I the first half, we will cosider the problem
CHAPTER 6 Polyomial idetity testig ad global miimum cut I this lecture we will cosider two further problems that ca be solved usig probabilistic algorithms. I the first half, we will cosider the problem
Lecture 14: Graph Entropy
 15-859: Iformatio Theory ad Applicatios i TCS Sprig 2013 Lecture 14: Graph Etropy March 19, 2013 Lecturer: Mahdi Cheraghchi Scribe: Euiwoog Lee 1 Recap Bergma s boud o the permaet Shearer s Lemma Number
15-859: Iformatio Theory ad Applicatios i TCS Sprig 2013 Lecture 14: Graph Etropy March 19, 2013 Lecturer: Mahdi Cheraghchi Scribe: Euiwoog Lee 1 Recap Bergma s boud o the permaet Shearer s Lemma Number
Lecture 4: April 10, 2013
 TTIC/CMSC 1150 Mathematical Toolkit Sprig 01 Madhur Tulsiai Lecture 4: April 10, 01 Scribe: Haris Agelidakis 1 Chebyshev s Iequality recap I the previous lecture, we used Chebyshev s iequality to get a
TTIC/CMSC 1150 Mathematical Toolkit Sprig 01 Madhur Tulsiai Lecture 4: April 10, 01 Scribe: Haris Agelidakis 1 Chebyshev s Iequality recap I the previous lecture, we used Chebyshev s iequality to get a
ECE 6980 An Algorithmic and Information-Theoretic Toolbox for Massive Data
 ECE 6980 A Algorithmic ad Iformatio-Theoretic Toolbo for Massive Data Istructor: Jayadev Acharya Lecture # Scribe: Huayu Zhag 8th August, 017 1 Recap X =, ε is a accuracy parameter, ad δ is a error parameter.
ECE 6980 A Algorithmic ad Iformatio-Theoretic Toolbo for Massive Data Istructor: Jayadev Acharya Lecture # Scribe: Huayu Zhag 8th August, 017 1 Recap X =, ε is a accuracy parameter, ad δ is a error parameter.
Design and Analysis of Algorithms
 Desig ad Aalysis of Algorithms Probabilistic aalysis ad Radomized algorithms Referece: CLRS Chapter 5 Topics: Hirig problem Idicatio radom variables Radomized algorithms Huo Hogwei 1 The hirig problem
Desig ad Aalysis of Algorithms Probabilistic aalysis ad Radomized algorithms Referece: CLRS Chapter 5 Topics: Hirig problem Idicatio radom variables Radomized algorithms Huo Hogwei 1 The hirig problem
# fixed points of g. Tree to string. Repeatedly select the leaf with the smallest label, write down the label of its neighbour and remove the leaf.
 Combiatorics Graph Theory Coutig labelled ad ulabelled graphs There are 2 ( 2) labelled graphs of order. The ulabelled graphs of order correspod to orbits of the actio of S o the set of labelled graphs.
Combiatorics Graph Theory Coutig labelled ad ulabelled graphs There are 2 ( 2) labelled graphs of order. The ulabelled graphs of order correspod to orbits of the actio of S o the set of labelled graphs.
On matchings in hypergraphs
 O matchigs i hypergraphs Peter Frakl Tokyo, Japa peter.frakl@gmail.com Tomasz Luczak Adam Mickiewicz Uiversity Faculty of Mathematics ad CS Pozań, Polad ad Emory Uiversity Departmet of Mathematics ad CS
O matchigs i hypergraphs Peter Frakl Tokyo, Japa peter.frakl@gmail.com Tomasz Luczak Adam Mickiewicz Uiversity Faculty of Mathematics ad CS Pozań, Polad ad Emory Uiversity Departmet of Mathematics ad CS
The Brunn-Minkowski Theorem and Influences of Boolean Variables
 Lecture 7 The Bru-Mikowski Theorem ad Iflueces of Boolea Variables Friday 5, 005 Lecturer: Nati Liial Notes: Mukud Narasimha Theorem 7.1 Bru-Mikowski). If A, B R satisfy some mild assumptios i particular,
Lecture 7 The Bru-Mikowski Theorem ad Iflueces of Boolea Variables Friday 5, 005 Lecturer: Nati Liial Notes: Mukud Narasimha Theorem 7.1 Bru-Mikowski). If A, B R satisfy some mild assumptios i particular,
 1 of 7 7/16/2009 6:06 AM Virtual Laboratories > 6. Radom Samples > 1 2 3 4 5 6 7 6. Order Statistics Defiitios Suppose agai that we have a basic radom experimet, ad that X is a real-valued radom variable
1 of 7 7/16/2009 6:06 AM Virtual Laboratories > 6. Radom Samples > 1 2 3 4 5 6 7 6. Order Statistics Defiitios Suppose agai that we have a basic radom experimet, ad that X is a real-valued radom variable
An Introduction to Randomized Algorithms
 A Itroductio to Radomized Algorithms The focus of this lecture is to study a radomized algorithm for quick sort, aalyze it usig probabilistic recurrece relatios, ad also provide more geeral tools for aalysis
A Itroductio to Radomized Algorithms The focus of this lecture is to study a radomized algorithm for quick sort, aalyze it usig probabilistic recurrece relatios, ad also provide more geeral tools for aalysis
Axioms of Measure Theory
 MATH 532 Axioms of Measure Theory Dr. Neal, WKU I. The Space Throughout the course, we shall let X deote a geeric o-empty set. I geeral, we shall ot assume that ay algebraic structure exists o X so that
MATH 532 Axioms of Measure Theory Dr. Neal, WKU I. The Space Throughout the course, we shall let X deote a geeric o-empty set. I geeral, we shall ot assume that ay algebraic structure exists o X so that
b i u x i U a i j u x i u x j
 M ath 5 2 7 Fall 2 0 0 9 L ecture 1 9 N ov. 1 6, 2 0 0 9 ) S ecod- Order Elliptic Equatios: Weak S olutios 1. Defiitios. I this ad the followig two lectures we will study the boudary value problem Here
M ath 5 2 7 Fall 2 0 0 9 L ecture 1 9 N ov. 1 6, 2 0 0 9 ) S ecod- Order Elliptic Equatios: Weak S olutios 1. Defiitios. I this ad the followig two lectures we will study the boudary value problem Here
The Boolean Ring of Intervals
 MATH 532 Lebesgue Measure Dr. Neal, WKU We ow shall apply the results obtaied about outer measure to the legth measure o the real lie. Throughout, our space X will be the set of real umbers R. Whe ecessary,
MATH 532 Lebesgue Measure Dr. Neal, WKU We ow shall apply the results obtaied about outer measure to the legth measure o the real lie. Throughout, our space X will be the set of real umbers R. Whe ecessary,
Lecture 9: Expanders Part 2, Extractors
 Lecture 9: Expaders Part, Extractors Topics i Complexity Theory ad Pseudoradomess Sprig 013 Rutgers Uiversity Swastik Kopparty Scribes: Jaso Perry, Joh Kim I this lecture, we will discuss further the pseudoradomess
Lecture 9: Expaders Part, Extractors Topics i Complexity Theory ad Pseudoradomess Sprig 013 Rutgers Uiversity Swastik Kopparty Scribes: Jaso Perry, Joh Kim I this lecture, we will discuss further the pseudoradomess
On the Number of 1-factors of Bipartite Graphs
 Math Sci Lett 2 No 3 181-187 (2013) 181 Mathematical Scieces Letters A Iteratioal Joural http://dxdoiorg/1012785/msl/020306 O the Number of 1-factors of Bipartite Graphs Mehmet Akbulak 1 ad Ahmet Öteleş
Math Sci Lett 2 No 3 181-187 (2013) 181 Mathematical Scieces Letters A Iteratioal Joural http://dxdoiorg/1012785/msl/020306 O the Number of 1-factors of Bipartite Graphs Mehmet Akbulak 1 ad Ahmet Öteleş
Application to Random Graphs
 A Applicatio to Radom Graphs Brachig processes have a umber of iterestig ad importat applicatios. We shall cosider oe of the most famous of them, the Erdős-Réyi radom graph theory. 1 Defiitio A.1. Let
A Applicatio to Radom Graphs Brachig processes have a umber of iterestig ad importat applicatios. We shall cosider oe of the most famous of them, the Erdős-Réyi radom graph theory. 1 Defiitio A.1. Let
Optimally Sparse SVMs
 A. Proof of Lemma 3. We here prove a lower boud o the umber of support vectors to achieve geeralizatio bouds of the form which we cosider. Importatly, this result holds ot oly for liear classifiers, but
A. Proof of Lemma 3. We here prove a lower boud o the umber of support vectors to achieve geeralizatio bouds of the form which we cosider. Importatly, this result holds ot oly for liear classifiers, but
f X (12) = Pr(X = 12) = Pr({(6, 6)}) = 1/36
 Probability Distributios A Example With Dice If X is a radom variable o sample space S, the the probability that X takes o the value c is Similarly, Pr(X = c) = Pr({s S X(s) = c}) Pr(X c) = Pr({s S X(s)
Probability Distributios A Example With Dice If X is a radom variable o sample space S, the the probability that X takes o the value c is Similarly, Pr(X = c) = Pr({s S X(s) = c}) Pr(X c) = Pr({s S X(s)
Ma/CS 6b Class 19: Extremal Graph Theory
 /9/05 Ma/CS 6b Class 9: Extremal Graph Theory Paul Turá By Adam Sheffer Extremal Graph Theory The subfield of extremal graph theory deals with questios of the form: What is the maximum umber of edges that
/9/05 Ma/CS 6b Class 9: Extremal Graph Theory Paul Turá By Adam Sheffer Extremal Graph Theory The subfield of extremal graph theory deals with questios of the form: What is the maximum umber of edges that
Notes for Lecture 11
 U.C. Berkeley CS78: Computatioal Complexity Hadout N Professor Luca Trevisa 3/4/008 Notes for Lecture Eigevalues, Expasio, ad Radom Walks As usual by ow, let G = (V, E) be a udirected d-regular graph with
U.C. Berkeley CS78: Computatioal Complexity Hadout N Professor Luca Trevisa 3/4/008 Notes for Lecture Eigevalues, Expasio, ad Radom Walks As usual by ow, let G = (V, E) be a udirected d-regular graph with
Online hypergraph matching: hiring teams of secretaries
 Olie hypergraph matchig: hirig teams of secretaries Rafael M. Frogillo Advisor: Robert Kleiberg May 29, 2008 Itroductio The goal of this paper is to fid a competitive algorithm for the followig problem.
Olie hypergraph matchig: hirig teams of secretaries Rafael M. Frogillo Advisor: Robert Kleiberg May 29, 2008 Itroductio The goal of this paper is to fid a competitive algorithm for the followig problem.
0, otherwise. EX = E(X 1 + X n ) = EX j = np and. Var(X j ) = np(1 p). Var(X) = Var(X X n ) =
 PROBABILITY MODELS 35 10. Discrete probability distributios I this sectio, we discuss several well-ow discrete probability distributios ad study some of their properties. Some of these distributios, lie
PROBABILITY MODELS 35 10. Discrete probability distributios I this sectio, we discuss several well-ow discrete probability distributios ad study some of their properties. Some of these distributios, lie
Bertrand s Postulate
 Bertrad s Postulate Lola Thompso Ross Program July 3, 2009 Lola Thompso (Ross Program Bertrad s Postulate July 3, 2009 1 / 33 Bertrad s Postulate I ve said it oce ad I ll say it agai: There s always a
Bertrad s Postulate Lola Thompso Ross Program July 3, 2009 Lola Thompso (Ross Program Bertrad s Postulate July 3, 2009 1 / 33 Bertrad s Postulate I ve said it oce ad I ll say it agai: There s always a
THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS
 THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS DEMETRES CHRISTOFIDES Abstract. Cosider a ivertible matrix over some field. The Gauss-Jorda elimiatio reduces this matrix to the idetity
THE ASYMPTOTIC COMPLEXITY OF MATRIX REDUCTION OVER FINITE FIELDS DEMETRES CHRISTOFIDES Abstract. Cosider a ivertible matrix over some field. The Gauss-Jorda elimiatio reduces this matrix to the idetity
It is always the case that unions, intersections, complements, and set differences are preserved by the inverse image of a function.
 MATH 532 Measurable Fuctios Dr. Neal, WKU Throughout, let ( X, F, µ) be a measure space ad let (!, F, P ) deote the special case of a probability space. We shall ow begi to study real-valued fuctios defied
MATH 532 Measurable Fuctios Dr. Neal, WKU Throughout, let ( X, F, µ) be a measure space ad let (!, F, P ) deote the special case of a probability space. We shall ow begi to study real-valued fuctios defied
Definition 2 (Eigenvalue Expansion). We say a d-regular graph is a λ eigenvalue expander if
 Expaer Graphs Graph Theory (Fall 011) Rutgers Uiversity Swastik Kopparty Throughout these otes G is a -regular graph 1 The Spectrum Let A G be the ajacecy matrix of G Let λ 1 λ λ be the eigevalues of A
Expaer Graphs Graph Theory (Fall 011) Rutgers Uiversity Swastik Kopparty Throughout these otes G is a -regular graph 1 The Spectrum Let A G be the ajacecy matrix of G Let λ 1 λ λ be the eigevalues of A
ON POINTWISE BINOMIAL APPROXIMATION
 Iteratioal Joural of Pure ad Applied Mathematics Volume 71 No. 1 2011, 57-66 ON POINTWISE BINOMIAL APPROXIMATION BY w-functions K. Teerapabolar 1, P. Wogkasem 2 Departmet of Mathematics Faculty of Sciece
Iteratioal Joural of Pure ad Applied Mathematics Volume 71 No. 1 2011, 57-66 ON POINTWISE BINOMIAL APPROXIMATION BY w-functions K. Teerapabolar 1, P. Wogkasem 2 Departmet of Mathematics Faculty of Sciece
Week 5-6: The Binomial Coefficients
 Wee 5-6: The Biomial Coefficiets March 6, 2018 1 Pascal Formula Theorem 11 (Pascal s Formula For itegers ad such that 1, ( ( ( 1 1 + 1 The umbers ( 2 ( 1 2 ( 2 are triagle umbers, that is, The petago umbers
Wee 5-6: The Biomial Coefficiets March 6, 2018 1 Pascal Formula Theorem 11 (Pascal s Formula For itegers ad such that 1, ( ( ( 1 1 + 1 The umbers ( 2 ( 1 2 ( 2 are triagle umbers, that is, The petago umbers
Random assignment with integer costs
 Radom assigmet with iteger costs Robert Parviaie Departmet of Mathematics, Uppsala Uiversity P.O. Box 480, SE-7506 Uppsala, Swede robert.parviaie@math.uu.se Jue 4, 200 Abstract The radom assigmet problem
Radom assigmet with iteger costs Robert Parviaie Departmet of Mathematics, Uppsala Uiversity P.O. Box 480, SE-7506 Uppsala, Swede robert.parviaie@math.uu.se Jue 4, 200 Abstract The radom assigmet problem
1 Review and Overview
 CS9T/STATS3: Statistical Learig Theory Lecturer: Tegyu Ma Lecture #6 Scribe: Jay Whag ad Patrick Cho October 0, 08 Review ad Overview Recall i the last lecture that for ay family of scalar fuctios F, we
CS9T/STATS3: Statistical Learig Theory Lecturer: Tegyu Ma Lecture #6 Scribe: Jay Whag ad Patrick Cho October 0, 08 Review ad Overview Recall i the last lecture that for ay family of scalar fuctios F, we
Lecture 2: April 3, 2013
 TTIC/CMSC 350 Mathematical Toolkit Sprig 203 Madhur Tulsiai Lecture 2: April 3, 203 Scribe: Shubhedu Trivedi Coi tosses cotiued We retur to the coi tossig example from the last lecture agai: Example. Give,
TTIC/CMSC 350 Mathematical Toolkit Sprig 203 Madhur Tulsiai Lecture 2: April 3, 203 Scribe: Shubhedu Trivedi Coi tosses cotiued We retur to the coi tossig example from the last lecture agai: Example. Give,
MASSACHUSETTS INSTITUTE OF TECHNOLOGY 6.436J/15.085J Fall 2008 Lecture 19 11/17/2008 LAWS OF LARGE NUMBERS II THE STRONG LAW OF LARGE NUMBERS
 MASSACHUSTTS INSTITUT OF TCHNOLOGY 6.436J/5.085J Fall 2008 Lecture 9 /7/2008 LAWS OF LARG NUMBRS II Cotets. The strog law of large umbers 2. The Cheroff boud TH STRONG LAW OF LARG NUMBRS While the weak
MASSACHUSTTS INSTITUT OF TCHNOLOGY 6.436J/5.085J Fall 2008 Lecture 9 /7/2008 LAWS OF LARG NUMBRS II Cotets. The strog law of large umbers 2. The Cheroff boud TH STRONG LAW OF LARG NUMBRS While the weak
Lecture 16: Monotone Formula Lower Bounds via Graph Entropy. 2 Monotone Formula Lower Bounds via Graph Entropy
 15-859: Iformatio Theory ad Applicatios i TCS CMU: Sprig 2013 Lecture 16: Mootoe Formula Lower Bouds via Graph Etropy March 26, 2013 Lecturer: Mahdi Cheraghchi Scribe: Shashak Sigh 1 Recap Graph Etropy:
15-859: Iformatio Theory ad Applicatios i TCS CMU: Sprig 2013 Lecture 16: Mootoe Formula Lower Bouds via Graph Etropy March 26, 2013 Lecturer: Mahdi Cheraghchi Scribe: Shashak Sigh 1 Recap Graph Etropy:
HOMEWORK 2 SOLUTIONS
 HOMEWORK SOLUTIONS CSE 55 RANDOMIZED AND APPROXIMATION ALGORITHMS 1. Questio 1. a) The larger the value of k is, the smaller the expected umber of days util we get all the coupos we eed. I fact if = k
HOMEWORK SOLUTIONS CSE 55 RANDOMIZED AND APPROXIMATION ALGORITHMS 1. Questio 1. a) The larger the value of k is, the smaller the expected umber of days util we get all the coupos we eed. I fact if = k
CS284A: Representations and Algorithms in Molecular Biology
 CS284A: Represetatios ad Algorithms i Molecular Biology Scribe Notes o Lectures 3 & 4: Motif Discovery via Eumeratio & Motif Represetatio Usig Positio Weight Matrix Joshua Gervi Based o presetatios by
CS284A: Represetatios ad Algorithms i Molecular Biology Scribe Notes o Lectures 3 & 4: Motif Discovery via Eumeratio & Motif Represetatio Usig Positio Weight Matrix Joshua Gervi Based o presetatios by
DECOMPOSITIONS OF COMPLETE UNIFORM HYPERGRAPHS INTO HAMILTON BERGE CYCLES
 DECOMPOSITIONS OF COMPLETE UNIFORM HYPERGRAPHS INTO HAMILTON BERGE CYCLES DANIELA KÜHN AND DERYK OSTHUS Abstract. I 1973 Bermod, Germa, Heydema ad Sotteau cojectured that if divides (, the the complete
DECOMPOSITIONS OF COMPLETE UNIFORM HYPERGRAPHS INTO HAMILTON BERGE CYCLES DANIELA KÜHN AND DERYK OSTHUS Abstract. I 1973 Bermod, Germa, Heydema ad Sotteau cojectured that if divides (, the the complete
Frequentist Inference
 Frequetist Iferece The topics of the ext three sectios are useful applicatios of the Cetral Limit Theorem. Without kowig aythig about the uderlyig distributio of a sequece of radom variables {X i }, for
Frequetist Iferece The topics of the ext three sectios are useful applicatios of the Cetral Limit Theorem. Without kowig aythig about the uderlyig distributio of a sequece of radom variables {X i }, for
4 The Sperner property.
 4 The Sperer property. I this sectio we cosider a surprisig applicatio of certai adjacecy matrices to some problems i extremal set theory. A importat role will also be played by fiite groups. I geeral,
4 The Sperer property. I this sectio we cosider a surprisig applicatio of certai adjacecy matrices to some problems i extremal set theory. A importat role will also be played by fiite groups. I geeral,
DECOMPOSITIONS OF COMPLETE UNIFORM HYPERGRAPHS INTO HAMILTON BERGE CYCLES
 DECOMPOSITIONS OF COMPLETE UNIFORM HYPERGRAPHS INTO HAMILTON BERGE CYCLES DANIELA KÜHN AND DERYK OSTHUS Abstract. I 1973 Bermod, Germa, Heydema ad Sotteau cojectured that if divides (, the the complete
DECOMPOSITIONS OF COMPLETE UNIFORM HYPERGRAPHS INTO HAMILTON BERGE CYCLES DANIELA KÜHN AND DERYK OSTHUS Abstract. I 1973 Bermod, Germa, Heydema ad Sotteau cojectured that if divides (, the the complete
An Asymptotic Expansion for the Number of Permutations with a Certain Number of Inversions
 A Asymptotic Expasio for the Number of Permutatios with a Certai Number of Iversios Lae Clark Departmet of Mathematics Souther Illiois Uiversity Carbodale Carbodale, IL 691-448 USA lclark@math.siu.edu
A Asymptotic Expasio for the Number of Permutatios with a Certai Number of Iversios Lae Clark Departmet of Mathematics Souther Illiois Uiversity Carbodale Carbodale, IL 691-448 USA lclark@math.siu.edu
Law of the sum of Bernoulli random variables
 Law of the sum of Beroulli radom variables Nicolas Chevallier Uiversité de Haute Alsace, 4, rue des frères Lumière 68093 Mulhouse icolas.chevallier@uha.fr December 006 Abstract Let be the set of all possible
Law of the sum of Beroulli radom variables Nicolas Chevallier Uiversité de Haute Alsace, 4, rue des frères Lumière 68093 Mulhouse icolas.chevallier@uha.fr December 006 Abstract Let be the set of all possible
ORIE 633 Network Flows September 27, Lecture 8
 ORIE 633 Network Flows September 7, 007 Lecturer: David P. Williamso Lecture 8 Scribe: Gema Plaza-Martíez 1 Global mi-cuts i udirected graphs 1.1 Radom cotractio Recall from last time we itroduced the
ORIE 633 Network Flows September 7, 007 Lecturer: David P. Williamso Lecture 8 Scribe: Gema Plaza-Martíez 1 Global mi-cuts i udirected graphs 1.1 Radom cotractio Recall from last time we itroduced the
Math 155 (Lecture 3)
 Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
Math 55 (Lecture 3) September 8, I this lecture, we ll cosider the aswer to oe of the most basic coutig problems i combiatorics Questio How may ways are there to choose a -elemet subset of the set {,,,
f X (12) = Pr(X = 12) = Pr({(6, 6)}) = 1/36
 Probability Distributios A Example With Dice If X is a radom variable o sample space S, the the probablity that X takes o the value c is Similarly, Pr(X = c) = Pr({s S X(s) = c} Pr(X c) = Pr({s S X(s)
Probability Distributios A Example With Dice If X is a radom variable o sample space S, the the probablity that X takes o the value c is Similarly, Pr(X = c) = Pr({s S X(s) = c} Pr(X c) = Pr({s S X(s)
Advanced Stochastic Processes.
 Advaced Stochastic Processes. David Gamarik LECTURE 2 Radom variables ad measurable fuctios. Strog Law of Large Numbers (SLLN). Scary stuff cotiued... Outlie of Lecture Radom variables ad measurable fuctios.
Advaced Stochastic Processes. David Gamarik LECTURE 2 Radom variables ad measurable fuctios. Strog Law of Large Numbers (SLLN). Scary stuff cotiued... Outlie of Lecture Radom variables ad measurable fuctios.
Math 216A Notes, Week 5
 Math 6A Notes, Week 5 Scribe: Ayastassia Sebolt Disclaimer: These otes are ot early as polished (ad quite possibly ot early as correct) as a published paper. Please use them at your ow risk.. Thresholds
Math 6A Notes, Week 5 Scribe: Ayastassia Sebolt Disclaimer: These otes are ot early as polished (ad quite possibly ot early as correct) as a published paper. Please use them at your ow risk.. Thresholds
CS 270 Algorithms. Oliver Kullmann. Growth of Functions. Divide-and- Conquer Min-Max- Problem. Tutorial. Reading from CLRS for week 2
 Geeral remarks Week 2 1 Divide ad First we cosider a importat tool for the aalysis of algorithms: Big-Oh. The we itroduce a importat algorithmic paradigm:. We coclude by presetig ad aalysig two examples.
Geeral remarks Week 2 1 Divide ad First we cosider a importat tool for the aalysis of algorithms: Big-Oh. The we itroduce a importat algorithmic paradigm:. We coclude by presetig ad aalysig two examples.
Introduction to Probability. Ariel Yadin
 Itroductio to robability Ariel Yadi Lecture 2 *** Ja. 7 ***. Covergece of Radom Variables As i the case of sequeces of umbers, we would like to talk about covergece of radom variables. There are may ways
Itroductio to robability Ariel Yadi Lecture 2 *** Ja. 7 ***. Covergece of Radom Variables As i the case of sequeces of umbers, we would like to talk about covergece of radom variables. There are may ways
Lecture 1 Probability and Statistics
 Wikipedia: Lecture 1 Probability ad Statistics Bejami Disraeli, British statesma ad literary figure (1804 1881): There are three kids of lies: lies, damed lies, ad statistics. popularized i US by Mark
Wikipedia: Lecture 1 Probability ad Statistics Bejami Disraeli, British statesma ad literary figure (1804 1881): There are three kids of lies: lies, damed lies, ad statistics. popularized i US by Mark
Basics of Probability Theory (for Theory of Computation courses)
 Basics of Probability Theory (for Theory of Computatio courses) Oded Goldreich Departmet of Computer Sciece Weizma Istitute of Sciece Rehovot, Israel. oded.goldreich@weizma.ac.il November 24, 2008 Preface.
Basics of Probability Theory (for Theory of Computatio courses) Oded Goldreich Departmet of Computer Sciece Weizma Istitute of Sciece Rehovot, Israel. oded.goldreich@weizma.ac.il November 24, 2008 Preface.
Definitions and Theorems. where x are the decision variables. c, b, and a are constant coefficients.
 Defiitios ad Theorems Remember the scalar form of the liear programmig problem, Miimize, Subject to, f(x) = c i x i a 1i x i = b 1 a mi x i = b m x i 0 i = 1,2,, where x are the decisio variables. c, b,
Defiitios ad Theorems Remember the scalar form of the liear programmig problem, Miimize, Subject to, f(x) = c i x i a 1i x i = b 1 a mi x i = b m x i 0 i = 1,2,, where x are the decisio variables. c, b,
Introduction to Probability. Ariel Yadin. Lecture 7
 Itroductio to Probability Ariel Yadi Lecture 7 1. Idepedece Revisited 1.1. Some remiders. Let (Ω, F, P) be a probability space. Give a collectio of subsets K F, recall that the σ-algebra geerated by K,
Itroductio to Probability Ariel Yadi Lecture 7 1. Idepedece Revisited 1.1. Some remiders. Let (Ω, F, P) be a probability space. Give a collectio of subsets K F, recall that the σ-algebra geerated by K,
Lecture 2 Long paths in random graphs
 Lecture Log paths i radom graphs 1 Itroductio I this lecture we treat the appearace of log paths ad cycles i sparse radom graphs. will wor with the probability space G(, p) of biomial radom graphs, aalogous
Lecture Log paths i radom graphs 1 Itroductio I this lecture we treat the appearace of log paths ad cycles i sparse radom graphs. will wor with the probability space G(, p) of biomial radom graphs, aalogous
Compositions of Random Functions on a Finite Set
 Compositios of Radom Fuctios o a Fiite Set Aviash Dalal MCS Departmet, Drexel Uiversity Philadelphia, Pa. 904 ADalal@drexel.edu Eric Schmutz Drexel Uiversity ad Swarthmore College Philadelphia, Pa., 904
Compositios of Radom Fuctios o a Fiite Set Aviash Dalal MCS Departmet, Drexel Uiversity Philadelphia, Pa. 904 ADalal@drexel.edu Eric Schmutz Drexel Uiversity ad Swarthmore College Philadelphia, Pa., 904
LONG SNAKES IN POWERS OF THE COMPLETE GRAPH WITH AN ODD NUMBER OF VERTICES
 J Lodo Math Soc (2 50, (1994, 465 476 LONG SNAKES IN POWERS OF THE COMPLETE GRAPH WITH AN ODD NUMBER OF VERTICES Jerzy Wojciechowski Abstract I [5] Abbott ad Katchalski ask if there exists a costat c >
J Lodo Math Soc (2 50, (1994, 465 476 LONG SNAKES IN POWERS OF THE COMPLETE GRAPH WITH AN ODD NUMBER OF VERTICES Jerzy Wojciechowski Abstract I [5] Abbott ad Katchalski ask if there exists a costat c >
A Hypergraph Extension. Bipartite Turán Problem
 A Hypergraph Extesio of the Bipartite Turá Problem Dhruv Mubayi 1 Jacques Verstraëte Abstract. Let t, be itegers with t. For t, we prove that i ay family of at least t 4( ) triples from a -elemet set X,
A Hypergraph Extesio of the Bipartite Turá Problem Dhruv Mubayi 1 Jacques Verstraëte Abstract. Let t, be itegers with t. For t, we prove that i ay family of at least t 4( ) triples from a -elemet set X,
Lecture 11: Channel Coding Theorem: Converse Part
 EE376A/STATS376A Iformatio Theory Lecture - 02/3/208 Lecture : Chael Codig Theorem: Coverse Part Lecturer: Tsachy Weissma Scribe: Erdem Bıyık I this lecture, we will cotiue our discussio o chael codig
EE376A/STATS376A Iformatio Theory Lecture - 02/3/208 Lecture : Chael Codig Theorem: Coverse Part Lecturer: Tsachy Weissma Scribe: Erdem Bıyık I this lecture, we will cotiue our discussio o chael codig
Chapter 7 Isoperimetric problem
 Chapter 7 Isoperimetric problem Recall that the isoperimetric problem (see the itroductio its coectio with ido s proble) is oe of the most classical problem of a shape optimizatio. It ca be formulated
Chapter 7 Isoperimetric problem Recall that the isoperimetric problem (see the itroductio its coectio with ido s proble) is oe of the most classical problem of a shape optimizatio. It ca be formulated
A Mean Paradox. John Konvalina, Jack Heidel, and Jim Rogers. Department of Mathematics University of Nebraska at Omaha Omaha, NE USA
 A Mea Paradox by Joh Kovalia, Jac Heidel, ad Jim Rogers Departmet of Mathematics Uiversity of Nebrasa at Omaha Omaha, NE 6882-243 USA Phoe: (42) 554-2836 Fax: (42) 554-2975 E-mail: joho@uomaha.edu A Mea
A Mea Paradox by Joh Kovalia, Jac Heidel, ad Jim Rogers Departmet of Mathematics Uiversity of Nebrasa at Omaha Omaha, NE 6882-243 USA Phoe: (42) 554-2836 Fax: (42) 554-2975 E-mail: joho@uomaha.edu A Mea
Lecture 3 The Lebesgue Integral
 Lecture 3: The Lebesgue Itegral 1 of 14 Course: Theory of Probability I Term: Fall 2013 Istructor: Gorda Zitkovic Lecture 3 The Lebesgue Itegral The costructio of the itegral Uless expressly specified
Lecture 3: The Lebesgue Itegral 1 of 14 Course: Theory of Probability I Term: Fall 2013 Istructor: Gorda Zitkovic Lecture 3 The Lebesgue Itegral The costructio of the itegral Uless expressly specified
Probability for mathematicians INDEPENDENCE TAU
 Probability for mathematicias INDEPENDENCE TAU 2013 28 Cotets 3 Ifiite idepedet sequeces 28 3a Idepedet evets........................ 28 3b Idepedet radom variables.................. 33 3 Ifiite idepedet
Probability for mathematicias INDEPENDENCE TAU 2013 28 Cotets 3 Ifiite idepedet sequeces 28 3a Idepedet evets........................ 28 3b Idepedet radom variables.................. 33 3 Ifiite idepedet
Model Theory 2016, Exercises, Second batch, covering Weeks 5-7, with Solutions
 Model Theory 2016, Exercises, Secod batch, coverig Weeks 5-7, with Solutios 3 Exercises from the Notes Exercise 7.6. Show that if T is a theory i a coutable laguage L, haso fiite model, ad is ℵ 0 -categorical,
Model Theory 2016, Exercises, Secod batch, coverig Weeks 5-7, with Solutios 3 Exercises from the Notes Exercise 7.6. Show that if T is a theory i a coutable laguage L, haso fiite model, ad is ℵ 0 -categorical,
Edge Disjoint Hamilton Cycles
 Edge Disjoit Hamilto Cycles April 26, 2015 1 Itroductio l +l l +c I the late 70s, it was show by Komlós ad Szemerédi ([7]) that for p =, the limit probability for G(, p) to cotai a Hamilto cycle equals
Edge Disjoit Hamilto Cycles April 26, 2015 1 Itroductio l +l l +c I the late 70s, it was show by Komlós ad Szemerédi ([7]) that for p =, the limit probability for G(, p) to cotai a Hamilto cycle equals
Disjoint set (Union-Find)
 CS124 Lecture 7 Fall 2018 Disjoit set (Uio-Fid) For Kruskal s algorithm for the miimum spaig tree problem, we foud that we eeded a data structure for maitaiig a collectio of disjoit sets. That is, we eed
CS124 Lecture 7 Fall 2018 Disjoit set (Uio-Fid) For Kruskal s algorithm for the miimum spaig tree problem, we foud that we eeded a data structure for maitaiig a collectio of disjoit sets. That is, we eed
Lecture 3: August 31
 36-705: Itermediate Statistics Fall 018 Lecturer: Siva Balakrisha Lecture 3: August 31 This lecture will be mostly a summary of other useful expoetial tail bouds We will ot prove ay of these i lecture,
36-705: Itermediate Statistics Fall 018 Lecturer: Siva Balakrisha Lecture 3: August 31 This lecture will be mostly a summary of other useful expoetial tail bouds We will ot prove ay of these i lecture,
γn 1 (1 e γ } min min
 Hug ad Giag SprigerPlus 20165:79 DOI 101186/s40064-016-1710-y RESEARCH O bouds i Poisso approximatio for distributios of idepedet egative biomial distributed radom variables Tra Loc Hug * ad Le Truog Giag
Hug ad Giag SprigerPlus 20165:79 DOI 101186/s40064-016-1710-y RESEARCH O bouds i Poisso approximatio for distributios of idepedet egative biomial distributed radom variables Tra Loc Hug * ad Le Truog Giag
Review Problems 1. ICME and MS&E Refresher Course September 19, 2011 B = C = AB = A = A 2 = A 3... C 2 = C 3 = =
 Review Problems ICME ad MS&E Refresher Course September 9, 0 Warm-up problems. For the followig matrices A = 0 B = C = AB = 0 fid all powers A,A 3,(which is A times A),... ad B,B 3,... ad C,C 3,... Solutio:
Review Problems ICME ad MS&E Refresher Course September 9, 0 Warm-up problems. For the followig matrices A = 0 B = C = AB = 0 fid all powers A,A 3,(which is A times A),... ad B,B 3,... ad C,C 3,... Solutio:
Topic 9: Sampling Distributions of Estimators
 Topic 9: Samplig Distributios of Estimators Course 003, 2016 Page 0 Samplig distributios of estimators Sice our estimators are statistics (particular fuctios of radom variables), their distributio ca be
Topic 9: Samplig Distributios of Estimators Course 003, 2016 Page 0 Samplig distributios of estimators Sice our estimators are statistics (particular fuctios of radom variables), their distributio ca be
Fall 2013 MTH431/531 Real analysis Section Notes
 Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
Fall 013 MTH431/531 Real aalysis Sectio 8.1-8. Notes Yi Su 013.11.1 1. Defiitio of uiform covergece. We look at a sequece of fuctios f (x) ad study the coverget property. Notice we have two parameters
Lecture 3 : Random variables and their distributions
 Lecture 3 : Radom variables ad their distributios 3.1 Radom variables Let (Ω, F) ad (S, S) be two measurable spaces. A map X : Ω S is measurable or a radom variable (deoted r.v.) if X 1 (A) {ω : X(ω) A}
Lecture 3 : Radom variables ad their distributios 3.1 Radom variables Let (Ω, F) ad (S, S) be two measurable spaces. A map X : Ω S is measurable or a radom variable (deoted r.v.) if X 1 (A) {ω : X(ω) A}
kp(x = k) = λe λ λ k 1 (k 1)! = λe λ r k e λλk k! = e λ g(r) = e λ e rλ = e λ(r 1) g (1) = E[X] = λ g(r) = kr k 1 e λλk k! = E[X]
![kp(x = k) = λe λ λ k 1 (k 1)! = λe λ r k e λλk k! = e λ g(r) = e λ e rλ = e λ(r 1) g (1) = E[X] = λ g(r) = kr k 1 e λλk k! = E[X] kp(x = k) = λe λ λ k 1 (k 1)! = λe λ r k e λλk k! = e λ g(r) = e λ e rλ = e λ(r 1) g (1) = E[X] = λ g(r) = kr k 1 e λλk k! = E[X]](/thumbs/81/82997186.jpg) Problem 1: (8 poits) Let X be a Poisso radom variable of parameter λ. 1. ( poits) Compute E[X]. E[X] = = kp(x = k) = k=1 λe λ λ k 1 (k 1)! = λe λ ke λλk λ k k! k =0 2. ( poits) Compute g(r) = E [ r X],
Problem 1: (8 poits) Let X be a Poisso radom variable of parameter λ. 1. ( poits) Compute E[X]. E[X] = = kp(x = k) = k=1 λe λ λ k 1 (k 1)! = λe λ ke λλk λ k k! k =0 2. ( poits) Compute g(r) = E [ r X],
Probabilistic Extensions of the Erdős-Ko-Rado Property
 Probabilistic Extesios of the Erdős-Ko-Rado Property Aa Celaya Departmet of Mathematics Uiversity of Wiscosi accelaya@yahoo.com Aat P. Godbole Departmet of Mathematics East Teessee State Uiversity godbolea@mail.etsu.edu
Probabilistic Extesios of the Erdős-Ko-Rado Property Aa Celaya Departmet of Mathematics Uiversity of Wiscosi accelaya@yahoo.com Aat P. Godbole Departmet of Mathematics East Teessee State Uiversity godbolea@mail.etsu.edu
Matrix Algebra 2.2 THE INVERSE OF A MATRIX Pearson Education, Inc.
 2 Matrix Algebra 2.2 THE INVERSE OF A MATRIX MATRIX OPERATIONS A matrix A is said to be ivertible if there is a matrix C such that CA = I ad AC = I where, the idetity matrix. I = I I this case, C is a
2 Matrix Algebra 2.2 THE INVERSE OF A MATRIX MATRIX OPERATIONS A matrix A is said to be ivertible if there is a matrix C such that CA = I ad AC = I where, the idetity matrix. I = I I this case, C is a
Convergence of random variables. (telegram style notes) P.J.C. Spreij
 Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Covergece of radom variables (telegram style otes).j.c. Spreij this versio: September 6, 2005 Itroductio As we kow, radom variables are by defiitio measurable fuctios o some uderlyig measurable space
Poisson approximations
 The Bi, p) ca be thought of as the distributio of a sum of idepedet idicator radom variables X +...+ X, with {X i = } deotig a head o the ith toss of a coi. The ormal approximatio to the Biomial works
The Bi, p) ca be thought of as the distributio of a sum of idepedet idicator radom variables X +...+ X, with {X i = } deotig a head o the ith toss of a coi. The ormal approximatio to the Biomial works
Chapter 3. Strong convergence. 3.1 Definition of almost sure convergence
 Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Chapter 3 Strog covergece As poited out i the Chapter 2, there are multiple ways to defie the otio of covergece of a sequece of radom variables. That chapter defied covergece i probability, covergece i
Lecture Notes for Analysis Class
 Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
Lecture Notes for Aalysis Class Topological Spaces A topology for a set X is a collectio T of subsets of X such that: (a) X ad the empty set are i T (b) Uios of elemets of T are i T (c) Fiite itersectios
1 Counting and Stirling Numbers
 1 Coutig ad Stirlig Numbers Natural Numbers: We let N {0, 1, 2,...} deote the set of atural umbers. []: For N we let [] {1, 2,..., }. Sym: For a set X we let Sym(X) deote the set of bijectios from X to
1 Coutig ad Stirlig Numbers Natural Numbers: We let N {0, 1, 2,...} deote the set of atural umbers. []: For N we let [] {1, 2,..., }. Sym: For a set X we let Sym(X) deote the set of bijectios from X to
The probability of generating the symmetric group when one of the generators is random
 Publ. Math. Debrece 69/3 (2006), 271 280 The probability of geeratig the symmetric group whe oe of the geerators is radom By LÁSZLÓ BABAI (Chicago) ad THOMAS P. HAYES (Berkeley) To the memory of Edit Szabó
Publ. Math. Debrece 69/3 (2006), 271 280 The probability of geeratig the symmetric group whe oe of the geerators is radom By LÁSZLÓ BABAI (Chicago) ad THOMAS P. HAYES (Berkeley) To the memory of Edit Szabó
CS 2750 Machine Learning. Lecture 22. Concept learning. CS 2750 Machine Learning. Concept Learning
 Lecture 22 Cocept learig Milos Hauskrecht milos@cs.pitt.edu 5329 Seott Square Cocept Learig Outlie: Learig boolea fuctios Most geeral ad most specific cosistet hypothesis. Mitchell s versio space algorithm
Lecture 22 Cocept learig Milos Hauskrecht milos@cs.pitt.edu 5329 Seott Square Cocept Learig Outlie: Learig boolea fuctios Most geeral ad most specific cosistet hypothesis. Mitchell s versio space algorithm
Almost-spanning universality in random graphs
 Almost-spaig uiversality i radom graphs David Colo Asaf Ferber Rajko Neadov Nemaja Škorić Abstract A graph G is said to be H(, )-uiversal if it cotais every graph o vertices with maximum degree at most.
Almost-spaig uiversality i radom graphs David Colo Asaf Ferber Rajko Neadov Nemaja Škorić Abstract A graph G is said to be H(, )-uiversal if it cotais every graph o vertices with maximum degree at most.
CS 2750 Machine Learning. Lecture 23. Concept learning. CS 2750 Machine Learning. Concept Learning
 Lecture 3 Cocept learig Milos Hauskrecht milos@cs.pitt.edu Cocept Learig Outlie: Learig boolea fuctios Most geeral ad most specific cosistet hypothesis. Mitchell s versio space algorithm Probably approximately
Lecture 3 Cocept learig Milos Hauskrecht milos@cs.pitt.edu Cocept Learig Outlie: Learig boolea fuctios Most geeral ad most specific cosistet hypothesis. Mitchell s versio space algorithm Probably approximately
Skip Lists. Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 S 3 S S 1
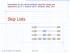 Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Skip Lists S 3 15 15 23 10 15 23 36 Skip Lists 1 What is a Skip List A skip list for
Presetatio for use with the textbook, Algorithm Desig ad Applicatios, by M. T. Goodrich ad R. Tamassia, Wiley, 2015 Skip Lists S 3 15 15 23 10 15 23 36 Skip Lists 1 What is a Skip List A skip list for
Topic 9: Sampling Distributions of Estimators
 Topic 9: Samplig Distributios of Estimators Course 003, 2018 Page 0 Samplig distributios of estimators Sice our estimators are statistics (particular fuctios of radom variables), their distributio ca be
Topic 9: Samplig Distributios of Estimators Course 003, 2018 Page 0 Samplig distributios of estimators Sice our estimators are statistics (particular fuctios of radom variables), their distributio ca be
6.895 Essential Coding Theory October 20, Lecture 11. This lecture is focused in comparisons of the following properties/parameters of a code:
 6.895 Essetial Codig Theory October 0, 004 Lecture 11 Lecturer: Madhu Suda Scribe: Aastasios Sidiropoulos 1 Overview This lecture is focused i comparisos of the followig properties/parameters of a code:
6.895 Essetial Codig Theory October 0, 004 Lecture 11 Lecturer: Madhu Suda Scribe: Aastasios Sidiropoulos 1 Overview This lecture is focused i comparisos of the followig properties/parameters of a code:
EDGE-COLORINGS AVOIDING RAINBOW STARS
 EDGE-COLORINGS AVOIDING RAINBOW STARS CARLOS HOPPEN, HANNO LEFMANN, KNUT ODERMANN, AND JULIANA SANCHES Abstract. We cosider a extremal problem motivated by a paper of Balogh [J. Balogh, A remark o the
EDGE-COLORINGS AVOIDING RAINBOW STARS CARLOS HOPPEN, HANNO LEFMANN, KNUT ODERMANN, AND JULIANA SANCHES Abstract. We cosider a extremal problem motivated by a paper of Balogh [J. Balogh, A remark o the
11. Hash Tables. m is not too large. Many applications require a dynamic set that supports only the directory operations INSERT, SEARCH and DELETE.
 11. Hash Tables May applicatios require a dyamic set that supports oly the directory operatios INSERT, SEARCH ad DELETE. A hash table is a geeralizatio of the simpler otio of a ordiary array. Directly
11. Hash Tables May applicatios require a dyamic set that supports oly the directory operatios INSERT, SEARCH ad DELETE. A hash table is a geeralizatio of the simpler otio of a ordiary array. Directly
( ) = p and P( i = b) = q.
 MATH 540 Radom Walks Part 1 A radom walk X is special stochastic process that measures the height (or value) of a particle that radomly moves upward or dowward certai fixed amouts o each uit icremet of
MATH 540 Radom Walks Part 1 A radom walk X is special stochastic process that measures the height (or value) of a particle that radomly moves upward or dowward certai fixed amouts o each uit icremet of
Fortgeschrittene Datenstrukturen Vorlesung 11
 Fortgeschrittee Datestruture Vorlesug 11 Schriftführer: Marti Weider 19.01.2012 1 Succict Data Structures (ctd.) 1.1 Select-Queries A slightly differet approach, compared to ra, is used for select. B represets
Fortgeschrittee Datestruture Vorlesug 11 Schriftführer: Marti Weider 19.01.2012 1 Succict Data Structures (ctd.) 1.1 Select-Queries A slightly differet approach, compared to ra, is used for select. B represets
Detailed proofs of Propositions 3.1 and 3.2
 Detailed proofs of Propositios 3. ad 3. Proof of Propositio 3. NB: itegratio sets are geerally omitted for itegrals defied over a uit hypercube [0, s with ay s d. We first give four lemmas. The proof of
Detailed proofs of Propositios 3. ad 3. Proof of Propositio 3. NB: itegratio sets are geerally omitted for itegrals defied over a uit hypercube [0, s with ay s d. We first give four lemmas. The proof of
Appendix to Quicksort Asymptotics
 Appedix to Quicksort Asymptotics James Alle Fill Departmet of Mathematical Scieces The Johs Hopkis Uiversity jimfill@jhu.edu ad http://www.mts.jhu.edu/~fill/ ad Svate Jaso Departmet of Mathematics Uppsala
Appedix to Quicksort Asymptotics James Alle Fill Departmet of Mathematical Scieces The Johs Hopkis Uiversity jimfill@jhu.edu ad http://www.mts.jhu.edu/~fill/ ad Svate Jaso Departmet of Mathematics Uppsala
