Fuzzy derivations KU-ideals on KU-algebras BY
|
|
|
- Piers Cox
- 6 years ago
- Views:
Transcription
1 Fu ervaons KU-eals on KU-algebras BY Sam M.Mosaa, Ahme Ab-elaem 2 sammosaa@ahoo.com ahmeabelaem88@ahoo.com,2deparmen o mahemacs -Facul o Eucaon -An Shams Unvers Ro, Caro, Egp Absrac. In hs manuscrp, we nrouce a new concep, whch s calle u le rgh ervaons KU- eals n KU-algebras. We sae an prove some heorems abou unamenal properes o. Moreover, we gve he conceps o he mage an he pre-mage o u le rgh ervaons KU-eals uner homomorphsm o KU- algebras an nvesgae some s properes. Furher, we have prove ha ever he mage an he pre-mage o u le rgh ervaons KU-eals uner homomorphsm o KU- algebras are u le rgh ervaons KU-eals. Furhermore, we gve he concep o he Caresan prouc o u le rgh ervaons KU - eals n Caresan prouc o KU algebras. AMS Subjec Classcaon: 3G25, 6F35 Kewors. KU-algebras,u le rgh ervaons o KU-eals, he mage an he per- mage o u le rgh ervaons KU eals, he Caresan prouc o u le rgh ervaons KU eals. Corresponng Auhor : Sam M. Mosaa sammosaa@ahoo.com. Inroucon As s well known, BCK an BCI-algebras are wo classes o algebras o logc. The were nrouce b Ima an Isek [,,2] an have been eensvel nvesgae b man researchers. I s known ha he class o BCK-algebras s a proper sub class o he BCI-algebras.The class o all BCK-algebras s a quasvare. Is ek pose an neresng problem solve b Wro nsk [24] wheher he class o BCK-algebras s a vare. In connecon wh hs problem, Komor [5] nrouce a noon o BCC-algebras, an Duek [7] reene he noon o BCC-algebras b usng a ual orm o he ornar enon n he sense o Komor. Duek an Zhang [8] nrouce a new noon o eals n BCCalgebras an escrbe connecons beween such eals an congruences.
2 C.Prabpaak an U.Leerawa [22 ], [23 ] nrouce a new algebrac srucure whch s calle KU - algebra. The gave he concep o homomorphsms o KUalgebras an nvesgae some relae properes. Several auhors [2,3,5,6,9,4] have sue ervaons n rngs an near rngs. Jun an Xn [3] apple he noon o ervaons n rng an near-rng heor o BCI-algebras, an he also nrouce a new concep calle a regular ervaon n BCI -algebras. The nvesgae some o s properes, ene a -ervaon eal an gave conons or an eal o be -ervaon. Laer, Hama an Al-Shehr [], ene a le ervaon n BCI-algebras an nvesgae a regular le ervaon. Zhan an Lu [27 ] sue -ervaons n BCI-algebras an prove some resuls. G. Muhun el [2,2] nrouce he noon o, -ervaon n a BCIalgebra an nvesgae relae properes. The prove a conon or a, - ervaon o be regular. The also nrouce he conceps o a, - nvaran, -ervaon an α-eal, an hen he nvesgae her relaons. Furhermore, he obane some resuls on regular, - ervaons. Moreover, he sue he noon o -ervaons on BCI-algebras an obane some o s relae properes. Furher, he characere he noon o p-semsmple BCI-algebra X b usng he noon o -ervaon. Laer, Mosaa e al [8,9], nrouce he noons o, r - r, -ervaon o a KU-algebra an some relae properes are eplore. The concep o u ses was nrouce b Zaeh [26]. In 99, X [25] apple he concep o u ses o BCI, BCK, MValgebras.Snce s ncepon, he heor o u ses, eal heor an s ucaon has evelope n man recons an s nng applcaons n a we vare o els. Mosaa e al, n 2[7] nrouce he noon o u KU-eals o KU-algebras an hen he nvesgae several basc properes whch are relae o u KU-eals. In hs paper, we nrouce he noon o u le rgh ervaons KU- eals n KU - algebras. The homomorphc mage premage o u le rgh - ervaons KU- eals n KU - algebras uner homomorprhsm o a KU-algebras are scusse. Man relae resuls have been erve. 2
3 2. Prelmnares In hs secon, we recall some basc enons an resuls ha are neee or our work. Denon 2. [22,23 ] Le X be a se wh a bnar operaon an a consan. X,, s calle KU-algebra he ollowng aoms hol :,, X : KU [ ] KU 2 KU 3 KU 4 mples Dene a bnar relaon b :, we can prove ha X, s a parall orere se. Throughou hs arcle, X wll enoe a KU-algebra unless oherwse menone Corollar 2.2 [7,22] In KU-algebra he ollowng enes are rue or all,, X : I mples ha v v [ ] Denon 2.3 [22,23] A subse S o KU-algebra X s calle sub algebra o X S, whenever, S Denon 2.4 [22,23 ] Anon emp subse A o KU-algebra X s calle eal o X s sase he ollowng conons: A A, A mples A, X. 3
4 Denon 2.5 [7] A non - emp subse A o a KU-algebra X s calle an KU eal o X sases he ollowng conons : A, 2 * * A, A mples * A, or all,, X Denon 2.6[7] Le X be a KU - algebra, a u se µ n X s calle u sub-algebra sases: S µ µ, S 2 µ {µ *, µ } or all, X. Denon 2.7 [7] Le X be a KU-algebra, a u se µ n X s calle a u KU-eal o X sases he ollowng conons: F µ µ, F 2 µ * mn {µ * *, µ }. Denon 2.8 For elemens an o KU-algebra X,,, we enoe. Denon 2.9[8] Le X be a KU-algebra. A sel map : X X s a le rgh ervaon brel,, r -ervaon o X sases he en, X I sases he en, X s calle rgh-le ervaon brel, r, -ervaon o X. Moreover, s boh, r an r, ervaon hen s calle a ervaon o X. Denon 2.[8] A ervaon o KU-algebra s sa o be regular. 4
5 Lemma 2.[8] A ervaon o KU-algebra X s regular. Eample 2.2 [8] Le X = {,,2,3. 4 } be a se n whch he operaon s ene as ollows: Usng he algorhms n Appen A, we can prove ha X, *, s a KU-algebra. Dene a map : X X b 4,,2,3 4 Then s eas o show ha s boh a, r an r, -ervaon o X. Eample 2.2. Le on bnar relaon on be he se o all posve negers an. The operaon * s ene as ollows: *=,where " " he mnus operaon.dene a b :. Then,*, X s a KU-algebra. We ene a map : X X b = or all.then, X,we have *= =.I, * = = =+ an * = = =, bu * * =+ * * = [ + ]= = + II From I an II, s no, r ervaon o X. On oher han 5
6 *= =, *= = =+, bu * * = [ ** *]* *= [ ] =. III From I an III, s r, ervaon o X. Hence r, -ervaon an, r ervaon are no conce. Proposon 2.3[8] Le X be a KU-algebra wh paral orer, an le be a ervaon o X. Then he ollowng hol, X :... v. v { X } s a sub algebra o X. Denon 2.4 [8] Le X be a KU-algebra an be a ervaon o X. Denoe F X { X : }. Proposon 2.5[8] Le X be a KU-algebra an be a ervaon o X.Then F X s a sub algebra o X. 6
7 3. Fu ervaons KU- eals o KU-algebras In hs secon, we wll scuss an nvesgae a new noon calle u- le ervaons KU - eals o KU - algebras an su several basc properes whch are relae o u le ervaons KU - eals. Denon 3. Le X be a KU-algebra an : X X be sel map.a non - emp subse A o a KU-algebra X s calle le ervaons KU eal o X sases he ollowng conons: A, 2 * * A, A mples * A, or all,, X Denon 3.2 Le X be a KU-algebra an : X X be sel map.a non - emp subse A o a KU-algebra X s calle rgh ervaons KU eal o X sases he ollowng conons: A, 2 * * A, A mples * A, or all,, X. Denon 3.3 Le X be a KU-algebra an : X X be sel map.a non - emp subse A o a KU-algebra X s calle ervaons KU -eal o X sases he ollowng conons: A, 2 * * A, A mples * A, or all,, X Denon 3.4 Le X be a KU-algebra an : X X be sel map. A u se : X [,] n X s calle a u le ervaons KU-ealbrel, F, -ervaon o X sases he ollowng conons: F µ µ, FL 2 µ * mn{ µ**, µ }. 7
8 Denon 3.5 Le X be a KU-algebra an : X X be sel map. A u se : X [,] n X s calle a u rgh ervaons KU-ealbrel, F, r o X sases he ollowng conons: F µ µ. -ervaon FR 2 µ * mn { µ**, µ }. Denon 3.6 Le X be a KU-algebra an : X X be sel map. A u se : X [,] n X s calle a u ervaons KU-eal, sases he ollowng conons F µ µ. F 2 µ * mn{ µ* *, µ }. Remark3.7 I I s e, he enons 3., 3.2,3.3 gves he enon KU-eal. II I s e, he enons 3.4,3.5, 3.6 gves he enon u KU-eal. Eample 3.8 Le X = {,,2,3. 4 } be a se n whch he operaon s ene as ollows: Usng he algorhms n Appen A, we can prove ha X, *, s a KU-algebra. * Dene a sel map : X X b 8
9 4,,2,3 4. Dene a u se µ : X [,],b µ =, µ =µ 2 =, µ 3 = µ 4 = 2, where,, 2 [,] wh > > 2.Roune calculaons gve ha µ s a u le rgh- ervaons KU- eal o KU- algebra X. Lemma 3.9 Le µ be a u le ervaons KU - eal o KU - algebra X, he nequal, * hols n X, hen µ mn {µ, µ }. Proo. Assume ha he nequal * hols n X, hen * * =, * * =, snce rom Proposon 2.3 an bfl 2, we have µ * mn{ µ**,µ }= mn{ µ, µ }= µ Pu =, we have µ * = µ mn{ µ*,µ }, bu µ * mn {µ * *, µ } = mn {µ * *, µ } =mn {µ, µ } = µ From,, we ge µ mn {µ, µ }, hs complees he proo. Lemma 3. I µ s a u le ervaons KU - eal o KU - algebra X an, hen μ μ. Proo. I,hen * =, *= snce rom Proposon 2.3 hs ogeher wh * = an μ μ,we ge µ * = µ mn {µ * *, µ } = mn {µ *, µ } = = mn {µ,µ } = µ. Proposon 3. The nersecon o an se o u le ervaons KU - eals o KU algebra X s also u le ervaons KU - eal. Proo. le be a aml o u le ervaons KU - eals o KU- algebra X, hen or an,, X, n n an 9
10 mn * n * nmn * *, n * *,n mn * *,. Ths complees he proo. Lemma 3.2 The nersecon o an se o u rgh ervaons KU - eals o KU algebra X s also u rgh ervaons KU - eal. proo. Clear Theorem3.3 Le µ be a u se n X hen µ s a u le ervaons KU- eal o X an onl sases : For all α [,],U μ, α φ mples Uμ,α s KU- eal o X A, where U μ, α = { X / μ α}. Proo. Assume ha µ s a u le ervaons KU- eal o X, le α [, ] be such ha U μ, α φ, an, X such ha U μ, α, hen µ α an so b FL 2, µ * = µ mn { µ * *, µ }= mn{µ *, µ } = mn {µ, µ } = α, hence U μ, α. Le * * U μ, α, U μ, α, I ollows romfl 2 ha µ * mn {µ * *, µ } = α, so ha * U µ, α. Hence U μ, α s KU - eal o X. Conversel, suppose ha µ sases A, le,, X be such ha µ * < mn {µ * *, µ },akng β = /2 {µ * + mn {µ * *, µ }, we have β [,] an µ * < β < mn {μ * *, µ }, ollows ha * * U μ, β an * U μ, β, hs s a conracon an hereore µ s a u le ervaons KU - eal o X. Theorem3.4 Le µ be a u se n X hen µ s a u rgh ervaons KU- eal o X an onl sases : For all α [,],U μ, α φ mples Uμ,α s KU- eal o X. Proposon 3.5 I µ s a u le ervaons KU - eal o X, hen µ * * µ
11 proo. Takng = * n FL2 an usng ku2 an F, we ge µ * * mn { µ * * *, µ } = mn {µ * * *, µ } = mn {µ * *, µ }= mn {µ, µ } = µ. Denon3.6 Le µ be a u le ervaons KU - eal o KU - algebra X,.he KU - eals, [,] are calle level KU - eal o µ. Corollar3.7 Le I be an KU - eal o KU - algebra X, hen or an e number n an open nerval,, here es a u le ervaons KU eal µ o X such ha = I. proo. The proo s smlar he corollar 4.4 [7]. 4 Image Pre-mage o u ervaons KU-eals uner homomorphsm In hs secon, we nrouce he conceps o he mage an he pre-mage o u le ervaons KU-eals n KU-algebras uner homomorphsm. Denon 4. Le be a mappng rom he se X o a se Y. I s a u subse o X, hen he u subse β o Y ene b sup, { X, } oherwse s sa o be he mage o uner. Smlarl β s a u subse o Y, hen he u subse µ = β n X.e he u subse ene b µ = β or all X s calle he prmage o β uner.
12 Theorem 4.2 An ono homomorphc premage o a u le ervaons KU - eal s also a u le ervaons KU - eal. Proo.Le : X X` be an ono homomorphsm o KU - algebras, β a u le ervaons KU - eal o X` an µ he premage o β uner, hen β = µ, or all X. Le X, hen µ = β β = µ. Now le,, X, hen µ * = β * mn {β *` *`, β } = mn { β * *,β }= mn {µ * *, µ }. The proo s complee. Denon 4.3 [4 ] A u subse µ o X has sup proper or an subse T o X, here es T such ha, SUP. T Theorem 4.4 Le : X Y be a homomorphsm beween KU - algebras X an Y. For ever u le ervaons KU - eal µ n X, µ s a u le ervaons KU - eal o Y. Proo. B enon sup or all Y an sup.we have o prove ha mn{, }, `, `, `Y. Le : X Y be an ono a homomorphsm o KU - algebras, µ a u le ervaons KU - eal o X wh sup proper an β he mage o μ uner, snce µ s a u le ervaons KU - eal o X, we have µ µ or all X. Noe ha `, where, ` are he ero o X an Y respecvel 2
13 3 Thus,, sup or all X, whch mples ha, sup or an Y. For an Y,,,le,, be Such ha sup, sup \ an sup } sup } {. Then sup }, mn{ =, sup mn sup \ = }, mn{. Hence β s a u le ervaons KU-eal o Y. Theorem 4.5 An ono homomorphc premage o a u rgh ervaons KU - eal s also a u rgh ervaons KU - eal Theorem 4.6 Le : X Y be a homomorphsm beween KU - algebras X an Y. For ever u rgh ervaons KU - eal µ n X, µ s a u rgh ervaons KU - eal o Y. proo. Clear
14 5. Caresan prouc o u le ervaons KU-eals Denon 5.[4] A u µ s calle a u relaon on an se S, µ s a u subse µ : S S [,]. Denon 5.2 [4] I µ s a u relaon on a se S an β s a u subse o S, hen μ s a u relaon on β μ, mn {β, β },, S. Denon 5.3 [4] Le µ an β be u subse o a se S, he Caresan prouc o μ an β s ene b μ β, = mn {μ, β },, S. Lemma 5.4[4] Le μ an β be u subse o a se S,hen s a u relaon on S. = or all [,]. Denon 5.5 I µ s a u le ervaons relaon on a se S an β s a u le ervaons subse o S, hen µ s a u le ervaons relaon on β µ, mn {β, β },, S. Denon 5.6 [4] Le µ an β be u le ervaons subse o a se S, he Caresan prouc o µ an β s ene b µ β, = mn {µ, β },, S Lemma 5.7[4] Le µ an β be u subse o a se S,hen s a u relaon on S, = or all [,]. 4
15 Denon 5.8 I β s a u le ervaons subse o a se S, he sronges u relaon on S, ha s a u ervaons relaon on β s µ β gven b µ β, = mn {β, β },, S. Lemma 5.9 For a gven u le ervaons subse S, le µ β be he sronges u le ervaons relaon on S,hen or [,], we have µ β = β β. Proposon 5. For a gven u subse β o KU - algebra X, le µ β be he sronges le u ervaons relaon on X. I µ β s a u le ervaons KU - eal o X X, hen β β = β or all X. Proo. Snce µ β s a u le ervaons KU- eal o X X, ollows rom F ha µ β, = mn {β, β } β, = mn {β, β }, where, X X hen β β = β. Remark5. Le X an Y be KU- algebras, we ene * on X Y b : For ever,, u, vx Y,, * u, v = * u, * v, hen clearl X Y, *,, s a KU- algebra. Theorem 5.2 Le µ an β be a u le ervaons KU- eals o KU - algebra X,hen µ β s a u le ervaons KU-eal o X X. Proo : or an, X X,we have, µ β, = mn {µ, β }= mn {µ, β} mn {µ, β } = µ β,. Now le, 2,, 2,, 2 X X, hen, µ β *, 2 * 2 = mn {µ,, β 2, 2 } mn{mn {µ * *, µ }}, mn {β 2 * 2 * 2, β 2 }} 5
16 = mn{mn{µ * *, µ 2 * 2 * 2 }, mn{µ, β 2 }} = mn{µ β * *, 2 * 2 * 2, µ β, 2 }. Hence µ β s a u le ervaons KU- eal o X X. Analogous o heorem 3.2 [ 6], we have a smlar resuls or u le ervaons KUeal, whch can be prove n smlar manner, we sae he resuls whou proo. Theorem 5.3 Le µ an β be a u le ervaons subse o KU-algebra X,such ha µ β s a u le ervaons KU-eal o X X, hen Eher µ µ or β β or all X, I µ µ or all X, hen eher µ β or β β, I β β or all X, hen eher µ µ or β µ, v Eher µ or β s a u le ervaons KU- eal o X. Theorem 5.4 Le β be a u subse o KU- algebra X an le µ β be he sronges u le ervaons relaon on X, hen β s a u le ervaons KU - eal o X an onl µ β s a u le ervaons KU- eal o X X. proo : Assume ha β s a u le ervaons KU- eal X, we noe rom F ha : µ β, = mn {β, β } =mn {β, β } mn {β, β } = µ β,. Now, or an, 2,, 2,, 2 X X, we have rom F 2 : µ β *, 2 * 2 = mn {β *, β 2 * 2 } mn {mn{β * *, β }, mn {β 2 * 2 * 2, β 2 }} = mn{mn{β * *, β 2 * 2 * 2 }, mn {β, β 2 }} = mn {µ β * *, 2 * 2 * 2, µ β, 2 }. 6
17 Hence µ β s a u le ervaons KU - eal o X X. Conversel. For all, X X, we have Mn {β, β } = µ β, = mn {β, β }. I ollows ha β β or all X, whch prove F. Now, le, 2,, 2,, 2 X X, hen mn {β *, β 2 * 2 } = µ β *, 2 * 2 mn {µ β, 2 *, 2 *, 2, µ β, 2 } = mn {µ β * *, 2 * 2 * 2, µ β, 2 } = mn {mn {β * *, β 2 * 2 * 2 }, mn {β, β 2 }} = mn {mn {β * *, β }, mn {β 2 * 2 * 2, β 2 }} In parcular, we ake 2 = 2 = 2 =, hen, β * mn { β * *, β } Ths prove FL 2 an complees he proo. Concluson Dervaon s a ver neresng an mporan area o research n he heor o algebrac srucures n mahemacs. In he presen paper, he noon o u le ervaons KU - eal n KU-algebra are nrouce an nvesgae he useul properes o u le ervaons KU - eals n KU-algebras. In our opnon, hese enons an man resuls can be smlarl eene o some oher algebrac ssems such as BCI-algebra, BCH-algebra,Hlber algebra,bf-algebra -Jalgebra,WS-algebra,CI-algebra, SU-algebra,BCL-algebra,BP-algebra,Coeer algebra,bo-algebra,pu- algebras an so orh. The man purpose o our uure work s o nvesgae: The nerval value, bpolar an nuonsc u le ervaons KU - eal n KUalgebra. 2 To conser he cubc srucure o le ervaons KU - eal n KU-algebra. We hope he u le ervaons KU - eals n KU-algebras, have applcaons n eren branches o heorecal phscs an compuer scence. 7
18 Algorhm or KU-algebras Inpu X : se, : bnar operaon Oupu X s a KU-algebra or no Begn I X hen go o.; En I I X hen go o.; En I Sop: =alse; : ; Whle X an no Sop o I hen Sop: = rue; En I j : Whle j X an no Sop o I hen j Sop: = rue; En I En I k : Whle k X an no Sop o I hen j j k k 8
19 Sop: = rue; En I En Whle En Whle En Whle I Sop hen. Oupu X s no a KU-algebra Else Oupu X s a KU-algebra En I En. Reerences [] H. A. S. Abujabal an N. O. Al-Shehr, On le ervaons o BCI-algebras, Soochow Journal o Mahemacs, vol. 33, no. 3, pp , 27. [2] H. E. Bell an L.-C. Kappe, Rngs n whch ervaons sas ceran algebrac conons, Aca Mahemaca Hungarca, vol. 53, no. 3-4, pp , 989. [3] H. E. Bell an G. Mason, On ervaons n near-rngs, near-rngs an Near-els, Norh-Hollan Mahemacs Sues, vol. 37, pp. 3 35, 987. [4] P.Bhaachare an N.P.Mukheree, Fu relaons an u group norm, sc,36985, [5] M. Breˇsar an J. Vukman, On le ervaons an relae mappngs, Proceengs o he Amercan Mahemacal Soce, vol., no., pp. 7 6, 99. [6] M. Breˇsar, On he sance o he composon o wo ervaons o he generale ervaons, Glasgow Mahemacal Journal, vol. 33, no., pp , 99. [7] W. A. Duek, The number o subalgebras o ne BCC-algebras, Bull. Ins. Mah. Aca. Snca, 2 992, [8] W. A. Duek an X. H. Zhang, On eals an congruences n BCCalgebras, Cechoslovak Mah. J., , [9] B. Hvala, Generale ervaons n rngs, Communcaons n Algebra, vol. 26, no. 4, pp , 998 9
20 [] Y.Ima an Isek K: On aom ssems o Proposonal calcul, XIV, Proc. Japan Aca. Ser A, Mah Sc., 42966,9-22. [] k.isek: An algebra relae wh a proposonal calcul, Proc. Japan Aca. Ser A Mah. Sc., , [2] K Isek an Tanaka S: An nroucon o heor o BCK-algebras, Mah. Japo., [3] Y. B. Jun an X. L. Xn, On ervaons o BCI-algebras, Inormaon Scences, vol. 59, no. 3-4, pp , 24. [4]A. A. M. Kamal, σ-ervaons on prme near-rngs, Tamkang Journal o Mahemacs, vol. 32, no. 2, pp , 2 [5]Y. Komor, The class o BCC-algebras s no a vare, Mah. Japonca, , [6 ] D.S.Malk an J.N.Moreson, Fu relaon on rngs an groups, u ses an ssems, 4399,7-23. [ 7] S. M. Mosaa M. A. Ab-Elnab- M.M. Youse, Fu eals o KU algebra Inernaonal Mahemacal Forum, Vol. 6, 2.no. 63, [8] S. M.Mosaa, R. A. K. Omar, A. Ab-elaem, Properes o ervaons on KUalgebras,gournal o avances n mahemacs Vol.9, No. [9]S. M. Mosaa, F. F.Kareem, Le e maps an α-ervaons o KU-algebra, gournal o avances n mahemacs Vol.9, No 7 [2] G. Muhun an Abullah M. Al-Roq On, -Dervaons n BCI-Algebras.Dscree Dnamcs n Naure an Soce Volume 22. [2] G. Muhun an Abullah M. Al-roq,On -Dervaons o BCI-Algebras Absrac an Apple Analss Volume 22, Arcle ID , 2 pages [22] C.Prabpaak an U.Leerawa, On eals an congruence n KU-algebras, scena Magna n- ernaonal book seres, Vol. 529, No., [23] C.Prabpaak an U.Leerawa, On somorphsms o KU-algebras, scena Magna nernaonal book seres, 529, no.3, [24] A. Wronsk, BCK-algebras o no orm a vare, Mah. Japonca, , [25] O.G.X, u BCK-algebras, Mah. Japan,
21 [26] L.A.Zaeh, Fu ses, norm. an conrol,8965, [27] J. Zhan an Y. L. Lu, On -ervaons o BCI-algebras, Inernaonal Journal o Mahemacs an Mahemacal Scences, no., pp , 25. Sam M. Mosaa sammosaa@ahoo.com Deparmen o Mahemacs, Facul o Eucaon, An Shams Unvers, Ro, Caro, Egp. Ahme Ab-elaem ahmeabelaem88@ahoo.com Deparmen o Mahemacs, Facul o Eucaon, An Shams Unvers, Ro, Caro, Egp. 2
TERNARY SEMIHYPERGROUPS IN TERMS OF BIPOLAR-VALUED FUZZY SETS
 IJRR 6 Jul wwwarpapresscom/volumes/vol6issue/ijrr_6 6pf TERNRY EMIHYPERGROUP IN TERM OF IPOLR-VLUED FUZZY ET Ibsam Masmal Deparmen of Mahemacs College of cence Jaan Unvers Jaan Kngom of aua raba E-mal:
IJRR 6 Jul wwwarpapresscom/volumes/vol6issue/ijrr_6 6pf TERNRY EMIHYPERGROUP IN TERM OF IPOLR-VLUED FUZZY ET Ibsam Masmal Deparmen of Mahemacs College of cence Jaan Unvers Jaan Kngom of aua raba E-mal:
Relative controllability of nonlinear systems with delays in control
 Relave conrollably o nonlnear sysems wh delays n conrol Jerzy Klamka Insue o Conrol Engneerng, Slesan Techncal Unversy, 44- Glwce, Poland. phone/ax : 48 32 37227, {jklamka}@a.polsl.glwce.pl Keywor: Conrollably.
Relave conrollably o nonlnear sysems wh delays n conrol Jerzy Klamka Insue o Conrol Engneerng, Slesan Techncal Unversy, 44- Glwce, Poland. phone/ax : 48 32 37227, {jklamka}@a.polsl.glwce.pl Keywor: Conrollably.
Comparison of Differences between Power Means 1
 In. Journal of Mah. Analyss, Vol. 7, 203, no., 5-55 Comparson of Dfferences beween Power Means Chang-An Tan, Guanghua Sh and Fe Zuo College of Mahemacs and Informaon Scence Henan Normal Unversy, 453007,
In. Journal of Mah. Analyss, Vol. 7, 203, no., 5-55 Comparson of Dfferences beween Power Means Chang-An Tan, Guanghua Sh and Fe Zuo College of Mahemacs and Informaon Scence Henan Normal Unversy, 453007,
GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS. Youngwoo Ahn and Kitae Kim
 Korean J. Mah. 19 (2011), No. 3, pp. 263 272 GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS Youngwoo Ahn and Kae Km Absrac. In he paper [1], an explc correspondence beween ceran
Korean J. Mah. 19 (2011), No. 3, pp. 263 272 GENERATING CERTAIN QUINTIC IRREDUCIBLE POLYNOMIALS OVER FINITE FIELDS Youngwoo Ahn and Kae Km Absrac. In he paper [1], an explc correspondence beween ceran
ON THE WEAK LIMITS OF SMOOTH MAPS FOR THE DIRICHLET ENERGY BETWEEN MANIFOLDS
 ON THE WEA LIMITS OF SMOOTH MAPS FOR THE DIRICHLET ENERGY BETWEEN MANIFOLDS FENGBO HANG Absrac. We denfy all he weak sequenal lms of smooh maps n W (M N). In parcular, hs mples a necessary su cen opologcal
ON THE WEA LIMITS OF SMOOTH MAPS FOR THE DIRICHLET ENERGY BETWEEN MANIFOLDS FENGBO HANG Absrac. We denfy all he weak sequenal lms of smooh maps n W (M N). In parcular, hs mples a necessary su cen opologcal
Solution in semi infinite diffusion couples (error function analysis)
 Soluon n sem nfne dffuson couples (error funcon analyss) Le us consder now he sem nfne dffuson couple of wo blocks wh concenraon of and I means ha, n a A- bnary sysem, s bondng beween wo blocks made of
Soluon n sem nfne dffuson couples (error funcon analyss) Le us consder now he sem nfne dffuson couple of wo blocks wh concenraon of and I means ha, n a A- bnary sysem, s bondng beween wo blocks made of
Existence and Uniqueness Results for Random Impulsive Integro-Differential Equation
 Global Journal of Pure and Appled Mahemacs. ISSN 973-768 Volume 4, Number 6 (8), pp. 89-87 Research Inda Publcaons hp://www.rpublcaon.com Exsence and Unqueness Resuls for Random Impulsve Inegro-Dfferenal
Global Journal of Pure and Appled Mahemacs. ISSN 973-768 Volume 4, Number 6 (8), pp. 89-87 Research Inda Publcaons hp://www.rpublcaon.com Exsence and Unqueness Resuls for Random Impulsve Inegro-Dfferenal
Cubic Bezier Homotopy Function for Solving Exponential Equations
 Penerb Journal of Advanced Research n Compung and Applcaons ISSN (onlne: 46-97 Vol. 4, No.. Pages -8, 6 omoopy Funcon for Solvng Eponenal Equaons S. S. Raml *,,. Mohamad Nor,a, N. S. Saharzan,b and M.
Penerb Journal of Advanced Research n Compung and Applcaons ISSN (onlne: 46-97 Vol. 4, No.. Pages -8, 6 omoopy Funcon for Solvng Eponenal Equaons S. S. Raml *,,. Mohamad Nor,a, N. S. Saharzan,b and M.
SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β
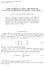 SARAJEVO JOURNAL OF MATHEMATICS Vol.3 (15) (2007), 137 143 SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β M. A. K. BAIG AND RAYEES AHMAD DAR Absrac. In hs paper, we propose
SARAJEVO JOURNAL OF MATHEMATICS Vol.3 (15) (2007), 137 143 SOME NOISELESS CODING THEOREMS OF INACCURACY MEASURE OF ORDER α AND TYPE β M. A. K. BAIG AND RAYEES AHMAD DAR Absrac. In hs paper, we propose
Approximate Analytic Solution of (2+1) - Dimensional Zakharov-Kuznetsov(Zk) Equations Using Homotopy
 Arcle Inernaonal Journal of Modern Mahemacal Scences, 4, (): - Inernaonal Journal of Modern Mahemacal Scences Journal homepage: www.modernscenfcpress.com/journals/jmms.aspx ISSN: 66-86X Florda, USA Approxmae
Arcle Inernaonal Journal of Modern Mahemacal Scences, 4, (): - Inernaonal Journal of Modern Mahemacal Scences Journal homepage: www.modernscenfcpress.com/journals/jmms.aspx ISSN: 66-86X Florda, USA Approxmae
V.Abramov - FURTHER ANALYSIS OF CONFIDENCE INTERVALS FOR LARGE CLIENT/SERVER COMPUTER NETWORKS
 R&RATA # Vol.) 8, March FURTHER AALYSIS OF COFIDECE ITERVALS FOR LARGE CLIET/SERVER COMPUTER ETWORKS Vyacheslav Abramov School of Mahemacal Scences, Monash Unversy, Buldng 8, Level 4, Clayon Campus, Wellngon
R&RATA # Vol.) 8, March FURTHER AALYSIS OF COFIDECE ITERVALS FOR LARGE CLIET/SERVER COMPUTER ETWORKS Vyacheslav Abramov School of Mahemacal Scences, Monash Unversy, Buldng 8, Level 4, Clayon Campus, Wellngon
In the complete model, these slopes are ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL. (! i+1 -! i ) + [(!") i+1,q - [(!
 ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL The frs hng o es n wo-way ANOVA: Is here neracon? "No neracon" means: The man effecs model would f. Ths n urn means: In he neracon plo (wh A on he horzonal
ANALYSIS OF VARIANCE FOR THE COMPLETE TWO-WAY MODEL The frs hng o es n wo-way ANOVA: Is here neracon? "No neracon" means: The man effecs model would f. Ths n urn means: In he neracon plo (wh A on he horzonal
Online Supplement for Dynamic Multi-Technology. Production-Inventory Problem with Emissions Trading
 Onlne Supplemen for Dynamc Mul-Technology Producon-Invenory Problem wh Emssons Tradng by We Zhang Zhongsheng Hua Yu Xa and Baofeng Huo Proof of Lemma For any ( qr ) Θ s easy o verfy ha he lnear programmng
Onlne Supplemen for Dynamc Mul-Technology Producon-Invenory Problem wh Emssons Tradng by We Zhang Zhongsheng Hua Yu Xa and Baofeng Huo Proof of Lemma For any ( qr ) Θ s easy o verfy ha he lnear programmng
Notes on the stability of dynamic systems and the use of Eigen Values.
 Noes on he sabl of dnamc ssems and he use of Egen Values. Source: Macro II course noes, Dr. Davd Bessler s Tme Seres course noes, zarads (999) Ineremporal Macroeconomcs chaper 4 & Techncal ppend, and Hamlon
Noes on he sabl of dnamc ssems and he use of Egen Values. Source: Macro II course noes, Dr. Davd Bessler s Tme Seres course noes, zarads (999) Ineremporal Macroeconomcs chaper 4 & Techncal ppend, and Hamlon
OP = OO' + Ut + Vn + Wb. Material We Will Cover Today. Computer Vision Lecture 3. Multi-view Geometry I. Amnon Shashua
 Comuer Vson 27 Lecure 3 Mul-vew Geomer I Amnon Shashua Maeral We Wll Cover oa he srucure of 3D->2D rojecon mar omograh Marces A rmer on rojecve geomer of he lane Eolar Geomer an Funamenal Mar ebrew Unvers
Comuer Vson 27 Lecure 3 Mul-vew Geomer I Amnon Shashua Maeral We Wll Cover oa he srucure of 3D->2D rojecon mar omograh Marces A rmer on rojecve geomer of he lane Eolar Geomer an Funamenal Mar ebrew Unvers
THE PREDICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS
 THE PREICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS INTROUCTION The wo dmensonal paral dfferenal equaons of second order can be used for he smulaon of compeve envronmen n busness The arcle presens he
THE PREICTION OF COMPETITIVE ENVIRONMENT IN BUSINESS INTROUCTION The wo dmensonal paral dfferenal equaons of second order can be used for he smulaon of compeve envronmen n busness The arcle presens he
A Deza Frankl type theorem for set partitions
 A Deza Frankl ype heorem for se parons Cheng Yeaw Ku Deparmen of Mahemacs Naonal Unversy of Sngapore Sngapore 117543 makcy@nus.edu.sg Kok Bn Wong Insue of Mahemacal Scences Unversy of Malaya 50603 Kuala
A Deza Frankl ype heorem for se parons Cheng Yeaw Ku Deparmen of Mahemacs Naonal Unversy of Sngapore Sngapore 117543 makcy@nus.edu.sg Kok Bn Wong Insue of Mahemacal Scences Unversy of Malaya 50603 Kuala
CS286.2 Lecture 14: Quantum de Finetti Theorems II
 CS286.2 Lecure 14: Quanum de Fne Theorems II Scrbe: Mara Okounkova 1 Saemen of he heorem Recall he las saemen of he quanum de Fne heorem from he prevous lecure. Theorem 1 Quanum de Fne). Le ρ Dens C 2
CS286.2 Lecure 14: Quanum de Fne Theorems II Scrbe: Mara Okounkova 1 Saemen of he heorem Recall he las saemen of he quanum de Fne heorem from he prevous lecure. Theorem 1 Quanum de Fne). Le ρ Dens C 2
The Shapley value for fuzzy games on vague sets
 WEA TRANACTIN on INFRMATIN CIENCE APPLICATIN The hapley value or uzzy games on vague ses Fan-Yong Meng* (Correspondng Auhor chool o Managemen Qngdao Technologcal nversy Qngdao 266520 hong Provnce P R Chna
WEA TRANACTIN on INFRMATIN CIENCE APPLICATIN The hapley value or uzzy games on vague ses Fan-Yong Meng* (Correspondng Auhor chool o Managemen Qngdao Technologcal nversy Qngdao 266520 hong Provnce P R Chna
HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD
 Journal of Appled Mahemacs and Compuaonal Mechancs 3, (), 45-5 HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD Sansław Kukla, Urszula Sedlecka Insue of Mahemacs,
Journal of Appled Mahemacs and Compuaonal Mechancs 3, (), 45-5 HEAT CONDUCTION PROBLEM IN A TWO-LAYERED HOLLOW CYLINDER BY USING THE GREEN S FUNCTION METHOD Sansław Kukla, Urszula Sedlecka Insue of Mahemacs,
Suyash Narayan Mishra, Piyush Kumar Tripathi & Alok Agrawal
 IOSR Journal o Mahemaics IOSR-JM e-issn: 78-578 -ISSN: 39-765X. Volume Issue Ver. VI Mar - Ar. 5 PP 43-5 www.iosrjournals.org A auberian heorem or C α β- Convergence o Cesaro Means o Orer o Funcions Suash
IOSR Journal o Mahemaics IOSR-JM e-issn: 78-578 -ISSN: 39-765X. Volume Issue Ver. VI Mar - Ar. 5 PP 43-5 www.iosrjournals.org A auberian heorem or C α β- Convergence o Cesaro Means o Orer o Funcions Suash
Displacement, Velocity, and Acceleration. (WHERE and WHEN?)
 Dsplacemen, Velocy, and Acceleraon (WHERE and WHEN?) Mah resources Append A n your book! Symbols and meanng Algebra Geomery (olumes, ec.) Trgonomery Append A Logarhms Remnder You wll do well n hs class
Dsplacemen, Velocy, and Acceleraon (WHERE and WHEN?) Mah resources Append A n your book! Symbols and meanng Algebra Geomery (olumes, ec.) Trgonomery Append A Logarhms Remnder You wll do well n hs class
Variants of Pegasos. December 11, 2009
 Inroducon Varans of Pegasos SooWoong Ryu bshboy@sanford.edu December, 009 Youngsoo Cho yc344@sanford.edu Developng a new SVM algorhm s ongong research opc. Among many exng SVM algorhms, we wll focus on
Inroducon Varans of Pegasos SooWoong Ryu bshboy@sanford.edu December, 009 Youngsoo Cho yc344@sanford.edu Developng a new SVM algorhm s ongong research opc. Among many exng SVM algorhms, we wll focus on
Track Properities of Normal Chain
 In. J. Conemp. Mah. Scences, Vol. 8, 213, no. 4, 163-171 HIKARI Ld, www.m-har.com rac Propes of Normal Chan L Chen School of Mahemacs and Sascs, Zhengzhou Normal Unversy Zhengzhou Cy, Hennan Provnce, 4544,
In. J. Conemp. Mah. Scences, Vol. 8, 213, no. 4, 163-171 HIKARI Ld, www.m-har.com rac Propes of Normal Chan L Chen School of Mahemacs and Sascs, Zhengzhou Normal Unversy Zhengzhou Cy, Hennan Provnce, 4544,
On Convergence Rate of Concave-Convex Procedure
 On Converence Rae o Concave-Conve Proceure Ian E.H. Yen Nanun Pen Po-We Wan an Shou-De Ln Naonal awan Unvers OP 202 Oulne Derence o Conve Funcons.c. Prora Applcaons n SVM leraure Concave-Conve Proceure
On Converence Rae o Concave-Conve Proceure Ian E.H. Yen Nanun Pen Po-We Wan an Shou-De Ln Naonal awan Unvers OP 202 Oulne Derence o Conve Funcons.c. Prora Applcaons n SVM leraure Concave-Conve Proceure
On elements with index of the form 2 a 3 b in a parametric family of biquadratic elds
 On elemens wh ndex of he form a 3 b n a paramerc famly of bquadrac elds Bora JadrevĆ Absrac In hs paper we gve some resuls abou prmve negral elemens p(c p n he famly of bcyclc bquadrac elds L c = Q ) c;
On elemens wh ndex of he form a 3 b n a paramerc famly of bquadrac elds Bora JadrevĆ Absrac In hs paper we gve some resuls abou prmve negral elemens p(c p n he famly of bcyclc bquadrac elds L c = Q ) c;
( ) () we define the interaction representation by the unitary transformation () = ()
 Hgher Order Perurbaon Theory Mchael Fowler 3/7/6 The neracon Represenaon Recall ha n he frs par of hs course sequence, we dscussed he chrödnger and Hesenberg represenaons of quanum mechancs here n he chrödnger
Hgher Order Perurbaon Theory Mchael Fowler 3/7/6 The neracon Represenaon Recall ha n he frs par of hs course sequence, we dscussed he chrödnger and Hesenberg represenaons of quanum mechancs here n he chrödnger
DEEP UNFOLDING FOR MULTICHANNEL SOURCE SEPARATION SUPPLEMENTARY MATERIAL
 DEEP UNFOLDING FOR MULTICHANNEL SOURCE SEPARATION SUPPLEMENTARY MATERIAL Sco Wsdom, John Hershey 2, Jonahan Le Roux 2, and Shnj Waanabe 2 Deparmen o Elecrcal Engneerng, Unversy o Washngon, Seale, WA, USA
DEEP UNFOLDING FOR MULTICHANNEL SOURCE SEPARATION SUPPLEMENTARY MATERIAL Sco Wsdom, John Hershey 2, Jonahan Le Roux 2, and Shnj Waanabe 2 Deparmen o Elecrcal Engneerng, Unversy o Washngon, Seale, WA, USA
Performance Analysis for a Network having Standby Redundant Unit with Waiting in Repair
 TECHNI Inernaonal Journal of Compung Scence Communcaon Technologes VOL.5 NO. July 22 (ISSN 974-3375 erformance nalyss for a Nework havng Sby edundan Un wh ang n epar Jendra Sngh 2 abns orwal 2 Deparmen
TECHNI Inernaonal Journal of Compung Scence Communcaon Technologes VOL.5 NO. July 22 (ISSN 974-3375 erformance nalyss for a Nework havng Sby edundan Un wh ang n epar Jendra Sngh 2 abns orwal 2 Deparmen
Key words: Fractional difference equation, oscillatory solutions,
 OSCILLATION PROPERTIES OF SOLUTIONS OF FRACTIONAL DIFFERENCE EQUATIONS Musafa BAYRAM * ad Ayd SECER * Deparme of Compuer Egeerg, Isabul Gelsm Uversy Deparme of Mahemacal Egeerg, Yldz Techcal Uversy * Correspodg
OSCILLATION PROPERTIES OF SOLUTIONS OF FRACTIONAL DIFFERENCE EQUATIONS Musafa BAYRAM * ad Ayd SECER * Deparme of Compuer Egeerg, Isabul Gelsm Uversy Deparme of Mahemacal Egeerg, Yldz Techcal Uversy * Correspodg
Testing a new idea to solve the P = NP problem with mathematical induction
 Tesng a new dea o solve he P = NP problem wh mahemacal nducon Bacground P and NP are wo classes (ses) of languages n Compuer Scence An open problem s wheher P = NP Ths paper ess a new dea o compare he
Tesng a new dea o solve he P = NP problem wh mahemacal nducon Bacground P and NP are wo classes (ses) of languages n Compuer Scence An open problem s wheher P = NP Ths paper ess a new dea o compare he
Linear Dynamic Models
 Linear Dnamic Models and Forecasing Reference aricle: Ineracions beween he muliplier analsis and he principle of acceleraion Ouline. The sae space ssem as an approach o working wih ssems of difference
Linear Dnamic Models and Forecasing Reference aricle: Ineracions beween he muliplier analsis and he principle of acceleraion Ouline. The sae space ssem as an approach o working wih ssems of difference
@FMI c Kyung Moon Sa Co.
 Annals of Fuzzy Mahemacs and Informacs Volume 8, No. 2, (Augus 2014), pp. 245 257 ISSN: 2093 9310 (prn verson) ISSN: 2287 6235 (elecronc verson) hp://www.afm.or.kr @FMI c Kyung Moon Sa Co. hp://www.kyungmoon.com
Annals of Fuzzy Mahemacs and Informacs Volume 8, No. 2, (Augus 2014), pp. 245 257 ISSN: 2093 9310 (prn verson) ISSN: 2287 6235 (elecronc verson) hp://www.afm.or.kr @FMI c Kyung Moon Sa Co. hp://www.kyungmoon.com
GORDON AND NEWELL QUEUEING NETWORKS AND COPULAS
 Yugoslav Journal of Operaons Research Vol 9 (009) Number 0- DOI:0.98/YUJOR0900C GORDON AND NEWELL QUEUEING NETWORKS AND COPULAS Danel CIUIU Facul of Cvl Indusral and Agrculural Buldngs Techncal Unvers
Yugoslav Journal of Operaons Research Vol 9 (009) Number 0- DOI:0.98/YUJOR0900C GORDON AND NEWELL QUEUEING NETWORKS AND COPULAS Danel CIUIU Facul of Cvl Indusral and Agrculural Buldngs Techncal Unvers
PHYS 1443 Section 001 Lecture #4
 PHYS 1443 Secon 001 Lecure #4 Monda, June 5, 006 Moon n Two Dmensons Moon under consan acceleraon Projecle Moon Mamum ranges and heghs Reerence Frames and relae moon Newon s Laws o Moon Force Newon s Law
PHYS 1443 Secon 001 Lecure #4 Monda, June 5, 006 Moon n Two Dmensons Moon under consan acceleraon Projecle Moon Mamum ranges and heghs Reerence Frames and relae moon Newon s Laws o Moon Force Newon s Law
Faα-Irresolute Mappings
 BULLETIN o he Bull. Malaysian Mah. Sc. Soc. (Second Series) 24 (2001) 193-199 MLYSIN MTHEMTICL SCIENCES SOCIETY Faα-Irresolue Mappings 1 R.K. SRF, 2 M. CLDS ND 3 SEEM MISHR 1 Deparmen o Mahemaics, Governmen
BULLETIN o he Bull. Malaysian Mah. Sc. Soc. (Second Series) 24 (2001) 193-199 MLYSIN MTHEMTICL SCIENCES SOCIETY Faα-Irresolue Mappings 1 R.K. SRF, 2 M. CLDS ND 3 SEEM MISHR 1 Deparmen o Mahemaics, Governmen
)-interval valued fuzzy ideals in BF-algebras. Some properties of (, ) -interval valued fuzzy ideals in BF-algebra, where
 Inernaonal Journal of Engneerng Advaned Researh Tehnology (IJEART) ISSN: 454-990, Volume-, Issue-4, Oober 05 Some properes of (, )-nerval valued fuzzy deals n BF-algebras M. Idrees, A. Rehman, M. Zulfqar,
Inernaonal Journal of Engneerng Advaned Researh Tehnology (IJEART) ISSN: 454-990, Volume-, Issue-4, Oober 05 Some properes of (, )-nerval valued fuzzy deals n BF-algebras M. Idrees, A. Rehman, M. Zulfqar,
A New Generalisation of Sam-Solai s Multivariate symmetric Arcsine Distribution of Kind-1*
 IOSR Journal o Mahemacs IOSRJM ISSN: 78-578 Volume, Issue May-June 0, PP 4-48 www.osrournals.org A New Generalsaon o Sam-Sola s Mulvarae symmerc Arcsne Dsrbuon o Knd-* Dr. G.S. Davd Sam Jayaumar. Dr.A.Solarau.
IOSR Journal o Mahemacs IOSRJM ISSN: 78-578 Volume, Issue May-June 0, PP 4-48 www.osrournals.org A New Generalsaon o Sam-Sola s Mulvarae symmerc Arcsne Dsrbuon o Knd-* Dr. G.S. Davd Sam Jayaumar. Dr.A.Solarau.
ON THE ADDITION OF UNITS AND NON-UNITS IN FINITE COMMUTATIVE RINGS
 ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 45, Number 6, 2015 ON THE ADDITION OF UNITS AND NON-UNITS IN FINITE COMMUTATIVE RINGS DARIUSH KIANI AND MOHSEN MOLLAHAJIAGHAEI ABSTRACT. Le R be a fne commuave
ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 45, Number 6, 2015 ON THE ADDITION OF UNITS AND NON-UNITS IN FINITE COMMUTATIVE RINGS DARIUSH KIANI AND MOHSEN MOLLAHAJIAGHAEI ABSTRACT. Le R be a fne commuave
COMPUTER SCIENCE 349A SAMPLE EXAM QUESTIONS WITH SOLUTIONS PARTS 1, 2
 COMPUTE SCIENCE 49A SAMPLE EXAM QUESTIONS WITH SOLUTIONS PATS, PAT.. a Dene he erm ll-ondoned problem. b Gve an eample o a polynomal ha has ll-ondoned zeros.. Consder evaluaon o anh, where e e anh. e e
COMPUTE SCIENCE 49A SAMPLE EXAM QUESTIONS WITH SOLUTIONS PATS, PAT.. a Dene he erm ll-ondoned problem. b Gve an eample o a polynomal ha has ll-ondoned zeros.. Consder evaluaon o anh, where e e anh. e e
. The geometric multiplicity is dim[ker( λi. number of linearly independent eigenvectors associated with this eigenvalue.
 Lnear Algebra Lecure # Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons
Lnear Algebra Lecure # Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons
DIFFERENTIAL SCHEMES
 DIFFERENTIAL SCHEMES RAYMOND T. HOOBLER Dedcated to the memory o Jerry Kovacc 1. schemes All rngs contan Q and are commutatve. We x a d erental rng A throughout ths secton. 1.1. The topologcal space. Let
DIFFERENTIAL SCHEMES RAYMOND T. HOOBLER Dedcated to the memory o Jerry Kovacc 1. schemes All rngs contan Q and are commutatve. We x a d erental rng A throughout ths secton. 1.1. The topologcal space. Let
On Derivations of BCC-algebras
 International Journal of Algebra, Vol. 6, 2012, no. 32, 1491-1498 On Derivations of BCC-algebras N. O. Alshehri Department of Mathematics, Faculty of Sciences(Girls) King Abdulaziz University, Jeddah,
International Journal of Algebra, Vol. 6, 2012, no. 32, 1491-1498 On Derivations of BCC-algebras N. O. Alshehri Department of Mathematics, Faculty of Sciences(Girls) King Abdulaziz University, Jeddah,
Online Appendix for. Strategic safety stocks in supply chains with evolving forecasts
 Onlne Appendx for Sraegc safey socs n supply chans wh evolvng forecass Tor Schoenmeyr Sephen C. Graves Opsolar, Inc. 332 Hunwood Avenue Hayward, CA 94544 A. P. Sloan School of Managemen Massachuses Insue
Onlne Appendx for Sraegc safey socs n supply chans wh evolvng forecass Tor Schoenmeyr Sephen C. Graves Opsolar, Inc. 332 Hunwood Avenue Hayward, CA 94544 A. P. Sloan School of Managemen Massachuses Insue
Advanced time-series analysis (University of Lund, Economic History Department)
 Advanced me-seres analss (Unvers of Lund, Economc Hsor Dearmen) 3 Jan-3 Februar and 6-3 March Lecure 4 Economerc echnues for saonar seres : Unvarae sochasc models wh Box- Jenns mehodolog, smle forecasng
Advanced me-seres analss (Unvers of Lund, Economc Hsor Dearmen) 3 Jan-3 Februar and 6-3 March Lecure 4 Economerc echnues for saonar seres : Unvarae sochasc models wh Box- Jenns mehodolog, smle forecasng
KEY. Math 334 Midterm I Fall 2008 sections 001 and 003 Instructor: Scott Glasgow
 1 KEY Mah 4 Miderm I Fall 8 secions 1 and Insrucor: Sco Glasgow Please do NOT wrie on his eam. No credi will be given for such work. Raher wrie in a blue book, or on our own paper, preferabl engineering
1 KEY Mah 4 Miderm I Fall 8 secions 1 and Insrucor: Sco Glasgow Please do NOT wrie on his eam. No credi will be given for such work. Raher wrie in a blue book, or on our own paper, preferabl engineering
. The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue.
![. The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue. . The geometric multiplicity is dim[ker( λi. A )], i.e. the number of linearly independent eigenvectors associated with this eigenvalue.](/thumbs/78/77822798.jpg) Mah E-b Lecure #0 Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons are
Mah E-b Lecure #0 Noes We connue wh he dscusson of egenvalues, egenvecors, and dagonalzably of marces We wan o know, n parcular wha condons wll assure ha a marx can be dagonalzed and wha he obsrucons are
On One Analytic Method of. Constructing Program Controls
 Appled Mahemacal Scences, Vol. 9, 05, no. 8, 409-407 HIKARI Ld, www.m-hkar.com hp://dx.do.org/0.988/ams.05.54349 On One Analyc Mehod of Consrucng Program Conrols A. N. Kvko, S. V. Chsyakov and Yu. E. Balyna
Appled Mahemacal Scences, Vol. 9, 05, no. 8, 409-407 HIKARI Ld, www.m-hkar.com hp://dx.do.org/0.988/ams.05.54349 On One Analyc Mehod of Consrucng Program Conrols A. N. Kvko, S. V. Chsyakov and Yu. E. Balyna
Li An-Ping. Beijing , P.R.China
 A New Type of Cpher: DICING_csb L An-Png Bejng 100085, P.R.Chna apl0001@sna.com Absrac: In hs paper, we wll propose a new ype of cpher named DICING_csb, whch s derved from our prevous sream cpher DICING.
A New Type of Cpher: DICING_csb L An-Png Bejng 100085, P.R.Chna apl0001@sna.com Absrac: In hs paper, we wll propose a new ype of cpher named DICING_csb, whch s derved from our prevous sream cpher DICING.
On computing differential transform of nonlinear non-autonomous functions and its applications
 On compung dfferenal ransform of nonlnear non-auonomous funcons and s applcaons Essam. R. El-Zahar, and Abdelhalm Ebad Deparmen of Mahemacs, Faculy of Scences and Humanes, Prnce Saam Bn Abdulazz Unversy,
On compung dfferenal ransform of nonlnear non-auonomous funcons and s applcaons Essam. R. El-Zahar, and Abdelhalm Ebad Deparmen of Mahemacs, Faculy of Scences and Humanes, Prnce Saam Bn Abdulazz Unversy,
Some Probability Inequalities for Quadratic Forms of Negatively Dependent Subgaussian Random Variables
 Joural of Sceces Islamc epublc of Ira 6(: 63-67 (005 Uvers of ehra ISSN 06-04 hp://scecesuacr Some Probabl Iequales for Quadrac Forms of Negavel Depede Subgaussa adom Varables M Am A ozorga ad H Zare 3
Joural of Sceces Islamc epublc of Ira 6(: 63-67 (005 Uvers of ehra ISSN 06-04 hp://scecesuacr Some Probabl Iequales for Quadrac Forms of Negavel Depede Subgaussa adom Varables M Am A ozorga ad H Zare 3
Continuous Indexed Variable Systems
 Ieraoal Joural o Compuaoal cece ad Mahemacs. IN 0974-389 Volume 3, Number 4 (20), pp. 40-409 Ieraoal Research Publcao House hp://www.rphouse.com Couous Idexed Varable ysems. Pouhassa ad F. Mohammad ghjeh
Ieraoal Joural o Compuaoal cece ad Mahemacs. IN 0974-389 Volume 3, Number 4 (20), pp. 40-409 Ieraoal Research Publcao House hp://www.rphouse.com Couous Idexed Varable ysems. Pouhassa ad F. Mohammad ghjeh
NONLOCAL BOUNDARY VALUE PROBLEM FOR SECOND ORDER ANTI-PERIODIC NONLINEAR IMPULSIVE q k INTEGRODIFFERENCE EQUATION
 Euroean Journal of ahemac an Comuer Scence Vol No 7 ISSN 59-995 NONLOCAL BOUNDARY VALUE PROBLE FOR SECOND ORDER ANTI-PERIODIC NONLINEAR IPULSIVE - INTEGRODIFFERENCE EQUATION Hao Wang Yuhang Zhang ngyang
Euroean Journal of ahemac an Comuer Scence Vol No 7 ISSN 59-995 NONLOCAL BOUNDARY VALUE PROBLE FOR SECOND ORDER ANTI-PERIODIC NONLINEAR IPULSIVE - INTEGRODIFFERENCE EQUATION Hao Wang Yuhang Zhang ngyang
Fuzzy Set Theory in Modeling Uncertainty Data. via Interpolation Rational Bezier Surface Function
 Appled Mahemacal Scences, Vol. 7, 013, no. 45, 9 38 HIKARI Ld, www.m-hkar.com Fuzzy Se Theory n Modelng Uncerany Daa va Inerpolaon Raonal Bezer Surface Funcon Rozam Zakara Deparmen of Mahemacs, Faculy
Appled Mahemacal Scences, Vol. 7, 013, no. 45, 9 38 HIKARI Ld, www.m-hkar.com Fuzzy Se Theory n Modelng Uncerany Daa va Inerpolaon Raonal Bezer Surface Funcon Rozam Zakara Deparmen of Mahemacs, Faculy
Delay-Range-Dependent Stability Analysis for Continuous Linear System with Interval Delay
 Inernaonal Journal of Emergng Engneerng esearch an echnology Volume 3, Issue 8, Augus 05, PP 70-76 ISSN 349-4395 (Prn) & ISSN 349-4409 (Onlne) Delay-ange-Depenen Sably Analyss for Connuous Lnear Sysem
Inernaonal Journal of Emergng Engneerng esearch an echnology Volume 3, Issue 8, Augus 05, PP 70-76 ISSN 349-4395 (Prn) & ISSN 349-4409 (Onlne) Delay-ange-Depenen Sably Analyss for Connuous Lnear Sysem
Method of upper lower solutions for nonlinear system of fractional differential equations and applications
 Malaya Journal of Maemak, Vol. 6, No. 3, 467-472, 218 hps://do.org/1.26637/mjm63/1 Mehod of upper lower soluons for nonlnear sysem of fraconal dfferenal equaons and applcaons D.B. Dhagude1 *, N.B. Jadhav2
Malaya Journal of Maemak, Vol. 6, No. 3, 467-472, 218 hps://do.org/1.26637/mjm63/1 Mehod of upper lower soluons for nonlnear sysem of fraconal dfferenal equaons and applcaons D.B. Dhagude1 *, N.B. Jadhav2
CHAPTER 5: MULTIVARIATE METHODS
 CHAPER 5: MULIVARIAE MEHODS Mulvarae Daa 3 Mulple measuremens (sensors) npus/feaures/arbues: -varae N nsances/observaons/eamples Each row s an eample Each column represens a feaure X a b correspons o he
CHAPER 5: MULIVARIAE MEHODS Mulvarae Daa 3 Mulple measuremens (sensors) npus/feaures/arbues: -varae N nsances/observaons/eamples Each row s an eample Each column represens a feaure X a b correspons o he
By HENRY H. KIM and KYU-HWAN LEE
 SPHERICAL HECKE ALGEBRAS OF SL OVER -DIMENSIONAL LOCAL FIELDS By HENRY H. KIM and KYU-HWAN LEE Absrac. In hs paper, we sudy sphercal Hece algebras of SL over wo dmensonal local felds. In order o defne
SPHERICAL HECKE ALGEBRAS OF SL OVER -DIMENSIONAL LOCAL FIELDS By HENRY H. KIM and KYU-HWAN LEE Absrac. In hs paper, we sudy sphercal Hece algebras of SL over wo dmensonal local felds. In order o defne
Lecture 16 (Momentum and Impulse, Collisions and Conservation of Momentum) Physics Spring 2017 Douglas Fields
 Lecure 16 (Momenum and Impulse, Collisions and Conservaion o Momenum) Physics 160-02 Spring 2017 Douglas Fields Newon s Laws & Energy The work-energy heorem is relaed o Newon s 2 nd Law W KE 1 2 1 2 F
Lecure 16 (Momenum and Impulse, Collisions and Conservaion o Momenum) Physics 160-02 Spring 2017 Douglas Fields Newon s Laws & Energy The work-energy heorem is relaed o Newon s 2 nd Law W KE 1 2 1 2 F
Ordinary Differential Equations in Neuroscience with Matlab examples. Aim 1- Gain understanding of how to set up and solve ODE s
 Ordnary Dfferenal Equaons n Neuroscence wh Malab eamples. Am - Gan undersandng of how o se up and solve ODE s Am Undersand how o se up an solve a smple eample of he Hebb rule n D Our goal a end of class
Ordnary Dfferenal Equaons n Neuroscence wh Malab eamples. Am - Gan undersandng of how o se up and solve ODE s Am Undersand how o se up an solve a smple eample of he Hebb rule n D Our goal a end of class
Inventory Analysis and Management. Multi-Period Stochastic Models: Optimality of (s, S) Policy for K-Convex Objective Functions
 Muli-Period Sochasic Models: Opimali of (s, S) Polic for -Convex Objecive Funcions Consider a seing similar o he N-sage newsvendor problem excep ha now here is a fixed re-ordering cos (> 0) for each (re-)order.
Muli-Period Sochasic Models: Opimali of (s, S) Polic for -Convex Objecive Funcions Consider a seing similar o he N-sage newsvendor problem excep ha now here is a fixed re-ordering cos (> 0) for each (re-)order.
12d Model. Civil and Surveying Software. Drainage Analysis Module Detention/Retention Basins. Owen Thornton BE (Mech), 12d Model Programmer
 d Model Cvl and Surveyng Soware Dranage Analyss Module Deenon/Reenon Basns Owen Thornon BE (Mech), d Model Programmer owen.hornon@d.com 4 January 007 Revsed: 04 Aprl 007 9 February 008 (8Cp) Ths documen
d Model Cvl and Surveyng Soware Dranage Analyss Module Deenon/Reenon Basns Owen Thornon BE (Mech), d Model Programmer owen.hornon@d.com 4 January 007 Revsed: 04 Aprl 007 9 February 008 (8Cp) Ths documen
Comb Filters. Comb Filters
 The smple flers dscussed so far are characered eher by a sngle passband and/or a sngle sopband There are applcaons where flers wh mulple passbands and sopbands are requred Thecomb fler s an example of
The smple flers dscussed so far are characered eher by a sngle passband and/or a sngle sopband There are applcaons where flers wh mulple passbands and sopbands are requred Thecomb fler s an example of
FI 3103 Quantum Physics
 /9/4 FI 33 Quanum Physcs Aleander A. Iskandar Physcs of Magnesm and Phooncs Research Grou Insu Teknolog Bandung Basc Conces n Quanum Physcs Probably and Eecaon Value Hesenberg Uncerany Prncle Wave Funcon
/9/4 FI 33 Quanum Physcs Aleander A. Iskandar Physcs of Magnesm and Phooncs Research Grou Insu Teknolog Bandung Basc Conces n Quanum Physcs Probably and Eecaon Value Hesenberg Uncerany Prncle Wave Funcon
Epistemic Game Theory: Online Appendix
 Epsemc Game Theory: Onlne Appendx Edde Dekel Lucano Pomao Marcano Snscalch July 18, 2014 Prelmnares Fx a fne ype srucure T I, S, T, β I and a probably µ S T. Le T µ I, S, T µ, βµ I be a ype srucure ha
Epsemc Game Theory: Onlne Appendx Edde Dekel Lucano Pomao Marcano Snscalch July 18, 2014 Prelmnares Fx a fne ype srucure T I, S, T, β I and a probably µ S T. Le T µ I, S, T µ, βµ I be a ype srucure ha
John Geweke a and Gianni Amisano b a Departments of Economics and Statistics, University of Iowa, USA b European Central Bank, Frankfurt, Germany
 Herarchcal Markov Normal Mxure models wh Applcaons o Fnancal Asse Reurns Appendx: Proofs of Theorems and Condonal Poseror Dsrbuons John Geweke a and Gann Amsano b a Deparmens of Economcs and Sascs, Unversy
Herarchcal Markov Normal Mxure models wh Applcaons o Fnancal Asse Reurns Appendx: Proofs of Theorems and Condonal Poseror Dsrbuons John Geweke a and Gann Amsano b a Deparmens of Economcs and Sascs, Unversy
A New Generalized Gronwall-Bellman Type Inequality
 22 Inernaonal Conference on Image, Vson and Comung (ICIVC 22) IPCSIT vol. 5 (22) (22) IACSIT Press, Sngaore DOI:.7763/IPCSIT.22.V5.46 A New Generalzed Gronwall-Bellman Tye Ineualy Qnghua Feng School of
22 Inernaonal Conference on Image, Vson and Comung (ICIVC 22) IPCSIT vol. 5 (22) (22) IACSIT Press, Sngaore DOI:.7763/IPCSIT.22.V5.46 A New Generalzed Gronwall-Bellman Tye Ineualy Qnghua Feng School of
3.1.3 INTRODUCTION TO DYNAMIC OPTIMIZATION: DISCRETE TIME PROBLEMS. A. The Hamiltonian and First-Order Conditions in a Finite Time Horizon
 3..3 INRODUCION O DYNAMIC OPIMIZAION: DISCREE IME PROBLEMS A. he Hamilonian and Firs-Order Condiions in a Finie ime Horizon Define a new funcion, he Hamilonian funcion, H. H he change in he oal value of
3..3 INRODUCION O DYNAMIC OPIMIZAION: DISCREE IME PROBLEMS A. he Hamilonian and Firs-Order Condiions in a Finie ime Horizon Define a new funcion, he Hamilonian funcion, H. H he change in he oal value of
Tight results for Next Fit and Worst Fit with resource augmentation
 Tgh resuls for Nex F and Wors F wh resource augmenaon Joan Boyar Leah Epsen Asaf Levn Asrac I s well known ha he wo smple algorhms for he classc n packng prolem, NF and WF oh have an approxmaon rao of
Tgh resuls for Nex F and Wors F wh resource augmenaon Joan Boyar Leah Epsen Asaf Levn Asrac I s well known ha he wo smple algorhms for he classc n packng prolem, NF and WF oh have an approxmaon rao of
Online Learning with Partial Feedback. 1 Online Mirror Descent with Estimated Gradient
 Avance Course in Machine Learning Spring 2010 Online Learning wih Parial Feeback Hanous are joinly prepare by Shie Mannor an Shai Shalev-Shwarz In previous lecures we alke abou he general framework of
Avance Course in Machine Learning Spring 2010 Online Learning wih Parial Feeback Hanous are joinly prepare by Shie Mannor an Shai Shalev-Shwarz In previous lecures we alke abou he general framework of
Chapter Lagrangian Interpolation
 Chaper 5.4 agrangan Inerpolaon Afer readng hs chaper you should be able o:. dere agrangan mehod of nerpolaon. sole problems usng agrangan mehod of nerpolaon and. use agrangan nerpolans o fnd deraes and
Chaper 5.4 agrangan Inerpolaon Afer readng hs chaper you should be able o:. dere agrangan mehod of nerpolaon. sole problems usng agrangan mehod of nerpolaon and. use agrangan nerpolans o fnd deraes and
Existence of Time Periodic Solutions for the Ginzburg-Landau Equations. model of superconductivity
 Journal of Mahemacal Analyss and Applcaons 3, 3944 999 Arcle ID jmaa.999.683, avalable onlne a hp:www.dealbrary.com on Exsence of me Perodc Soluons for he Gnzburg-Landau Equaons of Superconducvy Bxang
Journal of Mahemacal Analyss and Applcaons 3, 3944 999 Arcle ID jmaa.999.683, avalable onlne a hp:www.dealbrary.com on Exsence of me Perodc Soluons for he Gnzburg-Landau Equaons of Superconducvy Bxang
Periodic motions of a class of forced infinite lattices with nearest neighbor interaction
 J. Mah. Anal. Appl. 34 28 44 52 www.elsever.co/locae/jaa Peroc oons of a class of force nfne laces wh neares neghbor neracon Chao Wang a,b,, Dngban Qan a a School of Maheacal Scence, Suzhou Unversy, Suzhou
J. Mah. Anal. Appl. 34 28 44 52 www.elsever.co/locae/jaa Peroc oons of a class of force nfne laces wh neares neghbor neracon Chao Wang a,b,, Dngban Qan a a School of Maheacal Scence, Suzhou Unversy, Suzhou
LEVEL SET OF INTUITIONTISTIC FUZZY SUBHEMIRINGS OF A HEMIRING
 LEVEL SET OF INTUITIONTISTIC FUZZY SUBHEMIRINGS OF HEMIRING N. NITH ssstant Proessor n Mathematcs, Peryar Unversty PG Extn Centre, Dharmapur 636705. Emal : anthaarenu@gmal.com BSTRCT: In ths paper, we
LEVEL SET OF INTUITIONTISTIC FUZZY SUBHEMIRINGS OF HEMIRING N. NITH ssstant Proessor n Mathematcs, Peryar Unversty PG Extn Centre, Dharmapur 636705. Emal : anthaarenu@gmal.com BSTRCT: In ths paper, we
THEORETICAL AUTOCORRELATIONS. ) if often denoted by γ. Note that
 THEORETICAL AUTOCORRELATIONS Cov( y, y ) E( y E( y))( y E( y)) ρ = = Var( y) E( y E( y)) =,, L ρ = and Cov( y, y ) s ofen denoed by whle Var( y ) f ofen denoed by γ. Noe ha γ = γ and ρ = ρ and because
THEORETICAL AUTOCORRELATIONS Cov( y, y ) E( y E( y))( y E( y)) ρ = = Var( y) E( y E( y)) =,, L ρ = and Cov( y, y ) s ofen denoed by whle Var( y ) f ofen denoed by γ. Noe ha γ = γ and ρ = ρ and because
Survival Analysis and Reliability. A Note on the Mean Residual Life Function of a Parallel System
 Communcaons n Sascs Theory and Mehods, 34: 475 484, 2005 Copyrgh Taylor & Francs, Inc. ISSN: 0361-0926 prn/1532-415x onlne DOI: 10.1081/STA-200047430 Survval Analyss and Relably A Noe on he Mean Resdual
Communcaons n Sascs Theory and Mehods, 34: 475 484, 2005 Copyrgh Taylor & Francs, Inc. ISSN: 0361-0926 prn/1532-415x onlne DOI: 10.1081/STA-200047430 Survval Analyss and Relably A Noe on he Mean Resdual
UNIVERSITAT AUTÒNOMA DE BARCELONA MARCH 2017 EXAMINATION
 INTERNATIONAL TRADE T. J. KEHOE UNIVERSITAT AUTÒNOMA DE BARCELONA MARCH 27 EXAMINATION Please answer wo of he hree quesons. You can consul class noes, workng papers, and arcles whle you are workng on he
INTERNATIONAL TRADE T. J. KEHOE UNIVERSITAT AUTÒNOMA DE BARCELONA MARCH 27 EXAMINATION Please answer wo of he hree quesons. You can consul class noes, workng papers, and arcles whle you are workng on he
[ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5
![[ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5 [ ] 2. [ ]3 + (Δx i + Δx i 1 ) / 2. Δx i-1 Δx i Δx i+1. TPG4160 Reservoir Simulation 2018 Lecture note 3. page 1 of 5](/thumbs/85/92299540.jpg) TPG460 Reservor Smulaon 08 page of 5 DISCRETIZATIO OF THE FOW EQUATIOS As we already have seen, fne dfference appromaons of he paral dervaves appearng n he flow equaons may be obaned from Taylor seres
TPG460 Reservor Smulaon 08 page of 5 DISCRETIZATIO OF THE FOW EQUATIOS As we already have seen, fne dfference appromaons of he paral dervaves appearng n he flow equaons may be obaned from Taylor seres
A NEW INTERPRETATION OF INTERVAL-VALUED FUZZY INTERIOR IDEALS OF ORDERED SEMIGROUPS
 ScInLhore),7),9-37,4 ISSN 3-536; CODEN: SINTE 8 9 A NEW INTERPRETATION O INTERVAL-VALUED UZZY INTERIOR IDEALS O ORDERED SEMIGROUPS Hdy Ullh Khn, b, Nor Hnz Srmn, Asghr Khn c nd z Muhmmd Khn d Deprmen of
ScInLhore),7),9-37,4 ISSN 3-536; CODEN: SINTE 8 9 A NEW INTERPRETATION O INTERVAL-VALUED UZZY INTERIOR IDEALS O ORDERED SEMIGROUPS Hdy Ullh Khn, b, Nor Hnz Srmn, Asghr Khn c nd z Muhmmd Khn d Deprmen of
Appendix H: Rarefaction and extrapolation of Hill numbers for incidence data
 Anne Chao Ncholas J Goell C seh lzabeh L ander K Ma Rober K Colwell and Aaron M llson 03 Rarefacon and erapolaon wh ll numbers: a framewor for samplng and esmaon n speces dversy sudes cology Monographs
Anne Chao Ncholas J Goell C seh lzabeh L ander K Ma Rober K Colwell and Aaron M llson 03 Rarefacon and erapolaon wh ll numbers: a framewor for samplng and esmaon n speces dversy sudes cology Monographs
Improvement in Estimating Population Mean using Two Auxiliary Variables in Two-Phase Sampling
 Improvemen n Esmang Populaon Mean usng Two Auxlar Varables n Two-Phase amplng Rajesh ngh Deparmen of ascs, Banaras Hndu Unvers(U.P.), Inda (rsnghsa@ahoo.com) Pankaj Chauhan and Nrmala awan chool of ascs,
Improvemen n Esmang Populaon Mean usng Two Auxlar Varables n Two-Phase amplng Rajesh ngh Deparmen of ascs, Banaras Hndu Unvers(U.P.), Inda (rsnghsa@ahoo.com) Pankaj Chauhan and Nrmala awan chool of ascs,
MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES. Institute for Mathematical Research, Universiti Putra Malaysia, UPM Serdang, Selangor, Malaysia
 Malaysan Journal of Mahemacal Scences 9(2): 277-300 (2015) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Journal homeage: h://ensemumedumy/journal A Mehod for Deermnng -Adc Orders of Facorals 1* Rafka Zulkal,
Malaysan Journal of Mahemacal Scences 9(2): 277-300 (2015) MALAYSIAN JOURNAL OF MATHEMATICAL SCIENCES Journal homeage: h://ensemumedumy/journal A Mehod for Deermnng -Adc Orders of Facorals 1* Rafka Zulkal,
Linear Response Theory: The connection between QFT and experiments
 Phys540.nb 39 3 Lnear Response Theory: The connecon beween QFT and expermens 3.1. Basc conceps and deas Q: ow do we measure he conducvy of a meal? A: we frs nroduce a weak elecrc feld E, and hen measure
Phys540.nb 39 3 Lnear Response Theory: The connecon beween QFT and expermens 3.1. Basc conceps and deas Q: ow do we measure he conducvy of a meal? A: we frs nroduce a weak elecrc feld E, and hen measure
Scattering at an Interface: Oblique Incidence
 Course Insrucor Dr. Raymond C. Rumpf Offce: A 337 Phone: (915) 747 6958 E Mal: rcrumpf@uep.edu EE 4347 Appled Elecromagnecs Topc 3g Scaerng a an Inerface: Oblque Incdence Scaerng These Oblque noes may
Course Insrucor Dr. Raymond C. Rumpf Offce: A 337 Phone: (915) 747 6958 E Mal: rcrumpf@uep.edu EE 4347 Appled Elecromagnecs Topc 3g Scaerng a an Inerface: Oblque Incdence Scaerng These Oblque noes may
Improvement in Estimating Population Mean using Two Auxiliary Variables in Two-Phase Sampling
 Rajesh ngh Deparmen of ascs, Banaras Hndu Unvers(U.P.), Inda Pankaj Chauhan, Nrmala awan chool of ascs, DAVV, Indore (M.P.), Inda Florenn marandache Deparmen of Mahemacs, Unvers of New Meco, Gallup, UA
Rajesh ngh Deparmen of ascs, Banaras Hndu Unvers(U.P.), Inda Pankaj Chauhan, Nrmala awan chool of ascs, DAVV, Indore (M.P.), Inda Florenn marandache Deparmen of Mahemacs, Unvers of New Meco, Gallup, UA
WebAssign HW Due 11:59PM Tuesday Clicker Information
 WebAssgn HW Due 11:59PM Tuesday Clcker Inormaon Remnder: 90% aemp, 10% correc answer Clcker answers wll be a end o class sldes (onlne). Some days we wll do a lo o quesons, and ew ohers Each day o clcker
WebAssgn HW Due 11:59PM Tuesday Clcker Inormaon Remnder: 90% aemp, 10% correc answer Clcker answers wll be a end o class sldes (onlne). Some days we wll do a lo o quesons, and ew ohers Each day o clcker
Example: MOSFET Amplifier Distortion
 4/25/2011 Example MSFET Amplfer Dsoron 1/9 Example: MSFET Amplfer Dsoron Recall hs crcu from a prevous handou: ( ) = I ( ) D D d 15.0 V RD = 5K v ( ) = V v ( ) D o v( ) - K = 2 0.25 ma/v V = 2.0 V 40V.
4/25/2011 Example MSFET Amplfer Dsoron 1/9 Example: MSFET Amplfer Dsoron Recall hs crcu from a prevous handou: ( ) = I ( ) D D d 15.0 V RD = 5K v ( ) = V v ( ) D o v( ) - K = 2 0.25 ma/v V = 2.0 V 40V.
Lecture 18: The Laplace Transform (See Sections and 14.7 in Boas)
 Lecure 8: The Lalace Transform (See Secons 88- and 47 n Boas) Recall ha our bg-cure goal s he analyss of he dfferenal equaon, ax bx cx F, where we emloy varous exansons for he drvng funcon F deendng on
Lecure 8: The Lalace Transform (See Secons 88- and 47 n Boas) Recall ha our bg-cure goal s he analyss of he dfferenal equaon, ax bx cx F, where we emloy varous exansons for he drvng funcon F deendng on
Mechanics Physics 151
 Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm H ( q, p, ) = q p L( q, q, ) H p = q H q = p H = L Equvalen o Lagrangan formalsm Smpler, bu
Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm H ( q, p, ) = q p L( q, q, ) H p = q H q = p H = L Equvalen o Lagrangan formalsm Smpler, bu
EXISTENCE OF NON-OSCILLATORY SOLUTIONS TO FIRST-ORDER NEUTRAL DIFFERENTIAL EQUATIONS
 Elecronic Journal of Differenial Equaions, Vol. 206 (206, No. 39, pp.. ISSN: 072-669. URL: hp://ejde.mah.xsae.edu or hp://ejde.mah.un.edu fp ejde.mah.xsae.edu EXISTENCE OF NON-OSCILLATORY SOLUTIONS TO
Elecronic Journal of Differenial Equaions, Vol. 206 (206, No. 39, pp.. ISSN: 072-669. URL: hp://ejde.mah.xsae.edu or hp://ejde.mah.un.edu fp ejde.mah.xsae.edu EXISTENCE OF NON-OSCILLATORY SOLUTIONS TO
CS434a/541a: Pattern Recognition Prof. Olga Veksler. Lecture 4
 CS434a/54a: Paern Recognon Prof. Olga Veksler Lecure 4 Oulne Normal Random Varable Properes Dscrmnan funcons Why Normal Random Varables? Analycally racable Works well when observaon comes form a corruped
CS434a/54a: Paern Recognon Prof. Olga Veksler Lecure 4 Oulne Normal Random Varable Properes Dscrmnan funcons Why Normal Random Varables? Analycally racable Works well when observaon comes form a corruped
On Two Integrability Methods of Improper Integrals
 Inernaional Journal of Mahemaics and Compuer Science, 13(218), no. 1, 45 5 M CS On Two Inegrabiliy Mehods of Improper Inegrals H. N. ÖZGEN Mahemaics Deparmen Faculy of Educaion Mersin Universiy, TR-33169
Inernaional Journal of Mahemaics and Compuer Science, 13(218), no. 1, 45 5 M CS On Two Inegrabiliy Mehods of Improper Inegrals H. N. ÖZGEN Mahemaics Deparmen Faculy of Educaion Mersin Universiy, TR-33169
Mechanics Physics 151
 Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm Hqp (,,) = qp Lqq (,,) H p = q H q = p H L = Equvalen o Lagrangan formalsm Smpler, bu wce as
Mechancs Physcs 5 Lecure 9 Hamlonan Equaons of Moon (Chaper 8) Wha We Dd Las Tme Consruced Hamlonan formalsm Hqp (,,) = qp Lqq (,,) H p = q H q = p H L = Equvalen o Lagrangan formalsm Smpler, bu wce as
Upper Bound For Matrix Operators On Some Sequence Spaces
 Suama Uer Bou formar Oeraors Uer Bou For Mar Oeraors O Some Sequece Saces Suama Dearme of Mahemacs Gaah Maa Uersy Yogyaara 558 INDONESIA Emal: suama@ugmac masomo@yahoocom Isar D alam aer aa susa masalah
Suama Uer Bou formar Oeraors Uer Bou For Mar Oeraors O Some Sequece Saces Suama Dearme of Mahemacs Gaah Maa Uersy Yogyaara 558 INDONESIA Emal: suama@ugmac masomo@yahoocom Isar D alam aer aa susa masalah
Existence of positive solution for a third-order three-point BVP with sign-changing Green s function
 Elecronic Journal of Qualiaive Theory of Differenial Equaions 13, No. 3, 1-11; hp://www.mah.u-szeged.hu/ejqde/ Exisence of posiive soluion for a hird-order hree-poin BVP wih sign-changing Green s funcion
Elecronic Journal of Qualiaive Theory of Differenial Equaions 13, No. 3, 1-11; hp://www.mah.u-szeged.hu/ejqde/ Exisence of posiive soluion for a hird-order hree-poin BVP wih sign-changing Green s funcion
Chapter 6: AC Circuits
 Chaper 6: AC Crcus Chaper 6: Oulne Phasors and he AC Seady Sae AC Crcus A sable, lnear crcu operang n he seady sae wh snusodal excaon (.e., snusodal seady sae. Complee response forced response naural response.
Chaper 6: AC Crcus Chaper 6: Oulne Phasors and he AC Seady Sae AC Crcus A sable, lnear crcu operang n he seady sae wh snusodal excaon (.e., snusodal seady sae. Complee response forced response naural response.
Dynamic Team Decision Theory. EECS 558 Project Shrutivandana Sharma and David Shuman December 10, 2005
 Dynamc Team Decson Theory EECS 558 Proec Shruvandana Sharma and Davd Shuman December 0, 005 Oulne Inroducon o Team Decson Theory Decomposon of he Dynamc Team Decson Problem Equvalence of Sac and Dynamc
Dynamc Team Decson Theory EECS 558 Proec Shruvandana Sharma and Davd Shuman December 0, 005 Oulne Inroducon o Team Decson Theory Decomposon of he Dynamc Team Decson Problem Equvalence of Sac and Dynamc
II. Light is a Ray (Geometrical Optics)
 II Lgh s a Ray (Geomercal Opcs) IIB Reflecon and Refracon Hero s Prncple of Leas Dsance Law of Reflecon Hero of Aleandra, who lved n he 2 nd cenury BC, posulaed he followng prncple: Prncple of Leas Dsance:
II Lgh s a Ray (Geomercal Opcs) IIB Reflecon and Refracon Hero s Prncple of Leas Dsance Law of Reflecon Hero of Aleandra, who lved n he 2 nd cenury BC, posulaed he followng prncple: Prncple of Leas Dsance:
Supplement for Stochastic Convex Optimization: Faster Local Growth Implies Faster Global Convergence
 Supplemen for Sochasic Convex Opimizaion: Faser Local Growh Implies Faser Global Convergence Yi Xu Qihang Lin ianbao Yang Proof of heorem heorem Suppose Assumpion holds and F (w) obeys he LGC (6) Given
Supplemen for Sochasic Convex Opimizaion: Faser Local Growh Implies Faser Global Convergence Yi Xu Qihang Lin ianbao Yang Proof of heorem heorem Suppose Assumpion holds and F (w) obeys he LGC (6) Given
= s j Ui U j. i, j, then s F(U) with s Ui F(U) G(U) F(V ) G(V )
 1 Lecture 2 Recap Last tme we talked about presheaves and sheaves. Preshea: F on a topologcal space X, wth groups (resp. rngs, sets, etc.) F(U) or each open set U X, wth restrcton homs ρ UV : F(U) F(V
1 Lecture 2 Recap Last tme we talked about presheaves and sheaves. Preshea: F on a topologcal space X, wth groups (resp. rngs, sets, etc.) F(U) or each open set U X, wth restrcton homs ρ UV : F(U) F(V
