An Uniformly Minimum Variance Unbiased Point Estimator Using Fuzzy Observations
|
|
|
- Rudolph Skinner
- 6 years ago
- Views:
Transcription
1 AUSTRIAN JOURNAL OF STATISTICS Volume 36 (2007), Number 4, An Uniformly Minimum Variance Unbiased Point Estimator Using Fuzzy Observations Mohammad Ghasem Akbari and Abdolhamid Rezaei Ferdowsi University of Mashhad, Iran Abstract: This paper proposes a new method for uniformly minimum variance unbiased fuzzy point estimation. For this purpose we make use of a uniformly minimum variance unbiased estimator and we develop this new method for a fuzzy random sample X 1,..., X n is induced by X 1,..., X n on the same probability space. Zusammenfassung: In diesem Aufsatz schlagen wir eine neue Methode vor, um einen unverzerrten Fuzzy-Punktschätzer mit gleichmäßig minimaler Varianz zu bekommen. Dazu verwenden wir einen unverzerrten Punkt Schätzer mit gleichmäßig minimaler Varianz und entwickeln diese neue Methode für eine Fuzzy-Zufallsstichprobe X 1,..., X n, welche aus X 1,..., X n auf dem selben Wahrschenlichkeitsraum erzeugt ist. Keywords: Fuzzy Random Variable, Fuzzy Statistic, Signed Distance, Fuzzy Unbiased Estimator, Fuzzy Variance. 1 Introduction Statistical analysis in traditional form is based on crispness of data, random variables (RV s), point estimations, hypotheses, parameters, and so on. But there are many other situations in which the above mentioned concepts are imprecise. The point estimation approaches are frequently used in statistical inference. On the other hand, the theory of fuzzy sets is a well known tool for formulation and analysis of imprecise and subjective concepts. Therefore, the uniformly minimum variance unbiased fuzzy estimator (UMVUFE) with fuzzy data can be important. The problem of point estimation for an unknown parameter, using fuzzy data, is developed in different approaches. Kruse (1984) and Kruse and Meyer (1987) explained some methods for point and interval estimation for examples of fuzzy random variables (FRV s). Buckley (1983) studied the problem of estimation, with fuzzy data by a fuzzy decision making approach. Okuda (1987) considered fuzzy observations to estimate moments and parameters and he discusses maximum likelihood estimators and the loss of information due to fuzziness. Viertl (1996) studied nonparametric methods in estimation using fuzzy data. Lopez-Diaz and Gil (1998) derived some statistical inference methods, and studied their applications specially in statistical decision theory with fuzzy losses and fuzzy utilities. Cai et al. (1991) proposed a method for estimating parameters of membership functions through defining a likelihood function and studied its applications in fuzzy software reliability modelling. Cai (1993) discussed parameter estimation methods for normal membership functions. Lubiano et al. (1999) and Sadeghpour and Gien (2002) studied a Rao-Blackwell type theorem for FRV s. Lopez-Diaz and Gil (1998) defined a fuzzy unbiased estimator of the sample mean in random sampling with replacement from a finite population. Garcia
2 308 Austrian Journal of Statistics, Vol. 36 (2007), No. 4, et al. (2001) illustrated estimating the expected value of a FRV in the stratified random sampling. Some methods of statistical inference with fuzzy data are reviewed by Viertl (2002a, 2002b). There are some researches regarding the Bayesian point estimation methods combined with ideas from fuzzy set theory. Hryniewicz (2002) proposed the notion of fuzzy Bayes point estimation for fuzzy data. Gertner and Zhu (1997), based on two extensions of likelihood function, generalized Bayesian estimates for use when sample information and prior distribution are fuzzy. They applied their method to forest survey. Uemura (1991, 1993) formulated the fuzzy Bayes decision rule to facilitate determination of the loss function of a Bayes decision rule in a fuzzy environment. Wu (2003) studied fuzzy estimators of fuzzy parameters based on FRV s. Finally, Hong-Zhong et al. (2006) proposed a new method to determine the membership function of the parameter estimate of a multi-parameter distribution. This method can be used to determine the membership function of Bayesian estimates of a multi-parameter distribution. In this paper we organize the matter in the following way. In Section 2 we describe some basic concepts of canonical fuzzy numbers and FRV s. Also, we apply the ranking fuzzy numbers based on signed distance (Yao and Wu, 2000) between fuzzy canonical numbers. In Section 3 we summarize the research results report in the literature on uniformly minimum variance unbiased estimators (UMVUE s). Section 4 is devoted to describe UMVUE s using fuzzy data. Finally, some numerical examples are presented in Section 5 in order to illustrate our proposed method. 2 Preliminaries Let (Ω, F, P ) be a probability space. A RV X is a measurable function from (Ω, F, P ) to (X, B, P X ), where P X is the probability measure induced by X and is called the distribution of X, i.e., P X (A) = P (X A) = dp, A B. If P X is dominated by a σ finite measure υ, then by the Radon-Nikodym theorem (see Billingsley, 1995) we have P X (A) = f(x θ)dυ(x), A B, X A where f(x θ) is the Radon-Nikodym derivative of P X with respect to υ and is called probability density function (PDF) of X with respect to υ. In a statistical context the measure υ is usually a counting measure or a Lebesgue measure, hence P X (A) is calculated by x A f(x θ) or f(x θ)dx, respectively. A Let S X = {x X f(x θ) > 0} be the support or sample space of X, then a fuzzy subset x of S X is defined by its membership function µ x : S X [0, 1]. We denote by x α = {x : µ x (x) α} the α-cut set of x and x 0 is the closure of the set {x : µ x (x) > 0}. x is called normal fuzzy set if there exist x S X such that µ x (x) = 1 and is called convex fuzzy set if µ x (λx + (1 λ)y) min(µ x (x), µ x (y)) for λ [0, 1]. X A
3 M. Akbari and A. Rezaei 309 The fuzzy set x is called a fuzzy number if x is a normal convex fuzzy set and its α-cut set is bounded for all α 0. x is called a closed fuzzy number if x is a fuzzy number and its membership function µ x is upper semicontinous. x is called a bounded fuzzy number if x is a fuzzy number and its membership function µ x has compact support. If x is a closed and bounded fuzzy number with x L α = inf{x : x x α } and x U α = sup{x : x x α } and its membership function is strictly increasing on [x L α, x L 1 ] and strictly decreasing on [x U 1, x U α ], then x is called canonical fuzzy number. Given a real number x S X, we can induce a fuzzy number x with membership function µ x (r) such that µ x (x) = 1 and µ x (r) < 1 for r x. Let X be a RV with support S X and F(S X ) be a set of all fuzzy real numbers induced by the real numbers S X. If F(R) are canonical fuzzy real numbers on R then it is obvious that F(S X ) F(R). Definition 2.1 A FRV is a function X : Ω F(S X ), where such that X is induced by X. {(ω, x) : ω Ω, x X α (ω)} F B, α [0, 1], Lemma 2.1 Let F(R) be a canonical fuzzy real number system. Then X is a FRV iff X L α and X U α are RV s for all α [0, 1]. Definition 2.2 Let X be a RV with cumulative distribution function (CDF) F (x) and let X be a FRV induced by X. The fuzzy function F ( x) is called fuzzy cumulative distribution function of the FRV X, whenever its membership function equals where µ F ( x) (y) = sup αi [F L α ( x),fα U ( x)](y), F L α ( x) = F U α ( x) = inf {F (x) : x [xl β, x U β ]}, sup {F (x) : x [x L β, x U β ]}. The interval [Fα L ( x), Fα U ( x)] contains all of the CDF of each x L β and xu β for β α. To assert the fuzzy expectation of a FRV X, we first define E L α( X) and E U α ( X) as E L α( X) = E U α ( X) = inf {E(X) : X [XL β, Xβ U ]}, sup {E(X) : X [Xβ L, Xβ U ]}. The interval [E L α( X), E U α ( X)] will contain all of the expectations of each RV X L β and XU β for β α. Definition 2.3 Let X be a FRV induced by X. Then the fuzzy expectation of X is a fuzzy number Ẽ( X) with membership function µẽ( X) (y) = sup αi [E L α ( X),E U α ( X)] (y).
4 310 Austrian Journal of Statistics, Vol. 36 (2007), No. 4, Several ranking methods have been proposed so far by Cheng (1998), Modarres and Sadi-Nezhad (2001), and Nojavan and Ghazanfari (2006). Here we use another ranking system for canonical fuzzy numbers which is very realistic and is defined by Yao and Wu (2000) as follows. Definition 2.4 For any a, b R define their signed distance by d (a, b) = a b. Thus, we have the following possibilities to define the rank of any two numbers on R as d (a, b) > 0 d (a, 0) > d (b, 0) a > b, d (a, b) < 0 d (a, 0) < d (b, 0) a < b, d (a, b) = 0 d (a, 0) = d (b, 0) a = b. Definition 2.5 For each pair ã, b F(R) define the signed distance as d(ã, b) = 1 0 (M α (ã) M α ( b))dα = 1 0 d (M α (ã), M α ( b))dα, where M α (ã) and M α ( b) equal (a L α + a U α )/2 and (b L α + b U α )/2, respectively. Furthermore, d(ã, b) denotes the distance between ã and b. Definition 2.6 (Yao and Wu, 2000) For each ã, b F(R), define their ranking by d(ã, b) > 0 d(ã, 0) > d( b, 0) ã b, d(ã, b) < 0 d(ã, 0) < d( b, 0) ã b, d(ã, b) = 0 d(ã, 0) = d( b, 0) ã b. 3 The UMVUE with Crisp Data In this section, we describe concepts of UMVUE s with crisp data. Let X 1,..., X n be a random sample of size n, where the X i s have PDF f(x θ) with unknown parameter θ, θ Θ, and x 1,..., x n are realizations of X 1,..., X n, respectively. Recall that an estimator T (X 1,..., X n ) of θ is unbiased iff E[T (X 1,..., X n )] = θ for any θ Θ. If an unbiased estimator of θ exists, then θ is called an estimable parameter. Definition 3.1 An unbiased estimator T (X 1,..., X n ) of θ is called uniformly minimum variance unbiased estimator (UMV UE) iff var[(t (X 1,..., X n ))] var[(u(x 1,..., X n )], for any θ Θ and any other unbiased estimator U(X 1,..., X n ) of θ. The derivation of such an UMVUE is relatively simple if there exist a complete sufficient statistic for θ Θ. Theorem 3.1 (Lehmann-Scheffé) Suppose that there exists a complete sufficient statistic T (X 1,..., X n ) for θ Θ. If θ is estimable, then there exists an unique unbiased estimator of g(θ) of the form h(t ) with a Borel function h. Furthermore, h(t ) is the unique UMVUE of θ.
5 M. Akbari and A. Rezaei 311 There are two typically ways to derive a UMVUE when a complete sufficient statistic is available. The first one is to solve for h when the distribution of T is available. The second method to derive an UMVUE when there exists a complete sufficient statistic (used here), is to condition on T, i.e., if U(X 1,..., X n ) is an unbiased estimator of θ, then E[(U(X 1,..., X n ) T )] is the UMVUE of θ. To apply this method, we do not need the distribution of T but need to work out the conditional expectation E[U(X 1,..., X n T )]. From the uniqueness of the UMVUE, it does not matter which U(X 1,..., X n ) is used. We should choose U(X 1,..., X n ) to make the calculation of E[U(X 1,..., X n ) T ] as easy as possible. For a review in more details, see Shao (2003). 4 An UMVUE with Fuzzy Data Now we introduce concepts of an UMVUFE. Definition 4.1 Let X and Ỹ be two FRV s induced by X and Y. We say that X and Ỹ are independent iff each RV in the set {Xα L, Xα U : 0 α 1} is independent of each RV in the set {Yα L, Yα U : 0 α 1}. Definition 4.2 We say that X and Ỹ are identically distributed iff XL α, Yα L distributed, and Xα U, Yα U are identically distributed for all α [0, 1]. are identically Let X = ( X 1,..., X n ) be a fuzzy random sample induced by X = (X 1,..., X n ) on the sample probability space (Ω, F, P ), and with membership functions µ Xi (y). In traditional statistics, parameter estimates are functions of the sample. Formally, based on the sample X for a RV X with sample space S X, PDF f(x θ) and parameter space Θ, estimators are functions δ(x) defined on the sample space S X1 S Xn. For a realized sample x = (x 1,..., x n ) an estimation θ of the parameter θ is obtained by δ(x) = θ Θ. For a fuzzy random sample X induced by X with membership functions µ Xi (y) the function δ( x), where x = ( x 1,..., x n ), becomes a fuzzy element θ Θ, whose membership function µ δ( x) is derived by applying the extension principle (Klir and Yuan, 1995), i.e. { sup{min1 i n µ µ δ( x) (d) = Xi (x i ) : δ(x 1,..., x n ) = d}, δ 1 (d) 0, δ 1 (d) = for any d Θ. For a fuzzy random sample X, the fuzzy number δ( X) is called a fuzzy statistic, provided that it is not a function of any unknown parameter. Let X i and X i have CDF F and F, respectively. A fuzzy statistic δ( X) is said to be a (point) estimator of θ, if δ : F(S X1 ) F(S Xn ) Θ, where F(S Xi ) is the space of fuzzy values of X i.
6 312 Austrian Journal of Statistics, Vol. 36 (2007), No. 4, Each α-cut set of δ( X) depends on X. Suppose {δ(x) : X i estimator of θ that is obtained by α-cut of δ( X). Define ( X i ) α } is a crisp δ L α = δ L α(x) = δ U α inf {δ(x) : X i ( X i ) β }, = δα U (X) = sup {δ(x) : X i ( X i ) β }, where the interval I(δ α ) = [δα, L δα U ] contains all the crisp estimators of each RV Xiβ L and Xiβ U for β α. Definition 4.3 The fuzzy estimator δ( X) is unbiased for θ iff for all α [0, 1] and δ 0 [δ L α, δ U α ] there exists a θ 0 θ α such that E(δ 0 ) = θ 0. Let D be a nonempty set of all fuzzy unbiased estimators δ( X) for θ. Definition 4.4 The fuzzy estimator δ( X) is sufficient for θ iff for each α [0, 1] and δ I(δ α ), δ is a sufficient statistics for θ θ α. Now we define the membership function of the fuzzy variance function of δ( X), denoted by ṽar( δ( X)), as µṽar (y) = sup αi [var L α,var U α ](y), where var L α = inf {var(δ(x))}, var U α = sup {var(δ(x))}. (1) δ I(δ α ) δ I(δ α) Definition 4.5 δ ( X) is an UMVUFE of θ iff δ is unbiased and ṽar = ṽar( δ ) ṽar = ṽar( δ), δ D, where notation denotes signed distance. Theorem 4.1 Let X = (X 1,..., X n ) be a random sample and X = ( X 1,..., X n ) be a fuzzy random sample induced by X. If Ũ( X) is a fuzzy unbiased estimator for θ and T ( X) a fuzzy sufficient statistics for θ, then the UMVUFE δ ( X) has membership function in which E L α = E U α = µ δ ( X) (y) = sup αi [E L α,e U α ](y), inf {E[U(X) T (X)] : X i ( X i ) β }, sup {E[U(X) T (X)] : X i ( X i ) β }. Proof: We first prove that δ is a canonical fuzzy number. Define S α = {(x 1,..., x n ) : x i ( x i ) α } and k(x 1,..., x n ) = E[U(X) T (X)] for (x 1,..., x n ) S α and α [0, 1]. We know that x i s are canonical fuzzy numbers, k is continuous, S α is connected, closed, and bounded implying that the range of k is a closed and bounded interval of real
7 M. Akbari and A. Rezaei 313 numbers. Define δ α = k(s α ) for α [0, 1]. Furthermore δ 1 = E[U(X) T (X)]. Hence, δ α is a canonical fuzzy number. To proof unbiasedness, let α [0, 1] and δα [δα L, δα U ]. Thus there exists a X i X iα such that δα(x) = E[U(X) T (x)], E[δα(X)] = E[U(X)]. Now we know that Ũ( X) is an unbiased fuzzy estimator. By definition 4.3 there exists a θ 0 θ α such that E[δα(X)] = E[U(X)] = θ 0. As a result, δ ( X) is a fuzzy unbiased estimator. According to definition 4.4, T α is a sufficient statistic for θ 0 and in the other words, U(X) is unbiased for θ 0. Thus According to (1) we have and for δ ( X) we can write Thus, based on (2) we have var(δ α(x)) var(u(x)). (2) var L α(ũ(x)) = var L α( δ (X)) = inf {var(u(x))}, U I(U α ) inf {var(δ )}. δ [E L α,e U α ] var L α( δ ) var L α(ũ), and similarly it can be also shown that var U α ( δ ) var U α (Ũ). According to the function M in the Yao-Wu signed distance, we have d(ṽar, ṽar) = 1 0 (M α (ṽar ) M α (ṽar))dα 0, because M α (ṽar ) M α (ṽar). Hence, ṽar( δ ( X)) ṽar(ũ( X)). 5 Numerical Examples Now we illustrate the proposed approach for some distributions. Example 5.1 Let X be a RV from a N(θ, 1) population, i.e. f(x θ) = 1 exp ( 12 ) (x 2π θ)2, x, θ R. Consider x 1,..., x n with triangular membership functions (x i a, x i, x i + b) given by { (y xi + a)/a, x µ xi (y) = i a y x i, (x i + b y)/b, x i y x i + b for each 1 i n and a, b 0. We can interpret the canonical fuzzy numbers x i as the values of near to x i. We have µ δ ( X) (y) = sup αi [E L α,e U α ](y),
8 314 Austrian Journal of Statistics, Vol. 36 (2007), No. 4, such that E L α = x (1 α)a, E U α = x + (1 α)b, and we note that in crisp form for this example the UMVUE is δ (X) = X and also µ δ ( x) (x) = 1. For instance when a = b = 5 and our fuzzy observations x 1,..., x 6 have membership functions { { (y 40)/5, 40 y 45 (y 50)/5, 50 y 55 µ x1 (y) = (50 y)/5, 45 y 50, µ x 2 (y) = (60 y)/5, 55 y 60 { { (y 65)/5, 65 y 70 (y 80)/5, 80 y 85 µ x3 (y) = (75 y)/5, 70 y 75, µ x 4 (y) = (90 y)/5, 85 y 90 { { (y 110)/5, 110 y 115 (y 117)/5, 117 y 122 µ x5 (y) = (120 y)/5, 115 y 120, µ x 6 (y) = (127 y)/5, 122 y 127. We derive [E L α, E U α ] = [82 5(1 α), (1 α)]. Hence, δ ( x) is a canonical fuzzy number and µ δ ( x) (82) = 1. Example 5.2 Let X be a RV from a E(θ, 1) population, i.e., f(x θ) = exp( (x θ)), x > θ, θ > 0, and let x i be some fuzzy observations with membership functions { exp( (y xi ) µ xi (y) = 2 ), x i 0.5 y x i , otherwise for each 1 i n. We can interpret the canonical fuzzy numbers x i as the values of near to x i. We have µ δ ( x) (y) = sup αi [E L α,e U α ](y) such that { E L x(1) 1/n 0.5, 0 α exp( 0.25) α = x (1) 1/n log α, exp( 0.25) α 1, { E U x(1) 1/n + 0.5, 0 α exp( 0.25) α = x (1) 1/n + log α, exp( 0.25) α 1. We note that in crisp form for this example the UMVUE is δ (X) = X (1) 1/n and also µ δ ( x) (x (1) 1/n) = 1. Example 5.3 Let X be a RV from a U (θ, θ + 1) population i.e., f(x θ) = 1, θ x θ + 1, 0 < θ < 1, and x i are fuzzy observations with triangular membership functions (x i a, x i, x i + b). We have E L α = (x (1) + x (2) 1)/2 (1 α)a, E U α = (x (1) + x (2) 1)/2 + (1 α)b.
9 M. Akbari and A. Rezaei 315 Thus, the membership function of δ ( x) is µ δ ( x) (y) = sup αi [E L α,e U α ](y). Example 5.4 Let X be a RV from an exponential population with mean 1/θ, i.e., f(x θ) = θ exp( θx), x > 0, θ > 0, and let x i s be some fuzzy observations with membership functions { exp( (x xi ) µ xi (x) = 2 ), x i 0.5 x x i , otherwise for each 1 i n. Then we have n 1 E L n(x + 0.5), 0 α exp( 0.25) α = n 1 n(x + log α), exp( 0.25) α 1 n 1 E U n(x 0.5), 0 α exp( 0.25) α = n 1. n(x log α), exp( 0.25) α 1 Thus, the membership function of δ ( x) is Example 5.5 Let X be a RV with PDF µ δ ( x) (y) = sup αi [E L α,e U α ](y). f(x θ) = 1 θ, 0 < x < θ. Let x 1 and x 2 be two fuzzy canonical numbers with triangular membership functions (x i a, x i, x i + b ), then we have [ n + 1 [E L α, E U α ] = n (x (1) (1 α)a ), n + 1 ] n (x (1) + (1 α)b ). Furthermore, the parameter estimate at any α-cut level can be calculated with respect to membership function µ δ ( x) (y) = sup αi [E L α,e U α ](y). 6 Conclusion From the above discussion, it is clear that under Yao-Wu signed distance, the UMVUF estimator propose a canonical fuzzy number. The UMVUF estimator has the smallest fuzzy variance of the other fuzzy estimator for fuzzy parameter θ.
10 316 Austrian Journal of Statistics, Vol. 36 (2007), No. 4, Acknowledgements The authors thank the referees for their comments which helped us to improve the paper. References Billingsley, P.(1995). Probability and Measure (2nd ed.). New York: John Wiley. Buckley, J. J. (1983). Fuzzy decision making with data: applications to statistics. Fuzzy Sets and Systems, 16, Cai, K. Y. (1993). Parameter estimation of normal fuzzy variables. Fuzzy Sets and Systems, 55, Cai, K. Y., Wen, C. Y., and Zhang, M. L.(1991). Fuzzy variable as a basis for a theory of fuzzy reliability in the possibility context. Fuzzy Sets and Systems, 42, Cheng, C.(1998). A new approach for ranking fuzzy numbers by distance method. Fuzzy Sets and Systems, 95, Garcia, D., Lubiano, M. A., and Alonso, C. (2001). Estimating the expected value of fuzzy random variables in the stratified random sampling from finite populations. Information Sciences, 138, Gertner, G. Z., and Zhu, H.(1997). Bayesian estimation in forest survey when samples or prior information are fuzzy. Fuzzy Sets and Systems, 77, Hong-Zhong, H., Ming, J. Z., and Zhan-Quan, S.(2006). Bayesian reliability analysis for fuzzy lifetime data. Fuzzy Sets and Systems, 157, Hryniewicz, O.(2002). Possibilities approach to the Bayes statistical decisions. In P. Grzegorzewski, O. Hryniewicz, and M. A. Gil (Eds.), Soft Methods in Probability, Statistics and Data Analysis (p ). Heidelberg-New York: Physica Verlag. Klir, G., and Yuan, B. (1995). Fuzzy sets and fuzzy logic-theory and applications. Upper Saddle River, NJ: Prentice-Hall. Kruse, R. (1984). Statistical estimation with linguistic data. Information Science, 33, Kruse, R., and Meyer, K. D. (1987). Statistics with Vague Data (Vol. 33). Dordrecht: Reidel. Lopez-Diaz, M., and Gil, M. A. (1998). Reversing the order of integration in iterated expectations of fuzzy random variables, and statistical applications. Jornal of Statistical Planning and Inference, 74, Lubiano, M. A., Gil, M. A., and Lopez-Diaz, M. (1999). On the Rao-Blackwell theorem for fuzzy random variables. Kybernetica, 35, Modarres, M., and Sadi-Nezhad, S. (2001). Ranking fuzzy numbers by preference ratio. Fuzzy Sets and Systems, 118, Nojavan, M., and Ghazanfari, M. (2006). A fuzzy ranking method by desirability index. Journal of Intelligent and Fuzzy Systems, 17, Okuda, T. (1987). A statistical treatment of fuzzy observations: estimation problems. In Preprints of the 2nd IFSA Congress (p ). Sadeghpour, G. B., and Gien, D. (2002). d p,q -distance and Rao-Blackwell theorem for fuzzy random variables. In Proceedings of the 8th international Conference of Fuzzy Theory and Technology. Durham, USA.
11 M. Akbari and A. Rezaei 317 Shao, J.(2003). Mathematical Statistics (2nd ed.). New York: Springer-Verlag. Uemura, Y. (1991). A decision rule on fuzzy events. Japanese Journal of Fuzzy Theory and Systems, 3, Uemura, Y. (1993). A decision rule on fuzzy events under an observation. Journal of Fuzzy Mathematics, 1, Viertl, R.(1996). Statistical Methods for Non-Precise Data. Boca Raton: CRC Press. Viertl, R.(2002a). Statistics with one-dimensional fuzzy data. In C. B. et al. (Ed.), Statistical Modeling, Analysis and Management of Fuzzy Data (p ). Heidelberg: Physica-Verlag. Viertl, R. (2002b). Statistical inference with non-precise data. In Encyclopedia of Life Support Systems. Paris: UNESCO. Wu, H. C. (2003). The fuzzy estimators of fuzzy parameters based on fuzzy random variables. European Journal of Operation Research, 146, Yao, J. S., and Wu, K.(2000). Ranking fuzzy numbers based on decomposition principle and signed distance. Fuzzy Sets and Systems, 11, Authors Address: Mohammad Ghasem Akbari and Abdolhamid Rezaei Department of Statistics School of Mathematical Sciences Ferdowsi University of Mashhad , Mashhad Iran g z akbari@yahoo.com
Fuzzy Order Statistics based on α pessimistic
 Journal of Uncertain Systems Vol.10, No.4, pp.282-291, 2016 Online at: www.jus.org.uk Fuzzy Order Statistics based on α pessimistic M. GH. Akbari, H. Alizadeh Noughabi Department of Statistics, University
Journal of Uncertain Systems Vol.10, No.4, pp.282-291, 2016 Online at: www.jus.org.uk Fuzzy Order Statistics based on α pessimistic M. GH. Akbari, H. Alizadeh Noughabi Department of Statistics, University
Statistical Hypotheses Testing in the Fuzzy Environment
 Journal of Uncertain Systems Vol.6, No.3, pp.86-99, 22 Online at: www.jus.org.uk Statistical Hypotheses Testing in the Fuzzy Environment Mohammad Ghasem Akbari Department of Statistics, Faculty of Sciences,
Journal of Uncertain Systems Vol.6, No.3, pp.86-99, 22 Online at: www.jus.org.uk Statistical Hypotheses Testing in the Fuzzy Environment Mohammad Ghasem Akbari Department of Statistics, Faculty of Sciences,
Sequential Probability Ratio Test for Fuzzy Hypotheses Testing with Vague Data
 AUSTRIAN JOURNAL OF STATISTICS Volume 34 (2005), Number 1, 25 38 Sequential Probability Ratio Test for Fuzzy Hypotheses Testing with Vague Data Hamzeh Torabi and Javad Behboodian Shiraz University, Iran
AUSTRIAN JOURNAL OF STATISTICS Volume 34 (2005), Number 1, 25 38 Sequential Probability Ratio Test for Fuzzy Hypotheses Testing with Vague Data Hamzeh Torabi and Javad Behboodian Shiraz University, Iran
Ranking Fuzzy Random Variables Based on New Fuzzy Stochastic Orders
 Journal of Uncertain Systems Vol.8, No., pp.66-77, 04 Online at: www.jus.org.uk Ranking Fuzzy Random Variables Based on New Fuzzy Stochastic Orders R. Zarei, M. Amini, A.H. Rezaei Roknabadi Department
Journal of Uncertain Systems Vol.8, No., pp.66-77, 04 Online at: www.jus.org.uk Ranking Fuzzy Random Variables Based on New Fuzzy Stochastic Orders R. Zarei, M. Amini, A.H. Rezaei Roknabadi Department
Chi-square goodness-of-fit test for vague data
 Chi-square goodness-of-fit test for vague data Przemys law Grzegorzewski Systems Research Institute Polish Academy of Sciences Newelska 6, 01-447 Warsaw, Poland and Faculty of Math. and Inform. Sci., Warsaw
Chi-square goodness-of-fit test for vague data Przemys law Grzegorzewski Systems Research Institute Polish Academy of Sciences Newelska 6, 01-447 Warsaw, Poland and Faculty of Math. and Inform. Sci., Warsaw
Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic
 Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic Unbiased estimation Unbiased or asymptotically unbiased estimation plays an important role in
Chapter 3: Unbiased Estimation Lecture 22: UMVUE and the method of using a sufficient and complete statistic Unbiased estimation Unbiased or asymptotically unbiased estimation plays an important role in
ST5215: Advanced Statistical Theory
 Department of Statistics & Applied Probability Wednesday, October 19, 2011 Lecture 17: UMVUE and the first method of derivation Estimable parameters Let ϑ be a parameter in the family P. If there exists
Department of Statistics & Applied Probability Wednesday, October 19, 2011 Lecture 17: UMVUE and the first method of derivation Estimable parameters Let ϑ be a parameter in the family P. If there exists
An Evaluation of the Reliability of Complex Systems Using Shadowed Sets and Fuzzy Lifetime Data
 International Journal of Automation and Computing 2 (2006) 145-150 An Evaluation of the Reliability of Complex Systems Using Shadowed Sets and Fuzzy Lifetime Data Olgierd Hryniewicz Systems Research Institute
International Journal of Automation and Computing 2 (2006) 145-150 An Evaluation of the Reliability of Complex Systems Using Shadowed Sets and Fuzzy Lifetime Data Olgierd Hryniewicz Systems Research Institute
Process Capability Indices as Fuzzy Numbers
 AUSTRIAN JOURNAL OF STATISTICS Volume 34 2005, Number 4, 391 402 Process Capability Indices as Fuzzy Numbers Abbas Parchami, Mashaallah Mashinchi, Ali Reza Yavari, and Hamid Reza Maleki Shahid Bahonar
AUSTRIAN JOURNAL OF STATISTICS Volume 34 2005, Number 4, 391 402 Process Capability Indices as Fuzzy Numbers Abbas Parchami, Mashaallah Mashinchi, Ali Reza Yavari, and Hamid Reza Maleki Shahid Bahonar
Foundations of Fuzzy Bayesian Inference
 Journal of Uncertain Systems Vol., No.3, pp.87-9, 8 Online at: www.jus.org.uk Foundations of Fuzzy Bayesian Inference Reinhard Viertl Department of Statistics and Probability Theory, Vienna University
Journal of Uncertain Systems Vol., No.3, pp.87-9, 8 Online at: www.jus.org.uk Foundations of Fuzzy Bayesian Inference Reinhard Viertl Department of Statistics and Probability Theory, Vienna University
On Distribution Characteristics of a Fuzzy Random Variable
 Austrian Journal of Statistics February 218, Volume 47, 53 67. AJS http://www.ajs.or.at/ doi:1.17713/ajs.v47i2.581 On Distribution Characteristics of a Fuzzy Random Variable Jalal Chachi Semnan University
Austrian Journal of Statistics February 218, Volume 47, 53 67. AJS http://www.ajs.or.at/ doi:1.17713/ajs.v47i2.581 On Distribution Characteristics of a Fuzzy Random Variable Jalal Chachi Semnan University
Review and continuation from last week Properties of MLEs
 Review and continuation from last week Properties of MLEs As we have mentioned, MLEs have a nice intuitive property, and as we have seen, they have a certain equivariance property. We will see later that
Review and continuation from last week Properties of MLEs As we have mentioned, MLEs have a nice intuitive property, and as we have seen, they have a certain equivariance property. We will see later that
STA 732: Inference. Notes 10. Parameter Estimation from a Decision Theoretic Angle. Other resources
 STA 732: Inference Notes 10. Parameter Estimation from a Decision Theoretic Angle Other resources 1 Statistical rules, loss and risk We saw that a major focus of classical statistics is comparing various
STA 732: Inference Notes 10. Parameter Estimation from a Decision Theoretic Angle Other resources 1 Statistical rules, loss and risk We saw that a major focus of classical statistics is comparing various
Fuzzy histograms and fuzzy probability distributions
 Fuzzy histograms and fuzzy probability distributions R. Viertl Wiedner Hauptstraße 8 / 7-4 Vienna R.Viertl@tuwien.ac.at W. Trutschnig Wiedner Hauptstraße 8 / 7-4 Vienna trutschnig@statistik.tuwien.ac.at
Fuzzy histograms and fuzzy probability distributions R. Viertl Wiedner Hauptstraße 8 / 7-4 Vienna R.Viertl@tuwien.ac.at W. Trutschnig Wiedner Hauptstraße 8 / 7-4 Vienna trutschnig@statistik.tuwien.ac.at
Estimation theory. Parametric estimation. Properties of estimators. Minimum variance estimator. Cramer-Rao bound. Maximum likelihood estimators
 Estimation theory Parametric estimation Properties of estimators Minimum variance estimator Cramer-Rao bound Maximum likelihood estimators Confidence intervals Bayesian estimation 1 Random Variables Let
Estimation theory Parametric estimation Properties of estimators Minimum variance estimator Cramer-Rao bound Maximum likelihood estimators Confidence intervals Bayesian estimation 1 Random Variables Let
ST5215: Advanced Statistical Theory
 Department of Statistics & Applied Probability Wednesday, October 5, 2011 Lecture 13: Basic elements and notions in decision theory Basic elements X : a sample from a population P P Decision: an action
Department of Statistics & Applied Probability Wednesday, October 5, 2011 Lecture 13: Basic elements and notions in decision theory Basic elements X : a sample from a population P P Decision: an action
Spring 2012 Math 541A Exam 1. X i, S 2 = 1 n. n 1. X i I(X i < c), T n =
 Spring 2012 Math 541A Exam 1 1. (a) Let Z i be independent N(0, 1), i = 1, 2,, n. Are Z = 1 n n Z i and S 2 Z = 1 n 1 n (Z i Z) 2 independent? Prove your claim. (b) Let X 1, X 2,, X n be independent identically
Spring 2012 Math 541A Exam 1 1. (a) Let Z i be independent N(0, 1), i = 1, 2,, n. Are Z = 1 n n Z i and S 2 Z = 1 n 1 n (Z i Z) 2 independent? Prove your claim. (b) Let X 1, X 2,, X n be independent identically
Testing Statistical Hypotheses in Fuzzy Environment
 Mathware & Soft Computing 4 (1997) 203-217 Testing Statistical Hypotheses in Fuzzy Environment Przemys law Grzegorzewski, Olgierd Hryniewicz Systems Research Institute, Polish Academy of Sciences, l ul.
Mathware & Soft Computing 4 (1997) 203-217 Testing Statistical Hypotheses in Fuzzy Environment Przemys law Grzegorzewski, Olgierd Hryniewicz Systems Research Institute, Polish Academy of Sciences, l ul.
Some moment inequalities for fuzzy martingales and their applications
 Ahmadzade et al. Journal of Uncertainty Analysis and Applications 214, 2:7 RESEARCH Open Access Some moment inequalities for fuzzy martingales and their applications Hamed Ahmadzade 1, Mohammad Amini 1*,
Ahmadzade et al. Journal of Uncertainty Analysis and Applications 214, 2:7 RESEARCH Open Access Some moment inequalities for fuzzy martingales and their applications Hamed Ahmadzade 1, Mohammad Amini 1*,
Chapter 2: Fundamentals of Statistics Lecture 15: Models and statistics
 Chapter 2: Fundamentals of Statistics Lecture 15: Models and statistics Data from one or a series of random experiments are collected. Planning experiments and collecting data (not discussed here). Analysis:
Chapter 2: Fundamentals of Statistics Lecture 15: Models and statistics Data from one or a series of random experiments are collected. Planning experiments and collecting data (not discussed here). Analysis:
Fuzzy relation equations with dual composition
 Fuzzy relation equations with dual composition Lenka Nosková University of Ostrava Institute for Research and Applications of Fuzzy Modeling 30. dubna 22, 701 03 Ostrava 1 Czech Republic Lenka.Noskova@osu.cz
Fuzzy relation equations with dual composition Lenka Nosková University of Ostrava Institute for Research and Applications of Fuzzy Modeling 30. dubna 22, 701 03 Ostrava 1 Czech Republic Lenka.Noskova@osu.cz
40.530: Statistics. Professor Chen Zehua. Singapore University of Design and Technology
 Singapore University of Design and Technology Lecture 9: Hypothesis testing, uniformly most powerful tests. The Neyman-Pearson framework Let P be the family of distributions of concern. The Neyman-Pearson
Singapore University of Design and Technology Lecture 9: Hypothesis testing, uniformly most powerful tests. The Neyman-Pearson framework Let P be the family of distributions of concern. The Neyman-Pearson
Evaluating the Performance of Estimators (Section 7.3)
 Evaluating the Performance of Estimators (Section 7.3) Example: Suppose we observe X 1,..., X n iid N(θ, σ 2 0 ), with σ2 0 known, and wish to estimate θ. Two possible estimators are: ˆθ = X sample mean
Evaluating the Performance of Estimators (Section 7.3) Example: Suppose we observe X 1,..., X n iid N(θ, σ 2 0 ), with σ2 0 known, and wish to estimate θ. Two possible estimators are: ˆθ = X sample mean
Qualifying Exam in Probability and Statistics. https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf
 Part : Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Part : Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
New independence definition of fuzzy random variable and random fuzzy variable
 ISSN 1 746-7233, England, UK World Journal of Modelling and Simulation Vol. 2 (2006) No. 5, pp. 338-342 New independence definition of fuzzy random variable and random fuzzy variable Xiang Li, Baoding
ISSN 1 746-7233, England, UK World Journal of Modelling and Simulation Vol. 2 (2006) No. 5, pp. 338-342 New independence definition of fuzzy random variable and random fuzzy variable Xiang Li, Baoding
Testing Statistical Hypotheses
 E.L. Lehmann Joseph P. Romano Testing Statistical Hypotheses Third Edition 4y Springer Preface vii I Small-Sample Theory 1 1 The General Decision Problem 3 1.1 Statistical Inference and Statistical Decisions
E.L. Lehmann Joseph P. Romano Testing Statistical Hypotheses Third Edition 4y Springer Preface vii I Small-Sample Theory 1 1 The General Decision Problem 3 1.1 Statistical Inference and Statistical Decisions
Where are we? Operations on fuzzy sets (cont.) Fuzzy Logic. Motivation. Crisp and fuzzy sets. Examples
 Operations on fuzzy sets (cont.) G. J. Klir, B. Yuan, Fuzzy Sets and Fuzzy Logic: Theory and Applications, Prentice-Hall, chapters -5 Where are we? Motivation Crisp and fuzzy sets alpha-cuts, support,
Operations on fuzzy sets (cont.) G. J. Klir, B. Yuan, Fuzzy Sets and Fuzzy Logic: Theory and Applications, Prentice-Hall, chapters -5 Where are we? Motivation Crisp and fuzzy sets alpha-cuts, support,
Why Trapezoidal and Triangular Membership Functions Work So Well: Towards a Theoretical Explanation
 Journal of Uncertain Systems Vol.8, No.3, pp.164-168, 2014 Online at: www.jus.org.uk Why Trapezoidal and Triangular Membership Functions Work So Well: Towards a Theoretical Explanation Aditi Barua, Lalitha
Journal of Uncertain Systems Vol.8, No.3, pp.164-168, 2014 Online at: www.jus.org.uk Why Trapezoidal and Triangular Membership Functions Work So Well: Towards a Theoretical Explanation Aditi Barua, Lalitha
Intuitionistic Fuzzy Numbers and It s Applications in Fuzzy Optimization Problem
 Intuitionistic Fuzzy Numbers and It s Applications in Fuzzy Optimization Problem HASSAN MISHMAST NEHI a, and HAMID REZA MALEKI b a)department of Mathematics, Sistan and Baluchestan University, Zahedan,
Intuitionistic Fuzzy Numbers and It s Applications in Fuzzy Optimization Problem HASSAN MISHMAST NEHI a, and HAMID REZA MALEKI b a)department of Mathematics, Sistan and Baluchestan University, Zahedan,
Mathematical Statistics
 Mathematical Statistics Chapter Three. Point Estimation 3.4 Uniformly Minimum Variance Unbiased Estimator(UMVUE) Criteria for Best Estimators MSE Criterion Let F = {p(x; θ) : θ Θ} be a parametric distribution
Mathematical Statistics Chapter Three. Point Estimation 3.4 Uniformly Minimum Variance Unbiased Estimator(UMVUE) Criteria for Best Estimators MSE Criterion Let F = {p(x; θ) : θ Θ} be a parametric distribution
Numerical Solution of Fuzzy Differential Equations
 Applied Mathematical Sciences, Vol. 1, 2007, no. 45, 2231-2246 Numerical Solution of Fuzzy Differential Equations Javad Shokri Department of Mathematics Urmia University P.O. Box 165, Urmia, Iran j.shokri@mail.urmia.ac.ir
Applied Mathematical Sciences, Vol. 1, 2007, no. 45, 2231-2246 Numerical Solution of Fuzzy Differential Equations Javad Shokri Department of Mathematics Urmia University P.O. Box 165, Urmia, Iran j.shokri@mail.urmia.ac.ir
Information in Data. Sufficiency, Ancillarity, Minimality, and Completeness
 Information in Data Sufficiency, Ancillarity, Minimality, and Completeness Important properties of statistics that determine the usefulness of those statistics in statistical inference. These general properties
Information in Data Sufficiency, Ancillarity, Minimality, and Completeness Important properties of statistics that determine the usefulness of those statistics in statistical inference. These general properties
Chance Order of Two Uncertain Random Variables
 Journal of Uncertain Systems Vol.12, No.2, pp.105-122, 2018 Online at: www.jus.org.uk Chance Order of Two Uncertain andom Variables. Mehralizade 1, M. Amini 1,, B. Sadeghpour Gildeh 1, H. Ahmadzade 2 1
Journal of Uncertain Systems Vol.12, No.2, pp.105-122, 2018 Online at: www.jus.org.uk Chance Order of Two Uncertain andom Variables. Mehralizade 1, M. Amini 1,, B. Sadeghpour Gildeh 1, H. Ahmadzade 2 1
Qualifying Exam in Probability and Statistics. https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf
 Part 1: Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Part 1: Sample Problems for the Elementary Section of Qualifying Exam in Probability and Statistics https://www.soa.org/files/edu/edu-exam-p-sample-quest.pdf Part 2: Sample Problems for the Advanced Section
Monte Carlo Studies. The response in a Monte Carlo study is a random variable.
 Monte Carlo Studies The response in a Monte Carlo study is a random variable. The response in a Monte Carlo study has a variance that comes from the variance of the stochastic elements in the data-generating
Monte Carlo Studies The response in a Monte Carlo study is a random variable. The response in a Monte Carlo study has a variance that comes from the variance of the stochastic elements in the data-generating
ECE531 Lecture 8: Non-Random Parameter Estimation
 ECE531 Lecture 8: Non-Random Parameter Estimation D. Richard Brown III Worcester Polytechnic Institute 19-March-2009 Worcester Polytechnic Institute D. Richard Brown III 19-March-2009 1 / 25 Introduction
ECE531 Lecture 8: Non-Random Parameter Estimation D. Richard Brown III Worcester Polytechnic Institute 19-March-2009 Worcester Polytechnic Institute D. Richard Brown III 19-March-2009 1 / 25 Introduction
A Very Brief Summary of Statistical Inference, and Examples
 A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2008 Prof. Gesine Reinert 1 Data x = x 1, x 2,..., x n, realisations of random variables X 1, X 2,..., X n with distribution (model)
A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2008 Prof. Gesine Reinert 1 Data x = x 1, x 2,..., x n, realisations of random variables X 1, X 2,..., X n with distribution (model)
Key Renewal Theory for T -iid Random Fuzzy Variables
 Applied Mathematical Sciences, Vol. 3, 29, no. 7, 35-329 HIKARI Ltd, www.m-hikari.com https://doi.org/.2988/ams.29.9236 Key Renewal Theory for T -iid Random Fuzzy Variables Dug Hun Hong Department of Mathematics,
Applied Mathematical Sciences, Vol. 3, 29, no. 7, 35-329 HIKARI Ltd, www.m-hikari.com https://doi.org/.2988/ams.29.9236 Key Renewal Theory for T -iid Random Fuzzy Variables Dug Hun Hong Department of Mathematics,
Unbiased Estimation. Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others.
 Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Review Quiz. 1. Prove that in a one-dimensional canonical exponential family, the complete and sufficient statistic achieves the
 Review Quiz 1. Prove that in a one-dimensional canonical exponential family, the complete and sufficient statistic achieves the Cramér Rao lower bound (CRLB). That is, if where { } and are scalars, then
Review Quiz 1. Prove that in a one-dimensional canonical exponential family, the complete and sufficient statistic achieves the Cramér Rao lower bound (CRLB). That is, if where { } and are scalars, then
Hypothesis Test. The opposite of the null hypothesis, called an alternative hypothesis, becomes
 Neyman-Pearson paradigm. Suppose that a researcher is interested in whether the new drug works. The process of determining whether the outcome of the experiment points to yes or no is called hypothesis
Neyman-Pearson paradigm. Suppose that a researcher is interested in whether the new drug works. The process of determining whether the outcome of the experiment points to yes or no is called hypothesis
Mathematical statistics
 October 4 th, 2018 Lecture 12: Information Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation Chapter
October 4 th, 2018 Lecture 12: Information Where are we? Week 1 Week 2 Week 4 Week 7 Week 10 Week 14 Probability reviews Chapter 6: Statistics and Sampling Distributions Chapter 7: Point Estimation Chapter
Problem Selected Scores
 Statistics Ph.D. Qualifying Exam: Part II November 20, 2010 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. Problem 1 2 3 4 5 6 7 8 9 10 11 12 Selected
Statistics Ph.D. Qualifying Exam: Part II November 20, 2010 Student Name: 1. Answer 8 out of 12 problems. Mark the problems you selected in the following table. Problem 1 2 3 4 5 6 7 8 9 10 11 12 Selected
Lecture 4: UMVUE and unbiased estimators of 0
 Lecture 4: UMVUE and unbiased estimators of Problems of approach 1. Approach 1 has the following two main shortcomings. Even if Theorem 7.3.9 or its extension is applicable, there is no guarantee that
Lecture 4: UMVUE and unbiased estimators of Problems of approach 1. Approach 1 has the following two main shortcomings. Even if Theorem 7.3.9 or its extension is applicable, there is no guarantee that
Statistics with fuzzy random variables
 METRON - International Journal of Statistics 2007, vol. LXV, n. 3, pp. 277-303 ANA COLUBI RENATO COPPI PIERPAOLO D URSO MARÍA ÁNGELES GIL Statistics with fuzzy random variables Summary - The notion of
METRON - International Journal of Statistics 2007, vol. LXV, n. 3, pp. 277-303 ANA COLUBI RENATO COPPI PIERPAOLO D URSO MARÍA ÁNGELES GIL Statistics with fuzzy random variables Summary - The notion of
Week 5 Lectures 13-15
 Week 5 Lectures 13-15 Lecture 13 Definition 29 Let Y be a subset X. A subset A Y is open in Y if there exists an open set U in X such that A = U Y. It is not difficult to show that the collection of all
Week 5 Lectures 13-15 Lecture 13 Definition 29 Let Y be a subset X. A subset A Y is open in Y if there exists an open set U in X such that A = U Y. It is not difficult to show that the collection of all
The Proportional Likelihood Ratio Order for Lindley Distribution
 Communications of the Korean Statistical Society 2011, Vol. 18, No. 4, 485 493 DOI: 10.5351/CKSS.2011.18.4.485 The Proportional Likelihood Ratio Order for Lindley Distribution Jarrahiferiz, J. a, Mohtashami
Communications of the Korean Statistical Society 2011, Vol. 18, No. 4, 485 493 DOI: 10.5351/CKSS.2011.18.4.485 The Proportional Likelihood Ratio Order for Lindley Distribution Jarrahiferiz, J. a, Mohtashami
Compenzational Vagueness
 Compenzational Vagueness Milan Mareš Institute of information Theory and Automation Academy of Sciences of the Czech Republic P. O. Box 18, 182 08 Praha 8, Czech Republic mares@utia.cas.cz Abstract Some
Compenzational Vagueness Milan Mareš Institute of information Theory and Automation Academy of Sciences of the Czech Republic P. O. Box 18, 182 08 Praha 8, Czech Republic mares@utia.cas.cz Abstract Some
ASSESSING PROCESS PERFORMANCE WITH INCAPABILITY INDEX BASED ON FUZZY CRITICAL VALUE
 Iranian Journal of Fuzzy Systems Vol. 3, No. 5, (26). 2-34 2 ASSESSING PROCESS PERFORMANCE WITH INCAPABILITY INDEX BASED ON FUZZY CRITICAL VALUE Z. ABBASI GANJI AND B. SADEGHPOUR GILDEH Abstract. Process
Iranian Journal of Fuzzy Systems Vol. 3, No. 5, (26). 2-34 2 ASSESSING PROCESS PERFORMANCE WITH INCAPABILITY INDEX BASED ON FUZZY CRITICAL VALUE Z. ABBASI GANJI AND B. SADEGHPOUR GILDEH Abstract. Process
Review. December 4 th, Review
 December 4 th, 2017 Att. Final exam: Course evaluation Friday, 12/14/2018, 10:30am 12:30pm Gore Hall 115 Overview Week 2 Week 4 Week 7 Week 10 Week 12 Chapter 6: Statistics and Sampling Distributions Chapter
December 4 th, 2017 Att. Final exam: Course evaluation Friday, 12/14/2018, 10:30am 12:30pm Gore Hall 115 Overview Week 2 Week 4 Week 7 Week 10 Week 12 Chapter 6: Statistics and Sampling Distributions Chapter
Fundamentals of Statistics
 Chapter 2 Fundamentals of Statistics This chapter discusses some fundamental concepts of mathematical statistics. These concepts are essential for the material in later chapters. 2.1 Populations, Samples,
Chapter 2 Fundamentals of Statistics This chapter discusses some fundamental concepts of mathematical statistics. These concepts are essential for the material in later chapters. 2.1 Populations, Samples,
ECE 275B Homework # 1 Solutions Version Winter 2015
 ECE 275B Homework # 1 Solutions Version Winter 2015 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2
ECE 275B Homework # 1 Solutions Version Winter 2015 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2
Unbiased Estimation. Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others.
 Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
Unbiased Estimation Binomial problem shows general phenomenon. An estimator can be good for some values of θ and bad for others. To compare ˆθ and θ, two estimators of θ: Say ˆθ is better than θ if it
On intermediate value theorem in ordered Banach spaces for noncompact and discontinuous mappings
 Int. J. Nonlinear Anal. Appl. 7 (2016) No. 1, 295-300 ISSN: 2008-6822 (electronic) http://dx.doi.org/10.22075/ijnaa.2015.341 On intermediate value theorem in ordered Banach spaces for noncompact and discontinuous
Int. J. Nonlinear Anal. Appl. 7 (2016) No. 1, 295-300 ISSN: 2008-6822 (electronic) http://dx.doi.org/10.22075/ijnaa.2015.341 On intermediate value theorem in ordered Banach spaces for noncompact and discontinuous
Some Pre-filters in EQ-Algebras
 Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 1932-9466 Vol. 12, Issue 2 (December 2017), pp. 1057-1071 Applications and Applied Mathematics: An International Journal (AAM) Some Pre-filters
Available at http://pvamu.edu/aam Appl. Appl. Math. ISSN: 1932-9466 Vol. 12, Issue 2 (December 2017), pp. 1057-1071 Applications and Applied Mathematics: An International Journal (AAM) Some Pre-filters
Probability and Statistics qualifying exam, May 2015
 Probability and Statistics qualifying exam, May 2015 Name: Instructions: 1. The exam is divided into 3 sections: Linear Models, Mathematical Statistics and Probability. You must pass each section to pass
Probability and Statistics qualifying exam, May 2015 Name: Instructions: 1. The exam is divided into 3 sections: Linear Models, Mathematical Statistics and Probability. You must pass each section to pass
A Few Notes on Fisher Information (WIP)
 A Few Notes on Fisher Information (WIP) David Meyer dmm@{-4-5.net,uoregon.edu} Last update: April 30, 208 Definitions There are so many interesting things about Fisher Information and its theoretical properties
A Few Notes on Fisher Information (WIP) David Meyer dmm@{-4-5.net,uoregon.edu} Last update: April 30, 208 Definitions There are so many interesting things about Fisher Information and its theoretical properties
SOLUTIONS TO MATH68181 EXTREME VALUES AND FINANCIAL RISK EXAM
 SOLUTIONS TO MATH68181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question A1 a) The marginal cdfs of F X,Y (x, y) = [1 + exp( x) + exp( y) + (1 α) exp( x y)] 1 are F X (x) = F X,Y (x, ) = [1
SOLUTIONS TO MATH68181 EXTREME VALUES AND FINANCIAL RISK EXAM Solutions to Question A1 a) The marginal cdfs of F X,Y (x, y) = [1 + exp( x) + exp( y) + (1 α) exp( x y)] 1 are F X (x) = F X,Y (x, ) = [1
Charles Geyer University of Minnesota. joint work with. Glen Meeden University of Minnesota.
 Fuzzy Confidence Intervals and P -values Charles Geyer University of Minnesota joint work with Glen Meeden University of Minnesota http://www.stat.umn.edu/geyer/fuzz 1 Ordinary Confidence Intervals OK
Fuzzy Confidence Intervals and P -values Charles Geyer University of Minnesota joint work with Glen Meeden University of Minnesota http://www.stat.umn.edu/geyer/fuzz 1 Ordinary Confidence Intervals OK
LECTURE 5 NOTES. n t. t Γ(a)Γ(b) pt+a 1 (1 p) n t+b 1. The marginal density of t is. Γ(t + a)γ(n t + b) Γ(n + a + b)
 LECTURE 5 NOTES 1. Bayesian point estimators. In the conventional (frequentist) approach to statistical inference, the parameter θ Θ is considered a fixed quantity. In the Bayesian approach, it is considered
LECTURE 5 NOTES 1. Bayesian point estimators. In the conventional (frequentist) approach to statistical inference, the parameter θ Θ is considered a fixed quantity. In the Bayesian approach, it is considered
ECE 275B Homework # 1 Solutions Winter 2018
 ECE 275B Homework # 1 Solutions Winter 2018 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2 < < x n Thus,
ECE 275B Homework # 1 Solutions Winter 2018 1. (a) Because x i are assumed to be independent realizations of a continuous random variable, it is almost surely (a.s.) 1 the case that x 1 < x 2 < < x n Thus,
Fully fuzzy linear programming with inequality constraints
 Available online at http://ijim.srbiau.ac.ir/ Int. J. Industrial Mathematics (ISSN 2008-5621) Vol. 5, No. 4, 2013 Article ID IJIM-00280, 8 pages Research Article Fully fuzzy linear programming with inequality
Available online at http://ijim.srbiau.ac.ir/ Int. J. Industrial Mathematics (ISSN 2008-5621) Vol. 5, No. 4, 2013 Article ID IJIM-00280, 8 pages Research Article Fully fuzzy linear programming with inequality
Intersection and union of type-2 fuzzy sets and connection to (α 1, α 2 )-double cuts
 EUSFLAT-LFA 2 July 2 Aix-les-Bains, France Intersection and union of type-2 fuzzy sets and connection to (α, α 2 )-double cuts Zdenko Takáč Institute of Information Engineering, Automation and Mathematics
EUSFLAT-LFA 2 July 2 Aix-les-Bains, France Intersection and union of type-2 fuzzy sets and connection to (α, α 2 )-double cuts Zdenko Takáč Institute of Information Engineering, Automation and Mathematics
Math 494: Mathematical Statistics
 Math 494: Mathematical Statistics Instructor: Jimin Ding jmding@wustl.edu Department of Mathematics Washington University in St. Louis Class materials are available on course website (www.math.wustl.edu/
Math 494: Mathematical Statistics Instructor: Jimin Ding jmding@wustl.edu Department of Mathematics Washington University in St. Louis Class materials are available on course website (www.math.wustl.edu/
380 M.T. Moeti, A. Parchami and M. Mashinchi Figure 1. Fuzzy interval.. M(x) = 0 for all x ( 1;c], 3. M is strictly increasing and continuous on [c; a
![380 M.T. Moeti, A. Parchami and M. Mashinchi Figure 1. Fuzzy interval.. M(x) = 0 for all x ( 1;c], 3. M is strictly increasing and continuous on [c; a 380 M.T. Moeti, A. Parchami and M. Mashinchi Figure 1. Fuzzy interval.. M(x) = 0 for all x ( 1;c], 3. M is strictly increasing and continuous on [c; a](/thumbs/89/98092183.jpg) Scientia Iranica, Vol. 13, No. 4, pp 379{385 c Sharif University of Technology, October 00 Research Note A Note on Fuzzy Process Capability Indices M.T. Moeti 1, A. Parchami 1 and M. Mashinchi The notion
Scientia Iranica, Vol. 13, No. 4, pp 379{385 c Sharif University of Technology, October 00 Research Note A Note on Fuzzy Process Capability Indices M.T. Moeti 1, A. Parchami 1 and M. Mashinchi The notion
AN EASY COMPUTATION OF MIN AND MAX OPERATIONS FOR FUZZY NUMBERS
 J. Appl. Math. & Computing Vol. 21(2006), No. 1-2, pp. 555-561 AN EASY COMPUTATION OF MIN AND MAX OPERATIONS FOR FUZZY NUMBERS DUG HUN HONG* AND KYUNG TAE KIM Abstract. Recently, Chiu and WangFuzzy sets
J. Appl. Math. & Computing Vol. 21(2006), No. 1-2, pp. 555-561 AN EASY COMPUTATION OF MIN AND MAX OPERATIONS FOR FUZZY NUMBERS DUG HUN HONG* AND KYUNG TAE KIM Abstract. Recently, Chiu and WangFuzzy sets
STOCHASTIC COMPARISONS OF FUZZY
 CHAPTER FIVE STOCHASTIC COPARISONS OF FUZZY STOCHASTIC PROCESSES Abstract Chapter 5 investigates the stochastic comparison of fuzzy stochastic processes. This chapter introduce the concept of stochastic
CHAPTER FIVE STOCHASTIC COPARISONS OF FUZZY STOCHASTIC PROCESSES Abstract Chapter 5 investigates the stochastic comparison of fuzzy stochastic processes. This chapter introduce the concept of stochastic
Lecture 2: Basic Concepts of Statistical Decision Theory
 EE378A Statistical Signal Processing Lecture 2-03/31/2016 Lecture 2: Basic Concepts of Statistical Decision Theory Lecturer: Jiantao Jiao, Tsachy Weissman Scribe: John Miller and Aran Nayebi In this lecture
EE378A Statistical Signal Processing Lecture 2-03/31/2016 Lecture 2: Basic Concepts of Statistical Decision Theory Lecturer: Jiantao Jiao, Tsachy Weissman Scribe: John Miller and Aran Nayebi In this lecture
A Generalized Decision Logic in Interval-set-valued Information Tables
 A Generalized Decision Logic in Interval-set-valued Information Tables Y.Y. Yao 1 and Qing Liu 2 1 Department of Computer Science, University of Regina Regina, Saskatchewan, Canada S4S 0A2 E-mail: yyao@cs.uregina.ca
A Generalized Decision Logic in Interval-set-valued Information Tables Y.Y. Yao 1 and Qing Liu 2 1 Department of Computer Science, University of Regina Regina, Saskatchewan, Canada S4S 0A2 E-mail: yyao@cs.uregina.ca
λ(x + 1)f g (x) > θ 0
 Stat 8111 Final Exam December 16 Eleven students took the exam, the scores were 92, 78, 4 in the 5 s, 1 in the 4 s, 1 in the 3 s and 3 in the 2 s. 1. i) Let X 1, X 2,..., X n be iid each Bernoulli(θ) where
Stat 8111 Final Exam December 16 Eleven students took the exam, the scores were 92, 78, 4 in the 5 s, 1 in the 4 s, 1 in the 3 s and 3 in the 2 s. 1. i) Let X 1, X 2,..., X n be iid each Bernoulli(θ) where
557: MATHEMATICAL STATISTICS II BIAS AND VARIANCE
 557: MATHEMATICAL STATISTICS II BIAS AND VARIANCE An estimator, T (X), of θ can be evaluated via its statistical properties. Typically, two aspects are considered: Expectation Variance either in terms
557: MATHEMATICAL STATISTICS II BIAS AND VARIANCE An estimator, T (X), of θ can be evaluated via its statistical properties. Typically, two aspects are considered: Expectation Variance either in terms
A Note on Stochastic Orders
 Intern. J. Fuzzy Mathematical rchive Vol. 9, No. 2, 2015, 245-250 ISSN: 2320 3242 (P), 2320 3250 (online) Published on 8 October 2015 www.researchmathsci.org International Journal of Note on Stochastic
Intern. J. Fuzzy Mathematical rchive Vol. 9, No. 2, 2015, 245-250 ISSN: 2320 3242 (P), 2320 3250 (online) Published on 8 October 2015 www.researchmathsci.org International Journal of Note on Stochastic
A unified view of some representations of imprecise probabilities
 A unified view of some representations of imprecise probabilities S. Destercke and D. Dubois Institut de recherche en informatique de Toulouse (IRIT) Université Paul Sabatier, 118 route de Narbonne, 31062
A unified view of some representations of imprecise probabilities S. Destercke and D. Dubois Institut de recherche en informatique de Toulouse (IRIT) Université Paul Sabatier, 118 route de Narbonne, 31062
Math Camp II. Calculus. Yiqing Xu. August 27, 2014 MIT
 Math Camp II Calculus Yiqing Xu MIT August 27, 2014 1 Sequence and Limit 2 Derivatives 3 OLS Asymptotics 4 Integrals Sequence Definition A sequence {y n } = {y 1, y 2, y 3,..., y n } is an ordered set
Math Camp II Calculus Yiqing Xu MIT August 27, 2014 1 Sequence and Limit 2 Derivatives 3 OLS Asymptotics 4 Integrals Sequence Definition A sequence {y n } = {y 1, y 2, y 3,..., y n } is an ordered set
AN INTRODUCTION TO FUZZY SOFT TOPOLOGICAL SPACES
 Hacettepe Journal of Mathematics and Statistics Volume 43 (2) (2014), 193 204 AN INTRODUCTION TO FUZZY SOFT TOPOLOGICAL SPACES Abdülkadir Aygünoǧlu Vildan Çetkin Halis Aygün Abstract The aim of this study
Hacettepe Journal of Mathematics and Statistics Volume 43 (2) (2014), 193 204 AN INTRODUCTION TO FUZZY SOFT TOPOLOGICAL SPACES Abdülkadir Aygünoǧlu Vildan Çetkin Halis Aygün Abstract The aim of this study
Introduction to Intelligent Control Part 6
 ECE 4951 - Spring 2010 ntroduction to ntelligent Control Part 6 Prof. Marian S. Stachowicz Laboratory for ntelligent Systems ECE Department, University of Minnesota Duluth February 4-5, 2010 Fuzzy System
ECE 4951 - Spring 2010 ntroduction to ntelligent Control Part 6 Prof. Marian S. Stachowicz Laboratory for ntelligent Systems ECE Department, University of Minnesota Duluth February 4-5, 2010 Fuzzy System
Stability in multiobjective possibilistic linear programs
 Stability in multiobjective possibilistic linear programs Robert Fullér rfuller@abo.fi Mario Fedrizzi fedrizzi@cs.unitn.it Abstract This paper continues the authors research in stability analysis in possibilistic
Stability in multiobjective possibilistic linear programs Robert Fullér rfuller@abo.fi Mario Fedrizzi fedrizzi@cs.unitn.it Abstract This paper continues the authors research in stability analysis in possibilistic
Testing Statistical Hypotheses
 E.L. Lehmann Joseph P. Romano, 02LEu1 ttd ~Lt~S Testing Statistical Hypotheses Third Edition With 6 Illustrations ~Springer 2 The Probability Background 28 2.1 Probability and Measure 28 2.2 Integration.........
E.L. Lehmann Joseph P. Romano, 02LEu1 ttd ~Lt~S Testing Statistical Hypotheses Third Edition With 6 Illustrations ~Springer 2 The Probability Background 28 2.1 Probability and Measure 28 2.2 Integration.........
On various definitions of the variance of a fuzzy random variable
 5th International Symposium on Imprecise Probabilities and Their Applications, Prague, Czech Republic, 2007 On various definitions of the variance of a fuzzy random variable Inés Couso Dep. Statistics
5th International Symposium on Imprecise Probabilities and Their Applications, Prague, Czech Republic, 2007 On various definitions of the variance of a fuzzy random variable Inés Couso Dep. Statistics
Solution. (i) Find a minimal sufficient statistic for (θ, β) and give your justification. X i=1. By the factorization theorem, ( n
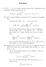 Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
Solution 1. Let (X 1,..., X n ) be a simple random sample from a distribution with probability density function given by f(x;, β) = 1 ( ) 1 β x β, 0 x, > 0, β < 1. β (i) Find a minimal sufficient statistic
EQUIVALENCE OF TOPOLOGIES AND BOREL FIELDS FOR COUNTABLY-HILBERT SPACES
 EQUIVALENCE OF TOPOLOGIES AND BOREL FIELDS FOR COUNTABLY-HILBERT SPACES JEREMY J. BECNEL Abstract. We examine the main topologies wea, strong, and inductive placed on the dual of a countably-normed space
EQUIVALENCE OF TOPOLOGIES AND BOREL FIELDS FOR COUNTABLY-HILBERT SPACES JEREMY J. BECNEL Abstract. We examine the main topologies wea, strong, and inductive placed on the dual of a countably-normed space
Lecture 7 October 13
 STATS 300A: Theory of Statistics Fall 2015 Lecture 7 October 13 Lecturer: Lester Mackey Scribe: Jing Miao and Xiuyuan Lu 7.1 Recap So far, we have investigated various criteria for optimal inference. We
STATS 300A: Theory of Statistics Fall 2015 Lecture 7 October 13 Lecturer: Lester Mackey Scribe: Jing Miao and Xiuyuan Lu 7.1 Recap So far, we have investigated various criteria for optimal inference. We
On the levels of fuzzy mappings and applications to optimization
 On the levels of fuzzy mappings and applications to optimization Y. Chalco-Cano Universidad de Tarapacá Arica - Chile ychalco@uta.cl H. Román-Fles Universidad de Tarapacá Arica - Chile hroman@uta.cl M.A.
On the levels of fuzzy mappings and applications to optimization Y. Chalco-Cano Universidad de Tarapacá Arica - Chile ychalco@uta.cl H. Román-Fles Universidad de Tarapacá Arica - Chile hroman@uta.cl M.A.
Optimal Unbiased Estimates of P {X < Y } for Some Families of Distributions
 Metodološki zvezki, Vol., No., 04, -9 Optimal Unbiased Estimates of P {X < } for Some Families of Distributions Marko Obradović, Milan Jovanović, Bojana Milošević Abstract In reliability theory, one of
Metodološki zvezki, Vol., No., 04, -9 Optimal Unbiased Estimates of P {X < } for Some Families of Distributions Marko Obradović, Milan Jovanović, Bojana Milošević Abstract In reliability theory, one of
Let us first identify some classes of hypotheses. simple versus simple. H 0 : θ = θ 0 versus H 1 : θ = θ 1. (1) one-sided
 Let us first identify some classes of hypotheses. simple versus simple H 0 : θ = θ 0 versus H 1 : θ = θ 1. (1) one-sided H 0 : θ θ 0 versus H 1 : θ > θ 0. (2) two-sided; null on extremes H 0 : θ θ 1 or
Let us first identify some classes of hypotheses. simple versus simple H 0 : θ = θ 0 versus H 1 : θ = θ 1. (1) one-sided H 0 : θ θ 0 versus H 1 : θ > θ 0. (2) two-sided; null on extremes H 0 : θ θ 1 or
Rough Approach to Fuzzification and Defuzzification in Probability Theory
 Rough Approach to Fuzzification and Defuzzification in Probability Theory G. Cattaneo and D. Ciucci Dipartimento di Informatica, Sistemistica e Comunicazione Università di Milano Bicocca, Via Bicocca degli
Rough Approach to Fuzzification and Defuzzification in Probability Theory G. Cattaneo and D. Ciucci Dipartimento di Informatica, Sistemistica e Comunicazione Università di Milano Bicocca, Via Bicocca degli
Probability and Measure
 Probability and Measure Robert L. Wolpert Institute of Statistics and Decision Sciences Duke University, Durham, NC, USA Convergence of Random Variables 1. Convergence Concepts 1.1. Convergence of Real
Probability and Measure Robert L. Wolpert Institute of Statistics and Decision Sciences Duke University, Durham, NC, USA Convergence of Random Variables 1. Convergence Concepts 1.1. Convergence of Real
Generalized Triangular Fuzzy Numbers In Intuitionistic Fuzzy Environment
 International Journal of Engineering Research Development e-issn: 2278-067X, p-issn : 2278-800X, www.ijerd.com Volume 5, Issue 1 (November 2012), PP. 08-13 Generalized Triangular Fuzzy Numbers In Intuitionistic
International Journal of Engineering Research Development e-issn: 2278-067X, p-issn : 2278-800X, www.ijerd.com Volume 5, Issue 1 (November 2012), PP. 08-13 Generalized Triangular Fuzzy Numbers In Intuitionistic
Measure-theoretic probability
 Measure-theoretic probability Koltay L. VEGTMAM144B November 28, 2012 (VEGTMAM144B) Measure-theoretic probability November 28, 2012 1 / 27 The probability space De nition The (Ω, A, P) measure space is
Measure-theoretic probability Koltay L. VEGTMAM144B November 28, 2012 (VEGTMAM144B) Measure-theoretic probability November 28, 2012 1 / 27 The probability space De nition The (Ω, A, P) measure space is
A General Overview of Parametric Estimation and Inference Techniques.
 A General Overview of Parametric Estimation and Inference Techniques. Moulinath Banerjee University of Michigan September 11, 2012 The object of statistical inference is to glean information about an underlying
A General Overview of Parametric Estimation and Inference Techniques. Moulinath Banerjee University of Michigan September 11, 2012 The object of statistical inference is to glean information about an underlying
STA 732: Inference. Notes 2. Neyman-Pearsonian Classical Hypothesis Testing B&D 4
 STA 73: Inference Notes. Neyman-Pearsonian Classical Hypothesis Testing B&D 4 1 Testing as a rule Fisher s quantification of extremeness of observed evidence clearly lacked rigorous mathematical interpretation.
STA 73: Inference Notes. Neyman-Pearsonian Classical Hypothesis Testing B&D 4 1 Testing as a rule Fisher s quantification of extremeness of observed evidence clearly lacked rigorous mathematical interpretation.
f (1 0.5)/n Z =
 Math 466/566 - Homework 4. We want to test a hypothesis involving a population proportion. The unknown population proportion is p. The null hypothesis is p = / and the alternative hypothesis is p > /.
Math 466/566 - Homework 4. We want to test a hypothesis involving a population proportion. The unknown population proportion is p. The null hypothesis is p = / and the alternative hypothesis is p > /.
Application of the Fuzzy Weighted Average of Fuzzy Numbers in Decision Making Models
 Application of the Fuzzy Weighted Average of Fuzzy Numbers in Decision Making Models Ondřej Pavlačka Department of Mathematical Analysis and Applied Mathematics, Faculty of Science, Palacký University
Application of the Fuzzy Weighted Average of Fuzzy Numbers in Decision Making Models Ondřej Pavlačka Department of Mathematical Analysis and Applied Mathematics, Faculty of Science, Palacký University
A Very Brief Summary of Statistical Inference, and Examples
 A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2009 Prof. Gesine Reinert Our standard situation is that we have data x = x 1, x 2,..., x n, which we view as realisations of random
A Very Brief Summary of Statistical Inference, and Examples Trinity Term 2009 Prof. Gesine Reinert Our standard situation is that we have data x = x 1, x 2,..., x n, which we view as realisations of random
Translation Invariant Experiments with Independent Increments
 Translation Invariant Statistical Experiments with Independent Increments (joint work with Nino Kordzakhia and Alex Novikov Steklov Mathematical Institute St.Petersburg, June 10, 2013 Outline 1 Introduction
Translation Invariant Statistical Experiments with Independent Increments (joint work with Nino Kordzakhia and Alex Novikov Steklov Mathematical Institute St.Petersburg, June 10, 2013 Outline 1 Introduction
On Semicontinuity of Convex-valued Multifunctions and Cesari s Property (Q)
 On Semicontinuity of Convex-valued Multifunctions and Cesari s Property (Q) Andreas Löhne May 2, 2005 (last update: November 22, 2005) Abstract We investigate two types of semicontinuity for set-valued
On Semicontinuity of Convex-valued Multifunctions and Cesari s Property (Q) Andreas Löhne May 2, 2005 (last update: November 22, 2005) Abstract We investigate two types of semicontinuity for set-valued
GENERALIZED KAPLAN MEIER ESTIMATOR FOR FUZZY SURVIVAL TIMES. Muhammad Shafiq. Reinhard Viertl. 1. Introduction
 GENERALIZED KAPLAN MEIER ESTIMATOR FOR FUZZY SURVIVAL TIMES ŚLĄSKI Muhammad Shafiq Department of Economics Kohat University of Science & Technology, Kohat, Pakistan Reinhard Viertl Institute of Statistics
GENERALIZED KAPLAN MEIER ESTIMATOR FOR FUZZY SURVIVAL TIMES ŚLĄSKI Muhammad Shafiq Department of Economics Kohat University of Science & Technology, Kohat, Pakistan Reinhard Viertl Institute of Statistics
Lecture 12 November 3
 STATS 300A: Theory of Statistics Fall 2015 Lecture 12 November 3 Lecturer: Lester Mackey Scribe: Jae Hyuck Park, Christian Fong Warning: These notes may contain factual and/or typographic errors. 12.1
STATS 300A: Theory of Statistics Fall 2015 Lecture 12 November 3 Lecturer: Lester Mackey Scribe: Jae Hyuck Park, Christian Fong Warning: These notes may contain factual and/or typographic errors. 12.1
Australian Journal of Basic and Applied Sciences, 5(9): , 2011 ISSN Fuzzy M -Matrix. S.S. Hashemi
 ustralian Journal of Basic and pplied Sciences, 5(9): 2096-204, 20 ISSN 99-878 Fuzzy M -Matrix S.S. Hashemi Young researchers Club, Bonab Branch, Islamic zad University, Bonab, Iran. bstract: The theory
ustralian Journal of Basic and pplied Sciences, 5(9): 2096-204, 20 ISSN 99-878 Fuzzy M -Matrix S.S. Hashemi Young researchers Club, Bonab Branch, Islamic zad University, Bonab, Iran. bstract: The theory
STATISTICAL METHODS FOR SIGNAL PROCESSING c Alfred Hero
 STATISTICAL METHODS FOR SIGNAL PROCESSING c Alfred Hero 1999 32 Statistic used Meaning in plain english Reduction ratio T (X) [X 1,..., X n ] T, entire data sample RR 1 T (X) [X (1),..., X (n) ] T, rank
STATISTICAL METHODS FOR SIGNAL PROCESSING c Alfred Hero 1999 32 Statistic used Meaning in plain english Reduction ratio T (X) [X 1,..., X n ] T, entire data sample RR 1 T (X) [X (1),..., X (n) ] T, rank
