Planar Symmetries. Chapter Introduction
|
|
|
- Spencer Sparks
- 6 years ago
- Views:
Transcription
1 Chapter 6 Planar Symmetries 6.1 Introduction The use of symmetry as an aspect of art goes back several millennia, and some early samples of artistic creations into which symmetry was consciously incorporated are displayed in Figure 6.1. The Greek mathematician Euclid (circa 300 BC), whose opus The Elements codified geometry for the following 2000 years, incorporated into this series of 13 books many propositions regarding both two- and three-dimensional symmetric figures. Interestingly, the first proposition of the first book concerns the construction of equilateral triangles and the last book is devoted to the description of the five regular solids (Fig. 7.1), all highly symmetric geometric objects. This endowed Euclid s work with a symmetry of its own. Given that he could have developed the subject matter in many other ways, it is arguable that this symmetric format was a result of a conscious decision on his part. Euclid and his successors viewed symmetries as merely aesthetically pleasing aspects of geometric objects rather than the subjects of mathematical investigations. In other words, the symmetries of these figures attracted their attention, but their technical investigations were restricted to the mathematical consequences of these symmetries rather than the symmetries themselves. It was not until the 18th century that mathematicians realized that symmetries per se could and should be subject to mathematical research. Since then, the mathematical study of symmetry, better known as group theory, has evolved into a deep and essential branch of mathematics with important applications to the physical sciences. This chapter is devoted to the description of the symmetries of plane figures. 6-1
2 6-2 Chapter 6 Planar Symmetries Figure 6.1 Symmetry in ancient art 6.2 Rigid Motions of the Plane The Oxford English Dictionary s definition of geometric symmetry is as follows: Exact correspondence in position of the several points or parts of a figure or body with reference to a dividing line, plane, or a point.
3 6.2 Rigid Motions of the Plane 6-3 The mathematical understanding is different: A geometric symmetry is a potential transformation of an object that would leave it in the same position. This requires a fair amount of clarification, and we begin with the notion of transformation or, more technically, a rigid motion. A rigid motion of the plane takes place when the plane is moved through space, without distortions, so that the plane as a whole ends up occupying its initial position, even though individual points and figures are deposited in new locations. Although the actual movement through space is a useful tool for visualizing a rigid motion, it is its final position that is of interest to us here, and consequently any two rigid motions that leave the points and figures of the plane in the same final positions are considered as identical, even though in their intermediary stages they may move the same points along different paths through space. Such is the case with the clockwise 90 and counterclockwise 270 turns: Both leave us facing to the right relative to our original position. In general, motions are visualized in the most efficient, or economical, manner possible. Moreover, rather than describe them as an actual movement through space, a difficult task within the confines of a textbook, the rigid motions are described by means of their final effect on some figures. The first type of rigid motions to be described are the translations. These are the rigid motions that keep all line segments parallel to their initial positions. The horizontal 3-inch shift to the right is a translation that carries the collection A of Figure 6.2 to location B. Of course, the horizontal 3-inch shift to the left is the translation that carries B to A. Similarly, there is a north-easterly translation that carries the mushroom M of Figure 6.3 to N. Before going on to discuss other types of rigid motions, it is necessary to make some more general definitions. If a rigid motion picks up a figure F and moves it to a new position G, it is said that G is the image of F under the action of that motion. Thus, B in Figure 6.2 is the image of A under the horizontal 3-inch rightward shift, whereas A is the image of B under the horizontal 3-inch leftward shift. Given a figure F and a rigid motion m, the collection of all the images generated from F by the iteration of both that motion and its reversal constitute the orbit of F generated by m. F in Figure 6.4 depicts an orbit generated by a horizontal translation. A B Figure 6.2 A figure with its image
4 6-4 Chapter 6 Planar Symmetries N M Figure 6.3 Another figure with its image F Figure 6.4 A translation Figure 6.5 depicts an orbit generated by a north-easterly translation. The orbits generated by any rigid motion and its reversal are, of course, identical, provided that they begin with the same figures. The second class of rigid motions are the rotations. These motions turn the plane through a certain signed angle about some pivot point (Fig. 6.6). When the specified angle is positive, the rotation moves counterclockwise from the point of view of the reader; when the angle is negative, the motion is clockwise. Although in general any angle can serve as an angle of rotation, the subsequent discussion is restricted to rotations whose angles measure 60, 90, 120, and 180. Typical orbits of such rotations appear in Figure 6.7. Their orbits are said to be 6-fold, 4-fold, 3-fold, and 2-fold, respectively. Because we are only interested in the question of where figures land Figure 6.5 A translation
5 6.2 Rigid Motions of the Plane 6-5 A 90 rotation A 90 rotation P Figure 6.6 Rotations about a pivot point P P rather than how they got there, rotations by angles of 180 and 180 with the same pivot points are equal to each other. Yet another class of rigid motions are the reflections, so called because their effect on geometric figures is akin to that of mirror reflections. They can be visualized as the effect of a 180 spatial rotation about a straight line, the axis, that lies in the rotated plane. The orbit of any figure generated by a reflection consists of two copies of that figure (Fig. 6.8). Because only the final position of the moving figure is of concern here, the fact that this rotation switches the sides of the plane is immaterial. A 6-fold orbit A 4-fold orbit A 3-fold orbit A 2-fold orbit Figure 6.7 Orbits of rotations
6 6-6 Chapter 6 Planar Symmetries Axis Axis Figure 6.8 Orbits of reflections The last type of rigid motion is the glide reflection (Fig. 6.9). As its name implies, this is a combination of a translation and a reflection whose axis is parallel to the direction of the translation. The orbit of a figure generated by a glide reflection consists of an infinite number of copies of the figure that are situated alternately on the two sides of the axis. As was the case for translations, the orbit of a figure generated by a glide reflection also includes the copies obtained by applying the reversal of the glide reflection, and so this orbit extends infinitely far in two directions (Fig. 6.10). The glide reflections complete the roster of all the rigid motions of the plane. Surprisingly, no new rigid motions are created by combining other rigid motions. This is not easy to visualize, but the combination of a translation with a rotation yields another rotation, and the combination of a rotation with a reflection generally yields a glide reflection. The following theorem is due to M. Chasles ( ). THEOREM The rigid motions of the plane consist of translations, rotations, reflections, and glide reflections. Just as 0 turns out to be a convenient number, so is it useful to consider the motion that does not move anything as a motion that is called the identity. Because Axis Figure 6.9 A glide reflection
7 6.2 Rigid Motions of the Plane Figure 6.10 The orbit of a glide reflection this motion does not change the distances between any two points, it qualifies as a rigid motion. The identity motion is denoted by Id. EXERCISES 6.2 Exercises 1 13 all refer to Figure Sketch six figures in the orbit of Δ ABC generated by a 1-inch translation in a direction parallel to the straight line m. 2. Sketch six figures in the orbit of Δ ABC generated by a 1-inch translation in a direction parallel to the straight line n. 3. Sketch the orbit of Δ ABC generated by a rotation that is pivoted at A and has angle a) 60 c) 120 b) 90 d) 180. P A Q B C S R m n Figure 6.11 Exercises 1 13
8 6-8 Chapter 6 Planar Symmetries 4. Sketch the orbit of Δ ABC generated by a rotation that is pivoted at B and has angle a) 60 b) 90 c) 120 d) Sketch the orbit of Δ ABC generated by a rotation that is pivoted at P and has angle a) 60 b) 90 c) 120 d) Sketch the orbit of Δ ABC generated by a rotation that is pivoted at Q and has angle a) 60 b) 90 c) 120 d) Sketch the orbit of Δ ABC generated by a rotation that is pivoted at R and has angle a) 60 b) 90 c) 120 d) Sketch the orbit of Δ ABC generated by the reflection with axis m. 9. Sketch the orbit of Δ ABC generated by the reflection with axis n. 10. Sketch the orbit of Δ ABC generated by the reflection with axis AB. 11. Sketch the orbit of Δ ABC generated by the reflection with axis BC. 12. Sketch the orbit of Δ ABC generated by the reflection with axis QR. 13. Sketch the orbit of Δ ABC generated by the reflection with axis RS. 14. Sketch six figures in the orbit of Δ ABC generated by a 1-inch glide reflection with axis m.
9 6.3 Symmetries of Polygons Sketch six figures in the orbit of Δ ABC generated by a 1-inch glide reflection with axis n. 16. Explain why the 360 rotation about a point P equals the identity motion. 6.3 Symmetries of Polygons A (mathematical) symmetry of a figure is a rigid motion that carries that figure onto itself. Alternately, a rigid motion is a symmetry of a figure provided this figure constitutes the entire orbit generated by the motion. Thus, the reflections with axes d, m, e, and n are all symmetries of the square (Fig. 6.12), and they are denoted by d, m, e, and n respectively. These reflections do not constitute all the square s symmetries. The 90, 180, and 270 (or 90 ) rotations about the center of the square are also such symmetries. If C denotes this center, then R C,90, R C,180, R C,270 denote these respective rotations. The identity rigid motion Id is another such symmetry. The set of all the symmetries of a figure is called its symmetry group, or just group. Thus, the symmetry group of the square is {Id, d, e, m, n, R C,90, R C,180, R C,270 } By definition, every plane figure F has a symmetry group that contains at least the identity motion Id. The isosceles triangle in Figure 6.13 has {Id, v } as its symmetry group, whereas that of the equilateral triangle is {Id, d, e, f, R C,120, R C,240 }. Because the orbits of translations and glide reflections are infinite in extent, it follows that no finite figure can have symmetries of either of these types. Infinitely extended figures, however, can have such symmetries. We first show how to create such figures and then examine the question of what their symmetry groups are like. m d n e Figure 6.12 Some symmetries of the square
10 6-10 Chapter 6 Planar Symmetries v e C f d Figure 6.13 An isosceles and an equilateral triangle EXERCISES Write down the symmetry groups of the following figures. a) The rectangle with unequal sides b) The regular pentagon c) The regular hexagon d) The regular heptagon e) The regular octagon 6.4 Frieze Patterns Orbits of finite figures generated by translations are called frieze patterns. These frieze patterns are the mathematical idealization of such decorative designs as borders used to accent wallpapers and trim sewn or printed around a cloth (Fig. 6.14). Unlike their physical manifestations, frieze patterns are understood to extend indefinitely in both directions, just like a straight line. The frieze pattern of a figure F necessarily has its generating translation as a symmetry, and in addition it inherits all the symmetries of F. This observation, however, does not account for all the symmetries of the frieze pattern. As shown in Figure 6.15, in the case of the figure F 1, there are no other symmetries, and so the pattern s symmetry group is denoted by Γ 1 = < τ >, where τ denotes the horizontal translation that generates the infinite frieze pattern Π(F 1 ). This is not meant to imply that τ is the only symmetry of Π(F 1 ). It is clear that the translation 2τ that denotes two consecutive applications of τ is also a symmetry of Π(F 1 ), and similarly, for each positive integer k, the translation kτ, which consists of k iterations of τ, is also a symmetry of Π(F 1 ). Frieze patterns always have infinite symmetry groups, and instead of listing their elements it is customary simply to list the types of symmetries they contain.
11 6.4 Frieze Patterns 6-11 Figure 6.14 Chinese frieze patterns Figure F 2 possesses the symmetry h (h for horizontal), which is of course also a symmetry of its frieze pattern Π(F 2 ). In addition, this pattern also necessarily possesses the glide reflection γ obtained by combining t with h as a symmetry. This Figure 6.15 A frieze pattern with symmetry group Γ. = < τ >
12 6-12 Chapter 6 Planar Symmetries Figure 6.16 A frieze pattern with symmetry group Γ 2 = < τ, h, γ > frieze s symmetry group is denoted by Γ 2 = < τ, h, γ > (Fig. 6.16). The symmetry v of F 3 results in a multitude of symmetries of the frieze Π(F 3 ), which are all essentially identical (Fig. 6.17). However, this frieze pattern possesses an additional symmetry, namely the reflection v, which has no counterpart in the generating figure F 3. Because of its similarity to v, the symmetry v is not listed in the symmetry group Γ 3 = < τ, v > of this frieze pattern. Such an additional reflection could not have appeared with the horizontal reflection of F 2, but similar accidental symmetries can arise in other cases, as seen below. The symmetry R C,180 of the figure F 4 results in the symmetries R = R C,180 of the frieze pattern. Once again, the frieze pattern has the additional symmetry R C,180. This frieze pattern s symmetry group is Γ 1 = < τ, R > (Fig. 6.18). The figure F 5 possesses all three of the above symmetries, as does the generated frieze pattern. Its symmetry group is Γ 5 = < τ, h, v, R, γ > (Fig. 6.19). This pattern of course also has the additional symmetries described for Γ 3 and Γ 4. The patterns shown in Figures 6.20 and 6.21 have symmetry groups Γ 6 = < τ, γ > and Γ 7 = < τ, γ, R > that contain glide reflections, just like Γ 2. Unlike the glide reflection of Γ 2, those of Γ 6 and Γ 7 do not have their component translation and reflection in the group. The following theorem, proved by P. Niggli in 1926, states that these are all the possible symmetry groups that frieze patterns can possess. THEOREM Every frieze pattern has a symmetry group that is identical with one of the groups Γ 1 = < τ >, Γ 2 = < τ, h, γ >, Γ 3 = <τ, v >, Γ 4 = < τ, R >, Γ 5 = < τ, h, v, R, γ >, Γ 6 = < τ, γ >, Γ 7 = < τ, γ, R >. Figure 6.17 A frieze pattern with symmetry group Γ 3 = < τ, v >
13 6.4 Frieze Patterns 6-13 Figure 6.18 A frieze pattern with symmetry group Γ 4 = < τ, R > F 5 Π(F ) 5 Figure 6.19 A frieze pattern with symmetry group Γ 5 = < τ, h, v, R, γ > Figure 6.20 A frieze pattern with symmetry group Γ 6 = < τ, γ > Figure 6.21 A frieze pattern with symmetry group Γ 7 = < τ, γ, R >
14 6-14 Chapter 6 Planar Symmetries EXERCISE 6.4 Identify the groups of the following frieze patterns Wallpaper Designs Wallpaper designs are the two-dimensional analogs of frieze patterns. More precisely, let Π(F) denote the frieze pattern generated by a figure F and a translation τ. If τ* is another translation whose direction is not parallel to that of τ, then the orbit Ω(F) = Π(Π(F)) of τ* generated by Π(F) is a wallpaper design. In other words, a wallpaper design is an orbit of an orbit. It is clear that both τ and τ* are symmetries of the wallpaper design they generate, and an illustration of this appears in Figures 6.22 and As was the case for frieze patterns, the generated design Π(F) may possess further symmetries that are not present in F. In contrast with the seven different groups of symmetries of frieze patterns, there are 17 different possibilities for the symmetry groups of wallpaper designs. Wallpaper designs exemplifying all these are exhibited in Figures 6.24 through
15 6.5 Wallpaper Designs 6-15 Figure 6.22 A wallpaper design In these diagrams, the presence of reflections and glide reflections is denoted by a dashed line with a label of either (for reflection) or γ (for glide translation). The centers of rotational symmetries are denoted by the symbols (180 ), (120 ), (90 ), (60 ). Table 6.1 lists the salient symmetry characteristics of each design. A rotation through an angle of 360 /n is said to have order n. A glide reflection is said to be nontrivial if its component translation and reflection are not symmetries of the pattern.
16 6-16 Chapter 6 Planar Symmetries Figure 6.23 Another wallpaper design The symbols p1, pgg, p31m, and so on listed in Table 6.1 under Type are used to denote both a type of wallpaper design and its symmetry group. They are known as the crystallographic notation for the symmetry groups. If the second character in this symbol is an integer, it is the highest order of all the rotations in that group. The significance of the other characters is too technical to explain here.
17 6.5 Wallpaper Designs 6-17 THEOREM There are exactly 17 wallpaper groups. The characteristics of the designs that correspond to these groups are displayed in Table 6.1. Figures each display one design for each of these groups. Theorem was first discovered in 1891 by E. S. Fedorov, 35 years before Niggli stated and proved its one-dimensional analog on frieze groups (Theorem 9.4.1). Curiously, this work had been preceded by Fedorov s and Arthur Schönflies s ( ) independent classifications of the 230 crystallographic groups, these being the three-dimensional analogs of the wallpaper groups. It has since been established that there are exactly 4783 classes of such groups in four-dimensional space. For spaces of more than four dimensions, it is only known that the number of such symmetry groups is finite. Highest Nontrivial order of glide Helpful Type rotation Reflections reflections distinguishing properties p1 1 No No p2 2 No No pm 1 Yes No pg 1 No Yes cm 1 Yes Yes pmm 2 Yes No pmg 2 Yes Yes Parallel reflection axes pgg 2 No Yes cmm 2 Yes Yes Perpendicular reflection axes p4 4 No No p4m 4 Yes Yes 4-fold centers on reflection axes p4g 4 Yes Yes 4-fold centers not on reflection axes p3 3 No No p3m1 3 Yes Yes All 3-fold centers on reflection axes p31m 3 Yes Yes Not all 3-fold centers on reflection axes p6 6 No No p6m 6 Yes Yes From Doris Schattschneider s article. Table 6.1 Recognition chart for plane periodic patterns
18 6-18 Chapter 6 Planar Symmetries p2 p3 p4 p6 pmm Figure 6.24 Six wallpaper designs p3m1
19 6.5 Wallpaper Designs 6-19 p4m p6m γ p4g p31m γ γ γ cmm Figure 6.25 Six more wallpaper designs pmg
20 6-20 Chapter 6 Planar Symmetries pm cm pg pgg p1 Figure 6.26 Five wallpaper designs
21 6.5 Wallpaper Designs 6-21 EXERCISES 6.5 Determine the crystallographic symbol of each of the following wallpaper designs In each case, a) Display a rotation of the highest order. b) Denote the presence of a glide reflection by drawing its axis with an accompanying γ. c) Denote the presence of a reflection by drawing its axis with an accompanying. d) Avoid redundancy by only drawing only one axis in any direction. e) In case you have to choose between a and a γ, display the γ
22 6-22 Chapter 6 Planar Symmetries
23 6.5 Wallpaper Designs
24 6-24 Chapter 6 Planar Symmetries
25 6.5 Wallpaper Designs
26 6-26 Chapter 6 Planar Symmetries
27 6.6 References and Further Readings References and Further Readings Ausdley, W. and G., Designs and Patterns from Historic Ornaments, Dover Publications, New York, Budden, F. J., Fascination of Groups, Cambridge University Press, Cambridge, Farmer, D. W., Groups and Symmetry: A Guide to Discovering Mathematics, American Mathematical Society, Washington DC, Grünbaum, B., and Shepard, G. C., Tilings and Patterns, W. H. Freeman and Co., Jones, O., The Grammar of Chinese Ornament, Studio Editions, London, Martin, G. E., Transformation Geometry: An Introduction to Symmetry, Springer-Veralg, New York, Schattschneider, D., The Plane Symmetry Groups, Their Recognition and Notation, Amer. Math. Monthly, 85(1978) no. 6, Weyl, H., Symmetry, Princeton University Press, Princeton, 1952.
The 17 Plane Symmetry Groups. Samantha Burns Courtney Fletcher Aubray Zell Boise State University
 The 17 Plane Symmetry Groups Samantha Burns Courtney Fletcher Aubray Zell Boise State University INTRODUCTION Our paper is going to be about the 17 plane Symmetry Groups, also called the wallpaper groups,
The 17 Plane Symmetry Groups Samantha Burns Courtney Fletcher Aubray Zell Boise State University INTRODUCTION Our paper is going to be about the 17 plane Symmetry Groups, also called the wallpaper groups,
WALLPAPER GROUPS. Julija Zavadlav
 WALLPAPER GROUPS Julija Zavadlav Abstract In this paper we present the wallpaper groups or plane crystallographic groups. The name wallpaper groups refers to the symmetry group of periodic pattern in two
WALLPAPER GROUPS Julija Zavadlav Abstract In this paper we present the wallpaper groups or plane crystallographic groups. The name wallpaper groups refers to the symmetry group of periodic pattern in two
14.1 INTRODUCTION. Nature. Architecture. Engineering. Compose a picture-album showing symmetry. Make some symmetrical paper-cut designs.
 14.1 INTRODUCTION Symmetry is an important geometrical concept, commonly exhibited in nature and is used almost in every field of activity. Artists, professionals, designers of clothing or jewellery, car
14.1 INTRODUCTION Symmetry is an important geometrical concept, commonly exhibited in nature and is used almost in every field of activity. Artists, professionals, designers of clothing or jewellery, car
2.4 Investigating Symmetry
 Locker LESSON 2.4 Investigating Symmetry Texas Math Standards The student is expected to: G.3.D Identify and distinguish between reflectional and rotational symmetry in a plane figure. Mathematical Processes
Locker LESSON 2.4 Investigating Symmetry Texas Math Standards The student is expected to: G.3.D Identify and distinguish between reflectional and rotational symmetry in a plane figure. Mathematical Processes
THE FIVE TYPES OF PLANAR 2-D LATTICES. (d) (e)
 THE FIVE TYPES OF PLANAR 2-D LATTICES (a) (d) (b) (d) and (e) are the same (e) (c) (f) (a) OBLIQUE LATTICE - NO RESTRICTIONS ON ANGLES BETWEEN THE UNIT CELL EDGES (b) RECTANGULAR LATTICE - ANGLE BETWEEN
THE FIVE TYPES OF PLANAR 2-D LATTICES (a) (d) (b) (d) and (e) are the same (e) (c) (f) (a) OBLIQUE LATTICE - NO RESTRICTIONS ON ANGLES BETWEEN THE UNIT CELL EDGES (b) RECTANGULAR LATTICE - ANGLE BETWEEN
NCERT Solutions for Class 7 Maths Chapter 14
 NCERT Solutions for Class 7 Maths Chapter 14 Symmetry Class 7 Chapter 14 Symmetry Exercise 14.1, 14.2, 14.3 Solutions Exercise 14.1 : Solutions of Questions on Page Number : 268 Q1 : Copy the figures with
NCERT Solutions for Class 7 Maths Chapter 14 Symmetry Class 7 Chapter 14 Symmetry Exercise 14.1, 14.2, 14.3 Solutions Exercise 14.1 : Solutions of Questions on Page Number : 268 Q1 : Copy the figures with
Investigation Of Plane Symmetry In Lattice Designs
 Salem State University Digital Commons at Salem State University Honors Theses Student Scholarship 2016-12-01 Investigation Of Plane Symmetry In Lattice Designs Katyana Sheridan Salem State University
Salem State University Digital Commons at Salem State University Honors Theses Student Scholarship 2016-12-01 Investigation Of Plane Symmetry In Lattice Designs Katyana Sheridan Salem State University
Lecture 1 Symmetry in the solid state -
 Lecture 1 Symmetry in the solid state - Part I: Simple patterns and groups 1 Symmetry operators: key concepts Operators: transform (move) the whole pattern (i.e., the attributes, or content, of all points
Lecture 1 Symmetry in the solid state - Part I: Simple patterns and groups 1 Symmetry operators: key concepts Operators: transform (move) the whole pattern (i.e., the attributes, or content, of all points
Symmetry in 2D. 4/24/2013 L. Viciu AC II Symmetry in 2D
 Symmetry in 2D 1 Outlook Symmetry: definitions, unit cell choice Symmetry operations in 2D Symmetry combinations Plane Point groups Plane (space) groups Finding the plane group: examples 2 Symmetry Symmetry
Symmetry in 2D 1 Outlook Symmetry: definitions, unit cell choice Symmetry operations in 2D Symmetry combinations Plane Point groups Plane (space) groups Finding the plane group: examples 2 Symmetry Symmetry
CHAPTER 8 WHY PRECISELY SEVENTEEN TYPES?
 2006 George Baloglou first draft: summer 2001 CHAPTER 8 WHY PRECISELY SEVENTEEN TYPES? 8.0 Classification of wallpaper patterns 8.0.1 The goal. Back in section 2.8 it was rather easy to explain why there
2006 George Baloglou first draft: summer 2001 CHAPTER 8 WHY PRECISELY SEVENTEEN TYPES? 8.0 Classification of wallpaper patterns 8.0.1 The goal. Back in section 2.8 it was rather easy to explain why there
A shape which can be divided by a straight line, so that each part is the mirror image of the other has reflective symmetry.
 SYMMETRY There are two kinds of symmetry: a) reflective symmetry b) rotational symmetry a) Reflective Symmetry A shape which can be divided by a straight line, so that each part is the image of the other
SYMMETRY There are two kinds of symmetry: a) reflective symmetry b) rotational symmetry a) Reflective Symmetry A shape which can be divided by a straight line, so that each part is the image of the other
INTRODUCTION. Fig. 1.1
 1 INTRODUCTION 1.1 SYMMETRY: AN INTRODUCTION In nature, when we see the fascinating world of plants, flowers, birds, architectural buildings (Lotus Temple of Delhi, Taj Mahal, Ashoka Pillar, Rastrapati
1 INTRODUCTION 1.1 SYMMETRY: AN INTRODUCTION In nature, when we see the fascinating world of plants, flowers, birds, architectural buildings (Lotus Temple of Delhi, Taj Mahal, Ashoka Pillar, Rastrapati
The Geometry of Root Systems. Brian C. Hall
 The Geometry of Root Systems A E Z S Brian C. Hall T G R S T G R S 1 1. I Root systems arise in the theory of Lie groups and Lie algebras, but can also be studied as mathematical objects in their own right.
The Geometry of Root Systems A E Z S Brian C. Hall T G R S T G R S 1 1. I Root systems arise in the theory of Lie groups and Lie algebras, but can also be studied as mathematical objects in their own right.
GM1.1 Answers. Reasons given for answers are examples only. In most cases there are valid alternatives. 1 a x = 45 ; alternate angles are equal.
 Cambridge Essentials Mathematics Extension 8 GM1.1 Answers GM1.1 Answers Reasons given for answers are examples only. In most cases there are valid alternatives. 1 a x = 45 ; alternate angles are equal.
Cambridge Essentials Mathematics Extension 8 GM1.1 Answers GM1.1 Answers Reasons given for answers are examples only. In most cases there are valid alternatives. 1 a x = 45 ; alternate angles are equal.
2.4 Investigating Symmetry
 Name Class Date 2.4 Investigating Symmetry Essential Question: How do you determine whether a figure has line symmetry or rotational symmetry? 1 Explore 1 Identifying Line Symmetry A figure has symmetry
Name Class Date 2.4 Investigating Symmetry Essential Question: How do you determine whether a figure has line symmetry or rotational symmetry? 1 Explore 1 Identifying Line Symmetry A figure has symmetry
Yanxi Liu.
 Yanxi Liu yanxi@cse.psu.edu Today s Theme: What is symmetry? From real world to mathematics, and back to the real world Real World Instances of Symmetry Symmetry Patterns from Real World (1) Symmetry Patterns
Yanxi Liu yanxi@cse.psu.edu Today s Theme: What is symmetry? From real world to mathematics, and back to the real world Real World Instances of Symmetry Symmetry Patterns from Real World (1) Symmetry Patterns
VERTEX-TRANSITIVE MAPS ON A TORUS. 1. Introduction
 VERTEX-TRANSITIVE MAPS ON A TORUS ONDREJ ŠUCH Abstract. We examine FVT (free, vertex transitive) actions of wallpaper groups on semiregular tilings. By taking quotients by lattices we then obtain various
VERTEX-TRANSITIVE MAPS ON A TORUS ONDREJ ŠUCH Abstract. We examine FVT (free, vertex transitive) actions of wallpaper groups on semiregular tilings. By taking quotients by lattices we then obtain various
Grade 8 Chapter 7: Rational and Irrational Numbers
 Grade 8 Chapter 7: Rational and Irrational Numbers In this chapter we first review the real line model for numbers, as discussed in Chapter 2 of seventh grade, by recalling how the integers and then the
Grade 8 Chapter 7: Rational and Irrational Numbers In this chapter we first review the real line model for numbers, as discussed in Chapter 2 of seventh grade, by recalling how the integers and then the
Chapter 3: Groups in science, art, and mathematics
 Chapter 3: Groups in science, art, and mathematics Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4120, Spring 2014 M. Macauley (Clemson)
Chapter 3: Groups in science, art, and mathematics Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4120, Spring 2014 M. Macauley (Clemson)
Symmetric spherical and planar patterns
 Symmetric spherical and planar patterns Jan van de Craats version August 3, 2011 1 Spherical patterns 1.1 Introduction Many objects in daily life exhibit various forms of symmetry. Balls, bowls, cylinders
Symmetric spherical and planar patterns Jan van de Craats version August 3, 2011 1 Spherical patterns 1.1 Introduction Many objects in daily life exhibit various forms of symmetry. Balls, bowls, cylinders
7. SYMMETRY GROUPS 7.1. What is Symmetry? rotational symmetry order
 7. SYMMETRY GROUPS 7.1. What is Symmetry? When we say that something is symmetric we re usually thinking of left-right symmetry. For example, a design is symmetric in this way if the right half is the
7. SYMMETRY GROUPS 7.1. What is Symmetry? When we say that something is symmetric we re usually thinking of left-right symmetry. For example, a design is symmetric in this way if the right half is the
Euclidean Geometry. The Elements of Mathematics
 Euclidean Geometry The Elements of Mathematics Euclid, We Hardly Knew Ye Born around 300 BCE in Alexandria, Egypt We really know almost nothing else about his personal life Taught students in mathematics
Euclidean Geometry The Elements of Mathematics Euclid, We Hardly Knew Ye Born around 300 BCE in Alexandria, Egypt We really know almost nothing else about his personal life Taught students in mathematics
Lesson 14: An Axiom System for Geometry
 219 Lesson 14: n xiom System for Geometry We are now ready to present an axiomatic development of geometry. This means that we will list a set of axioms for geometry. These axioms will be simple fundamental
219 Lesson 14: n xiom System for Geometry We are now ready to present an axiomatic development of geometry. This means that we will list a set of axioms for geometry. These axioms will be simple fundamental
English 5 th Grade A-L Vocabulary Cards and Word Walls Revised: 11/18/14
 English 5 th Grade A-L Vocabulary Cards and Word Walls Revised: 11/18/14 Important Notes for Teachers: The vocabulary cards in this file match the Common Core, the math curriculum adopted by the Utah State
English 5 th Grade A-L Vocabulary Cards and Word Walls Revised: 11/18/14 Important Notes for Teachers: The vocabulary cards in this file match the Common Core, the math curriculum adopted by the Utah State
GEOMETRY 3 BEGINNER CIRCLE 5/19/2013
 GEOMETRY 3 BEGINNER CIRCLE 5/19/2013 1. COUNTING SYMMETRIES A drawing has symmetry if there is a way of moving the paper in such a way that the picture looks after moving the paper. Problem 1 (Rotational
GEOMETRY 3 BEGINNER CIRCLE 5/19/2013 1. COUNTING SYMMETRIES A drawing has symmetry if there is a way of moving the paper in such a way that the picture looks after moving the paper. Problem 1 (Rotational
Crystallographic Point Groups and Space Groups
 Crystallographic Point Groups and Space Groups Physics 251 Spring 2011 Matt Wittmann University of California Santa Cruz June 8, 2011 Mathematical description of a crystal Definition A Bravais lattice
Crystallographic Point Groups and Space Groups Physics 251 Spring 2011 Matt Wittmann University of California Santa Cruz June 8, 2011 Mathematical description of a crystal Definition A Bravais lattice
Chapter 19. Symmetry and Patterns. Chapter Outline. Chapter Summary
 Chapter 9 Symmetry and Patterns Chapter Outline Introduction Section 9. Fibonacci Numbers and the Golden Ratio Section 9. Symmetries Preserve the Pattern Section 9.3 Rosette, Strip, and Wallpaper Patterns
Chapter 9 Symmetry and Patterns Chapter Outline Introduction Section 9. Fibonacci Numbers and the Golden Ratio Section 9. Symmetries Preserve the Pattern Section 9.3 Rosette, Strip, and Wallpaper Patterns
Lecture 1: Axioms and Models
 Lecture 1: Axioms and Models 1.1 Geometry Although the study of geometry dates back at least to the early Babylonian and Egyptian societies, our modern systematic approach to the subject originates in
Lecture 1: Axioms and Models 1.1 Geometry Although the study of geometry dates back at least to the early Babylonian and Egyptian societies, our modern systematic approach to the subject originates in
Lecture course on crystallography, 2015 Lecture 9: Space groups and International Tables for Crystallography
 Dr Semën Gorfman Department of Physics, University of SIegen Lecture course on crystallography, 2015 Lecture 9: Space groups and International Tables for Crystallography UNIT CELL and ATOMIC POSITIONS
Dr Semën Gorfman Department of Physics, University of SIegen Lecture course on crystallography, 2015 Lecture 9: Space groups and International Tables for Crystallography UNIT CELL and ATOMIC POSITIONS
Math 1230, Notes 2. Aug. 28, Math 1230, Notes 2 Aug. 28, / 17
 Math 1230, Notes 2 Aug. 28, 2014 Math 1230, Notes 2 Aug. 28, 2014 1 / 17 This fills in some material between pages 10 and 11 of notes 1. We first discuss the relation between geometry and the quadratic
Math 1230, Notes 2 Aug. 28, 2014 Math 1230, Notes 2 Aug. 28, 2014 1 / 17 This fills in some material between pages 10 and 11 of notes 1. We first discuss the relation between geometry and the quadratic
Chapter 3 Representations of a Linear Relation
 Chapter 3 Representations of a Linear Relation The purpose of this chapter is to develop fluency in the ways of representing a linear relation, and in extracting information from these representations.
Chapter 3 Representations of a Linear Relation The purpose of this chapter is to develop fluency in the ways of representing a linear relation, and in extracting information from these representations.
#785 Dr. Roger Roybal MATH October 2017 Project 1 A proof is a deliberate process where a mathematical concept is proven to be true using a
 #785 Dr. Roger Roybal MATH 331-02 24 October 2017 Project 1 A proof is a deliberate process where a mathematical concept is proven to be true using a step-by-step explanation and a lettered diagram. The
#785 Dr. Roger Roybal MATH 331-02 24 October 2017 Project 1 A proof is a deliberate process where a mathematical concept is proven to be true using a step-by-step explanation and a lettered diagram. The
Chapter 3 Representations of a Linear Relation
 Chapter 3 Representations of a Linear Relation The purpose of this chapter is to develop fluency in the ways of representing a linear relation, and in extracting information from these representations.
Chapter 3 Representations of a Linear Relation The purpose of this chapter is to develop fluency in the ways of representing a linear relation, and in extracting information from these representations.
Anticipations of Calculus - Archimedes
 Anticipations of Calculus - Archimedes Let ABC be a segment of a parabola bounded by the straight line AC and the parabola ABC, and let D be the middle point of AC. Draw the straight line DBE parallel
Anticipations of Calculus - Archimedes Let ABC be a segment of a parabola bounded by the straight line AC and the parabola ABC, and let D be the middle point of AC. Draw the straight line DBE parallel
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION COURSE II. Friday, January 26, :15 a.m. to 12:15 p.m.
 The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION THREE-YEAR SEQUENCE FOR HIGH SCHOOL MATHEMATICS COURSE II Friday, January 26, 2001 9:15 a.m. to 12:15 p.m., only Notice... Scientific
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION THREE-YEAR SEQUENCE FOR HIGH SCHOOL MATHEMATICS COURSE II Friday, January 26, 2001 9:15 a.m. to 12:15 p.m., only Notice... Scientific
Unit 15 Section 3 : Symmetry
 Unit 15 Section 3 : Symmetry In this section we revise the symmetry of objects and examine the symmetry of regular polygons. There are two types of symmetry: reflective symmetry and rotational symmetry.
Unit 15 Section 3 : Symmetry In this section we revise the symmetry of objects and examine the symmetry of regular polygons. There are two types of symmetry: reflective symmetry and rotational symmetry.
Integrated Math 1. Course Standards & Resource Guide
 Integrated Math 1 Course Standards & Resource Guide Integrated Math 1 Unit Overview Fall Spring Unit 1: Unit Conversion Unit 2: Creating and Solving Equations Unit 3: Creating and Solving Inequalities
Integrated Math 1 Course Standards & Resource Guide Integrated Math 1 Unit Overview Fall Spring Unit 1: Unit Conversion Unit 2: Creating and Solving Equations Unit 3: Creating and Solving Inequalities
Mathematics Behind the Construction of Islamic Geometric Patterns. Islamic art was born in a unique culture that predisposed it towards expression
 Theo Smith 391A-Math Gems Jenia Tevelev 4/28/15 Mathematics Behind the Construction of Islamic Geometric Patterns Islamic art was born in a unique culture that predisposed it towards expression through
Theo Smith 391A-Math Gems Jenia Tevelev 4/28/15 Mathematics Behind the Construction of Islamic Geometric Patterns Islamic art was born in a unique culture that predisposed it towards expression through
MEP Pupil Text 13-19, Additional Material. Gradients of Perpendicular Lines
 Graphs MEP Pupil Text -9, Additional Material.B Gradients of Perpendicular Lines In this section we explore the relationship between the gradients of perpendicular lines and line segments. Worked Example
Graphs MEP Pupil Text -9, Additional Material.B Gradients of Perpendicular Lines In this section we explore the relationship between the gradients of perpendicular lines and line segments. Worked Example
California Common Core State Standards for Mathematics Standards Map Mathematics I
 A Correlation of Pearson Integrated High School Mathematics Mathematics I Common Core, 2014 to the California Common Core State s for Mathematics s Map Mathematics I Copyright 2017 Pearson Education, Inc.
A Correlation of Pearson Integrated High School Mathematics Mathematics I Common Core, 2014 to the California Common Core State s for Mathematics s Map Mathematics I Copyright 2017 Pearson Education, Inc.
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION THREE-YEAR SEQUENCE FOR HIGH SCHOOL MATHEMATICS COURSE II
 The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION THREE-YEAR SEQUENCE FOR HIGH SCHOOL MATHEMATICS COURSE II Tuesday, August 13, 2002 8:30 to 11:30 a.m., only Notice... Scientific
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION THREE-YEAR SEQUENCE FOR HIGH SCHOOL MATHEMATICS COURSE II Tuesday, August 13, 2002 8:30 to 11:30 a.m., only Notice... Scientific
Tim Hughbanks CHEMISTRY 634. Two Covers. Required Books, etc.
 CHEMISTRY 634 This course is for 3 credits. Lecture: 2 75 min/week; TTh 11:10-12:25, Room 2122 Grades will be based on the homework (roughly 25%), term paper (15%), midterm and final exams Web site: http://www.chem.tamu.edu/rgroup/
CHEMISTRY 634 This course is for 3 credits. Lecture: 2 75 min/week; TTh 11:10-12:25, Room 2122 Grades will be based on the homework (roughly 25%), term paper (15%), midterm and final exams Web site: http://www.chem.tamu.edu/rgroup/
The Golden Ratio and Viète s Formula
 / (04), 43 54 The Golden Ratio and Viète s Formula Esther M. García Caballero, Samuel G. Moreno and Michael P. Prophet Abstract. Viète s formula uses an infinite product to express π. In this paper we
/ (04), 43 54 The Golden Ratio and Viète s Formula Esther M. García Caballero, Samuel G. Moreno and Michael P. Prophet Abstract. Viète s formula uses an infinite product to express π. In this paper we
Alaska Mathematics Standards Vocabulary Word List Grade 4
 1 add addend additive comparison area area model common factor common multiple compatible numbers compose composite number counting number decompose difference digit divide dividend divisible divisor equal
1 add addend additive comparison area area model common factor common multiple compatible numbers compose composite number counting number decompose difference digit divide dividend divisible divisor equal
THE GEOMETRY OF THALES
 THE GEOMETRY OF THALES BY PERCY J. HARDING. In this paper there will, of course, be found no new facts ; but merely a review of well-known historical statements and an attempt to connect them. It has often
THE GEOMETRY OF THALES BY PERCY J. HARDING. In this paper there will, of course, be found no new facts ; but merely a review of well-known historical statements and an attempt to connect them. It has often
Chem Symmetry and Introduction to Group Theory. Symmetry is all around us and is a fundamental property of nature.
 Symmetry and Introduction to Group Theory Symmetry is all around us and is a fundamental property of nature. Symmetry and Introduction to Group Theory The term symmetry is derived from the Greek word symmetria
Symmetry and Introduction to Group Theory Symmetry is all around us and is a fundamental property of nature. Symmetry and Introduction to Group Theory The term symmetry is derived from the Greek word symmetria
English 4 th Grade A-L Vocabulary Cards and Word Walls Revised: 2/10/14
 English 4 th Grade A-L Vocabulary Cards and Word Walls Revised: 2/10/14 Important Notes for Teachers: The vocabulary cards in this file match the Common Core, the math curriculum adopted by the Utah State
English 4 th Grade A-L Vocabulary Cards and Word Walls Revised: 2/10/14 Important Notes for Teachers: The vocabulary cards in this file match the Common Core, the math curriculum adopted by the Utah State
UNIT I SOLID STATE PHYSICS
 UNIT I SOLID STATE PHYSICS CHAPTER 1 CRYSTAL STRUCTURE 1.1 INTRODUCTION When two atoms are brought together, two kinds of forces: attraction and repulsion come into play. The force of attraction increases
UNIT I SOLID STATE PHYSICS CHAPTER 1 CRYSTAL STRUCTURE 1.1 INTRODUCTION When two atoms are brought together, two kinds of forces: attraction and repulsion come into play. The force of attraction increases
The Theorem of Pythagoras
 CONDENSED LESSON 9.1 The Theorem of Pythagoras In this lesson you will Learn about the Pythagorean Theorem, which states the relationship between the lengths of the legs and the length of the hypotenuse
CONDENSED LESSON 9.1 The Theorem of Pythagoras In this lesson you will Learn about the Pythagorean Theorem, which states the relationship between the lengths of the legs and the length of the hypotenuse
A plane in which each point is identified with a ordered pair of real numbers (x,y) is called a coordinate (or Cartesian) plane.
 Coordinate Geometry Rene Descartes, considered the father of modern philosophy (Cogito ergo sum), also had a great influence on mathematics. He and Fermat corresponded regularly and as a result of their
Coordinate Geometry Rene Descartes, considered the father of modern philosophy (Cogito ergo sum), also had a great influence on mathematics. He and Fermat corresponded regularly and as a result of their
GEO REVIEW TEST #1. 1. In which quadrilateral are the diagonals always congruent?
 GEO REVIEW TEST #1 Name: Date: 1. In which quadrilateral are the diagonals always congruent? (1) rectangle (3) rhombus 4. In the accompanying diagram, lines AB and CD intersect at point E. If m AED = (x+10)
GEO REVIEW TEST #1 Name: Date: 1. In which quadrilateral are the diagonals always congruent? (1) rectangle (3) rhombus 4. In the accompanying diagram, lines AB and CD intersect at point E. If m AED = (x+10)
EXERCISES IN QUATERNIONS. William Rowan Hamilton. (The Cambridge and Dublin Mathematical Journal, 4 (1849), pp ) Edited by David R.
 EXERCISES IN QUATERNIONS William Rowan Hamilton (The Cambridge and Dublin Mathematical Journal, 4 (1849), pp. 161 168.) Edited by David R. Wilkins 1999 EXERCISES IN QUATERNIONS. By Sir William Rowan Hamilton.
EXERCISES IN QUATERNIONS William Rowan Hamilton (The Cambridge and Dublin Mathematical Journal, 4 (1849), pp. 161 168.) Edited by David R. Wilkins 1999 EXERCISES IN QUATERNIONS. By Sir William Rowan Hamilton.
Analytical Methods for Materials
 Analytical Methods for Materials Lesson 11 Crystallography and Crystal Structures, Part 3 Suggested Reading Chapter 6 in Waseda Chapter 1 in F.D. Bloss, Crystallography and Crystal Chemistry: An Introduction,
Analytical Methods for Materials Lesson 11 Crystallography and Crystal Structures, Part 3 Suggested Reading Chapter 6 in Waseda Chapter 1 in F.D. Bloss, Crystallography and Crystal Chemistry: An Introduction,
TRIGONOMETRY REVIEW (PART 1)
 TRIGONOMETRY REVIEW (PART ) MATH 52, SECTION 55 (VIPUL NAIK) Difficulty level: Easy to moderate, given that you are already familiar with trigonometry. Covered in class?: Probably not (for the most part).
TRIGONOMETRY REVIEW (PART ) MATH 52, SECTION 55 (VIPUL NAIK) Difficulty level: Easy to moderate, given that you are already familiar with trigonometry. Covered in class?: Probably not (for the most part).
Spring 2015, Math 111 Lab 9: The Definite Integral as the Are. the Area under a Curve
 Spring 2015, Math 111 Lab 9: The Definite Integral as the Area under a Curve William and Mary April 14, 2015 Historical Outline Intuition Learning Objectives Today, we will be looking at applications of
Spring 2015, Math 111 Lab 9: The Definite Integral as the Area under a Curve William and Mary April 14, 2015 Historical Outline Intuition Learning Objectives Today, we will be looking at applications of
Structure of Materials Prof. Anandh Subramaniam Department of Material Science and Engineering Indian Institute of Technology, Kanpur
 Structure of Materials Prof. Anandh Subramaniam Department of Material Science and Engineering Indian Institute of Technology, Kanpur Lecture - 5 Geometry of Crystals: Symmetry, Lattices The next question
Structure of Materials Prof. Anandh Subramaniam Department of Material Science and Engineering Indian Institute of Technology, Kanpur Lecture - 5 Geometry of Crystals: Symmetry, Lattices The next question
HIGHER GEOMETRY. 1. Notation. Below is some notation I will use. KEN RICHARDSON
 HIGHER GEOMETRY KEN RICHARDSON Contents. Notation. What is rigorous math? 3. Introduction to Euclidean plane geometry 3 4. Facts about lines, angles, triangles 6 5. Interlude: logic and proofs 9 6. Quadrilaterals
HIGHER GEOMETRY KEN RICHARDSON Contents. Notation. What is rigorous math? 3. Introduction to Euclidean plane geometry 3 4. Facts about lines, angles, triangles 6 5. Interlude: logic and proofs 9 6. Quadrilaterals
Foundations of Basic Geometry
 GENERAL I ARTICLE Foundations of Basic Geometry Jasbir S Chahal Jasbir S Chahal is Professor of Mathematics at Brigham Young University, Provo, Utah, USA. His research interest is in number theory. The
GENERAL I ARTICLE Foundations of Basic Geometry Jasbir S Chahal Jasbir S Chahal is Professor of Mathematics at Brigham Young University, Provo, Utah, USA. His research interest is in number theory. The
KENDRIYA VIDYALAYA SANGATHAN, HYDERABAD REGION
 KENDRIYA VIDYALAYA SANGATHAN, HYDERABAD REGION SAMPLE PAPER 02 F PERIODIC TEST III EXAM (2017-18) SUBJECT: MATHEMATICS(041) BLUE PRINT : CLASS IX Unit Chapter VSA (1 mark) SA I (2 marks) SA II (3 marks)
KENDRIYA VIDYALAYA SANGATHAN, HYDERABAD REGION SAMPLE PAPER 02 F PERIODIC TEST III EXAM (2017-18) SUBJECT: MATHEMATICS(041) BLUE PRINT : CLASS IX Unit Chapter VSA (1 mark) SA I (2 marks) SA II (3 marks)
PREFACE. Synergy for Success in Mathematics 7 is designed for Grade 7 students. The textbook
 Synergy for Success in Mathematics 7 is designed for Grade 7 students. The textbook contains all the required learning competencies and is supplemented with some additional topics for enrichment. Lessons
Synergy for Success in Mathematics 7 is designed for Grade 7 students. The textbook contains all the required learning competencies and is supplemented with some additional topics for enrichment. Lessons
Molecular Spectroscopy. January 24, 2008 Introduction to Group Theory and Molecular Groups
 Molecular Spectroscopy January 24, 2008 Introduction to Group Theory and Molecular Groups Properties that define a group A group is a collection of elements that are interrelated based on certain rules
Molecular Spectroscopy January 24, 2008 Introduction to Group Theory and Molecular Groups Properties that define a group A group is a collection of elements that are interrelated based on certain rules
Dr Prya Mathew SJCE Mysore
 1 2 3 The word Mathematics derived from two Greek words Manthanein means learning Techne means an art or technique So Mathematics means the art of learning related to disciplines or faculties disciplines
1 2 3 The word Mathematics derived from two Greek words Manthanein means learning Techne means an art or technique So Mathematics means the art of learning related to disciplines or faculties disciplines
Descartes s Logarithm Machine
 Descartes s Logarithm Machine In the Geometry (1952), Descartes considered the problem of finding n mean proportionals (i.e. geometric means) between any two lengths a and b (with a < b). That is, the
Descartes s Logarithm Machine In the Geometry (1952), Descartes considered the problem of finding n mean proportionals (i.e. geometric means) between any two lengths a and b (with a < b). That is, the
Common Core State Standards for Mathematics - High School
 to the Common Core State Standards for - High School I Table of Contents Number and Quantity... 1 Algebra... 1 Functions... 3 Geometry... 6 Statistics and Probability... 8 Copyright 2013 Pearson Education,
to the Common Core State Standards for - High School I Table of Contents Number and Quantity... 1 Algebra... 1 Functions... 3 Geometry... 6 Statistics and Probability... 8 Copyright 2013 Pearson Education,
COUNTING AND SYMMETRY
 COUNTING AND SYMMETRY INTERMEDIATE GROUP NOVEMBER 6, 2016 Warm Up Problem 1. Examine the figure below. (1) How many lines of symmetry does the figure have? (2) How many symmetries does the figure have?
COUNTING AND SYMMETRY INTERMEDIATE GROUP NOVEMBER 6, 2016 Warm Up Problem 1. Examine the figure below. (1) How many lines of symmetry does the figure have? (2) How many symmetries does the figure have?
Higher Geometry Problems
 Higher Geometry Problems (1) Look up Eucidean Geometry on Wikipedia, and write down the English translation given of each of the first four postulates of Euclid. Rewrite each postulate as a clear statement
Higher Geometry Problems (1) Look up Eucidean Geometry on Wikipedia, and write down the English translation given of each of the first four postulates of Euclid. Rewrite each postulate as a clear statement
Mathematics 3210 Spring Semester, 2005 Homework notes, part 8 April 15, 2005
 Mathematics 3210 Spring Semester, 2005 Homework notes, part 8 April 15, 2005 The underlying assumption for all problems is that all points, lines, etc., are taken within the Poincaré plane (or Poincaré
Mathematics 3210 Spring Semester, 2005 Homework notes, part 8 April 15, 2005 The underlying assumption for all problems is that all points, lines, etc., are taken within the Poincaré plane (or Poincaré
Date: Math 7 Final Exam Review Name:
 Specific Outcome Achievement Indicators Chapter Got it?? the Solve a given problem involving the addition of two or more decimal numbers. addition, subtraction, multiplication and division of decimals
Specific Outcome Achievement Indicators Chapter Got it?? the Solve a given problem involving the addition of two or more decimal numbers. addition, subtraction, multiplication and division of decimals
(RC3) Constructing the point which is the intersection of two existing, non-parallel lines.
 The mathematical theory of ruller and compass constructions consists on performing geometric operation with a ruler and a compass. Any construction starts with two given points, or equivalently a segment
The mathematical theory of ruller and compass constructions consists on performing geometric operation with a ruler and a compass. Any construction starts with two given points, or equivalently a segment
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION COURSE II. Wednesday, August 16, :30 to 11:30 a.m.
 The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION THREE-YEAR SEQUENCE FOR HIGH SCHOOL MATHEMATICS COURSE II Wednesday, August 16, 000 8:30 to 11:30 a.m., only Notice... Scientific
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION THREE-YEAR SEQUENCE FOR HIGH SCHOOL MATHEMATICS COURSE II Wednesday, August 16, 000 8:30 to 11:30 a.m., only Notice... Scientific
California 3 rd Grade Standards / Excel Math Correlation by Lesson Number
 California 3 rd Grade Standards / Lesson (Activity) L1 L2 L3 L4 L5 L6 L7 L8 Excel Math Lesson Objective Learning about the tens place and the ones place; adding and subtracting two-digit numbers; learning
California 3 rd Grade Standards / Lesson (Activity) L1 L2 L3 L4 L5 L6 L7 L8 Excel Math Lesson Objective Learning about the tens place and the ones place; adding and subtracting two-digit numbers; learning
Algebraic Expressions
 ALGEBRAIC EXPRESSIONS 229 Algebraic Expressions Chapter 12 12.1 INTRODUCTION We have already come across simple algebraic expressions like x + 3, y 5, 4x + 5, 10y 5 and so on. In Class VI, we have seen
ALGEBRAIC EXPRESSIONS 229 Algebraic Expressions Chapter 12 12.1 INTRODUCTION We have already come across simple algebraic expressions like x + 3, y 5, 4x + 5, 10y 5 and so on. In Class VI, we have seen
Linear Independence x
 Linear Independence A consistent system of linear equations with matrix equation Ax = b, where A is an m n matrix, has a solution set whose graph in R n is a linear object, that is, has one of only n +
Linear Independence A consistent system of linear equations with matrix equation Ax = b, where A is an m n matrix, has a solution set whose graph in R n is a linear object, that is, has one of only n +
Preliminary chapter: Review of previous coursework. Objectives
 Preliminary chapter: Review of previous coursework Objectives By the end of this chapter the student should be able to recall, from Books 1 and 2 of New General Mathematics, the facts and methods that
Preliminary chapter: Review of previous coursework Objectives By the end of this chapter the student should be able to recall, from Books 1 and 2 of New General Mathematics, the facts and methods that
Geometric Structures
 Geometric Structures 3 Hour Exams & Final Fall 2003 Exam I Page 1 Exam II Page 6 Exam III Page 10 Final Exam Page 14 Oklahoma State University Terry Williams, Instructor Geometric Structures Exam I Fall
Geometric Structures 3 Hour Exams & Final Fall 2003 Exam I Page 1 Exam II Page 6 Exam III Page 10 Final Exam Page 14 Oklahoma State University Terry Williams, Instructor Geometric Structures Exam I Fall
PRACTICE TEST ANSWER KEY & SCORING GUIDELINES INTEGRATED MATHEMATICS I
 Ohio s State Tests PRACTICE TEST ANSWER KEY & SCORING GUIDELINES INTEGRATED MATHEMATICS I Table of Contents Questions 1 29: Content Summary and Answer Key... iii Question 1: Question and Scoring Guidelines...
Ohio s State Tests PRACTICE TEST ANSWER KEY & SCORING GUIDELINES INTEGRATED MATHEMATICS I Table of Contents Questions 1 29: Content Summary and Answer Key... iii Question 1: Question and Scoring Guidelines...
Homework Assignments Math /02 Fall 2014
 Homework Assignments Math 119-01/02 Fall 2014 Assignment 1 Due date : Friday, September 5 6th Edition Problem Set Section 6.1, Page 178: #1, 2, 3, 4, 5, 6. Section 6.2, Page 185: #1, 2, 3, 5, 6, 8, 10-14,
Homework Assignments Math 119-01/02 Fall 2014 Assignment 1 Due date : Friday, September 5 6th Edition Problem Set Section 6.1, Page 178: #1, 2, 3, 4, 5, 6. Section 6.2, Page 185: #1, 2, 3, 5, 6, 8, 10-14,
Rational Numbers and Exponents
 Rational and Exponents Math 7 Topic 4 Math 7 Topic 5 Math 8 - Topic 1 4-2: Adding Integers 4-3: Adding Rational 4-4: Subtracting Integers 4-5: Subtracting Rational 4-6: Distance on a Number Line 5-1: Multiplying
Rational and Exponents Math 7 Topic 4 Math 7 Topic 5 Math 8 - Topic 1 4-2: Adding Integers 4-3: Adding Rational 4-4: Subtracting Integers 4-5: Subtracting Rational 4-6: Distance on a Number Line 5-1: Multiplying
SKETCH 12 STARS FROM THE GREAT HAGIA SOPHIA 1
 SKETC 12 STARS ROM TE GREAT AGIA SOPIA 1 agia Sophia, or Aya Sofya in Turkish, is the largest Byzantine church in the world. Its current name is a shortened form of the full name The church of the oly
SKETC 12 STARS ROM TE GREAT AGIA SOPIA 1 agia Sophia, or Aya Sofya in Turkish, is the largest Byzantine church in the world. Its current name is a shortened form of the full name The church of the oly
6th Grade Mathematics
 Standard 1: Number & Operation and use numbers and use numbers 27-31% and use numbers 6.M.1.1.1 Compare magnitudes and relative magnitudes of positive rational numbers, including whole numbers through
Standard 1: Number & Operation and use numbers and use numbers 27-31% and use numbers 6.M.1.1.1 Compare magnitudes and relative magnitudes of positive rational numbers, including whole numbers through
IB STANDARD LEVEL MATHEMATICS FINAL REVIEW
 IB STANDARD LEVEL MATHEMATICS FINAL REVIEW 01 013 SECTION 1: STATISTICS 1. At a conference of 100 mathematicians there are 7 men and 8 women. The men have a mean height of 1.79 m and the women have a mean
IB STANDARD LEVEL MATHEMATICS FINAL REVIEW 01 013 SECTION 1: STATISTICS 1. At a conference of 100 mathematicians there are 7 men and 8 women. The men have a mean height of 1.79 m and the women have a mean
12 Rigid Transformations
 www.ck12.org CHAPTER 12 Rigid Transformations Chapter Outline 12.1 EXPLORING SYMMETRY 12.2 TRANSLATIONS AND VECTORS 12.3 REFLECTIONS 12.4 ROTATIONS 12.5 COMPOSITION OF TRANSFORMATIONS 12.6 EXTENSION: TESSELLATIONS
www.ck12.org CHAPTER 12 Rigid Transformations Chapter Outline 12.1 EXPLORING SYMMETRY 12.2 TRANSLATIONS AND VECTORS 12.3 REFLECTIONS 12.4 ROTATIONS 12.5 COMPOSITION OF TRANSFORMATIONS 12.6 EXTENSION: TESSELLATIONS
Common Core State Standards for Mathematics Integrated Pathway: Mathematics I
 A CORRELATION OF TO THE Standards for Mathematics A Correlation of Table of Contents Unit 1: Relationships between Quantities... 1 Unit 2: Linear and Exponential Relationships... 4 Unit 3: Reasoning with
A CORRELATION OF TO THE Standards for Mathematics A Correlation of Table of Contents Unit 1: Relationships between Quantities... 1 Unit 2: Linear and Exponential Relationships... 4 Unit 3: Reasoning with
(A B) 2 + (A B) 2. and factor the result.
 Transformational Geometry of the Plane (Master Plan) Day 1. Some Coordinate Geometry. Cartesian (rectangular) coordinates on the plane. What is a line segment? What is a (right) triangle? State and prove
Transformational Geometry of the Plane (Master Plan) Day 1. Some Coordinate Geometry. Cartesian (rectangular) coordinates on the plane. What is a line segment? What is a (right) triangle? State and prove
Chapter 3. Introducing Groups
 Chapter 3 Introducing Groups We need a super-mathematics in which the operations are as unknown as the quantities they operate on, and a super-mathematician who does not know what he is doing when he performs
Chapter 3 Introducing Groups We need a super-mathematics in which the operations are as unknown as the quantities they operate on, and a super-mathematician who does not know what he is doing when he performs
California 5 th Grade Standards / Excel Math Correlation by Lesson Number
 (Activity) L1 L2 L3 Excel Math Objective Recognizing numbers less than a million given in words or place value; recognizing addition and subtraction fact families; subtracting 2 threedigit numbers with
(Activity) L1 L2 L3 Excel Math Objective Recognizing numbers less than a million given in words or place value; recognizing addition and subtraction fact families; subtracting 2 threedigit numbers with
Midterm Review Packet. Geometry: Midterm Multiple Choice Practice
 : Midterm Multiple Choice Practice 1. In the diagram below, a square is graphed in the coordinate plane. A reflection over which line does not carry the square onto itself? (1) (2) (3) (4) 2. A sequence
: Midterm Multiple Choice Practice 1. In the diagram below, a square is graphed in the coordinate plane. A reflection over which line does not carry the square onto itself? (1) (2) (3) (4) 2. A sequence
Rigid Geometric Transformations
 Rigid Geometric Transformations Carlo Tomasi This note is a quick refresher of the geometry of rigid transformations in three-dimensional space, expressed in Cartesian coordinates. 1 Cartesian Coordinates
Rigid Geometric Transformations Carlo Tomasi This note is a quick refresher of the geometry of rigid transformations in three-dimensional space, expressed in Cartesian coordinates. 1 Cartesian Coordinates
Section 1: Sets and Interval Notation
 PART 1 From Sets to Functions Section 1: Sets and Interval Notation Introduction Set concepts offer the means for understanding many different aspects of mathematics and its applications to other branches
PART 1 From Sets to Functions Section 1: Sets and Interval Notation Introduction Set concepts offer the means for understanding many different aspects of mathematics and its applications to other branches
Higher Geometry Problems
 Higher Geometry Problems (1 Look up Eucidean Geometry on Wikipedia, and write down the English translation given of each of the first four postulates of Euclid. Rewrite each postulate as a clear statement
Higher Geometry Problems (1 Look up Eucidean Geometry on Wikipedia, and write down the English translation given of each of the first four postulates of Euclid. Rewrite each postulate as a clear statement
Integer (positive or negative whole numbers or zero) arithmetic
 Integer (positive or negative whole numbers or zero) arithmetic The number line helps to visualize the process. The exercises below include the answers but see if you agree with them and if not try to
Integer (positive or negative whole numbers or zero) arithmetic The number line helps to visualize the process. The exercises below include the answers but see if you agree with them and if not try to
Chapter 12: Ruler and compass constructions
 Chapter 12: Ruler and compass constructions Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4120, Spring 2014 M. Macauley (Clemson) Chapter
Chapter 12: Ruler and compass constructions Matthew Macauley Department of Mathematical Sciences Clemson University http://www.math.clemson.edu/~macaule/ Math 4120, Spring 2014 M. Macauley (Clemson) Chapter
Tetrads and their Counting
 Baltic J. Modern Computing, Vol. 6 (2018), No. 2, 96-106 https://doi.org/10.22364/bjmc.2018.6.2.01 Tetrads and their Counting Juris ČERŅENOKS, Andrejs CIBULIS Department of Mathematics, University of Latvia
Baltic J. Modern Computing, Vol. 6 (2018), No. 2, 96-106 https://doi.org/10.22364/bjmc.2018.6.2.01 Tetrads and their Counting Juris ČERŅENOKS, Andrejs CIBULIS Department of Mathematics, University of Latvia
Step-by-step and detailed demonstrations of how a specific concept or technique is applied in solving problems.
 PREFACE Synergy for Success in Mathematics 7 contains all the required learning competencies and is supplemented with some additional topics for enrichment. Lessons are presented using effective Singapore
PREFACE Synergy for Success in Mathematics 7 contains all the required learning competencies and is supplemented with some additional topics for enrichment. Lessons are presented using effective Singapore
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION COURSE II. Friday, January 26, :15 a.m. to 12:15 p.m.
 The University of the State of New York REGENTS HIGH SCHOOL EXMINTION THREE-YER SEQUENCE FOR HIGH SCHOOL MTHEMTICS COURSE II Friday, January 26, 2001 9:15 a.m. to 12:15 p.m., only Notice... Scientific
The University of the State of New York REGENTS HIGH SCHOOL EXMINTION THREE-YER SEQUENCE FOR HIGH SCHOOL MTHEMTICS COURSE II Friday, January 26, 2001 9:15 a.m. to 12:15 p.m., only Notice... Scientific
Homework Assignments Math /02 Fall 2017
 Homework Assignments Math 119-01/02 Fall 2017 Assignment 1 Due date : Wednesday, August 30 Section 6.1, Page 178: #1, 2, 3, 4, 5, 6. Section 6.2, Page 185: #1, 2, 3, 5, 6, 8, 10-14, 16, 17, 18, 20, 22,
Homework Assignments Math 119-01/02 Fall 2017 Assignment 1 Due date : Wednesday, August 30 Section 6.1, Page 178: #1, 2, 3, 4, 5, 6. Section 6.2, Page 185: #1, 2, 3, 5, 6, 8, 10-14, 16, 17, 18, 20, 22,
How to Make Impossible Wallpaper
 How to Make Impossible Wallpaper A tale of forbidden symmetries. By Erica Klarreich Figure 1. A wallpaper pattern, left, with six-fold rotational symmetry around each of the browngreen rosettes. Figure
How to Make Impossible Wallpaper A tale of forbidden symmetries. By Erica Klarreich Figure 1. A wallpaper pattern, left, with six-fold rotational symmetry around each of the browngreen rosettes. Figure
CHAPTER 12 HERON S FORMULA Introduction
 CHAPTER 1 HERON S FORMULA 1.1 Introduction You have studied in earlier classes about figures of different shapes such as squares, rectangles, triangles and quadrilaterals. You have also calculated perimeters
CHAPTER 1 HERON S FORMULA 1.1 Introduction You have studied in earlier classes about figures of different shapes such as squares, rectangles, triangles and quadrilaterals. You have also calculated perimeters
Classwork 8.1. Perform the indicated operation and simplify each as much as possible. 1) 24 2) ) 54w y 11) wy 6) 5 9.
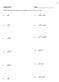 - 7 - Classwork 8.1 Name Perform the indicated operation and simplify each as much as possible. 1) 4 7) 16+ 5 49 ) 5 4 8) 11 6 81 ) 5 4x 9) 9 x + 49x 4) 75w 10) 6 5 54w y 5) 80wy 11) 15 6 6) 5 9 1) 15x
- 7 - Classwork 8.1 Name Perform the indicated operation and simplify each as much as possible. 1) 4 7) 16+ 5 49 ) 5 4 8) 11 6 81 ) 5 4x 9) 9 x + 49x 4) 75w 10) 6 5 54w y 5) 80wy 11) 15 6 6) 5 9 1) 15x
Constructions with ruler and compass
 Constructions with ruler and compass An application of algebra to geometry K. N. Raghavan http://www.imsc.res.in/ knr/ IMSc, Chennai July 2013 Cartesian geometry COORDINATE GEOMETRY FOLLOWING DESCARTES
Constructions with ruler and compass An application of algebra to geometry K. N. Raghavan http://www.imsc.res.in/ knr/ IMSc, Chennai July 2013 Cartesian geometry COORDINATE GEOMETRY FOLLOWING DESCARTES
