t, x 2 t above, using input-output modeling. Assume solute concentration is uniform in each tank. If x 1 0 = b 1
|
|
|
- Ronald Carroll
- 6 years ago
- Views:
Transcription
1 Mah Fri Apr 4 7 Sysems of differenial equaions - o model muli-componen sysems via comparmenal analysis: hp://enwikipediaorg/wiki/muli-comparmen_model Here's a relaively simple 2-ank problem o illusrae he ideas: Exercise ) Find differenial equaions for solue amouns, above, using inpu-oupu modeling Assume solue concenraion is uniform in each ank If = b, = b 2, wrie down he iniial value problem ha you expec would have a unique soluion answer (in marix-vecor form): 4 2 = 4 2 = b b 2
2 Geomeric inerpreaion of firs order sysems of differenial equaions The example on page is a special case of he general iniial value problem for a firs order sysem of differenial equaions: x = F, x x = x We will see how any single differenial equaion (of any order), or any sysem of differenial equaions (of any order) is equivalen o a larger firs order sysem of differenial equaions And we will discuss how he naural iniial value problems correspond Why we expec IVP's for firs order sysems of DE's o have unique soluions x : From eiher a mulivariable calculus course, or from physics, recall he geomeric/physical inerpreaion of x as he angen/velociy vecor o he parameric curve of poins wih posiion vecor x, as varies This picure should remind you of he discussion, bu ask quesions if his is new o you: Analyically, he reason ha he vecor of derivaives x compued componen by componen is acually a limi of scaled secan vecors (and herefore a angen/velociy vecor) is: x x x lim : : x n x n = lim : x n x n provided each componen funcion is differeniable Therefore, he reason you expec a unique soluion o he IVP for a firs order sysem is ha you know where you sar (x = x ), and you know your "velociy" vecor (depending on ime and curren locaion) you expec a unique soluion! (Plus, you could use somehing like a vecor version of Euler's mehod or he Runge-Kua mehod o approximae i! You jus conver he scalar quaniies in he code ino vecor quaniies And his is wha numerical solvers do) = x n :,
3 Exercise 2) Reurn o he page ank example = 4 2 = 4 2 = 9 = 2a) Inerpre he parameric soluion curve, T o his IVP, as indicaed in he pplane screen sho below ("pplane" is he siser program o "dfield", ha we were using in Chapers -2) Noice how i follows he "velociy" vecor field (which is ime-independen in his example), and how he "paricle moion" locaion, T is acually he vecor of solue amouns in each ank, a ime If your sysem involved en coupled anks raher han wo, hen his "paricle" is moving around in 2b) Wha are he apparen limiing solue amouns in each ank? 2c) How could your smar-alec younger sibling have old you he answer o 2b wihou considering any differenial equaions or "velociy vecor fields" a all?
4 Firs order sysems of differenial equaions of he form x = A x are called linear homogeneous sysems of DE's (Think of rewriing he sysem as x A x = in analogy wih how we wroe linear scalar differenial equaions) Then he inhomogeneous sysem of firs order DE's would be wrien as x A x = f or x = A x f Noice ha he operaor on vecor-valued funcions x defined by L x x A x is linear, ie L x y = L x L y L c x = c L x SO! The space of soluions o he homogeneous firs order sysem of differenial equaions x A x = is a subspace AND he general soluion o he inhomogeneous sysem x A x = f will be of he form x = x P x H where x P is any single paricular soluion and x H is he general homogeneous soluion Exercise 3) In he case ha A is a consan marix (ie enries don' depend on ), consider he homogeneous problem x = A x Look for soluions of he form x = e v, where v is a consan vecor Show ha x = e v solves he homogeneous DE sysem if and only if v is an eigenvecor of A, wih eigenvalue, ie A v = v Hin: In order for such an x o solve he DE i mus be rue ha and Se hese wo expressions equal x = e v A x = A e v = e A v
5 Exercise 4) Use he idea of Exercise 3 o solve he iniial value problem of Exercise 2!! Compare your soluion x o he parameric curve drawn by pplane, ha we looked a a couple of pages back Exercise 5) Lessons learned from ank example: Wha condiion on he marix A n n will allow you o uniquely solve every iniial value problem x = A x x = x n using he mehod in Exercise 3-4? Hin: Chaper 6 (If ha condiion fails here are oher ways o find he unique soluions)
6 Mah Week 4 April 7-2: secions 7-73 firs order sysems of linear differenial equaions; 74 mass-spring sysems Mon Apr 7 Coninue discussing sysems of differenial equaions, 7-73 Review exercises 3-5 in las Friday's noes, which foreshadow he eigenvalue-eigenvecor mehod for solving homogeneous firs order sysems of differenial equaion IVPs x = A x x = x ha he book covers in deail in secion 73 Then discuss he imporan fac ha every n h order differenial equaion or sysem of differenial equaions is acually equivalen o a (possibly quie large) sysem of firs order differenial equaions This discussion is in oday's noes and is he conen of secion 7 The exisence-uniqueness heorem for firs order sysems of differenial equaions will hen explain why he naural iniial value problems for higher order differenial equaions, ha we sudied in Chaper 5, also always have unique soluions Anoher mysery ha his correspondence will solve is why we used "characerisic polynomial" when looking for basis soluions e r o n h order consan coefficien homogeneous differenial equaions and hen used exacly he same erminology, "characerisic polynomial", when we were looking for marix eigenvalues (see secion 73) Along he way and omorrow as well, we will also be discussing how he heory and emplae for finding soluions o firs order sysems of linear differenial equaions precisely mirrors he emplae we developed for single n h -order linear differenial equaions in Chaper 5 This is he conen of secion 72
7 Convering higher order DE's or sysems of DE's o equivalen firs order sysems of DEs: Example: Consider his configuraion of wo coupled masses and springs: Exercise ) Use Newon's second law o derive a sysem of wo second order differenial equaions for,, he displacemens of he respecive masses from he equilibrium configuraion Wha iniial value problem do you expec yields unique soluions in his case?
8 Exercise 2) Consider he IVP from Exercise, wih he special values m = 2, m 2 = ; k = 4, k 2 = 2; F = 4 sin 3 : = 3 = sin 3 = b, = b 2 = c, = c 2 2a) Show ha if, solve he IVP above, and if we define v v 2 hen,, v, v 2 solve he firs order sysem IVP = v = v 2 v = 3 v 2 = sin 3 = b v = b 2 = c v 2 = c 2 2b) Conversely, show ha if,, v, v 2 solve he IVP of four firs order DE's, hen, solve he original IVP for wo second order DE's
9 I is always he case ha he naural iniial value problems for single or sysems of differenial equaions are equivalen o an iniial value problem for a larger sysem of firs order differenial equaions, as in he previous example A special case of his fac is ha if you have an IVP for single n h order DE for x, i is equivalen o an IVP for a sysem of n firs-order DE's, in which he funcions are = x, x, x 3 x,, x n x n For example, consider his second order underdamped IVP for x : x 5 x = x = 4 x = 4 Exercise 3) 3a) Conver his single second order IVP ino an equivalen firs order sysem IVP for x and x 3b) Solve he second order IVP in order o deduce a soluion o he firs order IVP Use Chaper 5 mehods even hough you love Laplace ransform more 3c) How does he Chaper 5 "characerisic polynomial" in 3b compare wih he Chaper 6 (eigenvalue) "characerisic polynomial" for he firs order sysem marix in 3a? hmmm 3d) Is your analyic soluion x, v in 3b consisen wih he parameric curve shown on he nex page, in a "pplane" screensho? The picure is called a "phase porrai" for posiion and velociy
10 If you've been using Wolfram alpha o solve second order differenial equaions you migh have noiced picures ha look jus like he one above, even hough you migh no have hough abou hem look a he plo a he lower righ corner of his screensho!
11
12 Theorem For he IVP x = F, x x = x If F, x is coninuous in he variable and differeniable in is x variable, hen here exiss a unique soluion o he IVP, a leas on some (possibly shor) ime inerval Theorem 2 For he special case of he firs order linear sysem of differenial equaions IVP x = A x f x = x If he marix A and he vecor funcion f are coninuous on an open inerval I conaining hen a soluion x exiss and is unique, on he enire inerval Remark: The soluions o hese sysems of DE's may be approximaed numerically using vecorized versions of Euler's mehod and he Runge Kua mehod The ideas are exacly he same as hey were for scalar equaions, excep ha hey now use vecors This is how commerical numerical DE solvers work For example, wih ime-sep h he Euler loop would incremen as follows: j = h j x j = x j h F j, x j Remark: These heorems are he rue explanaion for why he n h -order linear DE IVPs in Chaper 5 always have unique soluions - because each n h order linear DE IVP is equivalen o an IVP for a firs order sysem of n linear DE's In fac, when sofware finds numerical approximaions for soluions o higher order (linear or non-linear) DE IVPs ha can' be found by he echniques of Chaper 5 or oher mahemaical formulas, i works by convering hese IVPs o he equivalen firs order sysem IVPs, and uses algorihms like Euler and Runge-Kua o approximae he soluions
13 Theorem 3) Vecor space heory for firs order sysems of linear DEs (Noice he familiar hemeswe can compleely undersand hese facs if we ake he inuiively reasonable exisence-uniqueness Theorem 2 as fac) 3) For vecor funcions x differeniable on an inerval, he operaor L x x A x is linear, ie L x z = L x L z L c x = c L x check! 32) Thus, by he fundamenal heorem for linear ransformaions, he general soluion o he nonhomogeneous linear problem x A x = f I is x = x p x H where x p is any single paricular soluion and x H is he general soluion o he homogeneous problem x A x = We frequenly wrie he homogeneous linear sysem of DE's as x = A x
14 33) For A n n and x n he soluion space on he inerval I o he homogeneous problem x = A x is n-dimensional Here's why: Le X, X 2,X n be any n soluions o he homogeneous problem chosen so ha he Wronskian marix a I W X, X 2,, X n X X 2 X n is inverible (By he exisence heorem we can choose soluions for any collecion of iniial vecors - so for example, in heory we could pick he marix above o acually equal he ideniy marix In pracice we'll be happy wih any inverible marix ) Then for any b n he IVP x = A x x = b has soluion x = c X c 2 X 2 c n X n where he linear combinaion coefficiens are he soluion o he Wronskian marix equaion c b X X 2 X n c 2 : = b 2 : c n b n Thus, because he Wronskian marix a is inverible, every IVP can be solved wih a linear combinaion of X, X 2,X n, and since each IVP has only one soluion, X, X 2,X n span he soluion space The same marix equaion shows ha he only linear combinaion ha yields he zero funcion (which has iniial vecor b = ) is he one wih c = Thus X, X 2,X n are also linearly independen Therefore hey are a basis for he soluion space, and heir number n is he dimension of he soluion space
15 73 Eigenvecor mehod for finding he general soluion o he homogeneous consan marix firs order sysem of differenial equaions x = A x Here's how: We look for a basis of soluions x = e v, where v is a consan vecor Subsiuing his form of poenial soluion ino he sysem of DE's above yields he equaion e v = A e v = e A v Dividing boh sides of his equaion by he scalar funcion e gives he condiion v = A v We ge a soluion every ime v is an eigenvecor of A wih eigenvalue! If A is diagonalizable hen here is an n basis of eigenvecors v, v 2,v n and soluions X = e v, X 2 = e 2 v 2,, X n = e n v n which are a basis for he soluion space on he inerval I =, because he Wronskian marix a = is he inverible diagonalizing marix P = v v 2 v n ha we considered in Chaper 6 If A has complex number eigenvalues and eigenvecors i may sill be diagonalizable over n, and we will sill be able o exrac a basis of real vecor funcion soluions If A is no diagonalizable over n or over n he siuaion is more complicaed Exercise 4a) Use he mehod above o find he general homogeneous soluion o = 6 7 4b) Solve he IVP wih = 4
16 Exercise 5a) Wha second order overdamped iniial value problem is equivalen o he firs order sysem IVP on he previous page And wha is he soluion funcion o his IVP? 5b) Wha do you noice abou he Chaper 5 "Wronskian marix" for he second order DE in 4a, and he Chaper 7 "Wronskian marix" for he soluion o he equivalen firs order sysem? 5c) Since in he correspondence above, equals he mass velociy x = v, I've creaed he pplane phase porrai below using he leering x, v T raher han x, T Inepre he behavior of he overdamped mass-spring moion in erms of he pplane phase porrai 5d) How do he eigenvecors show up in he phase porrai, in erms of he direcion he origin is approached from as, and he direcion soluions came from (as )? hp://mahriceedu/~dfield/dfpphml
17 Mah Tues Apr Summary of wha is covered in Monday's and Tuesday's noes: Any iniial value problem for a differenial equaion or sysem of differenial equaions can be convered ino an equivalen iniial value problem for a sysem of firs order differenial equaions There is a "shor-ime" exisence-uniqueness heorem for firs order DE iniial value problems x = F, x x = x and soluions can be approximaed using Euler or Runge-Kua ype algorihms A special case of he IVP above is he one for a firs order linear sysem of differenial equaions : x = A x f x = x If he marix A and he vecor funcion f are coninuous on an open inerval I conaining hen a soluion x exiss and is unique, on he enire inerval The general soluion o an inhomogeneous linear sysem of DEs x = A x f ie x A x = f will be of he form x = x P homogeneous sysem x H where x P is a paricular soluion, and x H is he general soluion o he x = A x For A n n and x n he soluion space on he inerval I o he homogeneous problem is n-dimensional x = A x ie x A x = For A n n a consan marix, we ry o find a basis for he soluion space o x = A x consising of soluions of he form x = e v, where v is an eigenvecor of A wih eigenvalue We will succeed as long as A is diagonalizable Today: We will coninue using he eigenvalue-eigenvecor mehod for finding he general soluion o he homogeneous consan marix firs order sysem of differenial equaions x = A x ha we discussed yeserday, and is in Monday's noes Today we'll consider examples where he eigenvalues and eigenvecors are complex There is such an example in he homework due Wednesday problem w33
18
19 So far we've no considered he possibiliy of complex eigenvalues and eigenvecors Linear algebra heory works he same wih complex number scalars and vecors - one can alk abou complex vecor spaces, linear combinaions, span, linear independence, reduced row echelon form, deerminan, dimension, basis, ec Then he model space is n raher han n Definiion: v n (v ) is a complex eigenvecor of he marix A, wih eigenvalue if A v = v Jus as before, you find he possibly complex eigenvalues by finding he roos of he characerisic polynomial A I Then find he eigenspace bases by reducing he corresponding marix (using complex scalars in he elemenary row operaions) The bes way o see how o proceed in he case of complex eigenvalues/eigenvecors is o work an example There is a general discussion on he page afer his example ha we will refer o along he way: Glucose-insulin model (adaped from a discussion on page 339 of he ex "Linear Algebra wih Applicaions," by Oo Brescher) Le G be he excess glucose concenraion (mg of G per ml of blood, say) in someone's blood, a ime hours Excess means we are keeping rack of he difference beween curren and equilibrium ("fasing") concenraions Similarly, Le H be he excess insulin concenraion a ime hours When blood levels of glucose rise, say as food is digesed, he pancreas reacs by secreing insulin in order o uilize he glucose Researchers have developed mahemaical models for he glucose regulaory sysem Here is a simplified (linearized) version of one such model, wih paricular represenaive marix coefficiens I would be mean o apply beween meals, when no addiional glucose is being added o he sysem: G 4 G = H H Exercise 3a) Undersand why he signs of he marix enries are reasonable Now le's solve he iniial value problem, say righ afer a big meal, when G = H 3b) The firs sep is o ge he eigendaa of he marix Do his, and compare wih he Maple check on he nex page
20 > wih LinearAlgebra : 2 > A 5 ; Eigenvecors A ; 2 A := 5 5 I 5 I, 2 I 2 I () Noice ha Maple wries a capial I = 3c) Exrac a basis for he soluion space o his homogeneous sysem of differenial equaions from he eigenvecor informaion above: 3d) Solve he iniial value problem
21
22 Here are some picures o help undersand wha he model is predicing you could also consruc hese graphs using pplane () Plos of glucose vs insulin, a ime hours laer: > wih plos : > G exp cos 2 : H 5 exp sin 2 : plo plo G, = 3, color = green : plo2 plo H, = 3, color = brown : display plo, plo2, ile = `underdamped glucose-insulin ineracions` ; 6 underdamped glucose-insulin ineracions 2 3 2) A phase porrai of he glucose-insulin sysem: > pic fieldplo G 4 H, G H, G = 4, H = 5 4 : soln plo G, H, = 3, color = black : display pic, soln, ile = `Glucose vs Insulin phase porrai` ; H Glucose vs Insulin phase porrai G The example we jus worked is linear, and is vasly simplified Bu mahemaicians, docors, bioengineers, pharmaciss, are very ineresed in (especially more realisic) problems like hese
23 Soluions o homogeneous linear sysems of DE's when marix has complex eigenvalues: x = A x Le A be a real number marix Le = a b i C v = i n saisfy A v = v, wih a, b,, n Then z = e v is a complex soluion o x = A x because z = e v and his is equal o A z = A e v = e A v = e v Bu if we wrie z in erms of is real and imaginary pars, z = x i y hen he equaliy z = A z x i y = A x i y = A x i A y Equaing he real and imaginary pars on each side yields x = A x y = A y ie he real and imaginary pars of he complex soluion are each real soluions If A i = a b i i hen i is sraighforward o check ha A i = a b i i Thus he complex conjugae eigenvalue yields he complex conjugae eigenvecor The corresponding complex soluion o he sysem of DEs e a i b i = x i y so yields he same wo real soluions (excep wih a sign change on he second one) Anoher way o undersand how we ge he wo real soluions is o ake he wo complex soluions z = x i y w = x i y and recover x, y as linear combinaions of hese homogeneous soluions: x = 2 z w y = 2 i z w
24 Mah Wed Apr 9 Summary of Chaper 7 so far: Any iniial value problem for a differenial equaion or sysem of differenial equaions can be convered ino an equivalen iniial value problem for a sysem of firs order differenial equaions There is a "shor-ime" exisence-uniqueness heorem for firs order DE iniial value problems x = F, x x = x and soluions can be approximaed using Euler or Runge-Kua ype algorihms A special case of he IVP above is he one for a firs order linear sysem of differenial equaions : x = A x f x = x If he marix A and he vecor funcion f are coninuous on an open inerval I conaining hen a soluion x exiss and is unique, on he enire inerval The general soluion o an inhomogeneous linear sysem of DEs x = A x f ie x A x = f will be of he form x = x P homogeneous sysem x H where x P is a paricular soluion, and x H is he general soluion o he x = A x For A n n and x n he soluion space on he inerval I o he homogeneous problem x = A x ie x A x = is n-dimensional (This is also he "real" reason why he soluion spaces o nh order homogeneous linear DE's are n-dimensional, since hose DE's are equivalen o homogeneous syems of n firs order linear DE s) For A n n a consan marix, we ry o find a basis for he soluion space o x = A x consising of soluions of he form x = e v, where v is an eigenvecor of A wih eigenvalue We will succeed as long as A is diagonalizable Finish 73 Applicaions of firs order sysems of differenial equaions
25 Here are some of he deails from Tuesdday's discussion of he Glucose-insulin model G H = 4 Characerisic polynomial A I = 2 4 has roos = 2 i For he eigenvalue = 2 i we wish o solve he eigenvecor sysem A I v = : R 2 R, 5 R R 2 : 2 i 4 2 i 2 i i 2 Alhough i doesn' look like i, he second row is a muliple of he firs row, as i mus be: ir R 2 R 2 : 2 i So we may choose he eigenvecor v = 2 i, T This yields a complex funcion soluion z = e v = e 2 i 2 i If we rewrie z = x i y wih x, y real vecor funcions, hen each of x, y will be real soluions o he sysem of differenial equaions, and will in fac be a basis (See general discussion a end of Wednesday's noes) A he end of class we did his decomposiion of z ino real and imaginary pars: e 2 i 2 i = e 2 i cos 2 i sin 2 = e cos 2 i sin 2 2 i cos 2 i sin 2 This gives real soluions G H = e 2 sin 2 cos 2 i e x = e 2 sin 2, y = e 2 cos 2 cos 2 sin 2 and general homogeneous soluion using real funcions: x H = c x c 2 y = c e 2 sin 2 c cos 2 2 e 2 cos 2 sin 2 2 cos 2 cos 2
26 The Glucose-insulin example is linearized, and is vasly simplified Bu mahemaicians, docors, bioengineers, pharmaciss, are very ineresed in (especially more realisic) problems like hese Prof Fred Adler and a recen graduae suden Chris Remien in he Mah Deparmen, and collaboraing wih he Universiy Hospial recenly modeled liver poisoning by aceominophen (brand name Tyleonol), by sudying a non-linear sysem of 8 firs order differenial equaions They came up wih a sae of he ar and very useful diagnosic es: hp://unewsuahedu/news_releases/mah-can-save-ylenol-overdose-paiens-2/ Here's a link o heir published paper For fun, I copied and pased he non-linear sysem of firs order differenial equaions from a preprin of heir paper, below: hp://onlinelibrarywileycom/doi/2/hep25656/full hp://wwwmahuahedu/~korevaar/225spring2/adler-remien-preprinpdf
27 Example) consider he hree componen inpu-oupu model below: Exercise a) Derive he firs order sysem for he ank cascade above b) In case he ank volumes (in gallons) are V = 2, V 2 = 4, V 3 = 5, he flow rae r = gal min, and pure waer (wih no solue) is flowing ino he firs (op) ank, show ha your sysem in (a) can be wrien as x 3 = (This sysem is acually worked ou in he ex, page bu we'll modify he IVP, and hen consider a second case as well) x 3
28 c) Here's he eigenvecor daa for he marix in b You may wan o check or derive pars of i by hand, especially if you're sill no exper a finding eigenvalues and eigenvecors I enered he marix enries as raional numbers raher han decimals, alhough in oher problems you'd wan o use decimals Use he eigendaa o wrie down he general soluion o he sysem in b d) Solve he IVP for his ank cascade, assuming ha here are iniially 5 lb of sal in he firs ank, and no sal in he second and hird anks
29 Your answer o d should be 3 = 5 e e e 2 x e) We can plo he amouns of sal in each ank o figure ou wha's going on Make sure you undersand how he formulas below are relaed o he vecor equaion above, and inerpre he graphical resuls > wih plos : > x 5 exp 5 : plo plo x, = 3, color = black : x2 3 exp 5 3 exp 25 : plo2 plo x2, = 3, color = brown : x3 25 exp 5 5 exp exp 2 : plo3 plo x3, = 3, color = green : display plo, plo2, plo3, ile = `polluan flushing in ank cascade` ; > 5 5 polluan flushing in ank cascade 2 3 Exercise 2) Use he same ank cascade Only now, assume ha here is iniially 3 lb sal in he firs ank, none in he ohers, and ha when he waer sars flowing he inpu pipe conains saly waer, wih lb concenraion 5 gal 2a) Explain why his yields an IVP for an inhomogeneous sysem of linear DE's, namely x 3 = x 3 5 x 3 = 3
30 2b) Use a vecor analog of "undeermined coefficiens" o guess ha here migh be a paricular soluion ha is a consan vecor, ie x P = d Plug his guess ino he inhomgeneous sysem o deduce d In oher words, if we wrie he sysem wih he "linear operaor" par of he lef as in Chaper 5, we'd wrie x A x = b and we'd guess ha since he righ side was a consan vecor here migh be a paricular soluion ha was also a consan vecor (wih undeermined enries) 2c) Use x = x P x H o solve he IVP Compare your soluion o he plos below > x 3 exp 5 : plo plo x, = 5, color = black : x2 2 6 exp 5 4 exp 25 : plo2 plo x2, = 5, color = brown : x exp 5 7 exp 25 exp 2 : plo3 plo x3, = 5, color = green : display plo, plo2, plo3, ile = `polluan level sabilizing in ank cascade` ; 2 polluan level sabilizing in ank cascade >
31 Fri Apr 2 74 Mass-spring sysems and unehered mass-spring rains In your homework and lab for his week you sudy special cases of he spring sysems below, wih no damping Alhough we draw he picures horizonally, hey would also hold in verical configuraion if we measure displacemens from equilibrium in he underlying graviaional field Le's make sure we undersand why he naural sysem of DEs and IVP for his sysem is m = k k 2 m 2 = k 2 k 3 = a, = a 2 = b, = b 2 Exercise a) Wha is he dimension of he soluion space o his homogeneous linear sysem of differenial equaions? Why? b) Wha if one had a configuraion of n masses in series, raher han jus 2 masses? Wha would he dimension of he homogeneous soluion space be in his case? Why? Examples:
32 We can wrie he sysem of DEs for he sysem a he op of page in marix-vecor form: m x k k k 2 2 = m x k k k We denoe he diagonal marix on he lef as he "mass marix" M, and he marix on he righ as he spring consan marix K (alhough o be compleely in sync wih Chaper 5 i would be beer o call he spring marix K) All of hese configuraions of masses in series wih springs can be wrien as = M x = K x If we divide each equaion by he reciprocal of he corresponding mass, we can solve for he vecor of acceleraions: k k k 2 2 x m m k 2 m 2 k 2 k 3 m 2, which we wrie as x = A x (You can hink of A as he "acceleraion" marix) Noice ha he simplificaion above is mahemaically idenical o he algebraic operaion of muliplying he firs marix equaion by he (diagonal) inverse of he diagonal mass marix M In all cases: M x = K x x = A x, wih A = M K
33 How o find a basis for he soluion space o conserved-energy mass-spring sysems of DEs x = A x (*) Based on our previous experiences, he naural hing for his homogeneous sysem of linear differenial equaions is o ry and find a basis of soluions of he form x = f v (**) You migh guess ha f = e bu ha urns ou o no be he bes way o go Le's see wha f should equal by subsiuing in our guess! (We would maybe also hink abou firs convering he second order sysem o an equivalen firs order sysem of wice as many DE's, one for for each posiion funcion and one for each velociy funcion, and hen he exponenial guess would work, bu hey'd end up being complex exponenials) Subsiuing (**) ino (*) yields f v = A f v = f A v Since for each, he lef side is a scalar muliple of he consan vecor v, so mus be he righ side So v mus be an eigenvecor of A, A v = v, and if f is a real funcion and if v is a real (as opposed o complex) vecor, hen is also real Then f v = A f v = f v So we mus have So possible f 's are Case ) Case 2) Case 3) f f = f = c c 2 if = f = c cos c 2 sin if, = f = c e c 2 e 2 = if Case 3 will never happen for our mass-spring configuraions, because of conservaion of energy!
34 This leads o he Soluion space algorihm: Consider a very special case of a homogeneous sysem of linear differenial equaions, x = A x If A n n is a diagonalizable marix and if all of is eigenvalues are non-posiive hen for each eigenpair j, v wih here are wo linearly independen sinusoidal soluions o x = A x given by j j x j = cos j v y j j = sin j v j wih And for an eigenpair funcions j, v j wih j j = j = here are wo indpenden soluions given by consan and linear x j = v j y j = v j This procedure consrucs 2 n independen soluions o he sysem x soluion space = A x, ie a basis for he Remark: Wha's amazing is ha he fac ha if he sysem is conservaive, he acceleraion marix will always be diagonalizable, and all of is eigenvalues will be non-posiive In fac, if he sysem is ehered o a leas one wall (as in he firs wo diagrams on page ), all of he eigenvalues will be sricly negaive, and he algorihm above will always yield a basis for he soluion space (If he sysem is no ehered and is free o move as a rain, like he hird diagram on page, hen = will be one of he eigenvalues, and will yield he consan velociy and displacemen conribuion o he soluion space, c c 2 v, where v is he corresponding eigenvecor Togeher wih he soluions from sricly negaive eigenvalues his will sill lead o he general homogeneous soluion)
35 Exercise 2) Consider he special case of he configuraion on page one for which m = m 2 = m and k = k 2 = k 3 = k In his case, he equaion for he vecor of he wo mass acceleraions reduces o 2 k m k m = k m 2 k m a) Find he eigendaa for he marix = k m b) Deduce he eigendaa for he acceleraion marix A which is k imes his marix m c) Find he 4 dimensional soluion space o his wo-mass, hree-spring sysem
36 soluion The general soluion is a superposiion of wo "fundamenal modes" In he slower mode boh masses oscillae "in phase", wih equal ampliudes, and wih angular frequency = k In he faser m mode, boh masses oscillae "ou of phase" wih equal ampliudes, and wih angular frequency 2 = 3 k m The general soluion can be wrien as = C cos C 2 cos 2 2 = c cos c 2 sin c 3 cos 2 c 4 sin 2 Exercise 3) Show ha he general soluion above les you uniquely solve each IVP uniquely This should reinforce he idea ha he soluion space o hese wo second order linear homgeneous DE's is four dimensional 2 k k = m k m m 2 k m = a, = a 2 = b, = b 2
Announcements: Warm-up Exercise:
 Fri Apr 13 7.1 Sysems of differenial equaions - o model muli-componen sysems via comparmenal analysis hp//en.wikipedia.org/wiki/muli-comparmen_model Announcemens Warm-up Exercise Here's a relaively simple
Fri Apr 13 7.1 Sysems of differenial equaions - o model muli-componen sysems via comparmenal analysis hp//en.wikipedia.org/wiki/muli-comparmen_model Announcemens Warm-up Exercise Here's a relaively simple
Math Week 15: Section 7.4, mass-spring systems. These are notes for Monday. There will also be course review notes for Tuesday, posted later.
 Mah 50-004 Week 5: Secion 7.4, mass-spring sysems. These are noes for Monday. There will also be course review noes for Tuesday, posed laer. Mon Apr 3 7.4 mass-spring sysems. Announcemens: Warm up exercise:
Mah 50-004 Week 5: Secion 7.4, mass-spring sysems. These are noes for Monday. There will also be course review noes for Tuesday, posed laer. Mon Apr 3 7.4 mass-spring sysems. Announcemens: Warm up exercise:
Math Week 14 April 16-20: sections first order systems of linear differential equations; 7.4 mass-spring systems.
 Mah 2250-004 Week 4 April 6-20 secions 7.-7.3 firs order sysems of linear differenial equaions; 7.4 mass-spring sysems. Mon Apr 6 7.-7.2 Sysems of differenial equaions (7.), and he vecor Calculus we need
Mah 2250-004 Week 4 April 6-20 secions 7.-7.3 firs order sysems of linear differenial equaions; 7.4 mass-spring sysems. Mon Apr 6 7.-7.2 Sysems of differenial equaions (7.), and he vecor Calculus we need
t is a basis for the solution space to this system, then the matrix having these solutions as columns, t x 1 t, x 2 t,... x n t x 2 t...
 Mah 228- Fri Mar 24 5.6 Marix exponenials and linear sysems: The analogy beween firs order sysems of linear differenial equaions (Chaper 5) and scalar linear differenial equaions (Chaper ) is much sronger
Mah 228- Fri Mar 24 5.6 Marix exponenials and linear sysems: The analogy beween firs order sysems of linear differenial equaions (Chaper 5) and scalar linear differenial equaions (Chaper ) is much sronger
e a s a f t dt f t dt = p = p. t = a
 Mah 225-4 Fri Apr 7 5, EP76 Today we finish discussing Laplace ransform echniques: Impulse forcing ("dela funcions")oday's noes Convoluion formulas o solve any inhomogeneous consan coefficien linear DE,
Mah 225-4 Fri Apr 7 5, EP76 Today we finish discussing Laplace ransform echniques: Impulse forcing ("dela funcions")oday's noes Convoluion formulas o solve any inhomogeneous consan coefficien linear DE,
Mon Apr 9 EP 7.6 Convolutions and Laplace transforms. Announcements: Warm-up Exercise:
 Mah 225-4 Week 3 April 9-3 EP 7.6 - convoluions; 6.-6.2 - eigenvalues, eigenvecors and diagonalizabiliy; 7. - sysems of differenial equaions. Mon Apr 9 EP 7.6 Convoluions and Laplace ransforms. Announcemens:
Mah 225-4 Week 3 April 9-3 EP 7.6 - convoluions; 6.-6.2 - eigenvalues, eigenvecors and diagonalizabiliy; 7. - sysems of differenial equaions. Mon Apr 9 EP 7.6 Convoluions and Laplace ransforms. Announcemens:
Some Basic Information about M-S-D Systems
 Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
Some Basic Informaion abou M-S-D Sysems 1 Inroducion We wan o give some summary of he facs concerning unforced (homogeneous) and forced (non-homogeneous) models for linear oscillaors governed by second-order,
Two Coupled Oscillators / Normal Modes
 Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
Lecure 3 Phys 3750 Two Coupled Oscillaors / Normal Modes Overview and Moivaion: Today we ake a small, bu significan, sep owards wave moion. We will no ye observe waves, bu his sep is imporan in is own
dt = C exp (3 ln t 4 ). t 4 W = C exp ( ln(4 t) 3) = C(4 t) 3.
 Mah Rahman Exam Review Soluions () Consider he IVP: ( 4)y 3y + 4y = ; y(3) = 0, y (3) =. (a) Please deermine he longes inerval for which he IVP is guaraneed o have a unique soluion. Soluion: The disconinuiies
Mah Rahman Exam Review Soluions () Consider he IVP: ( 4)y 3y + 4y = ; y(3) = 0, y (3) =. (a) Please deermine he longes inerval for which he IVP is guaraneed o have a unique soluion. Soluion: The disconinuiies
Section 3.5 Nonhomogeneous Equations; Method of Undetermined Coefficients
 Secion 3.5 Nonhomogeneous Equaions; Mehod of Undeermined Coefficiens Key Terms/Ideas: Linear Differenial operaor Nonlinear operaor Second order homogeneous DE Second order nonhomogeneous DE Soluion o homogeneous
Secion 3.5 Nonhomogeneous Equaions; Mehod of Undeermined Coefficiens Key Terms/Ideas: Linear Differenial operaor Nonlinear operaor Second order homogeneous DE Second order nonhomogeneous DE Soluion o homogeneous
Chapter 6. Systems of First Order Linear Differential Equations
 Chaper 6 Sysems of Firs Order Linear Differenial Equaions We will only discuss firs order sysems However higher order sysems may be made ino firs order sysems by a rick shown below We will have a sligh
Chaper 6 Sysems of Firs Order Linear Differenial Equaions We will only discuss firs order sysems However higher order sysems may be made ino firs order sysems by a rick shown below We will have a sligh
Math 333 Problem Set #2 Solution 14 February 2003
 Mah 333 Problem Se #2 Soluion 14 February 2003 A1. Solve he iniial value problem dy dx = x2 + e 3x ; 2y 4 y(0) = 1. Soluion: This is separable; we wrie 2y 4 dy = x 2 + e x dx and inegrae o ge The iniial
Mah 333 Problem Se #2 Soluion 14 February 2003 A1. Solve he iniial value problem dy dx = x2 + e 3x ; 2y 4 y(0) = 1. Soluion: This is separable; we wrie 2y 4 dy = x 2 + e x dx and inegrae o ge The iniial
Lecture 2-1 Kinematics in One Dimension Displacement, Velocity and Acceleration Everything in the world is moving. Nothing stays still.
 Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
Lecure - Kinemaics in One Dimension Displacemen, Velociy and Acceleraion Everyhing in he world is moving. Nohing says sill. Moion occurs a all scales of he universe, saring from he moion of elecrons in
Predator - Prey Model Trajectories and the nonlinear conservation law
 Predaor - Prey Model Trajecories and he nonlinear conservaion law James K. Peerson Deparmen of Biological Sciences and Deparmen of Mahemaical Sciences Clemson Universiy Ocober 28, 213 Ouline Drawing Trajecories
Predaor - Prey Model Trajecories and he nonlinear conservaion law James K. Peerson Deparmen of Biological Sciences and Deparmen of Mahemaical Sciences Clemson Universiy Ocober 28, 213 Ouline Drawing Trajecories
( ) a system of differential equations with continuous parametrization ( T = R + These look like, respectively:
 XIII. DIFFERENCE AND DIFFERENTIAL EQUATIONS Ofen funcions, or a sysem of funcion, are paramerized in erms of some variable, usually denoed as and inerpreed as ime. The variable is wrien as a funcion of
XIII. DIFFERENCE AND DIFFERENTIAL EQUATIONS Ofen funcions, or a sysem of funcion, are paramerized in erms of some variable, usually denoed as and inerpreed as ime. The variable is wrien as a funcion of
EXERCISES FOR SECTION 1.5
 1.5 Exisence and Uniqueness of Soluions 43 20. 1 v c 21. 1 v c 1 2 4 6 8 10 1 2 2 4 6 8 10 Graph of approximae soluion obained using Euler s mehod wih = 0.1. Graph of approximae soluion obained using Euler
1.5 Exisence and Uniqueness of Soluions 43 20. 1 v c 21. 1 v c 1 2 4 6 8 10 1 2 2 4 6 8 10 Graph of approximae soluion obained using Euler s mehod wih = 0.1. Graph of approximae soluion obained using Euler
Chapter 2. First Order Scalar Equations
 Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
Chaper. Firs Order Scalar Equaions We sar our sudy of differenial equaions in he same way he pioneers in his field did. We show paricular echniques o solve paricular ypes of firs order differenial equaions.
10. State Space Methods
 . Sae Space Mehods. Inroducion Sae space modelling was briefly inroduced in chaper. Here more coverage is provided of sae space mehods before some of heir uses in conrol sysem design are covered in he
. Sae Space Mehods. Inroducion Sae space modelling was briefly inroduced in chaper. Here more coverage is provided of sae space mehods before some of heir uses in conrol sysem design are covered in he
Physics 235 Chapter 2. Chapter 2 Newtonian Mechanics Single Particle
 Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Chaper 2 Newonian Mechanics Single Paricle In his Chaper we will review wha Newon s laws of mechanics ell us abou he moion of a single paricle. Newon s laws are only valid in suiable reference frames,
Solutions of Sample Problems for Third In-Class Exam Math 246, Spring 2011, Professor David Levermore
 Soluions of Sample Problems for Third In-Class Exam Mah 6, Spring, Professor David Levermore Compue he Laplace ransform of f e from is definiion Soluion The definiion of he Laplace ransform gives L[f]s
Soluions of Sample Problems for Third In-Class Exam Mah 6, Spring, Professor David Levermore Compue he Laplace ransform of f e from is definiion Soluion The definiion of he Laplace ransform gives L[f]s
Single and Double Pendulum Models
 Single and Double Pendulum Models Mah 596 Projec Summary Spring 2016 Jarod Har 1 Overview Differen ypes of pendulums are used o model many phenomena in various disciplines. In paricular, single and double
Single and Double Pendulum Models Mah 596 Projec Summary Spring 2016 Jarod Har 1 Overview Differen ypes of pendulums are used o model many phenomena in various disciplines. In paricular, single and double
= ( ) ) or a system of differential equations with continuous parametrization (T = R
 XIII. DIFFERENCE AND DIFFERENTIAL EQUATIONS Ofen funcions, or a sysem of funcion, are paramerized in erms of some variable, usually denoed as and inerpreed as ime. The variable is wrien as a funcion of
XIII. DIFFERENCE AND DIFFERENTIAL EQUATIONS Ofen funcions, or a sysem of funcion, are paramerized in erms of some variable, usually denoed as and inerpreed as ime. The variable is wrien as a funcion of
u(x) = e x 2 y + 2 ) Integrate and solve for x (1 + x)y + y = cos x Answer: Divide both sides by 1 + x and solve for y. y = x y + cos x
 . 1 Mah 211 Homework #3 February 2, 2001 2.4.3. y + (2/x)y = (cos x)/x 2 Answer: Compare y + (2/x) y = (cos x)/x 2 wih y = a(x)x + f(x)and noe ha a(x) = 2/x. Consequenly, an inegraing facor is found wih
. 1 Mah 211 Homework #3 February 2, 2001 2.4.3. y + (2/x)y = (cos x)/x 2 Answer: Compare y + (2/x) y = (cos x)/x 2 wih y = a(x)x + f(x)and noe ha a(x) = 2/x. Consequenly, an inegraing facor is found wih
Differential Equations
 Mah 21 (Fall 29) Differenial Equaions Soluion #3 1. Find he paricular soluion of he following differenial equaion by variaion of parameer (a) y + y = csc (b) 2 y + y y = ln, > Soluion: (a) The corresponding
Mah 21 (Fall 29) Differenial Equaions Soluion #3 1. Find he paricular soluion of he following differenial equaion by variaion of parameer (a) y + y = csc (b) 2 y + y y = ln, > Soluion: (a) The corresponding
KINEMATICS IN ONE DIMENSION
 KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
KINEMATICS IN ONE DIMENSION PREVIEW Kinemaics is he sudy of how hings move how far (disance and displacemen), how fas (speed and velociy), and how fas ha how fas changes (acceleraion). We say ha an objec
System of Linear Differential Equations
 Sysem of Linear Differenial Equaions In "Ordinary Differenial Equaions" we've learned how o solve a differenial equaion for a variable, such as: y'k5$e K2$x =0 solve DE yx = K 5 2 ek2 x C_C1 2$y''C7$y
Sysem of Linear Differenial Equaions In "Ordinary Differenial Equaions" we've learned how o solve a differenial equaion for a variable, such as: y'k5$e K2$x =0 solve DE yx = K 5 2 ek2 x C_C1 2$y''C7$y
Finish reading Chapter 2 of Spivak, rereading earlier sections as necessary. handout and fill in some missing details!
 MAT 257, Handou 6: Ocober 7-2, 20. I. Assignmen. Finish reading Chaper 2 of Spiva, rereading earlier secions as necessary. handou and fill in some missing deails! II. Higher derivaives. Also, read his
MAT 257, Handou 6: Ocober 7-2, 20. I. Assignmen. Finish reading Chaper 2 of Spiva, rereading earlier secions as necessary. handou and fill in some missing deails! II. Higher derivaives. Also, read his
Concourse Math Spring 2012 Worked Examples: Matrix Methods for Solving Systems of 1st Order Linear Differential Equations
 Concourse Mah 80 Spring 0 Worked Examples: Marix Mehods for Solving Sysems of s Order Linear Differenial Equaions The Main Idea: Given a sysem of s order linear differenial equaions d x d Ax wih iniial
Concourse Mah 80 Spring 0 Worked Examples: Marix Mehods for Solving Sysems of s Order Linear Differenial Equaions The Main Idea: Given a sysem of s order linear differenial equaions d x d Ax wih iniial
Week 1 Lecture 2 Problems 2, 5. What if something oscillates with no obvious spring? What is ω? (problem set problem)
 Week 1 Lecure Problems, 5 Wha if somehing oscillaes wih no obvious spring? Wha is ω? (problem se problem) Sar wih Try and ge o SHM form E. Full beer can in lake, oscillaing F = m & = ge rearrange: F =
Week 1 Lecure Problems, 5 Wha if somehing oscillaes wih no obvious spring? Wha is ω? (problem se problem) Sar wih Try and ge o SHM form E. Full beer can in lake, oscillaing F = m & = ge rearrange: F =
Chapter 7: Solving Trig Equations
 Haberman MTH Secion I: The Trigonomeric Funcions Chaper 7: Solving Trig Equaions Le s sar by solving a couple of equaions ha involve he sine funcion EXAMPLE a: Solve he equaion sin( ) The inverse funcions
Haberman MTH Secion I: The Trigonomeric Funcions Chaper 7: Solving Trig Equaions Le s sar by solving a couple of equaions ha involve he sine funcion EXAMPLE a: Solve he equaion sin( ) The inverse funcions
HOMEWORK # 2: MATH 211, SPRING Note: This is the last solution set where I will describe the MATLAB I used to make my pictures.
 HOMEWORK # 2: MATH 2, SPRING 25 TJ HITCHMAN Noe: This is he las soluion se where I will describe he MATLAB I used o make my picures.. Exercises from he ex.. Chaper 2.. Problem 6. We are o show ha y() =
HOMEWORK # 2: MATH 2, SPRING 25 TJ HITCHMAN Noe: This is he las soluion se where I will describe he MATLAB I used o make my picures.. Exercises from he ex.. Chaper 2.. Problem 6. We are o show ha y() =
Math Wednesday March 3, , 4.3: First order systems of Differential Equations Why you should expect existence and uniqueness for the IVP
 Mah 2280 Wednesda March 3, 200 4., 4.3: Firs order ssems of Differenial Equaions Wh ou should epec eisence and uniqueness for he IVP Eample: Consider he iniial value problem relaed o page 4 of his eserda
Mah 2280 Wednesda March 3, 200 4., 4.3: Firs order ssems of Differenial Equaions Wh ou should epec eisence and uniqueness for he IVP Eample: Consider he iniial value problem relaed o page 4 of his eserda
ODEs II, Lecture 1: Homogeneous Linear Systems - I. Mike Raugh 1. March 8, 2004
 ODEs II, Lecure : Homogeneous Linear Sysems - I Mike Raugh March 8, 4 Inroducion. In he firs lecure we discussed a sysem of linear ODEs for modeling he excreion of lead from he human body, saw how o ransform
ODEs II, Lecure : Homogeneous Linear Sysems - I Mike Raugh March 8, 4 Inroducion. In he firs lecure we discussed a sysem of linear ODEs for modeling he excreion of lead from he human body, saw how o ransform
Section 7.4 Modeling Changing Amplitude and Midline
 488 Chaper 7 Secion 7.4 Modeling Changing Ampliude and Midline While sinusoidal funcions can model a variey of behaviors, i is ofen necessary o combine sinusoidal funcions wih linear and exponenial curves
488 Chaper 7 Secion 7.4 Modeling Changing Ampliude and Midline While sinusoidal funcions can model a variey of behaviors, i is ofen necessary o combine sinusoidal funcions wih linear and exponenial curves
!!"#"$%&#'()!"#&'(*%)+,&',-)./0)1-*23)
 "#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
"#"$%&#'()"#&'(*%)+,&',-)./)1-*) #$%&'()*+,&',-.%,/)*+,-&1*#$)()5*6$+$%*,7&*-'-&1*(,-&*6&,7.$%$+*&%'(*8$&',-,%'-&1*(,-&*6&,79*(&,%: ;..,*&1$&$.$%&'()*1$$.,'&',-9*(&,%)?%*,('&5
Solutions from Chapter 9.1 and 9.2
 Soluions from Chaper 9 and 92 Secion 9 Problem # This basically boils down o an exercise in he chain rule from calculus We are looking for soluions of he form: u( x) = f( k x c) where k x R 3 and k is
Soluions from Chaper 9 and 92 Secion 9 Problem # This basically boils down o an exercise in he chain rule from calculus We are looking for soluions of he form: u( x) = f( k x c) where k x R 3 and k is
In this chapter the model of free motion under gravity is extended to objects projected at an angle. When you have completed it, you should
 Cambridge Universiy Press 978--36-60033-7 Cambridge Inernaional AS and A Level Mahemaics: Mechanics Coursebook Excerp More Informaion Chaper The moion of projeciles In his chaper he model of free moion
Cambridge Universiy Press 978--36-60033-7 Cambridge Inernaional AS and A Level Mahemaics: Mechanics Coursebook Excerp More Informaion Chaper The moion of projeciles In his chaper he model of free moion
Math Final Exam Solutions
 Mah 246 - Final Exam Soluions Friday, July h, 204 () Find explici soluions and give he inerval of definiion o he following iniial value problems (a) ( + 2 )y + 2y = e, y(0) = 0 Soluion: In normal form,
Mah 246 - Final Exam Soluions Friday, July h, 204 () Find explici soluions and give he inerval of definiion o he following iniial value problems (a) ( + 2 )y + 2y = e, y(0) = 0 Soluion: In normal form,
Linear Response Theory: The connection between QFT and experiments
 Phys540.nb 39 3 Linear Response Theory: The connecion beween QFT and experimens 3.1. Basic conceps and ideas Q: How do we measure he conduciviy of a meal? A: we firs inroduce a weak elecric field E, and
Phys540.nb 39 3 Linear Response Theory: The connecion beween QFT and experimens 3.1. Basic conceps and ideas Q: How do we measure he conduciviy of a meal? A: we firs inroduce a weak elecric field E, and
MA Study Guide #1
 MA 66 Su Guide #1 (1) Special Tpes of Firs Order Equaions I. Firs Order Linear Equaion (FOL): + p() = g() Soluion : = 1 µ() [ ] µ()g() + C, where µ() = e p() II. Separable Equaion (SEP): dx = h(x) g()
MA 66 Su Guide #1 (1) Special Tpes of Firs Order Equaions I. Firs Order Linear Equaion (FOL): + p() = g() Soluion : = 1 µ() [ ] µ()g() + C, where µ() = e p() II. Separable Equaion (SEP): dx = h(x) g()
3.6 Derivatives as Rates of Change
 3.6 Derivaives as Raes of Change Problem 1 John is walking along a sraigh pah. His posiion a he ime >0 is given by s = f(). He sars a =0from his house (f(0) = 0) and he graph of f is given below. (a) Describe
3.6 Derivaives as Raes of Change Problem 1 John is walking along a sraigh pah. His posiion a he ime >0 is given by s = f(). He sars a =0from his house (f(0) = 0) and he graph of f is given below. (a) Describe
d 1 = c 1 b 2 - b 1 c 2 d 2 = c 1 b 3 - b 1 c 3
 and d = c b - b c c d = c b - b c c This process is coninued unil he nh row has been compleed. The complee array of coefficiens is riangular. Noe ha in developing he array an enire row may be divided or
and d = c b - b c c d = c b - b c c This process is coninued unil he nh row has been compleed. The complee array of coefficiens is riangular. Noe ha in developing he array an enire row may be divided or
Second Order Linear Differential Equations
 Second Order Linear Differenial Equaions Second order linear equaions wih consan coefficiens; Fundamenal soluions; Wronskian; Exisence and Uniqueness of soluions; he characerisic equaion; soluions of homogeneous
Second Order Linear Differenial Equaions Second order linear equaions wih consan coefficiens; Fundamenal soluions; Wronskian; Exisence and Uniqueness of soluions; he characerisic equaion; soluions of homogeneous
After the completion of this section the student. Theory of Linear Systems of ODEs. Autonomous Systems. Review Questions and Exercises
 Chaper V ODE V.5 Sysems of Ordinary Differenial Equaions 45 V.5 SYSTEMS OF FIRST ORDER LINEAR ODEs Objecives: Afer he compleion of his secion he suden - should recall he definiion of a sysem of linear
Chaper V ODE V.5 Sysems of Ordinary Differenial Equaions 45 V.5 SYSTEMS OF FIRST ORDER LINEAR ODEs Objecives: Afer he compleion of his secion he suden - should recall he definiion of a sysem of linear
Math 334 Fall 2011 Homework 11 Solutions
 Dec. 2, 2 Mah 334 Fall 2 Homework Soluions Basic Problem. Transform he following iniial value problem ino an iniial value problem for a sysem: u + p()u + q() u g(), u() u, u () v. () Soluion. Le v u. Then
Dec. 2, 2 Mah 334 Fall 2 Homework Soluions Basic Problem. Transform he following iniial value problem ino an iniial value problem for a sysem: u + p()u + q() u g(), u() u, u () v. () Soluion. Le v u. Then
Let us start with a two dimensional case. We consider a vector ( x,
 Roaion marices We consider now roaion marices in wo and hree dimensions. We sar wih wo dimensions since wo dimensions are easier han hree o undersand, and one dimension is a lile oo simple. However, our
Roaion marices We consider now roaion marices in wo and hree dimensions. We sar wih wo dimensions since wo dimensions are easier han hree o undersand, and one dimension is a lile oo simple. However, our
2.7. Some common engineering functions. Introduction. Prerequisites. Learning Outcomes
 Some common engineering funcions 2.7 Inroducion This secion provides a caalogue of some common funcions ofen used in Science and Engineering. These include polynomials, raional funcions, he modulus funcion
Some common engineering funcions 2.7 Inroducion This secion provides a caalogue of some common funcions ofen used in Science and Engineering. These include polynomials, raional funcions, he modulus funcion
Hint: There's a table of particular solutions at the end of today's notes.
 Mah 8- Fri Apr 4, Finish Wednesday's noes firs Then 94 Forced oscillaion problems via Fourier Series Today we will revisi he forced oscillaion problems of las Friday, where we prediced wheher or no resonance
Mah 8- Fri Apr 4, Finish Wednesday's noes firs Then 94 Forced oscillaion problems via Fourier Series Today we will revisi he forced oscillaion problems of las Friday, where we prediced wheher or no resonance
Solutions to Assignment 1
 MA 2326 Differenial Equaions Insrucor: Peronela Radu Friday, February 8, 203 Soluions o Assignmen. Find he general soluions of he following ODEs: (a) 2 x = an x Soluion: I is a separable equaion as we
MA 2326 Differenial Equaions Insrucor: Peronela Radu Friday, February 8, 203 Soluions o Assignmen. Find he general soluions of he following ODEs: (a) 2 x = an x Soluion: I is a separable equaion as we
5.1 - Logarithms and Their Properties
 Chaper 5 Logarihmic Funcions 5.1 - Logarihms and Their Properies Suppose ha a populaion grows according o he formula P 10, where P is he colony size a ime, in hours. When will he populaion be 2500? We
Chaper 5 Logarihmic Funcions 5.1 - Logarihms and Their Properies Suppose ha a populaion grows according o he formula P 10, where P is he colony size a ime, in hours. When will he populaion be 2500? We
Lab #2: Kinematics in 1-Dimension
 Reading Assignmen: Chaper 2, Secions 2-1 hrough 2-8 Lab #2: Kinemaics in 1-Dimension Inroducion: The sudy of moion is broken ino wo main areas of sudy kinemaics and dynamics. Kinemaics is he descripion
Reading Assignmen: Chaper 2, Secions 2-1 hrough 2-8 Lab #2: Kinemaics in 1-Dimension Inroducion: The sudy of moion is broken ino wo main areas of sudy kinemaics and dynamics. Kinemaics is he descripion
Chapter Three Systems of Linear Differential Equations
 Chaper Three Sysems of Linear Differenial Equaions In his chaper we are going o consier sysems of firs orer orinary ifferenial equaions. These are sysems of he form x a x a x a n x n x a x a x a n x n
Chaper Three Sysems of Linear Differenial Equaions In his chaper we are going o consier sysems of firs orer orinary ifferenial equaions. These are sysems of he form x a x a x a n x n x a x a x a n x n
2. Nonlinear Conservation Law Equations
 . Nonlinear Conservaion Law Equaions One of he clear lessons learned over recen years in sudying nonlinear parial differenial equaions is ha i is generally no wise o ry o aack a general class of nonlinear
. Nonlinear Conservaion Law Equaions One of he clear lessons learned over recen years in sudying nonlinear parial differenial equaions is ha i is generally no wise o ry o aack a general class of nonlinear
dy dx = xey (a) y(0) = 2 (b) y(1) = 2.5 SOLUTION: See next page
 Assignmen 1 MATH 2270 SOLUTION Please wrie ou complee soluions for each of he following 6 problems (one more will sill be added). You may, of course, consul wih your classmaes, he exbook or oher resources,
Assignmen 1 MATH 2270 SOLUTION Please wrie ou complee soluions for each of he following 6 problems (one more will sill be added). You may, of course, consul wih your classmaes, he exbook or oher resources,
MATH 4330/5330, Fourier Analysis Section 6, Proof of Fourier s Theorem for Pointwise Convergence
 MATH 433/533, Fourier Analysis Secion 6, Proof of Fourier s Theorem for Poinwise Convergence Firs, some commens abou inegraing periodic funcions. If g is a periodic funcion, g(x + ) g(x) for all real x,
MATH 433/533, Fourier Analysis Secion 6, Proof of Fourier s Theorem for Poinwise Convergence Firs, some commens abou inegraing periodic funcions. If g is a periodic funcion, g(x + ) g(x) for all real x,
Matlab and Python programming: how to get started
 Malab and Pyhon programming: how o ge sared Equipping readers he skills o wrie programs o explore complex sysems and discover ineresing paerns from big daa is one of he main goals of his book. In his chaper,
Malab and Pyhon programming: how o ge sared Equipping readers he skills o wrie programs o explore complex sysems and discover ineresing paerns from big daa is one of he main goals of his book. In his chaper,
Chapter #1 EEE8013 EEE3001. Linear Controller Design and State Space Analysis
 Chaper EEE83 EEE3 Chaper # EEE83 EEE3 Linear Conroller Design and Sae Space Analysis Ordinary Differenial Equaions.... Inroducion.... Firs Order ODEs... 3. Second Order ODEs... 7 3. General Maerial...
Chaper EEE83 EEE3 Chaper # EEE83 EEE3 Linear Conroller Design and Sae Space Analysis Ordinary Differenial Equaions.... Inroducion.... Firs Order ODEs... 3. Second Order ODEs... 7 3. General Maerial...
Simulation-Solving Dynamic Models ABE 5646 Week 2, Spring 2010
 Simulaion-Solving Dynamic Models ABE 5646 Week 2, Spring 2010 Week Descripion Reading Maerial 2 Compuer Simulaion of Dynamic Models Finie Difference, coninuous saes, discree ime Simple Mehods Euler Trapezoid
Simulaion-Solving Dynamic Models ABE 5646 Week 2, Spring 2010 Week Descripion Reading Maerial 2 Compuer Simulaion of Dynamic Models Finie Difference, coninuous saes, discree ime Simple Mehods Euler Trapezoid
Ordinary Differential Equations
 Ordinary Differenial Equaions 5. Examples of linear differenial equaions and heir applicaions We consider some examples of sysems of linear differenial equaions wih consan coefficiens y = a y +... + a
Ordinary Differenial Equaions 5. Examples of linear differenial equaions and heir applicaions We consider some examples of sysems of linear differenial equaions wih consan coefficiens y = a y +... + a
KEY. Math 334 Midterm III Winter 2008 section 002 Instructor: Scott Glasgow
 KEY Mah 334 Miderm III Winer 008 secion 00 Insrucor: Sco Glasgow Please do NOT wrie on his exam. No credi will be given for such work. Raher wrie in a blue book, or on your own paper, preferably engineering
KEY Mah 334 Miderm III Winer 008 secion 00 Insrucor: Sco Glasgow Please do NOT wrie on his exam. No credi will be given for such work. Raher wrie in a blue book, or on your own paper, preferably engineering
Exam 1 Solutions. 1 Question 1. February 10, Part (A) 1.2 Part (B) To find equilibrium solutions, set P (t) = C = dp
 Exam Soluions Februar 0, 05 Quesion. Par (A) To find equilibrium soluions, se P () = C = = 0. This implies: = P ( P ) P = P P P = P P = P ( + P ) = 0 The equilibrium soluion are hus P () = 0 and P () =..
Exam Soluions Februar 0, 05 Quesion. Par (A) To find equilibrium soluions, se P () = C = = 0. This implies: = P ( P ) P = P P P = P P = P ( + P ) = 0 The equilibrium soluion are hus P () = 0 and P () =..
Matrix Versions of Some Refinements of the Arithmetic-Geometric Mean Inequality
 Marix Versions of Some Refinemens of he Arihmeic-Geomeric Mean Inequaliy Bao Qi Feng and Andrew Tonge Absrac. We esablish marix versions of refinemens due o Alzer ], Carwrigh and Field 4], and Mercer 5]
Marix Versions of Some Refinemens of he Arihmeic-Geomeric Mean Inequaliy Bao Qi Feng and Andrew Tonge Absrac. We esablish marix versions of refinemens due o Alzer ], Carwrigh and Field 4], and Mercer 5]
23.2. Representing Periodic Functions by Fourier Series. Introduction. Prerequisites. Learning Outcomes
 Represening Periodic Funcions by Fourier Series 3. Inroducion In his Secion we show how a periodic funcion can be expressed as a series of sines and cosines. We begin by obaining some sandard inegrals
Represening Periodic Funcions by Fourier Series 3. Inroducion In his Secion we show how a periodic funcion can be expressed as a series of sines and cosines. We begin by obaining some sandard inegrals
15. Vector Valued Functions
 1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
1. Vecor Valued Funcions Up o his poin, we have presened vecors wih consan componens, for example, 1, and,,4. However, we can allow he componens of a vecor o be funcions of a common variable. For example,
Math 2142 Exam 1 Review Problems. x 2 + f (0) 3! for the 3rd Taylor polynomial at x = 0. To calculate the various quantities:
 Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Mah 4 Eam Review Problems Problem. Calculae he 3rd Taylor polynomial for arcsin a =. Soluion. Le f() = arcsin. For his problem, we use he formula f() + f () + f ()! + f () 3! for he 3rd Taylor polynomial
Math 315: Linear Algebra Solutions to Assignment 6
 Mah 35: Linear Algebra s o Assignmen 6 # Which of he following ses of vecors are bases for R 2? {2,, 3, }, {4,, 7, 8}, {,,, 3}, {3, 9, 4, 2}. Explain your answer. To generae he whole R 2, wo linearly independen
Mah 35: Linear Algebra s o Assignmen 6 # Which of he following ses of vecors are bases for R 2? {2,, 3, }, {4,, 7, 8}, {,,, 3}, {3, 9, 4, 2}. Explain your answer. To generae he whole R 2, wo linearly independen
Final Spring 2007
 .615 Final Spring 7 Overview The purpose of he final exam is o calculae he MHD β limi in a high-bea oroidal okamak agains he dangerous n = 1 exernal ballooning-kink mode. Effecively, his corresponds o
.615 Final Spring 7 Overview The purpose of he final exam is o calculae he MHD β limi in a high-bea oroidal okamak agains he dangerous n = 1 exernal ballooning-kink mode. Effecively, his corresponds o
Second-Order Differential Equations
 WWW Problems and Soluions 3.1 Chaper 3 Second-Order Differenial Equaions Secion 3.1 Springs: Linear and Nonlinear Models www m Problem 3. (NonlinearSprings). A bod of mass m is aached o a wall b means
WWW Problems and Soluions 3.1 Chaper 3 Second-Order Differenial Equaions Secion 3.1 Springs: Linear and Nonlinear Models www m Problem 3. (NonlinearSprings). A bod of mass m is aached o a wall b means
MATH 128A, SUMMER 2009, FINAL EXAM SOLUTION
 MATH 28A, SUMME 2009, FINAL EXAM SOLUTION BENJAMIN JOHNSON () (8 poins) [Lagrange Inerpolaion] (a) (4 poins) Le f be a funcion defined a some real numbers x 0,..., x n. Give a defining equaion for he Lagrange
MATH 28A, SUMME 2009, FINAL EXAM SOLUTION BENJAMIN JOHNSON () (8 poins) [Lagrange Inerpolaion] (a) (4 poins) Le f be a funcion defined a some real numbers x 0,..., x n. Give a defining equaion for he Lagrange
SOLUTIONS TO ECE 3084
 SOLUTIONS TO ECE 384 PROBLEM 2.. For each sysem below, specify wheher or no i is: (i) memoryless; (ii) causal; (iii) inverible; (iv) linear; (v) ime invarian; Explain your reasoning. If he propery is no
SOLUTIONS TO ECE 384 PROBLEM 2.. For each sysem below, specify wheher or no i is: (i) memoryless; (ii) causal; (iii) inverible; (iv) linear; (v) ime invarian; Explain your reasoning. If he propery is no
Welcome Back to Physics 215!
 Welcome Back o Physics 215! (General Physics I) Thurs. Jan 19 h, 2017 Lecure01-2 1 Las ime: Syllabus Unis and dimensional analysis Today: Displacemen, velociy, acceleraion graphs Nex ime: More acceleraion
Welcome Back o Physics 215! (General Physics I) Thurs. Jan 19 h, 2017 Lecure01-2 1 Las ime: Syllabus Unis and dimensional analysis Today: Displacemen, velociy, acceleraion graphs Nex ime: More acceleraion
4.5 Constant Acceleration
 4.5 Consan Acceleraion v() v() = v 0 + a a() a a() = a v 0 Area = a (a) (b) Figure 4.8 Consan acceleraion: (a) velociy, (b) acceleraion When he x -componen of he velociy is a linear funcion (Figure 4.8(a)),
4.5 Consan Acceleraion v() v() = v 0 + a a() a a() = a v 0 Area = a (a) (b) Figure 4.8 Consan acceleraion: (a) velociy, (b) acceleraion When he x -componen of he velociy is a linear funcion (Figure 4.8(a)),
Reading from Young & Freedman: For this topic, read sections 25.4 & 25.5, the introduction to chapter 26 and sections 26.1 to 26.2 & 26.4.
 PHY1 Elecriciy Topic 7 (Lecures 1 & 11) Elecric Circuis n his opic, we will cover: 1) Elecromoive Force (EMF) ) Series and parallel resisor combinaions 3) Kirchhoff s rules for circuis 4) Time dependence
PHY1 Elecriciy Topic 7 (Lecures 1 & 11) Elecric Circuis n his opic, we will cover: 1) Elecromoive Force (EMF) ) Series and parallel resisor combinaions 3) Kirchhoff s rules for circuis 4) Time dependence
Wall. x(t) f(t) x(t = 0) = x 0, t=0. which describes the motion of the mass in absence of any external forcing.
 MECHANICS APPLICATIONS OF SECOND-ORDER ODES 7 Mechanics applicaions of second-order ODEs Second-order linear ODEs wih consan coefficiens arise in many physical applicaions. One physical sysems whose behaviour
MECHANICS APPLICATIONS OF SECOND-ORDER ODES 7 Mechanics applicaions of second-order ODEs Second-order linear ODEs wih consan coefficiens arise in many physical applicaions. One physical sysems whose behaviour
Signal and System (Chapter 3. Continuous-Time Systems)
 Signal and Sysem (Chaper 3. Coninuous-Time Sysems) Prof. Kwang-Chun Ho kwangho@hansung.ac.kr Tel: 0-760-453 Fax:0-760-4435 1 Dep. Elecronics and Informaion Eng. 1 Nodes, Branches, Loops A nework wih b
Signal and Sysem (Chaper 3. Coninuous-Time Sysems) Prof. Kwang-Chun Ho kwangho@hansung.ac.kr Tel: 0-760-453 Fax:0-760-4435 1 Dep. Elecronics and Informaion Eng. 1 Nodes, Branches, Loops A nework wih b
SPH3U: Projectiles. Recorder: Manager: Speaker:
 SPH3U: Projeciles Now i s ime o use our new skills o analyze he moion of a golf ball ha was ossed hrough he air. Le s find ou wha is special abou he moion of a projecile. Recorder: Manager: Speaker: 0
SPH3U: Projeciles Now i s ime o use our new skills o analyze he moion of a golf ball ha was ossed hrough he air. Le s find ou wha is special abou he moion of a projecile. Recorder: Manager: Speaker: 0
T L. t=1. Proof of Lemma 1. Using the marginal cost accounting in Equation(4) and standard arguments. t )+Π RB. t )+K 1(Q RB
 Elecronic Companion EC.1. Proofs of Technical Lemmas and Theorems LEMMA 1. Le C(RB) be he oal cos incurred by he RB policy. Then we have, T L E[C(RB)] 3 E[Z RB ]. (EC.1) Proof of Lemma 1. Using he marginal
Elecronic Companion EC.1. Proofs of Technical Lemmas and Theorems LEMMA 1. Le C(RB) be he oal cos incurred by he RB policy. Then we have, T L E[C(RB)] 3 E[Z RB ]. (EC.1) Proof of Lemma 1. Using he marginal
WEEK-3 Recitation PHYS 131. of the projectile s velocity remains constant throughout the motion, since the acceleration a x
 WEEK-3 Reciaion PHYS 131 Ch. 3: FOC 1, 3, 4, 6, 14. Problems 9, 37, 41 & 71 and Ch. 4: FOC 1, 3, 5, 8. Problems 3, 5 & 16. Feb 8, 018 Ch. 3: FOC 1, 3, 4, 6, 14. 1. (a) The horizonal componen of he projecile
WEEK-3 Reciaion PHYS 131 Ch. 3: FOC 1, 3, 4, 6, 14. Problems 9, 37, 41 & 71 and Ch. 4: FOC 1, 3, 5, 8. Problems 3, 5 & 16. Feb 8, 018 Ch. 3: FOC 1, 3, 4, 6, 14. 1. (a) The horizonal componen of he projecile
Today: Falling. v, a
 Today: Falling. v, a Did you ge my es email? If no, make sure i s no in your junk box, and add sbs0016@mix.wvu.edu o your address book! Also please email me o le me know. I will be emailing ou pracice
Today: Falling. v, a Did you ge my es email? If no, make sure i s no in your junk box, and add sbs0016@mix.wvu.edu o your address book! Also please email me o le me know. I will be emailing ou pracice
) were both constant and we brought them from under the integral.
 YIELD-PER-RECRUIT (coninued The yield-per-recrui model applies o a cohor, bu we saw in he Age Disribuions lecure ha he properies of a cohor do no apply in general o a collecion of cohors, which is wha
YIELD-PER-RECRUIT (coninued The yield-per-recrui model applies o a cohor, bu we saw in he Age Disribuions lecure ha he properies of a cohor do no apply in general o a collecion of cohors, which is wha
4.6 One Dimensional Kinematics and Integration
 4.6 One Dimensional Kinemaics and Inegraion When he acceleraion a( of an objec is a non-consan funcion of ime, we would like o deermine he ime dependence of he posiion funcion x( and he x -componen of
4.6 One Dimensional Kinemaics and Inegraion When he acceleraion a( of an objec is a non-consan funcion of ime, we would like o deermine he ime dependence of he posiion funcion x( and he x -componen of
Hamilton- J acobi Equation: Explicit Formulas In this lecture we try to apply the method of characteristics to the Hamilton-Jacobi equation: u t
 M ah 5 2 7 Fall 2 0 0 9 L ecure 1 0 O c. 7, 2 0 0 9 Hamilon- J acobi Equaion: Explici Formulas In his lecure we ry o apply he mehod of characerisics o he Hamilon-Jacobi equaion: u + H D u, x = 0 in R n
M ah 5 2 7 Fall 2 0 0 9 L ecure 1 0 O c. 7, 2 0 0 9 Hamilon- J acobi Equaion: Explici Formulas In his lecure we ry o apply he mehod of characerisics o he Hamilon-Jacobi equaion: u + H D u, x = 0 in R n
Wed Apr continued: solving x = A x when the eigenvalues and eigenvectors are complex. More examples. Announcements: Warm-up Exercise:
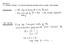 Wed Apr 18 7.3 continued: solving x = A x when the eigenvalues and eigenvectors are complex. More examples. Announcements: Warm-up Exercise: Consider this second order underdamped IVP for x t : x 2 x 5
Wed Apr 18 7.3 continued: solving x = A x when the eigenvalues and eigenvectors are complex. More examples. Announcements: Warm-up Exercise: Consider this second order underdamped IVP for x t : x 2 x 5
Traveling Waves. Chapter Introduction
 Chaper 4 Traveling Waves 4.1 Inroducion To dae, we have considered oscillaions, i.e., periodic, ofen harmonic, variaions of a physical characerisic of a sysem. The sysem a one ime is indisinguishable from
Chaper 4 Traveling Waves 4.1 Inroducion To dae, we have considered oscillaions, i.e., periodic, ofen harmonic, variaions of a physical characerisic of a sysem. The sysem a one ime is indisinguishable from
KEY. Math 334 Midterm III Fall 2008 sections 001 and 003 Instructor: Scott Glasgow
 KEY Mah 334 Miderm III Fall 28 secions and 3 Insrucor: Sco Glasgow Please do NOT wrie on his exam. No credi will be given for such work. Raher wrie in a blue book, or on your own paper, preferably engineering
KEY Mah 334 Miderm III Fall 28 secions and 3 Insrucor: Sco Glasgow Please do NOT wrie on his exam. No credi will be given for such work. Raher wrie in a blue book, or on your own paper, preferably engineering
( ) = Q 0. ( ) R = R dq. ( t) = I t
 ircuis onceps The addiion of a simple capacior o a circui of resisors allows wo relaed phenomena o occur The observaion ha he ime-dependence of a complex waveform is alered by he circui is referred o as
ircuis onceps The addiion of a simple capacior o a circui of resisors allows wo relaed phenomena o occur The observaion ha he ime-dependence of a complex waveform is alered by he circui is referred o as
72 Calculus and Structures
 72 Calculus and Srucures CHAPTER 5 DISTANCE AND ACCUMULATED CHANGE Calculus and Srucures 73 Copyrigh Chaper 5 DISTANCE AND ACCUMULATED CHANGE 5. DISTANCE a. Consan velociy Le s ake anoher look a Mary s
72 Calculus and Srucures CHAPTER 5 DISTANCE AND ACCUMULATED CHANGE Calculus and Srucures 73 Copyrigh Chaper 5 DISTANCE AND ACCUMULATED CHANGE 5. DISTANCE a. Consan velociy Le s ake anoher look a Mary s
Math 2214 Solution Test 1A Spring 2016
 Mah 14 Soluion Tes 1A Spring 016 sec Problem 1: Wha is he larges -inerval for which ( 4) = has a guaraneed + unique soluion for iniial value (-1) = 3 according o he Exisence Uniqueness Theorem? Soluion
Mah 14 Soluion Tes 1A Spring 016 sec Problem 1: Wha is he larges -inerval for which ( 4) = has a guaraneed + unique soluion for iniial value (-1) = 3 according o he Exisence Uniqueness Theorem? Soluion
STATE-SPACE MODELLING. A mass balance across the tank gives:
 B. Lennox and N.F. Thornhill, 9, Sae Space Modelling, IChemE Process Managemen and Conrol Subjec Group Newsleer STE-SPACE MODELLING Inroducion: Over he pas decade or so here has been an ever increasing
B. Lennox and N.F. Thornhill, 9, Sae Space Modelling, IChemE Process Managemen and Conrol Subjec Group Newsleer STE-SPACE MODELLING Inroducion: Over he pas decade or so here has been an ever increasing
KEY. Math 334 Midterm I Fall 2008 sections 001 and 003 Instructor: Scott Glasgow
 1 KEY Mah 4 Miderm I Fall 8 secions 1 and Insrucor: Sco Glasgow Please do NOT wrie on his eam. No credi will be given for such work. Raher wrie in a blue book, or on our own paper, preferabl engineering
1 KEY Mah 4 Miderm I Fall 8 secions 1 and Insrucor: Sco Glasgow Please do NOT wrie on his eam. No credi will be given for such work. Raher wrie in a blue book, or on our own paper, preferabl engineering
2.3 SCHRÖDINGER AND HEISENBERG REPRESENTATIONS
 Andrei Tokmakoff, MIT Deparmen of Chemisry, 2/22/2007 2-17 2.3 SCHRÖDINGER AND HEISENBERG REPRESENTATIONS The mahemaical formulaion of he dynamics of a quanum sysem is no unique. So far we have described
Andrei Tokmakoff, MIT Deparmen of Chemisry, 2/22/2007 2-17 2.3 SCHRÖDINGER AND HEISENBERG REPRESENTATIONS The mahemaical formulaion of he dynamics of a quanum sysem is no unique. So far we have described
18 Biological models with discrete time
 8 Biological models wih discree ime The mos imporan applicaions, however, may be pedagogical. The elegan body of mahemaical heory peraining o linear sysems (Fourier analysis, orhogonal funcions, and so
8 Biological models wih discree ime The mos imporan applicaions, however, may be pedagogical. The elegan body of mahemaical heory peraining o linear sysems (Fourier analysis, orhogonal funcions, and so
Math 334 Test 1 KEY Spring 2010 Section: 001. Instructor: Scott Glasgow Dates: May 10 and 11.
 1 Mah 334 Tes 1 KEY Spring 21 Secion: 1 Insrucor: Sco Glasgow Daes: Ma 1 and 11. Do NOT wrie on his problem saemen bookle, excep for our indicaion of following he honor code jus below. No credi will be
1 Mah 334 Tes 1 KEY Spring 21 Secion: 1 Insrucor: Sco Glasgow Daes: Ma 1 and 11. Do NOT wrie on his problem saemen bookle, excep for our indicaion of following he honor code jus below. No credi will be
Math 115 Final Exam December 14, 2017
 On my honor, as a suden, I have neiher given nor received unauhorized aid on his academic work. Your Iniials Only: Iniials: Do no wrie in his area Mah 5 Final Exam December, 07 Your U-M ID # (no uniqname):
On my honor, as a suden, I have neiher given nor received unauhorized aid on his academic work. Your Iniials Only: Iniials: Do no wrie in his area Mah 5 Final Exam December, 07 Your U-M ID # (no uniqname):
1. VELOCITY AND ACCELERATION
 1. VELOCITY AND ACCELERATION 1.1 Kinemaics Equaions s = u + 1 a and s = v 1 a s = 1 (u + v) v = u + as 1. Displacemen-Time Graph Gradien = speed 1.3 Velociy-Time Graph Gradien = acceleraion Area under
1. VELOCITY AND ACCELERATION 1.1 Kinemaics Equaions s = u + 1 a and s = v 1 a s = 1 (u + v) v = u + as 1. Displacemen-Time Graph Gradien = speed 1.3 Velociy-Time Graph Gradien = acceleraion Area under
Electrical Circuits. 1. Circuit Laws. Tools Used in Lab 13 Series Circuits Damped Vibrations: Energy Van der Pol Circuit
 V() R L C 513 Elecrical Circuis Tools Used in Lab 13 Series Circuis Damped Vibraions: Energy Van der Pol Circui A series circui wih an inducor, resisor, and capacior can be represened by Lq + Rq + 1, a
V() R L C 513 Elecrical Circuis Tools Used in Lab 13 Series Circuis Damped Vibraions: Energy Van der Pol Circui A series circui wih an inducor, resisor, and capacior can be represened by Lq + Rq + 1, a
Chapter Q1. We need to understand Classical wave first. 3/28/2004 H133 Spring
 Chaper Q1 Inroducion o Quanum Mechanics End of 19 h Cenury only a few loose ends o wrap up. Led o Relaiviy which you learned abou las quarer Led o Quanum Mechanics (1920 s-30 s and beyond) Behavior of
Chaper Q1 Inroducion o Quanum Mechanics End of 19 h Cenury only a few loose ends o wrap up. Led o Relaiviy which you learned abou las quarer Led o Quanum Mechanics (1920 s-30 s and beyond) Behavior of
EE100 Lab 3 Experiment Guide: RC Circuits
 I. Inroducion EE100 Lab 3 Experimen Guide: A. apaciors A capacior is a passive elecronic componen ha sores energy in he form of an elecrosaic field. The uni of capaciance is he farad (coulomb/vol). Pracical
I. Inroducion EE100 Lab 3 Experimen Guide: A. apaciors A capacior is a passive elecronic componen ha sores energy in he form of an elecrosaic field. The uni of capaciance is he farad (coulomb/vol). Pracical
Chapter 3 Boundary Value Problem
 Chaper 3 Boundary Value Problem A boundary value problem (BVP) is a problem, ypically an ODE or a PDE, which has values assigned on he physical boundary of he domain in which he problem is specified. Le
Chaper 3 Boundary Value Problem A boundary value problem (BVP) is a problem, ypically an ODE or a PDE, which has values assigned on he physical boundary of he domain in which he problem is specified. Le
Math Spring 2015 PRACTICE FINAL EXAM (modified from Math 2280 final exam, April 29, 2011)
 ame ID number Mah 8- Sring 5 PRACTICE FIAL EXAM (modified from Mah 8 final exam, Aril 9, ) This exam is closed-book and closed-noe You may use a scienific calculaor, bu no one which is caable of grahing
ame ID number Mah 8- Sring 5 PRACTICE FIAL EXAM (modified from Mah 8 final exam, Aril 9, ) This exam is closed-book and closed-noe You may use a scienific calculaor, bu no one which is caable of grahing
