Functions and Limits Peticolas / Megna, Fundamental Photographs, NYC
|
|
|
- Amie Melton
- 5 years ago
- Views:
Transcription
1 Functions and Limits A ball falls faster and faster as time passes. Galileo discovered that the distance fallen is proportional to the square of the time it has been falling. Calculus then enables us to calculate the speed of the ball at an time. 986 Peticolas / Megna, Fundamental Photographs, NYC The fundamental objects that we deal with in calculus are functions. We stress that a function can be represented in different was: b an equation, in a table, b a graph, or in words. We look at the main tpes of functions that occur in calculus and describe the process of using these functions as mathematical models of real-world phenomena. In A Preview of Calculus (page ) we saw how the idea of a it underlies the various branches of calculus. It is therefore appropriate to begin our stud of calculus b investigating its of functions and their properties. 9
2 CHAPTER FUNCTIONS AND LIMITS. Four Was to Represent a Function Year Population (millions) Functions arise whenever one quantit depends on another. Consider the following four situations. A. The area A of a circle depends on the radius r of the circle. The rule that connects r and A is given b the equation A r. With each positive number r there is associated one value of A, and we sa that A is a function of r. B. The human population of the world P depends on the time t. The table gives estimates of the world population P t at time t, for certain ears. For instance, P 95,56,, But for each value of the time t there is a corresponding value of P, and we sa that P is a function of t. C. The cost C of mailing an envelope depends on its weight w. Although there is no simple formula that connects w and C, the post office has a rule for determining C when w is known. D. The vertical acceleration a of the ground as measured b a seismograph during an earthquake is a function of the elapsed time t. Figure shows a graph generated b seismic activit during the Northridge earthquake that shook Los Angeles in 994. For a given value of t, the graph provides a corresponding value of a. a {cm/s@} t (seconds) FIGURE Vertical ground acceleration during the Northridge earthquake _5 Calif. Dept. of Mines and Geolog Each of these eamples describes a rule whereb, given a number ( r, t, w, or t), another number ( A, P, C, or a) is assigned. In each case we sa that the second number is a function of the first number. A function f is a rule that assigns to each element in a set D eactl one element, called f, in a set E. We usuall consider functions for which the sets D and E are sets of real numbers. The set D is called the domain of the function. The number f is the value of f at and is read f of. The range of f is the set of all possible values of f as varies throughout the domain. A smbol that represents an arbitrar number in the domain of a function f is called an independent variable. A smbol that represents a number in the range of f is called a dependent variable. In Eample A, for instance, r is the independent variable and A is the dependent variable.
3 SECTION. FOUR WAYS TO REPRESENT A FUNCTION (input) FIGURE Machine diagram for a function ƒ a f f(a) ƒ (output) ƒ It s helpful to think of a function as a machine (see Figure ). If is in the domain of the function f, then when enters the machine, it s accepted as an input and the machine produces an output f according to the rule of the function. Thus we can think of the domain as the set of all possible inputs and the range as the set of all possible outputs. The preprogrammed functions in a calculator are good eamples of a function as a machine. For eample, the square root ke on our calculator computes such a function. You press the ke labeled s (or s ) and enter the input. If, then is not in the domain of this function; that is, is not an acceptable input, and the calculator will indicate an error. If, then an approimation to s will appear in the displa. Thus the s ke on our calculator is not quite the same as the eact mathematical function f defined b f s. Another wa to picture a function is b an arrow diagram as in Figure 3. Each arrow connects an element of D to an element of E. The arrow indicates that f is associated with, f a is associated with a, and so on. The most common method for visualizing a function is its graph. If f is a function with domain D, then its graph is the set of ordered pairs D FIGURE 3 Arrow diagram for ƒ f E, f D (Notice that these are input-output pairs.) In other words, the graph of f consists of all points, in the coordinate plane such that f and is in the domain of f. The graph of a function f gives us a useful picture of the behavior or life histor of a function. Since the -coordinate of an point, on the graph is f, we can read the value of f from the graph as being the height of the graph above the point (see Figure 4). The graph of f also allows us to picture the domain of f on the -ais and its range on the -ais as in Figure 5. {, ƒ} ƒ range ƒ() f() f() domain FIGURE 4 FIGURE 5 FIGURE 6 The notation for intervals is given in Appendi A. EXAMPLE The graph of a function f is shown in Figure 6. (a) Find the values of f and f 5. (b) What are the domain and range of f? SOLUTION (a) We see from Figure 6 that the point, 3 lies on the graph of f, so the value of f at is f 3. (In other words, the point on the graph that lies above is 3 units above the -ais.) When 5, the graph lies about.7 unit below the -ais, so we estimate that f 5.7. (b) We see that f is defined when 7, so the domain of f is the closed interval, 7. Notice that f takes on all values from to 4, so the range of f is 4, 4
4 CHAPTER FUNCTIONS AND LIMITS - FIGURE 7 (_, ) FIGURE 8 =- (, 4) = EXAMPLE Sketch the graph and find the domain and range of each function. (a) f (b) t SOLUTION (a) The equation of the graph is, and we recognize this as being the equation of a line with slope and -intercept. (Recall the slope-intercept form of the equation of a line: m b. See Appendi B.) This enables us to sketch a portion of the graph of f in Figure 7. The epression is defined for all real numbers, so the domain of f is the set of all real numbers, which we denote b. The graph shows that the range is also. (b) Since t 4 and t, we could plot the points, 4 and,, together with a few other points on the graph, and join them to produce the graph (Figure 8). The equation of the graph is, which represents a parabola (see Appendi C). The domain of t is. The range of t consists of all values of t, that is, all numbers of the form. But for all numbers and an positive number is a square. So the range of t is,. This can also be seen from Figure 8. f a h f a EXAMPLE 3 If f 5 and h, evaluate. h SOLUTION We first evaluate f a h b replacing b a h in the epression for f : f a h a h 5 a h a ah h 5 a h a 4ah h 5a 5h Then we substitute into the given epression and simplif: The epression f a h f a h in Eample 3 is called a difference quotient and occurs frequentl in calculus. As we will see in Chapter, it represents the average rate of change of f between a and a h. f a h f a h a 4ah h 5a 5h a 5a h a 4ah h 5a 5h a 5a h 4ah h 5h h 4a h 5 Representations of Functions There are four possible was to represent a function: verball (b a description in words) numericall (b a table of values) visuall (b a graph) algebraicall (b an eplicit formula) If a single function can be represented in all four was, it s often useful to go from one representation to another to gain additional insight into the function. (In Eample, for instance, we started with algebraic formulas and then obtained the graphs.) But certain functions are described more naturall b one method than b another. With this in mind, let s reeamine the four situations that we considered at the beginning of this section.
5 P t Population (millions) SECTION. FOUR WAYS TO REPRESENT A FUNCTION 3 A. The most useful representation of the area of a circle as a function of its radius is probabl the algebraic formula A r r, though it is possible to compile a table of values or to sketch a graph (half a parabola). Because a circle has to have a positive radius, the domain is r r,, and the range is also,. B. We are given a description of the function in words: P t is the human population of the world at time t. Let s measure t so that t corresponds to the ear 9. The table of values of world population provides a convenient representation of this function. If we plot these values, we get the graph (called a scatter plot) in Figure 9. It too is a useful representation; the graph allows us to absorb all the data at once. What about a formula? Of course, it s impossible to devise an eplicit formula that gives the eact human population P t at an time t. But it is possible to find an epression for a function that approimates P t. In fact, using methods eplained in Section., we obtain the approimation P t f t t Figure shows that it is a reasonabl good fit. The function f is called a mathematical model for population growth. In other words, it is a function with an eplicit formula that approimates the behavior of our given function. We will see, however, that the ideas of calculus can be applied to a table of values; an eplicit formula is not necessar. P 5' 5' t t FIGURE 9 A function defined b a table of values is called a tabular function. w (ounces) w w w 3 3 w 4 4 w 5 C w (dollars) FIGURE The function P is tpical of the functions that arise whenever we attempt to appl calculus to the real world. We start with a verbal description of a function. Then we ma be able to construct a table of values of the function, perhaps from instrument readings in a scientific eperiment. Even though we don t have complete knowledge of the values of the function, we will see throughout the book that it is still possible to perform the operations of calculus on such a function. C. Again the function is described in words: Let C w be the cost of mailing a large envelope with weight w. The rule that the US Postal Service used as of is as follows: The cost is 88 cents for up to oz, plus 7 cents for each additional ounce (or less) up to 3 oz. The table of values shown in the margin is the most convenient representation for this function, though it is possible to sketch a graph (see Eample ). D. The graph shown in Figure is the most natural representation of the vertical acceleration function a t. It s true that a table of values could be compiled, and it is even possible to devise an approimate formula. But everthing a geologist needs to know amplitudes and patterns can be seen easil from the graph. (The same is true for the patterns seen in electrocardiograms of heart patients and polgraphs for lie-detection.)
6 4 CHAPTER FUNCTIONS AND LIMITS T FIGURE t In the net eample we sketch the graph of a function that is defined verball. EXAMPLE 4 When ou turn on a hot-water faucet, the temperature T of the water depends on how long the water has been running. Draw a rough graph of T as a function of the time t that has elapsed since the faucet was turned on. SOLUTION The initial temperature of the running water is close to room temperature because the water has been sitting in the pipes. When the water from the hot-water tank starts flowing from the faucet, T increases quickl. In the net phase, T is constant at the tempera ture of the heated water in the tank. When the tank is drained, T decreases to the temperature of the water suppl. This enables us to make the rough sketch of T as a function of t in Figure. In the following eample we start with a verbal description of a function in a phsical situation and obtain an eplicit algebraic formula. The abilit to do this is a useful skill in solving calculus problems that ask for the maimum or minimum values of quantities. h FIGURE w w 3 v EXAMPLE 5 A rectangular storage container with an open top has a volume of m. The length of its base is twice its width. Material for the base costs $ per square meter; material for the sides costs $6 per square meter. Epress the cost of materials as a function of the width of the base. SOLUTION We draw a diagram as in Figure and introduce notation b letting w and w be the width and length of the base, respectivel, and h be the height. The area of the base is w w w, so the cost, in dollars, of the material for the base is w. Two of the sides have area wh and the other two have area wh, so the cost of the material for the sides is 6 wh wh. The total cost is therefore C w 6 wh wh w 36wh To epress C as a function of w alone, we need to einate h and we do so b using the 3 fact that the volume is m. Thus w w h which gives h w 5 w PS In setting up applied functions as in Eample 5, it ma be useful to review the principles of problem solving as discussed on page 97, particularl Step : Understand the Problem. Domain Convention If a function is given b a formula and the domain is not stated eplicitl, the convention is that the domain is the set of all numbers for which the formula makes sense and defines a real number. Substituting this into the epression for C, we have Therefore the equation epresses C as a function of w. EXAMPLE 6 C w 36w 5 w w 8 C w w 8 w Find the domain of each function. w (a) f s (b) t SOLUTION (a) Because the square root of a negative number is not defined (as a real number), the domain of f consists of all values of such that. This is equivalent to, so the domain is the interval,. w
7 SECTION. FOUR WAYS TO REPRESENT A FUNCTION 5 (b) Since t and division b is not allowed, we see that t is not defined when or. Thus the domain of t is, which could also be written in interval notation as,,, The graph of a function is a curve in the -plane. But the question arises: Which curves in the -plane are graphs of functions? This is answered b the following test. The Vertical Line Test A curve in the -plane is the graph of a function of if and onl if no vertical line intersects the curve more than once. The reason for the truth of the Vertical Line Test can be seen in Figure 3. If each vertical line a intersects a curve onl once, at a, b, then eactl one functional value is defined b f a b. But if a line a intersects the curve twice, at a, b and a, c, then the curve can t represent a function because a function can t assign two different values to a. =a (a, c) =a (a, b) (a, b) FIGURE 3 a a For eample, the parabola shown in Figure 4(a) is not the graph of a function of because, as ou can see, there are vertical lines that intersect the parabola twice. The parabola, however, does contain the graphs of two functions of. Notice that the equation implies, so s. Thus the upper and lower halves of the parabola are the graphs of the functions f s [from Eample 6(a)] and t s. [See Figures 4(b) and (c).] We observe that if we reverse the roles of and, then the equation h does define as a function of (with as the independent variable and as the dependent variable) and the parabola now appears as the graph of the function h. (_, ) FIGURE 4 (a) = - (b) =œ + (c) =_œ +
8 6 CHAPTER FUNCTIONS AND LIMITS Piecewise Defined Functions The functions in the following four eamples are defined b different formulas in dif ferent parts of their domains. Such functions are called piecewise defined functions. v EXAMPLE 7 A function f is defined b f if if Evaluate f, f, and f and sketch the graph. SOLUTION Remember that a function is a rule. For this particular function the rule is the following: First look at the value of the input. If it happens that, then the value of f is. On the other hand, if, then the value of f is. Since, we have f 3. _ FIGURE 5 For a more etensive review of absolute values, see Appendi A. Since, we have f. Since, we have f. How do we draw the graph of f? We observe that if, then f, so the part of the graph of f that lies to the left of the vertical line must coincide with the line, which has slope and -intercept. If, then f, so the part of the graph of f that lies to the right of the line must coincide with the graph of, which is a parabola. This enables us to sketch the graph in Figure 5. The solid dot indicates that the point, is included on the graph; the open dot indicates that the point, is ecluded from the graph. The net eample of a piecewise defined function is the absolute value function. Recall that the absolute value of a number a, denoted b a, is the distance from a to on the real number line. Distances are alwas positive or, so we have For eample, a for ever number a s s 3 3 In general, we have a a a a if a if a = (Remember that if a is negative, then a is positive.) EXAMPLE 8 Sketch the graph of the absolute value function. SOLUTION From the preceding discussion we know that f if if FIGURE 6 Using the same method as in Eample 7, we see that the graph of f coincides with the line to the right of the -ais and coincides with the line to the left of the -ais (see Figure 6).
9 SECTION. FOUR WAYS TO REPRESENT A FUNCTION 7 EXAMPLE 9 Find a formula for the function f graphed in Figure 7. FIGURE 7 SOLUTION The line through, and, has slope m and -intercept b, so its equation is. Thus, for the part of the graph of f that joins, to,, we have f if Point-slope form of the equation of a line: See Appendi B. m The line through, and, has slope m, so its point-slope form is or So we have f if We also see that the graph of f coincides with the -ais for. Putting this information together, we have the following three-piece formula for f : f if if if C w FIGURE 8 EXAMPLE In Eample C at the beginning of this section we considered the cost C w of mailing a large envelope with weight w. In effect, this is a piecewise defined function because, from the table of values on page 3, we have C w if w if w if w 3 if 3 w 4 The graph is shown in Figure 8. You can see wh functions similar to this one are called step functions the jump from one value to the net. Such functions will be studied in Chapter. Smmetr If a function f satisfies f f for ever number in its domain, then f is called an even function. For instance, the function f is even because f f The geometric significance of an even function is that its graph is smmetric with respect
10 8 CHAPTER FUNCTIONS AND LIMITS to the -ais (see Figure 9). This means that if we have plotted the graph of f for, we obtain the entire graph simpl b reflecting this portion about the -ais. f(_) _ ƒ _ ƒ FIGURE 9 An even function FIGURE An odd function If f satisfies f f for ever number in its domain, then f is called an odd function. For eample, the function f 3 is odd because f 3 3 f The graph of an odd function is smmetric about the origin (see Figure ). If we alread have the graph of f for, we can obtain the entire graph b rotating this portion through 8 about the origin. v EXAMPLE Determine whether each of the following functions is even, odd, or neither even nor odd. (a) f 5 (b) t 4 (c) h SOLUTION (a) Therefore f f f is an odd function. (b) So t is even. (c) t 4 4 t h Since h h and h h, we conclude that h is neither even nor odd. The graphs of the functions in Eample are shown in Figure. Notice that the graph of h is smmetric neither about the -ais nor about the origin. f g h FIGURE (a) (b) (c)
11 SECTION. FOUR WAYS TO REPRESENT A FUNCTION 9 =ƒ A f( ) f( ) B C D Increasing and Decreasing Functions The graph shown in Figure rises from A to B, falls from B to C, and rises again from C to D. The function f is said to be increasing on the interval a, b, decreasing on b, c, and increasing again on c, d. Notice that if and are an two numbers between a and b with, then f f. We use this as the defining propert of an increasing function. a b c d A function f is called increasing on an interval I if FIGURE f f whenever in I It is called decreasing on I if = f f whenever in I FIGURE 3 In the definition of an increasing function it is important to realize that the inequalit f f must be satisfied for ever pair of numbers and in I with. You can see from Figure 3 that the function f is decreasing on the interval, and increasing on the interval,.. Eercises. If f s and t u u s u, is it true that f t?. If f is it true that f t? and 3. The graph of a function f is given. (a) State the value of f. (b) Estimate the value of f. (c) For what values of is f? (d) Estimate the value of such that f. (e) State the domain and range of f. (f) On what interval is f increasing? 4. The graphs of f and t are given. (a) State the values of f 4 and t 3. (b) For what values of is f t? t (c) Estimate the solution of the equation f. (d) On what interval is f decreasing? (e) State the domain and range of f. (f) State the domain and range of t. f 5. Figure was recorded b an instrument operated b the California Department of Mines and Geolog at the Universit Hospital of the Universit of Southern California in Los Angeles. Use it to estimate the range of the vertical ground acceleration function at USC during the Northridge earthquake. 6. In this section we discussed eamples of ordinar, everda functions: Population is a function of time, postage cost is a function of weight, water temperature is a function of time. Give three other eamples of functions from everda life that are described verball. What can ou sa about the domain and range of each of our functions? If possible, sketch a rough graph of each function. g. Homework Hints available at stewartcalculus.com
12 CHAPTER FUNCTIONS AND LIMITS 7 Determine whether the curve is the graph of a function of. If it is, state the domain and range of the function. in words what the graph tells ou about this race. Who won the race? Did each runner finish the race? (m) A B C 9.. t (s). The graph shown gives the weight of a certain person as a function of age. Describe in words how this person s weight varies over time. What do ou think happened when this person was 3 ears old? weight (pounds). The graph shows the height of the water in a bathtub as a function of time. Give a verbal description of what ou think happened. height (inches) age (ears) time (min) 3. You put some ice cubes in a glass, fill the glass with cold water, and then let the glass sit on a table. Describe how the temperature of the water changes as time passes. Then sketch a rough graph of the temperature of the water as a function of the elapsed time. 4. Three runners compete in a -meter race. The graph depicts the distance run as a function of time for each runner. Describe 5. The graph shows the power consumption for a da in September in San Francisco. ( P is measured in megawatts; t is mea - sured in hours starting at midnight.) (a) What was the power consumption at 6 AM? At 6 PM? (b) When was the power consumption the lowest? When was it the highest? Do these times seem reasonable? P t Pacific Gas & Electric 6. Sketch a rough graph of the number of hours of dalight as a function of the time of ear. 7. Sketch a rough graph of the outdoor temperature as a function of time during a tpical spring da. 8. Sketch a rough graph of the market value of a new car as a function of time for a period of ears. Assume the car is well maintained. 9. Sketch the graph of the amount of a particular brand of coffee sold b a store as a function of the price of the coffee.. You place a frozen pie in an oven and bake it for an hour. Then ou take it out and let it cool before eating it. Describe how the temperature of the pie changes as time passes. Then sketch a rough graph of the temperature of the pie as a function of time.. A homeowner mows the lawn ever Wednesda afternoon. Sketch a rough graph of the height of the grass as a function of time over the course of a four-week period.. An airplane takes off from an airport and lands an hour later at another airport, 4 miles awa. If t represents the time in minutes since the plane has left the terminal building, let t be
13 SECTION. FOUR WAYS TO REPRESENT A FUNCTION the horizontal distance traveled and t be the altitude of the plane. (a) Sketch a possible graph of t. (b) Sketch a possible graph of t. (c) Sketch a possible graph of the ground speed. (d) Sketch a possible graph of the vertical velocit. 35. h 36. s F p s sp f u u u 3. The number N (in millions) of US cellular phone subscribers is shown in the table. (Midear estimates are given.) (a) Use the data to sketch a rough graph of N as a function of (b) Use our graph to estimate the number of cell-phone subscribers at midear in and Temperature readings T (in F) were recorded ever two hours from midnight to : PM in Phoeni on September, 8. The time t was measured in hours from midnight. (a) Use the readings to sketch a rough graph of T as a function of t. (b) Use our graph to estimate the temperature at 9: AM. 5. If f 3, find f, f, f a, f a, f a, f a, f a, f a, [ f a ], and f a h. 6. A spherical balloon with radius r inches has volume V r 4 3 r 3. Find a function that represents the amount of air required to inflate the balloon from a radius of r inches to a radius of r inches. 7 3 Evaluate the difference quotient for the given function. Simplif our answer. 7. f 4 3, 8. f 3, 9. f, t N t T f a h f a h f f a a f 3 h f 3 h t. 38. Find the domain and range and sketch the graph of the function h s Find the domain and sketch the graph of the function. 39. f.4 4. F 4. f t t t t s G 3 f f 3 5 f 9 f 6 if if if if if if if 3 if 3 if Find an epression for the function whose graph is the given curve. 5. The line segment joining the points, 3 and 5, 7 5. The line segment joining the points 5, and 7, 53. The bottom half of the parabola 54. The top half of the circle H t 4 t t F t 3. f 3, f f 3 37 Find the domain of the function. 3. f f f t s 3 t 34. t t s3 t s t 57 6 Find a formula for the described function and state its domain. 57. A rectangle has perimeter m. Epress the area of the rect - angle as a function of the length of one of its sides.
14 CHAPTER FUNCTIONS AND LIMITS 58. A rectangle has area 6 m. Epress the perimeter of the rectangle as a function of the length of one of its sides. 59. Epress the area of an equilateral triangle as a function of the length of a side. 6. Epress the surface area of a cube as a function of its volume An open rectangular bo with volume m has a square base. Epress the surface area of the bo as a function of the length of a side of the base. 6. A Norman window has the shape of a rectangle surmounted b a semicircle. If the perimeter of the window is 3 ft, epress the area A of the window as a function of the width of the window. 67. In a certain countr, income ta is assessed as follows. There is no ta on income up to $,. An income over $, is taed at a rate of %, up to an income of $,. An income over $, is taed at 5%. (a) Sketch the graph of the ta rate R as a function of the income I. (b) How much ta is assessed on an income of $4,? On $6,? (c) Sketch the graph of the total assessed ta T as a function of the income I. 68. The functions in Eample and Eercise 67 are called step functions because their graphs look like stairs. Give two other eamples of step functions that arise in everda life Graphs of f and t are shown. Decide whether each function is even, odd, or neither. Eplain our reasoning g f f g 63. A bo with an open top is to be constructed from a rectangular piece of cardboard with dimensions in. b in. b cutting out equal squares of side at each corner and then folding up the sides as in the figure. Epress the vol ume V of the bo as a function of. 7. (a) If the point 5, 3 is on the graph of an even function, what other point must also be on the graph? (b) If the point 5, 3 is on the graph of an odd function, what other point must also be on the graph? 7. A function f has domain 5, 5 and a portion of its graph is shown. (a) Complete the graph of f if it is known that f is even. (b) Complete the graph of f if it is known that f is odd. 64. A cell phone plan has a basic charge of $35 a month. The plan includes 4 free minutes and charges cents for each additional minute of usage. Write the monthl cost C as a function of the number of minutes used and graph C as a function of for In a certain state the maimum speed permitted on freewas is 65 mi h and the minimum speed is 4 mi h. The fine for violating these its is $5 for ever mile per hour above the maimum speed or below the minimum speed. Epress the amount of the fine F as a function of the driving speed and graph F for. 66. An electricit compan charges its customers a base rate of $ a month, plus 6 cents per kilowatt-hour (kwh) for the first kwh and 7 cents per kwh for all usage over kwh. Epress the monthl cost E as a function of the amount of electricit used. Then graph the function E for. _ Determine whether f is even, odd, or neither. If ou have a graphing calculator, use it to check our answer visuall. 73. f f 76. f 4 f 77. f f
15 SECTION. MATHEMATICAL MODELS: A CATALOG OF ESSENTIAL FUNCTIONS If f and t are both even functions, is f t even? If f and t are both odd functions, is f t odd? What if f is even and t is odd? Justif our answers. 8. If f and t are both even functions, is the product ft even? If f and t are both odd functions, is ft odd? What if f is even and t is odd? Justif our answers.. Mathematical Models: A Catalog of Essential Functions A mathematical model is a mathematical description (often b means of a function or an equation) of a real-world phenomenon such as the size of a population, the demand for a product, the speed of a falling object, the concentration of a product in a chemical reaction, the life epectanc of a person at birth, or the cost of emission reductions. The purpose of the model is to understand the phenomenon and perhaps to make predictions about future behavior. Figure illustrates the process of mathematical modeling. Given a real-world problem, our first task is to formulate a mathematical model b identifing and naming the independent and dependent variables and making assumptions that simplif the phenomenon enough to make it mathematicall tractable. We use our knowledge of the phsical situation and our mathematical skills to obtain equations that relate the variables. In situations where there is no phsical law to guide us, we ma need to collect data (either from a librar or the Internet or b conducting our own eperiments) and eamine the data in the form of a table in order to discern patterns. From this numeri cal representation of a function we ma wish to obtain a graphical representation b plotting the data. The graph might even suggest a suitable algebraic formula in some cases. Real-world problem Formulate Mathematical Solve Mathematical Interpret model conclusions Real-world predictions Test FIGURE The modeling process The second stage is to appl the mathematics that we know (such as the calculus that will be developed throughout this book) to the mathematical model that we have formulated in order to derive mathematical conclusions. Then, in the third stage, we take those mathematical conclusions and interpret them as information about the original real-world phenomenon b wa of offering eplanations or making predictions. The final step is to test our predictions b checking against new real data. If the predictions don t compare well with realit, we need to refine our model or to formulate a new model and start the ccle again. A mathematical model is never a completel accurate representation of a phsical situation it is an idealization. A good model simplifies realit enough to permit mathematical calculations but is accurate enough to provide valuable conclusions. It is important to realize the itations of the model. In the end, Mother Nature has the final sa. There are man different tpes of functions that can be used to model relationships observed in the real world. In what follows, we discuss the behavior and graphs of these functions and give eamples of situations appropriatel modeled b such functions. The coordinate geometr of lines is reviewed in Appendi B. Linear Models When we sa that is a linear function of, we mean that the graph of the function is a line, so we can use the slope-intercept form of the equation of a line to write a formula for
16 4 CHAPTER FUNCTIONS AND LIMITS the function as f m b where m is the slope of the line and b is the -intercept. A characteristic feature of linear functions is that the grow at a constant rate. For instance, Figure shows a graph of the linear function f 3 and a table of sample values. Notice that whenever increases b., the value of f increases b.3. So f increases three times as fast as. Thus the slope of the graph 3, namel 3, can be interpreted as the rate of change of with respect to. _ =3- f FIGURE v EXAMPLE (a) As dr air moves upward, it epands and cools. If the ground temperature is C and the temperature at a height of km is C, epress the temperature T (in C) as a function of the height h (in kilometers), assuming that a linear model is appropriate. (b) Draw the graph of the function in part (a). What does the slope represent? (c) What is the temperature at a height of.5 km? SOLUTION (a) Because we are assuming that T is a linear function of h, we can write We are given that T when h, so T mh b m b b In other words, the -intercept is b. We are also given that T when h, so T m The slope of the line is therefore m and the required linear function is T=_h+ T h 3 h (b) The graph is sketched in Figure 3. The slope is m C km, and this represents the rate of change of temperature with respect to height. (c) At a height of h.5 km, the temperature is FIGURE 3 T.5 5 C
17 SECTION. MATHEMATICAL MODELS: A CATALOG OF ESSENTIAL FUNCTIONS 5 If there is no phsical law or principle to help us formulate a model, we construct an empirical model, which is based entirel on collected data. We seek a curve that fits the data in the sense that it captures the basic trend of the data points. v EXAMPLE Table lists the average carbon dioide level in the atmosphere, measured in parts per million at Mauna Loa Observator from 98 to 8. Use the data in Table to find a model for the carbon dioide level. SOLUTION We use the data in Table to make the scatter plot in Figure 4, where t represents time (in ears) and C represents the CO level (in parts per million, ppm). C TABLE 38 CO level CO level Year (in ppm) Year (in ppm) t FIGURE 4 Scatter plot for the average CO level Notice that the data points appear to lie close to a straight line, so it s natural to choose a linear model in this case. But there are man possible lines that approimate these data points, so which one should we use? One possibilit is the line that passes through the first and last data points. The slope of this line is and its equation is or C t 98 C.675t Equation gives one possible linear model for the carbon dioide level; it is graphed in Figure 5. C FIGURE 5 Linear model through first and last data points t
18 6 CHAPTER FUNCTIONS AND LIMITS A computer or graphing calculator finds the regression line b the method of least squares, which is to minimize the sum of the squares of the vertical distances between the data points and the line. The details are eplained in Section 4.7. Notice that our model gives values higher than most of the actual CO levels. A better linear model is obtained b a procedure from statistics called linear regression. If we use a graphing calculator, we enter the data from Table into the data editor and choose the linear regression command. (With Maple we use the fit[leastsquare] command in the stats package; with Mathematica we use the Fit command.) The machine gives the slope and -intercept of the regression line as m.6549 b So our least squares model for the CO level is C.6549t In Figure 6 we graph the regression line as well as the data points. Comparing with Figure 5, we see that it gives a better fit than our previous linear model. C FIGURE 6 The regression line t v EXAMPLE 3 Use the linear model given b Equa tion to estimate the average CO level for 987 and to predict the level for the ear 5. According to this model, when will the CO level eceed 4 parts per million? SOLUTION Using Equation with t 987, we estimate that the average CO level in 987 was C This is an eample of interpolation because we have estimated a value between observed values. (In fact, the Mauna Loa Observator reported that the average CO level in 987 was ppm, so our estimate is quite accurate.) With t 5, we get So we predict that the average CO level in the ear 5 will be ppm. This is an eample of etrapolation because we have predicted a value outside the region of observations. Consequentl, we are far less certain about the accurac of our prediction. Using Equation, we see that the CO level eceeds 4 ppm when Solving this inequalit, we get C t t
19 SECTION. MATHEMATICAL MODELS: A CATALOG OF ESSENTIAL FUNCTIONS 7 We therefore predict that the CO level will eceed 4 ppm b the ear 3. This pre diction is risk because it involves a time quite remote from our observations. In fact, we see from Figure 6 that the trend has been for CO levels to increase rather more rapidl in recent ears, so the level might eceed 4 ppm well before 3. Polnomials A function P is called a polnomial if P a n n a n n a a a where nis a nonnegative integer and the numbers a, a, a,..., a n are constants called the coefficients of the polnomial. The domain of an polnomial is,. If the leading coefficient a n, then the degree of the polnomial is n. For eample, the function P s is a polnomial of degree 6. A polnomial of degree is of the form P m b and so it is a linear function. A polnomial of degree is of the form P a b c and is called a quadratic function. Its graph is alwas a parabola obtained b shifting the parabola a, as we will see in the net section. The parabola opens upward if a and downward if a. (See Figure 7.) FIGURE 7 The graphs of quadratic functions are parabolas. (a) = ++ (b) =_ +3+ A polnomial of degree 3 is of the form P a 3 b c d a and is called a cubic function. Figure 8 shows the graph of a cubic function in part (a) and graphs of polnomials of degrees 4 and 5 in parts (b) and (c). We will see later wh the graphs have these shapes. FIGURE 8 (a) = -+ (b) =$-3 + (c) =3%-5 +6
20 8 CHAPTER FUNCTIONS AND LIMITS Polnomials are commonl used to model various quantities that occur in the natural and social sciences. For instance, in Section.7 we will eplain wh economists often use a polnomial P to represent the cost of producing units of a commodit. In the following eample we use a quadratic function to model the fall of a ball. Time (seconds) TABLE Height (meters) EXAMPLE 4 A ball is dropped from the upper observation deck of the CN Tower, 45 m above the ground, and its height h above the ground is recorded at -second intervals in Table. Find a model to fit the data and use the model to predict the time at which the ball hits the ground. SOLUTION We draw a scatter plot of the data in Figure 9 and observe that a linear model is inappropriate. But it looks as if the data points might lie on a parabola, so we tr a quadratic model instead. Using a graphing calculator or computer algebra sstem (which uses the least squares method), we obtain the following quadratic model: h (meters) 3 h t 4.9t h t (seconds) t FIGURE 9 Scatter plot for a falling ball FIGURE Quadratic model for a falling ball In Figure we plot the graph of Equation 3 together with the data points and see that the quadratic model gives a ver good fit. The ball hits the ground when h, so we solve the quadratic equation 4.9t.96t The quadratic formula gives t.96 s The positive root is t 9.67, so we predict that the ball will hit the ground after about 9.7 seconds. Power Functions A function of the form f a, where a is a constant, is called a power function. We consider several cases.
21 SECTION. MATHEMATICAL MODELS: A CATALOG OF ESSENTIAL FUNCTIONS 9 (i) a n, where n is a positive integer The graphs of f n for n,, 3, 4, and 5 are shown in Figure. (These are polnomials with onl one term.) We alread know the shape of the graphs of (a line through the origin with slope ) and [a parabola, see Eample (b) in Section.]. = = =# =$ =% FIGURE Graphs of ƒ= n for n=,, 3, 4, 5 The general shape of the graph of f n depends on whether n is even or odd. If n is even, then f n is an even function and its graph is similar to the parabola. If n is odd, then f n is an odd function and its graph is similar to that of 3. Notice from Figure, however, that as n increases, the graph of n becomes flatter near and steeper when. (If is small, then is smaller, 3 is even smaller, 4 is smaller still, and so on.) =$ (_, ) =^ (, ) = =# (, ) =% FIGURE Families of power functions (_, _) (ii) a n, where n is a positive integer The function f n s n is a root function. For n it is the square root function f s, whose domain is, and whose graph is the upper half of the parabola. [See Figure 3(a).] For other even values of n, the graph of s n is similar to that of s. For n 3 we have the cube root function f s 3 whose domain is (recall that ever real number has a cube root) and whose graph is shown in Figure 3(b). The graph of s n for n odd n 3 is similar to that of s 3. (, ) (, ) FIGURE 3 Graphs of root functions (a) ƒ=œ (b) ƒ=œ
22 3 CHAPTER FUNCTIONS AND LIMITS =Δ (iii) a The graph of the reciprocal function f is shown in Figure 4. Its graph has the equation, or, and is a hperbola with the coordinate aes as its asmptotes. This function arises in phsics and chemistr in connection with Bole s Law, which sas that, when the temperature is constant, the volume V of a gas is inversel proportional to the pressure P: V C P FIGURE 4 The reciprocal function where C is a constant. Thus the graph of V as a function of P (see Figure 5) has the same general shape as the right half of Figure 4. V FIGURE 5 Volume as a function of pressure at constant temperature P Power functions are also used to model species-area relationships (Eercises 6 7), illumination as a function of a distance from a light source (Eercise 5), and the period of revolution of a planet as a function of its distance from the sun (Eercise 8). Rational Functions A rational function f is a ratio of two polnomials: f P Q where P and Q are polnomials. The domain consists of all values of such that Q. A simple eample of a rational function is the function f, whose domain is ; this is the reciprocal function graphed in Figure 4. The function f 4 4 FIGURE 6 ƒ= $ is a rational function with domain. Its graph is shown in Figure 6. Algebraic Functions A function f is called an algebraic function if it can be constructed using algebraic operations (such as addition, subtraction, multiplication, division, and taking roots) starting with polnomials. An rational function is automaticall an algebraic function. Here are two more eamples: f s t 4 6 s s 3 When we sketch algebraic functions in Chapter 3, we will see that their graphs can assume a variet of shapes. Figure 7 illustrates some of the possibilities.
23 SECTION. MATHEMATICAL MODELS: A CATALOG OF ESSENTIAL FUNCTIONS 3 _3 5 FIGURE 7 (a) ƒ=œ +3 (b) =$œ -5 (c) h()=@?#(-)@ An eample of an algebraic function occurs in the theor of relativit. The mass of a particle with velocit v is m f v s v c where m is the rest mass of the particle and c 3. 5 km s is the speed of light in a vacuum. m The Reference Pages are located at the front and back of the book. Trigonometric Functions Trigonometr and the trigonometric functions are reviewed on Reference Page and also in Appendi D. In calculus the convention is that radian measure is alwas used (ecept when otherwise indicated). For eample, when we use the function f sin, it is understood that sin means the sine of the angle whose radian measure is. Thus the graphs of the sine and cosine functions are as shown in Figure 8. π _ 3π _π π _ π 3π _π _ π π π 5π 3π _ π 3π π 5π (a) ƒ=sin (b) =cos FIGURE 8 Notice that for both the sine and cosine functions the domain is, and the range is the closed interval,. Thus, for all values of, we have sin cos or, in terms of absolute values, sin cos Also, the zeros of the sine function occur at the integer multiples of ; that is, sin when n n an integer An important propert of the sine and cosine functions is that the are periodic functions and have period. This means that, for all values of, sin sin cos cos
24 3 CHAPTER FUNCTIONS AND LIMITS The periodic nature of these functions makes them suitable for modeling repetitive phenomena such as tides, vibrating springs, and sound waves. For instance, in Eample 4 in Section.3 we will see that a reasonable model for the number of hours of dalight in Philadelphia t das after Januar is given b the function L t.8 sin 365 t 8 The tangent function is related to the sine and cosine functions b the equation 3π π π _ π π 3π tan sin cos and its graph is shown in Figure 9. It is undefined whenever cos, that is, when, 3,... Its range is,. Notice that the tangent function has period : FIGURE 9 =tan (a) = FIGURE =log =log (b) =(.5) tan tan for all The remaining three trigonometric functions (cosecant, secant, and cotangent) are the reciprocals of the sine, cosine, and tangent functions. Their graphs are shown in Appendi D. Eponential Functions The eponential functions are the functions of the form f a, where the base a is a positive constant. The graphs of and.5 are shown in Figure. In both cases the domain is, and the range is,. Eponential functions will be studied in detail in Chapter 6, and we will see that the are useful for modeling man natural phenomena, such as population growth ( if a ) and radioactive deca ( if a. Logarithmic Functions The logarithmic functions f log a, where the base a is a positive constant, are the inverse functions of the eponential functions. The will be studied in Chapter 6. Figure shows the graphs of four logarithmic functions with various bases. In each case the domain is,, the range is,, and the function increases slowl when. =log =log EXAMPLE 5 Classif the following functions as one of the tpes of functions that we have discussed. (a) f 5 (b) t 5 (c) h s (d) u t t 5t 4 FIGURE SOLUTION (a) f 5 is an eponential function. (The is the eponent.) (b) t 5 is a power function. (The is the base.) We could also consider it to be a polnomial of degree 5. (c) h is an algebraic function. s (d) u t t 5t 4 is a polnomial of degree 4.
25 SECTION. MATHEMATICAL MODELS: A CATALOG OF ESSENTIAL FUNCTIONS 33. Eercises Classif each function as a power function, root function, polnomial (state its degree), rational function, algebraic function, trigonometric function, eponential function, or logarithmic function.. (a) f log (b) t s 4 (c) h 3 (e) v t 5 t (c) 3 (e) s s (d) (f) w sin cos. (a) (b) 3 4 Match each equation with its graph. Eplain our choices. (Don t use a computer or graphing calculator.) f f G 5. (a) Find an equation for the famil of linear functions with slope and sketch several members of the famil. (b) Find an equation for the famil of linear functions such that f and sketch several members of the famil. (c) Which function belongs to both families? (d) (f) 3. (a) (b) 5 (c) 8 4. (a) 3 (b) 3 (c) 3 (d) s 3 F u t.t.54t tan t cos t s 3 s 3 g h g 6. What do all members of the famil of linear functions f m 3 have in common? Sketch several members of the famil. 7. What do all members of the famil of linear functions f c have in common? Sketch several members of the famil. 8. Find epressions for the quadratic functions whose graphs are shown. f 3 (4, ) (_, ) 9. Find an epression for a cubic function f if f 6 and f f f.. Recent studies indicate that the average surface temperature of the earth has been rising steadil. Some scientists have modeled the temperature b the linear function T.t 8.5, where T is temperature in C and t represents ears since 9. (a) What do the slope and T-intercept represent? (b) Use the equation to predict the average global surface temperature in.. If the recommended adult dosage for a drug is D ( in mg), then to determine the appropriate dosage c for a child of age a, pharmacists use the equation c.47d a. Suppose the dosage for an adult is mg. (a) Find the slope of the graph of c. What does it represent? (b) What is the dosage for a newborn?. The manager of a weekend flea market knows from past eperience that if he charges dollars for a rental space at the market, then the number of spaces he can rent is given b the equation 4. (a) Sketch a graph of this linear function. (Remember that the rental charge per space and the number of spaces rented can t be negative quantities.) (b) What do the slope, the -intercept, and the -intercept of the graph represent? 3. The relationship between the Fahrenheit F and Celsius C temperature scales is given b the linear function F 9 5 C 3. (a) Sketch a graph of this function. (b) What is the slope of the graph and what does it represent? What is the F-intercept and what does it represent? 4. Jason leaves Detroit at : PM and drives at a constant speed west along I-96. He passes Ann Arbor, 4 mi from Detroit, at :5 PM. (a) Epress the distance traveled in terms of the time elapsed. g (, ) (, _.5) ; Graphing calculator or computer required. Homework Hints available at stewartcalculus.com
26 34 CHAPTER FUNCTIONS AND LIMITS (b) Draw the graph of the equation in part (a). (c) What is the slope of this line? What does it represent?. (a) (b) 5. Biologists have noticed that the chirping rate of crickets of a certain species is related to temperature, and the relationship appears to be ver nearl linear. A cricket produces 3 chirps per minute at 7 F and 73 chirps per minute at 8 F. (a) Find a linear equation that models the temperature T as a function of the number of chirps per minute N. (b) What is the slope of the graph? What does it represent? (c) If the crickets are chirping at 5 chirps per minute, estimate the temperature. 6. The manager of a furniture factor finds that it costs $ to manufacture chairs in one da and $48 to produce 3 chairs in one da. (a) Epress the cost as a function of the number of chairs produced, assuming that it is linear. Then sketch the graph. (b) What is the slope of the graph and what does it represent? (c) What is the -intercept of the graph and what does it represent? 7. At the surface of the ocean, the water pressure is the same as the air pressure above the water, 5 lb in. Below the surface, the water pressure increases b 4.34 lb in for ever ft of descent. (a) Epress the water pressure as a function of the depth below the ocean surface. (b) At what depth is the pressure lb in? 8. The monthl cost of driving a car depends on the number of miles driven. Lnn found that in Ma it cost her $38 to drive 48 mi and in June it cost her $46 to drive 8 mi. (a) Epress the monthl cost C as a function of the distance driven d, assuming that a linear relationship gives a suitable model. (b) Use part (a) to predict the cost of driving 5 miles per month. (c) Draw the graph of the linear function. What does the slope represent? (d) What does the C-intercept represent? (e) Wh does a linear function give a suitable model in this situation? 9 For each scatter plot, decide what tpe of function ou might choose as a model for the data. Eplain our choices. 9. (a) (b) ;. The table shows (lifetime) peptic ulcer rates (per population) for various famil incomes as reported b the National Health Interview Surve. Income Ulcer rate (per population) $4, 4. $6, 3. $8, 3.4 $,.5 $6,. $,.4 $3,.5 $45, 9.4 $6, 8. (a) Make a scatter plot of these data and decide whether a linear model is appropriate. (b) Find and graph a linear model using the first and last data points. (c) Find and graph the least squares regression line. (d) Use the linear model in part (c) to estimate the ulcer rate for an income of $5,. (e) According to the model, how likel is someone with an income of $8, to suffer from peptic ulcers? (f) Do ou think it would be reasonable to appl the model to someone with an income of $,? ;. Biologists have observed that the chirping rate of crickets of a certain species appears to be related to temperature. The table shows the chirping rates for various temperatures. Temperature Chirping rate Temperature Chirping rate ( F) (chirps min) ( F) (chirps min) (a) Make a scatter plot of the data. (b) Find and graph the regression line. (c) Use the linear model in part (b) to estimate the chirping rate at F.
27 SECTION. MATHEMATICAL MODELS: A CATALOG OF ESSENTIAL FUNCTIONS 35 ; 3. The table gives the winning heights for the men s Olmpic pole vault competitions up to the ear 4. Year Height (m) Year Height (m) (a) Make a scatter plot and decide whether a linear model is appropriate. (b) Find and graph the regression line. (c) Use the linear model to predict the height of the winning pole vault at the 8 Olmpics and compare with the actual winning height of 5.96 meters. (d) Is it reasonable to use the model to predict the winning height at the Olmpics? ; 4. The table shows the percentage of the population of Argentina that has lived in rural areas from 955 to. Find a model for the data and use it to estimate the rural percentage in 988 and. Percentage Percentage Year rural Year rural Man phsical quantities are connected b inverse square laws, that is, b power functions of the form f k. In particular, the illumination of an object b a light source is inversel proportional to the square of the distance from the source. Suppose that after dark ou are in a room with just one lamp and ou are tring to read a book. The light is too dim and so ou move halfwa to the lamp. How much brighter is the light? 6. It makes sense that the larger the area of a region, the larger the number of species that inhabit the region. Man ecologists have modeled the species-area relation with a power function and, in particular, the number of species S of bats living in caves in central Meico has been related to the surface area A of the caves b the equation S.7A.3. (a) The cave called Misión Imposible near Puebla, Meico, has a surface area of A 6 m. How man species of bats would ou epect to find in that cave? (b) If ou discover that four species of bats live in a cave, estimate the area of the cave. ; 7. The table shows the number N of species of reptiles and amphibians inhabiting Caribbean islands and the area A of the island in square miles. Island Saba 4 5 Monserrat 4 9 Puerto Rico 3,459 4 Jamaica 4,4 39 Hispaniola 9,48 84 Cuba 44,8 76 (a) Use a power function to model N as a function of A. (b) The Caribbean island of Dominica has area 9 m. How man species of reptiles and amphibians would ou epect to find on Dominica? ; 8. The table shows the mean (average) distances d of the planets from the sun (taking the unit of measurement to be the distance from the earth to the sun) and their periods T (time of revolution in ears). Planet d T Mercur Venus Earth.. Mars Jupiter Saturn Uranus Neptune (a) Fit a power model to the data. (b) Kepler s Third Law of Planetar Motion states that The square of the period of revolution of a planet is propor tional to the cube of its mean distance from the sun. Does our model corroborate Kepler s Third Law? A N
28 36 CHAPTER FUNCTIONS AND LIMITS.3 New Functions from Old Functions In this section we start with the basic functions we discussed in Section. and obtain new functions b shifting, stretching, and reflecting their graphs. We also show how to combine pairs of functions b the standard arithmetic operations and b composition. Transformations of Functions B appling certain transformations to the graph of a given function we can obtain the graphs of certain related functions. This will give us the abilit to sketch the graphs of man functions quickl b hand. It will also enable us to write equations for given graphs. Let s first consider translations. If c is a positive number, then the graph of f c is just the graph of f shifted upward a distance of c units (because each -coordinate is increased b the same number c). Likewise, if t f c, where c, then the value of t at is the same as the value of f at c (c units to the left of ). Therefore the graph of f c is just the graph of f shifted c units to the right (see Figure ). Vertical and Horizontal Shifts Suppose c. To obtain the graph of f c, shift the graph of f a distance c units upward f c, shift the graph of f a distance c units downward f c, shift the graph of f a distance c units to the right f c, shift the graph of f a distance c units to the left =ƒ+c =cƒ (c>) =f(+c) c =ƒ =f(-c) =f(_) =ƒ c c = ƒ c c =ƒ-c =_ƒ FIGURE Translating the graph of ƒ FIGURE Stretching and reflecting the graph of ƒ Now let s consider the stretching and reflecting transformations. If c, then the graph of cf is the graph of f stretched b a factor of c in the vertical direction (because each -coordinate is multiplied b the same number c). The graph of f is the graph of f reflected about the -ais because the point, is
29 SECTION.3 NEW FUNCTIONS FROM OLD FUNCTIONS 37 replaced b the point,. (See Figure and the following chart, where the results of other stretching, shrinking, and reflecting transformations are also given.) Vertical and Horizontal Stretching and Reflecting Suppose c. To obtain the graph of cf, stretch the graph of f verticall b a factor of c c f, shrink the graph of f verticall b a factor of c f c, shrink the graph of f horizontall b a factor of c f c, stretch the graph of f horizontall b a factor of c f, reflect the graph of f about the -ais f, reflect the graph of f about the -ais Figure 3 illustrates these stretching transformations when applied to the cosine function with c. For instance, in order to get the graph of cos we multipl the -coordinate of each point on the graph of cos b. This means that the graph of cos gets stretched verticall b a factor of. = cos =cos = cos =cos FIGURE 3 =cos =cos v EXAMPLE Given the graph of s, use transformations to graph s, s, s, s, and s. SOLUTION The graph of the square root function s, obtained from Figure 3(a) in Section., is shown in Figure 4(a). In the other parts of the figure we sketch s b shifting units downward, s b shifting units to the right, s b reflecting about the -ais, s b stretching verticall b a factor of, and s b reflecting about the -ais. _ (a) =œ FIGURE 4 (b) =œ - (c) =œ - (d) =_œ (e) =œ (f) =œ _
30 38 CHAPTER FUNCTIONS AND LIMITS EXAMPLE Sketch the graph of the function f () 6. SOLUTION Completing the square, we write the equation of the graph as 6 3 This means we obtain the desired graph b starting with the parabola and shifting 3 units to the left and then unit upward (see Figure 5). (_3, ) _3 _ FIGURE 5 (a) = (b) =(+3)@+ EXAMPLE 3 Sketch the graphs of the following functions. (a) sin (b) sin SOLUTION (a) We obtain the graph of sin from that of sin b compressing horizontall b a factor of. (See Figures 6 and 7.) Thus, whereas the period of sin is, the period of sin is. =sin =sin π π π 4 π π FIGURE 6 FIGURE 7 (b) To obtain the graph of sin, we again start with sin. We reflect about the -ais to get the graph of sin and then we shift unit upward to get sin. (See Figure 8.) =-sin FIGURE 8 π π 3π π EXAMPLE 4 Figure 9 shows graphs of the number of hours of dalight as functions of the time of the ear at several latitudes. Given that Philadelphia is located at approimatel 4 N latitude, find a function that models the length of dalight at Philadelphia.
31 SECTION.3 NEW FUNCTIONS FROM OLD FUNCTIONS Hours 8 N 3 N 4 N 5 N FIGURE 9 Graph of the length of dalight from March through December at various latitudes Lucia C. Harrison, Dalight, Twilight, Darkness and Time (New York, 935) page Mar. Apr. Ma June Jul Aug. Sept. Oct. Nov. Dec. 6 N SOLUTION Notice that each curve resembles a shifted and stretched sine function. B looking at the blue curve we see that, at the latitude of Philadelphia, dalight lasts about 4.8 hours on June and 9. hours on December, so the amplitude of the curve (the factor b which we have to stretch the sine curve verticall) is B what factor do we need to stretch the sine curve horizontall if we measure the time t in das? Because there are about 365 das in a ear, the period of our model should be 365. But the period of sin t is, so the horizontal stretching factor is c 365. We also notice that the curve begins its ccle on March, the 8th da of the ear, so we have to shift the curve 8 units to the right. In addition, we shift it units upward. Therefore we model the length of dalight in Philadelphia on the tth da of the ear b the function L t.8 sin 365 t 8 _ (a) = - _ (b) = - FIGURE Another transformation of some interest is taking the absolute value of a function. If f, then according to the definition of absolute value, f when f and f when f. This tells us how to get the graph of f from the graph of f : The part of the graph that lies above the -ais remains the same; the part that lies below the -ais is reflected about the -ais. v EXAMPLE 5 Sketch the graph of the function. SOLUTION We first graph the parabola in Figure (a) b shifting the parabola downward unit. We see that the graph lies below the -ais when, so we reflect that part of the graph about the -ais to obtain the graph of in Figure (b). Combinations of Functions Two functions f and t can be combined to form new functions f t, f t, ft, and f t in a manner similar to the wa we add, subtract, multipl, and divide real numbers. The sum and difference functions are defined b f t f t f t f t
32 4 CHAPTER FUNCTIONS AND LIMITS If the domain of f is A and the domain of t is B, then the domain of f t is the intersection A B because both f and t have to be defined. For eample, the domain of f s is A, and the domain of t s is B,, so the domain of f t s s is A B,. Similarl, the product and quotient functions are defined b t f f ft f t t The domain of ft is A B, but we can t divide b and so the domain of f t is A B t. For instance, if f and t, then the domain of the rational function f t is, or,,. There is another wa of combining two functions to obtain a new function. For eample, suppose that f u su and u t. Since is a function of u and u is, in turn, a function of, it follows that is ultimatel a function of. We compute this b substitution: f u f t f s (input) g f g The procedure is called composition because the new function is composed of the two given functions f and t. In general, given an two functions f and t, we start with a number in the domain of t and find its image t. If this number t is in the domain of f, then we can calculate the value of f t. Notice that the output of one function is used as the input to the net function. The result is a new function h f t obtained b substituting t into f. It is called the composition (or composite) of f and t and is denoted b f t ( f circle t ). f f{ } (output) Definition Given two functions f and t, the composite function f t (also called the composition of f and t) is defined b f t f t FIGURE The f g machine is composed of the g machine (first) and then the f machine. The domain of f t is the set of all in the domain of t such that t is in the domain of f. In other words, f t is defined whenever both t and f t are defined. Figure shows how to picture f t in terms of machines. EXAMPLE 6 If f and t 3, find the composite functions f t and t f. SOLUTION We have f t f t f 3 3 t f t f t 3 NOTE You can see from Eample 6 that, in general, f t t f. Remember, the notation f t means that the function t is applied first and then f is applied second. In Eample 6, f t is the function that first subtracts 3 and then squares; t f is the function that first squares and then subtracts 3.
33 SECTION.3 NEW FUNCTIONS FROM OLD FUNCTIONS 4 v EXAMPLE 7 If f s and t s, find each function and its domain. (a) f t (b) t f (c) f f (d) t t SOLUTION (a) f t f t f (s ) ss s 4 The domain of f t is,. (b) t f t f t(s ) s s For s to be defined we must have. For s s to be defined we must have If a b, then a b. s, that is, s, or 4. Thus we have 4, so the domain of t f is the closed interval, 4. (c) f f f f f (s ) ss s 4 The domain of f f is,. (d) t t t t t(s ) s s This epression is defined when both and s. The first inequalit means, and the second is equivalent to s, or 4, or. Thus, so the domain of t t is the closed interval,. It is possible to take the composition of three or more functions. For instance, the composite function f t h is found b first appling h, then t, and then f as follows: f t h f t h EXAMPLE 8 SOLUTION Find f t h if f, t, and h 3. f t h f t h f t 3 f So far we have used composition to build complicated functions from simpler ones. But in calculus it is often useful to be able to decompose a complicated function into simpler ones, as in the following eample. EXAMPLE 9 Given F cos 9, find functions f, t, and h such that F f t h. SOLUTION Since F cos 9, the formula for F sas: First add 9, then take the cosine of the result, and finall square. So we let h 9 t cos f Then f t h f t h f t 9 f cos 9 cos 9 F
34 4 CHAPTER FUNCTIONS AND LIMITS.3 Eercises. Suppose the graph of is given. Write equations for the graphs that are obtained from the graph of f as follows. s3 is given. Use transformations to create a function whose graph is as shown. (a) Shift 3 units upward. (b) Shift 3 units downward. (c) Shift 3 units to the right. (d) Shift 3 units to the left. (e) Reflect about the -ais. (f) Reflect about the -ais. (g) Stretch verticall b a factor of 3..5 =œ 3- (h) Shrink verticall b a factor of 3.. Eplain how each graph is obtained from the graph of f. 3 (a) f 8 (b) f 8 (c) 8f (d) f (e) f (f) 8f ( 8 ) 3 3. The graph of f is given. Match each equation with its _4 graph and give reasons for our choices. (a) f 4 (b) f 3 _.5 (c) 3 f (d) f 4 5 (e) f 6! 8. (a) How is the graph of sin related to the graph of sin? Use our answer and Figure 6 to sketch the f graph of sin. # 3 (b) How is the graph of s related to the graph of $ s? Use our answer and Figure 4(a) to sketch the graph of s. _6 _3 3 6 % _3 4. The graph of f is given. Draw the graphs of the following functions. (a) f (b) f (c) f (d) f ( 3 ) 5. The graph of f is given. Use it to graph the following functions. (a) f (b) f ( ) (c) f (d) f 9 4 Graph the function b hand, not b plotting points, but b starting with the graph of one of the standard functions given in Section., and then appling the appropriate transformations s s 4. 4 sin sin( ) 7. cos 8. s s tan 4 cos 5. The cit of New Orleans is located at latitude 3 N. Use Figure 9 to find a function that models the number of hours of dalight at New Orleans as a function of the time of ear. To check the accurac of our model, use the fact that on March 3 the sun rises at 5:5 AM and sets at 6:8 PM in New Orleans.. Homework Hints available at stewartcalculus.com
35 SECTION.3 NEW FUNCTIONS FROM OLD FUNCTIONS A variable star is one whose brightness alternatel increases and decreases. For the most visible variable star, Delta Cephei, the time between periods of maimum brightness is 5.4 das, the average brightness (or magnitude) of the star is 4., and its brightness varies b.35 magnitude. Find a function that models the brightness of Delta Cephei as a function of time. 7. (a) How is the graph of related to the graph of f? (b) Sketch the graph of sin. (c) Sketch the graph of. f ( ) s 8. Use the given graph of f to sketch the graph of f. Which features of f are the most important in sketching f? Eplain how the are used Epress the function in the form f t. 4. F 4 4. F cos s3 43. F 44. s v t sec t tan t 46. u t Epress the function in the form f t h. 47. R ss H sec 4 (s ) G 3 tan t tan t H s 8 5. Use the table to evaluate each epression. (a) f t (b) t f (c) (d) t t (e) t f 3 (f) f f f t Find (a) f t, (b) f t, (c) ft, and (d) f t and state their domains. 9. f 3, t 3 3. f s3, 3 36 Find the functions (a) f t, (b) t f, (c) f f, and (d) t t and their domains. 3. f, t 3. f, 33. f 3, 34. f s, 35. f, 36. f, t s t 3 4 t cos t s 3 t t sin f t Use the given graphs of f and t to evaluate each epression, or eplain wh it is undefined. (a) f t (b) t f (c) f t (d) t f 6 (e) t t (f) f f 4 g f 5. Use the given graphs of f and t to estimate the value of f t for 5, 4, 3,..., 5. Use these estimates to sketch a rough graph of f t Find f t h. 37. f 3, t sin, h 38., t, f 4 h s 39. f s 3, t, h 3 4. f tan, t, h s 3 f g
36 44 CHAPTER FUNCTIONS AND LIMITS 53. A stone is dropped into a lake, creating a circular ripple that travels outward at a speed of 6 cm s. (a) Epress the radius r of this circle as a function of the time t ( in seconds). (b) If A is the area of this circle as a function of the radius, find A r and interpret it. 54. A spherical balloon is being inflated and the radius of the balloon is increasing at a rate of cm s. (a) Epress the radius r of the balloon as a function of the time t ( in seconds). (b) If V is the volume of the balloon as a function of the radius, find V r and interpret it. 55. A ship is moving at a speed of 3 km h parallel to a straight shoreline. The ship is 6 km from shore and it passes a lighthouse at noon. (a) Epress the distance s between the lighthouse and the ship as a function of d, the distance the ship has traveled since noon; that is, find f so that s f d. (b) Epress d as a function of t, the time elapsed since noon; that is, find t so that d t t. (c) Find f t. What does this function represent? 56. An airplane is fling at a speed of 35 mi h at an altitude of one mile and passes directl over a radar station at time t. (a) Epress the horizontal distance d ( in miles) that the plane has flown as a function of t. (b) Epress the distance s between the plane and the radar station as a function of d. (c) Use composition to epress s as a function of t. 57. The Heaviside function H is defined b H t if t if t It is used in the stud of electric circuits to represent the sudden surge of electric current, or voltage, when a switch is instantaneousl turned on. (a) Sketch the graph of the Heaviside function. (b) Sketch the graph of the voltage V t in a circuit if the switch is turned on at time t and volts are applied instantaneousl to the circuit. Write a formula for V t in terms of H t. (c) Sketch the graph of the voltage V t in a circuit if the switch is turned on at time t 5 seconds and 4 volts are applied instantaneousl to the circuit. Write a formula for V t in terms of H t. (Note that starting at t 5 corre - sponds to a translation.) 58. The Heaviside function defined in Eercise 57 can also be used to define the ramp function cth t, which represents a gradual increase in voltage or current in a circuit. (a) Sketch the graph of the ramp function th t. (b) Sketch the graph of the voltage V t in a circuit if the switch is turned on at time t and the voltage is graduall increased to volts over a 6-second time interval. Write a formula for V t in terms of H t for t 6. (c) Sketch the graph of the voltage V t in a circuit if the switch is turned on at time t 7 seconds and the voltage is graduall increased to volts over a period of 5 seconds. Write a formula for V t in terms of H t for t Let f and t be linear functions with equations f m b and t m b. Is f t also a linear function? If so, what is the slope of its graph? 6. If ou invest dollars at 4% interest compounded annuall, then the amount A of the investment after one ear is A.4. Find A A, A A A, and A A A A. What do these compositions represent? Find a formula for the composition of n copies of A. 6. (a) If t and h 4 4 7, find a function f such that f t h. (Think about what operations ou would have to perform on the formula for t to end up with the formula for h.) (b) If f 3 5 and h 3 3, find a function t such that f t h. 6. If f 4 and h 4, find a function t such that t f h. 63. Suppose t is an even function and let h f t. Is h alwas an even function? 64. Suppose t is an odd function and let h f t. Is h alwas an odd function? What if f is odd? What if f is even?.4 The Tangent and Velocit Problems In this section we see how its arise when we attempt to find the tangent to a curve or the velocit of an object. The Tangent Problem The word tangent is derived from the Latin word tangens, which means touching. Thus a tangent to a curve is a line that touches the curve. In other words, a tangent line should have the same direction as the curve at the point of contact. How can this idea be made precise?
37 SECTION.4 THE TANGENT AND VELOCITY PROBLEMS 45 For a circle we could simpl follow Euclid and sa that a tangent is a line that intersects the circle once and onl once, as in Figure (a). For more complicated curves this definition is inadequate. Figure l(b) shows two lines land t passing through a point Pon a curve C. The line l intersects C onl once, but it certainl does not look like what we think of as a tangent. The line t, on the other hand, looks like a tangent but it intersects C twice. t P t C l FIGURE (a) (b) To be specific, let s look at the problem of tring to find a tangent line t to the parabola in the following eample. v EXAMPLE Find an equation of the tangent line to the parabola at the point P,. = Q{, } P(, ) t SOLUTION We will be able to find an equation of the tangent line t as soon as we know its slope m. The difficult is that we know onl one point, P, on t, whereas we need two points to compute the slope. But observe that we can compute an approimation to m b choosing a nearb point Q, on the parabola (as in Figure ) and computing the slope m PQ of the secant line PQ. [A secant line, from the Latin word secans, meaning cutting, is a line that cuts ( intersects) a curve more than once.] We choose so that Q P. Then FIGURE m PQ For instance, for the point Q.5,.5 we have m PQ m PQ m PQ The tables in the margin show the values of for several values of close to. The closer Q is to P, the closer is to and, it appears from the tables, the closer m PQ is to. This suggests that the slope of the tangent line t should be m. We sa that the slope of the tangent line is the it of the slopes of the secant lines, and we epress this smbolicall b writing m PQ m Q lp and Assuming that the slope of the tangent line is indeed, we use the point-slope form of the equation of a line (see Appendi B) to write the equation of the tangent line through, as m PQ or l
38 46 CHAPTER FUNCTIONS AND LIMITS Figure 3 illustrates the iting process that occurs in this eample. As Q approaches P along the parabola, the corresponding secant lines rotate about P and approach the tangent line t. Q t t t Q P P Q P Q approaches P from the right t t t Q P Q P Q P FIGURE 3 TEC In Visual.4 ou can see how the process in Figure 3 works for additional functions. t Q Q approaches P from the left Man functions that occur in science are not described b eplicit equations; the are defined b eperimental data. The net eample shows how to estimate the slope of the tangent line to the graph of such a function. v EXAMPLE The flash unit on a camera operates b storing charge on a capacitor and releasing it suddenl when the flash is set off. The data in the table describe the charge Q remaining on the capacitor (measured in microcoulombs) at time t (measured in seconds after the flash goes off ). Use the data to draw the graph of this function and estimate the slope of the tangent line at the point where t.4. [Note: The slope of the tangent line represents the electric current flowing from the capacitor to the flash bulb (measured in microamperes).] SOLUTION In Figure 4 we plot the given data and use them to sketch a curve that approimates the graph of the function. Q (microcoulombs) A P 6 5 B C FIGURE t (seconds)
39 SECTION.4 THE TANGENT AND VELOCITY PROBLEMS 47 Given the points P.4, 67.3 and R.,. on the graph, we find that the slope of the secant line PR is m PR R m PR (.,.) 84.5 (., 8.87) 74. (.6, 54.88) 67.5 (.8, 44.93) 55.5 (., 36.76) 54.5 The phsical meaning of the answer in Eample is that the electric current flowing from the capacitor to the flash bulb after.4 second is about 67 microamperes. The table at the left shows the results of similar calculations for the slopes of other secant lines. From this table we would epect the slope of the tangent line at t.4 to lie somewhere between 74 and In fact, the average of the slopes of the two closest secant lines is So, b this method, we estimate the slope of the tangent line to be 675. Another method is to draw an approimation to the tangent line at P and measure the sides of the triangle ABC, as in Figure 4. This gives an estimate of the slope of the tangent line as AB BC The Velocit Problem If ou watch the speedometer of a car as ou travel in cit traffic, ou see that the needle doesn t sta still for ver long; that is, the velocit of the car is not constant. We assume from watching the speedometer that the car has a definite velocit at each moment, but how is the instantaneous velocit defined? Let s investigate the eample of a falling ball. 3 Brand X Pictures/Jupiter Images/Fotosearch The CN Tower in Toronto was the tallest freestanding building in the world for 3 ears. v EXAMPLE 3 Suppose that a ball is dropped from the upper observation deck of the CN Tower in Toronto, 45 m above the ground. Find the velocit of the ball after 5 seconds. SOLUTION Through eperiments carried out four centuries ago, Galileo discovered that the distance fallen b an freel falling bod is proportional to the square of the time it has been falling. (This model for free fall neglects air resistance.) If the distance fallen after t seconds is denoted b s t and measured in meters, then Galileo s law is epressed b the equation s t 4.9t The difficult in finding the velocit after 5 s is that we are dealing with a single instant of time t 5, so no time interval is involved. However, we can approimate the desired quantit b computing the average velocit over the brief time interval of a tenth of a second from t 5 to t 5.: average velocit change in position time elapsed s 5. s m s
C H A P T E R 1. Functions and Models. PDF Created with deskpdf PDF Writer - Trial ::
 Licensed to: jsamuels@bmcc.cun.edu C H A P T E R A graphical representation of a function here the number of hours of dalight as a function of the time of ear at various latitudes is often the most natural
Licensed to: jsamuels@bmcc.cun.edu C H A P T E R A graphical representation of a function here the number of hours of dalight as a function of the time of ear at various latitudes is often the most natural
FUNCTIONS AND MODELS
 1 FUNCTIONS AND MODELS FUNCTIONS AND MODELS The fundamental objects that we deal with in calculus are functions. FUNCTIONS AND MODELS This chapter prepares the way for calculus by discussing: The basic
1 FUNCTIONS AND MODELS FUNCTIONS AND MODELS The fundamental objects that we deal with in calculus are functions. FUNCTIONS AND MODELS This chapter prepares the way for calculus by discussing: The basic
FUNCTIONS AND MODELS
 1 FUNCTIONS AND MODELS FUNCTIONS AND MODELS 1.2 MATHEMATICAL MODELS: A CATALOG OF ESSENTIAL FUNCTIONS In this section, we will learn about: The purpose of mathematical models. MATHEMATICAL MODELS A mathematical
1 FUNCTIONS AND MODELS FUNCTIONS AND MODELS 1.2 MATHEMATICAL MODELS: A CATALOG OF ESSENTIAL FUNCTIONS In this section, we will learn about: The purpose of mathematical models. MATHEMATICAL MODELS A mathematical
(2) Find the domain of f (x) = 2x3 5 x 2 + x 6
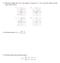 CHAPTER FUNCTIONS AND MODELS () Determine whether the curve is the graph of a function of. If it is state the domain and the range of the function. 5 8 Determine whether the curve is the graph of a function
CHAPTER FUNCTIONS AND MODELS () Determine whether the curve is the graph of a function of. If it is state the domain and the range of the function. 5 8 Determine whether the curve is the graph of a function
CHAPTER 1 FIGURE 22 increasing decreasing FIGURE 23
 . EXERCISES. The graph o a unction is given. (a) State the value o. (b) Estimate the value o 2. (c) For what values o is 2? (d) Estimate the values o such that. (e) State the domain and range o. () On
. EXERCISES. The graph o a unction is given. (a) State the value o. (b) Estimate the value o 2. (c) For what values o is 2? (d) Estimate the values o such that. (e) State the domain and range o. () On
2.4 Library of Functions; Piecewise-defined Functions. 1 Graph the Functions Listed in the Library of Functions
 80 CHAPTER Functions and Their Graphs Problems 8 88 require the following discussion of a secant line. The slope of the secant line containing the two points, f and + h, f + h on the graph of a function
80 CHAPTER Functions and Their Graphs Problems 8 88 require the following discussion of a secant line. The slope of the secant line containing the two points, f and + h, f + h on the graph of a function
Functions and Models 1.1. Functions and Their Representations
 _ptg_hr_-_23827_ch_ptg_hr_- 6/2/ :29 AM Page After learning a core group of basic functions, we will be armed with the tools to create formulas that describe scenarios as diverse as trends in the stock
_ptg_hr_-_23827_ch_ptg_hr_- 6/2/ :29 AM Page After learning a core group of basic functions, we will be armed with the tools to create formulas that describe scenarios as diverse as trends in the stock
Chapter 1 Functions and Models
 Chapter 1 Functions and Models 1.2 Mathematical Models: A catalog of Essential Functions A mathematical model is a mathematical description of a real world situations such as the size of a population,
Chapter 1 Functions and Models 1.2 Mathematical Models: A catalog of Essential Functions A mathematical model is a mathematical description of a real world situations such as the size of a population,
1.1 Exercises. (b) For what values of x is f x t x?
 CHAPTER FUNCTIONS AND MODELS. Eercises. The graph of a function f is given. (a) State the value of f. Estimate the value of f. (c) For what values of is f? (d) Estimate the values of such that f. (e) State
CHAPTER FUNCTIONS AND MODELS. Eercises. The graph of a function f is given. (a) State the value of f. Estimate the value of f. (c) For what values of is f? (d) Estimate the values of such that f. (e) State
LESSON #11 - FORMS OF A LINE COMMON CORE ALGEBRA II
 LESSON # - FORMS OF A LINE COMMON CORE ALGEBRA II Linear functions come in a variet of forms. The two shown below have been introduced in Common Core Algebra I and Common Core Geometr. TWO COMMON FORMS
LESSON # - FORMS OF A LINE COMMON CORE ALGEBRA II Linear functions come in a variet of forms. The two shown below have been introduced in Common Core Algebra I and Common Core Geometr. TWO COMMON FORMS
LESSON #12 - FORMS OF A LINE COMMON CORE ALGEBRA II
 LESSON # - FORMS OF A LINE COMMON CORE ALGEBRA II Linear functions come in a variet of forms. The two shown below have been introduced in Common Core Algebra I and Common Core Geometr. TWO COMMON FORMS
LESSON # - FORMS OF A LINE COMMON CORE ALGEBRA II Linear functions come in a variet of forms. The two shown below have been introduced in Common Core Algebra I and Common Core Geometr. TWO COMMON FORMS
LESSON #28 - POWER FUNCTIONS COMMON CORE ALGEBRA II
 1 LESSON #8 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
1 LESSON #8 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
1.2 Mathematical Models: A Catalog of Essential Functions
 1.2 Mathematical Models: A Catalog of Essential Functions A is a mathematical description of a real-world phenomenon. e.g., the size of a population, the demand for a product, the speed of a falling object,
1.2 Mathematical Models: A Catalog of Essential Functions A is a mathematical description of a real-world phenomenon. e.g., the size of a population, the demand for a product, the speed of a falling object,
Math 123 Summary of Important Algebra & Trigonometry Concepts Chapter 1 & Appendix D, Stewart, Calculus Early Transcendentals
 Math Summar of Important Algebra & Trigonometr Concepts Chapter & Appendi D, Stewart, Calculus Earl Transcendentals Function a rule that assigns to each element in a set D eactl one element, called f (
Math Summar of Important Algebra & Trigonometr Concepts Chapter & Appendi D, Stewart, Calculus Earl Transcendentals Function a rule that assigns to each element in a set D eactl one element, called f (
Infinite Limits. Let f be the function given by. f x 3 x 2.
 0_005.qd //0 :07 PM Page 8 SECTION.5 Infinite Limits 8, as Section.5, as + f() = f increases and decreases without bound as approaches. Figure.9 Infinite Limits Determine infinite its from the left and
0_005.qd //0 :07 PM Page 8 SECTION.5 Infinite Limits 8, as Section.5, as + f() = f increases and decreases without bound as approaches. Figure.9 Infinite Limits Determine infinite its from the left and
LESSON #24 - POWER FUNCTIONS COMMON CORE ALGEBRA II
 1 LESSON #4 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
1 LESSON #4 - POWER FUNCTIONS COMMON CORE ALGEBRA II Before we start to analze polnomials of degree higher than two (quadratics), we first will look at ver simple functions known as power functions. The
Polynomial and Rational Functions
 Polnomial and Rational Functions Figure -mm film, once the standard for capturing photographic images, has been made largel obsolete b digital photograph. (credit film : modification of work b Horia Varlan;
Polnomial and Rational Functions Figure -mm film, once the standard for capturing photographic images, has been made largel obsolete b digital photograph. (credit film : modification of work b Horia Varlan;
P.4 Lines in the Plane
 28 CHAPTER P Prerequisites P.4 Lines in the Plane What ou ll learn about Slope of a Line Point-Slope Form Equation of a Line Slope-Intercept Form Equation of a Line Graphing Linear Equations in Two Variables
28 CHAPTER P Prerequisites P.4 Lines in the Plane What ou ll learn about Slope of a Line Point-Slope Form Equation of a Line Slope-Intercept Form Equation of a Line Graphing Linear Equations in Two Variables
Linear and Nonlinear Systems of Equations. The Method of Substitution. Equation 1 Equation 2. Check (2, 1) in Equation 1 and Equation 2: 2x y 5?
 3330_070.qd 96 /5/05 Chapter 7 7. 9:39 AM Page 96 Sstems of Equations and Inequalities Linear and Nonlinear Sstems of Equations What ou should learn Use the method of substitution to solve sstems of linear
3330_070.qd 96 /5/05 Chapter 7 7. 9:39 AM Page 96 Sstems of Equations and Inequalities Linear and Nonlinear Sstems of Equations What ou should learn Use the method of substitution to solve sstems of linear
2.5 CONTINUITY. a x. Notice that Definition l implicitly requires three things if f is continuous at a:
 SECTION.5 CONTINUITY 9.5 CONTINUITY We noticed in Section.3 that the it of a function as approaches a can often be found simpl b calculating the value of the function at a. Functions with this propert
SECTION.5 CONTINUITY 9.5 CONTINUITY We noticed in Section.3 that the it of a function as approaches a can often be found simpl b calculating the value of the function at a. Functions with this propert
5.6 RATIOnAl FUnCTIOnS. Using Arrow notation. learning ObjeCTIveS
 CHAPTER PolNomiAl ANd rational functions learning ObjeCTIveS In this section, ou will: Use arrow notation. Solve applied problems involving rational functions. Find the domains of rational functions. Identif
CHAPTER PolNomiAl ANd rational functions learning ObjeCTIveS In this section, ou will: Use arrow notation. Solve applied problems involving rational functions. Find the domains of rational functions. Identif
In everyday speech, a continuous. Limits and Continuity. Critical Thinking Exercises
 062 Chapter Introduction to Calculus Critical Thinking Eercises Make Sense? In Eercises 74 77, determine whether each statement makes sense or does not make sense, and eplain our reasoning. 74. I evaluated
062 Chapter Introduction to Calculus Critical Thinking Eercises Make Sense? In Eercises 74 77, determine whether each statement makes sense or does not make sense, and eplain our reasoning. 74. I evaluated
LESSON #1 - BASIC ALGEBRAIC PROPERTIES COMMON CORE ALGEBRA II
 1 LESSON #1 - BASIC ALGEBRAIC PROPERTIES COMMON CORE ALGEBRA II Mathematics has developed a language all to itself in order to clarif concepts and remove ambiguit from the analsis of problems. To achieve
1 LESSON #1 - BASIC ALGEBRAIC PROPERTIES COMMON CORE ALGEBRA II Mathematics has developed a language all to itself in order to clarif concepts and remove ambiguit from the analsis of problems. To achieve
Review of Essential Skills and Knowledge
 Review of Essential Skills and Knowledge R Eponent Laws...50 R Epanding and Simplifing Polnomial Epressions...5 R 3 Factoring Polnomial Epressions...5 R Working with Rational Epressions...55 R 5 Slope
Review of Essential Skills and Knowledge R Eponent Laws...50 R Epanding and Simplifing Polnomial Epressions...5 R 3 Factoring Polnomial Epressions...5 R Working with Rational Epressions...55 R 5 Slope
1.5. Analyzing Graphs of Functions. The Graph of a Function. What you should learn. Why you should learn it. 54 Chapter 1 Functions and Their Graphs
 0_005.qd /7/05 8: AM Page 5 5 Chapter Functions and Their Graphs.5 Analzing Graphs of Functions What ou should learn Use the Vertical Line Test for functions. Find the zeros of functions. Determine intervals
0_005.qd /7/05 8: AM Page 5 5 Chapter Functions and Their Graphs.5 Analzing Graphs of Functions What ou should learn Use the Vertical Line Test for functions. Find the zeros of functions. Determine intervals
8.1 Exponents and Roots
 Section 8. Eponents and Roots 75 8. Eponents and Roots Before defining the net famil of functions, the eponential functions, we will need to discuss eponent notation in detail. As we shall see, eponents
Section 8. Eponents and Roots 75 8. Eponents and Roots Before defining the net famil of functions, the eponential functions, we will need to discuss eponent notation in detail. As we shall see, eponents
6. Graph each of the following functions. What do you notice? What happens when x = 2 on the graph of b?
 Pre Calculus Worksheet 1. Da 1 1. The relation described b the set of points {(-,5,0,5,,8,,9 ) ( ) ( ) ( )} is NOT a function. Eplain wh. For questions - 4, use the graph at the right.. Eplain wh the graph
Pre Calculus Worksheet 1. Da 1 1. The relation described b the set of points {(-,5,0,5,,8,,9 ) ( ) ( ) ( )} is NOT a function. Eplain wh. For questions - 4, use the graph at the right.. Eplain wh the graph
LESSON #48 - INTEGER EXPONENTS COMMON CORE ALGEBRA II
 LESSON #8 - INTEGER EXPONENTS COMMON CORE ALGEBRA II We just finished our review of linear functions. Linear functions are those that grow b equal differences for equal intervals. In this unit we will
LESSON #8 - INTEGER EXPONENTS COMMON CORE ALGEBRA II We just finished our review of linear functions. Linear functions are those that grow b equal differences for equal intervals. In this unit we will
3.7 InveRSe FUnCTIOnS
 CHAPTER functions learning ObjeCTIveS In this section, ou will: Verif inverse functions. Determine the domain and range of an inverse function, and restrict the domain of a function to make it one-to-one.
CHAPTER functions learning ObjeCTIveS In this section, ou will: Verif inverse functions. Determine the domain and range of an inverse function, and restrict the domain of a function to make it one-to-one.
KEY IDEAS. Chapter 1 Function Transformations. 1.1 Horizontal and Vertical Translations Pre-Calculus 12 Student Workbook MHR 1
 Chapter Function Transformations. Horizontal and Vertical Translations A translation can move the graph of a function up or down (vertical translation) and right or left (horizontal translation). A translation
Chapter Function Transformations. Horizontal and Vertical Translations A translation can move the graph of a function up or down (vertical translation) and right or left (horizontal translation). A translation
LESSON #42 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART 2 COMMON CORE ALGEBRA II
 LESSON #4 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART COMMON CORE ALGEBRA II You will recall from unit 1 that in order to find the inverse of a function, ou must switch and and solve for. Also,
LESSON #4 - INVERSES OF FUNCTIONS AND FUNCTION NOTATION PART COMMON CORE ALGEBRA II You will recall from unit 1 that in order to find the inverse of a function, ou must switch and and solve for. Also,
(b) Find the difference quotient. Interpret your result. 3. Find the average rate of change of ƒ(x) = x 2-3x from
 6360_ch0pp00-075.qd 0/6/08 4:8 PM Page 67 CHAPTER Summar 67 69. ƒ() = 3 70. ƒ() = -5 (b) Find the difference quotient. Interpret our result. 7. ƒ() = - 7. ƒ() = 0 73. ƒ() = + 74. ƒ() = -3 + 4 75. ƒ() =
6360_ch0pp00-075.qd 0/6/08 4:8 PM Page 67 CHAPTER Summar 67 69. ƒ() = 3 70. ƒ() = -5 (b) Find the difference quotient. Interpret our result. 7. ƒ() = - 7. ƒ() = 0 73. ƒ() = + 74. ƒ() = -3 + 4 75. ƒ() =
Study Guide and Intervention
 6- NAME DATE PERID Stud Guide and Intervention Graphing Quadratic Functions Graph Quadratic Functions Quadratic Function A function defined b an equation of the form f () a b c, where a 0 b Graph of a
6- NAME DATE PERID Stud Guide and Intervention Graphing Quadratic Functions Graph Quadratic Functions Quadratic Function A function defined b an equation of the form f () a b c, where a 0 b Graph of a
APPENDIXES. B Coordinate Geometry and Lines C. D Trigonometry E F. G The Logarithm Defined as an Integral H Complex Numbers I
 APPENDIXES A Numbers, Inequalities, and Absolute Values B Coordinate Geometr and Lines C Graphs of Second-Degree Equations D Trigonometr E F Sigma Notation Proofs of Theorems G The Logarithm Defined as
APPENDIXES A Numbers, Inequalities, and Absolute Values B Coordinate Geometr and Lines C Graphs of Second-Degree Equations D Trigonometr E F Sigma Notation Proofs of Theorems G The Logarithm Defined as
c) domain {x R, x 3}, range {y R}
 Answers Chapter 1 Functions 1.1 Functions, Domain, and Range 1. a) Yes, no vertical line will pass through more than one point. b) No, an vertical line between = 6 and = 6 will pass through two points..
Answers Chapter 1 Functions 1.1 Functions, Domain, and Range 1. a) Yes, no vertical line will pass through more than one point. b) No, an vertical line between = 6 and = 6 will pass through two points..
15.2 Graphing Logarithmic
 _ - - - - - - Locker LESSON 5. Graphing Logarithmic Functions Teas Math Standards The student is epected to: A.5.A Determine the effects on the ke attributes on the graphs of f () = b and f () = log b
_ - - - - - - Locker LESSON 5. Graphing Logarithmic Functions Teas Math Standards The student is epected to: A.5.A Determine the effects on the ke attributes on the graphs of f () = b and f () = log b
Exponential, Logistic, and Logarithmic Functions
 CHAPTER 3 Eponential, Logistic, and Logarithmic Functions 3.1 Eponential and Logistic Functions 3.2 Eponential and Logistic Modeling 3.3 Logarithmic Functions and Their Graphs 3.4 Properties of Logarithmic
CHAPTER 3 Eponential, Logistic, and Logarithmic Functions 3.1 Eponential and Logistic Functions 3.2 Eponential and Logistic Modeling 3.3 Logarithmic Functions and Their Graphs 3.4 Properties of Logarithmic
Answer Explanations. The SAT Subject Tests. Mathematics Level 1 & 2 TO PRACTICE QUESTIONS FROM THE SAT SUBJECT TESTS STUDENT GUIDE
 The SAT Subject Tests Answer Eplanations TO PRACTICE QUESTIONS FROM THE SAT SUBJECT TESTS STUDENT GUIDE Mathematics Level & Visit sat.org/stpractice to get more practice and stud tips for the Subject Test
The SAT Subject Tests Answer Eplanations TO PRACTICE QUESTIONS FROM THE SAT SUBJECT TESTS STUDENT GUIDE Mathematics Level & Visit sat.org/stpractice to get more practice and stud tips for the Subject Test
4.3 Exercises. local maximum or minimum. The second derivative is. e 1 x 2x 1. f x x 2 e 1 x 1 x 2 e 1 x 2x x 4
 SECTION 4.3 HOW DERIVATIVES AFFECT THE SHAPE OF A GRAPH 297 local maimum or minimum. The second derivative is f 2 e 2 e 2 4 e 2 4 Since e and 4, we have f when and when 2 f. So the curve is concave downward
SECTION 4.3 HOW DERIVATIVES AFFECT THE SHAPE OF A GRAPH 297 local maimum or minimum. The second derivative is f 2 e 2 e 2 4 e 2 4 Since e and 4, we have f when and when 2 f. So the curve is concave downward
Chapter Overview. 2.6 Modeling with Functions 2.7 Combining Functions 2.8 One-to-One Functions and Their Inverses
 . What Is a Function?. Graphs of Functions.3 Increasing and Decreasing Functions; Average Rate of Change.4 Transformations of Functions.5 Quadratic Functions; Maima and Minima.6 Modeling with Functions.7
. What Is a Function?. Graphs of Functions.3 Increasing and Decreasing Functions; Average Rate of Change.4 Transformations of Functions.5 Quadratic Functions; Maima and Minima.6 Modeling with Functions.7
One of the most common applications of Calculus involves determining maximum or minimum values.
 8 LESSON 5- MAX/MIN APPLICATIONS (OPTIMIZATION) One of the most common applications of Calculus involves determining maimum or minimum values. Procedure:. Choose variables and/or draw a labeled figure..
8 LESSON 5- MAX/MIN APPLICATIONS (OPTIMIZATION) One of the most common applications of Calculus involves determining maimum or minimum values. Procedure:. Choose variables and/or draw a labeled figure..
1.2 Functions and Their Properties PreCalculus
 1. Functions and Their Properties PreCalculus 1. FUNCTIONS AND THEIR PROPERTIES Learning Targets for 1. 1. Determine whether a set of numbers or a graph is a function. Find the domain of a function given
1. Functions and Their Properties PreCalculus 1. FUNCTIONS AND THEIR PROPERTIES Learning Targets for 1. 1. Determine whether a set of numbers or a graph is a function. Find the domain of a function given
Derivatives of Multivariable Functions
 Chapter 0 Derivatives of Multivariable Functions 0. Limits Motivating Questions In this section, we strive to understand the ideas generated b the following important questions: What do we mean b the limit
Chapter 0 Derivatives of Multivariable Functions 0. Limits Motivating Questions In this section, we strive to understand the ideas generated b the following important questions: What do we mean b the limit
Unit 10 - Graphing Quadratic Functions
 Unit - Graphing Quadratic Functions PREREQUISITE SKILLS: students should be able to add, subtract and multipl polnomials students should be able to factor polnomials students should be able to identif
Unit - Graphing Quadratic Functions PREREQUISITE SKILLS: students should be able to add, subtract and multipl polnomials students should be able to factor polnomials students should be able to identif
NCC Precalculus Partnership Program Final Examination, 2004
 NCC Precalculus Partnership Program Final Eamination, 2004 Part I: Answer onl 20 of the 25 questions below. Each question is worth 2 points. Place our answers on the answer sheet provided. Write the word
NCC Precalculus Partnership Program Final Eamination, 2004 Part I: Answer onl 20 of the 25 questions below. Each question is worth 2 points. Place our answers on the answer sheet provided. Write the word
Coordinate geometry. + bx + c. Vertical asymptote. Sketch graphs of hyperbolas (including asymptotic behaviour) from the general
 A Sketch graphs of = a m b n c where m = or and n = or B Reciprocal graphs C Graphs of circles and ellipses D Graphs of hperbolas E Partial fractions F Sketch graphs using partial fractions Coordinate
A Sketch graphs of = a m b n c where m = or and n = or B Reciprocal graphs C Graphs of circles and ellipses D Graphs of hperbolas E Partial fractions F Sketch graphs using partial fractions Coordinate
Lesson 4.1 Interpreting Graphs
 Lesson 4.1 Interpreting Graphs 1. Describe the pattern of the graph of each of the following situations as the graphs are read from left to right as increasing, decreasing, increasing and then decreasing,
Lesson 4.1 Interpreting Graphs 1. Describe the pattern of the graph of each of the following situations as the graphs are read from left to right as increasing, decreasing, increasing and then decreasing,
3.2 LOGARITHMIC FUNCTIONS AND THEIR GRAPHS
 Section. Logarithmic Functions and Their Graphs 7. LOGARITHMIC FUNCTIONS AND THEIR GRAPHS Ariel Skelle/Corbis What ou should learn Recognize and evaluate logarithmic functions with base a. Graph logarithmic
Section. Logarithmic Functions and Their Graphs 7. LOGARITHMIC FUNCTIONS AND THEIR GRAPHS Ariel Skelle/Corbis What ou should learn Recognize and evaluate logarithmic functions with base a. Graph logarithmic
3.1 Graph Quadratic Functions
 3. Graph Quadratic Functions in Standard Form Georgia Performance Standard(s) MMA3b, MMA3c Goal p Use intervals of increase and decrease to understand average rates of change of quadratic functions. Your
3. Graph Quadratic Functions in Standard Form Georgia Performance Standard(s) MMA3b, MMA3c Goal p Use intervals of increase and decrease to understand average rates of change of quadratic functions. Your
Linear Equations and Arithmetic Sequences
 CONDENSED LESSON.1 Linear Equations and Arithmetic Sequences In this lesson, ou Write eplicit formulas for arithmetic sequences Write linear equations in intercept form You learned about recursive formulas
CONDENSED LESSON.1 Linear Equations and Arithmetic Sequences In this lesson, ou Write eplicit formulas for arithmetic sequences Write linear equations in intercept form You learned about recursive formulas
Table of Contents. Module 1
 Table of Contents Module 1 11 Order of Operations 16 Signed Numbers 1 Factorization of Integers 17 Further Signed Numbers 13 Fractions 18 Power Laws 14 Fractions and Decimals 19 Introduction to Algebra
Table of Contents Module 1 11 Order of Operations 16 Signed Numbers 1 Factorization of Integers 17 Further Signed Numbers 13 Fractions 18 Power Laws 14 Fractions and Decimals 19 Introduction to Algebra
Precalculus Honors - AP Calculus A Information and Summer Assignment
 Precalculus Honors - AP Calculus A Information and Summer Assignment General Information: Competenc in Algebra and Trigonometr is absolutel essential. The calculator will not alwas be available for ou
Precalculus Honors - AP Calculus A Information and Summer Assignment General Information: Competenc in Algebra and Trigonometr is absolutel essential. The calculator will not alwas be available for ou
STANDARD FORM is a QUADRATIC FUNCTION and its graph is a PARABOLA. The domain of a quadratic function is the set of all real numbers.
 EXERCISE 2-3 Things to remember: 1. QUADRATIC FUNCTION If a, b, and c are real numbers with a 0, then the function f() = a 2 + b + c STANDARD FORM is a QUADRATIC FUNCTION and its graph is a PARABOLA. The
EXERCISE 2-3 Things to remember: 1. QUADRATIC FUNCTION If a, b, and c are real numbers with a 0, then the function f() = a 2 + b + c STANDARD FORM is a QUADRATIC FUNCTION and its graph is a PARABOLA. The
Chapter 1 Prerequisites for Calculus
 Section. Chapter Prerequisites for Calculus Section. Lines (pp. ) Quick Review.. + ( ) + () +. ( +). m. m ( ) ( ). (a) ( )? 6 (b) () ( )? 6. (a) 7? ( ) + 7 + Yes (b) ( ) + 9 No Yes No Section. Eercises.
Section. Chapter Prerequisites for Calculus Section. Lines (pp. ) Quick Review.. + ( ) + () +. ( +). m. m ( ) ( ). (a) ( )? 6 (b) () ( )? 6. (a) 7? ( ) + 7 + Yes (b) ( ) + 9 No Yes No Section. Eercises.
Functions. Introduction
 Functions,00 P,000 00 0 70 7 80 8 0 000 00 00 Figure Standard and Poor s Inde with dividends reinvested (credit "bull": modification of work b Praitno Hadinata; credit "graph": modification of work b MeasuringWorth)
Functions,00 P,000 00 0 70 7 80 8 0 000 00 00 Figure Standard and Poor s Inde with dividends reinvested (credit "bull": modification of work b Praitno Hadinata; credit "graph": modification of work b MeasuringWorth)
1.7 Inverse Functions
 71_0107.qd 1/7/0 10: AM Page 17 Section 1.7 Inverse Functions 17 1.7 Inverse Functions Inverse Functions Recall from Section 1. that a function can be represented b a set of ordered pairs. For instance,
71_0107.qd 1/7/0 10: AM Page 17 Section 1.7 Inverse Functions 17 1.7 Inverse Functions Inverse Functions Recall from Section 1. that a function can be represented b a set of ordered pairs. For instance,
Analytic Trigonometry
 CHAPTER 5 Analtic Trigonometr 5. Fundamental Identities 5. Proving Trigonometric Identities 5.3 Sum and Difference Identities 5.4 Multiple-Angle Identities 5.5 The Law of Sines 5.6 The Law of Cosines It
CHAPTER 5 Analtic Trigonometr 5. Fundamental Identities 5. Proving Trigonometric Identities 5.3 Sum and Difference Identities 5.4 Multiple-Angle Identities 5.5 The Law of Sines 5.6 The Law of Cosines It
Mini-Lecture 8.1 Solving Quadratic Equations by Completing the Square
 Mini-Lecture 8.1 Solving Quadratic Equations b Completing the Square Learning Objectives: 1. Use the square root propert to solve quadratic equations.. Solve quadratic equations b completing the square.
Mini-Lecture 8.1 Solving Quadratic Equations b Completing the Square Learning Objectives: 1. Use the square root propert to solve quadratic equations.. Solve quadratic equations b completing the square.
Rational Equations. You can use a rational function to model the intensity of sound.
 UNIT Rational Equations You can use a rational function to model the intensit of sound. Copright 009, K Inc. All rights reserved. This material ma not be reproduced in whole or in part, including illustrations,
UNIT Rational Equations You can use a rational function to model the intensit of sound. Copright 009, K Inc. All rights reserved. This material ma not be reproduced in whole or in part, including illustrations,
1. For each of the following, state the domain and range and whether the given relation defines a function. b)
 Eam Review Unit 0:. For each of the following, state the domain and range and whether the given relation defines a function. (,),(,),(,),(5,) a) { }. For each of the following, sketch the relation and
Eam Review Unit 0:. For each of the following, state the domain and range and whether the given relation defines a function. (,),(,),(,),(5,) a) { }. For each of the following, sketch the relation and
CHAPTER 2 Polynomial and Rational Functions
 CHAPTER Polnomial and Rational Functions Section. Quadratic Functions..................... 9 Section. Polnomial Functions of Higher Degree.......... Section. Real Zeros of Polnomial Functions............
CHAPTER Polnomial and Rational Functions Section. Quadratic Functions..................... 9 Section. Polnomial Functions of Higher Degree.......... Section. Real Zeros of Polnomial Functions............
3.2 Introduction to Functions
 8 CHAPTER Graphs and Functions Write each statement as an equation in two variables. Then graph each equation. 97. The -value is more than three times the -value. 98. The -value is - decreased b twice
8 CHAPTER Graphs and Functions Write each statement as an equation in two variables. Then graph each equation. 97. The -value is more than three times the -value. 98. The -value is - decreased b twice
Summary, Review, and Test
 944 Chapter 9 Conic Sections and Analtic Geometr 45. Use the polar equation for planetar orbits, to find the polar equation of the orbit for Mercur and Earth. Mercur: e = 0.056 and a = 36.0 * 10 6 miles
944 Chapter 9 Conic Sections and Analtic Geometr 45. Use the polar equation for planetar orbits, to find the polar equation of the orbit for Mercur and Earth. Mercur: e = 0.056 and a = 36.0 * 10 6 miles
WebAssign hw1.1 (Homework)
 WebAssign hw1.1 (Homework) Current Score : / 71 Due : Wednesday, May 31 2017 07:25 AM PDT Michael Lee Math261(Calculus I), section 1049, Spring 2017 Instructor: Michael Lee 1. /1 pointsscalc8 1.1.002.
WebAssign hw1.1 (Homework) Current Score : / 71 Due : Wednesday, May 31 2017 07:25 AM PDT Michael Lee Math261(Calculus I), section 1049, Spring 2017 Instructor: Michael Lee 1. /1 pointsscalc8 1.1.002.
Review Topics for MATH 1400 Elements of Calculus Table of Contents
 Math 1400 - Mano Table of Contents - Review - page 1 of 2 Review Topics for MATH 1400 Elements of Calculus Table of Contents MATH 1400 Elements of Calculus is one of the Marquette Core Courses for Mathematical
Math 1400 - Mano Table of Contents - Review - page 1 of 2 Review Topics for MATH 1400 Elements of Calculus Table of Contents MATH 1400 Elements of Calculus is one of the Marquette Core Courses for Mathematical
Glossary. Also available at BigIdeasMath.com: multi-language glossary vocabulary flash cards. An equation that contains an absolute value expression
 Glossar This student friendl glossar is designed to be a reference for ke vocabular, properties, and mathematical terms. Several of the entries include a short eample to aid our understanding of important
Glossar This student friendl glossar is designed to be a reference for ke vocabular, properties, and mathematical terms. Several of the entries include a short eample to aid our understanding of important
New Functions from Old Functions
 .3 New Functions rom Old Functions In this section we start with the basic unctions we discussed in Section. and obtain new unctions b shiting, stretching, and relecting their graphs. We also show how
.3 New Functions rom Old Functions In this section we start with the basic unctions we discussed in Section. and obtain new unctions b shiting, stretching, and relecting their graphs. We also show how
17 Exponential Functions
 Eponential Functions Concepts: Eponential Functions Graphing Eponential Functions Eponential Growth and Eponential Deca The Irrational Number e and Continuousl Compounded Interest (Section. &.A). Sketch
Eponential Functions Concepts: Eponential Functions Graphing Eponential Functions Eponential Growth and Eponential Deca The Irrational Number e and Continuousl Compounded Interest (Section. &.A). Sketch
Algebra II Notes Unit Six: Polynomials Syllabus Objectives: 6.2 The student will simplify polynomial expressions.
 Algebra II Notes Unit Si: Polnomials Sllabus Objectives: 6. The student will simplif polnomial epressions. Review: Properties of Eponents (Allow students to come up with these on their own.) Let a and
Algebra II Notes Unit Si: Polnomials Sllabus Objectives: 6. The student will simplif polnomial epressions. Review: Properties of Eponents (Allow students to come up with these on their own.) Let a and
Mathematics Placement Examination (MPE)
 Practice Problems for Mathematics Placement Eamination (MPE) Revised June, 011 When ou come to New Meico State Universit, ou ma be asked to take the Mathematics Placement Eamination (MPE) Your inital placement
Practice Problems for Mathematics Placement Eamination (MPE) Revised June, 011 When ou come to New Meico State Universit, ou ma be asked to take the Mathematics Placement Eamination (MPE) Your inital placement
M122 College Algebra Review for Final Exam
 M1 College Algebra Review for Final Eam Revised Fall 017 for College Algebra - Beecher All answers should include our work (this could be a written eplanation of the result, a graph with the relevant feature
M1 College Algebra Review for Final Eam Revised Fall 017 for College Algebra - Beecher All answers should include our work (this could be a written eplanation of the result, a graph with the relevant feature
CHAPTER 1 Functions and Their Graphs
 PART I CHAPTER Functions and Their Graphs Section. Lines in the Plane....................... Section. Functions........................... Section. Graphs of Functions..................... Section. Shifting,
PART I CHAPTER Functions and Their Graphs Section. Lines in the Plane....................... Section. Functions........................... Section. Graphs of Functions..................... Section. Shifting,
3.1 Graphing Quadratic Functions. Quadratic functions are of the form.
 3.1 Graphing Quadratic Functions A. Quadratic Functions Completing the Square Quadratic functions are of the form. 3. It is easiest to graph quadratic functions when the are in the form using transformations.
3.1 Graphing Quadratic Functions A. Quadratic Functions Completing the Square Quadratic functions are of the form. 3. It is easiest to graph quadratic functions when the are in the form using transformations.
Chapter 4. Introduction to Mathematical Modeling. Types of Modeling. 1) Linear Modeling 2) Quadratic Modeling 3) Exponential Modeling
 Chapter 4 Introduction to Mathematical Modeling Tpes of Modeling 1) Linear Modeling ) Quadratic Modeling ) Eponential Modeling Each tpe of modeling in mathematics is determined b the graph of equation
Chapter 4 Introduction to Mathematical Modeling Tpes of Modeling 1) Linear Modeling ) Quadratic Modeling ) Eponential Modeling Each tpe of modeling in mathematics is determined b the graph of equation
The American School of Marrakesh. Algebra 2 Algebra 2 Summer Preparation Packet
 The American School of Marrakesh Algebra Algebra Summer Preparation Packet Summer 016 Algebra Summer Preparation Packet This summer packet contains eciting math problems designed to ensure our readiness
The American School of Marrakesh Algebra Algebra Summer Preparation Packet Summer 016 Algebra Summer Preparation Packet This summer packet contains eciting math problems designed to ensure our readiness
Exponential and Logarithmic Functions
 7 Eponential and Logarithmic Functions In this chapter ou will stud two tpes of nonalgebraic functions eponential functions and logarithmic functions. Eponential and logarithmic functions are widel used
7 Eponential and Logarithmic Functions In this chapter ou will stud two tpes of nonalgebraic functions eponential functions and logarithmic functions. Eponential and logarithmic functions are widel used
6.4 graphs OF logarithmic FUnCTIOnS
 SECTION 6. graphs of logarithmic functions 9 9 learning ObjeCTIveS In this section, ou will: Identif the domain of a logarithmic function. Graph logarithmic functions. 6. graphs OF logarithmic FUnCTIOnS
SECTION 6. graphs of logarithmic functions 9 9 learning ObjeCTIveS In this section, ou will: Identif the domain of a logarithmic function. Graph logarithmic functions. 6. graphs OF logarithmic FUnCTIOnS
Module 3, Section 4 Analytic Geometry II
 Principles of Mathematics 11 Section, Introduction 01 Introduction, Section Analtic Geometr II As the lesson titles show, this section etends what ou have learned about Analtic Geometr to several related
Principles of Mathematics 11 Section, Introduction 01 Introduction, Section Analtic Geometr II As the lesson titles show, this section etends what ou have learned about Analtic Geometr to several related
3 Polynomial and Rational Functions
 3 Polnomial and Rational Functions 3.1 Quadratic Functions and Models 3.2 Polnomial Functions and Their Graphs 3.3 Dividing Polnomials 3.4 Real Zeros of Polnomials 3.5 Comple Zeros and the Fundamental
3 Polnomial and Rational Functions 3.1 Quadratic Functions and Models 3.2 Polnomial Functions and Their Graphs 3.3 Dividing Polnomials 3.4 Real Zeros of Polnomials 3.5 Comple Zeros and the Fundamental
Common Core State Standards for Activity 14. Lesson Postal Service Lesson 14-1 Polynomials PLAN TEACH
 Postal Service Lesson 1-1 Polynomials Learning Targets: Write a third-degree equation that represents a real-world situation. Graph a portion of this equation and evaluate the meaning of a relative maimum.
Postal Service Lesson 1-1 Polynomials Learning Targets: Write a third-degree equation that represents a real-world situation. Graph a portion of this equation and evaluate the meaning of a relative maimum.
2.2 SEPARABLE VARIABLES
 44 CHAPTER FIRST-ORDER DIFFERENTIAL EQUATIONS 6 Consider the autonomous DE 6 Use our ideas from Problem 5 to find intervals on the -ais for which solution curves are concave up and intervals for which
44 CHAPTER FIRST-ORDER DIFFERENTIAL EQUATIONS 6 Consider the autonomous DE 6 Use our ideas from Problem 5 to find intervals on the -ais for which solution curves are concave up and intervals for which
ALGEBRA 2 NY STATE COMMON CORE
 ALGEBRA NY STATE COMMON CORE Kingston High School 017-018 emathinstruction, RED HOOK, NY 1571, 015 Table of Contents U n i t 1 - Foundations of Algebra... 1 U n i t - Linear Functions, Equations, and their
ALGEBRA NY STATE COMMON CORE Kingston High School 017-018 emathinstruction, RED HOOK, NY 1571, 015 Table of Contents U n i t 1 - Foundations of Algebra... 1 U n i t - Linear Functions, Equations, and their
2.1 Evaluate and Graph Polynomial
 2. Evaluate and Graph Polnomial Functions Georgia Performance Standard(s) MM3Ab, MM3Ac, MM3Ad Your Notes Goal p Evaluate and graph polnomial functions. VOCABULARY Polnomial Polnomial function Degree of
2. Evaluate and Graph Polnomial Functions Georgia Performance Standard(s) MM3Ab, MM3Ac, MM3Ad Your Notes Goal p Evaluate and graph polnomial functions. VOCABULARY Polnomial Polnomial function Degree of
2-6. _ k x and y = _ k. The Graph of. Vocabulary. Lesson
 Chapter 2 Lesson 2-6 BIG IDEA The Graph of = _ k and = _ k 2 The graph of the set of points (, ) satisfing = k_, with k constant, is a hperbola with the - and -aes as asmptotes; the graph of the set of
Chapter 2 Lesson 2-6 BIG IDEA The Graph of = _ k and = _ k 2 The graph of the set of points (, ) satisfing = k_, with k constant, is a hperbola with the - and -aes as asmptotes; the graph of the set of
Instructor: Imelda Valencia Course: A3 Honors Pre Calculus
 Student: Date: Instructor: Imelda Valencia Course: A3 Honors Pre Calculus 01 017 Assignment: Summer Homework for those who will be taking FOCA 017 01 onl available until Sept. 15 1. Write the epression
Student: Date: Instructor: Imelda Valencia Course: A3 Honors Pre Calculus 01 017 Assignment: Summer Homework for those who will be taking FOCA 017 01 onl available until Sept. 15 1. Write the epression
Trigonometric Functions
 Trigonometric Functions This section reviews radian measure and the basic trigonometric functions. C ' θ r s ' ngles ngles are measured in degrees or radians. The number of radians in the central angle
Trigonometric Functions This section reviews radian measure and the basic trigonometric functions. C ' θ r s ' ngles ngles are measured in degrees or radians. The number of radians in the central angle
Polynomial and Rational Functions
 Name Date Chapter Polnomial and Rational Functions Section.1 Quadratic Functions Objective: In this lesson ou learned how to sketch and analze graphs of quadratic functions. Important Vocabular Define
Name Date Chapter Polnomial and Rational Functions Section.1 Quadratic Functions Objective: In this lesson ou learned how to sketch and analze graphs of quadratic functions. Important Vocabular Define
Answers Investigation 2
 Applications 1. a. Square Side Area 4 16 2 6 36 7 49 64 9 1 10 100 11 121 Rectangle Length Width Area 0 0 9 1 9 10 2 20 11 3 33 12 4 4 13 6 14 6 4 1 7 10 b. (See Figure 1.) c. The graph and the table both
Applications 1. a. Square Side Area 4 16 2 6 36 7 49 64 9 1 10 100 11 121 Rectangle Length Width Area 0 0 9 1 9 10 2 20 11 3 33 12 4 4 13 6 14 6 4 1 7 10 b. (See Figure 1.) c. The graph and the table both
8.4. If we let x denote the number of gallons pumped, then the price y in dollars can $ $1.70 $ $1.70 $ $1.70 $ $1.
 8.4 An Introduction to Functions: Linear Functions, Applications, and Models We often describe one quantit in terms of another; for eample, the growth of a plant is related to the amount of light it receives,
8.4 An Introduction to Functions: Linear Functions, Applications, and Models We often describe one quantit in terms of another; for eample, the growth of a plant is related to the amount of light it receives,
Lesson 9.1 Using the Distance Formula
 Lesson. Using the Distance Formula. Find the eact distance between each pair of points. a. (0, 0) and (, ) b. (0, 0) and (7, ) c. (, 8) and (, ) d. (, ) and (, 7) e. (, 7) and (8, ) f. (8, ) and (, 0)
Lesson. Using the Distance Formula. Find the eact distance between each pair of points. a. (0, 0) and (, ) b. (0, 0) and (7, ) c. (, 8) and (, ) d. (, ) and (, 7) e. (, 7) and (8, ) f. (8, ) and (, 0)
AP Calculus AB Summer Assignment Mrs. Berkson
 AP Calculus AB Summer Assignment Mrs. Berkson The purpose of the summer assignment is to prepare ou with the necessar Pre- Calculus skills required for AP Calculus AB. Net ear we will be starting off the
AP Calculus AB Summer Assignment Mrs. Berkson The purpose of the summer assignment is to prepare ou with the necessar Pre- Calculus skills required for AP Calculus AB. Net ear we will be starting off the
10.2 The Unit Circle: Cosine and Sine
 0. The Unit Circle: Cosine and Sine 77 0. The Unit Circle: Cosine and Sine In Section 0.., we introduced circular motion and derived a formula which describes the linear velocit of an object moving on
0. The Unit Circle: Cosine and Sine 77 0. The Unit Circle: Cosine and Sine In Section 0.., we introduced circular motion and derived a formula which describes the linear velocit of an object moving on
y = f(x + 4) a) Example: A repeating X by using two linear equations y = ±x. b) Example: y = f(x - 3). The translation is
 Answers Chapter Function Transformations. Horizontal and Vertical Translations, pages to. a h, k h, k - c h -, k d h 7, k - e h -, k. a A (-,, B (-,, C (-,, D (,, E (, A (-, -, B (-,, C (,, D (, -, E (,
Answers Chapter Function Transformations. Horizontal and Vertical Translations, pages to. a h, k h, k - c h -, k d h 7, k - e h -, k. a A (-,, B (-,, C (-,, D (,, E (, A (-, -, B (-,, C (,, D (, -, E (,
The speed the speed of light is 30,000,000,000 m/s. Write this number in scientific notation.
 Chapter 1 Section 1.1 Scientific Notation Powers of Ten 1 1 1.1.1.1.1 Standard Scientific Notation N n where 1 N and n is an integers Eamples of numbers in scientific notation. 8.17 11 Using Scientific
Chapter 1 Section 1.1 Scientific Notation Powers of Ten 1 1 1.1.1.1.1 Standard Scientific Notation N n where 1 N and n is an integers Eamples of numbers in scientific notation. 8.17 11 Using Scientific
Selected Answers and Solutions Go to Hotmath.com for step-by-step solutions of most odd-numbered exercises free of charge.
 Go to Hotmath.com for step-b-step solutions of most odd-numbered eercises free of charge. CHAPTER Functions from a Calculus Perspective Chapter Get Read. - -. - - - -. - 7. = + 9. = ± - 7. = - - 9. D =
Go to Hotmath.com for step-b-step solutions of most odd-numbered eercises free of charge. CHAPTER Functions from a Calculus Perspective Chapter Get Read. - -. - - - -. - 7. = + 9. = ± - 7. = - - 9. D =
Functions. Introduction CHAPTER OUTLINE
 Functions,00 P,000 00 0 970 97 980 98 990 99 000 00 00 Figure Standard and Poor s Inde with dividends reinvested (credit "bull": modification of work b Praitno Hadinata; credit "graph": modification of
Functions,00 P,000 00 0 970 97 980 98 990 99 000 00 00 Figure Standard and Poor s Inde with dividends reinvested (credit "bull": modification of work b Praitno Hadinata; credit "graph": modification of
Coached Instruction Supplement
 Practice Coach PLUS Coached Instruction Supplement Mathematics 8 Practice Coach PLUS, Coached Instruction Supplement, Mathematics, Grade 8 679NASP Triumph Learning Triumph Learning, LLC. All rights reserved.
Practice Coach PLUS Coached Instruction Supplement Mathematics 8 Practice Coach PLUS, Coached Instruction Supplement, Mathematics, Grade 8 679NASP Triumph Learning Triumph Learning, LLC. All rights reserved.
AP Calculus AB Summer Assignment Mrs. Berkson
 AP Calculus AB Summer Assignment Mrs. Berkson The purpose of the summer assignment is to prepare ou with the necessar Pre- Calculus skills required for AP Calculus AB. Net ear we will be starting off the
AP Calculus AB Summer Assignment Mrs. Berkson The purpose of the summer assignment is to prepare ou with the necessar Pre- Calculus skills required for AP Calculus AB. Net ear we will be starting off the
Section 1.2: A Catalog of Functions
 Section 1.: A Catalog of Functions As we discussed in the last section, in the sciences, we often tr to find an equation which models some given phenomenon in the real world - for eample, temperature as
Section 1.: A Catalog of Functions As we discussed in the last section, in the sciences, we often tr to find an equation which models some given phenomenon in the real world - for eample, temperature as
Explore 1 Graphing and Analyzing f(x) = e x. The following table represents the function ƒ (x) = (1 + 1 x) x for several values of x.
 1_ 8 6 8 Locker LESSON 13. The Base e Teas Math Standards The student is epected to: A.5.A Determine the effects on the ke attributes of the graphs of ƒ () = b and ƒ () = log b () where b is, 1, and e
1_ 8 6 8 Locker LESSON 13. The Base e Teas Math Standards The student is epected to: A.5.A Determine the effects on the ke attributes of the graphs of ƒ () = b and ƒ () = log b () where b is, 1, and e
