perfect mixing paradox
|
|
|
- Derek Dean
- 5 years ago
- Views:
Transcription
1 Using a slightly) more realistic model resolves the perfect mixing paradox arxiv: v1 [q-bio.pe] 8 Mar 2017 Rodrigo Ramos-Jiliberto 1,2 and Pablo Moisset de Espanés 3,4 1 Centro Nacional del Medio Ambiente. Universidad de Chile. Av. Alcalde Fernando Castillo Velasco 9975, La Reina, Santiago, Chile 2 Programas de Postgrado, Facultad de Ciencias, Pontificia Universidad Católica de Valparaíso. Av. Brasil 2950, Valparaíso, Chile 3 Instituto de Dinámica Celular y Biotecnología, Av. Beaucheff 850, Santiago, Chile 4 Centro de Modelamiento Matemático, FCFM, Universidad de Chile, Av. Beaucheff 850, Santiago, Chile November 5, 2018 Abstract In a recent paper published in Ecosphere, their authors suggest that extending the logistic growth model in its usual r K parameterization to a multi-patch environment results in undesirable properties, that were referred to as the perfect mixing paradox. ramos.jiliberto@gmail.com corresponding author) pmoisset@ing.uchile.cl 1
2 This led the authors to recommend using the Verhulst r α parameterization of the logistic model instead and abandoning the term carrying capacity in the context of population dynamics. In this study we show that the use of the logistic equation in its traditional r K parameterization is appropriate for representing the dynamics of populations in a simple spatial context with passive migration among patches. Furthermore, we show that the conclusions of the mentioned paper depend on the specific functional form for migration rates used for their analyses. In addition, we suggest that their specific migration model was not the best choice since biologically realistic options exist. Moreover, these alternatives require the same number of parameters. The model we present here is free of the paradoxical behaviors presented previously. This allows us to conclude that the logistic growth in its usual r K parameterization is useful in a spatial context if extended appropriately to a multi-patch scenario and consequently there are no reasons to abandon the concept of carrying capacity. Ecologists should pay great attention when using models in scenarios that are more complex or just different from the ones for which the models were created. Keywords Logistic model, migration rate, patch dynamics, space. Introduction In a recent paper, Arditi et al. [1] stated that a proper patch model of population dynamics must obey a basic logical property: If two patches are linked by migration, and if the migration rate becomes infinite, the two patches become perfectly mixed among each other, and the system must behave as a one-patch model for the total population. To illustrate the issue, they studied the following model: dn 1 dn 2 = r 1 N 1 1 N ) 1 K 1 = r 2 N 2 1 N 2 K 2 + β N 2 N 1 ) ) + β N 1 N 2 ), 1) where N i with i = 1, 2 being population size in patch i, r i the local intrinsic per capita
3 growth rate in patch i, K i the local carrying capacity in patch i and β the migration rate constant from and to any patch in the population. Note that each equation is the classical formula for logistic growth plus a term describing migration between patches. Arditi et al. [1] found that the asymptotic dynamics of system 1) in the case of perfect mixing i.e. with β ) is different from the asymptotic dynamics of the sum of the two populations in isolation i.e. with β = 0). In particular, they showed that the equilibrium population size of the system with perfect mixing is different either larger or smaller) that the sum of equilibrium sizes of the isolated populations. In the limiting but plausible case that the local populations differed in the value of their carrying capacities K i but not in the values of r i, merging two patches in a single one showed to be always detrimental for equilibrium population size. Although the analysis is correct, it is valid to ask whether the particular choice for describing migration in 1) was the best one for studying such a general ecological phenomenon. Apparently, the choice for migration model in [1] was made because of two main reasons: 1) this system was analyzed previously [5] [3] [7] [6] [4] [2] thus it has some tradition within the ecological literature, and 2) Arditi et al. [1] considered this model as a natural way to represent a two-patch system with logistic growth. All other things being equal, a well known and widely used model should be favored over its competitors. However this is only valid until we consider a model presenting some objective advantage e.g. better match with empirical observations) without compromising any substantial aspects such as number of parameters, mathematical tractability, etc.). In our opinion, model 1) is neither the most natural nor the best way to extend the logistic growth model to a two-patch scenario. Furthermore, we will show below that the paradoxical results reported by Arditi et al. [1] are only a consequence of using the specific model 1) and should not be considered to be a general fact. 3
4 a) b) Figure 1: Graphical representation of the flux of migrants in a two-patch population dynamics model. a): biologically unrealistic assumption of model1), where the net flux of migrants occurs from the less dense with higher absolute population size but with a much larger patch size) to the denser patch b): more realistic assumption, with migrant flux from the more dense to the less dense patch A more biologically plausible model Model 1), used in [1] to present the perfect mixing paradox contains as a key component a passive migration rate from patch i to patch j, βn i N j ). This formulation of passive migration rate assumes that there will be a positive flux of migrants from patch i to patch j whenever the absolute population size in patch i is larger than the absolute population size in patch j, no matter the differences in patch size or quality. This means that, given equal patch quality, it is possible to have a flux of migrants from a path with greater absolute population size but with lesser population density with a very large patch size) to a small and more dense patch which possesses a lower absolute population size Fig. 1a). This feature of model 1) represents an assumption of limited biological realism. Under the same scenario, a more reasonable assumption is that migrants should pass from the patch with higher population density absolute population size divided by patch size) to the patch with lower population density Fig. 1b). 4
5 We propose to re-evaluate the perfect mixing paradox using a slightly different system. This model is both amenable for analysis and contains a more realistic assumption about the direction of the net flux of migrants. dn 1 dn 2 = r 1 N 1 1 N ) 1 K 1 = r 2 N 2 1 N 2 K 2 + β ) + β N2 N ) 1 K 2 K 1 N1 N 2 K 1 K 2 ) 2) In this model the flux of migrants is governed by the differences between the ratios N i /K i. We will refer to the ratio N i /K i as the saturation of patch i, which is a balance between the local population size at time t and the local equilibrium population size K i. The value of K i depends on the quantity and quality of resources in patch i. The direction of the net flux of migrants in this model captures the intuition described in Fig. 1b. As shown below, this model does not exhibit the paradox presented in [1]. First, note that in isolation i.e., with β = 0), the system converges to N 1 = K 1, N 2 = K 2. This equilibrium is the same as the one of model 1). Using the same reasoning used in [1], if we assume perfect mixing of local populations i.e. with β ) in model 2), it can be shown that for all t > 0 N 1 K 1 = N 2 K 2 3) and therefore, for calculating the saturation of both patches combined: N 1 + N 2 = N K 1 K 1 K 1 + N 2 1 K 1 = N 1 = N 2 4) K 1 + K 2 K 1 + K 2 K 1 K 2 This shows that total population saturation under perfect mixing is equal to each of the local population saturations. Now, let us check whether the main paradoxical property presented in [1] holds for our model 2). This implies checking whether or not the long term total population size under perfect mixing is equal to total population size in isolation. Adding both equations of system 2) and using the equalities 4) which are valid for the 5
6 perfect mixing scenario, yields: dn T = dn 1 + dn 2 = r 1 N 1 + r 2 N 2 ) 1 N T = r 1K 1 + r 2 K 2 = r K T 1 N T K T K T 1 N T K T ) ) N T ) N T 5) where N T = N 1 + N 2, K T = K 1 + K 2 and r = r 1K 1 + r 2 K 2 K T. It is clear that, at equilibrium, the total population size under perfect mixing i.e. with β ) is K T = K 1 + K 2. Thus, using the more realistic model 2) resolves the main paradoxical behavior presented in [1] for mixed patches. Note also that in the logistic equation for N T the total intrinsic growth rate r is the weighted average of the local intrinsic growth rates, with weights K 1 and K 2. In the case that the patches differ only in their intrinsic growth rates r i and do not differ in their carrying capacities i.e., K 1 = K 2 ), the total intrinsic growth rate reduces to r = r 1 + r 2 )/2. Also, if r 1 = r 2 then r = r 1 = r 2. Another issue presented by Arditi et al. [1] is what they call an apparent spatial dependency of the equation parameters when the dynamics of the total population is represented by the Verhulst equation. The undesirable model property in a multi-patch context is that the value of the self-interference coefficient in the quadratic term decreases with number of patches S: dn T = rn T ᾱ S N T 2 6) To solve this issue, Arditi et al. [1] suggest to treat population size as density, in terms of mean population size per patch N = N T /S. When doing so, Eqn.6) becomes d N = r N ᾱ N 2 7) 6
7 which follows the Verhulst equation. Thus, the form of the equation is invariant in the number of patches in the metapopulation system and their parameters r and ᾱ) are simply the average of the corresponding local patch parameter values. In our case, and under the same reasoning, considering the average population in S well-mixed patches, N = NT /S, Eqn. 2) becomes: d N = r 1 N ) K N 8) with K = K T /S. That is, the carrying capacity of the average population is the average of the local carrying capacities. Like Eqn. 7), our Eqn. 8) is also invariant in the number patches, and their parameters r and K) are the weighted and aritmetic means, respectively, of the corresponding local patch parameters. Therefore there is no reason to favor the Verhulst s logistic equation over the classical formulation with the familiar r K parameterization in a multi-patch context, as argued by Arditi et al. [1]. Discussion The paper by Arditi et al. [1] argued that the logistic equation, in its usual r K parameterization, presents some undesirable properties when used in a multiple patch context. These properties configure what those authors called the perfect mixing paradox. Arditi et al. [1] also showed that the Verhulst s formulation of the logistic growth model dn / = rn αn 2 is less prone to these paradoxical features, as compared with the familiar Lotka formulation dn / = rn1 N /K), when generalized to a multi-patch environment. They conclude, on the basis of the analysis of these models extended to a metapopulation context by including a specific migration function, that the Verhulst formulation should be favored over the Lotka one, and that the term carrying capacity is misleading and should be abandoned in favor of the more correct equilibrium density. The supposedly paradoxical behavior of the metapopulation version of the Lotka-Gause 7
8 model rests, according to Arditi et al. [1], on two main features that were exemplified considering a two-patch environment as a study case. The first undesirable property is that the total mixed population equilibrium K T is in general different from the sum of the equilibria in the isolated patches K 1 +K 2. This major shortcoming of the analyzed model led Arditi et al. [1] to state that using the term carrying capacity is incorrect except in specific contexts. The second undesirable feature is the parameter dependence on the number of patches in the system, exhibited by the Verhulst form of the logistic growth model for the total population size. However, when population size is expressed as mean per patch) abundance the model parameters can be calculated as the average of the local parameters and do not depend on the number of patches. Nevertheless, Arditi et al. [1] claim that this scale-invariance is only exhibited by the Verhulst model and this gives it an advantage over the Lotka-Gause model. In this paper, we show that the paradoxical behaviors presented by Arditi et al. [1] belong only to the specific variant of the Lotka-Gause model they analyzed. Also, we suggest that the model used by Arditi et al. [1] is not the best choice regarding biological realism. In fact, we present a model as simple as the one they used two state-variables, five parameters) that is more realistic and is free of the alluded paradoxes exhibited by the Arditi s extensions to both the Lotka-Gause and the Verhulst logistic models. The most remarkable advantage of our model 2) is that, unlike both logistic forms used by Arditi et al. [1] in their analysis, total population size at equilibrium of a perfectly mixed metapopulation is equal to the sum of local equilibria. This feature immediately invalidates the criticism posed over the meaning and usefulness of the carrying capacity term. In our model 5), global intrinsic growth rate of the metapopulation is not the arithmetic average of local growth rates but it is equal to the weighted average of the local growth rate parameters. This is very reasonable, since under perfect mixing among patches, the ratios N i /K i are equated while their absolute abundances are not. So, it is possible to have patches with contrasting amount of resources e.g. space or nutrients) and therefore with unequal population abundances, say 3 individuals in patch 1 and 1000 individuals in patch 2. Under 8
9 this scenario, global intrinsic growth rate could not be the arithmetic mean of the local growth rates but it should be closer to the parameter value of the larger population. In the case of the Arditi s model, the absolute population abundances tend to be the same under perfect mixing and so the arithmetic mean and weighted mean are the same. Regarding the second issue stressed by Arditi et al. [1], we showed that our model 5) does not suffer from a lack of scale-invariance and that the dynamics of the per patch mean size of the metapopulation is fully consistent with the well known logistic dynamics within a single patch. In sum, we show here that the criticisms posed by Arditi et al. [1] to the familiar form of the logistic equation attributed to Lotka and Gause are only valid for the particular way in which those authors extended that equation to the multi-patch scenario. We also suggest that their model is not the best choice among other plausible models of the same complexity, and that their criticisms against the usefulness of the carrying capacity as a measure of patch size or richness is not well justified. However, the paper by Arditi et al. has the value of highlighting that modeling population, metapopulation or community dynamics requires more attention than is usually given to and that models should not be applied to any scenario without a rigorous theoretical analysis of their properties. Acknowledgments This study was supported by FONDECYT grant References [1] Roger Arditi, Louis-Flix Bersier, and Rudolf P. Rohr. The perfect mixing paradox and the logistic equation: Verhulst vs. lotka. Ecosphere, 711):e01599 n/a, e
10 [2] Roger Arditi, Claude Lobry, and Tewfik Sari. Is dispersal always beneficial to carrying capacity? new insights from the multi-patch logistic equation. Theoretical Population Biology, 106:45 59, [3] D. L. DeAngelis, C. C. Travis, and W. M. Post. Persistence and stability of seed-dispersed species in a patchy environment. Theoretical Population Biology, 162): , [4] Donald L. DeAngelis and Bo Zhang. Effects of dispersal in a non-uniform environment on population dynamics and competition: A patch model approach. Discrete and Continuous Dynamical Systems - Series B, 1910): , [5] H. I. Freedman and Paul Waltman. Mathematical models of population interactions with dispersal. i: Stability of two habitats with and without a predator. SIAM Journal on Applied Mathematics, 323): , [6] Ilkka Hanski. Metapopulation ecology. Oxford University Press, [7] Robert D. Holt. Population dynamics in two-patch environments: Some anomalous consequences of an optimal habitat distribution. Theoretical Population Biology, 282): ,
The perfect mixing paradox and the logistic equation: Verhulst vs. Lotka
 The perfect mixing paradox and the logistic equation: Verhulst vs. Lotka ROGER ARDITI, LOUIS-F ELIX BERSIER, AND RUDOLF P. ROHR Ecology and Evolution Department of Biology, University of Fribourg, Chemin
The perfect mixing paradox and the logistic equation: Verhulst vs. Lotka ROGER ARDITI, LOUIS-F ELIX BERSIER, AND RUDOLF P. ROHR Ecology and Evolution Department of Biology, University of Fribourg, Chemin
Is dispersal always beneficial to carrying capacity? New insights from the multi-patch logistic equation
 Is dispersal always beneficial to carrying capacity? New insights from the multi-patch logistic equation Roger Arditi, Claude Lobry, Tewfik Sari To cite this version: Roger Arditi, Claude Lobry, Tewfik
Is dispersal always beneficial to carrying capacity? New insights from the multi-patch logistic equation Roger Arditi, Claude Lobry, Tewfik Sari To cite this version: Roger Arditi, Claude Lobry, Tewfik
BIOS 5970: Plant-Herbivore Interactions Dr. Stephen Malcolm, Department of Biological Sciences
 BIOS 5970: Plant-Herbivore Interactions Dr. Stephen Malcolm, Department of Biological Sciences D. POPULATION & COMMUNITY DYNAMICS Week 10. Population models 1: Lecture summary: Distribution and abundance
BIOS 5970: Plant-Herbivore Interactions Dr. Stephen Malcolm, Department of Biological Sciences D. POPULATION & COMMUNITY DYNAMICS Week 10. Population models 1: Lecture summary: Distribution and abundance
ROLE OF TIME-DELAY IN AN ECOTOXICOLOGICAL PROBLEM
 CANADIAN APPLIED MATHEMATICS QUARTERLY Volume 6, Number 1, Winter 1997 ROLE OF TIME-DELAY IN AN ECOTOXICOLOGICAL PROBLEM J. CHATTOPADHYAY, E. BERETTA AND F. SOLIMANO ABSTRACT. The present paper deals with
CANADIAN APPLIED MATHEMATICS QUARTERLY Volume 6, Number 1, Winter 1997 ROLE OF TIME-DELAY IN AN ECOTOXICOLOGICAL PROBLEM J. CHATTOPADHYAY, E. BERETTA AND F. SOLIMANO ABSTRACT. The present paper deals with
dv dt Predator-Prey Models
 Predator-Prey Models This is a diverse area that includes general models of consumption: Granivores eating seeds Parasitoids Parasite-host interactions Lotka-Voterra model prey and predator: V = victim
Predator-Prey Models This is a diverse area that includes general models of consumption: Granivores eating seeds Parasitoids Parasite-host interactions Lotka-Voterra model prey and predator: V = victim
Interspecific Competition
 Interspecific Competition Intraspecific competition Classic logistic model Interspecific extension of densitydependence Individuals of other species may also have an effect on per capita birth & death
Interspecific Competition Intraspecific competition Classic logistic model Interspecific extension of densitydependence Individuals of other species may also have an effect on per capita birth & death
Gary G. Mittelbach Michigan State University
 Community Ecology Gary G. Mittelbach Michigan State University Sinauer Associates, Inc. Publishers Sunderland, Massachusetts U.S.A. Brief Table of Contents 1 Community Ecology s Roots 1 PART I The Big
Community Ecology Gary G. Mittelbach Michigan State University Sinauer Associates, Inc. Publishers Sunderland, Massachusetts U.S.A. Brief Table of Contents 1 Community Ecology s Roots 1 PART I The Big
The Dynamic Behaviour of the Competing Species with Linear and Holling Type II Functional Responses by the Second Competitor
 , pp. 35-46 http://dx.doi.org/10.14257/ijbsbt.2017.9.3.04 The Dynamic Behaviour of the Competing Species with Linear and Holling Type II Functional Responses by the Second Competitor Alemu Geleta Wedajo
, pp. 35-46 http://dx.doi.org/10.14257/ijbsbt.2017.9.3.04 The Dynamic Behaviour of the Competing Species with Linear and Holling Type II Functional Responses by the Second Competitor Alemu Geleta Wedajo
MA 777: Topics in Mathematical Biology
 MA 777: Topics in Mathematical Biology David Murrugarra Department of Mathematics, University of Kentucky http://www.math.uky.edu/~dmu228/ma777/ Spring 2018 David Murrugarra (University of Kentucky) Lecture
MA 777: Topics in Mathematical Biology David Murrugarra Department of Mathematics, University of Kentucky http://www.math.uky.edu/~dmu228/ma777/ Spring 2018 David Murrugarra (University of Kentucky) Lecture
Behaviour of simple population models under ecological processes
 J. Biosci., Vol. 19, Number 2, June 1994, pp 247 254. Printed in India. Behaviour of simple population models under ecological processes SOMDATTA SINHA* and S PARTHASARATHY Centre for Cellular and Molecular
J. Biosci., Vol. 19, Number 2, June 1994, pp 247 254. Printed in India. Behaviour of simple population models under ecological processes SOMDATTA SINHA* and S PARTHASARATHY Centre for Cellular and Molecular
Ecology Regulation, Fluctuations and Metapopulations
 Ecology Regulation, Fluctuations and Metapopulations The Influence of Density on Population Growth and Consideration of Geographic Structure in Populations Predictions of Logistic Growth The reality of
Ecology Regulation, Fluctuations and Metapopulations The Influence of Density on Population Growth and Consideration of Geographic Structure in Populations Predictions of Logistic Growth The reality of
Current controversies in Marine Ecology with an emphasis on Coral reef systems. Niche Diversification Hypothesis Assumptions:
 Current controversies in Marine Ecology with an emphasis on Coral reef systems Open vs closed populations (already Discussed) The extent and importance of larval dispersal Maintenance of Diversity Equilibrial
Current controversies in Marine Ecology with an emphasis on Coral reef systems Open vs closed populations (already Discussed) The extent and importance of larval dispersal Maintenance of Diversity Equilibrial
Current controversies in Marine Ecology with an emphasis on Coral reef systems
 Current controversies in Marine Ecology with an emphasis on Coral reef systems Open vs closed populations (already discussed) The extent and importance of larval dispersal Maintenance of Diversity Equilibrial
Current controversies in Marine Ecology with an emphasis on Coral reef systems Open vs closed populations (already discussed) The extent and importance of larval dispersal Maintenance of Diversity Equilibrial
Analysis of bacterial population growth using extended logistic Growth model with distributed delay. Abstract INTRODUCTION
 Analysis of bacterial population growth using extended logistic Growth model with distributed delay Tahani Ali Omer Department of Mathematics and Statistics University of Missouri-ansas City ansas City,
Analysis of bacterial population growth using extended logistic Growth model with distributed delay Tahani Ali Omer Department of Mathematics and Statistics University of Missouri-ansas City ansas City,
1. The growth of a cancerous tumor can be modeled by the Gompertz Law: dn. = an ln ( )
 1. The growth of a cancerous tumor can be modeled by the Gompertz Law: ( ) dn b = an ln, (1) dt N where N measures the size of the tumor. (a) Interpret the parameters a and b (both non-negative) biologically.
1. The growth of a cancerous tumor can be modeled by the Gompertz Law: ( ) dn b = an ln, (1) dt N where N measures the size of the tumor. (a) Interpret the parameters a and b (both non-negative) biologically.
BIOL 410 Population and Community Ecology. Predation
 BIOL 410 Population and Community Ecology Predation Intraguild Predation Occurs when one species not only competes with its heterospecific guild member, but also occasionally preys upon it Species 1 Competitor
BIOL 410 Population and Community Ecology Predation Intraguild Predation Occurs when one species not only competes with its heterospecific guild member, but also occasionally preys upon it Species 1 Competitor
Effective carrying capacity and analytical solution of a particular case of the Richards-like two-species population dynamics model
 Effective carrying capacity and analytical solution of a particular case of the Richards-like two-species population dynamics model Brenno Caetano Troca Cabella a,, Fabiano Ribeiro b and Alexandre Souto
Effective carrying capacity and analytical solution of a particular case of the Richards-like two-species population dynamics model Brenno Caetano Troca Cabella a,, Fabiano Ribeiro b and Alexandre Souto
COMPETITION OF FAST AND SLOW MOVERS FOR RENEWABLE AND DIFFUSIVE RESOURCE
 CANADIAN APPLIED MATHEMATICS QUARTERLY Volume 2, Number, Spring 22 COMPETITION OF FAST AND SLOW MOVERS FOR RENEWABLE AND DIFFUSIVE RESOURCE SILOGINI THANARAJAH AND HAO WANG ABSTRACT. In many studies of
CANADIAN APPLIED MATHEMATICS QUARTERLY Volume 2, Number, Spring 22 COMPETITION OF FAST AND SLOW MOVERS FOR RENEWABLE AND DIFFUSIVE RESOURCE SILOGINI THANARAJAH AND HAO WANG ABSTRACT. In many studies of
MA 137 Calculus 1 with Life Science Application A First Look at Differential Equations (Section 4.1.2)
 MA 137 Calculus 1 with Life Science Application A First Look at Differential Equations (Section 4.1.2) Alberto Corso alberto.corso@uky.edu Department of Mathematics University of Kentucky October 12, 2015
MA 137 Calculus 1 with Life Science Application A First Look at Differential Equations (Section 4.1.2) Alberto Corso alberto.corso@uky.edu Department of Mathematics University of Kentucky October 12, 2015
8 Ecosystem stability
 8 Ecosystem stability References: May [47], Strogatz [48]. In these lectures we consider models of populations, with an emphasis on the conditions for stability and instability. 8.1 Dynamics of a single
8 Ecosystem stability References: May [47], Strogatz [48]. In these lectures we consider models of populations, with an emphasis on the conditions for stability and instability. 8.1 Dynamics of a single
Chapter 5 Lecture. Metapopulation Ecology. Spring 2013
 Chapter 5 Lecture Metapopulation Ecology Spring 2013 5.1 Fundamentals of Metapopulation Ecology Populations have a spatial component and their persistence is based upon: Gene flow ~ immigrations and emigrations
Chapter 5 Lecture Metapopulation Ecology Spring 2013 5.1 Fundamentals of Metapopulation Ecology Populations have a spatial component and their persistence is based upon: Gene flow ~ immigrations and emigrations
BIOS 3010: ECOLOGY. Dr Stephen Malcolm. Laboratory 6: Lotka-Volterra, the logistic. equation & Isle Royale
 BIOS 3010: ECOLOGY Dr Stephen Malcolm Laboratory 6: Lotka-Volterra, the logistic equation & Isle Royale This is a computer-based activity using Populus software (P), followed by EcoBeaker analyses of moose
BIOS 3010: ECOLOGY Dr Stephen Malcolm Laboratory 6: Lotka-Volterra, the logistic equation & Isle Royale This is a computer-based activity using Populus software (P), followed by EcoBeaker analyses of moose
MA 138: Calculus II for the Life Sciences
 MA 138: Calculus II for the Life Sciences David Murrugarra Department of Mathematics, University of Kentucky. Spring 2016 David Murrugarra (University of Kentucky) MA 138: Section 11.4.2 Spring 2016 1
MA 138: Calculus II for the Life Sciences David Murrugarra Department of Mathematics, University of Kentucky. Spring 2016 David Murrugarra (University of Kentucky) MA 138: Section 11.4.2 Spring 2016 1
2 One-dimensional models in discrete time
 2 One-dimensional models in discrete time So far, we have assumed that demographic events happen continuously over time and can thus be written as rates. For many biological species with overlapping generations
2 One-dimensional models in discrete time So far, we have assumed that demographic events happen continuously over time and can thus be written as rates. For many biological species with overlapping generations
Age (x) nx lx. Population dynamics Population size through time should be predictable N t+1 = N t + B + I - D - E
 Population dynamics Population size through time should be predictable N t+1 = N t + B + I - D - E Time 1 N = 100 20 births 25 deaths 10 immigrants 15 emmigrants Time 2 100 + 20 +10 25 15 = 90 Life History
Population dynamics Population size through time should be predictable N t+1 = N t + B + I - D - E Time 1 N = 100 20 births 25 deaths 10 immigrants 15 emmigrants Time 2 100 + 20 +10 25 15 = 90 Life History
Oikos. Appendix A1. o20830
 1 Oikos o20830 Valdovinos, F. S., Moisset de Espanés, P., Flores, J. D. and Ramos-Jiliberto, R. 2013. Adaptive foraging allows the maintenance of biodiversity of pollination networks. Oikos 122: 907 917.
1 Oikos o20830 Valdovinos, F. S., Moisset de Espanés, P., Flores, J. D. and Ramos-Jiliberto, R. 2013. Adaptive foraging allows the maintenance of biodiversity of pollination networks. Oikos 122: 907 917.
Case Studies in Ecology and Evolution
 7 Competition (this chapter is still unfinished) Species compete in many ways. Sometimes there are dramatic contests, such as when male bighorns compete for access to mates. Territoriality. That kind of
7 Competition (this chapter is still unfinished) Species compete in many ways. Sometimes there are dramatic contests, such as when male bighorns compete for access to mates. Territoriality. That kind of
x 2 F 1 = 0 K 2 v 2 E 1 E 2 F 2 = 0 v 1 K 1 x 1
 ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 20, Number 4, Fall 1990 ON THE STABILITY OF ONE-PREDATOR TWO-PREY SYSTEMS M. FARKAS 1. Introduction. The MacArthur-Rosenzweig graphical criterion" of stability
ROCKY MOUNTAIN JOURNAL OF MATHEMATICS Volume 20, Number 4, Fall 1990 ON THE STABILITY OF ONE-PREDATOR TWO-PREY SYSTEMS M. FARKAS 1. Introduction. The MacArthur-Rosenzweig graphical criterion" of stability
THETA-LOGISTIC PREDATOR PREY
 THETA-LOGISTIC PREDATOR PREY What are the assumptions of this model? 1.) Functional responses are non-linear. Functional response refers to a change in the rate of exploitation of prey by an individual
THETA-LOGISTIC PREDATOR PREY What are the assumptions of this model? 1.) Functional responses are non-linear. Functional response refers to a change in the rate of exploitation of prey by an individual
population size at time t, then in continuous time this assumption translates into the equation for exponential growth dn dt = rn N(0)
 Appendix S1: Classic models of population dynamics in ecology and fisheries science Populations do not grow indefinitely. No concept is more fundamental to ecology and evolution. Malthus hypothesized that
Appendix S1: Classic models of population dynamics in ecology and fisheries science Populations do not grow indefinitely. No concept is more fundamental to ecology and evolution. Malthus hypothesized that
Final Project Descriptions Introduction to Mathematical Biology Professor: Paul J. Atzberger. Project I: Predator-Prey Equations
 Final Project Descriptions Introduction to Mathematical Biology Professor: Paul J. Atzberger Project I: Predator-Prey Equations The Lotka-Volterra Predator-Prey Model is given by: du dv = αu βuv = ρβuv
Final Project Descriptions Introduction to Mathematical Biology Professor: Paul J. Atzberger Project I: Predator-Prey Equations The Lotka-Volterra Predator-Prey Model is given by: du dv = αu βuv = ρβuv
Chapter 16: Competition. It s all mine, stay away!
 Chapter 16: Competition It s all mine, stay away! Species Interactions +/+ +/- -/- Basic interaction -/- Pop growth rate of species 1 (dn 1 /dt) is decreased by interaction Pop growth rate of species 2
Chapter 16: Competition It s all mine, stay away! Species Interactions +/+ +/- -/- Basic interaction -/- Pop growth rate of species 1 (dn 1 /dt) is decreased by interaction Pop growth rate of species 2
Exam 3. Principles of Ecology. April 14, Name
 Exam 3. Principles of Ecology. April 14, 2010. Name Directions: Perform beyond your abilities. There are 100 possible points (+ 9 extra credit pts) t N t = N o N t = N o e rt N t+1 = N t + r o N t (1-N
Exam 3. Principles of Ecology. April 14, 2010. Name Directions: Perform beyond your abilities. There are 100 possible points (+ 9 extra credit pts) t N t = N o N t = N o e rt N t+1 = N t + r o N t (1-N
Does spatial structure facilitate coexistence of identical competitors?
 Ecological Modelling 181 2005 17 23 Does spatial structure facilitate coexistence of identical competitors? Zong-Ling Wang a, Da-Yong Zhang b,, Gang Wang c a First Institute of Oceanography, State Oceanic
Ecological Modelling 181 2005 17 23 Does spatial structure facilitate coexistence of identical competitors? Zong-Ling Wang a, Da-Yong Zhang b,, Gang Wang c a First Institute of Oceanography, State Oceanic
BIOS 230 Landscape Ecology. Lecture #32
 BIOS 230 Landscape Ecology Lecture #32 What is a Landscape? One definition: A large area, based on intuitive human scales and traditional geographical studies 10s of hectares to 100s of kilometers 2 (1
BIOS 230 Landscape Ecology Lecture #32 What is a Landscape? One definition: A large area, based on intuitive human scales and traditional geographical studies 10s of hectares to 100s of kilometers 2 (1
Effect of Species 2 on Species 1 Competition - - Predator-Prey + - Parasite-Host + -
 Community Ecology Community - a group of organisms, of different species, living in the same area Community ecology is the study of the interactions between species The presence of one species may affect
Community Ecology Community - a group of organisms, of different species, living in the same area Community ecology is the study of the interactions between species The presence of one species may affect
Community Ecology. Classification of types of interspecific interactions: Effect of Species 1 on Species 2
 Community Ecology Community - a group of organisms, of different species, living in the same area Community ecology is the study of the interactions between species The presence of one species may affect
Community Ecology Community - a group of organisms, of different species, living in the same area Community ecology is the study of the interactions between species The presence of one species may affect
A Primer of Ecology. Sinauer Associates, Inc. Publishers Sunderland, Massachusetts
 A Primer of Ecology Fourth Edition NICHOLAS J. GOTELLI University of Vermont Sinauer Associates, Inc. Publishers Sunderland, Massachusetts Table of Contents PREFACE TO THE FOURTH EDITION PREFACE TO THE
A Primer of Ecology Fourth Edition NICHOLAS J. GOTELLI University of Vermont Sinauer Associates, Inc. Publishers Sunderland, Massachusetts Table of Contents PREFACE TO THE FOURTH EDITION PREFACE TO THE
Asynchronous and Synchronous Dispersals in Spatially Discrete Population Models
 SIAM J. APPLIED DYNAMICAL SYSTEMS Vol. 7, No. 2, pp. 284 310 c 2008 Society for Industrial and Applied Mathematics Asynchronous and Synchronous Dispersals in Spatially Discrete Population Models Abdul-Aziz
SIAM J. APPLIED DYNAMICAL SYSTEMS Vol. 7, No. 2, pp. 284 310 c 2008 Society for Industrial and Applied Mathematics Asynchronous and Synchronous Dispersals in Spatially Discrete Population Models Abdul-Aziz
Effects of fishing, market price, and climate on two South American clam species
 The following supplement accompanies the article Effects of fishing, market price, and climate on two South American clam species Leonardo Ortega 1, Juan Carlos Castilla 2, Marco Espino 3, Carmen Yamashiro
The following supplement accompanies the article Effects of fishing, market price, and climate on two South American clam species Leonardo Ortega 1, Juan Carlos Castilla 2, Marco Espino 3, Carmen Yamashiro
Ecology 302: Lecture VII. Species Interactions.
 Ecology 302: Lecture VII. Species Interactions. (Gotelli, Chapters 6; Ricklefs, Chapter 14-15) MacArthur s warblers. Variation in feeding behavior allows morphologically similar species of the genus Dendroica
Ecology 302: Lecture VII. Species Interactions. (Gotelli, Chapters 6; Ricklefs, Chapter 14-15) MacArthur s warblers. Variation in feeding behavior allows morphologically similar species of the genus Dendroica
Dynamical Systems and Chaos Part II: Biology Applications. Lecture 6: Population dynamics. Ilya Potapov Mathematics Department, TUT Room TD325
 Dynamical Systems and Chaos Part II: Biology Applications Lecture 6: Population dynamics Ilya Potapov Mathematics Department, TUT Room TD325 Living things are dynamical systems Dynamical systems theory
Dynamical Systems and Chaos Part II: Biology Applications Lecture 6: Population dynamics Ilya Potapov Mathematics Department, TUT Room TD325 Living things are dynamical systems Dynamical systems theory
Competition. Different kinds of competition Modeling competition Examples of competition-case studies Understanding the role of competition
 Competition Different kinds of competition Modeling competition Examples of competition-case studies Understanding the role of competition Competition The outcome of competition is that an individual suffers
Competition Different kinds of competition Modeling competition Examples of competition-case studies Understanding the role of competition Competition The outcome of competition is that an individual suffers
Modeling and Simulation Study of Mutuality Interactions with Type II functional Response and Harvesting
 American Journal of Applied Mathematics 201; 6(3): 109-116 http://www.sciencepublishinggroup.com/j/ajam doi: 10.116/j.ajam.2010603.12 ISSN: 2330-003 (Print); ISSN: 2330-006X (Online) Modeling and Simulation
American Journal of Applied Mathematics 201; 6(3): 109-116 http://www.sciencepublishinggroup.com/j/ajam doi: 10.116/j.ajam.2010603.12 ISSN: 2330-003 (Print); ISSN: 2330-006X (Online) Modeling and Simulation
Math 142-2, Homework 2
 Math 142-2, Homework 2 Your name here April 7, 2014 Problem 35.3 Consider a species in which both no individuals live to three years old and only one-year olds reproduce. (a) Show that b 0 = 0, b 2 = 0,
Math 142-2, Homework 2 Your name here April 7, 2014 Problem 35.3 Consider a species in which both no individuals live to three years old and only one-year olds reproduce. (a) Show that b 0 = 0, b 2 = 0,
Interspecific Competition
 Use Interspecific Competition 0.8 0.6 0.4 0. 0 0 0.5.5.5 3 Resource The niche and interspecific competition Species A Use Use 0.8 0.6 0.4 0. Species B 0 0 0.5.5.5 3 0.8 0.6 0.4 0. 0 0 0.5.5.5 3 Resource
Use Interspecific Competition 0.8 0.6 0.4 0. 0 0 0.5.5.5 3 Resource The niche and interspecific competition Species A Use Use 0.8 0.6 0.4 0. Species B 0 0 0.5.5.5 3 0.8 0.6 0.4 0. 0 0 0.5.5.5 3 Resource
SLOSS debate. reserve design principles. Caribbean Anolis. SLOSS debate- criticisms. Single large or several small Debate over reserve design
 SLOSS debate reserve design principles Single large or several small Debate over reserve design SLOSS debate- criticisms Caribbean Anolis Pattern not always supported Other factors may explain diversity
SLOSS debate reserve design principles Single large or several small Debate over reserve design SLOSS debate- criticisms Caribbean Anolis Pattern not always supported Other factors may explain diversity
1 (t + 4)(t 1) dt. Solution: The denominator of the integrand is already factored with the factors being distinct, so 1 (t + 4)(t 1) = A
 Calculus Topic: Integration of Rational Functions Section 8. # 0: Evaluate the integral (t + )(t ) Solution: The denominator of the integrand is already factored with the factors being distinct, so (t
Calculus Topic: Integration of Rational Functions Section 8. # 0: Evaluate the integral (t + )(t ) Solution: The denominator of the integrand is already factored with the factors being distinct, so (t
Logistic Model with Harvesting
 Logistic Model with Harvesting Model Here, we will talk about a model for the growth and harvesting of a fish population. Suppose that, absent any fishermen, the population grows logistically. That is,
Logistic Model with Harvesting Model Here, we will talk about a model for the growth and harvesting of a fish population. Suppose that, absent any fishermen, the population grows logistically. That is,
1.Introduction: 2. The Model. Key words: Prey, Predator, Seasonality, Stability, Bifurcations, Chaos.
 Dynamical behavior of a prey predator model with seasonally varying parameters Sunita Gakkhar, BrhamPal Singh, R K Naji Department of Mathematics I I T Roorkee,47667 INDIA Abstract : A dynamic model based
Dynamical behavior of a prey predator model with seasonally varying parameters Sunita Gakkhar, BrhamPal Singh, R K Naji Department of Mathematics I I T Roorkee,47667 INDIA Abstract : A dynamic model based
Metacommunities Spatial Ecology of Communities
 Spatial Ecology of Communities Four perspectives for multiple species Patch dynamics principles of metapopulation models (patchy pops, Levins) Mass effects principles of source-sink and rescue effects
Spatial Ecology of Communities Four perspectives for multiple species Patch dynamics principles of metapopulation models (patchy pops, Levins) Mass effects principles of source-sink and rescue effects
Student Background Readings for Bug Dynamics: The Logistic Map
 Student Background Readings for Bug Dynamics: The Logistic Map Figure 1 The population as a function of a growth rate parameter observed in the experiment of [Bugs]. Graphs such as this are called bifurcation
Student Background Readings for Bug Dynamics: The Logistic Map Figure 1 The population as a function of a growth rate parameter observed in the experiment of [Bugs]. Graphs such as this are called bifurcation
DYNAMICS OF A PREDATOR-PREY INTERACTION IN CHEMOSTAT WITH VARIABLE YIELD
 Journal of Sustainability Science Management Volume 10 Number 2, December 2015: 16-23 ISSN: 1823-8556 Penerbit UMT DYNAMICS OF A PREDATOR-PREY INTERACTION IN CHEMOSTAT WITH VARIABLE YIELD SARKER MD SOHEL
Journal of Sustainability Science Management Volume 10 Number 2, December 2015: 16-23 ISSN: 1823-8556 Penerbit UMT DYNAMICS OF A PREDATOR-PREY INTERACTION IN CHEMOSTAT WITH VARIABLE YIELD SARKER MD SOHEL
Na#onal Center for Theore#cal Sciences Mathema#cs Division, Taiwan
 Na#onal Center for Theore#cal Sciences Mathema#cs Division, Taiwan - TAMKANG JOURNAL OF MATHEMATICS Volume 47, Number 1, 127-141, March 2016 doi:10.5556/j.tkjm.47.2016.1984 This paper is available online
Na#onal Center for Theore#cal Sciences Mathema#cs Division, Taiwan - TAMKANG JOURNAL OF MATHEMATICS Volume 47, Number 1, 127-141, March 2016 doi:10.5556/j.tkjm.47.2016.1984 This paper is available online
Application of Cellular Automata in Conservation Biology and Environmental Management 1
 Application of Cellular Automata in Conservation Biology and Environmental Management 1 Miklós Bulla, Éva V. P. Rácz Széchenyi István University, Department of Environmental Engineering, 9026 Győr Egyetem
Application of Cellular Automata in Conservation Biology and Environmental Management 1 Miklós Bulla, Éva V. P. Rácz Széchenyi István University, Department of Environmental Engineering, 9026 Győr Egyetem
Stability analysis of a continuous model of mutualism with delay dynamics
 Stability analysis of a continuous model of mutualism with delay dynamics Item Type Article Authors Roberts, Jason A.; Joharjee, Najwa G. Citation Roberts, J. A., & Joharjee, N. G. (2016). Stability analysis
Stability analysis of a continuous model of mutualism with delay dynamics Item Type Article Authors Roberts, Jason A.; Joharjee, Najwa G. Citation Roberts, J. A., & Joharjee, N. G. (2016). Stability analysis
Natal versus breeding dispersal: Evolution in a model system
 Evolutionary Ecology Research, 1999, 1: 911 921 Natal versus breeding dispersal: Evolution in a model system Karin Johst 1 * and Roland Brandl 2 1 Centre for Environmental Research Leipzig-Halle Ltd, Department
Evolutionary Ecology Research, 1999, 1: 911 921 Natal versus breeding dispersal: Evolution in a model system Karin Johst 1 * and Roland Brandl 2 1 Centre for Environmental Research Leipzig-Halle Ltd, Department
An axiomatic theory for interaction between species in ecology: Gause s exclusion conjecture
 arxiv:q-bio/0611065v1 [q-bio.pe] 20 Nov 2006 An axiomatic theory for interaction between species in ecology: Gause s exclusion conjecture J. C. Flores a,b a Universidad de Tarapacá, Intituto de Alta Investigación,
arxiv:q-bio/0611065v1 [q-bio.pe] 20 Nov 2006 An axiomatic theory for interaction between species in ecology: Gause s exclusion conjecture J. C. Flores a,b a Universidad de Tarapacá, Intituto de Alta Investigación,
Towards a theory of ecotone resilience: coastal vegetation on a salinity gradient
 Towards a theory of ecotone resilience: coastal vegetation on a salinity gradient Jiang Jiang, Daozhou Gao and Donald L. DeAngelis Appendix A 1.1 The model without diffusion dn 1 = N 1 ρ 1 fs 11 N 1 1
Towards a theory of ecotone resilience: coastal vegetation on a salinity gradient Jiang Jiang, Daozhou Gao and Donald L. DeAngelis Appendix A 1.1 The model without diffusion dn 1 = N 1 ρ 1 fs 11 N 1 1
Interactions between predators and prey
 Interactions between predators and prey What is a predator? Predator An organism that consumes other organisms and inevitably kills them. Predators attack and kill many different prey individuals over
Interactions between predators and prey What is a predator? Predator An organism that consumes other organisms and inevitably kills them. Predators attack and kill many different prey individuals over
Modeling butterfly metapopulations: Does the logistic equation accurately model metapopulation dynamics? Ben Slager
 Modeling butterfly metapopulations: Does the logistic equation accurately model metapopulation dynamics? Ben Slager Introduction In 1798 Thomas Malthus constructed the theoretical framework for the logistic
Modeling butterfly metapopulations: Does the logistic equation accurately model metapopulation dynamics? Ben Slager Introduction In 1798 Thomas Malthus constructed the theoretical framework for the logistic
6 Metapopulations of Butterflies (sketch of the chapter)
 6 Metapopulations of Butterflies (sketch of the chapter) Butterflies inhabit an unpredictable world. Consider the checkerspot butterfly, Melitaea cinxia, also known as the Glanville Fritillary. They depend
6 Metapopulations of Butterflies (sketch of the chapter) Butterflies inhabit an unpredictable world. Consider the checkerspot butterfly, Melitaea cinxia, also known as the Glanville Fritillary. They depend
NOTES ON CHAOS. Chaotic dynamics stem from deterministic mechanisms, but they look very similar to random fluctuations in appearance.
 NOTES ON CHAOS. SOME CONCEPTS Definition: The simplest and most intuitive definition of chaos is the extreme sensitivity of system dynamics to its initial conditions (Hastings et al. 99). Chaotic dynamics
NOTES ON CHAOS. SOME CONCEPTS Definition: The simplest and most intuitive definition of chaos is the extreme sensitivity of system dynamics to its initial conditions (Hastings et al. 99). Chaotic dynamics
Multiple choice 2 pts each): x 2 = 18) Essay (pre-prepared) / 15 points. 19) Short Answer: / 2 points. 20) Short Answer / 5 points
 P 1 Biology 217: Ecology Second Exam Fall 2004 There should be 7 ps in this exam - take a moment and count them now. Put your name on the first p of the exam, and on each of the ps with short answer questions.
P 1 Biology 217: Ecology Second Exam Fall 2004 There should be 7 ps in this exam - take a moment and count them now. Put your name on the first p of the exam, and on each of the ps with short answer questions.
Chapter 6 Reading Questions
 Chapter 6 Reading Questions 1. Fill in 5 key events in the re-establishment of the New England forest in the Opening Story: 1. Farmers begin leaving 2. 3. 4. 5. 6. 7. Broadleaf forest reestablished 2.
Chapter 6 Reading Questions 1. Fill in 5 key events in the re-establishment of the New England forest in the Opening Story: 1. Farmers begin leaving 2. 3. 4. 5. 6. 7. Broadleaf forest reestablished 2.
Differential Equations ( DEs) MA 137 Calculus 1 with Life Science Application A First Look at Differential Equations (Section 4.1.
 /7 Differential Equations DEs) MA 37 Calculus with Life Science Application A First Look at Differential Equations Section 4..2) Alberto Corso alberto.corso@uky.edu Department of Mathematics University
/7 Differential Equations DEs) MA 37 Calculus with Life Science Application A First Look at Differential Equations Section 4..2) Alberto Corso alberto.corso@uky.edu Department of Mathematics University
On the stabilizing effect of specialist predators on founder-controlled communities
 On the stabilizing effect of specialist predators on founder-controlled communities Sebastian J. Schreiber Department of Mathematics Western Washington University Bellingham, WA 98225 May 2, 2003 Appeared
On the stabilizing effect of specialist predators on founder-controlled communities Sebastian J. Schreiber Department of Mathematics Western Washington University Bellingham, WA 98225 May 2, 2003 Appeared
How Philosophy Impacts on Mathematics
 .. How Philosophy Impacts on Mathematics Yang Rui Zhi Department of Philosophy Peking University Fudan University March 20, 2012 Yang Rui Zhi (PKU) Philosophical Impacts on Mathematics 20 Mar. 2012 1 /
.. How Philosophy Impacts on Mathematics Yang Rui Zhi Department of Philosophy Peking University Fudan University March 20, 2012 Yang Rui Zhi (PKU) Philosophical Impacts on Mathematics 20 Mar. 2012 1 /
Nonstandard Finite Difference Methods For Predator-Prey Models With General Functional Response
 Nonstandard Finite Difference Methods For Predator-Prey Models With General Functional Response Dobromir T. Dimitrov Hristo V. Kojouharov Technical Report 2007-0 http://www.uta.edu/math/preprint/ NONSTANDARD
Nonstandard Finite Difference Methods For Predator-Prey Models With General Functional Response Dobromir T. Dimitrov Hristo V. Kojouharov Technical Report 2007-0 http://www.uta.edu/math/preprint/ NONSTANDARD
Name Student ID. Good luck and impress us with your toolkit of ecological knowledge and concepts!
 Page 1 BIOLOGY 150 Final Exam Winter Quarter 2000 Before starting be sure to put your name and student number on the top of each page. MINUS 3 POINTS IF YOU DO NOT WRITE YOUR NAME ON EACH PAGE! You have
Page 1 BIOLOGY 150 Final Exam Winter Quarter 2000 Before starting be sure to put your name and student number on the top of each page. MINUS 3 POINTS IF YOU DO NOT WRITE YOUR NAME ON EACH PAGE! You have
BIOS 6150: Ecology Dr. Stephen Malcolm, Department of Biological Sciences
 BIOS 6150: Ecology Dr. Stephen Malcolm, Department of Biological Sciences Week 5: Interspecific Competition: Lecture summary: Definition. Examples. Outcomes. Lotka-Volterra model. Semibalanus balanoides
BIOS 6150: Ecology Dr. Stephen Malcolm, Department of Biological Sciences Week 5: Interspecific Competition: Lecture summary: Definition. Examples. Outcomes. Lotka-Volterra model. Semibalanus balanoides
4. Ecology and Population Biology
 4. Ecology and Population Biology 4.1 Ecology and The Energy Cycle 4.2 Ecological Cycles 4.3 Population Growth and Models 4.4 Population Growth and Limiting Factors 4.5 Community Structure and Biogeography
4. Ecology and Population Biology 4.1 Ecology and The Energy Cycle 4.2 Ecological Cycles 4.3 Population Growth and Models 4.4 Population Growth and Limiting Factors 4.5 Community Structure and Biogeography
On the status of the Michaelis-Menten equation and its implications for enzymology
 1 On the status of the Michaelis-Menten equation and its implications for enzymology Sosale Chandrasekhar 1 Department of Organic Chemistry, Indian Institute of Science, Bangalore 560 012, India 1 E-mail:
1 On the status of the Michaelis-Menten equation and its implications for enzymology Sosale Chandrasekhar 1 Department of Organic Chemistry, Indian Institute of Science, Bangalore 560 012, India 1 E-mail:
PERMANENCE IN LOGISTIC AND LOTKA-VOLTERRA SYSTEMS WITH DISPERSAL AND TIME DELAYS
 Electronic Journal of Differential Equations, Vol. 2005(2005), No. 60, pp. 1 11. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) PERMANENCE
Electronic Journal of Differential Equations, Vol. 2005(2005), No. 60, pp. 1 11. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) PERMANENCE
Mathematical Modelling Lecture 10 Difference Equations
 Lecture 10 Difference Equations phil.hasnip@york.ac.uk Overview of Course Model construction dimensional analysis Experimental input fitting Finding a best answer optimisation Tools for constructing and
Lecture 10 Difference Equations phil.hasnip@york.ac.uk Overview of Course Model construction dimensional analysis Experimental input fitting Finding a best answer optimisation Tools for constructing and
1 Computational problems
 80240233: Computational Complexity Lecture 1 ITCS, Tsinghua Univesity, Fall 2007 9 October 2007 Instructor: Andrej Bogdanov Notes by: Andrej Bogdanov The aim of computational complexity theory is to study
80240233: Computational Complexity Lecture 1 ITCS, Tsinghua Univesity, Fall 2007 9 October 2007 Instructor: Andrej Bogdanov Notes by: Andrej Bogdanov The aim of computational complexity theory is to study
Fundamentals of Dynamical Systems / Discrete-Time Models. Dr. Dylan McNamara people.uncw.edu/ mcnamarad
 Fundamentals of Dynamical Systems / Discrete-Time Models Dr. Dylan McNamara people.uncw.edu/ mcnamarad Dynamical systems theory Considers how systems autonomously change along time Ranges from Newtonian
Fundamentals of Dynamical Systems / Discrete-Time Models Dr. Dylan McNamara people.uncw.edu/ mcnamarad Dynamical systems theory Considers how systems autonomously change along time Ranges from Newtonian
Advanced Optical Communications Prof. R. K. Shevgaonkar Department of Electrical Engineering Indian Institute of Technology, Bombay
 Advanced Optical Communications Prof. R. K. Shevgaonkar Department of Electrical Engineering Indian Institute of Technology, Bombay Lecture No. # 15 Laser - I In the last lecture, we discussed various
Advanced Optical Communications Prof. R. K. Shevgaonkar Department of Electrical Engineering Indian Institute of Technology, Bombay Lecture No. # 15 Laser - I In the last lecture, we discussed various
BIOS 6150: Ecology Dr. Stephen Malcolm, Department of Biological Sciences
 BIOS 6150: Ecology Dr. Stephen Malcolm, Department of Biological Sciences Week 7: Dynamics of Predation. Lecture summary: Categories of predation. Linked prey-predator cycles. Lotka-Volterra model. Density-dependence.
BIOS 6150: Ecology Dr. Stephen Malcolm, Department of Biological Sciences Week 7: Dynamics of Predation. Lecture summary: Categories of predation. Linked prey-predator cycles. Lotka-Volterra model. Density-dependence.
Bifurcation and Stability Analysis of a Prey-predator System with a Reserved Area
 ISSN 746-733, England, UK World Journal of Modelling and Simulation Vol. 8 ( No. 4, pp. 85-9 Bifurcation and Stability Analysis of a Prey-predator System with a Reserved Area Debasis Mukherjee Department
ISSN 746-733, England, UK World Journal of Modelling and Simulation Vol. 8 ( No. 4, pp. 85-9 Bifurcation and Stability Analysis of a Prey-predator System with a Reserved Area Debasis Mukherjee Department
Principles of Ecology BL / ENVS 402 Exam II Name:
 Principles of Ecology BL / ENVS 402 Exam II 10-26-2011 Name: There are three parts to this exam. Use your time wisely as you only have 50 minutes. Part One: Circle the BEST answer. Each question is worth
Principles of Ecology BL / ENVS 402 Exam II 10-26-2011 Name: There are three parts to this exam. Use your time wisely as you only have 50 minutes. Part One: Circle the BEST answer. Each question is worth
Predation is.. The eating of live organisms, regardless of their identity
 Predation Predation Predation is.. The eating of live organisms, regardless of their identity Predation 1)Moves energy and nutrients through the ecosystem 2)Regulates populations 3)Weeds the unfit from
Predation Predation Predation is.. The eating of live organisms, regardless of their identity Predation 1)Moves energy and nutrients through the ecosystem 2)Regulates populations 3)Weeds the unfit from
Stability Analysis of Gompertz s Logistic Growth Equation Under Strong, Weak and No Allee Effects
 Stability Analysis of Gompertz s Logistic Growth Equation Under Strong, Weak and No Allee Effects J. LEONEL ROCHA ISEL - Instituto Superior de Engenharia de Lisboa ADM - Department of Mathematics Rua Conselheiro
Stability Analysis of Gompertz s Logistic Growth Equation Under Strong, Weak and No Allee Effects J. LEONEL ROCHA ISEL - Instituto Superior de Engenharia de Lisboa ADM - Department of Mathematics Rua Conselheiro
FIELDS INSTITUTE COMMUNICATIONS, VOLUME. 21, , 1999 RICH DYNAMICS OF GAUSE-TYPE RATIO-DEPENDENT PREDATOR-PREY SYSTEM
 FIELDS INSTITUTE COMMUNICATIONS, VOLUME. 21, 325-337, 1999 RICH DYNAMICS OF GAUSE-TYPE RATIO-DEPENDENT PREDATOR-PREY SYSTEM YANG KUANG abstract Ratio-dependent predator-prey models are increasingly favored
FIELDS INSTITUTE COMMUNICATIONS, VOLUME. 21, 325-337, 1999 RICH DYNAMICS OF GAUSE-TYPE RATIO-DEPENDENT PREDATOR-PREY SYSTEM YANG KUANG abstract Ratio-dependent predator-prey models are increasingly favored
Predator-prey interactions
 Predator-prey interactions Key concepts ˆ Predator-prey cycles ˆ Phase portraits ˆ Stabilizing mechanisms ˆ Linear stability analysis ˆ Functional responses ˆ The paradox of enrichment Predator-prey cycles
Predator-prey interactions Key concepts ˆ Predator-prey cycles ˆ Phase portraits ˆ Stabilizing mechanisms ˆ Linear stability analysis ˆ Functional responses ˆ The paradox of enrichment Predator-prey cycles
Stability Analysis of a Continuous Model of Mutualism with Delay Dynamics
 International Mathematical Forum, Vol. 11, 2016, no. 10, 463-473 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/imf.2016.616 Stability Analysis of a Continuous Model of Mutualism with Delay Dynamics
International Mathematical Forum, Vol. 11, 2016, no. 10, 463-473 HIKARI Ltd, www.m-hikari.com http://dx.doi.org/10.12988/imf.2016.616 Stability Analysis of a Continuous Model of Mutualism with Delay Dynamics
POPULATIONS and COMMUNITIES
 POPULATIONS and COMMUNITIES Ecology is the study of organisms and the nonliving world they inhabit. Central to ecology is the complex set of interactions between organisms, both intraspecific (between
POPULATIONS and COMMUNITIES Ecology is the study of organisms and the nonliving world they inhabit. Central to ecology is the complex set of interactions between organisms, both intraspecific (between
NONSTANDARD NUMERICAL METHODS FOR A CLASS OF PREDATOR-PREY MODELS WITH PREDATOR INTERFERENCE
 Sixth Mississippi State Conference on Differential Equations and Computational Simulations, Electronic Journal of Differential Equations, Conference 15 (2007), pp. 67 75. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu
Sixth Mississippi State Conference on Differential Equations and Computational Simulations, Electronic Journal of Differential Equations, Conference 15 (2007), pp. 67 75. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu
Population modeling of marine mammal populations
 Population modeling of marine mammal populations Lecture 1: simple models of population counts Eli Holmes National Marine Fisheries Service nmfs.noaa.gov Today s lecture topics: Density-independent growth
Population modeling of marine mammal populations Lecture 1: simple models of population counts Eli Holmes National Marine Fisheries Service nmfs.noaa.gov Today s lecture topics: Density-independent growth
Evidence for Competition
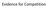 Evidence for Competition Population growth in laboratory experiments carried out by the Russian scientist Gause on growth rates in two different yeast species Each of the species has the same food e.g.,
Evidence for Competition Population growth in laboratory experiments carried out by the Russian scientist Gause on growth rates in two different yeast species Each of the species has the same food e.g.,
A REMARK ON THE GLOBAL DYNAMICS OF COMPETITIVE SYSTEMS ON ORDERED BANACH SPACES
 PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 00, Number 0, Pages 000 000 S 0002-9939(XX)0000-0 A REMARK ON THE GLOBAL DYNAMICS OF COMPETITIVE SYSTEMS ON ORDERED BANACH SPACES KING-YEUNG LAM
PROCEEDINGS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 00, Number 0, Pages 000 000 S 0002-9939(XX)0000-0 A REMARK ON THE GLOBAL DYNAMICS OF COMPETITIVE SYSTEMS ON ORDERED BANACH SPACES KING-YEUNG LAM
Marine Resources Development Foundation/MarineLab Grades: 9, 10, 11, 12 States: AP Biology Course Description Subjects: Science
 Marine Resources Development Foundation/MarineLab Grades: 9, 10, 11, 12 States: AP Biology Course Description Subjects: Science Highlighted components are included in Tallahassee Museum s 2016 program
Marine Resources Development Foundation/MarineLab Grades: 9, 10, 11, 12 States: AP Biology Course Description Subjects: Science Highlighted components are included in Tallahassee Museum s 2016 program
UNIVERSITY OF NOTTINGHAM. Discussion Papers in Economics CONSISTENT FIRM CHOICE AND THE THEORY OF SUPPLY
 UNIVERSITY OF NOTTINGHAM Discussion Papers in Economics Discussion Paper No. 0/06 CONSISTENT FIRM CHOICE AND THE THEORY OF SUPPLY by Indraneel Dasgupta July 00 DP 0/06 ISSN 1360-438 UNIVERSITY OF NOTTINGHAM
UNIVERSITY OF NOTTINGHAM Discussion Papers in Economics Discussion Paper No. 0/06 CONSISTENT FIRM CHOICE AND THE THEORY OF SUPPLY by Indraneel Dasgupta July 00 DP 0/06 ISSN 1360-438 UNIVERSITY OF NOTTINGHAM
LECTURE 1: Introduction and Brief History of Population Ecology
 WMAN 512 SPRING 2010 ADV WILDL POP ECOL LECTURE 1: Introduction and Brief History of Population Ecology Cappuccino, N. 1995. Novel approaches to the study of population dynamics. pp 2-16 in Population
WMAN 512 SPRING 2010 ADV WILDL POP ECOL LECTURE 1: Introduction and Brief History of Population Ecology Cappuccino, N. 1995. Novel approaches to the study of population dynamics. pp 2-16 in Population
Chapter 7. Evolutionary Game Theory
 From the book Networks, Crowds, and Markets: Reasoning about a Highly Connected World. By David Easley and Jon Kleinberg. Cambridge University Press, 2010. Complete preprint on-line at http://www.cs.cornell.edu/home/kleinber/networks-book/
From the book Networks, Crowds, and Markets: Reasoning about a Highly Connected World. By David Easley and Jon Kleinberg. Cambridge University Press, 2010. Complete preprint on-line at http://www.cs.cornell.edu/home/kleinber/networks-book/
Probe interval graphs and probe unit interval graphs on superclasses of cographs
 Author manuscript, published in "" Discrete Mathematics and Theoretical Computer Science DMTCS vol. 15:2, 2013, 177 194 Probe interval graphs and probe unit interval graphs on superclasses of cographs
Author manuscript, published in "" Discrete Mathematics and Theoretical Computer Science DMTCS vol. 15:2, 2013, 177 194 Probe interval graphs and probe unit interval graphs on superclasses of cographs
Evolutionary Dynamics and Extensive Form Games by Ross Cressman. Reviewed by William H. Sandholm *
 Evolutionary Dynamics and Extensive Form Games by Ross Cressman Reviewed by William H. Sandholm * Noncooperative game theory is one of a handful of fundamental frameworks used for economic modeling. It
Evolutionary Dynamics and Extensive Form Games by Ross Cressman Reviewed by William H. Sandholm * Noncooperative game theory is one of a handful of fundamental frameworks used for economic modeling. It
7.2. Differential Equations. Phase Plots. Example 1 The logistic equation. Phase Plots. Phase Plots. Phase Plots, Equilibria, and Stability
 Differential Equations 7 7.2, Equilibria, and Stability Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Phase plots provide a way to visualize the dynamics
Differential Equations 7 7.2, Equilibria, and Stability Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Phase plots provide a way to visualize the dynamics
PULSE-SEASONAL HARVESTING VIA NONLINEAR DELAY DIFFERENTIAL EQUATIONS AND APPLICATIONS IN FISHERY MANAGEMENT. Lev V. Idels
 PULSE-SEASONAL HARVESTING VIA NONLINEAR DELAY DIFFERENTIAL EQUATIONS AND APPLICATIONS IN FISHERY MANAGEMENT Lev V. Idels University-College Professor Mathematics Department Malaspina University-College
PULSE-SEASONAL HARVESTING VIA NONLINEAR DELAY DIFFERENTIAL EQUATIONS AND APPLICATIONS IN FISHERY MANAGEMENT Lev V. Idels University-College Professor Mathematics Department Malaspina University-College
The upper limit for the exponent of Taylor s power law is a consequence of deterministic population growth
 Evolutionary Ecology Research, 2005, 7: 1213 1220 The upper limit for the exponent of Taylor s power law is a consequence of deterministic population growth Ford Ballantyne IV* Department of Biology, University
Evolutionary Ecology Research, 2005, 7: 1213 1220 The upper limit for the exponent of Taylor s power law is a consequence of deterministic population growth Ford Ballantyne IV* Department of Biology, University
