A Reduction of Finitely Expandable Deep Pushdown Automata
|
|
|
- Myrtle Dennis
- 5 years ago
- Views:
Transcription
1 A Reduction of Finitely Expandable Deep Pushdown Automata Lucie Dvořáková Abstract For a positive integer n, n-expandable deep pushdown automata always contain no more than n occurrences of non-input symbols in their pushdowns during any computation. As its main result, the present paper demonstrates that these automata are as powerful as the same automata with only two non-input pushdown symbols $ and #, where # always appears solely as the pushdown bottom as it would in the regular pushdown automaton. The paper demonstrates an infinite hierarchy of language families that follows from this main result. In its conclusion, the paper suggests open problems and topics for the future investigation. Keywords: Deep Pushdown Automata, Finite Expandability, Reduction, Non-Input Pushdown Symbols Supplementary Material: N/A *xdvora1f@stud.fit.vutbr.cz, Faculty of Information Technology, Brno University of Technology 1. Introduction In essence, deep pushdown automata represent languageaccepting models based upon new stack-like structures, which can be modified deeper than on their top. As a result, these automata can make expansions deeper in their pushdown lists as opposed to ordinary pushdown automata, which can expand only the very pushdown top. At present, the study of deep pushdown automata represent a vivid trend in formal language theory (see [1, 2, 3, 4]). The present paper makes a contribution to this trend. This paper narrows its attention to n-expandable deep pushdown automata, where n is a positive integer. In essence, during any computation, their pushdown lists contain #, which always appears as the pushdown bottom, and no more than n 1 occurrences of other non-input symbols. As its main result, the paper demonstrates how to reduce the number of their non-input pushdown symbols different from # to one symbol, denoted by $, without affecting the power of these automata. Based on this main result, the paper establishes an infinite hierarchy of language families resulting from these reduced versions of n-expandable deep pushdown automata. More precisely, consider n- expandable deep pushdown automata with pushdown alphabets containing #, $, and input symbols. The paper shows that (n + 1)-expandable versions of these automata are stronger than their n-expandable versions, for every positive integer n. In addition, it points out that these automata with # as its only non-input symbol characterize the family of regular languages. In its conclusion, this paper formulates several open problem areas related to the subject of this paper for the future study. The paper is organized as follows. Section 2 gives all the definitions needed to follow the paper. Section 3 establishes all the results sketched above, and in its conclusion, it also brings the reader s attention to several open problems. 2. Preliminaries and Definitions We assume that the reader is familiar with formal language theory (see Harrison [5] or Meduna [6, 7]). Let N denote the set of all positive integers. For an alphabet Γ, Γ represents the free monoid generated by Γ under the operation of concatenation. The identity of Γ is denoted by ε. For w Γ, w denotes the length of w.
2 A deep pushdown automaton (Deep PDA) is a 7- tuple M = (Q,Σ,Γ,R,s,S, F), where Q is a finite set of states, Σ is a input alphabet, Γ is a pushdown alphabet, Σ Γ is an input alphabet, s Q is the start state, S Γ \ Σ is the start pushdown symbol, and F Q is the set of final states. Γ \ Σ contains the bottom pushdown symbol denoted by #. In what follows, N = Γ \ (Σ {#}). R is a finite subset of (N Q N Q (Γ \ {#}) + ) (N Q {#} Q (Γ \ {#}) {#}). R is called the set of rules; instead of (m,q,a,t,v) R, we write mqa tv throughout. A configuration of M is any member of Q Σ (Γ \ {#}) {#}. Let Ξ denote the set of all configurations of M. Next, we define three binary relations over Ξ p, e, and. Let q,t Q, x Σ, z (Γ \ {#}) {#}). 1. Let a Σ; then, (q,ax,az) p (q,x,z). 2. Let mqa tv R, z = uaw, u (Γ \ {#}), u contains m 1 occurrences of symbols from N, either A N, v (Γ \ {#}) + and w (Γ \ {#}) {#} or A = #, v (Γ \ {#}) {#}, and w = ε; then, (q,x,uaw) e (t,x,uvw). 3. Let α,β Ξ; α β if and only if α p β or α e β. Intuitively, in p and e, p and e stand for pop and expansion, respectively. Consider 2 above; to express that (q,x,uaw) e (q,x,uvw) is made according to mqa tv, write (q,x,uaw) e (t,x,uvw) [mqa tv]. If α,β Ξ, α β in M, we say that M makes a move from α to β. In the standard manner, extend e, p, and to e i, p i, and i, respectively, for i 0; then, based on e i, p i, and i, define e +, e, p +, p, +, and. The language of M, L(M), is defined as L(M) = {w (s,w,s#) ( f,ε,#) in M, w Σ, f F}. Let n N. If during any α β in M, α,β Ξ, M has no more than n occurrences of symbols form Γ\Σ in its pushdown, then M is an n-expandable Deep PDA. A right-linear grammar is a quadruple G = (N,T, P,S), where N is an alphabet of nonterminals, T is an alphabet of terminals such that N T = /0, P is a finite subset of N T (N {ε}), and S N. P is called the set of rules in G; instead of (A,x) P, we write A x. Define the language of G, L(G), as usual (see [6]). Let n,r N, n DPDA denotes the language family accepted by n-expandable Deep PDA. n DPDA r denotes the language family accepted by n-expandable deep pushdown automata with # and no more than (r 1) non-input pushdown symbols. Reg denotes the regular language family. Recall that Reg is characterized by right-linear grammars (see Theorem in [6]). 3. Result Next, we establish Lemma 3.1, which implies the main result of this paper. Lemma 3.1. Let n N. For every n-expandable Deep PDA M, there exists an n-expendable Deep PDA M R such that L(M) = L(M R ) and M R contains only two non-input pushdown symbols $ and #. Proof. Construction. Let n N. Let M = (Q,Σ,Γ,R,s,S,F) be an n-expandable Deep PDA. Recall that rules in R are of the form mqa tv, where m N, q,t Q, either A N and v (Γ \ {#}) + or A = # and v (Γ \ {#}) {#}, where # denotes the pushdown bottom. Let $ be a new symbol, $ / Q Γ, and let homomorphisms f and g over Γ be defined as f (A) = A and g(a) = $, for every A N, and f (a) = ε and g(a) = a, for every a (Σ {#}). Next, we construct an n-expandable Deep PDA M R = (Q R,Σ,Σ {$,#},R R,s R,$,F R ) by performing 1 through 4, given next: 1. Add m q;uaz $ t;u f (v)z g(v) to R R and add q;uaz, t;u f (v)z to Q R if mqa tv R, u,z N, u = m 1, z n m 1, u f (v)z < n, m N, q,t Q, A N, and v (Γ \ {#}) + ; 2. Add m q;u # t;u f (v) g(v)# to R R and add q;u, t;u f (v) to Q R if mq# tv# R, u N, u = m 1, u f (v) < n, m N, q,t Q, and v (Γ \ {#}) ; 3. Set s R = s;s ; 4. Add all t;u to F R, where t F, u N, u < n. Later in this proof, we demonstrate that L(M) = L(M R ). Basic Idea States in Q R include not only the states corresponding to the states in Q but also strings of noninput symbols. Whenever M pushes a non-input symbol onto the pushdown, M R records this information within its current state and pushes $ onto the pushdown instead. By Lemma 3.1. in [8], any n-expandable Deep PDA M can accept every w L(M) so all expansions precede all pops during the accepting process. Without any loss of generality, we assume that M and M R work in this way in what follows, too. To establish L(M) = L(M R ), we prove the following four claims.
3 Claim 3.1. Let (s,w,s#) j (q,v,x#) in M, where s,q Q, w,v Σ, and x (Γ\{#}). Then, ( s;s,w,$#) ( q; f (x),v,g(x)#) in M R, where s;s, q; f (x) Q R, and g(x) (Σ {$}). This claim is proved by induction on j 0. Basis Let j = 0, so (s,w,s#) 0 (s,w,s#) in M, where s Q and S N. Then, from 3 in the construction, we obtain ( s;s,w,$#) 0 ( s;s,w,$#) in M R, so the basis holds. Induction Hypothesis Assume there is i 0 such that Claim 3.1 holds true for all 0 j i. Induction Step Let (s,w,s#) i+1 (q,w,x#) in M, where x (Γ\{#}), s,q Q, w Σ, k,l 1, k+l < n. Since i + 1 1, we can express (s,w,s#) i+1 (q,w,x#) as (s,w,s#) i (t,w,x 0 A 1 x 1...A m...a k x k #) (q,w,x 0 A 1 x 1...A m 1 x m 1 y 0 B 1 y 1...B l y l x m A m+1...x k 1 A k x k #) [mta m qy 0 B 1 y 1...B l y l ] where A 1,...,A k,b 1,...,B l N and x 0 x 1...x k,y 0 y 1...y l Σ, t Q. By the induction hypothesis, we have ( s;s,w,$#) ( t;a 1...A m...a k,w,x 0 $x 1 $...$x k #) Since mta m qy 0 B 1 y 1...B l y l R, we also have m t;a 1...A m...a k $ q;a 1...A m 1 B 1...B l A m+1...a k y 0 $y 1 $...$y l R R (see 1 in the construction). Thus, ( t;a 1...A m...a k,w,x 0 $x 1 $...$x k #) ( q;a 1...A m 1 B 1...B l A m+1...a k,w, x 0 $x 1 $...$x m 1 y 0 $y 1 $...$y l x m $...$x k #) [m t;a 1...A m...a k $ q;a 1...A m 1 B 1...B l A m+1...a k y 0 $y 1 $...$y l ] Analogically, we can prove the induction step for the case when # is rewritten (see 2 in the construction). Therefore, Claim 3.1 holds true. Claim 3.2. L(M) L(M R ). Proof. Consider Claim 3.1 for v = ε, q F, and x = ε. Under this consideration Claim 3.1 implies Claim 3.2. Claim 3.3. Let ( s;s,w,$#) j ( q;a 1...A k,v,x#) in M R, where s R = s;s, q;a 1...A k Q R, w,v Σ, A 1,...,A k N, x = x 0 $x 1 $...$x k, and x 0...x k Σ. Then, (s,w,s#) (q,v,x 0 A 1 x 1...A k x k #) in M, where s,q Q. Proof. This claim is proved by induction on j 0. Basis. Let j = 0, so ( s;s,w,$#) 0 ( s;s,w,$#) in M R, where s R = s;s. From 3 in the construction, we have (s,w,s#) 0 (s,w,s#) in M, so the basis holds. Induction Hypothesis. Assume there is i 0 such that Claim 3.3 holds true for 0 j i. Induction Step. Let ( s;s,w,$#) i+1 ( q;a 1...A k, w, x 0 $x 1 $...$x k #) in M R, where s;s, q;a 1...A k Q R, A 1,..., A k N, w Σ, and x 0...x k Σ, k,l 1, k + l < n. Since i + 1 1, we can express ( s;s, w, $#) i+1 ( q;a 1...A k, w, x 0 $x 1 $...$x k #) as ( q;( s;s,w,$#) i ( t;a 1...A m...a k,w,x 0 $x 1 $...$x k #) A 1...A m 1 B 1...B l A m+1...a k,w,x 0 $x 1 $... $x m 1 y 0 $y 1 $...$y l x m $...$x k #) [m t;a 1...A m...a k $ q;a 1...A m 1 B 1...B l A m+1...a k y 0 $y 1 $...$y l ] By the induction hypothesis, we obtain (s,w,s#) i (t,w,x 0 A 1 x 1...A m...a k x k #) Since m t;a 1...A m...a k $ q;a 1...A m 1 B 1...B l A m+1...a k y 0 $y 1 $...$y l R R, we also have mta m qy 0 B 1 y 1...B l y l R as follows from 1 in the construction. We obtain (t,w,x 0 A 1 x 1...A m...a k x k #) (q,w,x 0 A 1 x 1...A m 1 x m 1 y 0 B 1 y 1... B l y l x m A m+1...x k 1 A k x k #) [mta m qy 0 B 1 y 1...B l y l ] Analogically, we can prove the case when # is expanded (see 2 in the construction). Therefore, Claim 3.3 holds true. Claim 3.4. L(M R ) L(M). Proof. Consider Claim 3.3 with v = ε, q;a 1...A k F R, and x = ε. Under this consideration, Claim 3.3 implies Claim 3.4.
4 As L(M) L(M R ) (see Claim 3.2) and L(M R ) L(M) (see Claim 3.4), L(M R ) = L(M). Thus, Lemma 3.1 holds. Example Take this three-expandable Deep PDA M = ({s,q,t},{a,b, c},{a,b,c,a,s,#}, R,s,S,{ f }) where R = {1sS qaa, 1qA f ab, 1 f A f c, 1qA taab, 2tA qac} Proof. This corollary follows from Theorem 3.1 in this paper and Corollary 3.1. in [8]. Can we reformulate Theorem 3.1 and Corollary 3.1 in terms of n DPDA 1? The answer is no as we show next. Lemma 3.2. Let M = (Q,Σ,Γ,R,s,S,F) be a Deep PDA with Γ \ Σ = {#}. Then, there is a right-linear grammar G such that L(G) = L(M). Proof. Let M = (Q,Σ,Γ,R,s,S,F) with Γ \ Σ = {#}. Thus, every rule in R is of the form 1q# px#, where q, p Q, x Σ. Next, we construct a right-linear grammar G = (Q,Σ,P,s) so L(M) = L(G). We construct P as follows: By the construction given in the proof of Lemma 3.1, we construct M R = (Q R, {a,b,c}, {a,b,c,$,#}, R R, s;s, $, { f ;A, f ;ε }), where Q R = { s;s, q;aa, f ;A, f ;ε, t;aa } and R R = {1 : 1 s;s $ For instance, M R makes q;aa $$, 2 : 1 q;aa $ f ;A ab, 3 : 1 f ;A $ f ;ε c, 4 : 1 q;aa $ t;aa a$b, 5 : 2 t;aa $ q;aa $c, 6 : 1 s;sa $ q;aaa $$, 7 : 1 s;ss $ q;aas $$, 8 : 1 q;aa $ f ;A ab, 9 : 1 q;as $ f ;S ab, 10 : 1 f ;AA $ f ;A c, 11 : 1 f ;AS $ f ;S c, 12 : 1 q;a $ t;a a$b, 13 : 1 q;as $ t;as a$b, 14 : 2 t;sa $ q;sa $c} ( s;s,aabbcc,$#) e ( q;aa,aabbcc,$$#) (1) e ( t;aa,aabbcc,a$b$#) (4) p ( t;aa,abbcc,$b$#) e ( q;aa,abbcc,$b$c#) (5) e ( f ;A,abbcc,abb$c#) (2) p ( f ;A,cc,$c#) e ( f ;ε,cc,cc#) (3) p ( f ;ε,ε,#) Theorem 3.1. For all n 1, n DPDA = n DPDA 2. Proof. This theorem follows from Lemma 3.1. Corollary 3.1. For all n 1, n DPDA 2 n+1 DPDA For every 1q# px# R, where p,q Q, x Σ, add q xp to P; 2. For every f F, add f ε to P. A rigorous proof that L(M) = L(G) is left to the reader. Theorem 3.2. Reg = 1 DPDA 1 = n DPDA 1, for any n 1. Proof. Let n 1. Reg 1 DPDA 1 = n DPDA 1 is clear. Recall that right-linear grammars characterize Reg, so n DPDA 1 Reg follows from Lemma 3.2. Thus, Reg = n DPDA 1. Corollary 3.2. Reg = 1 DPDA 1 = n DPDA 1 n DPDA 2, for all n 2. Proof. Let n 1. As obvious, 1 DPDA 1 = n DPDA 1 ndpda 2. Observe that {a n b n n 1} n DPDA 2 \ n DPDA 1 Therefore, Corollary 3.2 holds. 4. Conclusions In the present paper, we have reduced finitely expandable Deep PDAs with respect to the number of noninput pushdown symbols. Before closing this paper, we suggest some open problem areas related to this subject for the future investigation. 1. Can we reduce these automata with respect to the number of states? 2. Can we simultaneously reduce them with respect to the number of both states and non-input pushdown symbols? 3. Can we achieve the reductions described above in terms of general Deep PDAs, which are not finitely expandable?
5 Acknowledgements I would like to thank my supervisor prof. Alexander Meduna, CSc. for his help. RNDr. References [1] Nidhi Kalra and Ajay Kumar. Fuzzy state grammar and fuzzy deep pushdown automaton. Journal of Intelligent and Fuzzy Systems, 31(1): , [2] Nidhi Kalra and Ajay Kumar. State grammar and deep pushdown automata for biological sequences of nucleic acids. Current Bioinformatics, 11(4): , [3] Argimiro Arratia and Iain A. Stewart. Program schemes with deep pushdown storage. In Proc. of Logic and Theory of Algorithms, CiE 2008, volume 5028 of Lecture Notes in Computer Science, pages Springer, [4] Alexander Meduna. Deep pushdown automata. Acta Inf., 42(8-9): , [5] Michael A. Harrison. Introduction to Formal Language Theory. Addison-Wesley, [6] Alexander Meduna. Automata and Languages: Theory and Applications. Springer, [7] Alexander Meduna and Petr Zemek. Regulated Grammars and Automata. Springer, [8] Peter Leupold and Alexander Meduna. Finately expandable deep PDAs. In Proc. of Automata, Formal Languages and Algebraic Systems 2008, pages World Scientific, 2010.
How to Pop a Deep PDA Matters
 How to Pop a Deep PDA Matters Peter Leupold Department of Mathematics, Faculty of Science Kyoto Sangyo University Kyoto 603-8555, Japan email:leupold@cc.kyoto-su.ac.jp Abstract Deep PDA are push-down automata
How to Pop a Deep PDA Matters Peter Leupold Department of Mathematics, Faculty of Science Kyoto Sangyo University Kyoto 603-8555, Japan email:leupold@cc.kyoto-su.ac.jp Abstract Deep PDA are push-down automata
1. Draw a parse tree for the following derivation: S C A C C A b b b b A b b b b B b b b b a A a a b b b b a b a a b b 2. Show on your parse tree u,
 1. Draw a parse tree for the following derivation: S C A C C A b b b b A b b b b B b b b b a A a a b b b b a b a a b b 2. Show on your parse tree u, v, x, y, z as per the pumping theorem. 3. Prove that
1. Draw a parse tree for the following derivation: S C A C C A b b b b A b b b b B b b b b a A a a b b b b a b a a b b 2. Show on your parse tree u, v, x, y, z as per the pumping theorem. 3. Prove that
(pp ) PDAs and CFGs (Sec. 2.2)
 (pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
(pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
(pp ) PDAs and CFGs (Sec. 2.2)
 (pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
(pp. 117-124) PDAs and CFGs (Sec. 2.2) A language is context free iff all strings in L can be generated by some context free grammar Theorem 2.20: L is Context Free iff a PDA accepts it I.e. if L is context
Pushdown Automata. We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata.
 Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
Pushdown Automata We have seen examples of context-free languages that are not regular, and hence can not be recognized by finite automata. Next we consider a more powerful computation model, called a
Derivation in Scattered Context Grammar via Lazy Function Evaluation
 Derivation in Scattered Context Grammar via Lazy Function Evaluation Ota Jirák 1 and Dušan Kolář 2 1 FIT BUT, Brno, Czech Republic, ijirak@fit.vutbr.cz, WWW home page: http://www.fit.vutbr.cz/ ~ ijirak/
Derivation in Scattered Context Grammar via Lazy Function Evaluation Ota Jirák 1 and Dušan Kolář 2 1 FIT BUT, Brno, Czech Republic, ijirak@fit.vutbr.cz, WWW home page: http://www.fit.vutbr.cz/ ~ ijirak/
FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY
 15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
15-453 FORMAL LANGUAGES, AUTOMATA AND COMPUTABILITY REVIEW for MIDTERM 1 THURSDAY Feb 6 Midterm 1 will cover everything we have seen so far The PROBLEMS will be from Sipser, Chapters 1, 2, 3 It will be
October 6, Equivalence of Pushdown Automata with Context-Free Gramm
 Equivalence of Pushdown Automata with Context-Free Grammar October 6, 2013 Motivation Motivation CFG and PDA are equivalent in power: a CFG generates a context-free language and a PDA recognizes a context-free
Equivalence of Pushdown Automata with Context-Free Grammar October 6, 2013 Motivation Motivation CFG and PDA are equivalent in power: a CFG generates a context-free language and a PDA recognizes a context-free
Computational Models - Lecture 5 1
 Computational Models - Lecture 5 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 10/22, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
Computational Models - Lecture 5 1 Handout Mode Iftach Haitner and Yishay Mansour. Tel Aviv University. April 10/22, 2013 1 Based on frames by Benny Chor, Tel Aviv University, modifying frames by Maurice
5 Context-Free Languages
 CA320: COMPUTABILITY AND COMPLEXITY 1 5 Context-Free Languages 5.1 Context-Free Grammars Context-Free Grammars Context-free languages are specified with a context-free grammar (CFG). Formally, a CFG G
CA320: COMPUTABILITY AND COMPLEXITY 1 5 Context-Free Languages 5.1 Context-Free Grammars Context-Free Grammars Context-free languages are specified with a context-free grammar (CFG). Formally, a CFG G
Push-down Automata = FA + Stack
 Push-down Automata = FA + Stack PDA Definition A push-down automaton M is a tuple M = (Q,, Γ, δ, q0, F) where Q is a finite set of states is the input alphabet (of terminal symbols, terminals) Γ is the
Push-down Automata = FA + Stack PDA Definition A push-down automaton M is a tuple M = (Q,, Γ, δ, q0, F) where Q is a finite set of states is the input alphabet (of terminal symbols, terminals) Γ is the
Introduction to Formal Languages, Automata and Computability p.1/42
 Introduction to Formal Languages, Automata and Computability Pushdown Automata K. Krithivasan and R. Rama Introduction to Formal Languages, Automata and Computability p.1/42 Introduction We have considered
Introduction to Formal Languages, Automata and Computability Pushdown Automata K. Krithivasan and R. Rama Introduction to Formal Languages, Automata and Computability p.1/42 Introduction We have considered
The Pumping Lemma. for all n 0, u 1 v n u 2 L (i.e. u 1 u 2 L, u 1 vu 2 L [but we knew that anyway], u 1 vvu 2 L, u 1 vvvu 2 L, etc.
![The Pumping Lemma. for all n 0, u 1 v n u 2 L (i.e. u 1 u 2 L, u 1 vu 2 L [but we knew that anyway], u 1 vvu 2 L, u 1 vvvu 2 L, etc. The Pumping Lemma. for all n 0, u 1 v n u 2 L (i.e. u 1 u 2 L, u 1 vu 2 L [but we knew that anyway], u 1 vvu 2 L, u 1 vvvu 2 L, etc.](/thumbs/89/99844223.jpg) The Pumping Lemma For every regular language L, there is a number l 1 satisfying the pumping lemma property: All w L with w l can be expressed as a concatenation of three strings, w = u 1 vu 2, where u
The Pumping Lemma For every regular language L, there is a number l 1 satisfying the pumping lemma property: All w L with w l can be expressed as a concatenation of three strings, w = u 1 vu 2, where u
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET
 THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
THEORY OF COMPUTATION (AUBER) EXAM CRIB SHEET Regular Languages and FA A language is a set of strings over a finite alphabet Σ. All languages are finite or countably infinite. The set of all languages
Jumping Finite Automata
 Jumping Finite Automata Alexander Meduna and Petr Zemek Brno University of Technology, Faculty of Information Technology IT4Innovations Centre of Excellence Božetěchova 2, 612 00 Brno, Czech Republic http://www.fit.vutbr.cz/
Jumping Finite Automata Alexander Meduna and Petr Zemek Brno University of Technology, Faculty of Information Technology IT4Innovations Centre of Excellence Božetěchova 2, 612 00 Brno, Czech Republic http://www.fit.vutbr.cz/
SCHEME FOR INTERNAL ASSESSMENT TEST 3
 SCHEME FOR INTERNAL ASSESSMENT TEST 3 Max Marks: 40 Subject& Code: Automata Theory & Computability (15CS54) Sem: V ISE (A & B) Note: Answer any FIVE full questions, choosing one full question from each
SCHEME FOR INTERNAL ASSESSMENT TEST 3 Max Marks: 40 Subject& Code: Automata Theory & Computability (15CS54) Sem: V ISE (A & B) Note: Answer any FIVE full questions, choosing one full question from each
Pushdown Automata (Pre Lecture)
 Pushdown Automata (Pre Lecture) Dr. Neil T. Dantam CSCI-561, Colorado School of Mines Fall 2017 Dantam (Mines CSCI-561) Pushdown Automata (Pre Lecture) Fall 2017 1 / 41 Outline Pushdown Automata Pushdown
Pushdown Automata (Pre Lecture) Dr. Neil T. Dantam CSCI-561, Colorado School of Mines Fall 2017 Dantam (Mines CSCI-561) Pushdown Automata (Pre Lecture) Fall 2017 1 / 41 Outline Pushdown Automata Pushdown
PUSHDOWN AUTOMATA (PDA)
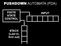 PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
PUSHDOWN AUTOMATA (PDA) FINITE STATE CONTROL INPUT STACK (Last in, first out) input pop push ε,ε $ 0,ε 0 1,0 ε ε,$ ε 1,0 ε PDA that recognizes L = { 0 n 1 n n 0 } Definition: A (non-deterministic) PDA
Left-Forbidding Cooperating Distributed Grammar Systems
 Left-Forbidding Cooperating Distributed Grammar Systems Filip Goldefus a, Tomáš Masopust b,, Alexander Meduna a a Faculty of Information Technology, Brno University of Technology Božetěchova 2, Brno 61266,
Left-Forbidding Cooperating Distributed Grammar Systems Filip Goldefus a, Tomáš Masopust b,, Alexander Meduna a a Faculty of Information Technology, Brno University of Technology Božetěchova 2, Brno 61266,
Theory of Computation
 Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 10: CF, PDAs and Beyond Greibach Normal Form I We want to show that all context-free
Thomas Zeugmann Hokkaido University Laboratory for Algorithmics http://www-alg.ist.hokudai.ac.jp/ thomas/toc/ Lecture 10: CF, PDAs and Beyond Greibach Normal Form I We want to show that all context-free
Pushdown Automata (2015/11/23)
 Chapter 6 Pushdown Automata (2015/11/23) Sagrada Familia, Barcelona, Spain Outline 6.0 Introduction 6.1 Definition of PDA 6.2 The Language of a PDA 6.3 Euivalence of PDA s and CFG s 6.4 Deterministic PDA
Chapter 6 Pushdown Automata (2015/11/23) Sagrada Familia, Barcelona, Spain Outline 6.0 Introduction 6.1 Definition of PDA 6.2 The Language of a PDA 6.3 Euivalence of PDA s and CFG s 6.4 Deterministic PDA
CS Pushdown Automata
 Chap. 6 Pushdown Automata 6.1 Definition of Pushdown Automata Example 6.2 L ww R = {ww R w (0+1) * } Palindromes over {0, 1}. A cfg P 0 1 0P0 1P1. Consider a FA with a stack(= a Pushdown automaton; PDA).
Chap. 6 Pushdown Automata 6.1 Definition of Pushdown Automata Example 6.2 L ww R = {ww R w (0+1) * } Palindromes over {0, 1}. A cfg P 0 1 0P0 1P1. Consider a FA with a stack(= a Pushdown automaton; PDA).
Introduction to Theory of Computing
 CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
CSCI 2670, Fall 2012 Introduction to Theory of Computing Department of Computer Science University of Georgia Athens, GA 30602 Instructor: Liming Cai www.cs.uga.edu/ cai 0 Lecture Note 3 Context-Free Languages
Einführung in die Computerlinguistik
 Einführung in die Computerlinguistik Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2016 1 / 22 CFG (1) Example: Grammar G telescope : Productions: S NP VP NP
Einführung in die Computerlinguistik Context-Free Grammars (CFG) Laura Kallmeyer Heinrich-Heine-Universität Düsseldorf Summer 2016 1 / 22 CFG (1) Example: Grammar G telescope : Productions: S NP VP NP
Pushdown Automata. Reading: Chapter 6
 Pushdown Automata Reading: Chapter 6 1 Pushdown Automata (PDA) Informally: A PDA is an NFA-ε with a infinite stack. Transitions are modified to accommodate stack operations. Questions: What is a stack?
Pushdown Automata Reading: Chapter 6 1 Pushdown Automata (PDA) Informally: A PDA is an NFA-ε with a infinite stack. Transitions are modified to accommodate stack operations. Questions: What is a stack?
MA/CSSE 474 Theory of Computation
 MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
MA/CSSE 474 Theory of Computation CFL Hierarchy CFL Decision Problems Your Questions? Previous class days' material Reading Assignments HW 12 or 13 problems Anything else I have included some slides online
Lecture Notes on Inductive Definitions
 Lecture Notes on Inductive Definitions 15-312: Foundations of Programming Languages Frank Pfenning Lecture 2 August 28, 2003 These supplementary notes review the notion of an inductive definition and give
Lecture Notes on Inductive Definitions 15-312: Foundations of Programming Languages Frank Pfenning Lecture 2 August 28, 2003 These supplementary notes review the notion of an inductive definition and give
Theory of Computation (IV) Yijia Chen Fudan University
 Theory of Computation (IV) Yijia Chen Fudan University Review language regular context-free machine DFA/ NFA PDA syntax regular expression context-free grammar Pushdown automata Definition A pushdown automaton
Theory of Computation (IV) Yijia Chen Fudan University Review language regular context-free machine DFA/ NFA PDA syntax regular expression context-free grammar Pushdown automata Definition A pushdown automaton
Lecture Notes on Inductive Definitions
 Lecture Notes on Inductive Definitions 15-312: Foundations of Programming Languages Frank Pfenning Lecture 2 September 2, 2004 These supplementary notes review the notion of an inductive definition and
Lecture Notes on Inductive Definitions 15-312: Foundations of Programming Languages Frank Pfenning Lecture 2 September 2, 2004 These supplementary notes review the notion of an inductive definition and
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs
 Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
Harvard CS 121 and CSCI E-207 Lecture 10: CFLs: PDAs, Closure Properties, and Non-CFLs Harry Lewis October 8, 2013 Reading: Sipser, pp. 119-128. Pushdown Automata (review) Pushdown Automata = Finite automaton
Pushdown Automata. Notes on Automata and Theory of Computation. Chia-Ping Chen
 Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
Pushdown Automata Notes on Automata and Theory of Computation Chia-Ping Chen Department of Computer Science and Engineering National Sun Yat-Sen University Kaohsiung, Taiwan ROC Pushdown Automata p. 1
Pushdown Automata. Chapter 12
 Pushdown Automata Chapter 12 Recognizing Context-Free Languages We need a device similar to an FSM except that it needs more power. The insight: Precisely what it needs is a stack, which gives it an unlimited
Pushdown Automata Chapter 12 Recognizing Context-Free Languages We need a device similar to an FSM except that it needs more power. The insight: Precisely what it needs is a stack, which gives it an unlimited
CPS 220 Theory of Computation Pushdown Automata (PDA)
 CPS 220 Theory of Computation Pushdown Automata (PDA) Nondeterministic Finite Automaton with some extra memory Memory is called the stack, accessed in a very restricted way: in a First-In First-Out fashion
CPS 220 Theory of Computation Pushdown Automata (PDA) Nondeterministic Finite Automaton with some extra memory Memory is called the stack, accessed in a very restricted way: in a First-In First-Out fashion
Pushdown automata. Twan van Laarhoven. Institute for Computing and Information Sciences Intelligent Systems Radboud University Nijmegen
 Pushdown automata Twan van Laarhoven Institute for Computing and Information Sciences Intelligent Systems Version: fall 2014 T. van Laarhoven Version: fall 2014 Formal Languages, Grammars and Automata
Pushdown automata Twan van Laarhoven Institute for Computing and Information Sciences Intelligent Systems Version: fall 2014 T. van Laarhoven Version: fall 2014 Formal Languages, Grammars and Automata
Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x where
 Recitation 11 Notes Context Free Grammars Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x A V, and x (V T)*. Examples Problem 1. Given the
Recitation 11 Notes Context Free Grammars Definition: A grammar G = (V, T, P,S) is a context free grammar (cfg) if all productions in P have the form A x A V, and x (V T)*. Examples Problem 1. Given the
Blackhole Pushdown Automata
 Fundamenta Informaticae XXI (2001) 1001 1020 1001 IOS Press Blackhole Pushdown Automata Erzsébet Csuhaj-Varjú Computer and Automation Research Institute, Hungarian Academy of Sciences Kende u. 13 17, 1111
Fundamenta Informaticae XXI (2001) 1001 1020 1001 IOS Press Blackhole Pushdown Automata Erzsébet Csuhaj-Varjú Computer and Automation Research Institute, Hungarian Academy of Sciences Kende u. 13 17, 1111
Computability and Complexity
 Computability and Complexity Push-Down Automata CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard Janicki Computability
Computability and Complexity Push-Down Automata CAS 705 Ryszard Janicki Department of Computing and Software McMaster University Hamilton, Ontario, Canada janicki@mcmaster.ca Ryszard Janicki Computability
Computational Models - Lecture 4
 Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
Computational Models - Lecture 4 Regular languages: The Myhill-Nerode Theorem Context-free Grammars Chomsky Normal Form Pumping Lemma for context free languages Non context-free languages: Examples Push
CS243, Logic and Computation Nondeterministic finite automata
 CS243, Prof. Alvarez NONDETERMINISTIC FINITE AUTOMATA (NFA) Prof. Sergio A. Alvarez http://www.cs.bc.edu/ alvarez/ Maloney Hall, room 569 alvarez@cs.bc.edu Computer Science Department voice: (67) 552-4333
CS243, Prof. Alvarez NONDETERMINISTIC FINITE AUTOMATA (NFA) Prof. Sergio A. Alvarez http://www.cs.bc.edu/ alvarez/ Maloney Hall, room 569 alvarez@cs.bc.edu Computer Science Department voice: (67) 552-4333
UNIT-VI PUSHDOWN AUTOMATA
 Syllabus R09 Regulation UNIT-VI PUSHDOWN AUTOMATA The context free languages have a type of automaton that defined them. This automaton, called a pushdown automaton, is an extension of the nondeterministic
Syllabus R09 Regulation UNIT-VI PUSHDOWN AUTOMATA The context free languages have a type of automaton that defined them. This automaton, called a pushdown automaton, is an extension of the nondeterministic
Miscellaneous. Closure Properties Decision Properties
 Miscellaneous Closure Properties Decision Properties 1 Closure Properties of CFL s CFL s are closed under union, concatenation, and Kleene closure. Also, under reversal, homomorphisms and inverse homomorphisms.
Miscellaneous Closure Properties Decision Properties 1 Closure Properties of CFL s CFL s are closed under union, concatenation, and Kleene closure. Also, under reversal, homomorphisms and inverse homomorphisms.
Chapter 1. Formal Definition and View. Lecture Formal Pushdown Automata on the 28th April 2009
 Chapter 1 Formal and View Lecture on the 28th April 2009 Formal of PA Faculty of Information Technology Brno University of Technology 1.1 Aim of the Lecture 1 Define pushdown automaton in a formal way
Chapter 1 Formal and View Lecture on the 28th April 2009 Formal of PA Faculty of Information Technology Brno University of Technology 1.1 Aim of the Lecture 1 Define pushdown automaton in a formal way
Lecture 17: Language Recognition
 Lecture 17: Language Recognition Finite State Automata Deterministic and Non-Deterministic Finite Automata Regular Expressions Push-Down Automata Turing Machines Modeling Computation When attempting to
Lecture 17: Language Recognition Finite State Automata Deterministic and Non-Deterministic Finite Automata Regular Expressions Push-Down Automata Turing Machines Modeling Computation When attempting to
Pushdown Automata: Introduction (2)
 Pushdown Automata: Introduction Pushdown automaton (PDA) M = (K, Σ, Γ,, s, A) where K is a set of states Σ is an input alphabet Γ is a set of stack symbols s K is the start state A K is a set of accepting
Pushdown Automata: Introduction Pushdown automaton (PDA) M = (K, Σ, Γ,, s, A) where K is a set of states Σ is an input alphabet Γ is a set of stack symbols s K is the start state A K is a set of accepting
Theory of Computation Lecture 1. Dr. Nahla Belal
 Theory of Computation Lecture 1 Dr. Nahla Belal Book The primary textbook is: Introduction to the Theory of Computation by Michael Sipser. Grading 10%: Weekly Homework. 30%: Two quizzes and one exam. 20%:
Theory of Computation Lecture 1 Dr. Nahla Belal Book The primary textbook is: Introduction to the Theory of Computation by Michael Sipser. Grading 10%: Weekly Homework. 30%: Two quizzes and one exam. 20%:
Automata Theory - Quiz II (Solutions)
 Automata Theory - Quiz II (Solutions) K. Subramani LCSEE, West Virginia University, Morgantown, WV {ksmani@csee.wvu.edu} 1 Problems 1. Induction: Let L denote the language of balanced strings over Σ =
Automata Theory - Quiz II (Solutions) K. Subramani LCSEE, West Virginia University, Morgantown, WV {ksmani@csee.wvu.edu} 1 Problems 1. Induction: Let L denote the language of balanced strings over Σ =
The Emptiness Problem for Valence Automata or: Another Decidable Extension of Petri Nets
 The Emptiness Problem for Valence Automata or: Another Decidable Extension of Petri Nets Georg Zetzsche Technische Universität Kaiserslautern Reachability Problems 2015 Georg Zetzsche (TU KL) Emptiness
The Emptiness Problem for Valence Automata or: Another Decidable Extension of Petri Nets Georg Zetzsche Technische Universität Kaiserslautern Reachability Problems 2015 Georg Zetzsche (TU KL) Emptiness
Foundations of Informatics: a Bridging Course
 Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
Foundations of Informatics: a Bridging Course Week 3: Formal Languages and Semantics Thomas Noll Lehrstuhl für Informatik 2 RWTH Aachen University noll@cs.rwth-aachen.de http://www.b-it-center.de/wob/en/view/class211_id948.html
What we have done so far
 What we have done so far DFAs and regular languages NFAs and their equivalence to DFAs Regular expressions. Regular expressions capture exactly regular languages: Construct a NFA from a regular expression.
What we have done so far DFAs and regular languages NFAs and their equivalence to DFAs Regular expressions. Regular expressions capture exactly regular languages: Construct a NFA from a regular expression.
Büchi Automata and their closure properties. - Ajith S and Ankit Kumar
 Büchi Automata and their closure properties - Ajith S and Ankit Kumar Motivation Conventional programs accept input, compute, output result, then terminate Reactive program : not expected to terminate
Büchi Automata and their closure properties - Ajith S and Ankit Kumar Motivation Conventional programs accept input, compute, output result, then terminate Reactive program : not expected to terminate
CFG and PDA accept the same languages
 Automata and Formal Languages CFG and PDA accept the same languages Sipser pages 115-122 Lecture 14 Tim Sheard 1 Equivalence of CFGs and PDAs The equivalence is expressed by two theorems. Theorem 1. Every
Automata and Formal Languages CFG and PDA accept the same languages Sipser pages 115-122 Lecture 14 Tim Sheard 1 Equivalence of CFGs and PDAs The equivalence is expressed by two theorems. Theorem 1. Every
CISC4090: Theory of Computation
 CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
CISC4090: Theory of Computation Chapter 2 Context-Free Languages Courtesy of Prof. Arthur G. Werschulz Fordham University Department of Computer and Information Sciences Spring, 2014 Overview In Chapter
Homework. Context Free Languages. Announcements. Before We Start. Languages. Plan for today. Final Exam Dates have been announced.
 Homework Context Free Languages PDAs and CFLs Homework #3 returned Homework #4 due today Homework #5 Pg 169 -- Exercise 4 Pg 183 -- Exercise 4c,e,i (use JFLAP) Pg 184 -- Exercise 10 Pg 184 -- Exercise
Homework Context Free Languages PDAs and CFLs Homework #3 returned Homework #4 due today Homework #5 Pg 169 -- Exercise 4 Pg 183 -- Exercise 4c,e,i (use JFLAP) Pg 184 -- Exercise 10 Pg 184 -- Exercise
Languages, regular languages, finite automata
 Notes on Computer Theory Last updated: January, 2018 Languages, regular languages, finite automata Content largely taken from Richards [1] and Sipser [2] 1 Languages An alphabet is a finite set of characters,
Notes on Computer Theory Last updated: January, 2018 Languages, regular languages, finite automata Content largely taken from Richards [1] and Sipser [2] 1 Languages An alphabet is a finite set of characters,
Intro to Theory of Computation
 Intro to Theory of Computation LECTURE 7 Last time: Proving a language is not regular Pushdown automata (PDAs) Today: Context-free grammars (CFG) Equivalence of CFGs and PDAs Sofya Raskhodnikova 1/31/2016
Intro to Theory of Computation LECTURE 7 Last time: Proving a language is not regular Pushdown automata (PDAs) Today: Context-free grammars (CFG) Equivalence of CFGs and PDAs Sofya Raskhodnikova 1/31/2016
Context-Free Languages
 CS:4330 Theory of Computation Spring 2018 Context-Free Languages Pushdown Automata Haniel Barbosa Readings for this lecture Chapter 2 of [Sipser 1996], 3rd edition. Section 2.2. Finite automaton 1 / 13
CS:4330 Theory of Computation Spring 2018 Context-Free Languages Pushdown Automata Haniel Barbosa Readings for this lecture Chapter 2 of [Sipser 1996], 3rd edition. Section 2.2. Finite automaton 1 / 13
CS5371 Theory of Computation. Lecture 7: Automata Theory V (CFG, CFL, CNF)
 CS5371 Theory of Computation Lecture 7: Automata Theory V (CFG, CFL, CNF) Announcement Homework 2 will be given soon (before Tue) Due date: Oct 31 (Tue), before class Midterm: Nov 3, (Fri), first hour
CS5371 Theory of Computation Lecture 7: Automata Theory V (CFG, CFL, CNF) Announcement Homework 2 will be given soon (before Tue) Due date: Oct 31 (Tue), before class Midterm: Nov 3, (Fri), first hour
Nondeterministic Finite Automata
 Nondeterministic Finite Automata Not A DFA Does not have exactly one transition from every state on every symbol: Two transitions from q 0 on a No transition from q 1 (on either a or b) Though not a DFA,
Nondeterministic Finite Automata Not A DFA Does not have exactly one transition from every state on every symbol: Two transitions from q 0 on a No transition from q 1 (on either a or b) Though not a DFA,
Grammars (part II) Prof. Dan A. Simovici UMB
 rammars (part II) Prof. Dan A. Simovici UMB 1 / 1 Outline 2 / 1 Length-Increasing vs. Context-Sensitive rammars Theorem The class L 1 equals the class of length-increasing languages. 3 / 1 Length-Increasing
rammars (part II) Prof. Dan A. Simovici UMB 1 / 1 Outline 2 / 1 Length-Increasing vs. Context-Sensitive rammars Theorem The class L 1 equals the class of length-increasing languages. 3 / 1 Length-Increasing
2.1 Solution. E T F a. E E + T T + T F + T a + T a + F a + a
 . Solution E T F a E E + T T + T F + T a + T a + F a + a E E + T E + T + T T + T + T F + T + T a + T + T a + F + T a + a + T a + a + F a + a + a E T F ( E) ( T ) ( F) (( E)) (( T )) (( F)) (( a)) . Solution
. Solution E T F a E E + T T + T F + T a + T a + F a + a E E + T E + T + T T + T + T F + T + T a + T + T a + F + T a + a + T a + a + F a + a + a E T F ( E) ( T ) ( F) (( E)) (( T )) (( F)) (( a)) . Solution
Chapter 3. Regular grammars
 Chapter 3 Regular grammars 59 3.1 Introduction Other view of the concept of language: not the formalization of the notion of effective procedure, but set of words satisfying a given set of rules Origin
Chapter 3 Regular grammars 59 3.1 Introduction Other view of the concept of language: not the formalization of the notion of effective procedure, but set of words satisfying a given set of rules Origin
SYLLABUS. Introduction to Finite Automata, Central Concepts of Automata Theory. CHAPTER - 3 : REGULAR EXPRESSIONS AND LANGUAGES
 Contents i SYLLABUS UNIT - I CHAPTER - 1 : AUT UTOMA OMATA Introduction to Finite Automata, Central Concepts of Automata Theory. CHAPTER - 2 : FINITE AUT UTOMA OMATA An Informal Picture of Finite Automata,
Contents i SYLLABUS UNIT - I CHAPTER - 1 : AUT UTOMA OMATA Introduction to Finite Automata, Central Concepts of Automata Theory. CHAPTER - 2 : FINITE AUT UTOMA OMATA An Informal Picture of Finite Automata,
Closure Properties of Regular Languages. Union, Intersection, Difference, Concatenation, Kleene Closure, Reversal, Homomorphism, Inverse Homomorphism
 Closure Properties of Regular Languages Union, Intersection, Difference, Concatenation, Kleene Closure, Reversal, Homomorphism, Inverse Homomorphism Closure Properties Recall a closure property is a statement
Closure Properties of Regular Languages Union, Intersection, Difference, Concatenation, Kleene Closure, Reversal, Homomorphism, Inverse Homomorphism Closure Properties Recall a closure property is a statement
Outline. CS21 Decidability and Tractability. Machine view of FA. Machine view of FA. Machine view of FA. Machine view of FA.
 Outline CS21 Decidability and Tractability Lecture 5 January 16, 219 and Languages equivalence of NPDAs and CFGs non context-free languages January 16, 219 CS21 Lecture 5 1 January 16, 219 CS21 Lecture
Outline CS21 Decidability and Tractability Lecture 5 January 16, 219 and Languages equivalence of NPDAs and CFGs non context-free languages January 16, 219 CS21 Lecture 5 1 January 16, 219 CS21 Lecture
Equivalence of CFG s and PDA s
 Equivalence of CFG s and PDA s Mridul Aanjaneya Stanford University July 24, 2012 Mridul Aanjaneya Automata Theory 1/ 53 Recap: Pushdown Automata A PDA is an automaton equivalent to the CFG in language-defining
Equivalence of CFG s and PDA s Mridul Aanjaneya Stanford University July 24, 2012 Mridul Aanjaneya Automata Theory 1/ 53 Recap: Pushdown Automata A PDA is an automaton equivalent to the CFG in language-defining
3.13. PUSHDOWN AUTOMATA Pushdown Automata
 3.13. PUSHDOWN AUTOMATA 317 3.13 Pushdown Automata We have seen that the regular languages are exactly the languages accepted by DFA s or NFA s. The context-free languages are exactly the languages accepted
3.13. PUSHDOWN AUTOMATA 317 3.13 Pushdown Automata We have seen that the regular languages are exactly the languages accepted by DFA s or NFA s. The context-free languages are exactly the languages accepted
60-354, Theory of Computation Fall Asish Mukhopadhyay School of Computer Science University of Windsor
 60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
60-354, Theory of Computation Fall 2013 Asish Mukhopadhyay School of Computer Science University of Windsor Pushdown Automata (PDA) PDA = ε-nfa + stack Acceptance ε-nfa enters a final state or Stack is
Automata Theory (2A) Young Won Lim 5/31/18
 Automata Theory (2A) Copyright (c) 2018 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later
Automata Theory (2A) Copyright (c) 2018 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later
cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska
 cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska LECTURE 14 SMALL REVIEW FOR FINAL SOME Y/N QUESTIONS Q1 Given Σ =, there is L over Σ Yes: = {e} and L = {e} Σ Q2 There are uncountably
cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska LECTURE 14 SMALL REVIEW FOR FINAL SOME Y/N QUESTIONS Q1 Given Σ =, there is L over Σ Yes: = {e} and L = {e} Σ Q2 There are uncountably
DM17. Beregnelighed. Jacob Aae Mikkelsen
 DM17 Beregnelighed Jacob Aae Mikkelsen January 12, 2007 CONTENTS Contents 1 Introduction 2 1.1 Operations with languages...................... 2 2 Finite Automata 3 2.1 Regular expressions/languages....................
DM17 Beregnelighed Jacob Aae Mikkelsen January 12, 2007 CONTENTS Contents 1 Introduction 2 1.1 Operations with languages...................... 2 2 Finite Automata 3 2.1 Regular expressions/languages....................
Section 1 (closed-book) Total points 30
 CS 454 Theory of Computation Fall 2011 Section 1 (closed-book) Total points 30 1. Which of the following are true? (a) a PDA can always be converted to an equivalent PDA that at each step pops or pushes
CS 454 Theory of Computation Fall 2011 Section 1 (closed-book) Total points 30 1. Which of the following are true? (a) a PDA can always be converted to an equivalent PDA that at each step pops or pushes
Computational Models: Class 5
 Computational Models: Class 5 Benny Chor School of Computer Science Tel Aviv University March 27, 2019 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
Computational Models: Class 5 Benny Chor School of Computer Science Tel Aviv University March 27, 2019 Based on slides by Maurice Herlihy, Brown University, and modifications by Iftach Haitner and Yishay
Properties of Context-Free Languages. Closure Properties Decision Properties
 Properties of Context-Free Languages Closure Properties Decision Properties 1 Closure Properties of CFL s CFL s are closed under union, concatenation, and Kleene closure. Also, under reversal, homomorphisms
Properties of Context-Free Languages Closure Properties Decision Properties 1 Closure Properties of CFL s CFL s are closed under union, concatenation, and Kleene closure. Also, under reversal, homomorphisms
Parikh s theorem. Håkan Lindqvist
 Parikh s theorem Håkan Lindqvist Abstract This chapter will discuss Parikh s theorem and provide a proof for it. The proof is done by induction over a set of derivation trees, and using the Parikh mappings
Parikh s theorem Håkan Lindqvist Abstract This chapter will discuss Parikh s theorem and provide a proof for it. The proof is done by induction over a set of derivation trees, and using the Parikh mappings
Remarks on Separating Words
 Remarks on Separating Words Erik D. Demaine, Sarah Eisenstat, Jeffrey Shallit 2, and David A. Wilson MIT Computer Science and Artificial Intelligence Laboratory, 32 Vassar Street, Cambridge, MA 239, USA,
Remarks on Separating Words Erik D. Demaine, Sarah Eisenstat, Jeffrey Shallit 2, and David A. Wilson MIT Computer Science and Artificial Intelligence Laboratory, 32 Vassar Street, Cambridge, MA 239, USA,
Theory of computation: initial remarks (Chapter 11)
 Theory of computation: initial remarks (Chapter 11) For many purposes, computation is elegantly modeled with simple mathematical objects: Turing machines, finite automata, pushdown automata, and such.
Theory of computation: initial remarks (Chapter 11) For many purposes, computation is elegantly modeled with simple mathematical objects: Turing machines, finite automata, pushdown automata, and such.
ECS 120: Theory of Computation UC Davis Phillip Rogaway February 16, Midterm Exam
 ECS 120: Theory of Computation Handout MT UC Davis Phillip Rogaway February 16, 2012 Midterm Exam Instructions: The exam has six pages, including this cover page, printed out two-sided (no more wasted
ECS 120: Theory of Computation Handout MT UC Davis Phillip Rogaway February 16, 2012 Midterm Exam Instructions: The exam has six pages, including this cover page, printed out two-sided (no more wasted
MTH401A Theory of Computation. Lecture 17
 MTH401A Theory of Computation Lecture 17 Chomsky Normal Form for CFG s Chomsky Normal Form for CFG s For every context free language, L, the language L {ε} has a grammar in which every production looks
MTH401A Theory of Computation Lecture 17 Chomsky Normal Form for CFG s Chomsky Normal Form for CFG s For every context free language, L, the language L {ε} has a grammar in which every production looks
Pushdown Automata. Pushdown Automata. Pushdown Automata. Pushdown Automata. Pushdown Automata. Pushdown Automata. The stack
 A pushdown automata (PDA) is essentially: An NFA with a stack A move of a PDA will depend upon Current state of the machine Current symbol being read in Current symbol popped off the top of the stack With
A pushdown automata (PDA) is essentially: An NFA with a stack A move of a PDA will depend upon Current state of the machine Current symbol being read in Current symbol popped off the top of the stack With
Chapter Five: Nondeterministic Finite Automata
 Chapter Five: Nondeterministic Finite Automata From DFA to NFA A DFA has exactly one transition from every state on every symbol in the alphabet. By relaxing this requirement we get a related but more
Chapter Five: Nondeterministic Finite Automata From DFA to NFA A DFA has exactly one transition from every state on every symbol in the alphabet. By relaxing this requirement we get a related but more
Sequences, Relations, and Functions
 Sequences, Relations, and Functions Alexander Meduna, Lukáš Vrábel, and Petr Zemek Brno University of Technology, Faculty of Information Technology Božetěchova 1/2, 612 00 Brno, CZ http://www.fit.vutbr.cz/
Sequences, Relations, and Functions Alexander Meduna, Lukáš Vrábel, and Petr Zemek Brno University of Technology, Faculty of Information Technology Božetěchova 1/2, 612 00 Brno, CZ http://www.fit.vutbr.cz/
CS481F01 Prelim 2 Solutions
 CS481F01 Prelim 2 Solutions A. Demers 7 Nov 2001 1 (30 pts = 4 pts each part + 2 free points). For this question we use the following notation: x y means x is a prefix of y m k n means m n k For each of
CS481F01 Prelim 2 Solutions A. Demers 7 Nov 2001 1 (30 pts = 4 pts each part + 2 free points). For this question we use the following notation: x y means x is a prefix of y m k n means m n k For each of
Theory of computation: initial remarks (Chapter 11)
 Theory of computation: initial remarks (Chapter 11) For many purposes, computation is elegantly modeled with simple mathematical objects: Turing machines, finite automata, pushdown automata, and such.
Theory of computation: initial remarks (Chapter 11) For many purposes, computation is elegantly modeled with simple mathematical objects: Turing machines, finite automata, pushdown automata, and such.
On the Regularity of Binoid Languages:
 On the Regularity of Binoid Languages: A Comparative Approach Zoltán L. Németh University of Szeged, Inst. of Informatics P.O.B. 652, 6701 Szeged, Hungary zlnemeth@inf.u-szeged.hu Abstract. A binoid is
On the Regularity of Binoid Languages: A Comparative Approach Zoltán L. Németh University of Szeged, Inst. of Informatics P.O.B. 652, 6701 Szeged, Hungary zlnemeth@inf.u-szeged.hu Abstract. A binoid is
CSE 105 THEORY OF COMPUTATION
 CSE 105 THEORY OF COMPUTATION Spring 2017 http://cseweb.ucsd.edu/classes/sp17/cse105-ab/ Review of CFG, CFL, ambiguity What is the language generated by the CFG below: G 1 = ({S,T 1,T 2 }, {0,1,2}, { S
CSE 105 THEORY OF COMPUTATION Spring 2017 http://cseweb.ucsd.edu/classes/sp17/cse105-ab/ Review of CFG, CFL, ambiguity What is the language generated by the CFG below: G 1 = ({S,T 1,T 2 }, {0,1,2}, { S
Theory of Computation Turing Machine and Pushdown Automata
 Theory of Computation Turing Machine and Pushdown Automata 1. What is a Turing Machine? A Turing Machine is an accepting device which accepts the languages (recursively enumerable set) generated by type
Theory of Computation Turing Machine and Pushdown Automata 1. What is a Turing Machine? A Turing Machine is an accepting device which accepts the languages (recursively enumerable set) generated by type
Homework 8. a b b a b a b. two-way, read/write
 Homework 8 309 Homework 8 1. Describe a TM that accepts the set {a n n is a power of 2}. Your description should be at the level of the descriptions in Lecture 29 of the TM that accepts {ww w Σ } and the
Homework 8 309 Homework 8 1. Describe a TM that accepts the set {a n n is a power of 2}. Your description should be at the level of the descriptions in Lecture 29 of the TM that accepts {ww w Σ } and the
Ogden s Lemma. and Formal Languages. Automata Theory CS 573. The proof is similar but more fussy. than the proof of the PL4CFL.
 CS 573 Automata Theory and Formal Languages Professor Leslie Lander Lecture # 24 December 4, 2000 Ogden s Lemma (6.2) Let L be a CFL, then there is a constant n such that if z is a word in L with z > n
CS 573 Automata Theory and Formal Languages Professor Leslie Lander Lecture # 24 December 4, 2000 Ogden s Lemma (6.2) Let L be a CFL, then there is a constant n such that if z is a word in L with z > n
Part 4 out of 5 DFA NFA REX. Automata & languages. A primer on the Theory of Computation. Last week, we showed the equivalence of DFA, NFA and REX
 Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 4 out of 5 ETH Zürich (D-ITET) October, 12 2017 Last week, we showed the equivalence of DFA, NFA and REX
Automata & languages A primer on the Theory of Computation Laurent Vanbever www.vanbever.eu Part 4 out of 5 ETH Zürich (D-ITET) October, 12 2017 Last week, we showed the equivalence of DFA, NFA and REX
Sri vidya college of engineering and technology
 Unit I FINITE AUTOMATA 1. Define hypothesis. The formal proof can be using deductive proof and inductive proof. The deductive proof consists of sequence of statements given with logical reasoning in order
Unit I FINITE AUTOMATA 1. Define hypothesis. The formal proof can be using deductive proof and inductive proof. The deductive proof consists of sequence of statements given with logical reasoning in order
UNIT-II. NONDETERMINISTIC FINITE AUTOMATA WITH ε TRANSITIONS: SIGNIFICANCE. Use of ε-transitions. s t a r t. ε r. e g u l a r
 Syllabus R9 Regulation UNIT-II NONDETERMINISTIC FINITE AUTOMATA WITH ε TRANSITIONS: In the automata theory, a nondeterministic finite automaton (NFA) or nondeterministic finite state machine is a finite
Syllabus R9 Regulation UNIT-II NONDETERMINISTIC FINITE AUTOMATA WITH ε TRANSITIONS: In the automata theory, a nondeterministic finite automaton (NFA) or nondeterministic finite state machine is a finite
cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska
 cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska LECTURE 11 CHAPTER 3 CONTEXT-FREE LANGUAGES 1. Context Free Grammars 2. Pushdown Automata 3. Pushdown automata and context -free
cse303 ELEMENTS OF THE THEORY OF COMPUTATION Professor Anita Wasilewska LECTURE 11 CHAPTER 3 CONTEXT-FREE LANGUAGES 1. Context Free Grammars 2. Pushdown Automata 3. Pushdown automata and context -free
Solution Scoring: SD Reg exp.: a(a
 MA/CSSE 474 Exam 3 Winter 2013-14 Name Solution_with explanations Section: 02(3 rd ) 03(4 th ) 1. (28 points) For each of the following statements, circle T or F to indicate whether it is True or False.
MA/CSSE 474 Exam 3 Winter 2013-14 Name Solution_with explanations Section: 02(3 rd ) 03(4 th ) 1. (28 points) For each of the following statements, circle T or F to indicate whether it is True or False.
Theory of Computation (VI) Yijia Chen Fudan University
 Theory of Computation (VI) Yijia Chen Fudan University Review Forced handles Definition A handle h of a valid string v = xhy is a forced handle if h is the unique handle in every valid string xhŷ where
Theory of Computation (VI) Yijia Chen Fudan University Review Forced handles Definition A handle h of a valid string v = xhy is a forced handle if h is the unique handle in every valid string xhŷ where
C6.2 Push-Down Automata
 Theory of Computer Science April 5, 2017 C6. Context-free Languages: Push-down Automata Theory of Computer Science C6. Context-free Languages: Push-down Automata Malte Helmert University of Basel April
Theory of Computer Science April 5, 2017 C6. Context-free Languages: Push-down Automata Theory of Computer Science C6. Context-free Languages: Push-down Automata Malte Helmert University of Basel April
Undecidable Problems and Reducibility
 University of Georgia Fall 2014 Reducibility We show a problem decidable/undecidable by reducing it to another problem. One type of reduction: mapping reduction. Definition Let A, B be languages over Σ.
University of Georgia Fall 2014 Reducibility We show a problem decidable/undecidable by reducing it to another problem. One type of reduction: mapping reduction. Definition Let A, B be languages over Σ.
HENNING FERNAU Fachbereich IV, Abteilung Informatik, Universität Trier, D Trier, Germany
 International Journal of Foundations of Computer Science c World Scientific Publishing Company PROGRAMMMED GRAMMARS WITH RULE QUEUES HENNING FERNAU Fachbereich IV, Abteilung Informatik, Universität Trier,
International Journal of Foundations of Computer Science c World Scientific Publishing Company PROGRAMMMED GRAMMARS WITH RULE QUEUES HENNING FERNAU Fachbereich IV, Abteilung Informatik, Universität Trier,
CS375: Logic and Theory of Computing
 CS375: Logic and Theory of Computing Fuhua (Frank) Cheng Department of Computer Science University of Kentucky 1 Table of Contents: Week 1: Preliminaries (set algebra, relations, functions) (read Chapters
CS375: Logic and Theory of Computing Fuhua (Frank) Cheng Department of Computer Science University of Kentucky 1 Table of Contents: Week 1: Preliminaries (set algebra, relations, functions) (read Chapters
Turing machines Finite automaton no storage Pushdown automaton storage is a stack What if we give the automaton a more flexible storage?
 Turing machines Finite automaton no storage Pushdown automaton storage is a stack What if we give the automaton a more flexible storage? What is the most powerful of automata? In this lecture we will introduce
Turing machines Finite automaton no storage Pushdown automaton storage is a stack What if we give the automaton a more flexible storage? What is the most powerful of automata? In this lecture we will introduce
Context Free Language Properties
 Context Free Language Properties Knowing that the context free languages are exactly those sets accepted by nondeterministic pushdown automata provides us a bit of information about them. We know that
Context Free Language Properties Knowing that the context free languages are exactly those sets accepted by nondeterministic pushdown automata provides us a bit of information about them. We know that
