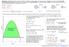
x 1 2 (v 0 v)t x v 0 t 1 2 at 2 Mechanics total distance total time Average speed CONSTANT ACCELERATION Maximum height y max v = 0

Size: px

Start display at page:

Download "x 1 2 (v 0 v)t x v 0 t 1 2 at 2 Mechanics total distance total time Average speed CONSTANT ACCELERATION Maximum height y max v = 0"

Rhoda Watts
5 years ago
Views:

1 Mechaics Aerae speed total distace total time t f i t f t i CONSAN ACCELERAION 0 at 0 a ( 0 )t 0 t at Maimum heiht y ma = 0 Phase a = 9.80 m/s Rocket fuel burs out +y Phase a = 9.4 m/s y = 0 Lauch Rocket crashes after falli from y ma

2 y 0 y θ 0 y = 0 0 y 0 θ 0 a t 0 t a t 0 a y 0y a y t y 0y t a y t y 0y a y y 0y θ θ θ 0 0y F : ma : y y 53.0 f s m cos u u m si u u F 3 F

3 a a m m m m a m m m a m

4 m f k m Motio y fs F fk F m m m m f m f s,ma f s = F m f k = mk Fiure Static reio Kietic reio F m M f s m f s m M M

5 W F ery is trasferred is importat i the desi ad use of pracs electrical appliaces ad eies of all kids. he issue mis par for lii creatures, W et m sice the maimum m 0 work per secod, or aimal aries reatly with output duratio. Power is defied as i = 0 rasfer with time: W et KE f KE i KE PE my F s k PE s k F et Fiure 5.7 orce is applied to a object ad if the work doe by this the time iteral t, the the aerae power deliered uri this iteral is the work doe diided by the time J/s) W t f = A object uderoes a KE i PE i KE f PE f the sum of the kietic eer ul to rewrite Equatio 5. by substituti W k F ad otic- m e aerae speed of the object duri the time t: i 0 [5.] d u h/ h W t F t F [5.3] tio 5.3, aerae power is a costat force times the aerae

Remarks he iitial elocity compoet of block is.50 m/s because the block is moi to the left. he eatie alue for f meas that block is still moi to the left at the istat uder cosideratio. Eercise 6.

5 m You ca chae the masses ad speeds of the blocks ad freeze the motio at the maimum compressio of the spri by loi ito PhysicsNow at www.cp7e.com ad oi to Iteractie Eample 6.

6 Remarks he iitial elocity compoet of block is.50 m/s because the block is moi to the left. he eatie alue for f meas that block is still moi to the left at the istat uder cosideratio. Eercise 6.7 Fid the elocity of block ad the compressio of the spri at the istat that block is at rest. : : I F t : F t p : m : f m : i Aswer 0.79 m/s to the riht 0.5 m You ca chae the masses ad speeds of the blocks ad freeze the motio at the maimum compressio of the spri by loi ito PhysicsNow at ad oi to Iteractie Eample GLANCING COLLISIONS d (k m/s) I Sectio 6. we showed that the total liear mometum of a system is cosered whe the system is isolated (that is, whe o eteral forces act o the system). For a eeral collisio of two objects i three-dimesioal space, the coseratio 0//04 8:58 AM Pae 73 of mometum priciple implies that the total mometum of the system i each directio is cosered. Howeer, a m : importat subset of collisios takes place i m : i a i m : f m : plae. he ame of billiards is a familiar eample ioli multiple collisios of objects moi o a two-dimesioal surface. We restrict our attetio to a sile f two-dimesioal collisio betwee two objects that takes place i a plae, ad iore ay possible rotatio. For such collisios, we obtai two compoet equatios for the coseratio of mometum: m i m i m f m f 6.3 Collisios 73 m iy m iy m f y m f y typical We must use problem three subscripts Elastic ioli this eeral Collisios elastic equatio, collisios, to represet, respectiely, there are () thetwo ukow quatid Equatios Now, cosider 6.0 ad object i questio, ad () the iitial ad fial alues of the compoets of elocity. m a two-dimesioal i 6. problem ca be soled m i which i a object simultaeously m of mass m f collides with a object of mass m to fid them. m f hese atios are liear ad that is iitially at rest, as i Actie Fiure 6.5. After quadratic, respectiely. A alterate approach simpliquadratic object moes equatio a ale with to respect aother to liear horizotal. equatio, his is called facilitati a lac- solutio. Ca- the collisio, object moes at a ale with respect to the horizotal, ad i collisio. Applyi the law of coseratio of mometum i compoet form, he factor i Equatio 6., we rewrite the equatio as ad oti that the iitial y-compoet of mometum is zero, we hae i i ( f f ) m ( i f ) m ( f i ) -compoet: m i 0 m f cos m f cos [6.5] y-compoet: 0 0 m f si m f si [6.6] e hae moed the terms cotaii m to oe side of the equatio ad otaii m to the other. Net, we factor both sides of f the equatio: +y m ( i f )( i f ) m ( f i )( f i ) i we separate the terms cotaii + m ad m f i the equatio for the co of mometum (Equatio 6.0) to et f cos f m m m ( i f ) m ( f i ) Before the collisio [6.3] btai our fial result, we diide Equatio 6. by Equatio 6.3, produci i f f i f si u f cos u f si f After the collisio u f ACIVE FIGURE 6.5 Before ad after a laci collisio betwee two balls. [6.] Lo ito PhysicsNow at ad o to Actie Fiure 6.5 to adjust the speed ad positio of the blue particle, adjust the masses of both particles, ad see the effects. Before collisio i i m + m f After collisio + ACIVE FIGURE 6.3 Before ad after a elastic head-o collisio betwee two hard spheres. Lo ito PhysicsNow at f

7 Liear Motio with a Costat Rotatioal Motio about a Fied (Variables: ad ) Ais with Costat (Variables: ad ) i at i t [7.7] i t at i t t [7.8] i a i [7.9] t r a t r a c r F c ma c m r

8 F G m m r PE G M Em r r = R E + h h PE m esc GM Em 0 R E PE esc GM E R E R E 4 GM S r 3 K S r 3

9 Now apply the first coditio of equilibrium to the beam: F R cos F y R y w B w M si Substituti the alue of foud i the preious step : ad the weihts, obtai the compoets of R: rf si Remarks ple, if the ais were to pass throuh the ceter Oof raity of the beam, the torque equatio would iole bo c R L/ 49 N L R y N Ee if we selected some other ais for the torque equatio, the solutio would be the same. F R y. oether with equatios () ad (), howeer, the ukows could still be foud a ood eercise. F Eercise 8.7 b A perso with mass 55.0 k stads.00 m away from the wall o a 6.00-m beam, as show i Fiure 8.d. of the beam is 40.0 k. Fid the hie force Fiure compoets 8.0 ad the tesio i the wire. w w Aswers 75 N, R N, R y 556 N R INERACIVE EXAMPLE 8.8 Do t Climb the Ladder Goal 53.0 Apply the two coditios of equilibrium. O Problem 50.0 N rests aaist a smooth ertical wall as i Fiure A uiform ladder 0.0 m 300 lo N ad weihi 600 N 8.3a. If the ladder is just o the ere of slippi whe it makes a 50.0 ale with the roud, fid the coefficiet R y si 53.0 of static frictio betwee the ladder ad roud. 0 m P d R cos 53.0 Stratey Fiure 8.3b O is the free-body diaram for 53.0 the ladder. he first coditio of equilibrium, F : i 0,.50 m 300 N ies two equatios 5.00 m for three.50 ukows: m the maitudes 600 N of the static frictio force f ad the ormal force, both (c) acti o the base of the ladder, ad the maitude of the force of the wall, P, acti o the top of the ladder N 50 O f O Fiure 8.3 (Iteractie Eample 8.8) A ladder lea aaist a frictioless wall. A free-body diaram of the la : (c) Leer arms for the force of raity ad P. d

CHAPTER 8 SYSTEMS OF PARTICLES

CHAPTER 8 SYSTEMS OF PARTICLES CHAPTER 8 SYSTES OF PARTICLES CHAPTER 8 COLLISIONS 45 8. CENTER OF ASS The ceter of mass of a system of particles or a rigid body is the poit at which all of the mass are cosidered to be cocetrated there