Verification of the Deutsch-Schorr-Waite Graph Marking Algorithm using Data Refinement
|
|
|
- Madlyn Sparks
- 5 years ago
- Views:
Transcription
1 Verification of the Deutsch-Schorr-Waite Graph Marking Algorithm using Data Refinement Viorel Preoteasa and Ralph-Johan Back February 16, 2013 Abstract The verification of the Deutsch-Schorr-Waite graph marking algorithm is used as a benchmark in many formalizations of pointer programs. The main purpose of this mechanization is to show how data refinement of invariant based programs can be used in verifying practical algorithms. The verification starts with an abstract algorithm working on a graph given by a relation next on nodes. Gradually the abstract program is refined into Deutsch-Schorr-Waite graph marking algorithm where only one bit per graph node of additional memory is used for marking. Contents 1 Introduction 2 2 Address Graph 3 3 Marking Using a Set Transitions Invariants Diagram Correctness of the transitions Diagram correctness Marking Using a Stack Transitions Invariants Data refinement relations Data refinement of the transitions Diagram data refinement Diagram correctness
2 5 Generalization of Deutsch-Schorr-Waite Algorithm Transitions Invariants Data refinement relations Diagram Data refinement of the transitions Diagram data refinement Diagram correctness Deutsch-Schorr-Waite Marking Algorithm Transitions Data refinement relation Data refinement of the transitions Diagram data refinement Diagram corectness Introduction The verification of the Deutsch-Schorr-Waite (DSW) [14, 10] graph marking algorithm is used as a benchmark in many formalizations of pointer programs [11, 1]. The main purpose of this mechanization is to show how data refinement [12] of invariant based programs [3, 4, 5, 6] can be used in verifying practical algorithms. The DSW algorithm marks all nodes in a graph that are reachable from a root node. The marking is achieved using only one extra bit of memory for every node. The graph is given by two pointer functions, left and right, which for any given node return its left and right successors, respectively. While marking, the left and right functions are altered to represent a stack that describes the path from the root to the current node in the graph. On completion the original graph structure is restored. We construct the DSW algorithm by a sequence of three successive data refinement steps. One step in these refinements is a generalization of the DSW algorithm to an algorithm which marks a graph given by a family of pointer functions instead of left and right only. Invariant based programming is an approach to construct correct programs where we start by identifying all basic situations (pre- and postconditions, and loop invariants) that could arise during the execution of the algorithm. These situations are determined and described before any code is written. After that, we identify the transitions between the situations, which together determine the flow of control in the program. The transitions are verified at the same time as they are constructed. The correctness of the program is thus established as part of the construction process. 2
3 Data refinement [9, 2, 7, 8] is a technique of building correct programs working on concrete data structures as refinements of more abstract programs working on abstract data structures. The correctness of the final program follows from the correctness of the abstract program and from the correctness of the data refinement. Both the semantics and the data refinement of invariant based programs were formalized in [13], and this verification is based on them. We use a simple model of pointers where addresses (pointers, nodes) are the elements of a set and pointer fields are global pointer functions from addresses to addresses. Pointer updates (x.left := y) are done by modifying the global pointer function left := left(x := y). Because of the nature of the marking algorithm where no allocation and disposal of memory are needed we do not treat these operations. A number of Isabelle techniques are used here. The class mechanism is used for extending the complete lattice theories as well as for introducing well founded and transitive relations. The polimorphism is used for the state of the computation. In [13] the state of computation was introduced as a type variable, or even more generaly, state predicates were introduced as elements of a complete (boolean) lattice. Here the state of the computation is instantiated with various tuples ranging from the abstract data in the first algorithm to the concrete data in the final refinement. The locale mechanism of Isabelle is used to introduce the specification variables and their invariants. These specification variables are used for example to prove that the main variables are restored to their initial values when the algorithm terminates. The locale extension and partial instantiation mechanisms turn out to be also very useful in the data refinements of DSW. We start with a locale which fixes the abstract graph as a relation next on nodes. This locale is first partially interpreted into a locale which replaces next by a union of a family of pointer functions. In the final refinement step the locale of the pointer functions is interpreted into a locale with only two pointer functions, left and right. 2 Address Graph theory Graph imports Main begin This theory introduces the graph to be marked as a relation next on nodes (addresses). We assume that we have a special node nil (the null address). We have a node root from which we start marking the graph. We also assume that nil is not related by next to any node and any node is not related by next to nil. locale node = 3
4 fixes nil fixes root :: node :: node locale graph = node + fixes next :: ( node node) set assumes next-not-nil-left: (!! x. (nil, x) / next) assumes next-not-nil-right: (!! x. (x, nil) / next) begin On lists of nodes we introduce two operations similar to existing hd and tl for getting the head and the tail of a list. The new function head applied to a nonempty list returns the head of the list, and it reurns nil when applied to the empty list. The function tail returns the tail of the list when applied to a non-empty list, and it returns the empty list otherwise. head S (if S = [] then nil else (hd S)) tail (S:: a list) (if S = [] then [] else (tl S)) lemma [simp]: ((nil, x) next) = False by (simp add: next-not-nil-left) lemma [simp]: ((x, nil) next) = False by (simp add: next-not-nil-right) theorem head-not-nil [simp]: (head S nil) = (head S = hd S tail S = tl S hd S nil S []) by (simp add: head-def tail-def ) theorem nonempty-head [simp]: head (x # S) = x by (simp add: head-def ) theorem nonempty-tail [simp]: tail (x # S) = S by (simp add: tail-def ) (in graph) reach x {y. (x, y) next y nil} theorem (in graph) reach-nil [simp]: reach nil = {} apply (simp add: reach-def, safe) apply (drule rtrancl-induct) theorem (in graph) reach-next: b reach a = (b, c) next = c reach a apply (simp add: reach-def ) 4
5 (in graph) path S mrk {x. ( s. s S (s, x) next O (next (( mrk) ( mrk))) )} end end 3 Marking Using a Set theory SetMark imports Graph../DataRefinementIBP/DataRefinement begin We construct in this theory a diagram which computes all reachable nodes from a given root node in a graph. The graph is defined in the theory Graph and is given by a relation next on the nodes of the graph. The diagram has only three ordered situation (init > loop > final). The termination variant is a pair of a situation and a natural number with the lexicographic ordering. The idea of this ordering is that we can go from a bigger situation to a smaller one, however if we stay in the same situation the second component of the variant must decrease. The idea of the algorithm is that it starts with a set X containing the root element and the root is marked. As long as X is not empty, if x X and y is an unmarked sucessor of x we add y to X. If x X has no unmarked sucessors it is removed from X. The algorithm terminates when X is empty. datatype I = init loop final declare I.split [split] instantiation I :: well-founded-transitive begin less-i-def : i < j (j = init (i = loop i = final)) (j = loop i = final) less-eq-i-def : (i::i ) (j ::I ) i = j i < j instance proof fix x y z :: I assume x < y and y < z then show x < z apply (simp add: less-i-def ) next 5
6 fix x y :: I show x y < > x = y x < y by (simp add: less-eq-i-def ) next fix P fix a::i show ( x. ( y. y < x P y) P x) = P a apply (case-tac P final) apply (case-tac P loop) apply (simp-all add: less-i-def ) by blast next qed (simp) end The set path S mrk contains all reachable nodes from S along paths with unmarked nodes. lemma trascl-less: x y = (a, x) R = ((a,x) (R ( {y}) ( {y})) (y,x) R O (R ( {y}) ( {y})) ) apply (drule-tac b = x and a = a and r = R and P = λ x. (x y ((a,x) (R ( {y}) ( {y})) (y,x) R O (R ( {y}) ( {y})) )) in rtrancl-induct) apply (auto simp: Compl-insert) apply (case-tac ya = y) apply auto apply (rule-tac x = a and y = ya and z = z and r = R ((UNIV {y}) (UNIV {y})) in rtrancl-trans) apply auto apply (case-tac za = y) apply auto apply (drule-tac x = ya and y = za and z = z and r = (R (UNIV {y}) (UNIV {y})) in rtrancl-trans) lemma (in graph) add-set [simp]: x y = x path S mrk = x path (insert y S) (insert y mrk) apply (simp add: path-def ) apply clarify apply (drule-tac x = x and y = y and a = ya and R = next ( mrk) ( mrk) in trascl-less) apply (case-tac (ya, x) (next ( mrk) mrk ( {y}) {y}) ) apply (rule-tac x = xa in exi ) apply (simp add: relcomp-unfold) apply (rule-tac x = ya in exi ) 6
7 apply (case-tac (next ( mrk) mrk ( {y}) {y}) = (next ( insert y mrk) insert y mrk)) apply (rule-tac x = y in exi ) apply (simp add: relcomp-unfold) apply (rule-tac x = yaa in exi ) apply (case-tac (next ( mrk) mrk ( {y}) {y}) = (next ( insert y mrk) insert y mrk)) lemma (in graph) add-set2 : x path S mrk = x / path (insert y S) (insert y mrk) = x = y apply (case-tac x y) apply (frule add-set) by simp-all lemma (in graph) del-stack [simp]: ( y. (t, y) next y mrk) = x / mrk = x path S mrk = x path (S {t}) mrk apply (simp add: path-def ) apply clarify apply (rule-tac x = xa in exi ) apply (case-tac x = y) apply auto apply (drule-tac a = y and b = x and R = (next ( mrk) mrk) in rtrancld) apply (drule-tac x = y and y = x in trancld) lemma (in graph) init-set [simp]: x reach root = x root = x path {root} {root} apply (simp add: reach-def path-def ) apply (case-tac root x) apply (drule-tac a = root and x = x and y = root and R = next in trascl-less) apply (simp-all add: Compl-insert) apply (drule-tac a = root and b = x and R = (next (UNIV {root}) (UNIV {root})) in rtrancld) apply (drule-tac x = root and y = x in trancld) lemma (in graph) init-set2 : x reach root = x / path {root} {root} = x = root 7
8 apply (case-tac root x) apply (drule init-set) by simp-all 3.1 Transitions (in graph) Q1-a [: X, mrk X, mrk. (root:: node) = nil X = {} mrk = mrk :] (in graph) Q2-a [: X, mrk X, mrk. (root:: node) nil X = {root:: node} mrk = {root:: node} :] (in graph) Q3-a [: X, mrk X, mrk. ( x X. y. (x, y) next y / mrk X = X {y} mrk = mrk {y}):] (in graph) Q4-a [: X, mrk X, mrk. ( x X. ( y. (x, y) next y mrk) X = X {x} mrk = mrk):] (in graph) Q5-a [: X, mrk X, mrk. X = {} mrk = mrk :] 3.2 Invariants (in graph) Loop { (X, mrk). finite ( mrk) finite X X mrk mrk reach root reach root mrk path X mrk} trm λ (X, mrk). 2 card ( mrk) + card X term-eq t w = {s. t s = w} term-less t w = {s. t s < w} lemma union-term-eq [simp]: ( w. term-eq t w) = UNIV apply (simp add: term-eq-def ) lemma union-less-term-eq [simp]: ( v {v. v < w}. term-eq t v) = term-less t w apply (simp add: term-eq-def term-less-def ) 8
9 (in graph) Init { (X ::( node set), mrk::( node set)). finite ( mrk) mrk = {}} (in graph) Final { (X ::( node set), mrk::( node set)). mrk = reach root} (in graph) SetMarkInv i = (case i of I.init Init I.loop Loop I.final Final) (in graph) SetMarkInvFinal i = (case i of I.final Final - {}) (in graph) [simp]: SetMarkInvTerm w i = (case i of I.init Init I.loop Loop {s. trm s = w} I.final Final) 3.3 Diagram (in graph) SetMark λ (i, j ). (case (i, j ) of (I.init, I.loop) Q1-a Q2-a (I.loop, I.loop) Q3-a Q4-a (I.loop, I.final) Q5-a - top) lemma (in graph) SetMark-dmono [simp]: dmono SetMark apply (unfold dmono-def SetMark-def Q1-a-def Q2-a-def Q3-a-def Q4-a-def Q5-a-def ) by simp 3.4 Correctness of the transitions lemma (in graph) init-loop-1-a[simp]: = Init { Q1-a } Loop apply (unfold hoare-demonic Init-def Q1-a-def Loop-def ) lemma (in graph) init-loop-2-a[simp]: = Init { Q2-a } Loop apply (simp add: hoare-demonic Init-def Q2-a-def Loop-def ) apply auto apply (simp-all add: reach-def ) apply (rule init-set2 ) by (simp-all add: reach-def ) 9
10 lemma (in graph) loop-loop-1-a [simp]: = (Loop {s. trm s = w}) { Q3-a } (Loop {s. trm s < w}) apply (simp add: hoare-demonic Q3-a-def Loop-def trm-def ) apply (simp-all) apply (simp-all add: reach-def subset-eq) apply (simp-all add: Compl-insert) apply (rule rtrancl-into-rtrancl) apply (simp-all add: Int-def ) apply (rule add-set2 ) apply (case-tac card ( b) > 0 ) lemma (in graph) loop-loop-2-a[simp]: = (Loop {s. trm s = w}) { Q4-a } (Loop {s. trm s < w}) apply (simp add: hoare-demonic Q4-a-def Loop-def trm-def ) apply auto apply (case-tac card a > 0 ) lemma (in graph) loop-final-a [simp]: = (Loop {s. trm s = w}) { Q5-a } Final apply (simp add: hoare-demonic Q5-a-def Loop-def Final-def subset-eq Int-def path-def ) lemma union-term-w[simp]: ( w. {s. t s = w}) = UNIV lemma union-less-term-w[simp]: ( v {v. v < w}. {s. t s = v}) = {s. t s < w} lemma sup-union[simp]: Sup (range A) i = ( w. A w i) by (simp-all add: Sup-fun-def ) lemma forall-simp [simp]: (!a b. x A. (a = (t x)) (h x) b u x) = ( x A. h x) lemma forall-simp2 [simp]: (!a b. x A.!y. (a = t x y) (h x y) (g x y) b u x y) = ( x A.! y. h x y g x y ) 10
11 3.5 Diagram correctness The termination ordering for the SetMark diagram is the lexicographic ordering on pairs (i, n) where i I and n nat. interpretation DiagramTermination λ (n::nat) (i :: I ). (i, n) done theorem (in graph) SetMark-correct: = SetMarkInv { pt SetMark } SetMarkInvFinal proof (rule-tac X = SetMarkInvTerm in hoare-diagram3 ) show dmono SetMark by simp show u i j. = SetMarkInvTerm u i{ SetMark (i, j ) } DiagramTermination.SUP-L-P (λn i. (i, n)) SetMarkInvTerm (i, u) j by (auto simp add: SUP-L-P-def less-pair-def less-i-def hoare-choice SetMark-def ) show SetMarkInv Sup (range SetMarkInvTerm) apply (simp add: le-fun-def, safe) apply (simp-all add: SetMarkInv-def ) apply (case-tac x) apply auto done show Sup (range SetMarkInvTerm) grd (step SetMark) SetMarkInvFinal apply (simp add: le-fun-def inf-fun-def SetMarkInvFinal-def ) apply (drule-tac x=i.loop in spec) apply (simp add: SetMark-def ) apply (simp add: Q1-a-def Q2-a-def ) apply auto[1 ] apply (frule-tac x=i.loop in spec) apply (drule-tac x=i.final in spec) apply (simp add: SetMark-def ) apply (simp add: Q3-a-def Q4-a-def Q5-a-def ) apply (auto) done qed theorem (in graph) SetMark-correct1 [simp]: Hoare-dgr SetMarkInv SetMark (SetMarkInv ( grd (step SetMark))) apply (simp add: Hoare-dgr-def ) apply (rule-tac x = SetMarkInvTerm in exi ) apply (subgoal-tac SetMarkInv = range SetMarkInvTerm) apply (simp-all add: SetMark-def SUP-L-P-def less-pair-def less-i-def hoare-choice uminus-apply) apply (simp-all add: fun-eq-iff ) apply (unfold SetMarkInv-def ) 11
12 theorem (in graph) stack-not-nil [simp]: (mrk, S) Loop = x S = x nil apply (simp add: Loop-def reach-def ) end 4 Marking Using a Stack theory StackMark imports SetMark../DataRefinementIBP/DataRefinement begin In this theory we refine the set marking diagram to a diagram in which the set is replaced by a list (stack). Iniatially the list contains the root element and as long as the list is nonempty and the top of the list has an unmarked successor y, then y is added to the top of the list. If the top does not have unmarked sucessors, it is removed from the list. The diagram terminates when the list is empty. The data refinement relation of the two diagrams is true if the list has distinct elements and the elements of the list and the set are the same. 4.1 Transitions (in graph) Q1 -a [:λ (stk::( node list), mrk::( node set)). {(stk ::( node list), mrk ). root = nil stk = [] mrk = mrk}:] (in graph) Q2 -a [:λ (stk::( node list), mrk::( node set)). {(stk, mrk ). root nil stk = [root] mrk = mrk {root}}:] (in graph) Q3 -a [:λ (stk, mrk). {(stk, mrk ). stk [] ( y. (hd stk, y) next y / mrk stk = y # stk mrk = mrk {y})}:] (in graph) Q4 -a [:λ (stk, mrk). {(stk, mrk ). stk [] ( y. (hd stk, y) next y mrk) stk = tl stk mrk = mrk}:] Q5 -a [:λ (stk, mrk). {(stk, mrk ). stk = [] mrk = mrk}:] 4.2 Invariants 12
13 Init UNIV Loop { (stk, mrk). distinct stk} Final UNIV [simp]: StackMarkInv i = (case i of I.init Init I.loop Loop I.final Final ) 4.3 Data refinement relations R1-a {: stk, mrk X, mrk. mrk = mrk :} R2-a {: stk, mrk X, mrk. X = set stk (stk, mrk) Loop mrk = mrk :} lemma [simp]: R1-a Apply.Disjunctive by (simp add: R1-a-def ) lemma [simp]: R2-a Apply.Disjunctive by (simp add: R2-a-def ) [simp]: R-a i = (case i of I.init R1-a I.loop R2-a I.final R1-a) lemma [simp]: Disjunctive-fun R-a by (simp add: Disjunctive-fun-def ) angelic-fun r = (λ i. {:r i:}) (in graph) StackMark-a = (λ (i, j ). (case (i, j ) of (I.init, I.loop) Q1 -a Q2 -a (I.loop, I.loop) Q3 -a Q4 -a (I.loop, I.final) Q5 -a - )) 4.4 Data refinement of the transitions theorem (in graph) init-nil [simp]: DataRefinement ({.Init.} o Q1-a) R1-a R2-a Q1 -a 13
14 by (simp add: data-refinement-hoare hoare-demonic Q1 -a-def Init-def Loop -def R1-a-def R2-a-def Q1-a-def angelic-def subset-eq) theorem (in graph) init-root [simp]: DataRefinement ({.Init.} o Q2-a) R1-a R2-a Q2 -a by (simp add: data-refinement-hoare hoare-demonic Q2 -a-def Init-def Loop -def R1-a-def R2-a-def Q2-a-def angelic-def subset-eq) theorem (in graph) step1 [simp]: DataRefinement ({.Loop.} o Q3-a) R2-a R2-a Q3 -a apply (simp add: data-refinement-hoare hoare-demonic Loop-def Loop -def R2-a-def Q3-a-def Q3 -a-def angelic-def subset-eq) apply (simp add: simp-eq-emptyset) by (metis List.set.simps(2 ) hd-in-set distinct.simps(2 )) theorem (in graph) step2 [simp]: DataRefinement ({.Loop.} o Q4-a) R2-a R2-a Q4 -a apply (simp add: data-refinement-hoare hoare-demonic Loop-def Loop -def R2-a-def Q4-a-def Q4 -a-def angelic-def subset-eq) apply (simp add: simp-eq-emptyset) apply clarify apply (case-tac a) theorem (in graph) final [simp]: DataRefinement ({.Loop.} o Q5-a) R2-a R1-a Q5 -a apply (simp add: data-refinement-hoare hoare-demonic Loop-def Loop -def R2-a-def R1-a-def Q5-a-def Q5 -a-def angelic-def subset-eq) by (simp add: simp-eq-emptyset) 4.5 Diagram data refinement lemma assert-comp-choice: {.p.} o (S T ) = ({.p.} o S) ({.p.} o T ) apply (rule antisym) apply (simp-all add: fun-eq-iff assert-def le-fun-def inf-fun-def inf-assoc) apply (rule-tac y = S x T x in order-trans) apply (rule inf-le2 ) apply (rule-tac y = S x T x in order-trans) apply (rule inf-le2 ) apply (rule-tac y = S x (p T x) in order-trans) apply (rule inf-le2 ) apply (rule-tac y = S x (p T x) in order-trans) apply (rule inf-le2 ) apply (rule-tac y = p T x in order-trans) apply (rule inf-le2 ) 14
15 by simp theorem (in graph) StackMark-DataRefinement [simp]: DgrDataRefinement2 SetMarkInv SetMark R-a StackMark-a by (simp add: DgrDataRefinement2-def StackMark-a-def SetMark-def demonic-sup-inf SetMarkInv-def data-refinement-choice2 assert-comp-choice) 4.6 Diagram correctness theorem (in graph) StackMark-correct: Hoare-dgr (R-a.. SetMarkInv) StackMark-a ((R-a.. SetMarkInv) ( grd (step (StackMark-a)))) apply (rule-tac D = SetMark in Diagram-DataRefinement2 ) apply auto by (rule SetMark-correct1 ) end 5 Generalization of Deutsch-Schorr-Waite Algorithm theory LinkMark imports StackMark begin In the third step the stack diagram is refined to a diagram where no extra memory is used. The relation next is replaced by two new variables link and label. The variable label : node index associates a label to every node and the variable link : index node node is a collection of pointer functions indexed by the set index of labels. For x node, link i x is the successor node of x along the function link i. In this context a node x is reachable if there exists a path from the root to x along the links link i such that all nodes in this path are not nil and they are labeled by a special label none index. The stack variable S is replaced by two new variables p and t ranging over nodes. Variable p stores the head of S, t stores the head of the tail of S, and the rest of S is stored by temporarily modifying the variables link and label. This algorithm is a generalization of the Deutsch-Schorr-Waite graph marking algorithm because we have a collection of pointer functions instead of left and right only. locale pointer = node + fixes none :: index fixes link0 :: index node node fixes label0 :: node index 15
16 assumes (nil:: node) = nil begin next = {(a, b). ( i. link0 i a = b) a nil b nil label0 a = none} end sublocale pointer link: graph nil root next apply unfold-locales apply (unfold next-def ) The locale pointer fixes the initial values for the variables link and label and it defines the relation next as the union of all link i functions, excluding the mappings to nil, the mappings from nil as well as the mappings from elements which are not labeled by none. The next two recursive functions, label 0, link 0 are used to compute the initial values of the variables label and link from their current values. context pointer begin primrec label-0 :: ( node index) ( node list) ( node index) where label-0 lbl [] = lbl label-0 lbl (x # l) = label-0 (lbl(x := none)) l lemma label-cong [cong]: f = g = xs = ys = pointer.label-0 n f xs = pointer.label-0 n g ys by simp primrec link-0 :: ( index node node) ( node index) node ( node list) ( index node node) where link-0 lnk lbl p [] = lnk link-0 lnk lbl p (x # l) = link-0 (lnk((lbl x) := ((lnk (lbl x))(x := p)))) lbl x l The function stack defined bellow is the main data refinement relation connecting the stack from the abstract algorithm to its concrete representation by temporarily modifying the variable link and label. primrec stack:: ( index node node) ( node index) node ( node list) bool where stack lnk lbl x [] = (x = nil) stack lnk lbl x (y # l) = (x nil x = y x set l stack lnk lbl (lnk (lbl x) x) l) lemma label-out-range0 [simp]: 16
17 x set S = label-0 lbl S x = lbl x apply (rule-tac P= label. x set S label-0 label S x = label x in mp) by (simp, induct-tac S, auto) lemma link-out-range0 [simp]: x set S = link-0 link label p S i x = link i x apply (rule-tac P= link p. x set S link-0 link label p S i x = link i x in mp) by (simp, induct-tac S, auto) lemma link-out-range [simp]: x set S = link-0 link (label(x := y)) p S = link-0 link label p S apply (rule-tac P= link p. x set S link-0 link (label(x := y)) p S = link-0 link label p S in mp) by (simp, induct-tac S, auto) lemma empty-stack [simp]: stack link label nil S = (S = []) by (case-tac S, simp-all) lemma stack-out-link-range [simp]: p set S = stack (link(i := (link i)(p := q))) label x S = stack link label x S apply (rule-tac P = link x. p set S stack (link(i := (link i)(p := q))) label x S = stack link label x S in mp) by (simp, induct-tac S, auto) lemma stack-out-label-range [simp]: p set S = stack link (label(p := q)) x S = stack link label x S apply (rule-tac P = link x. p set S stack link (label(p := q)) x S = stack link label x S in mp) by (simp, induct-tac S, auto) g mrk lbl ptr x ptr x nil ptr x / mrk lbl x = none lemma g-cong [cong]: mrk = mrk1 = lbl = lbl1 = ptr = ptr1 = x = x1 ==> pointer.g n m mrk lbl ptr x = pointer.g n m mrk1 lbl1 ptr1 x1 by simp 5.1 Transitions Q1 -a [: p, t, lnk, lbl, mrk p, t, lnk, lbl, mrk. root = nil p = nil t = nil lnk = lnk lbl = lbl mrk = mrk:] Q2 -a [: p, t, lnk, lbl, mrk p, t, lnk, lbl, mrk. root nil p = root t = nil lnk = lnk lbl = lbl mrk = mrk {root} :] 17
18 Q3 -a [: p, t, lnk, lbl, mrk p, t, lnk, lbl, mrk. p nil ( i. g mrk lbl (lnk i) p p = lnk i p t = p lnk = lnk(i := (lnk i)(p := t)) lbl = lbl(p := i) mrk = mrk {lnk i p}) :] Q4 -a [: p, t, lnk, lbl, mrk p, t, lnk, lbl, mrk. p nil ( i. g mrk lbl (lnk i) p) t nil p = t t = lnk (lbl t) t lnk = lnk(lbl t := (lnk (lbl t))(t := p)) lbl = lbl(t := none) mrk = mrk:] Q5 -a [: p, t, lnk, lbl, mrk p, t, lnk, lbl, mrk. p nil ( i. g mrk lbl (lnk i) p) t = nil p = nil t = t lnk = lnk lbl = lbl mrk = mrk:] Q6 -a [: p, t, lnk, lbl, mrk p, t, lnk, lbl, mrk. p = nil p = p t = t lnk = lnk lbl = lbl mrk = mrk :] 5.2 Invariants Init { (p, t, lnk, lbl, mrk). lnk = link0 lbl = label0 } Loop UNIV Final Init 5.3 Data refinement relations R1 -a {: p, t, lnk, lbl, mrk stk, mrk. (p, t, lnk, lbl, mrk) Init mrk = mrk:} R2 -a {: p, t, lnk, lbl, mrk stk, mrk. p = head stk t = head (tail stk) stack lnk lbl t (tail stk) link0 = link-0 lnk lbl p (tail stk) label0 = label-0 lbl (tail stk) 18
19 nil set stk mrk = mrk :} lemma [simp]: R1 -a Apply.Disjunctive by (simp add: R1 -a-def ) lemma [simp]: R2 -a Apply.Disjunctive by (simp add: R2 -a-def ) [simp]: R -a i = (case i of I.init R1 -a I.loop R2 -a I.final R1 -a) lemma [simp]: Disjunctive-fun R -a by (simp add: Disjunctive-fun-def ) 5.4 Diagram LinkMark = (λ (i, j ). (case (i, j ) of (I.init, I.loop) Q1 -a Q2 -a (I.loop, I.loop) Q3 -a (Q4 -a Q5 -a) (I.loop, I.final) Q6 -a - )) [simp]: LinkMarkInv i = (case i of I.init Init I.loop Loop I.final Final ) 5.5 Data refinement of the transitions theorem init1-a [simp]: DataRefinement ({.Init.} o Q1 -a) R1 -a R2 -a Q1 -a by (simp add: data-refinement-hoare hoare-demonic Q1 -a-def Init -def Init -def Loop -def R1 -a-def R2 -a-def Q1 -a-def tail-def head-def angelic-def subset-eq) theorem init2-a [simp]: DataRefinement ({.Init.} o Q2 -a) R1 -a R2 -a Q2 -a by (simp add: data-refinement-hoare hoare-demonic Q2 -a-def Init -def Init -def Loop -def R1 -a-def R2 -a-def Q2 -a-def tail-def head-def angelic-def subset-eq) theorem step1-a [simp]: DataRefinement ({.Loop.} o Q3 -a) R2 -a R2 -a Q3 -a apply (simp add: data-refinement-hoare hoare-demonic Q3 -a-def Init -def Init -def Loop -def R1 -a-def Q3 -a-def tail-def head-def angelic-def subset-eq) apply (unfold next-def ) 19
20 apply (simp add: R2 -a-def ) apply (simp add: data-refinement-hoare) apply (simp-all add: R2 -a-def angelic-def hoare-demonic simp-eq-emptyset) apply auto apply (rule-tac x = aa i (hd a) # a in exi ) apply (simp add: g-def neq-nil-conv) apply clarify apply (simp add: g-def neq-nil-conv) apply (case-tac a) apply (simp-all add: g-def neq-nil-conv) apply (case-tac a) apply (case-tac a) lemma neqif [simp]: x y = (if y = x then a else b) = b apply (case-tac y x) done theorem step2-a [simp]: DataRefinement ({.Loop.} o Q4 -a) R2 -a R2 -a Q4 -a apply (simp add: data-refinement-hoare hoare-demonic Q4 -a-def Init -def Init -def Loop -def Q4 -a-def tail-def head-def angelic-def subset-eq) apply (unfold next-def ) apply (simp add: R2 -a-def ) apply (simp add: data-refinement-hoare) apply (simp-all add: R2 -a-def angelic-def hoare-demonic simp-eq-emptyset) apply (simp-all add: neq-nil-conv) apply (unfold g-def ) apply (simp add: head-def ) apply auto [1 ] apply auto [1 ] apply (case-tac ysa) apply (case-tac ab ya = i) lemma setsimp: a = c = (x a) = (x c) done 20
21 theorem step3-a [simp]: DataRefinement ({.Loop.} o Q4 -a) R2 -a R2 -a Q5 -a apply (simp add: data-refinement-hoare hoare-demonic Q5 -a-def Init -def Init -def Loop -def Q4 -a-def angelic-def subset-eq) apply (unfold R2 -a-def ) apply (unfold next-def ) apply (simp add: data-refinement-hoare hoare-demonic angelic-def subset-eq simp-eq-emptyset g-def head-def tail-def ) theorem final-a [simp]: DataRefinement ({.Loop.} o Q5 -a) R2 -a R1 -a Q6 -a apply (simp add: data-refinement-hoare hoare-demonic Q6 -a-def Init -def Init -def Loop -def R2 -a-def R1 -a-def Q5 -a-def angelic-def subset-eq neq-nil-conv tail-def head-def ) apply (simp add: simp-eq-emptyset) by simp-all 5.6 Diagram data refinement lemma apply-fun-index [simp]: (r.. P) i = (r i) (P i) by (simp add: apply-fun-def ) lemma [simp]: Disjunctive-fun (r::( c a::complete-lattice b::complete-lattice)) = mono-fun r by (simp add: Disjunctive-fun-def mono-fun-def ) theorem LinkMark-DataRefinement-a [simp]: DgrDataRefinement2 (R-a.. SetMarkInv) StackMark-a R -a LinkMark apply (rule-tac P = StackMarkInv in DgrDataRefinement-mono) apply (simp add: le-fun-def SetMarkInv-def angelic-def R1-a-def R2-a-def Init -def Final -def ) apply (simp add: DgrDataRefinement2-def dgr-demonic-def LinkMark-def StackMark-a-def demonic-sup-inf data-refinement-choice2 assert-comp-choice) apply (rule data-refinement-choice2 ) apply (rule data-refinement-choice1 ) by simp-all lemma [simp]: mono Q1 -a by (simp add: Q1 -a-def ) lemma [simp]: mono Q2 -a by (simp add: Q2 -a-def ) lemma [simp]: mono Q3 -a by (simp add: Q3 -a-def ) lemma [simp]: mono Q4 -a by (simp add: Q4 -a-def ) lemma [simp]: mono Q5 -a by (simp add: Q5 -a-def ) 21
22 lemma [simp]: dmono StackMark-a apply (unfold dmono-def StackMark-a-def ) by simp 5.7 Diagram correctness theorem LinkMark-correct: Hoare-dgr (R -a.. (R-a.. SetMarkInv)) LinkMark ((R -a.. (R-a.. SetMarkInv)) ( grd (step LinkMark))) apply (rule-tac D = StackMark-a in Diagram-DataRefinement2 ) by (rule StackMark-correct) end end 6 Deutsch-Schorr-Waite Marking Algorithm theory DSWMark imports LinkMark begin Finally, we construct the Deutsch-Schorr-Waite marking algorithm by assuming that there are only two pointers (left, right) from every node. There is also a new variable, atom : node bool which associates to every node a Boolean value. The data invariant of this refinement step requires that index has exactly two distinct elements none and some, left = link none, right = link some, and atom x is true if and only if label x = some. We use a new locale which fixes the initial values of the variables left, right, and atom in left0, right0, and atom0 respectively. datatype Index = none some locale classical = node + fixes left0 :: node node fixes right0 :: node node fixes atom0 :: node bool assumes (nil:: node) = nil begin link0 i = (if i = (none::index) then left0 else right0 ) label0 x = (if atom0 x then (some::index) else none) end sublocale classical dsw: pointer nil root none::index link0 label0 proof qed auto 22
23 context classical begin lemma [simp]: (label0 = (λ x. if atom x then some else none)) = (atom0 = atom) apply (simp add: fun-eq-iff label0-def ) gg mrk atom ptr x ptr x nil ptr x / mrk atom x 6.1 Transitions QQ1-a [: p, t, left, right, atom, mrk p, t, left, right, atom, mrk. root = nil p = nil t = nil mrk = mrk left = left right = right atom = atom :] QQ2-a [: p, t, left, right, atom, mrk p, t, left, right, atom, mrk. root nil p = root t = nil mrk = mrk {root} left = left right = right atom = atom :] QQ3-a [: p, t, left, right, atom, mrk p, t, left, right, atom, mrk. p nil gg mrk atom left p p = left p t = p mrk = mrk {left p} left = left(p := t) right = right atom = atom:] QQ4-a [: p, t, left, right, atom, mrk p, t, left, right, atom, mrk. p nil gg mrk atom right p p = right p t = p mrk = mrk {right p} left = left right = right(p := t) atom = atom(p := True) :] QQ5-a [: p, t, left, right, atom, mrk p, t, left, right, atom, mrk. p nil ( not needed in the proof ) gg mrk atom left p gg mrk atom right p t nil atom t p = t t = left t mrk = mrk left = left(t := p) right = right atom = atom :] QQ6-a [: p, t, left, right, atom, mrk p, t, left, right, atom, mrk. p nil ( not needed in the proof ) gg mrk atom left p gg mrk atom right p 23
24 t nil atom t p = t t = right t mrk = mrk left = left right = right(t := p) atom = atom(t := False) :] QQ7-a [: p, t, left, right, atom, mrk p, t, left, right, atom, mrk. p nil gg mrk atom left p gg mrk atom right p t = nil p = nil t = t mrk = mrk left = left right = right atom = atom :] QQ8-a [: p, t, left, right, atom, mrk p, t, left, right, atom, mrk. p = nil p = p t = t mrk = mrk left = left right = right atom = atom:] 7 Data refinement relation RR-a {: p, t, left, right, atom, mrk p, t, lnk, lbl, mrk. lnk none = left lnk some = right lbl = (λ x. if atom x then some else none) p = p t = t mrk = mrk :} [simp]: R -a i = RR-a ClassicMark = (λ (i, j ). (case (i, j ) of (I.init, I.loop) QQ1-a QQ2-a (I.loop, I.loop) (QQ3-a QQ4-a) ((QQ5-a QQ6-a) QQ7-a) (I.loop, I.final) QQ8-a - )) 7.1 Data refinement of the transitions theorem init1-a [simp]: DataRefinement ({.Init.} o Q1 -a) RR-a RR-a QQ1-a by (simp add: data-refinement-hoare hoare-demonic angelic-def QQ1-a-def Q1 -a-def RR-a-def Init -def subset-eq) theorem init2-a [simp]: DataRefinement ({.Init.} o Q2 -a) RR-a RR-a QQ2-a by (simp add: data-refinement-hoare hoare-demonic angelic-def QQ2-a-def Q2 -a-def RR-a-def Init -def subset-eq) 24
25 lemma index-simp: (u = v) = (u none = v none u some = v some) by (safe, rule ext, case-tac x, auto) theorem step1-a [simp]: DataRefinement ({.Loop.} o Q3 -a) RR-a RR-a QQ3-a apply (simp add: data-refinement-hoare hoare-demonic angelic-def QQ3-a-def Q3 -a-def RR-a-def Loop -def subset-eq g-def gg-def simp-eq-emptyset) apply (rule-tac x=λ x. if x = some then ab some else (ab none)(a := aa) in exi ) apply (rule-tac x=none in exi ) apply (simp add: index-simp) done theorem step2-a[simp]: DataRefinement ({.Loop.} o Q3 -a) RR-a RR-a QQ4-a apply (simp add: data-refinement-hoare hoare-demonic angelic-def QQ4-a-def Q3 -a-def RR-a-def Loop -def subset-eq g-def gg-def simp-eq-emptyset) apply (rule-tac x=λ x. if x = none then ab none else (ab some)(a := aa) in exi ) apply (rule-tac x=some in exi ) apply (simp add: index-simp) apply (rule ext) apply auto done theorem step3-a [simp]: DataRefinement ({.Loop.} o Q4 -a) RR-a RR-a QQ5-a apply (simp add: data-refinement-hoare hoare-demonic angelic-def QQ5-a-def Q4 -a-def RR-a-def Loop -def subset-eq g-def gg-def simp-eq-emptyset) apply clarify apply (case-tac i) apply auto done lemma if-set-elim: (x (if b then A else B)) = ((b x A) ( b x B)) theorem step4-a [simp]: DataRefinement ({.Loop.} o Q4 -a) RR-a RR-a QQ6-a apply (simp add: data-refinement-hoare hoare-demonic angelic-def RR-a-def QQ6-a-def 25
26 Q4 -a-def Loop -def subset-eq simp-eq-emptyset g-def gg-def if-set-elim) apply (simp add: ext) apply (case-tac i) apply (case-tac i) apply (case-tac i) apply (case-tac i) by simp-all theorem step5-a [simp]: DataRefinement ({.Loop.} o Q5 -a) RR-a RR-a QQ7-a apply (simp add: data-refinement-hoare hoare-demonic angelic-def Q5 -a-def QQ7-a-def Loop -def subset-eq RR-a-def simp-eq-emptyset) apply (simp-all add: g-def gg-def ) apply (case-tac i) theorem final-step-a [simp]: DataRefinement ({.Loop.} o Q6 -a) RR-a RR-a QQ8-a by (simp add: data-refinement-hoare hoare-demonic angelic-def Q6 -a-def QQ8-a-def Loop -def subset-eq RR-a-def simp-eq-emptyset) 7.2 Diagram data refinement lemma [simp]: mono RR-a by (simp add: RR-a-def ) lemma [simp]: RR-a Apply.Disjunctive by (simp add: RR-a-def ) lemma [simp]: Disjunctive-fun R -a by (simp add: Disjunctive-fun-def ) lemma [simp]: mono-fun R -a by simp lemma [simp]: mono Q1 -a by (simp add: Q1 -a-def ) lemma [simp]: mono Q2 -a by (simp add: Q2 -a-def ) lemma [simp]: mono Q3 -a by (simp add: Q3 -a-def ) lemma [simp]: mono Q4 -a by (simp add: Q4 -a-def ) lemma [simp]: mono Q5 -a by (simp add: Q5 -a-def ) lemma [simp]: mono Q6 -a by (simp add: Q6 -a-def ) lemma [simp]: dmono LinkMark apply (unfold dmono-def LinkMark-def ) by simp theorem ClassicMark-DataRefinement-a [simp]: 26
27 DgrDataRefinement2 (R -a.. (R-a.. SetMarkInv)) LinkMark R -a ClassicMark apply (rule-tac P = LinkMarkInv in DgrDataRefinement-mono) apply (simp add: le-fun-def SetMarkInv-def angelic-def R1 -a-def R2 -a-def Init -def Loop -def Final -def ) apply auto apply (simp add: DgrDataRefinement2-def dgr-demonic-def ClassicMark-def LinkMark-def demonic-sup-inf data-refinement-choice2 assert-comp-choice) apply (rule data-refinement-choice2 ) apply (rule data-refinement-choice1 ) apply (rule data-refinement-choice2 ) apply (rule data-refinement-choice1 ) by simp-all 7.3 Diagram corectness theorem ClassicMark-correct-a [simp]: Hoare-dgr (R -a.. (R -a.. (R-a.. SetMarkInv))) ClassicMark ((R -a.. (R -a..(r-a.. SetMarkInv))) ( grd (step ClassicMark))) apply (rule-tac D = LinkMark in Diagram-DataRefinement2 ) apply auto by (rule LinkMark-correct) We have proved the correctness of the final algorithm, but the pre and the post conditions involve the angelic choice operator and they depend on all data refinement steps we have used to prove the final diagram. We simplify these conditions and we show that we obtained indead the corectness of the marking algorithm. The predicate ClassicInit which is true for the init situation states that initially the variables left, right, and atom are equal to their initial values and also that no node is marked. The predicate ClassicFinal which is true for the f inal situation states that at the end the values of the variables left, right, and atom are again equal to their initial values and the variable mrk records all reachable nodes. The reachable nodes are defined using our initial next relation, however if we unfold all locale interpretations and s we see easeily that a node x is reachable if there is a path from root to x along left and right functions, and all nodes in this path have the atom bit false. ClassicInit = {(p, t, left, right, atom, mrk). atom = atom0 left = left0 right = right0 finite ( mrk) mrk = {}} 27
28 ClassicFinal = {(p, t, left, right, atom, mrk). atom = atom0 left = left0 right = right0 mrk = reach root} theorem [simp]: ClassicInit (RR-a (R1 -a (R1-a (SetMarkInv init)))) apply (simp add: SetMarkInv-def ) apply (simp add: ClassicInit-def angelic-def RR-a-def R1 -a-def R1-a-def Init-def Init -def ) apply (unfold simp-eq-emptyset) apply (simp add: link0-def label0-def ) apply (simp add: fun-eq-iff ) by (simp add: label0-def ) theorem [simp]: (RR-a (R1 -a (R1-a (SetMarkInv final)))) ClassicFinal apply (simp add: SetMarkInv-def ) apply (simp add: ClassicFinal-def angelic-def RR-a-def R1 -a-def R1-a-def Final-def Final -def Init -def label0-def link0-def ) apply (simp add: simp-eq-emptyset inf-fun-def ) apply auto by (simp-all add: link0-def ) The indexed predicate ClassicPre is the precondition of the diagram, and since we are only interested in starting the marking diagram in the init situation we set ClassicPre loop = ClassicPre final =. [simp]: ClassicPre i = (case i of I.init ClassicInit I.loop {} I.final {}) We are interested on the other hand that the marking diagram terminates only in the final situation. In order to achieve this we define the postcondition of the diagram as the indexed predicate ClassicPost which is empty on every situation except f inal. [simp]: ClassicPost i = (case i of I.init {} I.loop {} I.final ClassicFinal) lemma exists-or: ( x. p x q x) = (( x. p x) ( x. q x)) lemma [simp]: 28
29 ( grd (step ClassicMark)) init = {} apply (simp add: grd-def step-def ) apply (drule-tac x = loop in spec) by (simp add: ClassicMark-def QQ1-a-def QQ2-a-def demonic-def, auto) lemma [simp]: grd = by (simp add: grd-def top-fun-def ) lemma [simp]: ( grd (step ClassicMark)) loop = {} apply (frule-tac x = final in spec) apply (drule-tac x = loop in spec) apply (unfold ClassicMark-def QQ1-a-def QQ2-a-def QQ3-a-def QQ4-a-def QQ5-a-def QQ6-a-def QQ7-a-def QQ8-a-def ) apply (case-tac a nil) The final theorem states the correctness of the marking diagram with respect to the precondition ClassicPre and the postcondition ClassicPost, that is, if the diagram starts in the initial situation, then it will terminate in the final situation, and it will mark all reachable nodes. lemma [simp]: mono QQ1-a by (simp add: QQ1-a-def ) lemma [simp]: mono QQ2-a by (simp add: QQ2-a-def ) lemma [simp]: mono QQ3-a by (simp add: QQ3-a-def ) lemma [simp]: mono QQ4-a by (simp add: QQ4-a-def ) lemma [simp]: mono QQ5-a by (simp add: QQ5-a-def ) lemma [simp]: mono QQ6-a by (simp add: QQ6-a-def ) lemma [simp]: mono QQ7-a by (simp add: QQ7-a-def ) lemma [simp]: mono QQ8-a by (simp add: QQ8-a-def ) lemma [simp]: dmono ClassicMark apply (unfold dmono-def ClassicMark-def ) by simp theorem = ClassicPre { pt ClassicMark } ClassicPost apply (rule-tac P = (R -a.. (R -a.. (R-a..SetMarkInv))) in hoare-pre) apply (subst le-fun-def ) apply (rule-tac Q = ((R -a.. (R -a.. (R-a.. SetMarkInv))) ( grd (step ((ClassicMark))))) in hoare-mono) apply (simp-all add: hoare-dgr-correctness) apply (rule le-funi ) apply (case-tac x) apply (simp-all add: inf-fun-def del: uminus-apply) 29
30 apply (rule-tac y = RR-a (R1 -a (R1-a (SetMarkInv final))) in order-trans) end end References [1] J.-R. Abrial. Event based sequential program development: Application to constructing a pointer program. In K. Araki, S. Gnesi, and D. Mandrioli, editors, FME, volume 2805 of Lecture Notes in Computer Science, pages Springer, [2] R. J. Back. Correctness preserving program refinements: proof theory and applications, volume 131 of Mathematical Centre Tracts. Mathematisch Centrum, Amsterdam, [3] R.-J. Back. Semantic correctness of invariant based programs. In International Workshop on Program Construction, Chateau de Bonas, France, [4] R.-J. Back. Invariant based programs and their correctness. In W. Biermann, G. Guiho, and Y. Kodratoff, editors, Automatic Program Construction Techniques, pages MacMillan Publishing Company, [5] R.-J. Back. Invariant based programming: Basic approach and teaching experience. Formal Aspects of Computing, [6] R.-J. Back and V. Preoteasa. Semantics and proof rules of invariant based programs. Technical Report 903, TUCS, Jul [7] R. J. Back and J. von Wright. Encoding, decoding and data refinement. Formal Aspects of Computing, 12: , [8] W. DeRoever and K. Engelhardt. Data Refinement: Model-Oriented Proof Methods and Their Comparison. Cambridge University Press, New York, NY, USA, [9] C. A. R. Hoare. Proof of correctness of data representations. Acta Informatica, 1(4), Dec [10] D. E. Knuth. The art of computer programming, volume 1 (3rd ed.): fundamental algorithms. Addison Wesley Longman Publishing Co., Inc., Redwood City, CA, USA,
31 [11] F. Mehta and T. Nipkow. Proving pointer programs in higher-order logic. Information and Computation, 199: , [12] V. Preoteasa and R.-J. Back. Data refinement of invariant based programs. Electronic Notes in Theoretical Computer Science, 259: , Proceedings of the 14th BCS-FACS Refinement Workshop (REFINE 2009). [13] V. Preoteasa and R.-J. Back. Semantics and data refinement of invariant based programs. In G. Klein, T. Nipkow, and L. Paulson, editors, Archive of Formal Proofs. DataRefinementIBP.shtml, May Formal proof development. Submitted. [14] H. Schorr and W. M. Waite. An efficient machine-independent procedure for garbage collection in various list structures. Commun. ACM, 10(8): ,
Imperative Insertion Sort
 Imperative Insertion Sort Christian Sternagel October 11, 2017 Contents 1 Looping Constructs for Imperative HOL 1 1.1 While Loops............................ 1 1.2 For Loops.............................
Imperative Insertion Sort Christian Sternagel October 11, 2017 Contents 1 Looping Constructs for Imperative HOL 1 1.1 While Loops............................ 1 1.2 For Loops.............................
Syntax and semantics of a GPU kernel programming language
 Syntax and semantics of a GPU kernel programming language John Wickerson April 17, 2016 Abstract This document accompanies the article The Design and Implementation of a Verification Technique for GPU
Syntax and semantics of a GPU kernel programming language John Wickerson April 17, 2016 Abstract This document accompanies the article The Design and Implementation of a Verification Technique for GPU
MP 5 Program Transition Systems and Linear Temporal Logic
 MP 5 Program Transition Systems and Linear Temporal Logic CS 477 Spring 2018 Revision 1.0 Assigned April 10, 2018 Due April 17, 2018, 9:00 PM Extension extend48 hours (penalty 20% of total points possible)
MP 5 Program Transition Systems and Linear Temporal Logic CS 477 Spring 2018 Revision 1.0 Assigned April 10, 2018 Due April 17, 2018, 9:00 PM Extension extend48 hours (penalty 20% of total points possible)
Design of Distributed Systems Melinda Tóth, Zoltán Horváth
 Design of Distributed Systems Melinda Tóth, Zoltán Horváth Design of Distributed Systems Melinda Tóth, Zoltán Horváth Publication date 2014 Copyright 2014 Melinda Tóth, Zoltán Horváth Supported by TÁMOP-412A/1-11/1-2011-0052
Design of Distributed Systems Melinda Tóth, Zoltán Horváth Design of Distributed Systems Melinda Tóth, Zoltán Horváth Publication date 2014 Copyright 2014 Melinda Tóth, Zoltán Horváth Supported by TÁMOP-412A/1-11/1-2011-0052
Dynamic Semantics. Dynamic Semantics. Operational Semantics Axiomatic Semantics Denotational Semantic. Operational Semantics
 Dynamic Semantics Operational Semantics Denotational Semantic Dynamic Semantics Operational Semantics Operational Semantics Describe meaning by executing program on machine Machine can be actual or simulated
Dynamic Semantics Operational Semantics Denotational Semantic Dynamic Semantics Operational Semantics Operational Semantics Describe meaning by executing program on machine Machine can be actual or simulated
Lattices and Orders in Isabelle/HOL
 Lattices and Orders in Isabelle/HOL Markus Wenzel TU München October 8, 2017 Abstract We consider abstract structures of orders and lattices. Many fundamental concepts of lattice theory are developed,
Lattices and Orders in Isabelle/HOL Markus Wenzel TU München October 8, 2017 Abstract We consider abstract structures of orders and lattices. Many fundamental concepts of lattice theory are developed,
A General Method for the Proof of Theorems on Tail-recursive Functions
 A General Method for the Proof of Theorems on Tail-recursive Functions Pasquale Noce Security Certification Specialist at Arjo Systems - Gep S.p.A. pasquale dot noce dot lavoro at gmail dot com pasquale
A General Method for the Proof of Theorems on Tail-recursive Functions Pasquale Noce Security Certification Specialist at Arjo Systems - Gep S.p.A. pasquale dot noce dot lavoro at gmail dot com pasquale
Structuring the verification of heap-manipulating programs
 Structuring the verification of heap-manipulating programs Aleksandar Nanevski (IMDEA Madrid) Viktor Vafeiadis (MSR / Univ. of Cambridge) Josh Berdine (MSR Cambridge) Hoare/Separation Logic Hoare logic
Structuring the verification of heap-manipulating programs Aleksandar Nanevski (IMDEA Madrid) Viktor Vafeiadis (MSR / Univ. of Cambridge) Josh Berdine (MSR Cambridge) Hoare/Separation Logic Hoare logic
Menger's Theorem. Christoph Dittmann August 16, Contents
 Menger's Theorem Christoph Dittmann isabelle@christoph-d.de August 16, 2018 We present a formalization of Menger's Theorem for directed and undirected graphs in Isabelle/HOL. This well-known result shows
Menger's Theorem Christoph Dittmann isabelle@christoph-d.de August 16, 2018 We present a formalization of Menger's Theorem for directed and undirected graphs in Isabelle/HOL. This well-known result shows
Program verification using Hoare Logic¹
 Program verification using Hoare Logic¹ Automated Reasoning - Guest Lecture Petros Papapanagiotou Part 2 of 2 ¹Contains material from Mike Gordon s slides: Previously on Hoare Logic A simple while language
Program verification using Hoare Logic¹ Automated Reasoning - Guest Lecture Petros Papapanagiotou Part 2 of 2 ¹Contains material from Mike Gordon s slides: Previously on Hoare Logic A simple while language
The Assignment Axiom (Hoare)
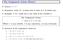 The Assignment Axiom (Hoare) Syntax: V := E Semantics: value of V in final state is value of E in initial state Example: X:=X+ (adds one to the value of the variable X) The Assignment Axiom {Q[E/V ]} V
The Assignment Axiom (Hoare) Syntax: V := E Semantics: value of V in final state is value of E in initial state Example: X:=X+ (adds one to the value of the variable X) The Assignment Axiom {Q[E/V ]} V
Verification of Recursive Programs. Andreas Podelski February 8, 2012
 Verification of Recursive Programs Andreas Podelski February 8, 2012 1 m(x) = x 10 if x > 100 m(m(x + 11)) if x 100 2 procedure m(x) returns (res) `0: if x>100 `1: res:=x-10 else `2: x m := x+11 `3: res
Verification of Recursive Programs Andreas Podelski February 8, 2012 1 m(x) = x 10 if x > 100 m(m(x + 11)) if x 100 2 procedure m(x) returns (res) `0: if x>100 `1: res:=x-10 else `2: x m := x+11 `3: res
Program Analysis Part I : Sequential Programs
 Program Analysis Part I : Sequential Programs IN5170/IN9170 Models of concurrency Program Analysis, lecture 5 Fall 2018 26. 9. 2018 2 / 44 Program correctness Is my program correct? Central question for
Program Analysis Part I : Sequential Programs IN5170/IN9170 Models of concurrency Program Analysis, lecture 5 Fall 2018 26. 9. 2018 2 / 44 Program correctness Is my program correct? Central question for
Miscellaneous Isabelle/Isar examples
 Miscellaneous Isabelle/Isar examples Makarius Wenzel With contributions by Gertrud Bauer and Tobias Nipkow October 8, 2017 Abstract Isar offers a high-level (and theory) language for Isabelle. We give
Miscellaneous Isabelle/Isar examples Makarius Wenzel With contributions by Gertrud Bauer and Tobias Nipkow October 8, 2017 Abstract Isar offers a high-level (and theory) language for Isabelle. We give
The Tortoise and the Hare Algorithm
 The Tortoise and the Hare Algorithm Peter Gammie October 11, 2017 Abstract We formalize the Tortoise and Hare cycle-finding algorithm ascribed to Floyd by Knuth (1981, p7, exercise 6), and an improved
The Tortoise and the Hare Algorithm Peter Gammie October 11, 2017 Abstract We formalize the Tortoise and Hare cycle-finding algorithm ascribed to Floyd by Knuth (1981, p7, exercise 6), and an improved
Hoare Logic (I): Axiomatic Semantics and Program Correctness
 Hoare Logic (I): Axiomatic Semantics and Program Correctness (Based on [Apt and Olderog 1991; Gries 1981; Hoare 1969; Kleymann 1999; Sethi 199]) Yih-Kuen Tsay Dept. of Information Management National Taiwan
Hoare Logic (I): Axiomatic Semantics and Program Correctness (Based on [Apt and Olderog 1991; Gries 1981; Hoare 1969; Kleymann 1999; Sethi 199]) Yih-Kuen Tsay Dept. of Information Management National Taiwan
Examples for program extraction in Higher-Order Logic
 Examples for program extraction in Higher-Order Logic Stefan Berghofer October 10, 2011 Contents 1 Auxiliary lemmas used in program extraction examples 1 2 Quotient and remainder 2 3 Greatest common divisor
Examples for program extraction in Higher-Order Logic Stefan Berghofer October 10, 2011 Contents 1 Auxiliary lemmas used in program extraction examples 1 2 Quotient and remainder 2 3 Greatest common divisor
A Termination Checker for Isabelle Hoare Logic
 A Termination Checker for Isabelle Hoare Logic Jia Meng 1, Lawrence C. Paulson 2, and Gerwin Klein 3 1 National ICT Australia jia.meng@nicta.com.au 2 Computer Laboratory, University of Cambridge lp15@cam.ac.uk
A Termination Checker for Isabelle Hoare Logic Jia Meng 1, Lawrence C. Paulson 2, and Gerwin Klein 3 1 National ICT Australia jia.meng@nicta.com.au 2 Computer Laboratory, University of Cambridge lp15@cam.ac.uk
Program Composition in Isabelle/UNITY
 Program Composition in Isabelle/UNITY Sidi O. Ehmety and Lawrence C. Paulson Cambridge University Computer Laboratory J J Thomson Avenue Cambridge CB3 0FD England Tel. (44) 1223 763584 Fax. (44) 1223 334678
Program Composition in Isabelle/UNITY Sidi O. Ehmety and Lawrence C. Paulson Cambridge University Computer Laboratory J J Thomson Avenue Cambridge CB3 0FD England Tel. (44) 1223 763584 Fax. (44) 1223 334678
Spring 2016 Program Analysis and Verification. Lecture 3: Axiomatic Semantics I. Roman Manevich Ben-Gurion University
 Spring 2016 Program Analysis and Verification Lecture 3: Axiomatic Semantics I Roman Manevich Ben-Gurion University Warm-up exercises 1. Define program state: 2. Define structural semantics configurations:
Spring 2016 Program Analysis and Verification Lecture 3: Axiomatic Semantics I Roman Manevich Ben-Gurion University Warm-up exercises 1. Define program state: 2. Define structural semantics configurations:
Gerwin Klein, June Andronick, Ramana Kumar S2/2016
 COMP4161: Advanced Topics in Software Verification {} Gerwin Klein, June Andronick, Ramana Kumar S2/2016 data61.csiro.au Content Intro & motivation, getting started [1] Foundations & Principles Lambda
COMP4161: Advanced Topics in Software Verification {} Gerwin Klein, June Andronick, Ramana Kumar S2/2016 data61.csiro.au Content Intro & motivation, getting started [1] Foundations & Principles Lambda
A Short Introduction to Hoare Logic
 A Short Introduction to Hoare Logic Supratik Chakraborty I.I.T. Bombay June 23, 2008 Supratik Chakraborty (I.I.T. Bombay) A Short Introduction to Hoare Logic June 23, 2008 1 / 34 Motivation Assertion checking
A Short Introduction to Hoare Logic Supratik Chakraborty I.I.T. Bombay June 23, 2008 Supratik Chakraborty (I.I.T. Bombay) A Short Introduction to Hoare Logic June 23, 2008 1 / 34 Motivation Assertion checking
Imperative Insertion Sort
 Imperative Insertion Sort Christian Sternagel April 17, 2016 Contents 1 Looping Constructs for Imperative HOL 1 1.1 While Loops............................ 1 1.2 For Loops.............................
Imperative Insertion Sort Christian Sternagel April 17, 2016 Contents 1 Looping Constructs for Imperative HOL 1 1.1 While Loops............................ 1 1.2 For Loops.............................
Lecture 4 Event Systems
 Lecture 4 Event Systems This lecture is based on work done with Mark Bickford. Marktoberdorf Summer School, 2003 Formal Methods One of the major research challenges faced by computer science is providing
Lecture 4 Event Systems This lecture is based on work done with Mark Bickford. Marktoberdorf Summer School, 2003 Formal Methods One of the major research challenges faced by computer science is providing
Stone Algebras. Walter Guttmann. September 6, 2016
 Stone Algebras Walter Guttmann September 6, 2016 Abstract A range of algebras between lattices and Boolean algebras generalise the notion of a complement. We develop a hierarchy of these pseudo-complemented
Stone Algebras Walter Guttmann September 6, 2016 Abstract A range of algebras between lattices and Boolean algebras generalise the notion of a complement. We develop a hierarchy of these pseudo-complemented
Positional Determinacy of Parity Games
 Positional Determinacy of Parity Games Christoph Dittmann christoph.dittmann@tu-berlin.de April 17, 2016 We present a formalization of parity games (a two-player game on directed graphs) and a proof of
Positional Determinacy of Parity Games Christoph Dittmann christoph.dittmann@tu-berlin.de April 17, 2016 We present a formalization of parity games (a two-player game on directed graphs) and a proof of
Discrete Mathematics Review
 CS 1813 Discrete Mathematics Discrete Mathematics Review or Yes, the Final Will Be Comprehensive 1 Truth Tables for Logical Operators P Q P Q False False False P Q False P Q False P Q True P Q True P True
CS 1813 Discrete Mathematics Discrete Mathematics Review or Yes, the Final Will Be Comprehensive 1 Truth Tables for Logical Operators P Q P Q False False False P Q False P Q False P Q True P Q True P True
Kleene Algebra with Tests and Demonic Refinement Algebras
 Kleene Algebra with Tests and Demonic Refinement Algebras Alasdair Armstrong Victor B. F. Gomes Georg Struth August 28, 2014 Abstract We formalise Kleene algebra with tests (KAT) and demonic refinement
Kleene Algebra with Tests and Demonic Refinement Algebras Alasdair Armstrong Victor B. F. Gomes Georg Struth August 28, 2014 Abstract We formalise Kleene algebra with tests (KAT) and demonic refinement
Amortized Complexity Verified
 Amortized Complexity Verified Tobias Nipkow August 28, 2014 Abstract A framework for the analysis of the amortized complexity of (functional) data structures is formalized in Isabelle/HOL and applied to
Amortized Complexity Verified Tobias Nipkow August 28, 2014 Abstract A framework for the analysis of the amortized complexity of (functional) data structures is formalized in Isabelle/HOL and applied to
HOL: Well-founded and Primitive Recursion
 Dipl.-Inf. Achim D. Brucker Dr. Burkhart Wolff Computer-supported Modeling and Reasoning http://www.infsec.ethz.ch/ education/permanent/csmr/ (rev. 16814) Submission date: HOL: Well-founded and Primitive
Dipl.-Inf. Achim D. Brucker Dr. Burkhart Wolff Computer-supported Modeling and Reasoning http://www.infsec.ethz.ch/ education/permanent/csmr/ (rev. 16814) Submission date: HOL: Well-founded and Primitive
The Tortoise and the Hare Algorithm
 The Tortoise and the Hare Algorithm Peter Gammie April 17, 2016 Abstract We formalize the Tortoise and Hare cycle-finding algorithm ascribed to Floyd by Knuth (1981, p7, exercise 6), and an improved version
The Tortoise and the Hare Algorithm Peter Gammie April 17, 2016 Abstract We formalize the Tortoise and Hare cycle-finding algorithm ascribed to Floyd by Knuth (1981, p7, exercise 6), and an improved version
Axiomatic Semantics. Lecture 9 CS 565 2/12/08
 Axiomatic Semantics Lecture 9 CS 565 2/12/08 Axiomatic Semantics Operational semantics describes the meaning of programs in terms of the execution steps taken by an abstract machine Denotational semantics
Axiomatic Semantics Lecture 9 CS 565 2/12/08 Axiomatic Semantics Operational semantics describes the meaning of programs in terms of the execution steps taken by an abstract machine Denotational semantics
List reversal: back into the frying pan
 List reversal: back into the frying pan Richard Bornat March 20, 2006 Abstract More than thirty years ago Rod Burstall showed how to do a proof of a neat little program, shown in a modern notation in figure
List reversal: back into the frying pan Richard Bornat March 20, 2006 Abstract More than thirty years ago Rod Burstall showed how to do a proof of a neat little program, shown in a modern notation in figure
Automata-Theoretic Model Checking of Reactive Systems
 Automata-Theoretic Model Checking of Reactive Systems Radu Iosif Verimag/CNRS (Grenoble, France) Thanks to Tom Henzinger (IST, Austria), Barbara Jobstmann (CNRS, Grenoble) and Doron Peled (Bar-Ilan University,
Automata-Theoretic Model Checking of Reactive Systems Radu Iosif Verimag/CNRS (Grenoble, France) Thanks to Tom Henzinger (IST, Austria), Barbara Jobstmann (CNRS, Grenoble) and Doron Peled (Bar-Ilan University,
The TLA + proof system
 The TLA + proof system Stephan Merz Kaustuv Chaudhuri, Damien Doligez, Leslie Lamport INRIA Nancy & INRIA-MSR Joint Centre, France Amir Pnueli Memorial Symposium New York University, May 8, 2010 Stephan
The TLA + proof system Stephan Merz Kaustuv Chaudhuri, Damien Doligez, Leslie Lamport INRIA Nancy & INRIA-MSR Joint Centre, France Amir Pnueli Memorial Symposium New York University, May 8, 2010 Stephan
Boolean Expression Checkers
 Boolean Expression Checkers Tobias Nipkow May 27, 2015 Abstract This entry provides executable checkers for the following properties of boolean expressions: satisfiability, tautology and equivalence. Internally,
Boolean Expression Checkers Tobias Nipkow May 27, 2015 Abstract This entry provides executable checkers for the following properties of boolean expressions: satisfiability, tautology and equivalence. Internally,
Proof Calculus for Partial Correctness
 Proof Calculus for Partial Correctness Bow-Yaw Wang Institute of Information Science Academia Sinica, Taiwan September 7, 2016 Bow-Yaw Wang (Academia Sinica) Proof Calculus for Partial Correctness September
Proof Calculus for Partial Correctness Bow-Yaw Wang Institute of Information Science Academia Sinica, Taiwan September 7, 2016 Bow-Yaw Wang (Academia Sinica) Proof Calculus for Partial Correctness September
THE AUSTRALIAN NATIONAL UNIVERSITY Second Semester COMP2600 (Formal Methods for Software Engineering)
 THE AUSTRALIAN NATIONAL UNIVERSITY Second Semester 2012 COMP2600 (Formal Methods for Software Engineering) Writing Period: 3 hours duration Study Period: 15 minutes duration Permitted Materials: One A4
THE AUSTRALIAN NATIONAL UNIVERSITY Second Semester 2012 COMP2600 (Formal Methods for Software Engineering) Writing Period: 3 hours duration Study Period: 15 minutes duration Permitted Materials: One A4
Mid-Semester Quiz Second Semester, 2012
 THE AUSTRALIAN NATIONAL UNIVERSITY Mid-Semester Quiz Second Semester, 2012 COMP2600 (Formal Methods for Software Engineering) Writing Period: 1 hour duration Study Period: 10 minutes duration Permitted
THE AUSTRALIAN NATIONAL UNIVERSITY Mid-Semester Quiz Second Semester, 2012 COMP2600 (Formal Methods for Software Engineering) Writing Period: 1 hour duration Study Period: 10 minutes duration Permitted
Analyse et Conception Formelle. Lesson 4. Proofs with a proof assistant
 Analyse et Conception Formelle Lesson 4 Proofs with a proof assistant T. Genet (ISTIC/IRISA) ACF-4 1 / 26 Prove logic formulas... to prove programs fun nth:: "nat => a list => a" where "nth 0 (x#_)=x"
Analyse et Conception Formelle Lesson 4 Proofs with a proof assistant T. Genet (ISTIC/IRISA) ACF-4 1 / 26 Prove logic formulas... to prove programs fun nth:: "nat => a list => a" where "nth 0 (x#_)=x"
Hoare Logic: Part II
 Hoare Logic: Part II COMP2600 Formal Methods for Software Engineering Jinbo Huang Australian National University COMP 2600 Hoare Logic II 1 Factorial {n 0} fact := 1; i := n; while (i >0) do fact := fact
Hoare Logic: Part II COMP2600 Formal Methods for Software Engineering Jinbo Huang Australian National University COMP 2600 Hoare Logic II 1 Factorial {n 0} fact := 1; i := n; while (i >0) do fact := fact
Mechanics of Static Analysis
 Escuela 03 III / 1 Mechanics of Static Analysis David Schmidt Kansas State University www.cis.ksu.edu/~schmidt Escuela 03 III / 2 Outline 1. Small-step semantics: trace generation 2. State generation and
Escuela 03 III / 1 Mechanics of Static Analysis David Schmidt Kansas State University www.cis.ksu.edu/~schmidt Escuela 03 III / 2 Outline 1. Small-step semantics: trace generation 2. State generation and
Automatic Verification of Parameterized Data Structures
 Automatic Verification of Parameterized Data Structures Jyotirmoy V. Deshmukh, E. Allen Emerson and Prateek Gupta The University of Texas at Austin The University of Texas at Austin 1 Outline Motivation
Automatic Verification of Parameterized Data Structures Jyotirmoy V. Deshmukh, E. Allen Emerson and Prateek Gupta The University of Texas at Austin The University of Texas at Austin 1 Outline Motivation
Space-aware data flow analysis
 Space-aware data flow analysis C. Bernardeschi, G. Lettieri, L. Martini, P. Masci Dip. di Ingegneria dell Informazione, Università di Pisa, Via Diotisalvi 2, 56126 Pisa, Italy {cinzia,g.lettieri,luca.martini,paolo.masci}@iet.unipi.it
Space-aware data flow analysis C. Bernardeschi, G. Lettieri, L. Martini, P. Masci Dip. di Ingegneria dell Informazione, Università di Pisa, Via Diotisalvi 2, 56126 Pisa, Italy {cinzia,g.lettieri,luca.martini,paolo.masci}@iet.unipi.it
Programming Languages and Compilers (CS 421)
 Programming Languages and Compilers (CS 421) Sasa Misailovic 4110 SC, UIUC https://courses.engr.illinois.edu/cs421/fa2017/cs421a Based in part on slides by Mattox Beckman, as updated by Vikram Adve, Gul
Programming Languages and Compilers (CS 421) Sasa Misailovic 4110 SC, UIUC https://courses.engr.illinois.edu/cs421/fa2017/cs421a Based in part on slides by Mattox Beckman, as updated by Vikram Adve, Gul
Roy L. Crole. Operational Semantics Abstract Machines and Correctness. University of Leicester, UK
 Midlands Graduate School, University of Birmingham, April 2008 1 Operational Semantics Abstract Machines and Correctness Roy L. Crole University of Leicester, UK Midlands Graduate School, University of
Midlands Graduate School, University of Birmingham, April 2008 1 Operational Semantics Abstract Machines and Correctness Roy L. Crole University of Leicester, UK Midlands Graduate School, University of
Amortized Complexity Verified
 Amortized Complexity Verified Tobias Nipkow Technische Universität München Abstract A framework for the analysis of the amortized complexity of (functional) data structures is formalized in Isabelle/HOL
Amortized Complexity Verified Tobias Nipkow Technische Universität München Abstract A framework for the analysis of the amortized complexity of (functional) data structures is formalized in Isabelle/HOL
Programming with Dependent Types in Coq
 Programming with Dependent Types in Coq Matthieu Sozeau LRI, Univ. Paris-Sud - Démons Team & INRIA Saclay - ProVal Project PPS Seminar February 26th 2009 Paris, France Coq A higher-order, polymorphic logic:
Programming with Dependent Types in Coq Matthieu Sozeau LRI, Univ. Paris-Sud - Démons Team & INRIA Saclay - ProVal Project PPS Seminar February 26th 2009 Paris, France Coq A higher-order, polymorphic logic:
Axiomatic Semantics. Operational semantics. Good for. Not good for automatic reasoning about programs
 Review Operational semantics relatively l simple many flavors (small vs. big) not compositional (rule for while) Good for describing language implementation reasoning about properties of the language eg.
Review Operational semantics relatively l simple many flavors (small vs. big) not compositional (rule for while) Good for describing language implementation reasoning about properties of the language eg.
Gödel s Incompleteness Theorems. Lawrence C. Paulson
 Gödel s Incompleteness Theorems Lawrence C. Paulson October 10, 2017 Abstract Gödel s two incompleteness theorems [2] are formalised, following a careful presentation by Świerczkowski [3], in the theory
Gödel s Incompleteness Theorems Lawrence C. Paulson October 10, 2017 Abstract Gödel s two incompleteness theorems [2] are formalised, following a careful presentation by Świerczkowski [3], in the theory
Fundamental Properties of Lambda-calculus
 Fundamental Properties of Lambda-calculus Tobias Nipkow Stefan Berghofer February 12, 2013 Contents 1 Basic definitions of Lambda-calculus 4 1.1 Lambda-terms in de Bruijn notation and substitution....
Fundamental Properties of Lambda-calculus Tobias Nipkow Stefan Berghofer February 12, 2013 Contents 1 Basic definitions of Lambda-calculus 4 1.1 Lambda-terms in de Bruijn notation and substitution....
An Isabelle/HOL Formalization of the Textbook Proof of Huffman s Algorithm
 An Isabelle/HOL Formalization of the Textbook Proof of Huffman s Algorithm Jasmin Christian Blanchette Institut für Informatik, Technische Universität München, Germany blanchette@in.tum.de March 12, 2013
An Isabelle/HOL Formalization of the Textbook Proof of Huffman s Algorithm Jasmin Christian Blanchette Institut für Informatik, Technische Universität München, Germany blanchette@in.tum.de March 12, 2013
Verifying Java-KE Programs
 Verifying Java-KE Programs A Small Case Study Arnd Poetzsch-Heffter July 22, 2014 Abstract This report investigates the specification and verification of a simple list class. The example was designed such
Verifying Java-KE Programs A Small Case Study Arnd Poetzsch-Heffter July 22, 2014 Abstract This report investigates the specification and verification of a simple list class. The example was designed such
NICTA Advanced Course. Theorem Proving Principles, Techniques, Applications
 NICTA Advanced Course Theorem Proving Principles, Techniques, Applications λ 1 CONTENT Intro & motivation, getting started with Isabelle Foundations & Principles Lambda Calculus Higher Order Logic, natural
NICTA Advanced Course Theorem Proving Principles, Techniques, Applications λ 1 CONTENT Intro & motivation, getting started with Isabelle Foundations & Principles Lambda Calculus Higher Order Logic, natural
Verified Characteristic Formulae for CakeML. Armaël Guéneau, Magnus O. Myreen, Ramana Kumar, Michael Norrish April 18, 2017
 Verified Characteristic Formulae for CakeML Armaël Guéneau, Magnus O. Myreen, Ramana Kumar, Michael Norrish April 18, 2017 CakeML Has: references, modules, datatypes, exceptions, a FFI,... Doesn t have:
Verified Characteristic Formulae for CakeML Armaël Guéneau, Magnus O. Myreen, Ramana Kumar, Michael Norrish April 18, 2017 CakeML Has: references, modules, datatypes, exceptions, a FFI,... Doesn t have:
SAT Solver verification
 SAT Solver verification By Filip Marić April 17, 2016 Abstract This document contains formall correctness proofs of modern SAT solvers. Two different approaches are used state-transition systems shallow
SAT Solver verification By Filip Marić April 17, 2016 Abstract This document contains formall correctness proofs of modern SAT solvers. Two different approaches are used state-transition systems shallow
Code Generation for a Simple First-Order Prover
 Code Generation for a Simple First-Order Prover Jørgen Villadsen, Anders Schlichtkrull, and Andreas Halkjær From DTU Compute, Technical University of Denmark, 2800 Kongens Lyngby, Denmark Abstract. We
Code Generation for a Simple First-Order Prover Jørgen Villadsen, Anders Schlichtkrull, and Andreas Halkjær From DTU Compute, Technical University of Denmark, 2800 Kongens Lyngby, Denmark Abstract. We
In this episode of The Verification Corner, Rustan Leino talks about Loop Invariants. He gives a brief summary of the theoretical foundations and
 In this episode of The Verification Corner, Rustan Leino talks about Loop Invariants. He gives a brief summary of the theoretical foundations and shows how a program can sometimes be systematically constructed
In this episode of The Verification Corner, Rustan Leino talks about Loop Invariants. He gives a brief summary of the theoretical foundations and shows how a program can sometimes be systematically constructed
A Formal Proof of Correctness of a Distributed Presentation Software System
 A Formal Proof of Correctness of a Distributed Presentation Software System Ievgen Ivanov, Taras Panchenko 1 Taras Shevchenko National University of Kyiv, 64/13, Volodymyrska st., Kyiv, 01601, Ukraine,
A Formal Proof of Correctness of a Distributed Presentation Software System Ievgen Ivanov, Taras Panchenko 1 Taras Shevchenko National University of Kyiv, 64/13, Volodymyrska st., Kyiv, 01601, Ukraine,
Hoare Logic and Model Checking
 Hoare Logic and Model Checking Kasper Svendsen University of Cambridge CST Part II 2016/17 Acknowledgement: slides heavily based on previous versions by Mike Gordon and Alan Mycroft Introduction In the
Hoare Logic and Model Checking Kasper Svendsen University of Cambridge CST Part II 2016/17 Acknowledgement: slides heavily based on previous versions by Mike Gordon and Alan Mycroft Introduction In the
Spring 2015 Program Analysis and Verification. Lecture 4: Axiomatic Semantics I. Roman Manevich Ben-Gurion University
 Spring 2015 Program Analysis and Verification Lecture 4: Axiomatic Semantics I Roman Manevich Ben-Gurion University Agenda Basic concepts of correctness Axiomatic semantics (pages 175-183) Hoare Logic
Spring 2015 Program Analysis and Verification Lecture 4: Axiomatic Semantics I Roman Manevich Ben-Gurion University Agenda Basic concepts of correctness Axiomatic semantics (pages 175-183) Hoare Logic
Proofs of Correctness: Introduction to Axiomatic Verification
 Proofs of Correctness: Introduction to Axiomatic Verification Introduction Weak correctness predicate Assignment statements Sequencing Selection statements Iteration 1 Introduction What is Axiomatic Verification?
Proofs of Correctness: Introduction to Axiomatic Verification Introduction Weak correctness predicate Assignment statements Sequencing Selection statements Iteration 1 Introduction What is Axiomatic Verification?
logical verification lecture program extraction and prop2
 logical verification lecture 7 2017-05-04 program extraction and prop2 overview program extraction program extraction: examples verified programs: alternative approach formulas of prop2 terminology proofs
logical verification lecture 7 2017-05-04 program extraction and prop2 overview program extraction program extraction: examples verified programs: alternative approach formulas of prop2 terminology proofs
Universität Augsburg
 Universität Augsburg Properties of Overwriting for Updates in Typed Kleene Algebras Thorsten Ehm Report 2000-7 Dezember 2000 Institut für Informatik D-86135 Augsburg Copyright c Thorsten Ehm Institut für
Universität Augsburg Properties of Overwriting for Updates in Typed Kleene Algebras Thorsten Ehm Report 2000-7 Dezember 2000 Institut für Informatik D-86135 Augsburg Copyright c Thorsten Ehm Institut für
Formal Methods in Software Engineering
 Formal Methods in Software Engineering An Introduction to Model-Based Analyis and Testing Vesal Vojdani Department of Computer Science University of Tartu Fall 2014 Vesal Vojdani (University of Tartu)
Formal Methods in Software Engineering An Introduction to Model-Based Analyis and Testing Vesal Vojdani Department of Computer Science University of Tartu Fall 2014 Vesal Vojdani (University of Tartu)
Functional Data Structures
 Functional Data Structures with Isabelle/HOL Tobias Nipkow Fakultät für Informatik Technische Universität München 2017-2-3 1 Part II Functional Data Structures 2 Chapter 1 Binary Trees 3 1 Binary Trees
Functional Data Structures with Isabelle/HOL Tobias Nipkow Fakultät für Informatik Technische Universität München 2017-2-3 1 Part II Functional Data Structures 2 Chapter 1 Binary Trees 3 1 Binary Trees
Automated Reasoning. Lecture 9: Isar A Language for Structured Proofs
 Automated Reasoning Lecture 9: Isar A Language for Structured Proofs Jacques Fleuriot jdf@inf.ed.ac.uk Acknowledgement: Tobias Nipkow kindly provided the slides for this lecture Apply scripts unreadable
Automated Reasoning Lecture 9: Isar A Language for Structured Proofs Jacques Fleuriot jdf@inf.ed.ac.uk Acknowledgement: Tobias Nipkow kindly provided the slides for this lecture Apply scripts unreadable
Iris: Higher-Order Concurrent Separation Logic. Lecture 6: Case Study: foldr
 1 Iris: Higher-Order Concurrent Separation Logic Lecture 6: Case Study: foldr Lars Birkedal Aarhus University, Denmark November 10, 2017 2 Overview Earlier: Operational Semantics of λ ref,conc e, (h, e)
1 Iris: Higher-Order Concurrent Separation Logic Lecture 6: Case Study: foldr Lars Birkedal Aarhus University, Denmark November 10, 2017 2 Overview Earlier: Operational Semantics of λ ref,conc e, (h, e)
Deductive Verification
 Deductive Verification Mooly Sagiv Slides from Zvonimir Rakamaric First-Order Logic A formal notation for mathematics, with expressions involving Propositional symbols Predicates Functions and constant
Deductive Verification Mooly Sagiv Slides from Zvonimir Rakamaric First-Order Logic A formal notation for mathematics, with expressions involving Propositional symbols Predicates Functions and constant
Axiomatic Semantics: Verification Conditions. Review of Soundness of Axiomatic Semantics. Questions? Announcements
 Axiomatic Semantics: Verification Conditions Meeting 18, CSCI 5535, Spring 2010 Announcements Homework 6 is due tonight Today s forum: papers on automated testing using symbolic execution Anyone looking
Axiomatic Semantics: Verification Conditions Meeting 18, CSCI 5535, Spring 2010 Announcements Homework 6 is due tonight Today s forum: papers on automated testing using symbolic execution Anyone looking
Program verification. 18 October 2017
 Program verification 18 October 2017 Example revisited // assume(n>2); void partition(int a[], int n) { int pivot = a[0]; int lo = 1, hi = n-1; while (lo
Program verification 18 October 2017 Example revisited // assume(n>2); void partition(int a[], int n) { int pivot = a[0]; int lo = 1, hi = n-1; while (lo
Chapter 3 Deterministic planning
 Chapter 3 Deterministic planning In this chapter we describe a number of algorithms for solving the historically most important and most basic type of planning problem. Two rather strong simplifying assumptions
Chapter 3 Deterministic planning In this chapter we describe a number of algorithms for solving the historically most important and most basic type of planning problem. Two rather strong simplifying assumptions
Axiomatic Semantics: Verification Conditions. Review of Soundness and Completeness of Axiomatic Semantics. Announcements
 Axiomatic Semantics: Verification Conditions Meeting 12, CSCI 5535, Spring 2009 Announcements Homework 4 is due tonight Wed forum: papers on automated testing using symbolic execution 2 Questions? Review
Axiomatic Semantics: Verification Conditions Meeting 12, CSCI 5535, Spring 2009 Announcements Homework 4 is due tonight Wed forum: papers on automated testing using symbolic execution 2 Questions? Review
Discrete Mathematics
 Discrete Mathematics Jeremy Siek Spring 2010 Jeremy Siek Discrete Mathematics 1 / 20 Outline of Lecture 4 1. Overview of First-Order Logic 2. Beyond Booleans: natural numbers, integers, etc. 3. Universal
Discrete Mathematics Jeremy Siek Spring 2010 Jeremy Siek Discrete Mathematics 1 / 20 Outline of Lecture 4 1. Overview of First-Order Logic 2. Beyond Booleans: natural numbers, integers, etc. 3. Universal
Hoare Logic: Reasoning About Imperative Programs
 Hoare Logic: Reasoning About Imperative Programs COMP1600 / COMP6260 Dirk Pattinson Australian National University Semester 2, 2018 Programming Paradigms Functional. (Haskell, SML, OCaml,... ) main paradigm:
Hoare Logic: Reasoning About Imperative Programs COMP1600 / COMP6260 Dirk Pattinson Australian National University Semester 2, 2018 Programming Paradigms Functional. (Haskell, SML, OCaml,... ) main paradigm:
COMP2111 Glossary. Kai Engelhardt. Contents. 1 Symbols. 1 Symbols 1. 2 Hoare Logic 3. 3 Refinement Calculus 5. rational numbers Q, real numbers R.
 COMP2111 Glossary Kai Engelhardt Revision: 1.3, May 18, 2018 Contents 1 Symbols 1 2 Hoare Logic 3 3 Refinement Calculus 5 1 Symbols Booleans B = {false, true}, natural numbers N = {0, 1, 2,...}, integers
COMP2111 Glossary Kai Engelhardt Revision: 1.3, May 18, 2018 Contents 1 Symbols 1 2 Hoare Logic 3 3 Refinement Calculus 5 1 Symbols Booleans B = {false, true}, natural numbers N = {0, 1, 2,...}, integers
Isabelle/FOL First-Order Logic
 Isabelle/FOL First-Order Logic Larry Paulson and Markus Wenzel August 15, 2018 Contents 1 Intuitionistic first-order logic 2 1.1 Syntax and axiomatic basis................... 2 1.1.1 Equality..........................
Isabelle/FOL First-Order Logic Larry Paulson and Markus Wenzel August 15, 2018 Contents 1 Intuitionistic first-order logic 2 1.1 Syntax and axiomatic basis................... 2 1.1.1 Equality..........................
Landau Symbols. Manuel Eberl. November 28, 2018
 Landau Symbols Manuel Eberl November 28, 2018 Contents 1 Sorting and grouping factors 1 2 Decision procedure for real functions 4 2.1 Eventual non-negativity/non-zeroness............. 4 2.2 Rewriting Landau
Landau Symbols Manuel Eberl November 28, 2018 Contents 1 Sorting and grouping factors 1 2 Decision procedure for real functions 4 2.1 Eventual non-negativity/non-zeroness............. 4 2.2 Rewriting Landau
The Divergence of the Prime Harmonic Series
 The Divergence of the Prime Harmonic Series Manuel Eberl April 17, 2016 Abstract In this work, we prove the lower bound ln(h n ) ln( 5 3 ) for the partial sum of the Prime Harmonic series and, based on
The Divergence of the Prime Harmonic Series Manuel Eberl April 17, 2016 Abstract In this work, we prove the lower bound ln(h n ) ln( 5 3 ) for the partial sum of the Prime Harmonic series and, based on
Axiomatic Semantics. Hoare s Correctness Triplets Dijkstra s Predicate Transformers
 Axiomatic Semantics Hoare s Correctness Triplets Dijkstra s Predicate Transformers Goal of a program = IO Relation Problem Specification Properties satisfied by the input and expected of the output (usually
Axiomatic Semantics Hoare s Correctness Triplets Dijkstra s Predicate Transformers Goal of a program = IO Relation Problem Specification Properties satisfied by the input and expected of the output (usually
Red-black Trees of smlnj Studienarbeit. Angelika Kimmig
 Red-black Trees of smlnj Studienarbeit Angelika Kimmig January 26, 2004 Contents 1 Introduction 1 2 Development of the Isabelle/HOL Theory RBT 2 2.1 Translation of Datatypes and Functions into HOL......
Red-black Trees of smlnj Studienarbeit Angelika Kimmig January 26, 2004 Contents 1 Introduction 1 2 Development of the Isabelle/HOL Theory RBT 2 2.1 Translation of Datatypes and Functions into HOL......
Lecture 2: Axiomatic semantics
 Chair of Software Engineering Trusted Components Prof. Dr. Bertrand Meyer Lecture 2: Axiomatic semantics Reading assignment for next week Ariane paper and response (see course page) Axiomatic semantics
Chair of Software Engineering Trusted Components Prof. Dr. Bertrand Meyer Lecture 2: Axiomatic semantics Reading assignment for next week Ariane paper and response (see course page) Axiomatic semantics
Reasoning About Imperative Programs. COS 441 Slides 10b
 Reasoning About Imperative Programs COS 441 Slides 10b Last time Hoare Logic: { P } C { Q } Agenda If P is true in the initial state s. And C in state s evaluates to s. Then Q must be true in s. Program
Reasoning About Imperative Programs COS 441 Slides 10b Last time Hoare Logic: { P } C { Q } Agenda If P is true in the initial state s. And C in state s evaluates to s. Then Q must be true in s. Program
Program Verification Using Separation Logic
 Program Verification Using Separation Logic Cristiano Calcagno Adapted from material by Dino Distefano Lecture 1 Goal of the course Study Separation Logic having automatic verification in mind Learn how
Program Verification Using Separation Logic Cristiano Calcagno Adapted from material by Dino Distefano Lecture 1 Goal of the course Study Separation Logic having automatic verification in mind Learn how
Acyclicity and Finite Linear Extendability: a Formal and Constructive Equivalence
 Acyclicity and Finite Linear Extendability: a Formal and Constructive Equivalence LIP, Stéphane Le Roux École normale supérieure de Lyon, France stephane.le.roux@ens-lyon.fr Abstract. Linear extension
Acyclicity and Finite Linear Extendability: a Formal and Constructive Equivalence LIP, Stéphane Le Roux École normale supérieure de Lyon, France stephane.le.roux@ens-lyon.fr Abstract. Linear extension
Ribbon Proofs for Separation Logic (Isabelle Formalisation)
 Ribbon Proofs for Separation Logic (Isabelle Formalisation) John Wickerson April 17, 2016 Abstract This document concerns the theory of ribbon proofs: a diagrammatic proof system, based on separation logic,
Ribbon Proofs for Separation Logic (Isabelle Formalisation) John Wickerson April 17, 2016 Abstract This document concerns the theory of ribbon proofs: a diagrammatic proof system, based on separation logic,
Lectures on Separation Logic. Lecture 2: Foundations
 Lectures on Separation Logic. Lecture 2: Foundations Peter O Hearn Queen Mary, University of London Marktoberdorf Summer School, 2011 Outline for this lecture Part I : Assertions and Their Semantics Part
Lectures on Separation Logic. Lecture 2: Foundations Peter O Hearn Queen Mary, University of London Marktoberdorf Summer School, 2011 Outline for this lecture Part I : Assertions and Their Semantics Part
Flow Interfaces Compositional Abstractions of Concurrent Data Structures. Siddharth Krishna, Dennis Shasha, and Thomas Wies
 Flow Interfaces Compositional Abstractions of Concurrent Data Structures Siddharth Krishna, Dennis Shasha, and Thomas Wies Background Verifying programs, separation logic, inductive predicates Verifying
Flow Interfaces Compositional Abstractions of Concurrent Data Structures Siddharth Krishna, Dennis Shasha, and Thomas Wies Background Verifying programs, separation logic, inductive predicates Verifying
Beyond First-Order Logic
 Beyond First-Order Logic Software Formal Verification Maria João Frade Departmento de Informática Universidade do Minho 2008/2009 Maria João Frade (DI-UM) Beyond First-Order Logic MFES 2008/09 1 / 37 FOL
Beyond First-Order Logic Software Formal Verification Maria João Frade Departmento de Informática Universidade do Minho 2008/2009 Maria João Frade (DI-UM) Beyond First-Order Logic MFES 2008/09 1 / 37 FOL
Disjunctive relational abstract interpretation for interprocedural program analysis
 Disjunctive relational abstract interpretation for interprocedural program analysis Nicolas Halbwachs, joint work with Rémy Boutonnet Verimag/CNRS, and Grenoble-Alpes University Grenoble, France R. Boutonnet,
Disjunctive relational abstract interpretation for interprocedural program analysis Nicolas Halbwachs, joint work with Rémy Boutonnet Verimag/CNRS, and Grenoble-Alpes University Grenoble, France R. Boutonnet,
Axiomatic Semantics. Semantics of Programming Languages course. Joosep Rõõmusaare
 Axiomatic Semantics Semantics of Programming Languages course Joosep Rõõmusaare 2014 Direct Proofs of Program Correctness Partial correctness properties are properties expressing that if a given program
Axiomatic Semantics Semantics of Programming Languages course Joosep Rõõmusaare 2014 Direct Proofs of Program Correctness Partial correctness properties are properties expressing that if a given program
Free Groups. Joachim Breitner. April 17, 2016
 Free Groups Joachim Breitner April 17, 2016 Abstract Free Groups are, in a sense, the most generic kind of group. They are defined over a set of generators with no additional relations in between them.
Free Groups Joachim Breitner April 17, 2016 Abstract Free Groups are, in a sense, the most generic kind of group. They are defined over a set of generators with no additional relations in between them.
Artificial Intelligence Chapter 7: Logical Agents
 Artificial Intelligence Chapter 7: Logical Agents Michael Scherger Department of Computer Science Kent State University February 20, 2006 AI: Chapter 7: Logical Agents 1 Contents Knowledge Based Agents
Artificial Intelligence Chapter 7: Logical Agents Michael Scherger Department of Computer Science Kent State University February 20, 2006 AI: Chapter 7: Logical Agents 1 Contents Knowledge Based Agents
COP4020 Programming Languages. Introduction to Axiomatic Semantics Prof. Robert van Engelen
 COP4020 Programming Languages Introduction to Axiomatic Semantics Prof. Robert van Engelen Assertions and Preconditions Assertions are used by programmers to verify run-time execution An assertion is a
COP4020 Programming Languages Introduction to Axiomatic Semantics Prof. Robert van Engelen Assertions and Preconditions Assertions are used by programmers to verify run-time execution An assertion is a
Recent developments in concurrent program logics
 Recent developments in concurrent program logics Viktor Vafeiadis University of Cambridge PSPL 2010 Why program logic? Reasoning framework Capture common reasoning principles Reduce accidental proof complexity
Recent developments in concurrent program logics Viktor Vafeiadis University of Cambridge PSPL 2010 Why program logic? Reasoning framework Capture common reasoning principles Reduce accidental proof complexity
Salembier s Min-tree algorithm turned into breadth first search
 Information Processing Letters 88 (2003) 225 229 www.elsevier.com/locate/ipl Salembier s Min-tree algorithm turned into breadth first search Wim H. Hesselink Department of Mathematics and Computing Science,
Information Processing Letters 88 (2003) 225 229 www.elsevier.com/locate/ipl Salembier s Min-tree algorithm turned into breadth first search Wim H. Hesselink Department of Mathematics and Computing Science,
Program verification. Hoare triples. Assertional semantics (cont) Example: Semantics of assignment. Assertional semantics of a program
 Program verification Assertional semantics of a program Meaning of a program: relation between its inputs and outputs; specified by input assertions (pre-conditions) and output assertions (post-conditions)
Program verification Assertional semantics of a program Meaning of a program: relation between its inputs and outputs; specified by input assertions (pre-conditions) and output assertions (post-conditions)
CIS (More Propositional Calculus - 6 points)
 1 CIS6333 Homework 1 (due Friday, February 1) 1. (Propositional Calculus - 10 points) --------------------------------------- Let P, Q, R range over state predicates of some program. Prove or disprove
1 CIS6333 Homework 1 (due Friday, February 1) 1. (Propositional Calculus - 10 points) --------------------------------------- Let P, Q, R range over state predicates of some program. Prove or disprove
Simply Typed Lambda Calculus
 Simply Typed Lambda Calculus Language (ver1) Lambda calculus with boolean values t ::= x variable x : T.t abstraction tt application true false boolean values if ttt conditional expression Values v ::=
Simply Typed Lambda Calculus Language (ver1) Lambda calculus with boolean values t ::= x variable x : T.t abstraction tt application true false boolean values if ttt conditional expression Values v ::=
Spring 2014 Program Analysis and Verification. Lecture 6: Axiomatic Semantics III. Roman Manevich Ben-Gurion University
 Spring 2014 Program Analysis and Verification Lecture 6: Axiomatic Semantics III Roman Manevich Ben-Gurion University Syllabus Semantics Static Analysis Abstract Interpretation fundamentals Analysis Techniques
Spring 2014 Program Analysis and Verification Lecture 6: Axiomatic Semantics III Roman Manevich Ben-Gurion University Syllabus Semantics Static Analysis Abstract Interpretation fundamentals Analysis Techniques
