2.20 Marine Hydrodynamics Lecture 3

Transcription

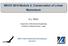
1 2.20 Marine Hyroynamics, Fall 2018 Lecture 3 Copyright c 2018 MIT - Department of Mechanical Engineering, All rights reserve. 1.7 Stress Tensor 2.20 Marine Hyroynamics Lecture Stress Tensor τ ij The stress (force per unit area) at a point in a flui nees nine components to be completely specifie, since each component of the stress must be efine not only by the irection in which it acts but also the orientation of the surface upon which it is acting. The first inex i specifies the irection in which the stress component acts, an the secon inex j ientifies the orientation of the surface upon which it is acting. Therefore, the i th component of the force acting on a surface whose outwar normal points in the j th irection is τ ij. X 2 τ 22 τ 32 τ 12 τ 33 τ 23 τ 13 τ 21 τ 31 τ 11 X 1 X 3 Figure 1: Shear stresses on an infinitesimal cube whose surfaces are parallel to the coorinate system. 1

2 Figure 2: Infinitesimal boy with surface PQR that is not perpenicular to any of the Cartesian axis. Consier an infinitesimal boy at rest with a surface PQR that is not perpenicular to any of the Cartesian axis. The unit normal vector to the surface PQR is ˆn = n 1ˆx 1 +n 2ˆx 2 +n 3ˆx 3. The area of the surface = A 0, an the area of each surface perpenicular to X i is A i = A 0 n i, for i = 1, 2, 3. Newton s law: F i = (volume force) i for i = 1, 2, 3 on all 4 faces Note: If δ is the typical imension of the boy : surface forces δ 2 : volume forces δ 3 An example of surface forces is the shear force an an example of volumetric forces is the gravity force. At equilibrium, the surface forces an volumetric forces are in balance. As the boy gets smaller, the mass of the boy goes to zero, which makes the volumetric forces equal to zero an leaving the sum of the surface forces equal zero. So, as δ 0, all4faces F i = 0 for i = 1, 2, 3 an τ i A 0 = τ i1 A 1 + τ i2 A 2 + τ i3 A 3 = τ ij A j. But the area of each surface to X i is A i = A 0 n i. Therefore τ i A 0 = τ ij A j = τ ij (A 0 n j ), where τ ij A j is the notation (represents the sum of all components). Thus τ i = τ ij n j for i = 1, 2, 3, where τ i is the component of stress in the i th irection on a surface with a normal n. We call τ i the stress vector an we call τ ij the stress matrix or tensor. 2

3 1.7.2 Example: Pascal s Law for Hyrostatics In a static flui, the stress vector cannot be ifferent for ifferent irections of the surface normal since there is no preferre irection in the flui. Therefore, at any point in the flui, the stress vector must have the same irection as the normal vector n an the same magnitue for all irections of n. Pascal s Law for hyrostatics: τ ij = τ = no summation {}}{ (p i ) (δ ij ) p p p 3 where p i is the pressure acting perpenicular to the i th surface. If p 0 is the pressure acting perpenicular to the surface PQR, then τ i = n i p 0, but: τ i = τ ij n j = (p i )δ ij n j = (p i )(n i ) Therefore p o = p i, i = 1, 2, 3 an n is arbitrary. 3

4 1.7.3 Symmetry of the Stress Tensor To prove the symmetry of the stress tensor we follow the steps: j τ ij τ ji δ τ ji o τ ij i Figure 3: Material element uner tangential stress. 1. The of surface forces = boy forces + mass acceleration. Assume no symmetry. Balance of the forces in the i th irection gives: (δ)(τ ij ) T OP (δ)(τ ij ) BOT T OM = O(δ 2 ), since surface forces are δ 2, where the O(δ 2 ) terms inclue the boy forces per unit epth. Then, as δ 0, (τ ij ) T OP = (τ ij ) BOT T OM. 2. The of surface torque = boy moment + angular acceleration. Assume no symmetry. Balance of moments about o gives: (τ ji δ)δ (τ ij δ)δ = O(δ 3 ), since the boy moment is proportional to δ 3. As δ 0, τ ij = τ ji. 4

5 1.8 Mass an Momentum Conservation Consier a material volume V m an recall that a material volume is a fixe mass of material. A material volume always encloses the same flui particles espite a change in size, position, volume or surface area over time Mass Conservation The mass insie the material volume is: M(V m ) = ρv S m (t) Figure 4: Material volume V m (t) with surface S m (t). Therefore the time rate of increase of mass insie the material volume is: t M(V m) = t V m (t) ρv = 0, which is the integral form of mass conservation for the material volume V m. 5

6 1.8.2 Momentum Conservation The flui velocity insie the material volume in the i th irection is enote as u i. Linear momentum of the material volume in the i th irection is ρu i V Newton s law of motion: The time rate of change of momentum of the flui in the material control volume must equal the sum of all the forces acting on the flui in that volume. Thus: Divergence Theorems t (momentum) i =(boy force) i + (surface force) i ρu i V = F i V + τ ij n j S t }{{} Vm(t) For vectors: For tensors: Using the ivergence theorems we obtain V V S m(t) τ i }{{ v } V = v j S x j τ ij V = x j S v.ˆn }{{} v j n j S τ ij n j S ρu i V = t ( F i + τ ) ij V x j which is the integral form of momentum conservation for the material volume V m. 6

7 1.8.3 Kinematic Transport Theorems Consier a flow through some moving control volume uring a small time interval t. Let f ( x, t) be any (Eulerian) flui property per unit volume of flui (e.g. mass, momentum, etc.). Consier the integral I(t): I(t) = f ( x, t) V Accoring to the efinition of the erivative, we can write I(t + t) I(t) I(t) = lim t t 0 t = lim t 0 1 t V(t+ t) f( x, t + t)v f( x, t)v S(t+ t) S(t) Figure 5: Control volume V an its bouning surface S at instants t an t + t. 7

8 Next, we consier the steps 1. Taylor series expansion of f( x, t + t) about ( x, t). 2. V = f( x, t + t) = f( x, t) + t f t ( x, t) + O(( t)2 ) V + V V(t+ t) where, V = V [U n ( x, t) t] S an U n ( x, t) is the normal velocity of S(t). V S(t) S(t+ t) S(t) U v 2 (x,t) t + O( t) n S Figure 6: Element of the surface S at instants t an t + t. Putting everything together: 1 I(t) = lim t t 0 t Vf + t V f t + t S(t) SU n f Vf + O( t) 2 (1) 8

9 From Equation (1) we obtain the Kinematic Transport Theorem (KTT), which is equivalent to Leibnitz rule in 3D. t f( x, t)v = f( x, t) V + t S(t) f( x, t)u n ( x, t)s For the special case that the control volume is a material volume it is = V m (t) an U n = v ˆn, where v is the flui particle velocity. The Kinematic Transport Theorem (KTT), then takes the form t f( x, t)v = Using the ivergence theorem, V f( x, t) V + t S m(t) }{{ α } V = α x i S i }{{} α ˆn S α i n i we obtain the 1 st Kinematic Transport Theorem (KTT) f( x, t)( v ˆn) S }{{} f(v i n i ) (Einstein Notation) t f ( x, t) V = [ ] f( x, t) + (f v) V, t }{{} (fv x i ) i where f is some flui property per unit volume. 9

10 1.8.4 Continuity Equation for Incompressible Flow Differential form of conservation of mass for all fluis Let the flui property per unit volume that appears in the 1 st KTT be mass per unit volume ( f = ρ): 0 = conservation of mass t ρv = 1 st KTT [ ] ρ t + (ρ v) V But since V m is arbitrary the integran must be 0 everywhere. (Because if it is not zero at any point then we can shrink the volume to that point an get a non-zero result which is a contraiction) Therefore: ρ t + (ρ v) = 0 ρ + [ v ρ + ρ v] = 0 } t {{} Dρ Dt Leaing to the ifferential form of Conservation of Mass: Dρ Dt + ρ v = 0 10

11 Continuity equation Conservation of mass for incompressible flow In general it is ρ = ρ(p, T,...), but we consier the special case of an incompressible flow, i.e. Dρ = 0 (Lecture 2). Dt Note: For a flow to be incompressible, the ensity of the entire flow nee not be constant (ρ( x, t) const). As an example consier a flow of more than one incompressible fluis, like water an oil, as illustrate in the picture below. Constant ρ flui particle ρ 1 oil water flui particle ρ 2 Figure 7: Interface of two fluis (oil-water) Since for incompressible flows Dρ = 0, substituting into the ifferential form of the Dt conservation of mass we obtain the Continuity Equation: v v i x }{{ i } = 0 rate of volume ilatation 11

12 1.8.5 Euler s Equation (Differential Form of Conservation of Momentum) 2 n Kinematic Transport Theorem 1 st KTT + ifferential form of conservation of mass for all fluis. If G = flui property per unit mass, then ρg = flui property per unit volume t ρgv = 1 st KT T [ ] (ρg) + (ρg v) V t after some algebra: = ( ) ρ G t + ρ v }{{} =0 from mass conservation ( G + ρ t ) + v G V } {{ } = DG Dt The 2 n Kinematic Transport Theorem (KTT) follows: ρgv = t V m V m DG ρ Dt V Note: The 2 n KTT is obtaine from the 1 st KTT (mathematical ientity) an the only assumption use is that mass is conserve. 12

13 Euler s Equation We consier G as the i th momentum per unit mass (v i ). Then, ( F i + τ ) ij V x j = conservation of momentum t ρv i V = 2 n KTT ρ Dv i Dt V But V m (t) is an arbitrary material volume, therefore the integral ientity gives Euler s equation: ρ Dv i Dt ρ v i t + v v i }{{} = F i + τ ij x j v j v i x j An in vector tensor form: ρ D v ( ) v Dt ρ + v v = F t + τ NOTE: Euler equation is the momentum equation for the flui in the ifferential form. Stress oes not make the flui to accelerate. It is the erivative of stress that makes the flui to accelerate. 13