Security Arguments for Digital Signatures and Blind Signatures
|
|
|
- Raymond Heath
- 5 years ago
- Views:
Transcription
1 J. Cryptology (2000) 13: DOI: /s International Association for Cryptologic Research Security Arguments for Digital Signatures and Blind Signatures David Pointcheval and Jacques Stern Laboratoire d Informatique, École Normale Supérieure, Paris Cedex 05, France {David.Pointcheval, Jacques.Stern}@ens.fr {pointche,stern} Communicated by Don Coppersmith Received 24 October 1997 and revised 22 May 1998 Online publication 21 March 2000 Abstract. Since the appearance of public-key cryptography in the seminal Diffie Hellman paper, many new schemes have been proposed and many have been broken. Thus, the simple fact that a cryptographic algorithm withstands cryptanalytic attacks for several years is often considered as a kind of validation procedure. A much more convincing line of research has tried to provide provable security for cryptographic protocols. Unfortunately, in many cases, provable security is at the cost of a considerable loss in terms of efficiency. Another way to achieve some kind of provable security is to identify concrete cryptographic objects, such as hash functions, with ideal random objects and to use arguments from relativized complexity theory. The model underlying this approach is often called the random oracle model. We use the word arguments for security results proved in this model. As usual, these arguments are relative to wellestablished hard algorithmic problems such as factorization or the discrete logarithm. In this paper we offer security arguments for a large class of known signature schemes. Moreover, we give for the first time an argument for a very slight variation of the wellknown El Gamal signature scheme. In spite of the existential forgery of the original scheme, we prove that our variant resists existential forgeries even against an adaptively chosen-message attack. This is provided that the discrete logarithm problem is hard to solve. Next, we study the security of blind signatures which are the most important ingredient for anonymity in off-line electronic cash systems. We first define an appropriate notion of security related to the setting of electronic cash. We then propose new schemes for which one can provide security arguments. Key words. Cryptography, Digital signatures, Blind signatures, Security arguments, Existential forgery, One-more forgery, Forking lemma. This paper is the full version of Security Proofs for Signature Schemes [43] presented at Eurocrypt 96 and Provably Secure Blind Signature Schemes [42] presented at Asiacrypt
2 362 D. Pointcheval and J. Stern Introduction Since the beginning of public-key cryptography with the Diffie Hellman paper [16], many new schemes have been proposed and many have been broken. Thus, the simple fact that a cryptographic algorithm withstands cryptanalytic attacks for several years is often considered as a kind of validation procedure. In this approach, cryptanalysis is viewed as a heuristic measure of the strength of a new proposal. A completely different paradigm is provided by the concept of provable security. A significant line of research has tried to provide proofs in the asymptotic framework of complexity theory. Stated in a more accurate way, this approach proposes computational reductions to well-established problems, such as factorization, RSA [49], the discrete logarithm problem, or any NP-complete problem [24]. Of course, these are not absolute proofs since cryptography ultimately relies on the existence of oneway functions and the P versus NP question. Moreover, in many cases, provable security is at the cost of an important loss in terms of efficiency [29], [27], [28], [1]. Recently, the scope of these methods has been considerably widened by using a model where concrete cryptographic objects, such as hash functions, are identified with ideal random objects, the so-called random oracle model formalized by Bellare and Rogaway [2]. In this model, DES [34] is viewed as a random permutation and SHA [36] as a random function with the appropriate range. Using this model, we offer security arguments for a large class of digital signatures. Moreover, we give, for the first time, an argument for a very slight variation of the well-known El Gamal signature scheme [17]. In spite of the existential forgery of the original scheme, we prove that our variant resists existential forgeries even against an adaptively chosen-message attack. This is provided that the discrete logarithm problem is hard to solve. Furthermore, we study the security of blind signatures, especially for their application in electronic cash systems: we first define adequate security notions for blind signatures, then we propose the first schemes for which security arguments can be given. We now briefly describe the organization of our paper. We first define the so-called random oracle model and explain why such a theoretical model can help in proving the validity of the design of a cryptographic scheme. We then recall the definition of a signature scheme together with the various attacks and forgeries that we consider. Also, we present the notion of blind signatures and its use for anonymity (and even revokable anonymity) in electronic cash schemes. Next, we consider the attacks that are relevant in the context of digital payments. In Section 2 we propose schemes for which one can provide security arguments. In order to simplify the proofs, we first explain our generic technique, the oracle replay attack and we present a simple probabilistic lemma, the splitting lemma. In Section 3 we prove two fundamental forking lemmas for digital signatures and blind signatures. They are our main ingredient for providing security arguments for many schemes.
3 Security Arguments for Digital Signatures and Blind Signatures Definitions 1.1. The Random Oracle Model Many cryptographic schemes use a hash function f (such as the Message Digest family MD4 [47], MD5 [48], and derived functions SHA-1 [36], HAVAL [40], RIPEMD [46], or RIPEMD-160 [5]). This use of hash functions was originally motivated by the wish to sign long messages with a single short signature. In order to achieve nonrepudiation, a minimal requirement on the hash function is to ask that it is impossible for the signer to find two different messages providing the same hash value, this property is called collision freeness. It was later realized that hash functions were an essential ingredient for the security of signature schemes. In order actually to obtain security arguments, while keeping the efficiency of the designs that use hash functions, several authors (e.g., [21], [2], [3], [43], [42], and [44]) have suggested using the hypothesis that f is actually a random function. We follow this suggestion by using the corresponding model, called the random oracle model. In this model the hash function can be seen as an oracle which produces a truly random value for each new query. Of course, if the same query is asked twice, identical answers are obtained. This is precisely the context of relativized complexity theory with oracles, hence the name. It is argued that proofs in this model ensure security of the overall design of a signature scheme provided that the hash function has no weakness. In the following we replace any hash function by a random oracle which outputs k-bit long elements, where k is a security parameter of the cryptographic scheme. In other words, k denotes both the security parameter of the cryptographic (signature) scheme and the length of the output of the random oracle. Roughly speaking, the security level is 2 k Digital Signature Schemes We now turn to digital signature schemes, the electronic version of handwritten signatures for digital documents: a user s signature on a message m is a string which depends on m, on public and secret data specific to the user and possibly on randomly chosen data, in such a way that anyone can check the validity of the signature by using public data only. The user s public data are called the public key, whereas his secret data are called the secret key. Obviously we would like to prevent the forgery of a user s signature without knowledge of his secret key. In this section we give a more precise definition of signature schemes and of the possible attacks against them. These definitions are based on [28]. Definition 1. A signature scheme is defined by the following (see Fig. 1): The key generation algorithm G. On input 1 k, where k is the security parameter, the algorithm G produces a pair (K p, K s ) of matching public and secret keys. We denote by n the length of the public key. Algorithm G is probabilistic (with random tape ω). The signing algorithm. Given a message m and a pair of matching public and secret keys (K p, K s ), produces a signature σ. The signing algorithm might be
4 364 D. Pointcheval and J. Stern Fig. 1. Signature schemes. probabilistic (with random tape ω), and in some schemes it might receive other inputs as well. The verification algorithm V. Given a signature σ, a message m, and a public key K p, V tests whether σ is a valid signature of m with respect to K p. In general, the verification algorithm need not be probabilistic Examples As shown in the Diffie Hellman paper [16], the trapdoor permutation paradigm allows us to create signatures in the public key setting. Two years later, Rivest et al. [49] proposed the first signature scheme based on the RSA trapdoor function: The RSA Signature. In the RSA context the generation algorithm produces a large composite number N = pq, a public key e, and a secret key d such that e d = 1 mod ϕ(n). The signature of a message m is the eth root of m, σ = m 1/e = m d mod N. The RSA scheme is not secure by itself since it is subject to existential forgery. In other words, it is easy to create a valid message signature pair, without any help of the signer, using the public verification relation m = σ e mod N. In many cases, this is not really dangerous because the resulting message is not intelligible or does not have the proper redundancy. Still such an RSA signature does not prove by itself the identity of the sender. In 1986 a new paradigm for signature schemes was introduced. It is derived from fair zero-knowledge identification protocols involving a prover and a verifier [26], and uses hash functions in order to create a kind of virtual verifier. In [21] Fiat and Shamir proposed a zero-knowledge identification protocol based on the hardness of extracting square roots. They also described the corresponding signature scheme and outlined its
5 Security Arguments for Digital Signatures and Blind Signatures 365 security. Similar security results for other signature schemes like Schnorr s [50], [51] are considered folklore results but have never appeared in print. We refer the reader to the literature for the precise description of those schemes, and we only recall the Schnorr signature: The Schnorr Signature. The generation algorithm produces two large primes p and q, such that q 2 k, where k is the security parameter, and q p 1, as well as an element g of (Z/pZ) of order q. It also creates a pair of keys, x (Z/qZ) and y = g x mod p. The signer publishes y and keeps x secret. The signature of a message m is a triple (r, e, s), where r = g K mod p, with a random K (Z/qZ), the challenge e = H(m, r) mod q and s = K + ex mod q. It satisfies r = g s y e mod p with e = H(m, r), or simply e = H(m, g s y e mod p), which is checked by the verifying algorithm Generic Digital Signature Schemes In this paper we consider signature schemes which, given the input message m, produce triples (σ 1, h,σ 2 ) where σ 1 randomly takes its values in a large set, h is the hash value of (m,σ 1 ), and σ 2 only depends on σ 1, the message m, and h. In particular, we can remark that each signature is independent of the previous ones. More precisely, in the proof of resistance against the strongest attacks, we assume that no σ 1 can appear with probability greater than 2/2 k, where k is the security parameter. This assumption is satisfied in the Schnorr signature scheme: σ 1 = g K mod p for a randomly chosen K in (Z/qZ) ; since g is of order q, and k log q, the probability for σ 1 to get a specific value is less than 1/(q 1) 2/2 k. In the same way, the Fiat Shamir [21] scheme and many others also satisfy this assumption. In some cases, in order to optimize the size of signatures, σ 1 or h can be omitted, since they can be correctly recovered during the verification process. For notational purposes we ignore these possible optimizations and keep σ 1, h as parts of the signature Attacks We focus on two specific kinds of attacks against signature schemes: the no-message attack and the known-message attack. In the first scenario the attacker only knows the public key of the signer. In the second one the attacker has access to a list of message signature pairs. According to the way this list was created, we distinguish four subclasses of known-message attacks: The plain known-message attack: the attacker has access to a list of signed messages, but he has not chosen them. The generic chosen-message attack: the attacker can choose the list of messages to be signed. However, this choice must be made before accessing the public key of the signer. We call this attack generic because the choice is independent of the signer. The oriented chosen-message attack: as above, the attacker chooses the list of messages to be signed, but the choice is made once the public key of the signer has been obtained. This attack is oriented against a specific signer.
6 366 D. Pointcheval and J. Stern Fig. 2. Attacks. The adaptively chosen-message attack: having knowledge of the public key of the signer, the attacker can ask the signer to sign any message that he wants. He can then adapt his queries according to previous message signature pairs. In the following we only consider the two extreme scenarios, the no-message attack and the adaptively chosen-message attack (see Fig. 2) Forgeries We now classify the expected results of an attack: Disclosing the secret key of the signer. It is the most serious attack. This attack is termed total break. Constructing an efficient algorithm which is able to sign any message. This is called universal forgery. Providing a new message signature pair. This is called existential forgery. In many cases this attack is not dangerous, because the output message is likely to be meaningless. Nevertheless, a signature scheme which is not existentially unforgeable does not guarantee by itself the identity of the signer. For example, it cannot be used to certify randomly looking elements, such as keys. Definition 2 (Secure Signature Scheme). A signature scheme is secure if an existential forgery is computationally impossible, even under an adaptively chosen-message attack. The first secure signature scheme was proposed by Goldwasser et al. [27] in It uses the notion of claw-free permutations pairs: informally, these are permutations f 0 and f 1 over a common domain for which it is computationally infeasible to find a triple (x, y, z) such that f 0 (x) = f 1 (y) = z. Furthermore, Goldwasser et al. proved that such claw-free permutations pairs exist if factoring is hard (see [27] and [28] for details).
7 Security Arguments for Digital Signatures and Blind Signatures 367 Fig. 3. Coin life Blind Signatures After this brief outline of signature schemes, we review another cryptographic primitive: blind signatures. We first motivate their use and give some well-known examples. We then define specific security properties of blind signatures related to the setting of electronic cash Motivation: Electronic Cash As early as 1982, Chaum s [13] pioneering work aimed at creating an electronic version of money. To achieve this goal, he introduced the notions of coins and randomized blind signatures (or simply blind signatures ). He claimed that this was the only way to ensure the required anonymity: in real life, a coin cannot be easily traced from the bank to the shop, furthermore, two spendings of a same user cannot be linked together. These are two main properties of real coins that Chaum wanted to mimic: untraceability and unlinkability. He proposed to define an electronic coin as a number with a certificate (a signature) produced by the bank; it is withdrawn from the bank, spent by the user, and deposited by the shop (see Fig. 3). On-line electronic cash. In his first scheme, Chaum used blind signatures for the production of coins. The user makes the bank blindly sign a coin. Then the user is in possession of a valid coin that the bank itself cannot recognize nor link with the user. When the user spends the coin, the shop immediately returns it to the bank. If the coin has already been spent, the bank detects the fact and informs the shop so that it refuses payment. It is an on-line context: there is a continuous communication between the shop and the bank in order to verify the validity of coins. In order to define the scheme, Chaum introduced the first blind signature scheme, based on the RSA hypothesis. It is a by now classical transformation of the original RSA signature scheme [49]: The Blind RSA Signature. The bank has a large composite number N = pq, a public key e, and a related secret key d. It also uses a public hash function H. In order to get the signature of a random number ρ, the user blinds it with a random value r e mod N, and sends m = H(ρ)r e mod N to the signer. The latter returns a signature σ of m such
8 368 D. Pointcheval and J. Stern that σ e = m = r e H(ρ) mod N. Then the user can unblind this signature computing σ = σ r 1 mod N. A coin is any pair (ρ, σ ) which satisfies σ e = H(ρ) mod N. In this scheme all coins have the same value, but in a real system different denominations might be encoded by different exponents e. Off-line electronic cash and the cut-and-choose methodology. In an off-line context we cannot prevent a user from spending a coin twice or even more, since the detection is made too late to refuse payment. This fraud is called double-spending. We only can hope that the double-spender will be discovered later and punished. Chaum et al. [14] were able to build such schemes by introducing the identity of the user in the coin in such a way that it remains concealed, unless double-spending happens. Once more, blind signatures were a critical point for anonymity, and, as before, the authors used the blind RSA signature, together with the cut-and-choose technique: in their proposition, a coin is a kind of list of k blind signatures, each having an embedded copy of the identity of the user. To be sure that double-spending will reveal the real identity of the user, the bank would like to verify that the signatures actually have the requested format, which would revoke anonymity. Then the bank helps the user to get 2k signatures, randomly chooses k of them, and verifies the inner structure of the selected signatures. Since these signatures are no longer anonymous, the user throws them away and constructs the coin with the k other ones. The probability for a cheater to be finally in possession of a fraudulous coin is about 2 2k. The main drawback of the cut-and-choose technique is that the coins are very large, as well as the amount of computations. In 1993 Ferguson [20] and Brands [7] proposed new schemes without cut-and-choose. The first one uses once again the blind RSA signature, whereas Brands scheme uses a new blind signature derived from the Schnorr signature scheme [50], [51]: The Blind Schnorr Signature. The generation algorithm produces two large prime integers p and q such that q p 1 as well as an element g of (Z/pZ) of order q. It also creates a pair of keys, (x, y), where x (Z/qZ) is the secret one, and y = g x mod p is the public one. The signer publishes y. In order to get the signature of a secret message m, the user asks the signer to initiate a communication. He chooses a random K (Z/qZ), computes, and sends the commitment r = g K mod p. The user then blinds this value with two random elements α, β Z/qZ, intor = rg α y β mod p, computes the value e = H(m, r ) mod q, and sends the challenge e = e +β mod q to the signer who returns the value s such that g s y e = r mod p. Finally, the user computes s = s α mod q. This way, the pair (e, s ) is a valid Schnorr signature of m since it satisfies e = H(m, g s y e mod p). In both schemes Ferguson and Brands managed to hide the identity of the user in a much more efficient way than the cut-and-choose methodology. Again, the identity is revealed after double-spending. Those blind signatures which hide a specific structure, such as the identity, are called restrictive blind signatures [11], [9], [8], [45]. Many extensions [19], [6], [10] have been proposed, followed by some attacks [8], [11] and repairs [9], [52]. All of them use blind signatures, and the security of the proposed
9 Security Arguments for Digital Signatures and Blind Signatures 369 schemes is totally dependent on the security of the blind signatures they use. Surprisingly, no security proofs have been proposed so far for blind signatures. Revokable anonymity. A few years ago [57], an undesirable feature of total anonymity in transactions was considered: perfect crimes (anonymous crimes without leaving any traces and consequently without any risk of being suspected later). Accordingly, a new line of research in electronic cash has investigated revokable anonymity [12], [22], [31] which proposes anonymity unless a Trusted Third Party (TTP) partially revokes it for some established reasons or in view of an obvious fraud (e.g., in case of doublespending). Again, those new schemes rely on the security of blind signature schemes Security As far as we know, no formal notion of security has ever been studied, or proved, in the context of blind signatures. However, it is a critical point in electronic cash systems. In the context of blind signatures, the previous definitions of security are no longer significant. In fact, existential forgery is somehow the basis for blind signatures. Nevertheless, a fundamental property for electronic cash systems is the guarantee that a user cannot forge more coins than the bank gives him. In other words, with l blind signatures of the bank, the user must not be able to create more than l coins. This form of security was more or less informally assumed in connection with several schemes, for example in [10], or under the unexpandability property of [23]. Definition 3 (The (l, l + 1)-Forgery). For any integer l, an(l, l + 1)-forgery comes from an attacker that produces l + 1 signatures after l interactions with the signer. Definition 4 (The One-More Forgery). For some integer l, polynomial in the security parameter k, an attacker can obtain l+1 valid signatures after fewer than l interactions with the signer. In other words, a one-more forgery is an (l, l + 1)-forgery for some polynomially bounded integer l. Definition 5 (The Strong One-More Forgery). An (l, l + 1)-forgery for a polylogarithmically bounded integer l (i.e., for some constant α, l (log k) α, where k is the security parameter) is called a strong one-more forgery. As usual, several scenarios can be envisioned. We focus on two kinds of attacks which naturally come from the use of blind signatures in electronic cash: The sequential attack (see Fig. 4): the attacker interacts sequentially with the signer. This attack can be performed by a user who withdraws coins, one after the other. It is clear that, in practical situations, many users might be allowed to withdraw money at the same time. The following attack must then be considered. The parallel attack (see Fig. 5): the attacker interacts l times in parallel with the signer. This attack is stronger. Indeed, the attacker can initiate new interactions with the signer before previous ones have ended. This attack can be performed by a group of users who withdraw many coins at the same time.
10 370 D. Pointcheval and J. Stern Fig. 4. The sequential attack. Fig. 5. The parallel attack. 2. Preliminaries 2.1. Complexity Theory and Oracle Replay Attack In this paper we offer several security arguments for digital signatures and blind signatures. All our results are given in the context of complexity theory. Hence, any participant is modeled by a probabilistic polynomial time Turing machine. Our paradigm is to use a supposedly efficient attacker in order to solve a difficult algorithmic problem. This goes through a generic reduction technique (see Fig. 6) which we call the oracle replay attack Fig. 6. Reduction of a difficult problem.
11 Security Arguments for Digital Signatures and Blind Signatures 371 Fig. 7. The oracle replay attack. (see Fig. 7): by a polynomial replay of the attack with different random oracles (the Q i s are the queries and the ρ i s are the answers), we make the attacker successfully forge signatures which are suitably related. More precisely, we want to obtain two signatures (σ 1, h,σ 2 ) and (σ 1, h,σ 2 ) of an identical message m such that σ 1 = σ 1,buth h. We then extract the solution of a difficult problem from the ability to forge such pairs. In the reductions, an important problem is to simulate properly the interactions that the attacker should have with other entities (with the random oracle f and particularly with the signer ). Those simulations should be indistinguishable from real interactions from the point of view of the attacker despite the obvious fact that no secret key is available Distinguishability of Distributions of Probability As explained above, in our reductions we have to provide indistinguishable simulations: the communication tapes between the attacker and the simulator and between the attacker and the signer (for example) will have to follow indistinguishable distributions of probability. In this subsection we define two notions of indistinguishability. Recall that a function f (k) is negligible in k if, for every polynomial p, f (k) is smaller than 1/ p(k), for k large enough; otherwise, it is nonnegligible. Definition 6. Let δ 0 and δ 1 be two distributions of probability. A distinguisher D is a probabilistic polynomial time Turing machine, with random tape ω, which, on input ρ, answers 0 or 1. The advantage of D with respect to two distributions δ 0 and δ 1 is defined as Adv(D,δ 0,δ 1 ) = 1 2 E [D(ω, ρ)] E [D(ω, ρ)]. ρ δ 0 ρ δ 1 It is easy to derive the following equality: Pr ω c {0,1} ρ δ c [D(ω, ρ) = c] = 1 2 ± Adv(D,δ0,δ 1 ). So, if this advantage is negligible, the answer of the distinguisher looks like the result of flipping a coin. Two distributions δ 0 and δ 1 are polynomially indistinguishable if there does not exist any distinguisher D with a nonnegligible advantage.
12 372 D. Pointcheval and J. Stern Two distributions δ 0 and δ 1 are statistically indistinguishable if Pr [x = y] Pr [x = y] is negligible. x δ 0 x δ 1 y Remark. It is clear that if two distributions are statistically indistinguishable, they are polynomially indistinguishable The Splitting Lemma Throughout this paper we repeatedly use the Splitting Lemma below. It translates the fact that when a subset A is large in a product space X Y, it has many large sections. Lemma 7 (The Splitting Lemma). Let A X Y such that Pr[(x, y) A] ε. For any α<ε, define { } B = (x, y) X Y Pr [(x, y Y y ) A] ε α and B = (X Y )\B, then the following statements hold: (i) Pr[B] α. (ii) (x, y) B, Pr y Y [(x, y ) A] ε α. (iii) Pr[B A] α/ε. Proof. In order to prove statement (i), we argue by contradiction. Assume that Pr[B] < α. Then ε Pr[B] Pr[A B] + Pr[ B] Pr[A B] <α (ε α) = ε. This implies a contradiction, hence the result. Statement (ii) is a straightforward consequence of the definition. We finally turn to the last assertion, using Bayes law: Pr[B A] = 1 Pr[ B A] = 1 Pr[A B] Pr[ B]/ Pr[A] 1 (ε α)/ε = α/ε. 3. Security Arguments for Digital Signatures This section is devoted to digital signatures and extends our previous results on their security [43]. Recall that an identification scheme [21] is an interactive protocol which involves a prover and a verifier. The prover tries to convince the verifier of his knowledge of a secret related to his identity. More specifically, a three-pass honest-verifier zero-knowledge identification protocol is an identification scheme with three interactions between the prover and the verifier, which leaks no information about the secret provided the verifier plays honestly, namely, randomly choosing his queries. The three
13 Security Arguments for Digital Signatures and Blind Signatures 373 interactions correspond to three messages: the commitment a sent by the prover, the challenge e randomly chosen by the verifier, and the answer r of the prover. The verifier finally accepts the proof if and only if this triple satisfies a test V (a, e, r) = 1. As described by Fiat and Shamir [21], any three-pass honest-verifier zero-knowledge identification protocol can be turned into a generic digital signature scheme: let (a, e, r) be a round of the identification protocol, we get a digital signature scheme by replacing the query of the verifier, which is a random value e, by the hash value of the message m to be signed together with the commitment a which is bound not to change, namely, e = f (m, a), where f is the hash function. If the identification protocol needs several sequential iterations in order to reach an adequate level of security, then, in the signature setting, one parallelizes the protocol. Accordingly, a signature of a message m is a triple (σ 1, h,σ 2 ), where σ 1 represents all successive commitments of the parallelized protocol, h = f (m,σ 1 ) and σ 2 represents all successive answers of the parallelized protocol. It satisfies a test V (σ 1, h,σ 2 ) = 1 as described above in the generic digital signature schemes section (see Section 1.2.2). For example, the Schnorr signature scheme is precisely the result of the above transformation applied to the Schnorr identification protocol. In what follows, we assume that f outputs k-bit long elements, where k is the security parameter of the signature scheme, as described above. We first prove the security of a generic digital signature scheme against no-message attacks. As an application, we directly obtain the security of the Schnorr signature scheme. Next, we extend our result to the adaptively chosen-message context. We close the section with a study of the El Gamal signature scheme [17]: in spite of the existential forgery of the original scheme, we present a slight variation which is existentially unforgeable under an adaptively chosen-message attack. This is provided that the discrete logarithm problem is hard to solve No-Message Attacks In this part we consider the no-message scenario. We propose a generic result and we apply our technique to the Schnorr signature scheme Generic Results Lemma 8. Let (G,,V) be a generic digital signature scheme with security parameter k. Let A be a probabilistic polynomial time Turing machine whose input only consists of public data and which can ask Q queries to the random oracle, with Q > 0. We assume that, within the time bound T, A produces, with probability ε 7Q/2 k, a valid signature (m,σ 1, h,σ 2 ). Then, within time T 16QT/ε, and with probability ε 1 9, a replay of this machine outputs two valid signatures (m,σ 1, h,σ 2 ) and (m,σ 1, h,σ 2 ) such that h h. Proof. We start with a no-message attacker A, which is a probabilistic polynomial time Turing machine with random tape ω. During the attack, this machine asks a polynomial number of questions to the random oracle f. We may assume that these questions are distinct: for instance, A can store questions and answers in a table. Let Q 1,...,Q Q be the Q distinct questions and let ρ = (ρ 1,...,ρ Q ) be the list of the Q answers of f.itis
14 374 D. Pointcheval and J. Stern clear that a random choice of f exactly corresponds to a random choice of ρ. Then, for a random choice of (ω, f ), with probability ε, A outputs a valid signature (m,σ 1, h,σ 2 ). Since f is a random oracle, it is easy to see that the probability for h to be equal to f (m,σ 1 ) is less than 1/2 k, unless it has been asked during the attack. So, it is likely that the question (m,σ 1 ) is actually asked during a successful attack. Accordingly, we define Ind(ω, f ) to be the index of this question: (m,σ 1 ) = Q Ind(ω, f ) (we let Ind(ω, f ) = if the question is never asked). We then define the sets and S ={(ω, f ) A f (ω) succeeds & Ind(ω, f ) }, S i ={(ω, f ) A f (ω) succeeds & Ind(ω, f ) = i} for i {1,...,Q}. We call S the set of the successful pairs (ω, f ), and we note that the set {S i i {1,...,Q}} is a partition of S. With those definitions, we find a lower bound for the probability of success, ν = Pr[S] ε 1/2 k 6ε/7. Let I be the set consisting of the most likely indices i, I ={i Pr[S i S] 1/2Q}. The following lemma claims that, in case of success, the index lies in I with probability at least 1 2. Lemma 9. Pr[Ind(ω, f ) I S] 1 2. Proof. By definition of the sets S i, Pr[Ind(ω, f ) I S] = i I Pr[S i S]. This probability is equal to 1 i I Pr[S i S]. Since the complement of I contains fewer than Q elements, this probability is at least 1 Q 1/2Q 1 2. We now run the attacker 2/ε times with random ω and random f. Since ν = Pr[S] 6ε/7, with probability greater than 1 (1 6ε/7) 2/ε, we get at least one pair (ω, f ) in S. It is easily seen that this probability is lower bounded by 1 e 12/ We now apply the Splitting Lemma (Lemma 7) for each integer i I : we denote by f i the restriction of f to queries of index strictly less than i. Since Pr[S i ] ν/2q, there exists a subset i of executions such that, for any (ω, f ) i, Pr f [(ω, f ) S i f i = f i ] ν/4q, Since all the subsets S i are disjoint, Pr[ i S i ] 1 2. Pr [( i I )(ω, f ) i S i S] ω, f [ ] = Pr ( i S i ) S = Pr[ i S i S] i I i I = ( ) Pr[ i S i ] Pr[S i S] Pr[S i S] / i I i I We let β denote the index Ind(ω, f ) corresponding to the successful pair. With probability at least 1 4, β I and (ω, f ) S β β. Consequently, with probability greater
15 Security Arguments for Digital Signatures and Blind Signatures 375 than 1, the 2/ε attacks have provided a successful pair (ω, f ), with β = Ind(ω, f ) I 5 and (ω, f ) S β. Furthermore, if we replay the attack, with fixed ω but randomly chosen oracle f such that f β = f β, we know that Pr f [(ω, f ) S β f β = f β] ν/4q. Then Pr [(ω, f ) S β and ρ β ρ f β f β = f β] Pr [(ω, f ) S β f f β = f β] Pr f [ρ β = ρ β] ν/4q 1/2 k ε/14q, where ρ β = f (Q β ) and ρ β = f (Q β ). We replay the attack 14Q/ε times with a new random oracle f such that f β = f β. With probability greater than 3, we get another 5 success. Finally, after less than 2/ε + 14Q/ε repetitions of the attack, with probability greater than , we have obtained two valid signatures (m,σ 1, h,σ 2 ) and (m,σ 1, h,σ 2 ) with Q β = (m,σ 1 ) = (m,σ 1 ) and distinct challenges h = f (Q β) f (Q β ) = h. The careful reader has noticed that the mechanics of our reduction depend on some parameters related to the attacker A, namely, its probability of success ε and the number Q of queries to the random oracle. This induces a lack of uniformity. In order to overcome this problem, we can use the reduction technique presented in our previous Eurocrypt 96 paper [43]. Unfortunately, the probability of success of the resulting reduction is much smaller: the expected time of success is of the order of Q 4 /ε 3 instead of Q/ε. Accordingly, we end up extremely far from any form of the exact security concept [3]. It is better to see the resulting machine M as an expected polynomial time Turing machine: 1. M initializes j = 0; 2. M runs A until it outputs a successful pair (ω, f ) S and denotes by N j the number of calls to A to obtain this success, and by β the index Ind(ω, f ); 3. M replays, at most 140N j α j times, A with fixed ω and random f such that f β = f β, where α = 8 7 ; 4. M increments j and returns to 2, until it gets a successful forking. For any execution of M, we denote by J the last value of j and by N the total number of calls to A. We want to compute the expectation of N. Since ν = Pr[S], and N j 1, then Pr[N j 1/5ν] 3 4. We define l = log α Q, so that 140N jα j 28Q/ε for any j l, whenever N j 1/5ν. Therefore, for any j l, when we have a first success in S, with probability greater than 1, the index β = Ind(ω, f ) is in the set I and 4 (ω, f ) S β β. Furthermore, with probability greater than 3 4, N j 1/5ν. Therefore, with the same conditions as before, that is ε 7Q/2 k, the probability of getting a successful fork after at most 28Q/ε iterations at step 3 is greater than 6 7. For any t l, the probability for J to be greater or equal to t is less than ( )t l, which is less than γ t l, with γ = 6 7. Furthermore, E[N J = t] j=t ( E[Nj ] + 140E[N j ]α j) 141 ν j=0 j=t j=0 α j 141 ν αt+1 α 1.
16 376 D. Pointcheval and J. Stern So, the expectation of N is E[N] = t E[N J = t] Pr[J = t] and then is 141 ν ( α t+1 ) Pr[J t] t α 1 [ 165 t=l 1 ( α t+1 ) ε + ( α t+1 ) ] γ t l α 1 α 1 t l t=0 165 ε α l+1 α ε α l+1 α 1 [ 1 α 1 + ] (αγ ) t t ( ) 1 α αγ Using the definition of l and the values of α and γ, we obtain E[N] 165 ε Hence the following theorem. 64Q 7 (7 + 49) = 84480Q. ε Theorem 10 (The Forking Lemma). Let (G,,V) be a generic digital signature scheme with security parameter k. Let A be a probabilistic polynomial time Turing machine whose input only consists of public data. We denote by Q the number of queries that A can ask to the random oracle. Assume that, within time bound T, A produces, with probability ε 7Q/2 k, a valid signature (m,σ 1, h,σ 2 ). Then there is another machine which has control over A and produces two valid signatures (m,σ 1, h,σ 2 ) and (m,σ 1, h,σ 2 ) such that h h, in expected time T 84480TQ/ε The Schnorr Digital Signature Scheme We now apply the previous result in the simple setting of the Schnorr signature scheme (see Fig. 8). Firstly, we briefly describe the protocol. For any security parameter k, an authority chooses two large prime integers p and q, such that 2 k 1 q < 2 k holds and q divides p 1 as well as an element g from (Z/pZ) of order q. The triple (p, q, g) is published Fig. 8. The Schnorr signature scheme.
17 Security Arguments for Digital Signatures and Blind Signatures 377 together with a public hash function f whose output domain is identified to (Z/qZ). The security parameter k is then equal to log q, whereas the size of the public key, denoted by n, is equal to log p. Furthermore, we assume that k log n. Any user randomly chooses his secret key x in (Z/qZ), and publishes y = g x mod p. In order to sign a message m, the user chooses a random element K in (Z/qZ) and computes the commitment r = g K mod p. He gets the challenge e = f (m, r) and computes s = K + xemod q. The signature is the triple (r, e, s), which satisfies the tests r? = g s y e mod p and e? = f (m, r). Theorem 11. Assume that, within a time bound T, an attacker A performs an existential forgery under a no-message attack against the Schnorr signature, with probability ε 7Q/q. We denote by Q the number of queries that A can ask to the random oracle. Then the discrete logarithm in subgroups of prime order can be solved in expected time less than 84480QT/ε. Proof. As we have previously seen, this scheme satisfies all the required properties of a generic signature scheme. From the Forking Lemma (Theorem 10), after a polynomial replay of the attacker A, we obtain two valid signatures (m, r, e, s) and (m, r, e, s ) with e e. Then we have the following equalities, r = g s y e mod p and r = g s y e mod p, from which we obtain the discrete logarithm log g y = (s s )/(e e) mod q Adaptively Chosen-Message Attacks We now focus on the adaptively chosen-message scenario. As in the previous section, we first give a generic result and we apply the technique to the Schnorr signature scheme Generic Results As was previously observed, in a no-message scenario, only the least powerful kind of adversaries is assumed to attack the signature scheme. For many applications, resistance to this type attack is not considered sufficient. If we want to assess the security of a signature scheme, we should prove its resistance against adaptively chosen-message attacks. In such a scenario, the attacker uses the signer as an oracle, and asks any signature he wants. If it is possible to simulate the signer by a simulator S who does not know the secret key (see Fig. 9), then we can make the attacker and the simulator collude in order to break the signature scheme, and, the same way as before, we can obtain two distinct signatures with a suitable relation. Lemma 12. Let A be a probabilistic polynomial time Turing machine whose input only consists of public data. We denote respectively by Q and R the number of queries that A can ask to the random oracle and the number of queries that A can ask to the signer. Assume that, within a time bound T, A produces, with probability ε 10(R + 1)(R + Q)/2 k, a valid signature (m,σ 1, h,σ 2 ). If the triples (σ 1, h,σ 2 ) can be simulated without knowing the secret key, with an indistinguishable distribution probability, then a replay of the attacker A, where interactions with the signer are simulated, outputs two valid
18 378 D. Pointcheval and J. Stern Fig. 9. Adaptively chosen message scenario. signatures (m,σ 1, h,σ 2 ) and (m,σ 1, h,σ 2 ) such that h h, within time T 23QT/ε and with probability ε 1 9. Proof. As in the previous proof, we let Q 1,..., Q Q denote the Q distinct queries to the random oracle, ρ 1,..., ρ Q the respective answers, and m 1,..., m R the R queries (possibly all the same) to the signing oracle. Using the simulator, we can simulate the answers of the signer without knowledge of the secret key. For a message m i, the simulator answers a triple (σ (i) 1, h(i),σ (i) 2 ). Then the attacker assumes that f (m i,σ (i) 1 ) = h(i) and stores it. The previous proof can be exactly mimicked, except for the problem added by the simulations: there is some risk of collisions of queries, or supposed queries, to the random oracle. Recall that in the definition of generic digital signature schemes, we made the assumption that the probability for a commitment σ (i) 1 to be output by the signing oracle is less than 2/2 k. Then two kinds of collisions can appear: A pair (m i,σ (i) 1 ) that the simulator outputs also appears in the list of questions asked to the random oracle by the attacker (some question Q j ). The probability of such an event is less than QR 2/2 k ε/5. A pair (m i,σ (i) 1 ) that the simulator outputs is exactly similar to another pair produced by this simulator (some question (m j,σ ( j) 1 )). The probability of such an event is less than R 2 /2 2/2 k ε/10. Altogether, the probability of collisions is less than 3ε/10. Therefore, Pr [A succeeds and no-collisions] ω, f 3 Pr [A succeeds] Pr [collisions] ε(1 ω, f ω, f 10 ) 7ε/10. This is clearly greater than 7Q/2 k. We can then apply the previous Forking Lemma (Lemma 8). Such a replay succeeds with probability ε 1 9, within time T 16QT 10/7ε 23QT/ε.
19 Security Arguments for Digital Signatures and Blind Signatures 379 Theorem 13 (The Forking Lemma). Let A be a probabilistic polynomial time Turing machine whose input only consists of public data. We denote respectively by Q and R the number of queries that A can ask to the random oracle and the number of queries that A can ask to the signer. Assume that, within a time bound T, A produces, with probability ε 10(R + 1)(R + Q)/2 k, a valid signature (m,σ 1, h,σ 2 ). If the triples (σ 1, h,σ 2 ) can be simulated without knowing the secret key, with an indistinguishable distribution probability, then there is another machine which has control over the machine obtained from A replacing interaction with the signer by simulation and produces two valid signatures (m,σ 1, h,σ 2 ) and (m,σ 1, h,σ 2 ) such that h h in expected time T QT/ε. Proof. The collusion of the attacker A and the simulator S defines a machine B which performs a no-message attack. An execution of B is successful if it outputs a forgery, and if there is no collisions of queries to the random oracle during the process. Then, within a time bound T, B has a probability of success greater than 7ε/10 7Q/2 k. Using Theorem 10, within an expected number of steps bounded by 84480Q/(7ε/10), one can provide two valid signatures Application to the Schnorr Digital Signature Scheme Theorem 14. Let A be an attacker which performs, within a time bound T, an existential forgery under an adaptively chosen-message attack against the Schnorr signature, with probability ε. We denote respectively by Q and R the number of queries that A can ask to the random oracle and the number of queries that A can ask to the signing oracle. Assume that ε 10(R + 1)(R + Q)/q, then the discrete logarithm in subgroups of prime order can be solved within expected time less than QT/ε. Proof. We only have to prove that the triples (r, e, s) produced by the signer and the random oracle can be simulated without the knowledge of the signer s secret. Once this is done, the result directly follows from Theorem 13, using the same proof as for Theorem 11. Lemma 15. The following distributions are the same: K R (Z/qZ) δ = (r, e, s) e R Z/qZ r = g K and δ = (r, e, s) mod p s = K + xemod q K R Z/qZ e R Z/qZ s = K r = g s y e mod p r 1 mod p. Proof. First we choose a triple (ε,β,γ)from the set of the signatures: let ε (Z/pZ), γ Z/qZ, and β Z/qZ such that g γ y β = ε 1 mod p. We then compute the probability of appearance of this triple following each distribution of probabilities: Pr δ [(r, e, s) = (ε,β,γ)] = Pr K 0,e [ ] g K = ε; e = β = K + xe = γ 1 q(q 1),
20 380 D. Pointcheval and J. Stern [ ] ε = r = g Pr[(r, e, s) = (ε,β,γ)] = Pr K y e δ r,e e = β; s = K = γ r 1 mod p 1 = q(q 1). From the above, the following simulator S produces triples (r, e, s) with an identical distribution from those produced by the signer. In order to sign the message m, S randomly chooses e Z/qZ and K R Z/qZ, and sets r = g K y e mod p and s = K. In the (unlikely) situation where r = 1 mod p, we discard the results and restart the simulation. Then it returns the triple (r, e, s) Further Results It is clear that identical results can be obtained for any signature scheme which is the transformation of a honest-verifier zero-knowledge identification protocol, and a fortiori of the parallelization of a zero-knowledge identification protocol (Fiat Shamir [21], Guillou Quisquater [30], the Permuted Kernel Problem [53], the Syndrome Decoding problem [54], the Constrained Linear Equations [55], the Permuted Perceptrons Problem [41], etc.). In fact, the zero-knowledge property is exactly what we need for our notion of simulation. For each of these schemes, existential forgery under an adaptively chosen-message attack in the random oracle model is equivalent to the mathematical problem on which the identification scheme relies. Furthermore, our results may also provide security arguments for other schemes. In the following section we study a signature scheme of the El Gamal type Application to the El Gamal Signature Scheme The original El Gamal signature scheme [17] was proposed in 1985 but its security was never proved equivalent to the discrete logarithm problem nor to the Diffie Hellman problem. As will be seen, the Forking Lemma provides a security argument for a very slight variant of this scheme The Original Scheme Description of the original scheme. We begin with a description of the original scheme [17], where k denotes, as usual, the security parameter: The key generation algorithm: it chooses a random large prime p, of length n polynomial in k, and a generator g of (Z/pZ), both public. Then, for a random secret key x Z/(p 1)Z, it computes the public key y = g x mod p. The signature algorithm: in order to sign a message m, one generates a pair (r, s) such that g m = y r r s mod p. To achieve this aim, one has to choose a random K (Z/(p 1)Z), to compute the exponentiation r = g K mod p and finally to solve the linear equation m = xr + Ksmod(p 1). The algorithm finally outputs (r, s). The verification algorithm checks both 1 < r < p and g m = y r r s mod p.
21 Security Arguments for Digital Signatures and Blind Signatures 381 Security. As already seen in the original paper, one cannot show that the scheme is fully secure because it is subject to existential forgery. Theorem 16. The original El Gamal signature scheme is existentially forgeable. Proof. This is a well-known result, but we describe two levels of forgeries: 1. The one-parameter forgery: let e R Z/(p 1)Z, ifweletr = g e y mod p and s = r mod p 1, it is easy to see that (r, s) is a valid signature for the message m = es mod p The two-parameter forgery: let e R Z/(p 1)Z and v R (Z/(p 1)Z),ifwe let r = g e y v mod p and s = rv 1 mod p 1, then (r, s) is a valid signature for the message m = es mod p 1. We now slightly modify the original scheme by using a hash function The Modified El Gamal Signature Scheme MEG In this variant we replace m by the hash value of the entire part of the computation bound not to change, once the commitment has been computed, namely, f (m, r), where f is a public hash function which outputs k-bit long elements. Definition 17. Let α be a fixed real. An α-hard prime number p is such that the factorization of p 1 yields p 1 = qrwith q prime and R p α, where p denotes the length of the integer p. Remark. Those prime moduli are precisely those used for cryptographic applications of the discrete logarithm problem. We describe the Modified El Gamal Signature Scheme: The key generation algorithm: it chooses a random large α-hard prime p, greater than 2 k, of length n polynomial in k. It also randomly chooses a generator g of (Z/pZ). They are both published. Then, for a random secret key x Z/(p 1)Z, it computes the public key y = g x mod p. The signature algorithm: in order to sign a message m, one generates a pair (r, s) such that g f (m,r) = y r r s mod p. To achieve this aim, one generates K and r the same way as before and solves the linear equation f (m, r) = xr + Ksmod(p 1). The algorithm outputs (r, f (m, r), s). The verification algorithm checks the signature equation with the obvious changes due to the hash function Security Results In this section we see that the above modification allows us to offer security arguments for the resulting scheme even against an adaptively chosen-message attack, at least for a large variety of moduli.
Security Proofs for Signature Schemes. Ecole Normale Superieure. 45, rue d'ulm Paris Cedex 05
 Security Proofs for Signature Schemes David Pointcheval David.Pointcheval@ens.fr Jacques Stern Jacques.Stern@ens.fr Ecole Normale Superieure Laboratoire d'informatique 45, rue d'ulm 75230 Paris Cedex 05
Security Proofs for Signature Schemes David Pointcheval David.Pointcheval@ens.fr Jacques Stern Jacques.Stern@ens.fr Ecole Normale Superieure Laboratoire d'informatique 45, rue d'ulm 75230 Paris Cedex 05
Outline. Provable Security in the Computational Model. III Signatures. Public-Key Encryption. Outline. David Pointcheval.
 Provable Security in the Computational Model III Signatures David Pointcheval Ecole normale supérieure, CNRS & INRI Public-Key Encryption Signatures 2 dvanced Security for Signature dvanced Security Notions
Provable Security in the Computational Model III Signatures David Pointcheval Ecole normale supérieure, CNRS & INRI Public-Key Encryption Signatures 2 dvanced Security for Signature dvanced Security Notions
Lecture 16 Chiu Yuen Koo Nikolai Yakovenko. 1 Digital Signature Schemes. CMSC 858K Advanced Topics in Cryptography March 18, 2004
 CMSC 858K Advanced Topics in Cryptography March 18, 2004 Lecturer: Jonathan Katz Lecture 16 Scribe(s): Chiu Yuen Koo Nikolai Yakovenko Jeffrey Blank 1 Digital Signature Schemes In this lecture, we introduce
CMSC 858K Advanced Topics in Cryptography March 18, 2004 Lecturer: Jonathan Katz Lecture 16 Scribe(s): Chiu Yuen Koo Nikolai Yakovenko Jeffrey Blank 1 Digital Signature Schemes In this lecture, we introduce
From Fixed-Length to Arbitrary-Length RSA Encoding Schemes Revisited
 From Fixed-Length to Arbitrary-Length RSA Encoding Schemes Revisited Julien Cathalo 1, Jean-Sébastien Coron 2, and David Naccache 2,3 1 UCL Crypto Group Place du Levant 3, Louvain-la-Neuve, B-1348, Belgium
From Fixed-Length to Arbitrary-Length RSA Encoding Schemes Revisited Julien Cathalo 1, Jean-Sébastien Coron 2, and David Naccache 2,3 1 UCL Crypto Group Place du Levant 3, Louvain-la-Neuve, B-1348, Belgium
Foundations of Cryptography
 - 111 - Foundations of Cryptography Notes of lecture No. 10B & 11 (given on June 11 & 18, 1989) taken by Sergio Rajsbaum Summary In this lecture we define unforgeable digital signatures and present such
- 111 - Foundations of Cryptography Notes of lecture No. 10B & 11 (given on June 11 & 18, 1989) taken by Sergio Rajsbaum Summary In this lecture we define unforgeable digital signatures and present such
Design Validations for Discrete Logarithm Based Signature Schemes
 Proceedings of the 2000 International Workshop on Practice and Theory in Public Key Cryptography (PKC 2000) (18 20 january 2000, Melbourne, Australia) H. Imai and Y. Zheng Eds. Springer-Verlag, LNCS 1751,
Proceedings of the 2000 International Workshop on Practice and Theory in Public Key Cryptography (PKC 2000) (18 20 january 2000, Melbourne, Australia) H. Imai and Y. Zheng Eds. Springer-Verlag, LNCS 1751,
ECash and Anonymous Credentials
 ECash and Anonymous Credentials CS/ECE 598MAN: Applied Cryptography Nikita Borisov November 9, 2009 1 E-cash Chaum s E-cash Offline E-cash 2 Anonymous Credentials e-cash-based Credentials Brands Credentials
ECash and Anonymous Credentials CS/ECE 598MAN: Applied Cryptography Nikita Borisov November 9, 2009 1 E-cash Chaum s E-cash Offline E-cash 2 Anonymous Credentials e-cash-based Credentials Brands Credentials
Schnorr Signature. Schnorr Signature. October 31, 2012
 . October 31, 2012 Table of contents Salient Features Preliminaries Security Proofs Random Oracle Heuristic PKS and its Security Models Hardness Assumption The Construction Oracle Replay Attack Security
. October 31, 2012 Table of contents Salient Features Preliminaries Security Proofs Random Oracle Heuristic PKS and its Security Models Hardness Assumption The Construction Oracle Replay Attack Security
Lecture 1: Introduction to Public key cryptography
 Lecture 1: Introduction to Public key cryptography Thomas Johansson T. Johansson (Lund University) 1 / 44 Key distribution Symmetric key cryptography: Alice and Bob share a common secret key. Some means
Lecture 1: Introduction to Public key cryptography Thomas Johansson T. Johansson (Lund University) 1 / 44 Key distribution Symmetric key cryptography: Alice and Bob share a common secret key. Some means
Introduction to Cryptography Lecture 13
 Introduction to Cryptography Lecture 13 Benny Pinkas June 5, 2011 Introduction to Cryptography, Benny Pinkas page 1 Electronic cash June 5, 2011 Introduction to Cryptography, Benny Pinkas page 2 Simple
Introduction to Cryptography Lecture 13 Benny Pinkas June 5, 2011 Introduction to Cryptography, Benny Pinkas page 1 Electronic cash June 5, 2011 Introduction to Cryptography, Benny Pinkas page 2 Simple
Katz, Lindell Introduction to Modern Cryptrography
 Katz, Lindell Introduction to Modern Cryptrography Slides Chapter 12 Markus Bläser, Saarland University Digital signature schemes Goal: integrity of messages Signer signs a message using a private key
Katz, Lindell Introduction to Modern Cryptrography Slides Chapter 12 Markus Bläser, Saarland University Digital signature schemes Goal: integrity of messages Signer signs a message using a private key
18734: Foundations of Privacy. Anonymous Cash. Anupam Datta. CMU Fall 2018
 18734: Foundations of Privacy Anonymous Cash Anupam Datta CMU Fall 2018 Today: Electronic Cash Goals Alice can ask for Bank to issue coins from her account. Alice can spend coins. Bank cannot track what
18734: Foundations of Privacy Anonymous Cash Anupam Datta CMU Fall 2018 Today: Electronic Cash Goals Alice can ask for Bank to issue coins from her account. Alice can spend coins. Bank cannot track what
Transitive Signatures Based on Non-adaptive Standard Signatures
 Transitive Signatures Based on Non-adaptive Standard Signatures Zhou Sujing Nanyang Technological University, Singapore, zhousujing@pmail.ntu.edu.sg Abstract. Transitive signature, motivated by signing
Transitive Signatures Based on Non-adaptive Standard Signatures Zhou Sujing Nanyang Technological University, Singapore, zhousujing@pmail.ntu.edu.sg Abstract. Transitive signature, motivated by signing
Cryptographic e-cash. Jan Camenisch. IBM Research ibm.biz/jancamenisch. IACR Summerschool Blockchain Technologies
 IACR Summerschool Blockchain Technologies Cryptographic e-cash Jan Camenisch IBM Research Zurich @JanCamenisch ibm.biz/jancamenisch ecash scenario & requirements Bank Withdrawal User Spend Deposit Merchant
IACR Summerschool Blockchain Technologies Cryptographic e-cash Jan Camenisch IBM Research Zurich @JanCamenisch ibm.biz/jancamenisch ecash scenario & requirements Bank Withdrawal User Spend Deposit Merchant
Group Undeniable Signatures
 Group Undeniable Signatures YUH-DAUH LYUU Department of Computer Science & Information Engineering and Department of Finance National Taiwan University No 1, Sec 4, Roosevelt Rd, Taipei, Taiwan lyuu@csie.ntu.edu.tw
Group Undeniable Signatures YUH-DAUH LYUU Department of Computer Science & Information Engineering and Department of Finance National Taiwan University No 1, Sec 4, Roosevelt Rd, Taipei, Taiwan lyuu@csie.ntu.edu.tw
Blind Signature Protocol Based on Difficulty of. Simultaneous Solving Two Difficult Problems
 Applied Mathematical Sciences, Vol. 6, 202, no. 39, 6903-690 Blind Signature Protocol Based on Difficulty of Simultaneous Solving Two Difficult Problems N. H. Minh, D. V. Binh 2, N. T. Giang 3 and N. A.
Applied Mathematical Sciences, Vol. 6, 202, no. 39, 6903-690 Blind Signature Protocol Based on Difficulty of Simultaneous Solving Two Difficult Problems N. H. Minh, D. V. Binh 2, N. T. Giang 3 and N. A.
Digital Signatures from Challenge-Divided Σ-Protocols
 Digital Signatures from Challenge-Divided Σ-Protocols Andrew C. Yao Yunlei Zhao Abstract Digital signature is one of the basic primitives in cryptography. A common paradigm of obtaining signatures, known
Digital Signatures from Challenge-Divided Σ-Protocols Andrew C. Yao Yunlei Zhao Abstract Digital signature is one of the basic primitives in cryptography. A common paradigm of obtaining signatures, known
1 Number Theory Basics
 ECS 289M (Franklin), Winter 2010, Crypto Review 1 Number Theory Basics This section has some basic facts about number theory, mostly taken (or adapted) from Dan Boneh s number theory fact sheets for his
ECS 289M (Franklin), Winter 2010, Crypto Review 1 Number Theory Basics This section has some basic facts about number theory, mostly taken (or adapted) from Dan Boneh s number theory fact sheets for his
Group Undeniable Signatures
 Group Undeniable Signatures YUH-DAUH LYUU Dept. of Computer Science & Information Engineering and Dept. of Finance National Taiwan University No 1, Sec 4, Roosevelt Rd, Taipei, Taiwan lyuu@csie.ntu.edu.tw
Group Undeniable Signatures YUH-DAUH LYUU Dept. of Computer Science & Information Engineering and Dept. of Finance National Taiwan University No 1, Sec 4, Roosevelt Rd, Taipei, Taiwan lyuu@csie.ntu.edu.tw
The Gap-Problems: a New Class of Problems for the Security of Cryptographic Schemes
 Proceedings of the 2001 International Workshop on Practice and Theory in Public Key Cryptography (PKC 2001) (13 15 february 2001, Cheju Islands, South Korea) K. Kim Ed. Springer-Verlag, LNCS 1992, pages
Proceedings of the 2001 International Workshop on Practice and Theory in Public Key Cryptography (PKC 2001) (13 15 february 2001, Cheju Islands, South Korea) K. Kim Ed. Springer-Verlag, LNCS 1992, pages
From Fixed-Length Messages to Arbitrary-Length Messages Practical RSA Signature Padding Schemes
 From Fixed-Length Messages to Arbitrary-Length Messages Practical RSA Signature Padding Schemes [Published in D. Naccache, Ed., Topics in Cryptology CT-RSA 2001, vol. 2020 of Lecture Notes in Computer
From Fixed-Length Messages to Arbitrary-Length Messages Practical RSA Signature Padding Schemes [Published in D. Naccache, Ed., Topics in Cryptology CT-RSA 2001, vol. 2020 of Lecture Notes in Computer
Constructing Provably-Secure Identity-Based Signature Schemes
 Constructing Provably-Secure Identity-Based Signature Schemes Chethan Kamath Indian Institute of Science, Bangalore November 23, 2013 Overview Table of contents Background Formal Definitions Schnorr Signature
Constructing Provably-Secure Identity-Based Signature Schemes Chethan Kamath Indian Institute of Science, Bangalore November 23, 2013 Overview Table of contents Background Formal Definitions Schnorr Signature
Secure and Practical Identity-Based Encryption
 Secure and Practical Identity-Based Encryption David Naccache Groupe de Cyptographie, Deṕartement d Informatique École Normale Supérieure 45 rue d Ulm, 75005 Paris, France david.nacache@ens.fr Abstract.
Secure and Practical Identity-Based Encryption David Naccache Groupe de Cyptographie, Deṕartement d Informatique École Normale Supérieure 45 rue d Ulm, 75005 Paris, France david.nacache@ens.fr Abstract.
Blind Collective Signature Protocol
 Computer Science Journal of Moldova, vol.19, no.1(55), 2011 Blind Collective Signature Protocol Nikolay A. Moldovyan Abstract Using the digital signature (DS) scheme specified by Belarusian DS standard
Computer Science Journal of Moldova, vol.19, no.1(55), 2011 Blind Collective Signature Protocol Nikolay A. Moldovyan Abstract Using the digital signature (DS) scheme specified by Belarusian DS standard
PAPER An Identification Scheme with Tight Reduction
 IEICE TRANS. FUNDAMENTALS, VOL.Exx A, NO.xx XXXX 200x PAPER An Identification Scheme with Tight Reduction Seiko ARITA, Member and Natsumi KAWASHIMA, Nonmember SUMMARY There are three well-known identification
IEICE TRANS. FUNDAMENTALS, VOL.Exx A, NO.xx XXXX 200x PAPER An Identification Scheme with Tight Reduction Seiko ARITA, Member and Natsumi KAWASHIMA, Nonmember SUMMARY There are three well-known identification
Lecture 22. We first consider some constructions of standard commitment schemes. 2.1 Constructions Based on One-Way (Trapdoor) Permutations
 CMSC 858K Advanced Topics in Cryptography April 20, 2004 Lecturer: Jonathan Katz Lecture 22 Scribe(s): agaraj Anthapadmanabhan, Ji Sun Shin 1 Introduction to These otes In the previous lectures, we saw
CMSC 858K Advanced Topics in Cryptography April 20, 2004 Lecturer: Jonathan Katz Lecture 22 Scribe(s): agaraj Anthapadmanabhan, Ji Sun Shin 1 Introduction to These otes In the previous lectures, we saw
Available online at J. Math. Comput. Sci. 6 (2016), No. 3, ISSN:
 Available online at http://scik.org J. Math. Comput. Sci. 6 (2016), No. 3, 281-289 ISSN: 1927-5307 AN ID-BASED KEY-EXPOSURE FREE CHAMELEON HASHING UNDER SCHNORR SIGNATURE TEJESHWARI THAKUR, BIRENDRA KUMAR
Available online at http://scik.org J. Math. Comput. Sci. 6 (2016), No. 3, 281-289 ISSN: 1927-5307 AN ID-BASED KEY-EXPOSURE FREE CHAMELEON HASHING UNDER SCHNORR SIGNATURE TEJESHWARI THAKUR, BIRENDRA KUMAR
An Anonymous Authentication Scheme for Trusted Computing Platform
 An Anonymous Authentication Scheme for Trusted Computing Platform He Ge Abstract. The Trusted Computing Platform is the industrial initiative to implement computer security. However, privacy protection
An Anonymous Authentication Scheme for Trusted Computing Platform He Ge Abstract. The Trusted Computing Platform is the industrial initiative to implement computer security. However, privacy protection
Lecture 9 Julie Staub Avi Dalal Abheek Anand Gelareh Taban. 1 Introduction. 2 Background. CMSC 858K Advanced Topics in Cryptography February 24, 2004
 CMSC 858K Advanced Topics in Cryptography February 24, 2004 Lecturer: Jonathan Katz Lecture 9 Scribe(s): Julie Staub Avi Dalal Abheek Anand Gelareh Taban 1 Introduction In previous lectures, we constructed
CMSC 858K Advanced Topics in Cryptography February 24, 2004 Lecturer: Jonathan Katz Lecture 9 Scribe(s): Julie Staub Avi Dalal Abheek Anand Gelareh Taban 1 Introduction In previous lectures, we constructed
ECS 189A Final Cryptography Spring 2011
 ECS 127: Cryptography Handout F UC Davis Phillip Rogaway June 9, 2011 ECS 189A Final Cryptography Spring 2011 Hints for success: Good luck on the exam. I don t think it s all that hard (I do believe I
ECS 127: Cryptography Handout F UC Davis Phillip Rogaway June 9, 2011 ECS 189A Final Cryptography Spring 2011 Hints for success: Good luck on the exam. I don t think it s all that hard (I do believe I
CPSC 467b: Cryptography and Computer Security
 CPSC 467b: Cryptography and Computer Security Michael J. Fischer Lecture 10 February 19, 2013 CPSC 467b, Lecture 10 1/45 Primality Tests Strong primality tests Weak tests of compositeness Reformulation
CPSC 467b: Cryptography and Computer Security Michael J. Fischer Lecture 10 February 19, 2013 CPSC 467b, Lecture 10 1/45 Primality Tests Strong primality tests Weak tests of compositeness Reformulation
Some Security Comparisons of GOST R and ECDSA Signature Schemes
 Some Security Comparisons of GOST R 34.10-2012 and ECDSA Signature Schemes Trieu Quang Phong Nguyen Quoc Toan Institute of Cryptography Science and Technology Gover. Info. Security Committee, Viet Nam
Some Security Comparisons of GOST R 34.10-2012 and ECDSA Signature Schemes Trieu Quang Phong Nguyen Quoc Toan Institute of Cryptography Science and Technology Gover. Info. Security Committee, Viet Nam
Optimal Security Reductions for Unique Signatures: Bypassing Impossibilities with A Counterexample
 Optimal Security Reductions for Unique Signatures: Bypassing Impossibilities with A Counterexample Fuchun Guo 1, Rongmao Chen 2, Willy Susilo 1, Jianchang Lai 1, Guomin Yang 1, and Yi Mu 1 1 Institute
Optimal Security Reductions for Unique Signatures: Bypassing Impossibilities with A Counterexample Fuchun Guo 1, Rongmao Chen 2, Willy Susilo 1, Jianchang Lai 1, Guomin Yang 1, and Yi Mu 1 1 Institute
Uncloneable Quantum Money
 1 Institute for Quantum Computing University of Waterloo Joint work with Michele Mosca CQISC 2006 1 Supported by NSERC, Sun Microsystems, CIAR, CFI, CSE, MITACS, ORDCF. Outline Introduction Requirements
1 Institute for Quantum Computing University of Waterloo Joint work with Michele Mosca CQISC 2006 1 Supported by NSERC, Sun Microsystems, CIAR, CFI, CSE, MITACS, ORDCF. Outline Introduction Requirements
Convertible Group Undeniable Signatures
 Convertible Group Undeniable Signatures Yuh-Dauh Lyuu 1 and Ming-Luen Wu 2 1 Dept. of Computer Science & Information Engineering and Dept. of Finance, National Taiwan University, Taiwan lyuu@csie.ntu.edu.tw
Convertible Group Undeniable Signatures Yuh-Dauh Lyuu 1 and Ming-Luen Wu 2 1 Dept. of Computer Science & Information Engineering and Dept. of Finance, National Taiwan University, Taiwan lyuu@csie.ntu.edu.tw
George Danezis Microsoft Research, Cambridge, UK
 George Danezis Microsoft Research, Cambridge, UK Identity as a proxy to check credentials Username decides access in Access Control Matrix Sometime it leaks too much information Real world examples Tickets
George Danezis Microsoft Research, Cambridge, UK Identity as a proxy to check credentials Username decides access in Access Control Matrix Sometime it leaks too much information Real world examples Tickets
Digital Signature Schemes and the Random Oracle Model. A. Hülsing
 Digital Signature Schemes and the Random Oracle Model A. Hülsing Today s goal Review provable security of in use signature schemes. (PKCS #1 v2.x) PAGE 1 Digital Signature Source: http://hari-cio-8a.blog.ugm.ac.id/files/2013/03/dsa.jpg
Digital Signature Schemes and the Random Oracle Model A. Hülsing Today s goal Review provable security of in use signature schemes. (PKCS #1 v2.x) PAGE 1 Digital Signature Source: http://hari-cio-8a.blog.ugm.ac.id/files/2013/03/dsa.jpg
Lecture 4 Chiu Yuen Koo Nikolai Yakovenko. 1 Summary. 2 Hybrid Encryption. CMSC 858K Advanced Topics in Cryptography February 5, 2004
 CMSC 858K Advanced Topics in Cryptography February 5, 2004 Lecturer: Jonathan Katz Lecture 4 Scribe(s): Chiu Yuen Koo Nikolai Yakovenko Jeffrey Blank 1 Summary The focus of this lecture is efficient public-key
CMSC 858K Advanced Topics in Cryptography February 5, 2004 Lecturer: Jonathan Katz Lecture 4 Scribe(s): Chiu Yuen Koo Nikolai Yakovenko Jeffrey Blank 1 Summary The focus of this lecture is efficient public-key
Dr George Danezis University College London, UK
 Dr George Danezis University College London, UK Identity as a proxy to check credentials Username decides access in Access Control Matrix Sometime it leaks too much information Real world examples Tickets
Dr George Danezis University College London, UK Identity as a proxy to check credentials Username decides access in Access Control Matrix Sometime it leaks too much information Real world examples Tickets
Designing Identification Schemes with Keys of Short Size *.
 Designing Identification Schemes with Keys of Short Size *. Jacques Stern Laboratoire d hformatique, kcole Normale SupCrieure Abstract. In the last few years, therc have been several attempts to build
Designing Identification Schemes with Keys of Short Size *. Jacques Stern Laboratoire d hformatique, kcole Normale SupCrieure Abstract. In the last few years, therc have been several attempts to build
Outline. The Game-based Methodology for Computational Security Proofs. Public-Key Cryptography. Outline. Introduction Provable Security
 The Game-based Methodology for Computational s David Pointcheval Ecole normale supérieure, CNRS & INRIA Computational and Symbolic Proofs of Security Atagawa Heights Japan April 6th, 2009 1/39 2/39 Public-Key
The Game-based Methodology for Computational s David Pointcheval Ecole normale supérieure, CNRS & INRIA Computational and Symbolic Proofs of Security Atagawa Heights Japan April 6th, 2009 1/39 2/39 Public-Key
Provable security. Michel Abdalla
 Lecture 1: Provable security Michel Abdalla École normale supérieure & CNRS Cryptography Main goal: Enable secure communication in the presence of adversaries Adversary Sender 10110 10110 Receiver Only
Lecture 1: Provable security Michel Abdalla École normale supérieure & CNRS Cryptography Main goal: Enable secure communication in the presence of adversaries Adversary Sender 10110 10110 Receiver Only
Digital Signatures. Adam O Neill based on
 Digital Signatures Adam O Neill based on http://cseweb.ucsd.edu/~mihir/cse207/ Signing by hand COSMO ALICE ALICE Pay Bob $100 Cosmo Alice Alice Bank =? no Don t yes pay Bob Signing electronically SIGFILE
Digital Signatures Adam O Neill based on http://cseweb.ucsd.edu/~mihir/cse207/ Signing by hand COSMO ALICE ALICE Pay Bob $100 Cosmo Alice Alice Bank =? no Don t yes pay Bob Signing electronically SIGFILE
A New Identification Scheme Based on the Perceptrons Problem
 Advances in Cryptology Proceedings of EUROCRYPT 95 (may 21 25, 1995, Saint-Malo, France) L.C. Guillou and J.-J. Quisquater, Eds. Springer-Verlag, LNCS 921, pages 319 328. A New Identification Scheme Based
Advances in Cryptology Proceedings of EUROCRYPT 95 (may 21 25, 1995, Saint-Malo, France) L.C. Guillou and J.-J. Quisquater, Eds. Springer-Verlag, LNCS 921, pages 319 328. A New Identification Scheme Based
Strongly Unforgeable Signatures Based on Computational Diffie-Hellman
 Strongly Unforgeable Signatures Based on Computational Diffie-Hellman Dan Boneh 1, Emily Shen 1, and Brent Waters 2 1 Computer Science Department, Stanford University, Stanford, CA {dabo,emily}@cs.stanford.edu
Strongly Unforgeable Signatures Based on Computational Diffie-Hellman Dan Boneh 1, Emily Shen 1, and Brent Waters 2 1 Computer Science Department, Stanford University, Stanford, CA {dabo,emily}@cs.stanford.edu
Cryptographic Protocols Notes 2
 ETH Zurich, Department of Computer Science SS 2018 Prof. Ueli Maurer Dr. Martin Hirt Chen-Da Liu Zhang Cryptographic Protocols Notes 2 Scribe: Sandro Coretti (modified by Chen-Da Liu Zhang) About the notes:
ETH Zurich, Department of Computer Science SS 2018 Prof. Ueli Maurer Dr. Martin Hirt Chen-Da Liu Zhang Cryptographic Protocols Notes 2 Scribe: Sandro Coretti (modified by Chen-Da Liu Zhang) About the notes:
A Fair and Efficient Solution to the Socialist Millionaires Problem
 In Discrete Applied Mathematics, 111 (2001) 23 36. (Special issue on coding and cryptology) A Fair and Efficient Solution to the Socialist Millionaires Problem Fabrice Boudot a Berry Schoenmakers b Jacques
In Discrete Applied Mathematics, 111 (2001) 23 36. (Special issue on coding and cryptology) A Fair and Efficient Solution to the Socialist Millionaires Problem Fabrice Boudot a Berry Schoenmakers b Jacques
Tightly-Secure Signatures From Lossy Identification Schemes
 Tightly-Secure Signatures From Lossy Identification Schemes Michel Abdalla, Pierre-Alain Fouque, Vadim Lyubashevsky, and Mehdi Tibouchi 2 École normale supérieure {michel.abdalla,pierre-alain.fouque,vadim.lyubashevsky}@ens.fr
Tightly-Secure Signatures From Lossy Identification Schemes Michel Abdalla, Pierre-Alain Fouque, Vadim Lyubashevsky, and Mehdi Tibouchi 2 École normale supérieure {michel.abdalla,pierre-alain.fouque,vadim.lyubashevsky}@ens.fr
Divisible E-cash Made Practical
 Divisible E-cash Made Practical Sébastien Canard (1), David Pointcheval (2), Olivier Sanders (1,2) and Jacques Traoré (1) (1) Orange Labs, Caen, France (2) École Normale Supérieure, CNRS & INRIA, Paris,
Divisible E-cash Made Practical Sébastien Canard (1), David Pointcheval (2), Olivier Sanders (1,2) and Jacques Traoré (1) (1) Orange Labs, Caen, France (2) École Normale Supérieure, CNRS & INRIA, Paris,
Lecture 10: Zero-Knowledge Proofs
 Lecture 10: Zero-Knowledge Proofs Introduction to Modern Cryptography Benny Applebaum Tel-Aviv University Fall Semester, 2011 12 Some of these slides are based on note by Boaz Barak. Quo vadis? Eo Romam
Lecture 10: Zero-Knowledge Proofs Introduction to Modern Cryptography Benny Applebaum Tel-Aviv University Fall Semester, 2011 12 Some of these slides are based on note by Boaz Barak. Quo vadis? Eo Romam
On the (In)security of the Fiat-Shamir Paradigm
 On the (In)security of the Fiat-Shamir Paradigm Shafi Goldwasser Yael Tauman February 2, 2004 Abstract In 1986, Fiat and Shamir proposed a general method for transforming secure 3-round public-coin identification
On the (In)security of the Fiat-Shamir Paradigm Shafi Goldwasser Yael Tauman February 2, 2004 Abstract In 1986, Fiat and Shamir proposed a general method for transforming secure 3-round public-coin identification
Provable Security for Public-Key Schemes. Outline. I Basics. Secrecy of Communications. Outline. David Pointcheval
 Provable Security for Public-Key Schemes I Basics David Pointcheval Ecole normale supérieure, CNRS & INRIA IACR-SEAMS School Cryptographie: Foundations and New Directions November 2016 Hanoi Vietnam Introduction
Provable Security for Public-Key Schemes I Basics David Pointcheval Ecole normale supérieure, CNRS & INRIA IACR-SEAMS School Cryptographie: Foundations and New Directions November 2016 Hanoi Vietnam Introduction
A Fully-Functional group signature scheme over only known-order group
 A Fully-Functional group signature scheme over only known-order group Atsuko Miyaji and Kozue Umeda 1-1, Asahidai, Tatsunokuchi, Nomi, Ishikawa, 923-1292, Japan {kozueu, miyaji}@jaist.ac.jp Abstract. The
A Fully-Functional group signature scheme over only known-order group Atsuko Miyaji and Kozue Umeda 1-1, Asahidai, Tatsunokuchi, Nomi, Ishikawa, 923-1292, Japan {kozueu, miyaji}@jaist.ac.jp Abstract. The
Ring Group Signatures
 Ring Group Signatures Liqun Chen Hewlett-Packard Laboratories, Long Down Avenue, Stoke Gifford, Bristol, BS34 8QZ, United Kingdom. liqun.chen@hp.com Abstract. In many applications of group signatures,
Ring Group Signatures Liqun Chen Hewlett-Packard Laboratories, Long Down Avenue, Stoke Gifford, Bristol, BS34 8QZ, United Kingdom. liqun.chen@hp.com Abstract. In many applications of group signatures,
1 What are Physical Attacks. 2 Physical Attacks on RSA. Today:
 Today: Introduction to the class. Examples of concrete physical attacks on RSA A computational approach to cryptography Pseudorandomness 1 What are Physical Attacks Tampering/Leakage attacks Issue of how
Today: Introduction to the class. Examples of concrete physical attacks on RSA A computational approach to cryptography Pseudorandomness 1 What are Physical Attacks Tampering/Leakage attacks Issue of how
Cryptographical Security in the Quantum Random Oracle Model
 Cryptographical Security in the Quantum Random Oracle Model Center for Advanced Security Research Darmstadt (CASED) - TU Darmstadt, Germany June, 21st, 2012 This work is licensed under a Creative Commons
Cryptographical Security in the Quantum Random Oracle Model Center for Advanced Security Research Darmstadt (CASED) - TU Darmstadt, Germany June, 21st, 2012 This work is licensed under a Creative Commons
An Introduction to Probabilistic Encryption
 Osječki matematički list 6(2006), 37 44 37 An Introduction to Probabilistic Encryption Georg J. Fuchsbauer Abstract. An introduction to probabilistic encryption is given, presenting the first probabilistic
Osječki matematički list 6(2006), 37 44 37 An Introduction to Probabilistic Encryption Georg J. Fuchsbauer Abstract. An introduction to probabilistic encryption is given, presenting the first probabilistic
Lecture Notes. (electronic money/cash) Michael Nüsken b-it. IPEC winter 2008
 Lecture Notes ee (electronic money/cash) Michael Nüsken b-it (Bonn-Aachen International Center for Information Technology) IPEC winter 2008 c 2008 Michael Nüsken Workshop
Lecture Notes ee (electronic money/cash) Michael Nüsken b-it (Bonn-Aachen International Center for Information Technology) IPEC winter 2008 c 2008 Michael Nüsken Workshop
An Efficient ID-based Digital Signature with Message Recovery Based on Pairing
 An Efficient ID-based Digital Signature with Message Recovery Based on Pairing Raylin Tso, Chunxiang Gu, Takeshi Okamoto, and Eiji Okamoto Department of Risk Engineering Graduate School of Systems and
An Efficient ID-based Digital Signature with Message Recovery Based on Pairing Raylin Tso, Chunxiang Gu, Takeshi Okamoto, and Eiji Okamoto Department of Risk Engineering Graduate School of Systems and
Entity Authentication
 Entity Authentication Sven Laur swen@math.ut.ee University of Tartu Formal Syntax Entity authentication pk (sk, pk) Gen α 1 β 1 β i V pk (α 1,...,α i 1 ) α i P sk (β 1,...,β i 1 ) Is it Charlie? α k The
Entity Authentication Sven Laur swen@math.ut.ee University of Tartu Formal Syntax Entity authentication pk (sk, pk) Gen α 1 β 1 β i V pk (α 1,...,α i 1 ) α i P sk (β 1,...,β i 1 ) Is it Charlie? α k The
Delegateable Signature Using Witness Indistinguishable and Witness Hiding Proofs
 Delegateable Signature Using Witness Indistinguishable and Witness Hiding Proofs Chunming Tang 1, Dingyi Pei 1,2 Zhuojun Liu 3 1 Institute of Information Security of Guangzhou University, P.R.China 2 State
Delegateable Signature Using Witness Indistinguishable and Witness Hiding Proofs Chunming Tang 1, Dingyi Pei 1,2 Zhuojun Liu 3 1 Institute of Information Security of Guangzhou University, P.R.China 2 State
Lecture 18 - Secret Sharing, Visual Cryptography, Distributed Signatures
 Lecture 18 - Secret Sharing, Visual Cryptography, Distributed Signatures Boaz Barak November 27, 2007 Quick review of homework 7 Existence of a CPA-secure public key encryption scheme such that oracle
Lecture 18 - Secret Sharing, Visual Cryptography, Distributed Signatures Boaz Barak November 27, 2007 Quick review of homework 7 Existence of a CPA-secure public key encryption scheme such that oracle
Provably Secure Partially Blind Signatures
 Provably Secure Partially Blind Signatures Masayuki ABE and Tatsuaki OKAMOTO NTT Laboratories Nippon Telegraph and Telephone Corporation 1-1 Hikari-no-oka Yokosuka-shi Kanagawa-ken, 239-0847 Japan E-mail:
Provably Secure Partially Blind Signatures Masayuki ABE and Tatsuaki OKAMOTO NTT Laboratories Nippon Telegraph and Telephone Corporation 1-1 Hikari-no-oka Yokosuka-shi Kanagawa-ken, 239-0847 Japan E-mail:
Computational Alternatives to Random Number Generators
 Proceedings of Selected Areas in Cryptography 98 (August 17 18, 1998, Kingston, Ontario, Canada) S. Tavares and H. Meijer Eds. Springer-Verlag, LNCS 1556, pages 72 80. Computational Alternatives to Random
Proceedings of Selected Areas in Cryptography 98 (August 17 18, 1998, Kingston, Ontario, Canada) S. Tavares and H. Meijer Eds. Springer-Verlag, LNCS 1556, pages 72 80. Computational Alternatives to Random
CPSC 467: Cryptography and Computer Security
 CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 11 October 7, 2015 CPSC 467, Lecture 11 1/37 Digital Signature Algorithms Signatures from commutative cryptosystems Signatures from
CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 11 October 7, 2015 CPSC 467, Lecture 11 1/37 Digital Signature Algorithms Signatures from commutative cryptosystems Signatures from
An Identification Scheme Based on KEA1 Assumption
 All rights are reserved and copyright of this manuscript belongs to the authors. This manuscript has been published without reviewing and editing as received from the authors: posting the manuscript to
All rights are reserved and copyright of this manuscript belongs to the authors. This manuscript has been published without reviewing and editing as received from the authors: posting the manuscript to
1 Cryptographic hash functions
 CSCI 5440: Cryptography Lecture 6 The Chinese University of Hong Kong 24 October 2012 1 Cryptographic hash functions Last time we saw a construction of message authentication codes (MACs) for fixed-length
CSCI 5440: Cryptography Lecture 6 The Chinese University of Hong Kong 24 October 2012 1 Cryptographic hash functions Last time we saw a construction of message authentication codes (MACs) for fixed-length
Provable Security Proofs and their Interpretation in the Real World
 Provable Security Proofs and their Interpretation in the Real World Vikram Singh Abstract This paper analyses provable security proofs, using the EDL signature scheme as its case study, and interprets
Provable Security Proofs and their Interpretation in the Real World Vikram Singh Abstract This paper analyses provable security proofs, using the EDL signature scheme as its case study, and interprets
Winter 2008 Introduction to Modern Cryptography Benny Chor and Rani Hod. Assignment #2
 0368.3049.01 Winter 2008 Introduction to Modern Cryptography Benny Chor and Rani Hod Assignment #2 Published Sunday, February 17, 2008 and very slightly revised Feb. 18. Due Tues., March 4, in Rani Hod
0368.3049.01 Winter 2008 Introduction to Modern Cryptography Benny Chor and Rani Hod Assignment #2 Published Sunday, February 17, 2008 and very slightly revised Feb. 18. Due Tues., March 4, in Rani Hod
Privacy and Computer Science (ECI 2015) Day 4 - Zero Knowledge Proofs Mathematics
 Privacy and Computer Science (ECI 2015) Day 4 - Zero Knowledge Proofs Mathematics F. Prost Frederic.Prost@ens-lyon.fr Ecole Normale Supérieure de Lyon July 2015 F. Prost Frederic.Prost@ens-lyon.fr (Ecole
Privacy and Computer Science (ECI 2015) Day 4 - Zero Knowledge Proofs Mathematics F. Prost Frederic.Prost@ens-lyon.fr Ecole Normale Supérieure de Lyon July 2015 F. Prost Frederic.Prost@ens-lyon.fr (Ecole
Digital signature schemes
 Digital signature schemes Martin Stanek Department of Computer Science Comenius University stanek@dcs.fmph.uniba.sk Cryptology 1 (2017/18) Content Introduction digital signature scheme security of digital
Digital signature schemes Martin Stanek Department of Computer Science Comenius University stanek@dcs.fmph.uniba.sk Cryptology 1 (2017/18) Content Introduction digital signature scheme security of digital
Zero-Knowledge Proofs and Protocols
 Seminar: Algorithms of IT Security and Cryptography Zero-Knowledge Proofs and Protocols Nikolay Vyahhi June 8, 2005 Abstract A proof is whatever convinces me. Shimon Even, 1978. Zero-knowledge proof is
Seminar: Algorithms of IT Security and Cryptography Zero-Knowledge Proofs and Protocols Nikolay Vyahhi June 8, 2005 Abstract A proof is whatever convinces me. Shimon Even, 1978. Zero-knowledge proof is
Homework 3 Solutions
 5233/IOC5063 Theory of Cryptology, Fall 205 Instructor Prof. Wen-Guey Tzeng Homework 3 Solutions 7-Dec-205 Scribe Amir Rezapour. Consider an unfair coin with head probability 0.5. Assume that the coin
5233/IOC5063 Theory of Cryptology, Fall 205 Instructor Prof. Wen-Guey Tzeng Homework 3 Solutions 7-Dec-205 Scribe Amir Rezapour. Consider an unfair coin with head probability 0.5. Assume that the coin
Lecture V : Public Key Cryptography
 Lecture V : Public Key Cryptography Internet Security: Principles & Practices John K. Zao, PhD (Harvard) SMIEEE Amir Rezapoor Computer Science Department, National Chiao Tung University 2 Outline Functional
Lecture V : Public Key Cryptography Internet Security: Principles & Practices John K. Zao, PhD (Harvard) SMIEEE Amir Rezapoor Computer Science Department, National Chiao Tung University 2 Outline Functional
Introduction to Modern Cryptography Lecture 11
 Introduction to Modern Cryptography Lecture 11 January 10, 2017 Instructor: Benny Chor Teaching Assistant: Orit Moskovich School of Computer Science Tel-Aviv University Fall Semester, 2016 17 Tuesday 12:00
Introduction to Modern Cryptography Lecture 11 January 10, 2017 Instructor: Benny Chor Teaching Assistant: Orit Moskovich School of Computer Science Tel-Aviv University Fall Semester, 2016 17 Tuesday 12:00
Cryptographic Hardness Assumptions
 Chapter 2 Cryptographic Hardness Assumptions As noted in the previous chapter, it is impossible to construct a digital signature scheme that is secure against an all-powerful adversary. Instead, the best
Chapter 2 Cryptographic Hardness Assumptions As noted in the previous chapter, it is impossible to construct a digital signature scheme that is secure against an all-powerful adversary. Instead, the best
Authentication. Chapter Message Authentication
 Chapter 5 Authentication 5.1 Message Authentication Suppose Bob receives a message addressed from Alice. How does Bob ensure that the message received is the same as the message sent by Alice? For example,
Chapter 5 Authentication 5.1 Message Authentication Suppose Bob receives a message addressed from Alice. How does Bob ensure that the message received is the same as the message sent by Alice? For example,
Evaluation Report on the ECDSA signature scheme
 Evaluation Report on the ECDSA signature scheme Jacques Stern 1 Introduction This document is an evaluation of the ECDSA signature scheme. Our work is based on the analysis of various documents [1, 32,
Evaluation Report on the ECDSA signature scheme Jacques Stern 1 Introduction This document is an evaluation of the ECDSA signature scheme. Our work is based on the analysis of various documents [1, 32,
CS 355: Topics in Cryptography Spring Problem Set 5.
 CS 355: Topics in Cryptography Spring 2018 Problem Set 5 Due: June 8, 2018 at 5pm (submit via Gradescope) Instructions: You must typeset your solution in LaTeX using the provided template: https://crypto.stanford.edu/cs355/homework.tex
CS 355: Topics in Cryptography Spring 2018 Problem Set 5 Due: June 8, 2018 at 5pm (submit via Gradescope) Instructions: You must typeset your solution in LaTeX using the provided template: https://crypto.stanford.edu/cs355/homework.tex
Algorithmic Number Theory and Public-key Cryptography
 Algorithmic Number Theory and Public-key Cryptography Course 3 University of Luxembourg March 22, 2018 The RSA algorithm The RSA algorithm is the most widely-used public-key encryption algorithm Invented
Algorithmic Number Theory and Public-key Cryptography Course 3 University of Luxembourg March 22, 2018 The RSA algorithm The RSA algorithm is the most widely-used public-key encryption algorithm Invented
Group Blind Digital Signatures: A Scalable Solution to Electronic Cash
 Group Blind Digital Signatures: A Scalable Solution to Electronic Cash Anna Lysyanskaya 1 and Zulfikar Ramzan 1 Laboratory for Computer Science, Massachusetts Institute of Technology, Cambridge MA 02139,
Group Blind Digital Signatures: A Scalable Solution to Electronic Cash Anna Lysyanskaya 1 and Zulfikar Ramzan 1 Laboratory for Computer Science, Massachusetts Institute of Technology, Cambridge MA 02139,
Pairing-Based Identification Schemes
 Pairing-Based Identification Schemes David Freeman Information Theory Research HP Laboratories Palo Alto HPL-2005-154 August 24, 2005* public-key cryptography, identification, zero-knowledge, pairings
Pairing-Based Identification Schemes David Freeman Information Theory Research HP Laboratories Palo Alto HPL-2005-154 August 24, 2005* public-key cryptography, identification, zero-knowledge, pairings
Cryptography CS 555. Topic 23: Zero-Knowledge Proof and Cryptographic Commitment. CS555 Topic 23 1
 Cryptography CS 555 Topic 23: Zero-Knowledge Proof and Cryptographic Commitment CS555 Topic 23 1 Outline and Readings Outline Zero-knowledge proof Fiat-Shamir protocol Schnorr protocol Commitment schemes
Cryptography CS 555 Topic 23: Zero-Knowledge Proof and Cryptographic Commitment CS555 Topic 23 1 Outline and Readings Outline Zero-knowledge proof Fiat-Shamir protocol Schnorr protocol Commitment schemes
YALE UNIVERSITY DEPARTMENT OF COMPUTER SCIENCE
 YALE UNIVERSITY DEPARTMENT OF COMPUTER SCIENCE CPSC 467a: Cryptography and Computer Security Notes 23 (rev. 1) Professor M. J. Fischer November 29, 2005 1 Oblivious Transfer Lecture Notes 23 In the locked
YALE UNIVERSITY DEPARTMENT OF COMPUTER SCIENCE CPSC 467a: Cryptography and Computer Security Notes 23 (rev. 1) Professor M. J. Fischer November 29, 2005 1 Oblivious Transfer Lecture Notes 23 In the locked
CPSC 467: Cryptography and Computer Security
 CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 15 October 25, 2017 CPSC 467, Lecture 15 1/31 Primitive Roots Properties of primitive roots Lucas test Special form primes Functions
CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 15 October 25, 2017 CPSC 467, Lecture 15 1/31 Primitive Roots Properties of primitive roots Lucas test Special form primes Functions
ON DEFINING PROOFS OF KNOWLEDGE IN THE BARE PUBLIC-KEY MODEL
 1 ON DEFINING PROOFS OF KNOWLEDGE IN THE BARE PUBLIC-KEY MODEL GIOVANNI DI CRESCENZO Telcordia Technologies, Piscataway, NJ, USA. E-mail: giovanni@research.telcordia.com IVAN VISCONTI Dipartimento di Informatica
1 ON DEFINING PROOFS OF KNOWLEDGE IN THE BARE PUBLIC-KEY MODEL GIOVANNI DI CRESCENZO Telcordia Technologies, Piscataway, NJ, USA. E-mail: giovanni@research.telcordia.com IVAN VISCONTI Dipartimento di Informatica
Anonymous Credentials Light
 Anonymous Credentials Light Foteini Baldimtsi, Anna Lysyanskaya foteini,anna@cs.brown.edu Computer Science Department, Brown University Abstract. We define and propose an efficient and provably secure
Anonymous Credentials Light Foteini Baldimtsi, Anna Lysyanskaya foteini,anna@cs.brown.edu Computer Science Department, Brown University Abstract. We define and propose an efficient and provably secure
New Approach for Selectively Convertible Undeniable Signature Schemes
 New Approach for Selectively Convertible Undeniable Signature Schemes Kaoru Kurosawa 1 and Tsuyoshi Takagi 2 1 Ibaraki University, Japan, kurosawa@mx.ibaraki.ac.jp 2 Future University-Hakodate, Japan,
New Approach for Selectively Convertible Undeniable Signature Schemes Kaoru Kurosawa 1 and Tsuyoshi Takagi 2 1 Ibaraki University, Japan, kurosawa@mx.ibaraki.ac.jp 2 Future University-Hakodate, Japan,
CPSC 467: Cryptography and Computer Security
 CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 19 November 8, 2017 CPSC 467, Lecture 19 1/37 Zero Knowledge Interactive Proofs (ZKIP) ZKIP for graph isomorphism Feige-Fiat-Shamir
CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 19 November 8, 2017 CPSC 467, Lecture 19 1/37 Zero Knowledge Interactive Proofs (ZKIP) ZKIP for graph isomorphism Feige-Fiat-Shamir
II. Digital signatures
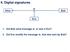 II. Digital signatures Alice m Bob Eve 1. Did Bob send message m, or was it Eve? 2. Did Eve modify the message m, that was sent by Bob? 1 Digital signatures Digital signature - are equivalent of handwritten
II. Digital signatures Alice m Bob Eve 1. Did Bob send message m, or was it Eve? 2. Did Eve modify the message m, that was sent by Bob? 1 Digital signatures Digital signature - are equivalent of handwritten
Parallel Coin-Tossing and Constant-Round Secure Two-Party Computation
 Parallel Coin-Tossing and Constant-Round Secure Two-Party Computation Yehuda Lindell Dept. of Computer Science and Applied Math. The Weizmann Institute of Science Rehovot 76100, Israel. lindell@wisdom.weizmann.ac.il
Parallel Coin-Tossing and Constant-Round Secure Two-Party Computation Yehuda Lindell Dept. of Computer Science and Applied Math. The Weizmann Institute of Science Rehovot 76100, Israel. lindell@wisdom.weizmann.ac.il
Impossibility Results for Universal Composability in Public-Key Models and with Fixed Inputs
 Impossibility Results for Universal Composability in Public-Key Models and with Fixed Inputs Dafna Kidron Yehuda Lindell June 6, 2010 Abstract Universal composability and concurrent general composition
Impossibility Results for Universal Composability in Public-Key Models and with Fixed Inputs Dafna Kidron Yehuda Lindell June 6, 2010 Abstract Universal composability and concurrent general composition
Lecture 17: Constructions of Public-Key Encryption
 COM S 687 Introduction to Cryptography October 24, 2006 Lecture 17: Constructions of Public-Key Encryption Instructor: Rafael Pass Scribe: Muthu 1 Secure Public-Key Encryption In the previous lecture,
COM S 687 Introduction to Cryptography October 24, 2006 Lecture 17: Constructions of Public-Key Encryption Instructor: Rafael Pass Scribe: Muthu 1 Secure Public-Key Encryption In the previous lecture,
Systèmes de preuve Groth-Sahai et applications
 Systèmes de preuve Groth-Sahai et applications Damien Vergnaud École normale supérieure C.N.R.S. I.N.R.I.A. 22 octobre 2010 Séminaire CCA D. Vergnaud (ENS) Groth-Sahai proof system and applications Oct.
Systèmes de preuve Groth-Sahai et applications Damien Vergnaud École normale supérieure C.N.R.S. I.N.R.I.A. 22 octobre 2010 Séminaire CCA D. Vergnaud (ENS) Groth-Sahai proof system and applications Oct.
Key-Exposure Free Chameleon Hashing and Signatures Based on Discrete Logarithm Systems
 Key-Exposure Free Chameleon Hashing and Signatures Based on Discrete Logarithm Systems Xiaofeng Chen, Fangguo Zhang, Haibo Tian, Baodian Wei, and Kwangjo Kim 1 School of Information Science and Technology,
Key-Exposure Free Chameleon Hashing and Signatures Based on Discrete Logarithm Systems Xiaofeng Chen, Fangguo Zhang, Haibo Tian, Baodian Wei, and Kwangjo Kim 1 School of Information Science and Technology,
Lecture 3: Interactive Proofs and Zero-Knowledge
 CS 355 Topics in Cryptography April 9, 2018 Lecture 3: Interactive Proofs and Zero-Knowledge Instructors: Henry Corrigan-Gibbs, Sam Kim, David J. Wu So far in the class, we have only covered basic cryptographic
CS 355 Topics in Cryptography April 9, 2018 Lecture 3: Interactive Proofs and Zero-Knowledge Instructors: Henry Corrigan-Gibbs, Sam Kim, David J. Wu So far in the class, we have only covered basic cryptographic
CPSC 467: Cryptography and Computer Security
 CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 18 November 3, 2014 CPSC 467, Lecture 18 1/43 Zero Knowledge Interactive Proofs (ZKIP) Secret cave protocol ZKIP for graph isomorphism
CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 18 November 3, 2014 CPSC 467, Lecture 18 1/43 Zero Knowledge Interactive Proofs (ZKIP) Secret cave protocol ZKIP for graph isomorphism
Analysis - "Post-Quantum Security of Fiat-Shamir" by Dominic Unruh
 Analysis - "Post-Quantum Security of Fiat-Shamir" by Dominic Unruh Bruno Produit Institute of Computer Science University of Tartu produit@ut.ee December 19, 2017 Abstract This document is an analysis
Analysis - "Post-Quantum Security of Fiat-Shamir" by Dominic Unruh Bruno Produit Institute of Computer Science University of Tartu produit@ut.ee December 19, 2017 Abstract This document is an analysis
Lecture th January 2009 Fall 2008 Scribes: D. Widder, E. Widder Today s lecture topics
 0368.4162: Introduction to Cryptography Ran Canetti Lecture 11 12th January 2009 Fall 2008 Scribes: D. Widder, E. Widder Today s lecture topics Introduction to cryptographic protocols Commitments 1 Cryptographic
0368.4162: Introduction to Cryptography Ran Canetti Lecture 11 12th January 2009 Fall 2008 Scribes: D. Widder, E. Widder Today s lecture topics Introduction to cryptographic protocols Commitments 1 Cryptographic
Augmented Black-Box Simulation and Zero Knowledge Argument for NP
 Augmented Black-Box Simulation and Zero Knowledge Argument for N Li Hongda, an Dongxue, Ni eifang The Data Assurance and Communication Security Research Center, School of Cyber Security, University of
Augmented Black-Box Simulation and Zero Knowledge Argument for N Li Hongda, an Dongxue, Ni eifang The Data Assurance and Communication Security Research Center, School of Cyber Security, University of
