SQUARES IN Z/NZ. q = ( 1) (p 1)(q 1)
|
|
|
- Malcolm Owens
- 5 years ago
- Views:
Transcription
1 SQUARES I Z/Z We study squares in the ring Z/Z from a theoretical and comutational oint of view. We resent two related crytograhic schemes. 1. SQUARES I Z/Z Consider for eamle the rime = 13. Write the liste of squares in (Z/Z). How many of them? Why? Let be an odd rime. For any integer one defines the Legendre symbol in the following way : = 0 if divides, = 1 if is a non-zero square modulo, = 1 if is not a square modulo. The ma induces a grou homomorhism from F onto {1, 1}. It is a character. Actually = 1 mod. This rovides a first method to comute this symbol efficiently. The famous quadratic recirocity law states that Theorem 1.1. If and q are odd (ositive) rime integers then ( q )( q ) = ( 1) ( 1)(q 1) 4. One can check this theorem on a few small eamles e.g. = 5 and q = 7 or = 5 and q = 3.. COMPUTIG SQUARE ROOTS I Z/Z Assume = 103 and = 46. One checks that mod 103 so 46 is a square modulo 103. We observe that is congruent to 3 modulo 4. So 1 = 51 is odd. The inverse of modulo 51 is 6. Indeed 6 = Set y = 6 mod 103. One has y = 1+51 = so y is a square root of. Comuting y = 6 is easy using fast eonentiation. On finds y = 46 mod 103. We thus have a very efficient method to comute square roots modulo a rime integer congruent to 3 modulo 4. 1
2 SQUARES I Z/Z Assume now that = 101 and = 13 mod 101. One checks that 50 1 mod 101 so is a square modulo 101. The order of in the grou (Z/101Z) divides de 50. The largest odd divisor of 50 is 5 but 5 1 mod 101. So the order of is even. We cannot comute a square root of as in the first eamle. To overcome this difficulty we assume that we know a non-quadratic residue z modulo 101. There are many of them since half of the non-zero residues are not squares. We ick a random integer z between and 1 and we comute z 50 mod 101. With robability 1 the result is 1 and we are done. For eamle z = 46 is fine since z 50 = 1 mod 101. Let us multily by z = 96 mod 101. We get X = z = 36 mod 101. And this time X 5 = 5 z 50 = 1 mod 101 so X has odd order. One easily comutes a square root of X by inverting modulo 5. Indeed 13 = 1+5 so X 13 is a square root of X. Set now y = X 13 z 1. One checks that y is a square root of. Attention : this is a robabilistic method. One does not know a general deterministic olynomial time algorithm to comute square roots modulo a rime. 3. SQUARES I Z/Z Let be an integer with rime decomosition = i e i i. From Chinese remainder theorem we know that an integer is a square modulo if and only if it is a square modulo every e i i. One can comute a square root of by first comuting square roots module every e i i then glue these square roots thanks to Chinese remainder theorem. This is efficient if we know the factorization of. In case = and = 3 we find four square roots in this way. In general, if is odd and has I rime factors one finds k square roots for each in (Z/Z). Conversely, if we have a black bo that returns a square root for any residue modulo then we can find non trivial factors of. Why? We say that there is a robabilistic reduction of the roblem of factoring integers to the roblem of comuting square roots modulo integers. There is also a robabilistic reduction of the roblem of comuting square roots modulo integers to the roblem of factoring integers. So these two roblems have similar comleity (at least in the robabilistic world). 4. THE JACOBI SYMBOL Assume 3 is an odd integer and les = i e i i be its rime decomosition. One defines the Jacobi symbol as = ei. i i The symbol only deends on the class of modulo. It has many evident multilicative roerties inherited from the Legendre symbol. For eamle = 0 if and only if a and a b b are not corime. The quadratic recirocity law can be etended to Jacobi symbols.
3 SQUARES I Z/Z 3 Theorem 4.1 (Gauss). Let M 3 and 3 be odd corime integers. One has 1 = ( 1) M 1 and = ( 1) M 1 8 M and = ( 1) (M 1)( 1) 4. M M M Using this theorem one can quickly comute Jacobi symbols. The algorithm is very similar to Euclidean algorithm. When is not a rime, the Jacobi symbol does not suffice to distinguish quadratic residues from non-quadratic residues. For eamle if = q is a roduct of two distinct odd rimes and is rime to then = 1 if and only if is either a square modulo and modulo q or is neither a square modulo nore modulo q. In this last case one says that is a false square. It is considered to be difficult to distinguish true and false squares. 5. A ZERO-KOWLEDGE IDETIFICATIO PROTOCOL Identification is a crucial need to secure communications. One needs to check the identity of one s contacts. Assume Carole belongs to a secret organization. She needs to contact James. She never met him. In order to avoid any infiltration of the organization, each of them must be able to check that he his dealing with the other. Here is a ossible rotocol. James gets close to Carole and tells her BELOTE. Carole answers REBELOTE. If everything goes well Carole and James know that they are in contact with the right erson. We assume of course that the two asswords (BELOTE and REBELOTE) have been rovided by the organization to each of them. These asswords should be used only once. Otherwise some enemy may intercet and re-use them. Another concern is the man-in-the-middle attack. A false Carole (say Karole) may contact James. James would give her the assword BELOTE to rove himself. Then Karole would quickly contact Carole and send her the assword BELOTE. Carole would accet this assword and answer REBELOTE to Karole. ow Karole would be able to convince James that she is Carole. All these difficulties are consequences of the following two self contradictory rinciles (1) The identity is defined by the knowledge of some information (e.g. a assword) that must be ket secret. () Proving oneself is achieved by unveiling this information (e.g. sending the assword). Biometric identification techniques (fingerrints, iris recognition, voice identification,... ) may be a solution, but this is not the scoe of this tet. The following identification scheme is due to Feige, Fiat and Shamir. It is a Zero-Knowledge identification scheme. James can rove that he knows a secret without unveiling it. To start with, each member X of the organization chooses two large rime integers X and q X and comutes their roduct X = X q X. Then X chooses a random quadratic residue r X modulo X with uniform robability and a square root f X of r X. So f X = r X mod X. Indeed it is simler to choose f X first. The collection of all triles (X, X, r X ) is ublished in the honebook of the organization. The rime factors X and q X and the square root f X are only known to X. It is the knowledge of f X that distinguishes X.
4 4 SQUARES I Z/Z Before contacting James, Carole looks for the trile (J, J, r J ) in the honebook. She contacts the alleged James and try to make sure that he knows a square root of r J modulo. They interact as follows. (1) James icks a random quadratic residue z = u mod J (with uniform robability) and comutes t = zr J mod J. He sends t to Carole. () Carole chooses a random element ɛ (with uniform robability) in {1, 1} and send it to James. (3) If ɛ = 1 James sends u to Carole. Otherwise he sends a square root s of t modulo J (he knows such a square root s = uf J because he knows a square root of r J and a square root of z.) (4) If ɛ = 1, Carole comutes z = t/r J mod J and checks that z = u mod J. (5) If ɛ = 0, Carole checks that s = t mod J. This rotocol runs in time olynomial in log J. It can and should be reeated many (e.g. 1000) times. Carole accets if the condition checked at the last ste has been always satisfied. Otherwise she rejects. If James wants to rove himself, he can answer Carole s questions. And Carole learns nothing about James secret because she only gets a series of random quadratic residues modulo J. She could roduce such a series herself without the suort of James. So she receives no information from him. Assume an enemy (say Octous) claims to be James. He doesn t know any square root of r J. So he cannot know at the same time an s and a u such that s = t and u = z. So he fails to answer correctly with robability 1. When the rotocol is iterated n times the robability for Octous to cheat Carole is 1/ n. The security of the scheme relies on the difficulty of comuting square roots modulo a comosite integer. This is a hard roblem as long as factoring integers is hard. 6. FLIPPIG COIS WITH A TELEPHOE Alice and Bob want to fli a coin to decide who is going to dust-swee tomorrow. However they are not in the same room and they only can interact with a telehone or by mail. They need to ick a random element in {heads, tails} with uniform robability. one of them should be able to influence on the result. The following rotocol rovides a solution under the assumtion that false squares cannot be distinguished from true ones efficiently. (1) Bob chooses two large numbers and q. He comutes the roduct = q and sends it ( to Alice ) (he does not send and q). Bob chooses a residue modulo such that = 1 (with uniform distribution)) and he sends to Alice. () Alice receives and but she doesn t know ans q. So she doesn t know if is a true or a false square. She ick a random element ɛ (with uniform distribution) in {1, 1} and she sends it to Bob.
5 SQUARES I Z/Z 5 (3) Bob comares ɛ and. If they are equal then the result of the rotocol is heads and if they are different the result is tails. Bob sends his conclusion to Alice. He justifies it by transmitting and q. (4) Alice checks ( that ) and ( q) are rime integers and = q. She comutes the Legendre symbols and and checks Bob s claim. q This rotocol runs in time olynomial in log. The robability distribution on the outut is uniform as soon as one of the layers is honest (meaning he eecutes the rotocol correctly). If Bob cheats but Alice is honest then the distribution is uniform because the grou comosition of two random variables, one of which is uniform, is uniform too. If Alice wants to influence on the result she must guess some information about whether is a true or a false square. One assume that it is imossible to get any information about this in olynomial time.
Jacobi symbols and application to primality
 Jacobi symbols and alication to rimality Setember 19, 018 1 The grou Z/Z We review the structure of the abelian grou Z/Z. Using Chinese remainder theorem, we can restrict to the case when = k is a rime
Jacobi symbols and alication to rimality Setember 19, 018 1 The grou Z/Z We review the structure of the abelian grou Z/Z. Using Chinese remainder theorem, we can restrict to the case when = k is a rime
Math 261 Exam 2. November 7, The use of notes and books is NOT allowed.
 Math 261 Eam 2 ovember 7, 2018 The use of notes and books is OT allowed Eercise 1: Polynomials mod 691 (30 ts In this eercise, you may freely use the fact that 691 is rime Consider the olynomials f( 4
Math 261 Eam 2 ovember 7, 2018 The use of notes and books is OT allowed Eercise 1: Polynomials mod 691 (30 ts In this eercise, you may freely use the fact that 691 is rime Consider the olynomials f( 4
MATH342 Practice Exam
 MATH342 Practice Exam This exam is intended to be in a similar style to the examination in May/June 2012. It is not imlied that all questions on the real examination will follow the content of the ractice
MATH342 Practice Exam This exam is intended to be in a similar style to the examination in May/June 2012. It is not imlied that all questions on the real examination will follow the content of the ractice
CPSC 467b: Cryptography and Computer Security
 Outline Authentication CPSC 467b: Cryptography and Computer Security Lecture 18 Michael J. Fischer Department of Computer Science Yale University March 29, 2010 Michael J. Fischer CPSC 467b, Lecture 18
Outline Authentication CPSC 467b: Cryptography and Computer Security Lecture 18 Michael J. Fischer Department of Computer Science Yale University March 29, 2010 Michael J. Fischer CPSC 467b, Lecture 18
x 2 a mod m. has a solution. Theorem 13.2 (Euler s Criterion). Let p be an odd prime. The congruence x 2 1 mod p,
 13. Quadratic Residues We now turn to the question of when a quadratic equation has a solution modulo m. The general quadratic equation looks like ax + bx + c 0 mod m. Assuming that m is odd or that b
13. Quadratic Residues We now turn to the question of when a quadratic equation has a solution modulo m. The general quadratic equation looks like ax + bx + c 0 mod m. Assuming that m is odd or that b
Math 4400/6400 Homework #8 solutions. 1. Let P be an odd integer (not necessarily prime). Show that modulo 2,
 MATH 4400 roblems. Math 4400/6400 Homework # solutions 1. Let P be an odd integer not necessarily rime. Show that modulo, { P 1 0 if P 1, 7 mod, 1 if P 3, mod. Proof. Suose that P 1 mod. Then we can write
MATH 4400 roblems. Math 4400/6400 Homework # solutions 1. Let P be an odd integer not necessarily rime. Show that modulo, { P 1 0 if P 1, 7 mod, 1 if P 3, mod. Proof. Suose that P 1 mod. Then we can write
MATH 361: NUMBER THEORY EIGHTH LECTURE
 MATH 361: NUMBER THEORY EIGHTH LECTURE 1. Quadratic Recirocity: Introduction Quadratic recirocity is the first result of modern number theory. Lagrange conjectured it in the late 1700 s, but it was first
MATH 361: NUMBER THEORY EIGHTH LECTURE 1. Quadratic Recirocity: Introduction Quadratic recirocity is the first result of modern number theory. Lagrange conjectured it in the late 1700 s, but it was first
The Hasse Minkowski Theorem Lee Dicker University of Minnesota, REU Summer 2001
 The Hasse Minkowski Theorem Lee Dicker University of Minnesota, REU Summer 2001 The Hasse-Minkowski Theorem rovides a characterization of the rational quadratic forms. What follows is a roof of the Hasse-Minkowski
The Hasse Minkowski Theorem Lee Dicker University of Minnesota, REU Summer 2001 The Hasse-Minkowski Theorem rovides a characterization of the rational quadratic forms. What follows is a roof of the Hasse-Minkowski
Math 104B: Number Theory II (Winter 2012)
 Math 104B: Number Theory II (Winter 01) Alina Bucur Contents 1 Review 11 Prime numbers 1 Euclidean algorithm 13 Multilicative functions 14 Linear diohantine equations 3 15 Congruences 3 Primes as sums
Math 104B: Number Theory II (Winter 01) Alina Bucur Contents 1 Review 11 Prime numbers 1 Euclidean algorithm 13 Multilicative functions 14 Linear diohantine equations 3 15 Congruences 3 Primes as sums
A CONCRETE EXAMPLE OF PRIME BEHAVIOR IN QUADRATIC FIELDS. 1. Abstract
 A CONCRETE EXAMPLE OF PRIME BEHAVIOR IN QUADRATIC FIELDS CASEY BRUCK 1. Abstract The goal of this aer is to rovide a concise way for undergraduate mathematics students to learn about how rime numbers behave
A CONCRETE EXAMPLE OF PRIME BEHAVIOR IN QUADRATIC FIELDS CASEY BRUCK 1. Abstract The goal of this aer is to rovide a concise way for undergraduate mathematics students to learn about how rime numbers behave
MATH 361: NUMBER THEORY ELEVENTH LECTURE
 MATH 361: NUMBER THEORY ELEVENTH LECTURE The subjects of this lecture are characters, Gauss sums, Jacobi sums, and counting formulas for olynomial equations over finite fields. 1. Definitions, Basic Proerties
MATH 361: NUMBER THEORY ELEVENTH LECTURE The subjects of this lecture are characters, Gauss sums, Jacobi sums, and counting formulas for olynomial equations over finite fields. 1. Definitions, Basic Proerties
CPSC 467: Cryptography and Computer Security
 CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 18 November 6, 2017 CPSC 467, Lecture 18 1/52 Authentication While Preventing Impersonation Challenge-response authentication protocols
CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 18 November 6, 2017 CPSC 467, Lecture 18 1/52 Authentication While Preventing Impersonation Challenge-response authentication protocols
MATH 3240Q Introduction to Number Theory Homework 7
 As long as algebra and geometry have been searated, their rogress have been slow and their uses limited; but when these two sciences have been united, they have lent each mutual forces, and have marched
As long as algebra and geometry have been searated, their rogress have been slow and their uses limited; but when these two sciences have been united, they have lent each mutual forces, and have marched
Practice Final Solutions
 Practice Final Solutions 1. True or false: (a) If a is a sum of three squares, and b is a sum of three squares, then so is ab. False: Consider a 14, b 2. (b) No number of the form 4 m (8n + 7) can be written
Practice Final Solutions 1. True or false: (a) If a is a sum of three squares, and b is a sum of three squares, then so is ab. False: Consider a 14, b 2. (b) No number of the form 4 m (8n + 7) can be written
MA3H1 TOPICS IN NUMBER THEORY PART III
 MA3H1 TOPICS IN NUMBER THEORY PART III SAMIR SIKSEK 1. Congruences Modulo m In quadratic recirocity we studied congruences of the form x 2 a (mod ). We now turn our attention to situations where is relaced
MA3H1 TOPICS IN NUMBER THEORY PART III SAMIR SIKSEK 1. Congruences Modulo m In quadratic recirocity we studied congruences of the form x 2 a (mod ). We now turn our attention to situations where is relaced
Introduction to Arithmetic Geometry Fall 2013 Lecture #10 10/8/2013
 18.782 Introduction to Arithmetic Geometry Fall 2013 Lecture #10 10/8/2013 In this lecture we lay the groundwork needed to rove the Hasse-Minkowski theorem for Q, which states that a quadratic form over
18.782 Introduction to Arithmetic Geometry Fall 2013 Lecture #10 10/8/2013 In this lecture we lay the groundwork needed to rove the Hasse-Minkowski theorem for Q, which states that a quadratic form over
Elliptic Curves Spring 2015 Problem Set #1 Due: 02/13/2015
 18.783 Ellitic Curves Sring 2015 Problem Set #1 Due: 02/13/2015 Descrition These roblems are related to the material covered in Lectures 1-2. Some of them require the use of Sage, and you will need to
18.783 Ellitic Curves Sring 2015 Problem Set #1 Due: 02/13/2015 Descrition These roblems are related to the material covered in Lectures 1-2. Some of them require the use of Sage, and you will need to
We collect some results that might be covered in a first course in algebraic number theory.
 1 Aendices We collect some results that might be covered in a first course in algebraic number theory. A. uadratic Recirocity Via Gauss Sums A1. Introduction In this aendix, is an odd rime unless otherwise
1 Aendices We collect some results that might be covered in a first course in algebraic number theory. A. uadratic Recirocity Via Gauss Sums A1. Introduction In this aendix, is an odd rime unless otherwise
Quadratic Residues, Quadratic Reciprocity. 2 4 So we may as well start with x 2 a mod p. p 1 1 mod p a 2 ±1 mod p
 Lecture 9 Quadratic Residues, Quadratic Recirocity Quadratic Congruence - Consider congruence ax + bx + c 0 mod, with a 0 mod. This can be reduced to x + ax + b 0, if we assume that is odd ( is trivial
Lecture 9 Quadratic Residues, Quadratic Recirocity Quadratic Congruence - Consider congruence ax + bx + c 0 mod, with a 0 mod. This can be reduced to x + ax + b 0, if we assume that is odd ( is trivial
Practice Final Solutions
 Practice Final Solutions 1. Find integers x and y such that 13x + 1y 1 SOLUTION: By the Euclidean algorithm: One can work backwards to obtain 1 1 13 + 2 13 6 2 + 1 1 13 6 2 13 6 (1 1 13) 7 13 6 1 Hence
Practice Final Solutions 1. Find integers x and y such that 13x + 1y 1 SOLUTION: By the Euclidean algorithm: One can work backwards to obtain 1 1 13 + 2 13 6 2 + 1 1 13 6 2 13 6 (1 1 13) 7 13 6 1 Hence
ERRATA AND SUPPLEMENTARY MATERIAL FOR A FRIENDLY INTRODUCTION TO NUMBER THEORY FOURTH EDITION
 ERRATA AND SUPPLEMENTARY MATERIAL FOR A FRIENDLY INTRODUCTION TO NUMBER THEORY FOURTH EDITION JOSEPH H. SILVERMAN Acknowledgements Page vii Thanks to the following eole who have sent me comments and corrections
ERRATA AND SUPPLEMENTARY MATERIAL FOR A FRIENDLY INTRODUCTION TO NUMBER THEORY FOURTH EDITION JOSEPH H. SILVERMAN Acknowledgements Page vii Thanks to the following eole who have sent me comments and corrections
Mersenne and Fermat Numbers
 NUMBER THEORY CHARLES LEYTEM Mersenne and Fermat Numbers CONTENTS 1. The Little Fermat theorem 2 2. Mersenne numbers 2 3. Fermat numbers 4 4. An IMO roblem 5 1 2 CHARLES LEYTEM 1. THE LITTLE FERMAT THEOREM
NUMBER THEORY CHARLES LEYTEM Mersenne and Fermat Numbers CONTENTS 1. The Little Fermat theorem 2 2. Mersenne numbers 2 3. Fermat numbers 4 4. An IMO roblem 5 1 2 CHARLES LEYTEM 1. THE LITTLE FERMAT THEOREM
.4. Congruences. We say that a is congruent to b modulo N i.e. a b mod N i N divides a b or equivalently i a%n = b%n. So a is congruent modulo N to an
 . Modular arithmetic.. Divisibility. Given ositive numbers a; b, if a 6= 0 we can write b = aq + r for aroriate integers q; r such that 0 r a. The number r is the remainder. We say that a divides b (or
. Modular arithmetic.. Divisibility. Given ositive numbers a; b, if a 6= 0 we can write b = aq + r for aroriate integers q; r such that 0 r a. The number r is the remainder. We say that a divides b (or
RECIPROCITY LAWS JEREMY BOOHER
 RECIPROCITY LAWS JEREMY BOOHER 1 Introduction The law of uadratic recirocity gives a beautiful descrition of which rimes are suares modulo Secial cases of this law going back to Fermat, and Euler and Legendre
RECIPROCITY LAWS JEREMY BOOHER 1 Introduction The law of uadratic recirocity gives a beautiful descrition of which rimes are suares modulo Secial cases of this law going back to Fermat, and Euler and Legendre
Mobius Functions, Legendre Symbols, and Discriminants
 Mobius Functions, Legendre Symbols, and Discriminants 1 Introduction Zev Chonoles, Erick Knight, Tim Kunisky Over the integers, there are two key number-theoretic functions that take on values of 1, 1,
Mobius Functions, Legendre Symbols, and Discriminants 1 Introduction Zev Chonoles, Erick Knight, Tim Kunisky Over the integers, there are two key number-theoretic functions that take on values of 1, 1,
By Evan Chen OTIS, Internal Use
 Solutions Notes for DNY-NTCONSTRUCT Evan Chen January 17, 018 1 Solution Notes to TSTST 015/5 Let ϕ(n) denote the number of ositive integers less than n that are relatively rime to n. Prove that there
Solutions Notes for DNY-NTCONSTRUCT Evan Chen January 17, 018 1 Solution Notes to TSTST 015/5 Let ϕ(n) denote the number of ositive integers less than n that are relatively rime to n. Prove that there
When do Fibonacci invertible classes modulo M form a subgroup?
 Calhoun: The NPS Institutional Archive DSace Reository Faculty and Researchers Faculty and Researchers Collection 2013 When do Fibonacci invertible classes modulo M form a subgrou? Luca, Florian Annales
Calhoun: The NPS Institutional Archive DSace Reository Faculty and Researchers Faculty and Researchers Collection 2013 When do Fibonacci invertible classes modulo M form a subgrou? Luca, Florian Annales
Cryptography. Lecture 8. Arpita Patra
 Crytograhy Lecture 8 Arita Patra Quick Recall and Today s Roadma >> Hash Functions- stands in between ublic and rivate key world >> Key Agreement >> Assumtions in Finite Cyclic grous - DL, CDH, DDH Grous
Crytograhy Lecture 8 Arita Patra Quick Recall and Today s Roadma >> Hash Functions- stands in between ublic and rivate key world >> Key Agreement >> Assumtions in Finite Cyclic grous - DL, CDH, DDH Grous
MATH 2710: NOTES FOR ANALYSIS
 MATH 270: NOTES FOR ANALYSIS The main ideas we will learn from analysis center around the idea of a limit. Limits occurs in several settings. We will start with finite limits of sequences, then cover infinite
MATH 270: NOTES FOR ANALYSIS The main ideas we will learn from analysis center around the idea of a limit. Limits occurs in several settings. We will start with finite limits of sequences, then cover infinite
QUADRATIC RECIPROCITY
 QUADRATIC RECIPROCITY JORDAN SCHETTLER Abstract. The goals of this roject are to have the reader(s) gain an areciation for the usefulness of Legendre symbols and ultimately recreate Eisenstein s slick
QUADRATIC RECIPROCITY JORDAN SCHETTLER Abstract. The goals of this roject are to have the reader(s) gain an areciation for the usefulness of Legendre symbols and ultimately recreate Eisenstein s slick
MAT 311 Solutions to Final Exam Practice
 MAT 311 Solutions to Final Exam Practice Remark. If you are comfortable with all of the following roblems, you will be very well reared for the midterm. Some of the roblems below are more difficult than
MAT 311 Solutions to Final Exam Practice Remark. If you are comfortable with all of the following roblems, you will be very well reared for the midterm. Some of the roblems below are more difficult than
YALE UNIVERSITY DEPARTMENT OF COMPUTER SCIENCE
 YALE UNIVERSITY DEPARTMENT OF COMPUTER SCIENCE CPSC 467a: Cryptography and Computer Security Notes 23 (rev. 1) Professor M. J. Fischer November 29, 2005 1 Oblivious Transfer Lecture Notes 23 In the locked
YALE UNIVERSITY DEPARTMENT OF COMPUTER SCIENCE CPSC 467a: Cryptography and Computer Security Notes 23 (rev. 1) Professor M. J. Fischer November 29, 2005 1 Oblivious Transfer Lecture Notes 23 In the locked
When do the Fibonacci invertible classes modulo M form a subgroup?
 Annales Mathematicae et Informaticae 41 (2013). 265 270 Proceedings of the 15 th International Conference on Fibonacci Numbers and Their Alications Institute of Mathematics and Informatics, Eszterházy
Annales Mathematicae et Informaticae 41 (2013). 265 270 Proceedings of the 15 th International Conference on Fibonacci Numbers and Their Alications Institute of Mathematics and Informatics, Eszterházy
Pseudorandom Sequence Generation
 YALE UNIVERSITY DEPARTMENT OF COMPUTER SCIENCE CPSC 467a: Crytograhy and Comuter Security Handout #21 Professor M. J. Fischer November 29, 2005 Pseudorandom Seuence Generation 1 Distinguishability and
YALE UNIVERSITY DEPARTMENT OF COMPUTER SCIENCE CPSC 467a: Crytograhy and Comuter Security Handout #21 Professor M. J. Fischer November 29, 2005 Pseudorandom Seuence Generation 1 Distinguishability and
Pythagorean triples and sums of squares
 Pythagorean triles and sums of squares Robin Chaman 16 January 2004 1 Pythagorean triles A Pythagorean trile (x, y, z) is a trile of ositive integers satisfying z 2 + y 2 = z 2. If g = gcd(x, y, z) then
Pythagorean triles and sums of squares Robin Chaman 16 January 2004 1 Pythagorean triles A Pythagorean trile (x, y, z) is a trile of ositive integers satisfying z 2 + y 2 = z 2. If g = gcd(x, y, z) then
Algebraic number theory LTCC Solutions to Problem Sheet 2
 Algebraic number theory LTCC 008 Solutions to Problem Sheet ) Let m be a square-free integer and K = Q m). The embeddings K C are given by σ a + b m) = a + b m and σ a + b m) = a b m. If m mod 4) then
Algebraic number theory LTCC 008 Solutions to Problem Sheet ) Let m be a square-free integer and K = Q m). The embeddings K C are given by σ a + b m) = a + b m and σ a + b m) = a b m. If m mod 4) then
QUADRATIC RECIPROCITY
 QUADRATIC RECIPROCITY JORDAN SCHETTLER Abstract. The goals of this roject are to have the reader(s) gain an areciation for the usefulness of Legendre symbols and ultimately recreate Eisenstein s slick
QUADRATIC RECIPROCITY JORDAN SCHETTLER Abstract. The goals of this roject are to have the reader(s) gain an areciation for the usefulness of Legendre symbols and ultimately recreate Eisenstein s slick
Cryptanalysis of Pseudorandom Generators
 CSE 206A: Lattice Algorithms and Alications Fall 2017 Crytanalysis of Pseudorandom Generators Instructor: Daniele Micciancio UCSD CSE As a motivating alication for the study of lattice in crytograhy we
CSE 206A: Lattice Algorithms and Alications Fall 2017 Crytanalysis of Pseudorandom Generators Instructor: Daniele Micciancio UCSD CSE As a motivating alication for the study of lattice in crytograhy we
CERIAS Tech Report The period of the Bell numbers modulo a prime by Peter Montgomery, Sangil Nahm, Samuel Wagstaff Jr Center for Education
 CERIAS Tech Reort 2010-01 The eriod of the Bell numbers modulo a rime by Peter Montgomery, Sangil Nahm, Samuel Wagstaff Jr Center for Education and Research Information Assurance and Security Purdue University,
CERIAS Tech Reort 2010-01 The eriod of the Bell numbers modulo a rime by Peter Montgomery, Sangil Nahm, Samuel Wagstaff Jr Center for Education and Research Information Assurance and Security Purdue University,
Lecture Notes, Week 6
 YALE UNIVERSITY DEPARTMENT OF COMPUTER SCIENCE CPSC 467b: Cryptography and Computer Security Week 6 (rev. 3) Professor M. J. Fischer February 15 & 17, 2005 1 RSA Security Lecture Notes, Week 6 Several
YALE UNIVERSITY DEPARTMENT OF COMPUTER SCIENCE CPSC 467b: Cryptography and Computer Security Week 6 (rev. 3) Professor M. J. Fischer February 15 & 17, 2005 1 RSA Security Lecture Notes, Week 6 Several
Advanced Cryptography Midterm Exam
 Advanced Crytograhy Midterm Exam Solution Serge Vaudenay 17.4.2012 duration: 3h00 any document is allowed a ocket calculator is allowed communication devices are not allowed the exam invigilators will
Advanced Crytograhy Midterm Exam Solution Serge Vaudenay 17.4.2012 duration: 3h00 any document is allowed a ocket calculator is allowed communication devices are not allowed the exam invigilators will
MAS 4203 Number Theory. M. Yotov
 MAS 4203 Number Theory M. Yotov June 15, 2017 These Notes were comiled by the author with the intent to be used by his students as a main text for the course MAS 4203 Number Theory taught at the Deartment
MAS 4203 Number Theory M. Yotov June 15, 2017 These Notes were comiled by the author with the intent to be used by his students as a main text for the course MAS 4203 Number Theory taught at the Deartment
NUMBER SYSTEMS. Number theory is the study of the integers. We denote the set of integers by Z:
 NUMBER SYSTEMS Number theory is the study of the integers. We denote the set of integers by Z: Z = {..., 3, 2, 1, 0, 1, 2, 3,... }. The integers have two oerations defined on them, addition and multilication,
NUMBER SYSTEMS Number theory is the study of the integers. We denote the set of integers by Z: Z = {..., 3, 2, 1, 0, 1, 2, 3,... }. The integers have two oerations defined on them, addition and multilication,
QUANTUM INFORMATION DELAY SCHEME USING ORTHOGONAL PRODUCT STATES
 0 th March 0. Vol. No. 00-0 JATIT & LLS. All rights reserved. ISSN: -86 www.jatit.org E-ISSN: 87- QUANTUM INFORMATION DELAY SCHEME USING ORTHOGONAL PRODUCT STATES XIAOYU LI, LIJU CHEN School of Information
0 th March 0. Vol. No. 00-0 JATIT & LLS. All rights reserved. ISSN: -86 www.jatit.org E-ISSN: 87- QUANTUM INFORMATION DELAY SCHEME USING ORTHOGONAL PRODUCT STATES XIAOYU LI, LIJU CHEN School of Information
CPSC 467: Cryptography and Computer Security
 CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 18 November 3, 2014 CPSC 467, Lecture 18 1/43 Zero Knowledge Interactive Proofs (ZKIP) Secret cave protocol ZKIP for graph isomorphism
CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 18 November 3, 2014 CPSC 467, Lecture 18 1/43 Zero Knowledge Interactive Proofs (ZKIP) Secret cave protocol ZKIP for graph isomorphism
HENSEL S LEMMA KEITH CONRAD
 HENSEL S LEMMA KEITH CONRAD 1. Introduction In the -adic integers, congruences are aroximations: for a and b in Z, a b mod n is the same as a b 1/ n. Turning information modulo one ower of into similar
HENSEL S LEMMA KEITH CONRAD 1. Introduction In the -adic integers, congruences are aroximations: for a and b in Z, a b mod n is the same as a b 1/ n. Turning information modulo one ower of into similar
#A47 INTEGERS 15 (2015) QUADRATIC DIOPHANTINE EQUATIONS WITH INFINITELY MANY SOLUTIONS IN POSITIVE INTEGERS
 #A47 INTEGERS 15 (015) QUADRATIC DIOPHANTINE EQUATIONS WITH INFINITELY MANY SOLUTIONS IN POSITIVE INTEGERS Mihai Ciu Simion Stoilow Institute of Mathematics of the Romanian Academy, Research Unit No. 5,
#A47 INTEGERS 15 (015) QUADRATIC DIOPHANTINE EQUATIONS WITH INFINITELY MANY SOLUTIONS IN POSITIVE INTEGERS Mihai Ciu Simion Stoilow Institute of Mathematics of the Romanian Academy, Research Unit No. 5,
Tanja Lange Technische Universiteit Eindhoven
 Crytanalysis Course Part I Tanja Lange Technische Universiteit Eindhoven 28 Nov 2016 with some slides by Daniel J. Bernstein Main goal of this course: We are the attackers. We want to break ECC and RSA.
Crytanalysis Course Part I Tanja Lange Technische Universiteit Eindhoven 28 Nov 2016 with some slides by Daniel J. Bernstein Main goal of this course: We are the attackers. We want to break ECC and RSA.
A Public-Key Cryptosystem Based on Lucas Sequences
 Palestine Journal of Mathematics Vol. 1(2) (2012), 148 152 Palestine Polytechnic University-PPU 2012 A Public-Key Crytosystem Based on Lucas Sequences Lhoussain El Fadil Communicated by Ayman Badawi MSC2010
Palestine Journal of Mathematics Vol. 1(2) (2012), 148 152 Palestine Polytechnic University-PPU 2012 A Public-Key Crytosystem Based on Lucas Sequences Lhoussain El Fadil Communicated by Ayman Badawi MSC2010
CPSC 467: Cryptography and Computer Security
 CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 19 November 8, 2017 CPSC 467, Lecture 19 1/37 Zero Knowledge Interactive Proofs (ZKIP) ZKIP for graph isomorphism Feige-Fiat-Shamir
CPSC 467: Cryptography and Computer Security Michael J. Fischer Lecture 19 November 8, 2017 CPSC 467, Lecture 19 1/37 Zero Knowledge Interactive Proofs (ZKIP) ZKIP for graph isomorphism Feige-Fiat-Shamir
CPSC 467b: Cryptography and Computer Security
 CPSC 467b: Cryptography and Computer Security Michael J. Fischer Lecture 16 March 19, 2012 CPSC 467b, Lecture 16 1/58 Authentication While Preventing Impersonation Challenge-response authentication protocols
CPSC 467b: Cryptography and Computer Security Michael J. Fischer Lecture 16 March 19, 2012 CPSC 467b, Lecture 16 1/58 Authentication While Preventing Impersonation Challenge-response authentication protocols
Privacy and Computer Science (ECI 2015) Day 4 - Zero Knowledge Proofs Mathematics
 Privacy and Computer Science (ECI 2015) Day 4 - Zero Knowledge Proofs Mathematics F. Prost Frederic.Prost@ens-lyon.fr Ecole Normale Supérieure de Lyon July 2015 F. Prost Frederic.Prost@ens-lyon.fr (Ecole
Privacy and Computer Science (ECI 2015) Day 4 - Zero Knowledge Proofs Mathematics F. Prost Frederic.Prost@ens-lyon.fr Ecole Normale Supérieure de Lyon July 2015 F. Prost Frederic.Prost@ens-lyon.fr (Ecole
1 Integers and the Euclidean algorithm
 1 1 Integers and the Euclidean algorithm Exercise 1.1 Prove, n N : induction on n) 1 3 + 2 3 + + n 3 = (1 + 2 + + n) 2 (use Exercise 1.2 Prove, 2 n 1 is rime n is rime. (The converse is not true, as shown
1 1 Integers and the Euclidean algorithm Exercise 1.1 Prove, n N : induction on n) 1 3 + 2 3 + + n 3 = (1 + 2 + + n) 2 (use Exercise 1.2 Prove, 2 n 1 is rime n is rime. (The converse is not true, as shown
Lecture Notes, Week 10
 YALE UNIVERSITY DEPARTMENT OF COMPUTER SCIENCE CPSC 467b: Cryptography and Computer Security Week 10 (rev. 2) Professor M. J. Fischer March 29 & 31, 2005 Lecture Notes, Week 10 1 Zero Knowledge Interactive
YALE UNIVERSITY DEPARTMENT OF COMPUTER SCIENCE CPSC 467b: Cryptography and Computer Security Week 10 (rev. 2) Professor M. J. Fischer March 29 & 31, 2005 Lecture Notes, Week 10 1 Zero Knowledge Interactive
Lecture 21: Quantum Communication
 CS 880: Quantum Information Processing 0/6/00 Lecture : Quantum Communication Instructor: Dieter van Melkebeek Scribe: Mark Wellons Last lecture, we introduced the EPR airs which we will use in this lecture
CS 880: Quantum Information Processing 0/6/00 Lecture : Quantum Communication Instructor: Dieter van Melkebeek Scribe: Mark Wellons Last lecture, we introduced the EPR airs which we will use in this lecture
Frobenius Elements, the Chebotarev Density Theorem, and Reciprocity
 Frobenius Elements, the Chebotarev Density Theorem, and Recirocity Dylan Yott July 30, 204 Motivation Recall Dirichlet s theorem from elementary number theory. Theorem.. For a, m) =, there are infinitely
Frobenius Elements, the Chebotarev Density Theorem, and Recirocity Dylan Yott July 30, 204 Motivation Recall Dirichlet s theorem from elementary number theory. Theorem.. For a, m) =, there are infinitely
arxiv: v1 [math.nt] 4 Nov 2015
![arxiv: v1 [math.nt] 4 Nov 2015 arxiv: v1 [math.nt] 4 Nov 2015](/thumbs/89/98642418.jpg) Wall s Conjecture and the ABC Conjecture George Grell, Wayne Peng August 0, 018 arxiv:1511.0110v1 [math.nt] 4 Nov 015 Abstract We show that the abc conjecture of Masser-Oesterlé-Sziro for number fields
Wall s Conjecture and the ABC Conjecture George Grell, Wayne Peng August 0, 018 arxiv:1511.0110v1 [math.nt] 4 Nov 015 Abstract We show that the abc conjecture of Masser-Oesterlé-Sziro for number fields
SQUAREFREE VALUES OF QUADRATIC POLYNOMIALS COURSE NOTES, 2015
 SQUAREFREE VALUES OF QUADRATIC POLYNOMIALS COURSE NOTES, 2015 1. Squarefree values of olynomials: History In this section we study the roblem of reresenting square-free integers by integer olynomials.
SQUAREFREE VALUES OF QUADRATIC POLYNOMIALS COURSE NOTES, 2015 1. Squarefree values of olynomials: History In this section we study the roblem of reresenting square-free integers by integer olynomials.
MA257: INTRODUCTION TO NUMBER THEORY LECTURE NOTES 2018
 MA257: INTRODUCTION TO NUMBER THEORY LECTURE NOTES 2018 J. E. CREMONA Contents 0. Introduction: What is Number Theory? 2 Basic Notation 3 1. Factorization 4 1.1. Divisibility in Z 4 1.2. Greatest Common
MA257: INTRODUCTION TO NUMBER THEORY LECTURE NOTES 2018 J. E. CREMONA Contents 0. Introduction: What is Number Theory? 2 Basic Notation 3 1. Factorization 4 1.1. Divisibility in Z 4 1.2. Greatest Common
MATH 371 Class notes/outline September 24, 2013
 MATH 371 Class notes/outline Setember 24, 2013 Rings Armed with what we have looked at for the integers and olynomials over a field, we re in a good osition to take u the general theory of rings. Definitions:
MATH 371 Class notes/outline Setember 24, 2013 Rings Armed with what we have looked at for the integers and olynomials over a field, we re in a good osition to take u the general theory of rings. Definitions:
Introduction to Modern Cryptography. Benny Chor
 Introduction to Modern Cryptography Benny Chor Hard Core Bits Coin Flipping Over the Phone Zero Knowledge Lecture 10 (version 1.1) Tel-Aviv University 18 March 2008. Slightly revised March 19. Hard Core
Introduction to Modern Cryptography Benny Chor Hard Core Bits Coin Flipping Over the Phone Zero Knowledge Lecture 10 (version 1.1) Tel-Aviv University 18 March 2008. Slightly revised March 19. Hard Core
ON POLYNOMIAL SELECTION FOR THE GENERAL NUMBER FIELD SIEVE
 MATHEMATICS OF COMPUTATIO Volume 75, umber 256, October 26, Pages 237 247 S 25-5718(6)187-9 Article electronically ublished on June 28, 26 O POLYOMIAL SELECTIO FOR THE GEERAL UMBER FIELD SIEVE THORSTE
MATHEMATICS OF COMPUTATIO Volume 75, umber 256, October 26, Pages 237 247 S 25-5718(6)187-9 Article electronically ublished on June 28, 26 O POLYOMIAL SELECTIO FOR THE GEERAL UMBER FIELD SIEVE THORSTE
Public Key Cryptosystems RSA
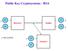 Public Key Crytosystems RSA 57 17 Receiver Sender 41 19 and rime 53 Attacker 47 Public Key Crytosystems RSA Comute numbers n = * 2337 323 57 17 Receiver Sender 41 19 and rime 53 Attacker 2491 47 Public
Public Key Crytosystems RSA 57 17 Receiver Sender 41 19 and rime 53 Attacker 47 Public Key Crytosystems RSA Comute numbers n = * 2337 323 57 17 Receiver Sender 41 19 and rime 53 Attacker 2491 47 Public
Quadratic Reciprocity
 Quadratic Recirocity 5-7-011 Quadratic recirocity relates solutions to x = (mod to solutions to x = (mod, where and are distinct odd rimes. The euations are oth solvale or oth unsolvale if either or has
Quadratic Recirocity 5-7-011 Quadratic recirocity relates solutions to x = (mod to solutions to x = (mod, where and are distinct odd rimes. The euations are oth solvale or oth unsolvale if either or has
Diophantine Equations
 Diohantine Equations Winter Semester 018/019 University of Bayreuth Michael Stoll Contents 1. Introduction and Examles 3. Aetizers 8 3. The Law of Quadratic Recirocity 1 Print version of October 5, 018,
Diohantine Equations Winter Semester 018/019 University of Bayreuth Michael Stoll Contents 1. Introduction and Examles 3. Aetizers 8 3. The Law of Quadratic Recirocity 1 Print version of October 5, 018,
Verifying Two Conjectures on Generalized Elite Primes
 1 2 3 47 6 23 11 Journal of Integer Sequences, Vol. 12 (2009), Article 09.4.7 Verifying Two Conjectures on Generalized Elite Primes Xiaoqin Li 1 Mathematics Deartment Anhui Normal University Wuhu 241000,
1 2 3 47 6 23 11 Journal of Integer Sequences, Vol. 12 (2009), Article 09.4.7 Verifying Two Conjectures on Generalized Elite Primes Xiaoqin Li 1 Mathematics Deartment Anhui Normal University Wuhu 241000,
HOMEWORK # 4 MARIA SIMBIRSKY SANDY ROGERS MATTHEW WELSH
 HOMEWORK # 4 MARIA SIMBIRSKY SANDY ROGERS MATTHEW WELSH 1. Section 2.1, Problems 5, 8, 28, and 48 Problem. 2.1.5 Write a single congruence that is equivalent to the air of congruences x 1 mod 4 and x 2
HOMEWORK # 4 MARIA SIMBIRSKY SANDY ROGERS MATTHEW WELSH 1. Section 2.1, Problems 5, 8, 28, and 48 Problem. 2.1.5 Write a single congruence that is equivalent to the air of congruences x 1 mod 4 and x 2
Chapter 3. Number Theory. Part of G12ALN. Contents
 Chater 3 Number Theory Part of G12ALN Contents 0 Review of basic concets and theorems The contents of this first section well zeroth section, really is mostly reetition of material from last year. Notations:
Chater 3 Number Theory Part of G12ALN Contents 0 Review of basic concets and theorems The contents of this first section well zeroth section, really is mostly reetition of material from last year. Notations:
Lecture 38: Secure Multi-party Computation MPC
 Lecture 38: Secure Multi-party Computation Problem Statement I Suppose Alice has private input x, and Bob has private input y Alice and Bob are interested in computing z = f (x, y) such that each party
Lecture 38: Secure Multi-party Computation Problem Statement I Suppose Alice has private input x, and Bob has private input y Alice and Bob are interested in computing z = f (x, y) such that each party
Probabilistic Algorithms
 Probabilistic Algorithms Klaus Sutner Carnegie Mellon University Fall 2017 1 Some Probabilistic Algorithms Probabilistic Primality Testing RP and BPP Where Are We? 3 Examle 1: Order Statistics 4 We have
Probabilistic Algorithms Klaus Sutner Carnegie Mellon University Fall 2017 1 Some Probabilistic Algorithms Probabilistic Primality Testing RP and BPP Where Are We? 3 Examle 1: Order Statistics 4 We have
MATH 210A, FALL 2017 HW 5 SOLUTIONS WRITTEN BY DAN DORE
 MATH 20A, FALL 207 HW 5 SOLUTIONS WRITTEN BY DAN DORE (If you find any errors, lease email ddore@stanford.edu) Question. Let R = Z[t]/(t 2 ). Regard Z as an R-module by letting t act by the identity. Comute
MATH 20A, FALL 207 HW 5 SOLUTIONS WRITTEN BY DAN DORE (If you find any errors, lease email ddore@stanford.edu) Question. Let R = Z[t]/(t 2 ). Regard Z as an R-module by letting t act by the identity. Comute
2 Asymptotic density and Dirichlet density
 8.785: Analytic Number Theory, MIT, sring 2007 (K.S. Kedlaya) Primes in arithmetic rogressions In this unit, we first rove Dirichlet s theorem on rimes in arithmetic rogressions. We then rove the rime
8.785: Analytic Number Theory, MIT, sring 2007 (K.S. Kedlaya) Primes in arithmetic rogressions In this unit, we first rove Dirichlet s theorem on rimes in arithmetic rogressions. We then rove the rime
2 Asymptotic density and Dirichlet density
 8.785: Analytic Number Theory, MIT, sring 2007 (K.S. Kedlaya) Primes in arithmetic rogressions In this unit, we first rove Dirichlet s theorem on rimes in arithmetic rogressions. We then rove the rime
8.785: Analytic Number Theory, MIT, sring 2007 (K.S. Kedlaya) Primes in arithmetic rogressions In this unit, we first rove Dirichlet s theorem on rimes in arithmetic rogressions. We then rove the rime
THE DIOPHANTINE EQUATION x 4 +1=Dy 2
 MATHEMATICS OF COMPUTATION Volume 66, Number 9, July 997, Pages 347 35 S 005-57897)0085-X THE DIOPHANTINE EQUATION x 4 +=Dy J. H. E. COHN Abstract. An effective method is derived for solving the equation
MATHEMATICS OF COMPUTATION Volume 66, Number 9, July 997, Pages 347 35 S 005-57897)0085-X THE DIOPHANTINE EQUATION x 4 +=Dy J. H. E. COHN Abstract. An effective method is derived for solving the equation
Representing Integers as the Sum of Two Squares in the Ring Z n
 1 2 3 47 6 23 11 Journal of Integer Sequences, Vol. 17 (2014), Article 14.7.4 Reresenting Integers as the Sum of Two Squares in the Ring Z n Joshua Harrington, Lenny Jones, and Alicia Lamarche Deartment
1 2 3 47 6 23 11 Journal of Integer Sequences, Vol. 17 (2014), Article 14.7.4 Reresenting Integers as the Sum of Two Squares in the Ring Z n Joshua Harrington, Lenny Jones, and Alicia Lamarche Deartment
Factor Rings and their decompositions in the Eisenstein integers Ring Z [ω]
![Factor Rings and their decompositions in the Eisenstein integers Ring Z [ω] Factor Rings and their decompositions in the Eisenstein integers Ring Z [ω]](/thumbs/79/79220303.jpg) Armenian Journal of Mathematics Volume 5, Number 1, 013, 58 68 Factor Rings and their decomositions in the Eisenstein integers Ring Z [ω] Manouchehr Misaghian Deartment of Mathematics, Prairie View A&M
Armenian Journal of Mathematics Volume 5, Number 1, 013, 58 68 Factor Rings and their decomositions in the Eisenstein integers Ring Z [ω] Manouchehr Misaghian Deartment of Mathematics, Prairie View A&M
Cryptography Assignment 3
 Crytograhy Assignment Michael Orlov orlovm@cs.bgu.ac.il) Yanik Gleyzer yanik@cs.bgu.ac.il) Aril 9, 00 Abstract Solution for Assignment. The terms in this assignment are used as defined in [1]. In some
Crytograhy Assignment Michael Orlov orlovm@cs.bgu.ac.il) Yanik Gleyzer yanik@cs.bgu.ac.il) Aril 9, 00 Abstract Solution for Assignment. The terms in this assignment are used as defined in [1]. In some
CONGRUENCE PROPERTIES MODULO 5 AND 7 FOR THE POD FUNCTION
 CONGRUENCE PROPERTIES MODULO 5 AND 7 FOR THE POD FUNCTION SILVIU RADU AND JAMES A. SELLERS Abstract. In this aer, we rove arithmetic roerties modulo 5 7 satisfied by the function odn which denotes the
CONGRUENCE PROPERTIES MODULO 5 AND 7 FOR THE POD FUNCTION SILVIU RADU AND JAMES A. SELLERS Abstract. In this aer, we rove arithmetic roerties modulo 5 7 satisfied by the function odn which denotes the
MATH 371 Class notes/outline October 15, 2013
 MATH 371 Class notes/outline October 15, 2013 More on olynomials We now consider olynomials with coefficients in rings (not just fields) other than R and C. (Our rings continue to be commutative and have
MATH 371 Class notes/outline October 15, 2013 More on olynomials We now consider olynomials with coefficients in rings (not just fields) other than R and C. (Our rings continue to be commutative and have
#A64 INTEGERS 18 (2018) APPLYING MODULAR ARITHMETIC TO DIOPHANTINE EQUATIONS
 #A64 INTEGERS 18 (2018) APPLYING MODULAR ARITHMETIC TO DIOPHANTINE EQUATIONS Ramy F. Taki ElDin Physics and Engineering Mathematics Deartment, Faculty of Engineering, Ain Shams University, Cairo, Egyt
#A64 INTEGERS 18 (2018) APPLYING MODULAR ARITHMETIC TO DIOPHANTINE EQUATIONS Ramy F. Taki ElDin Physics and Engineering Mathematics Deartment, Faculty of Engineering, Ain Shams University, Cairo, Egyt
A Modified Menezes-Vanstone Elliptic Curve Multi-Keys Cryptosystem
 A Modified Menezes-Vanstone Ellitic Curve Multi-Keys Crytosystem By K.H. Rahouma Electrical Technology Deartment Technical College in Riyadh Riyadh, Kingdom of Saudi Arabia E-mail: kamel_rahouma@yahoo.com
A Modified Menezes-Vanstone Ellitic Curve Multi-Keys Crytosystem By K.H. Rahouma Electrical Technology Deartment Technical College in Riyadh Riyadh, Kingdom of Saudi Arabia E-mail: kamel_rahouma@yahoo.com
LARGE GAPS BETWEEN CONSECUTIVE PRIME NUMBERS CONTAINING SQUARE-FREE NUMBERS AND PERFECT POWERS OF PRIME NUMBERS
 LARGE GAPS BETWEEN CONSECUTIVE PRIME NUMBERS CONTAINING SQUARE-FREE NUMBERS AND PERFECT POWERS OF PRIME NUMBERS HELMUT MAIER AND MICHAEL TH. RASSIAS Abstract. We rove a modification as well as an imrovement
LARGE GAPS BETWEEN CONSECUTIVE PRIME NUMBERS CONTAINING SQUARE-FREE NUMBERS AND PERFECT POWERS OF PRIME NUMBERS HELMUT MAIER AND MICHAEL TH. RASSIAS Abstract. We rove a modification as well as an imrovement
CDH/DDH-Based Encryption. K&L Sections , 11.4.
 CDH/DDH-Based Encrytion K&L Sections 8.3.1-8.3.3, 11.4. 1 Cyclic grous A finite grou G of order q is cyclic if it has an element g of q. { 0 1 2 q 1} In this case, G = g = g, g, g,, g ; G is said to be
CDH/DDH-Based Encrytion K&L Sections 8.3.1-8.3.3, 11.4. 1 Cyclic grous A finite grou G of order q is cyclic if it has an element g of q. { 0 1 2 q 1} In this case, G = g = g, g, g,, g ; G is said to be
Lecture 10. Public Key Cryptography: Encryption + Signatures. Identification
 Lecture 10 Public Key Cryptography: Encryption + Signatures 1 Identification Public key cryptography can be also used for IDENTIFICATION Identification is an interactive protocol whereby one party: prover
Lecture 10 Public Key Cryptography: Encryption + Signatures 1 Identification Public key cryptography can be also used for IDENTIFICATION Identification is an interactive protocol whereby one party: prover
arxiv: v2 [math.ho] 24 Nov 2014
![arxiv: v2 [math.ho] 24 Nov 2014 arxiv: v2 [math.ho] 24 Nov 2014](/thumbs/96/129262236.jpg) arxiv:88.48v2 [math.ho] 24 Nov 24 There are infinitely many rime numbers in all arithmetic rogressions with first term and difference corime. (By Mr. Lejeune-Dirichlet) [Read to the Academy of Sciences
arxiv:88.48v2 [math.ho] 24 Nov 24 There are infinitely many rime numbers in all arithmetic rogressions with first term and difference corime. (By Mr. Lejeune-Dirichlet) [Read to the Academy of Sciences
LECTURE 10: JACOBI SYMBOL
 LECTURE 0: JACOBI SYMBOL The Jcobi symbol We wish to generlise the Legendre symbol to ccomodte comosite moduli Definition Let be n odd ositive integer, nd suose tht s, where the i re rime numbers not necessrily
LECTURE 0: JACOBI SYMBOL The Jcobi symbol We wish to generlise the Legendre symbol to ccomodte comosite moduli Definition Let be n odd ositive integer, nd suose tht s, where the i re rime numbers not necessrily
Brownian Motion and Random Prime Factorization
 Brownian Motion and Random Prime Factorization Kendrick Tang June 4, 202 Contents Introduction 2 2 Brownian Motion 2 2. Develoing Brownian Motion.................... 2 2.. Measure Saces and Borel Sigma-Algebras.........
Brownian Motion and Random Prime Factorization Kendrick Tang June 4, 202 Contents Introduction 2 2 Brownian Motion 2 2. Develoing Brownian Motion.................... 2 2.. Measure Saces and Borel Sigma-Algebras.........
Characteristics of Fibonacci-type Sequences
 Characteristics of Fibonacci-tye Sequences Yarden Blausa May 018 Abstract This aer resents an exloration of the Fibonacci sequence, as well as multi-nacci sequences and the Lucas sequence. We comare and
Characteristics of Fibonacci-tye Sequences Yarden Blausa May 018 Abstract This aer resents an exloration of the Fibonacci sequence, as well as multi-nacci sequences and the Lucas sequence. We comare and
Outline. EECS150 - Digital Design Lecture 26 Error Correction Codes, Linear Feedback Shift Registers (LFSRs) Simple Error Detection Coding
 Outline EECS150 - Digital Design Lecture 26 Error Correction Codes, Linear Feedback Shift Registers (LFSRs) Error detection using arity Hamming code for error detection/correction Linear Feedback Shift
Outline EECS150 - Digital Design Lecture 26 Error Correction Codes, Linear Feedback Shift Registers (LFSRs) Error detection using arity Hamming code for error detection/correction Linear Feedback Shift
arxiv: v2 [math.nt] 11 Jun 2016
![arxiv: v2 [math.nt] 11 Jun 2016 arxiv: v2 [math.nt] 11 Jun 2016](/thumbs/91/105405277.jpg) Congruent Ellitic Curves with Non-trivial Shafarevich-Tate Grous Zhangjie Wang Setember 18, 018 arxiv:1511.03810v [math.nt 11 Jun 016 Abstract We study a subclass of congruent ellitic curves E n : y x
Congruent Ellitic Curves with Non-trivial Shafarevich-Tate Grous Zhangjie Wang Setember 18, 018 arxiv:1511.03810v [math.nt 11 Jun 016 Abstract We study a subclass of congruent ellitic curves E n : y x
Galois Fields, Linear Feedback Shift Registers and their Applications
 Galois Fields, Linear Feedback Shift Registers and their Alications With 85 illustrations as well as numerous tables, diagrams and examles by Ulrich Jetzek ISBN (Book): 978-3-446-45140-7 ISBN (E-Book):
Galois Fields, Linear Feedback Shift Registers and their Alications With 85 illustrations as well as numerous tables, diagrams and examles by Ulrich Jetzek ISBN (Book): 978-3-446-45140-7 ISBN (E-Book):
THE THEORY OF NUMBERS IN DEDEKIND RINGS
 THE THEORY OF NUMBERS IN DEDEKIND RINGS JOHN KOPPER Abstract. This aer exlores some foundational results of algebraic number theory. We focus on Dedekind rings and unique factorization of rime ideals,
THE THEORY OF NUMBERS IN DEDEKIND RINGS JOHN KOPPER Abstract. This aer exlores some foundational results of algebraic number theory. We focus on Dedekind rings and unique factorization of rime ideals,
Multiplicative group law on the folium of Descartes
 Multilicative grou law on the folium of Descartes Steluţa Pricoie and Constantin Udrişte Abstract. The folium of Descartes is still studied and understood today. Not only did it rovide for the roof of
Multilicative grou law on the folium of Descartes Steluţa Pricoie and Constantin Udrişte Abstract. The folium of Descartes is still studied and understood today. Not only did it rovide for the roof of
Analytic number theory and quadratic reciprocity
 Analytic number theory and quadratic recirocity Levent Aloge March 31, 013 Abstract What could the myriad tools of analytic number theory for roving bounds on oscillating sums ossibly have to say about
Analytic number theory and quadratic recirocity Levent Aloge March 31, 013 Abstract What could the myriad tools of analytic number theory for roving bounds on oscillating sums ossibly have to say about
Elementary Number Theory
 Elementary Number Theory WISB321 = F.Beukers 2012 Deartment of Mathematics UU ELEMENTARY NUMBER THEORY Frits Beukers Fall semester 2013 Contents 1 Integers and the Euclidean algorithm 4 1.1 Integers................................
Elementary Number Theory WISB321 = F.Beukers 2012 Deartment of Mathematics UU ELEMENTARY NUMBER THEORY Frits Beukers Fall semester 2013 Contents 1 Integers and the Euclidean algorithm 4 1.1 Integers................................
ON THE LEAST SIGNIFICANT p ADIC DIGITS OF CERTAIN LUCAS NUMBERS
 #A13 INTEGERS 14 (014) ON THE LEAST SIGNIFICANT ADIC DIGITS OF CERTAIN LUCAS NUMBERS Tamás Lengyel Deartment of Mathematics, Occidental College, Los Angeles, California lengyel@oxy.edu Received: 6/13/13,
#A13 INTEGERS 14 (014) ON THE LEAST SIGNIFICANT ADIC DIGITS OF CERTAIN LUCAS NUMBERS Tamás Lengyel Deartment of Mathematics, Occidental College, Los Angeles, California lengyel@oxy.edu Received: 6/13/13,
Factorability in the ring Z[ 5]
![Factorability in the ring Z[ 5] Factorability in the ring Z[ 5]](/thumbs/72/66373696.jpg) University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Dissertations, Theses, and Student Research Paers in Mathematics Mathematics, Deartment of 4-2004 Factorability in the ring
University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Dissertations, Theses, and Student Research Paers in Mathematics Mathematics, Deartment of 4-2004 Factorability in the ring
GOOD MODELS FOR CUBIC SURFACES. 1. Introduction
 GOOD MODELS FOR CUBIC SURFACES ANDREAS-STEPHAN ELSENHANS Abstract. This article describes an algorithm for finding a model of a hyersurface with small coefficients. It is shown that the aroach works in
GOOD MODELS FOR CUBIC SURFACES ANDREAS-STEPHAN ELSENHANS Abstract. This article describes an algorithm for finding a model of a hyersurface with small coefficients. It is shown that the aroach works in
GENERALIZED FACTORIZATION
 GENERALIZED FACTORIZATION GRANT LARSEN Abstract. Familiarly, in Z, we have unique factorization. We investigate the general ring and what conditions we can imose on it to necessitate analogs of unique
GENERALIZED FACTORIZATION GRANT LARSEN Abstract. Familiarly, in Z, we have unique factorization. We investigate the general ring and what conditions we can imose on it to necessitate analogs of unique
THE LEAST PRIME QUADRATIC NONRESIDUE IN A PRESCRIBED RESIDUE CLASS MOD 4
 THE LEAST PRIME QUADRATIC NONRESIDUE IN A PRESCRIBED RESIDUE CLASS MOD 4 PAUL POLLACK Abstract For all rimes 5, there is a rime quadratic nonresidue q < with q 3 (mod 4 For all rimes 3, there is a rime
THE LEAST PRIME QUADRATIC NONRESIDUE IN A PRESCRIBED RESIDUE CLASS MOD 4 PAUL POLLACK Abstract For all rimes 5, there is a rime quadratic nonresidue q < with q 3 (mod 4 For all rimes 3, there is a rime
