About Three Important Transformations Groups
|
|
|
- Claude Lucas
- 5 years ago
- Views:
Transcription
1 About Tree Important Transformatons Groups MONICA A.P. PURCARU Translvana Unversty of Braşov Department of Matematcs Iulu Manu Street Braşov ROMANIA m.purcaru@yaoo.com MIRELA TÂRNOVEANU Translvana Unversty of Braşov Department of Matematcs Iulu Manu Street Braşov ROMANIA m tarnoveanu@yaoo.com LAURA CIUPALĂ Translvana Unversty of Braşov Department of Computer Scence Iulu Manu Street Braşov ROMANIA laura cupala@yaoo.com Abstract: In te present paper e ntroduce te concepts of conformal metrcal d-structure and of conformal metrcal N-lnear connecton t respect to te conformal metrcal d-structure correspondng to an 1-form on a generalzed Hamlton space. We determne te set of all conformal metrcal N-lnear connectons n te case en te nonlnear connecton s arbtrary and e fnd mportant examples and partcular cases. We fnd te transformatons group of tese connectons. We study te role of te torson d-tensor felds T S and S n ts teory especally n te determnaton of te set of all semsymmetrc conformal metrcal N-lnear connectons t respect to te conformal metrcal d-structure correspondng to te same nonlnear connecton N. We gve te transformatons group of tese connectons and oter to mportant groups and e fnd ter remarable nvarants. Fnally e determne te set of all metrcal N-lnear connectons n te case en te nonlnear connecton s arbtrary e gve mportant examples and partcular cases and for te case en te nonlnear connecton s fxed e fnd te transformatons group of tese connectons. Key Words: second order cotangent bundle nonlnear connecton N-lnear connecton metrcal d-structure conformal metrcal d-structure conformal metrcal N-lnear connecton semsymmetrc conformal metrcal N-lnear connecton metrcal N-lnear connecton transformatons group subgroup nvarants. 1 Introducton Te geometry of te cotangent bundle T M π M as been studed by R.Mron S.Watanabe and S.Yeda n [5] by K.Yano and S.Isara n [14] by R.Mron D.Hrmuc H.Smada and S.Sabău n [4] C. Udrşte and O. Şandru n [12] etc. Contrbutons n development of ts teory ad also: Te dfferental geometry of te second order cotangent bundle T 2 M π 2 M as ntroduced and studed by R. Mron n [2] R. Mron D. Hrmuc H. Smada V.S. Sabău n [4] G. Atanasu and M. Târnoveanu n [1] C. Udrşte M.Popescu and P.Popescu n [11] C. Udrşte n [8] [9] C. Udrşte D. Oprş n [1] C. Udrşte I. Tevy n [13] etc. In te present secton e eep te general settng from R. Mron D. Hrmuc H. Smada V.S. Sabău [4] and subsequently e recall only some needed notons. For more detals see [4]. Let M be a real n dmensonal manfold and let T 2 M π 2 M be te dual of te 2 tangent bundle or 2 cotangent bundle. A pont u T 2 M can be rtten n te form u = x y p avng te local coordnates x y p = n. A cange of local coordnates on te 3n dmensonal manfold T 2 M s x = x x 1... x n det x x j ȳ = x y j 1 x j p = xj p x j j = n. We denote by T 2 M = T 2 M \ {} ere : M T 2 M s te null secton of te projecton π 2. Let us consder te tangent bundle of te dfferentable manfold T 2 M T T 2 M τ 2 T 2 M ere τ 2 s te canoncal projecton and te vertcal dstrbuton V : u T 2 M V u T{ u T 2 M locally } generated by te vector felds u u y p u T 2 M. lnear mappng Te follong F T 2 M J : χ T 2 M χ T 2 M defned by: J = J x y u T 2 M = J y p = 2 ISSN: Issue 9 Volume 9 September 21
2 s a tangent structure on T 2 M. We denote t N a nonlnear connecton on te manfold T 2 M t te local coeffcents N j x y p N j x y p j = n. Hence te tangent space of T 2 M n te pont u T 2 M s gven by te drect sum of vector spaces: T u T 2 M = N u W 1 u W 2 u u T 2 M. 3 A local adapted bass to te drect decomposton 3 s gven by: { δ δx y p } = n 4 δ δx = N j x + N y j j p j. 5 Wt respect to te coordnates transformatons 1 e ave te rules: by: δ δx y p = xj δ ; x δ x j = xj ; x ȳ j = x x j p j. 5 Te dual bass of te adapted bass 4 s gven { δx δy δp } 6 δx = dx δy = dy + N jdx j 6 δp = dp N j dx j. Wt respect to 1 te covector felds 6 are transformed by te rules: δ x = x x j δx j δȳ = x x j δy j δ p = xj x δp j. 6 Let D be an N lnear connecton on T 2 M t te local coeffcents n te adapted bass: DΓ N = H C C. An N lnear connecton D s unquely represented n te adapted bass 4 n te follong form: δ D δ = H δx j δx j δ δx D δ = H δx j y j y D δ δx j p = H j p δ D = C y j δx j δ δx D = C y j y j y 7 D y j p = C j p δ = C j δ δx D p j D p j D p j δx y = C j y p = C j p. An N-lnear connecton D t te local coeffcents DΓ N = H C C determnes te 1 2 covarant dervatves n te tensor algebra of d-tensor felds. Defnton 1 [1] An N-lnear connecton on T 2 M s called semsymmetrc f: T = 1 2 δj σ + δ σ j S = 1 2 δj τ + δ τ j S = 1 2 δ j v + δ vj ere σ τ χ T 2 M and v χ T 2 M. 8 2 Conformal metrcal N-lnear connectons n a generalzed Hamlton space Defnton 2 [4] A generalzed Hamlton space of order to s a par GH 2n = M g j x y p 1 g j s a d tensor feld of type 2 symmetrc and nondegenerate on te manfold T 2 M. 2 Te quadratc form g j X X j as a constant sgnature on T 2 M. g j s called te fundamental tensor or metrc tensor of te space GH 2n. In te case en T 2 M s a paracompact manfold ten on T 2 M tere exst te metrc tensors g j x y p postvely defned suc tat M g j s a generalzed Hamlton space. Defnton 3 [4] A generalzed Hamlton metrc g j x y p of order to on sort GH metrc s ISSN: Issue 9 Volume 9 September 21
3 called reductble to an Hamlton metrc H metrc of order to f tere exsts a functon H x y p on T 2 M suc tat: 2 H g j = 1 2 p p j. 9 Te covarant tensor feld g j s obtaned from te equatons: g j g = δ. 1 g j s a symmetrc nondegenerate and covarant of order to d tensor feld. Defnton 4 [4] An N lnear connecton D s called metrcal t respect to GH metrc g j f: g j = g j = g j =. 11 Te tensoral equatons 11 mply: g j = g j = g j =. 12 Teorem 5 [4]1. Tere exsts a unque N lnear connecton D Γ N = H C C avng te propertes: 1. Te nonlnear connecton N s a pror gven. 2. D Γ N s metrcal t respect to GHmetrc g j.e.12 are verfed. S 3. Te torson tensors T S and vans. 2. Te prevous connecton as te coeffcents C and C gven by and C = 1 2 gm g m C = 1 2 g m y j g m p j + g jm y + gjm p g y m g p m H are generalzed Crstoffel symbols: 13 H = 1 2 gm δg m + δg jm δg δx j δx δx. 14 m Te operators of Obata s type are gven by: Ω j = 1 2 Ω j = 1 2 δ δj g g j δ δj + g g j. 15 Te operators of Obata s type ave te same propertes as te one assocated t a Fnsler space [3]. Let S 2 T 2 M be te set of all symmetrc d- tensor felds of te type 2. As s easly son te relatons for a j b j S 2 T 2 M defned by: a j b j λx y p FT 2 M a j x y p = e 2λxyp b j x y p s an equvalence relaton on S 2 T 2 M. 16 Defnton 6 Te equvalent class ĝ of S 2 T 2 M/ to c te fundamental d-tensor feld g j belongs s called conformal metrcal d-structure. Tus: ĝ = {g g j x y p = e2λxyp g j x y p λx y p FT 2 M}. 17 Defnton 7 An N-lnear connecton D t local coeffcents: DΓ N = H C C for c tere exsts te 1-form ω ω = ω dx + ω δy + ω δp suc tat: { gj = 2ω g j g j = 2 ω g j g j = 2 ω 18 g j ere and denote te 1 and 2 covarant dervatves t respect to D s called conformal metrcal N-lnear connecton t respect to te conformal metrcal d-structure ĝ correspondng to te 1-form ω and s denoted by: DΓN ω. Proposton 8 If DΓN ω = H C C are te local coeffcents of a conformal metrcal N- lnear connecton n T 2 M t respect to te conformal metrcal structure ĝ correspondng to te 1- form ω ten: { g j = 2ω g j g j = 2 ω g j g j = 2 ω g j 19. Proof. Usng te relatons 18 by covarant dervaton from 1 e ave te results. Proposton 9 Te operators of Obata s type are covarant constant t respect to any conformal metrcal N-lnear connecton D: { Ω r sj l = Ω r sj l = Ω r Ω r sj l = Ω r sj l = Ω r sj l = sj l = 2 ere l l and l denote te 1 and 2 covarant dervatves t respect to D. ISSN: Issue 9 Volume 9 September 21
4 Proof. Usng te relatons 18 and 19 by covarant dervaton from 15 e ave te results. For any representatve g ĝ e ave: Teorem 1 For g j = e 2λ g j a conformal metrcal N-lnear connecton t respect to te conformal metrcal structure ĝ correspondng to te 1-form ω DΓN ω satsfes: { g j = 2ω g j g j = 2 ω g j g j = 2 ω g j 21 ere ω = ω + dλ. Snce n Teorem 1 ω = s equvalent to ω = d λ e ave: Teorem 11 A conformal metrcal N-lnear connecton t respect to ĝ correspondng to te 1-form ω DΓN ω s metrcal t respect to g ĝ.e. g j = g j = g j = f and only f ω s exact. We sall determne te set of all conformal metrcal N-lnear connectons t respect to ĝ. Let D Γ N = H C C be te local coeffcents of a fxed N- lnear connecton D on T 2 M ere N j x y p N j x y p j = n are te local coeffcents of te nonlnear connecton N. Ten any N-lnear connecton D on T 2 M t te local coeffcents DΓN = H C C ere N j x y p N j x y p j = n are te local coeffcents of te nonlnear connecton N can be expressed n te form [6]: N j = N j A j N j = N j A j H = H + A l C jl A l C l j B 22 C = C D C = C D j = n t A = A = j = n j 23 j ere denotes te -covarant dervatve t respect to D and A j A j B D D are te components of te dfference tensor felds of D from D. Teorem 12 Let D be a gven N -lnear connecton t local coeffcents D Γ N = H C C. Te set of all conformal metrcal N-lnear connectons t respect to ĝ correspondng to te 1-form ω t local coeffcents DΓN ω = H C C s gven by: N j = N j X j N j = N j X j H = H + X l C jl X l C l j gm g 2ω g mj + g mj l X l mj g mj l X l + Ω r sj Xs r C = C gm g mj 2 ω g mj + +Ω r sj Y s r C = C g m 2 ω g m + +Ω rj j = n 24 t: s Z r s X = X j j = j = n 25 ere and denote te 1 and 2 covarant dervatves t respect to D X j X j X Y Z are arbtrary d-tensor felds ω = ω dx + ω δy + ω δp s an arbtrary 1-form and Ω s te operator of Obata s type gven by 15. Proof. Usng te relatons by extenson of te metod gven by R.Mron n [3] for te case of Fnsler connectons e obtan te results. Partcular cases: 1. If X j = X j = X = Y = Z = n Teorem 12 e ave: Teorem 13 Let D be a gven N -lnear connecton on T 2 M t local coeffcents D Γ N = H C C. Ten te follong N-lnear conecton K t local coeffcents KΓ N ω = ISSN: Issue 9 Volume 9 September 21
5 H C C gven by 26 s conformal metrcal t respect to ĝ correspondng to te 1-form ω: H = H gm g 2ω g mj mj C = C gm g mj 2 ω g mj C = C gjm g m 2 ω g m j = n 26 ere and denote te 1 and 2 covarant dervatves t respect to D and ω = ω dx + ω δy + ω δp s an arbtrary 1-form. 2. If e tae a metrcal N-lnear connecton as D n Teorem 13 ten 26 becomes: H = H δj ω C = C δj ω 27 C = C δ j ω j = n. As an exemple of D e tae te N-lnear connecton gven n Teorem Teorem 14 Te follong N-lnear connecton W t local coeffcents W ΓN ω = H C C s a conformal metrcal N- lnear connecton t respect to ĝ correspondng to te 1-form ω: H = 1 2 gm δg m + δg jm δg δx j δx δx m δj ω 2Ω m ω m C = 1 2 gm g m + g jm g y j y y m j ω 2Ω m ω m C = 1 2 g g m m p j + gjm p g p m j ω 2Ω m ωm j = n 28 ere ω = ω dx + ω δy + ω δp s an arbtrary 1-form. 4. If e tae a conformal metrcal N-lnear connecton t respect to ĝ e.g. W as D n Teorem 12 e ave: Teorem 15 Let D be a fxed conformal metrcal N- lnear connecton t respect to ĝ correspondng to te 1-form ω t te local coeffcents D Γ N ω = H C C. Te set of all conformal metrcal N-lnear connectons t respect to ĝ correspondng to te 1-form ω t local coeffcents DΓN ω = H C C s gven by: N j = N j X j N j = N j X j H = H + C jl + ω l δj X l C l j + ω l δj X l + Ω r sj Xs r 29 t C = C + Ω r sj Y s r C = C + Ω jr j = n X = X j j s Z r s = j = n 3 ere and denote te 1 and 2 covarant dervatves t respect to D ω = ω dx + ω δy + ω δp s an arbtrary 1-form and X j X j X Y Z are arbtrary d-tensor felds. 5. Fnally f e tae X j = X j = n Teorem 15 e obtan: Teorem 16 Let D be a fxed conformal metrcal N- lnear connecton t respect to ĝ correspondng to te 1-form ω t local coeffcents D Γ N ω = H C C. Te set of all conformal met- rcal N-lnear connectons t respect to ĝ correspondng to te 1-form ω correspondng to te same nonlnear connecton N t local coeffcents DΓ N ω = H C C s gven by: H = H + Ω r sj Xs r C = C + Ω r sj Y s r 31 C = C + Ω jr j = n s Z r s ISSN: Issue 9 Volume 9 September 21
6 ere X Y Z are arbtrary d-tensor felds on T 2 M and ω = ω dx + ω δy + ω δp s an arbtrary 1-form. 3 Some specal classes of conformal metrcal N-lnear connectons We sall try to replace te arbtrary tensor felds X Y and Z n Teorem 16 by te torson tensor felds T S and S. We put: T = 1 2 gm g m T g jt m + +g T jm S = 1 2 gm g m S g js m + +g S jm S = 1 2 g mg m S +g S jm. gj S m + 32 Teorem 17 Let T S and S be tree gven se symmetrc tensor felds of type and 21 respectvely and let ω be a gven 1-form n T 2 M. Ten tere exsts a unque conformal metrcal N-lnear connecton t respect to ĝ correspondng to te 1-form ω t local coeffcents DΓN ω = H C C avng T S and S as te torson tensor felds. It s gven by: H = H + T C = C + S C = C + S 33 ere W ΓN ω = H C C are te local coeffcents of conformal metrcal N-lnear connecton t respect to ĝ correspondng to te 1-form ω gven n 28. Remar 18 Te conformal metrcal N-lnear connecton t respect to ĝ W correspondng to te 1-form ω t local coeffcents W ΓN ω = H C C gven n 28 s consdered as te semsymmetrc conformal metrcal N-lnear connecton t te vansng 1 and 2 torson vector felds. Usng te Defnton 1 te relatons 32 become: T = 2Ωr σ r S = 2Ωr τ r 34 S = 2Ω r vr. Usng te Teorem 17 and te relatons 34 e ave: Teorem 19 Te set of all semsymmetrc conformal metrcal N-lnear connectons t respect to ĝ correspondng to te 1-form ω t local coeffcents DΓN ω σ = H C C s gven by: H = H + 2Ω r σ r C = C + 2Ω r τ r 35 C = C + 2Ω r vr j = n ere W ΓN ω = H C C are te local coeffcents of te semsymmetrc conformal metrcal N-lnear connecton W gven n 28 and σ = σ dx + τ δy + v δp s an arbtrary 1-form. 4 Te group of transformatons of conformal metrcal N-lnear connectons We study te transformatons DΓN ω DΓ N ω of te conformal metrcal N-lnear connectons t respect to ĝ. If e replace D Γ N and DΓN ω n Teorem 12 by DΓN ω and DΓ N ω respectvely to conformal metrcal N- and respectvely N-lnear connectons t respect to ĝ e obtan: Teorem 2 To conformal metrcal N- and respectvely N- lnear connectons t respect to ĝ: D and D t local coeffcents DΓN ω = H C C and DΓ N ω = H C related as follos: N j = N j X j N j = N j X j C H = H + Xl C jl X lcj l δj p + δ j ω lx l δ j ωl X l + Ω r C = C δj ṗ + Ωr sj Y s r C = C δ j p + Ω jr s Z s j = n r respectvely are sj Xs r 36 ISSN: Issue 9 Volume 9 September 21
7 t: X j = X j = j = n 37 ere p = ω ω ω = ω dx + ω δy + ω δp and ω = ω dx + ω δy + ω δp are to 1-forms denote te -covarant dervatve t respect to D and X j X j X Y Z are arbtrary d-tensor felds. Proof. Usng n 24 te relatons 18 by drect calculaton e ave te results. Conversely gven te d-tensor felds X j X j X Y Z and one gven 1-form p = p dx + ṗ δy + p δp te above 36 s tougt to be a transformaton of a conformal metrcal N- lnear connecton DΓN ω to a conformal metrcal N-lnear connecton DΓ N ω = DΓ N ω + p. We sall denote ts transformaton by tx j X j X Y Z p. Tus e ave: Teorem 21 Te set C of all transformatons tx j X j X Y Z p gven by 36 and 37 s a transformatons group of te set of all conformal metrcal N-lnear connectons t respect to ĝ togeter t te mappng product: tx j X j X Y Z p tx j X j X Y Z p = tx j + X j X j + X j X + X Y + Y Z + Z p + p. 5 Te group of transformatons of semsymmetrc conformal metrcal N-lnear connectons We nqure about a subgroup of te group of transformatons of conformal metrcal n-lnear connecton: about te subgroup of transformatons of te semsymmetrc comformal metrcal N-lnear connectons correspondng to te same nonlnear connecton N. Let N be a gven nonlnear connecton. Ten any semsymmetrc conformal metrcal N-lnear connecton t local coeffcents DΓN ω σ = H C C t respect to ĝ s gven by 33 t 34. Teorem 22 To semsymmetrc conformal metrcal N-lnear connectons t respect to ĝ t local coeffcents DΓN ω σ = H C C and DΓ N ω σ = H C are related as follos: C H = H δ j p + 2Ωr q r C = C δj ṗ + 2Ωr q r C = C j = n δ j p + 2Ω r qr respectvely 38 ere p = ω ω q = σ σ p p = p dx + ṗ δy + p δp and q = q dx + q δy + q δp. Proof. Usng n 35 te relatons 28 by drect calculaton e ave te results. Conversely gven 1-forms p and q n T 2 M te above 38 s tougt to be a transformaton of a semsymmetrc conformal metrcal N-lnear connecton D t local coeffcents DΓN ω σ = H C C to a semsymmetrc conformal metrcal N- lnear connecton D t local coeffcents DΓN ω + p σ + p + q = H C C. We sall denote ts transformaton by tp q. Tus e ave: Teorem 23 Te set CN s of all transformatons tp q gven by 38 s a transformatons group of te set of all semsymmetrc conformal metrcal N-lnear connectons t respect to ĝ avng te same nonlnear connecton N togeter t te mappng product: tp q tp q = tp + p q + q. Ts group CN s s an Abelan subgroup of C and acts on te set of all semsymmetrc conformal metrcal N-lnear connectons avng te same nonlnear connecton N transtvely. Te transformaton tp q : DΓN ω σ DΓN ω + p σ + p + q gven by 38 s expressed by te product of te follong to transformatons: H = H δ j p C = C δ jṗ C = C δ j 39 p j = n H = H + 2Ωr q r C = C + 2Ωr q r C = C + 2Ω 4 r qr j = n Defnton 24 Te transformaton t : DΓN DΓN of N-lnear connecton on T 2 M defned by ISSN: Issue 9 Volume 9 September 21
8 39 s called co-parallel transformaton ere p s a gven 1-form. Teorem 25 Te set C p N of all co-parallel transformatons t gven by 39 s an Abelan group togeter t te mappng product. Defnton 26 Te transformaton t : DΓN DΓN of N-lnear connectons gven by 4 s called Mron transformaton as te name gven by M.Hasguc [3] for Fnsler spaces. Teorem 27 Te set CN m of all Mron transformatons t gven by 4 s a transformatons group togeter t te mappng product. Teorem 28 Te group CN s of all transformatons tp q gven by 38 s te drect product of te group C p N of all co-paralel transformatons and te group of all Mron transformatons. C m N It s noted tat te nvarants of te group CN s ll be te nvarants of eac of tese subgroups and recprocally. It s drectly son tat by a co-parallel transformaton 39 te curvature tensor felds R P and S are transformed as follos: R = R δ p P = P δ ṗ S = S δ p 41 ere p ṗ and p are te components of dp expressed t respect to D. Elmnatng p ṗ and p from 41 e ave: R = R S Tus e ave: P = P = S R = R 1 n δ R s s s s. P = P 1 n δ P s S = S 1 n δ S s Teorem 29 Te tensor felds R P and S gven by 43 are nvarants of te group C p N. Also e obtan: Teorem 3 Te tensor feld C gven by 44 s an nvarant of te group C p N. C = C 1 n δj C s s. 44 In our prevous paper [Bull Mat Buc] startng from te tensor felds: K = R C m Rm 1 C m R 2m P = P C m N jm p C m N m j y 45 e obtaned te follong mportant nvarants of te group of semsymmetrc metrcal N-lnear connectons avng te same nonlnear connecton N T ms N for n > 2: H = K + 2 n 2 A {Ω r j K r g rk 2n 1 } N = P + 2 n 2 A {Ω r j P r g rp 2n 1 } M = S + 2 n 2 A {Ω r j S r g rs M 2n 1 } = S + 2 n 2 A {Ω j r Sr grj S 2n 1 } K j = K j K = gj K j P j = P P = g j P j S j = S j S = gj S j S j = Sm jm S = g j S j j If e replace tese K P S j and S by te tensor felds K P S and S respectvely defned by: K = K 1 n δ K m m m m m P = P 1 n δ P m S = S 1 n δ S m S = S 1 n δ S m 48 e can obtan te nvarants of te group of transformatons of semsymmetrc conformal metrcal N- lnear connectons avng te same nonlnear connecton N C s N : Teorem 31 For n > 2 te follong tensor felds H N M and M are nvarants of te group CN s of transformatons of semsymmetrc conformal metrcal N-lnear connectons avng te same nonlnear connecton N: ISSN: Issue 9 Volume 9 September 21
9 H = K + 2 n 2 A {Ω r j K r g rk 2n 1 } N = P + 2 n 2 A {Ω r j P r g rp 2n 1 } M = S + 2 n 2 A {Ω r M g rs 2n 1 } = S + 2 n 2 A {Ω j r S r gr S 2n 1 } j S r K j = K j K = g j K j P j = P j P = g j P j S j = S j S = g j S j S j = S jm m S = g j S j. Fnally e gve anoter nvarant of te group C s N : 49 5 Teorem 32 Te follong tensor feld s an nvarant of te group C s N : C 2 n 1 Ωj r j = n ere C s gven by 44. C rm m 51 6 Metrcal N-lnear connectons n a generalzed Hamlton space We sall determne te set of all metrcal N-lnear connectons n te case en te nonlnear connecton N s arbtrary. Teorem 33 Let D be gven N-lnear connecton on T 2 M t local coeffcents D Γ N = = H C C ere te local coeffcents of te nonlnear connecton N are: N j x y p N j x y p j = n. Te set of all metrcal N-lnear connectons t respect to g j t local coeffcents DΓN = H C C s gven by: N j = N j X j N j = N j X j H = H + X l t: C jl X l C j l gm g + g mj l X l mj g mj l X l + Ω r sj Xs r C = C gm g mj + Ω r sj Y s r C = C gmj g m + Ω rj s Z r s j = n 52 X = X = j = n 53 j j ere and denote te 1 and 2 covarant dervatves t respect to D X j X j X Y Z are arbtrary d-tensor felds and Ω s te operator of Obata s type gven by 15. Proof. Usng te relatons by extenson of te metod gven by R.Mron n [3] for te case of Fnsler connectons e can deduce te results. Partcular cases: 1. If X j = X j = X = Y = Z = n Teorem 33 e ave: Teorem 34 Let D be a gven N-lnear connecton on T 2 M t local coeffcents D Γ N = H C C. Ten te follong N-lnear connecton D t local coeffcents DΓ N = H C C gven by 54 s metrcal: N j = N j N j = N j H = H gm g mj C = C gm g mj C = C gmj g m j = n 54 ISSN: Issue 9 Volume 9 September 21
10 ere and denote te 1 and 2 covarant dervatves t respect to D. 2. If e tae a metrcal N-lnear connecton as D n Teorem 33 e obtan: Teorem 35 Te set of all metrcal N- lnear connectons t local coeffcents DΓN = H C C s gven by: N j = N j X j N j = N j X j H = t: H + X l C jl X l C l j + Ω r sj Xs r C = C + Ω r C = C + Ω rj j = n X = X j ere j and sj Y s r s Z r s 55 = j = n 56 denote te 1 and 2 covarant dervatves t respect to D X j X j X Y Z are arbtrary d-tensor felds and Ω s te operator of Obata s type gven by If n Teorem 35 e consder X = X j = o e obtan te set of all metrcal N-lnear connectons avng te same nonlnear connecton N gven by R.Mron D.Hrmuc H.Smada and V.S. Sabău n ter boo [4] Teorem 2.3 p Te group of transformatons of metrcal N-lnear connectons Let N be a gven nonlnear connecton. Ten any metrcal N-lnear connecton correspondng to te same nonlnear connecton N as te local coeffcents DΓN = H C C. gven by: H = H + Ωr sj Xs r C = C + Ωr sj Y s r C = C + Ω rj s Zr s j = n 57 ere X Y Z are arbtrary d-tensor felds Ω s te operator of Obata s type gven by 15 and DΓN = H C C are te local coeffcents of a metrcal N-lnear connecton D. Conversely gven te tensor felds X Y Z te above 57 s tougt to be a transformaton of a metrcal N-lnear connecton DΓN to a metrcal N-lnear connecton DΓN. We sall denote ts transformaton by tx Y Z. Tus e ave: m T N Teorem 36 Te set of all transformatons tx Y Z gven by 57 togeter t te mappng product: tx Y Z tx = tx + X Y + Y Z Y Z Z + s a transformatons group of te set of all metrcal N-lnear connectons avng te same nonlnear connecton N. References: [1] G. Atanasu and M. Târnoveanu Ne Aspects n te Dfferental Geometry of te Second Order Cotangent BundleUnv. Tmşoara No [2] R. Mron Hamlton Geometry Semnarul de Mecancă Unv. Tmşoara [3] R. Mron and M. Hasguc Conformal Fnsler Connectons Rev.Roumane Mat.Pures Appl [4] R. Mron D. Hrmuc H. Smada and V. S. Sabău Te Geometry of Hamlton and Lagrange Spaces Kluer Acad.Publ. Vol 118FTPH 21. [5] R. Mron S. Watanabe and S. Ieda Cotangent Bundle Geometry Memorle Secţlor ştnţfce Bucureşt Acad. R.S.Romana Sera IVIX I [6] M. Purcaru and M. Târnoveanu On Transformatons Groups of N-Lnear Connectons on Second Order Cotangent Bundle Acta Unverstats Apulenss Specal Issue [7] M. Purcaru and M. Târnoveanu Metrcal Semsymmetrc N-Lnear Connectons on a Generalzed Hamlton Space Bull. Mat. Soc. Sc. Mat. Roum to appear. [8] C. Udrşte Mult-Tme Optmal Control WSEAS Transactons on Matematcs Issue 12 Volume 6 December 27 ISSN: ISSN: Issue 9 Volume 9 September 21
11 [9] C. Udrşte Non-classcal Lagrangan dynamcs and potental maps WSEAS Transactons on Matematcs Volume ISSN: [1] C. Udrşte and D. Oprş Euler-Lagrange- Hamlton dynamcs t fractonal acton WSEAS Transactons on Matematcs Volume ISSN: [11] C. Udrşte M. Popescu and P. Popescu Generalzed Multtme Lagrangans and Hamltonans WSEAS Transactons on Matematcs Volume Scopus Scmago ISSN: [12] C. Udrşte and O. Şandru Dual Nonlnear Connectons communcate to te 22 nd Conference on Dfferental Geometry and Topology Polytecnc Insttute of Bucarest Romana Sept [13] C. Udrste I. Tevy Mult-Tme Euler-Lagrange- Hamlton Teory WSEAS Transactons on Matematcs Volume ISSN: [14] K. Yano and S. Isara Tangent and Cotangent Bundles. Dfferental Geometry M.Deer Inc. Ne-Yor ISSN: Issue 9 Volume 9 September 21
ABOUT THE GROUP OF TRANSFORMATIONS OF METRICAL SEMISYMMETRIC N LINEAR CONNECTIONS ON A GENERALIZED HAMILTON SPACE OF ORDER TWO
 Bulletn of the Translvana Unversty of Braşov Vol 554 No. 2-202 Seres III: Mathematcs Informatcs Physcs 75-88 ABOUT THE GROUP OF TRANSFORMATIONS OF METRICAL SEMISYMMETRIC N LINEAR CONNECTIONS ON A GENERALIZED
Bulletn of the Translvana Unversty of Braşov Vol 554 No. 2-202 Seres III: Mathematcs Informatcs Physcs 75-88 ABOUT THE GROUP OF TRANSFORMATIONS OF METRICAL SEMISYMMETRIC N LINEAR CONNECTIONS ON A GENERALIZED
SOME RESULTS ON TRANSFORMATIONS GROUPS OF N-LINEAR CONNECTIONS IN THE 2-TANGENT BUNDLE
 STUDIA UNIV. BABEŞ BOLYAI MATHEMATICA Volume LIII Number March 008 SOME RESULTS ON TRANSFORMATIONS GROUPS OF N-LINEAR CONNECTIONS IN THE -TANGENT BUNDLE GHEORGHE ATANASIU AND MONICA PURCARU Abstract. In
STUDIA UNIV. BABEŞ BOLYAI MATHEMATICA Volume LIII Number March 008 SOME RESULTS ON TRANSFORMATIONS GROUPS OF N-LINEAR CONNECTIONS IN THE -TANGENT BUNDLE GHEORGHE ATANASIU AND MONICA PURCARU Abstract. In
2-π STRUCTURES ASSOCIATED TO THE LAGRANGIAN MECHANICAL SYSTEMS UDC 531.3: (045)=111. Victor Blãnuţã, Manuela Gîrţu
 FACTA UNIVERSITATIS Seres: Mechancs Automatc Control and Robotcs Vol. 6 N o 1 007 pp. 89-95 -π STRUCTURES ASSOCIATED TO THE LAGRANGIAN MECHANICAL SYSTEMS UDC 531.3:53.511(045)=111 Vctor Blãnuţã Manuela
FACTA UNIVERSITATIS Seres: Mechancs Automatc Control and Robotcs Vol. 6 N o 1 007 pp. 89-95 -π STRUCTURES ASSOCIATED TO THE LAGRANGIAN MECHANICAL SYSTEMS UDC 531.3:53.511(045)=111 Vctor Blãnuţã Manuela
M-LINEAR CONNECTION ON THE SECOND ORDER REONOM BUNDLE
 STUDIA UNIV. AEŞ OLYAI, MATHEMATICA, Volume XLVI, Number 3, September 001 M-LINEAR CONNECTION ON THE SECOND ORDER REONOM UNDLE VASILE LAZAR Abstract. The T M R bundle represents the total space of a tme
STUDIA UNIV. AEŞ OLYAI, MATHEMATICA, Volume XLVI, Number 3, September 001 M-LINEAR CONNECTION ON THE SECOND ORDER REONOM UNDLE VASILE LAZAR Abstract. The T M R bundle represents the total space of a tme
Acta Mathematica Academiae Paedagogicae Nyíregyháziensis 24 (2008), ISSN
 Acta Mathematca Academae Paedagogcae Nyíregyházenss 24 (2008), 65 74 www.ems.de/journals ISSN 1786-0091 ON THE RHEONOMIC FINSLERIAN MECHANICAL SYSTEMS CAMELIA FRIGIOIU Abstract. In ths paper t wll be studed
Acta Mathematca Academae Paedagogcae Nyíregyházenss 24 (2008), 65 74 www.ems.de/journals ISSN 1786-0091 ON THE RHEONOMIC FINSLERIAN MECHANICAL SYSTEMS CAMELIA FRIGIOIU Abstract. In ths paper t wll be studed
NATURAL 2-π STRUCTURES IN LAGRANGE SPACES
 AALELE ŞTIIŢIFICE ALE UIVERSITĂŢII AL.I. CUZA DI IAŞI (S.. MATEMATICĂ, Tomul LIII, 2007, Suplment ATURAL 2-π STRUCTURES I LAGRAGE SPACES Y VICTOR LĂUŢA AD VALER IMIEŢ Dedcated to Academcan Radu Mron at
AALELE ŞTIIŢIFICE ALE UIVERSITĂŢII AL.I. CUZA DI IAŞI (S.. MATEMATICĂ, Tomul LIII, 2007, Suplment ATURAL 2-π STRUCTURES I LAGRAGE SPACES Y VICTOR LĂUŢA AD VALER IMIEŢ Dedcated to Academcan Radu Mron at
Canonical transformations
 Canoncal transformatons November 23, 2014 Recall that we have defned a symplectc transformaton to be any lnear transformaton M A B leavng the symplectc form nvarant, Ω AB M A CM B DΩ CD Coordnate transformatons,
Canoncal transformatons November 23, 2014 Recall that we have defned a symplectc transformaton to be any lnear transformaton M A B leavng the symplectc form nvarant, Ω AB M A CM B DΩ CD Coordnate transformatons,
On the geometry of higher order Lagrange spaces.
 On the geometry of hgher order Lagrange spaces. By Radu Mron, Mha Anastase and Ioan Bucataru Abstract A Lagrange space of order k 1 s the space of acceleratons of order k endowed wth a regular Lagrangan.
On the geometry of hgher order Lagrange spaces. By Radu Mron, Mha Anastase and Ioan Bucataru Abstract A Lagrange space of order k 1 s the space of acceleratons of order k endowed wth a regular Lagrangan.
Monica Purcaru and Nicoleta Aldea. Abstract
 FILOMAT (Nš) 16 (22), 7 17 GENERAL CONFORMAL ALMOST SYMPLECTIC N-LINEAR CONNECTIONS IN THE BUNDLE OF ACCELERATIONS Monca Purcaru and Ncoeta Adea Abstract The am of ths paper 1 s to fnd the transformaton
FILOMAT (Nš) 16 (22), 7 17 GENERAL CONFORMAL ALMOST SYMPLECTIC N-LINEAR CONNECTIONS IN THE BUNDLE OF ACCELERATIONS Monca Purcaru and Ncoeta Adea Abstract The am of ths paper 1 s to fnd the transformaton
ENERGY-DEPENDENT MINKOWSKI METRIC IN SPACE-TIME
 ENERGY-DEPENDENT MINKOWSKI METRIC IN SPACE-TIME R. Mron, A. Jannusss and G. Zet Abstract The geometrcal propertes of the space-tme endowed wth a metrc dependng on the energy E of the consdered process
ENERGY-DEPENDENT MINKOWSKI METRIC IN SPACE-TIME R. Mron, A. Jannusss and G. Zet Abstract The geometrcal propertes of the space-tme endowed wth a metrc dependng on the energy E of the consdered process
Finslerian Nonholonomic Frame For Matsumoto (α,β)-metric
 Internatonal Journal of Mathematcs and Statstcs Inventon (IJMSI) E-ISSN: 2321 4767 P-ISSN: 2321-4759 ǁ Volume 2 ǁ Issue 3 ǁ March 2014 ǁ PP-73-77 Fnsleran Nonholonomc Frame For Matsumoto (α,)-metrc Mallkarjuna
Internatonal Journal of Mathematcs and Statstcs Inventon (IJMSI) E-ISSN: 2321 4767 P-ISSN: 2321-4759 ǁ Volume 2 ǁ Issue 3 ǁ March 2014 ǁ PP-73-77 Fnsleran Nonholonomc Frame For Matsumoto (α,)-metrc Mallkarjuna
η-einstein Complex Finsler-Randers Spaces
 Open Access Journal of Matematcal and Statstcal Analyss RESEARCH ARTICLE η-ensten Complex Fnsler-Randers Spaces Roopa MK * and Narasmamurty SK Department of PG Studes and Researc n Matematcs Kuvempu Unversty
Open Access Journal of Matematcal and Statstcal Analyss RESEARCH ARTICLE η-ensten Complex Fnsler-Randers Spaces Roopa MK * and Narasmamurty SK Department of PG Studes and Researc n Matematcs Kuvempu Unversty
Projective change between two Special (α, β)- Finsler Metrics
 Internatonal Journal of Trend n Research and Development, Volume 2(6), ISSN 2394-9333 www.jtrd.com Projectve change between two Specal (, β)- Fnsler Metrcs Gayathr.K 1 and Narasmhamurthy.S.K 2 1 Assstant
Internatonal Journal of Trend n Research and Development, Volume 2(6), ISSN 2394-9333 www.jtrd.com Projectve change between two Specal (, β)- Fnsler Metrcs Gayathr.K 1 and Narasmhamurthy.S.K 2 1 Assstant
Affine and Riemannian Connections
 Affne and Remannan Connectons Semnar Remannan Geometry Summer Term 2015 Prof Dr Anna Wenhard and Dr Gye-Seon Lee Jakob Ullmann Notaton: X(M) space of smooth vector felds on M D(M) space of smooth functons
Affne and Remannan Connectons Semnar Remannan Geometry Summer Term 2015 Prof Dr Anna Wenhard and Dr Gye-Seon Lee Jakob Ullmann Notaton: X(M) space of smooth vector felds on M D(M) space of smooth functons
SUPER PRINCIPAL FIBER BUNDLE WITH SUPER ACTION
 talan journal of pure appled mathematcs n. 33 2014 (63 70) 63 SUPER PRINCIPAL FIBER BUNDLE WITH SUPER ACTION M.R. Farhangdoost Department of Mathematcs College of Scences Shraz Unversty Shraz, 71457-44776
talan journal of pure appled mathematcs n. 33 2014 (63 70) 63 SUPER PRINCIPAL FIBER BUNDLE WITH SUPER ACTION M.R. Farhangdoost Department of Mathematcs College of Scences Shraz Unversty Shraz, 71457-44776
TR/95 February Splines G. H. BEHFOROOZ* & N. PAPAMICHAEL
 TR/9 February 980 End Condtons for Interpolatory Quntc Splnes by G. H. BEHFOROOZ* & N. PAPAMICHAEL *Present address: Dept of Matematcs Unversty of Tabrz Tabrz Iran. W9609 A B S T R A C T Accurate end condtons
TR/9 February 980 End Condtons for Interpolatory Quntc Splnes by G. H. BEHFOROOZ* & N. PAPAMICHAEL *Present address: Dept of Matematcs Unversty of Tabrz Tabrz Iran. W9609 A B S T R A C T Accurate end condtons
Physics 5153 Classical Mechanics. D Alembert s Principle and The Lagrangian-1
 P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
Inner Product. Euclidean Space. Orthonormal Basis. Orthogonal
 Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
Some results on a cross-section in the tensor bundle
 Hacettepe Journa of Matematcs and Statstcs Voume 43 3 214, 391 397 Some resuts on a cross-secton n te tensor bunde ydın Gezer and Murat tunbas bstract Te present paper s devoted to some resuts concernng
Hacettepe Journa of Matematcs and Statstcs Voume 43 3 214, 391 397 Some resuts on a cross-secton n te tensor bunde ydın Gezer and Murat tunbas bstract Te present paper s devoted to some resuts concernng
TANGENT DIRAC STRUCTURES OF HIGHER ORDER. P. M. Kouotchop Wamba, A. Ntyam, and J. Wouafo Kamga
 ARCHIVUM MATHEMATICUM BRNO) Tomus 47 2011), 17 22 TANGENT DIRAC STRUCTURES OF HIGHER ORDER P. M. Kouotchop Wamba, A. Ntyam, and J. Wouafo Kamga Abstract. Let L be an almost Drac structure on a manfold
ARCHIVUM MATHEMATICUM BRNO) Tomus 47 2011), 17 22 TANGENT DIRAC STRUCTURES OF HIGHER ORDER P. M. Kouotchop Wamba, A. Ntyam, and J. Wouafo Kamga Abstract. Let L be an almost Drac structure on a manfold
Acta Mathematica Academiae Paedagogicae Nyíregyháziensis 24 (2008), ISSN
 Acta Mathematca Academae Paedagogcae Nyíregyházenss 24 2008), 33 49 www.ems.de/journals ISSN 1786-0091 A SPECIAL NONLINEAR CONNECTION IN SECOND ORDER GEOMETRY NICOLETA BRINZEI Abstract. We show that, for
Acta Mathematca Academae Paedagogcae Nyíregyházenss 24 2008), 33 49 www.ems.de/journals ISSN 1786-0091 A SPECIAL NONLINEAR CONNECTION IN SECOND ORDER GEOMETRY NICOLETA BRINZEI Abstract. We show that, for
3.1 Expectation of Functions of Several Random Variables. )' be a k-dimensional discrete or continuous random vector, with joint PMF p (, E X E X1 E X
 Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Statstcs 1: Probablty Theory II 37 3 EPECTATION OF SEVERAL RANDOM VARIABLES As n Probablty Theory I, the nterest n most stuatons les not on the actual dstrbuton of a random vector, but rather on a number
Three views of mechanics
 Three vews of mechancs John Hubbard, n L. Gross s course February 1, 211 1 Introducton A mechancal system s manfold wth a Remannan metrc K : T M R called knetc energy and a functon V : M R called potental
Three vews of mechancs John Hubbard, n L. Gross s course February 1, 211 1 Introducton A mechancal system s manfold wth a Remannan metrc K : T M R called knetc energy and a functon V : M R called potental
Elementary work, Newton law and Euler-Lagrange equations
 Elementary work, Newton law and Euler-Lagrange equatons Constantn Udrşte, Oltn Dogaru, Ionel Ţevy, Dumtru Bala Abstract. The am of ths paper s to show a geometrcal connecton between elementary mechancal
Elementary work, Newton law and Euler-Lagrange equatons Constantn Udrşte, Oltn Dogaru, Ionel Ţevy, Dumtru Bala Abstract. The am of ths paper s to show a geometrcal connecton between elementary mechancal
The Finite Element Method: A Short Introduction
 Te Fnte Element Metod: A Sort ntroducton Wat s FEM? Te Fnte Element Metod (FEM) ntroduced by engneers n late 50 s and 60 s s a numercal tecnque for solvng problems wc are descrbed by Ordnary Dfferental
Te Fnte Element Metod: A Sort ntroducton Wat s FEM? Te Fnte Element Metod (FEM) ntroduced by engneers n late 50 s and 60 s s a numercal tecnque for solvng problems wc are descrbed by Ordnary Dfferental
SL n (F ) Equals its Own Derived Group
 Internatonal Journal of Algebra, Vol. 2, 2008, no. 12, 585-594 SL n (F ) Equals ts Own Derved Group Jorge Macel BMCC-The Cty Unversty of New York, CUNY 199 Chambers street, New York, NY 10007, USA macel@cms.nyu.edu
Internatonal Journal of Algebra, Vol. 2, 2008, no. 12, 585-594 SL n (F ) Equals ts Own Derved Group Jorge Macel BMCC-The Cty Unversty of New York, CUNY 199 Chambers street, New York, NY 10007, USA macel@cms.nyu.edu
Causal Diamonds. M. Aghili, L. Bombelli, B. Pilgrim
 Causal Damonds M. Aghl, L. Bombell, B. Plgrm Introducton The correcton to volume of a causal nterval due to curvature of spacetme has been done by Myrhem [] and recently by Gbbons & Solodukhn [] and later
Causal Damonds M. Aghl, L. Bombell, B. Plgrm Introducton The correcton to volume of a causal nterval due to curvature of spacetme has been done by Myrhem [] and recently by Gbbons & Solodukhn [] and later
Lagrangian Field Theory
 Lagrangan Feld Theory Adam Lott PHY 391 Aprl 6, 017 1 Introducton Ths paper s a summary of Chapter of Mandl and Shaw s Quantum Feld Theory [1]. The frst thng to do s to fx the notaton. For the most part,
Lagrangan Feld Theory Adam Lott PHY 391 Aprl 6, 017 1 Introducton Ths paper s a summary of Chapter of Mandl and Shaw s Quantum Feld Theory [1]. The frst thng to do s to fx the notaton. For the most part,
ON A DETERMINATION OF THE INITIAL FUNCTIONS FROM THE OBSERVED VALUES OF THE BOUNDARY FUNCTIONS FOR THE SECOND-ORDER HYPERBOLIC EQUATION
 Advanced Mathematcal Models & Applcatons Vol.3, No.3, 2018, pp.215-222 ON A DETERMINATION OF THE INITIAL FUNCTIONS FROM THE OBSERVED VALUES OF THE BOUNDARY FUNCTIONS FOR THE SECOND-ORDER HYPERBOLIC EUATION
Advanced Mathematcal Models & Applcatons Vol.3, No.3, 2018, pp.215-222 ON A DETERMINATION OF THE INITIAL FUNCTIONS FROM THE OBSERVED VALUES OF THE BOUNDARY FUNCTIONS FOR THE SECOND-ORDER HYPERBOLIC EUATION
Linear Approximation with Regularization and Moving Least Squares
 Lnear Approxmaton wth Regularzaton and Movng Least Squares Igor Grešovn May 007 Revson 4.6 (Revson : March 004). 5 4 3 0.5 3 3.5 4 Contents: Lnear Fttng...4. Weghted Least Squares n Functon Approxmaton...
Lnear Approxmaton wth Regularzaton and Movng Least Squares Igor Grešovn May 007 Revson 4.6 (Revson : March 004). 5 4 3 0.5 3 3.5 4 Contents: Lnear Fttng...4. Weghted Least Squares n Functon Approxmaton...
General viscosity iterative method for a sequence of quasi-nonexpansive mappings
 Avalable onlne at www.tjnsa.com J. Nonlnear Sc. Appl. 9 (2016), 5672 5682 Research Artcle General vscosty teratve method for a sequence of quas-nonexpansve mappngs Cuje Zhang, Ynan Wang College of Scence,
Avalable onlne at www.tjnsa.com J. Nonlnear Sc. Appl. 9 (2016), 5672 5682 Research Artcle General vscosty teratve method for a sequence of quas-nonexpansve mappngs Cuje Zhang, Ynan Wang College of Scence,
12 MATH 101A: ALGEBRA I, PART C: MULTILINEAR ALGEBRA. 4. Tensor product
 12 MATH 101A: ALGEBRA I, PART C: MULTILINEAR ALGEBRA Here s an outlne of what I dd: (1) categorcal defnton (2) constructon (3) lst of basc propertes (4) dstrbutve property (5) rght exactness (6) localzaton
12 MATH 101A: ALGEBRA I, PART C: MULTILINEAR ALGEBRA Here s an outlne of what I dd: (1) categorcal defnton (2) constructon (3) lst of basc propertes (4) dstrbutve property (5) rght exactness (6) localzaton
More metrics on cartesian products
 More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
Salmon: Lectures on partial differential equations. Consider the general linear, second-order PDE in the form. ,x 2
 Salmon: Lectures on partal dfferental equatons 5. Classfcaton of second-order equatons There are general methods for classfyng hgher-order partal dfferental equatons. One s very general (applyng even to
Salmon: Lectures on partal dfferental equatons 5. Classfcaton of second-order equatons There are general methods for classfyng hgher-order partal dfferental equatons. One s very general (applyng even to
Poisson brackets and canonical transformations
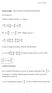 rof O B Wrght Mechancs Notes osson brackets and canoncal transformatons osson Brackets Consder an arbtrary functon f f ( qp t) df f f f q p q p t But q p p where ( qp ) pq q df f f f p q q p t In order
rof O B Wrght Mechancs Notes osson brackets and canoncal transformatons osson Brackets Consder an arbtrary functon f f ( qp t) df f f f q p q p t But q p p where ( qp ) pq q df f f f p q q p t In order
Representation theory and quantum mechanics tutorial Representation theory and quantum conservation laws
 Representaton theory and quantum mechancs tutoral Representaton theory and quantum conservaton laws Justn Campbell August 1, 2017 1 Generaltes on representaton theory 1.1 Let G GL m (R) be a real algebrac
Representaton theory and quantum mechancs tutoral Representaton theory and quantum conservaton laws Justn Campbell August 1, 2017 1 Generaltes on representaton theory 1.1 Let G GL m (R) be a real algebrac
SEYED MEHDI KAZEMI TORBAGHAN, MORTEZA MIRMOHAMMAD REZAII
 Bulletn of Mathematcal Analyss and Applcatons ISSN: 1821-1291, URL: http://www.bmathaa.org Volume 9 Issue 1(2017), Pages 19-30. f-harmonic MAPS FROM FINSLER MANIFOLDS SEYED MEHDI KAZEMI TORBAGHAN, MORTEZA
Bulletn of Mathematcal Analyss and Applcatons ISSN: 1821-1291, URL: http://www.bmathaa.org Volume 9 Issue 1(2017), Pages 19-30. f-harmonic MAPS FROM FINSLER MANIFOLDS SEYED MEHDI KAZEMI TORBAGHAN, MORTEZA
Lecture 6/7 (February 10/12, 2014) DIRAC EQUATION. The non-relativistic Schrödinger equation was obtained by noting that the Hamiltonian 2
 P470 Lecture 6/7 (February 10/1, 014) DIRAC EQUATION The non-relatvstc Schrödnger equaton was obtaned by notng that the Hamltonan H = P (1) m can be transformed nto an operator form wth the substtutons
P470 Lecture 6/7 (February 10/1, 014) DIRAC EQUATION The non-relatvstc Schrödnger equaton was obtaned by notng that the Hamltonan H = P (1) m can be transformed nto an operator form wth the substtutons
Mechanics Physics 151
 Mechancs Physcs 151 Lecture 3 Lagrange s Equatons (Goldsten Chapter 1) Hamlton s Prncple (Chapter 2) What We Dd Last Tme! Dscussed mult-partcle systems! Internal and external forces! Laws of acton and
Mechancs Physcs 151 Lecture 3 Lagrange s Equatons (Goldsten Chapter 1) Hamlton s Prncple (Chapter 2) What We Dd Last Tme! Dscussed mult-partcle systems! Internal and external forces! Laws of acton and
Lectures - Week 4 Matrix norms, Conditioning, Vector Spaces, Linear Independence, Spanning sets and Basis, Null space and Range of a Matrix
 Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
n α j x j = 0 j=1 has a nontrivial solution. Here A is the n k matrix whose jth column is the vector for all t j=0
 MODULE 2 Topcs: Lnear ndependence, bass and dmenson We have seen that f n a set of vectors one vector s a lnear combnaton of the remanng vectors n the set then the span of the set s unchanged f that vector
MODULE 2 Topcs: Lnear ndependence, bass and dmenson We have seen that f n a set of vectors one vector s a lnear combnaton of the remanng vectors n the set then the span of the set s unchanged f that vector
THE CARTIER ISOMORPHISM. These are the detailed notes for a talk I gave at the Kleine AG 1 in April Frobenius
 THE CARTIER ISOMORPHISM LARS KINDLER Tese are te detaled notes for a talk I gave at te Klene AG 1 n Aprl 2010. 1. Frobenus Defnton 1.1. Let f : S be a morpsm of scemes and p a prme. We say tat S s of caracterstc
THE CARTIER ISOMORPHISM LARS KINDLER Tese are te detaled notes for a talk I gave at te Klene AG 1 n Aprl 2010. 1. Frobenus Defnton 1.1. Let f : S be a morpsm of scemes and p a prme. We say tat S s of caracterstc
CHAPTER 5: Lie Differentiation and Angular Momentum
 CHAPTER 5: Le Dfferentaton and Angular Momentum Jose G. Vargas 1 Le dfferentaton Kähler s theory of angular momentum s a specalzaton of hs approach to Le dfferentaton. We could deal wth the former drectly,
CHAPTER 5: Le Dfferentaton and Angular Momentum Jose G. Vargas 1 Le dfferentaton Kähler s theory of angular momentum s a specalzaton of hs approach to Le dfferentaton. We could deal wth the former drectly,
Randers Space with Special Nonlinear Connection
 ISSN 1995-0802, obachevsk Journal of Mathematcs, 2008, Vol. 29, No. 1, pp. 27 31. c Pleades Publshng, td., 2008. Rers Space wth Specal Nonlnear Connecton H. G. Nagaraja * (submtted by M.A. Malakhaltsev)
ISSN 1995-0802, obachevsk Journal of Mathematcs, 2008, Vol. 29, No. 1, pp. 27 31. c Pleades Publshng, td., 2008. Rers Space wth Specal Nonlnear Connecton H. G. Nagaraja * (submtted by M.A. Malakhaltsev)
On Pfaff s solution of the Pfaff problem
 Zur Pfaff scen Lösung des Pfaff scen Probles Mat. Ann. 7 (880) 53-530. On Pfaff s soluton of te Pfaff proble By A. MAYER n Lepzg Translated by D. H. Delpenc Te way tat Pfaff adopted for te ntegraton of
Zur Pfaff scen Lösung des Pfaff scen Probles Mat. Ann. 7 (880) 53-530. On Pfaff s soluton of te Pfaff proble By A. MAYER n Lepzg Translated by D. H. Delpenc Te way tat Pfaff adopted for te ntegraton of
PHYS 705: Classical Mechanics. Calculus of Variations II
 1 PHYS 705: Classcal Mechancs Calculus of Varatons II 2 Calculus of Varatons: Generalzaton (no constrant yet) Suppose now that F depends on several dependent varables : We need to fnd such that has a statonary
1 PHYS 705: Classcal Mechancs Calculus of Varatons II 2 Calculus of Varatons: Generalzaton (no constrant yet) Suppose now that F depends on several dependent varables : We need to fnd such that has a statonary
Zeros and Zero Dynamics for Linear, Time-delay System
 UNIVERSITA POLITECNICA DELLE MARCHE - FACOLTA DI INGEGNERIA Dpartmento d Ingegnerua Informatca, Gestonale e dell Automazone LabMACS Laboratory of Modelng, Analyss and Control of Dynamcal System Zeros and
UNIVERSITA POLITECNICA DELLE MARCHE - FACOLTA DI INGEGNERIA Dpartmento d Ingegnerua Informatca, Gestonale e dell Automazone LabMACS Laboratory of Modelng, Analyss and Control of Dynamcal System Zeros and
The Multiple Classical Linear Regression Model (CLRM): Specification and Assumptions. 1. Introduction
 ECONOMICS 5* -- NOTE (Summary) ECON 5* -- NOTE The Multple Classcal Lnear Regresson Model (CLRM): Specfcaton and Assumptons. Introducton CLRM stands for the Classcal Lnear Regresson Model. The CLRM s also
ECONOMICS 5* -- NOTE (Summary) ECON 5* -- NOTE The Multple Classcal Lnear Regresson Model (CLRM): Specfcaton and Assumptons. Introducton CLRM stands for the Classcal Lnear Regresson Model. The CLRM s also
Yong Joon Ryang. 1. Introduction Consider the multicommodity transportation problem with convex quadratic cost function. 1 2 (x x0 ) T Q(x x 0 )
 Kangweon-Kyungk Math. Jour. 4 1996), No. 1, pp. 7 16 AN ITERATIVE ROW-ACTION METHOD FOR MULTICOMMODITY TRANSPORTATION PROBLEMS Yong Joon Ryang Abstract. The optmzaton problems wth quadratc constrants often
Kangweon-Kyungk Math. Jour. 4 1996), No. 1, pp. 7 16 AN ITERATIVE ROW-ACTION METHOD FOR MULTICOMMODITY TRANSPORTATION PROBLEMS Yong Joon Ryang Abstract. The optmzaton problems wth quadratc constrants often
On a direct solver for linear least squares problems
 ISSN 2066-6594 Ann. Acad. Rom. Sc. Ser. Math. Appl. Vol. 8, No. 2/2016 On a drect solver for lnear least squares problems Constantn Popa Abstract The Null Space (NS) algorthm s a drect solver for lnear
ISSN 2066-6594 Ann. Acad. Rom. Sc. Ser. Math. Appl. Vol. 8, No. 2/2016 On a drect solver for lnear least squares problems Constantn Popa Abstract The Null Space (NS) algorthm s a drect solver for lnear
R n α. . The funny symbol indicates DISJOINT union. Define an equivalence relation on this disjoint union by declaring v α R n α, and v β R n β
 Readng. Ch. 3 of Lee. Warner. M s an abstract manfold. We have defned the tangent space to M va curves. We are gong to gve two other defntons. All three are used n the subject and one freely swtches back
Readng. Ch. 3 of Lee. Warner. M s an abstract manfold. We have defned the tangent space to M va curves. We are gong to gve two other defntons. All three are used n the subject and one freely swtches back
Stanford University CS254: Computational Complexity Notes 7 Luca Trevisan January 29, Notes for Lecture 7
 Stanford Unversty CS54: Computatonal Complexty Notes 7 Luca Trevsan January 9, 014 Notes for Lecture 7 1 Approxmate Countng wt an N oracle We complete te proof of te followng result: Teorem 1 For every
Stanford Unversty CS54: Computatonal Complexty Notes 7 Luca Trevsan January 9, 014 Notes for Lecture 7 1 Approxmate Countng wt an N oracle We complete te proof of te followng result: Teorem 1 For every
The Order Relation and Trace Inequalities for. Hermitian Operators
 Internatonal Mathematcal Forum, Vol 3, 08, no, 507-57 HIKARI Ltd, wwwm-hkarcom https://doorg/0988/mf088055 The Order Relaton and Trace Inequaltes for Hermtan Operators Y Huang School of Informaton Scence
Internatonal Mathematcal Forum, Vol 3, 08, no, 507-57 HIKARI Ltd, wwwm-hkarcom https://doorg/0988/mf088055 The Order Relaton and Trace Inequaltes for Hermtan Operators Y Huang School of Informaton Scence
A CHARACTERIZATION OF ADDITIVE DERIVATIONS ON VON NEUMANN ALGEBRAS
 Journal of Mathematcal Scences: Advances and Applcatons Volume 25, 2014, Pages 1-12 A CHARACTERIZATION OF ADDITIVE DERIVATIONS ON VON NEUMANN ALGEBRAS JIA JI, WEN ZHANG and XIAOFEI QI Department of Mathematcs
Journal of Mathematcal Scences: Advances and Applcatons Volume 25, 2014, Pages 1-12 A CHARACTERIZATION OF ADDITIVE DERIVATIONS ON VON NEUMANN ALGEBRAS JIA JI, WEN ZHANG and XIAOFEI QI Department of Mathematcs
Analytical classical dynamics
 Analytcal classcal ynamcs by Youun Hu Insttute of plasma physcs, Chnese Acaemy of Scences Emal: yhu@pp.cas.cn Abstract These notes were ntally wrtten when I rea tzpatrck s book[] an were later revse to
Analytcal classcal ynamcs by Youun Hu Insttute of plasma physcs, Chnese Acaemy of Scences Emal: yhu@pp.cas.cn Abstract These notes were ntally wrtten when I rea tzpatrck s book[] an were later revse to
On Four Dimensional Semi-C-reducible. Landsberg Space
 Internatonal Matematcal Forum Vol. 8 201 no. 191-200 On Four Dmensonal Sem--reducble Landsberg Space V. K. aubey and *Rakes Kumar Dwved Department of Matematcs & Statstcs D.D.U. Gorakpur Unversty Gorakpur
Internatonal Matematcal Forum Vol. 8 201 no. 191-200 On Four Dmensonal Sem--reducble Landsberg Space V. K. aubey and *Rakes Kumar Dwved Department of Matematcs & Statstcs D.D.U. Gorakpur Unversty Gorakpur
DIFFERENTIAL FORMS BRIAN OSSERMAN
 DIFFERENTIAL FORMS BRIAN OSSERMAN Dfferentals are an mportant topc n algebrac geometry, allowng the use of some classcal geometrc arguments n the context of varetes over any feld. We wll use them to defne
DIFFERENTIAL FORMS BRIAN OSSERMAN Dfferentals are an mportant topc n algebrac geometry, allowng the use of some classcal geometrc arguments n the context of varetes over any feld. We wll use them to defne
On C 0 multi-contractions having a regular dilation
 SUDIA MAHEMAICA 170 (3) (2005) On C 0 mult-contractons havng a regular dlaton by Dan Popovc (mşoara) Abstract. Commutng mult-contractons of class C 0 and havng a regular sometrc dlaton are studed. We prove
SUDIA MAHEMAICA 170 (3) (2005) On C 0 mult-contractons havng a regular dlaton by Dan Popovc (mşoara) Abstract. Commutng mult-contractons of class C 0 and havng a regular sometrc dlaton are studed. We prove
The Jacobsthal and Jacobsthal-Lucas Numbers via Square Roots of Matrices
 Internatonal Mathematcal Forum, Vol 11, 2016, no 11, 513-520 HIKARI Ltd, wwwm-hkarcom http://dxdoorg/1012988/mf20166442 The Jacobsthal and Jacobsthal-Lucas Numbers va Square Roots of Matrces Saadet Arslan
Internatonal Mathematcal Forum, Vol 11, 2016, no 11, 513-520 HIKARI Ltd, wwwm-hkarcom http://dxdoorg/1012988/mf20166442 The Jacobsthal and Jacobsthal-Lucas Numbers va Square Roots of Matrces Saadet Arslan
Perfect Competition and the Nash Bargaining Solution
 Perfect Competton and the Nash Barganng Soluton Renhard John Department of Economcs Unversty of Bonn Adenauerallee 24-42 53113 Bonn, Germany emal: rohn@un-bonn.de May 2005 Abstract For a lnear exchange
Perfect Competton and the Nash Barganng Soluton Renhard John Department of Economcs Unversty of Bonn Adenauerallee 24-42 53113 Bonn, Germany emal: rohn@un-bonn.de May 2005 Abstract For a lnear exchange
Lecture 20: Noether s Theorem
 Lecture 20: Noether s Theorem In our revew of Newtonan Mechancs, we were remnded that some quanttes (energy, lnear momentum, and angular momentum) are conserved That s, they are constant f no external
Lecture 20: Noether s Theorem In our revew of Newtonan Mechancs, we were remnded that some quanttes (energy, lnear momentum, and angular momentum) are conserved That s, they are constant f no external
Mechanics Physics 151
 Mechancs Physcs 5 Lecture 0 Canoncal Transformatons (Chapter 9) What We Dd Last Tme Hamlton s Prncple n the Hamltonan formalsm Dervaton was smple δi δ p H(, p, t) = 0 Adonal end-pont constrants δ t ( )
Mechancs Physcs 5 Lecture 0 Canoncal Transformatons (Chapter 9) What We Dd Last Tme Hamlton s Prncple n the Hamltonan formalsm Dervaton was smple δi δ p H(, p, t) = 0 Adonal end-pont constrants δ t ( )
A particle in a state of uniform motion remain in that state of motion unless acted upon by external force.
 The fundamental prncples of classcal mechancs were lad down by Galleo and Newton n the 16th and 17th centures. In 1686, Newton wrote the Prncpa where he gave us three laws of moton, one law of gravty,
The fundamental prncples of classcal mechancs were lad down by Galleo and Newton n the 16th and 17th centures. In 1686, Newton wrote the Prncpa where he gave us three laws of moton, one law of gravty,
9 Characteristic classes
 THEODORE VORONOV DIFFERENTIAL GEOMETRY. Sprng 2009 [under constructon] 9 Characterstc classes 9.1 The frst Chern class of a lne bundle Consder a complex vector bundle E B of rank p. We shall construct
THEODORE VORONOV DIFFERENTIAL GEOMETRY. Sprng 2009 [under constructon] 9 Characterstc classes 9.1 The frst Chern class of a lne bundle Consder a complex vector bundle E B of rank p. We shall construct
Fedosov s approach to deformation quantization
 Fedosov s approac to deformaton quantzaton Sean Poorence Introducton In classcal mecancs te order of measurements does not affect te results of te measurements. However, trougout te 19t and early 20t centures,
Fedosov s approac to deformaton quantzaton Sean Poorence Introducton In classcal mecancs te order of measurements does not affect te results of te measurements. However, trougout te 19t and early 20t centures,
Calculus of Variations Basics
 Chapter 1 Calculus of Varatons Bascs 1.1 Varaton of a General Functonal In ths chapter, we derve the general formula for the varaton of a functonal of the form J [y 1,y 2,,y n ] F x,y 1,y 2,,y n,y 1,y
Chapter 1 Calculus of Varatons Bascs 1.1 Varaton of a General Functonal In ths chapter, we derve the general formula for the varaton of a functonal of the form J [y 1,y 2,,y n ] F x,y 1,y 2,,y n,y 1,y
THEORY OF FINSLER SUBMANIFOLDS VIA BERWALD CONNECTION
 Internatonal Electronc Journal of Geometry Volume 7 No. 1 pp. 108 125 (2014) c IEJG THEORY OF FINSLER SUBMANIFOLDS VIA BERWALD CONNECTION AUREL BEJANCU AND HANI REDA FARRAN Dedcated to memory of Proffessor
Internatonal Electronc Journal of Geometry Volume 7 No. 1 pp. 108 125 (2014) c IEJG THEORY OF FINSLER SUBMANIFOLDS VIA BERWALD CONNECTION AUREL BEJANCU AND HANI REDA FARRAN Dedcated to memory of Proffessor
5 The Rational Canonical Form
 5 The Ratonal Canoncal Form Here p s a monc rreducble factor of the mnmum polynomal m T and s not necessarly of degree one Let F p denote the feld constructed earler n the course, consstng of all matrces
5 The Ratonal Canoncal Form Here p s a monc rreducble factor of the mnmum polynomal m T and s not necessarly of degree one Let F p denote the feld constructed earler n the course, consstng of all matrces
Uniqueness of Weak Solutions to the 3D Ginzburg- Landau Model for Superconductivity
 Int. Journal of Math. Analyss, Vol. 6, 212, no. 22, 195-114 Unqueness of Weak Solutons to the 3D Gnzburg- Landau Model for Superconductvty Jshan Fan Department of Appled Mathematcs Nanjng Forestry Unversty
Int. Journal of Math. Analyss, Vol. 6, 212, no. 22, 195-114 Unqueness of Weak Solutons to the 3D Gnzburg- Landau Model for Superconductvty Jshan Fan Department of Appled Mathematcs Nanjng Forestry Unversty
FACTORIZATION IN KRULL MONOIDS WITH INFINITE CLASS GROUP
 C O L L O Q U I U M M A T H E M A T I C U M VOL. 80 1999 NO. 1 FACTORIZATION IN KRULL MONOIDS WITH INFINITE CLASS GROUP BY FLORIAN K A I N R A T H (GRAZ) Abstract. Let H be a Krull monod wth nfnte class
C O L L O Q U I U M M A T H E M A T I C U M VOL. 80 1999 NO. 1 FACTORIZATION IN KRULL MONOIDS WITH INFINITE CLASS GROUP BY FLORIAN K A I N R A T H (GRAZ) Abstract. Let H be a Krull monod wth nfnte class
Mathematical Preparations
 1 Introducton Mathematcal Preparatons The theory of relatvty was developed to explan experments whch studed the propagaton of electromagnetc radaton n movng coordnate systems. Wthn expermental error the
1 Introducton Mathematcal Preparatons The theory of relatvty was developed to explan experments whch studed the propagaton of electromagnetc radaton n movng coordnate systems. Wthn expermental error the
Physics 5153 Classical Mechanics. Principle of Virtual Work-1
 P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
SEMI-BASIC 1-FORMS AND COURANT STRUCTURE FOR METRIZABILITY PROBLEMS. Mircea Crasmareanu
 PUBLICATIONS DE L INSTITUT MATHÉMATIQUE Nouvelle sére, tome 98112 2015, 153 163 DOI: 10.2298/PIM150203020C SEMI-BASIC 1-FORMS AND COURANT STRUCTURE FOR METRIZABILITY PROBLEMS Mrcea Crasmareanu Abstract.
PUBLICATIONS DE L INSTITUT MATHÉMATIQUE Nouvelle sére, tome 98112 2015, 153 163 DOI: 10.2298/PIM150203020C SEMI-BASIC 1-FORMS AND COURANT STRUCTURE FOR METRIZABILITY PROBLEMS Mrcea Crasmareanu Abstract.
Screen transversal conformal half-lightlike submanifolds
 Annals of the Unversty of Craova, Mathematcs and Computer Scence Seres Volume 40(2), 2013, Pages 140 147 ISSN: 1223-6934 Screen transversal conformal half-lghtlke submanfolds Wenje Wang, Yanng Wang, and
Annals of the Unversty of Craova, Mathematcs and Computer Scence Seres Volume 40(2), 2013, Pages 140 147 ISSN: 1223-6934 Screen transversal conformal half-lghtlke submanfolds Wenje Wang, Yanng Wang, and
12. The Hamilton-Jacobi Equation Michael Fowler
 1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
Affine transformations and convexity
 Affne transformatons and convexty The purpose of ths document s to prove some basc propertes of affne transformatons nvolvng convex sets. Here are a few onlne references for background nformaton: http://math.ucr.edu/
Affne transformatons and convexty The purpose of ths document s to prove some basc propertes of affne transformatons nvolvng convex sets. Here are a few onlne references for background nformaton: http://math.ucr.edu/
An efficient algorithm for multivariate Maclaurin Newton transformation
 Annales UMCS Informatca AI VIII, 2 2008) 5 14 DOI: 10.2478/v10065-008-0020-6 An effcent algorthm for multvarate Maclaurn Newton transformaton Joanna Kapusta Insttute of Mathematcs and Computer Scence,
Annales UMCS Informatca AI VIII, 2 2008) 5 14 DOI: 10.2478/v10065-008-0020-6 An effcent algorthm for multvarate Maclaurn Newton transformaton Joanna Kapusta Insttute of Mathematcs and Computer Scence,
2.3 Nilpotent endomorphisms
 s a block dagonal matrx, wth A Mat dm U (C) In fact, we can assume that B = B 1 B k, wth B an ordered bass of U, and that A = [f U ] B, where f U : U U s the restrcton of f to U 40 23 Nlpotent endomorphsms
s a block dagonal matrx, wth A Mat dm U (C) In fact, we can assume that B = B 1 B k, wth B an ordered bass of U, and that A = [f U ] B, where f U : U U s the restrcton of f to U 40 23 Nlpotent endomorphsms
Random Walks on Digraphs
 Random Walks on Dgraphs J. J. P. Veerman October 23, 27 Introducton Let V = {, n} be a vertex set and S a non-negatve row-stochastc matrx (.e. rows sum to ). V and S defne a dgraph G = G(V, S) and a drected
Random Walks on Dgraphs J. J. P. Veerman October 23, 27 Introducton Let V = {, n} be a vertex set and S a non-negatve row-stochastc matrx (.e. rows sum to ). V and S defne a dgraph G = G(V, S) and a drected
The Pseudoblocks of Endomorphism Algebras
 Internatonal Mathematcal Forum, 4, 009, no. 48, 363-368 The Pseudoblocks of Endomorphsm Algebras Ahmed A. Khammash Department of Mathematcal Scences, Umm Al-Qura Unversty P.O.Box 796, Makkah, Saud Araba
Internatonal Mathematcal Forum, 4, 009, no. 48, 363-368 The Pseudoblocks of Endomorphsm Algebras Ahmed A. Khammash Department of Mathematcal Scences, Umm Al-Qura Unversty P.O.Box 796, Makkah, Saud Araba
Erbakan University, Konya, Turkey. b Department of Mathematics, Akdeniz University, Antalya, Turkey. Published online: 28 Nov 2013.
 Ths artcle was downloaded by: [Necmettn Erbaan Unversty] On: 24 March 2015, At: 05:44 Publsher: Taylor & Francs Informa Ltd Regstered n England and Wales Regstered Number: 1072954 Regstered offce: Mortmer
Ths artcle was downloaded by: [Necmettn Erbaan Unversty] On: 24 March 2015, At: 05:44 Publsher: Taylor & Francs Informa Ltd Regstered n England and Wales Regstered Number: 1072954 Regstered offce: Mortmer
for author's use only
 CARPATHIA J. MATH. 25 2009, o. 2, 163-176 Onlne verson avalale at http://carpathan.um.ro Prnt Edton: ISS 1584-2851 Onlne Edton: ISS 1843-4401 Metrzale systems of autonomous second order dfferental equatons
CARPATHIA J. MATH. 25 2009, o. 2, 163-176 Onlne verson avalale at http://carpathan.um.ro Prnt Edton: ISS 1584-2851 Onlne Edton: ISS 1843-4401 Metrzale systems of autonomous second order dfferental equatons
The binomial transforms of the generalized (s, t )-Jacobsthal matrix sequence
 Int. J. Adv. Appl. Math. and Mech. 6(3 (2019 14 20 (ISSN: 2347-2529 Journal homepage: www.jaamm.com IJAAMM Internatonal Journal of Advances n Appled Mathematcs and Mechancs The bnomal transforms of the
Int. J. Adv. Appl. Math. and Mech. 6(3 (2019 14 20 (ISSN: 2347-2529 Journal homepage: www.jaamm.com IJAAMM Internatonal Journal of Advances n Appled Mathematcs and Mechancs The bnomal transforms of the
INVARIANT STABLY COMPLEX STRUCTURES ON TOPOLOGICAL TORIC MANIFOLDS
 INVARIANT STABLY COMPLEX STRUCTURES ON TOPOLOGICAL TORIC MANIFOLDS HIROAKI ISHIDA Abstract We show that any (C ) n -nvarant stably complex structure on a topologcal torc manfold of dmenson 2n s ntegrable
INVARIANT STABLY COMPLEX STRUCTURES ON TOPOLOGICAL TORIC MANIFOLDS HIROAKI ISHIDA Abstract We show that any (C ) n -nvarant stably complex structure on a topologcal torc manfold of dmenson 2n s ntegrable
CHAPTER 14 GENERAL PERTURBATION THEORY
 CHAPTER 4 GENERAL PERTURBATION THEORY 4 Introducton A partcle n orbt around a pont mass or a sphercally symmetrc mass dstrbuton s movng n a gravtatonal potental of the form GM / r In ths potental t moves
CHAPTER 4 GENERAL PERTURBATION THEORY 4 Introducton A partcle n orbt around a pont mass or a sphercally symmetrc mass dstrbuton s movng n a gravtatonal potental of the form GM / r In ths potental t moves
Multi-Time Euler-Lagrange Dynamics
 Proceedngs of the 7th WSEAS Internatonal Conference on Systems Theory and Scentfc Computaton, Athens, Greece, August 24-26, 2007 66 Mult-Tme Euler-Lagrange Dynamcs CONSTANTIN UDRISTE Unversty Poltehnca
Proceedngs of the 7th WSEAS Internatonal Conference on Systems Theory and Scentfc Computaton, Athens, Greece, August 24-26, 2007 66 Mult-Tme Euler-Lagrange Dynamcs CONSTANTIN UDRISTE Unversty Poltehnca
CENTROID (AĞIRLIK MERKEZİ )
 CENTOD (ĞLK MEKEZİ ) centrod s a geometrcal concept arsng from parallel forces. Tus, onl parallel forces possess a centrod. Centrod s tougt of as te pont were te wole wegt of a pscal od or sstem of partcles
CENTOD (ĞLK MEKEZİ ) centrod s a geometrcal concept arsng from parallel forces. Tus, onl parallel forces possess a centrod. Centrod s tougt of as te pont were te wole wegt of a pscal od or sstem of partcles
A new Approach for Solving Linear Ordinary Differential Equations
 , ISSN 974-57X (Onlne), ISSN 974-5718 (Prnt), Vol. ; Issue No. 1; Year 14, Copyrght 13-14 by CESER PUBLICATIONS A new Approach for Solvng Lnear Ordnary Dfferental Equatons Fawz Abdelwahd Department of
, ISSN 974-57X (Onlne), ISSN 974-5718 (Prnt), Vol. ; Issue No. 1; Year 14, Copyrght 13-14 by CESER PUBLICATIONS A new Approach for Solvng Lnear Ordnary Dfferental Equatons Fawz Abdelwahd Department of
Supplemental document
 Electronc Supplementary Materal (ESI) for Physcal Chemstry Chemcal Physcs. Ths journal s the Owner Socetes 01 Supplemental document Behnam Nkoobakht School of Chemstry, The Unversty of Sydney, Sydney,
Electronc Supplementary Materal (ESI) for Physcal Chemstry Chemcal Physcs. Ths journal s the Owner Socetes 01 Supplemental document Behnam Nkoobakht School of Chemstry, The Unversty of Sydney, Sydney,
ON HOLLAND S FRAME FOR RANDERS SPACE AND ITS APPLICATIONS IN PHYSICS
 Steps n Dfferental Geometry, Proceedngs of the Colloquum on Dfferental Geometry, 25 30 July, 2000, Debrecen, Hungary ON HOAND S FRAME FOR RANDERS SPACE AND ITS APPICATIONS IN PHYSICS P.. ANTONEI AND I.
Steps n Dfferental Geometry, Proceedngs of the Colloquum on Dfferental Geometry, 25 30 July, 2000, Debrecen, Hungary ON HOAND S FRAME FOR RANDERS SPACE AND ITS APPICATIONS IN PHYSICS P.. ANTONEI AND I.
Math 324 Advanced Financial Mathematics Spring 2008 Final Exam Solutions May 2, 2008
 Mat 324 Advanced Fnancal Matematcs Sprng 28 Fnal Exam Solutons May 2, 28 Ts s an open book take-ome exam. You may work wt textbooks and notes but do not consult any oter person. Sow all of your work and
Mat 324 Advanced Fnancal Matematcs Sprng 28 Fnal Exam Solutons May 2, 28 Ts s an open book take-ome exam. You may work wt textbooks and notes but do not consult any oter person. Sow all of your work and
Quantum Mechanics I Problem set No.1
 Quantum Mechancs I Problem set No.1 Septembe0, 2017 1 The Least Acton Prncple The acton reads S = d t L(q, q) (1) accordng to the least (extremal) acton prncple, the varaton of acton s zero 0 = δs = t
Quantum Mechancs I Problem set No.1 Septembe0, 2017 1 The Least Acton Prncple The acton reads S = d t L(q, q) (1) accordng to the least (extremal) acton prncple, the varaton of acton s zero 0 = δs = t
17. Coordinate-Free Projective Geometry for Computer Vision
 17. Coordnate-Free Projectve Geometry for Computer Vson Hongbo L and Gerald Sommer Insttute of Computer Scence and Appled Mathematcs, Chrstan-Albrechts-Unversty of Kel 17.1 Introducton How to represent
17. Coordnate-Free Projectve Geometry for Computer Vson Hongbo L and Gerald Sommer Insttute of Computer Scence and Appled Mathematcs, Chrstan-Albrechts-Unversty of Kel 17.1 Introducton How to represent
One can coose te bass n te 'bg' space V n te form of symmetrzed products of sngle partcle wavefunctons ' p(x) drawn from an ortonormal complete set of
 8.54: Many-body penomena n condensed matter and atomc pyscs Last moded: September 4, 3 Lecture 3. Second Quantzaton, Bosons In ts lecture we dscuss second quantzaton, a formalsm tat s commonly used to
8.54: Many-body penomena n condensed matter and atomc pyscs Last moded: September 4, 3 Lecture 3. Second Quantzaton, Bosons In ts lecture we dscuss second quantzaton, a formalsm tat s commonly used to
Convexity preserving interpolation by splines of arbitrary degree
 Computer Scence Journal of Moldova, vol.18, no.1(52), 2010 Convexty preservng nterpolaton by splnes of arbtrary degree Igor Verlan Abstract In the present paper an algorthm of C 2 nterpolaton of dscrete
Computer Scence Journal of Moldova, vol.18, no.1(52), 2010 Convexty preservng nterpolaton by splnes of arbtrary degree Igor Verlan Abstract In the present paper an algorthm of C 2 nterpolaton of dscrete
ON SEPARATING SETS OF WORDS IV
 ON SEPARATING SETS OF WORDS IV V. FLAŠKA, T. KEPKA AND J. KORTELAINEN Abstract. Further propertes of transtve closures of specal replacement relatons n free monods are studed. 1. Introducton Ths artcle
ON SEPARATING SETS OF WORDS IV V. FLAŠKA, T. KEPKA AND J. KORTELAINEN Abstract. Further propertes of transtve closures of specal replacement relatons n free monods are studed. 1. Introducton Ths artcle
Linear, affine, and convex sets and hulls In the sequel, unless otherwise specified, X will denote a real vector space.
 Lnear, affne, and convex sets and hulls In the sequel, unless otherwse specfed, X wll denote a real vector space. Lnes and segments. Gven two ponts x, y X, we defne xy = {x + t(y x) : t R} = {(1 t)x +
Lnear, affne, and convex sets and hulls In the sequel, unless otherwse specfed, X wll denote a real vector space. Lnes and segments. Gven two ponts x, y X, we defne xy = {x + t(y x) : t R} = {(1 t)x +
10. Canonical Transformations Michael Fowler
 10. Canoncal Transformatons Mchael Fowler Pont Transformatons It s clear that Lagrange s equatons are correct for any reasonable choce of parameters labelng the system confguraton. Let s call our frst
10. Canoncal Transformatons Mchael Fowler Pont Transformatons It s clear that Lagrange s equatons are correct for any reasonable choce of parameters labelng the system confguraton. Let s call our frst
CENTROID (AĞIRLIK MERKEZİ )
 CENTOD (ĞLK MEKEZİ ) centrod s a geometrcal concept arsng from parallel forces. Tus, onl parallel forces possess a centrod. Centrod s tougt of as te pont were te wole wegt of a pscal od or sstem of partcles
CENTOD (ĞLK MEKEZİ ) centrod s a geometrcal concept arsng from parallel forces. Tus, onl parallel forces possess a centrod. Centrod s tougt of as te pont were te wole wegt of a pscal od or sstem of partcles
5 The Laplace Equation in a convex polygon
 5 Te Laplace Equaton n a convex polygon Te most mportant ellptc PDEs are te Laplace, te modfed Helmoltz and te Helmoltz equatons. Te Laplace equaton s u xx + u yy =. (5.) Te real and magnary parts of an
5 Te Laplace Equaton n a convex polygon Te most mportant ellptc PDEs are te Laplace, te modfed Helmoltz and te Helmoltz equatons. Te Laplace equaton s u xx + u yy =. (5.) Te real and magnary parts of an
