LECTURE 1 Introduction to Mechanics of Materials. Geometrical Properties of Cross Sections of a Rod (Part 1)
|
|
|
- Jeffery Bradford
- 5 years ago
- Views:
Transcription
1 V. DEMENKO MECHNCS OF MTERLS 05 LECTURE ntroduton to Mehans of Materals. Geometral Propertes of Cross Setons of a Rod (Part ) Prolems and Methods n Mehans of Materals (syn. Strength of Materals) Mehans of materals s the sene of strength stffness and stalty of elements of engneerng strutures. Strength s understood as the alty of struture or ts elements to wthstand a spefed external loadng wthout frature. Stffness (or rgdty) s understood as the apalty of a ody or strutural element to resst deformaton.e. to prevent exeedng elongatons defletons and so on. Stalty s meant as the apalty of a struture to resst the fores whh tend to move t from the ntal state of equlrum.e. to prevent uklng. Mehans of materals s one of the ranhes of mehans of deformale solds. Mehans of deformale solds nludes also other ranhes suh as the mathematal theory of elastty theory of plates and shells. The mathematal theory of elastty studes the ehavor of deformale solds usng a omplex mathematal apparatus. Strength of materals uses a smple mathematal apparatus and smplfyng hypotheses. t reates smple approxmate alulaton of typal strutural elements for strength rgdty and stalty. The struture sn't ale to work at the level of frature.e. should not fal under appled external loads. t must have prelmnary grounded fator of safety. The lak of fator leads to frature ut nsuffent fator makes struture mperfet. The orret hoe of fator s a responsle prolem n mehanal engneerng. The geometral sheme n strength of materals s the sheme of a rod. rod generally mples a ody one of whose dmensons (length) s onsderaly greater than the materals. other two. Bars eams shafts shells are also onsdered n mehans of
2 V. DEMENKO MECHNCS OF MTERLS 05 Geometral Propertes of Cross Setons of a Rod n solvng the prolems n strength of materals t s neessary to operate wth some geometral propertes of ross setons of a rod whh nfluene on alty of engneerng struture to wthstand appled load. Smplest example of a rod proessng y weldng s shown n Fg... Cross-Seton rea Fg. Fg. Take a ross seton of a rod. Relate t to a system of oordnates y z. solate an element from the area wth oordnates y z. Consder the followng ntegral: = lm = d 0 () where the ndex eneath the ntegral sgn ndates that the ntegraton s arred out over the whole ross-setonal area. The ntegral () s alled as ross-seton area. Cross-setonal areas of smple fgures Сrle πd = πr = area. Сrular setor α =angle n radans ( α π ) = αr area. Fg. Fg.
3 V. DEMENKO MECHNCS OF MTERLS 05 Сrular segment Orgn of axes at enter of rle α π α =angle n radans ( ) r ( α snαosα) = area. Crle wth ore removed α =angle n radans ( α π ) aros a α = = r a ; r a = r α r area. Fg. 5 Fg. 6 Сrular segment Orgn of axes at enter of rle α π α =angle n radans ( ) r ( α snαosα) = area. Equlateral trangle a sde = a area. Fg. 7 Fg.
4 V. DEMENKO MECHNCS OF MTERLS 05 Ellpse Orgn of axes at entrod = π a a magor axs mnor axs; Crumferene π.5 ( a ) a + ( a/ a) ( ).7 / a+ a 0 a/. Hollow rular ross seton ( ) = π r r r nner radus r outer radus t = r r thkness. Fg. 9 Fg. 0 Hollow square ross seton (douly symmetr) = area C entrod. soseles trapezod ( + ) h = area C entrod h heght. Fg. Fg.
5 V. DEMENKO MECHNCS OF MTERLS 05 5 soseles rght trangle = area C entrod. soseles trangle = h / area h heght wdth. Fg. Fg. Paraol semsegment y= f( x) = h x h = area. Paraol spandrel hx y= f( x) = h = area. Fg. 5 Fg. 6 Retangle = h area. Rght trangle = h / area. Fg. 7 Fg.
6 6 V. DEMENKO MECHNCS OF MTERLS 05 Quarter rle = πr area. Quarter-rular spandrel π = r area. Fg. 9 Fg. 0 Regular hexagon sde C entrod = area. Regular hexagon hollow ross seton (syn. regular hexagon tue) t thkness = 6t area. Fg. Fg. Semrle r radus = πr area. Sne wave h = area. π Fg. Fg.
7 V. DEMENKO MECHNCS OF MTERLS 05 7 Regular polygon wth n sdes n length of a sde β entral angle for a sde α nteror angle (or vertex angle). n numer of sdes ( ) Semsegment of nth degree n n ( ) ( / ) = = ( 0) y f x h x ( / ) = h n n+ area. n > ; Fg. 5 Fg. 6 Square hmney Square ross seton square = π / area. = a area. d Fg. 7 Fg. Square tuular ross seton wdth t thkness = t area. Thn rular rng = πrt = πdt d r t << r. = ( ) Fg. 9 Fg. 0
8 V. DEMENKO MECHNCS OF MTERLS 05 Trangle h = area. Trapezod ( + ) ha = area. Fg. Fg.. Stat Moment (Frst Moment) of a Seton Consder the followng two ntegrals: S y = zd Sz = yd. () Eah of the ntegrals represents the sum of the produts of elements of area and the dstane to the respetve axs (y or z). The frst ntegral s alled the stat moment of the seton wth respet to the y axs and the seond to the z axs. The stat moment s measured n meter ued ( m ). ordng to expressons () the stat moment an e postve negatve or equal to zero. The stat moment of a ompound seton equals to the sum of the stat moments of the smplest fgures (omponents).. Central xes. Centrod Consder a plane seton and draw two pars of parallel axes y z and y z as shown n Fg.. Let a dstane etween the axes wll e and a. The area of ths seton and S y and S z are gven. t s neessary to fnd the stat moments wth respet to the y and z axes.e. S y and S z. ordng to formulas () the stat moments are S = zd y S = yd. () z
9 s may e seen from Fg. V. DEMENKO MECHNCS OF MTERLS 05 9 z = z y = y a. () Susttutng y and z from expressons () to formulas () we fnd Beause as we know y ( ) S = z d= zd d z ( ). (5) S = y a d= yd a d zd= Sy yd= Sz d= (6) then we rewrte (5) as S = S y y S = S a. (7) z z Consder the frst of the expressons derved aove: S = S. y y The quantty may e any numer whatever ether postve or negatve. t an therefore always e hosen to make the produt equal to S y. Then the stat moment wth respet to the y -axs vanshes that s 0 Sy = 0 = Sz a. () n axs wth respet to whh the stat moment s zero s alled entral axs or entrodal axs. The pont of nterseton of entral axes s alled the enter of gravty or entrod of ross-seton. Thus equatons () make t possle to determne the poston of the entrod f the stat moments are known: Sy S = Z = a= Y z =. (9)
10 0 V. DEMENKO MECHNCS OF MTERLS 05 where Z and Y are oordnates of the entrod. t s possle also to fnd the stat moments f the poston of the entrod s known. The entrod of a omposte seton s determned y Fg. Y = n n z n Z = n y (0) where y and z are oordnates of the geometral enters of the omponent fgures. Consder the smplest example. Example The alulaton of entrod oordnate of the trangular (Fg. ) Gven: s the ase of the trangle h s the heght. R.D.: dstane of the entrod of the trangle from ts ase.e. z. Fg. Sy Soluton By defnton z =. The trangle stat moment wth respet to the y axs s equal to S y = zd. n our ase d= ( z) dz = h. From trangles smlarty (z) equals to Thus ( z) = ( h z). h h h h Sy = ( h z) = 6 0 z h + 6 h = =+. h
11 V. DEMENKO MECHNCS OF MTERLS 05 The oordnate from the ase of the trangle to the entrod of gravty s h / (up dreted) and the entrodal horzontal entral axs s loated upwards at dstane / of alttude from ts ase. Example Centrodal axes of rght trangle (Fg. 5) the heght. Gven: s the ase of the trangle h s R.D.: dstane of the entrod of the trangle from ts ase.e. x and y. Fg. 5 xd Sy x 0 = = = d= hxdx ( ) ; = hx ( ) ( x) h = = hx ( ) = ( x) h h h 0 ( ) xxdx h = = = 6. h h h = Sx h By analogy y = =. n result x y axes are entrodal axes of rght trangle. Example Centrod of a omposte area (Fg. 6) seton. Gven: dmensons of an angular R.D.: x y oordnates. Fg. 6 Soluton The areas and frst moments of omposte areas may e alulated y summng the orrespondng propertes of the omponent parts. Let us assume that a omposte area s dvded nto a total of n
12 V. DEMENKO MECHNCS OF MTERLS 05 parts and let us denote the area of the th part as. Then we an otan the area and frst moments y the followng summatons: n = () = S n = y x = S n = x ; () y = n whh x and y are the oordnates of the entrod of the th part. The oordnates of the entrod of the omposte area are x Sy = = n = n = x S y x = = = n n = y. () Sne the omposte area s represented exatly y the n parts the preedng equatons gve exat results for the oordnates of the entrod. To llustrate the use of Eq. () onsder the L -shaped area (or angle seton) shown n Fg. 6 a. Ths area has sde dmensons and and thkness t. The area an e dvded nto two retangles of areas and wth entrods C and C respetvely (Fg. 6 ). The areas and entrodal oordnates of these two parts are = t ( ) = t t t x = x = y = ; t t y =. Therefore the area and frst moments of the omposte area (from Eqs. () and ()) are ( ) = + = t + t ( ) t Sx = y + y = + t t ( ) t Sy = x + x = t+ t.
13 V. DEMENKO MECHNCS OF MTERLS 05 Fnally we an otan the oordnates x and area (Fg. 6 ) from Eq. (): x Sy t+ t = = t y y of the entrod C of the omposte Sx + t t = = +. () ( + ) ( t) Note : When a omposte area s dvded nto only two parts the entrod C of the entre area les on the lne jonng the entrods C and C of the two parts (as shown n Fg. for the L-shaped area). Note : When usng the formulas for omposte areas (Eqs. () () and ()) we an handle the asene of an area y sutraton. Ths proedure s useful when there are utouts or holes n the fgure. Example Determnaton the oordnates of the entrod of the ompound seton (Fg. 7) y z h = 0mm. Gven: = 0 mm = 0 mm R.D.: x y oordnates. Soluton Dvde the area nto two smplest fgures: the rght trangle and the retangle for whh the entrods are know. Selet an artrary referene system of axes y and z and determne the oordnates of the entrod usng equaton (0). Susttutng the numeral values nto the foregong expresson we reeve: h y + h + z z z + h + h h h h z + + h + Sy Sy Sy + h + h S S + S = = = = =... Fg. 7 + = = = = =...
14 V. DEMENKO MECHNCS OF MTERLS 05 Centrods of smple fgures Crular setor Orgn of axes at enter of rle: α π α =angle n radans ( ) = αr x = rsnα rsnα y =. α Fg. Crular segment Orgn of axes at enter of rle: α π α =angle n radans ( ) = r ( α snαosα) y r sn α =. α snαosα Fg 9 soseles trangle Orgn of axes at entrod: h = x = h y =. Fg 0 Paraol semsegment paraol semsegment OB s ounded y the x axs the y axs and a paraol urve havng ts vertex at (Fg. ). The equaton of the urve s y= f ( x) = h x ()
15 V. DEMENKO MECHNCS OF MTERLS 05 5 n whh s the ase and h s the heght of the semsegment. Loate the entrod C of the semsegment. To determne the oordnates equatons: x and x y of the entrod C (Fg. ) we wll use Sy S = y x =. We egn y seletng an element of area d n the form of a thn vertal strp of wdth dx and heght y. The area of ths dfferental element s Therefore the area of the paraol semsegment s d ydx h x = = dx. () x h = d= h dx = 0 ( ). () Note: Ths area s / of the area of the surroundng retangle. Fg. Fg. The frst moment of an element of area d wth respet to an axs s otaned y multplyng the area of the element y the dstane from ts entrod to the axs. Sne the x and y oordnates of the entrod of the element shown n Fg. are x and y / respetvely the frst moments of the element wth respet to the x and y axes are
16 6 V. DEMENKO MECHNCS OF MTERLS 05 y h x h Sx = d= dx = 5 0 () x h Sy = xd= hx dx = 0 n whh we have susttuted for d from Eq. (). We an now determne the oordnates of the entrod C: (5) x y Sy = = (6) Sx h = =. (7) 5 Notes: The entrod C of the paraol semsegment may also e loated y takng the element of area d as a horzontal strp of heght dy and wdth y x=. () h Ths expresson s otaned y solvng Eq. () for x n terms of y. nother posslty s to take the dfferental element as a retangle of wdth dx and heght dy. Then the expressons for nstead of sngle ntegrals. S x and S y are n the form of doule ntegrals Fg Paraol spandrel Orgn of axes at vertex O: hx y= f ( x) = h = x = h y =. 0
17 V. DEMENKO MECHNCS OF MTERLS 05 7 Quarter rle Orgn of axes at enter of rle O: x = πr r = y =. π Fg Quarter-rular spandrel Orgn of axes at pont of tangeny: π = r r x= r π y ( ) ( 0 π ) ( π ) r = 0. r. Fg 5 Retangle Orgn of axes at entrod: = h x = h y =. Fg 6
18 V. DEMENKO MECHNCS OF MTERLS 05 Rght trangle Orgn of axes at entrod: h = x = h y =. Fg 7 Semrle Orgn of axes at entrod: = πr r y =. π Fg Fg 9 Sne wave Orgn of axes at entrod: h = π π h y =. Thn rular ar Orgn of axes at enter of rle. pproxmate formulas for ase when t s small: β angle n radans ( β π ) ; = βrt rsn β y =. β Fg 50
19 V. DEMENKO MECHNCS OF MTERLS 05 9 Centrod of a trapezod Orgn of axes at entrod: ha ( + ) = h( a+ ) y =. a+ ( ) Fg 5 Centrod of a trangle Orgn of axes at entrod: h = + x = h y =. Fg 5. xal Moments (Seond Moments) and Produt of nerta Take a ross seton of a rod. Relate t to a system of o-ordnates y z. solate an element d from the area wth o-ordnates y z. n addton to the stat moment onsder the followng four ntegrals: y = z d z = y d () yz ρ = yzd () = ρ d () Fg. 5 where the frst two ntegrals () are alled the axal moments of nerta of the seton wth respet to the y and z axes respetvely.
20 0 V. DEMENKO MECHNCS OF MTERLS 05 The thrd ntegral () s alled the produt of nerta of the seton wth respet to two mutually perpendular axes y and z. The fourth ntegral () s alled the polar moment of nerta of the seton. The dmenson of the moments of nerta s m (meters n a power of four). The axal and polar moments of nerta are always postve and annot e equal to zero. The produt of nerta may e postve negatve or equal to zero dependng on the poston of the axes. For example ths value wth respet to any par of axes s zero when ether of the axes s an axs of symmetry. Example 5 The alulaton of the axal moment of nerta of a retangle wth respet to the axes y and z passng through the entrod of the retangle (Fg. 5). Gven: and h ase and heght of the retangle respetvely. retangle. R.D.: entral axal moments of nerta of a Soluton Let us separate an elementary area d wth the ase and the heght dz at the dstane z from the axs. Sne d=dz then Fg. 5 h + h y = z d= zdz =. h The moment of nerta wth respet to the z-axs s found y a smlar way: + h z = y d= y hdy =.
21 V. DEMENKO MECHNCS OF MTERLS 05 Example 6 Calulaton of the entral moment of nerta of a rular shape (Fg. 55). Gven: d dameter of the rle. R.D.: entral axal moments of nerta. Soluton We take d as πρdρ. Thus d πd ρ = ρ d= πρ dρ =. 0 Referrng to Fg 5 we fnd ρ = y + z. ( ) That s ρ y z. Usng the symmetry we an wrte = d= y + z d= + ρ y πd = z =. 6 Example 7 Calulaton of axal moments and produt of nerta for rght trangle relatve to axs ondent wth trangle legs (Fg. 56). h z df z ( ) Fg. 55 fter susttuton Fg. 56 dz z ( ) y Gven: h R.D.: y Soluton z yz (a) Calulaton of axal moments of nerta s prelmnary determned y F = z d where d= z ( ) dz. Usng smlarty ondton z = h z ( z ) = z h h. h h z z z h h h 0 0 y = z dz = =.
22 V. DEMENKO MECHNCS OF MTERLS 05 Thus h y = y analogy h z =. () Calulaton of produt of nerta t s known that for produt of nerta yz = yzd (a) F where d= ydz. () Equaton of nlned oundary АВ s Fg. 57 z h y + = where z = h y or y z = h. () fter ths equaton (a) may e rewrtten: yz n result z z h h h h y h z h = yzdy dz = z dz = z dz = h h h 0 z z z h = + =. h yz =+. (d) Note that the propertes of strutural elements suh as hannels angles or - eams are gven n the tales of standard seton (assortments). For some geometr fgures entral moments of nerta are presented elow.
23 V. DEMENKO MECHNCS OF MTERLS 05 ssortments of steel produts Geometral propertes of angle setons wth equal legs (L shapes) (GOST 509-7) wdth of we d thkness moment of nerta radus of gyraton z 0 dstane to entrod. Desgnaton (numer) Fg. 5 d xes rea X X X0 X0 Y0 Y0 mm m x 0 max x x x 0 max y 0 mn y m сm m сm сm 0 mn сm z 0 сm Mass per meter kg
24 V. DEMENKO MECHNCS OF MTERLS 05 (fnshed)
25 V. DEMENKO MECHNCS OF MTERLS 05 5 Geometral propertes of angle setons wth unequal legs (L shapes) (GOST 50-7) B wdth of larger leg wdth of smaller leg d thkness of legs moment of nerta radus of gyraton x 0 y 0 dstanes from the entrod to the ak of the legs. Desgna ton (nume r) 5/6 / /5 5/ 5/ 56/6 6/0 7/5 75/5 /5 9/56 0/6 Fg. 59 B mm d xes rea X X Y Y 0 y 0 m x y x tan α y u mn u mn сm сm m сm m сm m сm Mass per meter kg
26 6 /7 5/ /9 6/0 V. DEMENKO MECHNCS OF MTERLS 05 (fnshed) / 0/5 5/ Geometral propertes of hannel setons (C shapes) (GOST 0-7) Fg. 60 Dmensons mm Desgnaton (numer) h s t rea m x m h heght of a eam wdth of a flange s thkness of a we t average thkness of a flange W setonal modulus radus of gyraton S x frst moment of area moment of nerta x 0 dstane from the entrod to the ak of the we. W x m x сm S x m y m W y m y сm x 0 сm Weght per meter kg
27 V. DEMENKO MECHNCS OF MTERLS 05 7 (fnshed) а а а 0 0а а а Desgnat on (numer ) 0 6 a 0 0а а Geometral propertes of S shapes (-eam setons) (GOST 9-7) Fg. 6 Dmensons mm h s t rea m x m h heght of a eam wdth of a flange s thkness of a we t average thkness of a flange axal moment of nerta W setonal modulus radus of gyraton S x frst moment of a half-seton. W x m x сm S x m y m W y m y сm Mass per meter kg
28 V. DEMENKO MECHNCS OF MTERLS 05 (fnshed) а 7 7а 0 0а Centrodal axal moments of nerta for smple fgures Crle Orgn of axes at enter of rle: πd = π r = x = 0 xy πr πd = y = = 6 p = πr = πd 5 5 x = πr = πd. 6 Fg. 6 Crle wth ore removed Orgn of axes at enter of rle: α =angle n radans ( α π /); α = aros a r = r a ; Fg. 6 x a = r α r r a a x = α 6 r r r a a = α r r xy = 0.
29 V. DEMENKO MECHNCS OF MTERLS 05 9 Fg. 6 Crular setor Orgn of axes at enter of rle: α =angle n radans ( α π /); rsnα = αr x = rsnα y = ; α r x = ( α + snαos α) r y = ( α snαos α) = = 0 xy xy αr ρ =. Fg. 65 Fg. 66 Crular segment Ellpse Orgn of axes at enter of rle: α =angle n radans ( α π /); r sn α y = α snαosα r x = ( α snαosα + sn α) = = 0 xy r y = (α snαosα sn αos α) xy Orgn of axes at entrod: = π a x π a πa = y = ; = 0 xy πa p = ( + a ). Crumferene π[.5( a+ ) a] ( a/ a).7 / a+ a (0 a/).
30 0 V. DEMENKO MECHNCS OF MTERLS 05 Fg. 67 Fg. 6 Fg. 69 Fg. 70 soseles trangle Paraol semsegment Orgn of axes at entrod: h h = x = y = ; h h x = y 6 = xy = 0 ; h ρ = (h ) + h x =. Note: For an equlateral trangle h= /. Orgn of axes at orner: y f( x) h x = = h h = x = y = ; 5 6h x = 05 Paraol spandrel Quarter rle h y = 5 Orgn of axes at vertex: h xy =. hx y= f( x) = h h = x = y = ; 0 h x = h y = 5 h xy =. Orgn of axes at enter of rle: = πr x x πr = y = 6 r = y = ; π r xy = ; (9π 6) r x = 0.05 y = r. π
31 V. DEMENKO MECHNCS OF MTERLS 05 Fg. 7 Quarter-rular spandrel Retangle Orgn of axes at pont of tangeny: π = r r x = r ( π ) (0 π ) r y = 0.r ( π ) 5π x = r 0.05r 6 π y = x = r 0.70r 6. a Fg 7 a) Orgn of axes at entrod: h = h x = y = ; h h x = y = xy = 0 ; h ρ = ( h ) +. ) Orgn of axes at orner: h x = h h y = xy = ; h ρ = ( h ) + x h =. 6( + h )
32 V. DEMENKO MECHNCS OF MTERLS 05 Fg. 7 Regular polygon wth n sdes Orgn of axes at entrod: C = entrod (at enter of polygon) n = numer of sdes ( n ) = length of a sde β = entral angle for a sde α = nteror angle (or vertex angle) 60 n β = α = 0 n n α + β = 0 ; R = radus of rumsred rle (lne C) R = radus of nsred rle (lne CB) β β R = s R = ot n β = ot ; moment of nerta aout any axs through C (the entrod C s a prnpal pont and every axs through C s a prnpal axs) Rght trangle n β β = ot ot + 9 ρ =. a Fg. 7
33 V. DEMENKO MECHNCS OF MTERLS 05 a) Orgn of axes at entrod: h h = x = y = ; h h x = y 6 = 6 = ( h)/7 ; xy h ρ = ( + ) h x h 6 Fg. 75 =. Semrle ) Orgn of axes at vertex: h x = h y = h p = ( h + ) h xy = ; h x =. Orgn of axes at entrod: = π r y r = ; π (9π 6) r = 0.09r 7π y = π r = 0 xy = x = πr. x xy Fg. 76 Fg. 77 Semsne wave Thn rular ar Orgn of axes at entrod: = h y π = π h ; x = ( π ) h h 9π 6 y = h 0.h π π xy = 0 xy = h x =. 9 π Orgn of axes at enter of rle. pproxmate formulas for ase when t s small: β angle n radans ( β π /) ; = βrt y = ( rsn β)/ β ; x = rtβ ( + sn β os β ) y = rtβ ( sn β os β ) = = 0 xy β + snβ osβ x = rt β. Note: For a semrular ar ( β = π /). xy
34 V. DEMENKO MECHNCS OF MTERLS 05 Thn rular rng Orgn of axes at entrod. pproxmate formulas for ase when t s small: = πrt = πdt x y πrt πdt = = = = 0 ρ xy = πrt= πdt. Fg. 7 Thn retangle Orgn of axes at entrod. pproxmate formulas for ase when t s small: = t x y x = t sn β = t os β = t sn β. Fg. 79 Fg. 0 Trapezod Orgn of axes at entrod: ha ( + ) = h( a+ ) y = ( a+ ) x h ( a + a+ ) = 6( a+ ) h ( a+ ) x =.
35 V. DEMENKO MECHNCS OF MTERLS 05 5 Trangle a Fg. a) Orgn of axes at entrod: h + h = x = y = ; h x = 6 h y = ( + ); 6 h xy = ( ) 7 h ρ = ( h ) ) Orgn of axes at vertex: h x = h y = ( + ) h xy = ( ) h x =.
e a = 12.4 i a = 13.5i h a = xi + yj 3 a Let r a = 25cos(20) i + 25sin(20) j b = 15cos(55) i + 15sin(55) j
 Vetors MC Qld-3 49 Chapter 3 Vetors Exerse 3A Revew of vetors a d e f e a x + y omponent: x a os(θ 6 os(80 + 39 6 os(9.4 omponent: y a sn(θ 6 sn(9 0. a.4 0. f a x + y omponent: x a os(θ 5 os( 5 3.6 omponent:
Vetors MC Qld-3 49 Chapter 3 Vetors Exerse 3A Revew of vetors a d e f e a x + y omponent: x a os(θ 6 os(80 + 39 6 os(9.4 omponent: y a sn(θ 6 sn(9 0. a.4 0. f a x + y omponent: x a os(θ 5 os( 5 3.6 omponent:
LECTURE 2 Geometrical Properties of Rod Cross Sections (Part 2) 1 Moments of Inertia Transformation with Parallel Transfer of Axes.
 V. DEMENKO MECHNCS OF MTERLS 05 LECTURE Geometrial Properties of Rod Cross Setions (Part ) Moments of nertia Transformation with Parallel Transfer of xes. Parallel-xes Theorems S Given: a b = S = 0. z
V. DEMENKO MECHNCS OF MTERLS 05 LECTURE Geometrial Properties of Rod Cross Setions (Part ) Moments of nertia Transformation with Parallel Transfer of xes. Parallel-xes Theorems S Given: a b = S = 0. z
GEL 446: Applied Environmental Geology
 GE 446: ppled Envronmental Geology Watershed Delneaton and Geomorphology Watershed Geomorphology Watersheds are fundamental geospatal unts that provde a physal and oneptual framewor wdely used by sentsts,
GE 446: ppled Envronmental Geology Watershed Delneaton and Geomorphology Watershed Geomorphology Watersheds are fundamental geospatal unts that provde a physal and oneptual framewor wdely used by sentsts,
PHYSICS 212 MIDTERM II 19 February 2003
 PHYSICS 1 MIDERM II 19 Feruary 003 Exam s losed ook, losed notes. Use only your formula sheet. Wrte all work and answers n exam ooklets. he aks of pages wll not e graded unless you so request on the front
PHYSICS 1 MIDERM II 19 Feruary 003 Exam s losed ook, losed notes. Use only your formula sheet. Wrte all work and answers n exam ooklets. he aks of pages wll not e graded unless you so request on the front
ˆ (0.10 m) E ( N m /C ) 36 ˆj ( j C m)
 7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
7.. = = 3 = 4 = 5. The electrc feld s constant everywhere between the plates. Ths s ndcated by the electrc feld vectors, whch are all the same length and n the same drecton. 7.5. Model: The dstances to
Section 8.3 Polar Form of Complex Numbers
 80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
Week 9 Chapter 10 Section 1-5
 Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
Week 9 Chapter 10 Secton 1-5 Rotaton Rgd Object A rgd object s one that s nondeformable The relatve locatons of all partcles makng up the object reman constant All real objects are deformable to some extent,
8.1 Arc Length. What is the length of a curve? How can we approximate it? We could do it following the pattern we ve used before
 .1 Arc Length hat s the length of a curve? How can we approxmate t? e could do t followng the pattern we ve used before Use a sequence of ncreasngly short segments to approxmate the curve: As the segments
.1 Arc Length hat s the length of a curve? How can we approxmate t? e could do t followng the pattern we ve used before Use a sequence of ncreasngly short segments to approxmate the curve: As the segments
CENTROID (AĞIRLIK MERKEZİ )
 CENTOD (ĞLK MEKEZİ ) centrod s a geometrcal concept arsng from parallel forces. Tus, onl parallel forces possess a centrod. Centrod s tougt of as te pont were te wole wegt of a pscal od or sstem of partcles
CENTOD (ĞLK MEKEZİ ) centrod s a geometrcal concept arsng from parallel forces. Tus, onl parallel forces possess a centrod. Centrod s tougt of as te pont were te wole wegt of a pscal od or sstem of partcles
Indeterminate pin-jointed frames (trusses)
 Indetermnate pn-jonted frames (trusses) Calculaton of member forces usng force method I. Statcal determnacy. The degree of freedom of any truss can be derved as: w= k d a =, where k s the number of all
Indetermnate pn-jonted frames (trusses) Calculaton of member forces usng force method I. Statcal determnacy. The degree of freedom of any truss can be derved as: w= k d a =, where k s the number of all
CENTROID (AĞIRLIK MERKEZİ )
 CENTOD (ĞLK MEKEZİ ) centrod s a geometrcal concept arsng from parallel forces. Tus, onl parallel forces possess a centrod. Centrod s tougt of as te pont were te wole wegt of a pscal od or sstem of partcles
CENTOD (ĞLK MEKEZİ ) centrod s a geometrcal concept arsng from parallel forces. Tus, onl parallel forces possess a centrod. Centrod s tougt of as te pont were te wole wegt of a pscal od or sstem of partcles
DUE: WEDS FEB 21ST 2018
 HOMEWORK # 1: FINITE DIFFERENCES IN ONE DIMENSION DUE: WEDS FEB 21ST 2018 1. Theory Beam bendng s a classcal engneerng analyss. The tradtonal soluton technque makes smplfyng assumptons such as a constant
HOMEWORK # 1: FINITE DIFFERENCES IN ONE DIMENSION DUE: WEDS FEB 21ST 2018 1. Theory Beam bendng s a classcal engneerng analyss. The tradtonal soluton technque makes smplfyng assumptons such as a constant
CHAPTER 10 ROTATIONAL MOTION
 CHAPTER 0 ROTATONAL MOTON 0. ANGULAR VELOCTY Consder argd body rotates about a fxed axs through pont O n x-y plane as shown. Any partcle at pont P n ths rgd body rotates n a crcle of radus r about O. The
CHAPTER 0 ROTATONAL MOTON 0. ANGULAR VELOCTY Consder argd body rotates about a fxed axs through pont O n x-y plane as shown. Any partcle at pont P n ths rgd body rotates n a crcle of radus r about O. The
Physics 181. Particle Systems
 Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Physcs 181 Partcle Systems Overvew In these notes we dscuss the varables approprate to the descrpton of systems of partcles, ther defntons, ther relatons, and ther conservatons laws. We consder a system
Lecture Torsion Properties for Line Segments and Computational Scheme for Piecewise Straight Section Calculations
 Lecture - 003 Torson Propertes for Lne Segments and Computatonal Scheme for Pecewse Straght Secton Calculatons ths conssts of four parts (and how we wll treat each) A - dervaton of geometrc algorthms for
Lecture - 003 Torson Propertes for Lne Segments and Computatonal Scheme for Pecewse Straght Secton Calculatons ths conssts of four parts (and how we wll treat each) A - dervaton of geometrc algorthms for
1 Matrix representations of canonical matrices
 1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
Formulas for the Determinant
 page 224 224 CHAPTER 3 Determnants e t te t e 2t 38 A = e t 2te t e 2t e t te t 2e 2t 39 If 123 A = 345, 456 compute the matrx product A adj(a) What can you conclude about det(a)? For Problems 40 43, use
page 224 224 CHAPTER 3 Determnants e t te t e 2t 38 A = e t 2te t e 2t e t te t 2e 2t 39 If 123 A = 345, 456 compute the matrx product A adj(a) What can you conclude about det(a)? For Problems 40 43, use
Math1110 (Spring 2009) Prelim 3 - Solutions
 Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
Math 1110 (Sprng 2009) Solutons to Prelm 3 (04/21/2009) 1 Queston 1. (16 ponts) Short answer. Math1110 (Sprng 2009) Prelm 3 - Solutons x a 1 (a) (4 ponts) Please evaluate lm, where a and b are postve numbers.
A Tale of Friction Basic Rollercoaster Physics. Fahrenheit Rollercoaster, Hershey, PA max height = 121 ft max speed = 58 mph
 A Tale o Frcton Basc Rollercoaster Physcs Fahrenhet Rollercoaster, Hershey, PA max heght = 11 t max speed = 58 mph PLAY PLAY PLAY PLAY Rotatonal Movement Knematcs Smlar to how lnear velocty s dened, angular
A Tale o Frcton Basc Rollercoaster Physcs Fahrenhet Rollercoaster, Hershey, PA max heght = 11 t max speed = 58 mph PLAY PLAY PLAY PLAY Rotatonal Movement Knematcs Smlar to how lnear velocty s dened, angular
The Schrödinger Equation
 Chapter 1 The Schrödnger Equaton 1.1 (a) F; () T; (c) T. 1. (a) Ephoton = hν = hc/ λ =(6.66 1 34 J s)(.998 1 8 m/s)/(164 1 9 m) = 1.867 1 19 J. () E = (5 1 6 J/s)( 1 8 s) =.1 J = n(1.867 1 19 J) and n
Chapter 1 The Schrödnger Equaton 1.1 (a) F; () T; (c) T. 1. (a) Ephoton = hν = hc/ λ =(6.66 1 34 J s)(.998 1 8 m/s)/(164 1 9 m) = 1.867 1 19 J. () E = (5 1 6 J/s)( 1 8 s) =.1 J = n(1.867 1 19 J) and n
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
 COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
COMPLEX NUMBERS AND QUADRATIC EQUATIONS INTRODUCTION We know that x 0 for all x R e the square of a real number (whether postve, negatve or ero) s non-negatve Hence the equatons x, x, x + 7 0 etc are not
Lecture 12: Discrete Laplacian
 Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
One Dimensional Axial Deformations
 One Dmensonal al Deformatons In ths secton, a specfc smple geometr s consdered, that of a long and thn straght component loaded n such a wa that t deforms n the aal drecton onl. The -as s taken as the
One Dmensonal al Deformatons In ths secton, a specfc smple geometr s consdered, that of a long and thn straght component loaded n such a wa that t deforms n the aal drecton onl. The -as s taken as the
MEASUREMENT OF MOMENT OF INERTIA
 1. measurement MESUREMENT OF MOMENT OF INERTI The am of ths measurement s to determne the moment of nerta of the rotor of an electrc motor. 1. General relatons Rotatng moton and moment of nerta Let us
1. measurement MESUREMENT OF MOMENT OF INERTI The am of ths measurement s to determne the moment of nerta of the rotor of an electrc motor. 1. General relatons Rotatng moton and moment of nerta Let us
Complex Variables. Chapter 18 Integration in the Complex Plane. March 12, 2013 Lecturer: Shih-Yuan Chen
 omplex Varables hapter 8 Integraton n the omplex Plane March, Lecturer: Shh-Yuan hen Except where otherwse noted, content s lcensed under a BY-N-SA. TW Lcense. ontents ontour ntegrals auchy-goursat theorem
omplex Varables hapter 8 Integraton n the omplex Plane March, Lecturer: Shh-Yuan hen Except where otherwse noted, content s lcensed under a BY-N-SA. TW Lcense. ontents ontour ntegrals auchy-goursat theorem
Inductance Calculation for Conductors of Arbitrary Shape
 CRYO/02/028 Aprl 5, 2002 Inductance Calculaton for Conductors of Arbtrary Shape L. Bottura Dstrbuton: Internal Summary In ths note we descrbe a method for the numercal calculaton of nductances among conductors
CRYO/02/028 Aprl 5, 2002 Inductance Calculaton for Conductors of Arbtrary Shape L. Bottura Dstrbuton: Internal Summary In ths note we descrbe a method for the numercal calculaton of nductances among conductors
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Physics 4B. Question and 3 tie (clockwise), then 2 and 5 tie (zero), then 4 and 6 tie (counterclockwise) B i. ( T / s) = 1.74 V.
 Physcs 4 Solutons to Chapter 3 HW Chapter 3: Questons:, 4, 1 Problems:, 15, 19, 7, 33, 41, 45, 54, 65 Queston 3-1 and 3 te (clockwse), then and 5 te (zero), then 4 and 6 te (counterclockwse) Queston 3-4
Physcs 4 Solutons to Chapter 3 HW Chapter 3: Questons:, 4, 1 Problems:, 15, 19, 7, 33, 41, 45, 54, 65 Queston 3-1 and 3 te (clockwse), then and 5 te (zero), then 4 and 6 te (counterclockwse) Queston 3-4
Implicit Integration Henyey Method
 Implct Integraton Henyey Method In realstc stellar evoluton codes nstead of a drect ntegraton usng for example the Runge-Kutta method one employs an teratve mplct technque. Ths s because the structure
Implct Integraton Henyey Method In realstc stellar evoluton codes nstead of a drect ntegraton usng for example the Runge-Kutta method one employs an teratve mplct technque. Ths s because the structure
Rotational Dynamics. Physics 1425 Lecture 19. Michael Fowler, UVa
 Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
Rotatonal Dynamcs Physcs 1425 Lecture 19 Mchael Fowler, UVa Rotatonal Dynamcs Newton s Frst Law: a rotatng body wll contnue to rotate at constant angular velocty as long as there s no torque actng on t.
So far: simple (planar) geometries
 Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Physcs 06 ecture 5 Torque and Angular Momentum as Vectors SJ 7thEd.: Chap. to 3 Rotatonal quanttes as vectors Cross product Torque epressed as a vector Angular momentum defned Angular momentum as a vector
Spring 2002 Lecture #13
 44-50 Sprng 00 ecture # Dr. Jaehoon Yu. Rotatonal Energy. Computaton of oments of nerta. Parallel-as Theorem 4. Torque & Angular Acceleraton 5. Work, Power, & Energy of Rotatonal otons Remember the md-term
44-50 Sprng 00 ecture # Dr. Jaehoon Yu. Rotatonal Energy. Computaton of oments of nerta. Parallel-as Theorem 4. Torque & Angular Acceleraton 5. Work, Power, & Energy of Rotatonal otons Remember the md-term
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 ME 270 Fall 2013 Fnal Exam NME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS
ME 270 Fall 2013 Fnal Exam NME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS
425. Calculation of stresses in the coating of a vibrating beam
 45. CALCULAION OF SRESSES IN HE COAING OF A VIBRAING BEAM. 45. Calulaton of stresses n the oatng of a vbratng beam M. Ragulsks,a, V. Kravčenken,b, K. Plkauskas,, R. Maskelunas,a, L. Zubavčus,b, P. Paškevčus,d
45. CALCULAION OF SRESSES IN HE COAING OF A VIBRAING BEAM. 45. Calulaton of stresses n the oatng of a vbratng beam M. Ragulsks,a, V. Kravčenken,b, K. Plkauskas,, R. Maskelunas,a, L. Zubavčus,b, P. Paškevčus,d
Chapter 3 Differentiation and Integration
 MEE07 Computer Modelng Technques n Engneerng Chapter Derentaton and Integraton Reerence: An Introducton to Numercal Computatons, nd edton, S. yakowtz and F. zdarovsky, Mawell/Macmllan, 990. Derentaton
MEE07 Computer Modelng Technques n Engneerng Chapter Derentaton and Integraton Reerence: An Introducton to Numercal Computatons, nd edton, S. yakowtz and F. zdarovsky, Mawell/Macmllan, 990. Derentaton
THE SMOOTH INDENTATION OF A CYLINDRICAL INDENTOR AND ANGLE-PLY LAMINATES
 THE SMOOTH INDENTATION OF A CYLINDRICAL INDENTOR AND ANGLE-PLY LAMINATES W. C. Lao Department of Cvl Engneerng, Feng Cha Unverst 00 Wen Hwa Rd, Tachung, Tawan SUMMARY: The ndentaton etween clndrcal ndentor
THE SMOOTH INDENTATION OF A CYLINDRICAL INDENTOR AND ANGLE-PLY LAMINATES W. C. Lao Department of Cvl Engneerng, Feng Cha Unverst 00 Wen Hwa Rd, Tachung, Tawan SUMMARY: The ndentaton etween clndrcal ndentor
Chapter Newton s Method
 Chapter 9. Newton s Method After readng ths chapter, you should be able to:. Understand how Newton s method s dfferent from the Golden Secton Search method. Understand how Newton s method works 3. Solve
Chapter 9. Newton s Method After readng ths chapter, you should be able to:. Understand how Newton s method s dfferent from the Golden Secton Search method. Understand how Newton s method works 3. Solve
7.2 Volume. A cross section is the shape we get when cutting straight through an object.
 7. Volume Let s revew the volume of smple sold, cylnder frst. Cylnder s volume=se re heght. As llustrted n Fgure (). Fgure ( nd (c) re specl cylnders. Fgure () s rght crculr cylnder. Fgure (c) s ox. A
7. Volume Let s revew the volume of smple sold, cylnder frst. Cylnder s volume=se re heght. As llustrted n Fgure (). Fgure ( nd (c) re specl cylnders. Fgure () s rght crculr cylnder. Fgure (c) s ox. A
π e ax2 dx = x 2 e ax2 dx or x 3 e ax2 dx = 1 x 4 e ax2 dx = 3 π 8a 5/2 (a) We are considering the Maxwell velocity distribution function: 2πτ/m
 Homework Solutons Problem In solvng ths problem, we wll need to calculate some moments of the Gaussan dstrbuton. The brute-force method s to ntegrate by parts but there s a nce trck. The followng ntegrals
Homework Solutons Problem In solvng ths problem, we wll need to calculate some moments of the Gaussan dstrbuton. The brute-force method s to ntegrate by parts but there s a nce trck. The followng ntegrals
Dr. James C.Y. Guo, P.E., Professor and Director Civil Engineering, U. of Colorado Denver Pitot-Static Tube
 Flow Measurement Dr. James C.Y. Guo, P.E., Professor and Dretor Cvl Engneerng, U. of Colorado Denver Ptot-Stat Tube 1 Ptot-tube for Veloty Measurement Operaton of Ptot-Tube Manometer and Pressure Dfferental
Flow Measurement Dr. James C.Y. Guo, P.E., Professor and Dretor Cvl Engneerng, U. of Colorado Denver Ptot-Stat Tube 1 Ptot-tube for Veloty Measurement Operaton of Ptot-Tube Manometer and Pressure Dfferental
Application to Plane (rigid) frame structure
 Advanced Computatonal echancs 18 Chapter 4 Applcaton to Plane rgd frame structure 1. Dscusson on degrees of freedom In case of truss structures, t was enough that the element force equaton provdes onl
Advanced Computatonal echancs 18 Chapter 4 Applcaton to Plane rgd frame structure 1. Dscusson on degrees of freedom In case of truss structures, t was enough that the element force equaton provdes onl
Chapter 11 Angular Momentum
 Chapter 11 Angular Momentum Analyss Model: Nonsolated System (Angular Momentum) Angular Momentum of a Rotatng Rgd Object Analyss Model: Isolated System (Angular Momentum) Angular Momentum of a Partcle
Chapter 11 Angular Momentum Analyss Model: Nonsolated System (Angular Momentum) Angular Momentum of a Rotatng Rgd Object Analyss Model: Isolated System (Angular Momentum) Angular Momentum of a Partcle
A computer-aided optimization method of bending beams
 WSES Internatonal Conferene on ENGINEERING MECHNICS, STRUCTURES, ENGINEERING GEOLOGY (EMESEG '8), Heraklon, Crete Island, Greee, July 22-24, 28 omputer-aded optmzaton method of bendng beams CRMEN E. SINGER-ORCI
WSES Internatonal Conferene on ENGINEERING MECHNICS, STRUCTURES, ENGINEERING GEOLOGY (EMESEG '8), Heraklon, Crete Island, Greee, July 22-24, 28 omputer-aded optmzaton method of bendng beams CRMEN E. SINGER-ORCI
EVALUATION OF SEISMIC ACTIVE EARTH PRESSURE USING HORIZONTAL SLICE METHOD AND LOG-SPIRAL FAILURE SURFACE
 EVALUATIO OF SEISMIC ACTIVE EARTH PRESSURE USIG HORIZOTAL SLICE METHOD AD LOG-SPIRAL FAILURE SURFACE S. BAISHYA orth Eastern Regonal Insttute of Sene and Tehnology (ERIST), Arunahal Pradesh, Inda A. SARKAR
EVALUATIO OF SEISMIC ACTIVE EARTH PRESSURE USIG HORIZOTAL SLICE METHOD AD LOG-SPIRAL FAILURE SURFACE S. BAISHYA orth Eastern Regonal Insttute of Sene and Tehnology (ERIST), Arunahal Pradesh, Inda A. SARKAR
ACTM State Calculus Competition Saturday April 30, 2011
 ACTM State Calculus Competton Saturday Aprl 30, 2011 ACTM State Calculus Competton Sprng 2011 Page 1 Instructons: For questons 1 through 25, mark the best answer choce on the answer sheet provde Afterward
ACTM State Calculus Competton Saturday Aprl 30, 2011 ACTM State Calculus Competton Sprng 2011 Page 1 Instructons: For questons 1 through 25, mark the best answer choce on the answer sheet provde Afterward
International Mathematical Olympiad. Preliminary Selection Contest 2012 Hong Kong. Outline of Solutions
 Internatonal Mathematcal Olympad Prelmnary Selecton ontest Hong Kong Outlne of Solutons nswers: 7 4 7 4 6 5 9 6 99 7 6 6 9 5544 49 5 7 4 6765 5 6 6 7 6 944 9 Solutons: Snce n s a two-dgt number, we have
Internatonal Mathematcal Olympad Prelmnary Selecton ontest Hong Kong Outlne of Solutons nswers: 7 4 7 4 6 5 9 6 99 7 6 6 9 5544 49 5 7 4 6765 5 6 6 7 6 944 9 Solutons: Snce n s a two-dgt number, we have
Lectures - Week 4 Matrix norms, Conditioning, Vector Spaces, Linear Independence, Spanning sets and Basis, Null space and Range of a Matrix
 Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 NME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS Begn each problem n the space
NME (Last, Frst): Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS Begn each problem n the space
On the unconditional Security of QKD Schemes quant-ph/
 On the unondtonal Seurty of QKD Shemes quant-ph/9953 alk Outlne ntroduton to Quantum nformaton he BB84 Quantum Cryptosystem ve s attak Boundng ve s nformaton Seurty and Relalty Works on Seurty C.A. Fuhs
On the unondtonal Seurty of QKD Shemes quant-ph/9953 alk Outlne ntroduton to Quantum nformaton he BB84 Quantum Cryptosystem ve s attak Boundng ve s nformaton Seurty and Relalty Works on Seurty C.A. Fuhs
PES 1120 Spring 2014, Spendier Lecture 6/Page 1
 PES 110 Sprng 014, Spender Lecture 6/Page 1 Lecture today: Chapter 1) Electrc feld due to charge dstrbutons -> charged rod -> charged rng We ntroduced the electrc feld, E. I defned t as an nvsble aura
PES 110 Sprng 014, Spender Lecture 6/Page 1 Lecture today: Chapter 1) Electrc feld due to charge dstrbutons -> charged rod -> charged rng We ntroduced the electrc feld, E. I defned t as an nvsble aura
Four Bar Linkages in Two Dimensions. A link has fixed length and is joined to other links and also possibly to a fixed point.
 Four bar lnkages 1 Four Bar Lnkages n Two Dmensons lnk has fed length and s oned to other lnks and also possbly to a fed pont. The relatve velocty of end B wth regard to s gven by V B = ω r y v B B = +y
Four bar lnkages 1 Four Bar Lnkages n Two Dmensons lnk has fed length and s oned to other lnks and also possbly to a fed pont. The relatve velocty of end B wth regard to s gven by V B = ω r y v B B = +y
Structure and Drive Paul A. Jensen Copyright July 20, 2003
 Structure and Drve Paul A. Jensen Copyrght July 20, 2003 A system s made up of several operatons wth flow passng between them. The structure of the system descrbes the flow paths from nputs to outputs.
Structure and Drve Paul A. Jensen Copyrght July 20, 2003 A system s made up of several operatons wth flow passng between them. The structure of the system descrbes the flow paths from nputs to outputs.
Solutions to Problem Set 6
 Solutons to Problem Set 6 Problem 6. (Resdue theory) a) Problem 4.7.7 Boas. n ths problem we wll solve ths ntegral: x sn x x + 4x + 5 dx: To solve ths usng the resdue theorem, we study ths complex ntegral:
Solutons to Problem Set 6 Problem 6. (Resdue theory) a) Problem 4.7.7 Boas. n ths problem we wll solve ths ntegral: x sn x x + 4x + 5 dx: To solve ths usng the resdue theorem, we study ths complex ntegral:
Physics 111: Mechanics Lecture 11
 Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
Physcs 111: Mechancs Lecture 11 Bn Chen NJIT Physcs Department Textbook Chapter 10: Dynamcs of Rotatonal Moton q 10.1 Torque q 10. Torque and Angular Acceleraton for a Rgd Body q 10.3 Rgd-Body Rotaton
Problem Do any of the following determine homomorphisms from GL n (C) to GL n (C)?
 Homework 8 solutons. Problem 16.1. Whch of the followng defne homomomorphsms from C\{0} to C\{0}? Answer. a) f 1 : z z Yes, f 1 s a homomorphsm. We have that z s the complex conjugate of z. If z 1,z 2
Homework 8 solutons. Problem 16.1. Whch of the followng defne homomomorphsms from C\{0} to C\{0}? Answer. a) f 1 : z z Yes, f 1 s a homomorphsm. We have that z s the complex conjugate of z. If z 1,z 2
Conservation of Angular Momentum = "Spin"
 Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
Page 1 of 6 Conservaton of Angular Momentum = "Spn" We can assgn a drecton to the angular velocty: drecton of = drecton of axs + rght hand rule (wth rght hand, curl fngers n drecton of rotaton, thumb ponts
Unit 5: Quadratic Equations & Functions
 Date Perod Unt 5: Quadratc Equatons & Functons DAY TOPIC 1 Modelng Data wth Quadratc Functons Factorng Quadratc Epressons 3 Solvng Quadratc Equatons 4 Comple Numbers Smplfcaton, Addton/Subtracton & Multplcaton
Date Perod Unt 5: Quadratc Equatons & Functons DAY TOPIC 1 Modelng Data wth Quadratc Functons Factorng Quadratc Epressons 3 Solvng Quadratc Equatons 4 Comple Numbers Smplfcaton, Addton/Subtracton & Multplcaton
1. Estimation, Approximation and Errors Percentages Polynomials and Formulas Identities and Factorization 52
 ontents ommonly Used Formulas. Estmaton, pproxmaton and Errors. Percentages. Polynomals and Formulas 8. Identtes and Factorzaton. Equatons and Inequaltes 66 6. Rate and Rato 8 7. Laws of Integral Indces
ontents ommonly Used Formulas. Estmaton, pproxmaton and Errors. Percentages. Polynomals and Formulas 8. Identtes and Factorzaton. Equatons and Inequaltes 66 6. Rate and Rato 8 7. Laws of Integral Indces
Spin-rotation coupling of the angularly accelerated rigid body
 Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
Spn-rotaton couplng of the angularly accelerated rgd body Loua Hassan Elzen Basher Khartoum, Sudan. Postal code:11123 E-mal: louaelzen@gmal.com November 1, 2017 All Rghts Reserved. Abstract Ths paper s
Complex Numbers. x = B B 2 4AC 2A. or x = x = 2 ± 4 4 (1) (5) 2 (1)
 Complex Numbers If you have not yet encountered complex numbers, you wll soon do so n the process of solvng quadratc equatons. The general quadratc equaton Ax + Bx + C 0 has solutons x B + B 4AC A For
Complex Numbers If you have not yet encountered complex numbers, you wll soon do so n the process of solvng quadratc equatons. The general quadratc equaton Ax + Bx + C 0 has solutons x B + B 4AC A For
I have not received unauthorized aid in the completion of this exam.
 ME 270 Sprng 2013 Fnal Examnaton Please read and respond to the followng statement, I have not receved unauthorzed ad n the completon of ths exam. Agree Dsagree Sgnature INSTRUCTIONS Begn each problem
ME 270 Sprng 2013 Fnal Examnaton Please read and respond to the followng statement, I have not receved unauthorzed ad n the completon of ths exam. Agree Dsagree Sgnature INSTRUCTIONS Begn each problem
VECTORS VECTORS VECTORS VECTORS. 2. Vector Representation. 1. Definition. 3. Types of Vectors. 5. Vector Operations I. 4. Equal and Opposite Vectors
 1. Defnton A vetor s n entt tht m represent phsl quntt tht hs mgntude nd dreton s opposed to slr tht ls dreton.. Vetor Representton A vetor n e represented grphll n rrow. The length of the rrow s the mgntude
1. Defnton A vetor s n entt tht m represent phsl quntt tht hs mgntude nd dreton s opposed to slr tht ls dreton.. Vetor Representton A vetor n e represented grphll n rrow. The length of the rrow s the mgntude
Experiment 1 Mass, volume and density
 Experment 1 Mass, volume and densty Purpose 1. Famlarze wth basc measurement tools such as verner calper, mcrometer, and laboratory balance. 2. Learn how to use the concepts of sgnfcant fgures, expermental
Experment 1 Mass, volume and densty Purpose 1. Famlarze wth basc measurement tools such as verner calper, mcrometer, and laboratory balance. 2. Learn how to use the concepts of sgnfcant fgures, expermental
Statistical Mechanics and Combinatorics : Lecture III
 Statstcal Mechancs and Combnatorcs : Lecture III Dmer Model Dmer defntons Defnton A dmer coverng (perfect matchng) of a fnte graph s a set of edges whch covers every vertex exactly once, e every vertex
Statstcal Mechancs and Combnatorcs : Lecture III Dmer Model Dmer defntons Defnton A dmer coverng (perfect matchng) of a fnte graph s a set of edges whch covers every vertex exactly once, e every vertex
P A = (P P + P )A = P (I P T (P P ))A = P (A P T (P P )A) Hence if we let E = P T (P P A), We have that
 Backward Error Analyss for House holder Reectors We want to show that multplcaton by householder reectors s backward stable. In partcular we wsh to show fl(p A) = P (A) = P (A + E where P = I 2vv T s the
Backward Error Analyss for House holder Reectors We want to show that multplcaton by householder reectors s backward stable. In partcular we wsh to show fl(p A) = P (A) = P (A + E where P = I 2vv T s the
8.6 The Complex Number System
 8.6 The Complex Number System Earler n the chapter, we mentoned that we cannot have a negatve under a square root, snce the square of any postve or negatve number s always postve. In ths secton we want
8.6 The Complex Number System Earler n the chapter, we mentoned that we cannot have a negatve under a square root, snce the square of any postve or negatve number s always postve. In ths secton we want
LAB 4: Modulus of elasticity
 LAB 4: Modulus of elastcty 1. Preparaton: modulus of elastcty (chapter15, p.79) Hook s law graphcal determnaton of modulus of elastcty (p.8) determnaton of modulus of elastcty n tenson and flexural stress
LAB 4: Modulus of elastcty 1. Preparaton: modulus of elastcty (chapter15, p.79) Hook s law graphcal determnaton of modulus of elastcty (p.8) determnaton of modulus of elastcty n tenson and flexural stress
More metrics on cartesian products
 More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
MAGNETISM MAGNETIC DIPOLES
 MAGNETISM We now turn to magnetsm. Ths has actually been used for longer than electrcty. People were usng compasses to sal around the Medterranean Sea several hundred years BC. However t was not understood
MAGNETISM We now turn to magnetsm. Ths has actually been used for longer than electrcty. People were usng compasses to sal around the Medterranean Sea several hundred years BC. However t was not understood
Please review the following statement: I certify that I have not given unauthorized aid nor have I received aid in the completion of this exam.
 Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: Instructor s Name and Secton: (Crcle Your Secton) Sectons:
Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: Instructor s Name and Secton: (Crcle Your Secton) Sectons:
Math 217 Fall 2013 Homework 2 Solutions
 Math 17 Fall 013 Homework Solutons Due Thursday Sept. 6, 013 5pm Ths homework conssts of 6 problems of 5 ponts each. The total s 30. You need to fully justfy your answer prove that your functon ndeed has
Math 17 Fall 013 Homework Solutons Due Thursday Sept. 6, 013 5pm Ths homework conssts of 6 problems of 5 ponts each. The total s 30. You need to fully justfy your answer prove that your functon ndeed has
U.C. Berkeley CS294: Beyond Worst-Case Analysis Luca Trevisan September 5, 2017
 U.C. Berkeley CS94: Beyond Worst-Case Analyss Handout 4s Luca Trevsan September 5, 07 Summary of Lecture 4 In whch we ntroduce semdefnte programmng and apply t to Max Cut. Semdefnte Programmng Recall that
U.C. Berkeley CS94: Beyond Worst-Case Analyss Handout 4s Luca Trevsan September 5, 07 Summary of Lecture 4 In whch we ntroduce semdefnte programmng and apply t to Max Cut. Semdefnte Programmng Recall that
PHYS 1101 Practice problem set 12, Chapter 32: 21, 22, 24, 57, 61, 83 Chapter 33: 7, 12, 32, 38, 44, 49, 76
 PHYS 1101 Practce problem set 1, Chapter 3: 1,, 4, 57, 61, 83 Chapter 33: 7, 1, 3, 38, 44, 49, 76 3.1. Vsualze: Please reer to Fgure Ex3.1. Solve: Because B s n the same drecton as the ntegraton path s
PHYS 1101 Practce problem set 1, Chapter 3: 1,, 4, 57, 61, 83 Chapter 33: 7, 1, 3, 38, 44, 49, 76 3.1. Vsualze: Please reer to Fgure Ex3.1. Solve: Because B s n the same drecton as the ntegraton path s
APPENDIX A Some Linear Algebra
 APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
PHYSICS - CLUTCH CH 28: INDUCTION AND INDUCTANCE.
 !! www.clutchprep.com CONCEPT: ELECTROMAGNETIC INDUCTION A col of wre wth a VOLTAGE across each end wll have a current n t - Wre doesn t HAVE to have voltage source, voltage can be INDUCED V Common ways
!! www.clutchprep.com CONCEPT: ELECTROMAGNETIC INDUCTION A col of wre wth a VOLTAGE across each end wll have a current n t - Wre doesn t HAVE to have voltage source, voltage can be INDUCED V Common ways
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM
 ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
ELASTIC WAVE PROPAGATION IN A CONTINUOUS MEDIUM An elastc wave s a deformaton of the body that travels throughout the body n all drectons. We can examne the deformaton over a perod of tme by fxng our look
Module 14: THE INTEGRAL Exploring Calculus
 Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
Module 14: THE INTEGRAL Explorng Calculus Part I Approxmatons and the Defnte Integral It was known n the 1600s before the calculus was developed that the area of an rregularly shaped regon could be approxmated
χ x B E (c) Figure 2.1.1: (a) a material particle in a body, (b) a place in space, (c) a configuration of the body
 Secton.. Moton.. The Materal Body and Moton hyscal materals n the real world are modeled usng an abstract mathematcal entty called a body. Ths body conssts of an nfnte number of materal partcles. Shown
Secton.. Moton.. The Materal Body and Moton hyscal materals n the real world are modeled usng an abstract mathematcal entty called a body. Ths body conssts of an nfnte number of materal partcles. Shown
First Law: A body at rest remains at rest, a body in motion continues to move at constant velocity, unless acted upon by an external force.
 Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
Secton 1. Dynamcs (Newton s Laws of Moton) Two approaches: 1) Gven all the forces actng on a body, predct the subsequent (changes n) moton. 2) Gven the (changes n) moton of a body, nfer what forces act
FUZZY FINITE ELEMENT METHOD
 FUZZY FINITE ELEMENT METHOD RELIABILITY TRUCTURE ANALYI UING PROBABILITY 3.. Maxmum Normal tress Internal force s the shear force, V has a magntude equal to the load P and bendng moment, M. Bendng moments
FUZZY FINITE ELEMENT METHOD RELIABILITY TRUCTURE ANALYI UING PROBABILITY 3.. Maxmum Normal tress Internal force s the shear force, V has a magntude equal to the load P and bendng moment, M. Bendng moments
Army Ants Tunneling for Classical Simulations
 Electronc Supplementary Materal (ESI) for Chemcal Scence. Ths journal s The Royal Socety of Chemstry 2014 electronc supplementary nformaton (ESI) for Chemcal Scence Army Ants Tunnelng for Classcal Smulatons
Electronc Supplementary Materal (ESI) for Chemcal Scence. Ths journal s The Royal Socety of Chemstry 2014 electronc supplementary nformaton (ESI) for Chemcal Scence Army Ants Tunnelng for Classcal Smulatons
kq r 2 2kQ 2kQ (A) (B) (C) (D)
 PHYS 1202W MULTIPL CHOIC QUSTIONS QUIZ #1 Answer the followng multple choce questons on the bubble sheet. Choose the best answer, 5 pts each. MC1 An uncharged metal sphere wll (A) be repelled by a charged
PHYS 1202W MULTIPL CHOIC QUSTIONS QUIZ #1 Answer the followng multple choce questons on the bubble sheet. Choose the best answer, 5 pts each. MC1 An uncharged metal sphere wll (A) be repelled by a charged
Important Dates: Post Test: Dec during recitations. If you have taken the post test, don t come to recitation!
 Important Dates: Post Test: Dec. 8 0 durng rectatons. If you have taken the post test, don t come to rectaton! Post Test Make-Up Sessons n ARC 03: Sat Dec. 6, 0 AM noon, and Sun Dec. 7, 8 PM 0 PM. Post
Important Dates: Post Test: Dec. 8 0 durng rectatons. If you have taken the post test, don t come to rectaton! Post Test Make-Up Sessons n ARC 03: Sat Dec. 6, 0 AM noon, and Sun Dec. 7, 8 PM 0 PM. Post
Section 8.1 Exercises
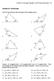 Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Secton 8.1 Non-rght Trangles: Law of Snes and Cosnes 519 Secton 8.1 Exercses Solve for the unknown sdes and angles of the trangles shown. 10 70 50 1.. 18 40 110 45 5 6 3. 10 4. 75 15 5 6 90 70 65 5. 6.
Moments of Inertia. and reminds us of the analogous equation for linear momentum p= mv, which is of the form. The kinetic energy of the body is.
 Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Moments of Inerta Suppose a body s movng on a crcular path wth constant speed Let s consder two quanttes: the body s angular momentum L about the center of the crcle, and ts knetc energy T How are these
Celestial Mechanics. Basic Orbits. Why circles? Tycho Brahe. PHY celestial-mechanics - J. Hedberg
 PHY 454 - celestal-mechancs - J. Hedberg - 207 Celestal Mechancs. Basc Orbts. Why crcles? 2. Tycho Brahe 3. Kepler 4. 3 laws of orbtng bodes 2. Newtonan Mechancs 3. Newton's Laws. Law of Gravtaton 2. The
PHY 454 - celestal-mechancs - J. Hedberg - 207 Celestal Mechancs. Basc Orbts. Why crcles? 2. Tycho Brahe 3. Kepler 4. 3 laws of orbtng bodes 2. Newtonan Mechancs 3. Newton's Laws. Law of Gravtaton 2. The
APPENDIX 2 FITTING A STRAIGHT LINE TO OBSERVATIONS
 Unversty of Oulu Student Laboratory n Physcs Laboratory Exercses n Physcs 1 1 APPEDIX FITTIG A STRAIGHT LIE TO OBSERVATIOS In the physcal measurements we often make a seres of measurements of the dependent
Unversty of Oulu Student Laboratory n Physcs Laboratory Exercses n Physcs 1 1 APPEDIX FITTIG A STRAIGHT LIE TO OBSERVATIOS In the physcal measurements we often make a seres of measurements of the dependent
6.3.4 Modified Euler s method of integration
 6.3.4 Modfed Euler s method of ntegraton Before dscussng the applcaton of Euler s method for solvng the swng equatons, let us frst revew the basc Euler s method of numercal ntegraton. Let the general from
6.3.4 Modfed Euler s method of ntegraton Before dscussng the applcaton of Euler s method for solvng the swng equatons, let us frst revew the basc Euler s method of numercal ntegraton. Let the general from
Affine transformations and convexity
 Affne transformatons and convexty The purpose of ths document s to prove some basc propertes of affne transformatons nvolvng convex sets. Here are a few onlne references for background nformaton: http://math.ucr.edu/
Affne transformatons and convexty The purpose of ths document s to prove some basc propertes of affne transformatons nvolvng convex sets. Here are a few onlne references for background nformaton: http://math.ucr.edu/
Modeling of Dynamic Systems
 Modelng of Dynamc Systems Ref: Control System Engneerng Norman Nse : Chapters & 3 Chapter objectves : Revew the Laplace transform Learn how to fnd a mathematcal model, called a transfer functon Learn how
Modelng of Dynamc Systems Ref: Control System Engneerng Norman Nse : Chapters & 3 Chapter objectves : Revew the Laplace transform Learn how to fnd a mathematcal model, called a transfer functon Learn how
INVESTIGATION ON THE SHEAR OF FIBER REINFORCED CONCRETE BEAMS CONSIDERING VARIOUS TYPES OF FIBERS
 - Tehnal Paper - INESTIGATION ON THE SHEAR OF FIBER REINFORCED CONCRETE BEAMS CONSIDERING ARIOUS TYPES OF FIBERS Ptha JONGIATSAKUL *, Koj MATSUMOTO *, Ken WATANABE * and Junhro NIWA * ABSTRACT Ths paper
- Tehnal Paper - INESTIGATION ON THE SHEAR OF FIBER REINFORCED CONCRETE BEAMS CONSIDERING ARIOUS TYPES OF FIBERS Ptha JONGIATSAKUL *, Koj MATSUMOTO *, Ken WATANABE * and Junhro NIWA * ABSTRACT Ths paper
12. The Hamilton-Jacobi Equation Michael Fowler
 1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
1. The Hamlton-Jacob Equaton Mchael Fowler Back to Confguraton Space We ve establshed that the acton, regarded as a functon of ts coordnate endponts and tme, satsfes ( ) ( ) S q, t / t+ H qpt,, = 0, and
PHYSICS - CLUTCH 1E CH 28: INDUCTION AND INDUCTANCE.
 !! www.clutchprep.com CONCEPT: ELECTROMAGNETIC INDUCTION A col of wre wth a VOLTAGE across each end wll have a current n t - Wre doesn t HAVE to have voltage source, voltage can be INDUCED V Common ways
!! www.clutchprep.com CONCEPT: ELECTROMAGNETIC INDUCTION A col of wre wth a VOLTAGE across each end wll have a current n t - Wre doesn t HAVE to have voltage source, voltage can be INDUCED V Common ways
Module 3: Element Properties Lecture 1: Natural Coordinates
 Module 3: Element Propertes Lecture : Natural Coordnates Natural coordnate system s bascally a local coordnate system whch allows the specfcaton of a pont wthn the element by a set of dmensonless numbers
Module 3: Element Propertes Lecture : Natural Coordnates Natural coordnate system s bascally a local coordnate system whch allows the specfcaton of a pont wthn the element by a set of dmensonless numbers
If the solution does not follow a logical thought process, it will be assumed in error.
 Group # Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS Begn each problem n the space provded
Group # Please revew the followng statement: I certfy that I have not gven unauthorzed ad nor have I receved ad n the completon of ths exam. Sgnature: INSTRUCTIONS Begn each problem n the space provded
Part C Dynamics and Statics of Rigid Body. Chapter 5 Rotation of a Rigid Body About a Fixed Axis
 Part C Dynamcs and Statcs of Rgd Body Chapter 5 Rotaton of a Rgd Body About a Fxed Axs 5.. Rotatonal Varables 5.. Rotaton wth Constant Angular Acceleraton 5.3. Knetc Energy of Rotaton, Rotatonal Inerta
Part C Dynamcs and Statcs of Rgd Body Chapter 5 Rotaton of a Rgd Body About a Fxed Axs 5.. Rotatonal Varables 5.. Rotaton wth Constant Angular Acceleraton 5.3. Knetc Energy of Rotaton, Rotatonal Inerta
INDETERMINATE STRUCTURES METHOD OF CONSISTENT DEFORMATIONS (FORCE METHOD)
 INETNTE STUTUES ETHO OF ONSISTENT EFOTIONS (FOE ETHO) If all the support reactons and nternal forces (, Q, and N) can not be determned by usng equlbrum equatons only, the structure wll be referred as STTIY
INETNTE STUTUES ETHO OF ONSISTENT EFOTIONS (FOE ETHO) If all the support reactons and nternal forces (, Q, and N) can not be determned by usng equlbrum equatons only, the structure wll be referred as STTIY
Physics 2A Chapter 3 HW Solutions
 Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C
Phscs A Chapter 3 HW Solutons Chapter 3 Conceptual Queston: 4, 6, 8, Problems: 5,, 8, 7, 3, 44, 46, 69, 70, 73 Q3.4. Reason: (a) C = A+ B onl A and B are n the same drecton. Sze does not matter. (b) C
One Dimension Again. Chapter Fourteen
 hapter Fourteen One Dmenson Agan 4 Scalar Lne Integrals Now we agan consder the dea of the ntegral n one dmenson When we were ntroduced to the ntegral back n elementary school, we consdered only functons
hapter Fourteen One Dmenson Agan 4 Scalar Lne Integrals Now we agan consder the dea of the ntegral n one dmenson When we were ntroduced to the ntegral back n elementary school, we consdered only functons
Professor Terje Haukaas University of British Columbia, Vancouver The Q4 Element
 Professor Terje Haukaas Unversty of Brtsh Columba, ancouver www.nrsk.ubc.ca The Q Element Ths document consders fnte elements that carry load only n ther plane. These elements are sometmes referred to
Professor Terje Haukaas Unversty of Brtsh Columba, ancouver www.nrsk.ubc.ca The Q Element Ths document consders fnte elements that carry load only n ther plane. These elements are sometmes referred to
