Hopf equation In Lecture 1 we considered propagation of sound in a compressible gas with the use of equation,
|
|
|
- Luke Hunter
- 5 years ago
- Views:
Transcription
1 Lecture 4 In preceding lectures we discussed dispersion effects defined as a nontrivial dependence of phase velocity of harmonic waves on their wave number. Due to dispersion effects, envelope of a wave pulse propagates with the group velocity. It also changes its form during propagation. In the lowest approimation, evolution of the envelop function is governed by the parabolic equation. Oscillations can also arise at sharp edges of the pulse. All these effects were considered in framework of linear theory. Now we shall study consequences of nonlinear effects neglecting dispersion. Hopf equation Hopf equation In Lecture we considered propagation of sound in a compressible gas with the use of equation, ρ t + (ρv) = 0, v t + (v )v = (/ρ) p. () where the pressure p and the density ρ were connected by a material state equation It is known from kinetic theory of gases that in the ideal gas p = p(ρ). (2) p = NkT = (ρ/m)kt. (3) Hence in the limit m the pressure vanishes and we get the equation of state p = 0. (4) of heavy dust particles. Correspondingly, the gas dynamics equations become independent of each other: the velocity field is governed by v t + (v )v = 0, (5) and when v(r, t) is known, the density can be found from the continuity equation ρ t + (ρv) = 0. (6) In case of one-dimensional flow, when all variables depend on one space coordinate only, equation (5) takes the form This equation is called the Hopf equation. v t + vv = 0. (7)
2 2 Solution Solution of Hopf equation As we know from Lecture, if the coefficient before v in Eq. (7) were constant, v t + cv = 0, then we would have the solution in the form v = v 0 ( ct), c const, where v 0 () is the initial distribution of the flow velocity at t = 0. Therefore, it seems natural to check whether the solution of equation is given implicitly by the epression v t + vv = 0. (8) v = v 0 ( vt). (9) Indeed, its differentiation gives v t = v 0v v 0v t t, v = v 0 v 0v t, where v 0() = dv 0 /d, and, hence, v t = vv 0 + v 0 t, v = v 0 + v 0 (0) t. Substitution of Eqs. (0) into Eq. (8) shows at once that Eq. (9) is the solution satisfying the initial condition v = v 0 () at t = 0. We have found the general solution of Eq. (8) in the form vt = w(v), () where w(v) is an arbitrary function. If we put here t = 0, we find that w(v) is an inverse function of the initial distribution v 0 (), and we denote this function as (v). Then the solution (9) of the Hopf equation can be written in the form = (v) + vt, which means that the velocity v is constant along the straight lines = + v 0 ( )t, v = v 0 ( ), (2) in the plane (, t), where is the value of at which the initial distribution has the value v of the initial velocity, i.e., it is the solution of the equation v = v 0 ( ). Let the initial distribution be given by the function v 0 ( ) = /( + 2 ). 2
3 _ u 0() _ Formula = + v 0 ( )t, v = v 0 ( ), gives the map of the initial points into the corresponding points at the moment of time t. = + v ()t b t = t b t > t b b t < t _ - At t = 0 this is the identical map =, but with growth of t its deviation from = increases proportionally to the values of v 0 ( ). We see that with growth of t the region of the plot ( ) corresponding to points with v 0 < 0 flattens, and at some moment t = t b the plot acquires a point with a horizontal tangent line. At greater times t > t b there arises a region < < +, where each value of corresponds to three values of. This means that after t = t b the faster particles begin to overtake the slower ones. Three values, 2, 3 corresponding to one value of give the three values of the initial velocities v 0 ( i ), i =, 2, 3, of particles which come to the point at the moment t. Hence, the plot of v() is three-valued in the region < < +. 3
4 v() t = 0 t = t b t > t b b t 2 t _ (t) M + (t) t b _ b 3 The boundaries of the multi-valued region can easily be found by noticing that at these points the plot of ( ) has a horizontal tangent line, / = + v 0( )t = 0. (3) Hence, Eqs. (2) and (3) define the functions ± (t) in a parametric form, ± = v 0 ( )/v 0( ), t = /v 0( ), (4) where plays the role of the parameter. The wave-breaking point b corresponds to the infleion point of the curve ( ), where 2 / 2 = 0, so the corresponding value of is determined by the equation v 0 ( b ) = 0. (5) If we find this value of b and substitute it into Eqs. (4), then we obtain the point ( b, t b ) in the plane (, t), where the boundary curves + (t) and (t) merge together. 4
5 It is useful to look at this figure from another point of view. At each value of Eq. (2) determines the straight line in the plane (, t) the characteristic of Eq. (8). Variation of gives the family of straight lines whose envelope is determined by the known from elementary differential geometry equations that is, just by Eqs. (4). t ( ) = 0, / = 0, Simple wave Simple wave Now we generalize the above consideration by relaing the condition p = 0. Namely, we look for the solution of the system for the one-dimensional flow ρ t + (ρv) = 0, v t + vv = (/ρ) p (6) under supposition that there is a relationship between the flow velocity v and the gas density ρ: v = v(ρ), ρ = ρ(v). Under this supposition, we may rewrite Eqs. (6) as ρ t + [d(ρv)/dρ] ρ = 0, (7) v t + [ v + (c 2 /ρ)(dρ/dv) ] v = 0. (8) Noticing that we obtain from Eq. (7) that ( ) t ρ t /ρ = ( / t) ρ, ρ = d(ρv) dρ = v + ρ dv dρ, 5
6 and in the same way from Eq. (8) that ( ) t = v + c2 ρ dρ dv. (9) Since ρ is a one-valued function of v, we have ( ) ( = t t and, hence, Thus, we have v ρ ) ρ dv dρ = c2 dρ ρ dv., v dv/dρ = ±c/ρ, (20) and the function v(ρ) (or v(p)) is determined by the relation ρ cdρ v = ± ρ. (2) After substitution of dρ/dv = ±ρ/c into Eq. (8) we obtain v t + (v ± c)v = 0 (22) similar to Hopf eq. v t + vv = 0. By analogy with Hopf equation we can write the solution of (22) = [v ± c(v)]t + (v), (23) where (v) is an arbitrary function, and c(v) can be found with the use of Eq. (2) and the formula c(ρ) = dp/dρ. The straight lines (23) in the plane (, t) are called characteristics of the system (7,8). Eq. (23) can be rewritten in the form v = v 0 [ (v ± c(v))t] (24) similar to Eq. (9), v 0 ( ) being the function inverse to (v); v 0 () defines the initial profile of the wave at t = 0. Points of the profile propagate with velocities V = v ± c. Since V varies from one point to another, the profile changes its form what can lead to the wave-breaking phenomenon. Therefore, the solution (23,24), which is called a simple wave solution, describes evolution up to the wave-breaking point. The time t b of wave breaking is determined by the condition that the profile has an infleion point with a vertical tangent line, ( / v) tb = 0, ( 2 / v 2) t b = 0. (25) 6
7 4 Polytropic gas Polytropic gas Polytropic gas has the equation of state (for air γ = 7/5) Hence the sound velocity c is equal to which substitution into (2) yields v = 2c 0 γ p = p 0 (ρ/ρ 0 ) γ. (26) c = c 0 (ρ/ρ 0 ) γ 2, (27) ( ( ρ ρ 0 ) γ ) 2, (28) and (27) and (28) give and Eq. (22) simplifies to c = c 0 ± 2 (γ )v. (29) v t + ( ±c (γ + )v) v = 0. (30) This equation coincides with Hopf equation. Its solution (23) becomes = ( ±c (γ + )v) t + (v), (3) and according to Eq. (27) the density ρ depends on the velocity v as ρ = ρ 0 ( ± 2 (γ )(v/c 0) ) 2/(γ ). (32) Substitution of Eq. (3) into Eq. (25) gives the conditions for the wave-breaking moment for a polytropic gas: t = 2 γ + (v), (v) = 0. (33) 5 Piston problem Piston problem Let a polytropic gas be located inside a pipe indefinitely long at one side ( ) and closed by a movable piston at the other side ( = 0). At some moment t = 0 the piston starts its motion according to the law = X(t), X(0) = 0. We have to calculate the corresponding flow of gas inside the pipe. We have to satisfy the boundary condition at the piston, v = Ẋ(t) at X(t) = ( c (γ + )v) t + (v), 7
8 which means that the flow velocity of the gas contacting with the piston is always equal to the piston s velocity. These two formulas define the function (v) in a parametric form: ) (τ) = X(τ) (c (γ + )Ẋ(τ) τ, v(τ) = Ẋ(τ). The substitution of the first formula into Eq. (3) yields the solution of the piston problem ] = X(τ) + [c (γ + )Ẋ(τ) (t τ), v = Ẋ(τ). (34) Let us specify these formulas for a simple case of the motion of the piston with constant acceleration, Then Eqs. (34) transform to X(t) = 2 at2, Ẋ(t) = at, a > 0. (35) = 2 aτ 2 + ( c (γ + )aτ) (t τ), v = aτ, and these two formulas give = (/2a)v 2 + ( c (γ + )v) (t v/a). (36) This is a quadratic equation with respect to v, its solution gives v = (/γ) ( c 0 2 (γ + )at) + (/γ) (c0 2 (γ + )at) 2 2γa( c0 t). The sign before the square root is chosen so that v = 0 at the boundary = c 0 t with the gas at rest. The plot of v() acquires a vertical tangent line at = c 0 t b at the moment t b = 2c 0 /[(γ + )a]. (37) v() t = t b t < t b 8
9 The characteristics of the flow are straight lines (36) parameterized by the values of v from the interval at v c 0 t, that is, they stem from the line = at 2 /2 corresponding to the piston s motion. t t b b 6 Problem Problem Problem 4.. Solve Hopf equation u t +uu = 0 for the initial condition u 0 () = /( + 2 ). Find the boundaries of the tree-valued solution and coordinates of the wave breaking point. 7 What to read? What to read? L.D. Landau and E.M. Lifshitz, Fluid mechanics, Section 0 G.B. Whitham, Linear and nonlinear waves, Section 2. A.M. Kamchatnov, Nonlinear periodic waves and their modulations An introductory course, Sections.3.2, Summary Summary of Lecture 4 Prototypic eample of nonlinear wave evolution is given by solution of Hopf equation u t + uu = 0 and simple wave solution of D fluid dynamics equations. 9
10 Typical behavior leads to wave breaking and formation of a non-physical multivalued region in the solution. This means that some other effects should be taken into account for regularizing the singularity. 0
Answers to Problem Set Number 04 for MIT (Spring 2008)
 Answers to Problem Set Number 04 for 18.311 MIT (Spring 008) Rodolfo R. Rosales (MIT, Math. Dept., room -337, Cambridge, MA 0139). March 17, 008. Course TA: Timothy Nguyen, MIT, Dept. of Mathematics, Cambridge,
Answers to Problem Set Number 04 for 18.311 MIT (Spring 008) Rodolfo R. Rosales (MIT, Math. Dept., room -337, Cambridge, MA 0139). March 17, 008. Course TA: Timothy Nguyen, MIT, Dept. of Mathematics, Cambridge,
Waves in a Shock Tube
 Waves in a Shock Tube Ivan Christov c February 5, 005 Abstract. This paper discusses linear-wave solutions and simple-wave solutions to the Navier Stokes equations for an inviscid and compressible fluid
Waves in a Shock Tube Ivan Christov c February 5, 005 Abstract. This paper discusses linear-wave solutions and simple-wave solutions to the Navier Stokes equations for an inviscid and compressible fluid
A Propagating Wave Packet The Group Velocity
 Lecture 7 A Propagating Wave Pacet The Group Velocity Phys 375 Overview and Motivation: Last time we looed at a solution to the Schrödinger equation (SE) with an initial condition (,) that corresponds
Lecture 7 A Propagating Wave Pacet The Group Velocity Phys 375 Overview and Motivation: Last time we looed at a solution to the Schrödinger equation (SE) with an initial condition (,) that corresponds
A Propagating Wave Packet The Group Velocity
 Lecture 7 A Propagating Wave Packet The Group Velocity Phys 375 Overview and Motivation: Last time we looked at a solution to the Schrödinger equation (SE) with an initial condition (,) that corresponds
Lecture 7 A Propagating Wave Packet The Group Velocity Phys 375 Overview and Motivation: Last time we looked at a solution to the Schrödinger equation (SE) with an initial condition (,) that corresponds
FLUID MECHANICS 3 - LECTURE 4 ONE-DIMENSIONAL UNSTEADY GAS
 FLUID MECHANICS 3 - LECTURE 4 ONE-DIMENSIONAL UNSTEADY GAS Consider an unsteady 1-dimensional ideal gas flow. We assume that this flow is spatially continuous and thermally isolated, hence, it is isentropic.
FLUID MECHANICS 3 - LECTURE 4 ONE-DIMENSIONAL UNSTEADY GAS Consider an unsteady 1-dimensional ideal gas flow. We assume that this flow is spatially continuous and thermally isolated, hence, it is isentropic.
Hydrodynamic modes of conducting liquid in random magnetic field
 arxiv:1602.08543v1 [physics.plasm-ph] 27 Feb 2016 Hydrodynamic modes of conducting liquid in random magnetic field A. A. Stupka November 7, 2017 Oles Honchar Dnipropetrovs k National University, Gagarin
arxiv:1602.08543v1 [physics.plasm-ph] 27 Feb 2016 Hydrodynamic modes of conducting liquid in random magnetic field A. A. Stupka November 7, 2017 Oles Honchar Dnipropetrovs k National University, Gagarin
20. Alfven waves. ([3], p ; [1], p ; Chen, Sec.4.18, p ) We have considered two types of waves in plasma:
![20. Alfven waves. ([3], p ; [1], p ; Chen, Sec.4.18, p ) We have considered two types of waves in plasma: 20. Alfven waves. ([3], p ; [1], p ; Chen, Sec.4.18, p ) We have considered two types of waves in plasma:](/thumbs/79/79935500.jpg) Phys780: Plasma Physics Lecture 20. Alfven Waves. 1 20. Alfven waves ([3], p.233-239; [1], p.202-237; Chen, Sec.4.18, p.136-144) We have considered two types of waves in plasma: 1. electrostatic Langmuir
Phys780: Plasma Physics Lecture 20. Alfven Waves. 1 20. Alfven waves ([3], p.233-239; [1], p.202-237; Chen, Sec.4.18, p.136-144) We have considered two types of waves in plasma: 1. electrostatic Langmuir
Lecture 4. Alexey Boyarsky. October 6, 2015
 Lecture 4 Alexey Boyarsky October 6, 2015 1 Conservation laws and symmetries 1.1 Ignorable Coordinates During the motion of a mechanical system, the 2s quantities q i and q i, (i = 1, 2,..., s) which specify
Lecture 4 Alexey Boyarsky October 6, 2015 1 Conservation laws and symmetries 1.1 Ignorable Coordinates During the motion of a mechanical system, the 2s quantities q i and q i, (i = 1, 2,..., s) which specify
The Euler Equation of Gas-Dynamics
 The Euler Equation of Gas-Dynamics A. Mignone October 24, 217 In this lecture we study some properties of the Euler equations of gasdynamics, + (u) = ( ) u + u u + p = a p + u p + γp u = where, p and u
The Euler Equation of Gas-Dynamics A. Mignone October 24, 217 In this lecture we study some properties of the Euler equations of gasdynamics, + (u) = ( ) u + u u + p = a p + u p + γp u = where, p and u
0.2. CONSERVATION LAW FOR FLUID 9
 0.2. CONSERVATION LAW FOR FLUID 9 Consider x-component of Eq. (26), we have D(ρu) + ρu( v) dv t = ρg x dv t S pi ds, (27) where ρg x is the x-component of the bodily force, and the surface integral is
0.2. CONSERVATION LAW FOR FLUID 9 Consider x-component of Eq. (26), we have D(ρu) + ρu( v) dv t = ρg x dv t S pi ds, (27) where ρg x is the x-component of the bodily force, and the surface integral is
On Fluid Maxwell Equations
 On Fluid Maxwell Equations Tsutomu Kambe, (Former Professor, Physics), University of Tokyo, Abstract Fluid mechanics is a field theory of Newtonian mechanics of Galilean symmetry, concerned with fluid
On Fluid Maxwell Equations Tsutomu Kambe, (Former Professor, Physics), University of Tokyo, Abstract Fluid mechanics is a field theory of Newtonian mechanics of Galilean symmetry, concerned with fluid
PHYS 643 Week 4: Compressible fluids Sound waves and shocks
 PHYS 643 Week 4: Compressible fluids Sound waves and shocks Sound waves Compressions in a gas propagate as sound waves. The simplest case to consider is a gas at uniform density and at rest. Small perturbations
PHYS 643 Week 4: Compressible fluids Sound waves and shocks Sound waves Compressions in a gas propagate as sound waves. The simplest case to consider is a gas at uniform density and at rest. Small perturbations
NANOSCALE SCIENCE & TECHNOLOGY
 . NANOSCALE SCIENCE & TECHNOLOGY V Two-Level Quantum Systems (Qubits) Lecture notes 5 5. Qubit description Quantum bit (qubit) is an elementary unit of a quantum computer. Similar to classical computers,
. NANOSCALE SCIENCE & TECHNOLOGY V Two-Level Quantum Systems (Qubits) Lecture notes 5 5. Qubit description Quantum bit (qubit) is an elementary unit of a quantum computer. Similar to classical computers,
A Very Brief Introduction to Conservation Laws
 A Very Brief Introduction to Wen Shen Department of Mathematics, Penn State University Summer REU Tutorial, May 2013 Summer REU Tutorial, May 2013 1 / The derivation of conservation laws A conservation
A Very Brief Introduction to Wen Shen Department of Mathematics, Penn State University Summer REU Tutorial, May 2013 Summer REU Tutorial, May 2013 1 / The derivation of conservation laws A conservation
n v molecules will pass per unit time through the area from left to
 3 iscosity and Heat Conduction in Gas Dynamics Equations of One-Dimensional Gas Flow The dissipative processes - viscosity (internal friction) and heat conduction - are connected with existence of molecular
3 iscosity and Heat Conduction in Gas Dynamics Equations of One-Dimensional Gas Flow The dissipative processes - viscosity (internal friction) and heat conduction - are connected with existence of molecular
0.3.4 Burgers Equation and Nonlinear Wave
 16 CONTENTS Solution to step (discontinuity) initial condition u(x, 0) = ul if X < 0 u r if X > 0, (80) u(x, t) = u L + (u L u R ) ( 1 1 π X 4νt e Y 2 dy ) (81) 0.3.4 Burgers Equation and Nonlinear Wave
16 CONTENTS Solution to step (discontinuity) initial condition u(x, 0) = ul if X < 0 u r if X > 0, (80) u(x, t) = u L + (u L u R ) ( 1 1 π X 4νt e Y 2 dy ) (81) 0.3.4 Burgers Equation and Nonlinear Wave
Salmon: Lectures on partial differential equations
 6. The wave equation Of the 3 basic equations derived in the previous section, we have already discussed the heat equation, (1) θ t = κθ xx + Q( x,t). In this section we discuss the wave equation, () θ
6. The wave equation Of the 3 basic equations derived in the previous section, we have already discussed the heat equation, (1) θ t = κθ xx + Q( x,t). In this section we discuss the wave equation, () θ
CapSel Euler The Euler equations. conservation laws for 1D dynamics of compressible gas. = 0 m t + (m v + p) x
 CapSel Euler - 01 The Euler equations keppens@rijnh.nl conservation laws for 1D dynamics of compressible gas ρ t + (ρ v) x = 0 m t + (m v + p) x = 0 e t + (e v + p v) x = 0 vector of conserved quantities
CapSel Euler - 01 The Euler equations keppens@rijnh.nl conservation laws for 1D dynamics of compressible gas ρ t + (ρ v) x = 0 m t + (m v + p) x = 0 e t + (e v + p v) x = 0 vector of conserved quantities
EP225 Note No. 4 Wave Motion
 EP5 Note No. 4 Wave Motion 4. Sinusoidal Waves, Wave Number Waves propagate in space in contrast to oscillations which are con ned in limited regions. In describing wave motion, spatial coordinates enter
EP5 Note No. 4 Wave Motion 4. Sinusoidal Waves, Wave Number Waves propagate in space in contrast to oscillations which are con ned in limited regions. In describing wave motion, spatial coordinates enter
Lecture 10: Whitham Modulation Theory
 Lecture 10: Whitham Modulation Theory Lecturer: Roger Grimshaw. Write-up: Andong He June 19, 2009 1 Introduction The Whitham modulation theory provides an asymptotic method for studying slowly varying
Lecture 10: Whitham Modulation Theory Lecturer: Roger Grimshaw. Write-up: Andong He June 19, 2009 1 Introduction The Whitham modulation theory provides an asymptotic method for studying slowly varying
8.01T Problem Set 2 Solutions Fall 2004
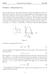 Problem 1. Measurement of g. a) The ball moves in the vertical direction under the influence of the constant force of gravity 1. Hence in our approximation the ball undergoes onedimensional motion with
Problem 1. Measurement of g. a) The ball moves in the vertical direction under the influence of the constant force of gravity 1. Hence in our approximation the ball undergoes onedimensional motion with
IV. Compressible flow of inviscid fluids
 IV. Compressible flow of inviscid fluids Governing equations for n = 0, r const: + (u )=0 t u + ( u ) u= p t De e = + ( u ) e= p u+ ( k T ) Dt t p= p(, T ), e=e (,T ) Alternate forms of energy equation
IV. Compressible flow of inviscid fluids Governing equations for n = 0, r const: + (u )=0 t u + ( u ) u= p t De e = + ( u ) e= p u+ ( k T ) Dt t p= p(, T ), e=e (,T ) Alternate forms of energy equation
Traffic Flow Problems
 Traffic Flow Problems Nicodemus Banagaaya Supervisor : Dr. J.H.M. ten Thije Boonkkamp October 15, 2009 Outline Introduction Mathematical model derivation Godunov Scheme for the Greenberg Traffic model.
Traffic Flow Problems Nicodemus Banagaaya Supervisor : Dr. J.H.M. ten Thije Boonkkamp October 15, 2009 Outline Introduction Mathematical model derivation Godunov Scheme for the Greenberg Traffic model.
Various lecture notes for
 Various lecture notes for 18311. R. R. Rosales (MIT, Math. Dept., 2-337) April 12, 2013 Abstract Notes, both complete and/or incomplete, for MIT s 18.311 (Principles of Applied Mathematics). These notes
Various lecture notes for 18311. R. R. Rosales (MIT, Math. Dept., 2-337) April 12, 2013 Abstract Notes, both complete and/or incomplete, for MIT s 18.311 (Principles of Applied Mathematics). These notes
Salmon: Lectures on partial differential equations
 4 Burger s equation In Lecture 2 we remarked that if the coefficients in u x, y,! "! "x + v x,y,! "! "y = 0 depend not only on x,y but also on!, then the characteristics may cross and the solutions become
4 Burger s equation In Lecture 2 we remarked that if the coefficients in u x, y,! "! "x + v x,y,! "! "y = 0 depend not only on x,y but also on!, then the characteristics may cross and the solutions become
Lecture 4 Notes: 06 / 30. Energy carried by a wave
 Lecture 4 Notes: 06 / 30 Energy carried by a wave We want to find the total energy (kinetic and potential) in a sine wave on a string. A small segment of a string at a fixed point x 0 behaves as a harmonic
Lecture 4 Notes: 06 / 30 Energy carried by a wave We want to find the total energy (kinetic and potential) in a sine wave on a string. A small segment of a string at a fixed point x 0 behaves as a harmonic
Longitudinal Waves. waves in which the particle or oscillator motion is in the same direction as the wave propagation
 Longitudinal Waves waves in which the particle or oscillator motion is in the same direction as the wave propagation Longitudinal waves propagate as sound waves in all phases of matter, plasmas, gases,
Longitudinal Waves waves in which the particle or oscillator motion is in the same direction as the wave propagation Longitudinal waves propagate as sound waves in all phases of matter, plasmas, gases,
Resonant excitation of trapped coastal waves by free inertia-gravity waves
 Resonant excitation of trapped coastal waves by free inertia-gravity waves V. Zeitlin 1 Institut Universitaire de France 2 Laboratory of Dynamical Meteorology, University P. and M. Curie, Paris, France
Resonant excitation of trapped coastal waves by free inertia-gravity waves V. Zeitlin 1 Institut Universitaire de France 2 Laboratory of Dynamical Meteorology, University P. and M. Curie, Paris, France
The region enclosed by the curve of f and the x-axis is rotated 360 about the x-axis. Find the volume of the solid formed.
 Section A ln. Let g() =, for > 0. ln Use the quotient rule to show that g ( ). 3 (b) The graph of g has a maimum point at A. Find the -coordinate of A. (Total 7 marks) 6. Let h() =. Find h (0). cos 3.
Section A ln. Let g() =, for > 0. ln Use the quotient rule to show that g ( ). 3 (b) The graph of g has a maimum point at A. Find the -coordinate of A. (Total 7 marks) 6. Let h() =. Find h (0). cos 3.
Introduction to Aerospace Engineering
 Introduction to Aerospace Engineering Lecture slides Challenge the future 3-0-0 Introduction to Aerospace Engineering Aerodynamics 5 & 6 Prof. H. Bijl ir. N. Timmer Delft University of Technology 5. Compressibility
Introduction to Aerospace Engineering Lecture slides Challenge the future 3-0-0 Introduction to Aerospace Engineering Aerodynamics 5 & 6 Prof. H. Bijl ir. N. Timmer Delft University of Technology 5. Compressibility
03. Simple Dynamical Systems
 University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 2015 03. Simple Dynamical Systems Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License
University of Rhode Island DigitalCommons@URI Classical Dynamics Physics Course Materials 2015 03. Simple Dynamical Systems Gerhard Müller University of Rhode Island, gmuller@uri.edu Creative Commons License
Simple waves and a characteristic decomposition of the two dimensional compressible Euler equations
 Simple waves and a characteristic decomposition of the two dimensional compressible Euler equations Jiequan Li 1 Department of Mathematics, Capital Normal University, Beijing, 100037 Tong Zhang Institute
Simple waves and a characteristic decomposition of the two dimensional compressible Euler equations Jiequan Li 1 Department of Mathematics, Capital Normal University, Beijing, 100037 Tong Zhang Institute
Numerical Simulation of Pressure Surge with the Method of Characteristics
 Numerical Simulation of Pressure Surge with the Method of Characteristics R. Fiereder 02.04.2009 Saint Petersburg, Russia Content Motivation Governing Equations Continuity Equation Momentum Equation Method
Numerical Simulation of Pressure Surge with the Method of Characteristics R. Fiereder 02.04.2009 Saint Petersburg, Russia Content Motivation Governing Equations Continuity Equation Momentum Equation Method
1. Introduction. 2. Basic equations. Theoretical and Mathematical Physics, 192(1): (2017) E. V. Trifonov
 Theoretical and Mathematical Physics, 9(): 974 98 (7) FAMILIES OF EXACT SOLUTIONS FOR LINEAR AND NONLINEAR WAVE EQUATIONS WITH A VARIABLE SPEED OF SOUND AND THEIR USE IN SOLVING INITIAL BOUNDARY VALUE
Theoretical and Mathematical Physics, 9(): 974 98 (7) FAMILIES OF EXACT SOLUTIONS FOR LINEAR AND NONLINEAR WAVE EQUATIONS WITH A VARIABLE SPEED OF SOUND AND THEIR USE IN SOLVING INITIAL BOUNDARY VALUE
Chapter 1. Introduction to Nonlinear Space Plasma Physics
 Chapter 1. Introduction to Nonlinear Space Plasma Physics The goal of this course, Nonlinear Space Plasma Physics, is to explore the formation, evolution, propagation, and characteristics of the large
Chapter 1. Introduction to Nonlinear Space Plasma Physics The goal of this course, Nonlinear Space Plasma Physics, is to explore the formation, evolution, propagation, and characteristics of the large
To study the motion of a perfect gas, the conservation equations of continuity
 Chapter 1 Ideal Gas Flow The Navier-Stokes equations To study the motion of a perfect gas, the conservation equations of continuity ρ + (ρ v = 0, (1.1 momentum ρ D v Dt = p+ τ +ρ f m, (1.2 and energy ρ
Chapter 1 Ideal Gas Flow The Navier-Stokes equations To study the motion of a perfect gas, the conservation equations of continuity ρ + (ρ v = 0, (1.1 momentum ρ D v Dt = p+ τ +ρ f m, (1.2 and energy ρ
2.5 Sound waves in an inhomogeneous, timedependent
 .5. SOUND WAVES IN AN INHOMOGENEOUS, TIME-DEPENDENT MEDIUM49.5 Sound waves in an inhomogeneous, timedependent medium So far, we have only dealt with cases where c was constant. This, however, is usually
.5. SOUND WAVES IN AN INHOMOGENEOUS, TIME-DEPENDENT MEDIUM49.5 Sound waves in an inhomogeneous, timedependent medium So far, we have only dealt with cases where c was constant. This, however, is usually
Introduction to Fluid Dynamics
 Introduction to Fluid Dynamics Roger K. Smith Skript - auf englisch! Umsonst im Internet http://www.meteo.physik.uni-muenchen.de Wählen: Lehre Manuskripte Download User Name: meteo Password: download Aim
Introduction to Fluid Dynamics Roger K. Smith Skript - auf englisch! Umsonst im Internet http://www.meteo.physik.uni-muenchen.de Wählen: Lehre Manuskripte Download User Name: meteo Password: download Aim
Waves in plasma. Denis Gialis
 Waves in plasma Denis Gialis This is a short introduction on waves in a non-relativistic plasma. We will consider a plasma of electrons and protons which is fully ionized, nonrelativistic and homogeneous.
Waves in plasma Denis Gialis This is a short introduction on waves in a non-relativistic plasma. We will consider a plasma of electrons and protons which is fully ionized, nonrelativistic and homogeneous.
Relativistic Physics of Force Fields in the Space-Time-Mass Domain
 Relativistic Physics of Force Fields in the Space-Time-Mass Domain Daniele Sasso * Abstract We consider physics of reference frames moving with any speed, starting from the inertial field. We point out
Relativistic Physics of Force Fields in the Space-Time-Mass Domain Daniele Sasso * Abstract We consider physics of reference frames moving with any speed, starting from the inertial field. We point out
Strongly nonlinear long gravity waves in uniform shear flows
 Strongly nonlinear long gravity waves in uniform shear flows Wooyoung Choi Department of Naval Architecture and Marine Engineering, University of Michigan, Ann Arbor, Michigan 48109, USA Received 14 January
Strongly nonlinear long gravity waves in uniform shear flows Wooyoung Choi Department of Naval Architecture and Marine Engineering, University of Michigan, Ann Arbor, Michigan 48109, USA Received 14 January
θ x = f ( x,t) could be written as
 9. Higher orer PDEs as systems of first-orer PDEs. Hyperbolic systems. For PDEs, as for ODEs, we may reuce the orer by efining new epenent variables. For example, in the case of the wave equation, (1)
9. Higher orer PDEs as systems of first-orer PDEs. Hyperbolic systems. For PDEs, as for ODEs, we may reuce the orer by efining new epenent variables. For example, in the case of the wave equation, (1)
3 Hydrostatic Equilibrium
 3 Hydrostatic Equilibrium Reading: Shu, ch 5, ch 8 31 Timescales and Quasi-Hydrostatic Equilibrium Consider a gas obeying the Euler equations: Dρ Dt = ρ u, D u Dt = g 1 ρ P, Dɛ Dt = P ρ u + Γ Λ ρ Suppose
3 Hydrostatic Equilibrium Reading: Shu, ch 5, ch 8 31 Timescales and Quasi-Hydrostatic Equilibrium Consider a gas obeying the Euler equations: Dρ Dt = ρ u, D u Dt = g 1 ρ P, Dɛ Dt = P ρ u + Γ Λ ρ Suppose
Thermodynamics ENGR360-MEP112 LECTURE 7
 Thermodynamics ENGR360-MEP11 LECTURE 7 Thermodynamics ENGR360/MEP11 Objectives: 1. Conservation of mass principle.. Conservation of energy principle applied to control volumes (first law of thermodynamics).
Thermodynamics ENGR360-MEP11 LECTURE 7 Thermodynamics ENGR360/MEP11 Objectives: 1. Conservation of mass principle.. Conservation of energy principle applied to control volumes (first law of thermodynamics).
ADIABATIC PROCESS Q = 0
 THE KINETIC THEORY OF GASES Mono-atomic Fig.1 1 3 Average kinetic energy of a single particle Fig.2 INTERNAL ENERGY U and EQUATION OF STATE For a mono-atomic gas, we will assume that the total energy
THE KINETIC THEORY OF GASES Mono-atomic Fig.1 1 3 Average kinetic energy of a single particle Fig.2 INTERNAL ENERGY U and EQUATION OF STATE For a mono-atomic gas, we will assume that the total energy
The first order quasi-linear PDEs
 Chapter 2 The first order quasi-linear PDEs The first order quasi-linear PDEs have the following general form: F (x, u, Du) = 0, (2.1) where x = (x 1, x 2,, x 3 ) R n, u = u(x), Du is the gradient of u.
Chapter 2 The first order quasi-linear PDEs The first order quasi-linear PDEs have the following general form: F (x, u, Du) = 0, (2.1) where x = (x 1, x 2,, x 3 ) R n, u = u(x), Du is the gradient of u.
2.25 Advanced Fluid Mechanics
 MIT Department of Mechanical Engineering.5 Advanced Fluid Mechanics Problem 4.05 This problem is from Advanced Fluid Mechanics Problems by A.H. Shapiro and A.A. Sonin Consider the frictionless, steady
MIT Department of Mechanical Engineering.5 Advanced Fluid Mechanics Problem 4.05 This problem is from Advanced Fluid Mechanics Problems by A.H. Shapiro and A.A. Sonin Consider the frictionless, steady
Simulation of nonlinear physical processes with the generalized phenomenological equation
 INTERNATIONAL JOURNAL OF MECHANICS Volume 9, 5 Simulation of nonlinear physical processes with the generalized phenomenological equation Sergey O. Gladkov, Sophie B. Bogdanova Abstract Using a phenomenologically
INTERNATIONAL JOURNAL OF MECHANICS Volume 9, 5 Simulation of nonlinear physical processes with the generalized phenomenological equation Sergey O. Gladkov, Sophie B. Bogdanova Abstract Using a phenomenologically
Thermodynamics I Chapter 2 Properties of Pure Substances
 Thermodynamics I Chapter 2 Properties of Pure Substances Mohsin Mohd Sies Fakulti Kejuruteraan Mekanikal, Universiti Teknologi Malaysia Properties of Pure Substances (Motivation) To quantify the changes
Thermodynamics I Chapter 2 Properties of Pure Substances Mohsin Mohd Sies Fakulti Kejuruteraan Mekanikal, Universiti Teknologi Malaysia Properties of Pure Substances (Motivation) To quantify the changes
Math Lecture 9
 Math 2280 - Lecture 9 Dylan Zwick Fall 2013 In the last two lectures we ve talked about differential equations for modeling populations Today we ll return to the theme we touched upon in our second lecture,
Math 2280 - Lecture 9 Dylan Zwick Fall 2013 In the last two lectures we ve talked about differential equations for modeling populations Today we ll return to the theme we touched upon in our second lecture,
Isentropic Duct Flows
 An Internet Book on Fluid Dynamics Isentropic Duct Flows In this section we examine the behavior of isentropic flows, continuing the development of the relations in section (Bob). First it is important
An Internet Book on Fluid Dynamics Isentropic Duct Flows In this section we examine the behavior of isentropic flows, continuing the development of the relations in section (Bob). First it is important
Minkowski spacetime. Pham A. Quang. Abstract: In this talk we review the Minkowski spacetime which is the spacetime of Special Relativity.
 Minkowski spacetime Pham A. Quang Abstract: In this talk we review the Minkowski spacetime which is the spacetime of Special Relativity. Contents 1 Introduction 1 2 Minkowski spacetime 2 3 Lorentz transformations
Minkowski spacetime Pham A. Quang Abstract: In this talk we review the Minkowski spacetime which is the spacetime of Special Relativity. Contents 1 Introduction 1 2 Minkowski spacetime 2 3 Lorentz transformations
Module 2: Governing Equations and Hypersonic Relations
 Module 2: Governing Equations and Hypersonic Relations Lecture -2: Mass Conservation Equation 2.1 The Differential Equation for mass conservation: Let consider an infinitely small elemental control volume
Module 2: Governing Equations and Hypersonic Relations Lecture -2: Mass Conservation Equation 2.1 The Differential Equation for mass conservation: Let consider an infinitely small elemental control volume
Gas Dynamics: Basic Equations, Waves and Shocks
 Astrophysical Dynamics, VT 010 Gas Dynamics: Basic Equations, Waves and Shocks Susanne Höfner Susanne.Hoefner@fysast.uu.se Astrophysical Dynamics, VT 010 Gas Dynamics: Basic Equations, Waves and Shocks
Astrophysical Dynamics, VT 010 Gas Dynamics: Basic Equations, Waves and Shocks Susanne Höfner Susanne.Hoefner@fysast.uu.se Astrophysical Dynamics, VT 010 Gas Dynamics: Basic Equations, Waves and Shocks
Thin airfoil theory. Chapter Compressible potential flow The full potential equation
 hapter 4 Thin airfoil theory 4. ompressible potential flow 4.. The full potential equation In compressible flow, both the lift and drag of a thin airfoil can be determined to a reasonable level of accuracy
hapter 4 Thin airfoil theory 4. ompressible potential flow 4.. The full potential equation In compressible flow, both the lift and drag of a thin airfoil can be determined to a reasonable level of accuracy
Continuum Mechanics Lecture 4 Fluid dynamics
 Continuum Mechanics Lecture 4 Flui ynamics Prof. http://www.itp.uzh.ch/~teyssier Outline - Flui kinematics - Mass an momentum conservation laws - The energy equation - Real fluis - Ieal fluis - Incompressible
Continuum Mechanics Lecture 4 Flui ynamics Prof. http://www.itp.uzh.ch/~teyssier Outline - Flui kinematics - Mass an momentum conservation laws - The energy equation - Real fluis - Ieal fluis - Incompressible
Study fluid dynamics. Understanding Bernoulli s Equation.
 Chapter Objectives Study fluid dynamics. Understanding Bernoulli s Equation. Chapter Outline 1. Fluid Flow. Bernoulli s Equation 3. Viscosity and Turbulence 1. Fluid Flow An ideal fluid is a fluid that
Chapter Objectives Study fluid dynamics. Understanding Bernoulli s Equation. Chapter Outline 1. Fluid Flow. Bernoulli s Equation 3. Viscosity and Turbulence 1. Fluid Flow An ideal fluid is a fluid that
Answers to Problem Set Number 02 for MIT (Spring 2008)
 Answers to Problem Set Number 02 for 18.311 MIT (Spring 2008) Rodolfo R. Rosales (MIT, Math. Dept., room 2-337, Cambridge, MA 02139). March 10, 2008. Course TA: Timothy Nguyen, MIT, Dept. of Mathematics,
Answers to Problem Set Number 02 for 18.311 MIT (Spring 2008) Rodolfo R. Rosales (MIT, Math. Dept., room 2-337, Cambridge, MA 02139). March 10, 2008. Course TA: Timothy Nguyen, MIT, Dept. of Mathematics,
Chapter 3 Burgers Equation
 Chapter 3 Burgers Equation One of the major challenges in the field of comple systems is a thorough understanding of the phenomenon of turbulence. Direct numerical simulations (DNS) have substantially
Chapter 3 Burgers Equation One of the major challenges in the field of comple systems is a thorough understanding of the phenomenon of turbulence. Direct numerical simulations (DNS) have substantially
Summary of the Equations of Fluid Dynamics
 Reference: Summary of the Equations of Fluid Dynamics Fluid Mechanics, L.D. Landau & E.M. Lifshitz 1 Introduction Emission processes give us diagnostics with which to estimate important parameters, such
Reference: Summary of the Equations of Fluid Dynamics Fluid Mechanics, L.D. Landau & E.M. Lifshitz 1 Introduction Emission processes give us diagnostics with which to estimate important parameters, such
First Order Equations
 10 1 Linear and Semilinear Equations Chapter First Order Equations Contents 1 Linear and Semilinear Equations 9 Quasilinear Equations 19 3 Wave Equation 6 4 Sstems of Equations 31 1 Linear and Semilinear
10 1 Linear and Semilinear Equations Chapter First Order Equations Contents 1 Linear and Semilinear Equations 9 Quasilinear Equations 19 3 Wave Equation 6 4 Sstems of Equations 31 1 Linear and Semilinear
Exam III Physics 101: Lecture 19 Elasticity and Oscillations
 Exam III Physics 101: Lecture 19 Elasticity and Oscillations Physics 101: Lecture 19, Pg 1 Overview Springs (review) Restoring force proportional to displacement F = -k x (often a good approximation) U
Exam III Physics 101: Lecture 19 Elasticity and Oscillations Physics 101: Lecture 19, Pg 1 Overview Springs (review) Restoring force proportional to displacement F = -k x (often a good approximation) U
I N T R O D U C T I O N T O P A R T I A L D I F F E R E N T I A L E Q U AT I O N S
 R U S S E L L L. H E R M A N I N T R O D U C T I O N T O P A R T I A L D I F F E R E N T I A L E Q U AT I O N S R. L. H E R M A N - V E R S I O N D AT E : S E P T E M B E R 3, 4 Copyright 4 by Russell
R U S S E L L L. H E R M A N I N T R O D U C T I O N T O P A R T I A L D I F F E R E N T I A L E Q U AT I O N S R. L. H E R M A N - V E R S I O N D AT E : S E P T E M B E R 3, 4 Copyright 4 by Russell
The Hopf equation. The Hopf equation A toy model of fluid mechanics
 The Hopf equation A toy model of fluid mechanics 1. Main physical features Mathematical description of a continuous medium At the microscopic level, a fluid is a collection of interacting particles (Van
The Hopf equation A toy model of fluid mechanics 1. Main physical features Mathematical description of a continuous medium At the microscopic level, a fluid is a collection of interacting particles (Van
Born of the Sound Wave Equation
 Corso di Laurea in Fisica - UNITS ISTITUZIONI DI FISICA PER IL SISTEMA TERRA Born of the Sound Wave Equation FABIO ROMANELLI Department of Mathematics & Geosciences University of Trieste romanel@units.it
Corso di Laurea in Fisica - UNITS ISTITUZIONI DI FISICA PER IL SISTEMA TERRA Born of the Sound Wave Equation FABIO ROMANELLI Department of Mathematics & Geosciences University of Trieste romanel@units.it
Lecture 3: Asymptotic Methods for the Reduced Wave Equation
 Lecture 3: Asymptotic Methods for the Reduced Wave Equation Joseph B. Keller 1 The Reduced Wave Equation Let v (t,) satisfy the wave equation v 1 2 v c 2 = 0, (1) (X) t2 where c(x) is the propagation speed
Lecture 3: Asymptotic Methods for the Reduced Wave Equation Joseph B. Keller 1 The Reduced Wave Equation Let v (t,) satisfy the wave equation v 1 2 v c 2 = 0, (1) (X) t2 where c(x) is the propagation speed
Waves and characteristics: Overview 5-1
 Waves and characteristics: Overview 5-1 Chapter 5: Waves and characteristics Overview Physics and accounting: use example of sound waves to illustrate method of linearization and counting of variables
Waves and characteristics: Overview 5-1 Chapter 5: Waves and characteristics Overview Physics and accounting: use example of sound waves to illustrate method of linearization and counting of variables
Where does Bernoulli's Equation come from?
 Where does Bernoulli's Equation come from? Introduction By now, you have seen the following equation many times, using it to solve simple fluid problems. P ρ + v + gz = constant (along a streamline) This
Where does Bernoulli's Equation come from? Introduction By now, you have seen the following equation many times, using it to solve simple fluid problems. P ρ + v + gz = constant (along a streamline) This
CONSERVATION OF MASS AND BALANCE OF LINEAR MOMENTUM
 CONSERVATION OF MASS AND BALANCE OF LINEAR MOMENTUM Summary of integral theorems Material time derivative Reynolds transport theorem Principle of conservation of mass Principle of balance of linear momentum
CONSERVATION OF MASS AND BALANCE OF LINEAR MOMENTUM Summary of integral theorems Material time derivative Reynolds transport theorem Principle of conservation of mass Principle of balance of linear momentum
Chapter 5 Performance analysis I Steady level flight (Lectures 17 to 20) Keywords: Steady level flight equations of motion, minimum power required,
 Chapter 5 Performance analysis I Steady level flight (Lectures 17 to 20) Keywords: Steady level flight equations of motion, minimum power required, minimum thrust required, minimum speed, maximum speed;
Chapter 5 Performance analysis I Steady level flight (Lectures 17 to 20) Keywords: Steady level flight equations of motion, minimum power required, minimum thrust required, minimum speed, maximum speed;
13.1 Ion Acoustic Soliton and Shock Wave
 13 Nonlinear Waves In linear theory, the wave amplitude is assumed to be sufficiently small to ignore contributions of terms of second order and higher (ie, nonlinear terms) in wave amplitude In such a
13 Nonlinear Waves In linear theory, the wave amplitude is assumed to be sufficiently small to ignore contributions of terms of second order and higher (ie, nonlinear terms) in wave amplitude In such a
Module-5: Hypersonic Boundary Layer theory. Lecture-20: Hypersonic boundary equation
 Module-5: Hypersonic Boundary Layer theory Lecture-0: Hypersonic boundary equation 0.1 Governing Equations for Viscous Flows The Navier-Stokes (NS) equaadtions are the governing equations for the viscous
Module-5: Hypersonic Boundary Layer theory Lecture-0: Hypersonic boundary equation 0.1 Governing Equations for Viscous Flows The Navier-Stokes (NS) equaadtions are the governing equations for the viscous
1/27/2010. With this method, all filed variables are separated into. from the basic state: Assumptions 1: : the basic state variables must
 Lecture 5: Waves in Atmosphere Perturbation Method With this method, all filed variables are separated into two parts: (a) a basic state part and (b) a deviation from the basic state: Perturbation Method
Lecture 5: Waves in Atmosphere Perturbation Method With this method, all filed variables are separated into two parts: (a) a basic state part and (b) a deviation from the basic state: Perturbation Method
If we plot the position of a moving object at increasing time intervals, we get a position time graph. This is sometimes called a distance time graph.
 Physics Lecture #2: Position Time Graphs If we plot the position of a moving object at increasing time intervals, we get a position time graph. This is sometimes called a distance time graph. Suppose a
Physics Lecture #2: Position Time Graphs If we plot the position of a moving object at increasing time intervals, we get a position time graph. This is sometimes called a distance time graph. Suppose a
Theoretical Question 3
 7 th Asian Physics Olympiad Theoretical Question 3 /Solutions Page /6 Theoretical Question 3 Solutions A The change of the pressure is related to the change in the density via V ρ P K K, () V ρ where ρ
7 th Asian Physics Olympiad Theoretical Question 3 /Solutions Page /6 Theoretical Question 3 Solutions A The change of the pressure is related to the change in the density via V ρ P K K, () V ρ where ρ
Lecture 5: Kinetic theory of fluids
 Lecture 5: Kinetic theory of fluids September 21, 2015 1 Goal 2 From atoms to probabilities Fluid dynamics descrines fluids as continnum media (fields); however under conditions of strong inhomogeneities
Lecture 5: Kinetic theory of fluids September 21, 2015 1 Goal 2 From atoms to probabilities Fluid dynamics descrines fluids as continnum media (fields); however under conditions of strong inhomogeneities
Sound Propagation through Media. Nachiketa Tiwari Indian Institute of Technology Kanpur
 Sound Propagation through Media Nachiketa Tiwari Indian Institute of Technology Kanpur LECTURE-17 HARMONIC PLANE WAVES Introduction In this lecture, we discuss propagation of 1-D planar waves as they travel
Sound Propagation through Media Nachiketa Tiwari Indian Institute of Technology Kanpur LECTURE-17 HARMONIC PLANE WAVES Introduction In this lecture, we discuss propagation of 1-D planar waves as they travel
Modified Schrödinger equation, its analysis and experimental verification
 Modified Schrödinger equation, its analysis and experimental verification arxiv:1202.1321v1 [quant-ph] 7 Feb 2012 Isaac Shnaid February 8, 2012 Abstract According to classical non-relativistic Schrödinger
Modified Schrödinger equation, its analysis and experimental verification arxiv:1202.1321v1 [quant-ph] 7 Feb 2012 Isaac Shnaid February 8, 2012 Abstract According to classical non-relativistic Schrödinger
For more info
 Characteristic of Ideal fluid:- (a) It is incompressible (b) It is non-viscous (c) Flow of ideal fluid is irrational (d) It is capable of exhibiting steady flow Stream line flow:- Flow of a liquid fluid
Characteristic of Ideal fluid:- (a) It is incompressible (b) It is non-viscous (c) Flow of ideal fluid is irrational (d) It is capable of exhibiting steady flow Stream line flow:- Flow of a liquid fluid
Phase Transitions. µ a (P c (T ), T ) µ b (P c (T ), T ), (3) µ a (P, T c (P )) µ b (P, T c (P )). (4)
 Phase Transitions A homogeneous equilibrium state of matter is the most natural one, given the fact that the interparticle interactions are translationally invariant. Nevertheless there is no contradiction
Phase Transitions A homogeneous equilibrium state of matter is the most natural one, given the fact that the interparticle interactions are translationally invariant. Nevertheless there is no contradiction
Notes on Entropy Production in Multicomponent Fluids
 Notes on Entropy Production in Multicomponent Fluids Robert F. Sekerka Updated January 2, 2001 from July 1993 Version Introduction We calculate the entropy production in a multicomponent fluid, allowing
Notes on Entropy Production in Multicomponent Fluids Robert F. Sekerka Updated January 2, 2001 from July 1993 Version Introduction We calculate the entropy production in a multicomponent fluid, allowing
Summary PHY101 ( 2 ) T / Hanadi Al Harbi
 الكمية Physical Quantity القانون Low التعريف Definition الوحدة SI Unit Linear Momentum P = mθ be equal to the mass of an object times its velocity. Kg. m/s vector quantity Stress F \ A the external force
الكمية Physical Quantity القانون Low التعريف Definition الوحدة SI Unit Linear Momentum P = mθ be equal to the mass of an object times its velocity. Kg. m/s vector quantity Stress F \ A the external force
The Bernoulli Equation
 The Bernoulli Equation The most used and the most abused equation in fluid mechanics. Newton s Second Law: F = ma In general, most real flows are 3-D, unsteady (x, y, z, t; r,θ, z, t; etc) Let consider
The Bernoulli Equation The most used and the most abused equation in fluid mechanics. Newton s Second Law: F = ma In general, most real flows are 3-D, unsteady (x, y, z, t; r,θ, z, t; etc) Let consider
Kinetic theory of the ideal gas
 Appendix H Kinetic theory of the ideal gas This Appendix contains sketchy notes, summarizing the main results of elementary kinetic theory. The students who are not familiar with these topics should refer
Appendix H Kinetic theory of the ideal gas This Appendix contains sketchy notes, summarizing the main results of elementary kinetic theory. The students who are not familiar with these topics should refer
Lecture 1: Introduction to Linear and Non-Linear Waves
 Lecture 1: Introduction to Linear and Non-Linear Waves Lecturer: Harvey Segur. Write-up: Michael Bates June 15, 2009 1 Introduction to Water Waves 1.1 Motivation and Basic Properties There are many types
Lecture 1: Introduction to Linear and Non-Linear Waves Lecturer: Harvey Segur. Write-up: Michael Bates June 15, 2009 1 Introduction to Water Waves 1.1 Motivation and Basic Properties There are many types
Introduction to Cosmology
 Introduction to Cosmology João G. Rosa joao.rosa@ua.pt http://gravitation.web.ua.pt/cosmo LECTURE 2 - Newtonian cosmology I As a first approach to the Hot Big Bang model, in this lecture we will consider
Introduction to Cosmology João G. Rosa joao.rosa@ua.pt http://gravitation.web.ua.pt/cosmo LECTURE 2 - Newtonian cosmology I As a first approach to the Hot Big Bang model, in this lecture we will consider
is conserved, calculating E both at θ = 0 and θ = π/2 we find that this happens for a value ω = ω given by: 2g
 UNIVERSITETET I STAVANGER Institutt for matematikk og naturvitenskap Suggested solutions, FYS 500 Classical Mechanics Theory 2016 fall Set 5 for 23. September 2016 Problem 27: A string can only support
UNIVERSITETET I STAVANGER Institutt for matematikk og naturvitenskap Suggested solutions, FYS 500 Classical Mechanics Theory 2016 fall Set 5 for 23. September 2016 Problem 27: A string can only support
Shock waves in the unitary Fermi gas
 Shock waves in the unitary Fermi gas Luca Salasnich Dipartimento di Fisica e Astronomia Galileo Galilei, Università di Padova Banff, May 205 Collaboration with: Francesco Ancilotto and Flavio Toigo Summary.
Shock waves in the unitary Fermi gas Luca Salasnich Dipartimento di Fisica e Astronomia Galileo Galilei, Università di Padova Banff, May 205 Collaboration with: Francesco Ancilotto and Flavio Toigo Summary.
Chapter 12. Recall that when a spring is stretched a distance x, it will pull back with a force given by: F = -kx
 Chapter 1 Lecture Notes Chapter 1 Oscillatory Motion Recall that when a spring is stretched a distance x, it will pull back with a force given by: F = -kx When the mass is released, the spring will pull
Chapter 1 Lecture Notes Chapter 1 Oscillatory Motion Recall that when a spring is stretched a distance x, it will pull back with a force given by: F = -kx When the mass is released, the spring will pull
Lecture 9: Waves in Classical Physics
 PHYS419 Lecture 9 Waves in Classical Physics 1 Lecture 9: Waves in Classical Physics If I say the word wave in no particular context, the image which most probably springs to your mind is one of a roughly
PHYS419 Lecture 9 Waves in Classical Physics 1 Lecture 9: Waves in Classical Physics If I say the word wave in no particular context, the image which most probably springs to your mind is one of a roughly
Module 4: One-Dimensional Kinematics
 4.1 Introduction Module 4: One-Dimensional Kinematics Kinematics is the mathematical description of motion. The term is derived from the Greek word kinema, meaning movement. In order to quantify motion,
4.1 Introduction Module 4: One-Dimensional Kinematics Kinematics is the mathematical description of motion. The term is derived from the Greek word kinema, meaning movement. In order to quantify motion,
Shock and Expansion Waves
 Chapter For the solution of the Euler equations to represent adequately a given large-reynolds-number flow, we need to consider in general the existence of discontinuity surfaces, across which the fluid
Chapter For the solution of the Euler equations to represent adequately a given large-reynolds-number flow, we need to consider in general the existence of discontinuity surfaces, across which the fluid
Macroscopic plasma description
 Macroscopic plasma description Macroscopic plasma theories are fluid theories at different levels single fluid (magnetohydrodynamics MHD) two-fluid (multifluid, separate equations for electron and ion
Macroscopic plasma description Macroscopic plasma theories are fluid theories at different levels single fluid (magnetohydrodynamics MHD) two-fluid (multifluid, separate equations for electron and ion
Quantum Black Hole and Information. Lecture (1): Acceleration, Horizon, Black Hole
 Quantum Black Hole and Information Soo-Jong Rey @ copyright Lecture (1): Acceleration, Horizon, Black Hole [Convention: c = 1. This can always be reinstated from dimensional analysis.] Today, we shall
Quantum Black Hole and Information Soo-Jong Rey @ copyright Lecture (1): Acceleration, Horizon, Black Hole [Convention: c = 1. This can always be reinstated from dimensional analysis.] Today, we shall
2 The incompressible Kelvin-Helmholtz instability
 Hydrodynamic Instabilities References Chandrasekhar: Hydrodynamic and Hydromagnetic Instabilities Landau & Lifshitz: Fluid Mechanics Shu: Gas Dynamics 1 Introduction Instabilities are an important aspect
Hydrodynamic Instabilities References Chandrasekhar: Hydrodynamic and Hydromagnetic Instabilities Landau & Lifshitz: Fluid Mechanics Shu: Gas Dynamics 1 Introduction Instabilities are an important aspect
2 Law of conservation of energy
 1 Newtonian viscous Fluid 1 Newtonian fluid For a Newtonian we already have shown that σ ij = pδ ij + λd k,k δ ij + 2µD ij where λ and µ are called viscosity coefficient. For a fluid under rigid body motion
1 Newtonian viscous Fluid 1 Newtonian fluid For a Newtonian we already have shown that σ ij = pδ ij + λd k,k δ ij + 2µD ij where λ and µ are called viscosity coefficient. For a fluid under rigid body motion
Limits and the derivative function. Limits and the derivative function
 The Velocity Problem A particle is moving in a straight line. t is the time that has passed from the start of motion (which corresponds to t = 0) s(t) is the distance from the particle to the initial position
The Velocity Problem A particle is moving in a straight line. t is the time that has passed from the start of motion (which corresponds to t = 0) s(t) is the distance from the particle to the initial position
12. MHD Approximation.
 Phys780: Plasma Physics Lecture 12. MHD approximation. 1 12. MHD Approximation. ([3], p. 169-183) The kinetic equation for the distribution function f( v, r, t) provides the most complete and universal
Phys780: Plasma Physics Lecture 12. MHD approximation. 1 12. MHD Approximation. ([3], p. 169-183) The kinetic equation for the distribution function f( v, r, t) provides the most complete and universal
2. Theory of Small Amplitude Waves
 . Theory of Small Amplitude Waves.1 General Discussion on Waves et us consider a one-dimensional (on -ais) propagating wave that retains its original shape. Assume that the wave can be epressed as a function
. Theory of Small Amplitude Waves.1 General Discussion on Waves et us consider a one-dimensional (on -ais) propagating wave that retains its original shape. Assume that the wave can be epressed as a function
Chapter 15. Mechanical Waves
 Chapter 15 Mechanical Waves A wave is any disturbance from an equilibrium condition, which travels or propagates with time from one region of space to another. A harmonic wave is a periodic wave in which
Chapter 15 Mechanical Waves A wave is any disturbance from an equilibrium condition, which travels or propagates with time from one region of space to another. A harmonic wave is a periodic wave in which
