pyoptfem Documentation
|
|
|
- Edgar Booth
- 5 years ago
- Views:
Transcription
1 pyoptfem Documentation Release V0.0.6 F. Cuvelier November 09, 2013
2
3 CONTENTS 1 Presentation Classical assembly algorithm (base version) Sparse matrix requirement Optimized classical assembly algorithm (OptV1 version) New Optimized assembly algorithm (OptV2 version) D benchmarks Benchmark usage Mass Matrix Stiffness Matrix Elastic Stiffness Matrix D benchmarks Benchmark usage Mass Matrix Stiffness Matrix Elastic Stiffness Matrix FEM2D module Assembly matrices (base, OptV1 and OptV2 versions) Element matrices (used by base and OptV1 versions) Vectorized tools (used by OptV2 version) Vectorized element matrices (used by OptV2 version) Mesh FEM3D module Assembly matrix (base, OptV1 and OptV2 versions) Element matrix (used by base and OptV1 versions) Vectorized tools (used by OptV2 version) Vectorized element matrix (used by OptV2 version) Mesh valid2d module Mass Matrix Stiffness matrix Elastic Stiffness Matrix valid3d module Mass Matrix Stiffness matrix Elastic Stiffness Matrix i
4 8 Quick testing 95 9 Testing and Working Requirements Installation License issues Indices and tables 105 Python Module Index 107 Index 109 ii
5 pyoptfem is a Python module which aims at measuring and comparing the performance of three programming techniques for assembling finite element matrices in 2D and 3D. For each of the matrices studied, three assembly versions are available: base, OptV1 and OptV2 Three matrices are currently implemented (more details are given in FEM2D module and FEM3D module) : Mass matrix : M i,j = φ j (q) φ i (q)dq, (i, j) {1,..., n q } 2. Ω h Stiffness matrix : S i,j = φ j (q). φ i (q)dq, (i, j) {1,..., n q } 2. Ω h Elastic stiffness matrix : K m,l = ε t (ψ l (q))σ(ψ m (q))dq, (m, l) {1,..., dn q } 2. Ω h Contents: where d is the space dimension. CONTENTS 1
6 2 CONTENTS
7 CHAPTER ONE PRESENTATION Let Ω h be a triangular (2d) or tetrahedral (3d) mesh of Ω R d corresponding to the following data structure: name type dimension description n q integer 1 number of vertices n me integer 1 number of elements q double d n q array of vertices coordinates. q(ν, j) is the ν-th coordinate of the j-th vertex, ν {1,..., d}, j {1,..., n q }. The j-th vertex will be also denoted by q j me integer (d + 1) n me connectivity array. me(β, k) is the storage index of the β-th vertex of the k-th element, in the array q, for β {1,..., (d + 1)} and k {1,..., n me } volumes double 1 n me array of volumes in 3d or areas in 2d. volumes(k) is the k-th element volume (3d) or element area (2d), k {1,..., n me } Scalar finite elements : Let H 1 h (Ω h) = {v C 0 (Ω h ), v T P 1 (T ), T T h }, be the finite dimensional space spanned by the P 1 -Lagrange (scalar) basis functions {φ i } i {1,...,nq} where P 1 (T ) denotes the space of all polynomials defined over T of total degree less than or equal to 1. The functions φ i satisfy φ i (q j ) = δ i,j, (i, j) {1,..., n q } 2 Then we have φ i 0 on T k, k {1,..., n me } such that q i / T k. A P 1 -Lagrange (scalar) finite element matrix is of the generic form D i,j = D(φ j, φ i )dω h, (i, j) {1,..., n q } 2 Ω h where D is the bilinear differential operator (order 1) defined for all u, v H 1 h (Ω h) by D(u, v) = A u, v (u b, v v u, c ) + duv and A (L (Ω h )) d d, b (L (Ω h )) d, c (L (Ω h )) d and d L (Ω h ) are given functions on Ω h. We can notice that D is a sparse matrix due to support properties of φ i functions. Let n dfe = d + 1. The element matrix D α,β (T k ), associated to D, is the n dfe n dfe matrix defined by D α,β (T k ) = D(φ k β, φ k α)(q)dq, (α, β) {1,..., n dfe } 2 T k 3
8 where φ k α = φ me(α,k) is the α-th local basis function associated to the k-th element. For examples, the Mass matrix is defined by M i,j = φ j φ i dω h Ω h The corresponding bilinear differential operator D is completely defined with A = 0, b = c = 0 and d = 1. the Stiffness matrix is defined by S i,j = φ j, φ i dω h Ω h The corresponding bilinear differential operator D is completely defined with A = I, b = c = 0 and d = 0. Vector finite elements : The dimension of the space (H 1 h (Ω h)) d is n df = d n q. in dimension d = 2, we have two natural basis : the global alternate basis B a defined by { ( φ1 B a = {ψ 1,..., ψ 2nq } = 0 ), ( 0, φ1) ( ) ( ( ) ( ) } φ2 0 φnq 0,,...,, 0 φ2) 0 φ nq and the global block basis B b defined by B b = {φ 1,..., φ 2nq } = { ( ) ( ) ( ) ( ( ( ) } φ1 φ2 φnq 0 0 0,,...,,,,..., φ1) φ2) φ nq in dimension d = 3, we have two natural basis : the global alternate basis B a defined by φ B a = {ψ 1,..., ψ 3nq } = 0, φ 1, 0,..., 0 0 φ 1 φ nq , φ nq, 0 0 φ nq and the global block basis B b defined by φ 1 B b = {φ 1,..., φ 3nq } = 0,..., 0 φ nq , φ 1,..., φ nq, 0,..., φ 1 φ nq 4 Chapter 1. Presentation
9 A P 1 -Lagrange (vector) finite element matrix in B a basis is of the generic form H l,m = H(ψ m, ψ l )dω h, (l, m) {1,..., dn q } 2 Ω h where H is the bilinear differential operator (order 1) defined by d H(u, v) = D α,β (u α, v β ) α,β=1 and D α,β is a bilinear differential operator of scalar type. For example, in dimension d = 2, the Elastic Stiffness matrix is defined by K m,l = ε t (ψ l (q))cε(ψ m (q)), (m, l) {1,..., 2n q } 2. Ω h where ε = (ε xx, ε yy, ε xy ) t is the strain tensor respectively and C is the Hooke matrix λ + 2μ λ 0 C = λ λ + 2μ μ Then the bilinear differential operator associated to this matrix is given by ( ) ( ) λ + 2μ 0 0 μ H(u, v) = 0 μ u 1, v 1 + λ 0 u 2, v 1 ( ) ( ) 0 λ μ 0 + μ 0 u 1, v λ + 2μ u 2, v 2 We present now three algorithms (base, OptV1 and OptV2 versions) for assembling this kind of matrix. Note: These algorithms can be successfully implemented in various interpreted languages under some assumptions. For all versions, it must have a sparse matrix implementation. For OptV1 and OptV2 versions, we also need a particular sparse matrix constructor (see Sparse matrix requirement). And, finally, OptV2 also required that the interpreted languages support classical vectorization operations. Here is the current list of interpreted languages for which we have successfully implemented these three algorithms : Python with Numpy and Scipy modules, Matlab, Octave, Scilab 5
10 1.1 Classical assembly algorithm (base version) Due to support properties of P 1 -Lagrange basis functions, we have the classical algorithm : Note: We recall the classical matrix assembly in dimension d with n dfe = d + 1. Figure 1.1: Classical matrix assembly in 2d or 3d In fact, for each element we add its element matrix to the global sparse matrix (lines 4 to 10 of the previous algorithm). This operation is illustrated in the following figure in 2d scalar fields case : Figure 1.2: Adding of an element matrix to global matrix in 2d scalar fields case The repetition of elements insertion in sparse matrix is very expensive. 6 Chapter 1. Presentation
11 1.2 Sparse matrix requirement The interpreted language must contain a function to generate a sparse matrix M from three 1d arrays of same length Ig, Jg and Kg such that M(Ig(k),Jg(k))=Kg(k). Furthermore, the elements of Kg having the same indices in Ig and Jg must be summed. We give for several interpreted languages the corresponding function : Python (scipy.sparse module) : M=sparse.<format>_matrix(Kg,(Ig,Jg),shape=(m,n) where <format> is the sparse matrix format chosen in csc, csr, lil,... Matlab : M=sparse(Ig,Jg,Kg,m,n), only csc format. Octave : M=sparse(Ig,Jg,Kg,m,n), only csc format. Scilab : M=sparse([Ig,Jg],Kg,[m,n]), only row-by-row format. Obviously, this kind of function exists in compiled languages. For example, in C language, one can use the SuiteSparse from T. Davis and with Nvidia GPU, one can use Thrust library. 1.3 Optimized classical assembly algorithm (OptV1 version) The idea is to create three global 1d-arrays I g, J g and K g allowing the storage of the element matrices as well as the position of their elements in the global matrix. The length of each array is n 2 dfe n me. (i.e. 9n me for d = 2 and 16n me for d = 3 ). Once these arrays are created, the matrix assembly is obtained with one of the previous commands. To create these three arrays, we first define three local 1d-arrays K e k, Ie k and J e k of n2 dfe elements obtained from a generic element matrix E(T k ) of dimension n dfe : From these arrays, it is then possible to build the three global arrays I g, J g and K g, of size n 2 dfe n me 1 defined, k {1,..., n me }, l { 1,..., n 2 dfe}, by K(n 2 dfe (k 1) + l) = Ke k (l), I(n 2 dfe (k 1) + l) = Ie k (l) = Ik ((l 1) mod m + 1), J(n 2 dfe (k 1) + l) = J e k (l) = Ik (E((l 1)/m) + 1). So, for each triangle T k, we have Then, a simple algorithm can build these three arrays using a loop over each triangle. Note: We give the complete OptV1 algorithm 1.4 New Optimized assembly algorithm (OptV2 version) We present the optimized version 2 algorithm where no loop is used. We define three 2d-arrays that allow to store all the element matrices as well as their positions in the global matrix. We denote by K g, I g and J g these n 2 dfe by n me 1.2. Sparse matrix requirement 7
12 8 Chapter 1. Presentation
13 arrays, defined k {1,..., n me }, il {1,..., n 2 dfe } by K g (il, k) = K e k(il), I g (il, k) = I e k(il), J g (il, k) = J e k(il). (1.1) The three local arrays K e k, Ie k and J e k are thus stored in the kth column of the global arrays K g, I g and J g respectively. A natural way to build these three arrays consists in using a loop through the triangles T k in which we insert the local arrays column-wise Figure 1.3: Construction of K g, I g and J g with loop The natural construction of these three arrays is done column-wise. So, for each array there are n me columns to compute, which depends on the mesh size. To vectorize, we must fill these arrays by row-wise operations and then for each array there are n 2 dfe rows to compute. We recall that n dfe does not depend on the mesh size. These rows insertions are represented in Figure 1.4. We can also remark that, (α, β) {1,..., n dfe }, with m = n dfe, K g (m(β 1) + α, k) = e k α,β, I g (m(β 1) + α, k) = I k α, J g (m(β 1) + α, k) = I k β New Optimized assembly algorithm (OptV2 version) 9
14 where, in scalar fields case, Iα k = me(α, k), α {1,..., d + 1} and in vector fields case, Ida b k = d me(a, k) b, a {1,..., d + 1}, b {0,..., d 1}. Figure 1.4: Row-wise operations on global arrays I g, J g and K g As we can see in Figures 1.5 and 1.6, it is quite easy to vectorize I g and J g computations in scalar fields case by filling these arrays lines by lines : Figure 1.5: Construction of I g and J g : OptV2 version for 2d scalar matrix Using vectorization tools, we can compute I g and J g in one line. The vectorized algorithms in 2d and 3d scalar fields are represented by Figure 1.7. In vector fields case, we construct the tabular T such that T(α, k) = I k α, α {1,..., n dfe }. Then we can vectorize I g and J g computations in vector fields case. We represent in Figure 1.8 these operations in 2d. Now, it remains to vectorize the computation of K g array which contains all the element matrices associated to D or H : it should be done by row-wise vector operations. We now describe a vectorized construction of K g array associated to a generic bilinear form a. For the mesh element T k, the element matrix is then given by a(φ i k 1, φ i k 1 ) a(φ i k 1, φ i k 2 ) a(φ i k 1, φ i k 3 ) E(T k ) = a(φ i k 2, φ i k 1 ) a(φ i k 2, φ i k 2 ) a(φ i k 2, φ i k 3 ) a(φ i k 3, φ i k 1 ) a(φ i k 3, φ i k 2 ) a(φ i k 3, φ i k 3 ) 10 Chapter 1. Presentation
15 Figure 1.6: Construction of I g and J g : OptV2 version for 3d scalar matrix Figure 1.7: Vectorized algorithms for I g and J g computations 1.4. New Optimized assembly algorithm (OptV2 version) 11
16 Figure 1.8: Construction of I g and J g : OptV2 version in 2d vector fields case 12 Chapter 1. Presentation
17 Figure 1.9: Construction of K g for Mass matrix 1.4. New Optimized assembly algorithm (OptV2 version) 13
18 Figure 1.10: Construction of K g for Mass matrix 14 Chapter 1. Presentation
19 CHAPTER TWO 2D BENCHMARKS Contents Benchmark usage Mass Matrix Stiffness Matrix Elastic Stiffness Matrix 2.1 Benchmark usage pyoptfem.fem2d.assemblybench.assemblybench([assembly=<string>, version=<string>, LN=<array>, meshname=<string>, meshdir=<string>, nbruns=<int>, la=<float>, mu=<float>, Num=<int>, tag=<string>,...]) Benchmark code for P 1 -Lagrange finite element matrices defined in FEM2D. Parameters assembly Name of an assembly routine. The string should be : MassAssembling2DP1, StiffAssembling2DP1 (default) StiffElasAssembling2DP1 versions List of versions. Must be a list of any size whose elements may be { base, OptV1, OptV2 } (default : [ OptV2, OptV1, base ]) meshname Name of the mesh files. By default it is an empty string. It means it uses SquareMesh function to generate meshes. meshdir Directory location of FreeFEM++ mesh files. Used if meshname is not empty. LN array of integer values. <LN> contains the values of N. Used to generate meshes data via Th=SquareMesh(N) function if meshname is empty or via getmesh class to read FreeFEM++ meshes Th=getMesh(meshdir+ / +meshname+str(n)+.msh ) LN default value is range(50, 90, 10) nbruns Number of runs on each mesh (default : 1) save For saving benchmark results in a file (see parameters <output>, <outdir> and <tag>) 15
20 plot For plotting computation times (default : True) output Name used to set results file name (default : bench2d ) outdir Directory location of saved results file name (default :./results ). tag Specify a tag string added to filename la the first Lame coefficient in Hooke s law, denoted by λ. Used by functions for assembling the elastic stiffness matrix. (default : 2) mu the second Lame coefficient in Hooke s law, denoted by μ. Used by functions for assembling the elastic stiffness matrix. (default : 0.3) Num Numbering choice. Used by functions for assembling the elastic stiffness matrix. (default : 0) 2.2 Mass Matrix Benchmark of MassAssembling2DP1 with base, OptV1 and OptV2 versions (see Mass Matrix) Table 2.1: MassAssembling2DP1 benchmark summary N nq ndof OptV2 OptV1 base (s) (s) (s) x1.00 x19.50 x (s) (s) (s) x1.00 x20.02 x (s) (s) (s) x1.00 x20.32 x (s) (s) (s) x1.00 x20.33 x (s) (s) (s) x1.00 x19.66 x (s) (s) (s) x1.00 x19.89 x (s) (s) (s) x1.00 x19.88 x (s) (s) (s) x1.00 x20.21 x This tabular was built with the following code : >>> from pyoptfem.fem2d import assemblybench >>> assemblybench(assembly= MassAssembling2DP1,LN=range(50,130,10)) SquareMesh(50): -> MassAssembling2DP1OptV2(nq=2601, nme=5000) run ( 1/ 1) : cputime= (s) - matrix 2601-by SquareMesh(120): -> MassAssembling2DP1base(nq=14641, nme=28800) run ( 1/ 1) : cputime= (s) - matrix by We also obtain Benchmark of MassAssembling2DP1 with OptV2 and OptV1 versions 16 Chapter 2. 2D benchmarks
21 Figure 2.1: MassAssembling2DP1 benchmark 2.2. Mass Matrix 17
22 Table 2.2: MassAssembling2DP1 benchmark summary N nq ndof OptV2 OptV (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x17.52 This tabular was built with the following code : >>> from pyoptfem.fem2d import assemblybench >>> assemblybench(assembly= MassAssembling2DP1,versions=[ OptV2, OptV1 ],LN=range(100,1300,100 SquareMesh(100): -> MassAssembling2DP1OptV2(nq=10201, nme=20000) run ( 1/ 1) : cputime= (s) - matrix by SquareMesh(1200): -> MassAssembling2DP1OptV1(nq= , nme= ) run ( 1/ 1) : cputime= (s) - matrix by We also obtain 2.3 Stiffness Matrix Benchmark of StiffAssembling2DP1 with base, OptV1 and OptV2 versions 18 Chapter 2. 2D benchmarks
23 Figure 2.2: MassAssembling2DP1 benchmark 2.3. Stiffness Matrix 19
24 Table 2.3: StiffAssembling2DP1 benchmark summary N nq ndof OptV2 OptV1 base (s) (s) (s) x1.00 x45.35 x (s) (s) (s) x1.00 x47.38 x (s) (s) (s) x1.00 x48.33 x (s) (s) (s) x1.00 x46.11 x (s) (s) (s) x1.00 x45.57 x (s) (s) (s) x1.00 x44.77 x (s) (s) (s) x1.00 x45.61 x (s) (s) (s) x1.00 x44.69 x This tabular was built with the following code : >>> from pyoptfem.fem2d import assemblybench >>> assemblybench(assembly= StiffAssembling2DP1,LN=range(50,130,10)) SquareMesh(50): -> StiffAssembling2DP1OptV2(nq=2601, nme=5000) run ( 1/ 1) : cputime= (s) - matrix 2601-by SquareMesh(120): -> StiffAssembling2DP1base(nq=14641, nme=28800) run ( 1/ 1) : cputime= (s) - matrix by We also obtain Benchmark of StiffAssembling2DP1 with OptV2 and OptV1 versions 20 Chapter 2. 2D benchmarks
25 Figure 2.3: StiffAssembling2DP1 benchmark 2.3. Stiffness Matrix 21
26 Table 2.4: StiffAssembling2DP1 benchmark summary N nq ndof OptV2 OptV (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x34.14 This tabular was built with the following code : >>> from pyoptfem.fem2d import assemblybench >>> assemblybench(assembly= StiffAssembling2DP1,versions=[ OptV2, OptV1 ],LN=range(100,1300,10 SquareMesh(100): -> StiffAssembling2DP1OptV2(nq=10201, nme=20000) run ( 1/ 1) : cputime= (s) - matrix by SquareMesh(1200): -> StiffAssembling2DP1OptV1(nq= , nme= ) run ( 1/ 1) : cputime= (s) - matrix by We also obtain 2.4 Elastic Stiffness Matrix Benchmark of StiffElasAssembling2DP1 with base, OptV1 and OptV2 versions 22 Chapter 2. 2D benchmarks
27 Figure 2.4: StiffAssembling2DP1 benchmark 2.4. Elastic Stiffness Matrix 23
28 Table 2.5: StiffElasAssembling2DP1 benchmark summary N nq ndof OptV2 OptV1 base (s) (s) (s) x1.00 x26.29 x (s) (s) (s) x1.00 x28.37 x (s) (s) (s) x1.00 x28.92 x (s) (s) (s) x1.00 x29.26 x (s) (s) (s) x1.00 x29.04 x (s) (s) (s) x1.00 x29.39 x (s) (s) (s) x1.00 x29.21 x This tabular was built with the following code : >>> from pyoptfem.fem2d import assemblybench >>> assemblybench(assembly= StiffElasAssembling2DP1,LN=range(30,65,5)) SquareMesh(30): -> StiffElasAssembling2DP1OptV2(nq=961, nme=1800) run ( 1/ 1) : cputime= (s) - matrix 1922-by SquareMesh(30): -> StiffElasAssembling2DP1OptV2(nq=961, nme=1800) run ( 1/ 1) : cputime= (s) - matrix 1922-by We also obtain Benchmark of StiffElasAssembling2DP1 with OptV2 and OptV1 versions StiffElasAssembling2DP1 benchmark sum- Table 2.6: mary N nq ndof OptV2 OptV (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x Chapter 2. 2D benchmarks
29 Figure 2.5: StiffElasAssembling2DP1 benchmark 2.4. Elastic Stiffness Matrix 25
30 This tabular was built with the following code : >>> from pyoptfem.fem2d import assemblybench >>> assemblybench(assembly= StiffElasAssembling2DP1,versions=[ OptV2, OptV1 ],LN=range(100,900 SquareMesh(100): -> StiffElasAssembling2DP1OptV2(nq=10201, nme=20000) run ( 1/ 1) : cputime= (s) - matrix by SquareMesh(800): -> StiffElasAssembling2DP1OptV1(nq=641601, nme= ) run ( 1/ 1) : cputime= (s) - matrix by We also obtain Figure 2.6: StiffElasAssembling2DP1 benchmark 26 Chapter 2. 2D benchmarks
31 CHAPTER THREE 3D BENCHMARKS Contents Benchmark usage Mass Matrix Stiffness Matrix Elastic Stiffness Matrix 3.1 Benchmark usage pyoptfem.fem3d.assemblybench.assemblybench([assembly=<string>, version=<string>, LN=<array>, meshname=<string>, meshdir=<string>, nbruns=<int>, la=<float>, mu=<float>, Num=<int>, tag=<string>,...]) Benchmark code for P 1 -Lagrange finite element matrices defined in FEM3D. Parameters assembly Name of an assembly routine. The string should be : MassAssembling3DP1, StiffAssembling3DP1 (default) StiffElasAssembling3DP1 versions List of versions. Must be a list of any size whose elements may be { base, OptV1, OptV2 } (default : [ OptV2, OptV1, base ]) meshname Name of the medit mesh files. By default it is an empty string. It means it uses CubeMesh(N) function to generate meshes. meshdir Directory location of medit mesh files. Used if meshname is not empty. LN array of integer values. <LN> contains the values of N. Used to generate meshes data via Th=CubeMesh(N) function if meshname is empty or via getmesh class to read FreeFEM++ meshes Th=getMesh(meshdir+ / +meshname+str(n)+.mesh ) LN default value is range(5, 14, 2) nbruns Number of runs on each mesh (default : 1) save For saving benchmark results in a file (see parameters <output>, <outdir> and <tag>). (default : False) 27
32 plot For plotting computation times (default : True) output Name used to set results file name (default : bench2d ) outdir Directory location of saved results file name (default :./results ). tag Specify a tag string added to filename la the first Lame coefficient in Hooke s law, denoted by λ. Used by functions for assembling the elastic stiffness matrix. (default : 2) mu the second Lame coefficient in Hooke s law, denoted by μ. Used by functions for assembling the elastic stiffness matrix. (default : 0.3) Num Numbering choice. Used by functions for assembling the elastic stiffness matrix. (default : 0) 3.2 Mass Matrix Benchmark of MassAssembling3DP1 with base, OptV1 and OptV2 versions (see Mass Matrix) Table 3.1: MassAssembling23P1 benchmark summary N nq ndof OptV2 OptV1 base (s) (s) (s) x1.00 x28.29 x (s) (s) (s) x1.00 x44.96 x (s) (s) (s) x1.00 x42.55 x (s) (s) (s) x1.00 x40.26 x (s) (s) (s) x1.00 x36.38 x (s) (s) (s) x1.00 x36.99 x (s) (s) (s) x1.00 x35.57 x This tabular was built with the following code : >>> from pyoptfem.fem3d import assemblybench >>> assemblybench(assembly= MassAssembling3DP1,LN=range(5,40,5)) CubeMesh(5): -> MassAssembling3DP1OptV2(nq=216, nme=750) run ( 1/ 1) : cputime= (s) - matrix 216-by CubeMesh(35): -> MassAssembling3DP1base(nq=46656, nme=257250) run ( 1/ 1) : cputime= (s) - matrix by We also obtain Benchmark of MassAssembling3DP1 with OptV2 and OptV1 versions 28 Chapter 3. 3D benchmarks
33 Figure 3.1: MassAssembling3DP1 benchmark 3.2. Mass Matrix 29
34 Table 3.2: MassAssembling2DP1 benchmark summary N nq ndof OptV2 OptV (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x34.71 This tabular was built with the following code : >>> from pyoptfem.fem3d import assemblybench >>> assemblybench(assembly= MassAssembling3DP1,versions=[ OptV2, OptV1 ],LN=range(10,110,10)) CubeMesh(10): -> MassAssembling3DP1OptV2(nq=1331, nme=6000) run ( 1/ 1) : cputime= (s) - matrix 1331-by CubeMesh(100): -> MassAssembling3DP1OptV1(nq= , nme= ) run ( 1/ 1) : cputime= (s) - matrix by We also obtain 3.3 Stiffness Matrix Benchmark of StiffAssembling3DP1 with base, OptV1 and OptV2 versions 30 Chapter 3. 3D benchmarks
35 Figure 3.2: MassAssembling3DP1 benchmark 3.3. Stiffness Matrix 31
36 Table 3.3: StiffAssembling3DP1 benchmark summary N nq ndof OptV2 OptV1 base (s) (s) (s) x1.00 x23.22 x (s) (s) (s) x1.00 x60.68 x (s) (s) (s) x1.00 x58.08 x (s) (s) (s) x1.00 x53.55 x (s) (s) (s) x1.00 x51.61 x (s) (s) (s) x1.00 x47.85 x (s) (s) (s) x1.00 x44.37 x This tabular was built with the following code : >>> from pyoptfem.fem3d import assemblybench >>> assemblybench(assembly= StiffAssembling3DP1,LN=range(5,40,5)) CubeMesh(5): -> StiffAssembling3DP1OptV2(nq=216, nme=750) run ( 1/ 1) : cputime= (s) - matrix 216-by CubeMesh(35): -> StiffAssembling3DP1base(nq=46656, nme=257250) run ( 1/ 1) : cputime= (s) - matrix by We also obtain Benchmark of StiffAssembling3DP1 with OptV2 and OptV1 versions 32 Chapter 3. 3D benchmarks
37 Figure 3.3: StiffAssembling3DP1 benchmark 3.3. Stiffness Matrix 33
38 Table 3.4: StiffAssembling3DP1 benchmark summary N nq ndof OptV2 OptV (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x29.04 This tabular was built with the following code : >>> from pyoptfem.fem3d import assemblybench >>> assemblybench(assembly= StiffAssembling3DP1,versions=[ OptV2, OptV1 ],LN=range(10,110,10)) CubeMesh(10): -> StiffAssembling3DP1OptV2(nq=1331, nme=6000) run ( 1/ 1) : cputime= (s) - matrix 1331-by CubeMesh(100): -> StiffAssembling3DP1OptV1(nq= , nme= ) run ( 1/ 1) : cputime= (s) - matrix by We also obtain 3.4 Elastic Stiffness Matrix Benchmark of StiffAssembling3DP1 with base, OptV1 and OptV2 versions 34 Chapter 3. 3D benchmarks
39 Figure 3.4: StiffAssembling3DP1 benchmark 3.4. Elastic Stiffness Matrix 35
40 Table 3.5: StiffAssembling3DP1 benchmark summary N nq ndof OptV2 OptV1 base (s) (s) (s) x1.00 x11.23 x (s) (s) (s) x1.00 x33.87 x (s) (s) (s) x1.00 x43.43 x (s) (s) (s) x1.00 x46.91 x (s) (s) (s) x1.00 x47.89 x (s) (s) (s) x1.00 x46.86 x (s) (s) (s) x1.00 x43.22 x This tabular was built with the following code : >>> from pyoptfem.fem3d import assemblybench >>> from numpy import * >>> assemblybench(assembly= StiffElasAssembling3DP1,LN=array([3,5,7,10,13,17,20])) CubeMesh(3): -> StiffElasAssembling3DP1OptV2(nq=64, nme=162) run ( 1/ 1) : cputime= (s) - matrix 192-by CubeMesh(20): -> StiffElasAssembling3DP1base(nq=9261, nme=48000) run ( 1/ 1) : cputime= (s) - matrix by We also obtain Benchmark of StiffAssembling3DP1 with OptV1 and OptV2 versions Table 3.6: StiffAssembling3DP1 benchmark summary N nq ndof OptV2 OptV (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x (s) (s) x1.00 x27.88 This tabular was built with the following code : 36 Chapter 3. 3D benchmarks
41 Figure 3.5: StiffElasAssembling3DP1 benchmark 3.4. Elastic Stiffness Matrix 37
42 >>> from pyoptfem.fem3d import assemblybench >>> assemblybench(assembly= StiffElasAssembling3DP1,versions=[ OptV2, OptV1 ],LN=range(10,80,1 CubeMesh(10): -> StiffElasAssembling3DP1OptV2(nq=1331, nme=6000) run ( 1/ 1) : cputime= (s) - matrix 3993-by CubeMesh(70): -> StiffElasAssembling3DP1OptV1(nq=357911, nme= ) run ( 1/ 1) : cputime= (s) - matrix by We also obtain Figure 3.6: StiffElasAssembling3DP1 benchmark 38 Chapter 3. 3D benchmarks
43 CHAPTER FOUR FEM2D MODULE Author Francois Cuvelier Date 15/09/2013 Contains functions to build some finite element matrices using P 1 -Lagrange finite elements on a 2D mesh. Each assembly matrix is computed by three different versions called base, OptV1 and OptV2 (see here) Contents Assembly matrices (base, OptV1 and OptV2 versions) Mass Matrix Stiffness Matrix Elastic Stiffness Matrix Element matrices (used by base and OptV1 versions) Element Mass Matrix Element Stiffness Matrix Element Elastic Stiffness Matrix Vectorized tools (used by OptV2 version) Vectorized computation of basis functions gradients Vectorized element matrices (used by OptV2 version) Element Mass Matrix Element Stiffness Matrix Element Elastic Stiffness Matrix Mesh 39
44 4.1 Assembly matrices (base, OptV1 and OptV2 versions) Let T h be a triangular mesh of Ω. We denote by Ω h structure: = T k T h T k a triangulation of Ω with the following data name type dimension description Python n q integer 1 number of vertices nq n me integer 1 number of elements nme q double 2 n q array of vertices coordinates. q(ν, j) is the ν-th coordinate of the j-th vertex, ν {1, 2}, j {1,..., n q }. The j-th vertex will be also denoted by q j me integer 3 n me connectivity array. me(β, k) is the storage index of the β-th vertex of the k-th element, in the array q, for β {1, 2, 3} and k {1,..., n me } areas double 1 n me array of areas. areas(k) is the k-th triangle area, k {1,..., n me } q (transposed) q[j-1] = q j me (transposed) areas The P 1 -Lagrange basis functions associated to Ω h are denoted by φ i for all i {1,..., n q } and defined by φ i (q j ) = δ i,j, (i, j) {1,..., n q } 2 We also define the global alternate basis B a by B a = {ψ 1,..., ψ 2nq } = { ( φ1 0 ), ( ) 0, φ 1 ( ) ( ) ( ) ( ) } φ2 0 φnq 0,,...,, 0 φ 2 0 φ nq and the global block basis B b by B b = {φ 1,..., φ 2nq } = { ( ) ( ) ( ) ( ( ( ) } φ1 φ2 φnq 0 0 0,,...,,,,..., φ1) φ2) φ nq Mass Matrix Assembly of the Mass Matrix by P 1 -Lagrange finite elements using base, OptV1 and OptV2 versions respectively (see report). The Mass Matrix M is given by M i,j = φ j (q) φ i (q)dq, (i, j) {1,..., n q } 2. Ω h Note: generic syntax: M = MassAssembling2DP1<version>(nq,nme,me,areas) nq: total number of nodes of the mesh, also denoted by n q, nme: total number of triangles, also denoted by n me, 40 Chapter 4. FEM2D module
45 me: Connectivity array, (nme,3) array, areas: Array of areas, (nme,) array, returns a Scipy CSC sparse matrix of size n q n q where <version> is base, OptV1 or OptV2 Benchmarks of theses functions are presented in Mass Matrix. We give a simple usage : >>> from pyoptfem.fem2d import * >>> Th=SquareMesh(5) >>> Mbase = MassAssembling2DP1base(Th.nq,Th.nme,Th.me,Th.areas) >>> MOptV1= MassAssembling2DP1OptV1(Th.nq,Th.nme,Th.me,Th.areas) >>> print(" NormInf(Mbase-MOptV1)=%e " % NormInf(Mbase-MOptV1)) NormInf(Mbase-MOptV1)= e-18 >>> MOptV2= MassAssembling2DP1OptV2(Th.nq,Th.nme,Th.me,Th.areas) >>> print(" NormInf(Mbase-MOptV2)=%e " % NormInf(Mbase-MOptV2)) NormInf(Mbase-MOptV2)= e-18 We can show sparsity of the Mass matrix : >>> from pyoptfem.fem2d import * >>> Th=SquareMesh(20) >>> M=MassAssembling2DP1base(Th.nq,Th.nme,Th.me,Th.areas) >>> showsparsity(m) Note: source code pyoptfem.fem2d.assembly.massassembling2dp1base(nq, nme, me, areas) Assembly of the Mass Matrix by P 1 -Lagrange finite elements using base version (see report). pyoptfem.fem2d.assembly.massassembling2dp1optv1(nq, nme, me, areas) Assembly of the Mass Matrix by P 1 -Lagrange finite elements using OptV1 version (see report). pyoptfem.fem2d.assembly.massassembling2dp1optv2(nq, nme, me, areas) Assembly of the Mass Matrix by P 1 -Lagrange finite elements using OptV2 version (see report) Stiffness Matrix Assembly of the Stiffness Matrix by P 1 -Lagrange finite elements using base, OptV1 and OptV2 versions respectively (see report). The Stiffness Matrix S is given by S i,j = φ j (q). φ i (q)dq, (i, j) {1,..., n q } 2. Ω h Note: generic syntax: M = StiffAssembling2DP1<version>(nq,nme,q,me,areas) nq: total number of nodes of the mesh, also denoted by n q, nme: total number of triangles, also denoted by n me, q: Array of vertices coordinates, (nq,2) array 4.1. Assembly matrices (base, OptV1 and OptV2 versions) 41
46 Figure 4.1: Sparsity of Mass Matrix generated with command showsparsity(m) 42 Chapter 4. FEM2D module
47 me: Connectivity array, (nme,3) array, areas: Array of areas, (nme,) array, returns a Scipy CSC sparse matrix of size n q n q where <version> is base, OptV1 or OptV2 Benchmarks of theses functions are presented in Stiffness Matrix. We give a simple usage : >>> pyoptfem.fem2d import * >>> Th=SquareMesh(5) >>> Sbase = StiffAssembling2DP1base(Th.nq,Th.nme,Th.q,Th.me,Th.areas) >>> SOptV1= StiffAssembling2DP1OptV1(Th.nq,Th.nme,Th.q,Th.me,Th.areas) >>> print(" NormInf(Sbase-SOptV1)=%e " % NormInf(Sbase-SOptV1)) NormInf(Sbase-SOptV1)= e+00 >>> SOptV2= StiffAssembling2DP1OptV2(Th.nq,Th.nme,Th.q,Th.me,Th.areas) >>> print(" NormInf(Sbase-SOptV2)=%e " % NormInf(Sbase-SOptV2)) NormInf(Sbase-SOptV1)= e-16 Note: source code pyoptfem.fem2d.assembly.stiffassembling2dp1base(nq, nme, q, me, areas) Assembly of the Stiffness Matrix by P 1 -Lagrange finite elements using base version (see report). pyoptfem.fem2d.assembly.stiffassembling2dp1optv1(nq, nme, q, me, areas) Assembly of the Stiffness Matrix by P 1 -Lagrange finite elements using OptV1 version (see report). pyoptfem.fem2d.assembly.stiffassembling2dp1optv2(nq, nme, q, me, areas) Assembly of the Stiffness Matrix by P 1 -Lagrange finite elements using OptV2 version (see report) Elastic Stiffness Matrix Assembly of the Elastic Stiffness Matrix by P 1 -Lagrange finite elements using base, OptV1 and OptV2 versions respectively (see report). The Elastic Stiffness Matrix K is given by K m,l = ε t (ψ l (q))σ(ψ m (q)), (m, l) {1,..., 2n q } 2. Ω h where σ = (σ xx, σ yy, σ xy ) t and ε = (ε xx, ε yy, ε xy ) t are the elastic stress and strain tensors respectively. Note: generic syntax: M = StiffElasAssembling2DP1<version>(nq,nme,q,me,areas,la,mu,Num) nq: total number of nodes of the mesh, also denoted by n q, nme: total number of triangles, also denoted by n me, q: array of vertices coordinates, (nq,2) array for base and OptV1, (2,nq) array for OptV2 version, me: Connectivity array, (nme,3) array for base and OptV1, 4.1. Assembly matrices (base, OptV1 and OptV2 versions) 43
48 (3,nme) array for OptV2 version, areas: (nme,) array of areas, la: the first Lame coefficient in Hooke s law, denoted by λ, mu: the second Lame coefficient in Hooke s law, denoted by μ, Num: 0: global alternate numbering with local alternate numbering (classical method), 1: global block numbering with local alternate numbering, 2: global alternate numbering with local block numbering, 3: global block numbering with local block numbering. returns a Scipy CSC sparse matrix of size 2n q 2n q where <version> is base, OptV1 or OptV2 Benchmarks of theses functions are presented in Elastic Stiffness Matrix. We give a simple usage : >>> from pyoptfem.fem2d import * >>> Th=SquareMesh(5) >>> Kbase = StiffElasAssembling2DP1base(Th.nq,Th.nme,Th.q,Th.me,Th.areas,2,0.5,0) >>> KOptV1= StiffElasAssembling2DP1OptV1(Th.nq,Th.nme,Th.q,Th.me,Th.areas,2,0.5,0) >>> print(" NormInf(Kbase-KOptV1)=%e " % NormInf(Kbase-KOptV1)) NormInf(Kbase-KOptV1)= e-16 >>> KOptV2= StiffElasAssembling2DP1OptV2(Th.nq,Th.nme,Th.q,Th.me,Th.areas,2,0.5,0) >>> print(" NormInf(Kbase-KOptV2)=%e " % NormInf(Kbase-KOptV2)) NormInf(Kbase-KOptV2)= e-15 We now illustrate the consequences of the choice of the global basis on matrix sparsity global alternate basis B a (Num=0 or Num=2) >>> from pyoptfem.fem2d import * >>> Th=SquareMesh(15) >>> K0=StiffElasAssembling2DP1OptV1(Th.nq,Th.nme,Th.q,Th.me,Th.areas,2,0.5,0) >>> showsparsity(k0) >>> K3=StiffElasAssembling2DP1OptV1(Th.nq,Th.nme,Th.q,Th.me,Th.areas,2,0.5,3) >>> showsparsity(k3) global block basis B a (Num=1 or Num=3) Note: source code pyoptfem.fem2d.assembly.stiffelasassembling2dp1base(nq, nme, q, me, areas, la, mu, Num) Assembly of the Elasticity Stiffness Matrix by P 1 -Lagrange finite elements using OptV2 version (see report). pyoptfem.fem2d.assembly.stiffelasassembling2dp1optv1(nq, nme, q, me, areas, la, mu, Num) Assembly of the Elasticity Stiffness Matrix by P 1 -Lagrange finite elements using OptV1 version (see report). pyoptfem.fem2d.assembly.stiffelasassembling2dp1optv2(nq, nme, q, me, areas, la, mu, Num) Assembly of the Elasticity Stiffness Matrix by P 1 -Lagrange finite elements using OptV2 version (see report). 44 Chapter 4. FEM2D module
49 Figure 4.2: Sparsity of the Elastic Stiffness Matrix generated with global alternate numbering (Num=0 or 2) 4.1. Assembly matrices (base, OptV1 and OptV2 versions) 45
50 Figure 4.3: Sparsity of the Elastic Stiffness Matrix generated with global block numbering (Num=1 or 3) 46 Chapter 4. FEM2D module
51 4.2 Element matrices (used by base and OptV1 versions) Let T be a triangle, of area T and with q 1, q 2 and q 3 its three vertices. We denote by φ 1, φ 2 and φ 3 the P 1 -Lagrange local basis functions such that φ i (q j ) = δ i,j, (i, j) {1, 2, 3} 2. We also define the local alternate basis B a by B a = { ψ ψ ψ1,..., ψ ψ ψ6 } = { ( φ1 0 ) (,, 0 φ1) ( ) ( φ2,, 0 0 φ2) ( ) ( φ3 0 φ3) }, 0 and the local block basis B b by { ( ) B b = { φ φ φ1,..., φ φ φ6 φ1 } =, 0 ( ) φ2, 0 ( ) ( ( ( φ3 0 φ3) },,,. 0 0 φ1) 0 φ2) The elasticity tensor, H, obtained from Hooke s law with an isotropic material, defined with the Lamé parameters λ and μ is given by λ + 2μ λ 0 H = λ λ + 2μ μ and, for a function u = (u 1, u 2 ) the strain tensors is given by ( u1 ε(u) = x, u 2 y, u 2 x + u 1 y ) t Element Mass Matrix The element Mass matrix M e (T ) for the triangle T is defined by M e i,j(t ) = φ i (q) φ j (q) dq, (i, j) {1, 2, 3} 2 T We obtain : M e (T ) = T (4.1) Note: pyoptfem.fem2d.elemmatrix.elemmassmat2dp1(area) Computes the element mass matrix M e (T ) for a given triangle T of area T Parameters area (float) area of the triangle. Returns 3 3 numpy array of floats Element matrices (used by base and OptV1 versions) 47
52 4.2.2 Element Stiffness Matrix The element stiffness matrix, S e (T ), for the T is defined by S e i,j(t ) = < φ i (q), φ j (q) > dq, (i, j) {1, 2, 3} 2 T We have : S e (T ) = 1 4 T < u, u > < u, v > < u, w > < v, u > < v, v > < v, w >. < w, u > < w, v > < w, w > where u = q 2 q 3, v = q 3 q 1 and w = q 1 q 2. Note: pyoptfem.fem2d.elemmatrix.elemstiffmat2dp1(q1, q2, q3, area) Computes the element stiffness matrix S e (T ) for a given triangle T Parameters Returns Type q1,q2,q3 (2 1 numpy array) the three vertices of the triangle, area (float) area of the triangle. 3 3 numpy array of floats Element Elastic Stiffness Matrix Let u = q 2 q 3, v = q 3 q 1 and w = q 1 q 2. The element elastic stiffness matrix, K e (T ), for a given triangle T in the local alternate basis B a is defined by K e i,j(t ) = ε( ψ j ) t (q)hε( ψ i )(q) dq, (i, j) {1,..., 6} 2. T We also have K e (T ) = 1 4 T Bt HB where H is the elasticity tensor and B = u 2 0 v 2 0 w u 1 0 v 1 0 w 1 u 1 u 2 v 1 v 2 w 1 w 2 Note: 48 Chapter 4. FEM2D module
53 pyoptfem.fem2d.elemmatrix.elemstiffelasmat2dp1ba(ql, area, H) Returns the element elastic stiffness matrix K e (T ) for a given triangle T in the local alternate basis B a Parameters ql (3 2 numpy array) contains the three vertices of the triangle : ql[0], ql[1] and ql[2], area (float) area of the triangle, H (3 3 numpy array) Elasticity tensor, H. Returns K e (T ) in B a basis. Type 6 6 numpy array of floats. The element elastic stiffness matrix, K e (T ), for a given triangle T in the local block basis B b is defined by K e i,j(t ) = ε( φ j ) t (q)hε( φ i )(q) dq, (i, j) {1,..., 6} 2. T We also have K e (T ) = 1 4 T Bt HB where H is the elasticity tensor and u 2 v 2 w B = u 1 v 1 w 1 u 1 v 1 w 1 u 2 v 2 w 2 Note: pyoptfem.fem2d.elemmatrix.elemstiffelasmat2dp1bb(ql, area, H) Returns the element elastic stiffness matrix K e (T ) for a given triangle T in the local block basis B b Parameters ql (3 2 numpy array) contains the three vertices of the triangle : ql[0], ql[1] and ql[2], area (float) area of the triangle, H (3 3 numpy array) Elasticity tensor, H. Returns K e (T ) in B b basis. Type 6 6 numpy array of floats 4.2. Element matrices (used by base and OptV1 versions) 49
54 4.3 Vectorized tools (used by OptV2 version) Vectorized computation of basis functions gradients By construction, the gradients of basis functions are constants on each element T k. So, we denote, α {1,..., 3}, by G α the 2 n me array defined, k {1,..., n me }, by G α (:, k) = φ me(α,k) (q), q T k. On a triangle T k, we define D 12 = q me(1,k) q me(2,k), D 13 = q me(1,k) q me(3,k) and D 23 = q me(2,k) q me(3,k). Then, we have φ k 1(q) = 1 ( ) D 23 y 2 T k D 23, φ k 2(q) = 1 ( ) D 13 y x 2 T k D 13, φ k 3(q) = 1 ( ) D 12 y x 2 T k D 12. x With these formulas, we obtain the vectorized algorithm given in Algorithm 4.4. Algorithm 4.4 Figure 4.4: Vectorized algorithm for computation of basis functions gradients in 2d 50 Chapter 4. FEM2D module
55 4.4 Vectorized element matrices (used by OptV2 version) Element Mass Matrix We have M e (T k ) = T k Then with K g definition (see Section New Optimized assembly algorithm (OptV2 version)), we obtain K g (3(i 1) + j, k) = T k 1 + δ i,j 12 1 i, j 3, We represent in figure 4.5 the corresponding row-wise operations. Figure 4.5: Construction of K g associated to 2d Mass matrix in So the vectorized algorithm for K g computation is simple and given in Algorithm 4.6. Algorithm 4.6 Note: pyoptfem.fem2d.elemmatrixvec.elemmassmat2dp1vec(areas) Computes all the element Mass matrices M e (T k ) for k {0,..., n me 1} Parameters areas (n me numpy array of floats) areas of all the mesh elements Vectorized element matrices (used by OptV2 version) 51
56 Figure 4.6: Vectorized algorithm for K g associated to 2d Mass matrix Returns a one dimensional numpy array of size 9n me Element Stiffness Matrix We have (α, β) {1,..., 3} 2 S e α,β(t k ) = T k φ k β, φ k α. Using vectorized algorithm function GRADIENTVEC2D given in Algorithm 4.4, we obtain the vectorized algorithm 4.7 for K g computation for the Stiffness matrix in 2d. Algorithm 4.7 Figure 4.7: Vectorized algorithm for K g associated to 2d Stiffness matrix Note: pyoptfem.fem2d.elemmatrixvec.elemstiffmat2dp1vec(nme, q, me, areas) Computes all the element stiffness matrices S e (T k ) for k {0,..., n me 1} Parameters nme (int) number of mesh elements, q (n q 2 numpy array of floats) mesh vertices, me (n me 3 numpy array of integers) mesh connectivity, 52 Chapter 4. FEM2D module
57 areas (n me numpy array of floats) areas of all the mesh elements. Returns a one dimensional numpy array of size 9n me Element Elastic Stiffness Matrix We define on T k the local alternate basis B k a by B k a = {ψ k 1,..., ψ k 6} = { ( φ k 1 0 ) ( ) ( ) ( ) ( ) ( ) } 0 φ k, φ k, 2 0 φ k, 1 0 φ k, 3 0, 2 0 φ k 3 where φ k α = φ me(α,k). With notations of Presentation, we have (α, β) {1,..., 6} 2 K e α,β(t k ) = ε t (ψ k β)cε(ψ k α)dq = T k H(ψ k β, ψ k α)(q)dq T k with, u = (u 1, u 2 ) H 1 (Ω) 2, v = (v 1, v 2 ) H 1 (Ω) 2, ( ) γ 0 H(u, v) = 0 μ u 1, v 1 ( ) 0 μ + λ 0 u 1, v 2 + ( 0 + ) λ μ 0 u 2, v 1 ) (4.2) u 2, v 2 ( μ 0 0 γ For example, we can explicitly compute the first two terms in the first column of K e (T k ) which are given by K e 1,1(T k ) = T k H(ψ k 1, ψ k 1)(q)dq = ( ( ) ( ) ) φ k T k H 1 φ k, 1 (q)dq ( 0 ) 0 γ 0 = T k 0 μ φ k 1, φ k 1 = T k ( γ φk 1 φ k 1 x x + μ φk 1 y ) φ k 1 y. and K e 2,1(T k ) = T k H(ψ k 1, ψ k 2)(q)dq = ( ( ) ( ) ) φ k T k H 1 0, 0 φ k (q)dq ( ) 1 0 μ = T k λ 0 φ k 1, φ k 1 = T k (λ + μ) φk 1 x φ k 1 y. Using vectorized algorithm function GRADIENTVEC2D given in Algorithm 4.4, we obtain the vectorized algorithm 4.7 for K g computation for the Elastic Stiffness matrix in 2d. Algorithm 4.8 Note: pyoptfem.fem2d.elemmatrixvec.elemstiffelasmatbavec2dp1(nme, q, me, areas, L, M, **kwargs) Computes all the element elastic stiffness matrices K e (T k ) for k {0,..., n me 1} in local alternate basis Vectorized element matrices (used by OptV2 version) 53
58 Figure 4.8: Vectorized algorithm for K g associated to 2d Elastic Stiffness matrix Parameters nme (int) number of mesh elements, q ((2,nq) numpy array of floats) mesh vertices, me ((3,nme) numpy array of integers) mesh connectivity, areas ((nme,) numpy array of floats) areas of all the mesh elements. L (float) the λ Lame parameter, M (float) the μ Lame parameter. Returns a (36*nme,) numpy array of floats. We define on T k the local block basis Bb k by { ( ) ( ) ( ) ( ) ( ) ( ) } Bb k = {φ k 1,..., φ k φ k 6} = 1 φ k, 2 φ k, , φ k, 1 φ k, 2 φ k 3 where φ k α = φ me(α,k). For example, using formula (4.2), we can explicitly compute the first two terms in the first column of K e (T k ) which are given by K e 1,1(T k ) = T k H(φ k 1, φ k 1)(q)dq = ( ( ) ( ) ) φ k T k H 1 φ k, 1 (q)dq ( 0 ) 0 γ 0 = T k 0 μ φ k 1, φ k 1 = T k ( γ φk 1 φ k 1 x x + μ φk 1 y ) φ k 1 y. 54 Chapter 4. FEM2D module
59 and K e 2,1(T k ) = T k H(φ k 1, φ k 2)(q)dq = ( ( ) ( ) ) φ k T k H 1 φ k, 2 (q)dq ( 0 ) 0 γ 0 = T k 0 μ φ k 1, φ k 2 = T k ( γ φk 1 φ k 2 x x + μ φk 1 y ) φ k 2 y. Using vectorized algorithm function GRADIENTVEC2D given in Algorithm 4.4, we obtain the vectorized algorithm 4.9 for K g computation for the Elastic Stiffness matrix in 2d. Algorithm 4.9 Figure 4.9: Vectorized algorithm for K g associated to 2d Elastic Stiffness matrix Note: pyoptfem.fem2d.elemmatrixvec.elemstiffelasmatbbvec2dp1(nme, q, me, areas, L, M, **kwargs) Computes all the element elastic stiffness matrices K e (T k ) for k {0,..., n me 1} in local block basis. Parameters nme (int) number of mesh elements, q ((2,nq) numpy array of floats) mesh vertices, me ((3,nme) numpy array of integers) mesh connectivity, areas ((nme,) numpy array of floats) areas of all the mesh elements. L (float) the λ Lame parameter, M (float) the μ Lame parameter. Returns a (36*nme,) numpy array of floats Vectorized element matrices (used by OptV2 version) 55
60 4.5 Mesh class pyoptfem.fem2d.mesh.squaremesh(n, **kwargs) Creates meshes of the unit square [0, 1] [0, 1]. Class attributes are : nq, total number of mesh vertices (points), also denoted n q. nme, total number of mesh elements (triangles in 2d), version, mesh structure version, q, Numpy array of vertices coordinates, dimension (nq,2) (version 0) or (2,nq) (version 1). q[j] (version 0) or q[:,j] (version 1) are the two coordinates of the j-th vertex, j {0,.., nq 1} me, Numpy connectivity array, dimension (nme,3) (version 0) or (3,nme) (version 1). me[k] (version 0) or me[:,k] (version 1) are the storage index of the three vertices of the k-th triangle in the array q of vertices coordinates, k {0,..., nme 1}. areas, Array of mesh elements areas, (nme,) Numpy array. areas[k] is the area of k-th triangle, k in range(0,nme) Parameters N number of points on each side of the square optional parameter : version=0 or version=1 >>> from pyoptfem.fem2d import * >>> Th=SquareMesh(3) >>> Th.nme,Th.nq (18, 16) >>> Th.q array([[ 0., 0. ], [ , 0. ], [ , 0. ], [ 1., 0. ], [ 0., ], [ , ], [ , ], [ 1., ], [ 0., ], [ , ], [ , ], [ 1., ], [ 0., 1. ], [ , 1. ], [ , 1. ], [ 1., 1. ]]) >>> PlotMesh(Th) class pyoptfem.fem2d.mesh.getmesh(meshfile, **kwargs) Reads a FreeFEM++ mesh from file meshfile. Class attributes are : nq, total number of mesh vertices (points), also denoted n q. nme, total number of mesh elements (triangles in 2d), version, mesh structure version, q, Numpy array of vertices coordinates, dimension (nq,2) (version 0) or (2,nq) (version 1). q[j] (version 0) or q[:,j] (version 1) are the two coordinates of the j-th vertex, j {0,.., nq 1} 56 Chapter 4. FEM2D module
61 Figure 4.10: SquareMesh(3) visualisation 4.5. Mesh 57
62 me, Numpy connectivity array, dimension (nme,3) (version 0) or (3,nme) (version 1). me[k] (version 0) or me[:,k] (version 1) are the storage index of the three vertices of the k-th triangle in the array q of vertices coordinates, k {0,..., nme 1}. areas, Array of mesh elements areas, (nme,) Numpy array. areas[k] is the area of k-th triangle, k in range(0,nme) Parameters N number of points on each side of the square optional parameter : version=0 or version=1 >>> from pyoptfem.fem2d import * >>> Th=getMesh( mesh/disk4-1-5.msh ) >>> PlotMesh(Th) Figure 4.11: Visualisation of a FreeFEM++ mesh (disk unit) 58 Chapter 4. FEM2D module
63 CHAPTER FIVE FEM3D MODULE Author Francois Cuvelier Date 15/09/2013 Contains functions to build some finite element matrices using P 1 -Lagrange finite elements on a 3D mesh. Each assembly matrix is computed by three differents versions called base, OptV1 and OptV2 (see here) Contents Assembly matrix (base, OptV1 and OptV2 versions) Mass Matrix Stiffness Matrix Elastic Stiffness Matrix Element matrix (used by base and OptV1 versions) Element Mass Matrix Element Stiffness Matrix Element Elastic Stiffness Matrix Vectorized tools (used by OptV2 version) Vectorized computation of basis functions gradients Vectorized element matrix (used by OptV2 version) Element Mass Matrix Element Stiffness Matrix Element Elastic Stiffness Matrix Mesh 59
64 5.1 Assembly matrix (base, OptV1 and OptV2 versions) Let Ω h be a tetrahedral mesh of Ω corresponding to the following structure data: name type dimension description Python n q integer 1 number of vertices nq n me integer 1 number of elements nme q double 3 n q array of vertices coordinates. q(ν, j) is the ν-th coordinate of the j-th vertex, ν {1, 2, 3}, j {1,..., n q }. The j-th vertex will be also denoted by q j me integer 4 n me connectivity array. me(β, k) is the storage index of the β-th vertex of the k-th element, in the array q, for β {1,..., 4} and k {1,..., n me } volumes double 1 n me array of volumes. volumes(k) is the k-th tetrahedron volume, k {1,..., n me } q (transposed) q[j-1] = q j me (transposed) volumes The P 1 -Lagrange basis functions associated to Ω h are denoted by φ i for all i {1,..., n q } and are defined by φ i (q j ) = δ i,j, (i, j) {1,..., n q } 2 We also define the global alternate basis B a by φ B a = {ψ 1,..., ψ 3nq } = 0, φ 1, 0,..., 0 0 φ 1 φ nq 0 0 0, φ nq, φ nq and the global block basis B b by φ 1 B b = {φ 1,..., φ 3nq } = 0,..., 0 φ nq , φ 1,..., φ nq, φ 1,..., 0 0 φ nq Mass Matrix Assembly of the Mass Matrix by P 1 -Lagrange finite elements using base, OptV1 and OptV2 versions respectively (see report). The Mass Matrix M is given by M i,j = φ j (q) φ i (q)dq, (i, j) {1,..., n q } 2. Ω h Note: generic syntax: M = MassAssembling3DP1<version>(nq,nme,me,volumes) nq: total number of nodes of the mesh, also denoted by n q, nme: total number of tetrahedra, also denoted by n me, 60 Chapter 5. FEM3D module
65 me: Connectivity array, (nme,4) array, volumes: Array of tetrahedra volumes, (nme,) array, returns a Scipy CSC sparse matrix of size n q n q where <version> is base, OptV1 or OptV2 >>> from pyoptfem.fem3d import * >>> Th=CubeMesh(5) >>> Mbase = MassAssembling3DP1base(Th.nq,Th.nme,Th.me,Th.volumes) >>> MOptV1= MassAssembling3DP1OptV1(Th.nq,Th.nme,Th.me,Th.volumes) >>> print(" NormInf(Mbase-MOptV1)=%e " % NormInf(Mbase-MOptV1)) NormInf(Mbase-MOptV1)= e-18 >>> MOptV2= MassAssembling3DP1OptV2(Th.nq,Th.nme,Th.me,Th.volumes) >>> print(" NormInf(Mbase-MOptV2)=%e " % NormInf(Mbase-MOptV2)) NormInf(Mbase-MOptV2)= e-18 We can show sparsity of the Mass matrix : >>> from pyoptfem.fem3d import * >>> Th=CubeMesh(5) >>> M=MassAssembling3DP1OptV2(Th.nq,Th.nme,Th.me,Th.areas) >>> showsparsity(m) Figure 5.1: Sparsity of Mass Matrix generated with command showsparsity(m) 5.1. Assembly matrix (base, OptV1 and OptV2 versions) 61
66 Note: source code pyoptfem.fem3d.assembly.massassembling3dp1base(nq, nme, me, volumes) Assembly of the Mass Matrix by P 1 -Lagrange finite elements using base version (see report). pyoptfem.fem3d.assembly.massassembling3dp1optv1(nq, nme, me, volumes) Assembly of the Mass Matrix by P 1 -Lagrange finite elements using OptV1 version (see report). pyoptfem.fem3d.assembly.massassembling3dp1optv2(nq, nme, me, volumes) Assembly of the Mass Matrix by P 1 -Lagrange finite elements using OptV2 version (see report) Stiffness Matrix Assembly of the Stiffness Matrix by P 1 -Lagrange finite elements using base, OptV1 and OptV2 versions respectively (see report). The Stiffness Matrix S is given by S i,j = φ j (q). φ i (q)dq, (i, j) {1,..., n q } 2. Ω h Note: generic syntax M=StiffAssembling3DP1<version>(nq,nme,q,me,volumes) Compute the stiffness sparse matrix where <version> is base, OptV1 or OptV2 Parameters nq total number of nodes of the mesh, also denoted by n q, nme total number of tetrahedra, also denoted by n me, q (numpy array of float) array of vertices coordinates, (nq,3) array for base and OptV1 versions, (3,nq) array for OptV2 version, me (numpy array of int) Connectivity array, (nme,4) array for base and OptV1 versions, (4,nme) array for OptV2 version, volumes (numpy array of floats,) (nme,) array of tetrahedra volumes, Returns a Scipy CSC sparse matrix of size 2n q 2n q Benchmarks of theses functions are presented in Stiffness Matrix. We give a simple usage : >>> from pyoptfem.fem3d import * >>> Th=CubeMesh(5) >>> Sbase = StiffAssembling3DP1base(Th.nq,Th.nme,Th.q,Th.me,Th.volumes) >>> SOptV1= StiffAssembling3DP1OptV1(Th.nq,Th.nme,Th.q,Th.me,Th.volumes) >>> print(" NormInf(Sbase-SOptV1)=%e " % NormInf(Sbase-SOptV1)) NormInf(Sbase-SOptV1)= e Chapter 5. FEM3D module
67 >>> SOptV2= StiffAssembling3DP1OptV2(Th.nq,Th.nme,Th.q,Th.me,Th.volumes) >>> print(" NormInf(Sbase-SOptV2)=%e " % NormInf(Sbase-SOptV2)) NormInf(Sbase-SOptV2)= e-15 Note: source code pyoptfem.fem3d.assembly.stiffassembling3dp1base(nq, nme, q, me, volumes) Assembly of the Stiffness Matrix by P 1 -Lagrange finite elements using base version (see report). pyoptfem.fem3d.assembly.stiffassembling3dp1optv1(nq, nme, q, me, volumes) Assembly of the Stiffness Matrix by P 1 -Lagrange finite elements using OptV1 version (see report). pyoptfem.fem3d.assembly.stiffassembling3dp1optv2(nq, nme, q, me, volumes) Assembly of the Stiffness Matrix by P 1 -Lagrange finite elements using OptV2 version (see report) Elastic Stiffness Matrix Assembly of the Elastic Stiffness Matrix by P 1 -Lagrange finite elements using base, OptV1 and OptV2 versions respectively (see report). The Elastic Stiffness Matrix K is given by K m,l = ε t (ψ l (q)) σ(ψ m (q)), (m, l) {1,..., 3n q } 2. Ω h where σ = (σ xx, σ yy, σ zz, σ xy, σ yz, σ xz ) t and ε = (ε xx, ε yy, ε zz, 2ε xy, 2ε yz, 2ε xz ) t are the elastic stress and strain tensors respectively. Note: generic syntax M=StiffElasAssembling3DP1<version>(nq,nme,q,me,volumes,la,mu,Num) Compute the elastic stiffness sparse matrix where <version> is base, OptV1 or OptV2 Parameters nq total number of nodes of the mesh, nme total number of tetrahedrons, q (numpy array of float) vertices coordinates, (nq,3) array for base and OptV1 versions, (3,nq) array for OptV2 version, me (numpy array of int) connectivity array, (nme,4) array for base and OptV1 versions, (4,nme) array for OptV2 version, volumes (numpy array of floats,) (nme,) array of tetrahedra volumes, la the first Lame coefficient in Hooke s law, denoted by λ, mu the second Lame coefficient in Hooke s law, denoted by μ, Num 5.1. Assembly matrix (base, OptV1 and OptV2 versions) 63
68 0 global alternate numbering with local alternate numbering (classical method), 1 global block numbering with local alternate numbering, 2 global alternate numbering with local block numbering, 3 global block numbering with local block numbering. Returns a Scipy CSC sparse matrix of size 3nq 3nq >>> from pyoptfem.fem3d import * >>> Th=CubeMesh(5) >>> Kbase = StiffElasAssembling3DP1base(Th.nq,Th.nme,Th.q,Th.me,Th.volumes,2,0.5,0) >>> KOptV1= StiffElasAssembling3DP1OptV1(Th.nq,Th.nme,Th.q,Th.me,Th.volumes,2,0.5,0) >>> print(" NormInf(Kbase-KOptV1)=%e " % NormInf(Kbase-KOptV1)) NormInf(Kbase-KOptV1)= e-15 >>> KOptV2= StiffElasAssembling3DP1OptV2(Th.nq,Th.nme,Th.q,Th.me,Th.volumes,2,0.5,0) >>> print(" NormInf(Kbase-KOptV2)=%e " % NormInf(Kbase-KOptV2)) NormInf(Kbase-KOptV2)= e-15 We now illustrate the consequences of the choice of the global basis on matrix sparsity global alternate basis B a (Num=0 or Num=2) >>> from pyoptfem.fem3d import * >>> Th=CubeMesh(5) >>> K0=StiffElasAssembling3DP1OptV1(Th.nq,Th.nme,Th.q,Th.me,Th.volumes,2,0.5,0) >>> showsparsity(k0) global block basis B a (Num=1 or Num=3) >>> K3=StiffElasAssembling3DP1OptV1(Th.nq,Th.nme,Th.q,Th.me,Th.volumes,2,0.5,3) >>> showsparsity(k3) Note: source code pyoptfem.fem3d.assembly.stiffelasassembling3dp1base(nq, nme, q, me, volumes, la, mu, Num) Assembly of the Elasticity Stiffness Matrix by P 1 -Lagrange finite elements using base version (see report). pyoptfem.fem3d.assembly.stiffelasassembling3dp1optv1(nq, nme, q, me, volumes, la, mu, Num) Assembly of the Elasticity Stiffness Matrix by P 1 -Lagrange finite elements using OptV1 version (see report). pyoptfem.fem3d.assembly.stiffelasassembling3dp1optv2(nq, nme, q, me, volumes, la, mu, Num) Assembly of the Elasticity Stiffness Matrix by P 1 -Lagrange finite elements using OptV2 version (see report). 5.2 Element matrix (used by base and OptV1 versions) Let T be a tetrahedron of volume T and with q 1, q 2, q 3 and q 4 its four vertices. We denote by φ 1, φ 2, φ 3 and φ 4 the P 1 -Lagrange local basis functions such that φ i (q j ) = δ i,j, (i, j) {1,..., 4} Chapter 5. FEM3D module
69 Figure 5.2: Sparsity of the Elastic Stiffness Matrix generated with global alternate numbering (Num=0 or 2) 5.2. Element matrix (used by base and OptV1 versions) 65
70 Figure 5.3: Sparsity of the Elastic Stiffness Matrix generated with global block numbering (Num=1 or 3) 66 Chapter 5. FEM3D module
71 We also define the local alternate basis B a by φ φ B a = { ψ ψ ψ1,..., ψ ψ ψ12 } = 0, φ 1, 0,..., 0, φ 4, 0, 0 0 φ φ 4 and the local block basis B b by φ 1 φ 2 φ 3 φ B b = { φ φ φ1,..., φ φ φ12 } = 0, 0, 0, 0,..., 0, 0, φ 1 φ 2 φ 3 φ 4 The elasticity tensor, H, obtained from Hooke s law with an isotropic material, defined with the Lamé parameters λ and μ is given by λ + 2μ λ λ λ λ + 2μ λ H = λ λ λ + 2μ μ μ μ and, for a function u = (u 1, u 2, u 3 ) the strain tensors is given by ε(u) = ( u1 x, u 2 y, u 3 z, u 2 x + u 1 y, u 2 z + u 3 y, u 1 z + u ) t 3 x Element Mass Matrix The element Mass matrix M e (T ) for the tetrahedron T, is defined by M e i,j(t ) = φ i (q) φ j (q) dq, (i, j) {1, 2, 3, 4} 2 T We obtain : M e (T ) = T Note: source code pyoptfem.fem3d.elemmatrix.elemmassmat3dp1(v) Computes the element mass matrix M e (T ) for a given tetrahedron T of volume T 5.2. Element matrix (used by base and OptV1 versions) 67
72 Parameters V (float) volume of the tetrahedron. Returns 4 4 numpy array of floats Element Stiffness Matrix The element stiffness matrix, S e (T ), for the T is defined by S e i,j(t ) = < φ i (q), φ j (q) > dq, (i, j) {1, 2, 3, 4} 2 T Note: source code pyoptfem.fem3d.elemmatrix.elemstiffmat3dp1(ql, volume) Computes the element stiffness matrix S e (T ) for a given tetrahedron T Parameters Returns Type ql (2 4 numpy array) the four vertices of the tetrahedron, volume (float) volume of the tetrahedron. 4 4 numpy array of floats Element Elastic Stiffness Matrix The element elastic stiffness matrix, K e (T ), for a given tetrahedron T in the local alternate basis B a is defined by K e i,j(t ) = ε( ψ j ) t (q)hε( ψ i )(q) dq, (i, j) {1,..., 12} 2. T We also have K e (T ) = 1 4 T Bt HB where H is the elasticity tensor and B is a 6 12 matrix defined by B = ( ε( ψ 1 ) ε( ψ 2 )... ε( ψ 11 ) ε( ψ 12 ) ) 68 Chapter 5. FEM3D module
73 So in B a basis we obtain φ 1 φ x x 0 0 φ 0 1 φ y y 0 φ φ B = z z φ 1 φ 1 φ y x φ 4 y x 0 φ 0 1 φ 1 z φ 1 z 0 y 0 φ 1 x φ 4 z φ 4 z 0 φ 4 y φ 4 x Note: source code pyoptfem.fem3d.elemmatrix.elemstiffelasmatba3dp1(ql, V, C) Returns the element elastic stiffness matrix K e (T ) for a given tetrahedron T in the local alternate basis B a Parameters ql (4 2 numpy array) contains the four vertices of the tetrahedron, V (float) volume of the tetrahedron H (6 6 numpy array) Elasticity tensor, H. Returns K e (T ) in B a basis. Type numpy array of floats. The element elastic stiffness matrix, K e (T ), for a given triangle T in the local block basis B b is defined by K e i,j(t ) = ε( φ j ) t (q)hε( φ i )(q) dq, (i, j) {1,..., 6} 2. T We also have K e (T ) = 1 4 T Bt HB where H is the elasticity tensor and B is a 6 12 matrix defined by ( B = ε( φ 1 ). ε( φ 2 )... ε( φ 11 ) ). ε( φ 12 ) So in B b basis we obtain φ 1 φ x... 4 x φ φ y... 4 y φ φ B = z... 4 z φ 1 φ y... 4 φ 1 φ y x... 4 x φ φ z... 4 φ 1 φ z y... 4 y φ 1 φ z... 4 φ z φ x... 4 x Note: source code 5.2. Element matrix (used by base and OptV1 versions) 69
74 pyoptfem.fem3d.elemmatrix.elemstiffelasmatbb3dp1(ql, V, C) Returns the element elastic stiffness matrix K e (T ) for a given tetrahedron T in the local block basis B b Parameters ql (4 2 numpy array) contains the four vertices of the tetrahedron, V (float) volume of the tetrahedron H (6 6 numpy array) Elasticity tensor, H. Returns K e (T ) in B b basis. Type numpy array of floats. 5.3 Vectorized tools (used by OptV2 version) Vectorized computation of basis functions gradients By construction, the gradients of basis functions are constants on each element T k. So, we denote, α {1,..., 4}, by G α the 3 n me array defined, k {1,..., n me }, by On T k tetrahedra we set G α (:, k) = φ me(α,k) (q), q T k. D 12 = q me(1,k) q me(2,k), D 23 = q me(2,k) q me(3,k) D 13 = q me(1,k) q me(3,k), D 24 = q me(2,k) q me(4,k) D 14 = q me(1,k) q me(4,k), D 34 = q me(3,k) q me(4,k) Then, we have φ k 1(q) = 1 6 T k φ k 3(q) = 1 6 T k D 23 y D 24 z D 24 y z + D 23 D 23 x D 24 z D 23 z D 24 x x D 24 y + D 23 y D 24 x D 23 D 12 y D 14 z D 14 y z + D 12 D 12 x D 14 z D 12 z D 14 x D 12 x D 14 y + D 12 y D 14 x, φ k 2(q) = 1 6 T k, φ k 4(q) = 1 6 T k D 13 y D 14 z D 13 z D 14 y x D 14 z + D 13 z D 14 x D 13 D 13 x D 14 y D 13 y D 14 x D 12 y D 13 z D 12 z D 13 y x D 13 z + D 12 z D 13 x D 12 D 12 x D 13 y D 12 y D 13 x With these formulas, we obtain the vectorized algorithm given in Algorithm 5.4. Algorithm Chapter 5. FEM3D module
75 Figure 5.4: Vectorized algorithm for computation of basis functions gradients in 3d 5.3. Vectorized tools (used by OptV2 version) 71
76 5.4 Vectorized element matrix (used by OptV2 version) Element Mass Matrix We have M e (T ) = T Then with K g definition (see Section New Optimized assembly algorithm (OptV2 version)), we obtain K g (4(i 1) + j, k) = T k 1 + δ i,j 20 1 i, j 4, So the vectorized algorithm for K g computation is simple and given in Algorithm 5.5. Algorithm 5.5 Figure 5.5: Vectorized algorithm for K g associated to 3d Mass matrix Note: pyoptfem.fem3d.elemmatrixvec.elemmassmat3dp1vec(nme, volumes) Computes all the element Mass matrices M e (T k ) for k {0,..., n me 1} Parameters volumes (n me numpy array of floats) volumes of all the mesh elements. Returns a one dimensional numpy array of size 16n me Element Stiffness Matrix We have (α, β) {1,..., 4} 2 S e α,β(t k ) = T k φ k β, φ k α. 72 Chapter 5. FEM3D module
77 Using vectorized algorithm function GRADIENTVEC3D given in Algorithm 5.4, we obtain the vectorized algorithm 5.6 for K g computation for the Stiffness matrix in 3d. Algorithm 5.6 Figure 5.6: Vectorized algorithm for K g associated to 3d Stiffness matrix Note: pyoptfem.fem3d.elemmatrixvec.elemstiffmat3dp1vec(nme, q, me, volumes) Computes all the element stiffness matrices S e (T k ) for k {0,..., n me 1} Parameters nme (int) number of mesh elements, q (3 n q numpy array of floats) mesh vertices, me (4 n me numpy array of integers) mesh connectivity, areas (n me numpy array of floats) areas of all the mesh elements. Returns a one dimensional numpy array of size 9n me Element Elastic Stiffness Matrix We define on the tetrahedron T k the local alternate basis B k a by { ( φ k) ( 0 ) ( 0 ) 1 0, φ k 1, 0, 0 0 φ k 1 Ba k = {ψ k 1,..., ψ k 12} ) =, ( φ k) ( 0 ) ( 0 2 0, φ k 2, φ k 2 ( φ k ) ( 0 ) ( 0 ), φ k 3, 0, 0 φ k 3 ( φ k) ( 0 ) ( 0 ) } 4 0, φ k 4, φ k Vectorized element matrix (used by OptV2 version) 73
78 where φ k α = φ me(α,k). With notations of Presentation, we have (α, β) {1,..., 12} 2 K e α,β(t k ) = ε t (ψ k β)cε(ψ k α)dq = T k H(ψ k β, ψ k α)(q)dq T k with, u = (u 1, u 2, u 3 ) H 1 (Ω) 3, v = (v 1, v 2, v 3 ) H 1 (Ω) 3, by ( γ μ 0 ( 0 0 μ 0 μ 0 λ 0 0 ( μ λ ) u 1, v 1 + ) u 1, v 2 + ) u 1, v 3 + ( 0 λ 0 μ 0 0 ( μ γ 0 ( 0 0 μ μ 0 λ 0 H(u, v) ) = u 2, v 1 + ) u 2, v 2 + ) u 2, v 3 + ( 0 0 λ ( μ λ ( 0 μ 0 μ μ γ ) u 3, v 1 ) u 3, v 2 ) u 3, v 3 where λ and μ are the Lame coefficients and γ = λ + 2μ. For example, we can explicitly compute the first two terms in the first column of K e (T k ) which are given by K e 1,1(T k ) = T k H(ψ k 1, ψ k 1)(q)dq = ( ( φ k) ( T k H 1 φ k) ) 0, 1 0 (q)dq ( 0 0 γ 0 0 ) = T k φ k 1, φ k 1 0 μ μ ( ) = T k γ φk 1 φ k 1 x x + μ( φk 1 φ k 1 y y + φk 1 φ k 1 z z ). and K e 2,1(T k ) = T k H(ψ k 1, ψ k 2)(q)dq = ( ( φ k) ( 0 ) ) T k H 1 0, φ k 1 (q)dq ( μ 0 ) = T k φ k 1, φ k 1 λ = T k (λ + μ) φk 1 x φ k 1 y. Using vectorized algorithm function GRADIENTVEC3D given in Algorithm 5.4, we obtain the vectorized algorithm 5.7 for K g computation for the Elastic Stiffness matrix in 3d. Algorithm 5.7 Figure 5.7: Vectorized algorithm for K g associated to 3d Elastic Stiffness matrix Note: 74 Chapter 5. FEM3D module
79 pyoptfem.fem3d.elemmatrixvec.elemstiffelasmatba3dp1vec(nme, q, me, volumes, la, mu) Computes all the element elastic stiffness matrices K e (T k ) for k {0,..., n me 1} in local alternate basis. Parameters nme (int) number of mesh elements, q ((3,nq) numpy array of floats) mesh vertices, me ((4,nme) numpy array of integers) mesh connectivity, volumes ((nme,) numpy array of floats) volumes of all the mesh elements. la (float) the lambda Lame parameter, mu (float) the mu Lame parameter. Returns a (144*nme,) numpy array of floats. We define on T k the local block basis B k b by { ( φ k) 1 0, 0 ( φ k) 2 0, 0 ( φ k) 3 0, 0 Bb k = {φk 1,..., φ k 12} = ( φ k) ( 0 ) ( 0 ) 4 0, φ k 1, φ k 2, ( 0 ) φ k 3 0 ( 0 ) ( 0 ) ( 0 ) ( 0 ) ( 0 ) }, φ k 4, 0, 0, 0, 0 0 φ k 1 φ k 2 φ k 3 φ k 4 where φ k α = φ me(α,k). For example, using formula (??), we can explicitly compute the first two terms in the first column of K e (T k ) which are given by K e 1,1(T k ) = T k H(φ k 1, φ k 1)(q)dq = ( ( φ k) ( T k H 1 φ k) ) 0, 1 0 (q)dq ( 0 0 γ 0 0 ) = T k φ k 1, φ k 1 0 μ μ ( ) = T k γ φk 1 φ k 1 x x + μ( φk 1 φ k 1 y y + φk 1 φ k 1 z z ). and K e 2,1(T k ) = T k H(φ k 1, φ k 2)(q)dq = ( ( φ k) ( T k H 1 φ k) ) 0, 2 0 (q)dq ( 0 0 γ 0 0 ) = T k φ k 1, φ k 2 0 μ μ ( ) = T k γ φk 1 φ k 2 x x + μ( φk 1 φ k 2 y y + φk 1 φ k 2 z z ). Using vectorized algorithm function GRADIENTVEC3D given in Algorithm 5.4, we obtain the vectorized algorithm 5.8 for K g computation for the Elastic Stiffness matrix in 3d. Algorithm 5.8 Note: pyoptfem.fem3d.elemmatrixvec.elemstiffelasmatbb3dp1vec(nme, q, me, volumes, L, M) Compute all the element elastic stiffness matrices, K e (T k ) for k {0,..., n me 1} in local block basis Vectorized element matrix (used by OptV2 version) 75
80 Figure 5.8: Vectorized algorithm for K g associated to 3d Elastic Stiffness matrix Parameters nme (int) number of mesh elements, q ((3,nq) numpy array of floats) mesh vertices, me ((4,nme) numpy array of integers) mesh connectivity, volumes ((nme,) numpy array of floats) volumes of all the mesh elements. la (float) the lambda Lame parameter, mu (float) the mu Lame parameter. Returns a (144*nme,) numpy array of floats. 5.5 Mesh class pyoptfem.fem3d.mesh.cubemesh(n, **kwargs) Creates meshes of the unit cube [0, 1] 3. Class attributes are : nq, total number of mesh vertices (points), also denoted n q. nme, total number of mesh elements (tetrahedra in 3d), version, mesh structure version, q, Numpy array of vertices coordinates, dimension (nq,3) (version 0) or (3,nq) (version 1). q[j] (version 0) or q[:,j] (version 1) are the three coordinates of the j-th vertex, j {0,.., nq 1} me, Numpy connectivity array, dimension (nme,4) (version 0) or (4,nme) (version 1). me[k] (version 0) or me[:,k] (version 1) are the storage index of the four vertices of the k-th tetrahedron in the array q of vertices coordinates, k {0,..., nme 1}. volumes, Array of mesh elements volumes, (nme,) Numpy array. volumes[k] is the volume of k-th tetrahedron, k in range(0,nme) 76 Chapter 5. FEM3D module
An efficient way to perform the assembly of finite element matrices in vector languages
 An efficient way to perform the assembly of finite element matrices in vector languages François Cuvelier, Caroline Japhet, Gilles Scarella To cite this version: François Cuvelier, Caroline Japhet, Gilles
An efficient way to perform the assembly of finite element matrices in vector languages François Cuvelier, Caroline Japhet, Gilles Scarella To cite this version: François Cuvelier, Caroline Japhet, Gilles
A two-dimensional FE truss program
 A two-dimensional FE truss program 4M020: Design Tools Eindhoven University of Technology Introduction The Matlab program fem2d allows to model and analyze two-dimensional truss structures, where trusses
A two-dimensional FE truss program 4M020: Design Tools Eindhoven University of Technology Introduction The Matlab program fem2d allows to model and analyze two-dimensional truss structures, where trusses
ECE521 W17 Tutorial 1. Renjie Liao & Min Bai
 ECE521 W17 Tutorial 1 Renjie Liao & Min Bai Schedule Linear Algebra Review Matrices, vectors Basic operations Introduction to TensorFlow NumPy Computational Graphs Basic Examples Linear Algebra Review
ECE521 W17 Tutorial 1 Renjie Liao & Min Bai Schedule Linear Algebra Review Matrices, vectors Basic operations Introduction to TensorFlow NumPy Computational Graphs Basic Examples Linear Algebra Review
TMA4220: Programming project - part 1
 TMA4220: Programming project - part 1 TMA4220 - Numerical solution of partial differential equations using the finite element method The programming project will be split into two parts. This is the first
TMA4220: Programming project - part 1 TMA4220 - Numerical solution of partial differential equations using the finite element method The programming project will be split into two parts. This is the first
Practical Information
 MA2501 Numerical Methods Spring 2018 Norwegian University of Science and Technology Department of Mathematical Sciences Semester Project Practical Information This project counts for 30 % of the final
MA2501 Numerical Methods Spring 2018 Norwegian University of Science and Technology Department of Mathematical Sciences Semester Project Practical Information This project counts for 30 % of the final
Finite Element Method in Geotechnical Engineering
 Finite Element Method in Geotechnical Engineering Short Course on + Dynamics Boulder, Colorado January 5-8, 2004 Stein Sture Professor of Civil Engineering University of Colorado at Boulder Contents Steps
Finite Element Method in Geotechnical Engineering Short Course on + Dynamics Boulder, Colorado January 5-8, 2004 Stein Sture Professor of Civil Engineering University of Colorado at Boulder Contents Steps
Sparse Linear Systems. Iterative Methods for Sparse Linear Systems. Motivation for Studying Sparse Linear Systems. Partial Differential Equations
 Sparse Linear Systems Iterative Methods for Sparse Linear Systems Matrix Computations and Applications, Lecture C11 Fredrik Bengzon, Robert Söderlund We consider the problem of solving the linear system
Sparse Linear Systems Iterative Methods for Sparse Linear Systems Matrix Computations and Applications, Lecture C11 Fredrik Bengzon, Robert Söderlund We consider the problem of solving the linear system
Continuum Mechanics and the Finite Element Method
 Continuum Mechanics and the Finite Element Method 1 Assignment 2 Due on March 2 nd @ midnight 2 Suppose you want to simulate this The familiar mass-spring system l 0 l y i X y i x Spring length before/after
Continuum Mechanics and the Finite Element Method 1 Assignment 2 Due on March 2 nd @ midnight 2 Suppose you want to simulate this The familiar mass-spring system l 0 l y i X y i x Spring length before/after
MATERIAL ELASTIC HERRMANN INCOMPRESSIBLE command.
 MATERIAL ELASTIC HERRMANN INCOMPRESSIBLE command Synopsis The MATERIAL ELASTIC HERRMANN INCOMPRESSIBLE command is used to specify the parameters associated with an isotropic, linear elastic material idealization
MATERIAL ELASTIC HERRMANN INCOMPRESSIBLE command Synopsis The MATERIAL ELASTIC HERRMANN INCOMPRESSIBLE command is used to specify the parameters associated with an isotropic, linear elastic material idealization
Scientific Computing I
 Scientific Computing I Module 8: An Introduction to Finite Element Methods Tobias Neckel Winter 2013/2014 Module 8: An Introduction to Finite Element Methods, Winter 2013/2014 1 Part I: Introduction to
Scientific Computing I Module 8: An Introduction to Finite Element Methods Tobias Neckel Winter 2013/2014 Module 8: An Introduction to Finite Element Methods, Winter 2013/2014 1 Part I: Introduction to
Inverse Design (and a lightweight introduction to the Finite Element Method) Stelian Coros
 Inverse Design (and a lightweight introduction to the Finite Element Method) Stelian Coros Computational Design Forward design: direct manipulation of design parameters Level of abstraction Exploration
Inverse Design (and a lightweight introduction to the Finite Element Method) Stelian Coros Computational Design Forward design: direct manipulation of design parameters Level of abstraction Exploration
The Plane Stress Problem
 The Plane Stress Problem Martin Kronbichler Applied Scientific Computing (Tillämpad beräkningsvetenskap) February 2, 2010 Martin Kronbichler (TDB) The Plane Stress Problem February 2, 2010 1 / 24 Outline
The Plane Stress Problem Martin Kronbichler Applied Scientific Computing (Tillämpad beräkningsvetenskap) February 2, 2010 Martin Kronbichler (TDB) The Plane Stress Problem February 2, 2010 1 / 24 Outline
8 A pseudo-spectral solution to the Stokes Problem
 8 A pseudo-spectral solution to the Stokes Problem 8.1 The Method 8.1.1 Generalities We are interested in setting up a pseudo-spectral method for the following Stokes Problem u σu p = f in Ω u = 0 in Ω,
8 A pseudo-spectral solution to the Stokes Problem 8.1 The Method 8.1.1 Generalities We are interested in setting up a pseudo-spectral method for the following Stokes Problem u σu p = f in Ω u = 0 in Ω,
An efficient way to perform the assembly of finite element matrices in Matlab and Octave
 An efficient way to perform the assembly of finite element matrices in and Caroline Japhet, François Cuvelier, Gilles Scarella To cite this version: Caroline Japhet, François Cuvelier, Gilles Scarella.
An efficient way to perform the assembly of finite element matrices in and Caroline Japhet, François Cuvelier, Gilles Scarella To cite this version: Caroline Japhet, François Cuvelier, Gilles Scarella.
As an example we consider the stacking and analysis of a 2-ply symmetric laminate. First we clear the Matlab space and close figures.
 Program Lam 1 Introduction The collection of Matlab command and function files in the package lam allows the stacking and analysis of a laminate. In fact only a representative piece of a laminate is considered,
Program Lam 1 Introduction The collection of Matlab command and function files in the package lam allows the stacking and analysis of a laminate. In fact only a representative piece of a laminate is considered,
NumPy 1.5. open source. Beginner's Guide. v g I. performance, Python based free open source NumPy. An action-packed guide for the easy-to-use, high
 NumPy 1.5 Beginner's Guide An actionpacked guide for the easytouse, high performance, Python based free open source NumPy mathematical library using realworld examples Ivan Idris.; 'J 'A,, v g I open source
NumPy 1.5 Beginner's Guide An actionpacked guide for the easytouse, high performance, Python based free open source NumPy mathematical library using realworld examples Ivan Idris.; 'J 'A,, v g I open source
Scientific Computing WS 2017/2018. Lecture 18. Jürgen Fuhrmann Lecture 18 Slide 1
 Scientific Computing WS 2017/2018 Lecture 18 Jürgen Fuhrmann juergen.fuhrmann@wias-berlin.de Lecture 18 Slide 1 Lecture 18 Slide 2 Weak formulation of homogeneous Dirichlet problem Search u H0 1 (Ω) (here,
Scientific Computing WS 2017/2018 Lecture 18 Jürgen Fuhrmann juergen.fuhrmann@wias-berlin.de Lecture 18 Slide 1 Lecture 18 Slide 2 Weak formulation of homogeneous Dirichlet problem Search u H0 1 (Ω) (here,
The following syntax is used to describe a typical irreducible continuum element:
 ELEMENT IRREDUCIBLE T7P0 command.. Synopsis The ELEMENT IRREDUCIBLE T7P0 command is used to describe all irreducible 7-node enhanced quadratic triangular continuum elements that are to be used in mechanical
ELEMENT IRREDUCIBLE T7P0 command.. Synopsis The ELEMENT IRREDUCIBLE T7P0 command is used to describe all irreducible 7-node enhanced quadratic triangular continuum elements that are to be used in mechanical
Octave. Tutorial. Daniel Lamprecht. March 26, Graz University of Technology. Slides based on previous work by Ingo Holzmann
 Tutorial Graz University of Technology March 26, 2012 Slides based on previous work by Ingo Holzmann Introduction What is? GNU is a high-level interactive language for numerical computations mostly compatible
Tutorial Graz University of Technology March 26, 2012 Slides based on previous work by Ingo Holzmann Introduction What is? GNU is a high-level interactive language for numerical computations mostly compatible
Numerical Modelling in Geosciences. Lecture 1 Introduction and basic mathematics for PDEs
 Numerical Modelling in Geosciences Lecture 1 Introduction and basic mathematics for PDEs Useful information Slides and exercises: download at my homepage: http://www.geoscienze.unipd.it/users/faccenda-manuele
Numerical Modelling in Geosciences Lecture 1 Introduction and basic mathematics for PDEs Useful information Slides and exercises: download at my homepage: http://www.geoscienze.unipd.it/users/faccenda-manuele
Computational Materials Modeling FHLN05 Computer lab
 Motivation Computational Materials Modeling FHLN05 Computer lab In the basic Finite Element (FE) course, the analysis is restricted to materials where the relationship between stress and strain is linear.
Motivation Computational Materials Modeling FHLN05 Computer lab In the basic Finite Element (FE) course, the analysis is restricted to materials where the relationship between stress and strain is linear.
User's Guide. 0 Contents. François Cuvelier December 16, Introduction 2
 User's Guide François Cuvelier December 16, 2017 Abstract This Matlab toolbox uses a simesh object, comming from the fcsimesh toolbox, to display simplicial meshes or datas on simplicial meshes. Its kernel
User's Guide François Cuvelier December 16, 2017 Abstract This Matlab toolbox uses a simesh object, comming from the fcsimesh toolbox, to display simplicial meshes or datas on simplicial meshes. Its kernel
SMCP Documentation. Release Martin S. Andersen and Lieven Vandenberghe
 SMCP Documentation Release 0.4.5 Martin S. Andersen and Lieven Vandenberghe May 18, 2018 Contents 1 Current release 3 2 Future releases 5 3 Availability 7 4 Authors 9 5 Feedback and bug reports 11 5.1
SMCP Documentation Release 0.4.5 Martin S. Andersen and Lieven Vandenberghe May 18, 2018 Contents 1 Current release 3 2 Future releases 5 3 Availability 7 4 Authors 9 5 Feedback and bug reports 11 5.1
Gradient Descent Methods
 Lab 18 Gradient Descent Methods Lab Objective: Many optimization methods fall under the umbrella of descent algorithms. The idea is to choose an initial guess, identify a direction from this point along
Lab 18 Gradient Descent Methods Lab Objective: Many optimization methods fall under the umbrella of descent algorithms. The idea is to choose an initial guess, identify a direction from this point along
Lecture 4 Implementing material models: using usermat.f. Implementing User-Programmable Features (UPFs) in ANSYS ANSYS, Inc.
 Lecture 4 Implementing material models: using usermat.f Implementing User-Programmable Features (UPFs) in ANSYS 1 Lecture overview What is usermat.f used for? Stress, strain and material Jacobian matrix
Lecture 4 Implementing material models: using usermat.f Implementing User-Programmable Features (UPFs) in ANSYS 1 Lecture overview What is usermat.f used for? Stress, strain and material Jacobian matrix
fc-graphics4mesh Matlab toolbox, User's Guide under rhum-ubuntu lts computer
 fc-graphics4mesh Matlab toolbox, User's Guide under rhum-ubuntu-16-04-3lts computer François Cuvelier December 13, 2017 Abstract This Matlab toolbox allows to display simplicial meshes or datas on simplicial
fc-graphics4mesh Matlab toolbox, User's Guide under rhum-ubuntu-16-04-3lts computer François Cuvelier December 13, 2017 Abstract This Matlab toolbox allows to display simplicial meshes or datas on simplicial
Matlab toolbox, User's Guide
 Matlab toolbox, User's Guide François Cuvelier April 20, 2018 Abstract The more Matlab toolbox allows to benchmark functions and much Compiled with Matlab 2017a, with toolboxes fc-bench['dev'] and fc-tools['dev']
Matlab toolbox, User's Guide François Cuvelier April 20, 2018 Abstract The more Matlab toolbox allows to benchmark functions and much Compiled with Matlab 2017a, with toolboxes fc-bench['dev'] and fc-tools['dev']
A FINITE-VOLUME DISCRETIZATION FOR DEFORMATION OF FRACTURED MEDIA
 A FINITE-VOLUME DISCRETIZATION FOR DEFORMATION OF FRACTURED MEDIA Eren Ucar a, Eirik Keilegavlen a, Inga Berre a,b, Jan Martin Nordbotten a,c a Department of Mathematics, University of Bergen, Bergen,
A FINITE-VOLUME DISCRETIZATION FOR DEFORMATION OF FRACTURED MEDIA Eren Ucar a, Eirik Keilegavlen a, Inga Berre a,b, Jan Martin Nordbotten a,c a Department of Mathematics, University of Bergen, Bergen,
Building a finite element program in MATLAB Linear elements in 1d and 2d
 Building a finite element program in MATLAB Linear elements in 1d and 2d D. Peschka TU Berlin Supplemental material for the course Numerische Mathematik 2 für Ingenieure at the Technical University Berlin,
Building a finite element program in MATLAB Linear elements in 1d and 2d D. Peschka TU Berlin Supplemental material for the course Numerische Mathematik 2 für Ingenieure at the Technical University Berlin,
Bake, shake or break - and other applications for the FEM. 5: Do real-life experimentation using your FEM code
 Bake, shake or break - and other applications for the FEM Programming project in TMA4220 - part 2 by Kjetil André Johannessen TMA4220 - Numerical solution of partial differential equations using the finite
Bake, shake or break - and other applications for the FEM Programming project in TMA4220 - part 2 by Kjetil André Johannessen TMA4220 - Numerical solution of partial differential equations using the finite
Iterative Methods for Linear Systems
 Iterative Methods for Linear Systems 1. Introduction: Direct solvers versus iterative solvers In many applications we have to solve a linear system Ax = b with A R n n and b R n given. If n is large the
Iterative Methods for Linear Systems 1. Introduction: Direct solvers versus iterative solvers In many applications we have to solve a linear system Ax = b with A R n n and b R n given. If n is large the
Computational Inelasticity FHLN05. Assignment A non-linear elasto-plastic problem
 Computational Inelasticity FHLN05 Assignment 2017 A non-linear elasto-plastic problem General instructions A written report should be submitted to the Division of Solid Mechanics no later than October
Computational Inelasticity FHLN05 Assignment 2017 A non-linear elasto-plastic problem General instructions A written report should be submitted to the Division of Solid Mechanics no later than October
Content. Department of Mathematics University of Oslo
 Chapter: 1 MEK4560 The Finite Element Method in Solid Mechanics II (January 25, 2008) (E-post:torgeiru@math.uio.no) Page 1 of 14 Content 1 Introduction to MEK4560 3 1.1 Minimum Potential energy..............................
Chapter: 1 MEK4560 The Finite Element Method in Solid Mechanics II (January 25, 2008) (E-post:torgeiru@math.uio.no) Page 1 of 14 Content 1 Introduction to MEK4560 3 1.1 Minimum Potential energy..............................
libsupermesh version 1.0.1
 libsupermesh version 1.0.1 James R. Maddison School of Mathematics and Maxwell Institute for Mathematical Sciences, University of Edinburgh, UK Iakovos Panourgias EPCC, University of Edinburgh, UK, Patrick
libsupermesh version 1.0.1 James R. Maddison School of Mathematics and Maxwell Institute for Mathematical Sciences, University of Edinburgh, UK Iakovos Panourgias EPCC, University of Edinburgh, UK, Patrick
Numerical Solutions to Partial Differential Equations
 Numerical Solutions to Partial Differential Equations Zhiping Li LMAM and School of Mathematical Sciences Peking University Variational Problems of the Dirichlet BVP of the Poisson Equation 1 For the homogeneous
Numerical Solutions to Partial Differential Equations Zhiping Li LMAM and School of Mathematical Sciences Peking University Variational Problems of the Dirichlet BVP of the Poisson Equation 1 For the homogeneous
MATHEMATICAL OBJECTS in
 MATHEMATICAL OBJECTS in Computational Tools in a Unified Object-Oriented Approach Yair Shapira @ CRC Press Taylor & Francis Group Boca Raton London New York CRC Press is an imprint of the Taylor & Francis
MATHEMATICAL OBJECTS in Computational Tools in a Unified Object-Oriented Approach Yair Shapira @ CRC Press Taylor & Francis Group Boca Raton London New York CRC Press is an imprint of the Taylor & Francis
Python & Numpy A tutorial
 Python & Numpy A tutorial Devert Alexandre School of Software Engineering of USTC 13 February 2012 Slide 1/38 Table of Contents 1 Why Python & Numpy 2 First steps with Python 3 Fun with lists 4 Quick tour
Python & Numpy A tutorial Devert Alexandre School of Software Engineering of USTC 13 February 2012 Slide 1/38 Table of Contents 1 Why Python & Numpy 2 First steps with Python 3 Fun with lists 4 Quick tour
Constitutive models. Constitutive model: determines P in terms of deformation
 Constitutive models Constitutive model: determines P in terms of deformation Elastic material: P depends only on current F Hyperelastic material: work is independent of path strain energy density function
Constitutive models Constitutive model: determines P in terms of deformation Elastic material: P depends only on current F Hyperelastic material: work is independent of path strain energy density function
MODELS USING MATRICES WITH PYTHON
 MODELS USING MATRICES WITH PYTHON José M. Garrido Department of Computer Science May 2016 College of Computing and Software Engineering Kennesaw State University c 2015, J. M. Garrido Models Using Matrices
MODELS USING MATRICES WITH PYTHON José M. Garrido Department of Computer Science May 2016 College of Computing and Software Engineering Kennesaw State University c 2015, J. M. Garrido Models Using Matrices
Boundary Value Problems and Iterative Methods for Linear Systems
 Boundary Value Problems and Iterative Methods for Linear Systems 1. Equilibrium Problems 1.1. Abstract setting We want to find a displacement u V. Here V is a complete vector space with a norm v V. In
Boundary Value Problems and Iterative Methods for Linear Systems 1. Equilibrium Problems 1.1. Abstract setting We want to find a displacement u V. Here V is a complete vector space with a norm v V. In
Some improvements of Xfem for cracked domains
 Some improvements of Xfem for cracked domains E. Chahine 1, P. Laborde 2, J. Pommier 1, Y. Renard 3 and M. Salaün 4 (1) INSA Toulouse, laboratoire MIP, CNRS UMR 5640, Complexe scientifique de Rangueil,
Some improvements of Xfem for cracked domains E. Chahine 1, P. Laborde 2, J. Pommier 1, Y. Renard 3 and M. Salaün 4 (1) INSA Toulouse, laboratoire MIP, CNRS UMR 5640, Complexe scientifique de Rangueil,
LibMesh Experience and Usage
 LibMesh Experience and Usage John W. Peterson peterson@cfdlab.ae.utexas.edu Univ. of Texas at Austin January 12, 2007 1 Introduction 2 Weighted Residuals 3 Poisson Equation 4 Other Examples 5 Essential
LibMesh Experience and Usage John W. Peterson peterson@cfdlab.ae.utexas.edu Univ. of Texas at Austin January 12, 2007 1 Introduction 2 Weighted Residuals 3 Poisson Equation 4 Other Examples 5 Essential
Analytical Mechanics: Elastic Deformation
 Analytical Mechanics: Elastic Deformation Shinichi Hirai Dept. Robotics, Ritsumeikan Univ. Shinichi Hirai (Dept. Robotics, Ritsumeikan Univ.) Analytical Mechanics: Elastic Deformation 1 / 60 Agenda Agenda
Analytical Mechanics: Elastic Deformation Shinichi Hirai Dept. Robotics, Ritsumeikan Univ. Shinichi Hirai (Dept. Robotics, Ritsumeikan Univ.) Analytical Mechanics: Elastic Deformation 1 / 60 Agenda Agenda
GETTING STARTED WITH FENICS
 GETTING STARTED WITH FENICS DOUGLAS N. ARNOLD 1. A first program in FEniCS 1.1. The boundary value problem. As a first problem we consider the Neumann boundary value problem: (1) u + u = f in, u = 0 on,
GETTING STARTED WITH FENICS DOUGLAS N. ARNOLD 1. A first program in FEniCS 1.1. The boundary value problem. As a first problem we consider the Neumann boundary value problem: (1) u + u = f in, u = 0 on,
Contents as of 12/8/2017. Preface. 1. Overview...1
 Contents as of 12/8/2017 Preface 1. Overview...1 1.1 Introduction...1 1.2 Finite element data...1 1.3 Matrix notation...3 1.4 Matrix partitions...8 1.5 Special finite element matrix notations...9 1.6 Finite
Contents as of 12/8/2017 Preface 1. Overview...1 1.1 Introduction...1 1.2 Finite element data...1 1.3 Matrix notation...3 1.4 Matrix partitions...8 1.5 Special finite element matrix notations...9 1.6 Finite
Comparative Analysis of Mesh Generators and MIC(0) Preconditioning of FEM Elasticity Systems
 Comparative Analysis of Mesh Generators and MIC(0) Preconditioning of FEM Elasticity Systems Nikola Kosturski and Svetozar Margenov Institute for Parallel Processing, Bulgarian Academy of Sciences Abstract.
Comparative Analysis of Mesh Generators and MIC(0) Preconditioning of FEM Elasticity Systems Nikola Kosturski and Svetozar Margenov Institute for Parallel Processing, Bulgarian Academy of Sciences Abstract.
Using MATLAB and. Abaqus. Finite Element Analysis. Introduction to. Amar Khennane. Taylor & Francis Croup. Taylor & Francis Croup,
 Introduction to Finite Element Analysis Using MATLAB and Abaqus Amar Khennane Taylor & Francis Croup Boca Raton London New York CRC Press is an imprint of the Taylor & Francis Croup, an informa business
Introduction to Finite Element Analysis Using MATLAB and Abaqus Amar Khennane Taylor & Francis Croup Boca Raton London New York CRC Press is an imprint of the Taylor & Francis Croup, an informa business
Fig. 1. Circular fiber and interphase between the fiber and the matrix.
 Finite element unit cell model based on ABAQUS for fiber reinforced composites Tian Tang Composites Manufacturing & Simulation Center, Purdue University West Lafayette, IN 47906 1. Problem Statement In
Finite element unit cell model based on ABAQUS for fiber reinforced composites Tian Tang Composites Manufacturing & Simulation Center, Purdue University West Lafayette, IN 47906 1. Problem Statement In
B553 Lecture 5: Matrix Algebra Review
 B553 Lecture 5: Matrix Algebra Review Kris Hauser January 19, 2012 We have seen in prior lectures how vectors represent points in R n and gradients of functions. Matrices represent linear transformations
B553 Lecture 5: Matrix Algebra Review Kris Hauser January 19, 2012 We have seen in prior lectures how vectors represent points in R n and gradients of functions. Matrices represent linear transformations
Lehrstuhl Informatik V. Lehrstuhl Informatik V. 1. solve weak form of PDE to reduce regularity properties. Lehrstuhl Informatik V
 Part I: Introduction to Finite Element Methods Scientific Computing I Module 8: An Introduction to Finite Element Methods Tobias Necel Winter 4/5 The Model Problem FEM Main Ingredients Wea Forms and Wea
Part I: Introduction to Finite Element Methods Scientific Computing I Module 8: An Introduction to Finite Element Methods Tobias Necel Winter 4/5 The Model Problem FEM Main Ingredients Wea Forms and Wea
B-Spline Interpolation on Lattices
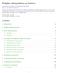 B-Spline Interpolation on Lattices David Eberly, Geometric Tools, Redmond WA 98052 https://www.geometrictools.com/ This work is licensed under the Creative Commons Attribution 4.0 International License.
B-Spline Interpolation on Lattices David Eberly, Geometric Tools, Redmond WA 98052 https://www.geometrictools.com/ This work is licensed under the Creative Commons Attribution 4.0 International License.
AFEM USER GUIDE R. VERFÜRTH
 AFEM USER GUIDE R. VERFÜRTH Contents 1. Introduction 1 2. Installing Scilab 2 3. Installing AFEM 2 4. Using AFEM 3 4.1. Data structures 3 4.2. Start 4 4.3. Help 4 5. Function afem 4 5.1. Overview 4 5.2.
AFEM USER GUIDE R. VERFÜRTH Contents 1. Introduction 1 2. Installing Scilab 2 3. Installing AFEM 2 4. Using AFEM 3 4.1. Data structures 3 4.2. Start 4 4.3. Help 4 5. Function afem 4 5.1. Overview 4 5.2.
Overlapping Schwarz preconditioners for Fekete spectral elements
 Overlapping Schwarz preconditioners for Fekete spectral elements R. Pasquetti 1, L. F. Pavarino 2, F. Rapetti 1, and E. Zampieri 2 1 Laboratoire J.-A. Dieudonné, CNRS & Université de Nice et Sophia-Antipolis,
Overlapping Schwarz preconditioners for Fekete spectral elements R. Pasquetti 1, L. F. Pavarino 2, F. Rapetti 1, and E. Zampieri 2 1 Laboratoire J.-A. Dieudonné, CNRS & Université de Nice et Sophia-Antipolis,
A Glimpse at Scipy FOSSEE. June Abstract This document shows a glimpse of the features of Scipy that will be explored during this course.
 A Glimpse at Scipy FOSSEE June 010 Abstract This document shows a glimpse of the features of Scipy that will be explored during this course. 1 Introduction SciPy is open-source software for mathematics,
A Glimpse at Scipy FOSSEE June 010 Abstract This document shows a glimpse of the features of Scipy that will be explored during this course. 1 Introduction SciPy is open-source software for mathematics,
(Multiscale) Modelling With SfePy
 (Multiscale) Modelling With SfePy Random Remarks... Robert Cimrman & Eduard Rohan & others Department of Mechanics & New Technologies Research Centre University of West Bohemia Plzeň, Czech Republic PANM
(Multiscale) Modelling With SfePy Random Remarks... Robert Cimrman & Eduard Rohan & others Department of Mechanics & New Technologies Research Centre University of West Bohemia Plzeň, Czech Republic PANM
GeoPDEs. An Octave/Matlab software for research on IGA. R. Vázquez. IMATI Enrico Magenes, Pavia Consiglio Nazionale della Ricerca
 GeoPDEs An Octave/Matlab software for research on IGA R. Vázquez IMATI Enrico Magenes, Pavia Consiglio Nazionale della Ricerca Joint work with C. de Falco and A. Reali Supported by the ERC Starting Grant:
GeoPDEs An Octave/Matlab software for research on IGA R. Vázquez IMATI Enrico Magenes, Pavia Consiglio Nazionale della Ricerca Joint work with C. de Falco and A. Reali Supported by the ERC Starting Grant:
3. Numerical integration
 3. Numerical integration... 3. One-dimensional quadratures... 3. Two- and three-dimensional quadratures... 3.3 Exact Integrals for Straight Sided Triangles... 5 3.4 Reduced and Selected Integration...
3. Numerical integration... 3. One-dimensional quadratures... 3. Two- and three-dimensional quadratures... 3.3 Exact Integrals for Straight Sided Triangles... 5 3.4 Reduced and Selected Integration...
2 Getting Started with Numerical Computations in Python
 1 Documentation and Resources * Download: o Requirements: Python, IPython, Numpy, Scipy, Matplotlib o Windows: google "windows download (Python,IPython,Numpy,Scipy,Matplotlib" o Debian based: sudo apt-get
1 Documentation and Resources * Download: o Requirements: Python, IPython, Numpy, Scipy, Matplotlib o Windows: google "windows download (Python,IPython,Numpy,Scipy,Matplotlib" o Debian based: sudo apt-get
Lecture notes Models of Mechanics
 Lecture notes Models of Mechanics Anders Klarbring Division of Mechanics, Linköping University, Sweden Lecture 7: Small deformation theories Klarbring (Mechanics, LiU) Lecture notes Linköping 2012 1 /
Lecture notes Models of Mechanics Anders Klarbring Division of Mechanics, Linköping University, Sweden Lecture 7: Small deformation theories Klarbring (Mechanics, LiU) Lecture notes Linköping 2012 1 /
Chapter Two: Numerical Methods for Elliptic PDEs. 1 Finite Difference Methods for Elliptic PDEs
 Chapter Two: Numerical Methods for Elliptic PDEs Finite Difference Methods for Elliptic PDEs.. Finite difference scheme. We consider a simple example u := subject to Dirichlet boundary conditions ( ) u
Chapter Two: Numerical Methods for Elliptic PDEs Finite Difference Methods for Elliptic PDEs.. Finite difference scheme. We consider a simple example u := subject to Dirichlet boundary conditions ( ) u
Lecture 9 Approximations of Laplace s Equation, Finite Element Method. Mathématiques appliquées (MATH0504-1) B. Dewals, C.
 Lecture 9 Approximations of Laplace s Equation, Finite Element Method Mathématiques appliquées (MATH54-1) B. Dewals, C. Geuzaine V1.2 23/11/218 1 Learning objectives of this lecture Apply the finite difference
Lecture 9 Approximations of Laplace s Equation, Finite Element Method Mathématiques appliquées (MATH54-1) B. Dewals, C. Geuzaine V1.2 23/11/218 1 Learning objectives of this lecture Apply the finite difference
Finite Elements. Colin Cotter. January 18, Colin Cotter FEM
 Finite Elements January 18, 2019 The finite element Given a triangulation T of a domain Ω, finite element spaces are defined according to 1. the form the functions take (usually polynomial) when restricted
Finite Elements January 18, 2019 The finite element Given a triangulation T of a domain Ω, finite element spaces are defined according to 1. the form the functions take (usually polynomial) when restricted
The Virtual Element Method: an introduction with focus on fluid flows
 The Virtual Element Method: an introduction with focus on fluid flows L. Beirão da Veiga Dipartimento di Matematica e Applicazioni Università di Milano-Bicocca VEM people (or group representatives): P.
The Virtual Element Method: an introduction with focus on fluid flows L. Beirão da Veiga Dipartimento di Matematica e Applicazioni Università di Milano-Bicocca VEM people (or group representatives): P.
BECAS - an Open-Source Cross Section Analysis Tool
 BECAS - an Open-Source Cross Section Analysis Tool José P. Blasques and Robert D. Bitsche Presented at DTU Wind Energy stand at the EWEA 2012 conference, Copenhagen, 16.4.2012 BECAS-DTUWind@dtu.dk Motivation
BECAS - an Open-Source Cross Section Analysis Tool José P. Blasques and Robert D. Bitsche Presented at DTU Wind Energy stand at the EWEA 2012 conference, Copenhagen, 16.4.2012 BECAS-DTUWind@dtu.dk Motivation
Sparse Matrices and Iterative Methods
 Sparse Matrices and Iterative Methods K. 1 1 Department of Mathematics 2018 Iterative Methods Consider the problem of solving Ax = b, where A is n n. Why would we use an iterative method? Avoid direct
Sparse Matrices and Iterative Methods K. 1 1 Department of Mathematics 2018 Iterative Methods Consider the problem of solving Ax = b, where A is n n. Why would we use an iterative method? Avoid direct
I. Numerical Computing
 I. Numerical Computing A. Lectures 1-3: Foundations of Numerical Computing Lecture 1 Intro to numerical computing Understand difference and pros/cons of analytical versus numerical solutions Lecture 2
I. Numerical Computing A. Lectures 1-3: Foundations of Numerical Computing Lecture 1 Intro to numerical computing Understand difference and pros/cons of analytical versus numerical solutions Lecture 2
Numerical methods for PDEs FEM convergence, error estimates, piecewise polynomials
 Platzhalter für Bild, Bild auf Titelfolie hinter das Logo einsetzen Numerical methods for PDEs FEM convergence, error estimates, piecewise polynomials Dr. Noemi Friedman Contents of the course Fundamentals
Platzhalter für Bild, Bild auf Titelfolie hinter das Logo einsetzen Numerical methods for PDEs FEM convergence, error estimates, piecewise polynomials Dr. Noemi Friedman Contents of the course Fundamentals
Module III: Partial differential equations and optimization
 Module III: Partial differential equations and optimization Martin Berggren Department of Information Technology Uppsala University Optimization for differential equations Content Martin Berggren (UU)
Module III: Partial differential equations and optimization Martin Berggren Department of Information Technology Uppsala University Optimization for differential equations Content Martin Berggren (UU)
FEniCS Course. Lecture 0: Introduction to FEM. Contributors Anders Logg, Kent-Andre Mardal
 FEniCS Course Lecture 0: Introduction to FEM Contributors Anders Logg, Kent-Andre Mardal 1 / 46 What is FEM? The finite element method is a framework and a recipe for discretization of mathematical problems
FEniCS Course Lecture 0: Introduction to FEM Contributors Anders Logg, Kent-Andre Mardal 1 / 46 What is FEM? The finite element method is a framework and a recipe for discretization of mathematical problems
1 Nonlinear deformation
 NONLINEAR TRUSS 1 Nonlinear deformation When deformation and/or rotation of the truss are large, various strains and stresses can be defined and related by material laws. The material behavior can be expected
NONLINEAR TRUSS 1 Nonlinear deformation When deformation and/or rotation of the truss are large, various strains and stresses can be defined and related by material laws. The material behavior can be expected
Computational Inelasticity FHLN05. Assignment A non-linear elasto-plastic problem
 Computational Inelasticity FHLN05 Assignment 2018 A non-linear elasto-plastic problem General instructions A written report should be submitted to the Division of Solid Mechanics no later than November
Computational Inelasticity FHLN05 Assignment 2018 A non-linear elasto-plastic problem General instructions A written report should be submitted to the Division of Solid Mechanics no later than November
Iterative solution methods and their rate of convergence
 Uppsala University Graduate School in Mathematics and Computing Institute for Information Technology Numerical Linear Algebra FMB and MN Fall 2007 Mandatory Assignment 3a: Iterative solution methods and
Uppsala University Graduate School in Mathematics and Computing Institute for Information Technology Numerical Linear Algebra FMB and MN Fall 2007 Mandatory Assignment 3a: Iterative solution methods and
Algorithms for Scientific Computing
 Algorithms for Scientific Computing Finite Element Methods Michael Bader Technical University of Munich Summer 2016 Part I Looking Back: Discrete Models for Heat Transfer and the Poisson Equation Modelling
Algorithms for Scientific Computing Finite Element Methods Michael Bader Technical University of Munich Summer 2016 Part I Looking Back: Discrete Models for Heat Transfer and the Poisson Equation Modelling
LibMesh Experience and Usage
 LibMesh Experience and Usage John W. Peterson peterson@cfdlab.ae.utexas.edu and Roy H. Stogner roystgnr@cfdlab.ae.utexas.edu Univ. of Texas at Austin September 9, 2008 1 Introduction 2 Weighted Residuals
LibMesh Experience and Usage John W. Peterson peterson@cfdlab.ae.utexas.edu and Roy H. Stogner roystgnr@cfdlab.ae.utexas.edu Univ. of Texas at Austin September 9, 2008 1 Introduction 2 Weighted Residuals
ABHELSINKI UNIVERSITY OF TECHNOLOGY
 ABHELSINKI UNIVERSITY OF TECHNOLOGY TECHNISCHE UNIVERSITÄT HELSINKI UNIVERSITE DE TECHNOLOGIE D HELSINKI A posteriori error analysis for the Morley plate element Jarkko Niiranen Department of Structural
ABHELSINKI UNIVERSITY OF TECHNOLOGY TECHNISCHE UNIVERSITÄT HELSINKI UNIVERSITE DE TECHNOLOGIE D HELSINKI A posteriori error analysis for the Morley plate element Jarkko Niiranen Department of Structural
Lazy matrices for contraction-based algorithms
 Lazy matrices for contraction-based algorithms Michael F. Herbst michael.herbst@iwr.uni-heidelberg.de https://michael-herbst.com Interdisziplinäres Zentrum für wissenschaftliches Rechnen Ruprecht-Karls-Universität
Lazy matrices for contraction-based algorithms Michael F. Herbst michael.herbst@iwr.uni-heidelberg.de https://michael-herbst.com Interdisziplinäres Zentrum für wissenschaftliches Rechnen Ruprecht-Karls-Universität
SOLVING LINEAR SYSTEMS
 SOLVING LINEAR SYSTEMS We want to solve the linear system a, x + + a,n x n = b a n, x + + a n,n x n = b n This will be done by the method used in beginning algebra, by successively eliminating unknowns
SOLVING LINEAR SYSTEMS We want to solve the linear system a, x + + a,n x n = b a n, x + + a n,n x n = b n This will be done by the method used in beginning algebra, by successively eliminating unknowns
Mechanics PhD Preliminary Spring 2017
 Mechanics PhD Preliminary Spring 2017 1. (10 points) Consider a body Ω that is assembled by gluing together two separate bodies along a flat interface. The normal vector to the interface is given by n
Mechanics PhD Preliminary Spring 2017 1. (10 points) Consider a body Ω that is assembled by gluing together two separate bodies along a flat interface. The normal vector to the interface is given by n
Scientific Computing WS 2018/2019. Lecture 15. Jürgen Fuhrmann Lecture 15 Slide 1
 Scientific Computing WS 2018/2019 Lecture 15 Jürgen Fuhrmann juergen.fuhrmann@wias-berlin.de Lecture 15 Slide 1 Lecture 15 Slide 2 Problems with strong formulation Writing the PDE with divergence and gradient
Scientific Computing WS 2018/2019 Lecture 15 Jürgen Fuhrmann juergen.fuhrmann@wias-berlin.de Lecture 15 Slide 1 Lecture 15 Slide 2 Problems with strong formulation Writing the PDE with divergence and gradient
Department of Chemical Engineering University of California, Santa Barbara Spring Exercise 2. Due: Thursday, 4/19/09
 Department of Chemical Engineering ChE 210D University of California, Santa Barbara Spring 2012 Exercise 2 Due: Thursday, 4/19/09 Objective: To learn how to compile Fortran libraries for Python, and to
Department of Chemical Engineering ChE 210D University of California, Santa Barbara Spring 2012 Exercise 2 Due: Thursday, 4/19/09 Objective: To learn how to compile Fortran libraries for Python, and to
LU Factorization. LU factorization is the most common way of solving linear systems! Ax = b LUx = b
 AM 205: lecture 7 Last time: LU factorization Today s lecture: Cholesky factorization, timing, QR factorization Reminder: assignment 1 due at 5 PM on Friday September 22 LU Factorization LU factorization
AM 205: lecture 7 Last time: LU factorization Today s lecture: Cholesky factorization, timing, QR factorization Reminder: assignment 1 due at 5 PM on Friday September 22 LU Factorization LU factorization
Gypsilab : a MATLAB toolbox for FEM-BEM coupling
 Gypsilab : a MATLAB toolbox for FEM-BEM coupling François Alouges, (joint work with Matthieu Aussal) Workshop on Numerical methods for wave propagation and applications Sept. 1st 2017 Facts New numerical
Gypsilab : a MATLAB toolbox for FEM-BEM coupling François Alouges, (joint work with Matthieu Aussal) Workshop on Numerical methods for wave propagation and applications Sept. 1st 2017 Facts New numerical
Higher-Order Compact Finite Element Method
 Higher-Order Compact Finite Element Method Major Qualifying Project Advisor: Professor Marcus Sarkis Amorn Chokchaisiripakdee Worcester Polytechnic Institute Abstract The Finite Element Method (FEM) is
Higher-Order Compact Finite Element Method Major Qualifying Project Advisor: Professor Marcus Sarkis Amorn Chokchaisiripakdee Worcester Polytechnic Institute Abstract The Finite Element Method (FEM) is
Parallel Discontinuous Galerkin Method
 Parallel Discontinuous Galerkin Method Yin Ki, NG The Chinese University of Hong Kong Aug 5, 2015 Mentors: Dr. Ohannes Karakashian, Dr. Kwai Wong Overview Project Goal Implement parallelization on Discontinuous
Parallel Discontinuous Galerkin Method Yin Ki, NG The Chinese University of Hong Kong Aug 5, 2015 Mentors: Dr. Ohannes Karakashian, Dr. Kwai Wong Overview Project Goal Implement parallelization on Discontinuous
The quasi-harmonic approximation (QHA)
 The quasi-harmonic approximation (QHA) M. Palumbo 19/01/2017 Trieste, Italy Limitations of the harmonic approximation E tot(r I, u I )=E tot(r I )+ I,α E tot u u Iα + 1 2 E tot Iα 2 I,α u u Iα u Iα u Jβ
The quasi-harmonic approximation (QHA) M. Palumbo 19/01/2017 Trieste, Italy Limitations of the harmonic approximation E tot(r I, u I )=E tot(r I )+ I,α E tot u u Iα + 1 2 E tot Iα 2 I,α u u Iα u Iα u Jβ
Integration using Gaussian Quadrature
 Integration using Gaussian Quadrature Tutorials November 25, 2017 Department of Aeronautics, Imperial College London, UK Scientific Computing and Imaging Institute, University of Utah, USA 2 Chapter 1
Integration using Gaussian Quadrature Tutorials November 25, 2017 Department of Aeronautics, Imperial College London, UK Scientific Computing and Imaging Institute, University of Utah, USA 2 Chapter 1
A Finite Difference Implementation of Phase Field Theory
 University of Connecticut DigitalCommons@UConn Master's Theses University of Connecticut Graduate School 12-16-2012 A Finite Difference Implementation of Phase Field Theory Nicholas W. Oren University
University of Connecticut DigitalCommons@UConn Master's Theses University of Connecticut Graduate School 12-16-2012 A Finite Difference Implementation of Phase Field Theory Nicholas W. Oren University
Mathematics for Engineers. Numerical mathematics
 Mathematics for Engineers Numerical mathematics Integers Determine the largest representable integer with the intmax command. intmax ans = int32 2147483647 2147483647+1 ans = 2.1475e+09 Remark The set
Mathematics for Engineers Numerical mathematics Integers Determine the largest representable integer with the intmax command. intmax ans = int32 2147483647 2147483647+1 ans = 2.1475e+09 Remark The set
Matrix-Vector Operations
 Week3 Matrix-Vector Operations 31 Opening Remarks 311 Timmy Two Space View at edx Homework 3111 Click on the below link to open a browser window with the Timmy Two Space exercise This exercise was suggested
Week3 Matrix-Vector Operations 31 Opening Remarks 311 Timmy Two Space View at edx Homework 3111 Click on the below link to open a browser window with the Timmy Two Space exercise This exercise was suggested
An exact reanalysis algorithm using incremental Cholesky factorization and its application to crack growth modeling
 INTERNATIONAL JOURNAL FOR NUMERICAL METHODS IN ENGINEERING Int. J. Numer. Meth. Engng 01; 91:158 14 Published online 5 June 01 in Wiley Online Library (wileyonlinelibrary.com). DOI: 10.100/nme.4 SHORT
INTERNATIONAL JOURNAL FOR NUMERICAL METHODS IN ENGINEERING Int. J. Numer. Meth. Engng 01; 91:158 14 Published online 5 June 01 in Wiley Online Library (wileyonlinelibrary.com). DOI: 10.100/nme.4 SHORT
Conjugate-Gradient. Learn about the Conjugate-Gradient Algorithm and its Uses. Descent Algorithms and the Conjugate-Gradient Method. Qx = b.
 Lab 1 Conjugate-Gradient Lab Objective: Learn about the Conjugate-Gradient Algorithm and its Uses Descent Algorithms and the Conjugate-Gradient Method There are many possibilities for solving a linear
Lab 1 Conjugate-Gradient Lab Objective: Learn about the Conjugate-Gradient Algorithm and its Uses Descent Algorithms and the Conjugate-Gradient Method There are many possibilities for solving a linear
CIV-E1060 Engineering Computation and Simulation Examination, December 12, 2017 / Niiranen
 CIV-E16 Engineering Computation and Simulation Examination, December 12, 217 / Niiranen This examination consists of 3 problems rated by the standard scale 1...6. Problem 1 Let us consider a long and tall
CIV-E16 Engineering Computation and Simulation Examination, December 12, 217 / Niiranen This examination consists of 3 problems rated by the standard scale 1...6. Problem 1 Let us consider a long and tall
AMS subject classifications. Primary, 65N15, 65N30, 76D07; Secondary, 35B45, 35J50
 A SIMPLE FINITE ELEMENT METHOD FOR THE STOKES EQUATIONS LIN MU AND XIU YE Abstract. The goal of this paper is to introduce a simple finite element method to solve the Stokes equations. This method is in
A SIMPLE FINITE ELEMENT METHOD FOR THE STOKES EQUATIONS LIN MU AND XIU YE Abstract. The goal of this paper is to introduce a simple finite element method to solve the Stokes equations. This method is in
16.20 HANDOUT #2 Fall, 2002 Review of General Elasticity
 6.20 HANDOUT #2 Fall, 2002 Review of General Elasticity NOTATION REVIEW (e.g., for strain) Engineering Contracted Engineering Tensor Tensor ε x = ε = ε xx = ε ε y = ε 2 = ε yy = ε 22 ε z = ε 3 = ε zz =
6.20 HANDOUT #2 Fall, 2002 Review of General Elasticity NOTATION REVIEW (e.g., for strain) Engineering Contracted Engineering Tensor Tensor ε x = ε = ε xx = ε ε y = ε 2 = ε yy = ε 22 ε z = ε 3 = ε zz =
Image Processing in Numpy
 Version: January 17, 2017 Computer Vision Laboratory, Linköping University 1 Introduction Image Processing in Numpy Exercises During this exercise, you will become familiar with image processing in Python.
Version: January 17, 2017 Computer Vision Laboratory, Linköping University 1 Introduction Image Processing in Numpy Exercises During this exercise, you will become familiar with image processing in Python.
6 Linear Systems of Equations
 6 Linear Systems of Equations Read sections 2.1 2.3, 2.4.1 2.4.5, 2.4.7, 2.7 Review questions 2.1 2.37, 2.43 2.67 6.1 Introduction When numerically solving two-point boundary value problems, the differential
6 Linear Systems of Equations Read sections 2.1 2.3, 2.4.1 2.4.5, 2.4.7, 2.7 Review questions 2.1 2.37, 2.43 2.67 6.1 Introduction When numerically solving two-point boundary value problems, the differential
CVXOPT Documentation. Release 1.2. Martin S. Andersen, Joachim Dahl, and Lieven Vandenberghe
 CVXOPT Documentation Release 1.2 Martin S. Andersen, Joachim Dahl, and Lieven Vandenberghe April 17, 2018 Contents 1 Copyright and License 3 2 Introduction 5 3 Dense and Sparse Matrices 7 3.1 Dense Matrices..............................................
CVXOPT Documentation Release 1.2 Martin S. Andersen, Joachim Dahl, and Lieven Vandenberghe April 17, 2018 Contents 1 Copyright and License 3 2 Introduction 5 3 Dense and Sparse Matrices 7 3.1 Dense Matrices..............................................
Hash tables. Hash tables
 Dictionary Definition A dictionary is a data-structure that stores a set of elements where each element has a unique key, and supports the following operations: Search(S, k) Return the element whose key
Dictionary Definition A dictionary is a data-structure that stores a set of elements where each element has a unique key, and supports the following operations: Search(S, k) Return the element whose key
MATRICES. a m,1 a m,n A =
 MATRICES Matrices are rectangular arrays of real or complex numbers With them, we define arithmetic operations that are generalizations of those for real and complex numbers The general form a matrix of
MATRICES Matrices are rectangular arrays of real or complex numbers With them, we define arithmetic operations that are generalizations of those for real and complex numbers The general form a matrix of
MATERIAL ELASTIC ANISOTROPIC command
 MATERIAL ELASTIC ANISOTROPIC command.. Synopsis The MATERIAL ELASTIC ANISOTROPIC command is used to specify the parameters associated with an anisotropic linear elastic material idealization. Syntax The
MATERIAL ELASTIC ANISOTROPIC command.. Synopsis The MATERIAL ELASTIC ANISOTROPIC command is used to specify the parameters associated with an anisotropic linear elastic material idealization. Syntax The
