SAMPLE. Chapter 8 LOGIC EXERCISE 8A.1 EXERCISE 8A.2
|
|
|
- Lawrence McCoy
- 5 years ago
- Views:
Transcription
1 Chapter 8 LOGIC EXERCISE 8A.1 1 A proposition is a statement whih may e true or false. A proposition is ineterminate if it oes not have the same answer for all people. a proposition, false proposition, false proposition, true proposition, false e proposition, true f proposition, true g a question, so not a proposition h proposition, true i a question, so not a proposition j proposition, false k proposition, ineterminate l a question, so not a proposition m proposition, ineterminate n proposition, ineterminate o proposition, ineterminate (only true when a transversal rosses two parallel lines) p proposition, false 2 a i :p: not all retangles are parallelograms. p is true. i :m: p 5 is a rational numer. m is true. i :r: 7 is an irrational numer. r is true. i :q: = 12 :q is true. e i :r: = 13 r is true. f i :s: The ifferene etween two o s is true. numers is not always even. g i :t: The prout of onseutive integers is t is true. not always even. h i :u: Not all otuse angles are equal. :u is true. i i :p: Not all trapeziums are parallelograms. :p is true. j i :q: Not all triangles with two equal angles are isoseles. q is true. 3 a x > 5 x<3 y > 8 y>10 4 a i No :r: Kania sore 60% or less. i Yes i No :r: Fari is not at soer pratie. i Yes e i No :r: I i not rink lak tea toay. 5 a x 2f1, 2, 3, 4g x<0, x 2 Z x 2fhorses, sheep, goats, eerg x is a female stuent e x is a female non-stuent EXERCISE 8A.2 SAMLE 1 a = f21, 24, 27g = f2, 4, 6, 8, 10g ' ' = f1, 2, 3, 6, 7, 14, 21, 42g
2 174 Mathematial Stuies SL (3r en), Chapter 8 LOGIC 2 a O M O M M O 3 a If is the truth set of p then = f6, 7, 8g. 4 a If is the truth set of p then = f0, 2, 4, 6, 8g ' ' EXERCISE 8B.1 The truth set of :p is 0 = f9, 10, 11, 12, 13, 14g. 1 a p ^ q: Te is a otor an Shelly is a entist. p ^ q: x is greater than 15 an less than 30. p ^ q: It is winy an it is raining. p ^ q: Kim has rown hair an lue eyes. 2 a p is true an q is true, so p ^ q is true. e The truth set of :p is 0 = f1, 3, 5, 7, 9g. p is true ut q is false (as triangles have three sies), so p ^ q is false. p is false (as 39 > 27) an q is false (as 16 < 23), so p ^ q is false. p is true an q is true, so p ^ q is true. p is false (as 5+8=13) an q is true, so p ^ q is false. 3 a The truth set of p ^ q is \ = f2, 4, 6g EXERCISE 8B.2 1 a p _ q: Tim owns a iyle or a sooter. p _ q: x is a multiple of 2 or a multiple of 5. p _ q: Dana stuies hysis or Chemistry. 2 a p is true an q is true, so p _ q is true. p is false (as a right angle has 90 ± ) ut q is true, so p _ q is true. p is false (as 8 < 5) an q is false (as 5 > 0), so p _ q is false. p is true ut q is false (as the mean of 8 an 14 is 11), so p _ q is true. 3 a p Y q: Meryn will visit Japan or Singapore, ut not oth, next year p Y q: Ann will invite Kate or Tray, ut not oth, to her party. p Y q: x is a fator of 56 or 40, ut not oth. SAMLE
3 4 a a is true an is true, so a Y is false. a is false (as 15 is o) an is true, so a Y is true. a is false (as 4:5 is not an integer) an is false (N oes not inlue negative numers), so a Y is false. a is true ut is false (as (2 8 ) 6 =2 8 6 =2 48 ), so a Y is true. 5 r: Kelly is a goo river an s: Kelly has a goo ar. a :r r ^ s :s ^:r r _ s 6 x: Sergio woul like to go swimming tomorrow an y: Sergio woul like to go owling tomorrow. a :x x ^ y x _ y :(x ^ y) e x Y y 7 a p: hillip likes ieream. q: hillip likes jelly. p ^ q: hillip likes ieream an jelly. p: hillip likes ieream. q: hillip likes jelly. p _:q: hillip likes ie ream or hillip oes not like jelly. p: x is greater than 10. q: x is a prime numer. p ^ q: x is oth greater than 10 an a prime numer. e p: The omputer is on. :p: The omputer is not on. f p: Angela has a wath. q: Angela has a moile phone. :p ^ q: Angela oes not have a wath ut oes have a moile phone. g p: Maya stuie Spanish. q: Maya stuie Frenh. p Y q: Maya stuie one of Spanish or Frenh. h p: I an hear thuner. q: I an hear an aeroplane. p _ q: I an hear thuner or an aeroplane. 8 Sine p Y q is false, p an q are either oth true or oth false. If p an q were oth false, then p _ q woul e false. But p _ q is true, so p is true an q is true. 9 a If is the truth set of p, then = f3, 6, 9, 12, 15, 18g. If is the truth set of q, then = f1, 3, 5, 7, 9, 11, 13, 15, 17, 19g. i The truth set of :q is 0 = f2, 4, 6, 8, 10, 12, 14, 16, 18, 20g. The truth set of p _ q is [ = f1, 3, 5, 6, 7, 9, 11, 12, 13, 15, 17, 18, 19g. i The truth set of p ^ q is \ = f3, 9, 15g. Mathematial Stuies SL (3r en), Chapter 8 LOGIC 175 p: Tuan an go to the mountains. q: Tuan an go to the eah. p Y q: Tuan an go to the mountains or to the eah, ut not oth. iv The truth set of p Y q is f1, 5, 6, 7, 11, 12, 13, 17, 18, 19g SAMLE 10 a If is the truth set of p, then = f2, 3, 5, 7, 11g. If is the truth set of q, then = f1, 2, 3, 4, 6, 12g i p ^ q: x is oth prime an a fator of 12. p _ q: x is prime or a fator of 12. i p Y q: x is prime or a fator of 12, ut not oth.
4 176 Mathematial Stuies SL (3r en), Chapter 8 LOGIC i p ^ q has the truth set \ = f2, 3g. p _ q has the truth set [ = f1, 2, 3, 4, 5, 6, 7, 11, 12g. i p Y q has the truth set f1, 4, 5, 6, 7, 11, 12g. 11 a p is false. s is true. q is true an u is true, so q ^ u is true. p is false ut w is true, so p _ w is true. e r is false ut s is true, so r _ s is true. f r is false an s is true, so r ^ s is false. g r is false an s is true, so r Y s is true. h t is false an v is false, so t _ v is false. 12 Let e the truth set of p an e the truth set of q. a p _ q means p or q or oth are true. So we want the region in or or oth, whih is [. :p _ q means :p or q or oth are true. So, p is false, or q is true, or oth. So we want the region in 0 or or oth, whih is 0 [. p Y q means p or q are true ut not oth. So, p is true an q is false, or p is false an q is true. We therefore want the region in ut not, or the region in ut not in. So, ( \ 0 ) [ ( \ 0 ). or p is true, q is true, ut exlue the region where p an q are true. So, ( [ ) \ (( \ ) 0 ) :p ^:q means :p is true an :q is true. So p is false an q is false. We want the region not in an not in, whih is 0 \ 0. SAMLE 13 a The shae region is \, whih is the region in an. So, oth p an q are true, whih is p ^ q. The shae region is the region in or, ut not oth. So, p or q is true, ut not oth, whih is p Y q. The shae region is 0, whih is the region not in. So, p is not true, whih is :p. 14 a The aptain is ol, ut not male. The aptain is ol or male. The aptain is ol. EXERCISE 8C.1 1 a p q :p :p ^ q T T F F T F F F F T T T F F T F p q p Y q :(p Y q) T T F T T F T F F T T F F F F T
5 Mathematial Stuies SL (3r en), Chapter 8 LOGIC 177 p q :p :q :p _:q T T F F F T F F T T F T T F T F F T T T p p _ p T T F F 2 a i p q :p :q :p ^:q T T F F F T F F T F F T T F F F F T T T neither (values in the :p ^:q olumn are neither all true nor all false). i p q p _ q :p (p _ q) _:p T T T F T T F T F T F T T T T F F F T T i p q p Y q p ^ (p Y q) T T F F T F T T F T T F F F F F i p q p ^ q p Y q (p ^ q) ^ (p Y q) T T T F F T F F T F F T F T F F F F F F tautology (values in the (p _ q) _:p olumn are all true). neither (values in the p ^ (p Y q) olumn are neither all true nor all false). logial ontraition (values in the (p ^ q) ^ (p Y q) olumn are all false). 3 a p ^:p is only true if oth p an :p are true at the same time, whih annot our. p :p p ^:p Sine the values in the p ^:p olumn are all false, T F F p ^:p is a logial ontraition. F T F 4 a p :p :(:p) T F T F T F p p ^ p T T F F SAMLE p q :p :p ^ q p _ (:p ^ q) p _ q T T F F T T T F F F T T F T T T T T F F T F F F Sine the truth tale olumns for p an :(:p) are iential, p an :(:p) are logially equivalent. So, :(:p) =p. Sine the truth tale olumns for p an p ^ p are iential, p an p ^ p are logially equivalent. So, p ^ p = p. Sine the truth tale olumns for p _ (:p ^ q) an p _ q are iential, p _ (:p ^ q) an p _ q are logially equivalent. So, p _ (:p ^ q) =p _ q. p q p Y q :(p Y q) :q p Y :q T T F T F T T F T F T F F T T F F F F F F T T T Sine the truth tale olumns for :(p Y q) an p Y :q are iential, :(p Y q) an p Y :q are logially equivalent. So, :(p Y q) =py :q.
6 178 Mathematial Stuies SL (3r en), Chapter 8 LOGIC e p q :p q _:p :(q _:p) :q p _ q :q ^ (p _ q) T T F T F F T F T F F F T T T T F T T T F F T F F F T T F T F F Sine the truth tale olumns for :(q _:p) an :q ^ (p _ q) are iential, :(q _:p) an :q ^ (p _ q) are logially equivalent. So, :(q _:p) =:q ^ (p _ q). f p q :p p _ q :p Y (p _ q) :q p _:q T T F T T F T T F F T T T T F T T T F F F F F T F T T T Sine the truth tale olumns for :p Y (p _ q) an p _:q are iential, :p Y (p _ q) an p _:q are logially equivalent. So, :p Y (p _ q) =p _:q. 5 a p q :p :q :p ^ q p ^:q (:p ^ q) _ (p ^:q) T T F F F F F T F F T F T T F T T F T F T F F T T F F F p Y q is logially equivalent to (:p ^ q) _ (p ^:q). 6 a i p _ q: I like apples or ananas. :(p _ q): I o not like apples or ananas. i :p: I o not like apples. iv :p ^:q: I o not like apples an I o not like ananas. p q p _ q :(p _ q) :p :q :p ^:q T T T F F F F T F T F F T F F T T F T F F F F F T T T T 7 a p q p Y q q ^ (p Y q) (p Y q) _ p T T F F T T F T F T F T T T T F F F F F i p Y q nees only one of p or q true, an not oth. So, 3 6 x 6 7 or x > 2, ut not oth. ) 3 6 x<2 or x>7. From the tale, q ^ (p Y q) nees p false an q true. So, 3 6 x 6 7 is not true, an x > 2 is true. ) x>7 i From the tale, (p Y q) _ p is true when p or q or oth are true. So, 3 6 x 6 7 or x > 2 or oth. ) x > 3 Sine the truth tale olumns for :(p _ q) an :p ^:q are iential, :(p _ q) an :p ^:q are logially equivalent. So, :(p _ q) =:p ^:q. SAMLE 8 a Any tautology has all the values in its truth tale olumn as true, so any two tautologies will have mathing (all true) truth tale olumns. Any logial ontraition has all the values in its truth tale olumn as false, so any two logial ontraitions will have mathing (all false) truth tale olumns. 9 a A logial ontraition has a truth tale olumn of all Fs, so its negation will have all Ts. ) the negation of a logial ontraition is a tautology.
1 a 4 b 14 c 6 d 18. e 11 f 19 g 29 h a = 5 2 = 3 b 3 7 = = 4. c 0 9 = = 9 d = = 17
 Camridge Essentials Mathematis Extension 8 N. Answers N. Answers a 6 d 8 e f 9 g 9 h a + = = = + = 0 9 = 0 + 9 = 9 d + 6 = + 6 = e + = + = f + 8 = + 8 = 0 a d 0 e f 0 g 8 h i j k l 96 x 8 8 0 6 y 6 9 0
Camridge Essentials Mathematis Extension 8 N. Answers N. Answers a 6 d 8 e f 9 g 9 h a + = = = + = 0 9 = 0 + 9 = 9 d + 6 = + 6 = e + = + = f + 8 = + 8 = 0 a d 0 e f 0 g 8 h i j k l 96 x 8 8 0 6 y 6 9 0
MAT 101 Exam 2 Logic (Part I) Fall Circle the correct answer on the following multiple-choice questions.
 Name: MA 101 Exam 2 Logic (Part I) all 2017 Multiple-Choice Questions [5 pts each] Circle the correct answer on the following multiple-choice questions. 1. Which of the following is not a statement? a)
Name: MA 101 Exam 2 Logic (Part I) all 2017 Multiple-Choice Questions [5 pts each] Circle the correct answer on the following multiple-choice questions. 1. Which of the following is not a statement? a)
WUCT121. Discrete Mathematics. Logic. Tutorial Exercises
 WUCT11 Discrete Mathematics Logic Tutorial Exercises 1 Logic Predicate Logic 3 Proofs 4 Set Theory 5 Relations and Functions WUCT11 Logic Tutorial Exercises 1 Section 1: Logic Question1 For each of the
WUCT11 Discrete Mathematics Logic Tutorial Exercises 1 Logic Predicate Logic 3 Proofs 4 Set Theory 5 Relations and Functions WUCT11 Logic Tutorial Exercises 1 Section 1: Logic Question1 For each of the
CSC Discrete Math I, Spring Propositional Logic
 CSC 125 - Discrete Math I, Spring 2017 Propositional Logic Propositions A proposition is a declarative sentence that is either true or false Propositional Variables A propositional variable (p, q, r, s,...)
CSC 125 - Discrete Math I, Spring 2017 Propositional Logic Propositions A proposition is a declarative sentence that is either true or false Propositional Variables A propositional variable (p, q, r, s,...)
Section 1.1: Propositions and Connectives
 Section 1.1: Propositions and Connectives Definition : Proposition: A statement that has exactly one truth value, i.e., either true (T) or false (F). Axiom (or Postulate): A statement about the primitive
Section 1.1: Propositions and Connectives Definition : Proposition: A statement that has exactly one truth value, i.e., either true (T) or false (F). Axiom (or Postulate): A statement about the primitive
1.1 Language and Logic
 c Oksana Shatalov, Fall 2017 1 1.1 Language and Logic Mathematical Statements DEFINITION 1. A proposition is any declarative sentence (i.e. it has both a subject and a verb) that is either true or false,
c Oksana Shatalov, Fall 2017 1 1.1 Language and Logic Mathematical Statements DEFINITION 1. A proposition is any declarative sentence (i.e. it has both a subject and a verb) that is either true or false,
1.1 Language and Logic
 c Oksana Shatalov, Spring 2018 1 1.1 Language and Logic Mathematical Statements DEFINITION 1. A proposition is any declarative sentence (i.e. it has both a subject and a verb) that is either true or false,
c Oksana Shatalov, Spring 2018 1 1.1 Language and Logic Mathematical Statements DEFINITION 1. A proposition is any declarative sentence (i.e. it has both a subject and a verb) that is either true or false,
Zero-Knowledge Protocols
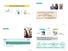 he People Zero-Knowlege Protools 2 he wars Prover (Peggy) Claim I Verifier (Vi) S Seret Deision 2 {true, false} zero-knowlege protool allows Peggy to Convine Vi that her laim is true an that she knows
he People Zero-Knowlege Protools 2 he wars Prover (Peggy) Claim I Verifier (Vi) S Seret Deision 2 {true, false} zero-knowlege protool allows Peggy to Convine Vi that her laim is true an that she knows
Proof by Contradiction
 Proof by Contradiction MAT231 Transition to Higher Mathematics Fall 2014 MAT231 (Transition to Higher Math) Proof by Contradiction Fall 2014 1 / 12 Outline 1 Proving Statements with Contradiction 2 Proving
Proof by Contradiction MAT231 Transition to Higher Mathematics Fall 2014 MAT231 (Transition to Higher Math) Proof by Contradiction Fall 2014 1 / 12 Outline 1 Proving Statements with Contradiction 2 Proving
The following techniques for methods of proofs are discussed in our text: - Vacuous proof - Trivial proof
 Ch. 1.6 Introduction to Proofs The following techniques for methods of proofs are discussed in our text - Vacuous proof - Trivial proof - Direct proof - Indirect proof (our book calls this by contraposition)
Ch. 1.6 Introduction to Proofs The following techniques for methods of proofs are discussed in our text - Vacuous proof - Trivial proof - Direct proof - Indirect proof (our book calls this by contraposition)
Logic Practice 2018 [95 marks]
![Logic Practice 2018 [95 marks] Logic Practice 2018 [95 marks]](/thumbs/82/84976503.jpg) Logic Practice 2018 [95 marks] Consider the following logic propositions. p: Sandi gets up before eight o clock q: Sandi goes for a run r: Sandi goes for a swim 1a. Write down in words the compound proposition
Logic Practice 2018 [95 marks] Consider the following logic propositions. p: Sandi gets up before eight o clock q: Sandi goes for a run r: Sandi goes for a swim 1a. Write down in words the compound proposition
HOMEWORK 1: SOLUTIONS - MATH 215 INSTRUCTOR: George Voutsadakis
 HOMEWORK 1: SOLUTIONS - MATH 215 INSTRUCTOR: George Voutsadakis Problem 1 Make truth tables for the propositional forms (P Q) (P R) and (P Q) (R S). Solution: P Q R P Q P R (P Q) (P R) F F F F F F F F
HOMEWORK 1: SOLUTIONS - MATH 215 INSTRUCTOR: George Voutsadakis Problem 1 Make truth tables for the propositional forms (P Q) (P R) and (P Q) (R S). Solution: P Q R P Q P R (P Q) (P R) F F F F F F F F
Exercise Set 1 Solutions Math 2020 Due: January 30, Find the truth tables of each of the following compound statements.
 1. Find the truth tables of each of the following compound statements. (a) ( (p q)) (p q), p q p q (p q) q p q ( (p q)) (p q) 0 0 0 1 1 1 1 0 1 0 1 0 0 0 1 0 0 1 1 1 1 1 1 1 0 0 1 0 (b) [p ( p q)] [( (p
1. Find the truth tables of each of the following compound statements. (a) ( (p q)) (p q), p q p q (p q) q p q ( (p q)) (p q) 0 0 0 1 1 1 1 0 1 0 1 0 0 0 1 0 0 1 1 1 1 1 1 1 0 0 1 0 (b) [p ( p q)] [( (p
Solutions Manual. Selected odd-numbered problems in. Chapter 2. for. Proof: Introduction to Higher Mathematics. Seventh Edition
 Solutions Manual Seleted odd-numbered problems in Chapter for Proof: Introdution to Higher Mathematis Seventh Edition Warren W. Esty and Norah C. Esty 5 4 3 1 Setion.1. Sentenes with One Variable Chapter
Solutions Manual Seleted odd-numbered problems in Chapter for Proof: Introdution to Higher Mathematis Seventh Edition Warren W. Esty and Norah C. Esty 5 4 3 1 Setion.1. Sentenes with One Variable Chapter
Introduction to Sets and Logic (MATH 1190)
 Introduction to Sets Logic () Instructor: Email: shenlili@yorku.ca Department of Mathematics Statistics York University Sept 18, 2014 Outline 1 2 Tautologies Definition A tautology is a compound proposition
Introduction to Sets Logic () Instructor: Email: shenlili@yorku.ca Department of Mathematics Statistics York University Sept 18, 2014 Outline 1 2 Tautologies Definition A tautology is a compound proposition
8. Given a rational number r, prove that there exist coprime integers p and q, with q 0, so that r = p q. . For all n N, f n = an b n 2
 MATH 135: Randomized Exam Practice Problems These are the warm-up exercises and recommended problems taken from all the extra practice sets presented in random order. The challenge problems have not been
MATH 135: Randomized Exam Practice Problems These are the warm-up exercises and recommended problems taken from all the extra practice sets presented in random order. The challenge problems have not been
5. Use a truth table to determine whether the two statements are equivalent. Let t be a tautology and c be a contradiction.
 Statements Compounds and Truth Tables. Statements, Negations, Compounds, Conjunctions, Disjunctions, Truth Tables, Logical Equivalence, De Morgan s Law, Tautology, Contradictions, Proofs with Logical Equivalent
Statements Compounds and Truth Tables. Statements, Negations, Compounds, Conjunctions, Disjunctions, Truth Tables, Logical Equivalence, De Morgan s Law, Tautology, Contradictions, Proofs with Logical Equivalent
Logical Operators. Conjunction Disjunction Negation Exclusive Or Implication Biconditional
 Logical Operators Conjunction Disjunction Negation Exclusive Or Implication Biconditional 1 Statement meaning p q p implies q if p, then q if p, q when p, q whenever p, q q if p q when p q whenever p p
Logical Operators Conjunction Disjunction Negation Exclusive Or Implication Biconditional 1 Statement meaning p q p implies q if p, then q if p, q when p, q whenever p, q q if p q when p q whenever p p
PROPOSITIONAL CALCULUS
 PROPOSITIONAL CALCULUS A proposition is a complete declarative sentence that is either TRUE (truth value T or 1) or FALSE (truth value F or 0), but not both. These are not propositions! Connectives and
PROPOSITIONAL CALCULUS A proposition is a complete declarative sentence that is either TRUE (truth value T or 1) or FALSE (truth value F or 0), but not both. These are not propositions! Connectives and
CHAPTER 1 - LOGIC OF COMPOUND STATEMENTS
 CHAPTER 1 - LOGIC OF COMPOUND STATEMENTS 1.1 - Logical Form and Logical Equivalence Definition. A statement or proposition is a sentence that is either true or false, but not both. ex. 1 + 2 = 3 IS a statement
CHAPTER 1 - LOGIC OF COMPOUND STATEMENTS 1.1 - Logical Form and Logical Equivalence Definition. A statement or proposition is a sentence that is either true or false, but not both. ex. 1 + 2 = 3 IS a statement
Chapter 9. There are 7 out of 50 measurements that are greater than or equal to 5.1; therefore, the fraction of the
 Pratie questions 6 1 a y i = 6 µ = = 1 i = 1 y i µ i = 1 ( ) = 95 = s n 95 555. x i f i 1 1+ + 5+ n + 5 5 + n µ = = = f 11+ n 11+ n i 7 + n = 5 + n = 6n n = a Time (minutes) 1.6.1.6.1.6.1.6 5.1 5.6 6.1
Pratie questions 6 1 a y i = 6 µ = = 1 i = 1 y i µ i = 1 ( ) = 95 = s n 95 555. x i f i 1 1+ + 5+ n + 5 5 + n µ = = = f 11+ n 11+ n i 7 + n = 5 + n = 6n n = a Time (minutes) 1.6.1.6.1.6.1.6 5.1 5.6 6.1
CS 2740 Knowledge Representation. Lecture 4. Propositional logic. CS 2740 Knowledge Representation. Administration
 Lecture 4 Propositional logic Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square dministration Homework assignment 1 is out Due next week on Wednesday, September 17 Problems: LISP programming a PL
Lecture 4 Propositional logic Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square dministration Homework assignment 1 is out Due next week on Wednesday, September 17 Problems: LISP programming a PL
MATH 225: Foundations of Higher Matheamatics. Dr. Morton. 3.4: Proof by Cases
 MATH 225: Foundations of Higher Matheamatics Dr. Morton 3.4: Proof y Cases Chapter 3 handout page 12 prolem 21: Prove that for all real values of y, the following inequality holds: 7 2y + 2 2y 5 7. You
MATH 225: Foundations of Higher Matheamatics Dr. Morton 3.4: Proof y Cases Chapter 3 handout page 12 prolem 21: Prove that for all real values of y, the following inequality holds: 7 2y + 2 2y 5 7. You
Mathematical Reasoning (Part I) 1
 c Oksana Shatalov, Spring 2017 1 Mathematical Reasoning (art I) 1 Statements DEFINITION 1. A statement is any declarative sentence 2 that is either true or false, but not both. A statement cannot be neither
c Oksana Shatalov, Spring 2017 1 Mathematical Reasoning (art I) 1 Statements DEFINITION 1. A statement is any declarative sentence 2 that is either true or false, but not both. A statement cannot be neither
Compound Propositions
 Discrete Structures Compound Propositions Producing new propositions from existing propositions. Logical Operators or Connectives 1. Not 2. And 3. Or 4. Exclusive or 5. Implication 6. Biconditional Truth
Discrete Structures Compound Propositions Producing new propositions from existing propositions. Logical Operators or Connectives 1. Not 2. And 3. Or 4. Exclusive or 5. Implication 6. Biconditional Truth
EECS 1028 M: Discrete Mathematics for Engineers
 EECS 1028 M: Discrete Mathematics for Engineers Suprakash Datta Office: LAS 3043 Course page: http://www.eecs.yorku.ca/course/1028 Also on Moodle S. Datta (York Univ.) EECS 1028 W 18 1 / 26 Why Study Logic?
EECS 1028 M: Discrete Mathematics for Engineers Suprakash Datta Office: LAS 3043 Course page: http://www.eecs.yorku.ca/course/1028 Also on Moodle S. Datta (York Univ.) EECS 1028 W 18 1 / 26 Why Study Logic?
MATH 215 DISCRETE MATHEMATICS INSTRUCTOR: P. WENG
 MATH 215 DISCRETE MATHEMATICS INSTRUCTOR: P. WENG Suggested Problems for Sets and Functions The following problems are from Discrete Mathematics and Its Applications by Kenneth H. Rosen. 1. Define the
MATH 215 DISCRETE MATHEMATICS INSTRUCTOR: P. WENG Suggested Problems for Sets and Functions The following problems are from Discrete Mathematics and Its Applications by Kenneth H. Rosen. 1. Define the
SETS. Chapter Overview
 Chapter 1 SETS 1.1 Overview This chapter deals with the concept of a set, operations on sets.concept of sets will be useful in studying the relations and functions. 1.1.1 Set and their representations
Chapter 1 SETS 1.1 Overview This chapter deals with the concept of a set, operations on sets.concept of sets will be useful in studying the relations and functions. 1.1.1 Set and their representations
Discrete Mathematics and Its Applications
 Discrete Mathematics and Its Applications Lecture 1: Proposition logic MING GAO DASE @ ECNU (for course related communications) mgao@dase.ecnu.edu.cn Sep. 12, 2017 Outline 1 Propositions 2 Connectives
Discrete Mathematics and Its Applications Lecture 1: Proposition logic MING GAO DASE @ ECNU (for course related communications) mgao@dase.ecnu.edu.cn Sep. 12, 2017 Outline 1 Propositions 2 Connectives
The statement calculus and logic
 Chapter 2 Contrariwise, continued Tweedledee, if it was so, it might be; and if it were so, it would be; but as it isn t, it ain t. That s logic. Lewis Carroll You will have encountered several languages
Chapter 2 Contrariwise, continued Tweedledee, if it was so, it might be; and if it were so, it would be; but as it isn t, it ain t. That s logic. Lewis Carroll You will have encountered several languages
Midterm: Sample 3. ECS20 (Fall 2017) 1) Using truth tables, establish for each of the two propositions below if it is a tautology, a contradiction
 Midterm: Sample 3 ECS20 (Fall 2017) Part I: logic 1) Using truth tables, establish for each of the two propositions below if it is a tautology, a contradiction or neither. 1) [p (q r)] [((r p) q) q] Let
Midterm: Sample 3 ECS20 (Fall 2017) Part I: logic 1) Using truth tables, establish for each of the two propositions below if it is a tautology, a contradiction or neither. 1) [p (q r)] [((r p) q) q] Let
MATH 114 Fall 2004 Solutions to practice problems for Final Exam
 MATH 11 Fall 00 Solutions to practice problems for Final Exam Reminder: the final exam is on Monday, December 13 from 11am - 1am. Office hours: Thursday, December 9 from 1-5pm; Friday, December 10 from
MATH 11 Fall 00 Solutions to practice problems for Final Exam Reminder: the final exam is on Monday, December 13 from 11am - 1am. Office hours: Thursday, December 9 from 1-5pm; Friday, December 10 from
radical symbol 1 Use a Calculator to Find Square Roots 2 Find Side Lengths
 Page 1 of 5 10.1 Simplifying Square Roots Goal Simplify square roots. Key Words radial radiand Square roots are written with a radial symbol m. An epression written with a radial symbol is alled a radial
Page 1 of 5 10.1 Simplifying Square Roots Goal Simplify square roots. Key Words radial radiand Square roots are written with a radial symbol m. An epression written with a radial symbol is alled a radial
2. Properties of Functions
 2. PROPERTIES OF FUNCTIONS 111 2. Properties of Funtions 2.1. Injetions, Surjetions, an Bijetions. Definition 2.1.1. Given f : A B 1. f is one-to-one (short han is 1 1) or injetive if preimages are unique.
2. PROPERTIES OF FUNCTIONS 111 2. Properties of Funtions 2.1. Injetions, Surjetions, an Bijetions. Definition 2.1.1. Given f : A B 1. f is one-to-one (short han is 1 1) or injetive if preimages are unique.
Review. Propositions, propositional operators, truth tables. Logical Equivalences. Tautologies & contradictions
 Review Propositions, propositional operators, truth tables Logical Equivalences. Tautologies & contradictions Some common logical equivalences Predicates & quantifiers Some logical equivalences involving
Review Propositions, propositional operators, truth tables Logical Equivalences. Tautologies & contradictions Some common logical equivalences Predicates & quantifiers Some logical equivalences involving
PSU MATH RELAYS LOGIC & SET THEORY 2017
 PSU MATH RELAYS LOGIC & SET THEORY 2017 MULTIPLE CHOICE. There are 40 questions. Select the letter of the most appropriate answer and SHADE in the corresponding region of the answer sheet. If the correct
PSU MATH RELAYS LOGIC & SET THEORY 2017 MULTIPLE CHOICE. There are 40 questions. Select the letter of the most appropriate answer and SHADE in the corresponding region of the answer sheet. If the correct
STRATEGIES OF PROBLEM SOLVING
 STRATEGIES OF PROBLEM SOLVING Second Edition Maria Nogin Department of Mathematics College of Science and Mathematics California State University, Fresno 2014 2 Chapter 1 Introduction Solving mathematical
STRATEGIES OF PROBLEM SOLVING Second Edition Maria Nogin Department of Mathematics College of Science and Mathematics California State University, Fresno 2014 2 Chapter 1 Introduction Solving mathematical
7 Algebra. 7.1 Manipulation of rational expressions. 5x x x x 2 y x xy y. x +1. 2xy. 13x
 7 Algera 7.1 Manipulation of rational expressions Exercise 7A 1 a x y + 8 x 7x + c 1x + 5 15 5x -10 e xy - 8 y f x + 1 g -7x - 5 h - x i xy j x - x 10 k 1 6 l 1 x m 1 n o 1x + 7 10 p x + a 7x + 9 (x +1)(x
7 Algera 7.1 Manipulation of rational expressions Exercise 7A 1 a x y + 8 x 7x + c 1x + 5 15 5x -10 e xy - 8 y f x + 1 g -7x - 5 h - x i xy j x - x 10 k 1 6 l 1 x m 1 n o 1x + 7 10 p x + a 7x + 9 (x +1)(x
Final Exam Study Guide and Practice Problems Solutions
 Final Exam Stuy Guie an Practice Problems Solutions Note: These problems are just some of the types of problems that might appear on the exam. However, to fully prepare for the exam, in aition to making
Final Exam Stuy Guie an Practice Problems Solutions Note: These problems are just some of the types of problems that might appear on the exam. However, to fully prepare for the exam, in aition to making
Unit 6 Logic Math 116
 Unit 6 Logic Math 116 Logic Unit Statement: A group words or symbols that can be classified as true or false. Examples of statements Violets are blue Five is a natural number I like Algebra 3 + 7 = 10
Unit 6 Logic Math 116 Logic Unit Statement: A group words or symbols that can be classified as true or false. Examples of statements Violets are blue Five is a natural number I like Algebra 3 + 7 = 10
COT 2104 Homework Assignment 1 (Answers)
 1) Classify true or false COT 2104 Homework Assignment 1 (Answers) a) 4 2 + 2 and 7 < 50. False because one of the two statements is false. b) 4 = 2 + 2 7 < 50. True because both statements are true. c)
1) Classify true or false COT 2104 Homework Assignment 1 (Answers) a) 4 2 + 2 and 7 < 50. False because one of the two statements is false. b) 4 = 2 + 2 7 < 50. True because both statements are true. c)
Direct Proof Divisibility
 Direct Proof Divisibility Lecture 15 Section 4.3 Robb T. Koether Hampden-Sydney College Fri, Feb 7, 2014 Robb T. Koether (Hampden-Sydney College) Direct Proof Divisibility Fri, Feb 7, 2014 1 / 23 1 Divisibility
Direct Proof Divisibility Lecture 15 Section 4.3 Robb T. Koether Hampden-Sydney College Fri, Feb 7, 2014 Robb T. Koether (Hampden-Sydney College) Direct Proof Divisibility Fri, Feb 7, 2014 1 / 23 1 Divisibility
https://vu5.sfc.keio.ac.jp/slide/
 1 FUNDAMENTALS OF LOGIC NO.2 PROPOSITION AND TRUTH VALUE Tatsuya Hagino hagino@sfc.keio.ac.jp lecture URL https://vu5.sfc.keio.ac.jp/slide/ Proposition A Proposition is a statement of which truth does
1 FUNDAMENTALS OF LOGIC NO.2 PROPOSITION AND TRUTH VALUE Tatsuya Hagino hagino@sfc.keio.ac.jp lecture URL https://vu5.sfc.keio.ac.jp/slide/ Proposition A Proposition is a statement of which truth does
Math.3336: Discrete Mathematics. Propositional Equivalences
 Math.3336: Discrete Mathematics Propositional Equivalences Instructor: Dr. Blerina Xhabli Department of Mathematics, University of Houston https://www.math.uh.edu/ blerina Email: blerina@math.uh.edu Fall
Math.3336: Discrete Mathematics Propositional Equivalences Instructor: Dr. Blerina Xhabli Department of Mathematics, University of Houston https://www.math.uh.edu/ blerina Email: blerina@math.uh.edu Fall
Mat 243 Exam 1 Review
 OBJECTIVES (Review problems: on next page) 1.1 Distinguish between propositions and non-propositions. Know the truth tables (i.e., the definitions) of the logical operators,,,, and Write truth tables for
OBJECTIVES (Review problems: on next page) 1.1 Distinguish between propositions and non-propositions. Know the truth tables (i.e., the definitions) of the logical operators,,,, and Write truth tables for
2. Find all combinations of truth values for p, q and r for which the statement p (q (p r)) is true.
 1 Logic Questions 1. Suppose that the statement p q is false. Find all combinations of truth values of r and s for which ( q r) ( p s) is true. 2. Find all combinations of truth values for p, q and r for
1 Logic Questions 1. Suppose that the statement p q is false. Find all combinations of truth values of r and s for which ( q r) ( p s) is true. 2. Find all combinations of truth values for p, q and r for
Logic and Propositional Calculus
 CHAPTER 4 Logic and Propositional Calculus 4.1 INTRODUCTION Many algorithms and proofs use logical expressions such as: IF p THEN q or If p 1 AND p 2, THEN q 1 OR q 2 Therefore it is necessary to know
CHAPTER 4 Logic and Propositional Calculus 4.1 INTRODUCTION Many algorithms and proofs use logical expressions such as: IF p THEN q or If p 1 AND p 2, THEN q 1 OR q 2 Therefore it is necessary to know
Chapter 5: Section 5-1 Mathematical Logic
 Chapter 5: Section 5-1 Mathematical Logic D. S. Malik Creighton University, Omaha, NE D. S. Malik Creighton University, Omaha, NE Chapter () 5: Section 5-1 Mathematical Logic 1 / 29 Mathematical Logic
Chapter 5: Section 5-1 Mathematical Logic D. S. Malik Creighton University, Omaha, NE D. S. Malik Creighton University, Omaha, NE Chapter () 5: Section 5-1 Mathematical Logic 1 / 29 Mathematical Logic
Lecture Note 2. 1 Bonferroni Principle. 1.1 Idea. 1.2 Want. Material covered today is from Chapter 1 and chapter 4
 Lecture Note 2 Material covere toay is from Chapter an chapter 4 Bonferroni Principle. Iea Get an iea the frequency of events when things are ranom billion = 0 9 Each person has a % chance to stay in a
Lecture Note 2 Material covere toay is from Chapter an chapter 4 Bonferroni Principle. Iea Get an iea the frequency of events when things are ranom billion = 0 9 Each person has a % chance to stay in a
Propositional Calculus. Problems. Propositional Calculus 3&4. 1&2 Propositional Calculus. Johnson will leave the cabinet, and we ll lose the election.
 1&2 Propositional Calculus Propositional Calculus Problems Jim Woodcock University of York October 2008 1. Let p be it s cold and let q be it s raining. Give a simple verbal sentence which describes each
1&2 Propositional Calculus Propositional Calculus Problems Jim Woodcock University of York October 2008 1. Let p be it s cold and let q be it s raining. Give a simple verbal sentence which describes each
Sec$on Summary. Tautologies, Contradictions, and Contingencies. Logical Equivalence. Normal Forms (optional, covered in exercises in text)
 Section 1.3 1 Sec$on Summary Tautologies, Contradictions, and Contingencies. Logical Equivalence Important Logical Equivalences Showing Logical Equivalence Normal Forms (optional, covered in exercises
Section 1.3 1 Sec$on Summary Tautologies, Contradictions, and Contingencies. Logical Equivalence Important Logical Equivalences Showing Logical Equivalence Normal Forms (optional, covered in exercises
Homework 3: Solutions
 Homework 3: Solutions ECS 20 (Fall 2014) Patrice Koehl koehl@cs.ucdavis.edu October 16, 2014 Exercise 1 Show that this implication is a tautology, by using a table of truth: [(p q) (p r) (q r)] r. p q
Homework 3: Solutions ECS 20 (Fall 2014) Patrice Koehl koehl@cs.ucdavis.edu October 16, 2014 Exercise 1 Show that this implication is a tautology, by using a table of truth: [(p q) (p r) (q r)] r. p q
2/2/2018. CS 103 Discrete Structures. Chapter 1. Propositional Logic. Chapter 1.1. Propositional Logic
 CS 103 Discrete Structures Chapter 1 Propositional Logic Chapter 1.1 Propositional Logic 1 1.1 Propositional Logic Definition: A proposition :is a declarative sentence (that is, a sentence that declares
CS 103 Discrete Structures Chapter 1 Propositional Logic Chapter 1.1 Propositional Logic 1 1.1 Propositional Logic Definition: A proposition :is a declarative sentence (that is, a sentence that declares
Knowledge Representation. Propositional logic
 CS 2710 Foundations of AI Lecture 10 Knowledge Representation. Propositional logic Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square Knowledge-based agent Knowledge base Inference engine Knowledge
CS 2710 Foundations of AI Lecture 10 Knowledge Representation. Propositional logic Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square Knowledge-based agent Knowledge base Inference engine Knowledge
Recall that the expression x > 3 is not a proposition. Why?
 Predicates and Quantifiers Predicates and Quantifiers 1 Recall that the expression x > 3 is not a proposition. Why? Notation: We will use the propositional function notation to denote the expression "
Predicates and Quantifiers Predicates and Quantifiers 1 Recall that the expression x > 3 is not a proposition. Why? Notation: We will use the propositional function notation to denote the expression "
Equations and Solutions
 Section 2.1 Solving Equations: The Addition Principle 1 Equations and Solutions ESSENTIALS An equation is a number sentence that says that the expressions on either side of the equals sign, =, represent
Section 2.1 Solving Equations: The Addition Principle 1 Equations and Solutions ESSENTIALS An equation is a number sentence that says that the expressions on either side of the equals sign, =, represent
Full file at
 1 Logic and Proofs 1.1 Propositions and Connectives 1. (a) true (b) false (c) true (d) false (e) false (f) false (g) false (h) false 2. (a) Not a proposition (b) False proposition (c) Not a proposition.
1 Logic and Proofs 1.1 Propositions and Connectives 1. (a) true (b) false (c) true (d) false (e) false (f) false (g) false (h) false 2. (a) Not a proposition (b) False proposition (c) Not a proposition.
Math 13, Spring 2013, Lecture B: Midterm
 Math 13, Spring 2013, Lecture B: Midterm Name Signature UCI ID # E-mail address Each numbered problem is worth 12 points, for a total of 84 points. Present your work, especially proofs, as clearly as possible.
Math 13, Spring 2013, Lecture B: Midterm Name Signature UCI ID # E-mail address Each numbered problem is worth 12 points, for a total of 84 points. Present your work, especially proofs, as clearly as possible.
1. Given the public RSA encryption key (e, n) = (5, 35), find the corresponding decryption key (d, n).
 MATH 135: Randomized Exam Practice Problems These are the warm-up exercises and recommended problems taken from all the extra practice sets presented in random order. The challenge problems have not been
MATH 135: Randomized Exam Practice Problems These are the warm-up exercises and recommended problems taken from all the extra practice sets presented in random order. The challenge problems have not been
Announcements CompSci 102 Discrete Math for Computer Science
 Announcements CompSci 102 Discrete Math for Computer Science Read for next time Chap. 1.4-1.6 Recitation 1 is tomorrow Homework will be posted by Friday January 19, 2012 Today more logic Prof. Rodger Most
Announcements CompSci 102 Discrete Math for Computer Science Read for next time Chap. 1.4-1.6 Recitation 1 is tomorrow Homework will be posted by Friday January 19, 2012 Today more logic Prof. Rodger Most
Chapter 2: The Logic of Quantified Statements. January 22, 2010
 Chapter 2: The Logic of Quantified Statements January 22, 2010 Outline 1 2.1- Introduction to Predicates and Quantified Statements I 2 2.2 - Introduction to Predicates and Quantified Statements II 3 2.3
Chapter 2: The Logic of Quantified Statements January 22, 2010 Outline 1 2.1- Introduction to Predicates and Quantified Statements I 2 2.2 - Introduction to Predicates and Quantified Statements II 3 2.3
(b) Exercise 3 of Section 1.6 (c) Theorem (d) The PMI, Section 2.4 (e) Theorem (0 Theorem (g) Theorem4.2.2
 16 (HAPTER 1 logic and Proofs ). 3. (h) (i) The fish bite only when the moon is full, A time of 3 minutes, 48 seconds or less is necessary to qualify for the Olympic team. Write the converse and contrapositive
16 (HAPTER 1 logic and Proofs ). 3. (h) (i) The fish bite only when the moon is full, A time of 3 minutes, 48 seconds or less is necessary to qualify for the Olympic team. Write the converse and contrapositive
Part Two: The Basic Components of the SOFL Specification Language
 Part Two: The Basic Components of the SOFL Specification Language SOFL logic Module Condition Data Flow Diagrams Process specification Function definition and specification Process decomposition Other
Part Two: The Basic Components of the SOFL Specification Language SOFL logic Module Condition Data Flow Diagrams Process specification Function definition and specification Process decomposition Other
1 The Well Ordering Principle, Induction, and Equivalence Relations
 1 The Well Ordering Principle, Induction, and Equivalence Relations The set of natural numbers is the set N = f1; 2; 3; : : :g. (Some authors also include the number 0 in the natural numbers, but number
1 The Well Ordering Principle, Induction, and Equivalence Relations The set of natural numbers is the set N = f1; 2; 3; : : :g. (Some authors also include the number 0 in the natural numbers, but number
a + b = b + a and a b = b a. (a + b) + c = a + (b + c) and (a b) c = a (b c). a (b + c) = a b + a c and (a + b) c = a c + b c.
 Properties of the Integers The set of all integers is the set and the subset of Z given by Z = {, 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5, }, N = {0, 1, 2, 3, 4, }, is the set of nonnegative integers (also called
Properties of the Integers The set of all integers is the set and the subset of Z given by Z = {, 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5, }, N = {0, 1, 2, 3, 4, }, is the set of nonnegative integers (also called
Properties of the Integers
 Properties of the Integers The set of all integers is the set and the subset of Z given by Z = {, 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5, }, N = {0, 1, 2, 3, 4, }, is the set of nonnegative integers (also called
Properties of the Integers The set of all integers is the set and the subset of Z given by Z = {, 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5, }, N = {0, 1, 2, 3, 4, }, is the set of nonnegative integers (also called
Tautologies, Contradictions, and Contingencies
 Section 1.3 Tautologies, Contradictions, and Contingencies A tautology is a proposition which is always true. Example: p p A contradiction is a proposition which is always false. Example: p p A contingency
Section 1.3 Tautologies, Contradictions, and Contingencies A tautology is a proposition which is always true. Example: p p A contradiction is a proposition which is always false. Example: p p A contingency
Knowledge Representation. Propositional logic.
 CS 1571 Introduction to AI Lecture 10 Knowledge Representation. Propositional logic. Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square Announcements Homework assignment 3 due today Homework assignment
CS 1571 Introduction to AI Lecture 10 Knowledge Representation. Propositional logic. Milos Hauskrecht milos@cs.pitt.edu 5329 Sennott Square Announcements Homework assignment 3 due today Homework assignment
Solutions to Exercises (Sections )
 s to Exercises (Sections 1.1-1.10) Section 1.1 Exercise 1.1.1: Identifying propositions (a) Have a nice day. : Command, not a proposition. (b) The soup is cold. : Proposition. Negation: The soup is not
s to Exercises (Sections 1.1-1.10) Section 1.1 Exercise 1.1.1: Identifying propositions (a) Have a nice day. : Command, not a proposition. (b) The soup is cold. : Proposition. Negation: The soup is not
Austin is the capital of Texas, and Texas shares a border with Louisiana. is true because p is true and r is true. 2-2 Logic
 Use the following statements and figure to write a compound statement for each conjunction or disjunction. Then find its truth value. Explain your reasoning. p : is the angle bisector of. q: Points C,
Use the following statements and figure to write a compound statement for each conjunction or disjunction. Then find its truth value. Explain your reasoning. p : is the angle bisector of. q: Points C,
2k n. k=0. 3x 2 7 (mod 11) 5 4x 1 (mod 9) 2 r r +1 = r (2 r )
 MATH 135: Randomized Exam Practice Problems These are the warm-up exercises and recommended problems take from the extra practice sets presented in random order. The challenge problems have not been included.
MATH 135: Randomized Exam Practice Problems These are the warm-up exercises and recommended problems take from the extra practice sets presented in random order. The challenge problems have not been included.
Homework assignment 1: Solutions
 Math 240: Discrete Structures I Due 4:30pm Friday 29 September 2017. McGill University, Fall 2017 Hand in to the mailbox at Burnside 1005. Homework assignment 1: Solutions Discussing the assignment with
Math 240: Discrete Structures I Due 4:30pm Friday 29 September 2017. McGill University, Fall 2017 Hand in to the mailbox at Burnside 1005. Homework assignment 1: Solutions Discussing the assignment with
2 Conditional and Biconditional Propositions
 18 FUNDAMENTALS OF MATHEMATICAL LOGIC 2 Conditional and Biconditional Propositions Let p and q be propositions. The implication p! q is the proposition that is false only when p is true and q is false;
18 FUNDAMENTALS OF MATHEMATICAL LOGIC 2 Conditional and Biconditional Propositions Let p and q be propositions. The implication p! q is the proposition that is false only when p is true and q is false;
DISCRETE MATHEMATICS BA202
 TOPIC 1 BASIC LOGIC This topic deals with propositional logic, logical connectives and truth tables and validity. Predicate logic, universal and existential quantification are discussed 1.1 PROPOSITION
TOPIC 1 BASIC LOGIC This topic deals with propositional logic, logical connectives and truth tables and validity. Predicate logic, universal and existential quantification are discussed 1.1 PROPOSITION
Chapter 1: The Logic of Compound Statements. January 7, 2008
 Chapter 1: The Logic of Compound Statements January 7, 2008 Outline 1 1.1 Logical Form and Logical Equivalence 2 1.2 Conditional Statements 3 1.3 Valid and Invalid Arguments Central notion of deductive
Chapter 1: The Logic of Compound Statements January 7, 2008 Outline 1 1.1 Logical Form and Logical Equivalence 2 1.2 Conditional Statements 3 1.3 Valid and Invalid Arguments Central notion of deductive
Recitation 4: Quantifiers and basic proofs
 Math 299 Recitation 4: Quantifiers and basic proofs 1. Quantifiers in sentences are one of the linguistic constructs that are hard for computers to handle in general. Here is a nice pair of example dialogues:
Math 299 Recitation 4: Quantifiers and basic proofs 1. Quantifiers in sentences are one of the linguistic constructs that are hard for computers to handle in general. Here is a nice pair of example dialogues:
Midterm Preparation Problems
 Midterm Preparation Problems The following are practice problems for the Math 1200 Midterm Exam. Some of these may appear on the exam version for your section. To use them well, solve the problems, then
Midterm Preparation Problems The following are practice problems for the Math 1200 Midterm Exam. Some of these may appear on the exam version for your section. To use them well, solve the problems, then
MATH 271 Summer 2016 Practice problem solutions Week 1
 Part I MATH 271 Summer 2016 Practice problem solutions Week 1 For each of the following statements, determine whether the statement is true or false. Prove the true statements. For the false statement,
Part I MATH 271 Summer 2016 Practice problem solutions Week 1 For each of the following statements, determine whether the statement is true or false. Prove the true statements. For the false statement,
RED. Name: Instructor: Pace Nielsen Math 290 Section 1: Winter 2014 Final Exam
 RED Name: Instructor: Pace Nielsen Math 290 Section 1: Winter 2014 Final Exam Note that the first 10 questions are true-false. Mark A for true, B for false. Questions 11 through 20 are multiple choice
RED Name: Instructor: Pace Nielsen Math 290 Section 1: Winter 2014 Final Exam Note that the first 10 questions are true-false. Mark A for true, B for false. Questions 11 through 20 are multiple choice
2-2 Logic ANSWER: A week has seven days, and there are 20 hours in a day. is false, because q is false. 3. ANSWER:
 Use the following statements to write a compound statement for each conjunction or disjunction. Then find its truth value. Explain your reasoning. p : A week has seven days. q: There are 20 hours in a
Use the following statements to write a compound statement for each conjunction or disjunction. Then find its truth value. Explain your reasoning. p : A week has seven days. q: There are 20 hours in a
More examples of mathematical. Lecture 4 ICOM 4075
 More examples of mathematical proofs Lecture 4 ICOM 4075 Proofs by construction A proof by construction is one in which anobjectthat proves the truth value of an statement is built, or found There are
More examples of mathematical proofs Lecture 4 ICOM 4075 Proofs by construction A proof by construction is one in which anobjectthat proves the truth value of an statement is built, or found There are
At least one of us is a knave. What are A and B?
 1. This is a puzzle about an island in which everyone is either a knight or a knave. Knights always tell the truth and knaves always lie. This problem is about two people A and B, each of whom is either
1. This is a puzzle about an island in which everyone is either a knight or a knave. Knights always tell the truth and knaves always lie. This problem is about two people A and B, each of whom is either
Unit 1 Logic Unit Math 114
 Unit 1 Logic Unit Math 114 Section 1.1 Deductive and Induction Reasoning Deductive Reasoning: The application of a general statement to a specific instance. Deductive reasoning goes from general to specific
Unit 1 Logic Unit Math 114 Section 1.1 Deductive and Induction Reasoning Deductive Reasoning: The application of a general statement to a specific instance. Deductive reasoning goes from general to specific
Euler and Hamilton Paths
 Euler an Hamilton Paths The town of Königserg, Prussia (now know as Kaliningra an part of the Russian repuli), was ivie into four setion y ranhes of the Pregel River. These four setions C A D B Figure:
Euler an Hamilton Paths The town of Königserg, Prussia (now know as Kaliningra an part of the Russian repuli), was ivie into four setion y ranhes of the Pregel River. These four setions C A D B Figure:
Methods Higher Tier Practice Paper Unit 1 Markscheme
 Methods Higher Tier Pratie Paper Unit Marksheme GCSE MATHEMATICS LINKED PAIR METHODS FOUNDATION NOTES ON MARKING PRINCIPLES Types of mark M marks: method marks A marks: auray marks B marks: unonditional
Methods Higher Tier Pratie Paper Unit Marksheme GCSE MATHEMATICS LINKED PAIR METHODS FOUNDATION NOTES ON MARKING PRINCIPLES Types of mark M marks: method marks A marks: auray marks B marks: unonditional
Write the negation of each of the following propositions without using any form of the word not :
 Write the negation of each of the following propositions without using any form of the word not : Today is Thursday Today is Monday or Tuesday or Wednesday or Friday or Saturday or Sunday 2 + 1 = 3 2+1
Write the negation of each of the following propositions without using any form of the word not : Today is Thursday Today is Monday or Tuesday or Wednesday or Friday or Saturday or Sunday 2 + 1 = 3 2+1
Section 1.2 Propositional Equivalences. A tautology is a proposition which is always true. A contradiction is a proposition which is always false.
 Section 1.2 Propositional Equivalences A tautology is a proposition which is always true. Classic Example: P P A contradiction is a proposition which is always false. Classic Example: P P A contingency
Section 1.2 Propositional Equivalences A tautology is a proposition which is always true. Classic Example: P P A contradiction is a proposition which is always false. Classic Example: P P A contingency
Chapter 1: Formal Logic
 Chapter 1: Formal Logic Dr. Fang (Daisy) Tang ftang@cpp.edu www.cpp.edu/~ftang/ CS 130 Discrete Structures Logic: The Foundation of Reasoning Definition: the foundation for the organized, careful method
Chapter 1: Formal Logic Dr. Fang (Daisy) Tang ftang@cpp.edu www.cpp.edu/~ftang/ CS 130 Discrete Structures Logic: The Foundation of Reasoning Definition: the foundation for the organized, careful method
Chapter 1 Elementary Logic
 2017-2018 Chapter 1 Elementary Logic The study of logic is the study of the principles and methods used in distinguishing valid arguments from those that are not valid. The aim of this chapter is to help
2017-2018 Chapter 1 Elementary Logic The study of logic is the study of the principles and methods used in distinguishing valid arguments from those that are not valid. The aim of this chapter is to help
2/13/2012. Logic: Truth Tables. CS160 Rosen Chapter 1. Logic?
 Logic: Truth Tables CS160 Rosen Chapter 1 Logic? 1 What is logic? Logic is a truth-preserving system of inference Truth-preserving: If the initial statements are true, the inferred statements will be true
Logic: Truth Tables CS160 Rosen Chapter 1 Logic? 1 What is logic? Logic is a truth-preserving system of inference Truth-preserving: If the initial statements are true, the inferred statements will be true
Chapter 1 Logic Unit Math 114
 Chapter 1 Logic Unit Math 114 Section 1.1 Deductive and Induction Reasoning Statements Definition: A statement is a group of words or symbols that can be classified as true or false. Examples of statements
Chapter 1 Logic Unit Math 114 Section 1.1 Deductive and Induction Reasoning Statements Definition: A statement is a group of words or symbols that can be classified as true or false. Examples of statements
CSCI Homework Set 1 Due: September 11, 2018 at the beginning of class
 CSCI 3310 - Homework Set 1 Due: September 11, 2018 at the beginning of class ANSWERS Please write your name and student ID number clearly at the top of your homework. If you have multiple pages, please
CSCI 3310 - Homework Set 1 Due: September 11, 2018 at the beginning of class ANSWERS Please write your name and student ID number clearly at the top of your homework. If you have multiple pages, please
~ p is always false. Based on the basic truth table for disjunction, if q is true then p ~
 MAT 101 Solutions Exam 2 (Logic, Part I) Multiple-Choice Questions 1. D Because this sentence contains exactly ten words, it is stating that it is false. But if it is taken to be false, then it has to
MAT 101 Solutions Exam 2 (Logic, Part I) Multiple-Choice Questions 1. D Because this sentence contains exactly ten words, it is stating that it is false. But if it is taken to be false, then it has to
1.3 Propositional Equivalences
 1 1.3 Propositional Equivalences The replacement of a statement with another statement with the same truth is an important step often used in Mathematical arguments. Due to this methods that produce propositions
1 1.3 Propositional Equivalences The replacement of a statement with another statement with the same truth is an important step often used in Mathematical arguments. Due to this methods that produce propositions
Level 5 Entry Test SAMPLE A 5. Lis en and check ( ). Then wri e. (34 points) a b c. a b c. a b c. a b c. He s from the U. He s B. He s from A. He s A.
 Level 5 Entry Test Score / 100 A 5 Lis en an check ( ). Then wri e. (34 points) 1 He s from the U. He s B. 2 He s from A. He s A. 3 He s from E. He s E. 4 What was he oing yesteray at 4:00? He in. Our
Level 5 Entry Test Score / 100 A 5 Lis en an check ( ). Then wri e. (34 points) 1 He s from the U. He s B. 2 He s from A. He s A. 3 He s from E. He s E. 4 What was he oing yesteray at 4:00? He in. Our
Section Summary. Section 1.5 9/9/2014
 Section 1.5 Section Summary Nested Quantifiers Order of Quantifiers Translating from Nested Quantifiers into English Translating Mathematical Statements into Statements involving Nested Quantifiers Translated
Section 1.5 Section Summary Nested Quantifiers Order of Quantifiers Translating from Nested Quantifiers into English Translating Mathematical Statements into Statements involving Nested Quantifiers Translated
ANS: If you are in Kwangju then you are in South Korea but not in Seoul.
 Math 15 - Spring 2017 - Homework 1.1 and 1.2 Solutions 1. (1.1#1) Let the following statements be given. p = There is water in the cylinders. q = The head gasket is blown. r = The car will start. (a) Translate
Math 15 - Spring 2017 - Homework 1.1 and 1.2 Solutions 1. (1.1#1) Let the following statements be given. p = There is water in the cylinders. q = The head gasket is blown. r = The car will start. (a) Translate
Foundations of Mathematics Worksheet 2
 Foundations of Mathematics Worksheet 2 L. Pedro Poitevin June 24, 2007 1. What are the atomic truth assignments on {a 1,..., a n } that satisfy: (a) The proposition p = ((a 1 a 2 ) (a 2 a 3 ) (a n 1 a
Foundations of Mathematics Worksheet 2 L. Pedro Poitevin June 24, 2007 1. What are the atomic truth assignments on {a 1,..., a n } that satisfy: (a) The proposition p = ((a 1 a 2 ) (a 2 a 3 ) (a n 1 a
Section L.1- Introduction to Logic
 Section L.1- Introduction to Logic Definition: A statement, or proposition, is a declarative sentence that can be classified as either true or false, but not both. Example 1: Which of the following are
Section L.1- Introduction to Logic Definition: A statement, or proposition, is a declarative sentence that can be classified as either true or false, but not both. Example 1: Which of the following are
1-2 Study Guide and Intervention
 1- Study Guide and Intervention Real Numbers All real numbers can be classified as either rational or irrational. The set of rational numbers includes several subsets: natural numbers, whole numbers, and
1- Study Guide and Intervention Real Numbers All real numbers can be classified as either rational or irrational. The set of rational numbers includes several subsets: natural numbers, whole numbers, and
