國立交通大學機械工程學系碩士論文 研究生 : 江振賓 指導教授 : 戈正銘教授 中華民國九十九年六月. 雙 Ge-Ku 系統,Sprott 4 系統及 Rossler 系統的 渾沌與渾沌同步. Chaos and Chaos Synchronization of Double Ge-Ku
|
|
|
- Elmer McDowell
- 5 years ago
- Views:
Transcription
1 國立交通大學機械工程學系碩士論文 雙 Ge-Ku 系統,Sprott 4 系統及 Rossler 系統的 渾沌與渾沌同步 Chaos and Chaos Synchronzaton of Double Ge-Ku System, Sprott 4 System and Rossler System 研究生 : 江振賓 指導教授 : 戈正銘教授 中華民國九十九年六月
2 雙 Ge-Ku 系統,Sprott 4 系統及 Rossler 系統的 渾沌與渾沌同步 Chaos and Chaos Synchronzaton of Double Ge-Ku System,Sprott 4 Systems and Rossler System 研究生 : 江振賓 指導教授 : 戈正銘 Student: Chen- Bn Chang Advsor: Zheng-Mng Ge 國立交通大學機械工程學系碩士論文 A Thess Submtted to Department of Mechancal Engneerng College of Engneerng Natonal Chao Tung Unversty In Partal Fulfllment of the Requrement For the Degree of master of scence In Mechancal Engneerng June 00 Hsnchu, Tawan, Republc of Chna 中華民國九十九年六月
3 雙 Ge-Ku 系統, Sprott 4 系統及 Rossler 系統的渾沌與渾沌同步 學生 : 江振賓 指導教授 : 戈正銘 國立交通大學 機械工程學系 摘要 本篇論文以相圖 龐卡萊映射圖 李亞普洛夫指數以及分歧圖等數值方法研究新 Double Ge-Ku 系統的渾沌現象 應用主動控制獲得雙重及多重渾沌交織同步 對此系統應用部分區域穩定性理論和實用漸進穩定理論來達成廣義同步 更進一步使用新模糊模型來研究 Sprott 4 系統以及 Rossler 系統的模糊模型和渾沌同步 此外, 將探討新模糊邏輯常數控制器應用在投影同步及含有不確定度的渾沌系統 在以上研究中, 皆可由相圖和時間歷程圖得到驗證
4 Chaos and Chaos Synchronzaton of Double Ge-Ku System, Sprott 4 System and Rossler System Student:Chen- Bn Chang Advsor:Zheng-Mng Ge Department of Mechancal Engneerng, Natonal Chao Tung Unversty Abstract In ths thess, the chaotc behavor of new Double Ge-Ku system s studed by phase portrats, tme hstores, Poncaré maps, Lyapunov exponents and bfurcaton dagrams. New type for chaotc synchronzaton, double and multple symplectc synchronzaton, are obtaned by actve control. A new knd of chaotc generalzed synchronzaton, dfferent translaton pragmatcal generalzed synchronzaton, s obtaned by pragmatcal asymptotcal stablty theorem and partal regon stablty theory. A new method, usng new fuzzy model, s studed for fuzzy modelng and synchronzaton of Sprott 4 system and Rossler system. Moreover, the new fuzzy logc constant controller s studed for projectve synchronzaton and chaotc system wth uncertanty. Numercal analyses, such as phase portrats and tme hstores are provded to verfy the effectveness of all above studes.
5 誌謝 此篇論文及碩士學業之完成, 首先必須感謝指導教授 戈正銘老師的 耐心指導與教誨 老師在專業領域上的成就以及對於文學和史學上的熱情, 都令學生印象深刻且受益匪淺 戈老師在學生的碩士生涯中扮演了很重要的角色 在研究上, 戈老師給了許多意見指引學生正確的研究方向, 在研究過程中, 也讓學生學習到當發現問題時, 解決問題的能力 在研究所的後段時間, 小宇學長更是不辭辛勞教導我們研究新的題目, 並且與老師共同傳授做研究的技巧, 著實讓我上了一課 經由這兩年的相處, 讓學生發現在學術研究之餘也能體會到古典文學之美, 這都使學生開拓了不一樣的視野 在這段研究的日子當中, 承蒙張晉銘 李仕宇 徐瑜韓 張育銘 陳志銘 陳聰文學長的熱心指導, 同時也感謝泳厚 尚恩 翔平同學的相互勉勵及幫忙, 使得本篇論文能夠順利完成 最後感謝我的家人, 讓我可以不必擔心課業以外的事物, 無後顧之憂的完成學業 最後, 僅以此論文獻給你們
6 CONTENTS CHINESE ABSTRACT.. ABSTRACT Acknowledgment.. CONTENTS..v LIST OF FIGURES...v Chapter Introducton Chapter Double Symplectc Synchronzaton for Double Ge-Ku System. Prelmnary.6. Double Symplectc Synchronzaton Scheme 6. Synchronzaton of Two Dfferent New Chaotc Systems...8 Chapter Multple Symplectc Synchronzaton for Double Ge-Ku System. Prelmnary.... Multple Symplectc Synchronzaton Scheme.... Synchronzaton of Three Dfferent Chaotc Systems... Chapter 4 Usng Partal Regon Stablty Theory for Dfferent Translaton Pragmatcal Generalzed Synchronzaton 4. Prelmnary The Scheme of Dfferent Translaton Pragmatc Generalzed by Partal Regon Theory 7 4. Dfferent Translaton Pragmatcal Synchronzaton of new DoubleGe-Ku Chaotc System 40 Chapter 5 Robust Projectve Ant-Synchronzaton of Non-autonomous and Chaotc Uncertan Stochastc Systems Va Fuzzy Logc Constant Controller 5. Prelmnary Projectve Ant-Synchronzaton by FLCC Scheme Smulaton Results 6 Chapter 6 Fuzzy Modelng and Synchronzaton of Chaotc Systems by a New Fuzzy Model 6. Prelmnary...79 v
7 6. New Fuzzy Model Theory New Fuzzy Model of Chaotc Systems Fuzzy Synchronzaton Scheme Smulaton Results 89 Chapter 7 Conclusons...98 Appendx A GYC Partal Regon Stablty Theory...00 Appendx B Pragmatcal Asymptotcal Stablty Theory.08 References v
8 LIST OF FIGURES Fg.. The chaotc attractor of a new Ge-Ku-Duffng system..4 Fg.. The chaotc attractor of uncontrolled new Double Ge-Ku system.4 Fg.. The bfurcaton dagram of uncontrolled new Double Ge-Ku system 5 Fg..4.The Lyapunov exponents of uncontrolled new Double Ge-Ku system..5 Fg..5 The phase portrat of the controlled new Double Ge-Ku system for CASE. 6 Fg..6 Tme hstores of the state errors for CASE.6 Fg..7 Tme hstores of x y and x y for CASE.7 Fg..8 The chaotc attractor of a new Ge-Ku-van der Pol system.7 Fg..9 The phase portrat of the controlled new Double Ge-Ku system for CASE 8 Fg..0 Tme hstores of the state errors for CASE 8 Fg.. Tme hstores of x y and x y for CASE...9 Fg.. The chaotc attractor of a new Ge-Ku Matheu system 9 Fg.. The phase portrat of the controlled new Double Ge-Ku system for CASE...0 Fg..4 Tme hstores of the state errors for CASE 0 Fg..5 Tme hstores of x y and x y for CASE Fg.. The chaotc attractor of the Lorenz system.0 Fg.. The chaotc attractor of the Chen system...0 Fg.. The phase portrat of the controlled DGK system Fg..4 Tme hstores of the state errors for Case Fg..5 Tme hstores of G( xy,, z, t) and F( x, y, zt, ) for Case v
9 Fg..6 The chaotc attractor of the Rossler system Fg..7 The phase portrat of the controlled DGK system... Fg..8 Tme hstores of the state errors for Case... Fg..9 Tme hstores of G( xy,, z, t) and F( x, y, zt, ) for Case..4 Fg..0 The chaotc attractor of a Sprott system 4 Fg.. The phase portrat of the controlled DGK system...5 Fg.. Tme hstores of the state errors for Case 5 Fg.. Tme hstores of G( xy,, z, t) and F( x, y, zt, ) for Case 6 Fg. 4. Coordnate translaton of state x 49 Fg. 4. Coordnate translaton of state y.49 Fg. 4. Phase portrat of the error dynamcs for Case 50 Fg. 4.4 Tme hstores of errors for Case..50 Fg. 4.5 Tme hstores of x, y for Case..5 Fg. 4.6 Tme hstores of parameter errors for Case.5 Fg. 4.7 Phase portrat of the error dynamc for Case 5 Fg. 4.8 Tme hstores of errors for Case..5 Fg. 4.9 Tme hstores of x, y for Case 5 Fg. 4.0 Tme hstores of parameter errors for Case 5 Fg. 4. Phase portrat of the error dynamc for Case 54 Fg. 4. The chaotc attractor of the Ge-Ku-van der Pol system...54 Fg. 4. Tme hstores of errors for Case 55 Fg. 4.4 Tme hstores of x, y for Case 55 Fg. 4.5 Tme hstores of parameter errors for Case...56 Fg. 5. The confguraton of fuzzy logc controller 70 Fg. 5. Membershp functon..70 Fg. 5. The chaotc behavor of Sprott 4 system [50].7 v
10 Fg. 5.4 Projectons of phase portrat of Eq (5.9)...7 Fg. 5.5 Tme hstores of error dervatves for master and slave chaotc systems wthout controllers 7 Fg. 5.6 Tme hstores of states for Example the FLCC s comng nto after 0s 7 Fg. 5.7 Tme hstores of errors for Example the FLCC s comng nto after 0s 7 Fg. 5.8 Tme hstores of states for the tradtonal controller s comng nto after 0s 7 Fg. 5.9 Tme hstores of states for the tradtonal controller s comng nto after 0s 74 Fg. 5.0 The Raylegh nose used...74 Fg. 5. Projecton of phase portrat of Eq (5.8)..75 Fg. 5. Projectons of phase portrat of chaotc DGK systems.75 Fg. 5. Tme hstores of error dervatves for master and slave chaotc uncertan stochastc systems wthout controllers.76 Fg. 5.4 Tme hstores of states for Example the FLCC s comng nto after 0s 76 Fg. 5.5 Tme hstores of errors for Example the FLCC s comng nto after 0s 77 Fg. 5.6 Tme hstores of states for the tradtonal controller s comng nto after 0s 77 Fg. 5.7 Tme hstores of states for the tradtonal controller s comng nto after 0s 78 Fg. 6. Chaotc behavor of Sprott 4 system...9 Fg. 6. Chaotc behavor of Sprott 4 system wth uncertanty 9 v
11 Fg. 6. Chaotc behavor of new fuzzy Sprott 4 system wth uncertanty..94 Fg. 6.4 Chaotc behavor of Rossler system 94 Fg. 6.5 Chaotc behavor of Rossler system wth uncertanty.95 Fg. 6.6 The Raylegh nose used 95 Fg. 6.7 Chaotc behavor of new fuzzy Rossler system wth uncertanty 96 Fg. 6.8 Tme hstores of errors for Example 96 Fg. 6.9 Tme hstores of errors for Example...97 x
12 Chapter Introducton Chaos s a very nterestng nonlnear phenomenon. Chaos as a modern theory s dscovered by the age of computer n the mddle of the past century, whch has an epoch-makng sgnfcance n exact scence. Generally speakng, desgnng a system to mmc the behavor of another chaotc system s called synchronzaton. Synchronzaton of chaotc systems has receved a sgnfcant attenton, snce Pecora and Carroll presented the chaos synchronzaton method to synchronze two dentcal chaotc systems wth dfferent ntal values n 990 []. In recent years, synchronzaton n chaotc dynamc system s a very nterestng problem and has been wdely studed. Chaos synchronzaton has been appled n bologcal systems [,], secure communcaton [4,5], and many other dscplnes. By lnear and nonlnear control [6-] dfferent types of synchronzaton for nteractng chaotc systems, such as complete synchronzaton [], phase synchronzaton [], lag synchronzaton [4], generalzed synchronzaton [5-0], antcpatng synchronzaton can be obtaned. Varous approaches for achevng chaos synchronzaton usng fuzzy systems have been proposed []. Fuzzy set theory was frst presented by Zadeh [], whle fuzzy logc control (FLC) schemes have been wdely developed and successfully deployed n many applcatons []. Furthermore, adaptve fuzzy controllers have been used to control and synchronze chaotc systems [4,5]. Uncertantes assocated wth the mathematcal characterzaton of a system can lead to unrelable damage [6]. Probablstc analyss provdes a tool for ncorporatng randoms n the analyss of frequency response by generally descrbng the randoms as
13 randoms varables. Whle the studes dscussed above addressed measurement nose, some researchers have started lookng at the effect of nose present n the model. Collns et al. [7] proposed a statstcal dentfcaton procedure by treatng the ntal parameters as normally dstrbuted random varables. In recent years, some chaos synchronzatons based on fuzzy systems have been proposed snce the fuzzy set theory was ntated by Zadeh [], such as fuzzy sldng mode controllng technque [8,9], LMI-based synchronzaton [0] and extended backsteppng sldng mode controllng technque []. The fuzzy logc control (FLC) scheme have been wdely developed and have been successfully appled to many applcatons []. Recently, Yau and Sheh [] proposed a new dea n desgnng fuzzy logc controllers - constructng fuzzy rules subject to a common Lyapunov functon such that the master-slave chaotc systems satsfy stablty condton n the Lyapunov sense. In [], there are two man controllers n ther slave system. One s used n elmnaton of nonlnear terms and the other s bult by fuzzy rules subject to a common Lyapunov functon. Therefore, the resultng controllers are n nonlnear form. In [], the regular form s necessary. In order to carry out the new method, the orgnal system must to be transformed nto ther regular form. In recent years, fuzzy logc proposed [4] has receved much attenton as a powerful tool for the nonlnear control. Among varous knds of fuzzy methods, Takag-Sugeno fuzzy (T-S fuzzy) system s wdely accepted as a useful tool for desgn and analyss of fuzzy control system [5-40]. Currently, some chaos control and synchronzaton based on T-S fuzzy systems have been proposed, such as fuzzy sldng mode controllng technque, LMI-based synchronzaton [4-4] and robust control [44]. Furthermore, two dfferent nonlnear systems may have dfferent numbers of nonlnear terms. It causes dfferent numbers of lnear subsystems. For synchronzaton of two dfferent nonlnear systems, the tradtonal method usng the
14 dea of PDC to desgn the fuzzy control law for stablzaton of the error dynamcs can not be used here, snce the number of subsystems becomes very large. Ge and Ku [45] gave a chaotc system formed by a smple pendulum wth ts pvot rotatng about an axs as Fg... Ths chaotc system s x x x ax sn x[ b( c cos x ) d sn wt] where a, b, c, d are parameters. After smplfcaton, sn x x, addton of couplng terms, we get the Double Ge-Ku system x x x fx x g h x kx x fx x g h x lx (.) x cos x and (.) where a, b, c, d, g are parameters. In Chapter, a new type of synchronzaton, double symplectc synchronzaton, G( x, y, t) F( x, y, t) s studed. Tradtonal generalzed synchronzaton and symplectc synchronzaton are specal cases of the double symplectc synchronzaton. Snce the symplectc functons are presented at both the rght hand sde and the left hand sde of the equalty. The double symplectc synchronzaton may be appled to ncrease the securty of secret communcaton due to the complexty of ts synchronzaton form. By usng the Barbalat s lemma[46], the double symplectc synchronzaton can be acheved. Fnally, the effectveness and feasblty of our proposed scheme are verfed by numercal smulatons. In Chapter, a new type of synchronzaton, multple symplectc synchronzaton s studed. When the double symplectc functons are extended to a more general form, G(x,y,z w,t) = F(x,y,z w,t), multple symplectc synchronzaton s acheved. The multple symplectc synchronzaton may be appled to ncrease the securty of
15 secret communcaton more effectvely than double symplectc synchronzaton due to more complexty of ts synchronzaton form. In Chapter 4, a new chaos generalzed synchronzaton strategy of dfferent translaton pragmatcal synchronzaton by stablty theory of partal regon [47-49] s proposed. By usng the stablty theory of partal regon, the Lyapunov functon s a smple lnear homogeneous functon of error states, the controllers are more smple snce they are n lower degree than that of tradtonal controllers, whle the tradtonal Lyapunov functon s a quadratc form of error states. In Chapter 5, we propose a new strategy whch s also constructng fuzzy rules subject to a Lyapunov drect method. Error dervatves are used to be upper bound and lower bound. Through ths new approach, a smplest controller,.e. constant controller, can be obtaned and the dffculty n realzaton of complcated controllers n chaos synchronzaton by Lyapunov drect method can be also overcome. Unlke conventonal approaches, the resultng control law has less maxmum magntude of the nstantaneous control command and t can reduce the actuator saturaton phenomenon n real physcal system. Some computer smulaton examples are gven n ths Chapter. In Chapter 6, the new fuzzy model s proposed. It gves a new way to lnearze complcated nonlnear system and only two subsystems are concluded. In smulaton examples, Sprott 4 system [50] and Rossler system are used. Fnally, conclusons are presented n Chapter 7. 4
16 Fg. The pendulum on rotatng arm. 5
17 Chapter Double Symplectc Synchronzaton for Double Ge-Ku System. Prelmnary In ths Chapter, a new type of synchronzaton, double symplectc synchronzaton, G( x, y, t) F( x, y, t) s proposed. Double symplectc synchronzaton s an extenson of symplectc synchronzaton, y F( x, y, t). Because the symplectc functons are presented at both the rght hand sde and the left hand sde of the equalty, t s called double symplectc synchronzaton. Snce the synchronzaton form s more complex than generalzed and symplectc synchronzatons, so we usually use t on the purpose of secret communcaton. The scheme s effectve as shown by three examples as follows.. Double Symplectc Synchronzaton Scheme Consder two dfferent nonlnear chaotc systems, Partner A and Partner B, descrbed by x f( x, t), (.) y C( t) y + g( u, t) u, (.) where x [,,, ] T n x x xn R and y [,,, ] are the state vectors of T n y y yn R Partner A (.) and Partner B (.), n n C R s the gven matrx, f and g are contnuous nonlnear vector functons, and u s the controller. Our goal s to desgn the controller u such that G( x, y, t) asymptotcally approaches F( x, y, t).for smplcty take G( x, y, t) x y and F( x, y, t) s a contnuous nonlnear vector functon. 6
18 Property [5]: An m n matrx A of real elements defnes a lnear mappng y Ax from n R nto m R, and the nduced p-norm of A for p,, and s gven by m n T max j, max ( ), max j. j (.) j A a A A A A a The useful property of nduced matrx norms for real matrx A s as follow: A A A. (.4) Theorem: For chaotc systems Partner A (.) and Partner B (.), f the controller u s desgned as u I D F D Ff x D F C y g y D F f x g y ( y ) [ x (, t) y ( ( t) (, t)) t (, t) (, t) C( t)( x F) K( x y F)], (.5) where DF x, DF y, DF t are the Jacoban matrces of F( x, y, t), K dag(,,, ), and satsfes k k k m mn( k ), (.6) C() t then the double symplectc synchronzaton wll be acheved. Proof: Defne the error vectors as e x y F( x, y, t), (.7) then the followng error dynamcs can be obtaned by ntroducng the desgned controller de e x y DxFx DyFy DtF dt f ( x, t) C( t) y g( y, t) D Ff ( x, t) D F( C( t) y g( y, t)) D F ( I D F) u ( C( t) K) e. y x y t (.8) Choose a non-negatve Lyapunov functon of the form 7
19 T Vt () ee. (.9) Takng the tme dervatve of Vt () along the trajectory of Eq. (.8), we have Vt () T ee T T e C() t e e Ke C( t) e mn( k ) e ( C( t) mn( k )) e. (.0) Snce M mn( k ) C ( t) 0, then V ( t) M e MV ( t). Therefore, t can be obtaned that V t ( ) V (0)e Mt (.) and t lm V( ) d t s bounded. Besdes, () 0 Vt s unformly contnuous. Accordng to Barbalat s lemma [46], the concluson can be drawn that lm Vt ( ) 0,.e. t lm e ( t) 0 t. Thus, the double symplectc synchronzaton can be acheved asymptotcally.. Synchronzaton of Two Dfferent New Chaotc Systems CASE Consder a new Ge-Ku-Duffng(GKD) system as Partner A descrbed by x x x hx x l p x kx x x x fx gx (.) where h=0.; l=; p=40; k=54; f=6; g=0; and the ntal condtons are x (0), x (0).4, x (0) 5. Eq. (.) can be rewrtten n the form of Eq. (.), 8
20 x t hx x l p x kx x x fx gx where fx (, ). The chaotc attractor of the new GKD system s shown n Fg... The controlled new Double Ge-Ku (DGK) system s consdered as Partner B descrbed by y y u y ay y bc y dy u y ay y bc y ey u where a=-0.5; b=-.4; c=.9; d=-4.5; e=6.;, u, u, u T (.) u s the controller, and the ntal condton s y (0), y (0).4, y (0) 5. The chaotc attractor of uncontrolled new DGK system s shown n Fg.., Bfurcaton dagram n Fg.. and Lyapunov exponents n Fg..4. Eq. (.) can be rewrtten n the form of Eq. (.), where 0 0 C ( t) bc a 0 and 0 0 a bc 0 gy (, t) by dyy. By applyng Property, t s derved that C() t a bc by ey y C () t a bc C ( t) ( a bc) Then C ( t). s estmated. Defne x y F( x, y, t) x y, and our goal s to acheve the double symplectc x y synchronzaton x y F( x, y, t). Accordng to Theorem, the nequalty mn( ) C() t must be satsfed. It can be obtaned that mn( k ). f we choose 9 k
21 k K 0 k and desgn the controller as 0 0 k u x y x x y x y x y x y u x y { hx x [ l( p x ) kx ]} x { ay y [ b( c y ) dy ]} hx x [ l( p x ) kx ] ay y [ b( c y ) dy ] x y x y u x y ( x x fx gx ) x { ay y [ b( c y ) ey ]} x x fx gx ay y [ b( c y ) ey ] x y x y The Theorem s satsfed and the double symplectc synchronzaton s acheved. The phase portrat of the controlled DGK system and the tme hstores of the state errors are shown n Fg..5 and Fg..6 and Fg..7, respectvely. CASE Consder a new Ge-Ku-van der Pol(GKv) system as Partner A descrbed by x x x fx x p k x mx x gx h x x lx (.4) where f=0.08; p=-0.5; k=00.56; m=-000.0; g=0.6; h=0.08; l=0.0; and the ntal condtons are x (0) 0.0, x(0) 0.0, x(0) 0.0. Eq. (.4) can be rewrtten n the form of Eq. (.), where x fx (, t) fx x[ p( k x ) mx. gx h( x ) x lx The chaotc attractor of the GKv system s shown n Fg..8. The controlled DGK system s consdered as Partner B descrbed by y y u y ay y bc y dy u y ay y bc y ey u 0 (.5)
22 where a=-0.5; b=-.4; c=.9; d=-4.5; e=6.;, u, u, u T u s the vector controller, and the ntal condtons are y (0) 0.0, y (0) 0.0, y (0) 0.0. Eq. (.5) can be rewrtten n the form of Eq. (.), where 0 0 C ( t) bc a 0 0 l g and 0 gy (, t) by dyy by ey y. By applyng Property, t s derved that C ( t) a bc, C () t a bc, and C ( t) ( a bc) Then C ( t). s estmated. Defne x y F( x, y, t) x y, and our goal s to acheve the double symplectc x y synchronzaton x y F( x, y, t). Accordng to Theorem, the nequalty mn( k ) C() t must be satsfed. It can be obtaned that mn( k ).. Thua we k choose K 0 k and desgn the controller as 0 0 k u x y x x y x y x y x y u x y { fx x [ p( k x ) mx ]} x { ay y [ b( c y ) dy ]} fx x [ p( k x ) mx ] ay y [ b( c y ) dy ] x y x y u x y [ gx h( x ) x lx ] x { ay y [ b( c y ) ey ]} gx h( x ) x lx ay y [ b( c y ) ey ] x y x y The Theorem s satsfed and the double symplectc synchronzaton s acheved.
23 The phase portrat of the controlled DGK system and the tme hstores of the errors are shown n Fg..9, Fg..0 and Fg.., respectvely. CASE Consder the Ge-Ku Matheu(GKM) system as Partner A descrbed by x x x kx x f m x nxx x ( g hx ) x lx pxx (.6) where k=-0.6; f=5; m=; n=0.; g=8; h=0; l=0.5; p=0.; and the ntal condtons are x (0) 0.0, x(0) 0.0, x(0) 0.0 Eq. (.6) can be rewrtten n x t kx x f m x nx x ( g hx ) x lx px x the form of Eq. (.), where fx (, ) attractor of the GKM system s shown n Fg... The controlled DGK system s consdered as Partner B descrbed by.the chaotc y y u y ay y bc y dy u y ay y bc y ey u (.7) where a=-0.5; b=-.4; c=.9; d=-4.5; e=6.;, u, u, u T u s the vector controller, and the ntal condtons are y (0) 0.0, y (0) 0.0, y (0) 0.0. Eq. (.7) can be rewrtten n the form of Eq. (.), where 0 0 C ( t) bc a 0 0 l g and 0 gy (, t) by dyy by ey y. By applyng Property, t s derved that
24 C ( t) a bc, C () t a bc, and C ( t) ( a bc) Then C( t). s estmated. Defne x y F( x, y, t) x y, and our goal s to acheve the x y double symplectc synchronzaton x y F( x, y, t). Accordng to Theorem, the nequalty mn( k ) C() t must be satsfed. It can be obtaned that mn( k ).. k Thus we choose K 0 k and desgn the controller as 0 0 k u x y x x y x y x y x y u x y { kx x [ f ( m x ) nx x ]} x { ay y [ b( c y ) dy ]} kx x [ f ( m x ) nx x ] ay y [ b( c y ) dy ] x y x y u x y [ ( g hx ) x lx px x ] x { ay y [ b( c y ) ey ]} ( g hx ) x lx px x ay y [ b( c y ) ey ] x y x y The Theorem s satsfed and the double symplectc synchronzaton s acheved. The phase portrat of the controlled DGK system and the tme hstores of the state errors are shown n Fg., Fg..4 and Fg..5, respectvely.
25 Fg.. The chaotc attractor of a new Ge-Ku-Duffng system. Fg.. The chaotc attractor of uncontrolled new Double Ge-Ku system. 4
26 b Fg.. The bfurcaton dagram of uncontrolled new Double Ge-Ku system. b Fg..4.The Lyapunov exponents of uncontrolled new Double Ge-Ku system. 5
27 Fg..5 The phase portrat of the controlled new Double Ge-Ku system for CASE. Fg..6 Tme hstores of x y and x y for CASE. 6
28 Fg..7 Tme hstores of the state errors for CASE. Fg..8 The chaotc attractor of a new Ge-Ku-van der Pol system. 7
29 Fg..9 The phase portrat of the controlled new Double Ge-Ku system for CASE. Fg..0 Tme hstores of x y and x y for CASE. 8
30 Fg.. Tme hstores of the state errors for CASE. Fg.. The chaotc attractor of a new Ge-Ku Matheu system. 9
31 Fg.. The phase portrat of the controlled new Double Ge-Ku system for CASE. Fg..4 Tme hstores of x y and x y for CASE. 0
32 Fg..5 Tme hstores of the state errors for CASE.
33 Chapter Multple Symplectc Synchronzaton for Double Ge-Ku System. Prelmnary In ths Chapter, a new type of synchronzaton, multple symplectc synchronzaton s studed. Symplectc synchronzaton and double symplectc synchronzaton are specal cases of the multple symplectc synchronzaton. When the double symplectc functons s extended to a more general form, G(x,y,z w,t) = F(x,y,z w,t), t s called multple symplectc synchronzaton. The multple symplectc synchronzaton may be appled to ncrease the securty of secret communcaton due to the complexty of ts synchronzaton form.. Multple Symplectc Synchronzaton Scheme Chaos synchronzaton, frst proposed by Fujsaka and Yamada n 98, dd not receved great attenton untl 990. Among many knds of synchronzatons, the generalzed synchronzaton s nvestgated. It means there exst a functonal relatonshp between the states of the master and those of the slave. Symplectc synchronzaton s defned as y H( x, y, t), where x, y are the state vectors of the master and of the slave, respectvely. The fnal desred state y of the slave not only depends upon the master state x but also depends upon the slave state y tself. Therefore the slave s not a tradtonal pure slave obeyng the master completely but plays a role to determne the fnal desred state of the slave system. We call ths knd of synchronzaton, symplectc synchronzaton, and call the master system Partner A, the slave system Partner B. Snce the symplectc functons are presented at both the rght hand sde and the
34 left hand sde of the equalty, t s called double symplectc synchronzaton, G( x, y, t) F( x, y, t), where x, y are state vectors of Partner A and Partner B, respectvely, G( x, y, t) and F( x, y, t) are gven vector functons of x, y and tme. When the double symplectc functons s extended to a more general form, G(x,y,z w,t) = F(x,y,z w,t), s called multple symplectc synchronzaton, where xy,, z,, ware state vectors of Partner A and Partner B, respectvely, G(x,y,z w,t)and F(x,y,z w,t)are gven vector functons of xy,, z,, w and tme.. Synchronzaton of Three Dfferent Chaotc Systems CASE. Defne x y z G( x, y, z, t) x y z, x y z sn sn sn sn sn sn x y z x y z x y z F( x, y, z, t) x sn y z x sn y z x sn y z, x y z x y z x y z and we wsh to acheve the multple symplectc synchronzaton G(x,y,z,t) = F(x,y,z,t). Let e = G(x,y,z,t) - F(x,y,z,t) Consder a Lorenz system s descrbed by x w x w x x w x x x x x w x xx (.) 8 where w 0, w, w 8, and the ntal condton s x (0) 0.0, x (0) 0.0, x (0) 0.0. The chaotc attractor of the Lorenz system s shown n Fg... The Chen system s descrbed by z h ( z z) z h h z z z h z z zz h z
35 (.) where h 5, h 7., h, and the ntal condton s z (0) 0.5, z (0) 0.6,z (0) 0.5. The chaotc attractor of the Chen system s shown n Fg... The controlled Double Ge-Ku (DGK) system s descrbed by y y u y ay y bc y dy u y ay y bc y ey u (.) where a=-0.5; b=-.4; c=.9; d=-4.5; e=6., s the controller parameters, and the ntal condton s y (0) 0.0, y (0) 0.0,y (0) 0.0,. Thus we desgn the controller as sn cos sn sn x ay y bc y dy cos y z x sn y h z z sn cos x sn y h z z u w x w x y h z z w x w x y z x y y z x y h z z w x x x x y z w x x x y z x ay y b c y ey y z u w x x x x ay y b c y dy sn cos sn sn cos sn sn cos sn h h z z z h z w x w x y z x y y z x y h h z z z h z w x x x x y z x ay y b c y dy y z x y h h z zz hz w x x x y z x ay y b c y ey y z x y h h z zz h z 4
36 u w x xx ay y b c y ey zz h z w x w x sn y z x y cos y z x sn y zz h z w x x xx sn y z x ay y bc y dy cos y z x sn y zz hz w x xx sn y z x ay y bc y ey cos y x sn y z z h z The Theorem n Chapter s satsfed and the multple symplectc synchronzaton s acheved. The phase portrat of the controlled DGK system and the tme hstores of the state errors and the tme hstores of G( xy,, z, t) and F( x, y, zt, ) are shown n Fg.. and Fg..4 and Fg..5, respectvely. z CASE. Defne x y z cos x yz cos x yz cos x yz G( x, y, z, t) x y z, F( x, y, z, t), cos x yz cos x yz cos x yz x y z cos x yz cos x yz cos x yz and we wsh to acheve the multple symplectc synchronzaton G(x,y,z,t) = F(x,y,z,t). Let e = G(x,y,z,t) - F(x,y,z,t) Consder a Rossler system s descrbed by x x x x x w x x w x x w x (.4) where w 0.5, w 0., w 0, and the ntal condton s x (0), x (0).4, x (0) 5,. The chaotc attractor of the Rossler system s shown n Fg..6. 5
37 The Chen system s descrbed z h ( z z) z h h z z z h z z zz h z (.5) where h 5, h 7., h, and the ntal condton s z (0) 0.5, z (0) 0.6,z (0) 0.5. The controlled DGK system s descrbed by (.6) where a=-0.5; b=-.4; c=.9; d=-4.5; e=6., s the controller parameters, and the ntal condton s y (0) 0.0, y (0) 0.0,y (0) 0.0,. Thus we desgn the controller as sn cos cos sn u x x y h z z x x x y z x y z x y h z z x w x x y z cos sn cos cos x ay y b c y dy z x y h z z w x x w x x y z x ay y b c y ey z y y u y ay y bc y dy u y ay y bc y ey u cos x y h z z u x w x ay y b c y dy h h z zz h z sn cos cos x x x yz x yz x y h h z zz h z sn cos x w x x y z x ay y b c y dy z cos x y h h z zz h z w xx w x sn x cos cos y z x ay y b c y ey z x y h h z zz hz 6
38 u w x x w x ay y b c y ey z z h z x x sn x y z cos x y z cos x y z z h z sn cos x w x x y z x ay y b c y dy z cos sn x y z z h z w x x w x x y z cos x ay y b c y ey z cos x y z z h z The Theorem n Chapter s satsfed and the multple symplectc synchronzaton s acheved. The phase portrat of the controlled DGK system and the tme hstores of the state errors and the tme hstores of G( xy,, z, t) and F( x, y, zt, ) are shown n Fg..7 and Fg..8 and Fg..9, respectvely. CASE. Defne x y z x yz x yz x yz G( x, y, z, t) x y z, F( x, y, z, t) x yz x yz x yz, x y z x yz x yz x yz and we wsh to acheve the multple symplectc synchronzaton. G(x,y,z,t) = F(x,y,z,t). Let e = G(x,y,z,t) - F(x,y,z,t) Consder a Sprott E system s descrbed by x xx x x x x w x (.7) where w 4, and the ntal condton s x (0), x(0), x(0),. The chaotc attractor of the Sprott E system s shown n Fg..0. The Chen system s descrbed 7
39 z h ( z z) z h h z z z h z z zz h z (.8) where h 5, h 7., h, and the ntal condton s z (0) 0.5, z (0) 0.6, z (0) 0.5. The controlled DGK system s descrbed by y y u y ay y bc y dy u y ay y bc y ey u (.9) where a=-0.5; b=-.4; c=.9; d=-4.5; e=6., are the controller parameters, and the ntal condton s y (0) 0.0, y (0) 0.0,y (0) 0.0,. Thus we desgn the controller as u xx y h z z xx yz x yz x y h z z x x y z x ay y b c y dy z x y h z z w x y z x ay y b c y ey z x y h z z w x yz x ay y bc y ey z x y u x x ay y b c y dy h h z zz hz x x y z x y z x y h h z z z h z x x y z x ay y b c y dy z x y h h z zz hz u w x ay y b c y ey z z h z x x y z x y z x y z z h z x x y z h h z z z h z w x yz x ay y b c y ey z x y zz h z x ay y b c y dy z x y z z h z The Theorem n Chapter s satsfed and the multple symplectc synchronzaton 8
40 s acheved. The phase portrat of the controlled DGK system and the tme hstores of the state errors and the tme hstores of G( xy,, z, t) and F( x, y, zt, ) are shown n Fg.. and Fg.. and Fg.., respectvely. 9
41 Fg.. The chaotc attractor of the Lorenz system. Fg.. The chaotc attractor of the Chen system. 0
42 Fg.. The phase portrat of the controlled DGK system. Fg..4 Tme hstores of G( xy,, z, t) and F( x, y, zt, ) for Case.
43 Fg..5 Tme hstores of the errors for Case. Fg..6 The chaotc attractor of the Rossler system.
44 Fg..7 The phase portrat of the controlled DGK system. Fg..8 Tme hstores of G( xy,, z, t) and F( x, y, zt, ) for Case.
45 Fg..9 Tme hstores of the errors for Case. Fg..0 The chaotc attractor of a Sprott E system. 4
46 Fg.. The phase portrat of the controlled DGK system. Fg.. Tme hstores of G( xy,, z, t) and F( x, y, zt, ) for Case. 5
47 Fg.. Tme hstores of the errors for Case. 6
48 Chapter 4 Dfferent Translaton Pragmatcal Generalzed Synchronzaton by Stablty Theory of Partal Regon for Double Ge-Ku System 4. Prelmnary In ths Chapter, a new strategy to acheve dfferent translaton generalzed synchronzaton by stablty theory of partal regon by whch the Lyapunov functon s smple lnear homogeneous functon of error states, the controllers are more smple snce they are n lower degree than that of tradtonal controllers. By a pragmatcal theorem of asymptotcal stablty based on an assumpton of equal probablty of ntal pont, an adaptve control law s derved such that t can be proved strctly that the common zero soluton of error dynamcs and of parameter dynamcs s asymptotcally stable. Numercal smulatons of a new Double Ge-Ku(DGK) system are gven to show the effectveness of the proposed scheme. 4. The Scheme of Dfferent Translaton Pragmatcal Generalzed Synchronzaton by Stablty Theory of Partal Regon There are two dentcal nonlnear dynamcal systems, and the master system synchronzes the slave system. The master system s gven by x Ax ( f, x ) B (4.) The master system after the orgn of x-coordnate system s translated to ( k, k,, k ) s x Ax ( f, x ) B (4.) n x [ x, x,, x ] x k [ x k, x k,, x k ] R denotes a state T where n n 7
49 vector where k [ k, k,, k] s a constant vector wth postve coeffcent k as shown n Fg.4.. A s an n n uncertan constant coeffcents matrx, f s a nonlnear vector functon, and B s a vector of uncertan constant coeffcents n f. The slave system s gven by y Ay ( f, y ) B ( u) t (4.) The slave system after the orgn of y-coordnate system s translated to ( k, k,, k ) s y Ay ( f, y ) B ( u) t (4.) n y [ y, y,, y ] y k [ y k, y k,, y k ] R denotes a state T where n n vector where k s a constant vector wth postve coeffcent k as shown n Fg.4.. A s an n n estmated coeffcent matrx, B s a vector of estmated coeffcents n f, and u( t) [ u( t), u( t),, u ( )] T n n t R s a control nput vector. Our goal s to desgn a controller ut () so that the state vector of the translated slave system (4.) asymptotcally approaches the state vector of the translated master system (4.) plus a gven nonchaotc or chaotc vector functon F( t) [ F ( t), F ( t),, F ( t)] T : n y G( x) x F(.) t (4.) Ths generalzed synchronzaton can be accomplshed when t, the lmt of the error vector e( t) [ e, e,, e ] T n approaches zero: lme 0 (4.4) t where e x F( ) t y x y ( F. ) t (4.5) From Eq. (4.5) we have 8
50 e xy F() t (4.6) e Ax Ay ( f, x) B ( f, y) B ( F) t. ( u) t (4.7) where k and k are chosen to guarantee that the error dynamcs always occurs n the frst quadrant of e coordnate system. A Lyapunov functon V ( e, Ac, Bc) s chosen as a postve defnte functon n frst quadrant of e coordnate system by stablty theory n partal regon as shown n Appendx A: V( e, Ac, Bc ) e ca cb (4.8) where Ac A A, Bc B B, A c and B c are two column matrces whose elements are all the elements of matrx A c and of matrx B c, respectvely. Its dervatve along any soluton of the dfferental equaton system consstng of Eq. (4.7) and update parameter dfferental equatons for A c and B c s V ( e, A B, ) Ax Ay f x( B, f) y B(, F ) t u ( t ) A ( B) (4.9) c c c c where ut (), A c, and B c are chosen so that V Ce, C s a dagonal negatve defnte matrx, and V s a negatve sem-defnte functon of e and parameter dfferences A c and B c. By pragmatcal asymptotcally stablty theorem n Appendx B, the Lyapunov functon used s a smple lnear homogeneous functon of states and the controllers are smpler because they n lower order than that of tradtonal controllers. In many papers [5-55], tradtonal Lyapunov stablty theorem and Babalat lemma are used to prove the error vector approaches zero, as tme approaches nfnty. But the queston, why the estmated parameters also approach to the uncertan parameters, remans no answer. By pragmatcal asymptotcal stablty theorem, the queston can be answered strctly. 9
51 4. Dfferent Translaton Pragmatcal Generalzed Synchronzaton of New Double Ge-Ku Chaotc System Case The followng chaotc systems are two translated DGK systems of whch the old orgn s translated to ( x, x, x) (50,50,50), ( y, y, y) (50,50,50) to guarantee the error dynamcs always happens n the frst quadrant of e coordnate system. x x 50 x a( x 50) ( x 50){ b[ c ( x 50) ] d( x 50)} x a( x 50) ( x 50){ b[ c ( x 50) ] g( x 50)} y y 50 u y a( y 50) ( y 50){ b[ c ( y 50) ] d( y 50)} u y a( y 50) ( y 50){ b[ c ( y 50) ] g( y 50)} u (4.0) (4.) Let ntal states be ( x, x, x) (50.0,50.0,50.0), ( y, y, y ) (50.0,50.0,50.0) and system parameters a 0.5, b.4, c.9, d 4.5, g 6.. The state error s e x y F() t x y e cos t where F() t cost e s a nonchaotc gven functon of tme. We fnd that the error dynamc wthout controller always exsts n frst quadrant as shown n Fg.4..,,, (4.) cos t lme lm( x y e ) t t Our am s lm e 0. We obtan the error dynamcs: t 40
52 cost e x 50 y 50 u (sn t) e e a( x 50) ( x 50){ b[ c ( x 50) ] d( x 50)} a( y 50) ( y 50){ b[ c ( y 50) ] d( y 50)} u (sn t) e e a( x 50) ( x 50){ b[ c ( x 50) ] g( x 50)} ay ( 50) ( y 50){ b[ c ( y 50) ] g( y 50)} u (sn t) e cost cost (4.) where a a aˆ, b b bˆ, c c cˆ, d d dˆ, g g gˆ, and a, b, c, d, g are estmates of uncertan parameters a, b, c, d and g respectvely. Usng dfferent translaton pragmatcal synchronzaton by stablty theory of partal regon, we can choose a Lyapunov functon n the form of a postve defnte functon n frst quadrant: V e e e a b c d g (4.4) Its tme dervatve s V e e e a b c d g cost ( x 50 y 50 u (sn t) e ) a( x 50) ( x 50){ b[ c ( x 50) ] d( x 50)} a( y 50) ( y 50){ b[ c ( y 50) ] d( y 50)} u (sn t) e cost a( x 50) ( x 50){ b[ c ( x 50) ] g( x 50)} a( y 50) ( y 50){ b[ c ( y 50) ] g( y 50)} u (sn t) e cost wz a b c d g (4.5) Choose a aˆ ae b bˆ be c cˆ ce d dˆ de g gˆ ge (4.6) 4
53 cost u x 50 y 50 (sn t) e e u a( x 50) ( x 50){ b[ c ( x 50) ] d( x 50)} a( y 50) ( y 50){ b[ c ( y 50) ] d( y 50)} (sn t) e e ae be ce u a( x 50) ( x 50){ b[ c ( x 50) ] gx ( 50)} a( y 50) ( y 50){ b[ c ( y 50) ] g( y 50)} (sn t) e e de ge We obtan cost cost (4.7) V e e e 0 (4.8) whch s a negatve sem-defnte functon of e, e, e, a, b, c, d, g, n the frst quadrant. The Lyapunov asymptotcal stablty theorem s not satsfed. We can not obtan that common orgn of error dynamcs () and parameter dynamcs (6) s asymptotcally stable. By pragmatcal asymptotcally stablty theorem, D s a 8-manfold, n=8 and the number of error state varables p=. When e e e 0 and a, b, c, d, g take arbtrary values, V 0, so X s of dmensons, m=n-p=8-=5, m+<n s satsfed. Accordng to the pragmatcal asymptotcally stablty theorem, error vector e approaches zero and the estmated parameters also approach the uncertan parameters. The equlbrum pont s pragmatcally asymptotcally stable. Under the assumpton of equal probablty, t s actually asymptotcally stable. The smulaton results are shown n Fgs Case The followng chaotc systems are two translated DGK systems of whch the old orgn s translated to ( x, x, x) (50,50,50), ( y, y, y) (50,50,50) to guarantee that the error dynamcs always happens n the frst quadrant of e coordnate system. 4
54 x x 50 x a( x 50) ( x 50){ b[ c ( x 50) ] d( x 50)} x a( x 50) ( x 50){ b[ c ( x 50) ] g( x 50)} y y 50 u y a( y 50) ( y 50){ b[ c ( y 50) ] d( y 50)} u y a( y 50) ( y 50){ b[ c ( y 50) ] g( y 50)} u (4.9) (4.0) Let ntal states be ( x, x, x) (50.0,50.0,50.0), ( y, y, y ) (50.0,50.0,50.0) and system parameters a 0.5, b.4, c.9, d 4.5, g 6.. The state error s e x y F() t, where Ft () z [ z, z, z] s the state vector of Chen system: zh( z z ) z ( w h) z z z wz z z z lz (4.) Let ntal states be z [ z, z, z] [0.5,0.6,0.5] and system parameters h 5, l, w 7.. The Chen system s chaotc, Ft () z [ z, z, z] s a gven chaotc vector functon of tme. Defne e x y z We fnd that the error dynamcs wthout controller always exsts n frst quadrant as shown n Fg.4.7. lm e lm[ x y z ],,, (4.) t t Our am s lm e 0. t We obtan the error dynamcs: 4
55 e x 50 y 50 u h( z z) e a( x 50) ( x 50){ b[ c ( x 50) ] d( x 50)} a( y 50) ( y 50){ b[ c ( y 50) ] d( y 50)} u ( w h) z zz wz e a( x 50) ( x 50){ b[ c ( x 50) ] g( x 50)} a( y 50) ( y 50){ b[ c ( y 50) ] g( y 50)} u zz lz (4.) where a a aˆ, b b bˆ, c c cˆ, d d dˆ, g g gˆ, and a, b, c, d, g, are estmates of uncertan parameters a, b, c, d and g respectvely. Usng dfferent translaton pragmatcal synchronzaton by stablty theory of partal regon, we can choose a Lyapunov functon n the form of a postve defnte functon n frst quadrant: V e e e a b c d g (4.4) Its tme dervatve s V e e e a b c d g ( x 50 y 50 u h( z z )) a( x 50) ( x 50){ b[ c ( x 50) ] d( x 50)} a( y 50) ( y 50){ b[ c ( y 50) ] d( y 50)} u ( w h) z z z wz a( x 50) ( x 50) { b[ c ( x 50) ] g( x 50)} a( y 50) ( y 50){ b[ c ( y 50) ] g( y 50)} u z z lz a b c d g (4.5) Choose a aˆ ae b bˆ be c cˆ ce d dˆ de g gˆ ge (4.6) 44
56 u x 50 y 50 h( z z) e u a( x 50) ( x 50){ b[ c ( x 50) ] d( x 50)} a( y 50) ( y 50){ b[ c ( y 50) ] d( y 50)} ( w h) z zz wz e ae be ce u a( x 50) ( x 50){ b[ c ( x 50) ] gx ( 50)} a( y 50) ( y 50){ b[ c ( y 50) ] g( y 50)} zz lz e de ge (4.7) We obtan V e e e 0 (4.8) whch s a negatve sem-defnte functon of e, e, e, a, b, c, d, g n the frst quadrant. The Lyapunov asymptotcal stablty theorem s not satsfed. We can not obtan that common orgn of error dynamcs () and parameter dynamcs (6) s asymptotcally stable. By pragmatcal asymptotcally stablty theorem, D s a 8-manfold, n=8 and the number of error state varables p=. When e e e 0 and a, b, c, d, g, take arbtrary values, V 0, so X s of dmensons, m=n-p=8-=5, m+<n s satsfed. Accordng to the pragmatcal asymptotcally stablty theorem, error vector e approaches zero and the estmated parameters also approach the uncertan parameters. The equlbrum pont s pragmatcally asymptotcally stable. Under the assumpton of equal probablty, t s actually asymptotcally stable. The smulaton results are shown n Fgs Case The followng chaotc systems are the two translated DGK systems of whch the old orgn s translated to ( x, x, x) (50,50,50), ( y, y, y) (50,50,50) to guarantee error dynamcs always happens n the frst quadrant of e coordnate system. 45
57 x x 50 x a( x 50) ( x 50){ b[ c ( x 50) ] d( x 50)} x a( x 50) ( x 50){ b[ c ( x 50) ] g( x 50)} y y 50 u y a( y 50) ( y 50){ b[ c ( y 50) ] d( y 50)} u y a( y 50) ( y 50){ b[ c ( y 50) ] g( y 50)} u (4.9) (4.0) Let ntal states be ( x, x, x) (50.0,50.0,50.0), ( y, y, y ) (50.0,50.0,50.0) and system parameters a 0.5, b.4, c.9, d 4.5, g 6.. The state error s e x y F() t, where Ft () z [ z, z, z] s state vector the new Ge-Ku-van der Pol(GKv) system: z z z fz z[ f( f z ) f4z] z gz h( z ) z lz (4.) Let ntal states be ( z, z, z) (0.0,0.0,0.0) and system parameters f 0.08, f 0.5, f 00.56, f , h 0.6, l 0.08, w 0.0, the Ge-Ku-van der Pol system [56] s chaotc n Fg.4., Ft () z [ z, z, z] s a gven chaotc vector functon of tme. Defne e x y z We fnd that the error dynamc wthout controller always exsts n frst quadrant as shown n Fg. 4.. lm e lm[ x y z ],,, (4.) t t Our am s lm e 0. t We obtan the error dynamcs: 46
58 e x 50 y 50 u z e a( x 50) ( x 50){ b[ c ( x 50) ] d( x 50)} a( y 50) ( y 50){ b[ c ( y 50) ] d( y 50)} u fz z[ f( f z ) f4z] e a( x 50) ( x 50){ b[ c ( x 50) ] g( x 50)} a( y 50) ( y 50){ b[ c ( y 50) ] g( y 50)} u hz l( z ) z wz (4.) where a a aˆ, b b bˆ, c c cˆ, d d dˆ, g g gˆ, and a, b, c, d, g, are estmates of uncertan parameters a, b, c, d and g respectvely. Usng dfferent translaton pragmatcal synchronzaton by stablty theory of partal regon, we can choose a Lyapunov functon n the form of a postve defnte functon n frst quadrant: V e e e a b c d g (4.4) Its tme dervatve s V e e e a b c d g ( x 50 y 50 u z ) a( x 50) ( x 50){ b[ c ( x 50) ] d( x 50)} a( y 50) ( y 50){ b[ c ( y 50) ] d( y 50)} u f z z [ f ( f z ) f z ] 4 a( x 50) ( x 50){ b[ c ( x 50) ] g( x 50)} a( y 50) ( y 50){ b[ c ( y 50) ] g( y 50)} u hz l( z ) z wz a b c d g (4.5) Choose 47
59 a aˆ ae b bˆ be c cˆ ce d dˆ de g gˆ ge u x 50 y 50 z e u a( x 50) ( x 50){ b[ c ( x 50) ] d( x 50)} a( y 50) ( y 50){ b[ c ( y 50) ] d( y 50)} fz z[ f( f z ) f4z] e ae be ce u a( x 50) ( x 50){ b[ c ( x 50) ] gx ( 50)} a( y 50) ( y 50){ b[ c ( y 50) ] g( y 50)} hz l( z ) z wz e de ge We obtan (4.6) (4.7) V e e e 0 (4.8) whch s a negatve sem-defnte functon of e, e, e, a, b, c, d, g, n the frst quadrant. The Lyapunov asymptotcal stablty theorem s not satsfed. We can not obtan that common orgn of error dynamcs () and parameter dynamcs (6) s asymptotcally stable. By pragmatcal asymptotcally stablty theorem, D s a 8-manfold, n=8 and the number of error state varables p=. When e e e 0 and a, b, c, d, g, take arbtrary values, V 0, so X s of dmensons, m=n-p=8-=5, m+<n s satsfed. Accordng to the pragmatcal asymptotcally stablty theorem, error vector e approaches zero and the estmated parameters also approach the uncertan parameters. The equlbrum pont s pragmatcally asymptotcally stable. Under the assumpton of equal probablty, t s actually asymptotcally stable. The smulaton results are shown n Fgs
60 Fg. 4. Coordnate translaton of state x. Fg. 4. Coordnate translaton of state y. 49
61 Fg. 4. Phase portrat of the error dynamcs for Case. Fg. 4.4 Tme hstores of x, y for Case. 50
62 Fg. 4.5 Tme hstores of errors for Case. Fg. 4.6 Tme hstores of parameter errors for Case. 5
63 Fg. 4.7 Phase portrat of the error dynamc for Case. Fg. 4.8 Tme hstores of x, y for Case. 5
64 Fg. 4.9 Tme hstores of errors for Case. Fg. 4.0 Tme hstores of parameter errors for Case. 5
65 Fg. 4. The chaotc attractor of the Ge-Ku-van der Pol system. Fg. 4. Phase portrat of the error dynamc for Case. 54
66 Fg. 4. Tme hstores of x, y for Case. Fg. 4.4 Tme hstores of errors for Case. 55
67 Fg. 4.5 Tme hstores of parameter errors for Case. 56
68 Chapter 5 Robust Projectve Ant-Synchronzaton of Non-autonomous and Chaotc Uncertan Stochastc Systems Va Fuzzy Logc Constant Controller 5. Prelmnary In ths Chapter, the smplest controller fuzzy logc constant controller (FLCC) whch s derved by fuzzy logc desgn and Lyapunov drect method s ntroduced. Controllers n tradtonal method are always complcated or nonlnear. FLCC proposed are such smple controllers whch are constructed by constant number decded by the values of the upper and lower bound of the error dervatves. Therefore ths tool s further used n projectve ant-synchronzaton of chaotc uncertan and stochastc systems wth to show the robustness and effectveness of FLCC. There are two cases llustrated n smulaton results to show the feasblty of the FLCC Sprott 4 system and Double Ge-Ku (DGK) system. Comparson of the effcency and complexty for the FLCC for tradtonal nonlnear controllers are gven n tables and fgures. 5. Projectve Ant-Synchronzaton by FLCC Scheme Consder the followng non-autonomous or uncertan chaotc system x Ax f(x) (5.) where x [ x, x, x ] T n n R denotes a state vector, A s an n n constant coeffcent matrx and f s a nonlnear vector functon, s uncertan term. The goal system whch can be ether chaotc or regular, s y By g(y) u (5.) 57
69 where y [ y, y, y ] T n n R denotes a state vector, B s an n n constant coeffcent matrx, g s a nonlnear vector functon, and u [ u, u, u ] T n n R s the fuzzy logc controller needed to be desgned. In order to make the chaotc state x approachng the goal state y, defne e xy as the state error, here s projectve constant. The projectve chaos ant-synchronzaton s accomplshed n the sense that [57]: where lme lm( x y ) 0 (5.) t t e xy (5.4) From Eq. (-4) we have the followng error dynamcs: e x y [ A x f (x) ] B[ y g (y) u] (5.5) Accordng to Lyapunov drect method, we have the followng Lyapunov functon to derve the fuzzy logc controller for ant-synchronzaton: V f ( e,... em,... en ) ( e... em... en ) 0 (5.6) The dervatve of the Lyapunov functon n Eq. (5.5) s: V e e... me me... nene (5.7) If the controllers ncluded n e... em... en can be sutably desgned to acheve the target: V 0, then the two chaotc systems are asymptotcally stable. The desgn process of FLCC s ntroduced n the followng secton. We use one sgnal, error dervatves e ( t) e, e e, e m n T, as the antecedent part of the proposed FLCC to desgn the control nput u that wll be used n the consequent part of the proposed FLCC as follows: T, u um, un u u (5.8) 58
70 where u s a constant column vector and the FLCC accomplshes the objectve to stablze the error dynamcs (5.5). The strategy of the FLCC desgnng s proposed as follow and the confguraton of the strategy s shown n Fg. 5.. Assume the upper bound and lower bound of e m are Z m and Z m, then the FLCC can be desgn step by step as follow: () If e m s detected as postve ( em 0 ), we have to desgn a controller for e 0, thenv e e 0can be acheved. Therefore we have the followng th f then m fuzzy rule as: m m Rule : IF Rule : IF em s M THEN u m = -Z m (5.9) em s M THEN u m = -Z m (5.0) Rule : IF em s M THEN u m = e m (5.) () If e m s detected as negatve ( em 0 ), we have to desgn a controller for e 0, thenv e e 0can be acheved. Therefore we have the followng th f then m fuzzy rule as: m m Rule : IF Rule : IF em s M THEN u m = Z m (5.) em s M THEN u m = Z m (5.) Rule :IF em s M THEN u m = e m (5.4) () If em approaches to zero, then the ant-synchronzaton s nearly acheved. Therefore we have the followng th f then fuzzy rule as: Rule :IF Rule : IF e s M THEN u m = e 0 (5.5) m m m e s M THEN u m = e 0 (5.6) m Rule : IF e s M THEN u m = e 0 (5.7) m em em Zm em em Zm where M, M and M sgn( ) sgn( ), M, M and M Z Z Z Z m m refer to the membershp functons of postve (P), negatve (N) and zero (Z) separately 59 m m m
71 whch are presented n Fg. 5. For each case, u m, = ~ s the -rd output of e m whch s a constant controller. The centrod defuzzfer evaluates the output of all rules as follows: M um u m (5.8) M The fuzzy rule base s lsted n Table 5., n whch the nput varables n the antecedent part of the rules are e m and the output varable n the consequent part s u m. Table 5. Rule-table of FLCC Rule Antecedent Consequent Part e m u m Negatve (N) u m Postve (P) u m Zero (Z) u m After desgnng approprate fuzzy logc constant controllers and beng substtuted nto Eq. (5.7), a negatve defnte of dervatves of Lyapunov functon V can be obtaned and the asymptotcally stablty of Lyapunov theorem can be acheved. Consequently, the processes of FLCC desgnng to control a system followng the trajectory of a goal system s - gettng the upper bound and lower bound of the error dervatves of the goal and control systems wthout any controller,.e. Z e Z. Through the fuzzy logc system whch follows the rules of Eq. (5.9) m m m ~ Eq. (5.7), a negatve defnte of dervatves of Lyapunov functon V can be obtaned and the asymptotcally stablty of Lyapunov theorem can be acheved. 5. Smulaton Results 60
72 There are two cases n ths secton. Each example s dvded nto two parts projecton ant-synchronzaton by FLCC and tradtonal method. In the end of each example, we further conclude the smulaton results of the two controllers and lst tables and fgures to show the effectveness and robustness of our method. 5.. Example. Projectve Ant-synchronzaton of Non-autonomous Chaotc Systems by FLCC The master Sprott 4 system [50] wth uncertanty s : dx () t x dt dx () t x dt dx () t ax x x x dt (5.9) For ntal condton x, x, ) = (0,, ), s Bsn(wt), =Csn(wt) and ( 0 0 x0 parameters a=-0.5, B=0.0, C=.0, w=0.0, chaos of the Sprott 4 system [50] appears. The chaotc behavor of Sprott 4 system [50] s shown n Fg 5.. And Eq. (5.9) s shown n Fg 5.4. The dentcal slave DGK system s: dy () t y u dt dy() t b y y [ b ( b y ) b y ] u dt dy() t b y y [ b ( b y ) b y ] u dt 4 5 (5.0) For ntal condton y, y, ) = (0.0, 0.0, 0.0) and parameters b = -0.5, ( 0 0 y0 b = -.4, b =.9, b 4 = -4.5, b 5 =6., chaos of the slave DGK system appears as well. u, u and u are FLCC to ant-synchronze the slave DGK system to master one,.e., the projecton of phase portrats of system (5.0) wth chaotc behavors s shown 6
73 n Fg. 5.. lm e 0 t (5.) where the error vector e ( t) x ( t) y( t) e e ( t) A x ( t) y ( t) e ( t) x( t) y( t) (5.) Let A. From Eq. (5.), we have the followng error dynamcs: e A[ x ] ( y u) e A[ x ] ( b y y[ b ( b y ) b4 y] u) e A[ ax x x x ] ( b y y[ b ( b y ) b5 y ] u) (5.) Choosng Lyapunov functon as: V ( e e e ) (5.4) Its tme dervatve s: V e e e e e e e { A[ x ] ( y u )} e { A[ x ] ( b y y [ b ( b y ) b y ] u )} 4 e { A[ a x x x x ] ( b y y [ b ( b y ) b y ] u )} 5 (5.5) In order to desgn FLCC, we dvde Eq. (5.5) nto three parts as follows: Assume V ( e e e ) V V V, then V ee ee ee V V V, where V e. Part : V ee e{ A[ x ] ( y u)} V e, V e and Part : V e e e { A[ x ] ( b y y [ b ( b y ) b y ] u )} 4 6
74 Part : V e e e A( a x x x x ) ( b y y [ b ( b y ) b y ] u ) 5 FLCC n Part, and can be obtaned va the fuzzy rules n Table. The maxmum value and mnmum value wthout any controller can be observed n tme hstores of error dervatves shown n Fg 5.5: Z, Z, Z 6. The ant-synchronzaton scheme s proposed n Part, and and let e e 0, e e 0 and e e 0. Hence we have V V V V V V V 0. It s clear that all of the rules n FLCC can lead the Lyapunov functon satsfes the asymptotcally stable theorem. The smulaton results are shown n Fg. 5.6 and Fg Projectve Ant-synchronzaton of Sprott 4 System [50]and DGK System by Tradtonal Method In order to lead the dervatve of Lyapunov functon n Eq. (5.5) to negatve defnte, we choose tradtonal nonlnear controller as: u [ A( x ) y e ] u { A( x ) b y y[ b ( b y ) b4 y] e} u { A( 0.5 x x x x ) b y y[ b ( b y ) b5 y ] e} (5.6) then we can obtan V e e e e e e0 (5.7) The dervatve of Lyapunov functon s negatve defnte and the error dynamcs n Eq. (5.) are gong to acheve asymptotcally stable. The smulaton results are shown n Fg. 5.8 and Fg Robust FLCC Compared wth Tradtonal Method In ths secton, we compare the numercal smulaton results n 5.. and 5.. 6
75 whch are lsted n Tables 5. and 5.. Comparng the two smulaton results n Tables 5. and 5., t s clear to fnd out that: () The performance of the error convergence of states by FLCC s much better than by tradtonal method; () The controller n FLCC desgnng are much smpler than tradtonal ones. Consequently, even the system contans parameter uncertanty, the FLCC can stll reman the hgh performance to ant-synchronze the two chaotc systems wth uncertanty and exactly and effcently. Table 5.. Controllers are compared between the tradtonal method and FLCC method. Controller FLCC Tradtonal u u u Z, e 0 Z, e 0 A( x ) y e { A( x ) b y y [ b ( b y ) b y ] e } 4 Z 6, e 0 { A[ a( ) x bx x x ] cy y sn y e } Table 5.. FLCC s compared to tradtonal method between errors data. Tme(s) FLCC Tradtonal 64
76 e e e e e e Example. Chaos Projectve Ant-synchronzaton of Uncertan Stochastc Sprott 4 System [50] and DGK System The uncertan stochastc Sprott 4 system [50] wth nose s: dx () t x dt dx() t x dt dx () t a x ( ) x x x dt (5.8) For ntal condton x, x, ) = (0,, ), the uncertan term s Dsn(wt), ( 0 0 x0 the stochastc term s Raylegh nose and parameters a=-0.5, D=0., w=0.5, chaos of the uncertan stochastc Sprott 4 system appears. Raylegh nose s shown n Fg 65
77 5.0. The chaotc behavor of Eq. (5.8) s shown n Fg 5.. The dentcal slave DGK system s: dy () t y u dt dy() t b y y [ b ( b y ) b y ] u dt dy() t b y y [ b ( b y ) b y ] u dt 4 5 (5.9) When ntal condton y, y, ) = (0.0, 0.0, 0.0) and parameters b = -0.5, ( 0 0 y0 b = -.4, b =.9, b 4 = -4.5, b 5 =6., chaos of the slave DGK system appears as well. u, u and u are FLCC to ant-synchronze the slave DGK system to the master one,.e., the projecton of phase portrats of system (-) wth chaotc behavors s shown n Fg. 5.. lm e 0 t (5.0) where the error vector e ( t) x ( t) y( t) e e ( t) A x ( t) y ( t) e ( t) x( t) y( t) (5.) Let A. From Eq. (5.), we have the followng error dynamcs: e A[ x ( y u)] e A[ x ( b y y[ b ( b y ) b4 y] u)] e A[ ax ( ) x x x ( b y y[ b ( b y ) b5 y] u)] (5.) Choosng Lyapunov functon as: V ( e e e) (5.) Its tme dervatve s: 66
78 V e e e e e e e { A[ x ( y u )]} e { A[ x ( b y y [ b ( b y ) b y ] u )]} 4 e { A[ a x ( ) x x x ( b y y [ b ( b y ) b y ] u )]} 5 (5.4) In order to desgn FLCC, we dvde Eq. (5.4) nto three parts as follows: AssumeV ( e e e ) V V V, then V e e ee ee V V V Part : V ee e A[ x ( y u)], wherev e, V e andv e. Part : Part : V e e e A[ x ( b y y [ b ( b y ) b y ] u )] 4 V e e e A[ a x ( ) x x x ( b y y [ b ( b y ) b y ] u )] 5 FLCC n Part, and can be obtaned va the fuzzy rules n Table 5.. The maxmum value and mnmum value wthout any controller can be observed n tme hstores of error dervatves shown n Fg 5.: Z, Z, Z 5. FLCC are proposed n Part, and and make e e 0, e e 0 and V V e e 0. Hence, we have V V V 0. It s clear that all of the rules n V V our FLCC can lead the Lyapunov functon satsfes the asymptotcally stable theorem. The smulaton results are shown n Fg. 5.4 and Chaos Projectve Ant-synchronzaton of Uncertanty Stochastc Sprott 4 System [50] and DGK System by Tradtonal Method Accordng to Eq. (5.4), we desgn complcated controllers to ant-synchronze chaotc system wth uncertanty by tradtonal method. We choose the controllers as follows 67
79 u [ A( x ) y e ] u { Ax b y y[ b ( b y ) b4 y] e} u { A( 0.5 x ( ) x x x ) b y y[ b ( b y ) b5 y] e} (5.5) then we can obtan V e e e e e e0 (5.6) The dervatve of Lyapunov functon s negatve defnte and the error dynamcs n Eq. (5.) are gong to acheve asymptotcally stable. The smulaton results are shown n Fg. 5.6 and Fg Robust FLCC Compared to Tradtonal Method In ths case, we compare the numercal smulaton results n 5..4 and 5..5 whch are lsted n Table 5.4 and 5.5. The two man superortes are stll exsted () The performance of the error convergence of states by FLCC are much better than by tradtonal method; () The controllers n FLCC desgnng are much smpler than tradtonal ones Table 5.4. Controllers are compared between the tradtonal method and FLCC method. Controller FLCC Tradtonal u u Z 4, e 0 A( x ) y e u Z, e 0 Z 5, e 0 { Ax b y y [ b ( b y ) b y ] e } 4 { A( 0.5 x ( ) x x x ) b y y [ b ( b y ) b y ] e } 5 68
80 Table 5.5. FLCC s compared to tradtonal method between errors data. Tme(s) FLCC Tradtonal e e e e 69
81 e e
82 Fg. 5. The confguraton of fuzzy logc controller. Fg. 5. Membershp functon. 7
83 Fg. 5. The chaotc behavor of Sprott 4 system [50] Fg. 5.4 Projectons of phase portrat of Eq (5.9). 7
84 Fg. 5.5 Tme hstores of error dervatves for master and slave chaotc systems wthout controllers. Fg. 5.6 Tme hstores of states for Example the FLCC s comng nto after 0s. 7
85 Fg. 5.7 Tme hstores of errors for Example the FLCC s comng nto after 0s. Fg. 5.8 Tme hstores of states for the tradtonal controller s comng nto after 0s. 74
86 Fg. 5.9 Tme hstores of states for the tradtonal controller s comng nto after 0s. Fg. 5.0 The Raylegh nose used. 75
87 Fg. 5. Projecton of phase portrat of Eq (5.8). Fg. 5. Projectons of phase portrat of chaotc DGK systems. 76
88 Fg. 5. Tme hstores of error dervatves for master and slave chaotc uncertan stochastc systems wthout controllers. Fg. 5.4 Tme hstores of states for Example the FLCC s comng nto after 0s. 77
89 Fg. 5.5 Tme hstores of errors for Example the FLCC s comng nto after 0s. Fg. 5.6 Tme hstores of states for the tradtonal controller s comng nto after 0s. 78
90 Fg. 5.7 Tme hstores of states for the tradtonal controller s comng nto after 0s. 79
91 Chapter 6 Fuzzy Modelng and Synchronzaton of Chaotc Systems by a New Fuzzy Model 6. Prelmnary In ths paper, a new fuzzy model [58] s used to smulate and synchronze two totally dfferent chaotc systems, Sprott systems and Rossler system. Va the new fuzzy model, a complex nonlnear system s lnearzed to a smple form. Only two lnear subsystems are needed and the numbers of fuzzy rules can be decreased from N to N. Sprott systems and Rossler system are used for examples n numercal smulaton results to show the effectveness and feasblty of our new model. 6. New Fuzzy Model Theory In system analyss and desgn, t s mportant to select an approprate model representng a real system. As an expresson model of a real plant, the fuzzy mplcatons and the fuzzy reasonng method suggested by Takag and Sugeno are tradtonally used. The new fuzzy model s also descrbed by fuzzy IF-THEN rules. The core of the new fuzzy model s that we express each nonlnear equaton nto two lnear sub-equatons by fuzzy IF-THEN rules and take all the frst lnear sub-equatons to form one lnear subsystem and all the second lnear sub-equatons to form another lnear subsystem. The overall fuzzy model of the system s acheved by fuzzy blendng of ths two lnear subsystem models. Consder a contnuous-tme nonlnear dynamc system as follows: Equaton : 80
92 rule : rule : where IF z (t) s M THEN (t) A x(t) B u(t), x IF z (t) s M THEN (t) A x(t) B u(t), (6.) x T (t), x (t),..., x n(t)] x(t) [x, T (t), u (t),..., u n(t)] u(t) [u,,...n, where n s the number of nonlnear terms. z (t) s nonlnear term, M, M are fuzzy sets,, B A are column vectors and x (t) A x(t) B u(t), j j j,, s the output from the frst and the second IF-THEN rules. ut () s vector controller. Gven a par of ( x ( t),u( t)) and take all the frst lnear sub-equatons to form one lnear subsystem and all the second lnear sub-equatons to form another lnear subsystem, the fnal output of the fuzzy system s nferred as follows: Ax(t) Bu(t) Ax(t) Bu(t) Ax(t) Bu(t) Ax(t) Bu(t) x(t) M M (6.) Ax(t) Bu(t) Ax(t) Bu(t) where M and M are dagonal matrces as followng: da ( M ) M M..., da ( M ) M M... M Note that for each equaton : j M j(z(t)), M j (z (t)) 0, =,,, n and j=,. 8 M
93 Va the new fuzzy model, the fnal form of the fuzzy model becomes very smple. The new model provdes a much more convenent approach for fuzzy model research and fuzzy applcaton. The smulaton results of chaotc systems are dscussed n next Secton. 6. New Fuzzy Model of Chaotc Systems In ths Secton, the new fuzzy models of two dfferent chaotc systems, Sprott 4 system [50] and Rossler system, are gven for Model and Model. Model : New fuzzy model of Sprott 4 system wth uncertanty The Sprott 4 system wth uncertanty s: x x x x x 0.5x x x x (6.) wth ntal states (0.0,, 0.0). Uncertan terms are = 0.sn(50t) and = 0.0cos(50t). The chaotc attractor of the Sprott 4 system s shown n Fg. 6. and the chaotc attractor of Eq.(6.) s shown n Fg. 6.. If T-S fuzzy model s used for representng local lnear models of Sprott 4 system, N, N 8, 8 fuzzy rules and 8 lnear subsystems are need. The process of modelng s shown as follows: T-S fuzzy model: Assume that: () Z Z [, ] and Z 0 () Z Z [, ] and Z 0 () x Z Z [, ] and Z 0 8
94 Then we have the followng T-S fuzzy rules: Rule : IF s M, s M and x s M THEN X A X, Rule : IF s M, s M and x s M THEN X A X, Rule : IF s M, s M and x s M THEN X A X, Rule 4: IF s M, s M and x s M THEN X A4 X, Rule 5: IF s M, s M and x s M THEN X A5 X, Rule 6: IF s M, s M and x s M THEN X A6 X, Rule 7: IF s M, s M and x s M THEN X A7 X, Rule 8: IF s M, s M and x s M THEN X A8 X, Then the fnal output of the Sprott 4 system can be composed by fuzzy lnear subsystems mentoned above. It s obvously an neffcent and complcated work. New fuzzy model: By usng the new fuzzy model, Sprott 4 system can be lnearzed as smple lnear equatons. The steps of fuzzy modelng are shown as follows: Steps of fuzzy modelng: Step : Assume that [ Z, Z] and Z 0, then the frst equaton of (-) can be represented by new fuzzy model as followng: Rule: IF s M, THEN x x Z, (6.4) where R u l e : I F s M, T H E N x x Z, ( 6. 5 ) M ( ), M ( ), Z Z 8
95 and Z 0.. M and M are fuzzy sets of the frst equaton of (-) and M M. Step : Assume that [ Z, Z] and Z 0, then the second equaton of (-) can be exactly represented by new fuzzy model as followng: where Rule : IF s M, THEN x x Z, (6.6) Rule : IF s M, THEN x x Z (6.7) M ( ), M ( ), Z Z and Z 0.0. M and M are fuzzy sets of the second equaton of (6.) and M M Step :. Assume that x [ Z, Z] and Z 0, then the thrd equaton of (6.) can be exactly represented by new fuzzy model as followng: where Rule : IF x s M, THEN x 0.5x x x xz, (6.8) Rule : IF x s M, THEN x 0.5x x x x Z (6.9) M x ( x ), M ( ), Z Z and Z.5. M and M are fuzzy sets of the thrd equaton of (6.) and M M. Here, we call Eqs.(6.4), (6.6) and (6.8) the frst lnear subsystem under the fuzzy rules, and Eqs.(6.5), (6.7) and (6.9) the second lnear subsystem under the fuzzy rules. The frst lnear subsystem s 84
96 x x Z x x Z x 0.5x x x x Z (6.0) The second lnear subsystem s x x Z x x Z x 0.5x x x x Z (6.) The fnal output of the fuzzy Sprott 4 system s nferred as follows and the chaotc behavor of fuzzy system s shown n Fg. 6.. Now we have: x M 0 0 x Z x 0 M 0 x Z x 0 0 M 0.5x x x xz M 0 0 x Z 0 M 0 x Z 0 0 M 0.5x x x xz (6.) Eq. (6.) can be rewrtten as a smple mathematcal expresson: ~ X (t) (A X(t) b ) (6.) where are dagonal matrces as follows: M M, da( M M M da( M ) ) 0 0 A 0 0, Z 0.5 Z b Z 0 A , Z 0.5 b Z Z 0 Va new fuzzy model, the number of fuzzy rules can be greatly reduced. Only two lnear subsystems are enough to express such complex chaotc behavors. The smulaton results are smlar the orgnal chaotc behavor of the Sprott 4 system as 85
97 show n Fg. 6.. Model : New fuzzy model of Rossler system wth uncertanty The Rossler system wth uncertanty s: y y y 0. y y 0.5y4 y 0. y y 9y (6.4) where uncertanty terms s whte nose (PSD=0.), 4 s Raylegh nose and ntal condtons are chosen as (,.4, 5). The chaotc attractor of Rossler system s shown n Fg. 6.4, the chaotc attractor of Eq.(6.4) s shown n Fg. 6.5 and the Raylegh nose s shown n Fg New fuzzy model: Assume that: () Z4 Z4 0. [, ] and Z 4 0, () 4 Z5 Z5 [, ] and Z 5 0, () y Z6 Z6 [, ] and Z 6 0, then we have the followng new fuzzy rules: Rule : IF 0. s N, THEN y y y Z4, (6.5) Rule : IF 0. s N, THEN y y y Z4 (6.6) where N 0. ( ), Z 4 N 0. Z ( ) 4 and Rule : IF 4 s N,THEN y y 0.5yZ5, (6.7) Rule : IF 4 s N,THEN y y 0.5yZ5, (6.8) 86
98 where N ( 4 ), Z 5 N ( 4 ). Z 5 and Rule : IF x s N,THEN y 0. yz 6 9y, (6.9) Rule : IF x s N,THEN y 0. yz 6 9y, (6.0) where N x ( ), Z 6 N x ( ). Z 6 n Eqs. (6.5)~(6.0), Z4 0.4, Z5 4 and Z N, N, N, N, N and N are fuzzy sets of Eq.(6.4) and N N, N N and N N Here, we call (6.5),(6.7) and (6.9) the frst lner subsystem under the fuzzy rules and (6.6), (6.8) and (6.0) the second lner subsystem under the fuzzy rules. The frst lnear subsystem s y y y Z4 y y 0.5yZ5 y 0. y Z 9y 6 (6.) The second lnear subsystem s y y y Z4 y y 0.5yZ5 y 0. y Z 9y 6 (6.) The fnal output of the fuzzy Rossler system s nferred as follows and the chaotc behavor of fuzzy system s shown n Fg
99 T y N 0 0 y y Z4 y 0 N 0 y 0.5yZ 5 y 0 0 N 0. y Z 9x 6 T N 0 0 y y Z4 0 N 0 y 0.5yZ N 0. y Z 9x 6 (6.) where Eq. (6.) can be rewrtten as a smple mathematcal expresson: Y ( t) ( C Y ( t) c~ ) (6.4) N N, da( N N N da( N ) ) 0 C 0.5Z5 0, Z Z4 c 0 0. C 0 0.5Z 0, Z c Z Va new fuzzy model, two lnear subsystems are enough to express such complex chaotc behavors. The smulaton results are smlar the orgnal chaotc behavor of the Rossler system. 6.4 Fuzzy Synchronzaton Scheme In ths Secton, we derve the new fuzzy synchronzaton scheme based on our new fuzzy model to synchronze two totally dfferent fuzzy chaotc systems. The followng fuzzy systems as the master and slave systems are gven: master system: ~ X (t) (A X(t) b ) (6.5) slave system: 88
100 Y (t) (C Y(t) ~ c ) BU(t) (6.6) Eq. (6.5) and Eq. (6.6) represent the two dfferent chaotc systems, and n Eq. (6.6) there s control nput U(t). Defne the error sgnal as e(t) X(t) Y(t), we have: where ~ e (t) X(t) Y(t) (A X(t) b ) (C Y(t) ~ c ) BU(t) (6.7) 89 The fuzzy controllers are desgned as follows: U (t) u (t) u (t) (6.8) u (t) FX(t) PY(t ), ~ u (t) b ~ c such that e(t) 0 as t. Our desgn s to determne the feedback gans F and P. By substtutng U(t) nto Eq.(6.7), we obtan: (A BF )X(t) (C BP )Y(t e (t) ) (6.9) Theorem : The error system n Eq. (6.9) s asymptotcally stable and the slave system n Eq. (6.6) can synchronze the master system n Eq. (6.5) under the fuzzy controller n Eq. (6.8) f the followng condtons below can be satsfed: Proof: G (A BF ) (A BF ) (C BP ) 0, =~. (6.0) The errors n Eq. (6.9) can be exactly lnearzed va the fuzzy controllers n Eq. (6.8) f there exst the feedback gans F such that ( A BF ) (A BF ) (C BP ) (C BP ) 0. (6.) Then the overall control system s lnearzed as e (t) Ge (t), (6.) where (A BF ) (A BF ) (C BP ) (C BP ) 0. G As a consequence, the zero soluton of the error system (6.) lnearzed va the
101 90 fuzzy controller (6.8) s asymptotcally stable. 6.5 Smulaton Results There are two examples n ths Secton to nvestgate the effectveness and feasblty of our new fuzzy model. Example : Synchronzaton of Master and Slave Sprott 4 system The fuzzy Sprott 4 system n Eq. (6.) s chosen as the master system and the fuzzy slave Sprott 4 system, wth fuzzy controllers s as follows: ) ( ~ ) ) ( ( ) ( t BU c t C Y t Y (6.) where are dagonal matrces ) ( N N N da, ) ( N N N da and C Z, 0 Z c Z C Z, 0 Z c Z. Therefore, the error and error dynamcs are: y x y x y x e e e, ) ( ~ ) ) ( ( ) ( ) ~ ) ( ( t BU c t C Y t Y b t A X y x y x y x e e e (6.4) B s chosen as an dentty matrx and the fuzzy controllers n Eq. (6.8) are used:
102 e x x e A BF x A BF x e x x y y C BP y C BP y y y (6.5) Accordng to Eq. (6.0), we have G A BF A BF C BP C BP. G s chosen as: G 0 0 (6.6) 0 0 Thus, the feedback gans F, F, P and P can be determned by the followng equatons: 0 F B A G F B A G (6.7) 0 P B C G P B C G The synchronzaton errors are shown n Fg
103 9 Example : Synchronzaton of Sprott 4 system and Rossler system. The fuzzy Sprott 4 system n Eq. (6.) s chosen as the master system and the fuzzy slave Rossler system, wth fuzzy controllers s as follows: ) ( ~ ) ) ( ( ) ( t BU c t C Y t Y (6.8) where are dagonal matrces, and C Z Z, Z c C Z Z, Z c Therefore, the error and error dynamcs are:, (6.9) B s chosen as an dentty matrx and the fuzzy controllers n Eq. (6.8) are used: y y C BP y C BP y y y (6.40) ) ( N N N da ) ( N N N da y x y x y x e e e ) ( ~ ) ) ( ( ) ( ) ~ ) ( ( t BU c t C Y t Y b t A X y x y x y x e e e x x x BF A x x x BF A e e e
104 Accordng to Eq. (6.0), we have G A BF A BF C BP C. G s chosen as: BP 0 G (6.4) Thus, the feedback gans F, F, P and P can be determned by the followng equaton: 0 F B A G F B A G (6.4) P B C G P B C G The synchronzaton errors are shown n Fg
105 Fg. 6. Chaotc behavor of Sprott 4 system. Fg. 6. Chaotc behavor of Sprott 4 system wth uncertanty. 94
106 Fg. 6. Chaotc behavor of new fuzzy Sprott 4 system wth uncertanty. Fg. 6.4 Chaotc behavor of Rossler system. 95
107 Fg. 6.5 Chaotc behavor of Rossler system wth uncertanty. Fg. 6.6 The Raylegh nose used. 96
108 Fg. 6.7 Chaotc behavor of new fuzzy Rossler system wth uncertanty. Fg. 6.8 Tme hstores of errors for Example. 97
授課大綱 課號課程名稱選別開課系級學分 結果預視
 授課大綱 課號課程名稱選別開課系級學分 B06303A 流體力學 Fluid Mechanics 必 結果預視 課程介紹 (Course Description): 機械工程學系 三甲 3 在流體力學第一課的學生可能會問 : 什麼是流體力學? 為什麼我必須研究它? 我為什麼要研究它? 流體力學有哪些應用? 流體包括液體和氣體 流體力學涉及靜止和運動時流體的行為 對流體力學的基本原理和概念的了解和理解對分析任何工程系統至關重要,
授課大綱 課號課程名稱選別開課系級學分 B06303A 流體力學 Fluid Mechanics 必 結果預視 課程介紹 (Course Description): 機械工程學系 三甲 3 在流體力學第一課的學生可能會問 : 什麼是流體力學? 為什麼我必須研究它? 我為什麼要研究它? 流體力學有哪些應用? 流體包括液體和氣體 流體力學涉及靜止和運動時流體的行為 對流體力學的基本原理和概念的了解和理解對分析任何工程系統至關重要,
生物統計教育訓練 - 課程. Introduction to equivalence, superior, inferior studies in RCT 謝宗成副教授慈濟大學醫學科學研究所. TEL: ext 2015
 生物統計教育訓練 - 課程 Introduction to equivalence, superior, inferior studies in RCT 謝宗成副教授慈濟大學醫學科學研究所 tchsieh@mail.tcu.edu.tw TEL: 03-8565301 ext 2015 1 Randomized controlled trial Two arms trial Test treatment
生物統計教育訓練 - 課程 Introduction to equivalence, superior, inferior studies in RCT 謝宗成副教授慈濟大學醫學科學研究所 tchsieh@mail.tcu.edu.tw TEL: 03-8565301 ext 2015 1 Randomized controlled trial Two arms trial Test treatment
國立中正大學八十一學年度應用數學研究所 碩士班研究生招生考試試題
 國立中正大學八十一學年度應用數學研究所 碩士班研究生招生考試試題 基礎數學 I.(2%) Test for convergence or divergence of the following infinite series cos( π (a) ) sin( π n (b) ) n n=1 n n=1 n 1 1 (c) (p > 1) (d) n=2 n(log n) p n,m=1 n 2 +
國立中正大學八十一學年度應用數學研究所 碩士班研究生招生考試試題 基礎數學 I.(2%) Test for convergence or divergence of the following infinite series cos( π (a) ) sin( π n (b) ) n n=1 n n=1 n 1 1 (c) (p > 1) (d) n=2 n(log n) p n,m=1 n 2 +
Linear Regression. Applied Linear Regression Models (Kutner, Nachtsheim, Neter, Li) hsuhl (NUK) SDA Regression 1 / 34
 Linear Regression 許湘伶 Applied Linear Regression Models (Kutner, Nachtsheim, Neter, Li) hsuhl (NUK) SDA Regression 1 / 34 Regression analysis is a statistical methodology that utilizes the relation between
Linear Regression 許湘伶 Applied Linear Regression Models (Kutner, Nachtsheim, Neter, Li) hsuhl (NUK) SDA Regression 1 / 34 Regression analysis is a statistical methodology that utilizes the relation between
The equation of motion of a dynamical system is given by a set of differential equations. That is (1)
 Dynamcal Systems Many engneerng and natural systems are dynamcal systems. For example a pendulum s a dynamcal system. State l The state of the dynamcal system specfes t condtons. For a pendulum n the absence
Dynamcal Systems Many engneerng and natural systems are dynamcal systems. For example a pendulum s a dynamcal system. State l The state of the dynamcal system specfes t condtons. For a pendulum n the absence
Chapter 1 Linear Regression with One Predictor Variable
 Chapter 1 Linear Regression with One Predictor Variable 許湘伶 Applied Linear Regression Models (Kutner, Nachtsheim, Neter, Li) hsuhl (NUK) LR Chap 1 1 / 41 Regression analysis is a statistical methodology
Chapter 1 Linear Regression with One Predictor Variable 許湘伶 Applied Linear Regression Models (Kutner, Nachtsheim, Neter, Li) hsuhl (NUK) LR Chap 1 1 / 41 Regression analysis is a statistical methodology
= lim(x + 1) lim x 1 x 1 (x 2 + 1) 2 (for the latter let y = x2 + 1) lim
 1061 微乙 01-05 班期中考解答和評分標準 1. (10%) (x + 1)( (a) 求 x+1 9). x 1 x 1 tan (π(x )) (b) 求. x (x ) x (a) (5 points) Method without L Hospital rule: (x + 1)( x+1 9) = (x + 1) x+1 x 1 x 1 x 1 x 1 (x + 1) (for the
1061 微乙 01-05 班期中考解答和評分標準 1. (10%) (x + 1)( (a) 求 x+1 9). x 1 x 1 tan (π(x )) (b) 求. x (x ) x (a) (5 points) Method without L Hospital rule: (x + 1)( x+1 9) = (x + 1) x+1 x 1 x 1 x 1 x 1 (x + 1) (for the
Chapter 5. Solution of System of Linear Equations. Module No. 6. Solution of Inconsistent and Ill Conditioned Systems
 Numercal Analyss by Dr. Anta Pal Assstant Professor Department of Mathematcs Natonal Insttute of Technology Durgapur Durgapur-713209 emal: anta.bue@gmal.com 1 . Chapter 5 Soluton of System of Lnear Equatons
Numercal Analyss by Dr. Anta Pal Assstant Professor Department of Mathematcs Natonal Insttute of Technology Durgapur Durgapur-713209 emal: anta.bue@gmal.com 1 . Chapter 5 Soluton of System of Lnear Equatons
More metrics on cartesian products
 More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
More metrcs on cartesan products If (X, d ) are metrc spaces for 1 n, then n Secton II4 of the lecture notes we defned three metrcs on X whose underlyng topologes are the product topology The purpose of
Dynamic Systems on Graphs
 Prepared by F.L. Lews Updated: Saturday, February 06, 200 Dynamc Systems on Graphs Control Graphs and Consensus A network s a set of nodes that collaborates to acheve what each cannot acheve alone. A network,
Prepared by F.L. Lews Updated: Saturday, February 06, 200 Dynamc Systems on Graphs Control Graphs and Consensus A network s a set of nodes that collaborates to acheve what each cannot acheve alone. A network,
Chapter 20 Cell Division Summary
 Chapter 20 Cell Division Summary Bk3 Ch20 Cell Division/1 Table 1: The concept of cell (Section 20.1) A repeated process in which a cell divides many times to make new cells Cell Responsible for growth,
Chapter 20 Cell Division Summary Bk3 Ch20 Cell Division/1 Table 1: The concept of cell (Section 20.1) A repeated process in which a cell divides many times to make new cells Cell Responsible for growth,
1 Matrix representations of canonical matrices
 1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
1 Matrx representatons of canoncal matrces 2-d rotaton around the orgn: ( ) cos θ sn θ R 0 = sn θ cos θ 3-d rotaton around the x-axs: R x = 1 0 0 0 cos θ sn θ 0 sn θ cos θ 3-d rotaton around the y-axs:
Yong Joon Ryang. 1. Introduction Consider the multicommodity transportation problem with convex quadratic cost function. 1 2 (x x0 ) T Q(x x 0 )
 Kangweon-Kyungk Math. Jour. 4 1996), No. 1, pp. 7 16 AN ITERATIVE ROW-ACTION METHOD FOR MULTICOMMODITY TRANSPORTATION PROBLEMS Yong Joon Ryang Abstract. The optmzaton problems wth quadratc constrants often
Kangweon-Kyungk Math. Jour. 4 1996), No. 1, pp. 7 16 AN ITERATIVE ROW-ACTION METHOD FOR MULTICOMMODITY TRANSPORTATION PROBLEMS Yong Joon Ryang Abstract. The optmzaton problems wth quadratc constrants often
Week3, Chapter 4. Position and Displacement. Motion in Two Dimensions. Instantaneous Velocity. Average Velocity
 Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Week3, Chapter 4 Moton n Two Dmensons Lecture Quz A partcle confned to moton along the x axs moves wth constant acceleraton from x =.0 m to x = 8.0 m durng a 1-s tme nterval. The velocty of the partcle
Inner Product. Euclidean Space. Orthonormal Basis. Orthogonal
 Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
Inner Product Defnton 1 () A Eucldean space s a fnte-dmensonal vector space over the reals R, wth an nner product,. Defnton 2 (Inner Product) An nner product, on a real vector space X s a symmetrc, blnear,
Lectures - Week 4 Matrix norms, Conditioning, Vector Spaces, Linear Independence, Spanning sets and Basis, Null space and Range of a Matrix
 Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Lectures - Week 4 Matrx norms, Condtonng, Vector Spaces, Lnear Independence, Spannng sets and Bass, Null space and Range of a Matrx Matrx Norms Now we turn to assocatng a number to each matrx. We could
Introduction. - The Second Lyapunov Method. - The First Lyapunov Method
 Stablty Analyss A. Khak Sedgh Control Systems Group Faculty of Electrcal and Computer Engneerng K. N. Toos Unversty of Technology February 2009 1 Introducton Stablty s the most promnent characterstc of
Stablty Analyss A. Khak Sedgh Control Systems Group Faculty of Electrcal and Computer Engneerng K. N. Toos Unversty of Technology February 2009 1 Introducton Stablty s the most promnent characterstc of
適應控制與反覆控制應用在壓電致動器之研究 Adaptive and Repetitive Control of Piezoelectric Actuators
 行 精 類 行 年 年 行 立 林 參 理 劉 理 論 理 年 行政院國家科學委員會補助專題研究計畫成果報告 適應控制與反覆控制應用在壓電致動器之研究 Adaptive and Repetitive Control of Piezoelectric Actuators 計畫類別 : 個別型計畫 整合型計畫 計畫編號 :NSC 97-2218-E-011-015 執行期間 :97 年 11 月 01
行 精 類 行 年 年 行 立 林 參 理 劉 理 論 理 年 行政院國家科學委員會補助專題研究計畫成果報告 適應控制與反覆控制應用在壓電致動器之研究 Adaptive and Repetitive Control of Piezoelectric Actuators 計畫類別 : 個別型計畫 整合型計畫 計畫編號 :NSC 97-2218-E-011-015 執行期間 :97 年 11 月 01
Report on Image warping
 Report on Image warpng Xuan Ne, Dec. 20, 2004 Ths document summarzed the algorthms of our mage warpng soluton for further study, and there s a detaled descrpton about the mplementaton of these algorthms.
Report on Image warpng Xuan Ne, Dec. 20, 2004 Ths document summarzed the algorthms of our mage warpng soluton for further study, and there s a detaled descrpton about the mplementaton of these algorthms.
Differential Equations (DE)
 工程數學 -- 微分方程 51 Differenial Equaions (DE) 授課者 : 丁建均 教學網頁 :hp://djj.ee.nu.edu.w/de.hm 本著作除另有註明外, 採取創用 CC 姓名標示 - 非商業性 - 相同方式分享 台灣 3. 版授權釋出 Chaper 8 Sysems of Linear Firs-Order Differenial Equaions 另一種解 聯立微分方程式
工程數學 -- 微分方程 51 Differenial Equaions (DE) 授課者 : 丁建均 教學網頁 :hp://djj.ee.nu.edu.w/de.hm 本著作除另有註明外, 採取創用 CC 姓名標示 - 非商業性 - 相同方式分享 台灣 3. 版授權釋出 Chaper 8 Sysems of Linear Firs-Order Differenial Equaions 另一種解 聯立微分方程式
Algorithms and Complexity
 Algorithms and Complexity 2.1 ALGORITHMS( 演算法 ) Def: An algorithm is a finite set of precise instructions for performing a computation or for solving a problem The word algorithm algorithm comes from the
Algorithms and Complexity 2.1 ALGORITHMS( 演算法 ) Def: An algorithm is a finite set of precise instructions for performing a computation or for solving a problem The word algorithm algorithm comes from the
Power law and dimension of the maximum value for belief distribution with the max Deng entropy
 Power law and dmenson of the maxmum value for belef dstrbuton wth the max Deng entropy Bngy Kang a, a College of Informaton Engneerng, Northwest A&F Unversty, Yanglng, Shaanx, 712100, Chna. Abstract Deng
Power law and dmenson of the maxmum value for belef dstrbuton wth the max Deng entropy Bngy Kang a, a College of Informaton Engneerng, Northwest A&F Unversty, Yanglng, Shaanx, 712100, Chna. Abstract Deng
DO NOT DO HOMEWORK UNTIL IT IS ASSIGNED. THE ASSIGNMENTS MAY CHANGE UNTIL ANNOUNCED.
 EE 539 Homeworks Sprng 08 Updated: Tuesday, Aprl 7, 08 DO NOT DO HOMEWORK UNTIL IT IS ASSIGNED. THE ASSIGNMENTS MAY CHANGE UNTIL ANNOUNCED. For full credt, show all work. Some problems requre hand calculatons.
EE 539 Homeworks Sprng 08 Updated: Tuesday, Aprl 7, 08 DO NOT DO HOMEWORK UNTIL IT IS ASSIGNED. THE ASSIGNMENTS MAY CHANGE UNTIL ANNOUNCED. For full credt, show all work. Some problems requre hand calculatons.
Convexity preserving interpolation by splines of arbitrary degree
 Computer Scence Journal of Moldova, vol.18, no.1(52), 2010 Convexty preservng nterpolaton by splnes of arbtrary degree Igor Verlan Abstract In the present paper an algorthm of C 2 nterpolaton of dscrete
Computer Scence Journal of Moldova, vol.18, no.1(52), 2010 Convexty preservng nterpolaton by splnes of arbtrary degree Igor Verlan Abstract In the present paper an algorthm of C 2 nterpolaton of dscrete
0 0 = 1 0 = 0 1 = = 1 1 = 0 0 = 1
 0 0 = 1 0 = 0 1 = 0 1 1 = 1 1 = 0 0 = 1 : = {0, 1} : 3 (,, ) = + (,, ) = + + (, ) = + (,,, ) = ( + )( + ) + ( + )( + ) + = + = = + + = + = ( + ) + = + ( + ) () = () ( + ) = + + = ( + )( + ) + = = + 0
0 0 = 1 0 = 0 1 = 0 1 1 = 1 1 = 0 0 = 1 : = {0, 1} : 3 (,, ) = + (,, ) = + + (, ) = + (,,, ) = ( + )( + ) + ( + )( + ) + = + = = + + = + = ( + ) + = + ( + ) () = () ( + ) = + + = ( + )( + ) + = = + 0
Canonical transformations
 Canoncal transformatons November 23, 2014 Recall that we have defned a symplectc transformaton to be any lnear transformaton M A B leavng the symplectc form nvarant, Ω AB M A CM B DΩ CD Coordnate transformatons,
Canoncal transformatons November 23, 2014 Recall that we have defned a symplectc transformaton to be any lnear transformaton M A B leavng the symplectc form nvarant, Ω AB M A CM B DΩ CD Coordnate transformatons,
Lecture Notes on Linear Regression
 Lecture Notes on Lnear Regresson Feng L fl@sdueducn Shandong Unversty, Chna Lnear Regresson Problem In regresson problem, we am at predct a contnuous target value gven an nput feature vector We assume
Lecture Notes on Lnear Regresson Feng L fl@sdueducn Shandong Unversty, Chna Lnear Regresson Problem In regresson problem, we am at predct a contnuous target value gven an nput feature vector We assume
Module 3 LOSSY IMAGE COMPRESSION SYSTEMS. Version 2 ECE IIT, Kharagpur
 Module 3 LOSSY IMAGE COMPRESSION SYSTEMS Verson ECE IIT, Kharagpur Lesson 6 Theory of Quantzaton Verson ECE IIT, Kharagpur Instructonal Objectves At the end of ths lesson, the students should be able to:
Module 3 LOSSY IMAGE COMPRESSION SYSTEMS Verson ECE IIT, Kharagpur Lesson 6 Theory of Quantzaton Verson ECE IIT, Kharagpur Instructonal Objectves At the end of ths lesson, the students should be able to:
Econ107 Applied Econometrics Topic 3: Classical Model (Studenmund, Chapter 4)
 I. Classcal Assumptons Econ7 Appled Econometrcs Topc 3: Classcal Model (Studenmund, Chapter 4) We have defned OLS and studed some algebrac propertes of OLS. In ths topc we wll study statstcal propertes
I. Classcal Assumptons Econ7 Appled Econometrcs Topc 3: Classcal Model (Studenmund, Chapter 4) We have defned OLS and studed some algebrac propertes of OLS. In ths topc we wll study statstcal propertes
Linear Approximation with Regularization and Moving Least Squares
 Lnear Approxmaton wth Regularzaton and Movng Least Squares Igor Grešovn May 007 Revson 4.6 (Revson : March 004). 5 4 3 0.5 3 3.5 4 Contents: Lnear Fttng...4. Weghted Least Squares n Functon Approxmaton...
Lnear Approxmaton wth Regularzaton and Movng Least Squares Igor Grešovn May 007 Revson 4.6 (Revson : March 004). 5 4 3 0.5 3 3.5 4 Contents: Lnear Fttng...4. Weghted Least Squares n Functon Approxmaton...
Transfer Functions. Convenient representation of a linear, dynamic model. A transfer function (TF) relates one input and one output: ( ) system
 Transfer Functons Convenent representaton of a lnear, dynamc model. A transfer functon (TF) relates one nput and one output: x t X s y t system Y s The followng termnology s used: x y nput output forcng
Transfer Functons Convenent representaton of a lnear, dynamc model. A transfer functon (TF) relates one nput and one output: x t X s y t system Y s The followng termnology s used: x y nput output forcng
Appendix B. The Finite Difference Scheme
 140 APPENDIXES Appendx B. The Fnte Dfference Scheme In ths appendx we present numercal technques whch are used to approxmate solutons of system 3.1 3.3. A comprehensve treatment of theoretcal and mplementaton
140 APPENDIXES Appendx B. The Fnte Dfference Scheme In ths appendx we present numercal technques whch are used to approxmate solutons of system 3.1 3.3. A comprehensve treatment of theoretcal and mplementaton
Anti-Synchronization of two Different Chaotic Systems via Optimal Control with Fully Unknown Parameters *
 ISSN 76-7659, England, UK Journal of Informaton and Computng Scence Vol. 5, No., 00, pp. 0-08 Ant-Synchronzaton of two Dfferent Chaotc Systems va Optmal Control wth Fully Unknown Parameters * Honglan Zhu
ISSN 76-7659, England, UK Journal of Informaton and Computng Scence Vol. 5, No., 00, pp. 0-08 Ant-Synchronzaton of two Dfferent Chaotc Systems va Optmal Control wth Fully Unknown Parameters * Honglan Zhu
Physics 5153 Classical Mechanics. Principle of Virtual Work-1
 P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
P. Guterrez 1 Introducton Physcs 5153 Classcal Mechancs Prncple of Vrtual Work The frst varatonal prncple we encounter n mechancs s the prncple of vrtual work. It establshes the equlbrum condton of a mechancal
NON-CENTRAL 7-POINT FORMULA IN THE METHOD OF LINES FOR PARABOLIC AND BURGERS' EQUATIONS
 IJRRAS 8 (3 September 011 www.arpapress.com/volumes/vol8issue3/ijrras_8_3_08.pdf NON-CENTRAL 7-POINT FORMULA IN THE METHOD OF LINES FOR PARABOLIC AND BURGERS' EQUATIONS H.O. Bakodah Dept. of Mathematc
IJRRAS 8 (3 September 011 www.arpapress.com/volumes/vol8issue3/ijrras_8_3_08.pdf NON-CENTRAL 7-POINT FORMULA IN THE METHOD OF LINES FOR PARABOLIC AND BURGERS' EQUATIONS H.O. Bakodah Dept. of Mathematc
ECE559VV Project Report
 ECE559VV Project Report (Supplementary Notes Loc Xuan Bu I. MAX SUM-RATE SCHEDULING: THE UPLINK CASE We have seen (n the presentaton that, for downlnk (broadcast channels, the strategy maxmzng the sum-rate
ECE559VV Project Report (Supplementary Notes Loc Xuan Bu I. MAX SUM-RATE SCHEDULING: THE UPLINK CASE We have seen (n the presentaton that, for downlnk (broadcast channels, the strategy maxmzng the sum-rate
國立交通大學 電子工程學系電子研究所碩士班 碩士論文
 國立交通大學 電子工程學系電子研究所碩士班 碩士論文 萃取接觸阻抗係數方法之比較研究 CBKR 結構與改良式 TLM 結構 A Comparison Study of the Specific Contact Resistivity Extraction Methods: CBKR Method and Modified TLM Method 研究生 : 曾炫滋 指導教授 : 崔秉鉞教授 中華民國一
國立交通大學 電子工程學系電子研究所碩士班 碩士論文 萃取接觸阻抗係數方法之比較研究 CBKR 結構與改良式 TLM 結構 A Comparison Study of the Specific Contact Resistivity Extraction Methods: CBKR Method and Modified TLM Method 研究生 : 曾炫滋 指導教授 : 崔秉鉞教授 中華民國一
Adaptive sliding mode reliable excitation control design for power systems
 Acta Technca 6, No. 3B/17, 593 6 c 17 Insttute of Thermomechancs CAS, v.v.. Adaptve sldng mode relable exctaton control desgn for power systems Xuetng Lu 1, 3, Yanchao Yan Abstract. In ths paper, the problem
Acta Technca 6, No. 3B/17, 593 6 c 17 Insttute of Thermomechancs CAS, v.v.. Adaptve sldng mode relable exctaton control desgn for power systems Xuetng Lu 1, 3, Yanchao Yan Abstract. In ths paper, the problem
國立交通大學 電信工程學系 碩士論文 考慮晶片上互感及電阻 電感 電容雜訊之漏話 導向電路佈局. Crosstalk-Driven Placement with Considering On-Chip Mutual. Inductance and RLC Noise 研究生 : 邱震軒
 國立交通大學 電信工程學系 碩士論文 考慮晶片上互感及電阻 電感 電容雜訊之漏話 導向電路佈局 Crosstalk-Driven Placement with Considering On-Chip Mutual Inductance and RLC Noise 研究生 : 邱震軒 指導教授 : 李育民教授 中華民國九十四年十月 考慮晶片上互感與電阻 電感 電容雜訊之漏話導向電路佈局 Crosstalk-Driven
國立交通大學 電信工程學系 碩士論文 考慮晶片上互感及電阻 電感 電容雜訊之漏話 導向電路佈局 Crosstalk-Driven Placement with Considering On-Chip Mutual Inductance and RLC Noise 研究生 : 邱震軒 指導教授 : 李育民教授 中華民國九十四年十月 考慮晶片上互感與電阻 電感 電容雜訊之漏話導向電路佈局 Crosstalk-Driven
Ch.9 Liquids and Solids
 Ch.9 Liquids and Solids 9.1. Liquid-Vapor Equilibrium 1. Vapor Pressure. Vapor Pressure versus Temperature 3. Boiling Temperature. Critical Temperature and Pressure 9.. Phase Diagram 1. Sublimation. Melting
Ch.9 Liquids and Solids 9.1. Liquid-Vapor Equilibrium 1. Vapor Pressure. Vapor Pressure versus Temperature 3. Boiling Temperature. Critical Temperature and Pressure 9.. Phase Diagram 1. Sublimation. Melting
The Two-scale Finite Element Errors Analysis for One Class of Thermoelastic Problem in Periodic Composites
 7 Asa-Pacfc Engneerng Technology Conference (APETC 7) ISBN: 978--6595-443- The Two-scale Fnte Element Errors Analyss for One Class of Thermoelastc Problem n Perodc Compostes Xaoun Deng Mngxang Deng ABSTRACT
7 Asa-Pacfc Engneerng Technology Conference (APETC 7) ISBN: 978--6595-443- The Two-scale Fnte Element Errors Analyss for One Class of Thermoelastc Problem n Perodc Compostes Xaoun Deng Mngxang Deng ABSTRACT
Scroll Generation with Inductorless Chua s Circuit and Wien Bridge Oscillator
 Latest Trends on Crcuts, Systems and Sgnals Scroll Generaton wth Inductorless Chua s Crcut and Wen Brdge Oscllator Watcharn Jantanate, Peter A. Chayasena, and Sarawut Sutorn * Abstract An nductorless Chua
Latest Trends on Crcuts, Systems and Sgnals Scroll Generaton wth Inductorless Chua s Crcut and Wen Brdge Oscllator Watcharn Jantanate, Peter A. Chayasena, and Sarawut Sutorn * Abstract An nductorless Chua
The lower and upper bounds on Perron root of nonnegative irreducible matrices
 Journal of Computatonal Appled Mathematcs 217 (2008) 259 267 wwwelsevercom/locate/cam The lower upper bounds on Perron root of nonnegatve rreducble matrces Guang-Xn Huang a,, Feng Yn b,keguo a a College
Journal of Computatonal Appled Mathematcs 217 (2008) 259 267 wwwelsevercom/locate/cam The lower upper bounds on Perron root of nonnegatve rreducble matrces Guang-Xn Huang a,, Feng Yn b,keguo a a College
Parameter Estimation for Dynamic System using Unscented Kalman filter
 Parameter Estmaton for Dynamc System usng Unscented Kalman flter Jhoon Seung 1,a, Amr Atya F. 2,b, Alexander G.Parlos 3,c, and Klto Chong 1,4,d* 1 Dvson of Electroncs Engneerng, Chonbuk Natonal Unversty,
Parameter Estmaton for Dynamc System usng Unscented Kalman flter Jhoon Seung 1,a, Amr Atya F. 2,b, Alexander G.Parlos 3,c, and Klto Chong 1,4,d* 1 Dvson of Electroncs Engneerng, Chonbuk Natonal Unversty,
Integrals and Invariants of Euler-Lagrange Equations
 Lecture 16 Integrals and Invarants of Euler-Lagrange Equatons ME 256 at the Indan Insttute of Scence, Bengaluru Varatonal Methods and Structural Optmzaton G. K. Ananthasuresh Professor, Mechancal Engneerng,
Lecture 16 Integrals and Invarants of Euler-Lagrange Equatons ME 256 at the Indan Insttute of Scence, Bengaluru Varatonal Methods and Structural Optmzaton G. K. Ananthasuresh Professor, Mechancal Engneerng,
Design and Optimization of Fuzzy Controller for Inverse Pendulum System Using Genetic Algorithm
 Desgn and Optmzaton of Fuzzy Controller for Inverse Pendulum System Usng Genetc Algorthm H. Mehraban A. Ashoor Unversty of Tehran Unversty of Tehran h.mehraban@ece.ut.ac.r a.ashoor@ece.ut.ac.r Abstract:
Desgn and Optmzaton of Fuzzy Controller for Inverse Pendulum System Usng Genetc Algorthm H. Mehraban A. Ashoor Unversty of Tehran Unversty of Tehran h.mehraban@ece.ut.ac.r a.ashoor@ece.ut.ac.r Abstract:
Numerical Heat and Mass Transfer
 Master degree n Mechancal Engneerng Numercal Heat and Mass Transfer 06-Fnte-Dfference Method (One-dmensonal, steady state heat conducton) Fausto Arpno f.arpno@uncas.t Introducton Why we use models and
Master degree n Mechancal Engneerng Numercal Heat and Mass Transfer 06-Fnte-Dfference Method (One-dmensonal, steady state heat conducton) Fausto Arpno f.arpno@uncas.t Introducton Why we use models and
Physics 5153 Classical Mechanics. D Alembert s Principle and The Lagrangian-1
 P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
P. Guterrez Physcs 5153 Classcal Mechancs D Alembert s Prncple and The Lagrangan 1 Introducton The prncple of vrtual work provdes a method of solvng problems of statc equlbrum wthout havng to consder the
Salmon: Lectures on partial differential equations. Consider the general linear, second-order PDE in the form. ,x 2
 Salmon: Lectures on partal dfferental equatons 5. Classfcaton of second-order equatons There are general methods for classfyng hgher-order partal dfferental equatons. One s very general (applyng even to
Salmon: Lectures on partal dfferental equatons 5. Classfcaton of second-order equatons There are general methods for classfyng hgher-order partal dfferental equatons. One s very general (applyng even to
Irregular vibrations in multi-mass discrete-continuous systems torsionally deformed
 (2) 4 48 Irregular vbratons n mult-mass dscrete-contnuous systems torsonally deformed Abstract In the paper rregular vbratons of dscrete-contnuous systems consstng of an arbtrary number rgd bodes connected
(2) 4 48 Irregular vbratons n mult-mass dscrete-contnuous systems torsonally deformed Abstract In the paper rregular vbratons of dscrete-contnuous systems consstng of an arbtrary number rgd bodes connected
The Study of Teaching-learning-based Optimization Algorithm
 Advanced Scence and Technology Letters Vol. (AST 06), pp.05- http://dx.do.org/0.57/astl.06. The Study of Teachng-learnng-based Optmzaton Algorthm u Sun, Yan fu, Lele Kong, Haolang Q,, Helongang Insttute
Advanced Scence and Technology Letters Vol. (AST 06), pp.05- http://dx.do.org/0.57/astl.06. The Study of Teachng-learnng-based Optmzaton Algorthm u Sun, Yan fu, Lele Kong, Haolang Q,, Helongang Insttute
THE GUARANTEED COST CONTROL FOR UNCERTAIN LARGE SCALE INTERCONNECTED SYSTEMS
 Copyrght 22 IFAC 5th rennal World Congress, Barcelona, Span HE GUARANEED COS CONROL FOR UNCERAIN LARGE SCALE INERCONNECED SYSEMS Hroak Mukadan Yasuyuk akato Yoshyuk anaka Koch Mzukam Faculty of Informaton
Copyrght 22 IFAC 5th rennal World Congress, Barcelona, Span HE GUARANEED COS CONROL FOR UNCERAIN LARGE SCALE INERCONNECED SYSEMS Hroak Mukadan Yasuyuk akato Yoshyuk anaka Koch Mzukam Faculty of Informaton
On simultaneous parameter identification and state estimation for cascade state affine systems
 Amercan Control Conference Westn Seattle Hotel, Seattle, Washngton, USA June 11-13, WeAI1.9 On smultaneous parameter dentfcaton and state estmaton for cascade state affne systems M. GHANES, G. ZHENG and
Amercan Control Conference Westn Seattle Hotel, Seattle, Washngton, USA June 11-13, WeAI1.9 On smultaneous parameter dentfcaton and state estmaton for cascade state affne systems M. GHANES, G. ZHENG and
tan θ(t) = 5 [3 points] And, we are given that d [1 points] Therefore, the velocity of the plane is dx [4 points] (km/min.) [2 points] (The other way)
![tan θ(t) = 5 [3 points] And, we are given that d [1 points] Therefore, the velocity of the plane is dx [4 points] (km/min.) [2 points] (The other way) tan θ(t) = 5 [3 points] And, we are given that d [1 points] Therefore, the velocity of the plane is dx [4 points] (km/min.) [2 points] (The other way)](/thumbs/74/69694342.jpg) 1051 微甲 06-10 班期中考解答和評分標準 1. (10%) A plane flies horizontally at an altitude of 5 km and passes directly over a tracking telescope on the ground. When the angle of elevation is π/3, this angle is decreasing
1051 微甲 06-10 班期中考解答和評分標準 1. (10%) A plane flies horizontally at an altitude of 5 km and passes directly over a tracking telescope on the ground. When the angle of elevation is π/3, this angle is decreasing
A new Approach for Solving Linear Ordinary Differential Equations
 , ISSN 974-57X (Onlne), ISSN 974-5718 (Prnt), Vol. ; Issue No. 1; Year 14, Copyrght 13-14 by CESER PUBLICATIONS A new Approach for Solvng Lnear Ordnary Dfferental Equatons Fawz Abdelwahd Department of
, ISSN 974-57X (Onlne), ISSN 974-5718 (Prnt), Vol. ; Issue No. 1; Year 14, Copyrght 13-14 by CESER PUBLICATIONS A new Approach for Solvng Lnear Ordnary Dfferental Equatons Fawz Abdelwahd Department of
國立交通大學 電子工程學系電子研究所碩士班 碩士論文
 國立交通大學 電子工程學系電子研究所碩士班 碩士論文 適用於快閃記憶體之 (9216,8195) 拉丁方陣 低密度奇偶校驗碼解碼器 A (9216,8195) LDPC Decoder based on Latin Square for NAND Flash Memory 學生 : 曾士家 指導教授 : 張錫嘉教授 中華民國一百年十二月 適用於快閃記憶體之 (9216,8195) 拉丁方陣 低密度奇偶校驗碼解碼器
國立交通大學 電子工程學系電子研究所碩士班 碩士論文 適用於快閃記憶體之 (9216,8195) 拉丁方陣 低密度奇偶校驗碼解碼器 A (9216,8195) LDPC Decoder based on Latin Square for NAND Flash Memory 學生 : 曾士家 指導教授 : 張錫嘉教授 中華民國一百年十二月 適用於快閃記憶體之 (9216,8195) 拉丁方陣 低密度奇偶校驗碼解碼器
Boundary Influence On The Entropy Of A Lozi-Type Map. Cellular Neural Networks : Defect Patterns And Stability
 Boundary Influence On The Entropy Of A Lozi-Type Map Yu-Chuan Chang and Jonq Juang Abstract: Let T be a Henon-type map induced from a spatial discretization of a Reaction-Diffusion system With the above-mentioned
Boundary Influence On The Entropy Of A Lozi-Type Map Yu-Chuan Chang and Jonq Juang Abstract: Let T be a Henon-type map induced from a spatial discretization of a Reaction-Diffusion system With the above-mentioned
Solutions HW #2. minimize. Ax = b. Give the dual problem, and make the implicit equality constraints explicit. Solution.
 Solutons HW #2 Dual of general LP. Fnd the dual functon of the LP mnmze subject to c T x Gx h Ax = b. Gve the dual problem, and make the mplct equalty constrants explct. Soluton. 1. The Lagrangan s L(x,
Solutons HW #2 Dual of general LP. Fnd the dual functon of the LP mnmze subject to c T x Gx h Ax = b. Gve the dual problem, and make the mplct equalty constrants explct. Soluton. 1. The Lagrangan s L(x,
COMPARISON OF SOME RELIABILITY CHARACTERISTICS BETWEEN REDUNDANT SYSTEMS REQUIRING SUPPORTING UNITS FOR THEIR OPERATIONS
 Avalable onlne at http://sck.org J. Math. Comput. Sc. 3 (3), No., 6-3 ISSN: 97-537 COMPARISON OF SOME RELIABILITY CHARACTERISTICS BETWEEN REDUNDANT SYSTEMS REQUIRING SUPPORTING UNITS FOR THEIR OPERATIONS
Avalable onlne at http://sck.org J. Math. Comput. Sc. 3 (3), No., 6-3 ISSN: 97-537 COMPARISON OF SOME RELIABILITY CHARACTERISTICS BETWEEN REDUNDANT SYSTEMS REQUIRING SUPPORTING UNITS FOR THEIR OPERATIONS
Ministry of Sciences and Technology, Chinese Academy of Sciences as well as some international pharmaceutical companies.
 Ren-Xiao WANG Professor, PhD Macau Institute for Applied Research in Medicine and Health, State Key Laboratory for Quality Research in Chinese Medicines Macau University of Science and Technology Prof.
Ren-Xiao WANG Professor, PhD Macau Institute for Applied Research in Medicine and Health, State Key Laboratory for Quality Research in Chinese Medicines Macau University of Science and Technology Prof.
Kernel Methods and SVMs Extension
 Kernel Methods and SVMs Extenson The purpose of ths document s to revew materal covered n Machne Learnng 1 Supervsed Learnng regardng support vector machnes (SVMs). Ths document also provdes a general
Kernel Methods and SVMs Extenson The purpose of ths document s to revew materal covered n Machne Learnng 1 Supervsed Learnng regardng support vector machnes (SVMs). Ths document also provdes a general
Chapter 1 Physics and Measurement
 Chapter 1 Physics and Measurement We have always been curious about the world around us. Classical Physics It constructs the concepts Galileo (1564-1642) and Newton s space and time. It includes mechanics
Chapter 1 Physics and Measurement We have always been curious about the world around us. Classical Physics It constructs the concepts Galileo (1564-1642) and Newton s space and time. It includes mechanics
APPENDIX A Some Linear Algebra
 APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
APPENDIX A Some Lnear Algebra The collecton of m, n matrces A.1 Matrces a 1,1,..., a 1,n A = a m,1,..., a m,n wth real elements a,j s denoted by R m,n. If n = 1 then A s called a column vector. Smlarly,
Chapter 9: Statistical Inference and the Relationship between Two Variables
 Chapter 9: Statstcal Inference and the Relatonshp between Two Varables Key Words The Regresson Model The Sample Regresson Equaton The Pearson Correlaton Coeffcent Learnng Outcomes After studyng ths chapter,
Chapter 9: Statstcal Inference and the Relatonshp between Two Varables Key Words The Regresson Model The Sample Regresson Equaton The Pearson Correlaton Coeffcent Learnng Outcomes After studyng ths chapter,
Statistics and Econometrics I
 Statistics and Econometrics I Probability Model Shiu-Sheng Chen Department of Economics National Taiwan University October 4, 2016 Shiu-Sheng Chen (NTU Econ) Statistics and Econometrics I October 4, 2016
Statistics and Econometrics I Probability Model Shiu-Sheng Chen Department of Economics National Taiwan University October 4, 2016 Shiu-Sheng Chen (NTU Econ) Statistics and Econometrics I October 4, 2016
Erratum: A Generalized Path Integral Control Approach to Reinforcement Learning
 Journal of Machne Learnng Research 00-9 Submtted /0; Publshed 7/ Erratum: A Generalzed Path Integral Control Approach to Renforcement Learnng Evangelos ATheodorou Jonas Buchl Stefan Schaal Department of
Journal of Machne Learnng Research 00-9 Submtted /0; Publshed 7/ Erratum: A Generalzed Path Integral Control Approach to Renforcement Learnng Evangelos ATheodorou Jonas Buchl Stefan Schaal Department of
Exercises of Chapter 2
 Exercses of Chapter Chuang-Cheh Ln Department of Computer Scence and Informaton Engneerng, Natonal Chung Cheng Unversty, Mng-Hsung, Chay 61, Tawan. Exercse.6. Suppose that we ndependently roll two standard
Exercses of Chapter Chuang-Cheh Ln Department of Computer Scence and Informaton Engneerng, Natonal Chung Cheng Unversty, Mng-Hsung, Chay 61, Tawan. Exercse.6. Suppose that we ndependently roll two standard
EEE 241: Linear Systems
 EEE : Lnear Systems Summary #: Backpropagaton BACKPROPAGATION The perceptron rule as well as the Wdrow Hoff learnng were desgned to tran sngle layer networks. They suffer from the same dsadvantage: they
EEE : Lnear Systems Summary #: Backpropagaton BACKPROPAGATION The perceptron rule as well as the Wdrow Hoff learnng were desgned to tran sngle layer networks. They suffer from the same dsadvantage: they
Performing Modulation Scheme of Chaos Shift Keying with Hyperchaotic Chen System
 6 th Internatonal Advanced echnologes Symposum (IAS 11), 16-18 May 011, Elazığ, urkey Performng Modulaton Scheme of Chaos Shft Keyng wth Hyperchaotc Chen System H. Oğraş 1, M. ürk 1 Unversty of Batman,
6 th Internatonal Advanced echnologes Symposum (IAS 11), 16-18 May 011, Elazığ, urkey Performng Modulaton Scheme of Chaos Shft Keyng wth Hyperchaotc Chen System H. Oğraş 1, M. ürk 1 Unversty of Batman,
國立交通大學 機械工程學系 碩士論文 應用適應控制之 H 型壓電陀螺儀的設計與控制. Design and Control of the H-type Piezoelectric. Gyroscope via Adaptive Control Strategies 研究生 : 黃建評
 國立交通大學 機械工程學系 碩士論文 應用適應控制之 H 型壓電陀螺儀的設計與控制 Design and Control of the H-type Piezoelectric Gyroscope via Adaptive Control Strategies 研究生 : 黃建評 指導教授 : 陳宗麟博士 中華民國九十四年七月 應用適應控制之 H 型壓電陀螺儀的設計與控制 Design and Control
國立交通大學 機械工程學系 碩士論文 應用適應控制之 H 型壓電陀螺儀的設計與控制 Design and Control of the H-type Piezoelectric Gyroscope via Adaptive Control Strategies 研究生 : 黃建評 指導教授 : 陳宗麟博士 中華民國九十四年七月 應用適應控制之 H 型壓電陀螺儀的設計與控制 Design and Control
KWUN TONG GOVERNMENT SECONDARY SCHOOL 觀塘官立中學 (Office) Shun Lee Estate Kwun Tong, Kowloon 上學期測驗
 觀塘官立中學 Tel.: 2343 7772 (Principal) 9, Shun Chi Street, 2343 6220 (Office) Shun Lee Estate Kwun Tong, Kowloon 各位中一至中三級學生家長 : 上學期測驗 上學期測驗將於二零一二年十月二十四日至十月三十日進行 安排如下 : 1. 測驗於 24/10, 25/10, 26/10, 29/10 早上八時三十五分至十時四十分進行
觀塘官立中學 Tel.: 2343 7772 (Principal) 9, Shun Chi Street, 2343 6220 (Office) Shun Lee Estate Kwun Tong, Kowloon 各位中一至中三級學生家長 : 上學期測驗 上學期測驗將於二零一二年十月二十四日至十月三十日進行 安排如下 : 1. 測驗於 24/10, 25/10, 26/10, 29/10 早上八時三十五分至十時四十分進行
Foundations of Arithmetic
 Foundatons of Arthmetc Notaton We shall denote the sum and product of numbers n the usual notaton as a 2 + a 2 + a 3 + + a = a, a 1 a 2 a 3 a = a The notaton a b means a dvdes b,.e. ac = b where c s an
Foundatons of Arthmetc Notaton We shall denote the sum and product of numbers n the usual notaton as a 2 + a 2 + a 3 + + a = a, a 1 a 2 a 3 a = a The notaton a b means a dvdes b,.e. ac = b where c s an
Odd/Even Scroll Generation with Inductorless Chua s and Wien Bridge Oscillator Circuits
 Watcharn Jantanate, Peter A. Chayasena, Sarawut Sutorn Odd/Even Scroll Generaton wth Inductorless Chua s and Wen Brdge Oscllator Crcuts Watcharn Jantanate, Peter A. Chayasena, and Sarawut Sutorn * School
Watcharn Jantanate, Peter A. Chayasena, Sarawut Sutorn Odd/Even Scroll Generaton wth Inductorless Chua s and Wen Brdge Oscllator Crcuts Watcharn Jantanate, Peter A. Chayasena, and Sarawut Sutorn * School
CSci 6974 and ECSE 6966 Math. Tech. for Vision, Graphics and Robotics Lecture 21, April 17, 2006 Estimating A Plane Homography
 CSc 6974 and ECSE 6966 Math. Tech. for Vson, Graphcs and Robotcs Lecture 21, Aprl 17, 2006 Estmatng A Plane Homography Overvew We contnue wth a dscusson of the major ssues, usng estmaton of plane projectve
CSc 6974 and ECSE 6966 Math. Tech. for Vson, Graphcs and Robotcs Lecture 21, Aprl 17, 2006 Estmatng A Plane Homography Overvew We contnue wth a dscusson of the major ssues, usng estmaton of plane projectve
壓差式迴路式均熱片之研製 Fabrication of Pressure-Difference Loop Heat Spreader
 壓差式迴路式均熱片之研製 Fabrication of Pressure-Difference Loop Heat Spreader 1 2* 3 4 4 Yu-Tang Chen Shei Hung-Jung Sheng-Hong Tsai Shung-Wen Kang Chin-Chun Hsu 1 2* 3! "# $ % 4& '! " ( )* +, -. 95-2622-E-237-001-CC3
壓差式迴路式均熱片之研製 Fabrication of Pressure-Difference Loop Heat Spreader 1 2* 3 4 4 Yu-Tang Chen Shei Hung-Jung Sheng-Hong Tsai Shung-Wen Kang Chin-Chun Hsu 1 2* 3! "# $ % 4& '! " ( )* +, -. 95-2622-E-237-001-CC3
Chapter 6. Series-Parallel Circuits ISU EE. C.Y. Lee
 Chapter 6 Series-Parallel Circuits Objectives Identify series-parallel relationships Analyze series-parallel circuits Determine the loading effect of a voltmeter on a circuit Analyze a Wheatstone bridge
Chapter 6 Series-Parallel Circuits Objectives Identify series-parallel relationships Analyze series-parallel circuits Determine the loading effect of a voltmeter on a circuit Analyze a Wheatstone bridge
Earth System Science Programme. Academic Counseling 2018
 Earth System Science Programme Academic Counseling 2018 1 Global Environmental Change 全球環境變化 Climate Change Air pollution Food Security Public Health Biodiversity Water pollution Natural Disasters 2 課程內容
Earth System Science Programme Academic Counseling 2018 1 Global Environmental Change 全球環境變化 Climate Change Air pollution Food Security Public Health Biodiversity Water pollution Natural Disasters 2 課程內容
Composite Hypotheses testing
 Composte ypotheses testng In many hypothess testng problems there are many possble dstrbutons that can occur under each of the hypotheses. The output of the source s a set of parameters (ponts n a parameter
Composte ypotheses testng In many hypothess testng problems there are many possble dstrbutons that can occur under each of the hypotheses. The output of the source s a set of parameters (ponts n a parameter
國立交通大學 顯示科技研究所 碩士論文 在二氧化矽基板上具有小圖形尺寸的光子晶體奈米結構雷射特性. Laser Emissions from Photonic Crystal Nanostructures with. Small Footprints on SiO 2 Substrate
 國立交通大學 顯示科技研究所 碩士論文 在二氧化矽基板上具有小圖形尺寸的光子晶體奈米結構雷射特性 Laser Emissions from Photonic Crystal Nanostructures with Small Footprints on SiO 2 Substrate 研究生 : 蔡為智 指導教授 : 李柏璁教授 中華民國 101 年 8 月 在二氧化矽基板上具有小圖形尺寸的光子晶體奈米結構雷射特性
國立交通大學 顯示科技研究所 碩士論文 在二氧化矽基板上具有小圖形尺寸的光子晶體奈米結構雷射特性 Laser Emissions from Photonic Crystal Nanostructures with Small Footprints on SiO 2 Substrate 研究生 : 蔡為智 指導教授 : 李柏璁教授 中華民國 101 年 8 月 在二氧化矽基板上具有小圖形尺寸的光子晶體奈米結構雷射特性
國立中山大學物理研究所 碩士論文. 運用第一原理研究矽原子團 (Sin, n=1-16) 參雜金原子 (Au) 之原子與電子結構. Atomic and electronic structures of AuSin(n=1-16) clusters. from first-principles
 國立中山大學物理研究所 碩士論文 運用第一原理研究矽原子團 (Sin, n=1-16) 參雜金原子 (Au) 之原子與電子結構 Atomic and electronic structures of AuSin(n=1-16) clusters from first-principles 研究生 : 許志強撰 指導教授 : 莊豐權 中華民國九十八年一月 Acknowledgment 首先, 當然要先感謝我的指導教授莊豐權,
國立中山大學物理研究所 碩士論文 運用第一原理研究矽原子團 (Sin, n=1-16) 參雜金原子 (Au) 之原子與電子結構 Atomic and electronic structures of AuSin(n=1-16) clusters from first-principles 研究生 : 許志強撰 指導教授 : 莊豐權 中華民國九十八年一月 Acknowledgment 首先, 當然要先感謝我的指導教授莊豐權,
The Second Anti-Mathima on Game Theory
 The Second Ant-Mathma on Game Theory Ath. Kehagas December 1 2006 1 Introducton In ths note we wll examne the noton of game equlbrum for three types of games 1. 2-player 2-acton zero-sum games 2. 2-player
The Second Ant-Mathma on Game Theory Ath. Kehagas December 1 2006 1 Introducton In ths note we wll examne the noton of game equlbrum for three types of games 1. 2-player 2-acton zero-sum games 2. 2-player
NUMERICAL DIFFERENTIATION
 NUMERICAL DIFFERENTIATION 1 Introducton Dfferentaton s a method to compute the rate at whch a dependent output y changes wth respect to the change n the ndependent nput x. Ths rate of change s called the
NUMERICAL DIFFERENTIATION 1 Introducton Dfferentaton s a method to compute the rate at whch a dependent output y changes wth respect to the change n the ndependent nput x. Ths rate of change s called the
A Robust Method for Calculating the Correlation Coefficient
 A Robust Method for Calculatng the Correlaton Coeffcent E.B. Nven and C. V. Deutsch Relatonshps between prmary and secondary data are frequently quantfed usng the correlaton coeffcent; however, the tradtonal
A Robust Method for Calculatng the Correlaton Coeffcent E.B. Nven and C. V. Deutsch Relatonshps between prmary and secondary data are frequently quantfed usng the correlaton coeffcent; however, the tradtonal
The Order Relation and Trace Inequalities for. Hermitian Operators
 Internatonal Mathematcal Forum, Vol 3, 08, no, 507-57 HIKARI Ltd, wwwm-hkarcom https://doorg/0988/mf088055 The Order Relaton and Trace Inequaltes for Hermtan Operators Y Huang School of Informaton Scence
Internatonal Mathematcal Forum, Vol 3, 08, no, 507-57 HIKARI Ltd, wwwm-hkarcom https://doorg/0988/mf088055 The Order Relaton and Trace Inequaltes for Hermtan Operators Y Huang School of Informaton Scence
Lecture 12: Discrete Laplacian
 Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
Lecture 12: Dscrete Laplacan Scrbe: Tanye Lu Our goal s to come up wth a dscrete verson of Laplacan operator for trangulated surfaces, so that we can use t n practce to solve related problems We are mostly
General viscosity iterative method for a sequence of quasi-nonexpansive mappings
 Avalable onlne at www.tjnsa.com J. Nonlnear Sc. Appl. 9 (2016), 5672 5682 Research Artcle General vscosty teratve method for a sequence of quas-nonexpansve mappngs Cuje Zhang, Ynan Wang College of Scence,
Avalable onlne at www.tjnsa.com J. Nonlnear Sc. Appl. 9 (2016), 5672 5682 Research Artcle General vscosty teratve method for a sequence of quas-nonexpansve mappngs Cuje Zhang, Ynan Wang College of Scence,
Difference Equations
 Dfference Equatons c Jan Vrbk 1 Bascs Suppose a sequence of numbers, say a 0,a 1,a,a 3,... s defned by a certan general relatonshp between, say, three consecutve values of the sequence, e.g. a + +3a +1
Dfference Equatons c Jan Vrbk 1 Bascs Suppose a sequence of numbers, say a 0,a 1,a,a 3,... s defned by a certan general relatonshp between, say, three consecutve values of the sequence, e.g. a + +3a +1
Estimation: Part 2. Chapter GREG estimation
 Chapter 9 Estmaton: Part 2 9. GREG estmaton In Chapter 8, we have seen that the regresson estmator s an effcent estmator when there s a lnear relatonshp between y and x. In ths chapter, we generalzed the
Chapter 9 Estmaton: Part 2 9. GREG estmaton In Chapter 8, we have seen that the regresson estmator s an effcent estmator when there s a lnear relatonshp between y and x. In ths chapter, we generalzed the
Improved delay-dependent stability criteria for discrete-time stochastic neural networks with time-varying delays
 Avalable onlne at www.scencedrect.com Proceda Engneerng 5 ( 4456 446 Improved delay-dependent stablty crtera for dscrete-tme stochastc neural networs wth tme-varyng delays Meng-zhuo Luo a Shou-mng Zhong
Avalable onlne at www.scencedrect.com Proceda Engneerng 5 ( 4456 446 Improved delay-dependent stablty crtera for dscrete-tme stochastc neural networs wth tme-varyng delays Meng-zhuo Luo a Shou-mng Zhong
A PROCEDURE FOR SIMULATING THE NONLINEAR CONDUCTION HEAT TRANSFER IN A BODY WITH TEMPERATURE DEPENDENT THERMAL CONDUCTIVITY.
 Proceedngs of the th Brazlan Congress of Thermal Scences and Engneerng -- ENCIT 006 Braz. Soc. of Mechancal Scences and Engneerng -- ABCM, Curtba, Brazl,- Dec. 5-8, 006 A PROCEDURE FOR SIMULATING THE NONLINEAR
Proceedngs of the th Brazlan Congress of Thermal Scences and Engneerng -- ENCIT 006 Braz. Soc. of Mechancal Scences and Engneerng -- ABCM, Curtba, Brazl,- Dec. 5-8, 006 A PROCEDURE FOR SIMULATING THE NONLINEAR
Linear Feature Engineering 11
 Lnear Feature Engneerng 11 2 Least-Squares 2.1 Smple least-squares Consder the followng dataset. We have a bunch of nputs x and correspondng outputs y. The partcular values n ths dataset are x y 0.23 0.19
Lnear Feature Engneerng 11 2 Least-Squares 2.1 Smple least-squares Consder the followng dataset. We have a bunch of nputs x and correspondng outputs y. The partcular values n ths dataset are x y 0.23 0.19
Chapter 22 Lecture. Essential University Physics Richard Wolfson 2 nd Edition. Electric Potential 電位 Pearson Education, Inc.
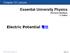 Chapter 22 Lecture Essential University Physics Richard Wolfson 2 nd Edition Electric Potential 電位 Slide 22-1 In this lecture you ll learn 簡介 The concept of electric potential difference 電位差 Including
Chapter 22 Lecture Essential University Physics Richard Wolfson 2 nd Edition Electric Potential 電位 Slide 22-1 In this lecture you ll learn 簡介 The concept of electric potential difference 電位差 Including
Fuzzy Boundaries of Sample Selection Model
 Proceedngs of the 9th WSES Internatonal Conference on ppled Mathematcs, Istanbul, Turkey, May 7-9, 006 (pp309-34) Fuzzy Boundares of Sample Selecton Model L. MUHMD SFIIH, NTON BDULBSH KMIL, M. T. BU OSMN
Proceedngs of the 9th WSES Internatonal Conference on ppled Mathematcs, Istanbul, Turkey, May 7-9, 006 (pp309-34) Fuzzy Boundares of Sample Selecton Model L. MUHMD SFIIH, NTON BDULBSH KMIL, M. T. BU OSMN
A New Refinement of Jacobi Method for Solution of Linear System Equations AX=b
 Int J Contemp Math Scences, Vol 3, 28, no 17, 819-827 A New Refnement of Jacob Method for Soluton of Lnear System Equatons AX=b F Naem Dafchah Department of Mathematcs, Faculty of Scences Unversty of Gulan,
Int J Contemp Math Scences, Vol 3, 28, no 17, 819-827 A New Refnement of Jacob Method for Soluton of Lnear System Equatons AX=b F Naem Dafchah Department of Mathematcs, Faculty of Scences Unversty of Gulan,
The Chaotic Robot Prediction by Neuro Fuzzy Algorithm (2) = θ (3) = ω. Asin. A v. Mana Tarjoman, Shaghayegh Zarei
 The Chaotc Robot Predcton by Neuro Fuzzy Algorthm Mana Tarjoman, Shaghayegh Zare Abstract In ths paper an applcaton of the adaptve neurofuzzy nference system has been ntroduced to predct the behavor of
The Chaotc Robot Predcton by Neuro Fuzzy Algorthm Mana Tarjoman, Shaghayegh Zare Abstract In ths paper an applcaton of the adaptve neurofuzzy nference system has been ntroduced to predct the behavor of
First Year Examination Department of Statistics, University of Florida
 Frst Year Examnaton Department of Statstcs, Unversty of Florda May 7, 010, 8:00 am - 1:00 noon Instructons: 1. You have four hours to answer questons n ths examnaton.. You must show your work to receve
Frst Year Examnaton Department of Statstcs, Unversty of Florda May 7, 010, 8:00 am - 1:00 noon Instructons: 1. You have four hours to answer questons n ths examnaton.. You must show your work to receve
Control of Uncertain Bilinear Systems using Linear Controllers: Stability Region Estimation and Controller Design
 Control of Uncertan Blnear Systems usng Lnear Controllers: Stablty Regon Estmaton Controller Desgn Shoudong Huang Department of Engneerng Australan Natonal Unversty Canberra, ACT 2, Australa shoudong.huang@anu.edu.au
Control of Uncertan Blnear Systems usng Lnear Controllers: Stablty Regon Estmaton Controller Desgn Shoudong Huang Department of Engneerng Australan Natonal Unversty Canberra, ACT 2, Australa shoudong.huang@anu.edu.au
Formulas for the Determinant
 page 224 224 CHAPTER 3 Determnants e t te t e 2t 38 A = e t 2te t e 2t e t te t 2e 2t 39 If 123 A = 345, 456 compute the matrx product A adj(a) What can you conclude about det(a)? For Problems 40 43, use
page 224 224 CHAPTER 3 Determnants e t te t e 2t 38 A = e t 2te t e 2t e t te t 2e 2t 39 If 123 A = 345, 456 compute the matrx product A adj(a) What can you conclude about det(a)? For Problems 40 43, use
Section 8.3 Polar Form of Complex Numbers
 80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
80 Chapter 8 Secton 8 Polar Form of Complex Numbers From prevous classes, you may have encountered magnary numbers the square roots of negatve numbers and, more generally, complex numbers whch are the
