IIE Transactions Publication details, including instructions for authors and subscription information:
|
|
|
- Darrell West
- 5 years ago
- Views:
Transcription
1 This artice was downoaded by: [Professor Barry Neson] On: 24 March 205, At: 09:50 Pubisher: Tayor & Francis Informa Ltd Registered in Engand and Waes Registered Number: Registered office: Mortimer House, 37-4 Mortimer Street, London WT 3JH, UK IIE Transactions Pubication detais, incuding instructions for authors and subscription information: Quicky Assessing Contributions to Input Uncertainty Eunhye Song a & Barry L. Neson a a Department of Industria Engineering & Management Sciences Northwestern University Evanston, IL USA E-mai: Accepted author version posted onine: 7 Nov 204.Pubished onine: 7 Nov 204. Cick for updates To cite this artice: Eunhye Song & Barry L. Neson (204): Quicky Assessing Contributions to Input Uncertainty, IIE Transactions, DOI: 0.080/074087X To ink to this artice: PLEASE SCROLL DOWN FOR ARTICLE Tayor & Francis makes every effort to ensure the accuracy of a the information (the Content ) contained in the pubications on our patform. However, Tayor & Francis, our agents, and our icensors make no representations or warranties whatsoever as to the accuracy, competeness, or suitabiity for any purpose of the Content. Any opinions and views expressed in this pubication are the opinions and views of the authors, and are not the views of or endorsed by Tayor & Francis. The accuracy of the Content shoud not be reied upon and shoud be independenty verified with primary sources of information. Tayor and Francis sha not be iabe for any osses, actions, caims, proceedings, demands, costs, expenses, damages, and other iabiities whatsoever or howsoever caused arising directy or indirecty in connection with, in reation to or arising out of the use of the Content. This artice may be used for research, teaching, and private study purposes. Any substantia or systematic reproduction, redistribution, reseing, oan, sub-icensing, systematic suppy, or distribution in any form to anyone is expressy forbidden. Terms & Conditions of access and use can be found at
2 IIE Transactions (205) 47, 7 Copyright C IIE ISSN: X print / onine DOI: 0.080/074087X Quicky assessing contributions to input uncertainty EUNHYE SONG and BARRY L. NELSON Department of Industria Engineering & Management Sciences, Northwestern University, Evanston, IL 60208, USA E-mai: nesonb@northwestern.edu Received February 204 and accepted October 204 Input uncertainty refers to the (often unmeasured) variabiity in simuation-based performance estimators that is a consequence of driving the simuation with input modes that are based on rea-word data. Severa methods have been proposed to assess the overa effect of input uncertainty, and some aso support attributing this uncertainty to the various input modes. However, these methods require a engthy sequence of diagnostic experiments. This paper provides a method to obtain an estimator of the overa variance due to input uncertainty, the reative contribution to this variance of each input distribution, and a measure of the sensitivity of overa uncertainty to increasing the rea-word sampe-size used to fit each distribution, a from a singe diagnostic experiment. The approach expoits a metamode that reates the means and variances of the input distributions to the mean response of the simuation output, and aso empoys bootstrapping of the rea-word data to represent input-mode uncertainty. Furthermore, whether and how the simuation outputs from the nomina and diagnostic experiments may be combined to obtain a better performance estimator is investigated. For the case when the anayst obtains additiona rea-word data, refines the input modes, and runs a foow-up experiment, an anaysis of whether and how the simuation outputs from a three experiments shoud be combined is presented. Numerica iustrations are provided. Keywords: Stochastic simuation, input modeing, input uncertainty, output anaysis. Introduction There is increasing recognition of the need to quantify a sources of error in mathematica and computer modes, incuding stochastic simuations. Every simuation anguage measures the statistica error due to samping from the input modes, typicay via Confidence Intervas (CIs) on the performance measures. However, these CIs do not account for the possibe (in fact, ikey) misspecification of the input modes when they are estimated from rea-word data. For instance, ater in this artice we consider the simuation of a remote order-taking system for customers using a drive-in service at a chain of fast-food restaurants; this simuation was created to estimate a measure of customer deay. Rea-word data on customer arrivas, the time it takes an agent to obtain a customer s order, and the time needed for a car to move beyond the order board are used to fit input modes that drive the simuation. Because we ony have a finite quantity of rea-word data, these input modes are imperfect representations of the actua processes. As shown in many papers (e.g., Barton (202), Barton et a. (204), Cheng and Hoand (998, 2004), Chick (200), and Zouaoui and Wison (2003, 2004) the error Corresponding author due to input uncertainty can overwhem the simuation samping error. These papers provide overa measures of input uncertainty, such as adjusted CIs or Bayesian credibe intervas, where as we focus on assessing the contribution of each input mode to input uncertainty as a guide to coecting more rea-word data. A predecessor of this artice, Ankenman and Neson (202) presented a quick-and-easy diagnostic experiment to assess the overa effect of input uncertainty reative to simuation samping variabiity, and a foow-up method for estimating contributions. Unfortunatey, their method for identifying the input modes that contribute the most to input uncertainty requires a sequence of additiona diagnostic experiments; in the worst case it requires as many experiments as there are input modes, and each of these experiments can be substantia. Furthermore, the variance mode that underies their diagnostic experiments has no rigorous justification. In this artice, we provide a new anaysis that requires ony one diagnostic experiment to assess the overa effect of input uncertainty, the reative contribution of each input distribution, and a measure of sampe size sensitivity of each distribution. Using these resuts, the anayst can decide whether it is worth the time and expense to coect additiona data and on which input processes to do so. If the anayst decides to coect additiona rea-word X C 205 IIE
3 2 Song and Neson input data to refine the input modes, then yet another simuation experiment woud be conducted. Thus, there are potentiay three sets of simuation output data: nomina experiment, diagnostic experiment, and foow-up experiment. We study when and how these data may be combined to produce better performance estimates. We obtain our measures of overa input uncertainty, contributions, and sampe size sensitivities using the foowing approach:. Foowing the nomina experiment, we take repeated bootstrap sampes from the rea-word data and use these data to create aternative sets of input distributions representing what coud have occurred with different rea-word sampes. 2. Using these aternative input distributions we fit a regression metamode that reates the mean of the simuation output to the means and variances of the input distributions. 3. From the metamode, we derive expressions for the overa variance in the simuation output due to input uncertainty, the contribution to this variance of each input distribution, and the reduction in overa variance that woud resut from one additiona rea-word sampe of data to fit each input distribution. The measures computed in step 3 can be used to guide additiona rea-word data coection and to heuristicay adjust measures of error, such as CIs, to account for both input and simuation variabiity. Ours is not the first attempt to decide from which input processes to coect more rea-word data to reduce input uncertainty. Freimer and Schruben (2002) considered uncertainty in the estimated parameters of parametric input distributions (e.g., exponentia with parameter λ, gamma with parameters α and β). Simiar to the present artice, they used bootstrapping of rea-word input data to mimic the effect of different possibe rea-word sampes and the corresponding input-parameter estimates they woud yied. The basic premise of Freimer and Schruben (2002) was that sufficient rea-word data on the parameters have been coected when their samping distributions, as represented by bootstrap vaues, have no statisticay detectabe effect on the simuation output. After what we ca the nomina experiment, Ng and Chick (200, 2006) attempted to optimay aocate a finite amount of additiona effort additiona rea-word input-data coection and additiona repications of the simuation to reduce overa uncertainty about the simuated system performance. Simiar to our approach, they empoyed a regression mode to reate the inputs to the outputs. Their goa was to coect additiona rea-word input observations and additiona simuation repications to minimize the posterior variance of the simuation point estimator subject to a budget constraint. Freimer and Schruben (2002) coected additiona input data unti they coud estabish that input uncertainty was negigibe, whereas Ng and Chick (200, 2006) optimay aocated the data-coection and simuation-repication budget to minimize overa uncertainty. Both assumed that it was possibe to coect input data from any of the input distributions in whatever quantity was desired or affordabe. We take the perspective that additiona rea-word data are often unattainabe, at east for some of the input processes, and the quantity that can be obtained is more ikey to be constrained by time than cost per observation; therefore, if we can get more data, we wi get as much as possibe. The insight we deiver starts with an overa assessment of input uncertainty, which is usefu for understanding risk even if there is no foow-up experiment. When additiona input data are to be coected, then our reative contributions and sensitivities provide guidance about the best targets. This artice is organized as foows. Section 2 defines the input uncertainty probem and sets up our mode of it. In Section 3 we describe the sequence of experiments nomina, diagnostic, and foow-up focusing on the diagnostic experiment for assessing input uncertainty and the contribution of each input distribution. When and how to combine output data from these experiments is addressed in Section 4. Section 5 provides guideines for the design of the diagnostic experiment. Section 6 summarizes resuts from an empirica study and an iustrative exampe, foowed by concusions in Section Probem formuation In this section we present a definition of input uncertainty and introduce our mode of it. 2.. Definition of input uncertainty In this artice, we consider mutuay independent input processes that are each independent and identicay distributed (i.i.d.) random variabes whose margina distributions are unknown. We use estimated or fitted distributions based on rea-word data as stand-ins for the unknown, true distributions. We do not consider mutivariate or time-dependent input processes here. Suppose that there are L mutuay independent input processes characterized by a coection of true rea-word margina distributions F c ={F c, F 2 c,...,f L c },wherec denotes correct. Since these distributions are unknown, we use a corresponding coection of estimated distributions F ={ F, F 2,..., F L } to drive the simuation. The th estimated margina distribution, F, can be either a parametric or an empirica distribution, but in either case it is inferred from observed rea-word data X, X 2,...,X m i.i.d. F c,wherem indicates the number of observations for the th input mode. We ony consider m > 0 and thus do not address subjectivey specified distributions for which we have no data.
4 Quicky assessing input uncertainty 3 Given a coection of input distributions F, the simuation generates performance output Y j ( F) on i.i.d. repication j =, 2,...,n. Ankenman and Neson (202) represented Y j ( F) as Y j ( F) = E[Y( F) F] + ε j, () where ε,ε 2,...,ε n are i.i.d. with mean zero and variance σ 2 representing the natura stochastic variabiity from repication to repication in the simuation. They assumed that ε j does not depend on the input mode F, which is ceary an approximation and one which we aso adopt. It is important to notice that E[Y( F) F] is a random variabe since it is a functiona of F, which is estimated from rea-word data. In other words, depending on the rea-word observations thatareusedtoinferf c, we coud have different vaues of E[Y( F) F]. The goa of our simuation is to estimate E[Y(F c )], which we typicay do with the sampe mean Ȳ( F) = n j= Y j( F)/n for given F. This artice focuses on how to assess the reative impact of each F on the variabiity of the simuation estimator Ȳ( F). As the number of simuation repications n increases, Ȳ( F) converges to E[Y( F) F], which is not necessariy the same as E[Y(F c )]. In fact, there is typicay a bias in the estimator Ȳ( F) coming from the fact that F is inferred from a finite number of observations and the simuation is a noninear transformation. The traditiona confidence interva captures ony Var[Ȳ( F) F] = σ 2 /n for given F. Therefore, we need a different approach to account for the variabiity of the simuation estimator depending on the input modes, which we refer to as the input uncertainty. Formay, the input uncertainty σi 2 of the simuation estimator Ȳ( F) is defined as σ 2 I = Var [E[Ȳ( F) F]], (2) where the Var[ ] is with respect to the samping distribution of F. Therefore, Var[Ȳ( F)] can be decomposed as Var[Ȳ( F)] = Var [E[Ȳ( F) F]] + E[Var[Ȳ( F) F]] = σ 2 I + σ 2 /n, (3) where the first expression is genera, and the second foows from the definition of σi 2 and the homoscedasticity assumption in Mode (). Ankenman and Neson (202) introduced the ratio γ = σ I /(σ/ n) as a measure of the reative significance of input uncertainty to the simuation-based estimator variabiity. Suppose that the anayst chooses n arge enough so that the estimator variance σ 2 /n is reasonaby sma. Then a very sma γ impies that σi 2 σ 2 /n; i.e., the input uncertainty is insignificant. On the other hand, if γ is arge, then σi 2 σ 2 /n; i.e., there is significant input uncertainty in the simuation estimator. In the atter case, a natura question is: Which modes contribute the most to the input uncertainty? Our proposed definition of the contribution of F to input uncertainty is V (m ) Var [ E [ Y ( F c, F 2 c,...,f c, F, F+ c,...,fl) c ]] F. (4) In other words, V (m ) is the variabiity in the simuation s expected vaue when a of the true input distributions except F c are known and F c is estimated by F. Notice that V is a function of the sampe size m to make it cear that the contribution depends on the number of observations; the arger m is, the smaer V (m ) becomes as F approaches F c.thereative contribution of the th input mode is V (m ) L i= V i(m i ). We aso define the (sampe size) sensitivity of the variance of Ȳ( F) with respect to th input mode by approximating m as rea vaued and taking Var[Ȳ( F)] m, (5) m =m which is the same as σ2 I m m =m if we assume homoscedastic simuation variance. The sensitivity can be interpreted as a measure of how much input uncertainty can be reduced by observing one more rea-word sampe from the th input process given that we aready have m observations. The input uncertainty probem is reated to goba sensitivity anaysis. Here we briefy describe simiarities and differences. Suppose we have a response y = g(x) thatis a function of some parameters x = (x, x 2,...,x L ). The response y might be the objective-function vaue in an optimization probem or the key output from a deterministic numerica simuation, for instance. However, the parameters x are not actuay known with certainty and therefore coud be modeed as a random vector X with known distribution F c. Loosey speaking, the goa of goba sensitivity anaysis is to assign to each parameter X, X 2,...,X L a measure of impact on the random variabe Y = g(x); the focus is often on decomposing Var[Y]. Many of these measures are computationay expensive to compute. For instance, Wagner (995) defined two goba sensitivity measures for the objective function of an optimization probem with uncertain parameters. One measure of sensitivity for the th parameter was based on the variance of the conditionaexpectation of g(x) given a parameters except X, whereas the other was the variance of the conditiona expectation of g(x) given ony X. Homma and Satei (996) proposed a reated variance-based sensitivity measure: the ratio of the variance of the tota effect (main effect and a the interaction effects of the parameter of interest) to the variance of Y. Oakey and O Hagan (2004) introduced the idea of repacing evauations of g(x) with evauations of a Gaussian
5 4 Song and Neson process metamode ĝ(x) thatisfittoachosensetofparameters and outputs (x i, g(x i )), i =, 2,...,k. Because generation of X F c and evauation of ĝ(x) are fast, this faciitates computing any of the goba sensitivity measures described above as we as others; furthermore, the Gaussian process metamode supports incorporating uncertainty about the true function g( ) into the anaysis. Marre et a. (202) extended this idea to stochastic simuations in which we can ony observe g with noise: g(x) + ɛ(x). They used joint metamodes for g( ) andvar[ɛ( )] to estimate a variance-based sensitivity measure using a functiona anaysis of variance (ANOVA) decomposition of g. Their setting is the cosest to ours in that they do sensitivity anaysis in the presence of stochastic simuation output. Returning to deterministic outputs, Pischke et a. (203) proposed density-based sensitivity measures as an aternative to variance-based measures. They evauated the expected difference between the unconditiona probabiity density of Y and its conditiona density given X = x.the arger the expected difference is, the more sensitive the output is to this parameter. From our perspective, goba sensitivity tries to assess the effect of each distribution F c, F c 2,...,F c L on Y(Fc ); that is, it decomposes the (simuation) variabiity represented by ε. Input uncertainty arises when F c is estimated by F, andan assessment tries to measure the impact of variabiity in F (and in this paper, each F ) in the presence of simuation variabiity. Input uncertainty due to F can depend on how sensitive the output is to the th distribution but aso on how we that distribution is estimated The mean-variance effects mode As noted earier, E[Y( F) F]is a random variabe depending on F; therefore, we can think of it as a functiona of F; i.e., g( F) = E[Y( F) F]. We suggest (and justify beow) the foowing mean-variance effects mode for g( F): g( F) = β 0 + β μ( F ) + ν σ 2 ( F ), (6) where μ( F )andσ 2 ( F ) represent the mean and the variance of a random variabe with distribution F, respectivey, and β and ν are constant coefficients. The phiosophy behind this mode is that sensitivity of the mean simuation output to the particuar reaization of F is argey captured by the reaized center (mean) and spread (variance) of the distribution. This mode coud be extended to incude higher moments such as skewness and kurtosis, or the 25th and the 75th percenties coud be chosen instead of mean and variance. However, the essence of the mode is to represent the reationship between each F and E[Y( F) F] through some characteristic properties of F.Asweshow ater, there are advantages to using the mean and variance when we want to estimate the contribution of each input mode. This mode does not incude interaction terms; we expect that in many cases the main effects are more significant than the interaction effects and can capture a arge part of the impact of F on the output. The contribution of F can be derived by pugging this mode into the definition in Equation (4). Let F c = {F c, F 2 c,...,f c, F, F+ c,...,f L c }; i.e., the set of a true distributions except F c.thenv (m ) becomes V (m ) = Var [ E[Y(F c ) F ] ] [ = Var β 0 + β i μ(fi c ) + ν i σ 2 (Fi c ) i=,i ] + β μ( F ) + ν σ 2 ( F ) = Var[β μ( F ) + ν σ 2 ( F )] i=,i = β 2 Var[μ( F )] + ν 2 Var[σ 2 ( F )] + 2β ν Cov[μ( F ),σ 2 ( F )]. (7) The third equaity hods because μ(fi c)andσ2 (Fi c)are constants. The overa input uncertainty σi 2 can be derived by pugging Mode (6) into the definition in Equation (2): σ 2 I = Var[g( F)] = = β 2 Var[μ( F )] + + ν 2 Var[σ 2 ( F )] 2β ν Cov[μ( F ),σ 2 ( F )] { β 2 Var[μ( F )] + ν 2 Var[σ 2 ( F )] + 2β ν Cov[μ( F ),σ 2 ( F )] } (8) = V (m ). The second equaity foows from independent samping from the input modes and the ast equaity foows directy from Equation (7). This resut shows that under Mode (6) the overa input uncertainty is the summation of individua contributions; i.e., σi 2 = L V (m ). Thus, under our mode the overa input uncertainty can be decomposed into the individua contributions, and the individua contributions are independent of each other. Aso, under this mode the sensitivity of F becomes σi 2 = V (m ), m =m m =m m m which makes the sensitivity simpy the derivative of the contribution with respect to the sampe size, evauated at the current number of sampes m. The variance decomposition in Equation (8) coincides with a resut in Cheng and Hoand (998) that was obtained by a different argument. They approximated the input uncertainty variance σi 2 as a function of the variances
6 Quicky assessing input uncertainty 5 of parameter estimators of parametric input distributions. If we et F c ( θ) be the true parametric famiy of input distributions, θ c be the coection of true parameters, and θ be an estimator of θ c, then a Tayor series expansion of g( θ) around θ c gives Var[g( θ)] (g(θ c )) T Var[ θ] (g(θ c )), (9) where Var[ θ] is the variance covariance matrix of θ and (g(θ c )) is the gradient of g( ) atθ c. By further assuming θ is a Maximum Likeihood Estimator (MLE) for θ c,they argued that Var[g( θ)] (g(θ c )) T V[ θ] (g(θ c )), where V[ θ] is the asymptotic variance covariance matrix of θ under some reguarity conditions. To connect this to our formuation, assume that each input distribution F c can be parameterized by μ(f c) and σ 2 (F c ). Then we can represent g( F) as a function of the parameters g( θ), where θ ={μ( F ),σ 2 ( F ),μ( F 2 ),σ 2 ( F 2 ),..., μ( F L ),σ 2 ( F L )}. Simiary, θ c ={μ(f c),σ2 (F c),μ(f 2 c),σ2 (F2 c),...,μ(f L c), σ 2 (FL c)} and the gradient (g(θ c )) under Mode (6) is (β,ν,β 2,ν 2,...,β L,ν L ) T. In fact, in our case the approximation in Equation (9) is an equaity because Mode (6) is inear in θ and therefore the first-order Tayor approximation is the mode itsef. A feature of our approach is that we can directy compute Var[ θ] without making further assumptions. Since we have independence among input processes, Var[ θ] is a bock diagona matrix: Var[μ( F )] Cov[μ( F ),σ 2 ( F )] 0 0 Cov[μ( F ),σ 2 ( F )] Var[σ 2 ( F )] 0 0 Var[ θ] = Var[μ( F L )] Cov[μ( F L ),σ 2 ( F L )] 0 0 Cov[μ( F L ),σ 2 ( F L )] Var[σ 2 ( F L )] Pugging Var[ θ] into Equation (9) gives the same expression as in Equation (8). Cheng and Hoand (998) provided an approximate anaysis of an exact mode that requires parametric input distributions and MLEs; we provide an exact anaysis of an approximate mode using any form of input distribution but assuming that most of the sensitivity of the simuation response to the input distributions is captured by their means and variances. To evauate the contribution of each input mode, we wi use east-squares regression to estimate β 0,β,...,β L,ν,ν 2,...,ν L. In the next section we introduce a sequence of experiments to estimate these coefficients and to evauate the contribution and sensitivity of each input mode. 3. The sequence of experiments In this section we describe a sequence of experiments that an anayst might conduct: nomina, diagnostic, andfoowup. Current simuation practice is to run ony the nomina experiment. The nomina experiment invoves the anayst coecting input data, choosing input modes F to use, buiding the simuation mode, and running n repications to obtain the point estimator Ȳ( F) of system performance E[Y(F c )]. From this experiment, the anayst obtains the traditiona CI for E[Y( F) F], which is typicay not the same as a CI for E[Y(F c )], as discussed earier. The number of repications n is either chosen arbitrariy, to achieve a certain eve of simuation error, or because it can be competed in the avaiabe time. We are suggesting that this be foowed by a diagnostic experiment to evauate the contribution and sensitivity of each input mode as we as the overa input uncertainty. The contributions can be cacuated from Equation (7) given the coefficients β,β 2,...,β L,ν,ν 2,...,ν L and the variance and covariance of μ( F )andσ 2 ( F ). We describe a method for estimating them in the next section. Upon competion of the diagnostic experiment, the anayst is either satisfied that input uncertainty is not substantia or is concerned that it is substantia and has a better understanding of how significant it is. In either case, the anayst has simuation resuts from the diagnostic experiment that coud perhaps be used to improve the estimate of E[Y(F c )]; we study whether and how to do this as we. When input uncertainty is substantia, the anayst may aso undertake a foow-up experiment, which invoves coecting additiona rea-word input data (with our sensitivities providing the most vauabe targets), refining the estimated input modes, and conducting another simuation with the refined input modes. Concusions coud be based on this fina experiment ony, but we investigate whether simuation outputs from the nomina and diagnostic experiments shoud aso be incorporated. Of course, there coud be additiona cyces of diagnostic and foow-up experiments as desired. 3.. Diagnostic experiment The diagnostic experiment is conducted to fit the meanvariance effects mode (6) and derive our measures of input uncertainty. To estimate the unknown coefficients β 0,β,...,β L,ν,ν 2,...,ν L by east squares, we need at east 2L + 2 design points, which means we need 2L + 2 different Fs. However, this is typicay impossibe since we do not have more than one data set to fit F; evenifwe did have mutipe data sets they woud usuay be pooed to enhance the precision of F. Instead, Song and Neson (203) suggested a bootstrap approach by treating F as the true rea-word distribution F c and samping mutipe times from F instead of gathering mutipe rea-word sampes. In our context, a bootstrap is an i.i.d. sampe X, X 2,...,X m from F. We use the notation Xj to denote a sampe from the empirica cumuative distribution
7 6 Song and Neson (ecdf) or fitted parametric distribution F, as opposed to X j, which is a sampe from the true rea-word distribution F c. More generay, a denotes a quantity defined by a bootstrap sampe. In our method a bootstrap sampe X, X 2,...,X m from F is treated as a rea-word sampe X, X 2,...,X m from F c. From the bootstrap sampe we can fit an ecdf F, which pays the roe of F, and cacuate μ( F )and σ 2 ( F ). Repeating this for =, 2,...,L, a coection of ecdfs F ={ F, F 2,..., F L } is obtained and we can run repications of the simuation with F to obtain the estimator Ȳ( F ). If we repeat this process B times, we wi get F (), F (2),..., F (B) and the corresponding means and variances of input modes, as we as the simuation estimators Ȳ( F () ), Ȳ( F (2) ),...,Ȳ( F (B) ) by which we can fit Mode (6). Why use bootstrap sampes to create design points for fitting the mean-variance effects mode (6) instead of a cassic designed experiment? First, this is not a simpe design space: it is the space of possibe fitted input distributions that coud resut from samping from the true distribution F c. Even if parametric distributions are used (which we do not require) so that the design space becomes the space of parameter vaues, some sets of parameters are far more ikey than others, and our mean-variance mode wi be most effective if we get a good fit near F c rather than a goba fit across the space. By using bootstrap sampes from F we create design points that are representative of what is ikey, providing a good fit where it matters most. Furthermore, simuating at bootstrap random sampes, rather than chosen design points, aows us to combine simuation resuts from the nomina and diagnostic experiments without introducing ack-of-fit bias; see Section 4. There are additiona advantages, which we describe beow. The anaogy between rea-word samping and bootstrap samping is equivaent to assuming that the input uncertainty σi 2 = Var[g( F)] is approximated as Var[g( F)] = Var[g( F) F c ] Var[g( F ) F]. (0) Under Mode (6), σi 2 is the sum of the contributions of a input modes as in Equation (8). Therefore, in view of the approximation (0): β 2 Var[μ( F )] + ν 2 Var[σ 2 ( F )] + 2β ν Cov[μ( F ),σ 2 ( F )] β 2 Var[μ( F ) F ] +ν 2 Var[σ 2 ( F ) F ] + 2β ν Cov[μ( F ),σ2 ( F ) F ], which wi be true if Var[μ( F )] Var[μ( F ) F ] Var[σ 2 ( F )] Var[σ 2 ( F ) F ] () Cov[μ( F ),σ 2 ( F )] Cov[μ( F ),σ2 ( F ) F ]. As the rea-word sampe size m increases, this approximation is asymptoticay justified under some conditions on F, as discussed in Section 3.3. A vauabe advantage of the approximation () is that it provides expressions for the variance and covariance components in Equation (7) that we need to cacuate the contributions. Since we use an empirica distribution F, μ( F )andσ2 ( F ) are simpy the sampe mean and the second sampe centra moment of X, X 2,...,X m, which is an i.i.d. sampe from the known distribution F. Therefore, as shown in Appendix A of the onine suppement, we can derive expressions for Var[μ( F ) F ], Var[σ 2 ( F ) F ], and Cov[μ( F ),σ2 ( F ) F ] as Var[μ( F ) F ] = M2 m Var[σ 2 ( F ) F ] = (m ) 2 m 3 M 4 (m 3)(m ) m 3 M4 (M2 )2 m Cov[μ( F ),σ2 ( F ) F ] = (m ) 2 m 3 M 3 (M 2 )2 M3 m, where M k is kth centra moment of F.If F is an empirica distribution, then M k = m i= (X i X ) k /m.if F is a parametric distribution, then we can cacuate the centra moments from the known representation; for instance, if F is a gamma distribution with estimated shape parameter α and rate parameter β, then the second, third, and fourth moments are α/ β 2,2 α/ β 3,and3 α 2 / β α/ β 4, respectivey. One of the major advantages of our approach is that these variance/covariance expressions are not approximations, which improves the estimation of the contributions. Aso notice that this is a very genera method that is appicabe to any empirica distribution and many parametric distributions; the ony time we face difficuty is when F is a parametric distribution whose parameters are in the range for which not a moments up to the fourth exist (e.g., a og-ogistic distribution with shape parameter ess than four). Even then, we can use our method provided that the offending distribution can be represented as a transformation of another distribution whose first four moments aways exist. In this case we fit the mean-variance mode to the moments of the underying distribution. For instance, the og-ogistic distribution is a transformation of a ogistic distribution whose first four moments are finite, so we fit to the moments of the underying ogistic distribution. Since every distribution can be viewed as a transformation of the uniform (0, ) distribution, our method is (at east in theory) competey genera. Inserting the moment expressions into Equation (7), the contribution of F with m sampes can be written as V (m ) { β 2 m M 2 + ( ν2 M 4 (M 2 )2) + 2β ν M 3 }, (2)
8 Quicky assessing input uncertainty 7 impying that the sampe size sensitivity of F is V (m ) m = { β 2 m =m (m ) 2 M 2 + ( ν2 M 4 ( M 2 ) 2 ) + 2β ν M 3 } = V (m ). (3) m Notice that the sensitivity is aways negative since input uncertainty is reduced with additiona rea-word data. Notice aso that the rank order of contributions and sensitivities of distributions do not aways coincide; even if F has the argest contribution, if m is aso arge then input uncertainty may be ess sensitive to F than some other input modes. In other words, an additiona sampe from F c may not make much difference to the input uncertainty variance since we aready have a arge sampe. The agorithm for the diagnostic experiment is as foows: Diagnostic Experiment. Given the estimated input modes F, do the foowing: 2. For bootstrap sampe b = tob a. For input mode = tol i.generate X (b), X (b) 2,...,X (b) by samping m times from F. ii.let F (b) be the ecdf of X (b), X (b) 2,...,X (b) m and cacuate the mean μ( F (b) ) and variance σ 2 ( F (b) ). b. Using input modes F (b) ={ F (b), F (b) 2,..., F (b) L }, simuate R i.i.d. repications Y j ( F (b) ), j =, 2,...,Rand cacuate the sampe mean Ȳ( F (b) ). 3. Fit the mode Ȳ( F (b) ) = β 0 + β μ( F (b) ) + m ν σ 2 ( F (b) ) + ε b (4) with Ȳ( F (b) ) from step 2b and μ( F (b) ),μ( F (b) 2 ),...,μ( F (b) L )andσ2 ( F (b) ),σ 2 ( F (b) 2 ),...,σ 2 ( F (b) L )from step 2a for b =, 2,...,B to estimate the coefficients β 0,β,...,β L,ν,ν 2,...,ν L. 4. Estimate the overa input uncertainty σ I 2 = L V (m ) and the ratio γ = σ I σ/ n = n L V (m ) σ 5. Estimate the contribution V (m ) and the sensitivity for =, 2,...,L. We estimate σ 2 in step 4 using the sampe variance from the nomina experiment, rather than using the residua meansquared error (MSE) of the fitted mode in step 3; this avoids bias due to ack of fit. Of course, n in step 4 is the. number of repications used in the nomina experiment and need not be the same as R. As discussed in Section 2., the ratio γ expresses input uncertainty in units of the simuation estimation error. If γ = 0.5, for instance, it impies that the input uncertainty is ony haf of the simuation estimation error, which may be acceptabe depending on the type of decision that the simuation is expected to support. If γ is arge e.g., γ = 20 then we can concude that the simuation estimation error as measured, say, by the width of a CI, shoud be infated by a factor of roughy + γ 2. Whether or not this is acceptabe depends on the situation: If the simuation estimation error is very sma as woud occur if the number of repications n is very arge then a CI that is roughy 20 times onger might have itte effect on the decision that the simuation mode is designed to support. We beieve that it wi often be the case that such an infation is unacceptabe, so the anayst may choose to coect more rea-word data for the input modes that have greater (more negative) sensitivities. This decision aso depends on the feasibiity and the cost of additiona data coection. The key insight is that γ must be interpreted in ight of the remaining simuation estimation error, not as an absoute number, and wi be the most meaningfu when n was expicity chosen chosen to achieve a specified eve of error. For instance if n was chosen (perhaps sequentiay) to attain a CI whose width is no more than ±,then γ can be interpreted as arge or sma reative to + γ Foow-up experiment If the anayst coects more rea-word data from some or a of the input processes, then they wi have an updated coection of input modes with m > m for at east one {, 2,...,L}. Using updated input modes that are fit to a of the accumuated data, the anayst can run a foow-up experiment to obtain an estimator of E[Y(F c )] with reduced input uncertainty. We assume that the foow-up experiment empoys at east as many simuation repications as the nomina experiment, so n n. If needed, this sequence of experiments can be repeated by regarding the resuts from the foow-up experiment in the previous sequence as a new nomina experiment. The primary question with respect the foow-up experiment is whether we shoud use simuation outputs from the nomina or diagnostic experiments in the overa estimator. We address this question in a ater section Vaidity of the bootstrap approximation Here we consider the vaidity of the approximation, introduced above, where we suggested that Var[g( F)] = Var[g( F) F c ] Var[g( F ) F].
9 8 Song and Neson Given our mode, this is equivaent to order statistic. Then Var[μ( F )] Var[μ( F ) F ] Var[σ 2 ( F )] Var[σ 2 ( F ) F ] Cov[μ( F ),σ 2 ( F )] Cov[μ( F ),σ2 ( F ) F ]. This assumption can be asymptoticay justified under certain conditions as the sampe size m gets arge; we describe some cases beow. Reca that in our method the bootstrap distribution F is an ecdf. Let μk = E[(X j E(X j )) k ], the kth centra moment of F c. Assuming that F is aso an ecdf, and the reevant moments exist, the asymptotic variance and covariance of μ( F )andσ2 ( F )given F are, with probabiity : im m Var[μ( F m ) F ] = im m M2 = μ2 im m Var[σ 2 ( F m ) F ] = im m M4 ( M 2 ) 2 = μ 4 ( μ 2 im m Cov[μ( F m ),σ2 ( F ) F ] = im m M3 = μ3. (5) Furthermore, when F is an ecdf it is easy to show that im m m Var[μ( F )] = μ 2 im m Var[σ 2 ( F )] = μ 4 m ( μ 2 im m Cov[μ( F ),σ 2 ( F )] = μ 3 m. ) 2 ) 2 (6) See Zhang (2007), Cho and Cho (2008), and the onine suppement. However, if F is a parametric distribution whose parameters are estimated from the observed rea-word data then neither Equation (5) nor Equation (6) is guaranteed to hod. For instance, if we fit the wrong parametric famiy to the data then differences can occur. A sufficient condition for both Equation (5) and (6) to hod when F is a parametric distribution is that F is fexibe enough to match any first four moments of the data, and the distribution is fit using the Method of Moments (MMs) up to at east the fourth moment. Even when we have the correct parametric famiy, there coud sti be differences depending on how we estimate the parameters. As mentioned above, if we use the MMs then the moments of the fitted distribution are the sampe moments. And in many cases, the MLEs and MMs are asymptoticay equivaent (e.g., norma). This is not aways the case, however. Suppose that F c is a uniform (0, ) distribution and we have m i.i.d. rea-word observations X, X 2,...,X m.the MLEs are α = X () and β = X (m ),wherex (i) is the ith im m m Var[μ( F )] = 0 < 2 = μ2 im m Var[σ 2 ( F )] = 0 < m 80 = μ4 (μ2 )2 im m Cov[μ( F ),σ 2 ( F )] = 0 = μ 3 m. Except for the covariance term, the asymptotic variances are smaer than those of the MMs estimators because the MLEs are asymptoticay more efficient. Nevertheess, even in this case our bootstrap approximation provides a vaid representation of the variabiity of the rea-word data that coud have been obtained, athough not a perfect representation of the variabiity of the estimated parameters. As a practica matter, we woud appy our method for any sampe sizes m,=, 2,...L that the anayst is comfortabe using to fit distributions if the aternative is to ignore input uncertainty. Based on the bootstrapping iterature (e.g., Ha (992, Appendix I)), the performance of sampe moment estimators, and our own experience in empirica studies, we are comfortabe with m Combining resuts from the nomina, diagnostic, and foow-up experiments In some situations it is not feasibe to gather additiona rea-word input data even if there is substantia input uncertainty; in others the input uncertainty is so sma that there is itte vaue in reducing it further. In either of these situations the anayst terminates the experiment at the diagnostic phase that generated Ȳ( F (b) ), b =, 2,...,B to fit Mode (6). The first question we address is whether these resuts can be utiized to improve the estimator Ȳ( F) from the nomina experiment by using a weighted estimator: Ỹ = αȳ( F) + ( α)ȳ( F), where Ȳ( F) = B b= Ȳ( F (b) )/B and α [0, ]. This estimator ony makes sense because the bootstrap distributions F (b) are samped directy from F and therefore indirecty from F c. Deterministicay chosen design points woud introduce an unknown and ikey significant bias. We answer this question by seeking α that minimizes MSE[Ỹ F], rather than minimizing MSE[Ỹ]. Minimizing MSE[Ỹ] woudmakesenseifwewereactuayabeto obtain mutipe rea-word data sets, whereas minimizing MSE[Ỹ F] acknowedges that we ony have one rea-word data set and therefore cannot improve our estimate of F c beyond F. From the derivation in Appendix B of the onine suppement, and under the assumption that Mode (6) hods, we have ( MSE[Ỹ F] = ( α) 2 (b ) 2 + σ I 2 B + σ 2 ) + α 2 σ 2 BR n, (7)
10 Quicky assessing input uncertainty 9 where b = Bias[Ȳ( F) F] = E[Y( F (b) ) F] E[Y( F) F] which is the bias from bootstrapping. Therefore, the optima α is α = (b ) 2 + σ 2 I /B + σ 2 /(BR) (b ) 2 + σ 2 I /B + σ 2 /(BR) + σ 2 /n. (8) experiment for a of the unknown quantities. As a rough CI we coud mutipy this by an appropriate norma quantie. We next consider the case when a three experiments have been conducted. Now it makes sense to try to minimize the MSE of the fina point estimator with respect to both input and simuation uncertainty. For this reason we discard the simuation resuts from the diagnostic experiment since they introduce additiona bias due to bootstrapping. For a cear distinction, et F m denote the coection of input modes used in the nomina experiment that were estimated from m ={m, m 2,...,m L } rea-word observations, and et Ȳ n ( F m ) denote the estimator from n repications using F m. Simiary, F m denotes the coection of input modes used in the foow-up experiment that were estimated from m ={m, m 2,...,m L } rea-word observations, where m m for a, andȳ n ( F m ) is the corresponding estimator from n n repications. Notice that it is very ikey that Ȳ n ( F m )andȳ n ( F m ) are positivey correated since the foow-up m rea-word observations incude the nomina m observations. The weighted estimator Ŷ is defined as Ŷ = αȳ n ( F m ) + ( α)ȳ n ( F m ). Due to the correation between Ȳ n ( F m )andȳ n ( F m ), finding α to minimize MSE(Ŷ) is more compicated than the previous case. As shown in Appendix D of the onine suppement, if we et b m and b m denote the bias of Ȳ n ( F m )and Ȳ n ( F m ), respectivey, as estimators of E[Y(F c )], and et σ 2 I and (σ I )2 denote the input uncertainty of the nomina and the foow-up experiments, respectivey, then α becomes α = (σ I )2 + (σ 2 /n ) + b m (b m b m ) Cov[Ȳ n ( F m ), Ȳ n ( F m )] σ 2 I + (σ I )2 + (σ 2 /n) + (σ 2 /n ) + (b m b m ) 2 2Cov[Ȳ n ( F m ), Ȳ n ( F m )]. Notice that α is stricty ess than one; hence, it is aways better to poo Ȳ( F) andȳ( F). The key term is σ 2 If α /n < 0weuseα = 0. In genera it is not easy to find a usefu expression for that represents the simuation variance: the arger it is, the Cov[Ȳ more weight is given to the diagnostic resuts, which are n ( F m ), Ȳ n ( F m )]. However, if we assume a input distributions are ecdfs, then under Mode (6) we can show biased but reduce simuation variance. An unbiased estimator of b is Ȳ( F) Ȳ( F), so every term in α that is either known or estimabe from the nomina and diagnostic Cov[Ȳ n ( F m ), Ȳ n ( F m )] (σ I experiments. )2. Previousy we suggested that the diagnostic experiment Under this condition we can aso get an expression for the coud be used to provide a heuristic adjustment to the CI or bias term as standard error of the mean of the nomina experiment by mutipying them by + γ 2. In Appendix C of the onine ν σ 2 (F c b m = ) suppement, we justify using σ I 2 + MSE as a pug-in m, approximation for the MSE of the combined estimator Ỹ, where MSE is Equation (7) with optima weight α where σ 2 (F c ) represents the variance of the true distribution F c. These expressions are derived in Appendix D of from Equation (8) but inserting estimates from the diagnostic the onine suppement. Therefore, for this specia case α becomes α (σ 2 /n ) + { L ν σ 2 (F c)/(m )}{ L ν σ 2 (F c)( (/(m )) (/(m )) )} (σ 2 /n)+(σ 2 /n )+ L ( V (m ) V (m )) + { L ν σ 2 (F c)( (/(m )) (/(m )) )} 2. (9) From this resut, we can immediatey observe that as n gets bigger, α gets smaer, which impies that the more repications we make from the foow-up experiment, the ess we vaue the repications from the nomina experiment, which makes sense. For the simpest case, suppose that the anayst did not coect additiona rea-word input data and ran the foowup experiment with the same input modes F m.thenα = n/(n + n ) because m = m for a. This is ceary the weight we woud use to poo two estimators from n and n repications generated by the same input modes. More generay, when m > m for at east one there is a trade-off because pooing eads to more bias as Ȳ n ( F m ) tends to have a arger bias than Ȳ n ( F m ). If Ȳ n ( F m ) is significanty more biased than Ȳ n ( F m ) then it is ess attractive to poo the two estimators and we suspect this is often the case. To iustrate this point, suppose that overa input uncertainty is substantia (e.g., γ = 20) and F has the argest contribution among a input modes whie others have negigibe contributions. In this case, the anayst might coect a arge additiona sampe (m m )fromf c to update F, whie keeping a other input modes the same as in the
11 0 Song and Neson nomina experiment. When this happens α becomes α (σ 2 /n ) + ((ν σ 2 (F c = ))2 /(m ))((/(m )) (/(m ))) (σ 2 /n) + (σ 2 /n ) + (V (m ) V (m )) +{ν σ 2 (F c)((/(m )) (/(m )))}. (20) 2 The denominator in Equation (20) is stricty positive as V (m ) > V (m ). However, the numerator can be negative if σ 2 ( n < ν σ 2 (F c )) 2 ( m m ) m, in which case α = 0. Even if the numerator is greater than zero, we suspect α wi be near zero for the foowing reasons.. The anayst may run more repications for the foow-up experiment than the nomina experiment (n n) asit provides a ess biased (more accurate) estimator, which makes σ 2 /n <σ 2 /n. 2. (σ 2 /n ) + ((ν σ 2 (F c ))2 /(m ))((/(m )) (/(m ))) <σ 2 /n ; 3. since m m, we expect V (m ) V (m ) V (m ); and 4. since γ is arge and F has the biggest contribution, V (m ) σ 2 n. From to 4; V (m ) σ 2 + (ν σ 2 (F c))2 n m ( m ), m and, therefore, α becomes sma. Hence, the more we reaword data we coect for the foow-up experiment, the ess benefit there is in variance reduction from pooing the two estimators, whereas the reative disadvantage from introducing additiona bias increases. As mentioned earier, the resut in Equation (9) hods under Mode (6) when we assume that F m and F m are coections of ecdfs. We beieve that α is typicay near zero in this case, which impies that it is better to use the estimator from the foow-up experiment without pooing. We aso suspect a simiar concusion hods when any of the input distributions are parametric. 5. Design of the diagnostic experiment The diagnostic experiment is an essentia component of our method. There are three key experiment design questions.. How shoud we seect design points? As discussed in Section 3., to fit Equation (4) we have chosen bootstrap generated empirica distributions F, F 2,..., F B as design points. This concentrates the design where we need to fit we, and it faciitates combining resuts from the nomina and diagnostic experiment. 2. Shoud we use Common Random Numbers (CRNs) across the diagnostic simuations? The bootstrap design points F (), F (2),..., F (B) must be samped independenty from F, but we can choose to use the same random numbers for the simuations conducted with each F (b). Keijnen (988) and others have shown that CRN tend to reduce the variance of the sope-parameter estimators in east-squares regression, which are β, ν, =, 2,...,L in Mode (6). Since the variance of V is an increasing function of the variances of β and ν,it seems cear that using CRNs is desirabe. 3. Given a budget of N simuation repications, how shoud it be divided between design points (B) and simuation repications per design point (R) so that RB = N? Ankenman and Neson (202) showed that with their method for assessing overa input uncertainty, if N is not too sma then B 0 is optima in terms of minimizing the expected width of the CI for γ. However, our objective is different: we focus on providing estimates of the contribution of each input mode. Beow we argue that B = N (R = ) is the best choice in terms of statistica efficiency, but B = 2L + 3 is best for computation. Therefore, we provide a recommendation that baances these two objectives. First, B = N is the optima design to minimize the MSE of the combined estimator from the nomina experiment (Ȳ( F))and the diagnostic experiment (Ȳ( F)). This is because the conditiona variance of Ȳ( F) can be approximated as Var[Ȳ( F) F] σi 2/B + σ 2 /N under the bootstrap approximation in Equation (0); see Appendix B of the onine suppement. Second, as described in Section 3, we estimate the parameters β 0,β,...,β L and ν,ν 2,...,ν L in Mode (6) by regressing B simuation output estimators on the means and variances of bootstrapped ecdfs. The design matrix for the regression is μ( F () ) σ 2 ( F () ) μ( F () L ) σ 2 ( F () L ) μ( F (2) ) σ 2 ( F (2) ) μ( F (2) L ) σ 2 ( F (2) L ) μ( F (B) ) σ 2 ( F (B) ) μ( F (B) L ) σ 2 ( F (B) L ) As we have 2L + parameters, we need at east 2L + 2 unique rows in the design matrix, which impies that it is necessary to have B 2L + 2. However, B 2L + 2 is not aways sufficient to obtain the required number of unique rows. If our input modes incude at east one continuous parametric distribution among F, F 2,..., F L, then with prob-
12 Quicky assessing input uncertainty abiity one a rows in the design matrix wi be unique because the probabiity of two bootstrap sampes with the same sampe moments is zero for a continuous distribution. On the other hand, if a input modes in F, F 2,..., F L are ecdfs or discrete parametric distributions, then we need to be more cautious. Bernoui distributions, particuary when the probabiity of success is extreme, are the most chaenging cases since ties in the sampe moments are quite ikey when m is sma. Thus, a arger m gives more opportunities for unique rows. Aso worth noting is that the ikeihood of identica rows diminishes as the number of input modes L increases, so the probem is ess pronounced in simuations with many input modes. Finay, the contribution estimator V in Equation (2) is a function of β and ν, so a good stand-in for the properties of V are the properties of β and ν. To iustrate why B = N is statisticay best, we temporariy simpify Mode (6) to ony incude the mean effects and no CRN: Y j ( F) = β 0 + β μ( F ) + ε j. (2) Then V (m ) = β 2Var[ μ( F )]. If we assume that both μ( F ) and ε j are normay distributed which is pausibe since μ( F ) is asymptoticay normay distributed with arge sampe size m then standard resuts show that Var[ β ] = ( ) B σ 2 (22) N B L 2 Var[μ( F )] when we force RB = N. Notice aso that E[ β 2 ] = β2 + Var [ β ] = β 2 + ( ) B N B L 2 σ 2 Var [μ( F )]. (23) Ceary, B = N is best for minimizing variance and bias, but the margina impact of increasing B diminishes when BR = N is fixed. If we extend this anaysis in the natura way to incude the variance effects as in Mode (6), then the L terms in the denominators of Equation (22) and (23) become 2L. On the other hand, from a computationa efficiency point of view using B < N (R > ) has advantages over B = N (R = ). There is typicay a computationa set-up cost for simuating a new design point (which is reay a new simuation mode) but very itte setup required for each additiona repication at a design point. If B < N then there are fewer setups. Furthermore, the number of rows in the design matrix is B, impying the need to manipuate a B (2L + ) matrix to fit the regression mode. This argues for smaer B. We must have B 2L + 2. When arger N is feasibe, we recommend making B arge enough so that the incrementa decrease in the variance and bias is sma, say <δ. Therefore, we seect the smaest B such that ( ) d B > δ, db B 2L 2 which impies seecting the smaest B such that 2L + 2 B > 2L δ and R = N/B. For instance, if L = 5andδ = 0.0 a % margina decrease then B = Empirica resuts This section summarizes an empirica study of the proposed method appied to two simpe exampes and aso an iustration on a reaistic probem. In the two simpe exampes we appy our method and provide intuitive expanations for the resuts, as we as compare them to true input-mode contributions as defined in Equation (4) that were estimated precisey from side experiments. These side experiments expoit the fact that the true, correct rea-word distributions are known, which is obviousy not the case in practice. In both exampes we define F c for each input and then sampe m observations that we treat as the rea-word data. We first evauate the method using a we-known Stochastic Activity Network (SAN); see Fig.. The goa is to estimate the mean time to compete the network. We defined a set of rea-word input distributions for the activity times F c ={F c, F 2 c,...,f 5 c }. Experiments under different settings of sampe size and mean and variance of the activity-time distributions were conducted and the variance contribution and sensitivity of each input distribution was estimated. The second exampe is an M/M// k queueing system simuation that has two input distributions: interarriva time and service time. The goa of the simuation is to estimate the mean steady-state queue ength, which is known to be a highy noninear function of the means of the two Fig.. AsmaSAN.
Proceedings of the 2014 Winter Simulation Conference A. Tolk, S. Y. Diallo, I. O. Ryzhov, L. Yilmaz, S. Buckley, and J. A. Miller, eds.
 Proceedings of the 2014 Winter Simuation Conference A. Tok, S. Y. Diao, I. O. Ryzhov, L. Yimaz, S. Buckey, and J. A. Mier, eds. ADVANCED TUTORIAL: INPUT UNCERTAINTY QUANTIFICATION Eunhye Song Barry L.
Proceedings of the 2014 Winter Simuation Conference A. Tok, S. Y. Diao, I. O. Ryzhov, L. Yimaz, S. Buckey, and J. A. Mier, eds. ADVANCED TUTORIAL: INPUT UNCERTAINTY QUANTIFICATION Eunhye Song Barry L.
A Brief Introduction to Markov Chains and Hidden Markov Models
 A Brief Introduction to Markov Chains and Hidden Markov Modes Aen B MacKenzie Notes for December 1, 3, &8, 2015 Discrete-Time Markov Chains You may reca that when we first introduced random processes,
A Brief Introduction to Markov Chains and Hidden Markov Modes Aen B MacKenzie Notes for December 1, 3, &8, 2015 Discrete-Time Markov Chains You may reca that when we first introduced random processes,
A QUICKER ASSESSMENT OF INPUT UNCERTAINTY. Eunhye Song Barry L. Nelson
 Proceedings of the 2013 Winter Simulation Conference R. Pasupathy, S.-H. Kim, A. Tolk, R. Hill, and M. E. Kuhl, eds. A QUICKER ASSESSMENT OF INPUT UNCERTAINTY Eunhye Song Barry. Nelson Department of Industrial
Proceedings of the 2013 Winter Simulation Conference R. Pasupathy, S.-H. Kim, A. Tolk, R. Hill, and M. E. Kuhl, eds. A QUICKER ASSESSMENT OF INPUT UNCERTAINTY Eunhye Song Barry. Nelson Department of Industrial
Do Schools Matter for High Math Achievement? Evidence from the American Mathematics Competitions Glenn Ellison and Ashley Swanson Online Appendix
 VOL. NO. DO SCHOOLS MATTER FOR HIGH MATH ACHIEVEMENT? 43 Do Schoos Matter for High Math Achievement? Evidence from the American Mathematics Competitions Genn Eison and Ashey Swanson Onine Appendix Appendix
VOL. NO. DO SCHOOLS MATTER FOR HIGH MATH ACHIEVEMENT? 43 Do Schoos Matter for High Math Achievement? Evidence from the American Mathematics Competitions Genn Eison and Ashey Swanson Onine Appendix Appendix
CS229 Lecture notes. Andrew Ng
 CS229 Lecture notes Andrew Ng Part IX The EM agorithm In the previous set of notes, we taked about the EM agorithm as appied to fitting a mixture of Gaussians. In this set of notes, we give a broader view
CS229 Lecture notes Andrew Ng Part IX The EM agorithm In the previous set of notes, we taked about the EM agorithm as appied to fitting a mixture of Gaussians. In this set of notes, we give a broader view
A Multivariate Input Uncertainty in Output Analysis for Stochastic Simulation
 A Mutivariate Input Uncertainty in Output Anaysis for Stochastic Simuation WEI XIE, Rensseaer Poytechnic Institute BARRY L. NELSON, Northwestern University RUSSELL R. BARTON, The Pennsyvania State University
A Mutivariate Input Uncertainty in Output Anaysis for Stochastic Simuation WEI XIE, Rensseaer Poytechnic Institute BARRY L. NELSON, Northwestern University RUSSELL R. BARTON, The Pennsyvania State University
NEW DEVELOPMENT OF OPTIMAL COMPUTING BUDGET ALLOCATION FOR DISCRETE EVENT SIMULATION
 NEW DEVELOPMENT OF OPTIMAL COMPUTING BUDGET ALLOCATION FOR DISCRETE EVENT SIMULATION Hsiao-Chang Chen Dept. of Systems Engineering University of Pennsyvania Phiadephia, PA 904-635, U.S.A. Chun-Hung Chen
NEW DEVELOPMENT OF OPTIMAL COMPUTING BUDGET ALLOCATION FOR DISCRETE EVENT SIMULATION Hsiao-Chang Chen Dept. of Systems Engineering University of Pennsyvania Phiadephia, PA 904-635, U.S.A. Chun-Hung Chen
SydU STAT3014 (2015) Second semester Dr. J. Chan 18
 STAT3014/3914 Appied Stat.-Samping C-Stratified rand. sampe Stratified Random Samping.1 Introduction Description The popuation of size N is divided into mutuay excusive and exhaustive subpopuations caed
STAT3014/3914 Appied Stat.-Samping C-Stratified rand. sampe Stratified Random Samping.1 Introduction Description The popuation of size N is divided into mutuay excusive and exhaustive subpopuations caed
A. Distribution of the test statistic
 A. Distribution of the test statistic In the sequentia test, we first compute the test statistic from a mini-batch of size m. If a decision cannot be made with this statistic, we keep increasing the mini-batch
A. Distribution of the test statistic In the sequentia test, we first compute the test statistic from a mini-batch of size m. If a decision cannot be made with this statistic, we keep increasing the mini-batch
STA 216 Project: Spline Approach to Discrete Survival Analysis
 : Spine Approach to Discrete Surviva Anaysis November 4, 005 1 Introduction Athough continuous surviva anaysis differs much from the discrete surviva anaysis, there is certain ink between the two modeing
: Spine Approach to Discrete Surviva Anaysis November 4, 005 1 Introduction Athough continuous surviva anaysis differs much from the discrete surviva anaysis, there is certain ink between the two modeing
(This is a sample cover image for this issue. The actual cover is not yet available at this time.)
 (This is a sampe cover image for this issue The actua cover is not yet avaiabe at this time) This artice appeared in a journa pubished by Esevier The attached copy is furnished to the author for interna
(This is a sampe cover image for this issue The actua cover is not yet avaiabe at this time) This artice appeared in a journa pubished by Esevier The attached copy is furnished to the author for interna
Explicit overall risk minimization transductive bound
 1 Expicit overa risk minimization transductive bound Sergio Decherchi, Paoo Gastado, Sandro Ridea, Rodofo Zunino Dept. of Biophysica and Eectronic Engineering (DIBE), Genoa University Via Opera Pia 11a,
1 Expicit overa risk minimization transductive bound Sergio Decherchi, Paoo Gastado, Sandro Ridea, Rodofo Zunino Dept. of Biophysica and Eectronic Engineering (DIBE), Genoa University Via Opera Pia 11a,
A Statistical Framework for Real-time Event Detection in Power Systems
 1 A Statistica Framework for Rea-time Event Detection in Power Systems Noan Uhrich, Tim Christman, Phiip Swisher, and Xichen Jiang Abstract A quickest change detection (QCD) agorithm is appied to the probem
1 A Statistica Framework for Rea-time Event Detection in Power Systems Noan Uhrich, Tim Christman, Phiip Swisher, and Xichen Jiang Abstract A quickest change detection (QCD) agorithm is appied to the probem
Statistical Inference, Econometric Analysis and Matrix Algebra
 Statistica Inference, Econometric Anaysis and Matrix Agebra Bernhard Schipp Water Krämer Editors Statistica Inference, Econometric Anaysis and Matrix Agebra Festschrift in Honour of Götz Trenker Physica-Verag
Statistica Inference, Econometric Anaysis and Matrix Agebra Bernhard Schipp Water Krämer Editors Statistica Inference, Econometric Anaysis and Matrix Agebra Festschrift in Honour of Götz Trenker Physica-Verag
Schedulability Analysis of Deferrable Scheduling Algorithms for Maintaining Real-Time Data Freshness
 1 Scheduabiity Anaysis of Deferrabe Scheduing Agorithms for Maintaining Rea-Time Data Freshness Song Han, Deji Chen, Ming Xiong, Kam-yiu Lam, Aoysius K. Mok, Krithi Ramamritham UT Austin, Emerson Process
1 Scheduabiity Anaysis of Deferrabe Scheduing Agorithms for Maintaining Rea-Time Data Freshness Song Han, Deji Chen, Ming Xiong, Kam-yiu Lam, Aoysius K. Mok, Krithi Ramamritham UT Austin, Emerson Process
FRST Multivariate Statistics. Multivariate Discriminant Analysis (MDA)
 1 FRST 531 -- Mutivariate Statistics Mutivariate Discriminant Anaysis (MDA) Purpose: 1. To predict which group (Y) an observation beongs to based on the characteristics of p predictor (X) variabes, using
1 FRST 531 -- Mutivariate Statistics Mutivariate Discriminant Anaysis (MDA) Purpose: 1. To predict which group (Y) an observation beongs to based on the characteristics of p predictor (X) variabes, using
Uniprocessor Feasibility of Sporadic Tasks with Constrained Deadlines is Strongly conp-complete
 Uniprocessor Feasibiity of Sporadic Tasks with Constrained Deadines is Strongy conp-compete Pontus Ekberg and Wang Yi Uppsaa University, Sweden Emai: {pontus.ekberg yi}@it.uu.se Abstract Deciding the feasibiity
Uniprocessor Feasibiity of Sporadic Tasks with Constrained Deadines is Strongy conp-compete Pontus Ekberg and Wang Yi Uppsaa University, Sweden Emai: {pontus.ekberg yi}@it.uu.se Abstract Deciding the feasibiity
MARKOV CHAINS AND MARKOV DECISION THEORY. Contents
 MARKOV CHAINS AND MARKOV DECISION THEORY ARINDRIMA DATTA Abstract. In this paper, we begin with a forma introduction to probabiity and expain the concept of random variabes and stochastic processes. After
MARKOV CHAINS AND MARKOV DECISION THEORY ARINDRIMA DATTA Abstract. In this paper, we begin with a forma introduction to probabiity and expain the concept of random variabes and stochastic processes. After
XSAT of linear CNF formulas
 XSAT of inear CN formuas Bernd R. Schuh Dr. Bernd Schuh, D-50968 Kön, Germany; bernd.schuh@netcoogne.de eywords: compexity, XSAT, exact inear formua, -reguarity, -uniformity, NPcompeteness Abstract. Open
XSAT of inear CN formuas Bernd R. Schuh Dr. Bernd Schuh, D-50968 Kön, Germany; bernd.schuh@netcoogne.de eywords: compexity, XSAT, exact inear formua, -reguarity, -uniformity, NPcompeteness Abstract. Open
Bayesian Learning. You hear a which which could equally be Thanks or Tanks, which would you go with?
 Bayesian Learning A powerfu and growing approach in machine earning We use it in our own decision making a the time You hear a which which coud equay be Thanks or Tanks, which woud you go with? Combine
Bayesian Learning A powerfu and growing approach in machine earning We use it in our own decision making a the time You hear a which which coud equay be Thanks or Tanks, which woud you go with? Combine
Asynchronous Control for Coupled Markov Decision Systems
 INFORMATION THEORY WORKSHOP (ITW) 22 Asynchronous Contro for Couped Marov Decision Systems Michae J. Neey University of Southern Caifornia Abstract This paper considers optima contro for a coection of
INFORMATION THEORY WORKSHOP (ITW) 22 Asynchronous Contro for Couped Marov Decision Systems Michae J. Neey University of Southern Caifornia Abstract This paper considers optima contro for a coection of
Some Measures for Asymmetry of Distributions
 Some Measures for Asymmetry of Distributions Georgi N. Boshnakov First version: 31 January 2006 Research Report No. 5, 2006, Probabiity and Statistics Group Schoo of Mathematics, The University of Manchester
Some Measures for Asymmetry of Distributions Georgi N. Boshnakov First version: 31 January 2006 Research Report No. 5, 2006, Probabiity and Statistics Group Schoo of Mathematics, The University of Manchester
Two-sample inference for normal mean vectors based on monotone missing data
 Journa of Mutivariate Anaysis 97 (006 6 76 wwweseviercom/ocate/jmva Two-sampe inference for norma mean vectors based on monotone missing data Jianqi Yu a, K Krishnamoorthy a,, Maruthy K Pannaa b a Department
Journa of Mutivariate Anaysis 97 (006 6 76 wwweseviercom/ocate/jmva Two-sampe inference for norma mean vectors based on monotone missing data Jianqi Yu a, K Krishnamoorthy a,, Maruthy K Pannaa b a Department
Proceedings of the 2014 Winter Simulation Conference A. Tolk, S. Y. Diallo, I. O. Ryzhov, L. Yilmaz, S. Buckley, and J. A. Miller, eds.
 Proceedings of the 2014 Winter Simuation Conference A. Tok, S. Y. Diao, I. O. Ryzhov, L. Yimaz, S. Buckey, and J. A. Mier, eds. STATISTICAL UNCERTAINTY ANALYSIS FOR STOCHASTIC SIMULATION WITH DEPENDENT
Proceedings of the 2014 Winter Simuation Conference A. Tok, S. Y. Diao, I. O. Ryzhov, L. Yimaz, S. Buckey, and J. A. Mier, eds. STATISTICAL UNCERTAINTY ANALYSIS FOR STOCHASTIC SIMULATION WITH DEPENDENT
Alberto Maydeu Olivares Instituto de Empresa Marketing Dept. C/Maria de Molina Madrid Spain
 CORRECTIONS TO CLASSICAL PROCEDURES FOR ESTIMATING THURSTONE S CASE V MODEL FOR RANKING DATA Aberto Maydeu Oivares Instituto de Empresa Marketing Dept. C/Maria de Moina -5 28006 Madrid Spain Aberto.Maydeu@ie.edu
CORRECTIONS TO CLASSICAL PROCEDURES FOR ESTIMATING THURSTONE S CASE V MODEL FOR RANKING DATA Aberto Maydeu Oivares Instituto de Empresa Marketing Dept. C/Maria de Moina -5 28006 Madrid Spain Aberto.Maydeu@ie.edu
Schedulability Analysis of Deferrable Scheduling Algorithms for Maintaining Real-Time Data Freshness
 1 Scheduabiity Anaysis of Deferrabe Scheduing Agorithms for Maintaining Rea- Data Freshness Song Han, Deji Chen, Ming Xiong, Kam-yiu Lam, Aoysius K. Mok, Krithi Ramamritham UT Austin, Emerson Process Management,
1 Scheduabiity Anaysis of Deferrabe Scheduing Agorithms for Maintaining Rea- Data Freshness Song Han, Deji Chen, Ming Xiong, Kam-yiu Lam, Aoysius K. Mok, Krithi Ramamritham UT Austin, Emerson Process Management,
Expectation-Maximization for Estimating Parameters for a Mixture of Poissons
 Expectation-Maximization for Estimating Parameters for a Mixture of Poissons Brandon Maone Department of Computer Science University of Hesini February 18, 2014 Abstract This document derives, in excrutiating
Expectation-Maximization for Estimating Parameters for a Mixture of Poissons Brandon Maone Department of Computer Science University of Hesini February 18, 2014 Abstract This document derives, in excrutiating
Stochastic Complement Analysis of Multi-Server Threshold Queues. with Hysteresis. Abstract
 Stochastic Compement Anaysis of Muti-Server Threshod Queues with Hysteresis John C.S. Lui The Dept. of Computer Science & Engineering The Chinese University of Hong Kong Leana Goubchik Dept. of Computer
Stochastic Compement Anaysis of Muti-Server Threshod Queues with Hysteresis John C.S. Lui The Dept. of Computer Science & Engineering The Chinese University of Hong Kong Leana Goubchik Dept. of Computer
AST 418/518 Instrumentation and Statistics
 AST 418/518 Instrumentation and Statistics Cass Website: http://ircamera.as.arizona.edu/astr_518 Cass Texts: Practica Statistics for Astronomers, J.V. Wa, and C.R. Jenkins, Second Edition. Measuring the
AST 418/518 Instrumentation and Statistics Cass Website: http://ircamera.as.arizona.edu/astr_518 Cass Texts: Practica Statistics for Astronomers, J.V. Wa, and C.R. Jenkins, Second Edition. Measuring the
Asymptotic Properties of a Generalized Cross Entropy Optimization Algorithm
 1 Asymptotic Properties of a Generaized Cross Entropy Optimization Agorithm Zijun Wu, Michae Koonko, Institute for Appied Stochastics and Operations Research, Caustha Technica University Abstract The discrete
1 Asymptotic Properties of a Generaized Cross Entropy Optimization Agorithm Zijun Wu, Michae Koonko, Institute for Appied Stochastics and Operations Research, Caustha Technica University Abstract The discrete
Akaike Information Criterion for ANOVA Model with a Simple Order Restriction
 Akaike Information Criterion for ANOVA Mode with a Simpe Order Restriction Yu Inatsu * Department of Mathematics, Graduate Schoo of Science, Hiroshima University ABSTRACT In this paper, we consider Akaike
Akaike Information Criterion for ANOVA Mode with a Simpe Order Restriction Yu Inatsu * Department of Mathematics, Graduate Schoo of Science, Hiroshima University ABSTRACT In this paper, we consider Akaike
SUPPLEMENTARY MATERIAL TO INNOVATED SCALABLE EFFICIENT ESTIMATION IN ULTRA-LARGE GAUSSIAN GRAPHICAL MODELS
 ISEE 1 SUPPLEMENTARY MATERIAL TO INNOVATED SCALABLE EFFICIENT ESTIMATION IN ULTRA-LARGE GAUSSIAN GRAPHICAL MODELS By Yingying Fan and Jinchi Lv University of Southern Caifornia This Suppementary Materia
ISEE 1 SUPPLEMENTARY MATERIAL TO INNOVATED SCALABLE EFFICIENT ESTIMATION IN ULTRA-LARGE GAUSSIAN GRAPHICAL MODELS By Yingying Fan and Jinchi Lv University of Southern Caifornia This Suppementary Materia
A Comparison Study of the Test for Right Censored and Grouped Data
 Communications for Statistica Appications and Methods 2015, Vo. 22, No. 4, 313 320 DOI: http://dx.doi.org/10.5351/csam.2015.22.4.313 Print ISSN 2287-7843 / Onine ISSN 2383-4757 A Comparison Study of the
Communications for Statistica Appications and Methods 2015, Vo. 22, No. 4, 313 320 DOI: http://dx.doi.org/10.5351/csam.2015.22.4.313 Print ISSN 2287-7843 / Onine ISSN 2383-4757 A Comparison Study of the
Lecture Note 3: Stationary Iterative Methods
 MATH 5330: Computationa Methods of Linear Agebra Lecture Note 3: Stationary Iterative Methods Xianyi Zeng Department of Mathematica Sciences, UTEP Stationary Iterative Methods The Gaussian eimination (or
MATH 5330: Computationa Methods of Linear Agebra Lecture Note 3: Stationary Iterative Methods Xianyi Zeng Department of Mathematica Sciences, UTEP Stationary Iterative Methods The Gaussian eimination (or
On the evaluation of saving-consumption plans
 On the evauation of saving-consumption pans Steven Vanduffe Jan Dhaene Marc Goovaerts Juy 13, 2004 Abstract Knowedge of the distribution function of the stochasticay compounded vaue of a series of future
On the evauation of saving-consumption pans Steven Vanduffe Jan Dhaene Marc Goovaerts Juy 13, 2004 Abstract Knowedge of the distribution function of the stochasticay compounded vaue of a series of future
Efficiently Generating Random Bits from Finite State Markov Chains
 1 Efficienty Generating Random Bits from Finite State Markov Chains Hongchao Zhou and Jehoshua Bruck, Feow, IEEE Abstract The probem of random number generation from an uncorreated random source (of unknown
1 Efficienty Generating Random Bits from Finite State Markov Chains Hongchao Zhou and Jehoshua Bruck, Feow, IEEE Abstract The probem of random number generation from an uncorreated random source (of unknown
General Certificate of Education Advanced Level Examination June 2010
 Genera Certificate of Education Advanced Leve Examination June 2010 Human Bioogy HBI6T/Q10/task Unit 6T A2 Investigative Skis Assignment Task Sheet The effect of using one or two eyes on the perception
Genera Certificate of Education Advanced Leve Examination June 2010 Human Bioogy HBI6T/Q10/task Unit 6T A2 Investigative Skis Assignment Task Sheet The effect of using one or two eyes on the perception
Separation of Variables and a Spherical Shell with Surface Charge
 Separation of Variabes and a Spherica She with Surface Charge In cass we worked out the eectrostatic potentia due to a spherica she of radius R with a surface charge density σθ = σ cos θ. This cacuation
Separation of Variabes and a Spherica She with Surface Charge In cass we worked out the eectrostatic potentia due to a spherica she of radius R with a surface charge density σθ = σ cos θ. This cacuation
Statistics for Applications. Chapter 7: Regression 1/43
 Statistics for Appications Chapter 7: Regression 1/43 Heuristics of the inear regression (1) Consider a coud of i.i.d. random points (X i,y i ),i =1,...,n : 2/43 Heuristics of the inear regression (2)
Statistics for Appications Chapter 7: Regression 1/43 Heuristics of the inear regression (1) Consider a coud of i.i.d. random points (X i,y i ),i =1,...,n : 2/43 Heuristics of the inear regression (2)
Data Mining Technology for Failure Prognostic of Avionics
 IEEE Transactions on Aerospace and Eectronic Systems. Voume 38, #, pp.388-403, 00. Data Mining Technoogy for Faiure Prognostic of Avionics V.A. Skormin, Binghamton University, Binghamton, NY, 1390, USA
IEEE Transactions on Aerospace and Eectronic Systems. Voume 38, #, pp.388-403, 00. Data Mining Technoogy for Faiure Prognostic of Avionics V.A. Skormin, Binghamton University, Binghamton, NY, 1390, USA
<C 2 2. λ 2 l. λ 1 l 1 < C 1
 Teecommunication Network Contro and Management (EE E694) Prof. A. A. Lazar Notes for the ecture of 7/Feb/95 by Huayan Wang (this document was ast LaT E X-ed on May 9,995) Queueing Primer for Muticass Optima
Teecommunication Network Contro and Management (EE E694) Prof. A. A. Lazar Notes for the ecture of 7/Feb/95 by Huayan Wang (this document was ast LaT E X-ed on May 9,995) Queueing Primer for Muticass Optima
6.434J/16.391J Statistics for Engineers and Scientists May 4 MIT, Spring 2006 Handout #17. Solution 7
 6.434J/16.391J Statistics for Engineers and Scientists May 4 MIT, Spring 2006 Handout #17 Soution 7 Probem 1: Generating Random Variabes Each part of this probem requires impementation in MATLAB. For the
6.434J/16.391J Statistics for Engineers and Scientists May 4 MIT, Spring 2006 Handout #17 Soution 7 Probem 1: Generating Random Variabes Each part of this probem requires impementation in MATLAB. For the
II. PROBLEM. A. Description. For the space of audio signals
 CS229 - Fina Report Speech Recording based Language Recognition (Natura Language) Leopod Cambier - cambier; Matan Leibovich - matane; Cindy Orozco Bohorquez - orozcocc ABSTRACT We construct a rea time
CS229 - Fina Report Speech Recording based Language Recognition (Natura Language) Leopod Cambier - cambier; Matan Leibovich - matane; Cindy Orozco Bohorquez - orozcocc ABSTRACT We construct a rea time
Determining The Degree of Generalization Using An Incremental Learning Algorithm
 Determining The Degree of Generaization Using An Incrementa Learning Agorithm Pabo Zegers Facutad de Ingeniería, Universidad de os Andes San Caros de Apoquindo 22, Las Condes, Santiago, Chie pzegers@uandes.c
Determining The Degree of Generaization Using An Incrementa Learning Agorithm Pabo Zegers Facutad de Ingeniería, Universidad de os Andes San Caros de Apoquindo 22, Las Condes, Santiago, Chie pzegers@uandes.c
More Scattering: the Partial Wave Expansion
 More Scattering: the Partia Wave Expansion Michae Fower /7/8 Pane Waves and Partia Waves We are considering the soution to Schrödinger s equation for scattering of an incoming pane wave in the z-direction
More Scattering: the Partia Wave Expansion Michae Fower /7/8 Pane Waves and Partia Waves We are considering the soution to Schrödinger s equation for scattering of an incoming pane wave in the z-direction
T.C. Banwell, S. Galli. {bct, Telcordia Technologies, Inc., 445 South Street, Morristown, NJ 07960, USA
 ON THE SYMMETRY OF THE POWER INE CHANNE T.C. Banwe, S. Gai {bct, sgai}@research.tecordia.com Tecordia Technoogies, Inc., 445 South Street, Morristown, NJ 07960, USA Abstract The indoor power ine network
ON THE SYMMETRY OF THE POWER INE CHANNE T.C. Banwe, S. Gai {bct, sgai}@research.tecordia.com Tecordia Technoogies, Inc., 445 South Street, Morristown, NJ 07960, USA Abstract The indoor power ine network
Manipulation in Financial Markets and the Implications for Debt Financing
 Manipuation in Financia Markets and the Impications for Debt Financing Leonid Spesivtsev This paper studies the situation when the firm is in financia distress and faces bankruptcy or debt restructuring.
Manipuation in Financia Markets and the Impications for Debt Financing Leonid Spesivtsev This paper studies the situation when the firm is in financia distress and faces bankruptcy or debt restructuring.
Optimal Control of Assembly Systems with Multiple Stages and Multiple Demand Classes 1
 Optima Contro of Assemby Systems with Mutipe Stages and Mutipe Demand Casses Saif Benjaafar Mohsen EHafsi 2 Chung-Yee Lee 3 Weihua Zhou 3 Industria & Systems Engineering, Department of Mechanica Engineering,
Optima Contro of Assemby Systems with Mutipe Stages and Mutipe Demand Casses Saif Benjaafar Mohsen EHafsi 2 Chung-Yee Lee 3 Weihua Zhou 3 Industria & Systems Engineering, Department of Mechanica Engineering,
Efficient Generation of Random Bits from Finite State Markov Chains
 Efficient Generation of Random Bits from Finite State Markov Chains Hongchao Zhou and Jehoshua Bruck, Feow, IEEE Abstract The probem of random number generation from an uncorreated random source (of unknown
Efficient Generation of Random Bits from Finite State Markov Chains Hongchao Zhou and Jehoshua Bruck, Feow, IEEE Abstract The probem of random number generation from an uncorreated random source (of unknown
Rate-Distortion Theory of Finite Point Processes
 Rate-Distortion Theory of Finite Point Processes Günther Koiander, Dominic Schuhmacher, and Franz Hawatsch, Feow, IEEE Abstract We study the compression of data in the case where the usefu information
Rate-Distortion Theory of Finite Point Processes Günther Koiander, Dominic Schuhmacher, and Franz Hawatsch, Feow, IEEE Abstract We study the compression of data in the case where the usefu information
c 2016 Georgios Rovatsos
 c 2016 Georgios Rovatsos QUICKEST CHANGE DETECTION WITH APPLICATIONS TO LINE OUTAGE DETECTION BY GEORGIOS ROVATSOS THESIS Submitted in partia fufiment of the requirements for the degree of Master of Science
c 2016 Georgios Rovatsos QUICKEST CHANGE DETECTION WITH APPLICATIONS TO LINE OUTAGE DETECTION BY GEORGIOS ROVATSOS THESIS Submitted in partia fufiment of the requirements for the degree of Master of Science
Testing for the Existence of Clusters
 Testing for the Existence of Custers Caudio Fuentes and George Casea University of Forida November 13, 2008 Abstract The detection and determination of custers has been of specia interest, among researchers
Testing for the Existence of Custers Caudio Fuentes and George Casea University of Forida November 13, 2008 Abstract The detection and determination of custers has been of specia interest, among researchers
Approximated MLC shape matrix decomposition with interleaf collision constraint
 Approximated MLC shape matrix decomposition with intereaf coision constraint Thomas Kainowski Antje Kiese Abstract Shape matrix decomposition is a subprobem in radiation therapy panning. A given fuence
Approximated MLC shape matrix decomposition with intereaf coision constraint Thomas Kainowski Antje Kiese Abstract Shape matrix decomposition is a subprobem in radiation therapy panning. A given fuence
ASummaryofGaussianProcesses Coryn A.L. Bailer-Jones
 ASummaryofGaussianProcesses Coryn A.L. Baier-Jones Cavendish Laboratory University of Cambridge caj@mrao.cam.ac.uk Introduction A genera prediction probem can be posed as foows. We consider that the variabe
ASummaryofGaussianProcesses Coryn A.L. Baier-Jones Cavendish Laboratory University of Cambridge caj@mrao.cam.ac.uk Introduction A genera prediction probem can be posed as foows. We consider that the variabe
Statistical Learning Theory: A Primer
 Internationa Journa of Computer Vision 38(), 9 3, 2000 c 2000 uwer Academic Pubishers. Manufactured in The Netherands. Statistica Learning Theory: A Primer THEODOROS EVGENIOU, MASSIMILIANO PONTIL AND TOMASO
Internationa Journa of Computer Vision 38(), 9 3, 2000 c 2000 uwer Academic Pubishers. Manufactured in The Netherands. Statistica Learning Theory: A Primer THEODOROS EVGENIOU, MASSIMILIANO PONTIL AND TOMASO
A simple reliability block diagram method for safety integrity verification
 Reiabiity Engineering and System Safety 92 (2007) 1267 1273 www.esevier.com/ocate/ress A simpe reiabiity bock diagram method for safety integrity verification Haitao Guo, Xianhui Yang epartment of Automation,
Reiabiity Engineering and System Safety 92 (2007) 1267 1273 www.esevier.com/ocate/ress A simpe reiabiity bock diagram method for safety integrity verification Haitao Guo, Xianhui Yang epartment of Automation,
Automobile Prices in Market Equilibrium. Berry, Pakes and Levinsohn
 Automobie Prices in Market Equiibrium Berry, Pakes and Levinsohn Empirica Anaysis of demand and suppy in a differentiated products market: equiibrium in the U.S. automobie market. Oigopoistic Differentiated
Automobie Prices in Market Equiibrium Berry, Pakes and Levinsohn Empirica Anaysis of demand and suppy in a differentiated products market: equiibrium in the U.S. automobie market. Oigopoistic Differentiated
Cryptanalysis of PKP: A New Approach
 Cryptanaysis of PKP: A New Approach Éiane Jaumes and Antoine Joux DCSSI 18, rue du Dr. Zamenhoff F-92131 Issy-es-Mx Cedex France eiane.jaumes@wanadoo.fr Antoine.Joux@ens.fr Abstract. Quite recenty, in
Cryptanaysis of PKP: A New Approach Éiane Jaumes and Antoine Joux DCSSI 18, rue du Dr. Zamenhoff F-92131 Issy-es-Mx Cedex France eiane.jaumes@wanadoo.fr Antoine.Joux@ens.fr Abstract. Quite recenty, in
Partial permutation decoding for MacDonald codes
 Partia permutation decoding for MacDonad codes J.D. Key Department of Mathematics and Appied Mathematics University of the Western Cape 7535 Bevie, South Africa P. Seneviratne Department of Mathematics
Partia permutation decoding for MacDonad codes J.D. Key Department of Mathematics and Appied Mathematics University of the Western Cape 7535 Bevie, South Africa P. Seneviratne Department of Mathematics
Online Load Balancing on Related Machines
 Onine Load Baancing on Reated Machines ABSTRACT Sungjin Im University of Caifornia at Merced Merced, CA, USA sim3@ucmerced.edu Debmaya Panigrahi Duke University Durham, NC, USA debmaya@cs.duke.edu We give
Onine Load Baancing on Reated Machines ABSTRACT Sungjin Im University of Caifornia at Merced Merced, CA, USA sim3@ucmerced.edu Debmaya Panigrahi Duke University Durham, NC, USA debmaya@cs.duke.edu We give
Age of Information: The Gamma Awakening
 Age of Information: The Gamma Awakening Eie Najm and Rajai Nasser LTHI, EPFL, Lausanne, Switzerand Emai: {eie.najm, rajai.nasser}@epf.ch arxiv:604.086v [cs.it] 5 Apr 06 Abstract Status update systems is
Age of Information: The Gamma Awakening Eie Najm and Rajai Nasser LTHI, EPFL, Lausanne, Switzerand Emai: {eie.najm, rajai.nasser}@epf.ch arxiv:604.086v [cs.it] 5 Apr 06 Abstract Status update systems is
VALIDATED CONTINUATION FOR EQUILIBRIA OF PDES
 VALIDATED CONTINUATION FOR EQUILIBRIA OF PDES SARAH DAY, JEAN-PHILIPPE LESSARD, AND KONSTANTIN MISCHAIKOW Abstract. One of the most efficient methods for determining the equiibria of a continuous parameterized
VALIDATED CONTINUATION FOR EQUILIBRIA OF PDES SARAH DAY, JEAN-PHILIPPE LESSARD, AND KONSTANTIN MISCHAIKOW Abstract. One of the most efficient methods for determining the equiibria of a continuous parameterized
Componentwise Determination of the Interval Hull Solution for Linear Interval Parameter Systems
 Componentwise Determination of the Interva Hu Soution for Linear Interva Parameter Systems L. V. Koev Dept. of Theoretica Eectrotechnics, Facuty of Automatics, Technica University of Sofia, 1000 Sofia,
Componentwise Determination of the Interva Hu Soution for Linear Interva Parameter Systems L. V. Koev Dept. of Theoretica Eectrotechnics, Facuty of Automatics, Technica University of Sofia, 1000 Sofia,
Problem set 6 The Perron Frobenius theorem.
 Probem set 6 The Perron Frobenius theorem. Math 22a4 Oct 2 204, Due Oct.28 In a future probem set I want to discuss some criteria which aow us to concude that that the ground state of a sef-adjoint operator
Probem set 6 The Perron Frobenius theorem. Math 22a4 Oct 2 204, Due Oct.28 In a future probem set I want to discuss some criteria which aow us to concude that that the ground state of a sef-adjoint operator
In-plane shear stiffness of bare steel deck through shell finite element models. G. Bian, B.W. Schafer. June 2017
 In-pane shear stiffness of bare stee deck through she finite eement modes G. Bian, B.W. Schafer June 7 COLD-FORMED STEEL RESEARCH CONSORTIUM REPORT SERIES CFSRC R-7- SDII Stee Diaphragm Innovation Initiative
In-pane shear stiffness of bare stee deck through she finite eement modes G. Bian, B.W. Schafer June 7 COLD-FORMED STEEL RESEARCH CONSORTIUM REPORT SERIES CFSRC R-7- SDII Stee Diaphragm Innovation Initiative
A proposed nonparametric mixture density estimation using B-spline functions
 A proposed nonparametric mixture density estimation using B-spine functions Atizez Hadrich a,b, Mourad Zribi a, Afif Masmoudi b a Laboratoire d Informatique Signa et Image de a Côte d Opae (LISIC-EA 4491),
A proposed nonparametric mixture density estimation using B-spine functions Atizez Hadrich a,b, Mourad Zribi a, Afif Masmoudi b a Laboratoire d Informatique Signa et Image de a Côte d Opae (LISIC-EA 4491),
THE REACHABILITY CONES OF ESSENTIALLY NONNEGATIVE MATRICES
 THE REACHABILITY CONES OF ESSENTIALLY NONNEGATIVE MATRICES by Michae Neumann Department of Mathematics, University of Connecticut, Storrs, CT 06269 3009 and Ronad J. Stern Department of Mathematics, Concordia
THE REACHABILITY CONES OF ESSENTIALLY NONNEGATIVE MATRICES by Michae Neumann Department of Mathematics, University of Connecticut, Storrs, CT 06269 3009 and Ronad J. Stern Department of Mathematics, Concordia
Formulas for Angular-Momentum Barrier Factors Version II
 BNL PREPRINT BNL-QGS-06-101 brfactor1.tex Formuas for Anguar-Momentum Barrier Factors Version II S. U. Chung Physics Department, Brookhaven Nationa Laboratory, Upton, NY 11973 March 19, 2015 abstract A
BNL PREPRINT BNL-QGS-06-101 brfactor1.tex Formuas for Anguar-Momentum Barrier Factors Version II S. U. Chung Physics Department, Brookhaven Nationa Laboratory, Upton, NY 11973 March 19, 2015 abstract A
C. Fourier Sine Series Overview
 12 PHILIP D. LOEWEN C. Fourier Sine Series Overview Let some constant > be given. The symboic form of the FSS Eigenvaue probem combines an ordinary differentia equation (ODE) on the interva (, ) with a
12 PHILIP D. LOEWEN C. Fourier Sine Series Overview Let some constant > be given. The symboic form of the FSS Eigenvaue probem combines an ordinary differentia equation (ODE) on the interva (, ) with a
Fast Blind Recognition of Channel Codes
 Fast Bind Recognition of Channe Codes Reza Moosavi and Erik G. Larsson Linköping University Post Print N.B.: When citing this work, cite the origina artice. 213 IEEE. Persona use of this materia is permitted.
Fast Bind Recognition of Channe Codes Reza Moosavi and Erik G. Larsson Linköping University Post Print N.B.: When citing this work, cite the origina artice. 213 IEEE. Persona use of this materia is permitted.
Chemical Kinetics Part 2
 Integrated Rate Laws Chemica Kinetics Part 2 The rate aw we have discussed thus far is the differentia rate aw. Let us consider the very simpe reaction: a A à products The differentia rate reates the rate
Integrated Rate Laws Chemica Kinetics Part 2 The rate aw we have discussed thus far is the differentia rate aw. Let us consider the very simpe reaction: a A à products The differentia rate reates the rate
Discrete Techniques. Chapter Introduction
 Chapter 3 Discrete Techniques 3. Introduction In the previous two chapters we introduced Fourier transforms of continuous functions of the periodic and non-periodic (finite energy) type, as we as various
Chapter 3 Discrete Techniques 3. Introduction In the previous two chapters we introduced Fourier transforms of continuous functions of the periodic and non-periodic (finite energy) type, as we as various
Emmanuel Abbe Colin Sandon
 Detection in the stochastic bock mode with mutipe custers: proof of the achievabiity conjectures, acycic BP, and the information-computation gap Emmanue Abbe Coin Sandon Abstract In a paper that initiated
Detection in the stochastic bock mode with mutipe custers: proof of the achievabiity conjectures, acycic BP, and the information-computation gap Emmanue Abbe Coin Sandon Abstract In a paper that initiated
A CLUSTERING LAW FOR SOME DISCRETE ORDER STATISTICS
 J App Prob 40, 226 241 (2003) Printed in Israe Appied Probabiity Trust 2003 A CLUSTERING LAW FOR SOME DISCRETE ORDER STATISTICS SUNDER SETHURAMAN, Iowa State University Abstract Let X 1,X 2,,X n be a sequence
J App Prob 40, 226 241 (2003) Printed in Israe Appied Probabiity Trust 2003 A CLUSTERING LAW FOR SOME DISCRETE ORDER STATISTICS SUNDER SETHURAMAN, Iowa State University Abstract Let X 1,X 2,,X n be a sequence
Process Capability Proposal. with Polynomial Profile
 Contemporary Engineering Sciences, Vo. 11, 2018, no. 85, 4227-4236 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/ces.2018.88467 Process Capabiity Proposa with Poynomia Profie Roberto José Herrera
Contemporary Engineering Sciences, Vo. 11, 2018, no. 85, 4227-4236 HIKARI Ltd, www.m-hikari.com https://doi.org/10.12988/ces.2018.88467 Process Capabiity Proposa with Poynomia Profie Roberto José Herrera
New Efficiency Results for Makespan Cost Sharing
 New Efficiency Resuts for Makespan Cost Sharing Yvonne Beischwitz a, Forian Schoppmann a, a University of Paderborn, Department of Computer Science Fürstenaee, 3302 Paderborn, Germany Abstract In the context
New Efficiency Resuts for Makespan Cost Sharing Yvonne Beischwitz a, Forian Schoppmann a, a University of Paderborn, Department of Computer Science Fürstenaee, 3302 Paderborn, Germany Abstract In the context
MONOCHROMATIC LOOSE PATHS IN MULTICOLORED k-uniform CLIQUES
 MONOCHROMATIC LOOSE PATHS IN MULTICOLORED k-uniform CLIQUES ANDRZEJ DUDEK AND ANDRZEJ RUCIŃSKI Abstract. For positive integers k and, a k-uniform hypergraph is caed a oose path of ength, and denoted by
MONOCHROMATIC LOOSE PATHS IN MULTICOLORED k-uniform CLIQUES ANDRZEJ DUDEK AND ANDRZEJ RUCIŃSKI Abstract. For positive integers k and, a k-uniform hypergraph is caed a oose path of ength, and denoted by
An Algorithm for Pruning Redundant Modules in Min-Max Modular Network
 An Agorithm for Pruning Redundant Modues in Min-Max Moduar Network Hui-Cheng Lian and Bao-Liang Lu Department of Computer Science and Engineering, Shanghai Jiao Tong University 1954 Hua Shan Rd., Shanghai
An Agorithm for Pruning Redundant Modues in Min-Max Moduar Network Hui-Cheng Lian and Bao-Liang Lu Department of Computer Science and Engineering, Shanghai Jiao Tong University 1954 Hua Shan Rd., Shanghai
$, (2.1) n="# #. (2.2)
 Chapter. Eectrostatic II Notes: Most of the materia presented in this chapter is taken from Jackson, Chap.,, and 4, and Di Bartoo, Chap... Mathematica Considerations.. The Fourier series and the Fourier
Chapter. Eectrostatic II Notes: Most of the materia presented in this chapter is taken from Jackson, Chap.,, and 4, and Di Bartoo, Chap... Mathematica Considerations.. The Fourier series and the Fourier
Mat 1501 lecture notes, penultimate installment
 Mat 1501 ecture notes, penutimate instament 1. bounded variation: functions of a singe variabe optiona) I beieve that we wi not actuay use the materia in this section the point is mainy to motivate the
Mat 1501 ecture notes, penutimate instament 1. bounded variation: functions of a singe variabe optiona) I beieve that we wi not actuay use the materia in this section the point is mainy to motivate the
Approximated MLC shape matrix decomposition with interleaf collision constraint
 Agorithmic Operations Research Vo.4 (29) 49 57 Approximated MLC shape matrix decomposition with intereaf coision constraint Antje Kiese and Thomas Kainowski Institut für Mathematik, Universität Rostock,
Agorithmic Operations Research Vo.4 (29) 49 57 Approximated MLC shape matrix decomposition with intereaf coision constraint Antje Kiese and Thomas Kainowski Institut für Mathematik, Universität Rostock,
MATH 172: MOTIVATION FOR FOURIER SERIES: SEPARATION OF VARIABLES
 MATH 172: MOTIVATION FOR FOURIER SERIES: SEPARATION OF VARIABLES Separation of variabes is a method to sove certain PDEs which have a warped product structure. First, on R n, a inear PDE of order m is
MATH 172: MOTIVATION FOR FOURIER SERIES: SEPARATION OF VARIABLES Separation of variabes is a method to sove certain PDEs which have a warped product structure. First, on R n, a inear PDE of order m is
Limits on Support Recovery with Probabilistic Models: An Information-Theoretic Framework
 Limits on Support Recovery with Probabiistic Modes: An Information-Theoretic Framewor Jonathan Scarett and Voan Cevher arxiv:5.744v3 cs.it 3 Aug 6 Abstract The support recovery probem consists of determining
Limits on Support Recovery with Probabiistic Modes: An Information-Theoretic Framewor Jonathan Scarett and Voan Cevher arxiv:5.744v3 cs.it 3 Aug 6 Abstract The support recovery probem consists of determining
Two-Stage Least Squares as Minimum Distance
 Two-Stage Least Squares as Minimum Distance Frank Windmeijer Discussion Paper 17 / 683 7 June 2017 Department of Economics University of Bristo Priory Road Compex Bristo BS8 1TU United Kingdom Two-Stage
Two-Stage Least Squares as Minimum Distance Frank Windmeijer Discussion Paper 17 / 683 7 June 2017 Department of Economics University of Bristo Priory Road Compex Bristo BS8 1TU United Kingdom Two-Stage
Combining reaction kinetics to the multi-phase Gibbs energy calculation
 7 th European Symposium on Computer Aided Process Engineering ESCAPE7 V. Pesu and P.S. Agachi (Editors) 2007 Esevier B.V. A rights reserved. Combining reaction inetics to the muti-phase Gibbs energy cacuation
7 th European Symposium on Computer Aided Process Engineering ESCAPE7 V. Pesu and P.S. Agachi (Editors) 2007 Esevier B.V. A rights reserved. Combining reaction inetics to the muti-phase Gibbs energy cacuation
IE 361 Exam 1. b) Give *&% confidence limits for the bias of this viscometer. (No need to simplify.)
 October 9, 00 IE 6 Exam Prof. Vardeman. The viscosity of paint is measured with a "viscometer" in units of "Krebs." First, a standard iquid of "known" viscosity *# Krebs is tested with a company viscometer
October 9, 00 IE 6 Exam Prof. Vardeman. The viscosity of paint is measured with a "viscometer" in units of "Krebs." First, a standard iquid of "known" viscosity *# Krebs is tested with a company viscometer
Discrete Techniques. Chapter Introduction
 Chapter 3 Discrete Techniques 3. Introduction In the previous two chapters we introduced Fourier transforms of continuous functions of the periodic and non-periodic (finite energy) type, we as various
Chapter 3 Discrete Techniques 3. Introduction In the previous two chapters we introduced Fourier transforms of continuous functions of the periodic and non-periodic (finite energy) type, we as various
AALBORG UNIVERSITY. The distribution of communication cost for a mobile service scenario. Jesper Møller and Man Lung Yiu. R June 2009
 AALBORG UNIVERSITY The distribution of communication cost for a mobie service scenario by Jesper Møer and Man Lung Yiu R-29-11 June 29 Department of Mathematica Sciences Aaborg University Fredrik Bajers
AALBORG UNIVERSITY The distribution of communication cost for a mobie service scenario by Jesper Møer and Man Lung Yiu R-29-11 June 29 Department of Mathematica Sciences Aaborg University Fredrik Bajers
STABLE GRAPHS BENJAMIN OYE
 STABLE GRAPHS BENJAMIN OYE Abstract. In Reguarity Lemmas for Stabe Graphs [1] Maiaris and Sheah appy toos from mode theory to obtain stronger forms of Ramsey's theorem and Szemeredi's reguarity emma for
STABLE GRAPHS BENJAMIN OYE Abstract. In Reguarity Lemmas for Stabe Graphs [1] Maiaris and Sheah appy toos from mode theory to obtain stronger forms of Ramsey's theorem and Szemeredi's reguarity emma for
8 Digifl'.11 Cth:uits and devices
 8 Digif'. Cth:uits and devices 8. Introduction In anaog eectronics, votage is a continuous variabe. This is usefu because most physica quantities we encounter are continuous: sound eves, ight intensity,
8 Digif'. Cth:uits and devices 8. Introduction In anaog eectronics, votage is a continuous variabe. This is usefu because most physica quantities we encounter are continuous: sound eves, ight intensity,
On Non-Optimally Expanding Sets in Grassmann Graphs
 ectronic Cooquium on Computationa Compexity, Report No. 94 (07) On Non-Optimay xpanding Sets in Grassmann Graphs Irit Dinur Subhash Khot Guy Kinder Dor Minzer Mui Safra Abstract The paper investigates
ectronic Cooquium on Computationa Compexity, Report No. 94 (07) On Non-Optimay xpanding Sets in Grassmann Graphs Irit Dinur Subhash Khot Guy Kinder Dor Minzer Mui Safra Abstract The paper investigates
Turbo Codes. Coding and Communication Laboratory. Dept. of Electrical Engineering, National Chung Hsing University
 Turbo Codes Coding and Communication Laboratory Dept. of Eectrica Engineering, Nationa Chung Hsing University Turbo codes 1 Chapter 12: Turbo Codes 1. Introduction 2. Turbo code encoder 3. Design of intereaver
Turbo Codes Coding and Communication Laboratory Dept. of Eectrica Engineering, Nationa Chung Hsing University Turbo codes 1 Chapter 12: Turbo Codes 1. Introduction 2. Turbo code encoder 3. Design of intereaver
APPENDIX C FLEXING OF LENGTH BARS
 Fexing of ength bars 83 APPENDIX C FLEXING OF LENGTH BARS C.1 FLEXING OF A LENGTH BAR DUE TO ITS OWN WEIGHT Any object ying in a horizonta pane wi sag under its own weight uness it is infinitey stiff or
Fexing of ength bars 83 APPENDIX C FLEXING OF LENGTH BARS C.1 FLEXING OF A LENGTH BAR DUE TO ITS OWN WEIGHT Any object ying in a horizonta pane wi sag under its own weight uness it is infinitey stiff or
High Spectral Resolution Infrared Radiance Modeling Using Optimal Spectral Sampling (OSS) Method
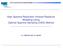 High Spectra Resoution Infrared Radiance Modeing Using Optima Spectra Samping (OSS) Method J.-L. Moncet and G. Uymin Background Optima Spectra Samping (OSS) method is a fast and accurate monochromatic
High Spectra Resoution Infrared Radiance Modeing Using Optima Spectra Samping (OSS) Method J.-L. Moncet and G. Uymin Background Optima Spectra Samping (OSS) method is a fast and accurate monochromatic
Iterative Decoding Performance Bounds for LDPC Codes on Noisy Channels
 Iterative Decoding Performance Bounds for LDPC Codes on Noisy Channes arxiv:cs/060700v1 [cs.it] 6 Ju 006 Chun-Hao Hsu and Achieas Anastasopouos Eectrica Engineering and Computer Science Department University
Iterative Decoding Performance Bounds for LDPC Codes on Noisy Channes arxiv:cs/060700v1 [cs.it] 6 Ju 006 Chun-Hao Hsu and Achieas Anastasopouos Eectrica Engineering and Computer Science Department University
General Certificate of Education Advanced Level Examination June 2010
 Genera Certificate of Education Advanced Leve Examination June 2010 Human Bioogy HBI6T/P10/task Unit 6T A2 Investigative Skis Assignment Task Sheet The effect of temperature on the rate of photosynthesis
Genera Certificate of Education Advanced Leve Examination June 2010 Human Bioogy HBI6T/P10/task Unit 6T A2 Investigative Skis Assignment Task Sheet The effect of temperature on the rate of photosynthesis
Maximum eigenvalue versus trace tests for the cointegrating rank of a VAR process
 Econometrics Journa (2001), voume 4, pp. 287 310. Maximum eigenvaue versus trace tests for the cointegrating rank of a VAR process HELMUT LÜTKEPOHL, PENTTI SAIKKONEN, AND CARSTEN TRENKLER Institut für
Econometrics Journa (2001), voume 4, pp. 287 310. Maximum eigenvaue versus trace tests for the cointegrating rank of a VAR process HELMUT LÜTKEPOHL, PENTTI SAIKKONEN, AND CARSTEN TRENKLER Institut für
LECTURE NOTES 9 TRACELESS SYMMETRIC TENSOR APPROACH TO LEGENDRE POLYNOMIALS AND SPHERICAL HARMONICS
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Eectromagnetism II October 7, 202 Prof. Aan Guth LECTURE NOTES 9 TRACELESS SYMMETRIC TENSOR APPROACH TO LEGENDRE POLYNOMIALS AND SPHERICAL
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Physics Department Physics 8.07: Eectromagnetism II October 7, 202 Prof. Aan Guth LECTURE NOTES 9 TRACELESS SYMMETRIC TENSOR APPROACH TO LEGENDRE POLYNOMIALS AND SPHERICAL
The distribution of the number of nodes in the relative interior of the typical I-segment in homogeneous planar anisotropic STIT Tessellations
 Comment.Math.Univ.Caroin. 51,3(21) 53 512 53 The distribution of the number of nodes in the reative interior of the typica I-segment in homogeneous panar anisotropic STIT Tesseations Christoph Thäe Abstract.
Comment.Math.Univ.Caroin. 51,3(21) 53 512 53 The distribution of the number of nodes in the reative interior of the typica I-segment in homogeneous panar anisotropic STIT Tesseations Christoph Thäe Abstract.
Stochastic Variational Inference with Gradient Linearization
 Stochastic Variationa Inference with Gradient Linearization Suppementa Materia Tobias Pötz * Anne S Wannenwetsch Stefan Roth Department of Computer Science, TU Darmstadt Preface In this suppementa materia,
Stochastic Variationa Inference with Gradient Linearization Suppementa Materia Tobias Pötz * Anne S Wannenwetsch Stefan Roth Department of Computer Science, TU Darmstadt Preface In this suppementa materia,
