arxiv:math/ v1 [math.mg] 13 Mar 2007
|
|
|
- Gervais Peters
- 5 years ago
- Views:
Transcription
1 arxiv:math/ v1 [math.mg] 13 Mar 2007 NOTES ON THE ROOTS OF STEINER POLYNOMIALS MARTIN HENK AND MARÍA A. HERNÁNDEZ CIFRE Dedicated to Jörg M. Wills on the occasion of his 70th birthday Abstract. We study the location and the size of the roots of Steiner polynomials of convex bodies in the Minkowski relative geometry. Based on a problem of Teissier on the intersection numbers of Cartier divisors of compact algebraic varieties it was conjectured that these roots have certain geometric properties related to the in- and circumradius of the convex body. We show that the roots of 1-tangential bodies fulfill the conjecture, but we also present convex bodies violating each of the conjectured properties. 1. Introduction Let K n be the set of all convex bodies, i.e., compact convex sets, in the n- dimensional Euclidean space R n, and let B n be the n-dimensional unit ball. The subset of K n consisting of all convex bodies with non-empty interior is denoted by K0 n. The volume of a set M Rn, i.e., its n-dimensional Lebesgue measure, is denoted by V(M). For two convex bodies K,E K n and a non-negative real number ρ the volume of K +ρe is a polynomial of degree n in ρ and it can be written as n ( ) n (1.1) V(K +ρe) = W i (K;E)ρ i. i i=0 This polynomial is called the Minkowski-Steiner polynomial or the relative Steiner polynomial of K. The coefficients W i (K;E) are called the relative quermassintegrals of K, and they are just a special case of the more general defined mixed volumes for which we refer to [12, s. 5.1]. In particular, we have W 0 (K;E) = V(K), W n (K;E) = V(E) and W i (K;E) = W n i (E;K). If E = B n the polynomial (1.1) becomes the classical Steiner polynomial or Steiner formula [13], and W i (K;B n ), for short denoted by W i (K), is the classical i-th quermassintegral of K. In this case, nw 1 (K) is the surface area of K, W n (K) = V(B n ) = κ n is the n-dimensional volume of B n and (2/κ n )W n 1 (K) is the mean width of K [12, p. 42] Mathematics Subject Classification. Primary 52A20, 52A39; Secondary 30C15. Key words and phrases. Steiner polynomial, Teissier s problem, tangential bodies, circumradius, inradius. Second author is supported in part by Dirección General de Investigación (MEC) MTM C04-02 and by Fundación Séneca (C.A.R.M.) 00625/PI/04. 1
2 2 MARTIN HENK AND MARÍA A. HERNÁNDEZ CIFRE The relative inradius r(k;e) and relative circumradius R(K;E) of K with respect to E are defined, respectively, by r(k;e) = max{r : x R n with x+re K}, R(K;E) = min{r : x R n with K x+re}. Notice that it always holds (1.2) r(k;e)r(e;k) = 1. In the planar case the inradius, circumradius and the quermassintegrals are related by the well-known Bonnesen inequality (1.3) W 1 (K;E) 2 W 0 (K;E)W 2 (K;E) W 2(K;E) 2 ( 2. R(K;E) r(k;e)) 4 Bonnesen [3] proved this result for E = B 2, the proof of the general case is due to Blaschke [2, pp ]. This inequality sharpens (in the plane) the Aleksandrov-Fenchel and the isoperimetric inequalities and there is no known generalization of it to higher dimensions. In fact(1.3) is an immediate consequence of the following stronger relations [2, pp ] (see also [6]) (1.4) W 0 (K;E)+2W 1 (K;E)ρ+W 2 (K;E)ρ 2 0 if R(K;E) ρ r(k;e). The left hand side is just the relative Steiner polynomial (1.1), and so (1.4) says that the (relative) Steiner polynomial n ( ) n f(k,e,s) = W i (K;E)s i, i i=0 regarded as a formal polynomial in a complex variable s C, has in the case n = 2 two real (negative) roots, one root less than or equal R(K;E) and the other root not less than r(k;e). In [14] Teissier studied Bonnesen-Type inequalities in Algebraic Geometry, more precisely, intersection numbers of Cartier divisors of n-dimensional compact algebraic varieties. These intersection numbers behave similarly as the (relative) quermassintegrals and, in particular, in the case n = 2 they satisfy an inequality as (1.4) with suitable defined in- and circumradius. Teissier raised the problem to find extensions of these two dimensional properties to higher dimensions (see also [9, p. 103]). In view of the properties derived from (1.4) in the planar case, in [10] and [11, p. 65] the following conjecture was posed which we formulate in terms of the relative Steiner polynomial: Conjecture 1.1. Let K,E K n. If a 1 a n are the real parts of the roots of f(k,e,s), then a 1 R(K;E) r(k;e) a n 0. As mentioned before, (1.4) implies the conjecture in dimension 2. A first systematic study of the roots of the classical Steiner polynomial in the 3- dimensional case as well as their relations to the so called Blaschke diagram
3 NOTES ON THE ROOTS OF STEINER POLYNOMIALS 3 can be found in [7]. There it is also shown that the conjecture is correct for some special 3-dimensional convex bodies. But no further progress has been made on it; only some results have been obtained by Wills [15] for a closely related polynomial, the so called Wills functional. In the following we will call the conjectured property that all real parts of the roots of f(k,e,s) are non-positive the negativity property of the roots, and the conjectured bounds related to r(k;e) and R(K;E) will be referred to as the inradius and circumradius bound, respectively. In Section 3 we study the above conjecture for the class of p-tangential bodies; for a definition see also Section 3. Among others we show that n-dimensional 1-tangential bodies, the so called cap-bodies, verify the conjecture. Theorem 1.1. Let K K0 n be a 1-tangential body of E Kn 0. Then the roots of f(k,e,s) satisfy Conjecture 1.1. If we move, however, to 2-tangential bodies then we loose, in general, the negativity property of the real parts of the roots. Theorem 1.2. There exists a 2-tangential body K K 15 such that f(k,b 15,s) has a root with positive real part. We remark that the minimum dimension of a convex body K such that f(k,e,s) violates the negativity property of the roots is at least 6. Based on the well-known inequalities (1.5) W i (K;E) 2 W i 1 (K;E)W i+1 (K;E) 0, 1 i n 1, which are particular cases of the Aleksandrov-Fenchel inequality(see e.g. [12, s. 6.3]), and on the Routh-Hurwitz criterion (see e.g. [8, p. 181]) one can check that f(k,e,s) is a Hurwitz polynomial for n 5, i.e., all its roots lie in the left half plane (see also [14, p. 103]). In Section 4 we construct a 3-dimensional convex body violating the conjectured circumradius bound, more precisely, Theorem 1.3. There exists K K0 3 such that all the real parts of the roots of f(k,b 3,s) are greater than R(K;B 3 ). Since W i (K,E) = W n i (E,K) we have f(k,e,s) = s n f(e,k,1/s). Hence, and on account of (1.2) it is not surprising that the body K of the theorem above leads also to a counterexample for the inradius bound. Corollary 1.1. There exists K K0 3 such that all the real parts of the roots of f(b 3,K,s) are less than r(b 3 ;K). Before giving the proofs of the theorems above we study in Section 2 the size of the roots of the relative Steiner polynomial f(k,e,s). We prove upper and lower bounds for them in terms of the circumradius and the inradius.
4 4 MARTIN HENK AND MARÍA A. HERNÁNDEZ CIFRE 2. Bounds for the roots of the Steiner polynomial In the following we will use the inequalities (2.1) r(k;e)w i+1 (K;E) W i (K;E) R(K;E)W i+1 (K;E), for i {0,...,n 1}. Since, up to translations, r(k;e)e K and K R(K; E)E these inequalities are a direct consequence of the monotonicity of the mixed volumes (cf. e.g. [12, p. 277]). Furthermore, for a complex number s we denote by Re(s) its real part. Proposition 2.1. Let K K n, E K n 0, and let γ i, i = 1,...,n, be the roots of the Steiner polynomial f(k,e,s). i) If dimk = m, m 1, the non-zero roots γ i are bounded by n m+1 m W n m (K;E) W n m+1 (K;E) γ i n W n 1(K;E) W n (K;E). The upper bound is best possible. In particular, we have r(k;e)/n γ i nr(k;e). ii) Re(γ1 ) + + Re(γn ) nr(k;e). iii) If Re(γ i ) 0 for all i = 1,...,n, then Re(γ1 ) + + Re(γn ) nr(k;e). Proof. Since dimk = m we have W i (K;E) = 0 for i = 0,...,n m 1 and W i (K;E) > 0 for i = n m,...,n (see [12, p. 277]). Hence the Steiner polynomial of K is m ( f(k,e,s) = s n m i=0 n n m+i ) W n m+i (K;E)s i = s n m h m (K,E,s) andthenon-zeroroots of f(k,e,s) aretheroots of h m (K,E,s). Itis known that the roots of a polynomial f(s) = a 0 +a 1 s+ +a m s m with positive real coefficients a j lie in the ring ρ 1 s ρ 2, where ρ 1 = min{a j /a j+1 } and ρ 2 = max{a j /a j+1 }, for j = 0,1,...,m 1, see e.g. [8, p. 137]. Hence in the case of h m (K,E,s) we just have to find the minimum and maximum of ( n) j Wj (K;E)/ (( n j+1) Wj+1 (K;E) ), j = n m,...,n 1. By (1.5) we see that W j (K;E)/W j+1 (K;E) is increasing in j, and since ( n) ( j / n j+1) is also increasing we get n m+1 m W n m (K;E) W n m+1 (K;E) ( n ) j Wj (K;E) ( n ) j+1 Wj+1 (K;E) nw n 1(K;E) W n (K;E), for j = n m,...,n 1, which shows the inequalities in i). The bounds in i) in terms of the inradius and the circumradius follow immediately with (2.1). Notice that if m < n then r(k;e) = 0. Hence the only non-trivial lower bound is obtained when m = n. By i) we see that the only non-zero root of the Steiner polynomial of a line segment K, i.e., dimk = 1, is given by γ = nw n 1 (K;E)/W n (K;E).
5 NOTES ON THE ROOTS OF STEINER POLYNOMIALS 5 This shows that the upper bound in i) is best possible for any choice of the body E K n 0. Since f(k,e,s) = W n (K;E) n i=1 (s γ i) we find that Together with (2.1) we get γ 1 + +γ n = n W n 1(K;E) W n (K;E). nr(k;e) γ 1 + +γ n = Re(γ1 )+ +Re(γ n ) Re(γ1 ) + + Re(γn ), which shows ii). Finally, if all the roots have negative real part (as conjectured), we even have Re(γ 1 ) + + Re(γ n ) = Re(γ 1 )+ +Re(γ n ) and as above we get by (2.1) the upper bound stated in iii). 3. Roots of the Steiner polynomial and tangential bodies A convex body K K n containing the convex body E K n is called a p-tangential body of E, p {0,...,n 1}, if each support plane of K that is not a support plane of E contains only (p 1)-singular points of K [12, p. 76]. Here a boundary point x of K is said to be an r-singular point of K if the dimension of the normal cone in x is at least n r. For further characterizations and properties of p-tangential bodies we refer to [12, Section 2.2]. So a 0-tangential body of E is just the bodye itself and each p-tangential body of E is also a q-tangential body for p < q n 1. A 1-tangential body is usually called cap-body, and it can be seen as the convex hull of E and countably many points such that the line segment joining any pair of those points intersects E. If K is a p-tangential body of E then r(k;e) = 1, and the following theorem gives a characterization of n-dimensional p-tangential bodies in terms of the quermassintegrals (cf. (2.1)). Theorem 3.1 (Favard [5], [12, p. 367]). Let K,E K0 n and p {0,...,n 1}. Then W 0 (K;E) = W 1 (K;E) = = W n p (K;E) if and only if K is a p-tangential body of E. The next proposition shows that n-dimensional p-tangential bodies always satisfy the inradius bound of Conjecture 1.1. Proposition 3.1. Let p {0,...,n 1}, and let K K0 n be a p-tangential body of E K0 n. Then there exists a root γ of f(k,e,s) such that Re(γ) r(k;e). Proof. Let γ i, for 1 i n, be the roots of f(k,e,s). From f(k,e,s) = W n (K;E) n i=1 (s γ i) we get ( 1) n W 0 (K;E) = W n (K;E)γ 1... γ n and n ( 1) n 1 nw 1 (K;E) = W n (K;E) γ j. i=1 j i
6 6 MARTIN HENK AND MARÍA A. HERNÁNDEZ CIFRE By Theorem 3.1 we have W 0 (K;E) = W 1 (K;E) for any p-tangential body, and thus n = n W 1(K;E) W 0 (K;E) = ( ) ( ) 1 1 = Re + +Re. γ 1 γ n γ 1 γ n Therefore, there exists a root γ j, say, such that Re(1/γ j ) 1, and so Re(γ j ) 1 = r(k;e). Remark 3.1. Let γ j with Re(1/γ j ) 1 be the root of the above proof of the polynomial f(k,e,s). Since W i (K;E) = W n i (E;K) and thus f(k,e,s) = s n f(e,k,1/s) we see that 1/γ j is a root of f(e,k,s). By (1.2) we have R(E;K) = 1 and so we get that the polynomial f(e,k,s) satisfies the circumradius bound. Now we come to the proof of Theorem 1.1 and show that 1-tangential bodies (cap-bodies) fulfill the conjecture. We remark that the analogous 3-dimensional result for E = B 3 was already mentioned in [11, p. 65]. Proof of Theorem 1.1. If K K0 n is a cap-body of E Kn 0 Theorem 3.1 asserts that W 0 (K;E) = W i (K;E), for all i = 1,...,n 1, and so we can rewrite the Steiner polynomial in the following way [ n 1 ( ) ] n f(k,e,s) = W 0 (K;E) s i + W n(k;e) i W i=0 0 (K;E) sn [ = W 0 (K;E) (1+s) n ( 1 α(k,e) ) s n], where α(k,e) = W n (K;E)/W 0 (K;E). Observe that 0 < α(k,e) 1 since E K. So in this case all the roots γ k of f(k,e,s) have to satisfy the equation (1/s+1) n = 1 α(k,e) and so we obtain 1 γ k = 1+ n 1 α(k,e) e 2πk n i for k = 0,...,n 1. Hence all the real parts of 1/γ k, and thus of γ k are nonpositive which shows the negativity property of the roots stated in Conjecture 1.1. The inradius bound of the conjecture is guaranteed by Proposition 3.1 and it remains to verify the circumradius bound. The smallest real part among the roots γ k corresponds to k = 0, i.e., it is γ 0 = 1 1 n 1 α(k,e), and we have to show that 1/ ( 1 n 1 α(k,e) ) R(K;E), which is equivalent to (3.1) 1 W ( ) n(k;e) W 0 (K;E) 1 n 1. R(K; E)
7 NOTES ON THE ROOTS OF STEINER POLYNOMIALS 7 In order to prove (3.1) we use the following inequality ( ) n [ (Wn 1 Wn 1 (K;E) n 1 W n (K;E) W 0 (K;E) W 0 (K;E) (K;E) W 0 (K;E) ) 1 n 1 1 R(K; E) obtained in [10, Corollary 22]. Since W n 1 (K;E) = W 0 (K;E) we get immediately (3.1). In contrast to 1-tangential bodies, the roots of Steiner polynomials of 2-tangential bodies do not fulfill all the properties of Conjecture 1.1, more precisely, some of their roots can have a positive real part if the dimension is large enough. Proof of Theorem 1.2. On account of Theorem 3.1 we may write the Steiner polynomial f(k,b n,s) of a 2-tangential body K K0 n of B n as [ n 2 ( ) ] n f(k,b n,s) = W 0 (K) s i +n W n 1(K) i W 0 (K) sn 1 + W n(k) W 0 (K) sn. i=0 We write β(k) = W n 1 (K)/W 0 (K) and α(k) = W n (K)/W 0 (K). All the roots of such a polynomial are non-zero. Since we are only interested in the negativity property of its roots we may divide by s n and with µ = 1/s it suffices to consider the polynomial h(k,µ) = n i=2 ( n i ) µ i +nβ(k)µ+α(k). Now it can be checked with a computer or by applying the Routh-Hurwitz criterion that the polynomial n n i=2( i) µ i has a root with positive real part for n = 15. Hence, if we find a 2-tangential body K K0 15 for which β(k) and α(k) can be arbitrarily small we get a counterexample to the negativity property of Conjecture 1.1. Observe that the roots of a polynomial are continuous functions of the coefficients of the polynomial (cf. e.g. [8, p. 3]). In order to construct such a body let P λ K0 3, λ 2, be the pyramid over a square basis with vertices (±λ,±λ, 1) (, 0,0,1+2/(λ 2 1) ). The coordinates are chosen such that the largest ball contained in P λ is B 3 and that all 2-faces (facets) of P λ touch B 3. Next we embed P λ in the canonical way into R 15 and consider K λ = conv{p λ,b 15 } K0 15. If H is a supportplaneof K λ whichis not a supportplane of B 15 it must beasupport plane of P λ and it can not contain any of the 2-faces of P λ. Thus H contains only 1-singular points of K λ and this shows that K λ is a 2-tangential body of B 15. It is easy to see that for the pyramid P λ there exists a constant c such that its 3-dimensional volume is not smaller than cλ 2. Hence there exists a constant c n dependingonly on the dimension such that V(K λ ) = W 0 (K λ ) c n λ 2. On the other hand, the circumradius of K λ is certainly less than 2λ ] n,
8 8 MARTIN HENK AND MARÍA A. HERNÁNDEZ CIFRE and so by (2.1) we have the bound W n 1 (K λ ) 2λV(B 15 ) = 2λW n (K λ ). Thus lim β(k λ) = lim α(k λ) = 0, λ λ which shows that h(k λ,µ) and thus f(k λ,b 15,s) has a root with positive real part if λ is large enough. Remark 3.2. It can be also checked that the polynomial n n i=3( i) µ i has a root with positive real part in dimension n = 12. Hence by an analogous argument and construction as above one can show that there exists a 3-tangential body K K0 12 of B 12 violating the negativity property of Conjecture 1.1. Since the construction of this 12-dimensional counterexample is a bit more involved we omit it here. To close the section we give a 20-dimensional numerical counterexample based on an almost regular crosspolytope. For 0 < λ 1 λ n we denote by C n (λ 1,...,λ n ) the orthogonal crosspolytope given by C n(λ 1,...,λ n ) = conv{±λ i e i : i = 1,...,n}, where e i denotes thei-th canonical unitvector. Analogously totheproofoflemma 2.1 in [1] it can be shown: Lemma 3.1. Let F i (λ l1,...,λ li+1 ) = conv{λ l1 e l1,...,λ li+1 e li+1 }, 0 i n, be an i-dimensional face of C n(λ 1,...,λ n ), 1 l 1 < < l i+1 n. The external angle of the face F i (λ l1,...,λ li+1 ) is given by i+1 2 n i 1 k=1 π (n i)/2 n j=1 λ j j k λ2 l j 0 P i+1 k=1 e 1 λ 2 l k!x 2 j {l 1,...,l i+1 } x 0 2 e y λ 2 jdy dx. The i-face F i (λ l1,...,λ li+1 ) is the i-simplex conv{λ l1 e l1,...,λ li+1 e li+1 }, and its i-th volume is given by 1 i+1 λ 2 i! l j. k=1j k Since C n(λ 1,...,λ n ) has 2 i+1 equal i-faces of the type F i (λ l1,...,λ li+1 ) we get the following formulae for the quermassintegrals. Theorem 3.2. Let 0 < λ 1 λ n. The quermassintegrals of the orthogonal crosspolytope C n (λ 1,...,λ n ) are given by: ( W 0 C n (λ 1,...,λ n ) ) = 2n n! λ 1... λ n, ( W 1 C n (λ 1,...,λ n ) ) = 2n n λ 2 j n!, i=1 j i
9 and for 0 i n 2, NOTES ON THE ROOTS OF STEINER POLYNOMIALS 9 ( W n i C n (λ 1,...,λ n ) ) = κ n i ( n i) 0 2 n i!π (n i)/2 P i+1 k=1 e 1 λ 2 l k 1 l 1 < <l i+1 n!x 2 j {l 1,...,l i+1 } i+1 k=1 n j=1 λ j x 0 j k λ2 l j 2 e y λ 2 j dy dx. Numerical computations show that the Steiner polynomial of the crosspolytope Cn( λ, (n/2)...,λ,1, (n/2)...,1 ), n even, has roots with positive real parts for different values of λ and n, e.g., for n = 20 and λ = The in- and circumradius bound Now we deal with the part of Conjecture 1.1 regarding the inradius and the circumradius bounds and we are going to show that the conjectured properties do not hold in dimension 3. To this end we consider first planar convex bodiesin R 3 andshow that thecircumradiusboundis false ingeneral for that class of bodies. From such a planar body we can easily construct a 3-dimensional counterexample which also fails the inradius bound. The inradius and circumradius of a convex body with respect to the unit ball will be denoted by r(k) and R(K). For a planar convex body we denote, as usual, by A(K) and p(k) its area and perimeter, respectively. With this notation (1.4) can be rewritten in the case E = B 2 as (4.1) A(K)+p(K)ρ+πρ 2 0, if R(K) ρ r(k). The next lemma gives a characterization of those planar convex bodies in R 3 failing the circumradius bound. Lemma 4.1. Let K K 3 be a planar convex body. All the roots of its Steiner polynomial f(k,b 3,s) have real part greater than R(K) if and only if p(k) 2 < ( 128/(3π) ) A(K) and p(k) < (16/3)R(K). Proof. SinceK K 3 is a planar body we have W 0 (K)=0, 3W 1 (K) = 2A(K) and 3W 2 (K) = (π/2)p(k). Hence f(k,b 3,s) = s (2A(K)+ π2 p(k)s+ 43 ) πs2. The non-zero roots γ 1,2 are given by γ 1,2 = 3 p(k)± p(k) π A(K). 16
10 10 MARTIN HENK AND MARÍA A. HERNÁNDEZ CIFRE If p(k) 2 ( 128/(3π) ) A(K) 0, i.e., if f(k,b 3,s) has only real roots, then we have 3 p(k) p(k) π A(K) p(k) p(k) 2 4πA(K) R(K), 16 2π where the last inequality follows from (4.1). Hence all the roots of the Steiner polynomial of K have real parts greater than R(K) if and only if p(k) 2 ( 128/(3π) ) A(K) < 0 and (3/16)p(K) > R(K). In order to find a convex body satisfying the conditions of the previous lemma we consider a symmetric lens L with circumradius R(L) = 1 and perimeter p(l) = 5.2 < 16/3. It is well known (see e.g. [4, p ]) that symmetric lenses are the extremal sets of the inequality 8φA(K) p(k) ( p(k) 4R(K)cosφ ), where φ is determined as the positive solution of the equation p(k)sinφ = 4R(K)φ. In the case of a lens, φ is the half angle between the two circles of the lens, see Figure 1. φ R(L) Figure 1. A symmetric lens L. For our lens L we obtain by the equality case in the above inequality A(L) = , which satisfies also the second inequality p(k) 2 < ( 128/(3π) ) A(K) of Lemma 4.1. Hence L is a 2-dimensional convex body in R 3 violating the circumradius bound. The roots of f(l,b 3,s) are given by (4.2) γ 1,2 = 0.975± i and γ 3 = 0, whose real parts are greater than R(L) = 1. From such a set it is easy to obtain 3-dimensional convex bodies K for which all the roots of f(k,b 3,s) have real part greater than R(K). Proof of Theorem 1.3. Observe, in general, we have for ν, ρ 0 that V(K+ νe +ρe) = V ( K +(ν +ρ)e ) and thus n ( ) n f(k +νe,e,s) = W i (K;E)(s+ν) i = f(k,e,s+ν). i i=0 Hence the roots of f(k+νe,e,s) are given by γ i ν, whereγ i are the roots of f(k,e,s). Now let L ν = L+νB 3, where L is the above 2-dimensional
11 NOTES ON THE ROOTS OF STEINER POLYNOMIALS 11 lens. Then L ν K0 3 for ν > 0 and the roots of f(l ν,b 3,s) are γ i ν, where γ i are given in (4.2). Thus all the real parts of γ i ν are greater than 1 ν = R(L ν,b 3 ). Finally we deal with the inradius bound. To this end let L ν be as in the proof above. Since W i (L ν ;B 3 ) = W 3 i (B 3 ;L ν ) we get f(b 3,L ν,s) = (2A(L)ν + π2 p(l)ν ) πν3 s 3 + ( 2A(L)+πp(L)ν +4πν 2) ( π ) s p(l)+4πν s+ 4 3 π. For instance, for ν = 1 it can be checked that the roots of this polynomial are γ 1,2 = ± i and γ 3 = 1, whose real parts are smaller than 1/2 = 1/R(L 1,B 3 ) = r(b 3,L 1 ). This provides the required counterexample to the inradius bound of Conjecture 1.1 stated in Corollary 1.1. We remark that the above construction in the proof of Theorem 1.3 and Corollary 1.1 works with any symmetriclens L with R(L) = 1 and perimeter p(l) [p 0,16/3], where p 0 = 4φ 0 /sinφ 0 = and φ 0 is the smallest positive solution of φ sinφcosφ = (3π/16)φ 2. Acknowledgements. This work has been developed during a research stay of the second author at the Otto-von-Guericke Universität Magdeburg, Germany, supported by Programa Nacional de ayudas para la movilidad de profesores de universidad e investigadores españoles y extranjeros (MEC), Ref. PR References [1] U. Betke and M. Henk, Intrinsic volumes and lattice points of crosspolytopes, Monatsh. Math. 115 (1 2) (1993), [2] W. Blaschke, Vorlesungen über Integralgeometrie, Deutscher Verlag der Wissenschaften, Berlin, 1995, 3rd ed. (1st ed.: 1949). [3] T. Bonnesen, Les problèmes des isopérimètres et des isépiphanes, Collection de monographies sur la théorie des fonctions, Gauthier-Villars, Paris [4] T. Bonnesen and W. Fenchel, Theorie der konvexen Körper. Springer, Berlin, 1934, English translation: Theory of convex bodies. Edited by L. Boron, C. Christenson and B. Smith. BCS Associates, Moscow, ID, [5] J. Favard, Sur les corps convexes, J. Math. Pures Appl. 12 (9) (1933), [6] H. Flanders, A proof of Minkowski s inequality for convex curves, Amer. Math. Monthly 75 (1968) [7] M. A. Hernández Cifre, E. Saorín, On the roots of the Steiner polynomial of a 3- dimensional convex body, Adv. Geom. 7 (2007), [8] M. Marden, Geometry of polynomials, Mathematical Surveys, No. 3, American Mathematical Society, Providence, R.I., 1966, 2nd ed. [9] T. Oda, Convex bodies and algebraic geometry. An introduction to the theory of toric varieties. Springer-Verlag, Berlin, [10] J. R. Sangwine-Yager, Bonnesen-style inequalities for Minkowski relative geometry. Trans. Amer. Math. Soc. 307 (1) (1988),
12 12 MARTIN HENK AND MARÍA A. HERNÁNDEZ CIFRE [11] J. R. Sangwine-Yager, Mixed volumes. In: Handbook of convex geometry (P. M. Gruber and J. M. Wills eds.), North-Holland, Amsterdam, 1993, [12] R. Schneider, Convex Bodies: The Brunn-Minkowski Theory, Cambridge University Press, Cambridge, [13] J. Steiner, Über parallele Flächen, Monatsber. Preuss. Akad. Wiss. (1840), , [Ges. Werke, Vol II (Reimer, Berlin, 1882) ]. [14] B. Teissier, Bonnesen-type inequalities in algebraic geometry I. Introduction to the problem. Seminar on Differential Geometry, Princeton Univ. Press, Princeton, N. J., 1982, [15] J. M. Wills, Minkowski s successive minima and the zeros of a convexity-function. Monatsh. Math. 109 (1990), Institut für Algebra und Geometrie, Otto-von-Guericke Universität Magdeburg, Universitätsplatz 2, D Magdeburg, Germany address: henk@math.uni-magdeburg.de Departamento de Matemáticas, Universidad de Murcia, Campus de Espinardo, Murcia, Spain address: mhcifre@um.es
ON SUCCESSIVE RADII AND p-sums OF CONVEX BODIES
 ON SUCCESSIVE RADII AND p-sums OF CONVEX BODIES BERNARDO GONZÁLEZ AND MARÍA A. HERNÁNDEZ CIFRE Abstract. We study the behavior of the so called successive inner and outer radii with respect to the p-sums
ON SUCCESSIVE RADII AND p-sums OF CONVEX BODIES BERNARDO GONZÁLEZ AND MARÍA A. HERNÁNDEZ CIFRE Abstract. We study the behavior of the so called successive inner and outer radii with respect to the p-sums
THE ISODIAMETRIC PROBLEM AND OTHER INEQUALITIES IN THE CONSTANT CURVATURE 2-SPACES
 THE ISODIAMETRIC PROBLEM AND OTHER INEQUALITIES IN THE CONSTANT CURVATURE -SPACES MARÍA A HERNÁNDEZ CIFRE AND ANTONIO R MARTÍNEZ FERNÁNDEZ Abstract In this paper we prove several new inequalities for centrally
THE ISODIAMETRIC PROBLEM AND OTHER INEQUALITIES IN THE CONSTANT CURVATURE -SPACES MARÍA A HERNÁNDEZ CIFRE AND ANTONIO R MARTÍNEZ FERNÁNDEZ Abstract In this paper we prove several new inequalities for centrally
REFINEMENTS OF THE BRUNN-MINKOWSKI INEQUALITY
 REFINEMENTS OF THE BRNN-MINKOWSKI INEQALITY Abstract. Brunn-Minkowski theorem says that vol 1 λk +λl 1/n, for K, L convex bodies, is a concave function in λ, and assuming a common hyperplane projection
REFINEMENTS OF THE BRNN-MINKOWSKI INEQALITY Abstract. Brunn-Minkowski theorem says that vol 1 λk +λl 1/n, for K, L convex bodies, is a concave function in λ, and assuming a common hyperplane projection
Deviation Measures and Normals of Convex Bodies
 Beiträge zur Algebra und Geometrie Contributions to Algebra Geometry Volume 45 (2004), No. 1, 155-167. Deviation Measures Normals of Convex Bodies Dedicated to Professor August Florian on the occasion
Beiträge zur Algebra und Geometrie Contributions to Algebra Geometry Volume 45 (2004), No. 1, 155-167. Deviation Measures Normals of Convex Bodies Dedicated to Professor August Florian on the occasion
L p -Width-Integrals and Affine Surface Areas
 LIBERTAS MATHEMATICA, vol XXX (2010) L p -Width-Integrals and Affine Surface Areas Chang-jian ZHAO and Mihály BENCZE Abstract. The main purposes of this paper are to establish some new Brunn- Minkowski
LIBERTAS MATHEMATICA, vol XXX (2010) L p -Width-Integrals and Affine Surface Areas Chang-jian ZHAO and Mihály BENCZE Abstract. The main purposes of this paper are to establish some new Brunn- Minkowski
Banach Journal of Mathematical Analysis ISSN: (electronic)
 Banach J. Math. Anal. 2 (2008), no., 70 77 Banach Journal of Mathematical Analysis ISSN: 735-8787 (electronic) http://www.math-analysis.org WIDTH-INTEGRALS AND AFFINE SURFACE AREA OF CONVEX BODIES WING-SUM
Banach J. Math. Anal. 2 (2008), no., 70 77 Banach Journal of Mathematical Analysis ISSN: 735-8787 (electronic) http://www.math-analysis.org WIDTH-INTEGRALS AND AFFINE SURFACE AREA OF CONVEX BODIES WING-SUM
The Stong Isoperimetric Inequality of Bonnesen
 Department of Mathematics Undergraduate Colloquium University of Utah January, 006 The Stong Isoperimetric Inequality of Bonnesen Andres Treibergs University of Utah Among all simple closed curves in the
Department of Mathematics Undergraduate Colloquium University of Utah January, 006 The Stong Isoperimetric Inequality of Bonnesen Andres Treibergs University of Utah Among all simple closed curves in the
Journal of Inequalities in Pure and Applied Mathematics
 section Journal of in Pure and Applied Mathematics COMPLETE SYSTEMS OF INEQUALITIES M.A. HERNÁNDEZ CIFRE, G. SALINAS AND S.S. GOMIS Departamento de Matemáticas, Universidad de Murcia, Campus de Espinardo,
section Journal of in Pure and Applied Mathematics COMPLETE SYSTEMS OF INEQUALITIES M.A. HERNÁNDEZ CIFRE, G. SALINAS AND S.S. GOMIS Departamento de Matemáticas, Universidad de Murcia, Campus de Espinardo,
SUCCESSIVE RADII OF FAMILIES OF CONVEX BODIES
 SUCCESSIVE RADII OF FAMILIES OF CONVEX BODIES BERNARDO GONZÁLEZ, MARÍA A. HERNÁNDEZ CIFRE, AND AICKE HINRICHS Abstract. We study properties of the so called in- and outer successive radii of special families
SUCCESSIVE RADII OF FAMILIES OF CONVEX BODIES BERNARDO GONZÁLEZ, MARÍA A. HERNÁNDEZ CIFRE, AND AICKE HINRICHS Abstract. We study properties of the so called in- and outer successive radii of special families
ON A DISCRETE BRUNN-MINKOWSKI TYPE INEQUALITY
 ON DISCRETE BRUNN-MINKOWSKI TYPE INEQULITY MRÍ. HERNÁNDEZ CIFRE, DVID IGLESIS, ND JESÚS YEPES NICOLÁS bstract. The Brunn-Minkowski inequality states that the volume of compact sets K, L R n satisfies volk
ON DISCRETE BRUNN-MINKOWSKI TYPE INEQULITY MRÍ. HERNÁNDEZ CIFRE, DVID IGLESIS, ND JESÚS YEPES NICOLÁS bstract. The Brunn-Minkowski inequality states that the volume of compact sets K, L R n satisfies volk
LATTICE POINT COVERINGS
 LATTICE POINT COVERINGS MARTIN HENK AND GEORGE A. TSINTSIFAS Abstract. We give a simple proof of a necessary and sufficient condition under which any congruent copy of a given ellipsoid contains an integral
LATTICE POINT COVERINGS MARTIN HENK AND GEORGE A. TSINTSIFAS Abstract. We give a simple proof of a necessary and sufficient condition under which any congruent copy of a given ellipsoid contains an integral
NAKAJIMA S PROBLEM: CONVEX BODIES OF CONSTANT WIDTH AND CONSTANT BRIGHTNESS
 NAKAJIMA S PROBLEM: CONVEX BODIES OF CONSTANT WIDTH AND CONSTANT BRIGHTNESS RALPH HOWARD AND DANIEL HUG Dedicated to Rolf Schneider on the occasion of his 65th birthday ABSTRACT. For a convex body K R
NAKAJIMA S PROBLEM: CONVEX BODIES OF CONSTANT WIDTH AND CONSTANT BRIGHTNESS RALPH HOWARD AND DANIEL HUG Dedicated to Rolf Schneider on the occasion of his 65th birthday ABSTRACT. For a convex body K R
Star bodies with completely symmetric sections
 Star bodies with completely symmetric sections Sergii Myroshnychenko, Dmitry Ryabogin, and Christos Saroglou Abstract We say that a star body is completely symmetric if it has centroid at the origin and
Star bodies with completely symmetric sections Sergii Myroshnychenko, Dmitry Ryabogin, and Christos Saroglou Abstract We say that a star body is completely symmetric if it has centroid at the origin and
Valuations on Polytopes containing the Origin in their Interiors
 Valuations on Polytopes containing the Origin in their Interiors Monika Ludwig Abteilung für Analysis, Technische Universität Wien Wiedner Hauptstraße 8-10/1142, 1040 Wien, Austria E-mail: monika.ludwig@tuwien.ac.at
Valuations on Polytopes containing the Origin in their Interiors Monika Ludwig Abteilung für Analysis, Technische Universität Wien Wiedner Hauptstraße 8-10/1142, 1040 Wien, Austria E-mail: monika.ludwig@tuwien.ac.at
SUCCESSIVE-MINIMA-TYPE INEQUALITIES. U. Betke, M. Henk and J.M. Wills
 SUCCESSIVE-MINIMA-TYPE INEQUALITIES U. Betke, M. Henk and J.M. Wills Abstract. We show analogues of Minkowski s theorem on successive minima, where the volume is replaced by the lattice point enumerator.
SUCCESSIVE-MINIMA-TYPE INEQUALITIES U. Betke, M. Henk and J.M. Wills Abstract. We show analogues of Minkowski s theorem on successive minima, where the volume is replaced by the lattice point enumerator.
THE MEAN MINKOWSKI MEASURES FOR CONVEX BODIES OF CONSTANT WIDTH. HaiLin Jin and Qi Guo 1. INTRODUCTION
 TAIWANESE JOURNAL OF MATHEMATICS Vol. 8, No. 4, pp. 83-9, August 04 DOI: 0.650/tjm.8.04.498 This paper is available online at http://journal.taiwanmathsoc.org.tw THE MEAN MINKOWSKI MEASURES FOR CONVEX
TAIWANESE JOURNAL OF MATHEMATICS Vol. 8, No. 4, pp. 83-9, August 04 DOI: 0.650/tjm.8.04.498 This paper is available online at http://journal.taiwanmathsoc.org.tw THE MEAN MINKOWSKI MEASURES FOR CONVEX
ON A LINEAR REFINEMENT OF THE PRÉKOPA-LEINDLER INEQUALITY
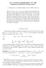 ON A LINEAR REFINEMENT OF TE PRÉKOPA-LEINDLER INEQUALITY A. COLESANTI, E. SAORÍN GÓMEZ, AND J. YEPES NICOLÁS Abstract. If f, g : R n R 0 are non-negative measurable functions, then the Prékopa-Leindler
ON A LINEAR REFINEMENT OF TE PRÉKOPA-LEINDLER INEQUALITY A. COLESANTI, E. SAORÍN GÓMEZ, AND J. YEPES NICOLÁS Abstract. If f, g : R n R 0 are non-negative measurable functions, then the Prékopa-Leindler
ON THE ISOTROPY CONSTANT OF PROJECTIONS OF POLYTOPES
 ON THE ISOTROPY CONSTANT OF PROJECTIONS OF POLYTOPES DAVID ALONSO-GUTIÉRREZ, JESÚS BASTERO, JULIO BERNUÉS, AND PAWE L WOLFF Abstract. The isotropy constant of any d-dimensional polytope with n vertices
ON THE ISOTROPY CONSTANT OF PROJECTIONS OF POLYTOPES DAVID ALONSO-GUTIÉRREZ, JESÚS BASTERO, JULIO BERNUÉS, AND PAWE L WOLFF Abstract. The isotropy constant of any d-dimensional polytope with n vertices
GAUSSIAN MEASURE OF SECTIONS OF DILATES AND TRANSLATIONS OF CONVEX BODIES. 2π) n
 GAUSSIAN MEASURE OF SECTIONS OF DILATES AND TRANSLATIONS OF CONVEX BODIES. A. ZVAVITCH Abstract. In this paper we give a solution for the Gaussian version of the Busemann-Petty problem with additional
GAUSSIAN MEASURE OF SECTIONS OF DILATES AND TRANSLATIONS OF CONVEX BODIES. A. ZVAVITCH Abstract. In this paper we give a solution for the Gaussian version of the Busemann-Petty problem with additional
INEQUALITIES FOR DUAL AFFINE QUERMASSINTEGRALS
 INEQUALITIES FOR DUAL AFFINE QUERMASSINTEGRALS YUAN JUN AND LENG GANGSONG Received 18 April 2005; Revised 2 November 2005; Accepted 8 November 2005 For star bodies, the dual affine quermassintegrals were
INEQUALITIES FOR DUAL AFFINE QUERMASSINTEGRALS YUAN JUN AND LENG GANGSONG Received 18 April 2005; Revised 2 November 2005; Accepted 8 November 2005 For star bodies, the dual affine quermassintegrals were
The small ball property in Banach spaces (quantitative results)
 The small ball property in Banach spaces (quantitative results) Ehrhard Behrends Abstract A metric space (M, d) is said to have the small ball property (sbp) if for every ε 0 > 0 there exists a sequence
The small ball property in Banach spaces (quantitative results) Ehrhard Behrends Abstract A metric space (M, d) is said to have the small ball property (sbp) if for every ε 0 > 0 there exists a sequence
Bulletin of the. Iranian Mathematical Society
 ISSN: 1017-060X (Print) ISSN: 1735-8515 (Online) Bulletin of the Iranian Mathematical Society Vol. 41 (2015), No. 3, pp. 581 590. Title: Volume difference inequalities for the projection and intersection
ISSN: 1017-060X (Print) ISSN: 1735-8515 (Online) Bulletin of the Iranian Mathematical Society Vol. 41 (2015), No. 3, pp. 581 590. Title: Volume difference inequalities for the projection and intersection
SHORTEST PERIODIC BILLIARD TRAJECTORIES IN CONVEX BODIES
 SHORTEST PERIODIC BILLIARD TRAJECTORIES IN CONVEX BODIES MOHAMMAD GHOMI Abstract. We show that the length of any periodic billiard trajectory in any convex body K R n is always at least 4 times the inradius
SHORTEST PERIODIC BILLIARD TRAJECTORIES IN CONVEX BODIES MOHAMMAD GHOMI Abstract. We show that the length of any periodic billiard trajectory in any convex body K R n is always at least 4 times the inradius
Estimates for the affine and dual affine quermassintegrals of convex bodies
 Estimates for the affine and dual affine quermassintegrals of convex bodies Nikos Dafnis and Grigoris Paouris Abstract We provide estimates for suitable normalizations of the affine and dual affine quermassintegrals
Estimates for the affine and dual affine quermassintegrals of convex bodies Nikos Dafnis and Grigoris Paouris Abstract We provide estimates for suitable normalizations of the affine and dual affine quermassintegrals
Brunn-Minkowski type inequalities for L p Blaschke- Minkowski homomorphisms
 Available online at www.tjnsa.com J. Nonlinear Sci. Appl. 9 (206), 6034 6040 Research Article Brunn-Minkowski type inequalities for L p Blaschke- Minkowski homomorphisms Feixiang Chen a,b,, Gangsong Leng
Available online at www.tjnsa.com J. Nonlinear Sci. Appl. 9 (206), 6034 6040 Research Article Brunn-Minkowski type inequalities for L p Blaschke- Minkowski homomorphisms Feixiang Chen a,b,, Gangsong Leng
arxiv:math/ v1 [math.co] 6 Dec 2005
![arxiv:math/ v1 [math.co] 6 Dec 2005 arxiv:math/ v1 [math.co] 6 Dec 2005](/thumbs/93/113728211.jpg) arxiv:math/05111v1 [math.co] Dec 005 Unimodality and convexity of f-vectors of polytopes Axel Werner December, 005 Abstract We consider unimodality and related properties of f-vectors of polytopes in various
arxiv:math/05111v1 [math.co] Dec 005 Unimodality and convexity of f-vectors of polytopes Axel Werner December, 005 Abstract We consider unimodality and related properties of f-vectors of polytopes in various
On self-circumferences in Minkowski planes
 extracta mathematicae Article in press On self-circumferences in Minkowski planes Mostafa Ghandehari, Horst Martini Department of Mathematics, University of Texas at Arlington, TX 76019, U.S.A. Faculty
extracta mathematicae Article in press On self-circumferences in Minkowski planes Mostafa Ghandehari, Horst Martini Department of Mathematics, University of Texas at Arlington, TX 76019, U.S.A. Faculty
Note on shortest and nearest lattice vectors
 Note on shortest and nearest lattice vectors Martin Henk Fachbereich Mathematik, Sekr. 6-1 Technische Universität Berlin Straße des 17. Juni 136 D-10623 Berlin Germany henk@math.tu-berlin.de We show that
Note on shortest and nearest lattice vectors Martin Henk Fachbereich Mathematik, Sekr. 6-1 Technische Universität Berlin Straße des 17. Juni 136 D-10623 Berlin Germany henk@math.tu-berlin.de We show that
Minkowski Valuations
 Minkowski Valuations Monika Ludwig Abstract Centroid and difference bodies define SL(n) equivariant operators on convex bodies and these operators are valuations with respect to Minkowski addition. We
Minkowski Valuations Monika Ludwig Abstract Centroid and difference bodies define SL(n) equivariant operators on convex bodies and these operators are valuations with respect to Minkowski addition. We
Affine surface area and convex bodies of elliptic type
 Affine surface area and convex bodies of elliptic type Rolf Schneider Abstract If a convex body K in R n is contained in a convex body L of elliptic type (a curvature image), then it is known that the
Affine surface area and convex bodies of elliptic type Rolf Schneider Abstract If a convex body K in R n is contained in a convex body L of elliptic type (a curvature image), then it is known that the
arxiv: v2 [math.dg] 7 May 2016
![arxiv: v2 [math.dg] 7 May 2016 arxiv: v2 [math.dg] 7 May 2016](/thumbs/95/125772896.jpg) THE IMPROVED ISOPERIMETRIC INEQUALITY AND THE WIGNER CAUSTIC OF PLANAR OVALS arxiv:151.6684v [math.dg] 7 May 16 MICHA L ZWIERZYŃSKI Abstract. The classical isoperimetric inequality in the Euclidean plane
THE IMPROVED ISOPERIMETRIC INEQUALITY AND THE WIGNER CAUSTIC OF PLANAR OVALS arxiv:151.6684v [math.dg] 7 May 16 MICHA L ZWIERZYŃSKI Abstract. The classical isoperimetric inequality in the Euclidean plane
III. CONGRESO DE JÓVENES INVESTIGADORES de la Real Sociedad Matemática Española. Universidad de Murcia, 7-11 Septiembre, 2015
 III CONGRESO DE JÓVENES INVESTIGADORES de la Real Sociedad Matemática Española Universidad de Murcia, 7-11 Septiembre, 2015 SESIÓN GEOMETRÍA CONVEXA Financiado por: Fundación Séneca-Agencia de Ciencia
III CONGRESO DE JÓVENES INVESTIGADORES de la Real Sociedad Matemática Española Universidad de Murcia, 7-11 Septiembre, 2015 SESIÓN GEOMETRÍA CONVEXA Financiado por: Fundación Séneca-Agencia de Ciencia
Helly s Theorem with Applications in Combinatorial Geometry. Andrejs Treibergs. Wednesday, August 31, 2016
 Undergraduate Colloquium: Helly s Theorem with Applications in Combinatorial Geometry Andrejs Treibergs University of Utah Wednesday, August 31, 2016 2. USAC Lecture on Helly s Theorem The URL for these
Undergraduate Colloquium: Helly s Theorem with Applications in Combinatorial Geometry Andrejs Treibergs University of Utah Wednesday, August 31, 2016 2. USAC Lecture on Helly s Theorem The URL for these
Bonnesen-type inequalities for surfaces of constant curvature
 Advances in Applied Mathematics 39 (2007) 143 154 www.elsevier.com/locate/yaama Bonnesen-type inequalities for surfaces of constant curvature Daniel A. Klain 1 Department of Mathematical Sciences, University
Advances in Applied Mathematics 39 (2007) 143 154 www.elsevier.com/locate/yaama Bonnesen-type inequalities for surfaces of constant curvature Daniel A. Klain 1 Department of Mathematical Sciences, University
DAR S CONJECTURE AND THE LOG-BRUNN-MINKOSKI INEQUALITY
 DAR S CONJECTURE AND THE LOG-BRUNN-MINKOSKI INEQUALITY DONGMENG XI AND GANGSONG LENG Abstract. In 999, Dar conjectured if there is a stronger version of the celebrated Brunn-Minkowski inequality. However,
DAR S CONJECTURE AND THE LOG-BRUNN-MINKOSKI INEQUALITY DONGMENG XI AND GANGSONG LENG Abstract. In 999, Dar conjectured if there is a stronger version of the celebrated Brunn-Minkowski inequality. However,
NOTE. On the Maximum Number of Touching Pairs in a Finite Packing of Translates of a Convex Body
 Journal of Combinatorial Theory, Series A 98, 19 00 (00) doi:10.1006/jcta.001.304, available online at http://www.idealibrary.com on NOTE On the Maximum Number of Touching Pairs in a Finite Packing of
Journal of Combinatorial Theory, Series A 98, 19 00 (00) doi:10.1006/jcta.001.304, available online at http://www.idealibrary.com on NOTE On the Maximum Number of Touching Pairs in a Finite Packing of
A New Approach to Covering
 A New Approach to Covering Ulrich Betke Martin Henk Jörg M. Wills September 0, 007 Abstract For finite coverings in euclidean d-space E d we introduce a parametric density function. Here the parameter
A New Approach to Covering Ulrich Betke Martin Henk Jörg M. Wills September 0, 007 Abstract For finite coverings in euclidean d-space E d we introduce a parametric density function. Here the parameter
On minimal solutions of linear Diophantine equations
 On minimal solutions of linear Diophantine equations Martin Henk Robert Weismantel Abstract This paper investigates the region in which all the minimal solutions of a linear diophantine equation ly. We
On minimal solutions of linear Diophantine equations Martin Henk Robert Weismantel Abstract This paper investigates the region in which all the minimal solutions of a linear diophantine equation ly. We
TitleHYPERELLIPTIC SURFACES WITH K^2 < 4. Author(s) Rito, Carlos; Sánchez, María Martí. Citation Osaka Journal of Mathematics.
 TitleHYPERELLIPTIC SURFACES WITH K^2 < 4 Author(s) Rito, Carlos; Sánchez, María Martí Citation Osaka Journal of Mathematics. 52(4) Issue 2015-10 Date Text Version publisher URL http://hdl.handle.net/11094/57673
TitleHYPERELLIPTIC SURFACES WITH K^2 < 4 Author(s) Rito, Carlos; Sánchez, María Martí Citation Osaka Journal of Mathematics. 52(4) Issue 2015-10 Date Text Version publisher URL http://hdl.handle.net/11094/57673
A Short Note on Gage s Isoperimetric Inequality
 A Short Note on Gage s Isoperimetric Inequality Hong Lu Shengliang Pan Department of Mathematics, East China Normal University, Shanghai, 262, P. R. China email: slpan@math.ecnu.edu.cn December 7, 24 Abstract
A Short Note on Gage s Isoperimetric Inequality Hong Lu Shengliang Pan Department of Mathematics, East China Normal University, Shanghai, 262, P. R. China email: slpan@math.ecnu.edu.cn December 7, 24 Abstract
ALMOST DISJOINT AND INDEPENDENT FAMILIES. 1. introduction. is infinite. Fichtenholz and Kantorovich showed that there is an independent family
 ALMOST DISJOINT AND INDEPENDENT FAMILIES STEFAN GESCHKE Abstract. I collect a number of proofs of the existence of large almost disjoint and independent families on the natural numbers. This is mostly
ALMOST DISJOINT AND INDEPENDENT FAMILIES STEFAN GESCHKE Abstract. I collect a number of proofs of the existence of large almost disjoint and independent families on the natural numbers. This is mostly
Quotient for radial Blaschke-Minkowski homomorphisms by Chang-Jian Zhao (1), Wing-Sum Cheung (2)
 Bull. Math. Soc. Sci. Math. Roumanie Tome 60 108) No. 2 2017 147 157 Quotient for radial Blaschke-Minkowski homomorphisms by Chang-Jian Zhao 1) Wing-Sum Cheung 2) Abstract Some new inequalities for quotient
Bull. Math. Soc. Sci. Math. Roumanie Tome 60 108) No. 2 2017 147 157 Quotient for radial Blaschke-Minkowski homomorphisms by Chang-Jian Zhao 1) Wing-Sum Cheung 2) Abstract Some new inequalities for quotient
A representation for convex bodies
 Armenian Journal of Mathematics Volume 5, Number 1, 2013, 69 74 A representation for convex bodies R. H. Aramyan* * Russian-Armenian State University; Institute of mathematics of National Academy of Sciences
Armenian Journal of Mathematics Volume 5, Number 1, 2013, 69 74 A representation for convex bodies R. H. Aramyan* * Russian-Armenian State University; Institute of mathematics of National Academy of Sciences
On families of anticommuting matrices
 On families of anticommuting matrices Pavel Hrubeš December 18, 214 Abstract Let e 1,..., e k be complex n n matrices such that e ie j = e je i whenever i j. We conjecture that rk(e 2 1) + rk(e 2 2) +
On families of anticommuting matrices Pavel Hrubeš December 18, 214 Abstract Let e 1,..., e k be complex n n matrices such that e ie j = e je i whenever i j. We conjecture that rk(e 2 1) + rk(e 2 2) +
Convergence in shape of Steiner symmetrized line segments. Arthur Korneychuk
 Convergence in shape of Steiner symmetrized line segments by Arthur Korneychuk A thesis submitted in conformity with the requirements for the degree of Master of Science Graduate Department of Mathematics
Convergence in shape of Steiner symmetrized line segments by Arthur Korneychuk A thesis submitted in conformity with the requirements for the degree of Master of Science Graduate Department of Mathematics
Diophantine approximations and integer points of cones
 Diophantine approximations and integer points of cones Martin Henk Robert Weismantel Abstract The purpose of this note is to present a relation between directed best approximations of a rational vector
Diophantine approximations and integer points of cones Martin Henk Robert Weismantel Abstract The purpose of this note is to present a relation between directed best approximations of a rational vector
SELECTIVELY BALANCING UNIT VECTORS AART BLOKHUIS AND HAO CHEN
 SELECTIVELY BALANCING UNIT VECTORS AART BLOKHUIS AND HAO CHEN Abstract. A set U of unit vectors is selectively balancing if one can find two disjoint subsets U + and U, not both empty, such that the Euclidean
SELECTIVELY BALANCING UNIT VECTORS AART BLOKHUIS AND HAO CHEN Abstract. A set U of unit vectors is selectively balancing if one can find two disjoint subsets U + and U, not both empty, such that the Euclidean
THE IMPLICIT FUNCTION THEOREM FOR CONTINUOUS FUNCTIONS. Carlos Biasi Carlos Gutierrez Edivaldo L. dos Santos. 1. Introduction
 Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 32, 2008, 177 185 THE IMPLICIT FUNCTION THEOREM FOR CONTINUOUS FUNCTIONS Carlos Biasi Carlos Gutierrez Edivaldo L.
Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 32, 2008, 177 185 THE IMPLICIT FUNCTION THEOREM FOR CONTINUOUS FUNCTIONS Carlos Biasi Carlos Gutierrez Edivaldo L.
Problems in additive number theory, V: Affinely inequivalent MSTD sets
 W N North-Western European Journal of Mathematics E M J Problems in additive number theory, V: Affinely inequivalent MSTD sets Melvyn B Nathanson 1 Received: November 9, 2016/Accepted: June 26, 2017/Online:
W N North-Western European Journal of Mathematics E M J Problems in additive number theory, V: Affinely inequivalent MSTD sets Melvyn B Nathanson 1 Received: November 9, 2016/Accepted: June 26, 2017/Online:
Convex Geometry. Otto-von-Guericke Universität Magdeburg. Applications of the Brascamp-Lieb and Barthe inequalities. Exercise 12.
 Applications of the Brascamp-Lieb and Barthe inequalities Exercise 12.1 Show that if m Ker M i {0} then both BL-I) and B-I) hold trivially. Exercise 12.2 Let λ 0, 1) and let f, g, h : R 0 R 0 be measurable
Applications of the Brascamp-Lieb and Barthe inequalities Exercise 12.1 Show that if m Ker M i {0} then both BL-I) and B-I) hold trivially. Exercise 12.2 Let λ 0, 1) and let f, g, h : R 0 R 0 be measurable
SOME REMARKS ON THE SPACE OF DIFFERENCES OF SUBLINEAR FUNCTIONS
 APPLICATIONES MATHEMATICAE 22,3 (1994), pp. 419 426 S. G. BARTELS and D. PALLASCHKE (Karlsruhe) SOME REMARKS ON THE SPACE OF DIFFERENCES OF SUBLINEAR FUNCTIONS Abstract. Two properties concerning the space
APPLICATIONES MATHEMATICAE 22,3 (1994), pp. 419 426 S. G. BARTELS and D. PALLASCHKE (Karlsruhe) SOME REMARKS ON THE SPACE OF DIFFERENCES OF SUBLINEAR FUNCTIONS Abstract. Two properties concerning the space
THE STEINER FORMULA FOR EROSIONS. then one shows in integral geometry that the volume of A ρk (ρ 0) is a polynomial of degree n:
 THE STEINER FORMULA FOR EROSIONS. G. MATHERON Abstract. If A and K are compact convex sets in R n, a Steiner-type formula is valid for the erosion of A by K if and only if A is open with respect to K.
THE STEINER FORMULA FOR EROSIONS. G. MATHERON Abstract. If A and K are compact convex sets in R n, a Steiner-type formula is valid for the erosion of A by K if and only if A is open with respect to K.
ON FREE PLANES IN LATTICE BALL PACKINGS ABSTRACT. 1. Introduction
 ON FREE PLANES IN LATTICE BALL PACKINGS MARTIN HENK, GÜNTER M ZIEGLER, AND CHUANMING ZONG ABSTRACT This note, by studying relations between the length of the shortest lattice vectors and the covering minima
ON FREE PLANES IN LATTICE BALL PACKINGS MARTIN HENK, GÜNTER M ZIEGLER, AND CHUANMING ZONG ABSTRACT This note, by studying relations between the length of the shortest lattice vectors and the covering minima
Geometric and isoperimetric properties of sets of positive reach in E d
 Geometric and isoperimetric properties of sets of positive reach in E d Andrea Colesanti and Paolo Manselli Abstract Some geometric facts concerning sets of reach R > 0 in the n dimensional Euclidean space
Geometric and isoperimetric properties of sets of positive reach in E d Andrea Colesanti and Paolo Manselli Abstract Some geometric facts concerning sets of reach R > 0 in the n dimensional Euclidean space
ISOPERIMETRIC INEQUALITY FOR FLAT SURFACES
 Proceedings of The Thirteenth International Workshop on Diff. Geom. 3(9) 3-9 ISOPERIMETRIC INEQUALITY FOR FLAT SURFACES JAIGYOUNG CHOE Korea Institute for Advanced Study, Seoul, 3-7, Korea e-mail : choe@kias.re.kr
Proceedings of The Thirteenth International Workshop on Diff. Geom. 3(9) 3-9 ISOPERIMETRIC INEQUALITY FOR FLAT SURFACES JAIGYOUNG CHOE Korea Institute for Advanced Study, Seoul, 3-7, Korea e-mail : choe@kias.re.kr
Brunn-Minkowski inequality for the 1-Riesz capacity and level set convexity for the 1/2-Laplacian
 Brunn-Minkowski inequality for the 1-Riesz capacity and level set convexity for the 1/2-Laplacian M. Novaga, B. Ruffini January 13, 2014 Abstract We prove that that the 1-Riesz capacity satisfies a Brunn-Minkowski
Brunn-Minkowski inequality for the 1-Riesz capacity and level set convexity for the 1/2-Laplacian M. Novaga, B. Ruffini January 13, 2014 Abstract We prove that that the 1-Riesz capacity satisfies a Brunn-Minkowski
Volumes of projection bodies of some classes of convex bodies
 Volumes of projection bodies of some classes of convex bodies Christos Saroglou University of Crete Department of Mathematics Abstract Schneider posed the problem of determining the maximal value of the
Volumes of projection bodies of some classes of convex bodies Christos Saroglou University of Crete Department of Mathematics Abstract Schneider posed the problem of determining the maximal value of the
Topics in Stochastic Geometry. Lecture 4 The Boolean model
 Institut für Stochastik Karlsruher Institut für Technologie Topics in Stochastic Geometry Lecture 4 The Boolean model Lectures presented at the Department of Mathematical Sciences University of Bath May
Institut für Stochastik Karlsruher Institut für Technologie Topics in Stochastic Geometry Lecture 4 The Boolean model Lectures presented at the Department of Mathematical Sciences University of Bath May
DOUGLAS J. DAILEY AND THOMAS MARLEY
 A CHANGE OF RINGS RESULT FOR MATLIS REFLEXIVITY DOUGLAS J. DAILEY AND THOMAS MARLEY Abstract. Let R be a commutative Noetherian ring and E the minimal injective cogenerator of the category of R-modules.
A CHANGE OF RINGS RESULT FOR MATLIS REFLEXIVITY DOUGLAS J. DAILEY AND THOMAS MARLEY Abstract. Let R be a commutative Noetherian ring and E the minimal injective cogenerator of the category of R-modules.
Rolle s Theorem for Polynomials of Degree Four in a Hilbert Space 1
 Journal of Mathematical Analysis and Applications 265, 322 33 (2002) doi:0.006/jmaa.200.7708, available online at http://www.idealibrary.com on Rolle s Theorem for Polynomials of Degree Four in a Hilbert
Journal of Mathematical Analysis and Applications 265, 322 33 (2002) doi:0.006/jmaa.200.7708, available online at http://www.idealibrary.com on Rolle s Theorem for Polynomials of Degree Four in a Hilbert
Chapter 1. Measure Spaces. 1.1 Algebras and σ algebras of sets Notation and preliminaries
 Chapter 1 Measure Spaces 1.1 Algebras and σ algebras of sets 1.1.1 Notation and preliminaries We shall denote by X a nonempty set, by P(X) the set of all parts (i.e., subsets) of X, and by the empty set.
Chapter 1 Measure Spaces 1.1 Algebras and σ algebras of sets 1.1.1 Notation and preliminaries We shall denote by X a nonempty set, by P(X) the set of all parts (i.e., subsets) of X, and by the empty set.
Cylindrical Partitions of Convex Bodies
 Combinatorial and Computational Geometry MSRI Publications Volume 52, 2005 Cylindrical Partitions of Convex Bodies ALADÁR HEPPES AND W LODZIMIERZ KUPERBERG Abstract. A cylindrical partition of a convex
Combinatorial and Computational Geometry MSRI Publications Volume 52, 2005 Cylindrical Partitions of Convex Bodies ALADÁR HEPPES AND W LODZIMIERZ KUPERBERG Abstract. A cylindrical partition of a convex
From the Brunn-Minkowski inequality to a class of Poincaré type inequalities
 arxiv:math/0703584v1 [math.fa] 20 Mar 2007 From the Brunn-Minkowski inequality to a class of Poincaré type inequalities Andrea Colesanti Abstract We present an argument which leads from the Brunn-Minkowski
arxiv:math/0703584v1 [math.fa] 20 Mar 2007 From the Brunn-Minkowski inequality to a class of Poincaré type inequalities Andrea Colesanti Abstract We present an argument which leads from the Brunn-Minkowski
An extended version of the Carathéodory extension Theorem
 An extended version of the Carathéodory extension Theorem Alexandre G. Patriota Departamento de Estatística, Universidade de São Paulo, São Paulo/SP, 05508-090, Brazil Abstract In this paper, we show that
An extended version of the Carathéodory extension Theorem Alexandre G. Patriota Departamento de Estatística, Universidade de São Paulo, São Paulo/SP, 05508-090, Brazil Abstract In this paper, we show that
BLOCH FUNCTIONS ON THE UNIT BALL OF AN INFINITE DIMENSIONAL HILBERT SPACE
 BLOCH FUNCTIONS ON THE UNIT BALL OF AN INFINITE DIMENSIONAL HILBERT SPACE OSCAR BLASCO, PABLO GALINDO, AND ALEJANDRO MIRALLES Abstract. The Bloch space has been studied on the open unit disk of C and some
BLOCH FUNCTIONS ON THE UNIT BALL OF AN INFINITE DIMENSIONAL HILBERT SPACE OSCAR BLASCO, PABLO GALINDO, AND ALEJANDRO MIRALLES Abstract. The Bloch space has been studied on the open unit disk of C and some
Gaussian Measure of Sections of convex bodies
 Gaussian Measure of Sections of convex bodies A. Zvavitch Department of Mathematics, University of Missouri, Columbia, MO 652, USA Abstract In this paper we study properties of sections of convex bodies
Gaussian Measure of Sections of convex bodies A. Zvavitch Department of Mathematics, University of Missouri, Columbia, MO 652, USA Abstract In this paper we study properties of sections of convex bodies
On mixed discriminants of positively definite matrix
 Also available at http://amc-journal.eu ISSN 1855-3966 printed edn., ISSN 1855-3974 electronic edn. ARS MATHEMATICA CONTEMPORANEA 9 2015 261 266 On mixed discriminants of positively definite matrix Chang-Jian
Also available at http://amc-journal.eu ISSN 1855-3966 printed edn., ISSN 1855-3974 electronic edn. ARS MATHEMATICA CONTEMPORANEA 9 2015 261 266 On mixed discriminants of positively definite matrix Chang-Jian
Convex Analysis and Economic Theory AY Elementary properties of convex functions
 Division of the Humanities and Social Sciences Ec 181 KC Border Convex Analysis and Economic Theory AY 2018 2019 Topic 6: Convex functions I 6.1 Elementary properties of convex functions We may occasionally
Division of the Humanities and Social Sciences Ec 181 KC Border Convex Analysis and Economic Theory AY 2018 2019 Topic 6: Convex functions I 6.1 Elementary properties of convex functions We may occasionally
ON THE TOTAL CURVATURE OF A KNOTTED SPACE CURVE.
 ON THE TOTAL CURVATURE OF A KNOTTED PACE CURVE. ITVÁN FÁRY (TRANLATION BY E. DENNE.) 1. Introduction 1. M. Fenchel 1 has proved a theorem saying that a closed curve (in ordinary space) has total curvature
ON THE TOTAL CURVATURE OF A KNOTTED PACE CURVE. ITVÁN FÁRY (TRANLATION BY E. DENNE.) 1. Introduction 1. M. Fenchel 1 has proved a theorem saying that a closed curve (in ordinary space) has total curvature
An example of a convex body without symmetric projections.
 An example of a convex body without symmetric projections. E. D. Gluskin A. E. Litvak N. Tomczak-Jaegermann Abstract Many crucial results of the asymptotic theory of symmetric convex bodies were extended
An example of a convex body without symmetric projections. E. D. Gluskin A. E. Litvak N. Tomczak-Jaegermann Abstract Many crucial results of the asymptotic theory of symmetric convex bodies were extended
A sharp Rogers Shephard type inequality for Orlicz-difference body of planar convex bodies
 Proc. Indian Acad. Sci. (Math. Sci. Vol. 124, No. 4, November 2014, pp. 573 580. c Indian Academy of Sciences A sharp Rogers Shephard type inequality for Orlicz-difference body of planar convex bodies
Proc. Indian Acad. Sci. (Math. Sci. Vol. 124, No. 4, November 2014, pp. 573 580. c Indian Academy of Sciences A sharp Rogers Shephard type inequality for Orlicz-difference body of planar convex bodies
QUASINORMAL FAMILIES AND PERIODIC POINTS
 QUASINORMAL FAMILIES AND PERIODIC POINTS WALTER BERGWEILER Dedicated to Larry Zalcman on his 60th Birthday Abstract. Let n 2 be an integer and K > 1. By f n we denote the n-th iterate of a function f.
QUASINORMAL FAMILIES AND PERIODIC POINTS WALTER BERGWEILER Dedicated to Larry Zalcman on his 60th Birthday Abstract. Let n 2 be an integer and K > 1. By f n we denote the n-th iterate of a function f.
The edge-diametric theorem in Hamming spaces
 Discrete Applied Mathematics 56 2008 50 57 www.elsevier.com/locate/dam The edge-diametric theorem in Hamming spaces Christian Bey Otto-von-Guericke-Universität Magdeburg, Institut für Algebra und Geometrie,
Discrete Applied Mathematics 56 2008 50 57 www.elsevier.com/locate/dam The edge-diametric theorem in Hamming spaces Christian Bey Otto-von-Guericke-Universität Magdeburg, Institut für Algebra und Geometrie,
LARGE DEVIATIONS OF TYPICAL LINEAR FUNCTIONALS ON A CONVEX BODY WITH UNCONDITIONAL BASIS. S. G. Bobkov and F. L. Nazarov. September 25, 2011
 LARGE DEVIATIONS OF TYPICAL LINEAR FUNCTIONALS ON A CONVEX BODY WITH UNCONDITIONAL BASIS S. G. Bobkov and F. L. Nazarov September 25, 20 Abstract We study large deviations of linear functionals on an isotropic
LARGE DEVIATIONS OF TYPICAL LINEAR FUNCTIONALS ON A CONVEX BODY WITH UNCONDITIONAL BASIS S. G. Bobkov and F. L. Nazarov September 25, 20 Abstract We study large deviations of linear functionals on an isotropic
On bisectors in Minkowski normed space.
 On bisectors in Minkowski normed space. Á.G.Horváth Department of Geometry, Technical University of Budapest, H-1521 Budapest, Hungary November 6, 1997 Abstract In this paper we discuss the concept of
On bisectors in Minkowski normed space. Á.G.Horváth Department of Geometry, Technical University of Budapest, H-1521 Budapest, Hungary November 6, 1997 Abstract In this paper we discuss the concept of
Pythagorean Property and Best Proximity Pair Theorems
 isibang/ms/2013/32 November 25th, 2013 http://www.isibang.ac.in/ statmath/eprints Pythagorean Property and Best Proximity Pair Theorems Rafa Espínola, G. Sankara Raju Kosuru and P. Veeramani Indian Statistical
isibang/ms/2013/32 November 25th, 2013 http://www.isibang.ac.in/ statmath/eprints Pythagorean Property and Best Proximity Pair Theorems Rafa Espínola, G. Sankara Raju Kosuru and P. Veeramani Indian Statistical
arxiv: v1 [math.mg] 27 Jan 2016
![arxiv: v1 [math.mg] 27 Jan 2016 arxiv: v1 [math.mg] 27 Jan 2016](/thumbs/74/69760634.jpg) On the monotonicity of the moments of volumes of random simplices arxiv:67295v [mathmg] 27 Jan 26 Benjamin Reichenwallner and Matthias Reitzner University of Salzburg and University of Osnabrueck Abstract
On the monotonicity of the moments of volumes of random simplices arxiv:67295v [mathmg] 27 Jan 26 Benjamin Reichenwallner and Matthias Reitzner University of Salzburg and University of Osnabrueck Abstract
NAKAJIMA S PROBLEM FOR GENERAL CONVEX BODIES
 NAKAJIMA S PROBLEM FOR GENERAL CONVEX BODIES DANIEL HUG ABSTRACT. For a convex body K R n, the kth projection function of K assigns to any k-dimensional linear subspace of R n the k-volume of the orthogonal
NAKAJIMA S PROBLEM FOR GENERAL CONVEX BODIES DANIEL HUG ABSTRACT. For a convex body K R n, the kth projection function of K assigns to any k-dimensional linear subspace of R n the k-volume of the orthogonal
Max-min (σ-)additive representation of monotone measures
 Noname manuscript No. (will be inserted by the editor) Max-min (σ-)additive representation of monotone measures Martin Brüning and Dieter Denneberg FB 3 Universität Bremen, D-28334 Bremen, Germany e-mail:
Noname manuscript No. (will be inserted by the editor) Max-min (σ-)additive representation of monotone measures Martin Brüning and Dieter Denneberg FB 3 Universität Bremen, D-28334 Bremen, Germany e-mail:
SOME NEW BONNESEN-STYLE INEQUALITIES
 J Korean Math Soc 48 (2011), No 2, pp 421 430 DOI 104134/JKMS2011482421 SOME NEW BONNESEN-STYLE INEQUALITIES Jiazu Zhou, Yunwei Xia, and Chunna Zeng Abstract By evaluating the containment measure of one
J Korean Math Soc 48 (2011), No 2, pp 421 430 DOI 104134/JKMS2011482421 SOME NEW BONNESEN-STYLE INEQUALITIES Jiazu Zhou, Yunwei Xia, and Chunna Zeng Abstract By evaluating the containment measure of one
arxiv:math/ v1 [math.fa] 26 Oct 1993
![arxiv:math/ v1 [math.fa] 26 Oct 1993 arxiv:math/ v1 [math.fa] 26 Oct 1993](/thumbs/72/67608278.jpg) arxiv:math/9310217v1 [math.fa] 26 Oct 1993 ON COMPLEMENTED SUBSPACES OF SUMS AND PRODUCTS OF BANACH SPACES M.I.Ostrovskii Abstract. It is proved that there exist complemented subspaces of countable topological
arxiv:math/9310217v1 [math.fa] 26 Oct 1993 ON COMPLEMENTED SUBSPACES OF SUMS AND PRODUCTS OF BANACH SPACES M.I.Ostrovskii Abstract. It is proved that there exist complemented subspaces of countable topological
Congruences involving product of intervals and sets with small multiplicative doubling modulo a prime
 Congruences involving product of intervals and sets with small multiplicative doubling modulo a prime J. Cilleruelo and M. Z. Garaev Abstract We obtain a sharp upper bound estimate of the form Hp o(1)
Congruences involving product of intervals and sets with small multiplicative doubling modulo a prime J. Cilleruelo and M. Z. Garaev Abstract We obtain a sharp upper bound estimate of the form Hp o(1)
New series expansions of the Gauss hypergeometric function
 New series expansions of the Gauss hypergeometric function José L. López and Nico. M. Temme 2 Departamento de Matemática e Informática, Universidad Pública de Navarra, 36-Pamplona, Spain. e-mail: jl.lopez@unavarra.es.
New series expansions of the Gauss hypergeometric function José L. López and Nico. M. Temme 2 Departamento de Matemática e Informática, Universidad Pública de Navarra, 36-Pamplona, Spain. e-mail: jl.lopez@unavarra.es.
PERIODS IMPLYING ALMOST ALL PERIODS FOR TREE MAPS. A. M. Blokh. Department of Mathematics, Wesleyan University Middletown, CT , USA
 PERIODS IMPLYING ALMOST ALL PERIODS FOR TREE MAPS A. M. Blokh Department of Mathematics, Wesleyan University Middletown, CT 06459-0128, USA August 1991, revised May 1992 Abstract. Let X be a compact tree,
PERIODS IMPLYING ALMOST ALL PERIODS FOR TREE MAPS A. M. Blokh Department of Mathematics, Wesleyan University Middletown, CT 06459-0128, USA August 1991, revised May 1992 Abstract. Let X be a compact tree,
Sung-Wook Park*, Hyuk Han**, and Se Won Park***
 JOURNAL OF THE CHUNGCHEONG MATHEMATICAL SOCIETY Volume 16, No. 1, June 2003 CONTINUITY OF LINEAR OPERATOR INTERTWINING WITH DECOMPOSABLE OPERATORS AND PURE HYPONORMAL OPERATORS Sung-Wook Park*, Hyuk Han**,
JOURNAL OF THE CHUNGCHEONG MATHEMATICAL SOCIETY Volume 16, No. 1, June 2003 CONTINUITY OF LINEAR OPERATOR INTERTWINING WITH DECOMPOSABLE OPERATORS AND PURE HYPONORMAL OPERATORS Sung-Wook Park*, Hyuk Han**,
SOME EXAMPLES IN VECTOR INTEGRATION
 SOME EXAMPLES IN VECTOR INTEGRATION JOSÉ RODRÍGUEZ Abstract. Some classical examples in vector integration due to R.S. Phillips, J. Hagler and M. Talagrand are revisited from the point of view of the Birkhoff
SOME EXAMPLES IN VECTOR INTEGRATION JOSÉ RODRÍGUEZ Abstract. Some classical examples in vector integration due to R.S. Phillips, J. Hagler and M. Talagrand are revisited from the point of view of the Birkhoff
A NEW ELLIPSOID ASSOCIATED WITH CONVEX BODIES
 A NEW ELLIPSOID ASSOCIATED WITH CONVEX BODIES Erwin Lutwak, Deane Yang, and Gaoyong Zhang Department of Mathematics Polytechnic University Brooklyn, NY 11201 Abstract. It is shown that corresponding to
A NEW ELLIPSOID ASSOCIATED WITH CONVEX BODIES Erwin Lutwak, Deane Yang, and Gaoyong Zhang Department of Mathematics Polytechnic University Brooklyn, NY 11201 Abstract. It is shown that corresponding to
Reflections of planar convex bodies
 Reflections of planar convex bodies Rolf Schneider Abstract. It is proved that every convex body in the plane has a point such that the union of the body and its image under reflection in the point is
Reflections of planar convex bodies Rolf Schneider Abstract. It is proved that every convex body in the plane has a point such that the union of the body and its image under reflection in the point is
A Simplex Contained in a Sphere
 J. Geom. Online First c 2008 Birkhäuser Verlag Basel/Switzerland DOI 10.1007/s00022-008-1907-5 Journal of Geometry A Simplex Contained in a Sphere Andrew Vince Abstract. Let Δ be an n-dimensional simplex
J. Geom. Online First c 2008 Birkhäuser Verlag Basel/Switzerland DOI 10.1007/s00022-008-1907-5 Journal of Geometry A Simplex Contained in a Sphere Andrew Vince Abstract. Let Δ be an n-dimensional simplex
Local strong convexity and local Lipschitz continuity of the gradient of convex functions
 Local strong convexity and local Lipschitz continuity of the gradient of convex functions R. Goebel and R.T. Rockafellar May 23, 2007 Abstract. Given a pair of convex conjugate functions f and f, we investigate
Local strong convexity and local Lipschitz continuity of the gradient of convex functions R. Goebel and R.T. Rockafellar May 23, 2007 Abstract. Given a pair of convex conjugate functions f and f, we investigate
GROWTH OF RANK 1 VALUATION SEMIGROUPS
 GROWTH OF RANK 1 VALUATION SEMIGROUPS STEVEN DALE CUTKOSKY, KIA DALILI AND OLGA KASHCHEYEVA Let (R, m R ) be a local domain, with quotient field K. Suppose that ν is a valuation of K with valuation ring
GROWTH OF RANK 1 VALUATION SEMIGROUPS STEVEN DALE CUTKOSKY, KIA DALILI AND OLGA KASHCHEYEVA Let (R, m R ) be a local domain, with quotient field K. Suppose that ν is a valuation of K with valuation ring
ON INTERSECTION OF SIMPLY CONNECTED SETS IN THE PLANE
 GLASNIK MATEMATIČKI Vol. 41(61)(2006), 159 163 ON INTERSECTION OF SIMPLY CONNECTED SETS IN THE PLANE E. D. Tymchatyn and Vesko Valov University of Saskatchewan, Canada and Nipissing University, Canada
GLASNIK MATEMATIČKI Vol. 41(61)(2006), 159 163 ON INTERSECTION OF SIMPLY CONNECTED SETS IN THE PLANE E. D. Tymchatyn and Vesko Valov University of Saskatchewan, Canada and Nipissing University, Canada
OPERATIONS BETWEEN SETS IN GEOMETRY RICHARD J. GARDNER, DANIEL HUG, AND WOLFGANG WEIL
 OPERATIONS BETWEEN SETS IN GEOMETRY January 4, 2013 RICHARD J. GARDNER, DANIEL HUG, AND WOLFGANG WEIL Abstract. An investigation is launched into the fundamental characteristics of operations on and between
OPERATIONS BETWEEN SETS IN GEOMETRY January 4, 2013 RICHARD J. GARDNER, DANIEL HUG, AND WOLFGANG WEIL Abstract. An investigation is launched into the fundamental characteristics of operations on and between
Math 341: Convex Geometry. Xi Chen
 Math 341: Convex Geometry Xi Chen 479 Central Academic Building, University of Alberta, Edmonton, Alberta T6G 2G1, CANADA E-mail address: xichen@math.ualberta.ca CHAPTER 1 Basics 1. Euclidean Geometry
Math 341: Convex Geometry Xi Chen 479 Central Academic Building, University of Alberta, Edmonton, Alberta T6G 2G1, CANADA E-mail address: xichen@math.ualberta.ca CHAPTER 1 Basics 1. Euclidean Geometry
MINKOWSKI AREAS AND VALUATIONS. Monika Ludwig. Abstract
 MINKOWSKI AREAS AND VALUATIONS Monika Ludwig Abstract All continuous GL(n) covariant valuations that map convex bodies to convex bodies are completely classified. This establishes a characterization of
MINKOWSKI AREAS AND VALUATIONS Monika Ludwig Abstract All continuous GL(n) covariant valuations that map convex bodies to convex bodies are completely classified. This establishes a characterization of
arxiv: v1 [math.co] 25 Jun 2014
![arxiv: v1 [math.co] 25 Jun 2014 arxiv: v1 [math.co] 25 Jun 2014](/thumbs/84/90873676.jpg) THE NON-PURE VERSION OF THE SIMPLEX AND THE BOUNDARY OF THE SIMPLEX NICOLÁS A. CAPITELLI arxiv:1406.6434v1 [math.co] 25 Jun 2014 Abstract. We introduce the non-pure versions of simplicial balls and spheres
THE NON-PURE VERSION OF THE SIMPLEX AND THE BOUNDARY OF THE SIMPLEX NICOLÁS A. CAPITELLI arxiv:1406.6434v1 [math.co] 25 Jun 2014 Abstract. We introduce the non-pure versions of simplicial balls and spheres
Asymptotic Behaviour of λ-convex Sets in the Hyperbolic Plane
 Geometriae Dedicata 76: 75 89, 1999. 1999 Kluwer Academic Publishers. Printed in the Netherlands. 75 Asymptotic Behaviour of λ-convex Sets in the Hyperbolic Plane EDUARDO GALLEGO and AGUSTÍ REVENTÓS Departament
Geometriae Dedicata 76: 75 89, 1999. 1999 Kluwer Academic Publishers. Printed in the Netherlands. 75 Asymptotic Behaviour of λ-convex Sets in the Hyperbolic Plane EDUARDO GALLEGO and AGUSTÍ REVENTÓS Departament
General Affine Surface Areas
 General Affine Surface Areas Monika Ludwig Abstract Two families of general affine surface areas are introduced. Basic properties and affine isoperimetric inequalities for these new affine surface areas
General Affine Surface Areas Monika Ludwig Abstract Two families of general affine surface areas are introduced. Basic properties and affine isoperimetric inequalities for these new affine surface areas
TORIC WEAK FANO VARIETIES ASSOCIATED TO BUILDING SETS
 TORIC WEAK FANO VARIETIES ASSOCIATED TO BUILDING SETS YUSUKE SUYAMA Abstract. We give a necessary and sufficient condition for the nonsingular projective toric variety associated to a building set to be
TORIC WEAK FANO VARIETIES ASSOCIATED TO BUILDING SETS YUSUKE SUYAMA Abstract. We give a necessary and sufficient condition for the nonsingular projective toric variety associated to a building set to be
A unique representation of polyhedral types. Centering via Möbius transformations
 Mathematische Zeitschrift manuscript No. (will be inserted by the editor) A unique representation of polyhedral types. Centering via Möbius transformations Boris A. Springborn Boris Springborn Technische
Mathematische Zeitschrift manuscript No. (will be inserted by the editor) A unique representation of polyhedral types. Centering via Möbius transformations Boris A. Springborn Boris Springborn Technische
