GRADED QUESTIONS ON COMPLEX NUMBER
|
|
|
- Steven Hunt
- 5 years ago
- Views:
Transcription
1 E /Math-I/ GQ/Comple umer GRADED QUESTINS N CMPEX NUMBER. The umer of the form + i y where ad y are real umers ad i = - i. e.( i ) is called a comple umer ad it is deoted y z i.e. z = + i y.the comple umer z is represeted y a poit P(,y) o XY - plae. is called real part ad is deoted Re z = & y is called imaiary part ad is deoted y Im z y.. If z = + i y e a y comple umer the its cojuate is deoted y z ad z iy.. 6. (Z + z), y (Z - z) i Euler' s ormulae i - i i) e cos i si ii) e cos i si Polar form i r e y ta y / z = r cos + i si Where r =,. 7. r = y is said to e modulus of the comple umer z ad is deoted y z iy y - 8. = ta y / is said to e amplitude or arumet of the comple umer z = + iy ad is deoted y ar z = amp z ta y / The value such that - is said to e priciple value of the arumet. 9. Properties of modulus ad arumet. z z z z. z z z - z z z. zz z z. z z. ar z z 6. ar z z z z z ar ar ar ar z. Hyperolic uctios et e real or comple the e e is called h yperolic sie of ad is deoted y sih ad e e is called h yperolic cosie of ad is deoted cosh sih = e ; cosh = e e e
2 E /Math-I/ GQ/Comple umer tah = sih cosh coth = cosh sih e e sech = e e cosh e e e e cosech = sih = e e e e. Relatios etwee circular fuctio ad hyperolic fuctios. Square Relatios (i) Si i = i sih (iii) ta i = i tah (v) Cosh i = cos (ii) cos i = cosh (i v) Sih i = i si (vi) tah i = i ta (i) Cosh - si h = (ii) sech + tah = (iii) coth - cosech =. Hyperolic Idetities. (i) sih (-) = - sih ( ii) cosh (-) = cosh (iii) tah - = -tah (i v) e cosh sih cosh sih. Additio formulae Sih (A B) = sih A cosh B cosh A sih B Cosh (A B) = cosha coshb sih A sih B tah A B tah A tah B tah A tah B 6. Product ormulae (i) sih ( A + B) + sih (A - B) = sih A cosh B. (ii) sih (A + B) - sih (A - B) = cosh A sih B (iii) cosh (A + B) + cosh (A - B) = cosh A cosh B (iv) cosh (A + B) - cosh (A - B) = sih A sih B C + DI C - D (v) sih C + sih D = sih cosh K J H G I K J C + DI C - D (vi) sih C - sih D = cosh sih K J H G I K J C + DI C - D (vii) cosh C + cosh D = cosh cosh K J H G I K J C + D C - D (viii) cosh C - cosh D = sih sih I K J H G I K J
3 E /Math-I/ GQ/Comple umer 7. ormulae for ad i) sih = sih cosh ii) cosh = cosh sih iii) cosh cosh iv) sih cosh tah v) tah = vi) sih = sih + sih + tah vii) cosh = cosh cosh viii) tah = i) sih = tah - tah ) cosh = tah + + tah tah tah tah 8. Values of Hyperolic fuctios X sih cosh tah EXAMPES: a i a. If iy the provethat y c d c id. If i the prove that a a i. id the comple umers whose sum is ad whose product is 8.. id the comple umer z such that z + i H G I z ad ar z KJ i) ar z+ ad ar z- 6 ii) id z if z + i / iii) id z if ar z+i = / ad ar z-i =. id the loci represeted y ii) z + i z - i = 6 ii) z - z + = iii) z - + i = iv) z -- 6i =
4 E /Math-I/ GQ/Comple umer. Simplify C.N. Cos - i si cos 7 + i si 7 Cos - i si cos + i si. id the mod ul us ad ar umet of 9 + si + i cos. Pro ve that cos i si + si - i cos. Evaluate. Sho w that + si + i cos + si - i cos + cos + i si + cos - i si DE MIVRE S THEREM Cos + i si cos - i si. Epress i the form a + i + i si /9 I cos K J Cos isi 8 i d i i. E press i the form a+i 8 i d i i. It z = i 0 0 The simplif y z d z i + i i I K J cos + i si /. Show that + cos + i si + cos - i si = cos cos + - cos - + I K J H G I K J + -I + + = si cos K J H G I K J. Show that + si + i cos + + si - i cos = cos 6. Show that cos - cos + i si - si + cos - cos - i si - si C.N.. If z = cos +i si the pro ve that i) ta ii) +z i icot +z -z. Pro ve that () po wer of +7i th is eq ual to (-) where is positi ve iteer (-i) d d i i I K J I K J 0
5 i i z z. If z e ad z e the pro ve that si - i z z. If a + c & ic ( a)z the prove that a + i iz + c iz ta. If si ita the prove that cos isi ta 6. If si ita the prove that cos isi ta H G I K J E /Math-I/ GQ/Comple umer I KJ C.N.. If z ad z are a y t wo comple umers such that z z ad z z the sho w that z z z z is p urel y imaiar y. If z ad z are a y t wo comple umers the pro ve that z z z z z z. Prove that the statemet Rez 0 & z z are equivalet where z iy. If z ad z are a y t wo comple umers such that z + z z z ad the show that arz. Prove that z z arz ar z C.N.. Pro ve that e a i cot -. If i, i & cot prove that.si.cosec. Pro ve that +cosec / a i- i+ i i c e h c e h
6 E /Math-I/ GQ/Comple umer C.N.. If ad are the roots of the eq uatio + = 0 The pro ve that 0 /. If ad are the roots of the eq uatio - +=0 The pro ve that. H G I cos K J 8 8 hece ded uce that. If ad are the roots of the eq uatio 0 The pro ve that cos H G I 6 6 Hece fid the val ue K J of +. If ad are the roots of the eq uatio 0 the pro ve that H G I cos Hece pro ve that 6 K J. If ad are the roots of the eq uatio z si -z si + = 0 the pro ve that cos cosec ) 6. If z=-+i & is iteer, the prove that z z 0 if is ot a mutiple of. 7. If + r = cos, pro ve that cos r r 8. If + = cos ad y + cos the pro ve that oe of the val ues of y m is cos m + ad that of + y is cos m - m y m y m y 9. If + = cos, y cos ad z+ Z cos y the pro ve that i) y z + = cos + + ii) m + y yz y m = cos m - 0. If - s = si, y - i & z- si the pro ve that y Z i) y z + = cos + + ii) the oe of yz m y + m y is cos m - I K J 6
7 C.N.6 E /Math-I/ GQ/Comple umer. If is a positive iteer the show that e j - a + i + a - i = a + cos ta Hece fid the value of + i + - i m m m m - e j. Prove that a + i a i a cos Hece fid the value of + i - i. Prove that + i i cos. Prove that C.N. 7 N M / / d i d i N M I I R S T -+ i i if = k! KJ KJ if = k a I K J ta / a Where k is a positive iteer 6. If is a positi ve iteer ad + p + p p... p the pro ve that. p0 p p... cos. p p p... si. p p p... cos 0 8 H G I K J 0 H G I K J H G I K J C.N. 8. If = e, y = e ad z = e ad + y + z = 0 the pro ve that + y + i i i z = 0. If si + si = 0 ad cos + cos = 0 the pro ve that i. cos + cos = cos + + ii. si + si = si + +. If cos + cos + cos = 0 ad si +si +si =0 the pro ve that i. cos + cos + cos = 0 ii. si + si + si = 0. If cos +cos +cos = si +si +si =0 the pro ve that i. cos cos cos ii. si si si = / si si iii. cos + cos cos 0 i v. si + 0 C.N. 9 Epasio of cos, si i powers of si, cos 7
8 E /Math-I/ GQ/Comple umer. Usi De-Moi vre s theorem sho w that si = cos si si. Use De-Moi ver s theorem to pro ve the follo wi result cos = cos 6cos si si. tai the e pasios of cos ad si i terms of po wers of cos ad si. Pro ve that si = si-0 si +6 si. Pro ve that cos = cos-0 cos +6 cos 6. tai the e pasio of cos 6 i terms of po wers of si ad cos 7. Pro ve that cos 6 = -8 si 8si si 6 8. If si6 = A cos si - B cos si + C cos si id the val ues of A, B ad C Prove that si7 = 7cos si - cos si cos si si 0. Prove that si 6cos cos + si si7 6. Prove that 7-6 si si 6si si si7 6. Prove that 6 cos 80 cos cos si. ta Prove that ta = ta -0 ta Hece deduce that ta ta 0 0 ta ta 7 Pro ve that ta 7 = 7t-t t t. where t = ta 6 t t 7t Hece ded uce that -ta 7 6 ta ta 0 C.N. 0 Epasio of cos, si i terms of sies or cosies of multiples of 8
9 E /Math-I/ GQ/Comple umer. Pro ve that si si si 0si tai the e pasios of cos ad si i terms of cosies of multiples of 6 6. Pro ve that cos si 8 cos 6 6. Use De-Moi vrers theorem to pro ve that cos si cos 6 cos 6 7. Pro ve that - si si 7 7si si-si 8 6. E press cos as a series i cosies of m ultiples of Pro ve that cos si cos8 + 8 cos E press cos si as a series i sies of m ultiples of cos si = - 9. Prove that si 8 + si6 - si -6 si 7 0. Pro ve that cos si = - 7 si - si0 - si si 6 +si-0 si 6 7. Pro ve that - cos si si - si - 6 si9 + 6 si7 + si - si - 0 si. Sho w that si cos = cos6 - cos - cos +.. If si cos = A cos A cos A cos A cos7 7 Pro ve that A 9A A 9 A 0 7. Pro ve that +cos7 where = cos +cos. Usi De-Moi vre s theorem sho w that +cos8 where cos 6. Use De-Moi vre s theorem to sho w that e +cos 9 = +cos 6cos 8cos cos cos j c h c h C.N. Roots of Comple Numer. id all the values of i ad show that their cotiued product is -. id all the values of + ad show that their cotiued product is.. id all the values of + i ad show that their cotiued product is + i. Show that the cotiued product of all the values of + i is + i. / / id the cotiued product of all the values of - i I KJ C.N. Solve the followi equatio / 8 / 9
10 E /Math-I/ GQ/Comple umer 6. i 0. i i c h C.N. Roots of Comple Numer. id the cue roots of uity ad show that they ca e epressed as,,. Prove that the roots of uity are i eometric proressio & their sum is zero & product is - th - 6. If is the comple cue root of uit y the sho w that - 7. th id the roots of - ad show that they ca e epressed as,,... Also fid their cotiued product. Sho w that the roots of the eq uatio 0 ca e writte as,,,,. c hc hc h Hece pro ve that If,,... are the roots of the eq uatio 0 the pro ve that 6 - c- hc- h c- hc- hc- h 7 7. Sol ve the eq uatio 0 ad sho w that = - + cos c I K J I h cos K J C.N. 0
11 E /Math-I/ GQ/Comple umer. Pro ve that a+i + a-i has real val ues ad fid those of +i + -i. Sho w that the roots of the eq uatio - are i ve y I K J H G I K J -+i si = cos r r where r = 0,,,,. id the commo roots of 0 & 6 i 0. Sol ve the eq uatio 0 ad fid which of its roots satisf y the eq uatio 6 6. Sho w that e ver y root of + 0 has for its real part. 6 6 p+ 6. Sho w that the roots of + 0 are i ve y -i cot N M Sho w that the roots of the eq uatio + are i ve y k 7 H G I icot K J, k =,, Wh y k 0? 0, p=0,,,,, 8. Sho w that the roots of the eq uatio z- z are i ve y z = i k cot, k =,,, k 0 H G I K J 9. id the three c ue roots of -cos -i si 0. Sol ve the eq uatio z i C.N.. If + i is a root of the equatio id all other roots. If oe of the roots of the equatio is + i id all other roots. C.N. 6 Hyperolic uctios Seperate the real ad imaiary parts of i. si + iy ii. cos + iy iii. sih + iy i v. cosh + iy iv. ta + iy v. tah + iy C.N. 7
12 E /Math-I/ GQ/Comple umer. Sho w that cosh -sih +tah. Pro ve that cosh -tah sih +tah. Pro ve that cosh 6 6 -tah sih cosh +sih. Pro ve that cosh cosh -sih sih. Pro ve that cosec h + coth = coth / 6. If sih cosh, fid tah cosh sih 7. Pr ove that 6cosh cosh cosh 0cosh - 8. If =tah 0. the pro ve that sih = / ad cosh = / 9. If si = tah Pro ve that ta = sih 0. Pro ve that - - -cosh C.N. 8 cosh ( M'96 ). Pro ve that - - +sih sih.. If cosh + i i y the prove that i. y y ii. cosh sih cos si i. sec y cosec ii. sec h y cosech. If si + i y. If cos i y i the prove that i. u cosec v sec ii. u sec h y + v cosech y If sih a + i i. - u i v the prove that i y the prove that y y ii. sih a cosh a si cos
13 E /Math-I/ GQ/Comple umer C.N. 9. If ta + i = + i y the pro ve that i. + y + cot = ii. + y - y coth = -. If tah a + i = + i y the pro ve that i. + + y = coth a ii. + y + y cot =. If + i y = ta. If tah + i 6 C.N. 0 + i the pro ve that + y 6 I K J + = I K J = + i y the pro ve that + y + y = i. If si +i e the pro ve that cos = si i. If sih i e the pro ve that sih cos cos. If cosh +i cos i si the pro ve that si si sih C.N.. If si + i Pcos + isi the prove that i. P cosh - cos ii. ta = tah cos z. If e si u + iv ad z = + iy the prove that e = cosh v - cosu. If + iy = cos + i the epress ad y i terms of ad. Hece show that cos ad. cosh are the roots of the equatio. y If si i iy the show that si ad cosh y are the roots of the equatio p c h p + 0. If cos + i cos i si the prove that cos cosh c h C.N.
14 . If ta +i y i the pro ve that. If +i y = c cot u+i v the pro ve that E /Math-I/ GQ/Comple umer - cos cosh y y si u v = c sih cosh v-cos u. If ta +i y = si u+i v the pro ve that si sih y ta u tah v C.N.. If +i = tah + i I the pro ve that K J. If cosec +i = u+i v the pro ve that u v = u I K J v I K J c h c h If +i y= cosh + i. the pro ve that y C.N.. If fa +i the pro ve that i. = + ta i sec ii. e cot I K JI KJ. If u = lo ta + the pro ve that i. tah u/ = ta ii. cosh u.cos. If ta = tah u the pro ve that i. sih u = ta ii. cosh u = sec N M Q P. If cos +i r e the sho w that = i lo si - si. If lo ta = y the pro ve that i. sih y = ta cot ii. cosh + y + cosh - y = cosh y.cosec 6. If cosh = sec the pro ve that i. tah = ta I ii. sih = ta iii. = lo ta + iv. ta ( e ) K J
15 C.N. +i y-c u+iv. If = e where, y, u ad v are real the pro ve that +i y+c i. = -c sih u cosh u - cos v ii. y = c si v cosh u - cos v E /Math-I/ GQ/Comple umer r e i. If ta /+i v the sho w that r=, ta =sih v ad tah v = ta. If = si cosh ad y = cos sih the pro ve that i y i. cosec -i + cosec +i = ii. cosec -i - cosec +i = y y. If = cos cosh ad y = si sih the pro ve that i y i. sec i + sec -i = ii. sec +i - sec i = y y. If +i y = cos u+i v the pro ve that i. + y cosh v cosu ii. - y cosh v-cosu Pro ve that ta If u- u+ ta tah ta tah + ta ta cot coth ta tah ta tah si +i y the sho w that the ar umet of u is + where cos sih y ta = +si cosh y, - - cos sih y ta = -si cosh y C.N. 6 Pro ve that e j e j - -. sih = lo + +. cosh = lo + - cosech = lo sech = lo tah = lo + coth = - I - - lo K J H G I - K J
16 E /Math-I/ GQ/Comple umer C.N. 7 Pro ve the follo wi relatios I - -. tah si = cosh sec + KJ I - KJ ta I = lo ta + / tah cos = cosh cosec K J. cosh + = tah - -. sech si = lo cot. tah = sih sih cosh + = sih 8. sih = cosec - + C.N. 8. Seperate the real ad Imaiar y parts of ta. c h i i Pro ve that ta e lo ta c h - i i. Pro ve that ta e lo ta c h - i. Pro ve that si e cos si i lo si si c h - i. Pro ve that cos e si si i lo si si - i ce h 6. Seperate the real ad imaiar y parts of i. ta - iy ii. tah - iy I K J I K J C.N. 9 Pro ve that. si z= - - lo iz z. si i i lo i -.cos i = i lo +. cos z = -i lo z+ z. sih 7. ta z = i lo e j e j e j e j i cosh i 6. cosh i sih i - - i+zi 8. si cosec i-z K J i lo cot 6
17 C.N. 0 E /Math-I/ GQ/Comple umer Epress i the form a + i I K J i i. cos - ii. cos - i iii. si - i / i v. si - i C.N. I. If + iy = i + i e lo the show that = ad y = lo sec + ta i i KJ i e I. If cos cosh + the show that = lo + K J H G I ia i KJ d i. Pr ove that tah(lo ). If ta +i y i where ad y are real the pro ve that is idetermiate ad y is ifiite. I K J - a. Pro ve that ta i lo a/ i a C.N. GARITHMS CMPEX NUMBER E press i the form a+ i i. lo - ii. lo - iii. lo + i i v. lo + i H- I K H - i I K m+ v. Prove that lo i i = + C.N. si +i y -. Pro ve that lo M P i ta cot tah y si iy N a+i -. Pro ve that lo i ta / a a-i. Pro ve that ta i lo. Pro ve that cos i lo. Pro ve that si i lo Q I K J a-ii a K J a a+ii a-i K J a a a-ii a+i K J a a 7
18 C.N. I -e cosec i K J H G I K J I lo i K J. Pro ve that lo p iy y ta / a. If a+i m the pro ve that loca h iy +i -. If i the pro ve that ta / y lo iy. Pro ve that lo +cos i si lo cos i E /Math-I/ GQ/Comple umer C.N.. Seperate the real ad imaiary parts y cosideri the pricipal values oly. C.N. 6 d i d i i I i K J i i i) + i ii) iii) i - i i i iv) i v) + i vi) -i lo. id the pricipal val ue of i i - /8 ad sho w that its real part is e cos lo. If lo lo +i y p iq the pro ve that y= ta taq lo y. d i H G I K J d ii Seperate i ito real ad imaiar y parts y cosideri pricipal val ues ol y C.N. 7. If i i the pro ve that e +i. i A ib, Pro ve that i) ta. A i-- i - B H G I K J A i B If i i the pro ve that i A B + = B A ii) A + B = e i. Pro ve that i cos i si where = +/ e. id the pricipal val ue of +i ta i m 6. Pr ove that the eeral value of ( i ta ) is e cos(lo ) i si(lo ) 7. id the pricipal val ue of +i d i d i i i - m+/ 8
19 C.N. 8. If lo si +i y = a+i the pro ve that a i) e cosh y - cos ii) ta = cot tah y I K J E /Math-I/ GQ/Comple umer -. Sho w that lo ta i i ta sih a. If ta lo+i y a i the pro ve that ta lo c y h where a a i ta sec e j. If +i ta ca ha ve real val ue the sho w that it is sec Eamples P. ANSWERS. i 6. i. z i ii z i. y y i ii iii 7 y DE MIVRE S THM I K J H G I K J cos + i si 6. modulus = i, arumet = / 6 C.N.. Modulus = cos sec C.N. I KJ I K J. i z i iii. z.. - Arumet = C.N. 6 Cos. -. cos ta C.N. 9. cos = cos 0 cos si cos si si = cos si - 0 cos si + si cos 6 = cos - cos si + cos si - si 8. A = 6, B = 0, C = 6 9
20 C.N si cos 6-6 cos + cos -0 6 cos cos cos + cos cos cos cos 6 8cos 6cos 8 8. cos Si si 8 + si 6 - si - 6 si 8 E /Math-I/ GQ/Comple umer C.N.. = cos k + + i si k +, k = 0,,,,,. = cos k + + i si k +, k = 0,, 6 6. =, i. = cos k + i si k +, k = 0,,,,. = cos k + + i si k +, k = 0,,,, ad ki k = cos + i si k = 0,,,, K J H G I K J 6. = cos k + + i si k +, k = 0,,,,, ad 6 6 = cos k + + i si k +, k = 0,, 7. = cos k + + i si k +, k = 0,,,,, ad 6 6 = cos k + + i si k +, k = 0,, 8. = cos k + - i si k +, k = 0,,,, ad 8 8 = cos k + + i si k +, k = 0,, 0
21 E /Math-I/ GQ/Comple umer. = cos k + i si k, k =,,,, k 0. = cos k + i si k, k =,,,, k 0 9. = cos k + + i si k +, k = 0,,, ad / = cos k + + i si k + k = 0,,, 0 = cos k + + i si k +, k = 0,,,, ad / = 0 cos k + + i si k + k = 0,,,,. = cos k + i si k +, k = 0,,,, k. = cos k + i si k +, k = 0,,,,, 6, k 7 7. = cos k + i si k +, k = 0,,,, k. = cos k + i si k, k =,,,, k 0. = cos k + i si k, k =,,,, k 0 6. = k + i si k cos, k =,,,, k 0 7. =, k = 0,,,,,, 6, 7 cos k + i sik = cos k + i si k +, k = 0,,, k, 6 6 C.N. I K J / k + /. cos, k 0,,. = cos k + i si k +, k = 0,,,,, ad 6 6 = cos k k i si, k = 0,,,,, commo roots are = k + i si k, k =,,, k 0,
22 E /Math-I/ GQ/Comple umer / k - k - 8. si / cos isi, k = 0,, Z = cos k + i si k + k = 0,,,, 0 0 C.N.. -i, i. -i, i C.N. 6. Si cosh y + i cos sih y. cos cosh y - i si sih y. sih cos y + i cosh si y. cosh cos y + i sih si y. si + i sih y cos + cosh y C.N. 8 i + si. lo - si 6.. i. C.N. 0 H G I K J N M Q P M P N Q ta - + i lo y + y y ii. lo + y - ta M P i y y y 6. N M sih + i si y cos + cos y ilo. ilo. i lo. lo + Q P d i d i C.N. a f. lo + i k + lo lo + am + fa + f i am f lo - a + f lo. lo a f a f lo i lo -. lo + i k + ta /. 6 lo 6
23 E /Math-I/ GQ/Comple umer C.N.. e - / lo - / I K J I K J I K J I K J I cos lo i si lo K J I K J. e Cos lo i si lo. e. ie. e cos lo i si lo 6. C.N. 6 - / / / i / - /. e cos i si C.N. 7 k +. e cos lo cos - i si lo cos I K J e
 COMPLEX NUMBERS AND DE MOIVRE'S THEOREM SYNOPSIS. Ay umber of the form x+iy where x, y R ad i = - is called a complex umber.. I the complex umber x+iy, x is called the real part ad y is called the imagiary
COMPLEX NUMBERS AND DE MOIVRE'S THEOREM SYNOPSIS. Ay umber of the form x+iy where x, y R ad i = - is called a complex umber.. I the complex umber x+iy, x is called the real part ad y is called the imagiary
Chapter 13: Complex Numbers
 Sectios 13.1 & 13.2 Comple umbers ad comple plae Comple cojugate Modulus of a comple umber 1. Comple umbers Comple umbers are of the form z = + iy,, y R, i 2 = 1. I the above defiitio, is the real part
Sectios 13.1 & 13.2 Comple umbers ad comple plae Comple cojugate Modulus of a comple umber 1. Comple umbers Comple umbers are of the form z = + iy,, y R, i 2 = 1. I the above defiitio, is the real part
Name of the Student:
 SUBJECT NAME : Trasforms ad Partial Diff Eq SUBJECT CODE : MA MATERIAL NAME : Problem Material MATERIAL CODE : JM8AM6 REGULATION : R8 UPDATED ON : April-May 4 (Sca the above QR code for the direct dowload
SUBJECT NAME : Trasforms ad Partial Diff Eq SUBJECT CODE : MA MATERIAL NAME : Problem Material MATERIAL CODE : JM8AM6 REGULATION : R8 UPDATED ON : April-May 4 (Sca the above QR code for the direct dowload
1. Complex numbers. Chapter 13: Complex Numbers. Modulus of a complex number. Complex conjugate. Complex numbers are of the form
 Comple umbers ad comple plae Comple cojugate Modulus of a comple umber Comple umbers Comple umbers are of the form Sectios 3 & 32 z = + i,, R, i 2 = I the above defiitio, is the real part of z ad is the
Comple umbers ad comple plae Comple cojugate Modulus of a comple umber Comple umbers Comple umbers are of the form Sectios 3 & 32 z = + i,, R, i 2 = I the above defiitio, is the real part of z ad is the
VITEEE 2018 MATHEMATICS QUESTION BANK
 VITEEE 8 MTHEMTICS QUESTION BNK, C = {,, 6}, the (B C) Ques. Give the sets {,,},B {, } is {} {,,, } {,,, } {,,,,, 6} Ques. s. d ( si cos ) c ta log( ta 6 Ques. The greatest umer amog 9,, 7 is ) c c cot
VITEEE 8 MTHEMTICS QUESTION BNK, C = {,, 6}, the (B C) Ques. Give the sets {,,},B {, } is {} {,,, } {,,, } {,,,,, 6} Ques. s. d ( si cos ) c ta log( ta 6 Ques. The greatest umer amog 9,, 7 is ) c c cot
Presentation of complex number in Cartesian and polar coordinate system
 a + bi, aεr, bεr i = z = a + bi a = Re(z), b = Im(z) give z = a + bi & w = c + di, a + bi = c + di a = c & b = d The complex cojugate of z = a + bi is z = a bi The sum of complex cojugates is real: z +
a + bi, aεr, bεr i = z = a + bi a = Re(z), b = Im(z) give z = a + bi & w = c + di, a + bi = c + di a = c & b = d The complex cojugate of z = a + bi is z = a bi The sum of complex cojugates is real: z +
Lecture 7: Polar representation of complex numbers
 Lecture 7: Polar represetatio of comple umbers See FLAP Module M3.1 Sectio.7 ad M3. Sectios 1 ad. 7.1 The Argad diagram I two dimesioal Cartesia coordiates (,), we are used to plottig the fuctio ( ) with
Lecture 7: Polar represetatio of comple umbers See FLAP Module M3.1 Sectio.7 ad M3. Sectios 1 ad. 7.1 The Argad diagram I two dimesioal Cartesia coordiates (,), we are used to plottig the fuctio ( ) with
(ii) Q.2 Reduce the following matrix to normal form and find its rank.
 B. E. Semester- (All Brach ecept Aero. Questio Bak Each questio has marks. Q. Fid the rak o 9 Q. Reduce the ollowig matri to ormal orm ad id its rak. Q. Fid iverse o a matri b Gauss Jorda Reductio method
B. E. Semester- (All Brach ecept Aero. Questio Bak Each questio has marks. Q. Fid the rak o 9 Q. Reduce the ollowig matri to ormal orm ad id its rak. Q. Fid iverse o a matri b Gauss Jorda Reductio method
Notation List. For Cambridge International Mathematics Qualifications. For use from 2020
 Notatio List For Cambridge Iteratioal Mathematics Qualificatios For use from 2020 Notatio List for Cambridge Iteratioal Mathematics Qualificatios (For use from 2020) Mathematical otatio Eamiatios for CIE
Notatio List For Cambridge Iteratioal Mathematics Qualificatios For use from 2020 Notatio List for Cambridge Iteratioal Mathematics Qualificatios (For use from 2020) Mathematical otatio Eamiatios for CIE
Chapter 10 Partial Differential Equations and Fourier Series
 Math-33 Chapter Partial Differetial Equatios November 6, 7 Chapter Partial Differetial Equatios ad Fourier Series Math-33 Chapter Partial Differetial Equatios November 6, 7. Boudary Value Problems for
Math-33 Chapter Partial Differetial Equatios November 6, 7 Chapter Partial Differetial Equatios ad Fourier Series Math-33 Chapter Partial Differetial Equatios November 6, 7. Boudary Value Problems for
CHAPTER 5: FOURIER SERIES PROPERTIES OF EVEN & ODD FUNCTION PLOT PERIODIC GRAPH
 CHAPTER : FOURIER SERIES PROPERTIES OF EVEN & ODD FUNCTION POT PERIODIC GRAPH PROPERTIES OF EVEN AND ODD FUNCTION Fuctio is said to be a eve uctio i: Fuctio is said to be a odd uctio i: Fuctio is said
CHAPTER : FOURIER SERIES PROPERTIES OF EVEN & ODD FUNCTION POT PERIODIC GRAPH PROPERTIES OF EVEN AND ODD FUNCTION Fuctio is said to be a eve uctio i: Fuctio is said to be a odd uctio i: Fuctio is said
Lecture 4. Properties of Logarithmic Function (Contd ) y Log z tan constant x. It follows that
 Lecture 4 Properties of Logarithmic Function (Contd ) Since, Logln iarg u Re Log ln( ) v Im Log tan constant It follows that u v, u v This shows that Re Logand Im Log are (i) continuous in C { :Re 0,Im
Lecture 4 Properties of Logarithmic Function (Contd ) Since, Logln iarg u Re Log ln( ) v Im Log tan constant It follows that u v, u v This shows that Re Logand Im Log are (i) continuous in C { :Re 0,Im
De Moivre s Theorem - ALL
 De Moivre s Theorem - ALL. Let x ad y be real umbers, ad be oe of the complex solutios of the equatio =. Evaluate: (a) + + ; (b) ( x + y)( x + y). [6]. (a) Sice is a complex umber which satisfies = 0,.
De Moivre s Theorem - ALL. Let x ad y be real umbers, ad be oe of the complex solutios of the equatio =. Evaluate: (a) + + ; (b) ( x + y)( x + y). [6]. (a) Sice is a complex umber which satisfies = 0,.
An application of a subset S of C onto another S' defines a function [f(z)] of the complex variable z.
![An application of a subset S of C onto another S' defines a function [f(z)] of the complex variable z. An application of a subset S of C onto another S' defines a function [f(z)] of the complex variable z.](/thumbs/82/84763354.jpg) Diola Bagaoko (1 ELEMENTARY FNCTIONS OFA COMPLEX VARIABLES I Basic Defiitio of a Fuctio of a Comple Variable A applicatio of a subset S of C oto aother S' defies a fuctio [f(] of the comple variable z
Diola Bagaoko (1 ELEMENTARY FNCTIONS OFA COMPLEX VARIABLES I Basic Defiitio of a Fuctio of a Comple Variable A applicatio of a subset S of C oto aother S' defies a fuctio [f(] of the comple variable z
02 - COMPLEX NUMBERS Page 1 ( Answers at the end of all questions ) l w l = 1, then z lies on
 0 - COMPLEX NUMBERS Page ( ) If the cube roots of uity are,,, the the roots of the equatio ( x - ) + 8 = 0 are ( a ) -, - +, - - ( b ) -, -, -, ( c ) -, -, - ( d ) -, +, + [ AIEEE 005 ] ( ) If z ad z are
0 - COMPLEX NUMBERS Page ( ) If the cube roots of uity are,,, the the roots of the equatio ( x - ) + 8 = 0 are ( a ) -, - +, - - ( b ) -, -, -, ( c ) -, -, - ( d ) -, +, + [ AIEEE 005 ] ( ) If z ad z are
, 4 is the second term U 2
 Balliteer Istitute 995-00 wwwleavigcertsolutioscom Leavig Cert Higher Maths Sequeces ad Series A sequece is a array of elemets seperated by commas E,,7,0,, The elemets are called the terms of the sequece
Balliteer Istitute 995-00 wwwleavigcertsolutioscom Leavig Cert Higher Maths Sequeces ad Series A sequece is a array of elemets seperated by commas E,,7,0,, The elemets are called the terms of the sequece
where c is a scaling constant, 0, 0,. r c sinh cos csinh cos cos, csinh cos sin, ccosh sin U csinh sin sin, csinh sin cos,0
 MATH 38:Partial Differetial Equatios Solutios to The Secod Midterm DEGENERATE ELLIPSOID COORDINATES. Problem PROOF: Give csih si cos, y csihsi si, z ccoshcos, where c is a scalig costat,,,. r We compute
MATH 38:Partial Differetial Equatios Solutios to The Secod Midterm DEGENERATE ELLIPSOID COORDINATES. Problem PROOF: Give csih si cos, y csihsi si, z ccoshcos, where c is a scalig costat,,,. r We compute
n=0 f n(z) converges, we say that f n (z) = lim N s N(z) (37)
 10 Power Series A fuctio defied by a series of fuctios Let {f } be defied o A C The formal sum f is called a series of fuctios If for ay z A, the series f (z) coverges, we say that f coverges o A I this
10 Power Series A fuctio defied by a series of fuctios Let {f } be defied o A C The formal sum f is called a series of fuctios If for ay z A, the series f (z) coverges, we say that f coverges o A I this
APPENDIX F Complex Numbers
 APPENDIX F Complex Numbers Operatios with Complex Numbers Complex Solutios of Quadratic Equatios Polar Form of a Complex Number Powers ad Roots of Complex Numbers Operatios with Complex Numbers Some equatios
APPENDIX F Complex Numbers Operatios with Complex Numbers Complex Solutios of Quadratic Equatios Polar Form of a Complex Number Powers ad Roots of Complex Numbers Operatios with Complex Numbers Some equatios
Complex Numbers. Brief Notes. z = a + bi
 Defiitios Complex Numbers Brief Notes A complex umber z is a expressio of the form: z = a + bi where a ad b are real umbers ad i is thought of as 1. We call a the real part of z, writte Re(z), ad b the
Defiitios Complex Numbers Brief Notes A complex umber z is a expressio of the form: z = a + bi where a ad b are real umbers ad i is thought of as 1. We call a the real part of z, writte Re(z), ad b the
Assignment ( ) Class-XI. = iii. v. A B= A B '
 Assigmet (8-9) Class-XI. Proe that: ( A B)' = A' B ' i A ( BAC) = ( A B) ( A C) ii A ( B C) = ( A B) ( A C) iv. A B= A B= φ v. A B= A B ' v A B B ' A'. A relatio R is dified o the set z of itegers as:
Assigmet (8-9) Class-XI. Proe that: ( A B)' = A' B ' i A ( BAC) = ( A B) ( A C) ii A ( B C) = ( A B) ( A C) iv. A B= A B= φ v. A B= A B ' v A B B ' A'. A relatio R is dified o the set z of itegers as:
Topic 1 2: Sequences and Series. A sequence is an ordered list of numbers, e.g. 1, 2, 4, 8, 16, or
 Topic : Sequeces ad Series A sequece is a ordered list of umbers, e.g.,,, 8, 6, or,,,.... A series is a sum of the terms of a sequece, e.g. + + + 8 + 6 + or... Sigma Notatio b The otatio f ( k) is shorthad
Topic : Sequeces ad Series A sequece is a ordered list of umbers, e.g.,,, 8, 6, or,,,.... A series is a sum of the terms of a sequece, e.g. + + + 8 + 6 + or... Sigma Notatio b The otatio f ( k) is shorthad
Appendix F: Complex Numbers
 Appedix F Complex Numbers F1 Appedix F: Complex Numbers Use the imagiary uit i to write complex umbers, ad to add, subtract, ad multiply complex umbers. Fid complex solutios of quadratic equatios. Write
Appedix F Complex Numbers F1 Appedix F: Complex Numbers Use the imagiary uit i to write complex umbers, ad to add, subtract, ad multiply complex umbers. Fid complex solutios of quadratic equatios. Write
19 Fourier Series and Practical Harmonic Analysis
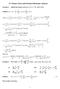 9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
9 Fourier Series ad Practica Harmoic Aaysis Eampe : Obtai the Fourier series of f ( ) e a i. a Soutio: Let f ( ) acos bsi sih a a a a a a e a a where a f ( ) d e d e e a a e a f ( ) cos d e cos d ( a cos
Chapter 4. Fourier Series
 Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Chapter 4. Fourier Series At this poit we are ready to ow cosider the caoical equatios. Cosider, for eample the heat equatio u t = u, < (4.) subject to u(, ) = si, u(, t) = u(, t) =. (4.) Here,
Math 4107: Abstract Algebra I Fall Webwork Assignment1-Groups (5 parts/problems) Solutions are on Webwork.
 Math 4107: Abstract Algebra I Fall 2017 Assigmet 1 Solutios 1. Webwork Assigmet1-Groups 5 parts/problems) Solutios are o Webwork. 2. Webwork Assigmet1-Subgroups 5 parts/problems) Solutios are o Webwork.
Math 4107: Abstract Algebra I Fall 2017 Assigmet 1 Solutios 1. Webwork Assigmet1-Groups 5 parts/problems) Solutios are o Webwork. 2. Webwork Assigmet1-Subgroups 5 parts/problems) Solutios are o Webwork.
Fundamental Concepts: Surfaces and Curves
 UNDAMENTAL CONCEPTS: SURACES AND CURVES CHAPTER udametal Cocepts: Surfaces ad Curves. INTRODUCTION This chapter describes two geometrical objects, vi., surfaces ad curves because the pla a ver importat
UNDAMENTAL CONCEPTS: SURACES AND CURVES CHAPTER udametal Cocepts: Surfaces ad Curves. INTRODUCTION This chapter describes two geometrical objects, vi., surfaces ad curves because the pla a ver importat
Taylor Series Mixed Exercise 6
 Taylor Series Mied Eercise Let f() cot ad a f(a) f () ( cos ec ) + cot f (a) f''() cotcosec + ( cosec ) f''(a) f'''() ( cosec cot cosec ) + cotcosec Substitutig ito the Taylor series epasio gives f() +
Taylor Series Mied Eercise Let f() cot ad a f(a) f () ( cos ec ) + cot f (a) f''() cotcosec + ( cosec ) f''(a) f'''() ( cosec cot cosec ) + cotcosec Substitutig ito the Taylor series epasio gives f() +
2012 GCE A Level H2 Maths Solution Paper Let x,
 GCE A Level H Maths Solutio Pape. Let, y ad z be the cost of a ticet fo ude yeas, betwee ad 5 yeas, ad ove 5 yeas categoies espectively. 9 + y + 4z =. 7 + 5y + z = 8. + 4y + 5z = 58.5 Fo ude, ticet costs
GCE A Level H Maths Solutio Pape. Let, y ad z be the cost of a ticet fo ude yeas, betwee ad 5 yeas, ad ove 5 yeas categoies espectively. 9 + y + 4z =. 7 + 5y + z = 8. + 4y + 5z = 58.5 Fo ude, ticet costs
Topic 9 - Taylor and MacLaurin Series
 Topic 9 - Taylor ad MacLauri Series A. Taylors Theorem. The use o power series is very commo i uctioal aalysis i act may useul ad commoly used uctios ca be writte as a power series ad this remarkable result
Topic 9 - Taylor ad MacLauri Series A. Taylors Theorem. The use o power series is very commo i uctioal aalysis i act may useul ad commoly used uctios ca be writte as a power series ad this remarkable result
Calculus 2 - D. Yuen Final Exam Review (Version 11/22/2017. Please report any possible typos.)
 Calculus - D Yue Fial Eam Review (Versio //7 Please report ay possible typos) NOTE: The review otes are oly o topics ot covered o previous eams See previous review sheets for summary of previous topics
Calculus - D Yue Fial Eam Review (Versio //7 Please report ay possible typos) NOTE: The review otes are oly o topics ot covered o previous eams See previous review sheets for summary of previous topics
ANSWERSHEET (TOPIC = ALGEBRA) COLLECTION #2
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC ALGEBRA) COLLECTION # Questio Type A.Sigle Correct Type Q. (B) Sol ( 5 7 ) ( 5 7 9 )!!!! C
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC ALGEBRA) COLLECTION # Questio Type A.Sigle Correct Type Q. (B) Sol ( 5 7 ) ( 5 7 9 )!!!! C
ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 4 Solutions [Numerical Methods]
![ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 4 Solutions [Numerical Methods] ENGI 4430 Advanced Calculus for Engineering Faculty of Engineering and Applied Science Problem Set 4 Solutions [Numerical Methods]](/thumbs/89/97848596.jpg) ENGI 3 Advaced Calculus or Egieerig Facult o Egieerig ad Applied Sciece Problem Set Solutios [Numerical Methods]. Use Simpso s rule with our itervals to estimate I si d a, b, h a si si.889 si 3 si.889
ENGI 3 Advaced Calculus or Egieerig Facult o Egieerig ad Applied Sciece Problem Set Solutios [Numerical Methods]. Use Simpso s rule with our itervals to estimate I si d a, b, h a si si.889 si 3 si.889
The Simplest Proofs of Both Arbitrarily Long. Arithmetic Progressions of primes. Abstract
 The Simplest Proofs of Both Arbitrarily Lo Arithmetic Proressios of primes Chu-Xua Jia P. O. Box 94, Beiji 00854 P. R. Chia cxjia@mail.bcf.et.c Abstract Usi Jia fuctios J ( ω ), J ( ω ) ad J ( ) 4 ω we
The Simplest Proofs of Both Arbitrarily Lo Arithmetic Proressios of primes Chu-Xua Jia P. O. Box 94, Beiji 00854 P. R. Chia cxjia@mail.bcf.et.c Abstract Usi Jia fuctios J ( ω ), J ( ω ) ad J ( ) 4 ω we
MA1200 Exercise for Chapter 7 Techniques of Differentiation Solutions. First Principle 1. a) To simplify the calculation, note. Then. lim h.
 MA00 Eercise for Chapter 7 Techiques of Differetiatio Solutios First Priciple a) To simplify the calculatio, ote The b) ( h) lim h 0 h lim h 0 h[ ( h) ( h) h ( h) ] f '( ) Product/Quotiet/Chai Rules a)
MA00 Eercise for Chapter 7 Techiques of Differetiatio Solutios First Priciple a) To simplify the calculatio, ote The b) ( h) lim h 0 h lim h 0 h[ ( h) ( h) h ( h) ] f '( ) Product/Quotiet/Chai Rules a)
[ 11 ] z of degree 2 as both degree 2 each. The degree of a polynomial in n variables is the maximum of the degrees of its terms.
![[ 11 ] z of degree 2 as both degree 2 each. The degree of a polynomial in n variables is the maximum of the degrees of its terms. [ 11 ] z of degree 2 as both degree 2 each. The degree of a polynomial in n variables is the maximum of the degrees of its terms.](/thumbs/82/84777652.jpg) [ 11 ] 1 1.1 Polyomial Fuctios 1 Algebra Ay fuctio f ( x) ax a1x... a1x a0 is a polyomial fuctio if ai ( i 0,1,,,..., ) is a costat which belogs to the set of real umbers ad the idices,, 1,...,1 are atural
[ 11 ] 1 1.1 Polyomial Fuctios 1 Algebra Ay fuctio f ( x) ax a1x... a1x a0 is a polyomial fuctio if ai ( i 0,1,,,..., ) is a costat which belogs to the set of real umbers ad the idices,, 1,...,1 are atural
Polynomial and Rational Functions. Polynomial functions and Their Graphs. Polynomial functions and Their Graphs. Examples
 Polomial ad Ratioal Fuctios Polomial fuctios ad Their Graphs Math 44 Precalculus Polomial ad Ratioal Fuctios Polomial Fuctios ad Their Graphs Polomial fuctios ad Their Graphs A Polomial of degree is a
Polomial ad Ratioal Fuctios Polomial fuctios ad Their Graphs Math 44 Precalculus Polomial ad Ratioal Fuctios Polomial Fuctios ad Their Graphs Polomial fuctios ad Their Graphs A Polomial of degree is a
Quiz. Use either the RATIO or ROOT TEST to determine whether the series is convergent or not.
 Quiz. Use either the RATIO or ROOT TEST to determie whether the series is coverget or ot. e .6 POWER SERIES Defiitio. A power series i about is a series of the form c 0 c a c a... c a... a 0 c a where
Quiz. Use either the RATIO or ROOT TEST to determie whether the series is coverget or ot. e .6 POWER SERIES Defiitio. A power series i about is a series of the form c 0 c a c a... c a... a 0 c a where
MATHEMATICS Code No. 13 INSTRUCTIONS
 DO NOT OPEN THIS TEST BOOKLET UNTIL YOU ARE ASKED TO DO SO COMBINED COMPETITIVE (PRELIMINARY) EXAMINATION, 0 Serial No. MATHEMATICS Code No. A Time Allowed : Two Hours Maimum Marks : 00 INSTRUCTIONS. IMMEDIATELY
DO NOT OPEN THIS TEST BOOKLET UNTIL YOU ARE ASKED TO DO SO COMBINED COMPETITIVE (PRELIMINARY) EXAMINATION, 0 Serial No. MATHEMATICS Code No. A Time Allowed : Two Hours Maimum Marks : 00 INSTRUCTIONS. IMMEDIATELY
Objective Mathematics
 . If sum of '' terms of a sequece is give by S Tr ( )( ), the 4 5 67 r (d) 4 9 r is equal to : T. Let a, b, c be distict o-zero real umbers such that a, b, c are i harmoic progressio ad a, b, c are i arithmetic
. If sum of '' terms of a sequece is give by S Tr ( )( ), the 4 5 67 r (d) 4 9 r is equal to : T. Let a, b, c be distict o-zero real umbers such that a, b, c are i harmoic progressio ad a, b, c are i arithmetic
LIMIT. f(a h). f(a + h). Lim x a. h 0. x 1. x 0. x 0. x 1. x 1. x 2. Lim f(x) 0 and. x 0
 J-Mathematics LIMIT. INTRODUCTION : The cocept of it of a fuctio is oe of the fudametal ideas that distiguishes calculus from algebra ad trigoometr. We use its to describe the wa a fuctio f varies. Some
J-Mathematics LIMIT. INTRODUCTION : The cocept of it of a fuctio is oe of the fudametal ideas that distiguishes calculus from algebra ad trigoometr. We use its to describe the wa a fuctio f varies. Some
Solutions for May. 3 x + 7 = 4 x x +
 Solutios for May 493. Prove that there is a atural umber with the followig characteristics: a) it is a multiple of 007; b) the first four digits i its decimal represetatio are 009; c) the last four digits
Solutios for May 493. Prove that there is a atural umber with the followig characteristics: a) it is a multiple of 007; b) the first four digits i its decimal represetatio are 009; c) the last four digits
PhysicsAndMathsTutor.com
 PhysicsAdMathsTutor.com physicsadmathstutor.com Jue 005 3. The fuctio f is defied by (a) Show that 5 + 1 3 f:, > 1. + + f( ) =, > 1. 1 (4) (b) Fid f 1 (). (3) The fuctio g is defied by g: + 5, R. 1 4 (c)
PhysicsAdMathsTutor.com physicsadmathstutor.com Jue 005 3. The fuctio f is defied by (a) Show that 5 + 1 3 f:, > 1. + + f( ) =, > 1. 1 (4) (b) Fid f 1 (). (3) The fuctio g is defied by g: + 5, R. 1 4 (c)
Mathematics Extension 2
 009 HIGHER SCHOOL CERTIFICATE EXAMINATION Mathematics Etesio Geeral Istructios Readig time 5 miutes Workig time hours Write usig black or blue pe Board-approved calculators may be used A table of stadard
009 HIGHER SCHOOL CERTIFICATE EXAMINATION Mathematics Etesio Geeral Istructios Readig time 5 miutes Workig time hours Write usig black or blue pe Board-approved calculators may be used A table of stadard
ANSWERS SOLUTIONS iiii i. and 1. Thus, we have. i i i. i, A.
 013 ΜΑΘ Natioal Covetio ANSWERS (1) C A A A B (6) B D D A B (11) C D D A A (16) D B A A C (1) D B C B C (6) D C B C C 1. We have SOLUTIONS 1 3 11 61 iiii 131161 i 013 013, C.. The powers of i cycle betwee
013 ΜΑΘ Natioal Covetio ANSWERS (1) C A A A B (6) B D D A B (11) C D D A A (16) D B A A C (1) D B C B C (6) D C B C C 1. We have SOLUTIONS 1 3 11 61 iiii 131161 i 013 013, C.. The powers of i cycle betwee
Mathematics Extension 2
 004 HIGHER SCHOOL CERTIFICATE EXAMINATION Mathematics Etesio Geeral Istructios Readig time 5 miutes Workig time hours Write usig black or blue pe Board-approved calculators may be used A table of stadard
004 HIGHER SCHOOL CERTIFICATE EXAMINATION Mathematics Etesio Geeral Istructios Readig time 5 miutes Workig time hours Write usig black or blue pe Board-approved calculators may be used A table of stadard
Notes 19 Bessel Functions
 ECE 638 Fall 17 David R. Jackso Notes 19 Bessel Fuctios Notes are from D. R. Wilto, Dept. of ECE 1 Cylidrical Wave Fuctios Helmholtz equatio: ψ + k ψ = I cylidrical coordiates: ψ 1 ψ 1 ψ ψ ρ ρ ρ ρ φ z
ECE 638 Fall 17 David R. Jackso Notes 19 Bessel Fuctios Notes are from D. R. Wilto, Dept. of ECE 1 Cylidrical Wave Fuctios Helmholtz equatio: ψ + k ψ = I cylidrical coordiates: ψ 1 ψ 1 ψ ψ ρ ρ ρ ρ φ z
Poornima University, For any query, contact us at: ,18
 AIEEE/1/MAHS 1 S. No Questios Solutios Q.1 he circle passig through (1, ) ad touchig the axis of x at (, ) also passes through the poit (a) (, ) (b) (, ) (c) (, ) (d) (, ) Q. ABCD is a trapezium such that
AIEEE/1/MAHS 1 S. No Questios Solutios Q.1 he circle passig through (1, ) ad touchig the axis of x at (, ) also passes through the poit (a) (, ) (b) (, ) (c) (, ) (d) (, ) Q. ABCD is a trapezium such that
Consortium of Medical Engineering and Dental Colleges of Karnataka (COMEDK) Undergraduate Entrance Test(UGET) Maths-2012
 Cosortium of Medical Egieerig ad Detal Colleges of Karataka (COMEDK) Udergraduate Etrace Test(UGET) Maths-0. If the area of the circle 7 7 7 k 0 is sq. uits, the the value of k is As: (b) b) 0 7 K 0 c)
Cosortium of Medical Egieerig ad Detal Colleges of Karataka (COMEDK) Udergraduate Etrace Test(UGET) Maths-0. If the area of the circle 7 7 7 k 0 is sq. uits, the the value of k is As: (b) b) 0 7 K 0 c)
) + 2. Mathematics 2 Outcome 1. Further Differentiation (8/9 pers) Cumulative total = 64 periods. Lesson, Outline, Approach etc.
 Further Differetiatio (8/9 pers Mathematics Outcome Go over the proofs of the derivatives o si ad cos. [use y = si => = siy etc.] * Ask studets to fid derivative of cos. * Ask why d d (si = (cos see graphs.
Further Differetiatio (8/9 pers Mathematics Outcome Go over the proofs of the derivatives o si ad cos. [use y = si => = siy etc.] * Ask studets to fid derivative of cos. * Ask why d d (si = (cos see graphs.
Special Involute-Evolute Partner D -Curves in E 3
 Special Ivolute-Evolute Parter D -Curves i E ÖZCAN BEKTAŞ SAL IM YÜCE Abstract I this paper, we take ito accout the opiio of ivolute-evolute curves which lie o fully surfaces ad by taki ito accout the
Special Ivolute-Evolute Parter D -Curves i E ÖZCAN BEKTAŞ SAL IM YÜCE Abstract I this paper, we take ito accout the opiio of ivolute-evolute curves which lie o fully surfaces ad by taki ito accout the
MEI Conference 2009 Stretching students: A2 Core
 MEI Coferece 009 Stretchig studets: A Core Preseter: Berard Murph berard.murph@mei.org.uk Workshop G How ca ou prove that these si right-agled triagles fit together eactl to make a 3-4-5 triagle? What
MEI Coferece 009 Stretchig studets: A Core Preseter: Berard Murph berard.murph@mei.org.uk Workshop G How ca ou prove that these si right-agled triagles fit together eactl to make a 3-4-5 triagle? What
Elementary Algebra and Geometry
 1 Elemetary Algera ad Geometry 1.1 Fudametal Properties (Real Numers) a + = + a Commutative Law for Additio (a + ) + c = a + ( + c) Associative Law for Additio a + 0 = 0 + a Idetity Law for Additio a +
1 Elemetary Algera ad Geometry 1.1 Fudametal Properties (Real Numers) a + = + a Commutative Law for Additio (a + ) + c = a + ( + c) Associative Law for Additio a + 0 = 0 + a Idetity Law for Additio a +
FUNCTIONS. Note: Example of a function may be represented diagrammatically. The above example can be written diagrammatically as follows.
 FUNCTIONS Def : A relation f from a set A into a set is said to be a function or mapping from A into if for each A there eists a unique such that (, ) f. It is denoted b f : A. Note: Eample of a function
FUNCTIONS Def : A relation f from a set A into a set is said to be a function or mapping from A into if for each A there eists a unique such that (, ) f. It is denoted b f : A. Note: Eample of a function
2. Fourier Series, Fourier Integrals and Fourier Transforms
 Mathematics IV -. Fourier Series, Fourier Itegrals ad Fourier Trasforms The Fourier series are used for the aalysis of the periodic pheomea, which ofte appear i physics ad egieerig. The Fourier itegrals
Mathematics IV -. Fourier Series, Fourier Itegrals ad Fourier Trasforms The Fourier series are used for the aalysis of the periodic pheomea, which ofte appear i physics ad egieerig. The Fourier itegrals
(Figure 2.9), we observe x. and we write. (b) as x, x 1. and we write. We say that the line y 0 is a horizontal asymptote of the graph of f.
 The symbol for ifiity ( ) does ot represet a real umber. We use to describe the behavior of a fuctio whe the values i its domai or rage outgrow all fiite bouds. For eample, whe we say the limit of f as
The symbol for ifiity ( ) does ot represet a real umber. We use to describe the behavior of a fuctio whe the values i its domai or rage outgrow all fiite bouds. For eample, whe we say the limit of f as
Definition 2.1 (The Derivative) (page 54) is a function. The derivative of a function f with respect to x, represented by. f ', is defined by
 Chapter DACS Lok 004/05 CHAPTER DIFFERENTIATION. THE GEOMETRICAL MEANING OF DIFFERENTIATION (page 54) Defiitio. (The Derivative) (page 54) Let f () is a fctio. The erivative of a fctio f with respect to,
Chapter DACS Lok 004/05 CHAPTER DIFFERENTIATION. THE GEOMETRICAL MEANING OF DIFFERENTIATION (page 54) Defiitio. (The Derivative) (page 54) Let f () is a fctio. The erivative of a fctio f with respect to,
GCE Further Mathematics (6360) Further Pure Unit 2 (MFP2) Textbook. Version: 1.5
 GCE Further Mathematics (660) Further Pure Uit (MFP) Tetbook Versio: 5 MFP Tetbook A-level Further Mathematics 660 Further Pure : Cotets Chapter : Comple umbers 4 Itroductio 5 The geeral comple umber 5
GCE Further Mathematics (660) Further Pure Uit (MFP) Tetbook Versio: 5 MFP Tetbook A-level Further Mathematics 660 Further Pure : Cotets Chapter : Comple umbers 4 Itroductio 5 The geeral comple umber 5
} is said to be a Cauchy sequence provided the following condition is true.
 Math 4200, Fial Exam Review I. Itroductio to Proofs 1. Prove the Pythagorea theorem. 2. Show that 43 is a irratioal umber. II. Itroductio to Logic 1. Costruct a truth table for the statemet ( p ad ~ r
Math 4200, Fial Exam Review I. Itroductio to Proofs 1. Prove the Pythagorea theorem. 2. Show that 43 is a irratioal umber. II. Itroductio to Logic 1. Costruct a truth table for the statemet ( p ad ~ r
Sequences, Sums, and Products
 CSCE 222 Discrete Structures for Computig Sequeces, Sums, ad Products Dr. Philip C. Ritchey Sequeces A sequece is a fuctio from a subset of the itegers to a set S. A discrete structure used to represet
CSCE 222 Discrete Structures for Computig Sequeces, Sums, ad Products Dr. Philip C. Ritchey Sequeces A sequece is a fuctio from a subset of the itegers to a set S. A discrete structure used to represet
PAPER : IIT-JAM 2010
 MATHEMATICS-MA (CODE A) Q.-Q.5: Oly oe optio is correct for each questio. Each questio carries (+6) marks for correct aswer ad ( ) marks for icorrect aswer.. Which of the followig coditios does NOT esure
MATHEMATICS-MA (CODE A) Q.-Q.5: Oly oe optio is correct for each questio. Each questio carries (+6) marks for correct aswer ad ( ) marks for icorrect aswer.. Which of the followig coditios does NOT esure
PHYSICS 116A Homework 2 Solutions
 PHYSICS 6A Homework 2 Solutios I. [optioal] Boas, Ch., 6, Qu. 30 (proof of the ratio test). Just follow the hits. If ρ, the ratio of succcessive terms for is less tha, the hits show that the terms of the
PHYSICS 6A Homework 2 Solutios I. [optioal] Boas, Ch., 6, Qu. 30 (proof of the ratio test). Just follow the hits. If ρ, the ratio of succcessive terms for is less tha, the hits show that the terms of the
x x x Using a second Taylor polynomial with remainder, find the best constant C so that for x 0,
 Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
Math Activity 9( Due with Fial Eam) Usig first ad secod Taylor polyomials with remaider, show that for, 8 Usig a secod Taylor polyomial with remaider, fid the best costat C so that for, C 9 The th Derivative
SOLUTION SET VI FOR FALL [(n + 2)(n + 1)a n+2 a n 1 ]x n = 0,
![SOLUTION SET VI FOR FALL [(n + 2)(n + 1)a n+2 a n 1 ]x n = 0, SOLUTION SET VI FOR FALL [(n + 2)(n + 1)a n+2 a n 1 ]x n = 0,](/thumbs/94/119566625.jpg) 4. Series Solutios of Differetial Equatios:Special Fuctios 4.. Illustrative examples.. 5. Obtai the geeral solutio of each of the followig differetial equatios i terms of Maclauri series: d y (a dx = xy,
4. Series Solutios of Differetial Equatios:Special Fuctios 4.. Illustrative examples.. 5. Obtai the geeral solutio of each of the followig differetial equatios i terms of Maclauri series: d y (a dx = xy,
ANSWER KEY WITH SOLUTION PAPER - 2 MATHEMATICS SECTION A 1. B 2. B 3. D 4. C 5. B 6. C 7. C 8. B 9. B 10. D 11. C 12. C 13. A 14. B 15.
 TARGET IIT-JEE t [ACCELERATION] V0 to V BATCH ADVANCED TEST DATE : - 09-06 ANSWER KEY WITH SOLUTION PAPER - MATHEMATICS SECTION A. B. B. D. C 5. B 6. C 7. C 8. B 9. B 0. D. C. C. A. B 5. C 6. D 7. A 8.
TARGET IIT-JEE t [ACCELERATION] V0 to V BATCH ADVANCED TEST DATE : - 09-06 ANSWER KEY WITH SOLUTION PAPER - MATHEMATICS SECTION A. B. B. D. C 5. B 6. C 7. C 8. B 9. B 0. D. C. C. A. B 5. C 6. D 7. A 8.
Solutions to Final Exam Review Problems
 . Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
. Let f(x) 4+x. Solutios to Fial Exam Review Problems Math 5C, Witer 2007 (a) Fid the Maclauri series for f(x), ad compute its radius of covergece. Solutio. f(x) 4( ( x/4)) ( x/4) ( ) 4 4 + x. Sice the
: Transforms and Partial Differential Equations
 Trasforms ad Partial Differetial Equatios 018 SUBJECT NAME : Trasforms ad Partial Differetial Equatios SUBJECT CODE : MA 6351 MATERIAL NAME : Part A questios REGULATION : R013 WEBSITE : wwwharigaeshcom
Trasforms ad Partial Differetial Equatios 018 SUBJECT NAME : Trasforms ad Partial Differetial Equatios SUBJECT CODE : MA 6351 MATERIAL NAME : Part A questios REGULATION : R013 WEBSITE : wwwharigaeshcom
Sets. Sets. Operations on Sets Laws of Algebra of Sets Cardinal Number of a Finite and Infinite Set. Representation of Sets Power Set Venn Diagram
 Sets MILESTONE Sets Represetatio of Sets Power Set Ve Diagram Operatios o Sets Laws of lgebra of Sets ardial Number of a Fiite ad Ifiite Set I Mathematical laguage all livig ad o-livig thigs i uiverse
Sets MILESTONE Sets Represetatio of Sets Power Set Ve Diagram Operatios o Sets Laws of lgebra of Sets ardial Number of a Fiite ad Ifiite Set I Mathematical laguage all livig ad o-livig thigs i uiverse
SCHOOL OF MATHEMATICS AND STATISTICS. Mathematics II (Materials)
 Dt proie: Form Sheet MAS5 SCHOOL OF MATHEMATICS AND STATISTICS Mthemtics II (Mteris) Atm Semester -3 hors Mrks wi e wre or swers to qestios i Sectio A or or est THREE swers to qestios i Sectio. Sectio
Dt proie: Form Sheet MAS5 SCHOOL OF MATHEMATICS AND STATISTICS Mthemtics II (Mteris) Atm Semester -3 hors Mrks wi e wre or swers to qestios i Sectio A or or est THREE swers to qestios i Sectio. Sectio
P a g e 5 1 of R e p o r t P B 4 / 0 9
 P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
P a g e 5 1 of R e p o r t P B 4 / 0 9 J A R T a l s o c o n c l u d e d t h a t a l t h o u g h t h e i n t e n t o f N e l s o n s r e h a b i l i t a t i o n p l a n i s t o e n h a n c e c o n n e
physicsandmathstutor.com
 physicsadmathstuto.com physicsadmathstuto.com Jue 005. A cuve has equatio blak x + xy 3y + 16 = 0. dy Fid the coodiates of the poits o the cuve whee 0. dx = (7) Q (Total 7 maks) *N03B034* 3 Tu ove physicsadmathstuto.com
physicsadmathstuto.com physicsadmathstuto.com Jue 005. A cuve has equatio blak x + xy 3y + 16 = 0. dy Fid the coodiates of the poits o the cuve whee 0. dx = (7) Q (Total 7 maks) *N03B034* 3 Tu ove physicsadmathstuto.com
Mathematics Extension 1
 016 Bored of Studies Trial Eamiatios Mathematics Etesio 1 3 rd ctober 016 Geeral Istructios Total Marks 70 Readig time 5 miutes Workig time hours Write usig black or blue pe Black pe is preferred Board-approved
016 Bored of Studies Trial Eamiatios Mathematics Etesio 1 3 rd ctober 016 Geeral Istructios Total Marks 70 Readig time 5 miutes Workig time hours Write usig black or blue pe Black pe is preferred Board-approved
In number theory we will generally be working with integers, though occasionally fractions and irrationals will come into play.
 Number Theory Math 5840 otes. Sectio 1: Axioms. I umber theory we will geerally be workig with itegers, though occasioally fractios ad irratioals will come ito play. Notatio: Z deotes the set of all itegers
Number Theory Math 5840 otes. Sectio 1: Axioms. I umber theory we will geerally be workig with itegers, though occasioally fractios ad irratioals will come ito play. Notatio: Z deotes the set of all itegers
2 Geometric interpretation of complex numbers
 2 Geometric iterpretatio of complex umbers 2.1 Defiitio I will start fially with a precise defiitio, assumig that such mathematical object as vector space R 2 is well familiar to the studets. Recall that
2 Geometric iterpretatio of complex umbers 2.1 Defiitio I will start fially with a precise defiitio, assumig that such mathematical object as vector space R 2 is well familiar to the studets. Recall that
APPM 4360/5360 Exam #2 Solutions Spring 2015
 APPM 436/536 Exam # Solutios Sprig 5 O the frot of your bluebook, write your ame ad make a gradig table. You re allowed oe sheet (letter-sized, frot ad back of otes. You are ot allowed to use textbooks,
APPM 436/536 Exam # Solutios Sprig 5 O the frot of your bluebook, write your ame ad make a gradig table. You re allowed oe sheet (letter-sized, frot ad back of otes. You are ot allowed to use textbooks,
U8L1: Sec Equations of Lines in R 2
 MCVU U8L: Sec. 8.9. Equatios of Lies i R Review of Equatios of a Straight Lie (-D) Cosider the lie passig through A (-,) with slope, as show i the diagram below. I poit slope form, the equatio of the lie
MCVU U8L: Sec. 8.9. Equatios of Lies i R Review of Equatios of a Straight Lie (-D) Cosider the lie passig through A (-,) with slope, as show i the diagram below. I poit slope form, the equatio of the lie
9795 FURTHER MATHEMATICS
 CAMBRIDGE INTERNATIONAL EXAMINATIONS Pre-U Certificate MARK SCHEME for the May/Jue series 9795 FURTHER MATHEMATICS 9795/ Paper (Further Pure Mathematics, maximum raw mark This mark scheme is published
CAMBRIDGE INTERNATIONAL EXAMINATIONS Pre-U Certificate MARK SCHEME for the May/Jue series 9795 FURTHER MATHEMATICS 9795/ Paper (Further Pure Mathematics, maximum raw mark This mark scheme is published
Math 143 Review for Quiz 14 page 1
 Math Review for Quiz age. Solve each of the followig iequalities. x + a) < x + x c) x d) x x +
Math Review for Quiz age. Solve each of the followig iequalities. x + a) < x + x c) x d) x x +
SEQUENCE AND SERIES NCERT
 9. Overview By a sequece, we mea a arragemet of umbers i a defiite order accordig to some rule. We deote the terms of a sequece by a, a,..., etc., the subscript deotes the positio of the term. I view of
9. Overview By a sequece, we mea a arragemet of umbers i a defiite order accordig to some rule. We deote the terms of a sequece by a, a,..., etc., the subscript deotes the positio of the term. I view of
3 Show in each case that there is a root of the given equation in the given interval. a x 3 = 12 4
 C Worksheet A Show i each case that there is a root of the equatio f() = 0 i the give iterval a f() = + 7 (, ) f() = 5 cos (05, ) c f() = e + + 5 ( 6, 5) d f() = 4 5 + (, ) e f() = l (4 ) + (04, 05) f
C Worksheet A Show i each case that there is a root of the equatio f() = 0 i the give iterval a f() = + 7 (, ) f() = 5 cos (05, ) c f() = e + + 5 ( 6, 5) d f() = 4 5 + (, ) e f() = l (4 ) + (04, 05) f
PhysicsAndMathsTutor.com
 PhysicsAdMathsTutor.com physicsadmathstutor.com Jue 005 4. f(x) = 3e x 1 l x, x > 0. (a) Differetiate to fid f (x). (3) The curve with equatio y = f(x) has a turig poit at P. The x-coordiate of P is α.
PhysicsAdMathsTutor.com physicsadmathstutor.com Jue 005 4. f(x) = 3e x 1 l x, x > 0. (a) Differetiate to fid f (x). (3) The curve with equatio y = f(x) has a turig poit at P. The x-coordiate of P is α.
BRAIN TEASURES TRIGONOMETRICAL RATIOS BY ABHIJIT KUMAR JHA EXERCISE I. or tan &, lie between 0 &, then find the value of tan 2.
 EXERCISE I Q Prove that cos² + cos² (+ ) cos cos cos (+ ) ² Q Prove that cos ² + cos (+ ) + cos (+ ) Q Prove that, ta + ta + ta + cot cot Q Prove that : (a) ta 0 ta 0 ta 60 ta 0 (b) ta 9 ta 7 ta 6 + ta
EXERCISE I Q Prove that cos² + cos² (+ ) cos cos cos (+ ) ² Q Prove that cos ² + cos (+ ) + cos (+ ) Q Prove that, ta + ta + ta + cot cot Q Prove that : (a) ta 0 ta 0 ta 60 ta 0 (b) ta 9 ta 7 ta 6 + ta
COMM 602: Digital Signal Processing
 COMM 60: Digital Sigal Processig Lecture 4 -Properties of LTIS Usig Z-Trasform -Iverse Z-Trasform Properties of LTIS Usig Z-Trasform Properties of LTIS Usig Z-Trasform -ve +ve Properties of LTIS Usig Z-Trasform
COMM 60: Digital Sigal Processig Lecture 4 -Properties of LTIS Usig Z-Trasform -Iverse Z-Trasform Properties of LTIS Usig Z-Trasform Properties of LTIS Usig Z-Trasform -ve +ve Properties of LTIS Usig Z-Trasform
AIEEE 2004 (MATHEMATICS)
 AIEEE 00 (MATHEMATICS) Importat Istructios: i) The test is of hours duratio. ii) The test cosists of 75 questios. iii) The maimum marks are 5. iv) For each correct aswer you will get marks ad for a wrog
AIEEE 00 (MATHEMATICS) Importat Istructios: i) The test is of hours duratio. ii) The test cosists of 75 questios. iii) The maimum marks are 5. iv) For each correct aswer you will get marks ad for a wrog
Modern Algebra. Previous year Questions from 2017 to Ramanasri
 Moder Algebra Previous year Questios from 017 to 199 Ramaasri 017 S H O P NO- 4, 1 S T F L O O R, N E A R R A P I D F L O U R M I L L S, O L D R A J E N D E R N A G A R, N E W D E L H I. W E B S I T E
Moder Algebra Previous year Questios from 017 to 199 Ramaasri 017 S H O P NO- 4, 1 S T F L O O R, N E A R R A P I D F L O U R M I L L S, O L D R A J E N D E R N A G A R, N E W D E L H I. W E B S I T E
Chapter 1. Complex Numbers. Dr. Pulak Sahoo
 Chapter 1 Complex Numbers BY Dr. Pulak Sahoo Assistat Professor Departmet of Mathematics Uiversity Of Kalyai West Begal, Idia E-mail : sahoopulak1@gmail.com 1 Module-2: Stereographic Projectio 1 Euler
Chapter 1 Complex Numbers BY Dr. Pulak Sahoo Assistat Professor Departmet of Mathematics Uiversity Of Kalyai West Begal, Idia E-mail : sahoopulak1@gmail.com 1 Module-2: Stereographic Projectio 1 Euler
WBJEE Answer Keys by Aakash Institute, Kolkata Centre
 WBJEE - 7 Aswer Keys by, Kolkata Cetre MATHEMATICS Q.No. B A C B A C A B 3 D C B B 4 B C D D 5 D A B B 6 C D B B 7 B C C A 8 B B A A 9 A * B D C C B B D A A D B B C B 3 A D D D 4 C B A A 5 C B B B 6 C
WBJEE - 7 Aswer Keys by, Kolkata Cetre MATHEMATICS Q.No. B A C B A C A B 3 D C B B 4 B C D D 5 D A B B 6 C D B B 7 B C C A 8 B B A A 9 A * B D C C B B D A A D B B C B 3 A D D D 4 C B A A 5 C B B B 6 C
T h e C S E T I P r o j e c t
 T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
T h e P r o j e c t T H E P R O J E C T T A B L E O F C O N T E N T S A r t i c l e P a g e C o m p r e h e n s i v e A s s es s m e n t o f t h e U F O / E T I P h e n o m e n o n M a y 1 9 9 1 1 E T
Stanford Math Circle January 21, Complex Numbers
 Staford Math Circle Jauary, 007 Some History Tatiaa Shubi (shubi@mathsjsuedu) Complex Numbers Let us try to solve the equatio x = 5x + x = is a obvious solutio Also, x 5x = ( x )( x + x + ) = 0 yields
Staford Math Circle Jauary, 007 Some History Tatiaa Shubi (shubi@mathsjsuedu) Complex Numbers Let us try to solve the equatio x = 5x + x = is a obvious solutio Also, x 5x = ( x )( x + x + ) = 0 yields
HKDSE Exam Questions Distribution
 HKDSE Eam Questios Distributio Sample Paper Practice Paper DSE 0 Topics A B A B A B. Biomial Theorem. Mathematical Iductio 0 3 3 3. More about Trigoometric Fuctios, 0, 3 0 3. Limits 6. Differetiatio 7
HKDSE Eam Questios Distributio Sample Paper Practice Paper DSE 0 Topics A B A B A B. Biomial Theorem. Mathematical Iductio 0 3 3 3. More about Trigoometric Fuctios, 0, 3 0 3. Limits 6. Differetiatio 7
MOCK TEST - 02 COMMON ENTRANCE TEST 2012 SUBJECT: MATHEMATICS Time: 1.10Hrs Max. Marks 60 Questions 60. then x 2 =
 MOCK TEST - 0 COMMON ENTRANCE TEST 0 SUBJECT: MATHEMATICS Time:.0Hrs Max. Marks 60 Questios 60. The value of si cot si 3 cos sec + + 4 4 a) 0 b) c) 4 6 + x x. If Ta - α + x + x the x a) cos α b) Taα c)
MOCK TEST - 0 COMMON ENTRANCE TEST 0 SUBJECT: MATHEMATICS Time:.0Hrs Max. Marks 60 Questios 60. The value of si cot si 3 cos sec + + 4 4 a) 0 b) c) 4 6 + x x. If Ta - α + x + x the x a) cos α b) Taα c)
Some Basic Diophantine Equations
 Some Basic iophatie Equatios R.Maikada, epartmet of Mathematics, M.I.E.T. Egieerig College, Tiruchirappalli-7. Email: maimaths78@gmail.com bstract- - I this paper we preset a method for solvig the iophatie
Some Basic iophatie Equatios R.Maikada, epartmet of Mathematics, M.I.E.T. Egieerig College, Tiruchirappalli-7. Email: maimaths78@gmail.com bstract- - I this paper we preset a method for solvig the iophatie
LIMITS AND DERIVATIVES
 Capter LIMITS AND DERIVATIVES. Overview.. Limits of a fuctio Let f be a fuctio defied i a domai wic we take to be a iterval, say, I. We sall study te cocept of it of f at a poit a i I. We say f ( ) is
Capter LIMITS AND DERIVATIVES. Overview.. Limits of a fuctio Let f be a fuctio defied i a domai wic we take to be a iterval, say, I. We sall study te cocept of it of f at a poit a i I. We say f ( ) is
Matrix Algebra 2.2 THE INVERSE OF A MATRIX Pearson Education, Inc.
 2 Matrix Algebra 2.2 THE INVERSE OF A MATRIX MATRIX OPERATIONS A matrix A is said to be ivertible if there is a matrix C such that CA = I ad AC = I where, the idetity matrix. I = I I this case, C is a
2 Matrix Algebra 2.2 THE INVERSE OF A MATRIX MATRIX OPERATIONS A matrix A is said to be ivertible if there is a matrix C such that CA = I ad AC = I where, the idetity matrix. I = I I this case, C is a
3sin A 1 2sin B. 3π x is a solution. 1. If A and B are acute positive angles satisfying the equation 3sin A 2sin B 1 and 3sin 2A 2sin 2B 0, then A 2B
 1. If A ad B are acute positive agles satisfyig the equatio 3si A si B 1 ad 3si A si B 0, the A B (a) (b) (c) (d) 6. 3 si A + si B = 1 3si A 1 si B 3 si A = cosb Also 3 si A si B = 0 si B = 3 si A Now,
1. If A ad B are acute positive agles satisfyig the equatio 3si A si B 1 ad 3si A si B 0, the A B (a) (b) (c) (d) 6. 3 si A + si B = 1 3si A 1 si B 3 si A = cosb Also 3 si A si B = 0 si B = 3 si A Now,
CHAPTER 4 FOURIER SERIES
 CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
CHAPTER 4 FOURIER SERIES CONTENTS PAGE 4. Periodic Fuctio 4. Eve ad Odd Fuctio 3 4.3 Fourier Series for Periodic Fuctio 9 4.4 Fourier Series for Haf Rage Epasios 4.5 Approimate Sum of the Ifiite Series
If a subset E of R contains no open interval, is it of zero measure? For instance, is the set of irrationals in [0, 1] is of measure zero?
![If a subset E of R contains no open interval, is it of zero measure? For instance, is the set of irrationals in [0, 1] is of measure zero? If a subset E of R contains no open interval, is it of zero measure? For instance, is the set of irrationals in [0, 1] is of measure zero?](/thumbs/89/99848926.jpg) 2 Lebesgue Measure I Chapter 1 we defied the cocept of a set of measure zero, ad we have observed that every coutable set is of measure zero. Here are some atural questios: If a subset E of R cotais a
2 Lebesgue Measure I Chapter 1 we defied the cocept of a set of measure zero, ad we have observed that every coutable set is of measure zero. Here are some atural questios: If a subset E of R cotais a
Different kinds of Mathematical Induction
 Differet ids of Mathematical Iductio () Mathematical Iductio Give A N, [ A (a A a A)] A N () (First) Priciple of Mathematical Iductio Let P() be a propositio (ope setece), if we put A { : N p() is true}
Differet ids of Mathematical Iductio () Mathematical Iductio Give A N, [ A (a A a A)] A N () (First) Priciple of Mathematical Iductio Let P() be a propositio (ope setece), if we put A { : N p() is true}

 6. If si () + cos () =, the is equal to :. If <
6. If si () + cos () =, the is equal to :. If <