Robust Rate-Maximization Game Under Bounded Channel Uncertainty
|
|
|
- Prosper Benson
- 5 years ago
- Views:
Transcription
1 Robust Rate-Maximization Game Under Bounded Channel Uncertainty Amod JG Anandkumar, Student Member, IEEE, Animashree Anandkumar, Member, IEEE, Sangarapillai Lambotharan, Senior Member, IEEE, and Jonathon A Chambers, Fellow, IEEE arxiv:0566v csit] 30 Sep 0 Abstract We consider the problem of decentralized power allocation for competitive rate-maximization in a frequencyselective Gaussian interference channel under bounded channel uncertainty We formulate a distribution-free robust framework for the rate-maximization game We present the robustoptimization equilibrium for this game and derive sufficient conditions for its existence and uniqueness We show that an iterative waterfilling algorithm converges to this equilibrium under certain sufficient conditions We analyse the social properties of the equilibrium under varying channel uncertainty bounds for the two-user case We also observe an interesting phenomenon that the equilibrium moves towards a frequency-division multiple access solution for any set of channel coefficients under increasing channel uncertainty bounds We further prove that increasing channel uncertainty can lead to a more efficient equilibrium, and hence, a better sum rate in certain two-user communication systems Finally, we confirm, through simulations, this improvement in equilibrium efficiency is also observed in systems with a higher number of users Index Terms Game theory, rate-maximization, Nash equilibrium, waterfilling, CSI uncertainty, robust games I INTRODUCTION Rate-maximization is an important signal processing problem for power-constrained multi-user wireless systems It involves solving a power control problem for mutually interfering users operating across multiple frequencies in a Gaussian interference channel In modern wireless systems where users may enter or leave the system freely and make decisions independently, decentralized control approaches and distributed algorithms are necessary Game-theoretic methods provide an appropriate set of tools for the design of such algorithms and have been increasingly used for the analysis and study of communications problems 3] In multi-user systems, the users can either cooperate with each other to achieve a socially optimal solution or compete against one another to optimize their own selfish objectives Cooperative game-theoretic approaches to the problem of AJG Anandkumar, S Lambotharan and JA Chambers are with the Advanced Signal Processing Group, School of Electronic, Electrical and Systems Engineering, Loughborough University, Loughborough, LE 3TU, UK {AJGAnandkumar, SLambotharan, JAChambers}@lboroacuk A Anandkumar is with the Center for Pervasive Communications and Computing, Department of Electrical Engineering and Computer Science, Henry Samueli School of Engineering, University of California Irvine, Irvine, CA USA aanandkumar@uciedu This work was supported by EPSRC grant EP/F065477/ The second author was supported in part by ARO Grant W9NF Part of this work was presented at the 00 IEEE International Conference on Acoustics, Speech, and Signal Processing ] and the Fourty-Third Asilomar Conference on Signals, Systems and Computers ] power control in wireless networks have been investigated in 4], 5] and surveyed in 6] 8] In this paper, we are interested in the other scenario where the users are competing against one another and aiming to maximize their own information rates This competitive rate-maximization problem can be modelled as a strategic noncooperative game The Nash equilibrium 9] of this game can be achieved via a distributed waterfilling algorithm where each user performs waterfilling by considering the multi-user interference as an additive coloured noise However, most of the current results on rate-maximization and waterfilling algorithms assume the availability of perfect information which is a strong requirement and cannot be met by practical systems This paper addresses the following fundamental questions: i How can the users independently allocate power if the channel state information CSI they have is imperfect? How can we formulate a rate maximization game under channel uncertainty and what is the nature of the equilibrium of this game? ii What are the existence and uniqueness properties of such an equilibrium? How can such a solution be computed by a distributed algorithm and what are the conditions for asymptotic convergence of such an algorithm? iii How are these conditions affected by the channel uncertainty? iv What is the effect of uncertainty on the sum-rate and the price of anarchy of such a system? In answering these questions, we can gain further insight into the behaviour of waterfilling algorithms and methods to improve sum-rate in general A Summary of Main Results The main contributions of this paper are three-fold First, we provide a game-theoretic solution for the problem of competitive rate-maximization in the presence of channel uncertainty Secondly, we analyse the efficiency of the equilibrium as a function of the channel uncertainty bound and prove that the robust waterfilling solution proposed achieves a higher sum-rate with increasing uncertainty under certain conditions Finally, we verify these results via simulations We show that improved sum-rate under channel uncertainty entails a cost in terms of more stringent conditions for the uniqueness of the equilibrium and slower convergence of the iterative algorithm to the equilibrium For systems with bounded channel uncertainty, we present a distribution-free robust formulation of the rate-maximization game based on an ellipsoid approximation of the uncertainty in the CSI We present the robust-optimization equilibrium RE for this game At the equilibrium, the users perform a modified
2 waterfilling operation where frequency-overlap among users is penalized We derive sufficient conditions for the existence and uniqueness of the equilibrium and for the convergence of an asynchronous iterative waterfilling algorithm to the equilibrium of this game In our work, we investigate the effect of channel uncertainty on the sum-rate of the system for the two-user case under two scenarios, viz, a two-frequency system and a system with large number of frequencies For the two-frequency system, the equilibrium sum-rate improves and the price of anarchy decreases as the channel uncertainty increases under high interference On the other hand, the behavior is reversed at low interference Another important contribution of our work is to show that increasing channel uncertainty always drives the equilibrium closer to a frequency division multiple access FDMA solution for any set of channel coefficients for the system with asymptotic number of frequencies This is because the users become more conservative about causing interference under increased uncertainty and this leads to better partitioning of the frequencies among the users Under certain channel conditions, this also translates to an improvement in the sumrate and a decrease in the price of anarchy of the system Thus, we show an interesting phenomenon where increased channel uncertainty can lead to a more efficient equilibrium, and hence, a better sum-rate in certain multi-user communication systems B Related Work An iterative waterfilling algorithm for maximizing information rates in digital subscriber line systems 0] is an early application of a game-theoretic approach to designing a decentralized algorithm for multi-user dynamic power control This framework has been further analyzed and extended in ] 5] The inefficiency of the Nash equilibrium which need not be Pareto optimal has been addressed in 6] and 7] and methods to improve the sum-rate of the system by using various pricing schemes and modified utility functions have been presented in 5], 8], 9] A centralized controller maximizing the sum-rate of the system leads to a non-convex optimization problem and has been shown to be strongly NP hard in 0] The Pareto-optimality of the FDMA solution for this sum-rate maximization problem under certain channel conditions has been proved in ] Uncertainty in game theory and distributed optimization problems has only recently been investigated The issue of bounded uncertainty in specific distributed optimization problems in communication networks has been investigated in ] wherein techniques to define the uncertainty set such that they can be solved distributively by robust optimization techniques are presented In 3], incomplete-information finite games have been modelled as a distribution-free robust game where the players use a robust optimization approach to counter bounded payoff uncertainty This robust game model also introduced a distribution-free equilibrium concept called the robust-optimization equilibrium on which our approach is based A brief look at a robust optimization approach for the rate-maximization game with uncertainty in the noise-plusinterference estimate has been presented in 4], where the authors present a numerically computed algorithm unlike the closed form results presented here Such a numerical solution prevents further mathematical analysis of the equilibrium and its behaviour under different uncertainty bounds Also, this uncertainty model is different from ours, where we assume the availability of CSI of the interfering channels and that these quantities have a bounded uncertainty A similar problem of rate-maximization in the presence of uncertainty in the estimate of noise-plus-interference levels due to quantization in the feedback channel has been considered in 5] This problem has been solved using a probabilistically constrained optimization approach and as in our work, also results in the waterfilling solution moving closer to an FDMA solution, with corresponding improvement in sum-rate However, the effect of quantization on the conditions for existence and uniqueness of the equilibrium and convergence of the algorithm have not been considered The results presented in 5] are for a sequentially updated algorithm whereas our results allow asynchronous and thus sequential or simultaneous updates to the algorithm Also, the power allocations computed by such a probabilistic optimization formulation do not guarantee that the information rates expected will be achieved for all channel realizations, unlike our worstcase optimization formulation Furthermore, the relative error and not just the absolute error due to quantization in the interference estimate as defined in 5] is assumed to be bounded and drawn from a uniform distribution, which is inaccurate In addition, this bound on the relative error can only be computed if the noise variance at the receivers is assumed to be known which is not the case The bounds computed in such a fashion are very loose and will degrade system performance The other assumption that this relative error bound is in the range 0, means that the absolute quantization error has to be less than the noise variance at the receivers, which restricts the applicability of the approach Our problem formulation has no such limitation on the uncertainty bound based on the noise variances in the system Robust rate-maximization for a cognitive radio scenario with uncertainty in the channel to the primary user has been presented in 6] This leads to a noncooperative game formulation without any uncertainties in the payoff functions of the game unlike in our case with robust interference limits acting as a constraint on the admissible set of strategies This game is then solved by numerical optimization as there is no closed form solution Initial results of our work, involving the problem formulation of the robust rate-maximization game and the results for sufficient conditions for existence and uniqueness of the equilibrium, along with the conditions for asymptotic convergence of the waterfilling algorithm to the equilibrium, have been presented in ] Initial results on the analysis of the efficiency of the equilibrium was presented in ] We now extend this work to include detailed proofs and further analysis of the efficiency of the equilibrium as a function of the channel uncertainty bound
3 3 C Paper Outline This paper is organized as follows: Section II describes the system model and provides the necessary preliminaries Section III formulates the robust game model for the ratemaximization game for the single-input single-output SISO frequency-selective Gaussian interference channel Section IV presents the robust-optimization equilibrium for this game and conditions for its existence and uniqueness, along with the conditions for asymptotic convergence of the waterfilling algorithm to the equilibrium Section V presents the analysis on the effect of uncertainty on the sum-rate of the system for the two-user scenario Section VI presents simulation results and Section VII presents the conclusions from this work and possible future research directions II SYSTEM MODEL AND PRELIMINARIES Notations used: Vectors and matrices are denoted by lowercase and uppercase boldface letters respectively The operators T, T,E{ } and are respectively transpose, transpose of matrix inverse, statistical expectation and Euclidean norm operators The diagonal matrix with the arguments as diagonal elements is denoted by Diag The quantity A] ij refers to the i,j-th element of A R m n + is the set of m n matrices with real non-negative elements The spectral radius largest absolute eigenvalue of matrix A is denoted by ρa The operation x] b a is defined as x] b a = a if x a; x if a < x < b; b if x b and x + max0,x The matrix projection onto the convex set Q is denoted by x] Q argmin z Q z x The term w > 0 indicates that all elements of w are positive and X 0 indicates that the matrix X is positive definite We consider a system similar to the one in 4], which is a SISO frequency-selective Gaussian interference channel with N frequencies, composed of Q SISO links Ω {,,Q} is the set of the Q players ie SISO links The quantity H rq k denotes the frequency response of the k-th frequency bin of the channel between source r and destination q The variance of the zero-mean circularly symmetric complex Gaussian noise at receiver q in the frequency bin k is denoted by σ qk The channel is assumed to be quasi-stationary for the duration of the transmission Let σqk σ qk/ H qq k and the total transmit power of user q be P q Let the vector s q s q s q s q N] be the N symbols transmitted by user q on the N frequency bins and p q k E{ s q k } be the power allocated to the k-th frequency bin by user q and p q p q p q p q N] be the power allocation vector The power allocation of each user q has two constraints: Maximum total transmit power for each user E { s q } N = p q k P q, for q =,,Q, where P q is power in units of energy per transmitted symbol Spectral mask constraints E { s q k } = p q k p max q k, for k =,,N and q =,,Q, where p max q k is the maximum power that is allowed to be allocated by user q for the frequency bin k Each receiver estimates the channel between itself and all the transmitters, which is private information The power allocation vectors are public information, ie known to all users Each receiver computes the optimal power allocation across the frequency bins for its own link and transmits it back to the corresponding transmitter in a low bit-rate error-free feedback channel Note that this leads to sharing of more information compared to other works in literature such as 4] The channel state information estimated by each receiver is assumed to have a bounded uncertainty of unknown distribution Ellipsoid is often used to approximate unknown and potentially complicated uncertainty sets 7] The ellipsoidal approximation has the advantage of parametrically modelling complicated data sets and thus provides a convenient input parameter to algorithms Further, in certain cases, there are statistical reasons leading to ellipsoidal uncertainty sets and also results in optimization problems with convenient analytical structures 8], 9] We consider that at each frequency, the uncertainty in the channel state information of each user is deterministically modelled under an ellipsoidal approximation { F q = F rq k+ F rq,k : F rq,k ǫ q } k =,,N, where ǫ q 0 q Ω is the uncertainty bound and 3 F rq k H rqk H qq k, 4 with F rq k being the nominal value We can consider uncertainty in F rq k instead of H rq k because a bounded uncertainty in F rq k and H rq k are equivalent, but with different bounds The information rate of user q can be written as 30] R q = N log + p q k σ qk+ F rqkp r k, 5 where σ q k σ q k/ H qqk The two popular measures of inefficiency of the equilibria of a game are the price of anarchy and the price of stability The price of anarchy is defined as the ratio between the objective function value at the socially optimal solution and the worst objective function value at any equilibrium of the game 3] The price of stability is defined as the ratio between the objective function value at the socially optimal solution and the best objective function value at any equilibrium of the game 3] We consider the sum-rate of the system as the social objective More specifically, we have a spherical approximation in 3 The model considered here has some redundancy in the uncertainty for the case when F rqk = 0 which leads to including F rqk+ F rq,k < 0 in the model which can never happen in practice However, this does not affect the solution in our method due to the nature of the max-min problem formulation in which leads to selection of positive values of F rq,k
4 4 function The sum-rate of the system is given by S = Q R q 6 q= In our case, the price of stability and anarchy are the same as we prove the sufficient conditions for the existence of a unique equilibrium in Theorem Thus, the price of anarchy, PoA, is the ratio of the sum-rate of the system at the social optimal solution, S, and the sum-rate of the system at the robust-optimization equilibrium, S rob, ie, PoA = S 7 Srob Note that a lower price of anarchy indicates that the equilibrium is more efficient III ROBUST RATE-MAXIMIZATION GAME FORMULATION A Nominal Game - No Channel Uncertainty The problem of power allocation across the frequency bins is cast as a strategic noncooperative game with the SISO links as players and their information rates as pay-off functions 4] Mathematically, the nominal game G nom can be written as, q Ω, max p q N st p q P q, log + p q k σ qk+ F rq kp r k where Ω {,,Q} is the set of the Q players ie the SISO links and P q is the set of admissible strategies of user q, which is defined as { P q p q R N : 0 p q k p max q k, N } p q k = P q, k =,,N The inequality constraint in is replaced with the equality constraint in 9 as, at the optimum of each problem in 8, the constraint must be satisfied with equality 4] To avoid the trivial solution p q k = p max q k k, it is assumed that N pmax q > P q Further, the players can be limited to pure strategies instead of mixed strategies, as shown in 7] B Robust Game - With Channel Uncertainty According to the robust game model 3], each player formulates a best response as the solution of a robust worstcase optimization problem for the uncertainty in the payoff function information rate, given the other players strategies If all the players know that everyone else is using the robust optimization approach to the payoff uncertainty, they would then be able to mutually predict each other s behaviour The robust game G rob where each playerq formulates a worst-case 8 9 robust optimization problem can be written as, q Ω, N p q k max min log + p q F rq F q σ qk+ F rq kp r k st p q P q, 0 where F q is the uncertainty set which is modelled under ellipsoid approximation as shown in 3 This optimization problem using uncertainty sets can be equivalently written in a form represented by protection functions ] as, q Ω, N p q k max min log + p q F rq,k σqk+ rq k+ F rq,k p r k F st F rq,k ǫ q, p q P q From the Cauchy-Schwarz inequality 3], we get ] F rq,k p r k F rq,k p r k ǫ q p r k Using, we get the robust game G rob as, q Ω, N p q k max log + p q σq k+ F rq kp r k+ǫ q p r k st p q P q 3 Now that we have defined the problem for robust ratemaximization under bounded channel uncertainty, we present the solution to the optimization problem in 3 for a singleuser in the following section C Robust Waterfilling Solution The closed-form solution to the robust optimization problem in 3 for any particular user q is given by the following theorem: Lemma Given the set of power allocations of other users p q {p,,p q,p q+,,p Q }, the solution to N p q k max log + p q σq k+ F rq kp r k+ǫ q p r k st p q P q 4 is given by the waterfilling solution p q = RWF qp q, 5 where the waterfilling operator RWF q is defined as RWFq p q ] k µ q σ q k F rq kp r k ǫ q p r k ] p 0 max q k 6
5 5 for k =,,N, where µ q is chosen to satisfy the power constraint N p qk = P q Proof: This can be shown using the Karush-Kuhn-Tucker optimality conditions 7] of this problem The robust waterfilling operation for each user is a distributed worst-case optimization under bounded channel uncertainty Compared with the original waterfilling operation in 4] under perfect CSI ie ǫ q 0, we see that an additional term has appeared in 6 for ǫ q > 0 This additional term can be interpreted as a penalty for allocating power to frequencies having a large product of uncertainty bound and norm of the powers of the other players currently transmitting in those frequencies This is because the users assume the worst-case interference from other users and are thus conservative about allocating power to such channels where there is a strong presence of other users Having derived the robust waterfilling solution for a single user in the presence of channel uncertainty, we consider whether a stable equilibrium for the system exists and if so, what its properties are and how it can be computed in the multi-user scenario in the following section IV ROBUST-OPTIMIZATION EQUILIBRIUM The solution to the game G rob is the robust-optimization equilibrium RE At any robust-optimization equilibrium of this game, the optimum action profile of the players {p q} q Ω must satisfy the following set of simultaneous waterfilling equations: q Ω, p q = RWF q p,,p q,p q+,,p Q = RWF q p q 7 It can easily be verified that the RE reduces to the Nash equilibrium of the system 4] when there is no uncertainty in the system In Section V, we analyse the global efficiency of the RE and show that the RE has a higher efficiency than the Nash equilibrium due to a penalty for interference which encourages better partitioning of the frequency space among the users The robust asynchronous iterative waterfilling algorithm for computing the RE of game G rob in a distributed fashion is described in Algorithm A Analysis of the RE of Game G rob Let N = {,,N} be the set of frequency bins Let Dq denote the set of frequency bins that user q would never use as the best response to any set of strategies adopted by the other users, { Dq k {,,N} : RWFq p q ] } 8 k = 0 p q P q, where P q P P q P q+ P Q The nonnegative matrices E and S max R Q Q + are defined as { ǫq, if r q, E] qr 9 0, otherwise, Algorithm Robust Iterative Waterfilling Algorithm Input: Ω: Set of users in the system P q : Set of admissible strategies of user q of user q is updated T : Number of iterations for which the algorithm is run τrn: q Time of the most recent power allocation of user r available to user q at time n RWF q : Robust waterfilling operation in 6 and T q : Set of time instants n when the power vector p n q Initialization: n = 0 and p 0 q any p P q, q Ω for n = 0 to{ T do p q n+ RWFq p τq n q, if n T q, = q Ω p q n, otherwise, end for S max ] qr { max k D q D r F rq k, if r q, 0, otherwise, 0 where D q is any subset of {,,N} such that N D q D q {,,N} The sufficient condition for existence and uniqueness of the RE of game G rob and for the guaranteed convergence of Algorithm is given by the following theorem: Theorem Game G rob has at least one equilibrium for any set of channel values and transmit powers of the users Furthermore, the equilibrium is unique and the asynchronous iterative waterfilling algorithm described in Algorithm converges to the unique RE of game G rob as the number of iterations for which the algorithm is run, T for any set of feasible initial conditions if ρs max < ρe, where E and S are as defined in 9 and 0 respectively Proof: See Appendix C In the absence of uncertainty, ie when ǫ q = 0 q Ω, we can see that this condition reduces to condition C in 4] as expected Since ρe 0, the condition on S max becomes more stringent as the uncertainty bound increases, ie the set of channel coefficients for which the existence of a unique equilibrium and the convergence of the algorithm is guaranteed shrinks as the uncertainty bound increases Also, from Lemma 3, we can see that the modulus of the waterfilling contraction increases as uncertainty increases This indicates that the convergence of the iterative waterfilling algorithm becomes slower as the uncertainty increases, as shown in simulation results Corollary When the uncertainties of all the Q users are equal say ǫ, the RE of the game G rob is unique and Algorithm converges to the unique RE of game G rob as T for any set of feasible initial condition if ρs max < ǫq
6 6 Proof: When the uncertainties of all Q users is ǫ, we get ρe = ǫq The above corollary explicitly shows how the uncertainty bound and the number of users in the system affect the existence of the equilibrium and the convergence to the equilibrium using an iterative waterfilling algorithm For a fixed uncertainty bound, as the number of users in the system increases, there is a larger amount of uncertain information in the system Hence, the probability that a given system for a fixed uncertainty bound will converge will decrease as the number of users in the system increases Also, if ǫq, we will not have a guaranteed unique equilibrium and algorithmic convergence for non-zero uncertainty bounds regardless of the channel coefficients This will help designers plan for the appropriate uncertainty bounds based on the planned number of users in the system Tx,] α, mα] mα, α] Rx Tx Rx,] Fig : Anti-symmetric system with Q =, N =,ǫ = ǫ = ǫ and the noise variances for both users in both frequencies is σ The channel gains are: H = H = H = H = ; H = H = α and H = H = mα with m > and 0 < α < The power allocations for this system at the robust-optimization equilibrium are presented in 3 V EFFICIENCY AT THE EQUILIBRIUM TWO-USER CASE In this section, we analyse the effect of uncertainty on the social output of the system For the two user case, the worstcase interference in each frequency reduces to F rq k + ǫ q pr k with q,r =, and q r This means that the robust waterfilling operation for the two user case Q = is simply the standard waterfilling solution with the worst-case channel coefficients We restrict the analysis to the two-user case with identical noise variance σq k = σ k,q across all frequencies and identical uncertainty bounds ǫ = ǫ = ǫ and total power constraints N p k = N p k = P T for both users These results can be extended to the nonidentical case along similar lines In order to develop a clear understanding of the behaviour of the equilibrium, the sumrate of the system is first analyzed for a system with two frequencies N = and then extended to systems with large N number of frequencies A Two Frequency Case N = Consider a two-frequency anti-symmetric system as shown in Figure where the channel gains are H = H = H = H = ; H = H = α and H = H = mα with m > and 0 < α < From 6 the power allocations at the robustoptimization equilibrium of this system are, p = µ σ α+ǫp ] +, p = µ σ mα+ǫp ] +, p = µ σ mα+ǫp ] +, p = µ σ α+ǫp ] +, 3 and the total power constraint for each user is p +p = p + p = Let p = p, hence, by symmetry, p = p = p, p = p and µ = µ = µ The following theorem presents the effect of uncertainty on the sum-rate and price of anarchy of the system for the high interference and low interference cases Theorem For the two-user two-frequency anti-symmetric system described above, we have the following results: High interference: When σ α p, the sum-rate increases and the price of anarchy decreases as the channel uncertainty bound increases Low interference: When σ mαp, the sum-rate decreases and the price of anarchy increases as the channel uncertainty bound increases Proof: See Appendix D We can see from this result that the RE behaves in opposite ways when there is high interference and when there is low interference in the system This suggests that there might be a certain level of interference where the sum-rate and price of anarchy do not change with change in uncertainty This is given by the following proposition: Proposition At the level of interference α = α o, where α o = σ m+ + 4m m m σ, 4 the sum-rate and the price of anarchy are independent of the level of uncertainty or the power allocation used Furthermore, at this value of interference, the price of anarchy is equal to unity Proof: See Appendix E We can see that even for such a simple system, the global behaviour of the robust-optimization equilibrium appears to be quite complex This indicates that the global properties of the robust-optimization equilibrium for larger systems is quite strongly dependent on the level of interference in the system, which is seen in the following results with asymptotic number of frequencies However, the underlying nature of the algorithm for the two-frequency case is that the RE moves towards the FDMA solution as the uncertainty bound increases from 63 B Large Number of Frequencies N We consider Jk, defined as Jk p kp k, 5
7 7 as a measure of the extent of partitioning of the frequency k It is minimum Jk = when both the users allocate all their total power to the same frequency k and is maximum Jk = 0 when at most one user is occupying the frequency k Note that Jk = 0 k {,,N} when the users adopt an FDMA scheme The following lemma describes the effect of the uncertainty bound on the extent of partitioning of the system: Lemma When the number of frequencies, N, the extent of partitioning in every frequency is non-decreasing as the uncertainty bound of the system increases for any set of channel values, ie, Jk 0 k {,,N} when N, 6 ǫ with equality for frequencies where Jk = 0, where Jk is defined in 5 Proof: See Appendix F The above lemma suggests that the robust-optimization equilibrium moves towards greater frequency-space partitioning as the uncertainty bound increases when there is a large number of frequencies in the system In other words, the RE is moving closer to an FDMA solution under increased channel uncertainty When the FDMA solution is globally optimal, this will lead to an improvement in the performance of the equilibrium This is stated in the following theorem: Theorem 3 As the number of frequencies, N, the sumrate price of anarchy at the robust-optimization equilibrium of the system is non-decreasing non-increasing as the uncertainty bound increases if, k {,,N}, F k ǫf k ǫ > 4 7 Proof: Using, Corollary 3], we find that the sum of the rates of the two users in the frequency k is quasi-convex only if F kf k > /4 Let C be the minimum number of frequencies occupied by any user When there are only two users and a large number of frequencies, C If the condition F kf k > 4 + C is satisfied for some C for all frequencies k {,,N} thus satisfying F kf k > /4, then the Pareto optimal solution is FDMA, Theorem 33] This needs to be satisfied for the worst-case channel coefficients which leads to 7 Thus, the solution moving closer to FDMA will improve the sum-rate of the system From Lemma, the robust equilibrium moves closer to FDMA as uncertainty increases and thus will result in an improvement in sum-rate The Pareto optimal solution under this condition which is FDMA is constant under varying uncertainty bounds as such an uncertainty in the interference coefficients F k and F k does not affect the FDMA solution where there is no interference Thus, an increase in sum-rate will result in an decrease in price of anarchy Remar For the special case of frequency-flat systems, at the equilibrium, all users have equal power allocation to all frequencies and this is not dependent on the uncertainty in the CSI This leads to no change in the extent of partitioning and thus sum-rate and price of anarchy are not affected by uncertainty Remark The results of this section are not just limited to the robust-optimization equilibrium for the system presented here When the uncertaintyǫ = 0, the framework presented here can be used to analyse the behaviour of the Nash equilibrium of the iterative waterfilling algorithm as a function of the interference coefficients Remark 3 The modified waterfilling operation in 6 can also be used as a pricing mechanism to achieve improved sum-rate performance in a system with no uncertainty where ǫ is a design parameter, with all the analytical results presented here still being valid VI SIMULATION RESULTS In this section, we present some simulation results to study the impact of channel uncertainty on the RE by comparing it with the ideal scenario of NE under perfect CSI Figure shows the simulation results for the two user and two frequency scenario and Figures 3 0 show the results for a more general system under different settings In Figure a, we can see the sum-rate at high interference as a function of interference and uncertainty in the system shown in Figure The flat region corresponds to the sumrate at Pareto optimal solution FDMA and the edge of the surface corresponds to the sufficient condition in It can be seen that the Nash equilibrium uncertainty, ǫ = 0 moves closer to the Pareto optimal solution as the interference increases It is also evident that the sum-rate increases for a fixed interference as uncertainty increases, as expected from Theorem In Figure b, we can see the sum-rate at low interference as a function of interference and uncertainty As expected from Theorem, the sum-rate decreases as the uncertainty increases In Figures 3 0, the behaviour of the equilibrium under varying uncertainty bounds is investigated through numerical simulations The simulations are computed for a system with Q users and N frequencies averaged over 5000 channel realizations The channel gains are H rq k N C 0, for r q and H qq k N C 0,5 The channel uncertainty model has nominal value F rq k = Frq true k+e rq k with e rq k U δ, δ, δ < The specific parameter values used for the simulations are provided above each figure Note that the zero uncertainty solution corresponds to the Nash equilibrium and the nominal solution is the solution resulting from using the erroneous channel values in the traditional ratemaximization game G S without accounting for its uncertainty The effect of uncertainty, number of users and number of frequencies on the average sum-rate of the system, the average number of frequencies occupied by each user and the average number of iterations for convergence are examined In these figures, the Nash equilibrium point is when the uncertainty is zero In Figure 3, it can be observed that the sum-rate at the Nash equilibrium under perfect CSI is less than the sum-rate at the robust-optimization equilibrium under imperfect CSI and that the gap in performance increases as the uncertainty δ
8 8 Sum rate Interference, α Uncertainty, ε a Sum-rate of the system under high interference vs uncertainty and interference Sum rate v/s interference and uncertainty Sum rate Interference, α Uncertainty, ε b Sum-rate of the system under low interference vs uncertainty and interference Fig : Simulation results for the anti-symmetric system in Figure Note that the zero uncertainty corresponds to the Nash equilibrium Sum rate Nominal solution Robust solution Q=4, N= Degree of uncertainty Fig 3: Sum-rate of the system vs uncertainty δ 0 0 Sum rate δ=05, N=6 Nominal solution Robust solution Number of users Fig 4: Sum-rate of the system vs number of users, Q Sum rate Nominal solution Robust solution δ=05, Q= Number of frequencies Fig 5: Sum-rate of the system vs number of frequencies, N Average no of freq/user 95 9 Q=4, N=6 85 Nominal solution Robust solution Degree of uncertainty Fig 6: Average number of channels occupied per user vs uncertainty, δ Average no of freq/user δ=05, N=6 Nominal solution Robust solution Number of users Fig 7: Average number of channels occupied per user vs number of users, Q
9 9 Average number of iterations Q=4, N= Degree of uncertainty Fig 8: Average number of iterations vs uncertainty, δ Average number of iterations δ=05, N= Number of users Fig 9: Average number of iterations vs number of users, Q increases Under imperfect CSI, the power allocation using the robust-optimization equilibrium 3 in 6 and 7 has higher sum-rate as uncertainty increases, because the users are more cautious about using frequencies with significant interference, thus reducing the total amount of interference in the system The Pareto optimal solution in this scenario is some form of FDMA where the specific channels allocated to a particular user will depend on the actual channel gains, and does not depend on the channel uncertainty bound for a given system realization Thus, when the sum-rate of the system increases with rise in uncertainty, we can expect that the price of anarchy will decrease In Figure 4, it can be observed that the sum-rate of the system under the robust solution reduces when the number of users increases This is because having a greater number of users results in higher interference for all users and this effect is strong enough to counter user diversity which would have resulted in higher sum-rates if the users were on an FDMA scheme In Figure 5, it can be observed that the sum-rate of the system improves with increase in number of frequencies and also that the robust solution continues to perform better than the nominal solution even when the number of frequencies increases In Figure 6, it can be seen that the robust solution results in a lower average number of channels per user as the uncertainty, δ increases Also, the total number of channels 3 6 and 7 are in terms of absolute uncertainty ǫ while the simulations use relative uncertainty δ They are equivalent to one another Average number of iterations δ=05, Q= Number of frequencies Fig 0: Average number of iterations vs number of frequencies, N each user occupies at the robust-optimization equilibrium is lesser than at the nominal solution, regardless of the number of users, as can be seen in Figure 7 This implies that the users are employing a smaller number of frequencies, which demonstrates the improved partitioning of the frequency space among the users in order to reduce interference Hence, this leads to the higher sum-rates as observed in Figure 3 In Figures 8 and 9, it can be observed that the average number of iterations for convergence increases as the uncertainty δ, and the number of users Q increase respectively This is as expected from Lemma 3 and Corollary, as the modulus of the block-contraction in 39 increases as the uncertainty increases This indicates that the step size of each iteration reduces as uncertainty increases, leading to slower convergence In Figure 0, it can be observed that the average number of iterations increases with the number of frequencies This is due to the fact that when there are more frequencies, and as such there is a greater probability of a channel realization being drawn from the tail of the Gaussian distribution used to generate them, which results in a smaller modulus of the block-contraction in 39 on average, a greater number of iterations are required in order to converge to the equilibrium Thus, the trade-off for robust solutions with higher sum-rates is in a higher number of iterations before convergence VII CONCLUSIONS In this paper, we have presented a novel approach for ratemaximization games under bounded channel state information uncertainty We have introduced a distribution-free robust formulation for the rate-maximization game The solution to this game has been shown to be a modified waterfilling operation The robust-optimization equilibrium RE for this game has been presented and sufficient conditions for its existence, uniqueness and asymptotic convergence of the algorithm to the RE have been derived For the two-user case, the effect of uncertainty on the social output of the system has been analyzed We analytically prove that the RE moves towards an FDMA solution as the uncertainty bound increases, when the number of frequencies in the system becomes asymptotically large Thus, an interesting effect of improvement in
10 0 sum-rate as the uncertainty bound increases is observed In summary, for systems with significant interference, bounded channel uncertainty leads to an improved sum-rate but at the cost of greater number of iterations This framework can be extended to MIMO rate-maximization games, cognitive radio with various interference constraints and other noncooperative games APPENDIX A Robust Waterfilling as a Projection Operation Let Φ q k represent the denominator terms in 4, which is the worst-case noise+interference Φ q k σ q k+ F rq kp r k+ǫ q p r k 8 It has been shown in 33] that the waterfilling operation can be interpreted as the Euclidean projection of a vector onto a simplex Using this framework, the robust waterfilling operator in 6 can be expressed as the Euclidean projection of the vector Φ q Φ q,,φ q N] T onto the simplex P q defined in 9: RWF q p q = Φ q ]P q, 9 which can be conveniently written as RWF q p q = σ q F rq p r ǫ q f q, 30 ]P q where σ q σq,,σ qn ] T, 3 Diag F rq,,f rq N, 3 ] T f q p r,, p r N 33 F rq B Contraction Property of the Waterfilling Projection Given the waterfilling mapping RWF defined as RWFp = RWF q p q q Ω : P P, 34 where P P P Q, with P q and RWF q p q respectively defined in 9 and 30, the block-maximum norm is defined as 34] RWFp w max,block q Ω RWFq p q w q, 35 where w w,,w Q ] T > 0 is any positive weight vector The vector weighted maximum norm is given by 3] x w,vec max q Ω x q w q, w > 0, x R Q 36 The matrix weighted maximum norm is given by 3] A w,mat max q w q r= Q A] qr w r, A R Q Q 37 The mapping RWF is said to be a block-contraction 4 with modulus α with respect to the norm w if there,block exists α 0, such that, p,p P, RWFp RWFp w,block α p p w,block, 38 where p i = p q i,,p q i for i =, The contraction property of the waterfilling mapping is given by the following lemma: Lemma 3 Given w w,,w Q ] T > 0, the mapping RWF defined in 34 satisfies RWF p RWF p w,block S max +E w,mat p p w,block, 39 p,p P, where E and S as defined in 9 and 0 respectively Furthermore, if S max +E w,mat <, 40 for some w > 0, then the mapping RWF is a block contraction with modulus α = S max +E w,mat Proof: This proof is structured similar to that of 33, Proposition ] However the additional term ǫ q f q in 30 necessitates a separate treatment here For each q Ω and i =,, given f q i = ] T p r i,, p rn i, let p q k i p k i,,p q k i,p q+ k i,,p Q k i ] and f q f Then, q f q N f q = p r k p r k N = p q k p q k ] N p q k p q k N = p r k +p r k = p r p r ] p r k p r k ] ] 45 where 43 follows from 3, Lemma 5] Now, define for each q Ω, e RWFq RWF q p q RWFq p q e q p 46 q p q 4 The mapping T is called a block-contraction with modulus α 0, if it is a contraction in the block-maximum norm with modulus α 34]
11 Then, using 30 in 46, e RWFq can be written as e RWFq = σ q ] F rq p r ǫ q f q P q σ q ] F rq p r ǫ q f q P q 47 F rq p r +ǫ q f q F rq p r ǫ q f q 48 = F rq p r p r +ǫ q f q f q 49 F rq p r p r f +ǫ q q f q 50 F rq p r p r + ǫ q p r p r ] 5 p max F rq k r p r k + ǫ q p r p r ] 5 = ] max F rq k e r +ǫ q e r 53 k D q D r S max ] rq +ǫ q e r 54 p q,p q P q and q Ω, where: 48 follows from the nonexpansive property of the waterfilling projection 33, Lemma 3]; 50 follows from the triangle inequality 3]; 5 follows from 45; 5 and 53 follow from the definitions of F rq and e q respectively from 3 and 46; and 54 follows from the definition of S max in 0 and Jensen s inequality 7] The set of inequalities in 54 can be written in vector form as 0 e RWF S max +Ee 55 where E is defined in 9 and the vectors e RWF and e are defined as e RWF ] T e RWF,,e RWFQ, and e = e,e Q ] T Using the vector and matrix weighted maximum norms from 36 and 37 respectively, 55 can be written as erwf w,vec S max +Ee w,vec S max +E w,mat e w,vec, 56 w > 0 Using the block-maximum norm 35, we get RWF p RWF p w,block = erwf w,vec S max +E w p,mat r p r w,block 57 p,p P, with E and S as defined in 9 and 0 respectively It is clear that RWF is a block contraction when S max +E w,mat < C Proof of Theorem From 35], every concave game 5 has at least one equilibrium For the game G rob : The set of feasible strategy profiles, P q of each player q is compact and convex The payoff function of each player q in 3 is continuous in p P and concave in p q P q Thus, the game G rob has at least one robust equilibrium From Lemma 3, the waterfilling mapping RWF is a block-contraction if 40 is satisfied for some w > 0 Thus, the RE of game G rob is unique using 36, Theorem ] Since S max +E is a nonnegative matrix, there exists a positive vector w such that S max +E w,mat < 58 Using 34, Corollary 6] and the triangle inequality 3], this is satisfied when S max w,mat + E w,mat < ρs max < ρe 59 From Lemma 3 and 58 the waterfilling mapping RWF is a block-contraction From 36, Theorem ], the robust iterative waterfilling algorithm described in Algorithm converges to the unique RE of game G rob for any set of feasible initial conditions and any update schedule D Proof of Theorem Consider the interior operating points of the robust waterfilling operator RWF q where it is linear Eliminating µ from 3, we get p = α ǫ m+α/ ǫ The signal-to-interference-plus-noise ratio SINR for the two users in the two frequency bins is given by p SINR = SINR = σ +α p SINR = SINR = p 6 σ +mαp and the sum-rate of the system at the RE is S rob log + +log p σ +α p The gradient of p with respect to ǫ is + p σ +mαp 6 p ǫ = m α > m+α/ ǫ Thus, the RE moves towards the FDMA solution as the uncertainty bound increases 5 A game is said to be concave if the payoff functions are concave and the sets of admissible strategies are compact and convex
12 Case : High interference scenario: In the high interference scenario, σ α p Let ξ = p/α p Then, the SINR for the two users in the two frequency bins can be approximated as p SINR = SINR α p = ξ, SINR = SINR p mαp = 64 mα ξ The sum-rate of the system at high interference can be approximated as S log +ξ+ mα ξ = log + mα +ξ + mα ξ 65 Our aim is to analyse the behaviour of the sum-rate S as the uncertainty ǫ increases To this end, we show that the gradient of the sum-rate with respect toǫis positive Aslogx increases monotonically with x, we consider ǫ ξ + mα ξ = mα ξ ξ ǫ = p ξ mp ǫ, 66 and p mp > 0 since p 05 and m > Now, ξ ǫ = p α p ǫ 67 From 63, 66 and 67, we get S ǫ > 0 Thus, we see that the sum-rate of the system increases as the uncertainty ǫ increases This also shows that the robust-optimization equilibrium achieves a higher sum-rate in the presence of channel uncertainty ǫ > 0 than the Nash equilibrium at zero uncertainty ǫ = 0 The social optimal solution for this system at high interference is frequency division multiplexing ] In other words, the frequency space is fully partitioned at the social optimal solution The sum-rate at the social optimal solution for the given system at high interference, S, is given by S = log + σ 68 The price of anarchy at high interference, PoA, is log + σ PoA = log + mα +ξ + 69 mα ξ Since S ǫ > 0, we have PoA ǫ < 0 Case : Low interference scenario: In the low interference scenario, ie when mαp σ, the signal-tointerference+noise ratio SINR for the two users in the two frequency bins can be approximately written as SINR = SINR p σ, SINR = SINR p σ 70 The sum-rate of the system at low interference can be approximated as S log + p p σ+ σ = log + σ + p p 7 σ Now, S ǫ = + σ + p p p p σ σ < 0 7 ǫ At low interference, the system behaves similar to a parallel Gaussian channel system The social optimal solution in this scenario is the classical waterfilling solution and leads to equal power allocation, ie, p = p = p = p = p = 05 The sum-rate at the social optimal solution for the given system at low interference, S, is given by S = 4log + σ 73 The price of anarchy at low interference, PoA, is 4log + σ PoA = log + σ + p p σ = log + σ + 4σ 4 log + σ + p p σ 74 Note that, at low interference, mαp From 60, we get p 05 Thus the PoA is close to unity Since S ǫ < 0, we have PoA ǫ > 0 E Proof of Proposition The gradient of the sum-rate S rob with respect to ǫ is S rob ǫ = S rob p From 63, we have p ǫ > 0 Now, S rob p = σ +α p + + αp σ +α p p σ +α p p ǫ 75 σ +mαp + pmα σ +mαp + p σ +mαp 76 Setting S rob p = 0, we solve for α to get the following roots, 0, σ α = m m+± 4m/σ +m+, 77 σ p m p +p The positive root that is independent of ǫ and p which is a function of the uncertainty ǫ, from 60 is the required solution where the sum-rate is constant regardless of uncertainty Thus, the required interference value is given by α o = σ m 4m/σ +m+ m 78 Since the rootα o of S rob p is independent of p, different power allocation schemes resulting in different values of p will
13 3 result in the same sum-rate at α = α o Thus, the price of anarchy at α = α o is unity F Proof of Lemma From 6, the power allocations for the two users at the robust-optimization equilibrium in the k-th frequency are +, p k = µ σ F +ǫp k +, 79 p k = µ σ F +ǫp k with N p k = N p k = P T Let D,D and D ol be the sets of frequencies exclusively used by user, user and by both respectively and n D and n D be the number of frequencies exclusively used by user and user respectively at the equilibrium Then, from 79, we have p k = µ σ and p k = 0 k D and p k = 0 and p k = µ σ k D The power remaining for allocation to the frequencies in D ol {,, } by user and user is n µ and n µ respectively This separation of the frequency-space into exclusive-use and overlapped-use frequencies allows us to analyse the system without the nonlinear operation + Thus, we can write the power allocations at the fixed point in the overlapped-use frequency-space as a system of linear equations, p k+ F k+ǫ p k µ σ = 0, k D ol 80 F k+ǫ p k+p k µ σ = 0, k D ol 8 k D ol p k+n µ σ = P T, 8 k D ol p k+n µ σ = P T 83 Writing these in matrix form we get, A k 0 I p 0 A kol I p = I I D µ 0 0 p t where ] ] F A k k+ǫ n 0, D, F k+ǫ 0 n ] ] ] p k PT µ σ pk, p p k t µ P T µ σ Let A k 0 A 0 A kol, B I, I C I I ] and P pk p ] T so that we can write 84 as ] A B P 0 = 87 C D] µ pt] We can solve this system to get ] ] P A B 0 W X 0 = = = µ] C D] p t Y Z] p t ] Xpt, 88 Zp t where ] W X Y Z ] A B 89 C D Using 37, Fact 09] and differentiating 88 with respect to ǫ, we get ] P A B = ǫ ǫ µ] A 0 ] ] A B 0 90 C D 0 0 C D] p t W = ǫ AXp ] t Y ǫ AXp 9 t Due to the nature of the waterfilling function, n and n are non-decreasing piecewise-constant functions of ǫ The above derivative exists only in the regions where n and n are constant From 37, Proposition 87] and using A = DiagA,,A, we get W = A A ZA A ZA A ZA A A ZA,9 X = A Z A Z ] T, 93 Y = ZA ZA ], 94 Z = n + k D ol F i+ǫ k D ol F i+ǫ k D ol n + k D ol, 95 where deta i = F i+ǫ F i+ǫ, n + k D ol n + k D ol F i+ǫ k Dol k D ol, and A i = F i+ǫ Fi+ǫ Fi+ǫ Thus, from 88 and 9, we get P = Xp t = A Zp t ] A Zp t ] T, 98 and P ǫ = W A X, 99 ǫ A ZA i GA i Zp t A GA Zp t i= = 00 i GA i Zp t A Zp t where A ZA i= G = A i ǫ = ] 0 0 Therefore, for k =,,, GA i =,,N 0 pk = p k p k ] T = A k Zp t, 0
IEEE TRANSACTIONS ON VEHICULAR TECHNOLOGY, VOL. 60, NO. 9, NOVEMBER
 IEEE TRANSACTIONS ON VEHICULAR TECHNOLOGY, VOL. 60, NO. 9, NOVEMBER 0 447 Robust Rate Maximization Game Under Bounded Channel Uncertainty Amod J. G. Anandumar, Student Member, IEEE, Animashree Anandumar,
IEEE TRANSACTIONS ON VEHICULAR TECHNOLOGY, VOL. 60, NO. 9, NOVEMBER 0 447 Robust Rate Maximization Game Under Bounded Channel Uncertainty Amod J. G. Anandumar, Student Member, IEEE, Animashree Anandumar,
Optimal Linear Precoding Strategies for Wideband Non-Cooperative Systems based on Game Theory-Part II: Algorithms
 Optimal Linear Precoding Strategies for Wideband Non-Cooperative Systems based on Game Theory-Part II: Algorithms Gesualdo Scutari 1, Daniel P. Palomar 2, and Sergio Barbarossa 1 E-mail: {scutari,sergio}@infocom.uniroma1.it,
Optimal Linear Precoding Strategies for Wideband Non-Cooperative Systems based on Game Theory-Part II: Algorithms Gesualdo Scutari 1, Daniel P. Palomar 2, and Sergio Barbarossa 1 E-mail: {scutari,sergio}@infocom.uniroma1.it,
Optimal Linear Precoding Strategies for Wideband Non-Cooperative Systems based on Game Theory-Part I: Nash Equilibria
 Optimal Linear Precoding Strategies for Wideband Non-Cooperative Systems based on Game Theory-Part I: Nash Equilibria Gesualdo Scutari 1, Daniel P. Palomar 2, and Sergio Barbarossa 1 E-mail: {aldo.scutari,sergio}@infocom.uniroma1.it,
Optimal Linear Precoding Strategies for Wideband Non-Cooperative Systems based on Game Theory-Part I: Nash Equilibria Gesualdo Scutari 1, Daniel P. Palomar 2, and Sergio Barbarossa 1 E-mail: {aldo.scutari,sergio}@infocom.uniroma1.it,
Competitive Design of Multiuser MIMO Systems based on Game Theory: A Unified View
 JOURNAL OF SELECTED AREAS IN COMMUNICATIONS, VOL.?, NO.?, SEPTEMBER 2008 1 Competitive Design of Multiuser MIMO Systems based on Game Theory: A Unified View Gesualdo Scutari, Member, IEEE, Daniel P. Palomar,
JOURNAL OF SELECTED AREAS IN COMMUNICATIONS, VOL.?, NO.?, SEPTEMBER 2008 1 Competitive Design of Multiuser MIMO Systems based on Game Theory: A Unified View Gesualdo Scutari, Member, IEEE, Daniel P. Palomar,
IEEE JOURNAL ON SELECTED AREAS IN COMMUNICATIONS, VOL. 26, NO. 7, SEPTEMBER
 IEEE JOURNAL ON SELECTED AREAS IN COMMUNICATIONS, VOL. 26, NO. 7, SEPTEMBER 2008 1089 Competitive Design of Multiuser MIMO Systems Based on Game Theory: A Unified View Gesualdo Scutari, Member, IEEE, Daniel
IEEE JOURNAL ON SELECTED AREAS IN COMMUNICATIONS, VOL. 26, NO. 7, SEPTEMBER 2008 1089 Competitive Design of Multiuser MIMO Systems Based on Game Theory: A Unified View Gesualdo Scutari, Member, IEEE, Daniel
Characterization of Convex and Concave Resource Allocation Problems in Interference Coupled Wireless Systems
 2382 IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL 59, NO 5, MAY 2011 Characterization of Convex and Concave Resource Allocation Problems in Interference Coupled Wireless Systems Holger Boche, Fellow, IEEE,
2382 IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL 59, NO 5, MAY 2011 Characterization of Convex and Concave Resource Allocation Problems in Interference Coupled Wireless Systems Holger Boche, Fellow, IEEE,
Game Theoretic Solutions for Precoding Strategies over the Interference Channel
 Game Theoretic Solutions for Precoding Strategies over the Interference Channel Jie Gao, Sergiy A. Vorobyov, and Hai Jiang Department of Electrical & Computer Engineering, University of Alberta, Canada
Game Theoretic Solutions for Precoding Strategies over the Interference Channel Jie Gao, Sergiy A. Vorobyov, and Hai Jiang Department of Electrical & Computer Engineering, University of Alberta, Canada
Signaling Design of Two-Way MIMO Full-Duplex Channel: Optimality Under Imperfect Transmit Front-End Chain
 DRAFT 1 Signaling Design of Two-Way MIMO Full-Duplex Channel: Optimality Under Imperfect Transmit Front-End Chain Shuqiao Jia and Behnaam Aazhang, arxiv:1506.00330v1 [cs.it] 1 Jun 2015 Abstract We derive
DRAFT 1 Signaling Design of Two-Way MIMO Full-Duplex Channel: Optimality Under Imperfect Transmit Front-End Chain Shuqiao Jia and Behnaam Aazhang, arxiv:1506.00330v1 [cs.it] 1 Jun 2015 Abstract We derive
MIMO Cognitive Radio: A Game Theoretical Approach Gesualdo Scutari, Member, IEEE, and Daniel P. Palomar, Senior Member, IEEE
 IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 58, NO. 2, FEBRUARY 2010 761 MIMO Cognitive Radio: A Game Theoretical Approach Gesualdo Scutari, Member, IEEE, and Daniel P. Palomar, Senior Member, IEEE Abstract
IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 58, NO. 2, FEBRUARY 2010 761 MIMO Cognitive Radio: A Game Theoretical Approach Gesualdo Scutari, Member, IEEE, and Daniel P. Palomar, Senior Member, IEEE Abstract
MULTI-INPUT multi-output (MIMO) channels, usually
 3086 IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 57, NO. 8, AUGUST 2009 Worst-Case Robust MIMO Transmission With Imperfect Channel Knowledge Jiaheng Wang, Student Member, IEEE, and Daniel P. Palomar,
3086 IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 57, NO. 8, AUGUST 2009 Worst-Case Robust MIMO Transmission With Imperfect Channel Knowledge Jiaheng Wang, Student Member, IEEE, and Daniel P. Palomar,
Optimum Power Allocation in Fading MIMO Multiple Access Channels with Partial CSI at the Transmitters
 Optimum Power Allocation in Fading MIMO Multiple Access Channels with Partial CSI at the Transmitters Alkan Soysal Sennur Ulukus Department of Electrical and Computer Engineering University of Maryland,
Optimum Power Allocation in Fading MIMO Multiple Access Channels with Partial CSI at the Transmitters Alkan Soysal Sennur Ulukus Department of Electrical and Computer Engineering University of Maryland,
Applications of Robust Optimization in Signal Processing: Beamforming and Power Control Fall 2012
 Applications of Robust Optimization in Signal Processing: Beamforg and Power Control Fall 2012 Instructor: Farid Alizadeh Scribe: Shunqiao Sun 12/09/2012 1 Overview In this presentation, we study the applications
Applications of Robust Optimization in Signal Processing: Beamforg and Power Control Fall 2012 Instructor: Farid Alizadeh Scribe: Shunqiao Sun 12/09/2012 1 Overview In this presentation, we study the applications
Nash Bargaining in Beamforming Games with Quantized CSI in Two-user Interference Channels
 Nash Bargaining in Beamforming Games with Quantized CSI in Two-user Interference Channels Jung Hoon Lee and Huaiyu Dai Department of Electrical and Computer Engineering, North Carolina State University,
Nash Bargaining in Beamforming Games with Quantized CSI in Two-user Interference Channels Jung Hoon Lee and Huaiyu Dai Department of Electrical and Computer Engineering, North Carolina State University,
Game Theoretic Approach to Power Control in Cellular CDMA
 Game Theoretic Approach to Power Control in Cellular CDMA Sarma Gunturi Texas Instruments(India) Bangalore - 56 7, INDIA Email : gssarma@ticom Fernando Paganini Electrical Engineering Department University
Game Theoretic Approach to Power Control in Cellular CDMA Sarma Gunturi Texas Instruments(India) Bangalore - 56 7, INDIA Email : gssarma@ticom Fernando Paganini Electrical Engineering Department University
Under sum power constraint, the capacity of MIMO channels
 IEEE TRANSACTIONS ON COMMUNICATIONS, VOL 6, NO 9, SEPTEMBER 22 242 Iterative Mode-Dropping for the Sum Capacity of MIMO-MAC with Per-Antenna Power Constraint Yang Zhu and Mai Vu Abstract We propose an
IEEE TRANSACTIONS ON COMMUNICATIONS, VOL 6, NO 9, SEPTEMBER 22 242 Iterative Mode-Dropping for the Sum Capacity of MIMO-MAC with Per-Antenna Power Constraint Yang Zhu and Mai Vu Abstract We propose an
Uniform Power Allocation in MIMO Channels: A Game-Theoretic Approach
 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 49, NO. 7, JULY 2003 1707 Uniform Power Allocation in MIMO Channels: A Game-Theoretic Approach Daniel Pérez Palomar, Student Member, IEEE, John M. Cioffi,
IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 49, NO. 7, JULY 2003 1707 Uniform Power Allocation in MIMO Channels: A Game-Theoretic Approach Daniel Pérez Palomar, Student Member, IEEE, John M. Cioffi,
Lecture 7 MIMO Communica2ons
 Wireless Communications Lecture 7 MIMO Communica2ons Prof. Chun-Hung Liu Dept. of Electrical and Computer Engineering National Chiao Tung University Fall 2014 1 Outline MIMO Communications (Chapter 10
Wireless Communications Lecture 7 MIMO Communica2ons Prof. Chun-Hung Liu Dept. of Electrical and Computer Engineering National Chiao Tung University Fall 2014 1 Outline MIMO Communications (Chapter 10
Distributed power allocation for D2D communications underlaying/overlaying OFDMA cellular networks
 Distributed power allocation for D2D communications underlaying/overlaying OFDMA cellular networks Marco Moretti, Andrea Abrardo Dipartimento di Ingegneria dell Informazione, University of Pisa, Italy
Distributed power allocation for D2D communications underlaying/overlaying OFDMA cellular networks Marco Moretti, Andrea Abrardo Dipartimento di Ingegneria dell Informazione, University of Pisa, Italy
Schur-convexity of the Symbol Error Rate in Correlated MIMO Systems with Precoding and Space-time Coding
 Schur-convexity of the Symbol Error Rate in Correlated MIMO Systems with Precoding and Space-time Coding RadioVetenskap och Kommunikation (RVK 08) Proceedings of the twentieth Nordic Conference on Radio
Schur-convexity of the Symbol Error Rate in Correlated MIMO Systems with Precoding and Space-time Coding RadioVetenskap och Kommunikation (RVK 08) Proceedings of the twentieth Nordic Conference on Radio
Information Theory Meets Game Theory on The Interference Channel
 Information Theory Meets Game Theory on The Interference Channel Randall A. Berry Dept. of EECS Northwestern University e-mail: rberry@eecs.northwestern.edu David N. C. Tse Wireless Foundations University
Information Theory Meets Game Theory on The Interference Channel Randall A. Berry Dept. of EECS Northwestern University e-mail: rberry@eecs.northwestern.edu David N. C. Tse Wireless Foundations University
Minimum Mean Squared Error Interference Alignment
 Minimum Mean Squared Error Interference Alignment David A. Schmidt, Changxin Shi, Randall A. Berry, Michael L. Honig and Wolfgang Utschick Associate Institute for Signal Processing Technische Universität
Minimum Mean Squared Error Interference Alignment David A. Schmidt, Changxin Shi, Randall A. Berry, Michael L. Honig and Wolfgang Utschick Associate Institute for Signal Processing Technische Universität
Power Control in Multi-Carrier CDMA Systems
 A Game-Theoretic Approach to Energy-Efficient ower Control in Multi-Carrier CDMA Systems Farhad Meshkati, Student Member, IEEE, Mung Chiang, Member, IEEE, H. Vincent oor, Fellow, IEEE, and Stuart C. Schwartz,
A Game-Theoretic Approach to Energy-Efficient ower Control in Multi-Carrier CDMA Systems Farhad Meshkati, Student Member, IEEE, Mung Chiang, Member, IEEE, H. Vincent oor, Fellow, IEEE, and Stuart C. Schwartz,
Approximately achieving the feedback interference channel capacity with point-to-point codes
 Approximately achieving the feedback interference channel capacity with point-to-point codes Joyson Sebastian*, Can Karakus*, Suhas Diggavi* Abstract Superposition codes with rate-splitting have been used
Approximately achieving the feedback interference channel capacity with point-to-point codes Joyson Sebastian*, Can Karakus*, Suhas Diggavi* Abstract Superposition codes with rate-splitting have been used
The Optimality of Beamforming: A Unified View
 The Optimality of Beamforming: A Unified View Sudhir Srinivasa and Syed Ali Jafar Electrical Engineering and Computer Science University of California Irvine, Irvine, CA 92697-2625 Email: sudhirs@uciedu,
The Optimality of Beamforming: A Unified View Sudhir Srinivasa and Syed Ali Jafar Electrical Engineering and Computer Science University of California Irvine, Irvine, CA 92697-2625 Email: sudhirs@uciedu,
Minimax Problems. Daniel P. Palomar. Hong Kong University of Science and Technolgy (HKUST)
 Mini Problems Daniel P. Palomar Hong Kong University of Science and Technolgy (HKUST) ELEC547 - Convex Optimization Fall 2009-10, HKUST, Hong Kong Outline of Lecture Introduction Matrix games Bilinear
Mini Problems Daniel P. Palomar Hong Kong University of Science and Technolgy (HKUST) ELEC547 - Convex Optimization Fall 2009-10, HKUST, Hong Kong Outline of Lecture Introduction Matrix games Bilinear
Dirty Paper Coding vs. TDMA for MIMO Broadcast Channels
 TO APPEAR IEEE INTERNATIONAL CONFERENCE ON COUNICATIONS, JUNE 004 1 Dirty Paper Coding vs. TDA for IO Broadcast Channels Nihar Jindal & Andrea Goldsmith Dept. of Electrical Engineering, Stanford University
TO APPEAR IEEE INTERNATIONAL CONFERENCE ON COUNICATIONS, JUNE 004 1 Dirty Paper Coding vs. TDA for IO Broadcast Channels Nihar Jindal & Andrea Goldsmith Dept. of Electrical Engineering, Stanford University
Channel Allocation Using Pricing in Satellite Networks
 Channel Allocation Using Pricing in Satellite Networks Jun Sun and Eytan Modiano Laboratory for Information and Decision Systems Massachusetts Institute of Technology {junsun, modiano}@mitedu Abstract
Channel Allocation Using Pricing in Satellite Networks Jun Sun and Eytan Modiano Laboratory for Information and Decision Systems Massachusetts Institute of Technology {junsun, modiano}@mitedu Abstract
Clean relaying aided cognitive radio under the coexistence constraint
 Clean relaying aided cognitive radio under the coexistence constraint Pin-Hsun Lin, Shih-Chun Lin, Hsuan-Jung Su and Y.-W. Peter Hong Abstract arxiv:04.3497v [cs.it] 8 Apr 0 We consider the interference-mitigation
Clean relaying aided cognitive radio under the coexistence constraint Pin-Hsun Lin, Shih-Chun Lin, Hsuan-Jung Su and Y.-W. Peter Hong Abstract arxiv:04.3497v [cs.it] 8 Apr 0 We consider the interference-mitigation
Competitive Scheduling in Wireless Collision Channels with Correlated Channel State
 Competitive Scheduling in Wireless Collision Channels with Correlated Channel State Utku Ozan Candogan, Ishai Menache, Asuman Ozdaglar and Pablo A. Parrilo Abstract We consider a wireless collision channel,
Competitive Scheduling in Wireless Collision Channels with Correlated Channel State Utku Ozan Candogan, Ishai Menache, Asuman Ozdaglar and Pablo A. Parrilo Abstract We consider a wireless collision channel,
6.254 : Game Theory with Engineering Applications Lecture 7: Supermodular Games
 6.254 : Game Theory with Engineering Applications Lecture 7: Asu Ozdaglar MIT February 25, 2010 1 Introduction Outline Uniqueness of a Pure Nash Equilibrium for Continuous Games Reading: Rosen J.B., Existence
6.254 : Game Theory with Engineering Applications Lecture 7: Asu Ozdaglar MIT February 25, 2010 1 Introduction Outline Uniqueness of a Pure Nash Equilibrium for Continuous Games Reading: Rosen J.B., Existence
IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 52, NO. 5, MAY
 IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 52, NO. 5, MAY 2004 1179 Optimum Linear Joint ansmit-receive Processing for MIMO Channels with QoS Constraints Daniel Pérez Palomar, Member, IEEE, Miguel Angel
IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 52, NO. 5, MAY 2004 1179 Optimum Linear Joint ansmit-receive Processing for MIMO Channels with QoS Constraints Daniel Pérez Palomar, Member, IEEE, Miguel Angel
POWER ALLOCATION AND OPTIMAL TX/RX STRUCTURES FOR MIMO SYSTEMS
 POWER ALLOCATION AND OPTIMAL TX/RX STRUCTURES FOR MIMO SYSTEMS R. Cendrillon, O. Rousseaux and M. Moonen SCD/ESAT, Katholiee Universiteit Leuven, Belgium {raphael.cendrillon, olivier.rousseaux, marc.moonen}@esat.uleuven.ac.be
POWER ALLOCATION AND OPTIMAL TX/RX STRUCTURES FOR MIMO SYSTEMS R. Cendrillon, O. Rousseaux and M. Moonen SCD/ESAT, Katholiee Universiteit Leuven, Belgium {raphael.cendrillon, olivier.rousseaux, marc.moonen}@esat.uleuven.ac.be
Efficient Computation of the Pareto Boundary for the Two-User MISO Interference Channel with Multi-User Decoding Capable Receivers
 Efficient Computation of the Pareto Boundary for the Two-User MISO Interference Channel with Multi-User Decoding Capable Receivers Johannes Lindblom, Eleftherios Karipidis and Erik G. Larsson Linköping
Efficient Computation of the Pareto Boundary for the Two-User MISO Interference Channel with Multi-User Decoding Capable Receivers Johannes Lindblom, Eleftherios Karipidis and Erik G. Larsson Linköping
Interactive Interference Alignment
 Interactive Interference Alignment Quan Geng, Sreeram annan, and Pramod Viswanath Coordinated Science Laboratory and Dept. of ECE University of Illinois, Urbana-Champaign, IL 61801 Email: {geng5, kannan1,
Interactive Interference Alignment Quan Geng, Sreeram annan, and Pramod Viswanath Coordinated Science Laboratory and Dept. of ECE University of Illinois, Urbana-Champaign, IL 61801 Email: {geng5, kannan1,
The Water-Filling Game in Fading Multiple Access Channels
 The Water-Filling Game in Fading Multiple Access Channels Lifeng Lai and Hesham El Gamal arxiv:cs/05203v [cs.it] 3 Dec 2005 February, 2008 Abstract We adopt a game theoretic approach for the design and
The Water-Filling Game in Fading Multiple Access Channels Lifeng Lai and Hesham El Gamal arxiv:cs/05203v [cs.it] 3 Dec 2005 February, 2008 Abstract We adopt a game theoretic approach for the design and
ELEC E7210: Communication Theory. Lecture 10: MIMO systems
 ELEC E7210: Communication Theory Lecture 10: MIMO systems Matrix Definitions, Operations, and Properties (1) NxM matrix a rectangular array of elements a A. an 11 1....... a a 1M. NM B D C E ermitian transpose
ELEC E7210: Communication Theory Lecture 10: MIMO systems Matrix Definitions, Operations, and Properties (1) NxM matrix a rectangular array of elements a A. an 11 1....... a a 1M. NM B D C E ermitian transpose
Random Access Game. Medium Access Control Design for Wireless Networks 1. Sandip Chakraborty. Department of Computer Science and Engineering,
 Random Access Game Medium Access Control Design for Wireless Networks 1 Sandip Chakraborty Department of Computer Science and Engineering, INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR October 22, 2016 1 Chen
Random Access Game Medium Access Control Design for Wireless Networks 1 Sandip Chakraborty Department of Computer Science and Engineering, INDIAN INSTITUTE OF TECHNOLOGY KHARAGPUR October 22, 2016 1 Chen
Maximizing Sum Rate and Minimizing MSE on Multiuser Downlink: Optimality, Fast Algorithms and Equivalence via Max-min SIR
 1 Maximizing Sum Rate and Minimizing MSE on Multiuser Downlink: Optimality, Fast Algorithms and Equivalence via Max-min SIR Chee Wei Tan, Mung Chiang ¾ and R. Srikant City University of Hong Kong ¾ Princeton
1 Maximizing Sum Rate and Minimizing MSE on Multiuser Downlink: Optimality, Fast Algorithms and Equivalence via Max-min SIR Chee Wei Tan, Mung Chiang ¾ and R. Srikant City University of Hong Kong ¾ Princeton
2318 IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 54, NO. 6, JUNE Mai Vu, Student Member, IEEE, and Arogyaswami Paulraj, Fellow, IEEE
 2318 IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 54, NO. 6, JUNE 2006 Optimal Linear Precoders for MIMO Wireless Correlated Channels With Nonzero Mean in Space Time Coded Systems Mai Vu, Student Member,
2318 IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 54, NO. 6, JUNE 2006 Optimal Linear Precoders for MIMO Wireless Correlated Channels With Nonzero Mean in Space Time Coded Systems Mai Vu, Student Member,
Optimal Power Control in Decentralized Gaussian Multiple Access Channels
 1 Optimal Power Control in Decentralized Gaussian Multiple Access Channels Kamal Singh Department of Electrical Engineering Indian Institute of Technology Bombay. arxiv:1711.08272v1 [eess.sp] 21 Nov 2017
1 Optimal Power Control in Decentralized Gaussian Multiple Access Channels Kamal Singh Department of Electrical Engineering Indian Institute of Technology Bombay. arxiv:1711.08272v1 [eess.sp] 21 Nov 2017
5682 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 55, NO. 12, DECEMBER /$ IEEE
 5682 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 55, NO. 12, DECEMBER 2009 Hyperplane-Based Vector Quantization for Distributed Estimation in Wireless Sensor Networks Jun Fang, Member, IEEE, and Hongbin
5682 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 55, NO. 12, DECEMBER 2009 Hyperplane-Based Vector Quantization for Distributed Estimation in Wireless Sensor Networks Jun Fang, Member, IEEE, and Hongbin
Computing Solution Concepts of Normal-Form Games. Song Chong EE, KAIST
 Computing Solution Concepts of Normal-Form Games Song Chong EE, KAIST songchong@kaist.edu Computing Nash Equilibria of Two-Player, Zero-Sum Games Can be expressed as a linear program (LP), which means
Computing Solution Concepts of Normal-Form Games Song Chong EE, KAIST songchong@kaist.edu Computing Nash Equilibria of Two-Player, Zero-Sum Games Can be expressed as a linear program (LP), which means
OSNR Optimization in Optical Networks: Extension for Capacity Constraints
 5 American Control Conference June 8-5. Portland OR USA ThB3.6 OSNR Optimization in Optical Networks: Extension for Capacity Constraints Yan Pan and Lacra Pavel Abstract This paper builds on the OSNR model
5 American Control Conference June 8-5. Portland OR USA ThB3.6 OSNR Optimization in Optical Networks: Extension for Capacity Constraints Yan Pan and Lacra Pavel Abstract This paper builds on the OSNR model
Quality-Of-Service Provisioning in Decentralized Networks: A Satisfaction Equilibrium Approach
 1 Quality-Of-Service Provisioning in Decentralized Networs: A Satisfaction Equilibrium Approach S.M. Perlaza, H. Tembine, S. Lasaulce, and M. Debbah arxiv:1112.1730v1 [cs.it] 7 Dec 2011 Abstract This paper
1 Quality-Of-Service Provisioning in Decentralized Networs: A Satisfaction Equilibrium Approach S.M. Perlaza, H. Tembine, S. Lasaulce, and M. Debbah arxiv:1112.1730v1 [cs.it] 7 Dec 2011 Abstract This paper
Game theory is a field of applied mathematics that
 [ Gesualdo Scutari, Daniel P. Palomar, Jong-Shi Pang, and Francisco Facchinei ] Flexible Design of Cognitive Radio Wireless Systems [From game theory to variational inequality theory] Game theory is a
[ Gesualdo Scutari, Daniel P. Palomar, Jong-Shi Pang, and Francisco Facchinei ] Flexible Design of Cognitive Radio Wireless Systems [From game theory to variational inequality theory] Game theory is a
A Nash Equilibrium Analysis for Interference Coupled Wireless Systems
 A Nash Equilibrium Analysis for Interference Coupled Wireless Systems Siddharth Nai Technical University of Berlin Heinrich Hertz Chair for Mobile Communications Einsteinufer 25, 10587 Berlin, Germany
A Nash Equilibrium Analysis for Interference Coupled Wireless Systems Siddharth Nai Technical University of Berlin Heinrich Hertz Chair for Mobile Communications Einsteinufer 25, 10587 Berlin, Germany
Network Calculus. A General Framework for Interference Management and Resource Allocation. Martin Schubert
 Network Calculus A General Framework for Interference Management and Resource Allocation Martin Schubert Fraunhofer Institute for Telecommunications HHI, Berlin, Germany Fraunhofer German-Sino Lab for
Network Calculus A General Framework for Interference Management and Resource Allocation Martin Schubert Fraunhofer Institute for Telecommunications HHI, Berlin, Germany Fraunhofer German-Sino Lab for
Optimal Secondary Spectrum Auctions for Markets with Communication Constraints
 Optimal Secondary Spectrum Auctions for Markets with Communication Constraints Deepan Palguna, David J. Love, and Ilya Pollak Abstract Auctions have been proposed as a way to provide economic incentives
Optimal Secondary Spectrum Auctions for Markets with Communication Constraints Deepan Palguna, David J. Love, and Ilya Pollak Abstract Auctions have been proposed as a way to provide economic incentives
Equilibria of Channel Selection Games in Parallel Multiple Access Channels
 Equilibria of Channel Selection Games in Parallel Multiple Access Channels Samir Medina Perlaza, Samson Lasaulce, Mérouane Debbah To cite this version: Samir Medina Perlaza, Samson Lasaulce, Mérouane Debbah.
Equilibria of Channel Selection Games in Parallel Multiple Access Channels Samir Medina Perlaza, Samson Lasaulce, Mérouane Debbah To cite this version: Samir Medina Perlaza, Samson Lasaulce, Mérouane Debbah.
Optimization in Wireless Communication
 Zhi-Quan (Tom) Luo Department of Electrical and Computer Engineering University of Minnesota 200 Union Street SE Minneapolis, MN 55455 2007 NSF Workshop Challenges Optimization problems from wireless applications
Zhi-Quan (Tom) Luo Department of Electrical and Computer Engineering University of Minnesota 200 Union Street SE Minneapolis, MN 55455 2007 NSF Workshop Challenges Optimization problems from wireless applications
Game Theory Fall 2003
 Game Theory Fall 2003 Problem Set 1 [1] In this problem (see FT Ex. 1.1) you are asked to play with arbitrary 2 2 games just to get used to the idea of equilibrium computation. Specifically, consider the
Game Theory Fall 2003 Problem Set 1 [1] In this problem (see FT Ex. 1.1) you are asked to play with arbitrary 2 2 games just to get used to the idea of equilibrium computation. Specifically, consider the
Ü B U N G S A U F G A B E N. S p i e l t h e o r i e
 T E C H N I S C H E U N I V E R S I T Ä T D R E S D E N F A K U L T Ä T E L E K T R O T E C H N I K U N D I N F O R M A T I O N S T E C H N I K Ü B U N G S A U F G A B E N S p i e l t h e o r i e by Alessio
T E C H N I S C H E U N I V E R S I T Ä T D R E S D E N F A K U L T Ä T E L E K T R O T E C H N I K U N D I N F O R M A T I O N S T E C H N I K Ü B U N G S A U F G A B E N S p i e l t h e o r i e by Alessio
DOWNLINK transmit beamforming has recently received
 4254 IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 58, NO. 8, AUGUST 2010 A Dual Perspective on Separable Semidefinite Programming With Applications to Optimal Downlink Beamforming Yongwei Huang, Member,
4254 IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 58, NO. 8, AUGUST 2010 A Dual Perspective on Separable Semidefinite Programming With Applications to Optimal Downlink Beamforming Yongwei Huang, Member,
Basic Game Theory. Kate Larson. January 7, University of Waterloo. Kate Larson. What is Game Theory? Normal Form Games. Computing Equilibria
 Basic Game Theory University of Waterloo January 7, 2013 Outline 1 2 3 What is game theory? The study of games! Bluffing in poker What move to make in chess How to play Rock-Scissors-Paper Also study of
Basic Game Theory University of Waterloo January 7, 2013 Outline 1 2 3 What is game theory? The study of games! Bluffing in poker What move to make in chess How to play Rock-Scissors-Paper Also study of
Limited Feedback in Wireless Communication Systems
 Limited Feedback in Wireless Communication Systems - Summary of An Overview of Limited Feedback in Wireless Communication Systems Gwanmo Ku May 14, 17, and 21, 2013 Outline Transmitter Ant. 1 Channel N
Limited Feedback in Wireless Communication Systems - Summary of An Overview of Limited Feedback in Wireless Communication Systems Gwanmo Ku May 14, 17, and 21, 2013 Outline Transmitter Ant. 1 Channel N
Robust linear optimization under general norms
 Operations Research Letters 3 (004) 50 56 Operations Research Letters www.elsevier.com/locate/dsw Robust linear optimization under general norms Dimitris Bertsimas a; ;, Dessislava Pachamanova b, Melvyn
Operations Research Letters 3 (004) 50 56 Operations Research Letters www.elsevier.com/locate/dsw Robust linear optimization under general norms Dimitris Bertsimas a; ;, Dessislava Pachamanova b, Melvyn
Single-User MIMO systems: Introduction, capacity results, and MIMO beamforming
 Single-User MIMO systems: Introduction, capacity results, and MIMO beamforming Master Universitario en Ingeniería de Telecomunicación I. Santamaría Universidad de Cantabria Contents Introduction Multiplexing,
Single-User MIMO systems: Introduction, capacity results, and MIMO beamforming Master Universitario en Ingeniería de Telecomunicación I. Santamaría Universidad de Cantabria Contents Introduction Multiplexing,
CS 781 Lecture 9 March 10, 2011 Topics: Local Search and Optimization Metropolis Algorithm Greedy Optimization Hopfield Networks Max Cut Problem Nash
 CS 781 Lecture 9 March 10, 2011 Topics: Local Search and Optimization Metropolis Algorithm Greedy Optimization Hopfield Networks Max Cut Problem Nash Equilibrium Price of Stability Coping With NP-Hardness
CS 781 Lecture 9 March 10, 2011 Topics: Local Search and Optimization Metropolis Algorithm Greedy Optimization Hopfield Networks Max Cut Problem Nash Equilibrium Price of Stability Coping With NP-Hardness
Vector Channel Capacity with Quantized Feedback
 Vector Channel Capacity with Quantized Feedback Sudhir Srinivasa and Syed Ali Jafar Electrical Engineering and Computer Science University of California Irvine, Irvine, CA 9697-65 Email: syed@ece.uci.edu,
Vector Channel Capacity with Quantized Feedback Sudhir Srinivasa and Syed Ali Jafar Electrical Engineering and Computer Science University of California Irvine, Irvine, CA 9697-65 Email: syed@ece.uci.edu,
IN this paper, we show that the scalar Gaussian multiple-access
 768 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 50, NO. 5, MAY 2004 On the Duality of Gaussian Multiple-Access and Broadcast Channels Nihar Jindal, Student Member, IEEE, Sriram Vishwanath, and Andrea
768 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 50, NO. 5, MAY 2004 On the Duality of Gaussian Multiple-Access and Broadcast Channels Nihar Jindal, Student Member, IEEE, Sriram Vishwanath, and Andrea
Lagrange Duality. Daniel P. Palomar. Hong Kong University of Science and Technology (HKUST)
 Lagrange Duality Daniel P. Palomar Hong Kong University of Science and Technology (HKUST) ELEC5470 - Convex Optimization Fall 2017-18, HKUST, Hong Kong Outline of Lecture Lagrangian Dual function Dual
Lagrange Duality Daniel P. Palomar Hong Kong University of Science and Technology (HKUST) ELEC5470 - Convex Optimization Fall 2017-18, HKUST, Hong Kong Outline of Lecture Lagrangian Dual function Dual
Battery-State Dependent Power Control as a Dynamic Game
 1 Battery-State Dependent Power Control as a Dynamic Game Ishai Menache and Eitan Altman Faculty of Electrical Engineering, Technion, Haifa 32000, Israel INRIA, Sophia-Antipolis, 2004 Route des Lucioles,
1 Battery-State Dependent Power Control as a Dynamic Game Ishai Menache and Eitan Altman Faculty of Electrical Engineering, Technion, Haifa 32000, Israel INRIA, Sophia-Antipolis, 2004 Route des Lucioles,
Spectrum Sharing Games on the Interference Channel
 Spectrum Sharing Games on the Interference Channel Mehdi Bennis +, Mael Le Treust, Samson Lasaulce, Merouane Debbah and Jorma Lilleberg + Centre for Wireless Communications, University of Oulu, Oulu, Finland
Spectrum Sharing Games on the Interference Channel Mehdi Bennis +, Mael Le Treust, Samson Lasaulce, Merouane Debbah and Jorma Lilleberg + Centre for Wireless Communications, University of Oulu, Oulu, Finland
Exact and Approximate Equilibria for Optimal Group Network Formation
 Exact and Approximate Equilibria for Optimal Group Network Formation Elliot Anshelevich and Bugra Caskurlu Computer Science Department, RPI, 110 8th Street, Troy, NY 12180 {eanshel,caskub}@cs.rpi.edu Abstract.
Exact and Approximate Equilibria for Optimal Group Network Formation Elliot Anshelevich and Bugra Caskurlu Computer Science Department, RPI, 110 8th Street, Troy, NY 12180 {eanshel,caskub}@cs.rpi.edu Abstract.
Novel spectrum sensing schemes for Cognitive Radio Networks
 Novel spectrum sensing schemes for Cognitive Radio Networks Cantabria University Santander, May, 2015 Supélec, SCEE Rennes, France 1 The Advanced Signal Processing Group http://gtas.unican.es The Advanced
Novel spectrum sensing schemes for Cognitive Radio Networks Cantabria University Santander, May, 2015 Supélec, SCEE Rennes, France 1 The Advanced Signal Processing Group http://gtas.unican.es The Advanced
Diversity-Multiplexing Tradeoff in MIMO Channels with Partial CSIT. ECE 559 Presentation Hoa Pham Dec 3, 2007
 Diversity-Multiplexing Tradeoff in MIMO Channels with Partial CSIT ECE 559 Presentation Hoa Pham Dec 3, 2007 Introduction MIMO systems provide two types of gains Diversity Gain: each path from a transmitter
Diversity-Multiplexing Tradeoff in MIMO Channels with Partial CSIT ECE 559 Presentation Hoa Pham Dec 3, 2007 Introduction MIMO systems provide two types of gains Diversity Gain: each path from a transmitter
AN EXTERNALITY BASED DECENTRALIZED OPTIMAL POWER ALLOCATION SCHEME FOR WIRELESS MESH NETWORKS
 AN EXTERNALITY BASED DECENTRALIZED OPTIMAL POWER ALLOCATION SCHEME FOR WIRELESS MESH NETWORKS Shruti Sharma and Demos Teneketzis Department of Electrical Engineering and Computer Science University of
AN EXTERNALITY BASED DECENTRALIZED OPTIMAL POWER ALLOCATION SCHEME FOR WIRELESS MESH NETWORKS Shruti Sharma and Demos Teneketzis Department of Electrical Engineering and Computer Science University of
Morning Session Capacity-based Power Control. Department of Electrical and Computer Engineering University of Maryland
 Morning Session Capacity-based Power Control Şennur Ulukuş Department of Electrical and Computer Engineering University of Maryland So Far, We Learned... Power control with SIR-based QoS guarantees Suitable
Morning Session Capacity-based Power Control Şennur Ulukuş Department of Electrical and Computer Engineering University of Maryland So Far, We Learned... Power control with SIR-based QoS guarantees Suitable
Price and Capacity Competition
 Price and Capacity Competition Daron Acemoglu, Kostas Bimpikis, and Asuman Ozdaglar October 9, 2007 Abstract We study the efficiency of oligopoly equilibria in a model where firms compete over capacities
Price and Capacity Competition Daron Acemoglu, Kostas Bimpikis, and Asuman Ozdaglar October 9, 2007 Abstract We study the efficiency of oligopoly equilibria in a model where firms compete over capacities
A Framework for Training-Based Estimation in Arbitrarily Correlated Rician MIMO Channels with Rician Disturbance
 A Framework for Training-Based Estimation in Arbitrarily Correlated Rician MIMO Channels with Rician Disturbance IEEE TRANSACTIONS ON SIGNAL PROCESSING Volume 58, Issue 3, Pages 1807-1820, March 2010.
A Framework for Training-Based Estimation in Arbitrarily Correlated Rician MIMO Channels with Rician Disturbance IEEE TRANSACTIONS ON SIGNAL PROCESSING Volume 58, Issue 3, Pages 1807-1820, March 2010.
Selecting Efficient Correlated Equilibria Through Distributed Learning. Jason R. Marden
 1 Selecting Efficient Correlated Equilibria Through Distributed Learning Jason R. Marden Abstract A learning rule is completely uncoupled if each player s behavior is conditioned only on his own realized
1 Selecting Efficient Correlated Equilibria Through Distributed Learning Jason R. Marden Abstract A learning rule is completely uncoupled if each player s behavior is conditioned only on his own realized
A Price-Based Approach for Controlling Networked Distributed Energy Resources
 A Price-Based Approach for Controlling Networked Distributed Energy Resources Alejandro D. Domínguez-García (joint work with Bahman Gharesifard and Tamer Başar) Coordinated Science Laboratory Department
A Price-Based Approach for Controlling Networked Distributed Energy Resources Alejandro D. Domínguez-García (joint work with Bahman Gharesifard and Tamer Başar) Coordinated Science Laboratory Department
Communication Games on the Generalized Gaussian Relay Channel
 Communication Games on the Generalized Gaussian Relay Channel Dileep M. alathil Department of Electrical Engineering University of Southern California manisser@usc.edu Rahul Jain EE & ISE Departments University
Communication Games on the Generalized Gaussian Relay Channel Dileep M. alathil Department of Electrical Engineering University of Southern California manisser@usc.edu Rahul Jain EE & ISE Departments University
K User Interference Channel with Backhaul
 1 K User Interference Channel with Backhaul Cooperation: DoF vs. Backhaul Load Trade Off Borna Kananian,, Mohammad A. Maddah-Ali,, Babak H. Khalaj, Department of Electrical Engineering, Sharif University
1 K User Interference Channel with Backhaul Cooperation: DoF vs. Backhaul Load Trade Off Borna Kananian,, Mohammad A. Maddah-Ali,, Babak H. Khalaj, Department of Electrical Engineering, Sharif University
Degrees-of-Freedom for the 4-User SISO Interference Channel with Improper Signaling
 Degrees-of-Freedom for the -User SISO Interference Channel with Improper Signaling C Lameiro and I Santamaría Dept of Communications Engineering University of Cantabria 9005 Santander Cantabria Spain Email:
Degrees-of-Freedom for the -User SISO Interference Channel with Improper Signaling C Lameiro and I Santamaría Dept of Communications Engineering University of Cantabria 9005 Santander Cantabria Spain Email:
Mathematical Economics - PhD in Economics
 - PhD in Part 1: Supermodularity and complementarity in the one-dimensional and Paulo Brito ISEG - Technical University of Lisbon November 24, 2010 1 2 - Supermodular optimization 3 one-dimensional 4 Supermodular
- PhD in Part 1: Supermodularity and complementarity in the one-dimensional and Paulo Brito ISEG - Technical University of Lisbon November 24, 2010 1 2 - Supermodular optimization 3 one-dimensional 4 Supermodular
Decentralized Interference Channels with Noisy Feedback Possess Pareto Optimal Nash Equilibria
 Decentralized Interference Channels with Noisy Feedback Possess Pareto Optimal Nash Equilibria Samir M. Perlaza Ravi Tandon H. Vincent Poor To cite this version: Samir M. Perlaza Ravi Tandon H. Vincent
Decentralized Interference Channels with Noisy Feedback Possess Pareto Optimal Nash Equilibria Samir M. Perlaza Ravi Tandon H. Vincent Poor To cite this version: Samir M. Perlaza Ravi Tandon H. Vincent
LECTURE 18. Lecture outline Gaussian channels: parallel colored noise inter-symbol interference general case: multiple inputs and outputs
 LECTURE 18 Last time: White Gaussian noise Bandlimited WGN Additive White Gaussian Noise (AWGN) channel Capacity of AWGN channel Application: DS-CDMA systems Spreading Coding theorem Lecture outline Gaussian
LECTURE 18 Last time: White Gaussian noise Bandlimited WGN Additive White Gaussian Noise (AWGN) channel Capacity of AWGN channel Application: DS-CDMA systems Spreading Coding theorem Lecture outline Gaussian
Price of Stability in Survivable Network Design
 Noname manuscript No. (will be inserted by the editor) Price of Stability in Survivable Network Design Elliot Anshelevich Bugra Caskurlu Received: January 2010 / Accepted: Abstract We study the survivable
Noname manuscript No. (will be inserted by the editor) Price of Stability in Survivable Network Design Elliot Anshelevich Bugra Caskurlu Received: January 2010 / Accepted: Abstract We study the survivable
Optimality, Duality, Complementarity for Constrained Optimization
 Optimality, Duality, Complementarity for Constrained Optimization Stephen Wright University of Wisconsin-Madison May 2014 Wright (UW-Madison) Optimality, Duality, Complementarity May 2014 1 / 41 Linear
Optimality, Duality, Complementarity for Constrained Optimization Stephen Wright University of Wisconsin-Madison May 2014 Wright (UW-Madison) Optimality, Duality, Complementarity May 2014 1 / 41 Linear
On the complexity of maximizing the minimum Shannon capacity in wireless networks by joint channel assignment and power allocation
 On the complexity of maximizing the minimum Shannon capacity in wireless networks by joint channel assignment and power allocation Mikael Fallgren Royal Institute of Technology December, 2009 Abstract
On the complexity of maximizing the minimum Shannon capacity in wireless networks by joint channel assignment and power allocation Mikael Fallgren Royal Institute of Technology December, 2009 Abstract
Iterative Learning Control Analysis and Design I
 Iterative Learning Control Analysis and Design I Electronics and Computer Science University of Southampton Southampton, SO17 1BJ, UK etar@ecs.soton.ac.uk http://www.ecs.soton.ac.uk/ Contents Basics Representations
Iterative Learning Control Analysis and Design I Electronics and Computer Science University of Southampton Southampton, SO17 1BJ, UK etar@ecs.soton.ac.uk http://www.ecs.soton.ac.uk/ Contents Basics Representations
Distributed Joint Offloading Decision and Resource Allocation for Multi-User Mobile Edge Computing: A Game Theory Approach
 Distributed Joint Offloading Decision and Resource Allocation for Multi-User Mobile Edge Computing: A Game Theory Approach Ning Li, Student Member, IEEE, Jose-Fernan Martinez-Ortega, Gregorio Rubio Abstract-
Distributed Joint Offloading Decision and Resource Allocation for Multi-User Mobile Edge Computing: A Game Theory Approach Ning Li, Student Member, IEEE, Jose-Fernan Martinez-Ortega, Gregorio Rubio Abstract-
Internalization of Social Cost in Congestion Games
 Internalization of Social Cost in Congestion Games Igal Milchtaich * November 2017 Congestion models may be studied from either the users point of view or the social one. The first perspective examines
Internalization of Social Cost in Congestion Games Igal Milchtaich * November 2017 Congestion models may be studied from either the users point of view or the social one. The first perspective examines
Title. Author(s)Tsai, Shang-Ho. Issue Date Doc URL. Type. Note. File Information. Equal Gain Beamforming in Rayleigh Fading Channels
 Title Equal Gain Beamforming in Rayleigh Fading Channels Author(s)Tsai, Shang-Ho Proceedings : APSIPA ASC 29 : Asia-Pacific Signal Citationand Conference: 688-691 Issue Date 29-1-4 Doc URL http://hdl.handle.net/2115/39789
Title Equal Gain Beamforming in Rayleigh Fading Channels Author(s)Tsai, Shang-Ho Proceedings : APSIPA ASC 29 : Asia-Pacific Signal Citationand Conference: 688-691 Issue Date 29-1-4 Doc URL http://hdl.handle.net/2115/39789
Structural and Multidisciplinary Optimization. P. Duysinx and P. Tossings
 Structural and Multidisciplinary Optimization P. Duysinx and P. Tossings 2018-2019 CONTACTS Pierre Duysinx Institut de Mécanique et du Génie Civil (B52/3) Phone number: 04/366.91.94 Email: P.Duysinx@uliege.be
Structural and Multidisciplinary Optimization P. Duysinx and P. Tossings 2018-2019 CONTACTS Pierre Duysinx Institut de Mécanique et du Génie Civil (B52/3) Phone number: 04/366.91.94 Email: P.Duysinx@uliege.be
Distributed Power Control for Time Varying Wireless Networks: Optimality and Convergence
 Distributed Power Control for Time Varying Wireless Networks: Optimality and Convergence Tim Holliday, Nick Bambos, Peter Glynn, Andrea Goldsmith Stanford University Abstract This paper presents a new
Distributed Power Control for Time Varying Wireless Networks: Optimality and Convergence Tim Holliday, Nick Bambos, Peter Glynn, Andrea Goldsmith Stanford University Abstract This paper presents a new
CS 598RM: Algorithmic Game Theory, Spring Practice Exam Solutions
 CS 598RM: Algorithmic Game Theory, Spring 2017 1. Answer the following. Practice Exam Solutions Agents 1 and 2 are bargaining over how to split a dollar. Each agent simultaneously demands share he would
CS 598RM: Algorithmic Game Theory, Spring 2017 1. Answer the following. Practice Exam Solutions Agents 1 and 2 are bargaining over how to split a dollar. Each agent simultaneously demands share he would
Distributed Power Allocation with Rate Constraints in Gaussian Frequency-Selective Interference Channels
 Dipartimento di Informatica e Sistemistica Antonio Ruberti Università degli Studi di Roma La Sapienza Distributed Power Allocation with Rate Constraints in Gaussian Frequency-Selective Interference Channels
Dipartimento di Informatica e Sistemistica Antonio Ruberti Università degli Studi di Roma La Sapienza Distributed Power Allocation with Rate Constraints in Gaussian Frequency-Selective Interference Channels
Interior-Point Methods for Linear Optimization
 Interior-Point Methods for Linear Optimization Robert M. Freund and Jorge Vera March, 204 c 204 Robert M. Freund and Jorge Vera. All rights reserved. Linear Optimization with a Logarithmic Barrier Function
Interior-Point Methods for Linear Optimization Robert M. Freund and Jorge Vera March, 204 c 204 Robert M. Freund and Jorge Vera. All rights reserved. Linear Optimization with a Logarithmic Barrier Function
Improper Gaussian signaling for
 Improper Gaussian signaling for multiple-access channels in underlay cognitive radio Christian Lameiro, Member, IEEE, Ignacio Santamaría, Senior Member, IEEE, arxiv:7.09768v [cs.it] 27 Nov 207 and Peter
Improper Gaussian signaling for multiple-access channels in underlay cognitive radio Christian Lameiro, Member, IEEE, Ignacio Santamaría, Senior Member, IEEE, arxiv:7.09768v [cs.it] 27 Nov 207 and Peter
Degrees-of-Freedom Robust Transmission for the K-user Distributed Broadcast Channel
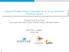 /33 Degrees-of-Freedom Robust Transmission for the K-user Distributed Broadcast Channel Presented by Paul de Kerret Joint work with Antonio Bazco, Nicolas Gresset, and David Gesbert ESIT 2017 in Madrid,
/33 Degrees-of-Freedom Robust Transmission for the K-user Distributed Broadcast Channel Presented by Paul de Kerret Joint work with Antonio Bazco, Nicolas Gresset, and David Gesbert ESIT 2017 in Madrid,
Decoupling Coupled Constraints Through Utility Design
 1 Decoupling Coupled Constraints Through Utility Design Na Li and Jason R. Marden Abstract The central goal in multiagent systems is to design local control laws for the individual agents to ensure that
1 Decoupling Coupled Constraints Through Utility Design Na Li and Jason R. Marden Abstract The central goal in multiagent systems is to design local control laws for the individual agents to ensure that
CDMA Systems in Fading Channels: Admissibility, Network Capacity, and Power Control
 962 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 46, NO. 3, MAY 2000 CDMA Systems in Fading Channels: Admissibility, Network Capacity, and Power Control Junshan Zhang, Student Member, IEEE, and Edwin
962 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 46, NO. 3, MAY 2000 CDMA Systems in Fading Channels: Admissibility, Network Capacity, and Power Control Junshan Zhang, Student Member, IEEE, and Edwin
Tutorial on Convex Optimization: Part II
 Tutorial on Convex Optimization: Part II Dr. Khaled Ardah Communications Research Laboratory TU Ilmenau Dec. 18, 2018 Outline Convex Optimization Review Lagrangian Duality Applications Optimal Power Allocation
Tutorial on Convex Optimization: Part II Dr. Khaled Ardah Communications Research Laboratory TU Ilmenau Dec. 18, 2018 Outline Convex Optimization Review Lagrangian Duality Applications Optimal Power Allocation
Virtual Robust Implementation and Strategic Revealed Preference
 and Strategic Revealed Preference Workshop of Mathematical Economics Celebrating the 60th birthday of Aloisio Araujo IMPA Rio de Janeiro December 2006 Denitions "implementation": requires ALL equilibria
and Strategic Revealed Preference Workshop of Mathematical Economics Celebrating the 60th birthday of Aloisio Araujo IMPA Rio de Janeiro December 2006 Denitions "implementation": requires ALL equilibria
Capacity of All Nine Models of Channel Output Feedback for the Two-user Interference Channel
 Capacity of All Nine Models of Channel Output Feedback for the Two-user Interference Channel Achaleshwar Sahai, Vaneet Aggarwal, Melda Yuksel and Ashutosh Sabharwal 1 Abstract arxiv:1104.4805v3 [cs.it]
Capacity of All Nine Models of Channel Output Feedback for the Two-user Interference Channel Achaleshwar Sahai, Vaneet Aggarwal, Melda Yuksel and Ashutosh Sabharwal 1 Abstract arxiv:1104.4805v3 [cs.it]
Uniqueness of Generalized Equilibrium for Box Constrained Problems and Applications
 Uniqueness of Generalized Equilibrium for Box Constrained Problems and Applications Alp Simsek Department of Electrical Engineering and Computer Science Massachusetts Institute of Technology Asuman E.
Uniqueness of Generalized Equilibrium for Box Constrained Problems and Applications Alp Simsek Department of Electrical Engineering and Computer Science Massachusetts Institute of Technology Asuman E.
Transmit Directions and Optimality of Beamforming in MIMO-MAC with Partial CSI at the Transmitters 1
 2005 Conference on Information Sciences and Systems, The Johns Hopkins University, March 6 8, 2005 Transmit Directions and Optimality of Beamforming in MIMO-MAC with Partial CSI at the Transmitters Alkan
2005 Conference on Information Sciences and Systems, The Johns Hopkins University, March 6 8, 2005 Transmit Directions and Optimality of Beamforming in MIMO-MAC with Partial CSI at the Transmitters Alkan
