arxiv: v1 [quant-ph] 12 Sep 2018
|
|
|
- Helen Allen
- 5 years ago
- Views:
Transcription
1 Optimal probabilistic storage and retrieval of unitary channels Michal Sedlák,, Alessandro Bisio, 3 and Mário Ziman, RCQI, Institute of Physics, Slovak Academy of Sciences, Dúbravská cesta 9, 845 Bratislava, Slovakia Faculty of Informatics, Masaryk University, Botanická 68a, 6000 Brno, Czech Republic 3 QUIT group, Dipartimento di Fisica, IF Sezione di Pavia, via Bassi 6, 700 Pavia, Italy arxiv: v [quant-ph] Sep 08 We address the question of a quantum memory storage of quantum dynamics. In particular, we design an optimal protocol for probabilistic storage-and-retrieval of unitary channels on d-dimensional quantum systems. If we may access the unknown unitary gate only -times, the optimal success probability of perfect retrieval of its single use is /( + d ). The derived size of the memory system exponentially improves the known upper bound on the size of the program register needed for probabilistic programmable quantum processors. Our results are closely related to probabilistic perfect alignment of reference frames and probabilistic port-based teleportation. PACS numbers: a, Ac, Fd Introduction. Since the discovery of the first quantum algorithms [, ] and protocols [3, 4] the information processing with quantum systems has challenged basic paradigms and existing limitations of computer science. In the last few decades we have discovered that quantum information cannot be cloned [5], its logical value cannot be inverted [6], quantum processors cannot be universally programmed [7], and universal multimeters do not exist [8, 9]. o doubt, any of these programmable devices would represent a very useful piece of quantum technology, thus, their approximate realisations are of foundational interest [8 ]. The no-go restrictions imposed by quantum theory are treated in two ways. Either we ask for an approximate performance, or we allow that the perfect performance happens with some probability of failure. Studies of optimal approximate cloners initiated by Hillery and Bužek [0] demonstrated that such non-ideal devices are of practical relevance and this motivated the study of other universal devices. In particular, it was shown that quantum theory limits the fidelity of clones of qubits to ( + )/3 [3]. For quantum processors ielsen and Chuang [7] proved that perfect (error free) implementation of k distinct unitary transformations requires at least k dimensional program register. Recently, the cloning was considered also for quantum transformations [4, 5]. This unveiled an unexpected feature called super-replication [6, 7]. In this protocol, starting with copies of a qubit unitary transformation U one deterministically generates up to copies of U with an exponentially small error rate. While studying cloning of unitaries it was realized there is a closely related task of storage-and-retrieval (SAR), which only differs in the causal order of available resources. While in the cloning the cloned device is available after the input states are at the disposal, one can consider also a task where this order is reversed, thus, the device is available only before the input states. In such case, we need to learn [8] and somehow store the action of the device and retrieve it once the input states are available. Problem formulation. The devices transforming states of d-dimensional quantum systems associated with Storing Quantum memory Retrieving Success FIG. S.: Optimal PSAR of unitary channels. Hilbert space H are formalized as quantum channels, i.e. completely positive trace-preserving linear maps on the space L(H) of linear operators on H. Suppose an unknown channel U is provided for experiments and we may access it times. However, we are asked to apply U on an unknown state ξ only after we lost the access to this channel. Therefore, our aim is to find an optimal strategy that stores U in a state of a quantum memory (associated with Hilbert space H M ) and allows us to retrieve its action when needed. In the approximative settings this task (for unitary channels) was studied in Ref.[9]. Our goal is to investigate the probabilistic version of the SAR problem, in particular, we aim to find the optimal probabilistic storage and retrieval procedure (PSAR). Moreover, we require the retrieved channel to be implemented perfectly and with the same probability of success ( covariance property) for all considered channels. We will design the strategy maximizing the probability for the set of unitary channels, i.e. U(ξ) = UξU for some unitary operator U. Due to no-programming theorem [7], the retrieving part of any PSAR strategy cannot be deterministic. Thus, the successful retrieval is described by a trace-non-increasing completely positive linear map (quantum operation) T U : L(H) L(H) proportional to the unknown unitary channel, T U = λ U U. Consequently, the success probability is λ U = tr[t U (ξ)] and the condition of covariance implies λ U = λ for all U. One-to-one probabilistic storage-and-retrieval. In such
2 case the unknown unitary U is applied on a suitably chosen state ψ (in general bipartite and entangled), which yields state ψ U H M and concludes the storing phase. Afterwards, once we want to apply unitary U on some state ξ, we employ a retrieving quantum instrument R = {R s, R f }, which acts on ξ ψ U ψ U and in case of success outputs an sub-normalized state λuξu, i.e. R s : L(H in H M ) L(H out ) with H = H in = H out. The retrieving quantum instrument plays the role of a probabilistic programmable processor and the state ψ U programs a unitary transformation U to be performed on a state ξ. Using the Choi isomorphism [0] we have that R s (ξ ψ U ψ U ) = tr in,m [(I ξ T ψ U ψ U T )R s ] = λtr in [(I ξ T ) U U ] = λuξu, where R s L(H out H in H M ) and U = d(u I) ψ + with ψ + = d / j j j (vectors { j } form an orthonormal basis of H = H in = H out ). Since the above identity must hold for any ξ and ψ U ψ U T = ψu ψ U (both the transposition and the conjugation are defined with respect to the same basis of H M ) we obtain the following perfect retrieval condition ψ U R s ψ U = λ U U U SU(d). (S.) Already this simple case shows that the maximization of probability of success λ involves the simultaneous optimization of the storing phase (choice of ψ ) and the retrieving phase (choice of quantum instrument R). It turns out that the optimal performance is achieved by the (incomplete) quantum teleportation protocol [4] that is a known example of a universal probabilistic quantum processor []. Let us note that this is similar to quantum gate teleportation invented by Gottesman and ielsen [], yet it is different, because PSAR must work perfectly for any unitary transformation. In particular, for the storing phase we set ψ = ψ +. Then the optimal retrieval is achieved by a quantum teleportation of state ξ using the stored state ψ U = d / U (see Fig. S.). The generalized Bell measurement performed on ξ and one part of ψ U results in an outcome k with probability /d. In such case we are left with the second part of ψ U in the state Uσ k ξσ k U, where σ k are generalized Pauli operators. In case of σ k = I (associated with the Bell measurement projection onto ψ + ) the stored unitary channel is successfully retrieved. For all the other outcomes, the unwanted σ k rotation can not be undone, because the unitary U is unknown. In conclusion, the teleportation-based PSAR succeeds with probability /d. Its optimality follows from our subsequent discussion of the optimal PSAR. -to-one probabilistic storage-and-retrieval. The general PSAR strategy with uses of a channel in the storing phase involves all combinations of their parallel, successive and adaptive processing and corresponds to a quantum circuit with open slots, where the uses of a channel can be inserted. Such framework is described within the theory of quantum networks [ 3, 4] and any quantum circuit with open slots is represented by a positive operator (see [7] for a short introduction). The Storing S Generalized quantum instrument A A Storing B M in in Retrieving R out Retrieving out Success or failure Success or failure FIG. S.: Illustration of PSAR Top: PSAR with the most general strategy. Bottom: PSAR with parallel use of unitary channels. storing network is described by an operator S. It accepts channels as its input and it outputs a memory state ψ U H M (see Fig. S.a). As in case the retrieving phase is described by a two-valued instrument R = {R s, R f }. The overall action of PSAR is a composition of S and R determining a generalized quantum instrument L = {L s, L f }. In the Choi picture the input of PSAR corresponds to U U L(H A H B ) and L s L(H A H B H out H in ), where H A = H B = H. The perfect retrieval condition (similarly to Eq. (S.)) is U L s U = λ U U U SU(d), (S.) where λ gives the success probability. Let us stress that the probability of success, i.e. the value of λ, is required to be the same for all U SU(d). Thanks to this assumption we can without loss of generality apply the methods of [9] to conclude that the optimal storing phase is parallel as illustrated in Fig. S.b. Consider the decomposition U = j Irr(U ) U j I mj into irreducible representations (IRRs), where U j is a unitary operator on H j and I mj denotes the identity operator on the multiplicity space. This corresponds to the following decomposition of the Hilbert space H A := j Irr(U ) H j H mj, and we set d j = dim(h j ). The result of [9] implies that the memory state ψ can be taken of the following form ψ := I j H M p j 0, p j =, d j j j (S.3) where I j denotes the identity operator on H j and H M := j Irr(U ) H j H j H A H A. The state ψ undergoes the action of the unitary channels and becomes
3 3 ψ U := j d j U j. Clearly, ψ U H M for any U. Let us now focus on the retrieving quantum instrument R from L(H in H M ) to L(H out ), where in/out labels the system on which the retrieved channel is applied. The perfect retrieval condition is again given by Eq. (S.) with ψu = j d j Uj. As a consequence of Eq. (S.) the optimal Choi operator R s can be chosen to satisfy the commutation relation [R s, U V U in V out] = 0, (S.4) where U := j U j I j, V := j I j V j. Thanks to Eq. (S.), U ψ = ψ U and ψi = ψ the perfect retrieval condition becomes ψ R s ψ = λ I I (S.5) and the success probability reads λ = d I ψ R s ψ I. Let us now consider the decomposition Uj U = U I (j) m, Irr(Uj U) (S.6) which induces the Hilbert space decomposition H j H = Irr(Uj U) H H (j) m. Let us denote by j K the set of values of j such that U V K is in the decomposition of Uj V j U V. Using Eqs. (S.) and (S.3) we can assume [7] that R s = I I s (), where s () := j,j j s () jj I I m (j) (j m ). Given this the left hand side of Eq. (S.) reads ψ R s ψ = λ I I + ν ( I d I I ), (S.7) where ν are specified in [7], λ = d d φ s () φ and φ = d j I (j) m. Since R s 0, the perfect learning condition of Eq. (S.) holds only if ν = 0 for all. Then, the success probability is λ = λ. The following result translates the optimisation of λ from an operator optimisation problem into a linear program. Theorem. For optimal PSAR the success probability λ is given by the following linear programming problem: maximize λ = d 3 µ,p j µ, C subject to 0 d µ p j p j 0 d j j Irr(U ) j j p j =, C where C = { Irr(U U ) dd = d j }. (S.8) Proof. We will sketch only the key steps. The complete proof is in [7]. First, one shows that / C implies s () = 0. Then, (for any C) ν = 0 and s () 0 imply that p j p j s () jj = µ d 3 j d3 j for some µ 0. Thus, λ = d µ C j,j j d d j d j = C d3 µ. The constraint that R s is a quantum operation gives tr out [R s ] I. Eq. (S.) implies [tr out [R s ], U V Uin ] = 0 and tr out [R s ] = d I I j dj s () jj. Thus, d d µ j p j must hold for all and j j. Conditions on p j are from Eq. (S.59). Case study: PSAR for qubit channels. In case of qubit (d = ) the decomposition of U into IRRs of SU() reads U = / j=( mod )/ U j I mj, where m j = j+ ( /+j+ /+j) [8] and Uj are the IRRs of spin j with dimension d j = j +. For convenience we work with even (for odd see [7]), so j = 0,,..., /. For SU() the complex conjugate representation Uj is equivalent to IRR U j. Thus, in Eq. (S.3) we get either = j +/ or = j /. Altogether, can have values C = {/,..., ( )/} or = ( + )/ / C, because d j = d / + d +/ = dd and d / d (+)/. The constraints in Eq. (S.5) imply for any j but j = 0, / the following two inequalities µ j+/ d jd j+/ p j, (S.9) µ j / d jd j / p j. (S.0) For j = 0, / only one of them exists. Let us define f j [0, ] for j = 0,..., as f ( j = j j+ j+ + ). Since f 0 = 0 and f / = we can multiply Eq. (S.9) by f j and Eq. (S.0) by f j, and take the sum for all j. A straightforward calculation gives the upper bound: + 3 = d 3 µ λ + 3. (S.) Finally, by choosing p j = (j+) /L, µ j+/ = /(L(j+ )) (where L = ( + )( + )( + 3)/6), one proves that that conditions in Eq. (S.5) are satisfied and the upper bound (S.) is achieved. The knowledge of µ and p j completely specifies the state ψ and the retrieving operation R s which can be explicitly expressed (see Fig. S.b). Let j, j z H j wit z { j,..., j} be an orthonormal basis of the spin j IRR. By definition I j = j j j, j z= j z j, j z. Consequently, from Eq. (S.59), the dimension of the quantum memory is dim H M = / j=0 d j for storage is ψ = / j=0 = L and the optimal input state j+ L I j. Optimal PSAR for qudit unitary transformations. The optimization of PSAR of qudit channels follows similar steps as for the qubit case and it exploits a combinatorial identity (Proposition 3 in [6]) which was discovered and proved as a byproduct of this analysis. Theorem. The optimal probability of success of probabilistic storage and retrieval of a unitary channel U(.) = U.U, U SU(d) equals λ = /( +d ). The optimal state for storage is ψ := d j j L I j H M where L := j d j and j Irr(U ).
4 Bob SWAP Alice 4 Success {,,} or failure {0} Success Storing Retrieving FIG. S.3: A modified optimal PSAR in which U is stored and the inverse transformation U is retrieved (SU() case). The generalisation to the is straightforward. Storing Retrieving FIG. S.4: Use of port-based teleportation scheme for PSAR. The proof is given in [7]. Clearly, as goes to infinity λ d, and λ implies d. Reminding that a d dimensional unitary transformation has d parameters, we see that roughly one use per unknown parameter is needed for reliable storage and retrieval of the transformation. Let us note that the storage state in Theorem is optimal also for the estimation of a group transformation in the maximum likelihood approach [30]. Further, it is worth to stress that the optimal PSAR protocol is achieved by a coherent retrieval, hence, the quantum memory is essential. In contrast, optimal approximate SAR [9] is equivalent to quantum estimation in the maximum fidelity approach and classical memory is sufficient as an output of the storing phase. Use of the optimal storage state in the design of an approximate SAR leads to fidelity that scales as O( ), however, for the optimal approximate SAR the fidelity scales as O( ) [9]. This O() difference is the price to pay for the perfect retrieval in case of PSAR. Alignment of reference frames [8]. (ARF) Let us note that the correction of alignment errors can be modeled as a PSAR protocol in which uses of an unknown U are stored and the aim is to retrieve the inverse transformation U. For SU(), we can show that, given uses of U, the inverse transformation U can be perfectly retrieved with the same optimal probability of success λ (see Fig. S.3 and [7]). It follows that the success probability of the probabilistic ARF protocol [8] achieves the optimal scaling O( ) (see [7]). Probabilistic port-based teleportation. (PPBT) As the first step of PPBT [3] Alice and Bob share suitably entangled pairs of quantum systems. Their goal is to teleport an unknown state ξ to Bob in a way that this state appears in one of his systems (called ports [33, 34]). In order to achieve this goal (see also Fig. S.4) Alice performs a specific measurement resulting in n {0,,..., } (0 labels the failure of the protocol), communicates this information to Bob who selects the system from the nth port to accomplish the teleportation. If Bob applies a channel U on each of his ports (storing phase) and Alice starts the teleportation (retrieving phase) of ξ afterwards, the nth port will output U(ξ). Strictly speaking, we swap nth port into a fixed quantum system and effectively we achieve PSAR. Let us stress that while any PPBT protocol can be turned into a PSAR protocol, the converse does not hold. In a sense, PPBT scheme provides a structurally simple realization of an optimal PSAR protocol. Our results show that the optimal probability of PPBT [35] coincides with the optimal success probability of PSAR. However, the memory dimension dim H M of the optimal PSAR is exponentially smaller (see the following paragraph) in comparison with qudits used in PPBT construction. Implications for covariant probabilistic programmable processors. Up to now the best bound on the size of the program register for universal covariant probabilistic processors was provided by family of PPBT processors for which dim H M (d (d ) ) /f, where f = λ is the failure probability. In contrast, the retrieving phase of optimal PSAR defines a class of processors for which the program register size reads dim H M = j Irr(U ) d j = ( ) +d, where we used Schur s result [36]. In terms of the failure probability it reads dim H M (/f) (d ), which is exponentially smaller (for fixed d and f 0) in comparison with PPBT-based processors. This result can be viewed as a quantification of achievable tradeoffs imposed by the no-programming theorem [7] on universal covariant probabilistic processors. Although PSAR provides only an upper bound on the size of the program register, we conjecture that the lower bound will have the same scaling. However, this question remains open. Summary. We showed that optimal probabilistic storage-and-retrieval of unknown unitary channels on d- dimensional quantum systems can be designed with success probability λ = /( +d ), where is the number of uses of the channel in the storing phase. This probability coincides with the success probability for probabilistic port-based teleportation [35], and, for the SU() case, with the probability of success for probabilistic alignment of reference frames. Optimal PPBT can be rephrased as an optimal protocol for PSAR, but for the PSAR protocol designed here the storing memory system is exponentially smaller and optimal in this parameter. On the other hand, PPBT-based PSAR implements all quantum channels (not only unitary ones), thus, its performance is universal. The question of potential reduction of memory system while keeping the universality for all channels remains open.
5 5 Acknowledgments MS and MZ acknowledge the support by the QuantERA project HIPHOP (project ID 73473), projects QETWORK (APVV ), MAXAP (VEGA /073/7), GRUPIK (MUI/G//07) and the support of the Czech Grant Agency (GAČR) project no. GA6-S. AB acknowledges the support of the ohn Templeton Foundation under the project ID# Causal Quantum Structures. The opinions expressed in this publication are those of the authors and do not necessarily reflect the views of the ohn Templeton Foundation. [] P. Shor, SIAM. Computing 6 (997), [] Lov K. Grover, Proceedings, 8th Annual ACM Symposium on the Theory of Computing (STOC), May 996, pages -9 [3] C. H. Bennett and G. Brassard, In Proceedings of IEEE International Conference on Computers, Systems and Signal Processing, volume 75, page 8. ew York, 984 [4] C. H. Bennett, G. Brassard, C. Crpeau, R. ozsa, A. Peres, W. K. Wootters, Phys. Rev. Lett. 70, (993) [5] W.K. Wootters and W.H. Zurek, ature 99, 80 (98) [6] V. Bužek, M. Hillery, and R. F. Werner, Phys. Rev. A 60, R66(R) (999) [7] M. A. ielsen and Isaac L. Chuang, Phys. Rev. Lett. 79, 3 (997) [8] Miloslav Dušek and Vladimir Bužek Phys. Rev. A 66, 0 (00) [9]. Fiurášek, M. Dušek, and R. Filip Phys. Rev. Lett. 89, 9040 (00) [0] V. Bužek and M. Hillery, Phys. Rev. A 54, 844 (996) [] V. Scarani, S. Iblisdir,. Gisin, A. Acin, Rev. Mod. Phys. 77, 5-56 (005) [] M. Hillery, V. Bužek,and M. Ziman, Phys. Rev. A 65, 030 (00) [3]. Gisin, S. Massar, Optimal Quantum Cloning Machines, Phys. Rev. Lett. 79, (997) [4] G. Chiribella, G.M. DAriano, and P. Perinotti, Phys. Rev. Lett. 0, (008) [5] A. Bisio, G.M. DAriano, P. Perinotti, and M. Sedlák, Phys. Lett. A 378, 797 (04) [6] W. Dur, P. Sekatski, and M. Skotiniotis, Phys. Rev. Lett. 4, 0503 (05). [7] G. Chiribella, Y. Yang, and C. Huang, Phys. Rev. Lett. 4, 0504 (05). [8] In the literature, the task of storage and retrieval is also called quantum learning. [9] A. Bisio, G. Chiribella, G. M. D Ariano, S. Facchini, P. Perinotti, Phys. Rev. A 8, 0334 (00) [0] M. Choi, Linear Algebra and its Applications, 0 (3): 85-90, (975), A. amiolkowski, Rep. Math. Phys. 3, 75 (97). [] T. Heinosaari, M. Ziman, The mathematical language og quantum theory, (Cambridge Universtiy Press, 0) [] D. Gottesman and I. Chuang, ature 40, 390 (999) [3] G. Chiribella, G. M. D Ariano, P. Perinotti, Phys. Rev. Lett. 0, (008). [4] G. Chiribella, G. M. D Ariano, P. Perinotti, Europhysics Letters 83, (008). [5] G. Chiribella, G. M. D Ariano, P. Perinotti, Phys. Rev. A 80, 0339 (009). [6] A. Bisio, G. Chiribella, G. M. D Ariano, P. Perinotti, Acta Physica Slovaca 6, o.3, (0). [7] see supplemental material [8]. I. Cirac, A. K. Ekert, and C. Macchiavello, Phys. Rev. Lett. 8, 4344 (999). [9] Michal Sedlák, Alessandro Bisio, On some new hookcontent identities, arxiv: [30] Giulio Chiribella, Giacomo Mauro DAriano, Paolo Perinotti, and Massimiliano F. Sacchi Phys. Rev. A 70, 0605 (004). [3] Stephen D. Bartlett, Terry Rudolph, Robert W. Spekkens and Peter S. Turner, ew. Phys., (009). [3] S. Ishizaka and T. Hiroshima, Phys. Rev. A 79, (009) [33] S. Ishizaka and T. Hiroshima, Phys. Rev. Lett. 0, 4050 (008) [34] M. Mozrzymas, M. Studziski, S. Strelchuk, and M. Horodecki, ew. Phys., Vol. 0, (08) [35] M. Studziski, S. Strelchuk, M. Mozrzymas, and M. Horodecki, Sci. Rep. Vol. 7, 087 (07) [36] Issai Schur, ber eine Klasse von Matrizen, die sich einer gegebenen Matrix zuordnen lassen, Doctoral dissertation, Universitt Berlin, 90; reprinted in Brauer k Rohrbach [7, Band I, pp. 7 (973)
6 6 I. SUPPLEMETAL MATERIAL This Supplemental Material provides a short introduction to theory of quantum networks, detailed proofs of Theorems, and more precise clarification of the relation of the presented work to the alignment of reference frames. II. QUATUM ETWORKS AD GEERALIZED ISTRUMETS The mathematical formalization of the perfect learning of a unitary channel can be easily given within the framework of quantum networks. In this section we provide a small review of the subject and we refer to the literature [ 3] for a complete presentation. We will start by introducing some notation. If H and K are finite-dimensional Hilbert spaces, then we denote with L(H) the set of linear operator on H and with L(H, K) the set of linear operator from H to K. We will use the one-to-one correspondence between linear operators A L(H, K) and vectors A K H and given by A = dim(k) m= dim(h) n= m A n m n, (S.) where { m } dim(k) m= and { n } dim(h) n= are two fixed orthonormal bases for K and H, respectively. For A, B and C operators on H one can verify the identity A B C = ABC T (S.3) where X T denotes the transpose of X with respect to the orthonormal basis n. A quantum operation O from L(H) to L(K) is a completely positive trace non increasing map which can be represented by its Choi operator O L(K H). The operator O must satisfy O 0, Tr K [O] I H (S.4) where Tr K denotes the partial trace on K and I H the identity operator on H. The two constraints in Eq. (S.4) correspond to the complete positivity and trace non increasing of the quantum operation O. By making use of the notation in Eq. (S.), the Choi operator for a unitary channel U can be written as the rank one projector U U. The action of the quantum operation O on a quantum state ρ L(H) can be described in terms of the Choi operator O as follows O(ρ) = Tr K [O(I K ρ T )] =: O ρ (S.5) where we introduce the link product between the operators O and ρ. The composition of two quantum operations can be represented in terms of their Choi operators too. Let us consider two quantum operations O, O with multipartite input and output, i.e. O goes from L(H H ) to L(H 3 K) and O goes from L(H 4 K) to L(H 5 H 6 ). We can connect the output of O on L(K) with the input of O on L(K) obtaining a new quantum operation from L(H H H 4 ) to L(H 3 H 5 H 6 ). The Choi operator of the resulting quantum operation is given by the link product of the two quantum operations, as follows: O O = Tr K [(O I 456 )(I 3 O T K )] (S.6) where O T K denotes the partial transposition of O on the Hilbert space K and I ijk denotes the identity operator on H i H j H k. We can interpret Eq. (S.5) as an instance of Eq. (S.6). A quantum network R consists in a sequence of multipartite quantum operations {O i, i =,... } where some output of a O i is connected to some input of the following quantum operation O i+ as we illustrate in the following diagram: 0 O O 3 O, (S.7) where the folating wires correspond to the input and output systems of the quantum network. R is called a deterministic quantum network if all the quantum operations in Eq. (S.7) are trace preserving, and it is called a probabilistic quantum network otherwise. A quantum network can be represented by a Choi operator (commonly called quantum comb) which is given by the link product of all the component quantum operations. The Choi operator R of a deterministic quantum network R obeys the following constraints Tr k [R (k) ] = I k R (k ) k =,..., (S.8) where, referring to the diagram in Eq. (S.7), the Hilbert space of the wire labelled by j is H j, R () = R, R (0) =, R (k) L(H oddk H evenk ) with H evenk = k j=0 H j and H oddk = k j=0 H j+. R (k) is the Choi operator of the reduced network R (k) obtained by discarding the last k teeth. The set of of positive operators satisfying Eq. (S.8) and the set of deterministic quantum networks are in one to one correspondence. On the other hand, a given deterministic quantum network R can be realized as a composition of quantum channels in many different ways. In the probabilistic case, the Choi operator of a probabilistic quantum network T, must satisfy 0 T R (S.9) where R is the Choi operator of a deterministic quantum network. A given probabilitic quantum network T can be realised as a composition of quantum operations in many different ways. In particular, any probabilitic quantum
7 7 network T can be realised by a composition of channels {C} and a final quantum operation O as follows: T = 0 C C 3 O. (S.0) A set of probabilistic quantum networks {R i }, with the same input and output wires, is called a generalised quantum instrument if the sum of their Choi operators i R i =: R is the Choi operator of a deterministic quantum networks. As in the analogous case of quantum instruments, the index i which labels the elements of a generalised quantum instrument represents the classical outcome which is available after the quantum network has been provided with some input. If the outcome i is obtained then it means that the probabilistic quantum network R i happened. Any generalised quantum instrument can always be realised by a a composition of channels followed by a final quantum intrument. We notice that for any probabilistic quantum network there exists a generalised quantum instrument which it belongs to. III. RELEVAT SUB-BLOCKS OF RETRIEVIG OPERATIO R s As we stated in the main text, Choi operator R s of the retrieving operation can be chosen to satisfy the commutation relation [R s, U V U in V out] = 0, (S.) where U := j U j I j, V := j I j V j. We remind also the perfect retrieving condition ψ R s ψ = λ I I. (S.) For convenience we placed here also the decomposition Uj U = U I (j) m, Irr(Uj U) (S.3) which induces the Hilbert space decomposition H j H = H H (j) m. (S.4) Irr(Uj U) First, we notice that the multiplicity spaces H m (j) H m (j) K are one dimensional and therefore I m (j) and are rank one. From the Schur-Weyl duality, any irreducible representation U j of SU(d) is in correspondence with a young diagram Y j. The defining representation U is represented by a single box. One can verify that there cannot be two equivalent Young diagrams in the decomposition Y j = K Y K. For a more detailed treatment we refer to [4]. Then we have that induces decomposition H mk = j j K H (j) m H (j) m, K where j K denotes the set of values of j such that U V K is in the decomposition of Uj V j U V. Since dim(h (j) m ) = we stress that I (j) m I (j m ) = δ j,j and H m = span({ I m (j) }, j j ). From Eq. (S.5) the commutation relation of Eq. (S.) becomes [R s, K U V K I mk ] = 0, which, thanks to the Schur s lemma, gives R s =,K I I K s (K), (S.6) where s (K) L(H mk ), s (K) 0. Due to I I being a rank one operator and R s being the sum of the positive operators from Eq. (S.6) we have that Eq. (S.) holds if and only if ψ I I K s (K) ψ = λ K I I, K. (S.7) From the identity I j I = Irr(Uj U) I I (j) m remind that I (j) m has rank one), we obtain ψ I = j φ : = Irr(U j U) I (j) d m j I I (j) d m j = (we I φ (S.8). (S.9) Using Eqs. (S.6), (S.8) into λ = d I ψ R s ψ I we obtain λ = λ λ = d d φ s () φ (S.30) where the λ K s were defined in Eq. (S.7). It is now easy to show that we can assume R s = I I s (), (S.3) where s () := j,j j s () jj I I m (j) (j m ). Indeed, let R s = K I I K s (K) be the optimal quantum operation and let us define the operators R s = I I s () where s () = s () and R s = K I I K s (K). Since both R s and R s are positive and R s + R s = R s, we have that Tr D [R s] I implies Tr D [R s ] I i.e. R s is a quantum operation. Finally, from Eq. (S.8) we have that ψ R s ψ = ψ R s ψ, thus proving that also {R s, ψ } is an optimal solution of our optimization problem. IV. EXPLICIT FORM OF THE RETRIEVED CHAEL U V U V = K U V K I mk (S.5) Due to commutation relation (S.) and the form of R s given by Eq. (S.3) the retrieved channel has the
8 8 following Choi operator ψ R s ψ = λ I I + ν ( I d I I ). (S.3) As we stated in the main text the perfect retrieving condition is satisfied if and only if ν = 0 for all. This happens because positive-semidefiniteness of R s () := I I s () implies ν 0 and the requirement ν = 0 implies that all the terms must vanish. Let us study separately every operator R s (), which by definition satisfies the commutation relation of Eq. (S.). We have that ψ R () s ψ = = ψ (U U U U)R s () (U U U U) ψ = (U U) ψ R s () ψ (U U) U (S.33) Thanks to the Schur s lemma Eq. (S.33) gives ψ R () s ψ = λ I I + ν ( I d I I ). By taking the trace of Eq. (S.34) we have Tr[ ψ R s () ψ ] = ψ Tr out in [R s () ] ψ = ψ I j I j q () j ψ = p j q () j = λ d + ν (d ) q () j := d d s () jj. j If we insert Eq. (S.9) into Eq. (S.30) we have λ = d p j d s () jj d j d. j j,j j From Eq. (S.35) and Eq. (S.36) we have ν = 0 p j δ j,j d d d s () jj j,j j j p j d j d j (S.34) (S.35) (S.36) s () jj = 0, (S.37) which is the most explicit form of the perfect retrieving condition that constraints the relation between the state ψ parametrized by probabilities p j and the structure of the retrieving operation parameterized by s () jk. V. PSAR AS A LIEAR PROGRAMMIG PROBLEM In this section we provide complete proof of Theorem from the main text. First, we prove the following technical lemma, which will be needed. Lemma. Suppose a matrix X = j,j X jj j j 0 obeys j,j X jj = j c j X jj, where c j > 0 and j c j =. This implies X χ χ, where χ = j c j j. Proof. Let us define v := j ρ := j A := j j Xjj j c j X jj j j (S.38) (S.39) (S.40) The condition j,j X jj = j c j X jj can be written as v A X v = 0. (S.4) Matrix H ij is positive semidefinite if and only if H ii 0 i and H ij H ii H jj i j. Using this criterion and j c j = one can easily show that both A X and A ρ ρ are positive semidefinite matrices. Moreover, using R(X jj ) X jj X jj X j j one can easily prove the inequality v (A X) v v (A ρ ρ ) v, which also gives v (A X) v = 0 = v (A ρ ρ ) v = 0, (S.4) (S.43) due to A ρ ρ 0. Moreover, let us rewrite expression v A v as As a consequence we have v A v = ρ B ρ B := j j c j j v (A ρ ρ ) v = ρ (B v v ) ρ. (S.44) (S.45) (S.46) Thanks to c j > 0 j we have that B v v is a positive matrix, which has either trivial or one dimensional kernel. This together with Eqs. (S.43),(S.46) allows us to write a necessary condition for matrix X ρ (B v v ) ρ = 0 (S.47) = B ρ v v ρ = 0 (S.48) Explicitly solving the above equation we get the only possible solution Xjj = Xj c j c j = X jj = µc j, (S.49) j which is unique up to a constant µ, as we expected due to the rank one deficiency of B v v. Once the diagonal elements X jj respect Eq. (S.49) we have
9 9 v (A ρ ρ ) v = 0, but to fulfill LHS of Eq. (S.43) we need also the saturation of the bound (S.4). This happens if and only if X jj = X jj Xj j, (S.50) which together with Eq. (S.49) proves the claim of the lemma. Let us restate Theorem from the main text. Theorem 3. For optimal PSAR the success probability λ is given by the following linear programming problem: maximize λ = d 3 µ,p j µ, C subject to 0 d µ p j p j 0 d j j Irr(U ) j j p j =, C where C = { Irr(U U ) dd = d j }. (S.5) Proof. We first need to examine relations between IRR s that appear in the decomposition of U and those that appear in j Irr(U ) U (j) U. We remind that from the Schur-Weyl duality, any irreducible representation U j of SU(d) is in correspondence with a young diagram Y j. The defining representation U is represented by a single box and IRR defined via U is represented by a column of d boxes. Decomposition of U into IRRs can be obtained by collecting the decompositions of the tensor products U k U of all Young diagrams k appearing with multiplicity m k in the decomposition of U and putting together equivalent IRRs (those with the same Young diagram). This can be mathematically stated as follows. Let Irr(U ) denote the set of Young diagrams that appear in the decomposition of U into IRRs of SU(d). We have that K Irr(U ) if and only if k Irr(U ) such that K Irr(U k U) and m K = k k K m k, where k K denotes the set of values of k such that U K is in the decomposition of U k U. On the other hand, thanks to Schur-Weyl duality the multiplicity m K = d K (m k = d k ) is given by the dimension of the IRRs of the symmetric group S() (S( )) with the Young diagram K (k), respectively. Hence, we obtained a known identity [4] d K = dk, (S.5) k k K where k K can be equivalently specified as those Young diagrams k, which by addition of a single box become K. ext, we consider decomposition of U j U (or more conveniently U U j ), where j Irr(U ). We denote Young diagram Y j with r rows and n i boxes in the i-th row as (n, n,..., n r ). A valid Young diagram of SU(d) IRR has r d, n r > 0 and n i n i+ i (we set n r+ = 0). Rows i in which n i > n i+ we call corners of (n, n,..., n r ) and we denote the number of corners by s and we write i Cor j. Suppose Y j (n, n,..., n r ) has r d. Then the decomposition of U U j contains s+ Young diagrams each with multiplicity one. One of them is given as Young diagram (n +, n +,..., n r +,,..., ) with d rows, which we denote Y j and for each i Cor j we have Young diagram Y j\ i (n,..., n i,..., n r ). The above statement follows from the Littlewood-Richardson rules [4] if one realizes, that either one of the corner boxes completes the first column into d boxes (the remaining boxes can be only attached to the right in the original order) or the whole Young diagram is attached from the right to the column of d boxes. If Y j (n, n,..., n r ) has r = d the situation is the same except for the diagram Y j not appearing in the decomposition, because it would not be a valid Young diagram. Let us note that Young diagram Y j can emerge in our setting only from diagram Y l, where l = j. We can also easily verify that dd j d j, which can be seen from the formula for the dimension of SU(d) IRRs [5] by calculating the fraction d j /d j for a general j. Therefore, we conclude that for = j Eq. (S.37) can be satisfied only if s ( j) jj = 0, which in turn thanks to Eq. (S.30) implies λ j = 0. Thus, Young diagrams C = {Y j, j Irr(U )} correspond to those that do not belong to the set C defined in the theorem. On the other hand, consistently with the notation for C, we define C = {Y j\ i, j Irr(U ), i Cor j }. Let us remind that Irr(U ) is exactly constituted by all Young diagrams consisting of boxes and having at most d rows. This implies C = Irr(U ), because by removing in any possible way a single box from Young diagrams in Irr(U ) we get all possible Young diagrams in Irr(U ). More operationally, for any Young diagram C we can add a box to the first row and get some element j Irr(U ), which can be reversed to prove the claim. Moreover, for every subset C j = {Y j\ i, i Cor j } of C we have that d j = d, (S.53) C j which is just a reformulation of Eq. (S.5), because Young diagrams C j have boxes and an addition of a single box changes them to Young diagram j consisting of boxes. Let us pick any element C. Let us now specify all the Young diagrams Y j, j Irr(U ), which contain in the decomposition of U j U. We denote such set j and it coincides wit defined below Eq. (S.5). These are such Young diagrams j in which by removing one corner box we get Y. This is the same as saying that j is the set of Young diagrams of SU(d) group that can be obtained from by addition of a single box, because Irr(U ) contains all possibly emerging Young diagrams. This implies that dd = j j d j, because this corresponds to the decomposition of an operator U U,
10 0 which acts on dd dimensional space. Thus, we proved that the set C can be equivalently defined as C = { Irr(U U ) dd = = {Y j\ i, j Irr(U ), i Cor j } d j } = Irr(U ) (S.54) Furthermore, we showed that for / C s = 0 and consequently λ = 0. In order to proceed we apply Lemma for every p C. Expression j d jd s() j jj plays the role of X jj, c j = dj dd and the remaining assumption is guaranteed by Eq. (S.37). As a consequence, we get that the condition (S.) of perfect retrieving and s () 0 is equivalent to s () jj = µ d 3 j d3 j p j p j µ 0 C (S.55) Thus, fulfillment of Eq. (S.55) guarantees the perfect retrieving of unitary transformations and we can rewrite the probability of success as λ = C j,j j d d µ d j d j = d 3 µ, C (S.56) where we used Eqs. (S.9),(S.30) and the defining property of the set C. The constraint that R s is a quantum operation translates into its Choi operator as Tr D [R s ] I. Since R s satisfies Eq. (S.), we obtain [Tr D [R s ], U V UC ] = 0, which implies Tr D [R s ] = d I I j dj s () jj. This implies Tr D [R s ] I d d j s () jj, j j. (S.57) VI. PSAR FOR QUBIT CHAELS - THE CASE OF ODD All the steps are completely analogical to the derivation valid for even presented in the main text. The main difference is that the IRR s with minimum and maximum spin ( = 0 and = + ) have only multiplicity one. For odd (identically as for even ) the investigation of the conditions of perfect learning reveals that s + has to be zero. On the other hand, = 0 can be involved in the perfect storing and retrieving. Other expressions remain identical, but now is an integer. In particular, we choose f according to the same formula as in the main text f j = ( ) j j + j + + (S.60) and the whole proof goes on analogically to the case of even. VII. PSAR FOR QUDIT CHAELS - THE GEERAL CASE OF SU(d) The goal of this section is to prove Theorem 4 from the main text. Theorem 4. The optimal probability of success of probabilistic storage and retrieval of a unitary channel U(.) = U.U, U SU(d) equals λ = /( +d ). The optimal state for storage is ψ := d j j L I j H M where L := j d j and j Irr(U ). Proof. The idea of the proof is analogical to the case of qubit unitary transformations. However, in the qudit case the relations between IRRs are more complicated and we will need some of the facts derived in the proof of Theorem 3 and a new combinatorial identities, which were derived in [6] by some of us. Let us define positive function Let us express the above condition via coefficients µ using Eq. (S.55) f(j, ) = d d j, (S.6) µ d j p j d, j j. (S.58) Let us remind the definition of state ψ from the main text. ψ := I j d H p j 0, p j =, j j j (S.59) Collecting Eqs.(S.56), (S.55),(S.58) and (S.59) we see that the optimization of probabilistic storage and retrieval is reduced to a linear program stated in the Theorem 3. for all j Irr(U ), C j or equivalently for all Irr(U ), j j = j. Let us note that thanks to Eq. (S.53) we have f(j, ) = j Irr(U ). (S.6) C j For the proof of the main theorem we need a new theorem from combinatorics [6] and a technical lemma. Theorem 5. For any Young diagram consisting of boxes it holds that (C j R j ) dj = ( ) d, (S.63) j
11 where the sum runs through all Young diagrams j that can be obtained from by addition of a single box, d, d j are dimensions of IRRs of the symmetric group S( ), S(), respectively C j is the number of the column of the added box, R j is the number of the row of the added box that leads from diagram to the diagram j. Lemma. For any Young diagram Irr(U ) the following identity for dimensions d, d j of IRRs of SU(d) group and for dimensions of d, d j of the symmetric group, holds d j d j = + d d d Irr(U ), where j = {j Irr(U ) Irr(U j U )}. (S.64) Proof. Let us remind expressions for the dimensions of IRRs that are involved (for detailed explanation see [4]): d j = l j d = l h dj =! d = ( )!, (S.65) h where, h denote the hook lengths factors and l j is box Y j (d R i + C i ) (here R i (C i ) is the row (column) of the current box from the Young diagram j). Using Eq. (S.65) we can write Eq. (S.64) as l j h = d + (S.66) l Thus, proving Lemma is equivalent to proving that Eq. (S.66) holds. We start by direct evaluation of the left hand side. We obtain: l j h l = (d R j + C j ) h (S.67) where R j is the row number and C j the column number of the additional box in Young diagram Y j with respect to Y. At this point it is useful to realize that for Young diagrams Irr(U ) with d-rows, there is a difference between the set j = j and the set of all Young diagrams that can be obtained from by addition of a single box. The difference is exactly one Young diagram, which is obtained from by adding the box into the d + -th row, in the first column. Luckily, the bracket (d R j + C j ) for this diagram evaluates to zero (d (d + ) + = 0), so we can sum also through this term in Eq. (S.67) without changing its value. This is useful especially for d <, because later on we want to apply Theorem 5, where the summation runs through the set. Thus, left hand side of Eq. (S.66) can be equivalently rewritten as l j h l = (d R j + C j ) h = F + G + H, j where we expanded the square and we defined F = d h G = (C j R j ) h j j H = h d(c j R j ). j It is known [7] that (S.68) (S.69) (S.70) j dj = d Irr(U ), (S.7) which can be using Eq. (S.65) equivalently rewritten as j h = Irr(U ). (S.7) Using the identity (S.7) we have that F = d. Moreover, we have j (d R j + C j ) h = j l j l h = d j d = d, (S.73) where we used Eq. (S.54) and the fact that d j = 0 if j has more than d rows. On the other hand j (d R j + C j ) h = d j = d + d H h + j (C j R j ) h (S.74) (S.75) and then H = 0. Combining the above considerations equation (S.68) reads l j h l = d + (C j R j ) h. j (S.76) Comparing Eq. (S.76) with Eq. (S.66) we conclude we still need to prove j (C j R j ) h =. (S.77) Luckily, the above equation is exactly the claim of Theorem 5 written using Eq. (S.65). Thus, relaying on Theorem 5 we conclude the proof.
12 Let us continue with the proof of Theorem 4. We multiply inequality (S.58) for every Irr(U ) and every j j by f(j, ). We sum these inequalities and thanks to Eqs. (S.6), (S.59) we get Irr(U ) Let us define z d f(j, ) d jd µ j Irr(U ) j Irr(U ) C j f(j, )p j p j =. f(j, ) d j Irr(U ), = d d d j d j = + d d 3 (S.78) (S.79) where we used Eq. (S.6) and Lemma. Using the definition (S.79) we can rewrite inequality (S.78) as z µ. (S.80) Irr(U ) We remind that Irr(U ) = C. Taking this into account inequality (S.80) directly implies + d d 3 µ λ = λ + d. C C (S.8) ext, we finish the proof of Theorem 4 by showing that the upper bound (S.8) can be saturated. One can choose p j = d j k Irr(U ) d k µ = d k Irr(U ) d k j Irr(U ) C (S.8) and insert them into Eqs. (S.5). It is easy to see that requirements on p j are satisfied and inequalities between p j and µ are actually all saturated. Let us now evaluate λ. Inserting Eq. (S.8) into Eq. (S.5) we obtain C λ = d k Irr(U ) d k = = = = + d k Irr(U ) d k + d k Irr(U ) d k + d k Irr(U ) d k + d, d j C d d j d j j Irr(U ) C j j Irr(U ) d j d d j (S.83) where we used Lemma, exchanged the order of the sums and used the Eq. (S.6). Thanks to knowledge of µ and p j we can completely specify the state ψ and the retrieving operation R s. Thus, we can build valid storing and retrieving strategy, which succeeds with probability /( + d ) saturating the upper bound (S.8) and concluding the proof. VIII. ALIGMET OF REFERECE FRAMES We now review the quantum protocol for the alignment of reference frames in a quantum communication scenario, as it was considered in Ref. [8]. Let us consider the scenario in which one party, called Alice, wants to send a qubit to another distant party, denoted as Bob. If the qubit is encoded into a spin-/ particle Bob can recover the quantum state ϕ if he and Alice share a reference frame for orientation. Otherwise, the lack of a shared frame amounts to having a noisy channel and Bob receives a decohered state ρ = SU() U ϕ ϕ U du. This problem can be circumvented if Alice, along with the quantum message ϕ, sends a state ψ as a token of her reference frame. Then Bob receives the state ρ ψ = SU() ψ U ψ U U ϕ ϕ U du, from which he tries to retrieve the message ϕ. In the perfect retrieving scenario, Bob wants to maximize the probability for recovering ϕ without any error. This scenario is equivalent to a storage and retrieval protocol: the token ψ plays the role of the storage state. ψ is a multipartite state ψ H The effect of the misalignment can be thought of as the storing phase in which the state ψ U := U ψ is created. In the retrieving phase, Bob exploits the state ψ U to retrieve the inverted channel U which is applied to the qubit U ϕ. There are two differences between this protocol and the SAR we consider in our work. The first difference is that uses of U are given, but we are required to retrieve U. However, for U SU(), we can show that our optimal PSAR protocol which stores U and retrieves U, can be turned into a PSAR protocol which retrieves U with the same probability of success. If we had ψ U, then the retrieval phase of our optimal PSAR protocol would recover U with the optimal probability of success λ (which is the same for any U SU()). In particular, for U SU(), the storage state ψ U can be created by exploiting uses of U as follows ψ U = U I ψ = I U ψ = = I (σ y Uσ y ) ψ where ψ is the optimal state for storage. (S.84)
13 3 The second difference between SAR and the alignment protocol is that we are not allowed to use an external reference system, i.e. the ancillary system H A in our protocol, since it would correspond to a partially shared reference frame. Since our protocol is less constraint than the alignment protocol, the probability of success λ of PSAR is an upper bound for the probability of success of perfect alignment. However both the strategy of Ref. [8] and the optimal PSAR protocol achieve the same O( ) scaling, which is then optimal. [] G. Chiribella, G. M. D Ariano, P. Perinotti, Phys. Rev. Lett. 0, (008). [] G. Chiribella, G. M. D Ariano, P. Perinotti, Phys. Rev. A 80, 0339 (009). [3] A. Bisio, G. Chiribella, G. M. D Ariano, P. Perinotti, Acta Physica Slovaca 6, o.3, (0). [4] W. Fulton,. Harris, Representation Theory: A First Course, Springer (03) [5] R. P. Stanley, S. Fomin, Enumerative Combinatorics, Vol. of Cambridge Studies in Advanced Mathematics, Cambridge University Press, 999. doi:0.07/cbo [6] Michal Sedlák Alessandro Bisio, On some new hookcontent identities, arxiv: [7] A. M. Vershik, Hook formula and related identities, ournal of Soviet Mathematics 59 (5) (99) doi:0.007/bf [8] Stephen D. Bartlett, Terry Rudolph, Robert W. Spekkens and Peter S. Turner, ew. Phys., (009).
Quantum-controlled measurement device for quantum-state discrimination
 PHYSICAL REVIEW A, 66, 022112 2002 Quantum-controlled measurement device for quantum-state discrimination Miloslav Dušek 1,2 and Vladimír Bužek 2,3 1 Department of Optics, Palacký University, 17. listopadu
PHYSICAL REVIEW A, 66, 022112 2002 Quantum-controlled measurement device for quantum-state discrimination Miloslav Dušek 1,2 and Vladimír Bužek 2,3 1 Department of Optics, Palacký University, 17. listopadu
Probabilistic exact cloning and probabilistic no-signalling. Abstract
 Probabilistic exact cloning and probabilistic no-signalling Arun Kumar Pati Quantum Optics and Information Group, SEECS, Dean Street, University of Wales, Bangor LL 57 IUT, UK (August 5, 999) Abstract
Probabilistic exact cloning and probabilistic no-signalling Arun Kumar Pati Quantum Optics and Information Group, SEECS, Dean Street, University of Wales, Bangor LL 57 IUT, UK (August 5, 999) Abstract
arxiv: v2 [quant-ph] 26 Mar 2012
![arxiv: v2 [quant-ph] 26 Mar 2012 arxiv: v2 [quant-ph] 26 Mar 2012](/thumbs/84/91205204.jpg) Optimal Probabilistic Simulation of Quantum Channels from the Future to the Past Dina Genkina, Giulio Chiribella, and Lucien Hardy Perimeter Institute for Theoretical Physics, 31 Caroline Street North,
Optimal Probabilistic Simulation of Quantum Channels from the Future to the Past Dina Genkina, Giulio Chiribella, and Lucien Hardy Perimeter Institute for Theoretical Physics, 31 Caroline Street North,
Dipartimento di Fisica - Università di Pavia via A. Bassi Pavia - Italy
 Paolo Perinotti paolo.perinotti@unipv.it Dipartimento di Fisica - Università di Pavia via A. Bassi 6 27100 Pavia - Italy LIST OF PUBLICATIONS 1. G. M. D'Ariano, M. Erba, P. Perinotti, and A. Tosini, Virtually
Paolo Perinotti paolo.perinotti@unipv.it Dipartimento di Fisica - Università di Pavia via A. Bassi 6 27100 Pavia - Italy LIST OF PUBLICATIONS 1. G. M. D'Ariano, M. Erba, P. Perinotti, and A. Tosini, Virtually
THE NUMBER OF ORTHOGONAL CONJUGATIONS
 THE NUMBER OF ORTHOGONAL CONJUGATIONS Armin Uhlmann University of Leipzig, Institute for Theoretical Physics After a short introduction to anti-linearity, bounds for the number of orthogonal (skew) conjugations
THE NUMBER OF ORTHOGONAL CONJUGATIONS Armin Uhlmann University of Leipzig, Institute for Theoretical Physics After a short introduction to anti-linearity, bounds for the number of orthogonal (skew) conjugations
Quantum entanglement and symmetry
 Journal of Physics: Conference Series Quantum entanglement and symmetry To cite this article: D Chrucisi and A Kossaowsi 2007 J. Phys.: Conf. Ser. 87 012008 View the article online for updates and enhancements.
Journal of Physics: Conference Series Quantum entanglement and symmetry To cite this article: D Chrucisi and A Kossaowsi 2007 J. Phys.: Conf. Ser. 87 012008 View the article online for updates and enhancements.
arxiv: v2 [quant-ph] 21 Oct 2013
![arxiv: v2 [quant-ph] 21 Oct 2013 arxiv: v2 [quant-ph] 21 Oct 2013](/thumbs/79/80226931.jpg) Genuine hidden quantum nonlocality Flavien Hirsch, 1 Marco Túlio Quintino, 1 Joseph Bowles, 1 and Nicolas Brunner 1, 1 Département de Physique Théorique, Université de Genève, 111 Genève, Switzerland H.H.
Genuine hidden quantum nonlocality Flavien Hirsch, 1 Marco Túlio Quintino, 1 Joseph Bowles, 1 and Nicolas Brunner 1, 1 Département de Physique Théorique, Université de Genève, 111 Genève, Switzerland H.H.
On PPT States in C K C M C N Composite Quantum Systems
 Commun. Theor. Phys. (Beijing, China) 42 (2004) pp. 25 222 c International Academic Publishers Vol. 42, No. 2, August 5, 2004 On PPT States in C K C M C N Composite Quantum Systems WANG Xiao-Hong, FEI
Commun. Theor. Phys. (Beijing, China) 42 (2004) pp. 25 222 c International Academic Publishers Vol. 42, No. 2, August 5, 2004 On PPT States in C K C M C N Composite Quantum Systems WANG Xiao-Hong, FEI
Lecture 11 September 30, 2015
 PHYS 7895: Quantum Information Theory Fall 015 Lecture 11 September 30, 015 Prof. Mark M. Wilde Scribe: Mark M. Wilde This document is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike
PHYS 7895: Quantum Information Theory Fall 015 Lecture 11 September 30, 015 Prof. Mark M. Wilde Scribe: Mark M. Wilde This document is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike
arxiv:quant-ph/ v1 20 Oct 2005
 Approximate programmable quantum processors Mark Hillery 1,2,Mário Ziman 2,3, and Vladimír Bužek 2,4 1 Department of Physics, Hunter College of CUY, 695 Park Avenue, ew York, Y 10021 USA 2 Research Center
Approximate programmable quantum processors Mark Hillery 1,2,Mário Ziman 2,3, and Vladimír Bužek 2,4 1 Department of Physics, Hunter College of CUY, 695 Park Avenue, ew York, Y 10021 USA 2 Research Center
Optimal copying of entangled two-qubit states
 Optimal copying of entangled two-qubit states J. Novotný, 1 G. Alber, 2 and I. Jex 1 1 Department of Physics, FJFI ČVUT, Břehová 7, 115 19 Praha 1-Staré Město, Czech Republic 2 Institut für Angewandte
Optimal copying of entangled two-qubit states J. Novotný, 1 G. Alber, 2 and I. Jex 1 1 Department of Physics, FJFI ČVUT, Břehová 7, 115 19 Praha 1-Staré Město, Czech Republic 2 Institut für Angewandte
Optimal discrimination of quantum measurements. Michal Sedlák. Department of Optics, Palacký University, Olomouc, Czech Republic
 Department of Optics, Palacký University, Olomouc, Czech Republic Optimal discrimination of quantum measurements Michal Sedlák joint work with M. Ziman Research Center for Quantum Information Institute
Department of Optics, Palacký University, Olomouc, Czech Republic Optimal discrimination of quantum measurements Michal Sedlák joint work with M. Ziman Research Center for Quantum Information Institute
arxiv: v2 [quant-ph] 16 Nov 2018
![arxiv: v2 [quant-ph] 16 Nov 2018 arxiv: v2 [quant-ph] 16 Nov 2018](/thumbs/90/104093222.jpg) aaacxicdvhlsgmxfe3hv62vvswncwelkrmikdlgi7cqc1yfwyro+mthmasibkjlgg+wk3u/s2/wn8wfsxs1qsjh3nuosckjhcuhb8fry5+yxfpejyawv1bx2jxnm8tto1hftcs23ui7aohciwcjnxieojjf/xphvrdcxortlqhqykdgj6u6ako5kjmwo5gtsc0fi/qtgbvtaxmolcnxuap7gqihlspyhdblqgbicil5q1atid3qkfhfqqo+1ki6e5f+cyrt/txh1f/oj9+skd2npbhlnngojzmpd8k9tyjdw0kykioniem9jfmxflvtjmjlaseio9n9llpk/ahkfldycthdga3aj3t58/gwfolthsqx2olgidl87cdyigsjusbud182x0/7nbjs9utoacgfz/g1uj2phuaubx9u6fyy7kljdts8owchowj1dsarmc6qvbi39l78ta8bw9nvoovjv1tsanx9rbsmy8zw==
aaacxicdvhlsgmxfe3hv62vvswncwelkrmikdlgi7cqc1yfwyro+mthmasibkjlgg+wk3u/s2/wn8wfsxs1qsjh3nuosckjhcuhb8fry5+yxfpejyawv1bx2jxnm8tto1hftcs23ui7aohciwcjnxieojjf/xphvrdcxortlqhqykdgj6u6ako5kjmwo5gtsc0fi/qtgbvtaxmolcnxuap7gqihlspyhdblqgbicil5q1atid3qkfhfqqo+1ki6e5f+cyrt/txh1f/oj9+skd2npbhlnngojzmpd8k9tyjdw0kykioniem9jfmxflvtjmjlaseio9n9llpk/ahkfldycthdga3aj3t58/gwfolthsqx2olgidl87cdyigsjusbud182x0/7nbjs9utoacgfz/g1uj2phuaubx9u6fyy7kljdts8owchowj1dsarmc6qvbi39l78ta8bw9nvoovjv1tsanx9rbsmy8zw==
Application of Structural Physical Approximation to Partial Transpose in Teleportation. Satyabrata Adhikari Delhi Technological University (DTU)
 Application of Structural Physical Approximation to Partial Transpose in Teleportation Satyabrata Adhikari Delhi Technological University (DTU) Singlet fraction and its usefulness in Teleportation Singlet
Application of Structural Physical Approximation to Partial Transpose in Teleportation Satyabrata Adhikari Delhi Technological University (DTU) Singlet fraction and its usefulness in Teleportation Singlet
Lecture 6: Quantum error correction and quantum capacity
 Lecture 6: Quantum error correction and quantum capacity Mark M. Wilde The quantum capacity theorem is one of the most important theorems in quantum hannon theory. It is a fundamentally quantum theorem
Lecture 6: Quantum error correction and quantum capacity Mark M. Wilde The quantum capacity theorem is one of the most important theorems in quantum hannon theory. It is a fundamentally quantum theorem
arxiv: v3 [quant-ph] 5 Jun 2015
![arxiv: v3 [quant-ph] 5 Jun 2015 arxiv: v3 [quant-ph] 5 Jun 2015](/thumbs/88/117676319.jpg) Entanglement and swap of quantum states in two qubits Takaya Ikuto and Satoshi Ishizaka Graduate School of Integrated Arts and Sciences, Hiroshima University, Higashihiroshima, 739-8521, Japan (Dated:
Entanglement and swap of quantum states in two qubits Takaya Ikuto and Satoshi Ishizaka Graduate School of Integrated Arts and Sciences, Hiroshima University, Higashihiroshima, 739-8521, Japan (Dated:
arxiv: v2 [quant-ph] 7 Apr 2014
![arxiv: v2 [quant-ph] 7 Apr 2014 arxiv: v2 [quant-ph] 7 Apr 2014](/thumbs/94/119025009.jpg) Quantum Chernoff bound as a measure of efficiency of quantum cloning for mixed states arxiv:1404.0915v [quant-ph] 7 Apr 014 Iulia Ghiu Centre for Advanced Quantum Physics, Department of Physics, University
Quantum Chernoff bound as a measure of efficiency of quantum cloning for mixed states arxiv:1404.0915v [quant-ph] 7 Apr 014 Iulia Ghiu Centre for Advanced Quantum Physics, Department of Physics, University
Flocks of Quantum Clones: Multiple Copying of Qubits
 Fortschr. Phys. 46 (998) 4 ±5, 5 ±5 Flocks of Quantum Clones: Multiple Copying of Qubits V. BuzÏek ;, M. Hillery and P. L. Knight 4 Institute of Physics, Slovak Academy of Sciences, DuÂbravska cesta 9,
Fortschr. Phys. 46 (998) 4 ±5, 5 ±5 Flocks of Quantum Clones: Multiple Copying of Qubits V. BuzÏek ;, M. Hillery and P. L. Knight 4 Institute of Physics, Slovak Academy of Sciences, DuÂbravska cesta 9,
Theory of Quantum Entanglement
 Theory of Quantum Entanglement Shao-Ming Fei Capital Normal University, Beijing Universität Bonn, Bonn Richard Feynman 1980 Certain quantum mechanical effects cannot be simulated efficiently on a classical
Theory of Quantum Entanglement Shao-Ming Fei Capital Normal University, Beijing Universität Bonn, Bonn Richard Feynman 1980 Certain quantum mechanical effects cannot be simulated efficiently on a classical
DECAY OF SINGLET CONVERSION PROBABILITY IN ONE DIMENSIONAL QUANTUM NETWORKS
 DECAY OF SINGLET CONVERSION PROBABILITY IN ONE DIMENSIONAL QUANTUM NETWORKS SCOTT HOTTOVY Abstract. Quantum networks are used to transmit and process information by using the phenomena of quantum mechanics.
DECAY OF SINGLET CONVERSION PROBABILITY IN ONE DIMENSIONAL QUANTUM NETWORKS SCOTT HOTTOVY Abstract. Quantum networks are used to transmit and process information by using the phenomena of quantum mechanics.
Optimal probabilistic cloning and purification of quantum states
 PHYSICAL REVIEW A 70, 032308 (2004) Optimal probabilistic cloning and purification of quantum states Jaromír Fiurášek,2 QUIC, Ecole Polytechnique, CP 65, Université Libre de Bruxelles, 050 Brussels, Belgium
PHYSICAL REVIEW A 70, 032308 (2004) Optimal probabilistic cloning and purification of quantum states Jaromír Fiurášek,2 QUIC, Ecole Polytechnique, CP 65, Université Libre de Bruxelles, 050 Brussels, Belgium
Estimation of Optimal Singlet Fraction (OSF) and Entanglement Negativity (EN)
 Estimation of Optimal Singlet Fraction (OSF) and Entanglement Negativity (EN) Satyabrata Adhikari Delhi Technological University satyabrata@dtu.ac.in December 4, 2018 Satyabrata Adhikari (DTU) Estimation
Estimation of Optimal Singlet Fraction (OSF) and Entanglement Negativity (EN) Satyabrata Adhikari Delhi Technological University satyabrata@dtu.ac.in December 4, 2018 Satyabrata Adhikari (DTU) Estimation
Port-based teleportation and its applications
 2 QUATUO Port-based teleportation and its applications Satoshi Ishizaka Graduate School of Integrated Arts and Sciences Hiroshima University Collaborator: Tohya Hiroshima (ERATO-SORST) Outline Port-based
2 QUATUO Port-based teleportation and its applications Satoshi Ishizaka Graduate School of Integrated Arts and Sciences Hiroshima University Collaborator: Tohya Hiroshima (ERATO-SORST) Outline Port-based
arxiv:quant-ph/ v2 17 Jun 1996
 Separability Criterion for Density Matrices arxiv:quant-ph/9604005v2 17 Jun 1996 Asher Peres Department of Physics, Technion Israel Institute of Technology, 32000 Haifa, Israel Abstract A quantum system
Separability Criterion for Density Matrices arxiv:quant-ph/9604005v2 17 Jun 1996 Asher Peres Department of Physics, Technion Israel Institute of Technology, 32000 Haifa, Israel Abstract A quantum system
1. Basic rules of quantum mechanics
 1. Basic rules of quantum mechanics How to describe the states of an ideally controlled system? How to describe changes in an ideally controlled system? How to describe measurements on an ideally controlled
1. Basic rules of quantum mechanics How to describe the states of an ideally controlled system? How to describe changes in an ideally controlled system? How to describe measurements on an ideally controlled
Lecture 4: Postulates of quantum mechanics
 Lecture 4: Postulates of quantum mechanics Rajat Mittal IIT Kanpur The postulates of quantum mechanics provide us the mathematical formalism over which the physical theory is developed. For people studying
Lecture 4: Postulates of quantum mechanics Rajat Mittal IIT Kanpur The postulates of quantum mechanics provide us the mathematical formalism over which the physical theory is developed. For people studying
arxiv:quant-ph/ v2 23 Aug 2003
 An Architecture of Deterministic Quantum Central Processing Unit arxiv:quant-ph/0207032v2 23 Aug 2003 Fei Xue a, Zeng-Bing Chen a Mingjun Shi a Xianyi Zhou a Jiangfeng Du a Rongdian Han a a Department
An Architecture of Deterministic Quantum Central Processing Unit arxiv:quant-ph/0207032v2 23 Aug 2003 Fei Xue a, Zeng-Bing Chen a Mingjun Shi a Xianyi Zhou a Jiangfeng Du a Rongdian Han a a Department
Quantum Error Correcting Codes and Quantum Cryptography. Peter Shor M.I.T. Cambridge, MA 02139
 Quantum Error Correcting Codes and Quantum Cryptography Peter Shor M.I.T. Cambridge, MA 02139 1 We start out with two processes which are fundamentally quantum: superdense coding and teleportation. Superdense
Quantum Error Correcting Codes and Quantum Cryptography Peter Shor M.I.T. Cambridge, MA 02139 1 We start out with two processes which are fundamentally quantum: superdense coding and teleportation. Superdense
Teleportation of Quantum States (1993; Bennett, Brassard, Crepeau, Jozsa, Peres, Wootters)
 Teleportation of Quantum States (1993; Bennett, Brassard, Crepeau, Jozsa, Peres, Wootters) Rahul Jain U. Waterloo and Institute for Quantum Computing, rjain@cs.uwaterloo.ca entry editor: Andris Ambainis
Teleportation of Quantum States (1993; Bennett, Brassard, Crepeau, Jozsa, Peres, Wootters) Rahul Jain U. Waterloo and Institute for Quantum Computing, rjain@cs.uwaterloo.ca entry editor: Andris Ambainis
QUANTUM INFORMATION -THE NO-HIDING THEOREM p.1/36
 QUANTUM INFORMATION - THE NO-HIDING THEOREM Arun K Pati akpati@iopb.res.in Instititute of Physics, Bhubaneswar-751005, Orissa, INDIA and Th. P. D, BARC, Mumbai-400085, India QUANTUM INFORMATION -THE NO-HIDING
QUANTUM INFORMATION - THE NO-HIDING THEOREM Arun K Pati akpati@iopb.res.in Instititute of Physics, Bhubaneswar-751005, Orissa, INDIA and Th. P. D, BARC, Mumbai-400085, India QUANTUM INFORMATION -THE NO-HIDING
A no-go theorem for theories that decohere to quantum mechanics
 A no-go theorem for theories that decohere to quantum mechanics Ciarán M. Lee University College London Joint work with John H. Selby arxiv:1701.07449 Motivation The more important fundamental laws and
A no-go theorem for theories that decohere to quantum mechanics Ciarán M. Lee University College London Joint work with John H. Selby arxiv:1701.07449 Motivation The more important fundamental laws and
Qubits vs. bits: a naive account A bit: admits two values 0 and 1, admits arbitrary transformations. is freely readable,
 Qubits vs. bits: a naive account A bit: admits two values 0 and 1, admits arbitrary transformations. is freely readable, A qubit: a sphere of values, which is spanned in projective sense by two quantum
Qubits vs. bits: a naive account A bit: admits two values 0 and 1, admits arbitrary transformations. is freely readable, A qubit: a sphere of values, which is spanned in projective sense by two quantum
Realization of positive-operator-valued measures using measurement-assisted programmable quantum processors
 Realization of positive-operator-valued measures using measurement-assisted programmable quantum processors Mário Ziman 1,2 and Vladimír Buže 1,3 1 Research Center for Quantum Information, Slova Academy
Realization of positive-operator-valued measures using measurement-assisted programmable quantum processors Mário Ziman 1,2 and Vladimír Buže 1,3 1 Research Center for Quantum Information, Slova Academy
Quantum Information Processing and Diagrams of States
 Quantum Information and Diagrams of States September 17th 2009, AFSecurity Sara Felloni sara@unik.no / sara.felloni@iet.ntnu.no Quantum Hacking Group: http://www.iet.ntnu.no/groups/optics/qcr/ UNIK University
Quantum Information and Diagrams of States September 17th 2009, AFSecurity Sara Felloni sara@unik.no / sara.felloni@iet.ntnu.no Quantum Hacking Group: http://www.iet.ntnu.no/groups/optics/qcr/ UNIK University
UNIVERSAL HYBRID QUANTUM PROCESSORS
 XJ0300183 Письма в ЭЧАЯ. 2003. 1[116] Particles and Nuclei, Letters. 2003. No. 1[116] UNIVERSAL HYBRID QUANTUM PROCESSORS A. Yu. Vlasov 1 FRC7IRH, St. Petersburg, Russia A quantum processor (the programmable
XJ0300183 Письма в ЭЧАЯ. 2003. 1[116] Particles and Nuclei, Letters. 2003. No. 1[116] UNIVERSAL HYBRID QUANTUM PROCESSORS A. Yu. Vlasov 1 FRC7IRH, St. Petersburg, Russia A quantum processor (the programmable
GROUP THEORY PRIMER. New terms: tensor, rank k tensor, Young tableau, Young diagram, hook, hook length, factors over hooks rule
 GROUP THEORY PRIMER New terms: tensor, rank k tensor, Young tableau, Young diagram, hook, hook length, factors over hooks rule 1. Tensor methods for su(n) To study some aspects of representations of a
GROUP THEORY PRIMER New terms: tensor, rank k tensor, Young tableau, Young diagram, hook, hook length, factors over hooks rule 1. Tensor methods for su(n) To study some aspects of representations of a
Ph 219/CS 219. Exercises Due: Friday 3 November 2006
 Ph 9/CS 9 Exercises Due: Friday 3 November 006. Fidelity We saw in Exercise. that the trace norm ρ ρ tr provides a useful measure of the distinguishability of the states ρ and ρ. Another useful measure
Ph 9/CS 9 Exercises Due: Friday 3 November 006. Fidelity We saw in Exercise. that the trace norm ρ ρ tr provides a useful measure of the distinguishability of the states ρ and ρ. Another useful measure
9. Distance measures. 9.1 Classical information measures. Head Tail. How similar/close are two probability distributions? Trace distance.
 9. Distance measures 9.1 Classical information measures How similar/close are two probability distributions? Trace distance Fidelity Example: Flipping two coins, one fair one biased Head Tail Trace distance
9. Distance measures 9.1 Classical information measures How similar/close are two probability distributions? Trace distance Fidelity Example: Flipping two coins, one fair one biased Head Tail Trace distance
Quantum Information Types
 qitd181 Quantum Information Types Robert B. Griffiths Version of 6 February 2012 References: R. B. Griffiths, Types of Quantum Information, Phys. Rev. A 76 (2007) 062320; arxiv:0707.3752 Contents 1 Introduction
qitd181 Quantum Information Types Robert B. Griffiths Version of 6 February 2012 References: R. B. Griffiths, Types of Quantum Information, Phys. Rev. A 76 (2007) 062320; arxiv:0707.3752 Contents 1 Introduction
ON THE ROLE OF THE BASIS OF MEASUREMENT IN QUANTUM GATE TELEPORTATION. F. V. Mendes, R. V. Ramos
 ON THE ROLE OF THE BASIS OF MEASREMENT IN QANTM GATE TELEPORTATION F V Mendes, R V Ramos fernandovm@detiufcbr rubens@detiufcbr Lab of Quantum Information Technology, Department of Teleinformatic Engineering
ON THE ROLE OF THE BASIS OF MEASREMENT IN QANTM GATE TELEPORTATION F V Mendes, R V Ramos fernandovm@detiufcbr rubens@detiufcbr Lab of Quantum Information Technology, Department of Teleinformatic Engineering
Quantum theory without predefined causal structure
 Quantum theory without predefined causal structure Ognyan Oreshkov Centre for Quantum Information and Communication, niversité Libre de Bruxelles Based on work with Caslav Brukner, Nicolas Cerf, Fabio
Quantum theory without predefined causal structure Ognyan Oreshkov Centre for Quantum Information and Communication, niversité Libre de Bruxelles Based on work with Caslav Brukner, Nicolas Cerf, Fabio
Local cloning of entangled states
 Local cloning of entangled states Vlad Gheorghiu Department of Physics Carnegie Mellon University Pittsburgh, PA 15213, U.S.A. March 16, 2010 Vlad Gheorghiu (CMU) Local cloning of entangled states March
Local cloning of entangled states Vlad Gheorghiu Department of Physics Carnegie Mellon University Pittsburgh, PA 15213, U.S.A. March 16, 2010 Vlad Gheorghiu (CMU) Local cloning of entangled states March
Quantum Gates, Circuits & Teleportation
 Chapter 3 Quantum Gates, Circuits & Teleportation Unitary Operators The third postulate of quantum physics states that the evolution of a quantum system is necessarily unitary. Geometrically, a unitary
Chapter 3 Quantum Gates, Circuits & Teleportation Unitary Operators The third postulate of quantum physics states that the evolution of a quantum system is necessarily unitary. Geometrically, a unitary
Perfect quantum teleportation and dense coding protocols via the 2N-qubit W state
 Perfect quantum teleportation and dense coding protocols via the -qubit W state Wang Mei-Yu( ) a)b) and Yan Feng-Li( ) a)b) a) College of Physics Science and Information Engineering, Hebei ormal University,
Perfect quantum teleportation and dense coding protocols via the -qubit W state Wang Mei-Yu( ) a)b) and Yan Feng-Li( ) a)b) a) College of Physics Science and Information Engineering, Hebei ormal University,
b) (5 points) Give a simple quantum circuit that transforms the state
 C/CS/Phy191 Midterm Quiz Solutions October 0, 009 1 (5 points) Short answer questions: a) (5 points) Let f be a function from n bits to 1 bit You have a quantum circuit U f for computing f If you wish
C/CS/Phy191 Midterm Quiz Solutions October 0, 009 1 (5 points) Short answer questions: a) (5 points) Let f be a function from n bits to 1 bit You have a quantum circuit U f for computing f If you wish
Entropy in Classical and Quantum Information Theory
 Entropy in Classical and Quantum Information Theory William Fedus Physics Department, University of California, San Diego. Entropy is a central concept in both classical and quantum information theory,
Entropy in Classical and Quantum Information Theory William Fedus Physics Department, University of California, San Diego. Entropy is a central concept in both classical and quantum information theory,
Optimal measurements for relative quantum information
 PHYSICAL REVIEW A 70, 032321 (2004) Optimal measurements for relative quantum information Stephen D. Bartlett, 1, * Terry Rudolph, 2, and Robert W. Spekkens 3, 1 School of Physical Sciences, The University
PHYSICAL REVIEW A 70, 032321 (2004) Optimal measurements for relative quantum information Stephen D. Bartlett, 1, * Terry Rudolph, 2, and Robert W. Spekkens 3, 1 School of Physical Sciences, The University
An Introduction to Quantum Information. By Aditya Jain. Under the Guidance of Dr. Guruprasad Kar PAMU, ISI Kolkata
 An Introduction to Quantum Information By Aditya Jain Under the Guidance of Dr. Guruprasad Kar PAMU, ISI Kolkata 1. Introduction Quantum information is physical information that is held in the state of
An Introduction to Quantum Information By Aditya Jain Under the Guidance of Dr. Guruprasad Kar PAMU, ISI Kolkata 1. Introduction Quantum information is physical information that is held in the state of
arxiv:quant-ph/ v1 14 Mar 2001
 Optimal quantum estimation of the coupling between two bosonic modes G. Mauro D Ariano a Matteo G. A. Paris b Paolo Perinotti c arxiv:quant-ph/0103080v1 14 Mar 001 a Sezione INFN, Universitá di Pavia,
Optimal quantum estimation of the coupling between two bosonic modes G. Mauro D Ariano a Matteo G. A. Paris b Paolo Perinotti c arxiv:quant-ph/0103080v1 14 Mar 001 a Sezione INFN, Universitá di Pavia,
Schur-Weyl duality, quantum data compression, tomography
 PHYSICS 491: Symmetry and Quantum Information April 25, 2017 Schur-Weyl duality, quantum data compression, tomography Lecture 7 Michael Walter, Stanford University These lecture notes are not proof-read
PHYSICS 491: Symmetry and Quantum Information April 25, 2017 Schur-Weyl duality, quantum data compression, tomography Lecture 7 Michael Walter, Stanford University These lecture notes are not proof-read
A scheme for protecting one-qubit information against erasure. error. Abstract
 A scheme for protecting one-qubit information against erasure error Chui-Ping Yang 1, Shih-I Chu 1, and Siyuan Han 1 Department of Chemistry, University of Kansas, and Kansas Center for Advanced Scientific
A scheme for protecting one-qubit information against erasure error Chui-Ping Yang 1, Shih-I Chu 1, and Siyuan Han 1 Department of Chemistry, University of Kansas, and Kansas Center for Advanced Scientific
Ph 219/CS 219. Exercises Due: Friday 20 October 2006
 1 Ph 219/CS 219 Exercises Due: Friday 20 October 2006 1.1 How far apart are two quantum states? Consider two quantum states described by density operators ρ and ρ in an N-dimensional Hilbert space, and
1 Ph 219/CS 219 Exercises Due: Friday 20 October 2006 1.1 How far apart are two quantum states? Consider two quantum states described by density operators ρ and ρ in an N-dimensional Hilbert space, and
Hilbert Space, Entanglement, Quantum Gates, Bell States, Superdense Coding.
 CS 94- Bell States Bell Inequalities 9//04 Fall 004 Lecture Hilbert Space Entanglement Quantum Gates Bell States Superdense Coding 1 One qubit: Recall that the state of a single qubit can be written as
CS 94- Bell States Bell Inequalities 9//04 Fall 004 Lecture Hilbert Space Entanglement Quantum Gates Bell States Superdense Coding 1 One qubit: Recall that the state of a single qubit can be written as
Manipulating Causal Order of Unitary Operations using Adiabatic Quantum Computation
 Manipulating Causal Order of Unitary Operations using Adiabatic Quantum Computation Kosuke Nakago, Quantum Information group, The University of Tokyo, Tokyo,Japan. Joint work with, Mio murao, Michal Hajdusek,
Manipulating Causal Order of Unitary Operations using Adiabatic Quantum Computation Kosuke Nakago, Quantum Information group, The University of Tokyo, Tokyo,Japan. Joint work with, Mio murao, Michal Hajdusek,
Introduction to Quantum Information Hermann Kampermann
 Introduction to Quantum Information Hermann Kampermann Heinrich-Heine-Universität Düsseldorf Theoretische Physik III Summer school Bleubeuren July 014 Contents 1 Quantum Mechanics...........................
Introduction to Quantum Information Hermann Kampermann Heinrich-Heine-Universität Düsseldorf Theoretische Physik III Summer school Bleubeuren July 014 Contents 1 Quantum Mechanics...........................
A Holevo-type bound for a Hilbert Schmidt distance measure
 Journal of Quantum Information Science, 205, *,** Published Online **** 204 in SciRes. http://www.scirp.org/journal/**** http://dx.doi.org/0.4236/****.204.***** A Holevo-type bound for a Hilbert Schmidt
Journal of Quantum Information Science, 205, *,** Published Online **** 204 in SciRes. http://www.scirp.org/journal/**** http://dx.doi.org/0.4236/****.204.***** A Holevo-type bound for a Hilbert Schmidt
arxiv:quant-ph/ v1 16 Jan 2006
 Cloning and Joint Measurements of Incompatible Components of Spin Thomas Brougham, Erika Andersson and Stephen M. Barnett 1 1 SUPA, Department of Physics, University of Strathclyde, Glasgow G4 0NG, UK
Cloning and Joint Measurements of Incompatible Components of Spin Thomas Brougham, Erika Andersson and Stephen M. Barnett 1 1 SUPA, Department of Physics, University of Strathclyde, Glasgow G4 0NG, UK
Linear-optical quantum information processing: A few experiments
 Linear-optical quantum information processing: A few experiments Miloslav Dušek Lucie Čelechovská, Karel Lemr, Michal Mičuda, Antonín Černoch, Jaromír Fiurášek, Miroslav Ježek, ek, Jan Soubusta, Radim
Linear-optical quantum information processing: A few experiments Miloslav Dušek Lucie Čelechovská, Karel Lemr, Michal Mičuda, Antonín Černoch, Jaromír Fiurášek, Miroslav Ježek, ek, Jan Soubusta, Radim
Quantum correlations with indefinite causal order
 Faculty of Physics, University of Vienna & Institute for Quantum Optics and Quantum Information, Vienna Quantum correlations with indefinite causal order Ognyan Oreshkov, Fabio Costa, Časlav Brukner Nature
Faculty of Physics, University of Vienna & Institute for Quantum Optics and Quantum Information, Vienna Quantum correlations with indefinite causal order Ognyan Oreshkov, Fabio Costa, Časlav Brukner Nature
Seminar 1. Introduction to Quantum Computing
 Seminar 1 Introduction to Quantum Computing Before going in I am also a beginner in this field If you are interested, you can search more using: Quantum Computing since Democritus (Scott Aaronson) Quantum
Seminar 1 Introduction to Quantum Computing Before going in I am also a beginner in this field If you are interested, you can search more using: Quantum Computing since Democritus (Scott Aaronson) Quantum
QUANTUM COMMUNICATIONS BASED ON QUANTUM HASHING. Alexander Vasiliev. Kazan Federal University
 QUANTUM COMMUNICATIONS BASED ON QUANTUM HASHING Alexander Vasiliev Kazan Federal University Abstract: In this paper we consider an application of the recently proposed quantum hashing technique for computing
QUANTUM COMMUNICATIONS BASED ON QUANTUM HASHING Alexander Vasiliev Kazan Federal University Abstract: In this paper we consider an application of the recently proposed quantum hashing technique for computing
The Minimax Fidelity for Quantum Channels: Theory and Some Applications
 The Minimax Fidelity for Quantum Channels: Theory and Some Applications Maxim Raginsky University of I!inois V.P. Belavkin, G.M. D Ariano and M. Raginsky Operational distance and fidelity for quantum channels
The Minimax Fidelity for Quantum Channels: Theory and Some Applications Maxim Raginsky University of I!inois V.P. Belavkin, G.M. D Ariano and M. Raginsky Operational distance and fidelity for quantum channels
arxiv: v3 [quant-ph] 17 Sep 2017
![arxiv: v3 [quant-ph] 17 Sep 2017 arxiv: v3 [quant-ph] 17 Sep 2017](/thumbs/82/86256787.jpg) Quantum Error Correction using Hypergraph States Shashanka Balakuntala and Goutam Paul # Department of Applied Mathematics and Computational Sciences, PSG College of Technology, Coimbatore 641 004, India,
Quantum Error Correction using Hypergraph States Shashanka Balakuntala and Goutam Paul # Department of Applied Mathematics and Computational Sciences, PSG College of Technology, Coimbatore 641 004, India,
arxiv:quant-ph/ v1 22 Aug 2005
 Conditions for separability in generalized Laplacian matrices and nonnegative matrices as density matrices arxiv:quant-ph/58163v1 22 Aug 25 Abstract Chai Wah Wu IBM Research Division, Thomas J. Watson
Conditions for separability in generalized Laplacian matrices and nonnegative matrices as density matrices arxiv:quant-ph/58163v1 22 Aug 25 Abstract Chai Wah Wu IBM Research Division, Thomas J. Watson
arxiv: v1 [quant-ph] 4 Jul 2013
![arxiv: v1 [quant-ph] 4 Jul 2013 arxiv: v1 [quant-ph] 4 Jul 2013](/thumbs/87/95035090.jpg) GEOMETRY FOR SEPARABLE STATES AND CONSTRUCTION OF ENTANGLED STATES WITH POSITIVE PARTIAL TRANSPOSES KIL-CHAN HA AND SEUNG-HYEOK KYE arxiv:1307.1362v1 [quant-ph] 4 Jul 2013 Abstract. We construct faces
GEOMETRY FOR SEPARABLE STATES AND CONSTRUCTION OF ENTANGLED STATES WITH POSITIVE PARTIAL TRANSPOSES KIL-CHAN HA AND SEUNG-HYEOK KYE arxiv:1307.1362v1 [quant-ph] 4 Jul 2013 Abstract. We construct faces
Unambiguous Discrimination Between Linearly Dependent States With Multiple Copies
 Unambiguous Discrimination Between Linearly Dependent States With Multiple Copies Anthony Chefles Department of Physical Sciences, University of Hertfordshire, Hatfield AL10 9AB, Herts, UK arxiv:quant-ph/0105016v3
Unambiguous Discrimination Between Linearly Dependent States With Multiple Copies Anthony Chefles Department of Physical Sciences, University of Hertfordshire, Hatfield AL10 9AB, Herts, UK arxiv:quant-ph/0105016v3
Permutations and quantum entanglement
 Journal of Physics: Conference Series Permutations and quantum entanglement To cite this article: D Chruciski and A Kossakowski 2008 J. Phys.: Conf. Ser. 104 012002 View the article online for updates
Journal of Physics: Conference Series Permutations and quantum entanglement To cite this article: D Chruciski and A Kossakowski 2008 J. Phys.: Conf. Ser. 104 012002 View the article online for updates
arxiv: v2 [quant-ph] 25 May 2018
![arxiv: v2 [quant-ph] 25 May 2018 arxiv: v2 [quant-ph] 25 May 2018](/thumbs/80/81904262.jpg) arxiv:79.79v2 [quant-ph] 25 May 28 A PRACTICAL QUANTUM ALGORITHM FOR THE SCHUR TRANSFORM WILLIAM M. KIRBY a Physics Department, Williams College Williamstown, MA 267, USA FREDERICK W. STRAUCH b Physics
arxiv:79.79v2 [quant-ph] 25 May 28 A PRACTICAL QUANTUM ALGORITHM FOR THE SCHUR TRANSFORM WILLIAM M. KIRBY a Physics Department, Williams College Williamstown, MA 267, USA FREDERICK W. STRAUCH b Physics
Quantum Teleportation Pt. 3
 Quantum Teleportation Pt. 3 PHYS 500 - Southern Illinois University March 7, 2017 PHYS 500 - Southern Illinois University Quantum Teleportation Pt. 3 March 7, 2017 1 / 9 A Bit of History on Teleportation
Quantum Teleportation Pt. 3 PHYS 500 - Southern Illinois University March 7, 2017 PHYS 500 - Southern Illinois University Quantum Teleportation Pt. 3 March 7, 2017 1 / 9 A Bit of History on Teleportation
Chapter 2 The Density Matrix
 Chapter 2 The Density Matrix We are going to require a more general description of a quantum state than that given by a state vector. The density matrix provides such a description. Its use is required
Chapter 2 The Density Matrix We are going to require a more general description of a quantum state than that given by a state vector. The density matrix provides such a description. Its use is required
On balance of information in bipartite quantum communication systems: entanglement-energy analogy
 On balance of information in bipartite quantum communication systems: entanglement-energy analogy Ryszard Horodecki 1,, Micha l Horodecki 1, and Pawe l Horodecki 2, 1 Institute of Theoretical Physics and
On balance of information in bipartite quantum communication systems: entanglement-energy analogy Ryszard Horodecki 1,, Micha l Horodecki 1, and Pawe l Horodecki 2, 1 Institute of Theoretical Physics and
Mixed-state sensitivity of several quantum-information benchmarks
 PHYSICAL REVIEW A 70, 05309 (004) Mixed-state sensitivity of several quantum-information benchmarks Nicholas A. Peters, Tzu-Chieh Wei, and Paul G. Kwiat Physics Department, University of Illinois, 1110
PHYSICAL REVIEW A 70, 05309 (004) Mixed-state sensitivity of several quantum-information benchmarks Nicholas A. Peters, Tzu-Chieh Wei, and Paul G. Kwiat Physics Department, University of Illinois, 1110
Max-Planck-Institut für Mathematik in den Naturwissenschaften Leipzig
 Max-Planck-Institut für Mathematik in den Naturwissenschaften Leipzig Coherence of Assistance and Regularized Coherence of Assistance by Ming-Jing Zhao, Teng Ma, and Shao-Ming Fei Preprint no.: 14 2018
Max-Planck-Institut für Mathematik in den Naturwissenschaften Leipzig Coherence of Assistance and Regularized Coherence of Assistance by Ming-Jing Zhao, Teng Ma, and Shao-Ming Fei Preprint no.: 14 2018
Tensor network simulations of strongly correlated quantum systems
 CENTRE FOR QUANTUM TECHNOLOGIES NATIONAL UNIVERSITY OF SINGAPORE AND CLARENDON LABORATORY UNIVERSITY OF OXFORD Tensor network simulations of strongly correlated quantum systems Stephen Clark LXXT[[[GSQPEFS\EGYOEGXMZMXMIWUYERXYQGSYVWI
CENTRE FOR QUANTUM TECHNOLOGIES NATIONAL UNIVERSITY OF SINGAPORE AND CLARENDON LABORATORY UNIVERSITY OF OXFORD Tensor network simulations of strongly correlated quantum systems Stephen Clark LXXT[[[GSQPEFS\EGYOEGXMZMXMIWUYERXYQGSYVWI
Transmitting and Hiding Quantum Information
 2018/12/20 @ 4th KIAS WORKSHOP on Quantum Information and Thermodynamics Transmitting and Hiding Quantum Information Seung-Woo Lee Quantum Universe Center Korea Institute for Advanced Study (KIAS) Contents
2018/12/20 @ 4th KIAS WORKSHOP on Quantum Information and Thermodynamics Transmitting and Hiding Quantum Information Seung-Woo Lee Quantum Universe Center Korea Institute for Advanced Study (KIAS) Contents
Quantum Cloning WOOTTERS-ZUREK CLONER
 Quantum Cloning Quantum cloning has been a topic of considerable interest for many years. It turns out to be quantum limit for copying an input state and is closely related to linear amplification when
Quantum Cloning Quantum cloning has been a topic of considerable interest for many years. It turns out to be quantum limit for copying an input state and is closely related to linear amplification when
arxiv: v3 [quant-ph] 11 Dec 2018
![arxiv: v3 [quant-ph] 11 Dec 2018 arxiv: v3 [quant-ph] 11 Dec 2018](/thumbs/88/116603231.jpg) The stabilizer for n-qubit symmetric states Xian Shi Institute of Mathematics, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China University of Chinese Academy
The stabilizer for n-qubit symmetric states Xian Shi Institute of Mathematics, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China University of Chinese Academy
arxiv: v1 [quant-ph] 3 Jan 2008
![arxiv: v1 [quant-ph] 3 Jan 2008 arxiv: v1 [quant-ph] 3 Jan 2008](/thumbs/81/83256169.jpg) A paradigm for entanglement theory based on quantum communication Jonathan Oppenheim 1 1 Department of Applied Mathematics and Theoretical Physics, University of Cambridge U.K. arxiv:0801.0458v1 [quant-ph]
A paradigm for entanglement theory based on quantum communication Jonathan Oppenheim 1 1 Department of Applied Mathematics and Theoretical Physics, University of Cambridge U.K. arxiv:0801.0458v1 [quant-ph]
arxiv:quant-ph/ v5 6 Apr 2005
 Nonunitary quantum circuit Hiroaki Terashima 1, and Masahito Ueda 1, arxiv:quant-ph/3461v5 6 Apr 5 1 Department of Physics, Tokyo Institute of Technology, Tokyo 15-8551, Japan CREST, Japan Science and
Nonunitary quantum circuit Hiroaki Terashima 1, and Masahito Ueda 1, arxiv:quant-ph/3461v5 6 Apr 5 1 Department of Physics, Tokyo Institute of Technology, Tokyo 15-8551, Japan CREST, Japan Science and
arxiv:quant-ph/ v2 3 Oct 2000
 Quantum key distribution without alternative measurements Adán Cabello Departamento de Física Aplicada, Universidad de Sevilla, 0 Sevilla, Spain January, 0 arxiv:quant-ph/990v Oct 000 Entanglement swapping
Quantum key distribution without alternative measurements Adán Cabello Departamento de Física Aplicada, Universidad de Sevilla, 0 Sevilla, Spain January, 0 arxiv:quant-ph/990v Oct 000 Entanglement swapping
Estimating entanglement in a class of N-qudit states
 Estimating entanglement in a class of N-qudit states Sumiyoshi Abe 1,2,3 1 Physics Division, College of Information Science and Engineering, Huaqiao University, Xiamen 361021, China 2 Department of Physical
Estimating entanglement in a class of N-qudit states Sumiyoshi Abe 1,2,3 1 Physics Division, College of Information Science and Engineering, Huaqiao University, Xiamen 361021, China 2 Department of Physical
TELEBROADCASTING OF ENTANGLED TWO-SPIN-1/2 STATES
 TELEBRODCSTING OF ENTNGLED TWO-SPIN-/ STTES IULI GHIU Department of Physics, University of Bucharest, P.O. Box MG-, R-775, Bucharest-Mãgurele, Romania Receive December, 4 quantum telebroacasting process
TELEBRODCSTING OF ENTNGLED TWO-SPIN-/ STTES IULI GHIU Department of Physics, University of Bucharest, P.O. Box MG-, R-775, Bucharest-Mãgurele, Romania Receive December, 4 quantum telebroacasting process
Representation Theory. Ricky Roy Math 434 University of Puget Sound
 Representation Theory Ricky Roy Math 434 University of Puget Sound May 2, 2010 Introduction In our study of group theory, we set out to classify all distinct groups of a given order up to isomorphism.
Representation Theory Ricky Roy Math 434 University of Puget Sound May 2, 2010 Introduction In our study of group theory, we set out to classify all distinct groups of a given order up to isomorphism.
Lecture: Quantum Information
 Lecture: Quantum Information Transcribed by: Crystal Noel and Da An (Chi Chi) November 10, 016 1 Final Proect Information Find an issue related to class you are interested in and either: read some papers
Lecture: Quantum Information Transcribed by: Crystal Noel and Da An (Chi Chi) November 10, 016 1 Final Proect Information Find an issue related to class you are interested in and either: read some papers
arxiv:quant-ph/ v2 18 Jan 2006
 Cloning of observables arxiv:quant-ph/0509170v2 18 Jan 2006 1. Introduction Alessandro Ferraro,, Matteo Galbiati, Matteo G. A. Paris Dipartimento di Fisica dell Università di Milano, Italia. STMicroelectronics,
Cloning of observables arxiv:quant-ph/0509170v2 18 Jan 2006 1. Introduction Alessandro Ferraro,, Matteo Galbiati, Matteo G. A. Paris Dipartimento di Fisica dell Università di Milano, Italia. STMicroelectronics,
arxiv:quant-ph/ v2 2 Jan 2007
 Revisiting controlled quantum secure direct communication using a non-symmetric quantum channel with quantum superdense coding arxiv:quant-ph/06106v Jan 007 Jun Liu 1, Yan Xia and Zhan-jun Zhang 1,, 1
Revisiting controlled quantum secure direct communication using a non-symmetric quantum channel with quantum superdense coding arxiv:quant-ph/06106v Jan 007 Jun Liu 1, Yan Xia and Zhan-jun Zhang 1,, 1
A review on quantum teleportation based on: Teleporting an unknown quantum state via dual classical and Einstein- Podolsky-Rosen channels
 JOURNAL OF CHEMISTRY 57 VOLUME NUMBER DECEMBER 8 005 A review on quantum teleportation based on: Teleporting an unknown quantum state via dual classical and Einstein- Podolsky-Rosen channels Miri Shlomi
JOURNAL OF CHEMISTRY 57 VOLUME NUMBER DECEMBER 8 005 A review on quantum teleportation based on: Teleporting an unknown quantum state via dual classical and Einstein- Podolsky-Rosen channels Miri Shlomi
Multilinear Singular Value Decomposition for Two Qubits
 Malaysian Journal of Mathematical Sciences 10(S) August: 69 83 (2016) Special Issue: The 7 th International Conference on Research and Education in Mathematics (ICREM7) MALAYSIAN JOURNAL OF MATHEMATICAL
Malaysian Journal of Mathematical Sciences 10(S) August: 69 83 (2016) Special Issue: The 7 th International Conference on Research and Education in Mathematics (ICREM7) MALAYSIAN JOURNAL OF MATHEMATICAL
Scheme for implementing perfect quantum teleportation with four-qubit entangled states in cavity quantum electrodynamics
 Scheme for implementing perfect quantum teleportation with four-qubit entangled states in cavity quantum electrodynamics Tang Jing-Wu( ), Zhao Guan-Xiang( ), and He Xiong-Hui( ) School of Physics, Hunan
Scheme for implementing perfect quantum teleportation with four-qubit entangled states in cavity quantum electrodynamics Tang Jing-Wu( ), Zhao Guan-Xiang( ), and He Xiong-Hui( ) School of Physics, Hunan
arxiv:quant-ph/ v1 8 May 2000
 On the Entangling Power of Quantum Evolutions Paolo Zanardi,3, Christof Zalka and Lara Faoro 2,3 Institute for Scientific Interchange (ISI) Foundation, Viale Settimio Severo 65, I-033 Torino, Italy 2 Dipartimento
On the Entangling Power of Quantum Evolutions Paolo Zanardi,3, Christof Zalka and Lara Faoro 2,3 Institute for Scientific Interchange (ISI) Foundation, Viale Settimio Severo 65, I-033 Torino, Italy 2 Dipartimento
Quantum Communication Complexity
 Quantum Communication Complexity Ronald de Wolf Communication complexity has been studied extensively in the area of theoretical computer science and has deep connections with seemingly unrelated areas,
Quantum Communication Complexity Ronald de Wolf Communication complexity has been studied extensively in the area of theoretical computer science and has deep connections with seemingly unrelated areas,
arxiv:quant-ph/ v1 13 Jan 2003
 Deterministic Secure Direct Communication Using Ping-pong protocol without public channel Qing-yu Cai Laboratory of Magentic Resonance and Atom and Molecular Physics, Wuhan Institute of Mathematics, The
Deterministic Secure Direct Communication Using Ping-pong protocol without public channel Qing-yu Cai Laboratory of Magentic Resonance and Atom and Molecular Physics, Wuhan Institute of Mathematics, The
Security Implications of Quantum Technologies
 Security Implications of Quantum Technologies Jim Alves-Foss Center for Secure and Dependable Software Department of Computer Science University of Idaho Moscow, ID 83844-1010 email: jimaf@cs.uidaho.edu
Security Implications of Quantum Technologies Jim Alves-Foss Center for Secure and Dependable Software Department of Computer Science University of Idaho Moscow, ID 83844-1010 email: jimaf@cs.uidaho.edu
Is Entanglement Sufficient to Enable Quantum Speedup?
 arxiv:107.536v3 [quant-ph] 14 Sep 01 Is Entanglement Sufficient to Enable Quantum Speedup? 1 Introduction The mere fact that a quantum computer realises an entangled state is ususally concluded to be insufficient
arxiv:107.536v3 [quant-ph] 14 Sep 01 Is Entanglement Sufficient to Enable Quantum Speedup? 1 Introduction The mere fact that a quantum computer realises an entangled state is ususally concluded to be insufficient
Private quantum subsystems and error correction
 Private quantum subsystems and error correction Sarah Plosker Department of Mathematics and Computer Science Brandon University September 26, 2014 Outline 1 Classical Versus Quantum Setting Classical Setting
Private quantum subsystems and error correction Sarah Plosker Department of Mathematics and Computer Science Brandon University September 26, 2014 Outline 1 Classical Versus Quantum Setting Classical Setting
Quantum algorithms for testing Boolean functions
 Quantum algorithms for testing Boolean functions Dominik F. Floess Erika Andersson SUPA, School of Engineering and Physical Sciences Heriot-Watt University, Edinburgh EH4 4AS, United Kingdom dominikfloess@gmx.de
Quantum algorithms for testing Boolean functions Dominik F. Floess Erika Andersson SUPA, School of Engineering and Physical Sciences Heriot-Watt University, Edinburgh EH4 4AS, United Kingdom dominikfloess@gmx.de
From Quantum Cellular Automata to Quantum Field Theory
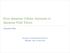 From Quantum Cellular Automata to Quantum Field Theory Alessandro Bisio Frontiers of Fundamental Physics Marseille, July 15-18th 2014 in collaboration with Giacomo Mauro D Ariano Paolo Perinotti Alessandro
From Quantum Cellular Automata to Quantum Field Theory Alessandro Bisio Frontiers of Fundamental Physics Marseille, July 15-18th 2014 in collaboration with Giacomo Mauro D Ariano Paolo Perinotti Alessandro
Quantum Entanglement- Fundamental Aspects
 Quantum Entanglement- Fundamental Aspects Debasis Sarkar Department of Applied Mathematics, University of Calcutta, 92, A.P.C. Road, Kolkata- 700009, India Abstract Entanglement is one of the most useful
Quantum Entanglement- Fundamental Aspects Debasis Sarkar Department of Applied Mathematics, University of Calcutta, 92, A.P.C. Road, Kolkata- 700009, India Abstract Entanglement is one of the most useful
arxiv:quant-ph/ v1 27 Dec 2004
 Multiparty Quantum Secret Sharing Zhan-jun Zhang 1,2, Yong Li 3 and Zhong-xiao Man 2 1 School of Physics & Material Science, Anhui University, Hefei 230039, China 2 Wuhan Institute of Physics and Mathematics,
Multiparty Quantum Secret Sharing Zhan-jun Zhang 1,2, Yong Li 3 and Zhong-xiao Man 2 1 School of Physics & Material Science, Anhui University, Hefei 230039, China 2 Wuhan Institute of Physics and Mathematics,
Structure of Unital Maps and the Asymptotic Quantum Birkhoff Conjecture. Peter Shor MIT Cambridge, MA Joint work with Anand Oza and Dimiter Ostrev
 Structure of Unital Maps and the Asymptotic Quantum Birkhoff Conjecture Peter Shor MIT Cambridge, MA Joint work with Anand Oza and Dimiter Ostrev The Superposition Principle (Physicists): If a quantum
Structure of Unital Maps and the Asymptotic Quantum Birkhoff Conjecture Peter Shor MIT Cambridge, MA Joint work with Anand Oza and Dimiter Ostrev The Superposition Principle (Physicists): If a quantum
