arxiv: v1 [math.ap] 29 Sep 2014
|
|
|
- Nelson Ferguson
- 5 years ago
- Views:
Transcription
1 GENERIC SELF-SIMILAR BLOWUP FOR EQUIVARIANT WAVE MAPS AND YANG-MILLS FIELDS IN HIGHER DIMENSIONS arxiv: v1 [math.ap] 29 Sep 2014 PAWE L BIERNAT AND PIOTR BIZOŃ Abstract. We consider equivariant wave maps from the (d + 1) dimensional Minkowski spacetime into the d-sphere for d 4. We find a new explicit stable self-similar solution and give numerical evidence that it plas the role of a universal attractor for generic blowup. An analogous result is obtained for the SO(d) smmetric Yang-Mills field for d Introduction This paper is concerned with the Cauch problem for the semilinear radial wave equation in (d + 1) dimensions u tt = u rr + d 1 r u r f(u) r 2, (1) where r 0 is the radial variable and u = u(t, r). For concretness, we shall focus on two specific and particularl interesting cases: { (d 1) sin(u) cos(u), (WM) f(u) = (2) d u(1 u)(2 u), (YM) which correspond to equivariant wave maps from the (d+1) dimensional Minkowski spacetime into the d-sphere and an SO(d + 2) smmetric Yang-Mills field in the (d + 3) dimensional Minkowski spacetime, respectivel (see e.g. [1] for the derivation). The basic question for equation (1) is whether solutions starting from smooth initial data can become singular ( blow up ) in finite time and, if so, how does the blowup occur. The ke feature, which plas a major role in answering this question, is the scale invariance of Eq.(1) with respect to the scaling tranformation u(t, r) u L (t, r) = u(t/l, r/l), Date: September 30,
2 GENERIC SELF-SIMILAR BLOWUP FOR EQUIVARIANT WAVE MAPS 2 where L is a positive constant. Under this scaling the conserved energ ( E(u) = u 2 t + u 2 r + F (u) ) r d 1 dr, (3) r 2 0 where F (u) = f(u), transforms as E(u L ) = L d 2 E(u), which means that Eq.(1) is energ critical for d = 2 and supercritical for d 3. The critical case d = 2 has been intensivel studied for the past decades leading to good understanding of the mechanism of blowup. Most notabl, Struwe proved that singularities necessaril have the form of self-shrinking harmonic maps (hence nonexistence of harmonic maps implies global regularit) and the rate of shrinking is faster than self-similar [2]. For the nonlinearities (2) the generic rates of shrinking were derived formall in [3, 4] and proved rigorousl in [5]. The understanding of the supercritical case d 3 is much less satisfactor. All known examples of blowup involve self-similar solutions [6, 7, 1, 8, 9], however it is not known if singularities must be selfsimilar. For d = 3 and the nonlinearities (2), the self-similar blowup was proved (under a certain spectral condition) to be stable [10, 11] and demonstrated numericall to be generic [12, 13]. In higher dimensions, as far as we know, nothing was known in even dimensions while for odd d 5 some self-similar solutions have been constructed [1, 8] but their stabilit and role in dnamics have not been studied. In this paper we present new explicit self-similar solutions of Eq.(1) in all dimensions d 4 (section 2), analze their linear stabilit (section 3), and finall give numerical evidence that the pla the role of universal attractors in the generic blowup (section 4). 2. Self-similar solutions B definition, self-similar solutions are invariant under the scaling, that is u(t/l, r/l) = u(t, r), hence the have the form u(t, r) = φ(), = r T t, (4) where a positive constant T, clearl allowed b the time translation smmetr, is introduced for later convenience. Inserting this ansatz into Eq.(1) one obtains the ordinar differential equation d 1 (1 2 )φ + 2 φ f(φ) 2 = 0. (5) We are interested in solutions that are smooth on the closed interval 0 1, which corresponds to the interior of the past light cone of
3 GENERIC SELF-SIMILAR BLOWUP FOR EQUIVARIANT WAVE MAPS 3 the point (t = T, r = 0). For such solutions n r r φ = (T t) n dn φ (0), (6) n T t r=0 dn hence the n-th derivative at the origin (such that dn φ (0) 0) diverges d n as t T. Thus, each self-similar solution φ() C [0, 1] is an example of a singularit developing in finite time from smooth initial data. We found the following explicit solutions of Eq.(5) 2 arctan, (WM) φ 0 () = d 2 a 2 (7) 2 + b, (YM) where a = 2(d + 4 3d(d 2)) 3d 2, b = 1 3d(d 2) (8 d) 3d(d 2) 3 3d 2 3d(d 2). For d = 3 these solutions have been known [7, 9], however for d 4 the appear to be new. In particular, the onl smooth self-similar solutions obtained previousl, for d = 5 (WM) and d {5, 7} (YM), b variational [1] and shooting [8] methods are different from φ 0. For both these methods it was essential that φ(1) = φ, where φ is the convexit radius of the target manifold, equal to π/2 for (WM) and 1 for (YM). In contrast, for our solutions φ 0 (1) < φ when d 4. Remark 1. A complete classification of smooth solutions of Eq.(5) for d 4 is not an eas problem; the main difficult being due to an involved smoothness condition at = 1 (see section 2.2 in [1] for the analsis of this condition in odd dimensions). Fortunatel, this hard ODE problem need not concern us here because, as will be shown in section 4, smooth solutions other than φ 0 do not seem to participate in the generic blowup, presumabl due to their instabilities. Remark 2. Clearl, solutions similar to φ 0 exist for a variet of nonlinearities other than (2) (albeit not in an explicit form, of course). In particular, b modifing (2) for φ > φ 0 (1) one can construct analogous smooth solutions for convex targets using the shooting method of [1]. Remark 3. It is instructive to compare the problem of blowup for Eq.(1) with the analogous problem for the heat flow u t = u rr + d 1 r u r f(u) r 2, (8)
4 GENERIC SELF-SIMILAR BLOWUP FOR EQUIVARIANT WAVE MAPS 4 with the same nonlinearities (2). This equation has self-similar blowup solutions for 3 d 6 (WM) [16] and 3 d 7 (YM) [17] but no such solutions exist in higher dimensions [18]. In accordance with that, it was found that the blowup for Eq.(8) changes character from self-similar [19] to non-self-similar [20] in sufficientl high dimensions. 3. Linear stabilit analsis As the first step towards understanding the role of the self-similar solution φ 0 ( r ) in dnamics we need to analze its linear stabilit. To T t this end it is convenient to define a new time coordinate s = ln(t t) and rewrite Eq.(1) in terms of U(s, ) = u(t, r) d 1 U ss + U s + 2 U s = (1 2 )U + 2 U f(u). (9) 2 In these variables the problem of finite time blowup in converted into the problem of asmptotic convergence for s towards the stationar solution φ 0 (). Following the standard procedure we seek solutions of Eq.(9) in the form U(s, ) = φ 0 () + e λs v(). Dropping nonlinear terms we get the quadratic eigenvalue equation d 1 (1 2 )v + 2(λ + 1) v λ(λ + 1)v V ()v = 0, (10) where V () := f (φ 0 ()) 2 = d 1 + (12 6d) 2 + (d 2) 2, 2 ( 2 + d 2) 2 (WM) d (3a 6a) 4 + (2 6ab) 2 + 2b 2 2 ( 2 + b) 2 (YM). We consider the eigenvalue problem (10) on the interval 0 1. B assumption, the solution U(s, ) is smooth for s <, hence we we demand that v C [0, 1]. This condition leads to the quantization of the eigenvalues. In order to determine the analticit properties of solutions of Eq.(10) it is convenient to introduce new variables x and w(x) defined b x = c c 1, v() = xµ (c x) λ 2 w(x), (11) where µ = 1/2, c = d 1 for (WM) and µ = 1, c = b + 1 for (YM). This change of variables brings Eq.(10) into the canonical form of the Heun equation [21] w + ( γ x + δ x 1 + ɛ ) w + x c αβx q x(x 1)(x c) w = 0, (12)
5 GENERIC SELF-SIMILAR BLOWUP FOR EQUIVARIANT WAVE MAPS 5 where in the case of (WM) γ = 1 + d/2, δ = (3 d)/2 + λ, ɛ = d/2, α = (λ + 5)/2, β = (λ 1)/2, q = (λ 1)(dλ + 5d 2λ 6)/4, and in the case of (YM) γ = 2 + d/2, δ = (3 d)/2 + λ, ɛ = 1/2, α = 3 + λ β, 1 ) β = (bλ + (3a 2 bd + 3a 2 d + b 2 + 2b + 1) b + λ + 3, 2b + 2 q = bλ 2 /4 3ad/2 + 5bλ/4 + dλ/4 + 3b/2 + d/2 + λ + 2. Equation (12) has four regular singularities at 0, 1, c,. The characteristic exponents at 0 and 1 are {0, 1 γ} and {0, 1 δ}, respectivel. The regular solutions at x = 0 and x = 1 are given b the local Heun functions (using the Maple notation) w 0 (x) = HeunG (c, q, α, β, γ, δ; x), (13) w 1 (x) = HeunG (1 c, q + αβ, α, β, δ, γ; 1 x). (14) The eigenvalues are given b zeros of the Wronskian W [w 1, w 2 ](λ) := w 1(x)w 2 (x) w 2(x)w 1 (x). (15) Unfortunatel, the connection problem for the Heun equation is unresolved and therefore (in contrast to the hpergeometric equation) no explicit formula for the Wronskian is available. Fortunatel, the Heun functions are built into Maple and the zeros of the Wronskian can be computed numericall with great precision 1. The results of this computation are displaed in Table 1 (WM) and Table 2 (YM). We remark that the eigenvalue λ 0 = 1 is due to the freedom of changing the blowup time T and does not correspond to an instabilit. The fact that the corresponding eigenfunction v 0 () = φ 0() has no zeros can be used to exclude rigorousl eigenvalues with R(λ) > d 2 (see [14, 15] for the proof in d = 3), however it seems hard to prove the nonexistence of eigenvalues with 0 < R(λ) < d 2. Nonetheless, we feel confident that if such an eigenvalue existed, we would have found it numericall. Consequentl, we assume that all the eigenvalues but λ 0 have negative real part 2. From this assumption it follows that the solution φ 0 is linearl asmptoticall stable [15]. 1 An alternative wa is to use the method of continued fractions [14]. We have verified that these two methods give identical results. 2 It is somewhat surprising that all eigenvalues are real.
6 GENERIC SELF-SIMILAR BLOWUP FOR EQUIVARIANT WAVE MAPS 6 n = 0 n = 1 n = 2 n = 3 n = 4 d = d = d = d = d = d = Table 1. The first few eigenvalues λ n (d) for the (WM) case. n = 0 n = 1 n = 2 n = 3 n = 4 d = d = d = d = d = d = Table 2. The first few eigenvalues λ n (d) for the (YM) case. 4. Dnamics of blowup In the lowest supercritical dimension d = 3 Donninger proved that the linear asmptotic stabilit of φ 0 implies its nonlinear asmptotic stabilit [10, 11]. It seems feasible that this result can be generalized to higher dimensions d 4 but we are not qualified to pursue this issue. We conjecture that the solution φ 0 is not onl nonlinearl stable but, in fact, it is a universal attractor for generic blowup. The numerical evidence for this conjecture in the case d = 3 was given in [12, 13]; here we give an analogous evidence for d 4. Consider a solution u(t, r) of Eq.(1) that starts from smooth initial data at t = 0 and becomes singular at (r = 0, t = T ) for some T > 0 (recall that singularities at r > 0 are impossible). We want to show that genericall u(t, r) converges to the self-similar solution φ 0 ( r ) as T t t T and the rate and profile of convergence are determined b the least damped mode e λ1s v 1 (), that is r u(t, r) φ 0 C (T t) λ 1 r v 1, (16) T t T t where the coefficient C and blowup time T depend on the initial data.
7 GENERIC SELF-SIMILAR BLOWUP FOR EQUIVARIANT WAVE MAPS 7 To verif (16), we solved Eq.(1) numericall for several large, randoml chosen, initial data leading to blowup. In order to keep track of the structure of the singularit developing on progressivel smaller scales, it is necessar to use an adaptive method which refines the spatio-temporal grid near the singularit. Our numerical method is based on the moving mesh method (known as MMPDE6, see [22]) combined with the Sundman transformation, as described in [23], with some minor modifications and improvements specific to the problem at hand. This method is ver efficient in computations of self-similar singularities. After obtaining a numerical solution u(r, t) we estimate the blowup time T and pass to the similarit variables s = log(t t), = r/(t t) and U(, s) = u(r, t) in order to compare analtical and numerical results. The results are illustrated in Figs. 1 and 2. s = 0.0 s = 1.3 s = 2.0 s = 4.0 π s = 6.3 s = 10.0 U(s, ) Figure 1. Snaphots from the evolution of sample initial data leading to blowup for the (WM) case in d = 4. The solution u(t, r) = U(s, ) converges to the self-similar solution φ 0 () = 2 arctan(/ 2) (dashed red curve).
8 GENERIC SELF-SIMILAR BLOWUP FOR EQUIVARIANT WAVE MAPS U(0, s) φ 0(0) Ce λ1s λ 1 = C = U(, s) φ 0 () Ce λ1s v 1 () s Figure 2. Numerical verification of the formula (16) for the solution depicted in Fig. 1. Left panel: we plot (T t) r u(t, 0) 2 in log-log scale and fit C(T t) λ 1. The value of λ 1 obtained from the fit agrees within one percent with the value given in Table 1. Right panel: for the parameters C and λ 1 determined above, the left and right hand sides of (16) are shown to agree at time s = 4. Acknowledgments. This work was supported in part b the NCN Grant No. DEC- 2012/06/A/ST2/ The second author acknowledges the hospitalit of the Banff International Research Station (Canada), where this work was initiated. References [1] T. Cazenave, J. Shatah, A.S. Tahvildar-Zadeh, Harmonic maps of the hperbolic space and the development of singularities in wave maps and Yang-Mills fields, Ann. Inst. Henri Poincaré 68, 315 (1998) [2] M. Struwe, Equivariant wave maps in two space dimensions, Commun. Pure Appl. Math. 56(7), 815 (2003) [3] P. Bizoń, Y.N. Ovchinnikov, I.M. Sigal, Collapse of an instanton, Nonlinearit 17, 1179 (2004) [4] Y.N. Ovchinnikov, I.M. Sigal, On collapse of wave maps, Phs. D 240, 1311 (2011) [5] P. Raphaël, I. Rodnianski, Stable blow up dnamics for the critical corotational wave maps and equivariant ang mills problems, Publ. Math. Inst. Hautes Etudes Sci. 115, 1 (2012) [6] J. Shatah, Weak solutions and development of singularities in the SU(2) σ- model, Comm. Pure Appl. Math. 41, 459 (1988) [7] N. Turok, D. Spergel, Global texture and the microwave background, Phs. Rev. Lett. 64, 2736 (1990)
9 GENERIC SELF-SIMILAR BLOWUP FOR EQUIVARIANT WAVE MAPS 9 [8] P. Bizoń, Equivariant self-similar wave maps from Minkowski spacetime into 3-sphere, Comm. Math. Phsics 215, 45 (2000) [9] P. Bizoń, Formation of singularities in Yang-Mills equations, Acta Phs. Polon. B 33, 1893 (2002) [10] R. Donninger, On stable self-similar blowup for equivariant wave maps, Comm. Pure Appl. Math. 64, 1095 (2011) [11] R. Donninger, Stable self-similar blowup in energ supercritical Yang-Mills theor, arxiv: [12] P. Bizoń, T. Chmaj, and Z. Tabor, Dispersion and collapse of wave maps, Nonlinearit 13, 1411 (2000) [13] P. Bizoń, Z. Tabor, On blowup of Yang-Mills fields, Phs. Rev. D 64, (2001) [14] P. Bizoń, An unusual eigenvalue problem, Acta. Phs. Polon. B 36, 5 (2005) [15] R. Donninger, B. Schörkhuber, P.C. Aichelburg, On stable self-similar blow up for equivariant wave maps: the linearized problem, Ann. Henri Poincaré 13, 103 (2012) [16] H. Fan, Existence of the self-similar solutions in the heat flow of harmonic maps, Sci. China Ser. A42, 113 (1999) [17] B. Weinkove, Singularit formation in the Yang-Mills flow, Calc. Var. Partial Differential Equations 19, 211 (2004) [18] P. Bizoń, A. Wasserman, Non-existence of shrinkers for the harmonic map flow in higher dimensions, arxiv: [19] P. Biernat, P. Bizoń, Shrinkers, expanders, and the unique continuation beond generic blowup in the heat flow for harmonic maps between spheres, Nonlinearit 24, 2211 (2011) [20] P. Biernat, Non-self-similar blow-up in the heat flow for harmonic maps in higher dimensions, arxiv: [21] NIST Digital Librar of Mathematical Functions, [22] W. Huang, Y. Ren, R. D. Russell, Moving mesh partial differential equations (MMPDES) based on the equidistribution principle, SIAM J. Numer. Anal. 31, 709 (1994) [23] C.J. Budd and J. F. Williams, How to adaptivel resolve evolutionar singularities in differential equations with smmetr, Journal of Engineering Mathematics 66, (2010) Institute of Mathematics, Jagiellonian Universit, Kraków, Poland address: pawel.biernat@gmail.com Institute of Phsics, Jagiellonian Universit, Kraków, Poland, and Max Planck Institute for Gravitational Phsics (Albert Einstein Institute), Golm, German address: piotr.bizon@aei.mpg.de
Equivariant self-similar wave maps from Minkowski spacetime into 3-sphere
 Equivariant self-similar wave maps from Minkowski spacetime into 3-sphere arxiv:math-ph/99126v1 17 Oct 1999 Piotr Bizoń Institute of Physics, Jagellonian University, Kraków, Poland March 26, 28 Abstract
Equivariant self-similar wave maps from Minkowski spacetime into 3-sphere arxiv:math-ph/99126v1 17 Oct 1999 Piotr Bizoń Institute of Physics, Jagellonian University, Kraków, Poland March 26, 28 Abstract
arxiv:math-ph/ v2 22 Jun 2001
 Formation of singularities for equivariant 2+1 dimensional wave maps into the two-sphere arxiv:math-ph/115v2 22 Jun 21 Piotr Bizoń, Tadeusz Chmaj, and Zbis law Tabor Institute of Physics, Jagellonian University,
Formation of singularities for equivariant 2+1 dimensional wave maps into the two-sphere arxiv:math-ph/115v2 22 Jun 21 Piotr Bizoń, Tadeusz Chmaj, and Zbis law Tabor Institute of Physics, Jagellonian University,
Formation of singularities for equivariant (2 + 1)-dimensional wave maps into the 2-sphere
 INSTITUTE OF PHYSICS PUBLISHING Nonlinearity 14 (2001) 1041 1053 NONLINEARITY PII: S0951-7715(01)18802-X Formation of singularities for equivariant (2 + 1)-dimensional wave maps into the 2-sphere Piotr
INSTITUTE OF PHYSICS PUBLISHING Nonlinearity 14 (2001) 1041 1053 NONLINEARITY PII: S0951-7715(01)18802-X Formation of singularities for equivariant (2 + 1)-dimensional wave maps into the 2-sphere Piotr
Long-term dynamics of nonlinear wave equations
 Long-term dynamics of nonlinear wave equations W. Schlag (University of Chicago) Recent Developments & Future Directions, September 2014 Wave maps Let (M, g) be a Riemannian manifold, and u : R 1+d t,x
Long-term dynamics of nonlinear wave equations W. Schlag (University of Chicago) Recent Developments & Future Directions, September 2014 Wave maps Let (M, g) be a Riemannian manifold, and u : R 1+d t,x
Threshold of singularity formation in the semilinear wave equation
 PHYSICAL REVIEW D 71, 044019 (2005) Threshold of singularity formation in the semilinear wave equation Steven L. Liebling Department of Physics, Long Island University-C.W. Post Campus, Brookville, New
PHYSICAL REVIEW D 71, 044019 (2005) Threshold of singularity formation in the semilinear wave equation Steven L. Liebling Department of Physics, Long Island University-C.W. Post Campus, Brookville, New
arxiv:math-ph/ v1 10 Jul 2003
 Collapse of an Instanton P. Bizoń Yu N. Ovchinnikov I.M. Sigal Jagellonian University L.D. Landau Institute University of Toronto Kraków Moscow Toronto arxiv:math-ph/3726v1 1 Jul 23 Abstract We construct
Collapse of an Instanton P. Bizoń Yu N. Ovchinnikov I.M. Sigal Jagellonian University L.D. Landau Institute University of Toronto Kraków Moscow Toronto arxiv:math-ph/3726v1 1 Jul 23 Abstract We construct
Exponential time differencing methods for nonlinear PDEs
 XXI Congreso de Ecuaciones Diferenciales Aplicaciones XI Congreso de Matemática Aplicada Ciudad Real, 1- septiembre 9 (pp. 1 8) Exponential time differencing methods for nonlinear PDEs F. de la Hoz 1,
XXI Congreso de Ecuaciones Diferenciales Aplicaciones XI Congreso de Matemática Aplicada Ciudad Real, 1- septiembre 9 (pp. 1 8) Exponential time differencing methods for nonlinear PDEs F. de la Hoz 1,
Late-time tails of self-gravitating waves
 Late-time tails of self-gravitating waves (non-rigorous quantitative analysis) Piotr Bizoń Jagiellonian University, Kraków Based on joint work with Tadek Chmaj and Andrzej Rostworowski Outline: Motivation
Late-time tails of self-gravitating waves (non-rigorous quantitative analysis) Piotr Bizoń Jagiellonian University, Kraków Based on joint work with Tadek Chmaj and Andrzej Rostworowski Outline: Motivation
Spotlight on the Extended Method of Frobenius
 113 Spotlight on the Extended Method of Frobenius See Sections 11.1 and 11.2 for the model of an aging spring. Reference: Section 11.4 and SPOTLIGHT ON BESSEL FUNCTIONS. Bessel functions of the first kind
113 Spotlight on the Extended Method of Frobenius See Sections 11.1 and 11.2 for the model of an aging spring. Reference: Section 11.4 and SPOTLIGHT ON BESSEL FUNCTIONS. Bessel functions of the first kind
c 1999 Society for Industrial and Applied Mathematics
 SIAM J. SCI. COMPUT. Vol., No. 6, pp. 978 994 c 999 Societ for Industrial and Applied Mathematics A STUDY OF MONITOR FUNCTIONS FOR TWO-DIMENSIONAL ADAPTIVE MESH GENERATION WEIMING CAO, WEIZHANG HUANG,
SIAM J. SCI. COMPUT. Vol., No. 6, pp. 978 994 c 999 Societ for Industrial and Applied Mathematics A STUDY OF MONITOR FUNCTIONS FOR TWO-DIMENSIONAL ADAPTIVE MESH GENERATION WEIMING CAO, WEIZHANG HUANG,
New approach to study the van der Pol equation for large damping
 Electronic Journal of Qualitative Theor of Differential Equations 2018, No. 8, 1 10; https://doi.org/10.1422/ejqtde.2018.1.8 www.math.u-szeged.hu/ejqtde/ New approach to stud the van der Pol equation for
Electronic Journal of Qualitative Theor of Differential Equations 2018, No. 8, 1 10; https://doi.org/10.1422/ejqtde.2018.1.8 www.math.u-szeged.hu/ejqtde/ New approach to stud the van der Pol equation for
arxiv: v1 [math.ap] 6 May 2010
![arxiv: v1 [math.ap] 6 May 2010 arxiv: v1 [math.ap] 6 May 2010](/thumbs/88/117715564.jpg) A CONTINUITY ARGUMENT FOR A SEMILINEAR SKYRME MODEL arxiv:005.095v [math.ap] 6 May 00 DAN-ANDREI GEBA AND S. G. RAJEEV Abstract. We investigate a semilinear modification for the wave map problem proposed
A CONTINUITY ARGUMENT FOR A SEMILINEAR SKYRME MODEL arxiv:005.095v [math.ap] 6 May 00 DAN-ANDREI GEBA AND S. G. RAJEEV Abstract. We investigate a semilinear modification for the wave map problem proposed
ON OSCILLATIONS OF SOLUTIONS OF THE FOURTH-ORDER THIN FILM EQUATION NEAR HETEROCLINIC BIFURCATION POINT
 ON OSCILLATIONS OF SOLUTIONS OF THE FOURTH-ORDER THIN FILM EQUATION NEAR HETEROCLINIC BIFURCATION POINT V.A. GALAKTIONOV arxiv:3.76v [math.ap] Dec 3 Abstract. The behaviour of solutions of the Cauch problem
ON OSCILLATIONS OF SOLUTIONS OF THE FOURTH-ORDER THIN FILM EQUATION NEAR HETEROCLINIC BIFURCATION POINT V.A. GALAKTIONOV arxiv:3.76v [math.ap] Dec 3 Abstract. The behaviour of solutions of the Cauch problem
Examples and counterexamples for Markus-Yamabe and LaSalle global asymptotic stability problems Anna Cima, Armengol Gasull and Francesc Mañosas
 Proceedings of the International Workshop Future Directions in Difference Equations. June 13-17, 2011, Vigo, Spain. PAGES 89 96 Examples and counterexamples for Markus-Yamabe and LaSalle global asmptotic
Proceedings of the International Workshop Future Directions in Difference Equations. June 13-17, 2011, Vigo, Spain. PAGES 89 96 Examples and counterexamples for Markus-Yamabe and LaSalle global asmptotic
Research Article Chaotic Attractor Generation via a Simple Linear Time-Varying System
 Discrete Dnamics in Nature and Societ Volume, Article ID 836, 8 pages doi:.//836 Research Article Chaotic Attractor Generation via a Simple Linear Time-Varing Sstem Baiu Ou and Desheng Liu Department of
Discrete Dnamics in Nature and Societ Volume, Article ID 836, 8 pages doi:.//836 Research Article Chaotic Attractor Generation via a Simple Linear Time-Varing Sstem Baiu Ou and Desheng Liu Department of
AN EFFICIENT MOVING MESH METHOD FOR A MODEL OF TURBULENT FLOW IN CIRCULAR TUBES *
 Journal of Computational Mathematics, Vol.27, No.2-3, 29, 388 399. AN EFFICIENT MOVING MESH METHOD FOR A MODEL OF TURBULENT FLOW IN CIRCULAR TUBES * Yin Yang Hunan Ke Laborator for Computation and Simulation
Journal of Computational Mathematics, Vol.27, No.2-3, 29, 388 399. AN EFFICIENT MOVING MESH METHOD FOR A MODEL OF TURBULENT FLOW IN CIRCULAR TUBES * Yin Yang Hunan Ke Laborator for Computation and Simulation
Two-sided Mullins-Sekerka flow does not preserve convexity
 Differential Equations and Computational Simulations III J. Graef, R. Shivaji, B. Soni, & J. Zhu (Editors) Electronic Journal of Differential Equations, Conference 01, 1997, pp. 171 179. ISSN: 1072-6691.
Differential Equations and Computational Simulations III J. Graef, R. Shivaji, B. Soni, & J. Zhu (Editors) Electronic Journal of Differential Equations, Conference 01, 1997, pp. 171 179. ISSN: 1072-6691.
arxiv:gr-qc/ v1 21 May 2006
 How to bypass Birkhoff through extra dimensions A simple framework for investigating the gravitational collapse in vacuum Piotr Bizoń 1,2 and Bernd G. Schmidt 2 1 M. Smoluchowski Institute of Physics,
How to bypass Birkhoff through extra dimensions A simple framework for investigating the gravitational collapse in vacuum Piotr Bizoń 1,2 and Bernd G. Schmidt 2 1 M. Smoluchowski Institute of Physics,
Math 4381 / 6378 Symmetry Analysis
 Math 438 / 6378 Smmetr Analsis Elementar ODE Review First Order Equations Ordinar differential equations of the form = F(x, ( are called first order ordinar differential equations. There are a variet of
Math 438 / 6378 Smmetr Analsis Elementar ODE Review First Order Equations Ordinar differential equations of the form = F(x, ( are called first order ordinar differential equations. There are a variet of
Elliptic Equations. Chapter Definitions. Contents. 4.2 Properties of Laplace s and Poisson s Equations
 5 4. Properties of Laplace s and Poisson s Equations Chapter 4 Elliptic Equations Contents. Neumann conditions the normal derivative, / = n u is prescribed on the boundar second BP. In this case we have
5 4. Properties of Laplace s and Poisson s Equations Chapter 4 Elliptic Equations Contents. Neumann conditions the normal derivative, / = n u is prescribed on the boundar second BP. In this case we have
arxiv: v1 [nlin.ps] 3 Sep 2009
![arxiv: v1 [nlin.ps] 3 Sep 2009 arxiv: v1 [nlin.ps] 3 Sep 2009](/thumbs/89/98633564.jpg) Soliton, kink and antikink solutions o a 2-component o the Degasperis-Procesi equation arxiv:0909.0659v1 [nlin.ps] 3 Sep 2009 Jiangbo Zhou, Liin Tian, Xinghua Fan Nonlinear Scientiic Research Center, Facult
Soliton, kink and antikink solutions o a 2-component o the Degasperis-Procesi equation arxiv:0909.0659v1 [nlin.ps] 3 Sep 2009 Jiangbo Zhou, Liin Tian, Xinghua Fan Nonlinear Scientiic Research Center, Facult
n n. ( t) ( ) = = Ay ( ) a y
 Sstems of ODE Example of sstem with ODE: = a+ a = a + a In general for a sstem of n ODE = a + a + + a n = a + a + + a n = a + a + + a n n n nn n n n Differentiation of matrix: ( t) ( t) t t = = t t ( t)
Sstems of ODE Example of sstem with ODE: = a+ a = a + a In general for a sstem of n ODE = a + a + + a n = a + a + + a n = a + a + + a n n n nn n n n Differentiation of matrix: ( t) ( t) t t = = t t ( t)
Solving Variable-Coefficient Fourth-Order ODEs with Polynomial Nonlinearity by Symmetric Homotopy Method
 Applied and Computational Mathematics 218; 7(2): 58-7 http://www.sciencepublishinggroup.com/j/acm doi: 1.11648/j.acm.21872.14 ISSN: 2328-565 (Print); ISSN: 2328-5613 (Online) Solving Variable-Coefficient
Applied and Computational Mathematics 218; 7(2): 58-7 http://www.sciencepublishinggroup.com/j/acm doi: 1.11648/j.acm.21872.14 ISSN: 2328-565 (Print); ISSN: 2328-5613 (Online) Solving Variable-Coefficient
LIST OF PUBLICATIONS. Mu-Tao Wang. March 2017
 LIST OF PUBLICATIONS Mu-Tao Wang Publications March 2017 1. (with P.-K. Hung, J. Keller) Linear stability of Schwarzschild spacetime: the Cauchy problem of metric coefficients. arxiv: 1702.02843v2 2. (with
LIST OF PUBLICATIONS Mu-Tao Wang Publications March 2017 1. (with P.-K. Hung, J. Keller) Linear stability of Schwarzschild spacetime: the Cauchy problem of metric coefficients. arxiv: 1702.02843v2 2. (with
Construction of concentrating bubbles for the energy-critical wave equation
 Construction of concentrating bubbles for the energy-critical wave equation Jacek Jendrej University of Chicago University of North Carolina February 13th 2017 Jacek Jendrej Energy-critical wave equations
Construction of concentrating bubbles for the energy-critical wave equation Jacek Jendrej University of Chicago University of North Carolina February 13th 2017 Jacek Jendrej Energy-critical wave equations
SYMMETRY RESULTS FOR PERTURBED PROBLEMS AND RELATED QUESTIONS. Massimo Grosi Filomena Pacella S. L. Yadava. 1. Introduction
 Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 21, 2003, 211 226 SYMMETRY RESULTS FOR PERTURBED PROBLEMS AND RELATED QUESTIONS Massimo Grosi Filomena Pacella S.
Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 21, 2003, 211 226 SYMMETRY RESULTS FOR PERTURBED PROBLEMS AND RELATED QUESTIONS Massimo Grosi Filomena Pacella S.
TRANSFER ORBITS GUIDED BY THE UNSTABLE/STABLE MANIFOLDS OF THE LAGRANGIAN POINTS
 TRANSFER ORBITS GUIDED BY THE UNSTABLE/STABLE MANIFOLDS OF THE LAGRANGIAN POINTS Annelisie Aiex Corrêa 1, Gerard Gómez 2, Teresinha J. Stuchi 3 1 DMC/INPE - São José dos Campos, Brazil 2 MAiA/UB - Barcelona,
TRANSFER ORBITS GUIDED BY THE UNSTABLE/STABLE MANIFOLDS OF THE LAGRANGIAN POINTS Annelisie Aiex Corrêa 1, Gerard Gómez 2, Teresinha J. Stuchi 3 1 DMC/INPE - São José dos Campos, Brazil 2 MAiA/UB - Barcelona,
From bell-shaped solitary wave to W/M-shaped solitary wave solutions in an integrable nonlinear wave equation
 PRAMANA c Indian Academ of Sciences Vol. 74, No. journal of Januar 00 phsics pp. 9 6 From bell-shaped solitar wave to W/M-shaped solitar wave solutions in an integrable nonlinear wave equation AIYONG CHEN,,,
PRAMANA c Indian Academ of Sciences Vol. 74, No. journal of Januar 00 phsics pp. 9 6 From bell-shaped solitar wave to W/M-shaped solitar wave solutions in an integrable nonlinear wave equation AIYONG CHEN,,,
Non-radial solutions to a bi-harmonic equation with negative exponent
 Non-radial solutions to a bi-harmonic equation with negative exponent Ali Hyder Department of Mathematics, University of British Columbia, Vancouver BC V6TZ2, Canada ali.hyder@math.ubc.ca Juncheng Wei
Non-radial solutions to a bi-harmonic equation with negative exponent Ali Hyder Department of Mathematics, University of British Columbia, Vancouver BC V6TZ2, Canada ali.hyder@math.ubc.ca Juncheng Wei
Stability Analysis for Linear Systems under State Constraints
 Stabilit Analsis for Linear Sstems under State Constraints Haijun Fang Abstract This paper revisits the problem of stabilit analsis for linear sstems under state constraints New and less conservative sufficient
Stabilit Analsis for Linear Sstems under State Constraints Haijun Fang Abstract This paper revisits the problem of stabilit analsis for linear sstems under state constraints New and less conservative sufficient
DISPERSIVE EQUATIONS: A SURVEY
 DISPERSIVE EQUATIONS: A SURVEY GIGLIOLA STAFFILANI 1. Introduction These notes were written as a guideline for a short talk; hence, the references and the statements of the theorems are often not given
DISPERSIVE EQUATIONS: A SURVEY GIGLIOLA STAFFILANI 1. Introduction These notes were written as a guideline for a short talk; hence, the references and the statements of the theorems are often not given
* τσ σκ. Supporting Text. A. Stability Analysis of System 2
 Supporting Tet A. Stabilit Analsis of Sstem In this Appendi, we stud the stabilit of the equilibria of sstem. If we redefine the sstem as, T when -, then there are at most three equilibria: E,, E κ -,,
Supporting Tet A. Stabilit Analsis of Sstem In this Appendi, we stud the stabilit of the equilibria of sstem. If we redefine the sstem as, T when -, then there are at most three equilibria: E,, E κ -,,
Lévy stable distribution and [0,2] power law dependence of. acoustic absorption on frequency
![Lévy stable distribution and [0,2] power law dependence of. acoustic absorption on frequency Lévy stable distribution and [0,2] power law dependence of. acoustic absorption on frequency](/thumbs/75/72606068.jpg) Lév stable distribution and [,] power law dependence of acoustic absorption on frequenc W. Chen Institute of Applied Phsics and Computational Mathematics, P.O. Box 89, Division Box 6, Beijing 88, China
Lév stable distribution and [,] power law dependence of acoustic absorption on frequenc W. Chen Institute of Applied Phsics and Computational Mathematics, P.O. Box 89, Division Box 6, Beijing 88, China
arxiv: v1 [math.ap] 28 Jun 2011
![arxiv: v1 [math.ap] 28 Jun 2011 arxiv: v1 [math.ap] 28 Jun 2011](/thumbs/85/92110193.jpg) GLOBAL WELL-POSEDNESS AND SCATTERING FOR SKYRME WAVE MAPS arxiv:1106.5750v1 [math.ap] 28 Jun 2011 DAN-ANDREI GEBA, KENJI NAKANISHI, AND SARADA G. RAJEEV Abstract. We study equivariant solutions for two
GLOBAL WELL-POSEDNESS AND SCATTERING FOR SKYRME WAVE MAPS arxiv:1106.5750v1 [math.ap] 28 Jun 2011 DAN-ANDREI GEBA, KENJI NAKANISHI, AND SARADA G. RAJEEV Abstract. We study equivariant solutions for two
Absorbing Boundary Conditions for Nonlinear Wave Equations
 Absorbing Boundary Conditions for Nonlinear Wave Equations R. B. Gibson December, 2010 1 1 Linear Wave Equations 1.1 Boundary Condition 1 To begin, we wish to solve where with the boundary condition u
Absorbing Boundary Conditions for Nonlinear Wave Equations R. B. Gibson December, 2010 1 1 Linear Wave Equations 1.1 Boundary Condition 1 To begin, we wish to solve where with the boundary condition u
Blow-up collocation solutions of nonlinear homogeneous Volterra integral equations
 Blow-up collocation solutions of nonlinear homogeneous Volterra integral equations R. Benítez 1,, V. J. Bolós 2, 1 Dpto. Matemáticas, Centro Universitario de Plasencia, Universidad de Extremadura. Avda.
Blow-up collocation solutions of nonlinear homogeneous Volterra integral equations R. Benítez 1,, V. J. Bolós 2, 1 Dpto. Matemáticas, Centro Universitario de Plasencia, Universidad de Extremadura. Avda.
Various behaviors of solutions for a semilinear heat equation after blowup
 Journal of Functional Analysis (5 4 7 www.elsevier.com/locate/jfa Various behaviors of solutions for a semilinear heat equation after blowup Noriko Mizoguchi Department of Mathematics, Tokyo Gakugei University,
Journal of Functional Analysis (5 4 7 www.elsevier.com/locate/jfa Various behaviors of solutions for a semilinear heat equation after blowup Noriko Mizoguchi Department of Mathematics, Tokyo Gakugei University,
Integro-differential equations: Regularity theory and Pohozaev identities
 Integro-differential equations: Regularity theory and Pohozaev identities Xavier Ros Oton Departament Matemàtica Aplicada I, Universitat Politècnica de Catalunya PhD Thesis Advisor: Xavier Cabré Xavier
Integro-differential equations: Regularity theory and Pohozaev identities Xavier Ros Oton Departament Matemàtica Aplicada I, Universitat Politècnica de Catalunya PhD Thesis Advisor: Xavier Cabré Xavier
arxiv: v1 [math.ap] 25 Jun 2008
![arxiv: v1 [math.ap] 25 Jun 2008 arxiv: v1 [math.ap] 25 Jun 2008](/thumbs/74/70611767.jpg) On the existence of smooth self-similar blow-up profiles for the wave-map equation arxiv:86.4148v1 [math.ap] 5 Jun 8 Pierre Germain October, 17 Abstract Consider the equivariant wave map equation from
On the existence of smooth self-similar blow-up profiles for the wave-map equation arxiv:86.4148v1 [math.ap] 5 Jun 8 Pierre Germain October, 17 Abstract Consider the equivariant wave map equation from
Symmetry Arguments and the Role They Play in Using Gauss Law
 Smmetr Arguments and the Role The la in Using Gauss Law K. M. Westerberg (9/2005) Smmetr plas a ver important role in science in general, and phsics in particular. Arguments based on smmetr can often simplif
Smmetr Arguments and the Role The la in Using Gauss Law K. M. Westerberg (9/2005) Smmetr plas a ver important role in science in general, and phsics in particular. Arguments based on smmetr can often simplif
OPTIMAL CONTROL FOR A PARABOLIC SYSTEM MODELLING CHEMOTAXIS
 Trends in Mathematics Information Center for Mathematical Sciences Volume 6, Number 1, June, 23, Pages 45 49 OPTIMAL CONTROL FOR A PARABOLIC SYSTEM MODELLING CHEMOTAXIS SANG UK RYU Abstract. We stud the
Trends in Mathematics Information Center for Mathematical Sciences Volume 6, Number 1, June, 23, Pages 45 49 OPTIMAL CONTROL FOR A PARABOLIC SYSTEM MODELLING CHEMOTAXIS SANG UK RYU Abstract. We stud the
Symmetry Properties of Autonomous Integrating Factors
 Smmetr, Integrabilit and Geometr: Methods and Applications Vol. 1 2005), Paper 024, 12 pages Smmetr Properties of Autonomous Integrating Factors Sibusiso MOYO and P.G.L. LEACH Department of Mathematics,
Smmetr, Integrabilit and Geometr: Methods and Applications Vol. 1 2005), Paper 024, 12 pages Smmetr Properties of Autonomous Integrating Factors Sibusiso MOYO and P.G.L. LEACH Department of Mathematics,
On the mesh relaxation time in the moving mesh method
 On the mesh relaxation time in the moving mesh method John Stockie http://www.math.sfu.ca/~stockie/ Department of Mathematics Simon Fraser University August 3, 2005 Adaptivity and Beyond Vancouver, August
On the mesh relaxation time in the moving mesh method John Stockie http://www.math.sfu.ca/~stockie/ Department of Mathematics Simon Fraser University August 3, 2005 Adaptivity and Beyond Vancouver, August
10 Back to planar nonlinear systems
 10 Back to planar nonlinear sstems 10.1 Near the equilibria Recall that I started talking about the Lotka Volterra model as a motivation to stud sstems of two first order autonomous equations of the form
10 Back to planar nonlinear sstems 10.1 Near the equilibria Recall that I started talking about the Lotka Volterra model as a motivation to stud sstems of two first order autonomous equations of the form
Some New Results on Global Nonexistence for Abstract Evolution Equations with Positive Initial Energy
 Some New Results on Global Nonexistence for Abstract Evolution Equations with Positive Initial Energy Patrizia Pucci 1 & James Serrin Dedicated to Olga Ladyzhenskaya with admiration and esteem 1. Introduction.
Some New Results on Global Nonexistence for Abstract Evolution Equations with Positive Initial Energy Patrizia Pucci 1 & James Serrin Dedicated to Olga Ladyzhenskaya with admiration and esteem 1. Introduction.
Research Article A New Four-Scroll Chaotic Attractor Consisted of Two-Scroll Transient Chaotic and Two-Scroll Ultimate Chaotic
 Mathematical Problems in Engineering Volume, Article ID 88, pages doi:.//88 Research Article A New Four-Scroll Chaotic Attractor Consisted of Two-Scroll Transient Chaotic and Two-Scroll Ultimate Chaotic
Mathematical Problems in Engineering Volume, Article ID 88, pages doi:.//88 Research Article A New Four-Scroll Chaotic Attractor Consisted of Two-Scroll Transient Chaotic and Two-Scroll Ultimate Chaotic
arxiv: v2 [math.ap] 30 Jul 2012
![arxiv: v2 [math.ap] 30 Jul 2012 arxiv: v2 [math.ap] 30 Jul 2012](/thumbs/82/86406811.jpg) Blow up for some semilinear wave equations in multi-space dimensions Yi Zhou Wei Han. arxiv:17.536v [math.ap] 3 Jul 1 Abstract In this paper, we discuss a new nonlinear phenomenon. We find that in n space
Blow up for some semilinear wave equations in multi-space dimensions Yi Zhou Wei Han. arxiv:17.536v [math.ap] 3 Jul 1 Abstract In this paper, we discuss a new nonlinear phenomenon. We find that in n space
Tobias Holck Colding: Publications. 1. T.H. Colding and W.P. Minicozzi II, Dynamics of closed singularities, preprint.
 Tobias Holck Colding: Publications 1. T.H. Colding and W.P. Minicozzi II, Dynamics of closed singularities, preprint. 2. T.H. Colding and W.P. Minicozzi II, Analytical properties for degenerate equations,
Tobias Holck Colding: Publications 1. T.H. Colding and W.P. Minicozzi II, Dynamics of closed singularities, preprint. 2. T.H. Colding and W.P. Minicozzi II, Analytical properties for degenerate equations,
BACKWARD FOKKER-PLANCK EQUATION FOR DETERMINATION OF MODEL PREDICTABILITY WITH UNCERTAIN INITIAL ERRORS
 BACKWARD FOKKER-PLANCK EQUATION FOR DETERMINATION OF MODEL PREDICTABILITY WITH UNCERTAIN INITIAL ERRORS. INTRODUCTION It is widel recognized that uncertaint in atmospheric and oceanic models can be traced
BACKWARD FOKKER-PLANCK EQUATION FOR DETERMINATION OF MODEL PREDICTABILITY WITH UNCERTAIN INITIAL ERRORS. INTRODUCTION It is widel recognized that uncertaint in atmospheric and oceanic models can be traced
CONCENTRATION COMPACTNESS FOR CRITICAL WAVE MAPS, BY JOACHIM KRIEGER AND WILHELM SCHLAG
 CONCENTRATION COMPACTNESS FOR CRITICAL WAVE MAPS, BY JOACHIM KRIEGER AND WILHELM SCHLAG Imagine a perfectly elastic d-dimensional sheet, infinite in extent, immersed (possibly with self-intersection) in
CONCENTRATION COMPACTNESS FOR CRITICAL WAVE MAPS, BY JOACHIM KRIEGER AND WILHELM SCHLAG Imagine a perfectly elastic d-dimensional sheet, infinite in extent, immersed (possibly with self-intersection) in
METHODS IN Mathematica FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS. Keçiören, Ankara 06010, Turkey.
 Mathematical and Computational Applications, Vol. 16, No. 4, pp. 784-796, 2011. Association for Scientific Research METHODS IN Mathematica FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS Ünal Göktaş 1 and
Mathematical and Computational Applications, Vol. 16, No. 4, pp. 784-796, 2011. Association for Scientific Research METHODS IN Mathematica FOR SOLVING ORDINARY DIFFERENTIAL EQUATIONS Ünal Göktaş 1 and
Sharp blow-up criteria for the Davey-Stewartson system in R 3
 Dynamics of PDE, Vol.8, No., 9-60, 011 Sharp blow-up criteria for the Davey-Stewartson system in R Jian Zhang Shihui Zhu Communicated by Y. Charles Li, received October 7, 010. Abstract. In this paper,
Dynamics of PDE, Vol.8, No., 9-60, 011 Sharp blow-up criteria for the Davey-Stewartson system in R Jian Zhang Shihui Zhu Communicated by Y. Charles Li, received October 7, 010. Abstract. In this paper,
SOME PROPERTIES OF CONJUGATE HARMONIC FUNCTIONS IN A HALF-SPACE
 SOME PROPERTIES OF CONJUGATE HARMONIC FUNCTIONS IN A HALF-SPACE ANATOLY RYABOGIN AND DMITRY RYABOGIN Abstract. We prove a multi-dimensional analog of the Theorem of Hard and Littlewood about the logarithmic
SOME PROPERTIES OF CONJUGATE HARMONIC FUNCTIONS IN A HALF-SPACE ANATOLY RYABOGIN AND DMITRY RYABOGIN Abstract. We prove a multi-dimensional analog of the Theorem of Hard and Littlewood about the logarithmic
Journal of Computational and Applied Mathematics
 Journal of Computational and Applied Mathematics 34 () 3 Contents lists available at ScienceDirect Journal of Computational and Applied Mathematics journal homepage:.elsevier.com/locate/cam A hperchaotic
Journal of Computational and Applied Mathematics 34 () 3 Contents lists available at ScienceDirect Journal of Computational and Applied Mathematics journal homepage:.elsevier.com/locate/cam A hperchaotic
Dynamics in Delay Cournot Duopoly
 Dnamics in Dela Cournot Duopol Akio Matsumoto Chuo Universit Ferenc Szidarovszk Universit of Arizona Hirouki Yoshida Nihon Universit Abstract Dnamic linear oligopolies are eamined with continuous time
Dnamics in Dela Cournot Duopol Akio Matsumoto Chuo Universit Ferenc Szidarovszk Universit of Arizona Hirouki Yoshida Nihon Universit Abstract Dnamic linear oligopolies are eamined with continuous time
Introduction to Differential Equations. National Chiao Tung University Chun-Jen Tsai 9/14/2011
 Introduction to Differential Equations National Chiao Tung Universit Chun-Jen Tsai 9/14/011 Differential Equations Definition: An equation containing the derivatives of one or more dependent variables,
Introduction to Differential Equations National Chiao Tung Universit Chun-Jen Tsai 9/14/011 Differential Equations Definition: An equation containing the derivatives of one or more dependent variables,
The Hopf Bifurcation Theorem: Abstract. Introduction. Transversality condition; the eigenvalues cross the imginary axis with non-zero speed
 Supercritical and Subcritical Hopf Bifurcations in Non Linear Maps Tarini Kumar Dutta, Department of Mathematics, Gauhati Universit Pramila Kumari Prajapati, Department of Mathematics, Gauhati Universit
Supercritical and Subcritical Hopf Bifurcations in Non Linear Maps Tarini Kumar Dutta, Department of Mathematics, Gauhati Universit Pramila Kumari Prajapati, Department of Mathematics, Gauhati Universit
Non-homogeneous semilinear elliptic equations involving critical Sobolev exponent
 Non-homogeneous semilinear elliptic equations involving critical Sobolev exponent Yūki Naito a and Tokushi Sato b a Department of Mathematics, Ehime University, Matsuyama 790-8577, Japan b Mathematical
Non-homogeneous semilinear elliptic equations involving critical Sobolev exponent Yūki Naito a and Tokushi Sato b a Department of Mathematics, Ehime University, Matsuyama 790-8577, Japan b Mathematical
Global well-posedness for semi-linear Wave and Schrödinger equations. Slim Ibrahim
 Global well-posedness for semi-linear Wave and Schrödinger equations Slim Ibrahim McMaster University, Hamilton ON University of Calgary, April 27th, 2006 1 1 Introduction Nonlinear Wave equation: ( 2
Global well-posedness for semi-linear Wave and Schrödinger equations Slim Ibrahim McMaster University, Hamilton ON University of Calgary, April 27th, 2006 1 1 Introduction Nonlinear Wave equation: ( 2
Bifurcations of the Controlled Escape Equation
 Bifurcations of the Controlled Escape Equation Tobias Gaer Institut für Mathematik, Universität Augsburg 86135 Augsburg, German gaer@math.uni-augsburg.de Abstract In this paper we present numerical methods
Bifurcations of the Controlled Escape Equation Tobias Gaer Institut für Mathematik, Universität Augsburg 86135 Augsburg, German gaer@math.uni-augsburg.de Abstract In this paper we present numerical methods
Generalized Least-Squares Regressions III: Further Theory and Classication
 Generalized Least-Squares Regressions III: Further Theor Classication NATANIEL GREENE Department of Mathematics Computer Science Kingsborough Communit College, CUNY Oriental Boulevard, Brookln, NY UNITED
Generalized Least-Squares Regressions III: Further Theor Classication NATANIEL GREENE Department of Mathematics Computer Science Kingsborough Communit College, CUNY Oriental Boulevard, Brookln, NY UNITED
16.5. Maclaurin and Taylor Series. Introduction. Prerequisites. Learning Outcomes
 Maclaurin and Talor Series 6.5 Introduction In this Section we eamine how functions ma be epressed in terms of power series. This is an etremel useful wa of epressing a function since (as we shall see)
Maclaurin and Talor Series 6.5 Introduction In this Section we eamine how functions ma be epressed in terms of power series. This is an etremel useful wa of epressing a function since (as we shall see)
The Coupled Three-Body Problem and Ballistic Lunar Capture
 The Coupled Three-Bod Problem and Ballistic Lunar Capture Shane Ross Martin Lo (JPL), Wang Sang Koon and Jerrold Marsden (Caltech) Control and Dnamical Sstems California Institute of Technolog Three Bod
The Coupled Three-Bod Problem and Ballistic Lunar Capture Shane Ross Martin Lo (JPL), Wang Sang Koon and Jerrold Marsden (Caltech) Control and Dnamical Sstems California Institute of Technolog Three Bod
INTRODUCTION TO DIFFERENTIAL EQUATIONS
 INTRODUCTION TO DIFFERENTIAL EQUATIONS. Definitions and Terminolog. Initial-Value Problems.3 Differential Equations as Mathematical Models CHAPTER IN REVIEW The words differential and equations certainl
INTRODUCTION TO DIFFERENTIAL EQUATIONS. Definitions and Terminolog. Initial-Value Problems.3 Differential Equations as Mathematical Models CHAPTER IN REVIEW The words differential and equations certainl
Subband Coding and Wavelets. National Chiao Tung University Chun-Jen Tsai 12/04/2014
 Subband Coding and Wavelets National Chiao Tung Universit Chun-Jen Tsai /4/4 Concept of Subband Coding In transform coding, we use N (or N N) samples as the data transform unit Transform coefficients are
Subband Coding and Wavelets National Chiao Tung Universit Chun-Jen Tsai /4/4 Concept of Subband Coding In transform coding, we use N (or N N) samples as the data transform unit Transform coefficients are
Convex ENO Schemes for Hamilton-Jacobi Equations
 Convex ENO Schemes for Hamilton-Jacobi Equations Chi-Tien Lin Dedicated to our friend, Xu-Dong Liu, notre Xu-Dong. Abstract. In one dimension, viscosit solutions of Hamilton-Jacobi (HJ equations can be
Convex ENO Schemes for Hamilton-Jacobi Equations Chi-Tien Lin Dedicated to our friend, Xu-Dong Liu, notre Xu-Dong. Abstract. In one dimension, viscosit solutions of Hamilton-Jacobi (HJ equations can be
The Attractors of the Rayleigh-Bénard Flowof ararefied Gas
 The Attractors of the Raleigh-Bénard Flowof ararefied Gas S.Stefanov, V. Roussinov and C. Cercignani Inst. of Mech., Bulg. Acad. of Sciences, Sofia, Bulgaria Dipart. di Matematica, Polit. di Milano, Ital
The Attractors of the Raleigh-Bénard Flowof ararefied Gas S.Stefanov, V. Roussinov and C. Cercignani Inst. of Mech., Bulg. Acad. of Sciences, Sofia, Bulgaria Dipart. di Matematica, Polit. di Milano, Ital
On Range and Reflecting Functions About the Line y = mx
 On Range and Reflecting Functions About the Line = m Scott J. Beslin Brian K. Heck Jerem J. Becnel Dept.of Mathematics and Dept. of Mathematics and Dept. of Mathematics and Computer Science Computer Science
On Range and Reflecting Functions About the Line = m Scott J. Beslin Brian K. Heck Jerem J. Becnel Dept.of Mathematics and Dept. of Mathematics and Dept. of Mathematics and Computer Science Computer Science
Sound Propagation in Ducts
 Sound Propagation in Ducts Hongbin Ju Department of Mathematics Florida State Universit, Tallahassee, FL.3306 www.aeroacoustics.info Please send comments to: hju@math.fsu.edu In this section we will discuss
Sound Propagation in Ducts Hongbin Ju Department of Mathematics Florida State Universit, Tallahassee, FL.3306 www.aeroacoustics.info Please send comments to: hju@math.fsu.edu In this section we will discuss
Amplitude-phase control of a novel chaotic attractor
 Turkish Journal of Electrical Engineering & Computer Sciences http:// journals. tubitak. gov. tr/ elektrik/ Research Article Turk J Elec Eng & Comp Sci (216) 24: 1 11 c TÜBİTAK doi:1.396/elk-131-55 Amplitude-phase
Turkish Journal of Electrical Engineering & Computer Sciences http:// journals. tubitak. gov. tr/ elektrik/ Research Article Turk J Elec Eng & Comp Sci (216) 24: 1 11 c TÜBİTAK doi:1.396/elk-131-55 Amplitude-phase
Limit cycles bifurcating from the periodic orbits of a discontinuous piecewise linear differential center with two zones
 This is a preprint of: Limit ccles bifurcating from the periodic orbits of a discontinuous piecewise linear differential center with two zones Jaume Llibre Douglas D. Novaes Marco Antonio Teixeira Internat.
This is a preprint of: Limit ccles bifurcating from the periodic orbits of a discontinuous piecewise linear differential center with two zones Jaume Llibre Douglas D. Novaes Marco Antonio Teixeira Internat.
Polynomial and Rational Functions
 Polnomial and Rational Functions Figure -mm film, once the standard for capturing photographic images, has been made largel obsolete b digital photograph. (credit film : modification of ork b Horia Varlan;
Polnomial and Rational Functions Figure -mm film, once the standard for capturing photographic images, has been made largel obsolete b digital photograph. (credit film : modification of ork b Horia Varlan;
THE WAVE MAPS EQUATION. 1. The equations Let us begin with the Laplace equation, R n
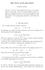 THE WAVE MAPS EQUATION DANIEL TATARU Abstract. The wave maps equation has become a very popular topic in recent years. The aim of these expository notes is to present a non-technical survey of the ideas
THE WAVE MAPS EQUATION DANIEL TATARU Abstract. The wave maps equation has become a very popular topic in recent years. The aim of these expository notes is to present a non-technical survey of the ideas
Physics of Tsunamis. This is an article from my home page: Ole Witt-Hansen 2011 (2016)
 Phsics of Tsunamis This is an article from m home page: www.olewitthansen.dk Ole Witt-Hansen 11 (16) Contents 1. Constructing a differential equation for the Tsunami wave...1. The velocit of propagation
Phsics of Tsunamis This is an article from m home page: www.olewitthansen.dk Ole Witt-Hansen 11 (16) Contents 1. Constructing a differential equation for the Tsunami wave...1. The velocit of propagation
On the Extension of Goal-Oriented Error Estimation and Hierarchical Modeling to Discrete Lattice Models
 On the Etension of Goal-Oriented Error Estimation and Hierarchical Modeling to Discrete Lattice Models J. T. Oden, S. Prudhomme, and P. Bauman Institute for Computational Engineering and Sciences The Universit
On the Etension of Goal-Oriented Error Estimation and Hierarchical Modeling to Discrete Lattice Models J. T. Oden, S. Prudhomme, and P. Bauman Institute for Computational Engineering and Sciences The Universit
Dynamics of energy-critical wave equation
 Dynamics of energy-critical wave equation Carlos Kenig Thomas Duyckaerts Franke Merle September 21th, 2014 Duyckaerts Kenig Merle Critical wave 2014 1 / 22 Plan 1 Introduction Duyckaerts Kenig Merle Critical
Dynamics of energy-critical wave equation Carlos Kenig Thomas Duyckaerts Franke Merle September 21th, 2014 Duyckaerts Kenig Merle Critical wave 2014 1 / 22 Plan 1 Introduction Duyckaerts Kenig Merle Critical
Dynamics of quantum vortices in a toroidal trap
 PHYSICAL REVIEW A 79, 4362 29 Dnamics of quantum vortices in a toroidal trap Peter Mason and Natalia G. Berloff Department of Applied Mathematics and Theoretical Phsics, Universit of Cambridge, Wilberforce
PHYSICAL REVIEW A 79, 4362 29 Dnamics of quantum vortices in a toroidal trap Peter Mason and Natalia G. Berloff Department of Applied Mathematics and Theoretical Phsics, Universit of Cambridge, Wilberforce
Polynomial and Rational Functions
 Polnomial and Rational Functions Figure -mm film, once the standard for capturing photographic images, has been made largel obsolete b digital photograph. (credit film : modification of ork b Horia Varlan;
Polnomial and Rational Functions Figure -mm film, once the standard for capturing photographic images, has been made largel obsolete b digital photograph. (credit film : modification of ork b Horia Varlan;
Simulation of Acoustic and Vibro-Acoustic Problems in LS-DYNA using Boundary Element Method
 10 th International LS-DYNA Users Conference Simulation Technolog (2) Simulation of Acoustic and Vibro-Acoustic Problems in LS-DYNA using Boundar Element Method Yun Huang Livermore Software Technolog Corporation
10 th International LS-DYNA Users Conference Simulation Technolog (2) Simulation of Acoustic and Vibro-Acoustic Problems in LS-DYNA using Boundar Element Method Yun Huang Livermore Software Technolog Corporation
Study on Nonlinear Vibration and Crack Fault of Rotor-bearing-seal Coupling System
 Sensors & Transducers 04 b IFSA Publishing S. L. http://www.sensorsportal.com Stud on Nonlinear Vibration and Crack Fault of Rotor-bearing-seal Coupling Sstem Yuegang LUO Songhe ZHANG Bin WU Wanlei WANG
Sensors & Transducers 04 b IFSA Publishing S. L. http://www.sensorsportal.com Stud on Nonlinear Vibration and Crack Fault of Rotor-bearing-seal Coupling Sstem Yuegang LUO Songhe ZHANG Bin WU Wanlei WANG
Simple Derivation of the Picard-Fuchs equations for the Seiberg-Witten Models
 hep-th/9703186 IPM-97 Simple Derivation of the Picard-Fuchs equations for the Seiberg-Witten Models Mohsen Alishahiha Institute for Studies in Theoretical Phsics and Mathematics, P.O.Box 19395-5531, Tehran,
hep-th/9703186 IPM-97 Simple Derivation of the Picard-Fuchs equations for the Seiberg-Witten Models Mohsen Alishahiha Institute for Studies in Theoretical Phsics and Mathematics, P.O.Box 19395-5531, Tehran,
Non-Analytic Solutions of Nonlinear Wave Models
 Non-Analtic Solutions of Nonlinear Wave Models Yi A. Li School of Mathematics Universit of Minnesota Minneapolis, MN 55455 ili@math.umn.edu Peter J. Olver School of Mathematics Universit of Minnesota Minneapolis,
Non-Analtic Solutions of Nonlinear Wave Models Yi A. Li School of Mathematics Universit of Minnesota Minneapolis, MN 55455 ili@math.umn.edu Peter J. Olver School of Mathematics Universit of Minnesota Minneapolis,
Problem set 6 Math 207A, Fall 2011 Solutions. 1. A two-dimensional gradient system has the form
 Problem set 6 Math 207A, Fall 2011 s 1 A two-dimensional gradient sstem has the form x t = W (x,, x t = W (x, where W (x, is a given function (a If W is a quadratic function W (x, = 1 2 ax2 + bx + 1 2
Problem set 6 Math 207A, Fall 2011 s 1 A two-dimensional gradient sstem has the form x t = W (x,, x t = W (x, where W (x, is a given function (a If W is a quadratic function W (x, = 1 2 ax2 + bx + 1 2
Interspecific Segregation and Phase Transition in a Lattice Ecosystem with Intraspecific Competition
 Interspecific Segregation and Phase Transition in a Lattice Ecosstem with Intraspecific Competition K. Tainaka a, M. Kushida a, Y. Ito a and J. Yoshimura a,b,c a Department of Sstems Engineering, Shizuoka
Interspecific Segregation and Phase Transition in a Lattice Ecosstem with Intraspecific Competition K. Tainaka a, M. Kushida a, Y. Ito a and J. Yoshimura a,b,c a Department of Sstems Engineering, Shizuoka
Critical Phenomena in Gravitational Collapse
 Critical Phenomena in Gravitational Collapse Yiruo Lin May 4, 2008 I briefly review the critical phenomena in gravitational collapse with emphases on connections to critical phase transitions. 1 Introduction
Critical Phenomena in Gravitational Collapse Yiruo Lin May 4, 2008 I briefly review the critical phenomena in gravitational collapse with emphases on connections to critical phase transitions. 1 Introduction
NUMERICAL STUDY OF QUANTIZED VORTEX INTERACTIONS IN THE NONLINEAR SCHRÖDINGER EQUATION ON BOUNDED DOMAINS
 MULTISCALE MODEL. SIMUL. Vol. 2, No. 2, pp. 4 439 c 24 Societ for Industrial and Applied Mathematics NUMERICAL STUDY OF QUANTIZED VORTEX INTERACTIONS IN THE NONLINEAR SCHRÖDINGER EQUATION ON BOUNDED DOMAINS
MULTISCALE MODEL. SIMUL. Vol. 2, No. 2, pp. 4 439 c 24 Societ for Industrial and Applied Mathematics NUMERICAL STUDY OF QUANTIZED VORTEX INTERACTIONS IN THE NONLINEAR SCHRÖDINGER EQUATION ON BOUNDED DOMAINS
PICONE S IDENTITY FOR A SYSTEM OF FIRST-ORDER NONLINEAR PARTIAL DIFFERENTIAL EQUATIONS
 Electronic Journal of Differential Equations, Vol. 2013 (2013), No. 143, pp. 1 7. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu PICONE S IDENTITY
Electronic Journal of Differential Equations, Vol. 2013 (2013), No. 143, pp. 1 7. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu PICONE S IDENTITY
3 First order nonlinear equations
 Separable equations 3 First order nonlinear equations d f dx = where f(x,) is not (in general) a linear function of. ( x, ) The equation is autonomous if there is no explicit dependence on the independent
Separable equations 3 First order nonlinear equations d f dx = where f(x,) is not (in general) a linear function of. ( x, ) The equation is autonomous if there is no explicit dependence on the independent
Asymptotics at regular singular points
 Ma 7, 2011 Asmptotics at regular singular points Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ Introduction 1. Examples 2. Regular singular points 3. Regular singular points at infinit
Ma 7, 2011 Asmptotics at regular singular points Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ Introduction 1. Examples 2. Regular singular points 3. Regular singular points at infinit
A NEW CHAOTIC ATTRACTOR FROM 2D DISCRETE MAPPING VIA BORDER-COLLISION PERIOD-DOUBLING SCENARIO
 A NEW CHAOTIC ATTRACTOR FROM D DISCRETE MAPPING VIA BORDER-COLLISION PERIOD-DOUBLING SCENARIO ZERAOULIA ELHADJ Received 1 April 5 The following map is studied: (, ) (1 + a( )+,b). It is proved numericall
A NEW CHAOTIC ATTRACTOR FROM D DISCRETE MAPPING VIA BORDER-COLLISION PERIOD-DOUBLING SCENARIO ZERAOULIA ELHADJ Received 1 April 5 The following map is studied: (, ) (1 + a( )+,b). It is proved numericall
The van Dommelen and Shen singularity in the Prandtl equations
 The van Dommelen and Shen singularit in the Prandtl equations Igor Kukavica, Vlad Vicol, and Fei Wang ABSTRACT. In 198, van Dommelen and Shen provided a numerical simulation that predicts the spontaneous
The van Dommelen and Shen singularit in the Prandtl equations Igor Kukavica, Vlad Vicol, and Fei Wang ABSTRACT. In 198, van Dommelen and Shen provided a numerical simulation that predicts the spontaneous
A. Derivation of regularized ERM duality
 A. Derivation of regularized ERM dualit For completeness, in this section we derive the dual 5 to the problem of computing proximal operator for the ERM objective 3. We can rewrite the primal problem as
A. Derivation of regularized ERM dualit For completeness, in this section we derive the dual 5 to the problem of computing proximal operator for the ERM objective 3. We can rewrite the primal problem as
ADAPTIVE NUMERICAL SCHEMES FOR A PARABOLIC PROBLEM WITH BLOW-UP
 ADAPTIVE NUMERICAL SCHEMES FOR A PARABOLIC PROBLEM WITH BLOW-UP RAÚL FERREIRA, PABLO GROISMAN AND JULIO D. ROSSI Abstract. In this paper we present adaptive procedures for the numerical study of positive
ADAPTIVE NUMERICAL SCHEMES FOR A PARABOLIC PROBLEM WITH BLOW-UP RAÚL FERREIRA, PABLO GROISMAN AND JULIO D. ROSSI Abstract. In this paper we present adaptive procedures for the numerical study of positive
Journal of Inequalities in Pure and Applied Mathematics
 Journal of Inequalities in Pure and Applied Mathematics http://jipam.vu.edu.au/ Volume 2, Issue 2, Article 15, 21 ON SOME FUNDAMENTAL INTEGRAL INEQUALITIES AND THEIR DISCRETE ANALOGUES B.G. PACHPATTE DEPARTMENT
Journal of Inequalities in Pure and Applied Mathematics http://jipam.vu.edu.au/ Volume 2, Issue 2, Article 15, 21 ON SOME FUNDAMENTAL INTEGRAL INEQUALITIES AND THEIR DISCRETE ANALOGUES B.G. PACHPATTE DEPARTMENT
DECAY ESTIMATES FOR THE KLEIN-GORDON EQUATION IN CURVED SPACETIME
 Electronic Journal of Differential Equations, Vol. 218 218), No. 17, pp. 1 9. ISSN: 172-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu DECAY ESTIMATES FOR THE KLEIN-GORDON EQUATION
Electronic Journal of Differential Equations, Vol. 218 218), No. 17, pp. 1 9. ISSN: 172-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu DECAY ESTIMATES FOR THE KLEIN-GORDON EQUATION
Note on the Chen-Lin Result with the Li-Zhang Method
 J. Math. Sci. Univ. Tokyo 18 (2011), 429 439. Note on the Chen-Lin Result with the Li-Zhang Method By Samy Skander Bahoura Abstract. We give a new proof of the Chen-Lin result with the method of moving
J. Math. Sci. Univ. Tokyo 18 (2011), 429 439. Note on the Chen-Lin Result with the Li-Zhang Method By Samy Skander Bahoura Abstract. We give a new proof of the Chen-Lin result with the method of moving
Two Dimensional Linear Systems of ODEs
 34 CHAPTER 3 Two Dimensional Linear Sstems of ODEs A first-der, autonomous, homogeneous linear sstem of two ODEs has the fm x t ax + b, t cx + d where a, b, c, d are real constants The matrix fm is 31
34 CHAPTER 3 Two Dimensional Linear Sstems of ODEs A first-der, autonomous, homogeneous linear sstem of two ODEs has the fm x t ax + b, t cx + d where a, b, c, d are real constants The matrix fm is 31
First Order Equations
 10 1 Linear and Semilinear Equations Chapter First Order Equations Contents 1 Linear and Semilinear Equations 9 Quasilinear Equations 19 3 Wave Equation 6 4 Sstems of Equations 31 1 Linear and Semilinear
10 1 Linear and Semilinear Equations Chapter First Order Equations Contents 1 Linear and Semilinear Equations 9 Quasilinear Equations 19 3 Wave Equation 6 4 Sstems of Equations 31 1 Linear and Semilinear
An exact solution for 2+1 dimensional critical collapse
 An exact solution for + dimensional critical collapse David Garfinkle Department of Physics, Oakland University, Rochester, Michigan 839 We find an exact solution in closed form for the critical collapse
An exact solution for + dimensional critical collapse David Garfinkle Department of Physics, Oakland University, Rochester, Michigan 839 We find an exact solution in closed form for the critical collapse
