arxiv: v1 [math.ap] 25 Jun 2008
|
|
|
- Nickolas Ray
- 6 years ago
- Views:
Transcription
1 On the existence of smooth self-similar blow-up profiles for the wave-map equation arxiv: v1 [math.ap] 5 Jun 8 Pierre Germain October, 17 Abstract Consider the equivariant wave map equation from Minkowski space to a rotationnally symmetric manifold N which has an equator (example: the sphere). In dimension 3, this article presents a necessary and sufficient condition on N for the existence of a smooth self-similar blow up profile. More generally, we study the relation between - the minimizing properties of the equator map for the Dirichlet energy corresponding to the (elliptic) harmonic map problem - and the existence of a smooth blow-up profile for the (hyperbolic) wave map problem. This has several applications to questions of regularity and uniqueness for the wave map equation. 1 Introduction 1.1 The geometric setting We will consider in the following equations on a map u, from the Euclidean space R d, with d 3 (which corresponds to the supercritical regime for harmonic maps and wave maps) to a manifold N embedded in R K Spherical symmetry and equator Thefirstassumptionthat wewill make isoneofsymmetry: onn, onecan take coordinates (which may be periodic in φ) (φ,χ) R S M 1 (M an integer) in which the metric reads dφ +g(φ) dχ, for a smooth odd function g such that g () = 1. We now impose that N has an equator; by this we simply mean φ > such that g (φ ) =, and minimal with this property. 1
2 1.1. Equivariance We further restrict u to the class of equivariant maps, that is, (r,ω) denoting polar coordinates on R d, u = R χ φ def : R d N (r,ω) (φ(r),χ(ω)). Here, χ : S d 1 S M 1 (M is an integer) is an eigenmap, that is a map satisfying, for a constant k χ = k and S d 1χ+kχ =. This can be achieved for some large enough M, provided see [3]. k = l(l+d ) with l N Of course, the most simple example of an eigenmap is provided by χ(ω) = ω, mapping S d 1 to itself, in which case k = d 1. We call equator map the map corresponding to φ φ ; it actually depends on χ, that is the equivariance class which is considered. 1. Harmonic maps and the equator map 1..1 The boundary value problem Harmonic maps from the ball B = B R d(,1) of the Euclidean space R d, to a manifold N embedded in R K, with Dirichlet boundary data h, satisfy the equation { u(x) Tu(x) N on B u = h on B (here, T u(x) N is the tangent space, at u(x), of N, and orthogonality is to be understood in the sense of R K ). In the equivariant setting discussed above, this Dirichlet problem becomes (1) (D α ) { φrr d 1 r φ r + k r g(φ)g (φ) = on [,1] φ(1) = α, where α is a given real number. 1.. The energy and the equator map Harmonic maps are critical points of the energy, which reads in the equivariant setting E e (φ) = 1 ( φ r + k ) r g (φ) r d 1 dr.
3 Solutions to the Dirichlet problem (D α ) are critical points of E e in the class F α = { } φ : [,1] R, φ r L (r d 1 dr), φ(1) = α It can easily be seen that the equator map φ φ is a solution of the Dirichlet problem with α = φ. A crucial point in this article will be the minimizing properties of φ. For a full answer to the question whether φ minimizes locally E e over F φ, see Proposition.1. Whether φ minimizes globally or not E e over F φ is a more difficult question. The answer is known in the case where χ = Id (covariant case) and N is an ellipse embedded in R d+1 given by (a [,1]). y 1 + +y d + y d+1 a = 1, and it is due to Jäger and Kaul [7], Baldes [1], Hélein [6]. These authors prove the following criterion: φ is the unique global minimizer of E e if and only if 1.3 Wave maps a 4(d 1) (d ). This paper addresses only some of the questions related to the wave map Cauchy problem. Other aspects, like the case of dimension, or optimal well-posedness results for wave maps without symmetries, are discussed in the review by Krieger [9] The initial value problem TheCauchyproblemforwavemapsfromMinkowskispaceR d+1 toamanifoldn embedded in R K reads tu(x,t) u(x,t) T u(x,t) N (WM) u(t = ) = u u t (t = ) = u 1. The weak formulation reads, for (u, u t ) L t (Ḣ1 L ), u(x,t) N for almost all (x, t), R d+1 [ u t, f t x u, x f ] dxdt = for f such that f t, x f L and for almost all (x, t), f(x,t) T u(x,t) N (u, u t ) t (u, u 1 ) weakly in Ḣ1 L. We can rewrite these equations in the equivariant setting. We obtain the following equation, which is to be understood in S if one considers weak solutions. (EWM) φ tt φ rr d 1 r φ r + k r g(φ)g (φ) = φ(t = ) = φ φ t (t = ) = φ 1. 3
4 1.3. Formation of singularities: the blow up profiles It is a basic problem to understand whether the wave map equation can develop singularities if the initial data are smooth. The approach followed by Shatah [1], Shatah and Tahvildar-Zadeh [13], and Cazenave, Shatah and Tahvildar-Zadeh [3] consists in building up smooth blow up profiles Definition 1.1 (blow up profiles) A (self-similar) blow up profile is a function ψ such that ( r φ(r,t) = ψ t) solves the wave-map equation. The profile ψ(ρ) has to be defined for ρ 1, and must have a smooth behavior at 1. Then one can extend the data (ψ,rψ ), defined on B R d(,1), smoothly to ( φ, φ 1 ), defined on R d. The solution to (EWM) with data ( φ, φ 1 ) equals ( ) r ψ 1 t inside the backward light cone, with basis B and vertex (x =,t = 1). In particular, a singularity appears at (x =,t = 1), even though the data were smooth. The PDE satisfied by φ turns into an ODE for ψ. More precisely, Proposition 1.1 Suppose that ψ is an integrable function, smooth at. Then R χ φ solves (WM) for t > if and only if ψ satisfies the equation () ρ (1 ρ )ψ (ρ)+ρ((d 1) ρ )ψ (ρ) kg(ψ)g (ψ) = in the classical sense on (,1) (1, ), and furthermore ψ(1 ) = ψ(1+). This proposition is proved in Section 7. A first approach to solving for ψ is to handle the above singular ODE. Another approach is variational, it was developed by the authors mentioned above. These authors observe that the equation satisfied by ψ is the harmonic map equation from the hyperbolic ball to N. Thus it can be solved by minimizing on E h (ψ) = G = B ( ψr k [ + g r (1 r (ψ) g (φ ) ]) r d 1 dr ) (1 r ) (d 3)/, {ψ : [,1] R, ψ r L ( r d 1 dr (1 r ) d 3 ), ψ(1) = φ } The functional E h corresponds to the Dirichlet energy for an equivariant map from the hyperbolic ball to N, except g (ψ) has been replaced by [ g (ψ) g (φ ) ]. This renormalization imposes the boundary condition ψ = φ for ρ = 1 - we will come back to this in the following. The following theorem summarizes results proved in [3]. 4.
5 Theorem 1.1 If inf E h(ψ) <, ψ G there exists a smooth ψ : [,1] [,R ] such that ψ() =. ψ(1) = φ. φ = ψ ( r t) solves (EWM) (where it is defined). u = R χ φ is smooth where it is defined. It should also be mentioned that self-similar blow-up profiles as given by the above theorem provide examples of non uniqueness for (EWM): see [13] [3]. We will use a similar argument in Theorem.1 for data equal to the equator map. In the absence of such a self-similar blow-up profile, there does not seem to be known examples of non-uniqueness. Finally, multiple solutions for the above variational problem are constructed in Jungen [8] Energy conservation and weak solutions A smooth solution of (EWM) satisfies the energy equality (we only give here the version which is centered at in space) (3) if R > T, E(T,R T,φ)+flux(,T,R,φ) = E(,R,φ) with the following notations R ( E(t,R,φ) def = φ r(t)+ k ) r g(φ(t)) +φ t(t) r d 1 dr ( flux(,t,r,φ) def 1 = φ t + k r g(φ) + 1 ) φ φ t φ n dσ, where S,T,R is the surface S,T,R S,T,R = {(r,s) such that t T and r = R s} (endowed with the metric coming from the natural embedding S R d+1 ), and where n is the outside normal of B(,R s). Notice that flux(,t,r,φ) is a positive quantity. In the case where the data are of finite energy, one can use energy conservation and a compactness argument to build up global weak solutions. Theorem 1. (Shatah [1], Freire [4]) Assume that the target manifold N is homogeneous and compact, and take data such that u L loc and u 1 L loc, i.e. for any R >, R ((φ ) r + kr ) R g(φ ) r d 1 dr + φ 1 rd 1 dr <. Then there exists a global solution of (WM) (u,u t ) L t (R,Ḣ1 loc ) L t (R,L loc ). 5
6 If one transposes this theorem in the equivariant setting, the following energy inequality can be proved to hold (4) if R > T, E(T,R T,φ)+flux(,T,R,φ) E(,R,φ). Indeed, it suffices to follow the steps of Shatah and Freire, who use a penalisation method. Since we consider equivariant functions, passing to the limit in the penalised problems is easy except for x = ; this is due to the energy bound which gives strong control anywhere else. Thus one can pass to the limit in (3) and obtain (4). Statement of the results.1 Local aspects Proposition.1 The three following facts are equivalent (i) kg(φ )g (φ ) (d ) 4 (ii) The second variation δ E e (φ )(w,w) for w F φ. (iii) The second variation δ E h (φ )(w,w) for w G. Besides, if we exclude the limit case where kg(φ )g (φ ) = (d ) 4, (i) becomes equivalent to (iv) The wave map equation with initial data equal to the equator map is linearly stable (in a sense to be made precise in Section 3.3). The proof of this proposition essentially consists in putting together already known results. It is interesting to notice that they all rely on different versions of Hardy s inequality. This proof will be given in Section 3.. The case of dimension 3 In dimension 3, we are able to analyze globally the relation between minimality of φ for E e and properties of the wave-map equation. However, we need to make some more hypotheses on the geometry of N. We do not claim that they are optimal, but they are simple, of sufficient generality, and will enable us to state our results in an elegant way. Recall that g is an odd smooth function. The further assumptions in dimension 3 are that either the φ coordinate is not periodic; φ and φ are the only zeros of g ; g is positive and decreasing on (φ, ). or the φ coordinate is 4φ periodic, and g(φ + ) is even. (Thus the manifold N has the symmetries of an ellipsoid with all semi-principal axes but one of the same length) Either of these assumptions ensures that Up to the symmetries of N, φ is unique with the property that g (φ ) =. Up to the symmetries of N, is unique with the property that g (φ ) =. 6
7 Up to the symmetries of N, (5) g(φ) < g(φ ) for any φ φ. We can now state the theorem. Theorem.1 If d = 3, and the above assumptions are satisfied, the three following facts are equivalent (i) The equator map is the unique global minimizer of E e on F φ. (ii) The only weak solution to (EWM) satisfying the energy inequality (4), and with initial data φ = φ φ 1 = is identically equal to the equator map φ. (iii) There does not exist a non-zero blow-up profile ψ such that R χ ψ C ( B R d(,1)). This theorem will be proved in Section 4. Let us mention quickly the main ideas of the proof. Starting from a smooth blow up profile ψ, it is possible to construct, using the equation it satisfies, a solution corresponding to data (φ, φ 1 ) = (φ, ) and non identically equal to φ. If the equator map minimizes the Dirichlet energy, it is intuitively clear that the equator map is the unique solution corresponding to data (φ, ) and satisfying the energy inequality. Indeed, any other solution would somehow have to make the energy grow, which is not allowed if the energy inequality is satisfied. Finally, if the equator map does not minimize the Dirichlet energy, we use the variational approach: Theorem 1.1 gives a smooth solution. Actually, the proof of Theorem.1 gives a little more than the statement above. In particular, we get the following very strong instability result, for data equal to the equator map, in case (i) above does not hold. Proposition. Suppose that the equator map φ is not the unique global minimizer of E e. Then there exists a smooth profile ψ : [,1] R such that for any T, φ(r,t) = { ) ψ( r t T φ if t T and r t T otherwise solves (EWM) with data (φ, φ 1 ) = (φ, ), and satisfies the energy equality (3). Finally, itisnaturaltoaskwhethernon-smoothprofilesmayexistevenif(i)intheorem.1 holds. In other words: can one replace in the statement of (iii) smooth by H s for some s? (Notice that the belonging of R χ ψ to any functional space can be easily defined using the embedding of N in R K.) 7
8 Proposition.3 (i) Suppose that ψ solves () on (,1), and that Then R χ ψ C ( B R 3(,1)). R χ ψ Ḣ3/ (B R 3(,1)). (ii) With only the assumptions made in Section 1.1 on g, there always exists a non zero ψ such that R χ ψ smooth near, R χ ψ Ḃ3/, (B R 3(,1)), (see [5] for a definition of the Besov space Ḃ3/, ) and solves (WM). u(x,t) = R χ ψ This proposition is proved in Section 6. Thus, for ψ, Ḣ 3/ and C regularity are equivalent. But if one goes down to Ḃ3/, the situation becomes drastically different: there always exist (no matter whether (i) in Theorem.1 holds true or not) a profile with this regularity. We would like to shed some light on the distinction between Ḣ3/ and Ḃ3/, appearing above. Notice first that the spaces Ḃ3/, Ḃ1/, or Ḣ3/ Ḣ1/ are at the scaling of the equation for the initial data. Global well-posedness for small data in Ḣ3/ Ḣ1/ for (WM) is due to Tao [15]. Global well posedness in the equivariant setting for a space similar to has been proved by the author [5]. Now let us point out a fundamental difference between considering solutions in the Sobolev space or in the Besov space. Space-time scaling invariant spaces corresponding to the spaces for the data mentioned above are Ḃ 3/, Ḃ1/, (u,u t ) L t Consider a smooth profile ψ and (Ḃ3/, Ḃ1/, ) u(x,t) = R χ ψ ( x t ) or L t ( ) x t Then (at least locally in space) (6) (u,u t ) L ( ) [ 1,1], Ḃ 3/, Ḃ1/, but (7) (u,u t ) / L ( [ 1,1], Ḣ 3/ Ḣ1/).. (Ḣ3/ Ḣ1/). Thus in some sense one sees the blow up in the Sobolev setting (7) but not in the Besov space setting (6). 8
9 .3 The case of dimension d 4 In the case of dimension d 4, we can only prove a weak version of Theorem.1. Theorem. Consider the following assertions (i) The equator map is the unique global minimizer of E e on F φ. (ii) The only weak solution to (EWM) satisfying the energy inequality (4), and with initial data φ = φ φ 1 = is identically equal to the equator map φ. (iii) There does not exist a blow-up profile ψ suchthat ψ(1) = φ and R χ ψ C ( B R d(,1)). There holds (i) (ii) (iii). The proof of this theorem is almost identical to the corresponding steps in Theorem.1; for this reason we do not include it here. The question of the regularity of the profile is much more involved in dimensions d 4: see [3]; we plan to come back to this and other aspects of the problem for d 4 in a subsequent paper. 3 Proof of Proposition.1 As mentioned above, the whole proof of Proposition.1 somehow relies on different versions of Hardy s inequality. It is interesting to recall here the whole space version, with the optimal constant Rd w x dx 4 (d ) w dx. R d 3.1 The second variation of E e : proof of (i) (ii) A small computation gives E e (φ +ǫw) = E e (φ )+ǫ 1 The conclusion follows due to the inequality (Baldes [1]) (w r + kr g(φ )g (φ )w ) r d 1 dr +O(ǫ 3 ). (8) if φ +ǫw F φ, where the constant is optimal. 1 w r d 3 dr 4 (d ) 1 w rr d 1 dr, 3. The second variation of E h : proof of (i) (iii) By a small computation one gets (since E h (φ ) = ) E h (φ +ǫw) = ǫ 1 ( w r + ) k r (1 r ) g(φ )g (φ )w 9 r d 1 dr (1 r ) (d 3)/ +O(ǫ3 ).
10 The conclusion follows due to the inequality (Cazenave Shatah Tahvildar-Zadeh [3]) (9) if φ +ǫw G, 1 w r d 3 (1 r ) d 1 dr 4 (d ) 1 wr r d 1 (1 r ) d 3 dr where the constant is optimal. 3.3 Linear stability of the equator map: proof of (i) (iv) The equation (EWM) can be rewritten using the new unknown function w = φ φ (1) w tt w rr d 1 w r + k r r g(φ +w)g (φ +w) =. Let us now linearize this equation in the limit w small: (11) w tt w rr d 1 w r + k r r g(φ )g (φ )w =. This is a linear wave equation with a singular(inverse square) potential. Dispersion for this class of potentials has been studied by Burq, Planchon, Stalker and Tahvildar Zadeh [], who prove the following result. Theorem 3.1 (Burq, Planchon, Stalker, Tahvildar-Zadeh) The solution of the equation w tt w rr d 1 r w r + a w = r w(t = ) = w w t (t = ) = w 1 satisfies the classical Strichartz estimates (1) ( ) σ w L p C( ) w t Lq x Ḣ1/ + w 1 Ḣ 1/ if with 1 p + d 1 q d 1 4 and σ = 1 p + d q d 1 (13) a > (d ) 4. In the case where a < (d ) 4, the point spectrum of the operator + a x extends to, see Remark 1.1 in Planchon, Stalker and Tahvildar-Zadeh [11]. In particular, in this case, there are no Strichartz estimates. What we mean by linearly stable in the statement of Proposition.1 is now clear: it means satisfying the Strichartz estimates given in Theorem 3.1. Applying the criterion(13) to the linearized equation(11), we get as expected the condition (i) in Proposition.1. Remark 3.1 (Nonlinear stability) Of course a much more interesting question than linear stability is non-linear stability, that is, well posedness of (1). For a certain range of kg(φ )g (φ ), a possible approach is the following: combine the Strichartz estimates with derivatives (that is, involving other regularities than what appears in (1)) of [] and the approach followed in [13] in order to get well posedness of (1). 1
11 This approach, however, does not cover all the cases where linear stability holds. The difficulty is that, if a is too close to (d ) 4, Strichartz estimates with derivatives are not available any more, and have to be replaced by estimates on ( )σ/( + a ) σ x w, LptL q x that is the relevant spaces involve fractional powers of the operator + a x. But as opposed to standard Sobolev spaces, product laws between such spaces are not known and need to be established in order to be able to handle nonlinear settings. Remark 3. Hardy s inequality did not appear explicitly in the present subsection, but it is one of the fundamental ingredients in the proof of Theorem Proof of Theorem Equivalence of (i) and (ii) (i) (ii) Let us suppose first that (i) holds, and consider φ a weak solution of (EWM) with data equal to the equator map, and satisfying the energy inequality (4). The equator map is smooth anywhere but in. By finite speed of propagation and weakstrong uniqueness for (EWM) (Struwe [14]), u must agree with the equator map outside of the forward light cone with vertex at (t,x) = (,) C = {(t,x), x t}. Let us write the energy equality (3) for the equator map (14) E(T,R T,φ )+flux(,t,r,φ ) = E(,R,φ ), where we choose T < R so that the flux term is computed on a surface which lies completely outside of the forward light cone C. For the weak solution φ, the energy inequality (4) holds, which reads (15) E(T,R T,φ)+flux(,T,R,φ) E(,R,φ). Comparing (14) and (15), and keeping in mind that φ and φ agree at time and outside of the light cone, one gets E(T,R T,φ ) E(T,R T,φ), which implies R T k R T r g(φ ) r dr (φ r (T)+ kr ) g(φ(t)) r dr. Thus, sinceφ(t,r T) = φ, theminimizingpropertyoftheequator mapgives φ(t) = φ. In other words (ii) holds true. 11
12 4.1. (i) (ii) Let us suppose that (i) does not hold, and prove that (EWM) with initial data equal to the equator map admits a solution which is not identically equal to the equator map. The alternative solution that we build up will be a self-similar solution ( r φ(r,t) = ψ t) Supposethat φ is not the uniqueglobal minimizer of E e in F φ. Thenthere exists φ F φ such that E e ( φ) E e (φ ). Since the space dimension is 3, F φ = G and therefore it makes sense to compute 1 E h ( φ) = E e ( φ) E e (φ k ( ) )+ 1 r g ( φ) g (φ ) r dr. Since φ is not identically φ, and by condition (5), E h ( φ) <. Hence Theorem 1.1 gives a self-similar profile ψ. Define the prolongation ψ(ρ) = { ψ(ρ) if ρ 1 φ if ρ 1. and ( r φ(r,t) = ψ t). By proposition 1.1, R χ φ solves (WM). It is easy to see that it takes the data φ(t = ) = φ and φ t (t = ) =. To conclude that (ii) is not true, it suffices to see that ψ satisfies the energy equality. This is precisely the statement of the next proposition, whose proof we postpone till Section 5. Proposition 4.1 ψ, as defined above, satisfies the energy equality (3). 4. Equivalence of (i) and (iii) 4..1 (i) (iii) Let us suppose that (i) does not hold. Proceeding as in Section 4.1., we get a profile ψ which is smooth on [,1]. Thus (iii) is not true. 4.. (iii) (i) Let us suppose that (iii) does not hold true, that is there exists a non zero blow up profile ψ such that R χ ψ C ( B R (,1)). Recall ψ satisfies the ODE ρ (1 ρ )ψ (ρ)+ρ(1 ρ )ψ (ρ) kg(ψ)g (ψ) = 1
13 Setting ρ = 1, we get g(ψ(1))g (ψ(1)) =. Thus, modulo the symmetries of the equation, either ψ(1) = or ψ(1) = φ. In order to show that the former case cannot occur, set and compute M(ρ) = 1 (ρ ρ 4 )ψ (ρ) kg(ψ(ρ)) M (ρ) = ρψ (ρ), so M is a decreasing quantity. Also, since the profile ψ corresponds to a smooth solution, one has necessarily ψ() = (modulo the symmetries of the equation), so M() =. Now, arguing by contradiction, suppose that ψ(1) =, then M(1) = and M has to be identically on [,1]. By the formula for M, this implies that ψ is constant on [,1], which is a contradiction. So ψ satisfies ψ(1) = φ, and if we define ψ(ρ) = { ψ(ρ) if ρ 1 φ if ρ 1, the associated space-time function ( r φ(r,t) = ψ t) solves (EWM) with data equal to the equator map, though it is not equal to the equator map itself. Thus (ii) does not hold true, and neither does (i) by the previous section. 5 Proof of Proposition 4.1 We are considering a smooth profile ψ, such that ψ() = and ψ(1) = φ, and { ( ψ r ) φ(r,t) = t if r t φ if r t. solves (EWM). Our aim is to show that φ satisfies the energy equality (3). We begin with the Claim 5.1 There holds g(φ)g (φ) r L 1 t loc L (r d 1 dr). Proof: Our function is non zero only for r < t. Thus we compute t [ g(φ)g ] (φ) t r r d 1 ψ dr C ( ) r t r r d 1 dr 1 Ct d 4 ψ(s) s s d 1 ds 1 Ct d 4 s d 3 ds Ct d 4. 13
14 Thus g(φ)g (φ) r L (r d 1 dr) Ct d 4, which is a locally integrable function of t for d 3. The proof of the energy equality is now standard. Define the mollification operator by the C function Z, [ f ǫ (x) = f 1 ( ) ] ǫ dz (x). ǫ Notice that this operator is defined for general functions of x, but we can apply it to radial functions, thus depending only on r, too. Now we mollify the equation, and take the L (r d 1 dr) scalar product with φ ǫ t over the truncated cone given by K,T,R = {(r,t) such that t T and r R t}. Thus we have (16) K [ φ tt φ rr d 1 φ r + k ] ǫ r r g(φ)g (φ) φ ǫ tr d 1 drdt =. Of course the idea is to let ǫ go to zero and recover the energy equality (3). It is easily seen that K [ R T φ tt φ rr d 1 ] ǫ φ r φ ǫ r tr d 1 drdt ǫ ( φ r (T)+φ t(t) ) r d 1 dr R ( φ r ()+φ t ()) r d 1 dr ( 1 + φ t + 1 ) φ φ t φ n dσ. S,R,T Only the last summand in (16) is problematic, and we rewrite it as K {r δ} [ ] k ǫ [ ] k ǫ r g(φ)g (φ) φ ǫ t rd 1 drdt+ K {r δ} r g(φ)g (φ) φ ǫ t rd 1 drdt def = I δ,ǫ +II δ,ǫ. The conclusion follows since I δ,ǫ ǫ R T δ R T δ k r g(φ(t)) r d 1 dr + R δ S,R,T \{r δ} R k r g(φ(t)) r d 1 dr k r g(φ()) r d 1 dr k r g(φ) dσ k r g(φ()) r d 1 dr + S,R,T k r g(φ) dσ and ǫ k II δ,ǫ K {r δ} r g(φ)g (φ)φ t r d 1 drdt δ. 14
15 6 Regularity of the profile 6.1 Profiles in Ḣ3/ In this subsection, we prove that if R χ ψ Ḣ3/ (B R 3(,1)) and ψ solves (), then R χ ψ C ( B R d(,1)). It is clear that ψ C ((,1)) so we simply need to examine the points and Smoothness of ψ around Define and observe that M(ρ) = 1 (ρ ρ 4 )ψ (ρ) kg(ψ(ρ)) M (ρ), hence M is decreasing. Assume first that M is bounded at. Then, as is proved in [5], ψ is continuous at and ψ() = or φ. Since M is decreasing, and g is maximal at φ, ψ() = φ is possible only if φ is identically equal to φ. But then R χ ψ does not belong to Ḣ3/. Thus necessarily ψ() =. Then R χ ψ is continuous at, and it satisfies the harmonic map equation from the hyperbolic ball to N. By elliptic regularity (see for instance [1]), R χ ψ is smooth in a neighborhood of. We now assume that M is not bounded at, and we will reach a contradiction. Since g is bounded, and M decreasing, M can be unbounded at if and only if for a constant C and close to ψ (ρ) C ρ. But this implies that r R χ ψ = (ψ (r), ) / L 3 (B R 3(,1)) (the coordinates correspond to the tangent space to N at ψ). This is a contradiction since R χ ψ Ḣ3/ (B R 3(,1)) x R χ ψ Ḣ1/ (B R 3(,1)) L 3 (B R 3(,1)) r R χ ψ = x x xr χ ψ L 3 (B R 3(,1)) Smoothness of ψ near 1 We notice first that if R χ ψ Ḣ3/, ψ is continuous at 1 thus ψ(1) is well-defined. If ψ(1) = φ, regularity can be proved as in [13], Lemma 4.. If ψ(1) =, one can show as in Subsection 4.. that ψ is constant. Thus the only remaining case is g(ψ(1))g (ψ(1)). We will assume that this holds and reach a contradiction. 15
16 Switching to the unknown function we get the new equation ψ(z) = ψ ( ) 1 z, (17) (z 1) ψ (z) = g( ψ(z))g ( ψ(z)) Integrating it twice yields successively Inserting this development in (17) gives ψ (z) g(ψ(1))g (ψ(1))log z 1 as z 1 ψ(z) = ψ(1)+o( z 1 log z 1 ) as z 1. ψ (z) = g(ψ(1))g (ψ(1)) z 1 Integrating this new equation yields ψ (z) = C + g(ψ(1))g (ψ(1)) +O(log z 1 ). log z 1 +D(z) where C is a constant and D (z) log z 1. Since we are considering an equivariant problem around r = 1, the regularity can be studied by reducing matters to the 1-dimensional case. It suffices to observe that but on the other hand (z D(z)) Ḣ1/ loc (R), z log z Ḃ1/, loc (R)\Ḣ1/ loc (R) (this is a simple computation, done in [5]) to conclude that (18) ψ (z) Ḃ 1/, loc (R)\Ḣ1/ loc (R) which is the desired contradiction. 6. Profiles in Ḃ3/, Our claim is that without any further assumptions than the ones of Section 1.1, there exist non-constant profiles such that and R χ ψ solves (WM). R χ ψ Ḃ3/, (R3 ) We sketch the proof, which simply consists of solving the ODE ψ + ρ ψ + kg(ψ)g (ψ) = ρ (1 ρ ) ψ() = = ψ (l 1) () = ψ (l) () = α (see [3], Lemma.5). One gets a solution which is smooth on [,1). We see as in (18) that ψ is in Ḃ3/, around 1. This concludes the proof. 16
17 7 Proof of Proposition 1.1 Let us recall the statement of Proposition 1.1: we aim at proving that if ψ is locally integrable, and smooth at, ( ) x u(x,t) = R χ ψ t solves the wave-map equation if and only if ψ solves (19) ρ (1 ρ )ψ (ρ)+ρ((d 1) ρ )ψ (ρ) kg(ψ)g (ψ) = classically on (,1) (1, ) and furthermore 7.1 From the PDE to the ODE ψ(1 ) = ψ(1 + ). A first step consists in proving that u as defined above solves (WM) for t > if and only if ψ solves (19) in S. This can be done in a straightforward manner, we refer to [5] for a proof in a less general situation. What remains is to see that the above ODE is solved in S if and only if it is solved classically on (,1) (1, ) and furthermore ψ(1 ) = ψ(1 + ). This is the aim of the next subsection. 7. Condition for solving the ODE in S (,1) Solving (19) in S or in the classical sense is equivalent in (,1) and (1, ). We now examine the situation of ρ = 1. The equation can be written away from 1 as ( ) d ρ d 1 ψ ρ d 3 = dρ (ρ 1) d 3 (ρ 1) d 1 kg(ψ)g (ψ). Integrating it starting from say 1/ or 3/, to ρ, gives { 1 () ψ C log(ρ 1) if d = 3 (ρ) (ρ 1) d 3 C + if d 4. C ρ 1 d 3 In any case, ψ is integrable on (,1) (1, ), and ψ is left and right-continuous at 1. Set ψ can be written as a def = ψ(1 + ) ψ(1 ). (1) ψ = ξ +aδ 1, where ξ belongs to L 1 and δ 1 is a Dirac weight at ρ = 1. Since (19) holds in the classical sense away from 1, we see that it holds in S (, ) if and only if for any f S, lim ǫ 1+ǫ 1 ǫ [ ρ (1 ρ )ψ (ρ)+ρ((d 1) ρ )ψ (ρ) kg(ψ)g (ψ) ] f(ρ)dρ = 17
18 (where the integral is to be understood in the distribution sense). Using the previous discussion, this can be rewritten as or, integrating by parts, (d 3)af(1)+ lim ǫ 1+ǫ 1 ǫ [ (d 3)af(1)+ lim ψ ρ (1 ρ )f ] 1+ǫ 1+ǫ ǫ 1 ǫ ρ (1 ρ )ψ (ρ)f(ρ)dρ = 1 ǫ which, by the estimates () and ([?]), is equivalent to (d 1)af(1) =. Thus we get a =, which is the desired result. ψ d dρ (ρ (1 ρ )f)dρ = Acknowledgements: The author is indebted to Jalal Shatah for very interesting discussions during the writing of this article. References [1] A. Baldes, Stability and uniqueness properties of the equator map from a ball into an ellipsoid Math. Z. 185 (1984), no. 4, [] N. Burq, F. Planchon, J. Stalker, S. Tahvildar-Zadeh, Strichartz estimates for the wave and Schrdinger equations with the inverse-square potential J. Funct. Anal. 3 (3), no., [3] T. Cazenave, J. Shatah, S. Tahvildar-Zadeh, Harmonic maps of the hyperbolic space and development of singularities in wave maps and Yang-Mills fields Ann. Inst. H. Poincar Phys. Thor. 68 (1998), no. 3, [4] A. Freire, Global weak solutions of the wave map system to compact homogeneous spaces, Manuscripta Math. 91 (1996), no. 4, [5] P. Germain, Besov spaces and self-similar solutions for the wave-map equation, to appear in Comm. P. D. E. [6] F. Hélein, Regularity and uniqueness of harmonic maps into an ellipsoid Manuscripta Math. 6 (1988), no., [7] W. Jäger, H. Kaul, Rotationally symmetric harmonic maps from a ball into a sphere and the regularity problem for weak solutions of elliptic systems J. Reine Angew. Math. 343 (1983), [8] M. Jungen, On equivariant self-similar wave maps, NoDEA Nonlinear Differential Equations Appl. 13 (6), no. 4, [9] J. Krieger, Global regularity and singularity development for wave maps., to appear in Surveys in Difftl. Geometry 18
19 [1] O. Ladyzhenskaya, N. Ural tseva, Linear and quasilinear elliptic equations Academic Press, New York-London (1968) [11] F. Planchon, J. Stalker, S. Tahvildar-Zadeh, L p estimates for the wave equation with the inverse-square potential. Discrete Contin. Dyn. Syst. 9 (3), no., [1] J. Shatah, Weak solutions and development of singularities of the SU() σ-model Comm. Pure Appl. Math. 41 (1988), no. 4, [13] J. Shatah, S. Tahvildar-Zadeh, On the Cauchy problem for equivariant wave maps Comm. Pure Appl. Math. 47 (1994), no. 5, [14] M. Struwe, Uniqueness for critical nonlinear wave equations and wave maps via the energy inequality Comm. Pure Appl. Math. 5 (1999), no. 9, [15] T. Tao, Global regularity of wave maps. II. Small energy in two dimensions Comm. Math. Phys. 4 (1), no.,
BIHARMONIC WAVE MAPS INTO SPHERES
 BIHARMONIC WAVE MAPS INTO SPHERES SEBASTIAN HERR, TOBIAS LAMM, AND ROLAND SCHNAUBELT Abstract. A global weak solution of the biharmonic wave map equation in the energy space for spherical targets is constructed.
BIHARMONIC WAVE MAPS INTO SPHERES SEBASTIAN HERR, TOBIAS LAMM, AND ROLAND SCHNAUBELT Abstract. A global weak solution of the biharmonic wave map equation in the energy space for spherical targets is constructed.
Equivariant self-similar wave maps from Minkowski spacetime into 3-sphere
 Equivariant self-similar wave maps from Minkowski spacetime into 3-sphere arxiv:math-ph/99126v1 17 Oct 1999 Piotr Bizoń Institute of Physics, Jagellonian University, Kraków, Poland March 26, 28 Abstract
Equivariant self-similar wave maps from Minkowski spacetime into 3-sphere arxiv:math-ph/99126v1 17 Oct 1999 Piotr Bizoń Institute of Physics, Jagellonian University, Kraków, Poland March 26, 28 Abstract
Non-radial solutions to a bi-harmonic equation with negative exponent
 Non-radial solutions to a bi-harmonic equation with negative exponent Ali Hyder Department of Mathematics, University of British Columbia, Vancouver BC V6TZ2, Canada ali.hyder@math.ubc.ca Juncheng Wei
Non-radial solutions to a bi-harmonic equation with negative exponent Ali Hyder Department of Mathematics, University of British Columbia, Vancouver BC V6TZ2, Canada ali.hyder@math.ubc.ca Juncheng Wei
Global well-posedness for semi-linear Wave and Schrödinger equations. Slim Ibrahim
 Global well-posedness for semi-linear Wave and Schrödinger equations Slim Ibrahim McMaster University, Hamilton ON University of Calgary, April 27th, 2006 1 1 Introduction Nonlinear Wave equation: ( 2
Global well-posedness for semi-linear Wave and Schrödinger equations Slim Ibrahim McMaster University, Hamilton ON University of Calgary, April 27th, 2006 1 1 Introduction Nonlinear Wave equation: ( 2
THE WAVE EQUATION. d = 1: D Alembert s formula We begin with the initial value problem in 1 space dimension { u = utt u xx = 0, in (0, ) R, (2)
 THE WAVE EQUATION () The free wave equation takes the form u := ( t x )u = 0, u : R t R d x R In the literature, the operator := t x is called the D Alembertian on R +d. Later we shall also consider the
THE WAVE EQUATION () The free wave equation takes the form u := ( t x )u = 0, u : R t R d x R In the literature, the operator := t x is called the D Alembertian on R +d. Later we shall also consider the
Long-term dynamics of nonlinear wave equations
 Long-term dynamics of nonlinear wave equations W. Schlag (University of Chicago) Recent Developments & Future Directions, September 2014 Wave maps Let (M, g) be a Riemannian manifold, and u : R 1+d t,x
Long-term dynamics of nonlinear wave equations W. Schlag (University of Chicago) Recent Developments & Future Directions, September 2014 Wave maps Let (M, g) be a Riemannian manifold, and u : R 1+d t,x
Blow-up on manifolds with symmetry for the nonlinear Schröding
 Blow-up on manifolds with symmetry for the nonlinear Schrödinger equation March, 27 2013 Université de Nice Euclidean L 2 -critical theory Consider the one dimensional equation i t u + u = u 4 u, t > 0,
Blow-up on manifolds with symmetry for the nonlinear Schrödinger equation March, 27 2013 Université de Nice Euclidean L 2 -critical theory Consider the one dimensional equation i t u + u = u 4 u, t > 0,
Solutions to the Nonlinear Schrödinger Equation in Hyperbolic Space
 Solutions to the Nonlinear Schrödinger Equation in Hyperbolic Space SPUR Final Paper, Summer 2014 Peter Kleinhenz Mentor: Chenjie Fan Project suggested by Gigliola Staffilani July 30th, 2014 Abstract In
Solutions to the Nonlinear Schrödinger Equation in Hyperbolic Space SPUR Final Paper, Summer 2014 Peter Kleinhenz Mentor: Chenjie Fan Project suggested by Gigliola Staffilani July 30th, 2014 Abstract In
Inégalités de dispersion via le semi-groupe de la chaleur
 Inégalités de dispersion via le semi-groupe de la chaleur Valentin Samoyeau, Advisor: Frédéric Bernicot. Laboratoire de Mathématiques Jean Leray, Université de Nantes January 28, 2016 1 Introduction Schrödinger
Inégalités de dispersion via le semi-groupe de la chaleur Valentin Samoyeau, Advisor: Frédéric Bernicot. Laboratoire de Mathématiques Jean Leray, Université de Nantes January 28, 2016 1 Introduction Schrödinger
DETERMINATION OF THE BLOW-UP RATE FOR THE SEMILINEAR WAVE EQUATION
 DETERMINATION OF THE LOW-UP RATE FOR THE SEMILINEAR WAVE EQUATION y FRANK MERLE and HATEM ZAAG Abstract. In this paper, we find the optimal blow-up rate for the semilinear wave equation with a power nonlinearity.
DETERMINATION OF THE LOW-UP RATE FOR THE SEMILINEAR WAVE EQUATION y FRANK MERLE and HATEM ZAAG Abstract. In this paper, we find the optimal blow-up rate for the semilinear wave equation with a power nonlinearity.
Heat equations with singular potentials: Hardy & Carleman inequalities, well-posedness & control
 Outline Heat equations with singular potentials: Hardy & Carleman inequalities, well-posedness & control IMDEA-Matemáticas & Universidad Autónoma de Madrid Spain enrique.zuazua@uam.es Analysis and control
Outline Heat equations with singular potentials: Hardy & Carleman inequalities, well-posedness & control IMDEA-Matemáticas & Universidad Autónoma de Madrid Spain enrique.zuazua@uam.es Analysis and control
The harmonic map flow
 Chapter 2 The harmonic map flow 2.1 Definition of the flow The harmonic map flow was introduced by Eells-Sampson in 1964; their work could be considered the start of the field of geometric flows. The flow
Chapter 2 The harmonic map flow 2.1 Definition of the flow The harmonic map flow was introduced by Eells-Sampson in 1964; their work could be considered the start of the field of geometric flows. The flow
Math The Laplacian. 1 Green s Identities, Fundamental Solution
 Math. 209 The Laplacian Green s Identities, Fundamental Solution Let be a bounded open set in R n, n 2, with smooth boundary. The fact that the boundary is smooth means that at each point x the external
Math. 209 The Laplacian Green s Identities, Fundamental Solution Let be a bounded open set in R n, n 2, with smooth boundary. The fact that the boundary is smooth means that at each point x the external
On m-accretive Schrödinger operators in L p -spaces on manifolds of bounded geometry
 On m-accretive Schrödinger operators in L p -spaces on manifolds of bounded geometry Ognjen Milatovic Department of Mathematics and Statistics University of North Florida Jacksonville, FL 32224 USA. Abstract
On m-accretive Schrödinger operators in L p -spaces on manifolds of bounded geometry Ognjen Milatovic Department of Mathematics and Statistics University of North Florida Jacksonville, FL 32224 USA. Abstract
Recent developments on the global behavior to critical nonlinear dispersive equations. Carlos E. Kenig
 Recent developments on the global behavior to critical nonlinear dispersive equations Carlos E. Kenig In the last 25 years or so, there has been considerable interest in the study of non-linear partial
Recent developments on the global behavior to critical nonlinear dispersive equations Carlos E. Kenig In the last 25 years or so, there has been considerable interest in the study of non-linear partial
CONCENTRATION COMPACTNESS FOR CRITICAL WAVE MAPS, BY JOACHIM KRIEGER AND WILHELM SCHLAG
 CONCENTRATION COMPACTNESS FOR CRITICAL WAVE MAPS, BY JOACHIM KRIEGER AND WILHELM SCHLAG Imagine a perfectly elastic d-dimensional sheet, infinite in extent, immersed (possibly with self-intersection) in
CONCENTRATION COMPACTNESS FOR CRITICAL WAVE MAPS, BY JOACHIM KRIEGER AND WILHELM SCHLAG Imagine a perfectly elastic d-dimensional sheet, infinite in extent, immersed (possibly with self-intersection) in
On the distance between homotopy classes of maps between spheres
 On the distance between homotopy classes of maps between spheres Shay Levi and Itai Shafrir February 18, 214 Department of Mathematics, Technion - I.I.T., 32 Haifa, ISRAEL Dedicated with great respect
On the distance between homotopy classes of maps between spheres Shay Levi and Itai Shafrir February 18, 214 Department of Mathematics, Technion - I.I.T., 32 Haifa, ISRAEL Dedicated with great respect
DECAY ESTIMATES FOR THE KLEIN-GORDON EQUATION IN CURVED SPACETIME
 Electronic Journal of Differential Equations, Vol. 218 218), No. 17, pp. 1 9. ISSN: 172-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu DECAY ESTIMATES FOR THE KLEIN-GORDON EQUATION
Electronic Journal of Differential Equations, Vol. 218 218), No. 17, pp. 1 9. ISSN: 172-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu DECAY ESTIMATES FOR THE KLEIN-GORDON EQUATION
Exact Solutions of the Einstein Equations
 Notes from phz 6607, Special and General Relativity University of Florida, Fall 2004, Detweiler Exact Solutions of the Einstein Equations These notes are not a substitute in any manner for class lectures.
Notes from phz 6607, Special and General Relativity University of Florida, Fall 2004, Detweiler Exact Solutions of the Einstein Equations These notes are not a substitute in any manner for class lectures.
A REMARK ON AN EQUATION OF WAVE MAPS TYPE WITH VARIABLE COEFFICIENTS
 A REMARK ON AN EQUATION OF WAVE MAPS TYPE WITH VARIABLE COEFFICIENTS DAN-ANDREI GEBA Abstract. We obtain a sharp local well-posedness result for an equation of wave maps type with variable coefficients.
A REMARK ON AN EQUATION OF WAVE MAPS TYPE WITH VARIABLE COEFFICIENTS DAN-ANDREI GEBA Abstract. We obtain a sharp local well-posedness result for an equation of wave maps type with variable coefficients.
REMARKS ON THE VANISHING OBSTACLE LIMIT FOR A 3D VISCOUS INCOMPRESSIBLE FLUID
 REMARKS ON THE VANISHING OBSTACLE LIMIT FOR A 3D VISCOUS INCOMPRESSIBLE FLUID DRAGOŞ IFTIMIE AND JAMES P. KELLIHER Abstract. In [Math. Ann. 336 (2006), 449-489] the authors consider the two dimensional
REMARKS ON THE VANISHING OBSTACLE LIMIT FOR A 3D VISCOUS INCOMPRESSIBLE FLUID DRAGOŞ IFTIMIE AND JAMES P. KELLIHER Abstract. In [Math. Ann. 336 (2006), 449-489] the authors consider the two dimensional
A Variational Analysis of a Gauged Nonlinear Schrödinger Equation
 A Variational Analysis of a Gauged Nonlinear Schrödinger Equation Alessio Pomponio, joint work with David Ruiz Dipartimento di Meccanica, Matematica e Management, Politecnico di Bari Variational and Topological
A Variational Analysis of a Gauged Nonlinear Schrödinger Equation Alessio Pomponio, joint work with David Ruiz Dipartimento di Meccanica, Matematica e Management, Politecnico di Bari Variational and Topological
CUTOFF RESOLVENT ESTIMATES AND THE SEMILINEAR SCHRÖDINGER EQUATION
 CUTOFF RESOLVENT ESTIMATES AND THE SEMILINEAR SCHRÖDINGER EQUATION HANS CHRISTIANSON Abstract. This paper shows how abstract resolvent estimates imply local smoothing for solutions to the Schrödinger equation.
CUTOFF RESOLVENT ESTIMATES AND THE SEMILINEAR SCHRÖDINGER EQUATION HANS CHRISTIANSON Abstract. This paper shows how abstract resolvent estimates imply local smoothing for solutions to the Schrödinger equation.
Laplace s Equation. Chapter Mean Value Formulas
 Chapter 1 Laplace s Equation Let be an open set in R n. A function u C 2 () is called harmonic in if it satisfies Laplace s equation n (1.1) u := D ii u = 0 in. i=1 A function u C 2 () is called subharmonic
Chapter 1 Laplace s Equation Let be an open set in R n. A function u C 2 () is called harmonic in if it satisfies Laplace s equation n (1.1) u := D ii u = 0 in. i=1 A function u C 2 () is called subharmonic
Minimization problems on the Hardy-Sobolev inequality
 manuscript No. (will be inserted by the editor) Minimization problems on the Hardy-Sobolev inequality Masato Hashizume Received: date / Accepted: date Abstract We study minimization problems on Hardy-Sobolev
manuscript No. (will be inserted by the editor) Minimization problems on the Hardy-Sobolev inequality Masato Hashizume Received: date / Accepted: date Abstract We study minimization problems on Hardy-Sobolev
ON WEAKLY NONLINEAR BACKWARD PARABOLIC PROBLEM
 ON WEAKLY NONLINEAR BACKWARD PARABOLIC PROBLEM OLEG ZUBELEVICH DEPARTMENT OF MATHEMATICS THE BUDGET AND TREASURY ACADEMY OF THE MINISTRY OF FINANCE OF THE RUSSIAN FEDERATION 7, ZLATOUSTINSKY MALIY PER.,
ON WEAKLY NONLINEAR BACKWARD PARABOLIC PROBLEM OLEG ZUBELEVICH DEPARTMENT OF MATHEMATICS THE BUDGET AND TREASURY ACADEMY OF THE MINISTRY OF FINANCE OF THE RUSSIAN FEDERATION 7, ZLATOUSTINSKY MALIY PER.,
Applied Math Qualifying Exam 11 October Instructions: Work 2 out of 3 problems in each of the 3 parts for a total of 6 problems.
 Printed Name: Signature: Applied Math Qualifying Exam 11 October 2014 Instructions: Work 2 out of 3 problems in each of the 3 parts for a total of 6 problems. 2 Part 1 (1) Let Ω be an open subset of R
Printed Name: Signature: Applied Math Qualifying Exam 11 October 2014 Instructions: Work 2 out of 3 problems in each of the 3 parts for a total of 6 problems. 2 Part 1 (1) Let Ω be an open subset of R
Isoperimetric Inequalities for the Cauchy-Dirichlet Heat Operator
 Filomat 32:3 (218), 885 892 https://doi.org/1.2298/fil183885k Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Isoperimetric Inequalities
Filomat 32:3 (218), 885 892 https://doi.org/1.2298/fil183885k Published by Faculty of Sciences and Mathematics, University of Niš, Serbia Available at: http://www.pmf.ni.ac.rs/filomat Isoperimetric Inequalities
Two dimensional exterior mixed problem for semilinear damped wave equations
 J. Math. Anal. Appl. 31 (25) 366 377 www.elsevier.com/locate/jmaa Two dimensional exterior mixed problem for semilinear damped wave equations Ryo Ikehata 1 Department of Mathematics, Graduate School of
J. Math. Anal. Appl. 31 (25) 366 377 www.elsevier.com/locate/jmaa Two dimensional exterior mixed problem for semilinear damped wave equations Ryo Ikehata 1 Department of Mathematics, Graduate School of
SYMMETRY OF POSITIVE SOLUTIONS OF SOME NONLINEAR EQUATIONS. M. Grossi S. Kesavan F. Pacella M. Ramaswamy. 1. Introduction
 Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 12, 1998, 47 59 SYMMETRY OF POSITIVE SOLUTIONS OF SOME NONLINEAR EQUATIONS M. Grossi S. Kesavan F. Pacella M. Ramaswamy
Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 12, 1998, 47 59 SYMMETRY OF POSITIVE SOLUTIONS OF SOME NONLINEAR EQUATIONS M. Grossi S. Kesavan F. Pacella M. Ramaswamy
Scattering theory for nonlinear Schrödinger equation with inverse square potential
 Scattering theory for nonlinear Schrödinger equation with inverse square potential Université Nice Sophia-Antipolis Based on joint work with: Changxing Miao (IAPCM) and Junyong Zhang (BIT) February -6,
Scattering theory for nonlinear Schrödinger equation with inverse square potential Université Nice Sophia-Antipolis Based on joint work with: Changxing Miao (IAPCM) and Junyong Zhang (BIT) February -6,
2 A Model, Harmonic Map, Problem
 ELLIPTIC SYSTEMS JOHN E. HUTCHINSON Department of Mathematics School of Mathematical Sciences, A.N.U. 1 Introduction Elliptic equations model the behaviour of scalar quantities u, such as temperature or
ELLIPTIC SYSTEMS JOHN E. HUTCHINSON Department of Mathematics School of Mathematical Sciences, A.N.U. 1 Introduction Elliptic equations model the behaviour of scalar quantities u, such as temperature or
Partial regularity for suitable weak solutions to Navier-Stokes equations
 Partial regularity for suitable weak solutions to Navier-Stokes equations Yanqing Wang Capital Normal University Joint work with: Quansen Jiu, Gang Wu Contents 1 What is the partial regularity? 2 Review
Partial regularity for suitable weak solutions to Navier-Stokes equations Yanqing Wang Capital Normal University Joint work with: Quansen Jiu, Gang Wu Contents 1 What is the partial regularity? 2 Review
SYMMETRY RESULTS FOR PERTURBED PROBLEMS AND RELATED QUESTIONS. Massimo Grosi Filomena Pacella S. L. Yadava. 1. Introduction
 Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 21, 2003, 211 226 SYMMETRY RESULTS FOR PERTURBED PROBLEMS AND RELATED QUESTIONS Massimo Grosi Filomena Pacella S.
Topological Methods in Nonlinear Analysis Journal of the Juliusz Schauder Center Volume 21, 2003, 211 226 SYMMETRY RESULTS FOR PERTURBED PROBLEMS AND RELATED QUESTIONS Massimo Grosi Filomena Pacella S.
Analysis in weighted spaces : preliminary version
 Analysis in weighted spaces : preliminary version Frank Pacard To cite this version: Frank Pacard. Analysis in weighted spaces : preliminary version. 3rd cycle. Téhéran (Iran, 2006, pp.75.
Analysis in weighted spaces : preliminary version Frank Pacard To cite this version: Frank Pacard. Analysis in weighted spaces : preliminary version. 3rd cycle. Téhéran (Iran, 2006, pp.75.
at time t, in dimension d. The index i varies in a countable set I. We call configuration the family, denoted generically by Φ: U (x i (t) x j (t))
 Notations In this chapter we investigate infinite systems of interacting particles subject to Newtonian dynamics Each particle is characterized by its position an velocity x i t, v i t R d R d at time
Notations In this chapter we investigate infinite systems of interacting particles subject to Newtonian dynamics Each particle is characterized by its position an velocity x i t, v i t R d R d at time
MULTIPLE SOLUTIONS FOR THE p-laplace EQUATION WITH NONLINEAR BOUNDARY CONDITIONS
 Electronic Journal of Differential Equations, Vol. 2006(2006), No. 37, pp. 1 7. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) MULTIPLE
Electronic Journal of Differential Equations, Vol. 2006(2006), No. 37, pp. 1 7. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) MULTIPLE
Existence of a ground state and blow-up problem for a nonlinear Schrödinger equation with critical growth
 Existence of a ground state and blow-up problem for a nonlinear Schrödinger equation with critical growth Takafumi Akahori, Slim Ibrahim, Hiroaki Kikuchi and Hayato Nawa 1 Introduction In this paper, we
Existence of a ground state and blow-up problem for a nonlinear Schrödinger equation with critical growth Takafumi Akahori, Slim Ibrahim, Hiroaki Kikuchi and Hayato Nawa 1 Introduction In this paper, we
EXISTENCE AND REGULARITY RESULTS FOR SOME NONLINEAR PARABOLIC EQUATIONS
 EXISTECE AD REGULARITY RESULTS FOR SOME OLIEAR PARABOLIC EUATIOS Lucio BOCCARDO 1 Andrea DALL AGLIO 2 Thierry GALLOUËT3 Luigi ORSIA 1 Abstract We prove summability results for the solutions of nonlinear
EXISTECE AD REGULARITY RESULTS FOR SOME OLIEAR PARABOLIC EUATIOS Lucio BOCCARDO 1 Andrea DALL AGLIO 2 Thierry GALLOUËT3 Luigi ORSIA 1 Abstract We prove summability results for the solutions of nonlinear
arxiv: v1 [math.fa] 26 Jan 2017
![arxiv: v1 [math.fa] 26 Jan 2017 arxiv: v1 [math.fa] 26 Jan 2017](/thumbs/82/85912765.jpg) WEAK APPROXIMATION BY BOUNDED SOBOLEV MAPS WITH VALUES INTO COMPLETE MANIFOLDS PIERRE BOUSQUET, AUGUSTO C. PONCE, AND JEAN VAN SCHAFTINGEN arxiv:1701.07627v1 [math.fa] 26 Jan 2017 Abstract. We have recently
WEAK APPROXIMATION BY BOUNDED SOBOLEV MAPS WITH VALUES INTO COMPLETE MANIFOLDS PIERRE BOUSQUET, AUGUSTO C. PONCE, AND JEAN VAN SCHAFTINGEN arxiv:1701.07627v1 [math.fa] 26 Jan 2017 Abstract. We have recently
arxiv: v2 [math.ap] 6 Sep 2007
![arxiv: v2 [math.ap] 6 Sep 2007 arxiv: v2 [math.ap] 6 Sep 2007](/thumbs/94/119011604.jpg) ON THE REGULARITY OF WEAK SOLUTIONS OF THE 3D NAVIER-STOKES EQUATIONS IN B 1, arxiv:0708.3067v2 [math.ap] 6 Sep 2007 A. CHESKIDOV AND R. SHVYDKOY ABSTRACT. We show that if a Leray-Hopf solution u to the
ON THE REGULARITY OF WEAK SOLUTIONS OF THE 3D NAVIER-STOKES EQUATIONS IN B 1, arxiv:0708.3067v2 [math.ap] 6 Sep 2007 A. CHESKIDOV AND R. SHVYDKOY ABSTRACT. We show that if a Leray-Hopf solution u to the
Nonlinear stabilization via a linear observability
 via a linear observability Kaïs Ammari Department of Mathematics University of Monastir Joint work with Fathia Alabau-Boussouira Collocated feedback stabilization Outline 1 Introduction and main result
via a linear observability Kaïs Ammari Department of Mathematics University of Monastir Joint work with Fathia Alabau-Boussouira Collocated feedback stabilization Outline 1 Introduction and main result
WELL-POSEDNESS OF THE TWO-DIMENSIONAL GENERALIZED BENJAMIN-BONA-MAHONY EQUATION ON THE UPPER HALF PLANE
 WELL-POSEDNESS OF THE TWO-DIMENSIONAL GENERALIZED BENJAMIN-BONA-MAHONY EQUATION ON THE UPPER HALF PLANE YING-CHIEH LIN, C. H. ARTHUR CHENG, JOHN M. HONG, JIAHONG WU, AND JUAN-MING YUAN Abstract. This paper
WELL-POSEDNESS OF THE TWO-DIMENSIONAL GENERALIZED BENJAMIN-BONA-MAHONY EQUATION ON THE UPPER HALF PLANE YING-CHIEH LIN, C. H. ARTHUR CHENG, JOHN M. HONG, JIAHONG WU, AND JUAN-MING YUAN Abstract. This paper
BLOWUP THEORY FOR THE CRITICAL NONLINEAR SCHRÖDINGER EQUATIONS REVISITED
 BLOWUP THEORY FOR THE CRITICAL NONLINEAR SCHRÖDINGER EQUATIONS REVISITED TAOUFIK HMIDI AND SAHBI KERAANI Abstract. In this note we prove a refined version of compactness lemma adapted to the blowup analysis
BLOWUP THEORY FOR THE CRITICAL NONLINEAR SCHRÖDINGER EQUATIONS REVISITED TAOUFIK HMIDI AND SAHBI KERAANI Abstract. In this note we prove a refined version of compactness lemma adapted to the blowup analysis
Inequalities for the ADM-mass and capacity of asymptotically flat manifolds with minimal boundary
 Inequalities for the ADM-mass and capacity of asymptotically flat manifolds with minimal boundary Fernando Schwartz Abstract. We present some recent developments involving inequalities for the ADM-mass
Inequalities for the ADM-mass and capacity of asymptotically flat manifolds with minimal boundary Fernando Schwartz Abstract. We present some recent developments involving inequalities for the ADM-mass
Foliations of hyperbolic space by constant mean curvature surfaces sharing ideal boundary
 Foliations of hyperbolic space by constant mean curvature surfaces sharing ideal boundary David Chopp and John A. Velling December 1, 2003 Abstract Let γ be a Jordan curve in S 2, considered as the ideal
Foliations of hyperbolic space by constant mean curvature surfaces sharing ideal boundary David Chopp and John A. Velling December 1, 2003 Abstract Let γ be a Jordan curve in S 2, considered as the ideal
DISPERSIVE EQUATIONS: A SURVEY
 DISPERSIVE EQUATIONS: A SURVEY GIGLIOLA STAFFILANI 1. Introduction These notes were written as a guideline for a short talk; hence, the references and the statements of the theorems are often not given
DISPERSIVE EQUATIONS: A SURVEY GIGLIOLA STAFFILANI 1. Introduction These notes were written as a guideline for a short talk; hence, the references and the statements of the theorems are often not given
arxiv: v1 [math.ap] 6 May 2010
![arxiv: v1 [math.ap] 6 May 2010 arxiv: v1 [math.ap] 6 May 2010](/thumbs/88/117715564.jpg) A CONTINUITY ARGUMENT FOR A SEMILINEAR SKYRME MODEL arxiv:005.095v [math.ap] 6 May 00 DAN-ANDREI GEBA AND S. G. RAJEEV Abstract. We investigate a semilinear modification for the wave map problem proposed
A CONTINUITY ARGUMENT FOR A SEMILINEAR SKYRME MODEL arxiv:005.095v [math.ap] 6 May 00 DAN-ANDREI GEBA AND S. G. RAJEEV Abstract. We investigate a semilinear modification for the wave map problem proposed
VANISHING-CONCENTRATION-COMPACTNESS ALTERNATIVE FOR THE TRUDINGER-MOSER INEQUALITY IN R N
 VAISHIG-COCETRATIO-COMPACTESS ALTERATIVE FOR THE TRUDIGER-MOSER IEQUALITY I R Abstract. Let 2, a > 0 0 < b. Our aim is to clarify the influence of the constraint S a,b = { u W 1, (R ) u a + u b = 1 } on
VAISHIG-COCETRATIO-COMPACTESS ALTERATIVE FOR THE TRUDIGER-MOSER IEQUALITY I R Abstract. Let 2, a > 0 0 < b. Our aim is to clarify the influence of the constraint S a,b = { u W 1, (R ) u a + u b = 1 } on
THE FORM SUM AND THE FRIEDRICHS EXTENSION OF SCHRÖDINGER-TYPE OPERATORS ON RIEMANNIAN MANIFOLDS
 THE FORM SUM AND THE FRIEDRICHS EXTENSION OF SCHRÖDINGER-TYPE OPERATORS ON RIEMANNIAN MANIFOLDS OGNJEN MILATOVIC Abstract. We consider H V = M +V, where (M, g) is a Riemannian manifold (not necessarily
THE FORM SUM AND THE FRIEDRICHS EXTENSION OF SCHRÖDINGER-TYPE OPERATORS ON RIEMANNIAN MANIFOLDS OGNJEN MILATOVIC Abstract. We consider H V = M +V, where (M, g) is a Riemannian manifold (not necessarily
Symmetry and monotonicity of least energy solutions
 Symmetry and monotonicity of least energy solutions Jaeyoung BYEO, Louis JEAJEA and Mihai MARIŞ Abstract We give a simple proof of the fact that for a large class of quasilinear elliptic equations and
Symmetry and monotonicity of least energy solutions Jaeyoung BYEO, Louis JEAJEA and Mihai MARIŞ Abstract We give a simple proof of the fact that for a large class of quasilinear elliptic equations and
COMBINED EFFECTS FOR A STATIONARY PROBLEM WITH INDEFINITE NONLINEARITIES AND LACK OF COMPACTNESS
 Dynamic Systems and Applications 22 (203) 37-384 COMBINED EFFECTS FOR A STATIONARY PROBLEM WITH INDEFINITE NONLINEARITIES AND LACK OF COMPACTNESS VICENŢIU D. RĂDULESCU Simion Stoilow Mathematics Institute
Dynamic Systems and Applications 22 (203) 37-384 COMBINED EFFECTS FOR A STATIONARY PROBLEM WITH INDEFINITE NONLINEARITIES AND LACK OF COMPACTNESS VICENŢIU D. RĂDULESCU Simion Stoilow Mathematics Institute
On the role of geometry in scattering theory for nonlinear Schrödinger equations
 On the role of geometry in scattering theory for nonlinear Schrödinger equations Rémi Carles (CNRS & Université Montpellier 2) Orléans, April 9, 2008 Free Schrödinger equation on R n : i t u + 1 2 u =
On the role of geometry in scattering theory for nonlinear Schrödinger equations Rémi Carles (CNRS & Université Montpellier 2) Orléans, April 9, 2008 Free Schrödinger equation on R n : i t u + 1 2 u =
A LOWER BOUND FOR THE GRADIENT OF -HARMONIC FUNCTIONS Edi Rosset. 1. Introduction. u xi u xj u xi x j
 Electronic Journal of Differential Equations, Vol. 1996(1996) No. 0, pp. 1 7. ISSN 107-6691. URL: http://ejde.math.swt.edu (147.6.103.110) telnet (login: ejde), ftp, and gopher access: ejde.math.swt.edu
Electronic Journal of Differential Equations, Vol. 1996(1996) No. 0, pp. 1 7. ISSN 107-6691. URL: http://ejde.math.swt.edu (147.6.103.110) telnet (login: ejde), ftp, and gopher access: ejde.math.swt.edu
BRUNN MINKOWSKI AND ISOPERIMETRIC INEQUALITY IN THE HEISENBERG GROUP
 Annales Academiæ Scientiarum Fennicæ Mathematica Volumen 28, 23, 99 19 BRUNN MINKOWSKI AND ISOPERIMETRIC INEQUALITY IN THE HEISENBERG GROUP Roberto Monti Universität Bern, Mathematisches Institut Sidlerstrasse
Annales Academiæ Scientiarum Fennicæ Mathematica Volumen 28, 23, 99 19 BRUNN MINKOWSKI AND ISOPERIMETRIC INEQUALITY IN THE HEISENBERG GROUP Roberto Monti Universität Bern, Mathematisches Institut Sidlerstrasse
arxiv: v1 [math.ap] 5 Nov 2018
![arxiv: v1 [math.ap] 5 Nov 2018 arxiv: v1 [math.ap] 5 Nov 2018](/thumbs/89/100785953.jpg) STRONG CONTINUITY FOR THE 2D EULER EQUATIONS GIANLUCA CRIPPA, ELIZAVETA SEMENOVA, AND STEFANO SPIRITO arxiv:1811.01553v1 [math.ap] 5 Nov 2018 Abstract. We prove two results of strong continuity with respect
STRONG CONTINUITY FOR THE 2D EULER EQUATIONS GIANLUCA CRIPPA, ELIZAVETA SEMENOVA, AND STEFANO SPIRITO arxiv:1811.01553v1 [math.ap] 5 Nov 2018 Abstract. We prove two results of strong continuity with respect
GLOBAL EXISTENCE FOR THE ONE-DIMENSIONAL SEMILINEAR TRICOMI-TYPE EQUATIONS
 GLOBAL EXISTENCE FOR THE ONE-DIMENSIONAL SEMILINEAR TRICOMI-TYPE EQUATIONS ANAHIT GALSTYAN The Tricomi equation u tt tu xx = 0 is a linear partial differential operator of mixed type. (For t > 0, the Tricomi
GLOBAL EXISTENCE FOR THE ONE-DIMENSIONAL SEMILINEAR TRICOMI-TYPE EQUATIONS ANAHIT GALSTYAN The Tricomi equation u tt tu xx = 0 is a linear partial differential operator of mixed type. (For t > 0, the Tricomi
A LOWER BOUND ON BLOWUP RATES FOR THE 3D INCOMPRESSIBLE EULER EQUATION AND A SINGLE EXPONENTIAL BEALE-KATO-MAJDA ESTIMATE. 1.
 A LOWER BOUND ON BLOWUP RATES FOR THE 3D INCOMPRESSIBLE EULER EQUATION AND A SINGLE EXPONENTIAL BEALE-KATO-MAJDA ESTIMATE THOMAS CHEN AND NATAŠA PAVLOVIĆ Abstract. We prove a Beale-Kato-Majda criterion
A LOWER BOUND ON BLOWUP RATES FOR THE 3D INCOMPRESSIBLE EULER EQUATION AND A SINGLE EXPONENTIAL BEALE-KATO-MAJDA ESTIMATE THOMAS CHEN AND NATAŠA PAVLOVIĆ Abstract. We prove a Beale-Kato-Majda criterion
Asymptotic Behavior of Marginally Trapped Tubes
 Asymptotic Behavior of Marginally Trapped Tubes Catherine Williams January 29, 2009 Preliminaries general relativity General relativity says that spacetime is described by a Lorentzian 4-manifold (M, g)
Asymptotic Behavior of Marginally Trapped Tubes Catherine Williams January 29, 2009 Preliminaries general relativity General relativity says that spacetime is described by a Lorentzian 4-manifold (M, g)
Diffraction by Edges. András Vasy (with Richard Melrose and Jared Wunsch)
 Diffraction by Edges András Vasy (with Richard Melrose and Jared Wunsch) Cambridge, July 2006 Consider the wave equation Pu = 0, Pu = D 2 t u gu, on manifolds with corners M; here g 0 the Laplacian, D
Diffraction by Edges András Vasy (with Richard Melrose and Jared Wunsch) Cambridge, July 2006 Consider the wave equation Pu = 0, Pu = D 2 t u gu, on manifolds with corners M; here g 0 the Laplacian, D
Wave equation on manifolds and finite speed of propagation
 Wave equation on manifolds and finite speed of propagation Ethan Y. Jaffe Let M be a Riemannian manifold (without boundary), and let be the (negative of) the Laplace-Beltrami operator. In this note, we
Wave equation on manifolds and finite speed of propagation Ethan Y. Jaffe Let M be a Riemannian manifold (without boundary), and let be the (negative of) the Laplace-Beltrami operator. In this note, we
On Chern-Simons-Schrödinger equations including a vortex point
 On Chern-Simons-Schrödinger equations including a vortex point Alessio Pomponio Dipartimento di Meccanica, Matematica e Management, Politecnico di Bari Workshop in Nonlinear PDEs Brussels, September 7
On Chern-Simons-Schrödinger equations including a vortex point Alessio Pomponio Dipartimento di Meccanica, Matematica e Management, Politecnico di Bari Workshop in Nonlinear PDEs Brussels, September 7
On Schrödinger equations with inverse-square singular potentials
 On Schrödinger equations with inverse-square singular potentials Veronica Felli Dipartimento di Statistica University of Milano Bicocca veronica.felli@unimib.it joint work with Elsa M. Marchini and Susanna
On Schrödinger equations with inverse-square singular potentials Veronica Felli Dipartimento di Statistica University of Milano Bicocca veronica.felli@unimib.it joint work with Elsa M. Marchini and Susanna
Nonlinear elliptic systems with exponential nonlinearities
 22-Fez conference on Partial Differential Equations, Electronic Journal of Differential Equations, Conference 9, 22, pp 139 147. http://ejde.math.swt.edu or http://ejde.math.unt.edu ftp ejde.math.swt.edu
22-Fez conference on Partial Differential Equations, Electronic Journal of Differential Equations, Conference 9, 22, pp 139 147. http://ejde.math.swt.edu or http://ejde.math.unt.edu ftp ejde.math.swt.edu
u xx + u yy = 0. (5.1)
 Chapter 5 Laplace Equation The following equation is called Laplace equation in two independent variables x, y: The non-homogeneous problem u xx + u yy =. (5.1) u xx + u yy = F, (5.) where F is a function
Chapter 5 Laplace Equation The following equation is called Laplace equation in two independent variables x, y: The non-homogeneous problem u xx + u yy =. (5.1) u xx + u yy = F, (5.) where F is a function
SCATTERING FOR THE TWO-DIMENSIONAL NLS WITH EXPONENTIAL NONLINEARITY
 SCATTERING FOR THE TWO-DIMENSIONAL NLS WITH EXPONENTIAL NONLINEARITY S. IBRAHIM, M. MAJDOUB, N. MASMOUDI, AND K. NAKANISHI Abstract. We investigate existence and asymptotic completeness of the wave operators
SCATTERING FOR THE TWO-DIMENSIONAL NLS WITH EXPONENTIAL NONLINEARITY S. IBRAHIM, M. MAJDOUB, N. MASMOUDI, AND K. NAKANISHI Abstract. We investigate existence and asymptotic completeness of the wave operators
Non-homogeneous semilinear elliptic equations involving critical Sobolev exponent
 Non-homogeneous semilinear elliptic equations involving critical Sobolev exponent Yūki Naito a and Tokushi Sato b a Department of Mathematics, Ehime University, Matsuyama 790-8577, Japan b Mathematical
Non-homogeneous semilinear elliptic equations involving critical Sobolev exponent Yūki Naito a and Tokushi Sato b a Department of Mathematics, Ehime University, Matsuyama 790-8577, Japan b Mathematical
Piecewise Smooth Solutions to the Burgers-Hilbert Equation
 Piecewise Smooth Solutions to the Burgers-Hilbert Equation Alberto Bressan and Tianyou Zhang Department of Mathematics, Penn State University, University Park, Pa 68, USA e-mails: bressan@mathpsuedu, zhang
Piecewise Smooth Solutions to the Burgers-Hilbert Equation Alberto Bressan and Tianyou Zhang Department of Mathematics, Penn State University, University Park, Pa 68, USA e-mails: bressan@mathpsuedu, zhang
THE L 2 -HODGE THEORY AND REPRESENTATION ON R n
 THE L 2 -HODGE THEORY AND REPRESENTATION ON R n BAISHENG YAN Abstract. We present an elementary L 2 -Hodge theory on whole R n based on the minimization principle of the calculus of variations and some
THE L 2 -HODGE THEORY AND REPRESENTATION ON R n BAISHENG YAN Abstract. We present an elementary L 2 -Hodge theory on whole R n based on the minimization principle of the calculus of variations and some
Hardy inequalities, heat kernels and wave propagation
 Outline Hardy inequalities, heat kernels and wave propagation Basque Center for Applied Mathematics (BCAM) Bilbao, Basque Country, Spain zuazua@bcamath.org http://www.bcamath.org/zuazua/ Third Brazilian
Outline Hardy inequalities, heat kernels and wave propagation Basque Center for Applied Mathematics (BCAM) Bilbao, Basque Country, Spain zuazua@bcamath.org http://www.bcamath.org/zuazua/ Third Brazilian
NONLINEAR SCHRÖDINGER ELLIPTIC SYSTEMS INVOLVING EXPONENTIAL CRITICAL GROWTH IN R Introduction
 Electronic Journal of Differential Equations, Vol. 014 (014), No. 59, pp. 1 1. ISSN: 107-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu NONLINEAR SCHRÖDINGER
Electronic Journal of Differential Equations, Vol. 014 (014), No. 59, pp. 1 1. ISSN: 107-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu NONLINEAR SCHRÖDINGER
The oblique derivative problem for general elliptic systems in Lipschitz domains
 M. MITREA The oblique derivative problem for general elliptic systems in Lipschitz domains Let M be a smooth, oriented, connected, compact, boundaryless manifold of real dimension m, and let T M and T
M. MITREA The oblique derivative problem for general elliptic systems in Lipschitz domains Let M be a smooth, oriented, connected, compact, boundaryless manifold of real dimension m, and let T M and T
CONVERGENCE OF EXTERIOR SOLUTIONS TO RADIAL CAUCHY SOLUTIONS FOR 2 t U c 2 U = 0
 Electronic Journal of Differential Equations, Vol. 206 (206), No. 266, pp. 6. ISSN: 072-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu CONVERGENCE OF EXTERIOR SOLUTIONS TO RADIAL CAUCHY
Electronic Journal of Differential Equations, Vol. 206 (206), No. 266, pp. 6. ISSN: 072-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu CONVERGENCE OF EXTERIOR SOLUTIONS TO RADIAL CAUCHY
AFFINE MAXIMAL HYPERSURFACES. Xu-Jia Wang. Centre for Mathematics and Its Applications The Australian National University
 AFFINE MAXIMAL HYPERSURFACES Xu-Jia Wang Centre for Mathematics and Its Applications The Australian National University Abstract. This is a brief survey of recent works by Neil Trudinger and myself on
AFFINE MAXIMAL HYPERSURFACES Xu-Jia Wang Centre for Mathematics and Its Applications The Australian National University Abstract. This is a brief survey of recent works by Neil Trudinger and myself on
PICARD S THEOREM STEFAN FRIEDL
 PICARD S THEOREM STEFAN FRIEDL Abstract. We give a summary for the proof of Picard s Theorem. The proof is for the most part an excerpt of [F]. 1. Introduction Definition. Let U C be an open subset. A
PICARD S THEOREM STEFAN FRIEDL Abstract. We give a summary for the proof of Picard s Theorem. The proof is for the most part an excerpt of [F]. 1. Introduction Definition. Let U C be an open subset. A
Various behaviors of solutions for a semilinear heat equation after blowup
 Journal of Functional Analysis (5 4 7 www.elsevier.com/locate/jfa Various behaviors of solutions for a semilinear heat equation after blowup Noriko Mizoguchi Department of Mathematics, Tokyo Gakugei University,
Journal of Functional Analysis (5 4 7 www.elsevier.com/locate/jfa Various behaviors of solutions for a semilinear heat equation after blowup Noriko Mizoguchi Department of Mathematics, Tokyo Gakugei University,
Lecture 5: Hodge theorem
 Lecture 5: Hodge theorem Jonathan Evans 4th October 2010 Jonathan Evans () Lecture 5: Hodge theorem 4th October 2010 1 / 15 Jonathan Evans () Lecture 5: Hodge theorem 4th October 2010 2 / 15 The aim of
Lecture 5: Hodge theorem Jonathan Evans 4th October 2010 Jonathan Evans () Lecture 5: Hodge theorem 4th October 2010 1 / 15 Jonathan Evans () Lecture 5: Hodge theorem 4th October 2010 2 / 15 The aim of
b) The system of ODE s d x = v(x) in U. (2) dt
 How to solve linear and quasilinear first order partial differential equations This text contains a sketch about how to solve linear and quasilinear first order PDEs and should prepare you for the general
How to solve linear and quasilinear first order partial differential equations This text contains a sketch about how to solve linear and quasilinear first order PDEs and should prepare you for the general
Compression on the digital unit sphere
 16th Conference on Applied Mathematics, Univ. of Central Oklahoma, Electronic Journal of Differential Equations, Conf. 07, 001, pp. 1 4. ISSN: 107-6691. URL: http://ejde.math.swt.edu or http://ejde.math.unt.edu
16th Conference on Applied Mathematics, Univ. of Central Oklahoma, Electronic Journal of Differential Equations, Conf. 07, 001, pp. 1 4. ISSN: 107-6691. URL: http://ejde.math.swt.edu or http://ejde.math.unt.edu
Instability of non-constant harmonic maps for the dimensional equivariant wave map system
 Instability of non-constant harmonic maps for the 1 + 2-dimensional equivariant wave map system Raphaël Côte Abstract In this paper we study (1+2)-dimensional equivariant wave maps to a surface N. This
Instability of non-constant harmonic maps for the 1 + 2-dimensional equivariant wave map system Raphaël Côte Abstract In this paper we study (1+2)-dimensional equivariant wave maps to a surface N. This
Sharp Sobolev Strichartz estimates for the free Schrödinger propagator
 Sharp Sobolev Strichartz estimates for the free Schrödinger propagator Neal Bez, Chris Jeavons and Nikolaos Pattakos Abstract. We consider gaussian extremisability of sharp linear Sobolev Strichartz estimates
Sharp Sobolev Strichartz estimates for the free Schrödinger propagator Neal Bez, Chris Jeavons and Nikolaos Pattakos Abstract. We consider gaussian extremisability of sharp linear Sobolev Strichartz estimates
Energy transfer model and large periodic boundary value problem for the quintic NLS
 Energy transfer model and large periodic boundary value problem for the quintic NS Hideo Takaoka Department of Mathematics, Kobe University 1 ntroduction This note is based on a talk given at the conference
Energy transfer model and large periodic boundary value problem for the quintic NS Hideo Takaoka Department of Mathematics, Kobe University 1 ntroduction This note is based on a talk given at the conference
Class Meeting # 13: Geometric Energy Estimates
 MATH 18.15 COURSE NOTES - CLASS MEETING # 13 18.15 Introduction to PDEs, Fall 011 Professor: Jared Speck Class Meeting # 13: Geometric Energy Estimates 1. m, the energy-momentum tensor, and compatible
MATH 18.15 COURSE NOTES - CLASS MEETING # 13 18.15 Introduction to PDEs, Fall 011 Professor: Jared Speck Class Meeting # 13: Geometric Energy Estimates 1. m, the energy-momentum tensor, and compatible
THE WAVE MAPS EQUATION. 1. The equations Let us begin with the Laplace equation, R n
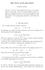 THE WAVE MAPS EQUATION DANIEL TATARU Abstract. The wave maps equation has become a very popular topic in recent years. The aim of these expository notes is to present a non-technical survey of the ideas
THE WAVE MAPS EQUATION DANIEL TATARU Abstract. The wave maps equation has become a very popular topic in recent years. The aim of these expository notes is to present a non-technical survey of the ideas
Variational Theory of Solitons for a Higher Order Generalized Camassa-Holm Equation
 International Journal of Mathematical Analysis Vol. 11, 2017, no. 21, 1007-1018 HIKAI Ltd, www.m-hikari.com https://doi.org/10.12988/ijma.2017.710141 Variational Theory of Solitons for a Higher Order Generalized
International Journal of Mathematical Analysis Vol. 11, 2017, no. 21, 1007-1018 HIKAI Ltd, www.m-hikari.com https://doi.org/10.12988/ijma.2017.710141 Variational Theory of Solitons for a Higher Order Generalized
1 Lyapunov theory of stability
 M.Kawski, APM 581 Diff Equns Intro to Lyapunov theory. November 15, 29 1 1 Lyapunov theory of stability Introduction. Lyapunov s second (or direct) method provides tools for studying (asymptotic) stability
M.Kawski, APM 581 Diff Equns Intro to Lyapunov theory. November 15, 29 1 1 Lyapunov theory of stability Introduction. Lyapunov s second (or direct) method provides tools for studying (asymptotic) stability
On Smoothness of Suitable Weak Solutions to the Navier-Stokes Equations
 On Smoothness of Suitable Weak Solutions to the Navier-Stokes Equations G. Seregin, V. Šverák Dedicated to Vsevolod Alexeevich Solonnikov Abstract We prove two sufficient conditions for local regularity
On Smoothness of Suitable Weak Solutions to the Navier-Stokes Equations G. Seregin, V. Šverák Dedicated to Vsevolod Alexeevich Solonnikov Abstract We prove two sufficient conditions for local regularity
A Hopf type lemma for fractional equations
 arxiv:705.04889v [math.ap] 3 May 207 A Hopf type lemma for fractional equations Congming Li Wenxiong Chen May 27, 208 Abstract In this short article, we state a Hopf type lemma for fractional equations
arxiv:705.04889v [math.ap] 3 May 207 A Hopf type lemma for fractional equations Congming Li Wenxiong Chen May 27, 208 Abstract In this short article, we state a Hopf type lemma for fractional equations
DIFFERENTIAL GEOMETRY, LECTURE 16-17, JULY 14-17
 DIFFERENTIAL GEOMETRY, LECTURE 16-17, JULY 14-17 6. Geodesics A parametrized line γ : [a, b] R n in R n is straight (and the parametrization is uniform) if the vector γ (t) does not depend on t. Thus,
DIFFERENTIAL GEOMETRY, LECTURE 16-17, JULY 14-17 6. Geodesics A parametrized line γ : [a, b] R n in R n is straight (and the parametrization is uniform) if the vector γ (t) does not depend on t. Thus,
PARTIAL REGULARITY OF BRENIER SOLUTIONS OF THE MONGE-AMPÈRE EQUATION
 PARTIAL REGULARITY OF BRENIER SOLUTIONS OF THE MONGE-AMPÈRE EQUATION ALESSIO FIGALLI AND YOUNG-HEON KIM Abstract. Given Ω, Λ R n two bounded open sets, and f and g two probability densities concentrated
PARTIAL REGULARITY OF BRENIER SOLUTIONS OF THE MONGE-AMPÈRE EQUATION ALESSIO FIGALLI AND YOUNG-HEON KIM Abstract. Given Ω, Λ R n two bounded open sets, and f and g two probability densities concentrated
A COUNTEREXAMPLE TO AN ENDPOINT BILINEAR STRICHARTZ INEQUALITY TERENCE TAO. t L x (R R2 ) f L 2 x (R2 )
 Electronic Journal of Differential Equations, Vol. 2006(2006), No. 5, pp. 6. ISSN: 072-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) A COUNTEREXAMPLE
Electronic Journal of Differential Equations, Vol. 2006(2006), No. 5, pp. 6. ISSN: 072-669. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) A COUNTEREXAMPLE
p-laplacian problems with critical Sobolev exponents
 Nonlinear Analysis 66 (2007) 454 459 www.elsevier.com/locate/na p-laplacian problems with critical Sobolev exponents Kanishka Perera a,, Elves A.B. Silva b a Department of Mathematical Sciences, Florida
Nonlinear Analysis 66 (2007) 454 459 www.elsevier.com/locate/na p-laplacian problems with critical Sobolev exponents Kanishka Perera a,, Elves A.B. Silva b a Department of Mathematical Sciences, Florida
MATH 220: MIDTERM OCTOBER 29, 2015
 MATH 22: MIDTERM OCTOBER 29, 25 This is a closed book, closed notes, no electronic devices exam. There are 5 problems. Solve Problems -3 and one of Problems 4 and 5. Write your solutions to problems and
MATH 22: MIDTERM OCTOBER 29, 25 This is a closed book, closed notes, no electronic devices exam. There are 5 problems. Solve Problems -3 and one of Problems 4 and 5. Write your solutions to problems and
EXISTENCE OF SOLUTIONS FOR A RESONANT PROBLEM UNDER LANDESMAN-LAZER CONDITIONS
 Electronic Journal of Differential Equations, Vol. 2008(2008), No. 98, pp. 1 10. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) EXISTENCE
Electronic Journal of Differential Equations, Vol. 2008(2008), No. 98, pp. 1 10. ISSN: 1072-6691. URL: http://ejde.math.txstate.edu or http://ejde.math.unt.edu ftp ejde.math.txstate.edu (login: ftp) EXISTENCE
GRAND SOBOLEV SPACES AND THEIR APPLICATIONS TO VARIATIONAL PROBLEMS
 LE MATEMATICHE Vol. LI (1996) Fasc. II, pp. 335347 GRAND SOBOLEV SPACES AND THEIR APPLICATIONS TO VARIATIONAL PROBLEMS CARLO SBORDONE Dedicated to Professor Francesco Guglielmino on his 7th birthday W
LE MATEMATICHE Vol. LI (1996) Fasc. II, pp. 335347 GRAND SOBOLEV SPACES AND THEIR APPLICATIONS TO VARIATIONAL PROBLEMS CARLO SBORDONE Dedicated to Professor Francesco Guglielmino on his 7th birthday W
A note on W 1,p estimates for quasilinear parabolic equations
 200-Luminy conference on Quasilinear Elliptic and Parabolic Equations and Systems, Electronic Journal of Differential Equations, Conference 08, 2002, pp 2 3. http://ejde.math.swt.edu or http://ejde.math.unt.edu
200-Luminy conference on Quasilinear Elliptic and Parabolic Equations and Systems, Electronic Journal of Differential Equations, Conference 08, 2002, pp 2 3. http://ejde.math.swt.edu or http://ejde.math.unt.edu
u( x) = g( y) ds y ( 1 ) U solves u = 0 in U; u = 0 on U. ( 3)
 M ath 5 2 7 Fall 2 0 0 9 L ecture 4 ( S ep. 6, 2 0 0 9 ) Properties and Estimates of Laplace s and Poisson s Equations In our last lecture we derived the formulas for the solutions of Poisson s equation
M ath 5 2 7 Fall 2 0 0 9 L ecture 4 ( S ep. 6, 2 0 0 9 ) Properties and Estimates of Laplace s and Poisson s Equations In our last lecture we derived the formulas for the solutions of Poisson s equation
Lecture 2: Isoperimetric methods for the curve-shortening flow and for the Ricci flow on surfaces
 Lecture 2: Isoperimetric methods for the curve-shortening flow and for the Ricci flow on surfaces Ben Andrews Mathematical Sciences Institute, Australian National University Winter School of Geometric
Lecture 2: Isoperimetric methods for the curve-shortening flow and for the Ricci flow on surfaces Ben Andrews Mathematical Sciences Institute, Australian National University Winter School of Geometric
The Helmholtz Equation
 The Helmholtz Equation Seminar BEM on Wave Scattering Rene Rühr ETH Zürich October 28, 2010 Outline Steklov-Poincare Operator Helmholtz Equation: From the Wave equation to Radiation condition Uniqueness
The Helmholtz Equation Seminar BEM on Wave Scattering Rene Rühr ETH Zürich October 28, 2010 Outline Steklov-Poincare Operator Helmholtz Equation: From the Wave equation to Radiation condition Uniqueness
A PHYSICAL SPACE PROOF OF THE BILINEAR STRICHARTZ AND LOCAL SMOOTHING ESTIMATES FOR THE SCHRÖDINGER EQUATION
 A PHYSICAL SPACE PROOF OF THE BILINEAR STRICHARTZ AND LOCAL SMOOTHING ESTIMATES FOR THE SCHRÖDINGER EQUATION TERENCE TAO Abstract. Let d 1, and let u, v : R R d C be Schwartz space solutions to the Schrödinger
A PHYSICAL SPACE PROOF OF THE BILINEAR STRICHARTZ AND LOCAL SMOOTHING ESTIMATES FOR THE SCHRÖDINGER EQUATION TERENCE TAO Abstract. Let d 1, and let u, v : R R d C be Schwartz space solutions to the Schrödinger
