arxiv: v3 [math.ds] 16 Jul 2013
|
|
|
- Morgan Stafford
- 5 years ago
- Views:
Transcription
1 ROTOPULSATORS OF THE CURVED N-BODY PROBLEM arxiv: v3 [math.ds] 16 Jul 013 Florin Diacu 1, and Shima Kordlou 1 Pacific Institute for the Mathematical Sciences and Department of Mathematics and Statistics University of Victoria P.O. Box 3060 STN CSC Victoria, BC, Canada, V8W 3R4 diacu@uvic.ca and shimak@uvic.ca October 19, 018 Abstract. We consider the N-body problem in spaces of constant curvature and study its rotopulsators, i.e. solutions for which the configuration of the bodies rotates and changes size during the motion. Rotopulsators fall naturally into five groups: positive elliptic, positive elliptic-elliptic, negative elliptic, negative hyperbolic, and negative elliptic-hyperbolic, depending on the nature and number of their rotations and on whether they occur in spaces of positive or negative curvature. After obtaining existence criteria for each type of rotopulsator, we derive their conservation laws. We further deal with the existence and uniqueness of some classes of rotopulsators in the - and 3-body case and prove two general results about the qualitative behaviour of rotopulsators. More precisely, for positive curvature we show that there is no foliation of the 3-sphere with Clifford tori such that the motion of each body is confined to some Clifford torus. For negative curvature, a similar result is proved relative to foliations of the hyperbolic 3-sphere with hyperbolic cylinders. 1
2 Florin Diacu and Shima Kordlou Contents 1. Introduction 3. Motivation 3 3. A brief history of the curved N-body problem 4 4. Summary of results 5 5. Equations of motion 6 6. Basic definitions 8 7. Positive elliptic rotopulsators Criterion for positive elliptic rotopulsators or relative equilibria Conservation laws for positive elliptic rotopulsating orbits Positive elliptic Lagrangian rotopulsators Positive elliptic-elliptic rotopulsators Criterion for positive elliptic-elliptic rotopulsators or relative equilibria Conservation laws for positive elliptic-elliptic rotopulsators Positive elliptic-elliptic rotopulsators for N = Positive elliptic-elliptic Lagrangian relative equilibria 4 9. Qualitative behaviour of rotopulsators in S Clifford tori Geometry and dynamics of rotopulsators in S Negative elliptic rotopulsators Criterion for negative elliptic rotopulsators or relative equilibria Conservation laws for negative elliptic rotopulsating orbits Negative elliptic Lagrangian rotopulsators Negative hyperbolic rotopulsators Criterion for negative hyperbolic rotopulsators or relative equilibria Conservation laws for negative hyperbolic rotopulsators Negative hyperbolic Eulerian rotopulsators for N = Negative hyperbolic Eulerian relative equilibria for N = Negative elliptic-hyperbolic rotopulsators Criterion for negative elliptic-hyperbolic rotopulsators or relative equilibria Conservation laws for negative elliptic-hyperbolic rotopulsators Negative elliptic-hyperbolic Eulerian rotopulsators for N = Negative elliptic-hyperbolic Eulerian relative equilibria for N = Qualitative behaviour of rotopulsators in H Hyperbolic cylinders Geometry and dynamics of rotopulsators in H Final remarks 48 References 49
3 Rotopulsators of the curved N-body problem 3 1. Introduction The goal of this paper is to study rotopulsators of the curved N-body problem, a type of solution that extends the concept of homographic orbit from the Euclidean space to spaces of constant curvature. In curved spaces, similar geometric figures are also congruent, so the word homographic is not suited for describing orbits that rotate and expand or contract during the motion. We will therefore introduce the concept of rotopulsator, which overlaps with the Euclidean notion of homographic solution of the N-body problem when the curvature of the space becomes zero. But before describing the results we prove in this paper, let us give the overall motivation of this research and provide a brief history of the N-body problem in spaces of constant curvature.. Motivation The curved N-body problem offers an opportunity to look into the nature of the physical space. How do we measure the shortest distance between two points: along a straight line, an arc of a great circle, or a geodesic of some other manifold? Apparently, Gauss tried to answer this question by measuring the angles of triangles formed by three mountain peaks, to decide whether their sum was smaller or larger than π radians. But his experiments failed because no deviation from π could be detected outside the unavoidable measurement errors. It thus became clear that if the physical space is not flat, the deviation from zero curvature is very small. Recent cosmological experiments involving the background radiation made physicists believe that space is Euclidean, although they have no proof so far, their results being as inconclusive as those of Gauss. In fact, from the mathematical point of view, zero curvature is highly unlikely, if compared to a continuum of possibilities for positive or negative curvature. The study of the curved N-body problem offers new insight since we can observe celestial motions from Earth. If we prove the existence of orbits that characterize only one of the positive, zero, or negative constant curvature spaces, i.e. such orbits don t occur in any of the two other possible spaces, and are stable too, then we can hope to decide the shape of physical space by astronomical observations. This dynamical approach towards understanding the geometry of the universe may succeed at the local, but not the global, level because celestial motions at large scales are mainly radial: galaxies and clusters of galaxies just move away from each other. Interesting celestial orbits occur only in solar systems. But the study of the curved N-body problem offers a new mathematical playfield that can shed some light on the Euclidian case through the study of the bifurcations that occur when the curvature tends to zero, and may lead to a better understanding of several mathematical questions, including those related to the singularities that occur in the motion of particle systems, [1], [4].
4 4 Florin Diacu and Shima Kordlou 3. A brief history of the curved N-body problem In the 1830s, János Bolyai and Nikolai Lobachevsky independently proposed a -body problem in the hyperbolic space H 3, [], [17]. They suggested the use of a force that is inversely proportional with the area of a sphere of radius r, where r is the distance between the bodies. Their line of thought followed that of Gauss, who had viewed gravitation as inversely proportional to the area of an Euclidean sphere in Euclidean space. But neither Bolyai nor Lobachevsky came up with an analytic expression for this new force. In 1870, Ernest Schering pointed out that, in H 3, the area of a sphere of radius r is proportional to sinh r, so he defined a potential that involves coth r, []. Wilhelm Killing naturaly extended this idea to the sphere S 3 with the help of a potential proportional to cot r, [13]. During the first couple of years of the 0th century, Heinrich Liebmann studied the Kepler problem (the motion of a body around a fixed centre) for the cotangent potential and recovered Kepler s laws in slightly modified form, [15]. Moreover, he found that a property earlier proved by Joseph Bertrand for the Newtonian potential, namely that all bounded orbits of the Kepler problem are closed, [1], was also true for the cotangent potential, [16]. These results, together with the fact that both the Newtonian and the cotangent potential of the Kepler problem are harmonic functions in the 3-dimensional case, established the cotangent potential among the problems worth researching in celestial mechanics. More recently, results in this direction were obtained by several Spanish and Russian mathematicians, [3], [14], [3]. It is interesting to note that, unlike in Euclidean space, the curved Kepler problem and the curved -body problem are not equivalent. The former is integrable, but the latter is not, [3], so its study appears to be more complicated than that of the classical case. Recently, we found a new setting that allowed the generalization of the -body case to any number N of bodies. We showed in several papers, [11], [6], [7], that the equations of motion can be simultaneously written for positive and negative curvature. The idea was to use the hyperbolic sphere, i.e. Weierstrass s model of hyperbolic geometry, given by the upper sheet of the hyperboloid of two sheets embedded in the Minkowski space. By suitable coordinate and time transformations, this study can be reduced to S 3 and H 3, or to S and H in the -dimensional case. For the latter, the equations in intrinsic coordinates were also obtained, [1], [10]. So far, we studied the singularities of the equations and of the solutions, the various classes of relative equilibria (i.e. orbits whose mutual distances are constant in time), and some rotopulsating orbits in the -dimensional case, [4], [5], [6], [7], [9], [10], [11], [1]. This paper provides a first investigation of the rotopulsating orbits in S 3 and H 3.
5 Rotopulsators of the curved N-body problem 5 4. Summary of results The remaining part of this paper is structured as follows. We first introduce in Section 5 the equations of motion in S 3 and H 3 and obtain their seven integrals of motion: one for the energy and six for the total angular momentum. In Section 6, we define the concept of rotopulsating orbit (or rotopulsator) and classify these solutions into five types, which we call positive elliptic, positive elliptic-elliptic, negative elliptic, negative hyperbolic, and negative elliptic-hyperbolic, depending on the manifold in which they move and on the nature and number of their rotations, which are determined by Lie groups of isometric transformations in S 3 and H 3. The main results are stated and proved in Sections 7 through 13. Sections 7, 8, 10, 11, and 1 have the same structure, each providing a criterion for the existence of the type of rotopulsator it analyzes, giving the corresponding conservation laws, and proving existence and uniqueness results for classes of rotopulsators or relative equilibria for systems of two or three bodies. Thus Section 7 deals with positive elliptic, Section 8 with positive elliptic-elliptic, Section 10 with negative elliptic, Section 11 with negative hyperbolic, and Section 1 with negative elliptic-hyperbolic rotopulsators and/or relative equilibria. The examples provided in each of these sections are of Lagrangian type (i.e. the bodes lie at the vertices of rotating equilateral triangles) for the positive elliptic, positive elliptic-elliptic, and negative elliptic rotopulsators, and of Eulerian type (i.e. the bodies lie on the same rotating geodesic) for the negative hyperbolic and negative elliptic-hyperbolic rotopulsators. Sections 10 and 13 offer a theorem each, whose object is to describe the qualitative behaviour of some classes of rotopulsators in S 3 and H 3, respectively. The first theorem shows that, for rotopulsators of S 3, for any foliation of the sphere with Clifford tori, none of the bodies can stay confined to some Clifford torus, so at least one body passes through a continuum of such surfaces. The second theorem proves a similar result for rotopulsators in H 3, where the Clifford tori are replaced by hyperbolic cylinders. An interesting finding is that of a class of Lagrangian relative equilibria (see Subsection 8.4) that cannot be generated from any single element of the underlying subgroup SO() SO() of the Lie group SO(4). (From the geometric-dynamical point of view this is very much like viewing the uniform motion of a point around a circle in its projection on some inclined plane. In projection, the motion appears elliptic and nonuniform.) Nevertheless, using suitable coordinate transformations, i.e. rotations of the frame, it is possible to find coordinates in which the solution can be generated by an element of the underlying torus SO() SO(). But the qualitative behaviour of the system can also be studied, without loss of information, in the original coordinates.
6 6 Florin Diacu and Shima Kordlou 5. Equations of motion Consider N bodies (point masses, point particles) of masses m 1,..., m N > 0 moving in S 3 (thought as embedded in the Euclidean space R 4 ) or H 3 (embedded in the Minkowski space R 3,1 ), where S 3 = {(w, x, y, z) w + x + y + z = 1}, H 3 = {(w, x, y, z) w + x + y z = 1, z > 0}. In previous work, we derived the equations of motion of the curved N-body problem using constrained Lagrangian dynamics and showed that, by suitable coordinate and time-rescaling transformations, the study of the problem can be reduced to S 3, for positive curvature, and to H 3, for negative curvature, as long as we deal only with qualitative properties, [6], [7]. The configuration of the system is described by the 4N-dimensional vector q = (q 1,..., q N ), where q i = (w i, x i, y i, z i ), i = 1,..., N, denote the position vectors of the bodies. The equations of motion are given by the second-order system m j [q j σ(q i q j )q i ] (1) q i = σ( q [σ σ(q i q j ) ] 3/ i q i )q i, i = 1,..., N,, with initial-condition constraints () q i (0) q i (0) = σ, q i (0) q i (0) = 0, i = 1,..., N. Here is the standard inner product of signature (+, +, +, +) in S 3, but the Lorentz inner product of signature (+, +, +, ) in H 3, and { +1, in S 3, σ = 1, in H 3, denotes the signum function. Since the equations of motion and the constraints on the initial conditions imply that q i q i = σ, q i q i = 0, i = 1,..., N, for all time, equations (1) can be viewed as a 6N-dimensional first-order system of ordinary differential equations. The gravitational force acting on each body has an attractive component (the above sum) and a term (involving the velocities) that corresponds to the constraints. As a consequence of Noether s theorem, system (1) has the scalar integral of energy, T (q, q) U(q) = h,
7 where Rotopulsators of the curved N-body problem 7 U(q) = 1 i<j N σm i m j q i q j [σ σ(q i q j ) ] 3/ is the force function ( U representing the potential), which stems from the cotangent of the distance, and T (q, q) = 1 m i ( q i q i )(σq i q i ) is the kinetic energy, with h representing an integration constant. System (1) also has the 6-dimensional integral of the total angular momentum, m i q i q i = c, where is the wedge product and c = (c wx, c wy, c wz, c xy, c xz, c yz ) denotes an integration vector, each component measuring the rotation of the system about the origin of the frame relative to the plane corresponding to the bottom indices. On components, the 6 integrals are given by the equations m i (w i ẋ i ẇ i x i ) = c wx, m i (w i ẏ i ẇ i y i ) = c wy, m i (w i ż i ẇ i z i ) = c wz, m i (x i ż i ẋ i z i ) = c xz, Using the notations m i (x i ẏ i ẋ i y i ) = c xy, m i (y i ż i ẏ i z i ) = c yz. q ij := q i q j and q ii := q i q i, we can explicitly write the equations of motion in S 3 as (3) q i = and in H 3 as (4) q i = m j (q j q ij q i ) (1 q ij )3/ q ii q i, q ii = 1, i = 1,,..., N, m j (q j + q ij q i ) (q ij 1)3/ + q ii q i, q ii = 1, i = 1,,..., N.
8 8 Florin Diacu and Shima Kordlou It is important to recall that the inner product that occurs in the expressions of q ij and q ii is not the same in the above two systems. From now on we will refer to equations (3) when we study motions in S 3 and to equations (4) when dealing with the dynamics of the bodies in H Basic definitions In this section we define several types of rotopulsating orbits of the curved N- body problem, a classification that follows naturally from the isometry groups of S 3 and H 3. The rotopulsating orbit extends the concept of Euclidean homographic solution to spaces of nonzero constant curvature. In two previous papers we introduced this concept in the -dimensional case and kept using the name homographic for it, [5], [9]. Our idea was that the configurations we studied (mostly polygons) remained homographic if viewed in the ambient Euclidean space. But it seems more natural to regard configurations in intrinsic terms, the more so when we move from two to three dimensions. In S, S 3, H, and H 3, however, the concept of similarity, which corresponds to the adjective homographic, makes little sense, since, for instance, the only similar triangles are the congruent ones. So to extend the concept of homographic orbit to spaces of constant curvature, the terminology needs, on one hand, to capture somehow the expansion/contraction aspect as well as the rotational component of the motion, and, on the other hand, to agree with the properties described by the original definition when the curvature tends to zero. We therefore introduce here a new adjective, rotopulsating, which preserves the features of the orbit without implying similarity of the configuration. For simplicity, rotopulsating orbits will also be called rotopulsators. The definitions we provide below follow naturally from the concept of relative equilibrium of the curved N-body problem, defined in [6], [7]. We introduced there various kinds of relative equilibria in terms of the isometric rotation groups of S 3 and H 3. The rotopulsators differ from relative equilibria by having nonuniform rotations and nonconstant mutual distances, as we will further see. To reconcile the two concepts, we also offer a new definition for relative equilibria. Definition 1 (Positive elliptic rotopulsators and relative equilibria). A solution of system (3) in S 3 is called a positive elliptic rotopulsator if it is of the form q = (q 1, q,..., q N ), q i = (w i, x i, y i, z i ), i = 1,,..., N, (5) w i = r i (t) cos[α(t) + a i ], x i = r i (t) sin[α(t) + a i ], y i = y i (t), z i = z i (t), where a i, i = 1,,..., N, are constants, α is a nonconstant function, r i, y i, and z i satisfy the conditions (6) 0 r i 1, 1 y i, z i 1, and r i + y i + z i = 1, i = 1,,..., N,
9 Rotopulsators of the curved N-body problem 9 and there are at least two indices i, j {1,,..., N}, i j, such that q ij is not constant. If the quantities q ij are constant for all i, j {1,,..., N}, i j, then the solution is called a positive elliptic relative equilibrium. Remark 1. The condition that α is nonconstant is imposed to ensure that the system has an elliptic rotation relative to the wx-plane; the fact that it has no rotation relative to the yz-plane follows from (6) and the corresponding integral of the angular momentum (see also Remark 7 below). Rotations relative to other base planes may occur. Definition (Positive elliptic-elliptic rotopulsators and relative equilibria). A solution of system (3) in S 3 is called a positive elliptic-elliptic rotopulsator if it is of the form (7) q = (q 1, q,..., q N ), q i = (w i, x i, y i, z i ), i = 1,,..., N, w i = r i (t) cos[α(t) + a i ], x i = r i (t) sin[α(t) + a i ], y i = ρ i (t) cos[β(t) + b i ], z i = ρ i (t) sin[β(t) + b i ], where a i, b i, i = 1,,..., N, are constants, α and β are nonconstant functions, and r i, ρ i satisfy the conditions 0 r i, ρ i 1 and r i + ρ i = 1, i = 1,,..., N, and there are at least two indices i, j {1,,..., N}, i j, such that q ij is not constant. If the quantities q ij are constant for all i, j {1,,..., N}, i j, then the solution is called a positive elliptic-elliptic relative equilibrium. Remark. The conditions that α and β are nonconstant are imposed to ensure that the system has two elliptic rotations, one relative to the wx-plane and the other relative to the yz-plane. Rotations relative to the other base planes may occur. Definition 3 (Negative elliptic rotopulsators and relative equilibria). A solution of system (4) in H 3 is called a negative elliptic rotopulsator if it is of the form (8) q = (q 1, q,..., q N ), q i = (w i, x i, y i, z i ), i = 1,,..., N, w i = r i (t) cos[α(t) + a i ], x i = r i (t) sin[α(t) + a i ], y i = y i (t), z i = z i (t), where a i, i = 1,,..., N, are constants, α is a nonconstant function, r i, y i, and z i satisfy the conditions (9) z i 1 and r i + y i z i = 1, i = 1,,..., N, and there are at least two indices i, j {1,,..., N}, i j, such that q ij is not constant. If the quantities q ij are constant for all i, j {1,,..., N}, i j, then the solution is called a negative elliptic relative equilibrium.
10 10 Florin Diacu and Shima Kordlou Remark 3. The condition that α is nonconstant is imposed to ensure that the system has an elliptic rotation relative to the wx-plane; the fact that it has no hyperbolic rotation relative to the yz-plane follows from (9) and the corresponding integral of the angular momentum (see also Remark 7 below). Rotations relative to other base planes may occur. Definition 4 (Negative hyperbolic rotopulsators and relative equilibria). A solution of system (4) in H 3 is called a negative hyperbolic rotopulsator if it is of the form (10) q = (q 1, q,..., q N ), q i = (w i, x i, y i, z i ), i = 1,,..., N, w i = w i (t), x i = x i (t), y i = ρ i (t) sinh[β(t) + b i ], z i = ρ i (t) cosh[β(t) + b i ], where b i, i = 1,,..., N, are constants, β is a nonconstant function, w i, x i, z i, and ρ i satisfy the conditions (11) z i 1 and w i + x i ρ i = 1, i = 1,,..., N, and there are at least two indices i, j {1,,..., N}, i j, such that q ij is not constant. If the quantities q ij are constant for all i, j {1,,..., N}, i j, then the solution is called a negative hyperbolic relative equilibrium. Remark 4. The condition that β is nonconstant is imposed to ensure that the system has a hyperbolic rotation relative to the yz-plane; the fact that it has no elliptic rotation relative to the wx-plane follows from (11) and the corresponding integral of the angular momentum (see also Remark 7 below). Rotations relative to other base planes may occur. Definition 5 (Negative elliptic-hyperbolic rotopulsators and relative equilibria). A solution of system (4) in H 3 is called a negative elliptic-hyperbolic rotopulsator if it is of the form (1) q = (q 1, q,..., q N ), q i = (w i, x i, y i, z i ), i = 1,,..., N, w i = r i (t) cos[α(t) + a i ], x i = r i (t) sin[α(t) + a i ], y i = ρ i (t) sinh[β(t) + b i ], z i = ρ i (t) cosh[β(t) + b i ], where a i, b i, i = 1,,..., N, are constants, α and β are nonconstant functions, r i, η i, z i satisfy the conditions z i 1 and r i ρ i = 1, i = 1,,..., N, and there are at least two indices i, j {1,,..., N}, i j, such that q ij is not constant. If the quantities q ij are constant for all i, j {1,,..., N}, i j, then the solution is called a negative elliptic-hyperbolic relative equilibrium.
11 Rotopulsators of the curved N-body problem 11 Remark 5. The conditions that α and β are not constant are imposed to ensure that the system has an elliptic rotation relative to the wx-plane and a hyperbolic rotation relative to the yz-plane. Rotations relative to other base planes may occur. Remark 6. Notice that we ignored a class of isometries in H 3 : the parabolic rotations, and did not provide a definition for solutions of this type. The reason for omitting this case is that, as proved in [6] and [7], relative equilibria that stem from parabolic rotations do not exist, and it is easy to show using the same idea that rotopulsators of parabolic type do not exist either. Remark 7. There are alternative ways to define the above classes of rotopulsating solutions of the curved N-body problem. Indeed, positive elliptic rotopulsators could be considered as positive elliptic-elliptic rotopulsators with β 0. Then y i (t) = ρ i (t) cos b i and z i (t) = ρ i (t) sin b i, i = 1,,..., N, with a i, b i constants, which makes sense, given that y i + z i = ρ i, i = 1,,..., N. Similarly, negative elliptic and negative hyperbolic rotopulsators could be defined as negative elliptic-hyperbolic rotopulsators with β 0 and α 0, respectively. But our choice of five distinct definitions is more convenient for computations and will help us emphasize, unambiguously, certain properties specific to each of these solutions. Nevertheless, we will use this remark later in the proofs of Theorems 1 and. Remark 8. In [9] we defined rotopulsators of the 3-body problem (called homographic orbits there for reasons we invoked earlier) in S and H in a narrower sense by asking that the Euclidean plane formed by the 3 bodies is all the time parallel with the xy-plane. In Definition 1 reduced to S, for instance, this implies that the condition for a relative equilibrium (which means that the mutual distances between the bodies remain constant during the motion) is equivalent to saying that r i is constant for all i = 1,,..., N. But, interesting enough, in Definition the functions r i (and consequently ρ i ) may vary in spite of the fact that the quantities q ij stay constant, i.e. the mutual distances don t vary in time. The reason for this behaviour is that the corresponding relative equilibrium cannot be generated from a single element of the natural subgroup SO() SO() of the Lie group SO(4) that arises from the wx and yz coordinate pairs of the chosen reference frame. Nevertheless, a classical result, which claims that in a semisimple compact Lie group every element is contained in a maximal torus, [0], shows that a suitable change of coordinates leads to a reference frame in which all functions r i are constant. In particular, SO(4) is a semisimple compact Lie group, so it satisfies the above result. Moreover, its maximal tori are the subgroups SO() SO(). But since it is impossible to know a priori which reference
12 1 Florin Diacu and Shima Kordlou system to choose in order to make the functions r i constant, it is easier to define relative equilibria by asking that the functions q ij, and not the functions r i, are constant, as we did in all the above definitions. 7. Positive elliptic rotopulsators In this section we analyze the solutions given in Definition 1. We first introduce a criterion for finding them, then obtain the conservation laws, and finally prove the existence of a particular class of orbits, namely the positive elliptic Lagrangian rotopulsators of the 3-body problem in S Criterion for positive elliptic rotopulsators or relative equilibria. The following result provides necessary and sufficient conditions for the existence of positive elliptic rotopulsators or relative equilibria in S 3. Criterion 1. A solution candidate of the form (5) is a positive elliptic rotopulsator for system (3) if and only if c (13) α = N m, jrj where c 0 is a constant, there are at least two distinct indices i, j {1,,..., N} such that q ij is not constant, and the variables y i, z i, r i, i = 1,,..., N, satisfy the first-order system of 5N equations (with N constraints: ri + yi + zi = 1, i = 1,,..., N), ẏ i = u i ż i = v i u (14) i = N m j (y j q ij y i ) F (1 q ij i (y, z, u i, v i )y i )3/ v i = N m j (z j q ij z i ) F (1 q ij i (y, z, u i, v i )z i )3/ r i α + ṙ i α = N where y = (y 1, y,..., y N ), z = (z 1, z,..., z N ), m j r j sin(a j a i ) (1 q ij )3/, (15) F i (y, z, u i, v i ) := u i + v i (y i v i z i u i ) 1 y i z i i = 1,,..., N, and, for any i, j {1,,..., N}, + q ij = r i r j cos(a i a j ) + y i y j + z i z j. c (1 y i z i ) [ N m j(1 y j z j )], If the quantities q ij are constant for all distinct indices i, j {1,,..., N}, then the solution is a relative equilibrium. If q ij = ±1 for some distinct i, j {1,,..., N}, then such solutions don t exist.
13 Rotopulsators of the curved N-body problem 13 Proof. Consider a solution candidate of the form (5). A straightforward computation shows that, for any i, j {1,,..., N}, q ij is of the form given in the above statement. Moreover, for any i = 1,,..., N, we find that q ij = ẏ i + żi (y i ż i z i ẏ i ) + (1 yi zi ) α 1 yi. z i For all i = 1,,..., N, each r i can be expressed in terms of y i and z i to obtain r i = (1 yi zi ) 1, ṙi = y iẏ i + z i ż i (1 yi z i ), 1 r i = (y iż i z i ẏ i ) ẏi żi (1 yi zi )(y i ÿ i + z i z i ) (1 yi z i ). 3 Substituting a candidate solution of the form (5) into system (3) and employing the above formulas, we obtain for the equations corresponding to ÿ i and z i that m j (y j q ij y i ) (16) ÿ i = (1 qij ) [ẏ i + żi (y i ż i z i ẏ i ) ]y i 3 1 yi (1 y z i zi )y i α, i (17) z i = m j (z j q ij z i ) (1 q ij ) 3 [ẏ i + ż i (y i ż i z i ẏ i ) ]z i 1 y i z i (1 y i z i )z i α. For the equations corresponding to ẅ i and ẍ i, after some long computations that also use (16) and (17), we are led to the equations m j r j sin(a j a i ) (18) r i α + ṙ i α = (1 qij ), i = 1,,..., N. 3 We will further show that equations (16), (17), and (18) lead to the system (14). For this purpose, we first compute α. For every i = 1,,..., N, multiply the ith equation in (18) by m i r i, add the resulting N equations, and notice that m i m j r i r j sin(a j a i ) = 0. Thus we obtain the equation α m i ri + α (1 q ij ) 3 m i r i ṙ i = 0,
14 14 Florin Diacu and Shima Kordlou which has the solution α = c N m ir i = c N m i(1 y i z i ), where c is an integration constant. Consequently, equations (16) and (17) become (19) m j (y j q ij y i ) ÿ i = (1 qij ) [ẏ i + żi (y i ż i z i ẏ i ) ]y i c (1 yi zi )y i 3 1 yi [ z N i m j(1 yj z j )], (0) z i = m j (z j q ij z i ) (1 q ij ) 3 [ẏ i + ż i (y i ż i z i ẏ i ) ]z i 1 y i z i c (1 y i z i )z i [ N m j(1 y j z j )], i = 1,,..., N. These equations are equivalent to the first 4N equations that appear in (14). We still need to show that (18) describes N first-order equations in the unknown functions r 1, r,..., r N. A straightforward computation shows that they can be written as e 1 ṙ 1 + b 1 ṙ + b 13 ṙ b 1N ṙ N = c 1 b 1 ṙ 1 + e ṙ + b 3 ṙ b N ṙ N = c (1). b N1 ṙ 1 + b N ṙ + b N3 ṙ e N ṙ N = c N, where e i = 1 m i r i, b ij = m j r j r i, c i = N m jr j c m j r j sin(a j a i ), 1 qij i = 1,,..., N, which is a first-order subsystem of N equations. (In general, this system can be simplified by solving the algebraic system in unknowns ṙ 1, ṙ,..., ṙ N leads.) The part of the criterion related to relative equilibria follows directly from Definition 1. The nonexistence of such solutions if some q ij = ±1 follows from the fact that at least a denominator cancels in the equations of motion. This remark completes the proof. 7.. Conservation laws for positive elliptic rotopulsating orbits. In addition to Criterion 1, we would also like to obtain the conservation laws specific to positive elliptic rotopulsators. They follow by straightforward computations using
15 Rotopulsators of the curved N-body problem 15 the above proof, the integral of energy, and the six integrals of the total angular momentum. Proposition 1. If system (3) has a solution of the form (5), then the following expressions are constant: energy, () + h = c m i [ẏ i + ż i (y i ż i z i ẏ i ) ] (1 y i z i ) N m i(1 y i z i ) 1 i<j N m i m j q ij (1 qij ) ; 1 total angular momentum relative to the wx-plane, (3) c wx = c, where c 0 is the constant in the expression (13) of α; total angular momentum relative to the wy-plane: (4) (5) (6) c wy = [ m i (1 yi zi ) 1 ẏi + (y ] iẏ i + z i ż i )y i (1 yi z i ) cos(α + a 1 i ) c N + N m i(1 yi z i ) m i (1 yi zi ) 1 yi sin(α + a i ); total angular momentum relative to the wz-plane, c wz = [ m i (1 yi zi ) 1 żi + (y ] iẏ i + z i ż i )z i (1 yi z i ) cos(α + a 1 i ) c N + N m j(1 yj z j ) m i (1 yi zi ) 1 zi sin(α + a i ); total angular momentum relative to the xy-plane, c xy = [ m i (1 yi zi ) 1 ẏi + (y ] iẏ i + z i ż i )y i (1 yi z i ) sin(α + a 1 i ) c N N m j(1 yj z j ) m i (1 yi zi ) 1 yi cos(α + a i );
16 16 Florin Diacu and Shima Kordlou (7) total angular momentum relative to the xz-plane: c xz = [ m i (1 yi zi ) 1 żi + (y ] iẏ i + z i ż i )z i (1 yi z i ) sin(α + a 1 i ) c N N m j(1 yj z j ) m i (1 yi zi ) 1 zi cos(α + a i ); total angular momentum relative to the yz-plane: (8) c yz = 0. The above result could be also used to prove the nonexistence of some candidates for positive elliptic rotopulsators, by showing that at least one of the above conservation laws is violated Positive elliptic Lagrangian rotopulsators. We further provide a class of specific examples of positive elliptic rotopulsators of the curved 3-body problem, namely Lagrangian orbits, i.e. bodies that lie at the vertices of a rotating equilateral triangle in S 3 that changes size, which means that it fails to be similar to itself but has congruent sides at every instant in time. As we will see, these systems rotate relative to the plane wx, but have no rotations with respect to the other base planes. Consider three equal masses, m 1 = m = m 3 =: m > 0, and a candidate solution of the form (9) q = (q 1, q, q 3 ), q i = (w i, x i, y i, z i ), i = 1,, 3, w 1 = r(t) cos α(t), x 1 = r(t) sin α(t), y 1 = y(t), z 1 = z(t), w = r(t) cos[α(t) + π/3], x = r(t) sin[α(t) + π/3], y = y(t), z = z(t), w 3 = r(t) cos[α(t) + 4π/3], x 3 = r(t) sin[α(t) + 4π/3], y 3 = y(t), z 3 = z(t). With the help of Criterion 1, we will further show that these are indeed solutions of curved 3-body problem in S 3. Proposition. Consider the curved 3-body problem in S 3 given by system (3) with N = 3. Then, except for a negligible set of orbits formed by positive elliptic Lagrangian relative equilibria, every candidate solution of the form (9) is a positive elliptic Lagrangian rotopulsator, which rotates relative to the plane wx, but has no rotation with respect to the planes wy, wz, xy, xz, and yz.
17 Rotopulsators of the curved N-body problem 17 Proof. Let us consider a candidate solution of the form (9). Then, using Criterion 1, straightforward computations show that q 1 = q 13 = q 3 = 3y + 3z 1, α = c 3mr, the equations in (14) involving α and α are identically satisfied, and that the variables y and z must satisfy the equations ẏ = u ż = v (30) u = F (y, z, u, v)y v = F (y, z, u, v)z, where F (y, z, u, v) = 8m 3(1 y z ) 1 (1 + 3y + 3z ) 3 u + v (yv uz) 1 y z. From (30), we can conclude that ÿz = y z, which implies that yż zẏ = k (constant). c 9m (1 y z ) But, since from (8) we have that 3m(yż zẏ) = c yz, it follows that k = c yz /3m. As, by Proposition 1, c yz = 0, we must take k = 0, so yż zẏ = 0, and therefore d y = 0 if z does not take zero values, so y(t) = γz(t), where γ is a constant. dt z Moreover, since sin α + sin(α + π/3) + sin(α + 4π/3) = cos α + cos(α + π/3) + cos(α + 4π/3) = 0, it follows from (4), (5), (6), and (7) that c wy = c wz = c xy = c xz = 0, so the triangle has no rotation relative to the planes wy, wz, xy, xz, and yz. If we denote δ = γ (which implies that u = γv), substitute y for γz (and therefore u for γv), make the change of variable z = δz, v = δv, and redenote z, v by z and v, respectively, system (30) reduces to the family of first order systems {ż = v (31) [ v = 8m c 3(1 z ) 1/ (1+3z ) 3/ 9m (1 z ) ]z. v 1 z The fixed points of this system correspond to relative equilibria. An obvious one is (z, v) = (0, 0), which is a Lagrangian relative equilibrium rotating on a great
18 18 Florin Diacu and Shima Kordlou circle of a great sphere of S 3. The other fixed points are given by the polynomial equation of degree six (3) 178m 3 (1 z ) = c (1 + 3z ) 3. This means that, for m and c fixed, there is a finite number of relative equilibria. Standard results of the theory of ordinary differential equations can now be applied to system (31) to prove the existence and uniqueness of analytic positive elliptic Lagrangian rotopulsators, for admissible initial conditions. This remark completes the proof. Although we proved the existence of the positive elliptic Lagrangian rotopulsators, it would be still interesting to learn more about their nature in terms of the energy constant. For this, we will first find the fixed points for the vector field of system (31) different from the obvious one, (z, v) = (0, 0), which is common to all equations in the family. Using the energy relation (), obtaining the solutions of equation (3) reduces to finding the zeroes of the family of polynomials P (z) = 7(9m 4 + h )z 8 18(15m 4 + h )z 4 8h z + 75m 4 h. According to Descartes s rule of signs, we have to distinguish between two cases: (i) h < 5 3m, when, for every fixed values of the parameters, P has either two positive roots or no positive root at all; (ii) h 5 3m, when, for every fixed values of the parameters, P has exactly one positive root. Case (ii) always leads to one fixed point since the unique positive root, z 0 := z 0 (m, h, ɛ), has the property z 0 < 1, since P (1) = 48m 4 > 0 and P (0) = 75m 4 h 0. Then the corresponding eigenvalues λ 1, are given by the equation λ + h 3m W (z 0, m, ɛ) = 0, where W (z 0, m, ɛ) is a finite number for every fixed value of the parameters. Independently of the values of W (z 0, m, ɛ), the eigenvalues show that z varies for every orbit that is not a fixed point. Similar conclusions can be drawn in case (i). Numerical experiments suggest that all the other orbits of system (31) are periodic, except for two homoclinic orbits. Since the periods of α and z don t usually match, the periodic orbits generate quasiperiodic positive elliptic Lagrangian rotopulsators, except for a negligible class, given by periodic positive elliptic Lagrangian rotopulsators (see Fig. 1). Remark 9. When y or z is a nonzero constant, the motion takes place on a -dimensional nongreat sphere. When y 0 or z 0, the motion is confined to a -dimensional great sphere, i.e. to S. The latter case corresponds to a class of Lagrangian orbits for which we gave a complete classification in [9].
19 Rotopulsators of the curved N-body problem 19 Figure 1. A typical phase portrait for system (31). 8. Positive elliptic-elliptic rotopulsators In this section we analyze the solutions given in Definition. We first prove a criterion for finding such solutions, then obtain the conservation laws, and finally analyze two particular class of examples. In the first case we prove the existence of positive elliptic-elliptic rotopulsators in the -body problem in S 3. In the second case we show that the positive elliptic-elliptic Lagrangian orbits of the 3-body problem in S 3 are always relative equilibria, so they cannot form rotopulsators Criterion for positive elliptic-elliptic rotopulsators or relative equilibria. The following result provides necessary and sufficient conditions for the existence of positive elliptic-elliptic rotopulsators or relative equilibria in S 3. Criterion. A solution candidate of the form (7) is a positive elliptic-elliptic rotopulsator for system (3) if and only if (33) α = c 1 N m ir i c, β = M N m, iri with c 1, c, M = N m i nonzero constants, there are at least two distinct indices i, j {1,,..., N} such that q ij is not constant, and the variables r 1, r,..., r N satisfy the first-order system of 4N equations, ṙ i = s i (34) ṡ i = G i (r, s i ) r i α + ṙ i α = N ρ i β + ρi β = N m j r j sin(a j a i ) (1 q ij )3/ m j ρ j sin(b j b i ) (1 q ij )3/,
20 0 Florin Diacu and Shima Kordlou where ri + ρ i = 1, i = 1,,..., N, r = (r 1, r,..., r N ), [ ] G i (r, s i ) = r i (1 ri c 1 ) ( c N m iri ) (M N m r is i iri ) 1 ri (35) m j [r j (1 ri ) cos(a i a j ) r i (1 ri ) 1 (1 rj ) 1 cos(b i b j )] + (1 qij ), 3 i = 1,,..., N, and for any i, j {1,,..., N} with i j, (36) q ij = r i r j cos(a i a j ) + (1 r i ) 1 (1 r j ) 1 cos(bi b j ). If q ij are constant for all distinct i, j {1,,..., N}, then the solution is a relative equilibrium. If q ij = ±1 for some distinct i, j {1,,..., N}, then such solutions don t exist. Proof. Consider a candidate solution of the form (7) for system (3). By expressing each ρ i in terms of r i, i = 1,,..., N, we obtain that ρ i = (1 r i ) 1, ρi = r iṙ i (1 r i ) 1 Then q ij takes the form (36), and ṙ i + r i (1 ri ) r i, ρ i = (1 ri ). 3 q ij = ṙ i + r i α + r i ṙ i 1 r i + (1 r i ) β. Substituting a solution candidate of the form (7) into system (3), and using the above formulas, we obtain for the equations corresponding to ẅ i and ẍ i the equations (37) + r i = r i (1 ri )( α β ) r iṙi 1 ri m j [r j (1 ri ) cos(a i a j ) r i (1 ri ) 1 (1 rj ) 1 cos(b i b j )] (1 ɛ ij ), 3 (38) r i α + ṙ i α = m j r j sin(a i a j ) (1 qij ), i = 1,,..., N, 3
21 Rotopulsators of the curved N-body problem 1 respectively, whereas for the equations corresponding to ÿ i, z i, we find equations (37) again as well as the equations N m j ρ j sin(b i b j ) (39) ρ i β + ρi β = (1 qij ), i = 1,,..., N. 3 We can solve equations (38) the same way we solved equations (18) and obtain c 1 α = N m, iri where c 1 is an integration constant. To solve equations (39), we proceed similarly, with the only change that for each i = 1,,..., N, the corresponding equation gets multiplied by m i (1 ri ) 1 instead of m i r i, to obtain after addition that c β = M N m, iri where M = N m i and c is an integration constant. Then equations (37), (38), (39) form system (34). Using the above expressions of α and β, we can conclude the same way as we did in the proof of Criterion 1 that (34) is a first-order system of 4N equations with no constraints. The part of the criterion related to relative equilibria follows directly from Definition. The nonexistence of such solutions if some q ij = ±1 follows from the fact that at least a denominator cancels in the equations of motion. This remark completes the proof. Remark 10. It follows from (33) that α and β are connected by the relationship (40) c 1 α + c β = M, written under the assumption that α and β are not constant. In particular, if α and β differ only by an additive constant, they are linear functions of time, i.e. α = β = c 1 + c M. 8.. Conservation laws for positive elliptic-elliptic rotopulsators. In addition to Criterion, we would also like to obtain the conservation laws specific to positive elliptic-elliptic rotopulsators. These laws follow by straightforward computations using the above proof, the integral of energy, and the six integrals of the total angular momentum. Proposition 3. If system (3) has a solution of the form (7), then the following expressions are constant:
22 Florin Diacu and Shima Kordlou energy: (41) h = m i ṙ i (1 r i ) + c 1 N m jr j c + (M N m jrj ) 1 i<j N m i m j q ij (1 qij ) ; 1 total angular momentum relative to the wx-plane, (4) c wx = c 1, where c 1 0 is the constant in the expression (33) of α; total angular momentum relative to the wy-plane, (43) c wy = 1 m i [r i (1 ri ) 1 ( α + β) sin(α β + ai b i ) +r i (1 ri ) 1 ( α β) sin(α + β + ai + b i ) (1 ri ) cos(α β + a 1 i b i ) ] ṙ i (1 ri ) cos(α + β + a 1 i + b i ) ; ṙ i total angular momentum relative to the wz-plane, (44) c wz = 1 m i [r i (1 ri ) 1 ( α + β) cos(α β + ai b i ) r i (1 ri ) 1 ( α β) cos(α + β + ai + b i ) + (1 ri ) sin(α β + a 1 i b i ) ] ṙ i (1 ri ) sin(α + β + a 1 i + b i ) ; ṙ i total angular momentum relative to the xy-plane, (45) c xy = 1 m i [r i (1 ri ) 1 ( α + β) cos(α β + ai b i ) +r i (1 ri ) 1 ( α β) cos(α + β + ai + b i ) + (1 ri ) sin(α β + a 1 i b i ) ] ṙ i + (1 ri ) sin(α + β + a 1 i + b i ) ; ṙ i
23 Rotopulsators of the curved N-body problem 3 total angular momentum relative to the xz-plane, c xz = 1 m i [r i (1 ri ) 1 ( α + β) sin(α β + ai b i ) (46) r i (1 ri ) 1 ( α β) sin(α + β + ai + b i ) (1 ri ) cos(α β + a 1 i b i ) ] ṙ i + (1 ri ) cos(α + β + a 1 i + b i ) ; total angular momentum relative to the yz-plane, (47) c yz = c, where c 0 is the constant in the expression (33) of β. The above result could also be used to prove the nonexistence of some candidates for positive elliptic rotopulsating orbits, by showing that at least one of the above conservation laws is violated Positive elliptic-elliptic rotopulsators for N =. We further show the existence of a class of positive elliptic-elliptic rotopulsators of the -body problem in S 3. These binary systems rotate relative to the planes wx and yz, but have no rotations with respect to the planes wy, wz, xy, and xz. Consider two equal masses, m 1 = m =: m > 0, and a candidate solution of the form q = (q 1, q ), q i = (w i, x i, y i, z i ), i = 1,, (48) w 1 = r(t) cos α(t), x 1 = r(t) sin α(t), y 1 = ρ(t) cos β(t), z 1 = ρ(t) sin β(t), w = r(t) cos[α(t) + π], x = r(t) sin[α(t) + π], y = ρ(t) cos β(t), z = ρ(t) sin β(t), with α and β nonconstant functions and r + ρ = 1. We can prove now the following result, which shows the existence of rotopulsators of the above form. Proposition 4. Consider the curved -body problem in S 3 given by system (3) with N =. Then, except for a negligible class of relative equilibria, every candidate solution of the form (48) is a positive elliptic-elliptic rotopulsator, which rotates relative to the planes wx and yz, but has no rotation with respect to the planes wy, wz, xy, and xz. Proof. From Criterion we notice that q 1 = r 1, α = c 1 mr, β = c m(1 r ), ṙ i
24 4 Florin Diacu and Shima Kordlou and that a candidate solution of the form (48) leads to the family of first-order systems (49) {ṙ = s [ ṡ = r(1 r ) c 1 4m r 4 ] c rs 4m (1 r ) 1 r m, 4r (1 r ) 1/ since the equations involving α, α and β, β, respectively, in system (34) are identically satisfied. Standard results of the theory of differential equations prove the existence and uniqueness of analytic solutions for nonsingular initial conditions attached to the above system. For fixed values of m > 0, c 1 0, and c 0, the number of fixed points of system (49) is obviously finite, so the set of fixed points is negligible when these constants vary. Therefore, except for the negligible set of orbits corresponding to fixed points, which are relative equilibria because r is constant, all the solutions of the form (48) are rotopulsators since r (and consequently the mutual distance q 1 between the bodies) varies. It follows from Proposition 3 that c wx = c 1, c yz = c, with c 1, c 0, and that c wy = c wz = c xy = c xz = 0, which proves that the binary system rotates relative to the planes wx and yz, but has no rotation with respect to the planes wy, wz, xy, and xz. This remark completes the proof Positive elliptic-elliptic Lagrangian relative equilibria. We further prove that the positive elliptic-elliptic Lagrangian orbits of the curved 3-body problem in S 3 (i.e. equilateral triangles having two rotations, one with respect to the plane wx and the other relative to the plane yz) are necessarily relative equilibria, and cannot be rotopulsators. Moreover, these orbits have no rotations relative to the other base planes. Consider three equal masses, m 1 = m = m 3 =: m > 0, and a candidate solution of the form (50) q = (q 1, q, q 3 ), q i = (w i, x i, y i, z i ), i = 1,, 3, w 1 = r(t) cos α(t), x 1 = r(t) sin α(t), y 1 = ρ(t) cos β(t), z 1 = ρ(t) sin β(t), w = r(t) cos[α(t) + π/3], x = r(t) sin[α(t) + π/3], y = ρ(t) cos[β(t) + π/3], z = ρ(t) sin[β(t) + π/3], w 3 = r(t) cos[α(t) + 4π/3], x 3 = r(t) sin[α(t) + 4π/3], y 3 = ρ(t) cos[β(t) + 4π/3], z 3 = ρ(t) sin[β(t) + 4π/3], with α and β nonconstant functions and r + ρ = 1. We can now prove the following result.
25 Rotopulsators of the curved N-body problem 5 Proposition 5. Consider the curved 3-body problem in S 3 given by system (3) with N = 3. Then every candidate solution of the form (50) is a positive ellipticelliptic Lagrangian relative equilibrium, which rotates relative to the planes wx and yz, but has no rotation with respect to the planes wy, wz, xy, and xz. Proof. To prove this result, we first apply Criterion to a candidate solution of the form (50) for system (3). Straightforward computations show that q 1 = q 13 = q 3 = 1/, which means that the sides of the equilateral triangle don t vary in time, so if this solution candidate proves to exist, then it is necessarily a positive elliptic-elliptic Lagrangian relative equilibrium. Notice further that (51) α = c 1 3mr, β = c 3m(1 r ), the equations in system (34) involving α, α and β, β, respectively, are identically satisfied, and that system (34) thus reduces to the family of first-order systems {ṙ = u, (5) u = c 1 (1 r ) r(9m u +c 9m r 3 ). 9m (1 r ) As in the proof of Proposition, the existence and uniqueness of analytic positive elliptic-elliptic rotopulsators for admissible initial conditions follows. From Proposition 3 we can conclude that c wx = c 1, c yz = c, with c 1, c 0, and that c wy = c wz = c xy = c xz = 0, which proves that the positive elliptic-elliptic Lagrangian relative equilibria rotate relative to the planes wx and yz, but have no rotation with respect to the planes wy, wz, xy, and xz. This remark completes the proof. Remark 11. As noted at the end of Section 4, since r varies, the above relative equilibria cannot be generated from an element of the underlying torus SO() SO() of the Lie group SO(4). Suitable rotations of the coordinate system, however, would make this possible, in which case r would become constant for each specific solution. To get some insight into the nature of these relative equilibria, let us first find the fixed points of system (5), which occur for (c 1 c )r 4 c 1r + c 1 = 0. For fixed values of c 1 and c, with c 1 c, there are at most two fixed points, r 1 = ( ) c 1 1/ c 1 c and r = ( ) c 1 1/, c 1 +c only one of which is between 0 and 1, whereas for c 1 = c there is a single fixed point, namely r 0 = 1/. So in both cases the fixed point is unique.
26 6 Florin Diacu and Shima Kordlou Numerical experiments suggest that the phase space picture of system (5) looks like in Fig.(), with r periodic, a fact in agreement with the Lie theory applied to the group SO(4). Consequently, the positive elliptic-elliptic Lagrangian orbits are expected to be quasiperiodic, since the periods of α and β differ, in general, except for a negligible set corresponding to periodic orbits. Figure. A typical flow of system (5) for c 1 = c = 1. For c 1 c, the flow looks qualitatively similar. Remark 1. From relations (51) we can see how the angular velocities α and β vary relative to r: when r is close to 0, α is large, while β is small, and the other way around when r is close to 1. Moreover, the expressions of α and β are consistent with relation (40). Remark 13. If we initially assume the masses to be distinct, but the bodies to correspond to the same function r, it follows that the solutions don t exist, which means that the masses must be always equal. If we additionally take distinct functions r 1, r, r 3, then q ij = r ir j + (1 r i ) 1/ (1 r j ) 1/ = (r i r j ) + [(1 ri ) 1/ (1 rj ) 1/ ], 4 which implies that the triangle is not necessarily equilateral, so the orbit may not be Lagrangian at all. Remark 14. The energy relation (41) takes the form h = 3mṙ (1 r ) + 1 [ ] c 1 6m r + c + 3m, 1 r so the energy constant, h, is always positive.
arxiv: v2 [math.ds] 1 Oct 2013
![arxiv: v2 [math.ds] 1 Oct 2013 arxiv: v2 [math.ds] 1 Oct 2013](/thumbs/77/76307545.jpg) RECTANGULAR ORBITS OF THE CURVED 4-BODY PROBLEM arxiv:1302.5352v2 [math.ds] 1 Oct 2013 Florin Diacu 1,2 and Brendan Thorn 2 1 Pacific Institute for the Mathematical Sciences and 2 Department of Mathematics
RECTANGULAR ORBITS OF THE CURVED 4-BODY PROBLEM arxiv:1302.5352v2 [math.ds] 1 Oct 2013 Florin Diacu 1,2 and Brendan Thorn 2 1 Pacific Institute for the Mathematical Sciences and 2 Department of Mathematics
ALL THE LAGRANGIAN RELATIVE EQUILIBRIA OF THE CURVED 3-BODY PROBLEM HAVE EQUAL MASSES. September 23, 2014
 ALL THE LAGRANGIAN RELATIVE EQUILIBRIA OF THE CURVED 3-BODY PROBLEM HAVE EQUAL MASSES Florin Diacu 1,2 and Sergiu Popa ( c /o 2 ) 1 Pacific Institute for the Mathematical Sciences and 2 Department of Mathematics
ALL THE LAGRANGIAN RELATIVE EQUILIBRIA OF THE CURVED 3-BODY PROBLEM HAVE EQUAL MASSES Florin Diacu 1,2 and Sergiu Popa ( c /o 2 ) 1 Pacific Institute for the Mathematical Sciences and 2 Department of Mathematics
BIFURCATIONS OF THE LAGRANGIAN ORBITS FROM THE CLASSICAL TO THE CURVED 3-BODY PROBLEM
 BIFURCATIONS OF THE LAGRANGIAN ORBITS FROM THE CLASSICAL TO THE CURVED 3-BODY PROBLEM Florin Diacu Pacific Institute for the Mathematical Sciences and Department of Mathematics and Statistics University
BIFURCATIONS OF THE LAGRANGIAN ORBITS FROM THE CLASSICAL TO THE CURVED 3-BODY PROBLEM Florin Diacu Pacific Institute for the Mathematical Sciences and Department of Mathematics and Statistics University
POLYGONAL HOMOGRAPHIC ORBITS OF THE CURVED n-body PROBLEM. Florin Diacu. February 9, 2011
 POLYGONAL HOMOGRAPHIC ORBITS OF THE CURVED n-body PROBLEM Florin Diacu Pacific Institute for the Mathematical Sciences and Department of Mathematics and Statistics University of Victoria PO Box 3060 STN
POLYGONAL HOMOGRAPHIC ORBITS OF THE CURVED n-body PROBLEM Florin Diacu Pacific Institute for the Mathematical Sciences and Department of Mathematics and Statistics University of Victoria PO Box 3060 STN
Kinematics. Chapter Multi-Body Systems
 Chapter 2 Kinematics This chapter first introduces multi-body systems in conceptual terms. It then describes the concept of a Euclidean frame in the material world, following the concept of a Euclidean
Chapter 2 Kinematics This chapter first introduces multi-body systems in conceptual terms. It then describes the concept of a Euclidean frame in the material world, following the concept of a Euclidean
arxiv: v1 [math.ca] 7 Jan 2018
![arxiv: v1 [math.ca] 7 Jan 2018 arxiv: v1 [math.ca] 7 Jan 2018](/thumbs/94/120119539.jpg) RELATIVE EQUILIBRIA IN CURVED RESTRICTED -BODY PROBLEMS arxiv:1801.016v1 math.ca 7 Jan 018 Florin Diacu 1,, and Sawsan Alhowaity, 1 Yangtze Center of Mathematics, Sichuan University, Chengdu, China Yale-NUS
RELATIVE EQUILIBRIA IN CURVED RESTRICTED -BODY PROBLEMS arxiv:1801.016v1 math.ca 7 Jan 018 Florin Diacu 1,, and Sawsan Alhowaity, 1 Yangtze Center of Mathematics, Sichuan University, Chengdu, China Yale-NUS
CHAPTER 3. Gauss map. In this chapter we will study the Gauss map of surfaces in R 3.
 CHAPTER 3 Gauss map In this chapter we will study the Gauss map of surfaces in R 3. 3.1. Surfaces in R 3 Let S R 3 be a submanifold of dimension 2. Let {U i, ϕ i } be a DS on S. For any p U i we have a
CHAPTER 3 Gauss map In this chapter we will study the Gauss map of surfaces in R 3. 3.1. Surfaces in R 3 Let S R 3 be a submanifold of dimension 2. Let {U i, ϕ i } be a DS on S. For any p U i we have a
7 Planar systems of linear ODE
 7 Planar systems of linear ODE Here I restrict my attention to a very special class of autonomous ODE: linear ODE with constant coefficients This is arguably the only class of ODE for which explicit solution
7 Planar systems of linear ODE Here I restrict my attention to a very special class of autonomous ODE: linear ODE with constant coefficients This is arguably the only class of ODE for which explicit solution
Stability of the Lagrange Points, L 4 and L 5
 Stability of the Lagrange Points, L 4 and L 5 Thomas Greenspan January 7, 014 Abstract A proof of the stability of the non collinear Lagrange Points, L 4 and L 5. We will start by covering the basics of
Stability of the Lagrange Points, L 4 and L 5 Thomas Greenspan January 7, 014 Abstract A proof of the stability of the non collinear Lagrange Points, L 4 and L 5. We will start by covering the basics of
Geometry beyond Euclid
 Geometry beyond Euclid M.S. Narasimhan IISc & TIFR, Bangalore narasim@math.tifrbng.res.in 1 Outline: Aspects of Geometry which have gone beyond Euclid Two topics which have played important role in development
Geometry beyond Euclid M.S. Narasimhan IISc & TIFR, Bangalore narasim@math.tifrbng.res.in 1 Outline: Aspects of Geometry which have gone beyond Euclid Two topics which have played important role in development
Chapter 7 Curved Spacetime and General Covariance
 Chapter 7 Curved Spacetime and General Covariance In this chapter we generalize the discussion of preceding chapters to extend covariance to more general curved spacetimes. 145 146 CHAPTER 7. CURVED SPACETIME
Chapter 7 Curved Spacetime and General Covariance In this chapter we generalize the discussion of preceding chapters to extend covariance to more general curved spacetimes. 145 146 CHAPTER 7. CURVED SPACETIME
Part IB GEOMETRY (Lent 2016): Example Sheet 1
 Part IB GEOMETRY (Lent 2016): Example Sheet 1 (a.g.kovalev@dpmms.cam.ac.uk) 1. Suppose that H is a hyperplane in Euclidean n-space R n defined by u x = c for some unit vector u and constant c. The reflection
Part IB GEOMETRY (Lent 2016): Example Sheet 1 (a.g.kovalev@dpmms.cam.ac.uk) 1. Suppose that H is a hyperplane in Euclidean n-space R n defined by u x = c for some unit vector u and constant c. The reflection
On the evolutionary form of the constraints in electrodynamics
 On the evolutionary form of the constraints in electrodynamics István Rácz,1,2 arxiv:1811.06873v1 [gr-qc] 12 Nov 2018 1 Faculty of Physics, University of Warsaw, Ludwika Pasteura 5, 02-093 Warsaw, Poland
On the evolutionary form of the constraints in electrodynamics István Rácz,1,2 arxiv:1811.06873v1 [gr-qc] 12 Nov 2018 1 Faculty of Physics, University of Warsaw, Ludwika Pasteura 5, 02-093 Warsaw, Poland
Geometric Modelling Summer 2016
 Geometric Modelling Summer 2016 Exercises Benjamin Karer M.Sc. http://gfx.uni-kl.de/~gm Benjamin Karer M.Sc. Geometric Modelling Summer 2016 1 Dierential Geometry Benjamin Karer M.Sc. Geometric Modelling
Geometric Modelling Summer 2016 Exercises Benjamin Karer M.Sc. http://gfx.uni-kl.de/~gm Benjamin Karer M.Sc. Geometric Modelling Summer 2016 1 Dierential Geometry Benjamin Karer M.Sc. Geometric Modelling
Classical Mechanics and Electrodynamics
 Classical Mechanics and Electrodynamics Lecture notes FYS 3120 Jon Magne Leinaas Department of Physics, University of Oslo 2 Preface FYS 3120 is a course in classical theoretical physics, which covers
Classical Mechanics and Electrodynamics Lecture notes FYS 3120 Jon Magne Leinaas Department of Physics, University of Oslo 2 Preface FYS 3120 is a course in classical theoretical physics, which covers
Tangent spaces, normals and extrema
 Chapter 3 Tangent spaces, normals and extrema If S is a surface in 3-space, with a point a S where S looks smooth, i.e., without any fold or cusp or self-crossing, we can intuitively define the tangent
Chapter 3 Tangent spaces, normals and extrema If S is a surface in 3-space, with a point a S where S looks smooth, i.e., without any fold or cusp or self-crossing, we can intuitively define the tangent
The Three Body Problem
 The Three Body Problem Joakim Hirvonen Grützelius Karlstad University December 26, 2004 Department of Engineeringsciences, Physics and Mathematics 5p Examinator: Prof Jürgen Füchs Abstract The main topic
The Three Body Problem Joakim Hirvonen Grützelius Karlstad University December 26, 2004 Department of Engineeringsciences, Physics and Mathematics 5p Examinator: Prof Jürgen Füchs Abstract The main topic
Noncollision Singularities in the n-body Problem
 Noncollision Singularities in the n-body Problem Danni Tu Department of Mathematics, Princeton University January 14, 2013 The n-body Problem Introduction Suppose we have n points in R 3 interacting through
Noncollision Singularities in the n-body Problem Danni Tu Department of Mathematics, Princeton University January 14, 2013 The n-body Problem Introduction Suppose we have n points in R 3 interacting through
Problem 1: Lagrangians and Conserved Quantities. Consider the following action for a particle of mass m moving in one dimension
 105A Practice Final Solutions March 13, 01 William Kelly Problem 1: Lagrangians and Conserved Quantities Consider the following action for a particle of mass m moving in one dimension S = dtl = mc dt 1
105A Practice Final Solutions March 13, 01 William Kelly Problem 1: Lagrangians and Conserved Quantities Consider the following action for a particle of mass m moving in one dimension S = dtl = mc dt 1
Stratification of 3 3 Matrices
 Stratification of 3 3 Matrices Meesue Yoo & Clay Shonkwiler March 2, 2006 1 Warmup with 2 2 Matrices { Best matrices of rank 2} = O(2) S 3 ( 2) { Best matrices of rank 1} S 3 (1) 1.1 Viewing O(2) S 3 (
Stratification of 3 3 Matrices Meesue Yoo & Clay Shonkwiler March 2, 2006 1 Warmup with 2 2 Matrices { Best matrices of rank 2} = O(2) S 3 ( 2) { Best matrices of rank 1} S 3 (1) 1.1 Viewing O(2) S 3 (
CALCULUS ON MANIFOLDS. 1. Riemannian manifolds Recall that for any smooth manifold M, dim M = n, the union T M =
 CALCULUS ON MANIFOLDS 1. Riemannian manifolds Recall that for any smooth manifold M, dim M = n, the union T M = a M T am, called the tangent bundle, is itself a smooth manifold, dim T M = 2n. Example 1.
CALCULUS ON MANIFOLDS 1. Riemannian manifolds Recall that for any smooth manifold M, dim M = n, the union T M = a M T am, called the tangent bundle, is itself a smooth manifold, dim T M = 2n. Example 1.
A crash course the geometry of hyperbolic surfaces
 Lecture 7 A crash course the geometry of hyperbolic surfaces 7.1 The hyperbolic plane Hyperbolic geometry originally developed in the early 19 th century to prove that the parallel postulate in Euclidean
Lecture 7 A crash course the geometry of hyperbolic surfaces 7.1 The hyperbolic plane Hyperbolic geometry originally developed in the early 19 th century to prove that the parallel postulate in Euclidean
0. Introduction 1 0. INTRODUCTION
 0. Introduction 1 0. INTRODUCTION In a very rough sketch we explain what algebraic geometry is about and what it can be used for. We stress the many correlations with other fields of research, such as
0. Introduction 1 0. INTRODUCTION In a very rough sketch we explain what algebraic geometry is about and what it can be used for. We stress the many correlations with other fields of research, such as
Introduction to Group Theory
 Chapter 10 Introduction to Group Theory Since symmetries described by groups play such an important role in modern physics, we will take a little time to introduce the basic structure (as seen by a physicist)
Chapter 10 Introduction to Group Theory Since symmetries described by groups play such an important role in modern physics, we will take a little time to introduce the basic structure (as seen by a physicist)
arxiv: v1 [math.dg] 28 Jun 2008
![arxiv: v1 [math.dg] 28 Jun 2008 arxiv: v1 [math.dg] 28 Jun 2008](/thumbs/90/101198950.jpg) Limit Surfaces of Riemann Examples David Hoffman, Wayne Rossman arxiv:0806.467v [math.dg] 28 Jun 2008 Introduction The only connected minimal surfaces foliated by circles and lines are domains on one of
Limit Surfaces of Riemann Examples David Hoffman, Wayne Rossman arxiv:0806.467v [math.dg] 28 Jun 2008 Introduction The only connected minimal surfaces foliated by circles and lines are domains on one of
Physical Dynamics (PHY-304)
 Physical Dynamics (PHY-304) Gabriele Travaglini March 31, 2012 1 Review of Newtonian Mechanics 1.1 One particle Lectures 1-2. Frame, velocity, acceleration, number of degrees of freedom, generalised coordinates.
Physical Dynamics (PHY-304) Gabriele Travaglini March 31, 2012 1 Review of Newtonian Mechanics 1.1 One particle Lectures 1-2. Frame, velocity, acceleration, number of degrees of freedom, generalised coordinates.
Accelerated Observers
 Accelerated Observers In the last few lectures, we ve been discussing the implications that the postulates of special relativity have on the physics of our universe. We ve seen how to compute proper times
Accelerated Observers In the last few lectures, we ve been discussing the implications that the postulates of special relativity have on the physics of our universe. We ve seen how to compute proper times
Spherical trigonometry
 Spherical trigonometry 1 The spherical Pythagorean theorem Proposition 1.1 On a sphere of radius, any right triangle AC with C being the right angle satisfies cos(c/) = cos(a/) cos(b/). (1) Proof: Let
Spherical trigonometry 1 The spherical Pythagorean theorem Proposition 1.1 On a sphere of radius, any right triangle AC with C being the right angle satisfies cos(c/) = cos(a/) cos(b/). (1) Proof: Let
Classical Mechanics and Electrodynamics
 Classical Mechanics and Electrodynamics Lecture notes FYS 3120 Jon Magne Leinaas Department of Physics, University of Oslo December 2009 2 Preface These notes are prepared for the physics course FYS 3120,
Classical Mechanics and Electrodynamics Lecture notes FYS 3120 Jon Magne Leinaas Department of Physics, University of Oslo December 2009 2 Preface These notes are prepared for the physics course FYS 3120,
POINCARE AND NON-EUCLIDEAN GEOMETRY
 Bulletin of the Marathwada Mathematical Society Vol. 12, No. 1, June 2011, Pages 137 142. POINCARE AND NON-EUCLIDEAN GEOMETRY Anant W. Vyawahare, 49, Gajanan Nagar, Wardha Road, NAGPUR - 440 015, M. S.
Bulletin of the Marathwada Mathematical Society Vol. 12, No. 1, June 2011, Pages 137 142. POINCARE AND NON-EUCLIDEAN GEOMETRY Anant W. Vyawahare, 49, Gajanan Nagar, Wardha Road, NAGPUR - 440 015, M. S.
274 Curves on Surfaces, Lecture 4
 274 Curves on Surfaces, Lecture 4 Dylan Thurston Notes by Qiaochu Yuan Fall 2012 4 Hyperbolic geometry Last time there was an exercise asking for braids giving the torsion elements in PSL 2 (Z). A 3-torsion
274 Curves on Surfaces, Lecture 4 Dylan Thurston Notes by Qiaochu Yuan Fall 2012 4 Hyperbolic geometry Last time there was an exercise asking for braids giving the torsion elements in PSL 2 (Z). A 3-torsion
Introduction to Cosmology
 Introduction to Cosmology João G. Rosa joao.rosa@ua.pt http://gravitation.web.ua.pt/cosmo LECTURE 2 - Newtonian cosmology I As a first approach to the Hot Big Bang model, in this lecture we will consider
Introduction to Cosmology João G. Rosa joao.rosa@ua.pt http://gravitation.web.ua.pt/cosmo LECTURE 2 - Newtonian cosmology I As a first approach to the Hot Big Bang model, in this lecture we will consider
RELATIVE EQUILIBRIA IN THE
 CANADIAN APPLIED MATHEMATICS QUARTERLY Volume 10, Number 1, Spring 2003 RELATIVE EQUILIBRIA IN THE CHARGED n-body PROBLEM Based on an invited presentation at the annual meeting of the Canadian Applied
CANADIAN APPLIED MATHEMATICS QUARTERLY Volume 10, Number 1, Spring 2003 RELATIVE EQUILIBRIA IN THE CHARGED n-body PROBLEM Based on an invited presentation at the annual meeting of the Canadian Applied
Hyperbolic Geometry on Geometric Surfaces
 Mathematics Seminar, 15 September 2010 Outline Introduction Hyperbolic geometry Abstract surfaces The hemisphere model as a geometric surface The Poincaré disk model as a geometric surface Conclusion Introduction
Mathematics Seminar, 15 September 2010 Outline Introduction Hyperbolic geometry Abstract surfaces The hemisphere model as a geometric surface The Poincaré disk model as a geometric surface Conclusion Introduction
General Relativity ASTR 2110 Sarazin. Einstein s Equation
 General Relativity ASTR 2110 Sarazin Einstein s Equation Curvature of Spacetime 1. Principle of Equvalence: gravity acceleration locally 2. Acceleration curved path in spacetime In gravitational field,
General Relativity ASTR 2110 Sarazin Einstein s Equation Curvature of Spacetime 1. Principle of Equvalence: gravity acceleration locally 2. Acceleration curved path in spacetime In gravitational field,
Critical points of the integral map of the charged 3-body problem
 Critical points of the integral map of the charged 3-body problem arxiv:1807.04522v1 [math.ds] 12 Jul 2018 Abstract I. Hoveijn, H. Waalkens, M. Zaman Johann Bernoulli Institute for Mathematics and Computer
Critical points of the integral map of the charged 3-body problem arxiv:1807.04522v1 [math.ds] 12 Jul 2018 Abstract I. Hoveijn, H. Waalkens, M. Zaman Johann Bernoulli Institute for Mathematics and Computer
1 Euclidean geometry. 1.1 The metric on R n
 1 Euclidean geometry This chapter discusses the geometry of n-dimensional Euclidean space E n, together with its distance function. The distance gives rise to other notions such as angles and congruent
1 Euclidean geometry This chapter discusses the geometry of n-dimensional Euclidean space E n, together with its distance function. The distance gives rise to other notions such as angles and congruent
HYPERBOLIC GEOMETRY AND PARALLEL TRANSPORT IN R 2 +
 HYPERBOLIC GEOMETRY ND PRLLEL TRNSPORT IN R + VINCENT GLORIOSO, BRITTNY LNDRY, ND PHILLIP WHITE bstract. We will examine the parallel transport of tangent vectors along a hyperbolic triangle containing
HYPERBOLIC GEOMETRY ND PRLLEL TRNSPORT IN R + VINCENT GLORIOSO, BRITTNY LNDRY, ND PHILLIP WHITE bstract. We will examine the parallel transport of tangent vectors along a hyperbolic triangle containing
the EL equation for the x coordinate is easily seen to be (exercise)
 Physics 6010, Fall 2016 Relevant Sections in Text: 1.3 1.6 Examples After all this formalism it is a good idea to spend some time developing a number of illustrative examples. These examples represent
Physics 6010, Fall 2016 Relevant Sections in Text: 1.3 1.6 Examples After all this formalism it is a good idea to spend some time developing a number of illustrative examples. These examples represent
I ve Got a Three-Body Problem
 I ve Got a Three-Body Problem Gareth E. Roberts Department of Mathematics and Computer Science College of the Holy Cross Mathematics Colloquium Fitchburg State College November 13, 2008 Roberts (Holy Cross)
I ve Got a Three-Body Problem Gareth E. Roberts Department of Mathematics and Computer Science College of the Holy Cross Mathematics Colloquium Fitchburg State College November 13, 2008 Roberts (Holy Cross)
Physics 6010, Fall Relevant Sections in Text: Introduction
 Physics 6010, Fall 2016 Introduction. Configuration space. Equations of Motion. Velocity Phase Space. Relevant Sections in Text: 1.1 1.4 Introduction This course principally deals with the variational
Physics 6010, Fall 2016 Introduction. Configuration space. Equations of Motion. Velocity Phase Space. Relevant Sections in Text: 1.1 1.4 Introduction This course principally deals with the variational
Geometric inequalities for black holes
 Geometric inequalities for black holes Sergio Dain FaMAF-Universidad Nacional de Córdoba, CONICET, Argentina. 3 August, 2012 Einstein equations (vacuum) The spacetime is a four dimensional manifold M with
Geometric inequalities for black holes Sergio Dain FaMAF-Universidad Nacional de Córdoba, CONICET, Argentina. 3 August, 2012 Einstein equations (vacuum) The spacetime is a four dimensional manifold M with
Classical Mechanics. Luis Anchordoqui
 1 Rigid Body Motion Inertia Tensor Rotational Kinetic Energy Principal Axes of Rotation Steiner s Theorem Euler s Equations for a Rigid Body Eulerian Angles Review of Fundamental Equations 2 Rigid body
1 Rigid Body Motion Inertia Tensor Rotational Kinetic Energy Principal Axes of Rotation Steiner s Theorem Euler s Equations for a Rigid Body Eulerian Angles Review of Fundamental Equations 2 Rigid body
Gromov s Proof of Mostow Rigidity
 Gromov s Proof of Mostow Rigidity Mostow Rigidity is a theorem about invariants. An invariant assigns a label to whatever mathematical object I am studying that is well-defined up to the appropriate equivalence.
Gromov s Proof of Mostow Rigidity Mostow Rigidity is a theorem about invariants. An invariant assigns a label to whatever mathematical object I am studying that is well-defined up to the appropriate equivalence.
Chapter 14: Vector Calculus
 Chapter 14: Vector Calculus Introduction to Vector Functions Section 14.1 Limits, Continuity, Vector Derivatives a. Limit of a Vector Function b. Limit Rules c. Component By Component Limits d. Continuity
Chapter 14: Vector Calculus Introduction to Vector Functions Section 14.1 Limits, Continuity, Vector Derivatives a. Limit of a Vector Function b. Limit Rules c. Component By Component Limits d. Continuity
8. Prime Factorization and Primary Decompositions
 70 Andreas Gathmann 8. Prime Factorization and Primary Decompositions 13 When it comes to actual computations, Euclidean domains (or more generally principal ideal domains) are probably the nicest rings
70 Andreas Gathmann 8. Prime Factorization and Primary Decompositions 13 When it comes to actual computations, Euclidean domains (or more generally principal ideal domains) are probably the nicest rings
arxiv: v1 [math.ca] 17 Jan 2019
![arxiv: v1 [math.ca] 17 Jan 2019 arxiv: v1 [math.ca] 17 Jan 2019](/thumbs/88/117182865.jpg) GLOBAL EXISTENCE AND SINGULARITY OF THE N-BODY PROBLEM WITH STRONG FORCE arxiv:1901.06001v1 [math.ca] 17 Jan 2019 Yanxia Deng 1, Slim Ibrahim 2 (In memory of Florin Diacu) Abstract. We use the idea of
GLOBAL EXISTENCE AND SINGULARITY OF THE N-BODY PROBLEM WITH STRONG FORCE arxiv:1901.06001v1 [math.ca] 17 Jan 2019 Yanxia Deng 1, Slim Ibrahim 2 (In memory of Florin Diacu) Abstract. We use the idea of
We have seen how to calculate forces and potentials from the smoothed density ρ.
 9. Orbits in stationary Potentials We have seen how to calculate forces and potentials from the smoothed density ρ. Now we can analyse how stars move in this potential. Because two body interactions can
9. Orbits in stationary Potentials We have seen how to calculate forces and potentials from the smoothed density ρ. Now we can analyse how stars move in this potential. Because two body interactions can
The Planar, Circular, Restricted Four-Body Problem
 The Planar, Circular, Restricted Four-Body Problem Gareth E. Roberts Julianne Kulevich Christopher J. Smith Department of Mathematics and Computer Science College of the Holy Cross NSF DMS-0708741 HC Faculty
The Planar, Circular, Restricted Four-Body Problem Gareth E. Roberts Julianne Kulevich Christopher J. Smith Department of Mathematics and Computer Science College of the Holy Cross NSF DMS-0708741 HC Faculty
Multi-Robotic Systems
 CHAPTER 9 Multi-Robotic Systems The topic of multi-robotic systems is quite popular now. It is believed that such systems can have the following benefits: Improved performance ( winning by numbers ) Distributed
CHAPTER 9 Multi-Robotic Systems The topic of multi-robotic systems is quite popular now. It is believed that such systems can have the following benefits: Improved performance ( winning by numbers ) Distributed
The Curved N-Body Problem: Risks and Rewards
 The Curved N-Body Problem: Risks and Rewards FLORIN DIACU Exploring new mathematical territory can be a risky adventure. With no landmarks in sight, it s easy to err, as all the giants, from Fermat and
The Curved N-Body Problem: Risks and Rewards FLORIN DIACU Exploring new mathematical territory can be a risky adventure. With no landmarks in sight, it s easy to err, as all the giants, from Fermat and
Phys 7221, Fall 2006: Midterm exam
 Phys 7221, Fall 2006: Midterm exam October 20, 2006 Problem 1 (40 pts) Consider a spherical pendulum, a mass m attached to a rod of length l, as a constrained system with r = l, as shown in the figure.
Phys 7221, Fall 2006: Midterm exam October 20, 2006 Problem 1 (40 pts) Consider a spherical pendulum, a mass m attached to a rod of length l, as a constrained system with r = l, as shown in the figure.
Physical Dynamics (SPA5304) Lecture Plan 2018
 Physical Dynamics (SPA5304) Lecture Plan 2018 The numbers on the left margin are approximate lecture numbers. Items in gray are not covered this year 1 Advanced Review of Newtonian Mechanics 1.1 One Particle
Physical Dynamics (SPA5304) Lecture Plan 2018 The numbers on the left margin are approximate lecture numbers. Items in gray are not covered this year 1 Advanced Review of Newtonian Mechanics 1.1 One Particle
4 Riemannian geometry
 Classnotes for Introduction to Differential Geometry. Matthias Kawski. April 18, 2003 83 4 Riemannian geometry 4.1 Introduction A natural first step towards a general concept of curvature is to develop
Classnotes for Introduction to Differential Geometry. Matthias Kawski. April 18, 2003 83 4 Riemannian geometry 4.1 Introduction A natural first step towards a general concept of curvature is to develop
Lecture 6 SPHERICAL GEOMETRY
 1 Lecture 6 SPHERICAL GEOMETRY So far we have studied finite and discrete geometries, i.e., geometries in which the main transformation group is either finite or discrete. In this lecture, we begin our
1 Lecture 6 SPHERICAL GEOMETRY So far we have studied finite and discrete geometries, i.e., geometries in which the main transformation group is either finite or discrete. In this lecture, we begin our
The first term involves the cross product of two parallel vectors and so it vanishes. We then get
 Physics 3550 Angular Momentum. Relevant Sections in Text: 3.4, 3.5 Angular Momentum You have certainly encountered angular momentum in a previous class. The importance of angular momentum lies principally
Physics 3550 Angular Momentum. Relevant Sections in Text: 3.4, 3.5 Angular Momentum You have certainly encountered angular momentum in a previous class. The importance of angular momentum lies principally
Lagrange Multipliers
 Optimization with Constraints As long as algebra and geometry have been separated, their progress have been slow and their uses limited; but when these two sciences have been united, they have lent each
Optimization with Constraints As long as algebra and geometry have been separated, their progress have been slow and their uses limited; but when these two sciences have been united, they have lent each
Arc Length and Riemannian Metric Geometry
 Arc Length and Riemannian Metric Geometry References: 1 W F Reynolds, Hyperbolic geometry on a hyperboloid, Amer Math Monthly 100 (1993) 442 455 2 Wikipedia page Metric tensor The most pertinent parts
Arc Length and Riemannian Metric Geometry References: 1 W F Reynolds, Hyperbolic geometry on a hyperboloid, Amer Math Monthly 100 (1993) 442 455 2 Wikipedia page Metric tensor The most pertinent parts
THE ENVELOPE OF LINES MEETING A FIXED LINE AND TANGENT TO TWO SPHERES
 6 September 2004 THE ENVELOPE OF LINES MEETING A FIXED LINE AND TANGENT TO TWO SPHERES Abstract. We study the set of lines that meet a fixed line and are tangent to two spheres and classify the configurations
6 September 2004 THE ENVELOPE OF LINES MEETING A FIXED LINE AND TANGENT TO TWO SPHERES Abstract. We study the set of lines that meet a fixed line and are tangent to two spheres and classify the configurations
5.2 The Levi-Civita Connection on Surfaces. 1 Parallel transport of vector fields on a surface M
 5.2 The Levi-Civita Connection on Surfaces In this section, we define the parallel transport of vector fields on a surface M, and then we introduce the concept of the Levi-Civita connection, which is also
5.2 The Levi-Civita Connection on Surfaces In this section, we define the parallel transport of vector fields on a surface M, and then we introduce the concept of the Levi-Civita connection, which is also
An introduction to General Relativity and the positive mass theorem
 An introduction to General Relativity and the positive mass theorem National Center for Theoretical Sciences, Mathematics Division March 2 nd, 2007 Wen-ling Huang Department of Mathematics University of
An introduction to General Relativity and the positive mass theorem National Center for Theoretical Sciences, Mathematics Division March 2 nd, 2007 Wen-ling Huang Department of Mathematics University of
In these chapter 2A notes write vectors in boldface to reduce the ambiguity of the notation.
 1 2 Linear Systems In these chapter 2A notes write vectors in boldface to reduce the ambiguity of the notation 21 Matrix ODEs Let and is a scalar A linear function satisfies Linear superposition ) Linear
1 2 Linear Systems In these chapter 2A notes write vectors in boldface to reduce the ambiguity of the notation 21 Matrix ODEs Let and is a scalar A linear function satisfies Linear superposition ) Linear
4 Orbits in stationary Potentials (BT 3 to page 107)
 -313see http://www.strw.leidenuniv.nl/ franx/college/ mf-sts13-c-1-313see http://www.strw.leidenuniv.nl/ franx/college/ mf-sts13-c Orbits in stationary Potentials (BT 3 to page 17) Now we have seen how
-313see http://www.strw.leidenuniv.nl/ franx/college/ mf-sts13-c-1-313see http://www.strw.leidenuniv.nl/ franx/college/ mf-sts13-c Orbits in stationary Potentials (BT 3 to page 17) Now we have seen how
ISOLATING BLOCKS NEAR THE COLLINEAR RELATIVE EQUILIBRIA OF THE THREE-BODY PROBLEM
 ISOLATING BLOCKS NEAR THE COLLINEAR RELATIVE EQUILIBRIA OF THE THREE-BODY PROBLEM RICHARD MOECKEL Abstract. The collinear relative equilibrium solutions are among the few explicitly known periodic solutions
ISOLATING BLOCKS NEAR THE COLLINEAR RELATIVE EQUILIBRIA OF THE THREE-BODY PROBLEM RICHARD MOECKEL Abstract. The collinear relative equilibrium solutions are among the few explicitly known periodic solutions
Solution Set Two. 1 Problem #1: Projectile Motion Cartesian Coordinates Polar Coordinates... 3
 : Solution Set Two Northwestern University, Classical Mechanics Classical Mechanics, Third Ed.- Goldstein October 7, 2015 Contents 1 Problem #1: Projectile Motion. 2 1.1 Cartesian Coordinates....................................
: Solution Set Two Northwestern University, Classical Mechanics Classical Mechanics, Third Ed.- Goldstein October 7, 2015 Contents 1 Problem #1: Projectile Motion. 2 1.1 Cartesian Coordinates....................................
Quasi-local Mass in General Relativity
 Quasi-local Mass in General Relativity Shing-Tung Yau Harvard University For the 60th birthday of Gary Horowtiz U. C. Santa Barbara, May. 1, 2015 This talk is based on joint work with Po-Ning Chen and
Quasi-local Mass in General Relativity Shing-Tung Yau Harvard University For the 60th birthday of Gary Horowtiz U. C. Santa Barbara, May. 1, 2015 This talk is based on joint work with Po-Ning Chen and
Marion and Thornton. Tyler Shendruk October 1, Hamilton s Principle - Lagrangian and Hamiltonian dynamics.
 Marion and Thornton Tyler Shendruk October 1, 2010 1 Marion and Thornton Chapter 7 Hamilton s Principle - Lagrangian and Hamiltonian dynamics. 1.1 Problem 6.4 s r z θ Figure 1: Geodesic on circular cylinder
Marion and Thornton Tyler Shendruk October 1, 2010 1 Marion and Thornton Chapter 7 Hamilton s Principle - Lagrangian and Hamiltonian dynamics. 1.1 Problem 6.4 s r z θ Figure 1: Geodesic on circular cylinder
From Wikipedia, the free encyclopedia
 1 of 8 27/03/2013 12:41 Quadratic form From Wikipedia, the free encyclopedia In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example, is a quadratic
1 of 8 27/03/2013 12:41 Quadratic form From Wikipedia, the free encyclopedia In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example, is a quadratic
THEODORE VORONOV DIFFERENTIABLE MANIFOLDS. Fall Last updated: November 26, (Under construction.)
 4 Vector fields Last updated: November 26, 2009. (Under construction.) 4.1 Tangent vectors as derivations After we have introduced topological notions, we can come back to analysis on manifolds. Let M
4 Vector fields Last updated: November 26, 2009. (Under construction.) 4.1 Tangent vectors as derivations After we have introduced topological notions, we can come back to analysis on manifolds. Let M
2.1 Basics of the Relativistic Cosmology: Global Geometry and the Dynamics of the Universe Part I
 1 2.1 Basics of the Relativistic Cosmology: Global Geometry and the Dynamics of the Universe Part I 2 Special Relativity (1905) A fundamental change in viewing the physical space and time, now unified
1 2.1 Basics of the Relativistic Cosmology: Global Geometry and the Dynamics of the Universe Part I 2 Special Relativity (1905) A fundamental change in viewing the physical space and time, now unified
Two-Body Problem. Central Potential. 1D Motion
 Two-Body Problem. Central Potential. D Motion The simplest non-trivial dynamical problem is the problem of two particles. The equations of motion read. m r = F 2, () We already know that the center of
Two-Body Problem. Central Potential. D Motion The simplest non-trivial dynamical problem is the problem of two particles. The equations of motion read. m r = F 2, () We already know that the center of
Non-existence of time-periodic dynamics in general relativity
 Non-existence of time-periodic dynamics in general relativity Volker Schlue University of Toronto University of Miami, February 2, 2015 Outline 1 General relativity Newtonian mechanics Self-gravitating
Non-existence of time-periodic dynamics in general relativity Volker Schlue University of Toronto University of Miami, February 2, 2015 Outline 1 General relativity Newtonian mechanics Self-gravitating
The harmonic map flow
 Chapter 2 The harmonic map flow 2.1 Definition of the flow The harmonic map flow was introduced by Eells-Sampson in 1964; their work could be considered the start of the field of geometric flows. The flow
Chapter 2 The harmonic map flow 2.1 Definition of the flow The harmonic map flow was introduced by Eells-Sampson in 1964; their work could be considered the start of the field of geometric flows. The flow
Möbius transformations Möbius transformations are simply the degree one rational maps of C: cz + d : C C. ad bc 0. a b. A = c d
 Möbius transformations Möbius transformations are simply the degree one rational maps of C: where and Then σ A : z az + b cz + d : C C ad bc 0 ( ) a b A = c d A σ A : GL(2C) {Mobius transformations } is
Möbius transformations Möbius transformations are simply the degree one rational maps of C: where and Then σ A : z az + b cz + d : C C ad bc 0 ( ) a b A = c d A σ A : GL(2C) {Mobius transformations } is
carroll/notes/ has a lot of good notes on GR and links to other pages. General Relativity Philosophy of general
 http://pancake.uchicago.edu/ carroll/notes/ has a lot of good notes on GR and links to other pages. General Relativity Philosophy of general relativity. As with any major theory in physics, GR has been
http://pancake.uchicago.edu/ carroll/notes/ has a lot of good notes on GR and links to other pages. General Relativity Philosophy of general relativity. As with any major theory in physics, GR has been
General Fourier Analysis and Gravitational Waves.
 General Fourier Analysis and Gravitational Waves. Johan Noldus April 0, 06 Abstract In a recent paper [] of this author, we generalized quantum field theory to any curved spacetime. The key idea of the
General Fourier Analysis and Gravitational Waves. Johan Noldus April 0, 06 Abstract In a recent paper [] of this author, we generalized quantum field theory to any curved spacetime. The key idea of the
CALC 3 CONCEPT PACKET Complete
 CALC 3 CONCEPT PACKET Complete Written by Jeremy Robinson, Head Instructor Find Out More +Private Instruction +Review Sessions WWW.GRADEPEAK.COM Need Help? Online Private Instruction Anytime, Anywhere
CALC 3 CONCEPT PACKET Complete Written by Jeremy Robinson, Head Instructor Find Out More +Private Instruction +Review Sessions WWW.GRADEPEAK.COM Need Help? Online Private Instruction Anytime, Anywhere
PURE Math Residents Program Gröbner Bases and Applications Week 3 Lectures
 PURE Math Residents Program Gröbner Bases and Applications Week 3 Lectures John B. Little Department of Mathematics and Computer Science College of the Holy Cross June 2012 Overview of this week The research
PURE Math Residents Program Gröbner Bases and Applications Week 3 Lectures John B. Little Department of Mathematics and Computer Science College of the Holy Cross June 2012 Overview of this week The research
APPM 2350 Section Exam points Wednesday September 26, 6:00pm 7:30pm, 2018
 APPM 2350 Section Exam 1 140 points Wednesday September 26, 6:00pm 7:30pm, 2018 ON THE FRONT OF YOUR BLUEBOOK write: (1) your name, (2) your student ID number, (3) lecture section/time (4) your instructor
APPM 2350 Section Exam 1 140 points Wednesday September 26, 6:00pm 7:30pm, 2018 ON THE FRONT OF YOUR BLUEBOOK write: (1) your name, (2) your student ID number, (3) lecture section/time (4) your instructor
δ-hyperbolic SPACES SIDDHARTHA GADGIL
 δ-hyperbolic SPACES SIDDHARTHA GADGIL Abstract. These are notes for the Chennai TMGT conference on δ-hyperbolic spaces corresponding to chapter III.H in the book of Bridson and Haefliger. When viewed from
δ-hyperbolic SPACES SIDDHARTHA GADGIL Abstract. These are notes for the Chennai TMGT conference on δ-hyperbolic spaces corresponding to chapter III.H in the book of Bridson and Haefliger. When viewed from
baryons+dm radiation+neutrinos vacuum curvature
 baryons+dm radiation+neutrinos vacuum curvature DENSITY ISN T DESTINY! The cosmologist T-shirt (if Λ>0): ΩM,0=0.9 ΩΛ,0=1.6 ΩR=0 ΩM,0=2.5 ΩM,0=2.0 ΩΛ,0=0.1 ΩM,0=2.0 TODAY Baryons 10 t0 68% Dark Energy 5%
baryons+dm radiation+neutrinos vacuum curvature DENSITY ISN T DESTINY! The cosmologist T-shirt (if Λ>0): ΩM,0=0.9 ΩΛ,0=1.6 ΩR=0 ΩM,0=2.5 ΩM,0=2.0 ΩΛ,0=0.1 ΩM,0=2.0 TODAY Baryons 10 t0 68% Dark Energy 5%
Nonlinear Control Lecture 2:Phase Plane Analysis
 Nonlinear Control Lecture 2:Phase Plane Analysis Farzaneh Abdollahi Department of Electrical Engineering Amirkabir University of Technology Fall 2010 r. Farzaneh Abdollahi Nonlinear Control Lecture 2 1/53
Nonlinear Control Lecture 2:Phase Plane Analysis Farzaneh Abdollahi Department of Electrical Engineering Amirkabir University of Technology Fall 2010 r. Farzaneh Abdollahi Nonlinear Control Lecture 2 1/53
arxiv: v4 [math.dg] 10 Feb 2018
![arxiv: v4 [math.dg] 10 Feb 2018 arxiv: v4 [math.dg] 10 Feb 2018](/thumbs/91/104497493.jpg) CYLINDERS AS LEFT INVARIANT CMC SURFACES IN Sol 3 AND E(κ, τ)-spaces DIFFEOMORPHIC TO R 3 MIROSLAV VRŽINA arxiv:1412.6820v4 [math.dg] 10 Feb 2018 ABSTRACT. In the present paper we give a geometric proof
CYLINDERS AS LEFT INVARIANT CMC SURFACES IN Sol 3 AND E(κ, τ)-spaces DIFFEOMORPHIC TO R 3 MIROSLAV VRŽINA arxiv:1412.6820v4 [math.dg] 10 Feb 2018 ABSTRACT. In the present paper we give a geometric proof
Higher Order Singularities in Piecewise Linear Vector Fields
 Higher Order Singularities in Piecewise Linear Vector Fields Xavier Tricoche, Gerik Scheuermann, Hans Hagen Computer Science Department, University of Kaiserslautern, Germany Summary. Piecewise linear
Higher Order Singularities in Piecewise Linear Vector Fields Xavier Tricoche, Gerik Scheuermann, Hans Hagen Computer Science Department, University of Kaiserslautern, Germany Summary. Piecewise linear
+ dxk. dt 2. dt Γi km dxm. . Its equations of motion are second order differential equations. with intitial conditions
 Homework 7. Solutions 1 Show that great circles are geodesics on sphere. Do it a) using the fact that for geodesic, acceleration is orthogonal to the surface. b ) using straightforwardl equations for geodesics
Homework 7. Solutions 1 Show that great circles are geodesics on sphere. Do it a) using the fact that for geodesic, acceleration is orthogonal to the surface. b ) using straightforwardl equations for geodesics
NIL. Let M be R 3 equipped with the metric in which the following vector. fields, U = and. are an orthonormal basis.
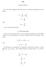 NIL KEVIN WHYTE Let M be R 3 equipped with the metric in which the following vector fields: U = x + y z V = y and W = z are an orthonormal basis. 1. Preliminaries Since we re given the metric via an orthonormal
NIL KEVIN WHYTE Let M be R 3 equipped with the metric in which the following vector fields: U = x + y z V = y and W = z are an orthonormal basis. 1. Preliminaries Since we re given the metric via an orthonormal
Lecture Introduction
 Lecture 1 1.1 Introduction The theory of Partial Differential Equations (PDEs) is central to mathematics, both pure and applied. The main difference between the theory of PDEs and the theory of Ordinary
Lecture 1 1.1 Introduction The theory of Partial Differential Equations (PDEs) is central to mathematics, both pure and applied. The main difference between the theory of PDEs and the theory of Ordinary
PHYM432 Relativity and Cosmology 17. Cosmology Robertson Walker Metric
 PHYM432 Relativity and Cosmology 17. Cosmology Robertson Walker Metric Cosmology applies physics to the universe as a whole, describing it s origin, nature evolution and ultimate fate. While these questions
PHYM432 Relativity and Cosmology 17. Cosmology Robertson Walker Metric Cosmology applies physics to the universe as a whole, describing it s origin, nature evolution and ultimate fate. While these questions
Variable separation and second order superintegrability
 Variable separation and second order superintegrability Willard Miller (Joint with E.G.Kalnins) miller@ima.umn.edu University of Minnesota IMA Talk p.1/59 Abstract In this talk we shall first describe
Variable separation and second order superintegrability Willard Miller (Joint with E.G.Kalnins) miller@ima.umn.edu University of Minnesota IMA Talk p.1/59 Abstract In this talk we shall first describe
Relativistic Electrodynamics
 Relativistic Electrodynamics Notes (I will try to update if typos are found) June 1, 2009 1 Dot products The Pythagorean theorem says that distances are given by With time as a fourth direction, we find
Relativistic Electrodynamics Notes (I will try to update if typos are found) June 1, 2009 1 Dot products The Pythagorean theorem says that distances are given by With time as a fourth direction, we find
Contravariant and Covariant as Transforms
 Contravariant and Covariant as Transforms There is a lot more behind the concepts of contravariant and covariant tensors (of any rank) than the fact that their basis vectors are mutually orthogonal to
Contravariant and Covariant as Transforms There is a lot more behind the concepts of contravariant and covariant tensors (of any rank) than the fact that their basis vectors are mutually orthogonal to
Definition 5.1. A vector field v on a manifold M is map M T M such that for all x M, v(x) T x M.
 5 Vector fields Last updated: March 12, 2012. 5.1 Definition and general properties We first need to define what a vector field is. Definition 5.1. A vector field v on a manifold M is map M T M such that
5 Vector fields Last updated: March 12, 2012. 5.1 Definition and general properties We first need to define what a vector field is. Definition 5.1. A vector field v on a manifold M is map M T M such that
Linear Regression and Its Applications
 Linear Regression and Its Applications Predrag Radivojac October 13, 2014 Given a data set D = {(x i, y i )} n the objective is to learn the relationship between features and the target. We usually start
Linear Regression and Its Applications Predrag Radivojac October 13, 2014 Given a data set D = {(x i, y i )} n the objective is to learn the relationship between features and the target. We usually start
Lecture Figure 4.5. Relating curvature to the circumference of a circle.
 Lecture 26 181 Figure 4.5. Relating curvature to the circumference of a circle. the plane with radius r (Figure 4.5). We will see that circumference = 2πr cr 3 + o(r 3 ) where c is a constant related to
Lecture 26 181 Figure 4.5. Relating curvature to the circumference of a circle. the plane with radius r (Figure 4.5). We will see that circumference = 2πr cr 3 + o(r 3 ) where c is a constant related to
Stable minimal cones in R 8 and R 9 with constant scalar curvature
 Revista Colombiana de Matemáticas Volumen 6 (2002), páginas 97 106 Stable minimal cones in R 8 and R 9 with constant scalar curvature Oscar Perdomo* Universidad del Valle, Cali, COLOMBIA Abstract. In this
Revista Colombiana de Matemáticas Volumen 6 (2002), páginas 97 106 Stable minimal cones in R 8 and R 9 with constant scalar curvature Oscar Perdomo* Universidad del Valle, Cali, COLOMBIA Abstract. In this
Mathematics 3210 Spring Semester, 2005 Homework notes, part 8 April 15, 2005
 Mathematics 3210 Spring Semester, 2005 Homework notes, part 8 April 15, 2005 The underlying assumption for all problems is that all points, lines, etc., are taken within the Poincaré plane (or Poincaré
Mathematics 3210 Spring Semester, 2005 Homework notes, part 8 April 15, 2005 The underlying assumption for all problems is that all points, lines, etc., are taken within the Poincaré plane (or Poincaré
GEOMETRIC QUANTIZATION
 GEOMETRIC QUANTIZATION 1. The basic idea The setting of the Hamiltonian version of classical (Newtonian) mechanics is the phase space (position and momentum), which is a symplectic manifold. The typical
GEOMETRIC QUANTIZATION 1. The basic idea The setting of the Hamiltonian version of classical (Newtonian) mechanics is the phase space (position and momentum), which is a symplectic manifold. The typical
Getting Some Big Air
 Getting Some Big Air Control #10499 February 14, 2011 Abstract In this paper we address the problem of optimizing a ramp for a snowboarder to travel. Our approach is two sided. We first address the forward
Getting Some Big Air Control #10499 February 14, 2011 Abstract In this paper we address the problem of optimizing a ramp for a snowboarder to travel. Our approach is two sided. We first address the forward
B.Sc. (Semester - 5) Subject: Physics Course: US05CPHY01 Classical Mechanics
 1 B.Sc. (Semester - 5) Subject: Physics Course: US05CPHY01 Classical Mechanics Question Bank UNIT: I Multiple choice questions: (1) The gravitational force between two masses is (a) Repulsive (b) Attractive
1 B.Sc. (Semester - 5) Subject: Physics Course: US05CPHY01 Classical Mechanics Question Bank UNIT: I Multiple choice questions: (1) The gravitational force between two masses is (a) Repulsive (b) Attractive
Properties of the Pseudosphere
 Properties of the Pseudosphere Simon Rubinstein Salzedo May 25, 2004 Euclidean, Hyperbolic, and Elliptic Geometries Euclid began his study of geometry with five axioms. They are. Exactly one line may drawn
Properties of the Pseudosphere Simon Rubinstein Salzedo May 25, 2004 Euclidean, Hyperbolic, and Elliptic Geometries Euclid began his study of geometry with five axioms. They are. Exactly one line may drawn
