A Quick Tour of Linear Algebra and Optimization for Machine Learning
|
|
|
- Damon Watkins
- 5 years ago
- Views:
Transcription
1 A Quick Tour of Linear Algebra and Optimization for Machine Learning Masoud Farivar January 8, / 28
2 Outline of Part I: Review of Basic Linear Algebra Matrices and Vectors Matrix Multiplication Operators and Properties Special Types of Matrices Vector Norms Linear Independence and Rank Matrix Inversion Range and Nullspace of a Matrix Determinant Quadratic Forms and Positive Semidefinite Matrices Eigenvalues and Eigenvectors Matrix Eigendecomposition 2 / 28
3 Outline of Part II: Review of Basic Optimization The Gradient The Hessian Least Squares Problem Gradient Descent Stochastic Gradient Descent Convex Optimization Special Classes of Convex Problems Example of Convex Problems in Machine learning Convex Optimization Tools 3 / 28
4 Matrices and Vectors Matrix: A rectangular array of numbers, e.g., A R m n : a 11 a a 1n a 21 a a 2n A =... a m1 a m2... a mn Vector: A matrix with only one column (default) or one row, e.g., x R n x = x 1 x 2. x n 4 / 28
5 Matrix Multiplication If A R m n, B R n p, C = AB, then C R m p : C ij = Properties of Matrix Multiplication: Associative: (AB)C = A(BC) n A ik B kj k=1 Distributive: A(B + C) = AB + AC Non-commutative: AB BA Block multiplication: If A = [A ik ], B = [B kj ], where A ik s and B kj s are matrix blocks, and the number of columns in A ik is equal to the number of rows in B kj, then C = AB = [C ij ] where C ij = k A ikb kj 5 / 28
6 Operators and properties Transpose: A R m n, then A T R n m : (A T ) ij = A ji Properties: (A T ) T = A (AB) T = B T A T (A + B) T = A T + B T Trace: A R n n, then: tr(a) = n i=1 A ii Properties: tr(a) = tr(a T ) tr(a + B) = tr(a) + tr(b) tr(λa) = λtr(a) If AB is a square matrix, tr(ab) = tr(ba) 6 / 28
7 Special types of matrices Identity matrix: I = I n R n n : { 1 i=j, I ij = 0 otherwise. A R m n : AI n = I m A = A Diagonal matrix: D = diag(d 1, d 2,..., d n ): { d i j=i, D ij = 0 otherwise. Symmetric matrices: A R n n is symmetric if A = A T. Orthogonal matrices: U R n n is orthogonal if UU T = I = U T U 7 / 28
8 Vector Norms A norm of a vector x is a measure of it s length or magnitude. The most common is the Euclidean or l 2 norm. ( n ) 1 l p norm : x p = x i p p i=1 n l 2 norm : x 2 = xi 2 i=1 used in ridge regression: y X β 2 + λ β 2 2 l 1 norm : x 1 = n x i i=1 used in l 1 penalized regression: y X β 2 + λ β 1 l norm : x = max x i i 8 / 28
9 Linear Independence and Rank A set of vectors {x 1,..., x n } is linearly independent if {α 1,..., α n }: n i=1 α ix i = 0 Rank: A R m n, then rank(a) is the maximum number of linearly independent columns (or equivalently, rows) Properties: rank(a) min{m, n} rank(a) = rank(a T ) rank(ab) min{rank(a), rank(b)} rank(a + B) rank(a) + rank(b) 9 / 28
10 Matrix Inversion If A R n n, rank(a) = n, then the inverse of A, denoted A 1 is the matrix that: AA 1 = A 1 A = I Properties: (A 1 ) 1 = A (AB) 1 = B 1 A 1 (A 1 ) T = (A T ) 1 The inverse of an orthogonal matrix is its transpose 10 / 28
11 Range and Nullspace of a Matrix Span: span({x 1,..., x n }) = { n i=1 α ix i α i R} Projection: Proj(y; {x i } 1 i n ) = argmin v span({xi } 1 i n ){ y v 2 } Range: A R m n, then R(A) = {Ax x R n } is the span of the columns of A Proj(y, A) = A(A T A) 1 A T y Nullspace: null(a) = {x R n Ax = 0} 11 / 28
12 Determinant A R n n, a 1,..., a n the rows of A, then det(a) is the volume of the S = { n i=1 α ia i 0 α i 1}. Properties: det(i ) = 1 det(λa) = λdet(a) det(a T ) = det(a) det(ab) = det(a)det(b) det(a) 0 if and only if A is invertible. If A invertible, then det(a 1 ) = det(a) 1 12 / 28
13 Quadratic Forms and Positive Semidefinite Matrices A R n n, x R n, x T Ax is called a quadratic form: x T Ax = A ij x i x j 1 i,j n A is positive definite if x R n : x T Ax > 0 A is positive semidefinite if x R n : x T Ax 0 A is negative definite if x R n : x T Ax < 0 A is negative semidefinite if x R n : x T Ax 0 13 / 28
14 Eigenvalues and Eigenvectors A R n n, λ C is an eigenvalue of A with the corresponding eigenvector x C n (x 0) if: Ax = λx eigenvalues: the n possibly complex roots of the polynomial equation det(a λi ) = 0, and denoted as λ 1,..., λ n Properties: tr(a) = n i=1 λ i det(a) = n i=1 λ i rank(a) = {1 i n λ i 0} 14 / 28
15 Matrix Eigendecomposition A R n n, λ 1,..., λ n the eigenvalues, and x 1,..., x n the eigenvectors. X = [x 1 x 2... x n ], Λ = diag(λ 1,..., λ n ), then AX = X Λ. A called diagonalizable if X invertible: A = X ΛX 1 If A symmetric, then all eigenvalues real, and X orthogonal (hence denoted by U = [u 1 u 2... u n ]): A = UΛU T = n λ i u i ui T i=1 A special case of Singular Value Decomposition 15 / 28
16 The Gradient Suppose f : R m n R is a function that takes as input a matrix A and returns a real value. Then the gradient of f is the matrix Note that the size of this matrix is always the same as the size of A. In particular, if A is the vector x R n, 16 / 28
17 The Hessian Suppose f : R n R is a function that takes a vector in R n and returns a real number. Then Hessian matrix with respect to x, the n n matrix: Gradient and Hessian of Quadratic and Linear Functions: 17 / 28
18 Least Squares Problem Solve the following minimization problem: Note that Taking the gradient with respect to x we have (and using the properties above): Setting this to zero and solving for x gives the following closed form solution (psuedo-inverse): 18 / 28
19 Gradient Descent Gradient Descent (GD): takes steps proportional to the negative of the gradient (first order method) Advantage: very general (we ll see it many times) Disadvantage: Local minima (sensitive to starting point) Step size not too large, not too small Common choices: Fixed Linear with iteration (May want step size to decrease with iteration) More advanced methods (e.g., Newton s method) 19 / 28
20 Gradient Descent A typical machine learning problem aims to minimize Error(loss) + Regularizer (penalty): Gradient Descent (GD): choose initial w (0) repeat until minf (w) = f (w; y, x) + g(w) w w (t+1) = w (t) η t F (w (t) ) w (t+1) w (t) ɛ or F (w (t) ) ɛ 20 / 28
21 Stochastic (Online) Gradient Descent Use updates based on individual data points chosen at random Applicable when minimizing an objective function is sum of differentiable functions: f (w; y, x) = 1 n n f (w; y i, x i ) i=1 Suppose we receive an stream of samples (y t, x t ) from the distribution, the idea of SGD is: w (t+1) = w (t) η t w f (w (t) ; y t, x t ) In practice, we typically shuffle data points in the training set randomly and use them one by one for the updates. 21 / 28
22 Stochastic (Online) Gradient Descent The objective does not always decrease for each step comparing to GD, SGD needs more steps, but each step is cheaper mini-batch (say pick up 100 samples and average) can potentially accelerate the convergence 22 / 28
23 Convex Optimization A set of points S is convex if, for any x, y S and for any 0 θ 1, θx + (1 θ)y S A function f : S R is convex if its domain S is a convex set and f (θx + (1 θ)y) θf (x) + (1 θ)f (y) for all x, y S, 0 θ 1. Convex functions can be efficiently minimized. 23 / 28
24 Convex Optimization A convex optimization problem in an optimization problem of the form where f is a convex function, C is a convex set, and x is the optimization variable. Or equivalently: where g i are convex functions, and h i are affine functions. Theorem All locally optimal points of a convex optimization problem are globally optimal. Note that the optimal solution is not necessarily unique. 24 / 28
25 Special Classes of Convex Problems Linear Programming: Quadratic Programming: Quadratically Constrained Quadratic Programming: Semidefinite Programming: 25 / 28
26 Example of Convex Problems in Machine learning Support Vector Machine (SVM) Classifier: This is a quadratic program with optimization variables ω R n, ξ R m, b R, and the input data x(i), y(i), i = 1,... m, and the parameter C R 26 / 28
27 Convex Optimization Tools In many applications, we can write an optimization problem in a convex form. Then we can use several software packages for convex optimization to efficiently solve these problems. These convex optimization engines include: MATLAB-based: CVX, SeDuMi, Matlab Optimization Toolbox (linprog, quadprog) Machine Learning: Weka (Java) libraries: CVXOPT (Python), GLPK (C), COIN-OR (C) SVMs: LIBSVM, SVM-light commerical packages: CPLEX, MOSEK 27 / 28
28 References The source of this review are the following: Boyd, S. and Vandenberghe, L. (2004). Convex Optimization. Cambridge University Press. Course notes from CMU s Course notes from Stanford s CS229, and CS224w Course notes from UCI s CS273a 28 / 28
Quick Tour of Linear Algebra and Graph Theory
 Quick Tour of Linear Algebra and Graph Theory CS224w: Social and Information Network Analysis Fall 2012 Yu Wayne Wu Based on Borja Pelato s version in Fall 2011 Matrices and Vectors Matrix: A rectangular
Quick Tour of Linear Algebra and Graph Theory CS224w: Social and Information Network Analysis Fall 2012 Yu Wayne Wu Based on Borja Pelato s version in Fall 2011 Matrices and Vectors Matrix: A rectangular
Knowledge Discovery and Data Mining 1 (VO) ( )
 Knowledge Discovery and Data Mining 1 (VO) (707.003) Review of Linear Algebra Denis Helic KTI, TU Graz Oct 9, 2014 Denis Helic (KTI, TU Graz) KDDM1 Oct 9, 2014 1 / 74 Big picture: KDDM Probability Theory
Knowledge Discovery and Data Mining 1 (VO) (707.003) Review of Linear Algebra Denis Helic KTI, TU Graz Oct 9, 2014 Denis Helic (KTI, TU Graz) KDDM1 Oct 9, 2014 1 / 74 Big picture: KDDM Probability Theory
Quick Tour of Linear Algebra and Graph Theory
 Quick Tour of Linear Algebra and Graph Theory CS224W: Social and Information Network Analysis Fall 2014 David Hallac Based on Peter Lofgren, Yu Wayne Wu, and Borja Pelato s previous versions Matrices and
Quick Tour of Linear Algebra and Graph Theory CS224W: Social and Information Network Analysis Fall 2014 David Hallac Based on Peter Lofgren, Yu Wayne Wu, and Borja Pelato s previous versions Matrices and
Linear Algebra Formulas. Ben Lee
 Linear Algebra Formulas Ben Lee January 27, 2016 Definitions and Terms Diagonal: Diagonal of matrix A is a collection of entries A ij where i = j. Diagonal Matrix: A matrix (usually square), where entries
Linear Algebra Formulas Ben Lee January 27, 2016 Definitions and Terms Diagonal: Diagonal of matrix A is a collection of entries A ij where i = j. Diagonal Matrix: A matrix (usually square), where entries
CS 246 Review of Linear Algebra 01/17/19
 1 Linear algebra In this section we will discuss vectors and matrices. We denote the (i, j)th entry of a matrix A as A ij, and the ith entry of a vector as v i. 1.1 Vectors and vector operations A vector
1 Linear algebra In this section we will discuss vectors and matrices. We denote the (i, j)th entry of a matrix A as A ij, and the ith entry of a vector as v i. 1.1 Vectors and vector operations A vector
Lecture 1 Review: Linear models have the form (in matrix notation) Y = Xβ + ε,
 2. REVIEW OF LINEAR ALGEBRA 1 Lecture 1 Review: Linear models have the form (in matrix notation) Y = Xβ + ε, where Y n 1 response vector and X n p is the model matrix (or design matrix ) with one row for
2. REVIEW OF LINEAR ALGEBRA 1 Lecture 1 Review: Linear models have the form (in matrix notation) Y = Xβ + ε, where Y n 1 response vector and X n p is the model matrix (or design matrix ) with one row for
Math Bootcamp An p-dimensional vector is p numbers put together. Written as. x 1 x =. x p
 Math Bootcamp 2012 1 Review of matrix algebra 1.1 Vectors and rules of operations An p-dimensional vector is p numbers put together. Written as x 1 x =. x p. When p = 1, this represents a point in the
Math Bootcamp 2012 1 Review of matrix algebra 1.1 Vectors and rules of operations An p-dimensional vector is p numbers put together. Written as x 1 x =. x p. When p = 1, this represents a point in the
2. Linear algebra. matrices and vectors. linear equations. range and nullspace of matrices. function of vectors, gradient and Hessian
 FE661 - Statistical Methods for Financial Engineering 2. Linear algebra Jitkomut Songsiri matrices and vectors linear equations range and nullspace of matrices function of vectors, gradient and Hessian
FE661 - Statistical Methods for Financial Engineering 2. Linear algebra Jitkomut Songsiri matrices and vectors linear equations range and nullspace of matrices function of vectors, gradient and Hessian
Introduction to Matrix Algebra
 Introduction to Matrix Algebra August 18, 2010 1 Vectors 1.1 Notations A p-dimensional vector is p numbers put together. Written as x 1 x =. x p. When p = 1, this represents a point in the line. When p
Introduction to Matrix Algebra August 18, 2010 1 Vectors 1.1 Notations A p-dimensional vector is p numbers put together. Written as x 1 x =. x p. When p = 1, this represents a point in the line. When p
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition
 Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2018 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2018 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
10-701/ Recitation : Linear Algebra Review (based on notes written by Jing Xiang)
 10-701/15-781 Recitation : Linear Algebra Review (based on notes written by Jing Xiang) Manojit Nandi February 1, 2014 Outline Linear Algebra General Properties Matrix Operations Inner Products and Orthogonal
10-701/15-781 Recitation : Linear Algebra Review (based on notes written by Jing Xiang) Manojit Nandi February 1, 2014 Outline Linear Algebra General Properties Matrix Operations Inner Products and Orthogonal
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition
 Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2016 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Linear Algebra review Powers of a diagonalizable matrix Spectral decomposition Prof. Tesler Math 283 Fall 2016 Also see the separate version of this with Matlab and R commands. Prof. Tesler Diagonalizing
Math Camp Lecture 4: Linear Algebra. Xiao Yu Wang. Aug 2010 MIT. Xiao Yu Wang (MIT) Math Camp /10 1 / 88
 Math Camp 2010 Lecture 4: Linear Algebra Xiao Yu Wang MIT Aug 2010 Xiao Yu Wang (MIT) Math Camp 2010 08/10 1 / 88 Linear Algebra Game Plan Vector Spaces Linear Transformations and Matrices Determinant
Math Camp 2010 Lecture 4: Linear Algebra Xiao Yu Wang MIT Aug 2010 Xiao Yu Wang (MIT) Math Camp 2010 08/10 1 / 88 Linear Algebra Game Plan Vector Spaces Linear Transformations and Matrices Determinant
Linear Algebra Review and Reference
 Linear Algebra Review and Reference Zico Kolter (updated by Chuong Do) October 7, 2008 Contents 1 Basic Concepts and Notation 2 11 BasicNotation 2 2 Matrix Multiplication 3 21 Vector-VectorProducts 4 22
Linear Algebra Review and Reference Zico Kolter (updated by Chuong Do) October 7, 2008 Contents 1 Basic Concepts and Notation 2 11 BasicNotation 2 2 Matrix Multiplication 3 21 Vector-VectorProducts 4 22
Mathematical Foundations of Applied Statistics: Matrix Algebra
 Mathematical Foundations of Applied Statistics: Matrix Algebra Steffen Unkel Department of Medical Statistics University Medical Center Göttingen, Germany Winter term 2018/19 1/105 Literature Seber, G.
Mathematical Foundations of Applied Statistics: Matrix Algebra Steffen Unkel Department of Medical Statistics University Medical Center Göttingen, Germany Winter term 2018/19 1/105 Literature Seber, G.
10-725/36-725: Convex Optimization Prerequisite Topics
 10-725/36-725: Convex Optimization Prerequisite Topics February 3, 2015 This is meant to be a brief, informal refresher of some topics that will form building blocks in this course. The content of the
10-725/36-725: Convex Optimization Prerequisite Topics February 3, 2015 This is meant to be a brief, informal refresher of some topics that will form building blocks in this course. The content of the
Linear Algebra Review. Vectors
 Linear Algebra Review 9/4/7 Linear Algebra Review By Tim K. Marks UCSD Borrows heavily from: Jana Kosecka http://cs.gmu.edu/~kosecka/cs682.html Virginia de Sa (UCSD) Cogsci 8F Linear Algebra review Vectors
Linear Algebra Review 9/4/7 Linear Algebra Review By Tim K. Marks UCSD Borrows heavily from: Jana Kosecka http://cs.gmu.edu/~kosecka/cs682.html Virginia de Sa (UCSD) Cogsci 8F Linear Algebra review Vectors
Jim Lambers MAT 610 Summer Session Lecture 1 Notes
 Jim Lambers MAT 60 Summer Session 2009-0 Lecture Notes Introduction This course is about numerical linear algebra, which is the study of the approximate solution of fundamental problems from linear algebra
Jim Lambers MAT 60 Summer Session 2009-0 Lecture Notes Introduction This course is about numerical linear algebra, which is the study of the approximate solution of fundamental problems from linear algebra
Matrix Algebra, part 2
 Matrix Algebra, part 2 Ming-Ching Luoh 2005.9.12 1 / 38 Diagonalization and Spectral Decomposition of a Matrix Optimization 2 / 38 Diagonalization and Spectral Decomposition of a Matrix Also called Eigenvalues
Matrix Algebra, part 2 Ming-Ching Luoh 2005.9.12 1 / 38 Diagonalization and Spectral Decomposition of a Matrix Optimization 2 / 38 Diagonalization and Spectral Decomposition of a Matrix Also called Eigenvalues
Math 315: Linear Algebra Solutions to Assignment 7
 Math 5: Linear Algebra s to Assignment 7 # Find the eigenvalues of the following matrices. (a.) 4 0 0 0 (b.) 0 0 9 5 4. (a.) The characteristic polynomial det(λi A) = (λ )(λ )(λ ), so the eigenvalues are
Math 5: Linear Algebra s to Assignment 7 # Find the eigenvalues of the following matrices. (a.) 4 0 0 0 (b.) 0 0 9 5 4. (a.) The characteristic polynomial det(λi A) = (λ )(λ )(λ ), so the eigenvalues are
Chapter 1. Matrix Algebra
 ST4233, Linear Models, Semester 1 2008-2009 Chapter 1. Matrix Algebra 1 Matrix and vector notation Definition 1.1 A matrix is a rectangular or square array of numbers of variables. We use uppercase boldface
ST4233, Linear Models, Semester 1 2008-2009 Chapter 1. Matrix Algebra 1 Matrix and vector notation Definition 1.1 A matrix is a rectangular or square array of numbers of variables. We use uppercase boldface
Math Linear Algebra Final Exam Review Sheet
 Math 15-1 Linear Algebra Final Exam Review Sheet Vector Operations Vector addition is a component-wise operation. Two vectors v and w may be added together as long as they contain the same number n of
Math 15-1 Linear Algebra Final Exam Review Sheet Vector Operations Vector addition is a component-wise operation. Two vectors v and w may be added together as long as they contain the same number n of
B553 Lecture 5: Matrix Algebra Review
 B553 Lecture 5: Matrix Algebra Review Kris Hauser January 19, 2012 We have seen in prior lectures how vectors represent points in R n and gradients of functions. Matrices represent linear transformations
B553 Lecture 5: Matrix Algebra Review Kris Hauser January 19, 2012 We have seen in prior lectures how vectors represent points in R n and gradients of functions. Matrices represent linear transformations
STAT200C: Review of Linear Algebra
 Stat200C Instructor: Zhaoxia Yu STAT200C: Review of Linear Algebra 1 Review of Linear Algebra 1.1 Vector Spaces, Rank, Trace, and Linear Equations 1.1.1 Rank and Vector Spaces Definition A vector whose
Stat200C Instructor: Zhaoxia Yu STAT200C: Review of Linear Algebra 1 Review of Linear Algebra 1.1 Vector Spaces, Rank, Trace, and Linear Equations 1.1.1 Rank and Vector Spaces Definition A vector whose
Linear Algebra for Machine Learning. Sargur N. Srihari
 Linear Algebra for Machine Learning Sargur N. srihari@cedar.buffalo.edu 1 Overview Linear Algebra is based on continuous math rather than discrete math Computer scientists have little experience with it
Linear Algebra for Machine Learning Sargur N. srihari@cedar.buffalo.edu 1 Overview Linear Algebra is based on continuous math rather than discrete math Computer scientists have little experience with it
Problem Set (T) If A is an m n matrix, B is an n p matrix and D is a p s matrix, then show
 MTH 0: Linear Algebra Department of Mathematics and Statistics Indian Institute of Technology - Kanpur Problem Set Problems marked (T) are for discussions in Tutorial sessions (T) If A is an m n matrix,
MTH 0: Linear Algebra Department of Mathematics and Statistics Indian Institute of Technology - Kanpur Problem Set Problems marked (T) are for discussions in Tutorial sessions (T) If A is an m n matrix,
Foundations of Matrix Analysis
 1 Foundations of Matrix Analysis In this chapter we recall the basic elements of linear algebra which will be employed in the remainder of the text For most of the proofs as well as for the details, the
1 Foundations of Matrix Analysis In this chapter we recall the basic elements of linear algebra which will be employed in the remainder of the text For most of the proofs as well as for the details, the
Linear Algebra - Part II
 Linear Algebra - Part II Projection, Eigendecomposition, SVD (Adapted from Sargur Srihari s slides) Brief Review from Part 1 Symmetric Matrix: A = A T Orthogonal Matrix: A T A = AA T = I and A 1 = A T
Linear Algebra - Part II Projection, Eigendecomposition, SVD (Adapted from Sargur Srihari s slides) Brief Review from Part 1 Symmetric Matrix: A = A T Orthogonal Matrix: A T A = AA T = I and A 1 = A T
Linear Algebra Review
 Linear Algebra Review Contents 1 Basic Concepts and Notations 2 2 Matrix Operations and Properties 3 21 Matrix Multiplication 3 211 Vector-Vector Products 3 212 Matrix-Vector Products 4 213 Matrix-Matrix
Linear Algebra Review Contents 1 Basic Concepts and Notations 2 2 Matrix Operations and Properties 3 21 Matrix Multiplication 3 211 Vector-Vector Products 3 212 Matrix-Vector Products 4 213 Matrix-Matrix
Machine Learning. Lecture 2: Linear regression. Feng Li. https://funglee.github.io
 Machine Learning Lecture 2: Linear regression Feng Li fli@sdu.edu.cn https://funglee.github.io School of Computer Science and Technology Shandong University Fall 2017 Supervised Learning Regression: Predict
Machine Learning Lecture 2: Linear regression Feng Li fli@sdu.edu.cn https://funglee.github.io School of Computer Science and Technology Shandong University Fall 2017 Supervised Learning Regression: Predict
Lecture 2: Linear Algebra Review
 EE 227A: Convex Optimization and Applications January 19 Lecture 2: Linear Algebra Review Lecturer: Mert Pilanci Reading assignment: Appendix C of BV. Sections 2-6 of the web textbook 1 2.1 Vectors 2.1.1
EE 227A: Convex Optimization and Applications January 19 Lecture 2: Linear Algebra Review Lecturer: Mert Pilanci Reading assignment: Appendix C of BV. Sections 2-6 of the web textbook 1 2.1 Vectors 2.1.1
Matrices and Linear Algebra
 Contents Quantitative methods for Economics and Business University of Ferrara Academic year 2017-2018 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2
Contents Quantitative methods for Economics and Business University of Ferrara Academic year 2017-2018 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2 3 4 5 Contents 1 Basics 2
CS 143 Linear Algebra Review
 CS 143 Linear Algebra Review Stefan Roth September 29, 2003 Introductory Remarks This review does not aim at mathematical rigor very much, but instead at ease of understanding and conciseness. Please see
CS 143 Linear Algebra Review Stefan Roth September 29, 2003 Introductory Remarks This review does not aim at mathematical rigor very much, but instead at ease of understanding and conciseness. Please see
Convex Optimization Overview (cnt d)
 Conve Optimization Overview (cnt d) Chuong B. Do November 29, 2009 During last week s section, we began our study of conve optimization, the study of mathematical optimization problems of the form, minimize
Conve Optimization Overview (cnt d) Chuong B. Do November 29, 2009 During last week s section, we began our study of conve optimization, the study of mathematical optimization problems of the form, minimize
Linear Algebra. Matrices Operations. Consider, for example, a system of equations such as x + 2y z + 4w = 0, 3x 4y + 2z 6w = 0, x 3y 2z + w = 0.
 Matrices Operations Linear Algebra Consider, for example, a system of equations such as x + 2y z + 4w = 0, 3x 4y + 2z 6w = 0, x 3y 2z + w = 0 The rectangular array 1 2 1 4 3 4 2 6 1 3 2 1 in which the
Matrices Operations Linear Algebra Consider, for example, a system of equations such as x + 2y z + 4w = 0, 3x 4y + 2z 6w = 0, x 3y 2z + w = 0 The rectangular array 1 2 1 4 3 4 2 6 1 3 2 1 in which the
Phys 201. Matrices and Determinants
 Phys 201 Matrices and Determinants 1 1.1 Matrices 1.2 Operations of matrices 1.3 Types of matrices 1.4 Properties of matrices 1.5 Determinants 1.6 Inverse of a 3 3 matrix 2 1.1 Matrices A 2 3 7 =! " 1
Phys 201 Matrices and Determinants 1 1.1 Matrices 1.2 Operations of matrices 1.3 Types of matrices 1.4 Properties of matrices 1.5 Determinants 1.6 Inverse of a 3 3 matrix 2 1.1 Matrices A 2 3 7 =! " 1
Introduction Eigen Values and Eigen Vectors An Application Matrix Calculus Optimal Portfolio. Portfolios. Christopher Ting.
 Portfolios Christopher Ting Christopher Ting http://www.mysmu.edu/faculty/christophert/ : christopherting@smu.edu.sg : 6828 0364 : LKCSB 5036 November 4, 2016 Christopher Ting QF 101 Week 12 November 4,
Portfolios Christopher Ting Christopher Ting http://www.mysmu.edu/faculty/christophert/ : christopherting@smu.edu.sg : 6828 0364 : LKCSB 5036 November 4, 2016 Christopher Ting QF 101 Week 12 November 4,
Preliminary Linear Algebra 1. Copyright c 2012 Dan Nettleton (Iowa State University) Statistics / 100
 Preliminary Linear Algebra 1 Copyright c 2012 Dan Nettleton (Iowa State University) Statistics 611 1 / 100 Notation for all there exists such that therefore because end of proof (QED) Copyright c 2012
Preliminary Linear Algebra 1 Copyright c 2012 Dan Nettleton (Iowa State University) Statistics 611 1 / 100 Notation for all there exists such that therefore because end of proof (QED) Copyright c 2012
Chapters 5 & 6: Theory Review: Solutions Math 308 F Spring 2015
 Chapters 5 & 6: Theory Review: Solutions Math 308 F Spring 205. If A is a 3 3 triangular matrix, explain why det(a) is equal to the product of entries on the diagonal. If A is a lower triangular or diagonal
Chapters 5 & 6: Theory Review: Solutions Math 308 F Spring 205. If A is a 3 3 triangular matrix, explain why det(a) is equal to the product of entries on the diagonal. If A is a lower triangular or diagonal
Matrices A brief introduction
 Matrices A brief introduction Basilio Bona DAUIN Politecnico di Torino Semester 1, 2014-15 B. Bona (DAUIN) Matrices Semester 1, 2014-15 1 / 44 Definitions Definition A matrix is a set of N real or complex
Matrices A brief introduction Basilio Bona DAUIN Politecnico di Torino Semester 1, 2014-15 B. Bona (DAUIN) Matrices Semester 1, 2014-15 1 / 44 Definitions Definition A matrix is a set of N real or complex
Matrices A brief introduction
 Matrices A brief introduction Basilio Bona DAUIN Politecnico di Torino Semester 1, 2014-15 B. Bona (DAUIN) Matrices Semester 1, 2014-15 1 / 41 Definitions Definition A matrix is a set of N real or complex
Matrices A brief introduction Basilio Bona DAUIN Politecnico di Torino Semester 1, 2014-15 B. Bona (DAUIN) Matrices Semester 1, 2014-15 1 / 41 Definitions Definition A matrix is a set of N real or complex
Linear Algebra Highlights
 Linear Algebra Highlights Chapter 1 A linear equation in n variables is of the form a 1 x 1 + a 2 x 2 + + a n x n. We can have m equations in n variables, a system of linear equations, which we want to
Linear Algebra Highlights Chapter 1 A linear equation in n variables is of the form a 1 x 1 + a 2 x 2 + + a n x n. We can have m equations in n variables, a system of linear equations, which we want to
. a m1 a mn. a 1 a 2 a = a n
 Biostat 140655, 2008: Matrix Algebra Review 1 Definition: An m n matrix, A m n, is a rectangular array of real numbers with m rows and n columns Element in the i th row and the j th column is denoted by
Biostat 140655, 2008: Matrix Algebra Review 1 Definition: An m n matrix, A m n, is a rectangular array of real numbers with m rows and n columns Element in the i th row and the j th column is denoted by
Properties of Matrices and Operations on Matrices
 Properties of Matrices and Operations on Matrices A common data structure for statistical analysis is a rectangular array or matris. Rows represent individual observational units, or just observations,
Properties of Matrices and Operations on Matrices A common data structure for statistical analysis is a rectangular array or matris. Rows represent individual observational units, or just observations,
1. Linear systems of equations. Chapters 7-8: Linear Algebra. Solution(s) of a linear system of equations (continued)
 1 A linear system of equations of the form Sections 75, 78 & 81 a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a 2n x n = b 2 a m1 x 1 + a m2 x 2 + + a mn x n = b m can be written in matrix
1 A linear system of equations of the form Sections 75, 78 & 81 a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a 2n x n = b 2 a m1 x 1 + a m2 x 2 + + a mn x n = b m can be written in matrix
Massachusetts Institute of Technology Department of Economics Statistics. Lecture Notes on Matrix Algebra
 Massachusetts Institute of Technology Department of Economics 14.381 Statistics Guido Kuersteiner Lecture Notes on Matrix Algebra These lecture notes summarize some basic results on matrix algebra used
Massachusetts Institute of Technology Department of Economics 14.381 Statistics Guido Kuersteiner Lecture Notes on Matrix Algebra These lecture notes summarize some basic results on matrix algebra used
Linear Algebra Review
 Linear Algebra Review ORIE 4741 September 1, 2017 Linear Algebra Review September 1, 2017 1 / 33 Outline 1 Linear Independence and Dependence 2 Matrix Rank 3 Invertible Matrices 4 Norms 5 Projection Matrix
Linear Algebra Review ORIE 4741 September 1, 2017 Linear Algebra Review September 1, 2017 1 / 33 Outline 1 Linear Independence and Dependence 2 Matrix Rank 3 Invertible Matrices 4 Norms 5 Projection Matrix
[3] (b) Find a reduced row-echelon matrix row-equivalent to ,1 2 2
![[3] (b) Find a reduced row-echelon matrix row-equivalent to ,1 2 2 [3] (b) Find a reduced row-echelon matrix row-equivalent to ,1 2 2](/thumbs/91/107233302.jpg) MATH Key for sample nal exam, August 998 []. (a) Dene the term \reduced row-echelon matrix". A matrix is reduced row-echelon if the following conditions are satised. every zero row lies below every nonzero
MATH Key for sample nal exam, August 998 []. (a) Dene the term \reduced row-echelon matrix". A matrix is reduced row-echelon if the following conditions are satised. every zero row lies below every nonzero
EE731 Lecture Notes: Matrix Computations for Signal Processing
 EE731 Lecture Notes: Matrix Computations for Signal Processing James P. Reilly c Department of Electrical and Computer Engineering McMaster University September 22, 2005 0 Preface This collection of ten
EE731 Lecture Notes: Matrix Computations for Signal Processing James P. Reilly c Department of Electrical and Computer Engineering McMaster University September 22, 2005 0 Preface This collection of ten
NOTES on LINEAR ALGEBRA 1
 School of Economics, Management and Statistics University of Bologna Academic Year 207/8 NOTES on LINEAR ALGEBRA for the students of Stats and Maths This is a modified version of the notes by Prof Laura
School of Economics, Management and Statistics University of Bologna Academic Year 207/8 NOTES on LINEAR ALGEBRA for the students of Stats and Maths This is a modified version of the notes by Prof Laura
10.34 Numerical Methods Applied to Chemical Engineering Fall Quiz #1 Review
 10.34 Numerical Methods Applied to Chemical Engineering Fall 2015 Quiz #1 Review Study guide based on notes developed by J.A. Paulson, modified by K. Severson Linear Algebra We ve covered three major topics
10.34 Numerical Methods Applied to Chemical Engineering Fall 2015 Quiz #1 Review Study guide based on notes developed by J.A. Paulson, modified by K. Severson Linear Algebra We ve covered three major topics
CP3 REVISION LECTURES VECTORS AND MATRICES Lecture 1. Prof. N. Harnew University of Oxford TT 2013
 CP3 REVISION LECTURES VECTORS AND MATRICES Lecture 1 Prof. N. Harnew University of Oxford TT 2013 1 OUTLINE 1. Vector Algebra 2. Vector Geometry 3. Types of Matrices and Matrix Operations 4. Determinants
CP3 REVISION LECTURES VECTORS AND MATRICES Lecture 1 Prof. N. Harnew University of Oxford TT 2013 1 OUTLINE 1. Vector Algebra 2. Vector Geometry 3. Types of Matrices and Matrix Operations 4. Determinants
Chap 3. Linear Algebra
 Chap 3. Linear Algebra Outlines 1. Introduction 2. Basis, Representation, and Orthonormalization 3. Linear Algebraic Equations 4. Similarity Transformation 5. Diagonal Form and Jordan Form 6. Functions
Chap 3. Linear Algebra Outlines 1. Introduction 2. Basis, Representation, and Orthonormalization 3. Linear Algebraic Equations 4. Similarity Transformation 5. Diagonal Form and Jordan Form 6. Functions
3 (Maths) Linear Algebra
 3 (Maths) Linear Algebra References: Simon and Blume, chapters 6 to 11, 16 and 23; Pemberton and Rau, chapters 11 to 13 and 25; Sundaram, sections 1.3 and 1.5. The methods and concepts of linear algebra
3 (Maths) Linear Algebra References: Simon and Blume, chapters 6 to 11, 16 and 23; Pemberton and Rau, chapters 11 to 13 and 25; Sundaram, sections 1.3 and 1.5. The methods and concepts of linear algebra
GATE Engineering Mathematics SAMPLE STUDY MATERIAL. Postal Correspondence Course GATE. Engineering. Mathematics GATE ENGINEERING MATHEMATICS
 SAMPLE STUDY MATERIAL Postal Correspondence Course GATE Engineering Mathematics GATE ENGINEERING MATHEMATICS ENGINEERING MATHEMATICS GATE Syllabus CIVIL ENGINEERING CE CHEMICAL ENGINEERING CH MECHANICAL
SAMPLE STUDY MATERIAL Postal Correspondence Course GATE Engineering Mathematics GATE ENGINEERING MATHEMATICS ENGINEERING MATHEMATICS GATE Syllabus CIVIL ENGINEERING CE CHEMICAL ENGINEERING CH MECHANICAL
Duke University, Department of Electrical and Computer Engineering Optimization for Scientists and Engineers c Alex Bronstein, 2014
 Duke University, Department of Electrical and Computer Engineering Optimization for Scientists and Engineers c Alex Bronstein, 2014 Linear Algebra A Brief Reminder Purpose. The purpose of this document
Duke University, Department of Electrical and Computer Engineering Optimization for Scientists and Engineers c Alex Bronstein, 2014 Linear Algebra A Brief Reminder Purpose. The purpose of this document
Math Camp II. Basic Linear Algebra. Yiqing Xu. Aug 26, 2014 MIT
 Math Camp II Basic Linear Algebra Yiqing Xu MIT Aug 26, 2014 1 Solving Systems of Linear Equations 2 Vectors and Vector Spaces 3 Matrices 4 Least Squares Systems of Linear Equations Definition A linear
Math Camp II Basic Linear Algebra Yiqing Xu MIT Aug 26, 2014 1 Solving Systems of Linear Equations 2 Vectors and Vector Spaces 3 Matrices 4 Least Squares Systems of Linear Equations Definition A linear
Introduction to Quantitative Techniques for MSc Programmes SCHOOL OF ECONOMICS, MATHEMATICS AND STATISTICS MALET STREET LONDON WC1E 7HX
 Introduction to Quantitative Techniques for MSc Programmes SCHOOL OF ECONOMICS, MATHEMATICS AND STATISTICS MALET STREET LONDON WC1E 7HX September 2007 MSc Sep Intro QT 1 Who are these course for? The September
Introduction to Quantitative Techniques for MSc Programmes SCHOOL OF ECONOMICS, MATHEMATICS AND STATISTICS MALET STREET LONDON WC1E 7HX September 2007 MSc Sep Intro QT 1 Who are these course for? The September
Linear algebra for computational statistics
 University of Seoul May 3, 2018 Vector and Matrix Notation Denote 2-dimensional data array (n p matrix) by X. Denote the element in the ith row and the jth column of X by x ij or (X) ij. Denote by X j
University of Seoul May 3, 2018 Vector and Matrix Notation Denote 2-dimensional data array (n p matrix) by X. Denote the element in the ith row and the jth column of X by x ij or (X) ij. Denote by X j
Mathematical foundations - linear algebra
 Mathematical foundations - linear algebra Andrea Passerini passerini@disi.unitn.it Machine Learning Vector space Definition (over reals) A set X is called a vector space over IR if addition and scalar
Mathematical foundations - linear algebra Andrea Passerini passerini@disi.unitn.it Machine Learning Vector space Definition (over reals) A set X is called a vector space over IR if addition and scalar
The Singular Value Decomposition
 The Singular Value Decomposition Philippe B. Laval KSU Fall 2015 Philippe B. Laval (KSU) SVD Fall 2015 1 / 13 Review of Key Concepts We review some key definitions and results about matrices that will
The Singular Value Decomposition Philippe B. Laval KSU Fall 2015 Philippe B. Laval (KSU) SVD Fall 2015 1 / 13 Review of Key Concepts We review some key definitions and results about matrices that will
Some notes on Linear Algebra. Mark Schmidt September 10, 2009
 Some notes on Linear Algebra Mark Schmidt September 10, 2009 References Linear Algebra and Its Applications. Strang, 1988. Practical Optimization. Gill, Murray, Wright, 1982. Matrix Computations. Golub
Some notes on Linear Algebra Mark Schmidt September 10, 2009 References Linear Algebra and Its Applications. Strang, 1988. Practical Optimization. Gill, Murray, Wright, 1982. Matrix Computations. Golub
Contents. 1 Introduction. 1.1 History of Optimization ALG-ML SEMINAR LISSA: LINEAR TIME SECOND-ORDER STOCHASTIC ALGORITHM FEBRUARY 23, 2016
 ALG-ML SEMINAR LISSA: LINEAR TIME SECOND-ORDER STOCHASTIC ALGORITHM FEBRUARY 23, 2016 LECTURERS: NAMAN AGARWAL AND BRIAN BULLINS SCRIBE: KIRAN VODRAHALLI Contents 1 Introduction 1 1.1 History of Optimization.....................................
ALG-ML SEMINAR LISSA: LINEAR TIME SECOND-ORDER STOCHASTIC ALGORITHM FEBRUARY 23, 2016 LECTURERS: NAMAN AGARWAL AND BRIAN BULLINS SCRIBE: KIRAN VODRAHALLI Contents 1 Introduction 1 1.1 History of Optimization.....................................
UNIT 6: The singular value decomposition.
 UNIT 6: The singular value decomposition. María Barbero Liñán Universidad Carlos III de Madrid Bachelor in Statistics and Business Mathematical methods II 2011-2012 A square matrix is symmetric if A T
UNIT 6: The singular value decomposition. María Barbero Liñán Universidad Carlos III de Madrid Bachelor in Statistics and Business Mathematical methods II 2011-2012 A square matrix is symmetric if A T
Linear Algebra. Christos Michalopoulos. September 24, NTU, Department of Economics
 Linear Algebra Christos Michalopoulos NTU, Department of Economics September 24, 2011 Christos Michalopoulos Linear Algebra September 24, 2011 1 / 93 Linear Equations Denition A linear equation in n-variables
Linear Algebra Christos Michalopoulos NTU, Department of Economics September 24, 2011 Christos Michalopoulos Linear Algebra September 24, 2011 1 / 93 Linear Equations Denition A linear equation in n-variables
Linear Algebra Practice Final
 . Let (a) First, Linear Algebra Practice Final Summer 3 3 A = 5 3 3 rref([a ) = 5 so if we let x 5 = t, then x 4 = t, x 3 =, x = t, and x = t, so that t t x = t = t t whence ker A = span(,,,, ) and a basis
. Let (a) First, Linear Algebra Practice Final Summer 3 3 A = 5 3 3 rref([a ) = 5 so if we let x 5 = t, then x 4 = t, x 3 =, x = t, and x = t, so that t t x = t = t t whence ker A = span(,,,, ) and a basis
MAT 610: Numerical Linear Algebra. James V. Lambers
 MAT 610: Numerical Linear Algebra James V Lambers January 16, 2017 2 Contents 1 Matrix Multiplication Problems 7 11 Introduction 7 111 Systems of Linear Equations 7 112 The Eigenvalue Problem 8 12 Basic
MAT 610: Numerical Linear Algebra James V Lambers January 16, 2017 2 Contents 1 Matrix Multiplication Problems 7 11 Introduction 7 111 Systems of Linear Equations 7 112 The Eigenvalue Problem 8 12 Basic
Online Exercises for Linear Algebra XM511
 This document lists the online exercises for XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Lecture 02 ( 1.1) Online Exercises for Linear Algebra XM511 1) The matrix [3 2
This document lists the online exercises for XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Lecture 02 ( 1.1) Online Exercises for Linear Algebra XM511 1) The matrix [3 2
Applied Mathematics 205. Unit V: Eigenvalue Problems. Lecturer: Dr. David Knezevic
 Applied Mathematics 205 Unit V: Eigenvalue Problems Lecturer: Dr. David Knezevic Unit V: Eigenvalue Problems Chapter V.2: Fundamentals 2 / 31 Eigenvalues and Eigenvectors Eigenvalues and eigenvectors of
Applied Mathematics 205 Unit V: Eigenvalue Problems Lecturer: Dr. David Knezevic Unit V: Eigenvalue Problems Chapter V.2: Fundamentals 2 / 31 Eigenvalues and Eigenvectors Eigenvalues and eigenvectors of
4 Linear Algebra Review
 4 Linear Algebra Review For this topic we quickly review many key aspects of linear algebra that will be necessary for the remainder of the course 41 Vectors and Matrices For the context of data analysis,
4 Linear Algebra Review For this topic we quickly review many key aspects of linear algebra that will be necessary for the remainder of the course 41 Vectors and Matrices For the context of data analysis,
Math 489AB Exercises for Chapter 1 Fall Section 1.0
 Math 489AB Exercises for Chapter 1 Fall 2008 Section 1.0 1.0.2 We want to maximize x T Ax subject to the condition x T x = 1. We use the method of Lagrange multipliers. Let f(x) = x T Ax and g(x) = x T
Math 489AB Exercises for Chapter 1 Fall 2008 Section 1.0 1.0.2 We want to maximize x T Ax subject to the condition x T x = 1. We use the method of Lagrange multipliers. Let f(x) = x T Ax and g(x) = x T
Mathematical foundations - linear algebra
 Mathematical foundations - linear algebra Andrea Passerini passerini@disi.unitn.it Machine Learning Vector space Definition (over reals) A set X is called a vector space over IR if addition and scalar
Mathematical foundations - linear algebra Andrea Passerini passerini@disi.unitn.it Machine Learning Vector space Definition (over reals) A set X is called a vector space over IR if addition and scalar
MATRIX ALGEBRA. or x = (x 1,..., x n ) R n. y 1 y 2. x 2. x m. y m. y = cos θ 1 = x 1 L x. sin θ 1 = x 2. cos θ 2 = y 1 L y.
 as Basics Vectors MATRIX ALGEBRA An array of n real numbers x, x,, x n is called a vector and it is written x = x x n or x = x,, x n R n prime operation=transposing a column to a row Basic vector operations
as Basics Vectors MATRIX ALGEBRA An array of n real numbers x, x,, x n is called a vector and it is written x = x x n or x = x,, x n R n prime operation=transposing a column to a row Basic vector operations
The University of Texas at Austin Department of Electrical and Computer Engineering. EE381V: Large Scale Learning Spring 2013.
 The University of Texas at Austin Department of Electrical and Computer Engineering EE381V: Large Scale Learning Spring 2013 Assignment Two Caramanis/Sanghavi Due: Tuesday, Feb. 19, 2013. Computational
The University of Texas at Austin Department of Electrical and Computer Engineering EE381V: Large Scale Learning Spring 2013 Assignment Two Caramanis/Sanghavi Due: Tuesday, Feb. 19, 2013. Computational
Review of Some Concepts from Linear Algebra: Part 2
 Review of Some Concepts from Linear Algebra: Part 2 Department of Mathematics Boise State University January 16, 2019 Math 566 Linear Algebra Review: Part 2 January 16, 2019 1 / 22 Vector spaces A set
Review of Some Concepts from Linear Algebra: Part 2 Department of Mathematics Boise State University January 16, 2019 Math 566 Linear Algebra Review: Part 2 January 16, 2019 1 / 22 Vector spaces A set
Linear Algebra & Analysis Review UW EE/AA/ME 578 Convex Optimization
 Linear Algebra & Analysis Review UW EE/AA/ME 578 Convex Optimization January 9, 2015 1 Notation 1. Book pages without explicit citation refer to [1]. 2. R n denotes the set of real n-column vectors. 3.
Linear Algebra & Analysis Review UW EE/AA/ME 578 Convex Optimization January 9, 2015 1 Notation 1. Book pages without explicit citation refer to [1]. 2. R n denotes the set of real n-column vectors. 3.
Lecture Summaries for Linear Algebra M51A
 These lecture summaries may also be viewed online by clicking the L icon at the top right of any lecture screen. Lecture Summaries for Linear Algebra M51A refers to the section in the textbook. Lecture
These lecture summaries may also be viewed online by clicking the L icon at the top right of any lecture screen. Lecture Summaries for Linear Algebra M51A refers to the section in the textbook. Lecture
Mobile Robotics 1. A Compact Course on Linear Algebra. Giorgio Grisetti
 Mobile Robotics 1 A Compact Course on Linear Algebra Giorgio Grisetti SA-1 Vectors Arrays of numbers They represent a point in a n dimensional space 2 Vectors: Scalar Product Scalar-Vector Product Changes
Mobile Robotics 1 A Compact Course on Linear Algebra Giorgio Grisetti SA-1 Vectors Arrays of numbers They represent a point in a n dimensional space 2 Vectors: Scalar Product Scalar-Vector Product Changes
EE/ACM Applications of Convex Optimization in Signal Processing and Communications Lecture 2
 EE/ACM 150 - Applications of Convex Optimization in Signal Processing and Communications Lecture 2 Andre Tkacenko Signal Processing Research Group Jet Propulsion Laboratory April 5, 2012 Andre Tkacenko
EE/ACM 150 - Applications of Convex Optimization in Signal Processing and Communications Lecture 2 Andre Tkacenko Signal Processing Research Group Jet Propulsion Laboratory April 5, 2012 Andre Tkacenko
AMS526: Numerical Analysis I (Numerical Linear Algebra)
 AMS526: Numerical Analysis I (Numerical Linear Algebra) Lecture 1: Course Overview & Matrix-Vector Multiplication Xiangmin Jiao SUNY Stony Brook Xiangmin Jiao Numerical Analysis I 1 / 20 Outline 1 Course
AMS526: Numerical Analysis I (Numerical Linear Algebra) Lecture 1: Course Overview & Matrix-Vector Multiplication Xiangmin Jiao SUNY Stony Brook Xiangmin Jiao Numerical Analysis I 1 / 20 Outline 1 Course
Linear Algebra Review
 January 29, 2013 Table of contents Metrics Metric Given a space X, then d : X X R + 0 and z in X if: d(x, y) = 0 is equivalent to x = y d(x, y) = d(y, x) d(x, y) d(x, z) + d(z, y) is a metric is for all
January 29, 2013 Table of contents Metrics Metric Given a space X, then d : X X R + 0 and z in X if: d(x, y) = 0 is equivalent to x = y d(x, y) = d(y, x) d(x, y) d(x, z) + d(z, y) is a metric is for all
Lecture 2: Linear operators
 Lecture 2: Linear operators Rajat Mittal IIT Kanpur The mathematical formulation of Quantum computing requires vector spaces and linear operators So, we need to be comfortable with linear algebra to study
Lecture 2: Linear operators Rajat Mittal IIT Kanpur The mathematical formulation of Quantum computing requires vector spaces and linear operators So, we need to be comfortable with linear algebra to study
Chapter 4 Euclid Space
 Chapter 4 Euclid Space Inner Product Spaces Definition.. Let V be a real vector space over IR. A real inner product on V is a real valued function on V V, denoted by (, ), which satisfies () (x, y) = (y,
Chapter 4 Euclid Space Inner Product Spaces Definition.. Let V be a real vector space over IR. A real inner product on V is a real valued function on V V, denoted by (, ), which satisfies () (x, y) = (y,
1. Select the unique answer (choice) for each problem. Write only the answer.
 MATH 5 Practice Problem Set Spring 7. Select the unique answer (choice) for each problem. Write only the answer. () Determine all the values of a for which the system has infinitely many solutions: x +
MATH 5 Practice Problem Set Spring 7. Select the unique answer (choice) for each problem. Write only the answer. () Determine all the values of a for which the system has infinitely many solutions: x +
TBP MATH33A Review Sheet. November 24, 2018
 TBP MATH33A Review Sheet November 24, 2018 General Transformation Matrices: Function Scaling by k Orthogonal projection onto line L Implementation If we want to scale I 2 by k, we use the following: [
TBP MATH33A Review Sheet November 24, 2018 General Transformation Matrices: Function Scaling by k Orthogonal projection onto line L Implementation If we want to scale I 2 by k, we use the following: [
Vectors To begin, let us describe an element of the state space as a point with numerical coordinates, that is x 1. x 2. x =
 Linear Algebra Review Vectors To begin, let us describe an element of the state space as a point with numerical coordinates, that is x 1 x x = 2. x n Vectors of up to three dimensions are easy to diagram.
Linear Algebra Review Vectors To begin, let us describe an element of the state space as a point with numerical coordinates, that is x 1 x x = 2. x n Vectors of up to three dimensions are easy to diagram.
Mathematical Methods wk 2: Linear Operators
 John Magorrian, magog@thphysoxacuk These are work-in-progress notes for the second-year course on mathematical methods The most up-to-date version is available from http://www-thphysphysicsoxacuk/people/johnmagorrian/mm
John Magorrian, magog@thphysoxacuk These are work-in-progress notes for the second-year course on mathematical methods The most up-to-date version is available from http://www-thphysphysicsoxacuk/people/johnmagorrian/mm
ACM 104. Homework Set 4 Solutions February 14, 2001
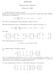 ACM 04 Homework Set 4 Solutions February 4, 00 Franklin Chapter, Problem 4, page 55 Suppose that we feel that some observations are more important or reliable than others Redefine the function to be minimized
ACM 04 Homework Set 4 Solutions February 4, 00 Franklin Chapter, Problem 4, page 55 Suppose that we feel that some observations are more important or reliable than others Redefine the function to be minimized
Math 205, Summer I, Week 4b:
 Math 205, Summer I, 2016 Week 4b: Chapter 5, Sections 6, 7 and 8 (5.5 is NOT on the syllabus) 5.6 Eigenvalues and Eigenvectors 5.7 Eigenspaces, nondefective matrices 5.8 Diagonalization [*** See next slide
Math 205, Summer I, 2016 Week 4b: Chapter 5, Sections 6, 7 and 8 (5.5 is NOT on the syllabus) 5.6 Eigenvalues and Eigenvectors 5.7 Eigenspaces, nondefective matrices 5.8 Diagonalization [*** See next slide
Convex Optimization Overview (cnt d)
 Convex Optimization Overview (cnt d) Chuong B. Do October 6, 007 1 Recap During last week s section, we began our study of convex optimization, the study of mathematical optimization problems of the form,
Convex Optimization Overview (cnt d) Chuong B. Do October 6, 007 1 Recap During last week s section, we began our study of convex optimization, the study of mathematical optimization problems of the form,
18.06 Problem Set 8 - Solutions Due Wednesday, 14 November 2007 at 4 pm in
 806 Problem Set 8 - Solutions Due Wednesday, 4 November 2007 at 4 pm in 2-06 08 03 Problem : 205+5+5+5 Consider the matrix A 02 07 a Check that A is a positive Markov matrix, and find its steady state
806 Problem Set 8 - Solutions Due Wednesday, 4 November 2007 at 4 pm in 2-06 08 03 Problem : 205+5+5+5 Consider the matrix A 02 07 a Check that A is a positive Markov matrix, and find its steady state
Elementary maths for GMT
 Elementary maths for GMT Linear Algebra Part 2: Matrices, Elimination and Determinant m n matrices The system of m linear equations in n variables x 1, x 2,, x n a 11 x 1 + a 12 x 2 + + a 1n x n = b 1
Elementary maths for GMT Linear Algebra Part 2: Matrices, Elimination and Determinant m n matrices The system of m linear equations in n variables x 1, x 2,, x n a 11 x 1 + a 12 x 2 + + a 1n x n = b 1
OHSx XM511 Linear Algebra: Solutions to Online True/False Exercises
 This document gives the solutions to all of the online exercises for OHSx XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Answers are in square brackets [. Lecture 02 ( 1.1)
This document gives the solutions to all of the online exercises for OHSx XM511. The section ( ) numbers refer to the textbook. TYPE I are True/False. Answers are in square brackets [. Lecture 02 ( 1.1)
LINEAR ALGEBRA REVIEW
 LINEAR ALGEBRA REVIEW SPENCER BECKER-KAHN Basic Definitions Domain and Codomain. Let f : X Y be any function. This notation means that X is the domain of f and Y is the codomain of f. This means that for
LINEAR ALGEBRA REVIEW SPENCER BECKER-KAHN Basic Definitions Domain and Codomain. Let f : X Y be any function. This notation means that X is the domain of f and Y is the codomain of f. This means that for
Large Scale Data Analysis Using Deep Learning
 Large Scale Data Analysis Using Deep Learning Linear Algebra U Kang Seoul National University U Kang 1 In This Lecture Overview of linear algebra (but, not a comprehensive survey) Focused on the subset
Large Scale Data Analysis Using Deep Learning Linear Algebra U Kang Seoul National University U Kang 1 In This Lecture Overview of linear algebra (but, not a comprehensive survey) Focused on the subset
Recall the convention that, for us, all vectors are column vectors.
 Some linear algebra Recall the convention that, for us, all vectors are column vectors. 1. Symmetric matrices Let A be a real matrix. Recall that a complex number λ is an eigenvalue of A if there exists
Some linear algebra Recall the convention that, for us, all vectors are column vectors. 1. Symmetric matrices Let A be a real matrix. Recall that a complex number λ is an eigenvalue of A if there exists
Mathematical Methods for Engineers 1 (AMS10/10A)
 Mathematical Methods for Engineers 1 (AMS10/10A) Quiz 5 - Friday May 27th (2016) 2:00-3:10 PM AMS 10 AMS 10A Name: Student ID: Multiple Choice Questions (3 points each; only one correct answer per question)
Mathematical Methods for Engineers 1 (AMS10/10A) Quiz 5 - Friday May 27th (2016) 2:00-3:10 PM AMS 10 AMS 10A Name: Student ID: Multiple Choice Questions (3 points each; only one correct answer per question)
Practice Final Exam. Solutions.
 MATH Applied Linear Algebra December 6, 8 Practice Final Exam Solutions Find the standard matrix f the linear transfmation T : R R such that T, T, T Solution: Easy to see that the transfmation T can be
MATH Applied Linear Algebra December 6, 8 Practice Final Exam Solutions Find the standard matrix f the linear transfmation T : R R such that T, T, T Solution: Easy to see that the transfmation T can be
A Brief Outline of Math 355
 A Brief Outline of Math 355 Lecture 1 The geometry of linear equations; elimination with matrices A system of m linear equations with n unknowns can be thought of geometrically as m hyperplanes intersecting
A Brief Outline of Math 355 Lecture 1 The geometry of linear equations; elimination with matrices A system of m linear equations with n unknowns can be thought of geometrically as m hyperplanes intersecting
Unit 3: Matrices. Juan Luis Melero and Eduardo Eyras. September 2018
 Unit 3: Matrices Juan Luis Melero and Eduardo Eyras September 2018 1 Contents 1 Matrices and operations 4 1.1 Definition of a matrix....................... 4 1.2 Addition and subtraction of matrices..............
Unit 3: Matrices Juan Luis Melero and Eduardo Eyras September 2018 1 Contents 1 Matrices and operations 4 1.1 Definition of a matrix....................... 4 1.2 Addition and subtraction of matrices..............
