Generalized flame balls
|
|
|
- Lambert Johns
- 5 years ago
- Views:
Transcription
1 Combustion Theory and Modelling Vol. 13, No., 9, Generalized flame balls Joel Daou 1,, Faisal Al-Malki 1 and Paul Ronney 1 School of Mathematics, University of Manchester, Manchester M13 9PL, UK; Department of Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA , USA (Received 1 June 8; final version received October 8) We consider generalized flame balls which correspond to stationary spherical flames with a flow of hot inert gas, either a source or a sink, at the origin. Depending on the flow, these flames can have positive, zero, or negative burning speeds, with zero speeds characterizing the Zeldovich flame balls. A full analytical description of these structures and their stability to radial perturbations is provided, using a large activation energy asymptotic approach and a thermo-diffusive approximation. The results are also complemented by a numerical study. The number and stability of the generalized flame balls are identified in various regions of the l-m-h space, where l is the (reduced) Lewis number, and M and h the flow rate and its enthalpy at the origin, respectively. It is typically found that, when the flow is a source, there is a maximum value of the flow rate M max depending on l and h, above which no stationary solutions exist, and below which there are two solutions characterizing a small stable flame ball and a large unstable flame ball; the implications of these results to the problem of ignition by a hot inert gas stream are discussed. When the flow is a sink, however, there is typically a single unstable solution, except for sufficiently large values of the Lewis number and large negative values of M, where three flame balls exist, the medium one being stable. Finally, the relation between the flame speed, positive or negative, and the flame curvature, small or large, is discussed. Keywords: flame balls; ignition by a hot stream; flame stability 1. Introduction Flame balls are non-propagating spherical flames, predicted by Zeldovich over sixty years ago, as stationary solutions of the heat conduction and diffusion equations in a motionless reactive mixture [1, p. 37]. These solutions are unstable under adiabatic conditions [1, p. 331], []. However, theoretical studies have shown that flame balls may be stabilized if account is taken of additional physical mechanisms such as volumetric heat-loss [3, 4], conductive heat-loss to walls [5] or suitably defined weakly non-uniform flow fields [6]. In these studies, two branches of solutions are typically found when the radius of the flame balls is plotted versus a control parameter such as the intensity of volumetric heat-loss, smaller than a critical value; the solutions on the lower branch representing small flames including Zeldovich flame balls are unstable, while those on the upper branch representing large flame balls are stable for a given range of the control parameter. In fact, much of the recent theoretical work on flame balls has been motivated by the observation of such Corresponding author. joel.daou@manchester.ac.uk ISSN: print / online C 9 Taylor & Francis DOI: 1.18/
2 7 J. Daou et al. apparently stable structures in lean hydrogen air mixtures in the experiments by Ronney and coworkers under micro-gravity conditions [7, 8]. In addition to the significance of flame balls as a possible mode of combustion in weakly flammable mixtures, an important related aspect, of particular relevance to the present work, is their significance in ignition problems involving heat addition by an external source such as an electric spark. In this context, they may indeed serve to estimate the minimum energy to be deposited by the source for successful ignition whereby an initially formed hot kernel generates an outwardly propagating flame front [1, p. 331]. For successful ignition to occur, however, both the power and the duration of the source need be taken into account [, 9, 1]. In the particular case of a point source of constant power, two branches of stationary solutions are obtained depending on the power of the source []; the lower branch representing small flame balls which are stable, the upper branch representing large flame balls, including Zeldovich flame balls, which are unstable. In this work, we extend these studies, by considering a model for flame balls in the presence of a flow of hot inert gas, either a source or a sink, at their origin. Depending on the direction and magnitude of the flow, these flames can have positive, zero or negative burning speeds, with zero speeds characterizing Zeldovich flame balls. We shall refer to these stationary solutions of the advection-diffusion-reaction heat and mass transport equations as generalized flame balls. One motivation for studying these solutions is that they provide a simple framework for analysing the important problem of flame initiation, intentional or accidental, by a hot gas stream; [11, p. 65] and [1]. They also provide valuable analytical information on the effect of convection, albeit for a specific radial flow, on the existence and stability of flame balls. Finally, the dependence of their burning velocity, positive or negative, on their curvature, small or large, may provide some insight into such dependence when studying the local behaviour of more complex premixed flames such as edge-flames in strained mixing layers or flamelets in turbulent flow fields. The paper is structured as follows. We begin by formulating the model and identifying its main non-dimensional parameters. An asymptotic analysis is then presented, where the stationary solutions, their multiplicity and their stability are fully described. This is followed by a numerical study which validates and illustrates the analytical results. Finally, a conclusion section where the main findings are summarized and additional extensions of the work suggested, closes the paper.. Formulation We consider a spherically symmetric flame around a point source of hot inert gas located at the origin, as shown in Figure 1. Within the thermo-diffusive approximation of constant density and constant transport properties, a relevant non-dimensional model consists of the equations θ t + M θ r r = 1 ( r θ r r r y F t + M r y F r = 1 1 Le r r ) + ω, (1) ( r y F r ) ω, () subject to the far-field boundary condition θ =, y F = 1 as r, (3)
3 Combustion Theory and Modelling 71 Flow rate: M Hot inert (burnt) gas Y = F Unburnt reactive gas Y F = Y Fu T = T u Figure 1. Spherical flame sustained by a point source of hot inert gas, with flow rate M>. Negative values of M correspond to a sink (not shown in this figure). and the requirement inside the ball that (θ,y F ) = (θ, ) for M> (θ,y F ) are bounded for M as r. Here θ and y F are the non-dimensional temperature and mass fraction of the fuel, respectively, and Le is the Lewis number. They are given by θ = (T T u )/(T ad T u ) and y F = Y F /Y Fu, where T u and Y Fu are the temperature and the fuel mass fraction of the reactive mixture in the far-field, and T ad is the adiabatic planar flame temperature. The fuel is assumed to limit the reaction rate ω, which is taken to follow the standard (non-dimensional) Arrhenius form ( ) ω = β β(θ 1) Le y F exp, 1 + α(θ 1) (4) where β is the non-dimensional activation energy or Zeldovich number, and α = (T ad T u )/T ad the heat release parameter. A convection term of strength M is included in the equations to account for the presence of a point-source radial flow at the origin if M>, where M represents the non-dimensional volumetric flow rate; when M<, we are in the presence of a sink which sucks the burnt gas. The units for speed and length chosen for the non-dimensionalization correspond to the propagation speed S L and the thickness δ L of the planar flame (more precisely to the asymptotic values of these as β ). The far-field boundary condition (3) corresponds to a frozen mixture with prescribed temperature and composition. The boundary condition (4) specifies the temperature of the fuel-free (inert) stream at the origin when M>; when M, θ and y F are simply required to be bounded.
4 7 J. Daou et al. We have now completed the formulation of the problem. The main task is to find timeindependent solutions to Equations (1) (4) which represent spherical flame balls whose radius R depend on the parameters Le, M and θ, in addition to β and α. We begin by reformulating the problem in the asymptotic limit β in the next section. This is followed by an analytical treatment which allows R to be determined in terms of three parameters representing Le, M and θ, along with the multiplicity of the solutions. The linear stability of these to one-dimensional perturbations is then addressed analytically. Finally, a numerical treatment of the problem with a finite value of β is provided, which supports and illustrates the analytical findings. We also discuss the application of the results to the problem of ignition by a hot inert gas flow and to clarifying the dependence of the speed and the burning rate of the flames encountered on their curvatures. 3. The large activation energy asymptotic limit In the limit β, the reaction is confined to an infinitely thin reaction sheet, located at r = r f, say. It is convenient to adopt the near-equidiffusion flame (NEF) approximation for which l β(le 1) is O(1), supplemented by the assumption that the temperature at the origin θ may deviate from unity by an amount at most of O(β 1 ), and thus may be written as θ = 1 + h /β, which defines h. These assumptions insure that the leading order temperature θ is unity in the burnt gas, θ (r r f ) = 1, and allow the problem to be reformulated in terms of θ and the (excess) enthalpy h θ 1 + yf 1 β(θ + y F 1); see e.g. [13, p. 38] and [14]. Here and below superscripts indicate expansions in terms of β 1. In terms of θ and h we have to solve θ + M θ t r r = 1 ) (r θ (r >r r f ) (5) r r h t + M h r r = 1 ( r h ) + l ) (r θ (r r r r r r f ) (6) r r subject to the far-field boundary condition θ =, h = as r (7) and the requirement inside the ball that h = h for M> h is bounded for M as r. (8) In addition, the jump conditions [θ ] =, [h] =, (9a) [ ] [ h θ ] + l =, (9b) r r [ θ ] ( h(r f = exp ), (9c) r
5 Combustion Theory and Modelling 73 must be satisfied; here [ ] = ( ) r ( ) f r +, indicate a jump at the reaction sheet located f at r = r f (see e.g. [13, p. 39] and [15, p. 59]). 4. Analytical results In this section, we consider the problem described by Equations (5) (9). We thus have three free parameters, namely, M (the flow rate), l (the reduced Lewis number), and h (the excess enthalpy at the origin) The stationary profiles Stationary solutions satisfying (5) (9), except the last jump condition 9c, are readily determined, and are given by h = θ = { 1 for r R 1 e M/r 1 e M/R for r R [ h + H (M) (h h ) 1 e M/r [ ] h + lm R e M/R 1 e M/r lm 1 e M/R 1 e M/R r e M/R ] for r R e M/r 1 e M/R for r R where h h(r), characterizing the departure of the flame temperature from the adiabatic planar flame value, is given by [ lm h h(r) = R(1 e M/R ) + H (M) h (1 e M/R ) + lm ] R and H (M) is the Heaviside function defined by for M H (M) = 1 for M>. (1) (11) (1) On using the remaining jump condition (9c), we obtain i.e. M e M/R ( = exp R 1 e M/R M e M/R = exp R 1 e M/R lm R(1 e M/R ) + H (M) ), ( h [ h (1 e M/R ) + lm ]), (13) R which allows the radius of the stationary flame R to be determined in terms of M, l, and h.
6 74 J. Daou et al. It can be noted that when M the enthalpy h inside the ball is a constant equal to h h(r) which is determined as part of the solution and is independent of the choice of h. In contrast, when M> corresponding to a source at the origin, h is of course essential in determining the profiles. 4.. Notation and preliminary remarks In order to facilitate the discussion of the results, we introduce here two quantities µ and S characterizing the flame by ( ) h µ = exp (burning rate) (14) and S = M R (flame speed). (15) The quantity µ represents the (non-dimensional) burning rate per unit flame area, a fact which follows from the jump condition (9c). 1 It is equal here to each side of Equation (13). The quantity S represents the flame speed or burning velocity defined as the speed with which the flame travels with respect to the unburnt gas ahead of it (or more precisely just ahead of its reaction sheet ), or equivalently, as minus the speed of the unburnt gas at r = R + with respect to the stationary flame ball, this speed being obviously given by the right-hand side of (15). It can be noted therefore that negative flame speeds S are obtained for M>, and positive flame speeds for M<. We note that Equation (1) can be written as h = lm 1 e + H (m) [ h m (1 e m ) + lm ] (16) showing that the perturbation in the flame temperature h is a function of the parameter m M/R, in addition to the reduced Lewis number l and the excess enthalpy h ; h = h (m; l,h ). Also, Equation (13) can be recast into the parametric form R = R(m; l,h ) = m exp ( l m H (m) [ h ]) 1 e m (1 e m ) + lm e m 1 M = M(m; l,h ) = mr(m; l,h ), (17a) (17b) involving the parameter m. Parametric plots of R versus M, and similarly of S = M/R = m/r and µ versus M, can thus be generated by varying m in the range (, ) for selected fixed values of l and h. For future reference we record the asymptotic behaviour R m, M m, µ 1, S 1 as m, (18) 1 Indeed, since θ + yf = 1 everywhere, and y F = in the burnt gas, the left-hand side of (9c) reduces to ( yf / r) r=r f +, which is the (non-dimensional) mass of fuel reaching the reaction sheet per unit area of the latter and unit time, in the limit β. Using the location of the reaction sheet to define the flame speed is a convenient and unambiguous choice in the limit β, although other choices are possible [16].
7 Combustion Theory and Modelling 75 which follows from (14) to (17). This shows that in the limit of infinitely strong sink, M, the radius of the stationary flame is large, R M, while its burning rate µ and speed S approach those of the planar flame as expected. On the other hand, we have R me m h,m m e m h,µ e h,s e m+ h as m, (19) so that, in particular, R and M asm ; this shows that all curves of R versus M must approach the point (R =,M = ) and that S takes infinitely large negative values in this limit The adiabatic case h = We begin with the adiabatic case h =, whose results are summarized in Figure 4.3. Plotted versus M are the flame radius R (top), the flame speed S (middle) and the burning rate per unit flame area µ (bottom), for selected values of l. These curves are generated as parametric plots, as explained in the previous paragraph, by varying the parameter m in the range (, ); for illustration, an arrow has been added to the curve R versus M corresponding to l = to indicate the direction of increasing m. It is observed that a maximum value of M depending on l exists, say M max, above which there are no stationary solutions. As will be demonstrated later, M max defines in fact a critical value of M for ignition to occur, with ignition defined as the transition from stationary to outwardly propagating flames. For M<M max, each curve R versus M has two branches of solutions, representing flame balls with burning speeds S. The upper branch intersects the vertical axis, M =, at a value of R corresponding to Zeldovich flame balls, 3 R = exp(l/), as can be verified by taking the limit m in (17). For solutions on this upper branch, R and S are decreasing functions of M, and so is µ if l<; µ is an increasing function of M if l>, and constant equal to one if l =. The lower branch intersects the vertical axis at the point (R =,M = ), in agreement with the asymptotic behaviour 19 obtained for m ; in this limit we have also S, and, in the present case with h =, µ 1. For solutions on this lower branch, R and S are increasing functions of M, and so is µ if l<; µ is a decreasing function of M if l>, and µ = 1ifl =. For M<, we have typically a unique solution, that is a single-valued dependence of R on M, as exemplified in the cases l =, l = and l =. As M, and irrespective of the value of l, the flame is rejected to infinity, and therefore behaves as a planar flame, in conformity with the asymptotic formulae (18) obtained in the limit m. It is notable however that this uniqueness of solution is lost when l is sufficiently large, as illustrated in the case l = 8forwhichR versus M takes the form of an S-shaped curve, for M<. It is instructive to determine in the l-m plane the locus of the turning points of the S-shaped curve obtained for M<and of the maximum flow rate M max. At these points, we must have dm/dm =, which can be solved for l to yield a relation of the form l = l(m; h ), namely, 4e m + (m 8)e m m + 4 m(me m + e m 1) l = [ (e m 1)(4 me m h ) + m ] (e m 1) me m (e m + m 1) (m <) (m >). () 3 See e.g. [15, p. 53].
8 76 J. Daou et al. R (Flame radius) l = 8 (rescaled) - M l = 8 l = 8 l = - l = - S (Flame speed) µ (Burning rate) M M Figure. Flame radius R versus M (top), flame speed S versus M (middle) and burning rate per unit flame area µ versus M (bottom), for selected values of l. In the top subfigure, R is divided by 1 for the particular case l = 8; also an arrow has been added to the curve corresponding to l = to indicate the direction of increasing m in the range (, ). When used with (17b), Equation () enables us to generate Figure 3. Plotted versus l are M max (upper half-plane) and the values of M corresponding to the turning points of R versus M for M< (curves in the lower half-plane). Four regions are thus delimited in the l-m plane, indicating the number of the stationary solutions. In the upper half plane, there are no solutions above the curve of M max and two solutions below it. In the
9 Combustion Theory and Modelling 77 M M max No solution solutions Reduced Lewis number l 1 solution 3 solutions Figure 3. Maximum flow rate M max allowing stationary solutions (curve in the upper half-plane), and the loci of the turning points of R versus M for M< (curves in the lower half-plane). lower half-plane, there is one solution, except in the cusp-region below the cusp, located at (l c = 7.83,M c = 15.6), approximately Effect of h In this paragraph, we examine the effect of h on the results, focusing our attention on the cases M>, since h plays no part when M ; see also the Appendix. This effect is illustrated in Figure 4. Plotted is the flame radius R versus M for selected values of l, and three values of h increasing from top to bottom. In the half-plane M>, all curves are inverse C-shaped passing through the origin, as found in the previous section. These curves shrink, with their tip located at the point I (M max,r(m max )) moving down and to the left, as h increases or l decreases. As already hinted, I plays the role of an ignition point, and this fact will become clearer after the stability of the solutions is examined in Section 5. The results then indicate that ignition, defined as the transition from stationary to propagating flames, is more readily obtained for larger values of h (i.e. hotter streams) and smaller values of l, since the source strength M max needed for ignition is then smaller. This remark, which is in line with our physical expectation, is further confirmed in Figure 5, where M max is plotted versus l for selected values of h. Another way to examine the existence and multiplicity of the stationary solutions is to plot R versus l, for fixed values of M and h. This is carried out in Figure 6, using the fact that Equation (13) provides an explicit expression of l in terms of M, R and h.
10 78 J. Daou et al. The curves labelled M = represent the classical Zeldovich flame balls. These curves and those corresponding to M< are of course unaffected by the value of h. It can be seen that two branches of solutions exist for M> provided that l is larger then a critical value l crit (M; h ), depending on M and h. For each fixed value of h, these critical values generate a curve which is obviously identical to the curve of M max versus l obtained for this particular value of h, as those in Figure Flame speed and burning rate dependence on curvature An interesting feature of the current problem is that it provides analytically the flame speed S and the burning rate per unit flame area µ in terms of the flame curvature ɛ R 1,for all values of ɛ ranging from vanishingly small to infinitely large. Such analytical results may be valuable as a guide in interpreting the local behaviour of curved flames in more complex situations where analytical expressions are usually nonexistent, notably for highly l = 3 - l = 3 - R R l = 3 R h - M Figure 4. R versus M for selected values of l and h = 3 (top), h = (middle), and h = 3 (bottom).
11 Combustion Theory and Modelling 79 M max h Figure 5. M max versus l for selected values of h. Reduced Lewis number l curved flames characterized by negative flame speeds. Examples of such situations include edge-flames in strained mixing layers referred to in the Appendix, and plausibly turbulent premixed flames. More specifically, using Equations (14) (17) and the fact that m M/R = S/ɛ, we obtain { S l S/ɛ = exp + H ( S) 1 e S/ɛ 1 es/ɛ [ h (1 es/ɛ ) l ]} S, (1) ɛ a formula which relates S to ɛ and involves the parameters l and h ; this also determines µ which is given by either side of (1). In the case of weakly curved flames, the flame properties approach those of the planar laminar flame, in particular, S 1 and µ 1, in the limit ɛ, as already indicated by the asymptotic results (18). The deviation of S and µ from their planar values due to the flame curvature are in fact negligible, transcendentally small, in the limit ɛ, in agreement with available knowledge on weakly stretched flames [17]; the flame-stretch being zero for the stationary spherical flames under consideration. In the case of highly curved flames, on the other hand, S and µ exp(h /) in the limit ɛ, as indicated by the asymptotic results (19). More precisely, Equation (1) implies that
12 8 J. Daou et al. h M = -1 1 M = -1 M = -1 Flame radius R 1 1 Reduced Lewis number l Figure 6. Flame radius R versus the reduced Lewis number l for selected values of M and h = (top), h = (middle), and h = (bottom). S exp S ( ɛ µ exp h l ɛ exp h ) as ɛ, () a formula which clarifies the dependence of negative flame speeds S, and the corresponding burning rates µ, on large flame curvatures ɛ, and the parameters h and l. We note that although the dependence of S on ɛ in () is not explicit, unlike that of µ, ɛ itself is an explicit function of S, namely ɛ = [ S + l exp ( h ) ] / [ h ln( S) ]. To close this section, we illustrate in Figure 7 the dependence of S and µ on ɛ, for selected values of l and h = 3 (top), h = (middle), and h = 3 (bottom). Concentrating first on the cases with h =, we observe that negative burning speeds are only possible for
13 Combustion Theory and Modelling 81 S (Flame speed) l = - 8 µ (Burning rate) l = - 8 S S l = - 8 l = - 8 h l = - 8 l = - 8 Flame curvature ε Figure 7. Flame speed S (left) and burning rate µ (right) versus flame curvature ɛ = R 1 for selected values of l and h = 3 (top), h = (middle), and h = 3 (bottom). sufficiently large values of the flame curvature ɛ, except for sufficiently large values of the Lewis number. Typically, for moderate deviation of l from zero, S versus ɛ is single valued, and is monotonically decreasing for non-negative values of l. The burning rate µ on the other is constant for l =, and has typically a non-monotonic dependence on ɛ. We note
14 8 J. Daou et al. in particular that the location of the maximum of µ, for negative values of l, corresponds to the Zeldovich flame balls for which S =, and does not coincide with the location of the maximum of S. The effect of h on the results, more precisely on those corresponding to negative values of S, can be assessed by comparing the top, middle, and bottom figures. Beside the obvious fact that a decrease in the value of h decreases both S and µ, it is observed that negative flame speeds and the corresponding burning rates may become typically multi-valued function of the flame curvature ɛ for h <. Finally, we note parenthetically that the relationships presented herein, relating the burning speed S or the burning rate µ to the flame curvature ɛ = R 1, can be nicely complemented by similar relationships pertaining to the well-studied problem of stationary spherical flames stabilized on a point source of Fuel. In the latter problem, the burning speed S cannot of course be negative, and, we have in fact S = µ, ifs is defined as the speed of the gas at the location of the reaction sheet. Without providing here the details of the derivation, we mention that the simple formula ( h e S/ɛ ) S = exp can be obtained, provided that the temperature θ of the ambient gas in the far field is close to unity (the adiabatic planar flame temperature) such that h β(θ 1) is O(1) as β. This formula is the counterpart of formula (1) and implies in particular that ( h S = 1 + EST as ɛ and S exp h ɛ exp h ) as ɛ. 5. Stability analysis In this section, we carry out a linear stability analysis of the stationary solution (θ,h,r f ) = ( θ, h, R) given by (1), (11) and (13) by considering perturbed solutions of the form r f = R + ɛ e σt, θ = θ + ɛ e σt ϕ(r), h = h + ɛ e σt ψ(r), (3) where r f is the radius of the perturbed flame and ɛ a small parameter characterizing the amplitude of the radial perturbations. By substitution into the equations and auxiliary conditions of Section 3, one ends up with ϕ(r <r f ) and the equations ϕ rr + r M r ϕ r σϕ = (r>r f ) (4) ψ rr + r M r ψ r σψ = lσϕ lm r ϕ r (r r f ) (5) subject to the boundary conditions ϕ =, ψ = as r (6) ψ = for M> as r (7) ψ is bounded for M
15 Combustion Theory and Modelling 83 and the jump conditions [ϕ] = µ, [ψ] = lµ (8a) [ψ r ] + l[ϕ r ] = lm R µ (8b) [ϕ r ] = ( ψ + R M R H (M) M ) R (h h ) µ (8c) at r = R.Hereψ ψ(r ), while h h(r) and µ exp(h /) are given by (1) and (14), respectively. It is to be noted that the jump conditions at the reaction sheet r = r f (t) have been transferred to r = R, using Taylor expansions about r = R, since r f R is small, of O(ɛ ), according to (3) 4. Equations (4) (8) constitute an eigen-boundary value problem, whose solution should, in principle, provide a dispersion relation between the eigen values σ and the parameters of the problem of the form F (σ ; l,m,h ) =. This relation should determine whether a particular solution is stable or unstable, based on whether all perturbations of this solution have Re(σ ) < and thus decay, or at least one perturbation has Re(σ ) > and thus grows. It is instructive to revisit first the particular case M = pertaining to the classical Zeldovich flame balls, for which the dispersion relation can be determined analytically as known in the literature, see e.g. [1, p. 37]. Indeed, in this case, we have h = l, µ = exp( l/) and R = exp(l/) on taking the limit M in (1) and (13). Thus, the stability problem reduces to solving (4) to (7) with M =, along with the jump conditions [ϕ] = 1/R, [ψ] = l/r, [ψ r ] + l[ϕ r ] =, and [ϕ r ] = ψ /R + /R at r = R = exp(l/). The solution satisfying all conditions, except the last jump condition, is given by ϕ = ψ = { ifr<r 1 r e(r r) σ l 4r e r σ e r σ e R σ R r e(r r) σ if r>r { ψ l R ( 1 + σ (R r) )} if r<r if r>r with ψ ψ(r ) = l(e R σ e R σ )/4Re R σ, provided that we assume that Re( σ ) >. The last jump condition then yields the dispersion relation l = 4(R σ 1)(1 + coth(r σ )), (9) 4 More explicitly, Taylor expansions to O(ɛ ) yield the relations [ϕ] = [ θ r ], [ψ] = [ h ( ) r ], [ψ r ] + l[ϕ r ] = [ h rr ] l[ θ rr ], and [ϕ r ] = ψ(r ) + h r (R ) exp ( h(r ) ) [ θ rr ], where the brackets designate jumps evaluated at r = R. These lead to the jump conditions (8) once the stationary solutions θ and h given by (1) and (11) are used.
16 84 J. Daou et al. which implies that for any value of l there exists an unstable mode characterized by a value of σ which is real and positive 5. Thus, we recover the known result that flame balls are always unstable, in the absence of other stabilizing effects, such as volumetric heat-losses, or the presence of a flow, M, considered next. Unfortunately, for M, analytical derivation of a dispersion relation is not straightforward since, to start with, the general solution to (4) does not seem to be expressible in terms of familiar elementary functions, as it is the case when M =. To make progress we may turn into a numerical treatment, as done in the next section, where it is found in particular that the transition from stable to unstable behaviours, occurs without oscillations, thus suggesting that Im(σ ) =, and hence σ =, for marginal stability. We may also continue the analytical treatment but limiting our objective to determining the stability/instability domains in the l-m-h space, without derivation of the dispersion relation itself. To this end, we look for marginal stability surfaces in the l-m-h space by anticipating, as suggested by the numerics, that these are characterized by σ =. Thus, we solve (4) to (8) with σ =. The solution satisfying all conditions, except the last jump condition, is given by with { ifr<r ϕ = µ 1 e M/r if r>r 1 e M/R ψ {1 H (M) ψ = ( ψ + lµ R lµ ) 1 e M/r ψ = ( )} 1 e M/r e M/R 1 e M/R lµ R r e M/r e M/R lm(r 1 µ) R(1 e M/R )[1 + H (M)Mµ 1 R ]. if r<r if r>r, The last jump condition then yields a relation of the form l = l(m; h ), which turns out to be identical to Equation (), valid at the turning points identified earlier. When this relation is used with Equation (17b) which is of the form M = M(l; m, h ), the marginal stability surfaces can be generated by varying the parameters m and h. We conclude that, for a fixed value of h, the marginal stability curves coincide with the curves depicting the extremum values of M versus l, as shown in Figure 3, in the particular case h =. Furthermore, since the solutions corresponding to the Zeldovich flame balls are unstable, any branch of solutions passing by these in Figure 4.3 (top) e.g. is unstable up to the turning points. In particular, in the domain M> in Figure 3 where two solutions are found, the one with the larger radius is unstable, the one with the smaller radius stable; when M< we are typically in the presence of a single solution which is unstable, except in the cusp region where three solutions exist, the middle one being stable, the others unstable. The picture is similar for h, since only the curve in the upper half plane in Figure 3 is shifted as h is changed, as illustrated in Figure 5. The results are conveniently summarized in Figure 8, where four regions are delimited in the l-m-h space, with the number of stationary solutions (flame balls) and their stability indicated in each region. 5 This conclusion follows, e.g., from a plot of the simple explicit relation (9) of l versus the variable R σ assumed real and positive. Also, the assumption Re( σ ) > which has just been made is consistent with this conclusion.
17 Combustion Theory and Modelling 85 Figure 8. Number of stationary solutions (flame balls) and their stability in different regions of the l-m-h space. 6. Numerical results Although the analytical analysis performed in the asymptotic limit β is rather complete and self-contained, it is complemented here by a numerical study carried out with a finite value of β. As we shall see, this study confirms the analytical predictions, at least from the qualitative point of view, and provides further illustrations. More specifically, the problem defined by Equations (1) (4) is solved numerically both as a time-dependent boundary value problem, with appropriate initial conditions, and as a stationary boundary value problem. A finite volume discretization in the space variable r is used to reduce the problem into a system of ordinary differential equations in the time-dependent case, and into a system of non-linear algebraic equations in the stationary case. The system of ordinary differential equations is solved by LSODA, a well tested robust solver with adaptive time-step which is suitable both for stiff and non-stiff problems [18]. The non-linear system of algebraic equations is solved with the NAG routine C5NBF [19], which is based on Powell s hybrid method []. The (non-dimensional) radial extent of the computational domain is typically from r = tor = 3, with a non-uniform spatial-grid comprising 5 points. A cutoff temperature θ c =.1 below which the reaction rate is set to zero is introduced to avoid the cold-boundary-difficulty. The values β = 1 and α =.85 are adopted, with other parameters specified in each case Stationary solutions Figure 9 shows the profiles of the temperature θ, the fuel mass fraction y F, and the reaction rate ω (normalized by its maximum value ω max ) in an illustrative case corresponding to
18 86 J. Daou et al. 1 θ M =.6 R =.5 ω max = 1.7 y F.5 ω / ω max r 4 Figure 9. The profiles of the temperature θ, the fuel mass fraction y F, and the normalized reaction rate ω/ω max for h =, M =.6andLe= 1. M =.6, h = and Le = 1. A flame ball of radius R.5 is observed with this choice of parameters, R being defined as the location where the reaction rate is maximum. A comparison between the analytical and numerical results is carried out in Figure 1 pertaining to h =. Shown is the maximum flow rate M max versus the Lewis number Le based on the numerics (solid curve) and the asymptotics (dashed curve). The agreement is excellent qualitatively, and good quantitatively provided the deviation of Le from unity are moderate, say Le in the range [.6, 1.3]. The effect of h is illustrated numerically in Figure 11 where R is plotted versus M,for selected values of h and Le = 1. The results are in agreement with the asymptotics, with a single stationary solution obtained for M<, and two solutions for M> less than a maximum value M max which decreases with increasing h. 4 3 Numerics Asymptotics M max Le 1.6 Figure 1. curve). M max versus Le for h = determined numerically (solid curve) and analytically (dashed
19 Combustion Theory and Modelling 87 Le = 1 1 h R h =.5 h = 1.5 M 1 Figure 11. Flame radius R versus M for selected values of h and Le = 1. In addition to the multiplicity of solutions obtained for M>, multiple solutions are also predicted in the analytical study for M< when Le is sufficiently larger than unity, as exemplified in Figure 4.3 (top subfigure, curve labelled l = 8). This fact is successfully confirmed numerically in Figure 1, where R is plotted versus M for Le =. 6.. Stability and time dependent calculations The stability of the stationary solutions to one-dimensional perturbations has been tested, using the following procedure. (1) The sparse non-linear algebraic problem is solved using the non-linear solver C5NBF to yield stationary solutions, each one being a vector with N 16 Le = R 8 M 11 Figure 1. Flame radius R versus M for Le =. Stars (on the middle branch in the left half-plane) and diamonds (on the lower branch in the right half-plane) are computed solutions which are found stable.
20 88 J. Daou et al. 1 Le = 1. h = 1 unstable stable R.5 3 Le =.8 Le = 1. Le = 1.4 M.8 h = R R Le =.8 Le = 1. Le =.8 Le = 1 Le = 1.5 M 1 h.6 1. M 1.8 Figure 13. Flame radius R versus M for selected values of Le and h = 1 (top), h = (middle), and h = 1 (bottom). Solid lines represent branches of stable solutions and dashed lines branches of unstable solutions. components, say y(n),n being twice the number of gridpoints. () Perturbations are added to the stationary solution y(n) to generate y perturbed (N) = y(n) + ɛ rand(n), where ɛ = 1 4 and rand(n) ann-dimensional vector of random numbers from the standard normal distribution produced using the NAG routine G5FDF [19]. (3) The system of ODEs corresponding to the time-dependent problem is solved using LSODA, starting from the perturbed solution y perturbed (N) as initial condition. When the resulting solution converges as time increases to a stationary solution y (N) such that y (N) y(n) < 1 5,the stationary solution y(n) is considered stable, otherwise unstable. 6 By applying the testing procedure just described, we end up with the following conclusions. (a) When M>, the solutions represented by the upper branch of R versus M in Figure 13 are found to be unstable, while those represented by the lower branch stable. (b) When M<, no stable solutions were found except for values of the Lewis number well above one and for sufficiently large negative values of M where multiple solutions are obtained as illustrated in Figure 1 pertaining to Le =. The middle branch of the 6 The notation stands here for the maximum norm.
21 Combustion Theory and Modelling 89 1 Le = 1 M = 1 R(t) M =.5 M = time, t Figure 14. Flame radius R versus time t for selected values of M, with h = andle= 1. S-shaped curve in the left half-plane of this figure is found to be stable as predicted by the asymptotics, except in a small neighbourhood of the lower turning point (the stars on this branch indicate stable solutions 7 ). Finally, we carry out the following numerical experiment to illustrate the ignition process, i.e. the transition from stationary stable flame balls (lying on the lower branch of R versus M) to outwardly propagating flames, as M is increased. Starting with an initial condition corresponding to a frozen mixture, we simulate the blowing of hot air at the adiabatic flame temperature (h = ) with a flow rate M =.3. After a transient, the solution settles to a stationary flame ball with radius R =.18, as illustrated in Figure 14 where R is plotted versus time (curve labelled M =.3). Starting from this stationary solution as initial condition, the calculation is repeated with a higher value of M =.5; the radius of the ball increases to a new stationary value R =.4. Starting from this new stationary solution as initial condition, and repeating the computation with M = 1, it is seen that the flame radius continually increases with time, illustrating the transition from stationary to expanding spherical flames. 7. Conclusions The problem under investigation has provided a complete analytical description of several fundamental aspects of combustion, made tractable by the simplifying assumptions of spherical symmetry and large activation energy. These aspects include the problem of ignition by a hot inert gas stream, the dependence of flame speeds, positive or negative, on the flame curvature, and the stability of the stationary solutions encountered which have been called generalized flame balls. In particular, as Zeldovich flame balls are used as criteria for successful ignition in stagnant reactive gases, generalized flame balls have been shown to provide similar criteria for ignition by a hot radial stream, a step towards understanding ignition by more practical flows of hot gases such as jets [1]. 7 We have checked that this small neighbourhood of the lower turning point with unstable solutions shrinks as β is increased (not shown here), improving thus the agreement with the asymptotics.
22 9 J. Daou et al. The main conclusions concerning the existence of generalized flame balls and their stability in the various regions of the l-m-h space have been summarized in Figure 8: for M smaller than a maximum value M max depending on l and h two flame balls are found the smaller one being stable; for M< we have typically a single solution which is stable unless the Lewis number Le is sufficiently greater than one and M has a sufficiently large negative value, in which case three flame balls exist the medium one being stable. The ignition process has been discussed and illustrated in connection with Figure 14; typically if a hot gas is blown with a weak flow rate M<M max, a stable stationary flame ball forms, which increases in size as M increases, and generates an expanding flame ball when M>M max. This transition from stationary stable to propagating flames typifies successful ignition and presents strong similarities with flame initiation by a constant power heat-source in a stagnant environment described in []. Finally the dependence of the burning rate per unit flame area µ and the flame speed S on the flame curvature ɛ = R 1 has been described in Section 4.5 and Figure 7, and may provide insight when analysing the local behaviour of more complex flames such as turbulent premixed flames or edge-flames in mixing layers, where both positive and negative flame speeds are encountered. Of course, the results established within our simple model can be extended in future studies to account for several additional effects, such as the size of the source (which has been modelled as a point-source in this paper), the presence of heat-losses coupled with the flow, a non-spherical geometry, etc. References [1] Ya. Zeldovich, G. Barenblatt, V. Librovich, and G. Makhviladze, The Mathematical Theory of Combustion and Explosions, Consultants Bureau, New York, [] B. Deshaies and G. Joulin, On the initiation of a spherical flame kernel, Combust. Sci. Technol. 37 (1984), pp [3] J. Buckmaster, G. Joulin, and P. Ronney, The structure and stability of nonadiabatic flame balls, Combust. Flame 79 (199), pp [4] J. Buckmaster, G. Joulin, and P. Ronney, The structure and stability of nonadiabatic flame balls: the effects of far-field losses, Combust. Flame 84 (1991), pp [5] G. Joulin and J.D. Buckmaster, Influence of boundary losses on structure and dynamics of flame-balls, Combust. Sci. Technol. 89 (1993), pp [6] J. Buckmaster and G. Joulin, Flame balls stabilized by suspension in fluid with a steady linear ambient velocity distribution, J. Fluid Mech. 7 (1991), pp [7] P. Ronney, Near-limit flame structures at low Lewis number, Combust. Flame 8 (199), pp [8] P. Ronney, M. Wu, H. Pearlman, and K. Weiland, Experimental study of flame balls in space: preliminary results from STS-83 space flight experiments, AIAA J. 36 (1998), pp [9] G. Joulin, Point-source initiation of lean spherical flames of light reactants an asymptotic theory, Combust. Sci. Technol. 43 (1985), pp [1] M. Champion, B. Deshaies, G. Joulin, and K. Kinoshita, Spherical flame initiation: theory versus experiments for lean propane-àair mixtures, Combust. Flame 65 (1986), pp [11] F.A. Williams, Combustion Theory,Benjamin-Cummings, Menlo Park, CA, [1] R. Sadanandan, D. Markus, R. Schießl, U. Maas, J. Olofsson, H. Seyfried, M. Richter, and M.Aldén, Detailed investigation of ignition by hot gas jets,proc.combust.inst.31 (7),pp [13] J.D. Buckmaster and G.S.S. Ludford, Lectures on Mathematical Combustion, Society for Industrial and Applied Mathematics, Philadelphia, [14] C. Lee and J. Buckmaster, The structure and stability of flame balls: a near-equidiffusional flame analysis, SIAM J. Appl. Math. 51 (1991), pp
23 Combustion Theory and Modelling 91 [15] G. Joulin and P. Vidal, Hydrodynamics and Nonlinear Instabilities, Cambridge University, Cambridge, [16] J.H. Tien and M. Matalon, On the burning velocity of stretched flames, Combust. Flame 84 (1991), pp [17] M. Matalon, On flame stretch, Combust. Sci. Technol. 31 (1983), pp [18] A. Hindmarsh, ODEPACK: A systematized collection of ODE solvers, in R.S. Stepleman et al., eds., Scientific Computing, North Holland, New York, 1983, pages [19] Numerical Algorithms Group (NAG), Fortran Library Mark, Oxford, 1. [] M.Powell, A hybrid method for nonlinear algebraic equations, in P. Rabinowitz, ed., Numerical Methods for Nonlinear Algebraic Equations, Gordon and Breach, New York, 197. [1] J. Daou and A. Liñán, The role of unequal diffusivities in ignition and extinction fronts in strained mixing layers, Combust. Theory Model. (1998), pp [] J. Daou and A. Liñán, Ignition and extinction fronts in counterflowing premixed reactive gases, Combust. Flame 118 (1999), pp Appendix: A special class of solutions There is a fundamental change in the character of the generalized flame balls described in this paper as M varies from negative to positive values. Namely, while h (and hence the temperature θ) is constant in the burnt gas for M, it is typically dependent on r and the enthalpy at the source h when M>, as implied by the boundary condition (8). We note however from (11) and (1) that the special choice h = lm/r(1 e M/R ) when M>leads to the constancy of h inside the ball, as for the cases M. The solutions with constant h in the burnt gas can be thus viewed as stationary solutions to a problem depending on the two parameters M and l, which is defined by Equations (5) and (6) applied in the domain r>r f, along with the requirements θ (r<r f ) = 1 and h(r <r f ) = const, the far-field boundary condition (7) and the jump conditions (9). The solutions corresponding to M = of this two-parameter problem (i.e. Zeldovich flame balls) can be extended smoothly to positive and negative values of M, unlike the solutions to the three-parameter problem discussed above, which are typically continuous but non-smooth functions of M as M. Of course, although the two-parameter problem is simpler to study than the three-parameter problem, its solutions are more difficult (but conceptually possible) to obtain experimentally, requiring a special choice of h. The object of this appendix is to present briefly the main results of this simpler, albeit less realistic, model. As before, stationary solutions satisfying all equations except the last jump condition 9c are readily determined, and are given by 1 for r R θ = 1 e M/r for r R 1 e M/R lm R h = lm R 1 1 e M/R for r R 1 e M/r lm 1 e M/R r e M/r 1 e M/R for r R. (3) (31) Using these solutions in (9c), we obtain M R e M/R ( = exp lm 1 e M/R R ) 1, (3) 1 e M/R
24 9 J. Daou et al. which allows the flame ball radius R to be determined in terms of M and l; in the particular case M = pertaining to Zeldovich flame balls, a Taylor expansion for small M provides R = exp(l/), as found in the literature [15, p. 53]. Also the effect of M on the flame radius R is easily obtained by recasting Equation (3) into the form R = R(m; l) = m exp ( l e m 1 ) m 1 e m, M = M(m; l) = mr(m, l) (33) involving the parameter m M/R. This allows parametric plots of R versus M for selected fixed values of l to be generated as in Figure 15. Since there is no difference between the three- and two-parameter models for M, we emphasize in this appendix only the case M>. In particular, we note that in the limit m,wehaver and M only if l< and R and M if l ; this explains the disappearance of the lower branch containing the origin for l = (or larger values, which are not shown). Thus l = appears as a critical value below which the curves of R versus M are multivalued, and above which they are single-valued. In the multi-valued cases corresponding to l<, two solutions are typically present for positive values of M, provided that M is smaller than a maximum value M max depending on l which characterizes the turning points in Figure 15. The curve depicting M max versus l, given in Figure 16, shows that M increases with l and tends to infinity as l. In the domain above this curve there are no solutions; in the domain below it, delimited by the vertical line l = and the horizontal line M =, two flame balls exit; everywhere else in the l-m domain, including in the half-plane M< (which is not shown), a single flame ball exists except outside the cusp region in Figure 3. Also, using Equation (3), we can plot R versus l for fixed values of M,asshown in Figure 17, where the curve labelled M = represent Zeldovich flame balls, for which R = exp(l/). Figure 15. R versus M for selected values of l.
25 Combustion Theory and Modelling M max Figure 16. M max versus l. 1 l Figure 17. R versus l for selected values of M.
26 94 J. Daou et al. 1 S l = 6 l = l = l = 1 l = ε Figure 18. Flame speed S versus ɛ = R 1 for selected values of l. Finally, a plot of the flame speed S versus the flame curvature ɛ = R 1 is provided for selected values of l in Figure 18, and can be compared with Figure 7 pertaining to the three-parameter model. We note that the range of flame curvatures ɛ and the range of negative speeds S cannot be arbitrarily large if l within the two-parameter model. However, the transition from positive to negative speeds occurs now smoothly as ɛ is increased. Furthermore, the curves plotted nicely mimic, when l<, the numerically observed variation of the propagation speed of edge-flames with a strain-related parameter ɛ determining their curvatures (compare with Figure 3 in [1] and Figure 6 in []).
Ignition and Extinction Fronts in Counterflowing Premixed Reactive Gases
 Ignition and Extinction Fronts in Counterflowing Premixed Reactive Gases J. DAOU* and A. LIÑÁN Dpto. Motopropulsion y Termofluidodinamica, Universidad Politécnica de Madrid, E.T.S.I. Aeronáuticos, Plaza
Ignition and Extinction Fronts in Counterflowing Premixed Reactive Gases J. DAOU* and A. LIÑÁN Dpto. Motopropulsion y Termofluidodinamica, Universidad Politécnica de Madrid, E.T.S.I. Aeronáuticos, Plaza
Laminar Premixed Flames: Flame Structure
 Laminar Premixed Flames: Flame Structure Combustion Summer School 2018 Prof. Dr.-Ing. Heinz Pitsch Course Overview Part I: Fundamentals and Laminar Flames Introduction Fundamentals and mass balances of
Laminar Premixed Flames: Flame Structure Combustion Summer School 2018 Prof. Dr.-Ing. Heinz Pitsch Course Overview Part I: Fundamentals and Laminar Flames Introduction Fundamentals and mass balances of
Flame Propagation in Poiseuille Flow under Adiabatic Conditions
 Flame Propagation in Poiseuille Flow under Adiabatic Conditions J. DAOU and M. MATALON* Department of Engineering Sciences and Applied Mathematics, Northwestern University, Evanston, IL 60208-3125, USA
Flame Propagation in Poiseuille Flow under Adiabatic Conditions J. DAOU and M. MATALON* Department of Engineering Sciences and Applied Mathematics, Northwestern University, Evanston, IL 60208-3125, USA
Effect of volumetric heat-loss on triple flame propagation
 Effect of volumetric heat-loss on triple flame propagation R. Daou, J. Daou, J. Dold Department of Mathematics, UMIST, Manchester M60 1QD, UK < John.Dold@umist.ac.uk > Abstract We present a numerical study
Effect of volumetric heat-loss on triple flame propagation R. Daou, J. Daou, J. Dold Department of Mathematics, UMIST, Manchester M60 1QD, UK < John.Dold@umist.ac.uk > Abstract We present a numerical study
Lecture 8 Laminar Diffusion Flames: Diffusion Flamelet Theory
 Lecture 8 Laminar Diffusion Flames: Diffusion Flamelet Theory 8.-1 Systems, where fuel and oxidizer enter separately into the combustion chamber. Mixing takes place by convection and diffusion. Only where
Lecture 8 Laminar Diffusion Flames: Diffusion Flamelet Theory 8.-1 Systems, where fuel and oxidizer enter separately into the combustion chamber. Mixing takes place by convection and diffusion. Only where
Premixed Edge-Flames under Transverse Enthalpy Gradients
 Premixed Edge-Flames under Transverse Enthalpy Gradients J. DAOU and M. MATALON* McCormick School of Engineering and Applied Science, Engineering Sciences and Applied Mathematics, Northwestern University,
Premixed Edge-Flames under Transverse Enthalpy Gradients J. DAOU and M. MATALON* McCormick School of Engineering and Applied Science, Engineering Sciences and Applied Mathematics, Northwestern University,
Lecture 6 Asymptotic Structure for Four-Step Premixed Stoichiometric Methane Flames
 Lecture 6 Asymptotic Structure for Four-Step Premixed Stoichiometric Methane Flames 6.-1 Previous lecture: Asymptotic description of premixed flames based on an assumed one-step reaction. basic understanding
Lecture 6 Asymptotic Structure for Four-Step Premixed Stoichiometric Methane Flames 6.-1 Previous lecture: Asymptotic description of premixed flames based on an assumed one-step reaction. basic understanding
S. Kadowaki, S.H. Kim AND H. Pitsch. 1. Motivation and objectives
 Center for Turbulence Research Annual Research Briefs 2005 325 The dynamics of premixed flames propagating in non-uniform velocity fields: Assessment of the significance of intrinsic instabilities in turbulent
Center for Turbulence Research Annual Research Briefs 2005 325 The dynamics of premixed flames propagating in non-uniform velocity fields: Assessment of the significance of intrinsic instabilities in turbulent
The Effect of Mixture Fraction on Edge Flame Propagation Speed
 8 th U. S. National Combustion Meeting Organized by the Western States Section of the Combustion Institute and hosted by the University of Utah May 19-22, 213 The Effect of Mixture Fraction on Edge Flame
8 th U. S. National Combustion Meeting Organized by the Western States Section of the Combustion Institute and hosted by the University of Utah May 19-22, 213 The Effect of Mixture Fraction on Edge Flame
Period Doubling Cascade in Diffusion Flames
 Period Doubling Cascade in Diffusion Flames Milan Miklavčič Department of Mathematics, Michigan State University, East Lansing, MI 48824, USA Combustion Theory and Modelling 11 No 1 (2007), 103-112 Abstract
Period Doubling Cascade in Diffusion Flames Milan Miklavčič Department of Mathematics, Michigan State University, East Lansing, MI 48824, USA Combustion Theory and Modelling 11 No 1 (2007), 103-112 Abstract
Lecture 7 Flame Extinction and Flamability Limits
 Lecture 7 Flame Extinction and Flamability Limits 7.-1 Lean and rich flammability limits are a function of temperature and pressure of the original mixture. Flammability limits of methane and hydrogen
Lecture 7 Flame Extinction and Flamability Limits 7.-1 Lean and rich flammability limits are a function of temperature and pressure of the original mixture. Flammability limits of methane and hydrogen
Stability Diagram for Lift-Off and Blowout of a Round Jet Laminar Diffusion Flame
 Stability Diagram for Lift-Off and Blowout of a Round Jet Laminar Diffusion Flame SANDIP GHOSAL* and LUC VERVISCH *Northwestern University, Mechanical Engineering, Evanston, IL 60208-311 USA INSA de Rouen
Stability Diagram for Lift-Off and Blowout of a Round Jet Laminar Diffusion Flame SANDIP GHOSAL* and LUC VERVISCH *Northwestern University, Mechanical Engineering, Evanston, IL 60208-311 USA INSA de Rouen
Asymptotic Structure of Rich Methane-Air Flames
 Asymptotic Structure of Rich Methane-Air Flames K. SESHADRI* Center for Energy and Combustion Research, Department of Mechanical and Aerospace Engineering, University of California at San Diego, La Jolla,
Asymptotic Structure of Rich Methane-Air Flames K. SESHADRI* Center for Energy and Combustion Research, Department of Mechanical and Aerospace Engineering, University of California at San Diego, La Jolla,
Structures of Turbulent Bunsen Flames in the Corrugated-Flamelet Regime
 25 th ICDERS August 2 7, 2015 Leeds, UK Structures of Turbulent Bunsen Flames in the Corrugated-Flamelet Regime Junichi Furukawa and Yasuko Yoshida Department of Mechanical Engineering Tokyo Metropolitan
25 th ICDERS August 2 7, 2015 Leeds, UK Structures of Turbulent Bunsen Flames in the Corrugated-Flamelet Regime Junichi Furukawa and Yasuko Yoshida Department of Mechanical Engineering Tokyo Metropolitan
REDIM reduced modeling of quenching at a cold inert wall with detailed transport and different mechanisms
 26 th ICDERS July 3 th August 4 th, 217 Boston, MA, USA REDIM reduced modeling of quenching at a cold inert wall with detailed transport and different mechanisms Christina Strassacker, Viatcheslav Bykov,
26 th ICDERS July 3 th August 4 th, 217 Boston, MA, USA REDIM reduced modeling of quenching at a cold inert wall with detailed transport and different mechanisms Christina Strassacker, Viatcheslav Bykov,
ACTIVATION ENERGY EFFECT ON FLAME PROPAGATION IN LARGE-SCALE VORTICAL FLOWS
 ACTIVATION ENERGY EFFECT ON FLAME PROPAGATION IN LARGE-SCALE VORTICAL FLOWS L. Kagan (a), P.D. Ronney (b) and G. Sivashinsky (a), Abstract (a) School of Mathematical Sciences, Tel Aviv University, Ramat
ACTIVATION ENERGY EFFECT ON FLAME PROPAGATION IN LARGE-SCALE VORTICAL FLOWS L. Kagan (a), P.D. Ronney (b) and G. Sivashinsky (a), Abstract (a) School of Mathematical Sciences, Tel Aviv University, Ramat
Effects of radiative heat loss on the extinction of counterflow premixed H 2 air flames
 Combust. Theory Modelling 4 (2000) 459 475. Printed in the UK PII: S1364-7830(00)09647-9 Effects of radiative heat loss on the extinction of counterflow premixed H 2 air flames Hongsheng Guo, Yiguang Ju
Combust. Theory Modelling 4 (2000) 459 475. Printed in the UK PII: S1364-7830(00)09647-9 Effects of radiative heat loss on the extinction of counterflow premixed H 2 air flames Hongsheng Guo, Yiguang Ju
The role of unequal diffusivities in ignition and extinction fronts in strained mixing layers
 Combust. Theory Modelling 2 (1998) 449 477. Printed in the UK PII: S1364-7830(98)94094-3 The role of unequal diffusivities in ignition and extinction fronts in strained mixing layers J Daou andaliñán Dpto
Combust. Theory Modelling 2 (1998) 449 477. Printed in the UK PII: S1364-7830(98)94094-3 The role of unequal diffusivities in ignition and extinction fronts in strained mixing layers J Daou andaliñán Dpto
Lecture 15. The Turbulent Burning Velocity
 Lecture 15 The Turbulent Burning Velocity 1 The turbulent burning velocity is defined as the average rate of propagation of the flame through the turbulent premixed gas mixture. In the laminar case, solutions
Lecture 15 The Turbulent Burning Velocity 1 The turbulent burning velocity is defined as the average rate of propagation of the flame through the turbulent premixed gas mixture. In the laminar case, solutions
Development of One-Step Chemistry Models for Flame and Ignition Simulation
 Development of One-Step Chemistry Models for Flame and Ignition Simulation S.P.M. Bane, J.L. Ziegler, and J.E. Shepherd Graduate Aerospace Laboratories California Institute of Technology Pasadena, CA 91125
Development of One-Step Chemistry Models for Flame and Ignition Simulation S.P.M. Bane, J.L. Ziegler, and J.E. Shepherd Graduate Aerospace Laboratories California Institute of Technology Pasadena, CA 91125
Interaction of Lewis number and heat loss effects for a laminar premixed flame propagating in a channel
 International Journal of Thermal Sciences 47 (2008) 84 92 www.elsevier.com/locate/ijts Interaction of Lewis number and heat loss effects for a laminar premixed flame propagating in a channel Subhadeep
International Journal of Thermal Sciences 47 (2008) 84 92 www.elsevier.com/locate/ijts Interaction of Lewis number and heat loss effects for a laminar premixed flame propagating in a channel Subhadeep
Edges of flames that do not exist: flame-edge dynamics in a non-premixed counterflow
 Combust. Theory Modelling 4 (2000) 435 457. Printed in the UK PII: S1364-7830(00)11525-6 Edges of flames that do not exist: flame-edge dynamics in a non-premixed counterflow R W Thatcher and J W Dold Mathematics
Combust. Theory Modelling 4 (2000) 435 457. Printed in the UK PII: S1364-7830(00)11525-6 Edges of flames that do not exist: flame-edge dynamics in a non-premixed counterflow R W Thatcher and J W Dold Mathematics
On the critical flame radius and minimum ignition energy for spherical flame initiation
 Available online at www.sciencedirect.com Proceedings of the Combustion Institute 33 () 9 6 Proceedings of the Combustion Institute www.elsevier.com/locate/proci On the critical flame radius and minimum
Available online at www.sciencedirect.com Proceedings of the Combustion Institute 33 () 9 6 Proceedings of the Combustion Institute www.elsevier.com/locate/proci On the critical flame radius and minimum
Faculty of Engineering. Contents. Introduction
 Faculty of Engineering Contents Lean Premixed Turbulent Flames vs. Hydrogen Explosion: A Short Survey on Experimental, Theoretical and Analytical Studies Dr.-Ing. Siva P R Muppala Lecturer Prof. Jennifer
Faculty of Engineering Contents Lean Premixed Turbulent Flames vs. Hydrogen Explosion: A Short Survey on Experimental, Theoretical and Analytical Studies Dr.-Ing. Siva P R Muppala Lecturer Prof. Jennifer
A comparison between two different Flamelet reduced order manifolds for non-premixed turbulent flames
 8 th U. S. National Combustion Meeting Organized by the Western States Section of the Combustion Institute and hosted by the University of Utah May 19-22, 2013 A comparison between two different Flamelet
8 th U. S. National Combustion Meeting Organized by the Western States Section of the Combustion Institute and hosted by the University of Utah May 19-22, 2013 A comparison between two different Flamelet
Lecture 9 Laminar Diffusion Flame Configurations
 Lecture 9 Laminar Diffusion Flame Configurations 9.-1 Different Flame Geometries and Single Droplet Burning Solutions for the velocities and the mixture fraction fields for some typical laminar flame configurations.
Lecture 9 Laminar Diffusion Flame Configurations 9.-1 Different Flame Geometries and Single Droplet Burning Solutions for the velocities and the mixture fraction fields for some typical laminar flame configurations.
AN ANALYSIS OF LEWIS NUMBER AND FLOW EFFECTS ON THE IGNITION OF PREMIXED GASES
 Twenty-first Symposium (International) on Combustion/The Combustion Institute, 1986/pp, 1891-1897 AN ANALYSIS OF LEWIS NUMBER AND FLOW EFFECTS ON THE IGNITION OF PREMIXED GASES P.S. TROMANS AND R.M. FURZELAND
Twenty-first Symposium (International) on Combustion/The Combustion Institute, 1986/pp, 1891-1897 AN ANALYSIS OF LEWIS NUMBER AND FLOW EFFECTS ON THE IGNITION OF PREMIXED GASES P.S. TROMANS AND R.M. FURZELAND
Extinction Limits of Premixed Combustion Assisted by Catalytic Reaction in a Stagnation-Point Flow
 44th AIAA Aerospace Sciences Meeting and Exhibit 9-12 January 2006, Reno, Nevada AIAA 2006-164 Extinction Limits of Premixed Combustion Assisted by Catalytic Reaction in a Stagnation-Point Flow Jingjing
44th AIAA Aerospace Sciences Meeting and Exhibit 9-12 January 2006, Reno, Nevada AIAA 2006-164 Extinction Limits of Premixed Combustion Assisted by Catalytic Reaction in a Stagnation-Point Flow Jingjing
Thermoacoustic Instabilities Research
 Chapter 3 Thermoacoustic Instabilities Research In this chapter, relevant literature survey of thermoacoustic instabilities research is included. An introduction to the phenomena of thermoacoustic instability
Chapter 3 Thermoacoustic Instabilities Research In this chapter, relevant literature survey of thermoacoustic instabilities research is included. An introduction to the phenomena of thermoacoustic instability
Keywords: Localised ignition, Homogeneous mixture, Width of energy deposition, Duration of energy deposition, Direct Numerical Simulation.
 Proceedings of the International Conference on Heat Transfer and Fluid Flow Prague, Czech Republic, August -, Paper No. 69 Effects of Energy Deposition Characteristics in Localised Forced Ignition of Turbulent
Proceedings of the International Conference on Heat Transfer and Fluid Flow Prague, Czech Republic, August -, Paper No. 69 Effects of Energy Deposition Characteristics in Localised Forced Ignition of Turbulent
Ignition and Combustion of Fuel Pockets Moving in an Oxidizing Atmosphere
 Ignition and Combustion of Fuel Pockets Moving in an Oxidizing Atmosphere JOEL DAOU Dpto. Motopropulsion y Termofluidodinamica, Universidad Politecnica De Madrid, E.T.S.I Aeronauticos, 28040 Madrid, Spain.
Ignition and Combustion of Fuel Pockets Moving in an Oxidizing Atmosphere JOEL DAOU Dpto. Motopropulsion y Termofluidodinamica, Universidad Politecnica De Madrid, E.T.S.I Aeronauticos, 28040 Madrid, Spain.
Quenching and propagation of combustion fronts in porous media
 Quenching and propagation of combustion fronts in porous media Peter Gordon Department of Mathematical Sciences New Jersey Institute of Technology Newark, NJ 72, USA CAMS Report 56-6, Spring 26 Center
Quenching and propagation of combustion fronts in porous media Peter Gordon Department of Mathematical Sciences New Jersey Institute of Technology Newark, NJ 72, USA CAMS Report 56-6, Spring 26 Center
Flame / wall interaction and maximum wall heat fluxes in diffusion burners
 Flame / wall interaction and maximum wall heat fluxes in diffusion burners de Lataillade A. 1, Dabireau F. 1, Cuenot B. 1 and Poinsot T. 1 2 June 5, 2002 1 CERFACS 42 Avenue Coriolis 31057 TOULOUSE CEDEX
Flame / wall interaction and maximum wall heat fluxes in diffusion burners de Lataillade A. 1, Dabireau F. 1, Cuenot B. 1 and Poinsot T. 1 2 June 5, 2002 1 CERFACS 42 Avenue Coriolis 31057 TOULOUSE CEDEX
High order effects in one step reaction sheet jump conditions for premixed flames
 INSTITUTE OF PHYSICS PUBLISHING Combust. Theory Modelling 7 3) 19 17 COMBUSTION THEORY AND MODELLING PII: S1364-7833)337-9 High order effects in one step reaction sheet jump conditions for premixed flames
INSTITUTE OF PHYSICS PUBLISHING Combust. Theory Modelling 7 3) 19 17 COMBUSTION THEORY AND MODELLING PII: S1364-7833)337-9 High order effects in one step reaction sheet jump conditions for premixed flames
Combustion. Indian Institute of Science Bangalore
 Combustion Indian Institute of Science Bangalore Combustion Applies to a large variety of natural and artificial processes Source of energy for most of the applications today Involves exothermic chemical
Combustion Indian Institute of Science Bangalore Combustion Applies to a large variety of natural and artificial processes Source of energy for most of the applications today Involves exothermic chemical
EINDHOVEN UNIVERSITY OF TECHNOLOGY Department of Mathematics and Computer Science. CASA-Report March2008
 EINDHOVEN UNIVERSITY OF TECHNOLOGY Department of Mathematics and Computer Science CASA-Report 08-08 March2008 The complexe flux scheme for spherically symmetrie conservation laws by J.H.M. ten Thije Boonkkamp,
EINDHOVEN UNIVERSITY OF TECHNOLOGY Department of Mathematics and Computer Science CASA-Report 08-08 March2008 The complexe flux scheme for spherically symmetrie conservation laws by J.H.M. ten Thije Boonkkamp,
Online publication date: 03 February 2010
 This article was downloaded by: [Chen, Zheng] On: 4 February 2010 Access details: Access Details: [subscription number 919069799] Publisher Taylor & Francis Informa Ltd Registered in England and Wales
This article was downloaded by: [Chen, Zheng] On: 4 February 2010 Access details: Access Details: [subscription number 919069799] Publisher Taylor & Francis Informa Ltd Registered in England and Wales
Chapter 13 Instability on non-parallel flow Introduction and formulation
 Chapter 13 Instability on non-parallel flow. 13.1 Introduction and formulation We have concentrated our discussion on the instabilities of parallel, zonal flows. There is the largest amount of literature
Chapter 13 Instability on non-parallel flow. 13.1 Introduction and formulation We have concentrated our discussion on the instabilities of parallel, zonal flows. There is the largest amount of literature
William A. Sirignano Mechanical and Aerospace Engineering University of California, Irvine
 Combustion Instability: Liquid-Propellant Rockets and Liquid-Fueled Ramjets William A. Sirignano Mechanical and Aerospace Engineering University of California, Irvine Linear Theory Nonlinear Theory Nozzle
Combustion Instability: Liquid-Propellant Rockets and Liquid-Fueled Ramjets William A. Sirignano Mechanical and Aerospace Engineering University of California, Irvine Linear Theory Nonlinear Theory Nozzle
Flamelet Analysis of Turbulent Combustion
 Flamelet Analysis of Turbulent Combustion R.J.M. Bastiaans,2, S.M. Martin, H. Pitsch,J.A.vanOijen 2, and L.P.H. de Goey 2 Center for Turbulence Research, Stanford University, CA 9435, USA 2 Eindhoven University
Flamelet Analysis of Turbulent Combustion R.J.M. Bastiaans,2, S.M. Martin, H. Pitsch,J.A.vanOijen 2, and L.P.H. de Goey 2 Center for Turbulence Research, Stanford University, CA 9435, USA 2 Eindhoven University
Numerical Simulation of Premixed V-Flame
 Proceedings of the World Congress on Engineering 7 Vol II WCE 7, July -, 7, London, U.K. Numerical Simulation of Premixed V-Flame C.K. Chan, B. Stewart, and C.W. Leung Abstract A Lagrangian front-tracking
Proceedings of the World Congress on Engineering 7 Vol II WCE 7, July -, 7, London, U.K. Numerical Simulation of Premixed V-Flame C.K. Chan, B. Stewart, and C.W. Leung Abstract A Lagrangian front-tracking
Mathematical modeling of critical conditions in the thermal explosion problem
 Mathematical modeling of critical conditions in the thermal explosion problem G. N. Gorelov and V. A. Sobolev Samara State University, Russia Abstract The paper is devoted to the thermal explosion problem
Mathematical modeling of critical conditions in the thermal explosion problem G. N. Gorelov and V. A. Sobolev Samara State University, Russia Abstract The paper is devoted to the thermal explosion problem
Lecture 12. Droplet Combustion Spray Modeling. Moshe Matalon
 Lecture 12 Droplet Combustion Spray Modeling Spray combustion: Many practical applications liquid fuel is injected into the combustion chamber resulting in fuel spray. Spray combustion involves many physical
Lecture 12 Droplet Combustion Spray Modeling Spray combustion: Many practical applications liquid fuel is injected into the combustion chamber resulting in fuel spray. Spray combustion involves many physical
Asymptotic Analysis of the Structure of Moderately Rich Methane-Air Flames
 Asymptotic Analysis of the Structure of Moderately Rich Methane-Air Flames K. SESHADRI,* X. S. BAI,** H. PITSCH, and N. PETERS Institut für Technische Mechanik, RWTH Aachen, D-52056 Aachen, Federal Republic
Asymptotic Analysis of the Structure of Moderately Rich Methane-Air Flames K. SESHADRI,* X. S. BAI,** H. PITSCH, and N. PETERS Institut für Technische Mechanik, RWTH Aachen, D-52056 Aachen, Federal Republic
Physics 342 Lecture 23. Radial Separation. Lecture 23. Physics 342 Quantum Mechanics I
 Physics 342 Lecture 23 Radial Separation Lecture 23 Physics 342 Quantum Mechanics I Friday, March 26th, 2010 We begin our spherical solutions with the simplest possible case zero potential. Aside from
Physics 342 Lecture 23 Radial Separation Lecture 23 Physics 342 Quantum Mechanics I Friday, March 26th, 2010 We begin our spherical solutions with the simplest possible case zero potential. Aside from
A Jet-Stirred Apparatus for Turbulent Combustion Experiments
 25 th ICDERS August 2 7, 2015 Leeds, UK A Jet-Stirred Apparatus for Turbulent Combustion Experiments Abbasali A. Davani; Paul D. Ronney University of Southern California Los Angeles, California, United
25 th ICDERS August 2 7, 2015 Leeds, UK A Jet-Stirred Apparatus for Turbulent Combustion Experiments Abbasali A. Davani; Paul D. Ronney University of Southern California Los Angeles, California, United
Equations of linear stellar oscillations
 Chapter 4 Equations of linear stellar oscillations In the present chapter the equations governing small oscillations around a spherical equilibrium state are derived. The general equations were presented
Chapter 4 Equations of linear stellar oscillations In the present chapter the equations governing small oscillations around a spherical equilibrium state are derived. The general equations were presented
Triple flame: Inherent asymmetries and pentasectional character
 Combustion Theory and Modelling, 2014 Vol. 18, No. 3, 454 473, http://dx.doi.org/10.1080/13647830.2014.923116 Triple flame: Inherent asymmetries and pentasectional character Albert Jordà Juanós and William
Combustion Theory and Modelling, 2014 Vol. 18, No. 3, 454 473, http://dx.doi.org/10.1080/13647830.2014.923116 Triple flame: Inherent asymmetries and pentasectional character Albert Jordà Juanós and William
LEWIS NUMBER EFFECTS ON THE STRUCTURE AND EXTINCTION OF DIFFUSION FLAMES DUE TO STRAIN. A. Liñan
 LEWIS NUMBER EFFECTS ON THE STRUCTURE AND EXTINCTION OF DIFFUSION FLAMES DUE TO STRAIN A. Liñan Escuela Técnica Superior de Ingenieros Aeronáuticos Universidad Politécnica de Madrid SPAIN In turbulent
LEWIS NUMBER EFFECTS ON THE STRUCTURE AND EXTINCTION OF DIFFUSION FLAMES DUE TO STRAIN A. Liñan Escuela Técnica Superior de Ingenieros Aeronáuticos Universidad Politécnica de Madrid SPAIN In turbulent
AME 513. " Lecture 8 Premixed flames I: Propagation rates
 AME 53 Principles of Combustion " Lecture 8 Premixed flames I: Propagation rates Outline" Rankine-Hugoniot relations Hugoniot curves Rayleigh lines Families of solutions Detonations Chapman-Jouget Others
AME 53 Principles of Combustion " Lecture 8 Premixed flames I: Propagation rates Outline" Rankine-Hugoniot relations Hugoniot curves Rayleigh lines Families of solutions Detonations Chapman-Jouget Others
The Role of Turbulence in Darrieus-Landau Instability
 The Role of Turbulence in Darrieus-Landau Instability G. Troiani 1, F. Creta 2, P. E. Lapenna 2, R. Lamioni 2 1 ENEA C.R. Casaccia, Rome, Italy 2 Dept. of Mechanical and Aerospace Eng., University of Rome
The Role of Turbulence in Darrieus-Landau Instability G. Troiani 1, F. Creta 2, P. E. Lapenna 2, R. Lamioni 2 1 ENEA C.R. Casaccia, Rome, Italy 2 Dept. of Mechanical and Aerospace Eng., University of Rome
CFD Analysis of Vented Lean Hydrogen Deflagrations in an ISO Container
 35 th UKELG Meeting, Spadeadam, 10-12 Oct. 2017 CFD Analysis of Vented Lean Hydrogen Deflagrations in an ISO Container Vendra C. Madhav Rao & Jennifer X. Wen Warwick FIRE, School of Engineering University
35 th UKELG Meeting, Spadeadam, 10-12 Oct. 2017 CFD Analysis of Vented Lean Hydrogen Deflagrations in an ISO Container Vendra C. Madhav Rao & Jennifer X. Wen Warwick FIRE, School of Engineering University
Effect of orientation on the ignition of stoichiometric ethylene mixtures by stationary hot surfaces
 Josue Melguizo-Gavilanes and Joseph E.Shepherd. Effect of orientation on the ignition of stoichiometric ethylene mixtures by stationary hot surfaces. Paper No. 981, 26th International Colloquium on the
Josue Melguizo-Gavilanes and Joseph E.Shepherd. Effect of orientation on the ignition of stoichiometric ethylene mixtures by stationary hot surfaces. Paper No. 981, 26th International Colloquium on the
Application of FGM to DNS of premixed turbulent spherical flames
 Application of FGM to DNS of premixed turbulent spherical flames R.J.M. Bastiaans, G.R.A Groot, J.A. van Oijen and L.P.H. de Goey, Section Combustion Technology, Department of Mechanical Engineering, Eindhoven
Application of FGM to DNS of premixed turbulent spherical flames R.J.M. Bastiaans, G.R.A Groot, J.A. van Oijen and L.P.H. de Goey, Section Combustion Technology, Department of Mechanical Engineering, Eindhoven
Two dimensional particle solution of the extended Hamilton Jacobi equation
 ANZIAM J. 50 (CTAC08) pp.c282 C291, 08 C282 Two dimensional particle solution of the extended Hamilton Jacobi equation D. V. Strunin 1 (Received 15 August 08; revised 17 October 08) Abstract In classical
ANZIAM J. 50 (CTAC08) pp.c282 C291, 08 C282 Two dimensional particle solution of the extended Hamilton Jacobi equation D. V. Strunin 1 (Received 15 August 08; revised 17 October 08) Abstract In classical
Lecture 7 Detonation Waves
 Lecture 7 etonation Waves p strong detonation weak detonation weak deflagration strong deflagration / 0 v =/ University of Illinois at Urbana- Champaign eflagrations produce heat Thermal di usivity th
Lecture 7 etonation Waves p strong detonation weak detonation weak deflagration strong deflagration / 0 v =/ University of Illinois at Urbana- Champaign eflagrations produce heat Thermal di usivity th
Analysis of lift-off height and structure of n-heptane tribrachial flames in laminar jet configuration
 Analysis of lift-off height and structure of n-heptane tribrachial flames in laminar jet configuration Stefano Luca*, Fabrizio Bisetti Clean Combustion Research Center, King Abdullah University of Science
Analysis of lift-off height and structure of n-heptane tribrachial flames in laminar jet configuration Stefano Luca*, Fabrizio Bisetti Clean Combustion Research Center, King Abdullah University of Science
Lecture 4. Laminar Premixed Flame Configura6on 4.- 1
 Lecture 4 Laminar Premixed Flame Configura6on 4.- 1 Bunsen Burner Classical device to generate a laminar premixed flame Gaseous fuel enters into the mixing chamber, into which air is entrained Velocity
Lecture 4 Laminar Premixed Flame Configura6on 4.- 1 Bunsen Burner Classical device to generate a laminar premixed flame Gaseous fuel enters into the mixing chamber, into which air is entrained Velocity
The Finite Difference Method
 Chapter 5. The Finite Difference Method This chapter derives the finite difference equations that are used in the conduction analyses in the next chapter and the techniques that are used to overcome computational
Chapter 5. The Finite Difference Method This chapter derives the finite difference equations that are used in the conduction analyses in the next chapter and the techniques that are used to overcome computational
Predicting NO Formation with Flamelet Generated Manifolds
 Predicting NO Formation with Flamelet Generated Manifolds J. A. van Oijen and L. P. H. de Goey Dept. Mechanical Engineering, Technische Universiteit Eindhoven P.O. Box, 6 MB Eindhoven, The Netherlands
Predicting NO Formation with Flamelet Generated Manifolds J. A. van Oijen and L. P. H. de Goey Dept. Mechanical Engineering, Technische Universiteit Eindhoven P.O. Box, 6 MB Eindhoven, The Netherlands
Calculation of critical conditions for the filtration combustion model
 Calculation of critical conditions for the filtration combustion model O. Vidilina 1, E. Shchepakina 1 1 Samara National Research University, 34 Moskovskoe Shosse, 443086, Samara, Russia Abstract The paper
Calculation of critical conditions for the filtration combustion model O. Vidilina 1, E. Shchepakina 1 1 Samara National Research University, 34 Moskovskoe Shosse, 443086, Samara, Russia Abstract The paper
Effects of Variation of the Flame Area and Natural Damping on Primary Acoustic Instability of Downward Propagating Flames in a Tube
 5 th ICDERS August 7, 015 Leeds, UK Effects of Variation of the Flame Area and Natural Damping on Primary Acoustic Instability of Downward Propagating Flames in a Tube Sung Hwan Yoon and Osamu Fujita Division
5 th ICDERS August 7, 015 Leeds, UK Effects of Variation of the Flame Area and Natural Damping on Primary Acoustic Instability of Downward Propagating Flames in a Tube Sung Hwan Yoon and Osamu Fujita Division
Poiseuille Advection of Chemical Reaction Fronts
 Utah State University DigitalCommons@USU All Physics Faculty Publications Physics 8- Poiseuille Advection of Chemical Reaction Fronts Boyd F. Edwards Utah State University Follow this and additional works
Utah State University DigitalCommons@USU All Physics Faculty Publications Physics 8- Poiseuille Advection of Chemical Reaction Fronts Boyd F. Edwards Utah State University Follow this and additional works
A Comparison of Ignition Phenomena Modelled with Detailed and Simplified Kinetics
 Combust. Sci. and Tech., 1992, Vol. 88. pp. 1-13 Photocopying permitted by license only Gordon and Breach Science Publishers S.A. Printed in United Kingdom A Comparison of Ignition Phenomena Modelled with
Combust. Sci. and Tech., 1992, Vol. 88. pp. 1-13 Photocopying permitted by license only Gordon and Breach Science Publishers S.A. Printed in United Kingdom A Comparison of Ignition Phenomena Modelled with
Topics in Other Lectures Droplet Groups and Array Instability of Injected Liquid Liquid Fuel-Films
 Lecture Topics Transient Droplet Vaporization Convective Vaporization Liquid Circulation Transcritical Thermodynamics Droplet Drag and Motion Spray Computations Turbulence Effects Topics in Other Lectures
Lecture Topics Transient Droplet Vaporization Convective Vaporization Liquid Circulation Transcritical Thermodynamics Droplet Drag and Motion Spray Computations Turbulence Effects Topics in Other Lectures
Department of Mechanical Engineering BM 7103 FUELS AND COMBUSTION QUESTION BANK UNIT-1-FUELS
 Department of Mechanical Engineering BM 7103 FUELS AND COMBUSTION QUESTION BANK UNIT-1-FUELS 1. Define the term fuels. 2. What are fossil fuels? Give examples. 3. Define primary fuels. Give examples. 4.
Department of Mechanical Engineering BM 7103 FUELS AND COMBUSTION QUESTION BANK UNIT-1-FUELS 1. Define the term fuels. 2. What are fossil fuels? Give examples. 3. Define primary fuels. Give examples. 4.
a 16 It involves a change of laminar burning velocity, widening or narrowing combustion limits for
 Peculiarities of filtration combustion of hydrogen-, propane- and methane-air mixtures in inert porous media. Kakutkina N.A., Korzhavin A.A., Mbarawa M. * Institute of chemical kinetics and combustion
Peculiarities of filtration combustion of hydrogen-, propane- and methane-air mixtures in inert porous media. Kakutkina N.A., Korzhavin A.A., Mbarawa M. * Institute of chemical kinetics and combustion
Effects of turbulence and flame instability on flame front evolution
 PHYSICS OF FLUIDS 18, 104105 2006 Effects of turbulence and flame instability on flame front evolution Jiao Yuan, Yiguang Ju, and Chung K. Law a Department of Mechanical and Aerospace Engineering, Princeton
PHYSICS OF FLUIDS 18, 104105 2006 Effects of turbulence and flame instability on flame front evolution Jiao Yuan, Yiguang Ju, and Chung K. Law a Department of Mechanical and Aerospace Engineering, Princeton
Physics 106a, Caltech 4 December, Lecture 18: Examples on Rigid Body Dynamics. Rotating rectangle. Heavy symmetric top
 Physics 106a, Caltech 4 December, 2018 Lecture 18: Examples on Rigid Body Dynamics I go through a number of examples illustrating the methods of solving rigid body dynamics. In most cases, the problem
Physics 106a, Caltech 4 December, 2018 Lecture 18: Examples on Rigid Body Dynamics I go through a number of examples illustrating the methods of solving rigid body dynamics. In most cases, the problem
Heat-recirculating combustors. Paul D. Ronney
 Heat-recirculating combustors Paul D. Ronney Department of Aerospace and Mechanical Engineering, 3650 McClintock Ave., OHE 430J University of Southern California, Los Angeles, CA, USA 90089-1453 1-213-740-0490
Heat-recirculating combustors Paul D. Ronney Department of Aerospace and Mechanical Engineering, 3650 McClintock Ave., OHE 430J University of Southern California, Los Angeles, CA, USA 90089-1453 1-213-740-0490
Laminar flame speed (burning velocity) reactants. propagating flame front. products. reactants
 Laminar flame speed (burning velocity) Introduction One of the most important parameters, influencing both, the combustion system design and combustion process control, is the flame speed. The flame speed
Laminar flame speed (burning velocity) Introduction One of the most important parameters, influencing both, the combustion system design and combustion process control, is the flame speed. The flame speed
Numerical Solution of Integral Equations in Solidification and Melting with Spherical Symmetry
 Numerical Solution of Integral Equations in Solidification and Melting with Spherical Symmetry V. S. Ajaev and J. Tausch 2 Southern Methodist University ajaev@smu.edu 2 Southern Methodist University tausch@smu.edu
Numerical Solution of Integral Equations in Solidification and Melting with Spherical Symmetry V. S. Ajaev and J. Tausch 2 Southern Methodist University ajaev@smu.edu 2 Southern Methodist University tausch@smu.edu
Combustion basics... We are discussing gaseous combustion in a mixture of perfect gases containing N species indexed with k=1 to N:
 Combustion basics... T. Poinsot poinsot@imft.fr Only the things you should know to understand the following courses Mainly elements of laminar flame theory for premixed and diffusion flames 1 Copyright
Combustion basics... T. Poinsot poinsot@imft.fr Only the things you should know to understand the following courses Mainly elements of laminar flame theory for premixed and diffusion flames 1 Copyright
Investigation of ignition dynamics in a H2/air mixing layer with an embedded vortex
 Paper # 070LT-0211 The 8th US National Meeting of the Combustion Institute, Park City, UT, May 19-22, 2013 Investigation of ignition dynamics in a H2/air mixing layer with an embedded vortex S.K. Menon
Paper # 070LT-0211 The 8th US National Meeting of the Combustion Institute, Park City, UT, May 19-22, 2013 Investigation of ignition dynamics in a H2/air mixing layer with an embedded vortex S.K. Menon
Pressure and Fuel Effects on the Flame Brush Thickness of H 2 /CO Flames
 Paper # 070LT-0011 Topic: Laminar & Turbulent Flames 8 th U. S. National Combustion Meeting Organized by the Western States Section of the Combustion Institute And hosted by the University of Utah May19-22,
Paper # 070LT-0011 Topic: Laminar & Turbulent Flames 8 th U. S. National Combustion Meeting Organized by the Western States Section of the Combustion Institute And hosted by the University of Utah May19-22,
Evaluation of Numerical Turbulent Combustion Models Using Flame Speed Measurements from a Recently Developed Fan- Stirred Explosion Vessel
 Paper # 070LT-0096 Topic: Turbulent Flames 8 th U. S. National Combustion Meeting Organized by the Western States Section of the Combustion Institute and hosted by the University of Utah May 19-22, 2013
Paper # 070LT-0096 Topic: Turbulent Flames 8 th U. S. National Combustion Meeting Organized by the Western States Section of the Combustion Institute and hosted by the University of Utah May 19-22, 2013
A Priori Model for the Effective Lewis Numbers in Premixed Turbulent Flames
 Paper # 070LT-0267 Topic: Turbulent Flames 8 th US National Combustion Meeting Organized by the Western States Section of the Combustion Institute and hosted by the University of Utah May 19-22, 2013.
Paper # 070LT-0267 Topic: Turbulent Flames 8 th US National Combustion Meeting Organized by the Western States Section of the Combustion Institute and hosted by the University of Utah May 19-22, 2013.
Overview spherical accretion
 Spherical accretion - AGN generates energy by accretion, i.e., capture of ambient matter in gravitational potential of black hole -Potential energy can be released as radiation, and (some of) this can
Spherical accretion - AGN generates energy by accretion, i.e., capture of ambient matter in gravitational potential of black hole -Potential energy can be released as radiation, and (some of) this can
EXPERIMENTAL AND NUMERICAL STUDIES FOR FLAME SPREAD OVER A FINITE-LENGTH PMMA WITH RADIATION EFFECT
 ISTP-16, 2005, PRAGUE 16 TH INTERNATIONAL SYMPOSIUM ON TRANSPORT PHENOMENA EXPERIMENTAL AND NUMERICAL STUDIES FOR FLAME SPREAD OVER A FINITE-LENGTH PMMA WITH RADIATION EFFECT Wen-Kuei Chang and Chiun-Hsun
ISTP-16, 2005, PRAGUE 16 TH INTERNATIONAL SYMPOSIUM ON TRANSPORT PHENOMENA EXPERIMENTAL AND NUMERICAL STUDIES FOR FLAME SPREAD OVER A FINITE-LENGTH PMMA WITH RADIATION EFFECT Wen-Kuei Chang and Chiun-Hsun
Self-similar solutions for the diffraction of weak shocks
 Self-similar solutions for the diffraction of weak shocks Allen M. Tesdall John K. Hunter Abstract. We numerically solve a problem for the unsteady transonic small disturbance equations that describes
Self-similar solutions for the diffraction of weak shocks Allen M. Tesdall John K. Hunter Abstract. We numerically solve a problem for the unsteady transonic small disturbance equations that describes
Overview of Turbulent Reacting Flows
 Overview of Turbulent Reacting Flows Outline Various Applications Overview of available reacting flow models LES Latest additions Example Cases Summary Reacting Flows Applications in STAR-CCM+ Ever-Expanding
Overview of Turbulent Reacting Flows Outline Various Applications Overview of available reacting flow models LES Latest additions Example Cases Summary Reacting Flows Applications in STAR-CCM+ Ever-Expanding
THE CONVECTION DIFFUSION EQUATION
 3 THE CONVECTION DIFFUSION EQUATION We next consider the convection diffusion equation ɛ 2 u + w u = f, (3.) where ɛ>. This equation arises in numerous models of flows and other physical phenomena. The
3 THE CONVECTION DIFFUSION EQUATION We next consider the convection diffusion equation ɛ 2 u + w u = f, (3.) where ɛ>. This equation arises in numerous models of flows and other physical phenomena. The
Modelling of transient stretched laminar flame speed of hydrogen-air mixtures using combustion kinetics
 Loughborough University Institutional Repository Modelling of transient stretched laminar flame speed of hydrogen-air mixtures using combustion kinetics This item was submitted to Loughborough University's
Loughborough University Institutional Repository Modelling of transient stretched laminar flame speed of hydrogen-air mixtures using combustion kinetics This item was submitted to Loughborough University's
Instabilities In A Reaction Diffusion Model: Spatially Homogeneous And Distributed Systems
 Applied Mathematics E-Notes, 10(010), 136-146 c ISSN 1607-510 Available free at mirror sites of http://www.math.nthu.edu.tw/ amen/ Instabilities In A Reaction Diffusion Model: Spatially Homogeneous And
Applied Mathematics E-Notes, 10(010), 136-146 c ISSN 1607-510 Available free at mirror sites of http://www.math.nthu.edu.tw/ amen/ Instabilities In A Reaction Diffusion Model: Spatially Homogeneous And
A theoretical study of spontaneous ignition of fuel jets in an oxidizing ambient with emphasis on hydrogen jets
 Combustion Theory and Modelling Vol. 12, No. 6, 2008, 1179 1196 A theoretical study of spontaneous ignition of fuel jets in an oxidizing ambient with emphasis on hydrogen jets K.B. Lim a, B.H. Chao b,
Combustion Theory and Modelling Vol. 12, No. 6, 2008, 1179 1196 A theoretical study of spontaneous ignition of fuel jets in an oxidizing ambient with emphasis on hydrogen jets K.B. Lim a, B.H. Chao b,
4 Oscillations of stars: asteroseismology
 4 Oscillations of stars: asteroseismology The HR diagram below shows a whole variety of different classes of variable or pulsating/oscillating stars. The study of these various classes constitutes the
4 Oscillations of stars: asteroseismology The HR diagram below shows a whole variety of different classes of variable or pulsating/oscillating stars. The study of these various classes constitutes the
Analysis of homogeneous combustion in Monolithic structures
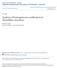 University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Papers in Chemical Reactions Chemical and Biomolecular Engineering Research and Publications 4-1-1996 Analysis of homogeneous
University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Papers in Chemical Reactions Chemical and Biomolecular Engineering Research and Publications 4-1-1996 Analysis of homogeneous
Best Practice Guidelines for Combustion Modeling. Raphael David A. Bacchi, ESSS
 Best Practice Guidelines for Combustion Modeling Raphael David A. Bacchi, ESSS PRESENTATION TOPICS Introduction; Combustion Phenomenology; Combustion Modeling; Reaction Mechanism; Radiation; Case Studies;
Best Practice Guidelines for Combustion Modeling Raphael David A. Bacchi, ESSS PRESENTATION TOPICS Introduction; Combustion Phenomenology; Combustion Modeling; Reaction Mechanism; Radiation; Case Studies;
Formation and Evolution of Distorted Tulip Flames
 25 th ICDERS August 2 7, 2015 Leeds, UK Formation and Evolution of Distorted Tulip Flames Huahua Xiao 1, 2, Ryan W. Houim 1, Elaine S. Oran 1, and Jinhua Sun 2 1 University of Maryland College Park, Maryland,
25 th ICDERS August 2 7, 2015 Leeds, UK Formation and Evolution of Distorted Tulip Flames Huahua Xiao 1, 2, Ryan W. Houim 1, Elaine S. Oran 1, and Jinhua Sun 2 1 University of Maryland College Park, Maryland,
n v molecules will pass per unit time through the area from left to
 3 iscosity and Heat Conduction in Gas Dynamics Equations of One-Dimensional Gas Flow The dissipative processes - viscosity (internal friction) and heat conduction - are connected with existence of molecular
3 iscosity and Heat Conduction in Gas Dynamics Equations of One-Dimensional Gas Flow The dissipative processes - viscosity (internal friction) and heat conduction - are connected with existence of molecular
A validation study of the flamelet approach s ability to predict flame structure when fluid mechanics are fully resolved
 Center for Turbulence Research Annual Research Briefs 2009 185 A validation study of the flamelet approach s ability to predict flame structure when fluid mechanics are fully resolved By E. Knudsen AND
Center for Turbulence Research Annual Research Briefs 2009 185 A validation study of the flamelet approach s ability to predict flame structure when fluid mechanics are fully resolved By E. Knudsen AND
Modeling of Wall Heat Transfer and Flame/Wall Interaction A Flamelet Model with Heat-Loss Effects
 9 th U. S. National Combustion Meeting Organized by the Central States Section of the Combustion Institute May 17-20, 2015 Cincinnati, Ohio Modeling of Wall Heat Transfer and Flame/Wall Interaction A Flamelet
9 th U. S. National Combustion Meeting Organized by the Central States Section of the Combustion Institute May 17-20, 2015 Cincinnati, Ohio Modeling of Wall Heat Transfer and Flame/Wall Interaction A Flamelet
Use of the graphical analytic methods of studying the combustion processes in the internal combustion
 Use of the graphical analytic methods of studying the combustion processes in the internal combustion engine combustion chamber on the basis of similarity criterion S. V. Krasheninnikov Samara State Aerospace
Use of the graphical analytic methods of studying the combustion processes in the internal combustion engine combustion chamber on the basis of similarity criterion S. V. Krasheninnikov Samara State Aerospace
Lecture 12 The Level Set Approach for Turbulent Premixed Combus=on
 Lecture 12 The Level Set Approach for Turbulent Premixed Combus=on 12.- 1 A model for premixed turbulent combus7on, based on the non- reac7ng scalar G rather than on progress variable, has been developed
Lecture 12 The Level Set Approach for Turbulent Premixed Combus=on 12.- 1 A model for premixed turbulent combus7on, based on the non- reac7ng scalar G rather than on progress variable, has been developed
Adaptive Time Space Discretization for Combustion Problems
 Konrad-Zuse-Zentrum fu r Informationstechnik Berlin Takustraße 7 D-14195 Berlin-Dahlem Germany JENS LANG 1,BODO ERDMANN,RAINER ROITZSCH Adaptive Time Space Discretization for Combustion Problems 1 Talk
Konrad-Zuse-Zentrum fu r Informationstechnik Berlin Takustraße 7 D-14195 Berlin-Dahlem Germany JENS LANG 1,BODO ERDMANN,RAINER ROITZSCH Adaptive Time Space Discretization for Combustion Problems 1 Talk
COMPUTATIONAL SIMULATION OF SPHERICAL DIFFUSION FLAME DYNAMICS AND EXTINCTION IN MICROGRAVITY TIANYING XIA. A thesis submitted to the
 COMPUTATIONAL SIMULATION OF SPHERICAL DIFFUSION FLAME DYNAMICS AND EXTINCTION IN MICROGRAVITY By TIANYING XIA A thesis submitted to the Graduate School-New Brunswick Rutgers, The State University of New
COMPUTATIONAL SIMULATION OF SPHERICAL DIFFUSION FLAME DYNAMICS AND EXTINCTION IN MICROGRAVITY By TIANYING XIA A thesis submitted to the Graduate School-New Brunswick Rutgers, The State University of New
arxiv: v1 [physics.chem-ph] 6 Oct 2011
![arxiv: v1 [physics.chem-ph] 6 Oct 2011 arxiv: v1 [physics.chem-ph] 6 Oct 2011](/thumbs/80/81226889.jpg) Calculation of the Minimum Ignition Energy based on the ignition delay time arxiv:1110.1163v1 [physics.chem-ph] 6 Oct 2011 Jens Tarjei Jensen a, Nils Erland L. Haugen b, Natalia Babkovskaia c a Department
Calculation of the Minimum Ignition Energy based on the ignition delay time arxiv:1110.1163v1 [physics.chem-ph] 6 Oct 2011 Jens Tarjei Jensen a, Nils Erland L. Haugen b, Natalia Babkovskaia c a Department
Well Stirred Reactor Stabilization of flames
 Well Stirred Reactor Stabilization of flames Well Stirred Reactor (see books on Combustion ) Stabilization of flames in high speed flows (see books on Combustion ) Stabilization of flames Although the
Well Stirred Reactor Stabilization of flames Well Stirred Reactor (see books on Combustion ) Stabilization of flames in high speed flows (see books on Combustion ) Stabilization of flames Although the
Theoretical Analysis of the Propagation of a Reaction Front in a Packed Bed
 Theoretical Analysis of the Propagation of a Reaction Front in a Packed Bed R. GORT, and J. J. H. BROUWERS* Department of Mechanical Engineering, Twente University, P.O. Box 217, 7500 AE Enschede, The
Theoretical Analysis of the Propagation of a Reaction Front in a Packed Bed R. GORT, and J. J. H. BROUWERS* Department of Mechanical Engineering, Twente University, P.O. Box 217, 7500 AE Enschede, The
Problem Set Number 2, j/2.036j MIT (Fall 2014)
 Problem Set Number 2, 18.385j/2.036j MIT (Fall 2014) Rodolfo R. Rosales (MIT, Math. Dept.,Cambridge, MA 02139) Due Mon., September 29, 2014. 1 Inverse function problem #01. Statement: Inverse function
Problem Set Number 2, 18.385j/2.036j MIT (Fall 2014) Rodolfo R. Rosales (MIT, Math. Dept.,Cambridge, MA 02139) Due Mon., September 29, 2014. 1 Inverse function problem #01. Statement: Inverse function
