A-POLYNOMIALS OF A FAMILY OF TWO-BRIDGE KNOTS
|
|
|
- Jordan Sherman
- 5 years ago
- Views:
Transcription
1 A-POLYNOMIALS OF A FAMILY OF TWO-BRIDGE KNOTS K. L. PETERSEN Abstract. The Jk, l knots, often called the double twist knots, are a subclass of two-bridge knots which contains the twist knots. We show that the A-polynomial of these knots can be determined by an explicit resultant. We present this resultant in two different ways. We determine a recursive definition for the A-polynomials of the J4, 2n and J5, 2n knots, and for the canonical component of the A-polynomials of the J2n, 2n knots. Our work also recovers the A-polynomials of the J1, 2n knots, and the recursive formulas for the A-polynomials of the A2, 2n and A3, 2n knots as computed by Hoste and Shanahan. Contents 1. Introduction 2 2. The A-polynomial 4 3. The Jk, l knots 5 4. Representations Reducible Representations Irreducible Representations The Longitude Proof of Theorem Resultants A Special Resultant Proof of Theorem Explicit computations for Jk, 2n knots for small k J1, 2n, torus knots J2, 2n, the twist knots J3, 2n J4, 2n J5, 2n J2m, 2m Appendix A4, 2n terms A5, 2n terms A2m, 2m terms Acknowledgements 32 References 32 1
2 2 K. L. PETERSEN 1. Introduction The A-polynomial of a 3-manifold M 3 with a single torus cusp was introduced in [4]. It is a two variable polynomial, usually written in terms of the variables M and L, which encodes how eigenvalues of a fixed meridian and longitude are related under representations from π 1 M 3 into SL 2 C. This polynomial is closely related to the SL 2 C character variety of M 3, and for hyperbolic manifolds it encodes information about the deformation of the hyperbolic structure of M 3, the existence of non-hyberbolic fillings of M 3, and can be used to determine boundary slopes of essential surfaces in M 3. Specifically, the boundary slopes of the Newton polygon of the A-polynomial are the boundary slopes detected by the SL 2 C character variety [4], and the Newton polygon is dual to the fundamental polygon of the Culler-Shalen seminorm [7]. This seminorm can be used to classify finite and exceptional surgeries of M 3 [1]. k l Figure 1. The knot Jk, l This polynomial has proven difficult to compute; data has been collected for most knots up to nine crossings see Knot Info [3] and calculations by Marc Culler [6], and a few families of knot complements in S 3 have proven amenable to computations. Tamura and Yokota [13] computed the A- polynomials of the 2, 3, 3 + 2n pretzel knots. Garoufalidis and Mattman [9] studied these A-polynomials, showing that they satisfy a specific type of linear recurrance relation. Hoste and Shanahan [10] established a recursively defined formula for the A-polynomials of the twist knots and the J3, 2n knots. This paper shows that the A-polynomial of the Jk, l knots can be computed as an explicit resultant, and recovers the work of Hoste and Shanahan. We also recursively determine the A-polynomial for the J4, 2n and J5, 2n knots, and the canonical component of the A-polynomial for the J2n, 2n knots.
3 A-POLYNOMIALS OF A FAMILY OF TWO-BRIDGE KNOTS 3 We consider the two-bridge knots Jk, l as described in Figure 1 where k and l are integers denoting the number of half twists in the labeled boxes; positive numbers correspond to right-handed twists and negative numbers correspond to left-handed twists. Such a projection determines a knot if kl is even, and we can reduce to considering the Jk, 2n knots as Jk, l = Jl, k. The knot J k, l is the mirror image of the knot Jk, l, and as a result the A-polynomial of J k, l is the A-polynomial of Jk, l with each M replaced by a M 1 [5]. Therefore we may assume k or l is positive. As discussed in 3 the Jk, l knots are a particularly attractive family as the fundamental groups of their complements have a relatively simple form. In Section 5.1 we show that the contribution to the A-polynomial from reducible representations is the term L 1. Therefore our main theorems focus on the term of the A-polynomials corresponding to irreducible representations. We write Ak, 2n to denote the contribution of factors of the A-polynomial corresponding to irreducible representations. This is welldefined up to multiplication by elements in Q and by powers of M and L. Our first main theorem is the following, where the polynomials F k,n and G k,n are defined in Definition 4.6 and Theorem 1.1. Assume k 1, 0, 1 and n 0. common vanishing set of F k,n r and G k,n r. Then Ak, 2n is the The A-polynomial can be determined by the resultant of these two polynomials, eliminating the variable r. This can be done, for example, using the Sylvester matrix and has been implemented in many computer algebra programs. The degree of F k,n as function of r is roughly 1 4 n k2 and the degree of G k,n is roughly 1 2 k. The next theorem demonstrates that the resultant can be computed using the polynomial H k,n, of degree about 2 n, which is defined in Definition 6.8, in place of F k,n. This resultant will differ from the resultant of F k,n and G k,n by factors of β = M 2 +l and γ = M 2 1l 1. As in Definition 3.3, l = L if k is even and l = LM 4n if k is odd. Theorem 1.2. Let ɛ = 1 if k is positive and 0 if k is negative, let ɛ = 1 if k is even and 0 if k is odd, and let ɛ = 1 ɛ1 ɛ. For k 1, 0, 1 and n 0 we have Ak, 2nγ m +ɛ n ɛ nk < 0 ResH k,n r, G k,n r = Ak, 2nβγ m +ɛ n ɛ n, k > 0 Ak, 2nδγ m +ɛ n ɛ n, k < 0 Theorem 1.1 is proven in Section 4.4 and Theorem 1.2 is proven in Section 6. In addition, we perform explicit computations in some special cases. If k = 0, then Jk, l is the unknot and the A-polynomial is L 1. The knots J±1, 2n are the torus knots whose A-polynomials are well known [4]. We present their A-polynomials in Theorem 7.1 for completeness. In Theorem 7.2 and Theorem 7.3 we recover the recursive formulas of Hoste
4 4 K. L. PETERSEN and Shanahan [10] for the A-polynomials of the twist knots the J±2, 2n knots and the J±3, 2n knots. We also compute recursive formulas for the A-polynomials of the J±4, 2n knots and the J±5, 2n knots. These are given in Theorem 7.5 and Theorem 7.7, respectively. Finally, we consider the J2n, 2n knots. These knots have an additional symmetry that the other Jk, l knots do not have, seen by flipping the corresponding four-plat upside down. This symmetry effectively factors the representation variety see [11] and this factorization can be seen on the level of the A-polynomial as well. A canonical component of the A-polynomial is an irreducible polynomial which contains the image of the discrete and faithful representation. We determine a recursive formula for the canonical component for these knots, given in Theorem The A-polynomial We follow the construction of the A-polynomial given in [5]. We consider a knot K in S 3, and let µ be a natural oriented meridian of K and λ a natural oriented longitude. Let Γ be the fundamental group of the complement of the knot K in S 3. For an oriented loop α S 3 K we write [α] Γ to be a base pointed homotopy class. We define R U to be the subset of the affine algebraic variety R = HomΓ, SL 2 C consisting of all representations ρ such that ρ[µ] and ρ[λ] are upper triangular. The set R U is an affine algebraic variety as well, since it simply has two additional equations specifying that these 2, 1 entries equal zero. Define the eigenvalue map ξ = ξ µ ξ λ : R U C 2 by setting ξρ = e µ, e λ where e µ is an eigenvalue of ρ[µ], and e λ is an eigenvalue of p[λ], both chosen consistently. We let M be the 1, 1 entry of ρ[µ] and L be the 1, 1 entry of ρ[λ]. We will use an alternate longitude, denoted by l, which we define below. If C is an algebraic component of R U, then the Zariski closure of ξc, ξc, is an algebraic subset of C 2. If ξc is a curve, then there is a polynomial that defines ξc which is unique up to constant multiples. The A-polynomial is defined as the product of all such polynomials. This polynomial may be taken to have integral coefficients with content zero, so it is well-defined up to sign. See [4]. There are an infinite number of abelian representations of Γ into SL 2 C. In such a representation every element of the commutator subgroup, including the longitude, is sent to the identity matrix. Therefore, L 1 is always a factor of the A-polynomial. This factor is often ignored in the definition of the A-polynomial. For the Jk, l knots, we will show that all reducible representations correspond only to the factor L 1, and we will usually omit this factor except when referring to the unknot.
5 A-POLYNOMIALS OF A FAMILY OF TWO-BRIDGE KNOTS 5 3. The Jk, l knots There are many relations amongst the Jk, l knots. The knot Jk, l is ambient isotopic to the knot Jl, k, so we will consider the knots Jk, 2n as if kl is odd then Jk, l is a two component link. The twist knots are the knots J±2, l. The figure-eight and the trefoil are J2, 2 and J2, 2, respectively. Also, J k, l is the mirror image of the knot Jk, l. The A-polynomial of a knot and its reflection differ only by replacing M with M 1 [5], so we may assume that k or l is positive. The Jk, l knots are hyperbolic unless k or l is less than 2 or k = l = ±2. We turn to the fundamental group of S 3 Jk, l. See [10, 11]. Proposition 3.1. The fundamental group of the complement of the knot Jk, 2n in S 3 is isomorphic to the group Γk, 2n = a, b : awk n = wn k b where { ab 1 m a 1 b m if k = 2m w k = ab 1 m aba 1 b m if k = 2m + 1. Among the relations mentioned above, the knot Jk, l is ambient isotopic to Jl, k, so the corresponding groups are isomorphic, but the above presentations are different. For a word v Γk, 2n written in powers of a and b, let v refer to the word obtained by reading v backwards. Definition 3.2. Let ɛv to be the exponent sum of v, written as a word in a and b, and let ɛk, n = ɛwk n. So that ɛ2m, n = 0 and ɛ2m+1, n = 2n. A natural meridian, µ, of the knot corresponds to a and a natural longitude, λ, to wk nwn k a 2ɛk,n. That is, [µ] = a and [λ] = wk nwn k a 2ɛk,n. We will also make use of an alternative longitude, which we now define. See [10]. Definition 3.3. Let λ 1 be the longitude corresponding to the word w n k wn k, so that [λ 1 ] = w n k wn k, and let l be a preferred eigenvalue of [λ 1 ]. This is chosen so that if k = 2m we have l = L and if k = 2m + 1 then l = LM 4n. 4. Representations First, we define a few polynomials we will use throughout. Definition 4.1. The j th Fibonacci polynomial, f j, is the Chebyshev polynomial defined recursively by the relation f j+1 x + f j 1 x = xf j x and initial conditions f 0 x = 0, and f 1 x = 1. With the substitution x = y + y 1 we have f j y + y 1 = y j y j /y y 1. Additionally, define the polynomials g j x = f j x f j 1 x. We will use the following several times. Lemma 4.2. If j 0, 1 then the polynomials f j x and f j 1 x share no common factors.
6 6 K. L. PETERSEN Proof. Let x = y + y 1 so that f j x = y j y j /y y 1. A root of f j x determines a solution to y 2j = 1. Similarly, a root of f j 1 f determines a solution to y 2j 2 = 1. Since gcd2j, 2j 2 = 2 the only simultaneous solutions are y = ±1. It follows that if f j x and f j 1 x share a root, it must be x = ±2. The Fibonacci recursion implies that f j 2 = j and f j 2 = ±j. Therefore, as j ±1, x = ±2 is not a root and the polynomials are relatively prime. Furthermore, we define certain terms in M and L to shorten some expressions. Definition 4.3. Let α = M 2 +1l+1, β = M 2 +l, γ = M 2 1l 1, δ = M 2 l+1, σ = β 2 +δ 2 and τ = l 1 2 M 2 + 4l + 2l M 2 + 4M 4 l + l 1 2 M 6. In many of the calculations to follow, we will use the Cayley-Hamilton theorem, which we now explicitly state for matrices in SL 2 C. Theorem 4.4 Cayley-Hamilton. Let X SL 2 C with trace x. For any integer j we have X j = f j xx f j 1 xi where I is the 2 2 identity matrix. For a matrix X, we will use X ij to denote the i, j th entry of X. As the eigenvalue map is invariant under conjugation, we consider representations ρ : Γk, 2n SL 2 C up to conjugation. A representation ρ : Γ SL 2 C is called reducible if all images share a one-dimensional eigenspace. Otherwise, a representation is called irreducible Reducible Representations. A reducible representation of Γk, 2n can be conjugated so that it is upper triangular with M s M t ρa = A = 0 M 1 and ρb = B = 0 M 1. We include the calculation of these terms of the A-polynomial for completeness. Proposition 4.5. The contribution to the A-polynomial from the reducible representations is the factor L 1. Proof. We use the presentation of the fundamental group from Proposition 3.1. Let W k = ρw k, Wk n = ρwn k, and let 0 denote the 2 2 zero matrix. First, consider k = 2m. The alternate longitude corresponds to ρ[λ 1 ] = Wk nw k n and is the identity in this case. That is, l = 1 for these representations. The defining word, in terms of matrices is AW2m n W 2m n B = 0. The matrix on the left is identically zero except for the 1, 2 entry which
7 A-POLYNOMIALS OF A FAMILY OF TWO-BRIDGE KNOTS 7 is nmm nm + nmm 2 s t. This equals zero for infinitely many representations, and M can be any value independent of l. Therefore, these representations contribute the factor l 1, which is L 1 to the A-polynomial. Similarly, consider k = 2m+1. The relation gives AWk n W k n B, a matrix whose only non-zero entry is the 1, 2 entry which is s t M 2n 1 + M 2n+1 mm M 1 M 2n M 2n /M + M 1 We conclude that there are infinitely many representations, and that M can be any value, independent of l. The 1, 1 entry of ρ[λ 1 ] is always M 4n, so l = M 4n. This is L = 1, and gives the factor L Irreducible Representations. To compute the A-polynomial, we now restrict attention to the irreducible representations ρ : Γ SL 2 C which map the meridian and longitude to upper triangular matrices. For such a representation, there are M and L in C such that M A = ρ[µ] = ρa = 0 M 1 and Λ = ρ[λ] = ρw n k wn k a 2ɛk,n = L 0 L 1. The alternative longitude, λ 1, corresponds to a matrix with 1, 1 entry l = LM 2ɛk,n. Let W k = ρw k, W = ρwk n and W = ρwk n. Up to conjugation all irreducible representations ρ : Γ SL 2 C are given by A = M 1 0 M 1 and B = ρ[b] = M 0 2 r M 1 where r 2. The 2,1 entry of W = ρwk n, W 21, equals 2 rw 12 for these groups. Therefore, the words W and W can be written as W W = 11 W 12 and W 2 rw 12 W W = 22 W rw 12 W 11 where W ij is W ij with all M s exchanged with M 1 s. This follows from [10]. The relation awk n = wn k b implies that, on the level of matrices, AW = W B. It follows by direct computation that the variables M and r define a valid representation if M M 1 W 12 + W 22 = 0. In fact, Riley [12] shows that a similar, more general statement is true for all two-bridge knots. Definition 4.6. Let F k,n r, t be defined by F k,n r = f n t k rf k,1 r f n 1 t k r
8 8 K. L. PETERSEN with F k,1 r defined by and t = t k r defined by F 2m,1 r = f m rg m rm 2 + M 2 r + 1 F 2m+1,1 r = f m rg m+1 rm 2 + M 2 r + 1 t 2m r = f m rg m+1 r g m rm 2 + M 2 r + 2 t 2m+1 r = g m+1 r 2 M 2 + M 2 r + 2. By [11] Proposition 3.7 the condition for ρ to be a representation can be encoded by these polynomials. Specifically, we have the following. Proposition 4.7. The map ρ as above determines a representation of Γk, 2n into SL 2 C if and only if F k,n r = The Longitude. The equation F k,n r = 0 with r 2 holds if and only if ρ is an irreducible representation of Γk, 2n. We now turn to the condition that the boundary subgroup is upper triangular. A natural meridian corresponds to the group element a, which was already taken to map to an upper triangular matrix A. Therefore, the remaining condition is to ensure that an element of Γk, 2n corresponding to a longitude, either λ or λ 1, also maps to an upper triangular matrix. The image ρ[λ] can be explicitly computed, as stated in the following lemma. We will let Λ = ρ[λ] henceforth. Lemma 4.8. With W = ρwk n, Λ = ρ[λ], Λ 11 = W 11 W 22 + W 12 W 122 r M 2ɛk,n Λ 12 = W 11 W 22 + W 12 W 122 r f 2ɛk,n M + M 1 + W 11 W 12 + W 12 W 11 M 2ɛk,n Λ 21 = 2 r W 12 W 22 + W 22 W 12 M 2ɛk,n Λ 22 = 2 r W 12 W 22 + W 22 W 12 f 2ɛk,n M + M 1 + W 22 W 11 + W 12 W 122 r M 2ɛk,n. Proof. Since [λ] = wk nwn k a 2ɛk,n one can compute Λ = W W A 2ɛk,n explicitly. A direct computation using the Cayley-Hamilton theorem confirms the above. From the lemma above, we now deduce an algebraic condition for Λ to be upper triangular. Lemma 4.9. For an irreducible representation ρ, Λ = ρ[λ] is upper triangular if and only if W 12 l + W 12 = 0, where l = LM 2ɛk,n. Proof. By Lemma 4.8, Λ 21 = 0 reduces to W 12 W 22 + W 22 W 12 = 0.
9 A-POLYNOMIALS OF A FAMILY OF TWO-BRIDGE KNOTS 9 Moreover, as L = Λ 11 by Lemma 4.8, L = W 11 W rw 12 W 12 M 2ɛk,n from which it follows that M 2ɛk,n L = W 11 W rw 12W 12. The alternate longitude is related by [λ 1 ] = a 2ɛk,n [λ]. By the Cayley-Hamilton theorem M 2ɛk,n = A 2ɛk,n 11, so that as ρa and ρ[λ] are upper triangular Therefore, l = ρ[λ 1 ] 11 = M 2ɛk,n L. 1 l = W 11 W rw 12 W 12. We consider this as the defining equation for l. Now we explore the condition for Λ to be upper triangular. We follow [10]. We multiply equation 1 by W 12, and have W 12 l = W 11 W 12 W rw 2 12W 12. Since W 12 W 22 = W 12 W 22 we rewrite this as W 12 l = W 11 W 12W rw 2 12W 12. Next, since detw = W 11 W 22 2 rw 2 12 = 1 W 12 l = W 11 W 12W 22 + W 11 W 22 1W 12 = W 12. Combining this, W 12 l + W 12 = 0. As l, M C this condition is equivalent to Λ 21 = 0. Now we show that the condition for Λ to be upper triangular can be expressed in terms of the entries of W k instead of W = W k n. Lemma For an irreducible representation ρ, Λ = ρ[λ] is upper triangular if and only if W k 12 l + W k 12 = 0, where l = LM 2ɛk,n. Proof. Using the Cayley-Hamilton theorem, W = W k n = f n t k rw k f n 1 t k ri. Therefore, W 12 = f n t k rw k 12 and W 12 = f nt k rw n 12 since f nt k r is symmetric in M and M 1. As a result, W 12 l + W 12 = f n t k r W k 12 l + W k 12. It suffices to show that f n t k r is not zero. If f n t k r = 0 then by Definition 4.6 F k,n r = f n 1 t k r = 0 and so f n 1 t k r = 0. This cannot occur if n 1, 0, 1 as by Lemma 4.2 f n and f n 1 are relatively prime. If n = 1, 0, 1 then either f n t k r or f n 1 t k r equals ±1 and cannot be zero.
10 10 K. L. PETERSEN 4.4. Proof of Theorem 1.1. We now use the Cayley-Hamilton theorem to determine explicit equations for the polynomials above. First, we determine explicit equations for the entries of W k. Lemma With W k = ρw k then W k 21 = 2 rw k 12. If k = 2m then W k 11 = f m r 2 2 rm 2 + [f m rr 1 f m 1 r] 2 W k 12 = f m r 2 [M + M 1 rm 1 ] + f m rf m 1 r[m 1 M] W k 22 = f m r 2 M 2 2 r + [f m r f m 1 r] 2. If k = 2m + 1 then W k 11 = f m r 2 [M 2 r 1 2 r 2r 2 ] + 2f m rf m 1 r[1 rm 2 + rr 2] + f m 1 r 2 [2 + M 2 r] W k 12 = f m r 2 [Mr 1 + r r 2 M 1 ] f m rf m 1 r[2r 1M 1 M] + f m 1 r 2 M 1 W k 22 = f m r 2 [r 1 2 M r] 2f m rf m 1 rr 1M 2 + f m 1 r 2 M 2. Proof. We calculate AB 1 r 1 M = r 2M 1 1 A 1 r 1 M 1 B = 2 rm 1 both of which have trace r, so that by the Cayley-Hamilton theorem AB 1 m r 1fm r f = m 1 r Mf m r r 2M 1 f m r f m r f m 1 r A 1 B m r 1fm r f = m 1 r M 1 f m r. 2 rmf m r f m r f m 1 r As W k = ρw k, using Proposition 3.1 for k = 2m we have and for k = 2m + 1, W k = AB 1 m A 1 B m W k = AB 1 m ABA 1 B m. Upon multiplying we obtain the stated expressions. In light of Lemma 4.10 we now compute W k 12 l + W k 12 using these equations. Definition Let G k,n r be defined by G 2m,n r = f m rrδ α γf m+1 r G 2m+1,n r = βf m+1 r δf m r.
11 A-POLYNOMIALS OF A FAMILY OF TWO-BRIDGE KNOTS 11 Using the Fibonacci identities, one can write these polynomials in different ways. For example, when k = 2m we also have G k,n r = f m rα rβ γf m 1 r. Lemma For an irreducible representation ρ, the condition for Λ = ρ[λ] to be upper triangular is equivalent to G k,n r = 0. Proof. By Lemma 4.10 it suffices to consider W k 12 l + W k 12. With Lemma 4.11 we see that for k = 2m, W k 12 l+w k 12 is exactly f mrm 1 times the expression for G k,n. When k = 2m + 1, by Lemma 4.11 similar to the above, W k 12 l + W k 12 is g m+1rm 1 times the expression for G k,n. It suffices to show that f m r 0 when k = 2m and that g m+1 r 0 when k = 2m+1. First, consider the even case. If f m r = 0 then F k,n r can be explicitly computed using Proposition 4.7 and is the A-polynomial. This implies that F k,1 r = 1 and t k r = 2. Therefore, F k,n r = f n 2 f n 1 2. As f j 2 = j for all j, we conclude that F k,n r = 1. Therefore the A- polynomial is L 1, with the inclusion of the reducible factor. By [2, 8] the only knot in S 3 with A-polynomial equal to L 1 is the unknot. Similarly, if k is odd we conclude that F k,1 r = 1 and t = 2 so that F k,n r = 1. Lemma For k 1, 0, 1 the polynomial G k,n r is an irreducible non-constant polynomial in Q[M ±1, l ±1 ]. Proof. Let R = Q[M ±1, l ±1 ]. Consider the case when k = 2m, so that G 2m,n r = f m rm 2 + 1l + 1 M 2 + lr + f m 1 rm 2 1l 1. Modulo the ideal generated by M 2 1, R can be identified with Q[l] and G 2m,n r = l + 1f m rr 2. As a result, any factorization of G 2m,n r in R[r] modulo M 2 1, gives a factorization of f m rr 2 in Q[r]. Modulo the ideal generated by M 2 + l we have G 2m,n r = l + 1l 1 f m+1 r f m r. Similarly, a factorization modulo M 2 + l gives a factorization of f m r f m+1 r in Q[r]. As f m rr 2 and f m r f m+1 r share no common roots by Lemma 4.2 we see that there is no factorization. We conclude that G 2m,n r is irreducible. Next consider k = 2m + 1, so that G 2m+1,n r = M 2 l + 1f m r + f m+1 rm 2 + l. First, assume that 2m+1 > 0, reducing modulo M 2 l+1 we have G 2m+1,n r = M 2 + lf m+1 r, and reducing modulo M 2 + 1l + 1 G 2m+1,n r = M 2 +l f m r+f m+1 r. Again, a factorization modulo either M 2 l+1 or M 2 + 1l + 1 gives a factorization of either f m+1 r or f m r + f m+1 r in Q[r]. But these are relatively prime by Lemma 4.2. Therefore G 2m+1,n r is irreducible in this case as well. Now consider the case when 2m + 1 < 0. Reducing modulo M 2 + l, G 2m+1,n r = M 2 l + 1f m r and reducing modulo M 2 1l 1, G 2m+1,n r = M 2 + l f m r f m+1 r. As before, we conclude that G 2m+1,n r is irreducible.
12 12 K. L. PETERSEN Theorem 1.1 now follows from Proposition 4.7, Lemma 4.13, and Lemma Remark Let K = QM, l. To determine the A-polynomial by eliminating the variable r from F k,n t k r and G k,n r using resultants, we require F k,n t k r and G k,n r to be non-constant polynomials in K[r]. The polynomial G k,n r is a non-constant polynomial in K[r] unless k = 1, 0, 1. For these values we have G 1,n r = δ, G 0,n r = γ, and G 1,n r = β. The polynomial F k,1 x is a non-constant polynomial in K[x] unless k = 0, 1. We have F 0,1 x = F 1,1 x = 1. The defining equation for t k r is nonconstant in K[r] unless k = 0, in which case t 0 r = 2. It is non-linear if k > 1 and if k = ±1 then t = M 2 + M r. It follows that F k,n t k r is constant only when n = 0, k = 0, or when n = k = 1. For these values there are no irreducible representations. These correspond to Jk, 0 = J0, 2n = J1, 2 which are all the unknot. We conclude that one of F k,n t k r and G k,n r is constant when k = 1, 0, 1 or n = 0. These values of k are the excluded values in Theorem Resultants In this section we collect facts about resultants that will be used later. If px and qx are polynomials with leading coefficients P and Q, the resultant of px and qx is Res px, qx = P deg q Q deg p r p r q where the product ranges over all roots r p of px and r q of qx. First, we summarize some basic facts about resultants. Lemma 5.1. Assume that px, qx, and rx are polynomials and the leading coefficient of qx is Q. 1 Resp, q = 1 deg p+deg q Resq, p. 2 Respr, q = Resp, qresr, q. 3 Q degp+rq Res p, q = Q deg p Res p + rq, q. The following polynomial will be useful in our calculations, as rational functions will naturally come out of our calculation. Definition 5.2. For a fixed x and y, and a polynomial ϕ, define the polynomial ϕx, y = y degϕ ϕ x y. We now collect a few useful lemmas. Lemma 5.3. Let ϕz be a polynomial of degree d and assume that tp 1 = p 2 + gp 3. Then p d 1 ϕt = ϕp 2, p 1 + gp 4 for some polynomial p 4.
13 A-POLYNOMIALS OF A FAMILY OF TWO-BRIDGE KNOTS 13 Proof. Notice that if ϕz = c d z d + c d 1 z d c 1 z + c 0 then since tp 1 = p 2 + gp 3 we have p d 1ϕt = c d p 1 t d + c d 1 p 1 p 1 t d c 1 p d 1 1 p 1 t + c 0 p d 1 = c d p 2 + gp 3 d + c d 1 p 1 p 2 + gp 3 d c 1 p d 1 1 p 2 + gp 3 + c 0 p d 1. For each n > 0 the term p 2 + gp 3 n = p n 2 + gp where p is a polynomial. Therefore, p d 1ϕt = c d p d 2 + c d 1 p 1 p d c 1 p d 1 1 p 2 + c 0 p d 1 + gp 4 = p d 1ϕ p 2 p 1 + gp 4 = ϕp 2, p 1 + gp 4. The following can be verified directly from the Fibonacci recursion. Lemma 5.4. Let A and B be constants. Then p k x, y = Af k x, y + Bf k 1 x, y satisfies the following recursion. We have p 1 x, y = A, p 2 x, y = Ax + B and for k > 2 the polynomial p k x, y = xp k 1 x, y y 2 p k 2 x, y. We have p 0 x, y = B, p 1 x, y = A xb and for k < 1 the polynomial p k x, y = xp k+1 x, y y 2 p k+2 x, y A Special Resultant. In this section we compute the resultant R j = Res f j xx + A + f j 1 xb, px where px = x 2 ax + b and a, b, A and B are constants. This type of resultant will be used several times in our computations. With X j = R j + R j+1 we will first show that X j satisfies a recursion, from which a recursion for R j follows. All of the proofs will rely on the recursive definition of the Fibonacci polynomials, f j+1 x + f j 1 x = xf j x. Let x 1 and x 2 be the two roots of px, so that x 1 x 2 = b and x 1 + x 2 = a. Let F j = f j x 1 f j x 2 = Resf j x, px G j = f j x 1 f j 1 x 2 + f j x 2 f j 1 x 1 H j = x 1 f j x 1 f j 1 x 2 + x 2 f j x 2 f j 1 x 1. In this section, let d 1 = b, d 2 = 2 a 2 + 2b, d 3 = b and d 4 = 1. Lemma 5.5. The following identities hold. 1 H j = F j+1 + bf j + F j 1 2 H j H j 2 = F j 1 a 2 2b 2bF j 2 3 F j = bf j a 2 + 2bF j 2 + bf j 3 F j 4 4 G j = af j 1 G j 1.
14 14 K. L. PETERSEN Proof. For the first identity, F j = x 1 f j 1 x 1 f j 2 x 1 x 2 f j 1 x 2 f j 2 x 2 = x 1 x 2 F j 1 + F j 2 x 1 f j 1 x 1 f j 2 x 2 + x 2 f j 1 x 2 f j 2 x 1 = bf j 1 + F j 2 H j 1. This proves the first assertion. Next, consider H j = x 1 x 1 f j 1 x 1 f j 2 x 1 f j 1 x 2 + x 2 x 2 f j 1 x 2 f j 2 x 2 f j 1 x 1 = F j 1 x x 2 2 x 1 f j 1 x 2 f j 2 x 1 + x 2 f j 1 x 1 f j 2 x 2 = F j 1 a 2 2b x 1 f j 2 x 1 x 2 f j 2 x 2 f j 3 x 2 + x 2 f j 2 x 2 x 1 f j 2 x 1 f j 3 x 1 = F j 1 a 2 2b 2x 1 x 2 F j 2 + x 1 f j 2 x 1 f j 3 x 2 + x 2 f j 3 x 1 f j 2 x 2 = F j 1 a 2 2b 2bF j 2 + H j 2. This shows the second assertion. With the above, we conclude that the third assertion holds. Finally, G j = f j 1 x 2 f j x 1 + f j 1 x 1 f j x 2 = f j 1 x 2 x 1 f j 1 x 1 f j 2 x 1 + f j 1 x 1 x 2 f j 1 x 2 f j 2 x 2 = x 1 + x 2 f j 1 x 2 f j 1 x 1 f j 1 x 2 f j 2 x 1 + f j 1 x 1 f j 2 x 2 = af j 1 G j 1 proving the final identity. Lemma 5.6. The following identity holds X j = BF j+2 + b + Aa + A 2 + bb BF j+1 + F j b + Aa + A 2 + bb + aab + B 2 + B + B 2 + BF j 1. Proof. The resultant R j is R j = f j x 1 x 1 + A + f j 1 x 1 B f j x 2 x 2 + A + f j 1 x 2 B = F j b + Aa + A 2 + B 2 F j 1 + ABG j + BH j. By Lemma 5.5, we can substitute H j and rewrite R j as R j = BF j+1 + F j b + Aa + A 2 + bb + B 2 + BF j 1 + ABG j. By another application of Lemma 5.5 we can substitute G j so that X j is as stated. Lemma 5.7. The term X j satisfies the recursion X j = bx j a 2 + 2bX j 2 + bx j 3 X j 4. Since X j = R j + R j 1 this implies the following recursion for R j.
15 A-POLYNOMIALS OF A FAMILY OF TWO-BRIDGE KNOTS 15 Proposition 5.8. The resultant R j of f j xx+a+f j 1 xb and x 2 ax+b satisfies the following recursion. R j = b 1R j 1 +2 a 2 +3bR j 2 +2 a 2 +3bR j 3 +b 1R j 4 R j 5 with initial conditions R 2 = b 2 + 2Bb + 2Bb 2 + B 2 + 2bB 2 + B 2 b 2 + Aab AaB + abba a 2 B a 2 B 2 + ba 2 R 1 = A 2 + Aa + AaB + b + 2Bb + bb 2 R 0 = B 2 R 1 = b + Aa + A 2 R 2 = B 2 2Bb + b 2 + AaB + Aab + a 2 B + ba 2. Proof. A recursion for X j of the form determines a recursion X j = c 1 X j 1 + c 2 X j 2 + c 3 X j 2 + c 4 X j 4 R j+1 = c 1 1R j + c 1 + c 2 R j 1 + c 2 + c 3 R j 2 + c 3 + c 4 R j 3 + c 4 R j 4. The following is immediate. Proposition 5.9. If S j = cd j R j then for j > 5, S j satisfies the recursion S j = db 1S j 1 + d 2 2 a 2 + 3bS j 2 + d 3 2 a 2 + 3bS j 3 + d 4 b 1S j 4 d 5 S j 5 and for j 5, S j satisfies the recursion S j = db 1S j+1 + d 2 2 a 2 + 3bS j+2 + d 3 2 a 2 + 3bS j+3 + d 4 b 1S j+4 d 5 S j+5. The initial conditions are determined by S j = cd j R j for j > 5 and j Proof of Theorem 1.2 By Theorem 1.1 the A-polynomial can be computed as ResF k,n t k r, G k,n r. The degree of F k,n is approximately 1 4 n k2 and the degree of G k,n is about 1 2 k. In this section we undergo a series of reductions replace F k,n with a polynomial of smaller degree, approximately 2 n. The terms α, β, γ and δ are defined in Definition 4.3. Definition 6.1. Let q 1 r = δβr σ and q 2 r = σr τ, and let g 0 be the leading coefficient of G k,n r. Specifically, g 0 = β if k > 0 and δ if k < 0. The following can be verified using the Fibonacci recursion.
16 16 K. L. PETERSEN Lemma 6.2. We have the following β m γ if k = 2m δ G k,n σ δβ = β m+1 δ m if k = 2m + 1 > 0 δ m β m 1 if k = 2m + 1 < 0. In the next few lemmas we rewrite key terms. Essentially we rewrite these terms as a multiple of G k,n r plus a remainder. This will allow us to simplify the resultant of F k,n r and G k,n r using Lemma 5.1. Let F = QM, L. First, we address F k,1 r. Let F k,1 = γ 1 α βt k r and let F k,n r = f nt k rf k,1 f n 1t k r. Lemma 6.3. For a fixed k 1, 0, 1, and n 0 there are polynomials R 1 r and R 2 r in F [r] such that and F k,1 r = F k,1 R 1rG k,n r F k,n r = F k,n r R 2rG k,n r. Proof. If k = 2m, let R 1 r = γ 1 f m rm 2 + M 2 r. If k = 2m + 1 let R 1 r = γ 1 g m+1 rm 2 + M 2 r. In each case, the first identity can be directly verified using the definition of F k,1 r and G k,n r with the substitution r = s + s 1 so that f j r = s j s j /s s 1. The second assertion follows from the definition of F k,n r and F k,n r letting R 2r = f n t k rr 1 r. This allows us to calculate the resultant of F k,n r and G k,n r in terms of F k,n r. Let A 1 = ResF k,n r, G k,n r and A 2 = ResF k,n r, G k,nr. Lemma 6.4. For a fixed k 1, 0, 1, and n 0 then A 1 nk < 0 A 2 = ±βa 1 n, k > 0. 1 k δa 1 n, k < 0 Proof. When n > 0 by Lemma 6.3 and Lemma 5.1 up to sign, we see that A 1 g degf k,n r 0 = g degf k,nr 0 A 2. Since degf k,n r = degt k r n 1 + degf k,1 r and degf k,n r = degt k r n we have A 1 g deg t kr 0 = A 2 g degf k,1r 0. The statement follows from calculating the degrees of t k r and F k,1 r. The other cases are similar.
17 A-POLYNOMIALS OF A FAMILY OF TWO-BRIDGE KNOTS 17 Now we turn to the defining equation for t k r. Lemma 6.5. Fix k 1, 0, 1 and n 0. R 3 r F [r] such that Proof. When k = 2m let t k rq 1 r = q 2 r G k,n rr 3 r. Then there is a polynomial R 3 r = M 2 + M 2 rf m rβr α + γf m+1 r and when k = 2m + 1 let R 3 r = r 2M 2 + M 2 rβf m r δf m+1 r. The statement follows immediately. Let A 3 = Resq 1 r n γf k,n r, G k,nr. Lemma 6.6. Fix k 1, 0, 1 and n 0. We have n A 1 γ m ɛ 2 δβ m ɛ 2 G k,n σ δβ nk < 0 n A 3 = ±A 1 βγ m ɛ 2 δβ m ɛ 2 G k,n σ δβ n, k > 0 n ±A 1 δγ m ɛ 2 δβ m ɛ 2 G k,n σ δβ n, k < 0 where ɛ 2 = 0 unless k is odd and negative, in which case ɛ 2 = 1. Proof. We use the identities in Lemma 5.1. First, notice that since deg G k,n = m ɛ 2, we have Next, A 2 γ degf k,nr A 2 γ m ɛ 2 = ResγF k,n r, G k,nr. ResγF k,n r, G k,nrresq 1 r, G k,n r n = A 3. Therefore, A 3 = Resq 1 r, G k,n r n γ m ɛ 2 A 2. By definition, q 1 r = δβr σ δβ. It follows that This simplifies to Resq 1 r, G k,n r = δβ m ɛ 2 G k,n σ δβ. n A 2 γ m ɛ 2 δβ m ɛ 2 G k,n σ δβ = A3. The lemma follows from combining this with the identity from Lemma 6.4. The term F k,n r has a factor of M 2 n in the denominator from the M 2 in the defining equation for t k r. The A-polynomial is well-defined up to multiples of M, so we will multiply by powers of M to make the powers of M all positive. To remove this factor of M 2 n, we compute A 0 = ResM 2 n F k,n r, G k,n r.
18 18 K. L. PETERSEN Therefore, A 0 = M 2 n deg Gk,nr A 1. By Lemma 6.6 we have n A 0 γ m ɛ 2 δβ m ɛ 2 G k,n σ δβ nk < 0 M 2 n deg Gk,nr n A 3 = ±A 0 βγ m ɛ 2 δβ m ɛ 2 G k,n σ δβ n, k > 0 n ±A 0 δγ m ɛ 2 δβ m ɛ 2 G k,n σ δβ n, k < 0 Since A 3 = Resq 1 r n γf k,n r, G k,nr, we conclude that M 2 n deg G k,nr A 3 = ResM 2 n q 1 r n γf k,n r, G k,nr. We conclude the following, with A 4 = ResM 2 n q 1 r n γf k,n r, G k,nr. Lemma 6.7. With ɛ 2 defined in Lemma 6.6, n A 0 γ m ɛ 2 δβ m ɛ 2 G k,n σ δβ nk < 0 n A 4 = ±A 0 βγ m ɛ 2 δβ m ɛ 2 G k,n σ δβ n, k > 0 n ±A 0 δγ m ɛ 2 δβ m ɛ 2 G k,n σ δβ n, k < 0 Now we define the polynomials H k,n r which differ from M 2 n q n 1 γf k,n r by a multiple of G k,n r. Definition 6.8. If n is positive let H k,n r = q 2 rm 2 H k,n 1 r q 1 r 2 M 4 H k,n 2 r with initial conditions H k,1 r = M 2 αq 1 r βq 2 r, and H k,2 r = M 4 αq 1 rq 2 r γq 1 r 2 βq 2 r 2. If n is negative let H k,n r = q 2 rm 2 H k,n+1 r q 1 r 2 M 4 H k,n+2 r with initial conditions H k,0 r = γ and H k, 1 r = M 2 βq 2 r αq 1 r + γq 2 r. The following follows directly from Lemma 5.4. Lemma 6.9. If n is positive, then H k,n r = M 2 n f n q 2, q 1 αq 1 r βq 2 r γq 1 r 2 f n 1 q 2, q 1 and if n is negative, then H k,n r = M 2 n f n q 2, q 1 αq 1 r βq 2 r γf n 1 q 2, q 1. Lemma Fix k 1, 0, 1 and n 0. R 4 r F [r] such that Then there is a polynomial M 2 n q 1 r n γf k,n r = H k,nr + G k,n rr 4 r.
19 A-POLYNOMIALS OF A FAMILY OF TWO-BRIDGE KNOTS 19 Proof. By Lemma 5.3 and Lemma 6.5 since tq 1 r = q 2 r G k,n R 3 r we have when n > 0 q 1 r n f n t α βt γf n 1 t = q 1 r n 1 f n t αq 1 r βq 2 r + βg k,n R 3 γq1 r n f n 1 t = H k,n rm 2 n + G k,n R 4. Here R 4 = βr 3 q1 n 1 f n t k r + P 4 αq 1 βq 2 γq1p 2 4 with P 4 and P 4 from Lemma 5.3. If n is negative, q 1 r n f n t α βt γf n 1 t = q 1 r n 1 f n t αq 1 βtq 1 γq1 r n f n 1 t = H k,n rm 2 n + G k,n R 4. Here R 4 = βr 3 q n 1 1 f n t k r + P 4 αq 1 βq 2 γp 4 with P 4 and P 4 as in the previous case. We are now ready to prove Theorem 1.2. Let A 5 = ResH k,n r, G k,n r. It is enough to show that up to sign, A 0 γ m +ɛ n 1 ɛ1 ɛ nk < 0 A 5 = A 0 βγ m +ɛ n 1 ɛ1 ɛ n, k > 0 A 0 δγ m +ɛ n 1 ɛ1 ɛ n, k < 0 where ɛ = 1 if k is even and ɛ = 0 if k is odd, and ɛ = 1 if k is positive and 0 if k is negative. Lemma 6.10 with Lemma 5.1 implies that A 4 g deg H k,nr 0 = g n +degf k,n r 0 A 5. Since the degree of H k,n r is n, we have A 4 = g degf k,n r 0 A 5. The degree of degf k,n r = n degt kr = nk so that A 4 = g nk 0 A 5. Using Lemma 6.7 it follows that n A 0 γ m ɛ 2 δβ m ɛ 2 G k,n σ δβ nk < 0 g nk n 0 A 5 = ±A 0 βγ m ɛ 2 δβ m ɛ 2 G k,n σ δβ n, k > 0 n ±A 0 δγ m ɛ 2 δβ m ɛ 2 G k,n σ δβ n, k < 0. n When k = 2m then ɛ 2 = 0 and δβ m ɛ 2 G k,n σ δβ = ±γ n g nk 0. This reduces to the stated form. When k = 2m + 1, then ɛ 2 depends on the sign
20 20 K. L. PETERSEN n of k. In both cases, δβ m ɛ 2 G k,n σ δβ nk = ±g 0. This reduces to the stated form. This completes the proof of Theorem Explicit computations for Jk, 2n knots for small k When k is small, we can recursively compute these resultants for all n. Here we calculate the A-polynomials for the J1, 2n, J2, 2n, J3, 2n, J4, 2n and J5, 2n knots. Since J k, l is the mirror image of Jk, l, the A-polynomial of J k, l can be determined from the A-polynomial of the Jk, l knot by replacing every M with an M 1. Therefore, these calculations also determine the A-polynomials of the J 1, 2n, J 2, 2n, J 3, 2n, J 4, 2n, and J 5, 2n knots. It is sufficient to determine the contribution from the irreducible representations, as the reducible representations contribute the factor L 1 to the A-polynomial J1, 2n, torus knots. The knot J1, 2n is the torus knot T 2, 2n 1 corresponding to the Schubert pair p, q = 1, 1 2k. By Remark 4.15 when k = ±1, G k,n r is constant. In particular, G 1,n = β and G 1,n = δ. Therefore this determines the irreducible contribution of the A-polynomial. The algebraic condition F 1,k r = 0 merely determines valid r values for ρ to be an irreducible representation. For n = 0, or 1 however, F 1,0 r and F 1,1 r are ±1. This indicates that there are no irreducible representations, which is clear as J1, 0 = J1, 2 are the unknot. Here l = LM 4n and since M 0, G 1,k r = β = 0 determines the factor β = M 2 + l = M 2 + LM 4n. Normalizing, by dividing by M 2, this is equivalent to the factor of 1 + LM 4n 2. We obtain the following, which has been observed before [4]. Theorem 7.1. The A-polynomial of the J1, 2n torus knot is given by { 1 + LM 4n 2 if n > 1 A1, 2n = M 2 4n + L if n J2, 2n, the twist knots. We will directly compute the A-polynomial as the common vanishing set of F 2,n and G 2,n using Theorem 1.1. Here m = 1 and we have the following F 2,n r = f n t 2 rf 2,1 r f n 1 t 2 r F 2,1 r = M 2 + M 2 r + 1 t 2 r = 2 rm 2 + M 2 r + 2 G 2,n r = M 2 + lr M 2 + 1l + 1. Since G 2,n r = 0 we conclude that r = M 2 + 1l + 1/M 2 + l. It follows that F 2,1 r = M 6 + l M 2 M 2 + l
21 and A-POLYNOMIALS OF A FAMILY OF TWO-BRIDGE KNOTS 21 t 2 = n 2 d 2 = 1 lm 8 + 2lM 6 + l M 4 + 2lM 2 + l 2 l M 2 + l 2 M 2. Therefore, M 6 + l F 2,n r = f n t 2 M 2 M 2 + l f n 1t 2. One can easily verify the following F 2, 1 = M 8 l + M 6 l + M 4 l M 2 l l /M 2 M 2 + l 2 F 2,0 = 1 F 2,1 = M 6 + l/m 2 M 2 + l F 2,2 = 1 lm lM 12 + l 2 + 2lM 10 M 8 l 2 lm 6 + 2l 2 + lm 4 + 2M 2 l 2 + l 3 l 2 /M 4 M 2 + l 3. The A-polynomial is given by the numerator of F k,n. Using Lemma 5.4 we conclude that the A-polynomials satisfy the recursion given by Hoste and Shanahan [10]. In this case l = L. Theorem 7.2. Let n 2 and d 2 be defined as above. For n positive with initial conditions A2, 2 = M 6 + l A2, 2n = n 2 A2, 2n 2 d 2 2A2, 2n 4 A2, 4 = 1 lm lM 12 + l 2 + 2lM 10 M 8 l 2 lm 6 For negative n with initial conditions + 2l 2 + lm 4 + 2M 2 l 2 + l 3 l 2. A2, 2n = n 2 A2, 2n + 2 d 2 2A2, 2n + 4 A2, 0 = 1 A2, 2 = M 8 l + lm 6 + 2l + l 2 + 1M 4 + M 2 l l J3, 2n. We will directly compute the A-polynomial as the common vanishing set of F 3,n and G 3,n using Theorem 1.1. Here, F 3,n r = f n t 3 rf 3,1 r f n 1 t 3 r F 3,1 r = r 1M 2 + M 2 r + 1 t 3 r = r 1 2 M 2 + M 2 r + 2 G 3,n r = M 2 + lr M 2 l + 1.
22 22 K. L. PETERSEN Since G 3,n r = 0 we have r = M 2 l + 1/M 2 + l. Using this, F 3,1 r = 1 lm 8 + lm 6 + 2M 4 l + M 2 l + l 2 l M 2 + l 2 M 2. Therefore, F 3,n is defined by 1 lm 8 + lm 6 + 2M 4 l + M 2 l + l 2 l F 3,n r = f n t 3 M 2 + l 2 M 2 f n 1 t 3 and t = n 3 /d 3 where n 3 = l 1 2 M l2 lm 8 + l 2 + 4l + 1M 6 + ll 2 + 4l + 1M 4 + 2l2l 1M 2 + ll 1 2 and d 3 = M 2 +l 3 M 2. The A-polynomial is given by the numerator of F k,n. Using Lemma 5.4 we see that the numerators satisfy the recursion given by Hoste and Shanahan [10]. Recall that since k = 3 we have l = LM 4n. The results that helped us determine the recursion for the resultant rely on the recursive definitions of F k,n r and G k,n r as polynomials in l, M ±2 and r. Therefore, to write A3, 2n in terms of the variables L and M, one uses the recursive definition below to determine the polynomial in l and M and then substitutes l = LM 4n. Theorem 7.3. Let n 3 and d 3 be defined as above. For n positive with initial conditions A3, 2n = n 3 A3, 2n 2 d 2 3A3, 2n 4 A3, 2 = 1 lm 8 + lm 6 + 2M 4 l + M 2 l + l 2 l A3, 4 = 1 3l + 3l 2 l 3 M l 2 + 3l 3 + 5lM 16 For n negative with initial conditions A3, 0 = 1 + 3l 2 l 3 + 5lM l 3 2l + 13l 2 l 4 M 12 + l + 2l l 2 3l 3 M l 3 3l 2 + 2l l 4 M l 3 l 5l 2 2l 4 M 6 + 3l 3 l 2 + 5l 4 M 4 + 8l 3 + 5l 4 + 3l 2 M 2 3l 4 + l 5 + 3l 3 l 2. A3, 2n = n 3 A3, 2n + 2 d 2 3A3, 2n + 4 A3, 2 = l 2 lm 10 + l 2 + 2lM lM 6 + 2l 2 + l 3 M 4 + l + 2l 2 M 2 + l l 2.
23 A-POLYNOMIALS OF A FAMILY OF TWO-BRIDGE KNOTS J4, 2n. We will show that the resultant defining A4, 2n is of the form considered in Section 5.1. Since k = 4 = 2m we have l = L for all of these knots. By Theorem 1.1 we can compute the A-polynomial as where ResF 4,n r, G 4,n r F 4,n r = f n t 4 rf 4,1 r f n 1 t 4 r F 4,1 r = rr 1M 2 + M 2 r + 1 t 4 r = rr 2 2rM 2 + M 2 r + 2 G 4,n r = M 2 + Lr 2 L + 1M 2 + 1r L 1M 2 1. Moreover, for this section, let a = β 4 M 2 LL 12L 2 L L1 4L + 5L 2 M 2 + L2L 3 + 5L L 1M 4 + 4L1 + 4L + L 2 M L + 10L 2 L 3 M 8 + 2L5 4L + L 2 M L2 L + L 2 M 12 b = β 4 M 4 LL LL 13L 1M 2 + 2LL 3 + L 2 + L 1M 4 + 2LL + 13L + 1M L + 14L 2 + 4L 3 + L 4 M 8 + 2LL + 1L + 3M L + L 2 L 3 M LL 1L 3M L3M 16 c = M 4 β 7 L 2 L 1 2 M M A = α/β C = β/γ B = 1/C. First we show that ResF 4,n r, G 4,n r is of the form considered in Proposition 5.9. Let R n = Res f n xx + A + f n 1 xb, x 2 ax + b and let A 1 = ResF 4,n r, G 4,n r. Lemma 7.4. Let ɛ = 1 if n > 0 and ɛ = 0 if n < 0. We have Proof. First, we define the following P 1 = M 6 + L rm 2 β/β 2 M 2 A 1 L 1 2 M = β 4 n +2 ɛ R n P 2 = M 2 r 2 β 2 M 2 + 1M 4 + Lβr L 1M 2 1M 6 + L/β 3 M 2 t = 2 + L 1 2 M M 6 + L L 1M M Lr /M 2 β 3 F 4,1 = L 1L M 8 + LM 2 M LM r /M 2 β 2.
24 24 K. L. PETERSEN With this, F 4,1 = F 4,1 + G 4,n P 1, and t = t + G 4,n P 2. Moreover, in terms of t we have F 4,1 = Ct +A, and G 4,n = ct 2 at +b. Additionally, let F 4,nr = f n t 4 F 4,1 f n 1 t 4, and F 4,nr = f n t F 4,1 f n 1 t. Let A 2 = ResF 4,n r, G 4,n. By the above, we have that and we conclude that F 4,n = F 4,nr + f n t 4 G 4,n P 1 A 1 g max{4 n 3,4 n 1 4} 0 = A 2 g max{4 n 1 4,4 n 1} 0. Therefore, when n > 0, A 1 = A 2 β 2 and when n < 0, A 1 = A 2. We also have F 4,nr = f n t + G 4,n P 2 F 4,1 f n 1 t + G 4,n P 2 = F 4,nr + G 4,n P 3. Let A 3 = ResF 4,n r, G k,nr as a function of r. The degree of F 4,n r is max{4 n 3, 4 n 1 4} and the degree of F 4,n r is n so we conclude that when n > 0 we have A 2 = β 3n 3 A 3 and when n < 0, A 2 = β 3 n A 3. By definition of A, B, C, a, b, and c, F 4,nr = C[f n t t + A + Bf n 1 t ] and G 4,n r = ct 2 at + b. Therefore, A 3 = A 4 where A 4 = ResC[f n t t + A + Bf n 1 t ], ct 2 at + b, and the resultant is taken with respect to the variable r. Let A 5 = ResC[f n xx + A + Bf n 1 x], cx 2 ax + b with respect to the variable x. The leading coefficient of t is t 0 = L1 LM M /M 2 β 3 and we conclude that these two resultants differ by this leading coefficient to the product of the powers of the two polynomials, A 4 = A 5 t 0 2 n. Explicitly, this is A 4 M 4 n β 6 n = A 5 L 2 n 1 L 2 n M n M n. Finally, since R n = Res f n xx+a+f n 1 xb, x 2 ax+b we conclude that R n = c degfnxx+a+f n 1xB C degx2 ax+b A 5, which reduces to the stated formulas. The M 2 factor in t 4 r introduces a factor of M 4 n into A 1. normalization, A4, 2n = M 4 n A 1 so that by Lemma 7.4 After A4, 2nL 1 2 M = M 4 n β 4 n +2 ɛ R n.
25 A-POLYNOMIALS OF A FAMILY OF TWO-BRIDGE KNOTS 25 We obtain a recursive formula for A4, 2n using Proposition 5.9. Let c 1 = b 1, and c 2 = 2 a 2 + 3b. Specifically, for n > 5, A4, 2n = c 1 M 4 β 4 A4, 2n 1 + c 2 M 4 β 4 2 A4, 2n 2 + c 2 M 4 β 4 3 A4, 2n 3 + c 1 M 4 β 4 4 A4, 2n 4 M 4 β 4 5 A4, 2n 5. where the initial conditions are A4, 2n = M 4n ResF 4,n r, G 4,n r for 1 n 5. in fact, setting A4, 0 = β 1 we can begin the recursion one step earlier. When n 5, using A4, 0 = 1 the recursion is A4, 2n = c 1 M 4 β 4 A4, 2n c 2 M 4 β 4 2 A4, 2n c 2 M 4 β 4 3 A4, 2n c 1 M 4 β 4 4 A4, 2n + 4 M 4 β 4 5 A4, 2n + 5. where initial terms A4, 2n for 4 n 0 are A4, 2n = M 4 n ResF 4,n r, G 4,n r. Finally, we write this as a self contained theorem, computing these coefficients explicitly. Theorem 7.5. With d 1, d 2, d 3, d 4, and d 5 as in the appendix, we have the following. For n positive A4, 2n = d 1 A4, 2n 1 + d 2 A4, 2n 2 + d 3 A4, 2n 3 + d 4 A4, 2n 4 + d 5 A4, 2n 5. The initial conditions are A4, 2n = ResM 2n F 4,n r, G 4,n r for 0 < n 5. For n negative A4, 2n = d 1 A4, 2n d 2 A4, 2n d 3 A4, 2n d 4 A4, 2n d 5 A4, 2n + 5. The initial conditions are A4, 2n = ResM 2 n F 4,n r, G 4,n r for 4 n J5, 2n. By Theorem 1.1 we can compute the A-polynomial of J5, 2n as ResF 5,n r, G 5,n r where F 5,n r = f n tf 5,1 r f n 1 t F 5,1 r = rr 2 r 1M 2 + M 2 r + 1 t 5 r = r 2 r 1 2 M 2 + M 2 r + 2 G 5,n r = M 2 + lr 2 M 2 l + 1r M 2 l.
26 26 K. L. PETERSEN We proceed in the same fashion as the A4, 2n case. For this section, we define the following a = l 4 2l 3 + 3l 2 4l + 2M l l 16l 2 2l 4 M 12 + l 4 12l l 2 + 6l + 2M l 3 + 5l + 30l 2 M l 3 + 5l 2 + 5l 4 M 6 + 6l l 3 12l 2 + l + 2l 5 M l 3 2l + 9l l 4 M 2 + 3l 3 2l 2 + 2l 5 + l 4l 4 M 2 β 5 b = 6l 2 + l 4 4l lM l 4 18l 2 + 8l + 12l 3 M l + 2l 4 6l 3 + 4l 2 M l 2l 4 8l l 2 M l l l 2 + 6lM 10 + l + l l 3 + 6l 4 + 6l 2 M 8 + 8l 2 2l + 8l l 3 M 6 + 2l 5 + 4l 3 6l 2 + 2l 4 + 2lM l 2 2l 18l 3 + 8l 4 M 2 + 6l 3 + l 4l 4 + l 5 4l 2 M 4 β 5 c = β 9 M 4 l 1 4 M M l 2 A = α/β B = γ/β C = β/γ. In addition, let and R n = Resf n xx + A + f m 1 xb, x 2 ax + b A 1 = ResF 5,n r, G 5,n r. Lemma 7.6. Let ɛ equal 1 when n > 0 and 2 when n < 0. Then A 1 γ 2 = β 5 n +ɛ R n. Proof. Let P 1 = r 2 M 2 M 2 + l 2 r1 + M 2 M 4 + lm 2 + l l 1M 2 1M 6 + l /β 3 M 2 P 2 = r 3 M 2 M 2 + l 3 + M 2 + l 2 l + 2M 2 l + 2M 4 + M 6 r 2 + M 2 + lm 6 + lm 2 l 2l 2M 2 + 1r + M 2 l + 1 2M 8 + M 8 l 2lM 6 2M 4 l 2M 2 l 2l 2 + l /M 2 β 4 F 5,1 = l1 + M 2 2 M l 1r M 2 + lm 8 l M 8 lm 6 2M 4 l M 2 l + l l 2 /β 3 M 2 t = ll M 2 2 M r
27 Moreover, let A-POLYNOMIALS OF A FAMILY OF TWO-BRIDGE KNOTS 27 + M 2 + lm 10 2M 10 l + M 10 l 2 2M 8 l 2 + 4M 8 l + 4lM 6 + M 6 + l 2 M 6 + M 4 l 3 + M 4 l + 4M 4 l 2 2M 2 l + 4M 2 l 2 + l 2l 2 + l 3 /M 2 β 4. F 5,nr = f n t 5 F 5,1 f n 1 t 5 and F 5,nr = f n t F 5,1 f n 1 t. A direct calculation shows that F 5,1 = F 5,1 + G 5,n P 1, and t = t + G 5,n P 2. Let A 2 = ResF 5,n r, G 5,n. We conclude that A 1 g max{5 n 4,5 n 1 5} 0 = A 2 g max{5 n 1,5 n 1 5} 0. Therefore when n > 0 we have A 1 = β 3 A 2 and when n 0, A 1 = A 2. Next, we see that F 5,nr = f n t + G 5,n P 2 F 5,1 f n 1 t + G 5,n P 2 = F 5,nr + G 5,n P 3. The degree of F 5,n r is max{5 n 4, 5 n 1 5} and the degree of F 5,n r is n. Let A 3 = ResF 5,n r, G 5,nr in terms of the variable r. Then A 2 = A 3 β 4n 1 when n > 0 and A 2 = A 3 β 4 n when n 0. With the terms as defined in the statement of the lemma, and F G 5,n = c t 2 at + b, 5,nr = C f n t t + A + Bf n 1 t. Let A 4 = Res Cf n t t + A + Bf n 1 t, ct 2 at + b, where the resultant is taken with respect to the variable r. Therefore, A 3 = A 4. Let A 5 = Res Cf n xx + A + Bf n 1 x, cx 2 ax + b. The leading coefficient of t is ll 1 2 M M M 2 β 4. Since the degree of Cf n xx + A + Bf n 1 x is n we conclude that A 4 M 2 β 4 2 n = ll 1 2 M M n A5. With A 6 = Resf n xx + A + Bf n 1 x, x 2 ax + b we see that A 5 = A 6 C 2 c n which is A 5 γ 2 l 1 4 n M n M n l 2 n = A 6 β 9 n +2 M 4 n. The lemma follows. Because of the M 2 in the t 5 r equation, A 1 is a polynomial divided by M 4 n. Therefore, we normalize such that the A-polynomial is A5, 2n = M 4 n A 1. By Lemma 7.6, A5, 2nγ 2 = M 4 n β 5 n +ɛ R n.
28 28 K. L. PETERSEN It now suffices to modify the recursion using Proposition 5.9 to remove the factors of γ 2 and β ɛ β 5 n. Let c 1 = b 1 and c 2 = 2 a 2 + 3b. As a result, for n > 5 A5, 2n = β 5 M 4 c 1 A5, 2n 1 + β 5 M 4 2 c 2 A5, 2n 2 + β 5 M 4 3 c 2 A5, 2n 3 + β 5 M 4 4 c 1 A5, 2n 4 β 5 M 4 5 A5, 2n 5. In fact, setting A5, 0 = β 1 we can begin the recursion one term earlier. For negative n, we have and A5, 2nγ 2 = M 4 n β 5 n +2 R n A5, 2n = β 5 M 4 c 1 A5, 2n β 5 M 4 2 c 2 A5, 2n β 5 M 4 3 c 2 A5, 2n β 5 M 4 4 c 1 A5, 2n + 4 β 5 M 4 5 A5, 2n + 5. As for the positives, setting A5, 0 = β 1 we can begin the recursion one term earlier. Finally, we write this as a self contained theorem. Recall that since k = 5 we have l = LM 4n. Similar to the case when k = 3, the results that helped us determine the recursion for the resultant rely on the recursive definitions of F 5,n r and G 5,n r as polynomials in l, M ±2 and r. Therefore, to write A5, 2n in terms of the variables L and M, one uses the recursive definition below to determine the polynomial in l and M and then substitutes l = LM 4n. Theorem 7.7. With d 1, d 2, d 3, d 4, and d 5 as in the appendix, we have the following. For n positive A5, 2n = d 1 A5, 2n 1 + d 2 A5, 2n 2 + d 3 A5, 2n 3 + d 4 A5, 2n 4 + d 5 A5, 2n 5. The initial conditions are A5, 2n = ResM 2n F 5,n r, G 5,n r for 0 < n 5. For n negative A5, 2n = d 1 A5, 2n d 2 A5, 2n d 3 A5, 2n d 4 A5, 2n d 5 A5, 2n + 5. The initial conditions are A5, 2n = ResM 2 n F 5,n r, G 5,n r for 5 n 0.
29 A-POLYNOMIALS OF A FAMILY OF TWO-BRIDGE KNOTS J2m, 2m. The knots J2m, 2m exhibit an additional symmetry, seen by turning the 4-plat diagram for these two-bridge knots upside down. This effectively factors the character variety, and the canonical component is birational to C see [11]. Moreover, the canonical component of the A- polynomial is determined by the resultant of t m r r and G 2m,m. In this case, l = L. The equations are, up to sign t m r = f m rg m+1 r g m rm 2 + M 2 r + 2 G 2m,m r = f m rα βr γf m 1 r. The polynomial t m r r is reducible. Since t m r r is given by f m rg m+1 r g m rm 2 + M 2 r + 2 r it suffices to see that 2 r is a factor of g m+1 r g m r. Since f j 2 = j for all j, it follows that g j 2 = f j 2 f j 1 2 = j j 1 = 1 and the fact that for all j, g j+1 2 g j 2 = 0 follows. Since r = 2 corresponds to the reducible representations, we do not want to include the contribution of these to the A-polynomial. However, the format of tr r as above is easy to use, so we will compute the resultant of G 2m,m r and tr r and then divide by the extra factor which corresponds to this extra term. The contribution of this extra factor is Resr 2, G 2m,m r = G 2m,m 2 = γ. For small values of m, the resultant can be computed directly using a computer algebra program. We show that this resultant can be computed recursively using Proposition 5.9. Let a = 2σ βδ, b = τ βδ, A = α β, and B = γ β. Let R m = Resr 2 ar+b, f m rr+a+bf m 1 r and let A 1 = Rest m r r, G 2m,m r. Lemma 7.8. For m 0 we have γg 0 Rest m r r, G 2m,m r = β 2 βδ m R m where g 0 is the leading coefficient of G 2m,m r. Proof. Let A 2 = Resδβr σt m r r, G 2m,m. First, notice that A 2 = A 1 Resδβr σ, G 2m,m and since degg 2m,m = m using Lemma 6.2 we have Resδβr σ, G 2m,m = γg 2 m 0. Therefore, A 2 = γg 2 m 0 A 1. By Lemma 6.5 there is a polynomial P 3 such that It follows that t m rδβr σ + τ σr + G 2m,m rp 3 r = 0. δβr σt m r r = βδr 2 + 2σr τ G 2m,m rp 3 r. Let A 3 = Resβδr 2 2σr + τ, G 2m,m r.
The Geometry of Character Varieties
 The Geometry of Character Varieties Kate Petersen Florida State December 10, 2011 Kate Petersen ( Florida State) Character Varieties December 10, 2011 1 / 22 The character variety, X (M), of a finite volume
The Geometry of Character Varieties Kate Petersen Florida State December 10, 2011 Kate Petersen ( Florida State) Character Varieties December 10, 2011 1 / 22 The character variety, X (M), of a finite volume
arxiv:math/ v2 [math.gt] 27 Feb 2004
![arxiv:math/ v2 [math.gt] 27 Feb 2004 arxiv:math/ v2 [math.gt] 27 Feb 2004](/thumbs/91/106823354.jpg) COMMENSURABILITY CLASSES OF TWIST KNOTS arxiv:math/0311051v2 [math.gt] 27 Feb 2004 JIM HOSTE Department of Mathematics Pitzer College Claremont, CA 91711, USA jhoste@pitzer.edu PATRICK D. SHANAHAN Department
COMMENSURABILITY CLASSES OF TWIST KNOTS arxiv:math/0311051v2 [math.gt] 27 Feb 2004 JIM HOSTE Department of Mathematics Pitzer College Claremont, CA 91711, USA jhoste@pitzer.edu PATRICK D. SHANAHAN Department
STAVROS GAROUFALIDIS AND THOMAS W. MATTMAN
 THE A-POLYNOMIAL OF THE ( 2, 3, 3 + 2n) PRETZEL KNOTS STAVROS GAROUFALIDIS AND THOMAS W. MATTMAN Abstract. We show that the A-polynomial A n of the 1-parameter family of pretzel knots K n = ( 2, 3,3+ 2n)
THE A-POLYNOMIAL OF THE ( 2, 3, 3 + 2n) PRETZEL KNOTS STAVROS GAROUFALIDIS AND THOMAS W. MATTMAN Abstract. We show that the A-polynomial A n of the 1-parameter family of pretzel knots K n = ( 2, 3,3+ 2n)
arxiv: v2 [math.gt] 2 Mar 2015
![arxiv: v2 [math.gt] 2 Mar 2015 arxiv: v2 [math.gt] 2 Mar 2015](/thumbs/71/65857478.jpg) THE AJ CONJECTURE FOR CABLES OF TWO-BRIDGE KNOTS NATHAN DRUIVENGA arxiv:14121053v2 [mathgt] 2 Mar 2015 Abstract The AJ-conjecture for a knot K S 3 relates the A-polynomial and the colored Jones polynomial
THE AJ CONJECTURE FOR CABLES OF TWO-BRIDGE KNOTS NATHAN DRUIVENGA arxiv:14121053v2 [mathgt] 2 Mar 2015 Abstract The AJ-conjecture for a knot K S 3 relates the A-polynomial and the colored Jones polynomial
HANS U. BODEN AND CYNTHIA L. CURTIS
 THE SL(2, C) CASSON INVARIANT FOR KNOTS AND THE Â-POLYNOMIAL HANS U. BODEN AND CYNTHIA L. CURTIS Abstract. In this paper, we extend the definition of the SL(2, C) Casson invariant to arbitrary knots K
THE SL(2, C) CASSON INVARIANT FOR KNOTS AND THE Â-POLYNOMIAL HANS U. BODEN AND CYNTHIA L. CURTIS Abstract. In this paper, we extend the definition of the SL(2, C) Casson invariant to arbitrary knots K
Detection of knots and a cabling formula for A-polynomials
 Detection of knots and a cabling formula for A-polynomials Yi Ni Department of Mathematics, Caltech 100 E California Blvd, Pasadena, CA 9115 Email: yini@caltech.edu Xingru Zhang Department of Mathematics,
Detection of knots and a cabling formula for A-polynomials Yi Ni Department of Mathematics, Caltech 100 E California Blvd, Pasadena, CA 9115 Email: yini@caltech.edu Xingru Zhang Department of Mathematics,
All roots of unity are detected by the A polynomial
 ISSN 1472-2739 (on-line) 1472-2747 (printed) 207 Algebraic & Geometric Topology Volume 5 (2005) 207 217 Published: 28 March 2005 ATG All roots of unity are detected by the A polynomial Eric Chesebro Abstract
ISSN 1472-2739 (on-line) 1472-2747 (printed) 207 Algebraic & Geometric Topology Volume 5 (2005) 207 217 Published: 28 March 2005 ATG All roots of unity are detected by the A polynomial Eric Chesebro Abstract
Course 311: Michaelmas Term 2005 Part III: Topics in Commutative Algebra
 Course 311: Michaelmas Term 2005 Part III: Topics in Commutative Algebra D. R. Wilkins Contents 3 Topics in Commutative Algebra 2 3.1 Rings and Fields......................... 2 3.2 Ideals...............................
Course 311: Michaelmas Term 2005 Part III: Topics in Commutative Algebra D. R. Wilkins Contents 3 Topics in Commutative Algebra 2 3.1 Rings and Fields......................... 2 3.2 Ideals...............................
SQUARE ROOTS OF 2x2 MATRICES 1. Sam Northshield SUNY-Plattsburgh
 SQUARE ROOTS OF x MATRICES Sam Northshield SUNY-Plattsburgh INTRODUCTION A B What is the square root of a matrix such as? It is not, in general, A B C D C D This is easy to see since the upper left entry
SQUARE ROOTS OF x MATRICES Sam Northshield SUNY-Plattsburgh INTRODUCTION A B What is the square root of a matrix such as? It is not, in general, A B C D C D This is easy to see since the upper left entry
Rings and groups. Ya. Sysak
 Rings and groups. Ya. Sysak 1 Noetherian rings Let R be a ring. A (right) R -module M is called noetherian if it satisfies the maximum condition for its submodules. In other words, if M 1... M i M i+1...
Rings and groups. Ya. Sysak 1 Noetherian rings Let R be a ring. A (right) R -module M is called noetherian if it satisfies the maximum condition for its submodules. In other words, if M 1... M i M i+1...
Theorem 5.3. Let E/F, E = F (u), be a simple field extension. Then u is algebraic if and only if E/F is finite. In this case, [E : F ] = deg f u.
![Theorem 5.3. Let E/F, E = F (u), be a simple field extension. Then u is algebraic if and only if E/F is finite. In this case, [E : F ] = deg f u. Theorem 5.3. Let E/F, E = F (u), be a simple field extension. Then u is algebraic if and only if E/F is finite. In this case, [E : F ] = deg f u.](/thumbs/81/83685479.jpg) 5. Fields 5.1. Field extensions. Let F E be a subfield of the field E. We also describe this situation by saying that E is an extension field of F, and we write E/F to express this fact. If E/F is a field
5. Fields 5.1. Field extensions. Let F E be a subfield of the field E. We also describe this situation by saying that E is an extension field of F, and we write E/F to express this fact. If E/F is a field
arxiv: v1 [math.gt] 8 Dec 2016
![arxiv: v1 [math.gt] 8 Dec 2016 arxiv: v1 [math.gt] 8 Dec 2016](/thumbs/96/128467353.jpg) ON THE VOLUME OF DOUBLE TWIST LINK CONE-MANIFOLDS ANH T. TRAN arxiv:62.02799v [math.gt] 8 Dec 206 Abstract. We consider the double twist link J2m +,2n + ) which is the twobridge link corresponding to the
ON THE VOLUME OF DOUBLE TWIST LINK CONE-MANIFOLDS ANH T. TRAN arxiv:62.02799v [math.gt] 8 Dec 206 Abstract. We consider the double twist link J2m +,2n + ) which is the twobridge link corresponding to the
Definitions, Theorems and Exercises. Abstract Algebra Math 332. Ethan D. Bloch
 Definitions, Theorems and Exercises Abstract Algebra Math 332 Ethan D. Bloch December 26, 2013 ii Contents 1 Binary Operations 3 1.1 Binary Operations............................... 4 1.2 Isomorphic Binary
Definitions, Theorems and Exercises Abstract Algebra Math 332 Ethan D. Bloch December 26, 2013 ii Contents 1 Binary Operations 3 1.1 Binary Operations............................... 4 1.2 Isomorphic Binary
Chapter 3. Rings. The basic commutative rings in mathematics are the integers Z, the. Examples
 Chapter 3 Rings Rings are additive abelian groups with a second operation called multiplication. The connection between the two operations is provided by the distributive law. Assuming the results of Chapter
Chapter 3 Rings Rings are additive abelian groups with a second operation called multiplication. The connection between the two operations is provided by the distributive law. Assuming the results of Chapter
Problems in Linear Algebra and Representation Theory
 Problems in Linear Algebra and Representation Theory (Most of these were provided by Victor Ginzburg) The problems appearing below have varying level of difficulty. They are not listed in any specific
Problems in Linear Algebra and Representation Theory (Most of these were provided by Victor Ginzburg) The problems appearing below have varying level of difficulty. They are not listed in any specific
Knot Groups with Many Killers
 Knot Groups with Many Killers Daniel S. Silver Wilbur Whitten Susan G. Williams September 12, 2009 Abstract The group of any nontrivial torus knot, hyperbolic 2-bridge knot, or hyperbolic knot with unknotting
Knot Groups with Many Killers Daniel S. Silver Wilbur Whitten Susan G. Williams September 12, 2009 Abstract The group of any nontrivial torus knot, hyperbolic 2-bridge knot, or hyperbolic knot with unknotting
On the positivity of linear weights in WENO approximations. Abstract
 On the positivity of linear weights in WENO approximations Yuanyuan Liu, Chi-Wang Shu and Mengping Zhang 3 Abstract High order accurate weighted essentially non-oscillatory (WENO) schemes have been used
On the positivity of linear weights in WENO approximations Yuanyuan Liu, Chi-Wang Shu and Mengping Zhang 3 Abstract High order accurate weighted essentially non-oscillatory (WENO) schemes have been used
Exercise Sheet 3 - Solutions
 Algebraic Geometry D-MATH, FS 2016 Prof. Pandharipande Exercise Sheet 3 - Solutions 1. Prove the following basic facts about algebraic maps. a) For f : X Y and g : Y Z algebraic morphisms of quasi-projective
Algebraic Geometry D-MATH, FS 2016 Prof. Pandharipande Exercise Sheet 3 - Solutions 1. Prove the following basic facts about algebraic maps. a) For f : X Y and g : Y Z algebraic morphisms of quasi-projective
disc f R 3 (X) in K[X] G f in K irreducible S 4 = in K irreducible A 4 in K reducible D 4 or Z/4Z = in K reducible V Table 1
![disc f R 3 (X) in K[X] G f in K irreducible S 4 = in K irreducible A 4 in K reducible D 4 or Z/4Z = in K reducible V Table 1 disc f R 3 (X) in K[X] G f in K irreducible S 4 = in K irreducible A 4 in K reducible D 4 or Z/4Z = in K reducible V Table 1](/thumbs/78/77977143.jpg) GALOIS GROUPS OF CUBICS AND QUARTICS IN ALL CHARACTERISTICS KEITH CONRAD 1. Introduction Treatments of Galois groups of cubic and quartic polynomials usually avoid fields of characteristic 2. Here we will
GALOIS GROUPS OF CUBICS AND QUARTICS IN ALL CHARACTERISTICS KEITH CONRAD 1. Introduction Treatments of Galois groups of cubic and quartic polynomials usually avoid fields of characteristic 2. Here we will
AZUMAYA ALGEBRAS AND CANONICAL COMPONENTS
 AZUMAYA ALGEBRAS AND CANONICAL COMPONENTS TED CHINBURG, ALAN W. REID, AND MATTHEW STOVER Abstract. Let M be a compact 3-manifold and Γ = π 1 (M). The work of Thurston and Culler Shalen established the
AZUMAYA ALGEBRAS AND CANONICAL COMPONENTS TED CHINBURG, ALAN W. REID, AND MATTHEW STOVER Abstract. Let M be a compact 3-manifold and Γ = π 1 (M). The work of Thurston and Culler Shalen established the
A connection between number theory and linear algebra
 A connection between number theory and linear algebra Mark Steinberger Contents 1. Some basics 1 2. Rational canonical form 2 3. Prime factorization in F[x] 4 4. Units and order 5 5. Finite fields 7 6.
A connection between number theory and linear algebra Mark Steinberger Contents 1. Some basics 1 2. Rational canonical form 2 3. Prime factorization in F[x] 4 4. Units and order 5 5. Finite fields 7 6.
(1) A frac = b : a, b A, b 0. We can define addition and multiplication of fractions as we normally would. a b + c d
 The Algebraic Method 0.1. Integral Domains. Emmy Noether and others quickly realized that the classical algebraic number theory of Dedekind could be abstracted completely. In particular, rings of integers
The Algebraic Method 0.1. Integral Domains. Emmy Noether and others quickly realized that the classical algebraic number theory of Dedekind could be abstracted completely. In particular, rings of integers
Varieties of characters and knot symmetries (I)
 Varieties of characters and knot symmetries (I) Joan Porti Universitat Autònoma de Barcelona June 2017 INdAM Meeting Geometric Topology in Cortona Organization Day 1 Character Varieties. Definition and
Varieties of characters and knot symmetries (I) Joan Porti Universitat Autònoma de Barcelona June 2017 INdAM Meeting Geometric Topology in Cortona Organization Day 1 Character Varieties. Definition and
Math 489AB Exercises for Chapter 2 Fall Section 2.3
 Math 489AB Exercises for Chapter 2 Fall 2008 Section 2.3 2.3.3. Let A M n (R). Then the eigenvalues of A are the roots of the characteristic polynomial p A (t). Since A is real, p A (t) is a polynomial
Math 489AB Exercises for Chapter 2 Fall 2008 Section 2.3 2.3.3. Let A M n (R). Then the eigenvalues of A are the roots of the characteristic polynomial p A (t). Since A is real, p A (t) is a polynomial
Basic Algebra. Final Version, August, 2006 For Publication by Birkhäuser Boston Along with a Companion Volume Advanced Algebra In the Series
 Basic Algebra Final Version, August, 2006 For Publication by Birkhäuser Boston Along with a Companion Volume Advanced Algebra In the Series Cornerstones Selected Pages from Chapter I: pp. 1 15 Anthony
Basic Algebra Final Version, August, 2006 For Publication by Birkhäuser Boston Along with a Companion Volume Advanced Algebra In the Series Cornerstones Selected Pages from Chapter I: pp. 1 15 Anthony
ADVANCED TOPICS IN ALGEBRAIC GEOMETRY
 ADVANCED TOPICS IN ALGEBRAIC GEOMETRY DAVID WHITE Outline of talk: My goal is to introduce a few more advanced topics in algebraic geometry but not to go into too much detail. This will be a survey of
ADVANCED TOPICS IN ALGEBRAIC GEOMETRY DAVID WHITE Outline of talk: My goal is to introduce a few more advanced topics in algebraic geometry but not to go into too much detail. This will be a survey of
Linear Algebra. Workbook
 Linear Algebra Workbook Paul Yiu Department of Mathematics Florida Atlantic University Last Update: November 21 Student: Fall 2011 Checklist Name: A B C D E F F G H I J 1 2 3 4 5 6 7 8 9 10 xxx xxx xxx
Linear Algebra Workbook Paul Yiu Department of Mathematics Florida Atlantic University Last Update: November 21 Student: Fall 2011 Checklist Name: A B C D E F F G H I J 1 2 3 4 5 6 7 8 9 10 xxx xxx xxx
Finite Fields. Sophie Huczynska. Semester 2, Academic Year
 Finite Fields Sophie Huczynska Semester 2, Academic Year 2005-06 2 Chapter 1. Introduction Finite fields is a branch of mathematics which has come to the fore in the last 50 years due to its numerous applications,
Finite Fields Sophie Huczynska Semester 2, Academic Year 2005-06 2 Chapter 1. Introduction Finite fields is a branch of mathematics which has come to the fore in the last 50 years due to its numerous applications,
SOLVING SOLVABLE QUINTICS. D. S. Dummit
 D. S. Dummit Abstract. Let f(x) = x 5 + px 3 + qx + rx + s be an irreducible polynomial of degree 5 with rational coefficients. An explicit resolvent sextic is constructed which has a rational root if
D. S. Dummit Abstract. Let f(x) = x 5 + px 3 + qx + rx + s be an irreducible polynomial of degree 5 with rational coefficients. An explicit resolvent sextic is constructed which has a rational root if
Fast Polynomial Multiplication
 Fast Polynomial Multiplication Marc Moreno Maza CS 9652, October 4, 2017 Plan Primitive roots of unity The discrete Fourier transform Convolution of polynomials The fast Fourier transform Fast convolution
Fast Polynomial Multiplication Marc Moreno Maza CS 9652, October 4, 2017 Plan Primitive roots of unity The discrete Fourier transform Convolution of polynomials The fast Fourier transform Fast convolution
Algebra Review. Instructor: Laszlo Babai Notes by Vincent Lucarelli and the instructor. June 15, 2001
 Algebra Review Instructor: Laszlo Babai Notes by Vincent Lucarelli and the instructor June 15, 2001 1 Groups Definition 1.1 A semigroup (G, ) is a set G with a binary operation such that: Axiom 1 ( a,
Algebra Review Instructor: Laszlo Babai Notes by Vincent Lucarelli and the instructor June 15, 2001 1 Groups Definition 1.1 A semigroup (G, ) is a set G with a binary operation such that: Axiom 1 ( a,
Putzer s Algorithm. Norman Lebovitz. September 8, 2016
 Putzer s Algorithm Norman Lebovitz September 8, 2016 1 Putzer s algorithm The differential equation dx = Ax, (1) dt where A is an n n matrix of constants, possesses the fundamental matrix solution exp(at),
Putzer s Algorithm Norman Lebovitz September 8, 2016 1 Putzer s algorithm The differential equation dx = Ax, (1) dt where A is an n n matrix of constants, possesses the fundamental matrix solution exp(at),
August 2015 Qualifying Examination Solutions
 August 2015 Qualifying Examination Solutions If you have any difficulty with the wording of the following problems please contact the supervisor immediately. All persons responsible for these problems,
August 2015 Qualifying Examination Solutions If you have any difficulty with the wording of the following problems please contact the supervisor immediately. All persons responsible for these problems,
NOTES ON FINITE FIELDS
 NOTES ON FINITE FIELDS AARON LANDESMAN CONTENTS 1. Introduction to finite fields 2 2. Definition and constructions of fields 3 2.1. The definition of a field 3 2.2. Constructing field extensions by adjoining
NOTES ON FINITE FIELDS AARON LANDESMAN CONTENTS 1. Introduction to finite fields 2 2. Definition and constructions of fields 3 2.1. The definition of a field 3 2.2. Constructing field extensions by adjoining
over a field F with char F 2: we define
 Chapter 3 Involutions In this chapter, we define the standard involution (also called conjugation) on a quaternion algebra. In this way, we characterize division quaternion algebras as noncommutative division
Chapter 3 Involutions In this chapter, we define the standard involution (also called conjugation) on a quaternion algebra. In this way, we characterize division quaternion algebras as noncommutative division
The Classification of Nonsimple Algebraic Tangles
 The Classification of Nonsimple Algebraic Tangles Ying-Qing Wu 1 A tangle is a pair (B, T ), where B is a 3-ball, T is a pair of properly embedded arcs. When there is no ambiguity we will simply say that
The Classification of Nonsimple Algebraic Tangles Ying-Qing Wu 1 A tangle is a pair (B, T ), where B is a 3-ball, T is a pair of properly embedded arcs. When there is no ambiguity we will simply say that
Rings. Chapter 1. Definition 1.2. A commutative ring R is a ring in which multiplication is commutative. That is, ab = ba for all a, b R.
 Chapter 1 Rings We have spent the term studying groups. A group is a set with a binary operation that satisfies certain properties. But many algebraic structures such as R, Z, and Z n come with two binary
Chapter 1 Rings We have spent the term studying groups. A group is a set with a binary operation that satisfies certain properties. But many algebraic structures such as R, Z, and Z n come with two binary
PRACTICE FINAL MATH , MIT, SPRING 13. You have three hours. This test is closed book, closed notes, no calculators.
 PRACTICE FINAL MATH 18.703, MIT, SPRING 13 You have three hours. This test is closed book, closed notes, no calculators. There are 11 problems, and the total number of points is 180. Show all your work.
PRACTICE FINAL MATH 18.703, MIT, SPRING 13 You have three hours. This test is closed book, closed notes, no calculators. There are 11 problems, and the total number of points is 180. Show all your work.
LINEAR ALGEBRA BOOT CAMP WEEK 1: THE BASICS
 LINEAR ALGEBRA BOOT CAMP WEEK 1: THE BASICS Unless otherwise stated, all vector spaces in this worksheet are finite dimensional and the scalar field F has characteristic zero. The following are facts (in
LINEAR ALGEBRA BOOT CAMP WEEK 1: THE BASICS Unless otherwise stated, all vector spaces in this worksheet are finite dimensional and the scalar field F has characteristic zero. The following are facts (in
THE GROUP OF UNITS OF SOME FINITE LOCAL RINGS I
 J Korean Math Soc 46 (009), No, pp 95 311 THE GROUP OF UNITS OF SOME FINITE LOCAL RINGS I Sung Sik Woo Abstract The purpose of this paper is to identify the group of units of finite local rings of the
J Korean Math Soc 46 (009), No, pp 95 311 THE GROUP OF UNITS OF SOME FINITE LOCAL RINGS I Sung Sik Woo Abstract The purpose of this paper is to identify the group of units of finite local rings of the
Algebra I. Book 2. Powered by...
 Algebra I Book 2 Powered by... ALGEBRA I Units 4-7 by The Algebra I Development Team ALGEBRA I UNIT 4 POWERS AND POLYNOMIALS......... 1 4.0 Review................ 2 4.1 Properties of Exponents..........
Algebra I Book 2 Powered by... ALGEBRA I Units 4-7 by The Algebra I Development Team ALGEBRA I UNIT 4 POWERS AND POLYNOMIALS......... 1 4.0 Review................ 2 4.1 Properties of Exponents..........
ELEMENTARY LINEAR ALGEBRA
 ELEMENTARY LINEAR ALGEBRA K R MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND First Printing, 99 Chapter LINEAR EQUATIONS Introduction to linear equations A linear equation in n unknowns x,
ELEMENTARY LINEAR ALGEBRA K R MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND First Printing, 99 Chapter LINEAR EQUATIONS Introduction to linear equations A linear equation in n unknowns x,
HASSE-MINKOWSKI THEOREM
 HASSE-MINKOWSKI THEOREM KIM, SUNGJIN 1. Introduction In rough terms, a local-global principle is a statement that asserts that a certain property is true globally if and only if it is true everywhere locally.
HASSE-MINKOWSKI THEOREM KIM, SUNGJIN 1. Introduction In rough terms, a local-global principle is a statement that asserts that a certain property is true globally if and only if it is true everywhere locally.
Matricial real algebraic geometry
 Magdeburg, February 23th, 2012 Notation R - a commutative ring M n (R) - the ring of all n n matrices with entries in R S n (R) - the set of all symmetric matrices in M n (R) Mn (R) 2 - the set of all
Magdeburg, February 23th, 2012 Notation R - a commutative ring M n (R) - the ring of all n n matrices with entries in R S n (R) - the set of all symmetric matrices in M n (R) Mn (R) 2 - the set of all
MATH 8253 ALGEBRAIC GEOMETRY WEEK 12
 MATH 8253 ALGEBRAIC GEOMETRY WEEK 2 CİHAN BAHRAN 3.2.. Let Y be a Noetherian scheme. Show that any Y -scheme X of finite type is Noetherian. Moreover, if Y is of finite dimension, then so is X. Write f
MATH 8253 ALGEBRAIC GEOMETRY WEEK 2 CİHAN BAHRAN 3.2.. Let Y be a Noetherian scheme. Show that any Y -scheme X of finite type is Noetherian. Moreover, if Y is of finite dimension, then so is X. Write f
Math 312/ AMS 351 (Fall 17) Sample Questions for Final
 Math 312/ AMS 351 (Fall 17) Sample Questions for Final 1. Solve the system of equations 2x 1 mod 3 x 2 mod 7 x 7 mod 8 First note that the inverse of 2 is 2 mod 3. Thus, the first equation becomes (multiply
Math 312/ AMS 351 (Fall 17) Sample Questions for Final 1. Solve the system of equations 2x 1 mod 3 x 2 mod 7 x 7 mod 8 First note that the inverse of 2 is 2 mod 3. Thus, the first equation becomes (multiply
GALOIS GROUPS OF CUBICS AND QUARTICS (NOT IN CHARACTERISTIC 2)
 GALOIS GROUPS OF CUBICS AND QUARTICS (NOT IN CHARACTERISTIC 2) KEITH CONRAD We will describe a procedure for figuring out the Galois groups of separable irreducible polynomials in degrees 3 and 4 over
GALOIS GROUPS OF CUBICS AND QUARTICS (NOT IN CHARACTERISTIC 2) KEITH CONRAD We will describe a procedure for figuring out the Galois groups of separable irreducible polynomials in degrees 3 and 4 over
a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2.
 Chapter 1 LINEAR EQUATIONS 11 Introduction to linear equations A linear equation in n unknowns x 1, x,, x n is an equation of the form a 1 x 1 + a x + + a n x n = b, where a 1, a,, a n, b are given real
Chapter 1 LINEAR EQUATIONS 11 Introduction to linear equations A linear equation in n unknowns x 1, x,, x n is an equation of the form a 1 x 1 + a x + + a n x n = b, where a 1, a,, a n, b are given real
CORRESPONDENCE BETWEEN ELLIPTIC CURVES IN EDWARDS-BERNSTEIN AND WEIERSTRASS FORMS
 CORRESPONDENCE BETWEEN ELLIPTIC CURVES IN EDWARDS-BERNSTEIN AND WEIERSTRASS FORMS DEPARTMENT OF MATHEMATICS AND STATISTICS UNIVERSITY OF OTTAWA SUPERVISOR: PROFESSOR MONICA NEVINS STUDENT: DANG NGUYEN
CORRESPONDENCE BETWEEN ELLIPTIC CURVES IN EDWARDS-BERNSTEIN AND WEIERSTRASS FORMS DEPARTMENT OF MATHEMATICS AND STATISTICS UNIVERSITY OF OTTAWA SUPERVISOR: PROFESSOR MONICA NEVINS STUDENT: DANG NGUYEN
ON THE MATRIX EQUATION XA AX = X P
 ON THE MATRIX EQUATION XA AX = X P DIETRICH BURDE Abstract We study the matrix equation XA AX = X p in M n (K) for 1 < p < n It is shown that every matrix solution X is nilpotent and that the generalized
ON THE MATRIX EQUATION XA AX = X P DIETRICH BURDE Abstract We study the matrix equation XA AX = X p in M n (K) for 1 < p < n It is shown that every matrix solution X is nilpotent and that the generalized
5 Quiver Representations
 5 Quiver Representations 5. Problems Problem 5.. Field embeddings. Recall that k(y,..., y m ) denotes the field of rational functions of y,..., y m over a field k. Let f : k[x,..., x n ] k(y,..., y m )
5 Quiver Representations 5. Problems Problem 5.. Field embeddings. Recall that k(y,..., y m ) denotes the field of rational functions of y,..., y m over a field k. Let f : k[x,..., x n ] k(y,..., y m )
Commensurability classes of 2-bridge knot complements
 Commensurability classes of 2-bridge knot complements A. W. Reid & G. S. Walsh Abstract We show that a hyperbolic 2-bridge knot complement is the unique knot complement in its commensurability class. We
Commensurability classes of 2-bridge knot complements A. W. Reid & G. S. Walsh Abstract We show that a hyperbolic 2-bridge knot complement is the unique knot complement in its commensurability class. We
Math 120 HW 9 Solutions
 Math 120 HW 9 Solutions June 8, 2018 Question 1 Write down a ring homomorphism (no proof required) f from R = Z[ 11] = {a + b 11 a, b Z} to S = Z/35Z. The main difficulty is to find an element x Z/35Z
Math 120 HW 9 Solutions June 8, 2018 Question 1 Write down a ring homomorphism (no proof required) f from R = Z[ 11] = {a + b 11 a, b Z} to S = Z/35Z. The main difficulty is to find an element x Z/35Z
1 Rings 1 RINGS 1. Theorem 1.1 (Substitution Principle). Let ϕ : R R be a ring homomorphism
 1 RINGS 1 1 Rings Theorem 1.1 (Substitution Principle). Let ϕ : R R be a ring homomorphism (a) Given an element α R there is a unique homomorphism Φ : R[x] R which agrees with the map ϕ on constant polynomials
1 RINGS 1 1 Rings Theorem 1.1 (Substitution Principle). Let ϕ : R R be a ring homomorphism (a) Given an element α R there is a unique homomorphism Φ : R[x] R which agrees with the map ϕ on constant polynomials
Q N id β. 2. Let I and J be ideals in a commutative ring A. Give a simple description of
 Additional Problems 1. Let A be a commutative ring and let 0 M α N β P 0 be a short exact sequence of A-modules. Let Q be an A-module. i) Show that the naturally induced sequence is exact, but that 0 Hom(P,
Additional Problems 1. Let A be a commutative ring and let 0 M α N β P 0 be a short exact sequence of A-modules. Let Q be an A-module. i) Show that the naturally induced sequence is exact, but that 0 Hom(P,
SOME FAMILIES OF MINIMAL ELEMENTS FOR A PARTIAL ORDERING ON PRIME KNOTS
 Nagasato, F. and Tran, A.T. Osaka J. Math. 53 (2016, 1029 1045 SOME FAMILIES OF MINIMAL ELEMENTS FOR A PARTIAL ORDERING ON PRIME KNOTS FUMIKAZU NAGASATO and ANH T. TRAN (Received September 30, 2014, revised
Nagasato, F. and Tran, A.T. Osaka J. Math. 53 (2016, 1029 1045 SOME FAMILIES OF MINIMAL ELEMENTS FOR A PARTIAL ORDERING ON PRIME KNOTS FUMIKAZU NAGASATO and ANH T. TRAN (Received September 30, 2014, revised
NOTES ON POLYNOMIAL REPRESENTATIONS OF GENERAL LINEAR GROUPS
 NOTES ON POLYNOMIAL REPRESENTATIONS OF GENERAL LINEAR GROUPS MARK WILDON Contents 1. Definition of polynomial representations 1 2. Weight spaces 3 3. Definition of the Schur functor 7 4. Appendix: some
NOTES ON POLYNOMIAL REPRESENTATIONS OF GENERAL LINEAR GROUPS MARK WILDON Contents 1. Definition of polynomial representations 1 2. Weight spaces 3 3. Definition of the Schur functor 7 4. Appendix: some
ELEMENTARY LINEAR ALGEBRA
 ELEMENTARY LINEAR ALGEBRA K. R. MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Corrected Version, 7th April 013 Comments to the author at keithmatt@gmail.com Chapter 1 LINEAR EQUATIONS 1.1
ELEMENTARY LINEAR ALGEBRA K. R. MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Corrected Version, 7th April 013 Comments to the author at keithmatt@gmail.com Chapter 1 LINEAR EQUATIONS 1.1
A field F is a set of numbers that includes the two numbers 0 and 1 and satisfies the properties:
 Byte multiplication 1 Field arithmetic A field F is a set of numbers that includes the two numbers 0 and 1 and satisfies the properties: F is an abelian group under addition, meaning - F is closed under
Byte multiplication 1 Field arithmetic A field F is a set of numbers that includes the two numbers 0 and 1 and satisfies the properties: F is an abelian group under addition, meaning - F is closed under
Quivers of Period 2. Mariya Sardarli Max Wimberley Heyi Zhu. November 26, 2014
 Quivers of Period 2 Mariya Sardarli Max Wimberley Heyi Zhu ovember 26, 2014 Abstract A quiver with vertices labeled from 1,..., n is said to have period 2 if the quiver obtained by mutating at 1 and then
Quivers of Period 2 Mariya Sardarli Max Wimberley Heyi Zhu ovember 26, 2014 Abstract A quiver with vertices labeled from 1,..., n is said to have period 2 if the quiver obtained by mutating at 1 and then
HMMT February 2018 February 10, 2018
 HMMT February 018 February 10, 018 Algebra and Number Theory 1. For some real number c, the graphs of the equation y = x 0 + x + 18 and the line y = x + c intersect at exactly one point. What is c? 18
HMMT February 018 February 10, 018 Algebra and Number Theory 1. For some real number c, the graphs of the equation y = x 0 + x + 18 and the line y = x + c intersect at exactly one point. What is c? 18
Homogeneous Coordinate Ring
 Students: Kaiserslautern University Algebraic Group June 14, 2013 Outline Quotients in Algebraic Geometry 1 Quotients in Algebraic Geometry 2 3 4 Outline Quotients in Algebraic Geometry 1 Quotients in
Students: Kaiserslautern University Algebraic Group June 14, 2013 Outline Quotients in Algebraic Geometry 1 Quotients in Algebraic Geometry 2 3 4 Outline Quotients in Algebraic Geometry 1 Quotients in
A matrix over a field F is a rectangular array of elements from F. The symbol
 Chapter MATRICES Matrix arithmetic A matrix over a field F is a rectangular array of elements from F The symbol M m n (F ) denotes the collection of all m n matrices over F Matrices will usually be denoted
Chapter MATRICES Matrix arithmetic A matrix over a field F is a rectangular array of elements from F The symbol M m n (F ) denotes the collection of all m n matrices over F Matrices will usually be denoted
Isotropic harmonic oscillator
 Isotropic harmonic oscillator 1 Isotropic harmonic oscillator The hamiltonian of the isotropic harmonic oscillator is H = h m + 1 mω r (1) = [ h d m dρ + 1 ] m ω ρ, () ρ=x,y,z a sum of three one-dimensional
Isotropic harmonic oscillator 1 Isotropic harmonic oscillator The hamiltonian of the isotropic harmonic oscillator is H = h m + 1 mω r (1) = [ h d m dρ + 1 ] m ω ρ, () ρ=x,y,z a sum of three one-dimensional
Points of Finite Order
 Points of Finite Order Alex Tao 23 June 2008 1 Points of Order Two and Three If G is a group with respect to multiplication and g is an element of G then the order of g is the minimum positive integer
Points of Finite Order Alex Tao 23 June 2008 1 Points of Order Two and Three If G is a group with respect to multiplication and g is an element of G then the order of g is the minimum positive integer
Homework 6 Solution. Math 113 Summer 2016.
 Homework 6 Solution. Math 113 Summer 2016. 1. For each of the following ideals, say whether they are prime, maximal (hence also prime), or neither (a) (x 4 + 2x 2 + 1) C[x] (b) (x 5 + 24x 3 54x 2 + 6x
Homework 6 Solution. Math 113 Summer 2016. 1. For each of the following ideals, say whether they are prime, maximal (hence also prime), or neither (a) (x 4 + 2x 2 + 1) C[x] (b) (x 5 + 24x 3 54x 2 + 6x
NOTES II FOR 130A JACOB STERBENZ
 NOTES II FOR 130A JACOB STERBENZ Abstract. Here are some notes on the Jordan canonical form as it was covered in class. Contents 1. Polynomials 1 2. The Minimal Polynomial and the Primary Decomposition
NOTES II FOR 130A JACOB STERBENZ Abstract. Here are some notes on the Jordan canonical form as it was covered in class. Contents 1. Polynomials 1 2. The Minimal Polynomial and the Primary Decomposition
 Algebra Qualifying Exam August 2001 Do all 5 problems. 1. Let G be afinite group of order 504 = 23 32 7. a. Show that G cannot be isomorphic to a subgroup of the alternating group Alt 7. (5 points) b.
Algebra Qualifying Exam August 2001 Do all 5 problems. 1. Let G be afinite group of order 504 = 23 32 7. a. Show that G cannot be isomorphic to a subgroup of the alternating group Alt 7. (5 points) b.
Mathematical Olympiad Training Polynomials
 Mathematical Olympiad Training Polynomials Definition A polynomial over a ring R(Z, Q, R, C) in x is an expression of the form p(x) = a n x n + a n 1 x n 1 + + a 1 x + a 0, a i R, for 0 i n. If a n 0,
Mathematical Olympiad Training Polynomials Definition A polynomial over a ring R(Z, Q, R, C) in x is an expression of the form p(x) = a n x n + a n 1 x n 1 + + a 1 x + a 0, a i R, for 0 i n. If a n 0,
Eighth Homework Solutions
 Math 4124 Wednesday, April 20 Eighth Homework Solutions 1. Exercise 5.2.1(e). Determine the number of nonisomorphic abelian groups of order 2704. First we write 2704 as a product of prime powers, namely
Math 4124 Wednesday, April 20 Eighth Homework Solutions 1. Exercise 5.2.1(e). Determine the number of nonisomorphic abelian groups of order 2704. First we write 2704 as a product of prime powers, namely
Lecture 17: The Alexander Module II
 Lecture 17: The Alexander Module II Notes by Jonier Amaral Antunes March 22, 2016 Introduction In previous lectures we obtained knot invariants for a given knot K by studying the homology of the infinite
Lecture 17: The Alexander Module II Notes by Jonier Amaral Antunes March 22, 2016 Introduction In previous lectures we obtained knot invariants for a given knot K by studying the homology of the infinite
ALGEBRA QUALIFYING EXAM PROBLEMS LINEAR ALGEBRA
 ALGEBRA QUALIFYING EXAM PROBLEMS LINEAR ALGEBRA Kent State University Department of Mathematical Sciences Compiled and Maintained by Donald L. White Version: August 29, 2017 CONTENTS LINEAR ALGEBRA AND
ALGEBRA QUALIFYING EXAM PROBLEMS LINEAR ALGEBRA Kent State University Department of Mathematical Sciences Compiled and Maintained by Donald L. White Version: August 29, 2017 CONTENTS LINEAR ALGEBRA AND
Undetected boundary slopes and roots of unity for the character variety of a 3-manifold
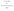 Copyright by Eric Bruce Chesebro 2006 The Dissertation Committee for Eric Bruce Chesebro certifies that this is the approved version of the following dissertation: Undetected boundary slopes and roots
Copyright by Eric Bruce Chesebro 2006 The Dissertation Committee for Eric Bruce Chesebro certifies that this is the approved version of the following dissertation: Undetected boundary slopes and roots
R S. with the property that for every s S, φ(s) is a unit in R S, which is universal amongst all such rings. That is given any morphism
 8. Nullstellensatz We will need the notion of localisation, which is a straightforward generalisation of the notion of the field of fractions. Definition 8.1. Let R be a ring. We say that a subset S of
8. Nullstellensatz We will need the notion of localisation, which is a straightforward generalisation of the notion of the field of fractions. Definition 8.1. Let R be a ring. We say that a subset S of
Topics in linear algebra
 Chapter 6 Topics in linear algebra 6.1 Change of basis I want to remind you of one of the basic ideas in linear algebra: change of basis. Let F be a field, V and W be finite dimensional vector spaces over
Chapter 6 Topics in linear algebra 6.1 Change of basis I want to remind you of one of the basic ideas in linear algebra: change of basis. Let F be a field, V and W be finite dimensional vector spaces over
Algebra SEP Solutions
 Algebra SEP Solutions 17 July 2017 1. (January 2017 problem 1) For example: (a) G = Z/4Z, N = Z/2Z. More generally, G = Z/p n Z, N = Z/pZ, p any prime number, n 2. Also G = Z, N = nz for any n 2, since
Algebra SEP Solutions 17 July 2017 1. (January 2017 problem 1) For example: (a) G = Z/4Z, N = Z/2Z. More generally, G = Z/p n Z, N = Z/pZ, p any prime number, n 2. Also G = Z, N = nz for any n 2, since
Simplifying Rational Expressions and Functions
 Department of Mathematics Grossmont College October 15, 2012 Recall: The Number Types Definition The set of whole numbers, ={0, 1, 2, 3, 4,...} is the set of natural numbers unioned with zero, written
Department of Mathematics Grossmont College October 15, 2012 Recall: The Number Types Definition The set of whole numbers, ={0, 1, 2, 3, 4,...} is the set of natural numbers unioned with zero, written
(a + b)c = ac + bc and a(b + c) = ab + ac.
 2. R I N G S A N D P O LY N O M I A L S The study of vector spaces and linear maps between them naturally leads us to the study of rings, in particular the ring of polynomials F[x] and the ring of (n n)-matrices
2. R I N G S A N D P O LY N O M I A L S The study of vector spaces and linear maps between them naturally leads us to the study of rings, in particular the ring of polynomials F[x] and the ring of (n n)-matrices
INTRODUCTION TO LIE ALGEBRAS. LECTURE 10.
 INTRODUCTION TO LIE ALGEBRAS. LECTURE 10. 10. Jordan decomposition: theme with variations 10.1. Recall that f End(V ) is semisimple if f is diagonalizable (over the algebraic closure of the base field).
INTRODUCTION TO LIE ALGEBRAS. LECTURE 10. 10. Jordan decomposition: theme with variations 10.1. Recall that f End(V ) is semisimple if f is diagonalizable (over the algebraic closure of the base field).
Yale University Department of Mathematics Math 350 Introduction to Abstract Algebra Fall Midterm Exam Review Solutions
 Yale University Department of Mathematics Math 350 Introduction to Abstract Algebra Fall 2015 Midterm Exam Review Solutions Practice exam questions: 1. Let V 1 R 2 be the subset of all vectors whose slope
Yale University Department of Mathematics Math 350 Introduction to Abstract Algebra Fall 2015 Midterm Exam Review Solutions Practice exam questions: 1. Let V 1 R 2 be the subset of all vectors whose slope
Spectra of Semidirect Products of Cyclic Groups
 Spectra of Semidirect Products of Cyclic Groups Nathan Fox 1 University of Minnesota-Twin Cities Abstract The spectrum of a graph is the set of eigenvalues of its adjacency matrix A group, together with
Spectra of Semidirect Products of Cyclic Groups Nathan Fox 1 University of Minnesota-Twin Cities Abstract The spectrum of a graph is the set of eigenvalues of its adjacency matrix A group, together with
Resultants. summary and questions. December 7, 2011
 Resultants summary and questions December 7, 2011 1 An exercise about free modules Let A be a unitary commutative integral ring. Let K be the fraction field of A. Let n 1 be an integer. Set V = A n and
Resultants summary and questions December 7, 2011 1 An exercise about free modules Let A be a unitary commutative integral ring. Let K be the fraction field of A. Let n 1 be an integer. Set V = A n and
COURSE SUMMARY FOR MATH 504, FALL QUARTER : MODERN ALGEBRA
 COURSE SUMMARY FOR MATH 504, FALL QUARTER 2017-8: MODERN ALGEBRA JAROD ALPER Week 1, Sept 27, 29: Introduction to Groups Lecture 1: Introduction to groups. Defined a group and discussed basic properties
COURSE SUMMARY FOR MATH 504, FALL QUARTER 2017-8: MODERN ALGEBRA JAROD ALPER Week 1, Sept 27, 29: Introduction to Groups Lecture 1: Introduction to groups. Defined a group and discussed basic properties
Optimization problems on the rank and inertia of the Hermitian matrix expression A BX (BX) with applications
 Optimization problems on the rank and inertia of the Hermitian matrix expression A BX (BX) with applications Yongge Tian China Economics and Management Academy, Central University of Finance and Economics,
Optimization problems on the rank and inertia of the Hermitian matrix expression A BX (BX) with applications Yongge Tian China Economics and Management Academy, Central University of Finance and Economics,
Polynomial Rings. (Last Updated: December 8, 2017)
 Polynomial Rings (Last Updated: December 8, 2017) These notes are derived primarily from Abstract Algebra, Theory and Applications by Thomas Judson (16ed). Most of this material is drawn from Chapters
Polynomial Rings (Last Updated: December 8, 2017) These notes are derived primarily from Abstract Algebra, Theory and Applications by Thomas Judson (16ed). Most of this material is drawn from Chapters
ELEMENTARY LINEAR ALGEBRA
 ELEMENTARY LINEAR ALGEBRA K. R. MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Second Online Version, December 1998 Comments to the author at krm@maths.uq.edu.au Contents 1 LINEAR EQUATIONS
ELEMENTARY LINEAR ALGEBRA K. R. MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Second Online Version, December 1998 Comments to the author at krm@maths.uq.edu.au Contents 1 LINEAR EQUATIONS
ELEMENTARY LINEAR ALGEBRA
 ELEMENTARY LINEAR ALGEBRA K R MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Second Online Version, December 998 Comments to the author at krm@mathsuqeduau All contents copyright c 99 Keith
ELEMENTARY LINEAR ALGEBRA K R MATTHEWS DEPARTMENT OF MATHEMATICS UNIVERSITY OF QUEENSLAND Second Online Version, December 998 Comments to the author at krm@mathsuqeduau All contents copyright c 99 Keith
COUNTING SEPARABLE POLYNOMIALS IN Z/n[x]
![COUNTING SEPARABLE POLYNOMIALS IN Z/n[x] COUNTING SEPARABLE POLYNOMIALS IN Z/n[x]](/thumbs/92/109397678.jpg) COUNTING SEPARABLE POLYNOMIALS IN Z/n[x] JASON K.C. POLAK Abstract. For a commutative ring R, a polynomial f R[x] is called separable if R[x]/f is a separable R-algebra. We derive formulae for the number
COUNTING SEPARABLE POLYNOMIALS IN Z/n[x] JASON K.C. POLAK Abstract. For a commutative ring R, a polynomial f R[x] is called separable if R[x]/f is a separable R-algebra. We derive formulae for the number
Letting be a field, e.g., of the real numbers, the complex numbers, the rational numbers, the rational functions W(s) of a complex variable s, etc.
 1 Polynomial Matrices 1.1 Polynomials Letting be a field, e.g., of the real numbers, the complex numbers, the rational numbers, the rational functions W(s) of a complex variable s, etc., n ws ( ) as a
1 Polynomial Matrices 1.1 Polynomials Letting be a field, e.g., of the real numbers, the complex numbers, the rational numbers, the rational functions W(s) of a complex variable s, etc., n ws ( ) as a
GALOIS GROUPS AS PERMUTATION GROUPS
 GALOIS GROUPS AS PERMUTATION GROUPS KEITH CONRAD 1. Introduction A Galois group is a group of field automorphisms under composition. By looking at the effect of a Galois group on field generators we can
GALOIS GROUPS AS PERMUTATION GROUPS KEITH CONRAD 1. Introduction A Galois group is a group of field automorphisms under composition. By looking at the effect of a Galois group on field generators we can
55 Separable Extensions
 55 Separable Extensions In 54, we established the foundations of Galois theory, but we have no handy criterion for determining whether a given field extension is Galois or not. Even in the quite simple
55 Separable Extensions In 54, we established the foundations of Galois theory, but we have no handy criterion for determining whether a given field extension is Galois or not. Even in the quite simple
Finite Fields. Sophie Huczynska (with changes by Max Neunhöffer) Semester 2, Academic Year 2012/13
 Finite Fields Sophie Huczynska (with changes by Max Neunhöffer) Semester 2, Academic Year 2012/13 Contents 1 Introduction 3 1 Group theory: a brief summary............................ 3 2 Rings and fields....................................
Finite Fields Sophie Huczynska (with changes by Max Neunhöffer) Semester 2, Academic Year 2012/13 Contents 1 Introduction 3 1 Group theory: a brief summary............................ 3 2 Rings and fields....................................
Quadratic reciprocity (after Weil) 1. Standard set-up and Poisson summation
 (December 19, 010 Quadratic reciprocity (after Weil Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ I show that over global fields k (characteristic not the quadratic norm residue symbol
(December 19, 010 Quadratic reciprocity (after Weil Paul Garrett garrett@math.umn.edu http://www.math.umn.edu/ garrett/ I show that over global fields k (characteristic not the quadratic norm residue symbol
ALGEBRA QUALIFYING EXAM SPRING 2012
 ALGEBRA QUALIFYING EXAM SPRING 2012 Work all of the problems. Justify the statements in your solutions by reference to specific results, as appropriate. Partial credit is awarded for partial solutions.
ALGEBRA QUALIFYING EXAM SPRING 2012 Work all of the problems. Justify the statements in your solutions by reference to specific results, as appropriate. Partial credit is awarded for partial solutions.
Problem 1A. Find the volume of the solid given by x 2 + z 2 1, y 2 + z 2 1. (Hint: 1. Solution: The volume is 1. Problem 2A.
 Problem 1A Find the volume of the solid given by x 2 + z 2 1, y 2 + z 2 1 (Hint: 1 1 (something)dz) Solution: The volume is 1 1 4xydz where x = y = 1 z 2 This integral has value 16/3 Problem 2A Let f(x)
Problem 1A Find the volume of the solid given by x 2 + z 2 1, y 2 + z 2 1 (Hint: 1 1 (something)dz) Solution: The volume is 1 1 4xydz where x = y = 1 z 2 This integral has value 16/3 Problem 2A Let f(x)
Ring Theory Problems. A σ
 Ring Theory Problems 1. Given the commutative diagram α A σ B β A σ B show that α: ker σ ker σ and that β : coker σ coker σ. Here coker σ = B/σ(A). 2. Let K be a field, let V be an infinite dimensional
Ring Theory Problems 1. Given the commutative diagram α A σ B β A σ B show that α: ker σ ker σ and that β : coker σ coker σ. Here coker σ = B/σ(A). 2. Let K be a field, let V be an infinite dimensional
ABSTRACT ALGEBRA 2 SOLUTIONS TO THE PRACTICE EXAM AND HOMEWORK
 ABSTRACT ALGEBRA 2 SOLUTIONS TO THE PRACTICE EXAM AND HOMEWORK 1. Practice exam problems Problem A. Find α C such that Q(i, 3 2) = Q(α). Solution to A. Either one can use the proof of the primitive element
ABSTRACT ALGEBRA 2 SOLUTIONS TO THE PRACTICE EXAM AND HOMEWORK 1. Practice exam problems Problem A. Find α C such that Q(i, 3 2) = Q(α). Solution to A. Either one can use the proof of the primitive element
1. Group Theory Permutations.
 1.1. Permutations. 1. Group Theory Problem 1.1. Let G be a subgroup of S n of index 2. Show that G = A n. Problem 1.2. Find two elements of S 7 that have the same order but are not conjugate. Let π S 7
1.1. Permutations. 1. Group Theory Problem 1.1. Let G be a subgroup of S n of index 2. Show that G = A n. Problem 1.2. Find two elements of S 7 that have the same order but are not conjugate. Let π S 7
Finite Fields: An introduction through exercises Jonathan Buss Spring 2014
 Finite Fields: An introduction through exercises Jonathan Buss Spring 2014 A typical course in abstract algebra starts with groups, and then moves on to rings, vector spaces, fields, etc. This sequence
Finite Fields: An introduction through exercises Jonathan Buss Spring 2014 A typical course in abstract algebra starts with groups, and then moves on to rings, vector spaces, fields, etc. This sequence
HILBERT FUNCTIONS. 1. Introduction
 HILBERT FUCTIOS JORDA SCHETTLER 1. Introduction A Hilbert function (so far as we will discuss) is a map from the nonnegative integers to themselves which records the lengths of composition series of each
HILBERT FUCTIOS JORDA SCHETTLER 1. Introduction A Hilbert function (so far as we will discuss) is a map from the nonnegative integers to themselves which records the lengths of composition series of each
