A versatile proof of Fermat s last theorem
|
|
|
- Sherilyn Carter
- 5 years ago
- Views:
Transcription
1 Abstract A versatile proof of Fermat s last theorem M.Meyyappan #1 Professor of Physics (Retd), Alagappa Government Arts College,Karaikudi , India A simple and multi-purpose proof is proposed with well known arithmetic axioms to explain not only the Fermat s assertion but also the non-existence of square triples (a,b,c) satisfying a n + b n = c n for all exponents including n = 2, reason for certain allowed and forbidden relations among equal sum of like powers and Beal conjecture (Mauldin/Tijdeman-Zagier conjecture) altogether successfully in a single frame. Key words Fermat s Last Theorem - arithmetic axioms equal power relations Multi-power relation - Beal conjecture. I. Introduction For all exponents greater than 2, the numerical relation in the form a n + b n = c n cannot exist when a,b and c are restricted to have whole integers which is called Fermat s Last Theorem (FLT), but is true when irrational and complex numbers are allowed for at least one or two members. After the Fermat s assertion, many people [1,2,3] attempted to prove FLT for different values of exponent and verified with the help of number theory. After the introduction of computer technology people attempted to support the proof of FLT for a wide range of exponents 3-4,000,000 [4]. A proof of FLT was given by Taylor and Wills [5,6] with the help of modern concepts of mathematics elliptic curve and modular theory. In general there must be two or more ways to get the same result for a given mathematical problem. Since the law of nature is always as simple as possible, there must be more natural and naive proof for FLT. This paper describes the attempt undertaken to disclose the naive and accessible proof of FLT with the help of well known arithmetic axioms and number theory. The unequivocal representation reveals its versatility of the methodology. II.Arithmetic axioms 1.In a n + b n = c n, c is always greater than both a and b but c m is less than a m + b m when m < n, and greater when m > n. This is true even when m is a fraction 2.The conservation of odd-evenness in the three member equal sum of like powers necessitates that the allowed and irreducible set of triples (a,b,c) must be with (odd, even, odd), where as the apparently allowed triples with (odd, odd, even) is forbidden due to non-conservation of odd-evenness of the relation, as a doubly even component cannot be balanced with a singly even component, and it is found to be true for all exponents. This restriction is given up in multi-power relations. 3.If a is prime in a three member equal power relation, then c - b will invariably be equal to 1 4.The product of any two powers to give a single power follows some rules. If a x x b y = c z, either the base numbers must be same or some of its power or the exponents must be same or some of its multiple. When b is equal to a α, where α may have any integer value, then z = x + α y and c = a. When y is equal to αx, then z = x and c = ab α. 5.In a x = b y, if a,b and the exponents are all whole integers, then a = α y and b = α x, so that a x = b y = α xy III.Proof of Fermat s Last Theorem In a n + b n = c n, a n is equal to a product of two factors (c n/2 - b n/2 ) (c n/2 + b n/2 ) and a n/2 > c n/2 - b n/2,, one can ingeniously separate these two factors as (c n/2 - b n/2 ) = a n/2 /k where k > 1, not necessary to be an integer and ISSN: Page 16
2 may have all possible values (axiom 1), then (c n/2 + b n/2 ) = k a n/2. Solving for b n and c n in terms of a n we get b n = a n [ (k 2 l) /2k] 2 and c n = a n [( k 2 + 1) / 2k] 2. In the same manner one can solve for a n and c n in terms of b n also, which gives mathematically identical result. a n + b n = c n is then rearranged with its internal constituents as [(2k) 2/n a] n + [(k 2-1) 2/n a] n = [ (k 2 + 1) 2/n a] n where a is found to be a common prime factor of the triple with an inherent condition 1 + [ (k 2 l) /2k] 2 = [( k 2 + 1) / 2k] 2. Mathematically speaking such equal power relations have a common prime factor, since any two members can be expressed in terms of the other member. They are reducible due to this common prime factor. An irreducible set of triple for an exponent n will not have any common prime factor at all. Besides that at least two members will be either irrational or complex instead of being whole integers. But the common prime factor remains in all the three member multi-power relations as stated in Beal conjecture, because it cannot be reduced as done in equal power relations. When reduced it becomes a generator of multi-power relation which will not have the common prime factor. Whatever may be the way by which a member is factorized with respect to the remaining members, the internal constituents may differ, but in general, the structure of the basic relation will be same. If a = p, a prime, then the relation becomes, p n + [(p n 1)/2] 2 = [(p n + 1)/2] 2, where the difference c - b = 1 (axiom-3), where no common prime factor exists. If a = pq where p < q, then (c n/2 - b n/2 ) = p n and (c n/2 + b n/2 ) = q n,it gives yet another form of the above expression (2 2/n pq) n + (q n p n ) 2 = (q n + p n ) 2, where the common prime factor may or may not exist. In fact all the three member equal or unequal power relations have the following general form a n + a n [x 2 ] = a n [y 2 ], where [x 2 ] and [y 2 ] may have any integer or a quantum of value or fractional value but with same denominator satisfying the condition 1 +[x 2 ] = [y 2 ]. For a given value of the exponent, one can change the base numbers only. Due to this limitation, the formation of a n + (βa) n = (γa) n is practically impossible as both β n and γ n cannot be whole integer simultaneously. By choosing a quantum of value for [x 2 ], one term can be converted into a modified power as required, but it is not possible for the other with (1 +[ x 2 ]). Even by adding any equal quantum of value in both side, the condition fails to support the relation. For example, by adding q both sides, the balance of the relation will not be affected. (a n β) + q = m n and a n ( 1 + β) + q = n x which demands 1 = n x - m x and for which no integer solutions are available. Any known relation with whole integers such as Pythagorean relation can even be considered for this purpose. It can be used as a key to solve problems related to equal sums of like and unlike powers with same or different number of terms in each side. The scope of this paper is restricted only to three member equal and unequal power relations. IV.General Proof of FLT Consider a basic relation (2k) 2 + (k 2-1) 2 = (k 2 + 1) 2,To convert it into an equal power relation with an exponent n, the requirements are k 2 = a n /4, (k 2-1) 2 = b n and (k 2 + 1) 2 = c n, with a condition c n/2 - b n/2 = 2.This is valid only when n = 2 for whole integral values of c and b. When a n + a n [x 2 ] = a n [y 2 ] represents the equal power relation, the condition is 1+ b n = c n. It is found that the relation becomes distinct when n 2 and n 3. When n = 2, the terms within each bracket will be whole integral number and will not have any common prime factor in its irreducible form and the condition reduces to c b = 2, which is practically possible. In the other case the condition is possible when b and c are fractions with equal denominator. When n is greater than 2, the condition becomes unrealistic and all the members cannot be expressed as whole integral number simultaneously. It is found that the terms inside each of the brackets can be made to be whole integer only when n = 2, which is the case of Pythagorean triples. When n 3, not all the three members will be whole integers simultaneously and one or more members will invariably be irrational or complex. It explains the argumentative support put forwarded by Pierre de Fermat for cubical and higher power relations and stands as valid proof of FLT. V.Non existence of square triples ISSN: Page 17
3 All the members of a triple (a,b,c) corresponding to any exponent n cannot be squares. It is true even when the exponent n = 2.In fact it is a direct consequence of FLT. The non-existence of square triples can also be taken as an indication of FLT. If all the members of a triple are squares (a 2, b 2,c 2 ) for an exponent n, then (a,b,c) would be a triple for the exponent 2n.If square triples exist for the exponent 2 than a fourth power must be equal to a sum of two fourth powers which is against the argument of the previous section. In a n + (a[x 2 ] 1/n ) n = (a[y 2 ] 1/n ) n,, if a is a square number say α 2, the other two members will be squares only if [x 2 ] = α 2n and [y 2 ] = β 2n, which gives again an impossible condition β 2n - α 2n = 1. It is not fulfilled even when n = 2.It predicts that all the members can be squares when the exponent is ½. The general form of the possible solution is given by 1 1/2 + (n 2 ) 1/2 = [(n+1) 2 ] 1/2. From (2k) 2 + (k 2-1) 2 = (k 2 + 1) 2 we can arrive at the same conclusion. The condition c n b n = 1 does not permit square triples for any exponent. VI.Forbidden power relations In general equal sum of like powers is possible with equal number of terms in each side of the expression for all exponents. Let us restrict our interest to a n + b n = c n + d n.the basic relation to explain its characteristics is [x 1 ] 2 +[ y 2 ] 2 = [x 2 ] 2 + [y 1 ] 2 where 1 + [x 1 ] 2 = [y 1 ] 2 and 1 + [x 2 ] 2 = [y 2 ] 2. In terms of independent variables k, k, m and n it can be expressed as [ (k 2 m 2 ) /2mk] 2 + [( k 2 + n 2 ) /2nk ] 2 = [ (k 2 n 2 ) /2nk ] 2 + [( k 2 + m 2 ) /2mk] 2. This can also be expressed as (a+b) 2 + (c-d) 2 = (a-b) 2 + (c+d) 2 with a condition ab = cd. For n th power relation each term must be n th power of an integer. If the two terms in one side of the relation are taken as a n + b n, then the terms in the other side will be (a n +/- 1) and (b n -/+ 1). By adding and subtracting a suitable number without affecting the balance, both the term in the other side can be made to be n th power of different numbers respectively. But there are some restrictions in the case of unequal number of like powers in each side of the relation. Fermat s assertion, a sum of two n th powers greater than equal to 3 equal to n th power of whole numbers is an unique restriction. This can also be proved algebraically (Annexure). The restrictions are found to be different for different exponents. For example, a sum three squares or three cubes can be shown to be a square or cube respectively (4kk ) 2 + [2k (k 2 1)] 2 + [(k 2 + 1)(k 2 + 1)] 2 = [(k 2 + 1)(k 2 + 1)] 2 where 1 + [(k 2-1) /2k] 2 = [(k 2 + 1) /2k] 2 and 1 + [(k 2-1) /2k ] 2 = [(k 2 + 1) /2k ] 2 But no such expression exists for the exponents n = 4 and 5.However a sum of four fourth or fifth powers equalling a fourth or fifth power respectively exists. It is the self adjustment that determines the possibility of formation of equal sum of like powers balanced with equal and unequal number of terms. Considering the case where a square is equal to a sum of three squares. [y 2 ] 2 = (1 +[ x 2 ]) 2 = 1 + [x 2 ] 2 + 2[x 2 ]. To make 2[x 2 ] to be a square, [x 2 ] must be equal to 2 α 2. For cubical relation [y 2 ] 3 = (1 +[ x 2 ]) 3 = 1 + [x 2 ] 3 + 3[x 2 ][y 2 ], and 3[x 2 ][y 2 ] to be a cube, it must be equal to 27α 3. The roots of the quadratic equation x 2 (1+ x 2 ) = 9 α 3 is given by x 2 = [-1 ± (1+ 36 α 3 )]/2, when α = 2, we get x 2 = 8 or 9 which gives a numeral relation 9 3 = Non-existence of equal sum of like powers in the form a 4 = b 4 + c 4 + d 4 conjectured by Euler can be explained successfully with the same fundamental expression- (c 2 ) 2 = ( a 2 + b 2 ) 2 = a 4 + b 4 + 2a 2 b 2,where 2a 2 b 2 cannot be expressed as a fourth power of a whole number with all possible values of a and b. VII.Beal conjecture Even though the conditional equal power relation with three members is unachievable for all exponents n 3, it is found that multi-power relations are obtainable. According to Beal conjecture [7,8,9] when the base numbers a,b and c and the exponents x,y and z greater than 2 in a x + b y = c z are all positive, then a,b,c will invariably have a common prime factor. The secret behind the multi-power relations is making up a power of an integer from the product of two terms - a power of an integer a m and a number of any kind [x 2 ] and [y 2 ] respectively obeying the condition 1 + [x 2 ] = [y 2 ].This can be accomplished under certain ways. The product a m. [x 2 ] becomes a m + n when [x 2 ] = ISSN: Page 18
4 a n, where the base number is unchanged but the exponent gets changed. The product is equal to (aα) m when [x 2 ] = α m where the exponent remains same but the base number is changed. It is equal to (aα) m + n when [x 2 ] = a n α n + m where both the base number and exponent are changed. It is (aα) n when [x 2 ] = a n - m α n where n > m and it is equal to α n / (a m n ) where m > n. In all the above cases, the base number of the product is some multiples of the base number in the multiplicand, i.e., the base of the multiplicand preserves the base of the product as its generic character. The product can be made to be equal to β n which may miss the generic character when [x 2 ] = β n /a m. In such cases both the base and exponent get changed. The acceptable multi-power relations are completely determined by the simultaneous fulfilment of the requirement by both the products a m [x 2 ] and a m [y 2 ] satisfying the condition 1 + [x 2 ] = [y 2 ]. Even though a m + b m = c m is not possible when a,b,c are all whole integers and m 3, multi-power relation in the form a x + b y = c z is possible for certain permissible values of x,y,z. Like equal power relations, all the three member multi-power relations have the same basic structure a x + a x [(k 2-1)/2k] 2 = a x [(k 2 +1)/2k] 2, where a and k are two independent variables. This can be converted into a multi-power relation by properly choosing the values of [x 2 ] and [y 2 ] and converting the products to a power of an integer. For example a x + a x + m = a x + n is not possible with same base number since 1 + a m a n for all possible values of a,m and n. But a x + a x + m = (aα) x is possible due to the soluble condition 1 + a m = α x. When a = 2,α = 3, m = 3 and x = 2, we get = 6 2. Similarly a x + (aα) x = a x + m is allowed due to attainable condition 1 + α x = a m which gives a multi-power relation = 3 5. From the general form of the three member equal power relation, one can derive one or more conditions for any particular requirement. Its numeral form can be used as a generator for the development of such multipower relations. In fact three member multi-power relation is not possible for all possible set of exponents due to insoluble condition. Table.1 shows some of the allowed and forbidden 3 member multi-power relations with a typical numerical example. Table.1.Allowed and Forbidden three member multi-power relations a x + b y = c z conditions numerical example a n + (aα) n = (aβ) n 1 + α n = β n not possible (FLT) a 3 + (aα) 3 = (aβ) α 3 = aβ = 9 4 (aα) 3 + (aβ) 3 = a 4 α 3 + β 3 = a = 35 4 a 3 + (aα) 4 = (aβ) a α 4 = β = 14 3 (aα) 3 + a 4 = (aβ) 3 α 3 + a = β = 57 3 a 3 + (aα) 3 = (aβ) α 3 = a 2 β = 3 5 (aα) 3 + (aβ) 3 = a 5 α 3 + β 3 = a = 4 5 a 5 + (aα) 3 = (aβ) 3 a 2 + α 3 = β = a 5 + α 3 = β 3 a 5 = (β α)(β 2 + βα +α 2 ) not possible ISSN: Page 19
5 a 3 + (aα) 5 = (aβ) a 2 α 5 = β = a 3 + (aα) 4 = (aβ) 5 1 = a(a β 5 α 4 ) not possible In fact multi-power relations can be obtained directly from the generator- any simple numeral expression, by multiplying each term with a common multiplier, which provides a common prime factor to the relation. For example, the condition = 2 when multiplied by 2 m gives 2 m + 2 m = 2 m + 1,and the common multiplier 2 2m gives 4 m + 4 m = 2 2m + 1 where as the condition = 2 3 gives = 14 3 with a common multiplier 7 3. a n + b n + 1 = c n is the most common type of multi-power relation. The general form of this type of relation is given by (2 n -1) n + (2 n -1) n + 1 = [2(2 n 1)] n A generator can provide many multi-power relations each with different multipliers. It is exemplified with few examples 1 + b y = c z = 3 2 Only certain common multiplier alone can make each term into a power of an integer. 1 is very convenient member as it is the only multiplicand to make product with multiplier of any form. In the above case either b z or c y or α zy will be the convenient multipliers. [1 + b y = c z ] x b z = b z + b y + z = (bc) z = 6 2 [1 + b y = c z ] x c y = c y + (cb) y = c y + z = 3 5 [1 + b y = c z ] x α zy = α zy + (α z b) y = (α y c) z (98) 3 = (1029) 2 Similarly, a x + b x = c = 28, multiplying with the common multiplier c x [a x + b x = c] x c x = (ac) x + (bc) x = c x = 28 4 with common multiplier = 28 7 with common multiplier 28 6 If a x + b y = c z itself is taken as generator, then one of the common multipliers will be α xyz (a x + b y = c z ) x α xyz = (aα yz ) x + (bα xz ) y = (cα xy ) z The generators usually do not have common prime factor, but will have in its reducible form. Hence the generators may or may not have a common prime factor depending upon its reducibility. In fact the generators are irreducible form of multi-power relations. When multiplied with a common multiplier to get a multi-power relation, it acquires a common prime factor. One can show that the common prime factor is compulsory for all the three member multi-power relations but vanishes in all the three member equal power relations.the common prime factor is not a compulsory requirement in multi-power relations with at least one member is a square or more than three members. The non-existence of common factor in equal power relations for all exponents n 3 can also be taken as an indirect proof of FLT VIII. Exempted multi-power relations Beal assertion is not a necessary condition in all multi-power relations with more than three members or one of the members is a square. e.g., ( with more than three members 9 4 = ; 3 5 = ; 5 4 = ) and ( with one member is a square 8 3 = ; = ; 17 4 = ). When one of the members is a square, then the three member multi-power relation becomes ISSN: Page 20
6 a 2 + a 2 [(k 2 1)/2k] 2 = a 2 [(k 2 + 1)/2k] 2 a 2 + a y [1/a y 2 ] [(k 2 1)/2k] 2 = a z [1/a z 2 ] [(k 2 + 1)/2k] 2 [1/a y 2 ] [(k 2 1)/2k] 2 = α y and [1/a z 2 ] [(k 2 + 1)/2k] 2 = β z, from which the required condition can be derived as 1= (a z 2 ) β z - (a y 2 ) α y = a y 2 [ a z y β z α y ] which has no integral solution. When it is converted into a form a 2 + b 3 = c 3, the common factor is either lost or changed by the denominator of [x 2 ] and [y 2 ]. When the common multiplier is some multiples of the common denominator of the fraction representing [x 2 ] and [y 2 ], the multi-power relation may lose its common prime factor. That is what is found in multi-power relation with one member is a square. Like three member equal power relations, in multi-power relations also all the members cannot be squares or any equal higher powers - a 2x + a 2x [x 2 ] = a 2x [y 2 ].Assuming x > y > z, one can construct a multi-power relation as a 2x + a 2y (a 2x -2y [x 2 ]) = a 2z (a 2x -2 z [y 2 ]) a x + (aβ) 2y = (aγ) 2z, with a condition 1 + β 2y /(a 2x 2y ) = γ 2z /(a 2x 2z ).Since the denominators are different β y must be divisible by (a x y ) and γ z by (a x z ) which gives a modified condition as 1 + m 2 = n 2, which has no practical solution for any integer values of m and n. Even by self adjustment also, one cannot make it to be true. Reference [1] Simon Singh, Fermat s Last Theorem Fourth Estate Ltd, (1997) [2] A.Jackson, Fermat s Enigma Review in AMS (1997). [3] H.M.Edward, Fermat s Last Theorem a genetic introduction to the Number Theorey, Germany,Springer,(1997). [4] S.Wagstaff, AMS Notices, 1976,167,p A-53,244 [5] Andrew Wills, Modular elliptic curve and Fermat s last theorem in Annals of Maths.1995, 141, [6] Gerd Faltings., The proof of Fermat s Last Theorem by R.Taylor and A.Wills AMS,1995,42 (7), [7] R.Daniel Mauldin, A generalization of Fermat s Last theorem: The Beal conjecture and prize problem in AMS, 1997, 44, [8] Golden G.Nyambuya, A simple and general proof of Beal conjecture in Adv.in Pure. Maths, 2014, 4, [9] wimhessellink.nl/fermat/wilesenglish.htm Annexure. The algebraic method also confirms FLT. In the case of cubical expression, a 3 + b 3 = (a+b)(a 2 - ab + b 2 ) = c 3 Since a+b > c, a+b= kc where k > 1 and a 2 - ab + b 2 = c 2 /k, Solving for a and b a = (kc/2) (ck/6)[ (12/k 3 ) 3] 1/2 and b = (kc/2) + (ck/6)[ (12/k 3 ) 3] 1/2 when k =1, the second term becomes c/2 and a = 0, b = c. For all values k > 1, the second term becomes irrational or complex. Acknowledgement The author is grateful to Pierre de Fermat who gave an open problem to think over at least if not to try to solve by people of all age group. This proof is dedicated to Mahatma Gandhi, a man I love most. ISSN: Page 21
x 9 or x > 10 Name: Class: Date: 1 How many natural numbers are between 1.5 and 4.5 on the number line?
 1 How many natural numbers are between 1.5 and 4.5 on the number line? 2 How many composite numbers are between 7 and 13 on the number line? 3 How many prime numbers are between 7 and 20 on the number
1 How many natural numbers are between 1.5 and 4.5 on the number line? 2 How many composite numbers are between 7 and 13 on the number line? 3 How many prime numbers are between 7 and 20 on the number
Shi Feng Sheng Danny Wong
 Exhibit C A Proof of the Fermat s Last Theorem Shi Feng Sheng Danny Wong Abstract: Prior to the Diophantine geometry, number theory (or arithmetic) was to study the patterns of the numbers and elementary
Exhibit C A Proof of the Fermat s Last Theorem Shi Feng Sheng Danny Wong Abstract: Prior to the Diophantine geometry, number theory (or arithmetic) was to study the patterns of the numbers and elementary
 Twitter: @Owen134866 www.mathsfreeresourcelibrary.com Prior Knowledge Check 1) Simplify: a) 3x 2 5x 5 b) 5x3 y 2 15x 7 2) Factorise: a) x 2 2x 24 b) 3x 2 17x + 20 15x 2 y 3 3) Use long division to calculate:
Twitter: @Owen134866 www.mathsfreeresourcelibrary.com Prior Knowledge Check 1) Simplify: a) 3x 2 5x 5 b) 5x3 y 2 15x 7 2) Factorise: a) x 2 2x 24 b) 3x 2 17x + 20 15x 2 y 3 3) Use long division to calculate:
JUST THE MATHS UNIT NUMBER 1.3. ALGEBRA 3 (Indices and radicals (or surds)) A.J.Hobson
 JUST THE MATHS UNIT NUMBER 1 ALGEBRA (Indices and radicals (or surds)) by AJHobson 11 Indices 12 Radicals (or Surds) 1 Exercises 14 Answers to exercises UNIT 1 - ALGEBRA - INDICES AND RADICALS (or Surds)
JUST THE MATHS UNIT NUMBER 1 ALGEBRA (Indices and radicals (or surds)) by AJHobson 11 Indices 12 Radicals (or Surds) 1 Exercises 14 Answers to exercises UNIT 1 - ALGEBRA - INDICES AND RADICALS (or Surds)
CHAPTER V Fermat s last theorem
 5.1 Introduction. CHAPTER V Fermat s last theorem We discuss elementary methods approaches to Fermat s last theorem, in which the game is we do not use complex numbers. In this chapter we use methods available
5.1 Introduction. CHAPTER V Fermat s last theorem We discuss elementary methods approaches to Fermat s last theorem, in which the game is we do not use complex numbers. In this chapter we use methods available
Proof of Beal s Conjecture. If, a x +b y =c z Where a,b,c,x,y,z are positive integers with x,y,z >2. Than a,b,c have a common prime factor.
 Global Journal of Pure and Applied Mathematics. ISSN 0973-1768 Volume 13, Number 5 (2017), pp. 1331-1336 Research India Publications http://www.ripublication.com Proof of Beal s Conjecture. If, a x +b
Global Journal of Pure and Applied Mathematics. ISSN 0973-1768 Volume 13, Number 5 (2017), pp. 1331-1336 Research India Publications http://www.ripublication.com Proof of Beal s Conjecture. If, a x +b
SUMS OF SQUARES WUSHI GOLDRING
 SUMS OF SQUARES WUSHI GOLDRING 1. Introduction Here are some opening big questions to think about: Question 1. Which positive integers are sums of two squares? Question 2. Which positive integers are sums
SUMS OF SQUARES WUSHI GOLDRING 1. Introduction Here are some opening big questions to think about: Question 1. Which positive integers are sums of two squares? Question 2. Which positive integers are sums
Algebraic Expressions
 Algebraic Expressions 1. Expressions are formed from variables and constants. 2. Terms are added to form expressions. Terms themselves are formed as product of factors. 3. Expressions that contain exactly
Algebraic Expressions 1. Expressions are formed from variables and constants. 2. Terms are added to form expressions. Terms themselves are formed as product of factors. 3. Expressions that contain exactly
3.0 INTRODUCTION 3.1 OBJECTIVES 3.2 SOLUTION OF QUADRATIC EQUATIONS. Structure
 UNIT 3 EQUATIONS Equations Structure 3.0 Introduction 3.1 Objectives 3.2 Solution of Quadratic Equations 3.3 Quadratic Formula 3.4 Cubic and Bioquadratic Equations 3.5 Answers to Check Your Progress 3.6
UNIT 3 EQUATIONS Equations Structure 3.0 Introduction 3.1 Objectives 3.2 Solution of Quadratic Equations 3.3 Quadratic Formula 3.4 Cubic and Bioquadratic Equations 3.5 Answers to Check Your Progress 3.6
Algebra I. Book 2. Powered by...
 Algebra I Book 2 Powered by... ALGEBRA I Units 4-7 by The Algebra I Development Team ALGEBRA I UNIT 4 POWERS AND POLYNOMIALS......... 1 4.0 Review................ 2 4.1 Properties of Exponents..........
Algebra I Book 2 Powered by... ALGEBRA I Units 4-7 by The Algebra I Development Team ALGEBRA I UNIT 4 POWERS AND POLYNOMIALS......... 1 4.0 Review................ 2 4.1 Properties of Exponents..........
Factorisation CHAPTER Introduction
 FACTORISATION 217 Factorisation CHAPTER 14 14.1 Introduction 14.1.1 Factors of natural numbers You will remember what you learnt about factors in Class VI. Let us take a natural number, say 30, and write
FACTORISATION 217 Factorisation CHAPTER 14 14.1 Introduction 14.1.1 Factors of natural numbers You will remember what you learnt about factors in Class VI. Let us take a natural number, say 30, and write
= 5 2 and = 13 2 and = (1) = 10 2 and = 15 2 and = 25 2
 BEGINNING ALGEBRAIC NUMBER THEORY Fermat s Last Theorem is one of the most famous problems in mathematics. Its origin can be traced back to the work of the Greek mathematician Diophantus (third century
BEGINNING ALGEBRAIC NUMBER THEORY Fermat s Last Theorem is one of the most famous problems in mathematics. Its origin can be traced back to the work of the Greek mathematician Diophantus (third century
PUTNAM TRAINING NUMBER THEORY. Exercises 1. Show that the sum of two consecutive primes is never twice a prime.
 PUTNAM TRAINING NUMBER THEORY (Last updated: December 11, 2017) Remark. This is a list of exercises on Number Theory. Miguel A. Lerma Exercises 1. Show that the sum of two consecutive primes is never twice
PUTNAM TRAINING NUMBER THEORY (Last updated: December 11, 2017) Remark. This is a list of exercises on Number Theory. Miguel A. Lerma Exercises 1. Show that the sum of two consecutive primes is never twice
LESSON 6.2 POLYNOMIAL OPERATIONS I
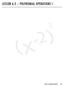 LESSON 6. POLYNOMIAL OPERATIONS I LESSON 6. POLYNOMIALS OPERATIONS I 63 OVERVIEW Here's what you'll learn in this lesson: Adding and Subtracting a. Definition of polynomial, term, and coefficient b. Evaluating
LESSON 6. POLYNOMIAL OPERATIONS I LESSON 6. POLYNOMIALS OPERATIONS I 63 OVERVIEW Here's what you'll learn in this lesson: Adding and Subtracting a. Definition of polynomial, term, and coefficient b. Evaluating
IES Parque Lineal - 2º ESO
 UNIT5. ALGEBRA Contenido 1. Algebraic expressions.... 1 Worksheet: algebraic expressions.... 2 2. Monomials.... 3 Worksheet: monomials.... 5 3. Polynomials... 6 Worksheet: polynomials... 9 4. Factorising....
UNIT5. ALGEBRA Contenido 1. Algebraic expressions.... 1 Worksheet: algebraic expressions.... 2 2. Monomials.... 3 Worksheet: monomials.... 5 3. Polynomials... 6 Worksheet: polynomials... 9 4. Factorising....
Ritangle - an A Level Maths Competition 2016
 Ritangle - an A Level Maths Competition 2016 Questions and Answers - 12-12-16 A. The Taster Questions Answer: this sequence cycles. The first eight terms are, r, i, t, a, n, g, l, e, 1 while the ninth
Ritangle - an A Level Maths Competition 2016 Questions and Answers - 12-12-16 A. The Taster Questions Answer: this sequence cycles. The first eight terms are, r, i, t, a, n, g, l, e, 1 while the ninth
CHMC: Finite Fields 9/23/17
 CHMC: Finite Fields 9/23/17 1 Introduction This worksheet is an introduction to the fascinating subject of finite fields. Finite fields have many important applications in coding theory and cryptography,
CHMC: Finite Fields 9/23/17 1 Introduction This worksheet is an introduction to the fascinating subject of finite fields. Finite fields have many important applications in coding theory and cryptography,
Algebra Revision Guide
 Algebra Revision Guide Stage 4 S J Cooper 1st Edition Collection of like terms... Solving simple equations... Factorisation... 6 Inequalities... 7 Graphs... 9 1. The straight line... 9. The quadratic curve...
Algebra Revision Guide Stage 4 S J Cooper 1st Edition Collection of like terms... Solving simple equations... Factorisation... 6 Inequalities... 7 Graphs... 9 1. The straight line... 9. The quadratic curve...
Chapter. Algebra techniques. Syllabus Content A Basic Mathematics 10% Basic algebraic techniques and the solution of equations.
 Chapter 2 Algebra techniques Syllabus Content A Basic Mathematics 10% Basic algebraic techniques and the solution of equations. Page 1 2.1 What is algebra? In order to extend the usefulness of mathematical
Chapter 2 Algebra techniques Syllabus Content A Basic Mathematics 10% Basic algebraic techniques and the solution of equations. Page 1 2.1 What is algebra? In order to extend the usefulness of mathematical
Fermat s Last Theorem
 Fermat s Last Theorem T. Muthukumar tmk@iitk.ac.in 0 Jun 014 An ancient result states that a triangle with vertices A, B and C with lengths AB = a, BC = b and AC = c is right angled at B iff a + b = c.
Fermat s Last Theorem T. Muthukumar tmk@iitk.ac.in 0 Jun 014 An ancient result states that a triangle with vertices A, B and C with lengths AB = a, BC = b and AC = c is right angled at B iff a + b = c.
Sharpening your algebra skills: Summer practice for students. Updated 2009
 Sharpening your algebra skills: Summer practice for students Updated 009 1 Summer Work: Enhancing Your Algebra Skills in Preparation for a Successful Year at Asheville School The mission of the Asheville
Sharpening your algebra skills: Summer practice for students Updated 009 1 Summer Work: Enhancing Your Algebra Skills in Preparation for a Successful Year at Asheville School The mission of the Asheville
Math Review. for the Quantitative Reasoning measure of the GRE General Test
 Math Review for the Quantitative Reasoning measure of the GRE General Test www.ets.org Overview This Math Review will familiarize you with the mathematical skills and concepts that are important for solving
Math Review for the Quantitative Reasoning measure of the GRE General Test www.ets.org Overview This Math Review will familiarize you with the mathematical skills and concepts that are important for solving
REVIEW Chapter 1 The Real Number System
 REVIEW Chapter The Real Number System In class work: Complete all statements. Solve all exercises. (Section.4) A set is a collection of objects (elements). The Set of Natural Numbers N N = {,,, 4, 5, }
REVIEW Chapter The Real Number System In class work: Complete all statements. Solve all exercises. (Section.4) A set is a collection of objects (elements). The Set of Natural Numbers N N = {,,, 4, 5, }
Polynomials and Polynomial Equations
 Polynomials and Polynomial Equations A Polynomial is any expression that has constants, variables and exponents, and can be combined using addition, subtraction, multiplication and division, but: no division
Polynomials and Polynomial Equations A Polynomial is any expression that has constants, variables and exponents, and can be combined using addition, subtraction, multiplication and division, but: no division
Algebraic Expressions and Identities
 ALGEBRAIC EXPRESSIONS AND IDENTITIES 137 Algebraic Expressions and Identities CHAPTER 9 9.1 What are Expressions? In earlier classes, we have already become familiar with what algebraic expressions (or
ALGEBRAIC EXPRESSIONS AND IDENTITIES 137 Algebraic Expressions and Identities CHAPTER 9 9.1 What are Expressions? In earlier classes, we have already become familiar with what algebraic expressions (or
Algebraic Expressions
 ALGEBRAIC EXPRESSIONS 229 Algebraic Expressions Chapter 12 12.1 INTRODUCTION We have already come across simple algebraic expressions like x + 3, y 5, 4x + 5, 10y 5 and so on. In Class VI, we have seen
ALGEBRAIC EXPRESSIONS 229 Algebraic Expressions Chapter 12 12.1 INTRODUCTION We have already come across simple algebraic expressions like x + 3, y 5, 4x + 5, 10y 5 and so on. In Class VI, we have seen
PREFACE. Synergy for Success in Mathematics 8 is designed for Grade 8 students. The textbook contains
 Synergy for Success in Mathematics 8 is designed for Grade 8 students. The textbook contains all the required learning competencies and is supplemented with some additional topics for enrichment. Lessons
Synergy for Success in Mathematics 8 is designed for Grade 8 students. The textbook contains all the required learning competencies and is supplemented with some additional topics for enrichment. Lessons
UNC Charlotte 2004 Algebra with solutions
 with solutions March 8, 2004 1. Let z denote the real number solution to of the digits of z? (A) 13 (B) 14 (C) 15 (D) 16 (E) 17 3 + x 1 = 5. What is the sum Solution: E. Square both sides twice to get
with solutions March 8, 2004 1. Let z denote the real number solution to of the digits of z? (A) 13 (B) 14 (C) 15 (D) 16 (E) 17 3 + x 1 = 5. What is the sum Solution: E. Square both sides twice to get
Use ordered pairs to locate points, to organize data,
 Eighth Grade Math Scope and Sequence Lesson Title Lesson Objective(s) TEKS First Six Weeks Problem Solving Use problem solving strategies including making a plan and choosing an appropriate method of 8.1B;
Eighth Grade Math Scope and Sequence Lesson Title Lesson Objective(s) TEKS First Six Weeks Problem Solving Use problem solving strategies including making a plan and choosing an appropriate method of 8.1B;
CONGRUENT NUMBERS AND ELLIPTIC CURVES
 CONGRUENT NUMBERS AND ELLIPTIC CURVES JIM BROWN Abstract. In this short paper we consider congruent numbers and how they give rise to elliptic curves. We will begin with very basic notions before moving
CONGRUENT NUMBERS AND ELLIPTIC CURVES JIM BROWN Abstract. In this short paper we consider congruent numbers and how they give rise to elliptic curves. We will begin with very basic notions before moving
DO NOT USE WITHOUT PERMISSION
 PROGRESSION FOR DEVELOPING ALGEBRA UNDERSTANDING THROUGH GENERALIZING ARITHMETIC ACROSS GRADES 3-7: This curricular progression is intended to develop algebra understanding through generalizing arithmetic.
PROGRESSION FOR DEVELOPING ALGEBRA UNDERSTANDING THROUGH GENERALIZING ARITHMETIC ACROSS GRADES 3-7: This curricular progression is intended to develop algebra understanding through generalizing arithmetic.
Math Topics in Algebra Course Notes: A Proof of Fermat s Last Theorem. Spring 2013
 Math 847 - Topics in Algebra Course Notes: A Proof of Fermat s Last Theorem Spring 013 January 6, 013 Chapter 1 Background and History 1.1 Pythagorean triples Consider Pythagorean triples (x, y, z) so
Math 847 - Topics in Algebra Course Notes: A Proof of Fermat s Last Theorem Spring 013 January 6, 013 Chapter 1 Background and History 1.1 Pythagorean triples Consider Pythagorean triples (x, y, z) so
Fantastic Factoring. Difference of Cubes. Difference of Squares. Sum of Cubes. Binomial Squares. Factor the following expressions
 Fantastic Factoring Following are some factoring patterns that you might already recognize. x and y can both represent variables in the expressions, or y might be a constant. These rules work for all real
Fantastic Factoring Following are some factoring patterns that you might already recognize. x and y can both represent variables in the expressions, or y might be a constant. These rules work for all real
A polynomial expression is the addition or subtraction of many algebraic terms with positive integer powers.
 LEAVING CERT Honours Maths notes on Algebra. A polynomial expression is the addition or subtraction of many algebraic terms with positive integer powers. The degree is the highest power of x. 3x 2 + 2x
LEAVING CERT Honours Maths notes on Algebra. A polynomial expression is the addition or subtraction of many algebraic terms with positive integer powers. The degree is the highest power of x. 3x 2 + 2x
Fermat s Last Theorem for Regular Primes
 Fermat s Last Theorem for Regular Primes S. M.-C. 22 September 2015 Abstract Fermat famously claimed in the margin of a book that a certain family of Diophantine equations have no solutions in integers.
Fermat s Last Theorem for Regular Primes S. M.-C. 22 September 2015 Abstract Fermat famously claimed in the margin of a book that a certain family of Diophantine equations have no solutions in integers.
5.1 Monomials. Algebra 2
 . Monomials Algebra Goal : A..: Add, subtract, multiply, and simplify polynomials and rational expressions (e.g., multiply (x ) ( x + ); simplify 9x x. x Goal : Write numbers in scientific notation. Scientific
. Monomials Algebra Goal : A..: Add, subtract, multiply, and simplify polynomials and rational expressions (e.g., multiply (x ) ( x + ); simplify 9x x. x Goal : Write numbers in scientific notation. Scientific
 1 Total Gadha s Complete Book of NUMBER SYSTEM TYPES OF NUMBERS Natural Numbers The group of numbers starting from 1 and including 1,,, 4, 5, and so on, are known as natural numbers. Zero, negative numbers,
1 Total Gadha s Complete Book of NUMBER SYSTEM TYPES OF NUMBERS Natural Numbers The group of numbers starting from 1 and including 1,,, 4, 5, and so on, are known as natural numbers. Zero, negative numbers,
Math 101 Study Session Spring 2016 Test 4 Chapter 10, Chapter 11 Chapter 12 Section 1, and Chapter 12 Section 2
 Math 101 Study Session Spring 2016 Test 4 Chapter 10, Chapter 11 Chapter 12 Section 1, and Chapter 12 Section 2 April 11, 2016 Chapter 10 Section 1: Addition and Subtraction of Polynomials A monomial is
Math 101 Study Session Spring 2016 Test 4 Chapter 10, Chapter 11 Chapter 12 Section 1, and Chapter 12 Section 2 April 11, 2016 Chapter 10 Section 1: Addition and Subtraction of Polynomials A monomial is
Algebra Review. Terrametra Resources. Lynn Patten
 Terrametra Resources Lynn Patten ALGEBRAIC EXPRESSION A combination of ordinary numbers, letter symbols, variables, grouping symbols and operation symbols. Numbers remain fixed in value and are referred
Terrametra Resources Lynn Patten ALGEBRAIC EXPRESSION A combination of ordinary numbers, letter symbols, variables, grouping symbols and operation symbols. Numbers remain fixed in value and are referred
Math 2 Variable Manipulation Part 2 Powers & Roots PROPERTIES OF EXPONENTS:
 Math 2 Variable Manipulation Part 2 Powers & Roots PROPERTIES OF EXPONENTS: 1 EXPONENT REVIEW PROBLEMS: 2 1. 2x + x x + x + 5 =? 2. (x 2 + x) (x + 2) =?. The expression 8x (7x 6 x 5 ) is equivalent to?.
Math 2 Variable Manipulation Part 2 Powers & Roots PROPERTIES OF EXPONENTS: 1 EXPONENT REVIEW PROBLEMS: 2 1. 2x + x x + x + 5 =? 2. (x 2 + x) (x + 2) =?. The expression 8x (7x 6 x 5 ) is equivalent to?.
Math From Scratch Lesson 28: Rational Exponents
 Math From Scratch Lesson 28: Rational Exponents W. Blaine Dowler October 8, 2012 Contents 1 Exponent Review 1 1.1 x m................................. 2 x 1.2 n x................................... 2 m
Math From Scratch Lesson 28: Rational Exponents W. Blaine Dowler October 8, 2012 Contents 1 Exponent Review 1 1.1 x m................................. 2 x 1.2 n x................................... 2 m
review To find the coefficient of all the terms in 15ab + 60bc 17ca: Coefficient of ab = 15 Coefficient of bc = 60 Coefficient of ca = -17
 1. Revision Recall basic terms of algebraic expressions like Variable, Constant, Term, Coefficient, Polynomial etc. The coefficients of the terms in 4x 2 5xy + 6y 2 are Coefficient of 4x 2 is 4 Coefficient
1. Revision Recall basic terms of algebraic expressions like Variable, Constant, Term, Coefficient, Polynomial etc. The coefficients of the terms in 4x 2 5xy + 6y 2 are Coefficient of 4x 2 is 4 Coefficient
A Brief Proof of the Riemann Hypothesis, Giving Infinite Results. Item Total Pages
 A Brief Proof of the Riemann Hypothesis, Giving Infinite Results Item 42 We will also show a positive proof of Fermat s Last Theorem, also related to the construction of the universe. 9 Total Pages 1 A
A Brief Proof of the Riemann Hypothesis, Giving Infinite Results Item 42 We will also show a positive proof of Fermat s Last Theorem, also related to the construction of the universe. 9 Total Pages 1 A
Discrete Logarithms. Let s begin by recalling the definitions and a theorem. Let m be a given modulus. Then the finite set
 Discrete Logarithms Let s begin by recalling the definitions and a theorem. Let m be a given modulus. Then the finite set Z/mZ = {[0], [1],..., [m 1]} = {0, 1,..., m 1} of residue classes modulo m is called
Discrete Logarithms Let s begin by recalling the definitions and a theorem. Let m be a given modulus. Then the finite set Z/mZ = {[0], [1],..., [m 1]} = {0, 1,..., m 1} of residue classes modulo m is called
Workshops: The heart of the MagiKats Programme
 Workshops: The heart of the MagiKats Programme Every student is assigned to a Stage, based on their academic year and assessed study level. Stage 5 students have completed all Stage 4 materials. The sheets
Workshops: The heart of the MagiKats Programme Every student is assigned to a Stage, based on their academic year and assessed study level. Stage 5 students have completed all Stage 4 materials. The sheets
Diophantine equations and beyond
 Diophantine equations and beyond lecture King Faisal prize 2014 Gerd Faltings Max Planck Institute for Mathematics 31.3.2014 G. Faltings (MPIM) Diophantine equations and beyond 31.3.2014 1 / 23 Introduction
Diophantine equations and beyond lecture King Faisal prize 2014 Gerd Faltings Max Planck Institute for Mathematics 31.3.2014 G. Faltings (MPIM) Diophantine equations and beyond 31.3.2014 1 / 23 Introduction
History of Mathematics
 History of Mathematics Paul Yiu Department of Mathematics Florida Atlantic University Summer 2011 6A: Fermat: Beginning of modern number theory (2) Fermat s little theorem Given a prime p, and any geometric
History of Mathematics Paul Yiu Department of Mathematics Florida Atlantic University Summer 2011 6A: Fermat: Beginning of modern number theory (2) Fermat s little theorem Given a prime p, and any geometric
Gaussian integers. 1 = a 2 + b 2 = c 2 + d 2.
 Gaussian integers 1 Units in Z[i] An element x = a + bi Z[i], a, b Z is a unit if there exists y = c + di Z[i] such that xy = 1. This implies 1 = x 2 y 2 = (a 2 + b 2 )(c 2 + d 2 ) But a 2, b 2, c 2, d
Gaussian integers 1 Units in Z[i] An element x = a + bi Z[i], a, b Z is a unit if there exists y = c + di Z[i] such that xy = 1. This implies 1 = x 2 y 2 = (a 2 + b 2 )(c 2 + d 2 ) But a 2, b 2, c 2, d
Prime Numbers and Irrational Numbers
 Chapter 4 Prime Numbers and Irrational Numbers Abstract The question of the existence of prime numbers in intervals is treated using the approximation of cardinal of the primes π(x) given by Lagrange.
Chapter 4 Prime Numbers and Irrational Numbers Abstract The question of the existence of prime numbers in intervals is treated using the approximation of cardinal of the primes π(x) given by Lagrange.
Section September 6, If n = 3, 4, 5,..., the polynomial is called a cubic, quartic, quintic, etc.
 Section 2.1-2.2 September 6, 2017 1 Polynomials Definition. A polynomial is an expression of the form a n x n + a n 1 x n 1 + + a 1 x + a 0 where each a 0, a 1,, a n are real numbers, a n 0, and n is a
Section 2.1-2.2 September 6, 2017 1 Polynomials Definition. A polynomial is an expression of the form a n x n + a n 1 x n 1 + + a 1 x + a 0 where each a 0, a 1,, a n are real numbers, a n 0, and n is a
Study Guide for Math 095
 Study Guide for Math 095 David G. Radcliffe November 7, 1994 1 The Real Number System Writing a fraction in lowest terms. 1. Find the largest number that will divide into both the numerator and the denominator.
Study Guide for Math 095 David G. Radcliffe November 7, 1994 1 The Real Number System Writing a fraction in lowest terms. 1. Find the largest number that will divide into both the numerator and the denominator.
27 Wyner Math 2 Spring 2019
 27 Wyner Math 2 Spring 2019 CHAPTER SIX: POLYNOMIALS Review January 25 Test February 8 Thorough understanding and fluency of the concepts and methods in this chapter is a cornerstone to success in the
27 Wyner Math 2 Spring 2019 CHAPTER SIX: POLYNOMIALS Review January 25 Test February 8 Thorough understanding and fluency of the concepts and methods in this chapter is a cornerstone to success in the
CONTENTS COLLEGE ALGEBRA: DR.YOU
 1 CONTENTS CONTENTS Textbook UNIT 1 LECTURE 1-1 REVIEW A. p. LECTURE 1- RADICALS A.10 p.9 LECTURE 1- COMPLEX NUMBERS A.7 p.17 LECTURE 1-4 BASIC FACTORS A. p.4 LECTURE 1-5. SOLVING THE EQUATIONS A.6 p.
1 CONTENTS CONTENTS Textbook UNIT 1 LECTURE 1-1 REVIEW A. p. LECTURE 1- RADICALS A.10 p.9 LECTURE 1- COMPLEX NUMBERS A.7 p.17 LECTURE 1-4 BASIC FACTORS A. p.4 LECTURE 1-5. SOLVING THE EQUATIONS A.6 p.
CHAPTER 1. Review of Algebra
 CHAPTER 1 Review of Algebra Much of the material in this chapter is revision from GCSE maths (although some of the exercises are harder). Some of it particularly the work on logarithms may be new if you
CHAPTER 1 Review of Algebra Much of the material in this chapter is revision from GCSE maths (although some of the exercises are harder). Some of it particularly the work on logarithms may be new if you
1.2. Indices. Introduction. Prerequisites. Learning Outcomes
 Indices 1.2 Introduction Indices, or powers, provide a convenient notation when we need to multiply a number by itself several times. In this Section we explain how indices are written, and state the rules
Indices 1.2 Introduction Indices, or powers, provide a convenient notation when we need to multiply a number by itself several times. In this Section we explain how indices are written, and state the rules
D-MATH Algebra I HS18 Prof. Rahul Pandharipande. Solution 1. Arithmetic, Zorn s Lemma.
 D-MATH Algebra I HS18 Prof. Rahul Pandharipande Solution 1 Arithmetic, Zorn s Lemma. 1. (a) Using the Euclidean division, determine gcd(160, 399). (b) Find m 0, n 0 Z such that gcd(160, 399) = 160m 0 +
D-MATH Algebra I HS18 Prof. Rahul Pandharipande Solution 1 Arithmetic, Zorn s Lemma. 1. (a) Using the Euclidean division, determine gcd(160, 399). (b) Find m 0, n 0 Z such that gcd(160, 399) = 160m 0 +
Preliminary in this section we obtain some identities that are required in below to achieve the main results. ( ) [ ( )] [ ( )] [ ]
![Preliminary in this section we obtain some identities that are required in below to achieve the main results. ( ) [ ( )] [ ( )] [ ] Preliminary in this section we obtain some identities that are required in below to achieve the main results. ( ) [ ( )] [ ( )] [ ]](/thumbs/94/121636343.jpg) The Bulletin of Society for Mathematical Services Stards Online: 2013-12-02 ISSN: 2277-8020, Vol. 8, pp 17-25 doi:10.18052/www.scipress.com/bsmass.8.17 2013 SciPress Ltd., Switzerl The methods of solving
The Bulletin of Society for Mathematical Services Stards Online: 2013-12-02 ISSN: 2277-8020, Vol. 8, pp 17-25 doi:10.18052/www.scipress.com/bsmass.8.17 2013 SciPress Ltd., Switzerl The methods of solving
ELLIPTIC CURVES BJORN POONEN
 ELLIPTIC CURVES BJORN POONEN 1. Introduction The theme of this lecture is to show how geometry can be used to understand the rational number solutions to a polynomial equation. We will illustrate this
ELLIPTIC CURVES BJORN POONEN 1. Introduction The theme of this lecture is to show how geometry can be used to understand the rational number solutions to a polynomial equation. We will illustrate this
Radical Expressions, Equations, and Functions
 Radical Expressions, Equations, and Functions 0 Real-World Application An observation deck near the top of the Sears Tower in Chicago is 353 ft high. How far can a tourist see to the horizon from this
Radical Expressions, Equations, and Functions 0 Real-World Application An observation deck near the top of the Sears Tower in Chicago is 353 ft high. How far can a tourist see to the horizon from this
Chapter 1: Foundations for Algebra
 Chapter 1: Foundations for Algebra 1 Unit 1: Vocabulary 1) Natural Numbers 2) Whole Numbers 3) Integers 4) Rational Numbers 5) Irrational Numbers 6) Real Numbers 7) Terminating Decimal 8) Repeating Decimal
Chapter 1: Foundations for Algebra 1 Unit 1: Vocabulary 1) Natural Numbers 2) Whole Numbers 3) Integers 4) Rational Numbers 5) Irrational Numbers 6) Real Numbers 7) Terminating Decimal 8) Repeating Decimal
Summary Slides for MATH 342 June 25, 2018
 Summary Slides for MATH 342 June 25, 2018 Summary slides based on Elementary Number Theory and its applications by Kenneth Rosen and The Theory of Numbers by Ivan Niven, Herbert Zuckerman, and Hugh Montgomery.
Summary Slides for MATH 342 June 25, 2018 Summary slides based on Elementary Number Theory and its applications by Kenneth Rosen and The Theory of Numbers by Ivan Niven, Herbert Zuckerman, and Hugh Montgomery.
ALGEBRA 1B GOALS. 1. The student should be able to use mathematical properties to simplify algebraic expressions.
 GOALS 1. The student should be able to use mathematical properties to simplify algebraic expressions. 2. The student should be able to add, subtract, multiply, divide, and compare real numbers. 3. The
GOALS 1. The student should be able to use mathematical properties to simplify algebraic expressions. 2. The student should be able to add, subtract, multiply, divide, and compare real numbers. 3. The
BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST, 2017 Junior Preliminary Problems & Solutions
 BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST, 017 Junior Preliminary Problems & s 1. If x is a number larger than, which of the following expressions is the smallest? (A) /(x 1) (B) /x (C) /(x
BRITISH COLUMBIA SECONDARY SCHOOL MATHEMATICS CONTEST, 017 Junior Preliminary Problems & s 1. If x is a number larger than, which of the following expressions is the smallest? (A) /(x 1) (B) /x (C) /(x
Proof of Beal s Conjecture
 Proof of Beal s Conjecture Stephen Marshall 26 Feb 14 Abstract: This paper presents a complete and exhaustive proof of the Beal Conjecture. The approach to this proof uses the Fundamental Theorem of Arithmetic
Proof of Beal s Conjecture Stephen Marshall 26 Feb 14 Abstract: This paper presents a complete and exhaustive proof of the Beal Conjecture. The approach to this proof uses the Fundamental Theorem of Arithmetic
Read the following definitions and match them with the appropriate example(s) using the lines provided.
 Algebraic Expressions Prepared by: Sa diyya Hendrickson Name: Date: Read the following definitions and match them with the appropriate example(s) using the lines provided. 1. Variable: A letter that is
Algebraic Expressions Prepared by: Sa diyya Hendrickson Name: Date: Read the following definitions and match them with the appropriate example(s) using the lines provided. 1. Variable: A letter that is
a 2 + b 2 = (p 2 q 2 ) 2 + 4p 2 q 2 = (p 2 + q 2 ) 2 = c 2,
 5.3. Pythagorean triples Definition. A Pythagorean triple is a set (a, b, c) of three integers such that (in order) a 2 + b 2 c 2. We may as well suppose that all of a, b, c are non-zero, and positive.
5.3. Pythagorean triples Definition. A Pythagorean triple is a set (a, b, c) of three integers such that (in order) a 2 + b 2 c 2. We may as well suppose that all of a, b, c are non-zero, and positive.
Exponents and Polynomials. (5) Page 459 #15 43 Second Column; Page 466 #6 30 Fourth Column
 Algebra Name: Date: Period: # Exponents and Polynomials (1) Page 453 #22 59 Left (2) Page 453 #25 62 Right (3) Page 459 #5 29 Odd (4) Page 459 #14 42 First Column; Page 466 #3 27 First Column (5) Page
Algebra Name: Date: Period: # Exponents and Polynomials (1) Page 453 #22 59 Left (2) Page 453 #25 62 Right (3) Page 459 #5 29 Odd (4) Page 459 #14 42 First Column; Page 466 #3 27 First Column (5) Page
Reteach Simplifying Algebraic Expressions
 1-4 Simplifying Algebraic Expressions To evaluate an algebraic expression you substitute numbers for variables. Then follow the order of operations. Here is a sentence that can help you remember the order
1-4 Simplifying Algebraic Expressions To evaluate an algebraic expression you substitute numbers for variables. Then follow the order of operations. Here is a sentence that can help you remember the order
Solve for the variable by transforming equations:
 Cantwell Sacred Heart of Mary High School Math Department Study Guide for the Algebra 1 (or higher) Placement Test Name: Date: School: Solve for the variable by transforming equations: 1. y + 3 = 9. 1
Cantwell Sacred Heart of Mary High School Math Department Study Guide for the Algebra 1 (or higher) Placement Test Name: Date: School: Solve for the variable by transforming equations: 1. y + 3 = 9. 1
CHAPTER 1 POLYNOMIALS
 1 CHAPTER 1 POLYNOMIALS 1.1 Removing Nested Symbols of Grouping Simplify. 1. 4x + 3( x ) + 4( x + 1). ( ) 3x + 4 5 x 3 + x 3. 3 5( y 4) + 6 y ( y + 3) 4. 3 n ( n + 5) 4 ( n + 8) 5. ( x + 5) x + 3( x 6)
1 CHAPTER 1 POLYNOMIALS 1.1 Removing Nested Symbols of Grouping Simplify. 1. 4x + 3( x ) + 4( x + 1). ( ) 3x + 4 5 x 3 + x 3. 3 5( y 4) + 6 y ( y + 3) 4. 3 n ( n + 5) 4 ( n + 8) 5. ( x + 5) x + 3( x 6)
UNC Charlotte Super Competition Level 3 Test March 4, 2019 Test with Solutions for Sponsors
 . Find the minimum value of the function f (x) x 2 + (A) 6 (B) 3 6 (C) 4 Solution. We have f (x) x 2 + + x 2 + (D) 3 4, which is equivalent to x 0. x 2 + (E) x 2 +, x R. x 2 + 2 (x 2 + ) 2. How many solutions
. Find the minimum value of the function f (x) x 2 + (A) 6 (B) 3 6 (C) 4 Solution. We have f (x) x 2 + + x 2 + (D) 3 4, which is equivalent to x 0. x 2 + (E) x 2 +, x R. x 2 + 2 (x 2 + ) 2. How many solutions
PRE-CALCULUS By: Salah Abed, Sonia Farag, Stephen Lane, Tyler Wallace, and Barbara Whitney
 PRE-CALCULUS By: Salah Abed, Sonia Farag, Stephen Lane, Tyler Wallace, and Barbara Whitney MATH 141/14 1 Pre-Calculus by Abed, Farag, Lane, Wallace, and Whitney is licensed under the creative commons attribution,
PRE-CALCULUS By: Salah Abed, Sonia Farag, Stephen Lane, Tyler Wallace, and Barbara Whitney MATH 141/14 1 Pre-Calculus by Abed, Farag, Lane, Wallace, and Whitney is licensed under the creative commons attribution,
Math Circle Beginners Group February 28, 2016 Euclid and Prime Numbers
 Math Circle Beginners Group February 28, 2016 Euclid and Prime Numbers Warm-up Problems 1. What is a prime number? Give an example of an even prime number and an odd prime number. (a) Circle the prime
Math Circle Beginners Group February 28, 2016 Euclid and Prime Numbers Warm-up Problems 1. What is a prime number? Give an example of an even prime number and an odd prime number. (a) Circle the prime
numbers and formulas
 1 1 numbers and formulas 1.1 numbers This is a difficult question to answer. However, we use numbers everyday and we live without problems concerning numbers (except during exams). But is does not mean
1 1 numbers and formulas 1.1 numbers This is a difficult question to answer. However, we use numbers everyday and we live without problems concerning numbers (except during exams). But is does not mean
LECTURE 10, MONDAY MARCH 15, 2004
 LECTURE 10, MONDAY MARCH 15, 2004 FRANZ LEMMERMEYER 1. Minimal Polynomials Let α and β be algebraic numbers, and let f and g denote their minimal polynomials. Consider the resultant R(X) of the polynomials
LECTURE 10, MONDAY MARCH 15, 2004 FRANZ LEMMERMEYER 1. Minimal Polynomials Let α and β be algebraic numbers, and let f and g denote their minimal polynomials. Consider the resultant R(X) of the polynomials
x y z 2x y 2y z 2z x n
 Integer Solutions, Rational solutions of the equations 4 4 4 x y z x y y z z x n 4 4 and x y z xy xz y z n; And Crux Mathematicorum Contest Corner problem CC4 Konstantine Zelator P.O. Box 480 Pittsburgh,
Integer Solutions, Rational solutions of the equations 4 4 4 x y z x y y z z x n 4 4 and x y z xy xz y z n; And Crux Mathematicorum Contest Corner problem CC4 Konstantine Zelator P.O. Box 480 Pittsburgh,
CHAPTER 3 BOOLEAN ALGEBRA
 CHAPTER 3 BOOLEAN ALGEBRA (continued) This chapter in the book includes: Objectives Study Guide 3.1 Multiplying Out and Factoring Expressions 3.2 Exclusive-OR and Equivalence Operations 3.3 The Consensus
CHAPTER 3 BOOLEAN ALGEBRA (continued) This chapter in the book includes: Objectives Study Guide 3.1 Multiplying Out and Factoring Expressions 3.2 Exclusive-OR and Equivalence Operations 3.3 The Consensus
Rational Points on Conics, and Local-Global Relations in Number Theory
 Rational Points on Conics, and Local-Global Relations in Number Theory Joseph Lipman Purdue University Department of Mathematics lipman@math.purdue.edu http://www.math.purdue.edu/ lipman November 26, 2007
Rational Points on Conics, and Local-Global Relations in Number Theory Joseph Lipman Purdue University Department of Mathematics lipman@math.purdue.edu http://www.math.purdue.edu/ lipman November 26, 2007
ALGEBRA. 1. Some elementary number theory 1.1. Primes and divisibility. We denote the collection of integers
 ALGEBRA CHRISTIAN REMLING 1. Some elementary number theory 1.1. Primes and divisibility. We denote the collection of integers by Z = {..., 2, 1, 0, 1,...}. Given a, b Z, we write a b if b = ac for some
ALGEBRA CHRISTIAN REMLING 1. Some elementary number theory 1.1. Primes and divisibility. We denote the collection of integers by Z = {..., 2, 1, 0, 1,...}. Given a, b Z, we write a b if b = ac for some
Algebra. Mathematics Help Sheet. The University of Sydney Business School
 Algebra Mathematics Help Sheet The University of Sydney Business School Introduction Terminology and Definitions Integer Constant Variable Co-efficient A whole number, as opposed to a fraction or a decimal,
Algebra Mathematics Help Sheet The University of Sydney Business School Introduction Terminology and Definitions Integer Constant Variable Co-efficient A whole number, as opposed to a fraction or a decimal,
ALGEBRAIC EXPRESSIONS AND POLYNOMIALS
 MODULE - ic Epressions and Polynomials ALGEBRAIC EXPRESSIONS AND POLYNOMIALS So far, you had been using arithmetical numbers, which included natural numbers, whole numbers, fractional numbers, etc. and
MODULE - ic Epressions and Polynomials ALGEBRAIC EXPRESSIONS AND POLYNOMIALS So far, you had been using arithmetical numbers, which included natural numbers, whole numbers, fractional numbers, etc. and
Graphing Square Roots - Class Work Graph the following equations by hand. State the domain and range of each using interval notation.
 Graphing Square Roots - Class Work Graph the following equations by hand. State the domain and range of each using interval notation. 1. y = x + 2 2. f(x) = x 1. y = x +. g(x) = 2 x 1. y = x + 2 + 6. h(x)
Graphing Square Roots - Class Work Graph the following equations by hand. State the domain and range of each using interval notation. 1. y = x + 2 2. f(x) = x 1. y = x +. g(x) = 2 x 1. y = x + 2 + 6. h(x)
Sect Least Common Denominator
 4 Sect.3 - Least Common Denominator Concept #1 Writing Equivalent Rational Expressions Two fractions are equivalent if they are equal. In other words, they are equivalent if they both reduce to the same
4 Sect.3 - Least Common Denominator Concept #1 Writing Equivalent Rational Expressions Two fractions are equivalent if they are equal. In other words, they are equivalent if they both reduce to the same
Intro to Algebra Today. We will learn names for the properties of real numbers. Homework Next Week. Due Tuesday 45-47/ 15-20, 32-35, 40-41, *28,29,38
 Intro to Algebra Today We will learn names for the properties of real numbers. Homework Next Week Due Tuesday 45-47/ 15-20, 32-35, 40-41, *28,29,38 Due Thursday Pages 51-53/ 19-24, 29-36, *48-50, 60-65
Intro to Algebra Today We will learn names for the properties of real numbers. Homework Next Week Due Tuesday 45-47/ 15-20, 32-35, 40-41, *28,29,38 Due Thursday Pages 51-53/ 19-24, 29-36, *48-50, 60-65
Proof of Beal s conjecture by deduction. Kamal Barghout PMU.
 Proof of Beal s conjecture by deduction Kamal Barghout PMU kbarghout@pmu.edu.sa Abstract Beal s conjecture solution is identified as an identity. Each term on the LHS of the solution is converted to an
Proof of Beal s conjecture by deduction Kamal Barghout PMU kbarghout@pmu.edu.sa Abstract Beal s conjecture solution is identified as an identity. Each term on the LHS of the solution is converted to an
5.1, 5.2, 5.3 Properites of Exponents last revised 6/7/2014. c = Properites of Exponents. *Simplify each of the following:
 48 5.1, 5.2, 5.3 Properites of Exponents last revised 6/7/2014 Properites of Exponents 1. x a x b = x a+b *Simplify each of the following: a. x 4 x 8 = b. x 5 x 7 x = 2. xa xb = xa b c. 5 6 5 11 = d. x14
48 5.1, 5.2, 5.3 Properites of Exponents last revised 6/7/2014 Properites of Exponents 1. x a x b = x a+b *Simplify each of the following: a. x 4 x 8 = b. x 5 x 7 x = 2. xa xb = xa b c. 5 6 5 11 = d. x14
ANSWERS. CLASS: VIII TERM - 1 SUBJECT: Mathematics. Exercise: 1(A) Exercise: 1(B)
 ANSWERS CLASS: VIII TERM - 1 SUBJECT: Mathematics TOPIC: 1. Rational Numbers Exercise: 1(A) 1. Fill in the blanks: (i) -21/24 (ii) -4/7 < -4/11 (iii)16/19 (iv)11/13 and -11/13 (v) 0 2. Answer True or False:
ANSWERS CLASS: VIII TERM - 1 SUBJECT: Mathematics TOPIC: 1. Rational Numbers Exercise: 1(A) 1. Fill in the blanks: (i) -21/24 (ii) -4/7 < -4/11 (iii)16/19 (iv)11/13 and -11/13 (v) 0 2. Answer True or False:
FOUNDATION MATHEMATICS
 FOUNDATION MATHEMATICS CLASS - IX Module - Sr. No. Chapters Page No.. Number System 60. Polynomials 6. Co-ordinate Geometry 6 4. Linear Equations in Two 7 7 Variables ETOOS EDUCATION PVT. LTD. Corporate
FOUNDATION MATHEMATICS CLASS - IX Module - Sr. No. Chapters Page No.. Number System 60. Polynomials 6. Co-ordinate Geometry 6 4. Linear Equations in Two 7 7 Variables ETOOS EDUCATION PVT. LTD. Corporate
On Fermat s marginal note: a suggestion
 On Fermat s marginal note: a suggestion Nico F. Benschop - Amspade Research - The Netherlands Annual Dutch Mathematics Congress N M C33 (U-Twente, Apr.1998) Abstract A suggestion is put forward regarding
On Fermat s marginal note: a suggestion Nico F. Benschop - Amspade Research - The Netherlands Annual Dutch Mathematics Congress N M C33 (U-Twente, Apr.1998) Abstract A suggestion is put forward regarding
Table of Contents. 2013, Pearson Education, Inc.
 Table of Contents Chapter 1 What is Number Theory? 1 Chapter Pythagorean Triples 5 Chapter 3 Pythagorean Triples and the Unit Circle 11 Chapter 4 Sums of Higher Powers and Fermat s Last Theorem 16 Chapter
Table of Contents Chapter 1 What is Number Theory? 1 Chapter Pythagorean Triples 5 Chapter 3 Pythagorean Triples and the Unit Circle 11 Chapter 4 Sums of Higher Powers and Fermat s Last Theorem 16 Chapter
Test 4 also includes review problems from earlier sections so study test reviews 1, 2, and 3 also.
 MATD 0370 ELEMENTARY ALGEBRA REVIEW FOR TEST 4 (1.1-10.1, not including 8.2) Test 4 also includes review problems from earlier sections so study test reviews 1, 2, and 3 also. 1. Factor completely: a 2
MATD 0370 ELEMENTARY ALGEBRA REVIEW FOR TEST 4 (1.1-10.1, not including 8.2) Test 4 also includes review problems from earlier sections so study test reviews 1, 2, and 3 also. 1. Factor completely: a 2
Algebra Using letters to represent numbers
 3 Algebra 1 Using letters to represent numbers 47 3.1 Using letters to represent numbers Algebra is the branch of mathematics in which letters are used to represent numbers. This can help solve some mathematical
3 Algebra 1 Using letters to represent numbers 47 3.1 Using letters to represent numbers Algebra is the branch of mathematics in which letters are used to represent numbers. This can help solve some mathematical
1.2. Indices. Introduction. Prerequisites. Learning Outcomes
 Indices.2 Introduction Indices, or powers, provide a convenient notation when we need to multiply a number by itself several times. In this section we explain how indices are written, and state the rules
Indices.2 Introduction Indices, or powers, provide a convenient notation when we need to multiply a number by itself several times. In this section we explain how indices are written, and state the rules
Mathematics: Year 12 Transition Work
 Mathematics: Year 12 Transition Work There are eight sections for you to study. Each section covers a different skill set. You will work online and on paper. 1. Manipulating directed numbers and substitution
Mathematics: Year 12 Transition Work There are eight sections for you to study. Each section covers a different skill set. You will work online and on paper. 1. Manipulating directed numbers and substitution
Review for Mastery. Integer Exponents. Zero Exponents Negative Exponents Negative Exponents in the Denominator. Definition.
 LESSON 6- Review for Mastery Integer Exponents Remember that means 8. The base is, the exponent is positive. Exponents can also be 0 or negative. Zero Exponents Negative Exponents Negative Exponents in
LESSON 6- Review for Mastery Integer Exponents Remember that means 8. The base is, the exponent is positive. Exponents can also be 0 or negative. Zero Exponents Negative Exponents Negative Exponents in
Elliptic Curves & Number Theory. R. Sujatha School of Mathematics TIFR
 Elliptic Curves & Number Theory R. Sujatha School of Mathematics TIFR Aim: To explain the connection between a simple ancient problem in number theory and a deep sophisticated conjecture about Elliptic
Elliptic Curves & Number Theory R. Sujatha School of Mathematics TIFR Aim: To explain the connection between a simple ancient problem in number theory and a deep sophisticated conjecture about Elliptic
In Exercises 1 12, list the all of the elements of the given set. 2. The set of all positive integers whose square roots are less than or equal to 3
 APPENDIX A EXERCISES In Exercises 1 12, list the all of the elements of the given set. 1. The set of all prime numbers less than 20 2. The set of all positive integers whose square roots are less than
APPENDIX A EXERCISES In Exercises 1 12, list the all of the elements of the given set. 1. The set of all prime numbers less than 20 2. The set of all positive integers whose square roots are less than
Academic-Clinic.com BASIC ARITHMETIC AND ALGEBRA POINTERS. Whole (natural) numbers. Arithmetical operations
 BASIC ARITHMETIC AND ALGEBRA POINTERS Whole (natural) numbers Natural numbers numbers, which appear as a result of calculus of single subjects: peoples, animals, birds, trees, different wares and so on.
BASIC ARITHMETIC AND ALGEBRA POINTERS Whole (natural) numbers Natural numbers numbers, which appear as a result of calculus of single subjects: peoples, animals, birds, trees, different wares and so on.
Grade 11/12 Math Circles Rational Points on an Elliptic Curves Dr. Carmen Bruni November 11, Lest We Forget
 Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 11/12 Math Circles Rational Points on an Elliptic Curves Dr. Carmen Bruni November 11, 2015 - Lest
Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 11/12 Math Circles Rational Points on an Elliptic Curves Dr. Carmen Bruni November 11, 2015 - Lest
Arithmetic Operations. The real numbers have the following properties: In particular, putting a 1 in the Distributive Law, we get
 MCA AP Calculus AB Summer Assignment The following packet is a review of many of the skills needed as we begin the study of Calculus. There two major sections to this review. Pages 2-9 are review examples
MCA AP Calculus AB Summer Assignment The following packet is a review of many of the skills needed as we begin the study of Calculus. There two major sections to this review. Pages 2-9 are review examples
