A BAYESIAN APPROACH TO SHRINKAGE ESTIMATORS
|
|
|
- Lee Morton
- 5 years ago
- Views:
Transcription
1 A BAYESIAN APPROACH TO SHRINKAGE ESTIMATORS Fle das Neves RIZZO Crstae Alvarega GAJO Deval Jaques de SOUZA Lucas Motero CHAVES ABSTRACT: Estmators obtaed by shrkg the least squares estmator are becomg wdely used sce the work of Ste, the early 60 s, where t s reseted a estmator for the mea of multvarate ormal that domates the samle mea, ad the work of Hoerl ad Keard, the early 70 s, o rdge estmators I ths work we reset a aroach usg Bayesa ad emrcal Bayesa rocedures to obta some mortat shrkage estmators KEYWORDS: shrkage estmators, emrcal Bayes, mmum mea square estmator Itroducto Two ladmark aers, oe by James-Ste (96), troducg the James-Ste estmators, ad aother by Hoerl ad Keard (970), troducg rdge estmators, exlore the dea that shrkg the usual least squares estmator, besdes the fact of troducg some bas, has the advatage of decreasg the mea square error (MSE) Both these works exlore the dea s to shrkg the estmates Ths s a coservatve rocedure used may areas of statstc Nowadays, that s kow as based estmato theory ad s used whe the least squared estmator ca t be used reaso, for examle, of multcollearty The theory of shrkage estmators s a very actve area of research ad we ca ot, as examles, the LASSO theory (TIBSHIRANI, 996) ad Elastc et theory (ZOU-HASTIE, 005) I ths short ote, we reset a systematc aroach to shrkage estmators usg Bayesa ad emrcal Bayes rocedures Examles for rdge regresso estmato ad James-Ste estmator are reset These rocedures are very well kow ad sread the lterature, but authors could t fd ay systematc smlar aroach Sce emrcal Bayes rocedure s ot of commo use, we revew, secto, a classcal examle We ed ths work wth a comutatoal smulato showg the behavor of some shrkage estmators Shrkage estmators Uversty Federal of Lavras UFLA, Deartmet of Exact Sceces, CP 37, CEP: , Lavras, MG, Brazl: rzzofle@gmalcom; crstaegajo@yahoocombr;devaljaques@dexuflabr; lucas@dexuflabr Rev Bras Bom, São Paulo, v33, 4, ,
2 Ubased estmators of a vector of arameter have a roblem that, geeral, s ot ˆ β ˆ β ˆ,, β a ubased estmator for the vector k metoed Cosder ( ) ( ) β β,, β,the, k E βˆ k k k E β E β var β + k var β + β ( ) ( E β ) We face here a uexected fact: eve though ˆ β s a ubased estmator of β, ˆβ s a based estmator for β, tedg to overestmate t Ths fact has motvated James-Ste to obta hs famous estmator The dea was to shrk the least squares estmator by a factor that deeds of the value observed Hoerl-Keard, workg wth multle lear regressos the resece of multcollearty, roosed a estmato deoted rdge regresso estmator, that s a kd of shrkage estmator Nowadays there s a huge theory about these estmators Emrcal Bayes method Whe the kowledge of the ror dstrbuto arameters s comlete or ukow, some formato may be obtaed from the data tself ad, ths way, t s ossble to make ferece about these arameters Ths s the so-called Bayesa emrcal methodto llustrate the emrcal Bayes methodology, cosder the classcal examle: Let X a Posso radom varable wth arameter µ ad ror π ( µ ) comletely ukow Gve a sze oe samle X x, the corresodg osteror dstrbuto, accordg to Bayes theorem, s x e µ µ π ( µ ) x e π ( µ x) x! where ( ) µ µ g x π ( µ ) d µ g x x ( ) 0! I relato to the mea square error, the Bayes estmator ˆB µ for µ s the mea of the osteror π ( µ x) : x e ˆ [ ] µ µ µ B E µ x µ π ( µ ) dµ x! g x x ( x )! g ( x ) e µ µ x! g ( x) ( x + )! g ( x + ) 0 ( ) ( ) ( ) x +! g x + π ( µ ) d µ x! g ( x) Rev Bras Bom, São Paulo, v33, 4, , 05
3 Now, oe ca use the kow ast observatos g ( x + ) Sce ( ) x x to estmate ( ),, g x ad g x s a dscrete dstrbuto t ca be estmated by the relatve frequeces card x gˆ ( x) card ; x x + gˆ ( x + ) where card{a} s the umber of elemets of set A The, the emrcal Bayes estmator s ( x + ) gˆ ( x + ) ˆ µ B gˆ x { ; x} { } 3 A aroxmato of the mmum mea squares error lear estmator for the mea Cosder deedet observatos ( ) Y,,,, wth model Y µ + ε, where µ s the arameter to be estmated ad the ε ' s are the assocated deedet errors The least square estmator for µ s ˆ µ Y Y Let s cosder all estmators of the form δ c( Y,, Y ) cy We wat to determe the artcular value of c that mmzes the mea squared error To do that we take the fucto MSE ( c ) E ( cy ) µ c E Y c µ E Y + µ σ c + µ c µ + µ The mmum value of ( ) MSE c defes the estmator ˆ µ µ, Y σ + µ Rev Bras Bom, São Paulo, v33, 4, ,
4 that deeds o oulato arameters µ ad σ, both ukow The atural way to byass ths roblem s to relace them by ther atural ubased estmators resultg ad the estmator Y ad S, Y Y ˆ µ Y S S + Y + Y that s a aroxmato of mmum mea square error lear estmator for the mea () I secto 8 we comare, va smulato, the behavor of these estmators 4 Shrkage estmators obtaed from ormalty The smlest examle of a shrkage estmator obtaed from ormalty s: suose Y ~ N ( θ,) ad ror ~ N ( 0,) mea, the osteror dstrbuto s y θ If a samle y ( y y ) π ( θ ) f ( y θ ) π ( θ ),, s take ad y, s t ( ) ex y θ ex θ y ex θ + + The the Bayes estmator s ˆ θ B Y, clearly a shrkage estmator + A more sohstcated argumet s to obta the estmator () usg emrcal Bayes aroach ~, µ ~ ormal 0, τ ad a samle If Y ormal ( µ σ ) wth ror ( ) ( ) y y,, y s observed, the osteror s ormal (GRUBER, 00-50), τ y π ( µ y ) ex µ τ σ τ σ + τ + σ The, usg the mea of the osteror as the Bayes estmator for µ 588 Rev Bras Bom, São Paulo, v33, 4, , 05
5 τ Y ˆ µ B Y τ + σ σ + τ We do t kowτ ad the dea s to use emrcal Bayes argumet The redctve dstrbuto s a ormal wth mea zero ad varace σ + τ (aedx) Observg that f Z ~ ormal ( 0, σ ) as ( [ ]) σ E Z E Z E Z, by the methods of momets, σ σ ca be estmated by oly oe observato, ˆ σ Z The we ca estmate + τ σ by Y It s reasoable to suose τ >> The we ca use Y as estmator of τ Relacg the arameters ˆ µ B by ts resectve estmators we get aga the estmator () The estmator () ca also be obtaed usg mxture Let s suose that, the model Y µ + ε, ~ (, ) ormal 0, τ Y ormal µ σ ad µ has a ror dstrbuto ( ) µ µ + µ, E cy E c Y cy We wat to comute the mea square error ( ) cosderg both Y ad µ as radom varables Comutg these exected values: f y Y y σ σ π f ( µ ) ex µ τ µ πτ ( ) ex ( µ ) ( ) ( ) µ ( ) E c Y cyµ + µ c y cyµ + µ f Y y f µ dµ dy Comutg each tegral: E c Y ( ) c y ex y µ ex µ dµ dy σ σ τ πτ π Rev Bras Bom, São Paulo, v33, 4, ,
6 c y ex y dy σ σ π τ τ + + c σ + τ ( ) E µ Y µ y ex y µ ex µ dy dµ σ σ τ πτ π µ ex µ E [ y] dµ πτ τ { µ Var [ µ ] ( E[ µ ]) E µ + τ All together: E c Y cyµ + µ σ c τ cτ τ + + So, the mmum value of the mea squared error ( ) c E cy µ s obtaed whe τ The, the MSE estmator for µ s: σ + τ ˆ τ µ Y σ + τ Relacg the arameters by ts estmators we, aga, get the estmator () * 0 5 A Bayesa terretato of rdge regresso estmators Cosder the multle lear regresso 590 Rev Bras Bom, São Paulo, v33, 4, , 05
7 Y ( ) X β + ε, ε ~ N 0, σ I We wll suoseσ kow ad a ror dstrbuto for the arameter vector β gve by a -varate ormal ~, σ β σ λ N 0 I λ The osteror dstrbuto gve data Y ad desg matrx X s f, β β σ, X, λ f Y Y X, β, σ f β β σ, λ ( Y ) ( ) ( ) σ ex ( Y X β ) ( Y X β ) σ λ σ ex ( Y X β ) ( Y X β ) σ ex β β σ σ ( + ) σ ex ( X β ) ( X β ) λβ β Y Y σ ( + ) σ ex [ X β β X β X X β λβ Y Y Y Y + + β] σ ( + ) σ ex X β β X + β [ X Xβ + λi] β Y Y Y Y σ To exlct the dstrbuto t s ecessary to comlete the square ( ) ( ) Y X β Y X β + λβ β Y Y Y X β β X Y + β X X β + λβ β ( ) Y Y Y X β + β X X + λ I β So, we eed to determe W such that ( β W ) ( X X + λi )( β W ) Y Y Y X β + β ( X X + λi ) β β ( + λ ) β ( + λ ) β + ( + λ ) X X I W X X I W X X I W The W ( X X + λi ) X Y ad Y X W ( X X I ) β + λ β ( Y X ) ( Y X ) + Y Y + ( X X + I ) W ( X X + I ) Y Y + ( X X + I ) W ( X X + I ) + W ( X X + λi ) W W ( X X + λi ) W β β λβ β β λ β λ β β λ β λ β ( β ) ( λ )( β ) ( λ ) W X X + I W + Y Y W X X + I W Rev Bras Bom, São Paulo, v33, 4, , 05 59
8 Therefore (,, fβ β σ Y X ) ex ( β W ) ( X X + λi )( β W ) + Y Y W ( X X + λi ) W ( β W ) ( X X λi )( β W ) + The osteror s a multvarate ormal wth mea ( ) the Bayes estmator s ( ) ˆ( β λ) X X + λi X Y W X X + λi X Y, therefore Ths s the rdge regresso estmator wth rdge arameter λ (Hoerl-Keard, 970) For λ 0 we have the ordary least square estmator ad ˆ β ( λ) < ˆ β (0) ad, for λ > 0 ˆ( β λ) s a shrkage estmator 6 The James-Ste estmator as a emrcal Bayes estmator Cosder the radom ormal vector ( ) X X,,, ~ (, ) X X N θ I ad suose deedet ormal rors dstrbutos for the arameters: θ ~ N(0, σ ) If oe observato X ( X,, X ) s take, the Bayes estmator s ˆ σ θ X X σ + σ + As σ s ukow, usg a emrcal Bayes rocedure t ca be estmate from the X X,, X The redctve dstrbuto s a multvarate deedet ormal data ( ) wth varace ( I ) σ +, N 0, ( σ + ) Cosder the radom varables X Z Z ~ (0,) N σ + Z X X X σ + ( σ + ) As sum of square deedet stadard ormal, t has ch-square dstrbuto wth X X arameter, that s Y ~ χ ( ) σ + X X As Y, takg exectato, σ + X X Y σ + E E X X ( σ ) Y σ E + + Y As 59 Rev Bras Bom, São Paulo, v33, 4, , 05
9 Y ~ Gama α, β y E y e dy Y y 0 Γ fy ( y) Γ y y e dy 0 Γ Γ Γ Γ Gama( α, β ) Γ Γ It follows that, E X X σ + ad, therefore, E X X σ + By the methods of momets we ca estmate σ + by As X X ˆ σ θ x, x σ + σ + relacg σ + by, the result s the famous James - Ste estmator (James-Ste, X X 96) ( ˆ θ JS ) X X X vectoral form ˆ θjs X X X Observe that the James Ste estmator s a shrkage estmator for > Rev Bras Bom, São Paulo, v33, 4, ,
10 7 A o-ormal examle I the examle (CASELLA-BERGER, 00, 95), suose X,, X d Beroull ( ) It s well kow that the maxmum lkelhood ad ubased estmator for the arameter s The MSE for ˆ s ˆ X X ( ˆ ) var [ ˆ ] E ( ˆ ) E ( ) ( ) var X To comute the Bayes estmator we cosder that, ad use a (, ) Y X s Bomal (, ) Beta α β as the ror for The, the osteror s gve by: y+ α y+ β π ( y) ( ) B y y ( + α, + β ) So, the osteror s a Beta ( y α, y β ) arameter s ts mea: + + ad the Bayes estmator for the y ˆ B + α α + β + The mea squared error for ths estmator s: ( ˆ ) B Var [ ˆ ] ( [ ˆ ]) B + E B ( ) ( α β ) E Observe that, takg + α α + β + α β, we get that the MSE s costat, that s, t 4 y + does t deed of the arameter I ths case the estmator ˆ 4 B + (MOOD et al, 963, theorem 4, age 350) ad s mmax 594 Rev Bras Bom, São Paulo, v33, 4, , 05
11 ( ) E ˆ B ( ) ( + ) + + ( ) ( + ) ( + ) ( ) 4 + E ˆ B Now, as ( ) 4( + ) ad E ( ˆ ) Fgure hels to choose betwee these two estmators ( ) Fgure - Comarso of MSE of ˆ (blue) ad ˆ B (red) for dfferet samle szes For small values of, clearly ˆ B s a better choce, excet f there s a strog reaso to beleve that s ear 0 or For hgh values of, the choce s the estmator ˆ, excet for a strog beleve that s ear 8 Comarg the estmator ˆµ ad the seudo-estmator ˆµ To emhasze the level of comlexty mled by the shrkg rocedure we µ comare the behavor of the seudo estmator ˆ µ Y ad the shrkage σ + µ estmator Rev Bras Bom, São Paulo, v33, 4, ,
12 ˆ µ Y S + Y Cosderg the dstrbutos Normal, Uform ad Double Exoetal, we comute the mea squared error usg 0000 samles of szes 0, 40 ad 00 wth varaces 4, 6 ad 36 The results are show Fgures, 3 ad 4 mea squared error Normal var mea squared error Normal var mea squared error Normal var real mea real mea real mea mea squared error Normal var mea squared error Normal var mea squared error Normal var real mea real mea real mea mea squared error Normal var mea squared error Normal var mea squared error Normal var real mea real mea real mea Fgure - MSE for Y (blue sold), ˆµ (red dotted) ad dstrbuto wth dfferet varaces ad samle szes ˆµ (gree log dash) for Normal 596 Rev Bras Bom, São Paulo, v33, 4, , 05
13 mea squared error Uform var mea squared error Uform var mea squared error Uform var real mea real mea real mea mea squared error Uform var mea squared error Uform var mea squared error Uform var real mea real mea real mea mea squared error Uform var mea squared error Uform var mea squared error Uform var real mea real mea real mea Fgure 3 - MSE for Y (blue sold), ˆµ (red dotted) ad dstrbuto wth dfferet varaces ad samle szes ˆµ (gree log dash) for Uform Rev Bras Bom, São Paulo, v33, 4, ,
14 m ea s quared error Double Exoetal var real mea m ea s quared error Double Exoetal var real mea m ea s quared error Double Exoetal var real mea m ea s quared error Double Exoetal var real mea m ea s quared error Double Exoetal var real mea m ea s quared error Double Exoetal var real mea m ea s quared error Double Exoetal var real mea m ea s quared error Double Exoetal var real mea m ea s quared error Double Exoetal var real mea Fgure 4 - MSE for Y (blue sold), ˆµ (red dotted) ad ˆµ (gree log dash) for Double Exoetal dstrbuto wth dfferet varaces ad samle szes 598 Rev Bras Bom, São Paulo, v33, 4, , 05
15 About fgures, 3 ad 4, observe that the seudo-estmator ˆµ behaves as t s suosed to, that s, excet for some fluctuato whe the real mea s far from the org, t has MSE lower tha the estmator Y O the other had, the estmator ˆµ has a comlex behavor ad oly for the real mea ear the org t has MSE lower tha the estmator Y We could t fd or guess a good reaso for that strage behavor Cocluso The shrkage rocedure shows to be fully comatble wth Bayesa ad emrcal Bayesa method The major roblem, whe shrkg a estmator, s to decde the amout of reducto to be aled The Bayesa method ca hel, gve a terretato of the ecessary reducto to be used The comlexty troduced by shrkage s far from bee comletely uderstood RIZZO, F N; GAJO, C A; SOUZA, D J; CHAVES, L M Uma abordagem Bayesaa do estmador de ecolhmeto Rev Bras Bom São Paulo, v33, 4, , 05 RESUMO: Estmadores obtdos or ecolhmeto do estmador de mímos quadrados usual têm sdo amlamete utlzados, desde os trabalhos de James-Ste (96) e Hoerl e Keard (970), sobre estmadores de cumeera Neste trabalho, aresetamos uma abordagem ara algus mortates estmadores de ecolhmeto, utlzado rocedmetos Bayesaos e Bayesaos emírcos PALAVRAS-CHAVE: Estmador de ecolhmeto, Bayes emírco, estmador de quadrados mímos Refereces CARLIN, B P; LOUIS, T A Bayes ad emrcal Bayes methods for data aalyss New York:Chama & Hall/CRC, 000 CASELLA, G; BERGER, R L Iferêca estatístca ed São Paulo: Cegage Learg, GRUBER, M H J Imrovgeffcecy by shrkage: the James-Ste ad rdge regresso estmators New York: CRC, GRUBER, M H J Regresso estmators: a comaratve study Baltmore: The Johs Hoks Press/CRC, 00 4 HOERL, A E; KENNARD, R W, Based Estmato for Noorthogoal Problems, Techometrcs, v,, 55-67, 970 MOOD, A M; BOES, F A; GRAYBILL, F A Itroducto to the theory of statstcs 3rd ed Columbus: McGraw-Hll, JAMES, W; STEIN, C Estmato wth Quadratc Loss Proc 4 th Berkeley Symos Math Statst Ad Prob, v, 96, Uv Calfora Press, Berkeley, Calf, , 96 Rev Bras Bom, São Paulo, v33, 4, ,
16 TIBSHIRANI, R Regresso shrkage ad selecto va the Lasso JR Stats Soc, v58,, 67-88, 996 ZOU, H; HASTIE, T Regularzato ad varable selecto va the elastc et JR Stats Soc, v 68,, 30-30, 005 Receved 0505 Aroved after revsed Rev Bras Bom, São Paulo, v33, 4, , 05
17 Aedx The redctve for ormal ad mea ror ormal f ( y) ( y µ ) π ( µ ) dµ ex ( y µ ) ex µ µ d πσ σ πτ τ ( µ µ ) µ µ π στ ex y y + d π σ τ yµ y µ π στ ex + + π σ τ σ σ dµ y yµτ ex ex µ π στ σ µ d π σ τ ( σ + τ ) σ τ + y yτ yτ ex ex µ π στ σ dµ π σ τ ( σ + τ ) ( σ + τ ) σ + τ 4 y y τ σ τ ex + πσ τ σ ( σ + τ ) σ τ σ + τ yτ ex µ µ d σ τ σ τ ( σ τ ) π + σ + τ σ + τ Rev Bras Bom, São Paulo, v33, 4, , 05 60
18 60 Rev Bras Bom, São Paulo, v33, 4, , 05 ( ) 4 4 ex τ τ σ σ τ σ σ τ π τ τ y ex ex σ τ σ τ π σ σ τ π τ y y
STK4011 and STK9011 Autumn 2016
 STK4 ad STK9 Autum 6 Pot estmato Covers (most of the followg materal from chapter 7: Secto 7.: pages 3-3 Secto 7..: pages 3-33 Secto 7..: pages 35-3 Secto 7..3: pages 34-35 Secto 7.3.: pages 33-33 Secto
STK4 ad STK9 Autum 6 Pot estmato Covers (most of the followg materal from chapter 7: Secto 7.: pages 3-3 Secto 7..: pages 3-33 Secto 7..: pages 35-3 Secto 7..3: pages 34-35 Secto 7.3.: pages 33-33 Secto
STK3100 and STK4100 Autumn 2017
 SK3 ad SK4 Autum 7 Geeralzed lear models Part III Covers the followg materal from chaters 4 ad 5: Sectos 4..5, 4.3.5, 4.3.6, 4.4., 4.4., ad 4.4.3 Sectos 5.., 5.., ad 5.5. Ørulf Borga Deartmet of Mathematcs
SK3 ad SK4 Autum 7 Geeralzed lear models Part III Covers the followg materal from chaters 4 ad 5: Sectos 4..5, 4.3.5, 4.3.6, 4.4., 4.4., ad 4.4.3 Sectos 5.., 5.., ad 5.5. Ørulf Borga Deartmet of Mathematcs
STK3100 and STK4100 Autumn 2018
 SK3 ad SK4 Autum 8 Geeralzed lear models Part III Covers the followg materal from chaters 4 ad 5: Cofdece tervals by vertg tests Cosder a model wth a sgle arameter β We may obta a ( α% cofdece terval for
SK3 ad SK4 Autum 8 Geeralzed lear models Part III Covers the followg materal from chaters 4 ad 5: Cofdece tervals by vertg tests Cosder a model wth a sgle arameter β We may obta a ( α% cofdece terval for
Dr. Shalabh Department of Mathematics and Statistics Indian Institute of Technology Kanpur
 Aalyss of Varace ad Desg of Exermets-I MODULE II LECTURE - GENERAL LINEAR HYPOTHESIS AND ANALYSIS OF VARIANCE Dr Shalabh Deartmet of Mathematcs ad Statstcs Ida Isttute of Techology Kaur Tukey s rocedure
Aalyss of Varace ad Desg of Exermets-I MODULE II LECTURE - GENERAL LINEAR HYPOTHESIS AND ANALYSIS OF VARIANCE Dr Shalabh Deartmet of Mathematcs ad Statstcs Ida Isttute of Techology Kaur Tukey s rocedure
CS 2750 Machine Learning Lecture 5. Density estimation. Density estimation
 CS 750 Mache Learg Lecture 5 esty estmato Mlos Hausrecht mlos@tt.edu 539 Seott Square esty estmato esty estmato: s a usuervsed learg roblem Goal: Lear a model that rereset the relatos amog attrbutes the
CS 750 Mache Learg Lecture 5 esty estmato Mlos Hausrecht mlos@tt.edu 539 Seott Square esty estmato esty estmato: s a usuervsed learg roblem Goal: Lear a model that rereset the relatos amog attrbutes the
Econometric Methods. Review of Estimation
 Ecoometrc Methods Revew of Estmato Estmatg the populato mea Radom samplg Pot ad terval estmators Lear estmators Ubased estmators Lear Ubased Estmators (LUEs) Effcecy (mmum varace) ad Best Lear Ubased Estmators
Ecoometrc Methods Revew of Estmato Estmatg the populato mea Radom samplg Pot ad terval estmators Lear estmators Ubased estmators Lear Ubased Estmators (LUEs) Effcecy (mmum varace) ad Best Lear Ubased Estmators
Training Sample Model: Given n observations, [[( Yi, x i the sample model can be expressed as (1) where, zero and variance σ
 Stat 74 Estmato for Geeral Lear Model Prof. Goel Broad Outle Geeral Lear Model (GLM): Trag Samle Model: Gve observatos, [[( Y, x ), x = ( x,, xr )], =,,, the samle model ca be exressed as Y = µ ( x, x,,
Stat 74 Estmato for Geeral Lear Model Prof. Goel Broad Outle Geeral Lear Model (GLM): Trag Samle Model: Gve observatos, [[( Y, x ), x = ( x,, xr )], =,,, the samle model ca be exressed as Y = µ ( x, x,,
Chapter 5 Properties of a Random Sample
 Lecture 3 o BST 63: Statstcal Theory I Ku Zhag, /6/006 Revew for the revous lecture Cocets: radom samle, samle mea, samle varace Theorems: roertes of a radom samle, samle mea, samle varace Examles: how
Lecture 3 o BST 63: Statstcal Theory I Ku Zhag, /6/006 Revew for the revous lecture Cocets: radom samle, samle mea, samle varace Theorems: roertes of a radom samle, samle mea, samle varace Examles: how
Point Estimation: definition of estimators
 Pot Estmato: defto of estmators Pot estmator: ay fucto W (X,..., X ) of a data sample. The exercse of pot estmato s to use partcular fuctos of the data order to estmate certa ukow populato parameters.
Pot Estmato: defto of estmators Pot estmator: ay fucto W (X,..., X ) of a data sample. The exercse of pot estmato s to use partcular fuctos of the data order to estmate certa ukow populato parameters.
Chapter 14 Logistic Regression Models
 Chapter 4 Logstc Regresso Models I the lear regresso model X β + ε, there are two types of varables explaatory varables X, X,, X k ad study varable y These varables ca be measured o a cotuous scale as
Chapter 4 Logstc Regresso Models I the lear regresso model X β + ε, there are two types of varables explaatory varables X, X,, X k ad study varable y These varables ca be measured o a cotuous scale as
BASIC PRINCIPLES OF STATISTICS
 BASIC PRINCIPLES OF STATISTICS PROBABILITY DENSITY DISTRIBUTIONS DISCRETE VARIABLES BINOMIAL DISTRIBUTION ~ B 0 0 umber of successes trals Pr E [ ] Var[ ] ; BINOMIAL DISTRIBUTION B7 0. B30 0.3 B50 0.5
BASIC PRINCIPLES OF STATISTICS PROBABILITY DENSITY DISTRIBUTIONS DISCRETE VARIABLES BINOMIAL DISTRIBUTION ~ B 0 0 umber of successes trals Pr E [ ] Var[ ] ; BINOMIAL DISTRIBUTION B7 0. B30 0.3 B50 0.5
2SLS Estimates ECON In this case, begin with the assumption that E[ i
 SLS Estmates ECON 3033 Bll Evas Fall 05 Two-Stage Least Squares (SLS Cosder a stadard lear bvarate regresso model y 0 x. I ths case, beg wth the assumto that E[ x] 0 whch meas that OLS estmates of wll
SLS Estmates ECON 3033 Bll Evas Fall 05 Two-Stage Least Squares (SLS Cosder a stadard lear bvarate regresso model y 0 x. I ths case, beg wth the assumto that E[ x] 0 whch meas that OLS estmates of wll
CHAPTER 6. d. With success = observation greater than 10, x = # of successes = 4, and
 CHAPTR 6 Secto 6.. a. We use the samle mea, to estmate the oulato mea µ. Σ 9.80 µ 8.407 7 ~ 7. b. We use the samle meda, 7 (the mddle observato whe arraged ascedg order. c. We use the samle stadard devato,
CHAPTR 6 Secto 6.. a. We use the samle mea, to estmate the oulato mea µ. Σ 9.80 µ 8.407 7 ~ 7. b. We use the samle meda, 7 (the mddle observato whe arraged ascedg order. c. We use the samle stadard devato,
Lecture 3. Sampling, sampling distributions, and parameter estimation
 Lecture 3 Samplg, samplg dstrbutos, ad parameter estmato Samplg Defto Populato s defed as the collecto of all the possble observatos of terest. The collecto of observatos we take from the populato s called
Lecture 3 Samplg, samplg dstrbutos, ad parameter estmato Samplg Defto Populato s defed as the collecto of all the possble observatos of terest. The collecto of observatos we take from the populato s called
Comparison of Dual to Ratio-Cum-Product Estimators of Population Mean
 Research Joural of Mathematcal ad Statstcal Sceces ISS 30 6047 Vol. 1(), 5-1, ovember (013) Res. J. Mathematcal ad Statstcal Sc. Comparso of Dual to Rato-Cum-Product Estmators of Populato Mea Abstract
Research Joural of Mathematcal ad Statstcal Sceces ISS 30 6047 Vol. 1(), 5-1, ovember (013) Res. J. Mathematcal ad Statstcal Sc. Comparso of Dual to Rato-Cum-Product Estmators of Populato Mea Abstract
Chapter 5 Properties of a Random Sample
 Lecture 6 o BST 63: Statstcal Theory I Ku Zhag, /0/008 Revew for the prevous lecture Cocepts: t-dstrbuto, F-dstrbuto Theorems: Dstrbutos of sample mea ad sample varace, relatoshp betwee sample mea ad sample
Lecture 6 o BST 63: Statstcal Theory I Ku Zhag, /0/008 Revew for the prevous lecture Cocepts: t-dstrbuto, F-dstrbuto Theorems: Dstrbutos of sample mea ad sample varace, relatoshp betwee sample mea ad sample
Lecture 7. Confidence Intervals and Hypothesis Tests in the Simple CLR Model
 Lecture 7. Cofdece Itervals ad Hypothess Tests the Smple CLR Model I lecture 6 we troduced the Classcal Lear Regresso (CLR) model that s the radom expermet of whch the data Y,,, K, are the outcomes. The
Lecture 7. Cofdece Itervals ad Hypothess Tests the Smple CLR Model I lecture 6 we troduced the Classcal Lear Regresso (CLR) model that s the radom expermet of whch the data Y,,, K, are the outcomes. The
STRONG CONSISTENCY FOR SIMPLE LINEAR EV MODEL WITH v/ -MIXING
 Joural of tatstcs: Advaces Theory ad Alcatos Volume 5, Number, 6, Pages 3- Avalable at htt://scetfcadvaces.co. DOI: htt://d.do.org/.864/jsata_7678 TRONG CONITENCY FOR IMPLE LINEAR EV MODEL WITH v/ -MIXING
Joural of tatstcs: Advaces Theory ad Alcatos Volume 5, Number, 6, Pages 3- Avalable at htt://scetfcadvaces.co. DOI: htt://d.do.org/.864/jsata_7678 TRONG CONITENCY FOR IMPLE LINEAR EV MODEL WITH v/ -MIXING
Multivariate Transformation of Variables and Maximum Likelihood Estimation
 Marquette Uversty Multvarate Trasformato of Varables ad Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Assocate Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Copyrght 03 by Marquette Uversty
Marquette Uversty Multvarate Trasformato of Varables ad Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Assocate Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Copyrght 03 by Marquette Uversty
å 1 13 Practice Final Examination Solutions - = CS109 Dec 5, 2018
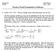 Chrs Pech Fal Practce CS09 Dec 5, 08 Practce Fal Examato Solutos. Aswer: 4/5 8/7. There are multle ways to obta ths aswer; here are two: The frst commo method s to sum over all ossbltes for the rak of
Chrs Pech Fal Practce CS09 Dec 5, 08 Practce Fal Examato Solutos. Aswer: 4/5 8/7. There are multle ways to obta ths aswer; here are two: The frst commo method s to sum over all ossbltes for the rak of
Lecture 9. Some Useful Discrete Distributions. Some Useful Discrete Distributions. The observations generated by different experiments have
 NM 7 Lecture 9 Some Useful Dscrete Dstrbutos Some Useful Dscrete Dstrbutos The observatos geerated by dfferet eermets have the same geeral tye of behavor. Cosequetly, radom varables assocated wth these
NM 7 Lecture 9 Some Useful Dscrete Dstrbutos Some Useful Dscrete Dstrbutos The observatos geerated by dfferet eermets have the same geeral tye of behavor. Cosequetly, radom varables assocated wth these
Bayes Estimator for Exponential Distribution with Extension of Jeffery Prior Information
 Malaysa Joural of Mathematcal Sceces (): 97- (9) Bayes Estmator for Expoetal Dstrbuto wth Exteso of Jeffery Pror Iformato Hadeel Salm Al-Kutub ad Noor Akma Ibrahm Isttute for Mathematcal Research, Uverst
Malaysa Joural of Mathematcal Sceces (): 97- (9) Bayes Estmator for Expoetal Dstrbuto wth Exteso of Jeffery Pror Iformato Hadeel Salm Al-Kutub ad Noor Akma Ibrahm Isttute for Mathematcal Research, Uverst
X X X E[ ] E X E X. is the ()m n where the ( i,)th. j element is the mean of the ( i,)th., then
![X X X E[ ] E X E X. is the ()m n where the ( i,)th. j element is the mean of the ( i,)th., then X X X E[ ] E X E X. is the ()m n where the ( i,)th. j element is the mean of the ( i,)th., then](/thumbs/83/87696552.jpg) Secto 5 Vectors of Radom Varables Whe workg wth several radom varables,,..., to arrage them vector form x, t s ofte coveet We ca the make use of matrx algebra to help us orgaze ad mapulate large umbers
Secto 5 Vectors of Radom Varables Whe workg wth several radom varables,,..., to arrage them vector form x, t s ofte coveet We ca the make use of matrx algebra to help us orgaze ad mapulate large umbers
Parameter Estimation
 arameter Estmato robabltes Notatoal Coveto Mass dscrete fucto: catal letters Desty cotuous fucto: small letters Vector vs. scalar Scalar: la Vector: bold D: small Hgher dmeso: catal Notes a cotuous state
arameter Estmato robabltes Notatoal Coveto Mass dscrete fucto: catal letters Desty cotuous fucto: small letters Vector vs. scalar Scalar: la Vector: bold D: small Hgher dmeso: catal Notes a cotuous state
Random Variables. ECE 313 Probability with Engineering Applications Lecture 8 Professor Ravi K. Iyer University of Illinois
 Radom Varables ECE 313 Probablty wth Egeerg Alcatos Lecture 8 Professor Rav K. Iyer Uversty of Illos Iyer - Lecture 8 ECE 313 Fall 013 Today s Tocs Revew o Radom Varables Cumulatve Dstrbuto Fucto (CDF
Radom Varables ECE 313 Probablty wth Egeerg Alcatos Lecture 8 Professor Rav K. Iyer Uversty of Illos Iyer - Lecture 8 ECE 313 Fall 013 Today s Tocs Revew o Radom Varables Cumulatve Dstrbuto Fucto (CDF
X ε ) = 0, or equivalently, lim
 Revew for the prevous lecture Cocepts: order statstcs Theorems: Dstrbutos of order statstcs Examples: How to get the dstrbuto of order statstcs Chapter 5 Propertes of a Radom Sample Secto 55 Covergece
Revew for the prevous lecture Cocepts: order statstcs Theorems: Dstrbutos of order statstcs Examples: How to get the dstrbuto of order statstcs Chapter 5 Propertes of a Radom Sample Secto 55 Covergece
STATISTICAL PROPERTIES OF LEAST SQUARES ESTIMATORS. x, where. = y - ˆ " 1
 STATISTICAL PROPERTIES OF LEAST SQUARES ESTIMATORS Recall Assumpto E(Y x) η 0 + η x (lear codtoal mea fucto) Data (x, y ), (x 2, y 2 ),, (x, y ) Least squares estmator ˆ E (Y x) ˆ " 0 + ˆ " x, where ˆ
STATISTICAL PROPERTIES OF LEAST SQUARES ESTIMATORS Recall Assumpto E(Y x) η 0 + η x (lear codtoal mea fucto) Data (x, y ), (x 2, y 2 ),, (x, y ) Least squares estmator ˆ E (Y x) ˆ " 0 + ˆ " x, where ˆ
( ) = ( ) ( ) Chapter 13 Asymptotic Theory and Stochastic Regressors. Stochastic regressors model
 Chapter 3 Asmptotc Theor ad Stochastc Regressors The ature of eplaator varable s assumed to be o-stochastc or fed repeated samples a regresso aalss Such a assumpto s approprate for those epermets whch
Chapter 3 Asmptotc Theor ad Stochastc Regressors The ature of eplaator varable s assumed to be o-stochastc or fed repeated samples a regresso aalss Such a assumpto s approprate for those epermets whch
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS
 UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postpoed exam: ECON430 Statstcs Date of exam: Jauary 0, 0 Tme for exam: 09:00 a.m. :00 oo The problem set covers 5 pages Resources allowed: All wrtte ad prted
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postpoed exam: ECON430 Statstcs Date of exam: Jauary 0, 0 Tme for exam: 09:00 a.m. :00 oo The problem set covers 5 pages Resources allowed: All wrtte ad prted
D KL (P Q) := p i ln p i q i
 Cheroff-Bouds 1 The Geeral Boud Let P 1,, m ) ad Q q 1,, q m ) be two dstrbutos o m elemets, e,, q 0, for 1,, m, ad m 1 m 1 q 1 The Kullback-Lebler dvergece or relatve etroy of P ad Q s defed as m D KL
Cheroff-Bouds 1 The Geeral Boud Let P 1,, m ) ad Q q 1,, q m ) be two dstrbutos o m elemets, e,, q 0, for 1,, m, ad m 1 m 1 q 1 The Kullback-Lebler dvergece or relatve etroy of P ad Q s defed as m D KL
1 Solution to Problem 6.40
 1 Soluto to Problem 6.40 (a We wll wrte T τ (X 1,...,X where the X s are..d. wth PDF f(x µ, σ 1 ( x µ σ g, σ where the locato parameter µ s ay real umber ad the scale parameter σ s > 0. Lettg Z X µ σ we
1 Soluto to Problem 6.40 (a We wll wrte T τ (X 1,...,X where the X s are..d. wth PDF f(x µ, σ 1 ( x µ σ g, σ where the locato parameter µ s ay real umber ad the scale parameter σ s > 0. Lettg Z X µ σ we
Chapter 8: Statistical Analysis of Simulated Data
 Marquette Uversty MSCS600 Chapter 8: Statstcal Aalyss of Smulated Data Dael B. Rowe, Ph.D. Departmet of Mathematcs, Statstcs, ad Computer Scece Copyrght 08 by Marquette Uversty MSCS600 Ageda 8. The Sample
Marquette Uversty MSCS600 Chapter 8: Statstcal Aalyss of Smulated Data Dael B. Rowe, Ph.D. Departmet of Mathematcs, Statstcs, ad Computer Scece Copyrght 08 by Marquette Uversty MSCS600 Ageda 8. The Sample
Qualifying Exam Statistical Theory Problem Solutions August 2005
 Qualfyg Exam Statstcal Theory Problem Solutos August 5. Let X, X,..., X be d uform U(,),
Qualfyg Exam Statstcal Theory Problem Solutos August 5. Let X, X,..., X be d uform U(,),
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS
 UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Exam: ECON430 Statstcs Date of exam: Frday, December 8, 07 Grades are gve: Jauary 4, 08 Tme for exam: 0900 am 00 oo The problem set covers 5 pages Resources allowed:
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Exam: ECON430 Statstcs Date of exam: Frday, December 8, 07 Grades are gve: Jauary 4, 08 Tme for exam: 0900 am 00 oo The problem set covers 5 pages Resources allowed:
STA302/1001-Fall 2008 Midterm Test October 21, 2008
 STA3/-Fall 8 Mdterm Test October, 8 Last Name: Frst Name: Studet Number: Erolled (Crcle oe) STA3 STA INSTRUCTIONS Tme allowed: hour 45 mutes Ads allowed: A o-programmable calculator A table of values from
STA3/-Fall 8 Mdterm Test October, 8 Last Name: Frst Name: Studet Number: Erolled (Crcle oe) STA3 STA INSTRUCTIONS Tme allowed: hour 45 mutes Ads allowed: A o-programmable calculator A table of values from
Dimensionality Reduction and Learning
 CMSC 35900 (Sprg 009) Large Scale Learg Lecture: 3 Dmesoalty Reducto ad Learg Istructors: Sham Kakade ad Greg Shakharovch L Supervsed Methods ad Dmesoalty Reducto The theme of these two lectures s that
CMSC 35900 (Sprg 009) Large Scale Learg Lecture: 3 Dmesoalty Reducto ad Learg Istructors: Sham Kakade ad Greg Shakharovch L Supervsed Methods ad Dmesoalty Reducto The theme of these two lectures s that
Two Fuzzy Probability Measures
 Two Fuzzy robablty Measures Zdeěk Karíšek Isttute of Mathematcs Faculty of Mechacal Egeerg Bro Uversty of Techology Techcká 2 66 69 Bro Czech Reublc e-mal: karsek@umfmevutbrcz Karel Slavíček System dmstrato
Two Fuzzy robablty Measures Zdeěk Karíšek Isttute of Mathematcs Faculty of Mechacal Egeerg Bro Uversty of Techology Techcká 2 66 69 Bro Czech Reublc e-mal: karsek@umfmevutbrcz Karel Slavíček System dmstrato
ENGI 4421 Joint Probability Distributions Page Joint Probability Distributions [Navidi sections 2.5 and 2.6; Devore sections
 ENGI 441 Jot Probablty Dstrbutos Page 7-01 Jot Probablty Dstrbutos [Navd sectos.5 ad.6; Devore sectos 5.1-5.] The jot probablty mass fucto of two dscrete radom quattes, s, P ad p x y x y The margal probablty
ENGI 441 Jot Probablty Dstrbutos Page 7-01 Jot Probablty Dstrbutos [Navd sectos.5 ad.6; Devore sectos 5.1-5.] The jot probablty mass fucto of two dscrete radom quattes, s, P ad p x y x y The margal probablty
Lecture Notes Types of economic variables
 Lecture Notes 3 1. Types of ecoomc varables () Cotuous varable takes o a cotuum the sample space, such as all pots o a le or all real umbers Example: GDP, Polluto cocetrato, etc. () Dscrete varables fte
Lecture Notes 3 1. Types of ecoomc varables () Cotuous varable takes o a cotuum the sample space, such as all pots o a le or all real umbers Example: GDP, Polluto cocetrato, etc. () Dscrete varables fte
VOL. 3, NO. 11, November 2013 ISSN ARPN Journal of Science and Technology All rights reserved.
 VOL., NO., November 0 ISSN 5-77 ARPN Joural of Scece ad Techology 0-0. All rghts reserved. http://www.ejouralofscece.org Usg Square-Root Iverted Gamma Dstrbuto as Pror to Draw Iferece o the Raylegh Dstrbuto
VOL., NO., November 0 ISSN 5-77 ARPN Joural of Scece ad Techology 0-0. All rghts reserved. http://www.ejouralofscece.org Usg Square-Root Iverted Gamma Dstrbuto as Pror to Draw Iferece o the Raylegh Dstrbuto
The Empirical Performances of the Selection Criteria for Nonparametric Regression Using Smoothing Spline
 Proceedgs of the 5th WSEAS It. Cof. o COMPUTATIONAL INTELLIGENCE, MAN-MACHINE SYSTEMS AND CYBERNETICS, Vece, Italy, November 0-, 006 8 The Emrcal Performaces of the Selecto Crtera for Noarametrc Regresso
Proceedgs of the 5th WSEAS It. Cof. o COMPUTATIONAL INTELLIGENCE, MAN-MACHINE SYSTEMS AND CYBERNETICS, Vece, Italy, November 0-, 006 8 The Emrcal Performaces of the Selecto Crtera for Noarametrc Regresso
Ordinary Least Squares Regression. Simple Regression. Algebra and Assumptions.
 Ordary Least Squares egresso. Smple egresso. Algebra ad Assumptos. I ths part of the course we are gog to study a techque for aalysg the lear relatoshp betwee two varables Y ad X. We have pars of observatos
Ordary Least Squares egresso. Smple egresso. Algebra ad Assumptos. I ths part of the course we are gog to study a techque for aalysg the lear relatoshp betwee two varables Y ad X. We have pars of observatos
Special Instructions / Useful Data
 JAM 6 Set of all real umbers P A..d. B, p Posso Specal Istructos / Useful Data x,, :,,, x x Probablty of a evet A Idepedetly ad detcally dstrbuted Bomal dstrbuto wth parameters ad p Posso dstrbuto wth
JAM 6 Set of all real umbers P A..d. B, p Posso Specal Istructos / Useful Data x,, :,,, x x Probablty of a evet A Idepedetly ad detcally dstrbuted Bomal dstrbuto wth parameters ad p Posso dstrbuto wth
Linear Regression Linear Regression with Shrinkage. Some slides are due to Tommi Jaakkola, MIT AI Lab
 Lear Regresso Lear Regresso th Shrkage Some sldes are due to Tomm Jaakkola, MIT AI Lab Itroducto The goal of regresso s to make quattatve real valued predctos o the bass of a vector of features or attrbutes.
Lear Regresso Lear Regresso th Shrkage Some sldes are due to Tomm Jaakkola, MIT AI Lab Itroducto The goal of regresso s to make quattatve real valued predctos o the bass of a vector of features or attrbutes.
TESTS BASED ON MAXIMUM LIKELIHOOD
 ESE 5 Toy E. Smth. The Basc Example. TESTS BASED ON MAXIMUM LIKELIHOOD To llustrate the propertes of maxmum lkelhood estmates ad tests, we cosder the smplest possble case of estmatg the mea of the ormal
ESE 5 Toy E. Smth. The Basc Example. TESTS BASED ON MAXIMUM LIKELIHOOD To llustrate the propertes of maxmum lkelhood estmates ad tests, we cosder the smplest possble case of estmatg the mea of the ormal
Application of Generating Functions to the Theory of Success Runs
 Aled Mathematcal Sceces, Vol. 10, 2016, o. 50, 2491-2495 HIKARI Ltd, www.m-hkar.com htt://dx.do.org/10.12988/ams.2016.66197 Alcato of Geeratg Fuctos to the Theory of Success Rus B.M. Bekker, O.A. Ivaov
Aled Mathematcal Sceces, Vol. 10, 2016, o. 50, 2491-2495 HIKARI Ltd, www.m-hkar.com htt://dx.do.org/10.12988/ams.2016.66197 Alcato of Geeratg Fuctos to the Theory of Success Rus B.M. Bekker, O.A. Ivaov
Lecture 3 Probability review (cont d)
 STATS 00: Itroducto to Statstcal Iferece Autum 06 Lecture 3 Probablty revew (cot d) 3. Jot dstrbutos If radom varables X,..., X k are depedet, the ther dstrbuto may be specfed by specfyg the dvdual dstrbuto
STATS 00: Itroducto to Statstcal Iferece Autum 06 Lecture 3 Probablty revew (cot d) 3. Jot dstrbutos If radom varables X,..., X k are depedet, the ther dstrbuto may be specfed by specfyg the dvdual dstrbuto
Median as a Weighted Arithmetic Mean of All Sample Observations
 Meda as a Weghted Arthmetc Mea of All Sample Observatos SK Mshra Dept. of Ecoomcs NEHU, Shllog (Ida). Itroducto: Iumerably may textbooks Statstcs explctly meto that oe of the weakesses (or propertes) of
Meda as a Weghted Arthmetc Mea of All Sample Observatos SK Mshra Dept. of Ecoomcs NEHU, Shllog (Ida). Itroducto: Iumerably may textbooks Statstcs explctly meto that oe of the weakesses (or propertes) of
LINEAR REGRESSION ANALYSIS
 LINEAR REGRESSION ANALYSIS MODULE V Lecture - Correctg Model Iadequaces Through Trasformato ad Weghtg Dr. Shalabh Departmet of Mathematcs ad Statstcs Ida Isttute of Techology Kapur Aalytcal methods for
LINEAR REGRESSION ANALYSIS MODULE V Lecture - Correctg Model Iadequaces Through Trasformato ad Weghtg Dr. Shalabh Departmet of Mathematcs ad Statstcs Ida Isttute of Techology Kapur Aalytcal methods for
ENGI 3423 Simple Linear Regression Page 12-01
 ENGI 343 mple Lear Regresso Page - mple Lear Regresso ometmes a expermet s set up where the expermeter has cotrol over the values of oe or more varables X ad measures the resultg values of aother varable
ENGI 343 mple Lear Regresso Page - mple Lear Regresso ometmes a expermet s set up where the expermeter has cotrol over the values of oe or more varables X ad measures the resultg values of aother varable
Lecture Note to Rice Chapter 8
 ECON 430 HG revsed Nov 06 Lecture Note to Rce Chapter 8 Radom matrces Let Y, =,,, m, =,,, be radom varables (r.v. s). The matrx Y Y Y Y Y Y Y Y Y Y = m m m s called a radom matrx ( wth a ot m-dmesoal dstrbuto,
ECON 430 HG revsed Nov 06 Lecture Note to Rce Chapter 8 Radom matrces Let Y, =,,, m, =,,, be radom varables (r.v. s). The matrx Y Y Y Y Y Y Y Y Y Y = m m m s called a radom matrx ( wth a ot m-dmesoal dstrbuto,
Probability and Statistics. What is probability? What is statistics?
 robablt ad Statstcs What s robablt? What s statstcs? robablt ad Statstcs robablt Formall defed usg a set of aoms Seeks to determe the lkelhood that a gve evet or observato or measuremet wll or has haeed
robablt ad Statstcs What s robablt? What s statstcs? robablt ad Statstcs robablt Formall defed usg a set of aoms Seeks to determe the lkelhood that a gve evet or observato or measuremet wll or has haeed
Lecture 9: Tolerant Testing
 Lecture 9: Tolerat Testg Dael Kae Scrbe: Sakeerth Rao Aprl 4, 07 Abstract I ths lecture we prove a quas lear lower boud o the umber of samples eeded to do tolerat testg for L dstace. Tolerat Testg We have
Lecture 9: Tolerat Testg Dael Kae Scrbe: Sakeerth Rao Aprl 4, 07 Abstract I ths lecture we prove a quas lear lower boud o the umber of samples eeded to do tolerat testg for L dstace. Tolerat Testg We have
Lecture Notes Forecasting the process of estimating or predicting unknown situations
 Lecture Notes. Ecoomc Forecastg. Forecastg the process of estmatg or predctg ukow stuatos Eample usuall ecoomsts predct future ecoomc varables Forecastg apples to a varet of data () tme seres data predctg
Lecture Notes. Ecoomc Forecastg. Forecastg the process of estmatg or predctg ukow stuatos Eample usuall ecoomsts predct future ecoomc varables Forecastg apples to a varet of data () tme seres data predctg
CHAPTER VI Statistical Analysis of Experimental Data
 Chapter VI Statstcal Aalyss of Expermetal Data CHAPTER VI Statstcal Aalyss of Expermetal Data Measuremets do ot lead to a uque value. Ths s a result of the multtude of errors (maly radom errors) that ca
Chapter VI Statstcal Aalyss of Expermetal Data CHAPTER VI Statstcal Aalyss of Expermetal Data Measuremets do ot lead to a uque value. Ths s a result of the multtude of errors (maly radom errors) that ca
Bias Correction in Estimation of the Population Correlation Coefficient
 Kasetsart J. (Nat. Sc.) 47 : 453-459 (3) Bas Correcto Estmato of the opulato Correlato Coeffcet Juthaphor Ssomboothog ABSTRACT A estmator of the populato correlato coeffcet of two varables for a bvarate
Kasetsart J. (Nat. Sc.) 47 : 453-459 (3) Bas Correcto Estmato of the opulato Correlato Coeffcet Juthaphor Ssomboothog ABSTRACT A estmator of the populato correlato coeffcet of two varables for a bvarate
Continuous Random Variables: Conditioning, Expectation and Independence
 Cotuous Radom Varables: Codtog, xectato ad Ideedece Berl Che Deartmet o Comuter cece & Iormato geerg atoal Tawa ormal Uverst Reerece: - D.. Bertsekas, J.. Tstskls, Itroducto to robablt, ectos 3.4-3.5 Codtog
Cotuous Radom Varables: Codtog, xectato ad Ideedece Berl Che Deartmet o Comuter cece & Iormato geerg atoal Tawa ormal Uverst Reerece: - D.. Bertsekas, J.. Tstskls, Itroducto to robablt, ectos 3.4-3.5 Codtog
Simulation Output Analysis
 Smulato Output Aalyss Summary Examples Parameter Estmato Sample Mea ad Varace Pot ad Iterval Estmato ermatg ad o-ermatg Smulato Mea Square Errors Example: Sgle Server Queueg System x(t) S 4 S 4 S 3 S 5
Smulato Output Aalyss Summary Examples Parameter Estmato Sample Mea ad Varace Pot ad Iterval Estmato ermatg ad o-ermatg Smulato Mea Square Errors Example: Sgle Server Queueg System x(t) S 4 S 4 S 3 S 5
Maximum Likelihood Estimation
 Marquette Uverst Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Coprght 08 b Marquette Uverst Maxmum Lkelhood Estmato We have bee sag that ~
Marquette Uverst Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Coprght 08 b Marquette Uverst Maxmum Lkelhood Estmato We have bee sag that ~
Module 7. Lecture 7: Statistical parameter estimation
 Lecture 7: Statstcal parameter estmato Parameter Estmato Methods of Parameter Estmato 1) Method of Matchg Pots ) Method of Momets 3) Mamum Lkelhood method Populato Parameter Sample Parameter Ubased estmato
Lecture 7: Statstcal parameter estmato Parameter Estmato Methods of Parameter Estmato 1) Method of Matchg Pots ) Method of Momets 3) Mamum Lkelhood method Populato Parameter Sample Parameter Ubased estmato
Comparison of Parameters of Lognormal Distribution Based On the Classical and Posterior Estimates
 Joural of Moder Appled Statstcal Methods Volume Issue Artcle 8 --03 Comparso of Parameters of Logormal Dstrbuto Based O the Classcal ad Posteror Estmates Raja Sulta Uversty of Kashmr, Sragar, Ida, hamzasulta8@yahoo.com
Joural of Moder Appled Statstcal Methods Volume Issue Artcle 8 --03 Comparso of Parameters of Logormal Dstrbuto Based O the Classcal ad Posteror Estmates Raja Sulta Uversty of Kashmr, Sragar, Ida, hamzasulta8@yahoo.com
ECONOMETRIC THEORY. MODULE VIII Lecture - 26 Heteroskedasticity
 ECONOMETRIC THEORY MODULE VIII Lecture - 6 Heteroskedastcty Dr. Shalabh Departmet of Mathematcs ad Statstcs Ida Isttute of Techology Kapur . Breusch Paga test Ths test ca be appled whe the replcated data
ECONOMETRIC THEORY MODULE VIII Lecture - 6 Heteroskedastcty Dr. Shalabh Departmet of Mathematcs ad Statstcs Ida Isttute of Techology Kapur . Breusch Paga test Ths test ca be appled whe the replcated data
Chapter 4 Multiple Random Variables
 Revew for the prevous lecture: Theorems ad Examples: How to obta the pmf (pdf) of U = g (, Y) ad V = g (, Y) Chapter 4 Multple Radom Varables Chapter 44 Herarchcal Models ad Mxture Dstrbutos Examples:
Revew for the prevous lecture: Theorems ad Examples: How to obta the pmf (pdf) of U = g (, Y) ad V = g (, Y) Chapter 4 Multple Radom Varables Chapter 44 Herarchcal Models ad Mxture Dstrbutos Examples:
best estimate (mean) for X uncertainty or error in the measurement (systematic, random or statistical) best
 Error Aalyss Preamble Wheever a measuremet s made, the result followg from that measuremet s always subject to ucertaty The ucertaty ca be reduced by makg several measuremets of the same quatty or by mprovg
Error Aalyss Preamble Wheever a measuremet s made, the result followg from that measuremet s always subject to ucertaty The ucertaty ca be reduced by makg several measuremets of the same quatty or by mprovg
Estimation of Stress- Strength Reliability model using finite mixture of exponential distributions
 Iteratoal Joural of Computatoal Egeerg Research Vol, 0 Issue, Estmato of Stress- Stregth Relablty model usg fte mxture of expoetal dstrbutos K.Sadhya, T.S.Umamaheswar Departmet of Mathematcs, Lal Bhadur
Iteratoal Joural of Computatoal Egeerg Research Vol, 0 Issue, Estmato of Stress- Stregth Relablty model usg fte mxture of expoetal dstrbutos K.Sadhya, T.S.Umamaheswar Departmet of Mathematcs, Lal Bhadur
Chapter 3 Experimental Design Models
 Chater 3 Exermetal Desg Models We cosder the models whch are used desgg a exermet. The exermetal codtos, exermetal setu ad the obectve of the study essetally determe that what tye of desg s to be used
Chater 3 Exermetal Desg Models We cosder the models whch are used desgg a exermet. The exermetal codtos, exermetal setu ad the obectve of the study essetally determe that what tye of desg s to be used
ESS Line Fitting
 ESS 5 014 17. Le Fttg A very commo problem data aalyss s lookg for relatoshpetwee dfferet parameters ad fttg les or surfaces to data. The smplest example s fttg a straght le ad we wll dscuss that here
ESS 5 014 17. Le Fttg A very commo problem data aalyss s lookg for relatoshpetwee dfferet parameters ad fttg les or surfaces to data. The smplest example s fttg a straght le ad we wll dscuss that here
Introduction to local (nonparametric) density estimation. methods
 Itroducto to local (oparametrc) desty estmato methods A slecture by Yu Lu for ECE 66 Sprg 014 1. Itroducto Ths slecture troduces two local desty estmato methods whch are Parze desty estmato ad k-earest
Itroducto to local (oparametrc) desty estmato methods A slecture by Yu Lu for ECE 66 Sprg 014 1. Itroducto Ths slecture troduces two local desty estmato methods whch are Parze desty estmato ad k-earest
Functions of Random Variables
 Fuctos of Radom Varables Chapter Fve Fuctos of Radom Varables 5. Itroducto A geeral egeerg aalyss model s show Fg. 5.. The model output (respose) cotas the performaces of a system or product, such as weght,
Fuctos of Radom Varables Chapter Fve Fuctos of Radom Varables 5. Itroducto A geeral egeerg aalyss model s show Fg. 5.. The model output (respose) cotas the performaces of a system or product, such as weght,
Generative classification models
 CS 75 Mache Learg Lecture Geeratve classfcato models Mlos Hauskrecht mlos@cs.ptt.edu 539 Seott Square Data: D { d, d,.., d} d, Classfcato represets a dscrete class value Goal: lear f : X Y Bar classfcato
CS 75 Mache Learg Lecture Geeratve classfcato models Mlos Hauskrecht mlos@cs.ptt.edu 539 Seott Square Data: D { d, d,.., d} d, Classfcato represets a dscrete class value Goal: lear f : X Y Bar classfcato
Some Statistical Inferences on the Records Weibull Distribution Using Shannon Entropy and Renyi Entropy
 OPEN ACCESS Coferece Proceedgs Paper Etropy www.scforum.et/coferece/ecea- Some Statstcal Ifereces o the Records Webull Dstrbuto Usg Shao Etropy ad Rey Etropy Gholamhosse Yar, Rezva Rezae * School of Mathematcs,
OPEN ACCESS Coferece Proceedgs Paper Etropy www.scforum.et/coferece/ecea- Some Statstcal Ifereces o the Records Webull Dstrbuto Usg Shao Etropy ad Rey Etropy Gholamhosse Yar, Rezva Rezae * School of Mathematcs,
Entropy, Relative Entropy and Mutual Information
 Etro Relatve Etro ad Mutual Iformato rof. Ja-Lg Wu Deartmet of Comuter Scece ad Iformato Egeerg Natoal Tawa Uverst Defto: The Etro of a dscrete radom varable s defed b : base : 0 0 0 as bts 0 : addg terms
Etro Relatve Etro ad Mutual Iformato rof. Ja-Lg Wu Deartmet of Comuter Scece ad Iformato Egeerg Natoal Tawa Uverst Defto: The Etro of a dscrete radom varable s defed b : base : 0 0 0 as bts 0 : addg terms
9 U-STATISTICS. Eh =(m!) 1 Eh(X (1),..., X (m ) ) i.i.d
 9 U-STATISTICS Suppose,,..., are P P..d. wth CDF F. Our goal s to estmate the expectato t (P)=Eh(,,..., m ). Note that ths expectato requres more tha oe cotrast to E, E, or Eh( ). Oe example s E or P((,
9 U-STATISTICS Suppose,,..., are P P..d. wth CDF F. Our goal s to estmate the expectato t (P)=Eh(,,..., m ). Note that ths expectato requres more tha oe cotrast to E, E, or Eh( ). Oe example s E or P((,
THE ROYAL STATISTICAL SOCIETY GRADUATE DIPLOMA
 THE ROYAL STATISTICAL SOCIETY EXAMINATIONS SOLUTIONS GRADUATE DIPLOMA PAPER II STATISTICAL THEORY & METHODS The Socety provdes these solutos to assst caddates preparg for the examatos future years ad for
THE ROYAL STATISTICAL SOCIETY EXAMINATIONS SOLUTIONS GRADUATE DIPLOMA PAPER II STATISTICAL THEORY & METHODS The Socety provdes these solutos to assst caddates preparg for the examatos future years ad for
Bayes (Naïve or not) Classifiers: Generative Approach
 Logstc regresso Bayes (Naïve or ot) Classfers: Geeratve Approach What do we mea by Geeratve approach: Lear p(y), p(x y) ad the apply bayes rule to compute p(y x) for makg predctos Ths s essetally makg
Logstc regresso Bayes (Naïve or ot) Classfers: Geeratve Approach What do we mea by Geeratve approach: Lear p(y), p(x y) ad the apply bayes rule to compute p(y x) for makg predctos Ths s essetally makg
Bayes Interval Estimation for binomial proportion and difference of two binomial proportions with Simulation Study
 IJIEST Iteratoal Joural of Iovatve Scece, Egeerg & Techology, Vol. Issue 5, July 04. Bayes Iterval Estmato for bomal proporto ad dfferece of two bomal proportos wth Smulato Study Masoud Gaj, Solmaz hlmad
IJIEST Iteratoal Joural of Iovatve Scece, Egeerg & Techology, Vol. Issue 5, July 04. Bayes Iterval Estmato for bomal proporto ad dfferece of two bomal proportos wth Smulato Study Masoud Gaj, Solmaz hlmad
Midterm Exam 1, section 1 (Solution) Thursday, February hour, 15 minutes
 coometrcs, CON Sa Fracsco State Uversty Mchael Bar Sprg 5 Mdterm am, secto Soluto Thursday, February 6 hour, 5 mutes Name: Istructos. Ths s closed book, closed otes eam.. No calculators of ay kd are allowed..
coometrcs, CON Sa Fracsco State Uversty Mchael Bar Sprg 5 Mdterm am, secto Soluto Thursday, February 6 hour, 5 mutes Name: Istructos. Ths s closed book, closed otes eam.. No calculators of ay kd are allowed..
Parameter, Statistic and Random Samples
 Parameter, Statstc ad Radom Samples A parameter s a umber that descrbes the populato. It s a fxed umber, but practce we do ot kow ts value. A statstc s a fucto of the sample data,.e., t s a quatty whose
Parameter, Statstc ad Radom Samples A parameter s a umber that descrbes the populato. It s a fxed umber, but practce we do ot kow ts value. A statstc s a fucto of the sample data,.e., t s a quatty whose
Linear Regression with One Regressor
 Lear Regresso wth Oe Regressor AIM QA.7. Expla how regresso aalyss ecoometrcs measures the relatoshp betwee depedet ad depedet varables. A regresso aalyss has the goal of measurg how chages oe varable,
Lear Regresso wth Oe Regressor AIM QA.7. Expla how regresso aalyss ecoometrcs measures the relatoshp betwee depedet ad depedet varables. A regresso aalyss has the goal of measurg how chages oe varable,
Estimation of the Loss and Risk Functions of Parameter of Maxwell Distribution
 Scece Joural of Appled Mathematcs ad Statstcs 06; 4(4): 9- http://www.scecepublshggroup.com/j/sjams do: 0.648/j.sjams.060404. ISSN: 76-949 (Prt); ISSN: 76-95 (Ole) Estmato of the Loss ad Rsk Fuctos of
Scece Joural of Appled Mathematcs ad Statstcs 06; 4(4): 9- http://www.scecepublshggroup.com/j/sjams do: 0.648/j.sjams.060404. ISSN: 76-949 (Prt); ISSN: 76-95 (Ole) Estmato of the Loss ad Rsk Fuctos of
STA 108 Applied Linear Models: Regression Analysis Spring Solution for Homework #1
 STA 08 Appled Lear Models: Regresso Aalyss Sprg 0 Soluto for Homework #. Let Y the dollar cost per year, X the umber of vsts per year. The the mathematcal relato betwee X ad Y s: Y 300 + X. Ths s a fuctoal
STA 08 Appled Lear Models: Regresso Aalyss Sprg 0 Soluto for Homework #. Let Y the dollar cost per year, X the umber of vsts per year. The the mathematcal relato betwee X ad Y s: Y 300 + X. Ths s a fuctoal
Chapter 3 Sampling For Proportions and Percentages
 Chapter 3 Samplg For Proportos ad Percetages I may stuatos, the characterstc uder study o whch the observatos are collected are qualtatve ature For example, the resposes of customers may marketg surveys
Chapter 3 Samplg For Proportos ad Percetages I may stuatos, the characterstc uder study o whch the observatos are collected are qualtatve ature For example, the resposes of customers may marketg surveys
Application of Calibration Approach for Regression Coefficient Estimation under Two-stage Sampling Design
 Authors: Pradp Basak, Kaustav Adtya, Hukum Chadra ad U.C. Sud Applcato of Calbrato Approach for Regresso Coeffcet Estmato uder Two-stage Samplg Desg Pradp Basak, Kaustav Adtya, Hukum Chadra ad U.C. Sud
Authors: Pradp Basak, Kaustav Adtya, Hukum Chadra ad U.C. Sud Applcato of Calbrato Approach for Regresso Coeffcet Estmato uder Two-stage Samplg Desg Pradp Basak, Kaustav Adtya, Hukum Chadra ad U.C. Sud
Chapter 2 General Linear Hypothesis and Analysis of Variance
 Chater Geeral Lear Hyothess ad Aalyss of Varace Regresso model for the geeral lear hyothess Let Y, Y,..., Y be a seuece of deedet radom varables assocated wth resoses. The we ca wrte t as EY ( ) = β x,
Chater Geeral Lear Hyothess ad Aalyss of Varace Regresso model for the geeral lear hyothess Let Y, Y,..., Y be a seuece of deedet radom varables assocated wth resoses. The we ca wrte t as EY ( ) = β x,
Mean is only appropriate for interval or ratio scales, not ordinal or nominal.
 Mea Same as ordary average Sum all the data values ad dvde by the sample sze. x = ( x + x +... + x Usg summato otato, we wrte ths as x = x = x = = ) x Mea s oly approprate for terval or rato scales, ot
Mea Same as ordary average Sum all the data values ad dvde by the sample sze. x = ( x + x +... + x Usg summato otato, we wrte ths as x = x = x = = ) x Mea s oly approprate for terval or rato scales, ot
CHAPTER 3 POSTERIOR DISTRIBUTIONS
 CHAPTER 3 POSTERIOR DISTRIBUTIONS If scece caot measure the degree of probablt volved, so much the worse for scece. The practcal ma wll stck to hs apprecatve methods utl t does, or wll accept the results
CHAPTER 3 POSTERIOR DISTRIBUTIONS If scece caot measure the degree of probablt volved, so much the worse for scece. The practcal ma wll stck to hs apprecatve methods utl t does, or wll accept the results
Solving Constrained Flow-Shop Scheduling. Problems with Three Machines
 It J Cotemp Math Sceces, Vol 5, 2010, o 19, 921-929 Solvg Costraed Flow-Shop Schedulg Problems wth Three Maches P Pada ad P Rajedra Departmet of Mathematcs, School of Advaced Sceces, VIT Uversty, Vellore-632
It J Cotemp Math Sceces, Vol 5, 2010, o 19, 921-929 Solvg Costraed Flow-Shop Schedulg Problems wth Three Maches P Pada ad P Rajedra Departmet of Mathematcs, School of Advaced Sceces, VIT Uversty, Vellore-632
Sampling Theory MODULE X LECTURE - 35 TWO STAGE SAMPLING (SUB SAMPLING)
 Samplg Theory ODULE X LECTURE - 35 TWO STAGE SAPLIG (SUB SAPLIG) DR SHALABH DEPARTET OF ATHEATICS AD STATISTICS IDIA ISTITUTE OF TECHOLOG KAPUR Two stage samplg wth uequal frst stage uts: Cosder two stage
Samplg Theory ODULE X LECTURE - 35 TWO STAGE SAPLIG (SUB SAPLIG) DR SHALABH DEPARTET OF ATHEATICS AD STATISTICS IDIA ISTITUTE OF TECHOLOG KAPUR Two stage samplg wth uequal frst stage uts: Cosder two stage
Chapter 13, Part A Analysis of Variance and Experimental Design. Introduction to Analysis of Variance. Introduction to Analysis of Variance
 Chapter, Part A Aalyss of Varace ad Epermetal Desg Itroducto to Aalyss of Varace Aalyss of Varace: Testg for the Equalty of Populato Meas Multple Comparso Procedures Itroducto to Aalyss of Varace Aalyss
Chapter, Part A Aalyss of Varace ad Epermetal Desg Itroducto to Aalyss of Varace Aalyss of Varace: Testg for the Equalty of Populato Meas Multple Comparso Procedures Itroducto to Aalyss of Varace Aalyss
Recursive linear estimation for discrete time systems in the presence of different multiplicative observation noises
 Recursve lear estmato for dscrete tme systems the resece of dfferet multlcatve observato oses C. Sáchez Gozález,*,.M. García Muñoz Deartameto de Métodos Cuattatvos ara la Ecoomía y la Emresa, Facultad
Recursve lear estmato for dscrete tme systems the resece of dfferet multlcatve observato oses C. Sáchez Gozález,*,.M. García Muñoz Deartameto de Métodos Cuattatvos ara la Ecoomía y la Emresa, Facultad
Lecture 02: Bounding tail distributions of a random variable
 CSCI-B609: A Theorst s Toolkt, Fall 206 Aug 25 Lecture 02: Boudg tal dstrbutos of a radom varable Lecturer: Yua Zhou Scrbe: Yua Xe & Yua Zhou Let us cosder the ubased co flps aga. I.e. let the outcome
CSCI-B609: A Theorst s Toolkt, Fall 206 Aug 25 Lecture 02: Boudg tal dstrbutos of a radom varable Lecturer: Yua Zhou Scrbe: Yua Xe & Yua Zhou Let us cosder the ubased co flps aga. I.e. let the outcome
Objectives of Multiple Regression
 Obectves of Multple Regresso Establsh the lear equato that best predcts values of a depedet varable Y usg more tha oe eplaator varable from a large set of potetal predctors {,,... k }. Fd that subset of
Obectves of Multple Regresso Establsh the lear equato that best predcts values of a depedet varable Y usg more tha oe eplaator varable from a large set of potetal predctors {,,... k }. Fd that subset of
Summary of the lecture in Biostatistics
 Summary of the lecture Bostatstcs Probablty Desty Fucto For a cotuos radom varable, a probablty desty fucto s a fucto such that: 0 dx a b) b a dx A probablty desty fucto provdes a smple descrpto of the
Summary of the lecture Bostatstcs Probablty Desty Fucto For a cotuos radom varable, a probablty desty fucto s a fucto such that: 0 dx a b) b a dx A probablty desty fucto provdes a smple descrpto of the
Midterm Exam 1, section 2 (Solution) Thursday, February hour, 15 minutes
 coometrcs, CON Sa Fracsco State Uverst Mchael Bar Sprg 5 Mdterm xam, secto Soluto Thursda, Februar 6 hour, 5 mutes Name: Istructos. Ths s closed book, closed otes exam.. No calculators of a kd are allowed..
coometrcs, CON Sa Fracsco State Uverst Mchael Bar Sprg 5 Mdterm xam, secto Soluto Thursda, Februar 6 hour, 5 mutes Name: Istructos. Ths s closed book, closed otes exam.. No calculators of a kd are allowed..
Chain Rules for Entropy
 Cha Rules for Etroy The etroy of a collecto of radom varables s the sum of codtoal etroes. Theorem: Let be radom varables havg the mass robablty x x.x. The...... The roof s obtaed by reeatg the alcato
Cha Rules for Etroy The etroy of a collecto of radom varables s the sum of codtoal etroes. Theorem: Let be radom varables havg the mass robablty x x.x. The...... The roof s obtaed by reeatg the alcato
{ }{ ( )} (, ) = ( ) ( ) ( ) Chapter 14 Exercises in Sampling Theory. Exercise 1 (Simple random sampling): Solution:
 Chapter 4 Exercses Samplg Theory Exercse (Smple radom samplg: Let there be two correlated radom varables X ad A sample of sze s draw from a populato by smple radom samplg wthout replacemet The observed
Chapter 4 Exercses Samplg Theory Exercse (Smple radom samplg: Let there be two correlated radom varables X ad A sample of sze s draw from a populato by smple radom samplg wthout replacemet The observed
Simple Linear Regression
 Statstcal Methods I (EST 75) Page 139 Smple Lear Regresso Smple regresso applcatos are used to ft a model descrbg a lear relatoshp betwee two varables. The aspects of least squares regresso ad correlato
Statstcal Methods I (EST 75) Page 139 Smple Lear Regresso Smple regresso applcatos are used to ft a model descrbg a lear relatoshp betwee two varables. The aspects of least squares regresso ad correlato
9.1 Introduction to the probit and logit models
 EC3000 Ecoometrcs Lecture 9 Probt & Logt Aalss 9. Itroducto to the probt ad logt models 9. The logt model 9.3 The probt model Appedx 9. Itroducto to the probt ad logt models These models are used regressos
EC3000 Ecoometrcs Lecture 9 Probt & Logt Aalss 9. Itroducto to the probt ad logt models 9. The logt model 9.3 The probt model Appedx 9. Itroducto to the probt ad logt models These models are used regressos
Overview. Basic concepts of Bayesian learning. Most probable model given data Coin tosses Linear regression Logistic regression
 Overvew Basc cocepts of Bayesa learg Most probable model gve data Co tosses Lear regresso Logstc regresso Bayesa predctos Co tosses Lear regresso 30 Recap: regresso problems Iput to learg problem: trag
Overvew Basc cocepts of Bayesa learg Most probable model gve data Co tosses Lear regresso Logstc regresso Bayesa predctos Co tosses Lear regresso 30 Recap: regresso problems Iput to learg problem: trag
Channel Models with Memory. Channel Models with Memory. Channel Models with Memory. Channel Models with Memory
 Chael Models wth Memory Chael Models wth Memory Hayder radha Electrcal ad Comuter Egeerg Mchga State Uversty I may ractcal etworkg scearos (cludg the Iteret ad wreless etworks), the uderlyg chaels are
Chael Models wth Memory Chael Models wth Memory Hayder radha Electrcal ad Comuter Egeerg Mchga State Uversty I may ractcal etworkg scearos (cludg the Iteret ad wreless etworks), the uderlyg chaels are
