Entropy, Relative Entropy and Mutual Information
|
|
|
- Hubert Patrick
- 6 years ago
- Views:
Transcription
1 Etro Relatve Etro ad Mutual Iformato rof. Ja-Lg Wu Deartmet of Comuter Scece ad Iformato Egeerg Natoal Tawa Uverst
2 Defto: The Etro of a dscrete radom varable s defed b : base : as bts 0 : addg terms of zero robablt chage the etro does ot Iformato Theor
3 Note that etro s a fucto of the dstrbuto of. It does ot deed o the actual values take b the r.v. but ol o the robabltes. If s wrtte as the the eected E g Eg Eectato value g value of the r. v. g Remark : The etro of the eected value of E Self-formato Iformato Theor 3
4 Lemma.: 0 Lemma.: b = b a a E: 0 0 def = bts whe =/ s a cocave fucto of 3 =0 f =0 or 4 ma occurs whe =/ Iformato Theor 4
5 Iformato Theor 5 Jot Etro ad Codtoal Etro Defto: The jot etro of a ar of dscrete radom varables wth a jot dstrbuto s defed as Defto: The codtoal etro s defed as E or as defed s E
6 Iformato Theor 6 Theorem. Cha Rule: or euvaletl we ca wrte : f
7 Corollar: Z = Z + Z Remark: II = Iformato Theor 7
8 Relatve Etro ad Mutual Iformato The etro of a radom varable s a measure of the ucertat of the radom varable; t s a measure of the amout of formato reured o the average to descrbe the radom varable. The relatve etro s a measure of the dstace betwee two dstrbutos. I statstcs t arses as a eected arthm of the lkelhood rato. The relatve etro D s a measure of the effcec of assumg that the dstrbuto s whe the true dstrbuto s. Iformato Theor 8
9 E: If we kew the true dstrbuto of the r.v. the we could costruct a code wth average descrto legth. If stead we used the code for a dstrbuto we would eed +D bts o the average to descrbe the r.v.. Iformato Theor 9
10 Iformato Theor 0 Defto: The relatve etro or Kullback Lebler dstace betwee two robablt mass fuctos ad s defes as E E E E D
11 Iformato Theor Defto: Cosder two r.v. s ad wth a jot robablt mass fucto ad margal robablt mass fuctos ad. The mutual formato I; s the relatve etro betwee the jot dstrbuto ad the roduct dstrbuto.e. ; E D I
12 E: Let = {0 } ad cosder two dstrbutos ad o. Let 0=-r =r ad let 0=-s =s. The ad D If r=s the D=D=0 Whle geeral D r s r s s r r s DD r s s r Iformato Theor
13 Iformato Theor 3 Relatosh betwee Etro ad Mutual Iformato Rewrte I; as ; I
14 Thus the mutual formato I; s the reducto the ucertat of due to the kowledge of. B smmetr t follows that I; = sas much about as sas about Sce = + I; = + I; = = The mutual formato of a r.v. wth tself s the etro of the r.v. etro : self-formato Iformato Theor 4
15 Theorem: Mutual formato ad etro:. I; = = = +. I; = I;. I; = I; Iformato Theor 5
16 Cha Rules for Etro Relatve Etro ad Mutual Iformato Theorem: Cha rule for etro Let be draw accordg to. The Iformato Theor 6
17 Iformato Theor 7 roof 3 3 3
18 Iformato Theor 8 We wrte the
19 Iformato Theor 9 Defto: The codtoal mutual formato of rv s. ad gve Z s defed b ; Z Z Z E Z Z Z I z
20 Iformato Theor 0 Theorem: cha rule for mutual-formato roof: I I ; ; I I ; ;
21 Defto: The codtoal relatve etro D s the average of the relatve etroes betwee the codtoal robablt mass fuctos ad averaged over the robablt mass fucto. D E Theorem: Cha rule for relatve etro D = D+ D Iformato Theor
22 Jese s Ieualt ad Its Coseueces Defto: A fucto s sad to be cove over a terval ab f for ever ab ad 0 f +- f +-f A fucto f s sad to be strctl cove f eualt holds ol f =0 or =. Defto: A fucto s cocave f f s cove. E: cove fuctos: e for 0 cocave fuctos: / for 0 both cove ad cocave: a+b; lear fuctos Iformato Theor
23 Theorem: If the fucto f has a secod dervatve whch s o-egatve ostve everwhere the the fucto s cove strctl cove. E E d : : dscrete case cotuous case Iformato Theor 3
24 Iformato Theor 4 Theorem : Jese s eualt: If f s cove fucto ad s a radom varable the Ef fe. roof: For a two mass ot dstrbuto the eualt becomes f + f f + + = whch follows drectl from the defto of cove fuctos. Suose the theorem s true for dstrbutos wth K- mass ots. The wrtg = /- K for = K- we have The roof ca be eteded to cotuous dstrbutos b cotut argumets. Mathematcal Iducto k k k k k k k k k k k k k k k k k k k k k k k f f f f f f f f f f
25 Iformato Theor 5 Theorem: Iformato eualt: Let be two robablt mass fuctos. The D 0 wth eualt ff = for all. roof: Let A={:>0} be the suort set of. The 0 cocave t s A A A A E E D
26 Corollar: No-egatvt of mutual formato: For a two rv s. I; 0 wth eualt ff ad are deedet. roof: Corollar: I; = D 0 wth eualt ff =.e. ad are deedet D 0 wth eualt ff = for all ad wth >0. Corollar: I;Z 0 wth eualt ff ad are codtoar deedet gve Z. Iformato Theor 6
27 Theorem: where deotes the umber of elemets the rage of wth eualt ff has a uform dstrbuto over. roof: Let u=/ be the uform robablt mass fucto over ad let be the robablt mass fucto for. The D u ece b theo - egatvt of 0 D u u relatve etro Iformato Theor 7
28 Theorem: codtog reduces etro: wth eualt ff ad are deedet. roof: 0 I;= Note that ths s true ol o the average; secfcall = ma be greater tha or less tha or eual to but o the average = =. Iformato Theor 8
29 E: Let have the followg jot dstrbuto 0 3/4 /8 /8 The =/8 7/8=0.544 bts ==0 bts == bts > owever = 3/4 =+/4 = = 0.5 bts < Iformato Theor 9
30 Theorem: Ideedece boud o etro: Let be draw accordg to. The wth eualt ff the are deedet. roof: B the cha rule for etroes wth eualt ff the s are deedet. Iformato Theor 30
31 The LOG SUM INEQUALIT AND ITS ALICATIONS Theorem: Log sum eualt For o-egatve umbers a a a ad b b.. b a a b wth eualt ff a /b = costat. some covetos : a a b 0 a a 0 f a 0 Iformato Theor 3
32 Iformato Theor 3 roof: Assume w.l.o.g that a >0 ad b >0. The fucto ft=tt s strctl cove sce for all ostve t. ece b Jese s eualt we have whch s the sum eualt. 0 " e t t f b a a b a a b b a b a b a b a b b b a b b b a b b b a b a b b b a t b b t f t f 0 ote that we obta ad.settg 0 for
33 Rerovg the theorem that D 0 wth eualt ff = D 0 from - sum eualt wth eualt ff /=c. Sce both ad are robablt mass fuctos c= =. Iformato Theor 33
34 Iformato Theor 34 Theorem: D s cove the ar.e. f ad are two ars of robablt mass fuctos the roof: 0 all for D D D D D b a a b a a the b b a a Let D -sum
35 Theorem: cocavt of etro: s a cocave fucto of. That s: λ +-λ λ +-λ roof: = Du where u s the uform dstrbuto o outcomes. The cocavt of the follows drectl from the covet of D. Iformato Theor 35
36 Theorem: Let ~ =. The mutual formato I; s a cocave fucto of for fed a cove fucto of for fed. roof: I;=-= = f s fed the s a lear fucto of. = = ece whch s a cocave fucto of s a cocave fucto of. The secod term of s a lear fucto of. ece the dfferece s a cocave fucto of. Iformato Theor 36
37 We f ad cosder two dfferet codtoal dstrbutos ad. The corresodg jot dstrbutos are = ad = ad ther resectve margals are ad. Cosder a codtoal dstrbuto = +- that s a mture of ad. The corresodg jot dstrbuto s also a mture of the corresodg jot dstrbutos whe s fed s lear wth = +- ad the dstrbuto of s also a mture = +-. ece f we let = = +-. The roduct of the margal dstrbutos s also lear wth whe s fed. I; = D cove of the mutual formato s a cove fucto of the codtoal dstrbuto. Therefore the covet of I; s the same as that of the D w.r.t. whe s fed. Iformato Theor 37
38 Data rocessg eualt: No clever maulato of the data ca mrove the fereces that ca be made from the data Defto: Rv s. Z are sad to form a Markov cha that order deoted b Z f the codtoal dstrbuto of Z deeds ol o ad s codtoall deedet of. That s Z form a Markov cha the z=z z=z : ad Z are codtoall deedet gve Z mles that Z If Z=f the Z Iformato Theor 38
39 Theorem: Data rocessg eualt f Z the I; I;Z No rocessg of determstc or radom ca crease the formato that cotas about. roof: I;Z = I;Z + I;Z : cha rule = I; + I;Z : cha rule Sce ad Z are deedet gve we have I;Z=0. Sce I;Z0 we have I;I;Z wth eualt ff I;Z=0.e. Z forms a Markov cha. Smlarl oe ca rove I;ZI;Z. Iformato Theor 39
40 Corollar: If Z forms a Markov cha ad f Z=g we have I;I;g : fuctos of the data caot crease the formato about. Corollar: If Z the I;ZI; roof: I;Z=I;Z+I;Z =I;+I;Z B Markovt I;Z=0 ad I;Z 0 I;ZI; The deedece of ad s decreased or remas uchaged b the observato of a dowstream r.v. Z. Iformato Theor 40
41 Note that t s ossble that I;Z>I; whe ad Z do ot form a Markov cha. E: Let ad be deedet far bar rv s ad let Z=+. The I;=0 but I;Z =Z Z =Z =Z=Z==/ bt. Iformato Theor 4
42 Fao s eualt: Fao s eualt relates the robablt of error guessg the r.v. to ts codtoal etro. Note that: The codtoal etro of a r.v. gve aother radom varable s zero ff s a fucto of. roof: W =0 mles there s o ucertat about f we kow for all wth >0 there s ol oe ossble value of wth >0 we ca estmate from wth zero robablt of error ff =0. we eect to be able to estmate wth a low robablt of error ol f the codtoal etro s small. Fao s eualt uatfes ths dea. Iformato Theor 4
43 Suose we wsh to estmate a r.v. wth a dstrbuto. We observe a r.v. whch s related to b the codtoal dstrbuto. From we calculate a fucto whch s a estmate of. We wsh to boud the robablt that. We observe that forms a Markov cha. Defe the robablt of error e r r g g Iformato Theor 43
44 Theorem: Fao s eualt For a estmator such that wth e = r we have e + e - Ths eualt ca be weakeed to or + e e Remark: e = 0 = 0 ^ ^ ^ e E: bar r.v. - Iformato Theor 44
45 roof: Defe a error rv. f E 0 f B the cha rule for etroes we have E ^ = ^ + E ^ ^ =0 =E + E e ^ e - Sce codtog reduces etro E E= e. Now sce E s a fucto of ad ^ E=0. ^ Sce E s a bar-valued r.v. E= e. The remag term E ^ ca be bouded as follows: E ^ = r E=0E=0+ ^ r E=E= ^ - e 0 + e - ^ Iformato Theor 45
46 ^ Sce gve E=0 = ad gve E= we ca uer boud the codtoal etro b the of the umber of remag outcomes -. e + e. ^ B the data rocessg eualt we have I; I; ^ sce ^ ad therefore ^. Thus we have e + e ^. Remark: Suose there s o kowledge of. Thus must be guessed wthout a formato. Let { m} ^ ad m. The the best guess of s = ad the resultg robablt of error s e = -. Fao s eualt becomes e + e m- The robablt mass fucto m = - e e /m- e /m- acheves ths boud wth eualt. Iformato Theor 46
47 Some roertes of the Relatve Etro. Let ad be two robablt dstrbutos o the state sace of a Markov cha at tme ad let + ad + be the corresodg dstrbutos at tme +. Let the corresodg jot mass fucto be deoted b ad. That s + = r + + = r + where r s the robablt trasto fucto for the Markov cha. Iformato Theor 47
48 The b the cha rule for relatve etro we have the followg two easos: D + + = D + D + + = D D + + Sce both ad are derved from the same Markov cha so + = + = r + ad hece D + + = 0 Iformato Theor 48
49 That s D = D D + + Sce D D D + + or D D + + Cocluso: The dstace betwee the robablt mass fuctos s decreasg wth tme for a Markov cha. Iformato Theor 49
50 . Relatve etro D betwee a dstrbuto o the states at tme ad a statoar dstrbuto decreases wth. I the last euato f we let be a statoar dstrbuto the + s the same statoar dstrbuto. ece D D + A state dstrbuto gets closer ad closer to each statoar dstrbuto as tme asses. D 0 lm Iformato Theor 50
51 3. Def:A robablt trasto matr [ j ] j = r { + =j =} s called doubl stochastc f j = = j= ad j j = = j= The uform dstrbuto s a statoar dstrbuto of ff the robablt trasto matr s doubl stochastc. Iformato Theor 5
52 4. The codtoal etro crease wth for a statoar Markov rocess. If the Markov rocess s statoar the s costat. So the etro s o-creasg. owever t ca be roved that creases wth. Ths mles that: the codtoal ucertat of the future creases. roof: codtog reduces etro = b Markovt = - b statoart Smlarl: 0 s creasg for a Markov cha. Iformato Theor 5
53 Suffcet Statstcs Suose we have a faml of robablt mass fucto {f } deed b ad let be a samle from a dstrbuto ths faml. Let T be a statstc fucto of the samle lke the samle mea or samle varace. The T Ad b the data rocessg eualt we have I;T I; for a dstrbuto o. owever f eualt holds o formato s lost. A statstc T s called suffcet for f t cotas all the formato about. Iformato Theor 53
54 Def: A fucto T s sad to be a suffcet statstc relatve to the faml {f } f s deedet of gve T.e. T forms a Markov cha. or: I; = I; T for all dstrbutos o Suffcet statstcs reserve mutual formato. Iformato Theor 54
55 Some eamles of Suffcet Statstcs. Let be a..d. seuece of co tosses of a co wth ukow arameter θ r. Gve the umber of s s a suffcet statstcs for θ. ere {0} T Gve T all seueces havg that ma s are euall lkel ad deedet of the arameter θ.. Iformato Theor 55
56 Iformato Theor r for statstcs suffcet a s T ad Thus otherwse k f k k
57 . If s ormall dstrbuted wth mea θ ad varace ; that s f f e N ad are draw deedetl accordg to a suffcet statstc for θ s the samle mea. Ths ca be verfed that s deedet of θ. f Iformato Theor 57
58 The mmal suffcet statstcs s a suffcet statstcs that s a fucto of all other suffcet statstcs. Def: A statc T s a mmal suffcet statstc related to f f t s a fucto of ever other suffcet statstc U : T U ece a mmal suffcet statstc mamall comresses the formato about θ the samle. Other suffcet statstcs ma cota addtoal rrelevat formato. The suffcet statstcs of the above eamles are mmal. Iformato Theor 58
59 Shuffles crease Etro: If T s a shuffle ermutato of a deck of cards ad s the tal radom osto of the cards the deck ad f the choce of the shuffle T s deedet of the T where T s the ermutato of the deck duced b the shuffle T o the tal ermutato. roof: T TT = T - TT wh? = T = f ad T are deedet! Iformato Theor 59
60 If ad are..d. wth etro the r = - wth eualt ff has a uform dstrbuto. f: suose ~. B Jese s eualt we have E E whch mles that - = = = r = Let ad be two..d. rv s wth etro. The rob. at = s gve b r = = Let be deedet wth ~ ~r The r = --Dr r = -r-dr *Notce that the fucto f= s cove f: --Dr = + r/ = r r = r = r = Iformato Theor 60
Chain Rules for Entropy
 Cha Rules for Etroy The etroy of a collecto of radom varables s the sum of codtoal etroes. Theorem: Let be radom varables havg the mass robablty x x.x. The...... The roof s obtaed by reeatg the alcato
Cha Rules for Etroy The etroy of a collecto of radom varables s the sum of codtoal etroes. Theorem: Let be radom varables havg the mass robablty x x.x. The...... The roof s obtaed by reeatg the alcato
Probability and Statistics. What is probability? What is statistics?
 robablt ad Statstcs What s robablt? What s statstcs? robablt ad Statstcs robablt Formall defed usg a set of aoms Seeks to determe the lkelhood that a gve evet or observato or measuremet wll or has haeed
robablt ad Statstcs What s robablt? What s statstcs? robablt ad Statstcs robablt Formall defed usg a set of aoms Seeks to determe the lkelhood that a gve evet or observato or measuremet wll or has haeed
3. Basic Concepts: Consequences and Properties
 : 3. Basc Cocepts: Cosequeces ad Propertes Markku Jutt Overvew More advaced cosequeces ad propertes of the basc cocepts troduced the prevous lecture are derved. Source The materal s maly based o Sectos.6.8
: 3. Basc Cocepts: Cosequeces ad Propertes Markku Jutt Overvew More advaced cosequeces ad propertes of the basc cocepts troduced the prevous lecture are derved. Source The materal s maly based o Sectos.6.8
Random Variables. ECE 313 Probability with Engineering Applications Lecture 8 Professor Ravi K. Iyer University of Illinois
 Radom Varables ECE 313 Probablty wth Egeerg Alcatos Lecture 8 Professor Rav K. Iyer Uversty of Illos Iyer - Lecture 8 ECE 313 Fall 013 Today s Tocs Revew o Radom Varables Cumulatve Dstrbuto Fucto (CDF
Radom Varables ECE 313 Probablty wth Egeerg Alcatos Lecture 8 Professor Rav K. Iyer Uversty of Illos Iyer - Lecture 8 ECE 313 Fall 013 Today s Tocs Revew o Radom Varables Cumulatve Dstrbuto Fucto (CDF
Continuous Random Variables: Conditioning, Expectation and Independence
 Cotuous Radom Varables: Codtog, xectato ad Ideedece Berl Che Deartmet o Comuter cece & Iormato geerg atoal Tawa ormal Uverst Reerece: - D.. Bertsekas, J.. Tstskls, Itroducto to robablt, ectos 3.4-3.5 Codtog
Cotuous Radom Varables: Codtog, xectato ad Ideedece Berl Che Deartmet o Comuter cece & Iormato geerg atoal Tawa ormal Uverst Reerece: - D.. Bertsekas, J.. Tstskls, Itroducto to robablt, ectos 3.4-3.5 Codtog
Lecture 3 Probability review (cont d)
 STATS 00: Itroducto to Statstcal Iferece Autum 06 Lecture 3 Probablty revew (cot d) 3. Jot dstrbutos If radom varables X,..., X k are depedet, the ther dstrbuto may be specfed by specfyg the dvdual dstrbuto
STATS 00: Itroducto to Statstcal Iferece Autum 06 Lecture 3 Probablty revew (cot d) 3. Jot dstrbutos If radom varables X,..., X k are depedet, the ther dstrbuto may be specfed by specfyg the dvdual dstrbuto
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS
 UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postpoed exam: ECON430 Statstcs Date of exam: Jauary 0, 0 Tme for exam: 09:00 a.m. :00 oo The problem set covers 5 pages Resources allowed: All wrtte ad prted
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Postpoed exam: ECON430 Statstcs Date of exam: Jauary 0, 0 Tme for exam: 09:00 a.m. :00 oo The problem set covers 5 pages Resources allowed: All wrtte ad prted
D KL (P Q) := p i ln p i q i
 Cheroff-Bouds 1 The Geeral Boud Let P 1,, m ) ad Q q 1,, q m ) be two dstrbutos o m elemets, e,, q 0, for 1,, m, ad m 1 m 1 q 1 The Kullback-Lebler dvergece or relatve etroy of P ad Q s defed as m D KL
Cheroff-Bouds 1 The Geeral Boud Let P 1,, m ) ad Q q 1,, q m ) be two dstrbutos o m elemets, e,, q 0, for 1,, m, ad m 1 m 1 q 1 The Kullback-Lebler dvergece or relatve etroy of P ad Q s defed as m D KL
å 1 13 Practice Final Examination Solutions - = CS109 Dec 5, 2018
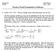 Chrs Pech Fal Practce CS09 Dec 5, 08 Practce Fal Examato Solutos. Aswer: 4/5 8/7. There are multle ways to obta ths aswer; here are two: The frst commo method s to sum over all ossbltes for the rak of
Chrs Pech Fal Practce CS09 Dec 5, 08 Practce Fal Examato Solutos. Aswer: 4/5 8/7. There are multle ways to obta ths aswer; here are two: The frst commo method s to sum over all ossbltes for the rak of
CHAPTER 3 POSTERIOR DISTRIBUTIONS
 CHAPTER 3 POSTERIOR DISTRIBUTIONS If scece caot measure the degree of probablt volved, so much the worse for scece. The practcal ma wll stck to hs apprecatve methods utl t does, or wll accept the results
CHAPTER 3 POSTERIOR DISTRIBUTIONS If scece caot measure the degree of probablt volved, so much the worse for scece. The practcal ma wll stck to hs apprecatve methods utl t does, or wll accept the results
STK3100 and STK4100 Autumn 2017
 SK3 ad SK4 Autum 7 Geeralzed lear models Part III Covers the followg materal from chaters 4 ad 5: Sectos 4..5, 4.3.5, 4.3.6, 4.4., 4.4., ad 4.4.3 Sectos 5.., 5.., ad 5.5. Ørulf Borga Deartmet of Mathematcs
SK3 ad SK4 Autum 7 Geeralzed lear models Part III Covers the followg materal from chaters 4 ad 5: Sectos 4..5, 4.3.5, 4.3.6, 4.4., 4.4., ad 4.4.3 Sectos 5.., 5.., ad 5.5. Ørulf Borga Deartmet of Mathematcs
Lecture 9. Some Useful Discrete Distributions. Some Useful Discrete Distributions. The observations generated by different experiments have
 NM 7 Lecture 9 Some Useful Dscrete Dstrbutos Some Useful Dscrete Dstrbutos The observatos geerated by dfferet eermets have the same geeral tye of behavor. Cosequetly, radom varables assocated wth these
NM 7 Lecture 9 Some Useful Dscrete Dstrbutos Some Useful Dscrete Dstrbutos The observatos geerated by dfferet eermets have the same geeral tye of behavor. Cosequetly, radom varables assocated wth these
2SLS Estimates ECON In this case, begin with the assumption that E[ i
 SLS Estmates ECON 3033 Bll Evas Fall 05 Two-Stage Least Squares (SLS Cosder a stadard lear bvarate regresso model y 0 x. I ths case, beg wth the assumto that E[ x] 0 whch meas that OLS estmates of wll
SLS Estmates ECON 3033 Bll Evas Fall 05 Two-Stage Least Squares (SLS Cosder a stadard lear bvarate regresso model y 0 x. I ths case, beg wth the assumto that E[ x] 0 whch meas that OLS estmates of wll
STK3100 and STK4100 Autumn 2018
 SK3 ad SK4 Autum 8 Geeralzed lear models Part III Covers the followg materal from chaters 4 ad 5: Cofdece tervals by vertg tests Cosder a model wth a sgle arameter β We may obta a ( α% cofdece terval for
SK3 ad SK4 Autum 8 Geeralzed lear models Part III Covers the followg materal from chaters 4 ad 5: Cofdece tervals by vertg tests Cosder a model wth a sgle arameter β We may obta a ( α% cofdece terval for
( ) = ( ) ( ) Chapter 13 Asymptotic Theory and Stochastic Regressors. Stochastic regressors model
 Chapter 3 Asmptotc Theor ad Stochastc Regressors The ature of eplaator varable s assumed to be o-stochastc or fed repeated samples a regresso aalss Such a assumpto s approprate for those epermets whch
Chapter 3 Asmptotc Theor ad Stochastc Regressors The ature of eplaator varable s assumed to be o-stochastc or fed repeated samples a regresso aalss Such a assumpto s approprate for those epermets whch
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS
 UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Exam: ECON430 Statstcs Date of exam: Frday, December 8, 07 Grades are gve: Jauary 4, 08 Tme for exam: 0900 am 00 oo The problem set covers 5 pages Resources allowed:
UNIVERSITY OF OSLO DEPARTMENT OF ECONOMICS Exam: ECON430 Statstcs Date of exam: Frday, December 8, 07 Grades are gve: Jauary 4, 08 Tme for exam: 0900 am 00 oo The problem set covers 5 pages Resources allowed:
2. Independence and Bernoulli Trials
 . Ideedece ad Beroull Trals Ideedece: Evets ad B are deedet f B B. - It s easy to show that, B deedet mles, B;, B are all deedet ars. For examle, ad so that B or B B B B B φ,.e., ad B are deedet evets.,
. Ideedece ad Beroull Trals Ideedece: Evets ad B are deedet f B B. - It s easy to show that, B deedet mles, B;, B are all deedet ars. For examle, ad so that B or B B B B B φ,.e., ad B are deedet evets.,
STK4011 and STK9011 Autumn 2016
 STK4 ad STK9 Autum 6 Pot estmato Covers (most of the followg materal from chapter 7: Secto 7.: pages 3-3 Secto 7..: pages 3-33 Secto 7..: pages 35-3 Secto 7..3: pages 34-35 Secto 7.3.: pages 33-33 Secto
STK4 ad STK9 Autum 6 Pot estmato Covers (most of the followg materal from chapter 7: Secto 7.: pages 3-3 Secto 7..: pages 3-33 Secto 7..: pages 35-3 Secto 7..3: pages 34-35 Secto 7.3.: pages 33-33 Secto
Econometric Methods. Review of Estimation
 Ecoometrc Methods Revew of Estmato Estmatg the populato mea Radom samplg Pot ad terval estmators Lear estmators Ubased estmators Lear Ubased Estmators (LUEs) Effcecy (mmum varace) ad Best Lear Ubased Estmators
Ecoometrc Methods Revew of Estmato Estmatg the populato mea Radom samplg Pot ad terval estmators Lear estmators Ubased estmators Lear Ubased Estmators (LUEs) Effcecy (mmum varace) ad Best Lear Ubased Estmators
Mean is only appropriate for interval or ratio scales, not ordinal or nominal.
 Mea Same as ordary average Sum all the data values ad dvde by the sample sze. x = ( x + x +... + x Usg summato otato, we wrte ths as x = x = x = = ) x Mea s oly approprate for terval or rato scales, ot
Mea Same as ordary average Sum all the data values ad dvde by the sample sze. x = ( x + x +... + x Usg summato otato, we wrte ths as x = x = x = = ) x Mea s oly approprate for terval or rato scales, ot
Lecture 3. Sampling, sampling distributions, and parameter estimation
 Lecture 3 Samplg, samplg dstrbutos, ad parameter estmato Samplg Defto Populato s defed as the collecto of all the possble observatos of terest. The collecto of observatos we take from the populato s called
Lecture 3 Samplg, samplg dstrbutos, ad parameter estmato Samplg Defto Populato s defed as the collecto of all the possble observatos of terest. The collecto of observatos we take from the populato s called
Summary of the lecture in Biostatistics
 Summary of the lecture Bostatstcs Probablty Desty Fucto For a cotuos radom varable, a probablty desty fucto s a fucto such that: 0 dx a b) b a dx A probablty desty fucto provdes a smple descrpto of the
Summary of the lecture Bostatstcs Probablty Desty Fucto For a cotuos radom varable, a probablty desty fucto s a fucto such that: 0 dx a b) b a dx A probablty desty fucto provdes a smple descrpto of the
Lecture 9: Tolerant Testing
 Lecture 9: Tolerat Testg Dael Kae Scrbe: Sakeerth Rao Aprl 4, 07 Abstract I ths lecture we prove a quas lear lower boud o the umber of samples eeded to do tolerat testg for L dstace. Tolerat Testg We have
Lecture 9: Tolerat Testg Dael Kae Scrbe: Sakeerth Rao Aprl 4, 07 Abstract I ths lecture we prove a quas lear lower boud o the umber of samples eeded to do tolerat testg for L dstace. Tolerat Testg We have
Pr[X (p + t)n] e D KL(p+t p)n.
![Pr[X (p + t)n] e D KL(p+t p)n. Pr[X (p + t)n] e D KL(p+t p)n.](/thumbs/87/95535752.jpg) Cheroff Bouds Wolfgag Mulzer 1 The Geeral Boud Let P 1,..., m ) ad Q q 1,..., q m ) be two dstrbutos o m elemets,.e.,, q 0, for 1,..., m, ad m 1 m 1 q 1. The Kullback-Lebler dvergece or relatve etroy of
Cheroff Bouds Wolfgag Mulzer 1 The Geeral Boud Let P 1,..., m ) ad Q q 1,..., q m ) be two dstrbutos o m elemets,.e.,, q 0, for 1,..., m, ad m 1 m 1 q 1. The Kullback-Lebler dvergece or relatve etroy of
Special Instructions / Useful Data
 JAM 6 Set of all real umbers P A..d. B, p Posso Specal Istructos / Useful Data x,, :,,, x x Probablty of a evet A Idepedetly ad detcally dstrbuted Bomal dstrbuto wth parameters ad p Posso dstrbuto wth
JAM 6 Set of all real umbers P A..d. B, p Posso Specal Istructos / Useful Data x,, :,,, x x Probablty of a evet A Idepedetly ad detcally dstrbuted Bomal dstrbuto wth parameters ad p Posso dstrbuto wth
Channel Models with Memory. Channel Models with Memory. Channel Models with Memory. Channel Models with Memory
 Chael Models wth Memory Chael Models wth Memory Hayder radha Electrcal ad Comuter Egeerg Mchga State Uversty I may ractcal etworkg scearos (cludg the Iteret ad wreless etworks), the uderlyg chaels are
Chael Models wth Memory Chael Models wth Memory Hayder radha Electrcal ad Comuter Egeerg Mchga State Uversty I may ractcal etworkg scearos (cludg the Iteret ad wreless etworks), the uderlyg chaels are
9 U-STATISTICS. Eh =(m!) 1 Eh(X (1),..., X (m ) ) i.i.d
 9 U-STATISTICS Suppose,,..., are P P..d. wth CDF F. Our goal s to estmate the expectato t (P)=Eh(,,..., m ). Note that ths expectato requres more tha oe cotrast to E, E, or Eh( ). Oe example s E or P((,
9 U-STATISTICS Suppose,,..., are P P..d. wth CDF F. Our goal s to estmate the expectato t (P)=Eh(,,..., m ). Note that ths expectato requres more tha oe cotrast to E, E, or Eh( ). Oe example s E or P((,
Point Estimation: definition of estimators
 Pot Estmato: defto of estmators Pot estmator: ay fucto W (X,..., X ) of a data sample. The exercse of pot estmato s to use partcular fuctos of the data order to estmate certa ukow populato parameters.
Pot Estmato: defto of estmators Pot estmator: ay fucto W (X,..., X ) of a data sample. The exercse of pot estmato s to use partcular fuctos of the data order to estmate certa ukow populato parameters.
Qualifying Exam Statistical Theory Problem Solutions August 2005
 Qualfyg Exam Statstcal Theory Problem Solutos August 5. Let X, X,..., X be d uform U(,),
Qualfyg Exam Statstcal Theory Problem Solutos August 5. Let X, X,..., X be d uform U(,),
Lecture Notes Types of economic variables
 Lecture Notes 3 1. Types of ecoomc varables () Cotuous varable takes o a cotuum the sample space, such as all pots o a le or all real umbers Example: GDP, Polluto cocetrato, etc. () Dscrete varables fte
Lecture Notes 3 1. Types of ecoomc varables () Cotuous varable takes o a cotuum the sample space, such as all pots o a le or all real umbers Example: GDP, Polluto cocetrato, etc. () Dscrete varables fte
Chapter 5 Properties of a Random Sample
 Lecture 6 o BST 63: Statstcal Theory I Ku Zhag, /0/008 Revew for the prevous lecture Cocepts: t-dstrbuto, F-dstrbuto Theorems: Dstrbutos of sample mea ad sample varace, relatoshp betwee sample mea ad sample
Lecture 6 o BST 63: Statstcal Theory I Ku Zhag, /0/008 Revew for the prevous lecture Cocepts: t-dstrbuto, F-dstrbuto Theorems: Dstrbutos of sample mea ad sample varace, relatoshp betwee sample mea ad sample
Lecture 7. Confidence Intervals and Hypothesis Tests in the Simple CLR Model
 Lecture 7. Cofdece Itervals ad Hypothess Tests the Smple CLR Model I lecture 6 we troduced the Classcal Lear Regresso (CLR) model that s the radom expermet of whch the data Y,,, K, are the outcomes. The
Lecture 7. Cofdece Itervals ad Hypothess Tests the Smple CLR Model I lecture 6 we troduced the Classcal Lear Regresso (CLR) model that s the radom expermet of whch the data Y,,, K, are the outcomes. The
Multiple Choice Test. Chapter Adequacy of Models for Regression
 Multple Choce Test Chapter 06.0 Adequac of Models for Regresso. For a lear regresso model to be cosdered adequate, the percetage of scaled resduals that eed to be the rage [-,] s greater tha or equal to
Multple Choce Test Chapter 06.0 Adequac of Models for Regresso. For a lear regresso model to be cosdered adequate, the percetage of scaled resduals that eed to be the rage [-,] s greater tha or equal to
Parameter Estimation
 arameter Estmato robabltes Notatoal Coveto Mass dscrete fucto: catal letters Desty cotuous fucto: small letters Vector vs. scalar Scalar: la Vector: bold D: small Hgher dmeso: catal Notes a cotuous state
arameter Estmato robabltes Notatoal Coveto Mass dscrete fucto: catal letters Desty cotuous fucto: small letters Vector vs. scalar Scalar: la Vector: bold D: small Hgher dmeso: catal Notes a cotuous state
STRONG CONSISTENCY FOR SIMPLE LINEAR EV MODEL WITH v/ -MIXING
 Joural of tatstcs: Advaces Theory ad Alcatos Volume 5, Number, 6, Pages 3- Avalable at htt://scetfcadvaces.co. DOI: htt://d.do.org/.864/jsata_7678 TRONG CONITENCY FOR IMPLE LINEAR EV MODEL WITH v/ -MIXING
Joural of tatstcs: Advaces Theory ad Alcatos Volume 5, Number, 6, Pages 3- Avalable at htt://scetfcadvaces.co. DOI: htt://d.do.org/.864/jsata_7678 TRONG CONITENCY FOR IMPLE LINEAR EV MODEL WITH v/ -MIXING
ρ < 1 be five real numbers. The
 Lecture o BST 63: Statstcal Theory I Ku Zhag, /0/006 Revew for the prevous lecture Deftos: covarace, correlato Examples: How to calculate covarace ad correlato Theorems: propertes of correlato ad covarace
Lecture o BST 63: Statstcal Theory I Ku Zhag, /0/006 Revew for the prevous lecture Deftos: covarace, correlato Examples: How to calculate covarace ad correlato Theorems: propertes of correlato ad covarace
X X X E[ ] E X E X. is the ()m n where the ( i,)th. j element is the mean of the ( i,)th., then
![X X X E[ ] E X E X. is the ()m n where the ( i,)th. j element is the mean of the ( i,)th., then X X X E[ ] E X E X. is the ()m n where the ( i,)th. j element is the mean of the ( i,)th., then](/thumbs/83/87696552.jpg) Secto 5 Vectors of Radom Varables Whe workg wth several radom varables,,..., to arrage them vector form x, t s ofte coveet We ca the make use of matrx algebra to help us orgaze ad mapulate large umbers
Secto 5 Vectors of Radom Varables Whe workg wth several radom varables,,..., to arrage them vector form x, t s ofte coveet We ca the make use of matrx algebra to help us orgaze ad mapulate large umbers
Third handout: On the Gini Index
 Thrd hadout: O the dex Corrado, a tala statstca, proposed (, 9, 96) to measure absolute equalt va the mea dfferece whch s defed as ( / ) where refers to the total umber of dvduals socet. Assume that. The
Thrd hadout: O the dex Corrado, a tala statstca, proposed (, 9, 96) to measure absolute equalt va the mea dfferece whch s defed as ( / ) where refers to the total umber of dvduals socet. Assume that. The
Lecture Notes Forecasting the process of estimating or predicting unknown situations
 Lecture Notes. Ecoomc Forecastg. Forecastg the process of estmatg or predctg ukow stuatos Eample usuall ecoomsts predct future ecoomc varables Forecastg apples to a varet of data () tme seres data predctg
Lecture Notes. Ecoomc Forecastg. Forecastg the process of estmatg or predctg ukow stuatos Eample usuall ecoomsts predct future ecoomc varables Forecastg apples to a varet of data () tme seres data predctg
Dr. Shalabh Department of Mathematics and Statistics Indian Institute of Technology Kanpur
 Aalyss of Varace ad Desg of Exermets-I MODULE II LECTURE - GENERAL LINEAR HYPOTHESIS AND ANALYSIS OF VARIANCE Dr Shalabh Deartmet of Mathematcs ad Statstcs Ida Isttute of Techology Kaur Tukey s rocedure
Aalyss of Varace ad Desg of Exermets-I MODULE II LECTURE - GENERAL LINEAR HYPOTHESIS AND ANALYSIS OF VARIANCE Dr Shalabh Deartmet of Mathematcs ad Statstcs Ida Isttute of Techology Kaur Tukey s rocedure
GEOMETRY OF JENSEN S INEQUALITY AND QUASI-ARITHMETIC MEANS
 IJRRS ugust 3 wwwararesscom/volumes/volissue/ijrrs 4d GEOMETRY OF JENSEN S INEQULITY ND QUSI-RITHMETIC MENS Zlato avć Mechacal Egeerg Facult Slavos Brod Uverst o Osje Trg Ivae Brlć Mažurać 35 Slavos Brod
IJRRS ugust 3 wwwararesscom/volumes/volissue/ijrrs 4d GEOMETRY OF JENSEN S INEQULITY ND QUSI-RITHMETIC MENS Zlato avć Mechacal Egeerg Facult Slavos Brod Uverst o Osje Trg Ivae Brlć Mažurać 35 Slavos Brod
1 Solution to Problem 6.40
 1 Soluto to Problem 6.40 (a We wll wrte T τ (X 1,...,X where the X s are..d. wth PDF f(x µ, σ 1 ( x µ σ g, σ where the locato parameter µ s ay real umber ad the scale parameter σ s > 0. Lettg Z X µ σ we
1 Soluto to Problem 6.40 (a We wll wrte T τ (X 1,...,X where the X s are..d. wth PDF f(x µ, σ 1 ( x µ σ g, σ where the locato parameter µ s ay real umber ad the scale parameter σ s > 0. Lettg Z X µ σ we
Ordinary Least Squares Regression. Simple Regression. Algebra and Assumptions.
 Ordary Least Squares egresso. Smple egresso. Algebra ad Assumptos. I ths part of the course we are gog to study a techque for aalysg the lear relatoshp betwee two varables Y ad X. We have pars of observatos
Ordary Least Squares egresso. Smple egresso. Algebra ad Assumptos. I ths part of the course we are gog to study a techque for aalysg the lear relatoshp betwee two varables Y ad X. We have pars of observatos
Simulation Output Analysis
 Smulato Output Aalyss Summary Examples Parameter Estmato Sample Mea ad Varace Pot ad Iterval Estmato ermatg ad o-ermatg Smulato Mea Square Errors Example: Sgle Server Queueg System x(t) S 4 S 4 S 3 S 5
Smulato Output Aalyss Summary Examples Parameter Estmato Sample Mea ad Varace Pot ad Iterval Estmato ermatg ad o-ermatg Smulato Mea Square Errors Example: Sgle Server Queueg System x(t) S 4 S 4 S 3 S 5
Chapter 14 Logistic Regression Models
 Chapter 4 Logstc Regresso Models I the lear regresso model X β + ε, there are two types of varables explaatory varables X, X,, X k ad study varable y These varables ca be measured o a cotuous scale as
Chapter 4 Logstc Regresso Models I the lear regresso model X β + ε, there are two types of varables explaatory varables X, X,, X k ad study varable y These varables ca be measured o a cotuous scale as
ECONOMETRIC THEORY. MODULE VIII Lecture - 26 Heteroskedasticity
 ECONOMETRIC THEORY MODULE VIII Lecture - 6 Heteroskedastcty Dr. Shalabh Departmet of Mathematcs ad Statstcs Ida Isttute of Techology Kapur . Breusch Paga test Ths test ca be appled whe the replcated data
ECONOMETRIC THEORY MODULE VIII Lecture - 6 Heteroskedastcty Dr. Shalabh Departmet of Mathematcs ad Statstcs Ida Isttute of Techology Kapur . Breusch Paga test Ths test ca be appled whe the replcated data
CHAPTER 6. d. With success = observation greater than 10, x = # of successes = 4, and
 CHAPTR 6 Secto 6.. a. We use the samle mea, to estmate the oulato mea µ. Σ 9.80 µ 8.407 7 ~ 7. b. We use the samle meda, 7 (the mddle observato whe arraged ascedg order. c. We use the samle stadard devato,
CHAPTR 6 Secto 6.. a. We use the samle mea, to estmate the oulato mea µ. Σ 9.80 µ 8.407 7 ~ 7. b. We use the samle meda, 7 (the mddle observato whe arraged ascedg order. c. We use the samle stadard devato,
Functions of Random Variables
 Fuctos of Radom Varables Chapter Fve Fuctos of Radom Varables 5. Itroducto A geeral egeerg aalyss model s show Fg. 5.. The model output (respose) cotas the performaces of a system or product, such as weght,
Fuctos of Radom Varables Chapter Fve Fuctos of Radom Varables 5. Itroducto A geeral egeerg aalyss model s show Fg. 5.. The model output (respose) cotas the performaces of a system or product, such as weght,
Chapter 4 Multiple Random Variables
 Revew for the prevous lecture: Theorems ad Examples: How to obta the pmf (pdf) of U = g (, Y) ad V = g (, Y) Chapter 4 Multple Radom Varables Chapter 44 Herarchcal Models ad Mxture Dstrbutos Examples:
Revew for the prevous lecture: Theorems ad Examples: How to obta the pmf (pdf) of U = g (, Y) ad V = g (, Y) Chapter 4 Multple Radom Varables Chapter 44 Herarchcal Models ad Mxture Dstrbutos Examples:
12.2 Estimating Model parameters Assumptions: ox and y are related according to the simple linear regression model
 1. Estmatg Model parameters Assumptos: ox ad y are related accordg to the smple lear regresso model (The lear regresso model s the model that says that x ad y are related a lear fasho, but the observed
1. Estmatg Model parameters Assumptos: ox ad y are related accordg to the smple lear regresso model (The lear regresso model s the model that says that x ad y are related a lear fasho, but the observed
CHAPTER VI Statistical Analysis of Experimental Data
 Chapter VI Statstcal Aalyss of Expermetal Data CHAPTER VI Statstcal Aalyss of Expermetal Data Measuremets do ot lead to a uque value. Ths s a result of the multtude of errors (maly radom errors) that ca
Chapter VI Statstcal Aalyss of Expermetal Data CHAPTER VI Statstcal Aalyss of Expermetal Data Measuremets do ot lead to a uque value. Ths s a result of the multtude of errors (maly radom errors) that ca
BASIC PRINCIPLES OF STATISTICS
 BASIC PRINCIPLES OF STATISTICS PROBABILITY DENSITY DISTRIBUTIONS DISCRETE VARIABLES BINOMIAL DISTRIBUTION ~ B 0 0 umber of successes trals Pr E [ ] Var[ ] ; BINOMIAL DISTRIBUTION B7 0. B30 0.3 B50 0.5
BASIC PRINCIPLES OF STATISTICS PROBABILITY DENSITY DISTRIBUTIONS DISCRETE VARIABLES BINOMIAL DISTRIBUTION ~ B 0 0 umber of successes trals Pr E [ ] Var[ ] ; BINOMIAL DISTRIBUTION B7 0. B30 0.3 B50 0.5
Comparison of Dual to Ratio-Cum-Product Estimators of Population Mean
 Research Joural of Mathematcal ad Statstcal Sceces ISS 30 6047 Vol. 1(), 5-1, ovember (013) Res. J. Mathematcal ad Statstcal Sc. Comparso of Dual to Rato-Cum-Product Estmators of Populato Mea Abstract
Research Joural of Mathematcal ad Statstcal Sceces ISS 30 6047 Vol. 1(), 5-1, ovember (013) Res. J. Mathematcal ad Statstcal Sc. Comparso of Dual to Rato-Cum-Product Estmators of Populato Mea Abstract
{ }{ ( )} (, ) = ( ) ( ) ( ) Chapter 14 Exercises in Sampling Theory. Exercise 1 (Simple random sampling): Solution:
 Chapter 4 Exercses Samplg Theory Exercse (Smple radom samplg: Let there be two correlated radom varables X ad A sample of sze s draw from a populato by smple radom samplg wthout replacemet The observed
Chapter 4 Exercses Samplg Theory Exercse (Smple radom samplg: Let there be two correlated radom varables X ad A sample of sze s draw from a populato by smple radom samplg wthout replacemet The observed
Class 13,14 June 17, 19, 2015
 Class 3,4 Jue 7, 9, 05 Pla for Class3,4:. Samplg dstrbuto of sample mea. The Cetral Lmt Theorem (CLT). Cofdece terval for ukow mea.. Samplg Dstrbuto for Sample mea. Methods used are based o CLT ( Cetral
Class 3,4 Jue 7, 9, 05 Pla for Class3,4:. Samplg dstrbuto of sample mea. The Cetral Lmt Theorem (CLT). Cofdece terval for ukow mea.. Samplg Dstrbuto for Sample mea. Methods used are based o CLT ( Cetral
Midterm Exam 1, section 2 (Solution) Thursday, February hour, 15 minutes
 coometrcs, CON Sa Fracsco State Uverst Mchael Bar Sprg 5 Mdterm xam, secto Soluto Thursda, Februar 6 hour, 5 mutes Name: Istructos. Ths s closed book, closed otes exam.. No calculators of a kd are allowed..
coometrcs, CON Sa Fracsco State Uverst Mchael Bar Sprg 5 Mdterm xam, secto Soluto Thursda, Februar 6 hour, 5 mutes Name: Istructos. Ths s closed book, closed otes exam.. No calculators of a kd are allowed..
Logistic regression (continued)
 STAT562 page 138 Logstc regresso (cotued) Suppose we ow cosder more complex models to descrbe the relatoshp betwee a categorcal respose varable (Y) that takes o two (2) possble outcomes ad a set of p explaatory
STAT562 page 138 Logstc regresso (cotued) Suppose we ow cosder more complex models to descrbe the relatoshp betwee a categorcal respose varable (Y) that takes o two (2) possble outcomes ad a set of p explaatory
STATISTICAL INFERENCE
 (STATISTICS) STATISTICAL INFERENCE COMPLEMENTARY COURSE B.Sc. MATHEMATICS III SEMESTER ( Admsso) UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION CALICUT UNIVERSITY P.O., MALAPPURAM, KERALA, INDIA -
(STATISTICS) STATISTICAL INFERENCE COMPLEMENTARY COURSE B.Sc. MATHEMATICS III SEMESTER ( Admsso) UNIVERSITY OF CALICUT SCHOOL OF DISTANCE EDUCATION CALICUT UNIVERSITY P.O., MALAPPURAM, KERALA, INDIA -
ENGI 4421 Joint Probability Distributions Page Joint Probability Distributions [Navidi sections 2.5 and 2.6; Devore sections
 ENGI 441 Jot Probablty Dstrbutos Page 7-01 Jot Probablty Dstrbutos [Navd sectos.5 ad.6; Devore sectos 5.1-5.] The jot probablty mass fucto of two dscrete radom quattes, s, P ad p x y x y The margal probablty
ENGI 441 Jot Probablty Dstrbutos Page 7-01 Jot Probablty Dstrbutos [Navd sectos.5 ad.6; Devore sectos 5.1-5.] The jot probablty mass fucto of two dscrete radom quattes, s, P ad p x y x y The margal probablty
MEASURES OF DISPERSION
 MEASURES OF DISPERSION Measure of Cetral Tedecy: Measures of Cetral Tedecy ad Dsperso ) Mathematcal Average: a) Arthmetc mea (A.M.) b) Geometrc mea (G.M.) c) Harmoc mea (H.M.) ) Averages of Posto: a) Meda
MEASURES OF DISPERSION Measure of Cetral Tedecy: Measures of Cetral Tedecy ad Dsperso ) Mathematcal Average: a) Arthmetc mea (A.M.) b) Geometrc mea (G.M.) c) Harmoc mea (H.M.) ) Averages of Posto: a) Meda
IS 709/809: Computational Methods in IS Research. Simple Markovian Queueing Model
 IS 79/89: Comutatoal Methods IS Research Smle Marova Queueg Model Nrmalya Roy Deartmet of Iformato Systems Uversty of Marylad Baltmore Couty www.umbc.edu Queueg Theory Software QtsPlus software The software
IS 79/89: Comutatoal Methods IS Research Smle Marova Queueg Model Nrmalya Roy Deartmet of Iformato Systems Uversty of Marylad Baltmore Couty www.umbc.edu Queueg Theory Software QtsPlus software The software
The number of observed cases The number of parameters. ith case of the dichotomous dependent variable. the ith case of the jth parameter
 LOGISTIC REGRESSION Notato Model Logstc regresso regresses a dchotomous depedet varable o a set of depedet varables. Several methods are mplemeted for selectg the depedet varables. The followg otato s
LOGISTIC REGRESSION Notato Model Logstc regresso regresses a dchotomous depedet varable o a set of depedet varables. Several methods are mplemeted for selectg the depedet varables. The followg otato s
CS 2750 Machine Learning Lecture 5. Density estimation. Density estimation
 CS 750 Mache Learg Lecture 5 esty estmato Mlos Hausrecht mlos@tt.edu 539 Seott Square esty estmato esty estmato: s a usuervsed learg roblem Goal: Lear a model that rereset the relatos amog attrbutes the
CS 750 Mache Learg Lecture 5 esty estmato Mlos Hausrecht mlos@tt.edu 539 Seott Square esty estmato esty estmato: s a usuervsed learg roblem Goal: Lear a model that rereset the relatos amog attrbutes the
Parameter, Statistic and Random Samples
 Parameter, Statstc ad Radom Samples A parameter s a umber that descrbes the populato. It s a fxed umber, but practce we do ot kow ts value. A statstc s a fucto of the sample data,.e., t s a quatty whose
Parameter, Statstc ad Radom Samples A parameter s a umber that descrbes the populato. It s a fxed umber, but practce we do ot kow ts value. A statstc s a fucto of the sample data,.e., t s a quatty whose
Chapter 5 Properties of a Random Sample
 Lecture 3 o BST 63: Statstcal Theory I Ku Zhag, /6/006 Revew for the revous lecture Cocets: radom samle, samle mea, samle varace Theorems: roertes of a radom samle, samle mea, samle varace Examles: how
Lecture 3 o BST 63: Statstcal Theory I Ku Zhag, /6/006 Revew for the revous lecture Cocets: radom samle, samle mea, samle varace Theorems: roertes of a radom samle, samle mea, samle varace Examles: how
Multiple Linear Regression Analysis
 LINEA EGESSION ANALYSIS MODULE III Lecture - 4 Multple Lear egresso Aalyss Dr. Shalabh Departmet of Mathematcs ad Statstcs Ida Isttute of Techology Kapur Cofdece terval estmato The cofdece tervals multple
LINEA EGESSION ANALYSIS MODULE III Lecture - 4 Multple Lear egresso Aalyss Dr. Shalabh Departmet of Mathematcs ad Statstcs Ida Isttute of Techology Kapur Cofdece terval estmato The cofdece tervals multple
Midterm Exam 1, section 1 (Solution) Thursday, February hour, 15 minutes
 coometrcs, CON Sa Fracsco State Uversty Mchael Bar Sprg 5 Mdterm am, secto Soluto Thursday, February 6 hour, 5 mutes Name: Istructos. Ths s closed book, closed otes eam.. No calculators of ay kd are allowed..
coometrcs, CON Sa Fracsco State Uversty Mchael Bar Sprg 5 Mdterm am, secto Soluto Thursday, February 6 hour, 5 mutes Name: Istructos. Ths s closed book, closed otes eam.. No calculators of ay kd are allowed..
TESTS BASED ON MAXIMUM LIKELIHOOD
 ESE 5 Toy E. Smth. The Basc Example. TESTS BASED ON MAXIMUM LIKELIHOOD To llustrate the propertes of maxmum lkelhood estmates ad tests, we cosder the smplest possble case of estmatg the mea of the ormal
ESE 5 Toy E. Smth. The Basc Example. TESTS BASED ON MAXIMUM LIKELIHOOD To llustrate the propertes of maxmum lkelhood estmates ad tests, we cosder the smplest possble case of estmatg the mea of the ormal
Test Paper-II. 1. If sin θ + cos θ = m and sec θ + cosec θ = n, then (a) 2n = m (n 2 1) (b) 2m = n (m 2 1) (c) 2n = m (m 2 1) (d) none of these
 Test Paer-II. If s θ + cos θ = m ad sec θ + cosec θ =, the = m ( ) m = (m ) = m (m ). If a ABC, cos A = s B, the t s C a osceles tragle a eulateral tragle a rght agled tragle. If cos B = cos ( A+ C), the
Test Paer-II. If s θ + cos θ = m ad sec θ + cosec θ =, the = m ( ) m = (m ) = m (m ). If a ABC, cos A = s B, the t s C a osceles tragle a eulateral tragle a rght agled tragle. If cos B = cos ( A+ C), the
Introducing Sieve of Eratosthenes as a Theorem
 ISSN(Ole 9-8 ISSN (Prt - Iteratoal Joural of Iovatve Research Scece Egeerg ad echolog (A Hgh Imact Factor & UGC Aroved Joural Webste wwwrsetcom Vol Issue 9 Setember Itroducg Seve of Eratosthees as a heorem
ISSN(Ole 9-8 ISSN (Prt - Iteratoal Joural of Iovatve Research Scece Egeerg ad echolog (A Hgh Imact Factor & UGC Aroved Joural Webste wwwrsetcom Vol Issue 9 Setember Itroducg Seve of Eratosthees as a heorem
Simple Linear Regression
 Statstcal Methods I (EST 75) Page 139 Smple Lear Regresso Smple regresso applcatos are used to ft a model descrbg a lear relatoshp betwee two varables. The aspects of least squares regresso ad correlato
Statstcal Methods I (EST 75) Page 139 Smple Lear Regresso Smple regresso applcatos are used to ft a model descrbg a lear relatoshp betwee two varables. The aspects of least squares regresso ad correlato
Nonparametric Density Estimation Intro
 Noarametrc Desty Estmato Itro Parze Wdows No-Parametrc Methods Nether robablty dstrbuto or dscrmat fucto s kow Haes qute ofte All we have s labeled data a lot s kow easer salmo bass salmo salmo Estmate
Noarametrc Desty Estmato Itro Parze Wdows No-Parametrc Methods Nether robablty dstrbuto or dscrmat fucto s kow Haes qute ofte All we have s labeled data a lot s kow easer salmo bass salmo salmo Estmate
Lecture 3 Naïve Bayes, Maximum Entropy and Text Classification COSI 134
 Lecture 3 Naïve Baes, Mamum Etro ad Tet Classfcato COSI 34 Codtoal Parameterzato Two RVs: ItellgeceI ad SATS ValI = {Hgh,Low}, ValS={Hgh,Low} A ossble jot dstrbuto Ca descrbe usg cha rule as PI,S PIPS
Lecture 3 Naïve Baes, Mamum Etro ad Tet Classfcato COSI 34 Codtoal Parameterzato Two RVs: ItellgeceI ad SATS ValI = {Hgh,Low}, ValS={Hgh,Low} A ossble jot dstrbuto Ca descrbe usg cha rule as PI,S PIPS
Parametric Density Estimation: Bayesian Estimation. Naïve Bayes Classifier
 arametrc Dest Estmato: Baesa Estmato. Naïve Baes Classfer Baesa arameter Estmato Suose we have some dea of the rage where arameters should be Should t we formalze such ror owledge hoes that t wll lead
arametrc Dest Estmato: Baesa Estmato. Naïve Baes Classfer Baesa arameter Estmato Suose we have some dea of the rage where arameters should be Should t we formalze such ror owledge hoes that t wll lead
best estimate (mean) for X uncertainty or error in the measurement (systematic, random or statistical) best
 Error Aalyss Preamble Wheever a measuremet s made, the result followg from that measuremet s always subject to ucertaty The ucertaty ca be reduced by makg several measuremets of the same quatty or by mprovg
Error Aalyss Preamble Wheever a measuremet s made, the result followg from that measuremet s always subject to ucertaty The ucertaty ca be reduced by makg several measuremets of the same quatty or by mprovg
Simple Linear Regression
 Correlato ad Smple Lear Regresso Berl Che Departmet of Computer Scece & Iformato Egeerg Natoal Tawa Normal Uversty Referece:. W. Navd. Statstcs for Egeerg ad Scetsts. Chapter 7 (7.-7.3) & Teachg Materal
Correlato ad Smple Lear Regresso Berl Che Departmet of Computer Scece & Iformato Egeerg Natoal Tawa Normal Uversty Referece:. W. Navd. Statstcs for Egeerg ad Scetsts. Chapter 7 (7.-7.3) & Teachg Materal
STA 108 Applied Linear Models: Regression Analysis Spring Solution for Homework #1
 STA 08 Appled Lear Models: Regresso Aalyss Sprg 0 Soluto for Homework #. Let Y the dollar cost per year, X the umber of vsts per year. The the mathematcal relato betwee X ad Y s: Y 300 + X. Ths s a fuctoal
STA 08 Appled Lear Models: Regresso Aalyss Sprg 0 Soluto for Homework #. Let Y the dollar cost per year, X the umber of vsts per year. The the mathematcal relato betwee X ad Y s: Y 300 + X. Ths s a fuctoal
Random Variables and Probability Distributions
 Radom Varables ad Probablty Dstrbutos * If X : S R s a dscrete radom varable wth rage {x, x, x 3,. } the r = P (X = xr ) = * Let X : S R be a dscrete radom varable wth rage {x, x, x 3,.}.If x r P(X = x
Radom Varables ad Probablty Dstrbutos * If X : S R s a dscrete radom varable wth rage {x, x, x 3,. } the r = P (X = xr ) = * Let X : S R be a dscrete radom varable wth rage {x, x, x 3,.}.If x r P(X = x
Multivariate Transformation of Variables and Maximum Likelihood Estimation
 Marquette Uversty Multvarate Trasformato of Varables ad Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Assocate Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Copyrght 03 by Marquette Uversty
Marquette Uversty Multvarate Trasformato of Varables ad Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Assocate Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Copyrght 03 by Marquette Uversty
Likelihood Ratio, Wald, and Lagrange Multiplier (Score) Tests. Soccer Goals in European Premier Leagues
 Lkelhood Rato, Wald, ad Lagrage Multpler (Score) Tests Soccer Goals Europea Premer Leagues - 4 Statstcal Testg Prcples Goal: Test a Hpothess cocerg parameter value(s) a larger populato (or ature), based
Lkelhood Rato, Wald, ad Lagrage Multpler (Score) Tests Soccer Goals Europea Premer Leagues - 4 Statstcal Testg Prcples Goal: Test a Hpothess cocerg parameter value(s) a larger populato (or ature), based
Chapter 8: Statistical Analysis of Simulated Data
 Marquette Uversty MSCS600 Chapter 8: Statstcal Aalyss of Smulated Data Dael B. Rowe, Ph.D. Departmet of Mathematcs, Statstcs, ad Computer Scece Copyrght 08 by Marquette Uversty MSCS600 Ageda 8. The Sample
Marquette Uversty MSCS600 Chapter 8: Statstcal Aalyss of Smulated Data Dael B. Rowe, Ph.D. Departmet of Mathematcs, Statstcs, ad Computer Scece Copyrght 08 by Marquette Uversty MSCS600 Ageda 8. The Sample
Mu Sequences/Series Solutions National Convention 2014
 Mu Sequeces/Seres Solutos Natoal Coveto 04 C 6 E A 6C A 6 B B 7 A D 7 D C 7 A B 8 A B 8 A C 8 E 4 B 9 B 4 E 9 B 4 C 9 E C 0 A A 0 D B 0 C C Usg basc propertes of arthmetc sequeces, we fd a ad bm m We eed
Mu Sequeces/Seres Solutos Natoal Coveto 04 C 6 E A 6C A 6 B B 7 A D 7 D C 7 A B 8 A B 8 A C 8 E 4 B 9 B 4 E 9 B 4 C 9 E C 0 A A 0 D B 0 C C Usg basc propertes of arthmetc sequeces, we fd a ad bm m We eed
Module 7. Lecture 7: Statistical parameter estimation
 Lecture 7: Statstcal parameter estmato Parameter Estmato Methods of Parameter Estmato 1) Method of Matchg Pots ) Method of Momets 3) Mamum Lkelhood method Populato Parameter Sample Parameter Ubased estmato
Lecture 7: Statstcal parameter estmato Parameter Estmato Methods of Parameter Estmato 1) Method of Matchg Pots ) Method of Momets 3) Mamum Lkelhood method Populato Parameter Sample Parameter Ubased estmato
MS exam problems Fall 2012
 MS exam problems Fall 01 (From: Rya Mart) 1. (Stat 401) Cosder the followg game wth a box that cotas te balls two red, three blue, ad fve gree. A player selects two balls from the box at radom, wthout
MS exam problems Fall 01 (From: Rya Mart) 1. (Stat 401) Cosder the followg game wth a box that cotas te balls two red, three blue, ad fve gree. A player selects two balls from the box at radom, wthout
Factorization of Finite Abelian Groups
 Iteratoal Joural of Algebra, Vol 6, 0, o 3, 0-07 Factorzato of Fte Abela Grous Khald Am Uversty of Bahra Deartmet of Mathematcs PO Box 3038 Sakhr, Bahra kamee@uobedubh Abstract If G s a fte abela grou
Iteratoal Joural of Algebra, Vol 6, 0, o 3, 0-07 Factorzato of Fte Abela Grous Khald Am Uversty of Bahra Deartmet of Mathematcs PO Box 3038 Sakhr, Bahra kamee@uobedubh Abstract If G s a fte abela grou
Bounds on the expected entropy and KL-divergence of sampled multinomial distributions. Brandon C. Roy
 Bouds o the expected etropy ad KL-dvergece of sampled multomal dstrbutos Brado C. Roy bcroy@meda.mt.edu Orgal: May 18, 2011 Revsed: Jue 6, 2011 Abstract Iformato theoretc quattes calculated from a sampled
Bouds o the expected etropy ad KL-dvergece of sampled multomal dstrbutos Brado C. Roy bcroy@meda.mt.edu Orgal: May 18, 2011 Revsed: Jue 6, 2011 Abstract Iformato theoretc quattes calculated from a sampled
Generative classification models
 CS 75 Mache Learg Lecture Geeratve classfcato models Mlos Hauskrecht mlos@cs.ptt.edu 539 Seott Square Data: D { d, d,.., d} d, Classfcato represets a dscrete class value Goal: lear f : X Y Bar classfcato
CS 75 Mache Learg Lecture Geeratve classfcato models Mlos Hauskrecht mlos@cs.ptt.edu 539 Seott Square Data: D { d, d,.., d} d, Classfcato represets a dscrete class value Goal: lear f : X Y Bar classfcato
PTAS for Bin-Packing
 CS 663: Patter Matchg Algorthms Scrbe: Che Jag /9/00. Itroducto PTAS for B-Packg The B-Packg problem s NP-hard. If we use approxmato algorthms, the B-Packg problem could be solved polyomal tme. For example,
CS 663: Patter Matchg Algorthms Scrbe: Che Jag /9/00. Itroducto PTAS for B-Packg The B-Packg problem s NP-hard. If we use approxmato algorthms, the B-Packg problem could be solved polyomal tme. For example,
Maximum Likelihood Estimation
 Marquette Uverst Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Coprght 08 b Marquette Uverst Maxmum Lkelhood Estmato We have bee sag that ~
Marquette Uverst Maxmum Lkelhood Estmato Dael B. Rowe, Ph.D. Professor Departmet of Mathematcs, Statstcs, ad Computer Scece Coprght 08 b Marquette Uverst Maxmum Lkelhood Estmato We have bee sag that ~
Unit 9. The Tangent Bundle
 Ut 9. The Taget Budle ========================================================================================== ---------- The taget sace of a submafold of R, detfcato of taget vectors wth dervatos at
Ut 9. The Taget Budle ========================================================================================== ---------- The taget sace of a submafold of R, detfcato of taget vectors wth dervatos at
Chapter 4 Multiple Random Variables
 Revew o BST 63: Statstcal Theory I Ku Zhag, /0/008 Revew for Chapter 4-5 Notes: Although all deftos ad theorems troduced our lectures ad ths ote are mportat ad you should be famlar wth, but I put those
Revew o BST 63: Statstcal Theory I Ku Zhag, /0/008 Revew for Chapter 4-5 Notes: Although all deftos ad theorems troduced our lectures ad ths ote are mportat ad you should be famlar wth, but I put those
Correlation and Simple Linear Regression
 Correlato ad Smple Lear Regresso Berl Che Departmet of Computer Scece & Iformato Egeerg Natoal Tawa Normal Uverst Referece:. W. Navd. Statstcs for Egeerg ad Scetsts. Chapter 7 (7.-7.3) & Teachg Materal
Correlato ad Smple Lear Regresso Berl Che Departmet of Computer Scece & Iformato Egeerg Natoal Tawa Normal Uverst Referece:. W. Navd. Statstcs for Egeerg ad Scetsts. Chapter 7 (7.-7.3) & Teachg Materal
i 2 σ ) i = 1,2,...,n , and = 3.01 = 4.01
 ECO 745, Homework 6 Le Cabrera. Assume that the followg data come from the lear model: ε ε ~ N, σ,,..., -6. -.5 7. 6.9 -. -. -.9. -..6.4.. -.6 -.7.7 Fd the mamum lkelhood estmates of,, ad σ ε s.6. 4. ε
ECO 745, Homework 6 Le Cabrera. Assume that the followg data come from the lear model: ε ε ~ N, σ,,..., -6. -.5 7. 6.9 -. -. -.9. -..6.4.. -.6 -.7.7 Fd the mamum lkelhood estmates of,, ad σ ε s.6. 4. ε
Unique Common Fixed Point of Sequences of Mappings in G-Metric Space M. Akram *, Nosheen
 Vol No : Joural of Facult of Egeerg & echolog JFE Pages 9- Uque Coo Fed Pot of Sequeces of Mags -Metrc Sace M. Ara * Noshee * Deartet of Matheatcs C Uverst Lahore Pasta. Eal: ara7@ahoo.co Deartet of Matheatcs
Vol No : Joural of Facult of Egeerg & echolog JFE Pages 9- Uque Coo Fed Pot of Sequeces of Mags -Metrc Sace M. Ara * Noshee * Deartet of Matheatcs C Uverst Lahore Pasta. Eal: ara7@ahoo.co Deartet of Matheatcs
Study of Correlation using Bayes Approach under bivariate Distributions
 Iteratoal Joural of Scece Egeerg ad Techolog Research IJSETR Volume Issue Februar 4 Stud of Correlato usg Baes Approach uder bvarate Dstrbutos N.S.Padharkar* ad. M.N.Deshpade** *Govt.Vdarbha Isttute of
Iteratoal Joural of Scece Egeerg ad Techolog Research IJSETR Volume Issue Februar 4 Stud of Correlato usg Baes Approach uder bvarate Dstrbutos N.S.Padharkar* ad. M.N.Deshpade** *Govt.Vdarbha Isttute of
Strong Convergence of Weighted Averaged Approximants of Asymptotically Nonexpansive Mappings in Banach Spaces without Uniform Convexity
 BULLETIN of the MALAYSIAN MATHEMATICAL SCIENCES SOCIETY Bull. Malays. Math. Sc. Soc. () 7 (004), 5 35 Strog Covergece of Weghted Averaged Appromats of Asymptotcally Noepasve Mappgs Baach Spaces wthout
BULLETIN of the MALAYSIAN MATHEMATICAL SCIENCES SOCIETY Bull. Malays. Math. Sc. Soc. () 7 (004), 5 35 Strog Covergece of Weghted Averaged Appromats of Asymptotcally Noepasve Mappgs Baach Spaces wthout
Bayes (Naïve or not) Classifiers: Generative Approach
 Logstc regresso Bayes (Naïve or ot) Classfers: Geeratve Approach What do we mea by Geeratve approach: Lear p(y), p(x y) ad the apply bayes rule to compute p(y x) for makg predctos Ths s essetally makg
Logstc regresso Bayes (Naïve or ot) Classfers: Geeratve Approach What do we mea by Geeratve approach: Lear p(y), p(x y) ad the apply bayes rule to compute p(y x) for makg predctos Ths s essetally makg
Lecture Note to Rice Chapter 8
 ECON 430 HG revsed Nov 06 Lecture Note to Rce Chapter 8 Radom matrces Let Y, =,,, m, =,,, be radom varables (r.v. s). The matrx Y Y Y Y Y Y Y Y Y Y = m m m s called a radom matrx ( wth a ot m-dmesoal dstrbuto,
ECON 430 HG revsed Nov 06 Lecture Note to Rce Chapter 8 Radom matrces Let Y, =,,, m, =,,, be radom varables (r.v. s). The matrx Y Y Y Y Y Y Y Y Y Y = m m m s called a radom matrx ( wth a ot m-dmesoal dstrbuto,
Analysis of System Performance IN2072 Chapter 5 Analysis of Non Markov Systems
 Char for Network Archtectures ad Servces Prof. Carle Departmet of Computer Scece U Müche Aalyss of System Performace IN2072 Chapter 5 Aalyss of No Markov Systems Dr. Alexader Kle Prof. Dr.-Ig. Georg Carle
Char for Network Archtectures ad Servces Prof. Carle Departmet of Computer Scece U Müche Aalyss of System Performace IN2072 Chapter 5 Aalyss of No Markov Systems Dr. Alexader Kle Prof. Dr.-Ig. Georg Carle
Unsupervised Learning and Other Neural Networks
 CSE 53 Soft Computg NOT PART OF THE FINAL Usupervsed Learg ad Other Neural Networs Itroducto Mture Destes ad Idetfablty ML Estmates Applcato to Normal Mtures Other Neural Networs Itroducto Prevously, all
CSE 53 Soft Computg NOT PART OF THE FINAL Usupervsed Learg ad Other Neural Networs Itroducto Mture Destes ad Idetfablty ML Estmates Applcato to Normal Mtures Other Neural Networs Itroducto Prevously, all
