Logistic regression analysis with multidimensional random effects: A comparison of three approaches
|
|
|
- Merilyn Morgan
- 6 years ago
- Views:
Transcription
1 Quality & Quantity manuscript No. (will be inserted by the editor) Logistic regression analysis with multidimensional random effects: A comparison of three approaches Olga Lukočienė Jeroen K. Vermunt Received: date / Accepted: date Abstract This paper investigates the performance of three types of random coefficients logistic regression models; that is, models using parametric, semi-parametric, and nonparametric specifications of the distribution of the random effects. Whereas earlier studies focussed on models with a single random effect, here we look at models with multidimensional random effects (intercepts and slopes). Moreover, also the performance of a semi-parametric approach using mixture regression models with number of latent classes is selected using the BIC is investigated. One of the main conclusions of our study is that the good results obtained with the nonparametric approach in the unidimensional case do not generalize to the multidimensional case. Parametric and semi-parametric approaches are much better in terms of bias and relative efficiency than the nonparametric approach. For the fixed-effects estimation, a parametric approach is the preferred method when the underlying assumption of the parametric model holds. In other situations, the semi-parametric approach is the best choice. Keywords Mixed models Hierarchical models Finite mixture models Multilevel logistic regression analysis Random coefficients EM algorithm Nonparametric maximum likelihood O. Lukočienė Department of Methodology and Statistics Tilburg University P.O. Box LE Tilburg The Netherlands. Tel.: Fax: o.lukociene@uvt.nl J.K. Vermunt Department of Methodology and Statistics Tilburg University P.O. Box LE Tilburg The Netherlands. Tel.: Fax: j.k.vermunt@uvt.nl
2 2 1 Introduction During the last decades, multilevel regression analysis has become part of the standard statistical toolbox of researchers in the social and behavioral sciences as well as in the biomedical field. This statistical method is used for the analysis of data sets in which lower-level units are nested within higher-level units (Hox, 2002; Skrondal and Rabe-Hesketh, 2004; Snijders and Bosker, 1999). Examples include data sets with a nesting of persons within families, survey respondents within geographical units, patients within therapists, pupils within schools, employees within firms, and repeated measurements within subjects. The lower level of the hierarchical structure is often referred to as level-1 and the higher level as level-2. Typical for multilevel data is that level-1 observations belonging to the same level-2 unit are more alike than level-1 units from different level-2 units, for example, because they share common environments, experiences, and interactions. The implications of this is that the responses of level-1 units within the same level-2 units are correlated and can thus not be treated as independent observations in the statistical analysis. Whereas in some applications this is perceived as a problem that should be dealt with when modeling multilevel data, in other applications the multilevel data structure is seen as containing valuable information on how groups (higher-level units) differ from each other, for example, in terms of the effects of explanatory variables on the outcome variable of interest (Bryk and Raudenbush, 1992; Hox, 1994; Snijders and Bosker, 1999). The most popular approach for the analysis of such data sets is by means of multilevel models, which are also referred to as hierarchical, mixed, random-effects, or randomcoefficients models (Bryk and Raudenbush, 1992; Hox, 1994; Longford, 1995; Snijders and Bosker, 1999). Whereas the terms multilevel and hierarchical refer to the data structure, the terms mixed, random-effects and random-coefficients indicate what these models are from a more technical point of view. More specifically, these models capture differences between level-2 units and thus also correlations between level-1 observations within level- 2 units by allowing one or more of the model parameters to vary randomly across level-2 units. Whereas the earliest developments and applications of multilevel regression models concerned linear models for continuous responses, these are nowadays also applied with discrete response variables. The most popular model for binary responses is the random-effects logistic regression model (Breslow and Clayton, 1993; Wolfinger and O Connell, 1993). A key issue in the specification of a multilevel regression model is that not only assumptions have to be made about the distribution of the residuals, but also about the distribution of the random effects, also referred to as the mixing distribution. The most common approach is to assume that it has a convenient parametric form, in most cases a normal distribution. However, as stressed by Aitkin (1999), parametric distributional assumptions about the random effects will usually not hold in practice, which may have serious implications for the parameter estimates. For example, various studies found that misspecification of the distribution of random effects results in a loss of efficiency of the fixed coefficient estimates (Agresti et al., 2004; Heagerty and Kurland, 2001; Maas and Hox, 2004; Neuhaus et al., 1992). Lukočienė (2008) not only confirmed this result for the random-intercept logistic regression model, but also showed that the estimate for the random-intercept variance may be severely biased when its distribution is misspecified. Rather than using a parametric random-effects approach, it is also possible to use either a nonparametric or a semi-parametric approach. These two alternatives have in common that they are both latent class models; that is, a discrete mixing distribution with K nodes (latent classes) is used to approximate the underlying distribution with an unknown shape. The locations and weights corresponding to the nodes are quantities to be estimated. Al-
3 3 though the nonparametric and semi-parametric approach are similar, they are fundamentally different in how they determine the number of latent classes. In the former, the number of latent classes is increased till the likelihood function is maximized, which yields what is called the nonparametric maximum likelihood (NPML) estimator of the random-effects distribution (Heckman and Singer, 1984; Laird, 1978; Lindsay, 1995). As indicated by Leroux (1992) and Leroux and Puterman (1992), the NPML estimate may yield unnecessarily large numbers of latent classes and well fitting models with fewer latent classes may be preferred. Rather than increasing the number of latent classes till a saturation point is reached, it is also possible to decide about the number of classes using information criteria such as AIC and BIC. Note that this is what is usually done in mixture regression analysis (Vermunt and van Dijk, 2001; Wedel and DeSarbo, 1994), as well as in other types of latent class analyses. To distinguish this approach from NPML, we call it a semi-parametric approach. This paper provides a comparison of the three random-effect approaches within the context of multilevel logistic regression analysis. It extends the work by (Lukočienė, 2008) on the comparison of parametric and NPML approaches for random-effects logistic regression analysis to the situation in which not only the intercept but also slopes are random coefficients, as is usual in social and behavioral science application of multilevel regression analysis (Kreft and de Leeuw, 1998; Singer, 1998; Snijders and Bosker, 1999). As far as we know, there are no studies investigating the performance of the NMPL approach when applied with multidimensional random effects. Moreover, we include the semi-parametric approach in the comparison. This is the commonly used latent-class based regression modeling approach for situations in which not only the intercept but also the slopes vary randomly across level-2 units. We focus on binary logistic regression models because these are more sensitive to specification issues in multilevel analysis than models for continuous response variables or counts (Agresti et al., 2000, 2004). Using a simulation study we wish to find out which of the three approaches parametric, semi-parametric or nonparametric should be used under different types of true randomeffects distributions and specific features of the sample. More specifically, we are interested in whether it makes sense to use a nonparametric or semi-parametric model as an alternative when the underlying assumptions of the parametric model do not hold? Moreover, we wish to know whether it harms to use a nonparametric or semi-parametric model say for practical reasons when the assumptions of the parametric model hold? The next section describes the multilevel logistic regression model of interest. Section 3 discusses the set up of the simulation study. Results of the simulation study are presented in Section 4. The last section summarizes the main conclusions and provides some practical recommendations. 2 The two-level logistic regression model This section describes the two-level logistic regression model using the single equation mixed model formulation (Skrondal and Rabe-Hesketh, 2004). An alternative would be to use the hierarchical model formulation, which contains separate regression equations for the various hierarchical levels (Bryk and Raudenbush, 1992; Hox, 2002; Snijders and Bosker, 1999). Let y i j denote the binary response (y i j = 0,1) of the level-1 unit i, i = 1,...,n j, belonging to the level-2 unit j, j = 1,...,n. Explanatory variables are referred to by x i j and z i j, where the former concern the fixed and the later the random effects. The vector with fixed effects is denoted by β and the vector with the unobservable common random coefficients shared
4 4 by all level-1 units belonging to the j th level-2 unit by u j. Let π i j = E(y i j x i j,z i j,u j ) be the conditional expectation of y i j. The multilevel logistic regression model for y i j takes on the following form: π i j log = β x i j + u j 1 π z i j. (1) i j The typical assumption for the random coefficients u j is that these are independently and identically distributed multivariate normal random variables with zero means and covariance matrix Σ u. Consistent with this distributional assumption, parameters of the two-level logistic regression model may be estimated by maximum likelihood (ML), where construction of the likelihood function is simplified by the fact that the y i j can be assumed to be independent within level-2 units conditionally on the observed predictors and the unobserved random effects. ML estimation involves maximizing the following marginal likelihood function: [ n n ] j L(β,Σ u ) = π y i j i j (1 π i j ) 1 y i j f (u j ;Σ u )du j, (2) j=1 i=1 u j where π y i j i j (1 π i j ) 1 y i j represents the Bernoulli distribution for the level-1 errors. Note that the fixed effects β and covariance matrix Σ u are the unknown parameters to be estimated. The integral should be solve numerically, for example, using Gauss-Hermite quadrature, which is basically a discrete approximation of the multivariate normal integral. Algorithms for maximizing the resulting numerically integrated marginal likelihood are the EM algorithm (Agresti et al., 2000; Bock and Aitkin, 1981; Dempster et al., 1977) and gradient methods, such as the Fisher scoring (Longford, 1987) and Newton-Raphson algorithm (Pan and Thompson, 2003; Rabe-Hesketh et al., 2004). In our study, we used numerical integration with 50 nodes per dimension. For maximization a combination of EM and Newton-Raphson was used, where the estimation process starts with EM iterations and switches to Newton- Raphson when the relative change in parameters is very small (Vermunt and Magidson, 2005). As was indicated in the introduction, usually nothing or very little it is known about the underlying distribution of the random effects (Aitkin, 1999). To prevent possible misspecification, it may therefore be attractive to assume the random effects u j come from an unspecified mixing distribution concentrated on a finite number of latent classes or mass points (Aitkin, 1999; Heckman and Singer, 1984; Laird, 1978; Vermunt, 1997). Let K denote the number of latent classes, k a particular latent class, and u k the unknown values of the random effects u j when level-2 unit j belongs to latent class k, and let π k = P(u j = u k ) represent the probability that a randomly selected level-2 unit belongs to latent class k or in other words that the random effects correspond to the location of class k. Using such a K-class discrete characterization of the random effects distribution yields the following marginal likelihood function: [ L(β,u n K n ] j,π) = π y i j i j k (1 π i j k) 1 y i j π k, (3) j=1 i=1 k=1 where π i j k is the conditional density function of y i j given that level-2 unit j belongs to latent class k. The two-level logistic regression model can now be written as a model for π i j k ; that is, π i j k log = β x i j + u k z i j. (4) 1 π i j k
5 5 The weights are restricted such that π k > 0 and K k=1 π k = 1. In addition one identifying location constraint should be imposed on each of the M + 1 random coefficients, e.g. K k=1 u mk π k = 0, which implies that the u k = (u 0k,...,u mk,...,u Mk ) are centered. The unknown parameters to be estimated are the fixed effects β, K 1 free mass point locations per dimension (u 0k,...,u Mk ) and K 1 free mass point weights π k. Note that although the variances and covariance of the random effects are not model parameters, they can easily be estimated as follows (Vermunt and van Dijk, 2001): ˆσ m 2 = K (u mk )2 π k and ˆσ mm = K u mk u m k π k. k=1 k=1 Maximization of the marginal likelihood function in equation (3) for a specific K, as in the parametric case, can be achieved by means of the EM and/or Newton-Raphson algorithm. It is usually advised to use of multiple sets of starting values to reduce the likelihood of ending up in a local maximum. To obtain the solution corresponding to the NPML estimate of the random effects distribution, we not only have to maximize (3) for specific values of K; but we simultaneously have to find the value of K say K NPML that yields the largest marginal likelihood value. In other words, we have to find the saturation point at which increasing K no longer results in an increase of the likelihood function. A method to find K NPML proposed by various authors involves introducing latent classes one by one using directional (Gateaux) derivatives (Böhning, 2000; Lindsay, 1983, 1995; Rabe-Hesketh et al., 2003). A much simpler alternative approach is to estimate the model with a large number of latent classes, K MAX. When K MAX > K NPML, the ML estimates for u k will be equal for some latent classes and/or the estimate for π k will be equal to zero for some latent classes (Böhning, 2000). In other words, classes may be merged (equal u k ) and/or removed (π k equal to zero). To prevent local maxima this procedure should be repeated with several sets of starting values. Moreover, to guarantee that also the more difficult to find mass points located at and + are encountered when needed in the NPML solution, it is advisable to include latent classes located at these values in each starting set (Hartzel et al., 2001; Wood and Hinde, 1987). As already mentioned, the NPML estimates may yield unnecessarily large K (Leroux, 1992; Leroux and Puterman, 1992) and estimates with a smaller number of latent classes that describe the data sufficiently may be preferred. Moreover, the latent classes may have substantive interpretations which are useful for the study concerned. This yields an approach in which the value of K should be estimated, yielding what we called the semi-parametric random-effects modeling approach. In this approach the value of K is increased till the criterion used for model selection no longer improves. In our study, we will use the BIC (Schwarz, 1978) for deciding about the number of classes, as was for example done by Vermunt and van Dijk (2001); Wedel and DeSarbo (1994). 3 Design of the simulation study This section describes the design of the simulation study. First, we discuss the design factors that were kept constant, and subsequently the ones that were varied. The key factors that were kept contant are the overall structure of the population model, the values of the fixedeffect parameters, and the values of the intraclass correlations for the random effects. The population model we used is a two-level random coefficients logistic regression model with one level-1 and one level-2 explanatory variable. This model can be formulated as follows: π i j log = β 0 + β 1 x 1i j + β 2 x 2 j + u 0 j + u 1 j z 1i j. (5) 1 π i j
6 6 Here, both x 1i j and z 1i j represent the level-1 predictor (in fact, x 1i j = z 1i j ), where x 1i j is used to define its fixed part and z 1i j its random part. The other fixed effects correspond to the intercept and the level-2 predictor x 2 j. The two explanatory variables are assumed to be binary predictors taking on the values 0 and 1 with probability 0.5 independently of one another. For the fixed intercept β 0 and slopes β 1 and β 2, we used the same values across simulation replications. More specifically, we set their values to: β 0 = 2, β 1 = β 2 = 2. This yields large enough but not too extreme differences between the response probabilities for u 0 j = 0 and u 1 j = 0. More specifically, the corresponding response probabilities for the four possible combinations of explanatory variables are P(y = 1 x 1 = 1,x 2 = 1,u 0 = u 1 = 0) = e 2 /(1 + e 2 ) = 0.88, P(y = 1 x 1 = 1,x 2 = 0,u 0 = u 1 = 0) = e 0 /(1 + e 0 ) = 0.5, P(y = 1 x 1 = 0,x 2 = 1,u 0 = u 1 = 0) = e 0 /(1 + e 0 ) = 0.5 and P(y = 1 x 1 = 0,x 2 = 0,u 0 = u 1 = 0) = e 2 /(1 + e 2 ) = A second element that was kept constant in the simulation study is the overall importance of the random part, which can be expressed by means of the intraclass correlation (ICC). Although Hox and Maas (2001) found that the value of the ICC may affect the impact of a misspecification of the random effects distribution, the study by Lukočienė (2008) on the random-intercept logistic regression model found that parametric and nonparametric approaches are almost indistinguible when the ICC value is small (e.g. 0.1). We will therefore not investigate this situation again, but instead focus on the condition with a moderate ICC value of 0.3. For this ICC value, Lukočienė (2008) found important differences in the performance of the parametric and nonparametric approaches. The ICC values can be set by using the fact that level-1 errors coming from a logistic distribution have a variance equal to π 2 /3. Since ICC = σ 2 /(σ 2 + π 2 /3), the variance of the random intercept σ0 2 can be obtained by σ 0 2 = ICC /(1 ICC)π2 /3, which for ICC = 0.3 yields σ0 2 = Similar to Busing (1993) and Maas and Hox (2004), we used the same variance for the random slope as for the random intercept (σ1 2 = 1.41 as well). So far, we discussed only the elements that were not varied in the simulations study. The three design factors that were varied are the random effects distribution, the level-1 sample size, and the level-2 sample size. We wish to assess how the parametric, nonparametric, and semi-parametric models perform under different true random-effect distributions and whether the performance depends on the level-1 and level-2 sample sizes. The study by Lukočienė (2008) on the random-intercept logistic regression model showed that these are the main factors affecting the performance of the parametric and nonparametric approaches. Data sets were generated using four distributional forms for the random effects, two continuous distributions (exponential and normal) and two discrete mixing distributions one five-class distribution with class membership probabilities of 0.1, 0.2, 0.4, 0.2, and 0.1, respectively, and another four-class distribution with equal membership probabilities of As demonstrated in Figure 1 and Figure 2, the locations of the classes of these two discrete mixing distribution were chosen in such a way that the random intercept and random slope would be uncorrelated, but strongly associated. With these four choices we have apart from the normal distribution, distributions that considerably deviate from normal in terms of skewness, kurtosis, discontinuity, and association between dimensions. The other two factors that were varied are the level-1 and level-2 sample sizes. More specifically, for the number of level-2 units we used n = 30, 100, and 1000 and for the
7 7 0.4 Random coefficient Random intercept Fig. 1 Discrete mixing distribution with five classes 0.25 Random coefficient Random intercept Fig. 2 Discrete mixing distribution with four classes number of level-1 units n j = 10, and 50. These sample sizes reflect the typical sample sizes in multilevel analysis (see also Kreft and de Leeuw (1998); Maas and Hox (2004); Lukočienė (2008)). Combining the 3 design factors distributional form, level-2 sample size, and level-1 sample size yielded a total of = 24 conditions. We generated 1000 simulated data sets for each of these conditions. For each simulated data set, the unknown model parameters were estimated using the parametric approach assuming that random effects come from a normal distribution, the NPML approach, and the semi-parametric approach using BIC as the model selection criterion.
8 8 4 Results of the simulation study The aim of the simulation study was to determine the bias and relative efficiency of the parametric, nonparametric, and semi-parametric random effects approaches under the different true random effects distributions and sample sizes. Let θ be one of the parameters of interest, which in our case are the fixed effects β 0, β 1, and β 2, and the standard deviations of the random effects distribution σ 0 and σ 1 which in the nonparametric and semi-parametric cases are computed from the nodes locations and weights. The ML estimate of θ obtained in replication s, s = 1,...,1000, is denoted by θ s. Rather than using the ] more standard definitions of bias and relative efficiency E( θ s θ) and E [( θ s θ) 2 we used a more robust definition to prevent that the results are affected by a small number of replications with boundary estimates. More specifically, when using the NPML estimator, especially in the conditions with large number of level-2 units and small number of level-1 units, there is a positive probability that one of the latent classes is located at infinity. In our case, latent classes can have 4 such possible locations: (, ), (, ), (, ), ] and/or (, ). When such boundary estimates may occur E( θ s θ) and E [( θ s θ) 2 do not exist. This not only applies to σ 0 and σ 1, but also to β 0, β 1, and β 2. To prevent this problem from occurring we define bias as the median of ( θ s θ) and relative efficiency as the median of θ s θ. For similar approaches, see Agresti et al. (2004) and Galindo-Garre et al. (2004). Below we first discuss the results for the fixed effects and then for the random effects. 4.1 Fixed effects The first evaluation criterion of interest is the bias in the parameter estimates. Table 1 provides the estimated biases of the fixed effects for the level-2 sample sizes of 1000 and 30. The first three columns of Table 1 indicate the values for the design factors: level-2 sample size, level-1 sample size, and the random-effects distribution used to generate the data sets. The fourth column indicates which of the three approaches parametric, nonparametric or semi-parametric was used for the estimation of the parameters. The last three columns present the biases in the estimates of the intercept and the two slopes. Reported biases are marked by a * when they are larger than 5% of the true parameter value, and smaller values are considered negligible. Table 1 shows that the bias of the fixed effects in the models estimated under the semiparametric approach is negligible for all cases with true discrete and exponential underlying distributions, except for the fixed effect β 1 when n = 30 and true underlying discrete distribution has 5 latent classes. When the semi-parametric approach is applied with the true bivariate normal distribution, we see biases only for β 2. The NPML approach yields biased estimates for almost every parameter, where it makes no difference whether the true distribution is discrete or continuous. The parametric approach performs very well when the true underlying distribution is bivariate normal, in which case the bias in the fixed effects is always negligible. However, for other true underlying distributions, the parametric approach gives biased estimates for at least one of the fixed effects. The results for the medium level-2 unit sample size n = 100 (which are not shown) are very similar to the results obtained with n = As was mentioned above, the second evaluation criterion of interest is the efficiency of the parameter estimates. Table 2 reports results on relative efficiency of the fixed effects obtained with the largest and smallest level-2 unit sample sizes n = 1000 and n = 30 (results
9 9 Table 1 Bias of the fixed effects for the conditions n = 1000 and 30 n n j True distribution Assumed ˆβ0s β 0 ˆβ1s β 1 ˆβ2s β Exponential Normal -0.12* Nonparametric * 0.04 Semi-parametric Normal Normal Nonparametric -0.17* 0.28* 0.05 Semi-parametric Discrete (4 classes) Normal Nonparametric -0.11* 0.24* 0.05 Semi-parametric Discrete (5 classes) Normal * 0.02 Nonparametric * 0.01 Semi-parametric Exponential Normal Nonparametric * 0.01 Semi-parametric Normal Normal Nonparametric * 0.03 Semi-parametric * Discrete (4 classes) Normal * Nonparametric * 0.02 Semi-parametric Discrete (5 classes) Normal * 0.05 Nonparametric * 0.01 Semi-parametric Exponential Normal -0.10* Nonparametric -0.58* 2.35* 0.29* Semi-parametric Normal Normal Nonparametric -0.94* 2.46* 0.32* Semi-parametric * Discrete (4 classes) Normal Nonparametric -0.88* 2.19* 0.28* Semi-parametric Discrete (5 classes) Normal 0.105* -0.16* Nonparametric -0.16* 2.09* 0.02 Semi-parametric * Exponential Normal Nonparametric -0.24* 1.59* -0.14* Semi-parametric Normal Normal Nonparametric -0.26* 0.92* -0.34* Semi-parametric * Discrete (4 classes) Normal * Nonparametric -0.15* 0.22* 0.04 Semi-parametric Discrete (5 classes) Normal 0.10* -0.16* Nonparametric -0.17* 2.20* 0.01 Semi-parametric * 0.00 Cases with medians absolute value over 5%. for n = 100 are again similar to the ones for n = 1000). Table 2 can be read similarly to Table 1. The semi-parametric approach clearly outperforms the parametric and nonparametric approaches in cases when the true underlying distribution of random effects is discrete. However, when the true underlying random effects distribution is bivariate normal the para-
10 10 Table 2 Efficiency of the fixed effects for the conditions n = 1000 and 30 n n j True distribution Assumed ˆβ 0s β 0 ˆβ 1s β 1 ˆβ 2s β Exponential Normal Nonparametric Semi-parametric Normal Normal Nonparametric Semi-parametric Discrete (4 classes) Normal Nonparametric Semi-parametric Discrete (5 classes) Normal Nonparametric Semi-parametric Exponential Normal Nonparametric Semi-parametric Normal Normal Nonparametric Semi-parametric Discrete (4 classes) Normal Nonparametric Semi-parametric Discrete (5 classes) Normal Nonparametric Semi-parametric Exponential Normal Nonparametric Semi-parametric Normal Normal Nonparametric Semi-parametric Discrete (4 classes) Normal Nonparametric Semi-parametric Discrete (5 classes) Normal Nonparametric Semi-parametric Exponential Normal Nonparametric Semi-parametric Normal Normal Nonparametric Semi-parametric Discrete (4 classes) Normal Nonparametric Semi-parametric Discrete (5 classes) Normal Nonparametric Semi-parametric metric approach is most efficient. For the true underlying exponential distribution, the parametric and semi-parametric approaches perform equally well in terms of efficiency. We find a considerable lower efficiency under the nonparametric approach for almost every condition.
11 11 Table 3 Bias and efficiency of the random effects for the conditions n = 1000 and 30 n n j True distribution Assumed ˆσ 0s σ 0 ˆσ 1s σ 1 ˆσ 0s σ 0 ˆσ 1s σ Exponential Normal 0.35* -0.17* Nonparametric 0.57* 6.15* Semi-parametric -0.12* -0.26* Normal Normal 0.26* 0.28* Nonparametric 1.20* 6.59* Semi-parametric -0.09* -0.17* Discrete (4 classes) Normal 0.29* 0.74* Nonparametric 0.16* 2.26* Semi-parametric Discrete (5 classes) Normal * Nonparametric * Semi-parametric Exponential Normal 0.13* -0.26* Nonparametric * Semi-parametric * Normal Normal 0.11* 0.18* Nonparametric * Semi-parametric * Discrete (4 classes) Normal 0.24* 0.89* Nonparametric * Semi-parametric Discrete (5 classes) Normal * Nonparametric * Semi-parametric Exponential Normal 0.15* -0.23* Nonparametric 2.45* 9.10* Semi-parametric -0.18* -0.47* Normal Normal * Nonparametric 3.40* 10.69* Semi-parametric -0.22* -0.42* Discrete (4 classes) Normal 0.14* 0.90* Nonparametric 2.78* 9.50* Semi-parametric -0.27* -0.33* Discrete (5 classes) Normal 0.23* -0.40* Nonparametric 0.18* 7.75* Semi-parametric * Exponential Normal 0.25* -0.24* Nonparametric 0.39* 6.87* Semi-parametric -0.11* -0.13* Normal Normal 0.23* 0.39* Nonparametric 0.95* 6.35* Semi-parametric -0.08* -0.10* Discrete (4 classes) Normal 0.37* 0.90* Nonparametric 0.14* 0.72* Semi-parametric Discrete (5 classes) Normal 0.22* -0.41* Nonparametric 0.21* 7.93* Semi-parametric * Cases with medians absolute value over 5%. If we have a closer look at results presented in Table 1 and Table 2 from the perspective of the effects of the level-1 and level-2 sample sizes, it can be observed is that the nonparametric approach perform very bad with the smaller level-2 sample size, and this is enforced when also the level-1 sample size is small. The quality of the other two approaches
12 12 is less strongly affected by the sample sizes. However, when misspecified, the normal model performs worse when the level-1 sample size increases. 4.2 Random effects Table 3 shows the results on bias and relative efficiency for the random effects obtained with sample sizes n = 1000 and n = 30. As in Table 1, biases larger than 5% of the true parameter value are marked by a *. The semi-parametric approach yields negligible biases for both random effects when the true underlying distribution is discrete and the sample size is The parametric approach yields moderate biases for almost every condition. However, the obtained biases of the parametric estimates with true continuous underlying distributions in the smallest samples (n = 30 and n j = 10) are smaller than for the semi-parametric and nonparametric estimates. In most other cases, the semi-parametric approach performs best showing the smallest bias for all true distributions. The last three columns of Table 3 report the information on the efficiency of the random effects estimates (of the standard deviations of the random effects). For the random intercept, the semi-parametric approach outperforms the parametric and nonparametric approaches in all investigated conditions. The same applies to the random slope, except for one situation; that is, when n j = 10 and the true underlying distribution is exponential, the parametric approach is the most efficient method. Results on bias and relative efficiency of random effects for the medium level-2 sample size (n = 100) are again not presented because they are rather similar to the results obtained with n = Remarks on semi-parametric and nonparametric approaches The results reported in Tables 1, 2, and 3 show that the nonparametric approach performs worse than the semi-parametric approach in almost all investigated conditions. As explained earlier, the difference between these two approaches is that they use different methods for determining the number of latent classes. To see how the use of BIC worked out in our simulation study, let us take a look at the number of latent classes selected according to this criterion when the true distribution is discrete. More specifically, Table 4 presents the percentage of simulation replications (out of 1000) in which a particular number of latent classes was selected using the semi-parametric approach. As can be seen, the number of latent classes is often underestimated with the smaller level-2 sizes, and this tendency is stronger when also the level-1 sample size is small. It can also be observed that the semiparametric specification never overestimates the number of latent classes, which confirms that BIC is a somewhat conservative measure when deciding about the number of classes (see, for example, Dias (2004)). As indicated earlier, in the nonparametric approach one increases the number of classes till a saturations point in reached, which seemingly lead to severely biased and much less efficient estimates. The NPML solution often consisted of a larger number of latent classes than the true discrete distribution even for the smallest level-2 sample size of 30. Such solutions contained nodes with small weights but very extreme locations, with explains the bias and inefficiency of this approach. In contrast, the semi-parametric approach will not accept such classes in the final solution because they do not yield a significantly better description of the data according to the BIC.
13 13 Table 4 Percentage of replications selecting a particular number of latent classes based on BIC in semiparametric approach n n j True distribution 2 classes 3 classes 4 classes 5 classes Discrete with 4 classes 100 Discrete with 5 classes Discrete with 4 classes 100 Discrete with 5 classes Discrete with 4 classes Discrete with 5 classes Discrete with 4 classes Discrete with 5 classes Discrete with 4 classes Discrete with 5 classes Discrete with 4 classes Discrete with 5 classes Conclusions The two questions that we wished to answer based on the simulation study are 1) whether the NPML and/or semi-parametric approaches perform better in terms of bias and efficiency compared to the parametric model when the latter is misspecified, and 2) whether the NPML and/or semi-parametric approaches perform equally well in terms of bias and efficiency compared to the parametric model when the latter is correctly specified. This was studied for small and large level-1 and level-2 sample sizes and different types of random effects distributions (with a moderate ICC value). We are now able to answer these two questions for the two-level logistic regression model. Our study showed that the NPML method gives the worst results in terms of bias and relative efficiency when compared to the parametric and semi-parametric methods, and this applies irrespective of the true random effects distribution. The semi-parametric approach performs best when the true underlying distribution of random effects is discrete. When the assumptions of the parametric model hold, the parametric approach is the best for the fixed effects estimation, but the semi-parametric approach is the preferred one for the random effects estimation. When the true distribution is exponential (continuous but not normal), the parametric model is still preferred with a small level-1 sample size, but the semi-parametric model is better with a larger level-1 sample size. We may finally compare our conclusions with those derived from the study by Lukočienė (2008) on multilevel logistic regression with only a random intercept. One important difference concerns the performance of the NPML method. Whereas this earlier study found that the NPML approach performs rather well as long as the level-1 sample size is not too small, here we have to conclude that it is by far the worst approach. In fact, the NPML method should not be used with multidimensional random effects. Another new element compared to this earlier study is that we also looked at the semi-parametric method which turned out to perform much better than the NPML method. As far as the parametric approach is concerned, similarly to the previous study it can be concluded that it is the preferred method when the normal distribution assumption holds, as well as when the distribution is continuous but not normal and the level-1 sample size is small. One limitation of our study is that it concerned two-level regression models, and it is not clear whether our findings can be generalized to models containing more hierarchical lev-
14 14 els. Another limitation is that we focussed on models for binary responses. The suggestion for the future research would be to look at other models from the generalized linear modeling family, as well as at models with more than two levels; that is, at the class of models described by (Vermunt, 2004). In our study we investigated three different specifications for the random effects distribution: a parametric approach with an underlying normal distribution, as well as nonparametric and semi-parametric approaches using an unspecified discrete mixing distribution. As a possible alternative one may use a combination of these, namely a finite mixture of normal distributions (Magder and Zeger, 1996; Verbeke and Molenberghs, 2000). Whereas such an approach may have particular advantages, such as that contrary to the nonparametric and semi-parametric approaches it yields nondiscrete random effects, Agresti et al. (2004) obtained somewhat disappointing results with this approach in the context of a log linear model for an odds ratio. Nevertheless, we believe that this hybrid approach may be promising in other situations, especially when the aim of the study is to obtain interpretable latent classes (Magidson and Vermunt, 2007). References Agresti, A., Booth, J.G., Hobert, J.P., Caffo, B., Random-effects modeling of categorical response data, Sociological Methodology 30, (2000). Agresti, A., Caffo, B., Ohman-Strickland, P., Examples in which misspecification of a random effects distribution reduces efficiency, and possible remedies, Computational Statistics and Data Analysis 47, (2004). Aitkin, M., A general maximum likelihood analysis of variance components in generalized linear models, Biometrics 55, (1999). Bock, R.D., Aitkin, M., Marginal maximum likelihood estimation of item parameters, Psychometrika 46, (1981). Böhning, D., Computer-assisted analysis of mixtures and applications. Meta-analysis, disease mapping and others. London: Chapman & Hall (2000). Breslow, N.E., Clayton, D.G., Approximate inference in generalized linear mixed models, Journal of the American Statistical Association 88, 9 25 (1993). Bryk, A.S., Raudenbush, S.W., Hierarchical linear models. Newbury Park: Sage (1992). Busing, F., Distribution characteristics of variance estimates in two-level models, Unpublished manuscript. Department of Psychometrics and Research Methodology, Leiden University (1993). Dempster, A.P., Laird, N.M., Rubin, D.B., Maximum likelihood estimation from incomplete data via the EM algorithm, Journal of the Royal Statistical Society 39(1), 1 38 (1977). Dias, J.G., Finite mixture models: review, applications and computer intensive methods. Doctoral dissertation, SOM Research School, University of Groningen, Netherlands (2004). Galindo-Garre, F., Vermunt, J.K., Bergsma, W., Bayesian posterior estimation of logit parameters with small samples, Sociological Methods and Research 39(33), (2004). Hartzel, J., Agresti, A., Caffo, B., Multinomial logit random effects models, Statistical Modelling 1(2), (2001). Heagerty, P.J., Kurland, B.F., Misspecified maximum likelihood estimates and generalized liner mixed models, Biometrica 88, (2001). Heckman, J.J., Singer, B., A method for minimizing the impact of distributional assumptions in econometric models of duration, Econometrica 52, (1984).
15 Hox, J., Multilevel analysis: techniques and applications. Mahwah, NJ: Lawrence Erlbaum (2002). Hox, J.J., Applied multilevel analysis. Amsterdam: TT (1994). Hox, J.J., Maas, C.J.M., The accuracy of multilevel structural equation modeling with pseudobalanced groups and small samples, Structural Equation Modeling 8, (2001). Kreft, I.G.G., de Leeuw, J., Introducing multilevel modeling. Sage, Newbury Park, CA (1998). Laird, N., Nonparametric maximum likelihood estimation of a mixture distribution, Journal of the American Statistical Association 73, (1978). Leroux, B.G., Maximum likelihood estimation for hidden Markov models. Stoch. Proc. and their appl. 40, (1992). Leroux, B.G., Puterman, M.L., Maximum-penalized-likelihood estimation for independent and Markov-dependent mixture models, Biometrics 48, (1992). Lindsay, B.G., The geometry of mixture likelihoods: a general theory, The Annals of Statistics 11, (1983). Lindsay, B.G., Mixture models: theory, geometry and applications. NSF-CBMS Regional Conference Series in Probability and Statistics, vol.5. Hayward, CA: Institute of Mathematical statistics (1995). Longford, N.T., A fast scoring algorithm for maximum likelihood estimation in unbalanced mixed models with nested random effects, Biometrika 74, (1987). Longford, N.T., Random coefficient models. Oxford: Clarendon (1995). Lukočienė, O., Vermunt, J.K., A Comparison of multilevel logistic regression models with parametric and nonparametric random intercepts, Manuscript submitted for publication (2008). Maas, C.J.M., Hox, J.J., The influence of violations of assumptions on multilevel parameter estimates and their standard errors, Computational Statistics and Data Analysis 46, (2004). Magder, L.S., Zeger, S.L., A smooth nonparametric estimate of mixing distribution using mixtures of Gaussians, Journal of the American Statistical Association 91, (1996). Magidson, J., Vermunt, J.K., Use of a random intercept in latent class regression models to remove response. Bulletin of the International Statistical Institute, 56th Session, paper 1604, 1 4 (2007). Neuhaus, J.M., Hauck, W.W., Kalbfleisch, J.D., The effects of mixture distribution misspecification when fitting mixed effects logistic models, Biometrika 79, (1992). Pan, J.X., Thompson, R., Gauss-Hermite quadrature approximation for estimationin in generalised linear mixed models, Computational Statistics 18, (2003). Rabe-Hesketh, S., Pickles, A., Skrondal, A., Correcting for covariate measurement error in logistic regression using nonparametric maximum likelihood estimation, Statistical Modelling 3, (2003). Rabe-Hesketh, S., Pickles, A., Skrondal, A., Generalized multilevel structural equation modeling, Psychometrica 69, (2004). Schwarz, G., Estimating the dimension of a model, The Annals of Statistics 6(2), (1978). Singer, J.D., Using SAS PROC MIXED to fit multilevel models, hierarchical models, and individual growth models, Journal of Educational and Behavioral Statistics 24, (1998). Skrondal, A., Rabe-Hesketh, S., Generalized latent variables modeling: multilevel, longitudinal, and structural equation models. Boca Raton, FL: Chapman & Hall/CRC (2004). 15
16 16 Snijders, T.A.B., Bosker, R.J., Multilevel analysis. London: Sage Publications (1999). Verbeke, G., Molenberghs, G., Linear mixed models for longitudinal data. Springer, Berlin (2000). Vermunt, J.K., Log-linear models for event histories. Advanced Quantitative Techniques in the Social Sciences Series 8. Sage Publications (1997). Vermunt, J.K., van Dijk, L., A nonparametric random-coefficients approach: the latent class regression model, Multilevel Modelling Newsletter 13, 6 13 (2001). Vermunt, J.K., An EM algorithm for the estimation of parametric and nonparametric hierarchical nonlinear models, Statistica Neerlandica 58, (2004). Vermunt, J.K., Magidson, J., Technical guide to Latent GOLD: basic and advanced. Belmont, MA: Statistical Innovations Inc (2005). Wedel, M., DeSarbo, W.S., A review of recent developments in latent class regression models. in Advanced Methods of Marketing Research, R.P. Bagozzi, ed. Cambridge: Blackwell Publishers, (1994). Wolfinger, R., O Connell, M., Generalized linear mixed models: a pseudo-likelihood approach, Journal of Statistical Computation and Simulation 48, (1993). Wood, A., Hinde, J., Binomial variance component models with a non-parametric assumption concerning random effects. In: Crouchley R, ed. Longitudinal data analysis. Avebury, Aldershot: Hants, (1987).
A Comparison of Multilevel Logistic Regression Models with Parametric and Nonparametric Random Intercepts
 A Comparison of Multilevel Logistic Regression Models with Parametric and Nonparametric Random Intercepts Olga Lukocien_e, Jeroen K. Vermunt Department of Methodology and Statistics, Tilburg University,
A Comparison of Multilevel Logistic Regression Models with Parametric and Nonparametric Random Intercepts Olga Lukocien_e, Jeroen K. Vermunt Department of Methodology and Statistics, Tilburg University,
Determining the number of components in mixture models for hierarchical data
 Determining the number of components in mixture models for hierarchical data Olga Lukočienė 1 and Jeroen K. Vermunt 2 1 Department of Methodology and Statistics, Tilburg University, P.O. Box 90153, 5000
Determining the number of components in mixture models for hierarchical data Olga Lukočienė 1 and Jeroen K. Vermunt 2 1 Department of Methodology and Statistics, Tilburg University, P.O. Box 90153, 5000
Growth models for categorical response variables: standard, latent-class, and hybrid approaches
 Growth models for categorical response variables: standard, latent-class, and hybrid approaches Jeroen K. Vermunt Department of Methodology and Statistics, Tilburg University 1 Introduction There are three
Growth models for categorical response variables: standard, latent-class, and hybrid approaches Jeroen K. Vermunt Department of Methodology and Statistics, Tilburg University 1 Introduction There are three
Mixed-Effects Logistic Regression Models for Indirectly Observed Discrete Outcome Variables
 MULTIVARIATE BEHAVIORAL RESEARCH, 40(3), 28 30 Copyright 2005, Lawrence Erlbaum Associates, Inc. Mixed-Effects Logistic Regression Models for Indirectly Observed Discrete Outcome Variables Jeroen K. Vermunt
MULTIVARIATE BEHAVIORAL RESEARCH, 40(3), 28 30 Copyright 2005, Lawrence Erlbaum Associates, Inc. Mixed-Effects Logistic Regression Models for Indirectly Observed Discrete Outcome Variables Jeroen K. Vermunt
Tilburg University. Mixed-effects logistic regression models for indirectly observed outcome variables Vermunt, Jeroen
 Tilburg University Mixed-effects logistic regression models for indirectly observed outcome variables Vermunt, Jeroen Published in: Multivariate Behavioral Research Document version: Peer reviewed version
Tilburg University Mixed-effects logistic regression models for indirectly observed outcome variables Vermunt, Jeroen Published in: Multivariate Behavioral Research Document version: Peer reviewed version
ROBUSTNESS OF MULTILEVEL PARAMETER ESTIMATES AGAINST SMALL SAMPLE SIZES
 ROBUSTNESS OF MULTILEVEL PARAMETER ESTIMATES AGAINST SMALL SAMPLE SIZES Cora J.M. Maas 1 Utrecht University, The Netherlands Joop J. Hox Utrecht University, The Netherlands In social sciences, research
ROBUSTNESS OF MULTILEVEL PARAMETER ESTIMATES AGAINST SMALL SAMPLE SIZES Cora J.M. Maas 1 Utrecht University, The Netherlands Joop J. Hox Utrecht University, The Netherlands In social sciences, research
BIBLIOGRAPHY. Azzalini, A., Bowman, A., and Hardle, W. (1986), On the Use of Nonparametric Regression for Model Checking, Biometrika, 76, 1, 2-12.
 BIBLIOGRAPHY Anderson, D. and Aitken, M. (1985), Variance Components Models with Binary Response: Interviewer Variability, Journal of the Royal Statistical Society B, 47, 203-210. Aitken, M., Anderson,
BIBLIOGRAPHY Anderson, D. and Aitken, M. (1985), Variance Components Models with Binary Response: Interviewer Variability, Journal of the Royal Statistical Society B, 47, 203-210. Aitken, M., Anderson,
Multilevel Modeling: When and Why 1. 1 Why multilevel data need multilevel models
 Multilevel Modeling: When and Why 1 J. Hox University of Amsterdam & Utrecht University Amsterdam/Utrecht, the Netherlands Abstract: Multilevel models have become popular for the analysis of a variety
Multilevel Modeling: When and Why 1 J. Hox University of Amsterdam & Utrecht University Amsterdam/Utrecht, the Netherlands Abstract: Multilevel models have become popular for the analysis of a variety
Generalized Linear Models for Non-Normal Data
 Generalized Linear Models for Non-Normal Data Today s Class: 3 parts of a generalized model Models for binary outcomes Complications for generalized multivariate or multilevel models SPLH 861: Lecture
Generalized Linear Models for Non-Normal Data Today s Class: 3 parts of a generalized model Models for binary outcomes Complications for generalized multivariate or multilevel models SPLH 861: Lecture
Discussion of Missing Data Methods in Longitudinal Studies: A Review by Ibrahim and Molenberghs
 Discussion of Missing Data Methods in Longitudinal Studies: A Review by Ibrahim and Molenberghs Michael J. Daniels and Chenguang Wang Jan. 18, 2009 First, we would like to thank Joe and Geert for a carefully
Discussion of Missing Data Methods in Longitudinal Studies: A Review by Ibrahim and Molenberghs Michael J. Daniels and Chenguang Wang Jan. 18, 2009 First, we would like to thank Joe and Geert for a carefully
Multilevel Regression Mixture Analysis
 Multilevel Regression Mixture Analysis Bengt Muthén and Tihomir Asparouhov Forthcoming in Journal of the Royal Statistical Society, Series A October 3, 2008 1 Abstract A two-level regression mixture model
Multilevel Regression Mixture Analysis Bengt Muthén and Tihomir Asparouhov Forthcoming in Journal of the Royal Statistical Society, Series A October 3, 2008 1 Abstract A two-level regression mixture model
Multilevel regression mixture analysis
 J. R. Statist. Soc. A (2009) 172, Part 3, pp. 639 657 Multilevel regression mixture analysis Bengt Muthén University of California, Los Angeles, USA and Tihomir Asparouhov Muthén & Muthén, Los Angeles,
J. R. Statist. Soc. A (2009) 172, Part 3, pp. 639 657 Multilevel regression mixture analysis Bengt Muthén University of California, Los Angeles, USA and Tihomir Asparouhov Muthén & Muthén, Los Angeles,
Model Estimation Example
 Ronald H. Heck 1 EDEP 606: Multivariate Methods (S2013) April 7, 2013 Model Estimation Example As we have moved through the course this semester, we have encountered the concept of model estimation. Discussions
Ronald H. Heck 1 EDEP 606: Multivariate Methods (S2013) April 7, 2013 Model Estimation Example As we have moved through the course this semester, we have encountered the concept of model estimation. Discussions
Computationally Efficient Estimation of Multilevel High-Dimensional Latent Variable Models
 Computationally Efficient Estimation of Multilevel High-Dimensional Latent Variable Models Tihomir Asparouhov 1, Bengt Muthen 2 Muthen & Muthen 1 UCLA 2 Abstract Multilevel analysis often leads to modeling
Computationally Efficient Estimation of Multilevel High-Dimensional Latent Variable Models Tihomir Asparouhov 1, Bengt Muthen 2 Muthen & Muthen 1 UCLA 2 Abstract Multilevel analysis often leads to modeling
Comparison between conditional and marginal maximum likelihood for a class of item response models
 (1/24) Comparison between conditional and marginal maximum likelihood for a class of item response models Francesco Bartolucci, University of Perugia (IT) Silvia Bacci, University of Perugia (IT) Claudia
(1/24) Comparison between conditional and marginal maximum likelihood for a class of item response models Francesco Bartolucci, University of Perugia (IT) Silvia Bacci, University of Perugia (IT) Claudia
LINEAR MULTILEVEL MODELS. Data are often hierarchical. By this we mean that data contain information
 LINEAR MULTILEVEL MODELS JAN DE LEEUW ABSTRACT. This is an entry for The Encyclopedia of Statistics in Behavioral Science, to be published by Wiley in 2005. 1. HIERARCHICAL DATA Data are often hierarchical.
LINEAR MULTILEVEL MODELS JAN DE LEEUW ABSTRACT. This is an entry for The Encyclopedia of Statistics in Behavioral Science, to be published by Wiley in 2005. 1. HIERARCHICAL DATA Data are often hierarchical.
Generalized Linear. Mixed Models. Methods and Applications. Modern Concepts, Walter W. Stroup. Texts in Statistical Science.
 Texts in Statistical Science Generalized Linear Mixed Models Modern Concepts, Methods and Applications Walter W. Stroup CRC Press Taylor & Francis Croup Boca Raton London New York CRC Press is an imprint
Texts in Statistical Science Generalized Linear Mixed Models Modern Concepts, Methods and Applications Walter W. Stroup CRC Press Taylor & Francis Croup Boca Raton London New York CRC Press is an imprint
PQL Estimation Biases in Generalized Linear Mixed Models
 PQL Estimation Biases in Generalized Linear Mixed Models Woncheol Jang Johan Lim March 18, 2006 Abstract The penalized quasi-likelihood (PQL) approach is the most common estimation procedure for the generalized
PQL Estimation Biases in Generalized Linear Mixed Models Woncheol Jang Johan Lim March 18, 2006 Abstract The penalized quasi-likelihood (PQL) approach is the most common estimation procedure for the generalized
Performance of Likelihood-Based Estimation Methods for Multilevel Binary Regression Models
 Performance of Likelihood-Based Estimation Methods for Multilevel Binary Regression Models Marc Callens and Christophe Croux 1 K.U. Leuven Abstract: By means of a fractional factorial simulation experiment,
Performance of Likelihood-Based Estimation Methods for Multilevel Binary Regression Models Marc Callens and Christophe Croux 1 K.U. Leuven Abstract: By means of a fractional factorial simulation experiment,
Chapter 4 Longitudinal Research Using Mixture Models
 Chapter 4 Longitudinal Research Using Mixture Models Jeroen K. Vermunt Abstract This chapter provides a state-of-the-art overview of the use of mixture and latent class models for the analysis of longitudinal
Chapter 4 Longitudinal Research Using Mixture Models Jeroen K. Vermunt Abstract This chapter provides a state-of-the-art overview of the use of mixture and latent class models for the analysis of longitudinal
A measure for the reliability of a rating scale based on longitudinal clinical trial data Link Peer-reviewed author version
 A measure for the reliability of a rating scale based on longitudinal clinical trial data Link Peer-reviewed author version Made available by Hasselt University Library in Document Server@UHasselt Reference
A measure for the reliability of a rating scale based on longitudinal clinical trial data Link Peer-reviewed author version Made available by Hasselt University Library in Document Server@UHasselt Reference
AVOIDING BOUNDARY ESTIMATES IN LATENT CLASS ANALYSIS BY BAYESIAN POSTERIOR MODE ESTIMATION
 Behaviormetrika Vol33, No1, 2006, 43 59 AVOIDING BOUNDARY ESTIMATES IN LATENT CLASS ANALYSIS BY BAYESIAN POSTERIOR MODE ESTIMATION Francisca Galindo Garre andjeroenkvermunt In maximum likelihood estimation
Behaviormetrika Vol33, No1, 2006, 43 59 AVOIDING BOUNDARY ESTIMATES IN LATENT CLASS ANALYSIS BY BAYESIAN POSTERIOR MODE ESTIMATION Francisca Galindo Garre andjeroenkvermunt In maximum likelihood estimation
SESSION 2 ASSIGNED READING MATERIALS
 Introduction to Latent Class Modeling using Latent GOLD SESSION 2 SESSION 2 ASSIGNED READING MATERIALS Copyright 2012 by Statistical Innovations Inc. All rights reserved. No part of this material may be
Introduction to Latent Class Modeling using Latent GOLD SESSION 2 SESSION 2 ASSIGNED READING MATERIALS Copyright 2012 by Statistical Innovations Inc. All rights reserved. No part of this material may be
Marginal Specifications and a Gaussian Copula Estimation
 Marginal Specifications and a Gaussian Copula Estimation Kazim Azam Abstract Multivariate analysis involving random variables of different type like count, continuous or mixture of both is frequently required
Marginal Specifications and a Gaussian Copula Estimation Kazim Azam Abstract Multivariate analysis involving random variables of different type like count, continuous or mixture of both is frequently required
Multilevel Statistical Models: 3 rd edition, 2003 Contents
 Multilevel Statistical Models: 3 rd edition, 2003 Contents Preface Acknowledgements Notation Two and three level models. A general classification notation and diagram Glossary Chapter 1 An introduction
Multilevel Statistical Models: 3 rd edition, 2003 Contents Preface Acknowledgements Notation Two and three level models. A general classification notation and diagram Glossary Chapter 1 An introduction
Continuous Time Survival in Latent Variable Models
 Continuous Time Survival in Latent Variable Models Tihomir Asparouhov 1, Katherine Masyn 2, Bengt Muthen 3 Muthen & Muthen 1 University of California, Davis 2 University of California, Los Angeles 3 Abstract
Continuous Time Survival in Latent Variable Models Tihomir Asparouhov 1, Katherine Masyn 2, Bengt Muthen 3 Muthen & Muthen 1 University of California, Davis 2 University of California, Los Angeles 3 Abstract
Confidence intervals for the variance component of random-effects linear models
 The Stata Journal (2004) 4, Number 4, pp. 429 435 Confidence intervals for the variance component of random-effects linear models Matteo Bottai Arnold School of Public Health University of South Carolina
The Stata Journal (2004) 4, Number 4, pp. 429 435 Confidence intervals for the variance component of random-effects linear models Matteo Bottai Arnold School of Public Health University of South Carolina
Multilevel and Related Models for Longitudinal Data
 7 Multilevel and Related Models for Longitudinal Data Anders Skrondal 1 and Sophia Rabe-Hesketh 2 1 Department of Statistics and Methodology Institute, London School of Economics & Division of Epidemiology,
7 Multilevel and Related Models for Longitudinal Data Anders Skrondal 1 and Sophia Rabe-Hesketh 2 1 Department of Statistics and Methodology Institute, London School of Economics & Division of Epidemiology,
Stat 542: Item Response Theory Modeling Using The Extended Rank Likelihood
 Stat 542: Item Response Theory Modeling Using The Extended Rank Likelihood Jonathan Gruhl March 18, 2010 1 Introduction Researchers commonly apply item response theory (IRT) models to binary and ordinal
Stat 542: Item Response Theory Modeling Using The Extended Rank Likelihood Jonathan Gruhl March 18, 2010 1 Introduction Researchers commonly apply item response theory (IRT) models to binary and ordinal
A class of latent marginal models for capture-recapture data with continuous covariates
 A class of latent marginal models for capture-recapture data with continuous covariates F Bartolucci A Forcina Università di Urbino Università di Perugia FrancescoBartolucci@uniurbit forcina@statunipgit
A class of latent marginal models for capture-recapture data with continuous covariates F Bartolucci A Forcina Università di Urbino Università di Perugia FrancescoBartolucci@uniurbit forcina@statunipgit
LOGISTIC REGRESSION Joseph M. Hilbe
 LOGISTIC REGRESSION Joseph M. Hilbe Arizona State University Logistic regression is the most common method used to model binary response data. When the response is binary, it typically takes the form of
LOGISTIC REGRESSION Joseph M. Hilbe Arizona State University Logistic regression is the most common method used to model binary response data. When the response is binary, it typically takes the form of
Type I and type II error under random-effects misspecification in generalized linear mixed models Link Peer-reviewed author version
 Type I and type II error under random-effects misspecification in generalized linear mixed models Link Peer-reviewed author version Made available by Hasselt University Library in Document Server@UHasselt
Type I and type II error under random-effects misspecification in generalized linear mixed models Link Peer-reviewed author version Made available by Hasselt University Library in Document Server@UHasselt
Conditional Inference Functions for Mixed-Effects Models with Unspecified Random-Effects Distribution
 Conditional Inference Functions for Mixed-Effects Models with Unspecified Random-Effects Distribution Peng WANG, Guei-feng TSAI and Annie QU 1 Abstract In longitudinal studies, mixed-effects models are
Conditional Inference Functions for Mixed-Effects Models with Unspecified Random-Effects Distribution Peng WANG, Guei-feng TSAI and Annie QU 1 Abstract In longitudinal studies, mixed-effects models are
H-LIKELIHOOD ESTIMATION METHOOD FOR VARYING CLUSTERED BINARY MIXED EFFECTS MODEL
 H-LIKELIHOOD ESTIMATION METHOOD FOR VARYING CLUSTERED BINARY MIXED EFFECTS MODEL Intesar N. El-Saeiti Department of Statistics, Faculty of Science, University of Bengahzi-Libya. entesar.el-saeiti@uob.edu.ly
H-LIKELIHOOD ESTIMATION METHOOD FOR VARYING CLUSTERED BINARY MIXED EFFECTS MODEL Intesar N. El-Saeiti Department of Statistics, Faculty of Science, University of Bengahzi-Libya. entesar.el-saeiti@uob.edu.ly
Model Selection for Semiparametric Bayesian Models with Application to Overdispersion
 Proceedings 59th ISI World Statistics Congress, 25-30 August 2013, Hong Kong (Session CPS020) p.3863 Model Selection for Semiparametric Bayesian Models with Application to Overdispersion Jinfang Wang and
Proceedings 59th ISI World Statistics Congress, 25-30 August 2013, Hong Kong (Session CPS020) p.3863 Model Selection for Semiparametric Bayesian Models with Application to Overdispersion Jinfang Wang and
WU Weiterbildung. Linear Mixed Models
 Linear Mixed Effects Models WU Weiterbildung SLIDE 1 Outline 1 Estimation: ML vs. REML 2 Special Models On Two Levels Mixed ANOVA Or Random ANOVA Random Intercept Model Random Coefficients Model Intercept-and-Slopes-as-Outcomes
Linear Mixed Effects Models WU Weiterbildung SLIDE 1 Outline 1 Estimation: ML vs. REML 2 Special Models On Two Levels Mixed ANOVA Or Random ANOVA Random Intercept Model Random Coefficients Model Intercept-and-Slopes-as-Outcomes
Fitting Multidimensional Latent Variable Models using an Efficient Laplace Approximation
 Fitting Multidimensional Latent Variable Models using an Efficient Laplace Approximation Dimitris Rizopoulos Department of Biostatistics, Erasmus University Medical Center, the Netherlands d.rizopoulos@erasmusmc.nl
Fitting Multidimensional Latent Variable Models using an Efficient Laplace Approximation Dimitris Rizopoulos Department of Biostatistics, Erasmus University Medical Center, the Netherlands d.rizopoulos@erasmusmc.nl
LSAC RESEARCH REPORT SERIES. Law School Admission Council Research Report March 2008
 LSAC RESEARCH REPORT SERIES Structural Modeling Using Two-Step MML Procedures Cees A. W. Glas University of Twente, Enschede, The Netherlands Law School Admission Council Research Report 08-07 March 2008
LSAC RESEARCH REPORT SERIES Structural Modeling Using Two-Step MML Procedures Cees A. W. Glas University of Twente, Enschede, The Netherlands Law School Admission Council Research Report 08-07 March 2008
Using Estimating Equations for Spatially Correlated A
 Using Estimating Equations for Spatially Correlated Areal Data December 8, 2009 Introduction GEEs Spatial Estimating Equations Implementation Simulation Conclusion Typical Problem Assess the relationship
Using Estimating Equations for Spatially Correlated Areal Data December 8, 2009 Introduction GEEs Spatial Estimating Equations Implementation Simulation Conclusion Typical Problem Assess the relationship
Longitudinal Analysis. Michael L. Berbaum Institute for Health Research and Policy University of Illinois at Chicago
 Longitudinal Analysis Michael L. Berbaum Institute for Health Research and Policy University of Illinois at Chicago Course description: Longitudinal analysis is the study of short series of observations
Longitudinal Analysis Michael L. Berbaum Institute for Health Research and Policy University of Illinois at Chicago Course description: Longitudinal analysis is the study of short series of observations
A Monte Carlo Power Analysis of Traditional Repeated Measures and Hierarchical Multivariate Linear Models in Longitudinal Data Analysis
 University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Developmental Cognitive Neuroscience Laboratory - Faculty and Staff Publications Developmental Cognitive Neuroscience Laboratory
University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Developmental Cognitive Neuroscience Laboratory - Faculty and Staff Publications Developmental Cognitive Neuroscience Laboratory
Class Notes: Week 8. Probit versus Logit Link Functions and Count Data
 Ronald Heck Class Notes: Week 8 1 Class Notes: Week 8 Probit versus Logit Link Functions and Count Data This week we ll take up a couple of issues. The first is working with a probit link function. While
Ronald Heck Class Notes: Week 8 1 Class Notes: Week 8 Probit versus Logit Link Functions and Count Data This week we ll take up a couple of issues. The first is working with a probit link function. While
Longitudinal Modeling with Logistic Regression
 Newsom 1 Longitudinal Modeling with Logistic Regression Longitudinal designs involve repeated measurements of the same individuals over time There are two general classes of analyses that correspond to
Newsom 1 Longitudinal Modeling with Logistic Regression Longitudinal designs involve repeated measurements of the same individuals over time There are two general classes of analyses that correspond to
Classification. Chapter Introduction. 6.2 The Bayes classifier
 Chapter 6 Classification 6.1 Introduction Often encountered in applications is the situation where the response variable Y takes values in a finite set of labels. For example, the response Y could encode
Chapter 6 Classification 6.1 Introduction Often encountered in applications is the situation where the response variable Y takes values in a finite set of labels. For example, the response Y could encode
Introducing Generalized Linear Models: Logistic Regression
 Ron Heck, Summer 2012 Seminars 1 Multilevel Regression Models and Their Applications Seminar Introducing Generalized Linear Models: Logistic Regression The generalized linear model (GLM) represents and
Ron Heck, Summer 2012 Seminars 1 Multilevel Regression Models and Their Applications Seminar Introducing Generalized Linear Models: Logistic Regression The generalized linear model (GLM) represents and
Longitudinal Data Analysis. Michael L. Berbaum Institute for Health Research and Policy University of Illinois at Chicago
 Longitudinal Data Analysis Michael L. Berbaum Institute for Health Research and Policy University of Illinois at Chicago Course description: Longitudinal analysis is the study of short series of observations
Longitudinal Data Analysis Michael L. Berbaum Institute for Health Research and Policy University of Illinois at Chicago Course description: Longitudinal analysis is the study of short series of observations
Label Switching and Its Simple Solutions for Frequentist Mixture Models
 Label Switching and Its Simple Solutions for Frequentist Mixture Models Weixin Yao Department of Statistics, Kansas State University, Manhattan, Kansas 66506, U.S.A. wxyao@ksu.edu Abstract The label switching
Label Switching and Its Simple Solutions for Frequentist Mixture Models Weixin Yao Department of Statistics, Kansas State University, Manhattan, Kansas 66506, U.S.A. wxyao@ksu.edu Abstract The label switching
Ron Heck, Fall Week 8: Introducing Generalized Linear Models: Logistic Regression 1 (Replaces prior revision dated October 20, 2011)
 Ron Heck, Fall 2011 1 EDEP 768E: Seminar in Multilevel Modeling rev. January 3, 2012 (see footnote) Week 8: Introducing Generalized Linear Models: Logistic Regression 1 (Replaces prior revision dated October
Ron Heck, Fall 2011 1 EDEP 768E: Seminar in Multilevel Modeling rev. January 3, 2012 (see footnote) Week 8: Introducing Generalized Linear Models: Logistic Regression 1 (Replaces prior revision dated October
Centering Predictor and Mediator Variables in Multilevel and Time-Series Models
 Centering Predictor and Mediator Variables in Multilevel and Time-Series Models Tihomir Asparouhov and Bengt Muthén Part 2 May 7, 2018 Tihomir Asparouhov and Bengt Muthén Part 2 Muthén & Muthén 1/ 42 Overview
Centering Predictor and Mediator Variables in Multilevel and Time-Series Models Tihomir Asparouhov and Bengt Muthén Part 2 May 7, 2018 Tihomir Asparouhov and Bengt Muthén Part 2 Muthén & Muthén 1/ 42 Overview
Micro-macro multilevel latent class models with multiple discrete individual-level variables
 Noname manuscript No. (will be inserted by the editor) Micro-macro multilevel latent class models with multiple discrete individual-level variables M. Bennink M. A. Croon B. Kroon J. K. Vermunt the date
Noname manuscript No. (will be inserted by the editor) Micro-macro multilevel latent class models with multiple discrete individual-level variables M. Bennink M. A. Croon B. Kroon J. K. Vermunt the date
A Nonlinear Mixed Model Framework for Item Response Theory
 Psychological Methods Copyright 2003 by the American Psychological Association, Inc. 2003, Vol. 8, No. 2, 185 205 1082-989X/03/$12.00 DOI: 10.1037/1082-989X.8.2.185 A Nonlinear Mixed Model Framework for
Psychological Methods Copyright 2003 by the American Psychological Association, Inc. 2003, Vol. 8, No. 2, 185 205 1082-989X/03/$12.00 DOI: 10.1037/1082-989X.8.2.185 A Nonlinear Mixed Model Framework for
Partitioning variation in multilevel models.
 Partitioning variation in multilevel models. by Harvey Goldstein, William Browne and Jon Rasbash Institute of Education, London, UK. Summary. In multilevel modelling, the residual variation in a response
Partitioning variation in multilevel models. by Harvey Goldstein, William Browne and Jon Rasbash Institute of Education, London, UK. Summary. In multilevel modelling, the residual variation in a response
T E C H N I C A L R E P O R T A SANDWICH-ESTIMATOR TEST FOR MISSPECIFICATION IN MIXED-EFFECTS MODELS. LITIERE S., ALONSO A., and G.
 T E C H N I C A L R E P O R T 0658 A SANDWICH-ESTIMATOR TEST FOR MISSPECIFICATION IN MIXED-EFFECTS MODELS LITIERE S., ALONSO A., and G. MOLENBERGHS * I A P S T A T I S T I C S N E T W O R K INTERUNIVERSITY
T E C H N I C A L R E P O R T 0658 A SANDWICH-ESTIMATOR TEST FOR MISSPECIFICATION IN MIXED-EFFECTS MODELS LITIERE S., ALONSO A., and G. MOLENBERGHS * I A P S T A T I S T I C S N E T W O R K INTERUNIVERSITY
Multilevel Analysis of Grouped and Longitudinal Data
 Multilevel Analysis of Grouped and Longitudinal Data Joop J. Hox Utrecht University Second draft, to appear in: T.D. Little, K.U. Schnabel, & J. Baumert (Eds.). Modeling longitudinal and multiple-group
Multilevel Analysis of Grouped and Longitudinal Data Joop J. Hox Utrecht University Second draft, to appear in: T.D. Little, K.U. Schnabel, & J. Baumert (Eds.). Modeling longitudinal and multiple-group
Variable Selection for Generalized Additive Mixed Models by Likelihood-based Boosting
 Variable Selection for Generalized Additive Mixed Models by Likelihood-based Boosting Andreas Groll 1 and Gerhard Tutz 2 1 Department of Statistics, University of Munich, Akademiestrasse 1, D-80799, Munich,
Variable Selection for Generalized Additive Mixed Models by Likelihood-based Boosting Andreas Groll 1 and Gerhard Tutz 2 1 Department of Statistics, University of Munich, Akademiestrasse 1, D-80799, Munich,
Stat 5101 Lecture Notes
 Stat 5101 Lecture Notes Charles J. Geyer Copyright 1998, 1999, 2000, 2001 by Charles J. Geyer May 7, 2001 ii Stat 5101 (Geyer) Course Notes Contents 1 Random Variables and Change of Variables 1 1.1 Random
Stat 5101 Lecture Notes Charles J. Geyer Copyright 1998, 1999, 2000, 2001 by Charles J. Geyer May 7, 2001 ii Stat 5101 (Geyer) Course Notes Contents 1 Random Variables and Change of Variables 1 1.1 Random
Multiple-Objective Optimal Designs for the Hierarchical Linear Model
 Journal of Of cial Statistics, Vol. 18, No. 2, 2002, pp. 291±303 Multiple-Objective Optimal Designs for the Hierarchical Linear Model Mirjam Moerbeek 1 and Weng Kee Wong 2 Optimal designs are usually constructed
Journal of Of cial Statistics, Vol. 18, No. 2, 2002, pp. 291±303 Multiple-Objective Optimal Designs for the Hierarchical Linear Model Mirjam Moerbeek 1 and Weng Kee Wong 2 Optimal designs are usually constructed
Efficient Analysis of Mixed Hierarchical and Cross-Classified Random Structures Using a Multilevel Model
 Efficient Analysis of Mixed Hierarchical and Cross-Classified Random Structures Using a Multilevel Model Jon Rasbash; Harvey Goldstein Journal of Educational and Behavioral Statistics, Vol. 19, No. 4.
Efficient Analysis of Mixed Hierarchical and Cross-Classified Random Structures Using a Multilevel Model Jon Rasbash; Harvey Goldstein Journal of Educational and Behavioral Statistics, Vol. 19, No. 4.
Exploiting TIMSS and PIRLS combined data: multivariate multilevel modelling of student achievement
 Exploiting TIMSS and PIRLS combined data: multivariate multilevel modelling of student achievement Second meeting of the FIRB 2012 project Mixture and latent variable models for causal-inference and analysis
Exploiting TIMSS and PIRLS combined data: multivariate multilevel modelling of student achievement Second meeting of the FIRB 2012 project Mixture and latent variable models for causal-inference and analysis
A NEW MODEL FOR THE FUSION OF MAXDIFF SCALING
 A NEW MODEL FOR THE FUSION OF MAXDIFF SCALING AND RATINGS DATA JAY MAGIDSON 1 STATISTICAL INNOVATIONS INC. DAVE THOMAS SYNOVATE JEROEN K. VERMUNT TILBURG UNIVERSITY ABSTRACT A property of MaxDiff (Maximum
A NEW MODEL FOR THE FUSION OF MAXDIFF SCALING AND RATINGS DATA JAY MAGIDSON 1 STATISTICAL INNOVATIONS INC. DAVE THOMAS SYNOVATE JEROEN K. VERMUNT TILBURG UNIVERSITY ABSTRACT A property of MaxDiff (Maximum
Introduction to. Multilevel Analysis
 Introduction to Multilevel Analysis Tom Snijders University of Oxford University of Groningen December 2009 Tom AB Snijders Introduction to Multilevel Analysis 1 Multilevel Analysis based on the Hierarchical
Introduction to Multilevel Analysis Tom Snijders University of Oxford University of Groningen December 2009 Tom AB Snijders Introduction to Multilevel Analysis 1 Multilevel Analysis based on the Hierarchical
Estimation in Generalized Linear Models with Heterogeneous Random Effects. Woncheol Jang Johan Lim. May 19, 2004
 Estimation in Generalized Linear Models with Heterogeneous Random Effects Woncheol Jang Johan Lim May 19, 2004 Abstract The penalized quasi-likelihood (PQL) approach is the most common estimation procedure
Estimation in Generalized Linear Models with Heterogeneous Random Effects Woncheol Jang Johan Lim May 19, 2004 Abstract The penalized quasi-likelihood (PQL) approach is the most common estimation procedure
Dynamic sequential analysis of careers
 Dynamic sequential analysis of careers Fulvia Pennoni Department of Statistics and Quantitative Methods University of Milano-Bicocca http://www.statistica.unimib.it/utenti/pennoni/ Email: fulvia.pennoni@unimib.it
Dynamic sequential analysis of careers Fulvia Pennoni Department of Statistics and Quantitative Methods University of Milano-Bicocca http://www.statistica.unimib.it/utenti/pennoni/ Email: fulvia.pennoni@unimib.it
Semiparametric Mixed Effects Models with Flexible Random Effects Distribution
 Semiparametric Mixed Effects Models with Flexible Random Effects Distribution Marie Davidian North Carolina State University davidian@stat.ncsu.edu www.stat.ncsu.edu/ davidian Joint work with A. Tsiatis,
Semiparametric Mixed Effects Models with Flexible Random Effects Distribution Marie Davidian North Carolina State University davidian@stat.ncsu.edu www.stat.ncsu.edu/ davidian Joint work with A. Tsiatis,
Semiparametric Generalized Linear Models
 Semiparametric Generalized Linear Models North American Stata Users Group Meeting Chicago, Illinois Paul Rathouz Department of Health Studies University of Chicago prathouz@uchicago.edu Liping Gao MS Student
Semiparametric Generalized Linear Models North American Stata Users Group Meeting Chicago, Illinois Paul Rathouz Department of Health Studies University of Chicago prathouz@uchicago.edu Liping Gao MS Student
Hierarchical Linear Models. Jeff Gill. University of Florida
 Hierarchical Linear Models Jeff Gill University of Florida I. ESSENTIAL DESCRIPTION OF HIERARCHICAL LINEAR MODELS II. SPECIAL CASES OF THE HLM III. THE GENERAL STRUCTURE OF THE HLM IV. ESTIMATION OF THE
Hierarchical Linear Models Jeff Gill University of Florida I. ESSENTIAL DESCRIPTION OF HIERARCHICAL LINEAR MODELS II. SPECIAL CASES OF THE HLM III. THE GENERAL STRUCTURE OF THE HLM IV. ESTIMATION OF THE
Repeated ordinal measurements: a generalised estimating equation approach
 Repeated ordinal measurements: a generalised estimating equation approach David Clayton MRC Biostatistics Unit 5, Shaftesbury Road Cambridge CB2 2BW April 7, 1992 Abstract Cumulative logit and related
Repeated ordinal measurements: a generalised estimating equation approach David Clayton MRC Biostatistics Unit 5, Shaftesbury Road Cambridge CB2 2BW April 7, 1992 Abstract Cumulative logit and related
Discrete Response Multilevel Models for Repeated Measures: An Application to Voting Intentions Data
 Quality & Quantity 34: 323 330, 2000. 2000 Kluwer Academic Publishers. Printed in the Netherlands. 323 Note Discrete Response Multilevel Models for Repeated Measures: An Application to Voting Intentions
Quality & Quantity 34: 323 330, 2000. 2000 Kluwer Academic Publishers. Printed in the Netherlands. 323 Note Discrete Response Multilevel Models for Repeated Measures: An Application to Voting Intentions
Power analysis for the Bootstrap Likelihood Ratio Test in Latent Class Models
 Power analysis for the Bootstrap Likelihood Ratio Test in Latent Class Models Fetene B. Tekle 1, Dereje W. Gudicha 2 and Jeroen. Vermunt 2 Abstract Latent class (LC) analysis is used to construct empirical
Power analysis for the Bootstrap Likelihood Ratio Test in Latent Class Models Fetene B. Tekle 1, Dereje W. Gudicha 2 and Jeroen. Vermunt 2 Abstract Latent class (LC) analysis is used to construct empirical
The consequences of misspecifying the random effects distribution when fitting generalized linear mixed models
 The consequences of misspecifying the random effects distribution when fitting generalized linear mixed models John M. Neuhaus Charles E. McCulloch Division of Biostatistics University of California, San
The consequences of misspecifying the random effects distribution when fitting generalized linear mixed models John M. Neuhaus Charles E. McCulloch Division of Biostatistics University of California, San
1 Introduction. 2 A regression model
 Regression Analysis of Compositional Data When Both the Dependent Variable and Independent Variable Are Components LA van der Ark 1 1 Tilburg University, The Netherlands; avdark@uvtnl Abstract It is well
Regression Analysis of Compositional Data When Both the Dependent Variable and Independent Variable Are Components LA van der Ark 1 1 Tilburg University, The Netherlands; avdark@uvtnl Abstract It is well
Machine Learning Linear Classification. Prof. Matteo Matteucci
 Machine Learning Linear Classification Prof. Matteo Matteucci Recall from the first lecture 2 X R p Regression Y R Continuous Output X R p Y {Ω 0, Ω 1,, Ω K } Classification Discrete Output X R p Y (X)
Machine Learning Linear Classification Prof. Matteo Matteucci Recall from the first lecture 2 X R p Regression Y R Continuous Output X R p Y {Ω 0, Ω 1,, Ω K } Classification Discrete Output X R p Y (X)
Correspondence Analysis of Longitudinal Data
 Correspondence Analysis of Longitudinal Data Mark de Rooij* LEIDEN UNIVERSITY, LEIDEN, NETHERLANDS Peter van der G. M. Heijden UTRECHT UNIVERSITY, UTRECHT, NETHERLANDS *Corresponding author (rooijm@fsw.leidenuniv.nl)
Correspondence Analysis of Longitudinal Data Mark de Rooij* LEIDEN UNIVERSITY, LEIDEN, NETHERLANDS Peter van der G. M. Heijden UTRECHT UNIVERSITY, UTRECHT, NETHERLANDS *Corresponding author (rooijm@fsw.leidenuniv.nl)
Hierarchical Generalized Linear Models. ERSH 8990 REMS Seminar on HLM Last Lecture!
 Hierarchical Generalized Linear Models ERSH 8990 REMS Seminar on HLM Last Lecture! Hierarchical Generalized Linear Models Introduction to generalized models Models for binary outcomes Interpreting parameter
Hierarchical Generalized Linear Models ERSH 8990 REMS Seminar on HLM Last Lecture! Hierarchical Generalized Linear Models Introduction to generalized models Models for binary outcomes Interpreting parameter
PIRLS 2016 Achievement Scaling Methodology 1
 CHAPTER 11 PIRLS 2016 Achievement Scaling Methodology 1 The PIRLS approach to scaling the achievement data, based on item response theory (IRT) scaling with marginal estimation, was developed originally
CHAPTER 11 PIRLS 2016 Achievement Scaling Methodology 1 The PIRLS approach to scaling the achievement data, based on item response theory (IRT) scaling with marginal estimation, was developed originally
The STS Surgeon Composite Technical Appendix
 The STS Surgeon Composite Technical Appendix Overview Surgeon-specific risk-adjusted operative operative mortality and major complication rates were estimated using a bivariate random-effects logistic
The STS Surgeon Composite Technical Appendix Overview Surgeon-specific risk-adjusted operative operative mortality and major complication rates were estimated using a bivariate random-effects logistic
For more information about how to cite these materials visit
 Author(s): Kerby Shedden, Ph.D., 2010 License: Unless otherwise noted, this material is made available under the terms of the Creative Commons Attribution Share Alike 3.0 License: http://creativecommons.org/licenses/by-sa/3.0/
Author(s): Kerby Shedden, Ph.D., 2010 License: Unless otherwise noted, this material is made available under the terms of the Creative Commons Attribution Share Alike 3.0 License: http://creativecommons.org/licenses/by-sa/3.0/
Rank Regression with Normal Residuals using the Gibbs Sampler
 Rank Regression with Normal Residuals using the Gibbs Sampler Stephen P Smith email: hucklebird@aol.com, 2018 Abstract Yu (2000) described the use of the Gibbs sampler to estimate regression parameters
Rank Regression with Normal Residuals using the Gibbs Sampler Stephen P Smith email: hucklebird@aol.com, 2018 Abstract Yu (2000) described the use of the Gibbs sampler to estimate regression parameters
Title: Testing for Measurement Invariance with Latent Class Analysis. Abstract
 1 Title: Testing for Measurement Invariance with Latent Class Analysis Authors: Miloš Kankaraš*, Guy Moors*, and Jeroen K. Vermunt Abstract Testing for measurement invariance can be done within the context
1 Title: Testing for Measurement Invariance with Latent Class Analysis Authors: Miloš Kankaraš*, Guy Moors*, and Jeroen K. Vermunt Abstract Testing for measurement invariance can be done within the context
boxcoxmix: An R Package for Response Transformations for Random Effect and Variance Component Models
 boxcoxmix: An R Package for Response Transformations for Random Effect and Variance Component Models Amani Almohaimeed and Jochen Einbeck Qassim University and Durham University Abstract Random effect
boxcoxmix: An R Package for Response Transformations for Random Effect and Variance Component Models Amani Almohaimeed and Jochen Einbeck Qassim University and Durham University Abstract Random effect
A Course in Applied Econometrics Lecture 14: Control Functions and Related Methods. Jeff Wooldridge IRP Lectures, UW Madison, August 2008
 A Course in Applied Econometrics Lecture 14: Control Functions and Related Methods Jeff Wooldridge IRP Lectures, UW Madison, August 2008 1. Linear-in-Parameters Models: IV versus Control Functions 2. Correlated
A Course in Applied Econometrics Lecture 14: Control Functions and Related Methods Jeff Wooldridge IRP Lectures, UW Madison, August 2008 1. Linear-in-Parameters Models: IV versus Control Functions 2. Correlated
Communications in Statistics - Simulation and Computation. Comparison of EM and SEM Algorithms in Poisson Regression Models: a simulation study
 Comparison of EM and SEM Algorithms in Poisson Regression Models: a simulation study Journal: Manuscript ID: LSSP-00-0.R Manuscript Type: Original Paper Date Submitted by the Author: -May-0 Complete List
Comparison of EM and SEM Algorithms in Poisson Regression Models: a simulation study Journal: Manuscript ID: LSSP-00-0.R Manuscript Type: Original Paper Date Submitted by the Author: -May-0 Complete List
Models for Longitudinal Analysis of Binary Response Data for Identifying the Effects of Different Treatments on Insomnia
 Applied Mathematical Sciences, Vol. 4, 2010, no. 62, 3067-3082 Models for Longitudinal Analysis of Binary Response Data for Identifying the Effects of Different Treatments on Insomnia Z. Rezaei Ghahroodi
Applied Mathematical Sciences, Vol. 4, 2010, no. 62, 3067-3082 Models for Longitudinal Analysis of Binary Response Data for Identifying the Effects of Different Treatments on Insomnia Z. Rezaei Ghahroodi
Discussion of Maximization by Parts in Likelihood Inference
 Discussion of Maximization by Parts in Likelihood Inference David Ruppert School of Operations Research & Industrial Engineering, 225 Rhodes Hall, Cornell University, Ithaca, NY 4853 email: dr24@cornell.edu
Discussion of Maximization by Parts in Likelihood Inference David Ruppert School of Operations Research & Industrial Engineering, 225 Rhodes Hall, Cornell University, Ithaca, NY 4853 email: dr24@cornell.edu
Dynamic logit model: pseudo conditional likelihood estimation and latent Markov extension
 Dynamic logit model: pseudo conditional likelihood estimation and latent Markov extension Francesco Bartolucci 1 Department of Economics, Finance and Statistics University of Perugia, IT bart@stat.unipg.it
Dynamic logit model: pseudo conditional likelihood estimation and latent Markov extension Francesco Bartolucci 1 Department of Economics, Finance and Statistics University of Perugia, IT bart@stat.unipg.it
Plausible Values for Latent Variables Using Mplus
 Plausible Values for Latent Variables Using Mplus Tihomir Asparouhov and Bengt Muthén August 21, 2010 1 1 Introduction Plausible values are imputed values for latent variables. All latent variables can
Plausible Values for Latent Variables Using Mplus Tihomir Asparouhov and Bengt Muthén August 21, 2010 1 1 Introduction Plausible values are imputed values for latent variables. All latent variables can
Misspecification of the covariance matrix in the linear mixed model: A monte carlo simulation
 Misspecification of the covariance matrix in the linear mixed model: A monte carlo simulation A DISSERTATION SUBMITTED TO THE FACULTY OF THE GRADUATE SCHOOL OF THE UNIVERSITY OF MINNESOTA BY Brandon LeBeau
Misspecification of the covariance matrix in the linear mixed model: A monte carlo simulation A DISSERTATION SUBMITTED TO THE FACULTY OF THE GRADUATE SCHOOL OF THE UNIVERSITY OF MINNESOTA BY Brandon LeBeau
Generalised Regression Models
 UNIVERSITY Of TECHNOLOGY, SYDNEY 35393 Seminar (Statistics) Generalised Regression Models These notes are an excerpt (Chapter 10) from the book Semiparametric Regression by D. Ruppert, M.P. Wand & R.J.
UNIVERSITY Of TECHNOLOGY, SYDNEY 35393 Seminar (Statistics) Generalised Regression Models These notes are an excerpt (Chapter 10) from the book Semiparametric Regression by D. Ruppert, M.P. Wand & R.J.
Investigating the Feasibility of Using Mplus in the Estimation of Growth Mixture Models
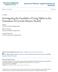 Journal of Modern Applied Statistical Methods Volume 13 Issue 1 Article 31 5-1-2014 Investigating the Feasibility of Using Mplus in the Estimation of Growth Mixture Models Ming Li University of Maryland,
Journal of Modern Applied Statistical Methods Volume 13 Issue 1 Article 31 5-1-2014 Investigating the Feasibility of Using Mplus in the Estimation of Growth Mixture Models Ming Li University of Maryland,
Applied Psychological Measurement 2001; 25; 283
 Applied Psychological Measurement http://apm.sagepub.com The Use of Restricted Latent Class Models for Defining and Testing Nonparametric and Parametric Item Response Theory Models Jeroen K. Vermunt Applied
Applied Psychological Measurement http://apm.sagepub.com The Use of Restricted Latent Class Models for Defining and Testing Nonparametric and Parametric Item Response Theory Models Jeroen K. Vermunt Applied
DIAGNOSTICS FOR STRATIFIED CLINICAL TRIALS IN PROPORTIONAL ODDS MODELS
 DIAGNOSTICS FOR STRATIFIED CLINICAL TRIALS IN PROPORTIONAL ODDS MODELS Ivy Liu and Dong Q. Wang School of Mathematics, Statistics and Computer Science Victoria University of Wellington New Zealand Corresponding
DIAGNOSTICS FOR STRATIFIED CLINICAL TRIALS IN PROPORTIONAL ODDS MODELS Ivy Liu and Dong Q. Wang School of Mathematics, Statistics and Computer Science Victoria University of Wellington New Zealand Corresponding
The equivalence of the Maximum Likelihood and a modified Least Squares for a case of Generalized Linear Model
 Applied and Computational Mathematics 2014; 3(5): 268-272 Published online November 10, 2014 (http://www.sciencepublishinggroup.com/j/acm) doi: 10.11648/j.acm.20140305.22 ISSN: 2328-5605 (Print); ISSN:
Applied and Computational Mathematics 2014; 3(5): 268-272 Published online November 10, 2014 (http://www.sciencepublishinggroup.com/j/acm) doi: 10.11648/j.acm.20140305.22 ISSN: 2328-5605 (Print); ISSN:
Linear Regression Models P8111
 Linear Regression Models P8111 Lecture 25 Jeff Goldsmith April 26, 2016 1 of 37 Today s Lecture Logistic regression / GLMs Model framework Interpretation Estimation 2 of 37 Linear regression Course started
Linear Regression Models P8111 Lecture 25 Jeff Goldsmith April 26, 2016 1 of 37 Today s Lecture Logistic regression / GLMs Model framework Interpretation Estimation 2 of 37 Linear regression Course started
Contents. Part I: Fundamentals of Bayesian Inference 1
 Contents Preface xiii Part I: Fundamentals of Bayesian Inference 1 1 Probability and inference 3 1.1 The three steps of Bayesian data analysis 3 1.2 General notation for statistical inference 4 1.3 Bayesian
Contents Preface xiii Part I: Fundamentals of Bayesian Inference 1 1 Probability and inference 3 1.1 The three steps of Bayesian data analysis 3 1.2 General notation for statistical inference 4 1.3 Bayesian
Investigating Models with Two or Three Categories
 Ronald H. Heck and Lynn N. Tabata 1 Investigating Models with Two or Three Categories For the past few weeks we have been working with discriminant analysis. Let s now see what the same sort of model might
Ronald H. Heck and Lynn N. Tabata 1 Investigating Models with Two or Three Categories For the past few weeks we have been working with discriminant analysis. Let s now see what the same sort of model might
ONE MORE TIME ABOUT R 2 MEASURES OF FIT IN LOGISTIC REGRESSION
 ONE MORE TIME ABOUT R 2 MEASURES OF FIT IN LOGISTIC REGRESSION Ernest S. Shtatland, Ken Kleinman, Emily M. Cain Harvard Medical School, Harvard Pilgrim Health Care, Boston, MA ABSTRACT In logistic regression,
ONE MORE TIME ABOUT R 2 MEASURES OF FIT IN LOGISTIC REGRESSION Ernest S. Shtatland, Ken Kleinman, Emily M. Cain Harvard Medical School, Harvard Pilgrim Health Care, Boston, MA ABSTRACT In logistic regression,
Performance Comparison of K-Means and Expectation Maximization with Gaussian Mixture Models for Clustering EE6540 Final Project
 Performance Comparison of K-Means and Expectation Maximization with Gaussian Mixture Models for Clustering EE6540 Final Project Devin Cornell & Sushruth Sastry May 2015 1 Abstract In this article, we explore
Performance Comparison of K-Means and Expectation Maximization with Gaussian Mixture Models for Clustering EE6540 Final Project Devin Cornell & Sushruth Sastry May 2015 1 Abstract In this article, we explore
Sparse Linear Models (10/7/13)
 STA56: Probabilistic machine learning Sparse Linear Models (0/7/) Lecturer: Barbara Engelhardt Scribes: Jiaji Huang, Xin Jiang, Albert Oh Sparsity Sparsity has been a hot topic in statistics and machine
STA56: Probabilistic machine learning Sparse Linear Models (0/7/) Lecturer: Barbara Engelhardt Scribes: Jiaji Huang, Xin Jiang, Albert Oh Sparsity Sparsity has been a hot topic in statistics and machine
The impact of covariance misspecification in multivariate Gaussian mixtures on estimation and inference
 The impact of covariance misspecification in multivariate Gaussian mixtures on estimation and inference An application to longitudinal modeling Brianna Heggeseth with Nicholas Jewell Department of Statistics
The impact of covariance misspecification in multivariate Gaussian mixtures on estimation and inference An application to longitudinal modeling Brianna Heggeseth with Nicholas Jewell Department of Statistics
Web-based Supplementary Materials for Multilevel Latent Class Models with Dirichlet Mixing Distribution
 Biometrics 000, 1 20 DOI: 000 000 0000 Web-based Supplementary Materials for Multilevel Latent Class Models with Dirichlet Mixing Distribution Chong-Zhi Di and Karen Bandeen-Roche *email: cdi@fhcrc.org
Biometrics 000, 1 20 DOI: 000 000 0000 Web-based Supplementary Materials for Multilevel Latent Class Models with Dirichlet Mixing Distribution Chong-Zhi Di and Karen Bandeen-Roche *email: cdi@fhcrc.org
