The cosmic distance scale
|
|
|
- Jerome Underwood
- 5 years ago
- Views:
Transcription
1 The cosmic distance scale Distance information is often crucial to understand the physics of astrophysical objects. This requires knowing the basic properties of such an object, like its size, its environment, its location in space... There are essentially two ways to derive distances to astronomical objects, through absolute distance estimators or through relative distance estimators Absolute distance estimators Objects for whose distance can be measured directly. They have physical properties which allow such a measurement. Examples are pulsating stars, supernovae atmospheres, gravitational lensing time delays from multiple quasar images, etc. Relative distance estimators These (ultimately) depend on directly measured distances, and are based on the existence of types of objects that share the same intrinsic luminosity (and whose distance has been determined somehow).
2 For example, there are types of stars that have all the same intrinsic luminosity. If the distance to a sample of these objects has been measured directly (e.g. through trigonometric parallax), then we can use these to determine the distance to a nearby galaxy by comparing their apparent brightness to those in the Milky Way. Essentially we use that log(d 1 /D 2 ) = 1/5 * [(m 1 m 2 ) - (A 1 A 2 )] where D 1 is the distance to system 1, D 2 is the distance to system 2, m 1 is the apparent magnitudes of stars in S 1 and S 2 respectively, and A 1 and A 2 corrects for the absorption towards the sources in S 1 and S 2. Stars or objects which have the same intrinsic luminosity are known as standard candles. If the distance to such a standard candle has been measured directly, then the relative distances will have been anchored to an absolute distance scale.
3 Plan of the day Distance determination for nearby objects (Few) Examples of absolute distance estimators (Many more) Examples of relative distance estimators
4 Brief review of distance determination in the Trigonometric parallax: Solar Neighbourhood Measures the displacement in position of a star on the celestial sphere as the Earth moves around the Sun. This angular displacement is dependent on the distance to the star: Π [arcsec] = 1/d[pc]. This method is currently restricted to nearby stars, within roughly 200 pc, for which the relative error in distance is of the order of 20%. Moving cluster method: All stars in an open cluster have the same velocity vector, which projected onto the celestial sphere is oriented towards a convergence point. The measurement of the proper motion, radial velocity and the convergence point the provides the distance to the cluster. Can be applied to nearby clusters spanning a wide angle on the sky, and for which proper motions can be accurately measured.
5 Absolute distance estimators These estimators can used for very distant objects, and so are not tied to the local calibration of distances using the nearby stars. They provide an additional check for the scales built up from relative distance indicators. This implies that a more robust distance scale is available when the two types of estimators are combined. The Baade-Wesselink method The luminosity of a star is given by L = 4 π R 2 σ T 4 eff Therefore, if the radius R is measured, and the T eff is obtained from the spectrum or color of a star, and the apparent magnitude is known then it would be possible to derive its distance. The most direct way of measuring the radii of stars is by using eclipsing binaries. However, these objects are not very common, and hence not very useful in constructing the ladder of distance scales.
6 It is possible to use this method on variable stars such as cepheids or RR Lyrae. The lines in the spectrum of such a star show periodic shifts that vary with the same period as the star's brightness. These shifts are due to the expansion and contraction of the atmosphere of the star. The amount by which the size of a star varies between t 1 and t 0 can be obtained by integrating the line-of-sight velocity in this time interval r = -p t0 t1 v los (t) dt The negative sign is due to the fact that when r increases the lines are blueshifted, indicating a negative radial velocity, and the other way round. The factor p takes into account that the line of sight velocity we measure comes from different regions from the stellar disc, and so it is not exactly equal to the expansion velocity of the atmosphere.
7 Thus if the star has a radius r 0 at t 0, and r 1 at t 1, the change in the bolometric apparent magnitude will be m 1 m 0 = M 1 M 0 = -2.5 log(l 1 /L 0 ) = -5 log(r 1 /r 0 ) - 10 log(t 1 /T 0 ) Since r 1 = r 0 + r, if we measure T 0 and T 1, and r using the lineshifts in the spectrum, we can solve for r 0, and thereby derive its total luminosity and so its distance. We may choose to compare two epochs when the colour of the star is the same, that is when T 0 = T 1. In that case, the above equation becomes r 0 = H r/(1 H) where H = 10 5(m 1 m0) This method relies on some simplifying assumptions which may not be fully correct v los corresponds to expanding atmosphere. But lines detected may originate from different layers moving at different speeds the stellar oscillations may be not purely radial A one-to-one relation between the colour of a star and its Teff. E.g., variable stars observed in different bands do not vary in the same way with time. Need to use realistic models of the atmospheres of variable stars to correct for systematic effects.
8 Distances from time delays If an object changes its brightness in time we may measure its distance D by the delay in the arrival of the time-varying signal. If the physical dimension of the source is d, then d ~ c t. If it is also possible to measure an angular scale, θ associated to the source size d then θ = d/d, and D ~ c t/θ Example: the ring around SN1987A Observations made by the IUE (a UV satellite) showed emission lines from highly ionized atoms in the spectrum of SN1987A. These lines were detected t 0 = 90 days after the initial explosion. Their intensity increased and reached a maximum at t 1 = 400 days. The simplest explanation is that the emission lines come from material that is located at some distance from the supernova. The presence of such material has been indeed observed, and is distributed in an inclined ring structure.
9 The delay in the detection of the first emission lines and their maximum intensity can be attributed to different light-paths (from B and C). t o = R ring /c (1 sin i) and t 1 = R ring /c (1 + sin i) Combining the equations and using the values of t 0 and t 1, one obtains R ring = / pc and i=42+/- 5 deg. Since the angular size of the ring is θ = / arcsec, we derive a distance of 52 +/- 3 kpc to the supernova (and hence to the LMC).
10 Relative distance indicators Luminosities of variable stars: RR Lyrae, cepheids Local Group, nearby groups Luminosity functions of globular clusters and planetary nebulae galaxies and nearby clusters Novae and supernovae galaxies and cosmological distances Kinematics of galaxies: Tully-Fisher and D n σ galaxies, groups of galaxies and clusters
11 Luminosities of variable stars The luminosities of some pulsating variables can be determined accurately from their periods. For example cepheids obey the relation <M V > ~ log (P/10 days) 4.13 with a scatter of 0.3 mag. This relation has been calibrated for cepheids whose distances could be measured directly, for example through trigonometric parallaxes and the Baade-Wesselink method. Cepheids have absolute magnitudes M V ~ - 3, so that they can be observed to distance moduli of (m V M V ) ~ 25 from the ground and (m V M V ) ~ 28 using HST. This allows one to reach the nearest galaxy cluster Virgo. Cepheids are particularly useful because of their characteristic light curves, implying that they can be identified unambiguously.
12 Another example are RR Lyrae stars whose absolute magnitude is M V ~ 0.6. This has been derived from nearby RR Lyrae (not very many because they are characteristic of metal-poor populations) for which the trigonometric parallax could be measured; and also using the main sequence fitting method for globular clusters, which in turn is based on the distance scale to local subdwarf stars. RR Lyrae are less bright, and do not allow us to measure distances beyond the Local Group.
13 Luminosity functions Objects that have a spread in intrinsic luminosities cannot be used as standard candles. However, if the luminosity function of these objects is universal, i.e. it does not vary from system to system, we can compare the distribution of apparent luminosities to derive a relative distance to the systems. By luminosity function we mean the number of objects with absolute magnitude in a given range (i.e. the distribution of absolute magnitudes). Globular clusters The average luminosity of the globular clusters around the Milky Way, the LMC and M31 seems to be the same. Hence we may assume that this should also apply to other systems. We can use the average luminosity of the globular clusters as a standard candle, and hence to derive the relative distance of a given host galaxy. This method is often used to derive distances to elliptical galaxies, because the globular clusters are very easy to identify in this case.
14 The globular cluster luminosity function is very similar in all galaxies φ GC exp[-(m <m GC >) 2 /(2 σ GC2 )] (N.B. we have accurate measurements of the absolute magnitude only for the globular clusters in the Milky Way). LF of globular clusters in four E in Virgo.. By fitting this functional formed to the apparent magnitudes of globular clusters around a given galaxy we can obtain <m GC >. The comparison of this quantity for different galaxies will give us a measure of their relative distances Note that to estimate <m GC > reliably implies that the observations should reach faint enough levels so that the turn-over is clearly visible in the distribution. So far, this method has allowed us to measure distances to the Coma cluster.
15 Luminosity functions: Planetary Nebulae Planetary nebulae are easily identifiable through their characteristic emission forbidden lines at 5007 A. They are very common in all types of galaxies, and so their luminosity function can be accurately determined for each host system. The PN luminosity function is very similar in all galaxies φ PN (m) e m [1 e 3(m PN cut m) ] There are no PN brighter than m PN cut, a cut-off apparent magnitude. The fact that there is such an abrupt cut-off at bright end implies that this method can be applied even when a limited number of PN (only the brightest) have been observed around a given system. The maximum luminosity in the PNLF in the bulge of M31 occurs at ± If we adopt a distance of 740 ± 40 kpc (derived from cepheids), then M cut PN = -4.6 ± 0.1.
16 Novae Novae are very bright, and reach peak absolute magnitudes of M v ~ -7, which makes them ideal to probe very large distances. Novae in our Galaxy are sufficiently close that it is possible to derive their distances directly, using the expansion of their shells. If a shell expands with a velocity v exp - measurable from the Doppler shifts in spectral lines-, after a time t, this shell will have an angular size δθ which corresponds to a physical dimension v exp t. Therefore the distance to the novae is v exp t/ δθ. The luminosities derived for novae in our Galaxy show that they are not standard candles, since their peak absolute magnitude range from -4.8 to However, they have a characteristic rate of decline in brightness M V (max) = log(t 2 /day) where M V (max) is the peak magnitude of the novae, and t 2 is the time the novae took to decline in brightness by two magnitudes from its maximum.
17 Supernovae Supernovae type Ia have very similar properties, which is not surprising given that they originate in essentially identical systems (C/O white dwarf that by accretion from a binary companion has reached a mass of 1.38 M sun, which leads to an instability and triggers the explosion.) They are ideal standard candles because of their extreme intrinsic luminosities, implying that they can be observed to cosmological distances M v (max) = /
18 Distances from galaxy kinematics Galaxies themselves are not standard candles, since their brightness vary strongly from system to system (as for example, evidenced by the population of galaxies in distant clusters). However, they obey certain scaling laws: the more massive a galaxy is, the larger its intrinsic luminosity. The more massive the galaxy, the larger the average speed of its stars. (This derives from the virial theorem). Tully-Fisher relation The luminosity of a spiral galaxy correlates strongly with its rotational velocity.
19 The rotational velocity of a spiral galaxy can be measured from the HI integrated spectrum. The HI gas in a spiral follows very closely circular orbits at a speed V c. If the galaxy is inclined at an angle i to the line of sight, the observed line of sight velocity will vary from + V c sin i to - V c sin i relative to the systemic velocity of the galaxy. This results in a double horn line profile. Thus measuring the width of the line we get a direct estimate of the circular velocity. Conventionally, this width is measured by finding the points in the line wings where the intensity has dropped by 20% of the peak value. The difference in Doppler shift between these 2 points is W 20. W 20 needs to be corrected for 2 effects. The first one is that HI does not follow perfectly circular orbits, but has some random motion, whose effect is to broaden the observed lines. This can be estimated to be typically 10 km/s. The second effect is due to the inclination. The width that we measure is essentially 2 V c sin i. Therefore, the quantity W R = (W 20 -W rand )/sin i is an inclination independent measure of the circular velocity of a spiral galaxy.
20 The best bands to measure the brightness of a spiral galaxy are the infrared bands. The reason is twofold: spiral galaxies have large amounts of dust, which produce extinction. The effect of extinction in the infrared is very small the light will be dominated by old stars, which are more representative of the overall stellar populations. The observed light does not depend therefore on current star formation activity. The relations obtained are M H = 9.5 (log W R 2.5) ± 0.08 M I = 8.72(log W R 2.5) ± 0.1 and have been calibrated using cepheid distances.
21 The D n - σ relation Elliptical galaxies also follow scaling laws which relate their size, velocity dispersion and luminosity (or surface brightness). The most useful relation to measure distances to elliptical galaxies is the D n - σ relation
22 The parameter D n is the diameter within which the mean surface brightness is µ n = mag/arcsec 2 in the blue. σ is the central velocity dispersion. The calibrated relation is D n = 2.05 (σ/100 km/s) 1.33 kpc To obtain the distance we only need to compare the angular size of D n to the scale predicted by this equation. There is a 15% scatter in the relation from galaxy to galaxy, which will imply a 15% intrinsic uncertainty in the distance. However, if one is interested in measuring the distance to a cluster of galaxies, the uncertainty to the cluster distance can be reduced by observing large numbers of elliptical galaxies.
23 Summary
24 Distances within the Local Group Distance to the Galactic center The only absolute distance estimator for the Galactic center are the water masers in star forming regions in SgrB2. In this case, we use the statistical parallax method: radial velocity and proper motions. The relative distance estimators that can be used are RR Lyrae in globular clusters (one looks for the maximum density of halo globular clusters. This point should coincide with the location of the Galactic center). RR Lyrae in the bulge Cepheids water masers 7.2 +/-.7 RR Lyrae 7.8 +/- 0.4 globular clusters 8.0 +/- 0.8 cepheids 8.0 +/- 0.5
25 Distance to the LMC: 50 +/- 2 kpc (It is the extragalactic zero-point of the distance scale) The absolute distance estimator for the LMC is SN 1987A using timedelay arguments, or the Baade-Wesselink method. The relative distance estimators that can be used are Main sequence fitting of globular clusters RR Lyrae stars SN 1987 A time delay Cepheids SN 1987A Baade- Wesselink RR Lyrae Cepheids main sequence fitting 52 +/- 3 kpc 55 +/- 5 kpc 44 +/- 2 kpc 50 +/- 2 kpc 50 +/- 5 kpc
26 Distance to the M31: 740 +/- 40 kpc Its distance is always referred to the LMC Comparison of cepheids in LMC and M31 show that the latter lies /- 0.8 times farther away. Comparison of RR Lyraes give a distance ratio of 15 +/- 1. The PN luminosity function also provides a distance ratio wrt LMC of 15 +/- 1. The peak in the GCLF can be compared to that of the Milky Way, and the distance derived in this way is 700 +/- 60 kpc. This is directly calibrated wrt Milky rather than the LMC. The fact that there is such good agreement between different estimators and zero-points gives good confidence that the scale is correct. Novae RR Lyrae Cepheids 710 +/- 80 kpc 750 +/- 50 kpc 760 +/- 50 kpc PNLF GCLF 750 +/- 50 kpc 700 +/- 60 kpc
27 Distances beyond the Local Group Different methods can be applied to nearby galaxies just outside the Local Group. These methods show good agreement for distances less than ~ 20 Mpc. PNLF and GCLF are generally in good agreement. Distances using the Tully-Fisher for spiral galaxies in clusters are in worse agreement with those distances derived from elliptical galaxies, which could be related to their different physical location in the clusters. The distance to the Virgo cluster is crucial in the extragalactic distance scale: nearest galaxy cluster contains large numbers of spirals and ellipticals has been the site of a few SN it has been recently possible to observe cepheids, and hence to derive a distance which involves less intermediate calibrations it is a fairly average type of cluster: distances beyond it are referred to it.
28 Comparison of various distance determination methods for galaxies in the Virgo cluster
Techniques for measuring astronomical distances generally come in two variates, absolute and relative.
 Chapter 6 Distances 6.1 Preliminaries Techniques for measuring astronomical distances generally come in two variates, absolute and relative. Absolute distance measurements involve objects possibly unique
Chapter 6 Distances 6.1 Preliminaries Techniques for measuring astronomical distances generally come in two variates, absolute and relative. Absolute distance measurements involve objects possibly unique
Practice Problem!! Assuming a uniform protogalactic (H and He only) cloud with a virial temperature of 10 6 K and a density of 0.
 Practice Problem Assuming a uniform protogalactic (H and He only) cloud with a virial temperature of 10 6 K and a density of 0.05 cm -3 (a) estimate the minimum mass that could collapse, (b) what is the
Practice Problem Assuming a uniform protogalactic (H and He only) cloud with a virial temperature of 10 6 K and a density of 0.05 cm -3 (a) estimate the minimum mass that could collapse, (b) what is the
The Next 2-3 Weeks. Important to read through Chapter 17 (Relativity) before I start lecturing on it.
 The Next 2-3 Weeks [27.1] The Extragalactic Distance Scale. [27.2] The Expansion of the Universe. [29.1] Newtonian Cosmology [29.2] The Cosmic Microwave Background [17] General Relativity & Black Holes
The Next 2-3 Weeks [27.1] The Extragalactic Distance Scale. [27.2] The Expansion of the Universe. [29.1] Newtonian Cosmology [29.2] The Cosmic Microwave Background [17] General Relativity & Black Holes
Page # Astronomical Distances. Lecture 2. Astronomical Distances. Cosmic Distance Ladder. Distance Methods. Size of Earth
 Size of Astronomical istances ecture 2 Astronomical istances istance to the Moon (1 sec) istance to the Sun (8 min) istance to other stars (years) istance to centre of our Galaxy ( 30,000 yr to centre)
Size of Astronomical istances ecture 2 Astronomical istances istance to the Moon (1 sec) istance to the Sun (8 min) istance to other stars (years) istance to centre of our Galaxy ( 30,000 yr to centre)
Lecture 32: The Expanding Universe Readings: Sections 26-5 and 28-2
 Lecture 32: The Expanding Universe Readings: Sections 26-5 and 28-2 Key Ideas Measuring the Distances to Galaxies and Determining the Scale of the Universe Distance Methods: Trigonometric Parallaxes Spectroscopic
Lecture 32: The Expanding Universe Readings: Sections 26-5 and 28-2 Key Ideas Measuring the Distances to Galaxies and Determining the Scale of the Universe Distance Methods: Trigonometric Parallaxes Spectroscopic
Outline. Go over AGN problem, again, should be rotating BH Go over problem 6.6 Olber's paradox Distances Parallax Distance ladder Direct checks
 Outline Go over AGN problem, again, should be rotating BH Go over problem 6.6 Olber's paradox Distances Parallax Distance ladder Direct checks Why is the night sky dark? (Olber s Paradox 1826) Or what
Outline Go over AGN problem, again, should be rotating BH Go over problem 6.6 Olber's paradox Distances Parallax Distance ladder Direct checks Why is the night sky dark? (Olber s Paradox 1826) Or what
Lecture 25: The Cosmic Distance Scale Sections 25-1, 26-4 and Box 26-1
 Lecture 25: The Cosmic Distance Scale Sections 25-1, 26-4 and Box 26-1 Key Ideas The Distance Problem Geometric Distances Trigonometric Parallaxes Luminosity Distances Standard Candles Spectroscopic Parallaxes
Lecture 25: The Cosmic Distance Scale Sections 25-1, 26-4 and Box 26-1 Key Ideas The Distance Problem Geometric Distances Trigonometric Parallaxes Luminosity Distances Standard Candles Spectroscopic Parallaxes
Set 5: Expansion of the Universe
 Set 5: Expansion of the Universe Cosmology Study of the origin, contents and evolution of the universe as a whole Expansion rate and history Space-time geometry Energy density composition Origin of structure
Set 5: Expansion of the Universe Cosmology Study of the origin, contents and evolution of the universe as a whole Expansion rate and history Space-time geometry Energy density composition Origin of structure
Galaxies. The majority of known galaxies fall into one of three major classes: spirals (78 %), ellipticals (18 %) and irregulars (4 %).
 Galaxies Collection of stars, gas and dust bound together by their common gravitational pull. Galaxies range from 10,000 to 200,000 light-years in size. 1781 Charles Messier 1923 Edwin Hubble The distribution
Galaxies Collection of stars, gas and dust bound together by their common gravitational pull. Galaxies range from 10,000 to 200,000 light-years in size. 1781 Charles Messier 1923 Edwin Hubble The distribution
The Extragalactic Distance Scale
 One of the important relations in Astronomy. It lets us Measure the distance to distance objects. Each rung on the ladder is calibrated using lower-rung calibrations. Distance Objects Technique 1-100 AU
One of the important relations in Astronomy. It lets us Measure the distance to distance objects. Each rung on the ladder is calibrated using lower-rung calibrations. Distance Objects Technique 1-100 AU
The Milky Way Galaxy (ch. 23)
 The Milky Way Galaxy (ch. 23) [Exceptions: We won t discuss sec. 23.7 (Galactic Center) much in class, but read it there will probably be a question or a few on it. In following lecture outline, numbers
The Milky Way Galaxy (ch. 23) [Exceptions: We won t discuss sec. 23.7 (Galactic Center) much in class, but read it there will probably be a question or a few on it. In following lecture outline, numbers
Galaxies and Cosmology
 4/28/17 The Discovery of Galaxies Up to the 1920 s, astronomers were not sure exactly how far away galaxies were, and thus didn t know how big they are! Spiral Nebulae could be assumed to be inside our
4/28/17 The Discovery of Galaxies Up to the 1920 s, astronomers were not sure exactly how far away galaxies were, and thus didn t know how big they are! Spiral Nebulae could be assumed to be inside our
The Cosmological Distance Ladder. It's not perfect, but it works!
 The Cosmological Distance Ladder It's not perfect, but it works! First, we must know how big the Earth is. Next, we must determine the scale of the solar system. Copernicus (1543) correctly determined
The Cosmological Distance Ladder It's not perfect, but it works! First, we must know how big the Earth is. Next, we must determine the scale of the solar system. Copernicus (1543) correctly determined
Lecture 9. Basics Measuring distances Parallax Cepheid variables Type Ia Super Novae. Gravitational lensing Sunyaev-Zeldovich effect
 Lecture 9 H 0 from the Hubble diagram Basics Measuring distances Parallax Cepheid variables Type Ia Super Novae H 0 from other methods Gravitational lensing Sunyaev-Zeldovich effect H 0 from the Hubble
Lecture 9 H 0 from the Hubble diagram Basics Measuring distances Parallax Cepheid variables Type Ia Super Novae H 0 from other methods Gravitational lensing Sunyaev-Zeldovich effect H 0 from the Hubble
Luminosity Functions of Planetary Nebulae & Globular Clusters. By Azmain Nisak ASTR 8400
 Luminosity Functions of Planetary Nebulae & Globular Clusters By Azmain Nisak ASTR 8400 Calculating Distance! m = apparent magnitude! M = absolute magnitude! r = distance in pc GLOBULAR CLUSTERS AS DISTANCE
Luminosity Functions of Planetary Nebulae & Globular Clusters By Azmain Nisak ASTR 8400 Calculating Distance! m = apparent magnitude! M = absolute magnitude! r = distance in pc GLOBULAR CLUSTERS AS DISTANCE
Star systems like our Milky Way. Galaxies
 Galaxies Star systems like our Milky Way Galaxies Contain a few thousand to tens of billions of stars,as well as varying amounts of gas and dust Large variety of shapes and sizes Gas and Dust in
Galaxies Star systems like our Milky Way Galaxies Contain a few thousand to tens of billions of stars,as well as varying amounts of gas and dust Large variety of shapes and sizes Gas and Dust in
Cosmic Distance Determinations
 Cosmic Distance Determinations Radar (works for inner solar system) Parallax D(pc) = 1 p(arcsec) GAIA satellite (2013) 20 micro-arcsec resolution! Thus D < 10 kpc Beyond Parallax: Standard Candles Use
Cosmic Distance Determinations Radar (works for inner solar system) Parallax D(pc) = 1 p(arcsec) GAIA satellite (2013) 20 micro-arcsec resolution! Thus D < 10 kpc Beyond Parallax: Standard Candles Use
Survey of Astrophysics A110
 Goals: Galaxies To determine the types and distributions of galaxies? How do we measure the mass of galaxies and what comprises this mass? How do we measure distances to galaxies and what does this tell
Goals: Galaxies To determine the types and distributions of galaxies? How do we measure the mass of galaxies and what comprises this mass? How do we measure distances to galaxies and what does this tell
Name Midterm Exam October 20, 2017
 Name Midterm Exam October 20, 2017 This test consists of three parts. For the first and second parts, you may write your answers directly on the exam, if you wish. For the other parts, use separate sheets
Name Midterm Exam October 20, 2017 This test consists of three parts. For the first and second parts, you may write your answers directly on the exam, if you wish. For the other parts, use separate sheets
Distance Measuring Techniques and The Milky Way Galaxy
 Distance Measuring Techniques and The Milky Way Galaxy Measuring distances to stars is one of the biggest challenges in Astronomy. If we had some standard candle, some star with a known luminosity, then
Distance Measuring Techniques and The Milky Way Galaxy Measuring distances to stars is one of the biggest challenges in Astronomy. If we had some standard candle, some star with a known luminosity, then
AST1100 Lecture Notes
 AST1100 Lecture Notes 11 12 The cosmic distance ladder How do we measure the distance to distant objects in the universe? There are several methods available, most of which suffer from large uncertainties.
AST1100 Lecture Notes 11 12 The cosmic distance ladder How do we measure the distance to distant objects in the universe? There are several methods available, most of which suffer from large uncertainties.
80 2 Observational Cosmology L and the mean energy
 80 2 Observational Cosmology fluctuations, short-wavelength modes have amplitudes that are suppressed because these modes oscillated as acoustic waves during the radiation epoch whereas the amplitude of
80 2 Observational Cosmology fluctuations, short-wavelength modes have amplitudes that are suppressed because these modes oscillated as acoustic waves during the radiation epoch whereas the amplitude of
The Extragalactic Distance Scale
 One of the important relations in Astronomy. It lets us Measure the distance to distance objects. Each rung on the ladder is calibrated using lower-rung calibrations. Distance Objects Technique 1-100 AU
One of the important relations in Astronomy. It lets us Measure the distance to distance objects. Each rung on the ladder is calibrated using lower-rung calibrations. Distance Objects Technique 1-100 AU
Relativity and Astrophysics Lecture 15 Terry Herter. RR Lyrae Variables Cepheids Variables Period-Luminosity Relation. A Stellar Properties 2
 Stellar Properties Relativity and Astrophysics Lecture 15 Terry Herter Outline Spectroscopic Parallax Masses of Stars Periodic Variable Stars RR Lyrae Variables Cepheids Variables Period-Luminosity Relation
Stellar Properties Relativity and Astrophysics Lecture 15 Terry Herter Outline Spectroscopic Parallax Masses of Stars Periodic Variable Stars RR Lyrae Variables Cepheids Variables Period-Luminosity Relation
Exam 4 Review EXAM COVERS LECTURES 22-29
 Exam 4 Review EXAM COVERS LECTURES 22-29 Theoretically is there a center of the universe? Is there an edge? Do we know where Earth is on this? There is no center to the Universe, What kind of light we
Exam 4 Review EXAM COVERS LECTURES 22-29 Theoretically is there a center of the universe? Is there an edge? Do we know where Earth is on this? There is no center to the Universe, What kind of light we
The Milky Way. Finding the Center. Milky Way Composite Photo. Finding the Center. Milky Way : A band of and a. Milky Way
 The Milky Way Milky Way : A band of and a The band of light we see is really 100 billion stars Milky Way probably looks like Andromeda. Milky Way Composite Photo Milky Way Before the 1920 s, astronomers
The Milky Way Milky Way : A band of and a The band of light we see is really 100 billion stars Milky Way probably looks like Andromeda. Milky Way Composite Photo Milky Way Before the 1920 s, astronomers
Chapter 14 The Milky Way Galaxy
 Chapter 14 The Milky Way Galaxy Spiral Galaxy M81 - similar to our Milky Way Galaxy Our Parent Galaxy A galaxy is a giant collection of stellar and interstellar matter held together by gravity Billions
Chapter 14 The Milky Way Galaxy Spiral Galaxy M81 - similar to our Milky Way Galaxy Our Parent Galaxy A galaxy is a giant collection of stellar and interstellar matter held together by gravity Billions
Astronomy from 4 Perspectives Bi-national Heraeus Sumer School Series for Teacher Students and Teachers
 Astronomy from 4 Perspectives Bi-national Heraeus Sumer School Series for Teacher Students and Teachers I. Cosmology Prof. Dr. Andreas Just Zentrum für Astronomie Heidelberg University Cosmic Distances
Astronomy from 4 Perspectives Bi-national Heraeus Sumer School Series for Teacher Students and Teachers I. Cosmology Prof. Dr. Andreas Just Zentrum für Astronomie Heidelberg University Cosmic Distances
Determining distance. L 4π f. d = d = R θ. Standard candle. Standard ruler
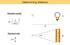 Determining distance Standard candle d = L 4π f 1 2 d L Standard ruler d = R θ θ R Determining distance: Parallax RULER tanπ = R d π R d π R = 1AU = 1.5 10 13 cm Define new distance unit: parsec (parallax-second)
Determining distance Standard candle d = L 4π f 1 2 d L Standard ruler d = R θ θ R Determining distance: Parallax RULER tanπ = R d π R d π R = 1AU = 1.5 10 13 cm Define new distance unit: parsec (parallax-second)
Big Galaxies Are Rare! Cepheid Distance Measurement. Clusters of Galaxies. The Nature of Galaxies
 Big Galaxies Are Rare! Potato Chip Rule: More small things than large things Big, bright spirals are easy to see, but least common Dwarf ellipticals & irregulars are most common Faint, hard to see Mostly
Big Galaxies Are Rare! Potato Chip Rule: More small things than large things Big, bright spirals are easy to see, but least common Dwarf ellipticals & irregulars are most common Faint, hard to see Mostly
AST2000 Lecture Notes
 AST2000 Lecture Notes Part 3A The cosmic distance ladder Questions to ponder before the lecture 1. How do we know that the distance to our closest star is 4 light years? 2. How do we know that our galaxy
AST2000 Lecture Notes Part 3A The cosmic distance ladder Questions to ponder before the lecture 1. How do we know that the distance to our closest star is 4 light years? 2. How do we know that our galaxy
INTRODUCTION TO SPACE
 INTRODUCTION TO SPACE 25.3.2019 The Galaxy II: Stars: Classification and evolution Various types of stars Interstellar matter: dust, gas Dark matter ELEC-E4530 Radio astronomy: the Sun, pulsars, microquasars,
INTRODUCTION TO SPACE 25.3.2019 The Galaxy II: Stars: Classification and evolution Various types of stars Interstellar matter: dust, gas Dark matter ELEC-E4530 Radio astronomy: the Sun, pulsars, microquasars,
Galaxy formation and evolution. Astro 850
 Galaxy formation and evolution Astro 850 Introduction What are galaxies? Systems containing many galaxies, e.g. 10 11 stars in the Milky Way. But galaxies have different properties. Properties of individual
Galaxy formation and evolution Astro 850 Introduction What are galaxies? Systems containing many galaxies, e.g. 10 11 stars in the Milky Way. But galaxies have different properties. Properties of individual
Chapter 19 Galaxies. Hubble Ultra Deep Field: Each dot is a galaxy of stars. More distant, further into the past. halo
 Chapter 19 Galaxies Hubble Ultra Deep Field: Each dot is a galaxy of stars. More distant, further into the past halo disk bulge Barred Spiral Galaxy: Has a bar of stars across the bulge Spiral Galaxy 1
Chapter 19 Galaxies Hubble Ultra Deep Field: Each dot is a galaxy of stars. More distant, further into the past halo disk bulge Barred Spiral Galaxy: Has a bar of stars across the bulge Spiral Galaxy 1
4.1 The Scale of the Universe: Basis of the Cosmological Distance Scale
 4.1 The Scale of the Universe: Basis of the Cosmological Distance Scale 1 The Scale of the Universe The Hubble length, D H = c/h 0, and the Hubble time, t H = 1/H 0 give the approximate spatial and temporal
4.1 The Scale of the Universe: Basis of the Cosmological Distance Scale 1 The Scale of the Universe The Hubble length, D H = c/h 0, and the Hubble time, t H = 1/H 0 give the approximate spatial and temporal
Lecture Outlines. Chapter 23. Astronomy Today 8th Edition Chaisson/McMillan Pearson Education, Inc.
 Lecture Outlines Chapter 23 Astronomy Today 8th Edition Chaisson/McMillan Chapter 23 The Milky Way Galaxy Units of Chapter 23 23.1 Our Parent Galaxy 23.2 Measuring the Milky Way Discovery 23-1 Early Computers
Lecture Outlines Chapter 23 Astronomy Today 8th Edition Chaisson/McMillan Chapter 23 The Milky Way Galaxy Units of Chapter 23 23.1 Our Parent Galaxy 23.2 Measuring the Milky Way Discovery 23-1 Early Computers
29:50 Stars, Galaxies, and the Universe Final Exam December 13, 2010 Form A
 29:50 Stars, Galaxies, and the Universe Final Exam December 13, 2010 Form A There are 40 questions. Read each question and all of the choices before choosing. Budget your time. No whining. Walk with Ursus!
29:50 Stars, Galaxies, and the Universe Final Exam December 13, 2010 Form A There are 40 questions. Read each question and all of the choices before choosing. Budget your time. No whining. Walk with Ursus!
The Stars. Background & History The Celestial Sphere: Fixed Stars and the Luminaries
 The Stars Background & History The Celestial Sphere: Fixed Stars and the Luminaries The Appearance of Stars on the Sky Brightness and Brightness Variations Atmospheric Effects: Twinkling Variable Stars
The Stars Background & History The Celestial Sphere: Fixed Stars and the Luminaries The Appearance of Stars on the Sky Brightness and Brightness Variations Atmospheric Effects: Twinkling Variable Stars
The Milky Way, Hubble Law, the expansion of the Universe and Dark Matter Chapter 14 and 15 The Milky Way Galaxy and the two Magellanic Clouds.
 The Milky Way, Hubble Law, the expansion of the Universe and Dark Matter Chapter 14 and 15 The Milky Way Galaxy and the two Magellanic Clouds. Image taken from the European Southern Observatory in Chile
The Milky Way, Hubble Law, the expansion of the Universe and Dark Matter Chapter 14 and 15 The Milky Way Galaxy and the two Magellanic Clouds. Image taken from the European Southern Observatory in Chile
24.1 Hubble s Galaxy Classification
 Chapter 24 Galaxies Units of Chapter 24 24.1 Hubble s Galaxy Classification 24.2 The Distribution of Galaxies in Space 24.3 Hubble s Law 24.4 XXActive Galactic Nuclei XXRelativistic Redshifts and Look-Back
Chapter 24 Galaxies Units of Chapter 24 24.1 Hubble s Galaxy Classification 24.2 The Distribution of Galaxies in Space 24.3 Hubble s Law 24.4 XXActive Galactic Nuclei XXRelativistic Redshifts and Look-Back
Chapter 23 The Milky Way Galaxy Pearson Education, Inc.
 Chapter 23 The Milky Way Galaxy The Milky Way is our own galaxy viewed from the inside. It is a vast collection of more than 200 billion stars, planets, nebulae, clusters, dust and gas. Our own sun and
Chapter 23 The Milky Way Galaxy The Milky Way is our own galaxy viewed from the inside. It is a vast collection of more than 200 billion stars, planets, nebulae, clusters, dust and gas. Our own sun and
AST1100 Lecture Notes
 AST1100 Lecture Notes 11-12 The cosmic distance ladder How do we measure the distance to distant objects in the universe? There are several methods available, most of which suffer from large uncertainties.
AST1100 Lecture Notes 11-12 The cosmic distance ladder How do we measure the distance to distant objects in the universe? There are several methods available, most of which suffer from large uncertainties.
Spatial distribution of stars in the Milky Way
 Spatial distribution of stars in the Milky Way What kinds of stars are present in the Solar neighborhood, and in what numbers? How are they distributed spatially? How do we know? How can we measure this?
Spatial distribution of stars in the Milky Way What kinds of stars are present in the Solar neighborhood, and in what numbers? How are they distributed spatially? How do we know? How can we measure this?
Part two of a year-long introduction to astrophysics:
 ASTR 3830 Astrophysics 2 - Galactic and Extragalactic Phil Armitage office: JILA tower A909 email: pja@jilau1.colorado.edu Spitzer Space telescope image of M81 Part two of a year-long introduction to astrophysics:
ASTR 3830 Astrophysics 2 - Galactic and Extragalactic Phil Armitage office: JILA tower A909 email: pja@jilau1.colorado.edu Spitzer Space telescope image of M81 Part two of a year-long introduction to astrophysics:
 COSMOLOGY PHYS 30392 OBSERVING THE UNIVERSE Part I Giampaolo Pisano - Jodrell Bank Centre for Astrophysics The University of Manchester - January 2013 http://www.jb.man.ac.uk/~gp/ giampaolo.pisano@manchester.ac.uk
COSMOLOGY PHYS 30392 OBSERVING THE UNIVERSE Part I Giampaolo Pisano - Jodrell Bank Centre for Astrophysics The University of Manchester - January 2013 http://www.jb.man.ac.uk/~gp/ giampaolo.pisano@manchester.ac.uk
Measuring the Hubble Constant through Cepheid Distances
 Measuring the Hubble Constant through Cepheid Distances Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant Freedman, Madore, Gibson, et al., Astrophysical Journal
Measuring the Hubble Constant through Cepheid Distances Final Results from the Hubble Space Telescope Key Project to Measure the Hubble Constant Freedman, Madore, Gibson, et al., Astrophysical Journal
5. A particular star has an angle of parallax of 0.2 arcsecond. What is the distance to this star? A) 50 pc B) 2 pc C) 5 pc D) 0.
 Name: Date: 1. How far away is the nearest star beyond the Sun, in parsecs? A) between 1 and 2 pc B) about 12 pc C) about 4 pc D) between 1/2 and 1 pc 2. Parallax of a nearby star is used to estimate its
Name: Date: 1. How far away is the nearest star beyond the Sun, in parsecs? A) between 1 and 2 pc B) about 12 pc C) about 4 pc D) between 1/2 and 1 pc 2. Parallax of a nearby star is used to estimate its
AST-1002 Section 0459 Review for Final Exam Please do not forget about doing the evaluation!
 AST-1002 Section 0459 Review for Final Exam Please do not forget about doing the evaluation! Bring pencil #2 with eraser No use of calculator or any electronic device during the exam We provide the scantrons
AST-1002 Section 0459 Review for Final Exam Please do not forget about doing the evaluation! Bring pencil #2 with eraser No use of calculator or any electronic device during the exam We provide the scantrons
The Cosmological Redshift. Cepheid Variables. Hubble s Diagram
 SOME NEGATIVE EFFECTS OF THE EXPANSION OF THE UNIVERSE. Lecture 22 Hubble s Law and the Large Scale Structure of the Universe PRS: According to modern ideas and observations, what can be said about the
SOME NEGATIVE EFFECTS OF THE EXPANSION OF THE UNIVERSE. Lecture 22 Hubble s Law and the Large Scale Structure of the Universe PRS: According to modern ideas and observations, what can be said about the
Galaxies & Introduction to Cosmology
 Galaxies & Introduction to Cosmology Other Galaxies: How many are there? Hubble Deep Field Project 100 hour exposures over 10 days Covered an area of the sky about 1/100 the size of the full moon Probably
Galaxies & Introduction to Cosmology Other Galaxies: How many are there? Hubble Deep Field Project 100 hour exposures over 10 days Covered an area of the sky about 1/100 the size of the full moon Probably
The King's University College Astronomy 201 Mid-Term Exam Solutions
 The King's University College Astronomy 201 Mid-Term Exam Solutions Instructions: The exam consists of two sections. Part A is 20 multiple choice questions - please record answers on the sheet provided.
The King's University College Astronomy 201 Mid-Term Exam Solutions Instructions: The exam consists of two sections. Part A is 20 multiple choice questions - please record answers on the sheet provided.
Hubble s Law. Tully-Fisher relation. The redshift. λ λ0. Are there other ways to estimate distances? Yes.
 Distances to galaxies Cepheids used by Hubble, 1924 to show that spiral nebulae like M31 were further from the Sun than any part of the Milky Way, therefore galaxies in their own right. Review of Cepheids
Distances to galaxies Cepheids used by Hubble, 1924 to show that spiral nebulae like M31 were further from the Sun than any part of the Milky Way, therefore galaxies in their own right. Review of Cepheids
Summary: Nuclear burning in stars
 Summary: Nuclear burning in stars Reaction 4 1 H 4 He 3 4 He 12 C 12 C + 4 He 16 O, Ne, Na, Mg Ne O, Mg O Mg, S Si Fe peak Min. Temp. 10 7 o K 2x10 8 8x10 8 1.5x10 9 2x10 9 3x10 9 Evolution through nuclear
Summary: Nuclear burning in stars Reaction 4 1 H 4 He 3 4 He 12 C 12 C + 4 He 16 O, Ne, Na, Mg Ne O, Mg O Mg, S Si Fe peak Min. Temp. 10 7 o K 2x10 8 8x10 8 1.5x10 9 2x10 9 3x10 9 Evolution through nuclear
The Discovery of Other Galaxies. 24. Normal Galaxies
 24. Normal Galaxies The discovery of other galaxies Edwin Hubble proved galaxies are very distant Edwin Hubble classified galaxies by shape Methods for determining distances to galaxies The Hubble Law
24. Normal Galaxies The discovery of other galaxies Edwin Hubble proved galaxies are very distant Edwin Hubble classified galaxies by shape Methods for determining distances to galaxies The Hubble Law
Building the cosmic distance scale: from Hipparcos to Gaia
 The Fundamental Distance Scale: state of the art and the Gaia perspectives 3-6 May 2011 Building the cosmic distance scale: from Hipparcos to Gaia Catherine TURON and Xavier LURI 1 ESA / ESO-H. Heyer Fundamental
The Fundamental Distance Scale: state of the art and the Gaia perspectives 3-6 May 2011 Building the cosmic distance scale: from Hipparcos to Gaia Catherine TURON and Xavier LURI 1 ESA / ESO-H. Heyer Fundamental
Astronomy Stars, Galaxies and Cosmology Exam 3. Please PRINT full name
 Astronomy 132 - Stars, Galaxies and Cosmology Exam 3 Please PRINT full name Also, please sign the honor code: I have neither given nor have I received help on this exam The following exam is intended to
Astronomy 132 - Stars, Galaxies and Cosmology Exam 3 Please PRINT full name Also, please sign the honor code: I have neither given nor have I received help on this exam The following exam is intended to
Astro 242. The Physics of Galaxies and the Universe: Lecture Notes Wayne Hu
 Astro 242 The Physics of Galaxies and the Universe: Lecture Notes Wayne Hu Syllabus Text: An Introduction to Modern Astrophysics 2nd Ed., Carroll and Ostlie First class Wed Jan 3. Reading period Mar 8-9
Astro 242 The Physics of Galaxies and the Universe: Lecture Notes Wayne Hu Syllabus Text: An Introduction to Modern Astrophysics 2nd Ed., Carroll and Ostlie First class Wed Jan 3. Reading period Mar 8-9
Lecture 29. Our Galaxy: "Milky Way"
 Lecture 29 The Milky Way Galaxy Disk, Bulge, Halo Rotation Curve Galactic Center Apr 3, 2006 Astro 100 Lecture 29 1 Our Galaxy: "Milky Way" Milky, diffuse band of light around sky known to ancients. Galileo
Lecture 29 The Milky Way Galaxy Disk, Bulge, Halo Rotation Curve Galactic Center Apr 3, 2006 Astro 100 Lecture 29 1 Our Galaxy: "Milky Way" Milky, diffuse band of light around sky known to ancients. Galileo
Addition to the Lecture on Galactic Evolution
 Addition to the Lecture on Galactic Evolution Rapid Encounters In case the encounter of two galaxies is quite fast, there will be not much dynamical friction due to lack of the density enhancement The
Addition to the Lecture on Galactic Evolution Rapid Encounters In case the encounter of two galaxies is quite fast, there will be not much dynamical friction due to lack of the density enhancement The
Distance measurements
 Distance measurements Pierre Hily-Blant 2018-19 Contents A current issue: The Hubble constant As you know, the Universe is expanding (this expansion is currently accelerating). The Hubble's law says that
Distance measurements Pierre Hily-Blant 2018-19 Contents A current issue: The Hubble constant As you know, the Universe is expanding (this expansion is currently accelerating). The Hubble's law says that
Astronomy A BEGINNER S GUIDE TO THE UNIVERSE EIGHTH EDITION
 Astronomy A BEGINNER S GUIDE TO THE UNIVERSE EIGHTH EDITION CHAPTER 14 The Milky Way Galaxy Lecture Presentation 14.0 the Milky Way galaxy How do we know the Milky Way exists? We can see it even though
Astronomy A BEGINNER S GUIDE TO THE UNIVERSE EIGHTH EDITION CHAPTER 14 The Milky Way Galaxy Lecture Presentation 14.0 the Milky Way galaxy How do we know the Milky Way exists? We can see it even though
Science Olympiad Astronomy C Division Event Golden Gate Invitational February 11, 2017
 Science Olympiad Astronomy C Division Event Golden Gate Invitational February 11, 2017 Team Name: Team Number: Directions: ~Answer all questions on the answer sheet provided. ~Please do NOT access the
Science Olympiad Astronomy C Division Event Golden Gate Invitational February 11, 2017 Team Name: Team Number: Directions: ~Answer all questions on the answer sheet provided. ~Please do NOT access the
AS1001: Galaxies and Cosmology
 AS1001: Galaxies and Cosmology Keith Horne kdh1@st-and.ac.uk http://www-star.st-and.ac.uk/~kdh1/eg/eg.html Text: Kutner Astronomy:A Physical Perspective Chapters 17-21 Cosmology Today Blah Title Current
AS1001: Galaxies and Cosmology Keith Horne kdh1@st-and.ac.uk http://www-star.st-and.ac.uk/~kdh1/eg/eg.html Text: Kutner Astronomy:A Physical Perspective Chapters 17-21 Cosmology Today Blah Title Current
Our Galaxy. We are located in the disk of our galaxy and this is why the disk appears as a band of stars across the sky.
 Our Galaxy Our Galaxy We are located in the disk of our galaxy and this is why the disk appears as a band of stars across the sky. Early attempts to locate our solar system produced erroneous results.
Our Galaxy Our Galaxy We are located in the disk of our galaxy and this is why the disk appears as a band of stars across the sky. Early attempts to locate our solar system produced erroneous results.
This Week in Astronomy
 Homework #8 Due Wednesday, April 18, 11:59PM Covers Chapters 15 and 16 Estimated time to complete: 40 minutes Read chapters, review notes before starting This Week in Astronomy Credit: NASA/JPL-Caltech
Homework #8 Due Wednesday, April 18, 11:59PM Covers Chapters 15 and 16 Estimated time to complete: 40 minutes Read chapters, review notes before starting This Week in Astronomy Credit: NASA/JPL-Caltech
Hubble s Law and the Cosmic Distance Scale
 Lab 7 Hubble s Law and the Cosmic Distance Scale 7.1 Overview Exercise seven is our first extragalactic exercise, highlighting the immense scale of the Universe. It addresses the challenge of determining
Lab 7 Hubble s Law and the Cosmic Distance Scale 7.1 Overview Exercise seven is our first extragalactic exercise, highlighting the immense scale of the Universe. It addresses the challenge of determining
The Hubble Constant. Measuring the Scale of the Universe. The Scale of the Universe. In this lecture:
 Ay 127, Spring 2013 Extragalactic Distance Scale In this lecture: S. G. Djorgovski Hubble constant: its definition and history The extragalactic distance ladder The HST Key Project and the more modern
Ay 127, Spring 2013 Extragalactic Distance Scale In this lecture: S. G. Djorgovski Hubble constant: its definition and history The extragalactic distance ladder The HST Key Project and the more modern
2019 Astronomy Team Selection Test
 2019 Astronomy Team Selection Test Acton-Boxborough Regional High School Written by Antonio Frigo Do not flip over this page until instructed. Instructions You will have 45 minutes to complete this exam.
2019 Astronomy Team Selection Test Acton-Boxborough Regional High School Written by Antonio Frigo Do not flip over this page until instructed. Instructions You will have 45 minutes to complete this exam.
The Milky Way Galaxy and Interstellar Medium
 The Milky Way Galaxy and Interstellar Medium Shape of the Milky Way Uniform distribution of stars in a band across the sky lead Thomas Wright, Immanuel Kant, and William Herschel in the 18th century to
The Milky Way Galaxy and Interstellar Medium Shape of the Milky Way Uniform distribution of stars in a band across the sky lead Thomas Wright, Immanuel Kant, and William Herschel in the 18th century to
MEASURING DISTANCES IN ASTRONOMY
 Basic Principles: MEASURING DISTANCES IN ASTRONOMY Geometric methods Standard candles Standard rulers [the last two methods relate quantities that are independent of distance to quantities that depend
Basic Principles: MEASURING DISTANCES IN ASTRONOMY Geometric methods Standard candles Standard rulers [the last two methods relate quantities that are independent of distance to quantities that depend
ASTRONOMY II Spring 1995 FINAL EXAM. Monday May 8th 2:00pm
 ASTRONOMY II - 79202 Spring 1995 FINAL EXAM Monday May 8th 2:00pm Name: You have three hours to complete this exam. I suggest you read through the entire exam before you spend too much time on any one
ASTRONOMY II - 79202 Spring 1995 FINAL EXAM Monday May 8th 2:00pm Name: You have three hours to complete this exam. I suggest you read through the entire exam before you spend too much time on any one
Lecture 27 Galaxy Types and the Distance Ladder December 3, 2018
 Lecture 27 Galaxy Types and the Distance Ladder December 3, 2018 1 2 Early Observations Some galaxies had been observed before 1900 s. Distances were not known. Some looked like faint spirals. Originally
Lecture 27 Galaxy Types and the Distance Ladder December 3, 2018 1 2 Early Observations Some galaxies had been observed before 1900 s. Distances were not known. Some looked like faint spirals. Originally
Name Class Date. Chapter 27. Stars and Galaxies. Review Choose the best response. Write the letter of that choice in the space provided.
 Stars and Galaxies Review Choose the best response. Write the letter of that choice in the space provided. 1. In the majority of stars, the most common element is a. oxygen. b. helium. c. hydrogen. d.
Stars and Galaxies Review Choose the best response. Write the letter of that choice in the space provided. 1. In the majority of stars, the most common element is a. oxygen. b. helium. c. hydrogen. d.
Ch. 25 In-Class Notes: Beyond Our Solar System
 Ch. 25 In-Class Notes: Beyond Our Solar System ES2a. The solar system is located in an outer edge of the disc-shaped Milky Way galaxy, which spans 100,000 light years. ES2b. Galaxies are made of billions
Ch. 25 In-Class Notes: Beyond Our Solar System ES2a. The solar system is located in an outer edge of the disc-shaped Milky Way galaxy, which spans 100,000 light years. ES2b. Galaxies are made of billions
Astronomy 100 Spring 2006 Lecture Questions Twelve Weeks Review
 Astronomy 100 Spring 2006 Lecture Questions Twelve Weeks Review 16-1 Fusion in the Sun The solar corona has temperatures roughly the same as temperatures in the Sun's core, where nuclear fusion takes place.
Astronomy 100 Spring 2006 Lecture Questions Twelve Weeks Review 16-1 Fusion in the Sun The solar corona has temperatures roughly the same as temperatures in the Sun's core, where nuclear fusion takes place.
* * The Astronomical Context. Much of astronomy is about positions so we need coordinate systems to. describe them. 2.1 Angles and Positions
 2-1 2. The Astronomical Context describe them. Much of astronomy is about positions so we need coordinate systems to 2.1 Angles and Positions Actual * q * Sky view q * * Fig. 2-1 Position usually means
2-1 2. The Astronomical Context describe them. Much of astronomy is about positions so we need coordinate systems to 2.1 Angles and Positions Actual * q * Sky view q * * Fig. 2-1 Position usually means
Lecture 33: Announcements
 Lecture 33: Announcements 1) Pick up graded hwk 5. Good job: Jessica, Jessica, and Elizabeth for a 100% score on hwk 5 and the other 25% of the class with an A. 2) Article and homework 7 were posted on
Lecture 33: Announcements 1) Pick up graded hwk 5. Good job: Jessica, Jessica, and Elizabeth for a 100% score on hwk 5 and the other 25% of the class with an A. 2) Article and homework 7 were posted on
Structure of Our Galaxy The Milkyway. More background Stars and Gas in our Galaxy
 Structure of Our Galaxy The Milkyway More background Stars and Gas in our Galaxy "What good are Mercator's North Poles and Equators Tropics, Zones, and Meridian Lines?" So the Bellman would cry, and the
Structure of Our Galaxy The Milkyway More background Stars and Gas in our Galaxy "What good are Mercator's North Poles and Equators Tropics, Zones, and Meridian Lines?" So the Bellman would cry, and the
The distance modulus in the presence of absorption is given by
 Problem 4: An A0 main sequence star is observed at a distance of 100 pc through an interstellar dust cloud. Furthermore, it is observed with a color index B-V = 1.5. What is the apparent visual magnitude
Problem 4: An A0 main sequence star is observed at a distance of 100 pc through an interstellar dust cloud. Furthermore, it is observed with a color index B-V = 1.5. What is the apparent visual magnitude
BROCK UNIVERSITY. Test 2, March 2015 Number of pages: 9 Course: ASTR 1P02 Number of Students: 420 Date of Examination: March 5, 2015
 BROCK UNIVERSITY Page 1 of 9 Test 2, March 2015 Number of pages: 9 Course: ASTR 1P02 Number of Students: 420 Date of Examination: March 5, 2015 Number of hours: 50 min Time of Examination: 18:00 18:50
BROCK UNIVERSITY Page 1 of 9 Test 2, March 2015 Number of pages: 9 Course: ASTR 1P02 Number of Students: 420 Date of Examination: March 5, 2015 Number of hours: 50 min Time of Examination: 18:00 18:50
The Milky Way. Mass of the Galaxy, Part 2. Mass of the Galaxy, Part 1. Phys1403 Stars and Galaxies Instructor: Dr. Goderya
 Foundations Chapter of Astronomy 15 13e Our Milky Way Seeds Phys1403 Stars and Galaxies Instructor: Dr. Goderya Selected Topics in Chapter 15 A view our Milky Way? The Size of our Milky Way The Mass of
Foundations Chapter of Astronomy 15 13e Our Milky Way Seeds Phys1403 Stars and Galaxies Instructor: Dr. Goderya Selected Topics in Chapter 15 A view our Milky Way? The Size of our Milky Way The Mass of
Lecture 14: Other Galaxies A2020 Prof. Tom Megeath. The Milky Way in the Infrared 3/17/10. NGC 7331: the Milky Way s Twins. Spiral Galaxy bulge halo
 Lecture 14: Other Galaxies A2020 Prof. Tom Megeath Our Galaxy: Side View We see our galaxy edge-on Primary features: Disk: young and old stars where we live. Bulge: older stars Halo: oldest stars, globular
Lecture 14: Other Galaxies A2020 Prof. Tom Megeath Our Galaxy: Side View We see our galaxy edge-on Primary features: Disk: young and old stars where we live. Bulge: older stars Halo: oldest stars, globular
View of the Galaxy from within. Lecture 12: Galaxies. Comparison to an external disk galaxy. Where do we lie in our Galaxy?
 Lecture 12: Galaxies View of the Galaxy from within The Milky Way galaxy Rotation curves and dark matter External galaxies and the Hubble classification scheme Plotting the sky brightness in galactic coordinates,
Lecture 12: Galaxies View of the Galaxy from within The Milky Way galaxy Rotation curves and dark matter External galaxies and the Hubble classification scheme Plotting the sky brightness in galactic coordinates,
M31 - Andromeda Galaxy M110 M32
 UNIT 4 - Galaxies XIV. The Milky Way galaxy - a huge collection of millions or billions of stars, gas, and dust, isolated in space and held together by its own gravity M110 M31 - Andromeda Galaxy A. Structure
UNIT 4 - Galaxies XIV. The Milky Way galaxy - a huge collection of millions or billions of stars, gas, and dust, isolated in space and held together by its own gravity M110 M31 - Andromeda Galaxy A. Structure
XII. The distance scale. h"p://sgoodwin.staff.shef.ac.uk/phy111.html
 XII. The distance scale h"p://sgoodwin.staff.shef.ac.uk/phy111.html 0. How far away are galaxies? We discussed galaxies without thinking about how we know the distances to these galaxies. Only in the past
XII. The distance scale h"p://sgoodwin.staff.shef.ac.uk/phy111.html 0. How far away are galaxies? We discussed galaxies without thinking about how we know the distances to these galaxies. Only in the past
Astronomy 113. Dr. Joseph E. Pesce, Ph.D. Dr. Joseph E. Pesce, Ph.D.
 Astronomy 113 Dr. Joseph E. Pesce, Ph.D. The Nature of Stars 8-2 Parallax For nearby stars - measure distances with parallax July 1 AU d p A A A January ³ d = 1/p (arcsec) [pc] ³ 1pc when p=1arcsec; 1pc=206,265AU=3
Astronomy 113 Dr. Joseph E. Pesce, Ph.D. The Nature of Stars 8-2 Parallax For nearby stars - measure distances with parallax July 1 AU d p A A A January ³ d = 1/p (arcsec) [pc] ³ 1pc when p=1arcsec; 1pc=206,265AU=3
Galaxies. Galaxy Diversity. Galaxies, AGN and Quasars. Physics 113 Goderya
 Galaxies, AGN and Quasars Physics 113 Goderya Chapter(s): 16 and 17 Learning Outcomes: Galaxies Star systems like our Milky Way Contain a few thousand to tens of billions of stars. Large variety of shapes
Galaxies, AGN and Quasars Physics 113 Goderya Chapter(s): 16 and 17 Learning Outcomes: Galaxies Star systems like our Milky Way Contain a few thousand to tens of billions of stars. Large variety of shapes
Dead & Variable Stars
 Dead & Variable Stars Supernovae Death of massive Stars As the core collapses, it overshoots and bounces A shock wave travels through the star and blows off the outer layers, including the heavy elements
Dead & Variable Stars Supernovae Death of massive Stars As the core collapses, it overshoots and bounces A shock wave travels through the star and blows off the outer layers, including the heavy elements
A 103 Notes, Week 14, Kaufmann-Comins Chapter 15
 NEARBY GALAXIES I. Brief History A 103 Notes, Week 14, Kaufmann-Comins Chapter 15 A. Kant B. Curtis-Shapley debate C. Distance to Andromeda II. Classification of nearby galaxies: Spirals, Ellipticals,
NEARBY GALAXIES I. Brief History A 103 Notes, Week 14, Kaufmann-Comins Chapter 15 A. Kant B. Curtis-Shapley debate C. Distance to Andromeda II. Classification of nearby galaxies: Spirals, Ellipticals,
Physics HW Set 3 Spring 2015
 1) If the Sun were replaced by a one solar mass black hole 1) A) life here would be unchanged. B) we would still orbit it in a period of one year. C) all terrestrial planets would fall in immediately.
1) If the Sun were replaced by a one solar mass black hole 1) A) life here would be unchanged. B) we would still orbit it in a period of one year. C) all terrestrial planets would fall in immediately.
Ay162, Spring 2006 Week 8 p. 1 of 15
 Astronomy 162, Week 8 Milky Way Galaxy, continued Patrick S. Osmer Spring, 2006 Rotation of Galaxy How do we know the galaxy is rotating, and how do we measure its rotation? Measure radial velocities of
Astronomy 162, Week 8 Milky Way Galaxy, continued Patrick S. Osmer Spring, 2006 Rotation of Galaxy How do we know the galaxy is rotating, and how do we measure its rotation? Measure radial velocities of
ASTR 1120 General Astronomy: Stars & Galaxies
 ASTR 1120 General Astronomy: Stars & Galaxies!NNOUNCEMENTS HOMEWORK #6 DUE TODAY, by 5pm HOMEWORK #7 DUE Nov. 10, by 5pm Dark matter halo for galaxies Dark matter extends beyond visible part of the galaxy
ASTR 1120 General Astronomy: Stars & Galaxies!NNOUNCEMENTS HOMEWORK #6 DUE TODAY, by 5pm HOMEWORK #7 DUE Nov. 10, by 5pm Dark matter halo for galaxies Dark matter extends beyond visible part of the galaxy
Milky Way S&G Ch 2. Milky Way in near 1 IR H-W Rixhttp://online.kitp.ucsb.edu/online/galarcheo-c15/rix/
 Why study the MW? its "easy" to study: big, bright, close Allows detailed studies of stellar kinematics, stellar evolution. star formation, direct detection of dark matter?? Milky Way S&G Ch 2 Problems
Why study the MW? its "easy" to study: big, bright, close Allows detailed studies of stellar kinematics, stellar evolution. star formation, direct detection of dark matter?? Milky Way S&G Ch 2 Problems
Set 1: Expansion of the Universe
 Set 1: Expansion of the Universe Syllabus Course text book: Ryden, Introduction to Cosmology, 2nd edition Olber s paradox, expansion of the universe: Ch 2 Cosmic geometry, expansion rate, acceleration:
Set 1: Expansion of the Universe Syllabus Course text book: Ryden, Introduction to Cosmology, 2nd edition Olber s paradox, expansion of the universe: Ch 2 Cosmic geometry, expansion rate, acceleration:
The Milky Way - Chapter 23
 The Milky Way - Chapter 23 The Milky Way Galaxy A galaxy: huge collection of stars (10 7-10 13 ) and interstellar matter (gas & dust). Held together by gravity. Much bigger than any star cluster we have
The Milky Way - Chapter 23 The Milky Way Galaxy A galaxy: huge collection of stars (10 7-10 13 ) and interstellar matter (gas & dust). Held together by gravity. Much bigger than any star cluster we have
The Milky Way Galaxy
 1/5/011 The Milky Way Galaxy Distribution of Globular Clusters around a Point in Sagittarius About 00 globular clusters are distributed in random directions around the center of our galaxy. 1 1/5/011 Structure
1/5/011 The Milky Way Galaxy Distribution of Globular Clusters around a Point in Sagittarius About 00 globular clusters are distributed in random directions around the center of our galaxy. 1 1/5/011 Structure
Lecture 19: Galaxies. Astronomy 111
 Lecture 19: Galaxies Astronomy 111 Galaxies What is a galaxy? Large assembly of stars, gas and dust, held together by gravity Sizes: Largest: ~1 Trillion stars (or more) Smallest: ~10 Million stars Milky
Lecture 19: Galaxies Astronomy 111 Galaxies What is a galaxy? Large assembly of stars, gas and dust, held together by gravity Sizes: Largest: ~1 Trillion stars (or more) Smallest: ~10 Million stars Milky
Chapter 20 Lecture. The Cosmic Perspective. Seventh Edition. Galaxies and the Foundation of Modern Cosmology Pearson Education, Inc.
 Chapter 20 Lecture The Cosmic Perspective Seventh Edition Galaxies and the Foundation of Modern Cosmology 20.1 Islands of Stars Our goals for learning: How do galaxies evolve? What are the three major
Chapter 20 Lecture The Cosmic Perspective Seventh Edition Galaxies and the Foundation of Modern Cosmology 20.1 Islands of Stars Our goals for learning: How do galaxies evolve? What are the three major
The Deaths of Stars. The Southern Crab Nebula (He2-104), a planetary nebula (left), and the Crab Nebula (M1; right), a supernova remnant.
 The Deaths of Stars The Southern Crab Nebula (He2-104), a planetary nebula (left), and the Crab Nebula (M1; right), a supernova remnant. Once the giant phase of a mediummass star ends, it exhales its outer
The Deaths of Stars The Southern Crab Nebula (He2-104), a planetary nebula (left), and the Crab Nebula (M1; right), a supernova remnant. Once the giant phase of a mediummass star ends, it exhales its outer
Neutron Stars. Neutron Stars and Black Holes. The Crab Pulsar. Discovery of Pulsars. The Crab Pulsar. Light curves of the Crab Pulsar.
 Chapter 11: Neutron Stars and Black Holes A supernova explosion of an M > 8 M sun star blows away its outer layers. Neutron Stars The central core will collapse into a compact object of ~ a few M sun.
Chapter 11: Neutron Stars and Black Holes A supernova explosion of an M > 8 M sun star blows away its outer layers. Neutron Stars The central core will collapse into a compact object of ~ a few M sun.
